高三理科数学第一轮第四单元导数及其应用专题训练测试卷及答案解析A卷
2023年新高考数学一轮复习4-4 导数的综合应用(真题测试)含详解

专题4.4 导数的综合应用(真题测试)一、单选题1.(2017·全国·高考真题(理))已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则=a ( ) A .12-B .13C .12D .12.(2015·陕西·高考真题(理))对二次函数(为非零整数),四位同学分别给出下列结论,其中有且仅有一个结 论是错误的,则错误的结论是 A .是的零点 B .1是的极值点 C .3是的极值D .点在曲线上3.(2022·青海·海东市第一中学模拟预测(理))已知函数()2e 2xx f x a x =-+,若有且仅有两个正整数,使得()0f x <成立,则实数a 的取值范围是( ) A .211,3e e ⎡⎫⎪⎢⎣⎭B .3291,5e e ⎡⎫⎪⎢⎣⎭C .391,5e 3e ⎡⎫⎪⎢⎣⎭D .212,2e e ⎡⎫⎪⎢⎣⎭4.(2014·全国·高考真题(文))已知函数,若存在唯一的零点,且,则的取值范围是( ) A .B .C .D .5.(2022·青海·海东市第一中学模拟预测(理))若函数()()22e e x x f x x ax a a R =+-∈有三个不同的零点,则实数a 的取值范围是( ) A .1,e ⎛⎫+∞ ⎪⎝⎭B .1,1e ⎛⎫ ⎪⎝⎭C .2110,,1e e e ⎛⎫⎛⎫⋃ ⎪ ⎪-⎝⎭⎝⎭D .210,e e ⎛⎫ ⎪-⎝⎭6.(2022·河南·开封市东信学校模拟预测(理))对任意0x >,不等式e ln()(1)0x ax a x -+-≥恒成立,则正数a 的最大值为( ) ABC .1eD .e7.(2015·全国·高考真题(理))设函数()(21)xf x e x ax a =--+,其中1a < ,若存在唯一的整数0x ,使得2()f x ax bx c =++a 1-()f x ()f x ()f x (2,8)()y f x =32()31f x ax x =-+()f x 0x 00x >a ()2,+∞()1,+∞(),2-∞-(),1-∞-0()0f x <,则a 的取值范围是( )A .3,12e ⎡⎫-⎪⎢⎣⎭B .33,2e 4⎡⎫-⎪⎢⎣⎭ C .33,2e 4⎡⎫⎪⎢⎣⎭ D .3,12e ⎡⎫⎪⎢⎣⎭8.(2022·内蒙古·海拉尔第二中学模拟预测(理))已知函数()()e ln e (0)xf x a a a =+>,若对任意实数1x >,不等式()()ln 1f x x ≥-总成立,则实数a 的取值范围为( ) A .210,e ⎛⎫ ⎪⎝⎭B .221,e e ⎛⎤⎥⎝⎦C .21,e ⎛⎫+∞ ⎪⎝⎭D .21,e ⎡⎫+∞⎪⎢⎣⎭二、多选题9.(2022·辽宁实验中学模拟预测)我们把形如(),,0f x y y '=的方程称为微分方程,符合方程的函数()y f x =称为微分方程的解,下列函数为微分方程0xy y xy +-'=的解的是( ) A .e x y = B .e x y x =C .e 1x y x =+D .e (R)x y c x c =⋅∈⋅10.(2022·河北沧州·二模)已知实数,a b 满足e e e a b a b ++=,则( ) A .0ab < B .1a b +> C .e e 4a b +D .e 1a b >11.(2022·湖南·模拟预测)已知1x >,1y >,且()()1e 11e y xx y ++=+,则下列结论一定正确的是( )A .()ln 0x y ->B .122x y +<C .226x y +>D .()ln ln3x y +<12.(2022·全国·高考真题)已知函数,则( )A .有两个极值点B .有三个零点C .点是曲线的对称中心D .直线是曲线的切线三、填空题13.(2020·河南高三其他(理))函数()2222ln x f x x e x ax =--,若0a =,则()f x 在[]1,2的最小值为_______;当0x >时,()1f x ≥恒成立,则a 的取值范围是_____. 14.(2022·全国·模拟预测(理))若曲线ln x y x =与212y kx =-仅有1个公共点,则k 的取值范围是3()1f x x x =-+()f x ()f x (0,1)()y f x =2y x =()y f x =___________.15.(2012·福建·高考真题(理))对于实数a 和b ,定义运算“*”: 设f (x )=(2x -1)*(x -1),且关于x 的方程为f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3的取值范围是_________________16.(2022·江苏·常州高级中学模拟预测)已知函数22()ln 2e f x x x mx =-+,若()0f x ≥的解集中恰有一个整数,则m 的取值范围为________. 四、解答题17.(2018·全国·高考真题(文))已知函数.(1)求曲线在点处的切线方程; (2)证明:当时,.18.(2017·全国·高考真题(理))已知函数(1)讨论的单调性;(2)若有两个零点,求的取值范围.19.(2017·全国·高考真题(文))已知函数.(1)讨论的单调性; (2)当时,证明. 20.(2016·全国·高考真题(文))设函数. (Ⅰ)讨论的单调性; (Ⅱ)证明当时,; (Ⅲ)设,证明当时,.21.(2015·全国·高考真题(理))设函数.(1)证明:在单调递减,在单调递增;(2)若对于任意,都有,求m 的取值范围.22.(2014·四川·高考真题(理))已知函数,其中,为自然对数的底数.(Ⅰ)设是函数的导函数,求函数在区间上的最小值;22,,a ab a ba b b ab a b ⎧-≠=⎨->⎩()21x ax x f x e +-=()y f x =()0,1-1a ≥()0f x e +≥()()2e 2e x xf x a a x =+--()f x ()f x a 2()ln (21)f x x ax a x =+++()f x 0a <3()24f x a≤--()ln 1f x x x =-+()f x (1,)x ∈+∞11ln x x x-<<1c >(0,1)x ∈1(1)xc x c +->2()e mx f x x mx =+-()f x (,0)-∞(0,)+∞12,[1,1]x x ∈-12|()()|1f x f x e -≤-2()1x f x e ax bx =---,a b R ∈ 2.71828e =()g x ()f x ()g x [0,1](Ⅱ)若,函数在区间内有零点,求的取值范围(1)0f ()f x (0,1)a专题4.4 导数的综合应用(真题测试)一、单选题1.(2017·全国·高考真题(理))已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则=a ( ) A .12-B .13C .12D .1【答案】C 【解析】 【分析】 【详解】因为()221111()2()1()1x x x x f x x x a e e x a e e --+--+=-++=-++-,设1t x =-,则()()()21t t f x g t t a e e -==++-,因为()()g t g t =-,所以函数()g t 为偶函数,若函数()f x 有唯一零点,则函数()g t 有唯一零点,根据偶函数的性质可知,只有当0=t 时,()0g t =才满足题意,即1x =是函数()f x 的唯一零点,所以210a -=,解得12a =.故选:C. 2.(2015·陕西·高考真题(理))对二次函数(为非零整数),四位同学分别给出下列结论,其中有且仅有一个结 论是错误的,则错误的结论是 A .是的零点 B .1是的极值点 C .3是的极值 D .点在曲线上【答案】A 【解析】 【详解】若选项A 错误时,选项B 、C 、D 正确,,因为是的极值点,是的极值,所以,即,解得:,因为点在曲线上,所以,即,解得:,所以,,所以,因为,所以不是的零点,所以选项A 错误,选项B 、C 、D 正确,故选A .3.(2022·青海·海东市第一中学模拟预测(理))已知函数()2e 2xx f x a x =-+,若有且仅有两个正整2()f x ax bx c =++a 1-()f x ()f x ()f x (2,8)()y f x =()2f x ax b ='+1()f x 3()f x ()()10{13f f '==203a b a b c +=⎧⎨++=⎩2{3b a c a =-=+()2,8()y f x =()42238a a a +⨯-++=5a =10b =-8c =()25108f x x x =-+()()()21511018230f -=⨯--⨯-+=≠1-()f x数,使得()0f x <成立,则实数a 的取值范围是( ) A .211,3e e ⎡⎫⎪⎢⎣⎭B .3291,5e e ⎡⎫⎪⎢⎣⎭C .391,5e 3e ⎡⎫⎪⎢⎣⎭D .212,2e e ⎡⎫⎪⎢⎣⎭【答案】C 【解析】 【分析】将()0f x <转化为2(2)exx a x +<,再分别求导分析2()e x x g x =和()(2)h x a x =+的图象,再分别求得1,1g ,()()2,2g ,()()3,3g 到()20-,的斜率,分析临界情况即可 【详解】由()0f x <且0x >,得2(2)exx a x +<,设2()e x x g x =,()(2)h x a x =+, 22()exx x g x '-=,已知函数()g x 在(0,2)上单调递增,在(2,)+∞上单调递减, 函数()(2)h x a x =+的图象过点(2,0)-,(1)11(2)3e g =--,2(2)12(2)e g =--,3(3)93(2)5e g =--,结合图象,因为329115e 3e e <<,所以3915e 3ea ≤<. 故选:C4.(2014·全国·高考真题(文))已知函数,若存在唯一的零点,且,则的取值范围是( ) A . B . C . D .【答案】C 【解析】 【详解】试题分析:当时,,函数和,不满足题意,舍去;当时,,令,得或.时,;时,;时,,且,此时在必有零点,故不满足题意,舍去;当时,时,32()31f x ax x =-+()f x 0x 00x >a ()2,+∞()1,+∞(),2-∞-(),1-∞-0a =2()31f x x =-+()f x 0a >2()36f x ax x '=-()0f x '=0x =2x a =(,0)x ∈-∞()0f x '>2(0,)x a ∈()0f x '<2(,)x a∈+∞()0f x '>(0)0f >(,0)x ∈-∞0a <2(,)x a∈-∞;时,;时,,且,要使得存在唯一的零点,且,只需,即,则,选C .5.(2022·青海·海东市第一中学模拟预测(理))若函数()()22e e x xf x x ax a a R =+-∈有三个不同的零点,则实数a 的取值范围是( ) A .1,e ⎛⎫+∞ ⎪⎝⎭B .1,1e ⎛⎫ ⎪⎝⎭C .2110,,1e e e ⎛⎫⎛⎫⋃ ⎪ ⎪-⎝⎭⎝⎭D .210,e e ⎛⎫ ⎪-⎝⎭【答案】D 【解析】 【分析】令()0f x =得20e e x xx xa a ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭,利用导数研究()e x x g x =的图像,由函数()f x 有三个零点可知,若令1e e xxt t ⎛⎫=≤ ⎪⎝⎭,则可知方程20t at a +-=的一根1t 必在10,e ⎛⎫ ⎪⎝⎭内,另一根21e t =或20t =或()2,0t ∈-∞上,分类讨论即可求解. 【详解】由22e e 0xxx ax a +-=得20e ex xx xa a ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭,令()e x x g x =, 由()10e xxg x -'==,得1x =,因此函数()g x 在(),1-∞上单调递增,在()1,+∞上单调递减,且()00g =,当0x >时,()0e x x g x =>,则()ex xg x =的图像如图所示: 即函数()g x 的最大值为()11eg =,令1e e xx t t ⎛⎫=≤ ⎪⎝⎭,则()20h t t at a =+-=,由二次函数的图像可知,二次方程的一根1t 必在10,e ⎛⎫ ⎪⎝⎭内,另一根21e t =或20t =或()2,0t ∈-∞上,当21e t =时,21e ea =-,则另一根111e t =-,不满足题意,当20t =时,a =0,则另一根10t =,不满足题意,()0f x '<2(,0)x a ∈()0f x '>(0,)x ∈+∞()0f x '<(0)0f >()f x 0x 00x >2()0f a>24a >2a <-当()2,0t ∈-∞时,由二次函数()20h t t at a =+-=的图像可知22000110e e a a a a ⎧+⋅-<⎪⎨⎛⎫+⋅->⎪ ⎪⎝⎭⎩, 解得210e ea <<-, 则实数a 的取值范围是210,e e ⎛⎫ ⎪-⎝⎭,故选:D.6.(2022·河南·开封市东信学校模拟预测(理))对任意0x >,不等式e ln()(1)0x ax a x -+-≥恒成立,则正数a 的最大值为( ) ABC .1eD .e【答案】D 【解析】 【分析】将不等式化为ln()e ln()e x ax x ax +≥+,构造()e x f x x =+有()(ln())f x f ax ≥,利用函数的单调性及参变分离法有e xa x ≤在0x >上恒成立,应用导数求右侧最小值,即可得结果.【详解】∵e ln()(1)0x ax a x -+-≥,∴ln()e ln()ln()e x ax x ax ax ax +≥+=+.令()e x f x x =+,则不等式化为()(ln())f x f ax ≥. ∵()e (0)x f x x x =+>为增函数,∴ln()x ax ≥,即e xa x≤.令e ()=x g x x ,则2(1)e ()x x g x x '-=,当01x <<时,()0g x '<,即()g x 递减;当1x >时,()0g x '>,即()g x 递增; 所以()()min 1e e g x g a ⇒≤==. ∴实数a 的最大值为e . 故选:D7.(2015·全国·高考真题(理))设函数()(21)xf x e x ax a =--+,其中1a < ,若存在唯一的整数0x ,使得0()0f x <,则a 的取值范围是( )A .3,12e ⎡⎫-⎪⎢⎣⎭B .33,2e 4⎡⎫-⎪⎢⎣⎭C .33,2e 4⎡⎫⎪⎢⎣⎭D .3,12e ⎡⎫⎪⎢⎣⎭【答案】D 【解析】 【分析】设()()21xg x e x =-,()1y a x =-,问题转化为存在唯一的整数0x 使得满足()()01g x a x <-,求导可得出函数()y g x =的极值,数形结合可得()01a g ->=-且()312g a e-=-≥-,由此可得出实数a 的取值范围.【详解】设()()21xg x e x =-,()1y a x =-,由题意知,函数()y g x =在直线y ax a =-下方的图象中只有一个点的横坐标为整数,()()21x g x e x '=+,当12x <-时,()0g x '<;当12x >-时,()0g x '>.所以,函数()y g x =的最小值为12122g e -⎛⎫-=- ⎪⎝⎭.又()01g =-,()10g e =>.直线y ax a =-恒过定点()1,0且斜率为a , 故()01a g ->=-且()31g a a e -=-≥--,解得312a e≤<,故选D.8.(2022·内蒙古·海拉尔第二中学模拟预测(理))已知函数()()e ln e (0)xf x a a a =+>,若对任意实数1x >,不等式()()ln 1f x x ≥-总成立,则实数a 的取值范围为( )A .210,e ⎛⎫ ⎪⎝⎭B .221,e e ⎛⎤⎥⎝⎦C .21,e ⎛⎫+∞ ⎪⎝⎭D .21,e ⎡⎫+∞⎪⎢⎣⎭【答案】D 【解析】 【分析】将所求不等式变形为()()ln 1ln eln eln 1x x ax a x -+++≥+-,构造函数()e xg x x =+,可知该函数在R 上为增函数,由此可得出()ln ln 1a x x ≥--,其中1x >,利用导数求出()()ln 1h x x x =--的最大值,即可求得实数a 的取值范围. 【详解】当1x >时,由()()ln 1f x x ≥-可得()ln eln 1ln 1x aa x +++≥-, 即()()()ln 1ln eln 1ln 1eln 1x x ax a x x x -+++≥-+-=+-,构造函数()e xg x x =+,其中x ∈R ,则()e 10x g x '=+>,所以,函数()g x 在R 上为增函数, 由()()ln 1ln eln eln 1x x ax a x -+++≥+-可得()()ln ln 1g x a g x +≥-⎡⎤⎣⎦,所以,()ln ln 1x a x +≥-,即()ln ln 1a x x ≥--,其中1x >, 令()()ln 1h x x x =--,其中1x >,则()12111xh x x x -'=-=--. 当12x <<时,()0h x '>,函数()h x 单调递增, 当2x >时,()0h x '<,函数()h x 单调递减, 所以,()()max ln 22a h x h ≥==-,21e a ∴≥. 故选:D.二、多选题9.(2022·辽宁实验中学模拟预测)我们把形如(),,0f x y y '=的方程称为微分方程,符合方程的函数()y f x =称为微分方程的解,下列函数为微分方程0xy y xy +-'=的解的是( ) A .e x y = B .e x y x =C .e 1x y x =+D .e (R)x y c x c =⋅∈⋅【答案】CD 【解析】 【分析】根据导数的运算求得导函数y ',代入微分方程检验即可. 【详解】选项A ,e x y =,则e x y '=,e e e e 0x x x x xy y xy x x '+-=+-=≠,不是解;选项B ,e x y x =,e e x x y x '=+,22e e e e 0x x x x xy y xy x x x x '+-=+--=,是方程的解;选项C ,e 1x y x =+,e e x x y x '=+,22e e 1e e 10x x x x xy y xy x x x x x x '+-=+++--=+≠,不是方程的解; 选项D ,e (R)x y c x c =⋅∈⋅,e e x x y c cx '=+,22e e e e 0x x x x xy y xy cx cx cx cx '+-=+--=,是方程的解. 故选:CD .10.(2022·河北沧州·二模)已知实数,a b 满足e e e a b a b ++=,则( ) A .0ab < B .1a b +> C .e e 4a b + D .e 1a b >【答案】BCD 【解析】 【分析】A.由e e e a b a b ++=得到111e ea b +=判断;BC.由e e e 2e e a b a b a b ++==2b 判断;D. 由111e e a b +=,得到e e e 1e 11e 1e 1b b b ab b b b b -+-=-=--,令()e e 1,0b b f b b b =-+>,用导数法判断. 【详解】 由e e e a b a b ++=得111e ea b +=,又e 0,e 0a b >>,所以e 1,e 1a b >>,所以0,0a b >>,所以0ab >,选项A 错误;因为e e e 2e e a b a b a b ++==2b ,即e e e 4a b a b ++=,所以ln41a b +>,选项B C ,正确,因为111e e a b +=,所以e e e 1b ab =-,所以e e e 1e 11e 1e 1b b b a bbb b b -+-=-=--.令()e e 1,0b b f b b b =-+>,则()e 0b f b b '=>,所以f b 在区间()0,∞+上单调递增,所以()()00f b f >=,即e e 10b b b -+>,又e 10b ->,所以e 10a b ->,即e 1a b >,选项D 正确. 故选:BCD11.(2022·湖南·模拟预测)已知1x >,1y >,且()()1e 11e y xx y ++=+,则下列结论一定正确的是( )A .()ln 0x y ->B .122x y +<C .226x y +>D .()ln ln3x y +<【答案】AC 【解析】 【分析】构造函数()e xf x x=,利用导数判断函数的单调性,得出1x y >+,结合不等式以及指、对数函数的性质逐一判断即可. 【详解】令()e x f x x=,则()()2e 1e e xx x x x f x x x --'==, 所以当1x >时,()0f x '>,所以()f x 在()1,+∞上单调递增; 由()()1e 11e yxx y ++=+得1e e 111x y x y y +=+++,即1e e 111x y x y y +-=++,∵1y >,∴11012y <<+, ∴1e e 1012x y x y +<-<+,即()()1012f x f y <-+<, ∴1x y >+,即1->x y ,∴()ln 0x y ->,A 正确;由1x y >+知12x y +>+,所以12222x y y ++>>,所以选项B 错误; 由1x y >+知12222326x y y y y ++>+=⋅>,所以选项C 正确.由1x y >+,1y >知213x y y +>+>,所以()()ln ln 21ln3x y y +>+>, 所以D 错误,故选:AC .12.(2022·全国·高考真题)已知函数,则( )A .有两个极值点B .有三个零点C .点是曲线的对称中心D .直线是曲线的切线【答案】AC 【解析】 【分析】利用极值点的定义可判断A ,结合的单调性、极值可判断B ,利用平移可判断C ;利用导数的几何意义3()1f x x x =-+()f x ()f x (0,1)()y f x =2y x =()y f x =()f x判断D. 【详解】由题,,令得或令得, 所以在上单调递减,在,上单调递增, 所以是极值点,故A 正确;因,,, 所以,函数在上有一个零点, 当时,,即函数在上无零点, 综上所述,函数有一个零点,故B 错误;令,该函数的定义域为,,则是奇函数,是的对称中心, 将的图象向上移动一个单位得到的图象, 所以点是曲线的对称中心,故C 正确;令,可得,又,当切点为时,切线方程为,当切点为时,切线方程为, 故D 错误.故选:AC.三、填空题13.(2020·河南高三其他(理))函数()2222ln x f x x e x ax =--,若0a =,则()f x 在[]1,2的最小值为_______;当0x >时,()1fx ≥恒成立,则a 的取值范围是_____.【答案】e (],1-∞ 【解析】当0a =时,∵()222ln x f x x ex =-,∴()222222x x f x xe x xe x'=+⋅-. 当1x >时,()0f x '>恒成立,()231f x x '=-()0fx '>x >x <()0f x '<x <()f x ((,-∞)+∞x =(10f =+>10f =>()250f -=-<()f x ,⎛-∞ ⎝⎭x ≥()0f x f ≥>⎝⎭()f x ⎫∞⎪⎪⎝⎭()f x 3()h x x x =-R ()()()()33h x x x x x h x -=---=-+=-()h x (0,0)()h x ()h x ()f x (0,1)()y f x =()2312f x x '=-=1x =±()(1)11f f =-=(1,1)21y x =-(1,1)-23y x =+∴()f x 在[]1,2上单调递增.∴()f x 在[]1,2上最小值为()1f e =.又0x >时,()1f x ≥恒成立,令 ()1xg x e x =--,()()100xg x e g ''=->=,所以()g x 在()0,∞+ 递增,()()00g x g >= 所以1x e x >+ ∴()22222ln 22ln 2ln x x x f x x e x ax e x ax +=--=--()2222ln 12ln 111x x x ax a x ≥++--=-+≥恒成立,∴1a ≤.故答案为e ;(],1-∞.14.(2022·全国·模拟预测(理))若曲线ln x y x =与212y kx =-仅有1个公共点,则k 的取值范围是___________. 【答案】(]1,02⎧⎫-∞⋃⎨⎬⎩⎭##1|02k k k ⎧⎫≤=⎨⎬⎩⎭或【解析】 【分析】将原问题转化为32ln 12x k x x =+只有一个解,令()()32ln 102x g x x x x =+>,利用导数求出()g x 的单调性及最值即可得答案. 【详解】 由题意可得:2ln 12x kx x =-只有一个解()0x >, 即32ln 12x k x x=+只有一个解. 令()32ln 12x g x x x=+, ()0x >原问题等价于y k =与()y g x =只有一个交点. 因为()43413ln 113ln x x xg x x x x '---=-= 因为13ln y x x =--在()0,∞+上单调递减, 且在1x =处的值为0 ,所以当()0,1x ∈时, ()()0,g x g x '>单调递增,当()1,x ∈+∞时, ()()0,g x g x '<单调递减且恒为正, 所以()()max 112g x g ==, 又因为y k =与()y g x =只有一个交点, 所以(]1,02k ⎧⎫∈-∞⎨⎬⎩⎭.故答案为: (]1,02⎧⎫-∞⋃⎨⎬⎩⎭.15.(2012·福建·高考真题(理))对于实数a 和b ,定义运算“*”: 设f (x )=(2x -1)*(x -1),且关于x 的方程为f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3的取值范围是_________________ 【答案】【解析】 【详解】由定义运算“*”可知 即,该函数图像如下:由,假设当关于x 的方程为f (x )=m (m ∈R )恰有三个互不相等的实数根时, m 的取值范围是,且满足方程,所以令则, 所以令22,,a ab a ba b b ab a b ⎧-≠=⎨->⎩⎫⎪⎪⎝⎭22(21)(21)(1)0()?(1)(21)(1)0x x x x f x x x x x ⎧----=⎨---->⎩2220()0x x x f x x x x ⎧-=⎨-+>⎩1124f ⎛⎫= ⎪⎝⎭1230x x x <<<10,4⎛⎫⎪⎝⎭23,x x 2-+=x x m 23=x x m 22-=x x m 1=x 123==x x x m 10,4⎛⎫=∈ ⎪⎝⎭y m所以, 又在递增的函数, 所以,所以,所以在递减, 则当时,;当时,所以.16.(2022·江苏·常州高级中学模拟预测)已知函数22()ln 2e f x x x mx =-+,若()0f x ≥的解集中恰有一个整数,则m 的取值范围为________.【答案】22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭【解析】【分析】由()0f x ≥且0x >,得出2ln 2e x x m x -+≥-,构造函数()ln =-xg x x,利用导数研究()g x 的单调性,画出()ln =-x g x x 和22e y x =-的大致图象,由图可知0m >,设0x 为()ln =-xg x x和22e y x m =-+的交点的横坐标,结合题意可知该整数为1,即012x ≤<,当直线22e y x m =-+过1,0A 和ln 22,2B ⎛⎫- ⎪⎝⎭时,即可求出求出m 的值,从而得出m 的取值范围.【详解】由题可知,22()ln 2e f x x x mx =-+,0x >, 由于()0f x ≥的解集中恰有一个整数,即22ln 2e 0x x mx -+≥,即222e ln x mx x -+≥-,因为0x >,所以2ln 2e xx m x-+≥-的解集中恰有一个整数, 令()ln =-x g x x ,则()2ln 1-'=x g x x , 当1e x <<时,()0g x '<;当e x >时,()0g x '>, 所以()g x 在()1,e 上单调递减,在()e,+∞上单调递增, 画出()ln xy xg x ==-和22e y x =-的大致图象,如图所示: 要使得2ln 2e xx m x-+≥-,可知0m >, 114'⎛= ⎝y ()=h m 10,4⎛⎫⎪⎝⎭()()01>=h m h 0y '<=y 10,4⎛⎫ ⎪⎝⎭0m =0y =14m ==y 123⎫∈⎪⎪⎝⎭x x x设0x 为()ln =-xg x x和22e y x m =-+的交点的横坐标, 而2ln 2e xx m x-+≥-的解集中恰有一个整数,可知该整数为1,即012x ≤<, 当01x =时,得()10g =;当02x =时,得()ln 222g =-, 即1,0A ,ln 22,2B ⎛⎫- ⎪⎝⎭,当直线22e y x m =-+过点1,0A 时,得22e m =,当直线22e y x m =-+过点ln 22,2B ⎛⎫- ⎪⎝⎭时,得2ln 24e 2m =-, 所以m 的取值范围为22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭.故答案为:22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭四、解答题17.(2018·全国·高考真题(文))已知函数.(1)求曲线在点处的切线方程; (2)证明:当时,.【答案】(1)切线方程是(2)证明见解析 【解析】 【分析】(1)求导,由导数的几何意义求出切线方程.(2)当时,,令,只需证明即可.【详解】()21x ax x f x e +-=()y f x =()0,1-1a ≥()0f x e +≥210x y --=a 1≥()12f x e 1x x e x x e +-+≥++-()12gx 1x e x x +=++-gx 0≥(1),.因此曲线在点处的切线方程是.(2)当时,.令,则,当时,,单调递减;当时,,单调递增; 所以 .因此.18.(2017·全国·高考真题(理))已知函数(1)讨论的单调性;(2)若有两个零点,求的取值范围. 【答案】(1)见解析;(2). 【解析】 【详解】试题分析:(1)讨论单调性,首先进行求导,发现式子特点后要及时进行因式分解,再对按,进行讨论,写出单调区间;(2)根据第(1)问,若,至多有一个零点.若,当时,取得最小值,求出最小值,根据,,进行讨论,可知当时有2个零点.易知在有一个零点;设正整数满足,则.由于,因此在有一个零点.从而可得的取值范围为.试题解析:(1)的定义域为,,(ⅰ)若,则,所以在单调递减. (ⅱ)若,则由得.当时,;当时,,所以在单调递减,在单调递增.(2)(ⅰ)若,由(1)知,至多有一个零点.(ⅱ)若,由(1)知,当时,取得最小值,最小值为. ()()2212xax a x f x e-++'-=()02f '=()y f x =()0,1-210x y --=1a ≥()()211x xf x e x x e e +-+≥+-+()211xg x x x e +=+-+()121x g x x e +=++'()120x g x e +''=+>1x <-()()10g x g '-'<=()g x 1x >-()()10g x g '-'>=()g x ()g x ()1=0g ≥-()0f x e +≥()()2e 2e x xf x a a x =+--()f x ()f x a (0,1)()f x a 0a ≤0a >0a ≤()f x 0a >ln x a =-()f x 1(ln )1ln f a a a-=-+1a =(1,)∈+∞a (0,1)a ∈(0,1)a ∈()f x (,ln )a -∞-0n 03ln(1)n a>-00000000()e (e 2)e 20n n n n f n a a n n n =+-->->->3ln(1)ln a a->-()f x (ln ,)a -+∞a (0,1)()f x (),-∞+∞()()()()2221121x x x xf x ae a e ae e =+---'=+0a ≤()0f x '<()f x (),-∞+∞0a >()0f x '=ln x a =-(),ln x a ∈-∞-()0f x '<()ln ,x a ∈-+∞()0f x '>()f x (),ln a -∞-()ln ,a -+∞0a ≤()f x 0a >ln x a =-()f x ()1ln 1ln f a a a-=-+①当时,由于,故只有一个零点; ②当时,由于,即,故没有零点; ③当时,,即. 又,故在有一个零点.设正整数满足,则.由于,因此在有一个零点. 综上,的取值范围为.19.(2017·全国·高考真题(文))已知函数.(1)讨论的单调性; (2)当时,证明. 【答案】(1)见解析;(2)见解析. 【解析】 【分析】(1)先求函数导数,再根据导函数符号的变化情况讨论单调性:当时,,则在单调递增;当时,在单调递增,在单调递减. (2)证明,即证,而,所以需证,设g (x )=ln x -x +1 ,利用导数易得,即得证. 【详解】(1) 的定义域为(0,+),. 若a ≥0,则当x ∈(0,+)时,,故f (x )在(0,+)单调递增.若a <0,则当时,时;当x ∈时,. 故f (x )在单调递增,在单调递减. (2)由(1)知,当a <0时,f (x )在取得最大值,最大值为. 1a =()ln 0f a -=()f x ()1,a ∈+∞11ln 0a a-+>()ln 0f a ->()f x ()0,1a ∈11ln 0a a-+<()ln 0f a -<()()4222e 2e 22e 20f a a ----=+-+>-+>()f x (),ln a -∞-0n 03ln 1n a ⎛⎫>- ⎪⎝⎭()()00000000e e 2e 20n n n nf n a a n n n =+-->->->3ln 1ln a a ⎛⎫->- ⎪⎝⎭()f x ()ln ,a -+∞a ()0,12()ln (21)f x x ax a x =+++()f x 0a <3()24f x a≤--(21)(1)'()(0)ax x f x x x++=>0a ≥'()0f x >()f x (0,)+∞0a <()f x 1(0,)2a -1(,)2a-+∞3()24f x a ≤--max 3()24f x a ≤--max 1()()2f x f a=-11ln()1022a a -++≤max ()(1)0g x g ==()f x ∞()()‘1211)22(1x ax f x ax a x x++=+++=∞’)(0f x >∞10,2x a ⎛⎫∈- ⎪⎝⎭()0f x '>1()2a ∞-+,’)(0f x <’)(0f x >1()2a∞-+,12x a=-111()ln()1224f a a a -=---所以等价于,即. 设g (x )=ln x -x +1,则. 当x ∈(0,1)时,;当x ∈(1,+)时,.所以g (x )在(0,1)单调递增,在(1,+)单调递减.故当x =1时,g (x )取得最大值,最大值为g (1)=0.所以当x >0时,g (x )≤0.从而当a <0时,,即. 20.(2016·全国·高考真题(文))设函数.(Ⅰ)讨论的单调性; (Ⅱ)证明当时,; (Ⅲ)设,证明当时,.【答案】(Ⅰ)当时,单调递增;当时,单调递减;(Ⅱ)见解析;(Ⅲ)见解析. 【解析】 【详解】试题分析:(Ⅰ)首先求出导函数,然后通过解不等式或可确定函数的单调性;(Ⅱ)左端不等式可利用(Ⅰ)的结论证明,右端将左端的换为即可证明;(Ⅲ)变形所证不等式,构造新函数,然后通过利用导数研究函数的单调性来处理. 试题解析:(Ⅰ)由题设,的定义域为,,令,解得. 当时,,单调递增;当时,,单调递减. (Ⅱ)由(Ⅰ)知,在处取得最大值,最大值为. 所以当时,. 故当时,,,即. (Ⅲ)由题设,设,则,令,解得.当时,,单调递增;当时,,单调递减. 由(Ⅱ)知,,故,又,故当时,. 所以当时,.3()24f x a≤--113ln()12244a a a ---≤--11ln()1022a a -++≤’1(1)g x x=-()0g x '>∞()0g x '<∞11ln()1022a a -++≤3()24f x a≤--()ln 1f x x x =-+()f x (1,)x ∈+∞11ln x x x-<<1c >(0,1)x ∈1(1)xc x c +->01x <<()f x 1x >()f x ()f x '()0f x '>()0f x '<()f x x 1x()f x (0,)+∞1()1f x x=-'()0f x '=1x =01x <<()0f x '>()f x 1x >()0f x '<()f x ()f x 1x =(1)0f =1x ≠ln 1x x <-(1,)x ∈+∞ln 1x x <-11ln1x x <-11ln x x x-<<1c >()1(1)x g x c x c =+--'()1ln xg x c c c =--'()0g x =01lnln ln c c x c-=0x x <'()0g x >()g x 0x x >'()0g x <()g x 11ln c c c-<<001x <<(0)(1)0g g ==01x <<()0g x >(0,1)x ∈1(1)xc x c +->21.(2015·全国·高考真题(理))设函数.(1)证明:在单调递减,在单调递增;(2)若对于任意,都有,求m 的取值范围.【答案】(1)在单调递减,在单调递增;(2).【解析】【详解】(Ⅰ).若,则当时,,;当时,,.若,则当时,,;当时,,.所以,在单调递减,在单调递增.(Ⅱ)由(Ⅰ)知,对任意的,在单调递减,在单调递增,故在处取得最小值.所以对于任意,的充要条件是:即①,设函数,则.当时,;当时,.故在单调递减,在单调递增.又,,故当时,.当时,,,即①式成立.当时,由的单调性,,即;当时,,即.综上,的取值范围是.22.(2014·四川·高考真题(理))已知函数,其中,为自然对数的底数.(Ⅰ)设是函数的导函数,求函数在区间上的最小值;(Ⅱ)若,函数在区间内有零点,求的取值范围【答案】(Ⅰ)当时, ;当 时, ; 当时, .(Ⅱ) 的范围为. 【解析】【详解】试题分析:(Ⅰ)易得,再对分情况确定的单调区间,根据在上的单调性即可得在上的最小值.(Ⅱ)设为在区间内的一个零点,注意到2()e mx f x x mx =+-()f x (,0)-∞(0,)+∞12,[1,1]x x ∈-12|()()|1f x f x e -≤-()f x (,0)-∞(0,)+∞[1,1]-()(1)2mx f x m e x -'=+0m ≥(,0)x ∈-∞10mx e -≤()0f x '<(0,)x ∈+∞10mx e -≥()0f x '>0m <(,0)x ∈-∞10mx e ->()0f x '<(0,)x ∈+∞10mx e -<()0f x '>()f x (,0)-∞(0,)+∞m ()f x [1,0]-[0,1]()f x 0x =12,[1,1]x x ∈-12()()1f x f x e -≤-(1)(0)1,{(1)(0)1,f f e f f e -≤---≤-1,{1,m m e m e e m e --≤-+≤-()1t g t e t e =--+()1t g t e =-'0t <()0g t '<0t >()0g t '>()g t (,0)-∞(0,)+∞(1)0g =1(1)20g e e --=+-<[1,1]t ∈-()0g t ≤[1,1]m ∈-()0g m ≤()0g m -≤1m >()g t ()0g m >1m e m e ->-1m <-()0g m ->1m e m e -+>-m [1,1]-2()1x f x e ax bx =---,a b R ∈ 2.71828e =()g x ()f x ()g x [0,1](1)0f =()f x (0,1)a 12a ≤()(0)1g x g b ≥=-122e a <≤()22ln(2)g x a a a b ≥--2e a >()2g x e a b ≥--a ()2,1e -()2,()2x x g x e ax b g x e a -='=--a ()g x ()g x [0,1]()g x [0,1]0x ()f x (0,1).联系到函数的图象可知,导函数在区间内存在零点,在区间内存在零点,即在区间内至少有两个零点. 由(Ⅰ)可知,当及时,在内都不可能有两个零点.所以.此时,在上单调递减,在上单调递增,因此,且必有.由得:,代入这两个不等式即可得的取值范围.试题解答:(Ⅰ)①当时,,所以.②当时,由得.若,则;若,则. 所以当时,在上单调递增,所以. 当时,在上单调递减,在上单调递增,所以. 当时,在上单调递减,所以. (Ⅱ)设为在区间内的一个零点,则由可知,在区间上不可能单调递增,也不可能单调递减.则不可能恒为正,也不可能恒为负.故在区间内存在零点.同理在区间内存在零点.所以在区间内至少有两个零点.由(Ⅰ)知,当时,在上单调递增,故在内至多有一个零点. 当时,在上单调递减,故在内至多有一个零点. 所以. 此时,在上单调递减,在上单调递增,因此,必有.由得:,有(0)0,(1)0f f ==()g x 0(0,)x 1x ()g x 0(),1x 2x ()g x (0,1)12a ≤2e a ≥()g x (0,1)122e a <<()g x [0,ln 2]a [ln 2,1]a 12(0,ln(2)],(ln(2),1)x a x a ∈∈(0)10,(1)20g b g e a b =->=-->(1)10f e a b =---=1b e a =--a ()2,()2x xg x e ax b g x e a -='=--0a ≤()20x g x e a -'=>()(0)1g x g b ≥=-0a >()20x g x e a -'=>2,ln(2)x e a x a >>12a >ln(2)0a >2e a >ln(2)1a >102a <≤()g x [0,1]()(0)1g x g b ≥=-122e a <≤()g x [0,ln 2]a [ln 2,1]a ()(ln 2)22ln 2g x g a a a a b ≥=--2e a >()g x [0,1]()(1)2g x g e a b ≥=--0x ()f x (0,1)0(0)()0f f x ==()f x 0(0,)x ()g x ()g x 0(0,)x 1x ()g x 0(),1x 2x ()g x (0,1)12a ≤()g x [0,1]()g x (0,1)2e a ≥()g x [0,1]()g x (0,1)122e a <<()g x [0,ln 2]a [ln 2,1]a 12(0,ln(2)],(ln(2),1)x a x a ∈∈(0)10,(1)20g b g e a b =->=-->(1)10f e a b =---=12a b e +=-<.解得.当时,在区间内有最小值.若,则,从而在区间上单调递增,这与矛盾,所以.又,故此时在和内各只有一个零点和.由此可知在上单调递增,在上单调递减,在上单调递增.所以,,故在内有零点.综上可知,的取值范围是. (0)120,(1)210g b a e g e a b a =-=-+>=--=->21e a -<<21e a -<<()g x [0,1](ln(2))g a (ln(2))0g a ≥()0([0,1])g x x ≥∈()f x [0,1](0)(1)0f f ==(ln(2))0g a <(0)20,(1)10g a e g a =-+>=->()g x (0,ln(2))a (ln(2),1)a 1x 2x ()f x 1[0,]x 1(,x 2)x 2[,1]x 1()(0)0f x f >=2()(1)0f x f <=()f x 1(,x 2)x a (2,1)e -。
高考数学一轮复习导数及其应用多选题复习题含答案

高考数学一轮复习导数及其应用多选题复习题含答案一、导数及其应用多选题1.关于函数()2ln f x x x=+,下列判断正确的是( )A .2x =是()f x 的极大值点B .函数yf xx 有且只有1个零点C .存在正实数k ,使得()f x kx >恒成立D .对任意两个正实数1x ,2x ,且21x x >,若()()12f x f x =,则124x x +> 【答案】BD 【分析】对于A ,利用导数研究函数()f x 的极值点即可; 对于B ,利用导数判断函数y f xx 的单调性,再利用零点存在性定理即得结论;对于C ,参变分离得到22ln xk x x <+,构造函数()22ln x g x x x=+,利用导数判断函数()g x 的最小值的情况;对于D ,利用()f x 的单调性,由()()12f x f x =得到1202x x <<<,令()211x t t x =>,由()()12f x f x =得21222ln t x x t t-+=,所以要证124x x +>,即证2224ln 0t t t -->,构造函数即得. 【详解】A :函数()f x 的定义域为0,,()22212x f x x x x-'=-+=,当()0,2x ∈时,0f x,()f x 单调递减,当()2,x ∈+∞时,0fx,()f x 单调递增,所以2x =是()f x 的极小值点,故A 错误.B :()2ln y f x x x x x=-=+-,22221210x x y x x x -+'=-+-=-<,所以函数在0,上单调递减.又()112ln1110f -=+-=>,()221ln 22ln 210f -=+-=-<,所以函数yf xx 有且只有1个零点,故B 正确.C :若()f x kx >,即2ln x kx x +>,则22ln x k x x <+.令()22ln x g x x x=+,则()34ln x x xg x x-+-'=.令()4ln h x x x x =-+-,则()ln h x x '=-,当()0,1∈x 时,()0h x '>,()h x 单调递增,当()1,∈+∞x 时,()0h x '<,()h x 单调递减,所以()()130h x h ≤=-<,所以0g x ,所以()22ln x g x x x=+在0,上单调递减,函数无最小值,所以不存在正实数k ,使得()f x kx >恒成立,故C 错误. D :因为()f x 在()0,2上单调递减,在2,上单调递增,∴2x =是()f x 的极小值点.∵对任意两个正实数1x ,2x ,且21x x >,若()()12f x f x =,则1202x x <<<. 令()211x t t x =>,则21x tx =,由()()12f x f x =,得121222ln ln x x x x +=+, ∴211222ln ln x x x x -=-,即()2121212ln x x x x x x -=,即()11121ln t x t x tx -=⋅,解得()121ln t x t t -=,()2121ln t t x tx t t-==,所以21222ln t x x t t-+=.故要证124x x +>,需证1240x x +->,需证22240ln t t t -->,需证2224ln 0ln t t tt t-->. ∵211x t x =>,则ln 0t t >, ∴证2224ln 0t t t -->.令()()2224ln 1H t t t t t =-->,()()44ln 41H t t t t '=-->,()()()414401t H t t t t-''=-=>>,所以()H t '在1,上是增函数.因为1t →时,()0H t '→,则()0H t '>,所以()H t 在1,上是增函数.因为1t →时,()0H t →,则()0H t >,所以2224ln 0ln t t tt t-->, ∴124x x +>,故D 正确. 故选:BD . 【点睛】关键点点睛:利用导数研究函数的单调性、极值点,结合零点存在性定理判断A 、B 的正误;应用参变分离,构造函数,并结合导数判断函数的最值;由函数单调性,应用换元法并构造函数,结合分析法、导数证明D 选项结论.2.函数()()320ax bx d a f x cx =+++≠有两个极值点1x 、()212x x x <,则下列结论正确的是( ) A .230b ac ->B .()f x 在区间()12,x x 上单调递减C .若()10af x <,则()f x 只有一个零点D .存在0x ,使得()()()1202f x f x f x +=【答案】ACD 【分析】利用极值点与导数的关系可判断A 选项的正误;取0a <,利用函数的单调性与导数的关系可判断B 选项的正误;分0a >、0a <两种情况讨论,分析函数()f x 的单调性,结合图象可判断C 选项的正误;计算出函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称,可判断D 选项的正误. 【详解】()()320f x ax bx cx d a =+++≠,则()232f x ax bx c '=++.对于A 选项,由题意可知,关于x 的二次方程()23200ax bx c a ++=≠有两个不等的实根,则24120b ac ∆=->,可得230b ac ->,A 选项正确;对于B 选项,当0a <时,且当()12,x x x ∈时,()0f x '>,此时函数()f x 在区间()12,x x 上单调递增,B 选项错误;对于C 选项,当0a >时,由()0f x '>,可得1x x <或2x x >;由()0f x '<,可得12x x x <<.所以,函数()f x 的单调递增区间为()1,x -∞、()2,x +∞,单调递减区间为()12,x x , 由()10af x <,可得()10<f x ,此时,函数()f x 的极大值为()10<f x ,极小值为()2f x ,且()()210f x f x <<,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内; 当0a <时,由()0f x '<,可得1x x <或2x x >;由()0f x '>,可得12x x x <<. 所以,函数()f x 的单调递减区间为()1,x -∞、()2,x +∞,单调递增区间为()12,x x ,由()10af x <,可得()10f x >,此时,函数()f x 的极小值为()10f x >,极大值为()2f x ,且()()210f x f x >>,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内,C 选项正确; 对于D 选项,由题意可知,1x 、2x 是方程2320ax bx c ++=的两根, 由韦达定理可得1223bx x a +=-,123c x x a=, ()()()()()()()()3232f t x f t x a t x b t x c t x d a t x b t x c t x d ⎡⎤⎡⎤-++=-+-+-++++++++⎣⎦⎣⎦()()()()()(322322322322332332a t t x tx x b t tx x c t x d a t t x tx x b t tx x c ⎡⎤⎡=-+-+-++-+++++++++⎣⎦⎣()()322223222a t tx b t x ct d =+++++,取3bt a=-,则322223222333333b b b b b b f x f x a x b x c d a a a a a a ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--+-+=-+⨯-+-++⋅-+⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦32222223333b b b b a b c d fa a a a ⎛⎫⎛⎫⎛⎫⎛⎫=-+⋅-+⋅-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以,函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称, 1223bx x a+=-,()()1223b f x f x f a ⎛⎫∴+=- ⎪⎝⎭,D 选项正确. 故选:ACD. 【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用; (2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.3.已知:()f x 是奇函数,当0x >时,()'()1f x f x ->,(1)3f =,则( )A .(4)(3)f ef >B .2(4)(2)f e f ->-C .3(4)41f e >-D .2(4)41f e -<--【答案】ACD 【分析】由已知构造得'()+10x x e f ⎡⎤>⎢⎥⎣⎦,令()()+1x f x g x e =,判断出函数()g x 在0x >时单调递增,由此得()()4>3g g ,化简可判断A ;()()4>2g g ,化简并利用()f x 是奇函数,可判断B ;()()4>1g g ,化简可判断C ;由C 选项的分析得32(4)41>4+1f e e >-,可判断D.【详解】 因为当0x >时,()'()1fx f x ->,所以()'()10f x f x -->,即()[]'()+10xf x f e x ->,所以'()+10x x e f ⎡⎤>⎢⎥⎣⎦, 令()()+1xf xg x e=,则当0x >时,()'>0g x ,函数()g x 单调递增, 所以()()4>3g g ,即43(4)+1(3)+1>f f e e,化简得(4)(3)1>(3)f f e e ef >+-,故A 正确;()()4>2g g ,即42(4)+1(2)+1>f f e e,化简得222(4)(2)1>(2)f f e e e f >+-,所以2(4)(2)e f f -<-,又()f x 是奇函数,所以2(4)(2)e f f -<-,故B 不正确;()()4>1g g ,即4(4)+1(1)+1>f f e e,又(1)3f =,化简得3(4)41f e >-,故C 正确; 由C 选项的分析得32(4)41>4+1f e e >-,所以2(4)41f e -<--,又()f x 是奇函数,所以2(4)41f e -<--,故D 正确, 故选:ACD. 【点睛】关键点点睛:解决本题中令有导函数的不等式,关键在于构造出某个函数的导函数,得出所构造的函数的单调性,从而可比较函数值的大小关系.4.在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它得名于荷兰数学家鲁伊兹布劳威尔(L.E.Brouwer )简单的讲就是对于满足一定条件的连续函数()f x ,存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点”函数,而称0x 为该函数的一个不动点,依据不动点理论,下列说法正确的是( ) A .函数()sin f x x =有3个不动点B .函数2()(0)f x ax bx c a =++≠至多有两个不动点C .若定义在R 上的奇函数()f x ,其图像上存在有限个不动点,则不动点个数是奇数D .若函数()f x =[0,1]上存在不动点,则实数a 满足l a e ≤≤(e 为自然对数的底数) 【答案】BCD 【分析】根据题目中的定义,结合导数、一元二次方程的性质、奇函数的性质进行判断即可. 【详解】令()sin g x x x =-,()1cos 0g x x '=-≥, 因此()g x 在R 上单调递增,而(0)0g =, 所以()g x 在R 有且仅有一个零点, 即()f x 有且仅有一个“不动点”,A 错误;0a ≠,20ax bx c x ∴++-=至多有两个实数根,所以()f x 至多有两个“不动点”,B 正确;()f x 为定义在R 上的奇函数,所以(0)0f =,函数()-y f x x =为定义在R 上的奇函数,显然0x =是()f x 的一个“不动点”,其它的“不动点”都关于原点对称,个数和为偶数, 因此()f x 一定有奇数个“不动点”,C 正确;因为()f x 在[0,1]存在“不动点”,则()f x x =在[0,1]有解,x =⇒2x a e x x =+-在[0,1]有解,令2()xm x e x x =+-,()12x m x e x '=+-,令()12x n x e x '=+-,()20x n x e '=-=,ln 2x =,()n x 在(0,ln 2)单调递减,在(ln 2,1)单调递增,∴min ()(ln 2)212ln 232ln 20n x n ==+-=->, ∴()0m x '>在[0,1]恒成立,∴()m x 在[0,1]单调递增,min ()(0)1m x m ==,max ()(1)m x m e ==,∴1a e ≤≤,D 正确,. 故选:BCD 【点睛】方法点睛:新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.5.设函数()()1x af x a x a =->的定义域为()0,∞+,已知()f x 有且只有一个零点,下列结论正确的有( ) A .a e =B .()f x 在区间()1,e 单调递增C .1x =是()f x 的极大值点D .()f e 是()f x 的最小值【答案】ACD 【分析】()f x 只有一个零点,转化为方程0x a a x -=在(0,)+∞上只有一个根,即ln ln x ax a=只有一个正根.利用导数研究函数ln ()xh x x=的性质,可得a e =,判断A ,然后用导数研究函数()x e f x e x =-的性质,求出()'f x ,令()0f x '=,利用新函数确定()'f x 只有两个零点1和e ,并证明出()'f x 的正负,得()f x 的单调性,极值最值.判断BCD .【详解】()f x 只有一个零点,即方程0x a a x -=在(0,)+∞上只有一个根,x a a x =,取对数得ln ln x a a x =,即ln ln x ax a=只有一个正根. 设ln ()x h x x =,则21ln ()x h x x-'=,当0x e <<时,()0h x '>,()h x 递增,0x →时,()h x →-∞,x e >时,()0h x '<,()h x 递减,此时()0h x >,max 1()()h x h e e==. ∴要使方程ln ln x ax a =只有一个正根.则ln 1a a e =或ln 0a a<,解得a e =或0a <,又∵1a >,∴a e =.A 正确;()x e f x e x =-,1()x e f x e ex -'=-,1()0x e f x e ex -'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.设()(1)ln 1p x e x x =--+,1()1e p x x-'=-,当01x e <<-时,()0p x '>,()p x 递增,1x e >-时,()0p x '<,()p x 递减,(1)p e -是极大值,又(1)()0p p e ==, 所以()p x 有且只有两个零点,01x <<或x e >时,()0p x <,即(1)ln 1e x x -<-,11e x x e --<,1e x ex e -<,()0f x '>,同理1x e <<时,()0f x '<,所以()f x 在(0,1)和(,)e +∞上递增,在(1,)e 上递减,所以极小值为()0f e =,极大值为(1)f ,又(0)1f =,所以()f e 是最小值.B 错,CD 正确. 故选:ACD . 【点睛】关键点点睛:本题考用导数研究函数的零点,极值,单调性.解题关键是确定()'f x 的零点时,利用零点定义解方程,1()0x e f x e ex -'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.然后证明方程只有这两个解即可.6.已知函数()sin xf x x=,(]0,x π∈,则下列结论正确的有( ) A .()f x 在区间(]0,π上单调递减B .若120x x π<<≤,则1221sin sin x x x x ⋅>⋅C .()f x 在区间(]0,π上的值域为[)0,1 D .若函数()()cos g x xg x x '=+,且()1g π=-,()g x 在(]0,π上单调递减【答案】ACD 【分析】先求出函数的导数,然后对四个选项进行逐一分析解答即可, 对于选项A :当0,2x π⎛⎫∈ ⎪⎝⎭时,可得()0f x '<,可得()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减;当,2x ππ⎡⎤∈⎢⎥⎣⎦,可得()0f x '<,可得()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减,最后作出判断; 对于选项B :由()f x 在区间(]0,π上单调递减可得()()12f x f x >,可得1212sin sin x x x x >,进而作出判断; 对于选项C :由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==,进而作出判断;对于选项D :()()()sin g x g x xg x x ''''=+-,可得()()sin xg x f x x''==,然后利用导数研究函数()g x '在区间(]0,π上的单调性,可得()()0g x g π''≤=,进而可得出函数()g x 在(]0,π上的单调性,最后作出判断.【详解】()2cos sin x x xf x x-'=, (]0,x π∈, 当0,2x π⎛⎫∈ ⎪⎝⎭时,cos 0x >,由三角函数线可知tan x x <, 所以sin cos xx x<,即cos sin x x x <,所以cos sin 0x x x -<, 所以()0f x '<,所以()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减, 当,2x ππ⎡⎤∈⎢⎥⎣⎦,cos 0x ≤,sin 0x ≥,所以cos sin 0x x x -<,()0f x '<, 所以()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减,所以()f x 在区间(]0,π上单调递减,故选项A 正确; 当120x x π<<≤时,()()12f x f x >, 所以1212sin sin x x x x >,即1221sin sin x x x x ⋅<⋅,故选项B 错误; 由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==, 所以当(]0,x π∈时,()[)0,1f x ∈,故选项C 正确;对()()cos g x xg x x '=+进行求导可得: 所以有()()()sin g x g x xg x x ''''=+-,所以()()sin xg x f x x''==,所以()g x ''在区间(]0,π上的值域为[)0,1, 所以()0g x ''≥,()g x '在区间(]0,π上单调递增,因为()0g π'=, 从而()()0g x g π''≤=,所以函数()g x 在(]0,π上单调递减,故选项D 正确.故选:ACD. 【点睛】方法点睛:本题考查导数的综合应用,对于函数()sin xf x x=的性质,可先求出其导数,然后结合三角函数线的知识确定导数的符号,进而确定函数的单调性和极值,最后作出判断,考查逻辑思维能力和运算求解能力,属于中档题.7.设函数()ln xf x x=,()ln g x x x =,下列命题,正确的是( ) A .函数()f x 在()0,e 上单调递增,在(),e +∞单调递减 B .不等关系33e e ππππ<<<成立C .若120x x <<时,总有()()()22212122a x x g x g x ->-恒成立,则1a ≥D .若函数()()2h x g x mx =-有两个极值点,则实数()0,1m ∈【答案】AC 【分析】利用函数的单调性与导数的关系可判断A 选项的正误;由函数()f x 在区间(),e +∞上的单调性比较3π、e π的大小关系,可判断B 选项的正误;分析得出函数()()22s x g x ax=-在()0,∞+上为减函数,利用导数与函数单调性的关系求出a 的取值范围,可判断C 选项的正误;分析出方程1ln 2xm x+=在()0,∞+上有两个根,数形结合求出m 的取值范围,可判断D 选项的正误. 【详解】对于A 选项,函数()ln x f x x =的定义域为()0,∞+,则()21ln xf x x -'=. 由()0f x '>,可得0x e <<,由()0f x '>,可得x e >.所以,函数()f x 在()0,e 上单调递增,在(),e +∞单调递减,A 选项正确; 对于B 选项,由于函数()ln xf x x=在区间(),e +∞上单调递减,且4e π>>, 所以,()()4f f π>,即ln ln 44ππ>,又ln 41ln 213ln 22043236--=-=>, 所以,ln ln 4143ππ>>,整理可得3e ππ>,B 选项错误; 对于C 选项,若120x x <<时,总有()()()22212122a x x g x g x ->-恒成立,可得()()22112222g x ax g x ax ->-,构造函数()()2222ln s x g x ax x x ax =-=-,则()()12s x s x >,即函数()s x 为()0,∞+上的减函数,()()21ln 20s x x ax '=+-≤对任意的()0,x ∈+∞恒成立, 即1ln x a x +≥对任意的()0,x ∈+∞恒成立, 令()1ln x t x x +=,其中0x >,()2ln x t x x'=-. 当01x <<时,()0t x '>,此时函数()t x 单调递增;当1x >时,()0t x '<,此时函数()t x 单调递减. 所以,()()max 11t x t ==,1a ∴≥,C 选项正确;对于D 选项,()()22ln h x g x mx x x mx =-=-,则()1ln 2h x x mx '=+-, 由于函数()h x 有两个极值点,令()0h x '=,可得1ln 2x m x+=, 则函数2y m =与函数()t x 在区间()0,∞+上的图象有两个交点,当1x e>时,()0t x >,如下图所示:当021m <<时,即当102m <<时,函数2y m =与函数()t x 在区间()0,∞+上的图象有两个交点.所以,实数m 的取值范围是10,2⎛⎫ ⎪⎝⎭,D 选项错误.故选:AC.【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用;(2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.8.若方程()2110x m x -+-=和()120x m e x -+-=的根分别为()1212,x x x x <和3x ,()434x x x <,则下列判断正确的是( )A .3201x x <<<B .1310x x -<<C .(),1m ∈-∞-D.1112x ⎛⎫-∈- ⎪ ⎪⎝⎭ 【答案】ABD【分析】根据题意将问题转化为,1x ,2x 和3x ,4x 分别是y m =与11y x x =--和12x x y e -=-交点的横坐标,再用导数研究函数11y x x =--和12x x y e -=-的单调性与取值情况,作出函数图象,数形结合即可解决问题.【详解】解:由题,1x ,2x 和3x ,4x 分别是11m x x =--和12x x m e -=-的两个根, 即y m =与11y x x =--和12x x y e -=-交点的横坐标. 对于函数11y x x =--,定义域为{}0x x ≠,21'10y x=+>,所以函数在(),0-∞和()0,∞+上单调递增,且1x =时,1y =-; 对于函数12x xy e -=-,11'x x y e--=,所以函数在(),1-∞上单调递增,在()1,+∞单调递减,且当,2x y →+∞→-,0x =时,2y =-,1x =时,1y =-; 故作出函数11y x x =--,12x x y e-=-的图像如图所示, 注意到:当()0,1x ∈时,11122x x x x x e ---<-<-, 由图可知,3201x x <<<,()2,1m ∈--, 从而()11112,1x x --∈--,解得11,12x ⎛⎫-∈- ⎪ ⎪⎝⎭, 所以选项AD 正确,选项C 错误,又121310x x x x -=<<.故选:ABD .本题考查利用导数研究函数的零点问题,考查化归转化思想与数形结合思想,是中档题.。
高考数学一轮复习单元检测四导数及其应用单元检测含解析

单元检测四 导数及其应用(时间:12019 满分:150分) 第Ⅰ卷(选择题 共40分)一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列求导运算正确的是( ) A.⎝ ⎛⎭⎪⎫x +1x2′=1+1x3B.(log 3x )′=1x lg3C .(3x )′=3x·ln3 D .(x 2sin x )′=2x cos x答案 C解析 由求导法则可知C 正确.2.已知函数f (x )=ln x +x 2f ′(a ),且f (1)=-1,则实数a 的值为( ) A .-12或1B.12 C .1 D .2答案 C解析 令x =1,则f (1)=ln1+f ′(a )=-1, 可得f ′(a )=-1.令x =a >0,则f ′(a )=1a+2af ′(a ),即2a 2-a -1=0,解得a =1或a =-12(舍去).3.若函数f (x )=x e x的图象的切线的倾斜角大于π2,则x 的取值范围是( )A .(-∞,0)B .(-∞,-1)C .(-∞,-1]D .(-∞,1)答案 B解析 f ′(x )=e x+x e x=(x +1)e x, 又切线的倾斜角大于π2,所以f ′(x )<0,即(x +1)e x<0,解得x <-1.4.函数f (x )=e|x |3x的部分图象大致为( )答案 C解析 由题意得f (x )为奇函数,排除B ; 又f (1)=e3<1,排除A ;当x >0时,f (x )=ex3x,所以f ′(x )=(x -1)ex 3x 2,函数f (x )在区间(0,1)内单调递减,在区间(1,+∞)内单调递增,排除D.5.若函数f (x )=ln x +ax 2-2在区间⎝ ⎛⎭⎪⎫12,2内存在单调递增区间,则实数a 的取值范围是( )A .(-∞,-2] B.⎝ ⎛⎭⎪⎫-18,+∞C.⎝ ⎛⎭⎪⎫-2,-18 D .(-2,+∞)答案 D解析 对f (x )求导得f ′(x )=1x +2ax =2ax 2+1x,由题意可得2ax 2+1>0在⎝ ⎛⎭⎪⎫12,2内有解,所以a >⎝ ⎛⎭⎪⎫-12x 2min . 因为x ∈⎝ ⎛⎭⎪⎫12,2,所以x 2∈⎝ ⎛⎭⎪⎫14,4,⎝ ⎛⎭⎪⎫-12x 2∈⎝ ⎛⎭⎪⎫-2,-18,所以a >-2.6.已知定义在R 上的函数f (x ),其导函数f ′(x )的大致图象如图所示,则下列叙述正确的是( )①f (b )>f (a )>f (c );②函数f (x )在x =c 处取得极小值,在x =e 处取得极大值; ③函数f (x )在x =c 处取得极大值,在x =e 处取得极小值; ④函数f (x )的最小值为f (d ).A .③B.①②C.③④D.④ 答案 A解析 由导函数的图象可知函数f (x )在区间(-∞,c ),(e ,+∞)内,f ′(x )>0, 所以函数f (x )在区间(-∞,c ),(e ,+∞)内单调递增,在区间(c ,e )内,f ′(x )<0, 所以函数f (x )在区间(c ,e )内单调递减. 所以f (c )>f (a ),所以①错;函数f (x )在x =c 处取得极大值,在x =e 处取得极小值,故②错,③对; 函数f (x )没有最小值,故④错.7.已知函数f (x )=(x 2-mx -m )e x+2m (m ∈R )在x =0处取得极小值,则f (x )的极大值是( )A .4e -2B .4e 2C .e -2D .e 2 答案 A解析 由题意知,f ′(x )=[x 2+(2-m )x -2m ]e x,f ′(0)=-2m =0,解得m =0,∴f (x )=x 2e x,f ′(x )=(x 2+2x )e x. 令f ′(x )>0,解得x <-2或x >0, 令f ′(x )<0,解得-2<x <0,则函数f (x )在区间(-∞,-2)和(0,+∞)上单调递增,在区间(-2,0)上单调递减, ∴函数f (x )的极大值为f (-2)=4e -2.故选A.8.设函数f (x )=min ⎩⎨⎧⎭⎬⎫x ln x ,x 2e x (min{a ,b }表示a ,b 中的较小者),则函数f (x )的最大值为( )A.32ln2B .2ln2C.1e D.4e 2 答案 D解析 函数f (x )的定义域为(0,+∞). 由y 1=x ln x 得y 1′=ln x +1, 令y 1′=0,解得x =1e,∴y 1=x ln x 在⎝ ⎛⎭⎪⎫0,1e 上单调递减,在⎝ ⎛⎭⎪⎫1e ,+∞上单调递增. 由y 2=x 2e x ,x >0得y 2′=2x -x2e x ,令y 2′=0,x >0,解得x =2,∴y 2=x 2ex 在(0,2)上单调递增,在(2,+∞)上单调递减,作出示意图如图,当x =2时,y 1=2ln2,y 2=4e2.∵2ln2>4e 2,∴y 1=x ln x 与y 2=x2e x 的交点在(1,2)内,∴函数f (x )的最大值为4e2.9.已知y =f (x )为(0,+∞)上的可导函数,且有f ′(x )+f (x )x>0,则对于任意的a ,b ∈ (0,+∞),当a >b 时,有( ) A .af (a )<bf (b ) B .af (a )>bf (b ) C .af (b )>bf (a ) D .af (b )<bf (a )答案 B解析 由f ′(x )+f (x )x >0,得xf ′(x )+f (x )x>0, 即[xf (x )]′x>0,即[xf (x )]′x >0.∵x >0,∴[xf (x )]′>0,即函数y =xf (x )为增函数,由a ,b ∈(0,+∞)且a >b ,得af (a )>bf (b ),故选B.10.(2018·温州“十五校联合体”联考)已知函数f (x )=2x -e 2x(e 为自然对数的底数),g (x )=mx +1(m ∈R ),若对于任意的x 1∈[-1,1],总存在x 0∈[-1,1],使得g (x 0)=f (x 1)成立,则实数m 的取值范围为( ) A .(-∞,1-e 2]∪[e 2-1,+∞) B .[1-e 2,e 2-1]C .(-∞,e -2-1]∪[1-e -2,+∞) D .[e -2-1,1-e -2] 答案 A解析 ∵f ′(x )=2-2e 2x,∴f (x )在区间[-1,0]上为增函数,在区间[0,1]上为减函数, ∵f (-1)-f (1)=(-2-e -2)-(2-e 2)=e 2-e -2-4>0, ∴f (-1)>f (1),又f (0)=-1,则函数f (x )在区间[-1,1]上的值域为A =[2-e 2,-1].当m >0时,函数g (x )在区间[-1,1]上的值域为B =[-m +1,m +1].依题意有A ⊆B ,则有⎩⎪⎨⎪⎧-m +1≤2-e 2,m +1≥-1,得m ≥e 2-1.当m =0时,函数g (x )在区间[-1,1]上的值域为B ={1},不符合题意. 当m <0时,函数g (x )在区间[-1,1]上的值域为B =[m +1,-m +1].依题意有A ⊆B ,则有⎩⎪⎨⎪⎧m +1≤2-e 2,-m +1≥-1,得m ≤1-e 2.综上,实数m 的取值范围为(-∞,1-e 2]∪[e 2-1,+∞).第Ⅱ卷(非选择题 共110分)二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.把答案填在题中横线上)11.已知直线y =kx 与函数f (x )=e x(其中e 为自然对数的底数)的图象相切,则实数k 的值为________;切点坐标为________. 答案 e (1,e)解析 设切点坐标为(x ,y ),需满足⎩⎪⎨⎪⎧e x=ye x=ky x =k ,所以解得x =1,y =e ,k =e , 所以k =e ,切点坐标为(1,e).12.设函数f (x )=x ln x ,则点(1,0)处的切线方程是________________;函数f (x )=x ln x 的最小值为________. 答案 x -y -1=0 -1e解析 由题意得f ′(x )=1+ln x , 所以f ′(1)=1,则所求切线方程为x -y -1=0. 由f ′(x )=1+ln x <0得0<x <1e ;由f ′(x )=1+ln x >0得x >1e,所以函数f (x )=x ln x 在⎝ ⎛⎭⎪⎫0,1e 上单调递减,在⎝ ⎛⎭⎪⎫1e ,+∞上单调递增, 所以函数f (x )=x ln x 在x =1e 处取得最小值,最小值为f ⎝ ⎛⎭⎪⎫1e =1e ln 1e=-1e .13.(2018·宁波九校期末)函数f (x )=x 3-2x +e x -e -x是________函数(填“奇”或“偶”),在R 上的增减性为________.(填“单调递增”、“单调递减”或“有增有减”) 答案 奇 单调递增解析 ∵函数f (x )=x 3-2x +e x -e -x, ∴它的定义域为R ,且满足f (-x )=-x 3+2x +e -x-e x=-f (x ), 故函数f (x )为奇函数.由于函数的导数f ′(x )=3x 2-2+(e x +e -x )≥3x 2-2+2=3x 2≥0, 故函数在R 上单调递增.14.(2018·诸暨检测)已知函数f (x )=x 3-3x ,函数f (x )的图象在x =0处的切线方程是________;函数f (x )在[0,2]内的值域是________. 答案 y =-3x [-2,2] 解析 ∵f (x )=x 3-3x , ∴f ′(x )=3x 2-3,又∵f (0)=0,f ′(0)=-3,∴函数f (x )在点(0,0)处的切线方程为y =-3x . 令f ′(x )=3x 2-3=0,得x =±1,当x 变化时,f (x )与f ′(x )的变化情况如下表.↗∴在[0,1]上,f (x )是减函数,其最小值为f (1)=-2,最大值为f (0)=0;在[1,2]上,f (x )是增函数,其最小值为f (1)=-2,最大值为f (2)=2.综上,在[0,2]上,f (x )的值域为[-2,2].15.已知函数f (x )=ln x 2+12,g (x )=e x -2,若g (m )=f (n )成立,则n -m 的最小值为________.答案 ln2解析 令f (n )=g (m )=k (k >0), 则由ln n 2+12=k ,解得n =2eke ,由em -2=k ,解得m =ln k +2, 则n -m =2e ke-ln k -2, 令h (k )=2eke-ln k -2,则h ′(k )=2eke-1k,由h ′(k )=0得k =12,且当k ∈⎝ ⎛⎭⎪⎫0,12时,h ′(k )<0,h (k )单调递减,当k ∈⎝ ⎛⎭⎪⎫12,+∞时,h ′(k )>0,h (k )单调递增,则h (k )min =h ⎝ ⎛⎭⎪⎫12=ln2,即n -m 的最小值是ln2.16.设实数λ>0,若对任意的x ∈(0,+∞),不等式e λx-ln x λ≥0恒成立,则λ的最小值为________. 答案 1e解析 当x ∈(0,1]时,λ>0,不等式e λx-ln x λ≥0显然成立,λ可取任意正实数;当x ∈(1,+∞)时,e λx -ln x λ≥0⇔λe λx ≥ln x ⇔λx ·e λx ≥ln x ·e ln x,设函数f (x )=x ·e x(x >0),而f ′(x )=(x +1)·e x>0, 则f (x )在(0,+∞)上单调递增,那么由λx ·e λx ≥ln x ·e ln x可得λx ≥ln x ⇔λ≥ln x x.令g (x )=ln xx(x >1),而g ′(x )=1-ln xx2, 易知函数g (x )在(1,e)上单调递增,在(e ,+∞)上单调递减, 那么g (x )max =g (e)=1e ,则有λ≥1e .综上分析可知,λ的最小值为1e.17.对于定义在R 上的函数f (x ),若存在非零实数x 0,使函数f (x )在(-∞,x 0)和(x 0,+∞)上均有零点,则称x 0为函数f (x )的一个“折点”.现给出下列四个函数: ①f (x )=3|x -1|+2;②f (x )=lg|x +2019|; ③f (x )=x 33-x -1;④f (x )=x 2+2mx -1(m ∈R ).则存在“折点”的函数是________.(填序号) 答案 ②④ 解析 因为f (x )=3|x -1|+2>2,所以函数f (x )不存在零点, 所以函数f (x )不存在“折点”;对于函数f (x )=lg|x +2019|,取x 0=-2019, 则函数f (x )在(-∞,-2019)上有零点x =-2020, 在(-2019,+∞)上有零点x =-2018,所以x 0=-2019是函数f (x )=lg|x +2019|的一个“折点”; 对于函数f (x )=x 33-x -1,则f ′(x )=x 2-1=(x +1)(x -1). 令f ′(x )>0,得x >1或x <-1; 令f ′(x )<0,得-1<x <1,所以函数f (x )在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递减. 又f (-1)=-13<0,所以函数f (x )只有一个零点,所以函数f (x )=x 33-x -1不存在“折点”;对于函数f (x )=x 2+2mx -1=(x +m )2-m 2-1, 由于f (-m )=-m 2-1≤-1,结合图象(图略)可知该函数一定有“折点”. 综上,存在“折点”的函数是②④.三、解答题(本大题共5小题,共74分.解答应写出文字说明,证明过程或演算步骤) 18.(14分)已知函数f (x )=e x+ln x .(1)求函数y =f ′(x )在区间[1,+∞)内的最小值;(2)若对任意x ∈[1,+∞),恒有f (x )≥e+m (x -1),求实数m 的取值范围. 解 (1)令y =h (x )=f ′(x )=e x+1x,则h ′(x )=e x-1x2,则当x ∈[1,+∞)时,e x≥e,1x2≤1,所以h ′(x )>0,即h (x )在区间[1,+∞)内是增函数, 于是y =f ′(x )在区间[1,+∞)内的最小值为h (1)=e +1.(2)令g (x )=f (x )-e -m (x -1),则g (x )≥0对任意x ∈[1,+∞)恒成立, 且发现g (1)=0,g ′(x )=1x+e x-m .由(1)知当m ≤e+1时,g ′(x )≥0,此时g (x )单调递增,于是g (x )≥g (1)=0,成立; 当m >e +1时,则存在t ∈(1,+∞),使得g ′(t )=0, 当x ∈(1,t )时,g ′(x )<0,当x ∈(t ,+∞)时,g ′(x )>0, 此时g (x )min =g (t )<g (1)=0,矛盾.综上得m ≤e+1,即实数m 的取值范围为(-∞,e +1]. 19.(15分)已知函数f (x )=2x +2x+a ln x ,a ∈R .(1)若函数f (x )在区间[1,+∞)内单调递增,求实数a 的取值范围;(2)记函数g (x )=x 2[f ′(x )+2x -2],若g (x )的最小值是-6,求函数f (x )的解析式. 解 (1)由题意知f ′(x )=2-2x 2+ax≥0在区间[1,+∞)内恒成立,所以a ≥2x-2x 在区间[1,+∞)内恒成立.令h (x )=2x-2x ,x ∈[1,+∞),因为h ′(x )=-2x2-2<0恒成立,所以h (x )在区间[1,+∞)内单调递减, 所以h (x )max =h (1)=0,所以a ≥0, 即实数a 的取值范围为[0,+∞). (2)g (x )=2x 3+ax -2,x >0.因为g ′(x )=6x 2+a ,当a ≥0时,g ′(x )>0恒成立,所以g (x )在区间(0,+∞)内单调递增,无最小值,不合题意,所以a <0. 令g ′(x )=0,则x =-a6或x =--a6(舍去), 由此可得函数g (x )在区间⎝ ⎛⎭⎪⎫0,-a 6内单调递减,在区间⎝⎛⎭⎪⎫-a 6,+∞内单调递增, 则x =-a6是函数g (x )的极小值点,也是最小值点, 所以g (x )min =g (x )极小值=g ⎝⎛⎭⎪⎫-a 6=-6, 解得a =-6,所以f (x )=2x +2x-6ln x .20.(15分)(2019·舟山模拟)已知函数f (x )=ln x -x ,g (x )=ax 2+2x (a <0).(1)求函数f (x )在区间⎣⎢⎡⎦⎥⎤1e ,e 上的最值; (2)求函数h (x )=f (x )+g (x )的极值点. 解 (1)依题意,f ′(x )=1x-1,令1x-1=0,解得x =1.因为f (1)=-1,f ⎝ ⎛⎭⎪⎫1e =-1-1e ,f (e)=1-e , 且1-e<-1-1e<-1,故函数f (x )在区间⎣⎢⎡⎦⎥⎤1e ,e 上的最大值为-1,最小值为1-e. (2)依题意,h (x )=f (x )+g (x )=ln x +ax 2+x (x >0), h ′(x )=1x +2ax +1=2ax 2+x +1x,当a <0时,令h ′(x )=0,则2ax 2+x +1=0. 因为Δ=1-8a >0,所以h ′(x )=2ax 2+x +1x =2a (x -x 1)(x -x 2)x, 其中x 1=-1-1-8a 4a ,x 2=-1+1-8a 4a. 因为a <0,所以x 1<0,x 2>0,所以当0<x <x 2时,h ′(x )>0;当x >x 2时,h ′(x )<0,所以函数h (x )在区间(0,x 2)内是增函数,在区间(x 2,+∞)内是减函数,故x 2=-1+1-8a 4a为函数h (x )的极大值点,无极小值点. 21.(15分)已知函数f (x )=5+ln x ,g (x )=kx x +1(k ∈R ). (1)若函数f (x )的图象在点(1,f (1))处的切线与函数y =g (x )的图象相切,求k 的值;(2)若k ∈N *,且x ∈(1,+∞)时,恒有f (x )>g (x ),求k 的最大值.(参考数据:ln5≈1.6094,ln6≈1.7918,ln(2+1)≈0.8814)解 (1)∵f (x )=5+ln x ,∴f (1)=5,且f ′(x )=1x, 从而得到f ′(1)=1.∴函数f (x )的图象在点(1,f (1))处的切线方程为y -5=x -1,即y =x +4.设直线y =x +4与g (x )=kxx +1(k ∈R )的图象相切于点P (x 0,y 0),从而可得g ′(x 0)=1,g (x 0)=x 0+4,又g ′(x )=k(x +1)2, ∴⎩⎪⎨⎪⎧ k (x 0+1)2=1,kx 0x 0+1=x 0+4,解得⎩⎪⎨⎪⎧ x 0=2,k =9或⎩⎪⎨⎪⎧ x 0=-2,k =1.∴k 的值为1或9.(2)由题意知,当x ∈(1,+∞)时,5+ln x >kx 1+x恒成立, 等价于当x ∈(1,+∞)时,k <(x +1)(5+ln x )x恒成立. 设h (x )=(x +1)(5+ln x )x(x >1), 则h ′(x )=x -4-ln x x 2(x >1),记p (x )=x -4-ln x (x >1),则p ′(x )=1-1x =x -1x>0, ∴p (x )在x ∈(1,+∞)上单调递增.又p (5)=1-ln5<0,p (6)=2-ln6>0,∴在x ∈(1,+∞)上存在唯一的实数m ,且m ∈(5,6),使得p (m )=m -4-ln m =0,①∴当x ∈(1,m )时,p (x )<0,即h ′(x )<0,则h (x )在x ∈(1,m )上单调递减,当x ∈(m ,+∞)时,p (x )>0,即h ′(x )>0,则h (x )在x ∈(m ,+∞)上单调递增,∴当x ∈(1,+∞)时,h (x )min =h (m )=(m +1)(5+ln m )m, 由①可得ln m =m -4,∴h (m )=(m +1)(m +1)m =m +1m+2, 而m ∈(5,6),∴m +1m +2∈⎝ ⎛⎭⎪⎫365,496, 又当m =3+22时,h (m )=8,p (3+22)=22-1-ln(3+22)>0,∴m ∈(5,3+22),∴h (m )∈⎝ ⎛⎭⎪⎫365,8. 又k ∈N *,∴k 的最大值是7.22.(15分)已知函数f (x )=ln x -m e x 的图象在点(1,f (1))处的切线与直线l :x +(1-e)y =0垂直,其中e 为自然对数的底数.(1)求实数m 的值及函数f (x )在区间[1,+∞)内的最大值.(2)①求证:函数f (x )有且仅有一个极值点.②求证:f (x )<x 2-2x -1.(1)解 由题意得f ′(x )=1x-m e x , 直线l :x +(1-e)y =0的斜率为-11-e, 故函数f (x )的图象在点(1,f (1))处的切线的斜率为1-e ,即f ′(1)=1-m e =1-e ,所以m =1.当x ∈[1,+∞)时,f ′(x )=1x-e x 单调递减,即f ′(x )≤f ′(1)=1-e<0,所以f (x )在区间[1,+∞)内单调递减,所以当x ∈[1,+∞)时,f (x )max =f (1)=ln1-e =-e.(2)证明 ①f ′(x )=1x-e x ,令h (x )=f ′(x ), 则h ′(x )=-1x 2-e x <0在(0,+∞)上恒成立, 即有h (x )在区间(0,+∞)内单调递减.又h ⎝ ⎛⎭⎪⎫12=2-12e >0,h (1)=1-e<0, 所以h (x )=0在区间(0,+∞)内有且仅有一个实根, 设此实根为x 0,则x 0∈⎝ ⎛⎭⎪⎫12,1. 当x ∈(0,x 0)时,h (x )>0,故f (x )单调递增; 当x ∈(x 0,+∞)时,h (x )<0,故f (x )单调递减, 所以函数f (x )在x =x 0处取得唯一的极大值, 即函数f (x )有且仅有一个极值点.②由①知f ′(x )=1x-e x 在区间(0,+∞)内为减函数, 又f ′(1)=1-e<0,f ′⎝ ⎛⎭⎪⎫12=2-e>0, 因此存在实数x 0∈⎝ ⎛⎭⎪⎫12,1满足方程f ′(x )=1x -e x =0, 此时f (x )在区间(0,x 0)内为增函数,在区间(x 0,+∞)内为减函数,且f ′(x 0)=1x 0-0e x =0, 由此得到1x 0=0e x ,x 0=-ln x 0. 由单调性知f (x )max =f (x 0)=ln x 0-0e x=-x 0-1x 0=-⎝ ⎛⎭⎪⎫x 0+1x 0, 又x 0∈⎝ ⎛⎭⎪⎫12,1,故-⎝⎛⎭⎪⎫x 0+1x 0<-2, 所以f (x )max <-2.又x 2-2x -1=(x -1)2-2≥-2,所以f (x )<x 2-2x -1.。
高考数学一轮复习导数及其应用多选题测试试题含答案

高考数学一轮复习导数及其应用多选题测试试题含答案一、导数及其应用多选题1.关于函数()e cos xf x a x =-,()π,πx ∈-下列说法正确的是( )A .当1a =时,()f x 在0x =处的切线方程为y x =B .若函数()f x 在()π,π-上恰有一个极值,则0a =C .对任意0a >,()0f x ≥恒成立D .当1a =时,()f x 在()π,π-上恰有2个零点 【答案】ABD 【分析】直接逐一验证选项,利用导数的几何意义求切线方程,即可判断A 选项;利用分离参数法,构造新函数和利用导数研究函数的单调性和极值、最值,即可判断BC 选项;通过构造新函数,转化为两函数的交点个数来解决零点个数问题,即可判断D 选项. 【详解】解:对于A ,当1a =时,()e cos xf x x =-,()π,πx ∈-,所以()00e cos00f =-=,故切点为(0,0),则()e sin xf x x '=+,所以()00e sin01f '=+=,故切线斜率为1,所以()f x 在0x =处的切线方程为:()010y x -=⨯-,即y x =,故A 正确; 对于B ,()e cos xf x a x =-,()π,πx ∈-,则()e sin xf x a x '=+,若函数()f x 在()π,π-上恰有一个极值,即()0f x '=在()π,π-上恰有一个解, 令()0f x '=,即e sin 0x a x +=在()π,π-上恰有一个解, 则sin xxa e -=在()π,π-上恰有一个解, 即y a =与()sin xxg x e -=的图象在()π,π-上恰有一个交点, ()sin cos xx xg x e -'=,()π,πx ∈-,令()0g x '=,解得:134x π=-,24x π=, 当3,,44x ππππ⎛⎫⎛⎫∈--⎪ ⎪⎝⎭⎝⎭时,()0g x '>,当3,44x ππ⎛⎫∈-⎪⎝⎭时,()0g x '<, ()g x ∴在3,4ππ⎛⎫--⎪⎝⎭上单调递增,在443,ππ⎛⎫- ⎪⎝⎭上单调递减,在,4ππ⎛⎫ ⎪⎝⎭上单调递增,所以极大值为3423204g e ππ-⎛⎫-=> ⎪⎝⎭,极小值为42204g e ππ-⎛⎫=< ⎪⎝⎭, 而()()()0,0,00g g g ππ-===, 作出()sinxg x e -=,()π,πx ∈-的大致图象,如下:由图可知,当0a =时,y a =与()sinx g x e-=的图象在()π,π-上恰有一个交点, 即函数()f x 在()π,π-上恰有一个极值,则0a =,故B 正确; 对于C ,要使得()0f x ≥恒成立,即在()π,πx ∈-上,()e cos 0xf x a x =-≥恒成立,即在()π,πx ∈-上,cos x xa e ≥恒成立,即maxcos x x a e ⎛⎫≥ ⎪⎝⎭,设()cos x x h x e =,()π,πx ∈-,则()sin cos xx xh x e--'=,()π,πx ∈-, 令()0h x '=,解得:14x π=-,234x π=, 当3,,44x ππππ⎛⎫⎛⎫∈--⎪⎪⎝⎭⎝⎭时,()0h x '>,当3,44x ππ⎛⎫∈- ⎪⎝⎭时,()0h x '<,()h x ∴在,4ππ⎛⎫--⎪⎝⎭上单调递增,在3,44ππ⎛⎫-⎪⎝⎭上单调递减,在3,4ππ⎛⎫⎪⎝⎭上单调递增, 所以极大值为42204h e ππ-⎛⎫-=> ⎪⎝⎭,()()11,h h e e ππππ--==,所以()cos x xh x e =在()π,πx ∈-上的最大值为42204h e ππ-⎛⎫-=> ⎪⎝⎭, 所以422a e π-≥时,在()π,πx ∈-上,()e cos 0xf x a x =-≥恒成立,即当422a e π-≥时,()0f x ≥才恒成立,所以对任意0a >,()0f x ≥不恒成立,故C 不正确; 对于D ,当1a =时,()e cos xf x x =-,()π,πx ∈-,令()0f x =,则()e cos 0xf x x =-=,即e cos x x =,作出函数xy e =和cos y x =的图象,可知在()π,πx ∈-内,两个图象恰有两个交点,则()f x 在()π,π-上恰有2个零点,故D 正确.故选:ABD. 【点睛】本题考查函数和导数的综合应用,考查利用导数的几何意义求切线方程,考查分离参数法的应用和构造新函数,以及利用导数研究函数的单调性、极值最值、零点等,考查化简运算能力和数形结合思想.2.在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它得名于荷兰数学家鲁伊兹布劳威尔(L.E.Brouwer )简单的讲就是对于满足一定条件的连续函数()f x ,存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点”函数,而称0x 为该函数的一个不动点,依据不动点理论,下列说法正确的是( ) A .函数()sin f x x =有3个不动点B .函数2()(0)f x ax bx c a =++≠至多有两个不动点C .若定义在R 上的奇函数()f x ,其图像上存在有限个不动点,则不动点个数是奇数D .若函数()f x =[0,1]上存在不动点,则实数a 满足l a e ≤≤(e 为自然对数的底数) 【答案】BCD 【分析】根据题目中的定义,结合导数、一元二次方程的性质、奇函数的性质进行判断即可. 【详解】令()sin g x x x =-,()1cos 0g x x '=-≥, 因此()g x 在R 上单调递增,而(0)0g =, 所以()g x 在R 有且仅有一个零点, 即()f x 有且仅有一个“不动点”,A 错误;0a ≠,20ax bx c x ∴++-=至多有两个实数根,所以()f x 至多有两个“不动点”,B 正确;()f x 为定义在R 上的奇函数,所以(0)0f =,函数()-y f x x =为定义在R 上的奇函数,显然0x =是()f x 的一个“不动点”,其它的“不动点”都关于原点对称,个数和为偶数, 因此()f x 一定有奇数个“不动点”,C 正确;因为()f x 在[0,1]存在“不动点”,则()f x x =在[0,1]有解,x =⇒2x a e x x =+-在[0,1]有解,令2()xm x e x x =+-,()12x m x e x '=+-,令()12x n x e x '=+-,()20x n x e '=-=,ln 2x =,()n x 在(0,ln 2)单调递减,在(ln 2,1)单调递增,∴min ()(ln 2)212ln 232ln 20n x n ==+-=->, ∴()0m x '>在[0,1]恒成立,∴()m x 在[0,1]单调递增,min ()(0)1m x m ==,max ()(1)m x m e ==,∴1a e ≤≤,D 正确,. 故选:BCD 【点睛】方法点睛:新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.3.定义在(0,)+∞上的函数()f x 的导函数为()'f x ,且()()f x f x x'<,则对任意1x 、2(0,)x ∈+∞,其中12x x ≠,则下列不等式中一定成立的有( )A .()()()1212f x x f x f x +<+B .()()()()21121212x xf x f x f x f x x x +<+ C .()1122(1)x x f f <D .()()()1212f x x f x f x <【答案】ABC 【分析】构造()()f x g x x=,由()()f x f x x '<有()0g x '<,即()g x 在(0,)+∞上单调递减,根据各选项的不等式,结合()g x 的单调性即可判断正误.【详解】 由()()f x f x x '<知:()()0xf x f x x'-<, 令()()f x g x x =,则()()()20xf x f x g x x '-='<,∴()g x 在(0,)+∞上单调递减,即122112121212()()()()0()g x g x x f x x f x x x x x x x --=<--当120x x ->时,2112()()x f x x f x <;当120x x -<时,2112()()x f x x f x >; A :121()()g x x g x +<,122()()g x x g x +<有112112()()x f x x f x x x +<+,212212()()x f x x f x x x +<+,所以()()()1212f x x f x f x +<+; B:由上得21121212()()()()x f x x x x f x x x -<-成立,整理有()()()()21121212x xf x f x f x f x x x +<+; C :由121x >,所以111(2)(1)(2)(1)21x x x f f g g =<=,整理得()1122(1)x x f f <; D :令121=x x 且121x x >>时,211x x =,12111()()()()g x g x f x f x =,12()(1)(1)g x x g f ==,有121()()g x x g x >,122()()g x x g x <,所以无法确定1212(),()()g x x g x g x 的大小.故选:ABC 【点睛】思路点睛:由()()f x f x x '<形式得到()()0xf x f x x'-<, 1、构造函数:()()f x g x x =,即()()()xf x f x g x x'-'=. 2、确定单调性:由已知()0g x '<,即可知()g x 在(0,)+∞上单调递减.3、结合()g x 单调性,转化变形选项中的函数不等式,证明是否成立.4.已知函数()sin xf x x=,(]0,x π∈,则下列结论正确的有( ) A .()f x 在区间(]0,π上单调递减B .若120x x π<<≤,则1221sin sin x x x x ⋅>⋅C .()f x 在区间(]0,π上的值域为[)0,1 D .若函数()()cos g x xg x x '=+,且()1g π=-,()g x 在(]0,π上单调递减【答案】ACD 【分析】先求出函数的导数,然后对四个选项进行逐一分析解答即可, 对于选项A :当0,2x π⎛⎫∈ ⎪⎝⎭时,可得()0f x '<,可得()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减;当,2x ππ⎡⎤∈⎢⎥⎣⎦,可得()0f x '<,可得()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减,最后作出判断; 对于选项B :由()f x 在区间(]0,π上单调递减可得()()12f x f x >,可得1212sin sin x x x x >,进而作出判断; 对于选项C :由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==,进而作出判断;对于选项D :()()()sin g x g x xg x x ''''=+-,可得()()sin xg x f x x''==,然后利用导数研究函数()g x '在区间(]0,π上的单调性,可得()()0g x g π''≤=,进而可得出函数()g x 在(]0,π上的单调性,最后作出判断.【详解】()2cos sin x x xf x x -'=, (]0,x π∈,当0,2x π⎛⎫∈ ⎪⎝⎭时,cos 0x >,由三角函数线可知tan x x <, 所以sin cos xx x<,即cos sin x x x <,所以cos sin 0x x x -<, 所以()0f x '<,所以()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减,当,2x ππ⎡⎤∈⎢⎥⎣⎦,cos 0x ≤,sin 0x ≥,所以cos sin 0x x x -<,()0f x '<, 所以()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以()f x 在区间(]0,π上单调递减,故选项A 正确; 当120x x π<<≤时,()()12f x f x >,所以1212sin sin x x x x >,即1221sin sin x x x x ⋅<⋅,故选项B 错误; 由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==, 所以当(]0,x π∈时,()[)0,1f x ∈,故选项C 正确;对()()cos g x xg x x '=+进行求导可得: 所以有()()()sin g x g x xg x x ''''=+-,所以()()sin xg x f x x''==,所以()g x ''在区间(]0,π上的值域为[)0,1, 所以()0g x ''≥,()g x '在区间(]0,π上单调递增,因为()0g π'=, 从而()()0g x g π''≤=,所以函数()g x 在(]0,π上单调递减,故选项D 正确. 故选:ACD. 【点睛】方法点睛:本题考查导数的综合应用,对于函数()sin xf x x=的性质,可先求出其导数,然后结合三角函数线的知识确定导数的符号,进而确定函数的单调性和极值,最后作出判断,考查逻辑思维能力和运算求解能力,属于中档题.5.已知函数()e sin xf x a x =+,则下列说法正确的是( )A .当1a =-时,()f x 在0,单调递增B .当1a =-时,()f x 在()()0,0f 处的切线为x 轴C .当1a =时,()f x 在()π,0-存在唯一极小值点0x ,且()010f x -<<D .对任意0a >,()f x 在()π,-+∞一定存在零点 【答案】AC 【分析】结合函数的单调性、极值、最值及零点,分别对四个选项逐个分析,可选出答案. 【详解】对于A ,当1a =-时,()e sin xf x x =-,()e cos xf x x '=-,因为()0,x ∈+∞时,e 1,cos 1xx >≤,即0fx,所以()f x 在0,上单调递增,故A 正确;对于B ,当1a =-时,()e sin xf x x =-,()e cos xf x x '=-,则()00e sin01f =-=,()00e cos00f '=-=,即切点为0,1,切线斜率为0,故切线方程为1y =,故B 错误;对于C ,当1a =时,()e sin xf x x =+,()e cos xf x x '+=,()e sin xf x x '=-',当()π,0x ∈-时,sin 0x <,e 0x >,则()e sin 0xx f x -'=>'恒成立,即()e cos x f x x '+=在()π,0-上单调递增,又ππ22ππe cos e 220f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝⎭+>,3π3π443π3πe cos e442f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝-⎭+,因为123π3π421e e 2e ---⎛⎫=<⎪⎭< ⎝,所以3π43πe 024f -⎛⎫'-= ⎪-⎭<⎝,所以存在唯一03ππ,42x ⎛⎫∈-- ⎪⎝⎭,使得()00f x '=成立,所以()f x 在()0π,x -上单调递减,在()0,0x 上单调递增,即()f x 在()π,0-存在唯一极小值点0x ,由()000e cos 0xf x x +'==,可得()000000πe sin cos sin 4x f x x x x x ⎛⎫=+=-+=- ⎪⎝⎭,因为03ππ,42x ⎛⎫∈-- ⎪⎝⎭,所以0π3ππ,44x ⎛⎫-∈-- ⎪⎝⎭,则()00π4f x x ⎛⎫=- ⎪⎝⎭()1,0∈-,故C 正确;对于选项D ,()e sin xf x a x =+,()π,x ∈-+∞,令()e sin 0xf x a x =+=,得1sin ex xa -=,()sin ex xg x =,()π,x ∈-+∞,则()πcos sin 4e e x xx x x g x ⎛⎫- ⎪-⎝⎭'==, 令0g x ,得πsin 04x ⎛⎫-= ⎪⎝⎭,则ππ4x k =+()1,k k ≥-∈Z ,令0g x,得πsin 04x ⎛⎫-> ⎪⎝⎭,则π5π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递减, 令0g x,得πsin 04x ⎛⎫-< ⎪⎝⎭,则5π9π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递增, 所以5π2π4x k =+()1,k k ≥-∈Z 时,()g x 取得极小值,极小值为5π5π2π2π445π5π2π5π4s 42in si πe e 4n k k g k k ++⎛⎫ ⎪⎛⎫⎝⎭== ⎪⎝⎭++()1,k k ≥-∈Z , 在()g x 的极小值中,3π4sin 3π45π5π42π4eg g -⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝+⎭-最小,当3ππ,4x ⎛⎫∈--⎪⎝⎭时,()g x 单调递减,所以函数()g x的最小值为3π3π445πsin 3π144eg --⎛⎫-==- ⎪⎝⎭,当3π411a--<-时,即3π40a -<<时,函数()g x 与1=-y a无交点,即()f x 在()π,-+∞不存在零点,故D 错误.故选:AC. 【点睛】本题考查利用导数研究函数的极值、零点、最值,及切线方程的求法,考查学生的推理能力与计算求解能力,属于难题.6.函数()ln f x x x =、()()f x g x x'=,下列命题中正确的是( ).A .不等式()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭B .函数()f x 在()0,e 上单调递增,在(,)e +∞上单调递减C .若函数()()2F x f x ax =-有两个极值点,则()0,1a ∈D .若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立,则m 1≥ 【答案】AD 【分析】对A ,根据()ln f x x x =,得到()()ln 1f x xg x x x'+==,然后用导数画出其图象判断;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<判断;对C ,将函数()()2F x f x ax =-有两个极值点,()ln 120x a x+=+∞在,有两根判断;对D ,将问题转化为22111222ln ln 22m m x x x x x x ->-恒成立,再构造函数()2ln 2m g x x x x =-,用导数研究单调性. 【详解】对A ,因为()()()ln 1ln f x x f x x x g x x x'+===、, ()2ln xg x x-'=, 令()0g x '>,得()0,1x ∈,故()g x 在该区间上单调递增;令()0g x '<,得()1x ∈+∞,,故()g x 在该区间上单调递减. 又当1x >时,()0g x >,()10,11g g e ⎛⎫== ⎪⎝⎭, 故()g x 的图象如下所示:数形结合可知,()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭,故正确; 对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<,所以函数()f x 在()0,e 上单调递减,在(,)e +∞上单调递增,错误;对C ,若函数()()2F x f x ax =-有两个极值点, 即()2ln F x x x ax =-有两个极值点,又()ln 21F x x ax '=-+, 要满足题意,则需()ln 2100x ax -+=+∞在,有两根, 也即()ln 120x a x+=+∞在,有两根,也即直线()2y a y g x ==与的图象有两个交点. 数形结合则021a <<,解得102a <<. 故要满足题意,则102a <<,故错误; 对D ,若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立, 即22111222ln ln 22m m x x x x x x ->-恒成立, 构造函数()2ln 2m g x x x x =-,()()12g x g x >,对任意的120x x >>恒成立, 故()g x ()0+∞,单调递增,则()ln 10g x mx x '=--≥()0+∞, 恒成立, 也即ln 1x m x+≤,在区间()0,∞+恒成立,则()max 1g x m =≤,故正确.故选:AD.【点睛】本题主要考查导数在函数图象和性质中的综合应用,还考查了数形结合的思想、转化化归思想和运算求解的能力,属于较难题.7.已知0a >,0b >,下列说法错误的是( )A .若1a b a b ⋅=,则2a b +≥B .若23a b e a e b +=+,则a b >C .()ln ln a a b a b -≥-恒成立D .2ln a a bb e e-<恒成立 【答案】AD【分析】对A 式化简,通过构造函数的方法,结合函数图象,说明A 错误;对B 不等式放缩22a b e a e b +>+,通过构造函数的方法,由函数的单调性,即可证明B 正确;对C 不等式等价变型()ln ln ln 1-≥-⇔≥-a b a a b a b b a ,通过10,ln 1∀>>-x x x恒成立,可得C 正确;D 求出ln -a a b b e 的最大值,当且仅当11a b e =⎧⎪⎨=⎪⎩时取等号,故D 错误. 【详解】A. 1ln ln 0⋅=⇔+=a b a b a a b b设()ln f x x x =,()()0∴+=f a f b由图可知,当1+→b 时,存在0+→a ,使()()0f a f b +=此时1+→a b ,故A 错误.B. 232+=+>+a b b e a e b e b设()2xf x e x =+单调递增,a b ∴>,B 正确 C. ()ln ln ln1-≥-⇔≥-a b a a b a b b a又10,ln 1∀>>-x x x ,ln 1∴≥-a b b a ,C 正确D. max 1=⇒=x x y y e e当且仅当1x =; min 1ln =⇒=-y x x y e 当且仅当1=x e; 所以2ln -≤a a b b e e ,当且仅当11a b e =⎧⎪⎨=⎪⎩时取等号,D 错误. 故选:AD【点睛】本题考查了导数的综合应用,考查了运算求解能力和逻辑推理能力,转化的数学思想和数形结合的数学思想,属于难题.8.已知函数1()2ln f x x x=+,数列{}n a 的前n 项和为n S ,且满足12a =,()()*1N n n a f a n +=∈,则下列有关数列{}n a 的叙述正确的是( )A .21a a <B .1n a >C .100100S <D .112n n n a a a +⋅+<【答案】AB【分析】A .计算出2a 的值,与1a 比较大小并判断是否正确;B .利用导数分析()f x 的最小值,由此判断出1n a >是否正确;C .根据n a 与1的大小关系进行判断;D .构造函数()()1ln 11h x x x x=+->,分析其单调性和最值,由此确定出1ln 10n n a a +->,将1ln 10n na a +->变形可得112n n a a ++>,再将112n n a a ++>变形可判断结果. 【详解】A 选项,3221112ln 2ln 4ln 2222a e =+=+<+=,A 正确; B 选项,因为222121()x f x x x x='-=-,所以当1x >时,()0f x '>,所以()f x 单增,所以()(1)1f x f >=, 因为121a =>,所以()11n n a f a +=>,所以1n a >,B 正确;C 选项,因为1n a >,所以100100S >,C 错误;D 选项,令1()ln 1(1)h x x x x =+->,22111()0x h x x x x-='=->, 所以()h x 在(1,)+∞单调递增,所以()(1)0h x h >=,所以1ln 10n n a a +->,则22ln 20n n a a +->,所以112ln 2n n n a a a ⎛⎫++> ⎪⎝⎭,即112n n a a ++>, 所以112n n n a a a ++>,所以D 错误.故选:AB.【点睛】易错点睛:本题主要考查导数与数列的综合问题,属于难题.解决该问题应该注意的事项: (1)转化以函数为背景的条件时,应该注意题中的限制条件,如函数的定义域,这往往是很容易被忽视的问题;(2)利用函数的方法研究数列中的相关问题时,应准确构造相应的函数,注意数列中相关限制条件的转化.。
(典型题)高中数学选修1-1第四章《导数应用》测试卷(有答案解析)

一、选择题1.已知函数()()22ln x x t f x x+-=,若对任意的[]2,3x ∈,()()0f x f x x '+>恒成立,则实数t 的取值范围是( )A .(),2-∞B .5,2⎛⎫-∞ ⎪⎝⎭C .103⎛⎫-∞ ⎪⎝⎭,D .()2,+∞2.已知函数32()22sin 524x f x x x π⎛⎫=++++ ⎪⎝⎭,且()22(34)12f t t f t -+-+<,则实数t 的取值范围是( ) A .(1,4) B .(,1)(4,)-∞⋃+∞ C .(4,1)-D .(,4)(1,)-∞-+∞3.已知函数3213()32f x x x c =++有3个不同的零点,则c 的取值范围是( ) A .9,02⎛⎫- ⎪⎝⎭ B .4,(0,)3⎫⎛-∞-⋃+∞ ⎪⎝⎭C .4,03⎛⎫-⎪⎝⎭ D .9,(0,)2⎫⎛-∞-⋃+∞ ⎪⎝⎭4.已知()f x 是可导函数,且()()ln f x x x f x '<⋅对于0x ∀>恒成立,则( ) A .()()()283462f f f << B .()()()623428f f f << C .()()()346229f f f <<D .()()()286234f f f <<5.已知函数ln ,0()(2),0x xx f x x x e x ⎧>⎪=⎨⎪+≤⎩,若函数()()g x f x a =-仅有一个零点,则实数a的取值范围为( ). A .(2,)+∞B .31(2,),e ⎛⎫+∞⋃-∞-⎪⎝⎭C .311,2,e e⎛⎤⎛⎫⋃-∞- ⎪⎥⎝⎦⎝⎭D .31,e ⎛⎫-∞-⎪⎝⎭6.已知定义在R 上的函数()f x 满足()()f x f x '<-,则下列式子成立的是( ) A .(2020)(2021)f ef > B .(2020)(2021)f ef < C .(2020)(2021)ef f >D .(2020)(2021)ef f <7.若函数32()x x x f x e e e a =---存在零点,则实数a 的取值范围为( ) A .[2,)-+∞B .[,)e C .2[,)e -+∞ D .[1,)-+∞8.对于R 上可导的任意函数()f x ,若当2x ≠时满足()02f x x '≤-,则必有( ) A .()()()1322f f f +< B .()()()1322f f f +≤ C .()()()1322f f f +≥ D .()()()1322f f f +>9.已知函数321()13f x x ax x =+++在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,则实数a 的取值范围为( )A .(,1]-∞-B .55,34⎡⎤--⎢⎥⎣⎦C .5,13⎛⎤-- ⎥⎝⎦D .55,34⎛⎫-- ⎪⎝⎭10.函数()()()()22ln 00x x x f x x e x -⎧-<⎪=⎨≥⎪⎩,若关于x 的方程()()2240f x af x a a -+-=有四个不等的实数根,则实数a 的取值范围为( ) A .()0,4 B .()(),44,-∞⋃+∞C .(){}4,04- D .(){},44-∞-11.已知函数()()()2122x x f x m e m R =+++∈有两个极值点,则实数m 的取值范围为( )A .10e ⎡⎤-⎢⎥⎣⎦,B .111e⎛⎫--- ⎪⎝⎭,C .1e ⎛⎫-∞- ⎪⎝⎭,D .()0+∞,12.已知函数()()()22ln 0f x a e x x a =->,1,1D e ⎡⎤=⎢⎥⎣⎦若所有点()(),s f t (s ,t D ∈)所构成的平面区域面积为2e 1-,则a =( )A .eB .1e 2- C .1 D .2e e - 二、填空题13.已知1a >,若对于任意的1[,)3x ∈+∞,不等式()4ln 3e ln xx x a a -≤-恒成立,则a的最小值为______.14.设函数()f x 是定义在R 上的偶函数,'()f x 为其导函数,当0x >时,()()0xf x f x +>',且(2)0f =,则不等式()0f x >的解集为__________.15.已知函数()()()3ln 06x f x a x x x a =-->,当0x >时,()0f x '≥(()f x '为函数()f x 的导函数),则实数a 的取值范围为______.16.若函数2sin y x ax =+在[]0,2π上单调递增,则实数a 的取值范围为______. 17.已知函数()f x 定义在R 上的函数,若2()()0x f x e f x --=,当0x ≤时,()()0f x f x '+<,则不等式21()(1)x f x e f x -≥-的解集为__________18.已知函数()()ln ,11,1x x x f x x e x ≥⎧=⎨-<⎩,若函数()()()2g x f x f x a =--⎡⎤⎣⎦有6个零点,则实数a 的取值范围是______.19.函数()2sin f x x ax =-在0,2π⎡⎤⎢⎥⎣⎦上的单调递减,则实数a 的取值范围为______. 20.过点(2,0)且与曲线y =1x相切的直线的方程为________ 三、解答题21.已知函数32()2f x x ax bx =+++在1x =-处取得极值7. (1)求,a b 的值;(2)求函数()f x 在区间[2,2]-上的最大值 22.已知函数1()ln1xf x x+=-. (1)求证:当(0,1)x ∈时,3()2()3x f x x >+;(2)设实数k 使得3()()3x f x k x >+对(0,1)x ∈恒成立,求k 的最大值.23.在①()14f -=-,()10f '=;②()10f =,()01f '=;③()f x 在()()1,1f --处的切线方程为84y x =+,这三个条件中任选一个,补充在下面问题中求解. 已知函数()32f x x ax bx =++,且______.(1)求a 、b 的值; (2)求函数()f x 的极小值. 24.设函数(),02alnxf x x a =->. (1)求()f x 的单调区间;(2)求证:当1,ax e ∈⎡⎤⎣⎦时,()22aaf x e ≤-25.已知函数()1ln f x x x =--. (1)求证:()0f x ≥;(2)求证:对于任意正整数n ,2111111222n e ⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. 26.设函数33,().()2,x x x af x a R x x a ⎧-=∈⎨->⎩(1)若0a =,则()f x 的最大值为;(2)若()f x 无最大值,则求实数a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】求导函数()f x ',化简()()0f x f x x'+>得10x t x+->在[]2,3x ∈恒成立,参变分离即可求参数范围. 【详解】∵()2222ln 2x x t f x x-+-'=, ∴对任意的[]2,3x ∈,()()0f x f x x'+>恒成立⇔对任意的[]2,3x ∈,()()0xf x f x '+>恒成立, ⇔对任意的[]2,3x ∈,10x t x+->恒成立, ⇔1x t x+>恒成立, 又()1g x x x =+在[]2,3上单调递增,∴()()225min g x g ==, ∴52t <.则实数t 的取值范围是5,2⎛⎫-∞ ⎪⎝⎭.故选:B 【点睛】对于恒成立问题,常用到以下两个结论: (1)()a f x ≥ 恒成立()max a f x ⇔≥; (2) ()a f x ≤ 恒成立()min a f x ⇔≤.2.A解析:A 【分析】先利用二倍角公式和诱导公式化简函数,构造()()6g x f x =-为R 上单调递增的奇函数,再转化不等式为()22(34)g t t g t -<-,利用单调性解不等式即得结果.【详解】解:33()26cos 2sin 62f x x x x x x x π⎛⎫=++-+=+++⎪⎝⎭令3()()62sin g x f x x x x =-=++,则2()32cos 0g x x x '=++>,()()g x g x -=-, 故()g x 在R 上单调递增,且()g x 为奇函数.不等式()22(34)12f t t f t -+-+<,即()226(34)60f t t f t --+-+-<, 即()22(34)0g t t g t -+-+<,则()22(34)g t t g t -<- 故2234t t t -<-,即2540t t -+<,所以14t <<. 故选:A. 【点睛】 方法点睛:利用函数奇偶性和单调性解不等式问题:(1)()f x 是奇函数,图像关于原点中心对称,利用奇函数性质将不等式()()12f g x f g x ⎡⎤⎡⎤<⎣⎦⎣⎦形式,再利用单调性得到()1g x 和()2g x 的大小关系,再解不等式即可;(2)()f x 是偶函数,图像关于y 轴对称,利用偶函数性质将不等式()()12f g x f g x ⎡⎤⎡⎤<⎣⎦⎣⎦形式,再利用单调性得到()1g x 和()2g x 的大小关系,再解不等式即可.3.A解析:A 【分析】求出三次函数的导数,根据导函数正负情况分析单调性和极值,图象要与x 轴三个交点,据此得出取值范围. 【详解】由条件得2()3(3)f x x x x x '=+=+, 令()0f x '>,可得解集为(,3)(0,)-∞-⋃+∞ 令()0f x '<,可得解集为(3,0)-则()f x 在(,3)-∞-和(0,)+∞上单调递增,在(3,0)-上单调递减,又9(3)2f c -=+,(0)f c =,要使()f x 有3个不同的零点,则902c c <<+,所以902c -<<. 故选:A 【点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.4.B解析:B 【分析】 构造函数()()ln f x g x x=,利用导数判断出函数()y g x =在区间()1,+∞上为增函数,可得出()()()248g g g <<,进而可得出结论. 【详解】令()()ln f x g x x=,则()()()()2ln ln xf x x f x g x x x '-'=. 当1x >时,由()()ln f x x x f x '<⋅得()0g x '>, 所以函数()()ln f x g x x=在()1,+∞上是增函数, 于是()()()248g g g <<,即()()()248ln 2ln 4ln 8f f f <<,即()()()248ln 22ln 23ln 2f f f <<. 化简得,()()()623428f f f <<, 故选:B.5.C解析:C 【分析】转化为()y f x =的图象与直线y a =仅有一个交点,利用导数得到函数的性质,根据函数的性质作出函数的图象,根据图象可得解. 【详解】当0x >时,ln ()x f x x=,21ln ()x x x f x x⋅-'=21ln xx -=,当0x e <<时,()'f x 0>,当x e >时,()0f x '<,所以()f x 在(0,)e 上递增,在(,)e +∞上递减,所以()f x 在x e =处取得极大值为1()f e e=,当0x ≤时,()(2)x f x x e =+,()(2)(3)x x xf x e x e x e '=++=+,当3x <-时,()0f x '<,当3x >-时,()0f x '>, 所以()f x 在(,3)-∞-上递减,在(3,0]-上递增,所以()f x 在3x =-处取得极小值为331(3)f e e--=-=-,又(0)2f =, 因为函数()()g x f x a =-仅有一个零点,所以()y f x =的图象与直线y a =仅有一个交点,作出函数()f x 的图象,如图:由图可知:12a e <≤或31a e<-. 故实数a 的取值范围为311,2,e e ⎛⎤⎛⎫⋃-∞- ⎪⎥⎝⎦⎝⎭.故选:C 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.6.A解析:A 【分析】构造函数()()xg x e f x =,求导判定函数单调性,根据单调性得(2020)(2021)g g >化简即可. 【详解】解:依题意()()0f x f x '+<,令()()xg x e f x =,则()(()())0xg x f x f x e ''=+<在R 上恒成立, 所以函数()()xg x e f x =在R 上单调递减, 所以(2020)(2021)g g >即20202021(2020)(2021)(2020)(2021)e e e f f f f >⇒>故选:A. 【点睛】四种常用导数构造法:(1)对于不等式()()0f x g x ''+> (或0<) ,构造函数()()()F x f x g x =+. (2)对于不等式()()0f x g x ''->(或0<) ,构造函数()()()F x f x g x =-.(3)对于不等式()()0f x f x '+>(或0<) ,构造函数()()xF x e f x =.(4)对于不等式()()0f x f x '->(或0<) ,构造函数()()xf x F x e =. 7.D解析:D 【分析】由题意得32x x x a e e e =--,令32()xxx g x e e e =--,求()g x 的取值范围可得答案.【详解】 由32()0xx x f x ee e a =---=,则32x x x a e e e =--,令32()xxx g x e ee =--,则()()()3223()3211213xxx x x x x x x g x e ee e e e e e e '=--=+-=--,当()0g x '>得0x >,()g x 单调递增,当()0g x '<得0x <,()g x 单调递减, 所以min()(0)1g x g ≥=-,()2215()124xxxxx g x e e e e e ⎡⎤⎛⎫=--=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,当x 趋向于正无穷大时,()g x 也趋向于正无穷大, 所以函数()f x 存在零点,则1a ≥-. 故选:D. 【点睛】方法点睛:本题考查函数零点问题.解题方法是把零点个数转化为方程解的个数,再转化为函数图象交点个数,由图象观察所需条件求得结论.考查了分析问题、解决问题的能力.8.B解析:B 【分析】根据()02f x x '≤-,得到2x >时,()f x 单调非递增函数,2x <时,()f x 单调非递减函数求解. 【详解】因为()02f x x '≤-, 所以当20x ->,即2x >时,()0f x '≤,则()f x 单调非递增函数,所以()()32f f ≤;当20x -<,即2x <时,()0f x '≥,()f x 单调非递减函数, 所以()()12f f ≤;由不等式的性质得:()()()1322f f f +≤. 故选:B【点睛】本题主要考查导数与函数的单调性以及不等式的基本性质,属于中档题.9.B解析:B 【分析】求导得到2()21'=++f x x ax ,然后根据()f x 在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,由(0)0(1)0(2)0(3)0f f f f ''≥⎧⎪≤⎪⎨''≤⎪⎪≥⎩求解.【详解】 已知函数321()13f x x ax x =+++, 则2()21'=++f x x ax ,因为()f x 在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,所以(0)0(1)0(2)0(3)0f f f f ''≥⎧⎪≤⎪⎨''≤⎪⎪≥⎩,即10121044109610a a a ≥⎧⎪++≤⎪⎨++≤⎪⎪++≥⎩,解得 5534a -≤≤-, 所以实数a 的取值范围为55,34⎡⎤--⎢⎥⎣⎦故选:B 【点睛】本题主要考查导数与函数的单调性以及二次函数与根的分布,还考查了逻辑推理和运算求解的能力,属于中档题.10.C解析:C 【分析】作出函数()f x 的大致图象,令()t f x =,则原问题可转为关于t 的方程2240t at a a -+-=有2个不等实根1t 和2t ,结合()f x 的图象可确定1t 和2t 符合两种情形:10t =,24t =或()10,4t ∈,()()2,04,t ∈-∞+∞,最后分两类讨论即可求得a 的取值范围. 【详解】当0x ≥时,()22xf x x e-=,∴()()222xf x x xe-'=-,∴当02x <<时,()0f x '>,()f x 单调递增; 当2x >时,()0f x '<,()f x 单调递减, 函数()f x 的大致图象如图所示:令()t f x =, 当0t =或4时,方程()t f x =有2个实根; 当()(),04,t ∈-∞+∞,方程()t f x =有1个实根.当t ∈(0,4)时,方程t =f (x )有3个实根; 则关于x 的方程()()2240fx af x a a -+-=有四个不等的实数根可等价于关于t 的方程2240t at a a -+-=有2个不等实根1t 和2t .∴1t 和2t 可符合两种情形:10t =,24t =或1t ∈(0,4),()()2,04,t ∈-∞+∞.若10t =,24t =,则124a t t =+=; 若1t ∈(0,4),()()2,04,t ∈-∞+∞,设g (t )=t 2﹣at +4a ﹣a 2,则g (0)•g (4)<0,∴()()22416440a aa a a -⋅-+-<,解得40a .综上,实数a 的取值范围为(){}4,04-.故选:C .【点睛】本题考查方程根的问题,利用导数研究函数的单调性与最值,考查学生的数形结合思想、转化与化归思想、逻辑推理能力和运算能力,属于中档题.11.B解析:B 【分析】求导()()1xf x x m e '=++,将问题转化为()()1xf x x m e '=++有两个不同的零点,也即是关于x 的方程1x xm e --=有两个不同的解,构造函数()xx g x e =,求导()1x xg x e-'=,分析导函数取得正负的区间,从而得函数()g x 的单调性和最值,从而可得选项. 【详解】函数()f x 的定义域为R ,()()'1x fx x m e =++,因为函数()f x 有两个极值点,所以()()1xf x x m e '=++有两个不同的零点, 故关于x 的方程1xxm e --=有两个不同的解, 令()x x g x e =,则()1xxg x e-'=,当(,1)x ∈-∞时, ()0g x '>,当(1,+)x ∈∞时,()0g x '<,所以函数()g x 在区间(,1)-∞上单调递增,在区间(1,+∞)上单调递减, 又当x →-∞时,()g x →-∞;当x →+∞时,()0g x →, 且0,()0x g x >>()11g e=,故101m e <--<,即111m e --<<-. 故选:B. 【点睛】本题考查运用导函数研究函数的单调性、最值、极值,关键在于构造合适的函数,参变分离的方法的运用,属于中档题.12.D解析:D 【分析】求得导函数()'f x ,确定()f x 在1,1e ⎡⎤⎢⎥⎣⎦上的单调性,()f x 在1,1e ⎡⎤⎢⎥⎣⎦上的值域,从而可得题中平面区域面积,解之可得a . 【详解】解:()()2222a e x f x a e x x -⎛⎫'=-= ⎪⎝⎭,因为1,1x e ⎡⎤∈⎢⎥⎣⎦,0a >,所以()0f x '>,()f x 在1,1e ⎡⎤⎢⎥⎣⎦上单调递增,则()f x 在1,1e ⎡⎤⎢⎥⎣⎦上的值域为()22,a e e a ⎡⎤+⎣⎦,因为所有点()(),s f t (s ,t D ∈)所构成的平面区域面积为2e 1-,所以()221211a e e e e ⎛⎫---=-⎪⎝⎭,解得2ea e =-, 故选:D . 【点睛】本题考查用导数求函数的值域,解题方法是求出导函数,用导数确定函数的单调性,求得值域区间,然后可计算出题设平面区域面积,得出结论.二、填空题13.【分析】不等式等价变形利用同构函数的单调性得解【详解】令∴在上单调递增∵∴∴恒成立令只需∴单调递增∴单调递减时的最大值为∴∴的最小值为故答案为:【点睛】不等式等价变形同构函数是解题关键解析:3e【分析】不等式等价变形()()()4ln 3ln 3ln 3ln xxxe x x a a x x a a e e-≤-⇔-≤-,利用同构函数()ln f x x x =-的单调性得解【详解】()()4ln 3ln 3ln 3ln x x e x x a a x x ae a x -≤-⇔-≤--()()3ln 3ln x x x x ae ae ⇔-≤-令()ln f x x x =-,()111x f x x x-'=-=, ∴()f x 在[)1,+∞上单调递增.∵1a >,1[,)3x ∈+∞,∴[)3,1,x e x a ∈+∞,∴33xx eae x x a ⇔≤⇔≤恒成立,令()3x x g x e =,只需max ()a g x ≥,()33xxg x e -'=, ∴1[,1),()0,()3x g x g x ∈'>单调递增,∴(1,),()0,()x g x g x ∈+∞'<单调递减,1x ∴=时,()g x 的最大值为3e,∴3a e ≥,∴a 的最小值为3e.故答案为:3e【点睛】不等式等价变形,同构函数()ln f x x x =-是解题关键.14.【详解】设则恒成立所以函数在上是增函数又因为是定义在上的偶函数所以上上的奇函数所以函数在上是增函数因为所以即所以化为当时不等式等价于即解得;当时不等式等价于即解得;综上不等式的解集为点睛:本题考查了 解析:(,2)(2,)-∞-+∞【详解】设()()g x xf x =,则()()()0g x f x xf x ''=+>恒成立, 所以函数()g x 在(0,)+∞上是增函数,又因为()f x 是定义在R 上的偶函数,所以()()g x xf x =上R 上的奇函数, 所以函数()g x 在(,0)-∞上是增函数,因为()20f =,所以()20f -=,即()()20,20g g =-=, 所以()0xf x >化为()0g x >,当0x >时,不等式()0f x >等价于()0g x >,即()()2g x g >,解得2x >; 当0x <时,不等式()0f x >等价于()0g x <,即()()2g x g <-,解得2x <-; 综上,不等式()0f x >的解集为(,2)(2,)-∞-+∞.点睛:本题考查了与函数有关的不等式的求解问题,其中解答中涉及到利用条件构造新函数和利用导数研究函数的单调性,以及根据单调性和奇偶性的关系对不等式进行转化,解答中一定要注意函数值为零时自变量的取值,这是题目的一个易错点,试题综合性强,属于中档试题.15.【分析】转化条件得设求导后求出函数的最小值令即可得解【详解】由题意得由于时故设则由于所以当时单调递减;当时单调递增于是所以即故实数的取值范围是故答案为:【点睛】本题考查了利用导数解决不等式恒成立问题 解析:(]0,e【分析】转化条件得()min 0f x '≥,设()()g x f x '=,求导后求出函数()g x 的最小值()min g x ,令()min 0g x ≥即可得解. 【详解】由题意得()2ln 2x f x a x '=-.由于0x >时,()0f x '≥,故()min 0f x '≥.设()()g x f x '=,则()(2x x x a g x xx+-'==.由于0x >,所以当(x ∈时,()0g x '<,()g x 单调递减;当)x ∈+∞时,()0g x '>,()g x 单调递增.于是()()()min min 1ln 022a af xg x ga a '===-=-≥, 所以ln 1a ≤即0a e <≤,故实数a 的取值范围是(]0,e . 故答案为:(]0,e 【点睛】本题考查了利用导数解决不等式恒成立问题,考查了推理能力,属于中档题.16.【分析】求出函数的导数问题转化为即可得到本题答案【详解】由题得因为函数在递增所以在恒成立即又当时所以故答案为:【点睛】本题主要考查根据函数的单调区间确定参数的取值范围考查学生的转化能力和运算求解能力 解析:[)2,+∞【分析】求出函数的导数,问题转化为()max 2cos a x ≥-,即可得到本题答案. 【详解】由题,得2cos y x a '=+, 因为函数在[]0,2π递增,所以2cos 0y x a '=+≥在[]0,2π恒成立, 即()max 2cos a x ≥-,又当[]0,2x π∈时,22cos 2x -≤-≤, 所以2a ≥, 故答案为:[)2,+∞【点睛】本题主要考查根据函数的单调区间确定参数的取值范围,考查学生的转化能力和运算求解能力.17.【分析】令根据题中条件得到为偶函数;对其求导根据题中条件判定在上单调递减;则在上单调递增;化所求不等式为求解即可得出结果【详解】令则因为所以即所以函数为偶函数;又当时所以即函数在上单调递减;则在上单解析:12x x ⎧⎫≥⎨⎬⎩⎭【分析】令()()xg x f x e =,根据题中条件,得到()g x 为偶函数;对其求导,根据题中条件,判定()g x 在(),0-∞上单调递减;则()g x 在()0,∞+上单调递增;化所求不等式为1x x ≥-,求解,即可得出结果.【详解】令()()xg x f x e =,则()()xg x f x e --=-,因为2()()0xf x ef x --=,所以()()x x f x e f x e -=-,即()()g x g x =-,所以函数()g x 为偶函数;又()[]()()()()x x xg x f x e f x e f x f x e '''=+=+,当0x ≤时,()()0f x f x '+<,所以()[]()()0xg x f x f x e ''=+<,即函数()g x 在(),0-∞上单调递减;则()g x 在()0,∞+上单调递增; 又不等式21()(1)x f x ef x -≥-可化为1()(1)x x f x e f x e -≥-,即()()1g x g x ≥-,所以只需1x x ≥-,则()221x x ≥-,解得12x ≥. 故答案为:12x x ⎧⎫≥⎨⎬⎩⎭. 【点睛】本题主要考查由函数单调性与奇偶性解不等式,考查导数的方法判定函数单调性,涉及绝对值不等式的解法,属于常考题型.18.【分析】当时利用导数法得到函数的单调性与极值再由时作出函数的大致图象令将问题转化为方程有两个不等根且即各有3个根求解【详解】当时所以当时递增当时递减所以当时取得最大值1又当时所以的大致图象如图所示:解析:1,04⎛⎫- ⎪⎝⎭【分析】当1x <时,()()1xf x x e =-,利用导数法得到函数的单调性与极值,再由1≥x 时,()ln f x x =,作出函数()f x 的大致图象,令()f x t =,将问题转化为方程20t t a --=有两个不等根12,t t ,且12,(0,1)t t ∈即()()12,f x t f x t ==各有3个根求解.【详解】当1x <时,()()1xf x x e =-,所以()xf x xe '=-,当0x <时,()0f x '>,()f x 递增,当01x <<时,()0f x '<,()f x 递减, 所以当0x =时, ()f x 取得最大值1, 又当1≥x 时,()ln f x x =,所以()f x 的大致图象如图所示:令()f x t =,则转化为方程20t t a --=有两个不等根12,t t , 且()()2121,(0,1),,t f x t f t x t ==∈各有3个根, 方程20t t a --=在(0,1)有两个不同的解,设2()g t t t a =--,所以(0)0140(1)0g a a g a =->⎧⎪∆=+>⎨⎪=->⎩,解得104a -<<. 故答案为:1,04⎛⎫- ⎪⎝⎭【点睛】本题主要方程的根与函数的零点问题,利用导数研究函数的单调性与极值,还考查了转化化归思想、数形结合思想和运算求解的能力,属于中档题.19.【分析】首先求出函数的导数依题意可得在上恒成立参变分离根据余弦函数的性质求出参数的取值范围;【详解】解:因为所以因为函数在上的单调递减所以在上恒成立即在上恒成立因为在上单调递减所以所以即故答案为:【 解析:[2,)+∞【分析】首先求出函数的导数,依题意可得()2cos 0f x x a '=-≤在0,2π⎡⎤⎢⎥⎣⎦上恒成立,参变分离,根据余弦函数的性质求出参数的取值范围; 【详解】解:因为()2sin f x x ax =-,0,2x π⎡⎤∈⎢⎥⎣⎦, 所以()2cos f x x a '=-, 因为函数()2sin f x x ax =-在0,2π⎡⎤⎢⎥⎣⎦上的单调递减, 所以()2cos 0f x x a '=-≤在0,2π⎡⎤⎢⎥⎣⎦上恒成立, 即2cos a x ≥在0,2x π⎡⎤∈⎢⎥⎣⎦上恒成立, 因为()2cos g x x =在0,2x π⎡⎤∈⎢⎥⎣⎦上单调递减,所以()()max 02cos02g x g === 所以2a ≥,即[)2,a ∈+∞ 故答案为:[)2,+∞ 【点睛】本题考查根据函数的单调性求参数的取值范围,利用导数研究函数的单调性,属于中档题.20.【解析】试题分析:设切点为所以切点为由点可知直线方程为考点:1直线方程;2导数的几何意义解析:20x y +-=. 【解析】试题分析:设切点为()0000220000111,2y x y y y x x x x -∴==-'∴-=-,所以切点为()1,1,由点()2,0可知直线方程为20x y +-= 考点:1.直线方程;2.导数的几何意义三、解答题21.(1)39a b =-⎧⎨=-⎩;(2)max ()7f x =.【分析】(1)先对函数求导,根据题中条件,列出方程组求解,即可得出结果;(2)先由(1)得到32()392f x x x x =--+,导数的方法研究其单调性,进而可求出最值. 【详解】(1)因为32()2f x x ax bx =+++,所以2()32f x x ax b '=++,又函数32()2f x x ax bx =+++在1x =-处取得极值7,(1)17(1)320f a b f a b -=+-=⎧⎨-=-+='⎩,解得39a b =-⎧⎨=-⎩;, 所以3()3693(3)(1)f x x x x x '=--=-+, 由()0f x '>得3x >或1x <-;由()0f x '<得13x ;满足题意;(2)又[2,2]x ∈-,由(1)得()f x 在(2,1)x ∈--上单调递增,在(1,2)x ∈-上单调递减, 因此max ()(1)7f x f =-=. 【点睛】方法点睛:该题考查的是有关利用导数研究函数的问题,解题方法如下:(1)先对函数求导,根据题意,结合函数在某个点处取得极值,导数为0,函数值为极值,列出方程组,求得结果;(2)将所求参数代入,得到解析式,利用导数研究其单调性,得到其最大值. 22.(1)证明见详解;(2)2 【分析】(1)构造新函数利用函数的单调性证明命题成立.(2)对k 进行讨论,利用新函数的单调性求参数k 的取值范围. 【详解】(1)证明:()()1()lnln 1ln 11xf x x x x+==+---, ()2112111f x x x x'=+=+-- 令()3()2()3x g x f x x =-+,则()()()4222211x g x f x x x ''=-+=-,因为()()001g x x '><<,所以()g x 在()0,1上单调递增, 所以()()00g x g >=,()0,1x ∈,即当()0,1x ∈时,3()2()3x f x x >+.(2)由(1)可知,当k 2≤时,3()()3x f x k x >+对(0,1)x ∈恒成立,当2k >时,令()3()()3x h x f x k x =-+,则()()2222()(1)1kx k h x f x k x x --''=-+=-,所以当0x <<()0h x '<,因此()h x 在区间⎛ ⎝上单调递减,当0x <<()()00h x h <=, 即3()()3x f x k x <+,所以当2k >时,3()()3x f x k x >+并非对(0,1)x ∈恒成立,综上可知,k 的最大值为2. 【点睛】关键点点睛:本题考查了构造新函数,利用导数判断函数的单调性,证明不等式,利用导数研究不等式恒成立,解题的关键是由(1)确定当k 2≤时,3()()3x f x k x >+对(0,1)x ∈恒成立,考查了运算求解能力.23.选①或②或③,(1)2a =-,1b =;(2)0. 【分析】(1)求出()232f x x ax b '=++,根据所选条件可得出关于a 、b 的方程组,即可解得a 、b 的值;(2)利用导数分析函数()f x 的单调性,由此可求得函数()f x 的极小值. 【详解】(1)方案一:选择①,()32f x x ax bx =++,则()232f x x ax b '=++,由已知可得()()1141320f a b f a b ⎧-=-+-=-⎪⎨=++='⎪⎩,解得21a b =-⎧⎨=⎩;方案二:选择②,()32f x x ax bx =++,则()232f x x ax b '=++,由已知可得()()11001f a b f b ⎧=++=⎪⎨=='⎪⎩,解得21a b =-⎧⎨=⎩;方案三:选择③,()32f x x ax bx =++,则()232f x x ax b '=++,因为函数()f x 在()()1,1f --处的切线方程为84y x =+,所以,()()1328114f a b f a b ⎧-=-+=⎪⎨-=-+-=-'⎪⎩,解得21a b =-⎧⎨=⎩;(2)由(1)得()322f x x x x =-+,()2341f x x x '∴=-+,由()0f x '=得:113x =,21x =,列表如下:所以,函数f x 的极小值为10f =. 【点睛】思路点睛:求函数()f x 的极值的步骤: (1)求函数()f x 的定义域; (2)求导()f x ';(3)解方程()00f x '=,当()00f x '=; (4)利用导数分析函数()f x 的单调性; (5)将极值点代入函数解析式计算即可. 24.(1)单调递增区间为,2a ⎛⎫+∞ ⎪⎝⎭,单调递减区间为0,2a ⎛⎫ ⎪⎝⎭;(2)证明见解析.【分析】(1)对()f x 求导,分别由()'0f x >和()'0f x <可求得单调递增和单调递减区间; (2)由题意只需证明()2max2aa f x e ≤-即可,讨论当12a ≤,即02a <≤,()f x 在1,a e ⎡⎤⎣⎦上单调递增,()()max a f x f e =;当2a >时先证明12aa e a >>>,可得()()max a f x f e =或()()max 11f x f ==,比较即可求证.【详解】(1)由题意得:()1,02af x x x'=->, 由()'0f x >,得2a x >, 由()'0f x <,得02a x <<, 所以()f x 的单调递增区间为,2a ⎛⎫+∞ ⎪⎝⎭,单调递减区间为0,2a ⎛⎫ ⎪⎝⎭.(2)若12a ≤,即02a <≤,由(1)知()f x 在1,a e ⎡⎤⎣⎦上单调递增,所以()()22max22a a a a a f x f e e e ==-≤-成立; 若12a >,即2a >,设()a g a e a =-, 则当2a >时,()'10a g a e =->,所以()()2220g a g e >=->, 所以2a a e a >>,从而1,2a a e ∈⎡⎤⎣⎦. 结合(1)可知,()f x 在1,2a ⎡⎤⎢⎥⎣⎦上单调递减,在,2a a e ⎛⎤ ⎥⎝⎦上单调递增, 下面比较()22a aa f e e =-和()11f =的大小, 设()22aa h a e =-,当2a >时,()'0,a h a e a =-> 所以()()2221h a h e >=->, 即()()1af e f >,而()()2max 2a a a f x f e e ==-, 所以当1,a x e ∈⎡⎤⎣⎦时,()22a a f x e ≤- 综上所述:当1,a x e ∈⎡⎤⎣⎦时,()22aa f x e ≤-. 【点睛】方法点睛:利用导数研究函数单调性的方法: (1)确定函数()f x 的定义域;求导函数()'f x ,由()0f x '>(或()0f x '<)解出相应的x 的范围,对应的区间为()f x 的增区间(或减区间);(2)确定函数()f x 的定义域;求导函数()'f x ,解方程()0f x '=,利用()0f x '=的根将函数的定义域分为若干个子区间,在这些子区间上讨论()'f x 的正负,由符号确定()f x 在子区间上的单调性.25.(1)证明见解析;(2)证明见解析.【分析】(1)求导根据导数()0f x '>,()0f x '<求出最小值()10f =进而有()0f x ≥成立 (2)有(1)得ln 1≤-x x ,令112n x =+得11ln 122n n ⎛⎫+< ⎪⎝⎭,不等式通项可加性相加,根据等比数列求和化简即可证明.【详解】解:(1)由题意得()111x f x x x-'=-= 当1x >时()0f x '>,()f x 单调增当01x <<时()0f x '<,()f x 单调减所以()f x 的最小值为()10f =,所以()()01x f f ≥=即()0f x ≥成立(2)由(1)知ln 1≤-x x 令112n x =+得11ln 122n n ⎛⎫+< ⎪⎝⎭ 所以2212111111ln 1ln 1ln 1222222n ⎛⎫⎛⎫⎛⎫+++++<++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭111221111212n n ⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎛⎫⎝⎭==-< ⎪⎝⎭- 即22111ln 1111ln 222e ⎛⎫⎛⎫⎛⎫⎛⎫+⋅++<= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以2111111222n e ⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ 【点睛】已知不等式证明问题常用的方法:(1)证明()min f x a ≥或()max f x a ≤;(3)构造两个函数()()f x g x <,证明()min max ()f x g x <26.(1)2;(2)(,1)-∞-.【分析】(1)将0a =代入,求出函数的导数,分析函数的单调性可得当1x =-时,()f x 有最大值2;(2)若()f x 无最大值,则3123a a a a ≤-⎧⎨->-⎩或312322a a a a a >-⎧⎪->-⎨⎪->⎩,解得可得答案. 【详解】(1)若0a =,33,0()2,0x x x f x x x ⎧-=⎨->⎩,所以233,0()2,0x x f x x ⎧-=⎨->⎩', 当1x <-时,()0f x '>,此时函数为单调递增函数,当1x >-时,()0f x '<,此时函数为单调递减函数,故当1x =-时()f x 有最大值为2 .(2)233,()2,x x a f x x a⎧-=⎨->'⎩,令()0f x '=,则1x =±,若()f x 无最大值,则 3123a a a a ≤-⎧⎨->-⎩ ① 或312322a a a a a >-⎧⎪->-⎨⎪->⎩②, 由①得(,1)a ∈-∞-,由②得无解,所以(,1)a ∈-∞-.故答案为:2;(,1)-∞-.【点睛】分段函数在高考中的常见题型有:已知分段函数求值、已知分段函数求值域、已知分段函数求不等式解集、已知分段函数求参数取值范围等,分段函数问题要注意分类讨论,涉及分段函数的单调性、奇偶性、周期性等问题,要善于利用数形结合的思想解决问题.。
高考数学一轮复习导数及其应用多选题单元测试含答案

高考数学一轮复习导数及其应用多选题单元测试含答案一、导数及其应用多选题1.对于函数()2ln 1f x x ax x a =+--+,其中a R ∈,下列4个命题中正确命题有( )A .该函数定有2个极值B .该函数的极小值一定不大于2C .该函数一定存在零点D .存在实数a ,使得该函数有2个零点【答案】BD 【分析】求出导函数,利用导数确定极值,结合零点存在定理确定零点个数. 【详解】函数定义域是(0,)+∞,由已知2121()2x ax f x x a x x+-'=+-=,280a ∆=+>,2210x ax +-=有两个不等实根12,x x ,但12102x x =-<,12,x x 一正一负.由于定义域是(0,)+∞,因此()0f x '=只有一个实根,()f x 只有一个极值,A 错; 不妨设120x x <<,则20x x <<时,()0f x '<,()f x 递减,2x x >时,()0f x '>,()f x 递增.所以2()f x 是函数的极小值.222210x ax +-=,22212x a x -=,22222()ln 1f x x ax x a =+--+=222222222222212112ln 12ln 2x x x x x x x x x -+---+=-+--+,设21()2ln 2g x x x x x =-+--+,则22111()22(1)(2)g x x x x x x'=-+-+=-+, 01x <<时,()0g x '>,()g x 递增,1x >时,()0g x '<,()g x 递减,所以()g x 极大值=(1)2g =,即()2g x ≤,所以2()2f x ≤,B 正确; 由上可知当()f x 的极小值为正时,()f x 无零点.C 错;()f x 的极小值也是最小值为2222221()2ln 2f x x x x x =-+--+, 例如当23x =时,173a =-,2()0f x <,0x →时,()f x →+∞,又2422217171714()21()03333f e e e e e =--++=-+>(217()3e >, 所以()f x 在(0,3)和(3,)+∞上各有一个零点,D 正确. 故选:BD . 【点睛】思路点睛:本题考查用导数研究函数的极值,零点,解题方法是利用导数确定函数的单调性,极值,但要注意在函数定义域内求解,对零点个数问题,注意结合零点存在定理,否则不能确定零点的存在性.2.已知:()f x 是奇函数,当0x >时,()'()1f x f x ->,(1)3f =,则( )A .(4)(3)f ef >B .2(4)(2)f e f ->-C .3(4)41f e >-D .2(4)41f e -<--【答案】ACD 【分析】由已知构造得'()+10x x e f ⎡⎤>⎢⎥⎣⎦,令()()+1x f x g x e =,判断出函数()g x 在0x >时单调递增,由此得()()4>3g g ,化简可判断A ;()()4>2g g ,化简并利用()f x 是奇函数,可判断B ;()()4>1g g ,化简可判断C ;由C 选项的分析得32(4)41>4+1f e e >-,可判断D.【详解】 因为当0x >时,()'()1fx f x ->,所以()'()10f x f x -->,即()[]'()+10xf x f e x ->,所以'()+10x x e f ⎡⎤>⎢⎥⎣⎦, 令()()+1xf xg x e=,则当0x >时,()'>0g x ,函数()g x 单调递增, 所以()()4>3g g ,即43(4)+1(3)+1>f f e e ,化简得(4)(3)1>(3)f f e e ef >+-,故A 正确;()()4>2g g ,即42(4)+1(2)+1>f f e e ,化简得222(4)(2)1>(2)f f e e e f >+-, 所以2(4)(2)e f f -<-,又()f x 是奇函数,所以2(4)(2)e f f -<-,故B 不正确;()()4>1g g ,即4(4)+1(1)+1>f f e e,又(1)3f =,化简得3(4)41f e >-,故C 正确; 由C 选项的分析得32(4)41>4+1f e e >-,所以2(4)41f e -<--,又()f x 是奇函数,所以2(4)41f e -<--,故D 正确, 故选:ACD. 【点睛】关键点点睛:解决本题中令有导函数的不等式,关键在于构造出某个函数的导函数,得出所构造的函数的单调性,从而可比较函数值的大小关系.3.已知函数()32f x x ax x c =+-+(x ∈R ),则下列结论正确的是( ).A .函数()f x 一定存在极大值和极小值B .若函数()f x 在1()x -∞,、2()x ,+∞上是增函数,则21x x -≥ C .函数()f x 的图像是中心对称图形D .函数()f x 的图像在点00())(x f x ,(0x R ∈)处的切线与()f x 的图像必有两个不同的公共点 【答案】ABC 【分析】首先求函数的导数2()3210f x x ax =+-=',再根据极值点与导数的关系,判断AB 选项;证明()()2()333a a af x f x f -++--=-,判断选项C ;令0a c ==,求切线与()f x 的交点个数,判断D 选项.【详解】A 选项,2()3210f x x ax =+-='的24120a ∆=+>恒成立,故()0f x '=必有两个不等实根,不妨设为1x 、2x ,且12x x <,令()0f x '>,得1x x <或2x x >,令()0f x '<,得12x x x <<,∴函数()f x 在12()x x ,上单调递减,在1()x -∞,和2()x ,+∞上单调递增, ∴当1x x =时,函数()f x 取得极大值,当2x x =时,函数()f x 取得极小值,A 对, B 选项,令2()3210f x x ax =+-=',则1223ax x +=-,1213x x ⋅=-,易知12x x <,∴213x x -==≥,B 对, C 选项,易知两极值点的中点坐标为(())33a a f --,,又23()(1)()333a a a f x x x f -+=-+++-,∴()()2()333a a af x f x f -++--=-, ∴函数()f x 的图像关于点(())33aa f --,成中心对称,C 对,D 选项,令0a c ==得3()f x x x =-,()f x 在(0)0,处切线方程为y x =-, 且3y xy x x =-⎧⎨=-⎩有唯一实数解, 即()f x 在(0)0,处切线与()f x 图像有唯一公共点,D 错, 故选:ABC . 【点睛】方法点睛:解决函数极值、最值综合问题的策略:1、求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小;2、求函数最值时,不可想当然地认为极值点就是最值点,要通过比较才能下结论;3、函数在给定闭区间上存在极值,一般要将极值与端点值进行比较才能确定最值.4.设函数()()()1f x x x x a =--,则下列结论正确的是( ) A .当4a =-时,()f x 在11,2⎡⎤-⎢⎥⎣⎦上的平均变化率为194B .当1a =时,函数()f x 的图像与直线427y =有2个交点 C .当2a =时,()f x 的图像关于点()1,0中心对称D .若函数()f x 有两个不同的极值点1x ,2x ,则当2a ≥时,()()120f x f x +≤ 【答案】BCD 【分析】运用平均变化率的定义可分析A ,利用导数研究()f x 的单调性和极值,可分析B 选项,证明()()20f x f x +-=可分析C 选项,先得出1x ,2x 为方程()23210x a x a -++=的两个实数根,结合韦达定理可分析D 选项. 【详解】对于A ,当4a =-时,()()()14f x x x x =-+,则()f x 在11,2⎡⎤-⎢⎥⎣⎦上的平均变化率为()()()119123192221412⎛⎫⨯-⨯--⨯-⨯ ⎪⎝⎭=---,故A 错误;对于B ,当1a =时,()()23212f x x x x x x =-=-+,()()()2341311f x x x x x '=-+=--,可得下表:因为14327f ⎛⎫= ⎪⎝⎭,()10f =,()42227f =>,结合()f x 的单调性可知, 方程()427f x =有两个实数解,一个解为13,另一个解在()1,2上,故B 正确; 对于C ,当2a =时,()()()()()()()231211111f x x x x x x x x ⎡⎤=--=---=---⎣⎦, 则有()()()()()()33211110f x f x x x x x +-=---+---=,故C 正确; 对于D ,()()()1f x x x x a =--,()()()()()2121321f x x x a x x a x a x a '=--+--=-++,令()0f x '=,可得方程()23210x a x a -++=,因为()()22412130a a a ∆=-+=-+>,且函数()f x 有两个不同的极值点1x ,2x ,所以1x ,2x 为方程()23210x a x a -++=的两个实数根,则有()12122132x x a a x x ⎧+=+⎪⎪⎨⎪=⎪⎩,则()()()()()()1211122211f x f x x x x a x x x a +=--+--()()()()33221212121x x a x x a x x =+-++++()()()()()22212112212121212x x x x x x a x x x x a x x ⎡⎤=+-++++-++⎣⎦()()()22211221212221233a x x x x x x x x a ⎡⎤=+-+-+++⎢⎥⎣⎦ ()()()()()21242212113327a a a x x a a --⎡⎤=+-++=-+⋅⎢⎥⎣⎦因为2a ≥,所以()()120f x f x +≤,故D 正确; 故选:BCD . 【点睛】关键点点睛:本题考查利用导数研究函数的单调性,平均变化率,极值等问题,本题的关键是选项D ,利用根与系数的关系,转化为关于a 的函数,证明不等式.5.在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它得名于荷兰数学家鲁伊兹布劳威尔(L.E.Brouwer )简单的讲就是对于满足一定条件的连续函数()f x ,存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点”函数,而称0x 为该函数的一个不动点,依据不动点理论,下列说法正确的是( ) A .函数()sin f x x =有3个不动点B .函数2()(0)f x ax bx c a =++≠至多有两个不动点C .若定义在R 上的奇函数()f x ,其图像上存在有限个不动点,则不动点个数是奇数D .若函数()f x =[0,1]上存在不动点,则实数a 满足l a e ≤≤(e 为自然对数的底数) 【答案】BCD 【分析】根据题目中的定义,结合导数、一元二次方程的性质、奇函数的性质进行判断即可. 【详解】令()sin g x x x =-,()1cos 0g x x '=-≥, 因此()g x 在R 上单调递增,而(0)0g =, 所以()g x 在R 有且仅有一个零点, 即()f x 有且仅有一个“不动点”,A 错误;0a ≠,20ax bx c x ∴++-=至多有两个实数根,所以()f x 至多有两个“不动点”,B 正确;()f x 为定义在R 上的奇函数,所以(0)0f =,函数()-y f x x =为定义在R 上的奇函数,显然0x =是()f x 的一个“不动点”,其它的“不动点”都关于原点对称,个数和为偶数, 因此()f x 一定有奇数个“不动点”,C 正确;因为()f x 在[0,1]存在“不动点”,则()f x x =在[0,1]有解,x =⇒2x a e x x =+-在[0,1]有解,令2()xm x e x x =+-,()12x m x e x '=+-,令()12x n x e x '=+-,()20x n x e '=-=,ln 2x =,()n x 在(0,ln 2)单调递减,在(ln 2,1)单调递增,∴min ()(ln 2)212ln 232ln 20n x n ==+-=->, ∴()0m x '>在[0,1]恒成立,∴()m x 在[0,1]单调递增,min ()(0)1m x m ==,max ()(1)m x m e ==,∴1a e ≤≤,D 正确,. 故选:BCD 【点睛】方法点睛:新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.6.已知函数()1ln f x x x x=-+,给出下列四个结论,其中正确的是( ) A .曲线()y f x =在1x =-处的切线方程为10x y ++=B .()f x 恰有2个零点C .()f x 既有最大值,又有最小值D .若120x x >且()()120f x f x +=,则121=x x 【答案】BD 【分析】本题首先可根据()10f -=以及13f判断出A 错误,然后根据当0x >时的函数单调性、当0x <时的函数单调性、()10f -=以及()10f =判断出B 正确和C 错误,最后根据()()120f x f x +=得出()121f x f x ⎛⎫= ⎪⎝⎭,根据函数单调性即可证得121=x x ,D 正确.【详解】函数()1ln f x x x x=-+的定义域为()(),00,-∞⋃+∞, 当0x >时,()1ln f x x x x=-+,()2221111x x f x x x x -+-'=--=;当0x <时,1ln f x x x x,()2221111x x f x x x x -+-'=--=,A 项:1ln 1110f,22111131f,则曲线()y f x =在1x =-处的切线方程为031y x ,即33y x =--,A 错误;B 项:当0x >时,222215124x x x f xx x ,函数()f x 是减函数,当0x <时,222215124x x x f xx x ,函数()f x 是减函数,因为()10f -=,()10f =,所以函数()f x 恰有2个零点,B 正确; C 项:由函数()f x 的单调性易知,C 错误; D 项:当1>0x 、20x >时, 因为()()120f x f x +=, 所以1222222221111ln lnf x f x x x x fx x x x , 因为()f x 在()0,∞+上为减函数,所以121x x =,120x x >, 同理可证得当10x <、20x <时命题也成立,D 正确,故选:BD. 【点睛】本题考查函数在某点处的切线求法以及函数单调性的应用,考查根据导函数求函数在某点处的切线以及函数单调性,导函数值即切线斜率,若导函数值大于0,则函数是增函数,若导函数值小于0,则函数是减函数,考查函数方程思想,考查运算能力,是难题.7.设函数()()1x af x a x a =->的定义域为()0,∞+,已知()f x 有且只有一个零点,下列结论正确的有( ) A .a e =B .()f x 在区间()1,e 单调递增C .1x =是()f x 的极大值点D .()f e 是()f x 的最小值【答案】ACD 【分析】()f x 只有一个零点,转化为方程0x a a x -=在(0,)+∞上只有一个根,即ln ln x ax a=只有一个正根.利用导数研究函数ln ()xh x x=的性质,可得a e =,判断A ,然后用导数研究函数()x e f x e x =-的性质,求出()'f x ,令()0f x '=,利用新函数确定()'f x 只有两个零点1和e ,并证明出()'f x 的正负,得()f x 的单调性,极值最值.判断BCD .【详解】()f x 只有一个零点,即方程0x a a x -=在(0,)+∞上只有一个根,x a a x =,取对数得ln ln x a a x =,即ln ln x ax a=只有一个正根. 设ln ()x h x x =,则21ln ()x h x x-'=,当0x e <<时,()0h x '>,()h x 递增,0x →时,()h x →-∞,x e >时,()0h x '<,()h x 递减,此时()0h x >,max 1()()h x h e e==. ∴要使方程ln ln x ax a =只有一个正根.则ln 1a a e =或ln 0a a<,解得a e =或0a <,又∵1a >,∴a e =.A 正确;()x e f x e x =-,1()x e f x e ex -'=-,1()0x e f x e ex -'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.设()(1)ln 1p x e x x =--+,1()1e p x x-'=-,当01x e <<-时,()0p x '>,()p x 递增,1x e >-时,()0p x '<,()p x 递减,(1)p e -是极大值,又(1)()0p p e ==,所以()p x 有且只有两个零点,01x <<或x e >时,()0p x <,即(1)ln 1e x x -<-,11e x x e --<,1e x ex e -<,()0f x '>,同理1x e <<时,()0f x '<,所以()f x 在(0,1)和(,)e +∞上递增,在(1,)e 上递减,所以极小值为()0f e =,极大值为(1)f ,又(0)1f =,所以()f e 是最小值.B 错,CD 正确. 故选:ACD . 【点睛】关键点点睛:本题考用导数研究函数的零点,极值,单调性.解题关键是确定()'f x 的零点时,利用零点定义解方程,1()0x e f x e ex -'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.然后证明方程只有这两个解即可.8.下列命题正确的有( ) A .已知0,0a b >>且1a b +=,则1222a b -<<B .34a b ==a bab+= C .323y x x x =--的极大值和极小值的和为6-D .过(1,0)A -的直线与函数3y x x =-有三个交点,则该直线斜率的取值范围是1(,2)(2,)4-+∞ 【答案】ACD 【分析】由等式关系、指数函数的性质可求2a b -的范围;利用指对数互化,结合对数的运算法求a b ab+;利用导数确定零点关系,结合原函数式计算极值之和即可;由直线与3y x x =-有三个交点,即可知2()h x x x k =--有两个零点且1x =-不是其零点即可求斜率范围. 【详解】A 选项,由条件知1b a =-且01a <<,所以21(1,1)a b a -=-∈-,即1222a b -<<;B 选项,34a b ==log a =4log b =1212112(log 3log 4)2a b ab a b+=+=+=; C 选项,2361y x x '=--中>0∆且开口向上,所以存在两个零点12,x x 且122x x +=、1213x x =-,即12,x x 为y 两个极值点,所以2212121212121212()[()3]3[()2]()6y y x x x x x x x x x x x x +=++--+--+=-;D 选项,令直线为(1)y k x =+与3y x x =-有三个交点,即2()()(1)g x x x k x =--+有三个零点,所以2()h x x x k =--有两个零点即可∴140(1)20k h k ∆=+>⎧⎨-=-≠⎩,解得1(,2)(2,)4k ∈-+∞故选:ACD 【点睛】本题考查了指对数的运算及指数函数性质,利用导数研究极值,由函数交点情况求参数范围,属于难题.9.已知函数()ln f x x mx =-有两个零点1x 、2x ,且12x x <,则下列结论不正确的是( ) A .10m e<<B .21x x -的值随m 的增大而减小C .101x <<D .2x e >【答案】C 【分析】由()0f x =得出ln xm x =,构造函数()ln x g x x=,利用导数分析函数()g x 的单调性与极值,数形结合可判断ACD 选项的正误;任取1m 、210,m e ⎛⎫∈ ⎪⎝⎭,且12m m <,设()()121g g m ξξ==,其中121e ξξ<<<;设()()122g g m ηη==,其中121e ηη<<<,利用函数()g x 的单调性结合不等式的基本性质得出2121ξξηη->-,可判断B 选项的正误. 【详解】令()0f x =,可得ln xm x =,构造函数()ln x g x x=,定义域为()0,∞+,()1ln xg x x-'=. 当0x e <<时, ()0g x '>,此时函数()g x 单调递增; 当x e >时,()0g x '<,此时函数()g x 单调递减. 所以,()()max 1g x g e e==,如下图所示:由图象可知,当10m e <<时,直线y m =与函数()ln x g x x=的图象有两个交点,A 选项正确;当1x >时,()0g x >,由图象可得11x e <<,2x e >,C 选项错误,D 选项正确; 任取1m 、210,m e ⎛⎫∈ ⎪⎝⎭,且12m m <,设()()121g g m ξξ==,其中121e ξξ<<<;设()()122g g m ηη==,其中121e ηη<<<.由于函数()g x 在区间()1,e 上单调递增,且()()11g g ξη<,11ξη∴<; 函数()g x 在区间(),e +∞上单调递减,且()()22g g ξη<,22ξη∴>. 由不等式的基本性质可得1212ξξηη-<-,则2121ξξηη->-. 所以,21x x -的值随m 的增大而减小,B 选项正确. 故选:C. 【点睛】在利用导数研究函数的零点问题个数中,可转化为判定()m g x =有两个实根时实数m 应满足的条件,并注意()g x 的单调性、奇偶性、最值的灵活应用.另外还可作出函数()y g x =的大致图象,直观判定曲线交点个数,但应注意严谨性,进行必要的论证.10.若方程()2110x m x -+-=和()120x m ex -+-=的根分别为()1212,x x x x <和3x ,()434x x x <,则下列判断正确的是( )A .3201x x <<<B .1310x x -<<C .(),1m ∈-∞-D .1151x ⎫--∈-⎪⎪⎝⎭【答案】ABD 【分析】根据题意将问题转化为,1x ,2x 和3x ,4x 分别是y m =与11y x x =--和12x xy e-=-交点的横坐标,再用导数研究函数11y xx=--和12xxye-=-的单调性与取值情况,作出函数图象,数形结合即可解决问题.【详解】解:由题,1x,2x和3x,4x分别是11m xx=--和12xxme-=-的两个根,即y m=与11y xx=--和12xxye-=-交点的横坐标.对于函数11y xx=--,定义域为{}0x x≠,21'10yx=+>,所以函数在(),0-∞和()0,∞+上单调递增,且1x=时,1y=-;对于函数12xxye-=-,11'xxye--=,所以函数在(),1-∞上单调递增,在()1,+∞单调递减,且当,2x y→+∞→-,0x=时,2y=-,1x=时,1y=-;故作出函数11y xx=--,12xxye-=-的图像如图所示,注意到:当()0,1x∈时,11122xxx xx e---<-<-,由图可知,3201x x<<<,()2,1m∈--,从而()11112,1xx--∈--,解得115,1x⎛⎫--∈-⎪⎪⎝⎭,所以选项AD正确,选项C错误,又121310x x x x-=<<.故选:ABD.【点睛】本题考查利用导数研究函数的零点问题,考查化归转化思想与数形结合思想,是中档题.。
(好题)高中数学选修1-1第四章《导数应用》测试卷(有答案解析)(4)

一、选择题1.已知函数()()ln 1xxf x x e e -=-++,则使不等式()()12f x f x +<成立的x 的取值范围是( ) A .()(),11,-∞-+∞B .()2,1--C .()1,1,3⎛⎫-∞-+∞ ⎪⎝⎭D .()(),21,-∞-⋃+∞2.已知函数()2()xxf x x e e x-=⋅-+,若()()()f x f y f x y <<+,则( )A .0xy >B .0xy <C .0x y +>D .0x y +<3.设函数()ln 2e f x x mx n x =--+.若不等式()0f x ≤对()0,x ∈+∞恒成立,则nm 的最大值为( ) A .4e B .2eC .eD .2e4.函数()cos f x x x =⋅的导函数为()f x ',则()f x 与()f x '在一个坐标系中的图象为( )A .B .C .D .5.现有橡皮泥制作的底面半径为4,高为3的圆锥一个.若将它重新制作成一个底面半径为r ,高为h 的圆柱(橡皮泥没有浪费),则该圆柱表面积的最小值为( )A .20πB .24πC .28πD .32π6.已知函数()ln f x x ax =-,其中[)1+x ∈∞,,若不等式()0f x ≤恒成立,则实数a 的取值范围为( )A .[)1,+∞B .1,1e⎛⎤-∞- ⎥⎦⎝C .1,e ⎡⎫+∞⎪⎢⎣⎭D .[)0,+∞7.已知函数21ln 22y x a x x =--在1,2⎡⎫+∞⎪⎢⎣⎭上单调递增,则实数a 的取值范围为( ) A .34a ≤-B .1a ≤-C .1a ≤D .01a ≤≤8.已知函数()()()110ln x f x x x++=>,若()1kf x x >+恒成立,则整数k 的最大值为( ) A .2B .3C .4D .59.已知函数()()22,02ln ,0x x f x a x x x x -⎧<⎪=⎨++>⎪⎩,若恰有3个互不相同的实数1x ,2x ,3x ,使得()()()1232221232f x f x f x x x x ===,则实数a 的取值范围为( ) A .1a e>-B .10a e-<< C .0a ≥ D .0a ≥或1a e=-10.设函数()x f x e x =-,直线y ax b =+是曲线()y f x =的切线,则+a b 的最大值是( ) A .11e-B .1C .1e -D .22e -11.已知定义域为R 的函数 f x () 的导函数为'f x () ,且满足'24f x f x ()﹣()> ,若 01f =()﹣ ,则不等式22x f x e +()> 的解集为( )A .∞(0,+)B .1+∞(﹣,)C .0∞(﹣,)D .1(﹣,﹣)∞ 12.若函数()(1)x f x x e a =--在(1,)-+∞上只有一个零点,则a 的取值范围为( ) A .21,e ⎛⎫--⎪⎝⎭B .2{1},e ⎡⎫-⋃-+∞⎪⎢⎣⎭ C .2,e ⎡⎫-+∞⎪⎢⎣⎭D .2{1},0e ⎡⎫-⋃-⎪⎢⎣⎭二、填空题13.已知函数1()ln (0)a x f x x a x x a e=++-<,若()0f x ≥在[)2,x ∈+∞上恒成立,则实数a 的取值范围为___________.14.对于函数22,0()12,02x x e x f x x x x ⎧⋅≤⎪=⎨-+>⎪⎩有下列命题: ①在该函数图象上一点(﹣2,f (﹣2))处的切线的斜率为22e -; ②函数f (x )的最小值为2e-;③该函数图象与x 轴有4个交点;④函数f (x )在(﹣∞,﹣1]上为减函数,在(0,1]上也为减函数. 其中正确命题的序号是_____.15.若函数()22ln 2f x x x a =++-在()1,e 上有零点,则实数a 的取值范围为______.16.已知a R ∈,对于任意的实数[]1,2x ∈,不等式()110xx e a x a e ⎛⎫+---≤ ⎪⎝⎭恒成立,则实数a 的取值范围是________________.17.定义在R 上的函数()f x 满足:()()22f x f x x -+=,且当0x ≤时,()2f x x '<,则不等式()()25510f x x x f +-+≥的解集为______.18.已知定义在R 上的函数()f x 关于y 轴对称,其导函数为()f x '. 当0x ≥时,()()1xf x f x '>-. 若对任意x ∈R ,不等式()()0x x x e f e e ax axf ax -+->恒成立,则正整数a 的最大值为_____.19.已知函数()2cos sin 2f x x x =+,则()f x 的最大值是__________.20.已知函数22(0)()4(0)x e x f x x x ⎧>=⎨+≤⎩,若x R ∀∈,()f x mx ≥,则实数m 的取值范围是________. 三、解答题21.已知函数()ln f x x x e =--. (1)求函数()f x 的单调区间;(2)若关于x 的不等式()xe f x mx ⋅在(0,)+∞上恒成立,求实数m 的取值范围.22.已知函数32()392f x x x x =-++-.(1)求函数()y f x =的图象在点()()1,1f 处的切线方程; (2)求()f x 的单调区间.23.“既要金山银山,又要绿水青山”.滨江风景区在一个直径AB 为100米的半圆形花园中设计一条观光线路(如图所示).在点A 与圆弧上的一点C (不同于A ,B 两点)之间设计为直线段小路,在直线段小路的两侧(注意是两侧)种植绿化带;再从点C 到点B 设计为沿弧的弧形小路,在弧形小路的内侧(注意是一侧)种植绿化带(注:小路及绿化带的宽度忽略不计).(1)设BAC θ∠= (弧度),将绿化带总长度表示为θ的函数()S θ;(2)试确定θ的值,使得绿化带总长度最大.(弧度公式:l r α=⋅,其中α为弧所对的圆心角)24.已知函数()ex af x x =+,其中a R ∈,e 是自然对数的底数. (1)当1a =-时,求函数()f x 在区间[)0,+∞上的零点个数; (2)若()2f x >对任意的实数x 恒成立,求a 的取值范围. 25.已知曲线3211()33f x x ax bx =+++在点()()1,1f 处的切线斜率为3,且2x =时()y f x =有极值.(1)求函数()f x 的解析式;(2)求函数()f x 在[]0,3上的极值和最小值. 26.已知函数()11f x x=-. (1)求曲线()y f x =在点()()1,1f 处的切线方程;(2)设函数()()ln g x f x t x =+,当1t ≤时,求()g x 零点的个数.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】先判断函数的奇偶性和单调性,从而可得关于x 的不等式,求出其解后可得正确的选项. 【详解】()f x 的定义域为()(),11,-∞-+∞,且()()()ln 1x x f x x e e f x --=--++=,又当1x >时,()()ln 1xxf x x e e -=-++,()11001x x f x e e e x e-'=+->+->-,故()f x 在()1,+∞为增函数, 故()()12f x f x +<即为11211112121x xx x x x ⎧<+<⎪+-+⎨⎪-⎩或或,解得2x <-或1x >,故选:D. 【点睛】方法点睛:解函数不等式,往往需要考虑函数的奇偶性和单调性,前者依据定义,后者可利用导数,注意定义域的要求.2.A解析:A 【分析】先判断函数的奇偶性和单调性,再分析得解. 【详解】由题得函数的定义域为R.()22())()(x x x x f x x e e x e e x x f x --=-+=-=-⋅-+,所以函数是偶函数.当0x >时,1()()2xx x x f x e xe xe x e-'=-+++, 因为0x >,所以()0f x '>,所以函数()f x 在(0,)+∞上单调递增,因为函数是偶函数,所以函数()f x 在(,0)-∞上单调递减,在(0,)+∞上单调递增. 如果0,0x y >>,则0x y +>,因为()()()f x f y f x y <<+,所以x y x y <<+,与已知相符; 如果0,0x y <<,则0x y +<,所以x y x y >>+,与已知相符; 如果0,0x y ><,因为()()f x f y <,所以0y x y <+<, 所以()()f y f x y >+,与已知矛盾;如果0,0x y <>,因为()()f x f y <,所以0y x y >+>, 所以()()f y f x y >+,与已知矛盾;当,x y 之中有一个为零时,不妨设0y =,()()f x y f x += ,()()()f x f y f x <<,显然不成立.故选:A 【点睛】方法点睛:对于函数的问题,要灵活利用函数的奇偶性和单调性分析函数的问题,利用函数的图象和性质分析函数的问题.3.D解析:D 【分析】 由题意可得ln 22e n x m x x m ⎛⎫-≤- ⎪⎝⎭对()0,x ∈+∞恒成立,设()ln e g x x x =-,()2,02n h x m x x m ⎛⎫=-> ⎪⎝⎭,根据它们的图象,结合的导数的几何意义,以及射线的性质,即可得到所求的最大值. 【详解】由不等式()0f x ≤对()0,x ∈+∞恒成立, 即为ln 20e x mx n x --+≤,即ln 22e n x m x x m ⎛⎫-≤- ⎪⎝⎭对()0,x ∈+∞恒成立,设()ln e g x x x =-,由()210eg x x x'=+>, 可得()g x 在()0,∞+上递增,且()0g e =,当0x →时,()g x →-∞;x →+∞,()g x →+∞, 作出()y g x =的图象,再设()2,02n h x m x x m ⎛⎫=-> ⎪⎝⎭,可得()h x 表示过,02n m ⎛⎫⎪⎝⎭,斜率为2m 的一条射线(不含端点), 要求nm 的最大值,且满足不等式恒成立,可得2n m的最大值, 由于点,02n m ⎛⎫⎪⎝⎭在x 轴上移动, 只需找到合适的0m >,且()ln e g x x x =-切于点,02n m ⎛⎫⎪⎝⎭,如图所示:此时2n e m =,即nm 的最大值为2e . 故选:D 【点睛】关键点点睛:本题考查不等式恒成立问题的解法,解题的关键是将问题转化为()ln e g x x x =-切于点,02n m ⎛⎫⎪⎝⎭,注意运用转化思想和数形结合思想,考查了导数的应用,求切线的斜率与单调性,考查了运算能力和推理能力.4.A解析:A 【分析】分析函数()f x 、()f x '的奇偶性,以及2f π⎛⎫' ⎪⎝⎭、()f π'的符号,利用排除法可得出合适的选项. 【详解】函数()cos f x x x =的定义域为R ,()()()cos cos f x x x x x f x -=--=-=-, 即函数()cos f x x x =为奇函数,()cos sin f x x x x '=-,函数()f x '的定义域为R ,()()()()cos sin cos sin f x x x x x x x f x ''-=-+-=-=,函数()f x '为偶函数,排除B 、C 选项;22f ππ⎛⎫'=- ⎪⎝⎭,()1f π'=-,则()02f f ππ⎛⎫<< ⎪⎝⎭''.对于D 选项,图中的偶函数为()f x ',由02f π⎛⎫'< ⎪⎝⎭,()0f π'<与题图不符,D 选项错误, 故选:A. 【点睛】思路点睛:函数图象的辨识可从以下方面入手: (1)从函数的定义域,判断图象的左右位置; (2)从函数的值域,判断图象的上下位置. (3)从函数的单调性,判断图象的变化趋势; (4)从函数的奇偶性,判断图象的对称性; (5)函数的特征点,排除不合要求的图象.5.B解析:B 【分析】利用体积相等可得出216r h ,再将圆柱表面积表示出来将216h r =代入求导即可得最值. 【详解】由题意可得圆柱和圆锥的体积相等,底面半径为4,高为3的圆锥为2143163ππ⨯⨯⨯=,底面半径为r ,高为h 的圆柱2r h π, 所以216r h ππ=,可得216r h ,即216h r =圆柱的表面积为:2222163222222S r rh r rr r rππππππ=+=+=+, 322324324r S r r r ππππ-'=-=, 令324320r S r ππ-'=>可得2r >,令324320r S r ππ-'=<可得02r <<,所以2r 时,表面积最小为23222242S πππ=⨯+=, 故选:B 【点睛】关键点点睛:本题解题的关键是利用体积相等得出h 和r 的关系,再将圆柱表面积用r 表示利用导数求最值.6.C解析:C 【分析】不等式()0f x ≤恒成立等价于ln xa x ≥在[)1,+∞上恒成立,则maxln x a x ⎛⎫≥ ⎪⎝⎭,运用导数求出函数ln xx在[)1,+∞上的最大值. 【详解】解:当[)1+x ∈∞,时,不等式()0f x ≤恒成立等价于ln xa x≥在[)1,+∞上恒成立, 令ln ()xg x x=,则21ln ()x g x x -'=当0x e <<时,()0g x '>;当x e >时,()0g x '<;所以max 1()()g x g e e==,所以1a e ≥故选:C. 【点睛】方法点睛:已知不等式恒成立求参数值(取值范围)问题常用的方法: (1)函数法:讨论参数范围,借助函数单调性求解;(2)分离参数法:先将参数分离,转化成求函数的值域或最值问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.7.B解析:B 【分析】由函数21ln 22y x a x x =--在1,2⎡⎫+∞⎪⎢⎣⎭上单调递增,知'0y ≥在1,2⎡⎫+∞⎪⎢⎣⎭上恒成立,分离参数,求最值得答案. 【详解】 因为函数21ln 22y x a x x =--在1,2⎡⎫+∞⎪⎢⎣⎭上单调递增, 所以22'20a x x ay x x x--=--=≥在1,2⎡⎫+∞⎪⎢⎣⎭上恒成立,所以222(1)1a x x x ≤-=--在1,2⎡⎫+∞⎪⎢⎣⎭上恒成立,所以1a ≤-, 故选:B. 【点睛】方法点睛:该题考查的是有关根据函数在给定区间上单调增求你参数的取值范围的问题,解题方法如下:(1)利用函数在给定区间上单调递增,得到其导数大于等于零在给定区间上恒成立; (2)求导;(3)分离参数,求最小值,得结果.8.B解析:B 【分析】 将不等式化为()()111ln x x k x +++>,令()()()111ln x g x xx ++=+,求出导函数,利用导数判断函数的单调性,从而可得()02,3x ∃∈使()00g x '=,进而可得()()001()g x x x g ≥=+,即求.【详解】()()()1ln 10x f x x x ++=>, ()1k f x x ∴>+可化为()111ln x k x x ++>+ 即()()111ln x x k x+++>, 令()()()111ln x g x xx ++=+,则()()()()21ln 11111x x x x ln x g x x +++---++⎡⎤⎣⎦'= ()211x ln x x--+=令()()11h x x ln x =--+, 则()111h x x '=-+,()0,x ∈+∞时, ()0h x '>,()g x '∴在()0,∞+单调递增.又()()1ln 32ln 420,30,49g g --''=<=> ()02,3x ∃∈使()00g x '=,即()0011ln x x +=-.当()00,x x ∈时,()()0,g x g x '<单调递减, 当0(,)x x ∈+∞时,()()0,g x g x '>单调递增,()()000001ln 1))1(()(1x x g x x x x g +∴≥==+++, ()02,3x ∈,()013,4x +∴∈,∴正整数k 的最大值为3.故选:B. 【点睛】关键点点睛:本题考查了导数研究不等式恒成立问题,解题的关键根据函数的单调性确定存在()02,3x ∈,使得()00g x '=,考查了分离参数法求范围.9.D解析:D 【分析】根据题意,令()()221,02ln 2,0x x f x x g x x x a x x ⎧<⎪⎪⋅==⎨⎪++>⎪⎩,得到函数()()2f xg x x =与直线2y =共有三个不同的交点;根据导数的方法,分别判断0x <和0x >时,函数的单调性,以及最值,结合题中条件,即可得出结果. 【详解】因为()()22,02ln ,0xx f x a x x x x -⎧<⎪=⎨++>⎪⎩,令()()221,02ln 2,0x x f x x g x x x a x x ⎧<⎪⎪⋅==⎨⎪++>⎪⎩,由题意,函数()()2f x g x x=与直线2y =共有三个不同的交点; 当0x <时,()212x g x x =⋅,则()()()()222232222ln 222ln 22222x x x x x x x x xx g x xx x '-⋅⋅+⋅+'==-=-⋅⋅⋅, 由()3ln 2202x x g x x +'=-=⋅解得222log ln 2x e =-=-; 所以()2,2log x e ∈-∞-时,()0g x '<,即函数()212x g x x =⋅单调递减; ()22log ,0x e ∈-时,()0g x '>,即函数()212x g x x=⋅单调递增; 所以()()()()222222min 2log 2212log 2422log 4log ee e g x g e e e -=-==<<⋅-,又2121122122g -⎛⎫-==> ⎪⎝⎭⎛⎫⋅- ⎪⎝⎭,()()271128724927g --==>⋅-, 所以()212x g x x=⋅与直线2y =有且仅有两个不同的交点; 当0x >时,()ln 2xg x a x =++,则()21ln x g x x -'=, 由()21ln 0xg x x-'==得x e =, 所以当()0,x e ∈时,()0g x '>,则函数()ln 2xg x a x=++单调递增; 当(),x e ∈+∞时,()0g x '<,则函数()ln 2xg x a x=++单调递减; 所以()()max 12g x g e a e==++, 又当1≥x 时,()ln 22xg x a a x=++≥+;当01x <<时,()2g x a <+; 当x e ≥时,()ln 22xg x a a x=++>+, 所以为使()ln 2xg x a x=++与直线2y =只有一个交点, 只需122a e ++=或22a +≥,即1a e=-或0a ≥. 故选:D.【点睛】本题主要考查由方程根的个数求参数,转化为函数交点个数问题求解即可,属于常考题型.10.C解析:C 【分析】先设切点写出曲线的切线方程,得出a 、b 的值,再利用构造函数利用导数求+a b 的最大值即可. 【详解】解:由题得()1x f x e '=-,设切点(t ,())f t ,则()t t f t e =-,()1tf t e '=-;则切线方程为:()(1)()t ty e t e x t --=--, 即(1)(1)tty e x e t =-+-,又因为y ax b =+, 所以1t a e =-,(1)tb e t =-, 则12t t a b e te +=-+-,令()12ttg t e te =-+-,则()(1)tg t t e '=-,则有1t >,()0g t '<;1t <,()0g t '>,即()g t 在(),1-∞上递增,在()1,+∞上递减, 所以1t =时,()g t 取最大值(1)121g e e e =-+-=-, 即+a b 的最大值为1e -. 故选:C. 【点睛】本题考查了利用导数求曲线的切线方程和研究函数的最值,属于中档题.11.A解析:A 【解析】 设()()22xf x F x e+=,则()()()224xf x f x F x e'--'=,∵f (x )−2f ′(x )−4>0,∴F ′(x )>0,即函数F (x )在定义域上单调递增, ∵f (0)=−1,∴F (0)=1,∴不等式f (x )+2>e 2x 等价为不等式()221e xf x +>等价为F (x )>F (0),解得x >0,故不等式的解集为(0,+∞), 本题选择A 选项.12.B解析:B 【分析】先对函数求导,可得当10x -<<时,()0f x '<;当0x >时,()0f x '>,从而得min ()(0)1f x f a ==--,而x →+∞时,()f x →+∞,所以要函数()(1)x f x x e a =--在(1,)-+∞上只有一个零点,只要满足10a --=或20a e--,从而可求出a 的取值范围 【详解】()x f x xe '=,当10x -<<时,()0f x '<;当0x >时,()0f x '>.从而min ()(0)1f x f a ==--,又2(1)f a e-=--,且x →+∞时,()f x →+∞, ∴10a --=或20a e --, 即1a =-或2a e-. 故选:B 【点睛】此题考查由导数解决函数零点问题,考查转化思想和计算能力,属于中档题二、填空题13.【分析】根据不等式恒成立得到在上恒成立令函数对其求导判定其在区间上的单调性得到在上恒成立再令利用导数的方法求出其最大值即可得出结果【详解】由在上恒成立得:在上恒成立易知当时令函数则在上恒成立则单调递 解析:[,0)e -【分析】根据不等式恒成立,得到ln ln a a x x x x e e ---≥-在[2,)x ∈+∞上恒成立,令函数()ln (01)g t t t t =-<<,对其求导,判定其在区间[2,)+∞上的单调性,得到ln x a x≥-在[2,)x ∈+∞上恒成立,再令()(2)ln xF x x x=-≥,利用导数的方法求出其最大值,即可得出结果. 【详解】由()0f x ≥在[2,)x ∈+∞上恒成立,得:ln ln a a x x x x e e ---≥-在[2,)x ∈+∞上恒成立,易知当[2,)x ∈+∞,0a <时,01a x <<,01x e -<<,令函数()ln (01)g t t t t =-<<,则1()10g t t'=->在()0,1t ∈上恒成立,则()g t 单调递增,故有a x x e -≥,则log ln xx xa ex-≥=-在[2,)x ∈+∞上恒成立, 令()(2)ln x F x x x=-≥,则21ln ()(ln )x F x x '-=,由()0F x '=得x e =,所以()2x e ∈,时,()0F x '>,则()F x 单调递增;,)[x e ∈+∞时,()0F x '<,则()F x 单调递减;故max ()()F x F e e ==-,则a e ≥-,所以0e a -≤<. 故答案为:[,0)e -. 【点睛】 方法点睛:由不等式恒成立(或能成立)求参数时,一般可对不等式变形,分离参数,根据分离参数后的结果,构造函数,由导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式,直接构成函数,根据导数的方法,利用分类讨论求函数的最值,即可得出结果.14.①②④【分析】求出导数代入-2可得判断①;利用函数的单调性求出极值可判断②④;分别求函数等于零的根可判断③【详解】x≤0时f(x)=2xe xf′(x)=2(1+x )ex 故f′(﹣2)=①正确;且f(解析:①②④ 【分析】求出导数代入-2可得判断①;利用函数的单调性求出极值可判断②④;分别求函数等于零的根可判断③. 【详解】x ≤0时,f (x )=2xe x ,f ′(x )=2(1+x )e x ,故f ′(﹣2)=22e-,①正确; 且f (x )在(﹣∞,﹣1)上单调递减,在(﹣1,0)上单调递增,故x ≤0时,f (x )有最小值f (﹣1)=2e-, x >0时,f (x )=2122x x -+在(0,1)上单调递减,在(1,+∞)上单调递增,故x >0时,f (x )有最小值f (1)=122e->- 故f (x )有最小值2e-,②④正确;令20x x e ⋅=得0x =,令21202x x -+=得22x =,故该函数图象与x 轴有3个交点,③错误; 故答案为:①②④ 【点睛】本题考查导数的几何意义,考查利用导数判断函数的单调性、求函数的最值一定注意定义域.15.【分析】令得构造函数并求值域可得答案【详解】由则令因为在上都递减所以在上是单调递减函数且可得故答案为:【点睛】方法点睛:本题考查由函数零点求参数问题解答时要先将函数的零点问题转化为方程有根的问题进而解析:21e a -<<【分析】 令0f x 得222ln a x x =--,构造函数2()22ln (0)g x x x x =-->并求值域可得答案. 【详解】由()22ln 20f x x x a =++-=,则222ln a x x =--,令2()22ln (0)g x x x x =-->,因为222ln ,y x y x =-=-在()1,e 上都递减,所以()g x 在()1,e 上是单调递减函数,且()()(1)g e g x g <<, 可得21e a -<<. 故答案为:21e a -<<. 【点睛】方法点睛:本题考查由函数零点求参数问题,解答时要先将函数的零点问题转化为方程有根的问题,进而分离参数,再运用函数思想将问题转化为研究函数图象的性质和最大最小值的问题,考查了分析问题解决问题的能力.16.【分析】当时证明出由题意可得出可得出结合函数的单调性可求得实数的取值范围【详解】当时先证明出构造函数则则函数在区间上单调递增所以所以函数在区间上单调递增当时所以由可得所以当时即令则所以函数在区间上单解析:11,e e ⎡⎤+⎢⎥⎣⎦【分析】当[]1,2x ∈时,证明出11xx e x e +>-,由题意可得出11xxx a e e-≤≤+,可得出()max min11xx x a e e ⎛⎫-≤≤+⎪⎝⎭,结合函数的单调性可求得实数a 的取值范围. 【详解】当[]1,2x ∈时,先证明出11xx e x e +>-,构造函数()11xxf x e x e =+-+, 则()11xx f x e e'=--,则函数()f x '在区间[]1,2上单调递增, 所以,()()1110f x f e e''≥=-->,所以,函数()f x 在区间[]1,2上单调递增, 当[]1,2x ∈时,()()110f x f e e ≥=+>,所以,11x x e x e+>-. 由()110xx e a x a e ⎛⎫+---≤ ⎪⎝⎭,可得11xx x a e e -≤≤+,所以,()max min11xx x a e e ⎛⎫-≤≤+⎪⎝⎭. 当[]1,2x ∈时,011x ≤-≤,即()max 11x -=, 令()1xx g x e e =+,则()10xxg x e e'=->,所以,函数()g x 在区间[]1,2上单调递增, 当[]1,2x ∈时,()()min 11g x g e e ==+,所以,11a e e≤≤+. 因此,实数a 的取值范围是11,e e⎡⎤+⎢⎥⎣⎦. 故答案为:11,e e ⎡⎤+⎢⎥⎣⎦. 【点睛】结论点睛:利用参变量分离法求解函数不等式恒(能)成立,可根据以下原则进行求解: (1)x D ∀∈,()()min m f x m f x ≤⇔≤; (2)x D ∀∈,()()max m f x m f x ≥⇔≥; (3)x D ∃∈,()()max m f x m f x ≤⇔≤; (4)x D ∃∈,()()min m f x m f x ≥⇔≥.17.【分析】令问题转化为根据函数的单调性求出不等式的解集即可【详解】因为所以令则所以为奇函数又因为当时所以在上单调递减即在上单调递减而不等式所以所以故答案为:【点睛】构造辅助函数是高中数学中一种常用的方解析:5,2⎛⎤-∞ ⎥⎝⎦ 【分析】令()()2g x f x x =-,问题转化为()()5g x x g -≥,根据函数的单调性求出不等式的解集即可. 【详解】因为()()22f x f x x -+=,所以()()()220f x x f x x ---+-=,令()()2g x f x x =-,则()()0g x g x -+=,所以()g x 为奇函数.又因为当0x ≤时,()()20g x f x x ''=-<, 所以()g x 在(],0-∞上单调递减, 即()g x 在R 上单调递减.而不等式()()()()()()()2225510555f x f x x f x x f x x g x g x +≥-+⇔-≥---⇔≥-,所以5x x ≤-,所以52x ≤. 故答案为:5,2⎛⎤-∞ ⎥⎝⎦【点睛】构造辅助函数是高中数学中一种常用的方法,解题中若遇到有关不等式、方程及最值之类问题,设法建立起目标函数,并确定变量的限制条件,通过研究函数的单调性、最值等问题,常可使问题变得明了,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点也是难点就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.18.2【分析】令利用可得在单调递增不等式恒成立等价于即当时分离参数可得可求出正整数的最大值为2再检验当时对于不等式恒成立即可求解【详解】因为定义在上的函数关于轴对称所以函数为上的偶函数令则因为当时即所以解析:2 【分析】令()()g x xf x x =-,利用()()1xf x f x '>-可得()g x 在[)0,+∞单调递增,不等式()()0x x x e f e e ax axf ax -+->恒成立等价于()()x g e g ax >,即e x ax >,当0x >时,分离参数可得()xe a h x x<=,可求出正整数a 的最大值为2,再检验当2a =时,对于0x <,不等式恒成立,即可求解. 【详解】因为定义在R 上的函数()f x 关于y 轴对称, 所以函数()f x 为R 上的偶函数,令()()g x xf x x =-,则()()()1g x f x xf x ''=+-,因为当0x ≥时,()()1xf x f x '>-,即()()()10g x f x xf x ''=+->, 所以()g x 在[)0,+∞单调递增, 不等式()()0xx xe f e eax axf ax -+->恒成立,即()()xxxe f eeaxf ax ax ->-,即()()x g e g ax >,所以e x ax >,当0x >时,()xe a h x x <=,则()()21x e x h x x-'=, 可得()h x 在()0,1单调递减,在()1,+∞单调递增, 所以()()min 1h x h e ==, 所以a e <,此时最大的正整数a 为2,2a =对于0x <时,e x ax >恒成立, 综上所述:正整数a 的最大值为2, 故答案为:2 【点睛】关键点点睛:本题的关键点是构造函数()()g x xf x x =-,利用导数判断出()g x 在[)0,+∞单调递增,不等式恒成立即()()x g e g ax >,利用单调性可得e x ax >,再分类参数求最值.19.【分析】求导后利用导数的正负求得函数的单调区间利用单调性求得函数的最大值【详解】由题意知是周期为的偶函数当时得的减区间为当时的增区间为所以当时取最大值故答案为:【点睛】本题主要考查利用导数求函数的最解析:2【分析】求导后利用导数的正负求得函数的单调区间,利用单调性求得函数的最大值. 【详解】2()2sin 2cos22sin 2(12sin )2(2sin 1)(sin 1)f x x x x x x x '=-+=-+-=--+由题意知()f x 是周期为2π的偶函数, 当()0f x '≤时,得()f x 的减区间为52,2()66k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦, 当()0f x '≥时,()f x 的增区间为5132,2()66Z k k k ππππ⎡⎤++⎢⎥∈⎣⎦,所以当2()6x k k Z ππ=+∈时,()f x 取最大值2.【点睛】本题主要考查利用导数求函数的最值,意在考查学生的数学运算的学科素养,属中档题.20.【分析】由函数的解析式分类讨论利用分离参数结合导数和基本不等式即可求解【详解】由题意函数(1)当时由可得即设可得当时单调递减;当时单调递增所以即;(2)当时由可得当时显然成立;当时可得因为当且仅当时 解析:[4,2]e -【分析】由函数的解析式,分类讨论,利用分离参数,结合导数和基本不等式,即可求解. 【详解】由题意,函数22,0,()4,0,x e x f x x x ⎧>=⎨+≤⎩,(1)当0x >时,由()f x mx ≥,可得2xe mx ≥,即2xe m x≤,设2()x e g x x =,可得22(21)()x e x g x x-'=, 当102x <<时,()0g x '<,()g x 单调递减;当12x >时,()0g x '>,()g x 单调递增, 所以min 1()22g x g e ⎛⎫==⎪⎝⎭,即2m e ≤; (2)当0x ≤时,由()f x mx ≥,可得24x mx +≥, 当0x =时显然成立; 当0x <时,可得4m x x ≥+,因为444x x x x ⎛⎫+=--+≤- ⎪-⎝⎭,当且仅当1x =-时取等号, 所以4m ≥-.综上可得,实数m 的取值范围是[4,2]e -, 故答案为:[4,2]e -. 【点睛】本题主要考查了函数的恒成立问题的求解,以及分段函数的性质的应用,其中解答中根据分段函数的分段条件,合理分类讨论,利用分离参数,结合导数和基本不等式求解是解答的关键,着重考查了转化思想,分类讨论思想,以及推理与运算能力.三、解答题21.(1)函数()f x 的单调递增区间为(1,)+∞,递减区间为(0,1);(2)(1,e e -⎤-∞-⎦.【分析】(1)解不等式()0f x '>与()0f x '<即可得单调区间; (2)先分离参数再利用导数研究函数最值即可得结果. 【详解】(1)依题意11(0,),()1x x f x x x'-∈+∞=-=, 令()0f x '>,解得1x >,令()0f x '<,解得01x <<,故函数()f x 的单调递增区间为(1,)+∞,递减区间为(0,1);(2)因为0x >,故不等式化为(ln )x x x e e m x --⋅,令(ln )()xx x e e h x x--⋅=,故min [()]m h x ,因为2(1)(ln 1)()xx x x e h x e x ---+'=,令11()ln 1,()1x x x x e x x xϕϕ'-=--+=-=,由(1)可知,当(0,1)x ∈时,()0x ϕ'>,当(1,)x ∈+∞时,()0x ϕ'<,又221130,(1)20,()0e e e e e ϕϕϕ⎛⎫=--<=->=⎪⎝⎭, 所以()ϕx 在(0,1)上存在唯一零点0x ,在(1,)+∞上存在唯一零点x e =,当00x x <<时,()0()0x h x ϕ'<<,,当01x x <<时,()0()0x h x ϕ'>>,,当1x e <<时,()0()0x h x ϕ'><,,当x e >时,()0,()0x h x ϕ'<>,所以函数()h x 在()00,x 和(1,)e 上为减函数,在()0,1x 和(,)e +∞上为增函数, 所以min [()]h x 是()0h x 与()h e 中的较小者,而1()e h e e -=-,因为()000ln 10x x x e ϕ=--+=,故010x e x e +-=, 故()()000100ln x x e x x e e h x ee x x ---=⋅=-=-,故1e m e --,综上所述,实数m 的取值范围为(1,e e -⎤-∞-⎦.【点晴】参变分离利用导数求解函数最值是解参数范围的关键.22.(1)1230x y --=;(2)单调递减区间为(,1)-∞-和(3,)+∞,单调递增区间为()1,3-.【分析】(1)求出导函数()'f x ,然后计算导数得斜率,从而得切线方程;(2)由()0f x '>得增区间,()0f x '<得减区间. 【详解】解:(1)∵32()392f x x x x =-++-,∴2()369f x x x '=-++, ∴()112f '=. 又∵()19f =,∴函数()y f x =的图象在点()()1,1f 处的切线方程为912(1)y x -=-, 即1230x y --=.(2)由(1),得2()3693(1)(3)f x x x x x '=-++=-+-,令()0f x '=,解得1x =-或3x =; 当()0f x '<时,1x <-或3x >;当()0f x '>时,13x .∴()f x 的单调递减区间为(,1)-∞-和(3,)+∞,单调递增区间为()1,3-.【点睛】关键点点睛:本题考查导数的几何意义,考查求函数的单调区间.解题方法是求出导函数()'f x ,计算0()f x '得切线斜率,由点斜式写出切线方程并整理成一般式.而求单调区间只要解不等式()0f x '>即得增区间,解不等式()0f x '<即得减区间.23.(1)()200cos 100,0,2S πθθθθ⎛⎫⎛⎫=+∈ ⎪ ⎪⎝⎭⎝⎭;(2)6πθ=. 【分析】(1)在直角三角形ABC 中,求出AC ,在扇形COB 中利用弧长公式求出弧BC 的长度,则可得函数()S θ;(2)利用导数可求得结果.【详解】(1)如图,连接,BC OC ,在直角三角形ABC 中,100,,AB BAC θ=∠=所以100cos ,AC θ=由于22,BOC BAC θ∠=∠=则弧BC 的长为250100,l r αθθ=⋅=⋅=()22100cos 100200cos 100,0,2S AC l πθθθθθθ⎛⎫⎛⎫∴=+=⨯+=+∈ ⎪ ⎪⎝⎭⎝⎭(2)由(1)可知()200sin 100S θθ'=-+, 令()0,S θ'= 得1sin 2θ=,因为(0,)2πθ∈所以6πθ=,当0,,()0,()6S S πθθθ'⎛⎫∈> ⎪⎝⎭单调递增, 当,,()0,()62S S ππθθθ'⎛⎫∈< ⎪⎝⎭单调递减, 所以当6πθ=时,使得绿化带总长度()S θ最大.【点睛】关键点点睛:仔细审题,注意题目中的关键词“两侧”和“一侧”是解题关键.24.(1)有1个零点;(2)(,)e +∞.【分析】(1)求导得到函数的单调性,再利用零点存在性定理得解;(2)分离参变量,不等式恒成立转化为求函数的最值得解.【详解】(1)当1a =-时,()1e x f x x =-, 则()110e xf x =+>', ∴()f x 在[)0,+∞上单调递增,又(0)10f =-<,1(1)10ef =->, 故0(0,1)x ∃∈,使得()00f x =,∴函数()f x 在区间[0,)+∞上有1个零点;(2)若()2f x >对任意的实数x 恒成立,即e (2)x a x >-恒成立,令()e (2)x g x x =-,则()e (1)x g x x '=-,令()0g x '>,得1x <;令()0g x '<,得1x >.∴()g x 在(,1)-∞上递增,在(1,)+∞上递减,∴max [()](1)e g x g ==,∴a 的取值范围为(e,)+∞.【点睛】方法点睛:不等式恒成立问题解决思路:一般参变量分离、转化为最值问题.25.(1)3211()8333f x x x x -=++;(2)极大值为(2)7f =,无极小值;最小值为1(0)3f =. 【分析】 (1)求出导数,根据题意有(1)123(2)440f a b f a b =++=⎧⎨=++=''⎩,解出,a b 代入解析式即可; (2)根据导数求出函数的单调区间,判定函数在区间[]0,3上的单调性,根据极值定义求出函数的极值,比较端点函数值即可解出最小值.【详解】解:(1)函数()f x 求导得2()2f x x ax b '=++因为函数()f x 在点()()1,1f 处的切线斜率为3,且2x =时()y f x =有极值所以(1)123(2)440f a b f a b =++=⎧⎨=++=''⎩解得38a b =-⎧⎨=⎩所以函数()f x 的解析式为3211()8333f x x x x -=++ (2)由(1)可知2()68(2)(4)f x x x x x '=-+=--所以当2x <或4x >时,()0,()f x f x '>单调递增;当24x <<时,()0f x '<,()f x 单调递减,则函数()f x 在[]0,3上有极大值为(2)7f =,无极小值 又因为119(0),(3),33f f == 所以(0)(3)f f < 则函数()f x 在[]0,3上的最小值为1(0)3f =. 【点睛】求函数的极值或极值点的步骤:(1)求导数()'f x ,不要忘记函数()f x 的定义域;(2)求方程()0f x '=的根;(3)检查在方程的根的左右两侧()'f x 的符号,确定极值点或函数的极值.26.(1)10x y +-=;(2)答案见解析.【分析】(1)求出()1f 和()1f '的值,结合点斜式可得出曲线()y f x =在点()()1,1f 处的切线方程;(2)求得()21tx g x x-'=,分0t ≤、01t <<、1t =三种情况讨论,由导数分析函数()g x 的单调性与极值,进而可得出实数t 在不同取值下函数()g x 零点的个数.【详解】(1)因为()11f x x =-,所以()21f x x'=-,所以()10f =,()11f '=-. 所以曲线()y f x =在点()()1,1f 处的切线方程是()1y x =--,即10x y +-=; (2)因为()()ln g x f x t x =+,所以()()1ln 10g x t x x x =+->, 所以()2211t tx g x x x x-'=-+=. ①当0t ≤时,()0g x '≤,所以()g x 在()0,∞+上单调递减.因为()10g =,所以()g x 有且仅有一个零点;②当01t <<时,令()0g x '>,得1x t>,令()0g x '<,得1x t <. 所以()g x 在10,t ⎛⎫ ⎪⎝⎭上单调递减,在1,t ⎛⎫+∞ ⎪⎝⎭上单调递增.因为()10g =,所以()g x 在10,t ⎛⎫ ⎪⎝⎭上有且仅有一个零点. 因为()110g g t ⎛⎫<= ⎪⎝⎭,即1ln 10t t t +-<,则111ln 1t t t <-<,所以,11t e t >, 则()1110t t g e e =>, 所以01,x t ⎛⎫∃∈+∞ ⎪⎝⎭,使得()00g x =,所以()g x 在1,t ⎛⎫+∞ ⎪⎝⎭上有且仅有一个零点. 所以当01t <<时,()g x 有两个零点;③当1t =时,()21x g x x-'=. 令()0g x '>,得1x >,令()0g x '<,得1x <.所以()g x 在()0,1上单调递减,在()1,+∞上单调递增.所以当1x =时,()g x 取得最小值,且()10g =,所以()g x 有且仅有一个零点. 综上所述,当0t ≤或1t =时,()g x 有且仅有一个零点;当01t <<时,()g x 有两个零点.【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用;(2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.。
浙江省2021届高考数学一轮复习第四章导数及其应用加强练四导数及其应用含解析

加强练(四) 导数及其应用一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f (x )=a ln x +x 在x =1处取到极值,则a 的值为( ) A.-1 B.-12C.0D.12解析 因为f (x )=a ln x +x ,所以f ′(x )=a x+1. 又因为f (x )在x =1处取到极植, 所以f ′(1)=a +1=0⇒a =-1. 经检验符合题意.故选A. 答案 A2.(2020·浙江新高考仿真卷二)已知函数g (x )=(x -1)f ′(x )的图象如图所示,则函数y =f (x )的图象有可能是( )解析 由函数g (x )=(x -1)f ′(x )的图象易得函数g (x )有两个零点,设其较大的零点为x 0.当x <1时,g (x )<0,x -1<0,则f ′(x )>0;当1<x <x 0时,g (x )>0,x -1>0,则f ′(x )>0;当x >x 0时,g (x )<0,x -1>0,则f ′(x )<0,所以函数f (x )在x =x 0左侧单调递增,在x =x 0右侧单调递减,故选C. 答案 C3.(2020·许昌、洛阳质检三)已知a >0,曲线f (x )=3x 2-4ax 与g (x )=2a 2ln x -b 有公共点,且在公共点处的切线相同,则实数b 的最小值为( ) A.0 B.-1e 2C.-2e2D.-4e2解析由f(x)=3x2-4ax,f′(x)=6x-4a,由g(x)=2a2ln x-b,g′(x)=2a2 x.设两曲线的公共点P(x0,y0),x0>0,因为两曲线在公共点处的切线相同,所以⎩⎪⎨⎪⎧6x0-4a=2a2x0,y0=3x20-4ax0,y0=2a2ln x0-b,由6x0-4a=2a2x0,x0=a,x0=-13a,又a>0,所以x0=a,消去y0得b=2a2ln a+a2,设b=h(a)=2a2ln a+a2,h′(a)=4a ln a+4a,令h′(a)=0,a=1e,又a>1e,h′(a)>0,0<a<1e时,h′(a)<0,所以a=1e是h(a)的极小值点,即b min=h⎝⎛⎭⎪⎫1e=-1e2.答案 B4.(2020·北京昌平区二模)已知函数f(x)是定义在R上的偶函数,且满足f(x)=⎩⎪⎨⎪⎧x2-x2(0≤x<1),x-1e x(x≥1),若函数F(x)=f(x)-m有6个零点,则实数m的取值范围是( )A.⎝⎛⎭⎪⎫-116,1e2B.⎝⎛⎭⎪⎫-116,0∪⎝⎛⎭⎪⎫0,1e2C.⎝⎛⎭⎪⎫0,1e2D.⎣⎢⎡⎭⎪⎫0,1e2解析函数F(x)=f(x)-m有6个零点,等价于函数y=f(x)与y=m有6个交点,当0≤x<1时,f(x)=x2-x2=⎝⎛⎭⎪⎫x-142-116,当x≥1时,f(x)=x-1e x,f′(x)=2-xe x,当x∈[1,2]时,f(x)递增,当x∈(2,+∞)时,f(x)递减,f(x)的极大值为f(2)=1e2,作出函数f(x)的图象如图,y =f (x )与y =m 的图象有6个交点,得0<m <1e2.答案 C5.(2020·温州适应性考试)已知实数a >0,b >0,a ≠1,且满足ln b =a -1a,则下列判断正确的是( ) A.a >b B.a <b C .log a b >1 D.log a b <1解析 由ln b =a -1a =a -1a 得lnb -a +1a =0,设f (x )=ln x -x +1x(x >0),则f ′(x )=1x -12x -12x x =-(x -1)22x x ,则函数f (x )=ln x -x +1x 在(0,+∞)上单调递减,且f (1)=0,所以当0<x <1时,ln x -x +1x >0,即ln x >x -1x;当x >1时,ln x -x +1x<0,即ln x <x -1x ,在平面直角坐标系内画出函数y =ln x 与y =x -1x的图象如图所示.由图易得若ln b =a -1a =a -1a,则0<b <a <1或1<a <b ,A ,B 错误;当a >1时,1<a <b ,函数y =log a x 为增函数,则log a b >log a a =1,当0<a <1时,0<b <a <1,函数y =log a x 为减函数,则log ab >log a a =1,C 正确,D 错误,故选C.答案 C6.(2020·浙江名校新高考研究联盟三联)已知a >b >0,则下列不等式正确的是( ) A.|ln a -b |>|ln b -a | B.|a -b |<|b -a | C.|ln a -b |<|ln b -a |D.|a -b |>|b -a |解析 因为|ln a -b |2-|ln b -a |2=(ln a -b -ln b +a )·(ln a -b +ln b -a ),构造函数f (x )=ln x +x ,则易知f (x )在(0,+∞)上单调递增,所以当a >b >0时,ln a +a >ln b+b ,所以ln a -b -ln b +a >0,由不等式ln x ≤x -1<x ,可得ln a -b +ln b -a <0,所以|ln a -b |2-|ln b -a |2<0,即|ln a -b |<|ln b -a |.同理,|a -b |2-|b -a |2=(a -b +b -a )(a -b -b +a ).因为a >b ,a >b ,所以a -b -b +a >0.构造函数f (x )=x -x ,则f ′(x )=12x-1,令f ′(x )=12x -1>0,得0<x <14,所以f (x )在⎝ ⎛⎭⎪⎫0,14上单调递增,在⎝ ⎛⎭⎪⎫14,+∞上单调递减.此时当a >b >0时,f (a ),f (b )大小不定,所以|a -b |、|b -a |大小不定,故选C. 答案 C7.(2019·天津卷)已知函数f (x )=⎩⎪⎨⎪⎧2x ,0≤x ≤1,1x,x >1.若关于x 的方程f (x )=-14x +a (a ∈R )恰有两个互异的实数解,则a 的取值范围为( )A.⎣⎢⎡⎦⎥⎤54,94B.⎝ ⎛⎦⎥⎤54,94C.⎝ ⎛⎦⎥⎤54,94∪{1} D.⎣⎢⎡⎦⎥⎤54,94∪{1} 解析 如图,分别画出两函数y =f (x )和y =-14x +a 的图象.(1)先研究当0≤x ≤1时,直线y =-14x +a 与y =2x 的图象只有一个交点的情况.当直线y =-14x +a 过点B (1,2)时,2=-14+a ,解得a =94.所以0≤a ≤94.(2)再研究当x >1时,直线y =-14x +a 与y =1x 的图象只有一个交点的情况:①相切时,由y ′=-1x 2=-14,得x =2,此时切点为⎝ ⎛⎭⎪⎫2,12,则a =1.②相交时,由图象可知直线y =-14x +a 从过点A 向右上方移动时与y =1x 的图象只有一个交点.过点A (1,1)时,1=-14+a ,解得a =54.所以a ≥54.结合图象可得,所求实数a 的取值范围为⎣⎢⎡⎦⎥⎤54,94∪{1}.故选D. 答案 D8.(2020·浙江名师预测卷二)已知函数f (x )=x 2+(x -1)·|x -a |,a ∈R ,x ≠a ,下列结论中正确的是( )A.存在实数a 使得f ′(x )=0有唯一解B.存在实数a 使得f ′(x )=0有两个解C.不存在实数a 使得f ′(x )=0无解D.不存在实数a 使得f ′(x )>0恒成立解析 f (x )=x 2+(x -1)|x -a |=⎩⎪⎨⎪⎧2x 2-(1+a )x +a ,x >a ,(1+a )x -a ,x <a ,当1+a 4≤a ,即a ≥13时,f (x )在R 上单调递增,∴f ′(x )>0恒成立,排除C ,D ;当-1<a <13时,f (x )在(-∞,a )上单调递增,在⎝ ⎛⎭⎪⎫a ,1+a 4上单调递减,在⎝ ⎛⎭⎪⎫1+a 4,+∞上单调递增,当且仅当x =1+a 4时,f ′(x )=0;当a <-1时,f (x )在⎝ ⎛⎭⎪⎫-∞,1+a 4上单调递减,在⎝ ⎛⎭⎪⎫1+a 4,+∞上单调递增,∴当且仅当x =1+a 4时,f ′(x )=0;当a =-1时,f (x )=⎩⎪⎨⎪⎧2x 2-1,x ≥-1,1,x <-1,∴f ′(x )=0有无数个解,综上,故选A. 答案 A9.(2020·广州综测一)已知函数f (x )=e |x |-ax 2,对任意x 1<0,x 2<0,都有(x 2-x 1)[f (x 2)-f (x 1)]<0,则实数a 的取值范围是( ) A.⎝⎛⎦⎥⎤-∞,e 2 B.⎝⎛⎦⎥⎤-∞,-e 2C.⎣⎢⎡⎦⎥⎤0,e 2D.⎣⎢⎡⎦⎥⎤-e 2,0 解析 因为对任意x 1<0,x 2<0,(x 2-x 1)[f (x 2)-f (x 1)]<0恒成立,所以f (x )在(-∞,0)上单调递减,即f (x )=e -x-ax 2在(-∞,0)上单调递减,故f ′(x )=-⎝ ⎛⎭⎪⎫1e x-2ax ≤0在(-∞,0)上恒成立,即-2ax ≤⎝ ⎛⎭⎪⎫1e x 在(-∞,0)上恒成立.因为⎝ ⎛⎭⎪⎫1e x>1,所以当a ≤0时上述不等式恒成立.当a >0时,若a =e 2,如图,作出函数y =-e x 对应的直线与y =⎝ ⎛⎭⎪⎫1e x 的图象,则两图象相切于点(-1,e),故当0<a ≤e 2时,-2ax ≤⎝ ⎛⎭⎪⎫1e x 在(-∞,0)上恒成立.故选A.答案 A10.(2020·宁波模拟)若关于x 的不等式⎝ ⎛⎭⎪⎫1x λx ≤127有正整数解,则实数λ的最小值为( )A.9B.8C.7D.6解析 由⎝ ⎛⎭⎪⎫1x λx ≤127,则两边取对数,得λx ln x ≥3ln 3存在正整数解,则λ>0,故ln x x ≥3ln 3λ.记函数f (x )=ln x x ,则由f ′(x )=1-ln xx2知函数f (x )在(0,e)上单调递增,在(e ,+∞)上单调递减,注意到2<e <3,故只需考虑f (2),f (3)的大小关系,因为f (2)=ln 22=f (4)<f (3),故f (3)=ln 33≥3ln 3λ,即λ≥9,故选A.答案 A二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)11.(2020·北京通州区三模)能够说明“在某个区间(a ,b )内,如果函数y =f (x )在这个区间内单调递增,那么f ′(x )>0恒成立”是假命题的一个函数是________(写出函数表达式和区间).解析 若f (x )=x 3,x ∈(-1,1), 易知f (x )=x 3在(-1,1)上恒增;但f ′(x )=3x 2,在x =0时f ′(x )=0,不满足f ′(x )>0恒成立;是假命题. 答案 f (x )=x 3,x ∈(-1,1)(答案不唯一) 12.设曲线y =x +1x -1在点(3,2)处的切线与直线ax +y +3=0垂直,则a =________,切线方程为________________. 解析 y ′=-2(x -1)2,所以曲线在(3,2)处的切线的斜率为-12,由题意知-a ×⎝ ⎛⎭⎪⎫-12=-1, 所以a =-2,切线方程为y -2=-12(x -3),即x +2y -7=0. 答案 -2 x +2y -7=013.若函数f (x )=ax 4-4ax 2+b (a >0,1≤x ≤2)的最大值为3,最小值为-5,则ab =________. 解析 令f ′(x )=4ax 3-8ax =4ax (x 2-2)=0, 解得x 1=0(舍去),x 2=2,x 3=-2(舍去). 又f (1)=a -4a +b =b -3a ,f (2)=16a -16a +b =b ,f (2)=b -4a ,所以⎩⎪⎨⎪⎧b -4a =-5,b =3.所以a =2,b =3,ab =6. 答案 614.(一题多解)在平面直角坐标系xOy 中,P 是曲线y =x +4x(x >0)上的一个动点,则点P 到直线x +y =0的距离的最小值是________;此时点P 的坐标为________. 解析 法一 由题意可设P ⎝⎛⎭⎪⎫x 0,x 0+4x(x 0>0), 则点P 到直线x +y =0的距离d =⎪⎪⎪⎪⎪⎪x 0+x 0+4x 02=⎪⎪⎪⎪⎪⎪2x 0+4x 02≥22x 0·4x 02=4,当且仅当2x 0=4x 0,即x 0=2时取等号, 此时y 0=2+42=32,即点P 的坐标为(2,32).法二 设P ⎝⎛⎭⎪⎫x 0,4x+x 0(x 0>0),则曲线在点P 处的切线的斜率为k =1-4x 20.令1-4x 20=-1,结合x 0>0得x 0=2,∴P (2,32),曲线y =x +4x(x >0)上的点P 到直线x +y =0的最短距离即为此时点P 到直线x +y =0的距离,故d min =|2+32|2=4.答案 4 (2,32)15.(2020·北京东城区期末)已知函数f (x )=ax e x -x 2-2x .(1)当a =1时,曲线y =f (x )在点(0,f (0))处的切线方程为________;(2)当x >0时,若曲线y =f (x )在直线y =-x 的上方,则实数a 的取值范围是________. 解析 (1)当a =1时,f (x )=x e x -x 2-2x ,其导数f ′(x )=e x(x +1)-2x -2,f ′(0)=-1. 又因为f (0)=0,所以曲线y =f (x )在点(0,f (0))处的切线方程为y =-x . (2)根据题意,当x >0时,“曲线y =f (x )在直线y =-x 的上方”等价于“ax e x -x 2-2x >-x 恒成立”, 又由x >0,则ax e x-x 2-2x >-x ⇒a e x-x -1>0⇒a >x +1ex,则原问题等价于a >x +1ex恒成立;设g (x )=x +1e x ,则g ′(x )=-xex , 又由x >0,则g ′(x )<0,则函数g (x )在区间(0,+∞)上递减, 又由g (0)=1e 0=1,则有x +1e x <1,若a >x +1ex恒成立,必有a ≥1,即a 的取值范围为[1,+∞). 答案 (1)y =-x (2)[1,+∞)16.已知函数F (x )=1-x x +k ln x (其中k <1e 且k ≠0),则F (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最大值为________,最小值为________.解析 ∵F (x )=1-x x +k ln x (x >0),∴F ′(x )=(1-x )′x -(1-x )x ′x 2+k x =kx -1x2. ①若k <0,在⎣⎢⎡⎦⎥⎤1e ,e 上,恒有k ⎝ ⎛⎭⎪⎫x -1k x 2<0,∴F (x )在⎣⎢⎡⎦⎥⎤1e ,e 上单调递减,F (x )min =F (e)=1-e e +k =1e+k -1,F (x )max =F ⎝ ⎛⎭⎪⎫1e=e -k -1.②k >0时,∵k <1e ,∴1k >e ,x -1k<0,∴k ⎝ ⎛⎭⎪⎫x -1k x 2<0,∴F (x )在⎣⎢⎡⎦⎥⎤1e ,e 上单调递减,∴F (x )min =F (e)=1-e e +k =1e +k -1,F (x )max =F ⎝ ⎛⎭⎪⎫1e =e -k -1.综上所述,当k ≠0且k <1e 时,F (x )max =e -k -1,F (x )min =1e +k -1.答案 e -k -1 1e+k -117.(2020·福州质检)已知函数f (x )=a ln(2x )-e 2xe 有且只有一个零点,则实数a 的取值范围是________.解析 由f (x )=a ln(2x )-e 2xe ,得f (x )=a ln 2x e +a -e 2xe .令t =2xe(t >0),则g (t )=a ln t +a -e t.当t =1e 时,g ⎝ ⎛⎭⎪⎫1e =-e 1e <0,所以t =1e 不是函数g (t )的零点;当t ≠1e 时,令g (t )=a ln t +a -e t=0,得a =e tln t +1,所以f (x )=a ln(2x )-e 2xe 有且只有一个零点,等价于直线y =a 与函数p (t )=e tln t +1(t >0且t ≠1e)的图象有且只有一个交点. p ′(t )=e t ⎝ ⎛⎭⎪⎫ln t +1-1t (ln t +1)2.令q (t )=ln t +1-1t (t >0且t ≠1e ),则q ′(t )=1t +1t 2>0,所以q (t )在⎝ ⎛⎭⎪⎫0,1e 和⎝ ⎛⎭⎪⎫1e ,+∞上单调递增,而ln 1e +1-11e=-e <0,q (1)=0,所以当t ∈⎝ ⎛⎭⎪⎫0,1e 时,p ′(t )<0,从而p (t )单调递减,且当t →0时,p (t )→0,t →1e 时,p (t )→-∞;当t ∈⎝ ⎛⎭⎪⎫1e ,1时,p ′(t )<0,从而p (t )单调递减,且t →1e 时,p (t )→+∞;当t ∈(1,+∞)时,p ′(t )>0,从而p (t )单调递增,且t →+∞时,p (t )→+∞, 又因为p (1)=e ,所以p (t )的图象如图所示. 直线y =a 与函数p (t )的图象的交点个数为1, 由图可知实数a 的取值范围是(-∞,0)∪{e}. 答案 (-∞,0)∪{e}三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤)18.(本小题满分14分)(2020·北京丰台区期末)设函数f (x )=a sin x -x cos x ,x ∈⎣⎢⎡⎦⎥⎤0,π2(1)当a =1时,求证:f (x )≥0;(2)如果f (x )≥0恒成立,求实数a 的最小值.(1)证明 因为a =1,所以f (x )=sin x -x cos x ,f ′(x )=x sin x ,当x ∈⎣⎢⎡⎦⎥⎤0,π2时,f ′(x )≥0恒成立,所以f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上单调递增,所以f (x )≥f (0)=0.(2)解 因为f (x )=a sin x -x cos x ,x ∈⎣⎢⎡⎦⎥⎤0,π2,所以f ′(x )=(a -1)cos x +x sin x .①当a =1时,由(1)知f (x )≥0对x ∈⎣⎢⎡⎦⎥⎤0,π2恒成立; ②当a >1时,因为x ∈⎣⎢⎡⎦⎥⎤0,π2,所以f ′(x )>0.因此f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上单调递增, 所以f (x )≥f (0)=0对x ∈⎣⎢⎡⎦⎥⎤0,π2恒成立;③当a <1时,令g (x )=f ′(x ),则g ′(x )=(2-a )sin x +x cos x ,因为x ∈⎣⎢⎡⎦⎥⎤0,π2,所以g ′(x )≥0恒成立,因此g (x )在区间⎣⎢⎡⎦⎥⎤0,π2上单调递增,且g (0)=a -1<0,g ⎝ ⎛⎭⎪⎫π2=π2>0,所以存在唯一x 0∈⎣⎢⎡⎦⎥⎤0,π2使得g (x 0)=0,即f ′(x 0)=0.所以任意x ∈(0,x 0)时,f ′(x )<0,所以f (x )在(0,x 0)上单调递减. 所以f (x )<f (0)=0,不合题意. 综上可知实数a 的最小值为1.19.(本小题满分15分)(2020·金丽衢十二校三联)已知函数f (x )=ln(2x +1)-kx (k >0). (1)若x =0时,函数f (x )取得一个极值,求实数k 的值;(2)在(1)的条件下,对任意n ∈N *,m >1,求证⎝ ⎛⎭⎪⎫1+1m ⎝ ⎛⎭⎪⎫1+1m 2…⎝ ⎛⎭⎪⎫1+1m n <e 1m -1(e 为自然对数的底数).(1)解 因为f (x )=ln(2x +1)-kx ⎝ ⎛⎭⎪⎫x >-12, 所以f ′(x )=22x +1-k ,由f ′(0)=0,得k =2.当k =2时,f ′(x )=-4x2x +1,它在x =0的两侧是异号的,所以k =2成立.(2)证明 由(1)进一步可以判断出f (0)是f (x )在⎝ ⎛⎭⎪⎫-12,+∞上的极大值,也是最大值,于是我们可以得到任意x >-12,ln(1+2x )≤2x , 所以任意x >-12,1+2x ≤e 2x . 于是⎝ ⎛⎭⎪⎫1+1m ⎝ ⎛⎭⎪⎫1+1m 2…⎝ ⎛⎭⎪⎫1+1m n ≤e 1m +1m 2+…+1m n =e 1m -1m n +11-1m <e 1m -1,即得证.20.(本小题满分15分)(2020·湖州适应性考试)已知函数f (x )=1-e -x x(x >0). (1)求函数f (x )的单调区间;(2)求证:f (x )>e -x 2(x >0). (1)解 已知函数f (x )=1-e -x x(x >0), 导函数为f ′(x )=1+x -e x x 2e x. 令h (x )=e x -x -1,则h ′(x )=e x -1,当x <0时,h ′(x )=e x -1<0;当x >0时,h ′(x )=e x -1>0,所以h (x )min =h (0)=0,即e x ≥x +1,当且仅当x =0时,等号成立.由已知x >0,得e x >x +1,所以f ′(x )=1+x -e x x 2e x<0, 所以函数f (x )的单调递减区间为(0,+∞),无单调递增区间.(2)证明 f (x )>e -x 2(x >0)等价于e -x +x e -x 2-1<0(x >0).令g (x )=e -x +x e -x 2-1,x >0, g ′(x )=-e -x +e -x 2+x ⎝ ⎛⎭⎪⎫-12e -x 2 =-e -x 2⎣⎢⎡⎦⎥⎤e -x 2-⎝ ⎛⎭⎪⎫-x 2+1, 由(1)易得e -x 2>-x 2+1,所以g ′(x )<0. 所以当x >0时,有g (x )<g (0)=0,即e -x +x e -x 2-1<0(x >0),故f (x )>e -x 2(x >0).21.(本小题满分15分)(2019·全国Ⅰ卷)已知函数f (x )=sin x -ln(1+x ),f ′(x )为f (x )的导数.证明:(1)f ′(x )在区间⎝⎛⎭⎪⎫-1,π2存在唯一极大值点; (2)f (x )有且仅有2个零点.证明 (1)设g (x )=f ′(x ),则g (x )=cos x -11+x ,g ′(x )=-sin x +1(1+x )2. 当x ∈⎝ ⎛⎭⎪⎫-1,π2时,g ′(x )单调递减,而g ′(0)>0,g ′⎝ ⎛⎭⎪⎫π2<0,可得g ′(x )在⎝⎛⎭⎪⎫-1,π2有唯一零点,设为α.则当x ∈(-1,α)时,g ′(x )>0;当x ∈⎝⎛⎭⎪⎫α,π2时,g ′(x )<0. 所以g (x )在(-1,α)单调递增,在⎝ ⎛⎭⎪⎫α,π2单调递减,故g (x )在⎝⎛⎭⎪⎫-1,π2存在唯一极大值点,即f ′(x )在⎝⎛⎭⎪⎫-1,π2存在唯一极大值点. (2)f (x )的定义域为(-1,+∞).①当x ∈(-1,0]时,由(1)知,f ′(x )在(-1,0)单调递增,而f ′(0)=0,所以当x ∈(-1,0)时,f ′(x )<0,故f (x )在(-1,0)单调递减,又f (0)=0,从而x =0是f (x )在(-1,0]的唯一零点.②当x ∈⎝ ⎛⎦⎥⎤0,π2时,由(1)知,f ′(x )在(0,α)单调递增,在⎝⎛⎭⎪⎫α,π2单调递减,而f ′(0)=0,f ′⎝ ⎛⎭⎪⎫π2<0,所以存在β∈⎝⎛⎭⎪⎫α,π2,使得f ′(β)=0,且当x ∈(0,β)时,f ′(x )>0;当x ∈⎝ ⎛⎭⎪⎫β,π2时,f ′(x )<0.故f (x )在(0,β)单调递增,在⎝ ⎛⎭⎪⎫β,π2单调递减.又f (0)=0,f ⎝ ⎛⎭⎪⎫π2=1-ln ⎝ ⎛⎭⎪⎫1+π2>0,所以当x ∈⎝ ⎛⎦⎥⎤0,π2时,f (x )>0.从而,f (x )在⎝ ⎛⎦⎥⎤0,π2上没有零点. ③当x ∈⎝ ⎛⎦⎥⎤π2,π时,f ′(x )<0,所以f (x )在⎝ ⎛⎭⎪⎫π2,π单调递减.而f ⎝ ⎛⎭⎪⎫π2>0,f (π)<0,所以f (x )在⎝ ⎛⎦⎥⎤π2,π有唯一零点. ④当x ∈(π,+∞)时,ln(x +1)>1.所以f (x )<0,从而f (x )在(π,+∞)没有零点.综上,f (x )有且仅有2个零点.22.(本小题满分15分)(2019·天津卷)设函数f (x )=e xcos x ,g (x )为f (x )的导函数.(1)求f (x )的单调区间; (2)当x ∈⎣⎢⎡⎦⎥⎤π4,π2时,证明f (x )+g (x )⎝ ⎛⎭⎪⎫π2-x ≥0; (3)设x n 为函数u (x )=f (x )-1在区间⎝⎛⎭⎪⎫2n π+π4,2n π+π2内的零点,其中n ∈N ,证明2n π+π2-x n <e -2n πsin x 0-cos x 0. (1)解 由已知,有f ′(x )=e x (cos x -sin x ).因此,当x ∈⎝⎛⎭⎪⎫2k π+π4,2k π+5π4(k ∈Z )时, 有sin x >cos x ,得f ′(x )<0,则f (x )单调递减;当x ∈⎝⎛⎭⎪⎫2k π-3π4,2k π+π4(k ∈Z )时,有sin x <cos x , 得f ′(x )>0,则f (x )单调递增.所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤2k π-3π4,2k π+π4(k ∈Z ), f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤2k π+π4,2k π+5π4(k ∈Z ). (2)证明 记h (x )=f (x )+g (x )⎝ ⎛⎭⎪⎫π2-x . 依题意及(1),有g (x )=e x (cos x -sin x ),从而g ′(x )=-2e x sin x .当x ∈⎝ ⎛⎭⎪⎫π4,π2时,g ′(x )<0, 故h ′(x )=f ′(x )+g ′(x )⎝ ⎛⎭⎪⎫π2-x +g (x )(-1) =g ′(x )⎝ ⎛⎭⎪⎫π2-x <0. 因此,h (x )在区间⎣⎢⎡⎦⎥⎤π4,π2上单调递减, 进而h (x )≥h ⎝ ⎛⎭⎪⎫π2=f ⎝ ⎛⎭⎪⎫π2=0. 所以当x ∈⎣⎢⎡⎦⎥⎤π4,π2时,f (x )+g (x )⎝ ⎛⎭⎪⎫π2-x ≥0. (3)证明 依题意,u (x n )=f (x n )-1=0,即e x n cos x n =1.记y n =x n -2n π,则y n ∈⎝ ⎛⎭⎪⎫π4,π2, 且f (y n )=e y n cos y n =e x n -2n πcos(x n -2n π)=e-2n π(n ∈N ). 由f (y n )=e -2n π≤1=f (y 0)及(1),得y n ≥y 0.由(2)知,当x ∈⎝ ⎛⎭⎪⎫π4,π2时,g ′(x )<0, 所以g (x )在⎣⎢⎡⎦⎥⎤π4,π2上为减函数, 因此g (y n )≤g (y 0)<g ⎝ ⎛⎭⎪⎫π4=0. 又由(2)知,f (y n )+g (y n )⎝ ⎛⎭⎪⎫π2-y n ≥0, 故π2-y n ≤-f (y n )g (y n )=-e -2n πg (y n )≤-e -2n πg (y 0)=e -2n πe y 0(sin y 0-cos y 0)<e -2n πsin x 0-cos x 0. 所以2n π+π2-x n <e -2n πsin x 0-cos x 0.。
高考数学一轮复习导数及其应用多选题测试试题及答案

高考数学一轮复习导数及其应用多选题测试试题及答案一、导数及其应用多选题1.已知函数()3sin f x x x ax =+-,则下列结论正确的是( )A .()f x 是奇函数B .当3a =-时,函数()f x 恰有两个零点C .若()f x 为增函数,则1a ≤D .当3a =时,函数()f x 恰有两个极值点【答案】ACD 【分析】利用函数奇偶性的定义可判断A 选项的正误;利用导数分析函数()f x 的单调性,可判断B 选项的正误;利用导数与函数单调性的关系可判断C 选项的正误;利用导数以及零点存在定理可判断D 选项的正误. 【详解】对于A 选项,函数()3sin f x x x ax =+-的定义域为R ,()()()()33sin sin f x x x ax x x ax f x -=-+-+=--+=-,函数()f x 为奇函数,A 选项正确;对于B 选项,当3a =-时,()3sin 3f x x x x =++,则()2cos 330f x x x '=++>,所以,函数()f x 在R 上为增函数,又()00f =,所以,函数()f x 有且只有一个零点,B 选项错误;对于C 选项,()2cos 3f x x x a '=+-,由于函数()f x 为增函数,则()0f x '≥对任意的x ∈R 恒成立,即23cos a x x ≤+. 令()23cos g x x x =+,则()6sin g x x x '=-,则()6cos 0g x x ''=->,所以,函数()g x '在R 上为增函数,当0x <时,()()00g x g ''<=,此时,函数()g x 为减函数; 当0x >时,()()00g x g ''>=,此时,函数()g x 为增函数. 所以,()()min 01g x g ==,1a ∴≤,C 选项正确;对于D 选项,当3a =时,()3sin 3f x x x x =+-,则()2cos 33f x x x '=+-.由B 选项可知,函数()f x '在(),0-∞上单调递减,在()0,∞+上单调递增,()()11cos10f f ''-==>,()020f '=-<,由零点存在定理可知,函数()f x '在()1,0-和()0,1上都存在一个零点, 因此,当3a =时,函数()f x 有两个极值点,D 选项正确. 故选:ACD. 【点睛】结论点睛:利用函数的单调性求参数,可按照以下原则进行:(1)函数()f x 在区间D 上单调递增()0f x '⇔≥在区间D 上恒成立; (2)函数()f x 在区间D 上单调递减()0f x '⇔≤在区间D 上恒成立; (3)函数()f x 在区间D 上不单调()f x '⇔在区间D 上存在极值点;(4)函数()f x 在区间D 上存在单调递增区间x D ⇔∃∈,使得()0f x '>成立; (5)函数()f x 在区间D 上存在单调递减区间x D ⇔∃∈,使得()0f x '<成立.2.对于定义在1D 上的函数()f x 和定义在2D 上的函数()g x ,若直线y kx b =+(),k b R ∈同时满足:①1x D ∀∈,()f x kx b ≤+,②2x D ∀∈,()g x kx b ≥+,则称直线y kx b =+为()f x 与()g x 的“隔离直线”.若()ln xf x x=,()1x g x e -=,则下列为()f x 与()g x 的隔离直线的是( )A .y x =B .12y x =-C .3ex y =D .1122y x =- 【答案】AB 【分析】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点,结合函数的图象和函数的单调性,以及直线的特征,逐项判定,即可求解. 【详解】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点, 由函数()ln x f x x =,可得()21ln xf x x-'=, 所以函数()f x 在()0,e 上单调递增,在(),e +∞上单调递减,因为()10f =,()11f '=,此时函数()f x 的点(1,0)处的切线方程为1y x =-, 且函数()f x 的图象在直线1y x =-的下方; 又由函数()1x g x e-=,可得()1e0x g x -'=>,()g x 单调递增,因为()()111g g '==,所以函数()g x 在点(1,1)处的切线方程为11y x -=-,即y x =, 此时函数()g x 的图象在直线y x =的上方,根据上述特征可以画出()y f x =和()y g x =的大致图象,如图所示,直线1y x =-和y x =分别是两条曲线的切线,这两条切线以及它们之间与直线y x =平行的直线都满足隔离直线的条件,所以A ,B 都符合;设过原点的直线与函数()y f x =相切于点00(,)P x y , 根据导数的几何意义,可得切线的斜率为021ln x k x -=,又由斜002000ln 0y x k x x -==-,可得002100ln 1ln x x x x -=,解得0x e =, 所以21ln 12()e k e e -==,可得切线方程为2x y e =, 又由直线3xy e=与曲()y f x =相交,故C 不符合; 由直线1122y x =-过点()1,0,斜率为12,曲线()y f x =在点()1,0处的切线斜率为1,明显不满足,排除D. 故选:AB.【点睛】对于函数的新定义试题:(1)认真审题,正确理解函数的新定义,合理转化;(2)根据隔离直线的定义,转化为函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方.3.若存在实常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”,已知函数()()2f x x R x =∈,()()10g x x x=<,()2eln h x x =(e 为自然对数的底数),则下列结论正确的是( ) A .()()()m x f x g x =-在32x ⎛⎫∈ ⎪⎝⎭内单调递增 B .()f x 和()g x 之间存在“隔离直线,且b 的最小值为4 C .()f x 和()g x 间存在“隔离直线”,且k 的取值范围是(]4,1- D .()f x 和()h x 之间存在唯一的“隔离直线”2e e y x =-【答案】AD 【分析】求出()()()m x f x g x =-的导数,检验在x ⎛⎫∈ ⎪⎝⎭内的导数符号,即可判断选项A ;选项B 、C 可设()f x 、()g x 的隔离直线为y kx b =+,2x kx b ≥+对一切实数x 都成立,即有10∆≤,又1kx b x≤+对一切0x <都成立,20∆≤,0k ≤,0b ≤,根据不等式的性质,求出k 、b 的范围,即可判断选项B 、C ;存在()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则隔离直线的方程为(y e k x -=,构造函数求出函数的导数,根据导数求出函数的最值.【详解】对于选项A :()()()21m x f x g x x x =-=-,()212m x x x'=+,当x ⎛⎫∈ ⎪⎝⎭时,()2120m x x x '=+>, 所以函数()()()m x f x g x =-在x ⎛⎫∈ ⎪⎝⎭内单调递增;故选项A 正确对于选项BC :设()f x 、()g x 的隔离直线为y kx b =+,则2x kx b ≥+对一切实数x 都成立,即有10∆≤,即240k b +≤,又1kx b x≤+对一切0x <都成立,则210kx bx +-≤,即 20∆≤,240b k +≤,0k ≤,0b ≤,即有24k b ≤-且24b k ≤-,421664k b k ≤≤-,可得40k -≤≤,同理可得:40b -≤≤,故选项B 不正确,故选项C 不正确;对于选项D :函数()f x 和()h x的图象在x =()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则隔离直线的方程为(y e k x -=,即y kx e =-,由()f x kx e ≥-,可得20x kx e -+≥对于x ∈R 恒成立,则0∆≤,只有k =y e =-,下面证明()h x e ≤-,令()2n ()l G x e h x e x e =--=--,()x G x x'=,当x =()0'=G x,当0x <<时,()0'<G x,当x >()0G x '>,则当x =()G x 取到极小值,极小值是0,也是最小值.所以()()0G x e h x =--≥,则()h x e ≤-当0x >时恒成立.所以()f x 和()g x之间存在唯一的“隔离直线”e y =-,故选项D 正确. 故选:AD 【点睛】本提以函数为载体,考查新定义,关键是对新定义的理解,考查函数的导数,利用导数求最值,属于难题.4.对于函数2ln ()xf x x =,下列说法正确的是( )A .()f x 在x =12eB .()f x 有两个不同的零点C .fff <<D .若()21f x k x <-在()0,∞+上恒成立,则2e k >【答案】ACD 【分析】求得函数的导数312ln ()-'=xf x x ,根据导数的符号,求得函数的单调区间和极值,可判定A 正确;根据函数的单调性和()10f =,且x >()0f x >,可判定B 不正确;由函数的单调性,得到f f >,再结合作差比较,得到f f >,可判定C 正确;分离参数得到()221ln 1x k f x x x+>+=在()0,∞+上恒成立,令()2ln 1x g x x +=,利用导数求得函数()g x 的单调性与最值,可判定D 正确. 【详解】由题意,函数2ln ()x f x x =,可得312ln ()(0)xf x x x -'=>,令()0f x '=,即312ln 0xx -=,解得x =当0x <<()0f x '>,函数()f x 在上单调递增;当x >()0f x '<,函数()f x 在)+∞上单调递减,所以当x =()f x 取得极大值,极大值为12f e=,所以A 正确; 由当1x =时,()10f =,因为()f x 在上单调递增,所以函数()f x 在上只有一个零点,当x >()0f x >,所以函数在)+∞上没有零点,综上可得函数在(0,)+∞只有一个零点,所以B 不正确;由函数()f x 在)+∞上单调递减,可得f f >,由于ln ln 2ln ,242f f πππ====,则2ln ln 2ln ln 22444f f ππππππ-=-=-,因为22ππ>,所以0f f ->,即f f >,所以ff f <<,所以C 正确;由()21f x k x<-在()0,∞+上恒成立,即()221ln 1x k f x x x +>+=在()0,∞+上恒成立, 设()2ln 1x g x x +=,则()32ln 1x g x x --'=, 令()0g x '=,即32ln 10x x --=,解得x =所以当0x<<()0g x '>,函数()g x 在上单调递增; 当x>()0g x '<,函数()g x 在)+∞上单调递减, 所以当x=()g x 取得最大值,最大值为22e eg e =-=, 所以2ek >,所以D 正确. 故选:ACD. 【点睛】本题主要考查导数在函数中的综合应用,以及恒成立问题的求解,着重考查了转化与化归思想、逻辑推理能力与计算能力,对于恒成立问题,通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;也可分离变量,构造新函数,直接把问题转化为函数的最值问题.5.已知函数()e sin xf x a x =+,则下列说法正确的是( )A .当1a =-时,()f x 在0,单调递增B .当1a =-时,()f x 在()()0,0f 处的切线为x 轴C .当1a =时,()f x 在()π,0-存在唯一极小值点0x ,且()010f x -<<D .对任意0a >,()f x 在()π,-+∞一定存在零点【答案】AC 【分析】结合函数的单调性、极值、最值及零点,分别对四个选项逐个分析,可选出答案. 【详解】对于A ,当1a =-时,()e sin xf x x =-,()e cos xf x x '=-,因为()0,x ∈+∞时,e 1,cos 1xx >≤,即0fx,所以()f x 在0,上单调递增,故A 正确;对于B ,当1a =-时,()e sin x f x x =-,()e cos xf x x '=-,则()00e sin01f =-=,()00e cos00f '=-=,即切点为0,1,切线斜率为0,故切线方程为1y =,故B 错误;对于C ,当1a =时,()e sin xf x x =+,()e cos xf x x '+=,()e sin xf x x '=-',当()π,0x ∈-时,sin 0x <,e 0x >,则()e sin 0xx f x -'=>'恒成立,即()e cos x f x x '+=在()π,0-上单调递增,又ππ22ππe cos e 220f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝⎭+>,3π3π443π3πe cos e 442f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝-⎭+,因为123π3π421e e 2e ---⎛⎫=<⎪⎭< ⎝,所以3π43πe 04f -⎛⎫'-= ⎪⎭<⎝,所以存在唯一03ππ,42x ⎛⎫∈-- ⎪⎝⎭,使得()00f x '=成立,所以()f x 在()0π,x -上单调递减,在()0,0x 上单调递增,即()f x 在()π,0-存在唯一极小值点0x ,由()000e cos 0xf x x +'==,可得()000000πe sin cos sin 4x f x x x x x ⎛⎫=+=-+=- ⎪⎝⎭,因为03ππ,42x ⎛⎫∈-- ⎪⎝⎭,所以0π3ππ,44x ⎛⎫-∈-- ⎪⎝⎭,则()00π4f x x ⎛⎫=- ⎪⎝⎭()1,0∈-,故C 正确;对于选项D ,()e sin xf x a x =+,()π,x ∈-+∞,令()e sin 0xf x a x =+=,得1sin ex xa -=, ()sin ex xg x =,()π,x ∈-+∞,则()πcos sin 4e e x xx x x g x ⎛⎫- ⎪-⎝⎭'==,令0g x ,得πsin 04x ⎛⎫-= ⎪⎝⎭,则ππ4x k =+()1,k k ≥-∈Z ,令0g x,得πsin 04x ⎛⎫-> ⎪⎝⎭,则π5π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递减, 令0g x,得πsin 04x ⎛⎫-< ⎪⎝⎭,则5π9π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递增, 所以5π2π4x k =+()1,k k ≥-∈Z 时,()g x 取得极小值,极小值为5π5π2π2π445π5π2π5π4s 42in si πe e 4n k k g k k ++⎛⎫ ⎪⎛⎫⎝⎭== ⎪⎝⎭++()1,k k ≥-∈Z , 在()g x 的极小值中,3π4sin 3π45π5π42π4eg g -⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝+⎭-最小,当3ππ,4x ⎛⎫∈--⎪⎝⎭时,()g x 单调递减,所以函数()g x的最小值为3π3π445πsin 3π144eg --⎛⎫-==- ⎪⎝⎭,当3π411a--<-时,即3π40a -<<时,函数()g x 与1=-y a无交点,即()f x 在()π,-+∞不存在零点,故D 错误.故选:AC. 【点睛】本题考查利用导数研究函数的极值、零点、最值,及切线方程的求法,考查学生的推理能力与计算求解能力,属于难题.6.已知函数()()()221x f x x e a x =-+-有两个零点,则a 的可能取值是( ) A .1- B .0C .1D .2【答案】CD 【分析】求出()f x 的导数,讨论a 的范围,结合函数的单调性和零点存在性定理可判断求出. 【详解】解:∵函数()()()221x f x x e a x =-+-, ∴()()()()()12112xxf x x e a x x e a '=-+-=-+,①若0a =,那么()()0202xf x x e x =⇔-=⇔=,函数()f x 只有唯一的零点2,不合题意; ②若0a >,那么20x e a +>恒成立, 当1x <时,()0f x '<,此时函数为减函数; 当1x >时,()0f x '>,此时函数为增函数; 此时当1x =时,函数()f x 取极小值e -,由()20f a =>,可得:函数()f x 在1x >存在一个零点; 当1x <时,x e e <,210x -<-<,∴()()()()()222121x f x x e a x x e a x =-+->-+-()()211a x e x e =-+--,令()()2110a x e x e -+--=的两根为1t ,2t ,且12t t <, 则当1x t <,或2x t >时,()()()2110f x a x e x e >-+-->, 故函数()f x 在1x <存在一个零点;即函数()f x 在R 上存在两个零点,满足题意; ③若02ea -<<,则()ln 2ln 1a e -<=, 当()ln 2x a <-时,()1ln 21ln 10x a e -<--<-=,()ln 2220a x e a e a -+<+=,即()()()120xf x x e a '=-+>恒成立,故()f x 单调递增,当()ln 21a x -<<时,10x -<,()ln 2220a x e a e a -+>+=, 即()()()120xf x x e a '=-+<恒成立,故()f x 单调递减,当1x >时,10x ->,()ln 2220a x e a e a -+>+=, 即()()(1)20xf x x e a '=-+>恒成立,故()f x 单调递增,故当()ln 2x a =-时,函数取极大值,由()()()()()2ln 2ln 222ln 21f a a a a a ⎡⎤⎡⎤-=---+--⎣⎦⎣⎦(){}2ln 2210a a ⎡⎤⎣⎦=--+<得:函数()f x 在R 上至多存在一个零点,不合题意;④若2ea =-,则()ln 21a -=, 当()1ln 2x a <=-时,10x -<,()ln 2220a x e a e a -+<+=, 即()()()120xf x x e a '=-+>恒成立,故()f x 单调递增,当1x >时,10x ->,()ln 2220a x e a e a -+>+=, 即()()()120xf x x e a '=-+>恒成立,故()f x 单调递增,故函数()f x 在R 上单调递增,函数()f x 在R 上至多存在一个零点,不合题意;⑤若2ea <-,则()ln 2ln 1a e ->=, 当1x <时,10x -<,()ln 2220a x e a e a -+<+=, 即()()()120xf x x e a '=-+>恒成立,故()f x 单调递增,当()1ln 2x a <<-时,10x ->,()ln 2220a x e a e a -+<+=, 即()()()120xf x x e a '=-+<恒成立,故()f x 单调递减,当()ln 2x a >-时,10x ->,()ln 2220a x e a e a -+>+=, 即()()()120xf x x e a '=-+>恒成立,故()f x 单调递增,故当1x =时,函数取极大值,由()10f e =-<得:函数()f x 在R 上至多存在一个零点,不合题意; 综上所述,a 的取值范围为()0,∞+, 故选:CD. 【点睛】本题考查利用导数研究函数的零点问题,属于较难题.7.函数()ln f x x x =、()()f x g x x'=,下列命题中正确的是( ).A .不等式()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭B .函数()f x 在()0,e 上单调递增,在(,)e +∞上单调递减C .若函数()()2F x f x ax =-有两个极值点,则()0,1a ∈D .若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立,则m 1≥ 【答案】AD 【分析】对A ,根据()ln f x x x =,得到()()ln 1f x x g x x x'+==,然后用导数画出其图象判断;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<判断;对C ,将函数()()2F x f x ax =-有两个极值点,()ln 120x a x+=+∞在,有两根判断;对D ,将问题转化为22111222ln ln 22m m x x x x x x ->-恒成立,再构造函数()2ln 2m g x x x x =-,用导数研究单调性.【详解】 对A ,因为()()()ln 1ln f x x f x x x g x x x'+===、, ()2ln x g x x-'=, 令()0g x '>,得()0,1x ∈,故()g x 在该区间上单调递增;令()0g x '<,得()1x ∈+∞,,故()g x 在该区间上单调递减. 又当1x >时,()0g x >,()10,11g g e ⎛⎫== ⎪⎝⎭,故()g x 的图象如下所示:数形结合可知,()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭,故正确; 对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<,所以函数()f x 在()0,e 上单调递减,在(,)e +∞上单调递增,错误;对C ,若函数()()2F x f x ax =-有两个极值点, 即()2ln F x x x ax =-有两个极值点,又()ln 21F x x ax '=-+, 要满足题意,则需()ln 2100x ax -+=+∞在,有两根, 也即()ln 120x a x+=+∞在,有两根,也即直线()2y a y g x ==与的图象有两个交点. 数形结合则021a <<,解得102a <<. 故要满足题意,则102a <<,故错误; 对D ,若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立, 即22111222ln ln 22m m x x x x x x ->-恒成立, 构造函数()2ln 2m g x x x x =-,()()12g x g x >,对任意的120x x >>恒成立, 故()g x ()0+∞,单调递增,则()ln 10g x mx x '=--≥()0+∞, 恒成立, 也即ln 1x m x+≤,在区间()0,∞+恒成立,则()max 1g x m =≤,故正确. 故选:AD.【点睛】 本题主要考查导数在函数图象和性质中的综合应用,还考查了数形结合的思想、转化化归思想和运算求解的能力,属于较难题.8.设函数()ln x f x x=,()ln g x x x =,下列命题,正确的是( ) A .函数()f x 在()0,e 上单调递增,在(),e +∞单调递减B .不等关系33e e ππππ<<<成立C .若120x x <<时,总有()()()22212122a x x g x g x ->-恒成立,则1a ≥ D .若函数()()2h x g x mx =-有两个极值点,则实数()0,1m ∈ 【答案】AC【分析】利用函数的单调性与导数的关系可判断A 选项的正误;由函数()f x 在区间(),e +∞上的单调性比较3π、e π的大小关系,可判断B 选项的正误;分析得出函数()()22s x g x ax =-在()0,∞+上为减函数,利用导数与函数单调性的关系求出a 的取值范围,可判断C 选项的正误;分析出方程1ln 2x m x +=在()0,∞+上有两个根,数形结合求出m 的取值范围,可判断D 选项的正误.【详解】对于A 选项,函数()ln x f x x =的定义域为()0,∞+,则()21ln x f x x-'=. 由()0f x '>,可得0x e <<,由()0f x '>,可得x e >.所以,函数()f x 在()0,e 上单调递增,在(),e +∞单调递减,A 选项正确;对于B 选项,由于函数()ln x f x x =在区间(),e +∞上单调递减,且4e π>>, 所以,()()4ff π>,即ln ln 44ππ>,又ln 41ln 213ln 22043236--=-=>, 所以,ln ln 4143ππ>>,整理可得3e ππ>,B 选项错误; 对于C 选项,若120x x <<时,总有()()()22212122a x x g x g x ->-恒成立, 可得()()22112222g x ax g x ax ->-,构造函数()()2222ln s x g x ax x x ax =-=-, 则()()12s x s x >,即函数()s x 为()0,∞+上的减函数,()()21ln 20s x x ax '=+-≤对任意的()0,x ∈+∞恒成立, 即1ln x a x+≥对任意的()0,x ∈+∞恒成立, 令()1ln x t x x +=,其中0x >,()2ln x t x x'=-. 当01x <<时,()0t x '>,此时函数()t x 单调递增;当1x >时,()0t x '<,此时函数()t x 单调递减. 所以,()()max 11t x t ==,1a ∴≥,C 选项正确;对于D 选项,()()22ln h x g x mx x x mx =-=-,则()1ln 2h x x mx '=+-, 由于函数()h x 有两个极值点,令()0h x '=,可得1ln 2x m x+=, 则函数2y m =与函数()t x 在区间()0,∞+上的图象有两个交点, 当1x e>时,()0t x >,如下图所示:当021m <<时,即当102m <<时,函数2y m =与函数()t x 在区间()0,∞+上的图象有两个交点.所以,实数m 的取值范围是10,2⎛⎫ ⎪⎝⎭,D 选项错误.故选:AC.【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用;(2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.。
2021届高考一轮专题重组卷第1部分专题4导数及其应用文含解析

专题四 导数及其应用本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷 (选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2019·全国卷Ⅱ)曲线y =2sinx +cosx 在点(π,-1)处的切线方程为( ) A .x -y -π-1=0 B .2x -y -2π-1=0 C .2x +y -2π+1=0 D .x +y -π+1=0答案 C解析 设y =f (x)=2sinx +cosx ,则f ′(x)=2cosx -sinx ,∴f′(π)=-2,∴曲线在点(π,-1)处的切线方程为y -(-1)=-2(x -π),即2x +y -2π+1=0.故选C.2.(2019·佛山模拟)若曲线y =e x在x =0处的切线,也是y =ln x +b 的切线,则b =( ) A .-1 B .1 C .2 D .e答案 C解析 y =e x的导数为y′=e x,曲线y =e x在x =0处的切线斜率为k =1,则曲线y =e x在x =0处的切线方程为y -1=x ,y =ln x +b 的导数为y′=1x ,设y =x +1和y =ln x +b 相切的切点为(m ,n),则1m =1,解得m =1,n =2,即有2=ln 1+b ,解得b =2.故选C.3.(2019·广东韶关调研)直线y =a 分别与曲线y =e x,y =ln x +1交于两点M ,N ,则|MN|的最小值为( )A .1B .1-ln 2C .ln 2D .1+ln 2答案 A解析 令e x=ln x +1=a>0,则x 1=ln a ,x 2=e a -1,从而|MN|=|x 1-x 2|=|ln a -ea -1|构造函数h(a)=ln a -ea -1,求导得h′(a)=1a-e a -1,解得极值点a =1.因此|MN|的最小值为|h(1)|=1.故选A.4.(2019·长沙模拟)满足f (x)=f′(x)的函数是( ) A .f (x)=3+x B .f (x)=-x C .f (x)=ln x D .f (x)=0答案 D解析 若f (x)=0,则f′(x)=0,从而有f (x)=f′(x).故选D. 5.(2019·成都二诊)函数y =x +1ex 的图象大致为( )答案 C解析 因为y =x +1e x ,所以y′=-xe x ,令y′>0,则x<0,令y′<0,则x>0,令y′=0,则x =0,所以函数y =x +1e x 在(-∞,0)上为增函数,在(0,+∞)上为减函数,且x =0是函数的极大值点,结合4个函数的图象,故选C.6.(2019·东北三省四市联考)设函数f (x)=e x(x 3-3x +3)-ae x-x(x≥-1),若不等式f (x)≤0有解,则实数a 的最小值为( )A.1e B .e C .1-1eD .e -1答案 C解析 ∵f (x)=e x (x 3-3x +3)-ae x -x≤0有解,∴a≥x 3-3x +3-x e x 有解.令g(x)=x 3-3x +3-x e x ,则g′(x)=3x 2-3+x -1e x =(x -1)⎝⎛⎭⎪⎫3x +3+1e x ,故当x ∈[-1,1)时,g′(x)<0,当x ∈(1,+∞)时,g′(x)>0,故g(x)在[-1,1)上单调递减,在(1,+∞)上单调递增,故g(x)min =g(1)=1-3+3-1e =1-1e ,∴a≥1-1e ,∴实数a 的最小值为1-1e.故选C.7.(2019·济南一中模拟)已知函数f (x)=-x 3+ax 2-x -1在(-∞,+∞)上是单调函数,则实数a 的取值范围是( )A .[-3,3]B .(-3,3)C .(-∞,-3)∪(3,+∞)D .(-∞,-3)答案 A解析 ∵函数f (x)=-x 3+ax 2-x -1的导函数为f′(x)=-3x 2+2ax -1,且函数f (x)在(-∞,+∞)上是单调函数,∴在(-∞,+∞)上f′(x)≤0恒成立,即-3x 2+2ax -1≤0恒成立,∴Δ=4a 2-12≤0,解得-3≤a≤3,∴实数a 的取值范围是[-3,3].故选A.8.(2019·南昌调研)已知函数f (x)是定义在R 上的偶函数,设函数f (x)的导函数为f′(x),若对任意的x>0都有2f (x)+xf′(x)>0恒成立,则( )A .4f (-2)<9f (3)B .4f (-2)>9f (3)C .2f (3)>3f (-2)D .3f (-3)<2f (-2) 答案 A解析 根据题意,令g(x)=x 2f (x),其导函数g′(x)=2xf (x)+x 2f′(x),又对任意的x>0都有2f (x)+xf′(x)>0恒成立,则当x>0时,有g′(x)=x[2f (x)+xf′(x)]>0恒成立,即函数g(x)在(0,+∞)上为增函数,又由函数f (x)是定义在R 上的偶函数,则f (-x)=f (x),则有g(-x)=(-x)2f (-x)=x 2f (x)=g(x),即函数g(x)也为偶函数,则有g(-2)=g(2),且g(2)<g(3),则有g(-2)<g(3),即有4f (-2)<9f (3).故选A.9.(2019·石家庄二中模拟)已知∀x ∈(0,+∞),不等式ln x +1≥m-n x (n>0)恒成立,则mn 的最大值是( )A .1B .-1C .eD .-e 答案 C解析 不等式ln x +1≥m-n x 可化为ln x +1-m +n x ≥0,令F (x)=ln x +1-m +nx (x>0),则F′(x)=1x -n x 2=x -n x 2,所以当x =n 时,F (x)min =ln n +2-m ,则ln n +2-m≥0⇒m≤2+ln n(n>0).所以mn ≤2+ln n n .令G(n)=2+ln n n ,则G′(n)=-1-ln n n 2,令G′(n)=0,可得n =1e ,故G(n)max =2-11e=e ,即m n ≤2+ln n n ≤e.所以m n的最大值为e.故选C. 10.(2019·安阳模拟)已知函数f (x)=x 33+x22与g(x)=6x +a 的图象有3个不同的交点,则a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤-223,272B.⎝ ⎛⎭⎪⎫-223,272C.⎝ ⎛⎦⎥⎤-272,223D.⎣⎢⎡⎦⎥⎤-272,223 答案 B解析 原问题等价于函数h(x)=x 33+x 22-6x 的图象与直线y =a 有三个不同的交点.h′(x)=x 2+x -6=(x -2)(x +3),当x ∈(-∞,-3)时,h′(x)>0,h(x)单调递增;当x ∈(-3,2)时,h′(x)<0,h(x)单调递减;当x ∈(2,+∞)时,h′(x)>0,h(x)单调递增.函数h(x)的图象如图所示.又h(-3)=272,h(2)=-223,数形结合可得a 的取值范围是⎝ ⎛⎭⎪⎫-223,272.故选B. 11.(2019·浙江高考)设a ,b ∈R ,函数f (x)=⎩⎪⎨⎪⎧x ,x<0,13x 3-12a +1x 2+ax ,x≥0.若函数y =f (x)-ax -b 恰有3个零点,则( )A .a<-1,b<0B .a<-1,b>0C .a>-1,b<0D .a>-1,b>0 答案 C解析 由题意,b =f (x)-ax =⎩⎪⎨⎪⎧1-a x ,x<0,13x 3-12a +1x 2,x≥0.设y =b ,g(x)=⎩⎪⎨⎪⎧1-a x ,x<0,13x 3-12a +1x 2,x≥0.即以上两个函数的图象恰有3个交点,根据选项进行讨论. ①当a<-1时,1-a>0,可知g(x)在(-∞,0)上单调递增;由g′(x)=x 2-(a +1)x =x[x -(a +1)](x≥0),a +1<0,可知g(x)在(0,+∞)上单调递增. 此时直线y =b 与g(x)的图象只有1个交点,不符合题意,故A ,B 排除. ②当a>-1,即a +1>0时, 因为g′(x)=x[x -(a +1)](x≥0), 所以当x≥0时,由g′(x)<0可得0<x<a +1,所以当x≥0时,g(x)在(0,a +1)上递减,g(x)在(a +1,+∞)上递增. 如图,y =b 与y =g(x)(x≥0)的图象至多有2个交点.当1-a>0,即-1<a<1时,由图象可得,若要y =g(x)与y =b 的图象有3个交点,必有b<0; 当1-a =0时,y =g(x)与y =b 的图象可以有1个、2个或无数个交点,但不存在有3个交点的情况,不符合题意,舍去;当1-a<0,即a>1时,y =g(x)与y =b 的图象可以有1个或2个交点,但不存在有3个交点的情况,不符合题意,舍去.综上,-1<a<1,b<0.故选C.12.(2019·拉萨中学月考)已知函数f (x)=ax 3-3x 2+1,若f (x)存在唯一的零点x 0,且x 0>0,则a 的取值范围是( )A .(2,+∞) B.(-∞,-2) C .(1,+∞) D.(-∞,-1) 答案 B解析 当a =0时,f (x)=-3x 2+1,令f (x)=0,解得x =±33,函数f (x)有两个零点,舍去.当a≠0时,f′(x)=3ax 2-6x =3ax ⎝ ⎛⎭⎪⎫x -2a ,令f′(x)=0,解得x =0或2a .①当a<0时,2a <0,当x<2a 或x>0时,f′(x)<0,此时函数f (x)单调递减;当2a <x<0时,f′(x)>0,此时函数f (x)单调递增.∴x =2a是函数f (x)的极小值点,x =0是函数f (x)的极大值点.∵函数f (x)=ax 3-3x 2+1存在唯一的零点x 0, 且x 0>0,则⎩⎪⎨⎪⎧2a <0,f ⎝ ⎛⎭⎪⎫2a >0,即⎩⎪⎨⎪⎧a<0,4a2<1,可得a<-2.②当a>0时,2a >0,当x>2a 或x<0时,f′(x)>0,此时函数f (x)单调递增;当0<x<2a时,f′(x)<0,此时函数f (x)单调递减.∴x =2a 是函数f (x)的极小值点,x =0是函数f (x)的极大值点.不满足函数f (x)=ax 3-3x 2+1存在唯一的零点x 0,且x 0>0,综上可得,实数a 的取值范围是(-∞,-2).故选B.第Ⅱ卷 (非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.(2019·泉州质检)若函数f (x)=xln x +a 的图象在点(1,f (1))处的切线过点(2,2),则a =________.答案 1解析 因为f′(x)=(xln x +a)′=ln x +1,所以f′(1)=ln 1+1=1,又f (1)=ln 1+a =a ,所以切点为(1,a),因此f (x)在点(1,f (1))处的切线方程为y =x -1+a ,又切线过点(2,2),所以2=2-1+a ,得a =1.14.(2019·江西九校联考)曲线y =x 2在点P(1,1)处的切线与直线l 平行且距离为5,则直线l 的方程为________.答案 2x -y +4=0或2x -y -6=0解析 曲线y =x 2在点P(1,1)处的切线为2x -y -1=0,直线l 和它平行,可设为y =2x -b ⇒2x -y -b =0,根据平行线间的距离公式得到|b -1|5=5⇒b =-4或6.代入化简得到方程为2x -y +4=0或2x-y -6=0.故答案为2x -y +4=0或2x -y -6=0.15.(2019·山西吕梁一模)定义在R 上的函数f (x)的导函数为f′(x),f (0)=0,若对任意x ∈R ,都有f (x)>f′(x)+1,则使得f (x)+e x>1成立的x 的取值范围为________.答案 (-∞,0) 解析 构造函数g(x)=fx -1e x,则g(0)=0-11=-1,对任意x ∈R ,都有f (x)>f′(x)+1,则g′(x)=f′x e x-[f x -1]e xe x 2=f′x +1-f xex<0. 则函数g(x)在R 上单调递减.由f (x)+e x >1化为f (x)-1>-e x,即f x -1ex>-1.所以g(x)=fx -1ex>g(0)=-1,结合g(x)的单调性,则x<0,故x 的取值范围为(-∞,0). 16.(2019·温州市高三2月高考适应性测试)已知f (x)=x 2-ax ,若对任意的a ∈R ,存在x 0∈[0,2],使得|f (x 0)|≥k 成立,则实数k 的最大值是________.答案 12-8 2解析 若存在x 0∈[0,2],使得|f (x 0)|≥k 成立, 则k≤|f (x 0)|max ,函数f (x)=x 2-ax =x(x -a), x ∈[0,2],其对称轴为x =a 2,①当a≤0时,f (x)在[0,2]上单调递增, 所以|f (x)|max =f (2)=4-2a , 所以k≤(4-2a)min =4, ②当a2≥2即a≥4时,f (x)在[0,2]上单调递减,f (0)=0, 所以|f (x)|max =|f (2)|=|4-2a|=2a -4, 所以k≤(2a-4)min =4,③当0<a<4时,函数f (x)在⎝ ⎛⎭⎪⎫0,a 2上单调递减,在⎝ ⎛⎭⎪⎫a 2,2上单调递增, f ⎝ ⎛⎭⎪⎫a 2=-a 24,f (2)=4-2a ,当2≤a<4时,4-2a≤0,所以此时|f (x)|max =⎪⎪⎪⎪⎪⎪-a 24=a24,所以k≤⎝ ⎛⎭⎪⎫a 24min =1, 当0<a<2时,4-2a>0,若⎪⎪⎪⎪⎪⎪-a 24≥|4-2a|,即a 24≥4-2a 时, 解得42-4≤a<2, 此时|f (x)|max =a24,所以k≤⎝ ⎛⎭⎪⎫a 24min =12-82, 当⎪⎪⎪⎪⎪⎪-a 24<|4-2a|,即a 24<4-2a 时, 解得0<a<42-4,此时|f (x)|max =4-2a ,所以k≤4-2a,4-2a ∈(12-82,4), 所以k≤12-82,因为12-82<1<4,且对任意的a ∈R 都成立, 所以k 的最大值为12-8 2.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)(2019·陕西省榆林市模拟)已知函数f (x)=x 2-x. (1)设g(x)=ln x -f (x)f′(x),求g(x)的最大值及相应的x 值;(2)对任意正数x 恒有f (x)+f ⎝ ⎛⎭⎪⎫1x ≥⎝ ⎛⎭⎪⎫x +1x ln m ,求m 的取值范围. 解 (1)∵f (x)=x 2-x ,∴f′(x)=2x -1,∴g(x)=ln x -f (x)f′(x)=ln x -(x 2-x)(2x -1)=ln x -2x 3+3x 2-x. 则g′(x)=1x-6x 2+6x -1=1-x6x 2+1x.∵g(x)的定义域为(0,+∞),∴6x 2+1x>0,①当0<x<1时,g′(x)>0;②当x =1时,g′(x)=0;③当x>1时,g′(x)<0. 因此g(x)在x ∈(0,1]上是增函数,在x ∈[1,+∞)上是减函数, 故当x =1时,g(x)取得最大值g(1)=0.(2)由(1)可知f (x)+f ⎝ ⎛⎭⎪⎫1x =x 2-x +1x 2-1x =⎝ ⎛⎭⎪⎫x +1x 2-2-⎝ ⎛⎭⎪⎫x +1x , 不等式f (x)+f ⎝ ⎛⎭⎪⎫1x ≥⎝ ⎛⎭⎪⎫x +1x ln m 可化为⎝ ⎛⎭⎪⎫x +1x 2-2-⎝ ⎛⎭⎪⎫x +1x ≥⎝ ⎛⎭⎪⎫x +1x ln m , ①因为x>0,所以x +1x ≥2(当且仅当x =1时取等号),设x +1x =s(s≥2),则①式可化为s 2-2-s≥sln m,即ln m≤s-2s-1(对s≥2恒成立),令h(s)=s -2s -1,此函数在[2,+∞)上是增函数,所以h(s)=s -2s -1的最小值为h(2)=0,于是l n m≤0,即0<m≤1.18.(本小题满分12分)(2019·全国卷Ⅰ)已知函数f (x)=2sinx -xcosx -x ,f′(x)为f (x)的导数.(1)证明:f′(x)在区间(0,π)存在唯一零点;(2)若x ∈[0,π]时,f (x)≥ax,求a 的取值范围. 解 (1)证明:设g(x)=f′(x),则g(x)=cosx +xsinx -1,g′(x)=xcosx.当x ∈⎝⎛⎭⎪⎫0,π2时,g′(x)>0;当x ∈⎝⎛⎭⎪⎫π2,π时,g′(x)<0, 所以g(x)在⎝ ⎛⎭⎪⎫0,π2上单调递增,在⎝ ⎛⎭⎪⎫π2,π上单调递减.又g(0)=0,g ⎝ ⎛⎭⎪⎫π2>0,g(π)=-2, 故g(x)在(0,π)存在唯一零点. 所以f′(x)在区间(0,π)存在唯一零点. (2)由题设知f (π)≥aπ,f (π)=0,可得a≤0.由(1)知,f′(x)在(0,π)只有一个零点,设为x 0,且当x ∈(0,x 0)时,f′(x)>0;当x ∈(x 0,π)时,f′(x)<0,所以f (x)在(0,x 0)上单调递增,在(x 0,π)上单调递减.又f (0)=0,f (π)=0,所以当x ∈[0,π]时,f (x)≥0.又当a≤0,x ∈[0,π]时,ax≤0,故f (x)≥ax. 因此,a 的取值范围是(-∞,0].19.(本小题满分12分)(2019·株洲模拟)已知函数f (x)=ln x +12ax 2-(a +1)x(其中a>0).(1)讨论f (x)的单调性;(2)若g(x)=-a +12x 2+f (x),设x 1,x 2(x 1<x 2)是函数g(x)的两个极值点,若a≥32,且g(x 1)-g(x 2)≥k恒成立,求实数k 的取值范围.解 (1)f (x)的定义域为(0,+∞),f′(x)=1x +ax -(a +1)=x -1ax -1x .①若0<a<1,则1a >1.由f′(x)>0得0<x<1或x>1a ;由f′(x)<0得1<x<1a,∴f (x)在区间(0,1),⎝ ⎛⎭⎪⎫1a ,+∞上单调递增,在区间⎝ ⎛⎭⎪⎫1,1a 上单调递减;②若a =1,则f′(x)≥0,∴f (x)在(0,+∞)上单调递增;③若a>1,则0<1a <1,由f′(x)>0得0<x<1a 或x>1;由f′(x)<0得1a<x<1,∴f (x)在⎝ ⎛⎭⎪⎫0,1a ,(1,+∞)上单调递增,在⎝ ⎛⎭⎪⎫1a ,1上单调递减. (2)∵g(x)=ln x +12x 2-(a +1)x ,g′(x)=1x +x -(a +1)=x 2-a +1x +1x,由g′(x)=0得x 2-(a +1)x +1=0,由a≥32,知Δ>0,∴x 1+x 2=a +1,x 1x 2=1, ∴x 2=1x 1,∵a≥32,x 1<x 2.∴⎩⎪⎨⎪⎧x 1+1x 1≥52,0<x 1<1x 1,解得0<x 1≤12,∴g(x 1)-g(x 2)=ln x 1x 2+12(x 21-x 22)-(a +1)(x 1-x 2)=2ln x 1-12⎝ ⎛⎭⎪⎫x 21-1x 21.设h(x)=2ln x -12⎝ ⎛⎭⎪⎫x 2-1x 2⎝ ⎛⎭⎪⎫0<x ≤12,则h′(x)=2x -x -1x3=-x 2-12x3<0,∴h(x)在⎝ ⎛⎦⎥⎤0,12上单调递减; 当x 1=12时,h(x)min =h ⎝ ⎛⎭⎪⎫12=158-2ln 2,∴k≤158-2ln 2,∴k 的最大值为158-2ln 2.20.(本小题满分12分)(2019·湘潭二模)已知函数f (x)=1+ln x -ax 2. (1)讨论函数f (x)的单调区间; (2)证明:xf (x)<2e2·e x +x -ax 3.解 (1)f (x)=1+ln x -ax 2的定义域为(0,+∞), f′(x)=1x -2ax =1-2ax2x.所以当a≤0时,f′(x)>0,f (x)在(0,+∞)上单调递增; 当a>0时,令f′(x)=0,得x =2a2a. 即当x ∈⎝ ⎛⎭⎪⎫0,2a 2a 时,f′(x)>0,所以f (x)的单调递增区间为⎝⎛⎭⎪⎫0,2a 2a . 当x ∈⎝⎛⎭⎪⎫2a 2a ,+∞时,f′(x)<0,f (x)的单调递减区间为⎝ ⎛⎭⎪⎫2a 2a ,+∞.(2)证明:要证xf (x)<2e 2·e x +x -ax 3,即证xln x<2e 2·e x,也即ln x x <2e xe 2x 2.令g(x)=2e 2·exx2(x>0),g′(x)=2e 2·e x·x 2-e x·2x x 4=2e2·exx -2x3, 当0<x<2时,g′(x)<0,g(x)单调递减; 当x>2时,g′(x)>0,g(x)单调递增, 所以g(x)的最小值为g(2)=12.令k(x)=ln x x ,则k′(x)=1-ln xx2, 当0<x<e 时,k′(x)>0,k(x)单调递增;当x>e 时,k′(x)<0,k(x)单调递减, 所以k(x)的最大值为k(e)=1e ,因为1e <12,所以k(x)<g(x),即ln x x <2e xe 2x 2.所以xf (x)<2e2·e x +x -ax 3.21.(本小题满分12分)(2019·北京高考)已知函数f (x)=14x 3-x 2+x.(1)求曲线y =f (x)的斜率为1的切线方程; (2)当x ∈[-2,4]时,求证:x -6≤f (x)≤x;(3)设F (x)=|f (x)-(x +a)|(a ∈R),记F (x)在区间[-2,4]上的最大值为M(a),当M(a)最小时,求a 的值.解 (1)由f (x)=14x 3-x 2+x 得f′(x)=34x 2-2x +1.令f′(x)=1,即34x 2-2x +1=1,得x =0或x =83.又f (0)=0,f ⎝ ⎛⎭⎪⎫83=827,所以曲线y =f (x)的斜率为1的切线方程是y =x 与y -827=x -83,即y =x 与y =x -6427.(2)证明:令g(x)=f (x)-x ,x ∈[-2,4]. 由g(x)=14x 3-x 2得g′(x)=34x 2-2x.令g′(x)=0得x =0或x =83.当x 变化时,g′(x),g(x)的变化情况如下:所以故-6≤g(x)≤0,即x -6≤f (x)≤x. (3)由(2)知,当a<-3时,M(a)=F (0)=|g(0)-a|=-a>3; 当a>-3时,M(a)=F (-2)=|g(-2)-a|=6+a>3; 当a =-3时,M(a)=3. 综上,当M(a)最小时,a =-3.22.(本小题满分12分)(2019·山东师大附中二模)已知函数f (x)=e x-aln x -e(a ∈R),其中e 为自然对数的底数.(1)若f (x)在x =1处取到极小值,求a 的值及函数f (x)的单调区间; (2)若当x ∈[1,+∞)时,f (x)≥0恒成立,求a 的取值范围. 解 (1)由f (x)=e x-aln x -e(a ∈R), 得f′(x)=e x-a x,因为f′(1)=0,所以a =e , 所以f′(x)=e x-e x =xe x-ex,令g(x)=xe x -e ,则g′(x)=e x(1+x),当x >0时,g′(x)>0,故g(x)在x ∈(0,+∞)上单调递增,且g(1)=0, 所以当x ∈(0,1)时,g(x)<0,当x ∈(1,+∞)时,g(x)>0. 即当x ∈(0,1)时,f′(x)<0,当x ∈(1,+∞)时,f′(x)>0. 所以函数f (x)在(0,1)上单调递减,在(1,+∞)上单调递增. (2)解法一:由f (x)=e x -aln x -e ,得f′(x)=e x-a x.当a≤0时,f′(x)=e x-a x >0,f (x)在x ∈[1,+∞)上单调递增,f (x)min =f (1)=0(符合题意);当a >0时,f′(x)=e x -a x,当x ∈[1,+∞)时,y =e x≥e,①当a ∈(0,e]时,因为x ∈[1,+∞),所以y =a x ≤e,f′(x)=e x-a x≥0,f (x)在x ∈[1,+∞)上单调递增,f (x)min =f (1)=0(符合题意). ②当a ∈(e ,+∞)时,存在x 0∈[1,+∞),满足f′(x 0)=e x 0 -ax 0=0,f (x)在x ∈[1,x 0)上单调递减,在x ∈(x 0,+∞)上单调递增,故f (x 0)<f (1)=0. 不满足x ∈[1,+∞)时,f (x)≥0恒成立, 综上所述,a 的取值范围是(-∞,e].解法二:由f (x)=e x-aln x -e ,可知f (1)=e 1-aln 1-e =0,因为f (x)=e x-aln x -e≥0在[1,+∞)上恒成立,所以其成立的必要条件是f′(1)≥0,而f′(x)=e x-a x,f′(1)=e -a≥0,即a≤e.①当a≤0时,f′(x)=e x-a x>0恒成立,此时f (x)在[1,+∞)上单调递增,f (x)≥f (1)=0(符合题意).②当0<a≤e 时,若x≥1,则有0<1x ≤1,-e≤-a≤-a x <0,而在x >1时,e x ≥e,f′(x)=e x-a x ≥0,所以f (x)在[1,+∞)上单调递增,即f (x)≥f (1)=0(符合题意).综上所述,a 的取值范围是(-∞,e].。
【最新】江苏省高三数学一轮典型专题训练:《导数及其应用》(含解析)

江苏省高三数学一轮复习典型题专题训练专题一、导数及其应用一、填空题1、(盐城上期中)若函数x x a x x f ln )3()(2+++=在区间(1,2)上存在唯一的极值点,则实数a 的取值范围为 ▲ .2、(南京市高三学情调研)若函数f (x )=12ax 2-e x +1在x =x 1和x =x 2两处取到极值, 且 x 2x 1≥2,则实数a 的取值范围是___3、(南京市六校联合体高三上学期12月联考)设直线l 是曲线x x y ln +=22的切线,则直线l 的斜率的最小值是 ▲ .4、(江苏省常州一中、泰兴中学、南菁高中高三10月月考)函数在点A (2,1)处切线的斜率为 ▲ .5、(江苏省常州一中、泰兴中学、南菁高中高三月考)若函数f(x)=kx-cosx 在区间()单调递增,则 k 的取值范围是 ▲ .6、(南师附中高三年级5月模拟)在平面直角坐标系xOy 中,点P 在曲线C :3103y x x =-+上,且在第四象限内.已知曲线C 在点P 处的切线为2y x b =+,则实数b 的值为 .7、(徐州市高三上期中考试)已知函数32()2f x x x a =--,若存在(]0,x a ∈-∞,使0()0f x ,则实数a 的取值范围为 ▲8、(常州上期末)已知函数()ln f x bx x =+,其中b ∈R .若过原点且斜率为k 的直线与曲线()y f x =相切,则k b -的值为 ▲ .9、(盐城市高三上学期期中)已知()f x 为奇函数,当0x <时,()2xf x e x =+,则曲线()y f x =在1x =处的切线斜率为 ▲ .10、(苏州市高三上学期期末)曲线2xy x e =+在0x =处的切线与两坐标轴围成的三角形面积为 .11、(盐城市高三上学期期中)在平面直角坐标系中,曲线21xy e x =++在x =0处的切线方程是 .12、(盐城市高三上学期期中)已知函数21()()(1)2xf x x m e x m x =+--+在R 上单调递增,则实数m 的取值集合为 .13、(南京市、镇江市高三上学期期中)已知e 为自然对数的底数,函数y =e x -lnx 在[1,e ]的最小值为__14、(苏锡常镇四市高三教学情况调查(二))已知点P 在曲线C :212y x =上,曲线C 在点P 处的切线为l ,过点P 且与直线l 垂直的直线与曲线C 的另一交点为Q ,O 为坐标原点,若OP ⊥OQ ,则点P 的纵坐标为 .15、(苏锡常镇四市高三教学情况调查(二))已已知e 为自然对数的底数,函数2()xf x e ax =-的图像恒在直线32y ax =上方,则实数a 的取值范围为 .二、解答题1、(南京市高三9月学情调研)已知函数f (x )=2x 3-3(a +1)x 2+6ax ,a ∈R . (1)曲线y =f (x )在x =0处的切线的斜率为3,求a 的值;(2)若对于任意x ∈(0,+∞),f (x )+f (-x )≥12ln x 恒成立,求a 的取值范围; (3)若a >1,设函数f (x )在区间[1,2]上的最大值、最小值分别为M (a )、m (a ), 记h (a )=M (a )-m (a ),求h (a )的最小值. 2、(南京市高三9月学情调研) 已知函数f (x )=ln x ,g (x )=x 2.(1)求过原点(0,0),且与函数f (x )的图象相切的直线l 的方程;(2)若a >0,求函数φ(x )=|g (x )-2a 2f (x )|在区间[1,+∞) 上的最小值. 3、(南京市六校联合体高三上学期12月联考)已知函数ln (),()xx xf xg x e x==. (1)求()f x 的极大值;(2)当0a >时,不等式()xg x ax b ≤+恒成立,求ba的最小值; (3)是否存在实数k N ∈,使得方程()(1)()f x x g x =+在(,1)k k +上有唯一的根,若存在,求出所有k 的值,若不存在,说明理由.4、(江苏省常州一中、泰兴中学、南菁高中高三10月月考)已知函数,a ∈R.⑴函数y= f(x)在点(2,f(2))处的切线与直线x-2y+1=0垂直,求a 的值; ⑵讨论函数f(x)的单调性; ⑶当a=1时,证明:不等式成立.(其中n!=1×2×3×…×n ,n ∈N*,n ≥2)5、(南京市高三12月联合调研)已知函数21()ln 2f x ax x =+,()g x bx =-,设()()()h x f x g x =-.(1)若()f x 在x 处取得极值,且(1)(1)2f g '=--,求函数()h x 的单调区间; (2)若0a =时函数()h x 有两个不同的零点12,x x .①求b 的取值范围;②求证:1221x x e >. 6、(南京市、盐城市高三上学期期末)若函数y =f (x )在x =x 0处取得极大值或极小值,则称x 0为函数y =f (x )的极值点.设函数f (x )=x 3-tx 2+1(t ∈R ). (1)若函数f (x )在(0,1)上无极值点,求t 的取值范围;(2)求证:对任意实数t ,在函数f (x )的图象上总存在两条切线相互平行;(3)当t =3时,若函数f (x )的图象上存在的两条平行切线之间的距离为4,问:这样的平行切线共有几组?请说明理由.7、(如皋市高三上学期期末)已知函数()ln 2f x x ax a =-+,其中a ∈R .(I )若函数()f x 的图象在1x =处的切线与直线20x ay --=垂直,求实数a 的值; (II )设函数()()22g x f x ax a =++. (1).求函数()g x 的单调区间;(2)若不等式()0g x >对任意的实数()1x ∈+∞,恒成立,求实数a 的取值范围. 8、(苏北三市(徐州、连云港、淮安)2019届高三期末)已知函数()()ln f x x a x =-()a ∈R . (1)若1a =,求()f x 在1x =处的切线方程;(2)若对于任意的正数x ,()0f x ≥恒成立,求实数a 的值; (3)若函数()f x 存在两个极值点,求实数a 的取值范围.9、(苏州市高三上学期期中)设函数()1ln f x ax x =--,a 为常数. (1)当2a =时,求()f x 在点(1,(1))f 处的切线方程; (2)若12,x x 为函数()f x 的两个零点,12x x >. ①求实数a 的取值范围; ②比较12x x +与2a的大小关系,并说明理由.10、(南京市高三第三次模拟)已知函数f (x )=ln x +a x +1,a ∈R .(1)若函数f (x )在x =1处的切线为y =2x +b ,求a ,b 的值;(2)记g (x )=f (x )+ax ,若函数g (x )在区间(0,12)上有最小值,求实数a 的取值范围;(3)当a =0时,关于x 的方程f (x )=bx 2有两个不相等的实数根,求实数b 的取值范围. 11、(七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)高三第一次模拟(2月)) 已知函数()()ln a f x x a x =+∈R .(1)讨论()f x 的单调性;(2)设()f x 的导函数为()f x ',若()f x 有两个不相同的零点12x x ,. ① 求实数a 的取值范围;② 证明:1122()()2ln 2x f x x f x a ''+>+.12、(七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第二次模拟) 已知函数21()2ln 2f x x x ax a =+-∈,R .(1)当3a =时,求函数()f x 的极值;(2)设函数()f x 在0x x =处的切线方程为()y g x =,若函数()()y f x g x =-是()0+∞,上 的单调增函数,求0x 的值;(3)是否存在一条直线与函数()y f x =的图象相切于两个不同的点?并说明理由.13、(七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第二次模拟(5月))已知函数2()1ln ax f x x =+(0a ≠),e 是自然对数的底数.(1)当0a >时,求()f x 的单调增区间;(2)若对任意的12x ≥,1()2e b f x -≥(b ∈R ),求b a 的最大值;(3)若()f x 的极大值为2-,求不等式()e 0x f x +<的解集.14、(苏锡常镇四市高三教学情况调查(一))已知函数()(1)ln (R)f x x x ax a =++∈. (1)若()y f x =在(1,(1)f )处的切线方程为0x y b ++=,求实数a ,b 的值; (2)设函数()()f x g x x=,x ∈[1,e](其中e 为自然对数的底数).①当a =﹣1时,求()g x 的最大值;②若()()exg x h x =是单调递减函数,求实数a 的取值范围.15、(盐城市2019届高三第三次模拟) 设函数x ae x x f -=)((e 为自然对数的底数,R a ∈). (1)当1=a 时,求函数)(x f 的图象在1=x 处的切线方程; (2)若函数)(x f 在区间(0,1)上具有单调性,求a 的取值范围;(3)若函数)()()(x f e e x g x -=有且仅有3个不同的零点321,,x x x ,且321x x x <<,113≤-x x ,求证: 1131-+≤+e e x x16、(南师附中高三年级5月模拟)设a 为实数,已知函数()xf x axe =,()lng x x x =+.(1)当a <0时,求函数()f x 的单调区间;(2)设b 为实数,若不等式2()2f x x bx ≥+对任意的a ≥1及任意的x >0恒成立,求b 的取值范围;(3)若函数()()()h x f x g x =+(x >0,x ∈R)有两个相异的零点,求a 的取值范围.参考答案一、填空题 1、 15(,6)2-- 2、[ 2ln2,+∞) 3、44、122㏑ 5、[-12∞,+) 6、-13 7、[1,0][2,)-+∞ 8、1e 9、12e-10、2311、32y x =+ 12、{}1- 13、e14、1 15、二、解答题1、解:(1)因为f (x )=2x 3-3(a +1)x 2+6ax ,所以f ′(x )=6x 2-6(a +1)x +6a ,所以曲线y =f (x )在x =0处的切线斜率k =f ′(0)=6a ,所以6a =3,所以a =12. ………………………2分(2)f (x )+f (-x )=-6(a +1)x 2≥12ln x 对任意x ∈(0,+∞)恒成立,所以-(a +1)≥2ln xx 2. ………………………4分令g (x )=2ln xx 2,x >0,则g '(x )=2(1-2ln x )x 3.令g '(x )=0,解得x =e .当x ∈(0,e)时,g '(x )>0,所以g (x )在(0,e)上单调递增;当x ∈(e ,+∞)时,g '(x )<0,所以g (x )在(e ,+∞)上单调递减.所以g (x )max =g (e)=1e , ………………………6分所以-(a +1)≥1e ,即a ≤-1-1e,所以a 的取值范围为(-∞,-1-1e ]. ………………………8分(3)因为f (x )=2x 3-3(a +1)x 2+6ax ,所以f ′(x )=6x 2-6(a +1)x +6a =6(x -1)(x -a ),f (1)=3a -1,f (2)=4.令f ′(x )=0,则x =1或a . ………………………10分 f (1)=3a -1,f (2)=4.①当1<a ≤53时,当x ∈(1,a )时,f '(x )<0,所以f (x )在(1,a )上单调递减; 当x ∈(a ,2)时,f '(x )>0,所以f (x )在(a ,2)上单调递增.又因为f (1)≤f (2),所以M (a )=f (2)=4,m (a )=f (a )=-a 3+3a 2, 所以h (a )=M (a )-m (a )=4-(-a 3+3a 2)=a 3-3a 2+4. 因为h ' (a )=3a 2-6a =3a (a -2)<0, 所以h (a )在(1,53]上单调递减,所以当a ∈(1,53]时,h (a )最小值为h (53)=827.………………………12分②当53<a <2时,当x ∈(1,a )时,f '(x )<0,所以f (x )在(1,a )上单调递减; 当x ∈(a ,2)时,f '(x )>0,所以f (x )在(a ,2)上单调递增.又因为f (1)>f (2),所以M (a )=f (1)=3a -1,m (a )=f (a )=-a 3+3a 2, 所以h (a )=M (a )-m (a )=3a -1-(-a 3+3a 2)=a 3-3a 2+3a -1. 因为h ' (a )=3a 2-6a +3=3(a -1)2≥0. 所以h (a )在(53,2)上单调递增,所以当a ∈(53,2)时,h (a )>h (53)=827. ………………………14分③当a ≥2时,当x ∈(1,2)时,f '(x )<0,所以f (x )在(1,2)上单调递减, 所以M (a )=f (1)=3a -1,m (a )=f (2)=4, 所以h (a )=M (a )-m (a )=3a -1-4=3a -5, 所以h (a )在[2,+∞)上的最小值为h (2)=1.综上,h (a )的最小值为827. ………………………16分2、解:(1)因为f (x )=ln x ,所以f ′(x )=1x (x >0).设直线l 与函数f (x )的图象相切于点(x 0,y 0),则直线l 的方程为 y -y 0=1x 0(x -x 0),即 y -ln x 0=1x 0(x -x 0).…………………… 3分因为直线l 经过点(0,0),所以0-ln x 0=1x 0(0-x 0),即ln x 0=1,解得x 0=e .因此直线l 的方程为 y =1e x ,即x -e y =0. …………………… 6分 (2)考察函数H (x )=g (x )-2a 2f (x )=x 2-2a 2ln x .H ′(x )=2x -2a 2x =2(x -a )( x +a )x(x >0). 因为a >0,故由H ′(x )=0,解得x =a . …………………… 8分 ① 当0<a ≤1时,H ′(x )≥0在[1,+∞)上恒成立,H (x )在区间[1,+∞)上递增,所以 H (x )min =H (1)=1>0,所以φ(x )min =1. …………………… 11分 ② 当a >1时,H (x )在区间[1,a ]上递减,在区间[a ,+∞)上递增, 所以 H (x )min =H (a )=a 2(1-2ln a ) .(ⅰ) 当1-2ln a ≤0,即a ∈[e ,+∞) 时,H (x )min =a 2(1-2ln a )≤0, 又H (1)=1>0,所以φ(x )min =0.(ⅱ) 当1-2ln a >0,a ∈(1,e) 时,H (x )min =a 2(1-2ln a )>0, 所以φ(x )min =a 2(1-2ln a ) .综上 φ(x )min =⎩⎪⎨⎪⎧1, 0<a ≤1,a 2(1-2ln a ),1<a <e ,0, a ≥e . …………………… 16分3、(1)1()x xf x e-'=,令()0f x '=,得1x =. …………………………………2分当1x <时,()0f x '>,则()f x 在(,1)-∞上单调递增,当1x >时,()0f x '>,则()f x 在(1,)+∞上单调递减,故当1x =时,()f x 的极大值为1e.………………………4分 (2)不等式()xg x ax b ≤+恒成立,即ln 0x ax b --≤恒成立,记()ln (0)m x x ax b x =-->,则1()(0)axm x x x -'=>,当0a >时,令()0m x '=,得1x a=,………………………………………………6分 当1(0,)x a ∈时,()0m x '>,此时()m x 单调递增,当1(,)x a∈+∞时,()0m x '<,此时()m x 单调递减,则max 1()()ln 10m x m a b a==---≤,即ln 1b a ≥--,…8分则ln 1b a a a +≥-, 记ln 1()a n a a+=-,则2ln ()(0)a n a a a '=>,令()0n a '=,得1a =当(0,1)a ∈时,()0n a '<,此时()n a 单调递减,当(1,)a ∈+∞时,()0n a '>,此时()n a 单调递增,min ()(1)1n a n ==-,故ba的最小值为1-. ………………………10分 (3)记(1)ln ()x x x x s x e x +=-,由2123ln 2(1)0,(2)1102s s e e =>=-<-=,……12分故存在1k =,使()(1)()f x x g x =+在(1,2)上有零点,下面证明唯一性:① 当01x <≤时,()0,(x 1)()0f x g x >+<,故()0s x >,0=)(x s 在(0,1]上无解…………………………………………………………………14分②当1x >时,211ln ()x x x x s x e x -+-'=-,而2110,1ln 0,0x x x x e x -<+->>,此时()0s x '<,()s x 单调递减,所以当1k=符合题意.……………………………16分4、5、解:(1)因为1()f x axx'=+,所以(1)1f a'=+,由(1)(1)2f g'=--可得a=b-3.又因为()f x在2x=处取得极值,所以22(20f'=,所以a= -2,b=1 . …………………………………2分所以2()lnh x x x x=-++,其定义域为(0,+∞)2121(21)(1)()21=x x x x h x x x x x-++-+-'=-++=令()0h x '=得121,12x x =-=,当x ∈(0,1)时,()>0h x ',当x ∈(1,+∞)()<0h x ',所以函数h (x )在区间(0,1)上单调增;在区间(1,+∞)上单调减. …………………………4分 (2)当0a =时,()ln h x x bx =+,其定义域为(0,+∞).①'1()h x b x=+,当0b ≥,则'()0h x >,()h x 在(0,)+∞上单调递增,不合题意。
(典型题)高中数学选修1-1第四章《导数应用》测试卷(答案解析)

一、选择题1.若关于x 的方程2lnx ax x -=在0,上有两个不等的实数根,则实数a 的取值范围为( ) A .(],1-∞-B .(),1-∞-C .[)1,-+∞D .()1,-+∞2.设函数()f x '是奇函数()()f x x R ∈的导函数,()10f -=,当0x >时,()()0xf x f x '-<,则使得()0f x >成立的x 的取值范围是( )A .()()0,11,+∞B .()(),11,-∞-+∞C .()(),10,1-∞-⋃D .()()1,01,-⋃+∞3.已知函数()2sin x m f x x +=-在30,4π⎡⎤⎢⎥⎣⎦上有两个不同的零点,则实数m 的取值范围是( ) A .3,44ππ⎫⎡--⎪⎢⎣⎭ B .3,44ππ⎛⎤⎥⎝⎦ C .,42ππ⎛⎫⎪⎝⎭ D .,24ππ⎛⎫-- ⎪⎝⎭ 4.已知函数()23ln f x x ax x =-+在其定义域内为增函数,则a 的最大值为( )A.4B .C .D .65.已知函数()f x 定义域为R ,其导函数为f x ,且()()30f x f x '->在R 上恒成立,则下列不等式定成立的是( ) A .()()310f e f <B .()()210f e f < C .()()310f e f >D .()()210f e f >6.已知函数()()()()221ln 10,,2a f x a x x a a xb x a b =-++--+>∈∈R R .若函数()f x 有三个零点,则( )A .1a >,0b <B .01a <<,0b >C .0a <,0b >D .01a <<,0b < 7.已知定义在R 上的函数()f x 满足()()f x f x '<-,则下列式子成立的是( )A .(2020)(2021)f ef >B .(2020)(2021)f ef <C .(2020)(2021)ef f >D .(2020)(2021)ef f <8.已知函数()()()110ln x f x x x++=>,若()1kf x x >+恒成立,则整数k 的最大值为( ) A .2B .3C .4D .59.对于正数k ,定义函数:()()()(),,f x f x k g x k f x k ⎧≤⎪=⎨>⎪⎩.若对函数()ln 22f x x x =-+,有()()g x f x =恒成立,则( )A .k 的最大值为1ln2+B .k 的最小值为1ln2+C .k 的最大值为ln 2D .k 的最小值为ln 210.甲乙两人进行乒乓球友谊赛,每局甲胜出概率是()01p p <<,三局两胜制,甲获胜概率是q ,则当q p -取得最大值时,p 的取值为( ) A .12B .1326-C .1326+ D .2311.函数()212x f x x -=+的值域是( ) A .30,⎡⎤⎢⎥⎣⎦B .3⎛⎫∞ ⎪ ⎪⎝⎭,+C .()0,3D .)3,⎡+∞⎣12.若函数32()21f x ax x x =+++在(1,2)上有最大值无最小值,则实数a 的取值范围为( ) A .34a >-B .53a <-C .5334a -<<- D .5334a -≤≤- 二、填空题13.已知函数()32133f x x x =++在区间(),3+m m 上存在极大值与极小值,则实数m 的取值范围是_________.14.已知函数()(ln )xe f x k x x x=+-,若1x =是函数()f x 的唯一极值点,则实数k 的取值范围是_______.15.已知函数()f x 与()f x '的图象如图所示,则函数()()x f x g x e=的单调递减区间为___________.16.已知函数()2ln(1)f x x ax =+-,对任意的(0,1),(0,1)m n ∈∈,当m n ≠时,(1)(1)1f m f n m n+-+<-,则实数a 的取值范围是____________.17.函数21f x x x 的极大值为_________.18.已知函数3223,01()21,1x x m x f x mx x ⎧-+≤≤=⎨-+>⎩,若函数()f x 的图象与x 轴有且只有两个不同的交点,则实数m 的取值范围为________.19.函数2sin y x x =-在[]0,2π上的递增区间是________.20.已知函数()321f x x x =++,若对于x R ∀∈不等式()21xf ax e a -+≤恒成立,则实数a 的取值范围为:____________.三、解答题21.已知函数()2ln f x x a x x=--. (1)已知()f x 在点()()1,1f 处的切线方程为2y x =-,求实数a 的值; (2)已知()f x 在定义域上是增函数,求实数a 的取值范围. 22.已知函数()xax f x e =. (1)当1a =时,判断函数()f x 的单调性; (2)若0a >,函数()()212g x f x x x =+-只有1个零点,求实数a 的取值范围. 23.已知函数32()691f x x x x =-++. (1)求曲线()y f x =在点()0,1处的切线方程.(2)证明:()()1ln 2cos x x f x x +->对1()2,x ∈+∞恒成立. 24.已知函数()()3f x alnx ax a R =--∈. (1)函数()f x 的单调区间;(2)当1a =-时,证明:当()1x ∈+∞,时,()20f x +>. 25.已知函数21()ln (1)12f x a x x a x =+-++. (I )当0a =时,求曲线()y f x =在点(2,(2))f 处的切线方程;(Ⅱ)若函数()f x 在1x =处取得极小值,求实数a 的取值范围.26.已知函数321()23f x x x ax =-++,21()42g x x =-. (1)若函数()f x 在()0,∞+上存在单调递增区间,求实数a 的取值范围;(2)设()()()G x f x g x =-.若02a <<,()G x 在[]1,3上的最小值为13-,求()G x 在[]1,3上取得最大值时,对应的x 值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】通过分离参数变成ln x a x x=-,构造函数()ln x f x xx =-,利用导数求其单调区间和值域,数形结合写出a 的取值范围. 【详解】2lnx ax x -=故ln xa x x=- 则()ln x f x xx=- ()2'221ln 1ln 1x x x f x x x---=-= 设()21ln g x x x =--,0x >故()'120g x x x=--< ()21ln g x x x =--在0,上为减函数,10g .故()0,1∈x 时()'0f x >;()1,∈+∞x 时()'0f x <.故()ln x f x xx=-在0,1上为增函数,在1,上为减函数.()()max 11f x f ==-,且0,x →时()f x →-∞;,x →+∞时()f x →-∞y a =与()ln x f x x x=-的图象要有两个交点则a 的取值范围为(),1-∞-. 故选:B 【点睛】方程在某区间上有解的问题,可通过分离参数,构造函数,利用导数求该区间上单调区间和值域,得出参数的取值范围.2.C解析:C 【分析】 构造函数()()f xg x x=,分析出函数()g x 为偶函数,且在()0,∞+上为减函数,由()0f x >可得出()00g x x ⎧>⎨>⎩或()00g x x ⎧<⎨<⎩,解这两个不等式组即可得解.【详解】构造函数()()f xg x x=,该函数的定义域为{}0x x ≠, 由于函数()f x 为奇函数,则()()()()()f x f x f x g x g x x x x---====--, 所以,函数()()f xg x x=为偶函数. 当0x >时,()()()20xf x f x g x x'-'=<,所以,函数()g x 在()0,∞+上为减函数, 由于函数()()f xg x x=为偶函数,则函数()g x 在(),0-∞上为增函数. ()10f -=,则()10f =且()00f =,所以,()()110g g -==.不等式()0f x >等价于()()010g x g x ⎧>=⎨>⎩或()()010g x g x ⎧<=-⎨<⎩,解得1x <-或01x <<.因此,不等式()0f x >的解集为()(),10,1-∞-⋃. 故选:C. 【点睛】方法点睛:利用函数的奇偶性与单调性求解抽象函数不等式,要设法将隐性划归为显性的不等式来求解,方法是:(1)把不等式转化为()()f g x f h x >⎡⎤⎡⎤⎣⎦⎣⎦;(2)判断函数()f x 的单调性,再根据函数的单调性把不等式的函数符号“f ”脱掉,得到具体的不等式(组),但要注意函数奇偶性的区别.3.A【分析】()0f x =有两解变形为2sin m xxe e =有两解, 设2sin ()xxg xe =,利用导数确定函数的单调性、极值,结合()g x 的大致图象可得结论. 【详解】 由()22sin x mf x e x +=-得2sin m xxe e =,设2sin ()xxg x e=,则2(cos sin )()x x g x -'=, 易知当04x π<<时,()0g x '>,()g x 递增,当344x ππ<<时,()0g x '<,()g x 递减,(0)0g =,414g e ππ⎛⎫= ⎪⎝⎭,34314g e ππ⎛⎫= ⎪⎝⎭,如图是()g x 的大致图象, 由2sin mx e =有两解得34411m e e eππ≤<,所以344m ππ-≤<-.故选:A .【点睛】关键点点睛:本题考查函数的零点问题,解题关键是转化.函数的零点转化为方程的解,再用分离参数变形为2sin m xe =2sin ()x g x =my e =有两个交点,利用导数研究函数()g x 的单调性、极值后可得.4.B解析:B 【分析】求导,则由题意导函数在0,上恒大于等于0,分参求a 范围.【详解】由题意可得()160f x x a x'=-+≥对()0,x ∈+∞恒成立,即16a x x ≤+,对()0,x ∈+∞因为16x x +≥16x x =即x =时取最小值所以a ≤ 故选:B 【点睛】(1)利用导数研究函数的单调性的关键在于准确判定导数的符号.关键是分离参数k ,把所求问题转化为求函数的最小值问题.(2)若可导函数f (x )在指定的区间D 上单调递增(减),求参数范围问题,可转化为f ′(x )≥0(或f ′(x )≤0)恒成立问题,从而构建不等式,要注意“=”是否可以取到.5.A解析:A 【分析】 构造函数()()3xf xg x e=,由()()30f x f x '->得0g x ,进而判断函数()g x 的单调性,判断各选项不等式. 【详解】()()3x f x g x e=,则()()()()()()3323333x x x x f x e f x e f x f x g x e e ⋅--==''', 因为()()30f x f x '->在R 上恒成立, 所以0g x在R 上恒成立,故()g x 在R 上单调递减, 所以()()10g g <,即()()3010f f e e <,即()()310f e f <, 故选:A. 【点睛】函数的单调性是函数的重要性质之一,它的应用贯穿于整个高中数学的教学之中.某些数学问题从表面上看似乎与函数的单调性无关,但如果我们能挖掘其内在联系,抓住其本质,那么运用函数的单调性解题,能起到化难为易、化繁为简的作用.因此对函数的单调性进行全面、准确的认识,并掌握好使用的技巧和方法,这是非常必要的.根据题目的特点,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.6.B解析:B 【分析】首先求出函数的导函数,要使函数()f x 有三个零点,则()0f x '=必定有两个正实数根,即可求出参数a 的取值范围,再求出函数的单调区间,从而得到()10f a ->,即可判断b 的范围; 【详解】解:因为()()()()221ln 10,,2a f x a x x a a xb x a b =-++--+>∈∈R R 所以()()()()()()()222111111ax a a x a a ax x a f x ax a a xxx+--+---+-'=++--==要使函数()f x 有三个零点,则()0f x '=必定有两个正实数根,即11x a=,21x a =-,所以1010a a->⎧⎪⎨>⎪⎩解得01a <<,此时111x a =>,211x a =-<,令()0f x '>,解得01x a <<-或1x a >,即函数在()0,1a -和1,a ⎛⎫+∞ ⎪⎝⎭上单调递增,令()0f x '<,解得11a x a -<<或1x a >,即函数在11,a a ⎛⎫- ⎪⎝⎭上单调递减,所以()f x 在1x a =-处取得极大值,在1x a=处取得极小值; 因为当0x →时,()f x →-∞;当x →+∞时,()f x →+∞,要使函数函数()f x 有三个零点,则()10f a ->,10f a ⎛⎫< ⎪⎝⎭即()()()()()()2211ln 11112a f a a a a a a ab -=--+-+---+ ()()()()211ln 102a a a a b -+⎡⎤=--++>⎢⎥⎣⎦且()()2211111ln 102a f a a a b a a a a ⎛⎫⎛⎫=-++--+< ⎪ ⎪⎝⎭⎝⎭ 因为01a <<,所以011a <-<,20a -<,所以()()2102a a -+<,()ln 10a -<,所以()()()()211ln 102a a a a -+⎡⎤--+<⎢⎥⎣⎦,又()()()()211ln 102a a a a b -+⎡⎤--++>⎢⎥⎣⎦,所以0b >故选:B 【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.7.A解析:A 【分析】构造函数()()xg x e f x =,求导判定函数单调性,根据单调性得(2020)(2021)g g >化简即可. 【详解】解:依题意()()0f x f x '+<,令()()x g x e f x =,则()(()())0xg x f x f x e ''=+<在R 上恒成立,所以函数()()xg x e f x =在R 上单调递减, 所以(2020)(2021)g g >即20202021(2020)(2021)(2020)(2021)e e e f f f f >⇒>故选:A. 【点睛】四种常用导数构造法:(1)对于不等式()()0f x g x ''+> (或0<) ,构造函数()()()F x f x g x =+. (2)对于不等式()()0f x g x ''->(或0<) ,构造函数()()()F x f x g x =-.(3)对于不等式()()0f x f x '+>(或0<) ,构造函数()()xF x e f x =.(4)对于不等式()()0f x f x '->(或0<) ,构造函数()()x f x F x e=. 8.B解析:B 【分析】 将不等式化为()()111ln x x k x +++>,令()()()111ln x g x xx ++=+,求出导函数,利用导数判断函数的单调性,从而可得()02,3x ∃∈使()00g x '=,进而可得()()001()g x x x g ≥=+,即求.【详解】()()()1ln 10x f x x x ++=>, ()1k f x x ∴>+可化为()111ln x k x x ++>+即()()111ln x x k x+++>, 令()()()111ln x g x xx ++=+, 则()()()()21ln 11111x x x x ln x g x x +++---++⎡⎤⎣⎦'= ()211x ln x x--+=令()()11h x x ln x =--+, 则()111h x x '=-+,()0,x ∈+∞时, ()0h x '>,()g x '∴在()0,∞+单调递增.又()()1ln 32ln 420,30,49g g --''=<=> ()02,3x ∃∈使()00g x '=,即()0011ln x x +=-.当()00,x x ∈时,()()0,g x g x '<单调递减, 当0(,)x x ∈+∞时,()()0,g x g x '>单调递增,()()000001ln 1))1(()(1x x g x x x x g +∴≥==+++, ()02,3x ∈,()013,4x +∴∈,∴正整数k 的最大值为3.故选:B. 【点睛】关键点点睛:本题考查了导数研究不等式恒成立问题,解题的关键根据函数的单调性确定存在()02,3x ∈,使得()00g x '=,考查了分离参数法求范围.9.B解析:B 【分析】利用导数求出函数()f x 的最大值,由函数()g x 的定义结合()()g x f x =恒成立可知()f x k ≤,由此可得出k 的取值范围,进而可得出合适的选项.【详解】对于正数k ,定义函数:()()()(),,f x f x kg x k f x k ⎧≤⎪=⎨>⎪⎩,且()()g x f x =恒成立,则()f x k ≤.函数()ln 22f x x x =-+的定义域为()0,∞+,且()111x f x x x-'=-=. 当01x <<时,()0f x '>,此时,函数()f x 单调递增; 当1x >时,()0f x '<,此时,函数()f x 单调递减. 所以,()()max 11ln 2f x f ==+,1ln 2k ∴≥+. 因此,k 的最小值为1ln2+. 故选:B. 【点睛】解决导数中的新定义的问题,要紧扣新定义的本质,将问题转化为导数相关的问题,本题将问题转为不等式()k f x ≥恒成立,从而将问题转化为求函数()f x 的最大值.10.C解析:C 【分析】采用三局两胜制,则甲在下列两种情况下获胜:甲净胜二局,前二局甲一胜一负,第三局甲胜,由此能求出甲胜概率,进而求得的最大值. 【详解】采用三局两胜制,则甲在下列两种情况下获胜: 甲净胜二局概率为2p ;前二局甲一胜一负,第三局甲胜概率为12(1)C p p p -⋅22(1)p p =-则22(1)q p p p =+-,得q p -222(1)p p p p =+--3223p p p =-+-(01)p <<, 设3223y p p p =-+-,(01)p <<,则2661y p p '=-+-6(p p =---则函数y 在单调递减,在单调递增,故函数在36p =+处取得极大值,也是最大值. 故选:C. 【点睛】本题考查了概率的求法和应用以及利用导数求函数最值的方法,解题时要认真审题,注意等价转化思想和分类讨论思想的合理运用,属于中档题.11.A解析:A 【分析】求出函数的定义域,然后求出导函数,确定单调性,得值域.【详解】由21020x x ⎧-≥⎨+≠⎩得11x -≤≤,()f x '==当112x -≤<-时,()0f x '>,()f x 递增,112x -<≤时,()0f x '<,()f x 递减, 所以12x =-时,max()22f x ==-+(1)(1)0f f -==, 所以()f x的值域是⎡⎢⎣⎦. 故选:A . 【点睛】本题考查用导数求函数的值域,解题方法是由导数确定函数的单调性,得出最大值和最小值,得值域.12.C解析:C 【详解】分析:函数()3221f x ax x x =+++在()1,2上有最大值无最小值,则极大值在()1,2之间,一阶导函数有根在()1,2,且左侧函数值小于0,右侧函数值大于0,列不等式求解 详解:f ′(x )=3ax 2+4x +1,x ∈(1,2).a =0时,f ′(x )=4x +1>0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去. a ≠0时,△=16﹣12a . 由△≤0,解得43a ≥,此时f ′(x )≥0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去.由△>0,解得a 43<(a ≠0),由f ′(x )=0,解得x1=,x2=.当403a <<时,x 1<0,x 2<0,因此f ′(x )≥0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去.当a <0时,x 1>0,x 2<0,∵函数f (x )=ax 3+2x 2+x +1在(1,2)上有最大值无最小值,∴必然有f ′(x 1)=0,∴123a-<2,a <0.解得:53-<a 34-<. 综上可得:53-<a 34-<. 故选:C .点睛:极值转化为最值的性质:1、若()[]f x x a,b ∈在上有唯一的极小值,且无极大值,那么极小值为()f x 的最小值;2、若()[]f x x a,b ∈在上有唯一的极大值,且无极小值,那么极大值为()f x 的最大值;二、填空题13.【分析】利用导数求出函数的极大值点和极小值点由题意可得出关于实数的不等式组由此可解得实数的取值范围【详解】则令可得列表如下: 极大值 极小值 所以函数的极大值点为 解析:()3,2--【分析】利用导数求出函数()f x 的极大值点和极小值点,由题意可得出关于实数m 的不等式组,由此可解得实数m 的取值范围. 【详解】()32133f x x x =++,则()()222f x x x x x '=+=+,令()0f x '=,可得12x =-,20x =,列表如下:所以,函数f x 的极大值点为2x =-,极小值点为0x =, 由于函数()32133f x x x =++在区间(),3+m m 上存在极大值与极小值, 所以,230m m <-⎧⎨+>⎩,解得32m -<<-.因此,实数m 的取值范围是()3,2--. 故答案为:()3,2--.【点睛】易错点点睛:已知极值点求参数的值,先计算()0f x '=,求得x 的值,再验证极值点.由于导数为0的点不一定是极值点,因此解题时要防止遗漏验证导致错误.14.【分析】首先求函数的导数由条件是函数的唯一极值点说明在无解或有唯一解求实数的取值【详解】∵∴∴x =1是函数f (x )的唯一极值点在上无解或有唯一解x=1①当x=1为其唯一解时k=e 令当时即h(x)的单 解析:(,]e -∞【分析】首先求函数的导数2(1)()()x x e kx f x x'--=,由条件1x =是函数()f x 的唯一极值点,说明0-=x e kx 在()0,x ∈+∞无解,或有唯一解1x =,求实数k 的取值. 【详解】∵()(ln )x e f x k x x x =+-,∴22(1)1(1)()()(1)x x x e x e kx f x k x x x'---=+-= ∴x =1是函数f (x )的唯一极值点,0x x e k ∴-=在(0,)x ∈+∞上无解,或有唯一解x =1,①当x =1为其唯一解时,k =e ,令()(0)x h x e ex x =->,()xh x e e '=-,当(0,1)x ∈时,()0h x '<,即h (x )的单调递减区间为(0,1), 当(1,)x ∈+∞时,()0h x '>,即()h x 的单调递增区间为(1,)+∞, ∴()h x 在x =1处,取得极小值, ∴k =e 时,x =1是f (x )的唯一极值点;②当xe k x=在(0,)x ∈+∞上无解,设()x e g x x =则2(1)()x e x g x x'-=, 当(0,1)x ∈时,()0g x '<,即g (x )的单调递减区间为(0,1),当(1,)x ∈+∞时,()0g x '>,即()g x 的单调递增区间为(1,)+∞, ∴()g x 在x =1处,取得极小值,也是其最小值,min ()(1)g x g e ==,又k xe x=在(0,)x ∈+∞上无解,e k ∴<,综上k e ≤ 故答案为:(,]e -∞. 【点睛】易错点睛:本题考查根据函数的极值点求参数的取值范围,容易忽略k e =的情况,此时x e ex ≥恒成立.15.【分析】利用图象得出不等式的解集再利用导数可求得函数的单调递减区间【详解】由图象可知不等式的解集为由可得解得因此函数的单调递减区间为故答案为:【点睛】思路点睛:利用导数求函数单调区间的步骤:(1)求解析:()0,1、()4,+∞ 【分析】利用图象得出不等式()()0f x f x '-<的解集,再利用导数可求得函数()()x f x g x e=的单调递减区间. 【详解】由图象可知,不等式()()0f x f x '-<的解集为()()0,14,+∞,()()x f x g x e =,()()()()()()()2x x x x f x e f x e f x f x g x e e ''-⋅'-==', 由()0g x '<,可得()()0f x f x '-<,解得()()0,14,x ∈+∞.因此,函数()()x f x g x e=的单调递减区间为()0,1、()4,+∞. 故答案为:()0,1、()4,+∞. 【点睛】思路点睛:利用导数求函数单调区间的步骤: (1)求函数()f x 的定义域; (2)求导数()f x ';(3)解不等式()0f x '>,并与定义域取交集得到的区间为函数()f x 的单调增区间; (4)解不等式()0f x '<,并与定义域取交集得到的区间为函数()f x 的单调减区间.16.【分析】把不等式恒成立转化为函数的导数小于1在内恒成立进而转化为在内恒成立结合函数的性质即可求解【详解】由题意分式的几何意义为:表示点与连线的斜率因为实数在区间内故和在区间内不等式恒成立所以函数图象解析:1,6⎡⎫-+∞⎪⎢⎣⎭【分析】 把不等式(1)(1)1f m f n m n+-+<-恒成立,转化为函数()f x 的导数小于1在(1,2)内恒成立,进而转化为()121a x ->+在(1,2)内恒成立,结合函数的性质,即可求解.【详解】 由题意,分式(1)(1)f m f n m n+-+-的几何意义为:表示点(1,(1))m f m ++与(1,(1))n f n ++连线的斜率, 因为实数,m n 在区间(0,1)内,故1m + 和1n +在区间(1,2)内, 不等式(1)(1)1f m f n m n+-+<-恒成立,所以函数图象上在区间(1,2)内任意两点连线的斜率小于1,故函数()2ln(1)f x x ax =+-的导数小于1在(1,2)内恒成立, 由函数()2ln(1)f x x ax =+-满足10x +>,即定义域为(1,)-+∞,即()2111f x ax x '=-<+在(1,2)内恒成立,即()121a x ->+在(1,2)内恒成立, 设函数()()121g x x -=+,根据函数的单调性可知函数()()121g x x -=+在(1,2)上是单调增函数,可得()()126g x g <=-,所以16a ≥-, 故答案为:1,6⎡⎫-+∞⎪⎢⎣⎭. 【点睛】对于利用导数研究不等式的恒成立问题的求解策略:1、通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.3、根据恒成立求解参数的取值时,一般涉及分类参数法,但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况,通常要设出导数的零点,难度较大.17.【分析】利用导数研究函数的单调性由此可求得该函数的极大值【详解】定义域为令可得或当或时此时函数单调递增;当时此时函数单调递减所以函数在处取得极大值且极大值为故答案为:【点睛】本题考查利用导数求解函数 解析:427【分析】利用导数研究函数21f x x x 的单调性,由此可求得该函数的极大值.【详解】()()21f x x x =-,定义域为R ,()()()()()2121311f x x x x x x '=-+-=--.令()0f x '=,可得13x =或1x =. 当13x <或1x >时,()0f x '>,此时,函数21f x x x 单调递增;当113x <<时,()0f x '<,此时,函数21f x x x 单调递减.所以,函数21f xx x 在13x =处取得极大值,且极大值为21114133327f ⎛⎫⎛⎫=⨯-=⎪ ⎪⎝⎭⎝⎭. 故答案为:427. 【点睛】本题考查利用导数求解函数的极值,考查计算能力,属于中等题.18.【分析】利用导数求得在区间上的单调性和最值对分成三种情况进行分类讨论由此求得的取值范围【详解】当时所以在区间上递减最大值为最小值为当时在区间上没有零点在区间上递增而所以在区间上没有零点所以不符合题意解析:1(0,)2【分析】利用导数求得()f x 在区间[]0,1上的单调性和最值,对m 分成0,0,0m m m <=>三种情况进行分类讨论,由此求得m 的取值范围. 【详解】当01x ≤≤时,()()'26661fx x x x x =-=-,所以()f x 在区间[]0,1上递减,最大值为()0f m =,最小值为()11f m =-.当0m <时,()f x 在区间[]0,1上没有零点,在区间()1,+∞上递增, 而2110m -⨯+>,所以()f x 在区间()1,+∞上没有零点.所以0m <不符合题意.当0m =时,3223,01()1,1x x x f x x ⎧-≤≤=⎨>⎩,所以()f x 在区间[)0,+∞上有唯一零点()00f =,所以0m =不符合题意.当0m >时,()f x 在区间[]0,1和区间()1,+∞上递减,要使()f x 的图象与x 轴有且只有两个不同的交点,则需0102110m m m >⎧⎪-≤⎨⎪-⨯+>⎩,解得102m <<.综上所述,m 的取值范围是10,2⎛⎫ ⎪⎝⎭. 故答案为:1(0,)2【点睛】本小题主要考查利用导数研究函数的零点,考查分类讨论的数学思想方法,属于中档题.19.【分析】根据函数求导解的解集即可【详解】因为函数所以令得或当时所以函数在上的递增区间是故答案为:【点睛】本题主要考查导数与函数的单调性还考查了转化问题和运算求解的能力属于中档题解析:5,33ππ⎡⎤⎢⎥⎣⎦【分析】根据函数2sin y x x =-,求导12cos y x '=-,解0y '>的解集即可. 【详解】因为函数2sin y x x =-, 所以12cos y x '=-, 令12cos 0y x '=-=,得3x π=或53x π=, 当533x ππ≤≤时,0y '>, 所以函数2sin y x x =-在[]0,2π上的递增区间是5,33ππ⎡⎤⎢⎥⎣⎦. 故答案为:5,33ππ⎡⎤⎢⎥⎣⎦【点睛】本题主要考查导数与函数的单调性,还考查了转化问题和运算求解的能力,属于中档题.20.【分析】根据在R 上递增结合将不等式恒成立转化为恒成立然后分和两种情况利用导数法求解【详解】因为所以成立所以在R 上递增又成立所以恒成立即恒成立当时转化为恒成立令当时单调递减当时单调递增所以当时求得最小解析:10a e≤≤ 【分析】根据()f x 在R 上递增,结合()01f =,将x R ∀∈不等式()21xf ax e a -+≤恒成立,转化为()2xa x e +≤ ,x R ∀∈恒成立,然后分20x +≤和20x +>两种情况,利用导数法求解. 【详解】因为()321f x x x =++,所以()2320f x x '=+>成立,所以()f x 在R 上递增,又()()01,21xf f ax e a =-+≤x R ∀∈成立,所以20x ax e a -+≤,x R ∀∈ 恒成立,即()2xa x e +≤,x R ∀∈恒成立,当20x +>时,转化为2xe a x ≤+恒成立,令()2xg x ex =+,()()()212x x e g x x +'=+,当21x -<<-时,()0g x '<,()g x 单调递减, 当1x >-时,()0g x '>,()g x 单调递增, 所以当1x =-时,()g x 求得最小值min 1()(1)g x g e=-=, 所以1a e≤, 当20x +≤时,转化为2xe a x ≥+恒成立,(),(,2)a g x x ≥∈-∞-上恒成立,(,2)x ∈-∞-时,()0,()g x g x '<单调递减,又(,2),()0x g x ∈-∞-<,所以0a ≥不等式恒成立, 综上:实数a 的取值范围为10a e≤≤ 故答案为:10a e≤≤ 【点睛】本题主要考查导数与函数的单调性,导数与不等式恒成立,还考查了转化化归的思想,分类讨论思想和运算求解的能力,属于中档题.三、解答题21.(1)2a =;(2)(-∞. 【分析】(1)由题意可得出()11f '=,由此可求得实数a 的值;(2)求出函数()f x 的定义域为()0,∞+,由题意可知,()2210af x x x'=+-≥在()0,∞+上恒成立,利用参变量分离法得出min2a x x ⎛⎫≤+ ⎪⎝⎭,利用基本不等式求出2x x +在()0,∞+上的最小值,由此可得出实数a 的取值范围.【详解】 (1)()2ln f x x a x x =--,()221af x x x'∴=+-,()13f a '∴=-,又()f x 在点()()1,1f 处的切线方程为2y x =-,()131f a '∴=-=,解得2a =; (2)()f x 的定义域为()0,∞+,()f x 在定义域上为增函数,()2210af x x x'∴=+-≥在()0,∞+上恒成立, 2a x x ∴≤+在()0,∞+上恒成立,min 2a x x ⎛⎫∴≤+ ⎪⎝⎭,由基本不等式2x x +=≥x时等号成立,故min2x x ⎛⎫+= ⎪⎝⎭ 故a的取值范围为(-∞. 【点睛】结论点睛:利用函数的单调性求参数,可按照以下原则进行:(1)函数()f x 在区间D 上单调递增()0f x '⇔≥在区间D 上恒成立; (2)函数()f x 在区间D 上单调递减()0f x '⇔≤在区间D 上恒成立; (3)函数()f x 在区间D 上不单调()f x '⇔在区间D 上存在异号零点; (4)函数()f x 在区间D 上存在单调递增区间x D ⇔∃∈,使得()0f x '>成立; (5)函数()f x 在区间D 上存在单调递减区间x D ⇔∃∈,使得()0f x '<成立. 22.(1)当1a =时,函数()f x 在区间(),1-∞上单调递增;在区间1,上单调递减;(2)当函数()g x 只有1个零点时,实数a 的取值范围是,2e ⎛⎫+∞ ⎪⎝⎭. 【分析】(1)先对函数求导,然后分别由0f x 和0f x 可求出函数的增区间和减区间;(2)由0g x,得1x =,或ln x a =,然后分ln 1a =,ln 1a <和ln 1a >三种情况讨论,当ln 1a =可得()g x 只有1个零点,当ln 1a <时,求出()g x 的单调区间,然后讨论其零点,当ln 1a >时,求出()g x 的单调区间,然后讨论其零点,从而可求出实数a 的取值范围 【详解】解:(1)当1a =时,()xxf x e =,定义域为R , 所以()1xxf x e -'=. 当1x <时,0f x,函数()f x 单调递增;当1x >时,0f x,函数()f x 单调递减.综上所述,当1a =时,函数()f x 在区间(),1-∞上单调递增; 在区间1,上单调递减.(2)因为0a >,函数()212x ax g x e x x =+-, 所以()()()111x xx a x e a g x x x e e -⎛⎫-'=+-=- ⎪⎝⎭. 当0g x时,得1x =,或ln x a =.①若ln 1a =,即a e =,则0g x恒成立,函数()g x 在R 上单调递增,因为()00g =,所以函数()g x 只有1个零点. ②若ln 1a <,即0a e <<, 当ln x a <时,0g x,函数()g x 单调递增; 当ln 1a x <<时,0g x ,函数()g x 单调递减;当1x >时,0g x,函数()g x 单调递增.(Ⅰ)当ln 0a <,即01a <<时,()()()ln 001g a g g >=>, 又因为()2220ag e =>,所以函数()g x 在区间1,2上有1个零点, 故函数()g x 在R 上至少有2个零点,不符合题意. (Ⅱ)当ln 0a =,即1a =时,()()()ln 001g a g g ==>, 又因为()2220g e =>,所以函数()g x 在区间1,2上有1个零点, 故函数()g x 在R 上至少有2个零点,不符合题意.(Ⅲ)当ln 0a >,即1a e <<时,()()()ln 001g a g g >=>, 若函数()g x 只有1个零点,需()1102a e g =->, 解得2ea e <<.③若ln 1a >,即a e >,当1x <时,0g x,函数()g x 单调递增;当1ln x a <<时,0g x ,函数()g x 单调递减; 当ln x a >时,0g x,函数()g x 单调递增.所以()()100g g >=,()21ln ln 02g a a =>所以函数()g x 在R 上只有1个零点.综上所述,当函数()g x 只有1个零点时,实数a 的取值范围是,2e ⎛⎫+∞ ⎪⎝⎭. 【点睛】关键点点睛:此题考查导数的应用,利用导数求函数的单调区间和求函数的零点,第二问解题的关键是由0g x求得1x =或ln x a =,然后分ln 1a =,ln 1a <和ln 1a >三种情况讨论函数的单调性,从而由零点的情况求出参数的取值范围,属于中档题 23.(1)91y x =+;(2)证明见解析. 【分析】(1)求出函数在0x =处的导数后可得切线方程.(2)设函数()1ln g x x x =+-,利用导数可证明在1(,)2+∞上有()()1,1f x g x ≥≥,但等号不同时成立,结合余弦函数的性质可证明()()1ln 2cos x x f x x +->在1()2,x ∈+∞恒成立.【详解】(1)解:2()3129f x x x -'=+,则()09f =,故曲线()y f x =在点()0,1处的切线方程为91y x =+. (2)证明:当1(,1)(3,)2x ∈⋃+∞时,()0f x '>, 则()f x 在1(,1),(3,)2+∞上单调递增;当()1,3x ∈时,()0f x '<,则()f x 在()1,3上单调递减. 因为133()(3)128f f =>=, 所以()f x 在1(,)2+∞上的最小值为()31f =.设函数()1ln g x x x =+-.则1()(0)x g x x x -'=>. 当1(,1)2x ∈时,()0g x '<,则()g x 在1(,1)2上单调递减;当(1,)x ∈+∞时,()0g x '>,则()g x 在(1,)+∞上单调递增. 故()()12g x g ≥=.从而()()1ln 2x x f x +-≥,但由于()1f x ≥与()2g x ≥的取等条件不同, 所以()()1ln 2x x f x +->.因为2cos 2x ≤,所以()()1ln 2cos x x f x x +->对1()2,x ∈+∞恒成立. 【点睛】方法点睛:对于不等式的恒成立的问题,如果该不等式中含有三角函数,那么可以利用三角函数的有界性把前者转化为与三角函数无关的不等式,这样便于问题的讨论与处理. 24.(1)答案见解析;(2)证明见解析. 【分析】 (1)求导()()1'(0)a x f x x x-=>,0a >,0a <,0a =讨论,令()'0f x >求解.(2)结合(1)将问题转化为()min 2f x >-求解. 【详解】(1)根据题意知,()()1'(0)a x f x x x-=>,当0a >时,当()01x ∈,时,()'0f x >,当()1x ∈+∞,时,()'0f x <, 所以()f x 的单调递增区间为()01,,单调递减区间为()1+∞,; 同理,当0a <时,()f x 的单调递增区间为()1+∞,,单调递减区间为()01,;当0a =时,()3f x =-,不是单调函数,无单调区间. (2)证明:当1a =-时,()ln 3f x x x =-+-, 所以12f ,由(1)知()ln 3f x x x =-+-在()1+∞,上单调递增, 所以当()1x ∈+∞,时,()()1f x f >. 即()2f x >-,所以()20f x +>. 【点睛】方法点睛:利用导数方法证明不等式f (x )>g (x )在区间D 上恒成立的基本方法是构造函数h (x )=f (x )-g (x ),然后根据函数的单调性,或者函数的最值证明函数h (x )>0,其中一个重要技巧就是找到函数h (x )在什么地方可以等于零,这往往就是解决问题的一个突破口. 25.(I )1y x =-;(Ⅱ)1a <. 【分析】(Ⅰ)当0a =时,利用导数的几何意义求切线方程;(Ⅱ)首先求函数的导数,2(1)()10a x a x af x x a x x'-++=+--==时,11x =和2x a =,并讨论a 与0,1的大小关系,求实数a 的取值范围. 【详解】(I )当0a =时,21()12f x x x =-+. 所以()1f x x '=-, 所以(2)1k f '==,因为21(2)22112f =⨯-+=. 所以切线方程为1y x =-.(Ⅱ)函数()f x 的定义域为(0,)+∞. 因为21()ln (1)12f x a x x a x =+-++ 所以2(1)()1a x a x af x x a x x'-++=+--=. 令()0f x '=,即2(1)0x a x a -++=,解得1x =或x a =.(1)当0a 时,当x 变化时,(),()f x f x '的变化状态如下表:所以0a 成立.(2)当01a <<时,当x 变化时,(),()f x f x '的变化状态如下表:所以01a <<成立.(3)当1a =时,()0f x '在(0,)+∞上恒成立,所以函数()f x 在(0,)+∞上单调递增,没有板小值,不成立. (4)当1a >时,当x 变化时,(),()f x f x '的变化状态如下表:所以1a >不成立. 综上所述,1a <. 【点睛】关键点点睛:本题考查根据极值点求a 的取值范围,本题容易求出导函数的零点1和a ,但需讨论a 的范围,这是易错的地方,容易讨论不全面,需注意.26.(1)12a >-;(2)最大值点为36+.36x +=. 【分析】(1)根据()f x 在()0,∞+上存在单调递增区间,由()2220f x x x a =-++>'在()0,∞+上有解求解.(2)由()0G x '=得1x =2x =,根据02a <<,易得10x <,213x <<,则()G x 在[]1,3上的最大值点为2x ,最小值为()1G 或()3G ,然后由()()143143G G a -=-+,分14403a -+<,14403a -+≥确定最小值进而求得a 即可 【详解】(1)∵()f x 在()0,∞+上存在单调递增区间, ∴()2220f x x x a =-++>'在()0,∞+上有解,即()max 0f x '>在()0,∞+上成立, 而()f x '的最大值为()112f a '=+, ∴120a +>, 解得:12a >-. (2)3211()()()2432G x f x g x x x ax =-=-+++, ∴()22G x x x a '=-++,由()0G x '=得:112x =,212x +=,则()G x 在()1,x -∞,()2,x +∞上单调递减,在()12,x x 上单调递增, 又∵当02a <<时,10x <,213x <<,∴()G x 在[]1,3上的最大值点为2x ,最小值为()1G 或()3G , 而()()143143G G a -=-+, 1︒当14403a -+<,即706a <<时,()113623G a =-=-,得136a =,此时,最大值点236x +=; 2︒ 当14403a -+≥,即726a ≤<时,()2511263G a =+=-,得94a =-(舍).综上()G x 在[]1,3 【点睛】方法点睛:(1)求解函数的最值时,要先求函数y =f (x )在[a ,b ]内所有使f ′(x )=0的点,再计算函数y =f (x )在区间内所有使f ′(x )=0的点和区间端点处的函数值,最后比较即得; (2)已知函数的最值求参数,一般先用参数表示最值,列方程求解参数.。
高三理科数学一轮单元卷:第四单元 导数及其应用 A卷

一轮单元训练金卷▪高三▪数学卷(A )第四单元 导数及其应用注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列求导数运算错误的是( ) A .()33ln 3x x '=B .()31log ln3x x '=C .2cos sin cos x x x x x x '-⎛⎫= ⎪⎝⎭D .()2ln 2ln x x x x x '=+2.函数22ln y x x =-的单调增区间为( )A .()()101-∞-,,B .()1+∞,C .()()101-+∞,,D .()01,3.函数()31443f x x x =-+-在[]03,上的最大值为( )A .4-B .4C .43D .24.若曲线()3f x x ax =+在点()()00f ,处的切线与210x y --=平行,则a 的值为( ) A .2-B .0C .1D .25.已知函数()y xf x =-'的图象如图所示,其中()f x '是函数()f x 的导函数,则函数()y f x =的大致图象可以是( )A .B .C .D .6.函数()ln f x a x x =+在区间[]23,上单调递增,则实数a 的取值范围为( ) A .3a >-B .2a >-C .3a ≥-D .2a ≥-7.若函数()()3261f x x ax a x =++++有极大值和极小值,则实数a 的取值范围是( )A .()12-,B .()()36-∞-+∞,,C .()36-,D .()()12-∞-+∞,,8.设点P 是曲线335y x =+上的任意一点,点P 处切线的倾斜角为α,则角α的取值范围是( ) A .2π03⎡⎤⎢⎥⎣⎦,B .2π0ππ23⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭,, C .23π2π⎛⎤⎥⎝⎦, D .33π2π⎡⎤⎢⎥⎣⎦,9.函数()33f x x x =-在()2a ,上有最小值,则实数a 的范围是( ) A .()1-∞,B .()11-,C .[)21-,D .[)11-,10.已知函数()37sin f x x x x =--+,若()()220f a f a +->,则实数a 的取值范围是( )A .()21-,B .()3-∞,C .()12-,D .()1-∞,11.(e 为自然对数的底数),若()0f x >在()0,+∞上恒成立,则实数m 的取值范围是( )A .(),2-∞B .(),e -∞C D 12.设函数()f x 的导函数为()'f x ,若对任意x ∈R 都有()()'f x f x >成立,则( ) A .()()ln 201520150f f < B .()()ln 201520150f f = C .()()ln 201520150f f >D .()ln 2015f 与()20150f 的大小关系不能确定二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.函数()sin f x x x =在πx =处的切线方程为______________.14.设函数()f x 满足()()()2311f x x f x f '=+-,则()'1f =___________. 15.已知函数()()2f x x x m =-在2x =处取得极小值,则m =__________. 16.已知函数()232ln xf x x x a=-+(0a >),若函数()f x 在[]12,上为单调函数,则a 的取值范围是__________.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(10分)已知曲线31433y x =+.求:(1)曲线在点()24P ,处的切线方程; (2)曲线过点()24P ,的切线方程. (参考数据:()()2323412x x x x -+=+-)18.(12分)已知函数()()321,3f x x ax bx a b =++∈R 在3x =-处取得极大值为9,(1)求a ,b 的值;(2)求函数()f x 在区间[]33-,上的最值.19.(12分)已知函数()2ln f x x x =-,(1)求曲线()y f x =在点(1,(1))f 处的切线方程; (2)求()y f x =的最小值.20.(12分)已知函数()2ln f x x a x =+的极值点为2.(1)求实数a 的值;(2)求函数()f x 的极值;(3)求函数()f x21.(12 (1)当1a =时,求()y f x =在0x =处的切线方程; (2)若函数()f x 在[]1,1-上单调递减,求实数a 的取值范围.22.(12分)已知函数()3232f x x ax =-.(1)若直线()0y ax a =≠与曲线()y f x =相切,求a 的值;(2)若函数()f x 在()13,上不单调,且函数()()g x f x a =+有三个零点,求a 的取值范围.一轮单元训练金卷▪高三▪数学卷答案(A )第四单元 导数及其应用一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.【答案】C【解析】()33ln 3x x '=,A 对;()()()222ln ln ln 2ln x x x x x x x x x ''=+=+,D 对; 2cos sin cos x x x xx x '--⎛⎫= ⎪⎝⎭,C 错;()3311log log ln3e x x x '==,B 对,故选C . 2.【答案】B【解析】函数22ln y x x =-的定义域为()0,+∞, 求函数22ln y x x =-的导数得2'2y x x=-,令0y '>,解得1x <-(舍)或1x >, ∴函数22ln y x x =-的单调增区间为()1+∞,,本题选择B 选项. 3.【答案】C【解析】函数()31443f x x x =-+-的导数为()24f x x '=-+,由()0f x '=,可得2x =(2-舍去),由()842433f =-=,()04f =-,()31f =-,可得()f x 在[0]3,上的最大值为43.本题选择C 选项. 4.【答案】D【解析】由函数()3f x x ax =+,得()23f x x a ='+,因为函数()3f x x ax =+在点()()00f ,的切线为210x y --=, 所以()02f '=,解得2a =,故选D . 5.【答案】A【解析】由函数()y xf x =-'的图象得到: 当1x <-时,()0f x '<,()f x 是减函数; 当10x -<<时,()0f x '>,()f x 是增函数; 当01x <<时,()0f x '>,()f x 是增函数;当1x >时,()0f x '<,()f x 是减函数.由此得到函数()y f x =的大致图象可以是A .故选A . 6.【答案】D【解析】根据函数的导数与单调性的关系,()ln f x a x x =+在区间[]23,上单调递增,只需()0f x '≥在区间[]23,上恒成立. 由导数的运算法则,()=10a f x x '+≥,移向得,1ax≥-,a x ≥-,a 只需大于等于x -的最大值即可,由2x -≤-,∴2a ≥-,故选D . 7.【答案】B【解析】∵()()3261f x x ax a x =++++,∴()()2326f x x ax a '=+++; 又∵函数()()3261f x x ax a x =++++有极大值和极小值, ∴()()224360a a ∆=⨯⨯+﹣>;故6a >或3a <-;故选B . 8.【答案】B【解析】∵曲线335y x =+,∴23y x =', ∵点P 是曲线上的任意一点,点P 处切线的倾斜角为α,∴tan α≥,∵[)0,πα∈,∴π2π0π23α⎡⎫⎡⎫∈⎪⎪⎢⎢⎣⎭⎣⎭,,,故选B . 9.【答案】C【解析】由函数()33f x x x =-,得()()()233311f x x x x ==+'--,当()()11x ∈-∞-+∞,,时,()0f x '>,所以()f x 在区间()1-∞-,,()1+∞,单调递增, 当()11x ∈-,时,()0f x '<,所以()f x 在区间()11-,单调递减, 又由()12f =-,令()2f x =-,即332x x -=-,解得2x =-或1x =,要使得函数()33f x x x =-在()2a ,上有最小值,结合函数的图象可得,实数a 的取值范围是[)21-,,故选C . 10.【答案】A【解析】∵()37sin f x x x x =--+,∴()()()337sin 7sin f x x x x x x x f x =--+=-+=---,则()f x 是奇函数, 函数的导数()237cos 0f x x x -'=-+<,则函数()f x 是减函数, 则由()()220f a f a +->,得()()()222f a f a f a -=->-, 得22a a <-,即220a a +-<,得21a -<<,即实数a 的取值范围是()21-,.故答案为A . 11.【答案】D【解析】()0,+∞上恒成立,故在()0,+∞当()0,2x ∈时,()'0g x <,故()g x 在()0,2上为减函数; 当()2,x ∈+∞时,()'0g x >,故()g x 在()2,+∞上为增函数;D .12.【答案】C 【解析】令()()ln f x g x x=,0x >,则()()()2ln ln f x f x g x x -='',因为对任意x ∈R 都有()()'f x f x >成立,所以()()()2ln ln 0f x f x g x x -''=>恒成立,即()()ln f x g x x=在()0+∞,上单调递增,则()()()ln 2015ln1020151f f f >=,即()()ln201520150f f >.二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】2ππy x =-+【解析】当πx =时,()πsi 0πn πf ==,求解函数的导数可得()'sin cos f x x x x =+,则()'sin ππcos πππf =+⨯=-,据此可知,切线过点()π0,,切线的斜率为πk =-, 切线方程为:()0ππy x -=--,即:2ππy x =-+. 14.【答案】1-【解析】∵()()()2311f x x f x f '=+-,∴()()231f x x f '=+', 令1x =,则()()1231f f ''=+,即()11f '=-,故答案为1-. 15.【答案】2【解析】∵函数()()2f x x x m =-,∴()2234f x x mx m =-+', ∵函数()f x 在2x =处取得极小值,∴()221280f m m =-+=', ∴2m =或6m =,当2m =时,()()()2384322f x x x x x =-+=--',函数在2x =处取得极小值,符合题意; 当6m =时,()()()232436326f x x x x x =-+=--',函数在2x =处取得极大值,不符合题意. ∴2m =,故答案为2. 16.【答案】[)2015⎛⎤+∞ ⎥⎝⎦,,【解析】由函数()232ln x f x x x a =-+,得()314f x x a x=-+', 因为函数()f x 在[]12,上为单调函数,所以[]12x ∈,时,()0f x '≥或()0f x '≤恒成立, 即314x a x ≥-或314x a x≤-在[]12x ∈,上恒成立,且0a >, 设()14h x x x=-,因为函数()h x 在[]12,上单调递增,所以()311524222h a ≥=⨯-=或()313h a≤=,解得205a <≤或1a ≥,即实数a 的取值范围是[)2015⎛⎤+∞ ⎥⎝⎦,,. 三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【答案】(1)440x y --=;(2)440x y --=或20x y -+=. 【解析】(1)因为()24P ,在曲线31433y x =+上,且2y x '=, ∴在点()24P ,处的切线的斜率2|4x k y ='==. ∴曲线在点()24P ,处的切线方程为()442y x -=-,即440x y --=. (2)设曲线31433y x =+与过点()24P ,的切线相切于点()00,A x y , 则切线的斜率220|x k y x ='==,∴切线方程为()320001433y x x x x --=-,∵点()24P ,在切线上,∴2300144233x x =+-,即3200340x x -+=, ∴322000440x x x +-+=,即()()200120x x +-=解得01x =-或02x =, ∴所求的切线方程为440x y --=或20x y -+=.18.【答案】(1)13a b ==-⎧⎨⎩;(2)最大值为9,最小值为53-.【解析】(1)()22f x x ax b =++',依题意得()()3039f f -=-='⎧⎪⎨⎪⎩,即9609939a b a b -+=-+-=⎧⎨⎩,解得13a b ==-⎧⎨⎩.经检验,上述结果满足题意. (2)由(1)得()32133f x x x x =+-,()()()223=31f x x x x x ∴=+-+-',令()0f x '>,得3x <-或1x >;令()0f x '<,得31x -<<,()f x ∴的单调递增区间为()1+∞,和(),3-∞-,()f x 的单调递增区间是()31-,, ()()=39f x f ∴-=极大值,()()5=13f x f =-极小值,又()39f =,所以函数()f x 在区间[]33-,上的最大值为9,最小值为53-.19.【答案】(1)20x y +-=;(2)22ln2-. 【解析】(1)()2ln f x x x =-,()21f x x∴=-',()11f '=-,()11f =,()f x ∴的切线方程为20x y +-=. (2)()22'1x f x x x-=-=,令()'0f x =,2x =, ()f x ∴在()02x ∈,递减,在()2x ∈+∞,递增,()()min 222ln 2f x f ∴==-. 20.【答案】(1)8a =-;(2)极小值为()248ln2f =-;(3 【解析】(1)∵()2ln f x x a x =+,0x >,∴()2a f x x x='+, 又函数()f x 的极值点为2,∴()22202af =⨯+=', 解得8a =-.经验证得8a =-符合题意,∴8a =-. (2)由(1)得()28ln f x x x =+.∴()()()22282x x f x x x x+-=-=', 当02x <<时,()0f x '<,()f x 单调递减, 当2x >时,()0f x '>,()f x 单调递增.∴当2x =时,()f x 有极小值,且极小值为()248ln2f =-. (3)由(2)得()f x 当单调递减,在(]2,e 上单调递增, ∴()()min 248ln 2f x f ==-,21.【答案】(1)10x y +-=;(2【解析】(1)1a = ()2e 22x f x x x ∴=---',()01k f ∴'==-,()01f =,∴()y f x =在0x =处的切线方程为()10y x -=--,即10x y +-=.(2)()222xf x ae x x =---',()f x 在[]1,1-上单调递减,∴()2e 220x f x a x x -'=--≤在[]1,1-上恒成立,[]1,1-()g x 不是常数函数.∴()g x 在[]1,1-∴实数a22.【答案】(1)169a =-;(23a <. 【解析】(1)设切点为()00x ax ,,则()200033f x x ax a '=-=,所以3232000003332ax x ax x ax =-=-,解得00x =或034x a =, 当00x =时,0a =,不合题意.当034x a =时,22279164a a a =-,因为0a ≠,所以169a =-. (2)()()2333f x x ax x x a '=-=-,因为()f x 在()13,上不是单调函数,所以13a <<.因为()f x 在()0-∞,,()a +∞,上单调递增,在()0a ,上单调递减, 所以()f x 的极大值为()00f =,()f x 的极小值为()312f a a =-,函数()()g x f x a =+有三个零点,即()f x 的图象与直线y a =-有三个交点,所以301213a a a a ⎧-<⎪⎪⎨->-<<⎪⎪⎩3a <<.。
高考数学一轮复习导数及其应用多选题单元测试及解析

高考数学一轮复习导数及其应用多选题单元测试及解析一、导数及其应用多选题1.已知偶函数()y f x =对于任意的0,2x π⎡⎫∈⎪⎢⎣⎭满足()()cos sin 0f x x f x x '+>(其中()f x '是函数()f x 的导函数),则下列不等式中不成立的是( )A34f ππ⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭B34f ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭C .()04f π⎛⎫>- ⎪⎝⎭ D.63f ππ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭【答案】ABC 【分析】 构造函数()()cos f x g x x =,结合导数和对称性可知()g x 为偶函数且在0,2x π⎡⎫∈⎪⎢⎣⎭上单调递2643f f πππ⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,从而可判断ABD 选项,由()04g g π⎛⎫< ⎪⎝⎭可判断C 选项.【详解】因为偶函数()y f x =对于任意的0,2x π⎡⎫∈⎪⎢⎣⎭满足()()cos sin 0f x x f x x '+>, 所以构造函数()()cos f x g x x =,则()()2cos sin ()0cos f x x f x x g x x'+'=>, ∴()g x 为偶函数且在0,2x π⎡⎫∈⎪⎢⎣⎭上单调递增,32333cos 3f g g f πππππ⎛⎫⎪⎛⎫⎛⎫⎛⎫⎝⎭∴-=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,4444cos 4f g g πππππ⎛⎫ ⎪⎛⎫⎛⎫⎛⎫⎝⎭-=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,666cos 6f g f ππππ⎛⎫ ⎪⎛⎫⎛⎫⎝⎭== ⎪ ⎪⎝⎭⎝⎭,由函数单调性可知643g g g πππ⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2643f f πππ⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 对于AB,4343f f ππππ⎛⎫⎛⎫⎛⎫<=- ⎪ ⎪⎛⎫-= ⎪⎝⎭⎝⎭⎝ ⎪⎭⎭⎝,故AB 错误; 对于C ,()04g g π⎛⎫<⎪⎝⎭,()044f ππ⎛⎫⎛⎫<=- ⎪ ⎪⎝⎭⎝⎭,故C 错误;对于D 263f fππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,即63f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,故D 正确; 故选:ABC. 【点睛】关键点点睛:本题考查了利用导数研究函数的单调性,解题的关键是利用已知条件构造对应的新函数()()cos f x g x x=,利用导数研究函数的单调性,从而比较大小,考查学生的逻辑推理能力与转化思想,属于较难题.2.关于函数()sin x f x e a x =+,(,)x π∈-+∞,下列说法正确的是( ) A .当1a =时,()f x 在(0,(0))f 处的切线方程为210x y -+=; B .当1a =时,()f x 存在唯一极小值点0x ,且()010f x -<<; C .对任意0a >,()f x 在(,)π-+∞上均存在零点; D .存在0a <,()f x 在(,)π-+∞上有且只有一个零点. 【答案】ABD 【分析】当1a =时,()sin x f x e x =+,求出(),(0),(0)f x f f '',得到()f x 在(0,(0))f 处的切线的点斜式方程,即可判断选项A ;求出()0,()0f x f x ''><的解,确定()f x 单调区间,进而求出()f x 极值点个数,以及极值范围,可判断选项B ;令()sin 0xf x e a x =+=,当0a ≠时,分离参数可得1sin x x ae -=,设sin (),(,)xxg x x e π=∈-+∞,求出()g x 的极值最值,即可判断选项C ,D 的真假. 【详解】A.当1a =时,()sin x f x e x =+,所以()cos x f x e x '=+,0(0)cos 02f e '=+=,0(0)01f e =+=,所以()f x 在(0,(0))f 处的切线方程为210x y -+=,故正确;B. 因为()sin 0x f x e x ''=->,所以()'f x 单调递增,又()202f π'-=>,334433()cos442f e e ππππ--⎛⎫'-=+-=- ⎪⎝⎭,又233442e e e ππ⎛⎫= ⎪⎝>>⎭,即34e π>,则3()04f π'-<,所以存在03,42x ππ⎛⎫∈-- ⎪⎝⎭,使得0()0f x '=,即 00cos 0x e x +=,则在()0,x π-上()0f x '<,在()0,x +∞上,()0f x '>,所以()f x 存在唯一极小值点0x,因为000000()sin sin cos 4x f x e x x x x π⎛⎫=+=-=- ⎪⎝⎭,03,42x ππ⎛⎫∈-- ⎪⎝⎭,所以03,44x πππ⎛⎫-∈-- ⎪⎝⎭()01,04x π⎛⎫-∈- ⎪⎝⎭,故正确; C.令()sin 0x f x e a x =+=,当0a ≠时,可得1sin x xa e-=,设sin (),(,)x xg x x eπ=∈-+∞,则cos sin 4()x x x x x g x e e π⎛⎫- ⎪-⎝⎭'==,令()0g x '=,解得,,14x k k Z k ππ=+∈≥-当52,244x k k ππππ⎡⎤∈++⎢⎥⎣⎦时()0g x '<,当592,244x k k ππππ⎡⎤∈++⎢⎥⎣⎦时,()0g x '>,所以当524x k ππ=+,,1k Z k ∈≥-时,()g x 取得极小值,即35,,...44x ππ=-,()g x 取得极小值,又35 (44)g g ππ⎛⎫⎛⎫-<> ⎪ ⎪⎝⎭⎝⎭,因为在3,4ππ⎡⎤--⎢⎥⎣⎦上,()g x 递减,所以()34342g x g e ππ⎛⎫≥-=- ⎪⎝⎭,所以当24x k ππ=+,,0k Z k ∈≥时, ()g x 取得极大值,即9,, (44)x ππ=,()g x 取得极大值,又9 (44)g g ππ⎛⎫⎛⎫>> ⎪⎪⎝⎭⎝⎭ ,所以 ()442g x g e ππ⎛⎫≤= ⎪⎝⎭,所以(),x π∈-+∞时,()34422g x e ππ-≤≤,当3412e a π-<-,即34a e π>时,()f x 在(,)π-+∞上不存在零点,故C 错误; D.当412ae -=4a e π=时,1=-y a 与()sin x xg x e =的图象只有一个交点,所以存在0a <,()f x 在(,)π-+∞上有且只有一个零点,故D 正确; 故选:ABD 【点睛】方法点睛:用导数研究函数的零点,一方面用导数判断函数的单调性,借助零点存在性定理判断;另一方面,也可将零点问题转化为函数图象的交点问题,利用数形结合来解决.3.已知(0,1)x ∈,则下列正确的是( ) A .cos 2x x π+<B .22xx <C.sin 2x >D .1ln 1x x <-【答案】ABC 【分析】构造函数()sin f x x x =-证明其在0,2π⎛⎫⎪⎝⎭单调递减,即可得sin 22x x ππ⎛⎫-<-⎪⎝⎭即可判断选项A ;作出2yx 和2x y =的函数图象可判断选项B ;作出()sin2xf x =,()224x h x x =+的图象可判断选项C ;构造函数()1ln 1x g x x =+-利用导数判断其在()0,1x ∈上的单调性即可判断选项D ,进而可得正确选项.【详解】对于选项A :因为()0,1x ∈,所以022x ππ<-<,令()sin f x x x =-,()cos 10f x x '=-≤,()sin f x x x =-在0,2π⎛⎫⎪⎝⎭单调递减,所以()()00f x f <=,即sin x x <,所以sin 22x x ππ⎛⎫-<- ⎪⎝⎭即cos 2x x π<-,可得cos 2x x π+<,故A 正确, 对于选项B :由图象可得()0,1x ∈,22x x <恒成立,故选项B 正确;对于选项C :要证22sin 24xx x >+ 令()sin 2x f x =,()224xh x x =+()()f x f x -=-,()sin2xf x =是奇函数, ()()h x h x -=,()224x h x x =+是偶函数,令2224144x t x x ==-++ ,则y t =, 因为24y x =+在()0,∞+单调递增,所以2414t x =-+在()0,∞+单调递增,而y t =单调递增,由符合函数的单调性可知()224x h x x =+在()0,∞+单调递增, 其函数图象如图所示:由图知当()0,1x ∈时22sin 24xx x >+C 正确; 对于选项D :令()1ln 1x g x x =+-,()01x <<,()221110x g x x x x-'=-=<, 所以()1ln 1x g x x=+-在()0,1单调递减,所以()()1ln1110g x g >=+-=, 即1ln 10x x+->,可得1ln 1x x >-,故选项D 不正确.故选:ABC 【点睛】思路点睛:证明不等式恒成立(或能成立)一般可对不等式变形,分离参数,根据分离参数后的结果,构造函数,由导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式,直接构成函数,根据导数的方法,利用分类讨论求函数的最值,即可得出结果.4.已知:()f x 是奇函数,当0x >时,()'()1f x f x ->,(1)3f =,则( )A .(4)(3)f ef >B .2(4)(2)f e f ->-C .3(4)41f e >-D .2(4)41f e -<--【答案】ACD 【分析】由已知构造得'()+10x x e f ⎡⎤>⎢⎥⎣⎦,令()()+1x f x g x e =,判断出函数()g x 在0x >时单调递增,由此得()()4>3g g ,化简可判断A ;()()4>2g g ,化简并利用()f x 是奇函数,可判断B ;()()4>1g g ,化简可判断C ;由C 选项的分析得32(4)41>4+1f e e >-,可判断D.【详解】 因为当0x >时,()'()1fx f x ->,所以()'()10f x f x -->,即()[]'()+10xf x f e x ->,所以'()+10x x e f ⎡⎤>⎢⎥⎣⎦, 令()()+1xf xg x e=,则当0x >时,()'>0g x ,函数()g x 单调递增, 所以()()4>3g g ,即43(4)+1(3)+1>f f e e ,化简得(4)(3)1>(3)f f e e ef >+-,故A 正确;()()4>2g g ,即42(4)+1(2)+1>f f e e ,化简得222(4)(2)1>(2)f f e e e f >+-, 所以2(4)(2)e f f -<-,又()f x 是奇函数,所以2(4)(2)e f f -<-,故B 不正确;()()4>1g g ,即4(4)+1(1)+1>f f e e,又(1)3f =,化简得3(4)41f e >-,故C 正确; 由C 选项的分析得32(4)41>4+1f e e >-,所以2(4)41f e -<--,又()f x 是奇函数,所以2(4)41f e -<--,故D 正确, 故选:ACD. 【点睛】关键点点睛:解决本题中令有导函数的不等式,关键在于构造出某个函数的导函数,得出所构造的函数的单调性,从而可比较函数值的大小关系.5.设函数cos 2()2sin cos xf x x x=+,则( )A .()()f x f x π=+B .()f x 的最大值为12C .()f x 在,04π⎛⎫- ⎪⎝⎭单调递增 D .()f x 在0,4π⎛⎫⎪⎝⎭单调递减 【答案】AD 【分析】先证明()f x 为周期函数,周期为π,从而A 正确,再利用辅助角公式可判断B 的正误,结合导数的符号可判断C D 的正误. 【详解】()f x 的定义域为R ,且cos 2()2sin cos xf x x x=+,()()()()cos 22cos 2()2sin cos 2sin cos x xf x f x x x x xππππ++===++++,故A 正确.又2cos 22cos 2()42sin cos 4sin 2x x f x x x x ==++,令2cos 24sin 2xy x=+,则()42cos 2sin 22y x y x x ϕ=-=+,其中cos ϕϕ==1≤即2415y ≤,故1515y -≤≤,当y =时,有1cos 4ϕϕ==,此时()cos 21x ϕ+=即2x k ϕπ=-,故max 15y =,故B 错误. ()()()()()22222sin 24sin 22cos 2414sin 2()4sin 24sin 2x x x x f x x x ⎡⎤-+--+⎣⎦'==++,当0,4x π⎛⎫∈ ⎪⎝⎭时,()0f x '<,故()f x 在0,4π⎛⎫⎪⎝⎭为减函数,故D 正确. 当,04x π⎛⎫∈- ⎪⎝⎭时,1sin20x -<<,故314sin 21x -<+<, 因为2t x =为增函数且2,02x π⎛⎫∈- ⎪⎝⎭,而14sin y t =+在,02π⎛⎫- ⎪⎝⎭为增函数,所以()14sin 2h x x =+在,04π⎛⎫- ⎪⎝⎭上为增函数, 故14sin 20x +=在,04π⎛⎫-⎪⎝⎭有唯一解0x , 故当()0,0x x ∈时,()0h x >即()0f x '<,故()f x 在()0,0x 为减函数,故C 不正确. 故选:AD 【点睛】方法点睛:与三角函数有关的复杂函数的研究,一般先研究其奇偶性和周期性,而单调性的研究需看函数解析式的形式,比如正弦型函数或余弦型函数可利用整体法来研究,而分式形式则可利用导数来研究,注意辅助角公式在求最值中的应用.6.关于函数()sin ,(,)x f e x x x π∈-=+∞+,下列结论正确的有( )A .()f x 在(0,)+∞上是增函数B .()f x 存在唯一极小值点0xC .()f x 在(,)π-+∞上有一个零点D .()f x 在(,)π-+∞上有两个零点 【答案】ABD 【分析】根据函数()f x 求得()'f x 与()f x '',再根据()0f x ''>在(,)π-+∞恒成立,确定()'f x 在(,)π-+∞上单调递增,及(0,)x ∈+∞()0f x '>,且存在唯一实数03(,)42x ππ∈--,使0()=0f x ',从而判断A ,B 选项正确;再据此判断函数()f x 的单调性,从而判断零点个数.【详解】由已知()sin ,(,)x f e x x x π∈-=+∞+得()cos x f x e x '=+,()sin xf x e x ''=-,(,)x π∈-+∞,()0f x ''>恒成立,()'f x 在(,)π-+∞上单调递增,又3423()0,()0,(0)20422f e f e f ππππ--'''-=-<-=>=>(0,)x ∴∈+∞时()(0)0f x f ''>>,且存在唯一实数03(,)42x ππ∈--,使0()=0f x ',即00cos x e x =-,所以()f x 在(0,)+∞上是增函数,且()f x 存在唯一极小值点0x ,故A,B 选项正确. 且()f x 在0(,)x π-单调递减,0(,)x +∞单调递增,又()00f eππ--=+>,000000()sin sin cos )04x f x e x x x x π=+=-=-<,(0)10=>f ,所以()f x 在(,)π-+∞上有两个零点,故D 选项正确,C 选项错误.故选:ABD. 【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.7.已知函数()f x 的定义域为()0,∞+,其导函数()f x '满足()1f x x'<,且()11f =,则下列结论正确的是( ) A .()2f e >B .10f e ⎛⎫> ⎪⎝⎭C .()1,x e ∀∈,()2f x <D .1,1x e ⎛⎫∀∈ ⎪⎝⎭, ()120x f x f ⎛⎫+> ⎪⎝⎭- 【答案】BCD 【分析】令()()ln F x f x x =-,求导得:'1()()0F x f x x'=-<,可得函数的单调性,再结合(1)1f =,可得(1)1F =,对选项进行一一判断,即可得答案;【详解】令()()ln F x f x x =-,∴'1()()0F x f x x'=-<, ()F x ∴在(0,)+∞单调递减, (1)1f =,(1)(1)1F f ∴==,对A ,()(1)()11()2F e F f e f e <⇒-<⇒<,故A 错误; 以B ,111(1)()110eF F f f e e ⎛⎫⎛⎫>⇒+>⇒> ⎪ ⎪⎝⎭⎝⎭,故B 正确; 对C ,(1,)()(1)()ln 1x e F x F f x x ∈∴<⇒-<,()1ln f x x ∴<+,(1.),ln (0,1)x e x ∈∈, 1ln (1,2)x ∴+∈,()2f x ∴<,故C 正确;对D ,111,1,,()x x F x F e x x ⎛⎫⎛⎫∈>> ⎪ ⎪⎝⎭⎝⎭()1ln ln f x x f x x ⎛⎫⇒->+ ⎪⎝⎭ 1()2ln f x f x x ⎛⎫⇒-> ⎪⎝⎭,1,1,ln (1,0)x x e ⎛⎫∈∴∈- ⎪⎝⎭,1()2f x f x ⎛⎫∴->- ⎪⎝⎭1()20f x f x ⎛⎫⇒-+> ⎪⎝⎭,故D 正确; 故选:BCD. 【点睛】根据条件构造函数,再利用导数的工具性研究函数的性质,是求解此类抽象函数问题的关键.8.对于函数2ln ()xf x x=,下列说法正确的是( )A .()f x 在x =12eB .()f x 有两个不同的零点C .ff f <<D .若()21f x k x<-在()0,∞+上恒成立,则2e k >【答案】ACD 【分析】求得函数的导数312ln ()-'=xf x x,根据导数的符号,求得函数的单调区间和极值,可判定A 正确;根据函数的单调性和()10f =,且x >()0f x >,可判定B 不正确;由函数的单调性,得到f f >,再结合作差比较,得到f f >,可判定C 正确;分离参数得到()221ln 1x k f x x x +>+=在()0,∞+上恒成立,令()2ln 1x g x x +=,利用导数求得函数()g x 的单调性与最值,可判定D 正确. 【详解】由题意,函数2ln ()x f x x=,可得312ln ()(0)xf x x x -'=>,令()0f x '=,即312ln 0xx-=,解得x =当0x <<()0f x '>,函数()f x 在上单调递增;当x >()0f x '<,函数()f x 在)+∞上单调递减,所以当x =()f x 取得极大值,极大值为12f e=,所以A 正确; 由当1x =时,()10f =,因为()f x 在上单调递增,所以函数()f x 在上只有一个零点,当x >()0f x >,所以函数在)+∞上没有零点,综上可得函数在(0,)+∞只有一个零点,所以B 不正确;由函数()f x 在)+∞上单调递减,可得f f >,由于ln 2ln ,42f f ππ====,则2ln ln 2ln ln 22444f f ππππππ-=-=-,因为22ππ>,所以0f f ->,即f f >,所以ff f <<,所以C 正确;由()21f x k x<-在()0,∞+上恒成立,即()221ln 1x k f x x x +>+=在()0,∞+上恒成立,设()2ln 1x g x x +=,则()32ln 1x g x x --'=, 令()0g x '=,即32ln 10x x --=,解得x = 所以当0x<<()0g x '>,函数()g x 在上单调递增; 当x>()0g x '<,函数()g x 在)+∞上单调递减, 所以当x=()g x 取得最大值,最大值为22e e g e =-=, 所以2e k >,所以D 正确. 故选:ACD.【点睛】本题主要考查导数在函数中的综合应用,以及恒成立问题的求解,着重考查了转化与化归思想、逻辑推理能力与计算能力,对于恒成立问题,通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;也可分离变量,构造新函数,直接把问题转化为函数的最值问题.9.已知函数()()()221x f x x e a x =-+-有两个零点,则a 的可能取值是( ) A .1-B .0C .1D .2 【答案】CD【分析】求出()f x 的导数,讨论a 的范围,结合函数的单调性和零点存在性定理可判断求出.【详解】解:∵函数()()()221x f x x e a x =-+-,∴()()()()()12112x x f x x e a x x e a '=-+-=-+, ①若0a =,那么()()0202xf x x e x =⇔-=⇔=, 函数()f x 只有唯一的零点2,不合题意;②若0a >,那么20x e a +>恒成立,当1x <时,()0f x '<,此时函数为减函数;当1x >时,()0f x '>,此时函数为增函数;此时当1x =时,函数()f x 取极小值e -,由()20f a =>,可得:函数()f x 在1x >存在一个零点;当1x <时,x e e <,210x -<-<,∴()()()()()222121x f x x e a x x e a x =-+->-+- ()()211a x e x e =-+--,令()()2110a x e x e -+--=的两根为1t ,2t ,且12t t <,则当1x t <,或2x t >时,()()()2110f x a x e x e >-+-->,故函数()f x 在1x <存在一个零点;即函数()f x 在R 上存在两个零点,满足题意;③若02e a -<<,则()ln 2ln 1a e -<=, 当()ln 2x a <-时,()1ln 21ln 10x a e -<--<-=,()ln 2220a x e a e a -+<+=,即()()()120x f x x e a '=-+>恒成立,故()f x 单调递增, 当()ln 21a x -<<时,10x -<,()ln 2220a x e a e a -+>+=,即()()()120xf x x e a '=-+<恒成立,故()f x 单调递减, 当1x >时,10x ->,()ln 2220a x e a e a -+>+=,即()()(1)20x f x x e a '=-+>恒成立,故()f x 单调递增, 故当()ln 2x a =-时,函数取极大值,由()()()()()2ln 2ln 222ln 21f a a a a a ⎡⎤⎡⎤-=---+--⎣⎦⎣⎦ (){}2ln 2210a a ⎡⎤⎣⎦=--+<得:函数()f x 在R 上至多存在一个零点,不合题意;④若2e a =-,则()ln 21a -=, 当()1ln 2x a <=-时,10x -<,()ln 2220a x e a e a -+<+=,即()()()120x f x x e a '=-+>恒成立,故()f x 单调递增, 当1x >时,10x ->,()ln 2220a x e a e a -+>+=,即()()()120xf x x e a '=-+>恒成立,故()f x 单调递增, 故函数()f x 在R 上单调递增,函数()f x 在R 上至多存在一个零点,不合题意;⑤若 2e a <-,则()ln 2ln 1a e ->=, 当1x <时,10x -<,()ln 2220a x e a e a -+<+=,即()()()120x f x x e a '=-+>恒成立,故()f x 单调递增, 当()1ln 2x a <<-时,10x ->,()ln 2220a x e a e a -+<+=, 即()()()120x f x x e a '=-+<恒成立,故()f x 单调递减, 当()ln 2x a >-时,10x ->,()ln 2220a x e a e a -+>+=,即()()()120x f x x e a '=-+>恒成立,故()f x 单调递增,故当1x =时,函数取极大值,由()10f e =-<得:函数()f x 在R 上至多存在一个零点,不合题意;综上所述,a 的取值范围为()0,∞+,故选:CD.【点睛】本题考查利用导数研究函数的零点问题,属于较难题.10.函数()ln f x x x =、()()f xg x x '=,下列命题中正确的是( ).A .不等式()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭B .函数()f x 在()0,e 上单调递增,在(,)e +∞上单调递减C .若函数()()2F x f x ax =-有两个极值点,则()0,1a ∈ D .若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立,则m 1≥ 【答案】AD【分析】 对A ,根据()ln f x x x =,得到()()ln 1f x x g x x x'+==,然后用导数画出其图象判断;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<判断;对C ,将函数()()2F x f x ax =-有两个极值点,()ln 120x a x+=+∞在,有两根判断;对D ,将问题转化为22111222ln ln 22m m x x x x x x ->-恒成立,再构造函数()2ln 2m g x x x x =-,用导数研究单调性.【详解】 对A ,因为()()()ln 1ln f x x f x x x g x x x'+===、, ()2ln x g x x-'=,令()0g x '>,得()0,1x ∈,故()g x 在该区间上单调递增;令()0g x '<,得()1x ∈+∞,,故()g x 在该区间上单调递减. 又当1x >时,()0g x >,()10,11g g e ⎛⎫== ⎪⎝⎭,故()g x 的图象如下所示:数形结合可知,()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭,故正确; 对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<,所以函数()f x 在()0,e 上单调递减,在(,)e +∞上单调递增,错误;对C ,若函数()()2F x f x ax =-有两个极值点, 即()2ln F x x x ax =-有两个极值点,又()ln 21F x x ax '=-+, 要满足题意,则需()ln 2100x ax -+=+∞在,有两根, 也即()ln 120x a x+=+∞在,有两根,也即直线()2y a y g x ==与的图象有两个交点. 数形结合则021a <<,解得102a <<. 故要满足题意,则102a <<,故错误; 对D ,若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立,即22111222ln ln 22m m x x x x x x ->-恒成立, 构造函数()2ln 2m g x x x x =-,()()12g x g x >,对任意的120x x >>恒成立, 故()g x ()0+∞,单调递增,则()ln 10g x mx x '=--≥()0+∞, 恒成立, 也即ln 1x m x+≤,在区间()0,∞+恒成立,则()max 1g x m =≤,故正确. 故选:AD.【点睛】 本题主要考查导数在函数图象和性质中的综合应用,还考查了数形结合的思想、转化化归思想和运算求解的能力,属于较难题.。
(压轴题)高中数学选修1-1第四章《导数应用》测试卷(含答案解析)
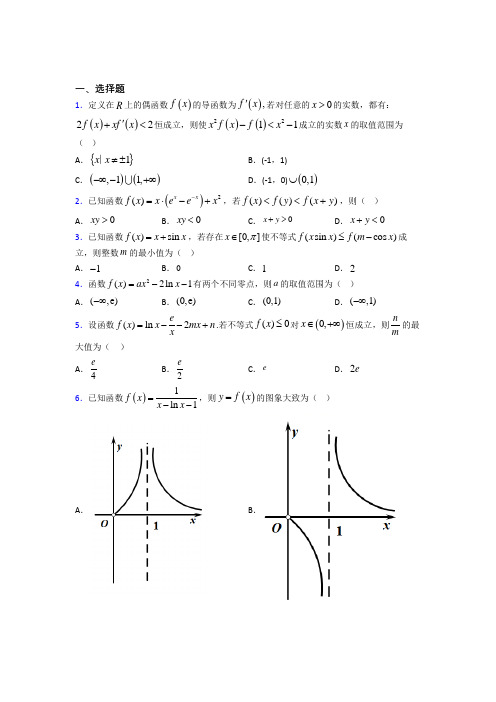
一、选择题1.定义在R 上的偶函数()f x 的导函数为(),f x '若对任意的0x >的实数,都有:()()22f x xf x '+<恒成立,则使()()2211x f x f x -<-成立的实数x 的取值范围为( )A .{}1xx ≠±∣ B .(-1,1) C .()(),11,-∞-+∞D .(-1,0)()0,1⋃2.已知函数()2()x xf x x e e x-=⋅-+,若()()()f x f y f x y <<+,则( )A .0xy >B .0xy <C .0x y +>D .0x y +<3.已知函数()sin f x x x =+,若存在[0,]x π∈使不等式(sin )(cos )f x x f m x ≤-成立,则整数m 的最小值为( ) A .1- B .0C .1D .2 4.函数2()2ln 1f x ax x =--有两个不同零点,则a 的取值范围为( )A .(,e)-∞B .(0,e)C .(0,1)D .(,1)-∞5.设函数()ln 2e f x x mx n x =--+.若不等式()0f x ≤对()0,x ∈+∞恒成立,则nm 的最大值为( ) A .4e B .2eC .eD .2e6.已知函数()1ln 1f x x x =--,则()y f x =的图象大致为( )A .B .C .D .7.已知定义在R 上的函数()f x 满足()()f x f x '<-,则下列式子成立的是( ) A .(2020)(2021)f ef > B .(2020)(2021)f ef < C .(2020)(2021)ef f >D .(2020)(2021)ef f <8.若定义在R 上的函数()f x 满足()()1f x f x '+>,(0)4f =,则不等式()3x x e f x e ⋅>+ (其中e 为自然对数的底数)的解集为( ) A .(0)(0)-∞+∞,, B .(0)(3)-∞⋃+∞,, C .(0)+∞,D .(3)+∞,9.已知函数()()22,02ln ,0xx f x a x x x x -⎧<⎪=⎨++>⎪⎩,若恰有3个互不相同的实数1x ,2x ,3x ,使得()()()1232221232f x f x f x x x x ===,则实数a 的取值范围为( ) A .1a e>-B .10a e-<< C .0a ≥ D .0a ≥或1a e=-10.已知函数321()13f x x ax x =+++在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,则实数a 的取值范围为( )A .(,1]-∞-B .55,34⎡⎤--⎢⎥⎣⎦C .5,13⎛⎤-- ⎥⎝⎦D .55,34⎛⎫--⎪⎝⎭11.若函数32()21f x ax x x =+++在(1,2)上有最大值无最小值,则实数a 的取值范围为( ) A .34a >-B .53a <-C .5334a -<<- D .5334a -≤≤- 12.若函数()xx f x ax ee -=+-在R 上单调递减,则实数a 的取值范围为( )A .2a ≤B .1a ≤C .1a ≥D .2a ≥二、填空题13.已知函数2()ln 3mf x x x x x=+-+.若函数()f x 在[1,2]上单调递减,则实数m 的最小值为________.14.函数()y f x =的导函数的图像如图所示,给出下列判断:①函数()y f x =在区间(3)5,内单调递增; ②函数()y f x =在区间1(3)2-,内单调递减; ③函数()y f x =在区间(22)-,内单调递增; ④当12x =-时,函数()y f x =有极大值;⑤当2x =时,函数()y f x =有极大值; 则上述判断中正确的是________.15.若函数32()f x x x =-在区间(,3)a a +内存在最大值,则实数a 的取值范围是____________.16.若0x ∀>,不等式ln 2(0)a x b a x ++≥>恒成立,则ba的最大值为________. 17.已知定义在R 上的函数()f x 关于y 轴对称,其导函数为()f x '. 当0x ≥时,()()1xf x f x '>-. 若对任意x ∈R ,不等式()()0x x x e f e e ax axf ax -+->恒成立,则正整数a 的最大值为_____.18.已知函数()x f x e alnx =-+2在[]1,4上单调递增,则a 的取值范围是__.19.如图,两条距离为4的直线都与y 轴平行,它们与抛物线()22014y px p =-<<和圆()2249x y -+=分别交于A ,B 和C ,D ,且抛物线的准线与圆相切,则22AB CD ⋅的最大值为______.20.已知a R ∈,设函数232,1()1,1x x a x f x x a nx x ⎧-+=⎨->⎩,若关于x 的不等式()0f x ≥在R上恒成立,则a 的取值范围是_________. 三、解答题21.已知函数()()21xf x x ae=-+.(1)讨论()f x 的单调性;(2)若()f x 存在零点,求a 的取值范围. 22.已知函数()1ln f x x x =--. (1)求证:()0f x ≥;(2)求证:对于任意正整数n ,2111111222n e ⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. 23.已知函数()(1)ln ()af x x a x a x=+-+∈R . (1)讨论函数()f x 的单调性;(2)当0a >时,若()2f x ≥恒成立,求实数a 的取值范围. 24.已知函数3()f x x x =-.(Ⅰ)求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间和极值; (Ⅲ)设函数()()2sin f x t x x x=-,(0,)x ∈π,试判断()t x 的零点个数,并证明你的结论. 25.设函数2()cos ,()sin a f x x x g x x=+=. (1)当[0,]x π∈时,判断()f x 的单调性; (2)若当,62x ππ⎡⎤∈⎢⎥⎣⎦时,不等式()()0f x g x -恒成立,求a 的取值范围. 26.已知函数()ln f x x ax =-有两个不同的零点()1212,x x x x <,其中e 2.71828=是自然对数的底数.(1)求实数a 的取值范围; (2)求证:(i )1x <;(ii )212x x ->.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据已知构造合适的函数,对函数求导,根据函数的单调性,求出函数的取值范围,并根据偶函数的性质的对称性,求出0x <的取值范围. 【详解】当0x >时,由2()()20f x xf x +'-<可知:两边同乘以x 得:22()()20xf x x f x x +'-< 设:22()()g x x f x x =-则2()2()()20g x xf x x f x x '=+'-<,恒成立:()g x ∴在(0,)+∞单调递减,由()()21x f x f -21x <-()()2211x f x x f ∴-<-即()()1g x g < 即1x >;当0x <时,函数是偶函数,同理得:1x <-综上可知:实数x 的取值范围为(-∞,1)(1-⋃,)+∞, 故选:C 【点睛】关键点点睛:主要根据已知构造合适的函数,函数求导,并应用导数法判断函数的单调性,偶函数的性质,属于中档题.2.A解析:A 【分析】先判断函数的奇偶性和单调性,再分析得解. 【详解】由题得函数的定义域为R.()22())()(x x x x f x x e e x e e x x f x --=-+=-=-⋅-+,所以函数是偶函数.当0x >时,1()()2xx x x f x e xe xe x e-'=-+++, 因为0x >,所以()0f x '>,所以函数()f x 在(0,)+∞上单调递增,因为函数是偶函数,所以函数()f x 在(,0)-∞上单调递减,在(0,)+∞上单调递增. 如果0,0x y >>,则0x y +>,因为()()()f x f y f x y <<+,所以x y x y <<+,与已知相符; 如果0,0x y <<,则0x y +<,所以x y x y >>+,与已知相符; 如果0,0x y ><,因为()()f x f y <,所以0y x y <+<, 所以()()f y f x y >+,与已知矛盾;如果0,0x y <>,因为()()f x f y <,所以0y x y >+>, 所以()()f y f x y >+,与已知矛盾;当,x y 之中有一个为零时,不妨设0y =,()()f x y f x += ,()()()f x f y f x <<,显然不成立.故选:A 【点睛】方法点睛:对于函数的问题,要灵活利用函数的奇偶性和单调性分析函数的问题,利用函数的图象和性质分析函数的问题.3.A解析:A 【分析】先对()f x 求导可得()1cos 0f x x '=+≥,()f x 单调递增,原不等式可化为存在[0,]x π∈ 使得sin cos x x m x ≤-有解,即sin cos m x x x ≥+对于[0,]x π∈有解,只需()min m g x ≥,利用导数判断()g x 的单调性求最小值即可. 【详解】由()sin f x x x =+可得()1cos 0f x x '=+≥, 所以()sin f x x x =+在[0,]x π∈单调递增,所以不等式(sin )(cos )f x x f m x ≤-成立等价于sin cos x x m x ≤-, 所以sin cos m x x x ≥+对于[0,]x π∈有解, 令()sin cos g x x x x =+,只需()min m g x ≥, 则()sin cos sin cos g x x x x x x x '=+-=,当02x π≤≤时,()cos 0g x x x '=≥,()g x 在0,2π⎡⎤⎢⎥⎣⎦单调递增,当2x ππ<≤时,()cos 0g x x x '=<,()g x 在,2ππ⎡⎤⎢⎥⎣⎦单调递减, ()0cos01g ==,()sin cos 1g ππππ=+=-,所以()()min 1g x g π==-, 所以1m ≥-, 整数m 的最小值为1-, 故选:A. 【点睛】方法点睛:若不等式(),0f x λ≥()x D ∈(λ是实参数)有解,将(),0f x λ≥转化为()g x λ≥或()()g x x D λ≤∈有解,进而转化为()max g x λ≤或()()min g x x D λ≥∈,求()g x 的最值即可.4.C解析:C 【分析】先令()0f x =,分离参数得到22ln 1x a x +=,令()22ln 1x g x x+=根据函数有两个不同零点,可得y a =与()22ln 1x g x x+=的图象有两个不同交点,对()g x 求导,判定其单调性,得出最值,画出大致图象,结合图象,即可得出结果. 【详解】因为函数2()2ln 1f x ax x =--有两个不同零点, 所以方程22ln 10ax x --=有两不同实根,即22ln 1x a x+=有两个不同的零点, 令()22ln 1x g x x +=,0x >,则得y a =与()22ln 1x g x x +=的图象有两个不同交点, 因为()()24322ln 124ln x x xx x g x x x ⋅-+⋅-'==,由()0g x '=可得1x =, 当()0,1x ∈时,()0g x '>,则()g x 单调递增; 当()1,x ∈+∞时,()0g x '<,则()g x 单调递减; 所以()()max 11g x g ==,又由()22ln 10x g x x +=>可得x >()22ln 10x g x x +=<可得0x <<, 画出()22ln 1x g x x+=的大致图象如下:由图像可得,当01a <<时,y a =与()22ln 1x g x x +=的图象有两个不同交点, 即原函数有两个不同零点. 故选:C. 【点睛】 思路点睛:利用导数的方法研究函数零点个数(方程根的个数)求参数问题时,一般需要先分离参数,根据分离后的结果,构造新的函数,利用导数的方法研究函数单调性,确定函数最值,利用数形结合的方法求解.5.D解析:D 【分析】 由题意可得ln 22e n x m x x m ⎛⎫-≤- ⎪⎝⎭对()0,x ∈+∞恒成立,设()ln e g x x x =-,()2,02n h x m x x m ⎛⎫=-> ⎪⎝⎭,根据它们的图象,结合的导数的几何意义,以及射线的性质,即可得到所求的最大值. 【详解】由不等式()0f x ≤对()0,x ∈+∞恒成立, 即为ln 20e x mx n x --+≤,即ln 22e n x m x x m ⎛⎫-≤- ⎪⎝⎭对()0,x ∈+∞恒成立,设()ln e g x x x =-,由()210eg x x x'=+>, 可得()g x 在()0,∞+上递增,且()0g e =,当0x →时,()g x →-∞;x →+∞,()g x →+∞, 作出()y g x =的图象, 再设()2,02n h x m x x m ⎛⎫=-> ⎪⎝⎭, 可得()h x 表示过,02n m ⎛⎫⎪⎝⎭,斜率为2m 的一条射线(不含端点),要求nm 的最大值,且满足不等式恒成立,可得2n m的最大值, 由于点,02n m ⎛⎫⎪⎝⎭在x 轴上移动, 只需找到合适的0m >,且()ln e g x x x =-切于点,02n m ⎛⎫⎪⎝⎭,如图所示:此时2n e m =,即nm 的最大值为2e . 故选:D 【点睛】关键点点睛:本题考查不等式恒成立问题的解法,解题的关键是将问题转化为()ln e g x x x =-切于点,02n m ⎛⎫⎪⎝⎭,注意运用转化思想和数形结合思想,考查了导数的应用,求切线的斜率与单调性,考查了运算能力和推理能力.6.A解析:A 【分析】利用导数分析函数ln 1y x x =--的单调性以及函数值符号,由此可得出函数()y f x =的图象. 【详解】对于函数ln 1y x x =--,该函数的定义域为()0,∞+,求导得111x y x x-'=-=. 当01x <<时,0y '<,此时函数ln 1y x x =--单调递减; 当1x >时,0y '>,此时函数ln 1y x x =--单调递增.所以,函数ln 1y x x =--的最小值为min 1ln110y =--=,即对任意的0x >,ln 10x x --≥.所以,函数()y f x =的定义域为()()0,11,+∞,且()0f x >,函数()y f x =的单调递增区间为()0,1,递减区间为()1,+∞. 所以,函数()y f x =的图象如A 选项中函数的图象. 故选:A. 【点睛】思路点睛:函数图象的辨识可从以下方面入手: (1)从函数的定义域,判断图象的左右位置; (2)从函数的值域,判断图象的上下位置. (3)从函数的单调性,判断图象的变化趋势; (4)从函数的奇偶性,判断图象的对称性; (5)函数的特征点,排除不合要求的图象.7.A解析:A 【分析】构造函数()()xg x e f x =,求导判定函数单调性,根据单调性得(2020)(2021)g g >化简即可. 【详解】解:依题意()()0f x f x '+<,令()()xg x e f x =,则()(()())0xg x f x f x e ''=+<在R 上恒成立, 所以函数()()xg x e f x =在R 上单调递减, 所以(2020)(2021)g g >即20202021(2020)(2021)(2020)(2021)e e e f f f f >⇒>故选:A. 【点睛】四种常用导数构造法:(1)对于不等式()()0f x g x ''+> (或0<) ,构造函数()()()F x f x g x =+. (2)对于不等式()()0f x g x ''->(或0<) ,构造函数()()()F x f x g x =-.(3)对于不等式()()0f x f x '+>(或0<) ,构造函数()()xF x e f x =.(4)对于不等式()()0f x f x '->(或0<) ,构造函数()()xf x F x e =. 8.C解析:C 【分析】构造函数()()3xxg x e f x e =⋅--,解不等式()0g x >即可,对()g x 求导得()[()()1]0x g x e f x f x ''=+->,可得()g x 在R 上单调递增,且(0)0g =,根据单调性可得0x >,即得正确答案. 【详解】令()()3x x g x e f x e =⋅--,则()()()[()()1]0xxxxg x e f x e f x e e f x f x '''=⋅+⋅-=+->, 所以()g x 在R 上单调递增, 又因为0(0)(0)30g e f e =⋅--=, 所以()0>g x ⇒0x >,即不等式的解集是(0)+∞,, 故选:C 【点睛】关键点点睛:本题的关键点是构造函数()()3xxg x e f x e =⋅--,所要解的不等式等价于()0g x >,且(0)0g =,所以()()0g x g >,因此需要对()g x 求导判断单调性即可. 9.D解析:D 【分析】根据题意,令()()221,02ln 2,0x x f x x g x x x a x x ⎧<⎪⎪⋅==⎨⎪++>⎪⎩,得到函数()()2f xg x x =与直线2y =共有三个不同的交点;根据导数的方法,分别判断0x <和0x >时,函数的单调性,以及最值,结合题中条件,即可得出结果. 【详解】因为()()22,02ln ,0xx f x a x x x x -⎧<⎪=⎨++>⎪⎩,令()()221,02ln 2,0x x f x x g x x x a x x ⎧<⎪⎪⋅==⎨⎪++>⎪⎩, 由题意,函数()()2f x g x x=与直线2y =共有三个不同的交点; 当0x <时,()212x g x x =⋅,则()()()()222232222ln 222ln 22222x x x x x x x x xx g x x x x '-⋅⋅+⋅+'==-=-⋅⋅⋅,由()3ln 2202x x g x x +'=-=⋅解得222log ln 2x e =-=-;所以()2,2log x e ∈-∞-时,()0g x '<,即函数()212x g x x =⋅单调递减; ()22log ,0x e ∈-时,()0g x '>,即函数()212x g x x =⋅单调递增; 所以()()()()222222min 2log 2212log 2422log 4log ee e g x g e e e -=-==<<⋅-,又2121122122g -⎛⎫-==> ⎪⎝⎭⎛⎫⋅- ⎪⎝⎭,()()271128724927g --==>⋅-, 所以()212x g x x =⋅与直线2y =有且仅有两个不同的交点; 当0x >时,()ln 2xg x a x =++,则()21ln x g x x-'=, 由()21ln 0xg x x-'==得x e =, 所以当()0,x e ∈时,()0g x '>,则函数()ln 2xg x a x=++单调递增; 当(),x e ∈+∞时,()0g x '<,则函数()ln 2xg x a x=++单调递减; 所以()()max 12g x g e a e==++, 又当1≥x 时,()ln 22xg x a a x=++≥+;当01x <<时,()2g x a <+; 当x e ≥时,()ln 22xg x a a x=++>+, 所以为使()ln 2xg x a x=++与直线2y =只有一个交点, 只需122a e ++=或22a +≥,即1a e=-或0a ≥. 故选:D. 【点睛】本题主要考查由方程根的个数求参数,转化为函数交点个数问题求解即可,属于常考题型.10.B解析:B 【分析】求导得到2()21'=++f x x ax ,然后根据()f x 在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,由(0)0(1)0(2)0(3)0f f f f ''≥⎧⎪≤⎪⎨''≤⎪⎪≥⎩求解.【详解】 已知函数321()13f x x ax x =+++, 则2()21'=++f x x ax ,因为()f x 在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,所以(0)0(1)0(2)0(3)0f f f f ''≥⎧⎪≤⎪⎨''≤⎪⎪≥⎩,即10121044109610a a a ≥⎧⎪++≤⎪⎨++≤⎪⎪++≥⎩,解得 5534a -≤≤-, 所以实数a 的取值范围为55,34⎡⎤--⎢⎥⎣⎦故选:B 【点睛】本题主要考查导数与函数的单调性以及二次函数与根的分布,还考查了逻辑推理和运算求解的能力,属于中档题.11.C解析:C 【详解】分析:函数()3221f x ax x x =+++在()1,2上有最大值无最小值,则极大值在()1,2之间,一阶导函数有根在()1,2,且左侧函数值小于0,右侧函数值大于0,列不等式求解 详解:f ′(x )=3ax 2+4x +1,x ∈(1,2).a =0时,f ′(x )=4x +1>0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去. a ≠0时,△=16﹣12a . 由△≤0,解得43a ≥,此时f ′(x )≥0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去.由△>0,解得a 43<(a ≠0),由f ′(x )=0,解得x123a--=,x2=.当403a <<时,x 1<0,x 2<0,因此f ′(x )≥0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去.当a <0时,x 1>0,x 2<0,∵函数f (x )=ax 3+2x 2+x +1在(1,2)上有最大值无最小值,∴必然有f ′(x 1)=0,∴12,a <0.解得:53-<a 34-<. 综上可得:53-<a 34-<. 故选:C .点睛:极值转化为最值的性质:1、若()[]f x x a,b ∈在上有唯一的极小值,且无极大值,那么极小值为()f x 的最小值;2、若()[]f x x a,b ∈在上有唯一的极大值,且无极小值,那么极大值为()f x 的最大值;12.A解析:A 【分析】 由()xx f x ax e e -=+-在R 上单调递减,可得:导函数()0x x f x a e e -'=--≤在R 上恒成立,参变分离后,求最值即可的解.【详解】 由()x x f x ax ee -=+-在R 上单调递减,可得:导函数()0xx f x a e e -'=--≤在R 上恒成立,因为0x e >,参变分离可得:min (+)x xa e e -≤,+2x x e e -≥=2a ≤故选:A 【点睛】本题考查了利用函数单调性求参数范围,考查了恒成立思想和基本不等式的应用,属于中档题.二、填空题13.6【分析】求导函数令恒成立变量分离转化为求新函数的最大值【详解】可得令若函数在上单调递减即当时单调增所以函数在上单调递增所以故答案为:6【点睛】关键点睛:变量分离转化为不等式恒成立问题进而求又一函数解析:6【分析】求导函数()f x ',令()0f x '≤恒成立,变量分离转化为求新函数的最大值. 【详解】21()23mf x x x x'=+--,()0f x '≤,可得3223m x x x ≥-+, 令()3223g x x x x =-+,若函数()f x 在[1,2]上单调递减,即()max m g x ≥ 当[1,2]x ∈时,()2661g x x x '=-+单调增,()()266110g x x x g ''=-+≥>,所以函数()g x 在[1,2]上单调递增()()max 26g x g ==,所以6m ≥.故答案为:6 【点睛】关键点睛:变量分离,转化为不等式恒成立问题,进而求又一函数的最值.14.③⑤【分析】根据导函数图像得出导数正负根据导数正负判定单调区间根据左正右负和左负有正判定极值【详解】解:对于①当时单调递减当时单调递增所以①错;对于②当时单调递增当时单调递减所以②错;对于③当时单调解析:③⑤ 【分析】根据导函数图像得出导数正负,根据导数正负判定单调区间,根据左正右负和左负有正判定极值. 【详解】解:对于①,当(34)x ∈,时()0f x '<,()f x 单调递减, 当(4,5)x ∈时()0f x '>,()f x 单调递增,所以①错;对于②,当1(2)2x ∈-,时()0f x '>,()f x 单调递增, 当(23)x ∈,时()0f x '<,()f x 单调递减,所以②错; 对于③,当(22)x ∈-,时()0f x '>,()f x 单调递增,所以③对; 对于④,当(22)x ∈-,时()0f x '>,()f x 单调递增,故当12x =-时()f x 不是极大值,所以④错;对于⑤,当1(2)2x ∈-,时()0f x '>,()f x 单调递增, 当(23)x ∈,时()0f x '<,()f x 单调递减,故2x =时函数()y f x =取得极大值,所以⑤对.故答案为:③⑤. 【点睛】求函数的极值或极值点的步骤:(1)求导数()'f x ,不要忘记函数()f x 的定义域;(2)求方程()0f x '=的根;(3)检查在方程的根的左右两侧()'f x 的符号,确定极值点或函数的极值.15.【分析】首先利用导数判断函数的单调性再根据函数在开区间内存在最大值可判断极大值点就是最大值点列式求解【详解】由题可知:所以函数在单调递减在单调递增故函数的极大值为所以在开区间内的最大值一定是又所以得 解析:(3,2]--【分析】首先利用导数判断函数的单调性,再根据函数在开区间(),3a a +内存在最大值,可判断极大值点就是最大值点,列式求解. 【详解】由题可知: 2()32(32)f x x x x x '=-=-所以函数()f x 在20,3⎛⎫ ⎪⎝⎭单调递减,在2(,0),,3⎛⎫-∞+∞⎪⎝⎭单调递增,故函数的极大值为 (0)0f =.所以在开区间(,3)a a +内的最大值一定是(0)0,f =又(1)(0)0f f ==, 所以03,31a a a <<+⎧⎨+≤⎩得实数a 的取值范围是(3,2].-- 故答案为:(]3,2-- 【点睛】关键点点睛:由函数在开区间内若存在最大值,即极大值点在区间内,同时还得满足极大值点是最大值,还需列不等式31a +≤,不要忽略这个不等式.16.【分析】先设对其求导求出其最小值为得到再令对其求导导数的方法研究其单调性得出最大值即可得出结果【详解】设则因为所以当时则函数单调递减;当时则函数单调递增;所以则令则;由可得;所以当时则函数单调递增; 解析:2e【分析】先设()ln 2af x x x=++,对其求导,求出其最小值为()min ln 3f x a =+,得到ln 3b a a a +≤,再令()ln 3a g a a +=,对其求导,导数的方法研究其单调性,得出最大值,即可得出结果. 【详解】设()ln 2a f x x x =++,则()221a x a f x x x x '-=-=,因为0a >, 所以当()0,x a ∈时,()20x af x x -'=<,则函数()f x 单调递减; 当(),x a ∈+∞时,()20x afx x '-=>,则函数()f x 单调递增; 所以()()min ln 3f x f a a b ==+≥, 则ln 3b a a a +≤,令()ln 3a g a a +=,则()221ln 32ln a a g a a a --+'==-; 由()0g a '=可得,2a e -=; 所以当()20,a e-∈时,()22ln 0a g a a +'=->,则函数()g a 单调递增;当()2,a e -∈+∞时,()22ln 0ag a a +'=-<,则函数()g a 单调递减; 所以()()2222max ln 3e g a g e e e---+===,即b a 的最大值为2e . 故答案为:2e 【点睛】 思路点睛:导数的方法研究函数最值时,通常需要先对函数求导,解对应的不等式,求出单调区间,得出函数单调性,得出极值,进而可得出最值.17.2【分析】令利用可得在单调递增不等式恒成立等价于即当时分离参数可得可求出正整数的最大值为2再检验当时对于不等式恒成立即可求解【详解】因为定义在上的函数关于轴对称所以函数为上的偶函数令则因为当时即所以解析:2 【分析】令()()g x xf x x =-,利用()()1xf x f x '>-可得()g x 在[)0,+∞单调递增,不等式()()0x x x e f e e ax axf ax -+->恒成立等价于()()x g e g ax >,即e x ax >,当0x >时,分离参数可得()xe a h x x<=,可求出正整数a 的最大值为2,再检验当2a =时,对于0x <,不等式恒成立,即可求解. 【详解】因为定义在R 上的函数()f x 关于y 轴对称, 所以函数()f x 为R 上的偶函数,令()()g x xf x x =-,则()()()1g x f x xf x ''=+-,因为当0x ≥时,()()1xf x f x '>-,即()()()10g x f x xf x ''=+->,所以()g x 在[)0,+∞单调递增, 不等式()()0xx xe f e eax axf ax -+->恒成立,即()()xx xe f eeaxf ax ax ->-,即()()x g e g ax >,所以e x ax >,当0x >时,()xe a h x x <=,则()()21x e x h x x-'=, 可得()h x 在()0,1单调递减,在()1,+∞单调递增, 所以()()min 1h x h e ==, 所以a e <,此时最大的正整数a 为2,2a =对于0x <时,e x ax >恒成立,综上所述:正整数a 的最大值为2, 故答案为:2 【点睛】关键点点睛:本题的关键点是构造函数()()g x xf x x =-,利用导数判断出()g x 在[)0,+∞单调递增,不等式恒成立即()()x g e g ax >,利用单调性可得e x ax >,再分类参数求最值.18.【分析】由函数在区间上单调递增即在上恒成立即在上恒成立设利用导数求得的单调性与最小值即可求解【详解】由题意函数则因为函数在区间上单调递增即在上恒成立即在上恒成立设则所以当时所以为单调递增函数所以函数 解析:a e ≤【分析】由函数()f x 在区间[]1,4上单调递增,即()0xaf x e x'=-≥在[]1,4上恒成立,即x a xe ≤在[]1,4上恒成立,设()xg x xe =,利用导数求得()g x 的单调性与最小值,即可求解. 【详解】由题意,函数()2xf x e alnx =-+,则()xa f x e x '=-, 因为函数()f x 在区间[]1,4上单调递增,即()0xa f x e x'=-≥在[]1,4上恒成立,即x a xe ≤在[]1,4上恒成立,设()xg x xe =,则()(1)x x xe xe e g x x ='=++,所以当[]1,4x ∈时,()(1)0xg x e x '=+≥,所以()g x 为单调递增函数,所以函数()xg x xe =的最小值为()1g e =,所以a e ≤.【点睛】本题主要考查了利用函数的单调性求参数问题,其中解答中把函数的转化为不等式的恒成立问题,利用导数求得新函数的单调性与最值是解答的关键,着重考查了推理与运算能力,属于基础题.19.【分析】先设直线的方程为再利用直线与圆锥曲线的位置关系将用表示再利用导数求函数的最值即可得解【详解】解:由抛物线的准线与圆相切得或7又∴设直线的方程为则直线的方程为则设令得;令得即函数在为增函数在为解析:【分析】先设直线AB 的方程为()03x t t =-<<,再利用直线与圆锥曲线的位置关系将AB CD ⋅用t 表示,再利用导数求函数的最值即可得解. 【详解】解:由抛物线的准线与圆相切得12p=或7,又014p <<,∴2p =. 设直线AB 的方程为()03x t t =-<<,则直线CD 的方程为4x t =-,则)03AB CD t ⋅==<<.设()()()2903f t t tt =-<<,()2'93f t t=-,令()'0f t >,得0t <<()'0f t <3t <<.即函数()f t 在(为增函数,在)为减函数,故()maxf t f ==22AB CD ⋅的最大值为28⨯=故答案为: 【点睛】本题考查了利用导数求函数的最值,重点考查了运算能力,属中档题.20.【分析】根据分段函数当时将恒成立转化为恒成立令利用二次函数的性质求得其最大值当时将转化为恒成立令用导数法求得其最小值然后两种情况取交集【详解】当时等价于恒成立令其中则所以当时等价于恒成立令则当时递增 解析:[]1,e【分析】根据分段函数,当1x ≤时,将()2320f x x x a =-+≥恒成立,转化为232x x a -恒成立,令23()2x x g x -=,利用二次函数的性质求得其最大值,当1x >时,将()ln 0f x x a x =-≥,转化为1xanx 恒成立,令()ln x h x x=,用导数法求得其最小值,然后两种情况取交集. 【详解】当1x ≤时,()2320f x x x a =-+≥等价于232x x a -恒成立,令()22231139()322228x x g x x x x -⎛⎫==--=--+ ⎪⎝⎭,其中1x ≤,则()max 1g x =, 所以1a ≥,当1x >时,()ln 0f x x a x =-≥等价于1xanx恒成立, 令()ln xh x x=,则221ln ln 1()(ln )(ln )x x x x h x x x -⋅-'==, 当x e >时,()()0,h x h x '>递增, 当1x e <<时,()()0,h x h x '<递减, ∴x e =时,()h x 取得最小值()h e e =, ∴()min a h x e ≤=, 综上:a 的取值范围是[]1,e . 故答案为:[]1,e . 【点睛】本题主要考查二次函数的最值,函数的最值与导数以及导数与不等式恒成立问题,还考查了运算求解的能力,属于中档题.三、解答题21.(1)()f x 在()2,1a -∞-上单调递减,在()21,a -+∞上单调递增;(2)(][),11,-∞-+∞.【分析】(1)先求导并解得()0f x '=的根,再判断根附近导数值的正负,即得单调性; (2)先判断极小值即最小值,再结合()210f a =>可知()min0f x ≤,解不等式即得结果. 【详解】解:(1)()()21xf x x a e '=-+,定义域为R ,由()0f x '=,得21x a =-,当21x a <-时,()0f x '<;当21x a >-时,()0f x '>, 故()f x 在()2,1a -∞-上单调递减,在()21,a -+∞上单调递增;(2)由(1)知()f x 在21x a =-处取得极小值,也是最小值, 则()()221min 11a f x f a e-=-=-,因为()f x 存在零点,且()210f a =>,故只需()21min 10a f x e -=-≤,即2101ae e -≥=,故210a -≥,解得1a ≤-或1a ≥, 所以a 的取值范围为(][),11,-∞-+∞.【点睛】 方法点睛:利用导数研究函数单调性的方法:(1)确定函数()f x 的定义域;求导函数()'f x ,由()0f x '>(或()0f x '<)解出相应的x 的范围,对应的区间为()f x 的增区间(或减区间);(2)确定函数()f x 的定义域;求导函数()'f x ,解方程()0f x '=,利用()0f x '=的根将函数的定义域分为若干个子区间,在这些子区间上讨论()'f x 的正负,由符号确定()f x 在子区间上的单调性.22.(1)证明见解析;(2)证明见解析. 【分析】(1)求导根据导数()0f x '>,()0f x '<求出最小值()10f =进而有()0f x ≥成立 (2)有(1)得ln 1≤-x x ,令112nx =+得11ln 122n n ⎛⎫+< ⎪⎝⎭,不等式通项可加性相加,根据等比数列求和化简即可证明. 【详解】解:(1)由题意得()111x f x x x-'=-= 当1x >时()0f x '>,()f x 单调增 当01x <<时()0f x '<,()f x 单调减 所以()f x 的最小值为()10f =, 所以()()01x f f ≥=即()0f x ≥成立 (2)由(1)知ln 1≤-x x 令112nx =+得11ln 122n n ⎛⎫+< ⎪⎝⎭所以2212111111ln 1ln 1ln 1222222n ⎛⎫⎛⎫⎛⎫+++++<++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭111221111212nn ⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎛⎫⎝⎭==-< ⎪⎝⎭-即22111ln 1111ln 222e ⎛⎫⎛⎫⎛⎫⎛⎫+⋅++<= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以2111111222n e ⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭【点睛】已知不等式证明问题常用的方法: (1)证明()min f x a ≥或()max f x a ≤;(3)构造两个函数()()f x g x <,证明()min max ()f x g x < 23.(1)答案见解析;(2)1a e ≤≤. 【分析】(1)求出导函数()'f x ,分类讨论确定()0f x '>的解得增区间,同时可由()0f x '<得减区间;(2)由(1)得()f x 的最小值为()f a ,解不等式()2f a ≥可得. 【详解】(1)函数定义域为(0,)+∞,由题意221(1)()()1a a x x a f x x x x -+-'=+-=, 当0a ≤时,在0x >时,()0f x '>恒成立,()f x 在(0,)+∞上单调递增,当0a >时,()0f x '>的解为x a >,()0f x '<的解为0x a <<, ()f x 在(,)a +∞上递增,在(0,)a 上递减.(2)由(1)知0a >时,()f x 在(,)a +∞上递增,在(0,)a 上递减.所以min ()()(1)ln 1f x f a a a a ==+-+,()2f x ≥恒成立,则(1)ln 12a a a +-+≥, 即(1)(ln 1)0a a --≤,由于01a <≤时,ln 0≤a ,不等式(1)(ln 1)0a a --≤不成立,所以1ln 1a a ≥⎧⎨≤⎩,解得1a e ≤≤. 【点睛】关键点点睛:本题考查用导数研究函数的单调性,研究不等式恒成立问题.一般地()f x m ≥恒成立等价于min ()f x m ≥,()f x m ≤恒成立,等价于max ()f x m ≤,然后解不等式可得参数范围.或者用分离参数法转化为()k g x ≤(其中k 不参数),则min ()k g x ≤,若()k g x ≥,则max ()x g x ≥.24.(Ⅰ)22y x =-;(Ⅱ)()f x 的单调递减区间是(,单调递增区间是(,-∞,)+∞;(Ⅲ)一个,证明见解析. 【分析】(Ⅰ)利用导数的几何意义求切线方程;(Ⅱ)根据()0f x '>和()0f x '<,求函数的单调递增和递减区间,根据极值的定义求极值;(Ⅲ)首先方程等价于212sin 0x x --=,设函数2()12sin ,(0,)g x x x x π=--∈,求函数的导数()22cos g x x x '=-,分0,2x π⎛⎫∈ ⎪⎝⎭和,2x ππ⎡⎫∈⎪⎢⎣⎭两个区间讨论函数的单调性,并结合零点存在性定理说明函数的零点个数. 【详解】(Ⅰ)由3()f x x x =-,得 2()31x f x '=-.因为(1)0f =,(1)2f '=,所以曲线()y f x =在点(1,(1))f 处的切线方程为22y x =-.(Ⅱ)令()0f x '=,得2310x -=,解得x =x =当x 变化时,()f x 和()'f x 变化情况如下表:)+∞;()f x 在x =x =处取得极小值. (Ⅲ)(0,)x π∈,()0t x =,即2120sin x x--=, 等价于212sin 0x x --=. 设2()12sin ,(0,)g x x x x π=--∈,则()22cos g x x x '=-.①当,2x ππ⎡⎫∈⎪⎢⎣⎭时,()0r g x >,()g x 在区间,2上单调递增.又2()3024g ππ=-<,2()10g π=π->, 所以()g x 在区间,2上有一个零点.②当(0,)2x π∈时,设()()22cos h x g x x x '==-.()22sin 0h x x '=+>,所以()'g x 在区间(0,)2π上单调递增.又(0)20g '=-<,()02g π'=π>,所以存在0(0,)2x π∈,使得00()g x '=.所以,当0(0,)x x ∈时,()0g x '<,()g x 单调递减; 当0(,)2x x π∈时,()0g x '>,()g x 单调递增.又(0)10g =-<,2()3024g ππ=-<, 所以()g x 在区间(0,)2π上无零点.综上所述,函数()t x 在定义域内只有一个零点. 【点睛】关键点点睛:本题第三问判断零点个数,首先要构造函数,当0,2x π⎛⎫∈ ⎪⎝⎭时,利用二次导数判断()g x '单调递增,存在0(0,)2x π∈,使得00()g x '=,再判断零点个数时,需结合函数的单调性和端点值共同判断. 25.(1)()f x 单调递增;(2)24a π.【分析】 (1)求导()'2sin fx x x =-,得出导函数的符号,从而可得函数()f x 单调性.(2)由已知将问题转化为不等式sin ()a x f x ⋅恒成立,令()sin ()k x x f x =⋅,求导''()cos ()sin ()k x x f x x f x =⋅+⋅,分析导函数的符号,得出()k x 单调递增,求得()k x 的最大值,由恒等式的思想可得出a 的取值范围. 【详解】 解:(1)()'2sin fx x x =-,令()2sin h x x x =-,当[0,]x π∈时,'()2cos 0h x x =->,所以当[0,]x π∈时,()2sin h x x x =-单调递增;所以()(0)0h x h =,即()0f x ',所以()f x 单调递增. (2)因为当,62x ππ⎡⎤∈⎢⎥⎣⎦时,不等式()()0f x g x -恒成立, 所以当,62x ππ⎡⎤∈⎢⎥⎣⎦时,不等式sin ()a x f x ⋅恒成立, 令()sin ()k x x f x =⋅,所以''()cos ()sin ()k x x f x x f x =⋅+⋅,因为当,62x ππ⎡⎤∈⎢⎥⎣⎦时,'cos 0,()0,sin 0,()0x f x x f x >>>>,所以'()0k x >,所以()k x 单调递增,所以2()24k x k ππ⎛⎫≤= ⎪⎝⎭,所以24a π≥. 【点睛】方法点睛:对于不等式恒成立问题,常常采用:()f x a >对一切x I ∈恒成立,等价于min ()f x a >;()f x α<对一切x I ∈恒成立,等价于max ()f x α<.26.(1)10,a e ⎛⎫∈ ⎪⎝⎭;(2)(i )证明见解析;(ii )证明见解析. 【分析】(1)函数()ln f x x ax =-有两个不同的零点,等价于ln xa x=在(0,)+∞上有两个不同的实根,记ln ()xg x x=,对函数求导判断单调性,可得实数a 的取值范围; (2)(i )将()1212,x x x x <代入方程并参变分离,利用分析法可知,需证明111ln 20x x x e -+>,构造()ln 2,(1,)h x x x x e x e =-+∈,求导判断单调性与最值即可证明不等式成立; (ii )设()()()21ln 11x x x x x ϕ-=->+,对函数求导判断单调性可得:()()21ln 011x x x x ->>>+,由1122ln ln x ax x ax =⎧⎨=⎩,两式作差可得2121ln x x a x x =-,利用证得的不等式进行放缩,可得不等式成立. 【详解】(1)函数()ln f x x ax =-有两个不同的零点()1212,x x x x <,变量分离得ln x a x=在(0,)+∞上有两个不同的实根,记ln ()xg x x =,则21ln ()x g x x -'=当(0,)x e ∈时,()0,()'>g x g x 单调递增;当(,)x e ∈+∞时,()0,()g x g x '<单调递减. 且0x →时,()g x →-∞;x →+∞时,()0g x → 故10,a e ⎛⎫∈ ⎪⎝⎭.(2)(i )因为12,x x 是ln x ax =的两根,由(1)可知121x e x <<<,且1122ln ln x ax x ax =⎧⎨=⎩(只涉及变量1x ,故只用11ln x ax =),所以11ln x a x =要证211111111120ln 20x ax ax x e x x x e a<⇔->⇔-+>⇔-+> 构造函数()ln 2,(1,)h x x x x e x e =-+∈,则()ln 10h x x '=-<,()h x 在()1,e 上递减 所以()()0>=h x h e ,原不等式成立. (ii )解析1:放缩设()()()21ln 11x x x x x ϕ-=->+,则()()()()222114011x x x x x x ϕ-'=-=>++恒成立, ()x ϕ∴在()1,+∞单调递增,()()10x ϕϕ>=,即()()21ln 011x x x x ->>>+ 由1122ln ln x ax x ax =⎧⎨=⎩,可得221211221212112121ln ln ln 121x x x x x x a x x x x x x x x x x ⎛⎫- ⎪-⎝⎭==>⋅=---++,从而212x x a >-,则21112x x x a ->->,要证明:212x x ->,只需证a>11ae a⇔>⇔<,证毕! 解析2:对数平均不等式由对数平均不等式2112211ln ln 2x x x x a x x -+=<-,所以122x x a+>,由(i)可知11x a-<,所以212x x a >->,从而21x x -=,即212x x -=,只需> 下同解法1. 【点睛】方法点睛:本题考查导数研究函数的单调性与零点问题,考查导数证明不等式,设函数()y f x =在[],a b 上连续,在(),a b 上可导,则:1.若()0f x '>,则()y f x =在[],a b 上单调递增;2.若()0f x '<,则()y f x =在[],a b 上单调递减.。
(常考题)北师大版高中数学选修1-1第四章《导数应用》测试卷(包含答案解析)(1)

一、选择题1.已知函数()22ln 3f x x ax x =+-在2x =处取得极小值,则()f x 在1,32⎡⎤⎢⎥⎣⎦的最大值为( ) A .52-B .92ln 32-C .1-D .2ln 24-2.已知函数21()ln 2f x x x a =--,若0x ∃>,()0f x ≥,则a 的取值范围是( ) A .1,2⎛⎤-∞- ⎥⎝⎦ B .1,2⎛⎤-∞ ⎥⎝⎦ C .(],1-∞D .(],e -∞3.函数3()1218f x x x =-+在区间[]3,3-上的最大值为( )A .34B .16C .24D .174.已知函数ln ,0()(2),0x xx f x x x e x ⎧>⎪=⎨⎪+≤⎩,若函数()()g x f x a =-仅有一个零点,则实数a的取值范围为( ). A .(2,)+∞B .31(2,),e ⎛⎫+∞⋃-∞-⎪⎝⎭C .311,2,e e⎛⎤⎛⎫⋃-∞- ⎪⎥⎝⎦⎝⎭D .31,e ⎛⎫-∞-⎪⎝⎭5.设函数()f x 为偶函数,且当0x ≥时,()cos x f x e x =-,则不等式(21)(2)0f x f x --->的解集为( )A .(1,1)-B .(,3)-∞-C .(3,)-+∞D .(1,)(,1)+∞⋃-∞-6.已知函数()()()22210,0x ax x x f x e ax e x ⎧-+<⎪=⎨-+-≥⎪⎩有两个零点,则实数a 的取值范围是( ) A .(),e +∞B .()2e ,+∞C .()20,eD .()0,e7.函数()2f x x =+的值域是( )A.⎡⎢⎣⎦B.3⎛⎫∞ ⎪ ⎪⎝⎭C.(D.)+∞8.()f x 是R 上的偶函数,当()0,x ∈+∞时,()()0xf x f x '->,且()30f =,则不等式()0f x x>的解集为( )A .()3,+∞B .()(),33,-∞-+∞C .()()3,03,-⋃+∞D .()()3,00,3-9.已知函数22(1)2,0()log 0x x f x x x ⎧-++≤⎪=⎨>⎪⎩,,若方程()f x a =有四个不同的解1x ,2x ,3x ,4x ,且1234x x x x <<<,则23423121()x x x x x +⋅+⋅的取值范围是( ) A .71(,]42-- B .37[,]24--C .71[,)42--D .313(,]42-- 10.已知函数2()f x x m =+与函数1()ln3g x x x =--,1,22x ⎡∈⎤⎢⎥⎣⎦的图象上恰有两对关于x 轴对称的点,则实数m 的取值范围是( ) A .5ln )4[2,2+ B .5[2ln 2,ln 2)4-+ C .5(ln 2,2ln 2)4+-D .(]2ln2,2-11.设函数()'f x 是奇函数()()f x x R ∈的导函数,(2)0f -=,当0x >时,()()03xf x f x '+>,则使得()0f x >成立的x 的取值范围是( ) A .(,2)(0,2)-∞-⋃ B .(,2)(2,2)-∞--C .(2,0)(2,)-+∞ D .(0,2)(2,)⋃+∞12.若函数()(1)x f x x e a =--在(1,)-+∞上只有一个零点,则a 的取值范围为( ) A .21,e ⎛⎫--⎪⎝⎭B .2{1},e ⎡⎫-⋃-+∞⎪⎢⎣⎭ C .2,e ⎡⎫-+∞⎪⎢⎣⎭D .2{1},0e ⎡⎫-⋃-⎪⎢⎣⎭二、填空题13.函数()y f x =的导函数的图像如图所示,给出下列判断:①函数()y f x =在区间(3)5,内单调递增; ②函数()y f x =在区间1(3)2-,内单调递减;③函数()y f x =在区间(22)-,内单调递增; ④当12x =-时,函数()y f x =有极大值;⑤当2x =时,函数()y f x =有极大值; 则上述判断中正确的是________. 14.已知函数()3x f x e -=,()1ln 22xg x =+,若()()f m g n =成立,则n m -的最小值为______.15.已知函数()cos sin f x x x x =-,下列结论中, ①函数()f x 的图象关于原点对称; ②当(0,)x π∈时,()0f x π-<<; ③若120x x π<<<,则1122sin sin x x x x >; ④若sin ax x bx <<对于0,2x π⎛⎫∀∈ ⎪⎝⎭恒成立,则a 的最大值为2π,b 的最小值为1. 所有正确结论的序号为______.16.函数2()ln f x x ax x =-在2(,2)e上不单调,则实数a 的取值范围是_____. 17.已知函数()2cos sin 2f x x x =+,则()f x 的最小值是______.18.已知a R ∈,设函数232,1()1,1x x a x f x x a nx x ⎧-+=⎨->⎩,若关于x 的不等式()0f x ≥在R上恒成立,则a 的取值范围是_________.19.已知函数()321f x x x =++,若对于x R ∀∈不等式()21xf ax e a -+≤恒成立,则实数a 的取值范围为:____________.20.已知函数()y f x =在R 上的图象是连续不断的一条曲线,并且关于原点对称,其导函数为()f x ',当0x >时,有不等式()()22x f x xf x '>-成立,若对x R ∀∈,不等式()()2220x x e f e a x f ax ->恒成立,则正整数a 的最大值为_______.三、解答题21.如图一边长为10cm 的正方形硬纸板,四角各截去一个大小相同的小正方形,然后折起,可以做成一个无盖长方体手工作品.所得作品的体积V (单位:cm 2)是关于截去的小正方形的边长x (单位:cm )的函数.(1)写出体积V 关于x 的函数表达式()f x .(2)截去的小正方形的边长为多少时,作品的体积最大?最大体积是多少? 22.设函数()(1)ln(1)f x x x x =-++ (1)若方程()f x t =在1,12⎡⎤-⎢⎥⎣⎦上有两个实数解,求t 的取值范围; (2)证明:当0m n >>时,(1)(1)n mm n +<+.23.已知函数2()ln (0)f x x a x a =->.(1)若2a =,求曲线()y f x =的斜率等于3的切线方程; (2)若()y f x =在区间1,e e ⎡⎤⎢⎥⎣⎦上恰有两个零点,求a 的取值范围.24.已知函数3()f x x x =-.(Ⅰ)求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间和极值; (Ⅲ)设函数()()2sin f x t x x x=-,(0,)x ∈π,试判断()t x 的零点个数,并证明你的结论. 25.(1)证明:1x e x ≥+; (2)证明:ln 1≤-x x ; (3)证明:1ln(1)x e x ->+. 26.已知函数321()23f x x x ax =-++,21()42g x x =-. (1)若函数()f x 在()0,∞+上存在单调递增区间,求实数a 的取值范围;(2)设()()()G x f x g x =-.若02a <<,()G x 在[]1,3上的最小值为13-,求()G x 在[]1,3上取得最大值时,对应的x 值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】由()20f '=求出a 的值,然后利用导数可求得函数()f x 在1,32⎡⎤⎢⎥⎣⎦的最大值.【详解】()22ln 3f x x ax x =+-,则()223f x ax x=+-', 由题意可得()2420f a '=-=,解得12a =,则()212ln 32f x x x x =+-, ()22323x x f x x x x-+'=+-=,令()0f x '=,可得1x =或2x =,列表如下:所以,函数()f x 的极大值为()12f =-,极小值为()22ln 24f =-, 又1112ln 228f ⎛⎫=-- ⎪⎝⎭,()932ln 32f =-,()()()95312ln 32ln 322ln 31022f f -=-+=-=->,则()()13f f <,所以,()()max 932ln 32f x f ==-. 故选:B. 【点睛】思路点睛:利用导数求函数()y f x =在[],a b 上的最大值和最小值的步骤如下: (1)求函数()y f x =在(),a b 内的极值;(2)将函数()y f x =的各极值与端点处的函数值()f a 、f b 比较,其中最大的一个是最大值,最小的一个是最小值.2.A解析:A由()f x 得21ln 2a x x ≤-,设21()ln 2g x x x =-,利用导数求()g x 的最大值可得答案. 【详解】 由21()ln 2f x x x a =--,得21ln 2a x x ≤-.设21()ln 2g x x x =-,则211()x g x x x x-'=-=.令()0g x '>,得01x <<;令()0g x '<,得1x >, 则()g x 在(0,1)上单调递增,在(1,)+∞上单调递减,从而1()(1)2g x g ≤=-, 故12a ≤-. 故选:A. 【点睛】本题考查了能成立求参数的问题,关键点是构造函数利用导数求最值,考查了分析问题、解决问题的能力.3.A解析:A 【分析】对函数求导,求出函数()y f x =的极值点,分析函数的单调性,再将极值与端点函数值比较大小,找出其中最大的作为函数()y f x =的最大值. 【详解】()31218f x x x =-+,则()2312f x x '=-,令'0f x,解得2x =±,列表如下:所以,函数y f x =的极大值为234f -=,极小值为22f =,又()327f -=,()39f =,因此,函数()y f x =在区间[]3,3-上的最大值为34, 故选:A . 【点睛】方法点睛:本题考查利用导数求函数在定区间上的最值,解题时严格按照导数求最值的基本步骤进行,考查计算能力,属于中等题.4.C解析:C转化为()y f x =的图象与直线y a =仅有一个交点,利用导数得到函数的性质,根据函数的性质作出函数的图象,根据图象可得解. 【详解】当0x >时,ln ()x fx x=,21ln ()x x x f x x ⋅-'=21ln xx -=, 当0x e <<时,()'f x 0>,当x e >时,()0f x '<,所以()f x 在(0,)e 上递增,在(,)e +∞上递减,所以()f x 在x e =处取得极大值为1()f e e=,当0x ≤时,()(2)x f x x e =+,()(2)(3)x x xf x e x e x e '=++=+,当3x <-时,()0f x '<,当3x >-时,()0f x '>, 所以()f x 在(,3)-∞-上递减,在(3,0]-上递增,所以()f x 在3x =-处取得极小值为331(3)f e e --=-=-,又(0)2f =, 因为函数()()g x f x a =-仅有一个零点,所以()y f x =的图象与直线y a =仅有一个交点,作出函数()f x 的图象,如图:由图可知:12a e <≤或31a e<-. 故实数a 的取值范围为311,2,e e ⎛⎤⎛⎫⋃-∞- ⎪⎥⎝⎦⎝⎭.故选:C 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.5.D【分析】利用导数判断函数在[)0,+∞的单调性,然后根据奇偶性判断()f x 在(],0-∞的单调性,再利用单调性与奇偶性结合求解不等式. 【详解】当0x ≥时,()cos x f x e x =-,所以()sin xf x e x '=+,因为0x ≥,所以1x e ≥,即()1sin 0f x x '≥+≥,所以函数()f x 在[)0,+∞上单调递增,又因为函数()f x 为R 上的偶函数,所以函数()f x 在(],0-∞上单调递减,在[)0,+∞上单调递增,则不等式(21)(2)0f x f x --->,等价于212x x ->-,所以1x <-或1x >.故选:D. 【点睛】对于求值或范围的问题,一般先利用函数的奇偶性得出区间上的单调性,再利用其单调性脱去函数的符号“f ”,转化为解不等式(组)的问题,若()f x 为偶函数,则()()()f x f x f x -==. 6.B解析:B 【分析】分离变量,利用导函数应用得到函数在0x <无零点,则0x >有两个零点,利用函数最值得到参数范围 【详解】当0x =时,()201e f =--,∴0x =不是函数()f x 的零点.当0x <时,由()0f x =,得221x a x -=,设()221x h x x -=,()()3210x h x x-'=<,则()h x 在(),0-∞上单调递减,且()0h x <.所以0x <时无零点当0x >时,()0f x =等价于2x e e a x +=,令()2x e e g x x +=,()22x x xe e e g x x--'=, 得()g x 在()0,2上单调递减,在()2,+∞上单调递增,()2min (2)g x g e ==,()2g x e ≥.因为()f x 有2个零点,所以2a e >. 故选:B. 【点睛】分离变量法,利用导数求函数的单调性,极值是解题关键.7.A解析:A 【分析】求出函数的定义域,然后求出导函数,确定单调性,得值域.由21020x x ⎧-≥⎨+≠⎩得11x -≤≤,()f x '==当112x -≤<-时,()0f x '>,()f x 递增,112x -<≤时,()0f x '<,()f x 递减, 所以12x =-时,max()22f x ==-+(1)(1)0f f -==, 所以()f x的值域是⎡⎢⎣⎦. 故选:A . 【点睛】本题考查用导数求函数的值域,解题方法是由导数确定函数的单调性,得出最大值和最小值,得值域.8.C解析:C 【分析】 构造函数()()f xg x x=,求导,利用()g x 的单调性和奇偶性解不等式. 【详解】 设()()f xg x x=(0x ≠), 则()()()2xf x f x g x x'-'=, ∵当()0,x ∈+∞时,()()0xf x f x '->, ∴()0g x '>,即()g x 在()0,∞+上单调递增, 又()f x 是R 上的偶函数, ∴()()()()f x f x g x g x x x--==-=--, 即()g x 是()(),00,-∞⋃+∞上的奇函数, ∴()g x 在(),0-∞上单调递增,∵()30f =, ∴()()()33303f g g -=-=-=. 而不等式()0f x x>等价于()0g x >, ∴30x -<<或3x >. 故选:C. 【点睛】本题主要考查函数的单调性与奇偶性的应用,利用条件构造函数,然后利用导数研究函数的单调性是解决本题的关键,属于中档题.9.D解析:D 【分析】画出图形,数形结合解答.注意到122x x +=-,2324log log x x -=,化简结论得32312x x -,311,42x ⎛⎤∈ ⎥⎝⎦,构造函数21()2f x x x =-,11,42x ⎛⎤∈ ⎥⎝⎦,利用导数判断出函数的单调性即可. 【详解】已知函数图象如下:方程()f x a =有四个不同的解1x ,2x ,3x ,4x ,且1234x x x x <<<, 则122x x +=-,2324log log x x -=,所以341x x ⋅=,且311,42x ⎛⎤∈ ⎥⎝⎦, 所以234322312311()2x x x x x x x ⋅=+⋅+-, 令21()2f x x x =-,11,42x ⎛⎤∈ ⎥⎝⎦, 则31()1f x x =+'在11,42⎛⎤⎥⎝⎦上恒大于0, 故()f x 在11,42x ⎛⎤∈⎥⎝⎦上单调递增,所以313(),42f x ⎡⎫∈--⎪⎢⎣⎭, 故选:D . 【点评】本题考查了函数的图像运用,利用数形结合判断函数交点问题,属于中档题.10.A解析:A 【分析】将问题转化为()()f x g x =-在1,22⎡⎤⎢⎥⎣⎦恰有两个不同的解,令()()()h x f x g x =+,将问题转化为()h x 在1,22⎡⎤⎢⎥⎣⎦上有两个零点的问题,利用导数可求得()h x 的单调性,进而确定区间端点值和最值,由此构造不等式求得结果. 【详解】()f x 与()g x 在1,22x ⎡∈⎤⎢⎥⎣⎦的图象上恰有两对关于x 轴对称的点,()()f x g x ∴=-在1,22⎡⎤⎢⎥⎣⎦恰有两个不同的解,即221ln3ln 30x m x x x x m x +--=+-+=在1,22⎡⎤⎢⎥⎣⎦上恰有两个不同的解, 令()2ln 3h x x x x m =+-+,则()()()2211123123x x x x h x x x x x---+'=+-==, ∴当1,12x ⎛⎫∈ ⎪⎝⎭时,()0h x '<;当()1,2x ∈时,()0h x '>,()h x ∴在1,12⎛⎫⎪⎝⎭上单调递减,在()1,2上单调递增,又15ln 224h m ⎛⎫=--+⎪⎝⎭,()12h m =-,()2ln 22h m =-+, 原问题等价于()h x 在1,22⎡⎤⎢⎥⎣⎦上恰有两个零点,则5ln 2024m m --+≥>-,解得:5ln 224m +≤<,即m 的取值范围为5ln 2,24⎡⎫+⎪⎢⎣⎭.故选:A . 【点睛】本题考查根据函数零点个数求解参数范围的问题,关键是能够将两函数图象对称点个数的问题转化为方程根的个数的问题,进一步通过构造函数的方式将问题转化为函数零点个数的问题.11.C解析:C 【分析】通过令3()()g x x f x =可知问题转化为解不等式()0>g x ,利用当0x >时32()3()0x f x x f x '+>及奇函数与偶函数的积函数仍为奇函数可知()g x 在(,0)-∞递减、在(0,)+∞上单调递增,进而可得结论.【详解】解:令3()()g x x f x =,则问题转化为解不等式()0>g x , 当0x >时,()3()0xf x f x '+>,∴当0x >时,233()()0x f x x f x +'>,∴当0x >时()0g x '>,即函数()g x 在(0,)+∞上单调递增,又(2)0f -=,()()f x x R ∈是奇函数,()()()()()()()333g x x f x x f x x f x g x ∴-=--=--== 故()g x 为偶函数,f ∴(2)0=,g (2)0=,且()g x 在(,0)-∞上单调递减, ∴当0x >时,()0>g x 的解集为(2,)+∞,当0x <时,()0(2)g x g >=-的解集为(2,0)-,∴使得f ()0x >成立的x 的取值范围是(2-,0)(2⋃,)+∞,故选C . 【点睛】本题考查利用导数研究函数的单调性,考查运算求解能力,构造新函数是解决本题的关键,注意解题方法的积累,属于中档题.12.B解析:B 【分析】先对函数求导,可得当10x -<<时,()0f x '<;当0x >时,()0f x '>,从而得min ()(0)1f x f a ==--,而x →+∞时,()f x →+∞,所以要函数()(1)x f x x e a =--在(1,)-+∞上只有一个零点,只要满足10a --=或20a e--,从而可求出a 的取值范围 【详解】()x f x xe '=,当10x -<<时,()0f x '<;当0x >时,()0f x '>.从而min ()(0)1f x f a ==--,又2(1)f a e-=--,且x →+∞时,()f x →+∞, ∴10a --=或20a e--,即1a =-或2a e-. 故选:B 【点睛】此题考查由导数解决函数零点问题,考查转化思想和计算能力,属于中档题二、填空题13.③⑤【分析】根据导函数图像得出导数正负根据导数正负判定单调区间根据左正右负和左负有正判定极值【详解】解:对于①当时单调递减当时单调递增所以①错;对于②当时单调递增当时单调递减所以②错;对于③当时单调解析:③⑤ 【分析】根据导函数图像得出导数正负,根据导数正负判定单调区间,根据左正右负和左负有正判定极值. 【详解】解:对于①,当(34)x ∈,时()0f x '<,()f x 单调递减, 当(4,5)x ∈时()0f x '>,()f x 单调递增,所以①错;对于②,当1(2)2x ∈-,时()0f x '>,()f x 单调递增, 当(23)x ∈,时()0f x '<,()f x 单调递减,所以②错; 对于③,当(22)x ∈-,时()0f x '>,()f x 单调递增,所以③对; 对于④,当(22)x ∈-,时()0f x '>,()f x 单调递增,故当12x =-时()f x 不是极大值,所以④错;对于⑤,当1(2)2x ∈-,时()0f x '>,()f x 单调递增, 当(23)x ∈,时()0f x '<,()f x 单调递减,故2x =时函数()y f x =取得极大值,所以⑤对.故答案为:③⑤. 【点睛】求函数的极值或极值点的步骤:(1)求导数()'f x ,不要忘记函数()f x 的定义域;(2)求方程()0f x '=的根;(3)检查在方程的根的左右两侧()'f x 的符号,确定极值点或函数的极值.14.【分析】根据得到mn 的关系利用消元法转化为关于t 的函数构造函数求函数的导数利用导数研究函数的最值即可得到结论【详解】解:不妨设∴()∴即故()令()所以在上是增函数且当时当时即当时取得极小值同时也是 解析:ln21-【分析】根据()()f m g n t ==得到m ,n 的关系,利用消元法转化为关于t 的函数,构造函数,求函数的导数,利用导数研究函数的最值即可得到结论. 【详解】解:不妨设()()f m g n t ==, ∴31ln 22m net -=+=,(0t >) ∴3ln m t -=,即3ln m t =+,122t n e -=⋅,故1223ln t n m e t --=⋅--(0t >), 令()1223ln t h t et -=⋅--(0t >),()1212t h t et-'=⋅-,()1221''20t h t e t -=⋅+>所以()h t '在()0,∞+上是增函数,且102h ⎛⎫'= ⎪⎝⎭, 当12t >时,()0h t '>, 当102t <<时,()0h t '<, 即当12t =时,()h t 取得极小值同时也是最小值, 此时1123ln ln 2122h ⎛⎫⎛⎫=-+=-⎪ ⎪⎝⎭⎝⎭,即n m -的最小值为ln21-, 故答案为:ln21-. 【点睛】本题考查利用导数求函数的最小值,考查化归转化思想与运算能力,是中档题.15.①②④【分析】首先对函数的奇偶性进行判断得出①正确;利用导数研究函数的单调性求得函数的值域判断②正确;利用导数研究函数的单调性进行变形得到③是错误的数形结合思想可以判断④是正确的【详解】因为所以所以解析:①②④ 【分析】首先对函数的奇偶性进行判断得出①正确;利用导数研究函数的单调性,求得函数的值域,判断②正确;利用导数研究函数sin ()xg x x=的单调性,进行变形得到③是错误的,数形结合思想可以判断④是正确的. 【详解】因为()cos sin f x x x x =-,所以()()cos()sin()cos sin ()f x x x x x x x f x -=----=-+=-, 所以()f x 为奇函数,所以函数()f x 的图象关于原点对称,所以①正确; 因为'()cos sin cos sin f x x x x x x x =--=-, 因为(0,)x π∈,所以'()0f x <, 所以()f x 在(0,)π上单调递减,所以()()(0)0f f x f ππ-=<<=,所以()0f x π-<<,所以②正确;令sin ()x g x x=,2cos sin '()x x xg x x -=, 由②可知,()f x 在(0,)π上单调递减,所以)'(0g x <,所以()g x 在(0,)π上单调递减, 若120x x π<<<,所以1212sin sin x x x x >, 即1122sin sin x x x x <,所以③错误; 若sin ax x bx <<对于0,2x π⎛⎫∀∈ ⎪⎝⎭恒成立,相当于sin y x =在0,2π⎛⎫⎪⎝⎭上落在直线y ax =的上方,落在直线y bx =的下方, 结合图形,可知a 的最大值为连接(0,0),(,1)2π的直线的斜率,即2π, b 的最小值为曲线sin y x =在(0,0)处的切线的斜率,即0'|1x y ==,所以④正确;故正确答案为:①②④. 【点睛】方法点睛:该题属于选择性填空题,解决此类问题的方法: (1)利用函数的奇偶性判断函数图象的对称性; (2)利用导数研究函数的单调性,从而求得其值域; (3)转化不等式,构造新函数,求导解决问题; (4)数形结合,找出范围.16.【分析】求得函数的导函数根据在区间上有极值求得的取值范围【详解】令得由于分离常数得构造函数所以在上递减在上递增下证:构造函数当时①而即所以所以由①可得所以当时单调递增由于所以当时故也即由于所以所以的解析:4(2,)ln 21+ 【分析】求得函数()f x 的导函数()'f x ,根据()f x 在区间2(,2)e上有极值,求得a 的取值范围. 【详解】()()'21ln 2ln f x x a x x a x a =-+=--,令'0f x得2ln 0x a x a --=,由于222,ln ln ln 2,ln 2ln 1ln 2x x x e e e<<<<<+<, 分离常数a 得21ln xa x=+.构造函数()21ln x h x x =+,()()'22ln 1ln x h x x =+,所以()h x 在2,1e ⎛⎫ ⎪⎝⎭上递减,在()1,2上递增,()()()424444,12,22ln 2ln 2ln 21ln 21ln eeh h h e e e e⎛⎫======⎪+⎝⎭+. 下证22e e >:构造函数()22xg x x =-,()'2ln 22xg x =-,当2x ≥时,22ln 222ln 22x -≥-①,而1ln 2ln 2e =<=<,即1ln 212<<,所以222ln 24<<,所以由①可得22ln 222ln 220x -≥->.所以当2x ≥时,()g x 单调递增.由于()20g =,所以当2x >时,()()20g x g >=,故()0g e >,也即22022e e e e ->⇒>.由于()22ln 2ln 2eee e >⇒>,所以()22h h e ⎛⎫<⎪⎝⎭. 所以a 的取值范围是4(2,)ln 21+ 故答案为:4(2,)ln 21+ 【点睛】本小题主要考查利用导数研究函数的单调性,属于中档题.17.【分析】由解析式可分析得到的一个周期为则只需考虑在上的值域即可利用导函数求得其最值即可【详解】由题的一个周期为故只需考虑在上的值域令解得或可得此时或或所以的最小值只能在点或或和边界点中取到因为所以的解析: 【分析】由解析式可分析得到()f x 的一个周期为2T π=,则只需考虑()f x 在[)0,2π上的值域即可,利用导函数求得其最值即可. 【详解】由题,()f x 的一个周期为2T π=, 故只需考虑()f x 在[)0,2π上的值域,()()()()22sin 2cos 22sin 212sin 22sin 1sin 1f x x x x x x x '=-+=-+-=--+,令()0f x '=,解得1sin 2x =或sin 1x =-, 可得此时6x π=或56π或π, 所以()2cos sin 2f x x x =+的最小值只能在点6x π=或56π或π和边界点0x =中取到,因为6f π⎛⎫=⎪⎝⎭,56f π⎛⎫= ⎪⎝⎭()2f π=-,()02f =,所以()f x 的最小值为故答案为:【点睛】本题考查导数的运算,考查利用导函数求最值,考查运算能力.18.【分析】根据分段函数当时将恒成立转化为恒成立令利用二次函数的性质求得其最大值当时将转化为恒成立令用导数法求得其最小值然后两种情况取交集【详解】当时等价于恒成立令其中则所以当时等价于恒成立令则当时递增 解析:[]1,e【分析】根据分段函数,当1x ≤时,将()2320f x x x a =-+≥恒成立,转化为232x x a -恒成立,令23()2x x g x -=,利用二次函数的性质求得其最大值,当1x >时,将()ln 0f x x a x =-≥,转化为1xanx 恒成立,令()ln x h x x=,用导数法求得其最小值,然后两种情况取交集. 【详解】当1x ≤时,()2320f x x x a =-+≥等价于232x x a -恒成立,令()22231139()322228x x g x x x x -⎛⎫==--=--+ ⎪⎝⎭,其中1x ≤,则()max 1g x =, 所以1a ≥,当1x >时,()ln 0f x x a x =-≥等价于1xanx恒成立, 令()ln xh x x=,则221ln ln 1()(ln )(ln )x x x x h x x x -⋅-'==, 当x e >时,()()0,h x h x '>递增, 当1x e <<时,()()0,h x h x '<递减, ∴x e =时,()h x 取得最小值()h e e =, ∴()min a h x e ≤=, 综上:a 的取值范围是[]1,e . 故答案为:[]1,e . 【点睛】本题主要考查二次函数的最值,函数的最值与导数以及导数与不等式恒成立问题,还考查了运算求解的能力,属于中档题.19.【分析】根据在R 上递增结合将不等式恒成立转化为恒成立然后分和两种情况利用导数法求解【详解】因为所以成立所以在R 上递增又成立所以恒成立即恒成立当时转化为恒成立令当时单调递减当时单调递增所以当时求得最小解析:10a e≤≤ 【分析】根据()f x 在R 上递增,结合()01f =,将x R ∀∈不等式()21xf ax e a -+≤恒成立,转化为()2xa x e +≤ ,x R ∀∈恒成立,然后分20x +≤和20x +>两种情况,利用导数法求解. 【详解】因为()321f x x x =++,所以()2320f x x '=+>成立,所以()f x 在R 上递增,又()()01,21xf f ax e a =-+≤x R ∀∈成立,所以20x ax e a -+≤,x R ∀∈ 恒成立,即()2xa x e +≤,x R ∀∈恒成立, 当20x +>时,转化为2xe a x ≤+恒成立,令()2xg x e x =+,()()()212x x e g x x +'=+,当21x -<<-时,()0g x '<,()g x 单调递减, 当1x >-时,()0g x '>,()g x 单调递增, 所以当1x =-时,()g x 求得最小值min 1()(1)g x g e=-=, 所以1a e≤, 当20x +≤时,转化为2xe a x ≥+恒成立,(),(,2)a g x x ≥∈-∞-上恒成立,(,2)x ∈-∞-时,()0,()g x g x '<单调递减,又(,2),()0x g x ∈-∞-<,所以0a ≥不等式恒成立, 综上:实数a 的取值范围为10a e≤≤ 故答案为:10a e≤≤ 【点睛】本题主要考查导数与函数的单调性,导数与不等式恒成立,还考查了转化化归的思想,分类讨论思想和运算求解的能力,属于中档题.20.【分析】令先判断函数g(x)的奇偶性和单调性得到在R 上恒成立再利用导数分析解答即得解【详解】因为当时有不等式成立所以令所以函数g(x)在(0+∞)上单调递增由题得所以函数g(x)是奇函数所以函数在R 解析:2【分析】令2()(),g x x f x =先判断函数g(x)的奇偶性和单调性,得到e x ax >在R 上恒成立,再利用导数分析解答即得解. 【详解】因为当0x >时,有不等式()()22x f x xf x '>-成立,所以()()22+20,[()]0x f x xf x x f x ''>∴>,令2()(),g x x f x =所以函数g(x)在(0,+∞)上单调递增, 由题得22()()()g(x),g x x f x x f x -=-=-=-所以函数g(x)是奇函数,所以函数在R 上单调递增. 因为对x R ∀∈,不等式()()2220xxe f e a x f ax ->恒成立,所以()()222,()()e xxxxe f ea x f ax g e g ax ax >∴>∴>,,因为a >0,所以当x≤0时,显然成立.当x >0时,()(0)xe a h x x x<=>,所以2(1)()xx e h x x-'=,所以函数h (x)在(0,1)单调递减,在(1,+∞)单调递增. 所以min ()(1)h x h e ==, 所以a <e,所以正整数a 的最大值为2. 故答案为2 【点睛】本题主要考查函数的奇偶性及其应用,考查函数单调性的判断及其应用,考查利用导数研究不等式的恒成立问题,意在考查学生对这些知识的理解掌握水平和分析推理能力.属于中档题.三、解答题21.(1)()()2102V f x x x ==-⋅,()0,5x ∈;(2)小正方形的边长为53cm 时,作品的体积最大,最大体积是200027cm 3. 【分析】(1)根据长方体的体积公式可得答案; (2)利用导数求()f x 单调区间及极值可得答案. 【详解】(1)由题意可得()()2102V f x x x ==-⋅,()0,5x ∈.(2)()()()()24320254355f x x x x x '=-+=--,令()0f x '=得53x =,5x =,∴53x =时,()f x 的最大值为327f ⎛⎫= ⎪⎝⎭,截去的小正方形的边长为53cm 时,作品的体积最大,最大体积是()3200027cm . 【点睛】思路点睛:解函数应用题的一般程序:第一步:审题——弄清题意,分清条件和结论,理顺数量关系;第二步:建模——将文字语言转化成数学语言,用数学知识建立相应的数学模型; 第三步:求模——求解数学模型,得到数学结论;第四步:还原——将用数学方法得到的结论还原为实际问题的意义;第五步:反思回顾——对于数学模型得到的数学结果,必须验证这个数学解对实际问题的合理性. 22.(1)11ln 2,022⎡⎫-+⎪⎢⎣⎭;(2)证明见解析. 【分析】(1)方程()f x t =在1,12⎡⎤-⎢⎥⎣⎦上有两个实数解,等价于函数()f x 在区间1,12⎡⎤-⎢⎥⎣⎦上的图像与直线y t =有两个交点,所以利用导数求出()f x 在1,02⎡⎤-⎢⎥⎣⎦上单调递增,在(]0,1上单调递减,再比较出(1)f 和12f ⎛⎫ ⎪⎝⎭的大小即可得答案; (2)由0m n >>,要证(1)(1)n mm n +<+,只需证ln(1)ln(1)n m m n +<+,只需证ln(1)ln(1)m n m n ++<,构造函数ln(1)(),(0)x g x x x +=>,然后利用导数证明()g x 是减函数即可 【详解】解:(1)由()(1)ln(1)f x x x x =-++,定义域为()1,-+∞,()ln(1)f x x '=-+,()ln(1)00f x x x '=-+=⇒=,当102x -≤<时,()()0,f x f x '>单调递增, 当01x <≤时,()()0,f x f x '<单调递减, 则()f x 在1,02⎡⎤-⎢⎥⎣⎦上单调递增,在(]0,1上单调递减,又111(0)0,(1)1ln 4,()ln 2222f f f ==--=-+, 135(1)()ln 20,222∴--=-<f f 1(1)2f f ⎛⎫∴< ⎪⎝⎭∴ 当11ln 2,022⎡⎫∈-+⎪⎢⎣⎭t 时,方程()f x t =有两解. (2)∵ 0m n >>.∴ 要证:(1)(1)n m m n +<+,只需证ln(1)ln(1)n m m n +<+, 只需证:ln(1)ln(1)m n m n ++<. 设ln(1)(),(0)x g x x x+=>, 则22ln(1)(1)ln(1)1()(1)xx x x x x g x x x x -+-+++=+'=. 由(1)知()(1)ln(1)f x x x x =-++在(0,)+∞单调递减, 又()00=f ,∴ (1)ln(1)0x x x -++<, 即()g x 是减函数,而m n >. ∴ ()()g m g n <,故原不等式成立. 【点睛】关键点点睛:此题考查导数的应用,考查利用导数证明不等式,考查数学转化思想,解题的关键是把(1)(1)n mm n +<+,转化为ln(1)ln(1)m n m n++<,再构造函数,再利用导数判断此函数为减函数即可,属于中档题23.(1)322ln 20x y ---=;(2)(22,e e ⎤⎦.【分析】(1)求出导函数,令()3f x '=求得切点坐标后可得切线方程;(2)求导函数()'f x ,确定()f x 在定义域内只有一个极值点,因此这个极值点必在区间1e e ⎛⎫⎪⎝⎭,上,然后得函数在1,e e ⎡⎤⎢⎥⎣⎦上的极小值,由极小值小于0,区间两个端点处函数值大于或等于0可得结论. 【详解】由已知函数()f x 定义域是(0,)+∞,(1)2()2ln f x x x =-,22(1)(1)()2x x f x x x x'+-=-=,由2()23f x x x'=-=解得2x =(12x =-舍去),又()422ln 2f =-,所以切线方程为(42ln 2)3(2)y x --=-,即322ln 20x y ---=;(2)222()2x x a x a f x x x x x⎛-+ -⎝⎭⎝⎭'=-==, 易知()f x()f x有两个零点,则1e e <<,即2222a e e<<,此时在1e ⎛ ⎝上()0f x '<,()f x递减,在e ⎫⎪⎪⎭上()0f x '>,()f x 递增, ()f x在x =时取得极小值2a f a =-,所以22111ln 0()ln 002f a e ee f e e a e a f a ⎧⎛⎫⎪=-≥ ⎪⎪⎝⎭⎪=-≥⎨⎪⎪=-<⎪⎩解得22e a e <≤.综上a 的范围是(22,e e ⎤⎦.【点睛】关键点点睛:本题考查导数的几何意义,考查用导数研究函数的零点问题.函数在某个区间上的零点,解题时先从大处入手,由导数确定函数的极值点,利用单调区间上的零点最多只有一个,因此函数的极值点必在给定区间内,从而缩小参数的a 范围,在此范围内计算()f x 的单调性与极值,结合零点存在定理可得结论.24.(Ⅰ)22y x =-;(Ⅱ)()f x的单调递减区间是(,单调递增区间是(,-∞,)+∞;(Ⅲ)一个,证明见解析. 【分析】(Ⅰ)利用导数的几何意义求切线方程;(Ⅱ)根据()0f x '>和()0f x '<,求函数的单调递增和递减区间,根据极值的定义求极值;(Ⅲ)首先方程等价于212sin 0x x --=,设函数2()12sin ,(0,)g x x x x π=--∈,求函数的导数()22cos g x x x '=-,分0,2x π⎛⎫∈ ⎪⎝⎭和,2x ππ⎡⎫∈⎪⎢⎣⎭两个区间讨论函数的单调性,并结合零点存在性定理说明函数的零点个数. 【详解】(Ⅰ)由3()f x x x =-,得 2()31x f x '=-.因为(1)0f =,(1)2f '=,所以曲线()y f x =在点(1,(1))f 处的切线方程为22y x =-.(Ⅱ)令()0f x '=,得2310x -=,解得3x =-或x =当x 变化时,()f x 和()'f x 变化情况如下表:)+∞;()f x 在x =x =处取得极小值. (Ⅲ)(0,)x π∈,()0t x =,即2120sin x x--=, 等价于212sin 0x x --=. 设2()12sin ,(0,)g x x x x π=--∈,则()22cos g x x x '=-.①当,2x ππ⎡⎫∈⎪⎢⎣⎭时,()0r g x >,()g x 在区间,2上单调递增.又2()3024g ππ=-<,2()10g π=π->, 所以()g x 在区间,2上有一个零点.②当(0,)2x π∈时,设()()22cos h x g x x x '==-.()22sin 0h x x '=+>,所以()'g x 在区间(0,)2π上单调递增.又(0)20g '=-<,()02g π'=π>,所以存在0(0,)2x π∈,使得00()g x '=.所以,当0(0,)x x ∈时,()0g x '<,()g x 单调递减; 当0(,)2x x π∈时,()0g x '>,()g x 单调递增.又(0)10g =-<,2()3024g ππ=-<, 所以()g x 在区间(0,)2π上无零点.综上所述,函数()t x 在定义域内只有一个零点. 【点睛】关键点点睛:本题第三问判断零点个数,首先要构造函数,当0,2x π⎛⎫∈ ⎪⎝⎭时,利用二次导数判断()g x '单调递增,存在0(0,)2x π∈,使得00()g x '=,再判断零点个数时,需结合函数的单调性和端点值共同判断.25.(1)证明见解析;(2)证明见解析;(3)证明见解析. 【分析】(1)令()(1)x f x e x =-+,求出导函数()'f x ,确定单调性得最小值,从而证得不等式成立;(2)令()ln (1)(0)g x x x x =-->,求导确定单调性得最大值后可证得不等式成立; (3)(1)变形得1x e x -≥,(2)变形可得ln(1)x x ,两个等号不同时成立,可证得不等式成立. 【详解】证明:(1)令()(1)x f x e x =-+,则有()1xf x e =-'.令()0f x '<得,0x <,令()0f x '>得,0x >所以()f x 在(,0)-∞单调递减,(0,)+∞上单调递增.所以0()(0)10f x f e ≥=-=,即(1)0x e x +≥-.所以1x e x ≥+.(2)令()ln (1)(0)g x x x x =-->,则1()1g x x'=-. 令()0g x '<得,0x >,令()0g x '>得,01x <<.所以()g x 在(0,1)单调递增,(1,)+∞上单调递减,所以()(1)ln1(11)0g x g ≤=--=,即ln (1)0x x --≤, 所以ln 1≤-x x .(3)由(1)得1x e x ≥+,所以1(1)1x e x x -≥-+=(当且仅当1x =时取等号)①. 由(2)得ln 1≤-x x ,所以ln(1)(1)1x x x +≤+-=(当且仅当0x =时取等号)② 因为①式与②式取等号的条件不同,所以1ln(1)x e x ->+. 【点睛】结论点睛:本题考查用导数证明不等式,证明方法是引入函数,用导数确定函数的单调性得到函数的最值,从而可证不等式成立.1x e x ≥+和ln 1≤-x x 是两个典型的不等式,例如它可变形得1x e x -≥,ln(1)x x ,有许多函数不等式都是考查这两个不等式的应用.请务必注意掌握.26.(1)12a >-;(2.x =. 【分析】(1)根据()f x 在()0,∞+上存在单调递增区间,由()2220f x x x a =-++>'在()0,∞+上有解求解.(2)由()0G x '=得112x =212x =,根据02a <<,易得10x <,213x <<,则()G x 在[]1,3上的最大值点为2x ,最小值为()1G 或()3G ,然后由()()143143G G a -=-+,分14403a -+<,14403a -+≥确定最小值进而求得a 即可 【详解】(1)∵()f x 在()0,∞+上存在单调递增区间, ∴()2220f x x x a =-++>'在()0,∞+上有解,即()max 0f x '>在()0,∞+上成立, 而()f x '的最大值为()112f a '=+, ∴120a +>, 解得:12a >-. (2)3211()()()2432G x f x g x x x ax =-=-+++, ∴()22G x x x a '=-++,由()0G x '=得:1x =2x =, 则()G x 在()1,x -∞,()2,x +∞上单调递减,在()12,x x 上单调递增, 又∵当02a <<时,10x <,213x <<,∴()G x 在[]1,3上的最大值点为2x ,最小值为()1G 或()3G ,而()()143143G G a -=-+, 1︒ 当14403a -+<,即706a <<时,()113623G a =-=-,得136a =,此时,最大值点236x +=; 2︒当14403a -+≥,即726a ≤<时,()2511263G a =+=-,得94a =-(舍).综上()G x 在[]1,3上的最大值点为36+. 【点睛】方法点睛:(1)求解函数的最值时,要先求函数y =f (x )在[a ,b ]内所有使f ′(x )=0的点,再计算函数y =f (x )在区间内所有使f ′(x )=0的点和区间端点处的函数值,最后比较即得; (2)已知函数的最值求参数,一般先用参数表示最值,列方程求解参数.。
高考理科数学第一轮专题导数及其应用测试题参考答案

高考理科数学第一轮专题《导数及其应用》测试题&参考答案测试时间:120分钟 满分:150分第Ⅰ卷 (选择题,共60分)一、选择题(本题共12小题,每小题5分,共60分,每小题只有一个选项符合题意)1.[2016·安庆二模]给出定义:设f ′(x )是函数y =f (x )的导函数,f ″(x )是函数f ′(x )的导函数,若方程f ″(x )=0有实数解x 0,则称点(x 0,f (x 0))为函数y =f (x )的“拐点”.已知函数f (x )=3x +4sin x -cos x 的拐点是M (x 0,f (x 0)),则点M ( )A .在直线y =-3x 上 B.在直线y =3x 上 C .在直线y =-4x 上 D.在直线y =4x 上答案 B解析 f ′(x )=3+4cos x +sin x ,f ″(x )=-4sin x +cos x =0,4sin x 0-cos x 0=0,所以f (x 0)=3x 0,故M (x 0,f (x 0))在直线y =3x 上.2.[2016·济南调研]设函数f ′(x )是f (x )(x ∈R )的导函数,f (0)=1,且3f (x )=f ′(x )-3,则4f (x )>f ′(x )的解集是( )A.⎝ ⎛⎭⎪⎫ln 43,+∞ B.⎝ ⎛⎭⎪⎫ln 23,+∞ C.⎝ ⎛⎭⎪⎫32,+∞ D.⎝ ⎛⎭⎪⎫e 3,+∞ 答案 B解析 根据f (0)=1,3f (x )=f ′(x )-3,导函数与原函数之间没有用变量x 联系,可知函数与y =e x 有关,可构造函数为f (x )=2e 3x -1,4f (x )>f ′(x )=3f (x )+3,即f (x )>3,2e 3x -1>3,解得x >ln 23,故选B.3.[2017·河北武邑期末]曲线f (x )=2x 2-1、直线x =2、x =3以及x 轴所围成的封闭图形的面积是( )A .ln 2 B.ln 3 C .2ln 2 D.ln 32答案 D 解析 因f (x )=1x -1-1x +1, 故⎠⎛23f (x )d x =⎠⎛23⎝⎛⎭⎪⎫1x -1-1x +1d x=[ln (x -1)-ln (x +1)] ⎪⎪⎪⎪32=lnx -1x +1⎪⎪⎪32=ln 12-ln 13=ln 32,故应选D .4.[2017·江西抚州联考]已知函数f(x)与f ′(x)的图象如图所示,则函数g(x)=f (x )e x 的递减区间为( )A .(0,4) B.(-∞,1),⎝ ⎛⎭⎪⎫43,4C .⎝ ⎛⎭⎪⎫0,43 D.(0,1),(4,+∞)答案 D解析 g ′(x)=f ′(x )e x -f (x )e x (e x )2=f ′(x )-f (x )e x ,令g ′(x)<0,即f ′(x)-f(x)<0,由图可得x ∈(0,1)∪(4,+∞),故函数单调递减区间为(0,1),(4,+∞),故选D .5.[2017·湖北联考]已知函数f(x)=ax 2-4ax -ln x ,则f(x)在(1,3)上不单调的一个充分不必要条件是( )A .a ∈⎝ ⎛⎭⎪⎫-∞,16B.a ∈⎝ ⎛⎭⎪⎫-12,+∞C .a ∈⎝ ⎛⎭⎪⎫-12,16D.a ∈⎝ ⎛⎭⎪⎫12,+∞答案 D解析 f ′(x)=2ax -4a -1x ,f(x)在(1,3)上不单调,则f ′(x)=2ax -4a -1x =0在(1,3)上有解,此方程可化为2ax 2-4ax -1=0,x 1+x 2=2,因此方程的两解不可能都大于1,从而它在(1,3)上只有一解,充要条件是(2a -4a -1)(18a -12a -1)<0,a<-12或a>16,因此D 是要求的一个充分不必要条件.故选D .6.[2016·甘肃五市联考]函数f(x)=x e cos x (x ∈[-π,π])的图象大致是( )答案 B解析 易得f(x)为奇函数,图象关于原点对称,故排除A ,C ;f ′(x)=e cos x +x e cos x ·(-sin x)=e cos x (1-x sin x),显然存在x 0∈(0,π),使得当x ∈(0,x 0)时,f ′(x)>0,x ∈(x 0,π)时,f ′(x)<0,即f(x)在[0,π]上先增后减,故排除D ,故选B .7.[2016·云南师大附中模拟]已知函数f(x)=|x|e x (x ∈R ),若关于x 的方程f (x )-m +1=0恰好有3个不相等的实数根,则实数m 的取值范围为( )A.⎝ ⎛⎭⎪⎫1,2e2e +1 B.⎝ ⎛⎭⎪⎫0,2e 2e C.⎝ ⎛⎭⎪⎫1,1e +1 D.⎝ ⎛⎭⎪⎫2e 2e ,1答案 A解析 当x ≤0时,f (x )=-xe x 为减函数,f (x )min =f (0)=0;当x >0时,f (x )=x e x ,f ′(x )=1-2x 2x e x ,则x >12时,f ′(x )<0,0<x <12时,f ′(x )>0,即f (x )在⎝ ⎛⎭⎪⎫0,12上递增,在⎝ ⎛⎭⎪⎫12,+∞上递减,f (x )极大值=f ⎝ ⎛⎭⎪⎫12=2e 2e .其大致图象如图所示,若关于x 的方程f (x )-m +1=0恰好有3个不相等的实数根,则0<m -1<2e2e ,即1<m <1+2e2e ,故选A.8.[2016·四川高考]设直线l 1,l 2分别是函数f (x )=⎩⎨⎧-ln x ,0<x <1,ln x ,x >1图象上点P 1,P 2处的切线,l 1与l 2垂直相交于点P ,且l 1,l 2分别与y 轴相交于点A ,B ,则△P AB 的面积的取值范围是( )A .(0,1) B.(0,2) C .(0,+∞) D.(1,+∞)答案 A解析 不妨设P 1(x 1,ln x 1),P 2(x 2,-ln x 2)(0<x 2<1<x 1),由于l 1⊥l 2,所以1x1×⎝ ⎛⎭⎪⎫-1x 2=-1,则x 1=1x 2.又切线l 1:y -ln x 1=1x 1(x -x 1),l 2:y +ln x 2=-1x 2(x -x 2),于是A (0,ln x 1-1),B (0,1+ln x 1),所以|AB |=2.联立⎩⎪⎨⎪⎧y -ln x 1=1x 1(x -x 1),y +ln x 2=-1x 2(x -x 2),解得x P =2x 1+1x 1.所以S △P AB =12×2×xP =2x 1+1x1,因为x 1>1,所以x 1+1x 1>2,所以S △P AB 的取值范围是(0,1),故选A.9.[2016·湖南七校联考]若函数f (x )=⎩⎪⎨⎪⎧a ln x -x 2-2(x >0),x +1x +a (x <0)的最大值为f (-1),则实数a 的取值范围为( ) A .[0,2e 2] B.[0,2e 3] C .(0,2e 2] D.(0,2e 3]答案 B解析 当x <0时,f (x )=x +1x +a =-⎝ ⎛⎭⎪⎫-x +1-x +a ≤f (-1)=a -2;若a <0时,f (x )=a ln x -x 2-2在区间(0,+∞)上为减函数,且当x →0时,f (x )→+∞;当a =0时,f (x )=-x 2-2≤-2恒成立;当a >0时,f ′(x )=ax -2x =a -2x 2x =-2⎝⎛⎭⎪⎫x -a 2⎝ ⎛⎭⎪⎫x +a 2x,即函数f (x )在⎝ ⎛⎭⎪⎫0,a 2上单调递增,在⎝ ⎛⎭⎪⎫a 2,+∞上单调递减,则需f ⎝⎛⎭⎪⎫a 2≤f (-1),即a ln a 2-a2-2≤a -2,即a lna 2≤32a ,即ln a2≤3,解得0<a ≤2e 3,综上所述,实数a 的取值范围为[0,2e 3],故选B.10.[2017·云南、四川、贵州联考]若存在两个正实数x ,y ,使得等式x 3e y x-ay 3=0成立,其中e 为自然对数的底数,则实数a 的取值范围为( )A.⎣⎢⎡⎭⎪⎫e 28,+∞ B.⎝ ⎛⎦⎥⎤0,e 327 C.⎣⎢⎡⎭⎪⎫e 327,+∞ D.⎝ ⎛⎦⎥⎤0,e 28 答案 C解析 由题意知a =e y x⎝ ⎛⎭⎪⎫y x 3,设y x =t (t >0),则a =e t t 3,令f (t )=e tt 3,则f ′(t )=e t (t -3)t 4,当t >3时,f ′(t )>0,当0<t <3时,f ′(t )<0,所以f (t )min =f (3)=e 327,∴a ≥e 327.11.[2016·山东高考]若函数y =f (x )的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y =f (x )具有T 性质.下列函数中具有T 性质的是( )A .y =sin x B.y =ln x C .y =e x D.y =x 3答案 A解析 设函数y =f (x )的图象上两点P (x 1,y 1),Q (x 2,y 2),则由导数的几何意义可知,点P ,Q 处切线的斜率分别为k 1=f ′(x 1),k 2=f ′(x 2),若函数具有T 性质,则k 1·k 2=f ′(x 1)·f ′(x 2)=-1.对于A 选项,f ′(x )=cos x ,显然k 1·k 2=cos x 1·cos x 2=-1有无数组解,所以该函数具有T 性质;对于B 选项,f ′(x )=1x (x >0),显然k 1·k 2=1x 1·1x 2=-1无解,故该函数不具有T 性质;对于C 选项,f ′(x )=e x >0,显然k 1·k 2=e x 1·e x 2=-1无解,故该函数不具有T 性质;对于D 选项,f ′(x )=3x 2≥0,显然k 1·k 2=3x 21·3x 22=-1无解,故该函数不具有T 性质.故选A.12.[2016·河南八市联考]已知函数f (x )=m e x2与函数g (x )=-2x 2-x +1的图象有两个不同的交点,则实数m 的取值范围为( )A .[0,1)B.[0,2)∪⎩⎨⎧⎭⎬⎫-18e 2C .(0,2)∪⎩⎨⎧⎭⎬⎫-18e 2D.[0,2e)∪⎩⎨⎧⎭⎬⎫-18e 2答案 D解析依题意,m e x2=-2x 2-x +1⇔m e x =-4x 2-2x +2⇔m =-4x 2-2x +2e x,故问题转化为函数y =m 的图象与函数h (x )=-4x 2-2x +2e x 的图象有两个交点,h ′(x )=2(2x +1)(x -2)e x ,故函数h (x )在⎝ ⎛⎭⎪⎫-∞,-12和(2,+∞)上单调递增,在⎝ ⎛⎭⎪⎫-12,2上单调递减,且当x →+∞时,h (x )→0,h ⎝ ⎛⎭⎪⎫-12=2e ,h (2)=-18e 2,作出函数h (x )的图象如图所示,观察图象可知,当函数f (x )=m e x2与函数g (x )=-2x 2-x +1的图象有两个不同的交点时,实数m ∈[0,2e)∪⎩⎨⎧⎭⎬⎫-18e 2,故选D.第Ⅱ卷 (非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.[2016·沈阳质检]函数f (x )=2x -ln x 的单调递增区间是________. 答案 ⎣⎢⎡⎭⎪⎫12,+∞(写成⎝ ⎛⎭⎪⎫12,+∞也给分) 解析 函数f (x )=2x -ln x 的定义域为(0,+∞),f ′(x )=2-1x ≥0,即x ≥12,所以函数f (x )=2x -ln x 的单调递增区间为⎣⎢⎡⎭⎪⎫12,+∞.14.[2016·长春质检]设函数f (x )=1-e x 的图象与x 轴的交点为P ,则曲线在点P 处的切线方程为________.答案 y =-x解析 由题意P (0,0),f ′(x )=-e x ,f ′(0)=-1,从而曲线在点P 处的切线方程为y =-x .15.[2016·北京高考改编]设函数f (x )=⎩⎨⎧x 3-3x ,x ≤a ,-2x ,x >a .若f (x )无最大值,则实数a 的取值范围是________.答案 (-∞,-1)解析 函数y =x 3-3x 与y =-2x 的大致图象如图所示,若函数f (x )=⎩⎨⎧x 3-3x ,x ≤a ,-2x ,x >a 无最大值,由图象可知-2a >2,解得a <-1.16.[2016·湖南七校联考]若函数f (x )=⎝ ⎛⎭⎪⎫1-14x 2(x 2+ax +b )的图象关于直线x=-1对称,则f (x )的最大值为________.答案 4解析 因为函数f (x )的图象关于直线x =-1对称,所以f (0)=f (-2),f (1)=f (-3),即⎩⎪⎨⎪⎧b =⎣⎢⎡⎦⎥⎤1-14×(-2)2[(-2)2-2a +b ],⎝ ⎛⎭⎪⎫1-14(1+a +b )=⎣⎢⎡⎦⎥⎤1-14×(-3)2[(-3)2-3a +b ],解得⎩⎨⎧a =4,b =0,所以f (x )=⎝ ⎛⎭⎪⎫1-14x 2(x 2+4x )=-14x 4-x 3+x 2+4x ,则f ′(x )=-x 3-3x 2+2x +4=-(x+1)(x 2+2x -4).令f ′(x )=0,解得x =-1或x =-1±5,易知函数f (x )在x =-1±5处取得极大值, 又f (-1+5)=f (-1-5)=4,所以f (x )max =4.三、解答题(共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.[2016·北京东城一模](本小题满分10分)已知函数f (x )=(x 2+mx )e x (其中e 为自然对数的底数).(1)当m =-2时,求函数f (x )的单调递增区间;(2)若函数f (x )在区间[1,3]上单调递减,求m 的取值范围. 解 (1)当m =-2时,f (x )=(x 2-2x )e x , f ′(x )=(2x -2)e x +(x 2-2x )e x =(x 2-2)e x ,(1分) 令f ′(x )≥0,即x 2-2≥0,解得x ≤-2或x ≥ 2.所以函数f (x )的单调递增区间是(-∞,-2]和[2,+∞).(4分) (2)依题意,f ′(x )=(2x +m )e x +(x 2+mx )e x =[x 2+(m +2)x +m ]e x ,(5分) 因为f ′(x )≤0对于x ∈[1,3]恒成立,所以x 2+(m +2)x +m ≤0,即m ≤-x 2+2x x +1=-(x +1)+1x +1.(7分)令g (x )=-(x +1)+1x +1,则g ′(x )=-1-1(x +1)2<0恒成立, 所以g (x )在区间[1,3]上单调递减,g (x )min =g (3)=-154,故m 的取值范围是⎝ ⎛⎦⎥⎤-∞,-154.(10分) 18.[2016·西安八校联考](本小题满分12分)已知函数f (x )=(x 3-6x 2+3x +t )e x ,t ∈R .(1)若函数f (x )在点(0,f (0))处的切线方程为4x -y +1=0,则求t 的值; (2)若函数y =f (x )有三个不同的极值点,求t 的值. 解 (1)函数f (x )=(x 3-6x 2+3x +t )e x , 则f ′(x )=(x 3-3x 2-9x +3+t )e x ,(2分)函数f (x )在点(0,f (0))处的切线斜率为f ′(0)=3+t , 由题意可得,3+t =4,解得t =1.(4分)(2)f ′(x )=(x 3-3x 2-9x +3+t )e x ,(5分)令g (x )=x 3-3x 2-9x +3+t ,则方程g (x )=0有三个不同的根,(6分) 又g ′(x )=3x 2-6x -9=3(x 2-2x -3)=3(x +1)(x -3), 令g ′(x )=0,得x =-1或3,且g (x )在区间(-∞,-1),(3,+∞)递增,在区间(-1,3)递减,(8分) 故问题等价于⎩⎨⎧ g (-1)>0,g (3)<0,即有⎩⎨⎧t +8>0,t -24<0,解得-8<t <24.(12分)19.[2017·河北石家庄联考](本小题满分12分)已知函数f (x )=e x -ax ,a >0. (1)记f (x )的极小值为g (a ),求g (a )的最大值; (2)若对任意实数x 恒有f (x )≥0,求a 的取值范围. 解 (1)函数f (x )的定义域是(-∞,+∞),f ′(x )=e x -a , 令f ′(x )>0,得x >ln a ,所以f (x )的单调递增区间是(ln a ,+∞); 令f ′(x )<0,得x <ln a ,所以f (x )的单调递减区间是(-∞,ln a ), 函数f (x )在x =ln a 处取极小值,g (a )=f (x )极小值=f (ln a )=e ln a -a ln a =a -a ln a .(3分) g ′(a )=1-(1+ln a )=-ln a ,当0<a <1时,g ′(a )>0,g (a )在(0,1)上单调递增; 当a >1时,g ′(a )<0,g (a )在(1,+∞)上单调递减,所以a =1是函数g (a )在(0,+∞)上唯一的极大值点,也是最大值点,所以g (a )max =g (1)=1.(6分)(2)当x≤0时,a>0,e x-ax≥0恒成立,(7分)当x>0时,f(x)≥0,即e x-ax≥0,即a≤e xx.(8分)令h(x)=e xx,x∈(0,+∞),h′(x)=e x x-e xx2=e x(x-1)x2,(10分)当0<x<1时,h′(x)<0,当x>1时,h′(x)>0,故h(x)的最小值为h(1)=e,所以a≤e,故实数a的取值范围是(0,e].(12分)20.[2016·广西三市调研](本小题满分12分)已知函数f(x)=ax+x ln x(a∈R).(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;(2)当a=1且k∈Z时,不等式k(x-1)<f(x)在x∈(1,+∞)上恒成立,求k 的最大值.解(1)f′(x)=a+ln x+1,(1分)由题意知f′(x)≥0在[e,+∞)上恒成立,(2分)即ln x+a+1≥0在[e,+∞)上恒成立,即a≥-(ln x+1)在[e,+∞)上恒成立,(3分)而[-(ln x+1)]max=-(ln e+1)=-2,∴a≥-2.(4分)(2)f(x)=x+x ln x,k<f(x)x-1,即k<x+x ln xx-1对任意x>1恒成立.(5分)令g(x)=x+x ln xx-1,则g′(x)=x-ln x-2(x-1)2.(6分)令h(x)=x-ln x-2(x>1),则h′(x)=1-1x=x-1x>0,∴h(x)在(1,+∞)上单调递增.(7分)∵h(3)=1-ln 3<0,h(4)=2-2ln 2>0,∴存在x0∈(3,4)使h(x0)=0.即当1<x<x0时,h(x)<0,即g′(x)<0,(8分)当x>x0时,h(x)>0,即g′(x)>0.∴g(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增.(9分)由h(x0)=x0-ln x0-2=0,得ln x0=x0-2,g(x)min=g(x0)=x0(1+ln x0)x0-1=x0(1+x0-2)x0-1=x0∈(3,4),(11分)∴k<g(x)min=x0且k∈Z,即k max=3.(12分)21.[2017·江苏模拟](本小题满分12分)已知函数f(x)=a ln x+1x-bx+1.(1)若2a-b=4,则当a>2时,讨论f(x)的单调性;(2)若b=-1,F(x)=f(x)-5x,且当a≥-4时,不等式F(x)≥2在区间[1,4]上有解,求实数a的取值范围.解(1)由2a-b=4,得f(x)=a ln x+1x+(4-2a)x+1,所以f′(x)=ax-1x2+(4-2a)=(4-2a)x2+ax-1x2=[(2-a)x+1](2x-1)x2.令f′(x)=0,得x1=12,x2=1a-2.(2分)当a=4时,f′(x)≤0,函数f(x)在定义域(0,+∞)内单调递减;当2<a <4时,在区间⎝ ⎛⎭⎪⎫0,12,⎝ ⎛⎭⎪⎫1a -2,+∞上,f ′(x )<0,f (x )单调递减,在区间⎝ ⎛⎭⎪⎫12,1a -2上,f ′(x )>0,f (x )单调递增; 当a >4时,在区间⎝ ⎛⎭⎪⎫0,1a -2,⎝⎛⎭⎪⎫12,+∞上,f ′(x )<0,f (x )单调递减,在区间⎝ ⎛⎭⎪⎫1a -2,12上,f ′(x )>0,f (x )单调递增.(6分) (2)由题意知,当a ≥-4时,F (x )在[1,4]上的最大值M ≥2.(7分)当b =-1时,F (x )=f (x )-5x =x -4x +a ln x +1,则F ′(x )=x 2+ax +4x 2(1≤x ≤4).(8分) ①当-4≤a ≤4时,F ′(x )=⎝ ⎛⎭⎪⎫x +a 22+4-a 24x 2≥0, 故F (x )在[1,4]上单调递增,M =F (4).(9分)②当a >4时,设x 2+ax +4=0(Δ=a 2-16>0)的两根分别为x 1,x 2,则⎩⎨⎧x 1+x 2=-a <0,x 1x 2=4,故x 1<0,x 2<0, 所以在[1,4]上,F ′(x )=x 2+ax +4x 2>0, 故F (x )在[1,4]上单调递增,M =F (4).(11分)综上,当a ≥-4时,F (x )在[1,4]上的最大值M =F (4)=4-1+a ln 4+1≥2,解得a ≥-1ln 2,所以实数a 的取值范围是⎣⎢⎡⎭⎪⎫-1ln 2,+∞.(12分) 22.[2016·长春质检](本小题满分12分)已知函数f (x )=e 1-x (-a +cos x )(a ∈R ).(1)若函数f (x )存在单调递减区间,求实数a 的取值范围;(2)若a =0,证明:∀x ∈⎣⎢⎡⎦⎥⎤-1,12,总有f (-x -1)+2f ′(x )·cos(x +1)>0. 解 (1)由题意得f ′(x )=-e 1-x (-a +sin x +cos x ),(1分)若函数f (x )存在单调减区间,则f ′(x )<0有解,而e 1-x >0恒成立,即-a +sin x +cos x >0有解,所以a <(sin x +cos x )max .又sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4∈[-2,2],所以a < 2.(4分)(2)证明:当a =0时,f (x )=e 1-x cos x ,f ′(x )=-e 1-x (sin x +cos x ),f (-x -1)+2f ′(x )·cos(x +1)=cos(x +1)·[ e x +2- ⎦⎥⎤22e 1-x ·sin ⎝ ⎛⎭⎪⎫x +π4.(5分) 由x ∈⎣⎢⎡⎦⎥⎤-1,12,有x +1∈⎣⎢⎡⎦⎥⎤0,32⊆⎣⎢⎡⎦⎥⎤0,π2, 从而cos(x +1)>0,要证原不等式成立,只要证e x +2-22e 1-x ·sin ⎝ ⎛⎭⎪⎫x +π4>0, 即证e 2x +1-22sin ⎝ ⎛⎭⎪⎫x +π4>0(6分) 对∀x ∈⎣⎢⎡⎦⎥⎤-1,12恒成立. 首先令g (x )=e 2x +1-(2x +2),由g ′(x )=2e 2x +1-2,可知,当x ∈⎝ ⎛⎭⎪⎫-12,+∞时g (x )单调递增, 当x ∈⎝ ⎛⎭⎪⎫-∞,-12时g (x )单调递减, 所以g (x )=e 2x +1-(2x +2)≥g ⎝ ⎛⎭⎪⎫-12=0,有e 2x +1≥2x +2⎝ ⎛⎭⎪⎫当且仅当x =-12时等号成立.(8分) 构造函数h (x )=2x +2-22sin ⎝ ⎛⎭⎪⎫x +π4,x ∈⎣⎢⎡⎦⎥⎤-1,12,因为h ′(x )=2-22cos ⎝ ⎛⎭⎪⎫x +π4=22[ 22-cos ( x +π4 ) ], 可见,在x ∈[]-1,0时,h ′(x )≤0,即h (x )在[-1,0]上是减函数,在x ∈⎝ ⎛⎦⎥⎤0,12时,h ′(x )>0,即h (x )在⎝ ⎛⎦⎥⎤0,12上是增函数, 所以,在⎣⎢⎡⎦⎥⎤-1,12上,h (x )min =h (0)=0,所以h (x )≥0. 所以,当且仅当x =0时,22sin ⎝ ⎛⎭⎪⎫x +π4≤2x +2,等号成立.(10分) 综上e 2x +1≥2x +2≥22sin ⎝ ⎛⎭⎪⎫x +π4,由于取等条件不同, 故e 2x +1-22sin ⎝ ⎛⎭⎪⎫x +π4>0,即e x +2-22e 1-x ·sin ⎝ ⎛⎭⎪⎫x +π4>0,所以原不等式成立.(12分)。
浙江专版2020届高考数学一轮复习单元检测四导数及其应用单元检测含解析

单元检测四导数及其应用(时间:分钟满分:分)第Ⅰ卷(选择题共分)一、选择题(本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的).下列求导运算正确的是( )′=+.()′=.()′=·.()′=答案解析由求导法则可知正确..已知函数()=+′(),且()=-,则实数的值为( ).-或..答案解析令=,则()=+′()=-,可得′()=-.令=>,则′()=+′(),即--=,解得=或=-(舍去)..若函数()=的图象的切线的倾斜角大于,则的取值范围是( ).(-∞,) .(-∞,-).(-∞,-] .(-∞,)答案解析′()=+=(+),又切线的倾斜角大于,所以′()<,即(+)<,解得<-..函数()=的部分图象大致为( )答案解析由题意得()为奇函数,排除;又()=<,排除;当>时,()=,所以′()=,函数()在区间()内单调递减,在区间(,+∞)内单调递增,排除. .若函数()=+-在区间内存在单调递增区间,则实数的取值范围是( ) .(-∞,-].(-,+∞)答案解析对()求导得′()=+=,由题意可得+>在内有解,所以>.因为∈,所以∈,∈,所以>-..已知定义在上的函数(),其导函数′()的大致图象如图所示,则下列叙述正确的是( )①()>()>();②函数()在=处取得极小值,在=处取得极大值;③函数()在=处取得极大值,在=处取得极小值;④函数()的最小值为()..③.①②.③④.④答案解析由导函数的图象可知函数()在区间(-∞,),(,+∞)内,′()>,所以函数()在区间(-∞,),(,+∞)内单调递增,在区间(,)内,′()<,所以函数()在区间(,)内单调递减.所以()>(),所以①错;函数()在=处取得极大值,在=处取得极小值,故②错,③对;函数()没有最小值,故④错..已知函数()=(--)+(∈)在=处取得极小值,则()的极大值是( ) .-..-.答案解析由题意知,′()=[+(-)-],′()=-=,解得=,∴()=,′()=(+).令′()>,解得<-或>,令′()<,解得-<<,则函数()在区间(-∞,-)和(,+∞)上单调递增,在区间(-)上单调递减,∴函数()的极大值为(-)=-.故选..设函数()=({,}表示,中的较小者),则函数()的最大值为( ).答案解析函数()的定义域为(,+∞).由=得′=+,令′=,解得=,∴=在上单调递减,在上单调递增.由=,>得′=,令′=,>,解得=,∴=在()上单调递增,在(,+∞)上单调递减,作出示意图如图,当=时,=,=.∵>,∴=与=的交点在()内,∴函数()的最大值为..已知=()为(,+∞)上的可导函数,且有′()+>,则对于任意的,∈(,+∞),当>时,有( ).()<() .()>().()>() .()<()答案解析由′()+>,得>,即>,即[()]′>.∵>,∴[()]′>,即函数=()为增函数,由,∈(,+∞)且>,得()>(),故选..(·温州“十五校联合体”联考)已知函数()=-(为自然对数的底数),()=+(∈),若对于任意的∈[-],总存在∈[-],使得()=()成立,则实数的取值范围为( ).(-∞,-]∪[-,+∞).[-,-].(-∞,--]∪[--,+∞).[----]答案解析∵′()=-,∴()在区间[-]上为增函数,在区间[]上为减函数,∵(-)-()=(---)-(-)=--->,∴(-)>(),又()=-,则函数()在区间[-]上的值域为=[-,-].当>时,函数()在区间[-]上的值域为=[-+,+].依题意有⊆,则有得≥-.当=时,函数()在区间[-]上的值域为={},不符合题意.当<时,函数()在区间[-]上的值域为=[+,-+].依题意有⊆,则有得≤-.综上,实数的取值范围为(-∞,-]∪[-,+∞).第Ⅱ卷(非选择题共分)二、填空题(本大题共小题,多空题每题分,单空题每题分,共分.把答案填在题中横线上) .已知直线=与函数()=(其中为自然对数的底数)的图象相切,则实数的值为;切点坐标为.答案(,)解析设切点坐标为(,),需满足所以解得=,=,=,所以=,切点坐标为(,)..设函数()=,则点()处的切线方程是;函数()=的最小值为.答案--=-解析由题意得′()=+,所以′()=,则所求切线方程为--=.由′()=+<得<<;由′()=+>得>,所以函数()=在上单调递减,在上单调递增,所以函数()=在=处取得最小值,最小值为==-..(·宁波九校期末)函数()=-+--是函数(填“奇”或“偶”),在上的增减性为.(填“单调递增”、“单调递减”或“有增有减”)答案奇单调递增解析∵函数()=-+--,∴它的定义域为,且满足(-)=-++--=-(),故函数()为奇函数.由于函数的导数′()=-+(+-)≥-+=≥,故函数在上单调递增..(·诸暨检测)已知函数()=-,函数()的图象在=处的切线方程是;函数()在[]内的值域是.答案=-[-]解析∵()=-,∴′()=-,又∵()=,′()=-,∴函数()在点()处的切线方程为=-.令′()=-=,得=±,当变化时,()与′()的变化情况如下表.(-∞,-)-(-)(,+∞)′()+-+()↗极大值↘极小值-↗∴在[]上,()是减函数,其最小值为()=-,最大值为()=;在[]上,()是增函数,其最小值为()=-,最大值为()=.综上,在[]上,()的值域为[-]..已知函数()=+,()=-,若()=()成立,则-的最小值为.答案解析令()=()=(>),则由+=,解得=,由-=,解得=+,则-=--,令()=--,则′()=-,由′()=得=,且当∈时,′()<,()单调递减,当∈时,′()>,()单调递增,则()==,即-的最小值是..设实数λ>,若对任意的∈(,+∞),不等式λ-≥恒成立,则λ的最小值为.答案解析当∈(]时,λ>,不等式λ-≥显然成立,λ可取任意正实数;当∈(,+∞)时,λ-≥⇔λλ≥⇔λ·λ≥·,设函数()=·(>),而′()=(+)·>,则()在(,+∞)上单调递增,那么由λ·λ≥·可得λ≥⇔λ≥.令()=(>),而′()=,易知函数()在(,)上单调递增,在(,+∞)上单调递减,那么()=()=,则有λ≥.综上分析可知,λ的最小值为..对于定义在上的函数(),若存在非零实数,使函数()在(-∞,)和(,+∞)上均有零点,则称为函数()的一个“折点”.现给出下列四个函数:①()=-+;②()=+;③()=--;④()=+-(∈).则存在“折点”的函数是.(填序号)答案②④解析因为()=-+>,所以函数()不存在零点,所以函数()不存在“折点”;对于函数()=+,取=-,则函数()在(-∞,-)上有零点=-,在(-,+∞)上有零点=-,所以=-是函数()=+的一个“折点”;对于函数()=--,则′()=-=(+)(-).令′()>,得>或<-;令′()<,得-<<,所以函数()在(-∞,-)和(,+∞)上单调递增,在(-,)上单调递减.又(-)=-<,所以函数()只有一个零点,所以函数()=--不存在“折点”;对于函数()=+-=(+)--,由于(-)=--≤-,结合图象(图略)可知该函数一定有“折点”.综上,存在“折点”的函数是②④.三、解答题(本大题共小题,共分.解答应写出文字说明,证明过程或演算步骤) .(分)已知函数()=+.()求函数=′()在区间[,+∞)内的最小值;()若对任意∈[,+∞),恒有()≥+(-),求实数的取值范围.解()令=()=′()=+,则′()=-,则当∈[,+∞)时,≥,≤,所以′()>,即()在区间[,+∞)内是增函数,于是=′()在区间[,+∞)内的最小值为()=+.()令()=()--(-),则()≥对任意∈[,+∞)恒成立,且发现()=,′()=+-.由()知当≤+时,′()≥,此时()单调递增,于是()≥()=,成立;当>+时,则存在∈(,+∞),使得′()=,当∈(,)时,′()<,当∈(,+∞)时,′()>,此时()=()<()=,矛盾.综上得≤+,即实数的取值范围为(-∞,+]..(分)已知函数()=++,∈.()若函数()在区间[,+∞)内单调递增,求实数的取值范围;()记函数()=[′()+-],若()的最小值是-,求函数()的解析式.解()由题意知′()=-+≥在区间[,+∞)内恒成立,所以≥-在区间[,+∞)内恒成立.令()=-,∈[,+∞),因为′()=--<恒成立,所以()在区间[,+∞)内单调递减,所以()=()=,所以≥,即实数的取值范围为[,+∞).()()=+-,>.因为′()=+,当≥时,′()>恒成立,所以()在区间(,+∞)内单调递增,无最小值,不合题意,所以<. 令′()=,则=或=-(舍去),由此可得函数()在区间内单调递减,在区间内单调递增,则=是函数()的极小值点,也是最小值点,所以()=()极小值==-,解得=-,所以()=+-..(分)(·舟山模拟)已知函数()=-,()=+(<).()求函数()在区间上的最值;()求函数()=()+()的极值点.解()依题意,′()=-,令-=,解得=.因为()=-,=--,()=-,且-<--<-,故函数()在区间上的最大值为-,最小值为-.()依题意,()=()+()=++(>),′()=++=,当<时,令′()=,则++=.因为Δ=->,所以′()==,其中=-,=-.因为<,所以<,>,所以当<<时,′()>;当>时,′()<,所以函数()在区间(,)内是增函数,在区间(,+∞)内是减函数,故=-为函数()的极大值点,无极小值点..(分)已知函数()=+,()=(∈).()若函数()的图象在点(,())处的切线与函数=()的图象相切,求的值;()若∈*,且∈(,+∞)时,恒有()>(),求的最大值.(参考数据:≈,≈,(+)≈)解()∵()=+,∴()=,且′()=,从而得到′()=.∴函数()的图象在点(,())处的切线方程为-=-,即=+. 设直线=+与()=(∈)的图象相切于点(,),从而可得′()=,()=+,又′()=,∴解得或∴的值为或.()由题意知,当∈(,+∞)时,+>恒成立,等价于当∈(,+∞)时,<恒成立.设()=(>),则′()=(>),记()=--(>),则′()=-=>,∴()在∈(,+∞)上单调递增.又()=-<,()=->,∴在∈(,+∞)上存在唯一的实数,且∈(),使得()=--=,①∴当∈(,)时,()<,即′()<,则()在∈(,)上单调递减,当∈(,+∞)时,()>,即′()>,则()在∈(,+∞)上单调递增,∴当∈(,+∞)时,()=()=,由①可得=-,∴()==++,而∈(),∴++∈,又当=+时,()=,(+)=--(+)>,∴∈(+),∴()∈.又∈*,∴的最大值是..(分)已知函数()=-的图象在点(,())处的切线与直线:+(-)=垂直,其中为自然对数的底数.()求实数的值及函数()在区间[,+∞)内的最大值.()①求证:函数()有且仅有一个极值点.②求证:()<--.()解由题意得′()=-,直线:+(-)=的斜率为-,故函数()的图象在点(,())处的切线的斜率为-,即′()=-=-,所以=.当∈[,+∞)时,′()=-单调递减,即′()≤′()=-<,所以()在区间[,+∞)内单调递减,所以当∈[,+∞)时,()=()=-=-.()证明①′()=-,令()=′(),则′()=--<在(,+∞)上恒成立,即有()在区间(,+∞)内单调递减.又=-12e>,()=-<,所以()=在区间(,+∞)内有且仅有一个实根,设此实根为,则∈.当∈(,)时,()>,故()单调递增;当∈(,+∞)时,()<,故()单调递减,所以函数()在=处取得唯一的极大值,即函数()有且仅有一个极值点.②由①知′()=-在区间(,+∞)内为减函数,又′()=-<,′=->,因此存在实数∈满足方程′()=-=,此时()在区间(,)内为增函数,在区间(,+∞)内为减函数,且′()=-=,由此得到=,=-.由单调性知()=()=-=--=-,又∈,故-<-,所以()<-.又--=(-)-≥-,所以()<--.。
(好题)高中数学选修1-1第四章《导数应用》检测卷(含答案解析)(1)

一、选择题1.已知,a b ∈R ,若函数()e =-x f x a bx 存在两个零点1x ,2x ,且210x x >>,则下列结论可能成立的是( ). A .0ae b >>B .0ae b >>C .0b ae >>D .0ae b >>2.若关于x 的方程2lnx ax x -=在0,上有两个不等的实数根,则实数a 的取值范围为( ) A .(],1-∞-B .(),1-∞-C .[)1,-+∞D .()1,-+∞3.已知函数()2()x xf x x e e x-=⋅-+,若()()()f x f y f x y <<+,则( )A .0xy >B .0xy <C .0x y +>D .0x y +<4.已知函数()sin f x x x =+,若存在[0,]x π∈使不等式(sin )(cos )f x x f m x ≤-成立,则整数m 的最小值为( ) A .1-B .0C .1D .25.已知函数4213(),42f x x x mx n =-++其中m ,n 为正整数,若函数()f x 有极大值,则m 的值为( ) A .1B .2C .3D .46.若定义在R 上的函数()f x 满足()()1f x f x '+>,(0)4f =,则不等式()3x x e f x e ⋅>+ (其中e 为自然对数的底数)的解集为( ) A .(0)(0)-∞+∞,, B .(0)(3)-∞⋃+∞,, C .(0)+∞,D .(3)+∞,7.下列不可能是函数()()()xx f x xee Z αα-=-∈的图象的是( )A .B .C .D .8.已知函数()()()22210,0x ax x x f x e ax e x ⎧-+<⎪=⎨-+-≥⎪⎩有两个零点,则实数a 的取值范围是( ) A .(),e +∞B .()2e ,+∞C .()20,eD .()0,e9.已知定义域为R 的函数 f x () 的导函数为'f x () ,且满足'24f x f x ()﹣()> ,若 01f =()﹣ ,则不等式22x f x e +()> 的解集为( )A .∞(0,+)B .1+∞(﹣,)C .0∞(﹣,)D .1(﹣,﹣)∞ 10.某生产厂家的年利润y (单位:万元)与年产量x (单位:万件)的函数关系式为31812863y x x =-+-,则该生产厂家获取的最大年利润为( )A .300万元B .252万元C .200万元D .128万元11.已知函数2()f x x m =+与函数1()ln3g x x x =--,1,22x ⎡∈⎤⎢⎥⎣⎦的图象上恰有两对关于x 轴对称的点,则实数m 的取值范围是( ) A .5ln )4[2,2+ B .5[2ln 2,ln 2)4-+ C .5(ln 2,2ln 2)4+-D .(]2ln2,2-12.若函数(1),()21,x x e x af x x x a⎧-+=⎨-->⎩有最大值,则实数a 的取值范围是( )A .211[,)22e --+∞ B .21[,)2e -+∞ C .[2-,)+∞ D .211(2,]22e --- 二、填空题13.已知定义在R 上的函数()f x 关于y 轴对称,其导函数为()f x '. 当0x ≥时,()()1xf x f x '>-. 若对任意x ∈R ,不等式()()0x x x e f e e ax axf ax -+->恒成立,则正整数a 的最大值为_____.14.函数2sin y x x =-在[]0,2π上的递增区间是________. 15.已知函数()2cos sin 2f x x x =+,则()f x 的最小值是______.16.设定义在R 上的连续函数()f x 的导函数为()f x ',已知函数()y x f x =⋅'的图象(如图)与x 轴的交点分别为()2,0-,()0,0,()2,0.给出下列四个命题:①函数()f x 的单调递增区间是()2,0-,(2,)+∞; ②函数()f x 的单调递增区间是(–,2)∞-,(2,)+∞; ③2x =-是函数()f x 的极小值点; ④2x =是函数()f x 的极小值点. 其中,正确命题的序号是__________.17.已知函数()f x 定义在R 上的函数,若2()()0x f x e f x --=,当0x ≤时,()()0f x f x '+<,则不等式21()(1)x f x e f x -≥-的解集为__________18.已知函数f (x )=2,(,0],(0,)xx x e x +∈-∞⎧⎨∈+∞⎩,若存在x 1,x 2(x 2>x 1)满足f (x 1)=f (x 2),则x 2﹣2x 1的取值范围为_____.19.已知函数()xf x e x =-,()22g x x mx =-,若对任意1x ∈R ,存在[]21,2x ∈,满足()()12f x g x ≥,则实数m 的取值范围为______. 20.已知随机变量X 的分布列为:X1 1k +P3k e -31k e--随机变量X 的数学期望为E X ,则满足E X k <的最大正整数k 的值是_____. (参考数据:ln 20.6931≈,ln3 1.0986≈,ln5 1.6094≈)三、解答题21.已知函数2()(41)43(0)xf x ax a x a e a ⎡⎤=-+++≠⎣⎦. (1)若1a =,求曲线()y f x =在(0,(0))f 处的切线方程; (2)若()f x 在2x =处取得极小值,求a 的取值范围.22.已知()()2log 1f x x =+.(1)若()()0121f x f x <--<,求x 的取值范围; (2)若关于x 的方程()40xf x m -+=有解,求实数m 的取值范围.23.已知函数()()2ln 211f x x ax a x =++++. (1)讨论()f x 的单调性; (2)当0a <时,证明:()314f x a≤-- 24.已知函数()()x f x x a e =+,其中a 为常数.(1)若函数()f x 在区间[1,)-+∞上是增函数,求实数a 的取值范围; (2)若3()x f x e xe ≥-在[0,1]x ∈时恒成立,求实数a 的取值范围.25.已知函数()ln 2f x x x x =-. (1)求函数()f x 的最小值;(2)求函数()()g x f x x e =+-的单调区间;(3)若函数()()h x f x mx =-在[)1,x ∈+∞单调递增,求实数m 的取值范围. 26.(1)证明:1x e x ≥+; (2)证明:ln 1≤-x x ; (3)证明:1ln(1)x e x ->+.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据题意将问题转化为方程xb e a x=在0,上有两个实数根,进而令()(),0,xe g x x x=∈+∞,再研究函数()g x 的单调性得0b e a >>,进而分0a >和0a <讨论即可得答案. 【详解】解:当0a =时,函数()f x 只有一个零点,故0a ≠,因为函数()e =-xf x a bx 存在两个零点1x ,2x ,且210x x >>所以方程xb e a x=在0,上有两个不相等的实数根.令()(),0,x e g x x x =∈+∞,()()21'x x e g x x-=, 所以当()1,∈+∞x 时()'0g x >,()0,1∈x 时()'0g x <,故函数()(),0,xe g x x x=∈+∞在1,上单调递增,在0,1上单调递减;所以()()min 1g x g e ==,所以0be a>>, 当0a >时,0b ae >>,当0a <时,0b ae <<. 故选:D. 【点睛】本题考查利用导数研究函数零点问题,解题的关键在于将问题转化为方程xb e a x=在0,上有两个不相等实数根,进而令()g x 研究函数的单调性即可.考查运算求解能力与化归转化思想,是中档题.2.B解析:B【分析】通过分离参数变成ln x a x x=-,构造函数()ln x f x xx =-,利用导数求其单调区间和值域,数形结合写出a 的取值范围. 【详解】2lnx ax x -=故ln xa x x=- 则()ln x f x xx=- ()2'221ln 1ln 1x x x f x x x ---=-=设()21ln g x x x =--,0x >故()'120g x x x=--< ()21ln g x x x =--在0,上为减函数,10g .故()0,1∈x 时()'0f x >;()1,∈+∞x 时()'0f x <.故()ln x f x xx=-在0,1上为增函数,在1,上为减函数.()()max 11f x f ==-,且0,x →时()f x →-∞;,x →+∞时()f x →-∞y a =与()ln x f x x x=-的图象要有两个交点则a 的取值范围为(),1-∞-. 故选:B 【点睛】方程在某区间上有解的问题,可通过分离参数,构造函数,利用导数求该区间上单调区间和值域,得出参数的取值范围.3.A解析:A 【分析】先判断函数的奇偶性和单调性,再分析得解. 【详解】由题得函数的定义域为R.()22())()(x x x x f x x e e x e e x x f x --=-+=-=-⋅-+,所以函数是偶函数.当0x >时,1()()2xx x x f x e xe xe x e-'=-+++, 因为0x >,所以()0f x '>,所以函数()f x 在(0,)+∞上单调递增,因为函数是偶函数,所以函数()f x 在(,0)-∞上单调递减,在(0,)+∞上单调递增. 如果0,0x y >>,则0x y +>,因为()()()f x f y f x y <<+,所以x y x y <<+,与已知相符; 如果0,0x y <<,则0x y +<,所以x y x y >>+,与已知相符; 如果0,0x y ><,因为()()f x f y <,所以0y x y <+<, 所以()()f y f x y >+,与已知矛盾;如果0,0x y <>,因为()()f x f y <,所以0y x y >+>, 所以()()f y f x y >+,与已知矛盾;当,x y 之中有一个为零时,不妨设0y =,()()f x y f x += ,()()()f x f y f x <<,显然不成立.故选:A 【点睛】方法点睛:对于函数的问题,要灵活利用函数的奇偶性和单调性分析函数的问题,利用函数的图象和性质分析函数的问题.4.A解析:A【分析】先对()f x 求导可得()1cos 0f x x '=+≥,()f x 单调递增,原不等式可化为存在[0,]x π∈ 使得sin cos x x m x ≤-有解,即sin cos m x x x ≥+对于[0,]x π∈有解,只需()min m g x ≥,利用导数判断()g x 的单调性求最小值即可. 【详解】由()sin f x x x =+可得()1cos 0f x x '=+≥, 所以()sin f x x x =+在[0,]x π∈单调递增,所以不等式(sin )(cos )f x x f m x ≤-成立等价于sin cos x x m x ≤-, 所以sin cos m x x x ≥+对于[0,]x π∈有解, 令()sin cos g x x x x =+,只需()min m g x ≥, 则()sin cos sin cos g x x x x x x x '=+-=, 当02x π≤≤时,()cos 0g x x x '=≥,()g x 在0,2π⎡⎤⎢⎥⎣⎦单调递增, 当2x ππ<≤时,()cos 0g x x x '=<,()g x 在,2ππ⎡⎤⎢⎥⎣⎦单调递减, ()0cos01g ==,()sin cos 1g ππππ=+=-,所以()()min 1g x g π==-, 所以1m ≥-, 整数m 的最小值为1-, 故选:A. 【点睛】方法点睛:若不等式(),0f x λ≥()x D ∈(λ是实参数)有解,将(),0f x λ≥转化为()g x λ≥或()()g x x D λ≤∈有解,进而转化为()max g x λ≤或()()min g x x D λ≥∈,求()g x 的最值即可.5.A解析:A 【分析】对()f x 进行求导得3()3f x x x m '=-+,构造新函数3()3,h x x x m x R =-+∈,利用导数研究函数()h x 的单调性,结合题意,可知函数()f x 有极大值,则()()1010h h ⎧->⎪⎨<⎪⎩,求解不等式且结合m ,n 为正整数,即可得出结果.【详解】由题可知,4213()42f x x x mx n =-++()x R ∈, 则3()3f x x x m '=-+,设3()3,h x x x m x R =-+∈,则2()33h x x '=-,令2()330h x x '=-=,解得:121,1x x =-=,则当1x <-或1x >时,()0h x '>;当11x -<<时,()0h x '<,所以()h x 在区间()(),1,1,-∞-+∞上单调递增;在区间()1,1-上单调递减, 又因为函数()f x 有极大值,则()()1010h h ⎧->⎪⎨<⎪⎩,即()()120120h m h m ⎧-=+>⎪⎨=-<⎪⎩,解得:22m -<<,而m ,n 为正整数,所以m 的值为1.故选:A. 【点睛】关键点点睛:本题考查利用导数研究函数的单调性和极值,从而求参数值,构造新函数且利用导数求出单调区间是解题的关键,考查转化思想和运用能力.6.C解析:C 【分析】构造函数()()3xxg x e f x e =⋅--,解不等式()0g x >即可,对()g x 求导得()[()()1]0x g x e f x f x ''=+->,可得()g x 在R 上单调递增,且(0)0g =,根据单调性可得0x >,即得正确答案. 【详解】令()()3x xg x e f x e =⋅--,则()()()[()()1]0xxxxg x e f x e f x e e f x f x '''=⋅+⋅-=+->, 所以()g x 在R 上单调递增, 又因为0(0)(0)30g e f e =⋅--=, 所以()0>g x ⇒0x >,即不等式的解集是(0)+∞,, 故选:C 【点睛】关键点点睛:本题的关键点是构造函数()()3xxg x e f x e =⋅--,所要解的不等式等价于()0g x >,且(0)0g =,所以()()0g x g >,因此需要对()g x 求导判断单调性即可. 7.B解析:B【分析】 由函数()()xx f x xee α-=-,分0a =, a 为正整数,a 为正偶数,a 为正奇数,a 为负整数分析其定义域,奇偶性和单调性判断. 【详解】当0α=时,()xxf x e e -=-其定义域为{}|0x x ≠,关于原点对称,又()()()xx x x f x ee e ef x ---=-=--=-,所以()f x 是奇函数,且单调递增,没有选项符合题意;当α为正整数时,()()xx f x xee α-=-的定义域为R ,图象经过原点,当0x >时, ()()11()())(x x x x x xf x x e e e e x e e x x x ααααα-----'⎡⎤⎡⎤==-+++⎣⎦+⎣-⎦,因为0,0x xx x e ee e --->+>,所以()0f x '>,则()f x 递增,又存在0M >,当x M >时,随着x 的增大,()'f x 的变化率越来越大, 若α为正偶数,则()f x 是奇函数,此时C 选项符合题意; 若α为正奇数,则()f x 是偶函数,此时A 选项符合题意; 当α为负整数时,()()xx f x xee α-=-的定义域为{}|0x x ≠,当α为负奇数,()()()()xx f x x e e f x α--=--=,()f x 为{}|0x x ≠上的偶函数,无选项符合;当α为负偶数时且4α≤-时,()()()()xx f x x ee f x α--=--=-,()f x 为{}|0x x ≠上的奇函数,当0x >时,()()211(())xx x x f x x e e x x x x x e e x ααααααα----+⎛⎫+--+⎪-⎝'⎡⎤=+=⎦⎭⎣, 令()2,0x x S x e x x αα-+=+>-, 则()()()()()2222222xxxxx x S x ex x e ααααα---+-'=-=-⨯--,令(),0x x x x αϕ->=,则()01xx ϕ'<=,故(),0xx x x αϕ->=为减函数,而()00ϕα=->,()()()23ln ln 2ln t t t αααϕ---+=+=-,其中2t =≥,令()232ln ,2u t t t t t =+-≥,则()()2223,2t t u t t t+-'=≥,则()()22232+440tt +-≤⨯-<,故()232ln ,2u t t t t t =+-≥为减函数,所以()2ln 240u t ≤-<,()()ln 0ϕα-<,所以存在()00x ∈+∞,,使得当()00,x x ∈时,()0x ϕ>即()0S x '<, 当()0,x x ∈+∞时,()0x ϕ<即()0S x '>, 故()S x 在()00,x 为减函数,在()0,x +∞为增函数, 因为()00S =,故()00S x <,而当x a >-时,()0S x >, 故存在()10,x ∈+∞,使得当()10,x x ∈时,()0S x <即()0f x '<, 当()1,x x ∈+∞时,()0S x >即()0f x '>,所以()f x 在()10,x 上为减函数,在()1,x +∞为增函数, 又当0x >时,()0f x >恒成立,故D 选项符合题意. 对任意的整数α,当α为非负整数时,()f x 在0x =处有定义,且()f x '在0x =不间断,故B 不符合题意,当α为负整数时,()f x 在0x =处没有定义,故B 不符合题意, 故选:B. 【点睛】方法点睛:对于知式选图问题的解法:1、从函数的定义域,判断函数图象的左右位置,从函数的值域判断图象的上下位置;2、从函数的单调性,判断函数图象的变换趋势;3、从函数的奇偶性,判断函数图象的对称性;4、从函数的周期性,判断函数图象图的循环往复;5、从函数的特殊点,排除不和要求的图象;8.B解析:B 【分析】分离变量,利用导函数应用得到函数在0x <无零点,则0x >有两个零点,利用函数最值得到参数范围 【详解】当0x =时,()201e f =--,∴0x =不是函数()f x 的零点.当0x <时,由()0f x =,得221x a x -=,设()221x h x x -=,()()3210x h x x-'=<,则()h x 在(),0-∞上单调递减,且()0h x <.所以0x <时无零点当0x >时,()0f x =等价于2x e e a x +=,令()2x e e g x x +=,()22x x xe e e g x x --'=,得()g x 在()0,2上单调递减,在()2,+∞上单调递增,()2min (2)g x g e ==,()2g x e ≥.因为()f x 有2个零点,所以2a e >. 故选:B. 【点睛】分离变量法,利用导数求函数的单调性,极值是解题关键.9.A解析:A 【解析】 设()()22xf x F x e+=,则()()()224xf x f x F x e'--'=,∵f (x )−2f ′(x )−4>0,∴F ′(x )>0,即函数F (x )在定义域上单调递增, ∵f (0)=−1,∴F (0)=1,∴不等式f (x )+2>e 2x 等价为不等式()221e xf x +>等价为F (x )>F (0),解得x >0,故不等式的解集为(0,+∞), 本题选择A 选项.10.C解析:C 【分析】求得函数的导数,得到函数的单调性,进而求解函数的最大值,即可得到答案. 【详解】由题意,函数31812863y x x =-+-,所以281y x '=-+,当09x <<时,0y '>,函数()f x 为单调递增函数; 当9x >时,0y '<,函数()f x 为单调递减函数,所以当9x =时,y 有最大值,此时最大值为200万元,故选C. 【点睛】本题主要考查了利用导数研究函数的单调性与最值问题,其中解答中熟记函数的导数在函数中的应用,准确判定函数的单调性是解答的关键,着重考查了推理与计算能力,属于基础题.11.A解析:A 【分析】将问题转化为()()f x g x =-在1,22⎡⎤⎢⎥⎣⎦恰有两个不同的解,令()()()h x f x g x =+,将问题转化为()h x 在1,22⎡⎤⎢⎥⎣⎦上有两个零点的问题,利用导数可求得()h x 的单调性,进而确定区间端点值和最值,由此构造不等式求得结果.【详解】()f x 与()g x 在1,22x ⎡∈⎤⎢⎥⎣⎦的图象上恰有两对关于x 轴对称的点,()()f x g x ∴=-在1,22⎡⎤⎢⎥⎣⎦恰有两个不同的解,即221ln3ln 30x m x x x x m x +--=+-+=在1,22⎡⎤⎢⎥⎣⎦上恰有两个不同的解, 令()2ln 3h x x x x m =+-+,则()()()2211123123x x x x h x x x x x---+'=+-==, ∴当1,12x ⎛⎫∈ ⎪⎝⎭时,()0h x '<;当()1,2x ∈时,()0h x '>,()h x ∴在1,12⎛⎫⎪⎝⎭上单调递减,在()1,2上单调递增,又15ln 224h m ⎛⎫=--+⎪⎝⎭,()12h m =-,()2ln 22h m =-+, 原问题等价于()h x 在1,22⎡⎤⎢⎥⎣⎦上恰有两个零点,则5ln 2024m m --+≥>-,解得:5ln 224m +≤<,即m 的取值范围为5ln 2,24⎡⎫+⎪⎢⎣⎭.故选:A . 【点睛】本题考查根据函数零点个数求解参数范围的问题,关键是能够将两函数图象对称点个数的问题转化为方程根的个数的问题,进一步通过构造函数的方式将问题转化为函数零点个数的问题.12.A解析:A 【分析】由x a >时,()21f x x =--递减,且无最大值,可得x a 时,()f x 取得最大值M ,且21M a --,求出x a 时,()f x 的导数和单调区间、极大值,讨论2a <-,判断单调性,可得最大值,解不等式判断无解,则2a -,求出最大值,解不等式即可得到所求a 的范围. 【详解】解:由x a >时,()21f x x =--递减,可得()21f x a <--,无最大值,函数(1),()21,x x e x af x x x a ⎧-+=⎨-->⎩有最大值,可得x a 时,()f x 取得最大值M ,且21M a --,由()(1)xf x x e =-+的导数为()(2)xf x x e '=-+,可得2x >-时,()0f x '<,()f x 递减;2x <-时,()0f x '>,()f x 递增. 即有()f x 在2x =-处取得极大值,且为最大值2e -.若2a <-,则()f x 在(-∞,]a 递增,可得()()f x f a (1)aa e =-+,由题意可得(1)21a a e a -+≥--,即得(1)210aa e a +--≤, 令(1))1(2aa e g a a +--=,则()(2)20ag a a e '=+-<,(2)a <-, 则()g a 在(),2-∞-递减,可得2(2)0()3g a g e ->-=-+>,则不等式(1)210aa e a +--≤无实数解.故2a -,此时在2x =-处()f x 取得最大值,为2e --,故221e a ----, 解得21122a e --, 综上可得,a 的范围是211[22e--,)+∞. 故选:A. 【点睛】本题考查了分段函数的最值问题,考查转化思想,以及分类讨论思想方法,注意运用导数,求出单调区间和极值、最值,考查化简整理的运算能力,属于中档题.二、填空题13.2【分析】令利用可得在单调递增不等式恒成立等价于即当时分离参数可得可求出正整数的最大值为2再检验当时对于不等式恒成立即可求解【详解】因为定义在上的函数关于轴对称所以函数为上的偶函数令则因为当时即所以解析:2 【分析】令()()g x xf x x =-,利用()()1xf x f x '>-可得()g x 在[)0,+∞单调递增,不等式()()0x x x e f e e ax axf ax -+->恒成立等价于()()x g e g ax >,即e x ax >,当0x >时,分离参数可得()xe a h x x<=,可求出正整数a 的最大值为2,再检验当2a =时,对于0x <,不等式恒成立,即可求解. 【详解】因为定义在R 上的函数()f x 关于y 轴对称, 所以函数()f x 为R 上的偶函数,令()()g x xf x x =-,则()()()1g x f x xf x ''=+-,因为当0x ≥时,()()1xf x f x '>-,即()()()10g x f x xf x ''=+->, 所以()g x 在[)0,+∞单调递增,不等式()()0xx xe f e eax axf ax -+->恒成立,即()()xxxe f eeaxf ax ax ->-,即()()x g e g ax >,所以e x ax >,当0x >时,()xe a h x x <=,则()()21x e x h x x-'=, 可得()h x 在()0,1单调递减,在()1,+∞单调递增, 所以()()min 1h x h e ==, 所以a e <,此时最大的正整数a 为2,2a =对于0x <时,e x ax >恒成立,综上所述:正整数a 的最大值为2, 故答案为:2 【点睛】关键点点睛:本题的关键点是构造函数()()g x xf x x =-,利用导数判断出()g x 在[)0,+∞单调递增,不等式恒成立即()()x g e g ax >,利用单调性可得e x ax >,再分类参数求最值.14.【分析】根据函数求导解的解集即可【详解】因为函数所以令得或当时所以函数在上的递增区间是故答案为:【点睛】本题主要考查导数与函数的单调性还考查了转化问题和运算求解的能力属于中档题解析:5,33ππ⎡⎤⎢⎥⎣⎦【分析】根据函数2sin y x x =-,求导12cos y x '=-,解0y '>的解集即可. 【详解】因为函数2sin y x x =-, 所以12cos y x '=-, 令12cos 0y x '=-=,得3x π=或53x π=, 当533x ππ≤≤时,0y '>, 所以函数2sin y x x =-在[]0,2π上的递增区间是5,33ππ⎡⎤⎢⎥⎣⎦.故答案为:5,33ππ⎡⎤⎢⎥⎣⎦【点睛】本题主要考查导数与函数的单调性,还考查了转化问题和运算求解的能力,属于中档题.15.【分析】由解析式可分析得到的一个周期为则只需考虑在上的值域即可利用导函数求得其最值即可【详解】由题的一个周期为故只需考虑在上的值域令解得或可得此时或或所以的最小值只能在点或或和边界点中取到因为所以的解析: 【分析】由解析式可分析得到()f x 的一个周期为2T π=,则只需考虑()f x 在[)0,2π上的值域即可,利用导函数求得其最值即可. 【详解】由题,()f x 的一个周期为2T π=, 故只需考虑()f x 在[)0,2π上的值域,()()()()22sin 2cos 22sin 212sin 22sin 1sin 1f x x x x x x x '=-+=-+-=--+,令()0f x '=,解得1sin 2x =或sin 1x =-, 可得此时6x π=或56π或π, 所以()2cos sin 2f x x x =+的最小值只能在点6x π=或56π或π和边界点0x =中取到,因为62f π⎛⎫=⎪⎝⎭,562f π⎛⎫=- ⎪⎝⎭()2f π=-,()02f =,所以()f x 的最小值为故答案为:【点睛】本题考查导数的运算,考查利用导函数求最值,考查运算能力.16.②④【分析】根据函数和图象可得的单调区间和单调性从而得到答案【详解】由函数和图象可得当时得所以函数单调递增当时得所以函数单调递减当时得所以函数单调递减当时得所以函数单调递增所以①错误;②正确;③是函解析:②④ 【分析】根据函数()y x f x =⋅'和图象可得()f x 的单调区间和单调性,从而得到答案. 【详解】由函数()y x f x =⋅'和图象可得,当2()–,x ∞-∈时,0y <,得()0f x '>,所以函数()f x 单调递增, 当()2,0x ∈-时,0y >,得()0f x '<,所以函数()f x 单调递减, 当(0,2)x ∈时,0y <,得()0f x '<,所以函数()f x 单调递减, 当(2,)x ∈+∞时,0y >,得()0f x '>,所以函数()f x 单调递增, 所以①错误;②正确;③2x =-是函数()f x 的极大值点,错误;④正确. 故答案为:②④. 【点睛】本题结合图象考查函数的单调性和判断极值,属于基础题.17.【分析】令根据题中条件得到为偶函数;对其求导根据题中条件判定在上单调递减;则在上单调递增;化所求不等式为求解即可得出结果【详解】令则因为所以即所以函数为偶函数;又当时所以即函数在上单调递减;则在上单解析:12x x ⎧⎫≥⎨⎬⎩⎭【分析】令()()xg x f x e =,根据题中条件,得到()g x 为偶函数;对其求导,根据题中条件,判定()g x 在(),0-∞上单调递减;则()g x 在()0,∞+上单调递增;化所求不等式为1x x ≥-,求解,即可得出结果.【详解】令()()xg x f x e =,则()()xg x f x e --=-,因为2()()0xf x ef x --=,所以()()x x f x e f x e -=-,即()()g x g x =-,所以函数()g x 为偶函数;又()[]()()()()x x xg x f x e f x e f x f x e '''=+=+,当0x ≤时,()()0f x f x '+<,所以()[]()()0xg x f x f x e ''=+<,即函数()g x 在(),0-∞上单调递减;则()g x 在()0,∞+上单调递增; 又不等式21()(1)x f x ef x -≥-可化为1()(1)x x f x e f x e -≥-,即()()1g x g x ≥-,所以只需1x x ≥-,则()221x x ≥-,解得12x ≥. 故答案为:12x x ⎧⎫≥⎨⎬⎩⎭. 【点睛】本题主要考查由函数单调性与奇偶性解不等式,考查导数的方法判定函数单调性,涉及绝对值不等式的解法,属于常考题型.18.ln22)【分析】用表示出得出关于的函数根据的范围判断函数单调性得出值域即可【详解】显然由题意可知故由可得故设则在上单调递减又故答案为:【点睛】本题主要考查利用导数研究函数的单调性和最值意在考查学生解析:[ln 2,2) 【分析】用2x 表示出1x ,得出212x x -关于2x 的函数2()g x ,根据2x 的范围,判断函数单调性得出值域即可. 【详解】显然10x ,20x >,由题意可知212x x e +=,故212x x e =-,2212224x x x x e ∴-=-+,由2121x x e +=>可得110x -<,故2120x e -<-,202x ln ∴<, 设()24(02)x g x x e x ln =-+<,则()120x g x e '=-<,()g x ∴在(0,2]ln 上单调递减, 又(0)2g =,(2)2g ln ln =, 2()2ln g x ∴<.故答案为:[2ln ,2). 【点睛】本题主要考查利用导数研究函数的单调性和最值,意在考查学生对这些知识的理解掌握水平.19.【分析】首先对进行求导利用导数研究函数的最值问题根据题意对任意存在使只要的最小值大于等于在指定区间上有解【详解】由得当时当时∴在上单调递减在上单调递增∴在上有解在上有解函数在上单调增故答案为:【点睛 解析:[)0,+∞【分析】首先对()f x 进行求导,利用导数研究函数()f x 的最值问题,根据题意对任意1x R ∈,存在[]21,2x ∈,使12()()f x g x ,只要()f x 的最小值大于等于()g x 在指定区间上有解 . 【详解】由()x f x e x =-,得()1xf x e '=-,当()1,0x ∈-时,()0f x '<,当()0,1x ∈时,()0f x '>, ∴()f x 在()1,0-上单调递减,在()0,1上单调递增, ∴()()min 01f x f ==()1g x ≤在[]1,2上有解,21212x mx m x x -≤⇔≥-在[]1,2上有解,函数1y x x =-在[]1,2上单调增,1101min y ∴=-=,20,0m m ≥≥.故答案为: [)0,+∞ 【点睛】不等恒成立与能成立的等价转换:任意1x A ∈,存在2x B ∈,使()()12min min ()()f x g x f x g x ⇔≥ 任意1x A ∈,任意2x B ∈,使()()12min max ()()f x g x f x g x ⇔= 存在1x A ∈,存在2x B ∈,使()()12max min ()()f x g x f x g x ⇔⇔20.【分析】根据期望的定义先得到将不等式化为构造函数利用导数的方法判断其单调性计算即可得出结果【详解】由题意所以可化为即其中显然成立;两边同时取以为底的对数得令则当时即函数单调递增;当时即函数单调递减; 解析:4【分析】根据期望的定义,先得到()31kE X ke k -=-++,将不等式()E X k <化为ln 3kk >,构造函数()ln ,03kf k k k =->,利用导数的方法判断其单调性,计算()4f ,()5f ,即可得出结果. 【详解】 由题意,()()333111kk k E X ek e ke k ---⎛⎫=++-=-++ ⎪⎝⎭,所以()E X k <可化为310kke --+<,即3kk e >,其中0k >显然成立; 两边同时取以e 为底的对数,得ln 3k k >, 令()ln ,03k f k k k =->,则()11333k f k k k-'=-=, 当()0,3k ∈时,()303k f k k -'=>,即函数()ln 3kf k k =-单调递增; 当()3,k ∈+∞时,()303k f k k -'=<,即函数()ln 3kf k k =-单调递减; 因此()()max 33ln 3ln 3103f k f ==-=->, 又()444ln 42ln 2 1.3862 1.3333033f =-≈-=->,()55ln 5 1.6094 1.666603f =-≈-<,因此满足ln 3kk >的最大正整数k 的值是4, 即满足()E X k <的最大正整数k 的值是4. 故答案为:4. 【点睛】本题主要考查导数的方法研究不等式能成立的问题,涉及离散型随机变量的期望,属于常考题型.三、解答题21.(1)27y x =+;(2)1,2⎛⎫+∞ ⎪⎝⎭. 【分析】(1)求出导函数()'f x ,得切线斜率(0)f ',从而可得切线方程; (2)求出()'f x ,求出()0f x '=的两根1a和2,根据两根的大小讨论()f x 的极值,由2是极小值点得出a 的范围. 【详解】本题考查利用导数研究函数性质.解析(1)若1a =,()2()57xf x x x e =-+, 所以()2()32xf x x x e '=-+, 所以(0)2 f '=,又(0)7f =,因此曲线()y f x =在(0,(0))f 处的切线方程为27y x =+. (2)2()(21)2(1)(2)xxf x ax a x e ax x e '⎡⎤=-++=--⎣⎦, 令()0 f x '=,得1x a=或2x =, 若102a <<,即12a > 则当1,2x a ⎛⎫∈ ⎪⎝⎭时,()0f x '<,当(2,)x ∈+∞时,()0f x '>, 所以()f x 在2x =处取得极小值..若12a ≤,且0a ≠,则当(0,2)x ∈时,112ax x ≤<, 所以10ax ,同时20x -<,所以()0f x '>,从而2x =不是()f x 的极小值点..综上可知,a 的取值范围是1,2⎛⎫+∞ ⎪⎝⎭. 【点睛】本题考查导数的几何意义,考查由极值点求参数范围.掌握极值的定义是解题关键.方法是:求出导函数()'f x ,确定()0f x '=的根,然后由根分实数为若干个区间,讨论各区间中()'f x 和正负,得单调区间,若在0x 左侧递减,右侧递增,则0x 是极小值点,若在0x 左侧递增,右侧递减,则0x 是极大值点. 22.(1)10,3⎛⎫ ⎪⎝⎭;(2)(],1-∞-. 【分析】(1)利用对数的运算法则化简,求解对数不等式. 注意化简前保证真数大于零.(2)分离参数,利用方程()2log 41xx m +-=-有解,构造函数()()2log 41x g x x =+-,求导,分析函数单调性,求出最值,得到m 的取值范围.【详解】(1)()()212log 22f x x -=-()()()()222lo 2212log 22g 1log 11f x x x x x xf ----+-=<+= 1220110222x x x x ⎧⎪->⎪+>⎨⎪-<+⎩<⎪ 则103x <<故x 的取值范围为10,3⎛⎫ ⎪⎝⎭.(2)()40xf x m -+=则()()2log 4104xxf x m m x =+-++=- ()2log 41xx m +-=- 设()()2log 41xg x x =+-()()'ln 444111441ln 2x x x x g x ⋅-=-=++⋅当(),0x ∈-∞时,'0gx当()0,x ∈+∞时,()'0g x > 且x →-∞时,()g x →+∞()2min log 21g x ==故1m -≥则1m ≤-故m 的取值范围为:(],1-∞-【点睛】利用导数求函数值域时,一种是利用导数判断函数的单调性,进而根据单调性求函数的值域;一种是利用导数与极值、最值的关系求函数的值域.23.(1)答案见解析;(2)证明见解析.【分析】(1)含参数的函数单调性,对0a ≥和0a <进行讨论;(2)对0a <时,先求出()f x 的最大值,构造关于a 的函数13111ln 12422f a a a a⎛⎫⎛⎫⎛⎫----=-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,利用导数讨论. 【详解】解:(1)()()2ln 211f x x ax a x =++++,()()()()()2221121112210ax a x ax x f x ax a x x x x+++++'∴=+++==>, 当0a ≥时,()0f x '≥恒成立,则()f x 在()0,∞+上单调递增当0a <时,令()0f x '>,则210ax +>, 所以102x a<<- 令()0f x '<,则210ax +< 所以12x a>- 综上:当0a ≥时,()f x 的增区间为()0,∞+;当0a <时,()f x 的增区间为10,2a ⎛⎫- ⎪⎝⎭,减区间为1,2a ⎛⎫-+∞ ⎪⎝⎭. (2)由(1)知,当0a <时,()max 12f x f a ⎛⎫=- ⎪⎝⎭13111ln 12422f a a a a⎛⎫⎛⎫⎛⎫----=-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 令()()ln 10g t t t t =-+>,则()111t g t t t-'=-=, 令()0g t '>,则01t <<.令()0g t '<,则1t >.故()()max 10g t g ==,所以ln 10t t -+≤ 又因为102a->, 所以11ln 1022a a ⎛⎫⎛⎫---+≤ ⎪ ⎪⎝⎭⎝⎭ 则13111ln 102422f a a a a ⎛⎫⎛⎫⎛⎫⎛⎫---+=---+≤ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 从而()max 314f x a ≤-+ 即()314f x a≤-+. 【点睛】 (1)含参数的导数的讨论:① 判断()0f x '=是否有根,② 比较()0f x '=的几个根的大小;(2)证明不等式通常作差,构造新函数,用导数进行讨论.24.(1)0a ≥;(2)3[,)e+∞.【分析】(1)求导函数()'f x ,令()0f x '≥恒成立,可求参数范围; (2)变量分离转化为32x a e x -≥-,求函数3()2x g x ex -=-最大值.【详解】 (1)由函数()()x f x x a e =+,得()(1)x f x x a e '=++,∵函数()f x 在区间[1,)-+∞上是增函数,∴()(1)0x f x x a e '=++≥,即1a x ≥--在区间[1,)-+∞上恒成立,∴当[1,)x ∈-+∞时,1(,0]x --∈-∞,∴0a ≥.(2)3()x f x e xe ≥-在[0,1]x ∈时恒成立,等价于32x a e x -≥-在[0,1]x ∈时恒成立,令3()2x g x e x -=-,则max ()a g x ≥,∵3()20x g x e -'=--<,∴()g x 在[0,1]上单调递减,∵()g x 在区间[0,1]上的最大值3max()(0)g x g e ==,∴3a e ≥, 即实数a 的取值范围是3[,)e+∞.【点睛】关键点睛:变量分离,转化为不等式恒成立问题,进而求又一函数的最值.25.(1)e -;(2)单调递减区间为()0,1,单调递增区间为()1,+∞;(3)1m ≤-.【分析】(1)求导可得()ln 1f x x '=-,令'()0f x =得x e =,分别讨论()0,x e ∈和(),x e ∈+∞时导函数的正负,可得()f x 的单调性,即可求得最小值;(2)求导可得()ln g x x e =-',由'()0g x =得1x =,分别讨论()0,1x ∈和()1,x ∈+∞时导函数的正负,可得()g x 单调区间;(3)所求等价于()()h x f x mx =-在[)1,x ∈+∞单调递增,即ln 1m x ≤-恒成立,根据x 的范围,即可求得ln 1x -的最小值,即可得答案.【详解】(1)函数()f x 的定义域为()0,∞+,()ln 1f x x '=-,由'()0f x =得x e =, 所以当()0,x e ∈时,'()0f x <,()f x 单调递减,当(),x e ∈+∞时,'()0f x >,()f x 单调递增,所以函数()f x 的最小值为()f e e =-;(2)()ln g x x x x ex =--,()ln g x x '=,由'()0g x =得1x =,所以当()0,1x ∈时,'()0g x <,()g x 单调递减, 当()1,x ∈+∞时,'()0g x >,()g x 单调递增, 所以()g x 的单调递减区间为()0,1,单调递增区间为()1,+∞;(3)()ln 1h x x m '=--,因为函数()()h x f x mx =-在[)1,x ∈+∞单调递增, 所以()ln 10h x x m =--≥'在[)1,x ∈+∞恒成立,即ln 1m x ≤-,因为[)1,x ∈+∞,所以min (ln 1)ln111x -=-=-,所以1m ≤-;【点睛】解题的关键是熟练掌握利用导数求解函数的单调区间、极值(最值)的方法,并灵活应用,在已知单调区间求参数时,可转化为恒成立问题,若()m t x <,需要min ()m t x <,若()m t x >,需max ()m t x >,考查计算化简的能力,属中档题.26.(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)令()(1)x f x e x =-+,求出导函数()'f x ,确定单调性得最小值,从而证得不等式成立;(2)令()ln (1)(0)g x x x x =-->,求导确定单调性得最大值后可证得不等式成立; (3)(1)变形得1x e x -≥,(2)变形可得ln(1)x x ,两个等号不同时成立,可证得不等式成立.【详解】证明:(1)令()(1)x f x e x =-+,则有()1x f x e =-'. 令()0f x '<得,0x <,令()0f x '>得,0x >所以()f x 在(,0)-∞单调递减,(0,)+∞上单调递增.所以0()(0)10f x f e ≥=-=,即(1)0x e x +≥-.所以1x e x ≥+.(2)令()ln (1)(0)g x x x x =-->,则1()1g x x'=-. 令()0g x '<得,0x >,令()0g x '>得,01x <<.所以()g x 在(0,1)单调递增,(1,)+∞上单调递减,所以()(1)ln1(11)0g x g ≤=--=,即ln (1)0x x --≤,所以ln 1≤-x x .(3)由(1)得1x e x ≥+,所以1(1)1x e x x -≥-+=(当且仅当1x =时取等号)①.由(2)得ln 1≤-x x ,所以ln(1)(1)1x x x +≤+-=(当且仅当0x =时取等号)② 因为①式与②式取等号的条件不同,所以1ln(1)x e x ->+.【点睛】结论点睛:本题考查用导数证明不等式,证明方法是引入函数,用导数确定函数的单调性得到函数的最值,从而可证不等式成立.1x e x ≥+和ln 1≤-x x 是两个典型的不等式,例如它可变形得1x e x -≥,ln(1)x x ,有许多函数不等式都是考查这两个不等式的应用.请务必注意掌握.。
