湖北省黄冈中学2013届高三11月月考地理试题
湖北黄冈市黄州中学2013届高考地理全真模拟卷(4)

湖北黄冈市黄州中学2013届高考地理全真模拟卷(4)一、选择题。
1.(广东省六校2013届高三第一次联考)藏族的传统服饰是掉袖藏袍,与这一服饰文化形成有关的自然条件是当地A.昼夜温差大 B.降水稀少 C.气压低 D.地形崎岖2.(江苏省扬州市2013届高三第一学期期中检测试题)据美国今日宇宙网站报道,科学家预计2012年太阳活动达到史无前例的高峰期,据此完成下列问题。
(1)太阳活动是A.有规律可循,但尚无法预报B.发生在太阳内部C.以黑子和耀斑为主要标志D.对人类生产、生活影响不大(2)这次太阳活动所产生的带电粒子流到达地球后,可能造成的影响有①地球各地出现极光现象②磁针不能正确指示方向③GPS定位系统将受到干扰④我国北方会出现极昼现象A.①② B.②③C.①③ D.③④3.(江苏省扬州市2013届高三第一学期期中检测试题)图1为“我国西北地区某地貌形态等高线示意图”,虚线表示不可见等高线,读图完成下列问题。
(1)图中P等高线的数值最有可能为A.711米 B.712米 C.713米 D.714米(2)图示地貌最有可能为A.风力侵蚀地貌B.风力沉积地貌 C.流水侵蚀地貌D.流水沉积地貌4.(江苏省扬州市2013届高三第一学期期中检测试题)图6为“世界某沿海城市城区分布图和海岸线变化模拟示意图”,读图完成下列问题。
(1)由图示信息可知,该城市主城区四个地点的地面坡度最大的可能是 A.e地 B.h地 C.q地 D.f地(2)据乙图可知,该地海岸线变化的主导原因是A.海水侵蚀增强 B.入海泥沙减少 C.全球气候变暖 D.修建水库平面上升后的海岸线最密集区f地。
(2)海平面上升导致该地海岸线变化,而导致海平面上升是由于全球气候变暖。
【考点定位】该题考查等值线和全球气候变暖。
5.(河北省衡水中学2013届高三第一次调研考试)该图为某时赤道南北天气状况示意图(单位:百帕),读图回答问题。
(1)下列说法正确的是A.甲天气系统东侧盛行偏南风,形成暖锋B.乙天气系统中心气流旋转下沉,东侧为暖锋C.①和②锋面分别向东南和西北方向移动D.m地晴朗,n地多雨(2)右图中正确反映②锋面过境期间a地温度变化过程的是A.A B.B C.C D.D6.(湖南省湘潭市2013届高三第一次模拟考试)每年的5月30日前后,日落时的金色阳光洒满美国纽约曼哈顿(西五区)的所有某走向的街道,呈现一幅壮观的景象,即“曼哈顿悬日”现象。
最新高三地理-【地理】湖北省黄冈中学高三月月考 精品
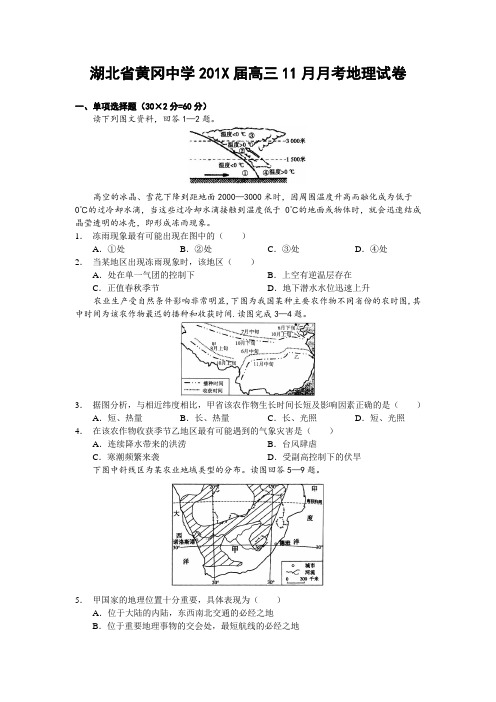
湖北省黄冈中学201X届高三11月月考地理试卷一、单项选择题(30×2分=60分)读下列图文资料,回答1—2题。
高空的冰晶、雪花下降到距地面2000—3000米时,因周围温度升高而融化成为低于0℃的过冷却水滴,当这些过冷却水滴接触到温度低于0℃的地面或物体时,就会迅速结成晶莹透明的冰壳,即形成冻雨现象。
1.冻雨现象最有可能出现在图中的()A.①处B.②处C.③处D.④处2.当某地区出现冻雨现象时,该地区()A.处在单一气团的控制下B.上空有逆温层存在C.正值春秋季节D.地下潜水水位迅速上升农业生产受自然条件影响非常明显,下图为我国某种主要农作物不同省份的农时图,其中时间为该农作物最迟的播种和收获时间.读图完成3—4题。
3.据图分析,与相近纬度相比,甲省该农作物生长时间长短及影响因素正确的是()A.短、热量B.长、热量C.长、光照D.短、光照4.在该农作物收获季节乙地区最有可能遇到的气象灾害是()A.连续降水带来的洪涝B.台风肆虐C.寒潮频繁来袭D.受副高控制下的伏旱下图中斜线区为某农业地域类型的分布。
读图回答5—9题。
5.甲国家的地理位置十分重要,具体表现为()A.位于大陆的内陆,东西南北交通的必经之地B.位于重要地理事物的交会处,最短航线的必经之地C.位于大陆南端,世界上某重要航线的必经之地D.位于两洋三洲五海之地,战略地位十分重要6.甲国家的地形特征为()A.以高原为主,地势西北高东南低B.以山地为主,地势东南高西北低C.以盆地为主,地势中部低四周高D.以高原为主,地势东南高西北低7.图中德班比诺洛斯港气温明显偏高,主要影响因素是()A.纬度位置B.洋流因素C.地形因素D.海陆位置8.图中分布最广的自然带是()A.热带荒漠带B.热带草原带C.亚热带常绿硬叶林带D.热带雨林带9.图中阴影部分为某种农业地域类型的分布,该农业地域类型是()A.水稻种植业B.混合农业C.商品谷物农业D.大牧场放牧业读黄河天然径流量与断流天数示意图,回答10—12题。
湖北省黄冈中学2013届高三11月月考数学理试题(解析版)

湖北省黄冈中学2013届高三上学期11月月考数学(理)试题(2012-11-3)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.sin(1920)-的值为( )A .32-B .12-C .32D .12解析:sin(1920)sin(2406360)sin(18060)-=-⨯=+,即原式sin60=-,故选A .答案:A2.命题“x ∀∈R ,20x >”的否定是( )A .x ∀∈R ,20x ≤B .x ∃∈R ,20x >C .x ∃∈R ,20x <D .x ∃∈R ,20x ≤解析:全称命题的否定是特称命题,易知应选D .答案:D3.已知集合{P =正奇数}和集合{|M x x ==,,}a b a P b P ⊕∈∈,若M P ⊆,则M 中的运算“⊕”是( )A .加法B .除法C .乘法D .减法解析:由已知集合M 是集合P 的子集,设*21,21(,)a m b n m n =-=-∈N ,∵(21)(21)a b m n ⋅=--42()12[2()1]1mn m n mn m n P =-++=-++-∈,∴M P ⊆,而其它运算均不使结果属于集合P ,故选C . 答案:C 4.已知某几何体的侧视图与其正视图相同,相关的尺寸如下图所示,则这个几何体的体积是( )A . 8πB . 7πC . 2π`D .74π 解析:依题意该几何体为一空心圆柱,故其体积2237[2()]124V ππ=-⨯=,选D .答案:D5.已知A 、B 两点分别在两条互相垂直的直线20x y -=和0x ay +=上,且AB 线段的中点为俯视图正 视 图 侧视图3 41P 10(0,)a,则线段AB 的长为( ) A .8B .9C .10D .11解析:由已知两直线互相垂直得2a =,∴线段AB 中点为P (0,5),且AB 为直角三角形AOB 的斜边,由直角三角形的性质得||2||10AB PO ==,选C .答案:C6.已知各项为正的等比数列{}n a 中,4a 与14a 的等比中项为22,则7112a a +的最小值为( ) A .16B .8C .22D .4解析:由已知2414(22)8a a ==,再由等比数列的性质有4147118a a a a ==,又70a >,110a >,7117112228a a a a +≥=,故选B .7.设函数2,0(),01x x bx c f x x ≥⎧++=⎨<⎩,若(4)(0)f f =,(2)2f =,则函数()()g x f x x =-的零点的个数是( )A .0B .1C .2D .3解析:已知即164422b c c b c ++=⎧⎨++=⎩,∴46b c =-⎧⎨=⎩,若0x ≥,则246x x x -+=,∴2x =,或3x =;若0x <,则1x =舍去,故选C .答案:C8.给出下列的四个式子:①1a b -,②1a b +,③1b a +,④1ba-;已知其中至少有两个式子的值与tan θ的值相等,则( )A .cos 2,sin 2a b θθ==B .sin 2,cos 2a b θθ==C .sin,cos22a b θθ==D .cos,sin22a b θθ==解析:sin sin 21cos2tan ,cos2,sin 2cos 1cos2sin 2a b θθθθθθθθθ-===∴==+时,式子①③与tan θ的值相等,故选A .答案:A9.设集合(){}(){},|||||1,,()()0A x y x y B x y y x y x =+≤=-+≤,M AB =,若动点(,)P x y M ∈,则22(1)x y +-的取值范围是( )A .15[,]22B .25[,]22C .110[,]22D .210[,]22解析:在同一直角坐标系中画出集合A 、B 所在区域,取交集后如图,故M 所表示的图象如图中阴影部分所示,而22(1)d x y =+-表示的是M 中的点到(0,1)的距离,从而易知所求范围是15[,]22,选A . 10.已知O 为平面上的一个定点,A 、B 、C 是该平面上不共线的三个动点,点P 满足条件2OB OC OP +=(),(0,)||cos ||cos AB ACAB B AC Cλλ++∈+∞,则动点P 的轨迹一定通过ABC ∆的( )A .重心B .垂心C .外心D .内心解析:设线段BC 的中点为D ,则2OB OCOD +=,∴2OB OC OP +=()||cos ||cos AB AC AB B AC C λ++()||cos ||cos AB ACOD AB B AC Cλ=++,∴()||cos ||cos AB ACOP OD DP AB B AC Cλ-=+=,∴()()||cos ||cos ||cos ||cos AB AC AB BC AC BCDP BC BC AB B AC C AB B AC Cλλ⋅⋅⋅=+⋅=+||||cos()||||cos ()(||||)0||cos ||cos AB BC B AC BC CBC BC AB B AC Cπλλ-=+=-+=,∴DP BC ⊥,即点P 一定在线段BC 的垂直平分线上,即动点P 的轨迹一定通过ABC ∆的外心,选C . 答案:C二.填空题:本大题共5小题,每小题5分,共25分,把答案直接填在题中横线上. 11.1220x e dx =⎰______________.解析:1122220011|(1)22xx e dx e e ==-⎰.答案:1(1)2e - 12.定义运算a c ad bcb d =-,复数z 满足11z ii i =+,则复数z 的模为_______________. 解析:由11z i i i=+得1212izi i i zi i +-=+⇒==-,∴222(1)5z =+-=.答案:513.已知方程22220x y kx y k ++++=所表示的圆有最大的面积,则直线(1)2y k x =-+的倾斜角α=_______________.解析:2214412r k k =+-≤,当有最大半径时有最大面积,此时0k =,1r =,∴直线方程为2y x =-+,设倾斜角为α,则由tan 1α=-且[0,)απ∈得34πα=.答案:34π14.已知函数2()m f x x -=是定义在区间2[3,]m m m ---上的奇函数,则()f m =_______. 解析:由已知必有23m m m -=+,即2230m m --=,∴3m =,或1m =-;当3m =时,函数即1()f x x -=,而[6,6]x ∈-,∴()f x 在0x =处无意义,故舍去; 当1m =-时,函数即3()f x x =,此时[2,2]x ∈-,∴3()(1)(1)1f m f =-=-=-.答案:1-15.在工程技术中,常用到双曲正弦函数2x xe e shx --=和双曲余弦函数2x x e e chx -+=,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 .解析:由右边2222x x y y x x y ye e e e e e e e ----++--=⋅-⋅1()4x yx y x y x y x y x y x y x y e e e e e e e e +--+--+--+--=+++-++-()()1(22)()42x y x y x y x y e e e e ch x y ------+=+==-=左边,故知.答案:填入()c c c s s h x y hx hy hx hy -=-,()c c c s s h x y hx hy hx hy +=+,()c s sh x y shx hy chx hy -=-,()c s sh x y shx hy chx hy +=+四个之一即可.三.解答题:本大题共6小题,共75分,请给出各题详细的解答过程.16.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且*41()n n S a n =+∈N .(1)求1a ,2a ;(2)设3log ||n n b a =,求数列{}n b 的通项公式.解答:(1)由已知1141S a =+,即1141a a =+,∴=1a 13,……………………2分 又2241S a =+,即1224()1a a a +=+,∴219a =-; ……………………5分 (2)当1n >时,1111(1)(1)44n n n n n a S S a a --=-=+-+,即13n n a a -=-,易证数列各项不为零(注:可不证),故有113n n a a -=-对2n ≥恒成立,∴{}n a 是首项为13,公比为13-的等比数列,∴1111()(1)333n n n n a ---=-=-, ……………………10分∴33log ||log 3n n n b a n -===-. ……………………12分17.(本小题满分12分)已知 1:(),3xp f x -=且|()|2f a <; q :集合2{|(2)10,}A x x a x x =+++=∈R ,且A ≠∅.若p ∨q 为真命题,p ∧q 为假命题,求实数a 的取值范围. 解答:若1|()|||23af a -=<成立,则616a -<-<, 即当57a -<<时p 是真命题; ……………………4分 若A ≠∅,则方程2(2)10x a x +++=有实数根,由2(2)40a ∆=+-≥,解得4a ≤-,或0a ≥,即当4a ≤-,或0a ≥时q 是真命题; ……………………8分 由于p ∨q 为真命题,p ∧q 为假命题,∴p 与q 一真一假,故知所求a 的取值范围是(,5](4,0)[7,)-∞--+∞. ……………………12分(注:结果中在端点处错一处扣1分,错两处扣2分,最多扣2分)18.(本小题满分12分)已知ABC ∆的两边长分别为25AB =,39AC =,且O 为ABC ∆外接圆的圆心.(注:39313=⨯,65513=⨯)(1)若外接圆O 的半径为652,且角B 为钝角,求BC 边的长; (2)求AO BC ⋅的值. 解答:(1)由正弦定理有2sin sin AB ACR C B==,∴253965sin sin C B ==,∴3sin 5B =,5sin 13C =, ……………………3分且B 为钝角,∴12cos 13C =,4cos 5B =-, ∴3125416sin()sin cos sin cos ()51313565B C B C C B +=+=⨯+⨯-=,又2sin BCR A=,∴2sin 65sin()16BC R A B C ==+=; ……………………6分 (2)由已知AO OC AC +=,∴22()AO OC AC +=,即2222||2||||39AO AO OC OC AC +⋅+== ……………………8分 同理AO OB AB +=,∴2222||2||||25AO AO OB OB AB +⋅+==, …………10分两式相减得22(3925)(3925)896AO OC AO OB ⋅-⋅=-+=,即2896AO BC ⋅=,∴448AO BC ⋅=. ……………………12分19.(本小题满分12分)在如图所示的多面体ABCDE中,AB ⊥平面ACD ,DE ⊥平面ACD ,AC=AD=CD=DE=2,AB=1,G 为AD 中点. (1)请在线段CE 上找到点F 的位置,使得恰有直线BF ∥平面ACD ,并证明这一事实; (2)求平面BCE 与平面ACD 所成锐二面角的大小;(3)求点G 到平面BCE 的距离. 解法一:以D 点为原点建立如图所示的空间直角坐标系,使得x 轴和z 轴的正半轴分别经过点A 和点E ,则各点的坐标为(0,0,0)D ,(2,0,0)A , (0,0,2)E ,(2,0,1)B ,(1,3,0)C ,(1)点F 应是线段CE 的中点,下面证明:设F 是线段CE 的中点,则点F 的坐标为13(,,1)22F ,∴33(,,0)22BF =-,显然BF 与平面xOy 平行,此即证得BF ∥平面ACD ; ……………………4分 (2)设平面BCE 的法向量为(,,)n x y z =, 则n CB ⊥,且n CE ⊥,由(1,3,1)CB =-,(1,3,2)CE =--,BA DCG EBADCG FEzx y∴30320x y z x y z ⎧-+=⎪⎨--+=⎪⎩,不妨设3y =,则12x z =⎧⎨=⎩,即(1,3,2)n =,∴所求角θ满足(0,0,1)2cos 2||n n θ⋅==,∴4πθ=; ……………………8分(3)由已知G 点坐标为(1,0,0),∴(1,0,1)BG =--,由(2)平面BCE 的法向量为(1,3,2)n =, ∴所求距离3||24||BG n d n ⋅==. ……………………12分解法二:(1)由已知AB ⊥平面ACD ,DE ⊥平面ACD ,∴AB//ED , 设F 为线段CE 的中点,H 是线段CD 的中点,连接FH ,则//FH =12ED ,∴//FH =AB , …………………2分∴四边形ABFH 是平行四边形,∴//BF AH , 由BF ⊄平面ACD 内,AH ⊂平面ACD ,//BF ∴平面ACD ; ……………4分 (2)由已知条件可知ACD ∆即为BCE ∆在平面ACD 上的射影,设所求的二面角的大小为θ,则cos ACDBCES S θ∆∆=, ……………………6分易求得BC=BE 5=,CE 22=,∴221||()622BCE CES CE BE ∆=⨯-=,而23||34ACD S AC ∆==,∴2cos 2ACD BCE S S θ∆∆==,而02πθ<<, ∴4πθ=;………………8分(3)连结BG 、CG 、EG ,得三棱锥C —BGE , 由ED ⊥平面ACD ,∴平面ABED ⊥平面ACD , 又CG AD ⊥,∴CG ⊥平面ABED ,设G 点到平面BCE 的距离为h ,则C BGE G BCE V V --=即1133BGE BCE S GC S h ∆∆⨯=⨯,由32BGE S ∆=,6BCE S ∆=,3CG =, BA DCGE∴3332246BGE BCE S GC h S ∆∆⨯===即为点G 到平面BCE 的距离.………………12分 20.(本小题满分13分)已知椭圆22221y x a b +=(0)a b >>的一个顶点为B (0,4),离心率e =55,直线l 交椭圆于M 、N 两点.(1)若直线l 的方程为4y x =-,求弦MN 的长;(2)如果ΔBMN 的重心恰好为椭圆的右焦点F ,求直线l 方程的一般式.解答:(1)由已知4b =,且55c a =,即2215c a=,∴22215a b a -=,解得220a =,∴椭圆方程为2212016y x +=; ……………………3分由224580x y +=与4y x =-联立,消去y 得29400x x -=,∴10x =,2409x =, ∴所求弦长221402||11||9MN x x =+-=; ……………………6分 (2)椭圆右焦点F 的坐标为(2,0), 设线段MN 的中点为Q 00(,)x y ,由三角形重心的性质知2BF FQ =,又(0,4)B , ∴00(2.4)2(2,)x y -=-,故得003,2x y ==-,求得Q 的坐标为(3,2)-; ……………………9分 设1122(,),(,)M x y N x y ,则12126,4x x y y +=+=-,且222211221,120162016x y x y +=+=, ……………………11分 以上两式相减得12121212()()()()02016x x x x y y y y +-+-+=,1212121244665545MN y y x x k x x y y -+==-=-=-+-∴,故直线MN 的方程为62(3)5y x +=-,即65280x y --=. ……………………13分 (注:直线方程没用一般式给出但结果正确的扣1分) 21.(本小题满分14分)已知函数[)1()ln 1,sin g x x x θ=++∞⋅在上为增函数,且(0,)θπ∈,12()ln m ef x mx x x-+=--,m ∈R . (1)求θ的值;(2)当0m =时,求函数()f x 的单调区间和极值; (3)若在[1,]e 上至少存在一个0x ,使得00()()f x g x >成立,求m 的取值范围. 解答:(1)由已知/211()0sin g x xx θ=-+≥⋅在[1,)+∞上恒成立, 即2sin 10sin x xθθ⋅-≥⋅,∵(0,)θπ∈,∴sin 0θ>, 故sin 10x θ⋅-≥在[1,)+∞上恒成立,只需sin 110θ⋅-≥, 即sin 1θ≥,∴只有sin 1θ=,由(0,)θπ∈知2πθ=; ……………………4分(2)∵0m =,∴12()ln ef x x x-+=--,(0,)x ∈+∞, ∴/2221121()e e x f x x x x---=-=, 令/()0f x =,则21x e =-(0,)∈+∞,∴x ,/()f x 和()f x 的变化情况如下表:x (0,21)e -21e -(21,)e -+∞/()f x+0 -()f x极大值(21)1ln(21)f e e -=---即函数的单调递增区间是(0,21)e -,递减区间为(21,)e -+∞,有极大值(21)1ln(21)f e e -=---; ……………………9分(3)令2()()()2ln m eF x f x g x mx x x +=-=--,当0m ≤时,由[1,]x e ∈有0m mx x -≤,且22ln 0e x x--<,∴此时不存在0[1,]x e ∈使得00()()f x g x >成立;当0m >时,2/222222()m e mx x m eF x m x x x +-++=+-=, ∵[1,]x e ∈,∴220e x -≥,又20mx m +>,∴/()0F x >在[1,]e 上恒成立, 故()F x 在[1,]e 上单调递增,∴max ()()4mF x F e me e==--, 令40m me e -->,则241e m e >-, 故所求m 的取值范围为24(,)1ee +∞-. ……………………14分。
湖北黄冈市黄州中学2013届高考地理全真模拟卷(8)

湖北黄冈市黄州中学2013届高考地理全真模拟卷(8)一、选择题。
1.【广东省普宁市城东中学2013届高三第三次月考】北京时间2012年6月27日11时47分,中国“蛟龙”在西太平洋的马里亚纳海沟(10°—15°N)再次刷新“中国深度”——下潜7062米。
结合该图完成问题。
(1)中国“蛟龙”7000米海试区表层洋流的流向为()A.自东向西 B.自西向东 C.自南向北 D.自北向南(2)探测期间,仅考虑风与洋流因素的影响,比较图中两条航线的航速。
下列说法正确的是()A.江阴→海试区的速度较快 B.海试区→青岛的速度较快C.两条航线速度相同 D.无法比较2.【广东佛山顺德区2013届高三第一学期期中教学质量检测】2012年10月中秋国庆双节期间,许多游客到浙江观看钱塘江大潮(是指大量海潮涌入钱塘江口形成的汹涌浪涛)。
读钱塘江河口位置图,回答下列问题。
(1)宋代文人苏轼云:“八月十八潮,壮观天下无”。
某一游客欲观赏气势磅礴的钱塘江大潮,最佳地点应在A.甲 B.乙 C.丙 D.丁(2)2011年6月30日,国务院正式批准设立浙江舟山群岛新区。
关于舟山群岛地理特征的叙述,正确的是A.夏季受东南信风影响,降水多 B.岛屿由河流泥沙堆积而成C.深水岸线多,宜发展港口物流业 D.有上升流,渔业资源丰富3.【四川省成都高新区2013届高三11月检测地理试卷】读所给两幅图,该城市地处平原地区,据此完成问题。
(1)若该城市功能分区合理,则其主导风向和河流的大致流向可能是:A.西风;自西向东流B.东北风;自东南向西北流C.北风;自北向南流D.西北风;自西北向东南流(2)右图中曲线能反映左图中甲乙一线地租变化的是:A.① B.② C.③ D.④4.【江苏省无锡一中2013届高三第一次质量检测】一组同学去我国东南沿海某地考察,行走过程中他们看到如下特征:“正前方和左侧各有一个山峰,其中一个山峰目测距离约2km (只考虑图示范围内的地形)”,据此回答问题。
湖北省黄冈市2013高三地理上学期期末考试版
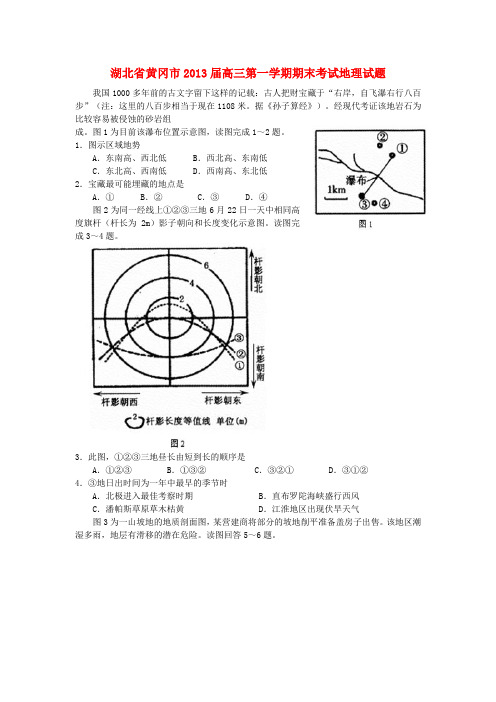
湖北省黄冈市2013届高三第一学期期末考试地理试题我国1000多年前的古文字留下这样的记载:古人把财宝藏于“右岸,自飞瀑右行八百步”(注:这里的八百步相当于现在1108米。
据《孙子算经》)。
经现代考证该地岩石为比较容易被侵蚀的砂岩组成。
图1为目前该瀑布位置示意图,读图完成1~2题。
1.图示区域地势A.东南高、西北低 B.西北高、东南低C.东北高、西南低 D.西南高、东北低2.宝藏最可能埋藏的地点是A.① B.② C.③ D.④图2为同一经线上①②③三地6月22日一天中相同高度旗杆(杆长为2m)影子朝向和长度变化示意图。
读图完成3~4题。
3.此图,①②③三地昼长由短到长的顺序是A.①②③ B.①③② C.③②① D.③①②4.③地日出时间为一年中最早的季节时A.北极进入最佳考察时期 B.直布罗陀海峡盛行西风C.潘帕斯草原草木枯黄 D.江淮地区出现伏旱天气图3为一山坡地的地质剖面图,某营建商将部分的坡地削平准备盖房子出售。
该地区潮湿多雨,地层有滑移的潜在危险。
读图回答5~6题。
5.上图所示甲、乙、丙三块营建基地中哪处危险性最高,其理由是A.甲基地最危险,因其位于顺向坡地 B.甲基地最危险,因其位于逆向坡地C.乙基地最危险,因其位于山顶 D.丙基地最危险,因其位于顺向坡地6.开挖甲基地所出露的岩石在古时代是如何生成的A.由岩浆冷却凝固形成 B.由生物遗骸堆积形成C.经沉积作用固结形成 D.在高温高压下变质形成阅读下列洋流名称,回答第7题。
①墨西哥湾暖流②本格拉寒流③千岛寒流④拉布拉多寒流⑤北大西洋暖流⑥阿拉斯加暖流⑦加那利寒流⑧北赤道暖流7.若由你率领船队沿当年哥伦布航线从西班牙前往西印度群岛并返回,为节省时间,顺次经过的洋流是A.⑦→⑧→①→⑤ B.⑧→⑥→⑤→④C.⑤→②→⑥→⑧ D.①→⑤→②→③图4为我国各大农业区分布示意图。
读图4回答8~9题。
8.下列说法正确的是A.①②属于不同的农业区B.⑥⑦⑧是我国重要的茶叶产区C.⑥地区最主要的农业类型是绿洲农业D.③地是我国重要的商品农业基地9.造成图中⑥、⑦两地区自然景观分异的主要原因是A.水分差异 B.热量差异C.非地带性因素 D.人类活动的影响读某工业部门区位要求及其所在地的地方条件比较表(“◎”号表示指向性因素,“×”号表示重要因素,“○”号表示一般因素)。
湖北黄冈市黄州中学2013届高考地理全真模拟卷

湖北黄冈市黄州中学2013届高考地理全真模拟卷(6)一、选择题。
1.【广东佛山顺德区2013届高三第一学期期中教学质量检测】2012年7月24日,我国最南端的地级市——三沙市(约16°50′N,ll2°20′E)在永兴岛正式成立,下辖西沙群岛、南沙群岛、中沙群岛的岛礁及其海域。
据此回答问题。
(1)三沙市成立时A.三沙市正午太阳高度大于北京市 B.去南极科考的最佳时期C.三沙市白昼时间长于广州市 D.地中海沿岸水循环活跃(2)三沙市管辖区域的珊瑚礁地貌景观非常典型,其形成的主要地质作用是A.海浪侵蚀 B.流水堆积 C.生物堆积 D.生物风化【答案】(1)A (2)C【解析】(1)2012年7月24日沙市在永兴岛正式成立,此时太阳直射在北半球,且向南移动,地中海沿岸在夏季高温少雨,水循环不活跃,三沙市纬度低于北京和广州市,三沙市正午太阳高度大于北京市,三沙市白昼时间短于广州市,去南极科考的最佳时期为北半球的冬季。
(1)珊瑚礁地貌是指造礁石珊瑚群体死后其遗骸构成的岩体,所以其形成的主要地质作用是生物堆积作用。
【考点定位】该题考查地球运动的地理意义和地质作用。
2.【2013届江苏省无锡一中高三第一次质量检测地理试卷】读南部非洲示意图,完成问题。
(1)图中M水文站测到的河水流量季节变化比往年有所减小,其原因最可能是()A.该河上游流域面积较小B.该河上游兴建水库C.该河流降水季节分配均匀D.该河上游雨林植被恢复较好(2)图中P处海域渔业资源丰富,其主要原因是()A.位于沿海大陆坡,阳光充足B.位于热带海域,海水交换能力强C.海水上涌,带来大量的营养物质D.寒暖流交汇,带来大量的营养物质【答案】(1)B(2)C【解析】本题考查世界区域地理和读图分析能力。
(1)图示M水文站所在河流上游流经热带草原气候,降水的季节变化大,但材料反映河流流量季节变化小,故可能为水库建设,能调节河流下游的径流量变化。
湖北省黄冈中学、孝感高中2013届高三上学期期末联考地理试题及答案

湖北省黄冈中学、孝感高中2013届高三上学期期末联考地理试题及答案湖北省黄冈中学、孝感高中2013届高三上学期期末联考地理试题第Ⅰ卷选择题读中国北亚热带柑橘生产的气候适宜度相对于多年平均值的变化图(图1)及2008年中国与美国、巴西柑橘产量与加工情况比较表(表1),回答1~2题。
国家产量(万吨)平均单产(吨/公顷)用途1吨浓缩汁需用原料果中国600.008.823%用于榨汁12~15吨鲜橙美国848.7031.9595%用于榨汁11~12吨鲜橙巴西1660.8022.9190%用于榨汁10~11吨鲜橙1.关于我国北亚热带地区柑橘生产发展变化的推测合理的是()A.气候适宜度不断增加,生产风险降低B.各气候要素的适宜度不断下降,生产风险增加C.柑橘生产的北界将不断北移,生产面积扩大D.全球气候变暖,使柑橘生产的气候条件更加适宜2.根据上表,关于我国柑橘生产的说法正确的是()A.我国柑橘生产区的纬度分布最低B.我国柑橘生产区的地形起伏最小C.我国柑橘的质量最优D.交通运输对我国柑橘生产的影响最大下图示意我国某地景观。
读图2,完成第3~4题。
3.根据图中信息,下列说法正确的是()A.处向斜槽部受挤压,物质坚硬不易被侵蚀而成山岭B.处岩层的断裂和错位是内外力共同作用的结果C.处地形平坦是流水侵蚀作用形成的冲积扇D.处岩层发生倾斜是内力作用的结果4.根据图示信息,推断该地区最可能位于()A.天山B.武夷山C.祁连山D.太行山下图为地中海地区冬季雨率等值线图(冬雨率为冬季降水量占全年降水量的百分率,单位:%)。
读图3,回答5~6题。
5.关于地中海地区冬雨率等值线的分布规律的叙述,正确的是()A.自北向南冬雨率递减B.从内陆向沿海冬雨率递减C.自沿海向内陆冬雨率递增D.自西北向东南冬雨率递增6.根据图示信息,下列说法正确的是()A.巴塞罗那的冬雨率与罗马相同B.东南部受西南季风影响时间长,冬雨率高C.西北部受盛行西风影响时间长,冬雨率低D.的黎波里的冬雨率远高于雅典图4表示某区域城市分布图,图5是该区域甲城市规划略图,读图回答7~8题。
黄冈中学2013届高三11月月考数学(理)

黄冈中学2013届11月月考数学试题(理)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.sin(1920)- 的值为( )A.2- B .12- C.2D .12解析:sin(1920)sin(2406360)sin(18060)-=-⨯=+ ,即原式sin 60=- ,故选A .答案:A2.命题“x ∀∈R ,20x >”的否定是( )A .x ∀∈R ,20x ≤B .x ∃∈R ,20x >C .x ∃∈R ,20x <D .x ∃∈R ,20x ≤解析:全称命题的否定是特称命题,易知应选D .答案:D3.已知集合{P =正奇数}和集合{|M x x ==,,}a b a P b P ⊕∈∈,若M P ⊆,则M 中的运算“⊕”是( ) A .加法 B .除法C .乘法D .减法解析:由已知集合M 是集合P 的子集,设*21,21(,)a m b n m n =-=-∈N ,∵(21)(21)a b m n ⋅=--42()12[2()1]1mn m n mn m n P =-++=-++-∈,∴M P ⊆,而其它运算均不使结果属于集合P ,故选C .答案:C4.已知某几何体的侧视图与其正视图相同,相关的尺寸如下图所示,则这个几何体的体积是( )A . 8πB . 7πC . 2π`D .74π解析:依题意该几何体为一空心圆柱,故其体积2237[2()]124V ππ=-⨯=,选D .答案:D5.已知A 、B 两点分别在两条互相垂直的直线20x y -=和0x ay +=上,且AB 线段的俯视图正 视 图 侧视图中点为P 10(0,)a,则线段AB 的长为( )A .8B .9C .10D .11解析:由已知两直线互相垂直得2a =,∴线段AB 中点为P (0,5),且AB 为直角三角形AO B 的斜边,由直角三角形的性质得||2||10AB PO ==,选C .答案:C6.已知各项为正的等比数列{}n a 中,4a 与14a 的等比中项为,则7112a a +的最小值为( )A .16B .8C .D .4解析:由已知24148a a ==,再由等比数列的性质有4147118a a a a ==,又70a >,110a >,71128a a +≥=,故选B .7.设函数2,0(),01x x bx c f x x ≥⎧++=⎨<⎩,若(4)(0)f f =,(2)2f =,则函数()()g x f x x=-的零点的个数是( ) A .0B .1C .2D .3解析:已知即164422b c c b c ++=⎧⎨++=⎩,∴46b c =-⎧⎨=⎩,若0x ≥,则246x x x -+=,∴2x =,或3x =;若0x <,则1x =舍去,故选C .答案:C8.给出下列的四个式子:①1a b-,②1a b+,③1b a+,④1b a-;已知其中至少有两个式子的值与tan θ的值相等,则( ) A .cos 2,sin 2a b θθ== B .sin 2,cos 2a b θθ== C .sin,cos22a b θθ==D .cos,sin22a b θθ==解析:sin sin 21cos 2tan ,cos 2,sin 2cos 1cos 2sin 2a b θθθθθθθθθ-===∴==+ 时,式子①③与tan θ的值相等,故选A .答案:A9.设集合(){}(){},|||||1,,()()0A x y x y B x y y x y x =+≤=-+≤,M A B = ,若动点(,)P x y M ∈,则22(1)x y +-的取值范围是( )A .15[,]22B .5]22C .1[,22D .[22解析:在同一直角坐标系中画出集合A 、B 所在区域,取交集后如图,故M所表示的图象如图中阴影部分所示,而d =表示的是M 中的点到(0,1)的距离,从而易知所求范围是15[,]22,选A .10.已知O 为平面上的一个定点,A 、B 、C 是该平面上不共线的三个动点,点P 满足条件2O B O C O P += (),(0,)||cos ||cos AB ACAB B AC C λλ++∈+∞ ,则动点P 的轨迹一定通过A B C ∆的( )A .重心B .垂心C .外心D .内心解析:设线段BC 的中点为D ,则2O B O CO D += ,∴2O B O C O P += ()||cos ||cos AB ACAB B AC Cλ++ ()||cos ||cos AB ACO D AB B AC Cλ=++,∴()||cos ||cos AB ACO P O D D P AB B AC Cλ-=+=,∴()()||cos ||cos ||cos ||cos AB AC AB BC AC BCD P BC BC AB B AC C AB B AC C λλ⋅⋅⋅=+⋅=+||||cos()||||cos ()(||||)0||cos ||cos AB BC B AC BC CBC BC AB B AC Cπλλ-=+=-+=, ∴D P BC ⊥,即点P 一定在线段B C 的垂直平分线上,即动点P 的轨迹一定通过A B C ∆的外心,选C . 答案:C二.填空题:本大题共5小题,每小题5分,共25分,把答案直接填在题中横线上.11.1220xe dx =⎰______________.解析:1122220011|(1)22xxe dx ee ==-⎰.答案:1(1)2e -12.定义运算a c ad bc bd=-,复数z 满足11z i i i=+,则复数z 的模为_______________.解析:由11z i i i=+得1212i zi i i z i i+-=+⇒==-,∴z ==.13.已知方程22220x y kx y k ++++=所表示的圆有最大的面积,则直线(1)2y k x =-+的倾斜角α=_______________.解析:1r =≤,当有最大半径时有最大面积,此时0k =,1r =,∴直线方程为2y x =-+,设倾斜角为α,则由tan 1α=-且[0,)απ∈得34πα=.答案:34π14.已知函数2()m f x x -=是定义在区间2[3,]m m m ---上的奇函数,则()f m =_______. 解析:由已知必有23m m m -=+,即2230m m --=,∴3m =,或1m =-; 当3m =时,函数即1()f x x -=,而[6,6]x ∈-,∴()f x 在0x =处无意义,故舍去; 当1m =-时,函数即3()f x x =,此时[2,2]x ∈-,∴3()(1)(1)1f m f =-=-=-.答案:1-15.在工程技术中,常用到双曲正弦函数2xxe e shx --=和双曲余弦函数2x xe echx -+=,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 .解析:由右边2222x xy yx xy ye ee ee ee e----++--=⋅-⋅1()4x yx yx yx yx y x yx yx ye eee eee e +--+--+--+--=+++-++-()()1(22)()42x yx y x yx y ee eech x y ------+=+==-=左边,故知.答案:填入()c c c s s h x y hx hy hx hy -=-,()c c c s s h x y hx hy hx hy +=+,()c s sh x y shx hy chx hy -=-,()c s sh x y shx hy chx hy +=+四个之一即可.三.解答题:本大题共6小题,共75分,请给出各题详细的解答过程.16.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且*41()n n S a n =+∈N .(1)求1a ,2a ;(2)设3log ||n n b a =,求数列{}n b 的通项公式. 解答:(1)由已知1141S a =+,即1141a a =+,∴=1a 13,……………………2分又2241S a =+,即1224()1a a a +=+,∴219a =-; ……………………5分(2)当1n >时,1111(1)(1)44n n n n n a S S a a--=-=+-+,即13n n a a -=-,易证数列各项不为零(注:可不证), 故有113n n a a -=-对2n ≥恒成立,∴{}n a 是首项为13,公比为13-的等比数列,∴1111()(1)333n n nn a ---=-=-, ……………………10分∴33log ||log 3nn n b a n -===-. ……………………12分17.(本小题满分12分)已知 1:(),3x p f x -=且|()|2f a <;q :集合2{|(2)10,}A x x a x x =+++=∈R ,且A ≠∅.若p ∨q 为真命题,p ∧q 为假命题,求实数a 的取值范围. 解答:若1|()|||23a f a -=<成立,则616a -<-<,即当57a -<<时p 是真命题; ……………………4分若A ≠∅,则方程2(2)10x a x +++=有实数根,由2(2)40a ∆=+-≥,解得4a ≤-,或0a ≥,即当4a ≤-,或0a ≥时q 是真命题; ……………………8分 由于p ∨q 为真命题,p ∧q 为假命题,∴p 与q 一真一假,故知所求a 的取值范围是(,5](4,0)[7,)-∞--+∞ . ……………………12分(注:结果中在端点处错一处扣1分,错两处扣2分,最多扣2分) 18.(本小题满分12分)已知A B C ∆的两边长分别为25A B =,39AC =,且O 为A B C∆外接圆的圆心.(注:39313=⨯,65513=⨯) (1)若外接圆O 的半径为652,且角B 为钝角,求BC 边的长;(2)求AO BC ⋅的值.解答:(1)由正弦定理有2sin sin A B A C R CB ==,∴253965sin sin CB==,∴3sin 5B =,5sin 13C =, ……………………3分且B 为钝角,∴12cos 13C =,4cos 5B =-,∴3125416sin()sin cos sin cos ()51313565B C B C C B +=+=⨯+⨯-=,又2sin B C R A=,∴2sin 65sin()16BC R A B C ==+=; ……………………6分(2)由已知AO OC AC += ,∴22()AO OC AC += ,即2222||2||||39AO AO O C O C AC +⋅+==……………………8分同理AO OB AB += ,∴2222||2||||25A O A O O B O B A B +⋅+==, …………10分两式相减得22(3925)(3925)896AO O C AO O B ⋅-⋅=-+=,即2896AO BC ⋅= ,∴448AO BC ⋅=. ……………………12分19.(本小题满分12分)在如图所示的多面体ABCDE中,AB ⊥平面ACD ,DE ⊥平面ACD ,AC=AD=CD=DE=2,AB=1,G 为AD 中点. (1)请在线段CE 上找到点F 的位置,使得恰有直线BF ∥平面ACD ,并证明这一事实; (2)求平面BCE 与平面ACD 所成锐二面角的大小;(3)求点G 到平面BCE 的距离.解法一:以D 点为原点建立如图所示的空间直角坐标系,使得x 轴和z 轴的正半轴分别经过点A 和点E ,则各点的坐标为(0,0,0)D ,(2,0,0)A ,(0,0,2)E ,(2,0,1)B,(1,0)C ,(1)点F 应是线段CE 的中点,下面证明:设F 是线段CE 的中点,则点F的坐标为1(,1)22F,∴3(,0)22B F =- ,显然BF与平面xOy 平行,此即证得BF ∥平面ACD ; ……………………4分 (2)设平面BCE 的法向量为(,,)n x y z =,则n CB ⊥ ,且n CE ⊥ ,由(1,C B =,(1,2)C E =-,∴020x z x z ⎧-+=⎪⎨--+=⎪⎩,不妨设y =12x z =⎧⎨=⎩,即2)n = ,∴所求角θ满足(0,0,1)cos 2||n n θ⋅==,∴4πθ=; ……………………8分 (3)由已知G 点坐标为(1,0,0),∴(1,0,1)BG =--,由(2)平面BCE的法向量为(1,2)n =,∴所求距离||||BG n d n ⋅==……………………12分解法二:(1)由已知AB ⊥平面ACD ,DE ⊥平面ACD ,∴AB//ED , 设F 为线段CE 的中点,H 是线段CD 的中点,连接FH ,则//FH =12ED ,∴//FH =AB ,…………………2分∴四边形ABFH 是平行四边形,∴//BF AH , 由B F ⊄平面ACD 内,AH ⊂平面ACD ,//B F ∴平面ACD ; ……………4分 (2)由已知条件可知A C D ∆即为B C E ∆在平面ACD 上的射影,设所求的二面角的大小为θ,则cos AC D BC ES S θ∆∆=, ……………………6分易求得BC=BE =CE =∴1||2BC E S C E ∆==而2||4AC D S AC ∆==∴cos 2AC D BC ES S θ∆∆==,而02πθ<<,∴4πθ=; ………………8分(3)连结BG 、CG 、EG ,得三棱锥C —BGE , 由ED ⊥平面ACD ,∴平面ABED ⊥平面ACD , 又C G A D ⊥,∴C G ⊥平面ABED ,设G 点到平面BCE 的距离为h ,则C BG E G BC E V V --=即1133BG E BC E S G C S h ∆∆⨯=⨯,E由32B G E S ∆=,BCE S ∆=C G =∴B G E B C ES G C h S ∆∆⨯===G 到平面BCE 的距离.………………12分20.(本小题满分13分)已知椭圆22221y x ab+=(0)a b >>的一个顶点为B (0,4),离心率e=5,直线l 交椭圆于M 、N 两点.(1)若直线l 的方程为4y x =-,求弦MN 的长;(2)如果ΔBMN 的重心恰好为椭圆的右焦点F ,求直线l 方程的一般式. 解答:(1)由已知4b =,且5c a =,即2215c a=,∴22215a b a-=,解得220a =,∴椭圆方程为2212016yx+=; ……………………3分由224580x y +=与4y x =-联立, 消去y 得29400x x -=,∴10x =,2409x =,∴所求弦长21||||9M N x x =-=; ……………………6分(2)椭圆右焦点F 的坐标为(2,0), 设线段MN 的中点为Q 00(,)x y ,由三角形重心的性质知2B F F Q =,又(0,4)B ,∴00(2.4)2(2,)x y -=-,故得003,2x y ==-,求得Q 的坐标为(3,2)-; ……………………9分 设1122(,),(,)M x y N x y ,则12126,4x x y y +=+=-,且222211221,120162016x y x y +=+=, ……………………11分以上两式相减得12121212()()()()02016x x x x y y y y +-+-+=,1212121244665545M N y y x x k x x y y -+==-=-=-+- ∴, 故直线MN 的方程为62(3)5y x +=-,即65280x y --=. ……………………13分(注:直线方程没用一般式给出但结果正确的扣1分) 21.(本小题满分14分)已知函数[)1()ln 1,sin g x x x θ=++∞⋅在上为增函数,且(0,)θπ∈,12()ln m ef x m x x x-+=--,m ∈R .(1)求θ的值;(2)当0m =时,求函数()f x 的单调区间和极值; (3)若在[1,]e 上至少存在一个0x ,使得00()()f x g x >成立,求m 的取值范围. 解答:(1)由已知/211()0sin g x xxθ=-+≥⋅在[1,)+∞上恒成立,即2sin 10sin x xθθ⋅-≥⋅,∵(0,)θπ∈,∴sin 0θ>,故sin 10x θ⋅-≥在[1,)+∞上恒成立,只需sin 110θ⋅-≥, 即sin 1θ≥,∴只有sin 1θ=,由(0,)θπ∈知2πθ=; ……………………4分(2)∵0m =,∴12()ln e f x x x-+=--,(0,)x ∈+∞,∴/2221121()e e xf x xxx---=-=,令/()0f x =,则21x e =-(0,)∈+∞,∴x ,/()f x 和()f x 的变化情况如下表:即函数的单调递增区间是(0,21)e -,递减区间为(21,)e -+∞,有极大值(21)1ln(21)f e e -=---; ……………………9分(3)令2()()()2ln m e F x f x g x m x x x+=-=--,当0m ≤时,由[1,]x e ∈有0m m x x-≤,且22ln 0e x x --<,∴此时不存在0[1,]x e ∈使得00()()f x g x >成立;当0m >时,2/222222()m e mx x m eF x m xxx+-++=+-=,∵[1,]x e ∈,∴220e x -≥,又20mx m +>,∴/()0F x >在[1,]e 上恒成立, 故()F x 在[1,]e 上单调递增,∴m ax ()()4m F x F e m e e==--,令40m m e e-->,则241e m e >-,故所求m 的取值范围为24(,)1e e +∞-. ……………………14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省黄冈中学2013届高三11月月考
地理试题
一、单项选择题
读“我国四大盆地地形剖面示意图”,回答1~2题。
1.关于四大盆地位置判断正确的是
A.都位于我国地势的第二级阶梯上B.盆地①位于最东面
C.盆地①、③都位于暖温带D.盆地②位于季风区
2.盆地①和盆地②相比较的叙述正确的是
A.盆地①和盆地②内能源资源丰富,但种类差异大
B.都属于外流区域,都有闻名于世的农业灌溉工程
C.两地所建林业生态工程的生态作用差异大
D.外力作用对地表形态的影响都以风力和流水作用为主
我国某中学地理研究性学习小组对霜冻现象进行探究性学习。
下图是他们通过长期收听天气预报绘制的我国东部地区的平均初霜、终霜日期曲线图。
据此回答3~4题:
3.图中初霜、终霜出现时间差异很大,造成这种差异的根本因素是
A.作物品种B.纬度位置C.海陆位置D.地形
4.不利于霜冻发生的条件是
A.天气严寒B.地面辐射强C.微风D.大气逆辐射强
读南极地区图,当英国伦敦日落时,阿蒙森一斯科特
考察站正当日出。
回答5~6题。
5.此刻,北京时间是
A.14点B.2点
C.8点D.20点
6.这一天,下列地理现象可信的是
A.长江中下游平原为“梅雨”期
B.我国开展值树活动的最佳时期
C.南极地区出现“南极臭氧洞”
D.澳大利亚正值最炎热的季节
右图为某地区1月、7月等温线示意图,m表示大陆海岸
线,读图回答7~8题。
7.有关图示区域的判断,不可能的是
A.甲位于大洋西岸B.甲位于大洋东岸
C.图示区域位于南半球D.图示区域位于北半球
8.若甲、乙两地的1月和7月温差分别为16 ℃和6 ℃,b、d两线数值分别为24 ℃、25 ℃,则a、c两线数值依次为
A.8 ℃18 ℃B.9 ℃19 ℃C.18 ℃8 ℃D.19 ℃9 ℃MN线为地球表面的一半圆弧,回答9~11题:
9.若MN线位于同一经线圈上,新年伊始,M点的正午太阳高度正好达90°,则A.M点比N点的线速度大B.M、N位于同一纬线上
C.M与N的纬度值相等D.M、N可能在同一经线上
10.若MN线位于晨昏线上,M点的地方时为8点,则
A.M点昼长大于N点昼长B.N点日出的地方时是4点
C.太阳直射点位于北半球D.M点的区时比N点的区时早12时11.若MN线位于70°N纬线上,6月22日晨昏线与M点距离最近时,下列说法错误的是A.M点的太阳高度为326'
︒
︒B.N点的正午太阳高度为4326' C.M点处于极昼D.N点的正午太阳高度达一年中最小
右图为我国某地局部降水(雪)分布图。
读图,完成12~13题。
12.导致图中雨雪分界线在甲、乙两处发生弯曲的主要因素是
A.纬度B.大气环流
C.地形D.海陆热力性质差异
13.下列对甲、乙两地天气的叙述,正确的有
①甲地中雨,乙地中雪
②甲地小雪,乙地小雨
③甲、乙两地风向均为偏北风,乙地风力较强
④甲、乙两地风均为偏南风,甲地风力较强
A.①③B.①④
C.②③D.②④
读某地区等高线地形图,完成14~16题。
14.关于图中规划公路叙述正确的是
A.最大高差可能为180米
B.走向为东北—西南
C.长度约为6千米
D.穿越山脊地区
15.沿图a—b剖面线绘制的地形剖面是下列的
16.在图示区域内拟建一座防火瞭望塔,在①②③④的选址方案中,瞭望范围最大的是
A.①B.②
C.③D.④
右图是我国某校地理兴趣小组根据当地楼房各朝向外
墙面接受的太阳辐射热量,绘制的一月和七月的太阳辐射日
总量变化方位图(单位:千焦/平方米〃日)。
读图回答17~
18题。
17.该地楼房
A.一月份东墙接受太阳辐射最多B.七月
份南墙接受太阳辐射最多
C.一月份南墙接受太阳辐射最多D.七月份北墙接受太阳辐射最多18.该地最有可能位于
A.三江平原B.黄河三角洲C.珠江三角洲D.长江三角洲2014年冬奥会计划于当年的2月7日至23日在俄罗斯南部城市索契举行。
下图为索契区域示意图和气候资料图,完成19~20题:
19.索契1月气温高于0℃的原因有
①纬度低,气温高②大高加索山对北方冷空气的阻挡作用
③受大西洋暖流的影响④受黑海和西风的影响
A.①②B.③④C.①③D.②④20.索契作为冬奥会举办地的优势条件主要是
A.冬季晴天多,阳光充足,便于开展户外运动
B.冬季降水多,北部有高山,积雪量大,有利于开展冰雪项目
C.黑海冬季结冰,有利于开展有冰雪项目
D.河网密布,便于开展水上项目
从河源到河口的河床最低点之间的纵截面称为河流纵剖面。
回答21~23题。
21.关于长江宜昌以西、以东河段纵剖面差异的成因,叙述正确的是A.长江宜昌以西河段流经三级地势阶梯,所以河段落差大
B.长江宜昌以东河段流速缓慢,泥沙沉积明显,所以河段落差小
C.长江宜昌以西河段流经地区降水量比以东河段大,所以河段落差大
D.长江宜昌以东河段人口、城市密集,所以河段落差小
22.关于黄河河段纵剖面的叙述正确的是
A.黄河落差最大的河段是宁夏至包头段
B.宁夏至包头河段水流缓慢,易出现凌汛现象
C.黄河下游地区水量小,流速慢,易出现海岸被侵蚀后退现象
D.黄河上游落差大,水流急,河水泥沙含量最大
23.关于河流综合开发治理的重点,叙述正确的是
A.长江宜昌以西段以整治河段,发展航运为主
B.长江宜昌以东段以防洪为首要任务
C.黄河宁夏以上段以水土保持为重点
D.黄河包头以下段以水电梯级开发为重点
下图是我国某区域按不同纬度所做的地形剖面图,读图完成24~25题。
24.图中L河的流向是
A.由东北流向西南B.由西南流向东北
C.由东南流向西北D.由西北流向东南
25.为使图示地区生态环境进一步改善,应建立保护区并注重
A.防治河水污染B.保护森林资源
C.防治土壤盐碱化D.治理酸雨危害
二、综合题(本大题共4小题,共50分)
26.(10分)图中的河流发源于岷山,是某大河的一级支流。
甲城市所在的地形区是著名的农业生产基地,其气候资料如下表,读图表资料回答下列问题:
甲城市(海拔505.9米)的气温、降水量统计表
(1)根据气候资料判断,该地的气候特点是,
气温年较差约为℃。
(4分)
(2)甲城市所在地形区名称是,该地形区的地势特征是,
判断依据是。
(6分)
27.(10分)读钓鱼岛附近海底地形图,回答下列问题。
(1)图B为
某同学绘制的沿甲乙线海底地形剖面示意图,图中距海岸千米附近有明显的差错,理由是。
(4分)
(2)从海底地形看,钓鱼岛东侧的海底地形主要为,西侧的海底地形为。
(2分)
(3)从钓鱼岛的位置和地质地形角度,分析说明钓鱼岛及其附属岛屿是我国固有领土的原因。
(4分)
28.(18分)读我国部分地区风能密度分布图,回答下列问题。
(1)分析图示地区风能密度在沿海最大的原因?(10分)
(2)分析南海在我国海洋运输中的交通地位。
(8分)
29.(12分)阅读材料,回答下列各题。
材料一下图为某中学地理研究性学习小组绘制的(25︒N,116︒E)附近某区域示意图,为正确标注该图的方向,同学们测得O城2011年6月10日日出、日落分别在X、Y方向。
高于阴坡。
(2)材料二中,甲、乙、丙、丁四地所在位置哪些在阳坡,哪些在阴坡?说明原因。
若
a为15℃等温线,则乙地气温的数值可能是多少?(10分)
湖北省黄冈中学2013届高三11月月考
地理考试答案
26.(10分)(1)夏季高温多雨,冬季温和少雨(或冬季低温少雨)(2分,冬、夏各1分,也可答亚热
带季风气候,雨热同期)20.1(2分)
(2)成都平原(或川西平原)(2分,答四川盆地只给1分)西北高、东南低(或由西北向东南倾斜;北高南低)(2分)河流主要由西北向东南流(或等高线的数值变化规律)(2分)
27.(10分)(1)35(2分)深度应该大于2000米(2分)
(2)大陆坡(1分)大陆架(1分)
(3)位于我国东海大陆架上,距我国台湾岛较近。
(4分)
28.(18分)(1)沿海地区位于海陆过渡地带,海陆热力差异大,气压差大、风力大。
(4分)受夏季风的影响;海洋表面平坦摩擦力小;位于夏秋季节台风登陆的前沿;台湾海峡的狭管效应,加大了风速。
(6分)
(2)海运交通位置极其重要,连接亚洲和大洋洲、太平洋和印度洋,(4分)是我国通往东南亚、印度洋直到非洲、欧洲的海上通道。
(4分)
29.(12分)(1)由东北流向西南。
(4分)
(2)丙、丁位于阳坡,甲、乙位于阴坡。
(4分)相同的海拔高度丙温度高于甲,丁温度高于乙。
(4分)约11℃。
(2分)。
