matlab实验题
数学实验matlab练习题

2015-2016数学实验练习题一、选择题1.清除Matlab工作空间(wordspace)变量的命令是(B )A. clcB. clearC. clfD.delete2. 清除当前屏幕上显示的所有内容,但不清除工作空间中的数据的命令是( A )A. clcB. clearC. clfD.delete3. 用来清除图形的命令( C )A. clcB. clearC. clfD.delete4. 在MATLAB程序中,使命令行不显示运算结果的符号是( A )A. ;B. %C. #D. &5. 在MATLAB程序中,可以将某行表示为注释行的符号是( B )A. ;B. %C. #D. &6.在循环结构中跳出循环,执行循环后面代码的命令为 ( B )A. returnB. breakC. continueD. Keyboard7.在循环结构中跳出循环,但继续下次循环的命令为( C )A. returnB. breakC. continueD. Keyboard8. MATLAB中用于声明全局变量的关键字是( C )A. infB. symsC. globalD. function9. 用户可以通过下面哪项获得指令的使用说明( A )A. helpB. loadC. demoD. lookfor10.在MATLAB命令窗口中键入命令S=zoros(3);可生成一个三行三列的零矩阵,如果省略了变量名S,MATLAB表现计算结果将用下面的哪一变量名做缺省变量名( A )A. ans;B. pi;C. NaN;D. Eps.11. 9/0的结果是( B )A. NAN;B. Inf;C. eps;D. 012.在MATLAB中程序或语句的执行结果都可以用不同格式显示,将数据结果显示为分数形式,用下面哪一条命令语句( D )A. format long;B. format long e;C. format bank;D. fromat rat13. 下列MATLAB命令中是构造1行3列的(-1,1)均匀分布随机矩阵的命令的是(D)A. randn(1,3);B. rand(1,3);C. ones(3);D. 以上都不对14. 产生四维元素都为1矩阵的语句为( A )A. ones(4)B. eye(4)C. zeros(4)D. rand(4)15. 用round 函数对数组[2.48 6.39 3.93 8.52]取整,结果为 ( C )A. [2 6 3 8]B. [2 6 4 8]C. [2 6 4 9]D. [3 7 4 9]16. y=dsolve(‘Dy=1/(1+x^2)-2*y^2’,’y(0)=0’,’x ’); ezplot(y)的功能是( A )A. 求微分方程特解并绘图;B. 解代数方程;C. 求定积分;D.求微分方程通解.17. MATLAB 命令roots([1,0,0,-1])的功能是 ( D )A. 产生向量[1,0,0,1];B. 求方程310x +=的根;C. 求多项式31x -的值;D. 求方程310x -=的根。
MATLAB实验题答案

1、求以下变量的值,并在MATLAB 中验证。
( 1 ) a = 1 : 2 : 5 a = 1 3 5 ( 2 ) b = [ a' , a' , a' ;a ] b = 1 1 1 3 3 3 5 5 5 1 3 5 ( 3 ) c = a + b ( 2 , : ) c = 4 6 82、下列运算是否合法,为什么?如合法,结果是多少? >> result2=a*b Error using * Inner matrix dimensions must agree. >> result3=a+b result3 = 3 6 25 8 11 >> result4=b*d result4 =31 22 22 40 49 13 >> result5=[b;c']*d result5 = 31 22 22 40 49 13-5 -8 7>> result6=a.*b result6 =2 8 -34 15 30 >> result7=a./b result7 =0.5000 0.5000 -3.0000 4.0000 1.6667 1.2000>> result8=a.c Attempt to reference field of non-structure array. >> result9=a.\b result9 = 2.0000 2.0000 -0.3333 0.2500 0.6000 0.8333 >> result10=a.^2 result10 = 1 4 9 16 25 36 >> result11=2.^a result11 =2 4 816 32 64 3、用MATLAB 求解下面的的方程组。
(1)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----017413231511222315921274321x x x x >> A=[7 2 1 -2;9 15 3 -2;-2 -2 11 5;1 3 2 13] >> B=[4 7 -1 0] >> B=B' >> x=inv(A)*B (2)⎪⎪⎩⎪⎪⎨⎧=-++=--=-++=++56533332821w z y x w y x w z y x z y x >> A1=[1 1 1 0;1 2 1 -1;2 -1 0 -3;3 3 5 -6]>> B2=[1;8;3;5] >> x2=inv(A1)*B24、已知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=1323151122231592127A (1)求矩阵A 的秩(rank) (2)求矩阵A 的行列式(determinant) (3)求矩阵A 的逆(inverse) (4)求矩阵A 的特征值及特征向量(eigenvalue and eigenvector) >> A3=[7 2 1 -2;9 15 3 -2;-2 -2 11 5;1 3 2 13] >> r=rank(A3) >> b=inv(A3) >> a=det(A3) >> [V,D]=eig(A3) 5、109910101022222++++==---=∑n n y ,求y=?(运行format long g 命令后,查看y 的值) m1=0; for m=-10:10 m1=m1+2^m; end m1 m1 = 2047.9990234375 6、求分段函数的值。
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
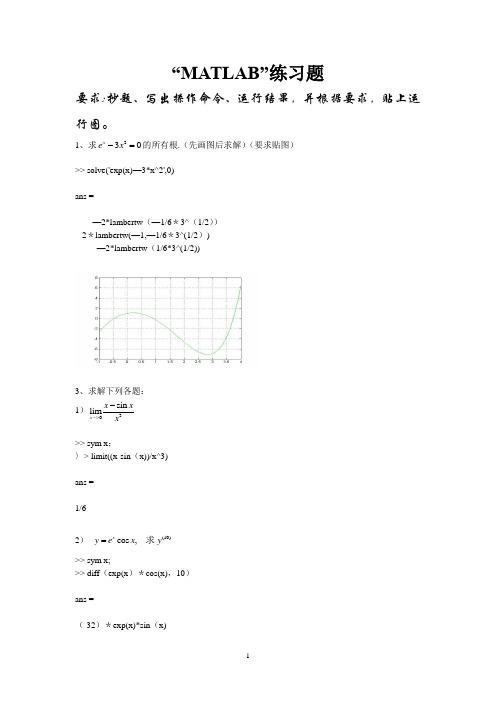
“MATLAB”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根.(先画图后求解)(要求贴图)>> solve('exp(x)—3*x^2',0)ans =—2*lambertw (—1/6*3^(1/2))-2*lambertw(—1,—1/6*3^(1/2))—2*lambertw (1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x ->->> sym x ;〉> limit((x-sin (x))/x^3)ans =1/62) (10)cos ,x y e x y =求>> sym x;>> diff (exp(x )*cos(x),10)ans =(-32)*exp(x)*sin (x)3)21/20(17x e dx ⎰精确到位有效数字)〉〉 sym x;〉〉 vpa((int(exp(x^2),x,0,1/2)),17)ans =0.544987104183622224)42254x dx x+⎰〉> sym x ;>〉 int (x^4/(25+x^2),x)ans =125*atan (x/5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
〉> sym t;>> x=log(sqrt (1+t^2));y=atan(t);〉> diff (y ,t )/diff (x ,t)ans =1/t6)设函数y =f (x )由方程xy +e y = e 所确定,求y ′(x ).>> syms x y ;f=x *y+exp(y )—exp (1);〉> -diff(f,x )/diff (f,y)ans =-y/(x + exp (y))7)0sin 2x e xdx +∞-⎰>〉 syms x ;>〉 y=exp(-x)*sin(2*x );〉> int(y ,0,inf )ans =2/58) 08x =展开(最高次幂为)〉> syms xf=sqrt(1+x);taylor(f,0,9)ans =— (429*x^8)/32768 + (33*x^7)/2048 — (21*x^6)/1024 +(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 19) 1sin (3)(2)x y e y =求〉> syms x y ;>〉 y=exp(sin (1/x));>〉 dy=subs (diff(y,3),x ,2)dy =—0.582610)求变上限函数2x x ⎰对变量x 的导数.>> syms a t ;>〉 diff (int(sqrt(a+t),t,x ,x^2))Warning: Explicit integral could not be found 。
matlab数学实验复习题(有答案)

复习题1、写出3个常用的绘图函数命令2、inv (A )表示A 的逆矩阵;3、在命令窗口健入clc4、在命令窗口健入clear 5、在命令窗口健入6、x=-1:0.2:17、det (A )表示计算A 的行列式的值;8、三种插值方法:拉格朗日多项式插值,分段线性插值,三次样条插值。
9、若A=123456789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,则fliplr (A )=321654987⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A-3=210123456--⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A .^2=149162536496481⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦tril (A )=100450789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦triu (A ,-1)=123456089⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦diag (A )=100050009⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A(:,2),=258A(3,:)=369 10、normcdf (1,1,2)=0.5%正态分布mu=1,sigma=2,x=1处的概率[t,x]=ode45(@f,[a,b],x0),中参数的涵义是@fun 是求解方程的函数M 文件,[a,b]是输入向量即自变量的范围a 为初值,x0为函数的初值,t 为输function 开头;17、二种数值积分的库函数名为:quad;quadl43,421、设x )的功能是作出将X 十等分的直方图 22、interp1([1,2,3],[3,4,5],2.5) Ans=4.523、建立一阶微分方程组⎩⎨⎧+='-='yx t y y x t x 34)(3)(2的函数M 文件。
(做不出来)二、写出运行结果:1、>>eye(3,4)=1000010000102、>>size([1,2,3])=1;33、设b=round (unifrnd (-5,5,1,4)),则=3 5 2 -5 >>[x,m]=min(b);x=-5;m=4 ,[x,n]=sort(b) -5 2 3 5 4 3 1 2mean(b)=1.25,median (b )=2.5,range (b )=10 4、向量b 如上题,则>>any(b),all(b<2),all(b<6) Ans=1 0 15、>>[5 6;7 8]>[7 8;5 6]=00116、若1234B ⎡⎤=⎢⎥⎣⎦,则 7、>>diag(diag(B))=10048、>>[4:-2:1].*[-1,6]=-4 12 9、>>acos(0.5),atan(1) ans=1.047197551196598 ans=0.785398163397448 10、>>norm([1,2,3]) Ans=3.74165738677394111、>>length ([1,3,-1])=312、>>x=0:0.4:2;plot(x,2*x,’k*’)13、>>zeros(3,1);ans=14、>>ones(3)=111111111,vander([2,3,5])=421931255116、>>floor(1:0.3:3)=1 1 1 12 2 218、>>subplot(2,2,1); fplot('sin',[0,2*pi]);subplot(2,2,2);plot([1,2,-1]);>>x=linspace(0,6*pi);subplot(2,2,3);plot3(cos(x),sin(x),x);>>subplot(2,2,4);polar(x,5*sin(4*x/3));19、>>t=linespace(0,2,11)0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.020、>>[a,b]=binostat(15,0.2)a=3 b=2.4>>y1=binopdf(5,10,0.7)=0.1029,y2=binocdf(5,10,0.7)=0.150321、>>log10([1,10,100])=[0 1 2]22、>>p=1;for k=2:3:9 p=p*k;end;p p=8023、>>s=0;for k=2:3:9 s=s+k;end;s s=1524、('^3exp(2*)3');(,1)=--+f inline x x feval fAns=3.864725、>>a1=norminv(0.6,3,4)a1=4.013426、>>unifinv(0.4,1,5),unifpdf(0.4,1,5),unifpdf(2,1,5)Ans=2.6 0 0.2527、>>A=[0 1-1;2 1 0;1-1 1];0 1 -11 -1 1>>A([1,3],:)1 -1 10 1 -1A([3,1],:)=1 -1 10 1 -1>>A(2,:)=2 1 0>>-2*A(1,:)= 0 -2 228、>>quad(‘sin(x)’,0,pi/2)=1.000029、>>trapz([3,4,6],[1,2,3])=6.500030、>> int('x-sin(x)',0,1)Ans=cos(1) - 1/231、>>round(3:0.4:5),ceil(3:0.4:5);floor(3:0.4:5)3 34 45 53 3 34 4 5>>limit(1+1/(3*x)^x,inf)=1>>diff(sin(3*x)+x^3,2)=6*x-9*sin(3*x)>>taylor(exp(3*x),5,1):命令输入: y=taylor(exp(3*x),x,1,'Order',5)Ans=exp(3) + 3*exp(3)*(x - 1) + (9*exp(3)*(x - 1)^2)/2 + (9*exp(3)*(x - 1)^3)/2 + (27*exp(3)*(x - 1)^4)/8>>a1=mod(15,4),b1=rem(15,4)=3,3>>a2=mod(-15,-4),b2=rem(-15,-4)=-3,-3>>a3=mod(15,-4),b3=rem(15,-4)=-1,-3>>a4=mod(-15,4),b4=rem(-15,4)=1,-334、>>x=binornd(20,0.4,2,4)8 7 10 810 7 9 12>>sign(x),1 1 1 11 1 1 1>>y=-poissrnd(8,2,4)-16 -10 8 -7-7 -8 -6 -9>>sign(y)-1 -1 -1 -1-1 -1 -1 -135、>>[a1,b1]=binostat(20,0.4) a1=8 b1=4.8 >>[a2,b2]=poisstat(8)ans=8,8>>[a3,b3]=chi2stat(15)ans=[15 30]36、运行M文件:chi2fign=5;a=0.9;xa=chi2inv(a,n);x=0:0.1:15;y=chi2pdf(x,n);plot(x,y,'b');hold on;xf=0:0.1:xa;yf=chi2pdf(xf,n);fill([xf,xa],[yf,0],'g');text(xa*1.01,0.005,num2str(xa));text(2.5,0.05,'alpha=0.9','fontsize',20); text(9,0.09,'X~{\chi}^2(4)','fontsize',16);37、>>t=linspace(0,2*pi);>>polar(t,3*t,’g*’)38、>>quadl(’exp(2*x).*log(3*x)’,1,3)ans =398.635239、x0=0:2*pi/6:2*pi;y0=sin(x0).*cos(x0);x=[linspace(0,2*pi,100)];y=sin(x).*cos(x);y1=spline(x0,y0,x);[x;y;y1]'plot(x,y,'k',x,y1,'b-')注:此处省略100组数据40、>>A=round(unifrnd(0,100,3,3));>>[L,U]=lu(A)L =0.9897 0.4699 1.0000 0.1649 1.0000 0 1.0000 0 0 U =97.0000 80.0000 92.0000 0 35.8041 26.8247 0 0 -89.656841、a=sparse([1 3 3],[2 3 5],[1 2 3],4,5);s=full(a) s =0 1 0 0 0 0 0 0 0 0 0 0 2 0 3 0 0 0 0 0 三、编程1、 分别用矩形公式、梯形公式、辛普森公式、Gauss-Lobatto 公式及随机模拟方法计算数值积分/230sin 2x e xdx π⎰,并与符号运算计算的结果进行比较。
数学实验(matlab版)过程考试试卷及答案完整版

试绘出三种产品产量与季度的三维垂直方向条形图(分组式). >> x=[8,8,9;11,7,8;12,6,9;10,6,10]; bar3(x,'group') 图形如下:
2/2
第一题:编程计算下面问题, x 值由键≥ 1 y = x 2 , −1 ≤ x < 1 2 x − 1, x < −1
>> x=input('输入 x:'); if x>=1 y=x^2+1; end if x<-1 y=x^2-1; end if x>=-1&x<1 y=x^2; end y 输入 x:5 y= 26 第二题:某人做一种材料的伸缩实验,t 为温度(℃),L 为长度(mm),实验数据见下表 t 20 25 30 35 40 L 81 82.3 84 86.8 89
f = x 4 − xy + y 2 ,求
>> syms x y
∂f ∂ 3 f , ∂x ∂y 3
1/1
f=x^4-x*y+y^2; dx=diff(f,x,1) dy3=diff(f,y,3) dx = 4*x^3-y dy3 = 0 第四题:某厂生产三种产品,某年四季度的产量如下 A 产品产量 笫一季度 笫二季度 笫三季度 笫四季度 8 11 12 10 B 产品产量 8 7 6 6 C 产品产量 9 8 9 10
用二阶拟合法,求 L 与 t 的表达式.要求:1.编程;2.写出 L 与 t 的关系式. >> t=[20,25,30,35,40]; L=[81,82.3,84,86.5,89]; k=polyfit(t,L,2) k= 0.0091 -0.1446 80.2114 L=0.0091 t^2 —0.1446t+ 80.2114 第三题:求微分与积分(编程)
MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤1、命令窗口的简单使用(1)简单矩阵的输入(2)求[12+2×(7-4)]÷32的算术运算结果2、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B与A.*B?A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9) 写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B3、 已知⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
Matlab实验报告题目

MATLAB 语言综合实验实验一 Matlab 运算基础一、实验目的1.熟悉启动和退出MATLAB 的方法。
2.熟悉MATLAB 命令窗口的组成。
3.掌握建立矩阵的方法。
4.掌握MATLAB 各种表达式的书写规则以及常用函数的使用。
二、实验内容1.求表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
⎥⎦⎤⎢⎣⎡-+=++=545.0212),1ln(212i x x x z 其中>> x=[2 1+2*i;-0.45 5];>> z=1/2*log(x+sqrt(1+x^2))z =0.7114 - 0.0253i 0.8968 + 0.3658i0.2139 + 0.9343i 1.1541 - 0.0044i>>2.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=723302131,76538773443412B A 求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵)>> A=[12 34 -4;34 7 87;3 65 7];>> B=[1 3 -1;2 0 3;3 -2 7];>> A+6*Bans =18 52 -1046 7 10521 53 49>> I=[1 1 1;1 1 1;1 1 1];>> A-B+Ians =12 32 -233 8 851 68 1>>(2)A*B和A.*B>> A=[12 34 -4;34 7 87;3 65 7];>> B=[1 3 -1;2 0 3;3 -2 7];>> A*Bans =68 44 62309 -72 596154 -5 241>> A.*Bans =12 102 468 0 2619 -130 49>>(3)A^3和A.^3>> A=[12 34 -4;34 7 87;3 65 7];>> B=[1 3 -1;2 0 3;3 -2 7];>> A^3ans =37226 233824 48604247370 149188 60076678688 454142 118820 >> A.^3ans =1728 39304 -6439304 343 65850327 274625 343 >>(4)A/B及B\A>> A=[12 34 -4;34 7 87;3 65 7];>> B=[1 3 -1;2 0 3;3 -2 7];>> A/Bans =16.4000 -13.6000 7.600035.8000 -76.2000 50.200067.0000 -134.0000 68.0000>> B\Aans =109.4000 -131.2000 322.8000-53.0000 85.0000 -171.0000-61.6000 89.8000 -186.2000>>(5)[A,B]和[A([1,3],:);B^2]>> A=[12 34 -4;34 7 87;3 65 7];>> B=[1 3 -1;2 0 3;3 -2 7];>> [A,B]ans =12 34 -4 1 3 -134 7 87 2 0 33 65 7 3 -2 7 >> [A([1,3],:); B^2]ans =12 34 -43 65 74 5 111 0 1920 -5 40>>实验二 Matlab 矩阵分析与处理一、实验目的1.掌握生成特殊矩阵的方法。
MATLAB数学实验100例题解
一元函数微分学实验1 一元函数的图形(基础实验)实验目的 通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析 函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧。
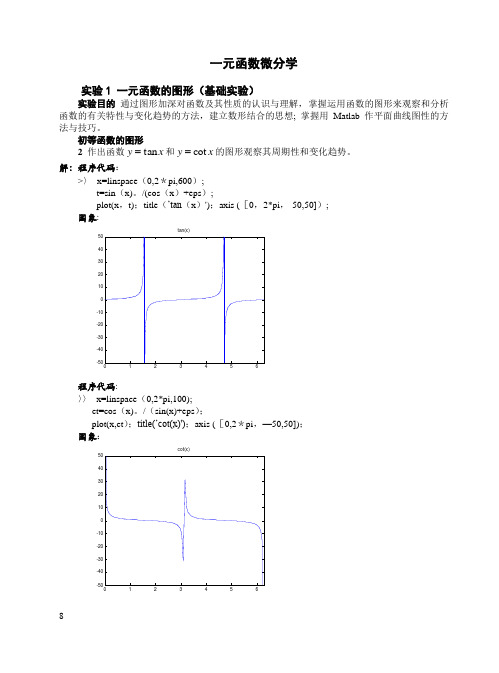
初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势。
解:程序代码:>〉 x=linspace (0,2*pi,600); t=sin (x)。
/(cos (x )+eps );plot(x ,t);title (’tan (x )');axis ([0,2*pi ,-50,50]); 图象:程序代码: 〉〉 x=linspace (0,2*pi,100); ct=cos (x)。
/(sin(x)+eps ); plot(x,ct );title(’cot(x)');axis ([0,2*pi ,—50,50]); 图象:cot(x)4在区间]1,1[-画出函数xy 1sin =的图形。
解:程序代码:>> x=linspace (-1,1,10000);y=sin(1。
/x ); plot (x,y ); axis ([-1,1,—2,2]) 图象:二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形:解:程序代码:>〉 t=linspace(0,2*pi,100); plot(cos(t ).*cos (5*t ),sin(t )。
*cos(3*t)); 图象:极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解:程序代码:〉〉 t=0:0.01:2*pi ; r=exp (t/10);polar(log(t+eps ),log (r+eps)); 图象:90270分段函数作图10 作出符号函数x y sgn =的图形。
MATLAB相关的实验以及答案

y=zeros(size(x)); i=numel(x); for j=1:i if (x(j)>=0) y(j)=-3*x(j)^2+5; else y(j)=3*x(j)^2+5; end end x y
4. 编写一程序,求出 编写一程序,求出[100 1000]以内的全部素数。 以内的全部素数。 以内的全部素数 num=[ ]; i=1; for k1=100:1000 k2=fix(sqrt(k1)); sign=1; for k3=2:k2 if mod(k1,k3)==0 sign=0; break end end if sign==1 num(i)=k1; i=i+1; end end num
6. 建立函数count(x),其中x为一个班的学生成绩,统 建立函数 ,其中 为一个班的学生成绩, 为一个班的学生成绩 计该班学生成绩,其中优秀:成绩≥90,良好:80≤ 计该班学生成绩,其中优秀:成绩 ,良好: 成绩<90,中等:70≤成绩 成绩<80,及格:60≤成绩 成绩<70, 成绩 ,中等: 成绩 ,及格: 成绩 , 不及格:成绩<60,分别输出优秀、良好、中等、不 不及格:成绩 ,分别输出优秀、良好、中等、 及格的人数,要求有输入、输出提示语句。例如: 及格的人数,要求有输入、输出提示语句。例如: >> count 请输入该班学生成绩: %输出提示 请输入该班学生成绩: 输出提示 [34 67 98 89 78] %输入成绩 输入成绩 成绩优秀: %输出结果 成绩优秀:1 输出结果 成绩良好: 成绩良好:1 成绩中等: 成绩中等:1 成绩及格: 成绩及格:1 成绩不及格: 成绩不及格:1
2. 输入三角形的三条边,求三角形的面积。如果输入 输入三角形的三条边,求三角形的面积。 的三个数不能构成三角形,要求输出“ 的三个数不能构成三角形,要求输出“不能构成一个 三角形”这样的提示信息。 三角形”这样的提示信息。 提示: 提示: area = s(s −a)(s −b)(s −c) s = (a +b + c) / 2 a=input('a='); b=input('b='); c=input('c='); if (a+b>c)&(a+c>b)&(b+c>a) s=(a+b+c)/2; area=sqrt(s*(s-a)*(s-b)*(s-c)) else fprintf(‘不能构成一个三角形 不能构成一个三角形\n’) 不能构成一个三角形 end
数学实验(matlab)样题及参考解答

东华大学高等数学实验试题A考试时间:90分钟(附参考解答)班级 学号 姓名 得分 上机考试说明:1. 开考前可将准备程序拷到硬盘, 开考后不允许用移动盘,也不允许上网;2. 领座考生试卷不同,开卷,可利用自己备用的书和其他资料,但不允许讨论,也不允许借用其他考生的书和资料。
3. 解答(指令行,答案等)全部用笔写在考卷上。
一、 计算题(70分)要求:写出M 函数(如果需要的话)、MATLAB 指令和计算结果。
1. 解线性方程组⎪⎪⎩⎪⎪⎨⎧-=+=+--=-+=-+14235231543421431321x x x x x x x x x x x 并求系数矩阵的行列式。
指令行:A=[5 1 –1 0;1 0 3 –1;-1 –1 0 5;0 0 2 4];b=[1;2;3;-1]; x=A\b,d=det(A) 结果:x 1=1.4, x 2= -5.9, x 3=0.1, x 4= -0.3. 行列式=70.2. 设 f(x,y) = 4 sin (x 3y),求 3,22==∂∂∂y x y x f 。
指令行:syms x y; f=diff(4*sin(x^3*y),x); f=diff(f,y); f=subs(f,x,2); f=subs(f,y,3)结果:1063.63. 求方程 3x 4+4x 3-20x+5 = 0 的所有解。
指令行:roots([3 4 0 –20 5])结果:-1.5003 - 1.5470i, -1.5003 + 1.5470i, 1.4134, 0.25394. 使用两种方法求积分dx e x 210221-⎰π的近似值。
方法一:指令行:syms x; s=int(1/sqrt(2*pi)*exp(-x^2/2),0,1); vpa(s,5)结果:0.34135方法二:指令行:x=0:0.01:1; y=1/sqrt(2*pi)*exp(-x.^2/2);trapz(x,y)结果:0.3413方法三:M 函数ex4fun.mfunction f=ex4fun(x)f=1/sqrt(2*pi)*exp(-x.^2/2);指令行:s=quadl(@ex4fun,0,1)结果:0.34135. 求函数 f(x,y) = 3x 2+10y 2+3xy-3x +2y 在原点附近的一个极小值点和极小值。
matlab数学实验练习题

Matlab 数学实验实验一 插值与拟合实验内容:预备知识:编制计算拉格朗日插值的M 文件。
1. 选择一些函数,在n 个节点上(n 不要太大,如5 ~ 11)用拉格朗日、分段线性、三次样条三种插值方法,计算m 个插值点的函数值(m 要适中,如50~100)。
通过数值和图形输出,将三种插值结果与精确值进行比较。
适当增加n ,再做比较,由此作初步分析。
下列函数任选一种。
(1)、 ;20,sin π≤≤=x x y (2)、;11,)1(2/12≤≤--=x x y(3)、;22,c os 10≤≤-=x x y(4)、22),ex p(2≤≤--=x x y2.用电压V=10伏的电池给电容器充电,电容器上t 时刻的电压为)(0)()(τteV V V t v ---=,其中0V 是电容器的初始电压,τ是充电常数。
试由下面一组t ,V 数据确定0V 和τ。
实验二 常微分方程数值解试验实验目的:1. 用MATLAB 软件求解微分方程,掌握Euler 方法和龙格-库塔方法;2. 掌握用微分方程模型解决简化的实际问题。
实验内容: 实验三 地图问题1. 下图是一个国家的地图,为了计算出它的国土面积,首先对地图作如下测量:以由西向东方向为x 轴,由南到北方向为y 轴,选择方便的原点,并将从最西边界点到最东边界点在x 轴上的区间适当地划分为若干段,在每个分点的y 方向测出南边界点和北边界点的y 坐标y1和y2,这样就得到了表中的数据(单位mm )。
根据地图的比例我们知道18mm相当于40km,试由测量数据计算该国土2实验四狼追兔问题狼猎兔问题是欧洲文艺复兴时代的著名人物达.芬奇提出的一个数学问题。
当一个兔子正在它的洞穴南面60码处觅食时,一只恶狼出现在兔子正东的100码处。
当两只动物同时发现对方以后,兔子奔向自己的洞穴,狼以快于兔子一倍的速度紧追兔子不放。
狼在追赶过程中所形成的轨迹就是追击曲线。
狼是否会在兔子跑回洞穴之前追赶上兔子?为了研究狼是否能够追上兔子,可以先考虑求出狼追兔子形成的追击曲线,然后根据曲线来确定狼是否能够追上兔子。
matlab简单编程21个题目及答案
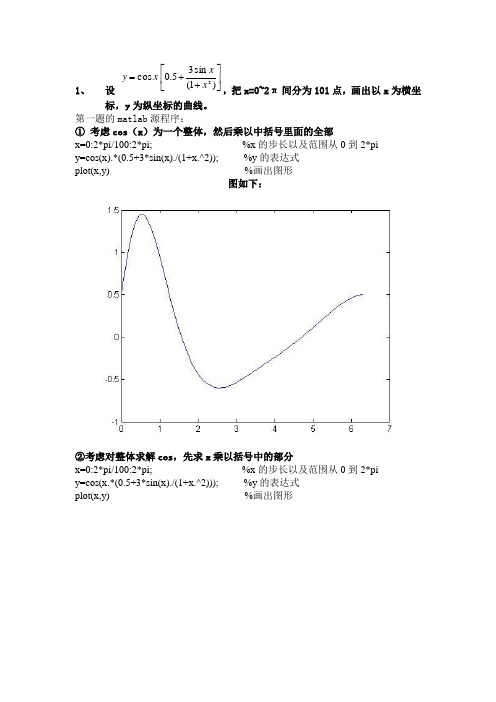
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
matlab课堂实验小测1带答案

课堂实验小测1◆1、MATLAB 中包含两个函数upper 和lower ,分别把字符串转化为大字和小写。
创建一个新的函数caps ,让字符串每个单词的第一个字母大写,其余为小写。
str=input('Please enter the words: ','s');str(1)=upper(str(1));str(2:end)=lower(str(2:end));disp(str);◆2、工程师们经常用分贝或dB 来描述两功率之比。
1dB 的定义如下:210110log P dB P = (2.13) P2 是已测量的功率, P1 代表参考功率。
假设参考功率P1 为1mw ,编写一个程序,接受一个输入功率P2 并把转化成为以1mw 为参考功率的dB.(它在工程上有一个特殊单位dBm)。
P2=input('Please enter the P2(mW): ');P1=1;PdB=10*log10(P2/P1)disp('The power is');disp(PdB);disp('mW');◆3、弹簧中的能量.压缩弹簧弹力的大小可由下面的公式计算出来F = kxF 代表弹力,单位为N 。
k 代表劲度系数单位为N/m.存储在压力弹簧中的势能为212E kx = E 代表势能,单位为焦。
下面是4个可用压缩弹簧的信息.编写一个程序,计算出每一个弹簧的压缩量和弹力势能.哪一个弹簧的弹力最大?F=[20,24,22,20];k=[500,600,700,800];x=F./k;disp('压缩量:');disp(x);E=1/2*k.*x.^2;disp('势能:')E[SE,ID]=sort(E);disp('最大弹力弹簧号:')ID(end)◆4、把角度的弧度格式转换为相应的度/分/秒。
MATLAB习题

MATLAB习题习题一1、通常情况下,MATLAB的工作界面主要由有哪几种窗口构成?答:指令窗口、历史指令窗口、工作空间浏览器、当前目录浏览器等窗口构成。
2、在MATLAB窗口中,可以键入各种指令、函数,并显示运行结果的窗口为【 A 】A、指令窗口B、当前目录浏览器C、工作空间浏览器D、历史指令窗口3、在MATLAB窗口中,可以对内存变量直接进行操作的窗口为【 C 】A、指令窗口B、当前目录浏览器C、工作空间浏览器D、历史指令窗口4、在MATLAB窗口中,记录在MATLAB命令窗口执行过的指令操作的窗口为【 D 】A、指令窗口B、当前目录浏览器C、工作空间浏览器D、历史指令窗口5、在MATLAB窗口中,用于搜索、查看和改变MATLAB路径和文件的窗口为【 B 】A、指令窗口B、当前目录浏览器C、工作空间浏览器D、历史指令窗口6、在MATLAB语言中,如果一个命令行很长,可以在物理行之后如下续行符【 B 】A、“,”B、“…”C、“、、、”D、“,”7、在MATLAB语言中,提示其后语句为输入指令的行提示符为【 D 】A、“;”B、“:”C、“,”D、“>>”8、在MATLAB语言中,在指令窗口运行过的指令再次调出运行的按键为【 B 】A、“;”B、“↑”或“↓”C、“,”D、“>>”9、在MATLAB语言中,若希望结果不被显示,可在语句之后加上符号【 A 】A、“;”B、“:”C、“,”D、“>>”10、在MATLAB语言中,下列常用操作命令解释错误的是【BE 】A、dir为显示当前目录下的文件B、clc为清除工作区中的变量C、path为显示搜索目录D、clf为清空当前图形窗口E、clear为清除命令窗口中的内容F、path为显示搜索路径11、若只知要搜索函数的前两个字母,可用lookfor 命令搜索此关键字的帮助信息。
12、在MATLAB语言中,可采用Tab 键进行模糊查询。
matlab所有实验及答案李楠资料

第二章 习题1、 矩阵Y= ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3472123100451150425,给出元素1的全下标和单下标,求出元素100的存储位置。
取出子矩阵⎥⎦⎤⎢⎣⎡21301,并求该矩阵的维数。
解:命令为:Y=[5,2,4;0,15,1;45,100,23;21,47,3] Y(2,3) Y(10)find(Y==100) sub2ind([4 3],3,2)B=Y(2:2:4,3:-2:1) 或 B=Y([2 4],[3 1]) [m n]=size(Y)2、已知矩阵A=[1 0 -1 ;2 4 1; -2 0 5],B=[0 -1 0;2 1 3;1 1 2] 求2A+B 、A 2-3B 、A*B 、B*A 、A .*B ,A/B 、A\B 解:命令为:A=[1 0 -1 ;2 4 1; -2 0 5] B=[0 -1 0;2 1 3;1 1 2] E=2*A+B F=A^2-3*B G=A*B H=B*A I=A.*B J=A/B K=A\B3、 利用函数产生3*4阶单位矩阵和全部元素都为8的4*4阶矩阵,并计算两者的乘积。
解:命令为: A=eye(3,4) B=8*ones(4) C=A*B4、创建矩阵a=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------7023021.5003.120498601,取出其前两列构成的矩阵b ,取出前两行构成矩阵c ,转置矩阵b 构成矩阵d ,计算a*b 、c<d ,c&d, c|d ,~c|~d 解:命令为:a=[-1,0,-6,8;-9,4,0,12.3;0,0,5.1,-2;0,-23,0,-7] b=a(:,[1 2]) c=a([1 2],:) d=b ’ e=a*b f=c<d g=c&d h=c|d i=~c|~d5、 使用函数,实现A 到B 、C 、D 、E 的转换A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡129631185210741 B=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡321654987121110 C=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡101112789456123,D=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡369122********* E=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡126311521041 解:命令为:A=[1 4 7 10;2 5 8 11;3 6 9 12] B=rot90(A) C=rot90(A,3) D=fliplr(A) A(:,3)=[] E=A7. 矩阵A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-410091021.5823.1204450002,用函数取出列向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100845和矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡410091001.582004450002 解:命令为:A=[2 0 0 0;45 4 0 12.3;2 8 5.2 -2;0 91 100 4] B=diag(A)C=tril(A)8.建立5阶魔方矩阵,求该矩阵的行列式和逆矩阵、秩以及any 和all 运算结果。
MATLAB练习题和答案

MATLAB练习题和答案MATLAB练习题和答案控制系统仿真实验Matlab部分实验结果⽬录实验⼀MATLAB基本操作 (1)实验⼆Matlab编程 (8)实验三Matlab底层图形控制 (10)实验四控制系统古典分析 (23)实验五控制系统现代分析 (28)实验六PID控制器的设计 (35)实验七系统状态空间设计 (40)实验九直流双闭环调速系统仿真 (44)实验⼀ MATLAB 基本操作1 ⽤MATLAB 可以识别的格式输⼊下⾯两个矩阵12332357135732391894A ??=??144367823355422675342189543ii B i +??+?=+?再求出它们的乘积矩阵C ,并将C 矩阵的右下⾓2×3⼦矩阵赋给D 矩阵。
赋值完成后,调⽤相应的命令查看MATLAB ⼯作空间的占⽤情况。
A=[1,2,3,3;2,3,5,7;1,3,5,7;3,2,3,9;1,8,9,4];B=[1+4i,4,3,6,7,8;2,3,3,5,5,4+2i;2,6+7i,5,3,4,2;1,8,9,5,4,3]; C=A*B;D=C(4:5,4:6); whosName Size Bytes Class AttributesA 5x4 160 doubleB 4x6 384 doublecomplexC 5x6 480 double complexD 2x3 96 double complex2 选择合适的步距绘制出下⾯的图形(,)t∈-sin(/)t,其中111t=[-1:0.1:1];y=sin(1./t);plot(t,y)3 对下⾯给出的各个矩阵求取矩阵的⾏列式、秩、特征多项式、范数、特征根、特征向量和逆矩阵。
75350 083341009103150037193......A =??-????,5765710876810957910B ??=12345678910111213141516C=,33245518118575131D --??-?=----A=[7.5,3.5,0,0;8,33,4.1,0;0,9,103,-1.5;0,0,3.7,19.3];B=[5,7,6,5;7,10,8,7;6,8,10,9;5,7,9,10];C=[1:4;5:8;9:12;13:1rtf6];D=[3,-3,-2,4;5,-5,1,8;11,8,5,-7;5,-1,-3,-1];det(A);det(B);det(C);det(D); rank(A); rank(B); rank(C); rank(D); a=poly(A); b=poly(B); c=poly(C); d=poly(D);norm(A);norm(B);norm(C);norm(D);[v,d]=eig(A,'nobalance');[v,d]=eig(B,'nobalance');[v,d]=eig(C,'nobalance');[v,d]=eig(D,'nobalance');m=inv(A);n=inv(B);p=inv(C);q=inv(D);4 求解下⾯的线性代数⽅程,并验证得出的解真正满⾜原⽅程。
Matlab实验习题集答案

1:用以上两种形式计算36sin 5e ++π算术运算结果。
>> 5^6+sin(pi)+exp(3)ans =1.5645e+004>> x=5^6+sin(pi)+exp(3)x = 1.5645e+0042:已知矩阵⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2211,2121B A ,对它们做简单的关系与逻辑运算C=(A<B)&(A= =B)>> A=[1 2;1 2];>> B=[1 1;2 2];>> C=(A<B)&(A==B) C =0 00 03:对数7sin 5+=a 用五位定点、十五位定点以及有理数形式表示出来。
>> a=5+sin(7);format short,aa =5.6570>> a=5+sin(7);>> format long,aa =5.6569865987187894:直接输入创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=98760154321A>> A=[1 2 3;4 15 60;7 8 9]A =1 2 34 15 607 8 95:输入矩阵111111111⎛⎫ ⎪ ⎪ ⎪⎝⎭。
%利用MATLAB 命令直接输入矩阵OneMatrix=ones(3,3,1)OneMatrix =1 1 1 1 1 1 1 1 16:输入矩阵00000 00000⎛⎫ ⎪⎝⎭>> OneMatrix=ones(2,5,1);ZeroMatrix=zeros(size(OneMatrix))ZeroMatrix =0 0 0 0 00 0 0 0 07:生成3阶魔方矩阵。
>> magic(3)ans =8 1 63 5 74 9 28:操作符冒号”:”的应用a)步长为1的等差数列b)步长为2的等差数列c)步长为-2的等差、递减数列>> 0:1:10ans =0 1 2 3 4 5 6 7 8 9 10 >> 0:2:10ans =0 2 4 6 8 10>> 10:(-2):0ans =10 8 6 4 2 09:已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=162ln973sin56231A,抽取与修改矩阵A的一些元素.a)求矩阵A的第二行第三列元素b)求矩阵A的第四个元素c)取矩阵A的A(2),A(3),A(4)d)取矩阵A的第一行e)取矩阵A的第三列f)把矩阵A的第一行第三列元素赋值给变量g)把矩阵A的第二行第一列元素修改为100>> A=[1 23 56;sin(3) 7 9;log(2) 6 1] >> A(2,3)ans =9>> A(4)ans =23>> A(2),A(3),A(4)ans =0.141120008059867ans =0.693147180559945ans =23>> A(1,:)ans =1 23 56>> A(:,3)ans =5691>> x=A(1,3)x =56>> A(2,1)=100A =1.0000 23.0000 56.0000 100.0000 7.0000 9.00000.6931 6.0000 1.000010:已知矩阵⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=851,9631BA,利用A与B生成矩阵13100690C⎛⎫= ⎪⎝⎭,() D A B=,AAAB⎛⎫= ⎪⎝⎭。
Matlab实验题目与答案

(温馨提示:实验课结束后,请将所有作业(题目、代码、结果)利用word 整理成一个完整的实验报告,加上封面,打印,纸质档于18周周一交)第一次上机作业目的:1. 掌握MATLAB 各种表达式的书写规则2. 运行课堂上讲过的例子,熟悉矩阵、表达式的基本操作和运算。
作业:1. 熟悉matlab 集成环境界面。
回答以下问题,并操作相关的指令:(1) 分别写出清除命令窗口和清除变量的指令。
答: clc 和clear(2)在命令行输入命令后,matlab 的搜索过程是怎样的?答: (1)检查该命令对象是不是一个变量。
(2)检查该命令对象是不是一个内部函数。
(3)检查该命令对象是否为当前目录下的程序文件。
(4)检查该命令对象是否为MATLAB 搜索路径中其他目录下的M 文件。
(3)什么是matlab 的当前工作目录?写出两种设置当前工作目录的方法? 答: 就是matlab 当前文件读取和存储的默认路径(1)在当前目录窗口中更改(2)在MATLAB 桌面工具栏中更改(3)使用cd 命令:cd c:\mydir---将c :\mydir 设置为当前目录(4)什么是matlab 的搜索路径?写出两种设置搜索路径的方法?答: 指Matlab 运行文件时进行搜索的目录。
(1)用path 命令设置:(2)用Set Path 对话框设置(5)help 命令和doc 命令有什么作用,它们有什么区别?答: help 命令:最基本的帮助命令,查询信息直接显示在命令窗口。
doc 命令:在帮助窗口中显示HTML 帮助文档,显示函数的详细用法及 例子,比help 命令更详细。
2. 在matlab 中输入下列表达式,并求各表达式的值,显示MATLAB 工作空间的使用情况并用两种方式保存全部变量,变量保存的文件名必须包含自己的学号后四位数:(1))1034245.01(26-⨯+⨯=w w=sqrt(2)*(1+0.34245*10^-6)w =1.4142(2),)tan(22ac b e abc c b a x ++-+++=ππ 其中a=3.5,b=5,c=9.8。
matlab实验习题

习题一:数据拟合1、某钢材厂从1990年到2010年的产量如下表所示,请利用三次样条插值的方法计算1999年该钢材厂的产量,并画出曲线,已知数据用‘*’表示。
要求写出达到题目要求的MATLAB 操作过程,不要求计算结果。
2、在一次化学动力学实验中,在某温度下乙醇溶液中,两种化合物反应的产物浓度与反应时间关系的原始数据如下,请对这组数据进行三次多项式拟合,并画出拟合曲线,已知数据如下。
time=[2.5 5.0 7.5 10.0 13.0 17.0 20.0 30.0 40.0 50.0 60.0 70.0]res=[0.29 0.56 0.77 1.05 1.36 1.52 2.00 2.27 2.81 3.05 3.25 3.56]3、通过测量得到一组数据:T=[1,2,3,4,5,6,7,8,9,10]Y=[4.842,4.362,3.754,3.368,3.169,3.083,]习题二:微积分1、计算极限011(1)lim sin sin x x x x x →⎛⎫+ ⎪⎝⎭2(2)lim x x x e →+∞ 30tan sin (3)lim x x x x →- 0(4)lim x x x →+ 0ln cot (5)lim ln x x x →+ 20(6)lim ln x x x →+ 20sin cos (7)lim sin x x x x x x→- 323325(8)lim 521x x x x x →∞-+++2、求下列函数的导数(1) y = (2) ln[tan()]24x y π=+; (3) 21cot ln sin 2y x x =+;(4) y x =. 3、求积分 (1)235(1).x x dx -⎰ (2) 2arctan .x xdx ⎰ (3)120().x x dx -⎰ 习题三:绘图1、作出函数tan y x =和cot y x =的图形观察其周期性和变化趋势.2、在区间[1,1]-画出函数1sin y x=的图形 3、作出函数2241z x y =++的图形4、作出函数22cos(49)z x y =+的图形5、画出参数曲面cos sin sin sin [0,4],[0.001,2]cos ln(tan /2/5)x u v y u vu v z v v u π=⎧⎪=∈∈⎨⎪=++⎩ 的图形.习题四:验证性实验(动画)1.画心行图案clear allclc[x,y,z]=meshgrid(linspace(-1.3,1.3));f=(x.^2+(9/4)*y.^2+z.^2-1).^3-x.^2.*z.^3-(9/80)*y.^2.*z.^3;p=patch(isosurface(x,y,z,f,0));set(p,'FaceColor','red','EdgeColor','none');daspect([1 1 1])view(3)camlight;lighting phongaxis off2.动态画曲线表白,(呵呵只需要把代码里的某人改成你的那个她的名字就行了)clc;h1=figure('name','爱的表达');axis([-1.5 1.5 -2 0.5]);axis off;set(gcf,'color','black');n=4;a=320;m=10^(-a);hll=line(NaN,NaN,'marker','.','linesty','-','erasemode','none','color','r');x1=[];y1=[];for theta=pi/2:-2*pi/999:-3*pi/2r1=1+cos(theta+pi/2);x1=[x1;r1*cos(theta)];y1=[y1;r1*sin(theta)];set(hll,'xdata',x1,'ydata',y1);pause(m);endpause(1);fill(x1,y1,'r');axis off;set(gcf,'color','black');text(-0.16*n,-0.85,'某人','fontsize',n*18,'color','b');title('心形线','fontsize',18,'color','m');disp('love you ');pause(1);x2=[];y2=[];h22=line(NaN,NaN,'marker','.','linesty','-','erasemode','none','color','b');for theta=pi/2:-2*pi/999:-3*pi/2r2=1+cos(theta+pi/2);x2=[x2;r2*cos(theta)];y2=[y2;r2*sin(theta)];set(h22,'xdata',x2,'ydata',y2);pause(m^19);endh2=figure('name','爱的表达');fill(x2,y2,'r');text(-0.58,-0.7,'我爱你','fontsize',40,'color','b');text(-0.17,-1.1,'张三','fontsize',18,'color','m');axis off;set(gcf,'color','black');pause(1);x3=[];y3=[];h33=line(NaN,NaN,'marker','.','linesty','-','erasemode','none','color','b'); for theta=pi/2:-2*pi/999:-3*pi/2r3=1+cos(theta+pi/2);x3=[x3;r3*cos(theta)];y3=[y3;r3*sin(theta)];set(h33,'xdata',x3,'ydata',y3);pause(m^19);end。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
sanxia
1. 画出衰减振荡曲线3sin 3t y e
t -=及其包络线30t y e -=,t 的取值范围是
[0,4]π
clear all;
t=(0:0.01:4*pi );
y=exp(-t/3).*sin(3*t);
y0=exp(-t/3);
plot(t,y);
hold on ;
plot(t,y0);
hold on ;
plot(t,-y0);
grid on ;
2.画出z=所表示的三维曲面,x,y的取值范围是[-8,8]。
clear;
clear all;
x=-8:0.5:8;
y=x';
X=ones(size(y))*x;
Y=y*ones(size(x));
R=sqrt(X.^2+Y.^2)+eps;
Z=sin(R)./R;
surf(X,Y,Z);
colormap(cool);
xlabel('X'),ylabel('Y'),zlabel('Z');
3、以.jpg图像为例,显示一幅真彩色图像的R,G,B分量图像,该图像放在D:\lydu\目录下
clear all;
A=imread('E:\sanxia.jpg');
J1(:,:,1)=A(:,:,1);
J1(:,:,2)=0;
J1(:,:,3)=0;
J2(:,:,2)=A(:,:,2);
J2(:,:,1)=0;
J2(:,:,3)=0;
J3(:,:,3)=A(:,:,3);
J3(:,:,1)=0;
J3(:,:,2)=0;
subplot(221);
imshow(A);
subplot(222);
imshow(J1);
subplot(223);
imshow(J2);
subplot(224);
imshow(J3);
4.以Matlab自带的图像cameraman.tif为例,使用imtransform函数实现图像平面扭曲功能。
注意:使用imtransform函数完成图像空间变换,imtransform(I,T),I 指要变换的图像,T是由maketform产生的变换结构,如T=maketform('affine',[.5 0 0;.5 1 0;0 0 1]);
clear all;
I=imread('cameraman.tif');
T=maketform('affine',[.5 0 0;.5 1 0;0 0 1]);
A=imtransform(I,T);
subplot(2,2,1);
imshow(I);
subplot(2,2,2);
imshow(A);
5.以图像uab.jpg为例,使用函数colfilt进行图像领域的distinct操作。
并将处理后的图像与原图像放在一起进行对比。
该图像放在D:\lydu\目录下.
原理:f=inline('ones(25,1)*mean(x)');函数inline(‘‘)是根据参数创建函数对象。
B=colfilt(A2,[5 5],'distinct',f);使用[5 5]的滑动块在A2上滑动,每滑动一次,就以滑动块遮住部分为参数X调用一次f.
clear all;
A=imread('E:\uab.jpg');
subplot(1,2,1); imshow(A);
A2=rgb2gray(A);
A2=double(A2);
f=inline('ones(25,1)*mean(x)');
B=uint8(colfilt(A2,[5 5],'distinct',f));
subplot(1,2,2); imshow(B);
6.以图像0043.jpg和0192.jpg为例,利用矩阵对应相乘把两个图像合成在一起。
clear all;
A = imread('E:\0043.jpg');
B = imread('E:\0192.jpg');
s=size(A);
subplot(1,3,1); imshow(A)
m=s(1),n=s(2);
B1=imresize(B,[m n]);
A=double(A);
C=double(B1);
D=A.*C/128;
D=uint8(D);
subplot(1,3,2); imshow(B)
subplot(1,3,3); imshow(D)。
