安徽省宿州市2014-2015学年高二上学期期末数学试卷(文科)
高中高二数学上学期第二次月考试卷 文(含解析)-人教版高二全册数学试题

2014-2015学年某某省某某市安吉县上墅私立高中高二(上)第二次月考数学试卷(文科)一、选择题:(本大题共10小题,每小题3分,共30分.)1.在△ABC中,“A=”是“cosA=”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件2.已知命题p:∃x∈R,x﹣2>0,命题q:∀x∈R,>x,则下列说法中正确的是() A.命题p∨q是假命题 B.命题p∧q是真命题C.命题p∨(¬q)是假命题 D.命题p∧(¬q)是真命题3.直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点,则该椭圆的离心率为()A. B. C. D.4.若直线(m+2)x+3y+3=0与直线x+(2m﹣1)y+m=0平行,则实数m=() A.﹣或1 B. 1 C. 1或2 D.﹣5.直线2x+3y+1=0与直线4x+my+7=0平行,则它们之间的距离为() A. 4 B. C. D.6.设l,m是不同的直线,α,β,γ是不同的平面()A.若l⊥α,l⊥m,则m∥α B.若l⊂α,m⊂β,α∥β,则l∥mC.若l∥α,m⊥α,则l⊥m D.若α∩β=l,l⊥γ,m⊥β,则m∥γ7.过P(2,0)的直线被圆(x﹣2)2+(y﹣3)2=9截得的线段长为2时,直线l的斜率为()A. B. C.±1 D.8.若双曲线的离心率为,则其渐近线方程为()A. y=±2x B. C. D.9.直线l:x+y﹣4=0与圆C:x2+y2=4的位置关系是()A.相交过圆心 B.相交不过圆心 C.相切 D.相离10.下列结论正确的是()A.命题“若a>b>0,则a2>b2”的逆命题是假命题B.若函数f(x)=sinx,则函数f(x)为周期函数的逆命题是真命题C.向量,的夹角为钝角的充要条件是•<0D.“x2>2”是“x2﹣3x+2≥0”的充分不必要条件二、填空题:(本大题共7小题,每小题3分,共21分.)11.由命题“存在x∈R,使x2+2x+m≤0”是假命题,则实数m的取值X围为.12.已知命题p:m<0,命题q:∀x∈R,x2+mx+1>0成立,若“p∧q”为真命题,则实数m 的取值X围是.13.两直线l1:ax+2y﹣1=0,l2:(a﹣1)x+ay+1=0垂直,则a=.14.两圆x2+y2﹣4x+6y=0和x2+y2﹣6x=0的连心线方程为.15.已知动圆M与圆C1:(x+3)2+y2=9外切且与圆C2:(x﹣3)2+y2=1内切,则动圆圆心M的轨迹方程是.16.一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.17.下列四个命题:①“∃x∈R,x2﹣x+1≤0”的否定;②“若x2+x﹣6≥0,则x>2”的否命题;③在△ABC中,“A>30°”是“sinA>”的充分不必要条件④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ.(k∈Z)”,其中真命题的序号是.三、解答题:(本大题共5小题,共49分.)18.设p:实数x满足x2+2ax﹣3a2<0(a>0),q:实数x满足x2+2x﹣8<0,且q是p的必要不充分条件,求a的取值X围.19.求满足下列条件的椭圆方程:(1)长轴在x轴上,长轴长等于12,离心率等于;(2)椭圆经过点(﹣6,0)和(0,8);(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.20.如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.(1)求证:AM⊥平面EBC;(2)求直线AB与平面EBC所成角的大小.21.已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为,且过点D(2,0).(1)求该椭圆的标准方程;(2)设点,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.22.已知圆C:x2+y2=4和直线l:3x+4y+12=0,点P是圆C上的一动点,直线与坐标轴的交点分别为点A、B,(1)求与圆C相切且平行直线l的直线方程;(2)求△PAB面积的最大值.2014-2015学年某某省某某市安吉县上墅私立高中高二(上)第二次月考数学试卷(文科)参考答案与试题解析一、选择题:(本大题共10小题,每小题3分,共30分.)1.在△ABC中,“A=”是“cosA=”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据充分必要条件的定义结合三角形的性质,分别证明充分性和必要性,从而得到答案.解答:解:在△ABC中,若A=,则cosA=,是充分条件,在△ABC中,若cosA=,则A=或A=,不是必要条件,故选:A.点评:本题考查了充分必要条件,考查了三角形中的三角函数值问题,是一道基础题.2.已知命题p:∃x∈R,x﹣2>0,命题q:∀x∈R,>x,则下列说法中正确的是() A.命题p∨q是假命题 B.命题p∧q是真命题C.命题p∨(¬q)是假命题 D.命题p∧(¬q)是真命题考点:复合命题的真假.专题:简易逻辑.分析:容易判断命题p是真命题,q是假命题,所以根据p∨q,p∧q,¬q的真假和p,q的关系即可找出正确选项.解答:解:∃x∈R,x﹣2>0,即不等式x﹣2>0有解,∴命题p是真命题;x<0时,无解,∴命题q是假命题;∴p∨q为真命题,p∧q是假命题,¬q是真命题,p∨(¬q)是真命题,p∧(¬q)是真命题;∴D正确.故选D.点评:考查真命题,假命题的概念,以及p∨q,p∧q,¬q的真假和p,q真假的关系.3.直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点,则该椭圆的离心率为()A. B. C. D.考点:椭圆的简单性质.专题:计算题.分析:直线x﹣2y+2=0与坐标轴的交点为(﹣2,0),(0,1),依题意得.解答:直线x﹣2y+2=0与坐标轴的交点为(﹣2,0),(0,1),直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点;故.故选A.点评:本题考查了椭圆的基本性质,只需根据已知条件求出a,b,c即可,属于基础题型.4.若直线(m+2)x+3y+3=0与直线x+(2m﹣1)y+m=0平行,则实数m=() A.﹣或1 B. 1 C. 1或2 D.﹣考点:直线的一般式方程与直线的平行关系.专题:直线与圆.分析:由直线的平行可得m的方程,解得m代回验证可得.解答:解:∵直线(m+2)x+3y+3=0与直线x+(2m﹣1)y+m=0平行,∴(m+2)(2m﹣1)﹣3×1=0,解得m=﹣或1经验证当m=1时,两直线重合,应舍去,故选:D点评:本题考查直线的一般式方程和平行关系,属基础题.5.直线2x+3y+1=0与直线4x+my+7=0平行,则它们之间的距离为() A. 4 B. C. D.考点:两条平行直线间的距离.专题:直线与圆.分析:通过直线的平行求出m,然后利用平行线之间的距离求解即可.解答:解:直线2x+3y+1=0与直线4x+my+7=0平行,所以m=6,直线4x+my+7=0化为直线4x+6y+7=0即2x+3y+3.5=0,它们之间的距离为:d==.故选:C.点评:本题考查两条平行线之间是距离的求法,基本知识的考查.6.设l,m是不同的直线,α,β,γ是不同的平面()A.若l⊥α,l⊥m,则m∥α B.若l⊂α,m⊂β,α∥β,则l∥mC.若l∥α,m⊥α,则l⊥m D.若α∩β=l,l⊥γ,m⊥β,则m∥γ考点:空间中直线与平面之间的位置关系.专题:空间位置关系与距离.分析:利用空间中线线、线面、面面间的位置关系求解.解答:解:若l⊥α,l⊥m,则m∥α或m⊂α,故A错误;若l⊂α,m⊂β,α∥β,则l与m平行或异面,故B错误;若l∥α,m⊥α,则由直线与平面平行的性质得l⊥m,故C正确;若α∩β=l,l⊥γ,m⊥β,则m∥γ或m⊂γ,故D错误.故选:C.点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.7.过P(2,0)的直线被圆(x﹣2)2+(y﹣3)2=9截得的线段长为2时,直线l的斜率为() A. B. C.±1 D.考点:直线与圆的位置关系.专题:直线与圆.分析:设直线l的方程为:y=kx﹣2k,由已知条件结合圆的性质和点到直线的距离公式推导出=2,由此能求出直线的斜率.解答:解:设直线l的斜率为k,则直线l的方程为:y=kx﹣2k,(x﹣2)2+(y﹣3)2=9的圆心C(2,3),半径r=3,∵过P(2,0)的直线被圆(x﹣2)2+(y﹣3)2=9截得的线段长为2,∴圆心C(2,3)到直线AB的距离d==2,∵点C(2,3)到直线y=kx﹣2k的距离d==2,∴•2=3,解得k=±.故选:A.点评:本题考查直线的斜率的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.8.若双曲线的离心率为,则其渐近线方程为()A. y=±2x B. C. D.考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:通过双曲线的离心率,推出a、b关系,然后直接求出双曲线的渐近线方程.解答:解:由双曲线的离心率,可知c=a,又a2+b2=c2,所以b=a,所以双曲线的渐近线方程为:y==±x.故选B.点评:本题考查双曲线的基本性质,渐近线方程的求法,考查计算能力.9.直线l:x+y﹣4=0与圆C:x2+y2=4的位置关系是()A.相交过圆心 B.相交不过圆心 C.相切 D.相离考点:直线与圆的位置关系.专题:直线与圆.分析:求出圆心(0,0)到直线l:x+y﹣4=0的距离d正好等于半径,可得直线和圆相切.解答:解:由于圆心(0,0)到直线l:x+y﹣4=0的距离为d==2=r(半径),故直线和圆相切,故选:C.点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于基础题.10.下列结论正确的是()A.命题“若a>b>0,则a2>b2”的逆命题是假命题B.若函数f(x)=sinx,则函数f(x)为周期函数的逆命题是真命题C.向量,的夹角为钝角的充要条件是•<0D.“x2>2”是“x2﹣3x+2≥0”的充分不必要条件考点:命题的真假判断与应用.专题:简易逻辑.分析: A.“若a>b>0,则a2>b2”的逆命题为“若a2>b2,则a>b>0”是假命题;B.函数f(x)=sinx,则函数f(x)为周期函数的逆命题为“函数f(x)为周期函数,则f (x)=sinx”,显然不正确;C.向量,的夹角为钝角⇒•<0,反之不成立,由于非零向量反向共线时,满足<0;D.“x2>2”⇒或x,而x2﹣3x+2=﹣≥﹣,反之也不成立.解答:解:A.“若a>b>0,则a2>b2”的逆命题为“若a2>b2,则a>b>0”是假命题,正确;B.函数f(x)=sinx,则函数f(x)为周期函数的逆命题为“函数f(x)为周期函数,则f (x)=sinx”是假命题,不正确;C.向量,的夹角为钝角⇒•<0,反之不成立,由于向量反向共线时,其<0,因此不正确;D.“x2>2”⇒或x,此时x2﹣3x+2=﹣≥﹣,反之也不成立,因此“x2>2”是“x2﹣3x+2≥0”的既不充分也不必要条件,不正确.综上可得:只有A.故选:A.点评:本题考查了函数的性质、简易逻辑的判定、向量的数量积及其夹角公式,考查了推理能力,属于基础题.二、填空题:(本大题共7小题,每小题3分,共21分.)11.由命题“存在x∈R,使x2+2x+m≤0”是假命题,则实数m的取值X围为(1,+∞).考点:特称命题.专题:计算题.分析:原命题为假命题,则其否命题为真命题,得出∀x∈R,都有x2+2x+m>0,再由△<0,求得m.解答:解:∵“存在x∈R,使x2+2x+m≤0”,∴其否命题为真命题,即是说“∀x∈R,都有x2+2x+m>0”,∴△=4﹣4m<0,解得m>1.∴m的取值X围为(1,+∞).故答案为:(1,+∞)点评:本题考查了存在命题的否定,不等式恒成立问题.考查转化、计算能力.12.已知命题p:m<0,命题q:∀x∈R,x2+mx+1>0成立,若“p∧q”为真命题,则实数m 的取值X围是﹣2<m<0 .考点:复合命题的真假.专题:简易逻辑.分析:根据复合命题的真假性判断出命题p、q都是真命题,再逐一求出m的X围,最后求它们的交集.解答:解:因为“p∧q”为真命题,所以命题p、q都是真命题,若命题q是真命题,则∀x∈R,x2+mx+1>0横成立,所以△=m2﹣4<0,解得﹣2<m<2,又命题p:m<0,也是真命题,所以实数m的取值X围是:﹣2<m<0,故答案为:﹣2<m<0.点评:本题考查了复合命题的真假性,以及二次函数的性质,属于基础题.13.两直线l1:ax+2y﹣1=0,l2:(a﹣1)x+ay+1=0垂直,则a= 0或﹣1 .考点:直线的一般式方程与直线的垂直关系.专题:直线与圆.分析:由已知得a(a﹣1)+2a=0,由此能求出a.解答:解:∵两直线l1:ax+2y﹣1=0,l2:(a﹣1)x+ay+1=0垂直,∴a(a﹣1)+2a=0,解得a=0或a=﹣1.故答案为:0或﹣1.点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意直线与直线垂直的性质的合理运用.14.两圆x2+y2﹣4x+6y=0和x2+y2﹣6x=0的连心线方程为3x﹣y﹣9=0 .考点:圆与圆的位置关系及其判定.专题:计算题;直线与圆.分析:求出圆心坐标,利用点斜式,可得方程.解答:解:两圆x2+y2﹣4x+6y=0和x2+y2﹣6x=0的圆心坐标分别为(2,﹣3),(3,0),∴连心线方程为y﹣0=(x﹣3),即3x﹣y﹣9=0.故答案为:3x﹣y﹣9=0.点评:本题考查圆与圆的位置关系及其判定,考查直线方程,比较基础.15.已知动圆M与圆C1:(x+3)2+y2=9外切且与圆C2:(x﹣3)2+y2=1内切,则动圆圆心M的轨迹方程是﹣=1(x≥2).考点:直线与圆的位置关系.专题:直线与圆.分析:找出两圆圆心坐标与半径,设设动圆圆心M(x,y),半径为r,根据动圆M与圆C1外切且与圆C2内切,即可确定出M轨迹方程.解答:解:由圆C1:(x+3)2+y2=9,圆心C1(﹣3,0),半径r1=3,圆C2:(x﹣3)2+y2=1,圆心C2(3,0),r2=1,设动圆圆心M(x,y),半径为r,根据题意得:,整理得:|MC1|﹣|MC2|=4,则动点M轨迹为双曲线,a=2,b=,c=3,其方程为﹣=1(x≥2).故答案为:﹣=1(x≥2)点评:此题考查了直线与圆的位置关系,以及动点轨迹方程,熟练掌握双曲线定义是解本题的关键.16.一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.考点:由三视图求面积、体积.专题:立体几何.分析:几何体是圆锥与圆柱的组合体,判断圆柱与圆锥的高及底面半径,代入圆锥与圆柱的体积公式计算.解答:解:由三视图知:几何体是圆锥与圆柱的组合体,其中圆柱的高为4,底面直径为2,圆锥的高为2,底面直径为4,∴几何体的体积V=π×12×4+×π×22×2=4π+π=π.故答案为:.点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.17.下列四个命题:①“∃x∈R,x2﹣x+1≤0”的否定;②“若x2+x﹣6≥0,则x>2”的否命题;③在△ABC中,“A>30°”是“sinA>”的充分不必要条件④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ.(k∈Z)”,其中真命题的序号是①②.考点:命题的真假判断与应用.专题:简易逻辑.分析:①按照特称命题的否定要求改写,然后判断真假;②先写出原命题,然后再按照否条件、否结论进行改写;③双向推理,然后进行判断,此例可以举反例;④结合奇函数的性质进行推导,从左推右,然后反推化简.解答:解:①原命题的否定是:∀x∈R,x2﹣x+1>0;因为,故①为真命题;②原命题的否命题是:若x2+x﹣6<0,则x≤2.由x2+x﹣6<0,得(x+3)(x﹣2)<0,所以﹣3<x<2,故②为真命题;③当A=150°时,.所以故在△ABC中,“A>30°”是“sinA>”的不充分条件.故③是假命题;④若函数f(x)为奇函数,则f(0)=tanφ=0,或y轴为图象的渐近线,所以φ=kπ(k∈Z);或tanφ不存在,则φ=,(k∈Z)所以前者是后者的不充分条件.故④为假命题.故答案为:①,②点评:本题以简易逻辑为载体,考查了命题的否定及否命题的写法以及真假判断,充分必要性的判断方法,属于基础题,难度不大.三、解答题:(本大题共5小题,共49分.)18.设p:实数x满足x2+2ax﹣3a2<0(a>0),q:实数x满足x2+2x﹣8<0,且q是p的必要不充分条件,求a的取值X围.考点:必要条件、充分条件与充要条件的判断.专题:不等式的解法及应用.分析:先分别化简两个不等式,再利用q是p的必要不充分条件,转化为,然后某某数a的取值X围.解答:解:由x2+2ax﹣3a2<0得(x+3a)(x﹣a)<0,又a>0,所以﹣3a<x<a,(2分)x2+2x﹣8<0,∴﹣4<x<2,p为真时,实数x的取值X围是:﹣3a<x<a;q为真时,实数x的取值X围是:﹣4<x<2(6分)因为q是p的必要不充分条件,所以有(10分)所以实数a的取值X围是≤a≤2.(14分)点评:本题考查一元二次不等式的解法,必要条件、充分条件与充要条件的判断,考查计算能力,转化思想,是中档题.19.求满足下列条件的椭圆方程:(1)长轴在x轴上,长轴长等于12,离心率等于;(2)椭圆经过点(﹣6,0)和(0,8);(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(1)设椭圆方程为+=1(a>b>0),运用离心率公式和a,b,c的关系,解得a,b,即可得到椭圆方程;(2)设椭圆方程为mx2+ny2=1,(m,n>0),由题意代入点(﹣6,0)和(0,8),解方程即可得到椭圆方程;(3)讨论椭圆的焦点的位置,由题意可得a﹣c=4,a+c=10,解方程可得a,c,再由a,b,c 的关系解得b,即可得到椭圆方程.解答:解:(1)设椭圆方程为+=1(a>b>0),由题意可得,2a=12,e=,即有a=6,=,即有c=4,b===2,即有椭圆方程为+=1;(2)设椭圆方程为mx2+ny2=1,(m,n>0),由题意代入点(﹣6,0)和(0,8),可得36m+0=1,且0+64n=1,解得m=,n=,即有椭圆方程为+=1;(3)当焦点在x轴上时,可设椭圆方程为+=1(a>b>0),由题意可得a﹣c=4,a+c=10,解得a=7,c=3,b==2,即有椭圆方程为+=1;同理,当焦点在y轴上时,可得椭圆方程为+=1.即有椭圆方程为+=1或+=1.点评:本题考查椭圆的方程和性质,主要考查椭圆的方程的求法,注意运用椭圆的方程的正确设法,以及椭圆性质的运用,属于基础题.20.如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.(1)求证:AM⊥平面EBC;(2)求直线AB与平面EBC所成角的大小.考点:直线与平面所成的角;平面与平面垂直的判定.专题:空间位置关系与距离;空间角;空间向量及应用.分析:(1)建立空间直角坐标,利用向量法证明线面垂直.(2)利用向量法求线面角的大小.解答:解:∵四边形ACDE是正方形,所以EA⊥AC,AM⊥EC,∵平面ACDE⊥平ABC,∴EA⊥平面ABC,∴可以以点A为原点,以过A点平行于BC的直线为x轴,分别以直线AC和AE为y轴和z轴,建立如图所示的空间直角坐标系A﹣xyz.设EA=AC=BC=2,则A(0,0,0),B(2,2,0),C(0,2,0),E(0,0,2),∵M是正方形ACDE的对角线的交点,∴M(0,1,1) (3)=(0,1,1),=(0,2,0)﹣(0,0,2)=(0,2,﹣2),=(2,2,0)﹣(0,2,0)=(2,0,0),∴,,∴AM⊥EC,AM⊥CB,∴AM⊥平面EBC.…(5分)(2)∵AM⊥平面EBC,∴为平面EBC的一个法向量,∵=(0,1,1),=(2,2,0),∴cos.∴=60°.∴直线AB与平面EBC所成的角为30°.…(12分)点评:本题主要考查向量法证明线面垂直以及利用向量法求线面角的大小,运算量较大.21.已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为,且过点D(2,0).(1)求该椭圆的标准方程;(2)设点,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.考点:轨迹方程;椭圆的标准方程.专题:计算题;圆锥曲线的定义、性质与方程.分析:(1)设椭圆方程为,根据题意可得a=2且c=,从而b==1,得到椭圆的标准方程;(2)设点P(x0,y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0,y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.解答:解:(1)由题意知椭圆的焦点在x轴上,设椭圆的标准方程是∵椭圆经过点D(2,0),左焦点为,∴a=2,,可得b==1因此,椭圆的标准方程为.(2)设点P的坐标是(x0,y0),线段PA的中点为M(x,y),由根据中点坐标公式,可得,整理得,∵点P(x0,y0)在椭圆上,∴可得,化简整理得,由此可得线段PA中点M的轨迹方程是.点评:本题给出椭圆满足的条件,求椭圆方程并求与之有关的一个轨迹方程,着重考查了椭圆的标准方程、简单几何性质和轨迹方程的求法等知识点,属于中档题.22.已知圆C:x2+y2=4和直线l:3x+4y+12=0,点P是圆C上的一动点,直线与坐标轴的交点分别为点A、B,(1)求与圆C相切且平行直线l的直线方程;(2)求△PAB面积的最大值.考点:直线和圆的方程的应用.专题:直线与圆.分析:(1)根据题意设所求方程为3x+4y+a=0,根据直线与圆相切时,圆心到直线的距离d=r求出a的值,即可确定出所求直线方程;(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,如图所示,求出|AB|与|MN|的长,即可确定出△PAB面积的最大值.解答:解:(1)设所求直线方程为3x+4y+a=0,由题意得:圆心(0,0)到直线的距离d=r,即=2,解得:a=±10,则所求直线方程为3x+4y±10=0;(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,此时直线方程为3x+4y﹣10=0,∵点C到直线AB的距离||=,CM=2,∴|MN|=+2=,∵A(﹣4,0),B(0,3),即OA=4,OB=3,∴|AB|=5,则△PAB面积最大值为×5×=11.点评:此题考查了直线与圆的方程的应用,涉及的知识有:点到直线的距离公式,两直线平行时斜率的关系,以及直线与圆相切的性质,熟练掌握公式及性质是解本题的关键.。
安徽省宿州市2014-2015学年高二上学期期中考试数学(文)试题 Word版含答案

高二期中数学试题(文)试题总分:150分 考试时间:120分钟一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置........ 1. 已知f (x )=x 2+ax +b ,满足f (1)=0,f (2)=0,则f (-1)= ▲ .2. 函数)4lg(2x x y -++=的定义域为 ▲ .3.30y +-=的斜率是 ▲4. 若直线210ax y ++=与直线20x y +-=互相平行,那么a 的值等于 ▲5. 经过点)0,1(-,且与直线y x +=0垂直的直线方程是 ▲6. 以)0,2(A ,)4,0(B 所连线段为直径的圆的方程是 ▲7. 直线0543=-+y x 到直线01543=++y x 的距离是 ▲8.直线032=-+y x 关于直线1=x 对称的直线的方程是 ▲9.设直线过点(0,),a 其斜率为1,且与圆222x y +=相切,则a 的值为 ▲10.直线250x y -+=与圆228x y +=相交于A 、B 两点,则AB ∣∣= ▲. 11.若某空间几何体的三视图如图所示,则该几何体的体积为 ▲12.已知一个球体的半径为1cm,若使其表面积增加到原来的2倍,则表面积增加后球的体积为 ▲13.设,m n 为空间的两条直线,,αβ为空间的两个平面,给出下列命题:①若m ∥α,m ∥β , 则α∥β; ②若m ⊥α,m ⊥β,则α∥β;③若m ∥α,n ∥α,则m ∥n ; ④若m ⊥α,n ⊥α,则m ∥n ;上述命题中,其中假命题...的序号是 ▲ . 14.在圆06222=--+y x y x 内,过点E (0,1)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积是 ▲二.解答题(本题总计80分)15.(本小题满分12分)已知直线1l :(2)(3)50m x m y +++-=和2l :6(21)5x m y +-=。
问m 为何值时,有:(1)1l ∥2l ?(2)1l ⊥2l ?16.(本小题满分12分)过点()2,5A ,且在坐标轴上截距互为相反数的直线l 的方程.17.(本小题满分14分)已知圆的方程是x 2 + y 2 = 5, 且圆的切线满足下列条件,求圆的切线方程(1)过圆外一点Q ( 3, 1 ) (2)过圆上一点P ( -2, 1 )18.(本小题满分14分)如图,在矩形ABCD 中,AB=2BC,P 、Q 分别为线段AB 、CD 的中点,EP ⊥平面ABCD.(Ⅰ)求证:AQ ∥平面CEP ;(Ⅱ)求证:平面AEQ ⊥平面DEP ;19、(本题满分14分)在平行四边形ABCD 中,(11)(71)(46)A B D ,,,,,,点M 是线段AB 的中点, 线段CM 与BD 交于点P ,(1)求直线CM 的方程(2)求点P 的坐标.20.(本题满分14分)已知圆C 的圆心C 在x 轴的正半轴上,半径为5,圆C 被直线03=+-y x 截得的弦长为172.(1)求圆C 的方程;(2)设直线50ax y -+=与圆相交于,A B 两点,求实数a 的取值范围;(3)在(2)的条件下,是否存在实数a ,使得B A ,关于过点(2, 4)P -的直线l对称?若存在,求出实数a 的值;若不存在,请说明理由.Q P E D C B A高二数学试题参考答案(文)一、填空题:1.62.「2,4)3. 3- 4、2 5、1+=x y 6、5)2()1(22=-+-y x7.4 8.012=+-y x 9. 2±. 10. 32 11.1 12.π332 13. ()1()3 14. 210二、解答题:15.解:由(2)(21)618m m m +-=+,得4m =或52m =-; ···········3分 当m =4时,l 1:6x +7y -5=0,l 2:6x +7y =5,即l 1与l 2重合; 当25-=m 时,,566:,052121:21=-=-+-y x l y x l 即l 1∥l 2. ∴当25-=m 时,l 1∥l 2. · ······························6分 (2)由6(2)(3)(21)0m m m +++-=得1m =-或92m =-; ∴当m =-1或m =-29时,l 1⊥ l 2. · ·····························12分 16.过点()2,5A ,且在坐标轴上截距互为相反数的直线l 的方程.解:(1)截距不为0时设l 的方程为1=-+a y a x l 过()0,3A ,∴ 125=-+aa ∴ 3=a ∴ l 的方程为:03=--y x ························8分(2)截距为0时,l 的方程为:052=-y x终上(1)、(2)可得:直线l 的方程是03=--y x 或052=-y x .························12分17.已知圆的方程是x 2 + y 2 = 5, 且圆的切线满足下列条件,求圆的切线方程(1)过圆外一点Q ( 3, 1 ) (2)过圆上一点P ( -2, 1 )解:(1) 若直线不与x 轴垂直时,设切线方程为y - 1 = k ( x -3 ), 则圆心( 0, 0 )到切线的距离等于半径5即 51|31|2=+-k k ⇒ ( 1 - 3k )2 = 5( k 2 + 1 ) ⇒ k =21-, k = 2若直线与x 轴垂直时,x =3,与圆相离,不合题意;综上所述,所求的切线方程是:x + 2y -5 = 0,2x -y -5 = 0························7分18、解:(1)AQ ∥PC ..···7分(2)AQ ⊥PDAQ ⊥平面EPD ········14分19、(1)3765-=x y ························7分 (2))38,6( ························14分20解:(1)设⊙C 的方程为22()25x m y -+=(0)m >解由题意设0m =>⎩……………………………2分 故1m =.故⊙C 的方程为22(1)25x y -+=. ……………………4分(2)5< ……………………………………6分故21250a a ->,所以0a <或512a >. 故,实数a 的取值范围为5(,0)(,)12-∞⋃+∞ ………………………………9分 (3)存在实数a ,使得,A B 关于l 对称.∴PC AB ⊥ ,又0a <或512a > 即⎪⎩⎪⎨⎧><-=-⋅12501)34(a a a 或 ……………………………………12分 ∴34a =,∴存在实数34a =,满足题设 ……………………14分。
2014-2015学年高二上学期期末考试数学试题
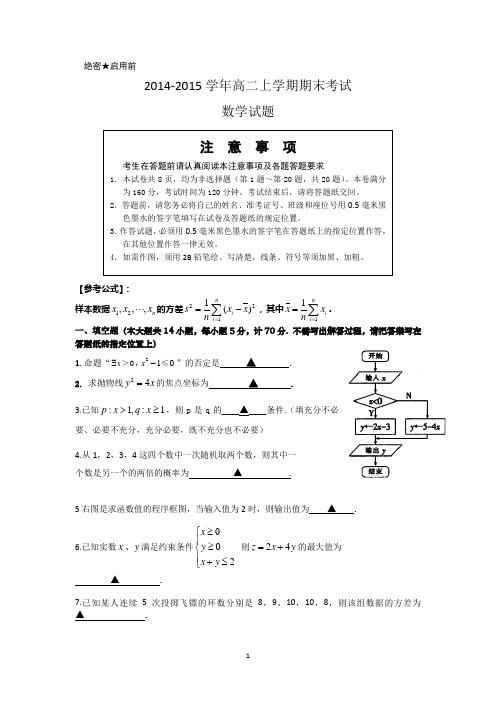
绝密★启用前2014-2015学年高二上学期期末考试数学试题【参考公式】:样本数据12,,,n x x x ⋅⋅⋅的方差2211()n i i s x x n ==-∑,其中11n i i x x n==∑.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1. 命题“2010x x ∃->≤,”的否定是 ▲ . 2. 求抛物线x y 42=的焦点坐标为 ▲ .3.已知1:,1:≥>x q x p ,则p 是q 的____▲____条件.(填充分不必要、必要不充分,充分必要,既不充分也不必要)4.从1,2,3,4这四个数中一次随机取两个数,则其中一 个数是另一个的两倍的概率为 ▲ .5右图是求函数值的程序框图,当输入值为2时,则输出值为_ ▲ .6.已知实数x y 、满足约束条件002x y x y ≥⎧⎪≥⎨⎪+≤⎩则24z x y =+的最大值为▲ .7.已知某人连续5次投掷飞镖的环数分别是8,9,10,10,8,则该组数据的方差为 ▲ .8.某学校选修羽毛球课程的学生中,高一,高二年级分别有80名,50名.现用分层抽样的方法在这130名学生中抽取一个样本,已知在高一年级学生中抽取了24 名,则在高二年级学生中应抽取的人数为 ▲ .9. 已知双曲线的对称轴为坐标轴,焦点坐标在x 轴上,离心率为2,b=2,则双曲线的标准方程是 ▲ .10.为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位cm ),所得数据均在区间[80,130]上,其频率分布直方图如下左图所示,则在抽测的60株树木中,有 ▲ 株树.木的底部周长小于100cm.11. 如上右图所示是一算法的伪代码,执行此算法时,输出的结果是 ▲ .12.若关于x 的不等式)2(22<+-+a ax ax 的解集为R ,则实数a 的取值范围是 ▲ .13.设椭圆)0(1:2222>>=+b a by a x C 的左、右焦点分别为F 1,F 2,P 是C 上的点,︒=∠⊥60,21212F PF F F PF ,则椭圆C 的离心率为______▲_______.14.已知0,0x y >>,且280x y xy +-=,则x y +的最小值为 ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)15.(本小题满分14分)已知椭圆的焦点在x 轴上,长轴长为4,焦距为2,求椭圆的标准方程.100 80 90 110 120 130 底部周长/cm16.(本小题满分14分)已知命题p:0>m ;命题q:不等式1,2+≤∈∀x m R x 恒成立. ①若命题q 为真命题,求实数m 的取值范围;②若命题”p 且q ”为真命题,求实数m 的取值范围.17.(本小题满分14分)已知方程12222=+--my m x 表示双曲线①求实数m 的取值范围;②当1=m 时,求双曲线的焦点到渐近线的距离。
2014-2015学年第一学期高二文科数学期末考试模拟卷

2014-2015学年第一学期高二文科数学期末考试模拟卷考试时间:120分钟;满分:150第I 卷(选择题)一、选择题1.已知向量2(4,1),(,2)a x b x =+=r ,则4x =是//a b r r 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.命题:“a b c d ≥⇒>”和“a b e f <⇔≤”,那么“c d ≤”是“e f ≤”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.对于平面α、β、γ和直线a 、b 、m 、n ,下列命题中真命题是 ( )A .若,,,,a m a n m n αα⊥⊥⊂⊂,则a α⊥B .若//,a b b α⊂,则//a αC .若,,//,//a b a b ββαα⊂⊂,则//βαD .若//,,,a b αβαγβγ==则//a b4.设e 是椭圆224x y k +=1的离心率,且e ∈(12,1),则实数k 的取值范围是 ( ) A .(0,3) B .(3,163) C .(0,3)∪(163,+∞) D .(0,2) 5.已知命题p :∀x ∈(0,∞+),3x >2x ,命题q :∃x ∈(∞-,0),x x ->2,则下列命题为真命题的是 ( )A . p ∧qB .(¬p )∧q C.(¬p )∧(¬q ) D.p ∧(¬q )6.抛物线22x y =的焦点到准线的距离为( )A.1B.12 C. 14 D. 18 7.命题“∀x >0,x 2+x >0”的否定是( ).A .2000x 0,x x 0>+>∃B .2000x 0,x x 0>+∃≤C .∀x >0,x 2+x ≤0D .∀x ≤0,x 2+x >08.、若一个圆台的的正视图如图所示,则其侧面积等于A.6 B .6πC .D .第8题9.已知正三棱柱ABC-A 1B 1C 1中,底面边长AB=2BB 1,则异面直线AB 1与BC 所成的角的余弦值是( )A .53B .55C . 32D .36 10.已知双曲线2222x y a b-=1(a >0,b >0)的一个焦点与抛物线y 2=的焦点重合,且双曲( ) A .x 2-29y =1 B .x 2-y 2=15 C.29x -y 2=1 D.29x -29y =1第II 卷(非选择题)二、填空题11.(全国Ⅰ文16)若直线m 被两平行线12:10:30l x y l x y -+=-+=与所截得的线段的长为22,则m 的倾斜角可以是①15 ②30 ③45 ④60 ⑤75其中正确答案的序号是 .(写出所有正确答案的序号)12.以椭圆1222=+y x 的顶点为焦点,以椭圆的焦点为顶点的双曲线方程为 13.已知两条直线y=ax-2和y=(a+2)x+1互相垂直,则a 等于_____ ___.14.已知过点)2,(m P 作直线l 与圆O :122=+y x 交于B A ,两点,且A 为线段PB 的中点,则m 的取值范围为 .15.已知圆C :22240x y x y m ++-+=与直线:2l y x =+相切,且圆D 与圆C 关于直线l 对。
安徽省宿州市2014-2015学年高中二年级上学期期末考试数学(理)试卷

2014-2015学年省市高二(上)期末数学试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1.将无盖正方体纸盒展开如图,则直线AB、CD在原正方体中的位置关系是()A.平行 B.相交且垂直 C.相交成60° D.异面2.“a=1”是“函数f(x)=cos2ax的最小正周期为π”的()A.充分条件 B.充分不必要条件C.必要不充分条件 D.充要条件3.若||=||=||=1,且<,>=,则(+﹣)•(++)=()A. 0 B. 1 C. 2 D. 34.经过圆x2+2x+y2=0的圆心C,且与直线x+y=0垂直的直线方程是()A. x+y+1=0 B. x+y﹣1=0 C. x﹣y﹣1=0 D. x﹣y+1=05.若双曲线的标准方程为﹣y2=1,则其渐近线方程是()A. y=±4x B. y=±x C. y=±2x D. y=±x6.已知点A(2,1),抛物线y2=4x的焦点F,P是抛物线上的一动点则|PA|+|PF|的最小值为()A. 1 B. 2 C. 3 D. 47.过椭圆+=1(a>b>0)的左焦点F1,作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为()A. B. C. D.8.体积为V的正方体,过不相邻四顶点连成一个正四面体,则该正四面体的体积是() A. B. C. D.9.如图,三棱柱ABC﹣A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为()A. 2 B. 2 C. D. 410.如图过椭圆+=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条角平分线,则称点M为该椭圆的“左特征点”,则椭圆+=1的“左特征点”M的坐标为()A.(﹣2,0) B.(﹣3,0) C.(﹣4,0) D.(﹣5,0)二、填空题(共5小题,每小题5分,满分25分)11.命题“存在实数x,使x2+2x+2≤0”的否定是.12.已知向量=(1,1,0),=(﹣1,0,2),且k+与2互相垂直,则k值是.13.直线l与椭圆+y2=1相交于A,B两点,若弦AB中点为(﹣1,),则直线l的方程为.14.抛物线y2=12x被直线x﹣y﹣3=0截得弦长为.15.如图所示正方体ABCD﹣A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=,给出下列五个结论①AC⊥BE②EF∥平面ABCD③异面直线AE,BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A﹣BEF的体积为定值其中正确的结论有:(写出所有正确结论的编号)三、解答题(共6小题,满分75分)16.已知p:对任意x∈R,不等式x2+ax+a>0恒成立,q:方程x2+ay2=a表示的是焦点在x 轴上的椭圆,如果命题“p且q”为假命题,命题“p或q”为真命题,数a的取值围.17.如图,在四棱柱P﹣ABCD中,底面是边长为2的正方形,侧棱PA⊥底面ABCD,PA=2,M,N分别为AD,BC的中点.(1)求证:平面PMN⊥平面PAD(2)求PM与平面PCD所成角的正弦值.18.已知圆x2+y2﹣6x﹣7=0与抛物线C:y2=2px(p>0)的准线相切(Ⅰ)求抛物线C的方程(Ⅱ)过抛物线C的焦点F的直线交抛物线于A,B两点,若|AB|=7,求线段AB的中点M到y轴的距离.19.已知圆心为C(﹣2,6)的圆经过点M(0,6﹣2)(1)求圆C的标准方程;(2)若直线l过点P(0,5)且被圆C截得的线段长为4,求直线l的方程.20.如图,已知四边形ABCD,EADM,MDCF都是边长为2的正方形,点P,Q分别是ED,AC 的中点.(1)求几何体EMF﹣ABCD的表面积;(2)证明:PQ∥平面BEF;(3)求平面BEF与平面ABCD夹角的余弦值.21.已知圆M:(x+)2+y2=24,定点N(,0),点P为圆M上的动点,点Q在NP上;点G在MP上,且满足=﹣2,•=0(1)求点G的轨迹C的方程(2)过点(2,0)作直线l与轴线C交于A,B两点;O是坐标原点,设=+;是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,请说明理由.2014-2015学年省市高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.将无盖正方体纸盒展开如图,则直线AB、CD在原正方体中的位置关系是()A.平行 B.相交且垂直 C.相交成60° D.异面考点:空间中直线与直线之间的位置关系;棱柱的结构特征.专题:空间位置关系与距离.分析:将正方体的展开图还原为正方体,得到对应的A,B,C,D,判断AB,CD的位置关系.解答:解:将正方体还原得到A,B,C,D的位置如图因为几何体是正方体,所以连接AC,得到三角形ABC是等边三角形,所以∠ABC=60°;故选:C.点评:本题考查了学生的空间想象能力以及正方体的性质.关键是将平面图形还原为几何体.2.“a=1”是“函数f(x)=cos2ax的最小正周期为π”的()A.充分条件 B.充分不必要条件C.必要不充分条件 D.充要条件考点:必要条件、充分条件与充要条件的判断;三角函数的周期性及其求法.专题:三角函数的图像与性质;简易逻辑.分析:根据充分条件和必要条件的定义结合三角函数的周期公式进行判断即可.解答:解:当a=1,则f(x)=cos2x,则函数的周期T=,若函数f(x)=cos2ax的最小正周期为π,则,解得a=±1,则“a=1”是“函数f(x)=cos2ax的最小正周期为π”的充分条件和必要条件,故选:B点评:本题主要考查充分条件和必要条件的判断,以及三角函数周期的计算,比较基础.3.若||=||=||=1,且<,>=,则(+﹣)•(++)=()A. 0 B. 1 C. 2 D. 3考点:平面向量数量积的运算.专题:平面向量及应用.分析:运用向量垂直的条件:数量积为0,以及向量的平方即为模的平方,计算即可得到所求.解答:解:若||=||=||=1,且<,>=,则=0,则(+﹣)•(++)=(+)2﹣2=++2﹣2=1+1﹣2=0,故选A.点评:本题考查向量的数量积的性质,向量垂直的条件:数量积为0,向量的平方即为模的平方,考查运算能力,属于基础题.4.经过圆x2+2x+y2=0的圆心C,且与直线x+y=0垂直的直线方程是()A. x+y+1=0 B. x+y﹣1=0 C. x﹣y﹣1=0 D. x﹣y+1=0考点:直线的一般式方程与直线的垂直关系;圆的一般方程.专题:直线与圆.分析:设与直线x+y=0垂直的直线方程为x﹣y+c=0,把圆心C(﹣1,0)代入,能求出所求直线方程.解答:解:设与直线x+y=0垂直的直线方程为x﹣y+c=0,把圆x2+2x+y2=0的圆心C(﹣1,0)代入,得c=1,∴所求直线方程为x﹣y+1=0.故选:D.点评:本题考查直线方程的求法,是基础题,解题时要注意直线与直线垂直的性质和圆的简单性质的合理运用.5.若双曲线的标准方程为﹣y2=1,则其渐近线方程是()A. y=±4x B. y=±x C. y=±2x D. y=±x考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:由双曲线﹣=1的渐近线方程为y=x,求出a,b即可得到渐近线方程.解答:解:双曲线﹣y2=1的a=2,b=1,由于渐近线方程为y=x,即为y=±x.故选D.点评:本题考查双曲线的方程和性质,考查渐近线方程的求法,考查运算能力,属于基础题.6.已知点A(2,1),抛物线y2=4x的焦点F,P是抛物线上的一动点则|PA|+|PF|的最小值为()A. 1 B. 2 C. 3 D. 4考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:利用抛物线的定义,将点P到其焦点的距离转化为它到其准线的距离即可.解答:解:根据题意,作图如右.设点P在其准线x=﹣1上的射影为M,有抛物线的定义得:|PF|=|PM|∴欲使|PA|+|PF|取得最小值,就是使|PA|+|PM|最小,∵|PA|+|PM|≥|AM|(当且仅当M,P,A三点共线时取“=”),∴|PA|+|PF|取得最小值时(M,P,A三点共线时),点P的纵坐标y0=1,设其横坐标为x0,∵P(x0,1)为抛物线y2=4x上的点,∴x0=,则有当P为(,1)时,|PA|+|PF|取得最小值,为3.故选C.点评:本题考查抛物线的定义和简单性质,将点P到其焦点的距离转化为它到其准线的距离是关键,考查转化思想的灵活应用,属于中档题.7.过椭圆+=1(a>b>0)的左焦点F1,作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为()A. B. C. D.考点:椭圆的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:把x=﹣c代入椭圆方程求得P的坐标,进而根据∠F1PF2=60°推断出=整理得e2+2e﹣=0,进而求得椭圆的离心率e.解答:解:由题意知点P的坐标为(﹣c,)或(﹣c,﹣),∵∠F1PF2=60°,∴=,即2ac=b2=(a2﹣c2).∴e2+2e﹣=0,∴e=或e=﹣(舍去).故选:D.点评:本题主要考查了椭圆的简单性质,考查了考生综合运用椭圆的基础知识和分析推理的能力,属中档题.8.体积为V的正方体,过不相邻四顶点连成一个正四面体,则该正四面体的体积是() A. B. C. D.考点:棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:如图所示,设正方体的棱长为a,则=﹣,即可得出.解答:解:如图所示,设正方体的棱长为a,则=﹣===.点评:本题考查了正方体与三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.9.如图,三棱柱ABC﹣A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为()A. 2 B. 2 C. D. 4考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:由三视图和题意可知三棱柱是正三棱柱,结合正视图,俯视图,不难得到侧视图,然后求出面积.解答:解:由三视图和题意可知三棱柱是正三棱柱,底面边长为2,侧棱长2,结合正视图,俯视图,得到侧视图是矩形,长为2,宽为面积为:2×=2故选:A.点评:本题考查由三视图求侧视图的面积,是基础题.10.如图过椭圆+=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条角平分线,则称点M为该椭圆的“左特征点”,则椭圆+=1的“左特征点”M的坐标为()A.(﹣2,0) B.(﹣3,0) C.(﹣4,0) D.(﹣5,0)考点:椭圆的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:设M(m,0)为椭圆的左特征点,根据椭圆左焦点,设直线AB方程代入椭圆方程,由∠AMB被x轴平分,k AM+k BM=0,利用韦达定理,即可求得结论.解答:解:设M(m,0)为椭圆+=1的左特征点,椭圆的左焦点F(﹣1,0),可设直线AB的方程为x=ky﹣1(k≠0)代入+=1得:3(ky﹣1)2+4y2=12,即(3k2+4)y2﹣6ky﹣9=0,设A(x1,y1),B(x2,y2)得y1+y2=,y1y2=﹣∵∠AMB被x轴平分,k AM+k BM=0,即,即y1(ky2﹣1)+y2(ky1﹣1)﹣(y1+y2)m=0∴2ky1y2﹣(y1+y2)(m+1)=0于是,2k×(﹣)﹣×(m+1)=0∵k≠0,∴﹣18﹣6(m+1)=0,即m=﹣4,∴M(﹣4,0).故选:C.点评:本题以新定义为载体主要考查了椭圆性质的应用,直线与椭圆相交关系的处理,要注意解题中直线AB得方程设为x=ky﹣2(k≠0)的好处在于避免讨论直线的斜率是否存在.二、填空题(共5小题,每小题5分,满分25分)11.命题“存在实数x,使x2+2x+2≤0”的否定是对任意实数x,使x2+2x+2>0..考点:特称命题;命题的否定.专题:规律型.分析:根据特称命题与全称命题是互为否定命题求解即可.解答:解:命题为特称命题,其否定为求出命题,其否定命题是:对任意实数x,使x2+2x+2>0.故答案是对任意实数x,使x2+2x+2>0.点评:本题考查特称命题的否定.12.已知向量=(1,1,0),=(﹣1,0,2),且k+与2互相垂直,则k值是.考点:向量语言表述线线的垂直、平行关系.专题:计算题.分析:由已知中向量=(1,1,0),=(﹣1,0,2),我们可以求出向量k+与2的坐标,根据k+与2互相垂直,两个向量的数量积为0,构造关于k的方程,解方程即可求出a值.解答:解:∵向量=(1,1,0),=(﹣1,0,2),∴k+=(k﹣1,k,2),2=(3,2,﹣2)∵k+与2互相垂直,则(k+)•(2)=3(k﹣1)+2k﹣4=5k﹣7=0解得k=故答案为:点评:本题考查的知识点是向量语言表述线线的垂直关系,其中根据k+与2互相垂直,两个向量的数量积为0,构造关于k的方程,是解答本题的关键.13.直线l与椭圆+y2=1相交于A,B两点,若弦AB中点为(﹣1,),则直线l的方程为x﹣2y+2=0 .考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:设A(x1,y1),B(x2,y2),则+=1,,两式相减,再利用中点坐标公式、斜率计算公式即可得出.解答:解:设A(x1,y1),B(x2,y2),则+=1,,两式相减可得:+(y1+y2)(y1﹣y2)=0,∵弦AB中点为(﹣1,),∴=0,∴k AB=.∴直线l的方程为y﹣=(x+1),解得x﹣2y+2=0.故答案为:x﹣2y+2=0.点评:本题考查了椭圆的标准方程及其性质、“点差法”、中点坐标公式、斜率计算公式,考查了推理能力与计算能力,属于中档题.14.抛物线y2=12x被直线x﹣y﹣3=0截得弦长为24 .考点:抛物线的简单性质.专题:直线与圆;圆锥曲线的定义、性质与方程.分析:直接把直线方程和抛物线方程联立,消去一个未知数,利用韦达定理和弦长公式求解.解答:解:假设直线和哦抛物线的两个交点分别为(x1,y1)、(x2,y2),由,得x2﹣18x+9=0,∴x1+x2=18,x1•x2=9,∴弦长为•=×=24.故答案为:24.点评:本题考查了直线与抛物线的关系,考查了韦达定理和弦长公式的应用,是中档题.15.如图所示正方体ABCD﹣A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=,给出下列五个结论①AC⊥BE②EF∥平面ABCD③异面直线AE,BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A﹣BEF的体积为定值其中正确的结论有:①②④⑤(写出所有正确结论的编号)考点:棱柱的结构特征.专题:综合题;空间位置关系与距离.分析:①AC⊥BE,可由线面垂直证两线垂直;②EF∥平面ABCD,可由线面平行的定义请线面平行;③由两个极端位置说明两异面直线所成的角不是定值;④A1点到面DD1B1B距离是定值,所以A1点到面BEF的距离为定值;⑤三棱锥A﹣BEF的体积为定值,可证明棱锥的高与底面积都是定值得出体积为定值.解答:解:①AC⊥BE,由题意及图形知,AC⊥面DD1B1B,故可得出AC⊥BE,此命题正确;②EF∥平面ABCD,由正方体ABCD﹣A1B1C1D1的两个底面平行,EF在其一面上,故EF与平面ABCD无公共点,故有EF∥平面ABCD,此命题正确;③由图知,当F与B1重合时,令上底面顶点为O,则此时两异面直线所成的角是∠A1AO,当E与D1重合时,此时点F与O重合,则两异面直线所成的角是∠OBC1,此二角不相等,故异面直线AE、BF所成的角不为定值,故不正确.④A1点到面DD1B1B距离是定值,所以A1点到面BEF的距离为定值,正确;⑤三棱锥A﹣BEF的体积为定值,由几何体的性质及图形知,三角形BEF的面积是定值,A 点到面DD1B1B距离是定值,故可得三棱锥A﹣BEF的体积为定值,此命题正确.故答案为:①②④⑤.点评:本题考查棱柱的结构特征,解答本题关键是正确理解正方体的几何性质,且能根据这些几何特征,对其中的点线面和位置关系作出正确判断.熟练掌握线面平行的判断方法,异面直线所成角的定义以及线面垂直的证明是解答本题的知识保证.三、解答题(共6小题,满分75分)16.已知p:对任意x∈R,不等式x2+ax+a>0恒成立,q:方程x2+ay2=a表示的是焦点在x 轴上的椭圆,如果命题“p且q”为假命题,命题“p或q”为真命题,数a的取值围.考点:复合命题的真假.专题:简易逻辑.分析:由p:对任意x∈R,不等式x2+ax+a>0恒成立,可得△<0,解得a的取值围.由q:方程x2+ay2=a表示的是焦点在x轴上的椭圆,得=1,a>1.由于命题“p且q”为假命题,命题“p或q”为真命题,故p、q一真一假,解出即可.解答:解:p:对任意x∈R,不等式x2+ax+a>0恒成立,∴△=a2﹣4a<0,解得0<a<4,得a的取值围是0<a<4.q:方程x2+ay2=a表示的是焦点在x轴上的椭圆,得=1,故a>1.∵命题“p且q”为假命题,命题“p或q”为真命题,故p、q一真一假,∴或,解得0<a≤1或a≥4.综上实数a的取值围是:0<a≤1或a≥4.点评:本题考查了一元二次不等式的解集与判别式的关系、椭圆的标准方程、复合命题的判定,考查了推理能力,属于基础题.17.如图,在四棱柱P﹣ABCD中,底面是边长为2的正方形,侧棱PA⊥底面ABCD,PA=2,M,N分别为AD,BC的中点.(1)求证:平面PMN⊥平面PAD(2)求PM与平面PCD所成角的正弦值.考点:直线与平面所成的角;平面与平面垂直的判定.专题:综合题;空间位置关系与距离;空间角.分析:(1)证明MN⊥平面PAD,即可证明平面PMN⊥平面PAD(2)过M作MO⊥平面PCD,连接PO,则∠MPO即为所求,利用V M﹣PCD=V P﹣MCD,求出OM,即可求PM与平面PCD所成角的正弦值.解答:(1)证明:∵PA⊥面ABCD,∴PA⊥MN,PA⊥AB,∵M、N分别为AD、BC中点,∴AB∥MN,∵AB⊥AD,AD∩MN=M,∴AB⊥平面PAD,∵AB∥MN,∴MN⊥平面PAD,∵MN⊂平面PMN,∴平面PMN⊥平面PAD﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)(2)解:过M作MO⊥平面PCD,连接PO,则∠MPO即为所求.∵V M﹣PCD=V P﹣MCD,∴=,∴OM=,∴sin∠MPO==﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)点评:本题考查平面与平面、直线与平面垂直的判定,考查线面角,考查学生分析解决问题的能力,属于中档题.18.已知圆x2+y2﹣6x﹣7=0与抛物线C:y2=2px(p>0)的准线相切(Ⅰ)求抛物线C的方程(Ⅱ)过抛物线C的焦点F的直线交抛物线于A,B两点,若|AB|=7,求线段AB的中点M 到y轴的距离.考点:圆与圆锥曲线的综合;抛物线的标准方程;直线与圆锥曲线的关系.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)求出圆的圆心与半径,利用y2=2px(p>0)的准线相切,求出p,得到抛物线方程.(Ⅱ)求出抛物线C的焦点坐标为(1,0),准线方程为x=﹣1,求出抛物线定义知线段AB 的中点M到准线的距离,然后求解线段AB的中点M到y轴的距离.解答:解:(Ⅰ)圆x2+y2﹣6x﹣7=0,即(x﹣3)2+y2=16,所以圆心(3,0),半径为4,抛物线的准线方程为x=,依题意,有3﹣(﹣)=4,得p=2,故抛物线方程为y2=4x;﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)由(Ⅰ)知,抛物线C的焦点坐标为(1,0),准线方程为x=﹣1,由抛物线定义知线段AB的中点M到准线的距离为,故线段AB的中点M到y轴的距离d=.﹣﹣﹣﹣﹣﹣(12分)点评:本题考查圆的方程与抛物线方程的综合应用,点到直线的距离,考查分析问题解决问题的能力.19.已知圆心为C(﹣2,6)的圆经过点M(0,6﹣2)(1)求圆C的标准方程;(2)若直线l过点P(0,5)且被圆C截得的线段长为4,求直线l的方程.考点:直线和圆的方程的应用;圆的标准方程.专题:直线与圆.分析:(1)根据题意求得圆的半径,则圆的方程可得.(2)先看当斜率不存在时,设出直线的方程,与圆的方程联立,消去y,得到关于x的一元二次方程,利用韦达定理和弦长公式建立等式求得k.则直线的方程可得.最后看斜率不存在时,进而验证.解答:解:(1)圆C的半径为|CM|=,∴圆C的标准方程为(x+2)2+(y﹣6)2=16.(2)当所求直线l的斜率存在时,设所求直线的方程为y=kx+5,即kx﹣y+5=0.联立直线与圆C的方程:,消去y得(1+k2)x2+(4﹣2k)x﹣11=0 ①设方程①的两根为x1,x2,由根与系数的关系得②由弦长公式得|x1﹣x2|==4③将②式代入③,并解得k=,此时直线l的方程为3x﹣4y+20=0.当直线l的斜率不存在时,直线l的方程为x=0,验算得方程为x=0的直线也满足题意.∴所求直线l的方程为3x﹣4y+20=0或x=0.点评:本题主要考查了直线与圆的方程问题.解题过程中对直线斜率不存在的情况一定不要疏漏.20.如图,已知四边形ABCD,EADM,MDCF都是边长为2的正方形,点P,Q分别是ED,AC 的中点.(1)求几何体EMF﹣ABCD的表面积;(2)证明:PQ∥平面BEF;(3)求平面BEF与平面ABCD夹角的余弦值.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定;二面角的平面角及求法.专题:空间位置关系与距离.分析:(1)设EMF﹣ABCD的表面积为S,利用S=S正方形ABCD+S正方形MDCF+S正方形EADM+S△EAB+S△FBC+S +S正△BEF,即可得出;△MEF(2)P是AM的中点,Q是AC的中点,由三角形中位线定理可得PQ∥BE,再利用线面平行的判定定理即可得出;(3)利用即可得出.解答:(1)解:设EMF﹣ABCD的表面积为S,则S=S正方形ABCD+S正方形MDCF+S正方形EADM+S△EAB+S△FBC+S△MEF+S正△BEF=22×3+3×+=18+2.(2)证明:∵P是AM的中点,Q是AC的中点,由三角形中位线定理可得:PQ∥BE,PQ⊄平面BEF,BE⊂平面BEF,∴PQ∥平面BEF.(3)解:设平面BEF与平面ABCD夹角为θ.由于△BEF在平面ABCD的射影是△ABC,∴==.点评:本题考查了三角形中位线定理、线面平行的判定定理、正方形与正三角形的面积计算公式、二面角的计算公式,考查了推理能力与计算能力,属于中档题.21.已知圆M:(x+)2+y2=24,定点N(,0),点P为圆M上的动点,点Q在NP上;点G在MP上,且满足=﹣2,•=0(1)求点G的轨迹C的方程(2)过点(2,0)作直线l与轴线C交于A,B两点;O是坐标原点,设=+;是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,请说明理由.考点:直线与圆锥曲线的综合问题;轨迹方程.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)据题意,G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=,半焦距c=,即可得到椭圆方程;(2)据题意,四边形OASB为矩形即•=0,即x1x2+y1y2=0.设出直线方程,将直线方程与椭圆方程联立,据韦达定理表示出则x1x2+y1y2=0,解方程求出参数,即得到直线方程.解答:解:(1)由=﹣2,•=0,可得Q为PN的中点且GQ⊥PN,∴GQ为PN的中垂线,∴|PG|=|GN|∴|GN|+|GM|=|MP|=2,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=,半焦距c=,∴短半轴长b=,∴点G的轨迹方程是﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(2)因为=+,所以四边形OASB为平行四边形若存在l使得||=||,则四边形OASB为矩形,∴•=0若l的斜率不存在,直线l的方程为x=2,则A(2,1),B(2,﹣1)∴•=3与•=0矛盾,故l的斜率存在.设l的方程为y=k(x﹣2),A(x1,y1),B(x2,y2),代入椭圆方程可得(2k2+1)x2﹣8k2x+8k2﹣6=0,∴x1+x2=,x1x2=,∴y1y2=k(x1﹣2)•k(x2﹣2)=﹣∴x1x2+y1y2=﹣=0,∴k=±1∴存在直线x﹣y﹣2=0或x+y﹣2=0使得四边形OASB的对角线相等.﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)点评:本题考查椭圆方程的求法;考查直线与椭圆的位置关系,解决的关键是将已知转化为x1x2+y1y2=0,属于一道中档题.。
2014-2015学年第一学期期末考试 高三数学(文科)试卷

2014-2015学年第一学期期末考试高三数学(文科)试卷一.选择题 (本大题共10小题,每小题5分,共50分) 1.若集合 A= {x | |x|1≤, x R ∈}, B= {y| y=x 2 ,x R ∈}, 则AB = ( )A. {x | 11x -≤≤};B. {x | 0x ≥};C. {x | 01x ≤≤} ;D. Φ 2. 若复数1z i =+, i 为虚数单位,则 ()1z z +=( ) A. 3i - ; B. 33i + ; C. 3 ; D. 13i +3. “ m=1/2 ”是 “直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直 ”的 ( )A.充分必要条件;B. 充分不必要条件;C. 必要不充分条件;D. 既不充分也不必要条件。
4. 1tan151tan15Oo+- 的值是( )A.2 B. C. 2 D. 5. 设{a n }是公比大于1的等比数列,若a 2011 与a 2012 是方程 24830x x -+=的两根,则a 2013 + a 2014 的值是 ( )A. 2 ;B. 9 ;C. 18 ;D. 20 ; 6. 已知函数 ()21log 11xf x x x-=-+++,则1120142014f f ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭的值为( )A. 0 ;B. -2 ;C. 2 ;D. 22013log 20157. 已知点P 在曲线 41x y e =+ 上,α 为曲线在点P 处切线的倾斜角,则角α的取值范围是 ( ) A. 0,4π⎛⎫⎪⎝⎭; B. ,42ππ⎛⎫⎪⎝⎭ ; C. 3,24ππ⎛⎫ ⎪⎝⎭ ; D. 3,4ππ⎛⎫ ⎪⎝⎭8. 直线 y x m =+(m 为参数)被椭圆 2214x y +=截得的弦的长度最大值是( ) A. 2 ; B.; C.; D.; 9. 沿对角线AC 将正方形A B C D 折成直二面角后,A B 与C D 所在的直线所成的角等于( )A. 90° ;B. 60° ;C. 45° ;D. 30°10. 已知O 是 △ABC 所在平面内的一点,角A 、B 、C 所对应的边长分别为a, b, c, 若aOA bOB cOC O ++= , 则O 是 △ABC 的( )A. 内心 ;B. 外心 ;C. 重心 ;D. 垂心 。
安徽省宿州市2012-2013学年高二上学期期末考试数学(文)试题(扫描版)

高二文科数学B 卷答案一.BBCCD ABBAD二.11. 存在实数x ,使得2210x x -+<1314. (0,1) 15. 2-三.16.解:(1)四棱锥P ABCD -的体积为1111133V =⨯⨯⨯= 6分 (2)PA ⎫⎪⊄⇒⎬⎪⊆⎭PA ∥OE面BDE PA ∥面BDE OE 面BDE 12分17. 解:(1)直线370x y ++=与32120x y --=的交点为(2,3)P - 所以半径5r CP == 故圆的标准方程为:22(1)(1)25x y ++-= 6分(2)圆心C 到与直线30x y --=的距离为:5d r =<= 故圆C 与直线30x y --=相交。
12分18.解: 命题p :函数()x f x a =在R 上递增;p 真⇒1a > 4分 命题q :关于x 的不等式2240x ax ++>对一切x R ∈恒成立;q 真⇒()22240a ∆=-<,即22a -<<所以q 假⇒22a a ≤-≥或 8分 ∵p 真q 假, ∴2a ≥综上所示a 的取值范围:[)2,+∞ 12分19.解: (1)2'()3123(2)(2)f x x x x =-=+- 3分'()022f x x x >⇒<->或 '()022f x x <⇒-<< 6分∴()f x 的单调递增区间是(,2)(2,)-∞-+∞和单调递减区间是(2,2)- 8分(2)(2)21,(2)11f f -==- 10分 ()f x 的极大值为21,()f x 的极小值为11- 12分20. 解:(1)2或-2 6分(2)由题意可设椭圆方程为22194x y k k+=++ (4)k >- 点(3,±2) 在椭圆上 ,∴94194k k +=++ 解得6=k 故所求椭圆方程为 1101522=+y x 13分 21. 解:(1)若函数()f x 在1(,)2+∞上是增加的,则'()f x 0≥在1(,)2+∞上恒成立,而'()f x =xm x -, 即2x m ≤在(,21+∞)上恒成立,故41≤m 6分 (2)当2=m 时,222'()x f x x x x-=-=,令'()f x =0得x =x ⎡∈⎣时'()0f x <,当x e ⎤∈⎦时'()f x >0,故2=x 是函数)(x f 在[]e ,1上唯一的极小值点,故)(x f min =1ln 2f =-. 11分 又221141(1),()22222e f f e e -==-=>, 故2max4()2e f x -= 14分。
宿州市2013-2014学年高二上学期期末考试数学试题及答案

第Ⅰ卷(选择题 共50分)一、选择题:(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的).1.数列1,23,35,47,59,…的一个通项公式a n 是( )A.n2n +1B.n2n -1C.n2n -3D.n2n +32.经过两点A (4,2y +1),B (2,-3)的直线的倾斜角为3π4,则y =( ). A .-1 B .0 C .-3 D .2 3.等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差为( ).A .1B .2C .3D .44.设集合A ={x |x 2-2x -3<0},B ={x |1≤x ≤4},则A ∩B = ( )A .{x |1≤x <3}B .{x |1≤x ≤3}C .{x |3<x ≤4}D .{x |3≤x ≤4}5.在等差数列{a n }中,已知a 4+a 8=16,则该数列前11项和S 11=( ).A .58B .88C .143D .1766.已知n m ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则( )A .βα//,且α//lB .βα⊥,且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l7.若a ,b ∈R ,且ab >0,则下列不等式恒成立的是( ).A .a 2+b 2>2abB .a +b ≥2abC.1a +1b>2abD.b a +ab≥28.圆x 2+y 2-2x -2y +1=0上的点到直线x -y =2的距离的最大值是( )A .2B .1+ 2C .2+22D .1+2 29.已知集合A ={(x ,y )|x ,y 为实数,且x 2+y 2=1},B ={(x ,y )|x ,y 为实数,且x +y =1},则A ∩B 的元素个数为( ).A .4B .3C .2D .110.(文)若1()2f x x x =+-(2)x >在x n =处取得最小值,则n =( ) A.52 B. 3C.72D. 4 (理).已知a >0,b >0,a +b =2,则y =1a +4b的最小值是 ( )A.72B .4 C.92D .5二、填空题:本大题共5小题,每小题5分,共25分.11.等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差为 12.已知数列{a n }的前n 项和为S n ,且S n =2(a n -1),则a 2等于 13.不等式(x+5)(3-2x )≥6的解集是14.若实数x ,y 满足224x y +=,求xy 的最大值15.已知f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=x 2+2x ,若f (2-a 2)>f (a ),则实数a 的取值范围是 .三、解答题:本大题共6题,共75分,写出文字说明、证明过程或演算步骤。
安徽省宿州市2015-2016学年高二上学期期末考试数学(文)试题(A卷)扫描版含答案

宿州市2015-2016学年度第一学期期末教学质量检测高二数学文科A 卷参考答案一、 选择题二、 填空题13.存在 x R ∈,使 210x x -+< 14.210x y --=15. 2:1 (填2不扣分) 16.①③⑤三、解答题17.解:p 为真,则1m >;………………..2分q 为真,则3m >或3m <-………………..4分若p 或q 真,p 且q 为假,故有“p 真q 假”和“p 假q 真”两种情况:当p 真q 假时 1-33m m >⎧⎨≤≤⎩ ,即 13m <≤………………..7分 当p 假q 真时 133m m m ≤⎧⎨><-⎩或,即3m <-………………..9分综上:13m <≤或3m <-.………………..10分18.解: (1)因为直线l 的斜率是21-,故所求直线的斜率为2 所以经过点P 且垂直于直线l 的直线方程是12-=x y .………………..6分(2)圆C :086422=+--+y x y x 化成标准方程是5)3()2(22=-+-y x 圆心(2,3),半径5=r设平行直线l 的圆的切线方程为20x y m ++=由55|62|=++m 可得3-=m 或13-=m平行直线l 的圆的切线方程为230x y +-=或0132=-+y x .………………..12分19.解:(1)2………………..4分(2)根据已知,A 1C 1 ⊥A 1A,A 1C 1 ⊥ A 1B 1∴ A 1C 1 ⊥平面A 1B 1 BA ∴A 1C 1 ⊥B 1A又∵在正方形A 1B 1 BA 中 ∴B 1A ⊥ A 1B∴B 1A ⊥面 A 1BC 1∴AB 1 ⊥ BC 1 . ………………………..8分(3)取BC 的中点M 易证平面EMF ∥平面A 1B 1 BA,又因为 直线EF 不在平面A 1B 1 BA 内 ∴EF ∥平面A 1B 1 BA. ………………..12分20.解:(1)因为圆C :2222120()24t x y t x ty t R +--+-=∈ 其标准方程为22222(1)()()24t t x y t +-+-=,………………..3分 所以22t a b t ⎧=⎪⎨⎪=⎩,即22b a =,故圆心的轨迹是以1(,0)2焦点的抛物线;………..8分(2)在(1)的基础上,按照抛物线定义即可证明.………………..12分(其他方法可酌情给分)21.解:(Ⅰ)定义域为R ,/(2)()x x x f x e --=, ………………..2分当0<x 或2>x 时,0)(/<x f ;当20<<x 时,0)(/>x f所以)(x f 的增区间是(0,2),减区间是),2(),0,(+∞-∞.………………..6分(Ⅱ))0()(2>=x e x x f x ,由ax x f >)(ln 得:x x x a -<ln 2………………..8分设x x x x g -=ln 2)(,则2/)ln 1(2)(xx x g -=,, 所以当e x <<0时,0)(/>x g ;当x e >时,0)(/<x g ,所以)(x g 在),0(e 上递增, 在),(+∞e 上递减,12)()(max -==e e g x g 所以a 的取值范围是)12,(--∞e . ………………..12分22.解: ⑴由题意,可得2ce a ==,代入(A 得22211a b +=,又222a b c =+, 解得2a =,b c ==,所以椭圆C 的方程22142y x +=.………………..5分⑵证明:设直线BD 的方程为y m =+,又A,B,D 三点不重合,∴0m ≠,设()11,D x y ,()22,B x y ,则由2224y m x y ⎧=+⎪⎨+=⎪⎩得22440x m ++-=,所以064-82>+=∆m ,∴所以m -<<.122x x m +=-,21244m x x -=,设直线AB,AD 的斜率分别为AB k ,AD k ,则()()122112121212110111AD ABm x m x y y k k x x x x x x +-++----+=+==----+; 所以0AD AB k k +=,即直线AB,AD 的斜率之和为定值. ………………..12分。
2014-2015学年第一学期期末考试高二数学试卷(文科)

2014-2015学年第一学期期末考试高二数学试卷(文科)注意事项:1.本卷答题时间90分钟,满分100分。
2.本卷不能使用计算器,答案一律做在答卷页上。
一、选择题:本小题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是最符合要求的.1、设合集的值为 ( )A .3B .4C .5D .62、已知m ,a 都是实数,且,则“”是“成立的” A .充分不必要条件 B .必要不充分条件C .充分必要条件D .不充分也不必要条件3、设5sin7a π=,2cos 7b π=,2tan 7c π=,则( ) A .a b c << B .a c b << C .b c a << D .b a c <<4、用、、表示三条不同的直线,表示平面,给出下列命题: ①若∥,∥,则∥;②若⊥,⊥,则⊥; ③若∥,∥,则∥;④若⊥,⊥,则∥. A. ①②B. ②③C. ①④D.③④5、等差数列,}{中n a n S a a a a ,,0,05665>><且为数列}{n a 的前n 项和,则使0>n S 的n 的最小值为( )A .11B .10C .6D .56、若0m n ->,1a >,则( )A. m m a a -- > n n a a --B. m m a a -- < n n a a --C. m m a a --≥ n n a a --D. m m a a -- ≤ n n a a --7、已知A (-2,0),B (0,2),C 是圆x 2+y 2-2x=0上任意一点,则△ABC 面积的最大值是 A.3+2B.3-2C.6D.48、已知变量x 、y 满足条件⎪⎩⎪⎨⎧≤-+≤-≥09201y x y x x 则x+y 的最大值是( )A.2B.5C.6D.8a A C a A U U 则集合},4,2{},5,2,1{},5,4,3,2,1{=-==0≠a },{a a m -∈a m =||abc y a b b c a c a b b c a c a y b y a b a y b y a b9、双曲线222x y a -=的左、右顶点分别为1A 、2A ,P 为其右支上一点,且12124A PA PA A ∠=∠,则12PA A ∠等于( )A .36πB .18π C .12π D .6π 10、设平面向量a =(x 1,y 1),b=(x 2,y 2) ,定义运算⊙:a ⊙b =x 1y 2-y 1x 2 .已知平面向量a ,b ,c ,则下列说法错误的是(A) (a ⊙b )+(b ⊙a )=0 (B) 存在非零向量a ,b 同时满足a ⊙b =0且a •b =0 (C) (a +b )⊙c =(a ⊙c )+(b ⊙c ) (D) |a ⊙b |2= |a |2|b |2-|a •b |2二.填空题:本大题共7小题,每小题4分,共28分.把答案填在答题卷上. 11、椭圆2255x ky +=的一个焦点是(0,2),则k =___ 12若,则的取值范围是13、一个体积为的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为14、若等差数列{}n a 中,37101148,4,a a a a a +-=-=则13__________.S = 15在中,PC BP BAC AC AB ABC ,,60,3,20==∠==∆16若)11(cos 12014220144)(≤≤-+++⋅=x x x x f xx 设的最大值是 最小值是 则=+N M17已知直线:21l y x =-与抛物线2:2(0)C y px p =>交于A 、B 两点,若抛物线上存在点M ,使△MAB 的重心恰好是抛物线C 的焦点F ,则p =02,sin απαα≤≤>α()f x ,M ,N 第 5 题NMAB DCO三.解答题:本大题共4小题,共42分.解答应写出文字说明,证明过程或演算步骤.18(本小题满分10分)已知函数f (x )=Asin (ωx+ϕ)(A>0,ω>0,||2πϕ<)在一个周期内的图象如图所示。
安徽省宿州市2014-2015学年高二上学期期末教学质量检测_地理试卷及答案

宿州市2014-15学年度第一学期期末教学质量检测
高二地理试题文科(A卷)参考答案
一、单项选择题(每小题2分,共50分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
二、综合题(共50分)
26.(14分)
(1)草地(2分)耕地(2分)
(2)风能(2分)太阳能(2分)
(3)①地势低平,②夏季高温,降水丰沛(雨热同期),③耕地面积广大。
(6分)
27.(14分)
(1)D (2分)
(2)人口众多,人均占有量少;工农业和居民生活用水量大;水资源污染和浪费严重。
(任答2点得4分)
节约用水;合理利用和保护水资源,防止水污染。
(4分)
(3)全程可自流;水质优良(4分)
28.(12分)
(1)17.6 ℃(2分)
(2)A (2分)
(3)BFE(2分)坡度更缓,工程量小,难度小(6分)
29.(10分)
(1)石油(或天然气)(2分) 管道运输(2分)
(2)①过度开垦,导致土壤荒漠化严重②不合理的灌溉导致土壤盐渍化③过度引用阿姆河河水灌溉,导致咸海面积萎缩,河流断流。
(6分)。
安徽省宿州市高二数学上学期期末考试试题 文(A卷,扫描

安徽省宿州市2015-2016学年高二数学上学期期末考试试题文(A卷,扫描版)宿州市2015-2016学年度第一学期期末教学质量检测高二数学文科A 卷参考答案一、 选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ABCDCBCAADCD二、 填空题13.存在 x R ∈,使 210x x -+< 14.210x y --= 15. 2:1 (填2不扣分) 16.①③⑤ 三、解答题17.解:p 为真,则1m >;………………..2分q 为真,则3m >或3m <-………………..4分若p 或q 真,p 且q 为假,故有“p 真q 假”和“p 假q 真”两种情况:当p 真q 假时 1-33m m >⎧⎨≤≤⎩,即 13m <≤………………..7分当p 假q 真时 133m m m ≤⎧⎨><-⎩或,即3m <-………………..9分综上:13m <≤或3m <-.………………..10分18.解: (1)因为直线l 的斜率是21-,故所求直线的斜率为2 所以经过点P 且垂直于直线l 的直线方程是12-=x y .………………..6分(2)圆C :086422=+--+y x y x 化成标准方程是5)3()2(22=-+-y x 圆心(2,3),半径5=r设平行直线l 的圆的切线方程为20x y m ++=由55|62|=++m 可得3-=m 或13-=m平行直线l 的圆的切线方程为230x y +-=或0132=-+y x .………………..12分19.解:(1)22+;………………..4分(2)根据已知,A 1C 1 ⊥A 1A,A 1C 1 ⊥ A 1B 1∴ A 1C 1 ⊥平面A 1B 1 BA ∴A 1C 1 ⊥B 1A 又∵在正方形A 1B 1 BA 中 ∴B 1A ⊥ A 1B ∴B 1A ⊥面 A 1BC 1∴AB 1 ⊥ BC 1 . ………………………..8分(3)取BC 的中点M 易证平面EMF ∥平面A 1B 1 BA,又因为 直线EF 不在平面A 1B 1 BA 内 ∴EF ∥平面A 1B 1 BA. ………………..12分20.解:(1)因为圆C :2222120()24t x y t x ty t R +--+-=∈其标准方程为22222(1)()()24t t x y t +-+-=,………………..3分所以22t a b t⎧=⎪⎨⎪=⎩,即22b a =,故圆心的轨迹是以1(,0)2焦点的抛物线;………..8分(2)在(1)的基础上,按照抛物线定义即可证明.………………..12分 (其他方法可酌情给分)21.解:(Ⅰ)定义域为R ,/(2)()x x x f x e --=, ………………..2分当0<x 或2>x 时,0)(/<x f ;当20<<x 时,0)(/>x f所以)(x f 的增区间是(0,2),减区间是),2(),0,(+∞-∞.………………..6分(Ⅱ))0()(2>=x e x x f x ,由ax x f >)(ln 得:x x x a -<ln 2………………..8分设x x x x g -=ln 2)(,则2/)ln 1(2)(x x x g -=,, 所以当e x <<0时,0)(/>x g ;当x e >时,0)(/<x g , 所以)(x g 在),0(e 上递增, 在),(+∞e 上递减,12)()(max -==ee g x g所以a 的取值范围是)12,(--∞e . ………………..12分22.解: ⑴由题意,可得22c e a ==,代入()1,2A 得22211a b+=,又222a b c =+, 解得2a =,2b c ==,所以椭圆C 的方程22142y x +=.………………..5分⑵证明:设直线BD 的方程为2y x m =+,又A,B,D 三点不重合,∴0m ≠,设()11,D x y ,()22,B x y ,则由22224y x m x y ⎧=+⎪⎨+=⎪⎩得2242240x mx m ++-=,所以064-82>+=∆m , ∴所以2222m -<<1222x x m +=-,21244m x x -=,设直线AB,AD 的斜率分别为AB k ,AD k ,则()()122112121212221221220111AD ABx m xx m x y y k k x x x x x x +--++--+=+==----+;所以0AD AB k k +=,即直线AB,AD 的斜率之和为定值. ………………..12分。
安徽省宿州市高二上学期期末教学质量检测 数学文 扫描

宿州市2014-2015学年度第一学期期末教学质量检测高二文科数学A 卷(参考答案)一、选择题二、填空题11.任意都有; 12.; 13.或; 14.; 15. ③⑤ 三、解答题16. 解::对任意,不等式恒成立, 由,得的取值范围是 ------3分:方程表示的是焦点在轴上的椭圆,得,故-------6分因为命题“且”为假命题,命题“或”为真命题,故、一真一假, ⑴当真假时,有;⑵当假真时,有; --------11分综上实数的取值范围是或. ---------12分 17. 解:由圆C :226440x y x y +-++=,即,故圆心半径, --------2分 因为,设圆心到直线的距离为,由,得 --------4分 (1)当的斜率存在时,设直线方程为.又圆的圆心为,半径, 由 , 解得.所以直线方程为, 即. ------9分(2)当的斜率不存在时,的方程为,经验证也满足条件. --11分综上直线的方程为或. ------12分18. 解:(Ⅰ)圆,即,所以圆心,半径为,抛物线的准线方程为,依题意,有,得,故抛物线方程为; ------6分(Ⅱ)由(Ⅰ)知,抛物线的焦点坐标为,准线方程为,由抛物线定义知线段的中点到准线的距离为117()222AF BF AB +==, 故线段的中点到轴的距离. ------12分19. 解:解:b ax x x f 363)(2++=',由该函数在处有极值, 故,即………………①又其图象在处的切线与直线平行 故,即………………②由①,②,解得 ------4分 ∴(Ⅰ)∵ 由得,列表如下故的单调递增区间是单调递增区间是 -----7分 (Ⅱ)由(1)可知列表如下∴在的最小值是∴或 ------12分 20. (Ⅰ)证明:取的中点,连接, 因为11,22MN EC DB EC ==∥∥,所以,故四边形为平行四边形,由,平面,平面,得平面. ------4分 (Ⅱ)因为平面,平面,所以,又因为为正三角形, 为的中点,所以,故由BN AC BN EC AC EC C ⊥⎧⎪⊥⎨⎪=⎩得平面,因为,所以平面, ----9分 又平面,所以平面平面.(Ⅲ)11(12)2332ABDEC A BDEC BDEC V V S h -+⋅==⋅⋅=⋅=分 21. 解:(Ⅰ)由题意不妨设切点,切点满足221211n mm n m n ⎧-⎪⎪=-⎨-⎪+=⎪⎩,解得.∴过切点的直线方程为,令得,即,令得,即.∴,∴椭圆方程为.椭圆的离心率 ------7分 (Ⅱ)设与直线的平行的直线方程为,由2222224205200154y x t x tx t x y =-+⎧⎪⇒-+-=⎨+=⎪⎩,22(20)424(520)0t t ∆=--⋅⋅-=,故当时,点到直线的最大距离为d ==,又因为,,所以AB ==故面积的最大值max 111)()225PAB S AB d ∆=⋅==------14分。
安徽省宿州市2014--2015学年高二上学期期末教学质量检测语文试题(A卷)(扫描版)

安徽省宿州市2014-2015学年高二上学期期末教学质量检测语文试题(扫描版)宿州市2014-2015学年度第一学期期末教学质量检测高二语文试题(A卷)参考答案一、1.B (原文并没有直接或间接地表达这样的观点,属无中生有。
)2.D (从意义的内在联系上来看是递进关系。
)3.A.(B. 原文:“中国”不是“中国文化”快步走过西方国家几百年的发展历史。
C.原文“不仅仅是技术危机”D.坚持了价值观上的普遍“正确性”,是电影得到观众认可,达到奥斯卡提名水平的必要条件而不是充要条件。
)二、4.B (埸,边境,边界。
)5.C .取独(A.递进/承接 B.凭借/因为D.祈使语气,还是/反问语气,难道)6.D.对江南春天草长莺飞、杂花生树的景象描写主要是为了勾起身处北方的陈伯之对江南美丽故土的思念。
7(1):推寻您离开梁朝投靠北魏的时候,并没有其它原因,只是因为没能在内心对自己仔细考察,外面又受到流言的蛊惑,以致(或因而)到了这个地步。
(共6分,“寻”“去”、“就”、“直”、“直以”的“以”、各1分,其它句意通达1分)(2)然而将军却像鱼一样在烧沸水的釜鼎之中游泳,像燕子一样在飞动摇荡的帐幕之上筑巢,不是令人迷惑不解吗?(共4分,“鱼”、“燕”名作状语,共1分,两个状语后置翻译时提到前面共1分,“巢”,名作动1分,其它句意通达1分)8、相同点:①突出“愁”之多,都暗含故国之思。
②比喻手法及艺术效果:以“江水”喻“愁”,化抽象为具体,形象生动。
(2分)不同点:李词自问自答,写法曲折,突出“愁”如东流之水,汹涌浩荡,无穷无尽。
屈词则以“不东流”突出“愁”之重。
(2分)9、①饱含愁情的飞花,偏偏依傍让遗民难于面对的景阳殿,传达出作者浓重的亡国之痛、故国之思。
②“只余”“空有”写出六代繁华都已消亡,现在只有年年重生的芳草和园中空啼的乳莺,诗人借景抒情,表达出昔盛今衰的感慨。
③用“白门”与“白头”都用一个“白”字做文章,说金陵故都往事令人愁生白发,表现一种历史的沧桑感与无奈感。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省宿州市2014-2015学年高二上学期期末数学试卷(文科)一、选择题(每小题5分,共50分)1.(5分)双曲线2x2﹣y2=8的实轴长是()A.2B.2C.4D.42.(5分)“x>3”的一个必要不充分条件是()A.x>4 B.x<4 C.x>2 D.x<23.(5分)一个长方体去掉一个小长方体,所得几何体的正视图与侧(左)视图分别如图所,则该几何体的俯视图为()A. B. C. D.4.(5分)设m为直线,α、β、γ为三个不同的平面,下列说法正确的是()A.若m∥α,α⊥β,则m⊥βB.若m⊂α,α∥β,则m∥βC.若m⊥α,α⊥β,则m∥βD.若α⊥β,α⊥γ,则β∥γ5.(5分)已知原命题:若a+b>2,则a,b至少有一个大于1,那么原命题与其逆命题的真假情况是()A.原命题真,逆命题假B.原命题假,逆命题真C.原命题与逆命题均为真命题D.原命题与逆命题均为假命题6.(5分)已知直线l1:x+my+6=0与直线l2:(m﹣2)x+3y+2m=0垂直,则实数m的值为()A.﹣1 B.C.3D.27.(5分)抛物线y2=12x被直线x﹣y﹣3=0截得弦长的值为()A.21 B.16 C.24 D.308.(5分)曲线y=e x lnx在x=1处的切线方程是()A.y=2e(x﹣1)B.y=ex﹣1 C.y=x﹣e D.y=e(x﹣1)9.(5分)函数f(x)=lnx﹣x的单调减区间为()A.(﹣∞,0),(1,+∞)B.(1,+∞)C.(﹣∞,0)D.(0,1)10.(5分)定义在R上的函数f(x)=sinx+2xf′(),f′(x)为f(x)的导函数,令a=﹣,b=log32,则下列关系正确的是()A.f(a)+f(b)<0 B.f(﹣a)+f(b)>0 C.f(a)+f(﹣b)<0 D.f(﹣a)+f(﹣b)<0二、填空题(每小题5分,共25分)11.(5分)已知命题p:存在n∈N,使得2n>1000,则p的否定为.12.(5分)已知球的表面积为16π,则该球的体积为.13.(5分)椭圆=1的离心率为,则实数k的值为.14.(5分)函数y=﹣在x=1处的导数为.15.(5分)已知曲线C:(t2﹣1)x2+t2y2=t4﹣t2(t≠0,t≠±1)以下结论正确的是(写出所有正确结论的序号)①曲线C有可能是圆;②曲线C有可能是抛物线;③当t<﹣1或t>1,曲线C是椭圆;④若曲线C是双曲线,则0<t<1;⑤不论t为何值,曲线C有相同的焦点.三、解答题16.(12分)已知p:a∈{a|对任意x∈R,不等式x2+ax+a>0恒成立},q:a∈{a|方程x2+ay2=a 表示的是焦点在x轴上的椭圆},如果命题“p且q”为假命题,命题“p或q”为真命题,求实数a的取值范围.17.(12分)已知点P(2,0)及圆C:x2+y2﹣6x+4y=0,若过点P的直线l与圆C交于M,N两点,且|MN|=4,求直线l的方程.18.(12分)已知圆x2+y2﹣6x﹣7=0与抛物线C:y2=2px(p>0)的准线相切(Ⅰ)求抛物线C的方程(Ⅱ)过抛物线C的焦点F的直线交抛物线于A,B两点,若|AB|=7,求线段AB的中点M 到y轴的距离.19.(12分)已知函数f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线与直线6x+2y+5=0平行.(Ⅰ)求a,b的值和函数f(x)的单调区间;(Ⅱ)当x∈时,f(x)>1﹣4c2恒成立,求实数c的取值范围.20.(13分)已知多面体ABDEC中,底面△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,M为EA的中点,CE=CA=2DB=2(Ⅰ)求证:DM∥平面ABC;(Ⅱ)求证:平面DEA⊥平面ECA;(Ⅲ)求此多面体ABDEC的体积.21.(14分)已知椭圆C:+=1(a>b>0),过点(1,)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆C的右焦点和上顶点(Ⅰ)求椭圆C的方程和离心率;(Ⅱ)点P为椭圆C上任意一点,求△PAB面积的最大值.安徽省宿州市2014-2015学年高二上学期期末数学试卷(文科)参考答案与试题解析一、选择题(每小题5分,共50分)1.(5分)双曲线2x2﹣y2=8的实轴长是()A.2B.2C.4D.4考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:化简双曲线方程为标准方程,求出a即可.解答:解:双曲线2x2﹣y2=8的标准方程为:,可得a=2,双曲线2x2﹣y2=8的实轴长是:4.故选:D.点评:本题考查双曲线的简单性质的应用,基本知识的考查.2.(5分)“x>3”的一个必要不充分条件是()A.x>4 B.x<4 C.x>2 D. x<2考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据充分条件和必要条件的定义进行判断即可.解答:解:x>4是x>3的充分不必要条件,x<4是x>3的既不充分也不必要条件,x>2是x>3的必要不充分条件,x<2是x<2的既不充分也不必要条件,故选:C点评:本题主要考查充分条件和必要条件的判断,比较基础.3.(5分)一个长方体去掉一个小长方体,所得几何体的正视图与侧(左)视图分别如图所,则该几何体的俯视图为()A. B. C. D.考点:简单空间图形的三视图.专题:立体几何.分析:从正视图和侧视图上分析,去掉的长方体的位置应该在的方位,然后判断俯视图的正确图形.解答:解:由正视图可知去掉的长方体在正视线的方向,从侧视图可以看出去掉的长方体在原长方体的左侧,由以上各视图的描述可知其俯视图符合C选项.故选:C.点评:本题考查几何体的三视图之间的关系,要注意记忆和理解“长对正、高平齐、宽相等”的含义.4.(5分)设m为直线,α、β、γ为三个不同的平面,下列说法正确的是()A.若m∥α,α⊥β,则m⊥βB.若m⊂α,α∥β,则m∥βC.若m⊥α,α⊥β,则m∥βD.若α⊥β,α⊥γ,则β∥γ考点:空间中直线与平面之间的位置关系;空间中直线与直线之间的位置关系.专题:空间位置关系与距离.分析:根据线面平行、面面平行、面面垂直等性质定理和判定定理对选项分别分析选择.解答:解:对于A,若m∥α,α⊥β,则m与β的位置关系不确定;故A错误;对于B,若m⊂α,α∥β,根据面面平行的性质定理可得m∥β;故B 正确;对于C,若m⊥α,α⊥β,则m∥β或者m⊂β;故C错误;对于D,若α⊥β,α⊥γ,则β与γ可能相交;故D错误;故选B.点评:本题考查了线面平行、面面平行、面面垂直等性质定理和判定定理的运用.5.(5分)已知原命题:若a+b>2,则a,b至少有一个大于1,那么原命题与其逆命题的真假情况是()A.原命题真,逆命题假B.原命题假,逆命题真C.原命题与逆命题均为真命题D.原命题与逆命题均为假命题考点:四种命题间的逆否关系.专题:简易逻辑.分析:根据题意,写出逆否命题,据不等式的性质判断出逆否命题是真命题,所以原命题是真命题;写出逆命题,通过举反例,说明逆命题是假命题.解答:解:逆否命题为:a,b都不大于1,则a+b≤2是真命题所以原命题是真命题逆命题为:若a,b至少有一个大于1,则a+b>2,例如,当a=2,b=﹣2时,满足条件,当a+b=2+(﹣2)=0,这与a+b>2矛盾,故为假命题故选A点评:判断一个命题的真假问题,若原命题不好判断,据原命题与其逆否命题的真假一致,常转化为判断其逆否命题的真假6.(5分)已知直线l1:x+my+6=0与直线l2:(m﹣2)x+3y+2m=0垂直,则实数m的值为()A.﹣1 B.C.3D.2考点:直线的一般式方程与直线的垂直关系.专题:直线与圆.分析:直接利用直线垂直的充要条件列出方程求解即可.解答:解:直线l1:x+my+6=0与直线l2:(m﹣2)x+3y+2m=0垂直,又知直线l2:(m﹣2)x+3y+2m=0的斜率存在,所以,解得m=.故选:B.点评:本题考查直线的垂直的充要条件的应用,判断直线的斜率是否存在是解题的关键.7.(5分)抛物线y2=12x被直线x﹣y﹣3=0截得弦长的值为()A.21 B.16 C.24 D.30考点:直线与圆锥曲线的关系.专题:函数的性质及应用.分析:直接把直线方程和抛物线方程联立,利用弦长公式求解.解答:解:直线方程为:x﹣y﹣3=0,假设两个交点(x1,y1)(x2,y2)由,得x2﹣18x+9=0,∴x1+x2=18,x1•x2=9,∴弦长等于•=×=24.故选:C.点评:本题考查了直线与圆锥曲线的关系,考查了弦长公式的应用,是中档题.8.(5分)曲线y=e x lnx在x=1处的切线方程是()A.y=2e(x﹣1)B.y=ex﹣1 C.y=x﹣e D.y=e(x﹣1)考点:利用导数研究曲线上某点切线方程.专题:导数的综合应用.分析:求导函数,切点切线的斜率,求出切点的坐标.,即可得到切线方程.解答:解:求曲线y=e x lnx导函数,可得f′(x)=e x lnx+∴f′(1)=e,∵f(1)=0,∴切点(1,0).∴函数f(x)=e x lnx在点(1,f(1))处的切线方程是:y﹣0=e(x﹣1),即y=e(x﹣1)故选:D.点评:本题考查导数的几何意义,考查学生的计算能力,属于基本知识的考查.9.(5分)函数f(x)=lnx﹣x的单调减区间为()A.(﹣∞,0),(1,+∞)B.(1,+∞)C.(﹣∞,0)D.(0,1)考点:利用导数研究函数的单调性.专题:导数的综合应用.分析:求出函数f(x)的定义域与导函数,令导函数小于0,求出x的范围,即为f(x)的单调递减区间.解答:解:函数f(x)=lnx﹣x的定义域为x>0,可得f′(x)=﹣1=令f′(x)<0,得x>1.∴函数f(x)=lnx﹣x的单调减区间是(1,+∞)故选:B.点评:求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间;令导函数小于0得到函数的递减区间.注意函数的定义域.10.(5分)定义在R上的函数f(x)=sinx+2xf′(),f′(x)为f(x)的导函数,令a=﹣,b=log32,则下列关系正确的是()A.f(a)+f(b)<0 B.f(﹣a)+f(b)>0 C.f(a)+f(﹣b)<0 D.f(﹣a)+f(﹣b)<0考点:导数的运算.专题:导数的概念及应用.分析:求出原函数的导函数,取x=求出f′(),代入原函数解析式后求出f(x),求导函数判断原函数的单调性,比较a与b的大小后运用单调性判断f(a)与f(b)的大小,再判断出函数的奇偶性,再判断各个选项.解答:解:由题意得,f(x)=sinx+2xf′(),则f′(x)=cosx+2f′(),令x=代入f′(x)得,f′()=cos+2f′(),解得f′()=,所以f(x)=sinx﹣x,由f′(x)=cosx﹣1≤0,得到f(x)为递减函数,因为a=﹣<b=log32,则f (a)>f (b),即f (a)﹣f (b)>0①,或f (b)﹣f (a)<0②,因为函数f(x)=sinx﹣x是奇函数,所以①等价于f (a)+f (﹣b)>0,则C错误;②等价于f (﹣a)+f (b)<0,则B错误;因为﹣a==<b=log32,则f (﹣a)>f (b),即f (﹣a)﹣f (b)>0,所以f (﹣a)+f (﹣b)>0,则D错误;由f (﹣a)+f (﹣b)>0得﹣f (a)﹣f (b)>0,即f (a)+f (b)<0,则A正确;故选:A.点评:本题考查了导数的运算,函数的奇偶性的定义、性质,利用导函数判断一个函数的单调性,由单调性比较两个函数值的大小,考查转化思想,属于中档题.二、填空题(每小题5分,共25分)11.(5分)已知命题p:存在n∈N,使得2n>1000,则p的否定为任意n∈N,都有2n≤1000.考点:命题的否定.专题:简易逻辑.分析:利用特称命题的否定是全称命题,写出结果即可.解答:解:因为特称命题的否定是全称命题,所以,命题p:存在n∈N,使得2n>1000,则p的否定为:任意n∈N,都有2n≤1000;故答案为:任意n∈N,都有2n≤1000.点评:本题考查命题的否定特称命题与全称命题的否定关系,基本知识的考查.12.(5分)已知球的表面积为16π,则该球的体积为.考点:球的体积和表面积.专题:计算题;空间位置关系与距离.分析:通过球的表面积求出球的半径,然后求出球的体积解答:解:一个球的表面积是16π,所以球的半径为:2,所以这个球的体积为:=.故答案为:.点评:本题是基础题,考查球的表面积、体积的计算,考查计算能力,公式的应用.13.(5分)椭圆=1的离心率为,则实数k的值为3或.考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:分类讨论,利用椭圆的离心率公式,即可求出k的值.解答:解:k>4,则,∴k=;0<k<4时,则=,∴k=3,故答案为:3或.点评:本题考查椭圆的简单性质,考查离心率是计算,考查分类讨论的数学思想,比较基础.14.(5分)函数y=﹣在x=1处的导数为.考点:导数的运算.专题:导数的概念及应用.分析:根据求导公式和复合函数的求导法则求函数的导数,再把x=1代入求值即可.解答:解:由题意得,y=﹣=﹣,所以y′=﹣=2x×=,则函数在x=1处的导数为=,故答案为:.点评:本题考查求导公式和复合函数的求导法则,属于基础题.15.(5分)已知曲线C:(t2﹣1)x2+t2y2=t4﹣t2(t≠0,t≠±1)以下结论正确的是③⑤(写出所有正确结论的序号)①曲线C有可能是圆;②曲线C有可能是抛物线;③当t<﹣1或t>1,曲线C是椭圆;④若曲线C是双曲线,则0<t<1;⑤不论t为何值,曲线C有相同的焦点.考点:命题的真假判断与应用.专题:计算题;不等式的解法及应用;直线与圆;圆锥曲线的定义、性质与方程.分析:将曲线C化为标准方程,对分母考虑,由于t2≠t2﹣1,则曲线C不表示圆,即可判断①;由于t2≠0,t2﹣1≠0,即可判断②;若为椭圆,则有t2>0,且t2﹣1>0,解不等式即可判断③;若曲线C表示双曲线,则t2>0且t2﹣1<0,解不等式即可判断④;分别讨论椭圆方程和双曲线方程,求得焦点,即可判断⑤.解答:解:曲线C:(t2﹣1)x2+t2y2=t4﹣t2(t≠0,t≠±1),即为+=1,对于①,由于t2≠t2﹣1,则曲线C不表示圆,则①错;对于②,由于t2≠0,t2﹣1≠0,则曲线C不可能表示抛物线,则②错;对于③,若为椭圆,则有t2>0,且t2﹣1>0,解得t>1或t<﹣1,则③对;对于④,若曲线C表示双曲线,则t2>0且t2﹣1<0,解得﹣1<t<0或0<t<1,则④错;对于⑤,若曲线C表示椭圆,由t2>t2﹣1,则焦点在x轴上,且为(±1,0),若曲线C为双曲线,则方程为﹣=1,则焦点在x轴上,且为(±1,0),则⑤对.故答案为:③⑤.点评:本题考查方程表示的曲线的形状,考查圆的方程以及圆锥曲线的方程和性质,考查不等式的解法,考查运算能力,属于基础题和易错题.三、解答题16.(12分)已知p:a∈{a|对任意x∈R,不等式x2+ax+a>0恒成立},q:a∈{a|方程x2+ay2=a 表示的是焦点在x轴上的椭圆},如果命题“p且q”为假命题,命题“p或q”为真命题,求实数a的取值范围.考点:复合命题的真假.专题:简易逻辑.分析:命题p:对任意x∈R,不等式x2+ax+a>0恒成立.可得△<0,解得a的取值范围.命题q:方程x2+ay2=a表示的是焦点在x轴上的椭圆,得,可得a>1.由于命题“p且q”为假命题,命题“p或q”为真命题,可得p、q必然一真一假.解答:解:命题p:对任意x∈R,不等式x2+ax+a>0恒成立.则△=a2﹣4a<0,解得0<a<4,可得a的取值范围是0<a<4.命题q:方程x2+ay2=a表示的是焦点在x轴上的椭圆,得,解得a>1.∵命题“p且q”为假命题,命题“p或q”为真命题,∴p、q必然一真一假,∴或,解得0<a≤1,或a≥4.∴实数a的取值范围是0<a≤1,或a≥4.点评:本题考查了一元二次不等式的解集与判别式的关系、椭圆的标准方程及其性质、简易逻辑的判定,属于基础题.17.(12分)已知点P(2,0)及圆C:x2+y2﹣6x+4y=0,若过点P的直线l与圆C交于M,N两点,且|MN|=4,求直线l的方程.考点:直线与圆的位置关系.专题:直线与圆.分析:求出圆的标准方程,利用直线和圆相交的弦长公式求出圆心到直线的距离即可求出直线方程.解答:解:由圆C:x2+y2﹣6x+4y=0,即(x﹣3)2+(y+2)2=9,故圆心C(3,﹣2),半径r=3,﹣﹣﹣﹣﹣﹣﹣﹣(2分)因为|MN|=4,设圆心到直线的距离为d,由|MN|=4=,得d=1﹣﹣﹣﹣﹣﹣﹣﹣(4分)(1)当l的斜率k存在时,设直线方程为y﹣0=k(x﹣2).又圆C的圆心为(3,﹣2),半径r=3,由,解得k=﹣.所以直线方程为y=﹣(x﹣2),即3x+4y﹣6=0.﹣﹣﹣﹣﹣﹣(9分)(2)当l的斜率不存在时,l的方程为x=2,经验证x=2也满足条件.﹣﹣(11分)综上直线l的方程为3x+4y﹣6=0或x=2.﹣﹣﹣﹣﹣﹣(12分)点评:本题主要考查直线方程的求解,根据直线和圆相交的弦长公式是解决本题的关键.18.(12分)已知圆x2+y2﹣6x﹣7=0与抛物线C:y2=2px(p>0)的准线相切(Ⅰ)求抛物线C的方程(Ⅱ)过抛物线C的焦点F的直线交抛物线于A,B两点,若|AB|=7,求线段AB的中点M 到y轴的距离.考点:圆与圆锥曲线的综合;抛物线的标准方程;直线与圆锥曲线的关系.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)求出圆的圆心与半径,利用y2=2px(p>0)的准线相切,求出p,得到抛物线方程.(Ⅱ)求出抛物线C的焦点坐标为(1,0),准线方程为x=﹣1,求出抛物线定义知线段AB 的中点M到准线的距离,然后求解线段AB的中点M到y轴的距离.解答:解:(Ⅰ)圆x2+y2﹣6x﹣7=0,即(x﹣3)2+y2=16,所以圆心(3,0),半径为4,抛物线的准线方程为x=,依题意,有3﹣(﹣)=4,得p=2,故抛物线方程为y2=4x;﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)由(Ⅰ)知,抛物线C的焦点坐标为(1,0),准线方程为x=﹣1,由抛物线定义知线段AB的中点M到准线的距离为,故线段AB的中点M到y轴的距离d=.﹣﹣﹣﹣﹣﹣(12分)点评:本题考查圆的方程与抛物线方程的综合应用,点到直线的距离,考查分析问题解决问题的能力.19.(12分)已知函数f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线与直线6x+2y+5=0平行.(Ⅰ)求a,b的值和函数f(x)的单调区间;(Ⅱ)当x∈时,f(x)>1﹣4c2恒成立,求实数c的取值范围.考点:导数在最大值、最小值问题中的应用;函数恒成立问题;利用导数研究函数的极值;利用导数研究曲线上某点切线方程.专题:函数的性质及应用;导数的综合应用.分析:(Ⅰ)先对函数进行求导,根据函数f(x)在x=2取得极值,说明导函数在x=2时值为0,再根据其图象在x=1处的切线斜率为﹣3,列出方程组即可求出a、b的值,进而可以求出函数的单调区间;(Ⅱ)可以求出函数在闭区间x∈上的最小值,这个最小值要大于1﹣4c2,解不等式可以得出实数c的取值范围.解答:解:f′(x)=3x2+6ax+3b,由该函数在x=2处有极值,故f′(2)=3•22+6a•2+3b=0即4a+b+4=0…①又其图象在图象在x=1处的切线与直线6x+2y+5=0平行所以f′(1)=3•12+6a•1+3b=﹣3即2a+b+2=0…②由①,②,解得a=﹣1,b=0﹣﹣﹣﹣﹣﹣(4分)∴f′(x)=x3﹣3x2+c(Ⅰ)∵f′(x)=3x2﹣6x=3x(x﹣2)由f′(x)=0得x1=0,x2=2.列表如下x (﹣∞,0)0(0,2)2(2,+∞)f′(x)+0 ﹣0 +f(x)↗极大值↘极小值↗故f(x)的单调递增区间是(﹣∞,0),(2,+∞)单调递增区间是(0,2)﹣﹣﹣﹣﹣(7分)(Ⅱ)由(1)可知列表如下x 1 (1,2)2(2,3)3f′(x)﹣0 +f(x)﹣2+c ↘﹣4+c ↗ c∴f(x)在的最小值是﹣4+c∴c﹣4>1﹣4c2解得c>1或c<﹣﹣﹣﹣﹣﹣﹣(12分)点评:本题主要考查函数在某点取得极值的条件和导数的几何意义,以及利用导数解决函数在闭区间上的最值问题和函数恒成立问题,综合性较强,属于难题.20.(13分)已知多面体ABDEC中,底面△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,M为EA的中点,CE=CA=2DB=2(Ⅰ)求证:DM∥平面ABC;(Ⅱ)求证:平面DEA⊥平面ECA;(Ⅲ)求此多面体ABDEC的体积.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定;平面与平面垂直的判定.专题:空间位置关系与距离.分析:(Ⅰ)取AC的中点N,连接MN,BN,利用三角形中位线定理与平行四边形的判定与性质定理可得DM∥BN,再利用线面平行的判定定理可得:DM∥平面ABC.(Ⅱ)由EC⊥平面ABC,可得EC⊥BN,利用△ABC为正三角形,可得BN⊥AC,可得BN⊥平面ECA,利用DM∥BN,可得DM⊥平面ECA,即可证明.(Ⅲ)取BC的中点O,连接AO,利用等边三角形的性质可得:AO⊥BC.利用面面垂直的性质定理可得:AO⊥平面BDEC.利用此多面体ABDEC的体积V=V A﹣BDEC=即可得出.解答:(Ⅰ)证明:取AC的中点N,连接MN,BN,∵,,∴DB,故四边形BDMN为平行四边形,由DM∥BN,DM⊄平面ABC,BN⊂平面ABC,∴DM∥平面ABC.(Ⅱ)证明:∵EC⊥平面ABC,BN⊂平面ABC,∴EC⊥BN,又∵△ABC为正三角形,N为AC的中点,∴BN⊥AC,又AC∩EC=C,∴BN⊥平面ECA,∵DM∥BN,∴DM⊥平面ECA,又DM⊂平面DEA,∴平面DEA⊥平面ECA.(Ⅲ)解:取BC的中点O,连接AO,∵△ABC是边长为2的等边三角形,∴AO⊥BC,AO=.∵平面BDEC⊥平面ABC,平面BDEC∩平面ABC=BC,∴AO⊥平面BDEC.S BDEC==3,∴此多面体ABDEC的体积V=V A﹣BDEC===.点评:本题考查了线面面面平行与垂直的判定性质定理、三角形的中位线定理、四棱锥的体积计算公式、平行四边形的判定与性质定理,考查了推理能力与计算能力,属于中档题.21.(14分)已知椭圆C:+=1(a>b>0),过点(1,)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆C的右焦点和上顶点(Ⅰ)求椭圆C的方程和离心率;(Ⅱ)点P为椭圆C上任意一点,求△PAB面积的最大值.考点:直线与圆锥曲线的综合问题;椭圆的标准方程;椭圆的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(Ⅰ)由题意可知:c=1,k OQ=,则k AB=﹣2,由此能求出椭圆的标准方程.(Ⅱ)设与直线AB的平行的直线方程为y=﹣2x+t,代入椭圆方程,由△=0得t=±2,故当t=﹣2时,求出点P到直线AB的最大距离,即可求△PAB面积的最大值.解答:解:(Ⅰ)由题意,Q(1,),可知:c=1,k OQ=,则k A B=﹣2,…(3分)所以直线AB的方程是y=﹣2(x﹣1),即y=﹣2x+2,即b=2.…(5分)所以a2=b2+c2=5,故椭圆的标准方程为.椭圆的离心率e==﹣﹣﹣﹣﹣﹣(7分)(Ⅱ)设与直线AB的平行的直线方程为y=﹣2x+t,代入椭圆方程得24x2﹣20tx+5t2﹣20=0,由△=0得t=±2,故当t=﹣2时,点P到直线AB的最大距离为d=,又因为A(1,0),B(,),所以|AB|=故△PAB积的最大值=×=﹣﹣﹣﹣﹣﹣(14分)点评:本题考查椭圆的方程与性质,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.。
