理论力学第4章点的运动和刚体基本运动习题解答
大学物理题库-第4章-刚体的转动习题(含答案解析)

刚体习题一、选择题 1、如图所示,A 、B 为两个相同的绕着轻绳的定滑轮.A 滑轮挂一质量为M 的物体,B 滑轮受拉力F ,而且F =Mg .设A 、B 两滑轮的角加速度分别为βA 和βB ,不计滑轮轴的摩擦,则有(A) βA =βB . (B) βA >βB .(C) βA <βB . (D) 开始时βA =βB ,以后βA <βB . [ ]2、关于刚体对轴的转动惯量,下列说法中正确的是(A )只取决于刚体的质量,与质量的空间分布和轴的位置无关.(B )取决于刚体的质量和质量的空间分布,与轴的位置无关.(C )取决于刚体的质量、质量的空间分布和轴的位置.(D )只取决于转轴的位置,与刚体的质量和质量的空间分布无关.[ ]3、有两个力作用在一个有固定转轴的刚体上:(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中,(A) 只有(1)是正确的.(B) (1) 、(2)正确,(3) 、(4) 错误.(C) (1)、(2) 、(3) 都正确,(4)错误.(D) (1) 、(2) 、(3) 、(4)都正确. [ ]4、如图所示,一质量为m 的匀质细杆AB ,A 端靠在粗糙的竖直墙壁上,B 端置于粗糙水平地面上而静止.杆身与竖直方向成θ角,则A 端对墙壁的压力大小 (A) 为 41mg cos θ. (B)为21mg tg θ. (C) 为 mg sin θ.(D) 不能唯一确定. [ ]5、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示.今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的?(A) 角速度从小到大,角加速度从大到小.(B) 角速度从小到大,角加速度从小到大.(C) 角速度从大到小,角加速度从大到小.(D) 角速度从大到小,角加速度从小到大. [ ]6、关于力矩有以下几种说法:(1) 对某个定轴而言,内力矩不会改变刚体的角动量.(2) 作用力和反作用力对同一轴的力矩之和必为零.(3) 质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的角加速度一定相等.在上述说法中,(A) 只有(2) 是正确的.(B) (1) 、(2) 是正确的.(C) (2) 、(3) 是正确的.(D) (1) 、(2) 、(3)都是正确的. [ ]7、一水平圆盘可绕通过其中心的固定竖直轴转动,盘上站着一个人.把人和圆盘取作系统,当此人在盘上随意走动时,若忽略轴的摩擦,此系统(A) 动量守恒.(B) 机械能守恒.(C) 对转轴的角动量守恒.(D) 动量、机械能和角动量都守恒.(E) 动量、机械能和角动量都不守恒. [ ]8、质量为m 的小孩站在半径为R 的水平平台边缘上.平台可以绕通过其中心的竖直光滑固定轴自由转动,转动惯量为J .平台和小孩开始时均静止.当小孩突然以相对于地面为v 的速率在台边缘沿逆时针转向走动时,则此平台相对地面旋转的角速度和旋转方向分别为(A) ⎪⎭⎫ ⎝⎛=R J mR v 2ω,顺时针. (B) ⎪⎭⎫ ⎝⎛=R J mR v 2ω,逆时针. (C) ⎪⎭⎫ ⎝⎛+=R mR J mR v 22ω,顺时针.(D) ⎪⎭⎫ ⎝⎛+=R mR J mR v 22ω,逆时针.[ ]9、一圆盘正绕垂直于盘面的水平光滑固定轴O 转动,如图射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度ω(A) 增大. (B) 不变.(C) 减小. (D) 不能确定 [ ]10、(0405)人造地球卫星,绕地球作椭圆轨道运动,地球在椭圆的一个焦点上,则卫星的(A)动量不守恒,动能守恒.(B)动量守恒,动能不守恒.(C)对地心的角动量守恒,动能不守恒.(D)对地心的角动量不守恒,动能守恒. [ ]11、一个圆盘在水平面内绕一竖直固定轴转动的转动惯量为J ,初始角速度为ω 0,后来变为021ω.在上述过程中,阻力矩所作的功为: (A) 2041ωJ . (B) 2081ωJ -. (C) 2041ωJ - (D) 2083ωJ -. [ ] 12、一均匀细杆可绕垂直它而离其一端l / 4 (l 为杆长)的水平固定轴O 在竖直平面内转动.杆 m m的质量为m ,当杆自由悬挂时,给它一个起始角速度ω 0,如杆恰能持续转动而不作往复摆动(一切摩擦不计)则需要 (A) ω 0≥l g 7/34. (B) ω 0≥l g /4.(C) ω 0≥()l g /3/4. (D) ω 0≥l g /12.[已知细杆绕轴O 的转动惯量J =(7/48)ml 2] [ ]13、假设卫星环绕地球中心作圆周运动,则在运动过程中,卫星对地球中心的(A) 角动量守恒,动能也守恒.(B) 角动量守恒,动能不守恒.(C) 角动量不守恒,动能守恒.(D) 角动量不守恒,动量也不守恒.(E) 角动量守恒,动量也守恒. [ ]14、一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力(A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断. [ ]15、如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统(A) 只有机械能守恒.(B) 只有动量守恒.(C) 只有对转轴O 的角动量守恒.(D) 机械能、动量和角动量均守恒. [ ]二、填空题1、如图4-23所示,质量为m 和m 2的两个质点A 和B ,用一长为l 的轻质细杆相连,系统绕通过杆上o 点且与杆垂直的轴转动。
《理论力学》第四章 静力学应用专题习题解
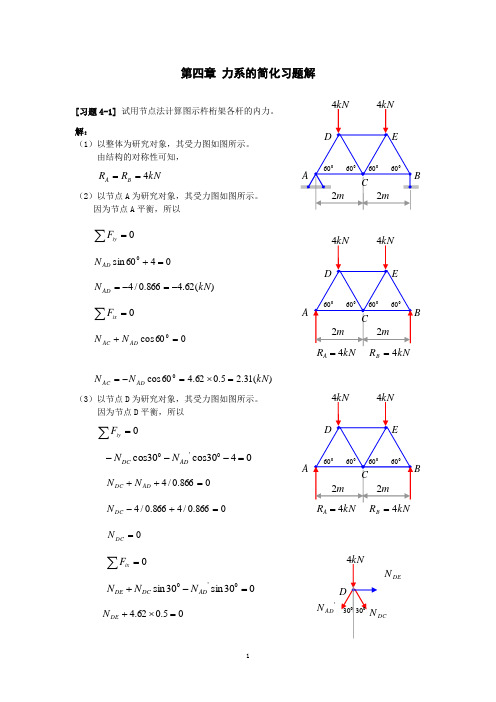
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
理论力学课后习题答案 第4章 运动分析基础

(b)第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环A 的运动规律。
解:Rv a a 2nsin ==θ,θsin 2R v a =θθtan cos d d 2tR v a tv a ===,⎰⎰=t v v t R vv 02d tan 1d 0θ t v R R v t s v 00tan tan d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0tan tan ln tan -=θθθ4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩⎪⎨⎧-=-=225.1324tt y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1) ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得2arccos 213arcsin y x =化简得轨迹方程:2942x y -=(2)轨迹如图(b ),其v 、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt sπ=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π==t ,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ==,12=∴tR a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮以匀角速度ω转动,如图所示。
理论力学题库第4章

理论力学题库——第四章一、填空题1. 科里奥利加速度 (“是”或“不是”)由科里奥利力产生的,二者方向 (“相同”或“不相同”)。
2. 平面转动参考系中某一点对静止参考系的加速度的表达式是 ,其中 是相对加速度, 是牵连加速度, 是科里奥利加速度。
4-1.非惯性系中,运动物体要受到 4种惯性力的作用它们是: 惯性力、惯性切向力、惯性离轴力、科里奥利力 。
4-2.在北半球,科里奥利力使运动的物体向 右 偏移,而南半球,科里奥利力使运动的物体向 左 偏移。
(填“左”或“右”)4-3.产生科里奥利加速度的条件是: 物体有相对速度υ'v及参照系转动,有角速度ωv ,且υ'v 与ωv不平行 。
4-4.科里奥利加速度是由参考系的 转动 和 物体的相对运动 相互影响产生的。
4-5.物体在 主动力、约束力和惯性力 的作用下在动系中保持平衡,称为相对平衡。
4-6.重力加速度随纬度增加的主要原因是:地球自转产生的惯性离轴力与地心引力有抵消作用 。
4-7.由于科里奥利力的原因北半球气旋(旋风)一般是 逆时针 旋转的.(顺时针或逆时针)4-8.地球的自转效应,在北半球会使球摆在水平面内 顺时针 转动.(顺时针或逆时针)二、选择题1. 关于平面转动参考系和平动参考系,正确的是( ) A. 平面转动参考系是非惯性系; B. 牛顿定律都不成立; C. 牛顿定律都成立;D.平动参考系中质点也受科里奥利力。
2. 下列关于非惯性系的说法中正确的是:【C 】A 惯性离心力与物体的质量无关;B 科里奥利力与物体的相对运动无关;C 科里奥利力是参考系的转动与物体相对与参考系的运动引起的;D 科里奥利力使地球上南半球河流右岸冲刷比左岸严重。
3. 科里奥利力的产生与下列哪个因素无关?【B 】A 参照系的转动;B 参照系的平动;C 物体的平动;D 物体的转动。
4. 在非惯性系中如果要克服科里奥利力的产生,需要:【D 】A 物体作匀速直线运动;B 物体作匀速定点转动;C 物体作匀速定轴转动;D 物体静止不动。
理论力学(刘又文 彭献)答案第4章
§4.2 思考解析
思考 4-1 已知平面图形 S 的运动方程,试写出 S 上给定点 M 的运动方程, 以及该点的速度和加速度解析表达式。 答:设已知 x A = f1 (t ),
y A = f 2 (t ), ϕ = f3 (t ) 。则 M 点运动方程为
xM = x A + AM cos ϕ = f1 (t ) + AM cos f3 (t ) yM = y A + AM sin ϕ = f 2 (t ) + AM sin f3 (t ) M 点速度和加速度分量分别为
n τ aCv = aO + aC + aC vO vO n τ 其中, aC = Rω 2 , aC = Rα = a0 ,方向与 a0 相反。 vO vO
110
故
n aCv = aC , aCv = Rω 2 = vO
2 v0 R
以 Cv 为基点,M 点的加速度如图 b 所示。 故
n 2 2 aM = (aMC − aCv ) + (aτ ( Rω 2 ) 2 + (2 Rα ) 2 = 2 a0 + MCv ) = v 4 v0 4R2
所以
xM = r cos ω t + AM cos ϕ , yM = r sin ω t − AM sin ϕ
对时间 t 求一阶和二阶导数便得 M 点的速度和加速度坐标分量。
思考 4-4
试求图 a、b、c 中各平面运动刚体的速度瞬心 Cv 。
ω
B
A B
C v
A
ω
(b) (c)
(a)
ω
C
A B
B
A
ω
Cv
vC vB
运动学习题解答

236d d t t t-==ϕωrad/s rad/s -31316时,12=⨯⨯==ωs t tt6-6d d ==ωα22rad/s rad/s -0166时,1=⨯==αs t rad/s 450rad/s 3013500300πππω=⨯==ntαωω+=022rad/s .rad/s πππωωα4850450300-=-=-=t rad/s rad/s -02326时,22=⨯⨯==ωs t 22rad/s 6-rad/s 26-62=⨯==α时,s t rad/srad/s πππω303090030=⨯==n 第一篇 运动学主要知识点:(1)点的运动学;(2)刚体基本运动; (3)点的合成运动; (4)刚体平面运动。
点的运动学1. 已知物体的转动方程为323t t -=ϕ,式中转角ϕ的单位为rad,时间t 的单位为s 。
试求t=1、2s 时物体的角速度和角加速度。
解:求角速度求角加速度2. 压气机原转速min /135000r n =,在50秒内转速降到min /900r n =。
若运动过程为匀减速转动,试求其角加速度。
解:压气机的初速度压气机的终了速度由匀变速转动的公式刚体基本运动3. 震动筛如图示,杆A O 1与B O 2相等且平行。
设在图示位置时,杆A O 1的角速度rad 1=ω,角加速度2/2s rad =α,转向如图所示。
已知m AM B O A O 121===,求此时M 点的速度和加速度的大小。
a) b)图15-3解:四连杆机构O 1ABO 2为平行四边形机构,AMB 杆做曲线平动,A 、M 、B 三点的速度、加速度完全相同。
s m A O v v A M /11=⋅==ω21/2s m A O a a A M =⋅==αττ,212/1s m A O a a n A n M =⋅==ω,全加速度222/24.2)()(s m a a a n MM M =+=τ,与n Ma 的夹角04.63arctan ==nMM a a τθ。
理论力学作业卷答案(第四章)

山东大学理论力学习题练习册班级学号姓名
4-12如图所示,轮O在水平面上作纯滚动,轮缘上固连销钉B,此销钉在摇杆O A的导槽内滑动,并带动摇
第 6 页共21 页
山东大学理论力学习题练习册班级学号姓名
r=,以等转速
4-21滚压机构的滚子沿水平面滚动而不滑动。
曲柄OA长为10cm
n=30r/min绕O轴转动。
如滚子的半径R=10cm,连杆AB长为103cm,求当曲柄与
水平面交角为60 时,滚子的角速度和角加速度。
4-24 半径为R的轮子沿水平面滚动而不滑动,如图所示。
在轮上有圆柱部分,其半径为r。
将线绕于圆柱上,线的
B端以速度v和加速度a沿水平方向运动。
求轮的轴心O的速度和加速度。
第7 页共21。
[分享]第四章刚体的转动问题与习题解答
![[分享]第四章刚体的转动问题与习题解答](https://img.taocdn.com/s3/m/c9e3663ccec789eb172ded630b1c59eef8c79aab.png)
第四章 刚体的转动 问题与习题解答问题:4-2、4-5、4-94-2如果一个刚体所受合外力为零,其合力矩是否也一定为零?如果刚体所受合外力矩为零,其合外力是否也一定为零?答:一个刚体所受合外力为零,其合力矩不一定为零,如图a 所示。
刚体所受合外力矩为零,其合外力不一定为零,例如图b 所示情形。
4-5为什么质点系动能的改变不仅与外力有关,而且也与内力有关,而刚体绕定轴转动动能的改变只与外力矩有关,而与内力矩无关?答:因为合外力对质点所作的功,等于质点动能的增量;而质点系中内力一般也做功,故内力对质点系的动能的增量有贡献。
而在刚体作定轴转动时,任何一对内力对转轴的力矩皆为一对大小相等、方向相反的力矩,且因定轴转动时刚体转过的角度d θ都一样,故其一对内力矩所作的功()0inij ij ji ij ji W M d M d M M d θθθ=+=+=,其内力功总和也为零,因而根据刚体定轴转动的动能定理可知:内力矩对其转动动能的增量无贡献。
4-9一人坐在角速度为0ω的转台上,手持一个旋转的飞轮,其转轴垂直地面,角速度为ω'。
如果突然使飞轮的转轴倒转,将会发生什么情况?设转台和人的转动惯量为J ,飞轮的转动惯量为J '。
答:(假设人坐在转台中央,且飞轮的转轴与转台的转轴重合)视转台、人和飞轮为同一系统。
(1)如开始时飞轮的转向与转台相同,则系统相对于中心轴的角动量为:10L J J ωω''=+飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的角动量为:21L J J ωω''=-在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''-=+即 102J Jωωω''=+,转台的转速变大了。
(2)如开始时飞轮的转向与转台相反,则系统相对于中心轴的角动量为:10L J J ωω''=-飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的F 1F 3ab角动量为:21L J J ωω''=+在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''+=-即 102J Jωωω''=-,转台的转速变慢了。
大学物理第四章-刚体的转动-习题及答案

1.刚体绕一定轴作匀变速转动,刚体上任一点是否有切向加速度?是否有法向加速度?切向和法 向加速度的大小是否随时间变化?
答:当刚体作匀变速转动时,角加速度 不变。刚体上任一点都作匀变速圆周运动,因此该点速
率在均匀变化,v l ,所以一定有切向加速度 at l ,其大小不变。又因该点速度的方向变化,
ω dr
(1)圆盘上半径为r、宽度为dr的同心圆环所受的摩擦力矩
为
dM
m
(
R2
2 rdr)grBiblioteka 2r 2 mgdr/
R2
负号表示摩擦力矩为阻力矩。对上式沿径向积分得圆盘所受
r dF
的总摩擦力矩大小为
M dM R 2r2mgdrdr 2 mgR
0
R2
3
(2)由于摩擦力矩是一恒力矩,圆盘的转动惯量 I 1 mr2 ,由角动量定理可得圆盘停止的 2
度.
解:碰撞过程满足角动量守恒:
2 3
mv0l
1 2
mv0
2 3
l
I
而
I m( 2 l)2 2m(1 l)2 2 ml2
3
33
所以
mv0l
2 3
ml 2
由此得到: 3v0 2l
2m
1 3
l
O⅓l
1 2
v
0
2 3
l
m
⅓l m v0
⅓l
15. 如图所示,A和B两飞轮的轴杆在同一中心线上,设两轮的转动惯量分别为 JA=10 kg·m2 和 JB
2
2
22
2
2
1 16
( Ld14
1 2
ad24
大学物理第四章习题及答案

第四章 刚体的转动4-1 一汽车发动机曲轴的转速在12s 内由3102.1⨯r.min -1增加到3107.2⨯r.min -1。
(1)求曲轴转动的角加速度;(2)在此时间内,曲轴转了多少转? 解:曲轴做匀变速转动。
(1)角速度n πω2=,根据角速度的定义dtd ωα=,则有:()=-=-=tn n t002πωωα13.1rad.s -2 (2)发动机曲轴转过的角度为t t t 221020ωωαωθ+=+=()t n n 0+=π在12秒内曲轴转过的圈数为 N 390220=+==t n n πθ圈。
4-2 一半径为0.25米的砂轮在电动机驱动下,以每分钟1800转的转速绕定轴作逆时针转动,现关闭电源,砂轮均匀地减速,15秒钟后停止转动.求(1)砂轮的角加速度;(2)关闭电源后10=t s 时砂轮的角速度,以及此时砂轮边缘上一点的速度和加速度大小.解:(1)4.1886060180020==⨯=ππω rad.s 1- 57.12415600=-=-=πα rad.s 2- (2)7.621057.124.1880=⨯-=+=t αωω rad.s 1-7.1525.07.62=⨯==r v ω m.s 1-14.3-==αr a t m.s 2- , 9872==ωr a n m. s 2-98822=+=n t a a a m. s 2-.4-3如图,质量201=m kg 的实心圆柱体A 其半径为20=r cm ,可以绕其固定水平轴转动,阻力忽略不计,一条轻绳绕在圆柱体上,另一端系一个质量102=m kg 的物体B ,求:(1)物体B 下落的加速度;(2)绳的张力T F 。
解: (1) 对实心圆柱体A ,利用转动定律αα2121r m J r F T == ——①对物体B ,利用牛顿定律a m F g m T 22=- ——② 有角量与线量之间的关系 αr a = 解得:9.422212=+=m m g m a m ·s -2(2)由②得 492)(2121=+=-=g m m m m a g m F T N4—3题图4-4如图,一定滑轮两端分别悬挂质量都是m 的物块A 和B ,图中R 和r ,已知滑轮的转动惯量为J ,求A 、B 两物体的加速度及滑轮的角加速度(列出方程即可)。
第4章点的运动和刚体的基本运动

aC aA 1m/s2,
R 0.5
vC vA 1.5m/s,
w0
vC R
10..55 3rad/s
(
)
w0t
1 2
t2
3 3 1 2 32 2
18rad, n
2
2.86(转)
② sr 0.3185.4m
③ w w0 t 3 2 3 9 rad/s
( ),
vB rw 0.392.7m/s
a
dv dt
d (v)
dt
dv
dt
v d
dt
a
an
①切向加速度 ---表示速度大小的变化
a
dv
dt
d 2s dt 2
大小: a 方向:d 2 s
dt 2
dv d2s dt dt 2
0,
正向;d 2 dt
s
2
0,反向。
②法向加速度 ---表示速度方向的变化
an
v d
dt
v lim
点的运动
加速度
a
an
a
v
匀 速0
0
0 vC
直 线
匀 变
a=C
a =C vv0 at 0
运
动
变 速
a
dv dt
0
a
dv dt
vv0 0tadt
s
s f (t) vt
sv0t
1 at 2 2
s 0tvdt
匀 曲速
0
an
v2
a
v2
vC
svt
线匀 运变
a=C
an
v2
a a2 an2
v v0 a t
理论力学(周衍柏)习题答案,第四章

第四章习题解答4.1解如题4.1.1图所示.坐标系的原点位于转动的固定点,轴沿轴与角速度的方向一致,即设点沿运动的相对速度为则有题意得:故在点时的绝对速度设与轴的夹角为,则故与边的夹角为,且指向左上方。
点时绝对速度设的夹角为,则,故与边的夹角为,且指向左下方。
4.2解如题4.2.1图所示,以转动的方向为极角方向建立坐标系。
轴垂直纸面向外,设点相对速度①设绝对速度的量值为常数,则:②对②式两边同时球时间导数得:依题意故解得通解当时,,将其带入①式游客的知:时,即最后有4.3解如题4.3.1图所示,直角坐标的原点位于圆锥顶点轴过圆锥的对称轴.点在轴上对应的一点,且有,所以点的绝对加速度:最后有4.4解如题4.4.1图所示,题4.4.1图坐标系是以轴转动的坐标系.图中画出的是曲线的一段,在任意一点处,假设某质点在此处静止,则该质点除了受重力、钢丝的约束力之外,还会受惯性离心力的作用,,方向沿轴正向,在作用下,致信处于平衡状态,则有①②有①得③又因为过原点.对上式积分得抛物线有③得将代入②的反作用力4.5以直管为参照系,方向沿管,沿竖直轴建立坐标系,则小球受力为:故沿方向运动的微分方程为:①有初始条件:可得①式解为故当邱刚离开管口时,即时.则得所以此时:故当球刚要离开管口时的相对速度为,绝对速度为,小球从开始运动到离开管口所需时间为4.6解以光滑细管为参考系,沿管,沿水平轴建立坐标系,如题4.6.1图所示,则小球受力为:故沿方向运动的微分方程为:①方程的通解而方程①的特解为:故方程①的通解为:初始条件为当时,故可得所以质点相对于管的运动规律为:4.7解以水平细管为参考系,沿管,沿竖直转动轴向上建立坐标系,如题图4.7.1图所示则易得质点反方向的运动微分方程为:①②将方程①②作简单变换可得:化简得其通解为:初始条件为:故可得:故4.8解以抛物线形金属丝为参照物沿抛物线在顶点的切线方向,沿竖直轴建立坐标系,则小环的运动微分方程为:①②故代入①②得化简即得4.9解一当小环相对平衡时,由上题可知即要求为常数,故故解二以地面为参照系,则小球受力,如图4-8所示.其中为固定地面的坐标系,故平衡时有:4.10解以地面为参考系,则小环的运动微分方程为:其中为与圆心的连线和通过点的直径间所夹的角化简得4.11解以地面为非惯性参考系,建立坐标系,指正南,竖直向上,发射点为原点,炮弹的运动微分方程为:①②③初始条件为故将①②③积分一次代入初始条件后得:④⑤⑥有⑥可得落地时间:⑦其中所以将展开可得由式及初始条件可得所以炮弹落地时的横向偏离为4.1 解以地面为非惯性,建立坐标系指向正南,竖直向上,上抛点为原点,质点的运动微分方程为:①初始条件为:如上题同理可得②③④代入①式得有④式求出落地时间为:有③式得:将代入得复落至地面时:。
大学物理习题参考解答物理习题参考解答刚体基本运动_转动定律_动能定理

选择题_03图示单元四 刚体基本运动 转动动能 1一 选择题01. 一刚体以每分钟60转绕z 轴做匀速转动(ω沿转轴正方向)。
设某时刻刚体上点P 的位置矢量为345r i j k =++,单位210m -,以210/m s -为速度单位,则该时刻P 点的速度为: 【 B 】(A) 94.2125.6157.0v i j k =++;(B) 25.118.8v i j =-+;(C) 25.118.8v i j =--;(D) 31.4v k =。
02. 轮圈半径为R ,其质量M 均匀布在轮缘上,长为R ,质量为m 的均质辐条固定在轮心和轮缘间,辐条共有2N 根。
今若将辐条数减少N 根但保持轮对通过轮心,垂直于轮平面轴的转动惯量保持不变,则轮圈的质量为 【 D 】(A)12N m M +; (B) 6N m M +; (C) 23N m M +; (D) 3Nm M +。
03. 如图所示,一质量为m 的均质杆长为l ,绕铅直轴OO '成θ角转动,其转动惯量为 【 C 】(A)2112ml ;(B) 221sin 4ml θ;(C) 221sin 3ml θ; (D) 213ml 。
04. 关于刚体对轴的转动惯量,下列说法中正确的是 【 C 】 (A) 只取决于刚体的质量,与质量的空间分布和轴的位置无关; (B) 取决于刚体的质量和质量的空间分布,与轴的位置无关; (C) 取决于刚体的质量、质量的空间分布和轴的位置;(D) 只取决于转轴的位置,与刚体的质量和质量的空间分布无关。
05. 两个匀质圆盘A 和B 的密度分别为A ρ和B ρ,若A B ρρ>,但两圆盘的质量与厚度相同,如两盘对通过盘心垂直于盘面轴的转动惯量各为A J 和B J ,则 【 B 】(A) A B J J >; (B) B A J J >;(C) A B J J =; (D) A J 和B J 哪个大,不能确定。
洪嘉振《理论力学》第3版习题详解第4章

4-1C 图示长方形,OA =1,2=OB ,OC =3。
初始其连体基b e r 与参考基r e r平行。
在某瞬时矩形的姿态坐标(欧拉角)为T2π2π2π⎟⎠⎞⎜⎝⎛−=q 。
试ry r 题4-1C (1)写出该瞬时连体基b e r关于参考基r e r 的方向余弦阵;(2)画出矩形的姿态图;(3)通过欧拉角的三次转动验证结果的正确性。
解:(1)根据方向余弦阵与欧拉角姿态坐标的关系,直接可得该瞬时的长方体的方向余弦阵⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=001010100rb A (2)以上方向余弦阵的第1、2和3列分别为基b e r 的基矢量b x r 、b y r 和b z r在基r e r 上的坐标阵可知,b x r 与r z r 同向,与同向,b y r r y r b z r与r x r 反向。
根据题图中长方体顶点A 、B 与C在连体基上b e r的位置,在题解图4-1Ca-c 中找到相应的位置,构成长方体的姿态坐标为T2π2π2π⎟⎠⎞⎜⎝⎛−=q 的当前姿态。
另一种方法是直接确定长方体顶点A 、B 与C 在参考基re r 上的当前位置。
根据已知条件可以定义给定点A 、B 与C 的矢径分别为A r r 、B r r 与C r r 。
在连体基b e r上的坐标阵分别为 ()T 001=′Ar ,,()T 020=′B r ()T 300=′C r 这些点在参考基r e r上的当前瞬时坐标阵为:,,⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛100001001010100A A A z y x ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛020020001010100B B B z y x ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛003300001010100C C C z y x直接根据上式给出的长方体顶点A 、B 与C 在基r e r 上的坐标阵,在基r e r上确定它的位置。
第四章刚体运动习题详解
mg 由(3)(4)(5)得
mgR sin
1 2
J02
1 2
J2
(5)
gh 2R2
cos2
g R
sin
1 2R
.
g 2
(h
4
3R)
M J
mgR 2mR2
g 2R
( 60 )
44
棒静止于水平位置,一质量为m'的小球,以速 度u垂直落到棒的端点,且与棒作弹性碰撞. 求:碰撞后小球的回跳速度以及棒的角速度.
解: 以棒和小球为系统. 在碰撞过程中, 对轴O的 外力矩只有小球的重力矩mgL .因碰撞时间
极短, 此重力矩对时间的累积L可t 忽略L不0 计.
碰前
o
碰后
o
u
m
Mdt dL
.
o
M J
J 1 mL2
质心平动
3 mg F mac
ac r
ac
1 2
L
3g 2L
F m(g
mg ac)
1 4
mg
问:若杆从上方转下来到水平位置时
0
此时 ? F ? 23
水平位置时力矩仍为
.Fo
此时
? F ?
0
M
1 2
mgL
M J
J
1 3
mL2
3g 2L
mg
此时质心的加速度为
解:
因摩擦力产生的力矩是恒定的,故角速度均匀 减小。
0
0
t
0
0 t
dt t
0
f dS
r
σ
m πR2
R
dθ o
r
M J 1 mR2
2
13-思考题

点的运动和刚体的基本运动思考题答案13.1动点作曲线运动时,其位移、路程、弧坐标是否相同?答:位移是矢量,路程是标量,弧坐标是代数量。
位移:动点在某一时间间隔△t 内的位置改变量,是一有向线段,是矢量; 路程:动点在某一时间间隔△t 内沿轨迹走过的弧线长度,其值和坐标原点的选择无关,是标量;弧坐标:动点沿轨迹运动时,动点离开坐标原点的弧长,其值和坐标原点的选择有关,是代数量。
13.2点作曲线运动时,若其速度大小保持不变,其加速度是否一定为零?为什么?答:点作曲线运动时,若其速度大小保持不变,其加速度不一定为零。
因为如速度的方向在改变,点仍然有法向加速度,比如点作匀速圆周运动,速度一直恒定,但有法向加速度的存在。
13.3动点运动切向加速度、法向加速度和全加速度的物理意义是什么?请指出在怎样的运动中会出现下述情况:(1)0=τa ,(2)0=n a ,(3)0=τa ,0=n a ,(4)0≠τa ,0≠n a答:动点运动切向加速度改变速度的大小即代数值,法向加速度改变速度的方向,全加速度是法向加速度和切向加速度的矢量和。
(1)切向加速度为零,点作匀速运动。
(2)法向加速度为零,点作直线运动。
(3)法向加速度和切向加速度都为零,点作匀速直线运动,或静止。
(4)法向加速度和切向加速度都不等于零,点作变速曲线运动。
13.4图中所示的一动点沿螺旋线自外向内运动,所走过的弧长与时间的一次方成正比。
试问(1)该动点是越走越快还是越走越慢?(2)该动点的加速度是越来越大还是越来越小?答:设弧长方程()是常数)和式中b k b kt t S (+=,则常数,===k dtt dS t v )()( ρρτ22,0)(k v a dt t dv a n ====。
(1)因为速度大小没有改变,是常数,因此该动点没有走快也没有走慢。
(2)切向加速度等于零,法向加速度根据推导结果,由于曲率半径越来越小,法向加速度越来越大,合加速度也越来越大。
理论力学重难点及相应题解

运动学部分:一、点的运动学重点难点分析1.重点:点的运动的基本概念(速度与加速度,切向加速度和法向加速度的物理意义等);选择坐标系,建立运动方程,求速度、加速度。
求点的运动轨迹。
2.难点:运动方程的建立。
解题指导:1.第一类问题(求导):建立运动方程然后求导。
若已知点的运动轨迹,且方程易于写出时,一般用自然法,否则用直角坐标法。
根据点的运动性质选取相应的坐标系,对于自然法要确定坐标原点和正向。
不管用哪种方法,注意将点置于一般位置,而不能置于特殊位置。
根据运动条件和几何关系把点的坐标表示为与时间有关的几何参数的函数,即可得点的运动方程。
2.第二类问题(积分):由加速度和初始条件求运动方程,即积分并确定积分常数。
二、刚体的简单运动重点难点分析:1.重点:刚体平移、定轴转动基本概念;刚体运动方程,刚体上任一点的速度和加速度。
2.难点:曲线平移。
解题指导:首先正确判断刚体运动的性质。
其后的分析与点的运动分析一样分两类问题进行。
建立刚体运动方程时,应将刚体置于一般位置。
三、点的合成运动(重要)重点难点分析:1.重点:动点和动系的选择;三种运动的分析。
速度合成与加速度合成定理的运用。
2.难点:动点和动系的选择。
解题指导:1.动点的选择、动系的确定和三种运动的分析常常是同时进行的,不可能按顺序完全分开。
2.常见的运动学问题中动点和动系的选择大致可分以下五类:(1)两个(或多个)不坟大小的物体独立运动,(如飞机、海上的船舶等)对该类问题,可根据情况任选一个物体为动点,而将动系建立在另一个物体上。
由于不考虑物体的大小,因此动系(刚体)与物体(点)只在一个点上连接,可视为铰接,建立的是平移动坐标系。
(2)一个小物体(点)相对一个大物体(刚体)运动,此时选小物体为动点,动系建立在大物体上。
(3)两个物体通过接触而产生运动关系。
其中一个物体的接触只发生在一个点上,而另一个物体的接触只发生在一条线上。
选动点为前一物体的接触点,动系则建立在后一物体上。
力学第4、5章习题及参考答案

AB C力学第4、5章习题及参考答案一、选择题1.力)(12SI i t F=作用在质量kg m 2=的物体上,使物体由原点从静止开始运动,则它在s 3末的动量应为[ B ].(检测题7)1..54.--s m kg i A 1..54.-s m kg i B 1..27.--s m kg i C 1..27.-s m kg i D 解:动量定理 10323030..54612-====⎰⎰s m kg i i t dt i t dt F p1..54-=s m kg i p选B .2.沙子从h =0.8m 高处落到以3m/s 速度水平向右运动的传送带上.设沙子落向传送带时受到的冲力远大于它的重力,取g=10m/s 2,则传送带给予沙子的作用力的方向[ B ].(附加题) (A) 与水平夹角 53向下 (B) 与水平夹角53向上(C) 与水平夹角 37向上 (D) 与水平夹角37向下解:如图所示,沙子落到传送带前瞬间的速度大小10.42-==s m gh v ,方向竖直向下. 沙子落到传送带后,随传送带向右运动的速率1.3-=s m v .设时间dt 内,落到传送带的沙子质量为dm .根据动量定 理有)43.(]4(3[)(0j i dm j i dm dm dt F+=--⋅=-⋅=v v)43(j i dt dm F +=设F与x 轴正方向的夹角为θ,则o x yF F 5334arctan arctan===θ 选B . 3.力N j i F )53( +=,其作用点的矢径为m j i r )34(-=,则该力对坐标原点的力矩大小为[ B ].(附加题)(A) .m N ⋅3 (B).m N ⋅29 (C).m N ⋅19 (D).m N ⋅9解:()m N k m N k k m N j i j i F r M .29.209.)34()53(-=--=-⨯+=⨯= 力矩的大小为m kN M .29=,方向沿z 轴负方向. 选B . 4.质量为m 的质点,以不变速率v 沿图中正三角形ABC 的水平 光滑轨道运动,质点越过A角时,轨道作用于质点的冲量的 大小为[ C ].(附加题)300v (A).v m (B).v m 2 (C).v m 3 (D).v m 2解:根据动量定理有 0p p I-=由此得出的矢量三角形如图所示. v v m m I o360sin 2== 选C5.质量为g 20的子弹,以s m /400的速率沿图示方向 射入一原来静止的质量为g 980的摆球中,摆线长度不可伸缩.子弹射入后与摆球一起运动的速率为[ A ](附加题)(A)s m /4 (B)s m /8 (C)s m /2 (D)s m /7解:子弹与摆球的系统,水平方向动量守恒.()v v M m m o +=30sin 010.430sin -=+=s m Mm m ov v 选A . 6.一个转动惯量为J 的圆盘绕一固定轴转动,初角速度为0ω.设它所受阻力矩与转动角速度成正比M =ωk -(k 为正常数),它的角速度从0ω变为0ω/2所需时间是[ C ].(附加题) (A) J /2 (B) J /k (C) (J /k )ln 2 (D) J /2k 解:(1)根据转动定律βJ M =有dtd Jk ωω=- 积分:⎰⎰=-2000ωωωωd t d J k t得 kJ t 2ln = 选C .7.一根质量为m 、长度为L 的匀质细直棒,平放在水平桌面上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 点的运动和刚体基本运动 习题解答4-1 图示曲线规尺的杆长200==AB OA mm ,50====AE AC DE CD mm 。
杆OA 绕O 轴转动的规律为t 5πϕ=rad ,并且当运动开始时,角0=ϕ,求尺上D 点的运动方程和轨迹。
解: 已知t πϕ2.0=,故点D 的运动方程为 m m 2.0cos 200D t x π= m m 2.0sin 100D t y π=消去时间t 得到点D 的轨迹方程为11002002222=+DD y x (椭圆)4-2 图示AB 杆长l ,以t ωϕ=的规律绕B 点转动,ω为常量。
而与杆连接的滑块B 以t b a s ωsin +=的规律沿水平线作谐振动,a 、b 为常量。
求A 点的轨迹。
解: 采用直角坐标法,取图示直角坐标系O xy , 则A 点位置坐标为ϕsin l s x += ,ϕcos l y -=,即()t l b a x ωsin ++= t l y ωcos -=. 消去时间t 得A 点轨迹方程为:2222()1()x a y b l l-+=+.(椭圆)4-3 套筒A 由绕过定滑轮B 的绳索牵引而沿导轨上升,滑轮中心到导轨的距离为l ,如图所示。
设绳索以等速0v 拉下,忽略滑轮尺寸。
求套筒A 的速度和加速度与距离x 的关系式。
解:设0=t 时,绳上C 点位于B 处,在瞬时t ,到达图示位置 则 =++=+t v l x BC AB 022常量,将上式求导,得到管套A 的速度和加速度为220d d l x xv t x v A +-==, 3220d d x l v t v a A A -==, 负号表示A A a v ,的实际方向与x 轴相反。
4-4 如图所示,半径为R 的圆形凸轮可绕O 轴转动,带动顶杆BC 作铅垂直线运动。
设凸轮圆心在A 点,偏心距e =OA ,t ωϕ=,其中ω为常量。
试求顶杆上B 点的运动方程、速度和加速度。
解:以O 点为原点建立坐标系,由余弦定理可得2222cos AB OA OB OA OB t ω=+-⋅⋅其中OA=e ,AB=R ,设B y =OB 代入上式题 4-1图题4-2图题4-3图可以得到 0cos 222B 2B =-+-R e t ey y ω, 解出2)(4)cos 2(cos 2222B R e t e t e y --+=ωωt e R t e ωω222sin cos -+= )sin 22sin (sin d d 222te R te t e t y v B B ωωωω-+-==))sin (4sin sin 2cos (cos d d 2322222222t e R te e R t e t e t v a B B ωωωωωω-+-+-==.4-5 若将题4-4中的顶杆换成平底的物块M ,其余条件不变。
试求物块上B 点的运动方程、速度和加速度。
解:由右图所示t e R y B ωcos +=,t e dtdy v BB ωωsin -==, t e dtdv a BB ωωcos 2==. 4-6 图示a 、b 、c 三种机构,已知机构尺寸h 和杆OA 与铅直线的夹角t ωϕ=,其中ω为常量,分析并比较它们的运动:1)穿过小环M 的杆OA 绕O 轴转动,同时拨动小环沿水平导杆滑动,求小环的速度和加速度。
2)绕O 轴转动的杆OA ,推动物块M 沿水平面滑动,求物块M 上一点的速度和加速度。
3)杆OA 绕O 轴转动时,通过套在杆上的套筒M 带动杆MN 沿水平轨道运动,求MN 上一点的速度和加速度。
a) b) c)题 4-6图解:经分析图a)、b) 、c) 中M 点速度和加速度相同。
以O 为原点,水平方向为x 轴,竖直方向为y 轴。
对图在a)、 b) 、c) 中M 点都有t h h x ωϕtg tg ⋅=⋅=, th x v ωω2cos ==&, t t h x a ωωω32cos sin 2==&&.题4-4图题4-5图4-7 图示滑道连杆机构。
已知10.BO =m ;10.OA =m ,滑道连杆BC 绕轴B 按t 10=ϕ的规律转动(ϕ以rad 计)。
试求滑块A 的速度和加速度。
解: 如右图所示。
以B 为极点和BO 为极轴建立极坐标系,则A 点的运动方程为()t OA 10cos 2⋅⋅=ρ , t 10=ϕ. A 点的速度为()t OA dt d v 10sin 20⋅⋅-==ρρ,()t OA dtd v 10cos 20⋅⋅==ϕρϕ, s m 220222==+=OA v v v ϕρ.A 点的加速度为()t OA tt a 10cos 400)d d (d d 222⋅⋅-=-=ϕρρρ,()t OA tt a 10sin 4)d d (d d 12⋅⋅-==ϕρρϕ. s m 4022=+=ϕρa a a .也可以用直角坐标法求解,并求出A 点地切向和法向加速度。
4-8 如图所示,一直杆以t 0ωϕ=绕其固定端O 转动,其中0ω为常量。
沿此杆有一滑块以匀速0v 滑动。
设运动开始时,杆在水平位置,滑块在O 点,试求滑块的轨迹(以极坐标表示)。
解: 以O 为极点,水平方向为极轴,点M 的运动方程为t v 0=ρ, t 0ωϕ=消去时间t ,得到滑块以极坐标表示的轨迹方程为ϕωρ0v =.4-9 点在平面上运动,其轨迹的参数方程为()m 32sintx π=()m 34sin4ty π+=,设0=t 时,0=s ;坐标s 的起点和0=t 时点的位置一致,s 的正方向相当于x 增大的方向。
试求轨迹的直角坐标方程)( x f y =、点沿轨迹运动的方程)( g t s =、点的速度和切向加速度与时间的函数关系。
解:由运动方程消去t ,得轨迹方程:42+=x y ,(22<<-x )题4-7图题4-8图0=t 时,由 t ty x s d 3cos203d d d 22ππ⋅⋅=+=,积分得点的运动方程t s 3sin472.4π=;点的速度和加速度在轨迹切线上的投影为:()s m 3cos683.4ts v π==&, t v a t 3sin 904.4π-==& ()2s m .4-10 点沿平面曲线轨迹xe y =向x 、y 增大的方向运动,其中x 、y 的单位皆为m ,速度大小为常量m/s 12=v 。
求动点经过m 1=y 处时,其速度和加速度在坐标轴上的投影。
解:点的切向加速度和法向加速度为0==dtdva t , ρ2v a n =; 式中 yy '''+=232)1(ρ, xe x y y ==d d &, x e x y y ==22d d && 当1=y 时, 0=x ,1=y &,1=y &&有 22=ρ, oy 45arctan '==θ,2362==ρv a n s m ∴ 当m y 1=时点的速度和加速度在坐标轴上的投影为:2622x y v v v m s === 2s m 3622-=-=n x a a ,2s m 3622==n y a a 4-11 如图所示,曲柄CB 以等角速度0ω绕C 轴转动,其转动方程为t 0ωϕ=。
通过滑块B 带动摇杆OA 转动。
设h OC =,r CB =。
求摇杆转动方程。
解:由题图所示:()θϕϕtan cos sin r h r -=由此解出杆的转动方程为 tr h tr 00cos sin arctanωωθ-=4-12 已知图示机构的尺寸如下:m 2021.r AM B O A O ====;AB O O =21。
如轮1O 按t π15=ϕ(ϕ单位为rad )的规律转动,求当50.=t s 时,杆AB 上的点M 的速度和加速度。
解: 点M 与点A 有相同的速度和加速度, 即s m 42.92.015=⋅===πωr v v M A 222s m 15.4442.0)15(=⋅===πωr a a M A题4-11图题4-12图4-13 机构如图所示,假设AB 杆以匀速u 运动,开始时0=ϕ。
试求当4πϕ=时,摇杆OC 的角速度和角加速度。
解:OC 杆转角ϕ满足lvt=ϕtan , 对时间t 求导得 ϕϕ2cos l v =&,ϕϕϕ&&&2sin lv -= 将 4πϕ=代入得2vlω=, 222v l α=-.负号表示α与ϕ方向相反。
4-14 纸盘由厚度为a 的纸条卷成,令纸盘的中心不动,而以等速v 拉纸条。
求纸盘的角加速度(以半径r 的函数表示)。
解: 设纸盘在t=0时刻的初始半径为R ,则在t 时 刻纸盘减少的面积为avt r R =-22ππ ωr v = 将以上两式分别对时间求导,得av dt drr=-π2 dtd rdt dr ωω+=0 纸盘的角加速度 322rav dt d πωα==.4-15 图示滚子传送带,已知滚子的直径0.2m =d ,转速为50r/min =n 。
求钢板在滚子上无滑动运动的速度和加速度,并求在滚子上与钢板接触点的加速度。
解:设钢板上的'M 点与滚子上的M 点接触,钢板平动速度s m ndv v v M M /524.06022'=⨯===π 钢板加速度 0==dtdva滚子上M 点的加速度0M =τa , 22n Ms m 74222/.dm v a==题4-13图题4-14图题4-15图4-16 图示机构中,杆AC 以匀速0v 沿水平导槽向右运动,通过滑块A 使杆OB 绕O 轴转动。
已知O 轴与导槽相距h 。
试求杆OB 的角速度和角加速度。
解: OA 杆转角ϕ满足htv 0tan =ϕ, 对时间t 求导得ϕϕ20cos h v =&,ϕϕ2sin 0hv-=&&ϕ&其中220222cos t v h h +=ϕ,2202022sin tv h htv +=ϕ∴ 22020t v h hv +==ϕω&, 2220230)(2t v h thv +=α.4-17 小环A 沿半径为R 的固定圆环以匀速0v 运动,带动穿过小环的摆杆OB 绕O 轴转动。
试求OB 的角速度和角加速度。
若l OB =,试求B 点的速度和加速度。
解: 设角ADC 为θ,由题义知R v ⋅=θ&0,R v 0=θ& 因D 为圆心,有角AOC =12ADC ,设角AOC 为ϕ,则OB 杆的角速度为0==22v Rθωϕ=&&角加速度0=α以O 为原点取直角坐标系,B 坐标为ϕϕsin y ,cos x B B l l ==B 点的速度为l R v v Rv l R v l 2y x 2cos y ,2sin -x 02B 2B 0B0B =+=⋅=⋅=&&&&ϕϕB 点的加速度为l Rv a R v l R v l 2202B 2B 22B 220B 4y x 4sin -y ,4cos -x =+=⋅=⋅=&&&&&&&&ϕϕ题4-16图题4-17图4-18 长度为l OA =的细杆可绕O 轴转动,其端点A 紧靠在物块B 的侧面上。
