浙江省嘉兴高三高考模拟试题数学(理科)附答案
浙江省嘉兴市2024届高三第一次模拟测试数学试题含答案

嘉兴市2024届高三第一模拟测试数学试卷(答案在最后)一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的.1.已知复数220231i i i z =++++ ,则z =()A.0B.1C.D.【答案】A 【解析】【分析】化简复数z ,继而求模即可.【详解】220231i i i z =++++ ()()23420172018201920202021202220231i+i i +i i i +i i +i i +i =+++⋅⋅⋅++++15050i 1i 0=+⨯+--=则0z =,故选:A .2.已知集合πsin ,044k A k k ⎧⎫=∈≤≤⎨⎬⎩⎭N 且,则集合A 的元素个数为()A.3 B.2C.4D.5【答案】A 【解析】【分析】将k 的所有可能取值逐个代入计算即可得出集合A ,即可得集合A 的元素个数.【详解】当0k =时,πsin sin004k ==,当1k =时,ππsinsin 442k ==,当2k =时,π2ππsin sin sin 1442k ===,当3k =时,π3πsin sin 442k ==,当4k =时,π4πsinsin sinπ044k ===,故0,,12A ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭,共三个元素.故选:A.3.已知向量()2,0a =,()0,3b = ,若实数λ满足()()b a a b λ-⊥+ ,则λ=()A.49B.94C.1- D.1【答案】A 【解析】【分析】先表示出,b a a b λ-+的坐标,然后根据垂直关系得到λ的方程,由此求解出结果.【详解】因为()()2,3,2,3b a a b λλ-=-+=,且()()b a a b λ-⊥+ ,所以22330λ-⨯+⨯=,所以49λ=,故选:A.4.已知1a x x=+,e e x x b -=+,sin c x x =,则下列结论错误的为()A.[1,1]x ∃∈-,a c >B.[1,1]x ∃∈-,b c >C.[1,1]x ∃∈-,a c <D.[1,1]x ∃∈-,b c<【答案】D 【解析】【分析】举例即可判断ABC ;再根据基本不等式及三角函数的性质即可判断D.【详解】对于A ,当π6x =时,π63626π64a =+>+=,13222c =+=,此时a c >,所以[1,1]x ∃∈-,a c >,故A 正确;对于B ,当0x =时,2b =,c =b c >,所以[1,1]x ∃∈-,b c >,故B 正确;对于C ,当π6x =-时,π606πa =--<,13122c =-+=,此时a c <,所以[1,1]x ∃∈-,a c <,故C 正确;对于D ,当[]1,1x ∈-时,2e e x x b -=≥=+,当且仅当e e x x-=,即0x =时取等号,πsin 2sin 3c x x x ⎛⎫=+=+ ⎪⎝⎭,由[]1,1x ∈-,得πππ1,1333x ⎡⎤+∈-++⎢⎥⎣⎦,而ππππ1π,012332<+<<-+<,所以当π3x +,即π6x =时,πsin 2sin 23c x x x ⎛⎫=+=+= ⎪⎝⎭,所以2≤c ,当且仅当π6x =时取等号,而π06≠,所以[1,1]x ∀∈-,b c >,故D 错误.故选:D.5.已知某物种t 年后的种群数量y 近似满足函数模型: 1.4e 0.1250ety k -=⋅(00k >,当0=t 时表示2023年初的种群数量).自2023年初起,经过n 年后(N)n ∈,当该物种的种群数量不足2023年初的10%时,n 的最小值为(参考数据:ln10 2.3026≈)()A.16B.17C.18D.19【答案】D 【解析】【分析】确定2023年初的种群数量为0=t 时的函数值,根据题意可列不等式 1.4e 0.125 1.4e 00e 10%e tk k -⋅<⋅⋅,结合对数运算即可求得答案.【详解】由题意可知2023年初的种群数量为0=t 时的函数值 1.4e0e k ⋅,故令 1.4e 0.125 1.4e 00e10%e ty k k -=⋅<⋅⋅,即0.1251e 10t -<,则0.125ln10t >,ln108ln108 2.302618.42080.125t ∴>=≈⨯=,由于*n ∈N ,故n 的最小值为19,故选:D6.已知数列{}n a 满足10a =,231a a ==,令()*12N n n n n b a a a n ++=++∈.若数列{}nb 是公比为2的等比数列,则2024a =()A.2024247- B.2024237+ C.2024247+ D.2024267+【答案】B 【解析】【分析】数列{}n b 是公比为2的等比数列,可得2nn b =,则有32nn n a a +-=,累加法结合等比数列求和公式,计算2024a .【详解】11230112b a a a =++=++=,数列{}n b 是公比为2的等比数列,则2nn b =,即()13123121222n n n n n n n n n n n n n a a a a a a a a b b ++++++++-=++-++=-=-=,()()()()2024202420212021201820182015522a a a a a a a a a a =-+-+-++-+ ()67423202420242021201820152212242322221111877⎡⎤--+⎢⎥⎣⎦=+++++=+=+=- .故选:B【点睛】关键点睛:本题关键点是利用数列{}n b 的通项得到32nn n a a +-=,用累加法即可计算2024a .7.正四面体的棱长为3,点M ,N 是它内切球球面上的两点,P 为正四面体表面上的动点,当线段MN 最长时,PM PN ⋅的最大值为()A.2B.94 C.3D.52【答案】C 【解析】【分析】设四面体ABCD 的内切球球心为O ,G 为BCD △的中心,E 为CD 的中点,连接,AG BE ,则O 在AG 上,连接BO ,根据题意求出内切球的半径,当MN 为内切球的直径时,MN 最长,再化简()()PM PN PO OM PO ON ⋅=+⋅+可求得其最大值.【详解】设正四面体ABCD 的内切球球心为O ,G 为BCD △的中心,E 为CD 的中点,连接,AG BE ,则O 在AG 上,连接BO ,则AO BO =.因为正四面体的棱长为3,所以223332BG BE ==⨯⨯=,所以AG ==r ,则()222AG r r BG -=+,)22rr =+,解得4r =,当MN 为内切球的直径时MN 最长,此时0+= OM ON,2348OM ON ⎛⋅=-=- ⎪⎝⎭ ,()()PM PN PO OM PO ON⋅=+⋅+ ()2238PO PO OM ON OM ON PO =+⋅++⋅=- ,因为P 为正四面体表面上的动点,所以当P 为正四体的顶点时,PO 最长,PO的最大值为44=,所以PM PN ⋅的最大值为23348⎛-= ⎝⎭.故选:C8.已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F ,2F ,P 为椭圆上不与左右顶点重合的任意一点,I ,G 分别为12PF F ∆的内心和重心,当IG x ⊥轴时,椭圆的离心率为A.13B.12C.2D.63【答案】A 【解析】【分析】结合图像,利用P 点坐标以及重心性质,得到G 点坐标,再由题目条件GI x ⊥轴,得到I 点横坐标,然后两次运用角平分线的相关性质得到MN ME的比值,再结合MIN ∆与MPE ∆相似,即可求得I 点纵坐标,也就是内切圆半径,再利用等面积法建立关于,,a b c 的关系式,从而求得椭圆离心率.【详解】如图,令P 点在第一象限(由椭圆对称性,其他位置同理),连接PO ,显然G 点在PO 上,连接PI 并延长交x 轴于点M ,连接G I 并延长交x 轴于点N ,GI x ⊥轴,过点P 作PE 垂直于x 轴于点E,设点00(,)P x y ,12(,0),(,0)F c F c -,则00,OE x PE y ==,因为G 为12PF F ∆的重心,所以00(,)33x y G ,因为IG x ⊥轴,所以I 点横坐标也为03x ,03xON =,因为PM 为12F PF ∠的角平分线,则有01212122()()23x PF PF F N NF F O ON OF ON ON -=-=+--==,又因为12+2PF PF a =,所以可得0012,33x xPF a PF a =+=-,又由角平分线的性质可得,011223=3x a F M PF x F M PF a +=-,而12=F M c OM F M c OM +-所以得03cxOM a=,所以0()3a c x MN ON OM a -=-=,0(3)3a c x ME OE OM a-=-=,所以3IN MN a c PEMEa c -==-,即0()3a c y IN a c-=-,因为1212121211()22PF F S PF PF F F IN F F PE ∆=++=即00()11(22)(2)232a c y a c c y a c -+=-,解得13c a =,所以答案为A.【点睛】本题主要考查离心率求解,关键是利用等面积法建立关于,,a b c 的关系式,同时也考查了重心坐标公式,以及内心的性质应用,属于难题.椭圆离心率求解方法主要有:(1)根据题目条件求出,a c ,利用离心率公式直接求解.(2)建立,,a b c 的齐次等式,转化为关于e 的方程求解,同时注意数形结合.二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列说法正确的是()A.正切函数是周期函数,最小正周期为πB.正切函数的图象是不连续的C.直线()ππZ 2x k k =+∈是正切曲线的渐近线D.把ππtan ,,)2(2y x x =∈-的图象向左、右平行移动πk 个单位,就得到tan y x =π(R,π)2x x k ∈≠+的图象【答案】ABC 【解析】【分析】根据正切函数的性质,以及它的的图象的特点,即可判断A ,B 。
浙江省嘉兴市高考数学模拟试卷(理科)

浙江省嘉兴市高考数学模拟试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)复数的值是()A .B .C .D . 12. (2分) (2017高二下·鸡西期末) 设集合 A={x|-1<x<2},集合 B={x|1<x<3},则 A∪B 等于()A . {x|-1<x<3}B . {x|-1<x<1}C . {x|1<x<2}D . {x|2<x<3}3. (2分)的展开式中,二次项系数最大的项是()A .B .C .D .4. (2分)(2019·呼和浩特模拟) 过坐标轴上一点作圆的两条切线,切点分别为、 .若,则的取值范围是()A .B .C .D .5. (2分) (2016高二上·芒市期中) 如图是某校举行歌唱比赛时,七位评委为某位选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数依次为()A . 87,86B . 83,85C . 88,85D . 82,866. (2分)在中,“”是“”的()A . 充分非必要条件B . 必要非充分条件C . 充要条件D . 既不充分也不必要条件7. (2分)下列四个函数中,以π为最小正周期的偶函数是()A . y=tanxB . y=cos2xC . y=sin2xD . y=xsinx8. (2分)已知不等式表示的平面区域的面积为2,则的最小值为()A .B .C . 2D . 49. (2分) (2020高一下·林州月考) 函数(且)的图像是下列图像中的()A .B .C .D .10. (2分)抛物线的焦点为F,A、B在抛物线上,且,弦AB的中点M 在其准线上的射影为N,则的最大值为()A .B .C . 1D .二、填空题 (共5题;共6分)11. (1分) (2017高一下·天津期末) 阅读如图的程序框图,运行相应的程序,则输出a的值是________.12. (1分) (2016高三上·山西期中) 如图,若n=4时,则输出的结果为________.13. (2分)若向量,则与平行的单位向量为________,与垂直的单位向量为________14. (1分)(2017·齐河模拟) 已知Ω={(x,y)||x|≤1,|y|≤1},A是曲线y=x3与围成的区域,若向区域Ω上随机投一点P,则点P落入区域A的概率为________.15. (1分) (2016高一上·右玉期中) 已知函数f(x)= ,若方程f(x)+k=0有三个不同的解a,b,c,且a<b<c,则ab+c的取值范围是________.三、解答题 (共6题;共60分)16. (10分) (2018高一下·长春期末) 在斜中,内角所对的边分别为 ,已知.(1)证明: ;(2)若的面积为边上的中点, ,求 .17. (10分) (2017高一上·汪清期末) 如图:在四棱锥V﹣ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为的等腰三角形.(1)求二面角V﹣AB﹣C的平面角的大小;(2)求四棱锥V﹣ABCD的体积.18. (10分)在等比数列{an}中,.(1)求数列{an}的通项公式;(2)设,且{bn}为递增数列,若,求证:.19. (5分)(2017·淄博模拟) 为弘扬传统文化,某校举行诗词大赛.经过层层选拔,最终甲乙两人进入决赛,争夺冠亚军.决赛规则如下:①比赛共设有五道题;②比赛前两人答题的先后顺序通过抽签决定后,双方轮流答题,每次回答一道,;③若答对,自己得1分;若答错,则对方得1分;④先得 3 分者获胜.已知甲、乙答对每道题的概率分别为和,且每次答题的结果相互独立.(Ⅰ)若乙先答题,求甲3:0获胜的概率;(Ⅱ)若甲先答题,记乙所得分数为 X,求X的分布列和数学期望 EX.20. (15分) (2017高二下·溧水期末) 定义在区间[﹣2,t](t>﹣2)上的函数f(x)=(x2﹣3x+3)ex (其中e为自然对数的底).(1)当t>1时,求函数y=f(x)的单调区间;(2)设m=f(﹣2),n=f(t),求证:m<n;(3)设g(x)=f(x)+(x﹣2)ex,当x>1时,试判断方程g(x)=x的根的个数.21. (10分)(2020·湖南模拟) 已知函数,,且与的图象有一个斜率为1的公切线(为自然对数的底数).(1)求;(2)设函数,讨论函数的零点个数.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题;共6分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共6题;共60分) 16-1、16-2、17-1、17-2、18-1、18-2、19-1、20-1、20-2、20-3、21-1、。
浙江省嘉兴市高考数学模拟试卷(一)(理科)

浙江省嘉兴市高考数学模拟试卷(一)(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)已知集合,则()A .B .C .D .2. (2分) (2015高二上·东莞期末) 已知正方体ABCD﹣A1B1C1D1 ,下列向量的数量积不为0的是()A .B .C .D .3. (2分)已知平面向量a=(2,1),b=(x,-2),若a∥b ,则a+b等于()A . (-2,-1)B . (2,1)C . (3,-1)D . (-3,1)4. (2分)(2016·海口模拟) 已知菱形ABCD的边长为6,∠ABD=30°,点E、F分别在边BC、DC上,BC=2BE,CD=λCF.若 =﹣9,则λ的值为()A . 2B . 3C . 4D . 55. (2分) (2017高一上·桂林月考) 已知函数的定义域为,则实数的取值范围为()A .B .C .D .6. (2分) (2016高二上·成都期中) 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是()A . 24B . 20+4C . 24+4D . 20+47. (2分) (2019高三上·广东月考) 已知函数的最小正周期为,且,则()A . 在单调递增B . 在单调递增C . 在单调递减D . 在单调递减8. (2分)如图所示,程序框图的输出结果为A .B .C .D .9. (2分) (2015高二下·临漳期中) 从正方体六个面的对角线中任取两条作为一对.其中所成的角为60°的共有()A . 24对B . 30对C . 48对D . 60对10. (2分)已知函数函数,其中,若函数恰有4个零点,则的取值范围是()A .B .C .D .11. (2分) (2017高二上·西安期末) 过抛物线y2=4x的焦点作直线交抛物线于A(x1 , y1),B(x2 , y2),如果x1+x2=6,那么|AB|=()A . 8B . 10C . 6D . 412. (2分)(2018·河南模拟) 已知函数,其中是自然对数的底数,若不等式恒成立,则的最小值为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2017高二下·鞍山期中) 已知i是虚数单位,计算的结果为________.14. (1分) (2016高二上·南通开学考) 设向量、是夹角为60°的两个单位向量,向量=x•+y• ,(x、y为实数).若△PMN是以点M为直角顶点的直角三角形,则x﹣y的值为________.15. (1分) (2018高三上·杭州月考) 已知函数若函数恰有4个不同的零点,则的取值范围为________.16. (1分) (2016高二上·阳东期中) 已知A、B两地的距离是10km,B、C两地的距离是20km,现测得∠ABC=120°,则A、C两地的距离是________ km.三、解答题 (共7题;共60分)17. (10分)(2019·东北三省模拟) 已知数列是等差数列,,,数列的前项和为,且 .(1)求数列、的通项公式;(2)记中,求数列的前项和 .18. (5分) (2017高三上·威海期末) 在△ABC中,角A,B,C的对边分别为a,b,c,且满足.(Ⅰ)求角C的值;(Ⅱ)若a=5,△ABC的面积为,求sinB的值.19. (5分) (2016高二上·淄川开学考) 在某校统考中,甲、乙两班数学学科前10名的成绩如表:(I)若已知甲班10位同学数学成绩的中位数为125,乙班10位同学数学成绩的平均分为130,求x,y的值;(Ⅱ)设定分数在135分之上的学生为数学尖优生,从甲、乙两班的所有数学尖优生中任两人,求两人在同一班的概率.20. (10分)(2017·莆田模拟) 如图,在梯形ABCD中,AB∥CD,,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.(1)求证:EF⊥平面BCF;(2)点M在线段EF(含端点)上运动,当点M在什么位置时,平面MAB与平面FCB所成锐二面角最大,并求此时二面角的余弦值.21. (10分)(2018·上饶模拟) 已知函数在处的切线方程为.(1)求实数的值;(2)设,若,且对任意的恒成立,求的最大值.22. (10分)(2018·株洲模拟) 在直角坐标系中,曲线的参数方程为: ,以坐标原点为极点,以轴正半轴为极轴,建立极坐标系.(1)若把曲线上的点的横坐标不变,纵坐标伸长到原来的2倍,得到曲线,求的极坐标方程;(2)直线的极坐标方程是 ,与曲线交于两点,求三角形的面积.23. (10分)受市场的影响,三峡某旅游公司的经济效益出现了一定程度的滑坡,现需要对某一景点进行改造升级,提高旅游增加值.经过市场调查,旅游增加值y万元与投入x万元之间满足y= x﹣ax2﹣lnx+ln10,且∈[1,+∞).当x=10时,y=9.2.(1)求y=f(x)的解析式和投入x的取值范围:(2)求旅游增加值y取得最大值时对应的x的值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共60分) 17-1、17-2、18-1、19-1、20-1、20-2、21-1、21-2、22-1、22-2、23-1、23-2、。
浙江省嘉兴市2024年数学(高考)部编版模拟(自测卷)模拟试卷

浙江省嘉兴市2024年数学(高考)部编版模拟(自测卷)模拟试卷一、单项选择题(本题包含8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题已知向量,则等于( ).A .B .6C .D .18第(2)题在中,,.若点满足,则( )A.B .C .D .第(3)题已知复数的模长为1,则的模长是( )A.1B .C .2D .第(4)题为得到函数的图象,只需将函数的图像A .向左平移个长度单位B .向右平移个长度单位C .向左平移个长度单位D .向右平移个长度单位第(5)题已知点在抛物线:()上,为的焦点,直线与的准线相交于点,则( )A.B .C .D .第(6)题已知等差数列的前n 项和为,若,则一定有( )A .B .C .D .第(7)题复数在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限第(8)题已知全集,集合,集合,则图中阴影部分所表示的集合为( )A .B .C .D .二、多项选择题(本题包含3小题,每小题6分,共18分。
在每小题给出的四个选项中,至少有两个选项正确。
全部选对的得6分,选对但不全的得3分,有选错或不答的得0分) (共3题)第(1)题已知曲线,则下面结论正确的是( )A .把曲线上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线问石平移个单位长度,得到曲线B .把曲线上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C .把曲线向左平移个单位长度,再把得到的曲线上各点的横坐标伸长到原来的2倍,纵坐标不变,得到曲线D .把曲线向左平移个单位长度,再把得到的曲线上各点的横坐标伸长到原来的2倍,纵坐标不变,最后把得到的曲线向右平移个单位长度,得到曲线第(2)题在正方体中,点P 在正方形内,且不在棱上,则下列说法错误的是( )A.在正方形内一定存在一点Q,使得B.在正方形内一定存在一点Q,使得C.在正方形内一定存在一点Q,使得平面平面D.在正方形内一定存在一点Q,使得平面第(3)题已知双曲线,则不因的变化而变化的是()A.顶点坐标B.渐近线方程C.焦距D.离心率三、填空(本题包含3个小题,每小题5分,共15分。
2021-2022学年浙江省嘉兴市大桥镇中学高三数学理模拟试卷含解析

2021-2022学年浙江省嘉兴市大桥镇中学高三数学理模拟试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 一个算法的程序框图如下,则其输出结果是()A.B.C.D.0参考答案:B由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量的值,是以为周期的周期函数,故又故选B.2. 函数,当时,,则的最小值是()A.1 B.2 C.D.参考答案:B因为,所以依题意,由即,得所以所以,整理得又,所以所以,所以的最小值为2.3. 已知向量,且,则的值为A.B.C.5 D.13参考答案:B4. 下图是一个空间几何体的三视图,则该几何体的表面三角形中为直角三角形的个数为()A.1 B.2 C.3 D.4参考答案:D由三视图可知,该几何体为一个如图所示的三棱锥,其中底面,底面是一个三边分别为的三角形,,由,可得,又底面,,平面,,因此该几何体的表面三角形中为直角三角形的个数为,故选D.5. 设是等差数列的前项和,,则参考答案:B略6. 对四组数据进行统计,获得以下散点图,关于其相关系数比较,正确的是( )相关系数为相关系数为相关系数为相关系数为A. B.C. D.参考答案:A7. 直线和圆的关系是()A.相离B.相交C.相交或相切D.相切参考答案:B略8. 设,(为虚数单位),则(A)(B)(C)或(D)不存在参考答案:B9.参考答案:D10. 函数的最小正周期和最大值分别为()A. B. C.,1 D.,参考答案:C二、填空题:本大题共7小题,每小题4分,共28分11. 如果执行下图所示的框图,输入,则输出的数等于()A .B .C .D .参考答案:A 略12. 已知空间一点A 的坐标是(5,2,﹣6),P 点在x 轴上,若PA=7,则P 点的坐标是 . 参考答案:(8,0,0)或(2,0,0) 考点: 空间中的点的坐标. 专题: 空间位置关系与距离.分析: 设出P 的坐标,利用PA=5,求解即可.解答: 解:设P 的坐标是(a ,0,0),点A 的坐标为(5,2,﹣6),PA=7, ∴ 解得a=8或2∴P 点的坐标是:(8,0,0)或(2,0,0) 故答案为:(8,0,0)或(2,0,0)点评: 本题考查空间两点间的距离公式的应用,考查计算能力. 13. 已知F 是双曲线的左焦点,过点F 倾斜角为30°的直线与C 的两条渐近线依次交于A ,B 两点,若,则C的离心率为.参考答案:214. 在△ABC 中,a 、b 、c 分别是∠A、B 、C 对应的边长.若cosA+sinA ﹣=0,则= .参考答案:【考点】HP :正弦定理.【分析】利用三角函数恒等变换的应用化简已知可得cos (A ﹣B )+sin (A+B )=2,由cos (A ﹣B ),sin (A+B )的范围,解得cos (A ﹣B )=1,sin (A+B )=1,解得A=B=45°,C=90°,利用正弦定理化简可得=,即可得解.【解答】解:在△ABC 中,∵cosA+sinA﹣=0,∴(cosA+sinA )(cosB+sinB )=2,∴cosAcosB+sinAsinB+sinAcosB+sinBcosA=2, ∴cos(A ﹣B )+sin (A+B )=2,∵cos(A ﹣B )∈[﹣1,1];sin (A+B )∈[﹣1,1], ∴当二者和为2时,只能是二者均为1, 即cos (A ﹣B )=1,sin (A+B )=1, ∵A、B 、C 为△ABC 内角, ∴A﹣B=0,A+B=90°, ∴解得A=B=45°,∴C=180°﹣45°﹣45°=90°, ∴==+=.故答案为:.15. 某几何体的三视图如图所示,则该几何体的体积为______.参考答案:【分析】由三视图可知,该几何体由上部四棱柱、下部圆柱组成的组合体,由柱体体积公式计算可得答案. 【详解】由三视图可知,该几何体由上部四棱柱、下部圆柱组成的组合体, 四棱柱的底面为边长为3的正方形,高为1,故体积为:,圆柱的底面圆直径为1,高为2,故体积为:,所求体积为,故答案为:【点睛】本题以三视图为载体考查几何体的体积,解题的关键是对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系,然后结合相应的公式求解.16. 不等式的解集是,则= 。
浙江省嘉兴市(新版)2024高考数学部编版模拟(综合卷)完整试卷

浙江省嘉兴市(新版)2024高考数学部编版模拟(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题若函数的定义域为,则函数的定义域是()A.B.C.D.第(2)题设集合,,则()A.B.C.D.第(3)题如图所示,是某三棱锥的三视图(由左至右,由上至下依次是主视图、左视图、俯视图),则该三棱锥的体积为()A.4B.C.D.1第(4)题已知双曲线的离心率为,则()A.B.C.D.第(5)题长方体的8个顶点在同一个球面上,且AB=2,AD=,,则顶点A、B间的球面距离是A.B.C.D.第(6)题已知F1,F2是双曲线的左右焦点,若直线与双曲线C交于P,Q两点,且四边形F1PF2Q是矩形,则双曲线的离心率为A.B.C.D.第(7)题已知体积为的球与正四棱锥的底面和4个侧面均相切,已知正四棱锥的底面边长为. 则该正四棱锥体积值是()A.B.C.D.第(8)题椭圆的离心率为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知R,复数,,则( )A .,B .若,时,C .若,,,则D .若,则第(2)题已知a ,b 都是正实数,则下列不等式中恒成立的是( )A.B.C.D.第(3)题在中,内角所对的边分别为,若的面积为16,则下列结论正确的是( )A.是直角三角形B.是等腰三角形C.的周长为32D.的周长为三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知四个数,,,的平均数为,则这四个数的中位数是________.第(2)题已知定义在上的函数的导函数是,对于任意的实数x 都有,当时,恒成立,则不等式的解集为______.第(3)题曲线在点处的切线方程为__________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知数列,,.(1)求证:数列是等差数列.(2)设,求证:数列的前n 项和.第(2)题已知在中,,(1)求A ;(2)若点D 是边BC 上一点,,△ABC 的面积为,求AD 的最小值.第(3)题如图,在四棱锥P ﹣ABCD 中,平面PAD ⊥平面ABCD ,PA =PD ,AB =AD ,PA ⊥PD ,AD ⊥CD ,∠BAD =60°,M ,N 分别为AD ,PA 的中点.(1)证明:平面BMN ∥平面PCD ;(2)若,求平面BMN 与平面BCP 所成锐二面角的余弦值.第(4)题已知抛物线,直线与的交点为(分别在x轴的上方和下方),与x轴的交点为,原点在以线段为直径的圆M上.(1)求a的值;(2)若,①求直线l的方程;②当过点的圆与直线相切时,求圆心的坐标.第(5)题若函数有且仅有一个极值点,函数有且仅有一个极值点,且,则称与具有性质.(1)函数与是否具有性质?并说明理由.(2)已知函数与具有性质.(i)求的取值范围;(ii)证明:.。
2020年浙江省嘉兴市新世纪学校高三数学理模拟试卷含解析
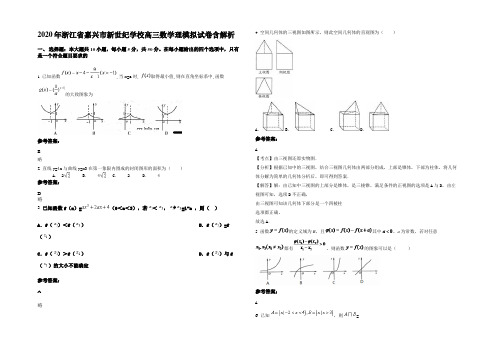
2020年浙江省嘉兴市新世纪学校高三数学理模拟试卷含解析一、 选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知函数,当x=a 时,取得最小值,则在直角坐标系中,函数的大致图象为参考答案:B 略2. 直线y=4x 与曲线y=x3在第一象限内围成的封闭图形的面积为( ) A . 2 B . 4 C . 2 D . 4 参考答案: D 略3. 已知函数f (x )=(0<a <3),若<,+=1-a ,则( )A .f ()<f ()B .f ()=f()C .f ()>f () D .f ()与f()的大小不能确定参考答案: A 略4. 空间几何体的三视图如图所示,则此空间几何体的直观图为( )A .B .C .D .参考答案:A【考点】由三视图还原实物图.【分析】根据已知中的三视图,结合三视图几何体由两部分组成,上部是锥体,下部为柱体,将几何体分解为简单的几何体分析后,即可得到答案.【解答】解:由已知中三视图的上部分是锥体,是三棱锥,满足条件的正视图的选项是A 与D ,由左视图可知,选项D 不正确,由三视图可知该几何体下部分是一个四棱柱 选项都正确, 故选A . 5. 函数的定义域为R ,且其中,a 为常数,若对任意都有,则函数的图象可以是( )参考答案:A6. 已知,则=A. B.C. D.参考答案:C略7. 已知命题:①函数y=2x(﹣1≤x≤1)的值域是[,2];②为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin2x图象上的所有点向右平移个单位长度;③当n=0或n=1时,幂函数y=x n的图象都是一条直线;④已知函数f(x)=,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是(2,4).其中正确的命题是()A.①③B.①④C.①③④D.①②③④参考答案:B【考点】命题的真假判断与应用.【分析】①根据指数函数的单调性进行判断.②根据三角函数的图象关系进行判断.③根据幂函数的定义和性质进行判断.④根据函数与方程的关系,利用数形结合进行判断.【解答】解:①∵y=2x是增函数,∴当﹣1≤x≤1时,函数的值域是[,2];故①正确,②函数y=sin2x图象上的所有点向右平移个单位长度,则y=sin2(x﹣)=sin(2x﹣,则无法得到函数y=sin(2x﹣)的图象,故②错误,③当n=0时,y=x0=1,(x≠0)是两条射线,当n=1时,幂函数y=x的图象都是一条直线;故③错误,④作出函数f(x)的图象如图,∴f(x)在(0,1]上递减,在(1,2)上递增,在(2,+∞)单调递减,又∵a,b,c互不相等,∴a,b,c在(0,2]上有两个,在(2,+∞)上有一个,不妨设a∈(0,1],b∈(1,2),c∈(2,+∞),则log2a+log2b=0,即ab=1,则abc的取值范围是c的取值范围,∵由﹣x+2=0,得x=4,则2<c<4,则2<abc<4,即abc的取值范围是(2,4).故④正确,故选:B.8. 设函数的导函数为,对任意x R都有成立,则()A. B.C. D. 与的大小不确定参考答案:【知识点】导数的应用. B12【答案解析】A 解析:设,则在x R上恒成立,所以是R上的减函数,所以,即,故选 A.【思路点拨】构造新函数,利用已知条件判断其单调性,从而得正确选项.9. 已知某几何体的三视图如图所示,则该几何体的体积为A. B.C. D.参考答案:【知识点】三视图G2B解析:根据三视图可知该几何体为一个四棱锥和三棱锥的组合体,如图所示,且平面,平面,底面为正方形,则有,所以和到平面的距离相等,且为,故,,则该几何体的体积为.【思路点拨】由三视图可知该几何体为一个四棱锥和三棱锥的组合体,分别按照四棱锥和三棱锥的体积公式求解即可.10. 设函数f(x)定义为如下数表,且对任意自然数n均有若,则的值为A.1B. 2 C .4 D.5参考答案:D略二、填空题:本大题共7小题,每小题4分,共28分11. 已知点P在圆x2+y2=1上运动,则P到直线3x+4y+15=0的距离的最小值为.参考答案:2略12. 若sin=,且,则sin 2的值为.参考答案:13. 已知数列满足,且对任意的正整数都有,若数列的前项和为,则= 。
浙江省嘉兴市高考数学一模试卷(理科)

浙江省嘉兴市高考数学一模试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2020·包头模拟) 设集合,则()A .B .C .D .2. (2分) (2019高二下·吉林期末) 已知复数为纯虚数,则()A . 0B . 3C . 0或3D . 43. (2分)执行如图所示的程序框图,若输出b的值为31,则图中判断框内①处应填()A . 3B . 4C . 5D . 64. (2分) (2018高一下·汕头期末) 一只蚂蚁在边长为4的正三角形区域内随机爬行,则它在离三个顶点距离都大于的区域内的概率为()A .B .C .D .5. (2分) (2019高三上·葫芦岛月考) 函数的图象大致为()A .B .C .D .6. (2分) (2016高二上·上杭期中) 数列{an}满足a1=3,an﹣an•an+1=1,An表示{an}前n项之积,则A2016的值为()A . ﹣B .C . ﹣1D . 17. (2分)(2018·重庆模拟) 已知向量,满足且,若向量在向量方向上的投影为,则()A .B .C .D .8. (2分)若函数的部分图象如图所示,则有()A .B .C .D .9. (2分)已知函数f(x)的图象关于y轴对称,并且是[0,+∞)上的减函数,若f(lgx)>f(1),则实数x的取值范围是()A .B .C .D . (0,1)10. (2分)(2017·衡阳模拟) 已知对任意平面向量 =(x,y),把绕其起点沿逆时针旋转θ角得到向量 =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转角θ得到点P,设平面内曲线C上的每一点绕原点逆时针方向旋转后得到点的轨迹是曲线x2﹣y2=2,则原来曲线C的方程是()A . xy=﹣1B . xy=1C . y2﹣x2=2D . y2﹣x2=111. (2分)过双曲线-=1的一个焦点F作一条渐线的垂线,垂足为点A,与另一条渐近线交于点B,若=2,则此双曲线的离心率为()A .B .C . 2D .12. (2分) (2015高二上·福建期末) 已知集合D= ,有下面四个命题:p1:∃(x,y)∈D,≥3 p2:∃(x,y)∈D,<1p3:∀(x,y)∈D,<4 p4:∀(x,y)∈D,≥2其中的真命题是()A . p1 , p3B . p1 , p4C . p2 , p3D . p2 , p4二、填空题 (共4题;共4分)13. (1分)(2017·抚顺模拟) 若实数x、y满足约束条件,则z=4x+y的最大值为________14. (1分)(2017·万载模拟) 若m= (6x2+tanx)dx,且(2x+ )m=a0+a1x+a2x2+…+amxm ,则(a0+a2+…+am)2﹣(a1+..+am﹣1)2的值为________.15. (1分)(2017·巢湖模拟) 已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A ﹣BCD的外接球,BC=3,AB=2 ,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是________.16. (1分)(2017·上饶模拟) 已知△ABC外接圆半径是2,,则△ABC的面积最大值为________三、解答题 (共7题;共65分)17. (10分)(2014·辽宁理) 在△ABC中,内角A、B、C的对边分别为a,b,c,且a>c,已知•=2,cosB= ,b=3,求:(1) a和c的值;(2) cos(B﹣C)的值.18. (10分)近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.(1)大气污染可引起心悸、呼吸困难等心肺疾病. 为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:患心肺疾病不患心肺疾病合计男20525女101525合计302050问有多大的把握认为是否患心肺疾病与性别有关?(2)空气质量指数PM2.5(单位:μg/ )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重. 某市在2016年年初着手治理环境污染,改善空气质量,检测到2016年1~5月的日平均PM2.5指数如下表:月份x12345PM2.5指数y7976757372试根据上表数据,求月份x与PM2.5指数y的线性回归直线方程,并预测2016年8月份的日平均PM2.5指数 (保留小数点后一位).19. (5分)如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE.20. (5分)(2020·吴江模拟) 在极坐标系中,直线的极坐标方程为.以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C的参数方程为(为参数).求直线l与曲线C交点P的直角坐标.21. (15分)(2017·淮北模拟) 已知函数发f(x)=(x+1)lnx﹣ax+2.(1)当a=1时,求在x=1处的切线方程;(2)若函数f(x)在定义域上具有单调性,求实数a的取值范围;(3)求证:,n∈N* .22. (10分)(2018·银川模拟) 选修4-4:极坐标与参数方程在极坐标系中,已直曲线 ,将曲线C上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C1 ,又已知直线,且直线与C1交于A、B两点,(1)求曲线C1的直角坐标方程,并说明它是什么曲线;(2)设定点 , 求的值;23. (10分)(2019·广西模拟) [选修4-5:不等式选讲]已知函数f(x)=|x+3|-2.(1)解不等式f(x)<|x-1|;(2)若x∈R,使得f(x)≥|2x-1|+b成立,求实数b的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共65分) 17-1、17-2、18-1、18-2、19-1、20-1、21-1、21-2、21-3、22-1、22-2、23-1、23-2、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
嘉兴高三三模数学理科试卷一.选择题(本题共10个小题,每题5分,共50分)1.设集合{1,2,3,4,5},{1,2,3},{2,4}U A B ===,则()U A C B I ( ) A .{1,3} B .{2,4} C .{1,2,3,5} D .{2,5} 2.若某多面体的三视图如图所示,则此多面体的体积是( )A .2B .4C .6D .123.已知等比数列{}n a 中,12345640,20a a a a a a ++=++=,则前9 项之和等于( )A .50B .70C .80D .904.已知m a 、都是实数,且0a ≠,则“{,}m a a ∈-”是“||m a =”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 5.右图所示的程序框图中的输出结果是 ( )A .2B .4C .8D .166.已知,m n 是两条不同直线,,,αβγ是三个不同平面,则下列正确的是( ) A .若m ∥,n α∥α,则m ∥n B .若,αγβγ⊥⊥,则α∥β C .若m ∥,n α∥β,则α∥β D . 若,m n αα⊥⊥,则m ∥n7.设向量,a b r r 满足||1,||3,()0a a b a a b =-=⋅-=r r r r r r ,则|2|a b +r r=( )A .2B .23C .4D .438.设变量,x y 满足约束条件22022010x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩,则11y s x +=+的取值范围是( )A .3[1,]2B .1[,1]2C .[1,2]D .1[,2]29.在正实数集上定义一种运算*:当a b ≥时,a *3b b =;当a b <时,a *2b b =, 则满足3*27x =的x 的值为( )A .3B .1或9C .1或2D .3或3310.过双曲线22221(0,0)x y a b a b-=>>的右焦点F 作圆222x y a +=的切线FM (切点为M ),交y 轴于点P ,若M 为线段FP 的中点, 则双曲线的离心率是( )(A) 2(B)3(C) 2 (D)5正视图3 22 侧视图俯视图2开始 S =1,k=1 结束 是 否S =S ×2 输出S k =k+1输入n=3 k ≤n二.填空题(本题共7个小题,每题4分,共28分) 11.曲线sin cos y x x =+在点(,1)2π处的切线斜率为 ▲ .12.已知复数1322z i =-+,满足210az bz ++=(a,b 为实数),则a b += ▲ . 13. 平面上两定点A,B 之间距离为4,动点P 满足2PA PB -=,则点P 到AB 中点的距离的最小值为 ▲ .14. 随机变量X 的分布列如下:其中a b c ,,成等差数列,若12EX =,则DX 的值是 ▲ .15.已知圆22:2O x y +=,圆22:(1)(3)1M x y -+-=,过圆M 上任一点P 作圆O 的切线PA ,若直线PA 与圆M 的另一个交点为Q ,则当弦PQ 的长度最大时,直线PA 的斜率是▲ .16.已知关于x 的方程22||90x a x a ++-=只有一个实数解,则实数a 的值为 ▲ . 17. 形如45132这样的数叫做“五位波浪数”,即十位数字、千位数字均比它们各自相邻的数字大,则由数字0,1,2,3,4,5,6,7可构成无重复数字的“五位波浪数”的个数为 . ▲ .三.解答题(本题共5题,满分72分)18.(本题满分14分)已知1(sin ,)2m A =u r 与(3,sin 3cos )n A A =+r 共线,其中A 是△ABC 的内角.(1)求角A 的大小;(2)若BC =2,求△ABC 面积S 的最大值,并判断S 取得最大值时△ABC 的形状.19.(本题满分14分)已知数列{}n a 满足113,33(*)nn n a a a n N +=-=∈,数列{}n b 满足3n n n b a -=.(1)求证:数列{}n b 是等差数列;(2)设3123452n n a a a a S n =+++++L ,求满足不等式2111284n n S S <<的所有正整数n 的值.20.(本题满分14分)如图,已知AB ⊥平面ACD ,DE ∥AB ,ACD ∆是正三角形,且2AD DE AB ==.(1)设M 是线段CD 的中点,求证:AM ∥平面BCE ; (2)求直线CB 与平面ABED 所成角的余弦值.21.(本题满分15分)如图,已知直线1:2(0)l y x m m =+<与抛物线21:(0)C y ax a =>和圆222:(1)5C x y ++=都相切,F 是1C 的焦点.(1)求m 与a 的值;(2)设A 是1C 上的一动点,以A 为切点作抛物线1C 的切线l ,直线l 交y 轴于点B ,以,FA FB 为邻边作平行四边形FAMB ,证明:点M 在一条定直线上;(3)在(2)的条件下,记点M 所在的定直线为2l ,直线2l 与y 轴交点为N ,连接MF 交抛物线1C 于,P Q 两点,求NPQ ∆的面积S 的取值范围.22。
(本题满分15分)已知函数()ln f x x x x =+. (1)求函数()f x 的图像在点(1,1)处的切线方程;(2)若k ∈Z ,且()(1)k x f x -<对任意1x >恒成立,求k 的最大值; (3)当4n m >≥时,证明()()mnn m mn nm >.参考答案:1-10 AABBC DBDDA 11. -1 12. 2 13. 1 14.51215. 1或-7 16. 3 17. 721 18.解:(1)因为m //n ,所以3sin (sin 3cos )02A A A ⋅+-=.所以31cos 23sin 2022A A -+-=,即31sin 2cos 212A A -=,即 ()πsin 216A -=. …………………4分因为(0,π)A ∈ , 所以()ππ11π2666A -∈-,. 故ππ262A -=,π3A =.……………7分 (2)由余弦定理,得 224b c bc =+-.又31sin 2ABC S bc A ∆==, …………………9分而222424b c bc bc bc bc +⇒+⇒≥≥≤,(当且仅当b c =时等号成立) …………11分所以331sin 432ABC S bc A ∆===. ………………………12分当△ABC 的面积取最大值时,b c =.又π3A =,故此时△ABC 为等边三角形.…14分19.(1)证明:由3n n n b a -=得3n n n a b =,则1113n n n a b +++=。
代入133n n n a a +-=中,得111333n n nn n b b +++-=,即得113n n b b +-=。
所以数列{}n b 是等差数列。
………………6分 (2)解:因为数列{}n b 是首项为11131b a -==,公差为13等差数列,则121(1)33n n b n +=+-=,则13(2)3n n n n a b n -==+⨯。
………………8分从而有132n n a n -=+,故21312133113333452132n n n n n a a a a S n ---=++++=++++==+-L L 。
…………11分 则223113131n n n nn S S -==-+,由2111284n n S S <<,得111128314n <<+。
即33127n<<,得14n <≤。
故满足不等式2111284n n S S <<的所有正整数n 的值为2,3,4。
………………14分20(I )证明:取CE 中点N,连接MN,BN则MN ∥DE ∥AB 且MN=21DE=AB∴四边形ABNM 为平行四边形∴AM ∥BN ………....4分 ∴AM ∥平面BCE ………………………....6分 (Ⅱ)解:取AD 中点H,连接BH ,∵ACD ∆是正三角形, ∴CH ⊥AD …....8分 又∵⊥AB 平面ACD ∴CH ⊥AB ∴CH ⊥平面ABED ....10分∴∠CBH 为直线 CB 与平面ABED 所成的角………....12分设AB=a,则AC=AD=2a , ∴BH=2a BC=5acos ∠CBH=51052==BC BH ………………....14分HDEBAN DEB A21.22。
(1)解:因为()ln 2f x x '=+,所以()12f '=,函数()f x 的图像在点(1,1)处的切线方程21y x =-;…………3分(2)解:由(1)知,()ln f x x x x =+,所以()(1)k x f x -<对任意1x >恒成立,即ln 1x x xk x +<-对任意1x >恒成立.…………4分 令()ln 1x x x g x x +=-,则()()2ln 21x x g x x --'=-,……………………4分 令()ln 2h x x x =--()1x >,则()1110x h x x x-'=-=>, 所以函数()h x 在()1,+∞上单调递增.………………………5分因为()()31ln30,422ln 20h h =-<=->,所以方程()0h x =在()1,+∞上存在唯一实根0x ,且满足()03,4x ∈.当01()0x x h x <<<时,,即()0g x '<,当0()0x x h x >>时,,即()0g x '>,…6分 所以函数()ln 1x x xg x x +=-在()01,x 上单调递减,在()0,x +∞上单调递增.所以()()()()()000000min001ln 123,411x x x x g x g x x x x ++-====∈⎡⎤⎣⎦--.…………7分所以()()0min 3,4k g x x <=∈⎡⎤⎣⎦.故整数k 的最大值是3.………………………8分 (3)由(2)知,()ln 1x x xg x x +=-是[)4,+∞上的增函数,……………9分所以当4n m >≥时,ln ln 11n n n m m mn m ++>--.…………………10分 即()()()()11ln 11ln n m n m n m -+>-+.整理,得()ln ln ln ln mn n m m mn m n n n m +>++-.………………11分 因为n m >, 所以ln ln ln ln mn n m m mn m n n +>+.…………………12分 即ln ln ln ln mnm mn n nm m n +>+.即()()ln ln mn m mn n n m m n >.………………13分所以()()mnn m mn nm >.………………………14分。
