微积分基本定理同步练习
数学选修2-2微积分基本定理练习题含答案

(2)
(3)
(4)
故
40.
【答案】
解: 原式
.
为纯虚数,
∴ 解得 ,
∴ ,
∴ .
【考点】
复数的模
微积分基本定理
复数代数形式的混合运算
复数的基本概念
【解析】
(1)利用导数的运算法则和微积分基本定理即可得出;
(2)利用复数的运算法则和纯虚数的意义即可得出.
【解答】
解: 原式
.
为纯虚数,
∴ 解得 ,
∴
(2)
【考点】
微积分基本定理
【解析】
(1)根据二倍角的余弦公式,得 ,因此将原式化为 在 上的定积分值,结合积分计算公式,不难算出原式的值;
(2)函数 在区间 上表达式为 ,在区间 上表达式为 .因此将所求积分转化为 在区间 上的积分值,加上 在区间 上的积分值,所得的和即为原式的值.
【解答】
解:(1)∵ ,
解:由于 ,定义当 时, ,
则
,
故答案为 .
19.
【答案】
【考点】
微积分基本定理
【解析】
求出原函数,即可求得定积分.
【解答】
解:
.
故答案为: .
20.
【答案】
【考点】
微积分基本定理
【解析】
利用积分的运算公式和积分的几何意义进行求值.
【解答】
解:因为 是奇函数,所以根据奇函数的积分性质可知, .
表示圆心在原点半径为 的上半圆,此时半圆的面积为 ,
1.
【答案】
B
【考点】
微积分基本定理
【解析】
由于 为 的一个原函数即 ,根据 公式即可求出值.
《微积分基本定理与应用》同步练习1

例2图 A
例 3图
BD 及 S1 的值;
(3)设由抛物线 C、直线 l1、l 2 所围成的图形的面积为 【课内练习 】
5
1. (2 x 4) dx = 0
S2,求证: S1∶ S2 的值为与 a 无关的常数.
(
)
A.5
B。4
C。 3
(
)
7. 设某物体一天的温度
T 是时间
t 的函数,
T
(t)=
at
3
+bt
2
+
ct
+
d(a
≠
0),其中温度的单位是
C,
时间的单位是小时, t=0 表示 12∶ 00 ,t 取正值表示 12 ∶ 00 以后.若测得该物体在 8∶ 00 的温度
为 8 C , 12∶ 00 的温度为 60 C , 13∶ 00 的温度为 58 C ,且已知该物体的温度在 8∶ 00 和
x
2
1
1
4
3
C。
D。
2
2
6
2
8 B 10
A . 21
B 。 22
C。 23
12 D。 24
3. 下列命题:
x
①若 f(x) 是定义在 R 上的奇函数,则
f ( t)dt 为 R 上的偶函数;
0
(
)
(
)
a
aT
②若 f(x) 是周期为 T (> 0)的周期函数,则
f ( x)dx
f ( x) dx ;
0
o
与抛物线 C2 所围成的图形面积为 9 a3 ,求直线 l 的方程.
1 定积分的概念、微积分基本定理(重点练)高二数学(理)十分钟同步课堂专练(人教A版选修2-2)

1.5~1.6 定积分的概念、微积分基本定理重点练一、单选题1.)10x dx =⎰( )A .22π+B .12π+ C .122π-D .142π- 2.已知函数()e3211(1)2f x x dx x f x x'=⋅--⎰,则()()11f f '+=( ) A .-1B .1C .-2D .23.已知311tan 4e dx x πα⎛⎫+=- ⎪⎝⎭⎰,则2sin cos cos sin αααα+=-( ) A .4-B .4C .5D .5-4.已知()()ln xxf x e e -=+,201sin 2a xdx π=⎰, 1.112b ⎛⎫= ⎪⎝⎭,2log 3c =,则下列选项中正确的是( ) A .()()()f a f b f c >> B .()()()f a f c f b >> C .()()()f c f a f b >>D .()()()f c f b f a >>二、填空题5.011edx x-+=⎰⎰______________.6.如图,在边长为1的正方形中随机撒一粒黄豆,则它落在阴影部分的概率为_______.三、解答题7.计算下列各式的值.(1)()0sin cos d x x x π-⎰;(2)1x⎰.参考答案1.【答案】D【解析】由定积分的运算法则,可得)111()x dx dx x dx =+-⎰⎰⎰,又由1dx ⎰相当于是以(1,0)为圆心,以1为半径的圆的面积的14,如图所示,可得104dx π=⎰, 又因为021011()1()|22x d x x --=-=⎰,所以)1110001()42x dx dx x dx π=+-=-⎰⎰⎰. 故选D.2.【答案】A【解析】因为e111ln |1edx x x ==⎰,所以()()3212f x x x f x '=--,所以()()232'12f x x xf '=--,令1x =,得()()13212f f ''=--,解得1(1)3f '=,所以321()23f x x x x =--,14(1)1233f =--=-, ()()1411133f f ⎛⎫'+=+-=- ⎪⎝⎭,故选A . 3.【答案】D【解析】由()()()331311ln ln ln13e e dx x C e C C x ⎰=+=+-+=,则tan 1tan 341tan πααα+⎛⎫+==- ⎪-⎝⎭,则tan 2α=,由2sin cos 2tan 15cos sin 1tan αααααα++==---故选D. 4.【答案】C【解析】()()ln xxf x e e-=+,x ∈R ,则()()()ln xx f x ee f x --=+=,所以()f x 为R 上的偶函数,并且()x xx xe ef x e e---'=+,则[)0,x ∈+∞时,()0f x '≥,当且仅当0x =时,“=”成立, 所以()f x 在[)0,x ∈+∞上单调递增,在(],0x ∈-∞上单调递减,()220111sin cos 222a xdx x ππ==-=⎰1.111110222b ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭,221log log 332c ==-, 又()22111log 3log 3222f c f f f ⎛⎫⎛⎫⎛⎫=-=> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以()()()f c f a f b >>.故选C 5.【答案】21π+【解析】11edx x⎰=ln 1e x ln ln1101e =-=-=,因为2-⎰表示的是圆224x y +=在x 轴及其上方的面积,所以2-⎰21222ππ=⨯⨯=,所以11edx x⎰2-+⎰=12π+.故填21π+. 6.【答案】13【解析】由题意,结合定积分可得阴影部分的面积为31120021(1()|33S dx x x ==-=⎰, 由几何概型的计算公式可得,黄豆在阴影部分的概率为113113p ==⨯. 故填137.【答案】(1) 2;(2) π【解析】(1)由题得()0sin cos d (cos sin )|(cos sin )(cos 0sin 0)x x x x x ππππ-=--=-----⎰=10102-++=;(2)令22(1)4(13,0)y x y x y =∴-+=≤≤≥,因为1x ⎰等于1,3,x x x ==轴和曲线ADB 所围成的曲边梯形的面积,如图扇形ACB , 扇形ACB 的面积为212=4ππ⨯⨯,所以1x π=⎰.。
微积分同步练习册(各节练习参考答案)

各章同步练习参考答案第二章 极限与连续 §2.1 答 案1.(1)πn sin ,0; (2)()nn 211--,0.2.(1)1; (2)i )⎪⎩⎪⎨⎧=≠--=+1,1,11q n q q q q x n n ,ii )当()1,1-∈q 时qq x n n -=∞→1lim ,当1,1-≠>q q 时∞=∞→n n x lim ,当1-=q 时n n x ∞→lim 不存在;(3)25; (4)2ln ; (5)41-;(6)5; (7)1; (8)23.3. 1lim =∞→n n x .4. 21lim =∞→n n x . 5. {}k a a ,,max 1Λ.§2.2 答 案1. 极限状态分别为0,∞+,不存在.2.2π,2π-,不存在.3. (1)21; (2)57-; (3)32-; (4)15854; (5)23;(6)21-; (7)9. 4. ()0lim 0=→x f x .5.极限不存在. 6. 23=a . 7.()x x x f 22-=()f x .§2.3 答 案1. 略. 2. 3. 3. 6. 4. 略.§2.4 答 案1.0. 2.1)32; 2)1.3.(1)43; (2)1-; (3)0. 4.1=a ,1-=b .§2.5 答 案1.(1)2-e ; (2)21-e ; (3)e ; (4)2e . 2.2=a ,2ln =b .3.()⎪⎩⎪⎨⎧>=<-=1,10,00,1x x x x f ,间断点0=x .§2.6 答 案1~5.略.第三章 导数与微分 §3.1 答 案1.(1)2+-=x y ; (2)0=y .2.(1)当 1≠x 时,2)1(1+-='x y ; (2)x y 3cos 3='.3. 当c a 2=且2c b -=时,)(x f 在c 可导.4.(1))(30x f '; (2))(0x f '-; (3))(20x f '.5.(1)函数)(x f 在0=x 处连续且可导,并且0)0(='f ;(2) 函数)(x f 在0=x 处可导,并且0)0(='f ;(3)⎪⎩⎪⎨⎧=≠-='0,00,1cos 1sin 2)(x x xx x x f 在0=x 处不连续,在其他点处连续.§3.2 答 案1.(1)221--+='x xy ; (2)1))((-++='b a ex b a e y ;(3)233225x x y π--='; (4))(212321--+-='x x y ;(5)x x x x x x y ln cos sin ln sin ⋅++⋅='; (6)12211)()(-+--+++='b a b a x b a ab x xab y ;(7)x x x x x x y cot csc tan sec sec -+=';(8)2)cos (sin sec 3x x x y +='; (9)22)1(4--='x xy .2.(1)2)(4x x e e y -+='; (2))11cot (2xx arc e y x+-='; (3))sin cos (cos x x x x x e y x--='-.§3.3 答 案1.(1)4234)1(34x x x x y -+-='; (2)2ln )(ln 1ln 22ln x x y xx -⋅='; (3)))2(cos 26sin()4sin(22x x y -='; (4)xxxe e e y 3332)cot()(csc 6-=';(5)()()x x x y ln ln ln 2=';(6)22a x y +='.2.(1) 34414341)1()6)(32(31)1)()6)(32(41)6(2(+-+-+-++--x x x x x x x ; (2)))ln(sin sin cos (cot )(sin cos x x x x x y x-⋅=';(3)xx x y x 2)2(ln +='.3.(1))](2)()[(22222x f x x f x xf dx dy'+=; (2)04==πx dxdy .4.(1)21; (2)y x y x dx dy -+=. 5.略.§3.4 答 案1.(1)dx xx dy 212--=; (2)dx x xe dy x)1(22+=; (3)dx x x e dy x)2sin (sin 2+=; (4)dx e e dy xx21+=. 2.(1)dx y a xb dy 22=; (2)dx y y y dy 112122---=.3.008.21.83≈.4.)22)(12()12(π--+-=a x y .5.t b ady dx t a b dx dy tan ,cot -=-=.§3.5 答 案1.(1)2222)1(62,12--=''-='x x y x x y ; (2)12124,2--=''='x x e y ey ;(3)32222)1(26,)1(2x x y x x y +-=''+-='; (4)3))cos(1()sin(,)cos(1)cos(y x y x y y x y x y +-+-=''+-+='. 2.(1)π21)1,0(-='-y ; (2)2)1,0(41-π=''-y . 3.)2)1(2sin(21)(π-+=-n x y n n .§3.6 答 案1.,2105,6162x MR x x MC -=+-=21499x x MC MR ML -+=-=.2.2,48400150-====x x ML ML . 3.(1)a E =; (2))9(2-=x xE .4.195)105(≈D 万(单位).第四章 中值定理与导数的应用§4.1 答 案1~4.略.§4.2 答 案1~2.略. 3.21. 4. 1.02020134e 0.02≈.§4.3 答 案1.(1)16; (2)12; (3)12; (4)2π; (5)1; (6)e ; (7)2ln 2; (8)2e ;(9)2e ; (10)13-; (11)16.§4.4 答 案1.(1)单增区间为(,1)(3,)-∞+∞U ,单减区间为(1,3);(2)单增区间为1(,)2+∞,单减区间为1(0,)2.2. 略.3.(1)拐点为2x =,上凸区间为(,2)-∞,下凸区间为(2,)+∞; (2)拐点为2x =,上凸区间为(,1)(1,2)-∞--U ,下凸区间为(2,)+∞. 4. 略.§4.5 答 案1.(1)2)1(=f 为极小值,2)1(-=-f 为极大值; (2)0)5(=f 为极小值,108)3(=f 为极大值.2.61,32-=-=b a ;1x 是极小值点,2x 是极大值点.3.(1)ee y 2)(2-=-为最小值,最大值不存在;(2)4)0(-=f 为最小值,2)3(=f 为最大值.4.36216)6(24222+-=-+=x x y x d ,)4,4(),(±=y x 时52min =d .§4.6 答 案1.(1)垂直渐近线为1-=x ;斜渐近线为1-=x y ; (2)垂直渐近线为1-=x 与1=x ;水平渐近线为0=y ; (3)水平渐近线为0=y .2.解:单调递增区间为)1,1(-,单调递减区间为)1,(--∞与),1(+∞;上凸区间为),2(+∞,下凸区间为)1,(--∞与)2,1(-.垂直渐近线为1-=x ,水平渐近线为0=y 。
高中数学北师大版选修2-2同步训练:(13)微积分基本定理

(13)微积分基本定理1、下列积分值等于1的是( )A. 1xdx ⎰B. ()11x dx +⎰C. 11dx ⎰D. 1012dx ⎰2、1-= ( )A. 3πB. 4πC. 2πD. π3、曲线3cos 02y x x π⎛⎫=≤≤ ⎪⎝⎭与坐标轴所围成的面积是()A. 2B. 3C. 52D. 44、()22sin cos x x dx ππ-+⎰的值是( )A. 0B. 4πC. 2D. 45、设()()()2,01,{2,12,x x f x x x ≤≤=-<≤则()2f x dx ⎰等于( ) A. 34B. 45C. 56D.不存在6、下列值等于1的积分是() A. 1012xdx ⎰B. ()11x dx +⎰C. 2012dx ⎰D. 1012dx ⎰7、()212x x dx +⎰等于()A. ()22|1x x +B. ()22ln 2|1x x +C. 222|12x x ⎛⎫+ ⎪⎝⎭D. 222|12ln 2x x ⎛⎫+ ⎪⎝⎭8、2231111dx x x x ⎛⎫++= ⎪⎝⎭⎰ ( ) A. 7ln 28+B. 7ln 22- C. 5ln 28- D. 17ln 28- 9、220sin 2x dx π=⎰ ( ) A. 4π B. 12π- C. 2D. 24π-10、自由落体的运动速度v gt = (g 为常数),则当[]1,2t ∈时,物体下落的距离为( )A.12g B. g C. 32g D. 2g11、设函数()()20f x ax c a =+≠,若()()1000,01f x dx f x x =≤≤⎰,则0x 的值为__________.12、若220a x dx =⎰,230b x dx =⎰,2sin c xdx =⎰,则,,a b c 的大小关系是__________. 13、由拋物线21y x =-,直线2x =,0x =,0y =所围成图形的面积是__________.14、若()122x k dx +=⎰,则k =__________.15、设()f x 是连续函数,且()()102f x x f t dt =+⎰,求()f x .答案以及解析1答案及解析:答案:C解析:2答案及解析:答案:C解析:3答案及解析:答案:B解析: 如图, 32202cos cos S xdx xdx πππ=+⎰⎰32sin |sin |123202x x πππ=-=+=.4答案及解析:答案:C解析:()22sin cos x x dx ππ-+⎰()2cos sin |22x x ππ=-+=-.5答案及解析:答案:C解析:6答案及解析:答案:C解析:7答案及解析:答案:D解析:8答案及解析:答案:A解析:9答案及解析:答案:D解析:10答案及解析:答案:C解析:物体下落的距离21s gtdt =⎰,则有221|12s gt =()22132122g g =-=.11答案及解析:答案:3解析:主要考查定积分的基本应用.由()()100f x dx f x =⎰,得()123011|03ax c dx ax cx +=+⎰2013a c ax c =+=+, ∴203a ax =, ∵0a ≠,∴2013x =,又001x ≤≤,∴03x =.12答案及解析:答案:c a b <<解析:13答案及解析:答案:2解析:14答案及解析:答案:1解析:15答案及解析:答案:因为()12f t dt ⎰是一个常数, 所以可设()f x x c =+,所以()()11200111|022f t dt t c dt t ct c ⎛⎫=+=+=+ ⎪⎝⎭⎰⎰,所以()112c f t dt c ==+⎰,所以1c =-, 所以()1f x x =-解析:由Ruize收集整理。
(完整版)7.微积分基本定理练习题

7、微积分基本定理一、选择题1.⎠⎛01(x 2+2x )d x 等于( )A.13B.23 C .1 D.43 2.∫2ππ(sin x -cos x )d x 等于( )A .-3B .-2C .-1D .03.自由落体的速率v =gt ,则落体从t =0到t =t 0所走的路程为( ) A.13gt 20 B .gt 20 C.12gt 20 D.16gt 20 4.曲线y =cos x ⎝ ⎛⎭⎪⎫0≤x ≤3π2与坐标轴所围图形的面积是( )A .4B .2 C.52 D .35.如图,阴影部分的面积是( )A .2 3B .2- 3 C.323 D.3536.⎠⎛03|x 2-4|d x =( )A.213B.223C.233D.253 7.⎠⎛241xd x 等于( )A .-2ln2B .2ln2C .-ln2D .ln2 8.若⎠⎛1a ⎝⎛⎭⎪⎫2x +1x d x =3+ln2,则a 等于( )A .6B .4C .3D .29.(2010·山东理,7)由曲线y =x 2,y =x 3围成的封闭图形面积为( ) A.112 B.14 C.13 D.71210.设f (x )=⎩⎪⎨⎪⎧x 20≤x <12-x1<x ≤2,则⎠⎛02f (x )d x 等于( )A.34B.45C.56 D .不存在 [解析] ⎠⎛02f (x )d x =⎠⎛01x 2d x +⎠⎛12(2-x )d x ,二、填空题11.从如图所示的长方形区域内任取一个点M (x ,y ),则点M 取自阴影部分的概率为________.12.一物体沿直线以v =1+t m/s 的速度运动,该物体运动开始后10s 内所经过的路程是________.13.求曲线y =sin x 与直线x =-π2,x =54π,y =0所围图形的面积为________.14.若a =⎠⎛02x 2d x ,b =⎠⎛02x 3d x ,c =⎠⎛02sin x d x ,则a 、b 、c 大小关系是________.三、解答题 15.求下列定积分:①⎠⎛02(3x 2+4x 3)d x ; ②sin 2x2d x .17.求直线y =2x +3与抛物线y =x 2所围成的图形的面积.18.(1)已知f (a )=⎠⎛01(2ax 2-a 2x )d x ,求f (a )的最大值;(2)已知f (x )=ax 2+bx +c (a ≠0),且f (-1)=2,f ′(0)=0,⎠⎛01f (x )d x =-2,求a ,b ,c的值.DBCDCCDDAC 11. 13 12. 23(1132-1) 13.4-22[解析] 所求面积为=1+2+⎝ ⎛⎭⎪⎫1-22=4-22. 14.[答案] c <a <b 三、解答题15.①⎠⎛02(3x 2+4x 3)d x ;②sin 2x2d x .[解析] ①⎠⎛02(3x 2+4x 3)d x =⎠⎛023x 2d x +⎠⎛024x 3d x =x 3| 20+x 4| 20=24.=12·⎝ ⎛⎭⎪⎫π2-0-12(1-0)=π-24. 17.求直线y =2x +3与抛物线y =x 2所围成的图形的面积.[解析] 由方程组⎩⎪⎨⎪⎧y =2x +3y =x 2得x 1=-1,x 2=3,则所求图形的面积为=(x 2+3x )| 3-1-13x 3| 3-1=323.18.(1)因为⎝ ⎛⎭⎪⎫23ax 3-12a 2x 2′=2ax 2-a 2x ,所以⎠⎛01(2ax 2-a 2x )d x =⎝ ⎛⎭⎪⎫23ax 3-12a 2x 2| 10=23a -12a 2.所以f (a )=23a -12a 2=-12⎝ ⎛⎭⎪⎫a 2-43a +49+29=-12⎝ ⎛⎭⎪⎫a -232+29.所以当a =23时,f (a )有最大值29 .(2)∵f (-1)=2,f ′(0)=0,∴⎩⎪⎨⎪⎧a -b +c =2b =0①而⎠⎛01f (x )d x =⎠⎛01(ax 2+bx +c )d x ,取F (x )=13ax 3+12bx 2+cx ,则F ′(x )=ax 2+bx +c .∴⎠⎛01f (x )d x =F (1)-F (0)=13a +12b +c =-2②解①②得a =6,b =0,c =-4.。
定积分及微积分基本定理练习题及答案

定积分与微积分基本定理练习题及答案1.(2011·宁夏银川一中月考)求曲线y =x2与y =x 所围成图形的面积,其中正确的是( )A .S =⎠⎛01(x2-x)dxB .S =⎠⎛01(x -x2)dxC .S =⎠⎛01(y2-y)dyD .S =⎠⎛01(y -y)dy [答案] B[分析] 根据定积分的几何意义,确定积分上、下限和被积函数.[解读] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x≥x2,故函数y =x2与y =x 所围成图形的面积S =⎠⎛01(x -x2)dx.2.(2010·山东日照模考)a =⎠⎛02xdx ,b =⎠⎛02exdx ,c =⎠⎛02sinxdx ,则a 、b 、c 的大小关系是( )A .a<c<bB .a<b<cC .c<b<aD .c<a<b [答案] D[解读] a =⎠⎛02xdx =12x2|02=2,b =⎠⎛02exdx =ex|02=e2-1>2,c =⎠⎛02sinxdx =-cosx|02=1-cos2∈(1,2),∴c<a<b.3.(2010·山东理,7)由曲线y =x2,y =x3围成的封闭图形面积为( )[答案] A[解读] 由⎩⎪⎨⎪⎧y =x2y =x3得交点为(0,0),(1,1).∴S =⎠⎛01(x2-x3)dx =⎪⎪⎪⎝ ⎛⎭⎪⎫13x3-14x401=112. [点评] 图形是由两条曲线围成的时,其面积是上方曲线对应函数表达式减去下方曲线对应函数表达式的积分,请再做下题:(2010·湖南师大附中)设点P 在曲线y =x2上从原点到A(2,4)移动,如果把由直线OP ,直线y =x2及直线x =2所围成的面积分别记作S1,S2.如图所示,当S1=S2时,点P 的坐标是( )[答案] A[解读] 设P(t ,t2)(0≤t≤2),则直线OP :y =tx ,∴S1=⎠⎛0t (tx -x2)dx =t36;S2=⎠⎛t2(x2-tx)dx =83-2t +t36,若S1=S2,则t =43,∴P ⎝ ⎛⎭⎪⎫43,169.4.由三条直线x =0、x =2、y =0和曲线y =x3所围成的图形的面积为( ) A .4 D .6 [答案] A[解读] S =⎠⎛02x3dx =⎪⎪⎪x4402=4. 5.(2010·湖南省考试院调研)⎠⎛1-1(sinx +1)dx 的值为( )A .0B .2C .2+2cos1D .2-2cos1 [答案] B[解读] ⎠⎛1-1(sinx +1)dx =(-cosx +x)|-11=(-cos1+1)-(-cos(-1)-1)=2.6.曲线y =cosx(0≤x≤2π)与直线y =1所围成的图形面积是( ) A .2π B.3π D .π [答案] A [解读] 如右图, S =∫02π(1-cosx)dx =(x -sinx)|02π=2π.[点评] 此题可利用余弦函数的对称性①②③④面积相等解决,但若把积分区间改为⎝ ⎛⎭⎪⎫π6,π,则对称性就无能为力了. 7.函数F(x)=⎠⎛0x t(t -4)dt 在[-1,5]上( )A .有最大值0,无最小值B .有最大值0和最小值-323C .有最小值-323,无最大值D .既无最大值也无最小值 [答案] B[解读] F′(x)=x(x -4),令F′(x)=0,得x1=0,x2=4, ∵F(-1)=-73,F(0)=0,F(4)=-323,F(5)=-253.∴最大值为0,最小值为-323. [点评] 一般地,F(x)=⎠⎛0x φ(t)dt 的导数F′(x)=φ(x).8.已知等差数列{an}的前n 项和Sn =2n2+n ,函数f(x)=⎠⎛1x 1t dt ,若f(x)<a3,则x的取值范围是( )B .(0,e21)C .(e -11,e)D .(0,e11) [答案] D[解读] f(x)=⎠⎛1x 1t dt =lnt|1x =lnx ,a3=S3-S2=21-10=11,由lnx<11得,0<x<e11.9.(2010·福建厦门一中)如图所示,在一个长为π,宽为2的矩形OABC 内,曲线y =sinx(0≤x≤π)与x 轴围成如图所示的阴影部分,向矩形OABC 内随机投一点(该点落在矩形OABC 内任何一点是等可能的),则所投的点落在阴影部分的概率是( )[答案] A[解读] 由图可知阴影部分是曲边图形,考虑用定积分求出其面积.由题意得S =⎠⎛0πsinxdx =-cosx|0π=-(cosπ-cos0)=2,再根据几何概型的算法易知所求概率P =S S 矩形OABC =22π=1π.10.(2010·吉林质检)函数f(x)=⎩⎪⎨⎪⎧x +2-2≤x<02cosx 0≤x≤π2的图象与x 轴所围成的图形面积S 为( )B .1C .4 [答案] C[解读] 面积S =∫π2-2f(x)dx =⎠⎛0-2(x +2)dx +∫π202cosxdx =2+2=4.11.(2010·沈阳二十中)设函数f(x)=x -[x],其中[x]表示不超过x 的最大整数,如[-]=-2,[]=1,[1]=1.又函数g(x)=-x3,f(x)在区间(0,2)上零点的个数记为m ,f(x)与g(x)的图象交点的个数记为n ,则⎠⎛mn g(x)dx 的值是( )A .-52B .-43C .-54D .-76[答案] A[解读] 由题意可得,当0<x<1时,[x]=0,f(x)=x ,当1≤x<2时,[x]=1,f(x)=x -1,所以当x ∈(0,2)时,函数f(x)有一个零点,由函数f(x)与g(x)的图象可知两个函数有4个交点,所以m =1,n =4,则⎠⎛m n g(x)dx =⎠⎛14⎝ ⎛⎭⎪⎫-x 3dx =⎪⎪⎪-x2614=-52. 11.(2010·江苏盐城调研)甲、乙两人进行一项游戏比赛,比赛规则如下:甲从区间[0,1]上随机等可能地抽取一个实数记为b ,乙从区间[0,1]上随机等可能地抽取一个实数记为c(b 、c 可以相等),若关于x 的方程x2+2bx +c =0有实根,则甲获胜,否则乙获胜,则在一场比赛中甲获胜的概率为( )[答案] A[解读] 方程x2+2bx +c =0有实根的充要条件为Δ=4b2-4c≥0,即b2≥c,由题意知,每场比赛中甲获胜的概率为p =⎠⎛01b2db1×1=13.12.(2010·吉林省调研)已知正方形四个顶点分别为O(0,0),A(1,0),B(1,1),C(0,1),曲线y =x2(x≥0)与x 轴,直线x =1构成区域M ,现将一个质点随机地投入正方形中,则质点落在区域M 内的概率是( )[答案] C[解读] 如图,正方形面积1,区域M 的面积为S =⎠⎛01x2dx=13x3|01=13,故所求概率p =13.2.如图,阴影部分面积等于( )A .23B .2-3[答案] C[解读] 图中阴影部分面积为S =⎠⎛-31 (3-x2-2x)dx =(3x -13x3-x2)|1-3=323.4-x2dx =( ) A .4π B.2π C .π [答案] C[解读] 令y =4-x2,则x2+y2=4(y≥0),由定积分的几何意义知所求积分为图中阴影部分的面积,∴S =14×π×22=π.4.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为v甲和v乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )A.在t1时刻,甲车在乙车前面B.在t1时刻,甲车在乙车后面C.在t0时刻,两车的位置相同D.t0时刻后,乙车在甲车前面[答案] A[解读] 判断甲、乙两车谁在前,谁在后的问题,实际上是判断在t0,t1时刻,甲、乙两车行驶路程的大小问题.根据定积分的几何意义知:车在某段时间内行驶的路程就是该时间段内速度函数的定积分,即速度函数v(t)的图象与t轴以及时间段围成区域的面积.从图象知:在t0时刻,v甲的图象与t轴和t=0,t=t0围成区域的面积大于v乙的图象与t 轴和t=0,t=t0围成区域的面积,因此,在t0时刻,甲车在乙车的前面,而且此时乙车的速度刚刚赶上甲车的速度,所以选项C,D错误;同样,在t1时刻,v甲的图象与t轴和t=t1围成区域的面积,仍然大于v乙的图象与t轴和t=t1围成区域的面积,所以,可以断定:在t1时刻,甲车还是在乙车的前面.所以选A.5.(2012·山东日照模拟)向平面区域Ω={(x ,y)|-π4≤x≤π4,0≤y≤1}内随机投掷一点,该点落在曲线y =cos2x 下方的概率是( )-1 [答案] D[解读] 平面区域Ω是矩形区域,其面积是π2,在这个区6. (sinx -cosx)dx 的值是( )A .0 C .2 D .-2 [答案] D[解读] (sinx -cosx)dx =(-cosx -sinx) =-2.7.(2010·惠州模拟)⎠⎛02(2-|1-x|)dx =________.[答案] 3[解读] ∵y =⎩⎪⎨⎪⎧1+x 0≤x≤13-x 1<x≤2,∴⎠⎛02(2-|1-x|)dx =⎠⎛01(1+x)dx +⎠⎛12(3-x)dx=(x +12x2)|10+(3x -12x2)|21=32+32=3.8.(2010·芜湖十二中)已知函数f(x)=3x2+2x +1,若⎠⎛1-1f(x)dx =2f(a)成立,则a =________.[答案] -1或13[解读] ∵⎠⎛1-1f(x)dx =⎠⎛1-1(3x2+2x +1)dx =(x3+x2+x)|1-1=4,⎠⎛1-1f(x)dx =2f(a),∴6a2+4a +2=4,∴a =-1或13.9.已知a =∫π20(sinx +cosx)dx ,则二项式(a x -1x )6的展开式中含x2项的系数是________.[答案] -192[解读] 由已知得a =∫π20(sinx +cosx)dx =(-cosx +sinx)|π20=(sin π2-cos π2)-(sin0-cos0)=2,(2x -1x)6的展开式中第r +1项是Tr +1=(-1)r×C r 6×26-r×x3-r ,令3-r =2得,r =1,故其系数为(-1)1×C 16×25=-192.10.有一条直线与抛物线y =x2相交于A 、B 两点,线段AB 与抛物线所围成图形的面积恒等于43,求线段AB 的中点P 的轨迹方程.[解读] 设直线与抛物线的两个交点分别为A(a ,a2),B(b ,b2),不妨设a<b , 则直线AB 的方程为y -a2=b2-a2b -a(x -a), 即y =(a +b)x -ab.则直线AB 与抛物线围成图形的面积为S =⎠⎛a b [(a +b)x -ab -x2]dx =(a +b2x2-abx -x33)|b a =16(b -a)3, ∴16(b -a)3=43, 解得b -a =2.设线段AB 的中点坐标为P(x ,y), 其中⎩⎪⎨⎪⎧x =a +b2,y =a2+b22.将b -a =2代入得⎩⎪⎨⎪⎧x =a +1,y =a2+2a +2.消去a 得y =x2+1.∴线段AB 的中点P 的轨迹方程为y =x2+1.能力拓展提升11.(2012·郑州二测)等比数列{an}中,a3=6,前三项和S3=⎠⎛034xdx ,则公比q 的值为( )A .1B .-12C .1或-12D .-1或-12[答案] C[解读] 因为S3=⎠⎛034xdx =2x2|30=18,所以6q +6q2+6=18,化简得2q2-q -1=0,解得q =1或q =-12,故选C.12.(2012·太原模拟)已知(xlnx)′=lnx +1,则⎠⎛1e lnxdx =( )A .1B .eC .e -1D .e +1 [答案] A[解读] 由(xlnx)′=lnx +1,联想到(xlnx -x)′=(lnx +1)-1=lnx ,于是⎠⎛1e lnxdx=(xlnx -x)|e 1=(elne -e)-(1×ln1-1)=1.13.抛物线y2=2x 与直线y =4-x 围成的平面图形的面积为________. [答案] 18[解读] 由方程组⎩⎪⎨⎪⎧y2=2x ,y =4-x ,解得两交点A(2,2)、B(8,-4),选y 作为积分变量x=y22、x =4-y ,∴S =⎠⎛-42 [(4-y)-y22]dy =(4y -y22-y36)|2-4=18.14.已知函数f(x)=ex -1,直线l1:x =1,l2:y =et -1(t 为常数,且0≤t≤1).直线l1,l2与函数f(x)的图象围成的封闭图形如图中区域Ⅱ所示,其面积用S2表示.直线l2,y 轴与函数f(x)的图象围成的封闭图形如图中区域Ⅰ所示,其面积用S1表示.当t 变化时,阴影部分的面积的最小值为________.[答案] (e -1)2[解读] 由题意得S1+S2=⎠⎛0t (et -1-ex +1)dx +⎠⎛t 1(ex -1-et +1)dx =⎠⎛0t (et -ex)dx +⎠⎛t 1(ex -et)dx =(xet -ex)|t 0+(ex -xet)|1t =(2t -3)et +e +1,令g(t)=(2t -3)et +e +1(0≤t≤1),则g′(t)=2et +(2t -3)et =(2t -1)et ,令g′(t)=0,得t =12,∴当t ∈[0,12)时,g′(t)<0,g(t)是减函数,当t ∈(12,1]时,g′(t)>0,g(t)是增函数,因此g(t)的最小值为g(12)=e +1-2e 12=(e -1)2.故阴影部分的面积的最小值为(e -1)2.15.求下列定积分.(1)⎠⎛1-1|x|dx 。
高中高三数学 定积分与微积分基本定理练习题-人教版高三全册数学试题

4.若 x2dx=9,则常数T的值为________.
解析:∵ ′=x2,
∴ x2dx= x3 = T3-0=9,∴T=3.
答案:3
5.如右图所示,则由两条曲线y=-x2,x2=-4y及直线y=-1所围成图形的面积为________.
解析:由图形的对称性,知所求图形的面积是位于y轴右侧图形面积的2倍.由 得C(1,-1).
同理,得D(2,-1).
故所求图形的面积S=2 [- -(-x2)]dx+ [- -(-1)]dx =2 dx- ( -1)dx =2 -( -x) = .
答案:
《定积分与微积分基本定理》
1.若S1= x2dx,S2= dx,S3= exdx,则S1,S2,S3的大小关系为( )
A. S1<S2<S3B. S2<S1<S3
C. S2<S3<S1D. S3<S2<S1
解析:S1= x2dx= x3 = ,
S2= dx=lnx =ln2,
S3= exdx=ex =e2-e=e(e-1)>e> ,
所以S2<S1<S3,故选B.
答案:B
2.设f(x)= 则
f(x)dx等于( )
A. B.
C. D. 不存在
解析:本题画图求解,更为清晰,如图,
f(x)dx= x2dx+ (2-x)dx
= x3+ )= .
答案:C
3.计算定积分 dx=________.
解析: dx表示圆x2+y2=22与x=0,x=2,y=0围成的图形的面积.根据定积分的几何意义,得 dx=π.
高中数学人教A版选修2-2同步训练:1.6 微积分基本定理

1.6 微积分基本定理1、直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积为( )A.B. C. 2 D. 42、1=⎰( )A. πB. 2πC. 3πD. 4π3、若()3241cos 2x a dx xdx π-=⎰⎰,则a =( )A.-1B.1C.2D.44、设()[][]20,121,2xx f x xx ⎧∈⎪=⎨-∈⎪⎩,则()2f x dx ⎰等于( )A. 34 B. 56C. 45D.不存在5、设()f x 是一次函数,且()15f x dx =⎰,()1176xf x dx =⎰,则()f x 的解析式为( ) A. 43x + B. 34x + C. 42x -+ D. 34x -+6、23012sin 2d πθθ⎛⎫- ⎪⎝⎭⎰的值为( )A. 2- B. 12- C.127、()12xex dx +⎰等于( )A. 1B. 1e -C. eD. 1e + 8、若1123ln 2ax dx x ⎛⎫+=+ ⎪⎝⎭⎰,则a 的值是( )A.6B.4C.3D.2 9、若1111ln 32ax dx x ⎛⎫-=- ⎪⎝⎭⎰,且1a >,则a 的值为( ) A. 3- B. ln 3D. 310、()4sin cos 2x a x dx π-=-⎰,则实数a 等于( ) A. 1C. 1-D.3-11、如图,在边长为e(e 为自然对数的底数)的正方形中,阴影部分的面积为__________.12、设函数()()20f x ax c a =+≠,若()()1000,01f x dx f x x =≤≤⎰,则0x 的值为__________.13、已知()21214kx dx ≤+≤⎰,则实数k 的取值范围为__________.14、()f x 是一次函数,且()105f x dx =⎰,117()6xf x dx =⎰,那么()f x 的解析式是__________ 15、已知()[](]2212,212,4x x f x xx ⎧+∈-⎪=⎨+∈⎪⎩若()3340k f x dx =⎰,求实数k 的值.答案以及解析1答案及解析: 答案:D 解析:由 34{y x y x ==,得2x =± ,或0x = ,所以两图象的交点坐标为()0,0,()2,8,()2,8--. 所以直线与曲线在第一象限内围成的封闭图形的面积:()2324021144|024S x x dx x x ⎛⎫=-=⨯- ⎪⎝⎭⎰11441684424=⨯⨯-⨯=-=,故选D.2答案及解析: 答案:B 解析:选B利用定积分几何意义和积分性质。
高中数学定积分与微积分基本定理练习题

定积分与微积分基本定理自我检测:1.设连续函数f(x)>0,则当a<b 时,定积分∫()ba f x dx 的符号( )A.一定是正的B.一定是负的C.当0<a<b 时是正的,当a<b<0时是负的D.以上结论都不对 2. ∫22ππ- (1+cosx)dx 等于( )A.πB.2C.π-2D.π+23.用S 表示图中阴影部分的面积,则S 的值是( )A. ∫()c a f x dxB.| ∫()c a f x dx|C. ∫()b a f x dx+∫()c b f x dxD. ∫()c b f x dx-∫()ba f x dx4.设函数()m f x x ax =+的导函数f′(x)=2x+1,则∫21()f x -dx 的值等于( )A.56 B.12 C.23 D.165.直线y=2x+3与抛物线2y x =所围成的图形面积为 .巩固练习:1. ∫412x dx 等于( )A.-2ln2B.2ln2C.-ln2D.ln22. ∫10(e 2)xx +dx 等于( )A.1B.e-1C.eD.e+13.已知f(x)= 210101x x x ⎧,-≤≤,⎨,<<,⎩则∫11()f x -dx 的值为 ( )A.32B.23-C.23 D.434.函数f(x)= 2110cosx 0x x x π+,-≤<,⎧⎨,≤≤⎩ 的图象与x 轴所围成的封闭图形的面积为( )A.32 B.1 C.2 D.125.函数y=∫(x x -cos 22)t t ++dt( )A.是奇函数B.是偶函数C.是非奇非偶函数D.以上都不正确6.由直线330x x y ππ=-,=,=与曲线y=cos x 所围成的封闭图形的面积为( )A.12 B.1 C.32 D.3 7.由曲线32y x y x =,=围成的封闭图形的面积为( )A.112B.14 C.13 D.7128.曲线1x y =与直线y=x,x=2所围成的图形面积为 .9.如果∫10()f x dx=1, ∫20()f x dx=-1,则∫21()f x dx= .10.由曲线2y x =和直线x=0,x=1,y=2(01)t t ,∈,所围成的图形(阴影部分)的面积的最小值为 .11.计算下列定积分.(1) ∫2211(2)x x -dx; (2) ∫3212()x x +dx; (3) ∫30π (sinx-sin2x)dx.12.已知f(x)为二次函数,且f(-1)=2,f′(0)=0,∫10()f x dx=-2.(1)求f(x)的解析式;(2)求f(x)在[-1,1]上的最大值与最小值.。
微积分基本定理同步练习题(理科)(学生版)

微积分基本定理同步练习题(理科)一、选择题1.已知物体做变速直线运动的位移函数s =s (t ),那么下列命题正确的是( )①它在时间段[a ,b ]内的位移是s =s (t )|ba ; ②它在某一时刻t =t 0时,瞬时速度是v =s ′(t 0);③它在时间段[a ,b ]内的位移是s =lim n →+∞i =1n b -ans ′(ξi );④它在时间段[a ,b ]内的位移是s =ʃb a s ′(t )d t .A .①B .①②C .①②④D .①②③④2. 若F ′(x )=x 2,则F (x )的解析式不正确的是( )A .F (x )=13x 3B .F (x )=x 3C .F (x )=13x 3+1D .F (x )=13x 3+c (c 为常数)3. ʃ10(e x+2x )d x 等于( ) A .1 B .e -1 C .eD .e +14.设函数f (x )=ax 2+b (a ≠0),若∫30f (x )d x =3f (x 0),则x 0=( ) A .±1B.2 C .± 3D .25.sin 2x2d x 等于( ) A.π4B.π2-1 C .2D.π-246.曲线y =x 2-1与x 轴所围成图形的面积等于( )A.13B.23C .1D.437.下列式子正确的是( )A. )()()(a f b f dx x f ba -=⎰ B. )()()(a fb f dx x f ba-='⎰ C.)()(x f dx x f ba=⎰D.)()(x f dx x f ba ='⎪⎭⎫ ⎝⎛⎰ 8.=⎰12dx x ( )A. 0B.31 C. 231x D. x 2 9.设函数f(x)=ax 2+1,若⎠⎛01f(x)d x =2,则a =( )A .1B .2C .3D .410. 由直线x =-π3,x =π3,y =0与曲线y =cos x 所围成的封闭图形的面积为( )A 12 B .1 C32D 3 11.=⎪⎭⎫⎝⎛+⎰-dx x x 22421( ) A.214B.54C.338D.21812.设f (x )=⎩⎪⎨⎪⎧x 2(0≤x <1)2-x (1≤x ≤2),则⎠⎛02f (x )d x 等于( )A.34B.45C.56D .不存在13.⎠⎛03|x 2-4|d x =( )A.213B.223C.233D.25314.θθπd ⎰⎪⎭⎫ ⎝⎛-3022sin 21 的值为( )A .-32B .-12 C.12D.3215.函数F (x )=⎠⎛0x cos t d t 的导数是( )A .cos xB .sin xC .-cos xD .-sin x16.若⎠⎛0k (2x -3x 2)d x =0,则k =( )A .0B .1C .0或1D .以上都不对17.a =⎠⎛02x d x ,b =⎠⎛02e xd x ,c =⎠⎛02sin x d x ,则a 、b 、c 的大小关系是( )A .a <c <bB .a <b <cC .c <b <aD .c <a <b18.由三条直线x =0、x =2、y =0和曲线y =x 3所围成的图形的面积为( ) A .4 B.43C.185D .6二、填空题 19.满足212)(xx x F -='的函数)(x F 为_____________。
【备战高考·理科数学】一轮复习同步训练:微积分基本定理(含答案)

同步训练17.微积分基本定理(含答案) 1.⎰42(x 3+x 2-30)dx =( )A .14B .28 C.563 D .562.⎰-22ππ(1+cosx)dx 等于( )A . 2 B.π C .π-2 D .π+2 3.定积分⎰10(2x +e x )dx 的值为( ) A .e +2 B .e -1 C .e D .e +14.求曲线y =x 3与y =x 所围成图形的面积,其中正确的是( ) A .S =⎰10(x 3-x)dxB .S =⎰10|(x -x 3)dxC .S =⎰10|(y 3-y)dy D .S =⎰10(y -3y )dy5.若函数f(x)=x 2+2x +a(a ,x ∈R)的最小值为-1,则⎰21|f(x)dx 等于( )A .2 B.163 C .6 D .76.若⎰10|(2x +a)dx =2,则a 等于( ) A .0 B .1 C .2 D .37.若F ′(x)=x 2,则F(x)的解析式不正确的是( )A .F(x)=13x 3B .F(x)=x 3C .F(x)=13x 3+2D .F(x)=13x 3+m(m 为常数)8.a =⎰1e x dx与b =⎰e11xdx 的大小关系是( ) A .a>b B .a<b C .a =b D .无法确定9.设f(x)=x 3+x ,则⎰-22f(x)dx 的值等于( ) A .0 B .1 C .2⎰20f(x)dx D.⎰20f(x)dx10.下列值等于1的是( ) A.⎰1x 2dx B.⎰1(x +1)dx C.⎰11dx D.⎰112dx 11.⎰-22|e|x|dx 值等于( )A .e 2-e -2B .2e 2C .2e 2-2D .e 2+e -2-2 12.若⎰b1(2x +1x)dx =3+ln2(b>1),则b 的值是( )A.2B.3C.4 D513.如图所示,由函数f(x)=e x -e 的图像,直线x =2及x 轴所围成阴影部分的面积等于14.若S 1=⎰21x 2dx ,S 2=⎰211xdx ,S 3=⎰21e x dx ,则S 1,S 2,S 3的大小关系为 15.设a>0.若曲线y =x 与直线x =a ,y =0所围成封闭图形的面积为a ,则a =________.16.函数y =x 2与y =kx(k >0)的图象所围成的图形的面积为92,则k 的值17.求由曲线y =x ,直线y =x -2及y 轴所围成的图形的面积.18.已知函数f(x)=-x 3+ax 2+bx(a ,b ∈R)的图象如图所示,它与x 轴在原点处相切,且x 轴与函数图象所围区域(图中阴影部分)的面积为112,求a 的值.参考答案: 1.答案C 解析⎰42(x 3+x 2-30)dx =⎝ ⎛⎭⎪⎫13x3+14x4-30x |42=14(44-24)-13(43-23)+30(4-2)=563.故选C.2.答案 D 解析 ⎰-22ππ(1+cosx)dx =2⎰20π(1+cosx)dx =2(x +sinx)|20π=2(π2+1)=π+2 3.答案 C 解析⎰1(2x +e x )dx =(x 2+e x )||10=(1+e)-(0+e 0)=e ,因此选C. 4.答案 B5.答案 B 解析 f(x)=(x +1)2+a -1,∵f(x)的最小值为-1,∴a -1=-1,即a =0.∴f(x)=x 2+2x.∴⎰21f(x)dx =⎰21|(x 2+2x)dx =(13x 3+x 2)|21=13×23+22-13-1=163.6.答案 B7.答案 B8.答案 A 解析 a =⎰1|e x dx =e x |10=e -1,b =⎰e1|1xdx =lnx |e1=1,则a>b. 答案 C 9.答案 A 解析 ⎰-22f(x)dx =(14x4+12x2)22-=0.10.答案 C 解析 ⎰101dx =x ||10=1.11答案 C 12.答案 A解析 由题意可知⎰b1(2x +1x)dx =(x2+lnx)||b 1=b2+lnb -1=3+ln2,解得b =2. 13. 解析 f(x)=e x -e =0时,x =1,∴S =⎰21(e x -e)dx =(e x -ex)|21=e 2-2e.14. 解析 S 1=13x 3|21=83-13=73,S 2=lnx|21=ln2<lne =1,S 3=e x |21|=e 2-e ≈2.72-2.7=4.59,所以S 2<S 1<S 315.答案 94解析 S =⎰axdx =23x 32||a0=23a 32=a ,解得a =94.16. 解析 根据题意,由函数y =x 2与y =kx(k >0)联立方程组得到交点坐标为x =0,x =k ,那么可知交点坐标为(0,0)(k ,k2),于是所求的面积为⎰k(kx -x 2)dx =⎝⎛⎪⎪⎪12kx2-⎭⎪⎫13x3k 0=92∴k =3,故答案为3. 17.解 y =x 与y =x -2以及y 轴所围成的图形为如图所示的阴影部分,联立⎩⎨⎧y =x ,y =x -2得交点坐标为(4,2),故所求面积为S =⎰40[x -(x -2)]dx=⎪⎪⎪⎪⎣⎢⎢⎡⎦⎥⎥⎤23x 32 -⎝ ⎛⎭⎪⎫x22-2x 4=163.18.解 f ′(x)=-3x 2+2ax +b ,∵f ′(0)=0,∴b =0.∴f(x)=-x 3+ax 2,令f(x)=0,得x =0或x =a(a<0).S 阴影=-⎰-0a(-x 3+ax 2)dx =112a 4=112,∴a=-1.。
高中数学 1.6 微积分基本定理同步练习 新人教A版选修2-2

精品 "正版〞资料系列 ,由本公司独创 .旨在将 "人教版〞、〞苏教版 "、〞北师 大版 "、〞华师大版 "等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和 检测题分享给需要的朋友 .本资源创作于2021年8月 ,是当前最|新版本的教材资源 .包含本课对应 内容 ,是您备课、上课、课后练习以及寒暑假预习的最|正确选择 .微积分根本定理一、选择题1.以下积分正确的选项是( )[答案] AA.214B.54 C.338D.218[答案] A[解析] ⎠⎛2-2⎝ ⎛⎭⎪⎫x 2+1x 4d x =⎠⎛2-2x 2d x +⎠⎛2-21x 4d x=13x 3| 2-2+⎝ ⎛⎭⎪⎫-13x -3| 2-2 =13(x 3-x -3)| 2-2 =13⎝ ⎛⎭⎪⎫8-18-13⎝ ⎛⎭⎪⎫-8+18=214.故应选A.3.⎠⎛1-1|x |d x 等于( )A.⎠⎛1-1x d xB.⎠⎛1-1d xC.⎠⎛0-1(-x )d x +⎠⎛01x d xD.⎠⎛0-1x d x +⎠⎛01(-x )d x[答案] C[解析] ∵|x |=⎩⎪⎨⎪⎧x (x ≥0)-x (x <0)∴⎠⎛1-1|x |d x =⎠⎛0-1|x |d x +⎠⎛01|x |d x=⎠⎛0-1(-x )d x +⎠⎛01x d x ,故应选C.4.设f (x )=⎩⎪⎨⎪⎧x 2(0≤x <1)2-x (1≤x ≤2) ,那么⎠⎛02f (x )d x 等于( )A.34B.45C.56D .不存在[答案] C[解析] ⎠⎛02f (x )d x =⎠⎛01x 2d x +⎠⎛12(2-x )d x取F 1(x )=13x 3 ,F 2(x )=2x -12x 2,那么F ′1(x )=x 2,F ′2(x )=2-x ∴⎠⎛02f (x )d x =F 1(1)-F 1(0)+F 2(2)-F 2(1)=13-0+2×2-12×22-⎝ ⎛⎭⎪⎫2×1-12×12=56.故应选C.5.⎠⎛ab f ′(3x )d x =( )A .f (b )-f (a )B .f (3b )-f (3a ) C.13[f (3b )-f (3a )]D .3[f (3b )-f (3a )][答案] C[解析] ∵⎣⎢⎡⎦⎥⎤13f (3x )′=f ′(3x ) ∴取F (x )=13f (3x ) ,那么⎠⎛abf ′(3x )d x =F (b )-F (a )=13[f (3b )-f (3a )].故应选C.6.⎠⎛03|x 2-4|d x =( )A.213B.223 C.233D.253[答案] C[解析] ⎠⎛03|x 2-4|d x =⎠⎛02(4-x 2)d x +⎠⎛23(x 2-4)d x=⎝ ⎛⎭⎪⎫4x -13x 3| 20+⎝ ⎛⎭⎪⎫13x 3-4x | 32=233.A .-32B .-12C.12D.32[答案] D[解析] ∵1-2sin2θ2=cos θ8.函数F (x )=⎠⎛0x cos t d t 的导数是( )A .cos xB .sin xC .-cos xD .-sin x[答案] A[解析] F (x )=⎠⎛0x cos t d t =sin t | x0=sin x -sin0=sin x .所以F ′(x )=cos x ,故应选A.9.假设⎠⎛0k (2x -3x 2)d x =0 ,那么k =( )A .0B .1C .0或1D .以上都不对[答案] C[解析] ⎠⎛0k (2x -3x 2)d x =(x 2-x 3)| k 0=k 2-k 3=0 ,∴k =0或1.10.函数F (x )=⎠⎛0x t (t -4)d t 在[-1,5]上( )A .有最|大值0 ,无最|小值B .有最|大值0和最|小值-323C .有最|小值-323 ,无最|大值D .既无最|大值也无最|小值 [答案] B[解析] F (x )=⎠⎛0x (t 2-4t )d t =⎝ ⎛⎭⎪⎫13t 3-2t 2| x 0=13x 3-2x 2(-1≤x ≤5).F ′(x )=x 2-4x ,由F ′(x )=0得x =0或x =4 ,列表如下:x (-1,0) 0 (0,4) 4 (4,5) F ′(x ) +-0 +F (x )极大值极小值可见极大值F (0)=0 ,极小值F (4)=-3.又F (-1)=-73 ,F (5)=-253∴最|大值为0 ,最|小值为-323.二、填空题 11.计算定积分: ①⎠⎛1-1x 2d x =________②⎠⎛23⎝ ⎛⎭⎪⎫3x -2x 2d x =________③⎠⎛02|x 2-1|d x =________ ④⎠⎛0-π2|sin x |d x =________[答案] 23;436;2;1[解析] ①⎠⎛1-1x 2d x =13x 3| 1-1=23.②⎠⎛23⎝⎛⎭⎪⎫3x -2x 2d x =⎝ ⎛⎭⎪⎫32x 2+2x | 32=436.③⎠⎛02|x 2-1|d x =⎠⎛01(1-x 2)d x +⎠⎛12(x 2-1)d x=⎝ ⎛⎭⎪⎫x -13x 3| 10+⎝ ⎛⎭⎪⎫13x 3-x | 21=2.[答案] 1+π213.(2021·陕西理 ,13)从如下图的长方形区域内任取一个点M (x ,y ) ,那么点M 取自阴影局部的概率为________.[答案] 13[解析] 长方形的面积为S 1=3 ,S 阴=⎠⎛013x 2dx =x 3| 10=1 ,那么P =S 1S 阴=13. 14.f (x )=3x 2+2x +1 ,假设⎠⎛1-1f (x )d x =2f (a )成立 ,那么a =________.[答案] -1或13[解析] 由F (x )=x 3+x 2+x ,F (1)=3 ,F (-1)=-1 , ∴⎠⎛1-1f (x )d x =F (1)-F (-1)=4 ,∴2f (a )=4 ,∴f (a )=2. 即3a 2+2aa =-1或13.三、解答题15.计算以下定积分: (1)⎠⎛052x d x ;(2)⎠⎛01(x 2-2x )d x ;(3)⎠⎛02(4-2x )(4-x 2)d x ;(4)⎠⎛12x 2+2x -3x d x .[解析] (1)⎠⎛052x d x =x 2| 50=25-0=25.(2)⎠⎛01(x 2-2x )d x =⎠⎛01x 2d x -⎠⎛012x d x=13x 3| 10-x 2| 10=13-1=-23. (3)⎠⎛02(4-2x )(4-x 2)d x =⎠⎛02(16-8x -4x 2+2x 3)d x=⎝⎛⎭⎪⎫16x -4x 2-43x 3+12x 4| 20=32-16-323+8=403.(4)⎠⎛12x 2+2x -3x d x =⎠⎛12⎝⎛⎭⎪⎫x +2-3x d x=⎝ ⎛⎭⎪⎫12x 2+2x -3ln x | 21=72-3ln2.16.计算以下定积分:[解析] (1)取F (x )=12sin2x ,那么F ′(x )=cos2x=12⎝ ⎛⎭⎪⎫1-32=14(2-3). (2)取F (x )=x 22+ln x +2x ,那么F ′(x )=x +1x+2.∴⎠⎛23⎝⎛⎭⎪⎫x +1x 2d x =⎠⎛23⎝⎛⎭⎪⎫x +1x+2d x =F (3)-F (2)=⎝ ⎛⎭⎪⎫92+ln3+6-⎝ ⎛⎭⎪⎫12×4+ln2+4=92+ln 32. (3)取F (x )=32x 2-cos x ,那么F ′(x )=3x +sin x17.计算以下定积分: (1)⎠⎛0-4|x +2|d x ;(2)f (x )=,求⎠⎛3-1f (x )d x 的值.[解析] (1)∵f (x )=|x +2|=∴⎠⎛0-4|x +2|d x =-⎠⎛-4-2(x +2)d x +⎠⎛0-2(x +2)d x=-⎝ ⎛⎭⎪⎫12x 2+2x | -2-4+⎝ ⎛⎭⎪⎫12x 2+2x | 0-2=2+2=4.(2)∵f (x )=∴⎠⎛3-1f (x )d x =⎠⎛0-1f (x )d x +⎠⎛01f (x )d x +⎠⎛12f (x )d x +⎠⎛23f (x )d x =⎠⎛01(1-x )d x +⎠⎛12(x -1)d x=⎝ ⎛⎭⎪⎫x -x 22| 10+⎝ ⎛⎭⎪⎫x 22-x | 21 =12+12=1. 18.(1)f (a )=⎠⎛01(2ax 2-a 2x )d x ,求f (a )的最|大值;(2)f (x )=ax 2+bx +c (a ≠0) ,且f (-1)=2 ,f ′(0)=0 ,⎠⎛01f (x )d x =-2 ,求a ,b ,c的值.[解析] (1)取F (x )=23ax 3-12a 2x 2那么F ′(x )=2ax 2-a 2x ∴f (a )=⎠⎛01(2ax 2-a 2x )d x=F (1)-F (0)=23a -12a 2=-12⎝ ⎛⎭⎪⎫a -232+29∴当a =23时 ,f (a )有最|大值29.(2)∵f (-1)=2 ,∴a -b +c =2① 又∵f ′(x )=2ax +b ,∴f ′(0)=b =0② 而⎠⎛01f (x )d x =⎠⎛01(ax 2+bx +c )d x取F (x )=13ax 3+12bx 2+cx那么F ′(x )=ax 2+bx +c∴⎠⎛01f (x )d x =F (1)-F (0)=13a +12b +c =-2③解①②③得a =6 ,b =0 ,c =-4.。
高中数学选修2-2同步练习题库:微积分基本定理(容易)
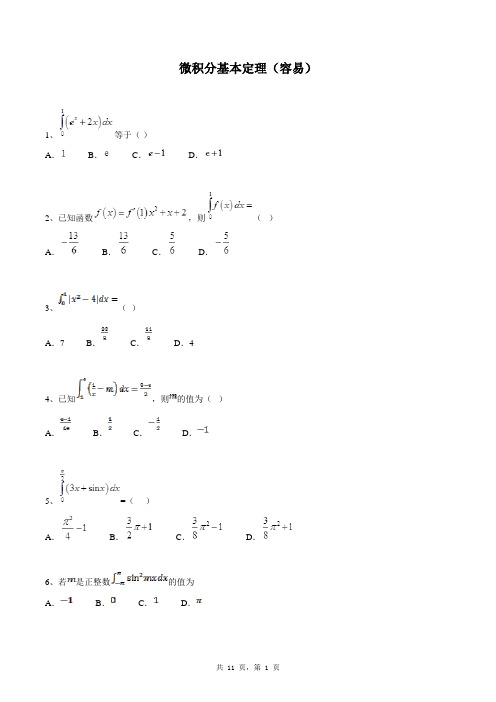
微积分基本定理(容易)1、等于()A. B. C. D.2、已知函数,则()A. B. C. D.3、()A.7 B. C. D.44、已知,则的值为()A. B. C. D.5、=()A. B. C. D.6、若是正整数的值为A. B. C. D.7、已知 (为常数),则()A.恒为0 B.恒为正 C.恒为负 D.取值不定8、已知(为常数),则()A.恒为 B.恒为正 C.恒为负 D.取值不定9、()A.0 B.-1 C. D.10、()A.1 B. C.0 D.11、的值为()A. B. C. D.112、的值为()A. B. C. D.113、()A.-1 B.1 C.0 D.-814、()A.1 B.e﹣1 C.e D.e+1 15、计算定积分=()A. B. C. D.16、定积分的值为()A. B. C. D.17、已知函数则=___________.18、若,则__________.19、若(),则__________.20、定积分__________.21、曲线与直线围成的封闭图形的面积为__________.22、我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系平面内,若函数的图象与轴围成一个封闭的区域,将区域沿轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域的面积相等,则此圆柱的体积为__________.23、若,则__________.24、_______________;25、dx= .参考答案1、B2、B3、C4、B5、D6、D7、A8、A9、A10、C11、D12、D13、C14、C15、B16、C17、18、319、120、21、-22、23、324、25、【解析】1、.故选择B.2、∵,∴,令,得,解得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微积分基本定理同步练习
一、选择题
1.(2010·山东日照模考)a =⎠⎛02x d x ,b =⎠⎛02e x d x ,c =⎠⎛0
2sin x d x ,则a 、b 、c 的大小关系是 A .a <c <b B .a <b <c C .c <b <a D .c <a <b
2.(2010·山东理,7)由曲线y =x 2,y =x 3围成的封闭图形面积为( )
A.112
B.14
C.13
D.712
3. (2010·湖南师大附中)设点P 在曲线y =x 2上从原点到A (2,4)移动,如果把由直线OP ,直线y =x 2及直线x
=2所围成的面积分别记作S 1,S 2.如图所示,当S 1=S 2时,点P 的坐标是( )
A.⎝⎛⎭⎫43,169
B.⎝⎛⎭⎫45,169
C.⎝⎛⎭⎫43,157
D.⎝⎛⎭⎫45,137
4.由三条直线x =0、x =2、y =0和曲线y =x 3所围成的图形的面积为( )
A .4 B.43 C.185 D .6
5.曲线y =cos x (0≤x ≤2π)与直线y =1所围成的图形面积是( )
A .2π
B .3π C.3π2 D .π
6.函数F (x )=⎠⎛0
x t (t -4)d t 在[-1,5]上( ) A .有最大值0,无最小值 B .有最大值0和最小值-323
C .有最小值-323
,无最大值 D .既无最大值也无最小值 7.已知等差数列{a n }的前n 项和S n =2n 2+n ,函数f (x )=⎠⎛1
x 1t d t ,若f (x )<a 3,则x 的取值范围是( ) A.⎝⎛⎭⎫36,+∞ B .(0,e 21) C .(e -11,e ) D .(0,e 11)
8.(2010·福建厦门一中)如图所示,在一个长为π,宽为2的矩形OABC 内,曲线y =
sin x (0≤x ≤π)与x 轴围成如图所示的阴影部分,向矩形OABC 内随机投一点(该点
落在矩形OABC 内任何一点是等可能的),则所投的点落在阴影部分的概率是( )
A.1π
B.2π
C.3π
D.π4
9.函数f (x )=⎩
⎪⎨⎪⎧
x +2(-2≤x <0)2cos x (0≤x ≤π2)的图象与x 轴所围成的图形面积S 为( ) A.32 B .1 C .4 D.12
10.已知正方形四个顶点分别为O (0,0),A (1,0),B (1,1),C (0,1), 曲 线y =x 2(x ≥0)
与x 轴,直线x =1构成区域M ,现将一个质点随机地投入正方形中,则质点落在区
域M 内的概率是( )
A.12
B.14
C.13
D.25
二、填空题
11.已知函数f (x )=3x 2+2x +1,若⎠
⎛1-1f (x )d x =2f (a )成立,则a =________. 12.抛物线y 2=2x 与直线y =4-x 围成的平面图形的面积为________.
13.(抛物线y 2=ax (a >0)与直线x =1围成的封闭图形的面积为43
,若直线l 与抛物线相切且平行于直线2x -y +6=0,则l 的方程为______.
14.已知函数f (x )=-x 3+ax 2+bx (a ,b ∈R )的图象如图所示,它与x 轴在原点处相切,且x 轴与函数图象所
围成区域(图中阴影部分)的面积为112
,则a 的值为________.
15.如图所示,在区间[0,1]上给定曲线y =x 2,试在此区间内确定t 的值,使图中阴影部
分的面积S 1+S 2最小.。
