n阶幻方的同心方阵构造法
构造幻方

构造幻方所谓幻方,也教纵横图,就是在n×n的方阵中放入1到n2个自然数:在一定的布局下,其各行、各列和两条对角线上的数字之和正好都相等。
这个和数就叫做“幻方常数”或幻和。
幻方分为奇数阶幻方、偶数阶幻方(单偶阶幻方、双偶阶幻方),下面就这三类幻方的构造分别示范。
奇数阶幻方的经典方法-罗伯奇数阶幻方,也就是3阶、5阶、7阶……幻方,那么如何构造这样的幻方呢?我们可以采取罗伯法(也叫连续摆数法),其法则如下:把“1”放在中间一列最上边的方格中,从它开始,按对角线方向(比如说按从左下到右上的方向)顺次把由小到大的各数放入各方格中,如果碰到顶,则折向底,如果到达右侧,则转向左侧,如果进行中轮到的方格中已有数或到达右上角,则退至前一格的下方。
按照这一法则建立5阶幻方的示例如下图:罗伯法(连续摆数法)的助记口诀:1居上行正中央,依次斜填切莫忘。
上出框界往下写,右出框时左边放。
重复便在下格填,角上出格一个样。
1居上行正中央——数字1放在首行最中间的格子中依次斜填切莫忘——向右上角斜行,依次填入数字上出框界往下写——如果右上方向出了上边界,就以出框后的虚拟方格位置为基准,将数字竖直降落至底行对应的格子中右出框时左边放——同上,向右出了边界,就以出框后的虚拟方格位置为基准,将数字平移至最左列对应的格子中重复便在下格填——如果数字{N}右上的格子已被其它数字占领,就将{N +1}填写在{N}下面的格子中角上出格一个样——如果朝右上角出界,和“重复”的情况做同样处理。
偶数阶幻方的一种制作方法——双偶阶、单偶阶幻方1.双偶阶幻方(中心对称交换法)n为偶数,且能被4整除(n=4,8,12,16,20……)(n=4k,k=1,2,3,4,5……)先说明一个定义。
互补:如果两个数字的和,等于幻方最大数和最小数的和,即n×n+1,称为互补。
先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:这个方阵的对角线,已经用颜色标出。
幻方的制作方法

奇数阶幻方,偶数阶幻方,六阶幻方的制作方法罗伯法(适合编制所有的奇阶幻方)一居上行正中央,依次斜填切莫忘,上出格时往下填,右出格时左边放,排重便在下格填,角上出格一个样。
六阶幻方,具体的做是:偶阶幻方分两类:双偶数阶幻方和单偶数阶幻方双偶数:四阶幻方,八阶幻方,……4K阶幻方,可用<对称交换法>,方法很简单:1) 把自然数依次排成方阵2) 把幻方划成4×4的小区,每个小区划对角线3) 把这些对角线所划到的数,保持不动4) 把没划到的数,按幻方的中心,以中心对称的方式,进行对调幻方完成!单偶数:六阶幻方,十阶幻方,……4K+2阶幻方方法是很繁的,有一种称<同心方阵法>:1) 把幻方分成两个区:一是边框一圈;二是里面一个双偶数方阵,2) 把(3+8K)到(16K2 +8K+2)按双偶数幻方方法填入双偶数方阵3) 把余下的数,在边上试填,调整到符合为止六阶幻方(4×1+2,k=1)就是把11~26填入中间4×4方格中传说在很久很久以前,黄河里跃起一匹龙马,马背上驮着一幅图;洛水里也浮出一只神龟,龟背上也驮着一幅图。
这两幅图上都用圆点来表示一组数字,马背上的那幅称为“河图”,龟背上的那幅称为“洛书”。
(参见图1)再后来,经过人们研究,发现图中右边的那幅“洛书”,其实是一幅纵横图,即用1到9这9个数字组成一幅数字图,使它横的每行相加、竖的每列相加以及对角线相加,其和都等于15(参见图2)。
我们知道,纵横图就是今天所说的“幻方”,一般地,是指把从1到十的自然数排成纵横各有m 个数,并且使同行、同列及同一对角线上的n个数的和都相等的一种方阵,其中涉及的是组合数学的问题。
而前面所说的“洛书”,就是我国最早的一个三阶幻方。
图1 河图洛书图2 纵横图长期以来,纵横图一直被看作是一种数字游戏。
一直到南宋时期的数学家杨辉,才真正把它作为一个数学问题而加以深入的研究。
幻方的规律和求法

幻方的规律和求法幻方的规律和求法:幻方可是个神奇的存在呀!简单来说,就是在一个正方形格子里,填上一些数字,让每行、每列以及对角线上的数字之和都相等。
我们可以把幻方想象成一个数字的大舞台,每个数字都像是一位演员,它们要在这个舞台上找到自己的位置,共同演绎出神奇的规律。
那些格子就像是演员们的站位,必须恰到好处,才能呈现出完美的表演。
比如说三阶幻方,就像是一个小型的数字音乐会,九个数字要在九个位置上完美配合,奏响和谐的数字乐章。
那幻方是怎么做到让每行、每列和对角线的数字和都相等的呢?这就像是一场精心编排的舞蹈,每个数字都要准确无误地迈出自己的舞步。
以三阶幻方为例,中间的数字就像是领舞的主角,它的位置至关重要。
其他数字则像是伴舞,围绕着中间数字旋转跳跃。
它们之间有着一种微妙的平衡和协调,就像一个默契十足的舞蹈团队。
我们来看看具体的规律。
首先,幻方中每行、每列和对角线上的数字之和是一个固定值,这个值是所有数字总和的三分之一。
比如三阶幻方,1 到9 这九个数字的总和是 45,那么每行、每列和对角线的和就是 15。
这就好像是一场比赛,每个队伍的目标总分是确定的,数字们要努力去达到这个目标。
其次,中间位置的数字有着特殊的地位,它往往是一个关键的平衡点。
而且,相对的两个数字之和通常等于另外两个相对数字之和,就像两队选手在进行拔河比赛,力量要保持平衡。
为了让大家更好地理解,我们来看一个具体的三阶幻方例子:4 9 23 5 78 1 6在这里,每行、每列和对角线的和都是 15。
4 和 6、9 和 1、2 和 8 等相对数字之和都是 10,是不是很神奇呢?幻方在生活中也有不少应用呢!比如在建筑设计中,一些古老的建筑可能会运用幻方的原理来布局,以求达到某种平衡和和谐。
在数学研究中,幻方更是一个重要的领域,数学家们不断探索着更复杂、更奇妙的幻方。
总之,幻方就像是一个隐藏在数字世界里的神秘宝藏,等待着我们去探索和发现。
它的规律既神奇又有趣,让我们感受到了数字的魅力和魔力。
第7讲.尖子班.例题详解

【分析】 方法一:第一步:求幻和:1239315++++÷=()第二步:求中心数:我们把幻方中对角线交点的数叫“中心数”,仔细观察可以发现:除了对角线外,第二行、第二列也分别经过中心数,那么,经过中心数的四条线段上的数字总和是幻和的4倍,即15460⨯=,显然,在这个总和中,中心数用了四次,其余各数正好各用一次,所以中心数应是:604535-÷=()第三步:确定四个角上的数.由于在同一条直线上的三个数的和是15,所以如果某格中的数是奇数,那么与这个数在同一条直线上的另两个数的奇偶性相同,所以四个角上的数必为偶数.第四步:用尝试法填一个基本解,以基本解为基础,可绕中心旋转与对调得到其它各解,共8解,下图为其中一解,其余解均可由其翻转或旋转得到:987654321方法二(对易法):南宋数学家杨辉概括为:“九子斜排,上下对易,左右相更,四维挺出”.即:先把1到9九个数字按顺序斜着排列,再把上下的数字1和9对调,左右的数字7和3对调,最后把4个不在边上也不在最中心的数字拉到角上,一个三阶幻方就形成了.33⨯的正方形中,在每个格子里分别填入1~9的9个数字,要求每行每列及对角线上的三个数的和相等(请给出至少一种填法).幻 方 的 构 造7数 表 与 幻 方 数表与幻方1789456123729654183381456927方法三(阶梯法):阶梯法也叫楼梯法,是法国数学家巴赫特创造的.这个方法看起来有点像对易法,但又完全不一样,十分简单而巧妙,适用于所有奇数阶幻方.这个方法把n 阶方阵从四周向外扩展成阶梯状,然后把2n 个自然数顺阶梯方向先码放好,再把方阵以外部分平移到方阵以内其对边部分去,即构成幻方.下图表示了如何用阶梯法构成3阶幻方.方法二和方法三中将1~9按8个不同的方位排列就可以得到本题8个不同的解. 方法四(罗伯法):把1(或最小的数)放在第一行正中,按以下规律排列剩下的数: ⑴ 每一个数放在前一个数的右上一格;⑵ 如果这个数所要放的格已经超出了最顶行,那么就把它放在最底行,仍然要放在右一列.⑶ 如果这个数所要放的格已经超出了最右列,那么就把它放在最左列,仍然要放在上一行.⑷ 如果这个数所要放的格已经填好了其它的数,或者同时超出了最顶行和最右列,那么就把它放在前一个数的下面,具体如下图:1121231234123456123456712345678123456789这是法国人罗伯特总结出的方法,所以叫“罗伯法”.罗伯法的口诀:一居上行正中央,后数依次右上连.上出框时往下填,右出框时往左填.排重便在下格填,右上排重一个样.它对于构造连续自然数(以及能构成等差数列的数)幻方是最简单易行的,适用于所有奇数阶幻方.276951438[练习]大家一起来练习用罗伯法写个七阶的幻方,注意强调细节.上出框与右出框的处理有时不容易把握,老师隆重推荐大家一种方法——“卷纸筒”,即把上下边重合在一线,则上出框后往右上填的位置正好在下边的对应点上.强调这种方法适用于任意奇数阶幻方.【分析】 ①罗伯法:教师边写边说口诀:“一居上行正中央,后数依次右上连.上出框时往下填,右出框时往左填.排重便在下格填,右上排重一个样”.见第二个图.这是法国人罗伯特总结出的“罗伯法”,它对于构造连续自然数(以及能构成等差数列的数)幻方是最简单易行的,适用于所有奇数阶幻方.25242322212019181716151413121110926584317②阶梯法:阶梯法也叫楼梯法,是法国数学家巴赫特创造的.这个方法十分简单而巧妙,适用于所有奇数阶幻方.这个方法把n 阶方阵从四周向外扩展成阶梯状,然后把2n 个自然数顺阶梯方向先码放好,再把方阵以外部分平移到方阵以内其对边部分去,即构成幻方.下面的图⑴和图⑵表示了如何用阶梯法构成5阶幻方.图⑴中顶边以上的4、5、10三个数在图⑵中被移入底边上方相应的3个原先为空的方格中,其余三侧照此处理.2524232221201918171615141312111098765432112345678910111213141516171819202122232425⑴ ⑵⑵练习:大家一起来练习用罗伯法写个七阶的幻方,注意强调细节.上出框与右出框的处理有时不容易把握,老师隆重推荐大家一种方法——“卷纸筒”,即把上下边重合在一线,则上出框后往右上填的位置正好在下边的对应点上.强调这种方法适用于任意奇数阶幻方.请你将1~25这二十五个自然数填入55 的空格内使每行、每列、每条对角线上的五数之和相等.2【分析】 对于偶数阶幻方的构造略微复杂一点,偶数阶幻方分为两类:双偶数阶幻方,即阶数是4的倍数的数;单偶数阶幻方,即阶数是2的倍数但不是4的倍数.构造双偶数阶幻方有一种简单而有趣的方法,叫做“对称法”.其构造方法如下:⑴ 把所求的数按从上到下、从左到右的次序顺序排成n 阶自然方阵,每个小四阶方阵中对角线上的数都不填.⑵ 按自下而上、从右到左的相反方向重复⑴的过程,但这次只填每个小四阶方阵中对角线穿过的方格,这样便可得到一个任意双偶数阶幻方. 用对称法编制四阶幻方,步骤如下:⑴ 在44 的方阵中都画上2条对角线,如图1;⑵ 按从上到下、从左到右的次序在方阵中填入1到16,但只填对角线不穿过的方格.凡有对角线通过的方格则跳过,如图2;⑶ 最后,按自下而上、从右到左的相反方向重复⑵的过程,但这次只填对角线穿过的方格,而跳过对角线所经过的方格(因为这些方格中已有数字),如图3. 此时整个方阵填入的数正好是1~16,而且正好形成一个四阶幻方.2358912141516131110764115141298532图1 图2 图3还有个类似与对称法的方法,我们叫它“对称交换法”.其构造方法如下: ⑴ 把所求的数按顺序排成n 阶自然方阵.⑵ 每个小四阶方阵中对角线上的数都不动.对角线以外的数在自然方阵中作中心对称变换,这用1~16编制一个四阶幻方.3样便可得到一个任意双偶数阶幻方. 用对称交换法编制四阶幻方,步骤如下: ⑴ 把1~16顺次填成如图1的形式. ⑵ 求幻和. 幻和12316434=++++÷=()⑶ 容易验证每条对角线上四个数之和恰为幻和.即16111613107434+++=+++=. 所以,对角线上的8个数字的位置保持不变.⑷ 把对角线以外的数字,以方阵对角线的交点为中心作对称换位(如图2). 这样,一个四阶幻方就编制出来了,如图3.123456789101112131415161234567891011121314151616151413121110987654321图1 图2 图3【分析】 方法一:给出的九个数形成一个等差数列,1~9也是一个等差数列.不难发现:中间方格里的数字应填等差数列的中间数,也就是第五个数,即应填19;填在四个角上方格中的数是位 于偶数项的数,即13,17,21,25,而且对角两数的和相等,即13251721+=+;余下 各数就不难填写了(见下图).幻 方 的 应 用用11,13,15,17,19,21,23,25,27编制成一个三阶幻方.4111723131925152127与幻方相反的问题是反幻方.将九个数填入33⨯(三行三列)的九个方格中,使得任一行、任一列以及两条对角线上的三个数之和互不相同,这样填好后的图称为三阶反幻方.方法二:用阶梯法,在三阶幻方的上下左右的中间添加一格,先将数字按从小到大的顺序,以斜行方向从左下向右上依次填写,再把添加格内的数填到本行(或本列)中相隔两行(或两列)的方格中.212313111927251517172311131519212527272521191513112317方法三:对易法:九子斜排,上下对易,左右相更,四维挺出.112727172713171317131713151923231915231915151923251121252125212521271111→→→方法四:用罗伯法的口诀:一居上行正中央,后数依次右上连.上出框时往下填,右出框时往左填.排重便在下格填,右上排重一个样.【分析】 因为每行的三数之和都等于k ,共有三行,所以九个数之和等于3k .如右上图所示,经过中心方格的有四条虚线,每条虚线上的三个数之和都等于k ,四条虚线上的所有数之和等于4k ,其中只有中心方格中的数是“重叠数”,九个数各被计算一次后,它又被重复计算了三次.所以有:将九个数填入下图的九个空格中,使得任一行、任一列以及两条对角线上的三个数之和都等于定数k ,则中心方格中的数必为3k ÷.5九数之和+中心方格中的数34k ⨯=, 3k +中心方格中的数34k ⨯=, 中心方格的数3k =÷注意:例题中对九个数及定数k 都没有特殊要求.这个结论对求解33⨯方格中的数阵问题很实用.ca b2*2c d b d a b d c -- 【分析】 设中心数为d (如右上图),因此每行、每列以及每条对角线上的三个数之和都等于3d ,第一行中间的数为2d b -,右下角的数为2d c -.根据第一行和第三列可求出右上图中*的数,由此可得:323232322d c d b d a d c d c d b d a d cd c b d a cc a b ---=-----+=--+-+=-+=+()()所以2c a b =+÷()56GFE65C D B A 1410613951284【分析】 为了叙述方便,我们将其余方格用字母表示,如上右图所示.根据题意可知: 5 27A B ++=⑴ 5 27C E ++=⑵ 5 27D G ++=⑶ 627C D ++=⑷ 627A E ++=⑸ 27A C G ++=⑹ 27B C F ++=⑺在九宫图中,第一行第三列的位置上填5,第二行第一列位置上填6,如下图.请你在其他方格中填上适当的数,使方阵横、纵、斜三个方向的三个数之和均为27.将九个数填入下图的空格中,使得每行、每列以及每条对角线上的三个数之和都相等,证明:2c a b =+÷()6727E F G ++=⑻由中心数=幻和3÷得知:2739C =÷=.将9C =代入⑷,得 12D =,将9C =代入⑵,则13E =.将 12D =代入⑶,则10G =.将13E =代入⑸,则 8A =.将 8A =代入⑴,则14B =.将14B =、9C =代入⑺,则4F =.由分析可知,中心方格必须填数字9,其他方格中也只有一种填法.见右上图.【分析】 这道题要构造的是一种比较特殊的幻方,叫三阶反幻方.它的特点就是将九个数填入33⨯的九个方格中,使得任一行、任一列以及两条对角线上的三个数之和互不相同.题目要求相邻的两个自然数在图中的位置也相邻,所以这9个自然数按照大小顺序在图中应能连成一条不相交的折线.经试验有下图所示的三种情况:按第一种填(如下图),不合题意.123654789——|——|—— 987456321——|——|—— 按第二种填(如下图),满足条件,有两解.123894|765——|—|—— 987216|345——|—|—— 将前9个自然数填入下图的9个方格中,使得任一行、任一列以及两条对角线上的三个数之和互不相同,并且相邻的两个自然数在图中的位置也相邻.8。
幻方制作方法

幻方制作方法一、什么是阶数?横竖各3格就是3阶,各4格就是4阶,依此类推。
二、奇数阶幻方的构造方法:把1放在中间,右上行走,上边出头往下落,右边出头往左走,占位或者对角出头往下落三、4×n阶幻方的构造(一)4×1阶幻方的构造方法一第一步:依次填数第二步:对角交换1 2 3 45 6 7 89 10 11 1213 14 15 16(二) 四阶幻方的构造方法二第一步:依次填数 第二步:不是对角的交换1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16总结:基本的四阶幻方的构造,是先依次填数,然后要么是对角的数据都交换,要么是对角的数据都不交换。
(三)4×n 阶幻方的构造我们已经知道了4×1阶幻方的构造方法:然后要么是对角的数据都交换,要么是对角的数据都不交换。
那么4×n 阶幻方的构造方法,完全与4阶幻方的构造一样,也是:要么是对角的数据都交换,要么是对角的数据都不交换。
但是,在构造4×2阶幻方时候,要把每2×2格作为一格,在构造4×3阶幻方时候,要把每3×3格作为一格,1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 5758 59 60 61 62 63 641 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 575859606162636416 2 3 13 34 5 11 10 8 34 9 7 6 12 34 4 14 15 1 34 34 34 34 341 15 14 4 34 12 6 7 9 34 8 10 11 5 34 13 3 2 16 34 34 34 34 3464 63 3 4 5 6 58 57 56 55 11 12 13 14 50 49 17 18 46 45 44 43 23 24 25 26 38 37 36 35 31 32 33 34 30 29 28 27 39 40 41 42 22 21 20 19 47 48 16 15 51 52 53 54 10 9 8 7 59 60 61 62 2 11 2 62 61 60 59 7 89 10 54 53 52 51 15 1648 47 19 20 21 22 42 4140 39 27 28 29 30 34 3332 31 35 36 37 38 26 2524 23 43 44 45 46 18 1749 50 14 13 12 11 55 5657 58 6 5 4 3 63 641 2 3 4 5 6 7 8 9 10 11 1213 14 15 16 17 18 19 20 21 22 23 2425 26 27 28 29 30 31 32 33 34 35 3637 38 39 40 41 42 43 44 45 46 47 4849 50 51 52 53 54 55 56 57 58 59 6061 62 63 64 65 66 67 68 69 70 71 7273 74 75 76 77 78 79 80 81 82 83 8485 86 87 88 89 90 91 92 93 94 95 9697 98 99 100 101 102 103 104 105 106 107 108109 110 111 112 113 114 115 116 117 118 119 120121 122 123 124 125 126 127 128 129 130 131 132133 134 135 136 137 138 139 140 141 142 143 1441 2 3 141 140 139 138 137 136 10 11 1213 14 15 129 128 127 126 125 124 22 23 2425 26 27 117 116 115 114 113 112 34 35 36108 107 106 40 41 42 43 44 45 99 98 9796 95 94 52 53 54 55 56 57 87 86 8584 83 82 64 65 66 67 68 69 75 74 7372 71 70 76 77 78 79 80 81 63 62 6160 59 58 88 89 90 91 92 93 51 50 4948 47 46 100 101 102 103 104 105 39 38 37109 110 111 33 32 31 30 29 28 118 119 120121 122 123 21 20 19 18 17 16 130 131 132133 134 135 9 8 7 6 5 4 142 143 144(三)如何在纸上快速填写4n阶幻方,参看上图1、我们假设对角不变。
构造幻方的技巧

构造幻方的技巧
1. 嘿,你知道吗,构造幻方有个超有用的技巧就是对称法呢!比如说,就像我们照镜子一样,让数字在相对的位置上保持对称,这样不就能快速搞定一部分啦!就像3x3 的幻方,把中位数放中间,其他数字两两对称放置,是不是很神奇呀!
2. 哇塞,还有个技巧叫等差序列法哟!想象一下,数字们排着队,有规律地前进。
比如 5x5 的幻方,先用等差序列把数字排好,再根据规则调整,你看,一个漂亮的幻方不就出来啦!
3. 嘿,别忘了巧用中心数呀!这就像是舞台的中心主角一样重要呢。
比如在奇数阶幻方里,中心数可是起着关键作用的呀,以它为基准去摆弄其他数字,多有意思呀!
4. 哈哈,还有一个神奇的技巧叫行列交换法呢!就好像小朋友交换玩具一样,把数字所在的行和列换一换位置,说不定就能构造成幻方啦,不信你试试呀!
5. 哇哦,奇数偶数分开考虑也是个很棒的方法呀!就像把不同的小伙伴分到不同的队伍里,分别对待它们,这样构造幻方会更清晰明了呢!
6. 哎呀呀,固定角落法也很赞哦!让一些关键数字固定在角落,就像给房子打下坚实的根基一样,再去填满其他地方,是不是很厉害呀!
7. 嘿,还有一种叫斜线填充法呢!想象一下沿着斜线把数字放进去,是不是很有创意呀。
比如在某些幻方里,先沿着斜线填好几个数字,剩下的就好办多啦!
8. 哇,逐步调整法也不能忽视呀!就跟我们慢慢调整自己的状态一样,一点一点地让幻方变得完美,很有意思吧!
9. 我觉得呀,构造幻方真的超有趣!这些技巧都各有各的奇妙之处,用起来就感觉自己像个小小的魔术师呢,能把数字变得那么神奇!赶紧去试试吧!。
幻方法则

幻方幻方法则南宋杨辉不仅精通数学,而且精通易学,在他1275年所著的《续古摘奇算法》中,就对河图和洛书的数学问题进行了详尽的研究。
其中对3阶幻方的排列,找出了一种奇妙的规律:“九子斜排,上下对易,左右相更,四维挺出,戴九履一,左三右七,二四为肩,六八为足”,清代,李光地的《周易折中》把杨辉所概括的这种排列排列原理为“阳动阴静”。
我们通常所说的幻方是平面和幻方。
n阶幻方就是在n×n的方格中填上n^2【n的平方】个数,行、列和对角线的和值相等为完美幻方,行、列和值相等为不完美幻方。
这一和值叫幻和值。
一个n阶幻方幻和值公式为:Nn=1/2xn(n2+1)【注:n2是n的平方】幻方分为奇阶幻方和偶阶幻方,构成方法也不同。
【奇阶幻方】一、Merzirac法生成奇阶幻方在第一行居中的方格内放1,依次向右上方填入2、3、4…,如果右上方已有数字,则向下移一格继续填写。
如下图用Merziral法生成的5阶幻方:17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9Merzirac法,有人也叫楼梯法,我管它叫斜步法,即走X+Y斜步(数字按右上方顺序填入),-Y跳步(如果右上方已有数字或出了对角线,则向下移一格继续填写)。
其实斜步法可以向4个方向依次填写数字,即右上、右下、左上、左下4个方向,每种斜步都可有2种跳步,即左(右)跳步、上(下)跳步。
对于X+Y斜步相应的跳步可以为-X,-Y。
【记住,跳步是X+Y斜步的X(或Y)相反方向即可。
如右上方向斜步,跳步就为向左(或向下)一步;左下方向斜步,跳步就为向右(或向上)一步;等等等等】二、loubere法生成奇阶幻方在居中的方格向上一格内放1,依次向右上方填入2、3、4…,如果右上方已有数字,则向上移两格继续填写。
如下图用Louberel法生成的5阶幻方:23 6 19 2 1510 18 1 14 2217 5 13 21 94 12 25 8 1611 24 7 20 3上述loubere法可以记作X+Y斜步(数字按右上方顺序填入),2Y跳步(如果右上方已有数字或出了对角线,则向上移二格继续填写)。
幻方填法之4n阶幻方
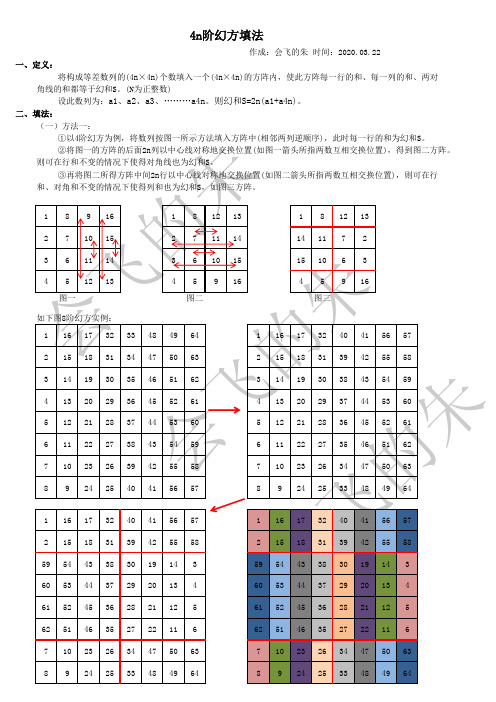
会飞的朱会飞的朱会飞的朱作成:会飞的朱时间:2020.03.22一、定义:将构成等差数列的(4n×4n)个数填入一个(4n×4n)的方阵内,使此方阵每一行的和、每一列的和、两对角线的和都等于幻和S。
(N为正整数)设此数列为:a1、a2、a3、………a4n。
则幻和S=2n(a1+a4n)。
二、填法:(一)方法一:①以4阶幻方为例,将数列按图一所示方法填入方阵中(相邻两列逆顺序),此时每一行的和为幻和S。
②将图一的方阵的后面2n列以中心线对称地交换位置(如图一箭头所指两数互相交换位置),得到图二方阵。
则可在行和不变的情况下使得对角线也为幻和S。
③再将图二所得方阵中间2n行以中心线对称地交换位置(如图二箭头所指两数互相交换位置),则可在行和、对角和不变的情况下使得列和也为幻和S,如图三方阵。
189161812131812132710152711141411723611143610151510634512134591645916图一图二图三如下图8阶幻方实例:116173233484964116173240415657215183134475063215183139425558314193035465162314193038435459413202936455261413202937445360512212837445360512212836455261611222738435459611222735465162710232639425558710232634475063892425404156578924253348496411617324041565711617324041565721518313942555821518313942555859544338301914359544338301914360534437292013460534437292013461524536282112561524536282112562514635272211662514635272211671023263447506371023263447506389242533484964892425334849644n阶幻方填法会飞的朱会飞的朱会飞的朱规律总结:六区间法:1、将方格按列左右均分成两部分,再按行上中下分成三部分共6个区间;2、从1区间左上角按列开始顺序填数,遇到列分线则跳到行分线对 称空格按顺序填。
n阶魔方阵解题思路

n阶魔方阵解题思路
解题思路如下:
1. 确定魔方阵的阶数n,魔方阵是一个n x n的矩阵,其中每一行、每一列以及对角线上的元素之和都相等。
2. 创建一个n x n的二维数组,表示魔方阵。
3. 将1放在第一行的中间位置,即第一行的中间列。
4. 从2开始,依次填充魔方阵。
规则如下:
a. 如果当前位置的右上方没有数字,则将当前数字放在右上方;
b. 如果当前位置的右上方有数字,则将当前数字放在下方。
5. 如果当前位置是第一行,则下一个位置应该是最后一列;如果当前位置是最后一列,则下一个位置应该是第一行。
否则,下一个位置是当前位置的右上方。
6. 重复步骤4和步骤5,直到魔方阵被填满。
7. 最后,输出填充完毕的魔方阵。
通过以上步骤,可以得到一个满足条件的n阶魔方阵。
改进镶边法构造任意奇阶同心幻方

文章编号 : 1 0 0 4—1 7 2 9 ( 2 0 1 3 ) 0 3— 0 1 9 9— 0 6
改 进 镶 边 法 构 造 任 意 奇 阶 同 心 幻 方
邓 湘 平
( 安徽 大学 化学化工学 院, 安徽 合肥 2 3 0 0 3 9 )
摘
要 :首先引入 了双关联等差 数列 的概念 , 借此提 出了一个 构造 n阶幻方的充分条件 , 然 后将奇 阶幻方分
为 n =4 m一1阶与 n=4 m+1 ( m=1 , 2, …, m∈N) 阶两类 , 介绍 了一种改进 的镶边法 , 分别构造两类奇 阶幻
方, 并 给出了严 格的证明 .此构造法简单易行 , 灵活多变 , 所构 造出的幻方具有独特的性质 .
关键词 : 幻方 ;同心幻方 ;镶边法 ;双关 联等差数列 ;十字旋转
进镶边法的一个最大特点是无需 已知一个较低阶幻方 , 可以由外及内或 由内及外 , 层层镶边 , 最终得到完
整 的 同心 幻方 .
1 构造广义 门阶幻方的一个充分条件
一
般 对 n阶幻 方 的定义 , 是将 1 , 2 , …, n 填 到 n×n的方格 中 , 使 其每 一横 行 、 竖 行 以及 2条对 角线 上
第3 1 卷第3 期
2 0 1 3年 9月
海 南 大 学 学 报 自 然 科 学 版
NATURAL S CI ENCE J OURNAL OF I - I AI NAN I i Ⅳ EI I T Y
V0 1 . 31 No . 3 S e p . 2 0 1 3
中图 分 类 号 :0 1 5 7 文 献 标 志 码 :A
幻 方是 一 个古 老而 著名 的组 合算 题 , 最 早起 源 于 中 国 .相 传 大 禹治 水 感 动 了上 天 , 一 只神 龟 从 河 中
n阶幻方构造方法

n阶幻方构造方法说实话n阶幻方构造这事,我一开始也是瞎摸索。
我就知道幻方就是把数字填到一个n乘n的格子里,让每行每列以及对角线上的数字之和都相等。
但真要动手构造啊,那可真不容易。
我试过那种最笨的方法,从1开始一个一个数字往里填。
可没填几个就乱套了。
就好比你盖房子,一块砖一块砖乱搭,最后肯定建不成好房子嘛。
后来我了解到一个叫做罗伯法的方法。
这个方法感觉就像是有了个小窍门。
比如说要构造一个奇数阶的幻方,首先是把1放在第一行中间的那个格子。
这就像是定了个小锚点一样。
接着呢,就是按照斜着往上走一格同时往右走一格的方法去填下一个数字。
要是碰到顶了,那就从最底行接着来;要是碰到最右边了,就从最左边那一列接着。
要是要填数字的格子已经有数字了,那就往下退一格再填。
就像走路遇到墙了,只能往回退一点寻找新的路。
我用这个方法试了试3阶幻方。
先把1放在第一行中间,然后按照规则去填2,发现要出顶了就从最底行接着填。
就这样慢慢地把9个数字都填进去了。
填完一看,每行每列以及对角线数字之和都相等,可高兴了。
不过对于偶数阶幻方,这个罗伯法就不行了。
我又摸索了好久。
听说有一种双偶阶幻方的构造方法。
就是把整个幻方的格子分成小的4×4的方格。
然后在每个小方格里面按一定顺序填数字。
但是这个一定顺序我就有点说不太清楚了。
我感觉就像是按照某种特殊的舞蹈步伐在填数字,但我还没能完全掌握。
还有那种单偶阶幻方的构造,我到现在都还觉得很复杂。
听说有个叫斯特雷奇法的,可我研究了半天也没完全搞明白。
感觉像进入一个迷宫一样,走了半天没能完全走通。
我觉得如果想构造n阶幻方,先把奇数阶的先拿下,用罗伯法多练习练习。
从简单的3阶幻方做起,就像学走路先从迈小步开始。
多做做例子,等把这个方法熟了再去研究偶数阶的,可能就不会那么难了。
我现在也还在探索偶数阶幻方怎么能轻松搞定的方法呢。
这个过程虽然有点波折,但每次成功构造出一个幻方的时候,那种成就感还是让我觉得挺值的。
n阶幻方的规律和方法

n阶幻方是指将数字填入n×n的方格中,使得每行、每列及对角线上的数字之和相等。
n阶幻方有多种填法,其中最经典的是罗伯特法(也有人称之为楼梯法)。
罗伯特法的填写步骤如下:
1. 将数字1放在第一行正中。
2. 如果这个数所要放的格已经超出了顶行,那么就把它放在底行,仍然要放在右一列。
3. 如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内。
4. 如果这个数所要放的格已经有数填入,处理方法同上。
除了罗伯特法,还有双偶阶幻方等其他方法。
双偶阶幻方是将数字从左到右、从上到下按顺序填写,这个方阵的对角线,已经用颜色标出,将对角线上的数字,换成与它互补(同色)的数字即可。
以上就是填写n阶幻方的一般规律和方法,可以根据实际情况进行调整和优化。
幻方的构造研究

幻方的构造研究尹春来2017年2月一、什么是幻方在一个由n排n列数连续自然数组成的正方形中,任一行、列及对角线的n个数之和都相等,具有这种性质的图表,称为“幻方”。
我国古代称为“河图”、“洛书”,又叫“纵横图”。
如下图,是一个六阶幻方。
幻方的几个概念。
奇幻方:当行(列)数n为奇数时,幻方称为奇幻方。
偶幻方:当行(列)数n为偶数时,幻方称为偶幻方。
双偶幻方:当n能被4整除时,幻方称为双偶幻方。
单偶幻方:当n被4整除时余2时,幻方称为单偶幻方。
完美幻方:任何泛对角线数字之和也相等时,也即将幻方看成是无限伸展的图形,则任何一个n×n方格内的数字都可以组成一个幻方,则称为完美幻方,又称魔鬼幻方。
幻和:幻方各行、列、对角线的和,为(n×n +1)×n/2二、幻方的构造方法在填幻方前,先约定几个规则。
一般将n阶幻方看作一个矩阵,记为A,其中的第i行j列方格内的数字记为a(i,j)。
幻方构造方法一般按某个规则,更多的以n个数为一组,一组最后一个数字到下一组第一个数字称为跳步。
如填写数字超出幻方格范围,则把幻方看成是可以并排放置无限伸展的图形,如下图所示,每个编号相同的对应方格视为等同位置,如果填写过程中超出了幻方原有空格位置,则自动转到对应位置继续填写。
即,按某种规则填写到a(i,j)时,若i>n,则i=i-n,若i<1则,i=i+n;j亦同。
下面,我们开始研究幻方的构造方法。
根据数字奇偶不同,我们将幻方分为奇幻方和偶幻方来分别研究。
2.1奇幻方奇幻方可以使用Merzirac法与loubere法。
1997年,我用国际象棋之马步试图构造完美幻方,故命名为horse法。
另外,幻方可以是多重嵌套的,用一定规则从低阶向高阶逐步构造,命名为Yinmagic法。
Merzirac法在第一行居中格(第(n+1)/2列)内放1,依次向左上方填入2、3、4…到n,跳步为下移一格,继续填写n+1,n+2……。
成功打造3n阶九宫幻方

“系统易学”成功打造3n 阶九宫幻方系列余 斌[1]电子信箱:ruyi999888@【提要】 现在是2005年末。
在运用“系统易学”的基本原理成功打造3n 阶九宫幻方系列[2]后,特撰写本文。
在向广大易学爱好者和幻方爱好者汇报、分享成果的同时,试图探索易学九宫系统更深的机理和九宫幻方与众不同的“幻”境。
【关键词】 “系统易学” 九宫幻方 3n 阶九宫幻方 元数 元通公式 阴数模式 阳数模式说到九宫数和幻方大多数人都不陌生,在金庸先生著名的武侠小说《射雕英雄传》中就有郭靖在黄蓉的指导下为英姑指点九宫数的排列:“戴九履一,左三右七,二四为肩,六八为足,五居中央。
”这当然只是金庸武侠小说中的一个小插曲。
事实上根据《论说》和《星子》的记载,传说在约3000年前的夏禹治水的时代有“神龟”背附神奇的星点图案出现在洛水,所以这个图案就被称为“洛书”。
“洛书”上的星点图案用数字表示再引入方格图案便形成了后来的九宫格或九宫数。
由于九宫数的数阵具有:“四正四维,皆合于十五”的特性,即三纵三横与对角三数相加之和都等于15的特殊机理,在中国古代更有“纵横图”的说法,于是也就揭开了幻方研究的序幕。
九宫数也就成为最具代表性的三三幻方,也是最早的幻方。
而“四正四维,皆合于十五”也就成为判定幻方的基本要素。
易学与幻方学由于“洛书”是幻方学的源头,同时也是传说中易学的源头之一,因此两者之间还是存在一定的同宗之缘。
在中国古代对幻方的研究大都伴有易学的影子;到了近代幻方学的发展开始走向纯数学化。
但同时也不断有人质疑:幻方研究来干什么用?这个看似简单的问题着实让人琢磨。
在笔者看来:纯数学化的问题是一个不可回避现实问题,当然这里存在诸多的历史和现实因素,但是顺着同宗之缘的线索寻求相互支撑平台也是一种选择,毕竟我们还不完全清楚“洛书”的真正内涵。
幻方学的研究与发展到现在已颇具规模。
在阶数[3]方面已经上千(据说还有上万的但笔者还未查到具体资料),另外还发展出了次方幻方[4]等幻方形式。
n阶幻方

N为4的倍数
• • • ⑵ N为4的倍数时 采用对称元素交换法。 首先把数1到n×n按从上至下,从左到右顺 序填入矩阵 • 然后将方阵的所有4×4子方阵中的两对角线 上位置的数关于方阵中心作对 • 称交换,即a(i,j)与a(n-1-i,n-1-j)交换,所有其 它位置上的数不变。 • (或者将对角线不变,其它位置对称交换也可)
• //释放动态内存 • for(i=0; i<n; i++) • { • delete[] array[i];//原来是 delete array[i]; • } • delete[] array; • }
程序执行结果
N阶幻方求解
N阶幻方历史
• 我国的纵横图通过东南亚国家,印度、阿 我国的纵横图通过东南亚国家,印度、 拉伯传到西方。 拉伯传到西方。由于纵横图具有十分奇幻 的特性,西方把纵横图叫作Magic Square, 的特性,西方把纵横图叫作 , 翻译成中文就是“幻方” 魔方” 翻译成中文就是“幻方”或“魔方”。
• • • • • • • • • • •
//输出n阶幻方 cout<<n<<"阶幻方:"<<endl; for(i=0; i<n; i++) { for(j=0;j<n;j++) { cout<<setw(int(log10(n*n))+2)<<array[i][j]; } cout<<endl; } cout<<endl;
• • • • • • • • • • • • • • • • • • • • • •
void showFangzhen(int n) { if(!(n%2)) return; int i,j,**array; //为指针分配动态内存 array=new int*[n]; for(i=0; i<n; i++) { array[i] = new int[n]; } //初始化数组 for(i=0; i<n; i++) { for(j=0; j<n; j++) { array[((n-1)/2+i-j+n)%n][(3*n-1+j-2*i)%n]=i*n+j+1; //or //array[(n+2*i-j)%n][((n-1)/2+n+j-i)%n]=i*n+j+1; } }
n阶幻方(n>4)的几种构造方法

n阶幻方(n>4)的几种构造方法
殷志祥
【期刊名称】《安徽理工大学学报(自然科学版)》
【年(卷),期】2000(020)001
【摘要】提出并证明了:1.递归构造n阶幻方(n>4)的方法;2.已知m阶幻方(m>2)、n阶幻方(n>2),求mn阶幻方的公式;3.已知m阶幻方(m>2),构造2m阶幻方的方法.
【总页数】6页(P67-72)
【作者】殷志祥
【作者单位】淮南工业学院数理系,安徽,淮南,232001
【正文语种】中文
【中图分类】O157
【相关文献】
1.3k阶拉丁幻方的构造方法 [J], 曹燕飞;刘兴祥
2.8t阶幻方及正交拉丁方的构造方法 [J], 俞万禧
3.任意奇阶和部分偶阶幻方的构造方法:宏微控制法和自我扩张法 [J], 温世清;王利达
4.双偶数阶完美和幻方的定义及其构造方法 [J], 张婧;刘兴祥;董朦朦
5.奇数阶始元臻美和幻方的构造方法 [J], 惠晶;刘兴祥
因版权原因,仅展示原文概要,查看原文内容请购买。
合数阶幻方的构造法

合数阶幻方的构造法一、概念和公式1、设n 阶矩阵()n ij n nA a ⨯=,,k b N ∈(1)定义()n ijn nkA ka ⨯=即()n ijn nA a ⨯=中的每个数都乘以k ; (2)()n ij n nA b a b⨯+=+,即()n ijn nA a ⨯=中的每个数都加上b ;由(1)(2)得出:()n ij n nkA b ka b ⨯+=+(3)()n m ij m mn mn A B a B ⨯⨯=⨯ 2 、()1n n n I ⨯= ,()n n n kI k ⨯= 二、用3幻方构造9阶幻方3492357816A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,33811246705A ⎛⎫ ⎪-= ⎪ ⎪⎝⎭,3111111111I ⎛⎫ ⎪= ⎪ ⎪⎝⎭ ,339999999999B I ⎛⎫⎪== ⎪ ⎪⎝⎭3333333333391(1)246705B B B A B B B B B B ⎛⎫⎪-⨯= ⎪ ⎪⎝⎭,()333333333333A A A A A A A A A A ⨯⎛⎫ ⎪= ⎪ ⎪⎝⎭()3333339333333333333333339(1)246705B A B A B A A A B A B A B A B A B AA B A ⨯+++⎛⎫⎪=-⨯+=+++ ⎪ ⎪+++⎝⎭就是9阶幻方。
其中33949992939597989196k k k kB A k k k k k k +++⎛⎫⎪+=+++ ⎪ ⎪+++⎝⎭表示由91,92,,99k k k +++ 这9个数构成的3阶幻方。
33333393333333333331362976817413181130323475777912141635283380737817101538222720404538586356246212325394143575961705261924443742625560677265492495447666870357485B A B A B A A B A B A B A B AA B A +++⎛⎫⎪=+++= ⎪ ⎪+++⎝⎭052716469816534651⎛⎫⎪⎪ ⎪⎪⎪ ⎪ ⎪⎪ ⎪⎪⎪ ⎪⎝⎭二、合数(3,;3,)n ab a a N b b N =≥∈≥∈ 已知a A ,b A ,1、 做出1a A -,就是把a A 中的每个数都减去12、 做出b I ,以及2b b B b I =3、 计算(1)a b A B -⨯4、 做出()b b b a abb a a A A A A A ⨯⨯⎛⎫ ⎪= ⎪ ⎪⎝⎭ 5、 那么()(1)n a b b a a A A B A ⨯=-⨯+就是一个n 阶幻方。
N阶幻方的一种简易解法

2
的关系仍然不会变化。
-3 4 -1
1 2 -3
总总总结结结我们的方法是制造出和幻方等价的归零幻方充分利用其各行列及对角线上数字之和为0的特点编排出各数的位置同时我们的方法避免了重复劳动使得第n阶幻方可以从第n2阶的结果加上外边各数的确定推出
N 阶幻方的一种简易解法
景士勇,张景元,景俊
江 苏 省 泰 州 市 海 陵 区 福 寿 苑1号 楼404室 ,225300 Email: jsy tz@ (Dated: January 8, 2005)
3 -4 1
-1 -2 3
2 0 -2 ←→ -4 0 4 ←→ -2 0 2 ←→ 4 0 -4
1 -4 3
3 -2 -1
-1 4 -3
-3 2 1
虽然不能认为这些解是平庸的,但由一个解马上可以得到4个解却是不争的事情。为了方 便起见,一般我们只考虑第一行首末两数为 同号且为负数的解(即以上4个解中左边第一 个,选哪个都无所谓),在本文中,称之为“规定解”。至于为什么考虑这两个数的特征, 那是因为首行第一个数与首列第一个数相同,而最后一个数又和首列最后一个数互为相反 数,具有非同寻常的意义。
Abstract
摘要
幻方问题既古老又新奇,迄今为止的解决方案要么过于繁琐,要么把奇数阶和偶数阶分开讨 论。本文旨在对各阶幻方提出一套简易的统一解法,使之可以方便的为读者掌握:阶数较小时, 花几分钟就可以填好;对于阶数较大的情况也不难应用计算机程序来处理。
幻方的构造方法

奇数阶幻方构造当n是奇数时,只需按以下步骤填写,即可得到一个n阶幻方.(1)先画一个n×n方格表;(2)把1填写在最顶行中间;(3)当k填好后,若k的右上方空,则把k+1填在此格,否则,把k+1填在k的下方.(注意,这里我们把最左列视作在最右列的右方,把最底行视作在最顶行的上方)例1填写一个3阶幻方这就是刚才的A3例2填写一个5可验证这是幻和为654k(双偶数)阶幻方的构造●4阶幻方的一种构造方法一般来说,偶数阶幻方的构造较难,但对于四阶幻方,我们有较简单的方法。
步骤如下:(1)先画一个4×4方格表;(2)在方格表中按顺序填写1~16;(3)兰.即1←→16,4←→13,6←→11,7←→10. 对换后,即得一个四阶幻方.●8阶幻方的构造幻和S8=260先按自然顺序填写8阶方阵;兰色不动,其余关于中心对称的两数互换位置.。
一般的4k 阶幻方仍可按此规律来构造.4k+2阶幻方的构造我们先来考察一个6阶幻方可以如何构造出来.第一步,先用上述介绍的方法构造出一个4阶幻方, 如图1所示,幻和为34; 第二步,把这个4阶幻方的每个数都加上10,得图2所示, 此时幻和为74;图2所用的数是11~26, 恰是1~36中间的16个数, 如图3所示;图1 图210−−−−→全部加图3第三步,观察剩余的20个数有这样的规律:+=+=+==+=,136235334102737而37+74=111=S 6, 于是,可把这20个数按“和为37”配成10对,如图4所示。
把第一行的数称为小头数,第二行的数称为大头数。
图4第四步,按每对在同一行或同一列或同一对角线的原则,把它们添加到图2的四周,但要满足: (a) 每边3个小头数;(b)对边的小头数之和相等。
这就可得到一个6阶幻方,如图5所示。
图5图5四周每边3个小头数(蓝色),第1行与第6行的小头数之和都是20; 第1列与第6列的小头数之和都是17.这种方法可以推广到一般4k+2阶幻方的构造,其步骤是:(1) 先构造出一个4k阶幻方;(2) 把这个4k阶幻方的每个数都加上8k+2,即把这16k2个数移到1~(4k+2)2的中间;(3) 把剩余的首尾两段小头数与大头数配对,每对之和为16k(k+1)+5;(4) 按每对在同一行或同一列或同一对角线的原则,把它们添加到上图的四周,但要满足: (a) 每边2k+1个小头数;(b)对边的小头数之和相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n 阶幻方的同心方阵构造法本文根据n 阶幻方的定义,首先利用线性方程组的理论证明了:利用同心方阵的办法可以构造出任意阶幻方,进而结合幻方的特点,给出了n 阶幻方的具体构造方法. 一 同心方阵构造法定义;将自然数1,2,3...n 2排成n 行n 列的方阵,若每行每列及每条对角线上的n 个数字的和皆为常数,称这样的n 阶方阵为n 阶幻方.这个常数称为幻方常数.同心方阵构造法是一种递推的方法.假定n 阶幻方已经做出,就依n 阶幻方为基础,在四周加上一层框子,即在第一行的上边,在第n 行的下边,各加上一行,在第一列的左边,在第n 列的右边,各加上一列.构造出一个n+2阶方阵,新的n+2阶幻方的中间部分是一个n 阶幻方,它是由原来的幻方的各元素分别加上2n+2x 形成的.n+2阶幻方的外围部分(即第一行,第n+2行,第一列,第n+2列所形成的正方形框子)是由数1,2,3, (2))2(+n 中的前2n+2个数,及后2n+2个数,按照下述要求构成的(1)使正方形各边上的n+2而数的和等于n+2阶的幻方常数k.(2) 使正方形上下两边,左右两边相对元素的和,及对角线两顶点元素的和都等于1)2(2++n . 这样构成的n+2阶幻方的方法称为同心方阵构造法容易证明二阶幻方是不存在的.三阶幻方容易做出,四阶阶幻方见[1].我们以三阶,四阶幻方为基础,根据本文所给出的方法,可以构造出任意阶幻方.二 同心方阵构造法的理论基础⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡++++++++++++++22122322211111233122212111131211...*...**............***...**...n n n n n n n n n n n n n n x x x x x x x x x x x x x x x x 根据同心方阵构造法得到以下4n+4个未知数2n+6个线性方程构成的线性方程组(令H n =++1)222()................2331222121211211231322122211........左右相对....右上角与左下角................上下相对.....左上角与右下角H x x H x x H x x H x x H x x H x x H x n n n n n n n n n n n =+=+=+=+=+=+=++++++++++++ 左)...上)...下)..右)........(.....(.....(....(....2121112112112222212222212111H x x x H x x x H x x x H x x x H x x n n n n n n n n n n n n n =+++=+++=+++=+++=++++++++++++++ (其中H 为幻方常数)这个线性方程组与常数项组成的增广矩阵如下:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡.00...00101...010100...00100...00000...000011...11111...11100...000000...00010...00010...101010...00000...00011...000000...000..........................00...00000...110000...00000...00000...001100...00000...00100...000010...00001...00000...000001...000........................00...10000...000000...10000...01000...000000...01010...00000...000000...001H H H H H H H H H H H H利用线性代数的知识,用矩阵的初等变换,将其化简(具体化简过程从略)成如下形式:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-------------00 (00)000...000000...000000...00000...000000...00011...11100...000000...0002221...11010...101000...00000...00011...000000...000............................................................00...00000...110000...0002221...11010...100100...00011...11000...000010 (0000)1 (00)000...000001...000............................................................00...10000...000000...10000...01000...000000...01010..00000...000000...001K H K H H K H K H H H H H由上面的矩阵可以看出;系数矩阵与增广矩阵的秩相等,可知线性方程组有解.这就证明了同心方阵构造法的可行性.同时还可以得到线性方程组的一般解.1221231322122211........................+++++++-=-=-=-=n n n n n n n x H x x H x x H x x H x 2212232221211124412331221223222124232222122322212423212212232221...........................2......22......22...++++++++++++++++++++++++++++++++++++++++-----=-=-=-=----------=+++++++++-=+++++-=n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n x x x x K x x H x x H x x H x x x x x x x x H K x x x x x x x x k H x x x x x K H x从而可知;这4n+4个未知数,其中2n+4个可由其它2n 个变量线性表出.即线性方程组中有2n 个自由未知量.这些自由未知量可以从数列1,2,…,2)2+n (中的前面2n+2个数,或从后面2n+2个数中选定.便可以由以上公式确定线性方程组的解.这就完成了证明.利用上述公式作具体的幻方,还有一些技术性的问题需要解决.就是要在指定的数集中求解.即自由未知量在4n+4个数中选定,其它未知量也必须在这4n+4个数中选定.4n+4个未知量与4n+4个自然数构成一一对应.下面给出一个具体的求解的办法.供读者参考.读者还可找到更巧妙的解.三 奇幻方的构造方法3.1奇幻方的构造法(n=2m+1)假定2m-1阶幻方已经做出,我们要作2m+1阶幻方. 3.2排序外围正方形四边数字的个数,m m m 8)12()1222=--+(前4m 个数字由小到大排序,后4m 个数字由大到小排序,两个数列构成一一对应如下:)1(..........).........41(14)12...(..........1)12....(2)12...(1)12...()12(4.................................................,.........3.............,.........2........,.........122222m i m m i m m m m mi 到从+-++-+-+-++上下两个相对的数的和都等于 1)12(2++=m H3.3配置上下两行从(1)中,将排好的4m 对数中截取前2m+1对,配置成上下两行,如下:(为方便计记a m =+2)12()1..........................12.............3......1...12....12....3.12...22......22.....2..................2...............2.........4.......2+-+-+----+-+--m m i m a i a a a m a m a i a a a m ii=12,……….m, i=1,2,……..m,m+1 (2) 由于幻方常数)122)(12(])12(....21[12122+++=+++++=m m m m m k计算上下两行的和)12()12)(12(12)12()132)(12(2)2(22++++=++++++=-++=m m k m m m m ma S m m k m m m m a a m S 少比下=多比上所以需要对配置的两行进行必要的调整.3.4调整对(2)作如下的调整,把第二行中的1换成1+2m+1,把3换成3+2m+1,…,把2i+1换成2i+1+2m+1,…,把2m-1换成2m-1+2m+1=4m,与它们对应的第一行的数也随着变化.调整后的两行成如下形式:)3,.......(1,......112............),........1(2,...122,.........1)(2.....,.........2m i m i m m i a m a i m a i 到从到从+++--++- km m m m i m i a S km m m m a i m a i S mi mi mi mi =+++=+++++-==+++=-+++-+=∑∑∑∑====)122)(12(12)(2)129)122)(12(2]1)2([2211211下上3.5 组合左右两列 确定四角元素从4m 对数中选出2m+1对后,余下2m-1对,组成在右两列如下:)4.......(2..........1122........22222.........12m i m i i m i a i m a i 到从到从+++-+---241464)122)(12(16412)122()22(23222321+=-+++=+++=-+=--+=++++-=∑∑=m S k m m m m m m k m m m m ma i m i a S mmi 右右由于4m+2可以拆成2m+2和2m,观察(3)中2m 在上面一行,2m+2在下面一行,就把2m 放在右上角,把2m+2放在右下角即可.其它两个角的元素是(3)中2m 和2m+2对应的另一行上的数,把上行中其余的数加在2m-1幻方的上面下行中对应的数放在下面相对应的位置上.(4)中的上行加在左边,下行对应的数加在右边相对的位置上.这就完成了加边的工作.作出了2m+1阶幻方. 四 偶幻方的构造方法(n=2m)4.1偶幻方的构造法(n=2m )假定2m 阶幻方已经做出,我们要作2m+2阶幻方. 4.2排序外围正方形四边数字的个数,48)2()2222+=-+m m m ( 前4m+2个数字由小到大排序,后4m+2个数字由大到小排序,两个数列构成一一对应如下:)5(..........).........241(14)22........(1)22....(2)22...(1)22...()22(24..............................................,.........3.............,.........2........,.........122222+--++-+-+-+++m i m m i m m m m m i 到从上下两个相对的数的和都等于 1)22(2++=m H4.3配置上下两行从(5)中,将排好的4m+2对数中截取前2m+2对,配置成上下两行,如下:(为方便计记b m =+2)22()).6...(..........1,....,2,1.....2.2..............2.............4.........2..........2....22....2....12....12........3...1.......12........12.........3.......1-=+-+----+---+-m i m i m b i b b b m b i b b b m i )1)(1()1)22)[(12(])22(....21[22122++=+++=+++++=b m m m m m k 计算上下两行的和1)2)(1(1)1(+++=++=m k b m S m k b m S 多比下少比上所以需要对配置的两行进行必要的调整.4.4 调整对(6)作如下的调整,把第一行中的2m+1换成2m+1+m+2=3m+3,那么第二行的b-2就换成b-3m-2,将第二行的2m+2换成2m+3,那么第一行的b-2m-1就换成b-2m-2,调整后的两行成如下形式:)7,.......(1,......1.32....23..........,.........2,...2222..........33,.......12,.........12m i m i m m b i i b m b m i b i 到从到从-+--+---++- kb m m b b m m m b i i b S kb m m b mb m b m i b i S mi mi mi mi =++=+-++=++--+++-==++=+++=--++++-+-=∑∑∑∑====)1)(1(1)2(32232)22()1)(1(12233]12[)12(1111下上4.5 组合左右两列 确定四角元素 n=2m,其中m 分为奇偶两种情况. 4.5.1 m=2t+1从4m+2对数中选出2m+2对后,余下2m 对,组成在右两列如下:)8..(....................12................................123...1)23(....1)(2...1)(2......22...2)23(................23)....(2.....).........(2...12..12+++++-++++-+-+-++-+--+t i i m i m b i m i m b m m b i m b i m i m b i m m b m 到从11)1)(1(2)2()2)(12()2()2()2()123()123()122()122(22212121212+-=-+++=++=+=+=++=+++++=++++--+++++--+++-=∑∑∑∑+=+=+=+=m b S k b m mb b m k m mb b m b t b t b t b i m i m b i m i m b m m b S t i t i t i t i 右右 从(7)中第一行找到b-2m-2,而3)22()1()22(+=---+-=----m m b m b m b S k 右由于第二行2,4,6,…,2m 中,必有m+3=2t+1+3=2t+4(为偶数)于是就把b-2m-2放在右上角,把m+3放在右下角即可.其它两个角的元素是(7)中b-2m-2和m+3对应的另一行上的数。
