第一部分专题一第2讲
第1部分 专题1 第2讲 第3节 考点3 词义猜测题-2023年新高考英语二轮专题复习冲刺

句意理解题——“意义吻合”法
典例片段 (2022·山西省高考一模) (第四段)By 1982, he had owned six chemist's shops, when Bhikhu, a then financial analyst, joined him, adding some “financial discipline” to his company. Vijay says: “I simply couldn't have done it without him.” As he puts it, “Brought up under one roof, we understand one another from A to Z.”
Since the restoration process began, at least 15 wells have been restored in the city of Delhi. The cost will be around $60,000, but by doing so, the water supply for the city could reach an additional 33,000 gallons. Rajkumar Sharma, a local citizen, said, “I was elated at the reuse of the stepwells. The stepwell in our village was the only source of water. With time, it had dried up and changed into a place for rubbish. We now have access to clean water for drinking and other purposes.”
高三化学复习:第一部分专题一第2讲专题针对训练

一、单项选择题1.(2011年聊城高三第一次)N A 表示阿伏加德罗常数的值。
下列叙述正确的是( )A .33.6 L(常温常压)氯气与2.7 g 铝充分反应,转移电子数为0.3N AB .标准状况下,22.4 L 乙烷含有共价键数目为8N AC .由N A 个CO 和N A 个N 2组成的混合物中含有10N A 个电子D. 1 L 1 mol·L -1的Na 2SO 4溶液中含有4N A 个离子解析:选A 。
A 项中氯气过量,铝全部被氧化,转移电子数为0.3N A ,该项正确;每个乙烷分子中含有6个碳氢键和1个碳碳键,共7个共价键,标准状况下的22.4 L 乙烷为1 mol ,共含共价键数目为7N A ,B 项错误;每个CO 分子和每个N 2分子均含有14个电子,故由N A 个CO 和N A 个N 2组成的混合物中共含有28N A 个电子,C 项错误;1 L 1 mol·L -1的Na 2SO 4溶液中含有3N A 个离子,D 项错误。
2.设N A 表示阿伏加德罗常数。
下列说法中,不.正确的是( ) A .标准状况下,22.4 L 氢气和氧气的混合气体,所含分子数为N AB .1 mol Al 3+含有的核外电子数为3N AC .常温常压下,1 mol 氦气含有的原子数为N AD .1 L 1 mol·L -1FeCl 3溶液中Fe 3+的数目小于N A解析:选B 。
标准状况下,22.4 L 任何气体所含分子都是1 mol ,A 项正确;1 mol Al 3+含有的核外电子数为10N A ,B 项错误;1 mol 氦气含有的原子数为N A ,与所处的温度、压强等条件无关,C 项正确;因FeCl 3溶液中Fe 3+的水解,故1 L 1 mol·L -1FeCl 3溶液中Fe 3+的数目小于N A ,D 项正确。
3.常温下,在密闭容器里分别充入两种气体各0.1 mol ,在一定条件下充分反应后,恢复到原温度时,压强降低为开始时的14。
第1部分 专题1 第2讲 第1节 考点1 细节理解题-2023年新高考英语二轮专题复习冲刺

5.__e_l_d_e_rl_y___ people=old people=__t_h_e_e_l_d_e_rl_y__=senior citizens 老人 6.___s_p_e_e_d_u_p____=increase speed=quicken up=___a_c_c_el_e_r_at_e___ speed 加速
3.be ___a_b_s_o_r_b_e_d_i_n_=be lost in=be _____b_u_ri_e_d_i_n___=be devoted to= be dedicated to=be ___c_o_m_m__it_te_d__to___ 专心致志于……
4 . be interested in = be keen on = have a great passion for = show enthusiasm to 对……感兴趣
...
The Old Man and the Sea was also inspired by an anecdote told by Hemingway's Cuban friend Carlos Gutierrez. In 1936, Hemingway wrote in a magazine ... about an old fisherman who caught a great marlin alone.
6.solve the problem=settle the problem=___d_e_al__w_i_th___ the problem= approach the problem=address the problem=___c_o_p_e__w_i_th____ the problem= do with the problem=tackle the problem 解决问题
2018版高考英语二轮教师用书:第1部分 专题1 第2讲 非谓语动词 含解析

第二讲非谓语动词(对应学生用书第6页)1.(2017·江苏高考卷)Many Chinese brands,________ their reputations over centuries,are facing new challenges from the modern market.A.having developed B.being developedC.developed D.developingA[考查非谓语动词。
句意:很多中国品牌历经几个世纪树立了声誉,它们正面临着当代市场带来的新挑战。
本句的主语“Many Chinese brands”与动词“develop”之间是主动关系,因此用现在分词,又根据句中的时间状语“over centuries”可知,此处应该使用现在分词的完成式。
故答案为A。
] 2.(2016·江苏高考卷)In art criticism,you must assume the artist has a secret message ________ within the work.A.to hide B.hiddenC.hiding D.being hiddenB[考查非谓语动词。
句意:在艺术评论中,你必须假设艺术家在作品中隐藏了一个秘密信息。
句中message与hide是逻辑上的被动关系,故用过去分词作后置定语。
]3.(2015·江苏高考卷)Much time ________ sitting at a desk,office workers are generally troubled by health problems.A.being spent B.having spentC.spent D.spendingC[考查非谓语动词。
句意:因为坐办公室的时间太长,所以工作人员一般都受健康问题的困扰。
句首用独立主格结构在句中作状语,表示原因。
专题一中国古代史(1)古代中国的政治制度

2.(2010· 上海单科3)汉代以来,某地出土了数 以千计的青铜重器,青铜铭文多涉及诸侯战争、 土地交换等内容。学者推断此地应是( B ) A.夏人的活动地域 B.周朝的重要都城 C.秦朝的阿房宫遗址 D.汉初同姓王的封国
此题考察春秋战国时期,连年征战,社会动荡,经济、政 治、文化等各个领域发生了急剧的变革。最深刻的变革来 自于经济领域。各国之间不断开辟农耕熟地,耕地不能转 让买卖的规定也逐渐失效。所以根据材料叙述,应该是B。 周朝,尤其是东周时期,正是分为春秋和战国两个时期。
c
6.(2010· 安徽文综14)柳宗元认为,秦末农民起义“咎 在人怨,非郡邑之制失也”;西汉七国之乱“有叛国而无 叛郡”,“秦制之得亦明矣”。下列哪种说法最符合材料 原意( ) A.郡县制与秦末农民战争没有关系 B.七国之乱因汉初分封而爆发 C.郡县制有利于中央集权统治 D.郡县制取代分封制是历史的必然 解析: 题目给了三句话,最后得出“秦制之得亦明矣”, 这里的秦制指的是秦朝的郡县制,郡县制有利加强对地方 的控制,加强了中央集权统治因此选C;A,B都是材料中的 一部分,不够全面。材料无法体现郡县取代分封的历史必 然,重在秦制中央集权之得,因此排除D.
c
7.(2010· 辽宁、湖南、宁夏文综25)柳宗元在《封建 论》中评价秦始皇废封建、行郡县说:“其为制,公之 大者也┅┅公天下之端自始皇。”郡县制为“公天下” 之开端,主要体现在( ) A.百姓不再是封君的属民 B.更有利于皇帝集权 C.制度法令的统一 D.依据才干政绩任免官吏 解析: 首先要清楚材料中的“封建”实指西周“分封 制”。分封制下,诸侯到卿、士,其权力、地位和财产 一切世袭,一般平民被排除在政治权利之外。秦始皇推 行郡县制,郡守、县令有皇帝任免,不得世袭,官吏任 免的标准是才干政绩。故地方政治权利向一般平民开放, 此即材料中所谓“公天下”。
2023年高考数学二轮复习第一部分专题攻略专题一小题专攻第二讲复数、平面向量

第二讲 复数、平面向量微专题1 复数常考常用结论1.已知复数z =a +b i(a ,b ∈R ),则(1)当b =0时,z ∈R ;当b ≠0时,z 为虚数;当a =0,b ≠0时,z 为纯虚数. (2)z 的共轭复数z ̅=a -b i. (3)z 的模|z |=√a 2+b 2. 2.已知i 是虚数单位,则 (1)(1±i)2=±2i ,1+i 1−i =i ,1−i1+i =-i.(2)i 4n =1,i 4n +1=i ,i 4n +2=-1,i 4n +3=-i.保 分 题1.[2022·新高考Ⅱ卷](2+2i)(1-2i)=( ) A .-2+4i B .-2-4i C .6+2i D .6-2i 2.[2022·全国甲卷]若z =1+i ,则|i z +3z ̅|=( ) A .4√5 B .4√2 C .2√5D .2√23.[2022·全国乙卷]已知z =1-2i ,且z +a z ̅+b =0,其中a ,b 为实数,则( ) A .a =1,b =-2 B .a =-1,b =2 C .a =1,b =2 D .a =-1,b =-2提 分 题例1 (1)[2022·福建漳州一模]已知z =|√3i -1|+11+i,则在复平面内z 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限(2)[2022·山东潍坊二模](多选)若复数z 1=2+3i ,z 2=-1+i ,其中i 是虚数单位,则下列说法正确的是( )A .z1z 2∈RB.z 1·z 2̅̅̅̅̅̅̅̅=z 1̅·z 2̅C .若z 1+m (m ∈R )是纯虚数,那么m =-2D .若z 1,z 2在复平面内对应的向量分别为OA ⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗ (O 为坐标原点),则|AB⃗⃗⃗⃗⃗ |=5 听课笔记:【技法领悟】复数的代数运算的基本方法是运用运算法则,可以通过对代数式结构特征的分析,灵活运用i 的幂的性质、运算法则来优化运算过程.巩固训练11.[2022·山东泰安二模]已知复数z =3−i 1−2i,i 是虚数单位,则复数z ̅-4在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.[2022·河北保定二模](多选)已知复数z 满足方程(z 2-4)(z 2-4z +5)=0,则( )A .z 可能为纯虚数B .方程各根之和为4C .z 可能为2-iD .方程各根之积为-20微专题2 平面向量常考常用结论1.平面向量的两个定理 (1)向量共线定理:向量a (a ≠0)与b 共线的充要条件是:存在唯一一个实数λ,使b =λa . (2)平面向量基本定理:如果e 1,e 2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a ,有且只有一对实数λ1,λ2,使a =λ1e 1+λ2e 2,其中e 1,e 2是一组基底.2.平面向量的坐标运算设a =(x 1,y 1),b =(x 2,y 2),其中b ≠0,θ为a 与b 的夹角. (1)a ∥b ⇔x 1y 2-x 2y 1=0.(2)a ·b =|a ||b |cos θ=x 1x 2+y 1y 2. (3)a ⊥b ⇔x 1x 2+y 1y 2=0.(4)|a |=√a ·a =√x 12+y 12.(5)cos θ=a·b|a ||b |=1212√x 1+y 1 √x 2+y 2.保 分 题1.△ABC 中,E 是边BC 上靠近B 的三等分点,则向量AE⃗⃗⃗⃗⃗ =( ) A .13AB ⃗⃗⃗⃗⃗ +13AC ⃗⃗⃗⃗⃗ B .13AB ⃗⃗⃗⃗⃗ +23AC ⃗⃗⃗⃗⃗ C .23AB⃗⃗⃗⃗⃗ +13AC ⃗⃗⃗⃗⃗ D .23AB ⃗⃗⃗⃗⃗ +23AC ⃗⃗⃗⃗⃗ 2.[2022·全国乙卷]已知向量a ,b 满足|a |=1,|b |=√3,|a -2b |=3,则a ·b =( ) A .-2 B .-1 C .1 D .2 3.[2022·全国甲卷]已知向量a =(m ,3),b =(1,m +1),若a ⊥b ,则m =________.提 分 题例2 (1)[2022·河北石家庄二模]在平行四边形ABCD 中,M ,N 分别是AD ,CD 的中点,若BM⃗⃗⃗⃗⃗⃗ =a ,BN ⃗⃗⃗⃗⃗ =b ,则BD ⃗⃗⃗⃗⃗ =( ) A .34a +23b B .23a +23bC .34a +34bD .23a +34b(2)[2022·山东济宁一模]等边三角形ABC 的外接圆的半径为2,点P 是该圆上的动点,则PA ⃗⃗⃗⃗ ·PB⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ 的最大值为( ) A .4 B .7 C .8 D .11 听课笔记:【技法领悟】求解向量数量积最值问题的两种思路1.直接利用数量积公式得出代数式,依据代数式求最值.2.建立平面直角坐标系,通过坐标运算得出函数式,转化为求函数的最值.巩固训练21.[2022·山东济南二模]在等腰梯形ABCD 中,AB ⃗⃗⃗⃗⃗ =-2CD ⃗⃗⃗⃗⃗ ,M 为BC 的中点,则AM ⃗⃗⃗⃗⃗⃗ =( )A .12AB ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ B .34AB ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ C .34AB ⃗⃗⃗⃗⃗ +14AD⃗⃗⃗⃗⃗ D .12AB ⃗⃗⃗⃗⃗ +34AD⃗⃗⃗⃗⃗ 2.[2022·福建漳州二模]已知△ABC 是边长为2的正三角形,P 为线段AB 上一点(包含端点),则PB⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ 的取值范围为( ) A .[-14,2] B .[-14,4] C .[0,2]D .[0,4]第二讲 复数、平面向量微专题1 复数保分题1.解析:(2+2i)(1-2i)=2-4i +2i -4i 2=2-2i +4=6-2i.故选D. 答案:D2.解析:因为z =1+i ,所以z ̅=1-i ,所以i z +3z ̅=i(1+i)+3(1-i)=2-2i ,所以|i z +3z ̅|=|2-2i|=√22+(−2)2=2√2.故选D. 答案:D3.解析:由z =1-2i 可知z ̅=1+2i.由z +a z ̅+b =0,得1-2i +a (1+2i)+b =1+a +b +(2a -2)i =0.根据复数相等,得{1+a +b =0,2a −2=0,解得{a =1,b =−2.故选A.答案:A提分题[例1] 解析:(1)∵z =|√3i -1|+11+i = √(√3)2+(−1)2+1−i1−i 2=2+1−i 2=52−12i ,∴复平面内z 对应的点(52,-12)位于第四象限. (2)对于A ,z1z 2=2+3i −1+i=(2+3i )(−1−i )(−1+i )(−1−i )=1−5i 2=12−52i ,A 错误;对于B ,∵z 1·z 2=(2+3i)(-1+i)=-5-i ,∴z 1·z 2̅̅̅̅̅̅̅̅=-5+i ;又z 1̅·z 2̅=(2-3i)(-1-i)=-5+i ,∴z 1·z 2̅̅̅̅̅̅̅̅=z 1̅·z 2̅,B 正确;对于C ,∵z 1+m =2+m +3i 为纯虚数,∴m +2=0,解得:m =-2,C 正确; 对于D ,由题意得:OA ⃗⃗⃗⃗⃗ =(2,3),OB ⃗⃗⃗⃗⃗ =(-1,-1),∴AB ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =(-3,-4),∴|AB ⃗⃗⃗⃗⃗ |=√9+16=5,D 正确.答案:(1)D (2)BCD [巩固训练1]1.解析:z =3−i1−2i =(3−i )(1+2i )(1−2i )(1+2i )=5+5i 5=1+i ,则z ̅-4=1-i -4=-3-i ,对应的点位于第三象限.故选C.答案:C2.解析:由(z 2-4)(z 2-4z +5)=0,得z 2-4=0或z 2-4z +5=0, 即z 2=4或(z -2)2=-1,解得:z =±2或z =2±i ,显然A 错误,C 正确; 各根之和为-2+2+(2+i)+(2-i)=4,B 正确; 各根之积为-2×2×(2+i)(2-i)=-20,D 正确. 答案:BCD微专题2 平面向量保分题1.解析:因为点E 是BC 边上靠近B 的三等分点,所以BE ⃗⃗⃗⃗⃗ =13BC ⃗⃗⃗⃗⃗ , 所以AE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +13BC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +13(BA ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=23AB ⃗⃗⃗⃗⃗ +13AC ⃗⃗⃗⃗⃗ .故选C. 答案:C2.解析:将|a -2b |=3两边平方,得a 2-4a ·b +4b 2=9.因为|a |=1,|b |=√3,所以1-4a ·b +12=9,解得a ·b =1.故选C.答案:C3.解析:由a ⊥b ,可得a ·b =(m ,3)·(1,m +1)=m +3m +3=0,所以m =-34. 答案:-34提分题[例2] 解析:(1)如图所示,设AB ⃗⃗⃗⃗⃗ =m ,AD⃗⃗⃗⃗⃗ =n ,且BD ⃗⃗⃗⃗⃗ =x a +y b ,则BD ⃗⃗⃗⃗⃗ =x a +y b =x (12n -m )+y (n -12m )=(12x +y )n -(x +12y )m , 又因为BD⃗⃗⃗⃗⃗ =n -m , 所以{12x +y =1x +12y =1,解得x =23,y =23,所以BD ⃗⃗⃗⃗⃗ =23a +23b . 故选B.(2)如图,等边三角形ABC ,O 为等边三角形ABC 的外接圆的圆心,以O 为原点,AO 所在直线为y 轴,建立直角坐标系.因为AO =2,所以A (0,2),设等边三角形ABC 的边长为a ,则asin A =asin 60°=2R =4,所以a =2√3,则B (-√3,-1),C (√3,-1).又因为P 是该圆上的动点,所以设P (2cos θ,2sin θ),θ∈[0,2π), PA ⃗⃗⃗⃗ =(-2cos θ,2-2sin θ),PB⃗⃗⃗⃗⃗ =(-√3-2cos θ,-1-2sin θ),PC ⃗⃗⃗⃗ =(√3-2cos θ,-1-2sin θ),PA ⃗⃗⃗⃗ ·PB ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ =-2cos θ(-√3-2cos θ)+(2-2sin θ)(-1-2sin θ)+(-√3-2cos θ)(√3-2cos θ)+(-1-2sin θ)(-1-2sin θ)=3+1+2sin θ+2√3cos θ=4+4sin (θ+π3),因为θ∈[0,2π),θ+π3∈[π3,7π3),sin (θ+π3)∈[-1,1],所以当sin (θ+π3)=1时,PA ⃗⃗⃗⃗ ·PB⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ 的最大值为8.故选C.答案:(1)B (2)C [巩固训练2]1.解析:取AD 中点N ,连接MN ,∵AB⃗⃗⃗⃗⃗ =-2CD ⃗⃗⃗⃗⃗ ,∴AB ∥CD ,|AB |=2|CD |, 又M 是BC 中点,∴MN ∥AB ,且|MN |=12(|AB |+|CD |)=34|AB |, ∴AM ⃗⃗⃗⃗⃗⃗ =AN ⃗⃗⃗⃗⃗ +NM ⃗⃗⃗⃗⃗⃗ =12AD ⃗⃗⃗⃗⃗ +34AB ⃗⃗⃗⃗⃗ ,故选B. 答案:B 2.解析:以AB 中点O 为坐标原点,OB ⃗⃗⃗⃗⃗ ,OC⃗⃗⃗⃗⃗ 正方向为x ,y 轴可建立如图所示平面直角坐标系,则A (-1,0),B (1,0),C (0,√3),设P (m ,0)(-1≤m ≤1),∴PB⃗⃗⃗⃗⃗ =(1-m ,0),PC ⃗⃗⃗⃗ =(-m ,√3), ∴PB⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ =m 2-m =(m -12)2-14, 则当m =12时,(PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ )min =-14;当m =-1时,(PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ )max =2; ∴PB⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ 的取值范围为[-14,2].故选A. 答案:A。
第1部分 专题1 第2讲 细胞的基本结构及功能

【答案】B
【解析】中心体的复制在有丝分裂间期, A错误;颤藻是原核生物,细胞中没
有高尔基体, B正确;线粒体是细胞进行有氧呼吸的主要场所,是细胞的“动力工
厂”,但并非细胞中的所有生命活动所需的能量都由线粒体提供,如光合作用暗反
应所需的能量由光反应供应, C错误;溶酶体中的水解酶是蛋白质,应该由核糖体
第一部分 专题突破
巧用索引法判断细胞类型
高考二轮专题析与练 ·生物
返回导航
第一部分 专题突破
细胞结构与功能中的几个“一定”与“不一定” (1)能进行光合作用的生物,不一定有叶绿体,但植物细胞的光合作用一定在叶 绿体中进行。 (2)能进行有氧呼吸的生物不一定有线粒体,但真核生物的有氧呼吸主要发生在 线粒体中。 (3)一切生物的蛋白质的合成场所一定是核糖体。 (4)有中心体的生物不一定为动物,但一定不是高等植物。 (5)高尔基体经膜泡分泌的物质不一定为分泌蛋白,但分泌蛋白一定经高尔基体 分泌。
高考二轮专题析与练 ·生物
返回导航
第一部分 专题突破
细胞膜成分的5点提醒 (1)不同种类的细胞,细胞膜的成分和含量不完全相同。如动物细胞膜中含有一 定量的胆固醇,而植物细胞膜中胆固醇含量很少或没有。 (2)细胞膜的组分并非是不可变的。例如,细胞癌变过程中,细胞膜组分发生变 化,糖蛋白含量下降,产生甲胎蛋白(AFP)、癌胚抗原(CEA)等物质。 (3)含量最高的成分:组成细胞膜的成分中,脂质含量最高,组成细胞膜的脂质 中,磷脂含量最丰富。
流动性
信息 物质
选择透过性
返回导航
第一部分 专题突破
(1)
(2)
高考二轮专题析与练 ·生物
2.几种主要细胞器的分类
中心体、核糖体 叶绿体、线粒体 高尔基体、内质网、液泡、溶酶体 叶绿体、线粒体 叶绿体、液泡 叶绿体、线粒体、核糖体
第1部分 专题1 第2讲 第4节 考点4 主旨大意题-2023年新高考英语二轮专题复习冲刺

①找主题词:定位到第一段中的“have banned texting by drivers”和 “persuade people to put down their phones when they are behind the wheel”。
②信息理解:第一段和第二段讲述了虽然大多数州已经尝试了各种各 样的方法来说服人们在开车时放下手机,可是问题却越来越严重。第三段 解释了该行为产生的部分原因。第四段至第五段介绍利用Textalyzer技术可 以监控司机在开车的时候是否使用了手机。最后一段讲述了相关人士呼吁 该项技术成为真正的法案才能改变人们的行为。
③总结概括:作者认为老师也应该向学生学习。故选D。
好题即练
(2022·河北省普通高中毕业班高考适应性考试)When both of Marcus Edwards' kidneys (肾) failed, he was put on a list of people in desperate need of finding a donor (捐献者). Until he could find one, he had to rely on dialysis (透 析), a treatment that would give him around five years of support. Marcus had to experience this timeconsuming process five days a week for three hours at a time.
He decided to use this as an opportunity to let people across the country know he was in search of a kidney! His sign never made it on television like he'd hoped, but it did catch the eye of a woman sitting near them in the stadium. She asked if she could take a photo of Marcus with the sign so she could share it online, and he happily agreed.
高三化学复习:第一部分专题一第2讲

1.(2011年高考大纲全国卷)N A 为阿伏加德罗常数,下列叙述错误的是( )A .18 g H 2O 中含有的质子数为10N AB .12 g 金刚石中含有的共价键数为4N AC .46 g NO 2和N 2O 4混合气体中含有原子总数为3N AD .1 mol Na 与足量O 2反应,生成Na 2O 和Na 2O 2的混合物,钠失去N A 个电子解析:选B 。
A 项,1 mol H 2O 中含有的质子数为10N A ,故正确;B 项,12 g 金刚石中含有的共价键数为2N A ,故错误;C 项,混合气体中N 和O 原子数之比等于1∶2,46 g 混合气体中所含原子总数为:4614×1+16×2×3N A =3N A ,故正确;D 项,1 mol Na 完全反应生成Na 2O 和Na 2O 2,钠均由0价变为+1价,故钠失去的电子数一定为N A ,故正确。
2.(2011年高考江苏卷)设N A 为阿伏加德罗常数的值。
下列叙述正确的是( )A .1 mol 甲醇中含有C —H 键的数目为4N AB. 25 ℃,pH =13的NaOH 溶液中含有OH -的数目为0.1N AC .标准状况下,2.24 L 己烷含有分子的数目为0.1N AD .常温常压下,Na 2O 2与足量H 2O 反应,共生成0.2 mol O 2,转移电子的数目为0.4N A 解析:选D 。
A 项,甲醇的结构式为,1 mol 甲醇中含C —H 键的数目为3N A ;B 项未注明溶液体积,C 项,己烷在标准状况下为液体。
3.(2010年高考江苏卷)设N A 为阿伏加德罗常数的值,下列叙述正确的是( )A .常温下,1 L 0.1 mol·L -1的NH 4NO 3溶液中氮原子数为0.2 N AB .1 mol 羟基中电子数为10 N AC .在反应KIO 3+6HI===KI +3I 2+3H 2O 中,每生成3 mol I 2转移的电子数为6N AD .常温常压下,22.4 L 乙烯中C —H 键数为4N A解析:选A 。
2019-2020版高考化学二轮教师用书第1部分 专题1 第2讲 阿伏加德罗常数 Word版含答案

第2讲 阿伏加德罗常数(对应学生用书第5页)■储知识——剖解重点难点备考·1.四个关键问题六大突破点阿伏加德罗常数应用的2. 求算N (微粒数)的基本思路:气体摩尔体积的适用条件1突破点 (1)角度:从V m =22.4 L·mol -1的适用条件和物质的状态突破。
(2)突破方法:一看气体是否处在“标准状况(0 ℃、101 kPa)”;二看标准状况下,物质是否为气态(如CCl 4、CHCl 3、CH 2Cl 2、H 2O 、溴、SO 3、己烷、HF 、苯、乙醇等在标准状况下均不为气态)。
与物质所处状况)或质量(物质的量 2突破点 (1)角度:设置与计算无关的一些干扰条件,给出非标准状况下气体的物质的量或质量,干扰正确判断。
(2)突破方法:排“干扰”,明确物质的量或质量与物质所处状况无关,物质的量或质量确定时,物质所含的粒子数与温度、压强等外界条件无关。
物质的组成与结构3突破点 (1)角度:从特殊物质的组成与结构特点突破。
(2)突破方法:①熟记特殊物质中所含微粒(分子、原子、电子、质子、中子等)的数目,常考查的特殊物质(如Ne 、D 2O 、18O 2、O 3、P 4、H 37Cl 、—OH 、OH -等)。
②记住最简式相同的物质,明确微粒数目特点(如NO 2和N 2O 4、乙烯和丙烯、O 2和O 3等)。
③记住物质中所含化学键的数目(如1 mol 硅中含Si —Si 键的数目为2N A,1 mol SiO 2中含Si —O 键的数目为4N A ,再如H 2O 2、C n H 2n +2中化学键的数目分别为3、3n +1等)。
④记住摩尔质量相同的物质(如N 2、CO 、C 2H 4等)。
电解质溶液中粒子数目4突破点 (1)角度:难电离、易水解的粒子的数目计算以及电解质组成、溶液体积等因素上突破。
(2)突破方法:细审题、抓“三看”:一看是否指明溶液的体积;二看是否有弱电解质或可水解的弱酸根离子(或弱碱阳离子),如1 L 0.1 mol·L -1的乙酸溶液和1 L 0.1 mol·L -1的乙酸钠溶液中含CH 3COO -的数目不相等且都小于0.1N A ;三看所给条件是否与电解质的组成有关,如pH =1的H 2SO 4溶液中c (H +)=0.1 mol·L -1(与电解质的组成无关),0.05 mol·L -1的Ba(OH)2溶液中c (OH -)=0.1 mol·L -1(与电解质的组成有关),不要忽略溶剂水中的H 、O 原子数目。
2023年高考英语二轮复习第一部分阅读能力突破篇专题一阅读理解第2讲推理判断题

第一部分 专题一 阅读理解
高考二轮总复习 • 英语 新教材
返回导航
该类型的命题方式常常以下列形式呈现: 1.It can be inferred/concluded from the text that ________. 2.What can we infer/learn from...? 3.We can learn from the passage that ________. 4.The passage/story...indicates/suggests/implies that ________.
them, had little privacy, rare baths, and a blanket of snow on their quilt when they woke up in the morning.(她们和一个当地家庭,哈里森一家一 起搬进去,并且和他们一样,几乎没有隐私,很少洗澡,早上醒来时被 子上覆盖着一层雪。)”以及“In spring, the snow was replaced by mud over ice.(在春天,覆盖在冰上的雪被泥替代。)”可知,女孩们的生活条 件非常艰苦,她们饱受磨难。故选D。
第一部分 专题一 阅读理解
高考二轮总复习 • 英语 新教材
返回导航
Wickenden is a very good storyteller.The sweep of the land and the stoicism (坚忍) of the people move her to some beautiful writing.Here is a picture of Dorothy Woodruff, on her horse, looking down from a hill top: “When the sun slipped behind the mountains, it shed a rosy glow all around them.Then a full moon rose.The snow was marked only by small animals: foxes, coyotes, mice, and varying hares, which turned white in the winter.”
2023高考历史二轮专题复习 第一部分 板块一 中国古代史 第2讲古代中国经济的基本结构与特点

线索三 古代商业 古代商业发展包括市场形成、市场管理、货币演变、国内外贸易、 城市商业功能发展等五大要素,其中市场管理是核心内容,时空限制 经历了一个由严格到松散的过程。
线索四 古代经济政策 古代的经济政策以重农抑商、闭关锁国为主,前者首倡于商鞅变法, 贯穿于封建社会始终,后者仅实行于明清两朝,两者均是导致资本主 义萌芽在中国发展缓慢的重要因素。
读材料,回答问题。 材料一 古代农书是我国丰富农业技术经验的总结,也是了解农业
(4)影响: ①对经济布局的影响。随着经济重心南移,南北差距日益缩小,南 北经济联系不断加强,共同促进我国古代经济的发展。
②对我国交通贸易的影响。由于经济重心的南移,造成了南方沿海 城市的迅速发展,海上交通和运输也有了很大的改善。在南宋完成经 济重心南移后,南方城市一直到现在都受益匪浅。一些有海港的城市 利用海上交通和河运得到了快速的发展,促进了与周边国家的经济和 政治交流。
2.古代农耕经济难以推动社会转型的原因 (1)政治因素:封建土地私有制很难实现社会财富的积累及向商业资 本的转化。“抑商”“闭关锁国”政策阻碍了资本主义萌芽的成长, 既不能积累财富,也不能拓展海外市场、刺激资本扩张,难以推动工 业化。 (2)经济因素:自给自足的小农经济占主导地位,不利于商品市场的 扩大和农产品的真正商品化。 (3)思想因素:以农立国的经济思想,导致民间资本不能成为工商业 资本。
②北方战乱频繁,南方相对稳定,为江南经济发展创造了稳定的环 境。
③北方人民大批南迁,增加了大量劳动力,并带来了先进的生产技 术和工具。
④南方统治者为巩固统治,重视发展经济,鼓励开垦荒地、兴修水 利。
⑤新的农作物在江南引种,推动了农业生产发展。 ⑥海外贸易的发展,促进了江南商品经济的繁荣。
第1部分 板块2 核心考点突破拿高分 专题1 第2讲 三角恒等变换与解三角形(小题)

第2讲 三角恒等变换与解三角形(小题)热点一 三角恒等变换 1.三角求值“三大类型”“给角求值”“给值求值”“给值求角”. 2.三角恒等变换“四大策略”(1)常值代换:常用到“1”的代换,1=sin 2θ+cos 2θ=tan 45°等.(2)项的拆分与角的配凑:如sin 2α+2cos 2α=(sin 2α+cos 2α)+cos 2α,α=(α-β)+β等. (3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次. (4)弦、切互化.例1 (1)(2019·榆林模拟)若α,β都是锐角,且cos α=55,sin(α+β)=35,则cos β等于( ) A.2525 B.255C.2525或255D.55或525(2)已知sin α=55,sin(α-β)=-1010,α,β均为锐角,则β等于( ) A.5π12 B.π3 C.π4D.π6(3)3sin 220°-1cos 220°+64sin 220°=________. 跟踪演练1 (1)已知sin ⎝⎛⎭⎫π6-α=33,则cos ⎝⎛⎭⎫2α+2 018π3等于( ) A.23 B.13 C.-23D.-13(2)(2019·吕梁模拟)已知α∈⎝⎛⎭⎫0,π2,β∈⎝⎛⎭⎫0,π2,tan α=cos 2β1-sin 2β,则( ) A.α+β=π2B.α-β=π4C.α+β=π4D.α+2β=π2热点二 利用正弦、余弦定理解三角形 1.正弦定理:在△ABC 中,a sin A =b sin B =c sin C=2R (R 为△ABC 的外接圆半径). 变形:a =2R sin A ,b =2R sin B ,c =2R sin C ,sin A =a 2R ,sin B =b 2R ,sin C =c2R,a ∶b ∶c =sin A ∶sin B ∶sin C 等.2.余弦定理:在△ABC 中,a 2=b 2+c 2-2bc cos A . 变形:b 2+c 2-a 2=2bc cos A ,cos A =b 2+c 2-a 22bc. 3.三角形的面积公式:S =12ab sin C =12ac sin B =12bc sin A .例2 (1)(2019·东北师大附中、重庆一中、吉大附中、长春十一中联考)在△ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,B =π3,AB →·BC →=-2,且满足sin A +sin C =2sin B ,则该三角形的外接圆的半径R 为( ) A.433 B.233C. 3D.2(2)(2019·葫芦岛调研)△ABC 的周长为10+27,且满足sin A ∶sin B ∶sin C =2∶3∶7,则△ABC 的面积为( ) A.6 3 B.47 C.87 D.12跟踪演练2 (1)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若△ABC 的面积为S ,且a =1,4S =b 2+c 2-1,则△ABC 外接圆的面积为( ) A.4π B.2π C.π D.π2(2)(2019·广州模拟)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若A =3B ,则ab 的取值范围是( )A.(0,3)B.(1,3)C.(0,1]D.(1,2] 热点三 正弦、余弦定理的实际应用1.用正弦定理和余弦定理可解决距离问题、高度问题、角度问题、计算面积问题、航海问题或物理问题等.2.解决三角形应用题的基本思路实际问题――→画图数学问题―――→解三角形数学问题的解――→检验实际问题的解. 3.用正、余弦定理解决问题的一般步骤:(1)选定或确定要创建的三角形,要首先确定所求量所在的三角形,若其他量已知,则直接解;若有未知量,则把未知量放在另一确定三角形中求解.(2)确定用正弦定理还是余弦定理,如果都可用,选择便于计算的定理.例3(1)某游轮在A处看灯塔B在A的北偏东75°的方向上,距A 12 6 海里处,灯塔C在A的北偏西30°的方向上,距A 8 3 海里处,游轮由A处向正北方向航行到D处时再看灯塔B在南偏东60°的方向上,则此时灯塔C与游轮的距离为()A.20 海里B.8 3 海里C.23 2 海里D.24 海里(2)如图,某学生社团在校园内测量远处某栋楼CD的高度,D为楼顶,线段AB的长度为600 m,在A处测得∠DAB=30°,在B处测得∠DBA=105°,且此时看楼顶D的仰角∠DBC=30°,已知楼底C和A,B在同一水平面上,则此楼高度CD=________m.(精确到1 m)跟踪演练3(1)如图所示,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15 000 m,速度为1 000 km/h,飞行员先看到山顶的俯角为15°,经过108 s后又看到山顶的俯角为75°,则山顶的海拔高度为________m.(取3=1.732)(2)如图所示,为测量竖直旗杆CD的高度,在旗杆底部C所在水平地面上选取相距421m 的两点A,B,在A处测得旗杆底部C在西偏北20°的方向上,旗杆顶部D的仰角为60°;在B处测得旗杆底部C在东偏北10°的方向上,旗杆顶部D的仰角为45°,则旗杆CD的高度为________m.真题体验1.(2017·山东,理,9)在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin A cos C+cos A sin C,则下列等式成立的是()A.a=2bB.b=2aC.A=2BD.B=2A2.(2019·全国Ⅱ,理,10)已知α∈⎝⎛⎭⎫0,π2,2sin 2α=cos 2α+1,则sin α等于( ) A.15 B.55 C.33 D.2553.(2019·全国Ⅱ,理,15)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若b =6,a =2c ,B =π3,则△ABC 的面积为________. 押题预测1.已知sin 2α=45,α∈⎝⎛⎭⎫0,π4,则sin ⎝⎛⎭⎫π4-α的值为________. 2.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若b cos C c cos B =1+cos 2C1+cos 2B ,C 是锐角,且a=27,cos A =13,则△ABC 的面积为________.3.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,A =30°,C =45°,c =3,点P 是平面ABC 内的一个动点,若∠BPC =60°,则△PBC 面积的最大值是________.A 组 专题通关1.(2019·沈阳市东北育才学校模拟)已知cos ⎝⎛⎭⎫π2-α=15,则cos 2α等于( ) A.725 B.-725C.2325D.-23252.tan 70°+tan 50°-3tan 70°tan 50°的值为( ) A. 3 B.33C.-33D.- 33.(2019·吕梁模拟)已知△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,若2cos B =ac ,则该三角形一定是( ) A.等腰三角形 B.直角三角形 C.等边三角形D.等腰直角三角形4.(2019·黄冈调研)已知a ,b ,c 分别为△ABC 的三个内角A ,B ,C 的对边,且C =π4,c =2,a =x ,若满足条件的三角形有两个,则x 的取值范围是( )A.2<x <1B.2<x <2C.1<x <2D.1<x < 25.(2019·甘肃省静宁县第一中学模拟)某船开始看见灯塔在南偏东30°方向,后来船沿南偏东60°的方向航行15 km 后,看见灯塔在正西方向,则这时船与灯塔的距离是( ) A.5 km B.5 2 km C.5 3 kmD.10 km6.(2019·韶关调研)已知2cos ()α-βcos β-cos ()α-2β=24,则1-tan 2α1+tan 2α等于( )A.-34B.-43C.34D.437.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,a cos B +b cos A =2c cos C ,c =7,且△ABC 的面积为332,则△ABC 的周长为( )A.1+7B.2+7C.4+7D.5+78.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若a cos B -b cos A =c2,则a cos A +b cos B a cos B 的最小值为( ) A. 3 B.433C.33D.2339.已知2sin θ=1-cos θ,则tan θ等于( ) A.-43或0B.43或0C.-43D.4310.(2019·安徽省合肥一中、马鞍山二中等六校联考)设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,则下列命题正确的是( ) ①若a 2+b 2<c 2,则C >π2;②若ab >c 2,则C >π3;③若a 3+b 3=c 3,则C <π2;④若2ab >(a +b )c ,则C >π2;⑤若()a 2+b 2c 2<2a 2b 2,则C <π3.A.①②③B.①②⑤C.①③④D.①③⑤11.在△ABC 中,A ,B ,C 的对边分别是a ,b ,c .若A =120°,a =1,则2b +3c 的最大值为( ) A.3 B.2213C.3 2D.35212.(2019·黄冈调研)已知圆C :x 2+(y -1)2=R 2与函数y =2sin x 的图象有唯一交点,且交点的横坐标为α,则4cos 2α2-α-2sin 2α等于( )A.-2B.2C.-3D.313.(2019·洛阳统考)已知tan ⎝⎛⎭⎫α+π4=2,则2sin α3sin α+cos α=________. 14.(2019·韶关调研)在△ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,且b +a sin C =2a sin B -csin B -sin A ,则A =________.15.(2019·茂名模拟)《九章算术》中记载了一个“折竹抵地”问题,今年超强台风“山竹”登陆时再现了这一现象(如图所示),不少大树被大风折断.某路边一树干被台风吹断后(没有完全断开),树干与底面成75°角,折断部分与地面成45°角,树干底部与树尖着地处相距10米,则大树原来的高度是________米(结果保留根号).16.如图,在△ABC 中,BC =2,∠ABC =π3,AC 的垂直平分线DE 与AB ,AC 分别交于点D ,E ,且DE =62,则BE 2=________.B 组 能力提高17.(2019·广东省中山一中等七校联考)如图所示,在平面直角坐标系xOy 中,点B, C 分别在x轴和y 轴非负半轴上,点A 在第一象限,且∠BAC =π2, AB =AC =4,那么O, A 两点间距离的( )A.最大值是42,最小值是4B.最大值是8,最小值是4C.最大值是42,最小值是2D.最大值是8,最小值是218.已知在△ABC 中,∠ABC =90°,AB =3,BC =2,P 为△ABC 内一点,∠BPC =135°,则AP 的最小值为________.。
高中物理大二轮物理复习专题目录

二轮物理
选择题48分专练(一) 选择题48分专练(二) 实验题15分专练(一) 实验题15分专练(二) 计算题32分专练(一) 计算题32分专练(二) 选考题15分专练(一) 选考题15分专练(二)
第二部分 考前冲刺增分练
二轮物理
小卷冲刺抢分练(一)——(8+2实验) 小卷冲刺抢分练(二)——(8+2实验) 小卷冲刺抢分练(三)——(8+2计算) 小卷冲刺抢分练(四)——(8+2计算) 高考模拟标准练
大二轮专题复习与测试
物理
二轮物理
第一部分 专题一 力与运动 第1讲 物体的平衡 考向一 力学中的平衡问题 考向二 电学中的平衡问题 考向三 平衡中的临界极值问题 第2讲 牛顿运动定律和直线运动 考向一 运动图象的理解及应用 考向二 匀变速直线运动应用规律 考向三 牛顿运动定律的综合应用
专题整合突破
二轮物理
第2讲 电学实验与创新 考向一 电表改装与读数、多用电表原理与使用 考向二 以伏安法测电阻为核心的实验 考向三 以测电源电动势和内阻为核心的实验 考向四 电学创新设计实验
二轮物理
专题七 选考部分 第1讲 (选修3-3) 分子动理论、气体及热力学定律 考向一 热学基础知识与气体实验定律的组合 考向二 热学基础知识、热力学定律与气体定律的组合 第2讲 (选修3-4) 机械振动和机械波 光 电磁波 考向一 振动(或波动)与光的折射、全反射的组合 考向二 光学基础知识与波动(或振动)的组合 考向三 电磁波、光学、波动(或振动)的组合
二轮物理
第三部分 一、物理学史和物理思想方法 (一)高中物理的重要物理学史 (二)高中物理的重要思想方法 二、高考必知的五大解题思想 (一)守恒的思想 (二)等效的思想 (三)分解的思想 (四)对称的思想 (五)数形结合的思想
高考数学二轮复习 第一部分 专题一 第二讲 函数的图象与性质 第二讲 函数的图象与性质教案
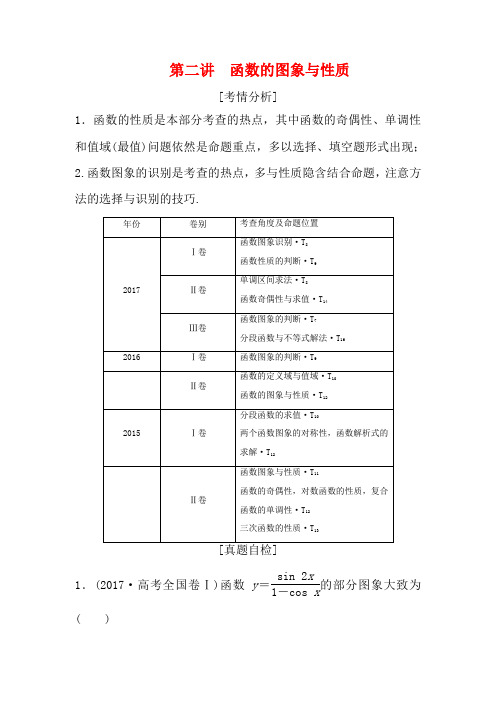
第二讲函数的图象与性质[考情分析]1.函数的性质是本部分考查的热点,其中函数的奇偶性、单调性和值域(最值)问题依然是命题重点,多以选择、填空题形式出现;2.函数图象的识别是考查的热点,多与性质隐含结合命题,注意方法的选择与识别的技巧.1.(2017·高考全国卷Ⅰ)函数y=sin 2x1-cos x的部分图象大致为( )解析:由题意,令函数f (x )=sin 2x 1-cos x ,其定义域为{x |x ≠2k π,k ∈Z },又f (-x )=sin -2x 1-cos -x =-sin 2x 1-cos x=-f (x ),所以f (x )=sin 2x 1-cos x 为奇函数,其图象关于原点对称,故排除B ;因为f (π2)=sin π1-cos π2=0, f (3π4)=sin 3π21-cos 3π4=-11+22<0,所以排除A ;f (π)=sin 2π1-cos π=0,排除D.故选C.答案:C2.(2016·高考全国卷Ⅱ)已知函数f (x )(x ∈R )满足f (x )=f (2-x ),若函数y =|x 2-2x -3|与y =f (x )图象的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则∑mi =1x i=( ) A .0B .mC .2mD .4m 解析:∵f (x )=f (2-x ),∴函数f (x )的图象关于直线x =1对称. 又y =|x 2-2x -3|=|(x -1)2-4|的图象关于直线x =1对称, ∴两函数图象的交点关于直线x =1对称.当m 为偶数时,m i =1x i =2×m2=m ;当m 为奇数时,m i =1x i =2×m -12+1=m .故选B.答案:B 3.(2016·高考全国卷Ⅱ)下列函数中,其定义域和值域分别与函数y =10lg x 的定义域和值域相同的是( )A .y =xB .y =lg xC .y =2xD .y =1x 解析:函数y =10lg x 的定义域与值域均为(0,+∞).函数y =x 的定义域与值域均为(-∞,+∞).函数y =lg x 的定义域为(0,+∞),值域为(-∞,+∞). 函数y =2x 的定义域为(-∞,+∞),值域为(0,+∞). 函数y =1x的定义域与值域均为(0,+∞).故选D. 答案:D函数及其表示[方法结论]求解函数的定义域时要注意三式——分式、根式、对数式,分式中的分母不为零,偶次方根中的被开方数非负,对数的真数大于零.解决此类问题的关键在于准确列出不等式(或不等式组),求解即可.确定条件时应先看整体,后看部分,约束条件一个也不能少.[题组突破]1.(2017·西安模拟)已知函数f (x )=⎩⎪⎨⎪⎧ log 2x ,x >03x +1,x ≤0,则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫14的值是( ) A.109B.19 C .-19D .-109 解析:由题意可得:函数f (x )=⎩⎪⎨⎪⎧ log 2x ,x >03x +1,x ≤0,∴f ⎝ ⎛⎭⎪⎫14=log 214=-2,∴f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫14=f (-2)=3-2+1=109.故选A.答案:A2.函数f (x )=-x 2+9x +10-2ln x -1的定义域为( ) A .[1,10]B .[1,2)∩(2,10]C .(1,10]D .(1,2)∪(2,10]解析:要使原函数有意义,则⎩⎪⎨⎪⎧ -x 2+9x +10≥0x -1>0x -1≠1,解得1<x ≤10且x ≠2,所以函数f (x )=-x 2+9x +10-2ln x -1的定义域为(1,2)∪(2,10],故选D.答案:D3.(2017·石家庄模拟)已知函数f (x )=⎩⎪⎨⎪⎧ 2e x -1,x <1x 3+x ,x ≥1,则f (f (x ))<2的解集为( )A .(1-ln 2,+∞)B .(-∞,1-ln 2)C .(1-ln 2,1)D .(1,1+ln 2) 解析:因为当x ≥1时,f (x )=x 3+x ≥2,当x <1时,f (x )=2ex -1<2,所以f (f (x ))<2等价于f (x )<1,即2e x -1<1,解得x <1-ln 2,所以f (f (x ))<2的解集为(-∞,1-ln 2),故选B.答案:B[误区警示]分段函数易被误认为是多个函数,其实质是一个函数,其定义域为各段的并集,其最值是各段函数最值中的最大者与最小者,求值时要注意判断自变量的取值,否则要分类讨论.函数图象及应用[典例] (1)函数y =e cos x (-π≤x ≤π)的大致图象为( )解析:当x =0时,则y =ecos 0=e ;当x =π时,则y =e cos π=1e.可排除A ,B ,D ,选C.答案:C (2)函数f (x )=ln(x -1x)的图象是( )解析:因为f (x )=ln(x -1x ),所以x -1x =x +1x -1x >0,解得-1<x <0或x >1,所以函数的定义域为(-1,0)∪(1,+∞),可排除A ,D.因为函数u =x -1x在(-1,0)和(1,+∞)上单调递增,函数y =ln u 在(0,+∞)上单调递增,根据复合函数的单调性可知,函数f (x )在(-1,0)和(1,+∞)上单调递增,选B. 答案:B(3)已知三次函数f (x )=2ax 3+6ax 2+bx 的导函数为f ′(x ),则函数f (x )与f ′(x )的图象可能是( )解析:因为f ′(x )=6ax 2+12ax +b ,则函数f ′(x )的图象的对称轴为x =-1,故可排除A ,D ;由选项C 的图形可知,当x >0时,f ′(x )>0,故函数f (x )=2ax 3+6ax 2+bx 在(0,+∞)上单调递增,但图象中函数f (x )在(0,+∞)上不具有单调性,故排除C.选B. 答案:B(4)已知函数f (x -1)是定义在R 上的奇函数,且在[0,+∞)上是增函数,则函数f (x )的图象可能是( )解析:函数f (x -1)的图象向左平移1个单位,即可得到函数f (x )的图象;因为函数f (x -1)是定义在R 上的奇函数,所以函数f (x -1)的图象关于原点对称,所以函数f (x )的图象关于点(-1,0)对称,排除A ,C ,D ,选B.答案:B[类题通法]函数图象的识别与判断技巧方法1 特殊点法用特殊点法破解函数图象问题需寻找特殊的点,即根据已知函数的图象或已知函数的解析式,取特殊点,判断各选项的图象是否经过该特殊点,从而得正确的选项.在求函数值的过程中运算一定要认真,从而准确进行判断.如本例中(1).方法2 性质检验法已知函数解析式,判断其图象的关键:由函数解析式明确函数的定义域、值域、单调性、奇偶性、周期性等性质,根据这些性质对函数图象进行具体的分析和判断,即可得出正确选项.若能熟记基本初等函数的性质,则此类题就不攻自破.如本例中(2).方法3 导数法判断复杂函数的图象,常借助导数这一工具,先对原函数进行求导,再利用导数判断函数的单调性、极值或最值,从而对选项进行筛选.要注意函数求导之后,导函数发生了变化,故导函数和原函数的定义域会有所不同,我们必须在原函数的定义域内研究函数的极值和最值.如本例中(3).方法4 图象变换法有关函数y=f(x)与函数y=af(bx+c)+h的图象问题的判断,熟练掌握图象的平移变换(左加右减,上加下减)、对称变换、伸缩变换等,便可顺利破解此类问题.如本例中(4).[演练冲关]1.(2017·长沙模拟)函数y =ln|x |-x 2的图象大致为( ) 解析:令f (x )=ln|x |-x 2,定义域为(-∞,0)∪(0,+∞)且f (-x )=ln |x |-x 2=f (x ),故函数y =ln|x |-x 2为偶函数,其图象关于y 轴对称,排除B ,D ;当x >0时,y =ln x -x 2,则y ′=1x-2x ,当x ∈(0,22)时,y ′=1x-2x >0,y =ln x -x 2单调递增,排除C.选A.答案:A2.(2017·惠州模拟)函数f (x )=(x -1x)cos x (-π≤x ≤π且x ≠0)的图象可能为( )解析:函数f (x )=(x -1x)cos x (-π≤x ≤π且x ≠0)为奇函数,排除选项A ,B ;当x =π时,f (x )=(π-1π)cos π=1π-π<0,排除选项C ,故选D.答案:D函数的性质及应用[方法结论]1.判断函数单调性的一般规律对于选择、填空题,若能画出图象一般用数形结合法;而对于由基本初等函数通过加、减运算或复合运算而成的函数常转化为基本初等函数单调性的判断问题;对于解析式为分式、指数函数式、对数函数式等较复杂的函数,用导数法;对于抽象函数,一般用定义法.2.函数的奇偶性(1)确定函数的奇偶性,务必先判断函数的定义域是否关于原点对称.(2)奇函数的图象关于原点对称,偶函数的图象关于y 轴对称.3.记住几个周期性结论(1)若函数f (x )满足f (x +a )=-f (x )(a >0),则f (x )为周期函数,且2a 是它的一个周期.(2)若函数f (x )满足f (x +a )=1f x (a >0),则f (x )为周期函数,且2a 是它的一个周期.[典例] (1)(2016·湖南六校联考)已知f (x )是偶函数,且在[0,+∞)上是减函数,若f (lg x )>f (2),则x 的取值范围是( ) A.⎝ ⎛⎭⎪⎫1100,1 B.⎝ ⎛⎭⎪⎫0,1100∪(1,+∞) C.⎝ ⎛⎭⎪⎫1100,100 D .(0,1)∪(100,+∞)解析:通解:不等式可化为⎩⎪⎨⎪⎧ lg x ≥0lg x <2或⎩⎪⎨⎪⎧ lg x <0-lg x <2,解得1≤x <100或1100<x <1, 所以x 的取值范围是⎝ ⎛⎭⎪⎫1100,100.优解:由偶函数的定义可知,f (x )=f (-x )=f (|x |),故不等式f (lg x )>f (2)可化为|lg x |<2,即-2<lg x <2,解得1100<x <100,故选C. 答案:C(2)(2017·安徽六安一中测试)已知函数y =3-|x |3+|x |的定义域为[a ,b ](a ,b ∈Z ),值域为[0,1],则满足条件的整数对(a ,b )共有( )A .6个B .7个C .8个D .9个解析:函数y =3-|x |3+|x |=63+|x |-1,易知函数是偶函数,x >0时是减函数,所以函数的图象如图所示,根据图象可知,函数y =3-|x |3+|x |的定义域可能为[-3,0],[-3,1],[-3,2],[-3,3],[-2,3],[-1,3],[0,3],共7种,所以满足条件的整数对(a ,b )共有7个.故选B.答案:B[类题通法]1.数学思想转化在函数性质的应用,主要是已知偶函数时注意f (x )=f (-x )=f (|x |).2.求解函数性质的综合问题时注意数形结合思想化抽象为直观.3.注意特殊值、特殊点法在性质中的应用.[演练冲关]1.(2017·甘肃会宁一中月考)已知函数f (x )=⎩⎪⎨⎪⎧ 1-2a x +3a ,x <1ln x ,x ≥1的值域为R ,则实数a 的取值范围是( )A .[-1,12) B .(-1,12) C .(-∞,-1] D .(0,12) 解析:通解:当x ≥1时,ln x ≥0,要使函数f (x )=⎩⎪⎨⎪⎧ 1-2a x +3a ,x <1ln x ,x ≥1的值域为R ,只需⎩⎪⎨⎪⎧ 1-2a >01-2a +3a ≥0,解得-1≤a <12,故选A. 优解:取a =-1,则函数f (x )的值域为R ,所以a =-1满足题意,排除B 、D ;取a =-2,则函数f (x )的值域为(-∞,-1)∪[0,+∞),所以a =-2不满足题意,排除C ,故选A.答案:A2.已知函数f (x )=2×4x-a 2x 的图象关于原点对称,g (x )=ln(e x +1)-bx 是偶函数,则log a b =( )A .1B .-1C .-12 D.14 解析:由题意得f (0)=0,∴a =2.∵g (1)=g (-1),∴ln(e +1)-b =ln(1e +1)+b ,∴b =12,∴log 2 12=-1. 故选B.答案:B3.(2017·衡阳四中月考)函数y =f (x )在区间[0,2]上单调递增,且函数f (x +2)是偶函数,则下列结论成立的是( )A .f (1)<f (52)<f (72) B .f (72)<f (1)<f (52) C .f (72)<f (52)<f (1) D .f (52)<f (1)<f (72) 解析:因为函数f (x +2)是偶函数,所以f (x +2)=f (-x +2),即函数f (x )的图象关于x =2对称,又因为函数y =f (x )在区间[0,2]上单调递增,所以函数y =f (x )在区间[2,4]上单调递减.因为f (1)=f (3),72>3>52,所以f (72)<f (3)<f (52),即f (72)<f (1)<f (52),故选B.答案:B新定义下的函数问题[方法结论]新定义函数问题主要包括两类:(1)概念型,即基于函数概念背景的新定义问题,此类问题常以函数的三要素(定义域、对应法则、值域)作为重点,考查考生对函数概念的深入理解;(2)性质型,即基于函数性质背景的新定义问题,主要涉及函数的单调性、奇偶性、周期性、有界性、对称性等性质及有关性质的延伸,旨在考查考生灵活应用函数性质的能力.[题组突破]1.对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为M函数:(ⅰ)对任意的x∈[0,1],恒有f(x)≥0;(ⅱ)当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.则下列3个函数中不是M函数的个数是( )①f(x)=x2②f(x)=x2+1 ③f(x)=2x-1A.0 B.1C.2 D.3解析:在[0,1]上,3个函数都满足f(x)≥0. 当x1≥0,x2≥0,x1+x2≤1时:对于①,f(x1+x2)-[f(x1)+f(x2)]=(x1+x2)2-(x21+x22)=2x1x2≥0,满足;对于②,f(x1+x2)-[f(x1)+f(x2)]=[(x1+x2)2+1]-[(x21+1)+(x22+1)]=2x1x2-1<0,不满足;对于③,f(x1+x2)-[f(x1)+f(x2)]=(212+-1)-(21x-1+22x-x x1)=21x22x-21x-22x+1=(21x-1)(22x-1)≥0,满足.故选B.答案:B2.(2017·哈尔滨四校联考)已知函数f(x)=⎩⎪⎨⎪⎧ 21-x ,0≤x ≤1,x -1,1<x ≤2,如果对任意的n ∈N *,定义f n (x )=f {f [f …fn 个 (x )]},那么f 2 016(2)的值为( ) A .0B .1C .2D .3解析:∵f 1(2)=f (2)=1,f 2(2)=f (1)=0,f 3(2)=f (0)=2,f 4(2)=f (2)=1,∴f n (2)的值具有周期性,且周期为3,∴f 2 016(2)=f 3×672(2)=f 3(2)=2,故选C.答案:C。
第一部分专题一第2讲

考向二 等压线的判读与应用 2.(2011·江苏地理)下图是某区域某时地面天气简图。读图
回答(1)~(2)题。
(1)图中 M 地的风向是
A.东北
B.东南
C.西北
D.西南
(2)产生图示区域降水的天气系统是
A.气旋
B.反气旋
C.暖锋
D.冷锋
() ()
解 析 第 (1) 题 , 从 图 中 所 示 经 纬 度 可 以 看 出 , 图 中 (50°N,100°E)附近的高压中心位于亚欧大陆。M 点位于北 半球高压中心的东部,根据水平气压梯度力由高压指向低 压,加上摩擦力、地转偏向力(向右偏)的影响,风向为西 北风。第(2)题,在高纬度吹来的西北风的影响下,形成冷 锋,产生了图示区域的降水。 答案 (1)C (2)D
波罗的海
低值区 成低压中心
由 高 压 指 从沿海向内 从 近 岸 向 远
向北递
向 低 压 陆地区,一 洋、从赤道向
减为北
数值变
处 , 垂 直 般降水逐渐 副热带海区、
半球,
化趋势
于 等 压 减少;赤道 从高纬度海区
向南递
及应用
线 , 产 生 地区和温带 向 副 热 带 海
减为南
水 平 气 压 地区降水较 区,盐度均变
月份相反 半球冬季,南半球夏季
预测演练 3.读下图,回答(1)~(2)题。
(1)假设该图为等高线地形图,L 为河流,则图中箭头正确表示
河流集水方向的是
()
A.①
B.②
C.③
D.④
(2)假设图中曲线为等高线,L 为河流,且图中等高距为 200 m,
则图中 a 和 b 的数值可能是
2023年新高考数学大一轮复习专题一函数与导数第2讲基本初等函数函数与方程

第2讲 基本初等函数、函数与方程[考情分析] 1.基本初等函数的图象、性质是高考考查的重点,利用函数性质比较大小是常见题型.2.函数零点的个数判断及参数范围是高考的热点,常以压轴题形式出现.考点一 基本初等函数的图象与性质核心提炼1.指数函数y=a x(a>0,a≠1)与对数函数y=log a x(a>0,a≠1)互为反函数,其图象关于y=x对称,它们的图象和性质分0<a<1,a>1两种情况,着重关注两函数图象的异同.2.幂函数y=xα的图象和性质,主要掌握α=1,2,3,,-1五种情况.例1 (1)已知f(x)=2x-1,g(x)=1-x2,规定:当|f(x)|≥g(x)时,h(x)=|f(x)|;当| f(x)|<g(x)时,h(x)=-g(x),则h(x)( )A.有最小值-1,最大值1B.有最大值1,无最小值C.有最小值-1,无最大值D.有最大值-1,无最小值答案 C解析 画出y=|f(x)|=|2x-1|与y=g(x)=1-x2的图象,它们交于A,B两点.由“规定”在A,B两侧,|f(x)|≥g(x),故h(x)=|f(x)|;在A,B之间,|f(x)|<g(x),故h(x)=-g(x).综上可知,y=h(x)的图象是图中的实线部分,因此h(x)有最小值-1,无最大值.(2)已知函数f(x)=e x+2(x<0)与g(x)=ln(x+a)+2的图象上存在关于y轴对称的点,则a的取值范围是( )A.B.(-∞,e)C. D.答案 B解析 由题意知,方程f(-x)-g(x)=0在(0,+∞)上有解,即e-x+2-ln(x+a)-2=0在(0,+∞)上有解,即函数y=e-x与y=ln(x+a)的图象在(0,+∞)上有交点.函数y=ln(x+a)可以看作由y=ln x左右平移得到,当a=0时,两函数有交点,当a<0时,向右平移,两函数总有交点,当a>0时,向左平移,由图可知,将函数y=ln x的图象向左平移到过点(0,1)时,两函数的图象在(0,+∞)上不再有交点,把(0,1)代入y=ln(x+a),得1=ln a,即a=e,∴a<e.规律方法 (1)对数函数与指数函数的单调性都取决于其底数的取值,当底数a的值不确定时,要注意分a>1和0<a<1两种情况讨论:当a>1时,两函数在定义域内都为增函数;当0<a<1时,两函数在定义域内都为减函数.(2)基本初等函数的图象和性质是统一的,在解题中可相互转化.跟踪演练1 (1)函数f(x)=ln(x2+2)-e x-1的大致图象可能是( )答案 A解析 当x→+∞时,f(x)→-∞,故排除D;函数f(x)的定义域为R,且在R上连续,故排除B;f(0)=ln2-e-1,由于ln2>ln=,e-1<,所以f(0)=ln2-e-1>0,故排除C. (2)已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<-的解集是( )A.(-∞,-1) B.(-∞,-1]C.(1,+∞) D.[1,+∞)答案 A解析 当x>0时,f(x)=1-2-x>0.又f(x)是定义在R上的奇函数,所以f(x)<-的解集和f(x)>的解集关于原点对称,由1-2-x>得2-x<=2-1,即x>1,则f(x)<-的解集是(-∞,-1).故选A.考点二 函数的零点核心提炼判断函数零点个数的方法:(1)利用零点存在性定理判断法.(2)代数法:求方程f(x)=0的实数根.(3)几何法:对于不易求根的方程,将它与函数y=f(x)的图象联系起来,利用函数的性质找出零点或利用两个函数图象的交点求解.在利用函数性质时,可用求导的方法判断函数的单调性.考向1 函数零点的判断例2 (1)(2020·长沙调研)已知函数f(x)=若函数g(x)=f(x)-m有两个不同的零点x1,x2,则x1+x2等于( )A.2B.2或2+C.2或3D.2或3或2+答案 D解析 当x≤0时,f′(x)=(x+1)e x,当x<-1时,f′(x)<0,故f(x)在(-∞,-1)上单调递减,当-1<x≤0时,f′(x)>0,故f(x)在(-1,0]上单调递增,所以x≤0时,f(x)的最小值为f(-1)=-.又当x≥1时,f(x)=3-x,当0<x<1时,f(x)=x+1.作出f(x)的图象,如图所示.因为g(x)=f(x)-m有两个不同的零点,所以方程f(x)=m 有两个不同的根,等价于直线y=m与f(x)的图象有两个不同的交点,且交点的横坐标分别为x1,x2,由图可知1<m<2或m=0或m=-.若1<m<2,则x1+x2=2;若m=0,则x1+x2=3;若m=-,则x1+x2=-1+3+=2+.(2)设函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(2-x),当x∈[-2,0]时,f(x)=x-1,则关于x的方程f(x)-log8(x+2)=0在区间(-2,6)上根的个数为( )A.1B.2C.3D.4答案 C解析 对于任意的x∈R,都有f(2+x)=f(2-x),∴f(x+4)=f[2+(x+2)]=f[2-(x+2)]=f(-x)=f(x),∴函数f(x)是一个周期函数,且T=4.又∵当x∈[-2,0]时,f(x)=x-1,且函数f(x)是定义在R上的偶函数,且f(6)=1,则函数y=f(x)与y=log8(x+2)在区间(-2,6)上的图象如图所示,根据图象可得y=f(x)与y=log8(x+2)在区间(-2,6)上有3个不同的交点,即f(x)-log8(x+2)=0在区间(-2,6)上有3个根.考向2 求参数的值或取值范围例3 (1)已知关于x的方程9-|x-2|-4·3-|x-2|-a=0有实数根,则实数a的取值范围是__ ______.答案 [-3,0)解析 设t=3-|x-2|(0<t≤1),由题意知a=t2-4t在(0,1]上有解,又t2-4t=(t-2)2-4(0<t≤1),∴-3≤t2-4t<0,∴实数a的取值范围是[-3,0).(2)已知函数f(x)=若函数g(x)=f(x)-2x恰有2个不同的零点,则实数a的取值范围为__ __________________.答案 [-3,-1)∪[3,+∞)解析 由题意得g(x)=即g(x)=如图所示,因为g(x)恰有两个不同的零点,即g(x)的图象与x轴有两个交点.若当x≤a时,g(x)=x2+4x+3有两个零点,则令x2+4x+3=0,解得x=-3或x=-1,则当x>a时,g(x)=3-x没有零点,所以a≥3.若当x≤a时,g(x)=x2+4x+3有一个零点,则当x>a时,g(x)=3-x必有一个零点,即-3≤a<-1,综上所述,a∈[-3,-1)∪[3,+∞).规律方法 利用函数零点的情况求参数值(或取值范围)的三种方法跟踪演练2 (1)已知偶函数y=f(x)(x∈R)满足f(x)=x2-3x(x≥0),若函数g(x)=则y=f(x)-g(x)的零点个数为( )A.1B.3C.2D.4答案 B解析 作出函数f(x)与g(x)的图象如图,由图象可知两个函数有3个不同的交点,所以函数y=f(x)-g(x)有3个零点.(2)(多选)已知函数f(x)=若关于x的方程f(f(x))=0有8个不同的实根,则a的值可能为( )A.-6B.8C.9D.12答案 CD解析 当a≤0时,f(x)仅有一个零点x=0,故f(f(x))=0有8个不同的实根不可能成立.当a >0时,f (x )的图象如图所示,当f (f (x ))=0时,f 1(x )=-2a ,f 2(x )=0,f 3(x )=a .又f (f (x ))=0有8个不同的实根,故f 1(x )=-2a 有三个根,f 2(x )=0有三个根,f 3(x )=a 有两个根,又x 2-ax =2-,所以-2a >-且a <2a ,解得a >8且a >0,综上可知,a >8.专题强化练一、单项选择题1.(2020·全国Ⅰ)设a log 34=2,则4-a 等于( )A.B.C.D.答案 B解析 方法一 因为a log 34=2,所以log 34a =2,所以4a =32=9,所以4-a ==.方法二 因为a log 34=2,所以a ==2log 43=log 432=log 49,所以4-a =14log 94-=9-1=.2.函数f (x )=ln x +2x -6的零点一定位于区间( )A .(1,2)B .(2,3)C .(3,4)D .(4,5)答案 B解析 函数f (x )=ln x +2x -6在其定义域上连续且单调,f (2)=ln2+2×2-6=ln2-2<0,f (3)=ln3+2×3-6=ln3>0,故函数f (x )=ln x +2x -6的零点在区间(2,3)上.3.在同一直角坐标系中,函数f (x )=2-ax 和g (x )=log a (x +2)(a >0且a ≠1)的大致图象可能为( )答案 A解析 由题意知,当a >0时,函数f (x )=2-ax 为减函数.若0<a <1,则函数f (x )=2-ax 的零点x 0=∈(2,+∞),且函数g (x )=log a (x +2)在(-2,+∞)上为减函数;若a >1,则函数f (x )=2-ax 的零点x 0=∈(0,2),且函数g (x )=log a (x +2)在(-2,+∞)上为增函数.故A 正确.4.(2020·广东省揭阳三中模拟)已知a ,b ,c 满足4a =6,b =log c 3=,则( )A .a <b <cB .b <c <aC .c <a <bD .c <b <a 答案 B解析 4a =6>4,a >1,b2,c 3=<1,0<c <1,故a >c >b .5.(2020·全国Ⅲ)Logistic 模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位:天)的Logistic 模型:I (t )=,其中K 为最大确诊病例数.当I (t *)=0.95K 时,标志着已初步遏制疫情,则t *约为(ln19≈3)( )A .60B .63C .66D .69答案 C解析 因为I (t )=,所以当I (t *)=0.95K0.95K ,即*0.235311e t ⎛⎫-- ⎪⎝⎭+=0.95,即1+*0.2353e t ⎛⎫-- ⎪⎝⎭=,即*0.2353e t ⎛⎫-- ⎪⎝⎭=-1,∴*0.2353e t ⎛⎫- ⎪⎝⎭=19,∴0.23(t *-53)=ln19,∴t *=+53≈+53≈66.6.(2020·泉州模拟)若函数y =log a (x 2-ax +1)有最小值,则a 的取值范围是( )A .1<a <2B .0<a <2,a ≠1C .0<a <1D .a ≥2答案 A解析 令u (x )=x 2-ax +1,函数y =log a (x 2-ax +1)有最小值,∴a >1,且u (x )min >0,∴Δ=a 2-4<0,∴1<a <2,∴a 的取值范围是1<a <2.7.(2020·太原质检)已知函数f (x )=(e 为自然对数的底数),若函数g (x )=f (x )+kx 恰好有两个零点,则实数k 等于( )A .-2eB .eC .-eD .2e答案 C解析 g (x )=f (x )+kx =0,即f (x )=-kx ,如图所示,画出函数y =f (x )和y =-kx 的图象,-2x 2+4x +1=-kx ,即2x 2-(4+k )x -1=0,设方程的两根为x 1,x 2,则Δ=(4+k )2+8>0,且x 1x 2=-,故g (x )在x <0时有且仅有一个零点,y =-kx 与y =f (x )在x >0时相切.当x >0时,设切点为(x 0,-kx 0),f (x )=e x ,f ′(x )=e x ,f ′(x 0)=0e x =-k kx 0,解得x0=1,k=-e.8.已知函数f(x)=若关于x的方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的解,则a的取值范围是( )A.(1,2) B.C. D.∪答案 D解析 作出f(x)=|x|+1,x≠0的图象如图所示.设t=f(x),则原方程化为2t2-(2a+3)t+3a=0,解得t1=a,t2=.由图象可知,若关于x的方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的实数解,只有当直线y=a与函数y=f(x)的图象有三个不同的交点时才满足条件,所以1<a<2.又方程2t2-(2a+3)t+3a=0有两个不相等的实数根,所以Δ=(2a+3)2-4×2×3a=(2a-3)2>0,解得a≠,综上,得1<a<2,且a≠.二、多项选择题9.(2020·临沂模拟)若10a=4,10b=25,则( )A.a+b=2B.b-a=1C.ab>8lg22D.b-a>lg6答案 ACD解析 由10a=4,10b=25,得a=lg4,b=lg25,则a+b=lg4+lg25=lg100=2,故A正确;b-a=lg25-lg4=lg>lg6且lg<1,故B错误,D正确;ab=lg4·lg25=4lg2·lg5>4lg2·lg4=8lg22,故C正确.10.已知函数f(x)=log a(x+1),g(x)=log a(1-x),a>0,a≠1,则( )A.函数f(x)+g(x)的定义域为(-1,1)B.函数f(x)+g(x)的图象关于y轴对称C.函数f(x)+g(x)在定义域上有最小值0D.函数f(x)-g(x)在区间(0,1)上是减函数答案 AB解析 ∵f(x)=log a(x+1),g(x)=log a(1-x),a>0,a≠1,∴f(x)+g(x)=log a(x+1)+log a(1-x),由x+1>0且1-x>0得-1<x<1,故A对;由f(-x)+g(-x)=log a(-x +1)+log a(1+x)=f(x)+g(x),得函数f(x)+g(x)是偶函数,其图象关于y轴对称,B对;∵-1<x<1,∴f(x)+g(x)=log a(1-x2),∵y=1-x2在[0,1)上单调递减,由复合函数的单调性可知,当0<a<1时,函数f(x)+g(x)在[0,1)上单调递增,有最小值f(0)+g(0)=log a(1-0)=0;当a>1时,函数f(x)+g(x)在[0,1)上单调递减,无最小值,故C错;∵f(x)-g(x)=log a(x+1)-log a(1-x),当0<a<1时,f(x)=log a(x+1)在(0,1)上单调递减,g(x)=log a(1-x)在(0,1)上单调递增,函数f(x)-g(x)在(0,1)上单调递减;当a>1时,f(x)=log a(x+1)在(0,1)上单调递增,g(x)=log a(1-x)在(0,1)上单调递减,函数f(x)-g(x)在(0,1)上单调递增,故D错.11.(2020·淄博模拟)已知函数y=f(x)是R上的奇函数,对于任意x∈R,都有f(x+4)=f(x)+f(2)成立.当x∈[0,2)时,f(x)=2x-1.给出下列结论,其中正确的是( )A.f(2)=0B.点(4,0)是函数y=f(x)图象的一个对称中心C.函数y=f(x)在区间[-6,-2]上单调递增D.函数y=f(x)在区间[-6,6]上有3个零点答案 AB解析 对于A,因为f(x)为奇函数且对任意x∈R,都有f(x+4)=f(x)+f(2),令x=-2,则f(2)=f(-2)+f(2)=0,故A正确;对于B,由A知,f(2)=0,则f(x+4)=f(x),则4为f(x)的一个周期,因为f(x)的图象关于原点(0,0)成中心对称,则(4,0)是函数f(x)图象的一个对称中心,故B正确;对于C,因为f(-6)=0,f(-5)=f(-5+4)=f(-1)=-f(1)=-1,-6<-5,而f(-6)>f(-5),所以f(x)在区间[-6,-2]上不是单调递增的,故C错误;对于D,因为f(0)=0,f(2)=0,所以f(-2)=0,又4为f(x)的一个周期,所以f(4)=0,f(6)=0,f(-4)=0,f(-6)=0,所以函数y=f(x)在区间[-6,6]上有7个零点,故D错误.12.对于函数f(x)=则下列结论正确的是( )A.任取x1,x2∈[2,+∞),都有|f(x1)-f(x2)|≤1B.函数y=f(x)在[4,5]上单调递增C.函数y=f(x)-ln(x-1)有3个零点D.若关于x的方程f(x)=m(m<0)恰有3个不同的实根x1,x2,x3,则x1+x2+x3=答案 ACD解析 f(x)=的图象如图所示,当x∈[2,+∞)时,f(x)的最大值为,最小值为-,∴任取x1,x2∈[2,+∞),都有|f(x1)-f(x2)|≤1恒成立,故A正确;函数y=f(x)在[4,5]上的单调性和在[0,1]上的单调性相同,则函数y=f(x)在[4,5]上不单调,故B错误;作出y=ln(x-1)的图象,结合图象,易知y =ln(x-1)的图象与f(x)的图象有3个交点,∴函数y=f(x)-ln(x-1)有3个零点,故C 正确;若关于x的方程f(x)=m(m<0)恰有3个不同的实根x1,x2,x3,不妨设x1<x2<x3,则x1+x2=3,x3=,∴x1+x2+x3=,故D正确.三、填空题13.(2019·全国Ⅱ)已知f(x)是奇函数,且当x<0时,f(x)=-e ax.若f(ln2)=8,则a=________.答案 -3解析 当x>0时,-x<0,f(-x)=-e-ax.因为函数f(x)为奇函数,所以当x>0时,f(x)=-f(-x)=e-ax,所以f(ln2)=e-a ln2=a=8,所以a=-3.14.已知函数f(x)=|lg x|,若f(a)=f(b)(a≠b),则函数g(x)=的最小值为________.答案 2解析 因为|lg a|=|lg b|,所以不妨令a<b,则有-lg a=lg b,所以ab=1,b=(0<a<1),所以g(x)=当x≤0时,g(x)=(x+)2+3≥3,取等号时x=-;当x>0时,g(x)=ax+≥2=2,当且仅当x=时,等号成立,综上可知,g(x)min=2.15.定义在R上的奇函数f(x),当x≥0时,f(x)=则函数F(x)=f(x)-的所有零点之和为_ _______.答案 解析 由题意知,当x<0时,f(x)=作出函数f(x)的图象如图所示,设函数y=f(x)的图象与y=交点的横坐标从左到右依次为x1,x2,x3,x4,x5,由图象的对称性可知,x1+x2=-6,x4+x5=6,x1+x2+x4+x5=0,令-=,解得x3=,所以函数F(x)=f(x)-的所有零点之和为.16.对于函数f(x)与g(x),若存在λ∈{x∈R|f(x)=0},μ∈{x∈R|g(x)=0},使得|λ-μ|≤1,则称函数f(x)与g(x)互为“零点密切函数”,现已知函数f(x)=e x-2+x-3与g(x)=x2-ax-x+4互为“零点密切函数”,则实数a的取值范围是________.答案 [3,4]解析 由题意知,函数f(x)的零点为x=2,设g(x)的零点为μ,满足|2-μ|≤1,因为|2-μ|≤1,所以1≤μ≤3.方法一 因为函数g(x)的图象开口向上,所以要使g(x)的至少一个零点落在区间[1,3]上,则需满足g(1)g(3)≤0,或解得≤a≤4,或3≤a<,得3≤a≤4.故实数a的取值范围为[3,4].方法二 因为g(μ)=μ2-aμ-μ+4=0,a==μ+-1,因为1≤μ≤3,所以3≤a≤4.故实数a的取值范围为[3,4].。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一部分 专题一 第2讲[随堂巩固]1.(2014·大纲全国)一质点沿x 轴做直线运动,其v -t 图象如图1-2-5所示.质点在t =0时位于x =5 m 处,开始沿x 轴正向运动.当t =8 s 时,质点在x 轴上的位置为图1-2-5A .x =3 mB .x =8 mC .x =9 mD .x =14 m解析 由图象知,质点在8 s 内的位移Δx =12×(2+4)×2 m -12×(2+4)×1 m =3 m .t =0时,质点位于x =5 m 处,故8 s 末质点位置x =5 m +Δx =8 m ,B 正确.答案 B2.两个质点A 、B 放在同一水平面上,由静止开始从同一位置沿相同方向同时开始做直线运动,其运动的v -t 图象如图1-2-6所示.对A 、B 运动情况的分析,下列结论正确的是A .A 、B 加速时的加速度大小之比为2∶1,A 、B 减速时的加速度 图1-2-6 大小之比为1∶1B .在t =3t 0时刻,A 、B 相距最远C .在t =5t 0时刻,A 、B 相距最远D .在t =6t 0时刻,A 、B 相遇解析 由v -t 图象可知,通过斜率可计算加速度大小,加速时A 、B 的加速度大小之比为10∶1,减速时A 、B 的加速度大小之比为1∶1,所以选项A 错误;由A 、B 运动关系可知,当A 、B 速度相同时距离最远,所以选项B 、C 错误;由题意可知A 、B 是从同一位置同时开始运动的,由速度-时间图象可以计算出运动位移,可知6t 0时刻,A 、B 位移相同,因此在此时刻A 、B 相遇,所以选项D正确.答案 D3.(2013·四川理综)甲、乙两物体在t=0时刻经过同一位置沿x轴运动,其v-t图象如图1-2-7所示,则图1-2-7A.甲、乙在t=0到t=1 s之间沿同一方向运动B.乙在t=0到t=7 s之间的位移为零C.甲在t=0到t=4 s之间做往复运动D.甲、乙在t=6 s时的加速度方向相同解析在t=0到t=1 s之间,甲、乙两物体的运动方向先相反,后相同,选项A错误,在t =0到t=7 s之间由乙物体的v-t图象的“线下面积”可知位移为0,选项B正确,在t=0到t =4 s之间甲物体沿x轴向同一个方向运动,选项C错误,由甲、乙两物体的v-t图象可知t=6 s 时图线的斜率均为负值,即它们的加速度方向相同,选项D正确.答案BD[课下作业][限时45分钟,满分100分]一、选择题(每小题6分,共60分)1.如图1-2-8所示,一个质点从O点开始做匀加速直线运动,连续经过1、2、3、…、2 012、2 013各个位置,通过这些位置的瞬时速度分别为v1、v2、v3、…、v2012和v2 013,v表示从1到2 013的平均速度,已知连续两点间距离都相等,即x12=x23=…,则关于v、v504和v1 007,的大小关系正确的是图1-2-8A.v<v504B.v504<v<v1 007C.v>v1 007D.无法比较解析设1和2两点间距离为L,v2504-v21=2a(503L)、v22 013-v21=2a(2 012L),联立可得v2504=503v22 013+1 509v212 012,又平均速度v=v2 013+v12.v2-v2504=1 006v1(v2 013-v1)2 012>0,则v>v504,又根据中点位移的瞬时速度大于中点时刻的瞬时速度即v<v1 007,正确选项为B.答案 B2.(2014·湖北八校联考)如图1-2-9为一质点沿直线运动的v-t图象,已知质点从零时刻出发,在2T时刻恰好返回出发点.则下列说法正确的是A.0~T与T~2T时间内的位移相同B.质点在1.5T时离出发点最远图1-2-9 C.T秒末与2T秒末速度大小之比为1∶2D.0~T与T~2T时间内的加速度大小之比为1∶3解析0~T内,对于质点有x=12a1T2,v=a1T,T~2T内,对于质点有-x=v T-12a2T2,联立有a2=3a1,选项D正确;质点速度减小为零时有0=v-a2t,则t=T3,质点在43T时离出发点最远,选项B错误;0~T与T~2T时间内的位移大小相等,方向相反,选项A错误;由图可知T 秒末与2T秒末速度大小之比为1∶2,选项C正确.答案CD3.(2014·东营二模)一个质点做直线运动的v-t图象如图1-2-10所示,下列判断正确的是图1-2-10A.质点在0~5 s内的位移大小为10 mB.质点在10 s末离出发点最远C.质点在整个0~12 s内的运动过程中,10~12 s内的加速度最大D .质点在0~8 s 内的平均速度为1 m/s答案 C4.(2014·课标Ⅱ)甲乙两汽车在一平直公路上同向行驶.在t =0到t =t 1的时间内,它们的v -t 图象如图1-2-11所示.在这段时间内A .汽车甲的平均速度比乙的大B .汽车乙的平均速度等于v 1+v 22图1-2-11 C .甲乙两汽车的位移相同D .汽车甲的加速度大小逐渐减小,汽车乙的加速度大小逐渐增大解析 在v -t 图象中,图线与坐标轴所围的面积表示位移,由题图知在0~t 1时间内,甲的位移大于乙的位移,C 错误.由v =x /t 知,甲的平均速度比乙的大,故A 正确.如图所示,汽车乙的v -t 图象中,实线下的面积小于上面那条虚线下的面积,故汽车乙的平均速度小于v 1+v 22,B 错误.v -t 图象中的斜率表示加速度,甲、乙图线上各点切线的斜率均逐渐减小,故加速度都逐渐减小,D 错误.答案 A5.(2014·效实中学摸底)如图1-2-12所示,将小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5所示小球运动过程中每次曝光的位置,连续两次曝光的时间间隔均为T ,每块砖的厚度为d .根据图中的信息,下列判断正确的是A .能判定位置“1”是小球释放的初始位置B .能求出小球下落的加速度为d T 2 图1-2-11C .能求出小球在位置“3”的速度为7d 2TD .如果已知d 和T 的数值,就能判定小球下落过程中机械能是否守恒解析 根据题图中的信息,利用Δx =aT 2,能求出小球下落的加速度为a =d T 2,选项B 正确;能求出小球在位置“3”的速度为v 3=7d 2T ,选项C 正确.若已知d 和T 的数值,代入a =d T 2,若计算得出a =g ,则小球做自由落体运动,小球下落过程中机械能守恒;若计算得出a <g ,则小球下落过程中机械能不守恒,选项D 正确.能判定位置“1”不是小球释放的初始位置,选项A 错误.答案 BCD6.(2014·豫东、豫北联考)如图1-2-13所示,直线a 和曲线b 分别是在平直公路上行驶的汽车a 和b 的位移—时间(x -t )图线.由图可知A .在t 1时刻,a 、b 两车运动方向相同B .在t 2时刻,a 、b 两车运动方向相反C .在t 1到t 2这段时间内,b 车的速率先减少后增大 图1-2-13D .在t 1到t 2这段时间内,b 车的速率一直比a 车的大解析 x -t 图线的斜率表示速度,从题图中看出,a 车始终静止,b 车先正向减速,速度为0后,再反向加速,因此A 、B 、D 选项错误,C 正确.答案 C7.如图1-2-14所示,在地面上一盘子C 的正上方A 处有一金属小球a 距C 为20 m ,在B 处有另一个金属小球b 距C 为15 m ,小球a 比小球b 提前1 s由静止释放(g 取10 m/s 2).则A .b 先落入C 盘中,不可能在下落过程中相遇B .a 先落入C 盘中,a 、b 下落过程相遇点发生在BC 之间某位置C .a 、b 两小球同时落入C 盘 图1-2-14D .在a 球下落过程中,a 、b 两小球相遇点恰好在B 处解析 小球a 、b 释放后均做自由落体运动,则有h =12gt 2,代入计算得t a =2 s ,t b = 3 s ,小球a 提前1 s 释放,所以b 释放后a 运动t a -1 s =1 s 落入C 盘,比b 球早落入.选项A 、C 错,b球释放时a 下落1 s ,此时下落的高度h =12gt ′2=5 m ,刚好到达小球b 的同高处,此时b 开始释放,所以二者在B 点相遇,然后a 球超过b 球先落入盘中.选项D 对、B 错.答案 D8.考驾照需要进行路考,路考中有一项是定点停车,路旁竖一标志杆,在车以10 m/s 的速度匀速行驶过程中,当车头与标志杆的距离为20 m 时,学员立即刹车,让车做匀减速直线运动,车头恰好停在标志杆处,忽略学员的反应时间,则A .汽车刹车过程的时间为4 sB .汽车刹车过程的时间为2 sC .汽车刹车时的加速度大小为5 m/s 2D .汽车刹车时的加速度大小为0.25 m/s 2解析 采用逆向思维法,刹车过程可以看做是初速度为零的匀加速直线运动,由x =12v t 可得t =4 s ,选项A 正确,B 错误;根据v 2=2ax 可得,a =2.5 m/s 2,选项C 、D 错误.本题答案为A.答案 A9.(2013·海南)一物体做直线运动,其加速度随时间变化的a -t 图象如图1-2-15所示.下图图象中,可能正确描述此物体运动的是图1-2-15解析 由图可知,在0~T 2时间内a =a 0>0,若v 0≥0,物体做匀加速运动;若v 0<0,物体做匀减速运动,故B 、C 皆错误;由于在T ~2T 时间内a =-a 0,故物体做匀减速运动且图线斜率的绝对值与0~T 2时间内相同,故A 错误、D 正确. 答案 D10.蹦极一直是勇敢者喜爱的运动项目,如图1-2-16所示,已知弹性绳的原长为L ,蹦极运动员从开始无初速下落到最低点过程中(不计空气阻力),下图中图象分别描述运动员的位移、速度、加速度、动能随时间的变化情况,其中正确的是图1-2-16解析 弹性绳被拉伸之前,运动员做自由落体运动,根据x =12gt 2可知选项 A 错误;弹性绳被拉伸后,运动员先做加速度逐渐减小的变加速直线运动,后做加速度反向逐渐增大的变减速直线运动,选项B 正确、C 错误;弹性绳被拉伸之前,运动员做自由落体直线运动,根据E k =12m v 2=12mg 2t 2可知选项D 错误. 答案 B二、计算题(共40分)11.(18分)(2014·成都高新区高三检测)某消防员在一次执行任务过程中,遇到突发事件,需从10 m 长的直杆顶端先从静止开始匀加速下滑,加速度大小a 1=8 m/s 2,然后立即匀减速下滑,减速时的最大加速度a 2=4 m/s 2,若落地时的速度不允许超过4 m/s ,把消防员看成质点,求该消防员下滑全过程的最短时间.解析 设直杆长为h ,加速下滑部分长为h 1,减速下滑部分长为h 2,最大速度为v ,落地速度为v 1,由速度-位移公式v 2-v 20=2ax ,再由h 1+h 2=h ,解得:v 22a 1+v 2-v 212a 2=h 又有速度-时间公式v =a 1t 1联立以上各式解得:v =8 m/s ,t 1=1 s落地前的速度为v1=4 m/s,由速度-时间公式v1=v-a2t2,解得:t2=1 s该消防员下滑全过程的最短时间为:t=t1+t2=2 s.答案 2 s12.(22分)(2014·池州高三月考)随着机动车数量的增加,交通安全问题日益凸显,分析交通违法事例,将警示我们遵守交通法规,珍惜生命,如图1-2-17所示为某型号货车紧急制动时(假设做匀减速直线运动)的v2-x图象(v为货车的速度,x为制动距离),其中图线1为满载时符合安全要求的制动图象,图线2为严重超载时的制动图象.某路段限速72 km/h,是根据该型号货车满载时安全制动时间和制动距离确定的,现有图1-2-17一辆该型号的货车严重超载并以54 km/h的速度行驶,通过计算求解:(1)驾驶员紧急制动时,该型号严重超载的货车制动时间和制动距离是否符合安全要求;(2)若驾驶员从发现险情到采取紧急制动措施的反应时间为1 s,则该型号货车满载时以72 km/h速度正常行驶的跟车距离至少应为多远.解析(1)根据速度位移公式v2-v20=2ax,有v2=2ax+v20,图线斜率的一半表示加速度;根据题图象得到:满载时,加速度为5 m/s2,严重超载时加速度为2.5 m/s2;设该型号货车满载时以72 km/h(20 m/s)的速度减速,制动距离x1=v22a1=4002×5m=40 m,制动时间为t1=va1=205s=4 s;设该型号货车严重超载时以54 km/h (15 m/s)的速度减速,制动距离x2=v′22a2=1522×2.5m=45m>x1,制动时间为t2=v′a2=152.5s=6 s>t1;所以驾驶员紧急制动时,该型号严重超载的货车制动时间和制动距离均不符合安全要求.(2)货车在反应时间内做匀速直线运动x3=v t3=20×1 m=20 m,跟车距离x=v22a1+x3=40 m+20 m=60 m.答案(1)不符合(2)60 m。
