排列组合中的分组分配
排列组合中的分组分配问题的有效解法

排列组合中的分组分配问题的有效解法排列组合中的分组分配问题是指将一组元素分成不同的组,每个组中的元素个数可以不同,同时每个元素只能属于一个组。
这类问题在实际生活中非常常见,比如将不同班级的学生分配到不同的宿舍,将不同商品分配到不同的仓库等。
在解决这类问题时,可以使用回溯法进行穷举搜索,具体步骤如下:1. 定义一个空的结果集,用来存储所有的有效分组分配方案。
2. 定义一个空的临时集合,用来存储当前正在处理的分组分配方案。
3. 使用回溯法进行搜索,从第一个元素开始,尝试将其放入不同的组中。
4. 对于每个选择,如果选择当前组的元素数量小于或等于规定的数量,则将该元素加入到临时集合中,并递归处理下一个元素。
5. 如果当前组的元素数量大于规定的数量,则回溯到上一层,并尝试选择其他组进行分配。
6. 当所有元素都被分配完毕时,将临时集合存入结果集中。
7. 返回结果集,即为所有的有效分组分配方案。
这种解法的时间复杂度为O(k^n),其中n为元素的个数,k为分组的个数。
在实际使用中,由于组合数目可能非常大,可能需要进行一些剪枝优化,以提高运行效率。
还可以使用动态规划方法解决分组分配问题。
动态规划方法将问题分为多个子问题,然后利用子问题的解来求解原问题。
具体步骤如下:1. 定义一个二维数组dp,dp[i][j]表示将前i个元素分配到j个组中的方案数。
2. 初始化dp数组,将所有元素分配到一个组中的方案数为1,其他地方为0。
3. 使用动态规划进行求解,从第一个元素开始,依次遍历所有可能的组合情况。
4. 对于每个元素,从1到j(j为组的数量)进行遍历,分别计算分配到该组和不分配到该组的方案数之和,并更新dp数组。
5. 当所有元素都遍历完毕后,dp[n][k]即为最终的解。
这种解法的时间复杂度为O(nk^2),可以在不超出计算能力的情况下求解大规模的分组分配问题。
排列组合中的分组分配问题可以使用回溯法和动态规划方法进行求解。
排列组合中的分组分配问题的有效解法

排列组合中的分组分配问题的有效解法排列组合中的分组分配问题在数学和计算机科学中是一个重要的问题,它涉及到如何将一组对象分配到不同的集合中,使得每个集合包含的对象满足特定的条件。
在实际生活中,这种问题也经常出现,比如在制定班级或团队分组、分配资源等方面。
在这篇文章中,我们将讨论排列组合中的分组分配问题,并介绍一些有效的解法,希望能够帮助读者更好地理解和解决这类问题。
1. 理解排列组合中的分组分配问题排列组合中的分组分配问题,通常可以描述为以下几种形式:(1)将N个对象分成K个组,每个组的大小不同;(2)将N个对象分成K个组,每个组的大小相同;(3)将N个对象分成K个组,每个组的大小不同,但满足一定条件。
在实际应用中,这些问题可能会涉及到一些约束条件,比如每个组中的对象之间有特定的关系,或者每个组中的对象有特定的属性,这将在具体问题中得到体现。
2. 有效解法为了解决排列组合中的分组分配问题,我们介绍一些有效的解法,包括暴力穷举、动态规划和回溯法等。
(1)暴力穷举暴力穷举是一种简单直接的方法,它通过遍历所有可能的组合来寻找符合条件的分组分配。
这种方法的优点是容易理解和实现,但是当问题规模较大时,时间复杂度会非常高,需要花费大量的计算资源。
暴力穷举一般适用于问题规模较小的情况。
(2)动态规划动态规划是一种常用的解决排列组合问题的方法,它通过将原问题分解成若干个子问题,并且这些子问题之间存在重叠的性质。
通过记录中间结果,可以避免重复计算,从而提高效率。
在分组分配问题中,动态规划可以用来求解不同组合的分配方案数量、找到最优的分组方案等。
通过定义状态转移方程和设计合适的算法,可以高效地解决大规模的分组分配问题。
(3)回溯法回溯法是一种递归地穷举所有可能的解决方案,通过不断地试探和回溯来寻找最优的解决方案。
在分组分配问题中,回溯法可以用来找到满足条件的分组方案,或者列举所有可能的分配方案。
回溯法的优点是能够找到所有可能的解,但是在问题规模较大时,时间复杂度会很高,需要耗费大量的计算资源。
6、排列组合问题之分组分配问题

排列组合问题之分组分配问题(一)(五个方面)一、非均匀分组(分步组合法)“非均匀分组”是指将所有元素分成元素个数彼此不相等的组。
例1、7人参加义务劳动,按下列方法分组有多少种不同的分法①分成3组,分别为1人、2人、4人;②选出5个人分成2组,一组2人,另一组3人。
解:①先选出1人,有C;种,再由剩下的6人选出2人,有C:种,最后由剩下的4人为一组,有C:种。
由分步计数原理得分组方法共有C;C:C: =105(种)。
②可选分同步。
先从7人中选出2人,有©种,再由剩下的5人中选出3人,有C;种,分组方法共有C;C:=210(种)。
也可先选后分。
先选出5人,再分为两组,由分步计数原理得分组方法共有C;C;C;=210 (种二、均匀分组(去除重复法)“均匀分组”是指将所有元素分成所有组元素个数相等或部分组元素个数相等的组。
㈠全部均匀分组(去除重复法)例2、7人参加义务劳动,选出6个人,分成2组,每组都是3人,有多少种不同的分法解:可选分同步。
先选3人为一组,有E种;再选3人为另一组,有C:种。
又有2 组都是3人,每Af种分法只能算一种,所以不同的分法共有亠L = 70 (种)。
C3C3也可先选后分。
不同的分法共有C;・-4^ = 70 (种)。
A?㈡部分均匀分组(去除重复法)例3、10个不同零件分成4堆,每堆分别有2、2、2、4个,有多少种不同的分法解:分成2、2、2、4个元素的4堆,分别有C:、C:、C;、C;种,又有3堆都C1 c2c2是2个元素,每&种分法只能算一种,所以不同的分组方法共有|()^ 6= 3150 (种)。
【小结:不论是全部均匀分组,还是部分均匀分组,如果有加个组的元素是均匀的,都有A:;种顺序不同的分法只能算一种分法。
】三、编号分组㈠非均匀编号分组(分步先组合后排列法)例4、7人参加义务劳动,选出2人一组、3人一组,轮流挖土、运土,有多少种分组方法解:分组方法共有C;C;A;=420 (种)。
排列组合中分组分配问题

分组分配问题一.基本内容1.案例分析:将4个不同的元素分为2份,每份2个,请问有多少不同的分法?解析:若按照2422C C 6=的方法进行分组,不妨设4个元素分别为,,,a b c d ,则会出现以下情况:①,ab cd ;②,cd ab ;③,ac bd ;④,bd ac ;⑤,ad bc ;⑥,bc ad .显然,用组合数公式计算出来的结果重复了三次,最终的分组结果应以为:242222C C 3A =2.基本原理2.1分组问题属于“组合”问题,常见的分组问题有三种:将n 个不同元素分成m 组,且每组的元素个数分别为m m m m m ,,,,321 ,记m m mm m m n mm m n mm n mn C C C C N )()(121321211-+++-+--⋅⋅⋅⋅= .(1)非均匀不编号分组:n 个不同元素分成m 组,每组元素数目均不相等,且不考虑各组间的顺序,其分法种数为N .(2)均匀不编号分组:将n 个不同元素分成不编号(即无序)的m 组,每组元素数目相等,其分法种数为m mA N .(3)部分均匀不编号分组:将n 个不同元素分成不编号的m 组,其中有r 组元素个数相等,其分法种数为r rA N ,如果再有k 组均匀分组,应再除以kk A .2.2分配问题属于“排列”问题,分配问题可以按要求逐个分配,也可以分组后再分配.3.相同元素的分组问题:挡板法及其应用:对于n 个相同元素分成m 组(m n <),且每组至少一个元素的分组问题,可采用“隔板法”解决:n 个元素之间形成1n -个空格,只需放入1m -个隔板即可,故不同的分配方案有11C m n --种,其等效于不定方程的非负整数解个数:不定方程r x x x n =+⋅⋅⋅++21的非负整数解.(1)方程r x x x n =+⋅⋅⋅++21的正整数解为11--n r C 个.(2)方程r x x x n =+⋅⋅⋅++21的非负整数解为11--+n r n C 个.二.例题分析例1.某校有5名大学生打算前往观看冰球,速滑,花滑三场比赛,每场比赛至少有1名学生且至多2名学生前往,则甲同学不去观看冰球比赛的方案种数有()A .48B .54C .60D .72【解析】将5名大学生分为1-2-2三组,即第一组1个人,第二组2个人,第三组2个人,共有2215312215C C C A ∙∙=种方法;由于甲不去看冰球比赛,故甲所在的组只有2种选择,剩下的2组任意选,所以由2224A =种方法;按照分步乘法原理,共有41560⨯=种方法;故选:C.例2.甲、乙、丙、丁、戊5名志愿者参加新冠疫情防控志愿者活动,现有,,A B C 三个小区可供选择,每个志愿者只能选其中一个小区.则每个小区至少有一名志愿者,且甲不在A 小区的概率为()A .193243B .100243C .23D .59【解析】首先求所有可能情况,5个人去3个地方,共有53243=种情况,再计算5个人去3个地方,且每个地方至少有一个人去,5人被分为3,1,1或2,2,1当5人被分为3,1,1时,情况数为3353C A 60⨯=;当5人被分为2,2,1时,情况数为12354322C C A 90A ⨯⨯=;所以共有6090150+=.由于所求甲不去A ,情况数较多,反向思考,求甲去A 的情况数,最后用总数减即可,当5人被分为3,1,1时,且甲去A ,甲若为1,则3242C A 8⨯=,甲若为3,则2242C A 12⨯=共计81220+=种,当5人被分为2,2,1时,且甲去A ,甲若为1,则224222C A 6A ⨯=,甲若为2,则112432C C A 24⨯⨯=,共计62430+=种,所以甲不在A 小区的概率为()1502030100243243-+=,故选:B.例3.安排5名大学生到三家企业实习,每名大学生只去一家企业,每家企业至少安排1名大学生,则大学生甲、乙到同一家企业实习的概率为()A .15B .310C .325D .625【解析】5名大学生分三组,每组至少一人,有两种情形,分别为2,2,1人或3,1,1人;当分为3,1,1人时,有3353C A 60=种实习方案,当分为2,2,1人时,有22353322C C A 90A ⋅=种实习方案,即共有6090150+=种实习方案,其中甲、乙到同一家企业实习的情况有13233333C A C A 36+=种,故大学生甲、乙到同一家企业实习的概率为36615025=,故选:D.例4.学校要安排2名班主任,3名科任老师共五人在本校以及另外两所学校去监考,要求在本校监考的老师必须是班主任,且每个学校都有人去,则有()种不同的分配方案.A .18B .20C .28D .34【解析】根据本校监考人数分为:本校1人监考,另外4人分配给两所学校,有2,2和3,1两种分配方案,所以总数为:28)(2233142222222412=+∙A C C A A C C C ;本校2人监考,另外3人分配给两所学校,有2,1一种分配方案,所以总数为:()212223226C C C A =,根据分类计数原理,所有分配方案总数为28+6=34;故选:D.例5.现有甲、乙、丙、丁、戊五位同学,分别带着A 、B 、C 、D 、E 五个不同的礼物参加“抽盲盒”学游戏,先将五个礼物分别放入五个相同的盒子里,每位同学再分别随机抽取一个盒子,恰有一位同学拿到自己礼物的概率为()A .45B .12C .47D .38【解析】先从五人中抽取一人,恰好拿到自己的礼物,有15C 种情况,接下来的四人分为两种情况,一种是两两一对,两个人都拿到对方的礼物,有224222C C A 种情况,另一种是四个人都拿到另外一个人的礼物,不是两两一对,都拿到对方的情况,由3211C C 种情况,综上:共有22111425322245C C C C C A ⎛⎫⋅+= ⎪⎝⎭种情况,而五人抽五个礼物总数为55120A =种情况,故恰有一位同学拿到自己礼物的概率为4531208=.故选:D 例6.为贯彻落实《中共中央国务院关于全面深化新时代教师队伍建设改革的意见》精神,加强义务教育教师队伍管理,推动义务教育优质均衡发展,安徽省全面实施中小学教师“县管校聘”管理改革,支持建设城乡学校共同体.2022年暑期某市教体局计划安排市区学校的6名骨干教师去4所乡镇学校工作一年,每所学校至少安排1人,则不同安排方案的总数为()A .2640B .1440C .2160D .1560【解析】将6人分组有2种情况:2211,3111,所以不同安排方案的总数为2234646422C C A 1560A C ⎛⎫+= ⎪⎝⎭.故选:D.例7.为促进援疆教育事业的发展,某省重点高中选派了3名男教师和2名女教师去支援边疆工作,分配到3所学校,每所学校至少一人,每人只去一所学校,则两名女教师分到同一所学校的情况种数为______.【解析】①若2位女老师和1名男老师分到一个学校有1333C A =18种情况;②若2位女老师分在一个学校,则3名男教师分为2组,再分到3所学校,有2333C A =18种情况,故两名女教师分到同一所学校的情况种数为181836+=种.故答案为:36.例8.2020年是脱贫攻坚决战决胜之年,某市为早日实现目标,现将甲、乙、丙、丁4名干部派遣到,,A B C 三个贫困县扶贫,要求每个贫困县至少分到一人,则甲、乙2名干部不被分到同一个贫困县的概率为___________.【解析】每个贫困县至少分到一人,4名干部分到三个县有211342132236C C C A A =种方案,其中甲、乙2名干部被分到同一个贫困县的方案有336A =种所以甲、乙2名干部不被分到同一个贫困县的概率为3665366P -==,故答案为:56例9.为弘扬学生志愿服务精神,某学校开展了形式多样的志愿者活动.现需安排5名学生,分别到3个地点(敬老院、幼儿园和交警大队)进行服务,要求每个地点至少安排1名学生,则有_______________________种不同的安排方案(用数字作答).【解析】先将5人分为三组,每组的人数分别为3、1、1或2、2、1,再将三组分配给三个地点,由分步乘法计数原理可知,不同的安排方案数为2233535322150C C C A A ⎛⎫+= ⎪⎝⎭种.故答案为:150.例10.6名教师分配到3所薄弱学校去支教,每个学校至少分配一名教师,甲乙两人不能去同一所学校,丙丁两人必须去同一所学校,共有________种分配方案(用数字作答).【解析】按题目要求可按4、1、1或3、2、1或2、2、2分配,若按4、1、1分配,丙丁必须在4人里,需要从其余剩下的4人里选2人,有24C 种,去掉选中甲乙的1种情况,有(24C -1)种选法,安排去3个学校,共有(24C -1)33A =30种;若按3、2、1分配有两类,丙丁为2,甲乙中选1人作1,分配到3个学校有1323C A ,丙丁在3人组中,从剩余4人中取1人,组成3人组,剩余3人取2人组成2人组,剩余1人构成1人组,去掉甲乙构成2人组的情况2种,共有12432C C -种取法,安排去3个学校有(12432C C -)33A 种,两类共有1323C A +(12432C C -)33A =72种;若按2、2、2分配有2·33A =12种,∴共有30+72+12=114种分配方案.下面是挡板法及其应用,仅做了解即可.例11.不定方程12x y z ++=的非负整数解的个数为()A .55B .60C .91D .540解析:不定方程12x y z ++=的非负整数解的个数⇔将12个相同小球放入三个盒子,允许有空盒的放法种数.现在在每个盒子里各加一个相同的小球,问题等价于将15个相同小球放入三个盒子,没有空盒的放法种数,则只需在15个小球中形成的空位(不包含两端)中插入两块板即可,因此,不定方程12x y z ++=的非负整数解的个数为21491C =.故选:C.例12.方程123412x x x x +++=的正整数解共有()组A .165B .120C .38D .35解析:如图,将12个完全相同的球排成一列,在它们之间形成的11个空隙中任选三个插入三块隔板,把球分成四组,每一种分法所得球的数目依次是1x 、2x 、3x 、4x ,显然满足123412x x x x +++=,故()1234,,,x x x x 是方程123412x x x x +++=的一组解,反之,方程123412x x x x +++=的每一组解都对应着一种在12个球中插入隔板的方式,故方程123412x x x x +++=的正整数解的数目为:31111109165321C ⨯⨯==⨯⨯,故选:A.。
排列组合中的分组分配问题的有效解法

排列组合中的分组分配问题的有效解法排列组合中的分组分配问题是数学中一个非常重要的问题,也是在实际生活中经常遇到的问题。
该问题主要涉及到将一组物品分配到若干个组中,或者将一组人员分配到不同的团队中。
解决这类问题通常需要使用排列组合的知识和技巧。
下面我们将介绍一些有效的解法,希望可以帮助您更好地解决这类问题。
一、隔板法隔板法是经典的排列组合问题解法之一,它在解决分组分配问题中非常实用。
这种方法的核心思想是在待分配的物品之间插入隔板,将物品分成若干组。
具体步骤如下:1. 确定分组数目:首先需要确定待分配的物品要分成几组,这取决于具体问题的要求。
2. 插入隔板:接下来,在待分配的物品之间插入隔板,每个隔板代表一个组的结束。
设共有n个物品和m-1个组隔板,那么总共有n+m-1个位置可以插入隔板。
其中一个特殊的情况是可以将物品和组隔板看作一共有n+m个位置中选择n个位置插入物品,这进一步转化成排列组合问题。
3. 解决问题:确定好每个物品的位置,将其分配到不同的组中即可得到分组分配问题的解。
二、多重集的分组分配多重集是集合的一个扩展,它包含了元素的重复出现次数。
在分组分配问题中,有时候待分配的物品会包含相同的元素,这时候就需要使用多重集的知识和技巧来解决问题。
多重集的分组分配通常需要使用生成函数、递推关系式等工具来求解。
具体步骤如下:1. 确定多重集:首先需要将待分配的物品表示成一个多重集,其中包含了元素的类型和重复出现次数。
通常可以使用集合的形式来表示多重集,例如{a, a, b, c, c, c}表示了元素a出现2次,b出现1次,c出现3次。
2. 利用生成函数求解:多重集的分组分配问题通常可以转化成生成函数的形式来求解,其中生成函数是一个形式化的表达式,它包含了待分配的物品的信息。
利用生成函数的性质和技巧,可以快速得到分组分配问题的解。
3. 使用递推关系式求解:对于一些复杂的多重集分组分配问题,可以使用递推关系式来求解。
排列组合中的分组分配问题及排列组合专项练习题

排列组合中的分组分配问题分组分配问题是排列组合教学中的一个重点和难点。
某些排列组合问题看似非分配问题,实际上可运用分配问题的方法来解决。
一、 提出分组与分配问题,澄清模糊概念n 个不同元素按照某些条件分配给k 个不同得对象,称为分配问题,分定向分配和不定向分配两种问题;将n 个不同元素按照某些条件分成k 组,称为分组问题.分组问题有不平均分组、平均分组、和部分平均分组三种情况。
分组问题和分配问题是有区别的,前者组与组之间只要元素个数相同是不区分的;而后者即使2组元素个数相同,但因对象不同,仍然是可区分的.对于后者必须先分组后排列。
二、基本的分组问题例1 六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?(1)每组两本.(2)一组一本,一组二本,一组三本. (3)一组四本,另外两组各一本.分析:(1)分组与顺序无关,是组合问题。
分组数是624222C C C =90(种) ,这90种分组实际上重复了6次。
我们不妨把六本不同的书写上1、2、3、4、5、6六个号码,考察以下两种分法:(1,2)(3,4)(5,6)与(3,4)(1,2)(5,6),由于书是均匀分组的,三组的本数一样,又与顺序无关,所以这两种分法是同一种分法。
以上的分组方法实际上加入了组的顺序,因此还应取消分组的顺序,即除以组数的全排列数33A,所以分法是22264233C C C A =15(种)。
(2)先分组,方法是615233C C C ,那么还要不要除以33A ?我们发现,由于每组的书的本数是不一样的,因此不会出现相同的分法,即共有615233C C C =60(种) 分法。
(3)分组方法是642111C C C =30(种) ,那么其中有没有重复的分法呢?我们发现,其中两组的书的本数都是一本,因此这两组有了顺序,而与四本书的那一组,由于书的本数不一样,不可能重复。
所以实际分法是41162122C C C A =15(种)。
排列组合中的分组分配问题完整

五非均分组分配对象确定问题
例6 六本不同的书按1∶2∶3分给甲、乙、丙三个人 有多少种不同的分法?
C61C52C33
非均分组有分配对象要把组数当作元素个数 再作排列。
五非均分组分配对象不固定问题
例7 六本不同的书分给3人,1人1本,1人2本,1人3本 有多少种分法
C
2 10
C
2 8
C
2 6
C
4 4
A
3 3
C
2 10
C
2 8
C
2 6
C
4 4
3 有六本不同的书分给甲、乙、丙三名同学,按下条 件,各有多少种不同的分法?
(1)每人各得两本; (2)甲得一本,乙得两本,丙得三本; (3)一人一本,一人两本,一人三本; (4)甲得四本,乙得一本,丙得一本; (5)一人四本,另两人各一本·
排列组合中的分组分配问题
ab
cd
ac
bd
ad
bc
bc
ad
bd
ac
cd
ab
一、 提出分组与分配问题,澄清模糊概念 n 个不同元素按照某些条件分配给 k 个不同得对象,称为
分配问题,分定向分配和不定向分配两种问题;将 n 个不同 元素按照某些条件分成 k 组,称为分组问题.分组问题有不平 均分组、平均分组、和部分平均分组三种情况。分组问题和 分配问题是有区别的,前者组与组之间只要元素个数相同是 不区分的;而后者即使 2 组元素个数相同,但因对象不同, 仍然是可区分的.对于后者必须先分组后排列。
C61C52C33 A33
练习1
1:12本不同的书平均分成四组有多少 种不同分法?
排列组合中的分组分配问题完整版

2 2
.
三:部分均分有分配 对象的问题
例3、 12支笔按3:3:2:2:2分给A、B、C、D、E 五个人有多少种不同的分法?
方法:先分再排法 。分成的组数看成元素的个数 · 把均分的五组看成是五个元素在五个位置上作排列
答(答:)
C132C
3 9
A
3 3
C62 A
C42
2 2
C22
A
5 5
三:部分均分无分配对象的问题
.
X
说明: 提出分组与分配问题,澄清模糊概念: n 个不同元素按照某些条件分配给 k 个不同的对象,称为
分配问题 ,分定向分配和不定向分配两种问题;将 n 个不同 元素按照某些条件分成 k 组,称为 分组问题.分组问题有不平 均分组、平均分组、和部分平均分组三种情况。 分组问题和 分配问题是有区别的 ,前者组与组之间只要元素个数相同是 不区分的;而后者即使 2 组元素个数相同,但因对象不同, 仍然是可区分的 .对于后者必须先分组后排列。
三个人有多少种不同的分法?答:C
61C 52C
3 3
注:非均分组有分配对象要把组数当作元素个数 ,
此与非均分 配结果一样。 五、非均分组分配对象不固定问题
例7 、六本不同的书分给 三人,1人1本,1人2本,1人3本
有多少种分法?
答:C61C
52C
3 3
.A33
思考: 有6本不同的书,按下条件,各有多少种不同
C160 ?C62 ?C42 ?C22 ?18900
种分法 ?
.
【讨论】:隔(插)板法
1、 某 运 输 公 司 有 7 个 车 队 , 每 队 的 车 都 多 于 四 辆 , 且 型 号 相 同 。 要 从 这 7个 车 队 中 抽 出10辆 车 组 成 一 运输队,每队至少抽一辆,问不同的抽法有多少种。
排列组合中的分组分配问题的有效解法

排列组合中的分组分配问题的有效解法
排列组合中的分组分配问题是一类常见的组合优化问题,其目标是将一组对象分配到不同的组中,并满足一定的条件或限制。
在实际应用中,这类问题常常涉及到资源分配、任务调度、人员安排等方面。
1. 贪心算法:贪心算法是一种简单而常用的解法,它根据问题的特点每次选择当前最优的解决方案,并逐步构建最终的解。
在分组分配问题中,贪心算法可以从初始状态开始,每次选择满足一定条件的对象,并将其分配到符合要求的组中,直到所有对象都被分配完毕或达到某种终止条件。
2. 动态规划:动态规划是一种使用备忘录或状态转移方程的方法,通过将原问题分解为若干个子问题,并记录子问题的解,最终通过子问题的解构造出原问题的解。
在分组分配问题中,可以使用动态规划求解最优解。
具体方法是定义一个状态转移方程来描述每个子问题的最优解,然后采用自底向上的方式逐步计算出最终解。
3. 回溯算法:回溯算法是一种逐步试探的算法,通过不断尝试所有可能的解,并及时剪枝来找到最优解。
在分组分配问题中,回溯算法可以通过递归的方式遍历所有可能的分组分配方案,并通过剪枝操作来减少搜索空间。
具体方法是定义一个递归函数,在每一步选择一个对象并加入到某个组中,直到所有对象被分配完成或达到某个终止条件。
4. 蚁群算法:蚁群算法是一种模拟蚂蚁觅食行为的启发式算法,通过模拟蚂蚁找到食物的行为,来寻找问题的最优解。
在分组分配问题中,蚁群算法可以通过定义蚂蚁的移动规则、信息素的更新规则等,来模拟蚂蚁在不同组中选择对象的过程,并通过信息素的增强来引导蚂蚁选择更优的解。
排列组合分组分配问题公式

排列组合分组分配问题公式排列组合分组分配问题,这可是数学里挺有意思的一块呢!咱先来说说排列。
比如说,从 5 个不同的水果里选 3 个排成一排,有多少种排法?这就是排列问题。
排列的公式是 A(n, m) = n! / (n - m)! 这里的“!”表示阶乘,比如 5! = 5 × 4 × 3 × 2 × 1 。
再讲讲组合。
还是从 5 个水果里选 3 个,不考虑顺序,这就是组合问题。
组合的公式是 C(n, m) = n! / [m!(n - m)!] 。
那分组分配问题又是什么呢?给您举个例子,有 6 本不同的书,分成 3 组,每组 2 本,这就是分组问题。
如果再把这 3 组书分别分给 3 个人,这就是分配问题啦。
我记得有一次,学校组织活动,要从班里选几个同学去参加不同的项目。
这可就用到了排列组合分组分配的知识。
当时老师说要从 20 个同学里选 5 个参加绘画比赛,选 8 个参加歌唱比赛,剩下的 7 个参加朗诵比赛。
这可把我难住了,我就在心里默默算着。
先算选 5 个参加绘画比赛,用组合公式 C(20, 5) 得出结果,再算选 8 个参加歌唱比赛的组合数 C(15, 8) ,最后选 7 个参加朗诵比赛的组合数 C(7, 7) 。
然后把这三个结果乘起来,就是总的分组方案数啦。
分组问题里还有平均分组的情况,要注意除以重复的组数的阶乘。
比如说把 8 个人平均分成 4 组,那就要先算出总的分组数 C(8, 2)×C(6,2)×C(4, 2)×C(2, 2) ,然后再除以 A(4, 4) ,这样才能得到不重复的分组方案数。
分配问题也有不同的情况,比如相同元素的分配,可以用隔板法。
比如说把 10 个相同的苹果分给 3 个小朋友,每人至少一个,那就在 9 个空隙里插 2 个隔板,方案数就是 C(9, 2) 。
总之,排列组合分组分配问题,看起来挺复杂,但是只要咱把公式弄明白,多做几道题,其实也不难。
排列组合中的分组分配问题

排列组合中的分组分配问题This model paper was revised by the Standardization Office on December 10, 2020排列组合中的分组分配问题分组分配问题是排列组合教学中的一个重点和难点。
某些排列组合问题看似非分配问题,实际上可运用分配问题的方法来解决。
一、 提出分组与分配问题,澄清模糊概念n 个不同元素按照某些条件分配给k 个不同得对象,称为分配问题,分定向分配和不定向分配两种问题;将n 个不同元素按照某些条件分成k 组,称为分组问题.分组问题有不平均分组、平均分组、和部分平均分组三种情况。
分组问题和分配问题是有区别的,前者组与组之间只要元素个数相同是不区分的;而后者即使2组元素个数相同,但因对象不同,仍然是可区分的.对于后者必须先分组后排列。
二、基本的分组问题例1 六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法(1)每组两本.(2)一组一本,一组二本,一组三本.(3)一组四本,另外两组各一本.分析:(1)分组与顺序无关,是组合问题。
分组数是624222C C C =90(种) ,这90种分组实际上重复了6次。
我们不妨把六本不同的书写上1、2、3、4、5、6六个号码,考察以下两种分法:(1,2)(3,4)(5,6)与(3,4)(1,2)(5,6),由于书是均匀分组的,三组的本数一样,又与顺序无关,所以这两种分法是同一种分法。
以上的分组方法实际上加入了组的顺序,因此还应取消分组的顺序,即除以组数的全排列数33A ,所以分法是22264233C C C A =15(种)。
(2)先分组,方法是615233C C C ,那么还要不要除以33A 我们发现,由于每组的书的本数是不一样的,因此不会出现相同的分法,即共有615233C C C =60(种) 分法。
(3)分组方法是642111C C C =30(种) ,那么其中有没有重复的分法呢我们发现,其中两组的书的本数都是一本,因此这两组有了顺序,而与四本书的那一组,由于书的本数不一样,不可能重复。
组合中的分组分配问题(应用)
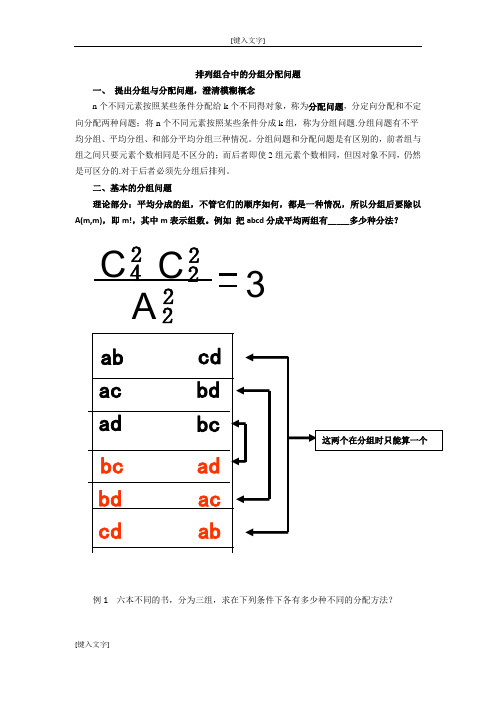
排列组合中的分组分配问题一、 提出分组与分配问题,澄清模糊概念n 个不同元素按照某些条件分配给k 个不同得对象,称为分配问题,分定向分配和不定向分配两种问题;将n 个不同元素按照某些条件分成k 组,称为分组问题.分组问题有不平均分组、平均分组、和部分平均分组三种情况。
分组问题和分配问题是有区别的,前者组与组之间只要元素个数相同是不区分的;而后者即使2组元素个数相同,但因对象不同,仍然是可区分的.对于后者必须先分组后排列。
二、基本的分组问题理论部分:平均分成的组,不管它们的顺序如何,都是一种情况,所以分组后要除以A(m,m),即m!,其中m 表示组数。
例如 把abcd 分成平均两组有_____多少种分法?例1 六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?C 4 2 C 22 A 2 2 3ab cd ac bd ad bccdbd bc ad ac ab这两个在分组时只能算一个①每组两本.22264233C C CA②一组一本,一组二本,一组三本.615233CCC③一组四本,另外两组各一本.41162122C C CA=15(种)定向分配④乙两本、丙两本.222642C C C=90(种⑤甲一本、乙两本、丙三本.615233CCC=60(种)⑥甲四本、乙一本、丙一本.411621C C C=30(种不定项分配⑦每人两本.22264233C C CA33A=90(种)⑧一人一本、一人两本、一人三本. 615233CCC33A=360⑨一人四本、一人一本、一人一本.41162122C C CA33A=90⑩6本不同的书,分给甲、乙、丙三人,每人至少一本。
540本不定向分配题的一般原则:先分组后排列11结论1:一般地,n个不同的元素分成p组,各组内元素数目分别为m1,m2,…,mp ,其中k组内元素数目相等,那么分组方法数是321112ppmmmmn n m n m m mkkC C C CA---⋯。
6、排列组合问题之分组分配问题

排列组合问题之分组分配问题(一)(五个方面)一、非平均分组 (分步组合法)“非平均分组”是指将全部元素分成元素个数互相不相等的组。
例 1、 7 人参加义务劳动,按以下方法分组有多少种不相同的分法?①分成 3组,分别为 1人、 2 人、 4 人;②选出 5个人分成 2 组,一组 2 人,另一组 3人。
解:①先选出 1人,有 C 17 种,再由剩下的 6 人选出 2 人,有 C 62 种,最后由剩下的 4 人为一组,有 C 44 种。
由分步计数原理得分组方法共有C 71C 62 C 44 105 (种)。
②可 选分同步 。
先从 7 人中选出 2 人,有 C 72 种,再由剩下的 5 人中选出 3 人,有 C 53种,分组方法共有 C 72C 53210 (种)。
也可 先选后分 。
先选出 5 人,再分为两组,由分步 计数原理得分组方法共有C 75C 52 C 33 210 (种)。
二、平均分组 (去除重复法)“平均分组”是指将全部元素分成全部组元素个数相等或部分组元素个数相等的组。
㈠全部平均分组 (去除重复法)23例 2、 7人参加义务劳动,选出6人,有多少种不相同的分法?个人,分成 组,每组都是 解: 可选分同步 。
先选 3 人为一组,有 C 73 种;再选 3 人为另一组,有 C 43 种。
又有 2 组都 是 3人,每 A 22 种分法只能算一种,因此不相同的分法共有 C 73C 43 70 (种)。
A 22也可 先选后分 。
不相同的分法共有 C 76 C 63C 3370 (种)。
A 22㈡部分平均分组 (去除重复法)例 3、 10个不相同零件分成 4 堆,每堆分别有 2 、 2 、 2 、 4 个,有多少种不相同的分法?解:分成 2 、 2 、 2 、 4 个元素的 4 堆,分别有 C 102 、 C 82 、 C 62 、 C 44 种,又有 3 堆都是 2个元素,每 A 33 种分法只能算一种,因此不相同的分组方法共有C 102C 82 C 62 C 44 3150 (种)。
排列组合中的分组分配问题
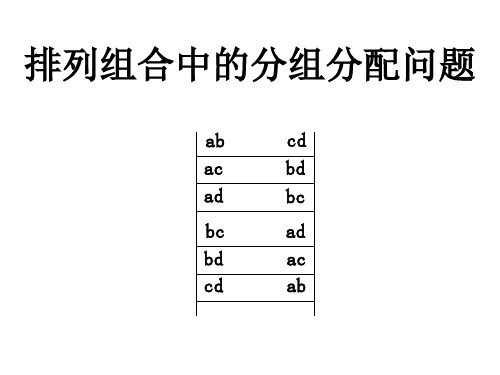
(1)
(2)按2∶2∶2∶4分给
甲、乙、丙、丁四个
人有多少种不同的分 (2)
法?
C120
C
2 8
C
2 6
4 4
A
3 3
C120
C
2 8
C
2 6
C
4 4
3 有六本不同的书分给甲、乙、丙三名同学,按下条 件,各有多少种不同的分法?
(1)每人各得两本; (2)甲得一本,乙得两本,丙得三本; (3)一人一本,一人两本,一人三本; (4)甲得四本,乙得一本,丙得一本; (5)一人四本,另两人各一本·
变式练习
按下列条件,从12人中选出5人,有多少种不同选法?
(((((12345)))))甲甲甲甲甲、必、、 、乙 须 乙乙 乙、 当 、、 、丙 选 丙丙 丙三 , 三三 三人乙人人人不、至必只能丙多须有当不当一2人选能选人当;当;当选选选C;;;33CCC921131CC94943C613032C76985 126
分析: (1)分组与顺序无关,是组合问题。分组数是C62C42C22=90(种)
这90种分组实际上重复了6次。 考察以下两种分法:(1,2)(3,4)(5,6)与(3,4)(1,2)(5,6),由于 书是均匀分组的,三组的本数一样,又与顺序无关,所以这两种分法是同 一种分法。以上的分组方法实际上加入了组的顺序,因此还应取消分组的 顺序,即除以组数的全排列数A33=6,所以分法是 90/6=15(种)。 (2)先分组,方法是C61C52C33=60,那么还要不要除以A33?我们发 现,由于每组的书的本数是不一样的,因此不会出现相同的分法,即共有 60(种) 分法。 (3)分组方法是C64*C21*C11=30(种)
1 把abcd分成平均两组 有_____多少种分法?
排列组合中的分组分配问题的有效解法

排列组合中的分组分配问题的有效解法排列组合是概率与统计中的基础知识点,其中包括排列、组合等概念。
在实际生活中,我们经常会遇到需要对一个集合内的元素进行分组和分配的问题,这些问题又被称为分组分配问题。
例如,在一个班级中,我们需要将学生分成若干组,或者在一个公司中,我们需要将员工分配到不同的部门,这些都属于分组分配问题,而排列组合则提供了有效的解决方法。
一、排列组合的基本概念1. 排列排列用于描述一组元素的各种排列方式。
例如,由 A、B、C 三个元素组成的集合,其所有排列包括 ABC、ACB、BAC、BCA、CAB、CBA 共 6 种。
排列的数量为 n!,其中 n 为集合中元素的个数。
排列与顺序有关,即不同顺序的排列被视为不同的结果。
2. 组合二、分组分配问题的解决方法1. 确定组数解决分组分配问题的第一步是确定分成几组,或者分配到几个部门。
这个数目通常由具体问题所确定,如班级分组时可能要求分成 2、3 或 4 组等。
2. 确定元素第二步是确定需要分组或分配的元素,即确定学生、员工、球队等。
这个数目也由具体问题所确定。
接下来,我们需要确定分成的每一组的元素个数,或者每个部门中的员工个数。
这个分组方式的确定关系到具体问题的解决。
4. 应用排列组合最后,我们可以应用排列组合的知识来解决分组分配问题。
例如,在班级分组时,如果确定分成 2 组,每组各 10 人,则分组的总方法数为 45。
这个计算过程可以用排列组合的方法来解决:先从 20 个学生中选出 10 个,共 C(20, 10) 种方法,然后将这 10 个学生划分到两个组中,使用排列的方法可以得到 2(10!) 种方案。
因此,班级分组的总方案数为2(10!)C(20, 10) = 45。
在公司分配员工到部门时,如果要求每个部门中的员工数量相同,且每个部门至少要有一个员工,则可以使用组合数目和整数划分的知识来解决问题。
具体方法如下:设共有 n 个员工,要分成 k 个部门,每个部门包含 m 个员工。
排列组合分组分配问题

(1)平均分组,没有分配对象
例6: 6本不同的书平均分成3组,有多少种分 法? 15种
(2)非平均分组,没有分配对象
例7: 6本不同的书分成3组,一组3本,一组2 本,一组1本,有多少种分法? 60种 例8: 6本不同的书,分成3组,一组4本,其余两 组各1本,有多少种分法? 15种
1.有分配对象的分组:元素分组后,又分配给具体对 象,而分组是确定
例1: 6本不同的书分给3人,甲得1本,乙得2 本,丙得3本,有多少种不同的分法?
60种
(2)各组元素数目确定,分配对象 不确定
例2: 6本不同的书分给3人,1人1本,1人2 本,1人3本,有多少种分法?
360种
(3)平均分配给具体对象
例3: 6本不同的书平均分给3人,有多少种分 法?
90种
(4)部分均分给若干对象
例4: 6本不同的书分给3人,1人4本,其余2人 各1本,有多少种分法? 90种 例5: 6本不同的书全部分给4名学生,每人至 多2本,至少1本,有多少种分法? 1080种
2.无分配对象的分组:元素分组以后,没有分配对象 或所分配给的对象不具体不确定,可以不加以区别.
排列组合中的分配分组问题

排列组合中的分配分组问题排列、组合以其独特的研究对象和研究方法,在高中数学教学中占有特殊的地位,是高考必考内容之一,它既是学习概率的预备知识,又是进一步学习数理统计、组合数学等高等数学的基础,因此排列与组合问题的应用题是高考的常见题型。
本文就笔者自己解决排列组合问题中的分配分组问题的一些浅见拙知与大家分享,不值一飧,还望批评与指正。
一、基本定义:1、排列:从n 个不同的元素中取出)(n m m ≤个元素,按照一定的顺序排成一列,叫做从n 个不同的元素中取出m 个元素的一个排列。
2、组合:从n 个不同的元素中取出)(n m m ≤个元素合成一组,叫做从n 个不同的元素中取出m 个元素的一个组合。
3、排列数与组合数公式:)1)......(1(A +--=m n n n mn!)1().........1(m m n n n C A C m n m n m n+--== 二、解题思路总析:从排列与组合的定义来看,这两个数学名词的相同之处在于“选”—从n 个不同的元素中取出)(n m m ≤个元素;不同之处在于:排列有“序”——取出的m 各元素之间有顺序,组合无“序”——取出的m 各元素之间无顺序。
所以根据题目的意思分析元素之间是否有序就成了解决问题是用排列数公式还是用组合数公式的关键。
另外,在分配分组问题中,还存在分成的各组元素个数相等或不相等的问题,各组元素个数相等的分配分组称为“均匀”,各组元素个数全不相等的分配分组称为“不均匀”。
综合以上两点,笔者把排列组合中的分配分组问题统分为四类:1、均匀有序:各组元素个数相等,各组之间有顺序;2、均匀无序:各组元素个数相等,各组之间没有顺序;3、不均匀无序:各组元素个数全不相等,各组之间没有顺序;4、不均匀有序:各组元素个数全不相等,各组之间有顺序。
其中均匀有序又称“双肯定”分法,不均匀无序又称“双否定”,均匀无序和不均匀有序称为“单肯定”下面就以具体例题来说明上面四类问题的一般解法:例1:有6本不同的书,(1)甲、乙、丙3人每人2本,有多少种不同的分法?(2)分成3堆,每堆2本,有多少种不同的分法?(3)分成3堆,一堆1本,一堆2本,一堆3本,有多少种不同的分法?(4)分给甲、乙、丙3人,一人1本,一人2本,一人3本,有多少种不同的分法?解析:对于问题(1),首先从6本不同的书中选出2本来给甲,选出的2本书之间无顺序,为26C ;其次,从剩下的4本书中选出2本来给乙,为24C ;最后剩下的2本给丙,为22C ;整个解题过程应用的是分步计数原理,所以最终的分法数为90C *C *C N 2224261==;对于问题(2),与问题(1)的相同在于都是均匀分组,差别仅仅在于,一个是分给3人,一个是分成3堆,即就是分成的3组之间一个是有顺序的,一个是没有顺序的,所以问题(2)的解决可以在问题(1)解决的基础上对3组进行“消序”,即15A C *C *C N 332224262==; 对于问题(3),解决方法与问题(1)一样,用分步计数原理,先从6本不同的书中选出1本来,再从剩下的5本书中选出2本来,最后剩下的3本作为一堆,最终的分法数为60C *C *C N 3325163==;对于问题(4),分析题目,可见问题(4)与问题(3)的相同在于都是不均匀分组,差别在于问题(3)是分成3堆,即分成的3组无序,问题(4)是分给3人,即分成的3组有序,所以问题(4)的解决可以在问题(3)解决的基础上对3组进行“排序”,即603A *C *C *C N 333325164==。
高中数学专题排列组合中的分组分配问题

高中数学专题排列组合中的分组分配问题Ⅰ.概述分组分配问题是排列、组合问题的综合,是排列组合问题中的一个重点和难点;某些排列组合问题看似非分配问题,实际上也可运用分配问题的方法来解决。
解决分组分配问题的一个基本指导思想就是先分组后分配。
分组分配问题特征:(1)分组分配特征:问题涉及把相关的元素进行分组然后再分配;(2)分组的类型:整体均分、部分均分和不等分三种;无论分成几组,都应注意只要有元素的个数相等的组存在,就需要考虑均分的现象(即:整体平均分组;或部分平均分组);(3)均分特征:只要出现所分组中的元素个数相等,则存在重复出现的情况,作为分组只能计为一种。
Ⅱ.排列组合中的分组与分配问题一.分组与分配有关概念1.将n个不同元素按照某些条件分成k组,称为分组问题;分组问题有不平均分组、整体平均分组和部分平均分组三种情况。
2.将n个不同元素按照某些条件分配给k个不同的对象(位置),称为分配问题;分配分定向分配和不定向分配两种问题;3.分组问题和分配问题的区别:前者组与组之间只要元素个数相同是不区分的;而后者即使2组元素个数相同,但因对象不同,仍然是有区分的,对于分配问题必须先分组后分配,而分组通常与组合相关,分配通常与排列相关。
二.基本的分组问题(一)分组问题的基础题例【题例1】六本不同的书,分为三组,求在下列条件下各有多少种不同的分组方法?(1)每组两本.(2)一组一本,一组二本,一组三本.(3)一组四本,另外两组各一本.【分析】:(1)分组与顺序无关,是组合问题。
注意,这里6个元素,分3组,每组2个元素,所求的分组种类:不是“从6个元素中取2个元素的组合数”,而是“6选2,选3次,分成3组,所得的组数”;在这样的分组中,由于要选3次,且平均选取,就存在选取的顺序,故所得组中出现重复的组,重复的种数即所分组的全排列数。
若一组分组为:(1,2)(3,4)(5,6),另一组分组为(3,4)(1,2)(5,6),则这样的两组只能算一组,不能算作两组;若一组分组为:(1,2)(3,4)(5,6),另一组分组为(1,3)(2,4)(5,6),则这样的两组应算作两个不同的分组;在(1,2)(3,4)(5,6)与(1,3)(2,4)(5,6)这两个分组中出现的“从6个元素中选取2个元素的组合”则有5个,且其中的组合(5,6)只能算作1个计数;三.基本的分配问题(一)定向分配问题:将所给元素按要求分配到指定对象【题例2】六本不同的书,分给甲、乙、丙三人,求在下列条件下各有多少种不同的分配方法?(1)甲两本、乙两本、丙两本.(2)甲一本、乙两本、丙三本.(3)甲四本、乙一本、丙一本.(二)不定向分配问题:将所给元素按要求分配到非指定对象【题例3】六本不同的书,分给甲、乙、丙三人,求在下列条件下各有多少种不同的分配方法?(1)每人两本.(2)一人一本、一人两本、一人三本.(3)一人四本、一人一本、一人一本.Ⅲ.分组-分配问题类型与方法探究一.分组问题的基本类型--思想方法(一)分组问题类型1--非均匀分组(分步-组合法):“非均匀分组”是指将所给元素分成元素个数彼此不相等的若干组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 练习:9件不同的玩具,按下列分配方案各有几
•
• • • • 种分法? ①甲得2件,乙得3件,丙得4件,有多少种分法 ? ②一人得2件,一人得3件,一人得4件,有多少 种分法? ③每人3件,有多少种分法? ④平均分成三堆,有多少种分法? ⑤分为2、2、2、3四堆,有多少种分法?
• 练习: 9件不同的玩具,按下列分配方案各有几种
9
C C C C C C C C C C C 2174
3 3 3 9 2 1 3 3 5 8 1 2 3 3 5 7 0 3 3 3 5 6
排列组合中的分组分配问题
ab ac ad bc bd cd
cd bd bc
ad ac ab
引旧育新
1 把abcd分成平均两组 有_____多少种分法? 2 C4 ab ac ad bc bd cd cd bd bc ad ac ab 2 C2 2 A2
3
这两个在分组时只能算一个
记住:
平均分成的组,不管 它们的顺序如何,都 是一种情况,所以分 组后要除以m!,其中m
2 每组中选正、副组长都有 A5 种方法.
5 5 C10 C5 2 2 A A 种. 5 5 50400 2 A2
由分步计数原理共有
二:均分有分配对象的问题
例2:6本不同的书按2∶2∶2平均分给甲、乙、 丙三个人,有多少种不同的分法? 方法:先分再排法。分成的组数看成元 素的个数· (1)均分的三组看成是三个元素在三 个位置上作排列
例7 六本不同的书分给甲、乙、丙3人,1人1本,1人2 本,1人3本有多少种分法?
C61C52C33A33
练习1
1:12本不同的书平均分成四组有多少 种不同分法?
C CCC 4 A4
3 12
3 9
3 6
3 3
练习2
2:10本不同的书
(1)按2∶2∶2∶4分成 四堆有多少种不同的 分法? (2)按2∶2∶2∶4分给 甲、乙、丙、丁四个 人有多少种不同的分 法?
mk mk
种.
如果 m1 , m2 mk 中有且仅有i个相等,则不同的分法为:
C C
m1 n
m2 n m1
C
m3 n ( m1 m2 ) i i
C
A
种.
基础探究
一:均分无分配对象的问题
例1:12本不同的书 (1)按4∶4∶4平均分成三堆有多少种不同的分法? (2)按2∶2∶2∶6分成四堆有多少种不同的分法? 4 4 4 C C C 8 4 12 (1) 3 A3 2 6 2 2 C 12C 10 C 8 C 6 (2) 3 A3
• 练习: 9件不同的玩具,按下列分配方案各有几种
分法? • ②一人得2件,一人得3件,一人得4件,有多少种分 法? • ③每人3件,有多少种分法? 解:②三个人中哪个得2件、哪个得3件、哪个得4件没 有确定,故这三个数字可以在甲、乙、丙中进行排列, 3 故应在第1问的前提下再进行一步排列,有 A3 种.
5 A5
四.非均分组无分配对象问题
例5 6本不同的书按1∶2∶3分成三堆有多少种 不同的分法?
C61C52C33
注意:非均分问题无分配对象只要按比例分完再用 乘法原理作积
五.非均分组分配对象确定问题
例6 六本不同的书按1∶2∶3分给甲、乙、丙三个人 有多少种不同的分法?
C61C52C33
五非均分组分配对象不固定问题
12! 8! 4!· 8! 4!· 4! 或
1 3!
5775
2 2 2 6 C 12C 6 C 4 C 2 3 A3
• 练习:把10人平均分成两组,再从每组中选出正、 副组长各一人,共有多少种选法? 解:分两步,先分组,再分别在每一组中选正、副 组长. 5 5 C10 C5 分组有 种方法, 2 A2
3 9 6
3 ⑤先分3件为一堆有 C9 种方法,然后6件平均分配应有
3 2 2 2 C C C C C C C 9 6 4 2 1260 种. 种方法,故共有 3 A3 A
2 6
2 4 3 3
2 2
三.多面手问题
例4 :有12名划船运动员,其中3人只会划左舷,4人只会划右 舷,其余5人既会划左舷也会划右舷。现在要从这12名运动员 中选出6人平均分在左、右舷划船参加比赛,有多少种不同的 选法? 分析:设集合A={只会划左舷的3个人},B={只会划右舷的4个 人},C={既会划左舷又会划右舷的5个人} 先分类,以集合A为基准,划左舷的3个人中,有以下几类情 况:①A中有3人;②A中有2人;C中有1人;③A中有1人,C 中有2人;④C中有3人。 第①类,划左舷的人已选定,划右舷的人可以在B,C中选3人, 有 C3 种 ,以下类同
2 C6 (1)
2 2 C4 C2 3 A3 3 A3 2 2 2 C6 C4 C2
三:部分均分无分配对象的问题
例4 六本不同的书分成3组一组4本其余各1本有多少种分法
C64C21C11 A22
三:部分均分有分配对象的问题
例3 12支笔按3:3:2:2:2分给A、B、C、D、 E五个人有多少种不同的分法? 方法:先分再排法。分成的组数看成元素的个数· (2)均分的五组看成是五个元素在五个位置上作 排列 2 3 2 2 3 C C 9 C6 C4 C2 12 (2) 3 2 A3 A2
(1) ( 2)
C CC C 3 A3 C C C C
2 10 2 8 2 6
2 10
2 8
2 6
4 4
பைடு நூலகம்
4 4
3 有六本不同的书分给甲、乙、丙三名同学,按下条 件,各有多少种不同的分法? (1)每人各得两本; (2)甲得一本,乙得两本,丙得三本; (3)一人一本,一人两本,一人三本; (4)甲得四本,乙得一本,丙得一本; (5)一人四本,另两人各一本· 2 2 2 C6C4 C2 1 2 3 (2) C 6 C5 C3 3 1 2 3 (3) C 6 C5 C3 A 3 (1) (4) 4 C6 1 C2 1 C1 1 C2
1 (5) A 3
4 C6
1 C1
4、12本不同的书分给甲、乙、丙三人按下列条件, 各有多少 种不同的分法? (1)一人三本,一人四本,一人五本; (2)甲三本,乙四本,丙五本; (3)甲两本,乙、丙各五本; (4)一人两本,另两人各五本· 3 4 5 3 (1) C 12 C9 C5 A 3 (2) C 3 C 4 C 5 9 5 12 5 5 2 (3) C 12 C 10 C 5 5 5 1 2 (4) A 3 C 12 C 10 C 5
分法? • ①甲得2件,乙得3件,丙得4件,有多少种分法?
解:①以人为主考虑,三个人去取玩具,据分步计数 原理求解. 2 第1步先由甲从9件不同的玩具中选2件有 C9 种.
3 种. 第2步由乙从剩下的7件中选3件有 C7 4 第3步余下4件全给丙有 C4 种.
3 4 由分步计数原理得 C92 C7 C4 1260 种.
表示组数。
1.(平均分组公式)
一般地平均分成n堆(组),必须除以n!,如若部 分平均分成m堆(组),必须再除以m!,即平均分组问 题,一般地来说,km个不同的元素分成k组,每组m个, 则不同的分法有
C C
m km
m ( k 1) m k k
C
m m
A
种.
故平均分配要除以分组数的全排列.
2.(不平均分组公式)
引伸:不平均分配问题:一般来说,把n个不同元素 分成k组,每组分别有 m1 , m2 , m3 m个, k
m1 m2 mk n, 且 m1, m2 m互不相等,且 k
则不同分法为
C
m1 n
C
m2 n m1
C
m3 n ( m1 m2 )
C
mk mk
2 3 4 3 故由分步计数原理有 C9 C7 C4 A3 7560 种.
③每人3件,即各人分得数相同,不需排列.则有 3 3 3 C9 C6 C3 3 A 3 1680 种. 3 A3
• 练习: 9件不同的玩具,按下列分配方案各有几种
分法? • ④平均分成三堆,有多少种分法? • ⑤分为2、2、2、3四堆,有多少种分法? 解:④设分三堆有x 种方法,因堆与堆之间没有差异, 而人却有差异,在第③问中,先分三堆再三人去拿. 故有 x A3 C 3 C 3 1680 x 280 种.
