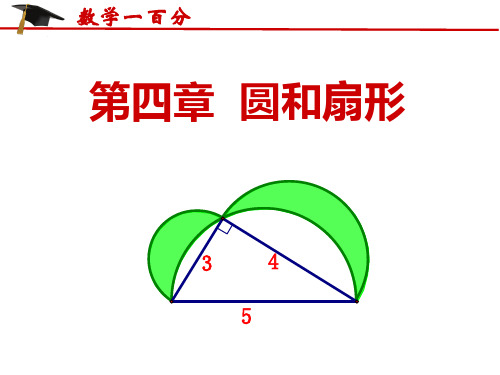
圆的面积和扇形的面积
2六年级数学圆的面积

圆面积一.考点,难点回顾1、圆面积2、圆环面积3、扇形面积二、知识点回顾1、圆的面积:圆所占面积的大小叫做圆的面积。
圆的面积一般用字母S表示。
R-π2r(R为大圆半径,r为小圆半径)2、圆环面积的计算公式:S环=π23、扇形:(1)弧:圆上任意两点间的部分叫做圆弧,简称弧(arc).大于半圆的弧称为优弧,优弧是用三个字母表示。
小于半圆的弧称为劣弧,劣弧用两个字母表示。
半圆既不是优弧,也不是劣弧。
优弧是大于180度的弧,劣弧是小于180度的弧。
(2)圆心角:顶点在圆心上的角叫做圆心角。
(3)扇形:由圆心角的两条半径和圆心角所对应的一段弧围成的图形叫做扇形。
圆心角越大,扇形越大;圆心角越小,扇形越小。
三.典型例题例1、一个周长是62.8米的圆形花坛,它的面积是多少平方米?例2、将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
例3、圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍;大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()倍;圆的半径增加5倍,圆的周长增加(),圆的面积增加()。
例4、一个半圆的周长是20.56分米,这个半圆的面积是多少平方分米?例5、校园圆形花池的半径是 6米,在花池的周围修一条1米宽的水泥路,求水泥路的面积是多少平方米?例6、半径是4厘米,圆心角是270°的扇形面积是多少平方厘米?四.课堂习题一、填空1.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
2.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
3.大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为()平方厘米。
4.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是()平方厘米。
圆面积扇形面积公式

圆面积扇形面积公式圆面积和扇形面积是几何学中常见的概念,它们分别表示圆的面积和由圆心和圆上两点所形成的扇形的面积。
本文将分别介绍圆面积和扇形面积的计算公式及应用。
一、圆面积的计算公式圆是几何学中的基本图形之一,它由一个圆心和一条等距于圆心的曲线组成。
圆的面积是圆内所有点构成的平面区域的大小。
计算圆的面积需要使用圆的半径或直径。
圆的面积计算公式为:S = πr²其中,S表示圆的面积,π是一个常数,约等于3.14159,r表示圆的半径。
例如,已知一个圆的半径为5cm,那么可以通过代入公式计算圆的面积:S = 3.14159 x 5² = 3.14159 x 25 = 78.54平方厘米因此,该圆的面积为78.54平方厘米。
二、扇形面积的计算公式扇形是由圆心、圆上两点和它们之间的弧所组成的图形。
扇形与圆的关系密切,它是圆的一部分。
计算扇形的面积需要使用扇形的半径和对应的圆心角。
扇形的面积计算公式为:S = 0.5r²θ其中,S表示扇形的面积,r表示扇形所在圆的半径,θ表示扇形的圆心角(单位为弧度)。
例如,已知一个扇形的半径为6cm,圆心角为60°,那么可以通过代入公式计算扇形的面积:θ = 60° = 60 x π/180 ≈ 1.047弧度S = 0.5 x 6² x 1.047 = 18 x 1.047 = 18.846平方厘米因此,该扇形的面积为18.846平方厘米。
三、圆面积和扇形面积的应用圆面积和扇形面积在现实生活中有着广泛的应用。
下面以几个例子来说明:1. 建筑设计:在建筑设计中,圆形的庭院、花坛等都需要计算其面积,以便合理规划和安排空间。
2. 农业种植:农业种植中,圆形的农田、水池等都需要计算其面积,以便合理安排种植和灌溉。
3. 工程测量:在工程测量中,扇形面积常用于计算某个区域的覆盖范围或扇形防护罩的面积。
4. 圆桌布草:圆桌布草的制作需要根据桌子的直径计算所需的面积,以便选购合适尺寸的布草。
圆的面积及扇形面积

圆的面积及扇形面积圆的面积:圆所占平面的大小叫圆的面积,圆的面积一般用字母“S”表示, S =πr ². 圆环的面积计算公式:S =πR ²-πr ²=π(R ²-r ²)扇形:由组成圆心角的两条半径以及圆心角所对的弧构成的图形叫扇形扇形面积公式:236036036012n S n n S S r S S lr π=⇒===例1、如图,已知正方形面积是60平方厘米,分别在两个图中求圆的面积。
练一练:已知右图中阴影部分的面积是300平方厘米,求圆的面积。
例2、一个圆形花坛的直径是20米,现在要在花坛的周围铺一条2米宽的石板路,这条石板路的周长是多少米?以及占地面积是多少平方米?2、已知右图中阴影部分的面积是40平方厘米,求圆环的面积。
例3、如右图,一个扇形的圆心角是90°,它的周长是14.28厘米,求它的面积。
练一练:1、右图中平行四边形的面积是100平方厘米,求阴影部分的面积。
2、如图,△ABC是一个等腰直角三角形,AB=BC=10,求图中阴影部分的面积。
(单位:分米)3、如图,∠AOB=90度,∠COB=45度,(1)若OB=20,求以OB为直径的半圆面积及扇形COB的面积(2)已知阴影甲的面积是 4.56平方厘米,那么阴影乙的面积是_______平方厘米。
4、已知,如图,∠AOC=120度,OA=5厘米,AB=3厘米求阴影部分的面积。
5、已知一个大正方形和两个同样大小的小正方形如图所示拼在一起,大正方形的边长为6,小正方形的边长为2.(π=3.14)(1)求扇形BCD的面积(2)求图中阴影部分的面积例4、我们学习了扇形的面积,试回忆扇形面积公式的推导过程,回答下列问题:(1)对于一个半径为r,圆心角为n度的扇形,其面积为______(2)扇形面积公式的推导过程与下列哪个公式的推导使用了基本相同的方法_____A.圆的面积公式B.圆的周长公式C.平行四边形的面积公式D.弧长公式(3)扇形面积的推导过程中,下列哪些知识起着重要的作用_____(可多选)A.圆的面积公式B.圆的周长公式C.弧长公式D.比的意义(4)已知一个扇形的弧长为l,半径为r,试用l和r表示该扇形的面积,并写出简要的推导过程。
(精品)数学讲义六年级秋季班-第16讲:圆和扇形的面积

圆和扇形的面积是六年级数学上学期第四章第二节的内容.本讲主要讲解圆的面积和扇形面积的求解方法,及它们之间的关系;重点是掌握圆的面积和扇形面积的基本计算方法,难点是在不同的图形中根据题目条件灵活解答相关问题.1、圆的面积圆所占平面的大小叫做圆的面积.设圆的半径长为r,面积为S,那么:圆的面积2S r r rππ=⨯=.圆和扇形的面积内容分析知识结构模块一:圆的面积知识精讲例题解析【例1】(1)圆的半径是4厘米,它的面积是______平方厘米;(结果保留π)(2)圆的直径是6米,它的周长是______米,它的面积是______平方米;(π取3.14)(3)圆的周长是25.12分米,它的面积是______平方分米.(π取3.14)【难度】★【答案】(1)50.24;(2)18.84;28.26;(3)50.24.【解析】(1)和(2)直接利用基本公式进行计算,(3)中先根据周长求出,圆的半径为:25.12÷3.14÷2 = 4米,故面积为:3.14×4×4 = 50.24平方米.【总结】考查圆的周长及面积的计算.【例2】有大小两个圆,如果大圆半径是小圆半径的3倍,则大圆的周长是小圆的______倍,大圆的面积是小圆的______倍;如果大圆直径是小圆半径的4倍,则小圆面积是与大圆面积的比是______.【难度】★【答案】3;9;1:16.【解析】圆的周长与半径成正比,圆的面积与半径的平方成正比.【总结】考查圆的面积与圆的周长与圆的半径的关系.【例3】有一只羊栓在草地的木柱上,绳子的长度是4米,这只羊最多可以吃到______平方米的草.(π取3.14)【难度】★【答案】50.24.【解析】S = 4×4×3.14 = 50.24平方米.【总结】考查圆的面积在实际问题中的运用.2/ 16【例4】在一个边长为20厘米的正方形纸板里剪出一个最大的圆,则圆的面积是______平方厘米.(π取3.14)【难度】★【答案】314.【解析】剪出的最大圆的直径即为正方形的边长,所以圆的半径为10厘米,所以圆的面积是:10×10×3.14 = 314平方厘米.【总结】本题主要考查正方形中剪出最大圆的问题.【例5】用一根长为16分米的铁丝围成一个圆,接头处长为0.3分米,这个圆的面积是多少?(π取3.14)【难度】★★【答案】19.625平方分米.【解析】由题意,可得圆的半径为:(16-0.3)÷3.14÷2 = 2.5分米,故这个圆的面积为:2.5×2.5×3.14 = 19.625平方分米.【总结】考查圆的面积的计算,注意本题中铁丝的总长度剪出接头处的长度即为圆的周长.【例6】一种铝制面盆是用直径20厘米的圆形铝板冲压而成的,要做100个这样的面盆至少需要铝板______平方米.(π取3.14)【难度】★★【答案】3.14.【解析】圆的半径为:20÷2 = 10厘米,要做100个这样的面盆至少需要铝板:100×3.14×10×10=31400平方厘米= 3.14平方米.【总结】考查圆的面积的计算的简单应用,注意单位的换算.【例7】周长相等的长方形、正方形和圆,______的面积最大.【难度】★★【答案】圆【解析】在所有周长相等的图形中,圆的面积最大.【总结】通过周长求面积,考查学生的转换能力.4 / 16【例8】 两个同心圆,大圆半径为5厘米,小圆半径为3厘米,求圆环的面积.(π取3.14)【难度】★★【答案】50.24平方厘米.【解析】圆环的面积为:3.14×(25-9)= 50.24平方厘米. 【总结】考查圆环的面积的计算.【例9】 一个圆形喷水池的周长是62.8米,绕着这个水池修一条宽2米的水泥路,求路面的面积.(π取3.14)【难度】★★【答案】138.16平方米.【解析】圆心水池的半径为:62.8÷3.14÷2=10米,则路面的面积为: 3.14×(144-100)= 138.16平方米. 【总结】考查圆环的面积在实际问题中的应用.【例10】 如图,已知大圆半径是6厘米,那么阴影部分面积占大圆面积的______.(用分数表示)【难度】★★ 【答案】41. 【解析】阴影部分的面积即为小圆的面积,故阴影部分面积占大圆面积的91364ππ【总结】考查圆的面积的计算.【例11】 两个圆的面积之和为1991平方厘米,小圆的周长是大圆周长的90%,则大圆的面积是_______平方厘米.(π取3.14)【难度】★★ 【答案】1100.【解析】设大圆的半径为10r ,小圆半径为9r ,所以大圆面积占两圆面积的100181,所以 大圆面积为:1991÷181×100=1100平方厘米. 【总结】考查圆的面积的计算【例12】 有5块圆形的花圃它们的直径分别是3米、4米、5米、8米、9米,请将这5块花圃分成两组,分别交给两个班级管理,使这两个班级管理的面积尽可能接近.【难度】★★【答案】直径4米和9米的两个花圃交给一个班管理,直径3米、5米和8米的三个花圃交 给另一个班管理.【解析】由于面积与半径的平方成正比,故几个花圃面积之比是9:16:25:64:81, 因为16+81=97;9+25+64=98, 所以符合要求,所以把直径4米和9米的两个花圃交给一个班管理,其余交给另一个班管理. 【总结】本题一方面考查圆的面积与半径的关系,另一方面考查圆面积计算的简单应用.【例13】 大小两圆的相交部分(如图所示的阴影部分)面积是大圆面积的415,是小圆面积的35,量得小圆的半径是5厘米,问大圆的半径是多少?(π取3.14)【难度】★★★ 【答案】7.5厘米.【解析】由题意,可得:415S S =阴影大圆,35S S =阴影小圆, 则43155S S =小圆大圆,设大圆半径为R ,则22435155R ππ⨯⨯=⨯⨯,解得:7.5R =. 即大圆的半径为7.5厘米.【总结】本题综合性较强,要根据阴影部分的面积表示出大圆面积和小圆面积的关系,从而 求出大圆的半径.【例14】 如图,正方形的面积是12平方厘米,求图中阴影部分的面积为多少平方厘米?(π取3.14)【难度】★★★ 【答案】2.58平方厘米.【解析】设正方形的边长为a ,则212a =,则圆的面积为: 223.14 3.14 3.1439.4224a a ⎛⎫⨯=⨯=⨯= ⎪⎝⎭,故阴影部分面积为:12-9.42 = 2.58平方厘米. 【总结】本题主要考查圆面积计算的简单应用.6 / 16ABO【例15】 如图中的圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,图中阴影部分的周长是多少厘米?(π取3.14)【难度】★★★ 【答案】20.5厘米.【解析】由图可知,这个长方形的宽等于圆的半径,长方形的面积等于圆的面积, 所以长方形的长等于圆的周长的一半,故阴影部分的周长=长方形的长×2+长方形的宽-圆的半径+41×圆的周长 =16.4+16.4÷4=20.5厘米.【总结】考查不规则图形的周长的计算,注意计算周长是要包含组成图形的所有的线段和弧 长.===1、 扇形的概念由组成圆心角的两条半径和圆心角所对的弧围成的图形,叫做扇形. 如图,空白部分记作扇形AOB . 2、 扇形的面积设组成扇形的半径为r ,圆心角为n °,弧长为l ,那么:213602n S r lr π==扇形.【例16】 一个扇形的面积是它所在圆面积的15,这个扇形的圆心角是______.【难度】★ 【答案】72°.【解析】360°÷5 = 72°.【总结】考查扇形的面积与所在的圆的面积的关系.模块二:扇形的面积知识精讲例题解析【例17】 一个扇形的半径是5厘米,圆心角是60°,则此扇形的面积是______平方厘米,周长是______厘米.(π取3.14)【难度】★【答案】13.08;15.23.【解析】扇形的面积为:60×3.14×5×5÷360=13.08平方厘米 ; 此扇形的周长为:60×3.14×5÷180 + 5×2 = 15.23厘米.【总结】考查扇形面积及周长的计算,注意扇形的周长还包含了两条半径的长.【例18】 已知扇形的弧长是31.4厘米,半径是10厘米,那么扇形的面积是______平方厘米.(π取3.14)【难度】★【答案】157.【解析】1131.41015722S lr ==⨯⨯=平方厘米.【总结】考查扇形面积的计算.【例19】 一扇形的半径不变,圆心角扩大为原来的3倍,则面积是原来的______倍;若它的圆心角不变,半径扩大为原来的3倍,则面积是原来的______倍.【难度】★ 【答案】3,9. 【解析】213602n S r lr π==扇形. 【总结】考查扇形的面积与扇形的圆心角及所在的圆的半径之间的关系.【例20】 一个圆心角为60°的扇形,其面积与一个直径为9的圆相等,求此扇形所在圆的面积.(结果保留π)【难度】★★ 【答案】121.5π.【解析】由题意,可得:22960()2360r ππ⨯⨯⨯=,解得:2121.5r =,故此扇形所在圆的面积为:2121.5r ππ=.【总结】考查扇形面积的计算,注意先根据题目中的条件计算出半径的平方,再求面积.8 / 16ABCDEFA BC D【例21】 一个圆心角为45°的扇形,它的周长为11.14厘米,求它的面积.(π取3.14) 【难度】★★【答案】6.28平方厘米.【解析】设扇形所在圆的半径为r ,则由题意可得:4522 3.1411.14360r r +⨯⨯⨯=, 解得:4r =厘米,故此扇形的面积为:245 3.144 6.28360⨯⨯=平方厘米.【总结】本题一方面考查扇形的半径的计算,另一方面考查扇形面积的计算.【例22】 如图,已知正方形边长为2,分别以正方形的两个对角顶点为圆心,以边长为半径作两段圆弧,求阴影部分的面积.(结果保留π)【难度】★★ 【答案】24π-. 【解析】229022S 2224360S S ππ⨯=-=⨯-=-正阴影扇形.【总结】本题主要考查形如“树叶”状的图形的面积的计算.【例23】 等腰直角三角形ABC 中,以直角顶点A 为圆心,以高AD 为半径,画一条弧,交AB 、AC 分别于E 、F ,AD = 2厘米,图中阴影部分的面积是______平方厘米.(π取3.14)【难度】★★ 【答案】0.86. 【解析】21124 3.1424 3.140.8624ABCAEF S SS =-=⨯⨯-⨯⨯=-=阴影扇形.【总结】考查阴影部分的面积的计算,注意用规则图形的面积去表示不规则图形的面积.【例24】 如图,扇形BAC 的面积是半圆ADB 面积的113倍,那么CAB ∠是______度.【难度】★★ 【答案】60【解析】因为半圆的直径为扇形的半径,所以设半圆的半径为r , 则扇形的半径为2r ,故由题意,可得:()22241803360360n r r ππ⎛⎫=⎪⎝⎭,解得:60n =.即CAB ∠是60度. 【总结】本题要认真观察,先分析半圆的半径与扇形半径的关系,然后再进行计算.ABCH【例25】 如图,三角形为任意三角形,三个圆的半径均为1厘米,则阴影部分的面积为______平方厘米.(π取3.14)【难度】★★【答案】1.57平方厘米.【解析】由图可知:阴影部分的面积是三个扇形的面积之和, 三个扇形的半径分别为1,圆心角之和为180°, 故阴影部分面积为:180×3.14×1×1÷360=1.572cm .【总结】考查阴影部分的面积,本题的关键是求出三个扇形的圆心角之和.【例26】 如图,ABC ∆的三条边都是6厘米,高AH 为5.2厘米,分别以A 、B 、C 三点为圆心,6厘米长为半径画弧,求这三段弧围成的图形的面积.(π取3.14)【难度】★★【答案】25.32平方厘米.【解析】一个小扇形的面积是:60×3.14×6×6÷360=18.84平方厘米, 等边三角形的面积为:6×5.2÷2=15.6(平方厘米), 所以这三段弧所围成的图形的面积是:18.84×3-15.6×2=56.52-31.2=25.32(平方厘米)【总结】本题主要是利用割补法将不规则图形的面积问题转化为规则图形的面积计算.【例27】 如图,长方形的宽为5,正好是大扇形半径的一半,求阴影部分的面积.(π取3.14)【难度】★★【答案】48.125.【解析】22113.1410105 3.14548.12544S =⨯⨯-⨯-⨯⨯=阴影().【总结】本题中阴影部分的面积等于大扇形的面积减去长方形的面积再加上小扇形的面积.10 / 16【例28】 如图,圆的半径是6厘米,阴影部分的面积是31.5π平方厘米,求图中三角形的面积.【难度】★★★ 【答案】18平方厘米.【解析】圆的面积为:6636ππ⨯⨯=,空白部分的扇形的面积为:3631.5 4.5πππ-=,设空白部分的扇形的圆心角为n ,则36 4.5360nππ⨯=,解得n =45,所以空白部分的三角形是等腰直角三角形, 故面积为6×6×0.5=18平方厘米.【总结】本题主要是根据扇形的面积公式求出圆心角的度数,从而求出三角形的面积.【例29】 有一只狗被系在一建筑物的墙角上,这个建筑物是边长6米的等边三角形,绳长是8米.当绳被狗拉紧时,狗活动范围的总面积为多少平方米?(π取3.14)【难度】★★★ 【答案】175.84平方米.【解析】根据图可知:大扇形的圆心角为360-60=300度, 小扇形的圆心角为:180-60=120度,故总面积为:22300120822175.84360360ππ⨯⨯+⨯⨯⨯=平方米.【总结】本题中要注意小狗活动的范围包含了三个扇形.【例30】 已知C 、D 两点在以AB 为直径的半圆周上且把半圆三等分,若已知AB 长为10,求阴影部分的面积.(结果保留π)【难度】★★★【答案】256π.【解析】连接CD 、OD 、OC ,则阴影部分面积为CD BDCS S 弓形+∆.因为C 、D 把半圆弧AB 三等分,所以AB CD ODC BCD ∆∆∥,所以、等底等高, 所以阴影部分面积=CD BDC S S 弓形+∆=()260102253606OCD S ππ⨯⨯÷==扇形. 【总结】本题综合性较强,考查了一些几何的内容,教师可以选择性的讲解.ABC D【习题1】 扇形的面积是314平方米,其所在圆的面积是1256平方米,则这个扇形的圆心角为______°.【难度】★ 【答案】90.【解析】314÷1256×360°= 90°. 【总结】考查扇形面积公式的逆运用.【习题2】 一种手榴弹爆炸后,有效杀伤范围的半径是6米,有效杀伤面积是______平方米.(π取3.14)【难度】★ 【答案】113.04.【解析】36×3.14=13.04平方米.【总结】考查圆的面积的计算在实际问题中的运用.【习题3】 若一扇形所在的圆心角缩小为原来的12,半径扩大为原来的2倍,则它的面积( )A .扩大为原来的2倍B .扩大为原来的4倍C .是原来的12 D .不变【难度】★ 【答案】A 【解析】213602n S r lr π==扇形. 【总结】考查扇形的面积与扇形的圆心角及扇形所在的圆的半径之间的关系.【习题4】 如果用整个圆来表示班级共有40名学生,那么被评为三好学生的8名同学应该用圆心角为______的扇形来表示.【难度】★★ 【答案】72°.【解析】8÷40×360°= 72°.【总结】考查圆心角在实际问题中的运用.随堂检测12 / 16【习题5】 环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积.(π取3.14) 【难度】★★【答案】15.7平方厘米.【解析】外圆的半径长为:18.84÷3.14÷2=3cm ;内圆半径长为:4÷2=2cm ; 故环形的面积为:3.14×(3×3-2×2)=15.7平方厘米. 【总结】考查圆环的面积的计算.【习题6】 两个圆的面积之差是209平方厘米,已知大圆的周长是小圆的周长的119倍,求小圆的面积.(π取3.14)【难度】★★【答案】891平方厘米.【解析】因为大圆的周长是小圆的周长的119倍,故大圆与小圆的面积之比为:100:81,因为两个圆的面积之差是209平方厘米,所以小圆的面积为: 209÷(100-81)×81 = 209÷19×81= 891平方厘米. 【总结】本题主要是根据大小两圆的周长比确定出面积比.【习题7】 一时钟的分针长6分米,从上午9点到上午10点40分,分针扫过的面积是多少平方分米?【难度】★★【答案】188.4平方分米.【解析】从上午9点到上午10点40分,分针走过的度数为:600°,故分针扫过的面积为:2600 3.146188.4360⨯⨯=平方分米.【总结】时针走过一小时,则分针走了360度,本题主要是确定出分针转过的度数.A B2 2【习题8】 如图,正方形的边长为4,求阴影部分的面积. 【难度】★★ 【答案】4.56.【解析】2145444822360S S S ππ=-=⨯⨯-⨯⨯=-空三角形扇形,14(82)48 4.562S S S πππ=-=⨯⨯--=-=阴影半圆空.【总结】本题主要考查阴影部分的面积计算.【习题9】 如图所示的阴影部分分别为三种标点符号:句号、逗号和问号.已知大圆半径为R ,小圆半径为r ,且R = 2r .哪一个标点符号的面积最小?【难度】★★★ 【答案】问号. 【解析】句号的面积:22243r r r ππ-=();逗号的面积:224r 22r ππ⨯÷=;问号的面积:22223134r 44r r r πππ-+=().【总结】本题中主要考查阴影部分的面积,注意计算方法.【习题10】 如图,A 与B 是两个圆的圆心,那么两个阴影部分的面积相差______平方厘米.(π取3.14)【难度】★★★ 【答案】1.42平方厘米.【解析】两个阴影部分的面积差为大扇形的面积减去长方形的面积, 再减去小扇形的面积,即:22113.144 3.1422444⨯⨯-⨯⨯-⨯= 1.42平方厘米.【总结】本题要注意认真审题,看清楚求的是两部分的面积差,然后转化为规则图形的面积的差.空14 / 16【作业1】 下列判断中,正确的是( )A .半径越大的扇形,面积越大B .所对圆心角越大的扇形,面积越大C .所对圆心角相同时,半径越大的扇形面积越大D .半径相等时,所对圆心角越大的扇形面积越小 【难度】★ 【答案】C 【解析】213602n S r lr π==扇形. 【总结】考查扇形面积的影响因素.【作业2】 圆的半径由6厘米增加到9厘米,圆的面积增加了______平方厘米.(π取3.14) 【难度】★ 【答案】141.3.【解析】3.14×(81-36)=141.3平方厘米. 【总结】考查圆的面积的计算【作业3】 一个扇形的半径是5厘米,圆心角是72°,这个扇形的周长是______分米.(π取3.14)【难度】★ 【答案】1.628【解析】72×3.14×5÷180+5+5=16.28厘米=1.628分米. 【总结】考查扇形周长的计算,注意单位的换算.课后作业【作业4】 一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆,还剩下______平方厘米的纸没有用.(π取3.14)【难度】★★ 【答案】286.【解析】30×20-3.14×10×10=286平方厘米. 【总结】考查长方形纸片上剪出最大圆的面积的计算.【作业5】 一个扇形的面积是78.5平方厘米,圆心角为36°,当这个扇形的半径不变而圆心角增加了108°以后,这个扇形的面积是______平方厘米.(π取3.14)【难度】★★ 【答案】314.【解析】扇形所在圆的面积是785平方厘米,故增加的面积为(108+36)÷360×785=314. 【总结】考查扇形的面积与所在圆的面积的计算.【作业6】 某大楼上有一石英制的时钟,已知时针与分针分别长60厘米和80厘米,则时针走1小时,时针与分针扫过的平面的面积差为多少平方分米?(π取3.14)【难度】★★【答案】191.54平方分米.【解析】时针走1小时,走过的圆心角度数为30°,而分针走过了360°,故面积差为: 3.14×80×80-30×3.14×60×60÷360=19154平方厘米=191.54平方分米. 【总结】本题考查扇形的面积在钟表问题中的运用,注意确定表针走过的度数.【作业7】 如图是三个半圆构成的图形,其中小半圆直径为8,中半圆直径为20,则阴影部分面积与大半圆的面积之比是多少?【难度】★★ 【答案】4:7.【解析】2221111410456222S ππππ=⨯⨯-⨯⨯-⨯⨯=阴影;2114982S ππ=⨯⨯=大半圆,故阴影部分面积与大半圆的面积之比是:56984:7ππ=:. 【总结】考查半圆面积的计算.16 / 16红红 红 红蓝 蓝蓝蓝 【作业8】 一辆汽车的车轮直径为1米,试计算当汽车以120千米/时的速度行驶时,车轮的转速是每秒多少周?(3π≈,结果保留整数位)【难度】★★ 【答案】11.【解析】车轮转速:120×10003113600÷=周. 【总结】考查圆的周长计算的简单应用【作业9】 如图是对称图形,红色部分的面积大还是蓝色部分的面积大? 【难度】★★★ 【答案】一样大【解析】设大圆R =2,则小圆r =1.蓝色部分的面积:211(21)42422r ππ-⨯⨯⨯=-;红色部分的面积为:()2244(424)24R r S ππππππ--=--+=-蓝色, 所以两部分面积一样大.【总结】考查不规则图形的面积,注意认真分析,转化为规则图形的计算.【作业10】 如图,扇形AOB 为14个圆,半径为4厘米,以它的两条半径为直径,在扇形内部画两个半圆,求阴影部分的面积.【难度】★★★ 【答案】4.56平方厘米.【解析】通过割补,可以将“树叶”状的阴影转化到上面两个弓形处,故13.14444424.564S S S =-=⨯⨯⨯-⨯÷=阴影扇形直角三角形平方厘米.【总结】本题主要考查利用割补法求阴影部分的面积.。
圆计算面积的公式

圆计算面积的公式圆的面积公式是由圆周率π来计算的。
圆的面积公式为:A=πr²,其中A表示圆的面积,r表示圆的半径。
圆是一个由无数个点组成的一个闭合曲线。
圆由圆心和圆周上的点组成,其中圆心是指从圆的任何一点出发画直线与圆周相交所形成的点。
圆的面积公式推导如下:首先,将圆分成无数个扇形,每个扇形的角度为θ。
则每个扇形的面积可以表示为扇形的圆心角度和整个圆的角度之比。
因此,每个扇形的面积可以表示为θ/360乘以整个圆的面积。
其次,我们可以将圆的周长表示为每个扇形的周长之和。
每个扇形的弧长可以表示为扇形的圆心角度和整个圆的角度之比。
因此,每个扇形的弧长可以表示为θ/360乘以整个圆的周长。
然后,我们可以将每个扇形的面积表示为扇形的弧长乘以半径。
因此,每个扇形的面积可以表示为(θ/360)*2πr,其中πr表示圆的周长。
由此,我们可以得到每个扇形的面积为(θ/360)*πr²。
最后,我们将无数个扇形的面积之和即整个圆的面积表示为A=Σ[(θ/360)*πr²]。
由于当扇形角度无穷小时,无数个扇形的面积之和趋近于整个圆的面积,因此可以用极限运算来表示。
当扇形角度无穷小时,极限运算可以表示为积分。
因此,整个圆的面积可以表示为A=∫[(θ/360)*πr²]。
根据积分的性质,我们可以将积分公式中的θ/360提取出来,并将其值替换为1、因此,整个圆的面积可以表示为A=(1/360)*∫[πr²dθ]。
根据θ的范围为0到360,我们可以将积分的上界和下界替换为0和360,得到A=(1/360)*∫[0,360][πr²dθ]。
对于一个完整的圆,θ的范围为0到360,θ的积分等于360,所以A=(1/360)*360*πr²。
化简后得到A=πr²,这就是圆的面积公式。
因此,我们可以利用圆的面积公式A=πr²来计算圆的面积。
根据给定的半径r,直接将其代入公式中即可计算出圆的面积。
圆的面积变形题

圆的面积变形题
圆的面积$S=\pi r^2$,根据面积公式可以衍生出很多变形题,以下是一些常见的类型:
1. 已知圆的半径,求圆的面积:这是最基本的问题,直接使用圆的面积公式$S=\pi r^2$即可。
2. 已知圆的直径,求圆的面积:因为直径是半径的两倍,所以可以先求出半径,再代入圆的面积公式。
3. 已知圆的周长,求圆的面积:根据圆的周长公式$C=2\pi r$,可以求出半径,再代入圆的面积公式。
4. 已知圆的面积,求圆的半径:将圆的面积公式$S=\pi r^2$变形为$r=\sqrt{\frac{S}{\pi}}$,即可求出半径。
5. 求圆环的面积:圆环的面积等于外圆的面积减去内圆的面积,即$S=\pi R^2-\pi r^2$,其中$R$为外圆半径,$r$为内圆半径。
6. 求扇形的面积:扇形的面积等于圆的面积乘以扇形的圆心角度数除以$360^\circ$,即$S=\frac{\pi r^2\theta}{360^\circ}$,其中
$\theta$为扇形的圆心角度数。
以上是一些常见的圆的面积变形题,解决这些问题需要熟练掌握圆的面积公式和相关的数学知识。
圆面积扇形面积公式

圆面积扇形面积公式圆是几何中的基本图形之一,它有许多重要的性质和公式。
其中,圆的面积和扇形的面积是我们经常需要计算的。
本文将介绍圆的面积和扇形的面积公式,以及它们的应用。
1. 圆的面积公式圆的面积公式是数学中最基本且最重要的公式之一。
在计算圆的面积时,我们需要知道圆的半径。
圆的半径是从圆心到圆上任意一点的距离,通常用字母r表示。
圆的面积公式为:S = πr^2,其中π是一个常数,约等于3.14159。
例如,如果一个圆的半径是5厘米,那么它的面积就是:S = 3.14159 * 5^2 = 78.54平方厘米。
2. 扇形的面积公式扇形是圆的一部分,它由圆心、圆弧和两条半径组成。
计算扇形的面积时,我们需要知道扇形的圆心角和圆的半径。
扇形的面积公式是:S = (θ/360) * πr^2,其中θ是扇形的圆心角,可以用度数或弧度表示。
例如,如果一个扇形的圆心角是60度,半径是5厘米,那么它的面积就是:S = (60/360) * 3.14159 * 5^2 = 13.09平方厘米。
3. 圆与扇形的应用圆和扇形的面积公式在日常生活和工作中有广泛的应用。
以下是一些例子:(1) 建筑设计:在建筑设计中,圆和扇形的面积公式可以用来计算房间的面积、花坛的面积等。
(2) 圆桌布料:如果我们知道圆桌的直径或半径,可以利用圆的面积公式计算所需的桌布面积,以便购买合适尺寸的桌布。
(3) 园艺设计:在园艺设计中,扇形的面积公式可以用来计算花坛或草坪的面积,以便购买足够的土壤或草坪。
(4) 圆形广告牌:如果我们想在一个圆形广告牌上放置广告,可以利用扇形的面积公式计算广告的面积,帮助我们确定广告的尺寸和设计。
总结:圆的面积和扇形的面积是几何中重要的概念和公式。
圆的面积公式是S = πr^2,扇形的面积公式是S = (θ/360) * πr^2,其中θ是扇形的圆心角。
这些公式在日常生活和工作中有广泛的应用,可以帮助我们计算房间面积、购买桌布、设计花坛等。
著名机构数学教案讲义六年级秋季班第14课时 圆和扇形的面积(教师)

第14课时 圆和扇形的面积知识精要1、圆的面积(1)圆的概念:圆所占平面的大小叫做圆的面积。
(2)圆的面积公式:设圆的半径为r ,面积为S ,那么圆的面积为2S r π=2、扇形的面积(1)扇形的概念:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。
(2)扇形的面积公式:设组成扇形的半径为r ,圆心角为0n ,弧长为l ,则213602n S r lr π==扇形 3、扇形统计图 扇形统计图是用圆的面积表示一组数据的整体,用圆中扇形面积与圆面积的比来表示各组成部分在总体中所占的百分比的统计图。
扇形统计图有时也称做饼分统计图,扇形统计图可以直观地反映出各个部分数量在总量中所占的份额。
热身练习1、已知圆的周长为12.56厘米,则这个圆的面积是__12.56___平方厘米。
2、已知圆的面积是50.24平方厘米,那么这个圆的半径是___4___厘米。
3、已知扇形面积是1.413平方分米,圆心角是72°,那么它的半径是__15___厘米。
4、一个雷达圆形屏幕的半径是50厘米,那么屏幕的面积是__7850__平方厘米。
5、在一边长是12厘米的正方形铁片上,剪一个最大的圆,剪去的面积是__113.04___平方厘米。
6、大圆半径是小圆半径的3倍,大圆的面积是84.78平方厘米,则小圆的面积是__9.42___平方厘米。
精解名题例1、新华学校有个圆形花池,池边周围栏杆长50.24米,那么这个花池的圆形底面积是多少平方米? 解:半径:50.24÷2÷3.14=8(米)面积:3.14×8×8=200.96(平方米)例2、某挂钟的分针长6厘米,如果走过20分钟,这根分针在钟面上扫过的面积是多少平方厘米? 解:68.37614.336012036022=⨯⨯==r n S π(平方厘米)例3、一所中学准备搬迁到新校舍,在迁入新校舍之前就该校500名学生如何到新校舍的问题进行了一次调查,得到如下数据:步行90人,骑自行车160人,坐公共汽车220人,其他30人,请算出各部分学生数占学生总数的百分比,并用扇形统计图表示。
六年级秋季班-第16讲:圆和扇形的面积(1)

圆和扇形的面积是六年级数学上学期第四章第二节的内容.本讲主要讲解圆的面积和扇形面积的求解方法,及它们之间的关系;重点是掌握圆的面积和扇形面积的基本计算方法,难点是在不同的图形中根据题目条件灵活解答相关问题.1、 圆的面积圆所占平面的大小叫做圆的面积.设圆的半径长为r ,面积为S ,那么:圆的面积2S r r r ππ=⨯=.圆和扇形的面积内容分析知识结构模块一:圆的面积知识精讲例题解析【例1】(1)圆的半径是4厘米,它的面积是______平方厘米;(结果保留π)(2)圆的直径是6米,它的周长是______米,它的面积是______平方米;(π取3.14)(3)圆的周长是25.12分米,它的面积是______平方分米.(π取3.14)【难度】★【答案】【解析】【例2】有大小两个圆,如果大圆半径是小圆半径的3倍,则大圆的周长是小圆的______倍,大圆的面积是小圆的______倍;如果大圆直径是小圆半径的4倍,则小圆面积与大圆面积的比是______.【难度】★【答案】【解析】【例3】有一只羊栓在草地的木柱上,绳子的长度是4米,这只羊最多可以吃到______平方米的草.(π取3.14)【难度】★【答案】【解析】【例4】在一个边长为20厘米的正方形纸板里剪出一个最大的圆,则圆的面积是______平方厘米.(π取3.14)【难度】★【答案】【解析】【例5】用一根长为16分米的铁丝围成一个圆,接头处长为0.3分米,这个圆的面积是多少?(π取3.14)【难度】★★【答案】【解析】【例6】一种铝制面盆是用直径20厘米的圆形铝板冲压而成的,要做100个这样的面盆至少需要铝板______平方米.(π取3.14)【难度】★★【答案】【解析】【例7】周长相等的长方形、正方形和圆,______的面积最大.【难度】★★【答案】【解析】【例8】两个同心圆,大圆半径为5厘米,小圆半径为3厘米,求圆环的面积.(π取3.14)【难度】★★【答案】【解析】【例9】一个圆形喷水池的周长是62.8米,绕着这个水池修一条宽2米的水泥路,求路面的面积.(π取3.14)【难度】★★【答案】【解析】【例10】如图,已知大圆半径是6厘米,那么阴影部分面积占大圆面积的______.(用分数表示)【难度】★★【答案】【解析】【例11】 两个圆的面积之和为1991平方厘米,小圆的周长是大圆周长的90%,则大圆的面积是_______平方厘米.(π取3.14)【难度】★★ 【答案】 【解析】【例12】 有5块圆形的花圃它们的直径分别是3米、4米、5米、8米、9米,请将这5块花圃分成两组,分别交给两个班级管理,使这两个班级管理的面积尽可能接近.【难度】★★ 【答案】 【解析】【例13】 大小两圆的相交部分(如图所示的阴影部分)面积是大圆面积的415,是小圆面积的35,量得小圆的半径是5厘米,问大圆的半径是多少?(π取3.14)【难度】★★★ 【答案】 【解析】【例14】 如图,正方形的面积是12平方厘米,求图中阴影部分的面积为多少平方厘米?(π取3.14)【难度】★★★ 【答案】 【解析】【例15】 如图中的圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,图中阴影部分的周长是多少厘米?(π取3.14)【难度】★★★ 【答案】 【解析】B1、 扇形的概念由组成圆心角的两条半径和圆心角所对的弧围成的图形,叫做扇形.如图,空白部分记作扇形AOB . 2、 扇形的面积设组成扇形的半径为r ,圆心角为n °,弧长为l ,那么:213602n S r lr π==扇形.【例16】 一个扇形的面积是它所在圆面积的15,这个扇形的圆心角是______.【难度】★ 【答案】 【解析】【例17】 一个扇形的半径是5厘米,圆心角是60°,则此扇形的面积是______平方厘米,周长是______厘米.(π取3.14)【难度】★ 【答案】 【解析】【例18】 已知扇形的弧长是31.4厘米,半径是10厘米,那么扇形的面积是______平方厘米.(π取3.14)【难度】★ 【答案】 【解析】模块二:扇形的面积知识精讲例题解析【例19】 一扇形的半径不变,圆心角扩大为原来的3倍,则面积是原来的______倍;若它的圆心角不变,半径扩大为原来的3倍,则面积是原来的______倍.【难度】★ 【答案】 【解析】【例20】 一个圆心角为60°的扇形,其面积与一个直径为9的圆相等,求此扇形所在圆的面积.(结果保留π)【难度】★★ 【答案】 【解析】【例21】 一个圆心角为45°的扇形,它的周长为11.14厘米,求它的面积.(π取3.14) 【难度】★★ 【答案】 【解析】【例22】 如图,已知正方形边长为2,分别以正方形的两个对角顶点为圆心,以边长为半径作两段圆弧,求阴影部分的面积.(结果保留π)【难度】★★ 【答案】 【解析】【例23】 等腰直角三角形ABC 中,以直角顶点A 为圆心,以高AD 为半径,画一条弧,交AB 、AC 分别于E 、F ,AD = 2厘米,图中阴影部分的面积是______平方厘米. (π取3.14)【难度】★★ 【答案】 【解析】ABCDABCH【例24】 如图,扇形BAC 的面积是半圆ADB 面积的113倍,那么CAB ∠是______度.【难度】★★ 【答案】 【解析】【例25】 如图,三角形为任意三角形,三个圆的半径均为1厘米,则阴影部分的面积为______平方厘米.(π取3.14)【难度】★★ 【答案】 【解析】【例26】 如图,ABC ∆的三条边都是6厘米,高AH 为5.2厘米,分别以A 、B 、C 三点为圆心,6厘米长为半径画弧,求这三段弧围成的图形的面积.(π取3.14)【难度】★★ 【答案】 【解析】【例27】 如图,长方形的宽为5,正好是大扇形半径的一半,求阴影部分的面积.(π取3.14) 【难度】★★ 【答案】 【解析】【例28】 如图,圆的半径是6厘米,阴影部分的面积是31.5π平方厘米,求图中三角形的面积.【难度】★★★ 【答案】 【解析】【例29】 有一只狗被系在一建筑物的墙角上,这个建筑物是边长6米的等边三角形,绳长是8米.当绳被狗拉紧时,狗活动范围的总面积为多少平方米?(π取3.14)【难度】★★★ 【答案】 【解析】【例30】 已知C 、D 两点在以AB 为直径的半圆周上且把半圆三等分,若已知AB 长为10,求阴影部分的面积.(结果保留π)【难度】★★★ 【答案】 【解析】【习题1】扇形的面积是314平方米,其所在圆的面积是1256平方米,则这个扇形的圆心角为______°.【难度】★【答案】【解析】【习题2】一种手榴弹爆炸后,有效杀伤范围的半径是6米,有效杀伤面积是______平方米.( 取3.14)【难度】★【答案】【解析】【习题3】若一扇形所在的圆心角缩小为原来的12,半径扩大为原来的2倍,则它的面积()A.扩大为原来的2倍B.扩大为原来的4倍C.是原来的12D.不变【难度】★【答案】【解析】【习题4】如果用整个圆来表示班级共有40名学生,那么被评为三好学生的8名同学应该用圆心角为______的扇形来表示.【难度】★★【答案】【解析】随堂检测【习题5】 环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积.(π取3.14) 【难度】★★ 【答案】 【解析】【习题6】 两个圆的面积之差是209平方厘米,已知大圆的周长是小圆的周长的119倍,求小圆的面积.(π取3.14)【难度】★★ 【答案】 【解析】【习题7】 一时钟的分针长6分米,从上午9点到上午10点40分,分针扫过的面积是多少平方分米?【难度】★★ 【答案】 【解析】【习题8】 如图,正方形的边长为4,求阴影部分的面积. 【难度】★★ 【答案】 【解析】【习题9】 如图所示的阴影部分分别为三种标点符号:句号、逗号和问号.已知大圆半径为R ,小圆半径为r ,且R = 2r .哪一个标点符号的面积最小?【难度】★★★ 【答案】 【解析】A B2 2【习题10】如图,A与B是两个圆的圆心,那么两个阴影部分的面积相差______平方厘米.(π取3.14)【难度】★★★【答案】【解析】【作业1】下列判断中,正确的是()A.半径越大的扇形,面积越大B.所对圆心角越大的扇形,面积越大C.所对圆心角相同时,半径越大的扇形面积越大D.半径相等时,所对圆心角越大的扇形面积越小【难度】★【答案】【解析】【作业2】圆的半径由6厘米增加到9厘米,圆的面积增加了______平方厘米.(π取3.14)【难度】★【答案】【解析】课后作业【作业3】一个扇形的半径是5厘米,圆心角是72°,这个扇形的周长是______分米.(π取3.14)【难度】★【答案】【解析】【作业4】一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆,还剩下______平方厘米的纸没有用.(π取3.14)【难度】★★【答案】【解析】【作业5】一个扇形的面积是78.5平方厘米,圆心角为36°,当这个扇形的半径不变而圆心角增加了108°以后,这个扇形的面积是______平方厘米.(π取3.14)【难度】★★【答案】【解析】【作业6】某大楼上有一石英制的时钟,已知时针与分针分别长60厘米和80厘米,则时针走1小时,时针与分针扫过的平面的面积差为多少平方分米?(π取3.14)【难度】★★【答案】【解析】【作业7】如图是三个半圆构成的图形,其中小半圆直径为8,中半圆直径为20,则阴影部分面积与大半圆的面积之比是多少?【难度】★★【答案】【解析】红红红红蓝蓝蓝蓝【作业8】一辆汽车的车轮直径为1米,试计算当汽车以120千米/时的速度行驶时,车轮的转速是每秒多少周?(3π≈,结果保留整数位)【难度】★★【答案】【解析】【作业9】如图是对称图形,红色部分的面积大还是蓝色部分的面积大?【难度】★★★【答案】【解析】【作业10】如图,扇形AOB为14个圆,半径为4厘米,以它的两条半径为直径,在扇形内部画两个半圆,求阴影部分的面积.【难度】★★★【答案】【解析】。
六年级秋季班-第16讲:圆和扇形的面积

圆和扇形的面积是六年级数学上学期第四章第二节的内容.本讲主要讲解圆的面积和扇形面积的求解方法,及它们之间的关系;重点是掌握圆的面积和扇形面积的基本计算方法,难点是在不同的图形中根据题目条件灵活解答相关问题.1、 圆的面积圆所占平面的大小叫做圆的面积.设圆的半径长为r ,面积为S ,那么:圆的面积2S r r r ππ=⨯=.圆和扇形的面积内容分析知识结构模块一:圆的面积知识精讲例题解析【例1】(1)圆的半径是4厘米,它的面积是______平方厘米;(结果保留π)(2)圆的直径是6米,它的周长是______米,它的面积是______平方米;(π取3.14)(3)圆的周长是25.12分米,它的面积是______平方分米.(π取3.14)【难度】★【答案】【解析】【例2】有大小两个圆,如果大圆半径是小圆半径的3倍,则大圆的周长是小圆的______倍,大圆的面积是小圆的______倍;如果大圆直径是小圆半径的4倍,则小圆面积与大圆面积的比是______.【难度】★【答案】【解析】【例3】有一只羊栓在草地的木柱上,绳子的长度是4米,这只羊最多可以吃到______平方米的草.(π取3.14)【难度】★【答案】【解析】【例4】在一个边长为20厘米的正方形纸板里剪出一个最大的圆,则圆的面积是______平方厘米.(π取3.14)【难度】★【答案】【解析】【例5】用一根长为16分米的铁丝围成一个圆,接头处长为0.3分米,这个圆的面积是多少?(π取3.14)【难度】★★【答案】【解析】【例6】一种铝制面盆是用直径20厘米的圆形铝板冲压而成的,要做100个这样的面盆至少需要铝板______平方米.(π取3.14)【难度】★★【答案】【解析】【例7】周长相等的长方形、正方形和圆,______的面积最大.【难度】★★【答案】【解析】【例8】两个同心圆,大圆半径为5厘米,小圆半径为3厘米,求圆环的面积.(π取3.14)【难度】★★【答案】【解析】【例9】一个圆形喷水池的周长是62.8米,绕着这个水池修一条宽2米的水泥路,求路面的面积.(π取3.14)【难度】★★【答案】【解析】【例10】如图,已知大圆半径是6厘米,那么阴影部分面积占大圆面积的______.(用分数表示)【难度】★★【答案】【解析】【例11】两个圆的面积之和为1991平方厘米,小圆的周长是大圆周长的90%,则大圆的面积是_______平方厘米.(π取3.14)【难度】★★【答案】【解析】【例12】有5块圆形的花圃它们的直径分别是3米、4米、5米、8米、9米,请将这5块花圃分成两组,分别交给两个班级管理,使这两个班级管理的面积尽可能接近.【难度】★★【答案】【解析】【例13】大小两圆的相交部分(如图所示的阴影部分)面积是大圆面积的415,是小圆面积的35,量得小圆的半径是5厘米,问大圆的半径是多少?(π取3.14)【难度】★★★【答案】【解析】【例14】如图,正方形的面积是12平方厘米,求图中阴影部分的面积为多少平方厘米?(π取3.14)【难度】★★★【答案】【解析】【例15】如图中的圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,图中阴影部分的周长是多少厘米?(π取3.14)【难度】★★★【答案】【解析】B1、 扇形的概念由组成圆心角的两条半径和圆心角所对的弧围成的图形,叫做扇形.如图,空白部分记作扇形AOB . 2、 扇形的面积设组成扇形的半径为r ,圆心角为n °,弧长为l ,那么:213602n S r lr π==扇形.【例16】 一个扇形的面积是它所在圆面积的15,这个扇形的圆心角是______.【难度】★ 【答案】 【解析】【例17】 一个扇形的半径是5厘米,圆心角是60°,则此扇形的面积是______平方厘米,周长是______厘米.(π取3.14)【难度】★ 【答案】 【解析】【例18】 已知扇形的弧长是31.4厘米,半径是10厘米,那么扇形的面积是______平方厘米.(π取3.14)【难度】★ 【答案】 【解析】模块二:扇形的面积知识精讲例题解析【例19】 一扇形的半径不变,圆心角扩大为原来的3倍,则面积是原来的______倍;若它的圆心角不变,半径扩大为原来的3倍,则面积是原来的______倍.【难度】★ 【答案】 【解析】【例20】 一个圆心角为60°的扇形,其面积与一个直径为9的圆相等,求此扇形所在圆的面积.(结果保留π)【难度】★★ 【答案】 【解析】【例21】 一个圆心角为45°的扇形,它的周长为11.14厘米,求它的面积.(π取3.14) 【难度】★★ 【答案】 【解析】【例22】 如图,已知正方形边长为2,分别以正方形的两个对角顶点为圆心,以边长为半径作两段圆弧,求阴影部分的面积.(结果保留π)【难度】★★ 【答案】 【解析】【例23】 等腰直角三角形ABC 中,以直角顶点A 为圆心,以高AD 为半径,画一条弧,交AB 、AC 分别于E 、F ,AD = 2厘米,图中阴影部分的面积是______平方厘米. (π取3.14)【难度】★★ 【答案】 【解析】ABCDABCH【例24】 如图,扇形BAC 的面积是半圆ADB 面积的113倍,那么CAB ∠是______度.【难度】★★ 【答案】 【解析】【例25】 如图,三角形为任意三角形,三个圆的半径均为1厘米,则阴影部分的面积为______平方厘米.(π取3.14)【难度】★★ 【答案】 【解析】【例26】 如图,ABC ∆的三条边都是6厘米,高AH 为5.2厘米,分别以A 、B 、C 三点为圆心,6厘米长为半径画弧,求这三段弧围成的图形的面积.(π取3.14)【难度】★★ 【答案】 【解析】【例27】 如图,长方形的宽为5,正好是大扇形半径的一半,求阴影部分的面积.(π取3.14) 【难度】★★ 【答案】 【解析】【例28】 如图,圆的半径是6厘米,阴影部分的面积是31.5π平方厘米,求图中三角形的面积.【难度】★★★ 【答案】 【解析】【例29】 有一只狗被系在一建筑物的墙角上,这个建筑物是边长6米的等边三角形,绳长是8米.当绳被狗拉紧时,狗活动范围的总面积为多少平方米?(π取3.14)【难度】★★★ 【答案】 【解析】【例30】 已知C 、D 两点在以AB 为直径的半圆周上且把半圆三等分,若已知AB 长为10,求阴影部分的面积.(结果保留π)【难度】★★★ 【答案】 【解析】【习题1】扇形的面积是314平方米,其所在圆的面积是1256平方米,则这个扇形的圆心角为______°.【难度】★【答案】【解析】【习题2】一种手榴弹爆炸后,有效杀伤范围的半径是6米,有效杀伤面积是______平方米.( 取3.14)【难度】★【答案】【解析】【习题3】若一扇形所在的圆心角缩小为原来的12,半径扩大为原来的2倍,则它的面积()A.扩大为原来的2倍B.扩大为原来的4倍C.是原来的12D.不变【难度】★【答案】【解析】【习题4】如果用整个圆来表示班级共有40名学生,那么被评为三好学生的8名同学应该用圆心角为______的扇形来表示.【难度】★★【答案】【解析】随堂检测【习题5】环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积.(π取3.14)【难度】★★【答案】【解析】【习题6】两个圆的面积之差是209平方厘米,已知大圆的周长是小圆的周长的119倍,求小圆的面积.(π取3.14)【难度】★★【答案】【解析】【习题7】一时钟的分针长6分米,从上午9点到上午10点40分,分针扫过的面积是多少平方分米?【难度】★★【答案】【解析】【习题8】如图,正方形的边长为4,求阴影部分的面积.【难度】★★【答案】【解析】【习题9】如图所示的阴影部分分别为三种标点符号:句号、逗号和问号.已知大圆半径为R,小圆半径为r,且R = 2r.哪一个标点符号的面积最小?【难度】★★★【答案】【解析】AB22【习题10】 如图,A 与B 是两个圆的圆心,那么两个阴影部分的面积相差______平方厘米.(π取3.14)【难度】★★★ 【答案】 【解析】【作业1】 下列判断中,正确的是( )A .半径越大的扇形,面积越大B .所对圆心角越大的扇形,面积越大C .所对圆心角相同时,半径越大的扇形面积越大D .半径相等时,所对圆心角越大的扇形面积越小 【难度】★ 【答案】 【解析】【作业2】 圆的半径由6厘米增加到9厘米,圆的面积增加了______平方厘米.(π取3.14) 【难度】★ 【答案】 【解析】课后作业【作业3】一个扇形的半径是5厘米,圆心角是72°,这个扇形的周长是______分米.(π取3.14)【难度】★【答案】【解析】【作业4】一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆,还剩下______平方厘米的纸没有用.(π取3.14)【难度】★★【答案】【解析】【作业5】一个扇形的面积是78.5平方厘米,圆心角为36°,当这个扇形的半径不变而圆心角增加了108°以后,这个扇形的面积是______平方厘米.(π取3.14)【难度】★★【答案】【解析】【作业6】某大楼上有一石英制的时钟,已知时针与分针分别长60厘米和80厘米,则时针走1小时,时针与分针扫过的平面的面积差为多少平方分米?(π取3.14)【难度】★★【答案】【解析】【作业7】如图是三个半圆构成的图形,其中小半圆直径为8,中半圆直径为20,则阴影部分面积与大半圆的面积之比是多少?【难度】★★【答案】【解析】红红红红蓝 蓝蓝 蓝【作业8】 一辆汽车的车轮直径为1米,试计算当汽车以120千米/时的速度行驶时,车轮的转速是每秒多少周?(3π≈,结果保留整数位)【难度】★★ 【答案】 【解析】【作业9】 如图是对称图形,红色部分的面积大还是蓝色部分的面积大? 【难度】★★★ 【答案】 【解析】【作业10】 如图,扇形AOB 为14个圆,半径为4厘米,以它的两条半径为直径,在扇形内部画两个半圆,求阴影部分的面积.【难度】★★★ 【答案】 【解析】。
扇形面积公式和

扇形面积公式扇形面积计算公式:S扇=(n/360)πR²,S扇=1/2lr(知道弧长时),S扇=(1/2)θR²(θ为以弧度表示的圆心角),S扇=(lR)/2(l为扇形弧长)。
R是扇形半径,n是弧所对圆心角度数,π是圆周。
注:π为圆周率约等于3.1415926535一般取3.14。
1、扇形的面积可以用圆的面积乘以弧度角和2π的比值。
2、如果用L来表示扇形的弧长,A可以通过L乘以总面积再除以2πr。
3、弧长公式:n是圆心角度数,r是半径,α是圆心角弧度。
l=nπr÷180或l=n/180·πr或l=|α|r在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°。
4、扇形是与圆形有关的一种重要图形,其面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n/360*πr^2。
如果其顶角采用弧度单位,则可简化为1/2×弧长×(半径)。
5、扇形还与三角形有相似之处,上述简化的面积公式亦可看成:1/2×弧长×(半径),与三角形面积:1/2×底×高相似。
6一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形。
显然,它是由圆周的一部分与它所对应的圆心角围成。
《几何原本》中这样定义扇形:由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形、弧长(L)=n/360·2πr=nπr/180,扇形的弧相似三角形的一条边。
扇形面积公式推导是:S扇=(lR)/2(l为扇形弧长)=(1/2)θR²(θ为以弧度表示的圆心角)。
扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。
由定理“等半径的两个扇形的面积之比等于它们的弧长之比”,将圆看作扇形,利用弧长公式和圆的面积公式即可。
第十五讲 圆和扇形的面积

第十五讲 圆和扇形的面积【典型例题1】在一个圆形喷水池的周长是62.8米,绕着这个水池修一条宽2米的水泥路.求路面的面积.解析:1014.328.622=⨯==πC r (米) S=S 大圆-S 小圆=πr 2-πR 2=3.14×(10+2)2-3.14×102=138.16(平方米)答:路面的面积是138.16平方米.点评:绕着这个水池修一条宽2米的水泥路的情况如图所示,因此路的面积就是大圆面积减小圆面积,其中大圆的半径是小圆半径加上2米.【知识点】1. 圆周长公式用字母C 表示圆的周长,d 表示直径,r 表示半径,那么C=πd 或C=2πr . 能解根据实际问题中的半径或直径求周长,能解根据圆的周长求圆的半径或直径.2.圆的面积圆所占的平面的大小叫做圆的面积.3.圆的面积公式设圆的半径为r ,面积为S ,那么圆的面积S=πr 2.【基本习题限时训练】1、一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆,还剩下( )平方厘米的纸没用A 、2226B 、106.5C 、286D 、656【解】C2、如图阴影部分的面积是( )A 、19.625B 、78.5C 、39.25D 、以上都不对【解】A3、将半径为3厘米的圆,扩大到半径为5厘米的大圆,面积增加了( )A 、9π平方厘米B 、725π平方厘米C 、15π平方厘米D 、16π平方厘米【解】D【拓展题1】用同样的铁丝分别围成一个正方形和一个圆,它们的面积是否相等?如果不相等,哪个面积大,为什么?【解析】面积不相等,圆的面积大.设铁丝的长为x,由此分别算出正方形的边长是a=x4,圆的半径r=x2π,那么S正方形=x216,S圆=x24π.因为16>4π,所以x216<x24π.【点评】圆的周长和面积的大小都由半径的长度决定,所以先由周长表示出半径,再由半径求出面积,再与正方形相比较。
【拓展题2】把三角板放在桌面上,绕着点C将三角板旋转一周后形成如下的图形,如果AB=4厘米,BC=3厘米,AC=5厘米,那么直角边AB所覆盖的面积是多少平方厘米?【解析】S= S大圆-S小圆=πAC2-πBC2=25π-9π=16π=50.24(平方厘米)【点评】AB所覆盖的面积是一个环形,其中外圆的半径是AC的长,内圆的半径是BC的长【典型例题2】一块正方形的草皮,边长为4米,在两个相对的角上各有一棵树,树上各栓一只羊,绳长4米,问两只羊都能吃到的草的草皮有多少?解析: πππ44414122=⨯⨯=r (平方米) 21绿色阴影部分=4π-21×4×4=4π-8(平方米) 阴影部分面积=2×(4π-8)=8π-16=8×3.14-16=9.12(平方米)答 阴影部分的面积是9.12平方米.点评:根据题意先画出图1,由于栓羊的绳长4米,所以一只羊只能草的的面积正好是以树心为圆心,4米长为半径的圆的四分之一,故两只羊都能吃到的草的面积就是绿色的阴影部分图2.先求阴影部分的一半如图3、图4.【知识点】圆的面积公式设圆的半径为r ,面积为S ,那么圆的面积S=πr 2.【基本习题限时训练】1、有一只羊栓在草地的木桩上,绳子的长度是4米,这只羊最多可以吃到( )平方米的草A 、50.24B 、25.12C 、12.56D 、 16【解】A2、学校的操场由一个长方形和两个半圆组成,则这个操场的面积是( )平方米。
圆与扇形的面积运算

圆与扇形的面积运算在几何学中,圆和扇形是常见的图形,它们的面积计算是基础知识。
下面我将分别介绍圆和扇形的面积运算方法。
一、圆的面积运算圆是一个闭合于一个平面上所有点到一个固定点的距离相等的图形。
圆的面积计算公式为:面积= π * r^2,其中π是一个常数,约等于3.14159,r是圆的半径。
例如,如果给定一个圆的半径为5 cm,则该圆的面积为:面积= π * 5^2= 3.14159 * 25≈ 78.53975 平方厘米二、扇形的面积运算扇形是由一个圆心角和与其相应的两条半径所围成的图形。
扇形的面积计算依赖于圆的面积,根据圆的面积比例可以得到扇形的面积计算公式。
扇形的面积计算公式为:面积= (θ/360°) * π * r^2,其中θ是圆心角的度数,r是扇形的半径。
例如,如果给定一个扇形的圆心角为60°,半径为5 cm,则该扇形的面积为:面积 = (60/360) * 3.14159 * 5^2≈ 0.16667 * 3.14159 * 25≈ 13.08996 平方厘米在实际问题中,我们常常需要计算不完整的扇形面积。
如果给定的圆心角θ小于360°,我们可以使用相应的圆心角和整个圆的面积比值,再乘以整个圆的面积,即可得到不完整扇形的面积。
例如,如果给定的圆心角θ为120°,半径仍为5 cm,我们可以计算不完整扇形的面积如下:面积 = (120/360) * 3.14159 * 5^2≈ 0.33333 * 3.14159 * 25≈ 26.17993 平方厘米结论:通过以上的解释与计算实例可知,圆和扇形的面积计算方法相对简单。
圆的面积只需根据圆的半径运用公式Area = π * r^2进行计算,而扇形的面积则需要额外考虑圆心角的影响,应用公式Area = (θ/360°) *π * r^2来计算。
这些计算方法在几何学和实际应用中具有广泛的使用场景,对于我们理解和解决与圆和扇形相关的问题非常有帮助。
关于初中数学圆方面的计算公式

1.圆的周长C=2πr=πd2.圆的面积S=πr²3.扇形弧长l=nπr/1804.扇形面积S=nπr²/360=rl/25.圆锥侧面积S=πrl6.圆锥的表面积S=πrl+πr²〖圆的定义〗几何说:平面上到定点的距离等于定长的所有点组成的图形叫做圆。
定点称为圆心,定长称为半径。
轨迹说:平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆。
集合说:到定点的距离等于定长的点的集合叫做圆。
〖圆的相关量〗1、圆周率:圆周长度与圆的直径长度的比叫做圆周率,值是3.79...,通常用π表示,计算中常取3.14为它的近似值(但奥数常取3或3.1416)。
2、圆弧和弦:圆上任意两点间的部分叫做圆弧,简称弧。
大于半圆的弧称为优弧,小于半圆的弧称为劣弧。
连接圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
3、圆心角和圆周角:顶点在圆心上的角叫做圆心角。
顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。
4、内心和外心:过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心。
和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心。
5、扇形:在圆上,由两条半径和一段弧围成的图形叫做扇形。
圆锥侧面展开图是一个扇形。
这个扇形的半径成为圆锥的母线。
〖圆和圆的相关量字母表示方法〗圆—⊙半径—r 弧—⌒直径—d 扇形弧长/圆锥母线—l 周长—C 面积—S〖圆和其他图形的位置关系〗圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r。
直线与圆有3种位置关系:无公共点为相离;有两个公共点为相交;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点。
以直线AB与圆O为例(设OP⊥AB于P,则PO是AB到圆心的距离):AB与⊙O相离,PO>r;AB与⊙O相切,PO=r;AB与⊙O相交,PO<r。
小学数学竞赛:圆与扇形(二).学生版解题技巧 培优 易错 难

【例 43】传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有10平方米.每当太阳西下,钟面就会出现奇妙的阴影(如右图).那么,阴影部分的面积是平方米.
【巩固】图中是一个钟表的圆面,图中阴影部分甲与阴影部分乙的面积之比是多少?
【例 22】如图所示, 是一边长为 的正方形, 是 的中点,而 是 的中点.以 为圆心、半径为 的四分之一圆的圆弧交 于 ,以 为圆心、半径为 的四分之一圆的圆弧交 于 点,若图中 和 两块面积之差为 (其中 、 为正整数),请问 之值为何?
【巩固】在图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差.(圆周率取 )
【例 48】将一块边长为 厘米的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,求剪成的正方形铁皮的面积的最大值.
图1图2图3
【例 8】用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?
【例 9】如图,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径都是1.求阴影部分的面积.
【例 10】如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.(圆周率取 )
【例 36】如下图所示,两个相同的正方形,左图中阴影部分是9个圆,右图中阴影部分是16个圆.哪个图中阴影部分的面积大?为什么?
【例 37】如图,在 方格表中,分别以 、 、 为圆心,半径为3、2、1,圆心角都是 的三段圆弧与正方形 的边界围成了两个带形,那么这两个带形的面积之比
【例 38】如图中,正方形的边长是 ,两个顶点正好在圆心上,求图形的总面积是多少?(圆周率取 )
【小学奥数】专题:如何计算圆和扇形组合的图形面积
面积的 2 ,那么这个扇形的圆心角是多少度?
5
解: 因为 S扇形 n
S 360
所以
2 n , 5 360
n 2, 360 5
解得 n=144
答:扇形的圆心角是144度.
二.应数用学举一例百分
例题5 解答题:
※(2)如果扇形的圆心角变为原来的5倍,半
径变为原来的 1/3 ,那么这个扇形的弧长变为
黄颜色部分的面积 R2 r2
R2 r2
数学一百分 三.巩固练习
2.在面积是720平方毫米的圆上,有一个 面积为45平方毫米的同半径的扇形,这个 扇形的圆心角的度数是多少度?
解: S=720平方毫米,S扇形 45 平方毫米, S扇形 = n , 45 = n , n 22.50. S 360 720 360
例题3 (1)圆的直径是4米,周长是多少米?面 积是多少平方米?
解:(1)d=4米,r=2米,
C=πd =3.14×4 =12.56(m) .
S r2 =3.14×4 =12.56(平方米).
答:圆的周长是12.56米,面积是12.56平方米.
数学一百分 二.应用举例
例题3 (2)扇形的半径为3厘米,圆心角为 120°,求扇形的面积及扇形的弧长.
20cm,求扇形的面积?
解:(3)r=6cm, l=20-2×6=8(cm),
S扇形
1 lr 2
1 86 2
24
或 l n r , 6 n 8, nπ=240,
180 180
S扇形
n r2
360
240 36 360
24(平方厘米).
答:扇形的面积为24平方厘米.
数学一百分
二.应用举例
六年级秋季班-第16讲圆和扇形的面积
圆和扇形的面积是六年级数学上学期第四章第二节的内容.本讲主要讲解圆的面积和扇形面积的求解方法,及它们之间的关系;重点是掌握圆的面积和扇形面积的基本计算方法,难点是在不同的图形中根据题目条件灵活解答相关问题.1、圆的面积圆所占平面的大小叫做圆的面积.设圆的半径长为r,面积为S,那么:圆的面积2S r r rππ=⨯=.圆和扇形的面积内容分析知识结构模块一:圆的面积知识精讲例题解析【例1】(1)圆的半径是4厘米,它的面积是______平方厘米;(结果保留π)(2)圆的直径是6米,它的周长是______米,它的面积是______平方米;(π取3.14)(3)圆的周长是25.12分米,它的面积是______平方分米.(π取3.14)【难度】★【答案】【解析】【例2】有大小两个圆,如果大圆半径是小圆半径的3倍,则大圆的周长是小圆的______倍,大圆的面积是小圆的______倍;如果大圆直径是小圆半径的4倍,则小圆面积与大圆面积的比是______.【难度】★【答案】【解析】【例3】有一只羊栓在草地的木柱上,绳子的长度是4米,这只羊最多可以吃到______平方米的草.(π取3.14)【难度】★【答案】【解析】【例4】在一个边长为20厘米的正方形纸板里剪出一个最大的圆,则圆的面积是______平方厘米.(π取3.14)【难度】★【答案】【解析】【例5】用一根长为16分米的铁丝围成一个圆,接头处长为0.3分米,这个圆的面积是多少?(π取3.14)【难度】★★【答案】【解析】【例6】一种铝制面盆是用直径20厘米的圆形铝板冲压而成的,要做100个这样的面盆至少需要铝板______平方米.(π取3.14)【难度】★★【答案】【解析】【例7】周长相等的长方形、正方形和圆,______的面积最大.【难度】★★【答案】【解析】【例8】两个同心圆,大圆半径为5厘米,小圆半径为3厘米,求圆环的面积.(π取3.14)【难度】★★【答案】【解析】【例9】一个圆形喷水池的周长是62.8米,绕着这个水池修一条宽2米的水泥路,求路面的面积.(π取3.14)【难度】★★【答案】【解析】【例10】如图,已知大圆半径是6厘米,那么阴影部分面积占大圆面积的______.(用分数表示)【难度】★★【答案】【解析】【例11】两个圆的面积之和为1991平方厘米,小圆的周长是大圆周长的90%,则大圆的面积是_______平方厘米.(π取3.14)【难度】★★【答案】【解析】【例12】有5块圆形的花圃它们的直径分别是3米、4米、5米、8米、9米,请将这5块花圃分成两组,分别交给两个班级管理,使这两个班级管理的面积尽可能接近.【难度】★★【答案】【解析】【例13】大小两圆的相交部分(如图所示的阴影部分)面积是大圆面积的415,是小圆面积的35,量得小圆的半径是5厘米,问大圆的半径是多少?(π取3.14)【难度】★★★【答案】【解析】【例14】如图,正方形的面积是12平方厘米,求图中阴影部分的面积为多少平方厘米?(π取3.14)【难度】★★★【答案】【解析】【例15】如图中的圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,图中阴影部分的周长是多少厘米?(π取3.14)【难度】★★★【答案】【解析】ABO1、 扇形的概念由组成圆心角的两条半径和圆心角所对的弧围成的图形,叫做扇形. 如图,空白部分记作扇形AOB . 2、 扇形的面积设组成扇形的半径为r ,圆心角为n °,弧长为l ,那么:213602n S r lr π==扇形.【例16】 一个扇形的面积是它所在圆面积的15,这个扇形的圆心角是______.【难度】★ 【答案】 【解析】【例17】 一个扇形的半径是5厘米,圆心角是60°,则此扇形的面积是______平方厘米,周长是______厘米.(π取3.14)【难度】★ 【答案】 【解析】【例18】 已知扇形的弧长是31.4厘米,半径是10厘米,那么扇形的面积是______平方厘米.(π取3.14)【难度】★ 【答案】 【解析】模块二:扇形的面积知识精讲例题解析ABCDEF【例19】 一扇形的半径不变,圆心角扩大为原来的3倍,则面积是原来的______倍;若它的圆心角不变,半径扩大为原来的3倍,则面积是原来的______倍.【难度】★ 【答案】 【解析】【例20】 一个圆心角为60°的扇形,其面积与一个直径为9的圆相等,求此扇形所在圆的面积.(结果保留π)【难度】★★ 【答案】 【解析】【例21】 一个圆心角为45°的扇形,它的周长为11.14厘米,求它的面积.(π取3.14) 【难度】★★ 【答案】 【解析】【例22】 如图,已知正方形边长为2,分别以正方形的两个对角顶点为圆心,以边长为半径作两段圆弧,求阴影部分的面积.(结果保留π)【难度】★★ 【答案】 【解析】【例23】 等腰直角三角形ABC 中,以直角顶点A 为圆心,以高AD 为半径,画一条弧,交AB 、AC 分别于E 、F ,AD = 2厘米,图中阴影部分的面积是______平方厘米. (π取3.14)【难度】★★ 【答案】 【解析】ABCDABCH【例24】 如图,扇形BAC 的面积是半圆ADB 面积的113倍,那么CAB ∠是______度.【难度】★★ 【答案】 【解析】【例25】 如图,三角形为任意三角形,三个圆的半径均为1厘米,则阴影部分的面积为______平方厘米.(π取3.14)【难度】★★ 【答案】 【解析】【例26】 如图,ABC ∆的三条边都是6厘米,高AH 为5.2厘米,分别以A 、B 、C 三点为圆心,6厘米长为半径画弧,求这三段弧围成的图形的面积.(π取3.14)【难度】★★ 【答案】 【解析】【例27】 如图,长方形的宽为5,正好是大扇形半径的一半,求阴影部分的面积.(π取3.14) 【难度】★★ 【答案】 【解析】ABCD【例28】 如图,圆的半径是6厘米,阴影部分的面积是31.5π平方厘米,求图中三角形的面积.【难度】★★★ 【答案】 【解析】【例29】 有一只狗被系在一建筑物的墙角上,这个建筑物是边长6米的等边三角形,绳长是8米.当绳被狗拉紧时,狗活动范围的总面积为多少平方米?(π取3.14)【难度】★★★ 【答案】 【解析】【例30】 已知C 、D 两点在以AB 为直径的半圆周上且把半圆三等分,若已知AB 长为10,求阴影部分的面积.(结果保留π)【难度】★★★ 【答案】 【解析】【习题1】扇形的面积是314平方米,其所在圆的面积是1256平方米,则这个扇形的圆心角为______°.【难度】★【答案】【解析】【习题2】一种手榴弹爆炸后,有效杀伤范围的半径是6米,有效杀伤面积是______平方米.( 取3.14)【难度】★【答案】【解析】【习题3】若一扇形所在的圆心角缩小为原来的12,半径扩大为原来的2倍,则它的面积()A.扩大为原来的2倍B.扩大为原来的4倍C.是原来的12D.不变【难度】★【答案】【解析】【习题4】如果用整个圆来表示班级共有40名学生,那么被评为三好学生的8名同学应该用圆心角为______的扇形来表示.【难度】★★【答案】【解析】随堂检测【习题5】环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积.(π取3.14)【难度】★★【答案】【解析】【习题6】两个圆的面积之差是209平方厘米,已知大圆的周长是小圆的周长的119倍,求小圆的面积.(π取3.14)【难度】★★【答案】【解析】【习题7】一时钟的分针长6分米,从上午9点到上午10点40分,分针扫过的面积是多少平方分米?【难度】★★【答案】【解析】【习题8】如图,正方形的边长为4,求阴影部分的面积.【难度】★★【答案】【解析】【习题9】如图所示的阴影部分分别为三种标点符号:句号、逗号和问号.已知大圆半径为R,小圆半径为r,且R = 2r.哪一个标点符号的面积最小?【难度】★★★【答案】【解析】A B 2 2 【习题10】 如图,A 与B 是两个圆的圆心,那么两个阴影部分的面积相差______平方厘米.(π取3.14)【难度】★★★【答案】【解析】【作业1】 下列判断中,正确的是( )A .半径越大的扇形,面积越大B .所对圆心角越大的扇形,面积越大C .所对圆心角相同时,半径越大的扇形面积越大D .半径相等时,所对圆心角越大的扇形面积越小【难度】★【答案】【解析】【作业2】 圆的半径由6厘米增加到9厘米,圆的面积增加了______平方厘米.(π取3.14)【难度】★【答案】【解析】课后作业【作业3】一个扇形的半径是5厘米,圆心角是72°,这个扇形的周长是______分米.(π取3.14)【难度】★【答案】【解析】【作业4】一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆,还剩下______平方厘米的纸没有用.(π取3.14)【难度】★★【答案】【解析】【作业5】一个扇形的面积是78.5平方厘米,圆心角为36°,当这个扇形的半径不变而圆心角增加了108°以后,这个扇形的面积是______平方厘米.(π取3.14)【难度】★★【答案】【解析】【作业6】某大楼上有一石英制的时钟,已知时针与分针分别长60厘米和80厘米,则时针走1小时,时针与分针扫过的平面的面积差为多少平方分米?(π取3.14)【难度】★★【答案】【解析】【作业7】如图是三个半圆构成的图形,其中小半圆直径为8,中半圆直径为20,则阴影部分面积与大半圆的面积之比是多少?【难度】★★【答案】【解析】红 红 红红 蓝 蓝 蓝 蓝 【作业8】 一辆汽车的车轮直径为1米,试计算当汽车以120千米/时的速度行驶时,车轮的转速是每秒多少周?(3π≈,结果保留整数位)【难度】★★【答案】【解析】【作业9】 如图是对称图形,红色部分的面积大还是蓝色部分的面积大?【难度】★★★【答案】【解析】【作业10】 如图,扇形AOB 为14个圆,半径为4厘米,以它的两条半径为直径,在扇形内部画两个半圆,求阴影部分的面积.【难度】★★★【答案】【解析】。
圆的面积计算与扇形问题

圆与扇形的面积关系
扇形的面积公式:1/2 * πr² * θ
扇形的面积是圆的面积 的一部分,取决于θ的
大小
当θ=180°时,扇形的 面积等于圆的面积的一
半
当θ=45°时,扇形的 面积等于圆的面积的八
分之一
当θ=15°时,扇形的 面积等于圆的面积的三
十二分之一
圆的面积公式:πr²
θ为扇形的圆心角
当θ=360°时,扇形的 面积等于圆的面积
圆与扇形的角度关系
圆心角:圆心与圆周上任意两点所形成的角 扇形角:扇形顶点与圆心所形成的角 扇形面积:扇形角与圆面积的比值 扇形面积公式:S扇形=(1/2)*r^2*θ(θ为扇形角)
圆与扇形的边长关系
圆心角:扇形与圆心之间的角度 半径:圆心到圆周上任意一点的距离 弧长:扇形与圆心之间的弧长 扇形面积:弧长与半径的乘积 圆面积:半径的平方乘以π 扇形与圆的面积关系:扇形面积等于圆面积乘以圆心角的正弦值
当θ=30°时,扇形的 面积等于圆的面积的十
六分之一
当θ=90°时,扇形的 面积等于圆的面积的四
分之一
圆与扇形的周长关系
圆的周长公式:C=2πr
扇形的周长公式:C=2πr+2R
扇形与圆的周长关系:扇形的周长等于圆的周长加上两个半径的长度 扇形与圆的面积关系:扇形的面积等于圆的面积乘以扇形的圆心角与360 度的比值
扇形是圆的一部分,可以用 来表示圆的一部分面积
扇形可以用来表示圆的一部 分弧长
扇形在生活中的应用
扇形在数学中的作用:计算圆 的面积、弧长、角度等
扇形在工程中的应用:建筑设 计、机械制造、电子电路等
扇形在艺术中的应用:绘画、 雕塑、装饰等
扇形在日常生活中的应用:钟 表、风扇、方向盘等
圆面积计算公式范文

圆面积计算公式范文圆的面积是数学中一个基本的概念,它被广泛应用于各个领域,如几何学、物理学和工程学等等。
本文将介绍两种计算圆面积的公式:πr²和½πd²。
公式推导:假设我们有一个圆,它的半径为r。
我们可以将这个圆分割成无数个非常小的扇形。
每个扇形的面积可以用一个三角函数来表示:A=½θr²,其中A表示扇形的面积,θ表示扇形的角度。
当我们将所有扇形的面积相加时,就得到了整个圆的面积。
由于圆的角度是360度,所以可以得到:A=½×360°×r²=180°r²然而,这个公式只适用于角度为度的情况,不适用于弧度。
于是,我们引入三角函数sin(x)和π,这样我们就可以用弧度来度量角度。
根据三角函数,我们有sin(180°) = sin(π) = 0。
所以,我们可以将上述公式简化为:A=0×r²=0因此,最终的圆的面积公式为:A=πr²下面我们来看第二种公式:½πd²。
其中,π仍然表示π无理数,d表示圆的直径。
公式推导:由于圆的直径是圆的半径的两倍,我们可以用半径的两倍来表示直径:d=2r,其中r表示圆的半径。
将该表达式代入圆的面积公式πr²中,我们可以得到:A=π(½d)²=¼πd²这就是计算圆面积的另一种公式。
需要注意的是,这两种公式只适用于平面上的二维圆。
如果你想计算三维圆柱体的表面积,你需要使用不同的公式。
在实际应用中,可以根据需要选择适合的公式进行计算。
例如,在计算圆形花坛的面积时,我们可以使用πr²;而在计算圆形光线的投影面积时,我们可以使用½πd²。
总结起来,计算圆的面积有两个常用公式:πr²和½πd²。
这两个公式可以根据实际情况灵活选择,以达到最准确的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天天学教育学员个性化辅导教案
学生姓名 辅导科目 数学 所在年级 六年级 所在课次 授课教师 付老师
教案编号
教材版本
授课时间
课题名称 圆的面积和扇形的面积
教学重点 教学难点
了解圆及扇形面积计算公式,并会运用公式解决具体问题; 求组合图形的面积.
教学过程 圆和扇形的面积
一、圆的面积:
1.圆是平面上的一种曲线图形,圆心决定圆的位置,半径决定圆的大小。
圆的面积的计算公式是:r
S 2
π
=。
2.解答圆的相关问题,关键在于理解圆的各部分名称和意义,掌握圆的相关计算公式,能够灵活运用和正确计
算。
例1.一个圆形鱼池,周长是47.1米,鱼池的面积是多少平方米?
例2.小丽用4根1m 的绳子围成4个圆、小明用2根2m 的绳子围成2个圆、小杰用1根4m 的绳子围成1个圆;三人围的圆中,谁的面积最大?
例3.一个圆半径增加2米,则周长如何变化?面积如何变化?
例4.有周长相等的正方形、圆,面积大小关系如何? 练习:
1. 求下面图形的面积。
2.草地上有一棵树,把一只羊用绳子拴在树下边,若绳长
3.5米,不算接头长度,这只羊最多可以吃到多少平方米范围的草?
二、扇形的面积:
如图所示,阴影部分的面积就是半径为R,圆心角为n°的扇形面积,显然扇形的面积是它所在圆的面积的一部分,因为圆心角是360°的扇形面积等于圆面积,所以圆心角为1°的扇形面积是,由此得圆心角为n°的扇形面积的计算公式是。
又因为扇形的弧长,扇形面积,所以又得到扇形面积的另一个计算公式:。
例1.扇形半径45mm,圆心角240°,则弧长________周长_________
例2.扇形水池半径3米,周长8.14米,则这个扇形的面积是_________
例3.如图所示,在同心圆中,两圆的半径分别为2,1,∠AOB=120°,则阴影部分的面积是()
A. B. C. D.
三、弓形的面积:
(1)弓形的定义:由弦及其所对的弧(包括劣弧、优弧、半圆)组成的图形叫做弓形。
(2)弓形的周长=弦长+弧长
(3)弓形的面积
如图所示,每个圆中的阴影部分的面积都是一个弓形的面积,从图中可以看出,只要把扇形OAmB的面积和△AOB的面积计算出来,就可以得到弓形AmB的面积。
当弓形所含的弧是劣弧时,如图1所示,
当弓形所含的弧是优弧时,如图2所示,
当弓形所含的弧是半圆时,如图3所示,
注意:
(1)圆周长、弧长、圆面积、扇形面积的计算公式。
圆周长弧长圆面积扇形面积
公
式
(2)扇形与弓形的联系与区别
图
示
面
积
四、组合图形简单计算:
例1、圆环外直径8cm,内直径6cm,圆环的面积?
例2、求阴影部分的面积。
练习:
1.如图,ABCD是一个长方形,两端是两个相等的半圆,求阴影部分的面积。
2.求下面图形阴影部分的面积。
3.一个圆形花圃,在花圃外围铺一条宽2米的水泥路面。
这条水泥路的面积是多少平方米?
4.⑴求下面各环形的面积。
(图中单位:厘米)
⑵求阴影部分的面积。
(图中单位:厘米)
5.求下面扇形的面积。
6.⑴在一个直径为6厘米的圆上剪下一个圆心角是60°的扇形,这个扇形的面积是多少?
⑵求阴影部分的面积。
(图中单位:厘米)
作业:
1、求阴影部分的面积。
(图中单位:厘米)
2、动物园猴山外圈是一个圆形,它的直径是50米,在它的圈外又修一条宽是5米的环形人行道,人行道的面积是多少平方米?
3、有一种冲锋枪有效射程是1200米,如果它在一平面上作60°的扫射,控制面积有多大?
4、有一种环形胶垫,内圈直径为6毫米,外圈直径为10毫米,做500个这样的胶垫共需要多少平方厘米的胶皮?
5、在一个长是10厘米,宽是8厘米的长方形铁皮上剪一个最大的圆,圆的面积是多少?
6、求组合图形的面积。
(图中单位:厘米)
7、求阴影部分的面积。
(图中单位:厘米)
8、右图是个半圆(图中单位:厘米),其阴影部分的周长是多少?
9、山羊妈妈在一块空旷的地上开垦种植了三块大小相同的圆形草地,它们的半径都是4米(如图)。
有一天山羊妈妈外出有事,为防止小山羊们走失,也为了给小山羊们有一片空地活动,就在三个圆之间围成一个三角形的栅栏.。
那么小山羊们可吃的草地面积是多少呢?
教
学
总
结
学员评价优秀□良好□一般□差□
下
次
课
安
排。
