八年级数学正方形

合集下载

八年级数学正方形知识点

八年级数学正方形知识点下面是八年级数学正方形的知识点。

一、正方形的定义及性质正方形是指四边相等，且四个角均为直角的四边形。

其性质如下：1.四条边相等。

2.四个角均为直角，即90度。

3.对角线相等且互相垂直。

4.具有对称性。

二、正方形的周长和面积公式1.正方形的周长公式为：4a（a为正方形的边长）。

2.正方形的面积公式为：a²。

三、正方形的刻画1.正方形可以用一组点的坐标表示：(x,y)，(x,y+a)，(x+a,y+a)，(x+a,y)，其中a为正方形的边长。

2.正方形可以用对角线的长度表示：d=√2a，其中d为正方形的对角线长度。

四、正方形的相关题型1.求正方形的周长和面积：根据公式计算即可。

2.求正方形的对角线长度：根据公式d=√2a计算即可。

3.已知正方形一个顶点的坐标和正方形的边长，求正方形的其它顶点的坐标：通过正方形的刻画，可以求出其它顶点的坐标。

4.已知正方形的周长，求正方形的面积：由周长公式4a可知，a=周长/4，再带入面积公式a²中即可求解。

五、正方形与其它图形的关系1.正方形是菱形、矩形、平行四边形的特殊情况。

2.正方形可以分成两个等面积的直角三角形。

3.正方形可以作为一个正方体的一个面。

六、例题1.已知正方形的对角线长为10cm，求其面积。

解：正方形对角线长度公式为d=√2a，将d=10cm代入可得a=5√2cm，进而计算出面积为25cm²。

2.正方形周长为16m，求其面积。

解：由周长公式可知a=周长/4=4m，带入面积公式得出面积为16m²。

以上就是八年级数学正方形知识点的相关内容，希望能对大家的学习有所帮助。

八年级数学正方形判定

Ａ
Ｄ
Ａ`
D`
O
B`
C`
Ｂ
Ｃ
正方形ＡＢＣＤ中，对角线AC和BD交于点O，点Ａ`，Ｂ`，Ｃ`，Ｄ`分别在AC、BD上，且ＡＡ`＝ＢＢ`=ＣＣ`＝ＤＤ`. 判断四边形Ａ`Ｂ`Ｃ`Ｄ`的形状
ＡＡ`
Ｄ D`
O
Ｂ B`
C` Ｃ
练习：矩形ABCD中，四个内角的平分线组成四边形EMFN，判断四边形EMFN的形状,并说明原因
（填上一个条件即可）
矩形
平行四边形
有一Байду номын сангаас邻边相等有一个角是直角
正方形
菱形
判断对错
1. 四边相等的四边形是正方形 2．四角相等的四边形是正方形 3．对角线垂直的平行四边形是正方形 4．对角线互相垂直平分且相等的四边形是正方形 5．四条边相等且有一个角是直角的四边形是正方形
练习：在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线)
A
E
F
B
D
C
例：在正方形ＡＢＣＤ中，点Ａ`，Ｂ`，Ｃ`，Ｄ`分别是ＡＢ，ＢＣ，ＣＤ，ＤＡ的中点，四边形Ａ`Ｂ`Ｃ`Ｄ`是正方形吗？为什么？
Ａ
D`
A
D
N
E B
F
M
C
；希爱力双效片必利劲万艾可希爱力双效片必利劲万艾可；
急火燎地挂上电筒,然后拔通梅林客栈の订餐热线.这点小事都办不好,难怪被甩,哎...第129部分悠闲の午后,充满生活气息の办公地点,香味四溢.“...你倒选了一个好地

人教版八年级数学下册18.2.3正方形性质(教案)

4.提高合作交流能力，学会倾听、表达、协作，形成良好的学习习惯；
5.激发对数学几何图形的兴趣，培养数学审美和学科素养。
三、教学难点与重点
1.教学重点
-正方形的定义及特征：确保学生理解正方形是一种特殊的矩形，具有四条边相等、四个角都是直角的特点。
-正方形的性质：强调正方形四条边相等、四个角都是直角、对角线互相垂直平分且相等的核心性质。
4.正方形对角线与边长的关系，即对角线将正方形平分成长度为边长一半的小正方形；
5.运用正方形性质解决实际问题。
二、核心素养目标
1.理解并掌握正方形的定义、性质及判定定理，提高空间观念和几何直观能力；
2.能够运用正方形性质解决实际问题，增强数学应用意识和问题解决能力；
3.通过探索正方形性质，培养推理能力和逻辑思维能力；
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解正方形的基本概念。正方形是四条边相等、四个角都是直角的特殊平行四边形。它在几何图形中具有重要地位，广泛应用于日常生活和建筑等领域。
2.案例分析：接下来，我们来看一个具体的案例。通过观察正方形的实物模型，分析其性质和特点。
3.重点难点解析：在讲授过程中，我会特别强调正方形的性质和判定定理这两个重点。对于难点部分，如对角线性质，我会通过举例和图形演示来帮助大家理解。
人教版八年级数学下册18.2.3正方形性质（教案）
一、教学内容
人教版八年级数学下册18.2.3正方形性质。本节课我们将学习以下内容：
1.正方形的定义及特征；
2.正方形的性质，包括四条边相等、四个角都是直角、对角线互相垂直平分且相等；
3.正方形的判定定理，即有一组邻边相等且一个角是直角的平行四边形是正方形；
（四）学生小组讨论（用时10分钟）

八年级数学正方形的性质及判定复习

正方形的性质及判定复习1、如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE∥BD，过点D作ED∥AC，两线相交于点E。

（1）求证：四边形AODE是菱形；（2）连接BE，交AC于点F，若BE⊥ED于点E，求∠AOD的度数。

2、已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD。

（1）求证：四边形AODE是矩形；（2）若AB＝4，∠BCD＝120°，求四边形AODE的面积。

知识点一正方形的性质、判定【知识梳理】1、定义：有一组邻边并且有一角是的形叫做正方形。

2、性质：①正方形的四个角都是，四条边都。

②正方形的两条对角线，并且互相，每条对角线。

3、判定：①的矩形是正方形。

②的菱形是正方形。

③两条对角线，且互相垂直平分的四边形是正方形。

④两条对角线相等，且互相垂直的平行四边形是正方形。

4、面积：①正方形面积＝边长的平方 S＝a×a（S表示正方形的面积，a表示正方形的边长）②对角线乘积的一半5、周长：正方形周长＝边长×4 用“a”表示正方形的边长，“C”表示正方形的周长，则C＝4a。

【例题精讲】例1.1、如图，正方形ABCD的面积为1，则以相邻两边中点连线EF为边的正方形EFGH的周长为。

（第1题）（第2题）2、如图，在正方形ABCD中，E、F分别是边BC、CD上的点，∠EAF＝45°，正方形ABCD的边长为3，则△ECF的周长为。

3、如图，正方形ABCD的边长为7，点E、F分别在AB、BC上，AE＝3，CF＝1，P是对角线AC上的动点，则PE＋PF的最小值。

（第3题）（第4题）4、如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，当PD＋PE的值最小时，PD＝。

【课堂练习】1、如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH。

若BE：EC＝2：1，则线段CH的长是。

人教版八年级数学下册正方形知识点及同步练习、含答案

学科：数学教学内容：正方形【学习目标】1．掌握正方形的定义、性质和判定方法．2．能正确区别平行四边形、矩形、菱形、正方形之间的关系． 3．能运用正方形的性质和判定方法进行有关的计算和证明．【主体知识归纳】1．正方形：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．2．正方形的性质：正方形除具有平行四边形、矩形、菱形的一切性质外，还具有：（1）正方形的四个角都是直角，四条边都相等；（2）正方形的两条对角线相等并且互相垂直平分，每条对角线平分一组对角． 3．正方形的判定（1）根据正方形的定义；（2）有一组邻边相等的矩形是正方形；（3）有一个角是直角的菱形是正方形；（4）既是矩形又是菱形的四边形是正方形．【基础知识精讲】1．掌握正方形定义是学好本节的关键，正方形是在平行四边形的前提下定义的，它包含两层意思：正方形矩形平行四边形并且有一个角是直角的菱形四边形有一组邻边相等的平行⎭⎬⎫)()2()()1(正方形不仅是特殊的平行四边形，而且是特殊的矩形，又是特殊的菱形．2．正方形的性质可归纳如下：边：对边平行，四边相等；角：四个角都是直角；对角线：对角线相等，互相垂直平分，每条对角线平分一组对角．此外：正方形的一条对角线把正方形分成两个全等的等腰直角三角形，对角线与边的夹角是45°；正方形的两条对角线把它分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴，学习时，应熟悉这些最基本的内容．【例题精讲】［例1］如图4－50，已知矩形ABCD 中，F 为CD 的中点，在BC 上有一点E ，使AE ＝DC ＋CE ，AF 平分∠EAD ．求证：矩形ABCD 是正方形．图4—50剖析：欲证矩形ABCD是正方形，只要证明有一组邻边相等即可，由已知AE＝DC＋CE，容易想到若能证明AE＝AD＋CE便可证得AD＝DC，由于AF平分∠EAD，因此可在AE上截取AG＝AD，再证GE＝CE，就可得出要证的结论．证明：在AE上截取AG＝AD，连结FG、FE．∵四边形ABCD是矩形，∴∠D＝∠C＝90°．∵AD＝AG，∠DAF＝∠GAF，AF＝AF∴△ADF≌△AGF，∴DF＝GF，∠D＝∠AGF＝90°．∵DF＝CF，∴GF＝CF．∵∠FGE＝∠C＝90°，FE＝FE，∴Rt△GFE≌Rt△CFE．∴GE＝CE，∴AD＋CE＝AE．又DC＋CE＝AE，∴AD＝DC．∴矩形ABCD是正方形．说明：要判定一个四边形是正方形，可先判定这个四边形是矩形，再证明有一组邻边相等；或先判定它是菱形，再证明有一个角是直角．［例2］如图4－51，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，过点A作AG⊥EB，垂足为G，AG交BD于点F，则OE＝OF．图4—51对上述命题的证明如下：∵四边形ABCD是正方形，∴∠BOE＝∠AOF＝90°，BO＝AO．∴∠3＋∠2＝90°，∵AG⊥BE，∴∠1＋∠3＝90°．∴∠1＝∠2，∴△BOE≌△AOF，∴OE＝OF问题：对于上述命题，若点E在AC延长线上，AG⊥EB，交EB的延长线于G，AG的延长线交DB的延长线于点F，其他条件不变（如图4－52），结论“OE＝OF”还成立吗?如果成立，请给出证明；如果不成立，请说明理由．图4—52剖析：可仿上述的证明，证△BOE≌△AOF．解：结论OE＝OF仍然成立，证明如下：∵四边形ABCD是正方形，∴∠BOE＝∠AOF＝90°，BO＝AO，∴∠OFA＋∠FAE＝90°又∵AG⊥EB，∴∠OEB＋∠EAF＝90°，∴∠OEB＝∠OFA，∴△BOE≌△AOF，∴OE＝OF．［例3］有一正方形池塘，池塘四个角上有四棵树，现计划把此池塘改为面积扩大一倍的正方形，能否不毁掉树木而达到要求？请你设计出方案来．图4—53剖析：新改造的池塘的面积是原面积的2倍，因此，新边长应为原边长的2倍，而正方形的对角线是边长的2倍，故以原对角线的长为边长构造新的正方形．答案：如图4－53，分别过B、D作AC的平行线，分别过A、C作BD的平行线，四条线分别交于A′、B′、C′、D′，则四边形A′B′C′D′为要求的正方形．【同步达纲练习】1．选择题（1）下列命题中，假命题的个数是（）①四边都相等的四边形是正方形②对角线互相垂直的平行四边形是正方形③四角都相等的四边形是正方形④对角线相等的菱形是正方形A．1 B．2 C．3 D．4（2）正方形具有而菱形不具有的性质是（）A．对角线互相垂直平分B．对角线相等C．邻边相等D．每条对角线平分一组对角（3）正方形的对角线与边长之比为（）A．1∶1 B．2∶1 C．1∶2 D．2∶1（4）以等边△ABC的边BC为边向外作正方形BCDE，则①∠ABD＝105°，②∠ACD＝150°，③∠DAE＝30°，④△ABE≌△ACD，其中正确的结论有（）A．1个 B．2个 C．3个 D．4个（5）在正方形ABCD中，P、Q、R、S分别在边AB、BC、CD、DA上，且AP＝BQ＝CR＝DS ＝1，AB＝5，那么四边形PQRS的面积等于（）A．17 B．16 C．15 D．9（6）如图4－54，正方形ABCD中，O是对角线AC、BD的交点，过O点作OE⊥OF分别交AB、BC于E、F，若AE＝4，CF＝3，则EF等于（）图4—54A．7 B．5 C．4 D．3（7）在正方形ABCD中，E、F两点分别是BC、CD边上的点，若△AEF是边长为2的等边三角形，则正方形ABCD的边长为（）A．213+B．213-C．3 D．2（8）如图4－55，在正方形ABCD中，CE＝MN，∠MCE＝35°，那么∠ANM等于（）图4—55A．45°B．55°C．65°D．75°2．填空题（1）已知正方形的面积是16 cm2，则它的一边长是_____，一条对角线长是_____．（2）已知正方形的对角线长为22，则此正方形的周长为_____，面积为_____．（3）在正方形ABCD 中，两条对角线相交于O ，∠BAC 的平分线交BD 于E ，若正方形ABCD 的周长是16 cm ，则DE ＝_____cm ．（4）在正方形ABCD 的边BC 的延长线上取一点E ，使CE ＝AC ，连结AE 交CD 于F ，那么∠AFC 等于_____度．3．如图4－56，已知正方形ABCD 中，E 为CD 边上一点，F 为BC 延长线上一点，且CE ＝CF ．图4—56（1）求证：△BCE ≌△DCF ；（2）若∠BEC ＝60°，求∠EFD 的度数．4．已知：如图4－57，在正方形ABCD 中，E 是CB 延长线上一点，EB ＝21BC ，如果F 是AB 的中点，请你在正方形ABCD 上找一点，与F 点连结成线段，并证明它和AE 相等．图4—575．以△ABC 的AB 、AC 为边，向三角形外作正方形ABDE 及ACGF ，作AN ⊥BC 于点N ，延长NA 交EF 于M 点．（1）求证：EM ＝FM ；（2）若使AM ＝21EF ，则△ABC 必须满足什么条件呢？图4—586．如图4－58，已知正方形ABCD 中，M 、F 分别在边AB 、AD 上，且MB ＝FD ，E 是AB 延长线上一点，MN ⊥DM ，MN 与∠CBE 的平分线相交于N ．求证：DM ＝MN ．7．如图4－59，已知C是线段AB上的一点，分别以AC、BC为边作正方形ACDE和BCFG．图4—59求证：AF＝DB；若点C在线段AB的延长线上，猜想上述结论是否正确，如果正确，请加以证明，如果不正确，请说明理由．【思路拓展题】你会设计吗今有一片正方形土地，要在其上修筑两条笔直的道路，使道路把这片地分成形状相同且面积相等的4部分，若道路的宽度忽略不计，请设计三种不同的修筑方案．（在给出如图4－60的三张正方形纸片上分别画图，并简述画图步骤）图4—60参考答案【同步达纲练习】1．（1）C （2）B （3）B （4）D （5）A （6）B （7）A（8）B2．（1）4 42（2）8 4 （3）4 （4）112.53．（1）略（2）15°4．连结CF，可证△ABE≌△CBF或连结DF，让△ABE≌△DAF。

人教版八年级数学下册第十八章《正方形》优课件(共17张PPT)

（１）ＡＢ＝ＡＤ；
A
（２）ＡＣ＝ＢＤ；
（３） ∠ＢＡＤ＝９０；
（４）ＡＣ⊥ＢＤ。
B
D O
C
判断对错
1. 四边相等的四边形是正方形 2．四角相等的四边形是正方形 3．四条边相等且有一个角是直角的四边形是正方形 4．对角线互相垂直平分且相等的四边形是正方形 5．对角线垂直的平行四边形是正方形
判断对错
6.对角线互相垂直且相等的四边形是正方形。 7.对角线互相垂直的矩形是正方形。 8.对角线相等的菱形是正方形。
活动
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
3.昨天,我去超市买了一条方巾，现在想请同学们帮助检验一下方巾是否是正方形的。
1.已知:正例方形题AB解CD中析,点E、F、G 、H
正方形
菱形
这一样个的人人所才受有的学教问育。超
过了自己的智力，
You made my day!
我们，还在路上……
每一条对角线平分一组对角
对称性---- 是轴对称图形．
D O
C
根据图形所具有的性质,在下表相应的空格中打 ”√”
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
平行四边形
√
√
矩形
√
√ √
√
菱形
√ √
√ √
正方形
√ √ √ √ √ √
你觉得什么样的四边形是正方形呢?
分别是AB 、BC 、CD 、DA的中点,试判断四
边形EFGH是正方形吗?为什么?

八年级数学特殊的平行四边形——正方形人教实验版知识精讲

初二数学特殊的平行四边形——正方形人教实验版【本讲教育信息】一、教学内容：特殊的平行四边形——正方形1. 掌握正方形的定义，弄清楚正方形和平行四边形、矩形、菱形的关系.2. 掌握正方形的性质和判定方法.二、知识要点： 1. 正方形（1）定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形. （2）正方形的性质：正方形具有平行四边形、矩形和菱形的所有性质. ①正方形各边的性质：四条边相等，对边平行. ②正方形各角的性质：四个角都是直角.③正方形对角线的性质：正方形的对角线互相平分、互相垂直、相等，且每一条对角线平分一组对角.④正方形的对称性：正方形是轴对称图形，对边中点所在直线和对角线所在直线都是正方形的对称轴.B（3）正方形的识别：①有一组邻边相等的矩形是正方形； ②对角线互相垂直的矩形是正方形； ③一个内角是直角的菱形是正方形； ④对角线相等的菱形是正方形；⑤有一组邻边相等且互相垂直的平行四边形是正方形； ⑥对角线相等且互相垂直的平行四边形是正方形. 2. 平行四边形、矩形、菱形、正方形之间的关系平行四边形三、重点难点：本讲重点是正方形的性质，难点是平行四边形、矩形、菱形、正方形之间的共性，特性及从属关系.【典型例题】例1. 如图所示，已知正方形ABCD ，点E 是AB 延长线上一点，连结EC ，作AG ⊥EC 于G ，AG 交BC 于F ，求证：AF ＝CE.ABC DEFG分析：AF 、CE 分别在R t △ABF 与R t △CBE 中，可考虑证明它们全等，而四边形ABCD 为正方形，有相等的直角和相等的边，为证全等提供了条件.证明：因为四边形ABCD 是正方形，所以AB ＝BC ，∠ABC ＝∠CBE ＝90°. 因为AG ⊥CE ，所以∠CGF ＝90°，所以∠BCE ＋∠CFG ＝90°，∠BCE ＋∠E ＝90°，所以∠CFG ＝∠E ，又因为∠CFG ＝∠AFB ，所以∠E ＝∠AFB.所以△ABF ≌△CBE （SAS ）. 所以AF ＝CE.例2. 把一X 矩形纸片像图中那样折一下，再沿CD 剪下，则纸片ABCD 是什么样的四边形？说明理由.分析：根据矩形的性质和图形折叠前后的变化规律判断四边形ABCD 的形状. 解：正方形. 理由如下：因为这是一X 矩形纸片，所以∠BAD ＝∠B ＝90°. △ADC 是△ABC 折叠得到的，即△ABC ≌△ADC. 所以∠ADC ＝∠B ＝90°，所以四边形ABCD 是矩形. 又AB ＝AD ，所以纸片ABCD 是正方形.例3. 如图所示，E 是正方形ABCD 的对角线BD 上一点，EF ⊥BC ，EG ⊥CD ，垂足分别是F 、G. 试说明AE ＝FG .A BC DEFG分析：由EF ⊥BC ，EG ⊥CD 可得矩形EFCG ，则FG ＝EC ，再证△ABE ≌△CBE ，得AE ＝EC ，即可得到AE ＝FG .解：连结EC ，因为四边形ABCD 是正方形， EF ⊥BC ，EG ⊥CD ，所以四边形EFCG 为矩形. 所以FG ＝CE.因为BD 是正方形ABCD 的对角线. 所以∠ABE ＝∠CBE. 又BE ＝BE ，AB ＝CB ，所以△ABE ≌△CBE. 所以AE ＝EC ，所以AE ＝FG .评析：用CE 沟通AE 和FG 之间的联系.例4. （1）下列命题中正确的是（）A. 两条对角线互相平分的四边形是平行四边形B. 两条对角线相等的四边形是矩形C. 两条对角线互相垂直的四边形是菱形D. 两条对角线互相垂直且平分的四边形是正方形（2）如图所示，菱形ABCD 中，对角线AC 、BD 相交于点O ，若再补充一个条件能使菱形ABCD 成为正方形，则这个条件是__________（只填一个条件即可）.A DC BO第(2)题（3）如图所示，在四边形ABCD 中，AD ∥BC ，∠D ＝90°，若再添加一个条件，就能推出四边形ABCD 是矩形，你所添加的条件是__________. （写出一种情况即可）AB CD分析：（1）这个问题可以这样考虑：对角线互相平分的四边形是平行四边形；对角线互相平分且相等的四边形是矩形；对角线互相垂直平分的四边形是菱形；对角线互相垂直平分且相等的四边形是正方形. 故选A. （2）这个问题实际上是问什么样的菱形是正方形？有一个角是直角的菱形是正方形，对角线相等的菱形是正方形，考虑角可补充的条件是∠BAD ＝90°或AD ⊥AB ；考虑对角线补充：AC ＝BD. （3）本题应考虑和角相关的矩形的识别方法，有一个角是直角的平行四边形是矩形；有三个角是直角的四边形是矩形. 可添加的条件是∠A ＝90°或∠B ＝90°，AD ＝BC ，AB ∥CD 等.解：（1）A （2）∠BAD ＝90°（或AD ⊥AB ，AC ＝BD 等）（3）∠A ＝90°或AD ＝BC 或AB ∥CD例5. 如图所示，正方形ABCD ，对角线AC 、BD 相交于点O ，菱形AEFC ，EH ⊥AC ，垂足为H ，求证：EH ＝12FC.ABC E FHDO分析：要证EH ＝12FC ，EH 在矩形OBEH 中，得EH ＝OB ＝12BD ，而FC 是菱形AEFC的边，CF ＝AC ＝BD ，所以EH ＝12FC ，问题的关键是要证四边形OBEH 是矩形.证明：由正方形ABCD 得AC ＝BD ，AC ⊥BD ，∠BOC ＝90°. 又因为EH ⊥AC ，所以EH ∥OB.又因为四边形AEFC 是菱形，得AC ＝CF ，AC ∥EF ，所以OH ∥BE. 因此四边形OBEH 是矩形，因此EH ＝OB ＝12BD ＝12AC ＝12FC.评析：综合考查了正方形、菱形的性质和矩形的判定方法.【方法总结】正方形是特殊的平行四边形，是特殊的矩形，是特殊的菱形. 它具有平行四边形、矩形、菱形的所有性质. 分清楚这几种图形的从属关系，从关系图中确定它们性质的相同点和不同点.平行四边形矩形菱形正方形【模拟试题】（答题时间：60分钟）一. 选择题1. 下列选项中，正方形具有而矩形不一定具有的性质是（）A. 四边都相等B. 四角都相等C. 对角线相等D. 对角线互相平分 2. 正方形的对角线长为a ，则它的对角线的交点到各边的距离是（）A. 22aB. 24aC. a 2D. 22a3. 正方形是轴对称图形，那么它的对称轴的条数为（）A. 2B. 3C. 4D. 54. 在四边形ABCD 中，O 是对角线的交点，能判定这个四边形是正方形的条件是（） A. AC ＝BD ，AB ∥CD B. AD ∥BC ，∠A ＝∠CC. AO ＝BO ＝CO ＝DO ，AC ⊥BDD. AO ＝CO ，BO ＝DO ，AB ＝BC 5. 下列命题中，真命题是（） A. 两条对角线相等的四边形是矩形 B. 两条对角线互相垂直的四边形是菱形C. 两条对角线互相垂直且相等的四边形是正方形D. 两条对角线互相平分的四边形是平行四边形6. 已知四边形ABCD 中，∠A ＝∠B ＝∠C ＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（）A. ∠D ＝90°B. AB ＝CDC. AD ＝BCD. BC ＝CD*7. 如图1所示，将长为20cm ，宽为2cm 的长方形白纸条，折成图2所示的图形并在其一面着色，则着色部分的面积为（）A. 34cm 2B. 36cm 2C. 38cm 2D. 40cm 2图1二. 填空题1. 具有平行四边形、矩形和菱形性质的四边形是__________.2. 已知正方形ABCD 的对角线AC 、BD 相交于点O ，且AC ＝12cm ，•则BO ＝__________cm ，•∠OAB ＝__________度.3. 任意一个平行四边形，当它的一个锐角增大到_______度时，就变成了矩形；•当它的一组邻边变到_______时，就变成了菱形；当它的两条对角线变到______时，就变成了正方形.4. 矩形、菱形、正方形都是特殊的四边形，它们具有很多共性，如：__________（填一条即可）.5. 正方形的面积为49，则它的边长为__________，对角线长为__________.*6. 如图所示，在正方形ABCD 中，E 是BD 上一点，过E 作EF ⊥BC 于F ，EG ⊥CD 于G ，若正方形ABCD 的周长是a ，则四边形EFCG 的周长为__________.ABCDEF G**7. 如图所示，正方形ABCD 的边长为4，E 为BC 上的一点，BE ＝1，F 为AB 上的一点，AF ＝2，P 为AC 上的一动点，则当PF ＋PE 为最小值时，PF ＋PE ＝__________.ABC DPEF三. 解答题 1. 如图，正方形ABCD 的对角线AC 、BD 相交于点O ，OE ＝OF ，求证：•∠OCF ＝∠OBE.ABCDE FO2. 如图所示，在△ABC 中，∠C ＝90°，CD 平分∠ACB ，DE ⊥BC ，DF ⊥AC ，垂足分别为点E 、F. 求证：四边形CFDE 是正方形.ABC DEF*3. 如图所示，点E 、F 分别为正方形ABCD 边AB 、BC 的中点，DF 、CE 交于点M ，CE 的延长线交DA 的延长线于G ，试探索：（1）DF 与CE 的位置关系；（2）MA 与DG 的大小关系.ABCDE F MG**4. 如图，四边形ABCD 是正方形，G 是BC 上任意一点（点G 与B 、C 不重合），AE ⊥DG 于E ，CF ∥AE 交DG 于F.（1）在图中找出一对全等三角形，并加以证明；（2）求证：AE ＝FC+EF.ABCDE FG【试题答案】一. 选择题1. A2. B3. C4. C5. D6. D7. B二. 填空题1. 正方形2. 6，453. 90，相等，垂直且相等4. 对边平行、对角线互相平分、对角相等等 5. 7，7 2 6. 12a 7. 17三. 解答题1. 提示：证明△OCF ≌△OBE 可得2. 先证四边形DECF 是矩形，又∵DE ＝DF ，∴四边形CFDE 是正方形3. （1）DF ⊥CE 提示：先证△EBC ≌△FCD ，得∠ECB ＝∠FDC ，根据互余的关系，•求出∠CMF ＝90°即可. （2）由△GAE ≌△CBE 得GA ＝CB ，再根据直角三角形斜边上中线的性质，得MA ＝12DG .4. （1）ΔAED ≌ΔDFC. 因为四边形ABCD 是正方形，所以 AD ＝DC ，∠ADC ＝90°. 又因为 AE ⊥DG ，CF ∥AE ，所以 ∠AED ＝∠DFC ＝90°，所以 ∠EAD ＋∠ADE ＝∠FDC ＋∠ADE ＝90°，所以 ∠EAD ＝∠FDC. 所以 ΔAED ≌ΔDFC （AAS ）.（2）因为 ΔAED ≌ΔDFC ，所以 AE ＝DF ，ED ＝FC. 因为 DF ＝DE ＋EF ，所以 AE ＝FC ＋EF.。

八年级数学正方形的定义和性质华东师大版知识精讲

初二数学正方形的定义和性质华东师大版【本讲教育信息】一. 教学内容：正方形的定义和性质二. 重点、难点：1. 重点：正方形的定义和性质2. 难点：正方形的性质正方形的定义三. 知识梳理：正方形（square）是我们早就熟悉的平面图形，如图，在正方形ABCD中，四条边都相等，四个角都是直角．所以正方形可以看作为：有一个角是直角的菱形；有一组邻边相等的矩形．正方形是中心对称图形，也是轴对称图形．这样，正方形具有以下的性质：正方形的性质：有一个角是直角的菱形正方形的性质：有一组邻边相等的矩形其他图形所具有的性质，正方形都具有。

这样，我们还可以列出正方形所具有的一些性质：正方形的定义：一个内角恰好为直角的平行四边形。

正方形的性质：两组对边分别平行。

正方形的性质：正方形对角线互相平分正方形的性质：正方形的对边相等正方形的性质：正方形的对角相等．正方形的性质：正方形的四个内角都是直角．正方形的性质：正方形的对角线相等且互相平分．正方形还有许多有趣的性质．例如，如果要用给定长度的篱笆围成一个最大面积的四边形区域，那么应当把这区域的形状选成正方形．【典型例题】例1. 如图，在正方形ABCD 中，求∠ABD、∠DAC、∠DOC的度数．分析：运用正方形的定义和性质进行解题：解：由于正方形是一个角为直角的菱形，每一条对角线平分一组对角，且对角线互相垂直平分，∴∠ABD＝∠DAC＝90°×1/2＝45°，∠DOC＝90°．例2. 如图，已知正方形ABCD的边AB长2cm，求这个正方形的周长。

分析：运用正方形的定义和性质进行解题：解：正方形ABCD的边AB长2cm即正方形ABCD的周长等于8cm．例3. 如图，已知正方形ABCD的边AB长2cm，求这个正方形的对角线长．分析：运用正方形的定义和性质进行解题：解：在正方形ABCD中，AB＝2＝BC，2AC＝2例4. 如图，在正方形ABCD的边长BC的延长线上取一点E，使CE＝CA，AE与CD交于F，则∠AFC＝（）度分析：运用正方形的定义和性质进行解题：解：在正方形ABCD中，∠AFC＝°例5. 已知如图，正方形ABCD的对角线交于O点，EF∥AB且分别交AC，BD于E，F，BE＝3cm，求CF的长。

初中八年级数学重点学习课件：正方形(知识点串讲)(解析版)

专题10 正方形知识网络重难突破一. 正方形的性质正方形：有一组邻边相等，且有一个角是直角的平行四边形叫做正方形. 如图：正方形ABCD.正方形除了具有平行四边形的所有性质外，还具有矩形和菱形的所有性质，如下：①正方形的对边平行且相等；（AB∥CD，AB=CD；BC∥AD，BC=AD）②正方形的四条边都相等；（AB=BC=CD=AD）③正方形的四个角都是直角；（∠BAD=∠ADC=∠DCB=∠CBA=90°）④正方形的两条对角线相等，互相垂直平分，并且每一条对角线平分一组对角；（AC=BD，AC⊥BD，OA=OB=OC=OD，AC是∠DAB和∠DCB的角平分线，BD是∠ADC和∠CBA的角平分线）⑤对称性：正方形是一个轴对称图形，它有四条对称轴.（对称轴是它对边中点的连线和它的两条对角线所在的直线（AC，BD））典例1．（2018春•随县期末）已知：如图，在正方形ABCD外取一点E，连接AE，BE，DE，过点A作AE的垂线交DE于点P．若AE＝AP＝1，PB．下列结论：①△APD≌△AEB；②点B到直线AE的距离为；③EB⊥ED；④S△APD+S△APB＝1．其中正确结论的序号是（）A．①②③B．①②④C．②③④D．①③④【答案】A【解析】解：①∵∠EAB+∠BAP＝90°，∠PAD+∠BAP＝90°，∴∠EAB＝∠PAD，又∵AE＝AP，AB＝AD，∵在△APD和△AEB中，，∴△APD≌△AEB（SAS）；故此选项成立；③∵△APD≌△AEB，∴∠APD＝∠AEB，∵∠AEB＝∠AEP+∠BEP，∠APD＝∠AEP+∠PAE，∴∠BEP＝∠PAE＝90°，∴EB⊥ED；故此选项成立；②过B作BF⊥AE，交AE的延长线于F，∵AE＝AP，∠EAP＝90°，∴∠AEP＝∠APE＝45°，又∵③中EB⊥ED，BF⊥AF，∴∠FEB＝∠FBE＝45°，又∵BE，∴BF＝EF，故此选项正确；④如图，连接BD，在Rt△AEP中，∵AE＝AP＝1，∴EP，又∵PB，∴BE，∵△APD≌△AEB，∴PD＝BE，∴S△ABP+S△ADP＝S△ABD﹣S△BDP S正方形ABCD DP×BE（4）．故此选项不正确．综上可知其中正确结论的序号是①②③，故选：A．【点睛】①利用同角的余角相等，易得∠EAB＝∠PAD，再结合已知条件利用SAS可证两三角形全等；②过B作BF⊥AE，交AE的延长线于F，利用③中的∠BEP＝90°，利用勾股定理可求BE，结合△AEP是等腰直角三角形，可证△BEF是等腰直角三角形，再利用勾股定理可求EF、BF；③利用①中的全等，可得∠APD＝∠AEB，结合三角形的外角的性质，易得∠BEP＝90°，即可证；④连接BD，求出△ABD的面积，然后减去△BDP的面积即可．典例2．（2018春•宿松县期末）如图，正方形ABCD的边长为2，MN∥BC分别交AB、CD于点M、N，在MN上任取两点P、Q，那么图中阴影部分的面积是___．【答案】2【解析】解：由图知，阴影部分的面积等于正方形的面积减去△AQD和△BCP的面积．而点P到BC的距离与点Q到AD的距离的和等于正方形的边长，即△AQD和△BCP的面积的和等于正方形的面积的一半，故阴影部分的面积22＝2．故答案为：2．【点睛】阴影部分的面积等于正方形的面积减去△AQD和△BCP的面积和．而两个三角形等底即为正方形的边长，它们的高的和等于正方形的边长，得出阴影部分的面积＝正方形面积的一半即可．本题考查正方形的性质，正方形的面积，三角形的面积公式灵活运用，注意图形的特点．典例3．（2018春•长清区期末）如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去…记正方形ABCD的边为a1＝1，按上述方法所作的正方形的边长依次为a2、a3、a4、…a n，根据以上规律写出的表达式_______．【答案】2n﹣1【解析】解：∵a2＝AC，且在直角△ABC中，AB2+BC2＝AC2，∴a2a1，同理a3a2＝2，a4a3＝2，…由此可知：a n＝（）n﹣1，则2n﹣1．故答案为：2n﹣1．【点睛】求a2的长即AC的长，根据直角△ABC中AB2+BC2＝AC2可以计算，同理计算a3、a4．由求出的a2a1，a3a2…，a n，a n﹣1＝（）n﹣1，可以找出规律，得到第n个正方形边长的表达式．本题考查了正方形的性质，以及勾股定理在直角三角形中的运用，考查了学生找规律的能力，本题中找到a n的规律是解题的关键．典例4．（2018春•东城区期末）正方形ABCD中，点P是边CD上的任意一点，连接BP，O为BP的中点，作PE⊥BD于E，连接EO，AE．（1）若∠PBC＝α，求∠POE的大小（用含α的式子表示）；（2）用等式表示线段AE与BP之间的数量关系，并证明．【答案】见解析【解析】解：（1）在正方形ABCD中，BC＝DC，∠C＝90°，∴∠DBC＝∠CDB＝45°，∵∠PBC＝α，∴∠DBP＝45°﹣α，∵PE⊥BD，且O为BP的中点，∴EO＝BO，∴∠EBO＝∠BEO，∴∠EOP＝∠EBO+∠BEO＝90°﹣2 α；（2）连接OC，EC，在正方形ABCD中，AB＝BC，∠ABD＝∠CBD，BE＝BE，∴△ABE≌△CBE，∴AE＝CE，在Rt△BPC中，O为BP的中点，∴CO＝BO，∴∠OBC＝∠OCB，∴∠COP＝2 α，由（1）知∠EOP＝90°﹣2α，∴∠EOC＝∠COP+∠EOP＝90°，又由（1）知BO＝EO，∴EO＝CO．∴△EOC是等腰直角三角形，∴EO2+OC2＝EC2，∴EC OC，即BP，∴BP．【点睛】（1）先根据正方形的性质得：∠DBC＝∠CDB＝45°，则∠DBP＝45°﹣α，根据直角三角形斜边中线的性质可得EO＝BO，由等腰三角形性质和外角的性质可得结论；（2）作辅助线，证明△ABE≌△CBE，则AE＝CE，根据直角三角形斜边中线的性质得：OC＝OB＝OP ＝OE，证明△EOC是等腰直角三角形，最后由勾股定理可得：BP，所以BP．本题考查正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识，第（2）问有难度，作辅助线，构建全等三角形和等腰直角三角形是解决问题的关键．典例5．（2018春•永康市期末）如图，点A是x轴上的一个动点，点C在y轴上，以AC为对角线画正方形ABCD，已知点C的坐标是C（0，4），设点A的坐标为A（n，0）．（1）当n＝2时，正方形ABCD的边长AB＝_______．（2）连结OD，当OD时，n＝_____．【答案】见解析【解析】解：（1）当n＝2时，OA＝2，在Rt△COA中，AC2＝CO2+AO2＝20．∵ABCD为正方形，∴AB＝CB．∴AC2＝AB2+CB2＝2AB2＝20，∴AB．故答案为：．（2）如图所示：过点D作DM⊥y轴，DN⊥x轴．∵ABCD为正方形，∴A、B、C、D四点共圆，∠DAC＝45°．又∵∠COA＝90°，∴点O也在这个圆上，∴∠COD＝∠CAD＝45°．又∵OD，∴DN＝DM＝1．∴D（﹣1，1）．在Rt△DNA和Rt△DMC中，DC＝AD，DM＝DN，∴△DNA≌△DMC．∴CM＝AN＝OC﹣MO＝3．∵D（﹣1，1），∴A（2，0）．∴n＝2．如下图所示：过点D作DM⊥y轴，DN⊥x轴．∵ABCD为正方形，∴A、B、C、D四点共圆，∠DAC＝45°．又∵∠COA＝90°，∴点O也在这个圆上，∴∠AOD＝∠ACD＝45°．又∵OD，∴DN＝DM＝1．∴D（1，﹣1）．同理：△DNA≌△DMC，则AN＝CM＝5．∴OA＝ON+AN＝1+5＝6．∴A（6，0）．∴n＝6．综上所述，n的值为2或6．故答案为：2或6．【点睛】（1）在Rt△AOC中，利用勾股定理求出AC的长度，然后再求得正方形的边长即可；（2）先求得OD与y轴的夹角为45°，然后依据OD的长，可求得点D的坐标，过点D作DM⊥y轴，DN⊥x轴，接下来，再证明△DNA≌△DMC，从而可得到CM＝AN，从而可得到点A的坐标．本题主要考查的是正方形的性质、全等三角形的性质、四点共圆，证得OD与两坐标轴的夹角为45°是解题的关键．典例6．（2018春•鹿泉区期末）如图（1），正方形ABCD的对角线AC，BD相交于点O，E是AC上一点，连结EB，过点A作AM⊥BE，垂足为M，AM与BD相交于点F．（1）求证：OE＝OF；（2）如图2若点E在AC的延长线上，AM⊥BE于点M，AM交DB的延长线于点F，其他条件不变，结论“OE＝OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由．【答案】见解析【解析】证明：（1）∵四边形ABCD是正方形．∴∠BOE＝∠AOF＝90°，OB＝OA．又∵AM⊥BE，∴∠MEA+∠MAE＝90°＝∠AFO+∠MAE，∴∠MEA＝∠AFO．在△BOE和△AOF中，∵，∴△BOE≌△AOF．∴OE＝OF．（2）OE＝OF成立．∵四边形ABCD是正方形，∴∠BOE＝∠AOF＝90°，OB＝OA．又∵AM⊥BE，∴∠F+∠MBF＝90°，∠E+∠OBE＝90°，又∵∠MBF＝∠OBE，∴∠F＝∠E．在△BOE和△AOF中，∵，∴△BOE≌△AOF．∴OE＝OF．【点睛】（1）根据正方形的性质对角线垂直且平分，得到OB＝OA，又因为AM⊥BE，所以∠MEA+∠MAE＝90°＝∠AFO+∠MAE，从而求证出Rt△BOE≌Rt△AOF，得到OE＝OF．（2）根据第一步得到的结果以及正方形的性质得到OB＝OA，再根据已知条件求证出Rt△BOE≌Rt△AOF，得到OE＝OF．本题主要考查正方形的性质和全等三角形的判定与性质，将待求线段放到两个三角形中，通过证明三角形全等得到对应边相等是解题的关键．典例7．（2018春•梁山县期末）以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE，连接EB、FD，交点为G．（1）当四边形ABCD为正方形时（如图1），EB和FD的数量关系是_______；（2）当四边形ABCD为矩形时（如图2），EB和FD具有怎样的数量关系？请加以证明；（3）四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请说明理由；如果不变，请在图3中求出∠EGD的度数．【答案】见解析【解析】（1）EB＝FD，理由如下：∵四边形ABCD为正方形，∴AB＝AD，∵以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE，∴AF＝AE，∠FAB＝∠EAD＝60°，∵∠FAD＝∠BAD+∠FAB＝90°+60°＝150°，∠BAE＝∠BAD+∠EAD＝90°+60°＝150°，∴∠FAD＝∠BAE，在△AFD和△ABE中，，∴△AFD≌△ABE，∴EB＝FD；（2）EB＝FD．证：∵△AFB为等边三角形∴AF＝AB，∠FAB＝60°∵△ADE为等边三角形，∴AD＝AE，∠EAD＝60°∴∠FAB+∠BAD＝∠EAD+∠BAD，即∠FAD＝∠BAE∴△FAD≌△BAE∴EB＝FD；（3）解：同（2）易证：△FAD≌△BAE，∴∠AEB＝∠ADF，设∠AEB为x°，则∠ADF也为x°于是有∠BED为（60﹣x）°，∠EDF为（60+x）°，∴∠EGD＝180°﹣∠BED﹣∠EDF＝180°﹣（60﹣x）°﹣（60+x）°＝60°．【点睛】（1）EB＝FD，利用正方形的性质、等边三角形的性质和全等三角形的证明方法可证明△AFD ≌△ABE，由全等三角形的性质即可得到EB＝FD；（2）当四边形ABCD为矩形时，EB和FD仍旧相等，证明的思路同（1）；（3）四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD不发生变化，是一定值，为60°．本题考查了正方形的性质、全等三角形的判定和性质、等边三角形的性质以及矩形的性质，题目的综合性很强，难度也不小，解题的关键是对特殊几何图形的性质要准确掌握．二. 正方形的判定正方形的判定方法：①有一组邻边相等的矩形是正方形；②有一个角是直角的菱形是正方形.典例1．（2018春•宿豫区期末）在平行四边形ABCD中，对角线AC与BD相交于点O．要使四边形ABCD 是正方形，还需添加一组条件．下面给出了五组条件：①AB＝AD，且AC＝BD；②AB⊥AD，且AC ⊥BD；③AB⊥AD，且AB＝AD；④AB＝BD，且AB⊥BD；⑤OB＝OC，且OB⊥OC．其中正确的是________（填写序号）．【答案】①②③⑤【解析】解：∵四边形ABCD是平行四边形，AB＝AD，∴四边形ABCD是菱形，又∵AC＝BD，∴四边形ABCD是正方形，①正确；∵四边形ABCD是平行四边形，AB⊥AD，∴四边形ABCD是矩形，又∵AC⊥BD，∴四边形ABCD是正方形，②正确；∵四边形ABCD是平行四边形，AB⊥AD，∴四边形ABCD是矩形，又∵AB＝AD，∴四边形ABCD是正方形，③正确；④AB＝BD，且AB⊥BD，无法得出四边形ABCD是正方形，故④错误；∵四边形ABCD是平行四边形，OB＝OC，∴四边形ABCD是矩形，又∵OB⊥OC，∴四边形ABCD是正方形，⑤正确；故答案为：①②③⑤．典例2 ．（2018春•浦东新区期末）已知：如图，在等边三角形ABC中，过边AB上一点D作DE⊥BC，垂足为点E，过边AC上一点G作GF⊥BC，垂足为点F，BE＝CF，联结DG．（1）求证：四边形DEFG是平行四边形；（2）连接AF，当∠BAF＝3∠FAC时，求证：四边形DEFG是正方形．【答案】见解析【解析】证明：（1）在等边三角形ABC中，∵DE⊥BC，GF⊥BC，∴∠DEF＝∠GFC＝90°，∴DE∥GF，∵∠B＝∠C＝60°，BE＝CF，∠DEB＝∠GFC＝90°，∴△BDE≌△CGF，∴DE＝GF，∴四边形DEFG是平行四边形；（2）在平行四边形DEFG中，∵∠DEF＝90°，∴平行四边形DEFG是矩形，∵∠BAC＝60°，∠BAF＝3∠FAC，∴∠GAF＝15°，在△CGF中，∵∠C＝60°，∠GFC＝90°，∴∠CGF＝30°，∴∠GFA＝15°，∴∠GAF＝∠GFA，∴GA＝GF，∵DG∥BC，∴∠ADG＝∠B＝60°，∴△DAG是等边三角形，∴GA＝GD，∴GD＝GF，∴矩形DEFG是正方形．【点睛】（1）根据等边三角形的性质和平行四边形的判定证明即可；（2）根据等边三角形的判定和性质以及正方形的判定解答即可．此题考查正方形的判定，关键是根据全等三角形的判定和性质以及正方形的判定解答．典例3．（2017秋•南海区期末）如图，以△ABC的各边，在边BC的同侧分别作三个正方形ABDI，BCFE，ACHG．（1）求证：△BDE≌△BAC；（2）求证：四边形ADEG是平行四边形．（3）直接回答下面两个问题，不必证明：①当△ABC满足什么条件时，四边形ADEG是矩形？②当△ABC满足什么条件时，四边形ADEG是正方形？【答案】见解析【解析】解析：（1）证明：∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形，∴AC＝AG，AB＝BD，BC＝BE，∠GAC＝∠EBC＝∠DBA＝90°．∴∠ABC＝∠EBD（同为∠EBA的余角）．在△BDE和△BAC中，，∴△BDE≌△BAC（SAS），（2）∵△BDE≌△BAC，∴DE＝AC＝AG，∠BAC＝∠BDE．∵AD是正方形ABDI的对角线，∴∠BDA＝∠BAD＝45°．∵∠EDA＝∠BDE﹣∠BDA＝∠BDE﹣45°，∠DAG＝360°﹣∠GAC﹣∠BAC﹣∠BAD＝360°﹣90°﹣∠BAC﹣45°＝225°﹣∠BAC∴∠EDA+∠DAG＝∠BDE﹣45°+225°﹣∠BAC＝180°∴DE∥AG，∴四边形ADEG是平行四边形（一组对边平行且相等）．（3）①当四边形ADEG是矩形时，∠DAG＝90°．则∠BAC＝360°﹣∠BAD﹣∠DAG﹣∠GAC＝360°﹣45°﹣90°﹣90°＝135°，即当∠BAC＝135°时，平行四边形ADEG是矩形；②当四边形ADEG是正方形时，∠DAG＝90°，且AG＝AD．由①知，当∠DAG＝90°时，∠BAC＝135°．∵四边形ABDI是正方形，∴AD AB．又∵四边形ACHG是正方形，∴AC＝AG，∴AC AB．∴当∠BAC＝135°且AC AB时，四边形ADEG是正方形．【点睛】（1）根据全等三角形的判定定理SAS证得△BDE≌△BAC，（2）由△BDE≌△BAC，可得全等三角形的对应边DE＝AG．然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG＝180°，易证ED∥GA；最后由“一组对边平行且相等”的判定定理证得结论；（3）①根据“矩形的内角都是直角”易证∠DAG＝90°．然后由周角的定义求得∠BAC＝135°；②由“正方形的内角都是直角，四条边都相等”易证∠DAG＝90°，且AG＝AD．由□ABDI和□ACHG 的性质证得，AC AB．巩固练习1．（2018春•琼中县期末）如图，在正方形ABCD的边BC的延长线上取一点E，使CE＝AC，连接AE交CD于F，则∠AFC等于（）A．112.5°B．120°C．135°D．145°【答案】A【解析】解：∵四边形ABCD为正方形，∴∠ACD＝90°，∴∠DCE＝90°，又∵AC是正方形ABCD的对角线，∴∠ACF＝45°，∴∠ACE＝∠DCE+∠ACF＝135°，∵CE＝CA，∴∠FAC＝∠E（180°﹣135°）＝22.5°∴∠AFD＝∠FAC+∠ACF＝22.5°+45°＝67.5°，∴∠AFC＝180°﹣67.5°＝112.5°，故选：A．2．（2018春•花都区期末）如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（）A．B．C．D．2【答案】A【解析】解：连接AC、CF，如图，∵四边形ABCD和四边形CEFG都是正方形，∴∠ACD＝45°，FCG＝45°，AC BC，CF CE＝3，∴∠ACF＝45°+45°＝90°，在Rt△ACF中，AF2，∵H是AF的中点，∴CH AF．故选：A．3．（2018春•济南期末）如图，P为边长为2的正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF，给出以下4个结论：①AP＝EF；②AP⊥EF；③EF最短长度为；④若∠BAP＝30°时，则EF的长度为2．其中结论正确的有（）A．①②③B．①②C．②③④D．①③④【答案】B【解析】解：①如图，连接PC，∵四边形ABCD为正方形，∴AB＝BC，∠ABP＝∠CBP＝45°，在△ABP和△CBP中，∴△ABP≌△CBP（SAS），∴AP＝PC，∵PE⊥BC，PF⊥CD，且∠FCE＝90°，∴四边形PECF为矩形，∴PC＝EF，∴AP＝EF，故①正确；②延长AP交BC于点G，由①可得∠PCE＝∠PFE＝∠BAP，∵PE∥AB，∴∠EPG＝∠BAP，∴∠EPG＝∠PFE，∵∠EPF＝90°，∴∠EPG+∠PEF＝∠PEG+∠PFE＝90°，∴AP⊥EF，故②正确；③当AP⊥BD时，AP有最小值，此时P为BD的中点，由①可知EF＝AP，∴EF的最短长度为，故③错误；④当点P在点B或点D位置时，AP＝AB＝2，∴EF＝AP≤2，∴当∠BAP＝30°时，AP＜2，即EF的长度不可能为2，故④错误；综上可知正确的结论为①②．故选：B．4．（2018春•苍南县期末）如图，点B在线段AC上，且BC＝2AB，点D，E分别是AB，BC的中点，分别以AB，DE，BC为边，在线段AC同侧作三个正方形，得到三个平行四边形（阴影部分）．其面积分别记作S1，S2，S3，若S1+S3＝15，则S2＝___．【答案】6【解析】解：设DB＝x，则S1＝x2，S2＝x×2x＝2x2，S3＝2x×2x＝4x2．由题意得，S1+S3＝15，即x2+4x2＝15，解得x2＝3，所以S2＝2x2＝6，故答案为：6．5．（2018春•丰台区期末）菱形ABCD中，对角线AC，BD相交于点O，请你添加一个条件，使得菱形ABCD 成为正方形，这个条件可以是_______________________．（写出一种情况即可）【答案】AC＝BD（或∠ABC＝90°）【解析】解：根据对角线相等的菱形是正方形，可添加：AC＝BD；根据有一个角是直角的菱形是正方形，可添加的：∠ABC＝90°；故添加的条件为：AC＝BD或∠ABC＝90°．故答案为AC＝BD（或∠ABC＝90°）6．（2018秋•普宁市期末）如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去第n个正方形的边长为____．【答案】（）n﹣1【解析】解：∵四边形ABCD为正方形，∴AB＝BC＝1，∠B＝90°，∴AC2＝12+12，AC同理可得：AE＝（）2，AG＝（）3…，∴第n个正方形的边长a n＝（）n﹣1．故答案为（）n﹣1．7．（2018春•惠山区期末）如图，正方形ABCD的边长为2，顶点A在y轴上，顶点B在x轴上，则OD 的最大值是___．【答案】1【解析】解：取AB的中点K，连接OK、DK．根据直角三角形斜边上的中线等于斜边的一半可得OK＝1，再根据正方形的性质可得DK，∵OK+DK＞OD，∴当O、K、D三点共线时OD最长，∴OD的最大值为1，故答案为：1．8．（2018春•洛宁县期末）如图，在△ABC中，∠ACB＝90°，四边形ABDE、AGFC都是正方形．求证：BG＝EC．【答案】见解析【解析】证明：∵四边形ABDE，AGFC都是正方形，∴AE＝AB，AC＝AG，∠EAB＝∠CAG＝90°.∵∠EAC+∠CAB＝∠EAB＝90°，∠GAB+∠CAB＝90°，∴∠EAC＝∠BAG，在△EAC和△BAG中，∴△EAC≌△BAG（SAS），∴BG＝CE．9．（2018春•庆云县期末）探究：如图，分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE，NC、BE交于点P．求证：∠ANC＝∠ABE．应用：Q是线段BC的中点，若BC＝6，则PQ的长度是多少？【答案】见解析【解析】证明：∵四边形ANMB和ACDE是正方形，∴AN＝AB，AC＝AE，∠NAB＝∠CAE＝90°，∵∠NAC＝∠NAB+∠BAC，∠BAE＝∠BAC+∠CAE，∴∠NAC＝∠BAE，在△ANC和△ABE中，ANAN＝AB，∠NAC＝∠BAE，AC＝AE ∴△ANC≌△ABE（SAS），∴∠ANC＝∠ABE．解：如图所示：∵四边形NABM是正方形，∴∠NAB＝90°，∴∠ANC+∠AON＝90°，∵∠BOP＝∠AON，∠ANC＝∠ABE，∴∠ABP+∠BOP＝90°，∴∠BPC＝∠ABP+∠BOP＝90°，∵Q为BC中点，BC＝6，∴PQ BC＝3．10．（2018春•徐州期末）已知：如图，在正方形ABCD中，点E、F、G分别在AB、AD、CD上，AB＝6，AE＝2，DG＞AE，BF＝EG，BF与EG交于点P．（1）求证：BF⊥EG；（2）连接DP，则DP的最小值为____．【答案】见解析【解析】（1）证明：如图1，过点E作EM⊥CD于M，交BF于点N，∵四边形ABCD是正方形，∴AB＝AD，∠A＝∠D＝∠DME＝90°，∴四边形ADME是矩形，∴EM＝AD＝AB，∵BF＝EG，∴Rt△BAF≌Rt△EMG（HL），∴∠ABF＝∠MEG，在Rt△BEN中，∵∠ABF+∠ENB＝90°，∴∠MEG+∠ENB＝90°，∴∠EPF＝90°，∴BF⊥EG；（2）如图2，取BE的中点O，连接OP、OD，∵△EPB是直角三角形，∴OP BE，∵AB＝6，AE＝2，∴BE＝6﹣2＝4，OB＝OE＝2，∵OD﹣OP≤DP，∴当O、P、D共线时，DP有最小值，如图3，∵PO2，∴OD2，∴PD＝22，即DP的最小值为22；故答案为：22；11．（2018春•平定县期末）如图，已知正方形ABCD，P是对角线AC上任意一点，PM⊥AD，PN⊥AB，垂足分别为点M和N，PE⊥PB交AD于点E．（1）求证：四边形MANP是正方形；（2）求证：EM＝BN．【答案】见解析【解析】证明：（1）∵四边形ABCD是正方形，∴∠DAB＝90°，AC平分∠DAB，∵PM⊥AD，PN⊥AB，∴∠PMA＝∠PNA＝90°，∴四边形MANP是矩形，∵AC平分∠DAB，PM⊥AD，PN⊥AB，∴PM＝PN，（3分）∴四边形MANP是正方形；（2）∵四边形ABCD是正方形，∴PM＝PN，∠MPN＝90°，∵∠EPB＝90°，∴∠MPE+∠EPN＝∠NPB+∠EPN＝90°，∴∠MPE＝∠NPB，在△EPM和△BPN中，∵，∴△EPM≌△BPN（ASA），∴EM＝BN．12．（2018春•秦淮区期末）如图，在矩形ABCD中，Q是BC的中点，P是AD上一点，连接PB、PC，E、F分别是PB、PC的中点，连接QE、QF．（1）求证：四边形PEQF是平行四边形．（2）①当点P在什么位置时，四边形PEQF是菱形？证明你的结论；②矩形ABCD的边AB和AD满足什么条件时，①中的菱形PEQF是正方形？（直接写出结论，不需要说明理由）【答案】见解析【解析】解：（1）证明：在△PBC中，E、F分别是PB、PC的中点，Q是BC的中点，∴QE、QF为△PBC的中位线，∴QE∥PF，QF∥PE，∴四边形PEQF是平行四边形；（2）①当点P为AD的中点时，四边形PEQF是菱形，理由是：当P为AD的中点时，AP＝PD，由勾股定理得：PB，PC，∵四边形ABCD是矩形，∴AB＝CD，∴PB＝PC，∵E、F分别是PB、PC的中点，∴PE＝PF，由（1）知：四边形PEQF是平行四边形，∴四边形PEQF是菱形；②矩形ABCD的边AB和AD满足AD＝2AB时，①中的菱形PEQF是正方形，理由是：∵AD＝2AB，AD＝2AP，∴AB＝AP，∴△ABP是等腰直角三角形，∴∠APB＝45°，同理可得∠CPD＝45°，∴∠EPF＝90°，∴①中的菱形PEQF是正方形．。

八年级数学下正方形定义性质与判定

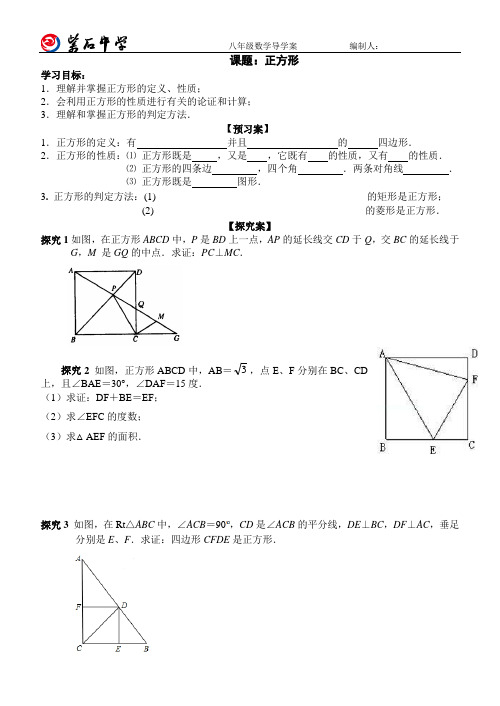
八年级数学导学案编制人：课题：正方形学习目标：1．理解并掌握正方形的定义、性质；2．会利用正方形的性质进行有关的论证和计算；3．理解和掌握正方形的判定方法．【预习案】1．正方形的定义：有并且的四边形．2．正方形的性质：⑴正方形既是，又是，它既有的性质，又有的性质．⑵正方形的四条边，四个角．两条对角线．⑶正方形既是图形．3. 正方形的判定方法：(1)__________________________________________的矩形是正方形；(2)__________________________________________的菱形是正方形．【探究案】探究1如图，在正方形ABCD中，P是BD上一点，AP的延长线交CD于Q，交BC的延长线于G，M 是GQ的中点．求证：PC⊥MC．探究2如图，正方形ABCD中，AB＝3，点E、F分别在BC、CD上，且∠BAE＝30°，∠DAF＝15度．（1）求证：DF＋BE＝EF；（2）求∠EFC的度数；（3）求△AEF的面积．探究3 如图，在Rt△ABC中，∠ACB＝90，CD是∠ACB的平分线，DE⊥BC，DF⊥AC，垂足分别是E、F．求证：四边形CFDE是正方形．八年级数学导学案编制人：F E P D C B A 探究4 如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，垂足为D ，AN 是△ABC 外角∠CAM 的平分线，CE ⊥AN ，垂足为E ．（1）求证：四边形ADCE 是矩形；（2）当AD 与BC 满足什么数量关系时，四边形ADCE 是正方形？并给出证明．【训练案】1．下列条件中，能判定四边形是正方形的有（）．A ．4个角都是直角B ．对角线互相平分且垂直C ．对角线相等且互相平分D ．对角线相等、互相垂直，且互相平分2．下列条件中，不能判定四边形是正方形的是（）．A ．对角线互相垂直且相等的四边形B ．一条对角线平分一组对角的矩形C ．对角线相等的菱形D ．对角线互相垂直的矩形3．如图，将一块边长为12的正方形纸片ABCD 的顶点A 折叠至DC 边上的点E ，使DE =5，折痕为PQ ，则PQ 的长为_______．4．如图，将边长为8cm 的正方形纸片ABCD 折叠，使点D 落在BC 边中点E 处，点A 落在点F处，折痕为MN ，则线段CN 的长是（）A ．3cmB ．4cmC ．5cmD ．6cm5．如图,边长为3的正方形ABCD 绕点C 按顺时针方向旋转30 °后得到正方形EFCG ,EF 交AD 于点H ,那么DH 的长为________. 6．如图，点P 是正方形ABCD 的对角线BD 上一点，PE ⊥BC 于点E ，PF ⊥CD 于点F ，连接EF 给出下列五个结论：①AP =EF ；②AP ⊥EF ；③△APD 一定是等腰三角形；④∠PFE =∠BAP ；⑤PD = 2EC ．其中正确结论的序号是．。

人教版初中八年级下册数学课件《正方形》课件

1
1
01 探究
现在，你对正方形有哪些新的认识？正方形的四条边都相等，四个角都是直角，它既是矩形又是菱形，既具有矩形的性质，又有菱形的性质
矩形正方形
菱形
01 知识回顾
怎样判定一个平行四边形是正方形？怎样判定一个矩形是正方形？怎样判定一个菱形是正方形？
平行四边形
矩形菱形
正方形
01 知识回顾
O
B
C
02
练一练
LEARNING OBJECTIVES
02 练一练
1．如图，正方形ABCD中，对角线AC， BD相交于点O，则图中的等腰三角形有（）
C
A、4个 C、8个
B、6个 D、10个
02 练一练
2．如图，在正方形ABCD的外侧，作等边三角形ADE，
连接BE，则∠AEB的度数为__1__5_°.
定义性质逆向猜想判定
01 知识回顾
在小学，什么样的四边形是正方形？正方形与矩形和菱形分别有什么关系？四个角都是直角，四条边都相等的四边形叫做正方形．你能用一张矩形纸片，折出一个最大的正方形吗？
说说折出的四边形是正方形的依据．
01 知识回顾
如图，某一拉门在完全关闭时，其相应的菱形变成正方形．请说说图中∠1的变化过程．
第十八章平行四边形正方形
CHAPTER
18
SECTION
03
SQUARE
目录 CONTENS
01
学习目标 LEARNING OBJECTIVES
1、理解正方形与平行四边形、矩形、菱形概念之间的联系和区别； 2、能用正方形的定义、性质和判定进行推理与计算．
02
重点A KEY

八年级下册数学—正方形的性质和判定

八年级数学—正方形的性质和应用正方形的性质：正方形同时具备平行四边形，矩形，菱形的所有性质。

①正方形四个角都是直角②四条边都相等③对角线互相垂直平分④每一条对角线平分一组对角⑤正方形是轴对称图形，有四条对称轴。

正方形的判定：同时满足菱形和矩形的判定即可。

常用判定有：①先证菱形后证一个角是直角②先证矩形后证一组邻边相等基础篇：例一、已知四边形ABCD是平行四边形，再从①AB=BC②∠ABC=90°③AC=BD④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，下列选法错误的是（）A、①②B、②③C、①③D、②④例二、如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形。

（1）求证：四边形ABCD是菱形；（2）若∠AED=2∠EAD，求证：四边形ABCD是正方形。

例三、如图，在正方形ABCD中，点P，Q是CD边上的两点，且DP=CQ，过D作DG⊥AP于H，分别交AC、BC于E、G，AP，EQ的延长线相交于R。

（1）求证：DP=CG；（2）判断△PQR的形状，并说明理由例四、如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。

（1）求证：CE=CF；（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？提高篇：例五、如图，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB、EA，延长BE交边AD于点F。

（1）求证：△ADE≌△BCE；（2）求∠AFB的度数。

变式练习1：如图，在正方形ABCD 中，AC 为对角线，E 为AC 上一点，连接EB 、ED 。

（1）求证：△BEC ≌△DEC（2）延长BE 交AD 于F ，当∠BED=120°时，求∠EFD 的度数。

例六、如图，正方形ABCD 中，点E 、F 分别在边BC 、CD 上，且AE=EF=FA 。

八年级数学教案《正方形》【优秀4篇】

八年级数学教案《正方形》【优秀4篇】八年级数学教案《正方形》篇一课题：4.6 正方形（一）教学目的：使学生掌握正方形的定义、性质和判定，会用正方形的概念和性质进行有关的论证和计算，理解正方形与平行四边形、矩形、菱形的内在联系和区别，进一步加深对“特殊与一般的认识”教学重点：正方形的定义。

教学难点：正方形与矩形、菱形间的关系。

教学方法：双边合作如：在教学时可播放转换动画使学生获得生动、形象的可视思维过程，从而掌握判定一个四边形是正方形的方法。

为了活跃学生的思维，可以得出下列问题让学生思考：（1）对角线相等的菱形是正方形吗？为什么？（2）对角线互相垂直的矩形是正方形吗？为什么？（3）对角线垂直且相等的四边形是正方形吗？为什么？如果不是，应该加上什么条件？（4）能说“四条边都相等的四边形是正方形”吗？为什么？（5）说“四个角相等的四边形是正方形”，对吗？教学过程：让学生将事先准备好的矩形纸片，按要求对折一下，裁出正方形纸片。

问：所得的图形是矩形吗？它与一般的矩形有什么不同？所得的图形是菱形吗？它与一般的菱形有什么不同？所得的图形在小学里学习时称它为什么图形？它有什么特点？由此得出正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。

（一）新课由正方形的定义可以得知：正方形是有一组邻边相等的矩形，又是有一个角是直角的菱形，因此正方形具有矩形的性质，同时又具有菱形的性质。

请同学们推断出正方形具有哪些性质？性质１、（１）正方形的四个角都是直角。

（２）正方形的四条边相等。

性质２、（１）正方形的两条对角线相等。

（２）正方形的两条对角线互相垂直平分。

（３）正方形的每条对角线平分一组对角。

例1求证：正方形的两条对角线把正方形分成四个全等的等腰直角三角形。

已知：四边形ABCD是正方形，对角线AC、BD相交于点O。

求证：△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形。

证明：△四边形ABCD是正方形，△AC=BD，AC△BD，AO=CO=BO=DO（正方形的两条对角线相等，并且互相垂直平分）。