角平分线和全等三角形证明分类
构造全等三角形的四种技巧

构造全等三角形的四种技巧在几何学中,全等三角形是一个非常重要的概念。
全等三角形是指两个或两个以上的三角形,它们的形状和大小完全相同。
理解并能够构造全等三角形,对于解决各种几何问题有着至关重要的作用。
以下是构造全等三角形的四种技巧:利用公理:全等三角形的公理是:如果两个三角形的三边对应相等,那么这两个三角形全等。
这个公理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后根据这些边长画出两个三角形。
这两个三角形的形状和大小将会完全相同。
利用角平分线:角平分线定理指出,一个角的平分线将对应的边分为两段,这两段与角的两边形成的两个小三角形是全等的。
通过这个定理,你可以通过一个角的平分线,构造出一个全等三角形。
利用中垂线:中垂线定理指出,一条中垂线将一个线段分为两段,这两段与线段的两端形成的两个小三角形是全等的。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后通过中垂线将这些边分为两段。
这样,你就可以得到两个全等的三角形。
利用平行线:平行线定理指出,如果两条平行线被第三条直线所截,那么截得的对应线段成比例。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后在两条平行线上画出对应的线段。
由于这些线段成比例,因此它们形成的两个小三角形是相似的。
如果这些相似三角形的对应边长度相等,那么它们就是全等的。
以上就是构造全等三角形的四种技巧。
理解和掌握这些技巧,对于解决各种几何问题有着重要的作用。
已知两个三角形全等,则它们对应边上的高也________;对应角平分线也________;对应边上的中线也________。
两个直角三角形全等,除了用定义外,还可以用以下________判定。
已知三角形ABC全等三角形DEF,且AB=18cm,BC=20cm,CA=15cm,则DE=________cm,DF=________cm,EF=________cm.做衣服需要依据身体部位的大小来选择布料,而教学则需要依据学生原有的知识基础来选择教学方法。
(完整版)利用角平分线构造全等三角形

善于构造 活用性质安徽 张雷几何问题中,若出现角平分线这一条件时,可联想角平分线的特性,灵活利用角平分线的特性来解决问题.1.显“距离”, 用性质很多时候,题意中只给角平分线这个条件,图上并没有出现“距离”,而角平分线性质的运用又离不开这个“距离”,所以同学们应大胆地让“距离”现身(过角平分线上的一点向角的两边作垂线段)例:三角形的三条角平分线交于一点,你知道这是为什么吗? 分析:我们知道两条直线是交于一点的,因此可以想办法证明第三条角平分线通过前两条角平分线的交点.已知:如图,△ABC 的角平分线AD 与BE 交于点I ,求证:点I 在∠ACB 的平分线上. 证明:过点I 作IH ⊥AB 、IG ⊥AC 、IF ⊥BC ,垂足分别是点H 、G 、F . ∵点I 在∠BAC 的角平分线AD 上,且IH ⊥AB 、IG ⊥AC ∴IH=IG (角平分线上的点到角的两边距离相等) 同理 IH=IF ∴IG=IF (等量代换) 又IG ⊥AC 、IF ⊥BC∴点I 在∠ACB 的平分线上(到一个角的两边的距离相等的点,在这个角的平分线上).即:三角形的三条角平分线交于一点.【例2】已知:如图,PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线,•它们交于点P ,PD ⊥BM 于D ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.【分析】要证BP 为∠MBN 的平分线,只需证PD=PF ,而PA 、PC 为外角平分线,•故可过P 作PE ⊥AC 于E .根据角平分线性质定理有PD=PE ,PF=PE ,则有PD=PF ,故问题得证.【证明】过P 作PE ⊥AC 于E .∵PA 、PC 分别为∠MAC 与∠NCA 的平分线.且PD ⊥BM ,PF ⊥BN ∴PD=PE ,PF=PE,∴PD=PF又∵PD ⊥BM ,PF ⊥BN,∴点P 在∠MBN 的平分线上,D C A EHI F G2DCBA35EF14即BP是∠MBN的平分线.2.构距离,造全等有角平分线时常过角平分线上的点向角两边引垂线,根据角平分线上的点到角两边距离相等,可构造处相应的全等三角形而巧妙解决问题.例3.△ABC中,∠C=90°,AC=BC,DA平分∠CAB交BC于D点,问能否在AB•上确定一点E使△BDE的周长等于AB的长.请说明理由.解:过D作DE⊥AB,交AB于E点,则E点即可满足要求.因为∠C=90°,AC=BC,又DE⊥AB,∴DE=EB.∵AD平分∠CAB且CD⊥AC、ED⊥AB,∴CD=DE.由“HL”可证Rt△ACD≌Rt△AED.∴AC=AE.∴L△BDE=BD+DE+EB =BD+DC+EB =BC+EB=AC+EB =AE+EB =AB.例4.如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB.求证:AD=CD+AB.证明:过M作ME⊥AD,交AD于E.∵DM平分∠ADC,∠C=90°.MC=ME.根据“HL”可以证得Rt△MCD≌Rt△MED,∴CD=ED.同理可得AB=AE.∴CD+AB=ED+AE=AD.即AD=CD+AB.3.巧翻折, 造全等以角平分线为对称轴,构造两三角形全等.即在角两边截取相等的线段,构造全等三角形.例5.如图,已知△ABC中∠BAC=90°,AB=AC,CD•垂直于∠ABC•的平分线BD 于D,BD交AC于E,求证:BE=2CD.分析:要证BE=2CD,想到要构造等于2CD的线段,结合角平分线,•利用翻折的方法把△CBD沿BD翻折,使BC重叠到BA所在的直线上,即构造全等三角形(△BCD ≌△BFD),然后证明BE和CF(2CD)所在的三角形全等.证明:延长BA、CD交于点F∵BD ⊥CF (已知) ∴∠BDC=∠BDF=90° ∵BD 平分∠ABC (已知) ∴∠1=∠2 在△BCD 和△BFD 中21()()()BD BD BDC BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩已知公共边已证∴△BCD ≌△BFD (ASA ) ∴CD=FD , 即CF=2CD∵∠5=∠4=90°,∠BDF=90° ∴∠3+∠F=90°,∠1+∠F=90°。
三角形中的五种常见证明类型

专训一:三角形中的五种常见证明类型名师点金:学习了全等三角形及等腰三角形的性质和判定后,与此相关的几何证明题的类型非常丰富,常见的类型有:证明数量关系、位置关系,线段的和差关系、倍分关系、不等关系等.证明数量关系题型1证明线段相等1.如图,在△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC 上的点,且AE=AF,求证:DE=DF.(第1题)题型2证明角相等2.如图,在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,AE⊥BD 于F交BC于E.求证:∠ADB=∠CDE.(第2题)证明位置关系3.如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AB,AC上,且BD=CF,BE=CD,点G是EF的中点,求证:DG⊥EF.(第3题)证明倍分关系4.如图,在△ABC中,AB=AC,AD,BE是△ABC的高,AD,BE相交于点H,且AE=BE,求证:AH=2BD.(第4题)证明和、差关系5.如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC.求证:AB+BD=AC.(第5题)证明不等关系6.如图,AD是△ABC中∠BAC的平分线,P是AD上的任意一点,且AB >AC,求证:AB-AC>PB-PC.(第6题)专训二:构造全等三角形的六种常用方法名师点金:在进行几何题的证明或计算时,需要在图形中添加一些辅助线,辅助线能使题目中的条件比较集中,能比较容易找到一些量之间的关系,使数学问题得以较轻松地解决.常见的辅助线作法有:构造法、平移法、旋转法、翻折法、加倍折半法和截长补短法,目的都是构造全等三角形.构造基本图形法1.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.(第1题)翻折法2.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.(第2题)旋转法3.如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE +DF=EF,求∠EAF的度数.(第3题)平移法4.在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC交AC于点Q,且AP与BQ相交于点O.求证:AB+BP=BQ+AQ.(第4题)加倍折半法5.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,求∠C的度数.(第5题)截长补短法6.如图所示,AB∥CD,BE、CE分别为∠ABC、∠BCD的平分线,点E 在AD上.求证:BC=AB+CD.(第6题)专训三:分类讨论思想在等腰三角形中的应用名师点金:分类讨论思想是解题的一种常用方法,在等腰三角形中,往往会遇到条件或结论不唯一的情况,此时就需要分类讨论.通过正确地分类讨论,可以使复杂的问题得到清晰、完整、严密的解答.其解题策略为:先分类,再画图,后计算.当顶角和底角不确定时,分类讨论1.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角度数为()A.40°B.100°C.40°或70°D.40°或100°2.已知等腰三角形ABC中,AD⊥BC于D,且AD=12BC,则等腰三角形ABC的底角的度数为()A.45°B.75°C.45°或75°D.65°3.若等腰三角形的一个外角为64°,则底角的度数为________.当底和腰不确定时,分类讨论4.(2015·荆门)已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为()A.8或10B.8C.10D.6或125.等腰三角形的两边长分别为7和9,则其周长为________.6.若实数x,y满足|x-5|+(10-y)2=0,则以x,y的值为边长的等腰三角形的周长为________.当高的位置关系不确定时,分类讨论7.等腰三角形一腰上的高与另一边的夹角为25°,求这个三角形的各个内角的度数.由腰的垂直平分线引起的分类讨论8.在三角形ABC中,AB=AC,AB边上的垂直平分线与AC所在的直线相交所得的锐角为40°,求∠B的度数.由腰上的中线引起的分类讨论9.等腰三角形ABC的底边BC长为5 cm,一腰上的中线BD把其分为周长差为3 cm的两部分.求腰长.点的位置不确定引起的分类讨论10.如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有()(第10题)A.7个B.6个C.5个D.4个11.如图,已知△ABC中,BC>AB>AC,∠ACB=40°,如果D,E是直线AB上的两点,且AD=AC,BE=BC,求∠DCE的度数.(第11题)专训四:三角形中常见的热门考点名师点金:本章主要学习了互逆命题与互逆定理,全等三角形的性质与判定,等腰三角形,线段垂直平分线与角平分线等常见的轴对称图形的性质与判定.本章的考点较多,也是中考的重点考查内容.互逆命题、基本事实、互逆定理1.下列命题是真命题的是()A.无限小数是无理数B.相反数等于它本身的数是0和1C.对顶角相等D.等边三角形既是轴对称图形,又是中心对称图形2.下列命题及其逆命题是互逆定理的是()A.全等三角形的对应角相等B.若两个角都是直角,则它们相等C.同位角相等,两直线平行D.若a=b,则|a|=|b|全等三角形的性质与判定3.如图所示,AB∥EF∥CD,∠ABC=90°,AB=DC,那么图中的全等三角形有()A.3对B.2对C.1对D.0对(第3题)(第4题)4.如图,在△ABC中,AC=5,F是高AD和BE的交点,AD=BD,则BF的长是()A.7 B.6 C.5 D.45.(2015·杭州)如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC,求证:DM=DN.(第5题)等腰三角形的判定与性质6.如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F分别为垂足,则下列四个结论:(1)∠DEF=∠DFE;(2)AE=AF;(3)DA平分∠EDF;(4)AD垂直平分EF.其中正确的有()A.1个B.2个C.3个D.4个(第6题)(第7题)(第8题)7.如图,AD是△ABC的中线,∠ADC=60°,BC=6,把△ABC沿直线AD折叠,点C落在C′处,连接BC′,则BC′的长为________.8.如图所示,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作MN∥BC,分别交AB,AC于点M,N.若AB=6 cm,AC=9 cm,则△AMN 的周长为________.9.(中考·淄博)如图,AD∥BC,BD平分∠ABC.求证:AB=AD.(第9题)尺规作图10.如图,已知线段a,h,作等腰三角形ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法如下:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC.△ABC即为所要求作的等腰三角形.上述作法的四个步骤中,你认为有错误的一步是()(第10题)A.(1) B.(2) C.(3) D.(4)线段垂直平分线与角平分线11.如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC 于点D,交AB于点E,则下列结论错误的是()A.BD平分∠ABCB.△BCD的周长等于AB+BCC.AD=BD=BCD.点D是线段AC的中点(第11题)(第12题)12.如图,已知在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=130°,那么∠CAB的大小是()A.80°B.50°C.40°D.20°13.如图,已知C是∠MAN的平分线上一点,CE⊥AB于E,点B,D分别在AM,AN上,且AE=12(AD+AB).问:∠1和∠2有何关系?并说明理由.(第13题)思想方法a.分类讨论思想14.等腰三角形的一个外角等于110°,则这个三角形的顶角度数为________.15.(2014·安顺)已知等腰三角形的两边长分别为a,b,且a,b满足2a-3b+5+(2a+3b-13)2=0,则此等腰三角形的周长为() A.7或8 B.6或10C.6或7 D.7或10b.方程思想16.如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,求∠A的度数.(第16题)c.转化思想17.如图,已知在△ABC中,∠ABC=3∠C,AD是∠BAC的平分线,BE⊥AD于E,求证:BE=12(AC-AB).(第17题)答案专训一1.证明:连接AD.∵AB =AC ,D 是BC 的中点,∴∠EAD =∠FAD.在△AED 和△AFD 中,⎩⎨⎧AE =AF ,∠EAD =∠FAD ,AD =AD ,∴△AED ≌△AFD(S .A .S .).∴DE =DF.2.证明:过点C 作CG ⊥AC 交AE 的延长线于G ,则CG ∥AB ,∴∠BAF =∠G.又∵AF ⊥BD ,AC ⊥CG ,∴∠BAF +∠ABF =90°,∠CAG +∠G =90°.∴∠ABF =∠CAG.在△ABD 和△CAG 中,⎩⎨⎧∠ABF =∠CAG ,AB =AC ,∠BAD =∠ACG =90°,∴△ABD ≌△CAG(A .S .A .).∴AD =CG ,∠ADB =∠G.又∵D 为AC 的中点,∴AD =CD ,∴CD =CG.∵AB =AC ,∴∠ABC =∠ACB.又∵AB ∥CG ,∴∠ABC =∠GCE.∴∠ACB =∠GCE.又∵CE =CE ,∴△CDE ≌△CGE(S .A .S .).∴∠G =∠CDE.∴∠ADB =∠CDE.(第3题)3.证明:如图,连接ED ,FD.∵AB =AC ,∴∠B =∠C.在△BDE 和△CFD 中,⎩⎨⎧BD =CF ,∠B =∠C ,BE =CD ,∴△BDE ≌△CFD(S .A .S .).∴DE =DF.又∵点G 是EF 的中点,∴DG ⊥EF.4.证明:∵AD ,BE 是△ABC 的高,∴∠ADB =∠AEB =90°,又∵∠BHD =∠AHE ,∴∠EBC =∠EAH.在△BCE 和△AHE 中,⎩⎨⎧∠EBC =∠EAH ,BE =AE ,∠BEC =∠AEH =90°,∴△BCE ≌△AHE(A .S .A .).∴AH =BC.又∵AB =AC ,AD ⊥BC ,∴BC =2BD ,∴AH =2BD.5.证明:如图,延长CB 至E ,使BE =BA ,则∠BAE =∠E.∵∠ABC =2∠C =2∠E ,∴∠E =∠C ,∴AE =AC.∵AD 平分∠BAC ,∴∠BAD =∠DAC.∵∠BAE =∠E ,∠E =∠C ,∴∠BAE =∠C.又∵∠EAD =∠BAE +∠BAD ,∠EDA =∠C +∠DAC ,∴∠EAD =∠EDA.∴AE =DE.∴AC =DE =BE +BD =AB +BD.(第5题)(第6题)6.证明:如图,在AB 上截取AE ,使AE =AC ,连接PE.∵AD 是∠BAC 的平分线,∴∠BAD =∠CAD.在△AEP 和△ACP 中,⎩⎨⎧AE =AC ,∠BAD =∠CAD ,AP =AP ,∴△AEP ≌△ACP(S .A .S .),∴PE =PC.在△PBE 中,BE >PB -PE ,∴AB -AC >PB -PC.专训二1.证明:如图,过点B 作BG ⊥BC 交CF 的延长线于点G.∵∠ACB =90°,∴∠2+∠ACF =90°.∵CE ⊥AD ,∴∠AEC =90°,∴∠1+∠ACF =180°-∠AEC =180°-90°=90°.∴∠1=∠2.在△ACD 和△CBG 中,⎩⎨⎧∠1=∠2,AC =CB ,∠ACD =∠CBG =90°,∴△ACD ≌△CBG(A .S .A .).∴∠ADC =∠G ,CD =BG.∵点D 为BC 的中点,∴CD =BD.∴BD =BG.又∵∠DBG =90°,∠DBF =45°,∴∠GBF =∠DBG -∠DBF =90°-45°=45°.∴∠DBF =∠GBF.在△BDF 和△BGF 中,⎩⎨⎧BD =BG ,∠DBF =∠GBF ,BF =BF ,∴△BDF ≌△BGF(S .A .S .).∴∠BDF =∠G.∴∠ADC =∠BDF.点拨:本题运用了构造基本图形法,通过作辅助线构造△CBG 、△BGF 是解题的关键.(第1题)(第2题)2.证明:如图,延长AD 交BC 于点F.(相当于将AB 边向下翻折,与BC 边重合,A 点落在F 点处,折痕为BE)∵BE 平分∠ABC ,∴∠ABE =∠CBE.∵BD ⊥AD ,∴∠ADB =∠BDF =90°.在△ABD 和△FBD 中,⎩⎨⎧∠ABD =∠FBD ,BD =BD ,∠ADB =∠FDB =90°,∴△ABD ≌△FBD(A .S .A .).∴∠2=∠DFB.又∵∠DFB =∠1+∠C ,∴∠2=∠1+∠C.(第3题)3.解:如图,延长CB 到点H ,使得BH =DF ,连接AH.∵∠ABE =90°,∠D =90°,∴∠ABH =∠D =90°.在△ABH 和△ADF 中,⎩⎨⎧AB =AD ,∠ABH =∠D =90°,BH =DF ,∴△ABH ≌△ADF.∴AH =AF ,∠BAH =∠DAF.∴∠BAH +∠BAF =∠DAF +∠BAF ,即∠HAF =∠BAD =90°. ∵BE +DF =EF ,∴BE +BH =EF ,即HE =EF.在△AEH 和△AEF 中,⎩⎨⎧AH =AF ,AE =AE ,EH =EF ,∴△AEH ≌△AEF.∴∠EAH =∠EAF.∴∠EAF =12∠HAF =45°.点拨:图中所作辅助线,相当于将△ADF 绕点A 顺时针旋转90°,使AD 边与AB 边重合,得到△ABH.4.证明:过点O 作OD ∥BC 交AB 于点D ,∴∠ADO =∠ABC. ∵∠BAC =60°,∠C =40°,∴∠ABC =80°.∴∠ADO =80°.∵BQ 平分∠ABC ,∴∠QBC =40°.∴∠AQB =∠C +∠QBC =80°.∴∠ADO =∠AQB.易知∠DAO =∠QAO ,OA =OA ,∴△ADO ≌△AQO.∴OD =OQ ,AD =AQ.∵OD ∥BP ,∴∠PBO =∠DOB ,又∵∠PBO =∠DBO ,∴∠DBO =∠DOB.∴BD =OD.∴BD =OQ.∵∠BAC =60°,∠ABC =80°,BQ 平分∠ABC ,AP 平分∠BAC , ∴∠BAP =30°,∠ABQ =40°,∴∠BOP =70°.∵∠BAP =30°,∠ABC =80°,∴∠APB =70°.∴∠BOP =∠APB ,∴BO =BP.∴AB +BP =AD +DB +BP =AQ +OQ +BO =BQ +AQ.5.解:在DC 上截取DE =BD ,连接AE ,∵AD ⊥BC ,BD =DE ,∴AD 是线段BE 的垂直平分线,∴AB =AE ,∠B =∠AEB.∵AB +BD =CD ,DE =BD ,∴AB +DE =CD.而CD =DE +EC ,∴AB =EC ,∴AE =EC.故设∠EAC =∠C =x ,∵∠AEB 为△AEC 的外角,∴∠AEB =∠EAC +∠C =2x ,∴∠B =2x ,∠BAE =180°-2x -2x =180°-4x.∵∠BAC =120°,∴∠BAE +∠EAC =120°,即180°-4x +x =120°,解得x =20°,则∠C =20°.6.证法一:用截长法,如图①所示,在BC 上截取BF =AB ,连接EF.(第6题)因为BE 平分∠ABC ,CE 平分∠BCD ,所以∠ABE =∠FBE ,∠FCE =∠DCE.在△ABE 和△FBE 中,因为⎩⎨⎧AB =FB ,∠ABE =∠FBE ,BE =BE ,所以△ABE ≌△FBE.所以∠A =∠EFB.因为AB ∥CD ,所以∠A +∠D =180°.因为∠BFE +∠EFC =180°,所以∠EFC =∠D.在△EFC 和△EDC 中,因为⎩⎨⎧∠FCE =∠DCE ,∠EFC =∠D ,EC =EC ,所以△EFC ≌△EDC.所以FC =DC.所以BC =BF +FC =AB +CD.证法二:用补短法,如图②所示,延长BE 交CD 的延长线于点G.因为AB ∥CD ,所以∠ABE =∠G.因为BE 平分∠ABC ,所以∠ABE =∠CBE.所以∠CBE =∠G.因为CE 平分∠BCD ,所以∠BCE =∠GCE.在△BEC 和△GEC 中,因为⎩⎨⎧∠CBE =∠G ,∠BCE =∠GCE ,CE =CE ,所以△BEC ≌△GEC.所以BC =GC ,BE =GE.在△ABE 和△DGE 中,因为⎩⎨⎧∠ABE =∠G ,∠AEB =∠DEG ,BE =GE ,所以△ABE ≌△DGE.所以AB =DG.所以BC =CG =GD +DC =AB +CD.专训三1.D 2.C 3.32°4.C 5.23或25 6.257.解:设等腰三角形ABC 中,AB =AC ,BD ⊥AC 于D.(1)当高与底边的夹角为25°时,高一定在△ABC 的内部,如图①,∵∠DBC =25°,∴∠C =90°-∠DBC =90°-25°=65°,∴∠ABC =∠C =65°,∠A =180°-2×65°=50°.(第7题)(2)当高与另一腰的夹角为25°时,如图②,高在△ABC 的内部时,∵∠ABD =25°,∴∠A =90°-∠ABD =65°,∴∠C =∠ABC =(180°-∠A)÷2=57.5°;如图③,高在△ABC 的外部时,∵∠ABD =25°,∴∠BAD =90°-∠ABD =90°-25°=65°,∴∠BAC=180°-65°=115°,∴∠ABC=∠C=(180°-115°)÷2=32.5°,故三角形各内角的度数为:65°,65°,50°或65°,57.5°,57.5°或115°,32.5°,32.5°.点拨:由于题目中的“另一边”没有指明是“腰”还是“底边”,因此必须进行分类讨论,另外,还要结合图形,分高在三角形内还是在三角形外.8.解:此题分两种情况:(1)如图①,AB边的垂直平分线与AC边交于点D,∠ADE=40°,则∠A=50°,∵AB=AC,∴∠B=(180°-50°)÷2=65°.(2)如图②,AB边的垂直平分线与CA的延长线交于点D,∠ADE=40°,则∠DAE=50°,∴∠BAC=130°.∵AB=AC,∴∠B=(180°-130°)÷2=25°.故∠B的大小为65°或25°.(第8题)9.解:∵BD为AC边上的中线,∴AD=CD.(1)当(AB+AD)-(BC+CD)=3 cm时,则AB-BC=3 cm,∵BC=5 cm,∴AB=8 cm;(2)当(BC+CD)-(AB+AD)=3 cm时,则BC-AB=3 cm,∵BC=5 cm,∴AB=2 cm;但是当AB=2 cm时,三边长为2 cm,2 cm,5 cm,而2+2<5,不符合三角形三边关系,故舍去,故腰长为8 cm.10.B11.解:(1)当点D,E在点A的同侧,且都在BA的延长线上时,如图①,(第11题)∵BE=BC,∴∠BEC=(180°-∠ABC)÷2,∵AD=AC,∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,∵∠DCE=∠BEC-∠ADC,∴∠DCE=(180°-∠ABC)÷2-∠BAC÷2=(180°-∠ABC-∠BAC)÷2=∠ACB÷2=40°÷2=20°.(2)当点D,E在点A的同侧,且点D在D′的位置,点E在E′的位置时,如图②,与(1)类似地可以求得∠D′CE′=∠ACB÷2=20°.(3)当点D,E在点A的两侧,且点E在E′的位置时,如图③,∵BE′=BC,∴∠BE′C=(180°-∠CBE′)÷2=∠ABC÷2,∵AD=AC,∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,又∵∠DCE′=180°-(∠BE′C+∠ADC),∴∠DCE′=180°-(∠ABC+∠BAC)÷2=180°-(180°-∠ACB)÷2=90°+∠ACB÷2=90°+40°÷2=110°.(4)当点D,E在点A的两侧,且点D在D′的位置时,如图④,∵AD′=AC,∴∠AD′C=(180°-∠BAC)÷2,∵BE=BC,∴∠BEC=(180°-∠ABC)÷2,∴∠D′CE=180°-(∠D′EC+∠ED′C)=180°-(∠BEC+∠AD′C)=180°-[(180°-∠ABC)÷2+(180°-∠BAC)÷2]=(∠BAC+∠ABC)÷2=(180°-∠ACB)÷2=(180°-40°)÷2=70°.综上所述,∠DCE的度数为20°或110°或70°.专训四1.C 2.C 3.A 4.C5.证明:∵AM=2MB,AN=2NC,∴AM=23AB,AN=23AC.又∵AB=AC,∴AM=AN.∵AD平分∠BAC,∴∠MAD=∠NAD.又∵AD=AD,∴△AMD≌△AND(S.A.S.).∴DM=DN.6.D7.38.15 cm9.证明:∵AD∥BC,∴∠DBC=∠ADB.又∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABD=∠ADB,∴AB =AD.10.C 11.D 12.D(第13题)13.解:∠1与∠2互补.理由:作CF ⊥AN 于F(如图),∵AC 平分∠MAN ,∴∠3=∠4,又∵CE ⊥AM ,CF ⊥AN ,∴CF =CE ,∠CFA =∠CEA =90°,∴Rt △ACF ≌Rt △ACE ,∴AF =AE.∵AE =12(AD +AB)=12(AF -DF +AE +BE)=AE +12(BE -DF),∴BE -DF =0,∴BE =DF ,又CE =CF ,∠CEB =∠CFD ,∴△DFC ≌△BEC(S .A .S .),∴∠5=∠2,∵∠1+∠5=180°,∴∠1+∠2=180°.即∠1与∠2互补.14.70°或40° 点拨:本题运用了分类讨论思想,将已知条件外角等于110°分为底角处的外角和顶角处的外角两种情况进行讨论,解题时要防止漏解.15.A 点拨:∵2a -3b +5+(2a +3b -13)2=0,∴⎩⎨⎧2a -3b +5=0,2a +3b -13=0,解得⎩⎨⎧a =2,b =3. 当a 为底边长时,三角形的三边长为2,3,3,则周长为8;当b 为底边长时,三角形的三边长为2,2,3,则周长为7.综上所述,此等腰三角形的周长为7或8.16.解:设∠ABD 的度数为x.∵AD =DE =EB ,∴∠A =∠AED =2∠ABD =2x.∵BC =BD ,∴∠C =∠BDC =∠ABD +∠A =3x.∵AB =AC ,∴∠ABC =∠C =3x.∴∠A +∠C +∠ABC =8x =180°.∴x =22.5°.∴∠A =2x =45°.17.证明:如图,延长BE 交AC 于F.∵AD 是∠BAC 的平分线,∴∠BAE =∠FAE.(第17题)在△ABE 和△AFE 中,⎩⎨⎧∠BAE =∠FAE ,AE =AE ,∠AEB =∠AEF =90°,∴△ABE ≌△AFE(A .S .A .).∴∠ABF =∠AFB ,BE =FE ,AB =AF.∴BE =12BF.∠ABC =∠ABF +∠FBC=∠AFB +∠FBC =∠C +∠FBC +∠FBC =∠C +2∠FBC ,又∵∠ABC =3∠C ,∴3∠C =∠C +2∠FBC.∴∠C =∠FBC.∴BF =CF.∴BE =12CF.∵CF =AC -AF =AC -AB ,∴BE =12(AC -AB).点拨:本题运用了转化思想,通过添加辅助线构造等腰三角形,然后利用等腰三角形的性质将AC 与AB 的差转化为AC 与AF 的差是解题的关键.。
全等三角形题型归类及解析

全等三角形难题题型归类及解析一、角平分线型角平分线是轴对称图形,所以我们要充分的利用它的轴对称性,常作的辅助线是:一利用截取一条线段构造全等三角形,二是经过平分线上一点作两边的垂线。
另外掌握两个常用的结论:角平分线与平行线构成等腰三角形,角平分线与垂线构成等腰三角形。
1. 如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC ,在AB 上截取AE=AC ,连结DE ,已知DE=2cm ,BD=3cm ,求线段BC 的长。
2. 已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在BD 上,PM ⊥AD 于M ,•PN ⊥CD 于N ,判断PM 与PN 的关系.3. 已知:如图E 在△ABC 的边AC 上,且∠AEB=∠ABC 。
(1) 求证:∠ABE=∠C ;(2) 若∠BAE 的平分线AF 交BE 于F ,FD ∥BC 交AC 于D ,设AB=5,AC=8,求DC 的长。
.AB C DE PD A CBM N5、如图所示,已知∠1=∠2,EF ⊥AD 于P ,交BC 延长线于M ,求证:2∠M=(∠ACB-∠B )21PFMDBA CE6、如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E .(1) 若BD 平分∠ABC ,求证CE=12BD ;(2) 若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由。
8、如图,在△ABC 中,∠ABC=60°,AD 、CE 分别平分∠BAC 、∠ACB ,求证:AC=AE+CD .二、中点型由中点应产生以下联想:ED C BA1、想到中线,倍长中线2、利用中心对称图形构造8字型全等三角形3、在直角三角形中联想直角三角形斜边上的中线4、三角形的中位线2、已知:如图,ABC △中,45ABC ∠=°,CD AB ⊥于D ,BE 平分ABC ∠,且BE A C ⊥于E ,与CD 相交于点F H ,是BC 边的中点,连结DH 与BE 相交于点G . (1)求证:BF AC =;(2)求证:12CE BF =D AE FCHGB3、如图,△ABC 中,D 是BC 的中点,DE ⊥DF ,试判断BE+CF 与EF 的大小关 系,并证明你的结论。
角平分线四大模型总结+习题+解析(最全版)
⾓平分线四⼤模型总结+习题+解析(最全版)⾓平分线四⼤辅助线模型⾓平分线的性质为证明线段或⾓相等开辟了新的途径,同时也是全等三⾓形知识的延续,⼜为后⾯⾓平分线的判定定理的学习奠定了基础.涉及到⾓平分线的考点主要是性质、判定以及四⼤辅助线模型,在初⼆上期中、期末考试中都是经常考察的⽅向。
⾓平分线性质:⾓平分线上的点到⾓两边的距离相等.⾓平分线判定:到⾓的两边距离相等的点在⾓的⾓平分线上.四⼤模型1、⾓平分线+平⾏线,等腰三⾓形必出现已知:OC平分∠AOB,CD∥OB交OA于D.则△ODC为等腰三⾓形,OD=CD.2、⾓平分线+两垂线,线等全等必出现已知:OC平分∠AOB.辅助线:过点C作CD⊥OA,CE⊥OB.则CD=CE,△ODC ≌△OEC.3、⾓平分线+⼀垂线,中点全等必出现已知:OC平分∠AOB,DC垂直OC于点C.辅助线:延长DC交OB于点E.则C是DE的中点,△ODC ≌△OEC.4、⾓平分线+截长补短线,对称全等必出现已知:OC平分∠AOB,截取OE=OD,连接CD、CE.则△ODC和△OCE关于OC对称,即△ODC ≌△OEC.【核⼼考点⼀】⾓平分线的性质与判定1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:163.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB ,另⼀把直尺压住射线OA 并且与第⼀把直尺交于点P ,⼩明说:“射线OP 就是BOA ∠的⾓平分线.”他这样做的依据是( )A .⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B .⾓平分线上的点到这个⾓两边的距离相等C .三⾓形三条⾓平分线的交点到三条边的距离相等D .以上均不正确6.(2019秋?梁平区期末)如图,若BD AE ⊥于B ,DC AF ⊥于C ,且DB DC =,40BAC ∠=?,130ADG ∠=?,则DGF ∠=.7.(2018春?开江县期末)如图,在Rt ABC ?中,90C ∠=?,以顶点A 为圆⼼,适当长为半径画弧,分别交AB 、AC 于点M 、N ,再分别以点M 、N 为圆⼼,⼤于12MN 的长为半径画弧,两弧交于点P ,射线AP 交边BC 于点D .下列说法错误的是( ) A .CAD BAD ∠=∠B .若2CD =,则点D 到AB 的距离为2C .若30B ∠=?,则CDA CAB ∠=∠D .2ABD ACD S S ??=8.(2014秋?西城区校级期中)如图,点E 是AOB ∠的平分线上⼀点,EC OA ⊥,ED OB ⊥,垂⾜分别是C ,D .下列结论中正确的有( )(1)ED EC =;(2)OD OC =;(3)ECD EDC ∠=∠;(4)EO 平分DEC ∠;(5)OE CD ⊥;(6)直线OE 是线段CD 的垂直平分线.A .3个B .4个C .5个D .6个9.(2019春?杜尔伯特县期末)如图:在ABC ?中,90C ∠=?,AD 是BAC ∠的平分线,DE AB ⊥于E ,F 在AC 上,BD DF =,证明:(1)CF EB =.(2)2AB AF EB =+.10.(2019秋?垦利区期中)如图,ABC⊥⊥且平分BC,DE AB中,AD平分BAC∠,DG BC于E,DF AC⊥于F.(1)判断BE与CF的数量关系,并说明理由;(2)如果8AB=,6AC=,求AE、BE的长.11.(2017秋?遂宁期末)某地区要在区域S内(即COD∠内部)建⼀个超市M,如图所⽰,按照要求,超市M到两个新建的居民⼩区A,B的距离相等,到两条公路OC,OD的距离也相等.这个超市应该建在何处?(要求:尺规作图,不写作法,保留作图痕迹)【核⼼考点⼆】⾓平分线+⾓两边垂线12.(2019秋?肥城市期末)如图,//AB CD ,BP 和CP 分别平分ABC ∠和DCB ∠,AD 过点P ,且与AB 垂直,垂⾜为A ,交CD 于D ,若8AD =,则点P 到BC 的距离是.13.(2015?湖州)如图,已知在ABC ?中,CD 是AB 边上的⾼线,BE 平分ABC ∠,交CD 于点E ,5BC =,2DE =,则BCE ?的⾯积等于( )A .10B .7C .5D .414.(2010秋?涵江区期末)如图所⽰,在Rt ABC ?中,90C ∠=?,BC AC =,AD 平分BAC ∠交BC 于D ,求证:AB AC CD =+.15.(2012秋?蓬江区校级期末)如图,已知90∠=∠=?,M是BC的中点,DM平分B C∠.求证:ADC(1)AM平分DAB∠;(2)DM AM⊥.16.(2016秋?西城区校级期中)已知:如图,12∠=∠,P为BN上的⼀点,PF BC⊥于F,=,PA PC(1)求证:180∠+∠=?;PCB BAP(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.【核⼼考点三】⾓平分线+垂线17.(2017秋?和平区校级⽉考)如图.在ABC ?中,BE 是⾓平分线,AD BE ⊥,垂⾜为D ,求证:21C ∠=∠+∠.18.(2013秋?昌平区期末)已知:如图,在ABC ?中,AD 平分BAC ∠,CD AD ⊥于点D ,DCB B ∠=∠,若10AC =,6AD=,求AB 的长.19.如图所⽰,ABC ?中,ACB ABC ∠>∠,AE 平分BAC ∠,CD AE ⊥于D ,求证:ACD B ∠>∠.20.已知:如图,在ABC ?中,3ABC C ∠=∠,12∠=∠,BE AE ⊥.求证:2AC AB BE -=.21.(2019秋?下陆区期中)如图,BD 是ABC ∠的⾓平分线,AD BD ⊥,垂⾜为D ,20DAC ∠=?,38C ∠=?,则BAD ∠=.22.(2019秋?曲⾩市校级⽉考)如图,在ABC ?中,AB AC =,90BAC ∠=?,BD 平分ABC ∠交AC 于D ,过C 作CE BD ⊥交BD 延长线于E .求证:12CE BD =.23.(2019?沂源县⼀模)(1)如图(a)所⽰,BD、CE分别是ABC的外⾓平分线,过点A作AD BD⊥,AE CE⊥,垂⾜分别为D、E,连接DE,求证:1() 2DE AB BC AC=++;(2)如图(b)所⽰,BD、CE分别是ABC的内⾓平分线,其他条件不变,DE与ABC三边有怎样的数量关系?并证明这个数量关系;(3)如图(c)所⽰,BD为ABC的内⾓平分线,CE为ABC的外⾓平分线,其他条件不变,DE与ABC三边⼜有怎样的数量关系?并证明这个数量关系.24.(2017秋?夏⾢县期中)如图,在ABC ?中,ABC ∠、ACB ∠的平分线相交于F ,过F 作//DE BC ,交AB 于D ,交AC 于E ,那么下列结论:①BDF ?、CEF ?都是等腰三⾓形;②DE DB CE =+;③AD DE AE AB AC ++=+;④BF CF =.正确的有.25.(2019秋?垦利区期末)如图,平⾏四边形ABCD 中,3AB cm =,5BC cm =;,BE 平分ABC ∠,交AD 于点E ,交CD 延长线于点F ,则DE DF +的长度为.26.(2010秋?海淀区期末)如图,BD 是ABC ?的⾓平分线,//DE BC ,DE 交AB 于E ,若AB BC =,则下列结论中错误的是( )A .BD AC ⊥B .A EDA ∠=∠C .2AD BC =D .BE ED =27.如图,若BD 、CD 分别平分ABC ∠和ACB ∠,过D 作//DE AB 交BC 于E ,作//DF AC 交BC 于F ,求证:BC 的长等于DEF ?的周长.28.(2018秋?邳州市期中)如图,在四边形ABCD中,对⾓线AC平分BAD >,∠,AB AD 下列结论正确的是()A.AB AD CB CD->-B.AB AD CB CD-=-C.AB AD CB CD-<-D.AB AD-与CB CD-的⼤⼩关系不确定29.(2012?⿇城市校级模拟)在ABC∠的外⾓平分线,P是AD上的任意中,AD是BAC⼀点,试⽐较PB PC+与AB AC+的⼤⼩,并说明理由.30.(2018秋?万州区期中)已知:如图,在四边形ABCD中,AC平分BAD ∠,CE AB⊥于=+.E,且180B D∠+∠=?,求证:AE AD BE31.(2017秋?海淀区期中)如图,已知AD是BAC∠=?,C=+,31的⾓平分线,AC AB BD 求B∠的度数.32.(2019秋?平⼭县期中)如图,90∠=?,OM平分AOB∠,将直⾓三⾓板的顶点PAOB在射线OM上移动,两直⾓边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.33.(2016秋?丰宁县期中)如图,在ABC ?中,100A ∠=?,40ABC ∠=?,BD 是ABC ∠的平分线,延长BD ⾄E ,使DE AD =.求证:BC AB CE =+.34.(2018秋?丰城市期中)在ABC ?中,2ACB B ∠=∠,(1)如图1,当90C ∠=?,AD 为BAC ∠的⾓平分线时,在AB 上截取AE AC =,连接DE ,求证:AB AC CD =+;(2)如图2,当90C ∠≠?,AD 为BAC ∠的⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请直接写出你的结论,不需要证明;(3)如图3,当AD 为ABC ?的外⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请写出你的猜想,并说明理由.35.(2019春?利津县期末)如图,在ABC∠平分线,AD的垂直平分线分中,AD是BAC别交AB、BC延长线于F、E.求证:(1)EAD EDA∠=∠;(2)//DF AC;(3)EAC B∠=∠.36.(2014?西城区⼆模)在ABC>,AD平分BAC∠交BC于点∠为锐⾓,AB AC,BACD.(1)如图1,若ABC是等腰直⾓三⾓形,直接写出线段AC,CD,AB之间的数量关系;(2)BC的垂直平分线交AD延长线于点E,交BC于点F.①如图2,若60∠=?,判断AC,CE,AB之间有怎样的数量关系并加以证明;ABE②如图3,若AC AB+,求BAC∠的度数.⾓平分线四⼤辅助线模型--解析⼀.⾓平分线的性质与判定(共11⼩题)1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .【分析】⾸先过点P 作PB OM ⊥于B ,由OP 平分MON ∠,PA ON ⊥,3PA =,根据⾓平分线的性质,即可求得PB 的值,⼜由垂线段最短,可求得PQ 的最⼩值.【解答】解:过点P 作PB OM ⊥于B , OP 平分MON ∠,PA ON ⊥,3PA =,3PB PA ∴==,PQ ∴的最⼩值为3.故选:C .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:16【分析】利⽤⾓平分线的性质,可得出ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼相等,估计三⾓形的⾯积公式,即可得出ABD ?与ACD ?的⾯积之⽐等于对应边之⽐.【解答】解:AD 是ABC ?的⾓平分线,∴设ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼分别为1h ,2h ,12h h ∴=,ABD ∴?与ACD ?的⾯积之⽐:8:64:3AB AC ===,故选:B .3.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm【分析】根据⾓平分线的性质得到ED EC =,计算即可.【解答】解:BE 平分ABC ∠,DE AB ⊥,90ACB ∠=?, ED EC ∴=,3AE DE AE EC AC cm ∴+=+==,故选:B .4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn【分析】过点D 作DE AB ⊥于E ,根据⾓平分线上的点到⾓的两边距离相等可得DE CD =,然后根据三⾓形的⾯积公式即可得到结论.【解答】解:如图,过点D 作DE AB ⊥于E ,BD 是ABC ∠的平分线,90C ∠=?,DE CD m ∴==,ABD ∴?的⾯积122n m mn =??=,故选:A.5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB,另⼀把直尺压住射线OA并且与第⼀把直尺交于点P,⼩明说:“射线OP就是BOA∠的⾓平分线.”他这样做的依据是()A.⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B.⾓平分线上的点到这个⾓两边的距离相等C.三⾓形三条⾓平分线的交点到三条边的距离相等D.以上均不正确【分析】过两把直尺的交点C作CE AO=,再根据⾓⊥,CF BO⊥,根据题意可得CE CF的内部到⾓的两边的距离相等的点在这个⾓的平分线上可得OP平分AOB∠;【解答】解:(1)如图所⽰:过两把直尺的交点P作PE AO⊥,⊥,PF BO两把完全相同的长⽅形直尺,PE PF∴=,∠(⾓的内部到⾓的两边的距离相等的点在这个⾓的平分线上),OP∴平分AOB故选:A.。
全等三角形证明判定方法分类总结

全等三角形一SSS知识要点1.全等图形定义:两个能够重合的图形称为全等图形. 2.全等图形的性质:1全等图形的形状和大小都相同;对应边相等;对应角相等 2全等图形的面积相等3.全等三角形:两个能够完全重合的三角形称为全等三角形1表示方法:两个三角形全等用符号“≌”来表示;读作“全等于” 如DEF ABC ∆∆与全等;记作ABC ∆≌DEF ∆2符号“≌”的含义:“∽”表示形状相同;“=”表示大小相等;合起来就是形状相同;大小也相等;这就是全等.3两个全等三角形重合时;互相重合的顶点叫做对应顶点;互相重合的边叫做对应边;互相重合的角叫做对应角.4证两个三角形全等时;通常把表示对应顶点的字母写在对应的位置上.4.全等三角形的判定一:三边对应相等的两个三角形全等;简与成“边边边”或“SSS ”. 典型例题例1.如图;ABC ∆≌ADC ∆;点B 与点D 是对应点;=∠BAC 且︒=∠20B ;1=∆ABC S ;求ACD D CAD ∠∠∠,,的度数ACD ∆的面积.例2.如图;ABC ∆≌DEF ∆;cm CE cm BC A 5,9,50==︒=∠;求EDF∠的度数及CF 的长.例3.如图;已知:AB=AD;AC=AE;BC=DE;求证:CAD BAE ∠=∠例4.如图AB=DE;BC=EF;AD=CF;求证:1ABC ∆≌DEF ∆2AB//DE;BC//EF例5.如图;在,90︒=∠∆C ABC 中D 、E 分别为AC 、AB 上的点;且BE=BC;DE=DC;求证:1AB DE ⊥;2BD 平分ABC ∠巩固练习1.下面给出四个结论:①若两个图形是全等图形;则它们形状一定相同;②若两个图形的形状相同;则它们一定是全等图形;③若两个图形的面积相等;则它们一定是全等图形;④若两个图形是全等图形;则它们的大小一定相同;其中正确的是A 、①④B 、①②C 、②③D 、③④ 2.如图;ABD ∆≌CDB ∆;且AB 和CD 是对应边;下面四个结论中 不正确的是A 、CDB ABD ∆∆和的面积相等 B 、CDB ABD ∆∆和的周长相等C 、CBD C ABD A ∠+∠=∠+∠ D 、AD//BC 且AD=BC3.如图;ABC ∆≌BAD ∆;A 和 B 以及C 和D 分别是对应点;如果︒=∠︒=∠35,60ABD C ;则BAD ∠的度数为A 、︒85B 、︒35C 、︒60D 、︒80 4.如图;ABC ∆≌DEF ∆;AD=8;BE=2;则AE 等于 A 、6 B 、5 C 、4 D 、35.如图;要使ACD ∆≌BCE ∆;则下列条件能满足的是 A 、AC=BC;AD=CE;BD=BE B 、AD=BD;AC=CE;BE=BD C 、DC=EC;AC=BC;BE=AD D 、AD=BE;AC=DC;BC=EC6.如图;ABE ∆≌DCF ∆;点A 和点D 、点E 和点F分别是对应点;则AB= ;=∠A ;AE= ;CE= ;AB// ;若BC AE ⊥;则DF与BC的关系是 . 7.如图;ABC ∆≌AED ∆;若=∠︒=∠︒=∠︒=∠BAC C EAB B 则,45,30,40 ;=∠D ;=∠DAC.8.如图;若AB=AC;BE=CD;AE=AD;则ABE ∆ ACD ∆;所以=∠AEB ;=∠BAE ;=∠BAD .9.如图;ABC ∆≌DEF ∆;︒=∠90C ;则下列说法错误的是互余与F C ∠∠互补与F C ∠∠互余与E A ∠∠互余与D B ∠∠D第4题图第5题图B第6题图第7题图 第8题图第9题题图10.如图;ACF ∆≌DBE ∆;cm CD cm AD ACF E 5.2,9,110,30==︒=∠︒=∠;求D ∠的度数及BC 的长.11.如图;在ABD ABC ∆∆与中;AC=BD;AD=BC;求证:ABC ∆≌ABD ∆全等三角形一作业1.如图;ABC ∆≌CDA ∆;AC=7cm;AB=5cm.;则AD 的长是 A 、7cm B 、5cm C 、8cm D 、无法确定2.如图;ABC ∆≌DCE ∆;︒=∠︒=∠62,48E A ;点B 、C 、E 在同一直线上;则ACD ∠的度数为A 、︒48B 、︒38C 、︒110D 、︒623.如图;ABC ∆≌DEF ∆;AF=2cm;CF=5cm;则AD= .4.如图;ABE ∆≌ACD ∆;︒=∠︒=∠25,100B A ;求BDC ∠的度数.5.如图;已知;AB=DE;BC=EF;AF=CD;求证:AB//CD6.如图;已知AB=EF;BC=DE;AD=CF;求证:①ABC ∆≌FED ∆②AB//EF7.如图;已知AB=AD;AC=AE;BC=DE;求证:CAE BAD ∠=∠AB CEAD CAB CDEACDFA C E FDE全等三角形二知识要点定义:SAS两边和它们的夹角对应相等的两个三角形全等;简写成“边角边”或“SAS ”;几何表示如图;在ABC ∆和DEF ∆中;ABC EF BC E B DE AB ∆∴⎪⎩⎪⎨⎧=∠=∠=≌)(SAS DEF ∆典型例题例1 已知:如图;AB=AC;AD=AE;求证:BE=CD.例2 如图;已知:点D 、E 在BC 上;且BD=CE;AD=AE;∠1=∠2;由此你能得出哪些结论 给出证明.例 3 如图已知:AE=AF;AB=AC;∠A=60°;∠B=24°;求∠BOE 的度数.例4 如图;B;C;D 在同一条直线上;△ABC;△ADE 是等边三角形; 求证:①CE=AC+DC ; ②∠ECD=60°.例5如图;已知△ABC 、△BDE 均为等边三角形..求证:BD +CD=AD..C ADBECABC E巩固练习1.在△ABC 和△C B A '''中;若AB=B A '';AC=C A '';还要加一个角的条件;使△ABC ≌△C B A ''';那么你加的条件是A .∠A=∠A ' B.∠B=∠B ' C.∠C=∠C ' D.∠A=∠B ' 2.下列各组条件中;能判断△ABC ≌△DEF 的是 A .AB=DE;BC=EF ;CA=CD B.CA=CD ;∠C=∠F ;AC=EFC .CA=CD ;∠B=∠E D.AB=DE ;BC=EF;两个三角形周长相等 3.阅读理解题:如图:已知AC;BD 相交于O;OA=OB;OC=OD.那么△AOD 与△BOC 全等吗 请说明理由.△ABC 与△BAD 全等吗 请说明理由. 小明的解答:21∠=∠ AOD ≌△BOC而△BAD=△AOD+△ADB △ABC=△BOC+△ 所以△ABC ≌△BAD1你认为小明的解答有无错误;2如有错误给出正确解答;4.如图;点C 是AB 中点;CD ∥BE;且CD=BE;试探究AD 与CE 的关系..5.如图;AE 是,BAC 的平分线∠AB=AC1若D 是AE 上任意一点;则△ABD ≌△ACD;说明理由.2若D 是AE 反向延长线上一点;结论还成立吗 请说明理由. 6.如图;已知AB=AC;EB=EC;请说明BD=CD 的理由DOA=OB OD=OC全等三角形二作业1.如图;已知AB=AC;AD=AE;BF=CF;求证:BDF ∆≌CEF ∆..2.如图;△ABC;△BDF 为等腰直角三角形..求证:1CF=AD ;2CE ⊥AD..3.如图;AB=AC;AD=AE;BE 和CD 相交于点O;AO 的延长线交BC 于点F.. 求证:BF=FC..4.已知:如图1;AD ∥BC;AE=CF;AD=BC;E 、F 在直线AC 上;求证:DE ∥BF..5. 如图;已知AB ⊥AC;AD ⊥AE;AB=AC;AD=AE; 求证:1BE=DC;2BE ⊥DC.6、已知;如图A 、F 、C 、D 四点在一直线上;AF=CD;AB//DE;且AB=DE;求证:1△ABC ≌△DEF 2∠CBF=∠FECAB CE D FA C BDE FAD E CBFO 1 2 DC ABE FD ABQCPE7、已知:如图;AB=AC;AD=AE;∠BAC=∠DAE.求证:BD=CE8、如图;正方形ABCD的边CD在正方形ECGF的边CE上;连接BE、DG;1观察猜想BE与DG之间的大小关系;并证明你的结论..2图中是否存在通过旋转能够互相重合的两个三角形若存在;请说出旋转过程;若不存在;说明理由..9、已知:如图;AD是BC上的中线 ;且DF=DE.求证:BE∥CF.10、已知C为AB上一点;△ACN和△BCM是正三角形.求证:1AM=BN2求∠AFN大小..11、已知如图;F在正方形ABCD的边BC边上;E在AB的延长线上;FB=EB;AF交CE于G;求∠AGC的度数.12、如图;△ABC是等腰直角三角形;其中CA=CB;四边形CDEF是正方形;连接AF、BD.1观察图形;猜想AF与BD之间有怎样的关系;并证明你的猜想;2若将正方形CDEF绕点C按顺时针方向旋转;使正方形CDEF的一边落在△ABC的内部;请你画出一个变换后的图形;并对照已知图形标记字母;题1中猜想的结论是否仍然成立若成立;直接写出结论;不必证明;若不成立;请说明理由.CNMBAEDFFDACE BFDACGEB全等三角形三ASA知识要点ASA如图;在ABC ∆与DEF ∆中EB DE AB D A ∠=∠=∠=∠ ∴)(ASA DEF ABC ∆≅∆ASA 公理推论AAS 公理:有两角和其中一角的对边对应相等的两个三角形全等.典型例题例1下列条件不可推得ABC ∆和'''C B A ∆全等的条件是 A 、 AB=A 'B ';'A A ∠=∠;'C C ∠=∠B 、 AB= A 'B ';AC=A 'C ';BC='B C 'C 、 AB= A 'B ';AC=A 'C ';'B B ∠=∠ D 、AB= A 'B ';'A A ∠=∠;'B B ∠=∠例2已知如图;DE AB DE AB D A //,,=∠=∠;求证:BC=EF例3如图;AB=AC;C B ∠=∠;求证:AD=AE例4已知如图;43,21∠=∠∠=∠;点P 在AB 上;可以得出PC=PD 吗 试证明之.例5如图;321∠=∠=∠;AC=AE;求证:DE=BCADAB例6如图;21,∠=∠∠=∠D A ;AC;BD 相交于O; 求证:①AB=CD ②OA=OD巩固练习1.如图;AB//CD;AF//DE;BE=CF;求证:AB=CD2.如图;AD//BC;O 为AC 中点;过点O 的直线分别交AD;BC 于点M;N;求证:AM=CN3.求证:两个全等三角形ABC 与A 'B 'C '的角平分线AD 、A 'D '相等4.如图;AB;CD 相交于O;E;F 分别在AD;BC 上;若FOB EOD ∆≅∆;求证:COF AOE ∆≅∆5.如图;AB//CD;AD//BC;求证:AB=CD6.已知;如图AB=DB;21,∠=∠∠=∠E C ;求证:AC=DEAD 'B D 'C 'BA BD全等三角形三作业1.已知;如图;CD AF D A =∠=∠∠=∠,21,;求证:AB=DE2.如图;已知CAD BAE ADE AED ∠=∠∠=∠,;求证:BE=CD3.已知如图;AB=AD;CAE BAD D B ∠=∠∠=∠,;求证:AC=AE4.已知如图;在ABC ∆中;AD 平分BC AD BAC ⊥∠,;求证:ABD ACD ∆≅∆5.已知如图;cm AC ABD DCA DBC ACB 10,,=∠=∠∠=∠;求BD 的长要求写出完整的过程6、如图ABC △中;∠B =∠C;D;E;F 分别在AB;BC;AC 上;且BD=CE;∠DEF=∠B 求证:ED=EFECEA D ECBF7、 1如图1;以的边、为边分别向外作正方形和正方形;连结;试判断△ABC 与△AEG 面积之间的关系;并说明理由.2园林小路;曲径通幽;如图2所示;小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a 平方米;内圈的所有三角形的面积之和是b 平方米;这条小路一共占地多少平方米8、已知:如图 ; AD 为CE 的垂直平分线 ; EF ∥BC.求证:△EDN ≌△CDN ≌△EMN .9、 已知:如图 ; AB=AC ; AD=AE ; 求证:△OBD ≌△OCE10、已知:如图 ; AB=CD ; AD=BC ;O 为BD 中点 ; 过O 作直线分别与DA 、BC 的延长线交于E 、F .求证:OE=OF11、如图在△ABC 和△DBC 中 ; ∠1=∠2 ; ∠3=∠4 ; P 是BC 上任意一点.求证:PA=PD.12、已知 :如图 ; 四边形 ABCD 中 ; AD ∥BC ; F 是AB 的中点 ; DF 交CB 延长线 于E ; CE=CD . 求证:∠ADE=∠EDC .13、已知:如图 ; OA=OE ; OB=OF ; 直线FA 与BE 交于C ; AB 和EF 交于O ;求证:∠1=∠2.AG FC BD E 图1全等三角形四 强化训练1、如图;△ABC 是等边三角形;点D 、E 、F 分别是线段AB 、BC 、CA 上的点; 1若AD BE CF ==;问△DEF 是等边三角形吗 试证明你的结论; 2若△DEF 是等边三角形;问AD BE CF ==成立吗 试证明你的结论.2、如图所示;已知∠1=∠2;EF ⊥AD 于P;交BC 延长线于M;求证:2∠M=∠ACB-∠B3、△ABC 中;∠A=90°;AB=AC;D 为BC 中点;E 、F 分别在AC 、AB 上;且DE ⊥DF;试判断DE 、DF 的数量关系;并说明理由.4、已知:如图;ABC△中;45ABC ∠=°;CD AB ⊥于D ;BE 平分ABC ∠;且BE AC ⊥于E ;与CD 相交于点F H ,是BC 边的中点;连结DH 与BE 相交于点G . 1求证:BF AC =;2求证:12CE BF =;5、 如图;点O 是等边ABC △内一点;110AOB BOC α∠=∠=,.将BOC △绕点C 按顺时针方向旋转60得ADC △;连接OD . 1求证:COD △是等边三角形;2当150α=时;试判断AOD △的形状;并说明理由;3探究:当α为多少度时;AOD △是等腰三角形BD A A BCDO110 α7、过等腰直角三角形直角顶点A 作直线AM 平行于斜边BC;在AM 上取点D;使BD=BC;且DB 与AC 所在直线交于E;求证:CD=CE..过A 作AF ⊥BC 于F;过D 作DG ⊥BC 于G;则DG=AF=1/2BC=1/2BD; 在Rt △BDG 中;DG=1/2BD =>∠DBC=30° =>∠BDC=∠BCD=1/2180°-30°=75°;即∠EDC=75° ∠DEC=∠DBC+∠BCA=30°+45°=75° ∴∠EDC=∠DEC =>CD=CE8、Rt △ABC;AB=AC;BM 是中线;AD ⊥BM 交BC 于D;求证:∠AMB=∠CMD..9、如图;已知△ABC 是等边三角形;∠BDC =120º;说明AD=BD+CD 的理由..10、已知:如图;点D 在△ABC 的边CA 的延长线上;点E 在BA 的延长线上;CF 、EF分别是∠ACB 、∠AED 的平分线;且∠B=30°;∠D=40°;求∠F 的度数..11、等边三角形ABC 和等边三角形DEC;D 在AC 边上..延长BD 交CE 延长线于N;延长AE 交BC 延长线于M..求证:CM=CN 易证△BCD ≌△ACE 所以∠DBC=∠EAC再证△BCN ≌△ACM ASA∴ CM=CNE CABM D AB MA BCE MND12、操作:如图①;△ABC是正三角形;△BDC是顶角∠BDC=120°的等腰三角形;以D为顶点作一个60°角;角的两边分别交AB、AC边于M、N两点;连接MN.探究:线段BM、MN、NC之间的关系;并加以证明.13、如图等边△ABC和等边△CDE;点P为射线BC一动点;角APK=60°;PK交直线CD 于K..(1)试探索AP、PK之间的数量关系;KD(2)当点P运动到BC延长线上时;上题结论是否依然成立为什么.. 14、涉及相似三角形若P为ABC△所在平面上一点;且120APB BPC CPA∠=∠=∠=°;则点P叫做ABC△的费马点. 如图;在锐角ABC△外侧作等边ACB△′连结BB′..求证:BB′过ABC△的费马点P;且BB′=PA PB PC++.15、如图;ABC∆是等腰直角三角形;∠C=900;点M;N分别是边AC和BC的中点;点D在射线BM上;且BD=2BM; 点E在射线NA上;且NE=2NA.求证:BD⊥DE.ACBB'K ADMNEDCBA第五章 全等三角形 拓展延伸分析:三角形全等的证明及其运用关键点在于“把相等的边角放入正确的三角形中”;去说明“相等的边角所在的三角形全等”;利用三角形全等来说明两个角相等两条边相等是初中里面一个非常常见而又重要的方法..例1:已知AE 既是∠BAC 的平分线;也是∠BDC 的平分线;试说明AB=AC思路:AB 在△ABD 中;AC 在△ACD 中;要说明AB=AC;尝试说明△ABD 与△ACD 全等..1. 观察图形发现两个三角形存在公共边AD2. 题目所给条件可以得到两组角相等;3. 再根据三个条件的位置;利用ASA;可得三角形全等 4. 再利用全等三角形的对应边相等;得到AB=AC例2:在△ABC 中;∠BAC=90°;AB=AC;AE 是过点A 的直线;BD ⊥AE;CE ⊥AE;如果CE=5;BD=11;请你求出DE 的长度..思路:抓住题目中所给的一组相等线段AB=AC 进行分析;对它们的位置进行分析;发现AB 、AC 分别位于一个Rt △中;所以尝试着去找条件;去说明它们所在的两个Rt △全等..那么:已经存在了两组等量关系:AB=AC;直角=直角.可以求证△ABD ≌△ACE..D CEAB练习1. 小明说:“三角形一边的两个端点到这边上的中线所在直线的距离相等..”你认为小明的话有道理吗为什么分析:如图;题目的意思是要你说明哪两条线段相等呢_______=_______∴我们只需要说明 ________≌________解:练习2.在△ABC中;∠ACB= 900;AC=BC;直线MN经过点C;且AD⊥MN于D;BE⊥MN于E..1当直线MN绕点C旋转到图1的位置时;△ADC≌△CEB;且DE=AD+BE..你能说出其中的道理吗2当直线MN绕点C旋转到图2的位置时; DE =AD-BE..说说你的理由..3当直线MN绕点C旋转到图3的位置时;试问DE;AD;BE 具有怎样的等量关系请写出这个等量关系..BA图1图3。
角平分线和全等三角形证明分类
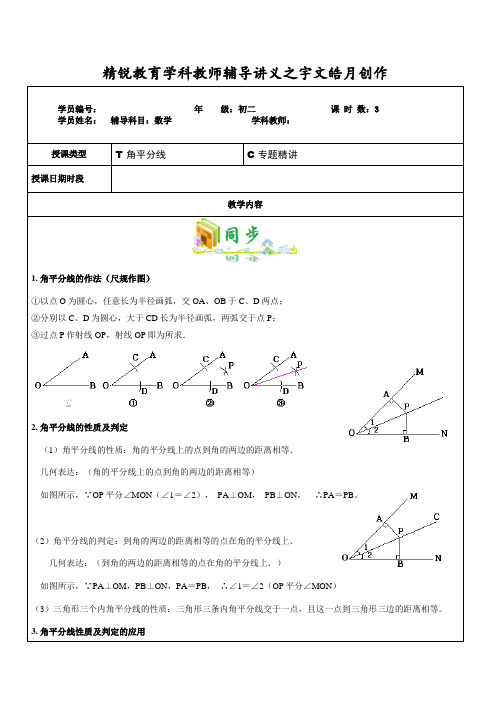
精锐教育学科教师辅导讲义之宇文皓月创作学员编号:年级:初二课时数:3学员姓名:辅导科目:数学学科教师:授课类型T 角平分线C专题精讲授课日期时段教学内容1. 角平分线的作法(尺规作图)①以点O为圆心,任意长为半径画弧,交OA、OB于C、D两点;②分别以C、D为圆心,大于CD长为半径画弧,两弧交于点P;③过点P作射线OP,射线OP即为所求.2. 角平分线的性质及判定(1)角平分线的性质:角的平分线上的点到角的两边的距离相等.几何表达:(角的平分线上的点到角的两边的距离相等)如图所示,∵OP平分∠MON(∠1=∠2),PA⊥OM,PB⊥ON,∴PA=PB。
(2)角平分线的判定:到角的两边的距离相等的点在角的平分线上.几何表达:(到角的两边的距离相等的点在角的平分线上.)如图所示,∵PA⊥OM,PB⊥ON,PA=PB,∴∠1=∠2(OP平分∠MON)(3)三角形三个内角平分线的性质:三角形三条内角平分线交于一点,且这一点到三角形三边的距离相等。
3. 角平分线性质及判定的应用①为推导线段相等、角相等提供依据和思路; ②实际生活中的应用.例:一个工厂,在公路西侧,到公路的距离与到河岸的距离相等,而且到河上公路桥头的距离为300米.在下图中标出工厂的位置,并说明理由.【例题讲解】1.在△ABC 中,AC ⊥BC ,AD 为∠BAC 的平分线,DE ⊥AB ,AB =7㎝,AC =3㎝,求BE 的长。
2.如图:在△ABC 中,∠C=90° AD 是∠BAC 的平分线,DE ⊥AB 于E ,F 在AC 上,BD=DF ; 求证:CF=EB3.如图,P 为∠AOB 内一点,OA=OB ,且△OPA 与△OPB 面积相等,求证∠AOP=∠BOP.4.如图,AB=AC ,AD=AE ,BD 、CE 交于O ,求证AO 平分∠BAC.EDCBAEABCD F【同步练习】1.在Rt △ABC 中,BD 平分∠ABC ,DE ⊥AB 于E ,则: ⑴图中相等的线段有哪些?相等的角呢? ⑵哪条线段与DE 相等?为什么?⑶若AB =10,BC =8,AC =6, 求BE ,AE 的长和△AED 的周长2.已知,如图DABC 中,AB=AC ,D 是BC 的中点。
(完整版)几种证明全等三角形添加辅助线的方法

教学过程构造全等三角形几种方法在几何解题中,常常需要添加辅助线构造全等三角形,以沟通题设与结论之间的联系。
现分类加以说明。
一、延长中线构造全等三角形例1. 如图1,AD是△ABC的中线,求证:AB+AC>2AD。
证明:延长AD至E,使AD=DE,连接CE。
如图2。
∵AD是△ABC的中线,∴BD=CD。
又∵∠1=∠2,AD=DE,∴△ABD≌△ECD(SAS)。
AB=CE。
∵在△ACE中,CE+AC>AE,∴AB+AC>2AD。
二、沿角平分线翻折构造全等三角形例2. 如图3,在△ABC中,∠1=∠2,∠ABC=2∠C。
求证:AB+BD=AC。
证明:将△ABD沿AD翻折,点B落在AC上的E点处,即:在AC上截取AE=AB,连接ED。
如图4。
∵∠1=∠2,AD=AD,AB=AE,∴△ABD≌△AED(SAS)。
∴BD=ED,∠ABC=∠AED=2∠C。
而∠AED=∠C+∠EDC,∴∠C=∠EDC。
所以EC=ED=BD。
∵AC=AE+EC,∴AB+BD=AC。
三、作平行线构造全等三角形例3. 如图5,△ABC中,AB=AC。
E是AB上异于A、B的任意一点,延长AC到D,使CD=BE,连接DE交BC于F。
求证:EF=FD。
证明:过E作EM∥AC交BC于M,如图6。
则∠EMB=∠ACB,∠MEF=∠CDF。
∵AB=AC,∴∠B=∠ACB。
∴∠B=∠EMB。
故EM=BE。
∵BE=CD,∴EM=CD。
又∵∠EFM=∠DFC,∠MEF=∠CDF,∴△EFM≌△DFC(AAS)。
EF=FD。
四、作垂线构造全等三角形例4. 如图7,在△ABC中,∠BAC=90°,AB=AC。
M是AC边的中点。
AD ⊥BM交BC于D,交BM于E。
求证:∠AMB=∠DMC。
证明:作CF⊥AC交AD的延长线于F。
如图8。
∵∠BAC=90°,AD⊥BM,∴∠FAC=∠ABM=90°-∠BAE。
∵AB=AC,∠BAM=∠ACF=90°,∴△ABM≌△CAF(ASA)。
三角形全等的五种判定方法及如何构造三角形全等
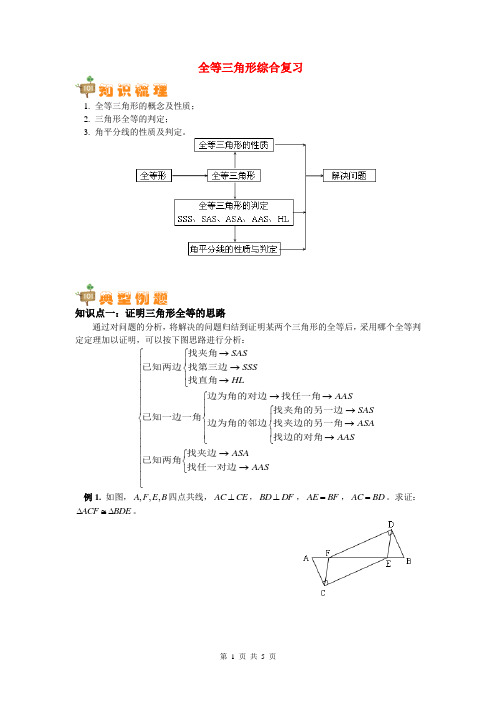
全等三角形综合复习1. 全等三角形的概念及性质;2. 三角形全等的判定;3. 角平分线的性质及判定。
知识点一:证明三角形全等的思路通过对问题的分析,将解决的问题归结到证明某两个三角形的全等后,采用哪个全等判定定理加以证明,可以按下图思路进行分析:⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩SAS SSSHL AAS SAS ASA AAS ASA AAS 找夹角已知两边找第三边找直角边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一对边 例1. 如图,,,,A F E B 四点共线,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =。
求证:ACF BDE ∆≅∆。
知识点二:构造全等三角形例 2. 如图,在ABC ∆中,BE 是∠ABC 的平分线,AD BE ⊥,垂足为D 。
求证:21C ∠=∠+∠。
例3. 如图,在ABC ∆中,AB BC =,90ABC ∠=。
F 为AB 延长线上一点,点E 在BC 上,BE BF =,连接,AE EF 和CF 。
求证:AE CF =。
知识点三:常见辅助线的作法1. 连接四边形的对角线例4. 如图,AB //CD ,AD //BC ,求证:AB CD =。
解题后的思考:连接四边形的对角线,是构造全等三角形的常用方法。
2. 作垂线,利用角平分线的知识例5.如图,,AP CP分别是ABC∆外角MAC∠和NCA∠的平分线,它们交于点P。
求证:BP为MBN∠的平分线。
解题后的思考:题目已知中有角平分线的条件,或者有要证明角平分线的结论时,常过角平分线上的一点向角的两边作垂线,利用角平分线的性质或判定来解答问题。
3. “截长补短”构造全等三角形例 6.如图,在ABC∆中,AB AC>,12∠=∠,P为AD上任意一点。
求证:AB AC PB PC->-。
AAS,HL证全等及角平分线的性质知识点总结和重难点精析

AAS,HL证全等及角平分线的性质知识点总结和重难点精析
知识点总结:
1、AAS定理:两个三角形中,如果两条对应边及其夹角相等,那么这两个三角形全等。
简写成对应角相等的角边角定理。
2、HL定理:两个直角三角形中,如果一条直角边和斜边相等,那么这两个三角形全等。
简写成对应边相等的直角边和斜边定理。
3、角平分线的性质:角平分线是将角分成两个相等的角的射线,角平分线上点到角的两边距离相等。
重难点精析:
1、AAS定理的应用难点在于如何通过已知条件构造出至少一组边角相等的关系,这对于推导证明过程至关重要。
对于初学者来说,可以尝试通过画图和模拟过程来理解,逐渐提高空间想象能力。
2、HL定理的应用主要难点在于直角三角形的判断,需要学生熟悉勾股定理的相关知识。
在解决实际问题时,需要灵活运用直角三角形的性质,如等角对等边等。
3、角平分线的性质在学习中容易被忽视,其重要性在于为证明线段相等提供了一种重要的方法。
对于初学者来说,需要加强对此性质的练习和理解,能够熟练地应用到各种几何问题中。
总结:
AAS,HL定理和角平分线的性质是八年级数学中的重要知识点,
它们在几何学中的应用广泛且具有挑战性。
通过对这些定理的深入学习和实践,学生可以提升自身的几何思维能力和问题解决能力。
角平分线的性质与全等三角形

角平分线的性质与全等三角形一、知识回顾1、角平分线的定义:从一个角的顶点出发把一个角分成两个相等的角的射线叫做角的平分线。
2、角的平分线的性质:角平分线上的点到角的两边的距离相等。
3、全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等。
∵△ABC≌△A'B'C'∴AB=A'B',BC=B'C',AC=A'C'; ∠A=∠A', ∠B=∠B', ∠C=∠C'二、典型例题例1:下列定理中逆定理不存在的是()A.角平分线上的点到这个角的两边距离相等B.在一个三角形中,如果两边相等,那么它们所对的角也相等C.同位角相等,两直线平行D.全等三角形的对应角相等分析:把每个选项的逆命题写出,然后利用相关的知识进行证明,不能证明的是错误的,选项D的逆定理是不存在的.解答:A、角平分线上的点到这个角的两边距离相等的逆定理存在,可通过三角形全等来证明,正确;B、在一个三角形中,如果两边相等,那么它们所对的角也相等逆定理存在,可通过证明三角形全等来证明,正确;C、同位角相等,两直线平行的逆定理是平行线的性质定理之一,正确;D、对应角相等的三角形不全等,及其逆命题不正确,也就是逆定理不存在.故选D.___________________________________________________________________________ ___例2:如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PA平分∠BAC,则△APD与△APE 全等的理由是()A.SAS B.AASC.SSS D.ASA分析:根据已知条件在三角形中的位置来选择判定方法,本题中有两角及一角的对边对应相等,所以应选择AAS,比较简单.解答:由已知得,AP=AP,∠DAP=∠EAP,∠ADP=∠AEP所以符合AAS判定.故选B.___________________________________________________________________________ ___例3:已知,如图,△ABC中,AD是角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F.下列说法,正确的有()①DE=DF,②AE=AF,③AD平分∠EDF;④AD⊥BC,⑤图**有3对全等三角形.A.B. 3个C.4个D.5个分析:根据题意可以推出DE=DF,△AED≌△AFD,即可推出说法①②③为正确.解答:∵AD是角平分线,DE⊥AB,DF⊥AC,∴DE=DF,∠EAD=∠FAD,∴△AED≌△AFD,∴AE=AF,AD平分∠EDF.故选B.___________________________________________________________________________ ___例4:(2002·四川)以下命题中,真命题是()①同一平面内的两条直线不平行就相交;②三角形的外角必定大于它的内角;③两边和其中一边的对角对应相等的两个三角形全等;④两个全等三角形的面积相等.A.①、③B.①、④C.①、②、④D.②、③、④分析:同一个平面内的两条直线的位置关系:平行、相交;三角形的外角大于任何一个和它不相邻的内角;全等三角形的判定方法:SSS、SAS、AAS、ASA;全等三角形的面积比相等.解答:A、根据平面内两条直线的位置关系,故正确;B、三角形的外角应大于任何一个和它不相邻的内角,故错误;C、不符合全等三角形的判定定理,故错误;D、根据全等三角形的定义,故正确.故选B.___________________________________________________________________________ ___例5:如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是()A.∠DAE=∠CBE B.CE=DEC.△DEA不全等于△CBE D.△EAB是等腰三角形分析:由题中条件可得,△ABD≌△BAC,由全等可得对应角相等,对应线段相等,即可得△ADE≌△BCE,所以C中说两个三角形不全等是错误的;再由角相等也可得△EAB为等腰三角形,进而可得出结论.解答:∵∠1=∠2,∠C=∠D,且AB为公共边,∴△ABD≌△BAC,∴∠DAB=∠CBA,AD=BC,又∠1=∠2,∴∠DAE=∠CBE,A正确;又AD=BC,∠D=∠C,∴△ADE≌△BCE,C错误;∴CE=DE,B正确;∵∠1=∠2△EAB为等腰三角形,D正确.故C错,选C.三、解题经验角平分线的性质很简单,也比较容易掌握。
三角形的全等判定(ASA、AAS、SSS、HL)和角的平分线
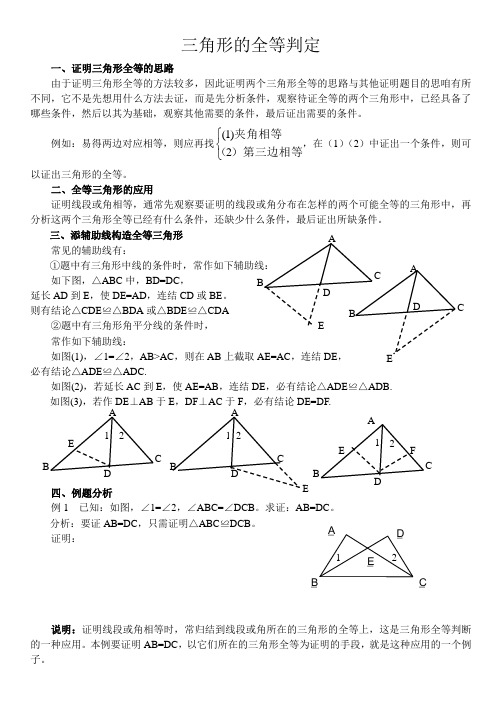
三角形的全等判定一、证明三角形全等的思路由于证明三角形全等的方法较多,因此证明两个三角形全等的思路与其他证明题目的思咱有所不同,它不是先想用什么方法去证,而是先分析条件,观察待证全等的两个三角形中,已经具备了哪些条件,然后以其为基础,观察其他需要的条件,最后证出需要的条件。
例如:易得两边对应相等,则应再找⎩⎨⎧)第三边相等(夹角相等2)1(,在(1)(2)中证出一个条件,则可以证出三角形的全等。
二、全等三角形的应用证明线段或角相等,通常先观察要证明的线段或角分布在怎样的两个可能全等的三角形中,再分析这两个三角形全等已经有什么条件,还缺少什么条件,最后证出所缺条件。
三、添辅助线构造全等三角形 常见的辅助线有:如下图,△ABC 中,BD=DC , 延长AD 到E ,使DE=AD ,连结CD 或BE 。
则有结论△CDE ≌△BDA 或△BDE ≌△CDA ②题中有三角形角平分线的条件时,常作如下辅助线:如图(1),∠1=∠2,AB>AC ,则在AB 必有结论△ADE ≌△ADC.如图(2),若延长AC 到E ,使AE=AB ,连结DE ,必有结论△ADE ≌△ADB.例1 已知:如图,∠1=∠2,∠ABC=∠DCB 。
求证:AB=DC 。
分析:要证AB=DC ,只需证明△ABC ≌DCB 。
证明:说明:证明线段或角相等时,常归结到线段或角所在的三角形的全等上,这是三角形全等判断的一种应用。
本例要证明AB=DC ,以它们所在的三角形全等为证明的手段,就是这种应用的一个例子。
_ C _例2 已知:如图,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF=AC ,FD=CD ,求证:BE ⊥AC 。
分析:本题考察“HL ”公理的应用。
要证BE ⊥AC ,可证∠C+∠1=90°,而∠2+∠1=90°,只需证∠2=∠C 。
从而转化为证明它们所在的△BDF 与△ADC 全等,而这由“HL ”公理不难得证。
八年级数学人教版上册第12章全等三角形12.3角平分线的性质(图文详解)

A
E F
B
D
c
八年级数学上册第12章全等三角形
解法一:添加条件:AE=AF, 在△AED与△AFD中,
∵AE=AF,∠EAD=∠FAD,AD=AD, ∴△AED≌△AFD(SAS). 解法二:添加条件:∠EDA=∠FDA,
在△AED与△AFD中, ∵∠EAD=∠FAD,AD=AD,∠EDA=∠FDA, ∴△AED≌△AFD(ASA).
八年级数学上册第12章全等三角形
通过本课时的学习,需要我们掌握: 1.角平分线的性质: 角的平分线上的点到角的两边的距离相等. 2.角平分线的判定: 到角的两边的距离相等的点在角平分线上.
A
为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
M
C
射线OC即为所求.
O
N
B
八年级数学上册第12章全等三角形
为什么OC是∠AOB的角平分线?
证明:连结MC,NC由作法知: 在△OMC和△ONC中
OM=ON MC=NC OC=OC
O ∵△OMC≌△ONC(SSS) ∴∠AOC=∠BOC 即OC 是∠AOB的角平分线.
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC
画一条射线AE,AE就是∠DAB的平分线.你能说明它的道
理吗?
B
E
C
A D
八年级数学上册第12章全等三角形
【证明】 在△ACD和△ACB中
B
E
C
AD=AB(已知)
DC=BC(已知)
A D
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的对应角相等)
全等三角形及角平分线难题ppt解答

1 这样的点共有_________ 个。 9、如图所示,在△ABC中,BC=5cm,BP、CP分别 是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC, 5 则△PDE的周长是_________________ cm。 10、在△ABC中,∠C=90°,BC=16cm,∠A的平分线AD交BC于D,且CD: 6cm DB=3:5,则D到AB的距离等于_________ 。
(二)填空题 6、如图所示,AB=AC,AD=AE,∠BAC=∠DAE, 55O ∠1=250,∠2=300,则∠3=________________
ห้องสมุดไป่ตู้
7、如图所示,DA⊥AB,EA⊥AC,AB=AD,AC=AE, 90O BET和CD相交于O,则∠DOE的度数是_______________. 角平分线 8、到三角形三边距离相等的点是三角形的___________ 交点,
∴△ADE≌△BCF(SAS) ∴∠E=∠F ∴DF∥BF 例2、如图所示,AD=BC,FD=EB,AB=CD,求证∠E=∠F. 证明:易证:△ADB≌△BCD(SSS) ∴ ∠ABD=∠CDB ∴ ∠BDF=∠EBD 又BE=DF,BD=BD ∴ △EDB≌△BFD(SAS)
例3、如图所示,在△ABC中,延长AC边上的中线BD到F, 使DF=BD,延长AB边上的中线CE到G,使EG=CE,求证: AF=AG. 证明:∵AE=BE,GE=CE, ∠AEG=∠CEB ∴ △ECB≌△GAE(SAS) 同理AF=BC ∴AG=AF
∴∠EDC=∠C=40O
易证△AEB≌△FEB(SAS),∴∠EFB=∠A=100O ∴ED=EF
∴BC=BD+DC=BE+AE.
例7、已知:如图所示PA、PC分别是△ABC的外角∠MAC、∠NCA的平分 线,它们交于P;PD⊥BM于D,PF⊥BN于E,则BP是∠MBN的平分线吗? 说明理由。 是。 ∵PA、PC分别是△ABC的外角∠MAC、∠NCA的平分线 又∵PD⊥BM,PF⊥BN ∴PM=PE=PF, ∴BP是∠MBN的平分线。
中考数学常见几何模型角平分线的基本模型(一)全等类

专题07 角平分线的重要模型(一)全等类角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的全等类模型作相应的总结,需学生反复掌握。
模型1.角平分线构造轴对称模型(角平分线+截线段等)【模型解读与图示】已知如图1,OP为AOB∠的角平分线、PM不具备特殊位置时,辅助线的作法大都为在OB上截取ON OM=,连结PN即可.即有OMP∆≌ONP∆,利用相关结论解决问题.图1 图21.(2022·湖北十堰·九年级期末)在△ABC中,△ACB=2△B,如图①,当△C=90°,AD为△BAC 的角平分线时,在AB上截取AE=AC,连结DE,易证AB=AC+CD.(1)如图②,当△C≠90°,AD为△BAC的角平分线时,线段AB,AC,CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;(2)如图③,当AD为△ABC的外角平分线时,线段AB,AC,CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.【答案】(1)AB AC CD=+;证明见解析;(2)AB AC CD+=;证明见解析.【分析】(1)首先在AB上截取AE=AC,连接DE,易证△ADE△△ADC(SAS),则可得△AED=△C,ED=CD,又由△AED=△ACB,△ACB=2△B,所以△AED=2△B,即△B=△BDE,易证DE=CD,则可求得AB=AC+CD;(2)首先在BA的延长线上截取AE=AC,连接ED,易证△EAD△△CAD,可得ED=CD,△AED =△ACD,又由△ACB=2△B,易证DE=EB,则可求得AC+AB=CD.【详解】(1)猜想:AB AC CD=+.AB∥CD⇒AB+CD=BCFDEBAC证明:如图②,在AB 上截取AE AC =,连结DE ,△AD 为ABC 的角平分线时,△BAD CAD ∠=∠,△AD AD =,△()SAS ADE ADC ≌△△, △AED C ∠=∠,ED CD =,△2ACB B ∠=∠,△2AED B ∠=∠.△B EDB ∠=∠,△EB ED =,△EB CD =,△AB AE DE AC CD =+=+.(2)猜想:AB AC CD +=.证明:在BA 的延长线上截取AE AC =,连结ED .△AD 平分FAC ∠,△EAD CAD ∠=∠.在EAD 与CAD 中,AE AC =,EAD CAD ∠=∠,AD AD =,△EAD CAD ≌△△.△ED CD =,AED ACD ∠=∠.△FED ACB ∠=∠.又2ACB B ∠=∠,FED B EDB ∠=∠+∠,EDB B ∠=∠.△EB ED =.△EA AB EB ED CD +===.△AC AB CD +=.【点睛】此题考查三角形综合题、全等三角形的判定与性质、等腰三角形的判定、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.(2022·山东烟台·九年级期末)已知在ABC 中,满足2ACB B ∠=∠,(1)【问题解决】如图1,当90C ∠=︒,AD 为BAC ∠的角平分线时,在AB 上取一点E 使得AE AC =,连接DE ,求证:AB AC CD =+.(2)【问题拓展】如图2,当90C ∠≠︒,AD 为BAC ∠的角平分线时,在AB 上取一点E 使得AE AC =,连接DE ,(1)中的结论还成立吗?若成立,请你证明:若不成立,请说明理由.(3)【猜想证明】如图3,当AD 为ABC 的外角平分线时,在BA 的延长线上取一点E 使得AE AC =,连接DE ,线段AB 、AC 、CD 又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明. 【答案】(1)证明见解析(2)成立,证明见解析 (3)猜想AB AC CD +=,证明见解析【分析】(1)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED ACD ∠=∠,再根据三角形的外角性质可得45B BDE ∠=∠=︒,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证; (2)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED C ∠=∠,再根据三角形的外角性质可得B BDE ∠=∠,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证;(3)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED ACD ∠=∠,从而可得FED ACB ∠=∠,再根据三角形的外角性质可得B BDE ∠=∠,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证.(1)证明:△AD 为BAC ∠的角平分线,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△ED CD =,AED ACD ∠=∠,又△90ACB ∠=︒,2ACB B ∠=∠,△45B ∠=︒,90AED ∠=︒,△45AED BDE B ∠=∠=∠-︒,△B BDE ∠=∠,△EB ED =,△EB CD =,△AB AE EB AC CD =+=+.(2)解:(1)中的结论还成立,证明如下:△AD 为BAC ∠的角平分线时,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△AED C ∠=∠,ED CD =,△2ACB B ∠=∠,△2AED B ∠=∠,又△AED B EDB ∠=∠+∠,△B EDB ∠=∠,△EB ED =,△EB CD =,△AB AE EB AC CD =+=+.(3)解:猜想AB AC CD +=,证明如下:△AD 平分EAC ∠,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△ED CD =,AED ACD ∠=∠,如图,△180180AED ACD ︒-∠=︒-∠,即FED ACB ∠=∠,△2ACB B ∠=∠,△2∠=∠,FED B又△FED B EDB∠=∠+∠,△EDB B∠=∠,△EB ED=,+===,△AB AE EB ED CD△AB AC CD+=.【点睛】本题主要考查了三角形全等的判定与性质、等腰三角形的判定,熟练掌握三角形全等的判定方法是解题关键.3.(2022·浙江·九年级期中)(1)如图1,在△ABC中,△ACB=2△B,△C=90°,AD为△BAC 的平分线交BC于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)(2)如图2,当△C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.(3)如图3,当△ACB≠90°,△ACB=2△B ,AD为△ABC的外角△CAF的平分线,交BC的延长线于点D,则线段AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.【答案】(1)见解析;(2)AB=AC+CD;(3)AB=CD﹣AC【分析】(1)在AB上截取AE=AC,连接DE,根据角平分线的定义得到△1=△2.推出△ACD△△AED (SAS).根据全等三角形的性质得到△AED=△C=90,CD=ED,根据已知条件得到△B=45°.求得△EDB=△B=45°.得到DE=BE,等量代换得到CD=BE.即可得到结论;(2)在AC取一点E使AB=AE,连接DE,易证△ABD△△AED,所以△B=△AED,BD=DE,又因为△B=2△C,所以△AED=2△C,因为△AED是△EDC的外角,所以△EDC=△C,所以ED=EC,BD=EC,进而可证明AB+BD=AE+EC=AC;(3)在AB的延长线AF上取一点E,使得AE=AC,连接DE.证明△ACD△△AED,根据全等三角形的性质得到DE=BE,BE=CD,即可得出结论.【详解】(1)证明:在AB上取一点E,使AE=AC△AD为△BAC的平分线△△BAD=△CAD.在△ACD和△AED中,AE ACBAD CADAD AD=⎧⎪∠=∠⎨⎪=⎩△△ACD△△AED(SAS).△△AED=△C=90°,CD=ED,又△△ACB=2△B,△C=90°,△△B=45°.△△EDB=△B=45°.△DE=BE,△CD=BE.△AB=AE+BE,△AB=AC+CD.(2)证明:在AB取一点E使AC=AE,在△ACD和△AED中,AC AEBAD EADAD AD===⎧⎪∠∠⎨⎪⎩,△△ACD△△AED,△△C=△AED,CD=DE,又△△C=2△B,△△AED=2△B,△△AED是△EDC的外角,△△EDB=△B,△ED=EB,△CD=EB,△AB=AC+CD;(3)猜想:AB=CD﹣AC证明:在BA的延长线上取一点E,使得AE=AC,连接DE,在△ACD和△AED中,AC AECAD EADAD AD=⎧⎪∠=∠⎨⎪=⎩,△△ACD△△AED(SAS),△△ACD=△AED,CD=DE,△△ACB=△FED,又△△ACB=2△B△△FED=2△B,又△△FED=△B+△EDB,△△EDB=△B,△DE=BE,△BE=CD,△AB=BE-AE△AB=CD﹣AC.【点睛】本题考查全等三角形的判定和性质,关于线段和差关系的证明,通常采用截长补短法.4.(2022·北京九年级专题练习)在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC 平分BAE ∠,90ACE ∠=︒,则线段AE 、AB 、DE 的长度满足的数量关系为______;(直接写出答案)(2)如图(2),AC 平分BAE ∠,EC 平分AED ∠,若120ACE ∠=︒,则线段AB 、BD 、DE 、AE 的长度满足怎样的数量关系?写出结论并证明.【答案】(1)AE =AB +DE ;(2)AE =AB +DE +12BD ,证明见解析.【分析】(1)在AE 上取一点F ,使AF =AB ,由三角形全等的判定可证得△ACB ≌△ACF ,根据全等三角形的性质可得BC =FC ,∠ACB =∠ACF ,根据三角形全等的判定证得△CEF ≌△CED ,得到EF =ED ,再由线段的和差可以得出结论;(2)在AE 上取点F ,使AF =AB ,连结CF ,在AE 上取点G ,使EG =ED ,连结CG ,根据全等三角形的判定证得△ACB ≌△ACF 和△ECD ≌△ECG ,由全等三角形的性质证得CF =CG ,进而证得△CFG 是等边三角形,就有FG =CG =12BD ,从而可证得结论.【详解】解:(1)如图(1),在AE 上取一点F ,使AF =AB .∵AC 平分∠BAE ,∴∠BAC =∠FAC .在△ACB 和△ACF 中,AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩===∴△ACB ≌△ACF (SAS ).∴BC =FC ,∠ACB =∠ACF .∵C 是BD 边的中点,∴BC =CD .∴CF =CD .∵∠ACE =90°,∴∠ACB +∠DCE =90°,∠ACF +∠ECF =90°.∴∠ECF =∠ECD .在△CEF 和△CED 中,CF CD ECF ECD CE CE ⎧⎪∠∠⎨⎪⎩===∴△CEF ≌△CED (SAS ).∴EF =ED .∵AE =AF +EF ,∴AE =AB +DE .故答案为:AE =AB +DE ;(2)AE =AB +DE +12BD .证明:如图(2),在AE 上取点F ,使AF =AB ,连结CF ,在AE 上取点G ,使EG =ED ,连结CG .∵C 是BD 边的中点,∴CB =CD =12BD .∵AC 平分∠BAE ,∴∠BAC =∠FAC . 在△ACB 和△ACF 中,AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩===∴△ACB ≌△ACF (SAS ).∴CF =CB ,∠BCA =∠FCA .同理可证:△ECD ≌△ECG ∴CD =CG ,∠DCE =∠GCE .∵CB =CD ,∴CG =CF .∵∠ACE =120°,∴∠BCA +∠DCE =180°−120°=60°.∴∠FCA +∠GCE =60°.∴∠FCG =60°.∴△FGC 是等边三角形.∴FG =FC =12BD .∵AE =AF +EG +FG ,∴AE =AB +DE +12BD .【点睛】本题主要考查了全等三角形的判定与性质的运用,能熟练应用三角形全等的判定和性质是解决问题的关键.模型2.角平分线垂两边(角平分线+外垂直)【模型解读与图示】已知如图1,OP 为OAB ∠的角平分线、PM OA ⊥于点M 时,辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等,利用相关结论解决问题. 图1图2图3D B邻等对补模型:已知如图2,AP 是∠CAB 的角平分线,EP =DP辅助线:过点P 作PG ⊥AC 、PF ⊥AB结论:①︒=∠+∠180EPD BAC (D P E A 、、、四点共圆);②EG DF =;③DF AE AD 2+=1.(2022·北京·中考真题)如图,在ABC ∆中,AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____.【答案】1【分析】作DF AC ⊥于点F ,由角平分线的性质推出1DF DE ==,再利用三角形面积公式求解即可.【详解】解:如图,作DF AC ⊥于点F ,△AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,△1DF DE ==, △1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1. 【点睛】本题考查角平分线的性质,通过作辅助线求出三角形ACD 中AC 边的高是解题的关键.2.(2022·山东泰安·中考真题)如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =( )A .40°B .45°C .50°D .60°【答案】C【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠FAP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC =∠ACD ﹣∠ABC =2x °﹣(x °﹣40°)﹣(x °﹣40°)=80°,∴∠CAF =100°, 在Rt △PFA 和Rt △PMA 中,{PA PAPM PF ==,∴Rt △PFA ≌Rt △PMA (HL ),∴∠FAP =∠PAC =50°.故选C .【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM =PN =PF 是解题的关键.3.(2022·江苏扬州·中考真题)如图,在ABCD 中,BE 、DG 分别平分ABC ADC ∠∠、,交AC 于点E G 、.(1)求证:,BE DG BE DG =∥;(2)过点E 作EF AB ⊥,垂足为F .若ABCD 的周长为56,6EF =,求ABC ∆的面积. 【答案】(1)见详解(2)84【分析】(1)由平行四边形的性质证()ABE CDG ASA ∆≅∆即可求证;(2)作EQ BC ⊥,由ΔΔΔABC ABE EBC S S S =+即可求解;(1)证明:在ABCD 中,△//AB CD ,△BAE DCG ∠=∠,△ABCD 的周长为56,AB BC +=BE 平分∠EQ EF ==ABC S S ∆∆=【点睛】本题主要考查平行四边形的性质、三角形的全等、角平分线的性质,掌握相关知识CD 交射线OA 于点F ,射线CE 交射线OB 于点G .(1)如图1,若CD △OA ,CE △OB ,请直接写出线段CF 与CG 的数量关系;(2)如图2,若△AOB =120°,△DCE =△AOC ,试判断线段CF 与CG 的数量关系,并说明理由.【答案】(1)CF=CG;(2)CF=CG,见解析【分析】(1)结论CF=CG,由角平分线性质定理即可判断.(2)结论:CF=CG,作CM△OA于M,CN△OB于N,证明△CMF△△CNG,利用全等三角形的性质即可解决问题.【详解】解:(1)结论:CF=CG;证明:△OP平分△AOB,CF△OA,CG△OB,△CF=CG(角平分线上的点到角两边的距离相等);(2)CF=CG.理由如下:如图,过点C作CM△OA,CN△OB,△OP平分△AOB,CM△OA,CN△OB,△AOB=120°,△CM=CN(角平分线上的点到角两边的距离相等),△△AOC=△BOC=60°(角平分线的性质),△△DCE=△AOC,△△AOC=△BOC=△DCE=60°,△△MCO=90°-60° =30°,△NCO=90°-60° =30°,△△MCN=30°+30°=60°,△△MCN=△DCE,△△MCF=△MCN-△DCN,△NCG=△DCE-△DCN,△△MCF=△NCG,在△MCF和△NCG中,CMF CNG CM CNMCF NCG ∠=∠⎧⎪=⎨⎪∠=∠⎩△△MCF △△NCG (ASA ),△CF =CG (全等三角形对应边相等).【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线的性质的应用,熟练证明三角形全等.模型3.角平分线垂中间(角平分线+内垂直)【模型解读与图示】已知如图1,OP 为AOB ∠的角平分线,PM OP ⊥于点P 时,辅助线的作法大都为延长MP 交OB 于点N 即可。
《角平分线》三角形的证明

03
角平分线在解三角形中 的应用
利用角平分线求三角形面积
要点一
结论
通过三角形的两条角平分线和对应的底边,可以快速 求出三角形的面积。
要点二
具体而言,如果我们已知三角 形的两条角平分线长度分别为 $… $S=\frac{ab}{c}\cdot S_{正方形}$,其中$S_{正方形
}$为以$c$为边长的正方形的面积。这个公式的证明可 以通过将三角形拆分为两个小的三角形,并分别求解 它们的面积得到。
THANKS
感谢观看
利用角平分线求三角形内切圆半径
结论:三角形的三条角平分线交于一点,该点到三角 形三边的距离相等,且等于三角形内切圆的半径。
三角形内切圆是与三角形三边都相切的圆,其半径可 以通过三角形的角平分线求得。具体而言,如果我们 已知三角形的三条角平分线长度分别为$a$、$b$和 $c$,那么三角形的内切圆半径$r$可以通过以下公式 求解:$r=\frac{abc}{4K}$,其中$K$为三角形的半周 长,即$K=\frac{a+b+c}{2}$。这个公式的证明可以 通过将三角形的面积表示为半周长与内切圆半径的乘 积得到。
总结词
角平分线等分底边
详细描述
在等腰三角形中,角平分线会将底边等分成两个相等的部分。因此,我们可以利用这个性质来证明一 个三角形是等腰三角形。具体来说,如果我们能证明三角形的底边被角平分线等分,并且这个角平分 线同时也是三角形的中线,那么就可以证明这是一个等腰三角形。
利用角平分线证明直角三角形
总结词
三角形的任意一条角平分线将三角形分成两个面积相等的小三角形。
02 03
关系2
三角形三个角的角平分线交于一点,这一点称为三角形的内心。三角形 的内心到三角形三边的距离相等,且内心与三角形顶点的连线平分相对 应的外角。
三角形全等角平分线模型例题及证明

三角形全等角平分线模型例题及证明好嘞,今天咱们就来聊聊三角形全等和角平分线的那些事儿。
哎,你有没有发现,三角形真的是个神奇的东西,简简单单的三个点,连起来就是个图形,偏偏它的性质可多了。
全等三角形就是那种长得一模一样的三角形,形状、大小都不差分毫,简直就是双胞胎兄弟,走到哪儿都能被认出来。
这可不是光靠眼力就能看出来的,得用几何的法则来推理推理。
你想啊,要是我把一块巧克力分成两半,照样能做出两个一模一样的巧克力,谁能不爱呢?然后咱们聊聊角平分线,听这个名字就觉得高大上,其实它就是把一个角一分为二,像是把一个大蛋糕切成两个均匀的部分。
角平分线的妙处在于,无论你这角多么刁钻,切开后左右两边总是各占一半,这就好比是把一块肉分给两只小狗,谁都不委屈。
这个东西在三角形里特别重要,尤其是当我们要证明一些三角形全等的时候,角平分线可是个好帮手。
来来,咱们用个例子来看看,想象一下一个三角形ABC,A点是个大老板,B和C 是他的两个小弟。
假如我们在A点那儿划一条角平分线,直接把这个角一分为二,结果B和C两兄弟就被各自分到了一份相等的“收益”。
这条角平分线还可以引出一些神奇的性质,比如说,平分线上的每一点到两条边的距离是相等的,就像是公园里的秋千,两边的绳子一样长。
咱们再说说证明的过程,想想看,我们要证明这条平分线把角一分为二,其实就是要把三角形的两个小部分给比出来。
用个简单的三角形来举个例子,假设你有个A点,B点和C点连起来,就是个三角形。
然后,你在A点做一个角平分线,往下拉到BC边,假设叫做D点。
这时候,ABD和ACD这两个小三角形就是咱们的主角了。
要证明它们全等,就要用到一些三角形全等的公理,比如边角边、边边边,这些可是几何的“黄金法则”。
拿到这两个小三角形,咱们就得找出相等的部分。
AD就是它们共同的边,然后,角BAD和角CAD是相等的,因为你就是那条角平分线,没跑。
BD和CD这两个小边也是相等的,因为D点就在BC边上嘛,这可太简单了。
证明两个全等三角形的角平分线相等

《证明两个全等三角形的角平分线相等》一、引言在高中数学学习中,我们经常会接触到三角形的相关知识。
而在三角形的性质中,全等三角形是一个重要的概念。
那么,当两个三角形全等时,它们的角平分线是否相等呢?接下来,我们将从深度和广度两个方面进行全面评估,探讨这一问题。
二、基础知识我们需要了解一些基础知识。
对于全等三角形来说,它们的对应边和对应角都相等。
而角平分线是指一条线段,它将一个角平分成两个相等的角。
在我们证明两个全等三角形的角平分线相等之前,我们需要先了解一下什么是角平分线,以及全等三角形的性质。
1. 什么是角平分线角平分线是指从角的顶点出发,将角平分成两个相等的角的线段。
在三角形中,我们经常遇到内角平分线,它将一个三角形内角平分为两个相等的角。
2. 全等三角形的性质全等三角形指的是具有相同形状和大小的三角形。
当两个三角形的对应边和对应角分别相等时,我们可以称它们为全等三角形。
全等三角形的性质包括对应边相等、对应角相等等。
三、证明角平分线相等接下来,我们将从证明的角度来探讨两个全等三角形的角平分线是否相等。
通过分析和推理,我们可以得出结论并进行证明。
1. 证明思路假设有两个全等三角形ABC和DEF,它们的对应边和对应角分别相等。
我们需要证明角A的平分线和角D的平分线相等。
我们可以利用全等三角形的性质和角平分线的定义来进行证明。
2. 证明过程我们可以根据全等三角形的性质得出三个对应边分别相等,即AB=DE,AC=DF,BC=EF。
根据角平分线的定义和角的性质,我们可以得出角A的平分线和角D的平分线分别是AO和DO。
由于三角形ABC和DEF是全等的,所以角A和角D是相等的,即∠A=∠D。
根据角平分线的性质,我们得出∠BAO=∠DAO。
同理,我们还可以得出∠CAO=∠DA0。
根据角的性质和等量关系,我们可以得出结论:两个全等三角形的角平分线是相等的。
四、总结与回顾通过以上的证明过程,我们得出了结论:两个全等三角形的角平分线是相等的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精锐教育学科教师辅导讲义
学员编号:年级:初二课时数:3
学员姓名:辅导科目:数学学科教师:
授课类型T 角平分线C专题精讲
授课日期时段
教学内容
1. 角平分线的作法(尺规作图)
①以点O为圆心,任意长为半径画弧,交OA、OB于C、D两点;
②分别以C、D为圆心,大于CD长为半径画弧,两弧交于点P;
③过点P作射线OP,射线OP即为所求.
2. 角平分线的性质及判定
(1)角平分线的性质:角的平分线上的点到角的两边的距离相等.
几何表达:(角的平分线上的点到角的两边的距离相等)
如图所示,∵OP平分∠MON(∠1=∠2), PA⊥OM, PB⊥ON,∴PA=PB。
(2)角平分线的判定:到角的两边的距离相等的点在角的平分线上.
几何表达:(到角的两边的距离相等的点在角的平分线上.)
如图所示,∵PA⊥OM,PB⊥ON,PA=PB,∴∠1=∠2(OP平分∠MON)
(3)三角形三个内角平分线的性质:三角形三条内角平分线交于一点,且这一点到三角形三边的距离相等。
3. 角平分线性质及判定的应用
①为推导线段相等、角相等提供依据和思路; ②实际生活中的应用.
例:一个工厂,在公路西侧,到公路的距离与到河岸的距离相等,并且到河上公路桥头的距离为300米.在下图中标出工厂的位置,并说明理由.
【例题讲解】
1.在△ABC 中,AC ⊥BC ,AD 为∠BAC 的平分线,DE ⊥AB ,AB =7㎝,AC =3㎝,求BE 的长。
2.如图:在△ABC 中,∠C=90° AD 是∠BAC 的平分线,DE ⊥AB 于E ,F 在AC 上,BD=DF ; 求证:CF=EB
3.如图,P 为∠AOB 内一点,OA=OB ,且△OPA 与△OPB 面积相等,求证∠AOP=∠BOP.
E
D
C
B
A
E
A
B
C
D
F
4.如图,AB=AC ,AD=AE ,BD 、CE 交于O ,求证AO 平分∠BAC.
【同步练习】
1.在Rt △ABC 中,BD 平分∠ABC ,DE ⊥AB 于E ,则: ⑴图中相等的线段有哪些?相等的角呢? ⑵哪条线段与DE 相等?为什么?
⑶若AB =10,BC =8,AC =6, 求BE ,AE 的长和△AED 的周长
2.已知,如图DABC 中,AB=AC ,D 是BC 的中点。
求证:D 到AB 、AC 的距离相等。
3.△ABC 中,∠C=90°,AD 为角平分线,BC=64,BD ∶DC=9∶7,求D 到AB 的距离.
A B
C
D
E
4.如图,在△ABC中,∠C=90°,AC=BC,AD是∠A是角平分线.求证:AC+CD=AB.
角平分线性质的应用
(一)证明线段相等
例1 已知:如图,∠B=∠C=90°,DM平分∠ADC,AM平分∠DAB。
求证:MB=MC
(二)证明角的平分线
例2已知,如图AF、CF是DABC的外角DAC、ACE的平分线
求证:点F必在B的平分线上。
(三)证明角相等
例3.如图,C、D是∠AOB平分线上的点,CE⊥OA于E,CF⊥OB于F.求证:∠CDE=∠CDF.
◆基础知识扫描
1.点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为( )
A.60°
B.90°
C.120°
D.150°
2.如图1,AB=AD,CB=CD,AC、BD相交于点O,则下列结论正确的是( )
A. OA=OC
B. 点O到AB、CD的距离相等
C. 点O到CB、CD的距离相等
D. ∠BDA=∠BDC
3.△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且
AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A.2cm 2cm 2cm;
B. 3cm 3cm 3cm;
C. 4cm 4cm 4cm;
D. 2cm 3cm 5cm
4.到一个角的两边距离相等的点在 ;角平分线上的点到这个角的两边的距离 .
5.如图2,△ABC中,∠B=90°, ∠A、∠C的平分线交于点O,则∠AOC的度数为 .
◆能力训练升级
6.如图3,P是∠AOB的平分线上的一点,PE⊥OA于E,PF⊥OB于F,OP与EF的位置关系是
7.如图4,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB
的周长为__ cm.
一、专题精讲
【题型一】公共边类型的全等三角形
图形1 图形2 图形3
注意隐含条件AD=AD 隐含条件AB=BA 隐含条件AC=CA
【例1】 在ABC ∆中,AB=AC,AD 平分∠BAC ,求证:ABD ∆≌ACD ∆
【例2】如图, ∠ABC=∠DCB, ∠ACB=∠DBC,求证:AC=DB.
【例3】已知:如图,AB ∥CD ,AB =CD .求证:AD ∥BC .
A B C
D A
B C
D B
C
A D
D C B A A
B C
D
【题型二】边加减类型的全等三角形
图形1 图形2 图形3 图形4
【例4】已知点B,E,C,F 在同一条直线上,AB=DF,AC=DE,BE=CF. 求证:∠A=∠D. .
【例5】如图,已知:.,,CF BE DE AC DF AB ===求证:DF AB //.
【例6】如图,已知:BF CE DF AE CD AB ===,,.求证:(1)DE AF =;(2)AE ∥DF.
【例7】已知:如图,A 、C 、F 、D 在同一直线上,AF =DC ,AB =DE ,BC =EF ,
求证:△ABC ≌△DEF .
B
C
D
E
F A A D B E F C
(1)
A
B
F
E C
D (4) A B F
E D C
(2) A B E F D C
(3) ∵ BE=CF ∴ BE-EF=CF-EF ∴ BF=CE ∵
BE=CF ∴ BE+EF=CF+EF
∴ BF=CE ∵ BE=CF ∴ BE+EF=CF+EF ∴ BF=CE ∵ BE=CF
∴ BE-EF=CF-EF ∴ BF=CE
A D
B
E C
F
【例8】如图,AB=AC,BE和CD相交于P,PB=PC,求证:PD=PE.
【题型四】对顶角类型的全等三角形
图形1 图形2
【例9】如图1,已知:AB=CD,AD=CB.求证:∠B=∠D.
【例10】如图,两条直线AC,BD相交于O,BO=DO,AO=CO,直线EF过点O且分别交AB、CD于点E,F,求证:OE=OF
图形1 图形2 图形3 图形4
【例10】已知:如图(1),AB=AD ,BC=DE ,∠1=∠2.求证:(1)AC=AE ; (2) ∠CAE=∠CDE.
【例11】已知:如图(2),∠E=∠F=90°,∠B=∠C ,AE=AF ,给出下列结论:①∠1=∠2;②BE=CF ;③△CAN ≌△ABM ;④CD=DN.其中正确的结论是__________________.
【例12】如图,已知AB=AD , ∠B=∠D ,∠1=∠2,证明:BC=DE
E
D
C
B
A N M
F
E
D C
B
A
E
D
C
B
A
【题型六】大山型的全等三角形
【例14】已知:如图,AB ⊥CD,ED ⊥BD ,AB=CD ,BC=DE ,求证:AC ⊥CE.
同步练习:
1. 如图所示,已知CD CB AD AB ==,,E 是AC 上一点. 求证:AED AEB ∠=∠.
2. 已知:如图,AB=DC,AC=DB,BE=CE.求证:AE=DE .
3.如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O. 求证:(1) △ABC ≌△AED ; (2) OB =OE .
4.如图,已知:E D ∠=∠,AM EM CN DN ===.
求证:点B 是线段AC 的中点.
5.已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM .
6.已知:如图,AE ⊥AB ,BC ⊥AB ,AE =AB ,ED =AC . 求证:ED ⊥AC .
学法提炼:
1、三角形全等的证题思路
(1)SAS
HL
SSS →⎧⎪→⎨⎪→⎩
找夹角已知两边找直角找另一边 (2)AAS SAS ASA AAS →→⎧⎪→⎧⎪⎨⎪→→⎨⎪⎪⎪→⎩⎩
边为角的对边找任意一角找夹角的另一边已知一边和一角边为角的邻边找夹边的另一角找边的对角 (3)ASA AAS
→⎧⎨→⎩找夹边已知两角找任意一边。
