弹性力学的变分解法
弹性力学的基本方程和变分原理

σ xx
( x,
y, z) +
∂σ xx
( x,
∂x
y, z)
dx +
∂
2σ
xx ( x,
2∂x2
y,
z
)
(
dx
)2
+
略去二阶以上微量,有
σ
xx
(x
+
dx,
y
)
=
σ
xx
(x,
y)
+Leabharlann ∂σxx (x,∂x
y
)
dx
故弹性体 V 域内任一点沿坐标轴 x, y, z 方向的平衡方程为
∂σ x ∂x
+
∂τ xy ∂y
(0.1.5)
其中 [A]是微分算子
∂
∂x
0
0
∂ ∂y
0
∂
∂z
[A]
=
0
∂ ∂y
0
∂∂ ∂x ∂z
0
0
0
∂ ∂z
0
∂ ∂y
∂
∂x
(0.1.6)
{F} 是体积力向量,{F} = Fx Fy Fz T
2. 几何方程——应变-位移关系 设一个变形体微小体元的平面直角在变形前为 APB,而变形后为 A’P’B’,P 点变形到 P’点的
PA′ − PP′ − PA PA
=
P= A + AA′ − PP′ − PA
dx +
u
+
∂u ∂x
dx
−u
− dx
=
∂u
PA
dx
∂x
(2)定义 y 方向的相对伸长量为
弹性力学的变分解法
七、弹性力学参量的下标表示法前面给出的力分量、应力分量、应变分量和位移分量,其表示方法引用的是记号法;这是一种公认的弹性力学参量表示方法。
下标表示法书写简洁,便于力学问题的理论推导。
1. 下标符号具有相同性质的一组物理量,可用一个带下标的字母表示:如:位移分量u, v, w 表示为u 1, u 2, u 3,缩写为u i (i =1,2,3)坐标x, y, z 表示为x 1, x 2, x 3,缩写为x i (i =1,2,3)单位矢量i, j, k 表示e i (i =1,2,3)。
体力分量X, Y, Z 表示为X 1, X 2, X 3,缩写为X i (i =1,2,3)应力分量:z zy zx yz y yxxz xy x 可表示为:333231232221131211 缩写为:)3,2,1;3,2,1( j i ij4. 克罗内克(Kroneker)符号具有如下性质 )cos(j i ij e ej i e eji ji ij 01 100010001333231232221131211 ij ij (1)3ii j i ij A A ij 也称换名算子同理:ijkj ik A a (2)选取可能位移:十、利用位移变分原理的近似解法m mm m mm mm m w C w w v B v v u A u u 000其中系数是完全任意的m m m C B A 、、1、瑞雷—里兹法(1)是在边界上满足位移边界条件的设定函数000w v u 、、(2)是在边界上为零的设定函数m m m w v u 、、可见,由(1)、(2)选取出来的是可能位移w v u 、、。
弹性力学用差分法和变分法解平面问题课件

目 录
• 引言 • 差分法解平面问题 • 变分法解平面问题 • 有限元法的基本原理 • 弹性力学问题的有限元解法实例 • 总结与展望
01
引言
弹性力学简介
01 弹性力学的定义和研究内容
02 弹性力学与其他力学分支的关系
03
弹性力学的发展历程和应用领域
差分法和变分法概述
根据边界条件和约束条件,建立约束方程f,如节点力平衡条件 、位移边界条件等。
通过求解线性方程组Kx=f,得到每个节点的位移。
三维弹性力学问题的有限元解法
建立刚度矩阵
根据每个三维单元的物理特性,建立刚度 矩阵K,该矩阵包含了材料的弹性常数和
每个节点的位移信息。
A 定义三维离散网格
将连续的弹性体离散化为Biblioteka 限个小 的三维单元,每个单元之间通过节
点连接。
B
C
D
求解节点位移
通过求解线性方程组Kx=f,得到每个节点 的位移。
建立约束方程
根据边界条件和约束条件,建立约束方程f ,如节点力平衡条件、位移边界条件等。
06
总结与展望
差分法和变分法的优缺点比较
直观易懂,易于编程实现
差分法优点
对于稳定问题,解的精度和收敛速 度一般较好
差分法和变分法的优缺点比较
差分法的定义和基本原理 变分法的定义和基本原理 差分法和变分法在弹性力学中的应用
平面问题概述
平面问题的定义和分 类
弹性力学中的平面问 题及其研究意义
平面问题的基本特点 和求解方法
02
差分法解平面问题
差分法的基本原理
01
有限差分法是一种将连续的物理问题离散化为网格上的数学问 题的方法。
弹性力学的变分法
F (i) j
=
0
j=1 i=1
i =1
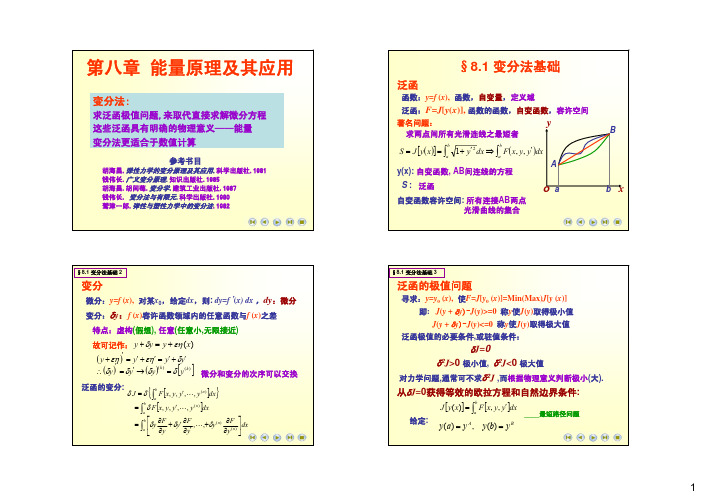
n:质点总数,mj:第j个质点上作用的外力的数量
虚位移原理与牛顿定理完全等价
质点系→弹性体
§8.2 虚位移原理、总位能最小原理3
证明充分性:
∫∫∫ − σ ijδε ij dV + ∫∫∫ X iδui dV ∫∫ + X Viδui dΣ = 0
Ω
Ω
Σ
∫∫∫ ∫∫∫ ∫∫∫ ( ) ∫∫∫ σ ijδε ij dV = σ ijδui, j dV =
S : 泛函
自变函数容许空间: 所有连接AB两点 光滑曲线的集合
oa
B
bx
§8.1 变分法基础 3
泛函的极值问题
寻求:y=y0 (x), 使F=J[y0 (x)]=Min(Max)J[y (x)] 即: J(y + δy)-J(y)>=0 称y使J(y)取得极小值 J(y + δy)-J(y)<=0 称y使J(y)取得极大值
∴
⎧δ ⎩⎨δ
X X
i Vi
=0 =0
Q
⎪⎧σ ⎪⎩⎨σ
ij ij
,j
n
+ Xi j−X
=
Vi
0 =
0
∴
⎪⎧δσ ⎪⎩⎨δσ
ij ij
,j
n
=0 j =0
引入本构关系,对于上述满足平衡方程的应变状态,显然:
δX i = 0, 但 δXVi ≠ 0 即δσij引入约束反力δXvi
虚应力原理可写作:
∫∫∫ − δσ ijε ij (σ )dV + ∫∫ δX Vi (σ )uidΣ = 0
U* U
第9章---弹性力学变分原理

§9-2 应变能与余应变能 热力学定律——导出应变能的表达式
物体在外荷载作用下的功能转换:
弹性力学的 变分原理
可逆过程——外荷载对物体所做的功全部转化为物体的
动能和物体因变形引起的应变能(内能)。
不可逆过程——外荷载对物体所做的功, 一部分转化为
物体的动能和应变能,另一部分转化为热能、声能等被耗散。
y y ( x) y( x) x [a, b]
(9-4)
§9-1 变分法的预备知识 二、函数的变分
弹性力学的 变分原理
通常函数要满足一定的边界条件, 函数的变分应满足齐 次边界条件
y(a) ya , y(b) yb
y(a) 0, y(b) 0
导数的变分
( y) y ( x) y( x) (y ) y ( x) y( x) ( y) (y)
应变能密度是应力分量的函数,而应力分量又是位 置 x、y、z的函数,因此,应变能密度是一个泛函。
泛函的一般形式
I [ y( x)] f ( x, y, y)dx
a
b
§9-1 变分法的预备Hale Waihona Puke 识 二、函数的变分函数的微分
弹性力学的 变分原理
dy y( x)dx
是增量的一阶小量!
函数的变分
热力学定律——导出应变能的表达式
弹性力学的变分原理
(σ u) il,iul il il ( σ ) u σ : ε
代(11-12a)
V ( σ f ) udv σ : εdv
V V
σ : εdv
若以广义虎克定律代入,得应力分量的应变能密度
§9-1 变分法的预备知识 一、函数与泛函
清华大学弹性力学-变分法

y'
)dx]
b
a
f
dx
与(c)比较可知:
I
b
a (
f
)dx
(c)
b
a
f dx
b
a (
f
)dx
积分上下限保持不变,变分和 定积分的运算可以交换顺序。
35
进一步化简:
b
a
f
(
x,
y,
y'
)dx
b
a [
f
(
x,
y
y ,
y'
y'
)
f
(
x,
y,
y'
)]dx
ab[f (y及y'的高阶项)]dx
b
a (
f
dx
)
(ab y及y'的高阶项)dx
泛函I 的变分为:
I
b
a (
f
)dx
(c)
(b)代入(c) ,得: 34
I
b
a (
f y
y
f y'
y'
)dx
I
[
b
a
f
(
x,
y,
例:求图示结构最大挠度。
l
x o
EI
P x
解:(1)设挠曲线为:
w
z
w b1x 2 b2 x3
满足边界条件: ( w )x0 0,
( w x
)x 0
0
(2)用最小势能原理确定b1 , b2
弯矩:
d 2w
M ( x ) EI dx 2 EI ( 2b1 6b2 x )
18
弹性力学用差分法和变分法解平面问题课件

05 弹性力学平面问题的变分 法求解
弹性力学平面问题的变分表示
总结词
通过将弹性力学平面问题转化为变分问题,可以更方便地应用数学工具求解。
详细描述
在弹性力学中,平面问题可以用变分法表示为求取某一泛函的极值问题。这个 泛函通常是由物体的能量泛函表示的,反映了物体的弹性和位移之间的关系。
差分法和变分法的联系
数学基础
两者都基于数学原理,差分法基于离散数学,变分法基于 连续数学。
求解过程
在求解过程中,差分法将连续问题离散化,而变分法则通 过极值条件寻找近似解。
应用领域
两者在弹性力学领域都有广泛应用,差分法更适用于数值模拟和 计算机辅助设计,而变分法更适用于理论分析和解析解的求解。
差分法和变分法的应用选择
差分法的原理
差分法的原理基于泰勒级数展开,将连续的物理量用离散的差商近似代替导数,从而将微分方程转化 为差分方程。
通过选择适当的离散方式和步长,可以使得差分方程的解收敛于原微分方程的解。
差分法的应用
在弹性力学中,差分法可以用于求解 各种平面问题和空间问题,如平面应 变问题、平面应力问题、弹性地基上 的平板问题等。
差分方程的收敛性
分析差分方程求解方法的收敛性,确保求解 过程的稳定性。
弹性力学平面问题的差分解法
差分解法的步骤
详细介绍使用差分法求解弹性力学平面问题的步骤,包括离散化、 建立差分方程、求解差分方程等。
差分解法的应用
举例说明差分解法在解决实际问题中的应用,如板、梁、薄膜等结 构的分析。
差分解法的优缺点
弹性力学平面问题的变分方程
总结词
通过变分法,可以建立弹性力学平面问 题的变分方程。
弹性力学-第十一章 弹性力学的变分原理

1 1 2 1 2 dw2 A = σ xε x = Eε x = Ez ( 2 ) 2 2 2 dx
2
1 L d 2w 2 V = ∫∫∫ Adxdydz = ∫ [∫∫ Ez 2 ( 2 ) dydz]dx 2 0 R dx 1 L d 2w 2 = ∫ EI ( 2 ) dx 2 0 dx
式中: 式中: 总势能为: 总势能为:
应变能为
ψ γ xz =α ( y ) x
ψ γ yz =α ( + x) y
ψ ψ 1 1 2 2 U = GL ∫ (γ xz + γ yz )dA = GLα 2 ∫ [( y )2 + ( + y )2 ]dA 2 2 x y A A
总势能为 ψ ψ 1 ∏ = GLα 2 ∫ [( y)2 + ( + y ) 2 ]dA α LM 2 x y A 令(11.5)变分 变分 为零,并利用 为零 并利用 格林公式得
T
(11.2) (11.9)
上式为一组以 方程组, 方程组,解出
Aim
(m=1,2,3,…)为未知数的线性非齐次代数 为未知数的线性非齐次代数 代入( 代入(11.8)就得到位移的近似解答. )就得到位移的近似解答.
Aim
这种方法称为瑞利 李兹法 这种方法称为瑞利-李兹法. 瑞利 李兹法.
弹性力学的变分原理§ 第十一章 弹性力学的变分原理§11-2 应用最小势能原理求近似解的方法
第十一章 弹性力学的变分原理 §11-1 最小势能原理
d2 d 2w d 2w [ 2 ( EI 2 ) q]δ wdx + ( EI 2 M )δ ( dw ) ∫0 dx dx L dx dx
L
d d 2w [ ( EI 2 ) + P]δ w = 0 dx dx L
弹性力学变分原理

fiuikdv
tiuik ds
s ij
ikj
dv
V
S
V
证明:
因为
s是静力容许的
ij
fiuik dv
s ij
,
juik
dv
V
V
s ij
n
juik
ds
us k
ij i ,
j
dv
S
V
移项后
tiuik ds
s
ij
k ij
dv
S
V
fiuikdv tiuikds isjikj dv
又 I ( b f ( x, y, y )dx) a
与上式比较,可得:
b
b
( f (x, y, y' )dx) f (x, y, y' )dx
a
a
结论:变分运算和积分运算可以交换次序
四、泛函的驻值与极值
1、函数的驻值和极值
如果函数y(x)在x=x0的邻近任一点上的值都 不大于或都不小于y(x0),即
三、泛函的变分
一般情况下,泛函可写为:
b
I a f (x, y, y)dx
1、按照泰勒级数展开法则,被积函数 f 的增 量可以写成
f f ( x, y y, y y ) f ( x, y, y )
f y f y ...
y y
上式中,右边的前两项是 f 的增量的主部, 定义为 f 的一阶变分,表示为
dv
V
S
V
并取
s ij
ij
fi (ui ui )dv ti (ui ui )ds
V
S
ij (ij ij )dv
V
(完整版)弹性力学第十一章弹性力学的变分原理

第十一章弹性力学的变分原理知识点静力可能的应力弹性体的功能关系功的互等定理弹性体的总势能虚应力应变余能函数应力变分方程最小余能原理的近似解法扭转问题最小余能近似解有限元原理与变分原理有限元原理的基本概念有限元整体分析几何可能的位移虚位移虚功原理最小势能原理瑞利-里茨(Rayleigh-Ritz)法伽辽金(Гапёркин)法最小余能原理平面问题最小余能近似解基于最小势能原理的近似计算方法基于最小余能原理的近似计算方法有限元单元分析一、内容介绍由于偏微分方程边值问题的求解在数学上的困难,因此对于弹性力学问题,只能采用半逆解方法得到个别问题解答。
一般问题的求解是十分困难的,甚至是不可能的。
因此,开发弹性力学的数值或者近似解法就具有极为重要的作用。
变分原理就是一种最有成效的近似解法,就其本质而言,是把弹性力学的基本方程的定解问题,转换为求解泛函的极值或者驻值问题,这样就将基本方程由偏微分方程的边值问题转换为线性代数方程组。
变分原理不仅是弹性力学近似解法的基础,而且也是数值计算方法,例如有限元方法等的理论基础。
本章将系统地介绍最小势能原理和最小余能原理,并且应用变分原理求解弹性力学问题。
最后,将介绍有限元方法的基本概念。
本章内容要求学习变分法数学基础知识,如果你没有学过上述课程,请学习附录3或者查阅参考资料。
二、重点1、几何可能的位移和静力可能的应力;2、弹性体的虚功原理;3、最小势能原理及其应用;4、最小余能原理及其应用;5、有限元原理的基本概念。
§11.1 弹性变形体的功能原理学习思路:本节讨论弹性体的功能原理。
能量原理为弹性力学开拓了新的求解思路,使得基本方程由数学上求解困难的偏微分方程边值问题转化为代数方程组。
而功能关系是能量原理的基础。
首先建立静力可能的应力和几何可能的位移概念;静力可能的应力和几何可能的位移可以是同一弹性体中的两种不同的受力状态和变形状态,二者彼此独立而且无任何关系。
能量原理与变分法(弹性力学)

§11-1 弹性体的形变势能
1. 形变势能的一般表达式
P
l0
单向拉伸:
P
外力所做的功:
由于在静载(缓慢加载)条件下, 其它能量损失很小,所外力功全部转 化杆件的形变势能(变形能)U:
l
O
l l
三向应力状态: 一点的应力状态:
P
x
令:
杆件的体积
—— 单位体积的变形能, 称为比能。
z y
x
三向应力状态:
2023最新整理收集 do
第十一章 能量原理与变分法
something
要点:(1)弹性体形变势能的计算、变分法 的基本思想
(2)位移变分法 —— 最小势能原理、里兹(Ritz)法、
伽辽金(Galerkin)法
(3)应力变分法 —— 最小余能原理、卡氏(Castigliano)
定理
(4)位移变分法、应力变分法的应用
主 要内容
§11-1 弹性体的形变势能 §11-2 位移变分方程 §11-3 位移变分法 §11-4 位移变分法应用于平面问题 §11-5 应力变分方程 §11-6 应力变分法 §11-7 应力变分法应于平面问题
§11-8 应力变分法应于扭转问题 §11-9 解答的唯一性 §11-10 功的互等定理
(b)对变分方程进行数值求解
基本思想:将求解区域离散, 离散成有限个小区域(单元), 在小区域(单元)上假设可能解,最后由能量原理
(变分原理)确定其最优解。 —— 将问题转变为求解大型的线性方程组。 —— 有限单元法、边界元法、离散元法 等
典型软件: ANSYS,MARC,ADINA,SAP,NASTRAN, ABAQUS 等; —— 基于有限元法的分析软件; UDEC —— 基于离散元法的分析软件;
弹性力学有限元第五章 变分法解平面问题

用V表示外力的势能(以u,v=0的自然状态下的势能为0),它等于外 力在实际位移上所做的功冠以负号,则:
d U V 0
第五章 变分法解平面问题
§5-3 位移变分方程
d U V 0
U+V是形变势能和外力势能的总和,可以看出,在给定的外力作 用下,实际存在的位移应使总势能的变分成为零。 最小势能原理
积分可得形变势能。 平面应变问题作弹性常数的替换。
第五章 变分法解平面问题
§5-3 位移变分方程
设有平面问题中的任一单位厚度的弹性体,在外力作用下平衡。
u,v为其实际位移分量,假设这些位移分量发生了位移变分(虚位 移)d u, d v,成为:u u d u v v d v
考察其能量方面的变化。
b a a
增量的主要部分定义为泛函的变分,则
f f 代入d f,则 d I d y d y dx a y y
b
d I d f dx
b a
显然,存在关系式: d
b
a
f dx d f dx
a
b
只要积分的上下限不变,变分的运算和定积分运算可以交换次序
U1 U1 U1 dxdy f xd u f yd v dxdy f xd u f yd v ds e x de x e y de y g xy dg xy
虚功方程:方程右边各项称为应力在虚应变上的虚功。 如果在虚位移发生之前,弹性体是出于平衡状态,那么在虚位移过程 中,外力在虚位移上所做的虚功等于应力在虚应变上所做的虚功。
b
第五章 变分法解平面问题
§5-1 变分法简介
弹性力学经典变分原理

E Eij
为 Lagrange-Green 应变张量(用 Lagrange 坐标系来描述),把
ij
称作为
Euler-Almansi 应变张量(用 Euler 坐标系来描述)。 如 果 我 们 在 Lagrange 坐 标 系 中 , 沿 着 某 一 个 特 定 的 坐 标 方 向 取 一 个 微 分 单 元
0 ny 0
0 0 nz
0 nz ny
nz 0 nx
ny nx 0
(3.1.29)
j 1
3
ij , j
f i 0,
i 1, 2,3
(3.1.30)
写成分量的形式为
x xy zx fx 0 x y z
xy x
y y
(3.1.24)
ε E T ( )u
其中
(3.1.25)
u [u v w]T
[ x y z yz zx xy ]T
x E ( ) = E ( , , ) 0 x y z 0
式中 代表梯度算子
0 y 0
(3.1.27)
也就是说
p E (n)
式中
(3.1.28)
p px
py
pz
T
[ x y z yz zx xy ]T
E (n) 就是将 E ( ) 中的梯度矢量替换成截面的法向单位矢量 n ,即 nx E ( n) 0 0
3.1.4 平衡方程 应力分量在物体内部的平衡方程为
3 3 3
dX i
X i dx j j 1 x j
3
ds 2 ds0 2
第7章弹性力学变分解法

ij ij
2
1 2
(2G ij ij ) ij 1 2 (K 2 3 G )
2
1 2 1 2
G ij ij
K
2
G ij ij
G
2
' ij
' ij
Wv W f
' ij
式中 Wv
K E
1 2
K
W f G
'ij
关于虚位移原理的注解 由虚位移原理(位移变分方程)
V
V
ij
ij dV fi ui dV T j u j dS
V S
ij ij dV
V
W
ij
ij dV WdV
V
W ( ij )dV
m 1
n
对i不求和 _ v0=v _ w0=w
_ u, v, w 满足边界条件:u0=u
且代入总势能变分方程 (U W ) 0 中 可解出系数am, bm, cm。
伽辽金法:由 (U V ) 0
有 展开上式
V
U V 0
1 2 ( ij ui , j ji u j ,i )dV ij ui , j dV
V S
令 U W ( ij )dV 称为变形势能;
V fi ui dV T j u j dS 称为外力势能。
V S
V
则对于 ( W ( ij )dV
V
f i ui dV T j u j dS ) 0
V S
有
(U V ) 0
变形体的虚功原理常用的一种形式
弹性力学的变分原理 ppt课件

ilil
σ u il,iul ilul,i il,iul ilil σu σ :ε
V f udv σ udv
V
V
σ f udv σ :εdv σ :εdv
理
理
§11-3 广义虚功原理
一、真实位移、真实应力和真实应变
即几何连续条件
即平衡条件 它们构成弹性力学问题的解。
二、容许位移、容许应变
比较
只对应于一个连续的位移场,但不一定 对应于一个平衡的应力状态,即与 对应的 应力不一定满足平衡条件;而真实位移必对 应一个平衡的应力状态。
容许位移和应变不一定是真实的位移和应 变。但反之,真实的位移和应变必然是容许 的。
一般情况下,泛函具有如下形式:
二、函数的微分 与变分
1、自变量的微分dx 2、函数的微分-因变量增量 3、函数的变分-与微分对应,仍为函数
注意到:
与(*)式比较,可见: 即:
结论:导数的变分等于变分的导数,或变分
记号与求导记号可以互换。
三、泛函的变分
一般情况下,泛函可写为:
1、按照泰勒级数展开法则,被积函数 f 的增 量可以写成
1 2
ij
ui, j
ui, j
1 2
ijui, j
ijui, j
1 2
ijui, j ijui, j
iju j,i
1 2
ij
ui, j
u j,i
ijij
V f udv t uds f udv n σ uds
弹簧
准静态加载
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七、弹性力学参量的下标表示法
前面给出的力分量、应力分量、应变分量和位移分量,其 表示方法引用的是记号法;这是一种公认的弹性力学参量表示 方法。 下标表示法书写简洁,便于力学问题的理论推导。 1. 下标符号 具有相同性质的一组物理量,可用一个带下标的字母表示: 如:位移分量 u, v, w 表示为 u1, u2, u3 ,缩写为ui(i=1,2,3) 体力分量 X, Y, Z 表示为X1, X2, X3 ,缩写为Xi(i=1,2,3) 坐标 x, y, z 表示为x1, x2, x3 ,缩写为xi(i=1,2,3) 单位矢量 i, j, k 表示ei(i=1,2,3)。
( G ) , i G 2ui X i 0 (i 1 , 2 , 3) E —— 拉梅常数 (1 )(1 2 )
x y z ij ij
—— 体积应变
(2) 几何方程
1 ij ui , j u j , i 2
二、变分法
变分法是研究求泛函的极大 值和极小值的方法
三、变分法发展的三个古典问题
1、最速降线问题 确定一条曲线,连接不在同一铅直线上所 给二点A和B,使它具有:当质点沿这条 线由A滑至B时所需的时间为最小。 即求泛函: 2 的极小值
y A
J
x1
1 y 2 gy
x0
dx
B
x
2、短程线问题 求曲面
S
2
t0
x y )dt ( xy
的极大值,且须满足
t1
t0
y dt l x
2 2
一般情况下,泛函具有如下形式:
F ( x, y, y)dx
a
b
其中被积函数 F ( x, y, y) 也是 y(x) 的泛函
四、函数的微分与泛函的变分 dy f dx ydx 函数的微分:
( x, y , z ) 0
x1
上所给二点间长度最短的曲线。
这是约束极值或条件极值问题。即求泛函:
J
x0
2 2 1 y z dx
的极小值,其中 y(x) 和 z(x) 应满足 ( x, y, z ) 0
3、等周问题 求长为一定的封闭线 l ,使其所围成的面积 S 为最大。 即求泛函: 1 t1
(i 1,2,3)
a a1e1 a2 e2 a3e3
求和指标
aij x j Pi
j 求和指标
i 非求和指标 称为自由指标
(i 1,2,3;
j 1,2,3)
a11 x1 a12 x2 a13 x3 P 1 a21 x1 a22 x2 a23 x3 P2 a x a x a x P 3 31 1 32 2 33 3
1 F 2g 1 y 2 y
Fy Fxy Fyy y Fyy y 0
d ( F Fy y) 而 dx y( Fy Fxy Fyy y Fyy y) 0
不显含 x
尤拉方程有初积分形式:
F Fy y C
F Fy y C
(3) 物理方程 用应力分量表示应变分量
x
1 ij ij kk ij E E
1 x E E 1 y y E E 1 z z E E
用应变分量表示应力分量
1 xy xy 2 E yz 1 yz yz 2 E zx 1 zx zx 2 E
假设函数 y(x) 的形式发生改变而成为 新的函数 Y(x) ,如果对应于 x 的一个 定值,y 有微小增量 y
y
Y(x) y dx dy y(x)
y Y ( x) y ( x)
—— y(x) 的变分
( y) Y ( x) y( x) d (y ) 而 (y ) Y ( x) y( x)
3. 求导数的简记方法 微分算符简记法:
例:
, i xi ui ui , i u11 u 22 u33 xi
求和约定
, i xi x j xi ui ui ui , j ui , jk x j x j xk
六、变分问题的直接解法(里兹法) 里兹法——从一族假定解中寻找满足泛函变分的“最佳”解
n
取满足边界条件的试函数 其中 Ci —— 待定系数
y ( x) CiU i
i 1
U i —— 基函数
确定 Ci 使泛函 达到极值 0 , (i 1 , 2 , , n) Ci
Ci
v u xy yx x y w v yz zy y z w u zx xz x z
u x x v y y w z z
求泛函 [ y ( x)]
x1
x0
F ( x, y ( x), y( x))dx
的极值,其中容许函数(能确定泛函的曲线)的边界点是固定 的,且 y ( x0 ) y0 , y ( x1 ) y1 ,函数 F ( x, y, y) 三阶可微 x1 F F 其变分为 [ y y]dx x0 y y dy dy dx d (y ) 看积分第2项 (y)dx ( )dx dx dx x1 不动边界 x1 F x1 d F F 分部积分 ydx ( )ydx y 0 x0 y x0 dx y y x0 x1 F d F [ ( )]ydx x0 y dx y F d F y(x) 能使 取得极值的必要条件是: ( ) 0 尤拉方程 y dx y 或 Fy Fxy Fyy y Fyy y 0
弹性力学的变分解法 一、泛函
定义:凡变量的值是由一个或几个函数的选取而确定者,这个 变量就叫做泛函 如:连接给定两点的曲线弧的长 l 是一个泛函(因这个量是由 函数 y=y(x) 的选取而确定的)
l[ y ( x)]
x1
y
x0
1 y2 dx
B(x1 ,y1 ) y=y(x) A(x0 ,y0 ) x
dx
( y) (y )
—— 导数的变分 = 变分的导数
x
泛函的变分:考察泛函 F(x, y, y’) 当函数 y(x) 具有变分 y 时, 泛函的增量可用泰勒展开:
y 也有变分y
F F F ( x, y y , y y) F ( x, y , y) y y (y及y高阶项) y y F F y y —— 泛函F 的变分 定义: F y y
例:最速降线问题 将坐标原点置于A点,质点的运动速度为 ds 2 gy dt 从 A(0,0) 滑至B(x1 ,y1 ) 所用时间为
1 t [ y ( x)] 2g 1 y 2 y
A
x
B y
x1
0
dy
y (0) 0 , y ( x1 ) y1
尤拉方程
求泛函 t 的极值函数 y(x)
考察泛函 [y(x)], 的增量为:
b b
a b
F ( x, y y, y y) dx F ( x, y, y) dx
a
[ F ( x, y y, y y) F ( x, y, y)]dx
a
[F (y及y的高阶项)]dx (F ) dx (y及y的高阶项)dx
应力分量:
x xy xz yx y yz zx zy z
11 12 13 21 22 23 31 32 33
可表示为:
缩写为: ij ( i 1 , 2 , 3 ; j 1 , 2 , 3 )
即
1 y y
2
y
2 2
2 y ( 1 y ) C1 化简后:
C
y (1 y )
引进参数 t ,使
y ctg t
C1 C1 C1 2 y C1 sin t (1 cos 2t ) 2 2 1 y 1 ctg t 2 dy 2C1 sin t cos tdt dx 2C1 sin 2 tdt C1 (1 cos 2t ) dt y ctg t sin 2t C1 x C1 (t ) C2 ( 2t sin 2t ) C2 2 2 C1 C1 x (t1 sin t1 ) x C2 (2t sin 2t ) 2 2 C1 C1 y (1 cos t1 ) y (1 cos 2t ) 2 2 —— 圆滚线 C2 0 令 2t t1 ,且因y=0, x=0 时,
x y z
xy
ij ij 2G ij
(4) 边界条件 力边界条件: 位移边界条件:
应变分量:
x yx zx
xy xz y yz zy z
13 x 1 23 yx 2 1 33 zx 2 1 xy 2 1 xz 2 1 yz 2 z
1 i j ij 0 i j
11 12 13 1 0 0 0 1 0 ij 22 23 21 31 32 33 0 0 1 ij 具有如下性质 (1) ii 3
(2) ij Ai A j 同理:
ij 也称换名算子
aik kj Aij
5. 弹性力学的下标表示法
(1) 平衡微分方程 应力分量表示:
ij , j X i 0 (i 1, 2, 3)
位移分量表示:
