三角函数的诱导公式(A卷)
三角函数的诱导公式练习题含答案

三角函数的诱导公式练习题(1)1. tan225∘的值为()A.1B.√22C.−√22D.−12. 已知3sin(θ+π2)+sin(θ+π)=0,θ∈(−π,0),则sinθ=( )A.−3√1010B.−√1010C.3√1010D.√10103. 若sin(π3−α)=−13,则cos(α+π6)=( )A.−13B.13C.−2√23D.2√234. 已知sin(α+π4)=35,则cos(π4−α)=( )A.4 5B.−45C.−35D.355. 已知α是第二象限角,若sin(π2−α)=−13,则sinα=()A.−2√23B.−13C.13D.2√236. 已知函数f(x)={1x,x0,log2x−3,x0,则f(−12)⋅f(16)=()A.3B.1C.−1D.−27. (5分)已知x∈R,则下列等式恒成立的是( )A.sin(−x)=sin xB.sin(3π2−x)=cos xC.cos(π2+x)=−sin x D.cos(x−π)=−cos x8. sin 14π3−cos (−25π4)=________.9. 已知sin α=45,则cos (α+π2)=________. 10. cos 85∘+sin 25∘cos 30∘cos 25∘等于________11. 已知cos θ=−35,则sin (θ+π2)=________.12. 已知cos (π−α)=35,α∈(0,π),则tan α=________.13. 已知f (α)=sin (α−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π),其中α≠12kπ(k ∈Z ).(1)化简f (α);(2)若f (π2+β)=−√33,且角β为第四象限角,求sin (2β+π6)的值.14. 已知α为第二象限角,且sin α+cos α=−713,分别求tan α,sin 2α−2sin αcos α的值.15. 如图,四边形ABCD 中,△ABC 是等腰直角三角形,其中AC ⊥BC ,AB =√6,又CD//AB ,cos ∠ABD =√63.(1)求BD 的长;(2)求△ACD的面积.参考答案与试题解析三角函数的诱导公式练习题(1)一、选择题(本题共计 6 小题,每题 5 分,共计30分)1.【答案】A【考点】运用诱导公式化简求值【解析】原式中的角度变形后,利用诱导公式及特殊角的三角函数值计算即可得到结果.【解答】解:原式=tan(180∘+45∘)=tan45∘=1,故选A.2.【答案】A【考点】同角三角函数间的基本关系诱导公式【解析】利用诱导公式,同角三角函数基本关系式即可求解.【解答】解:∵sin(θ+π2)=sinθcosπ2+cosθsinπ2=cosθ,sin(θ+π)=sinθcosπ+cosθsinπ=−sinθ,∴ 3cosθ−sinθ=0,∴cosθ=13sinθ,由于sin2θ+cos2θ=1,而θ∈(−π,0),∴sinθ<0,∴109sin2θ=1.∴sinθ=−3√1010.故选A.3.【答案】A【考点】运用诱导公式化简求值【解析】观察所求角和已知角可得cos(α+π6)=cos[π2−(π3−α)],再利用诱导公式即可求解.【解答】解:∵ (α+π6)+(π3−a)=π2,∴ cos (α+π6)=cos [π2−(π3−α)]=sin (π3−α)=−13.故选A .4.【答案】 D【考点】运用诱导公式化简求值 【解析】由题意利用利用诱导公式化简三角函数式的值,可得结果. 【解答】解:∵ sin (α+π4)=35, ∴ cos (π4−α)=sin [π2−(π4−α)] =sin (π4+α)=35. 故选D . 5. 【答案】 D【考点】同角三角函数间的基本关系 运用诱导公式化简求值【解析】直接利用诱导公式以及同角三角函数基本关系式转化求解即可. 【解答】α是第二象限角,若sin (π2−α)=−13 可得cos α=−13,所以sin α=√1−cos 2α=2√23. 6.【答案】 D【考点】 求函数的值 分段函数的应用 函数的求值 【解析】推导出f(−12)=1−12=−2,f(16)=log 216−3=4−3=1,由此能求出f(−12)⋅f(16)的值. 【解答】∵ 函数f(x)={1x,x0,log 2x −3,x0,∴ f(−12)=1−12=−2,f(16)=log 216−3=4−3=1, ∴ f(−12)⋅f(16)=(−2)×1=−2.二、 多选题 (本题共计 1 小题 ,共计5分 ) 7.【答案】 C,D【考点】运用诱导公式化简求值 【解析】 此题暂无解析 【解答】解:A ,sin (−x )=−sin x ,故 A 不成立; B ,sin (3π2−x)=−cos x ,故B 不成立; C ,cos (π2+x)=−sin x ,故C 成立;D ,cos (x −π)=−cos x ,故D 成立. 故选CD .三、 填空题 (本题共计 5 小题 ,每题 5 分 ,共计25分 ) 8.【答案】√3−√22【考点】运用诱导公式化简求值 【解析】本题考查利用诱导公式求值. 【解答】 解:sin14π3−cos (−25π4)=sin (4π+2π3)−cos (−6π−π4) =sin 2π3−cos π4=√3−√22. 故答案为:√3−√22.−4 5【考点】运用诱导公式化简求值【解析】原式利用诱导公式化简,将sinα的值代入计算即可求出值.【解答】解:∵sinα=45,∴cos(π2+α)=−sinα=−45.故答案为:−45.10.【答案】12【考点】三角函数的恒等变换及化简求值【解析】把cos85∘化为cos(60∘+25∘),由两角和的余弦公式化简即可.【解答】cos85∘+sin25∘cos30∘cos25∘=cos(60∘+25∘)+sin25∘cos30∘cos25∘=12cos25∘−√32sin25∘+√32sin25∘cos25∘=12.11.【答案】−3 5【考点】三角函数的恒等变换及化简求值【解析】由已知利用诱导公式即可化简求值得解.【解答】∵cosθ=−35,∴sin(θ+π2)=cosθ=−35.−43【考点】同角三角函数间的基本关系 运用诱导公式化简求值【解析】由诱导公式可得cos a 的值,及α的范围,利用同角三角函数间的基本关系求出tan α的值即可. 【解答】解: ∵ cos (π−α)=−cos α=35,α∈(0,π), ∴ cos α=−35<0,则α∈(π2,π),则sin α=√1−cos 2α=45, ∴ tan α=sin αcos α=45−35=−43.故答案为:−43.四、 解答题 (本题共计 3 小题 ,每题 5 分 ,共计15分 ) 13.【答案】 解:(1) f(α)=sin (a−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π)=(−cos α)⋅sin α⋅(−tan α)(−tan α)⋅sin α=−cos α.(2)由f (π2+β)=−cos (π2+β)=−√33,得sin β=−√33, 又角β为第四象限角,所以cos β−√63, sin 2β=−2√23,cos 2β=13,所以sin (2β+π6)=sin 2βcos π8+cos 2βsin π6 =(−2√23)⋅√32+13⋅12=1−2√66. 【考点】运用诱导公式化简求值同角三角函数间的基本关系 【解析】 此题暂无解析 【解答】 解:(1) f(α)=sin (a−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π)=(−cos α)⋅sin α⋅(−tan α)(−tan α)⋅sin α=−cos α.(2)由f (π2+β)=−cos (π2+β)=−√33,得sin β=−√33, 又角β为第四象限角,所以cos β−√63, sin 2β=−2√23,cos 2β=13,所以sin (2β+π6)=sin 2βcos π8+cos 2βsin π6=(−2√23)⋅√32+13⋅12=1−2√66. 14. 【答案】解:因为sin α+cos α=−713,所以(sin α+cos α)2=sin 2α+2sin αcos α+cos 2α=49169, 整理得2sin αcos α=−120169,则(sin α−cos α)2=1−2sin αcos α=289169. 因为α为第二象限角,所以sin α−cos α=1713,解得sin α=513,cos α=−1213. 所以tan =sin αcos α=−512, sin 2α−2sin αcos α=25169−(−120169)=145169. 【考点】同角三角函数间的基本关系 三角函数的恒等变换及化简求值 【解析】 【解答】解:因为sin α+cos α=−713,所以(sin α+cos α)2=sin 2α+2sin αcos α+cos 2α=49169, 整理得2sin αcos α=−120169,则(sin α−cos α)2=1−2sin αcos α=289169.因为α为第二象限角,所以sin α−cos α=1713, 解得sin α=513,cos α=−1213. 所以tan =sin αcos α=−512,sin 2α−2sin αcos α=25169−(−120169)=145169.15.【答案】解:(1)因为CD // AB ,AC ⊥BC ,△ABC 是等腰直角三角形, 所以∠ABC =∠CA =∠ACD =12×(180∘−90∘)=45∘, 所以∠BCD =90∘+45∘=135∘.所以sin ∠BDC =sin ∠ABD =√1−(√63)2=√33, 在△ABC 中,BC =AC =√3, 在△BCD 中,由正弦定理得, BD =BC⋅sin ∠BCD sin ∠BDC=√3×√22√33=3√22.(2)在△BCD 中,由正弦定理可得, CD =BC ⋅sin (45∘−∠ABD)sin ∠BDC=√3×√22×(√63−√33)√33=2√3−√62. 所以S △ACD =12AC ⋅CD ⋅sin ∠ACD =12×√3×2√3−√62×√22=3(√2−1)4. 【考点】正弦定理同角三角函数间的基本关系【解析】(1)由题意可求∠BCD =135∘,在△BCD 中,由正弦定理可得BD 的值.(2)在△BCD 中,由正弦定理可得CD 的值,根据三角形的面积公式即可求解. 【解答】解:(1)因为CD // AB ,AC ⊥BC ,△ABC 是等腰直角三角形, 所以∠ABC =∠CA =∠ACD =12×(180∘−90∘)=45∘, 所以∠BCD =90∘+45∘=135∘.所以sin ∠BDC =sin ∠ABD =(√63)=√33, 在△ABC 中,BC =AC =√3, 在△BCD 中,由正弦定理得, BD =BC⋅sin ∠BCD sin ∠BDC=√3×√22√33=3√22.(2)在△BCD 中,由正弦定理可得,CD=BC⋅sin(45∘−∠ABD)sin∠BDC=√3×√22×(√63−√33)√33=2√3−√62.所以S△ACD=12AC⋅CD⋅sin∠ACD=12×√3×2√3−√62×√22=3(√2−1)4.试卷第11页,总11页。
02三角函数诱导公式(含经典例题+答案)
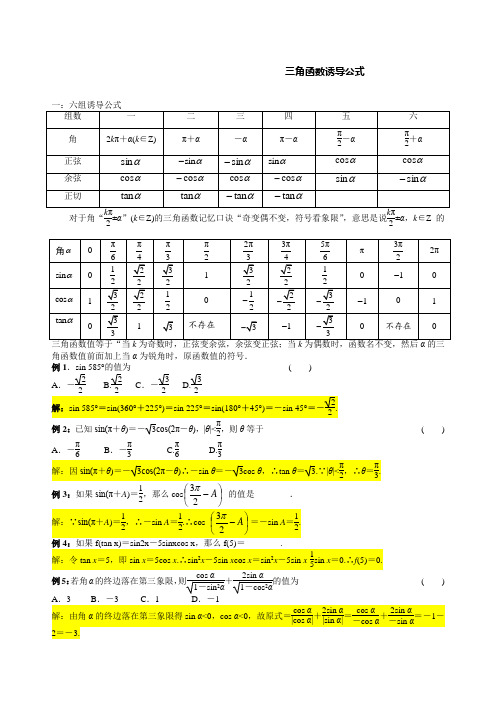
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说k π2±α,k ∈Z 的角函数值前面加上当α为锐角时,原函数值的符号.例1.sin 585°的值为 ( )A .-2 B.2 C .-3 D.3例2:已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于 ( )A .-πB .-π C.π D.π例3:如果sin(π+A )=12,那么cos ⎪⎫⎛-A 3 的值是________. 例5:若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 ( )例6:已知α∈(-π,0),tan(3π+α)=31,则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B .-1010 C.31010 D .-31010解:tan α=13,cos ⎪⎭⎫⎝⎛+απ23=sin α.∵α∈(-π,0),∴sin α=-1010. A .-32 B.32 C.3-12 D.3+12解:sin 600°+tan 240°=sin(720°-120°)+tan(180°+60°)=-sin 120°+tan 60°=-32+3=32. ( ) A .3 B .5 C .1 D .不能确定解:f(2 011)=asin(2 011π+α)+bcos(2 011π+β)+4=asin(π+α)+bcos(π+β)+4=-asin α-bcos β+4 =5.∴asin α+bcos β=-1.∴f(2 012)=asin(2 012π+α)+bcos(2 012π+β)+4=asin α+bcos β+4 =-1+4=3.1.诱导公式在三角形中经常应用,常用的变形结论有:A +B =π-C ; 2A +2B +2C =2π;A 2+B 2+C 2=π2.2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.例9:△ABC 中,cos A =13,则sin(B +C )=________.解:∵△ABC 中,A +B +C =π,∴sin(B +C )=sin(π-A )=sin A =1-cos 2A =223.例10:在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角. 解:由已知得⎩⎨⎧sin A =2sin B ①3cos A =2cos B ②①2+②2得2cos 2A =1,即cos A =22或cos A =-22.(1)当cos A =22时,cos B =32,又A 、B 是三角形的内角,∴A =π4,B =π6,∴C =π-(A +B )=712π. A .B .C .D .2.cos (﹣30°)的值是( ) A .B .C .D .3.下列能与sin20°的值相等的是( ) A .cos20° B .sin (﹣20°) C .sin70° D .sin160°4.已知,则下列各式中值为的是( )A .B .sin (π+α)C .D .sin (2π﹣α)换元法与诱导公式例11:已知41)3sin(=+απ,则=-)6cos(απ 。
三角函数的诱导公式

三角函数的诱导公式常用的诱导公式有以下几组:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为:对于k·π/2±α(k∈Z)的个三角函数值,①当k是偶数时,得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cotcot→tan.(奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)例如:sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
三角函数诱导公式练习题-带答案

三角函数的诱导公式(1)一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( )A .-2π+2k π≤x ≤2π+2k π B .-2π+2k π≤x ≤2π3+2k π C . 2π+2k π≤x ≤2π3+2k π D .(2k +1)π≤x ≤2(k +1)π(以上k ∈Z ) 2.sin (-6π19)的值是( ) A . 21 B .-21 C .23 D .-23 3.下列三角函数:①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π]; ⑤sin [(2n +1)π-3π](n ∈Z ). 其中函数值与sin3π的值相同的是( ) A .①② B .①③④ C .②③⑤ D .①③⑤4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为( ) A .-36 B .36 C .-26 D .26 5.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( )A .cos (A +B )=cosC B .sin (A +B )=sin C C .tan (A +B )=tan CD .sin2A B +=sin 2C 6.函数f (x )=cos3πx (x ∈Z )的值域为( ) A .{-1,-21,0,21,1} B .{-1,-21,21,1} C .{-1,-23,0,23,1} D .{-1,-23,23,1} 二、填空题7.若α.8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________.三、解答题9.求值:sin (-660°)cos420°-tan330°cot (-690°).11..12、求证:tan(2π)sin(2π)cos(6π)cos(π)sin(5π)q q qq q-----+=tanθ.三角函数的诱导公式(2)一、选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为( ) A. 21 B. —21 C. 23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A. 23 B. 21 C. 23± D. —23 3.化简:)2cos()2sin(21-•-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )A.sinα=sinβB. sin(α-π2) =sinβC.cosα=cosβD. cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4) 二、填空题:6.cos(π-x)= 23,x ∈(-π,π),则x 的值为 . 7.tanα=m ,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ . 8.|sinα|=sin (-π+α),则α的取值范围是 .三、解答题:9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5; (2)sin [(2n +1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.。
完整版)三角函数诱导公式总结

完整版)三角函数诱导公式总结三角函数诱导公式与同角的三角函数知识点1】诱导公式及其应用诱导公式是指通过一些特定的公式,将三角函数中的某些角度转化为其他角度,从而简化计算。
以下是常用的诱导公式:公式一:sin(-α) = -sinα;cos(-α) = cosα;tan(-α) = -tanα公式二:sin(π+α) = -sinα;cos(π+α) = -cosα;tan(π+α) =tanα公式三:sin(π-α) = sinα;cos(π-α) = -cosα;tan(π-α) = -tanα公式四:sin(2π-α) = -sinα;cos(2π-α) = cosα;tan(2π-α) = -tanα公式五:sin(π/2-α) = cosα;cos(π/2-α) = sinα公式六:sin(π/2+α) = cosα;cos(π/2+α) = -sinα公式七:sin(-π/2-α) = -cosα;cos(-π/2-α) = -sinα公式八:sin(-π/2+α) = -cosα;cos(-π/2+α) = sinα公式九:sin(α+2kπ) = sinα;cos(α+2kπ) = cosα;tan(α+2kπ) = tanα(其中k∈Z)。
以上公式可以总结为两条规律:1.前四组诱导公式可以概括为:函数名不变,符号看象限。
2.公式五到公式八总结为一句话:函数名改变,符号看象限(原函数所在象限)。
另外,还有一个规律是:奇变偶不变,符号看象限。
也就是说,将三角函数的角度全部化成kπ/2+α或是kπ/2-α的形式,如果k是奇数,那么符号要改变;如果k是偶数,符号不变。
例1、求值:(1)cos(2916π)= ________;(2)tan(-855)= ________;(3)sin(-π)= ________。
例2、已知tan(π+α)=3,求:(2cos(-α)-3sin(π+α))/(4cos(-α)+sin(2π-α))的值。
高一数学 知识点 三角函数 诱导公式 常考题 经典题 50道 含答案和解析

高一数学三角函数诱导公式50道常考题经典题一、单选题1.若角的终边上有一点(-4,a),则a的值是()A. B. C. D.【答案】A【考点】任意角的三角函数的定义,诱导公式一【解析】【解答】由三角函数的定义知:,所以,因为角的终边在第三象限,所以<0,所以的值是。
【分析】三角函数是用终边上一点的坐标来定义的,和点的位置没有关系。
属于基础题型。
================================================================================2.若,则的值是( )A. B. C. D.【答案】C【解析】【解答】即,所以,,=,故选C。
【分析】简单题,此类题解的思路是:先化简已知条件,再将所求用已知表示。
================================================================================3.若,则()A. B. C. D.【答案】C【考点】诱导公式一,同角三角函数间的基本关系【解析】【解答】,故选C.================================================================================4.函数图像的一条对称轴方程是()A. B. C. D.【答案】A【考点】诱导公式一,余弦函数的图象,余弦函数的对称性【解析】【分析】,由y=cosx的对称轴可知,所求函数图像的对称轴满足即,当k=-1时,,故选A.================================================================================5.已知,则()A. B. C. D.【答案】C【考点】诱导公式一,同角三角函数间的基本关系,弦切互化【解析】【解答】因为,所以,可得,故C符合题意.故答案为:C .【分析】利用诱导公式将已知条件化简可求出tan,将中分子分母同时除以cos.================================================================================6.函数()A. 是奇函数B. 是偶函数C. 既是奇函数,又是偶函数D. 是非奇非偶函数【答案】A【考点】奇函数,诱导公式一【解析】【解答】∵,∴,∴是奇函数.故答案为:A【分析】首先利用诱导公式整理化简f(x) 的解析式,再根据奇函数的定义即可得证出结果。
三角函数系列第四节诱导公式测试题(含答案)

诱导公式一、选择题( ) A .30° B .-30° C .630° D .-630°2.tan300°+00765sin )405cos( 的值是( ) A .1+3 B .1-3 C .-1-3 D .-1+33.计算cos330°的值为( ) A .﹣B .﹣C .D .4. cos510°的值为( )A .B . ﹣C . ﹣D .5.设,则tan (π+x )等于( )A . 0B .C . 1D .6.已知tan α=3,则=( )A . ﹣B . 0C .D .7.已知sin (﹣α)=,α∈(﹣,0),则tan α等于( )A .B . ﹣C . 2D . ﹣28.若sin (+θ)=,则cos (π﹣θ)等于( )A . ﹣B .C . ﹣D .9.已知,则sina=( )A .B .C .D .10.已知sinα=,α是第二象限的角,则cos(π﹣α)=()A.B.C.D.11.sin()的值等于()A.B.C.D.12.tan(﹣1410°)的值为()A.B.C.D.13.若且,则sin(π﹣α)()A.B.C.D.14.已知sinα=,则cos(﹣α)等于()A.B.﹣C.D.﹣15.代数式•化简后的值为()A.cosαB.﹣cosαC.sinαD.﹣sinα16.sin510°=()A.B.﹣C.D.﹣17.cos(﹣2040°)=()A.B.C.D.19.若函数f(θ)=,则f(﹣)= .20.已知sin(+α)=,那么cosα= .21.sin960°的值为.22.tan600°的值是.23.已知sin(π﹣θ)+3cos(π+θ)=0,其中,则cosθ=.24.已知,x∈(π,2π),则tanx=.25.求值:=.26.求值:sinπ=.27.计算cos315°的值是.28.已知α为第三象限角,且 sin(π﹣α)=﹣,f(α)==.29.sin+cos+tan(﹣)= .30.已知tanα=2,则= .31.若α的终边过点,(﹣1,2),则= .32.已知方程sin(α﹣3π)=2cos(α﹣4π),求的值.33.已知角a终边上一点P(﹣4,3),求的值.34.(1)计算:lg22+lg2lg5+lg5;(2)化简:.35.已知函数f(x)=(1)化简函数f(x)的解析式;(2)求出函数f(x)的最大值及取得最大值时x的值.36.已知f(α)=,(1)化简f(α);(2)若f(α)=,且<α<,求cosα﹣sinα的值;(3)求满足f(α)≥的α的取值集合.37.已知α为第二象限角,.(1)化简f(α);(2)若,求f(α)的值.38已知角a是第三象限角,且f(a)=(Ⅰ)化简f(a)(Ⅱ)若sin(2π﹣a)=,求f(a)的值.39.化简:•sin(α﹣2π)•cos(2π﹣α)+cos2(﹣α)﹣.40.已知(1)化简f(α)(2)若α是第三象限角,且,求f(α)的值.41.已知角α的终边与单位圆的交点P的坐标为(﹣,﹣),(1)求sinα和cosα的值,(2)求的值,(3)判断的符号并说明理由.42.(1)已知tanθ=2,求的值;(2)已知﹣<x<,sinx+cosx=,求tanx的值.43.已知角α顶点在原点,始边与x轴的正半轴重合,终边在函数y=﹣3x(x≤0)的图象上.(Ⅰ)求sinα、cosα和tanα的值;(Ⅱ)求的值.诱导公式试卷答案1.B2.B3.D4.C5.B6.C7.D8.A9.B10.A11.D12.A13.B14.A15.D16.A17.B18.220.21.22.23.24.25.26.27.28.29.030.﹣31.﹣132.∴原式====﹣…(12分)点评:本题考查三角函数的诱导公式及化简求值,熟练掌握诱导公式是化简的关键,属于中档题.33解答:∵角a终边上一点P(﹣4,3),∴cosα=﹣,sinα=,tanα=﹣,∴原式==﹣tanα=.34.解答:(1)lg22+lg2lg5+lg5=lg2(lg2+lg5)+lg5=lg2+lg5=1;(2)原式==﹣1.35解答:(1)f(x)==cosx;(2)∵f(x)=cosx,∴f(x)max=1,此时,x=2kπ,k∈Z.36..解答:解;(1)﹣(4分)(2),,∵,∴sinα>cosα,∴﹣﹣﹣﹣(8分)(3),∴,∴.∴﹣﹣﹣﹣﹣(12分)37.解答:(1)f(α)==﹣cosα;(2)∵cos(α﹣)=cos(﹣α)=sinα=,α为第二象限角,∴cosα=﹣=﹣,则f(α)=﹣cosα=.38.(I)﹣cosa.(II).解答:(Ⅰ)f(a)===﹣=﹣cosa.(Ⅱ)∵sin(2π﹣a)=﹣sina=,∴sina=﹣.又角a是第三象限角,∴cosa=﹣=﹣,∴f(a)=﹣cosa=.39.解答:原式=﹣•(﹣sinα)•cosα+cos2α+=sin2α+cos2α+=1+.40.解答:(1)==cosα(2)∵,∴,又∵α为第三象限角,∴,∴.41.解答:(1)∵角α的终边与单位圆的交点P的坐标为(﹣,﹣),∴sinα=﹣,cosα=﹣;(2)∵sinα=﹣,cosα=﹣,∴tanα=,则原式===+;(3)∵ta nα=,∴tan(α+)====﹣2﹣<0.42.解答:(1)∵tanθ=2,∴原式===﹣1;(2)∵sinx+cosx=,∴(sinx+cosx)2=,即2sinxcosx=﹣<0,∵﹣<x<,∴sinx<0,cosx>0,∴(sinx﹣cosx)2=1﹣2sinxcosx=,∴sinx﹣cosx=﹣,∴sinx=﹣,cosx=,∴tanx=﹣.43.解答:(Ⅰ)∵角α顶点在原点,始边与x轴的正半轴重合,终边在函数y=﹣3x(x≤0)的图象上∴sinα==,cosα==﹣,tanα==﹣3;(Ⅱ)原式==﹣tanα=3.。
三角函数诱导公式全集

三角函数诱导公式全集三角函数诱导公式一:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα三角函数诱导公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα三角函数诱导公式三:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα三角函数诱导公式四:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)三角函数诱导公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα三角函数诱导公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)注意:在做题时,将a看成锐角来做会比较好做。
三角函数的诱导公式【六公式】

)/ )
九倍角
sin9A=(sinA*(-3+4*sinA^2 )* ( 64*sinA^6-96*sinA^4+36*sinA^2-3 ))
cos9A=(cosA*(-3+4*cosA^2 )* ( 64*cosA^6-96*cosA^4+36*cosA^2-3 ))
tan9A=tanA* ( 9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8 ) / (1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8 )
例. c^3=c*c^2=c* (1-s^2 ), c^5=c*(c^2 ) ^2=c* ( 1-s^2 ) ^2 )
特殊公式
(sina+sin θ) * ( sina- sin θ) =sin (a+θ) *sin ( a- θ)
证明:(sina+sin θ) *( sina- sin θ) =2 sin[ (θ +a)/2] cos[(a - θ)/2] *2 cos[ (θ +a)/2] sin[(a- θ) /2]
tan (α +β+γ) =(tan α+tan β+tan γ - tan α· tan β· tan γ) / (1- tan α· tan β - tan β· tan γ - tan α· tan γ)
(α +β+γ≠π /2+2k π,α、β、γ≠π /2+2k π)
积化和差的四个公式
sina*cosb=(sin(a+b)+sin(a-b))/2
cosa*sinb=(sin(a+b)-sin(a-b))/2
高一三角函数公式及诱导公式习题(附答案)

2
2
D. { - 1,- 3 , 3 , 1}
2
2
7.若 α是第三象限角,则 1 2 sin( π ) cos( π ) =_________.
8. sin21°+sin22°+sin23° +… +si2n89°=_________ . 三、解答题 9.求值: sin(- 660°) cos420 °-tan330 °cot (- 690°).
B. sin( A+B) =sinC
C. tan( A+B) =tanC
D. sin A
B
C
=sin
2
2
6.函数 f( x) =cosπx ( x∈ Z)的值域为( )
3
A. { -1,- 1 , 0, 1 , 1}
2
2
B. { - 1,- 1 , 1 ,1}
22
C. { -1,- 二、填空题
3 , 0, 3 ,1}
tanα +tanβ tan( α +β )= 1- tanα tanβ
tanα - tanβ tan( α- β )= 1+ tanα tanβ
4. 二倍角公式
sin2α =2sinα cosα
2
2
2
2
cos2α =cosα- sin α = 2 cosα - 1= 1- 2 sin α
2tan α
cos
3
2
= 2 cos
1 cos
cos 3
2
2 2 cos
cos
3
2 cos
=
2
2
2 (cos
cos )
2
2 cos
三角函数诱导公式(人教A版)(含答案)1

三角函数诱导公式(人教A版)一、单选题(共15道,每道6分)1.已知,,则( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:三角函数的诱导公式2.,,则的值为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:三角函数的诱导公式3.若,则( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:三角函数的诱导公式4.已知,且为第四象限角,则为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:三角函数的诱导公式5.诱导公式=( )(其中)A. B.C. D.与的值为奇偶数有关答案:A解题思路:试题难度:三颗星知识点:三角函数的诱导公式6.已知,则( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:三角函数的诱导公式7.若,那么( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:三角函数的诱导公式8.已知,则( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:三角函数的诱导公式9.若,则( )A. B.C.0D.答案:D解题思路:试题难度:三颗星知识点:三角函数的诱导公式10.若,则的值为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:三角函数的诱导公式11.已知,则( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:三角函数的诱导公式12.已知,为锐角,则=( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:三角函数的诱导公式13.的值是( )A.1B.-1C. D.答案:B解题思路:试题难度:三颗星知识点:三角函数的诱导公式14.的值是( )A. B.45C.44D.答案:D解题思路:试题难度:三颗星知识点:三角函数的诱导公式15.在△中,已知,则=( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:三角函数的诱导公式。
高一三角函数公式及诱导公式习题(附答案)

三角函数公式1. 同角三角函数基本关系式sin 2α+cos 2α=1 sin αcos α =tan αtan αcot α=12. 诱导公式 (奇变偶不变,符号看象限)(一)sin(π-α)=sin α sin(π+α)=-sin α cos(π-α)=-cos α cos(π+α)=-cos α tan(π-α)=-tan α tan(π+α)=tan α sin(2π-α)=-sin α sin(2π+α)=sin α cos(2π-α)=cos α cos(2π+α)=cos α tan(2π-α)=-tan α tan(2π+α)=tan α(二) sin(π2 -α)=cos α sin(π2+α)=cos αcos(π2 -α)=sin α cos(π2+α)=- sin αtan(π2 -α)=cot α tan(π2 +α)=-cot αsin(3π2 -α)=-cos α sin(3π2 +α)=-cos αcos(3π2 -α)=-sin α cos(3π2 +α)=sin αtan(3π2 -α)=cot α tan(3π2+α)=-cot αsin(-α)=-sin α cos(-α)=cos α tan(-α)=-tan α3. 两角和与差的三角函数cos(α+β)=cos αcos β-sin αsin β cos(α-β)=cos αcos β+sin αsin β sin (α+β)=sin αcos β+cos αsin β sin (α-β)=sin αcos β-cos αsin β tan(α+β)= tan α+tan β1-tan αtan βtan(α-β)= tan α-tan β1+tan αtan β4.二倍角公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2αtan2α=2tanα1-tan2α5.公式的变形(1)升幂公式:1+cos2α=2cos2α 1—cos2α=2sin2α(2)降幂公式:cos2α=1+cos2α2sin2α=1-cos2α2(3)正切公式变形:tanα+tanβ=tan(α+β)(1-tanαtanβ) tanα-tanβ=tan(α-β)(1+tanαtan β)(4)万能公式(用tanα表示其他三角函数值)sin2α=2tanα1+tan2αcos2α=1-tan2α1+tan2αtan2α=2tanα1-tan2α6.插入辅助角公式asinx +bcosx=a 2+b 2 sin(x+φ) (tan φ= ba )特殊地:sinx ±cosx = 2 sin(x ±π4)7. 熟悉形式的变形(如何变形)1±sinx ±cosx 1±sinx 1±cosx tanx +cotx 1-tan α1+tan α 1+tan α1-tan α若A 、B 是锐角,A+B =π4,则(1+tanA )(1+tanB)=28. 在三角形中的结论若:A +B +C=π , A+B+C 2 =π2则有tanA +tanB +tanC=tanAtanBtanCtan A 2 tan B 2 +tan B 2 tan C 2 +tan C 2 tan A2=1三角函数的诱导公式1一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( )A .-2π+2k π≤x ≤2π+2k π B.-2π+2k π≤x ≤2π3+2k πC . 2π+2k π≤x ≤2π3+2k π D.(2k +1)π≤x ≤2(k +1)π(以上k ∈Z )2.sin (-6π19)的值是( )A . 21 B .-21 C .23D .-233.下列三角函数:①sin (n π+3π4);②cos (2n π+6π);③sin(2n π+3π);④cos [(2n +1)π-6π];⑤sin [(2n +1)π-3π](n∈Z ).其中函数值与sin 3π的值相同的是( )A .①②B .①③④C .②③⑤D .①③⑤4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为( )A .-36 B .36 C .-26D .26 5.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( )A .cos (A +B )=cosC B .sin (A +B )=sin C C .tan (A +B )=tan CD .sin 2B A +=sin 2C6.函数f (x )=cos 3πx (x ∈Z )的值域为( )A .{-1,-21,0,21,1} B .{-1,-21,21,1} C .{-1,-23,0,23,1} D .{-1,-23,23,1}二、填空题7.若α是第三象限角,则)πcos()πsin(21αα---=_________.8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________. 三、解答题9.求值:sin (-660°)cos420°-tan330°cot(-690°).10.证明:1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθθθ.11.已知cos α=31,cos (α+β)=1,求证:cos (2α+β)=31.12. 化简:︒+︒︒︒+790cos 250sin 430cos 290sin 21.13、求证:)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tan θ.14. 求证:(1)sin (2π3-α)=-cos α;(2)cos (2π3+α)=sin α.参考答案1一、选择题1.C 2.A 3.C 4.B 5.B 6.B 二、填空题7.-sin α-cos α 8.289三、解答题 9.43+1.10.证明:左边=θθθθ22sin cos cos sin 2-1-- =-θθθθθθθθθθcos sin cos sin )sin )(cos sin (cos )cos (sin 2-+=-++,右边=θθθθθθθθcos sin cos sin tan tan tan tan -+=1-1+=1+-1--,左边=右边,∴原等式成立.11.证明:∵cos (α+β)=1,∴α+β=2k π.∴cos (2α+β)=cos (α+α+β)=cos (α+2k π)=cos α=31.12.解:︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21=︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =-1.13.证明:左边=θθθθθθθθθθsin cos cos )sin )(tan ()sin )(cos ()cos()sin()tan(--=-----=tan θ=右边,∴原等式成立.14证明:(1)sin (2π3-α)=sin [π+(2π-α)]=-sin (2π-α)=-cos α.(2)cos (2π3+α)=cos [π+(2π+α)]=-cos (2π+α)=sin α.三角函数的诱导公式2一、选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为( ) A. 21 B. —21 C.23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A.23 B. 21C. 23±D. —23 3.化简:)2cos()2sin(21-•-+ππ得( )+cos2 D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )α=sinβ B. sin(α-π2) =sinβ α=cosβ D. cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ),A. 51(4+5) B. 51(4-5) C. 51(4±5) D.51(5-4)二、填空题:6.cos(π-x)=23,x ∈(-π,π),则x 的值为 . 7.tanα=m,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ .8.|sinα|=sin(-π+α),则α的取值范围是 . 三、解答题:9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin 3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5;(2)sin [(2n +1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.参考答案21.C 2.A 3.C 4.C 5.A6.±65π 7.11-+m m 8.[(2k-1) π,2k π] 9.原式=)cos (·sin()cos()n s (sin αα)παπα--+--αi =)cos ?(sin )cos (sin 2αααα--= sinα 10.161111.解:(1)sin 3π7=sin (2π+3π)=sin 3π=23.(2)cos 4π17=cos (4π+4π)=cos 4π=22.(3)tan (-6π23)=cos (-4π+6π)=cos 6π=23.(4)sin (-765°)=sin [360°×(-2)-45°]=sin (-45°)=-sin45°=-22.注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.12.解:(1)sin 3π4·cos6π25·tan 4π5=sin (π+3π)·cos(4π+6π)·tan(π+4π)=(-sin 3π)·cos 6π·tan 4π=(-23)·23·1=-43.(2)sin [(2n +1)π-3π2]=sin (π-3π2)=sin 3π=23.13.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++ =θθθθθcos cos 223cos cos 1cos 2223++-+-+ =θθθθθcos cos 22)cos (cos 2cos 2223++---=θθθθθcos cos 22)1(cos cos )1(cos 223++---=θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-=cos θ-1,∴f (3π)=cos 3π-1=21-1=-21.。
三角函数诱导公式练习题含答案

三角函数的诱导公式1一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( ) A .-2π+2k π≤x ≤2π+2k π B .-2π+2k π≤x ≤2π3+2k πC .2π+2k π≤x ≤2π3+2k π D .(2k +1)π≤x ≤2(k +1)π(以上k ∈Z )2.sin (-6π19)的值是( ) A .21 B .-21 C .23 D .-23 3.下列三角函数:①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π]; ⑤sin [(2n +1)π-3π](n ∈Z ). 其中函数值与sin 3π的值相同的是( ) A .①②B .①③④C .②③⑤D .①③⑤4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为( ) A .-36 B .36 C .-26D .26 5.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( )A .cos (A +B )=cosC B .sin (A +B )=sin C C .tan (A +B )=tan CD .sin 2B A +=sin 2C6.函数f (x )=cos 3πx(x ∈Z )的值域为( ) A .{-1,-21,0,21,1} B .{-1,-21,21,1} C .{-1,-23,0,23,1}D .{-1,-23,23,1} 二、填空题7.若α是第三象限角,则)πcos()πsin(21αα---=_________. 8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________. 三、解答题9.求值:sin (-660°)cos420°-tan330°cot (-690°).10.证明:1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθθθ.11.已知cos α=31,cos (α+β)=1,求证:cos (2α+β)=31.12. 化简:︒+︒︒︒+790cos 250sin 430cos 290sin 21.13、求证:)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tan θ.14. 求证:(1)sin (2π3-α)=-cos α; (2)cos (2π3+α)=sin α.参考答案1一、选择题1.C 2.A 3.C 4.B 5.B 6.B 二、填空题7.-sin α-cos α 8.289 三、解答题 9.43+1. 10.证明:左边=θθθθ22sin cos cos sin 2-1--=-θθθθθθθθθθcos sin cos sin )sin )(cos sin (cos )cos (sin 2-+=-++,右边=θθθθθθθθcos sin cos sin tan tan tan tan -+=1-1+=1+-1--, 左边=右边,∴原等式成立.11.证明:∵cos (α+β)=1,∴α+β=2k π.∴cos (2α+β)=cos (α+α+β)=cos (α+2k π)=cos α=31.12.解:︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21=︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =-1.13.证明:左边=θθθθθθθθθθsin cos cos )sin )(tan ()sin )(cos ()cos()sin()tan(--=-----=tan θ=右边, ∴原等式成立.14证明:(1)sin (2π3-α)=sin [π+(2π-α)]=-sin (2π-α)=-cos α. (2)cos (2π3+α)=cos [π+(2π+α)]=-cos (2π+α)=sin α.三角函数的诱导公式2一、选择题: 1.已知sin(4π+α)=23,则sin(43π-α)值为( )A.21 B. —21C. 23D. —232.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A.23 B. 21C. 23±D. —23 3.化简:)2cos()2sin(21-•-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2) 4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )A.sin α=sin βB. sin(α-π2) =sin βC.cos α=cos βD. cos(π2-α) =-cos β 5.设tan θ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4)二、填空题: 6.cos(π-x)=23,x ∈(-π,π),则x 的值为 . 7.tan α=m ,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ .8.|sin α|=sin (-π+α),则α的取值范围是 . 三、解答题: 9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin 3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin3π4·cos 6π25·tan 4π5;(2)sin [(2n +1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.参考答案21.C 2.A 3.C 4.C 5.A 6.±65π7.11-+m m 8.[(2k-1) π,2k π]9.原式=)cos (·sin()cos()n s (sin αα)παπα--+--αi =)cos ?(sin )cos (sin 2αααα--= sin α 10.161111.解:(1)sin 3π7=sin (2π+3π)=sin 3π=23.(2)cos4π17=cos (4π+4π)=cos 4π=22.(3)tan (-6π23)=cos (-4π+6π)=cos 6π=23.(4)sin (-765°)=sin [360°×(-2)-45°]=sin (-45°)=-sin45°=-22. 注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.12.解:(1)sin 3π4·cos 6π25·tan 4π5=sin (π+3π)·cos (4π+6π)·tan (π+4π)=(-sin3π)·cos 6π·tan 4π=(-23)·23·1=-43.(2)sin [(2n +1)π-3π2]=sin (π-3π2)=sin 3π=23.13.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++=θθθθθcos cos 223cos cos 1cos 2223++-+-+=θθθθθcos cos 22)cos (cos 2cos 2223++--- =θθθθθcos cos 22)1(cos cos )1(cos 223++---=θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-=cos θ-1, ∴f (3π)=cos 3π-1=21-1=-21.三角函数公式1. 同角三角函数基本关系式sin 2α+cos 2α=1 sin αcos α=tan α tan αcot α=12. 诱导公式 (奇变偶不变,符号看象限)(一) sin(π-α)=sin α sin(π+α)=-sin αcos(π-α)=-cos α cos(π+α)=-cos α tan(π-α)=-tan α tan(π+α)=tan α sin(2π-α)=-sin α sin(2π+α)=sin α cos(2π-α)=cos α cos(2π+α)=cos α tan(2π-α)=-tan α tan(2π+α)=tan α (二) sin(π2 -α)=cos α sin(π2+α)=cos αcos(π2 -α)=sin α cos(π2 +α)=- sin αtan(π2 -α)=cot α tan(π2 +α)=-cot αsin(3π2 -α)=-cos α sin(3π2 +α)=-cos αcos(3π2 -α)=-sin α cos(3π2 +α)=sin αtan(3π2 -α)=cot α tan(3π2+α)=-cot αsin(-α)=-sin α cos(-α)=cos α tan(-α)=-tan α3. 两角和与差的三角函数 cos(α+β)=cos αcos β-sin αsin β cos(α-β)=cos αcos β+sin αsin β sin (α+β)=sin αcos β+cos αsin β sin (α-β)=sin αcos β-cos αsin βtan(α+β)= tan α+tan β1-tan αtan β。
三角函数 诱导公式专项练习(含答案)

三角函数诱导公式专项练习(含答案) 三角函数诱导公式专项练一、单选题1.sin(-600°)的值为()A。
-√3/2B。
-1C。
1D。
√3/22.cos(11π/3)的值为()A。
-√3/2B。
-13/2C。
√2D。
23.已知sin(30°+α)=√3/2,则cos(60°-α)的值为A。
1/2B。
-1/2C。
√3/2D。
-√3/24.已知cos(π/3+α)=-5/2,且α∈(2π/5,π),则XXX(α-π)=()A。
-34/4B。
-3C。
4D。
35.已知sin(π-α)=-2/√3,且α∈(-2,0),则tan(2π-α)的值为A。
2√5/5B。
-2√5/2√5C。
±5D。
√5/26.已知cos(π/4-α)=√2/2,则sin(α+π/4)=()A。
-3B。
1C。
√2D。
√14/47.已知sinα=3/5,2<α<π/2,则sin(2-α)=()A。
3/5B。
-3/5C。
4/5D。
-4/58.已知tanx=-12/5π,x∈(π/2,π),则cos(-x+3π/2)=()A。
5/13B。
-5/12C。
13D。
-12/139.如果cos(π+A)=-1,那么sin(π/2+A)=A。
-1/2B。
2C。
1D。
-110.已知cos(π/2-α)-3cosα/(sinα-cos(π+α))=2,则tanα=()A。
12/5B。
-3C。
1/2D。
-511.化简cos480°的值是()A。
1B。
-1C。
√3/2D。
-√3/212.cos(-585°)的值是()A。
√2/2B。
√3/2C。
-√3/2D。
-√2/213.已知角α的终边经过点P(-5,-12),则sin(3π/2+α)的值等于()A。
-5B。
-12/13C。
13D。
12/1314.已知cos(π+α)=2/3,则tanα=()A。
√55/2B。
2√5/52.已知cosα=2/5,-2/5<α<0,则tan(α+α)cos(-α)tanα的值为()答案:D解析:由cosα=2/5可得sinα=-√(21)/5,代入公式可得tan(α+α)cos(-α)tanα=-1/√3=-√3/3,故选D。
考点06 诱导公式及恒等变换(新高考地区专用)(解析版)

考点06 诱导公式及恒等变换一.三角函数的诱导公式cos(α-β)=cos αcos β+sin αsin β cos(α+β)=cos αcos β-sin αsin β sin(α-β)=sin αcos β-cos αsin β sin(α+β)=sin αcos β+cos αsin β tan(α-β)=tan α-tan β1+tan αtan βtan(α+β)=tan α+tan β1-tan αtan β三.二倍角公式(1)sin 2α=2sin αcos α ↔12sin 2α=sin αcos α (2)cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α 222212cos 1cos2cos 1cos 2212sin 1cos 2sin 1c =22=os α⇔αααααααα⇔+=(+)-=(-)(3)tan 2α=2tan α1-tan 2α知识理解考向一 诱导公式【例1】(2020·四川射洪中学高三月考(理))已知角α的终边经过点()12,5P -. (1)求sin α,cos α;(2)求()()()()cos 2cos 2sin 2cos f παπααπαα⎛⎫+-+ ⎪⎝⎭=-+-的值. 【答案】(1)5sin 13α=-,12cos 13α=;(2)2919. 【解析】(1)由题意可得:13OP =,由角的终边上的点的性质可得5sin 13α=-,12cos 13α=; (2)由(1)可知5sin 13α=-,12cos 13α=,再结合诱导公式得:()()()()512cos 2cos 2sin 2cos 21313512sin 2cos sin 2cos 213121399f παπααααπαααα⎛⎫⎛⎫⎛⎫+-+--+ ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭====-+-+⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭,所以()2919f α=【举一反三】考向分析1.(2020·全国高三专题练习)化简:3sin()cos()tan()22tan()sin()ππααπαπαπα-++-+-. 【答案】cos α-.【解析】3sin()cos()tan()22tan()sin()ππααπαπαπα-++-+-cos sin cos sin cos sin sin ααααααα-⨯=⨯cos α=-. 2.(2020·全国高三专题练习)若角α的终边上有一点(),8P m -,且3cos 5α=-. (1)求m 的值;(2)求()()()sin cos 2tan cos ππαααπα⎛⎫++ ⎪⎝⎭---的值.【答案】(1)6-;(2)45. 【解析】(1)点P 到原点的距离为r ==根据三角函数的概念可得3cos 5α==-,解得6m =-,6m =(舍去).(2)原式()()()sin cos (sin )(sin )2sin tan cos (tan )cos ππααααααπααα⎛⎫++ ⎪--⎝⎭==-----,由(1)可得10r ==,84sin 5r α-==-,所以原式4sin 5α=-=. 3.(2020·全国高三专题练习)已知角α的终边经过点1(,33P -- (1)求sin ,cos ,tan ααα的值;(25sin(3)2cos()ππαα-++ 【答案】(1)1sin ,tan 3ααα==-=2) 【解析】(1)由题意角α的终边经过点1(,3P -,可得1r OP ==,根据三角函数的定义,可得1sin ,tan 33ααα=-=-=. (25sin(3)2cos()ππαα-++=tan (14α===-⨯=. 考向二 恒等变化【例2】(1)(2020·四川省阆中东风中学校高三月考)cos80cos130sin80sin130︒︒-︒︒等于( ) A. B .12-C .12D(2)(2020·甘肃高二单元测试)sin15︒=( ) ABCD(3)(2019·广东华南师大附中高三月考(理))若1tan 2α=,则tan 4πα⎛⎫+ ⎪⎝⎭的值为( )A .1B .3C .5D .7【答案】(1)A (2)C (3)B【解析】(1)cos80cos130sin80sin130︒︒-︒︒()cos 80130cos 210=+= ()cos 18030=+cos30=-=-.故选:A (2)∈154530︒=︒-︒,∈()1sin15sin 4530sin45cos30cos45sin302︒=︒-︒=︒︒-︒︒==C . (3)由tan tantan 14tan 41tan 1tan tan 4παπααπαα++⎛⎫+== ⎪-⎝⎭-⋅, 又1tan 2α=,原式1+1tan 12=311tan 1-2αα+==-.故选:B. 【举一反三】1.(2020·四川省广元市川师大万达中学高三月考(理))sin160cos10cos20sin10︒︒+︒︒=( ) A. B .12-C .12D【答案】C【解析】1sin160cos10cos 20sin10sin 20cos10cos 20sin10sin 302︒︒+︒︒=︒︒+︒︒==。
第四课时 三角函数诱导公式例题展示(笔记整理)

第四课时 三角函数诱导公式例题展示(笔记整理)知识点一:第一组诱导公式展示诱导公式二:关于原点对称.sin(180°+α)=-sinα,cos(180°+α)=-cosα.弧度时的关系式为:sin(π+α)=-sinα,cos(π+α)=-cosα,tan(π+α)=tanα.诱导公式三:可将求负角的三角函数值转化为求正角的三角函数值.sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα.诱导公式四:可将求π-α角的三角函数值转化为求角α的三角函数值.sin(π-α)=sinα,cos(π-α)=-cosα,tan(π-α)=-tanα.公式一—四:α+k·2π(k∈Z ),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.进一步简记为:“函数名不变,符号看象限”.点拨、引导学生注意公式中的α是任意角.例1 利用公式求下列三角函数值:(1)cos225°;(2)sin 311π;(3)sin(316π-);(4)cos(-2 040°). 解:(1)cos225°=cos(180°+45°)=-cos45°=22-;(2)sin 311π=sin(4π3π-)=-sin 3π=23-; (3)sin(316π-)=-sin 316π=-sin(5π+3π)=-(-sin 3π)=23; (4)cos(-2 040°)=cos2 040°=cos(6×360°-120°)=cos120°=cos(180°-60°)=-cos60°=21-. 点评:利用公式一—四把任意角的三角函数转化为锐角的三角函数,一般可按下列步骤进行:上述步骤体现了由未知转化为已知的转化与化归的思想方法.变式训练1.利用公式求下列三角函数值:(1)cos(-510°15′);(2)sin(317-π). 解:(1)cos(-510°15′)=cos510°15′=cos(360°+150°15′)=cos150°15′=cos(180°-29°45′) =-cos29°45′=-0.868 2; (2)sin(317-π)=sin(3π-3×2π)=sin 3π=23. 例2 (2007全国高考,1)cos330°等于( ) A.21 B.21- C.23 D.23-答案:C变式训练2.化简:οοοο790cos 250sin 430cos 290sin 21++ 解:οοοο790cos 250sin 430cos 290sin 21++ =)70720cos()70180sin()70360cos()70360sin(21οοοοοοοο++++-+ =οοοοοοοο70sin 70cos |70sin 70cos |70cos 70sin 70cos 70sin 21--=+-- =170sin 70cos 70cos 70sin -=--οοοο. 知识点二:第二组诱导公式展示诱导公式六:公式五、六公式左边的角分别是2π±α,23π-α.其中2π,23π是纵坐标轴上的角,因此这些公式可归结为纵坐标上的角±α,函数名称要改变.例3.证明(1)sin(23π-α)=-cosα;(2)cos(23π-α)=-sinα. 证明:(1)sin(23π-α)=sin[π+(2π-α)]=-sin(2π-α)=-cosα; (2)cos(23π-α)=cos[π+(2π-α)]=-cos(2π-α)=-sinα. 点评:由公式五及六推得23π±α的三角函数值与角α的三角函数值之间的关系,从而进一步可以推广到212+k π(k∈Z )的情形.本例的结果可以直接作为诱导公式直接使用.例4. 化简.)29sin()sin()3sin()cos()211cos()2cos()cos()2sin(a a a a a a a a +-----++-ππππππππ 解:原式=)]2(4sin[)]sin()[sin()cos ()]2(5cos[)sin )(cos )(sin (a a a a a a a a +++----+---ππππππ =)2sin()]sin ([sin )cos ()]2cos([cos sin 2a a a a a a a +------ππ=aa cos sin -=-tanα. 变式训练 3.已知cos(6π-α)=m(m≤1),求sin(32π-α)的值. 解:∈32π-α-(6π-α)=2π,∈32π-α=2π+(6π-α). ∈sin(32π-α)=sin [2π+(6π-α)]=cos(6π-α)=m. 4.已知sinα是方程5x 2-7x -6=0的根,且α为第三象限角, 求)2cos()2cos()tan()2(tan )23sin()23sin(2a a a a a a +•--•-•-•+ππππππ的值.解:∈5x 2-7x -6=0的两根x=2或x=53-, ∈-1≤x≤1,∈sinα=53-. 又∈α为第三象限角,∈cosα=2sin -1-=54-. ∈tanα=43. ∈原式=)sin (sin )tan (tan )cos ()cos (2a a a a a a -•-••-•-=tana=43。
三角函数诱导公式大全

常用的诱导公式有以下几组:1.sinα^2 +cosα^2=12.sinα/c osα=tanα3.tanα=1/c otα公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)3常用公式编辑口诀;奇变偶不变,符号看象限一般的最常用公式有:Sin(A+B)=SinA*CosB+SinB*CosASin(A-B)=SinA*CosB-SinB*CosACos(A+B)=CosA*CosB-SinA*SinBCos(A-B)=CosA*CosB+SinA*SinBTan(A+B)=(TanA+TanB)/(1-TanA*TanB)Tan(A-B)=(TanA-TanB)/(1+TanA*TanB)同角三角函数的关系(即同角八式)·平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系:sinα=tanα*c osαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1·商数关系:sina/cosa=tanacosa/sina=cota直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,sina=y/r余弦等于角A的邻边比斜边cosa=x/r正切等于对边比邻边,tana=y/x三角函数恒等变形公式·两角和与差的三角函数:cos(α+β)=cosα·c osβ-sinα·s inβcos(α-β)=cosα·c osβ+sinα·s inβsinα·cosβ-c osα·s inβsin(α+β)=sinα·c osβ+cosα·s inβ sin(α-β)=tan(α+β)=(tanα+tanβ)/(1-tanα·t anβ)tan(α-β)=(tanα-t anβ)/(1+tanα·t anβ)·辅助角公式:Asinα+B cosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)·倍角公式:sin(2α)=2sinα·c osα=2/(t anα+cotα)cos(2α)=cos^2(α)-s in^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-t an^2(α)]·三倍角公式:sin(3α)=3sinα-4sin^3(α)cos(3α)=4c os^3(α)-3cosα·半角公式:cosα)/2)sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/s inαtan(α/2)=±√((1-·降幂公式:sin^2(α)=(1-c os(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=vercos(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))万能公式:· sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·c osβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-s inβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-c osβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0。
三角函数 诱导公式的特殊情况

三角函数诱导公式的特殊情况
三角函数的诱导公式是指通过三角函数的和差化积,积化和差等方法,将一个三角函数表达式化简成另一个三角函数表达式的公式。
在特殊情况下,我们可以看到一些特殊的诱导公式,比如:
1. 正弦和余弦的诱导公式,sin(A ± B) = sinAcosB ± cosAsinB, cos(A ± B) = cosAcosB ∓ sinAsinB.
这些公式在解决三角函数的加减角问题时非常有用,可以将一个三角函数的和差表示成另外一种形式,从而简化计算。
2. 正切的诱导公式,tan(A ± B) = (tanA ± tanB)/(1 ∓tanAtanB)。
这个公式在处理正切函数的加减角时很有用,可以将一个正切函数的加减角表示为另一个正切函数的形式。
3. 余切的诱导公式,cot(A ± B) = (cotAcotB ∓ 1)/(cotB ± cotA)。
这个公式也可以帮助我们将一个余切函数的加减角表示为另一个余切函数的形式。
这些特殊情况下的诱导公式在解决三角函数相关的问题时起着重要作用,能够简化计算,化繁为简。
除了这些特殊情况下的诱导公式,还有其他一些三角函数的诱导公式,它们在不同的情况下都能发挥作用,帮助我们解决各种三角函数的运算和求解问题。
掌握这些诱导公式,可以更加灵活地运用三角函数的性质,解决各种数学问题。
三角函数诱导公式练习题-代答案

三角函数的诱导公式(1)一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( )A .-2π+2k π≤x ≤2π+2k π B .-2π+2k π≤x ≤2π3+2k π C . 2π+2k π≤x ≤2π3+2k π D .(2k +1)π≤x ≤2(k +1)π(以上k ∈Z ) 2.sin (-6π19)的值是( ) A . 21 B .-21 C .23 D .-23 3.下列三角函数:①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π]; ⑤sin [(2n +1)π-3π](n ∈Z ). 其中函数值与sin3π的值相同的是( ) A .①② B .①③④ C .②③⑤ D .①③⑤4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为( ) A .-36 B .36 C .-26 D .26 5.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( )A .cos (A +B )=cos CB .sin (A +B )=sinC C .tan (A +B )=tan CD .sin 2A B +=sin 2C 6.函数f (x )=cos3πx (x ∈Z )的值域为( ) A .{-1,-21,0,21,1} B .{-1,-21,21,1} C .{-1,-23,0,23,1} D .{-1,-23,23,1} 二、填空题7.若α.8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________.三、解答题9.求值:sin (-660°)cos420°-tan330°cot (-690°).11..12、求证:tan(2π)sin(2π)cos(6π)cos(π)sin(5π)q q qq q-----+=tanθ.三角函数的诱导公式(2)一、选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为( ) A. 21 B. —21 C. 23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A. 23 B. 21 C. 23± D. —23 3.化简:)2cos()2sin(21-•-+ππ得( )+cos2 D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( ) α=sinβ B. sin(α-π2) =sinβ α=cosβ D. cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4) 二、填空题:6.cos(π-x)= 23,x ∈(-π,π),则x 的值为 . 7.tanα=m ,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ . 8.|sinα|=sin (-π+α),则α的取值范围是 .三、解答题:9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5; (2)sin [(2n +1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班级 姓名 学号 分数(测试时间:120分钟 满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.sin11π6的值是( ) A.21 B.-21 C.23 D.-23 【答案】B 【解析】 试题分析:111sinsin(2)sin()sin 66662πππππ=-=-=-=-. 考点:诱导公式,特殊角的三角函数值.2.23sin()6π-的值是 ( )A.12 B .12- D .【答案】A 【解析】考点:诱导公式.3. 已知sin()0,cos()0θπθπ+<->,则θ是第( )象限角. A .一 B .二 C .三 D .四 【答案】B 【解析】试题分析:由sin()sin 0sin 0θπθθ+=-<⇒>,cos()cos 0cos 0θπθθ-=->⇒<,由sin 0cos 0θθ>⎧⎨<⎩可知θ是第二象限角,选B.考点:诱导公式及三角函数在各个象限的符号.4.已知α为锐角,且tan()30πα-+=,则sin α的值( )A.13【答案】B 【解析】考点:诱导公式 正弦余弦正切之间的关系5.已知cos 4πα⎛⎫+ ⎪⎝⎭=23,则sin 4πα⎛⎫- ⎪⎝⎭的值等于( )A .23B .-23C 【答案】A 【解析】试题分析:诱导公式ααπsin 2cos =⎪⎭⎫ ⎝⎛-,注意244ππαπα=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+,324sin 42.cos 4cos =⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛+παπαππα,所以选A考点:诱导公式6.sin 315cos 4952sin 210︒-︒+︒的值是( )A.1B.1- D. 【答案】B【解析】试题分析:sin315cos4952sin210sin(36045)cos(36018045)2sin(18030)︒-︒+︒=︒-︒-︒+︒-︒+︒+︒1sin45cos(18045)2sin30cos452112=-︒-︒-︒-︒=+︒-⨯==-,选B.考点:诱导公式及特殊角的三角函数值.7.sin300°+tan240°的值是( )(A)-(B)(C)-+ (D)+【答案】B考点:诱导公式及特殊角的三角函数值.8. 已知1sin2A=,那么3cos2Aπ⎛⎫-=⎪⎝⎭()A.12- B.12C. D【答案】A【解析】试题分析:因3cos2Aπ⎛⎫-=⎪⎝⎭21sin-=-A.故应选A.考点:诱导公式及运用.9.已知3cos()sin()22()cos()tan()fππ+α-αα=-π-απ-α,则25()3f-π的值为()A .12B .-12CD .【答案】A 【解析】试题分析: ()()()sin cos cos cos tan f αααααα--==--,25()3f -π=25cos 3π⎛⎫- ⎪⎝⎭=25cos 3π=cos 83ππ⎛⎫+ ⎪⎝⎭=cos 3π=12. 考点:诱导公式. 10. cos ()-sin()的值是( ). A.B .-C .0 D.【答案】A 【解析】考点:诱导公式及特殊角的三角函数值.11. 知α为锐角,且2tan()3cos()502ππαβ--++=,tan()6sin πα++()πβ+=1,则sin α=( )A B D .13【答案】C 【解析】试题分析:诱导公式化简为⎩⎨⎧=--=++01sin 6tan 05sin 3tan 2-βαβα,解得:,3tan =α⎪⎩⎪⎨⎧=+=1cos sin 3cos sin 22αααα,得10103sin =α,故选C. 考点:1.诱导公式;2.同角三角函数基本关系式. 12. 计算2sin(-600°)+tan(-855°)的值为( ) (A)(B)1 (C)2 (D)0【答案】C考点:诱导公式及特殊角的三角函数值.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 若53)sin(-=+απ,则=αcos .【答案】54±【解析】解:因为33sin()sin 55π+α=-∴α=,故利用平方和为1可知=αcos 54±考点:诱导公式及同角三角函数公式.14. 已知sin 52πα⎛⎫+ ⎪⎝⎭=15,那么cos α=________.【答案】15【解析】sin 52πα⎛⎫+ ⎪⎝⎭=sin 2πα⎛⎫+ ⎪⎝⎭=cos α=15考点:诱导公式及同角三角函数公式.15. 已知tan 2θ=,则()()sin cos 2sin sin 2πθπθπθπθ⎛⎫+-- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭_________. 【答案】2- 【解析】试题分析:()()sin cos 2sin sin 2πθπθπθπθ⎛⎫+-- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭2cos 22sin cos sin 1tan 1cos θθθθθθ==---,又tan 2θ=,则原式=2-. 考点:三角函数的诱导公式. 16. 已知32cos =a ,且02<<-a π,求)tan()cos()2sin()tan(a a a a +-+--πππ的值。
【答案】25- 【解析】考点:诱导公式化简三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知sin(3π+θ)=13,求233[)1])22cos cos cos cos sin cos sin πθθπππθπθθθπθ-⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭(+)(-)+(--(-+的值.【答案】18【解析】因为sin(3π+θ)=-sin θ=13,所以sin θ=-13.原式=213112cos cos cos cos cos sin cos cos θπθπθθθθπθθ⎛⎫⎪⎝⎭-(-)+=(--)+--(-)+ +22221122211113cos cos cos cos cos cos sin θθθθθθθ⎛⎫- ⎪⎝⎭=+===-++--=18. 考点:诱导公式,同角间的基本关系式.18.已知cos α=31,且-2π<α<0,求αααππαtan )cos()2sin()cot(-+∙--的值.【答案】原式=42cos sin sin cot tan )cos(sin )cot(=-=-=--ααααααααt 【解析】考点:1.诱导公式;2.三角化简.19.(1)化简()f α=)23cos()2cos(3)sin()2sin(απαπαπαπ-++--+-; (2)若tan 2α=,求()f α的值.【答案】(1) cos sin ()3cos sin f ααααα+=-;(2)12()332f α+==-.【解析】(1)cos sin ()3cos sin f ααααα+=- , 8分(每个公式2分,即符号1分,化对1分) (2)cos sin 1tan ()3cos sin 3tan f ααααααα++==--, 12分(每化对1个得1分)若tan 2α=,则12()332f α+==-, 14分 (说明:用其他方法做的同样酌情给分) 考点:诱导公式,同角间的基本关系式. 20.已知cos(π+α)=-12,且角α在第四象限,计算: (1)sin(2π-α); (2)[21]2sin n sin sin cos n αππαπααπ⋅+(+)+(+)(-)(+)(n∈Z).【答案】(1(2)-4考点:1.诱导公式;2.三角化简.21. 已知3cos()cos(2)sin()22()3sin()sin()2f ππαπαααππαα+⋅-⋅-+=--⋅+. (1)化简()f α;(2)若α是第三象限角,且31cos()25πα-=,求()f α的值. 【答案】(1)cos α-;(2)()f α=. 【解析】(1)原式sin cos()[sin()]sin cos cos 2cos sin cos sin()sin()2παααααααπααπαα----===--+⋅+(2)由51)23cos(=-πα得1sin 5α-=即1sin 5α=-,因为α是第三象限角,所以cos α==,所以)(αf cos α=-=. 考点:1.诱导公式;2.三角化简. 22. 已知()()απαπ-=+cos sin 2,计算: (1)ααααcos 2sin cos sin 2+-;(2)αααα22cos 2cos sin sin -+. 【答案】(1)34;(2)45.考点:诱导公式,求三角函数值.。
