天津大学物理化学第五版-第四章-多组分系统热力学
《物理化学》考点精讲(第4讲 多组分系统热力学)

第4讲多组分系统热力学《物理化学》考点精讲教程(天津大学第五版)主讲人:张彩丽网学天地《物理化学》(天大第五版)考点精讲教程第4讲多组分系统热力学4.1 偏摩尔量4.2 化学势4.3 气体组分的化学势4.4 逸度及逸度因子4.5 拉乌尔定律和亨利定律4.6 理想液态混合物4.7 理想稀溶液4.8 活度及活度因子4.9 稀溶液的依数性《物理化学》(天大第五版)考点精讲教程一、偏摩尔量二、偏摩尔量的测定法举例三、吉布斯−杜亥姆方程四、偏摩尔量之间的关系4.1 偏摩尔量《物理化学》(天大第五版)考点精讲教程结果:恒温、恒压下混合后,混合物的体积不等于混合前纯组分体积之和:**B m,B C m,CV n V n V ≠+原因:①水分子之间、乙醇分子之间和水分子与乙醇分子之间的分子间相互作用不同;②水分子与乙醇分子体积及形状不同。
对所有广度量X 均存在同样的结果:B BBX n X ≠∑*一、偏摩尔量《物理化学》(天大第五版)考点精讲教程(4)偏摩尔量:X ⎛⎞∂《物理化学》(天大第五版)考点精讲教程B VV ⎛⎞∂《物理化学》(天大第五版)考点精讲教程《物理化学》(天大第五版)考点精讲教程二、偏摩尔量的测定法举例以二组分系统偏摩尔体积测定为例:三、吉布斯恒温、恒压《物理化学》(天大第五版)考点精讲教程《物理化学》(天大第五版)考点精讲教程因此:B B B d =0n X ∑B B Bd =0x X ∑或此即吉布斯−杜亥姆方程。
该方程指出,系统中各组分的偏摩尔量并非完全独立,而是相互依存的。
在恒温、恒压下,当混合物的组成发生微小变化时,如果一组分的偏摩尔量增大,则另一组分的偏摩尔量必然减小,且增大与减小的比例与混合物中两组分的摩尔分数(或物质的量)成反比。
《物理化学》(天大第五版)考点精讲教程《物理化学》(天大第五版)考点精讲教程4.2 化学势一、化学势的定义二、多相多组分系统的热力学基本方程三、化学势判据及应用举例《物理化学》(天大第五版)考点精讲教程,,C defB B B T p n G G n μ⎛⎞∂⎜⎟===⎜⎟⎝⎠∂纯物质的化学势即为其摩尔吉布斯函数:B m, B G μ=*化学势是最重要的《物理化学》(天大第五版)考点精讲教程二、多相多组分系统的热力学基本方程μ+Vd况;不仅能应用于变组成的封闭系统,也适用于开放系统。
第4章 多组分系统热力学1(天津大5版)

系统热力学平衡的决定因素
系统热力学平衡--热平衡、力平衡、相平衡和 化学平衡 T决定热平衡 p决定力平衡
µ决定系统的相平衡和化学平衡
§4.3 气体组分的化学势
气体标准态: pӨ=100kPa、具有理想气体性质 的纯气体。 气体B在标准态下的化学势称为该气体的标准化 学势μӨ,它只是温度的函数。
1. 纯组分理想气体的化学势
2. 多相多组分系统的热力学基本方程
(1)单相多组分系统 )
G = G (T , p, nB, nC L)
可得 : ∂G ∂G ∂G dG = dT + dp + ∑ dnB ∂T p.nB ∂nB T . P.nC ∂p T .nB
偏摩尔量XB
VB = (∂V
UB = (∂U
∂nB
)T , p , nc
)T , p , nc
B物质的偏摩尔体积 物质的偏摩尔体积 B物质的偏摩尔热力学能 物质的偏摩尔热力学能 B物质的偏摩尔焓 物质的偏摩尔焓 B物质的偏摩尔熵 物质的偏摩尔熵 B物质的偏摩尔亥姆霍兹函数 物质的偏摩尔亥姆霍兹函数 B物质的偏摩尔吉布斯函数 物质的偏摩尔吉布斯函数
多组分单相系统的热力学公式
dU = TdS − pdV + ∑ µ BdnB
B
dH = TdS + Vdp + ∑ µ BdnB
B
dA = − SdT − pdV + ∑ µ BdnB
B
dG = − SdT + Vdp + ∑ µ BdnB
B
(2)多相多组分系统
dU = TdS − pdV + ∑∑ µ B (α ) dnB (α )
物理化学:第4章_多组分系统热力学_
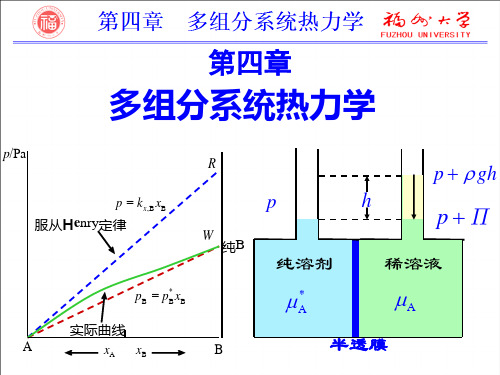
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
第四章 多组分系统热力学——【天津大学 物理化学 精】
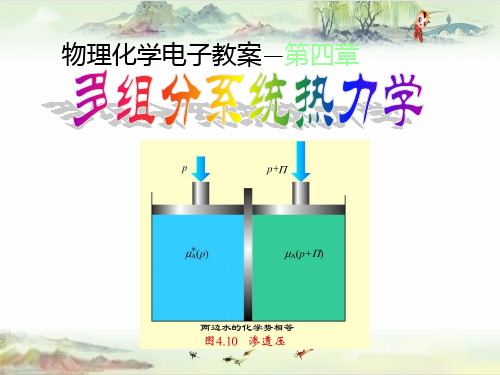
U nBUB B
H nBHB B
A nB AB
B
S nBSB B
G nBGB B
U
UB
( nB
)T , p,nc
HB
( H nB
)T , p,nc
A
AB
( nB
)T , p,nc
S
SB
( nB
)T , p,nc
G GB ( nB )T , p,nc
=B
化学势
3. 偏摩尔量的测定法举例
cm3mol-1;VBV,2A = V
2 n5BV.B340
nA
cm3mol-1
根据加合公式 V = nAVA+ nBVB
得:
由此可得,在两种溶液中H2O的偏摩尔体积分别为 VA=18.067 cm3mol-1;VA=18.045 cm3mol-1
2020/9/23
§4.2 化学势
化学势的定义
保持温度、压力和除B以外的其它组分不变, 体系的Gibbs自由能随nB的变化率称为化学势,所以 化学势就是偏摩尔Gibbs自由能。
T ,
p , nC
dnB
G S T p,nB
G p
T
,nB
V
G nB
T , p,nC
B
2020/9/23
同理
dG SdT Vdp BdnB B
dU TdS pdV BdnB B
dH TdS Vdp BdnB B
dA SdT pdV BdnB B
单相多组分系统 热力学基本方程
( nB
)T
, p,nC
若体系仅有一种组分(即纯物质),则根据摩尔量 的定义,XB就是摩尔量。
2020/9/23
物理化学 第四章 多组分系统热力学

Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B,C形成真实液态混合物: 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时,两组分的偏摩尔体积可用下法表示: 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线,此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB,VC。
B
系统中各广度量的偏摩尔量: 对于多组分系统中的组分B,有: 偏摩尔体积: VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能: UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓: HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵: SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数:AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数: GB=(ƽG/ƽnB)T,p,n
C
几点说明: (1)偏摩尔量为两个广度性质之比,所以为强度 性质; (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下,偏导数式的下标为T,p 时才是偏摩尔量; (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中,偏摩尔量不同; (4)若系统为单组分系统,则该组分的偏摩尔量 与该组分的摩尔量相等,即: XB=X*B,m
C
=VB (数学知识:二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势,用符号μB表示:
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质,其化学势等于它的摩尔吉布斯函 数。
物理化学(天津大学第五版)第一~五章总结

第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
解:根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 ︒C,另一个球则维持0 ︒C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 ︒C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算用van der Waals计算,查表得知,对于N2气(附录七),用MatLab fzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果1.16 25 ︒C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为138.7 kPa,于恒定总压下冷却到10 ︒C,使部分水蒸气凝结为水。
天津大学版物理化学课件第四章

即稀溶液中溶剂蒸气压下降值Δp与纯溶剂蒸气压之 比等于溶质的摩尔分数,而与溶质种类无关。 表4.4.1以甘露蜜醇的水溶液为例,列出了不同浓度下溶剂 蒸气压下降的实验值与拉乌尔定律的计算值。可以看出, 在所测的浓度范围内两者是很一致的。
表4.4.1 甘露蜜醇水溶液的蒸气压下降值(20℃)
溶质的摩尔分 数 103xB 1.769 蒸气压下降值△p/Pa 实验值 计算值 相对百分误差 %
dG -SdT Vdp B dnB
B
这四个方程时适用于均匀系统的更为普遍的热力学基本 方程,不仅适用于变组成的封闭系统,也适用于开放系 统。在封闭系统内的任一均匀部分(纯物质、混合物或 溶液)中组分B、C等的物质的量发生变化,是由于系统 内部发生了相变化或化学变化引起的。
如果将U、H、A表示成如下函数关系:
4.分配定律:
实验证明:在一定的温度、压力下,当溶质在共存的两互 不相溶液体间成平衡时,若形成的溶液的浓度不大,则 溶质在两液相中的质量浓度比为一常数。这就是能斯特 分配定律。比例系数称为分配系数,符号为K。
K bB ( ) / b( )
(4.6.18)
K是比例系数,称为分配系数。 这一经验定律可以由溶质在α、β两相间达到平衡时化学势 相等得出。
质量摩尔浓 度 b/(mol· -1) kg
0.0984
4.093
4.146
+1.3
0.2962
0.4938 0.6934 0.8913
5.307
8.817 12.34 15.80
12.29
20.48 28.83 37.23
12.41
20.60 28.83 36.95
+1.0
+0.6 0.0 -0.7
物理化学 4 多组分系统热力学

Physical Chemistry
河北联合大学
1
of 137
第四章 多组分系统热力学
河北联合大学
2
of 137
经 典 热 力 学 系 统
简单系统
(由纯物质形成的相及组成不变 的平衡系统)
多组分系统
(相组成改变的单相或多相系统)
河北联合大学
3
of 137
多组分系统可为单相或多相。若它为多相的,则可
全部浓度范围内及理想稀溶液在小范围内均有简
单的规律性。 对溶液,将组分区分为溶剂和溶质,对溶质 与溶剂用不同标准态研究;对混合物中任意组分
均选用同样的标准态加以研究。
河北联合大学
7
of 137
混合物(mixture) 多组分均匀体系中,溶剂和溶质不加区分,
各组分均可选用相同的标准态,使用相同的经验
V VB n B T , P ,nC
nC表示,除 B 以 外,其它组分的物质 的量均不变。
除了体积,其它广度量也有偏摩尔量。
河北联合大学
16 of 137
2.偏摩尔量:
在由组分 B, C, D…形成的混合系统中,任一广度量 X 是T, p , nB , nC , nD , …的函数,即:
20 of 137
河北联合大学
应当指出, 1)只有广度量才有偏摩尔量,强度量是不存在偏摩尔量的。 2)只有恒温恒压下,系统的某一广度量随某一组分的物质 的量的变化率,才能称为偏摩尔量,任何其它条件下的变化率 均不称为偏摩尔量。
G 例:尽管 A n n B T ,V ,nC B T , p ,nC
4.1.5b
积分得:
dX X
物理化学上册第五版天津大学出版社第四章多组分系统热力学习题答案

物理化学上册第五版天津大学出版社第四章多组分系统热力学习题答案4-1 由溶剂A 与溶质B 形成一定组成的溶液。
此溶液中B 的浓度为c B ,质量摩尔浓度为b B ,此溶液的密度为ρ。
以M A ,M B 分别代表溶剂和溶质的摩尔质量,若溶液的组成用B 的摩尔分数x B 表示时,试导出x B 与c B ,x B 与b B 之间的关系式。
解:对于A ,B 二组分溶液,溶液中物质B 的物质的量n B 与溶液的物质的量之比,称为物质B 的摩尔分数,符号x B 。
即AB B n n n +=B x物质B 的物质的量浓度为溶液V n B=B c 。
在二组分溶液中,溶质B的摩尔分数x B 与其浓度c B 之间的关系为溶液溶液溶液V M m c c V n c c n n V c AAB BA B B AB B /x B +=+=+=A B B B A B B B M c c V M c c +=+=溶液AB B B BA B B B B M M c c c M V M n c c )()/( -+=-+=ρρ式中ρ为溶液的密度,单位为kg·m -3;A 代表溶剂。
而物质B 的质量摩尔浓度则是溶液中溶质B 的物质的量除以溶剂的质量即ABB m n b =其单位为mol·kg -1。
在二组分溶液中溶质B 的摩尔分数x B 与质量摩尔浓度b B 的关系为AB BA A AB B A A A B A B M b b M n n b b m n m n m n /1)/(/// x B +=+=+=4-2 D-果糖C 6H 12O 6(B )溶于水(A )中形成的某溶液,质量分数W B =0.095,此溶液在20℃时的密度ρ=1.0365Mg·m -3。
求此果糖溶液的(1)摩尔分数;(2)浓度;(3)质量摩尔浓度。
解:(1)0104.018/905.0180/095.0180/095.0/)1(//=+=-+=B B B B B B B M W M W M W x(2)333547.0100365.1/1180/095.0dm mol dm mol c B ⋅=⋅⨯=(3)113583.0101000/)095.01(180/095.0--⋅=⋅⨯-=kg mol kg mol b B4-3 在25℃、1kg 水(A )溶解有醋酸(B ),当醋酸的质量摩尔浓度b B 介于0.16和 2.5mol·kg -1之间时,溶液的总体积V/cm 3=1002.935+51.832×(b B / mol·kg -1)+0.1394(b B / mol·kg -1)2。
天津大学高等教育出版社第五版《物理化学》第四章PPT课件

dG dG dG
dn B dnB B B
B B
dn B B
B
<0 自发过程 =0 平衡状态
恒温恒压下非体积功等于零的条件下: dG
★
dn B B
B
<0 自发过程 =0 平衡状态 >0 非自发过程
由享利定律可知,当溶质、溶剂和温度都一定时,亨利常数就为定值, 气体的分压越大,则该气体在溶液中的溶解度也就越大。所以增加气体的 压力有利于吸收操作。 由下表可知,随温度的升高,k值增大,因而当CO2分压相同时,随 着温度的升高,CO2的溶解度xCO2将下降。反之降低温度,则xCO2的溶解 度将增大,所以低温有利于吸收操作。
§4.3
1.纯理想气体的化学势
气体组分的化学势
( g ) B ▲标准状态下的化学势:
▲任意压力下的化学势:μ
*
纯理想气体:μ =GB =Gm
T
2.理想气体混合物中任一组分的化学势
3.纯真实气体的化学势
▲标准态规定:该温度及标准压力下的假想的纯态理想气体 ▲纯真实气体的化学势:可设计下面途径
p与p0相差不大
mix G T mix S
恒温恒压下液体混合过程的吉布斯函数变△mixG<0,说明混合过程 为自发过程。
§4.6
1.溶剂的化学势
理想稀溶液
理想稀溶液(无限稀薄溶液):溶质的相对含量趋于零的溶液。
T一定,若与理想稀溶液成平衡的气体为理想气体混合物, 溶剂遵循拉乌尔定律, 溶剂A的化学势:
故组成a的系统的体积: 混合物的组成改变时:※ 两组分的偏摩尔体积也在改变 ※ 组成越接近某一纯组分时,该组分的偏摩尔体积 也就越接近于该纯组分的摩尔体积;
物理化学 第四章 多组分系统热力学

AB
( nB
)T , p ,nC
G
GB
( nB
)T , p ,nC
注意:偏摩尔量的下脚标为:T,P,C(C≠ B)
使用偏摩尔量时应注意: 1.偏摩尔量的含义是:在等温、等压、保持B物质 以外的所有组分的物质的量不变的条件下,广度性 质X的随组分B的物质的量的变化率。
2.只有广度性质才有偏摩尔量,而偏摩尔量是强度 性质。
六、偏摩尔量之间的函数关系
对于组分B:VB、UB、HB、SB、AB、GB之间的关系:
HB= UB +PVB ,
AB= UB -TSB
GB = HB -TSB= UB +PVB -TSB UB =AB+PVB
(
GB P
)T
,nA
VB
(
GB T
)
P,nA
SB
( GB )
[T T
]P,nB
3.纯物质的偏摩尔量就是它的摩尔量。
4.任何偏摩尔量都是T,p和组成的函数。
偏摩尔量的集合公式
设一个均相体系由1、2、 、k个组分组成,则体 系任一广度量Z应是T,p及各组分物质的量的函数,即:
X X (T , p, n1, n2,, nk )
在等温、等压条件下:
X
X
dX
( n1
···········
dG= dG(α) + dG(β) +·········
恒T,p时 dG SdT Vdp
B
dnB
B
同理,有
dU TdS pdV B ( )dnB ( ) B
dH TdS Vdp B ( )dnB ( ) B
天津大学物理化学教研室《物理化学》(第5版)上册配套题库名校考研真题+课后习题+章节题库模拟试题

目 录第一部分 名校考研真题第1章 气体的pVT关系第2章 热力学第一定律第3章 热力学第二定律第4章 多组分系统热力学第5章 化学平衡第6章 相平衡第二部分 课后习题第1章 气体的ρVT关系第2章 热力学第一定律第3章 热力学第二定律第4章 多组分系统热力学第5章 化学平衡第6章 相平衡第三部分 章节题库第1章 气体的ρVT关系第2章 热力学第一定律第3章 热力学第二定律第4章 多组分系统热力学第5章 化学平衡第6章 相平衡第四部分 模拟试题天津大学物理化学教研室《物理化学》(第5版)配套模拟试题及详解第一部分 名校考研真题第1章 气体的pVT 关系一、填空题1.各种不同的真实气体的对比参数,反映了其所处状态偏离( )的倍数,在三个对比参数中,只要有( )分别相同,即可认为处于相同的对应状态。
[南京航空航天大学2012研]【解析】对比参数是指:,其中分别为临界压力、临界摩尔体积和临界温度。
当不同气体有两个对比参数相等时,第三个对比参数也将(大致)相等,称为对应状态原理。
2.一定温度时,真实气体的标准态是指( )压力( )理想气体。
[南京航空航天大学2012研]3.严格说来,只有在( )的极限情况下,真实气体才服从理想气体状态方程式;不过,在低于几MPa 的压力下,真实气体应用理想气体状态方程式其精度可满足一般的工程计算需要,对于难液化的真实气体,其适用的压力范围上限相对( )。
[南京航空航天大学2011研]临界点;两个对比参数【答案】标准;假想的【答案】压力趋近于零;较宽【答案】4.道尔顿分压定律适用于混合气体中的组分气体在单独存在于与混合气体具有相同( )、相同( )条件下,组分气体的分压与混合气体总压的关系。
[南京航空航天大学2011研]5.温度越( ),使气体液化所需的压力越大,对于一个确定的液体存在一个确定的温度,在此温度之上,压力再大,也不会使气体液化,该温度称为该气体的( )。
[南京航空航天大学2011研]6.当真实气体的压缩因子Z ( )1时,说明真实气体的V m 比相同条件下理想气体的V m 要大,此时的真实气体比理想气体( )被压缩。
Removed_物理化学 第四章 第五版 高等教育出版社 天津大学 刘俊吉 周亚平 上册

第四章多组分系统热力学4.1 有溶剂A与溶质B形成一定组成的溶液。
此溶液中B的浓度为c B,质量摩尔浓度为b B,此溶液的密度为。
以M A,M B分别代表溶剂和溶质的摩尔质量,若溶液的组成用B的摩尔分数x B表示时,试导出x B与c B,x B与b B之间的关系。
解:根据各组成表示的定义4.2 D-果糖溶于水(A)中形成的某溶液,质量分数,此溶液在20 °C时的密度。
求:此溶液中D-果糖的(1)摩尔分数;(2)浓度;(3)质量摩尔浓度。
解:质量分数的定义为4.3 在25 °C,1 kg水(A)中溶有醋酸(B),当醋酸的质量摩尔浓度b B介于和之间时,溶液的总体积。
求:(1)把水(A)和醋酸(B)的偏摩尔体积分别表示成b B的函数关系。
(2)时水和醋酸的偏摩尔体积。
解:根据定义当时4.4 60 °C时甲醇的饱和蒸气压是84.4 kPa,乙醇的饱和蒸气压是47.0 kPa。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50 %,求60 °C时此混合物的平衡蒸气组成,以摩尔分数表示。
解:质量分数与摩尔分数的关系为求得甲醇的摩尔分数为根据Raoult定律4.5 80 °C是纯苯的蒸气压为100 kPa,纯甲苯的蒸气压为38.7 kPa。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物,80 °C时气相中苯的摩尔分数,求液相的组成。
解:根据Raoult定律4.6 在18 °C,气体压力101.352 kPa下,1 dm3的水中能溶解O20.045 g,能溶解N2 0.02 g。
现将 1 dm3被202.65 kPa空气所饱和了的水溶液加热至沸腾,赶出所溶解的O2和N2,并干燥之,求此干燥气体在101.325 kPa,18 °C下的体积及其组成。
设空气为理想气体混合物。
其组成体积分数为:,解:显然问题的关键是求出O2和N2的Henry常数。
天津大学物理化学课程资料第四章多组分系统热力学

,
p,nC
dnB
18
在组成不变时:
G T
p,nB
S
,
G p
T ,nB
V
代入上式有:
dG SdT Vdp BdnB
B
结合 dU = d (G-pV +T S) dH = d (G +T S) , dA = d (G-pV)
19
dU TdS pdV BdnB dH TdS Vdp BdnB dA SdT pdV BdnB
dp
X
nB
T , p,nC
dnB
下标 nB表示:各组分的摩尔数都没改变; 下标 nc 表示:除B组外,其它各组分的摩尔数都未变
7
定义:
XB
X nB
T ,P ,nC
XB 偏摩尔量
意义: 在恒T、p及其它组分都不变时,加入极微量dnB的B 组分后,引起系统 X 性质的改变 dX。
或: 在恒T、p下,于足够大量的某一定组成的溶液中加入 1 mol B组分,而溶液浓度可视为不变时,1 mol B组 分对此种溶液中 X 性质的贡献。
第四章 多组分系统热力学
1
多组分系统
气态混合物
混合物 液态混合物
溶液
固态混合物
(第六章)
固态溶液
液态溶液 非电解质溶液
电解质溶液 (第七章)
混合物:各组分标准态相同; 溶液:溶质、溶剂标准态不同
研究方法:理想 实际
2
组成表示法:
1. 物质B的摩尔分数:
xB xB xB
B
xB 1
B
2. 物质B的质量分数:
wB mB
mB
B
wB 1
B
天津大学-第五版-物理化学上习题答案

第一章 气体的pVT 关系1-1物质的体膨胀系数V α与等温压缩系数T κ的定义如下:1 1T T pV p V V T V V⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫⎝⎛∂∂=κα 试导出理想气体的V α、T κ与压力、温度的关系 解:对于理想气体,pV=nRT111 )/(11-=⋅=⋅=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T TVV p nR V T p nRT V T V V p p V α 1211 )/(11-=⋅=⋅=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=p p V V pnRT V p p nRT V p V V T T T κ 1-2 气柜内有、27℃的氯乙烯(C 2H 3Cl )气体300m 3,若以每小时90kg 的流量输往使用车间,试问贮存的气体能用多少小时解:设氯乙烯为理想气体,气柜内氯乙烯的物质的量为mol RT pV n 623.1461815.300314.8300106.1213=⨯⨯⨯== 每小时90kg 的流量折合p 摩尔数为133153.144145.621090109032-⋅=⨯=⨯=h mol M v Cl H C n/v=(÷)=小时1-3 0℃、的条件常称为气体的标准状况。
试求甲烷在标准状况下的密度。
解:33714.015.273314.81016101325444--⋅=⨯⨯⨯=⋅=⋅=m kg M RT p M V n CH CH CHρ 1-4 一抽成真空的球形容器,质量为。
充以4℃水之后,总质量为。
若改用充以25℃、的某碳氢化合物气体,则总质量为。
试估算该气体的摩尔质量。
解:先求容器的容积33)(0000.10010000.100000.250000.1252cm cm V l O H ==-=ρn=m/M=pV/RTmol g pV RTm M ⋅=⨯-⨯⨯==-31.301013330)0000.250163.25(15.298314.841-5 两个体积均为V 的玻璃球泡之间用细管连接,泡内密封着标准状况条件下的空气。
物理化学天津大学第五版课件第四章

例4-1、25℃时有x(甲醇)=0.400的甲醇水溶液。若向大量的该溶液 中加入1mol水(A) ,则溶液的体积增加17.35cm3;加入1mol甲醇 (B),则溶液体积增加39.01cm3。 试求将0.600mol水与0.400mol甲醇混合,计算混合过程体积变化了 多少? 已知:25℃下ρA=0.997g· cm-3 ,ρB=0.791g· cm-3 。
—— 混合物总体积随B组分物质量的变化率
——m3/mol
——偏导 8
液体中发生的混合过程多为定温定压过程,则
V V V V dV dp dnB dnC ... dT T p ,nB p T ,nB nB T , p ,nc nC T , p ,nD
§4-1
液态混合物及溶液组成的标度
nB bB mA
1.混合物及溶液中组分B的组成标度
(1)B的质量摩尔浓度: (2)B的体积摩尔浓度: 单位:mol· kg-1
nB cB 单位:mol· m-3 V
nB B (3)B的摩尔分数: x B B nB B
mB (4)B的质量分数: wB mB
AB U B TSB GB H B TSB ... ... G B p VB T , nB T , nB
... ... S B VB p T p , nB ... ...
H B GB T 2 T T p
例:水与乙醇的混合物体积,Vm或V 均小于理想情况。主要 是偶极分子强烈吸引及本身缔合度发生变化——形成氢键。 60 Vm0 20 H2O 60
Vm
Vm ,水 =18.09mL/mol, Vm ,乙醇 =58.35mL/mol
第四章-多组分系统热力学-天大第五版

即,系统广度量为系统各组分物质的量的一次齐次函数。
③ 齐次函数的欧拉公式:
X (T , p , n B , n C, n D , L ) =
å
B
骣X ¶ nB 琪 琪 琪n ¶ 桫
B T , p ,n C
④ 偏摩尔量:
骣X ¶ X B == 琪 琪n 桫 B ¶
def T ,p ,n C
⑤ 偏摩尔量集合公式:
$
2. 理想气体混合物中任一组分的化学势 由理想气体模型可知,理想气体混合物中 B 组分的性质 并不受其它组分的影响,故其化学势表达式与纯理想气体 化学势表达式相同:
pB y Bp $ mB(pg ) = mB(g ) + R T ln $ = mB(g ) + R T ln $ p p
$
式中 p B = y B p 为混合理想气体中 B 组分的分压。 3. 纯真实气体的化学势 标准态:温度 T,标准压力 p 下假想的纯态理想气体。
① 化学平衡 首先假定系统已处于相平衡,有
mB (a ) = mB ( b ) = mB (d) = L
用 mB 表示 B 组分的化学势,从而
邋
a B
骣 mB (a )dn B (a ) = 邋mB 琪 dn B (a ) = 0 琪 琪a 桫 B
dn B
故化学平衡条件
å
mB dn B = 0
B
该平衡条件与化学反应达到平衡的方式无关。
偏摩尔熵
T ,p ,n C
偏摩尔亥姆霍兹函数
T ,p ,n C
偏摩尔吉布斯函数
T ,p ,n C
3.偏摩尔量的测定法举例 以二组分系统偏摩尔体积测定为例:
5.吉布斯 − 杜亥姆方程
最新物理化学课件(天大第五版)04-01溶液热力学

Chapter 4 the Thermodynamics of Multicomponent System
1
系统按照所含组分数和相数可划分为:
单组分均相系统 多组分均相系统
单组分多相系统 多组分多相系统
多组分均相系统 :由两种或两种以上物质以分子状态 相互混合而成的均匀系统
与该组分在混合物中摩尔分数的乘积。
30
p 0 VB
RT p
dp
定义:
~pB
pB
exp
p 0
VB RT
1 p
dp
对于纯气体
~p*
p exp
p 0
Vm* RT
1 p
dp
对于理想气体积分项为0
~pB pB
22
逸度因子
B
def
~p B pB
对于理想气体 ~pB pB
1
(1)线的差异
~p
Pa
(2)标准态
23
2.逸度因子的计算及普遍化逸度因子图
11
5.吉布斯–杜亥姆方程(Gibbs-Duhem)
X nB X B
B
dX (nBdX B X BdnB )
B
dX
X T
p,nC
dT
X p
T ,nC
dp
B
X B dn B
恒温恒压: dX XBdnB
B
nBdX B 0
B
xBdX B 0
B
二元系统: xAdX A xBdXB 0
p
G G1 G2 G3 RT ln p
p 0
Vm*
RT p
dp
* ( g)
RT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
G ( ) T , nB V B p
B ( ) T , x VB p
B ( ) T Vm ,B p
结论:几种纯液体在恒温恒压下,混合成理想液态混合物时,混合前 后系统的体积不变。
( 2)
mix H 0
结论:几种纯液体在恒温恒压了混合成理想液态混合物时,混合前 后系统的焓不变,因而混合(焓)热等于零。
4.偏摩尔量与摩尔量的差别 [1]若B,C形成理想混合物 V*m,B和V*m,C为两纯液体的摩尔体积
Vm~xc作图得一条直线(见图中虚线) 截距:V*m,B 斜率:V*m,C-V*m,B
[2]若B,C形成了真实混合物 Vm~xc作图得一条曲线(见图中实线) 过d作Vm~xc曲线的切线,此切线在纵坐标轴上的 截距为该组成下两组分的偏摩尔体积VB,Vc
>0 非自发过程
化学势判据
★
3、化学势判据及应用举例 在恒温恒压下,若系统中存在有多相(α,β…),多组分(B,C …) 则:
dG dG dG
dn dn B B B B dn B B
B B B
<0 自发过程 =0 平衡状态
由享利定律可知,当溶质、溶剂和温度都一定时,亨利常数就为定值, 气体的分压越大,则该气体在溶液中的溶解度也就越大。所以增加气体的 压力有利于吸收操作。 由下表可知,随温度的升高,k值增大,因而当CO2分压相同时,随 着温度的升高,CO2的溶解度xCO2将下降。反之降低温度,则xCO2的溶解 度将增大,所以低温有利于吸收操作。
3.拉乌尔定律和亨利定律的微观解释 ※拉乌尔定律的微观解释 溶液中加入溶质 B ,单位液面上 A 分子数占液面总分子数的分数从纯 溶剂时的1下降至溶液的xA,致使单位液面上溶剂 A的蒸发速率按比例下降, 溶液中溶剂A的饱和蒸气压也相应地按比例下降。 pA=p*AxA ※亨利定律的微观解释 在溶解平衡时,气相中B在单位表面上的凝结速率与蒸发速率相等,故 气相中B的平衡分压力正比于溶液中B的摩尔分数。
全微分形式:
压力及混合 物中各组分 的物质的量 均不变时, 系统广度量 X 随温度的 变化率
温度及混合 物中各组分 的物质的量 均不变时, 系统广度量 X 随压力的 变化率;
温度、压力及除了组分 B 以外其余各组分的物 质的量均不变时,组分 B的物质的量发生了微 小的变化引起系统广度 量X 随组分B 的物质的 量的变化率。
表示纯液体B(xB=1),在温度T,压力p下的化学势
* B (l )
▲纯液体B的化学势:
▲理想液态混合物中任一分B的化学势:
如何表示纯液体 B在标准状态下(T,P0)的化学势 B (l )
纯液体 B在标准状态下的化学势
0 B ( l ) (T,P )
纯液体B在T, p下的化学势
* B (l )
恒温恒压下非体积功等于零的条件下: dG
dn B B
B
<0 自发过程 =0 平衡状态 >0 非自发过程
>0 非自发过程
化学势判据
★
★
若此相变化能自发进行 若两相处于相平衡状态
在恒温恒压下,若任一物质B在两相中具有相同的分子形式,但化学势不等,则 相变化自发朝着化学势减少的方向进行;若两相的化学势相等,则两相处于相平 衡状态。
或
恒温、恒压下, 在足够大量的某 一定组成的混合 物中加入单位物 质的量的组分B 时所引起系统广 度量 X的增量
组分B偏摩尔量
●偏摩尔量:在温度、压力及除了组分B以外其余各组分的物质的量均不改 变时,广度量X 随组分B的物质的量nB的变化率XB称为组分B 的偏摩尔量。
注意: ▲纯物质的偏摩尔量等于其摩尔量 ▲只有广度量才有偏摩尔量 ▲只有恒温恒压下系统的广度量随某一组分的物质的量的变 化率才能称为偏摩尔量 ▲偏摩尔量和摩尔量一样,是强度量。
※一定温度、压力下,向物质的量为nc的液体组分C中,不断地加入组分B
※测量加入不同nB时,混合物的体积 V ※V-nB作图 ※过曲线上任一点作曲线的切线,此切线的斜率即为:
V ( )T , p ,nc VB nB
※组分C在此组成下的偏摩尔体积Vc
V nBVB nCVC
V n BVB VC nC
★化学势判据 (恒温恒压) ★气体的化学势 ●理想气体
B
B
dnB
<0 自发过程 =0 平衡状态 >0 非自发过程
总结2
纯
混合物 纯
●真实气体 混合物 ★拉乌尔定律 适用条件:理想液态混合物 或理想稀溶液中的溶剂 pA(溶剂)~ xA ★亨利定律 适用条件:稀溶液中的挥发性溶质 pB(溶质)~ xB
多组分系统热力 xue §4.1 偏摩尔量 1.问题的提出: ★在20℃,纯水的摩尔体积为18.09cm3/mol ,纯乙醇的摩尔体积为cm3/mol 将0.5摩尔的水与0.5摩尔的水混合,溶液体积: V=(0.5×18.09十0.5×18.09)cm3 =18.09cm3 V nBVm , B nCVm,C 理想混合溶液
⑤拉乌尔定律的微观解释 溶液中加入溶质B,单位液面上A分子数占液面总分子数的分数从纯溶 剂时的1下降至溶液的xA,致使单位液面上溶剂A的蒸发速率按比例下降, 溶液中溶剂A的饱和蒸气压也相应地按比例下降。
2.亨利定律 ①定律: 一定温度下,稀溶液中挥发性溶质在气相中的平衡分压与其在溶液中 的摩尔分数(或质量摩尔浓度、物质的量浓度)成正比
恒温恒压下液体混合过程的吉布斯函数变△mixG<0,说明混合过程 为自发过程。
§4.6
1.溶剂的化学势
理想稀溶液
理想稀溶液(无限稀薄溶液):溶质的相对含量趋于零的溶液。
T一定,若与理想稀溶液成平衡的气体为理想气体混合物, 溶剂遵循拉乌尔定律, 溶剂A的化学势:
§ 4. 2
化学势
化学势:混合物(或溶液)中组分B的偏摩尔吉布斯函数GB称之
1.多组分单相系统的热力学公式 若: 则:
更为普遍的热力学基本方程 适用条件:均匀(单相)系统
若U、H、A将表示成如下函数关系
比较可得:
偏摩尔量
2.多组分多相系统的热力学公式 对多组分多相系统中的α、β…每一个相,有
对系统内所有的相求和 因各相的T,p均相同
故组成a的系统的体积: 混合物的组成改变时:※ 两组分的偏摩尔体积也在改变 ※ 组成越接近某一纯组分时,该组分的偏摩尔体积 也就越接近于该纯组分的摩尔体积;
5.吉布斯一杜亥姆方程 T,p一定时, 对此式求全微分: 故必然有: 吉布斯—杜亥姆方程 偏摩尔的集合公式 已知
若为二组分混合物,则有 xBdXB+xcdXC=0
①定律 稀溶液中溶剂的蒸气压等于同一温度下纯溶剂的饱和蒸气压与溶液 中溶剂的摩尔分数的乘积。 ②数学表达式
p*A:纯溶剂的饱和蒸气压 pA :溶液中溶剂的饱和蒸气压 xA : 溶液中溶剂的摩尔分数
③适用条件:理想液态混合物
或理想稀溶液中的溶剂 ④注意: 适用于溶液达气液平衡的体系
pA =气相中溶剂组分的分压
③对于其他热力学性质如H、G、S、
U等亦有类似情况。 ★0.5摩尔的水与0.5摩尔的乙醇混合中, 水 和 乙 醇的 偏 摩 尔体 积 分 别为 VB=17.0cm3/mol,Vc=57.4 cm3/mol, V=(0.5×17. 0+0.5 ×57.4)cm3=37.2 cm3
2、偏摩尔量 组分B,C,D,…形成的混合系统中,任一广度量X
标准状态下的假想的纯态理想气体
→
压力为p的真实气体
压力为p的理想气体
→
将气体变为p→0的气体
↓
纯真实气体与理想 气体化学势的差别 是由于两者在同样 温度压力下摩尔体 积不同造成的。
↓
4.真实气体混合物中任一组分的化学势
纯 理想气体 混合物
纯 真实气体
混合物
§4 .4
拉乌尔定律和亨利定律
1.拉乌尔定律
结论:在恒温恒压下,当混合物的组成发生微小 变化时,若一组分的偏摩尔量增大,则另一组分 的偏摩尔量必然减小,且增大与减小的比例与混 合物中两组分的摩尔分数(或物质的量)成反比。
6、偏摩尔量之间的函数关系 热力学函数之间存在有一定的函数关系 :
H =U+pV, A =U-TS, G =U+pV-TS=H-TS=A+pV 将这些公式 对混合物中 任一组分B 取偏导数, 各偏摩尔量 之间也有着 同样的关系
理想液态混合物中任一分 B的化学势为:
G ( B ) P , nB S B T
( B ) P, x S B T
B ( ) P, x S m ,B T
摩尔混合熵为: 恒压、恒温下液体的混合过程是一个自发过程
恒温下:
混合过程中:
mix H 0
mix G T mix S
(T,P)
当压力从p0变至p时 理想液态混合物中任一组分B的化学势与混合物组成的关系式
p与p0相差不大 忽略积分项
3.理想液态混合物的混合性质 相互混合 纯液体 B(n )
B
纯液体 C( nC) (1)
恒温恒压
理想液态混合物 (n= nB +nC)
mixV 0
理想液态混合物中任一分B的化学势为:
●偏摩尔量的集合公式
在恒温恒压条件下, dT=0,dp=0
若按混合物原有组成的比例同时微量地加入组分 B,C,…以形成混合物, 此过程中组成恒定,积分上式:
偏摩尔量的集合公式 表明:在一定温度、压力下,某一组成混合物的任一广度量等于各组分 对应的偏摩尔量与其物质的量的乘积之和
3、偏摩尔量的测定法举例
②数学表达式
pB 挥发性溶质在气相中的平衡分压 xB 挥发性溶质在溶液中的摩尔分数 kx,B 亨利系数
