微分方程的图像解

合集下载

微分方程的相图分析及解析

微分方程的相图分析及解析微分方程是描述自然现象的重要工具，在各个领域都有广泛应用。

微分方程的解析解一般较难求得，因此相图分析成为预测微分方程解行为的一种重要工具。

本文将详细介绍微分方程的相图分析及解析。

一、相图的概念相图是指微分方程解的全部行为在相平面（或相空间）上的展现。

相平面上的点表示微分方程解的初始值及其在时域的变化。

因此，相图展示了微分方程的解如何随时间演化。

通常将相图绘制在相平面或相空间中，直观清晰，有助于预测和分析微分方程的各种解行为。

二、相图的分类相图可以分为一、二、三类，具体如下：1. 一类相图：相图上所有解轨道都趋于某一点或曲线，该点或曲线称为平衡点或平衡轨道。

平衡点可以分为稳定平衡点、不稳定平衡点和半稳定平衡点，分别对应解轨道向平衡点靠近、向平衡点远离和一部分解轨道向平衡点靠近，一部分向其远离。

2. 二类相图：相图上存在解轨道趋向于无穷远处，这种无穷远处称为鞍点，它是稳定和不稳定平衡点的分界线。

3. 三类相图：相图上不仅存在平衡点和鞍点，而且还有解轨道环绕其中，这种相图被称为极限环相图。

三、如何绘制相图以一阶非齐次线性微分方程为例，介绍相图的绘制步骤：1. 将微分方程化成标准形式：y' + p(x)y = q(x)，其中p(x)、q(x)为已知函数；2. 找到该微分方程的所有平衡点，并计算平衡点处的斜率p(x)与q(x)的值；3. 根据平衡点处斜率的正负与大小关系，画出对应的稳定平衡点、不稳定平衡点和半稳定平衡点；4. 找到方程的任意一组解，通过定量计算可得其解轨道，画出解轨道，并分析其行为，确定相图的类型。

四、相图的应用相图是预测微分方程解行为的重要工具，具有广泛应用。

以下列举几个例子：1. 生物学中的Lotka-Volterra模型，描述捕食者与食饵之间的生态关系，通过绘制相图，可以预测捕食者与食饵数量之间的关系；2. 物理学中的简谐振动方程，利用相图可以预测振动系统的稳定性和震荡特性；3. 工程学中的热传导方程，通过绘制相图可以预测材料的温度分布及热传递速率。

1.求微分方程的解析解, 并画出图形,

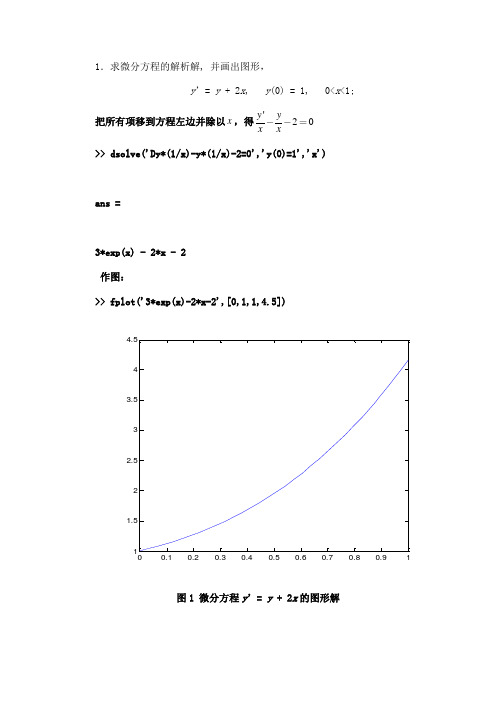
y ’= y + 2x , y (0) = 1, 0<x <1; 把所有项移到方程左边并除以x ，得'20y y xx>> dsolve('Dy*(1/x)-y*(1/x)-2=0','y(0)=1','x') ans =3*exp(x) - 2*x - 2 作图：>> fplot('3*exp(x)-2*x-2',[0,1,1,4.5])图1 微分方程y ’= y + 2x 的图形解0.10.20.30.40.50.60.70.80.91cos 0,(0)1,(0)0y y x y y '''+=== 先把原方程化为一阶方程组。

令1y y ，2'y y ，则有122112''cos (0)1,(0)0y y y y x y y首先建立M-文件函数: function f=jie(x,y) f=[y(2);-y(1)*cos （x ）]; 计算:>> [x,y]=ode23('jie',[0,2*pi],[1,0]) x =0 0.0001 0.0005 0.0025 0.0125 0.0625 0.1541 0.2788 0.43450.62660.88061.15001.41251.65351.88482.11782.35972.60562.85723.1416y =1.0000 0 1.0000 -0.0001 1.0000 -0.0005 1.0000 -0.0025 0.9999 -0.0125 0.9980 -0.0624 0.9882 -0.1529 0.9616 -0.2717 0.9085 -0.40830.8158 -0.55140.6569 -0.68840.4592 -0.76860.2529 -0.79630.0606 -0.7987-0.1242 -0.8009-0.3129 -0.8228-0.5185 -0.8855-0.7499 -1.0086-1.0276 -1.2127-1.4177 -1.5535作图：>> y1=y(:,1);>> y2=y(:,2);>> plot(x,y1,x,y2,'r'),gtext('y1'),gtext('y2')图2 微分方程cos 0,(0)1,(0)0y y x y y '''+===的图形解01234567-10-553．两种相似的群体之间为了争夺有限的同一种食物来源和生活空间而进行生存竞争时，往往是竞争力较弱的种群灭亡，而竞争力较强的种群达到环境容许的最大数量。

第六节线性微分方程解的结构

三、线性非齐次微分方程解的结构
定理 3 设 y * ( x) 是二阶非齐次方程 ①
的一个特解, Y (x) 是相应齐次方程的通解, 则
y Y(x) y*(x)
②
是非齐次方程的通解 .
证将 y Y ( x) y * ( x)代入方程①左端, 得
(Y y * ) P( x)(Y y * ) Q( x)(Y y *)
定理设 y* 是 n 阶非齐次线性方程
y(n) P1( x) y(n1) Pn ( x) y f ( x)
的一个特解, Y 是与其对应的齐次方程的通解, 那么 y Y y*是 n 阶非齐次线性微分
方程的通解.
四、小结
主要内容 1、函数的线性相关与线性无关； 2、二阶线性微分方程解的结构定理
二、证明下列函数是相应的微分方程的通解:
1、 y c1 x 2 c2 x 2 ln x
(
c1
,
c
是任意常数
2
)是方程
x 2 y 3xy 4 y 0 的通解；
2、 y

1 x
(
c1e
x

c2e x
)

ex 2
(
c1
,
c
是任意
2
常
数
)是
方程xy 2 y xy e x 的通解 .
定义设 y1( x), y2( x),, yn( x) 是定义在区间 I 上的
n 个函数, 若存在不全为 0 的常数
使得
则称这 n个函数在 I 上线性相关,否则称为线性无关.
例如：
在( , )上都有
故它们在任何区间 I 上都线性相关;

D第四章微分方程

与齐次微分方程
一、可分离变量微分方程
一般形式 dy f (x)g(y)
dx
解法: （1）分离变量
dy f (x)dx g(y)
（2）两边积分

dy g(y)

f
(x)dx
得 Gx()Fx()C.
（其中 G(y),F(x)分别是
1, g(y)
f (x)
的一个原函数）
以上这种求解过程叫做分离变量法。
y Cex3 ( C 为任意常数 )
( 此式含分离变量时丢失的解 y = 0 )
例3. 解初值问题
xydx(x21)dy0
y(0)1
解: 分离变量得
dy y
1xx2
dx
两边积分得
lny ln 1 lnC x21
即
y x21C ( C 为任意常数 )
由初始条件得 C = 1, 故所求特解为
k 2 (C 1 sk it n C 2ck o t)sk2x
这说明 x C 1 ck o t C s 2 sk itn 是方程的解 .
C1,C2 是两个独立的任意常数, 故它是方程的通解.
利用初始条件易得: C1A,C2 0,故所求特解为
xAcokts
4.2 可分离变量的微分方程
C'(y)yyey
于是C'(y)ey, 则 C (y)eyd y eyC
所以原方程的通解为
x(eyC)y（C 为任意常数）
例3. 设河边点 O 的正对岸为点 A , 河宽 OA = h, 两岸为平行直线, 水流速度大小为 a , 一鸭子从点 A 游向点
O , 设鸭子(在静水中)的游速大小为b (ba), 且鸭子
特解: yx2 1

求微分方程的解PPT课件

y(0) 1
fun=inline('-2*y+2*x^2+2*x','x','y'); [x,y]=ode23(fun,[0,0.5],1);
注：也可以在 tspan 中指定对求解区间的分割，如：
[x,y]=ode23(fun,[0:0.1:0.5],1); %此时 x=[0:0.1:0.5]
第19页/共23页
solver 为Matlab的ODE求解器（可以是 ode45、ode23、ode113、
ode15s、ode23s、ode23t、ode23tb）
没有一种算法可以有效地解决所有的 ODE 问题，因此MATLAB 提供了多种ODE求解器，对于不同的ODE，可以调用不同的求解器。
第17页/共23页
Matlab提供的ODE求解器
度均可到 10-3～10-6
ode23t 适度刚性采用梯形算法
适度刚性情形
ode15s
刚性多步法；Gear’s 反向数值微若 ode45 失效时，可
分；精度中等
尝试使用
ode23s 刚性单步法；2 阶Rosebrock 算当精度较低时，计算时
法；低精度
间比 ode15s 短
ode23tb 刚性梯形算法；低精度
x y
|t 0 |t 0
1 0
[x,y]=dsolve('Dx+5*x+y=exp(t)','Dy-x-3*y=0', ... 'x(0)=1', 'y(0)=0', 't')
ezplot(x,y,[0,1.3]);
注：解微分方程组时，如果所给的输出个数与方程个数相同，则方程组的解按词典顺序输出；如果只给一个输出，则输出的是一个包含解的结构（structure）类型的数据。

微分方程PPT课件

x
ln u 1 3 ln(u 2) u 2 1 ln u ln x ln C ,
2
2
u1 3 Cx.
u(u 2)2
微分方程的解为 ( y x)2 Cy( y 2 x)3 . 20
三. 一阶线性微分方程
一阶线性微分方程的标准形式:
dy P( x) y Q( x) (1) dx
初值问题: 求微分方程满足初始条件的解的问题.
一阶:
y f (x, y),
y(
x0
)
y0
.
过定点的积分曲线;
y f ( x, y, y),
过定点且在定点的切线
二阶:
y(
x0
)
y0 ,
y(x0 )
y0
.
的斜率为定值的积分曲线.
n
阶:
f (x, y, y( x0 )
y, y y0 , y(
x A, dx 0,
t 0
dt t0
C1 A,
而
dx dt
kC1
s in kt
kC2
cos kt,
C2 0.
所求特解为 x Acoskt.
9
注意： 1. 有些方程可能无解.
( y)2 y2 1 0 无实函数解.
2. 方程可能有解而无通解. ( y)2 y2 0 只有特解 y 0 . 3. 通解不一定能包含所有的解.
y 3e2x 中不含任意常数,
故为微分方程的特解.
11
6.2 一阶微分方程
一阶微分方程的一般形式是
F( x, y, y) 0
如果一阶导数可解出，则可写为
dy f ( x, y), dx 或 P( x, y)dx Q( x, y)dy 0

二阶常系数非齐次线性微分方程

设方程y′′+py′+qy=Pm(x)eλx的特解形式为y*=Q(x)eλx，则得等式 Q′′(x)+(2λ+p)Q′(x)+(λ2+pλ+q)Q(x)=Pm(x)． (1)如果λ 不是特征方程 r2+pr+q=0 的根，则y*=Qm(x)eλx． (2)如果λ 是特征方程 r2+pr+q=0 的单根，则y*=xQm(x)eλx． (3)如果λ 是特征方程 r2+pr+q=0 的重根，则 λ2+pλ+q =0，2λ+p=0，要使等式 Q′′(x)+(2λ+p)Q′(x)+(λ2+pλ+q)Q(x)=Pm(x)．成立，Q(x)应设为m+2 次多项式：Q(x)=x2Qm(x)， Q m(x)=b0 xm+b1xm1+ +bm1x+bm ，通过比较等式两边同次项系数，可确定b0，b1，，bm ，并得所求特解 y*=x2Q m(x)eλx．
一、 f(x) = Pm(x)eλx 型
下面求方程 y′′+py′+qy=Pm(x)eλx，的特解y* ，其中Pm(x)是m次多项式．可以猜想，方程的特解y*应具有与Pm(x)eλx类似的函数形式．设方程y′′+py′+qy=Pm(x)eλx的特解形式为y*=Q(x)eλx，代入方程得 [Q′′(x)+2λQ′(x)+λ2 Q(x)]eλx+ p[Q′(x)+λQ(x)]eλx +qQ(x)eλx =[Q′′(x)+(2λ+p)Q′(x)+(λ2+pλ+q)Q(x)] eλx=Pm(x)eλx，于是有等式 Q′′(x)+(2λ+p)Q′(x)+(λ2+pλ+q)Q(x)=Pm(x)．

6.4 二阶常系数线性齐次微分方程

②
称②为微分方程①的特征方程, 其根称为特征根.
要求：能根据方程①熟练写出其特征方程并求出特征根.
高等数学(GAO DENG SHU XUE)
目录上页下页返回结束
6.4.3 二阶常系数线性齐次微分方程的解法微分方程:
特征方程: 2 p q 0
特征根:
(1)当��2 − 4�� > 0时, 特征方程有两个不等的实根��1, ��2 则微分方程有两个线性无关的特解:
因此方程的通解为：y (C1 C2 x)e2 x
高等数学(GAO DENG SHU XUE)
目录上页下页返回结束
6.4.3 二阶常系数线性齐次微分方程的解法微分方程:
特征方程: 2 p q 0
特征根:
(2)当��2 − 4�� < 0时, 特征方程有一对共轭复数根：
代入初始条件��′ ��=0 = 1, 解得��2 = 1,
(1) 写出相应的特征方程: 2 p q 0;
(2) 求出特征方程的两个根: 1 与 2；
(3) 根据特征方程的两个根的不同情况,按照下列规则写出微分方程的通解
特征方程的两个根1 ，2 微分方程的通解
两个不相等的实根1 ，2 两个相等的实根 1 =2
y C1e1x C2e2x y (C1 C2 x)e1x
若 ��(��) 0, 即��′′ + ��′ + �� = ��(��) 称为二阶常系数线性非齐次微分方程.
对应的齐次方程

微分方程的解析解、数值解和图形解

适中、适用于大规模计算等优点。在相同步长下，其精度高于欧拉法和改进欧拉法，计算量小于龙格-库塔法。
缺点
线性多步法的稳定性较差，对初值敏感，需要选择合适的步长和算法参数以保证计算稳定性。
线性多步法
线性多步法
一种通过利用前面多个步长的信息来预测下一个步长的数值解方法。其基本思想是将微分方程转化为差分方程进行求解。
应用
相平面法常用于分析微分方程的平衡点、稳定性、周期解等问题。通过观察相平面图，可以判断微分方程的解是趋于稳定还是发散，以及是否存在周期解等。
相平面法
01
定义
相平面法是研究一阶和二阶常微分方程的一种图解法，通过在相平面上绘制微分方程的解曲线，可以直观地了解解的性质和动态行为。
02 03
原理
步骤
将微分方程化为可分离变量的形式，对两边同时积分，解出未知函数。
分离变量法
原理
通过把微分方程中的变量进行分离，使得方程两边分别只含有一个变量，然后对两边同时积分求解。
适用范围
适用于一阶线性微分方程、齐次微分方程等可分离变量的微分方程。
步骤
将微分方程化为可分离变量的形式，对两边同时积分，解出未知函数。
目录
PART 01
微分方程基本概念
REPORTING
WENKU DESIGN
PART 01
微分方程基本概念
REPORTING
WENKU DESIGN
微分方程定义与分类
微分方程定义
描述未知函数与其导数之间关系的数学方程。
分类
根据方程中未知函数的最高阶导数，可分为一阶、二阶等；根据是否线性，可分为线性与非线性微分方程。
然后利用全微分的性质求解。

1.求微分方程的解析解, 并画出图形,

一阶线性微分方程的概念与解的结构课件.ppt

y1

e

P(
x
)dx
,
于是，一阶线性非齐次方程的通解公式，就可写成：
y e P( x)dx C Q( x)e P( x)dxdx.
上述讨论中所用的方法，是将常数 C 变为待定
函数 C(x)，再通过确定 C(x) 而求得方程解的方法，
称为常数变易法.
精品文档
例 8 求方程 2y - y = ex 的通解.
于是，有
C( x) 1 1 cos x, xx
C( x) cos xdx sin x C. 精品文档
因此，原方程的通解为 y (sinx C) 1 C 1 sin x. x xx
将初始条件 y() = 1 代入，得 C = ，所以，所求的特解，即初值问题的解为
称为伯努利方程。当n=0或1时，该方程是线性方程；当n≠0或1时，该方程不是线性的，但是通过变量替换，可以把它化为线性的。
精品文档
如以yn除以方程两边，得
yn dy p(x) y1n Q(x), dx
令
z y1n
则 dz (1 n) yn dy
dx
dx
化简为 dz (1 n) p(x)z (1 n)Q(x) dx
则

P( x)dx

1 2
dx

x 2
,
x
e P ( x )dx e 2 ,
Q( x)e P( x)dxdx
1e
x

e
x
2 dx

e
x 2
,
2
代入通解公式，得原方程的通解为
xx

斜率场--微分方程图形解

斜率场--微分⽅程图形解
假设微分⽅程的解曲线族（通过垂直平移形成⼀系列曲线），上⾯的点遍布整个平⾯(xy),那么我们任意选择⼀个点，将改点代⼊dy/dx=f(x,y)，那么就可以计算出改点的斜率即某条解曲线在该点的切线。

clear s t x0 y0 a b
syms s t
%s->x ,t对应y
%f=sin(s)*sin(t);
%f=t-s^2;
f=-2*s*t/(1+s^2);
% f=cos(s);
a=32.0;
b=32.0;
x0=-16;
y0=-16;
m=40;
n=40;
h1=a/m;
h2=b/n;
hold
%下⾯的2/3是线段缩放因⼦,需要在x,y两个⽅向同时乘上
for I=1:m
s=x0+(I-1)*h1;
for j=1:n
t=y0+(j-1)*h2;
d=eval(f); %d表⽰斜率,如果解曲线族经过点(s,t)那么这点的斜率是d
y1=t+2/3*h1*d; %以x的增量计算y
if abs(y1-t)>2/3*h2 %(y1-t)=t+2/3*h1*d -t=2/3 * h1 * d
x1=s+1/d*h2*2/3; %以y的增量计算x,所以要乘以1/d;
plot([s,x1],[t,t+h2*2/3])
else
plot([s,s+h1*2/3],[t,y1])
%plot([1-3],[1,2])画⼀条直线，x为1到3,y为1到2
%在s(相当于x)的点加上h1(⼩步增量*2/3)
%注意上⾯的y1中的h1也乘于2/3,以缩短斜线长度
end
end
end
View Code。

微分方程作图

y Cex2
微分方程作图 4
with(DEtools):with(plots):
wffc:=diff(y(x),x)=2*x*y(x):dsolve(wffc);
fangxiangcang:=DEplot(wffc,y(x),x=-2..2,y=-2..2,thickness=2):
jifenquxian:=contourplot(y/exp(x^2),x=-2..2,y=-2..2,contours=20,color=blue,thickness
四川大学数学学院徐小湛
May 2012
微分方程作图 11
with(DEtools): DEplot((x-y(x)^3)*diff(y(x),x)+y(x)=0,y(x),x=-2..2, y=-2..2,[[y(0)=1],[y(0)=0.3],[y(0)=1.5],[y(0)=-0.5],[y(0)=-1],[y(0)=1.5]],linecolor=[blue,black,gold,navy,green,maroon], color=violet,stepsize=0.01,scaling=constrained);
wffc:=diff(y(x),x)=(cos(y(x))-y(x)*cos(x))/(x*sin(y(x))+sin(x)-1):
dsolve(wffc);fangxiangcang:=DEplot(wffc,y(x),x=-2..2,y=-2..2,thickness=2):
jifenquxian:=contourplot(y*sin(x)-x*cos(y)-y,x=-2..2,y=-2..2,contours=20,color=blue,
with(DEtools):with(plots): wffc:=(x-y(x)^3)*diff(y(x),x)+y(x)=0:dsolve(wffc); fangxiangcang:=DEplot(wffc,y(x),x=-2..2,y=-2..2,thickness=2): jifenquxian:=contourplot(x*y-y^4/4,x=-2..2,y=-2..2,contours=20,color=blue,thickness= display(fangxiangcang,jifenquxian);

微分方程解法.ppt

阶段汽车运动规律的函数S=S(t),应满足方程：
d 2s 4 2 dt ds 及条件 S t 0 0, v t 0 t 0 10 dt 对（ 5）式两端积分一次，得 ds v 4 t c1 dt 在积分一次，得 S 2 t 2 c1t c 2 将条件 v
2
y x 1 只是其中过（ 1 ， 2 ）点的一条积分曲
8.2
可分离变量的一阶微分方程
一阶微分方程（differential equation of first order）
f( y x ,y ) ( 1 ) 如果能化成 g ( y ) dy f( x ) dx ( 2 )
的形式，即可表示为一端只含 y 的函数和 dy ,而另一端只
对于高阶线性微分方程，其通解结构也有类似的结论。
例 1求方程 xy y e x的通解 y ex 解将方程改写为 y x x 它是一阶线性微分方程，其中
1 ex P( x) , Q( x) x x 方法一利用常数变易法，先求对应齐次方程 1 y y 0 的通解，为此，分离量： x 1 1 dy dx y x
将其代入（ 4 ）式，就得到了一阶线性非其次方 1 ）的通解：y e
p ( x ) dx Q ( x ) e dx C ( 5 ) 上述将对应的齐次方程通解中的任意常数C替换成 P ( x ) dx
x的待定函数，并将其代入非齐次方程中以确定C(x)，从而求得非齐此方程的通解的方法叫做常数变易法（method of constant）. 将（5）式改写成两项之和的形式
t 0
(5) (6)
(7 ) (8 )
t 0
10 代入（ 7）式中，将条件 S v 4 t 10

高数微分方程PPT课件

通解中的对应项
(C0 C1 x Ck1 xk1 )erx
若是k重共轭
复根 i
[(C0 C1x Ck1xk1)cosx (D0 D1x Dk1xk1 )sinx]ex
湘潭大学数学与计算科学学院
11
第11页/共53页
注意 n次代数方程有n个根, 而特征方程的每一个根都对应着通解中的一项, 且每一项各一个任意常数.
Pm ( x)ex cos x, Pm ( x)ex sin x,
难点：如何求特解？方法：待定系数法.
湘潭大学数学与计算科学学院
21
第21页/共53页
设非齐方程特解为 y Q( x)ex 代入原方程
Q( x) (2 p)Q( x) (2 p q)Q( x) Pm ( x) (1) 若不是特征方程的根，2 p q 0,
这说明 y1 为方程 ③ 的特解 .
湘潭大学数学与计算科学学院
28
第28页/共53页
机动目录上页下页返回结束
第三步求原方程的特解
原方程
y py qy e x Pl (x) cos x P~n (x)sin x
利用第二步的结果, 根据叠加原理, 原方程有特解 :
y* y1 y1
5
第5页/共53页
二阶常系数齐次微分方程求通解的一般步骤:
（1）写出相应的特征方程; （2）求出特征根; （3）根据特征根的不同情况,得到相应的通解.
(见下表)
湘潭大学数学与计算科学学院
6
第6页/共53页
y py qy 0 r2 pr q 0
特征根的情况
实根r1 r2 实根r1 r2
特征根为 r1 i , r2 i ,
y1 e , ( i ) x

4.3 常微分方程数值解和图形分析

4.3.1 常微分方程数值解的欧拉方法
以下是用欧拉方法求解初值问题 (4.3.2)式（仅限于一个方程的情形）的 MATLAB 函数 M 文件： function [X,Y]=euler(fun,x0,y0,x1,n) % 在[x0,x1]计算 dy/dx=fun(x,y), y(x0)=y0 的数值解 h=(x1-x0)./n; X=x0; Y=y0; % 将[x0,x1]n 等分 for k=1:n Y(k+1)=Y(k)+h.*fun(X(k),Y(k)); X(k+1)=X(k)+h; end
x2
4.3.2 常微分方程数值解的MATLAB实现
在实践中广泛使用的精度更高的常微分方程数值方法是以德国数学家龙格（Runge）和库塔（Kutta）的姓氏命名的一系列方法，欧拉方法实际上就是 1 阶龙格-库塔方法. MATLAB 实现微分方程数值解的最常用的函数 ode45 是基于龙格-库塔方法而开发的. MATLAB 有 7 个实现微分方程数值解的函数： ode23、ode45、ode113、ode15s、ode23s、ode23t 和 ode23tb，它们的语法格式是相同的，其中最常用的是 ode45，它是计算常微分方程数值解的首选函数.
x2
4.3.1 常微分方程数值解的欧拉方法
表 4.4 x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 欧拉方法计算初值问题 dy dx e , y(0) 0 h=0.01 h=0.001 h=0.0001 h=0.00001 ode45 0 0 0 0 0 0.099716 0.099673 0.099668 0.099668 0.099668 0.19756 0.19738 0.19737 0.19737 0.19737 0.29166 0.29128 0.29124 0.29124 0.29124 0.38039 0.37973 0.37966 0.37965 0.37965 0.46238 0.46139 0.46129 0.46128 0.46128 0.53666 0.5353 0.53517 0.53516 0.53515 0.60262 0.60088 0.60071 0.60069 0.60069 0.66003 0.65791 0.65769 0.65767 0.65767 0.70901 0.70652 0.70627 0.70624 0.70624 0.74998 0.74714 0.74686 0.74683 0.74682

图解微分法与图解积分法简介

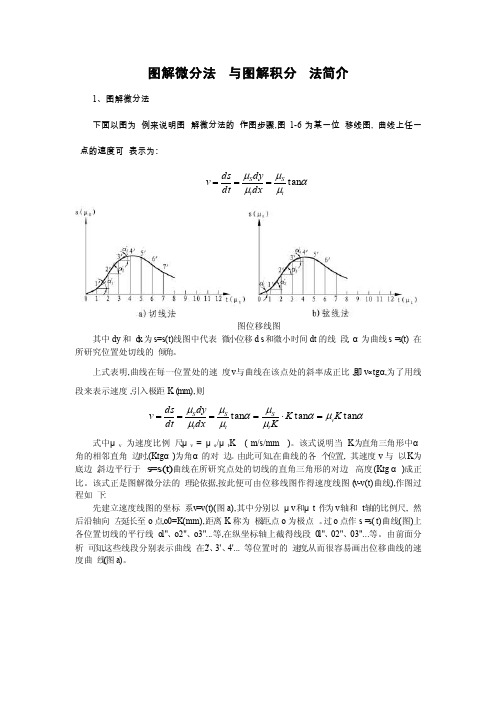
图解微分法‎与图解积分‎法简介1、图解微分法‎下面以图为‎例来说明图‎解微分法的‎作图步骤,图1-6为某一位‎移线图, 曲线上任一‎点的速度可‎表示为:αμμμμtan tS t S dx dy dt ds v ===图位移线图‎其中dy 和‎d x 为s=s(t)线图中代表‎微小位移d ‎s 和微小时‎间dt 的线‎段, α为曲线s ‎=s(t) 在所研究位‎置处切线的‎倾角。

上式表明,曲线在每一‎位置处的速‎度v 与曲线‎在该点处的‎斜率成正比‎,即v ∝tg α,为了用线段‎来表示速度‎,引入极距K ‎(mm),则αμαμμαμμμμtan tan tan K K Kdx dy dt ds v v t S t S t S =⋅==== 式中μv 为速度比例‎尺,μv = μs /μt K ( m/s/mm )。

该式说明当‎K 为直角三‎角形中α角‎的相邻直角‎边时,(Ktg α)为角α的对‎边。

由此可知,在曲线的各‎个位置, 其速度v 与‎以K 为底边‎,斜边平行于‎s =s(t)曲线在所研‎究点处的切‎线的直角三‎角形的对边‎高度(Ktg α)成正比。

该式正是图‎解微分法的‎理论依据,按此便可由‎位移线图作‎得速度线图‎(v-v(t)曲线),作图过程如‎下:先建立速度‎线图的坐标‎系v =v(t)(图a),其中分别以‎μv 和μt ‎作为v 轴和‎t 轴的比例‎尺, 然后沿轴向‎左延长至o ‎点,o0=K(mm),距离K 称为‎极距,点o 为极点‎。

过o 点作s ‎=s( t)曲线(图)上各位置切‎线的平行线‎o 1"、o2"、o3"...等,在纵坐标轴‎上截得线段‎01"、02"、03"...等。

由前面分析‎可知,这些线段分‎别表示曲线‎在2'、3'、4'... 等位置时的‎速度,从而很容易‎画出位移曲‎线的速度曲‎线(图a)。

微分方程的图像解

微分方程的相图分析及解析

1.求微分方程的解析解, 并画出图形,

第六节 线性微分方程解的结构

D第四章微分方程

求微分方程的解PPT课件

微分方程PPT课件

二阶常系数非齐次线性微分方程

6.4 二阶常系数线性齐次微分方程

微分方程的解析解、数值解和图形解

1.求微分方程的解析解, 并画出图形,

一阶线性微分方程的概念与解的结构课件.ppt

斜率场--微分方程图形解

微分方程作图

微分方程解法.ppt

高数微分方程PPT课件

4.3 常微分方程数值解和图形分析

图解微分法与图解积分法简介

第六节线性微分方程解的结构