有趣的七桥问题

七桥问题SevenBridgesProblem

著名古典数学问题之一.在哥尼斯堡地一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图).问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点?欧勒于年研究并解决了此问题，他把问题归结为如下右图地“一笔画”问题，证明上述走法是不可能地.

有关图论研究地热点问题.世纪初普鲁士地柯尼斯堡，普雷格尔河流经此镇，奈发夫岛位于河中，共有座桥横跨河上，把全镇连接起来.当地居民热衷于一个难题：是否存在一条路线，可不重复地走遍七座桥.这就是柯尼斯堡七桥问题..欧拉用点表示岛和陆地，两点之间地连线表示连接它们地桥，将河流、小岛和桥简化为一个网络，把七桥问题化成判断连通网络能否一笔画地问题.他不仅解决了此问题，且给出了连通网络可一笔画地充要条件是它们是连通地，且奇顶点(通过此点弧地条数是奇数)地个数为或.资料个人收集整理，勿做商业用途当在年访问, ( )时，他发现当地地市民正从事一项非常有趣地消遣活动.城中有一条名叫地河流横经其中，这项有趣地消遣活动是在星期六作一次走过所有七座桥地散步，每座桥只能经过一次而且起点与终点必须是同一地点.资料个人收集整理，勿做商业用途

把每一块陆地考虑成一个点，连接两块陆地地桥以线表示.

后来推论出此种走法是不可能地.他地论点是这样地，除了起点以外，每一次当一个人由一座桥进入一块陆地（或点）时，他（或她）同时也由另一座桥离开此点.所以每行经一点时，计算两座桥（或线），从起点离开地线与最后回到始点地线亦计算两座桥，因此每一个陆地与其他陆地连接地桥数必为偶数.资料个人收集整理，勿做商业用途

趣味数学七桥问题

单击添加大标题
Your text
18世纪，在（现俄罗斯）哥尼斯堡城风景秀美的普莱格尔河上有7座别致的拱桥，将河中的两个岛和河岸连结（如左图）。城中的居民经常沿河过桥散步。城中有位青年很聪明，爱思考，有一天，这位青年给大家提出了这样一个问题：能否一次走遍7座桥，而每座桥只许通过一次，最后仍回到起始地点。这就是数学史上著名的七桥问题。
小热身七桥问题
单击添加大标题
Your text
1836年，瑞士著名的数学家——欧拉，欧拉发现了这个问题的本质：这个问题与岛的形状和大小无关，与河岸的形状长短无关、与桥的形状、长短无关，重要的是桥、河岸、岛之间的位置关系。把两岸和小岛缩成一个点，桥当作连接这些点的一条线。
小热身七桥问题
② 有偶数条边相连的点叫偶点。如：
小热身七桥问题一笔画
欧拉定理：
①凡是由偶点组成的连通图，一定可以一笔画成。画时可以任一偶点为起点，最后一定能以这个点为终点画完此图。 ②只有两个奇点的连通图，一定可以一笔画完。画时必须以一个奇点为起点，另一个奇点为终点。 ③其他情况的图，都不能一笔画出。
问题转化为：笔尖不离开纸面，一笔画出给定的图形，不允许重复任何一条线，这样的图形简称为“一笔画”
小热身七桥问题
能一笔画的图形必须是连通图。从图的一点出发，笔不离纸，经过每条边恰好一次，不能重复。但是，并不是所有的连通图都可以一笔画出。它是由图的奇、偶点的数目来决定的。 ① 有奇数条边相连的点叫奇点。如：

哥尼斯堡七桥问题

1736年，在经过一年的研究之后，29岁的欧拉提交了《哥尼斯堡七桥》的论文，圆满解决了这一问题。
同时开创了数学新分支---图论以及拓扑学。
欧拉解题方法
在论文中，欧拉将七桥问题抽象出来，把每一块陆地考虑成一个点，连接两块陆地的桥以线表示。并由此得到了如图一样的几何图形。若我们分别用A、B、C、D四个点表示为哥尼斯堡的四个区域。这样著名的“七桥问题”便转化为是否能够用一笔不重复的画出过此七条线的问题了。
有一天，他被这个问题弄得头昏脑涨了，便到野外去散步。新鲜的空气，清凉的风，使他顿时感到轻松舒适，但他头脑里仍然只有那个尚未找到的圈儿。
一片片肥大的玉米叶子，在他眼里变成了“绿色的纸条儿”，他不由自主地蹲下去，摆弄着、观察着。叶子弯曲着耸拉下来，有许多扭成半圆形的，他随便撕下一片，顺着叶子自然扭的方向对接成一个圆圈儿，他惊喜地发现，这“绿色的圆圈儿”就是他梦寐以求的那种圆圈。
七桥问题的历史贡献
欧拉的这个考虑非常重要，也非常巧妙，它正表明了数学家处理实际问题的独特之处——把一个实际问题抽象成合适的“数学模型”。这种研究方法就是“数学模型方法”。
这并不需要运用多么深奥的理论，但想到这一点，却是解决难题的关键。
1736年，欧拉在交给彼得堡科学院的《哥尼斯堡7座桥》的论文报告中，阐述了他中，阐述了他的解题方法。
网络的“连通性”

哥尼斯堡七桥问题

欧拉在数学、物理、天文、建筑以至音乐、哲学方面都取得了辉煌的成就。在数学的各个领域，常常见到以欧来命名的公式、定理、和重要常数。课本上常见的如π、i、e、sin、cos、 tg、△x、Σ、f(x)等，都是他创立并推广的。欧拉还首先完成了月球绕地球运动的精确理论，创立了分析力学、刚体力学等力学学科，深化了望远镜、显微镜的设计计算理论。
哈里发的题目是这样的：请用线把下图中写有相同数字的小圆圈连接起来，但所连的线不许相交，也不许与图中的线相交。
上述问题的解决，似乎不费吹灰之力。但实际上求婚者们全都乘兴而来，败兴而去！
据说后来哈里发终于醒悟，发现自己所提的问题是不可能实现的，因而后来又改换了题目。也有的说，哈里发固执已见，美丽的公主因此终生未嫁。事情究竟如何，现在
欧拉注意到每个点都是若干条线的端点，他把图形上的点分为两类：奇点和偶点。要想不重复地一笔画出某个图形，除去起始点和终止点外，其余点，如果画进去一条线，就一定要画出一条线，从而必须是偶点。
一笔画原理：
一个图如果可以一笔画成，那么这个图中奇数顶点的个数不是0就是2。反之亦然。
当图形中有两个顶点时，以其中一个为起始点，另一个为终止点，就能一笔画；当图形中没有奇点时，从任何一个起始点都可以完成一笔画。
现今俄罗斯的加里宁格勒，旧称哥尼斯堡，是一座历史名城。在十八、十九世纪，那里是东普鲁士的首府，曾经诞生和培育过许多伟大的人物。著名的哲学家，古典唯心主义的创始人康德，终生没有离开过哥尼斯堡一步!二十世纪最伟大的数学家之一，德国的希尔伯特也出生于此地。

七桥问题等

“七大千年数学难题”之一的庞加莱猜想，是本次国际数学家大会讨论的焦点。其实，除了“七大千年数学难题”之外，数学史上还有一些有趣的数学难题给人留下深刻印象。

哥德巴赫猜想

提出者：德国教师哥德巴赫；提出时间：1742年；内容表述：任何一个大于2的偶数都可以表示为

两个素数之和；研究进展：尚未完全破解。

费马大定理

提出者：法国数学家费马；

提出时间：1637年；

内容表述：x的n次方加y的n次方等于z的n次方，在n是大于2的自然数时没有正整数解；

研究进展：由英国数学家安德鲁·怀尔斯和他的学生理查·泰勒于1995年成功证明。

四色猜想

提出者：英国学生格思里；

提出时间：1852年；

内容表述：每幅地图都可以用4种颜色着色，使得有共同边界的国家着上不同的颜色；

研究进展：于1976年被计算机验证。

女生散步问题

提出者：英国数学家柯克曼；

提出时间：1850年；

内容表述：某学生宿舍共有15位女生，每天3人一组进行散步，问怎样安排，才能使每位女生有机会与其他每一位女生在同一组中散步，并恰好每周一次；

研究进展：已获证明。

七桥问题

提出者：起源于普鲁士柯尼斯堡镇（今俄罗斯加里宁格勒）；

提出时间：18世纪初；

内容表述：一条河的两条支流绕过一个岛，有7座桥横跨这两条支流，问一名散步者能否走过每一座桥，而且每座桥只能走一次，就让这名散步者回到原地。

故事背景

七桥问题

七桥问题Seven Bridges Problem 18世纪著名古典数学问题之一。在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点？欧拉于1736年研究并解决了此问题，他把问题归结为如下右图的“一笔画”问题，证明上述走法是不可能的。有关图论研究的热点问题。18世纪初普鲁士的柯尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来（如左图上）。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点后来大数学家欧拉把它转化成一个几何问题（如左图下）——一笔画问题。他不仅解决了此问题，且给出了连通图可以一笔画的充要条件是它们是连通的，且奇顶点(通过此点弧的条数是奇数)的个数为0或2.

有趣的七桥问题课件

详细描述
在七桥问题中，欧拉发现了一个重要的定理：对于任何连通图，都存在一个欧拉回路。这个定理对于解决七桥问题至关重要，因为它证明了从哥尼斯堡的一个地方开始，可以遍历所有的桥并回到起点。
03
七桥问题的解决方案
欧拉的贡献
欧拉是第一个深入研究七桥问题的人，他通过数学模型和逻辑推理，得出了著名的欧拉定理，为解决七桥问题奠定了基础。
一个重要分支。
七桥问题的解决方案也成为了计算机科学中算法设计和数据结构
研究的重要基础。
04
七桥问题的扩展和实际应用
其他有趣的几何问题
欧拉路径和欧拉回路
几何图形的匹配问题
与七桥问题类似的几何问题，涉及到在一个图形中找出路径，使得路径起点和终点重合，且每条边只过一次。
在几何图形中寻找一种模式或结构，使得图形中的某些部分能够匹配或对齐。
几何图形的染色问题
给定一个几何图形，使用最少的颜色进行染色，使得相邻区域颜色不同。这是一个经典的NP完全问题。
在现实生活中的应用
城市规划
七桥问题在城市规划中有着广泛的应用，例如在道路规划和交通流优化方面。通过模拟和分析交通流和路径选择，可以优化城市
交通系统。
物流和运输
七桥问题在物流和运输领域也有应用，例如在最优路径选择、车辆调度和配送路线规划等方面。
对未来科技发展的启示

七桥问题小短文

摘要：

1.七桥问题的起源和背景

2.七桥问题的解决方法

3.七桥问题的意义和影响

正文：

七桥问题起源于18 世纪初的波兰，它是一个有趣的图论问题。这个问题描述了波兰一个城市的维斯瓦河上的七座桥，市民们想要知道是否存在一条路径，使得他们可以从某座桥走到另一座桥，同时不重复经过任何一座桥。这个问题看似简单，实际上却引发了图论这一数学分支的诞生。

七桥问题的解决方法是通过图论中的“欧拉回路”概念。欧拉回路是指在一个图中，经过每条边一次且回到起点的一条路径。通过分析七桥问题，数学家欧拉发现，只有当图中所有顶点的度数都是偶数时，才存在欧拉回路。在七桥问题中，由于每个顶点的度数都是奇数，因此不存在欧拉回路，市民们无法通过七座桥走一遍回到起点。

七桥问题的意义和影响深远。它不仅使得图论这一数学分支得到了发展，还对现实生活中的许多问题产生了影响。例如，在计算机网络、交通运输、电路设计等领域，图论的应用都发挥了重要作用。同时，七桥问题也成为了图论发展史上的一个经典案例，启发了无数数学家和工程师去研究更多有趣的图论问题。

总之，七桥问题作为一个历史悠久的数学问题，它的解决方法和意义对图

论的发展产生了深远影响。

七桥问题在生活中的应用应用

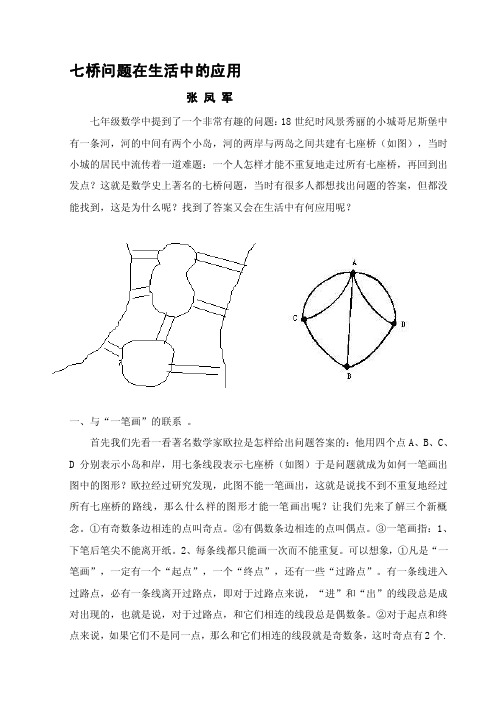
七桥问题在生活中的应用

张凤军

七年级数学中提到了一个非常有趣的问题：18世纪时风景秀丽的小城哥尼斯堡中有一条河，河的中间有两个小岛，河的两岸与两岛之间共建有七座桥（如图），当时小城的居民中流传着一道难题：一个人怎样才能不重复地走过所有七座桥，再回到出发点？这就是数学史上著名的七桥问题，当时有很多人都想找出问题的答案，但都没能找到，这是为什么呢？找到了答案又会在生活中有何应用呢？

一、与“一笔画”的联系。

首先我们先看一看著名数学家欧拉是怎样给出问题答案的：他用四个点A、B、C、D分别表示小岛和岸，用七条线段表示七座桥（如图）于是问题就成为如何一笔画出图中的图形？欧拉经过研究发现，此图不能一笔画出，这就是说找不到不重复地经过所有七座桥的路线，那么什么样的图形才能一笔画出呢？让我们先来了解三个新概念。①有奇数条边相连的点叫奇点。②有偶数条边相连的点叫偶点。③一笔画指：1、下笔后笔尖不能离开纸。2、每条线都只能画一次而不能重复。可以想象，①凡是“一笔画”，一定有一个“起点”，一个“终点”，还有一些“过路点”。有一条线进入过路点，必有一条线离开过路点，即对于过路点来说，“进”和“出”的线段总是成对出现的，也就是说，对于过路点，和它们相连的线段总是偶数条。②对于起点和终点来说，如果它们不是同一点，那么和它们相连的线段就是奇数条，这时奇点有2个.

如果起点和终点是同一点，那么就没有奇点，即奇点个数为0.简单说：能够一笔画的图形奇点的个数只能是0或2，而七桥问题中不符合一笔画的条件，也就无法不重复的经过所有七座桥，通过上面的分析，我们今后能很快看出哪些图形可以一笔画，那些不能。

五年级下册数学教案-8.5 有趣的七桥问题丨苏教版

五年级下册数学教案-8.5 有趣的七桥问题丨苏教版教学内容

本课教学内容为苏教版五年级下册数学第8.5节“有趣的七桥问题”。本节课将引导学生通过探索历史上著名的七桥问题，理解图论的基本概念，并尝试解决简单的图论问题。

教学目标

1. 让学生理解并掌握七桥问题的背景及数学意义。

2. 培养学生通过观察、分析解决实际问题的能力。

3. 引导学生运用图论思想解决实际问题，培养学生的逻辑思维和创新思维。

教学难点

1. 图论的基本概念对于小学生来说较为抽象，如何让学生理解并运用图论思想解决问题是一大挑战。

2. 引导学生从实际问题中抽象出数学模型，并运用所学知识解决问题。

教具学具准备

1. 教师准备：多媒体教学设备，用于展示七桥问题的背景及相关知识。

2. 学生准备：纸、笔等学习用品。

教学过程

1. 导入

利用多媒体设备展示哥尼斯堡七桥问题的背景，引发学生的兴趣和好奇心。

2. 探究

- 让学生分组讨论，尝试找出所有可能的路径。

- 引导学生观察并发现规律，从而理解图论的基本概念。

3. 实践

- 让学生尝试解决类似的图论问题，如“五桥问题”、“六桥问题”等。

- 引导学生从实际问题中抽象出数学模型，并运用所学知识解决问题。

4. 总结

- 让学生总结本节课所学内容，并分享自己的学习心得。

- 教师对学生的表现进行评价和总结。

板书设计

1. 有趣的七桥问题

2. 副图论的基本概念及应用

3. 正文：

- 七桥问题的背景及数学意义

- 图论的基本概念

- 解决图论问题的方法

作业设计

1. 完成课后练习题，巩固所学知识。

2. 尝试解决一个新的图论问题，并记录解决过程。

奥林匹克数学七桥问题

B
B为奇点， A和C为偶点。
与奇数条线相连的点叫“奇点”; 与偶数条线相连的点叫“偶点”。
在连通图中，奇点的个数是0或2，这幅图可以一笔画，否则不能一笔画。
①奇点的个数是0时，可以任一偶点为起点，最后还回到这一点。 ②奇点的个数是2时，必须以一个奇点为起点，另一个奇点为终点。
1.下图是国际奥委会的会标，你能一笔把它
wenku.baidu.com
直到1836年，瑞士著名的数学家欧拉才证明了这个问题的不可能性。欧拉解决这个问题的方法非常巧妙.他认为：人们关心的只是一次不重复地走遍这七座桥，而并不关心桥的长短和岛的大小，因此，岛和岸都可以看作一个点，而桥则可以看成是连接这些点的一条线.这样，一个实际问题就转化为一个几何图形（如下图）能否一笔画出的问题了. C A D
画出来吗？
2.下图是某展览厅的平面图，它由五个展室组成，任
两展室之间都有门相通，整个展览厅还有一个进口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出？
B
C
D
E A
F
谢谢观赏
奥林匹克数学
一笔画你能笔尖不离纸,一笔画出下面的每个图形吗? 试试看.（不走重复路线）
故事发生在18世纪的哥尼斯堡城.流经那里的一条河中有两个小岛，还有七座桥把这两个小岛与河岸联系起来那里风景优美，游人众多。

有趣的七桥问题课件

运用编程技术
现代编程技术也可以用于解决七桥问题。例如，使用遗传算法、模拟退火等优化算法，可以在较短的时间内找到最优解。
证明
01
02
03
数学证明
程序证明
实验验证
七桥问题的解的存在性和唯一性可以通过数学证明得到证明。例如，可以利用欧拉定理证明七桥问题只有一种解法。
通过编写程序来求解七桥问题，可以直观地看到程序输出的结果，从而证明了答案的正确性。
通过实验验证七桥问题的答案是否正确，是最直接的方法之一。可以通过模拟走桥的过程或者使用真实的模型来进行验证。
04
七桥问题的扩展和引申
扩展
复杂网络
可以将七桥问题扩展到更为复杂的网络问题，例如，如何从某个节点出发，经过每条边恰好一次
，并返回到起始节点。
图形理论
七桥问题可以作为图形理论中的一个经典问题，它涉及到图的连通性、欧拉路径和哈密顿回路等概念。
问题是要找到一条路径，这条路径可以遍历所有的桥和岛屿一次并回到起点。
然而，数学家们经过论证发现，这样的路径是不存在的。
03
七桥问题的解法与证明
解法
01
使用穷举法
七桥问题的一个经典解法是使用穷举法，即列举出所有可能的走Biblioteka Baidu，然
后逐一判断是否能够走完所有的桥且不重复。
02 03

校本教材配套课件—有趣的七桥问题(托起美的数学)

怎样散步才能一次不重复的走过每座桥，并且最后回到出发点呢？
哥尼斯堡七桥问题
• 故事发生在18 世纪欧洲东普鲁士（现为俄罗斯的加里宁格
勒）有个名叫哥尼斯堡的城市近郊。这里的普雷盖尔河穿城而过，河中有两个岛，两岸与两岛之间架有七座桥（如图） • • • • 当时城中居民热烈地讨论着这样一个问题：一个散步者怎样走才能不重复地走遍所有的七座桥而回到原出发点？
Baidu Nhomakorabea
这个问题初看起来似乎不太难，所以很多人都想试一试，寻找这种走法，但谁出找不出问题的答案，均以失败
告终。
当时大数学家殴拉从众多人的失败中想到，这样的走
法可能就根本不存在，随后他用数学的方法证实了自己的
猜想是正确的，并于1736 年发表了图论（组合数学的一个
分支）的第一篇论文“哥尼斯堡的七座桥”。
C
A
B
D
C
A
B
D

有趣的数学——七桥问题与网状图

拓扑学起源于对1736年的一个著名问题的解答——哥尼斯堡（KSnigsberg)的七桥问题。

哥尼斯堡®是一座城市的名字，它位于普雷格尔河Preger River)上，共有七座桥梁，小城有两座小岛，被河流包围在中间，河岸上有多处桥梁通向两座小岛，而两岛之间由一座桥梁连接。小城有个叫做“周日环城游”的传统，人们在环游时候都想每座桥梁只经过一次。这个问题一直没有得到解答，后来它引起瑞士数学家列昂哈德欧拉（Leonhard Euler，1707—1783)的关注。那时，欧拉在圣彼得堡效忠于俄国凯瑟琳大帝。在解答这个问题的过程中，欧拉发明了一个数学分支，那就是拓扑学。他利用拓扑学知识——我们今天通常称做网状图——解答了哥尼斯堡的七桥问题。借助网状图，他证明了这个每个桥梁只想穿越一次的做法是不可行的，做不到的。

这个问题及欧拉的解答，使得世界上兴起了对拓扑学的研究。拓扑是一个相对较新的学科领域，19世纪的数学家将拓扑与非欧几里得几何一并进行了深入探究，关于拓扑的第一篇论文写于1847年。

网状图就是解答问题的基本图形。下图中是关于哥尼斯堡（K6nigsberg)的七桥问题。

网状图由顶点和弧线构成，要求一次穿越弧线部分就能走完全程，而顶点可以重复经过，如上图中的顶点A、B、C、D。注意每个顶点连接着多少条弧线——A有3条，B有5条，C有3条，D有3条。由于它们都是奇数，所以这些顶点也叫做奇数顶点，那么偶数顶点就有偶数条弧线相连。欧拉（Leonhard Euler)发现了网状图的很多性质，要想继续走下去，网状图得有多少个奇数顶点和偶数顶点。具体地，欧拉注意到一定要在奇数顶点开始或结束行程。随着这个想法，他推理出既然网状图只有一个开始和一个结束，那么它也只可能有两个奇数顶点。因此，哥尼斯堡的七桥问题有四个奇数顶点，那这个问题就是不可解答的。

五年级下册数学说课稿-8.5 有趣的七桥问题丨苏教版

一、背景

七桥问题是欧拉在1736年首次提出的。当时欧拉在普鲁士柏林的皇家学院任职。这个问题是这样的：柯尼斯堡市（今俄罗斯加里宁格勒）有七座桥将两岸分割成两半，如图所示。一个人想要从某一个地方出发，走过每座桥恰好一次，最后回到出发点。问是否可能？

七桥问题

通过这个问题，欧拉发现了图论的基本思想，并开创了图论的研究。现在，图论是运筹学和计算机科学中的一个重要分支。

二、教学目标

1.了解七桥问题的提出和求解过程，激发学生的数学兴趣；

2.培养学生的分析问题的能力、解决问题的思路；

3.引导学生探究图与图论的基础知识，并掌握相关概念。

三、教学过程

1. 导入

老师可以用一个小游戏或一个趣味启发式例子引入七桥问题。比如：《三个水桶如何准确地分出4、5、6升水》等问题。引入七桥问题后，可以让学生猜想解题思路。

2. 讲解

接着，老师可以结合ppt或白板，介绍欧拉发现七桥问题时，是如何用图论方法解决问题的。引导学生明确图的定义，图的相关概念和术语。

3. 实践

接下来，老师可以让学生自己制作柯尼斯堡市的地图，用各种颜色的线连接桥和两岸，再尝试走一遍符合要求的路径。这样可以提高学生的动手实践能力，同时激发学生的学习兴趣。

4. 拓展

为了让学生更好地理解图的基础概念，老师可以将此问题扩展到随机图的情况。以一个具体的小例子展示随机图的生成方式和性质，再引出相关的基本概念和算法。

四、教学互动

1.学生在自己设计柯尼斯堡市地图时，可以相互交流，分享自己的解法和思路；

2.在引入图的相关概念时，老师可以和学生一起模拟简单的图、完全图、孤立点、连通图等，让学生理解并熟悉这些术语；

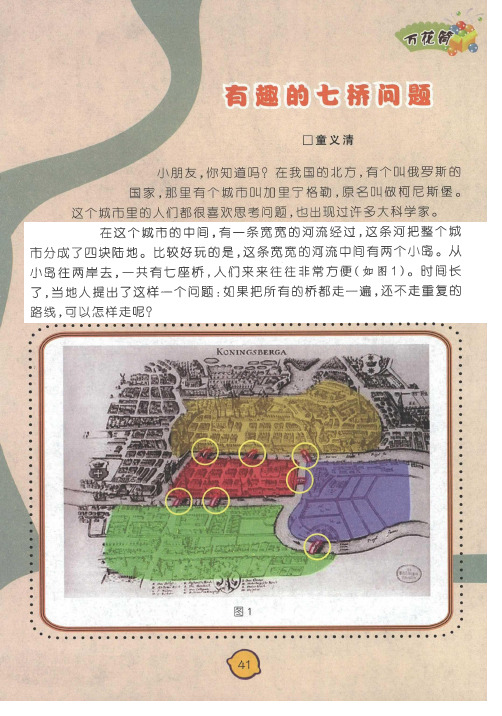
来，大数学家欧拉把这个七桥景物画成了简单图形，用
最简单的点、线来表示这个问题于是七桥问题就被
，
，
转化成友笔题啦小朋
画“ 一
画 ”的问
如页图（
２）
！
大数学家欧拉根据七桥问题还总结出任意 “ 河桥图 ” 的解决方
亩趣的七挢阀题
□ 童义清
小朋友你知道吗？，
在我国的北方有个叫俄罗斯的，
国家那里有个城市叫加里宁格勒原名叫做柯尼斯堡。
，
，
这个城市里的人们都很喜欢思考问题，也出现过许多大科学家。
法有兴趣的小朋友可以在练习本上接着研究一下：如果是 “ 六桥问，
题 ”“ 九桥问题 ” ，可不可以不重复地走一遍所有的桥呢？
（
作者
单位：
安徽省合肥市
屯溪路小学
）
了当地人提出了这样一个问题：如果把所有的桥都走一遍，还不走重复的，

哥尼斯堡七桥问题

当中取圈
将6个一样的铁圈用绳子串着，绳子的两端如下图那样开着。你能把当中的两个铁圈取出来，却又不让两端的铁圈脱离绳子吗？
把绳的两头扣起来，将其一端上的两只铁圈通过绳结移到另一端去，然后再将绳子解开，现在取走中间的两只铁圈便很容易了。
博物馆中的拓扑游戏道具
变。例如点变化后仍然是点；线变化后依旧为线；相交的图形绝不因橡皮的拉伸和弯曲而变得不相交!
拓扑学正是研究诸如此类，使图形在橡皮膜上保持不变性质的几何学。
拓扑学是在19世纪末兴起并在20世纪蓬勃发展的数学分支，与近世代数、近代分析共同成为数学的三大支柱。
拓扑学已在物理、化学、生物一些工程技术中得到越来越广泛的应用。拓扑学主要研究几何图形在一对一的双方连续变换下不同的性质，这种性质称为“拓扑性质”。
——拓扑学
拓扑学研究的课题是极为有趣的。在拓扑学中人们感兴趣的只是图形的位置而不是它的大小。有人把拓扑学说成是橡皮膜上的几何学是很恰当的。因为橡皮膜上的图形，随着橡皮膜的拉动，其长度、曲直、面积等等都将发生变化。此时谈论 “有多长？”、“有多大？”之类的问题，是毫无意义的!
不过，在橡皮膜几何里也有一些图形的性质保持不
想不到轰动一时的哥尼斯堡七桥问题，竟然与孩子们的游戏，想用一笔画画出“串 "字和“田”字这类问题一样，而后者并不比前者更为简单!
事实上，中国民间很早就流传着这种一笔画的游戏，只是很可惜，长期以来，人们只把它作为一类有趣的游戏，没有对它引起重视，也没有数学家对它进行经验总结和研究，这不能不说是一种遗憾。