考点精讲16

合集下载

一建【公路】第16讲-附属设施3及路基工程质量通病及防治措施

2020年一级建造师《公路工程管理与实务》考点精讲（二）加筋土挡土墙工程施工技术1.特点及适用条件一般不宜使用。

特点：柔性结构物，能够适应地基轻微的变形；是一种很好的抗震结构物。

2.施工要求的。

面方向进行，严禁平行于拉筋方向碾压。

（41m范围内，应使用小型机具夯实或人工夯实，不得使用（2）类型：分为柱板式锚杆挡土墙和壁板式锚杆挡土墙两类，多用于岩石边坡防护。

（1）柱板式组成：挡土板、肋柱、锚杆；力的传递：土压力→挡土板→肋柱→锚杆（2）壁板式组成：墙面板（壁面板）、锚杆；力的传递：土压力→墙面板→锚杆2.施工要求工艺流程：施工准备→基坑开挖→基础浇（砌）筑→锚杆制作→钻孔→锚杆安放与注浆锚固→柱。

1.施工前、应采取卸载、反压、排水等措施使滑坡体保持基本稳定，严禁在滑坡急剧变形阶段进行抗滑施工。

2.12）开挖应分节进行。

分节不宜过长，每节宜为0.5～1.0m。

不得在土石层变化处和滑动面处分节。

（3）应开挖一节、支护一节。

（4）开挖应在上一节护壁混凝土终凝后进行，护壁混凝土模板支撑应在混凝土强度达到能保持护壁结构不变形后方可拆除。

3.桩身混凝土施工应符合下列规定：钢筋笼搭接接头不得设在土石分界和滑动面处。

钢筋保护层厚度应满足设计要求。

灌注应连续进行，不得中断。

4.桩板式抗滑挡土墙施工应符合下列规定：（1）挡土板应在桩身混凝土达到设计强度后安装。

挡土板安装时，应边安装并做好挡土板后排水设施。

（2）施工过程中应对地下水位、滑坡体位移和变形进行监测。

（五）挡土墙质量检验项目（1）浆砌挡土墙实测项目：砂浆强度（△）、平面位置、墙面坡度、断面尺寸（△）、顶面高程、表面平整度。

（2）干砌挡土墙实测项目：平面位置、墙面坡度、断面尺寸（△）、顶面高程、表面平整度。

（3）片石混凝土挡土墙实测项目：混凝土强度（△）、平面位置、墙面坡度、断面尺寸（△）、顶面高程、表面平整度。

装防护罩。

3.4.5.4〜6根）缆风索，每增高的地铺应牢固。

中考考点专题16翻译填空

目录
首页
上一页
下一页
末页
宇轩图书
考点解读考点知识精讲中考典例精析考点训练
7．It's impossible to do sth. 做某事是不可能的 It's_impossible_for Taiwan_to_break away from our motherland. 台湾从祖国分裂出去是不可能的。 8．It's one's duty to do sth. 做某事是某人的责任 It's_our_duty_to_protect the environment. 保护环境是我们的责任。 9．as soon as 一„„就„„ I'll tell you as soon_as_she comes. 她一来，我就告诉你。 10．as...as 和„„一样 English is_as_important as maths. 英语和数学一样重要。 11．either...or... 要么„„，要么„„ I left it either on the table or in the drawer. 我要么把它放桌子上了，要么放在抽屉里了。 12．neither...nor... 既不„„，也不„„ Mary can_neither sing_nor_dance. 玛丽既不会唱歌，也不会跳舞。
目录首页上一页下一页末页
宇轩图书
考点解读考点知识精讲中考典例精析考点训练
6．be late for 迟到 She_was_late_for_school yesterday. 她昨天上学迟到了。 7．be good /bad for...对……有益/害 Eating more fruit_is_good_for our health. 多吃水果对我们的健康有益。 8．keep...from.../prevent...from...(防止„„做„„) Forests help to_keep_the water from running away. 森林有助于防止水的流失。 9．be proud of 以有„„感到自豪 one of the best...最好的„„之一 We are_proud_of_Yao Ming who is one_of_the_best basketball players in the world. 我们以有世界上最优秀的篮球运动员之一——姚明，而感到自豪。 10．give up 放弃 Though he was so tired, he didn't give_up_the competition. 尽管他很累了，但他并没有放弃比赛。

高教版公共英语3级精讲班讲义16

公共英语 3 级精讲班第 16 讲讲义Dialogue我正在找旅行咨询中心。

locate1) 找出，指出(某人、某事物)的准确位置或地点locate an electrical faultlocate a town on a mapI’m trying to locate Mr. Smith.2) be located 将(某物)设置在某处A new factory is to be located on this site.The information office is located in the city center.当我听从别人方向时，总是迷路。

我一进地铁就没有方向感。

lose the sense of direction我正朝着那个方向走，我告诉你它在什么地方。

I’ll show you where it is.宾语从句用陈述句语序。

没关系。

它到处充满生机，在晚上有很多地方可以参观有很多方式可以娱乐。

看起来我在即将到来的日子里可以在这儿充分享受了。

the coming day 即将到来的日子我到会议去注册并且准备我的展览摊位。

一切都顺利。

我们摆放好我们的宣传书册等着正式开幕。

setout 安排或摆放We’ll need to set out chairs for the meeting.She set out the pieces on the chess-board.记者莎莉·布朗正在和负责交通规划的政府官员彼得· 史密斯关于他正在计划的交通政策进行交谈。

1) in chargeof 处于控制或支配某人、某物的地位Who’s in charge here?He was left in charge of the shop while the manager was away.2) workon 忙于做某事He is working on a new novel.到 1700 年，英国已经有了一个运河和湖泊交通的一个完整的系统。

初中毕业道德与法治总复习精讲第一篇考点梳理板块二法律第十六讲崇尚法治精神(八下第四单元)

关键词：平等 ※1.平等的内涵。(P101) (1)同等情况同等对待，比如男女同工同酬、一次选举一人一票等。 (2)不同情况差别对待，比如老人、儿童、孕妇、残疾人在乘坐公共交通工具时应获得优先权和得到特殊关照。[2020B.14(1)]
※2.法律面前人人平等。(P101～103)[2020A.8D，B.14(1)] (1)我国宪法规定：中华人民共和国公民在法律面前一律平等。 (2)重要性：是社会文明进步的标志，也是社会主义法治的基本原则之一。
(2)期盼正义、实现正义、维护正义，是我们的共同心声。 (3)公平正义是人类追求的永恒目标，是法治社会的核心价值。 (4)实现公平正义，是国家、社会和全体公民的共同责任。
※6.我们应怎样守护正义？(P117～118) (1)个人守护正义。守护正义需要勇气和智慧，面对非正义行为，一方面要敢于斗争，相信正义必定战胜邪恶；另一方面要讲究策略，寻找有效的方法，做到见义“智”为。(2019A.8B) (2)司法维护正义。司法是捍卫社会公平正义的最后一道防线。司法机关必须坚持以事实为根据，以法律为准绳，严格遵循诉讼程序，平等对待当事人，确保司法过程和结果合法、公正。
4.维护和实现社会正义有什么意义？(P113) (1)有利于恰当地调整和处理人与人之间的关系，充分发挥人们的主动性和创造性。 (2)有利于营造和谐、稳定、安宁的社会环境，为社会发展注入不竭的动力。
5.我们为什么要做有正义感的人？(守护正义的重要性)(P116～ 119)
(1)追求正义是社会生活的一个重要主题。正义感是公民的21B.14(2)； 2019A.14(1)]
(1)自由不是为所欲为，是有限制的、相对的。必要的限制是对自由的保护。无限制的自由只会走向自由的反面，导致混乱与伤害。(2)无论现实世界还是网络空间，自由都是法律之内的自由。

2023学年沪教版上海八年级数学上学期同步考点精讲精练16-3-2二次根式的加减及混合运算带讲解

16.3.2二次根式的加减及混合运算考点一、二次根式的加减1.二次根式的加减实质就是合并同类二次根式，即先把各个二次根式化成最简二次根式，再把其中的同类二次根式进行合并.对于没有合并的二次根式，仍要写到结果中.要点：（1）在进行二次根式的加减运算时，整式加减运算中的交换律、结合律及去括号、添括号法则仍然适用. （2）二次根式加减运算的步骤：1)将每个二次根式都化简成为最简二次根式；2)判断哪些二次根式是同类二次根式，把同类的二次根式结合为一组；3)合并同类二次根式.考点二、二次根式的混合运算二次根式的混合运算是对二次根式的乘除及加减运算法则的综合运用.要点：(1)二次根式的混合运算顺序与实数中的运算顺序一样，先乘方，后乘除，最后算加减，有括号要先算括号里面的；(2)在实数运算和整式运算中的运算律和乘法公式在二次根式的运算中仍然适用；(3)二次根式混合运算的结果要写成最简形式.题型1：二次根式的加减法1-数字型182）A．5 B10C．32D．42C【分析】根据二次根式的运算法则即可求解．82822232==故选C．【点睛】此题主要考查二次根式的运算，解题的关键是熟知其运算法则．2273______．23先进行化简，然后作差求解即可．解：原式333==【点睛】本题考查了二次根式的化简与减法运算．解题的关键在于正确的计算．3______．首先化简二次根式，进而合并求出即可．解：原式==故答案为：【点睛】此题主要考查了二次根式的加减运算，正确化简二次根式是解题关键．题型2：二次根式的加减法2-字母型4．计算：（1________；（2）=_________．根据合并同类二次根式的法则计算即可；解：（1=，（2）-=故答案为：【点睛】本题考查了二次根式的加减法，熟练掌握合并同类二次根式的法则是解题的关键5．计算；（1(=________；（2）5-________．-【分析】（1）先化简二次根式，然后根据合并同类二次根式的法则计算即可；（2）讨论x和a同时大于0和同时小于0，利用二次根式的性质化简即可．解：（1(=（2）ax≥∴0当0x >，0a ≥时55x ---当0x <，0a ≤时55x -+=故答案为：-【点睛】本题考查了二次根式的加减法，熟练掌握合并同类二次根式的法则是解题的关键．6．计算二次根式________．合并同类二次根式得：故答案：7．1642 ） A ．正数B ．非正数C ．非负数D ．负数B【分析】先化为最简二次根式，然后合并同类项，再根据二次根式有意义确定0x ≥0≥，最后确定值的符号即可．解:1642=1642x x ⋅24==-∴0x ≥0≥，∴0-≤，故选：B ．【点睛】本题考查了二次根式的化简，及二次根式的加减运算，二次根式有意义条件，熟知此知识点是解题的关键．题型3：二次根式的混合运算1-数字型8=_____________． 2【分析】先把分子中的二次根式化为最简二次根式，然后合并后进行二次根式的除法运算．2=．故答案为：2．【点睛】本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，再合并同类二次根式，然后进行二次根式的乘除运算．9．计算：=（）A ．4B ．5C ．6D ．8C【分析】先根据二次根式的性质化简括号内的式子，再进行减法运算，最后进行除法运算即可．原式6=÷==．故选C ．【点睛】本题考查了二次根式的混合运算，利用二次根式的性质化简是解题的关键．1002019)-=________． 1【分析】根据二次根式的运算法则和零指数的性质进行计算即可．解：原式1= 4211=--=故答案为1．【点睛】本题考查了二次根式的运算法则和零指数，解题关键是熟练运用相关法则，准确进行计算．11-+⨯ ）A ．+B ．32C ．D ．A【分析】先化简各个二次根式再合并即可.=故选A.【点睛】本题考查了二次根式的混合运算，熟练掌握二次根式的化简与同类二次根式的合并是解题的关键.12=______．44 【分析】利用二次根式的混合运算法则计算即可．=4==4故答案为：4【点睛】本题考查二次根式的混合运算法则，解题的关键是熟练掌握二次根式的混合运算法则．13 ）A ．-B C ．36-D ．6-D【分析】根据二次根式的混合运算法则进行计算即可原6==-故选D ．【点睛】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．=______．14先分母有理化，再根据二次根式的加减运算法则求解即可．==11【点睛】本题考查分母有理化、二次根式的加减运算，熟练掌握分母有理化的方法是解答的关键．15-分别根据分母有理化、二次根式的乘法和二次根式的性质化简与计算，再合并同类二次根式即可．-=-262【点睛】本题考查了二次根式的混合运算，属于基础题型，熟练掌握运算法则是解题的关键．题型4：二次根式的大小比较16．请用“>，=，<”符号比较大小：＞【分析】求出=解：==∵18＞12，∴故答案为：＞．【点睛】本题考查了二次根式的大小比较，能选择适当的方法比较两个数的大小是解此题的关键．17910＝______．> 2##2【分析】根据45<<可推出101711210510，从而可比较两数大小；利用平方差公式分母有理化即可．解：∵45<<，∴516<<， ∴51716555即101711210510，910>；2==故答案为：>； 2．【点睛】本题考查实数的大小比较，和二次根式的化简．能正确得出45<<和利用平方差公式分母有理化是解题关键．18．比较大小：（1）（2）4_________2+（3；（4> ， < ， > ， <【分析】（1）先将，有4532>，即可比较大小；（2）利用作差法，即可比较大小；（3）利用作商法，即可比较大小；（4>解：（1）∵==4532>，>∴>（2）∵(4(24222(1-+=--=-，又1，∴2(10<，即(4(20-+<，∴42+（3）1 ===>，>；（4）><故答案为：（1）>；（2）<；（3）>；（4）<．【点睛】本题主要考查了二次根式比较大小，二次根式的运算，熟练掌握二次根式的性质是解题的关键．题型5：二次根式的混合运算2-字母型及复合型19．若m，n+mn=_____.1【分析】利用二次根式的运算法则将已知等式化简，求出m、n的值，代入mn即可求解.1414∴4m=1, 4n=16,∴m=14， n=4，mn=414⨯= 1. 故答案为1.【点睛】本题考查二次根式的化简求值.20．若a 、b a +=a ________，b =________． 0 214 【分析】先把等式的左边化简，再合并同类二次根式，再利用实数的无理数性质可得答案．解： a =+，∴a =+a =+ ∴a =0，b =214．故答案为：0;214．【点睛】本题考查的是二次根式的加减运算，实数中无理数的性质，掌握合并同类二次根式与实数中无理数的性质是解题的关键．21．已知22a b ==，则（）A ．a b =B ．1ab =C ．1ab =-D ．0a b +=D【分析】根据a 与b 的值结合选项进行一一比较及计算即可结论．∵2a =(22b ==-，∴a b ，A 选项不正确；∴(227ab =-=-+∴B 、C 选项都不正确；∴220a b +==，D 选项正确．故选D ．【点睛】此题考查了二次根式求值运算，掌握二次根式的运算法则是解题关键．22．已知：5a b +=-，1ab = ） A ．5B ．-5C ．25D ．5或-5A【分析】首先由a+b=-5，ab=1得出a 、b 的取值范围，然后使原式分母有理化，再由a 、b 的取值范围确定所求值的符号，通分化简代入求值；解：∵ab=1＞0，∴a 、b 同号，又∵a+b=-5＜0，∴a ＜0，b ＜0．115a b ⎫==+==⎪⎭；故选：A【点睛】此题考查的知识点是二次根式的化简求值，关键是体现了整体代入思想，还要注意字母的取值．23．已知x =y =y x x y+=______． 8【分析】先把所求代数式通分，再把x 、y 的值代入进行计算即可．解：22y x y x x y xy++=，将x =y =得：原式=22(53)(53)1682(53)(53)++-==+-，故答案为：8．【点睛】本题考查了二次根式的化简求值，结合平方差公式以及完全平方公式是解题的关键．题型6：二次根式的混合运算与分式24．先化简，再求值：223112-⎛⎫-÷⎪++⎝⎭a a a a ，其中3a =． 2aa+，233- 【分析】根据分式的加减乘除法则进行化简，然后代入数值计算即可．解：原式1(1)2(1)(1)-+=⨯++-a a a a a a 2=+a a 当3a =时，原式323=+ 233=-．【点睛】本题考查了分式加减乘除的混合运算，分式的化简求值，二次根式的加减运算，解题的关键是熟练掌握运算法则，正确进行化简．25．已知1526x =-，则21055x x x -+-的值．63【分析】先根据分母有理化化简x ，再把原式变形即可求解． ∵1526x =-()()526526226526+==+-⨯+ ∴21055x x x -+-21025205x x x -+-=-25+2652065+26526--．【点睛】此题主要考查分式的化简求值，解题的关键是熟知二次根式、分式及完全平方公式的运算． 26．先化简，再求值：已知a 23+2221211a a a a a -+-+- 11a a-+，3【分析】先化简得11aa-+，再将a=11aa-+即可得．解：原式=2(1)1aa--=11(1)aaa a----=11aa -+当a=代入11aa-+得：111221231+=++．【点睛】本题考查了整式的化简求值，二次根式的混合运算，正确计算是解题的关键．题型7：复杂的二次根式混合运算275【分析】先把二次根式进行化简，再合并同类二次根式即可求得结果．55==【点睛】本题考查了二次根式的混合运算，在进行此类运算时，一般先把二次根式化为最简二次根式的形式后再运算．28．计算：(1)；(2)．(1)4(2)【分析】（1）先把括号内的二次根式化简及除法运算，再计算二次根式的除法运算，最后合并同类二次根式即可；（2）先计算括号内的二次根式的减法运算，再计算二次根式的除法运算，从而可得答案.(1)解：2332332232322322626262626 464(2)解：ab a ab ab a b a ab a ab ab aa ab a ba ab ab a2a ab a bab aa ab a baba b a【点睛】本题考查的是二次根式的混合运算，掌握“二次根式的混合运算的运算顺序”是解本题的关键.292式的性质和二次根式的加减计算法则进行化简即可．2===【点睛】本题主要考查了平方差公式，完全平方公式，分式的化简，二次根式的加减计算，解题的关键在于能够熟练掌握平方差公式和完全平方公式．30．计算：（1（2）（12．【分析】（1）先化为最简二次根式，再利用二次根式的加减法则进行计算；（2）利用二次根式的乘除法则及分式乘法运算法则进行计算即可．解：（1）原式=4= （2）原式22213a m n m n =+-222133a m n m n=⨯+- )212a m n m n=+-2=2== 【点睛】本题考查了二次根式的混合运算，分式的乘法运算，熟练掌握各运算法则是解题的关键．题型8：二次根式混合运算的应用31=________．根据长+宽列式，利用二次根式的性质化简，再进行二次根式的加法计算即可．解：这个长方形的长与宽的和．故答案为【点睛】本题考查了二次根式的加减法，解答本题的关键是掌握二次根式的化简方法．32．解不等式：11)x x +>-2x +＜根据解不等式的步骤解不等式即可．解：去括号，得1x +>，移项、合并同类项，得(11x >- 系数化为1，得x <2x <+【点睛】本题考查了一元一次不等式的解法和分母有理化，本题的易错点是易忽略10．33．如图是一个简单的数值运算程序，若输入x _________．24x x →→→输入减输出-根据题意可得：程序所代表的代数式为24x -，再由x 1x =，代入即可求解．解：程序所代表的代数式为24x -， ∵x∴1x =，当1x =时，输出的值为21)4314-=--=-故答案为：- 【点睛】本题主要考查了二次根式的混合运算，根据程序图得到程序所代表的代数式为24x -是解题的关键． 34．宋代数学家秦九韶，古希腊数字家海伦在探究三角形面积的求解过程中发现，若一个三角形的三边长分别为a ，b ，c ，设1()2p a b c =++，则这个三角形面积为：S =明，这个公式叫海伦秦九韶公式，当4a =，5b =，6c =时，三角形边a 上的高等于（）A B C D A【分析】由题意易得()11522p a b c =++=，则有S a 边上的高为h ，进而问题可求解．解：由题意，得：4a =，5b =，6c =；()11522p a b c ∴=++=；S ∴==；设a 边上的高为h ，则12ah S =，22424s h a∴==故选：A．【点睛】本题主要考查二次根式的应用，熟练掌握二次根式的运算是解题的关键．35．若22248t t---＝2.5，则22248t t-+-的值为_____．325【分析】设224t-=a，将原等式变形后可求得a的值，代入所求式子可得结论．设224t-=a，则24-t2=a2，8-t2=a2-16，∵224t-−28t-=2.5，a-216a-=52，a−52＝216a-，两边同时平方得：(a−52)2＝a2−16，解得：a=89 20，则22248t t-+-，=8920+216a-，=8920+289()1620-，=8920+1521400，=8920+3920，=325，故答案为325．【点睛】本题是二次根式的化简求值问题，利用换元法，将原方程转化为关于a的方程，解方程可解决问题，计算量大，要细心．一、单选题1．下列运算正确的是（）A222B222233=C．333D633=B【分析】根据二次根式的化简、加法与乘除法法则逐项判断即可得．解：A=B==C1>，所以，则此项错误，不符题意；D=故选：B．【点睛】本题考查了二次根式的运算以及化简，熟练掌握运算法则是解题关键．2．下列等式成立的是（）A=B=C=3C【分析】用二次根式的加减法的法则，二次根式的乘除法的法则对各项进行运算即可．A A不符合题意；B=B不符合题意；C=C符合题意；D=D不符合题意；故选：C．【点睛】本题主要考查二次根式的混合运算，解答的关键是对相应的运算法则的掌握．3）A．2与3之间B．3与4之间C．4与5之间D．5与6之间C【分析】由二次根式的性质，二次根式的乘法、加法进行计算，再进无理数的估算即可．==3∵12<<，∴435<+；故选：C【点睛】本题考查了二次根式的性质，二次根式的乘法、加法运算法则，以及无理数的估算，解题的关键是掌握运算法则进行计算．4．当x=222x x++的值为（）A．14 B．17 C．533D．5+D【分析】将x=解：由题意得：当x=22++=+=+22225x x故选：D．【点睛】本题考查了二次根式的混合运算及求代数式的值，熟练掌握二次根式的混合运算法则是解题的关键．m，小数部分为n，则（2m+n）（2m﹣n）的值是（）5A．B．-C．2D．2-A【分析】m、n的值，再用平方差公式计算（2m+n）（2m﹣n），最后再再代入求值即可．2，解：∵1m=1，小数部分为n，∴（2m+n）（2m﹣n）=224m n-=)22411⨯-=()431--=故选：A．【点睛】本题考查估算无理数的大小、二次根式的计算及平方差公式，理解算术平方根的定义是正确估算的前提．6）A．0 B．3 CD．不存在B【分析】先根据二次根式有意义，求出xx的增大而增大，则在x取值范围内x取最小值时代入计算，即可求解．则102020xxx-≥⎧⎪-≥⎨⎪+≥⎩，解得：x≥2，∵x的增大而增大，∴当x＝2时，代数式的值最小，1+0+2＝3．故选：B．【点睛】此题考查了函数的最值问题，考查了二次根式的意义．此题难度适中，解题的关键是根据题意求得x的取值范围．7．已知ab11a b+的值为（） A ．﹣B ．C ．﹣D ．A 【分析】先进行通分计算，然后代入求值即可．解：原式＝b a ab ab+＝a bab + 当ab＝﹣故选：A ．【点睛】本题主要考查了分式的化简求值以及二次根式的混合运算，掌握二次根式的混合运算成为解答本题的关键． 8．若0a <，0b <，化简） A ．(23-b a B ．(23--b a C ．(23-+b a D ．(23+b a C 【分析】a 化简，注意0a <，0b <，最后加减运算即可．解：223,ab a ab =-0a <，0b <，(2223332ab a abb a ∴-=-=-+故选：C ．【点睛】a 是解题关键．9．已知a b =c =a ，b ，c 的大小关系是（）A ．a b c <<B ．a c b <<C ．c b a <<D ．b c a << A【分析】先把,,a b c再结合2021+20202020+2019,从而可得答案．解：∵a ==，b =，c ==，2021+20202020+2019, ∴.a b c <<故选A ．【点睛】本题考查的是二次根式的大小比较，二次根式的混合运算，掌握“二次根式的大小比较的方法”是解本题的关键．10．设12211112a =++，22211123a =++，32211134a =++，……，22111(1)n a n n =+++．其中n 为正整数，则）A ．201920202020 B ．202020202021 C ．202020212021 D ．202120212022D【分析】11(1)n n =++，然后把代数式进行化简，再进行计算，即可得到答案．解：∵n 为正整数，＝21(1)n n n n +++ ＝11(1)n n ++；2021a +＝（1+112⨯）+（1+123⨯）+（1+134⨯）+…+（1+120212022⨯）＝2021+1﹣11111112233420212022+-+-++- ＝2021+1﹣12022 ＝202120212022．故选：D ．【点睛】本题考查了二次根式的化简求值，解题的关键是用裂项法将分数1n(n 1)+化成111n n -+抵消规律求和．二、填空题11=________．33【分析】先根据二次根式的性质化简，同时进行二次根式的乘法运算，然后合并即可．解：原式＝33=故答案为：3本题考查了二次根式的混合运算，熟练掌握运算法则是解题的关键．12＝ ____．4--4-【分析】根据二次根式的混合运算可进行求解．解：原式=2⎝=31--=4--故答案为4--【点睛】本题主要考查二次根式的混合运算，熟练掌握二次根式的混合运算是解题的关键．13，一矩形的长为，若该圆的面积与矩形的面积相等，则矩形的宽为____cm．【分析】园的面积=2rπ，矩形的面积=长×宽，根据圆的面积与矩形的面积相等可得2rπ=长×宽，代入数据即可求解．设矩形的宽为x cm∵圆的面积与矩形的面积相等，∴2rπ=长×宽2π=，解得：x=故答案为：【点睛】本题主要考查了圆的面积与矩形面积得等量代换，熟练地掌握圆的面积公式与矩形的面积公式，根据题意找出等量关系列出等式是解题的关键．14==ab=_________2【分析】运用二次根式化简的法则先化简，再得出a，b的值即可．解：246-==∴== 2.2,1,a b∴=故答案为：2．ab本题考查了二次根式的化简求值，解题的关键是掌握二次根式运算法则．15．已知52x =+，52y =-，求下列各式的值：（1）x y +=______；（2）222x xy y -+=______；（3）22x y -=______．25 16 85【分析】（1）把52x =+，52y =-代入x y +进行计算即可；（2）先计算x y -，再把222x xy y -+化为()2x y -，再代入计算即可；（3）把22x y -化为()()x y x y +-，再整体代入计算即可．解：（1）∵52x =+，52y =-，2 5.x y（2）∵52x =+，52y =-， 52524,x y ∴()22222416.x xy y x y -+=-==（3）∵25,x y4,x y -= ∴()()222548 5.x y x y x y -=+-=⨯=故答案为：（1）25；（2）16；（3）85【点睛】本题考查的是二次根式的加减运算，二次根式的乘法运算，掌握“利用完全平方公式与平方差公式进行简便运算”是解本题的关键．16．现有一块长25dm ，宽23dm 的长方形木板，能否采用如图的方式，在这块木板上截出两个面积分别是4dm 2和9dm 2的正方形木板？______（填“能”或者“否”）．否根据正方形的面积可以分别求得两个正方形的边长是2dm 和3dm ，然后进行比较相应的边长即可．解：，由于，∴不能够在这块木板上截出两个面积分别是4dm 2和9dm 2的正方形木板．故答案为：否．【点睛】本题考查了二次根式的应用，正确求得每个正方形的边长，并能够正确比较实数的大小是解题的关键．17．对任意的正数a ，b ，定义运算“*”如下：)),*.a b a b a b ⎧≥⎪=⎨<⎪⎩计算()()3*23*5+的结果为______．【分析】根据新定义，将所给数值代入计算即可．解：∵))*a b a b a b ⎧≥⎪=⎨>⎪⎩， ∴()()3*23*5+==故答案为：【点睛】本题考查实数的计算，解题的关键是读懂新定义的运算法则．180.618≈这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设a =b =11111S a b =+++，2222211S a b =+++，…，10010010010010011S a b =+++，则12100S S S +++=_______．5050【分析】利用分式的加减法则分别可求S 1=1，S 2=2，S 100=100，•••，利用规律求解即可．解：a =b =1ab ==∴， 1112211112a b a b a b b b a bS a a ++++=+===+++++++， 222222222222222222221112a b a b S a b a b a b a b ++++=+=⨯=⨯=+++++++， …，10010010010010010010010010010010011100100111a b S a b a b a b +++=+=⨯=+++++∴12100S S S +++=121005050++⋯⋯+=故答案为：5050【点睛】本题考查了分式的加减法，二次根式的混合运算，求得1ab =，找出的规律是本题的关键．三、解答题19．计算：﹣(22+（3）（ (1)-5(2)-6【分析】（1）先利用完全平方公式和平方差公式计算，然后化简后合并即可；（2）先把各二次根式化为最简二次根式，然后把括号内合并后进行二次根式的除法运算．(1)解：原式））7﹣﹣1=﹣5(2)原式=﹣6．【点睛】本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．20．计算：⎛ ⎝-【分析】先化简括号内的二次根式，同步计算后面的分母化，再计算二次根式的除法运算，最后合并同类二次根式即可.解：⎛ ⎝2222326322222222222222=-【点睛】本题考查的是二次根式的混合运算，掌握“二次根式的加减乘除运算的运算法则与混合运算的运算顺序”是解本题的关键.21．计算：)21⎭．-根据二次根式的性质、二次根式的加减混合运算法则计算．解：原式=31-=31231---+=-【点睛】本题考查了二次根式的加减运算、乘法运算，掌握二次根式的加减运算法则是解题的关键．22==的值．4 【分析】根据二次根式分母有理化计算即可；2=+2==原式===224=；【点睛】本题主要考查了二次根式分母有理化和乘除运算，准确化简是解题的关键．23-【分析】通分并利用同分母分式的减法法则合并，再利用平方差公式简便计算即可求解．=((1218⨯=-==-【点睛】本题考查了二次根式的混合运算，正确运用乘法公式是解题关键．24．已知：11,x y--==，求值：x2﹣y2．先利用分母有理化把二次根式化简，再利用平方差公式分解因式，进而即可求解．解：∵11,x y--==，∴x y====∴x2﹣y2=（x+y）（x-y）=⎝⎭∙535322=【点睛】本题主要考查二次根式的混合运算，掌握负整数指数幂和分母有理化是解题的关键．25．三角形的周长为(cm，面积为(2cm，求：（1）第三边的长；（2）第三边上的高．（1）；（2）()4cm【分析】（1）首先化简二次根式，进而合并同类二次根式得出答案；（2）设第三边上的高为x，列出等式12x⨯，求解即可．解：（1）三角形周长为(cm，∴第三边的长是：(故第三边的长为：；（2）设第三边上的高为x，则12x⨯，解得：x=，故第三边上的高为：()4cm．【点睛】本题考查了二次根式的加减运算，解题的关键是掌握正确化简二次根式运算法则．26．算即可===本题考查了因式分解，二次根式的加减，将分式的分子因式分解是解题的关键．27先将各项分别化简，再合并同类二次根式．=【点睛】本题考查了二次根式的混合运算，解题的关键是掌握运算法则以及二次根式的性质．28．计算：（1）129+）0115-⎛⎫- ⎪⎝⎭；（2）41a⎫+⎪⎪-⎭．（1）3-；（2【分析】（1）分别计算分数指数幂，零指数幂，负指数幂以及化简二次根式，再算加减法；（2）根据二次根式和分母有理化以及约分进行计算即可．解：（1）)1121915-⎛⎫+- ⎪⎝⎭=(3152+--=3-（2）41a⎫+⎪⎪-⎭=13⎤21-21本题考查的是二次根式的化简求值，熟知二次根式混合运算的法则是解答此题的关键．29．在二次根式的计算和比较大小中，有时候用“平方法”会取得很好的效果，例如，比较a ＝b ＝的大小，我们可以把a 和b 分别平方，∵a 2＝12，b 2＝18，则a 2＜b 2，∴a ＜b ．请利用“平方法”解决下面问题：(1)比较c ＝，d ＝c d （填写＞，＜或者＝）．(2)猜想m ＝n ＝(3)＝（直接写出答案）．(1)c >d(2)m <n ，证明过程见解析(3)4或【分析】（1）根据题干中“平方法”比较实数大小；（2）根据题干中“平方法”比较二次根式的大小；（3）根据题干中“平方法”找出21)p =-21)p =+质结合完全平方公式进而开平方分类讨论得出答案．(1)解：∵c 2=32，d 2=28，则c 2>d 2，∴c >d ；故答案为：>．(2)解：猜想：m <n ，证明：∵m ＝n ＝∴m 2=(2 n 2＝(2∴m 2<n 2，∴m <n ；(3)解：∵21)p =-21)p =+11∴p ≥1，分情况讨论：①1≤0，即1≤p ≤2时，原式=2(1+21)，=4；②1>0，即p >2时，原式=21)+21)，综合①②得：当1≤p ≤2时，原式=4；当p >2时，原式故答案为：4或．【点睛】此题考查了实数的大小比较，二次根式的大小比较和化简二次根式，解题的关键是熟练运用题干中“平方法”，第（3）题注意分情况讨论．30．综合与实践：在学习二次根式时，发现一些含有根号的式子可以结合完全平方式化成另一个式子的平方，如：()(2224131211+++=+⨯=+，()2225322-=+--=．1==(1)请你依上述方法将4-(2)(3)=a 、m 、n 均为正整数，则=a ________．(1))211 (2)2(3)5或7【分析】（1）参照题目例子，将4拆分为1和3，把4-转化为2()a b -的形式，即可求解；（2）用（1）中方法把被开方数是无理数的式子依次化简，再进行二次根式的加减运算即可；（3的平方，与a +进行对比即可求出a 值． (1)解：())22243121-=+-=-=，1． (2)解：()2228215532-+-=-===3=132=． (3)解：222()m n m n =+=+=++26a +a 、m 、n 均为正整数，()m n a ∴++=+m n a ∴+=，6mn =，当2m =，3n =或3m =，2n =时，5a m n =+=；当1m =，6n =或6m =，1n =时，7a m n =+=；故答案为：5或7．【点睛】本题考查完全平方公式、二次根式的混合运算，题目较为新颖，能够灵活运用完全平公式对二次根式进行化简是解题的关键．。

2022-2023学年沪教版上海八年级数学上学期同步考点精讲精练16-3-1二次根式的乘除带讲解

16.3.1二次根式的乘除考点一、二次根式的乘法及积的算术平方根1.法则：（a≥0，b≥0）,即两个二次根式相乘，根指数不变，只把被开方数相乘.要点：(1)在运用二次根式的乘法法则进行运算时，一定要注意：公式中a、b都必须是非负数；(在本章中，如果没有特别说明，所有字母都表示非负数).(2)该法则可以推广到多个二次根式相乘的运算：;≥0，≥0，…..≥0）;(3)若二次根式相乘的结果能写成的形式，则应化简，如.2.积的算术平方根（a≥0，b≥0）,即积的算术平方根等于积中各因式的算术平方根的积.要点： (1)在这个性质中，a、b可以是数，也可以是代数式，无论是数，还是代数式，都必须满足a≥0，b≥0,才能用此式进行计算或化简，如果不满足这个条件，等式右边就没有意义，等式也就不能成立了；(2)二次根式的化简关键是将被开方数分解因数，把含有形式的a移到根号外面.考点二、二次根式的除法及商的算术平方根1.除法法则：（a≥0，b>0）,即两个二次根式相除，根指数不变，把被开方数相除..要点：(1)在进行二次根式的除法运算时，对于公式中被开方数a、b的取值范围应特别注意，a≥0，b>0，因为b在分母上，故b不能为0.(2)运用二次根式的除法法则，可将分母中的根号去掉，二次根式的运算结果要尽量化简，最后结果中分母不能带根号.2.商的算术平方根的性质（a≥0，b>0），即商的算术平方根等于被除式的算术平方根除以除式的算术平方根.要点：运用此性质也可以进行二次根式的化简，运用时仍要注意符号问题.题型1：二次根式的乘法1-数字型10.4 1.6）A．0.2 B．0.4 C．0.6 D．0.8D【分析】根据二次根式乘法法则计算即可．原式0.8===．故选：D ．【点睛】本题考查了二次根式乘法法则：算术平方根的积等于各个被开方数积的算术平方根．2_________． 20 【分析】根据二次根式的乘法法则计算即可．解：原式==20=，故答案为：20．【点睛】本题考查了二次根式的乘法法则，熟练掌握二次根式的乘法法则是解决本题的关键．题型2：二次根式的乘法2-字母型及复合型3__________．4a 【分析】根据二次根式的乘法进行求解即可．4a =；故答案为：4a 【点睛】本题主要考查二次根式的乘法，熟练掌握二次根式的乘法法则是解题的关键． 4．下列计算正确的是( )A ．B ()()35=15-⨯-C ．-DDA 选项：24，计算错误，故与题意不符；B 3515=⨯=，计算步骤有误，故与题意不符;C 选项：22233633，计算错误，故与题意不符；D ，计算正确，故与题意相符. 故选D.5．计算（- ） A ．4 B ．8 C ．16 D ．32B 【分析】利用平方差公式进行计算即可．解：（=22=-20128.=-=故选B ．【点睛】本题考查的是利用平方差公式进行二次根式的乘法运算，掌握公式特点是解题的关键．题型3：二次根式的乘法法则成立的条件6230x -=成立的x 的值为（）A ．-2B ．3C ．-2或3D ．以上都不对B 【分析】根据二次根式有意义的条件以及二次根式的乘法进行分析即可得答案. 2x 30-=，0=0=， ∴x=-2或x=3，又∵2030x x +≥⎧⎨-≥⎩，∴x=3，故选B. 【点睛】本题考查了二次根式的乘法以及二次根式有意义的条件，熟练掌握相关知识是解题的关键.题型4：二次根式的除法1-数字型7___．用二次根式除法法则计算即可．=故答案为：【点睛】本题考查了二次根式的除法，解题关键是熟练掌握二次根式除法法则，准确进行计算．8_____． 3 【分析】直接利用二次根式的除法运算计算得出即可．3=．故答案为：3．【点睛】本题主要考察了二次根式的除法，熟悉掌握运算的法则是解题的关键．9_____． 2 【分析】根据二次根式的除法法则计算即可求解．÷2=，故答案为：2．【点睛】本题考查了二次根式的除法运算，熟知二次根式的除法法则是解题关键．题型5：二次根式除法法则成立的条件10x 的取值范围是（） A ．x ≠2 B ．x ≥0C ．x ≥2D ．x ＞2D【分析】根据被开方数为非负数，且分式的分母不能为0，列不等式组求出x 的取值范围即可．由题意可得：020x x ≥⎧⎨-⎩＞，解得：x ＞2．故选D ．【点睛】二次根式的被开方数是非负数，分母不为0，是本题确定取值范围的主要依据．11=成立的条件时，则x 的取值范围为 ___．32x -≤<【分析】由二次根式有意义的条件可得30,20x x 再解不等式组即可得到答案.解： 3020x x ①②由①得：3,x ≥-由②得：2,x <所以则x 的取值范围为3 2.x 故答案为：32x -≤< 【点睛】本题考查的是商的算术平方根的运算法则与二次根式有意义的条件，掌握0,0ba b a”是解本题的关键.12．下列各式：==a ＞0，b≥0）；=-，其中一定成立的是________（填序号）． ②③④ 【分析】根据二次根式的性质及运算法则逐项分析即可．①00，a b ≥>≠=00，a b ≥>；③当00，a b >≥时，3133b a a a a== ④3a 成立时，0a ≤3a aaaa ，故一定成立；故答案为：②③④．【点睛】本题考查二次根式的性质以及乘除远算法则，熟练掌握基本性质计算法则是解题关键．题型6：二次根式的除法2-字母型及复合型13____．根据二次根式的除法法则解决此题．===故答案为：【点睛】本题主要考查二次根式的除法，解题的关键是熟练掌握二次根式的除法法则．14___．根据二次根式的除法运算法则计算即可；原式255yx x y==；【点睛】本题主要考查了二次根式的除法法则，准确计算是解题的关键．15=_________． x 【分析】根据二次根式的除法法则计算即可．=123⎛÷ ⎝=x ．【点睛】本题考查了二次根式的除法，熟练掌握除法法则是解答本题的关键．二次根式相除，把系数相除作为商的系数，被开方数相除，作为商的被开方数，并化为最简二次根式．16．计算：43434(32)⨯=______24 【分析】运用积的乘方的逆运算：(ab )n =anbn ，把43434(32)⨯写成433434432⨯⨯⨯左到右的顺序运算．解：43434(32)⨯ =433434432⨯⨯⨯ =3×23 =3×8=24=故答案为：24，【点睛】此题考查了实数的运算，解决问题的关键是掌握正确的运算顺序． 17．当0x >= _________________．94先根据二次根式的定义和除法的性质可得0y >，再根据二次根式的性质化简，然后计算二次根式的除法即可得．由二次根式的定义得：2500x y y x ⎧≥⎪⎨≥⎪⎩，0x，0y ∴≥，又除法运算的除数不能为0，0y ∴≠， 0y ∴>，35xy =3xy==49=94本题考查了二次根式的定义与除法运算，熟练掌握二次根式的运算法则是解题关键．题型7：二次根式的乘除法1-数字型18．下列运算错误的是（） A=B=C．25= D．2D 【分析】利用二次根式的运算性质分别运算后即可确定错误的选项，从而确定正确的答案．解：A=BC、25=，正确，不符合题意； D、2故选：D．【点睛】本题考查了二次根式的运算，解题的关键是了解二次根式的有关的运算性质，难度不大．19___．先把除法转化为乘法，再计算即可完成．=【点睛】本题考查了二次根式的乘除混合运算，注意运算顺序不要出错．题型8：二次根式的乘除法2-字母型及复合型20．下列结论中，对于实数a、b，成立的个数有（）=a=±；2a．A．0个B．1个C．2个D．3个C【分析】根据二次根式有意义的条件结合二次根式的乘除法及二次根式的性质逐一分析四条结论的正误，由此即可得出结论．①当a、b∴①不成立；②∵a＞0，b≥0，∴ba≥0，②成立；＝|a|，∴③不成立；＝|a 2|＝a 2， ∴④成立．综上可知：成立的结论有②④．故选C ．【点睛】本题考查了二次根式有意义的条件、二次根式的乘除法以及二次根式的性质与化简，熟练掌握二次根式的乘除法及二次根式的性质是解题的关键．21=（）A B C D ．【分析】直接利用二次根式的乘除运算法则化简求出即可．原式==故选：A 【点睛】此题主要考查了二次根式的乘除运算，正确掌握运算法则是解题关键． 22．计算：（1（20)a >（334÷（4（5）2(0,0)a b >>．（1）19；（2）3a ；（34）5）312-a b【分析】（1）根据二次根式的除法运算法则计算即可；（2）根据二次根式的乘除法混合运算法则计算即可；（3）根据二次根式的乘除法混合运算法则计算即可；（4）根据二次根式的乘除法混合运算法则计算即可；（5）根据二次根式的乘除法混合运算法则计算即可．（1）原式19==；（2）原式=3a ==；（3）原式331(2442=÷=⨯÷；（4）原式=（5）原式1 23()2ab =⨯÷-12ab =-212ab a =-⨯312a b =-．【点睛】本题考查了二次根式的混合运算，熟练化简二次根式后，在加减的过程中，有同类二次根式的要合并；相乘的时候，被开方数简单的直接让被开方数相乘，再化简；较大的也可先化简，再相乘，灵活对待． 23．计算:（1）（2）(（3）0,0)a b >>（1）2）154-；（3 【分析】（1）根据二次根式乘除法法则计算即可；（2）根据二次根式乘除法法则计算即可；（3）根据二次根式乘除法法则计算即可．（1）原式233=⨯2=（2）原式13153()5=844⨯-⨯=-⨯-；（3）原式== 【点睛】本题考查了二次根式的混合运算，主要考查学生的化简能力，题目比较典型，但是一道比较容易出错的题目．题型9：有理化因式241的一个有理化因式是（）A B C 1 D ． 1- D【分析】根据有理化因式的定义进行求解即可．两个含有根式的代数式相乘，如果它们的积不含有根式，那么这两个代数式相互叫做有理化因式．解：∵由平方差公式，)111x =-，11-．故选：D ．【点睛】本题主要考查了对有理化因式的理解，正确选择两个二次根式，使它们的积符合平方差公式是解答问题的关键．25的有理化因式是 ___．根据有理化因式的定义（两个根式相乘的积不含根号）即可得答案．3x =-，【点睛】本题考查了有理化因式，熟练掌握有理化的方法是解题关键．26．写出n 的一个有理化因式：_______．n 【分析】根据平方差公式即可得出答案．解：n的有理化因式n，故答案为n．【点睛】此题考查了有理化因式的定义：两个含有根式的代数式相乘，如果它们的积不含有根式，那么这两个代数式相互叫做有理化因式，及平方差计算公式，熟记有理化因式的定义是解题的关键．27．）B C DAC【分析】根据有理化因式定义：如果两个含有二次根式的非零代数式相乘，它们的积不含有二次根式，就说这两个非零代数式互为有理化因式，结合各个选项中两个代数式特征作出判断即可．解：∵3(2)x=-，∴故选：C．【点睛】本题考查了有理化因式的定义：两个含二次根式的非零代数式相乘时，它们的积不含二次根式，这样的两个代数式成互为有理化因式．一般地，282的有理化因式可以是___．2【分析】利用平方差公式进行有理化即可得．解：因为2)5=--=-，14x x22，2．【点睛】本题考查了有理化因式，熟练掌握有理化的方法是解题关键．题型10：与分母有理化计算变形问题292的倒数是（）A 2B ．2C ．2D A【分析】根据二次根式分母有理化的方法进行化简即可．22，故选：A ．【点睛】本题考查了二次根式的分母有理化，解题关键是熟练运用二次根式性质进行分母有理化．30．已知a=1则a 与b 的关系是( ) A ．互为相反数B ．互为倒数C ．相等D ．互为负倒数A【分析】把的分子分母同乘（1a 比较得出结论即可．1b1=--（1a=1∴a 与b 互为相反数.故选A.【点睛】本题考查分母有理化.31m ＞0，n ＞0)分别作了如下变形：()m n-====关于这两种变形过程的说法正确的是( )A ．甲，乙都正确B ．甲，乙都不正确C ．只有甲正确D ．只有乙正确D【分析】甲的做法是先把分母有理化，再约分；乙的做法是先把分子分解因式，再约分．计算过程中，要考虑m=n 这种情况．甲的做法是先把分母有理化，再约分，如果m=n 则化简不成立；乙的做法是先把分子分解因式，再约分，正确．故本题选D ．【点睛】本题考查的是分母有理化的计算方法．32．若a ，b ＝a b 的值为（） A ．12B ．14CD B【分析】将a b 的式子，从而得到a 和b 的关系，继而能得出a b 的值．a ＝=b 44=． ∴14a b =．故选B ．【点睛】本题考查二次根式的乘除法，有一定难度，关键是在分母有理化时要观察b 的形式．题型11：二次根式乘除的应用33．若一个长方体的长为_______．12【分析】直接根据长方体体积公式求解可得．∵长方体的长为∴长方体的体积=12故答案为：12【点睛】本题考查求长方体的体积，注意正方体的体积求法与长方体类似，为棱长×棱长×棱长．34．站在竖直高度 h m 的地方，看见的水平距离是 d m ，它们近似地符合公式85h d =.某一登山者登上海拔2000 m 的山顶，那么他看到的水平距离是________m . 160 【分析】把h=2000代入公式85h d =进行即可. 解：把h=2000代入公式85h d =得 2000884008201605d ===⨯=所以答案是：160. 【点睛】本题考查了二次根式的计算.熟练掌握二次根式的性质是运算的关键.35．若3的整数部分是a ，小数部分是b ，则22a b +的值是___________．523-【分析】首先根据3的取值范围得出a ，b 的值进而求出即可．解：∵123<<，3的整数部分是a ，小数部分是b ，∴a =1，b =3-1∴()222=1+3-1=5-23a b + 故答案为：523-【点睛】此题主要考查了估算无理数的大小，得出a ，b 的值是解题关键．一、单选题11128 ） A 2B ．2C ．2D 2B【分析】直接根据二次根式的除法计算法则求解即可得到答案．解：原式2=．故选B ．【点睛】本题主要考查了二次根式的乘除计算，解题的关键在于能够熟练掌握二次根式的乘除计算法则． 2．下列各运算，正确的是（）A ．=B 35=CD x y + B【分析】根据二次根式的运算法则和二次根式有意义的条件进行计算即可．解：A 、30=，故本选项错误；B 35，本选项正确；CD故选：B ．【点睛】本题考查了二次根式的运算法则，二次根式有意义的条件，掌握这些知识点是解题关键．3．计算）A B C D ．C【分析】根据二次根式的运算法则即可求出答案．原式=故选C ．【点睛】本题考查二次根式的乘除法，解题的关键是熟练运用二次根式的乘除法法则，本题属于基础题型．4（）（a ＞0，b ＞0）A ．10b a B ．10a b C ．2a D ．2a 2C【分析】根据二次根式的除法法则计算可得．解：原式2a ===，故选C ．【点睛】本题主要考查二次根式的乘除法，解题的关键是掌握二次根式的除法运算法则．5其中0,a b ≥满足的条件是（）A ．b ＜0B ．b ≥0C ．b 必须等于零D ．不能确定B【分析】根据二次根式乘法法则的条件解答即可．解：=0a ≥，∴b ≥0．故选：B ．【点睛】本题考查了二次根式的定义和乘法法则的理解，属于基础题型，熟知二次根式的被开方数非负是解答的关键．6 ） A ．10到11之间B ．9到10之间C ．8到9之间D ．7到8之间D【分析】先根据二次根式的乘法计算得到原式为4的范围，即可得出答案．解：原式==4∵34<，∴748<+<，故选：D．【点睛】本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，在进行二次根式的乘除运算，然后合并同类二次根式．7）B C DAC【分析】三角形面积计算既可以用直角边计算，又可以用斜边和斜边上的高计算，根据这个等量关系即可求斜边上的高．直角三角形中，两直角边长的乘积等于斜边长与斜边上的高（h=，∴h=．故选：C．【点睛】本题考查了二次根式的运算，根据面积相等的方法巧妙地计算斜边上的高是解本题的关键．8n的最小值是（）A．3 B．2 C．48 D．6A【分析】先将所给二次根式化为最简二次根式，然后再判断n的最小正整数值．∴是一个完全平方数，正整数n的最小值为3．48n是正整数，3n故选：A．【点睛】本题考查了二次根式的定义，解答本题的关键是能够正确的对二次根式进行化简．9．计算201820192)2)的结果是（）A ．2+B 2 C ．2 D B【分析】原式利用积的乘方变形为201820182)2)2)，再利用平方差公式计算，从而得出答案．201820192)2)=201820182)2)2)=))2018222⎡⎤⎣⎦=())201812-2故选B ．【点睛】本题考查了二次根式的混合运算，熟练掌握运算法则是解题的关键．10．已知226a b ab +=，且a >b >0，则a b a b +-的值为( )AB ．C ．2D ．±2 A【分析】已知a 2+b 2=6ab ，变形可得（a +b ）2=8ab ，（a -b ）2=4ab ，可以得出（a +b ）和（a -b ）的值，即可得出答案．解：∵a 2+b 2=6ab ，∴（a +b ）2=8ab ，（a -b ）2=4ab ，∵a ＞b ＞0，∴a +b a -b∴a b a b +-= 故选A ．【点睛】本题考查了分式的化简求值问题，完全平方公式的变形求值，二次根式的除法，观察式子可以得出应该运用完全平方式来求解，要注意a 、b 的大小关系以及本身的正负关系．二、填空题11．计算；（1=__________________；（2=_________；（3=_________；（4=__________，（5=__________；（6=____________；（7=__________；（8=__________．（1（2 （3；（4 （5 （6 （7，（8）【分析】=00a b ≥>、），反过来，可=00a b ≥>、）．（1= （2=（3=4（5=（6=（7=；（8=．【点睛】本题考查了二次根式的除法运算，掌握二次根数的除法法则是解题的关键．12=______．44 【分析】利用二次根式的混合运算法则计算即可．=4==4故答案为：4【点睛】本题考查二次根式的混合运算法则，解题的关键是熟练掌握二次根式的混合运算法则．13．化简；（1）_____________；（2___________()0a >；（3）10111)1)=_____________；45 31．【分析】（1）根据二次根式的乘法运算法则计算，然后利用二次根式性质化简即可；（2）先把被开方式因式分解，利用二次根式性质化简，化简结果也可3（3）利用乘方的逆运算分出一次幂与10次幂即))1110111=，再利用积的乘方逆运将底数用平方差公式化简后再与一次幂因式相乘．解:（1）45==；（23==()0a >；（3）)))101011101)1)111111⎡⎤==⨯=⎣⎦故答案为（1）452）331．【点睛】本题考查二次根式的乘法乘方混合运算，掌握二次根式性质，二次根式乘方与乘法运算法则是解题关键．14y0xy的值为________．=，那么()20201【分析】根据非负数的性质列出方程求出x，y的值，代入所求代数式计算即可．解：由题意得，x0=，y0，解得，x=，y=则xy1=，∴()2020=．xy1故答案为：1.【点睛】本题考查的是算术平方根的非负性，绝对值的非负性，二次根式的乘法运算，有理数乘方的含义，代数式的值，一元一次方程的解法，掌握以上知识是解题的关键．15．不等式>____________．x<利用解不等式的方法与步骤求得解集，进一步化简即可．xx＜x＜故答案为：x＜【点睛】本题考查了二次根式的实际运用，掌握解不等式的方法与二次根式的化简是解答本题的关键．16a b=，用含a、b=_________．ab【分析】的形式，即可求解．=ab故答案为ab【点睛】此题考查了二次根式乘法的逆用，熟练掌握二次根式是解题的关键．17．交通警察在处理事故时，车辆是否超速是划分责任的一个主要依据，根据实际工作经验，刹车后车轮滑过的距离可以用来推算当时的车速，所用的公式为其中v 表示车速=v d 表示刹车后车轮滑过的距离（单位：m ），f 表示摩擦系数.在一段限速80km /h 的地段，发生了一起交通事故，警察在现场调查中测得24d m =， 1.3f =，则肇事汽车当时______超速.（填“已经”或“没有”）已经【分析】把d 、f 的值代入公式进行计算即可得解．∵d =24m ，f =1.3，∴v 16×5.59≈89.4km/h ．∵89.4＞80，∴肇事汽车当时已经超速．故答案为已经．【点睛】本题考查了二次根式的应用，把已知数据代入公式进行计算即可，计算时要用计算器．18．==……请你将发现的规律用含自然数n （n ≥1）的等式表示出来__________________．(1)n n =+≥【分析】(2=+(3=+n (n ≥1)(1)n n =+≥=(2=+(3+……，发现的规律用含自然数n (n ≥1)(1)n n =+≥．(1)n n =+≥ 【点睛】本题主要考查二次根式，找出题中的规律是解题的关键，观察各式，归纳总结得到一般性规律，写出用n 表示的等式即可．三、解答题19⎛÷ ⎝2a -根据二次根式的乘除计算法则和化简法则求解即可．解：当0a >，0b >时，原式232b b ⎛=⋅- ⎝322⎛=- ⎝2a =- 当0a <，0b <时，原式232b b ⎛=⋅ ⎝⎭ 322⎛= ⎝2a =-∴原式2a =-【点睛】本题主要考查了利用二次根式的性质化简，二次根式的乘除计算，熟知相关计算法则是解题的关键． 20．计算：（1）（25；（3）)21；（4）)33；（5）（6（1）；（2）1；（3）6+4）4；（5）5；（6）5．【分析】（1）根据二次根式的乘法运算法则进行计算；（2）根据二次根式的乘法运算法则进行计算；（3）利用完全平方公式进行计算；（4）利用平方差公式进行计算；（5）根据二次根式的乘法运算法则进行计算；（6）根据二次根式的除法运算法则进行计算；解：（1）32⨯=（2555651===-=；（3）)22211516=+=+=+（4）)223331394=-=-=；（5）615==-=；（6235==+=．【点睛】本题考查二次根式的乘除法，理解二次根式的性质，掌握二次根式乘除运算法则是解题关键．21【分析】根据二次根式的乘法与除法法则进行计算即可．3112n m m m =⨯m n=362= 本题考查了二次根式的乘除运算及二次根式的化简，掌握二次根式乘除运算的法则并正确化简二次根式是解题的关键．22．【分析】根据二次根式的乘除运算法则进行即可．12=12==根据题意知：x 与y 同号== 本题考查了二次根式的乘除混合运算，掌握二次根式的乘除运算法则是关键，最后二次根式要化成最简二次根式．23．计算（1（2（x ＜2y ＜0） (1) 203;(2)-21xy 试题分析:(1)根据二次根式的乘法和除法法则计算,(2)根据二次根式的性质进行化简.试题解析÷ =203,（2x ＜2y ＜0） =2122y x y x xy -⨯--, =21xy -. 24．阅读下面问题：1；＝1×1× 试求：________； (2)当n________； (3)…的值．(3)9【分析】（1）根据题目中的例子，可以将所求式子化简；（2）根据题目中的例子，可以将所求式子化简；（3）先将所求式子变形，然后计算即可．【小题1】=【小题2】=【小题3】....+11=101=-9=．【点睛】本题考查二次根式的化简求值、分母有理化、平方差公式，解答本题的关键是明确它们各自的计算方法．。

中考数学专题16 函数与其他实际运用问题【考点精讲】(解析版)

题型一：拱桥类问题【例1】（2021·贵州）甲秀楼是贵阳市一张靓丽的名片．如图①，甲秀楼的桥拱截面OBA 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽8m OA =，桥拱顶点B 到水面的距离是4m ．（1）按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；（2）一只宽为1.2m 的打捞船径直向桥驶来，当船驶到桥拱下方且距O 点0.4m 时，桥下水位刚好在OA 处．有一名身高1.68m 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；（3）如图③，桥拱所在的函数图象是抛物线()20y ax bx c a =++≠，该抛物线在x 轴下方部分与桥拱OBA 在平静水面中的倒影组成一个新函数图象．将新函数图象向右平移()0m m >个单位长度，平移后的函数图象在89x ≤≤时，y 的值随x 值的增大而减小，结合函数图象，求m 的取值范围．【答案】（1）y =14-x 2+2x （0≤x ≤8）；（2）他的头顶不会触碰到桥拱，理由见详解；（3）5≤m ≤8 【分析】（1）设二次函数的解析式为：y =a (x -8)x ，根据待定系数法，即可求解；专题16 函数与其他实际运用问题（2）把：x =1，代入y =14-x 2+2x ，得到对应的y 值，进而即可得到结论；（3）根据题意得到新函数解析式，并画出函数图像，进而即可得到m 的范围．【详解】（1）根据题意得：A (8，0)，B (4，4)，设二次函数的解析式为：y =a (x -8)x ，把(4，4)代入上式，得：4=a ×(4-8)×4，解得：14a =-，∴二次函数的解析式为：y =14-(x -8)x =14-x 2+2x （0≤x ≤8）；（2）由题意得：x =0.4+1.2÷2=1，代入y =14-x 2+2x ，得y =14-×12+2×1=74＞1.68，答：他的头顶不会触碰到桥拱；（3）由题意得：当0≤x ≤8时，新函数表达式为：y =14x 2-2x ，当x ＜0或x ＞8时，新函数表达式为：y =-14x 2+2x ， ∴新函数表达式为：2212(08)412(08)4x x x y x x x x ⎧-≤≤⎪⎪=⎨⎪-+⎪⎩或，∵将新函数图象向右平移()0m m >个单位长度，∴O '（m ，0），A '（m +8，0），m +4，-4），如图所示，根据图像可知：当m +4≥9且m ≤8时，即：5≤m ≤8时，平移后的函数图象在89x ≤≤时，y 的值随x 值的增大而减小．题型二：实际运用类问题【例2】（2021·湖北）如今我国的大棚（如图1）种植技术已十分成熟．小明家的菜地上有一个长为16米的蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在离地面高1米的墙体A 处，另一端固定在离地面高2米的墙体B 处，现对其横截面建立如图2所示的平面直角坐标系．已知大棚上某处离地面的高度y （米）与其离墙体A 的水平距离x （米）之间的关系满足216y x bx c =-++，现测得A ，B 两墙体之间的水平距离为6米．图2（1）直接写出b ，c 的值；（2）求大棚的最高处到地面的距离；（3）小明的爸爸欲在大棚内种植黄瓜，需搭建高为3724米的竹竿支架若干，已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿，则共需要准备多少根竹竿？【答案】（1）76b =，1c =；（2）7324米；（3）352【分析】（1）根据题意，可直接写出点A 点B 坐标，代入216y x bx c =-++，求出b 、c 即可；（2）根据（1）中函数解析式直接求顶点坐标即可；（3根据2173716624y x x =-++=，先求得大棚内可以搭建支架的土地的宽，再求得需搭建支架的面积，最后根据每平方米需要4根竹竿计算即可．【详解】解：（1）由题意知点A 坐标为(0)1，，点B 坐标为(6)2，，将A 、B 坐标代入216y x bx c =-++得：21=12666c b c ⎧⎪⎨=-⨯++⎪⎩解得：761b c ⎧=⎪⎨⎪=⎩，故76b =，1c =；（2）由221717731666224y x x x ⎛⎫=-++=--+ ⎪⎝⎭，可得当72x =时，y 有最大值7324，即大棚最高处到地面的距离为7324米；（3）由2173716624y x x =-++=，解得112x =，2132x =，又因为06x ≤≤，可知大棚内可以搭建支架的土地的宽为111622-=（米），又大棚的长为16米，故需要搭建支架部分的土地面积为1116882⨯=（平方米）共需要884352⨯=（根）竹竿．题型三：体育活动类问题【例3】（2021·广西）2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为轴，过跳台终点作水平线的垂线为轴，建立平面直角坐标系．图中的抛物线近似表示滑雪场地上的一座小山坡，某运动员从点正上方米处的点滑出，滑出后沿一段抛物线运动．（1）当运动员运动到离处的水平距离为米时，离水平线的高度为米，求抛物线的函数解析式（不要求写出自变量的取值范围）；（2）在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为米？x A y 2117C :1126y x x =-++O 4A 221:8C y x bx c =-++A 482C x 1（3）当运动员运动到坡顶正上方，且与坡顶距离超过米时，求的取值范围．【答案】（1）；（2）12米；（3）．【分析】（1）根据题意可知：点A （0，4）点B （4，8），利用待定系数法代入抛物线即可求解；（2）高度差为1米可得可得方程，由此即可求解；（3）由抛物线可知坡顶坐标为，此时即当时，运动员运动到坡顶正上方，若与坡顶距离超过米，即，由此即可求出b的取值范围．【详解】解：（1）根据题意可知：点A （0，4），点B （4，8）代入抛物线得，，解得：，∴抛物线的函数解析式；（2）∵运动员与小山坡的竖直距离为米， ∴，解得：（不合题意，舍去），，故当运动员运动水平线的水平距离为12米时，运动员与小山坡的竖直距离为米；（3）∵点A （0，4）， ∴抛物线，∵抛物线， ∴坡顶坐标为， ∵当运动员运动到坡顶正上方，且与坡顶距离超过米时，3b 213482y x x =-++3524b ≥221:8C y x bx c =-++21=1C C -2117C :1126y x x =-++61(7,)127x =32161773812y b c =-⨯++≥+221:8C y x bx c =-++2=4144=88c b c ⎧⎪⎨-⨯++⎪⎩=43=2c b ⎧⎪⎨⎪⎩2C 213482y x x =-++1221317(4)(1)182126x x x x -++--++=14x =-212x =1221:48C y x bx =-++22117161C :1=(7)1261212y x x x =-++--+61(7,)123∴，解得：．1．（2021·浙江）如图1是一座抛物线型拱桥侧面示意图．水面宽AB与桥长CD均为24m，在距离D点6米的E处，测得桥面到桥拱的距离EF为1.5m，以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系．（1）求桥拱项部O离水面的距离．（2）如图2，桥面上方有3根高度均为4m的支柱CG，OH，DI，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1m．①求出其中一条钢缆抛物线的函数表达式．②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值．【答案】（1）6m；（2）①；②2m【分析】（1）设，由题意得，求出抛物线图像解析式，求当x=12或x=-12时y1的值即可；（2）①由题意得右边的抛物线顶点为，设，将点H代入求值即可；21617743812y b=-⨯++≥+3524b≥21'(6)112y x=++211y a x=(6, 1.5)F-(6,1)222(6)1y a x=-+提分训练②设彩带长度为h ，则，代入求值即可．【详解】解（1）设，由题意得，，，，当时，，桥拱顶部离水面高度为6m ．（2）①由题意得右边的抛物线顶点为，设，，，，， (左边抛物线表达式：) ②设彩带长度为h ，则，当时，，答：彩带长度的最小值是2m ．2．（2021·河北）下图是某同学正在设计的一动画示意图，轴上依次有，，三个点，且，在上方有五个台阶（各拐角均为），每个台阶的高、宽分别是1和1．5，台阶到轴距离．从点处向右上方沿抛物线：发出一个带光的点．12h y y =-211y a x =(6, 1.5)F -11.536a ∴-=1124a ∴=-21124y x ∴=-∴12x =21112624y =-⨯=-∴(6,1)∴222(6)1y a x =-+(0,4)H 224(06)1a ∴=-+2112a ∴=221(6)112y x ∴=-+21'(6)112y x =++22221111(6)1()412248h y y x x x x =-=-+--=-+∴4x =2min h =x A O N 2AO =ON 15~T T 90︒1T x 10OK =A L 2412y x x =-++P（1）求点的横坐标，且在图中补画出轴，并直接指出点会落在哪个台阶上；（2）当点落到台阶上后立即弹起，又形成了另一条与形状相同的抛物线，且最大高度为11，求的解析式，并说明其对称轴是否与台阶有交点；（3）在轴上从左到右有两点，，且，从点向上作轴，且．在沿轴左右平移时，必须保证（2）中沿抛物线下落的点能落在边（包括端点）上，则点横坐标的最大值比最小值大多少？（注：（2）中不必写的取值范围）【答案】（1），见解析，点会落在的台阶上；（2），其对称轴与台阶有交点；（3．【分析】（1）二次函数与坐标轴的交点坐标可以直接算出，根据点的坐标可以确定轴，利用函数的性质可以判断落在那个台阶上；（2）利用二次函数图象的平移来求解抛物线，再根据函数的对称轴的值来判断是否与台阶有交点；（3）抓住二次函数图象不变，是在左右平移，要求点横坐标的最大值比最小值大多少，利用临界点法，可以确定什么时候横坐标最大，什么时候横坐标最小，从而得解．【详解】解：（1）当，，解得：，在左侧，，关于对称， A y P P L C C 5T x D E 1DE =E EB x ⊥2BE =BDE x C P BD B x (2,0)A -P 4T 2(7)11y x =--+5T 2-A y C 5T BDE B 0y =24120x x -++=2,6x x =-=A (2,0)A ∴-2412y x x =-++ 22bx a=-=轴与重合，如下图：由题意在坐标轴上标出相关信息，当时，，解得：，，∴点会落在的台阶上，坐标为，（2）设将抛物线，向下平移5个单位，向右平移的单位后与抛物线重合，则抛物线的解析式为：，由（1）知，抛物线过，将代入，，解得：（舍去，因为是对称轴左边的部分过），抛物线:，关于，且，其对称轴与台阶有交点．（3）由题意知，当沿轴左右平移，恰使抛物线下落的点过点时，此时点的横坐标值最大；当，，解得：（取舍），故点的横坐标最大值为：y ∴OK 7y =24127x x -++=1,5x x =-=4.556<< P 4T (5,7)P L a C C 2(2)11y x a =---+C (5,7)P (5,7)P 2(2)11y x a =---+27(3)11a =--+5,1a a ==(5,7)P C 2(7)11y x =--+2(7)11y x =--+ 72bx a=-=677.5<<∴5T BDE x C P D B 0y =2(7)110x --+=1277x x ==B 8当沿轴左右平移，恰使抛物线下落的点过点时，此时点的横坐标值最小；当，，解得：（舍去），故点的横坐标最小值为：，则点横坐标的最大值比最小值大：，．3．（2021·黑龙江大庆市·中考真题）如图①是甲，乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形实心铁块立放其中（圆柱形实心铁块的下底面完全落在乙槽底面上），现将甲槽中的水匀速注入乙槽，甲，乙两个水槽中水的深度()cm y 与注水时间()min x 之间的关系如图②所示，根据图象解答下列问题：（1）图②中折线EDC 表示_____________槽中水的深度与注入时间之间的关系；线段AB 表示_____________槽中水的深度与注入时间之间的关系；铁块的高度为_____________cm ．（2）注入多长时间，甲､乙两个水槽中水的深度相同？（请写出必要的计算过程）【答案】（1）乙，甲，16；（2）2分钟【分析】（1）根据图象分析可知水深减少的图象为甲槽的，水深增加的为乙槽的，并水深16cm 之后增加的变慢，即可得到铁块的高度；（2）利用待定系数法求出两个水槽中水深与时间的解析式，即可求解．【详解】解：（1）图②中折线EDC 表示乙槽中水的深度与注入时间之间的关系；线段AB 表示甲槽中水的深度与放出时间之间的关系；铁块的高度为16cm ．BDE x C P B B 2y =2(7)112x --+=1210,4x x ==B 10B 81022（2）设甲槽中水的深度为111y k x b =+，把()0,14A ，()7,0B 代入，可得 1111470b k b =⎧⎨+=⎩，解得11214k b =-⎧⎨=⎩， ∴甲槽中水的深度为1214y x =-+，根据图象可知乙槽和甲槽水深相同时，在DE 段，设乙槽DE 段水的深度为222y k x b =+，把()0,4E ，()4,16D 代入，可得 2224416b k b =⎧⎨+=⎩，解得2234k b =⎧⎨=⎩， ∴甲槽中水的深度为234y x =+，∴甲､乙两个水槽中水的深度相同时，21434x x -+=+，解得2x =，故注入2分钟时，甲､乙两个水槽中水的深度相同。

初中英语中考考点词汇精讲(共16个)

中考英语考点词汇精讲rmationinformation是不可数名词，意为“信息，情报”，常用some，much，a great deal of等修饰。

表示“一条消息”用 a piece of information。

例如：A great deal of information can be stored in the computer.计算机能储存大量的信息。

【拓展】辨析information，news与messageinformation 表示通过打听、观察及学习获得的资料。

news是不可数名词，意为“消息，新闻”,指通过广播、电视及报纸报道的事。

message是可数名词，意为“口信，消息”，指通过口头或笔头传递给他人的消息。

I like listening to news on the radio.我喜欢听广播新闻。

Sorry，he isn’t in.Could you leave a message?对不起，他不在家，请你留个口信好吗？2.past（1）past作介词，意为“经过，穿过”。

例如：Go past the hospital, and you will see the post office.经过医院，你就会看到邮局。

（2）past作名词，意为“过去”。

例如：Alice has traveled a lot in the past.爱丽丝在过去旅游了许多地方。

（3）past作形容词，意为“过去的，前任的”。

例如：Great changes have taken place in the past 20 years.在过去的20年里发生了巨大的变化。

【拓展】pass作动词，意为“经过，传递”；pass作名词，意为“关口，通过”。

例如：The school bus passed our garden.校车经过了我们的花园。

Please pass me the book.请把书递给我。

中级财务会计核心考点精讲第十六章财务报告

第十六章财务报告【内容提示】1.财务报表概述2.资产负债表3.利润表4.现金流量表5.所有者权益变动表6.财务报表附注7.合并报表基本知识第一节财务报表概述财务报表列报的基本要求（一）依据各项会计准则确认和计量的结果编制财务报表（二）列报基础（三）权责发生制（四）列报的一致性（五）依据重要性原则单独或汇总列报项目（六）财务报表项目金额间的相互抵销财务报表项目应当以总额列报，资产和负债、收入和费用不能相互抵销，即不得以净额列报，但企业会计准则另有规定的除外。

以下三种情况不属于抵销：1.一组类似交易形成的利得和损失以净额列示，但具有重要性的除外；2.资产或负债项目按扣除备抵项目后的净额列示；3.非日常活动的产生的利得和损失，以同一交易形成的收益扣减相关费用后的净额列示更能反映交易实质的。

（七）比较信息的列报（八）财务报表表首的列报要求（九）报告期间第二节资产负债表一、资产负债表的编制（一）资产和负债按流动性列报1.资产的流动性划分资产满足下列条件之一的，应当归类为流动资产：（1）预计在一个正常营业周期中变现、出售或耗用。

（2）主要为交易目的而持有。

（3）预计在资产负债表日起一年内（含一年）变现。

（4）自资产负债表日起一年内，交换其他资产或清偿负债的能力不受限制的现金或现金等价物。

【提示】并非所有交易性金融资产均为流动资产，比如自资产负债表日起超过12个月到期且预期持有超过12个月的衍生工具应当划分为非流动资产或非流动负债。

2.负债满足下列条件之一的，应当归类为流动负债：（1）预计在一个正常营业周期中清偿。

（2）主要为交易目的而持有。

（3）自资产负债日起一年内到期应予以清偿。

（4）企业无权自主地将清偿推迟至资产负债表日后一年以上。

此外，企业在判断负债的流动性划分时，对于资产负债表日后事项的有关影响需要特别的加以考虑。

【提示1】经营性负债项目即使在资产负债表日后超过一年才予清偿，仍划分为流动负债。

【提示2】关于可转换工具负债成份的分类，负债在其对手方选择的情况下可通过发行权益进行清偿的条款与在资产负债表日负债的流动性划分无关。

2020年九年级英语课件下册名师测控教案考点精讲 (16)

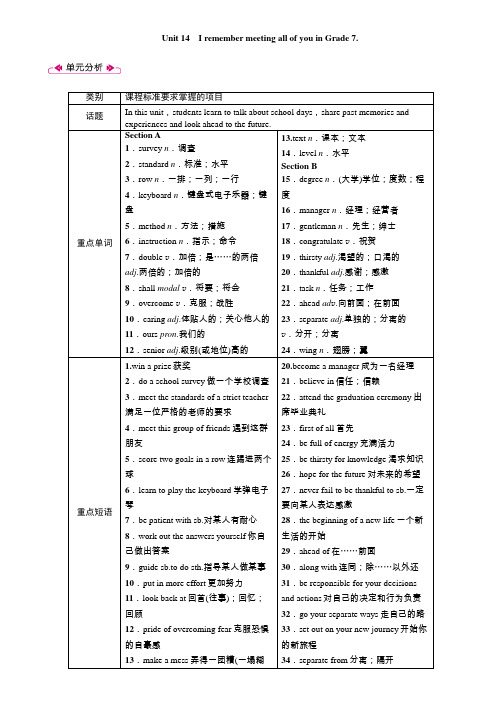
Unit 14I remember meeting all of you in Grade 7.类别课程标准要求掌握的项目话题In this unit，students learn to talk about school days，share past memories and experiences and look ahead to the future.重点单词Section A1．survey n．调查2．standard n．标准；水平3．row n．一排；一列；一行4．keyboard n．键盘式电子乐器；键盘5．method n．方法；措施6．instruction n．指示；命令7．double v．加倍；是……的两倍adj.两倍的；加倍的8．shall modal v．将要；将会9．overcome v．克服；战胜10．caring adj.体贴人的；关心他人的11．ours pron.我们的12．senior adj.级别(或地位)高的13.text n．课本；文本14．level n．水平Section B15．degree n．(大学)学位；度数；程度16．manager n．经理；经营者17．gentleman n．先生；绅士18．congratulate v．祝贺19．thirsty adj.渴望的；口渴的20．thankful adj.感谢；感激21．task n．任务；工作22．ahead ad v.向前面；在前面23．separate adj.单独的；分离的v．分开；分离24．wing n．翅膀；翼重点短语1.win a prize获奖2．do a school survey做一个学校调查3．meet the standards of a strict teacher满足一位严格的老师的要求4．meet this group of friends遇到这群朋友5．score two goals in a row连踢进两个球6．learn to play the keyboard学弹电子琴7．be patient with sb.对某人有耐心8．work out the answers yourself你自己做出答案9．guide sb.to do sth.指导某人做某事10．put in more effort更加努力11．look back at回首(往事)；回忆；回顾12．pride of overcoming fear克服恐惧的自豪感13．make a mess弄得一团糟(一塌糊20.become a manager成为一名经理21．believe in信任；信赖22．attend the graduation ceremony出席毕业典礼23．first of all首先24．be full of energy充满活力25．be thirsty for knowledge渴求知识26．hope for the future对未来的希望27．never fail to be thankful to sb.一定要向某人表达感激28．the beginning of a new life一个新生活的开始29．ahead of在……前面30．along with连同；除……以外还31．be responsible for your decisionsand actions对自己的决定和行为负责32．go your separate ways走自己的路33．set out on your new journey开始你的新旅程34．separate from分离；隔开涂)14．keep one's cool沉住气；保持冷静15．try to be on time for morningreadings尽力赶上早读16．look forward to doing sth.期望做某事17．join the school swim team加入学校游泳队18．go by(时间)逝去；过去19．get a business degree取得一个商业学位35．give sb.wings to fly给某人飞翔的翅膀36．the last day of junior high school初中的最后一天37．share so many good memories分享如此多美好的记忆重点句型1.—What happened in Grade 7 that was special？在七年级时发生了什么特别的事？—Our team won the school basketball competition.我们队赢了学校的篮球比赛。

专题16 函数与导数常见经典压轴小题全归类(精讲精练)(原卷版)

专题16函数与导数常见经典压轴小题全归类【命题规律】1、导数的计算和几何意义是高考命题的热点，多以选择题、填空题形式考查，难度较小．2、应用导数研究函数的单调性、极值、最值多在选择题、填空题靠后的位置考查，难度中等偏上，属综合性问题．【核心考点目录】核心考点一：函数零点问题之分段分析法模型核心考点二：函数嵌套问题核心考点三：函数整数解问题核心考点四：唯一零点求值问题核心考点五：等高线问题核心考点六：分段函数零点问题核心考点七：函数对称问题核心考点八：零点嵌套问题核心考点九：函数零点问题之三变量问题核心考点十：倍值函数核心考点十一：函数不动点问题核心考点十二：函数的旋转问题核心考点十三：构造函数解不等式核心考点十四：导数中的距离问题核心考点十五：导数的同构思想核心考点十六：不等式恒成立之分离参数、分离函数、放缩法核心考点十七：三次函数问题核心考点十八：切线问题核心考点十九：任意存在性问题核心考点二十：双参数最值问题核心考点二十一：切线斜率与割线斜率核心考点二十二：最大值的最小值问题（平口单峰函数、铅锤距离）核心考点二十三：两边夹问题和零点相同问题核心考点二十四：函数的伸缩变换问题【真题回归】1．（2022·全国·统考高考真题）当1x =时，函数()ln bf x a x x=+取得最大值2-，则(2)f '=（） A ．1-B ．12-C ．12D ．12．（2022·全国·统考高考真题）函数()()cos 1sin 1f x x x x =+++在区间[]0,2π的最小值、最大值分别为（）A ．ππ22-，B ．3ππ22-， C ．ππ222-+，D ．3ππ222-+， 3．（多选题）（2022·全国·统考高考真题）已知函数3()1f x x x =-+，则（） A ．()f x 有两个极值点B ．()f x 有三个零点C ．点(0,1)是曲线()y f x =的对称中心D ．直线2y x =是曲线()y f x =的切线4．（2022·天津·统考高考真题）设a ∈R ，对任意实数x ，记(){}2min 2,35f x x x ax a =--+-．若()f x 至少有3个零点，则实数a 的取值范围为______.5．（2022·全国·统考高考真题）已知1x x =和2x x =分别是函数2()2e x f x a x =-（0a >且1a ≠）的极小值点和极大值点．若12x x <，则a 的取值范围是____________．6．（2022·全国·统考高考真题）若曲线()e x y x a =+有两条过坐标原点的切线，则a 的取值范围是________________．7．（2022·浙江·统考高考真题）已知函数()22,1,11,1,x x f x x x x ⎧-+≤⎪=⎨+->⎪⎩则12f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭________；若当[,]x a b ∈时，1()3f x ≤≤，则b a -的最大值是_________．8．（2022·全国·统考高考真题）曲线ln ||y x =过坐标原点的两条切线的方程为____________，____________． 9．（2022·北京·统考高考真题）设函数()()21,,2,.ax x a f x x x a -+<⎧⎪=⎨-≥⎪⎩若()f x 存在最小值，则a 的一个取值为________；a 的最大值为___________．【方法技巧与总结】1、求分段函数的函数值，要先确定要求值的自变量属于哪一段区间，然后代入该段的解析式求值，当出现()()f f a 的形式时，应从内到外依次求值；当给出函数值求自变量的值时，先假设所求的值在分段函数定义区间的各段上，然后求出相应自变量的值，切记要代入检验，看所求的自变量的值是否满足相应段自变量的取值范围．2、含有抽象函数的分段函数，在处理时首先要明确目标，即让自变量向有具体解析式的部分靠拢，其次要理解抽象函数的含义和作用（或者对函数图象的影响）．3、含分段函数的不等式在处理上通常有两种方法：一种是利用代数手段，通过对x 进行分类讨论将不等式转变为具体的不等式求解；另一种是通过作出分段函数的图象，数形结合，利用图象的特点解不等式．4、分段函数零点的求解与判断方法：（1）直接法：直接根据题设条件构造关于参数的不等式，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成球函数值域的问题加以解决；（3）数形结合法：先将解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．5、动态二次函数中静态的值：解决这类问题主要考虑二次函数的有关性质及式子变形，注意二次函数的系数、图象的开口、对称轴是否存在不变的性质，二次函数的图象是否过定点，从而简化解题．6、动态二次函数零点个数和分布问题：通常转化为相应二次函数的图象与x 轴交点的个数问题，结合二次函数的图象，通过对称轴，根的判别式，相应区间端点函数值等来考虑．7、求二次函数最值问题，应结合二次函数的图象求解，有三种常见类型：（1）对称轴变动，区间固定；（2）对称轴固定，区间变动；（3）对称轴变动，区间也变动．这时要讨论对称轴何时在区间之内，何时在区间之外．讨论的目的是确定对称轴和区间的关系，明确函数的单调情况，从而确定函数的最值．8、由于三次函数的导函数为我们最熟悉的二次函数，所以基本的研究思路是：借助导函数的图象来研究原函数的图象．如借助导函数的正负研究原函数的单调性；借助导函数的（变号）零点研究原函数的极值点（最值点）；综合借助导函数的图象画出原函数的图象并研究原函数的零点…具体来说，对于三次函数()()32 0f x ax bx cx d a =+++＞，其导函数为()()232 0f x ax bx c a '=++＞，根的判别式()243b ac ∆=-．增区间：(), x -∞，0∆≤恒成立，三次函数()f x 在R 上为增函数，没有极值点，有且只有一个零点；（2）当0∆≥时，()0f x '=有两根1x ，2x ，不妨设12x x ＜，则1223b x x a+=-，可得三次函数()f x 在()1, x -∞，()2, x +∞上为增函数，在()12, x x 上为减函数，则1x ，2x 分别为三次函数()32f x ax bx cx d=+++的两个不相等的极值点，那么：① 若()()120f x f x ⋅＞，则()f x 有且只有1个零点； ② 若()()120f x f x ⋅＜，则()f x 有3个零点； ③ 若()()120f x f x ⋅=，则()f x 有2个零点．特别地，若三次函数()()32 0f x ax bx cx d a =+++＞存在极值点0x ，且()00f x =，则()f x 地解析式为()()()20f x a x x x m =--．同理，对于三次函数()()32 0f x ax bx cx d a =+++＜，其性质也可类比得到．9、由于三次函数()()32 0f x ax bx cx d a =+++≠的导函数()232f x ax bx c '=++为二次函数，其图象变化规律具有对称性，所以三次函数图象也应当具有对称性，其图象对称中心应当为点, 33bb faa ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，此结论可以由对称性的定义加以证明．事实上，该图象对称中心的横坐标正是三次函数导函数的极值点．10、对于三次函数图象的切线问题，和一般函数的研究方法相同．导数的几何意义就是求图象在该店处切线的斜率，利用导数研究函数的切线问题，要区分“在”与“过”的不同，如果是过某一点，一定要设切点坐标，然后根据具体的条件得到方程，然后解出参数即可．11、恒成立（或存在性）问题常常运用分离参数法，转化为求具体函数的最值问题．12、如果无法分离参数，可以考虑对参数或自变量进行分类讨论，利用函数性质求解，常见的是利用函数单调性求解函数的最大、最小值．13、当不能用分离参数法或借助于分类讨论解决问题时，还可以考虑利用函数图象来求解，即利用数形结合思想解决恒成立（或存在性）问题，此时应先构造函数，作出符合已知条件的图形，再考虑在给定区间上函数图象之间的关系，得出答案或列出条件，求出参数的范围．14、两类零点问题的不同处理方法利用零点存在性定理的条件为函数图象在区间[a ，b ]上是连续不断的曲线，且()()0f a f b ⋅<．．①直接法：判断-一个零点时，若函数为单调函数，则只需取值证明()()0f a f b ⋅<．②分类讨论法：判断几个零点时，需要先结合单调性，确定分类讨论的标准，再利用零点存在性定理，在每个单调区间内取值证明()()0f a f b ⋅<．15、利用导数研究方程根（函数零点）的技巧（1）研究方程根的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等．（2）根据题目要求，画出函数图象的走势规律，标明函数极（最）值的位置．（3）利用数形结合的思想去分析问题，可以使问题的求解有一个清晰、直观的整体展现． 16、已知函数零点个数求参数的常用方法（1）分离参数法：首先分离出参数，然后利用求导的方法求出构造的新函数的最值，根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围．（2）分类讨论法：结合单调性，先确定参数分类的标准，在每个小范围内研究零点的个数是否符合题意，将满足题意的参数的各小范围并在一起，即为所求参数范围．【核心考点】核心考点一：函数零点问题之分段分析法模型【典型例题】例1．（2023·浙江奉化·高二期末）若函数322ln ()x ex mx xf x x -+-=至少存在一个零点，则m 的取值范围为（） A ．21,e e ⎛⎤-∞+ ⎥⎝⎦B ．21,e e ⎡⎫++∞⎪⎢⎣⎭C ．1,e e ⎛⎤-∞+ ⎥⎝⎦D ．1,e e ⎡⎫++∞⎪⎢⎣⎭例2．（2023·天津·耀华中学高二期中）设函数()322ln f x x ex mx x =-+-，记()()f xg x x=，若函数()g x 至少存在一个零点，则实数m 的取值范围是 A ．21,e e ⎛⎤-∞+ ⎥⎝⎦B ．210,e e ⎛⎤+ ⎥⎝⎦C ．21e ,e ⎛⎫++∞ ⎪⎝⎭D ．2211e ,e e e ⎛⎤--+ ⎥⎝⎦例3．（2023·湖南·长沙一中高三月考（文））设函数()22x xf x x x a e=--+（其中e 为自然对数的底数），若函数()f x 至少存在一个零点，则实数a 的取值范围是（） A ．1(0,1]e+B ．1(0,]e e +C ．1[,)e e ++∞D ．1(,1]e-∞+核心考点二：函数嵌套问题【典型例题】例4．（2023·全国·高三专题练习）已知函数2()(1)x f x x x e =--，设关于x 的方程25()()()f x mf x m R e-=∈有n 个不同的实数解，则n 的所有可能的值为A ．3B ．1或3C ．4或6D ．3或4或6例5．（2023·全国·高三专题练习（文））已知函数()||12x f x e =-，()()11,021ln ,0x x g x x x x ⎧+≤⎪=⎨⎪->⎩若关于x 的方程()()0g f x m -=有四个不同的解，则实数m 的取值集合为（） A ．ln 20,2⎛⎫ ⎪⎝⎭B ．ln 2,12⎛⎫⎪⎝⎭C ．ln 22⎧⎫⎨⎬⎩⎭D ．()0,1例6．（2023·河南·高三月考（文））已知函数()ln x f x x=，若关于x 的方程()()210f x af x a ++-=⎡⎤⎣⎦有且仅有三个不同的实数解，则实数a 的取值范围是( ) A ．()2e,1e --B ．()1e,0-C ．(),1e -∞-D ．()1e,2e -核心考点三：函数整数解问题【典型例题】例7．（2023·福建宁德·高三）当1x >时，()41ln ln 3k x x x x --<-+恒成立，则整数k 的最大值为（） A ．2-B ．1-C ．0D ．1例8．（2023·江苏·苏州大学附属中学高三月考）已知a Z ∈，关于x 的一元二次不等式260x x a -+≤的解集中有且仅有3个整数，则所有符合条件的a 的值之和是（） A ．13B ．21C ．26D ．30例9．（2023·江苏宿迁·高一月考）用符号[x ]表示不超过x 的最大整数（称为x 的整数部分），如[﹣1.2]=﹣2，[0.2]=0，[1]=1，设函数f （x ）=（1﹣ln x ）（ln x ﹣ax ）有三个不同的零点x 1，x 2，x 3，若[x 1]+[x 2]+[x 3]=6，则实数a 的取值范围是（） A ．10,e ⎛⎫⎪⎝⎭B ．ln 31,3e ⎛⎫⎪⎝⎭ C ．ln 21,2e ⎡⎫⎪⎢⎣⎭ D ．ln 2ln 3,23⎡⎫⎪⎢⎣⎭ 核心考点四：唯一零点求值问题【典型例题】例10．（2023·安徽蚌埠·模拟预测（理））已知函数()()()2ln 1ln f x x x a x =-+--有唯一零点，则a =（）A ．0B ．12-C ．1D ．2例11．（2023·辽宁沈阳·模拟预测）已知函数()(),g x h x 分别是定义在R 上的偶函数和奇函数，且()()x g x h x e x +=+，若函数()()12216x f x g x λλ-=+--有唯一零点，则正实数λ的值为（）A ．12B ．13C ．2D ．3例12．（2023·新疆·莎车县第一中学高三期中）已知函数()g x ，()h x 分别是定义在R 上的偶函数和奇函数，且()()sin xg x h e x x x ++=-，若函数()()20202320202x f g x x λλ-=---有唯一零点，则实数λ的值为 A ．1-或12B ．1或12-C ．1-或2D ．2-或1核心考点五：等高线问题【典型例题】例13．（2023·陕西·千阳县中学模拟预测（理））已知函数2()log 1f x x =-，若方程()f x a =(0)a >的4个不同实根从小到大依次为1x ，2x ，3x ，4x ，有以下三个结论：①142x x +=且232x x +=；②当1a =时，12111x x +=且34111x x +=；③21340x x x x +=．其中正确的结论个数为（） A ．0 B ．1 C ．2 D ．3例14．（2023·江苏省天一中学高三月考）已知函数2()(2)x f x x x e =-，若方程()f x a =有3个不同的实根()123123x x x x x x <<，，，则22ax -的取值范围为（） A ．10e⎡⎫-⎪⎢⎣⎭，B．1e⎡-⎢⎣⎭C．()D．(例15．（2023·浙江·高一单元测试）已知函数(){}2max ,32f x x x =-，其中{},max ,,p p q p q q p q ≥⎧=⎨<⎩，若方程()()302f x ax a =+>有四个不同的实根1x 、2x 、3x 、()41234x x x x x <<<，则1423x x x x ++的取值范围是（）A ．93,102⎫⎛-- ⎪⎝⎭B ．193,102⎫⎛-- ⎪⎝⎭C ．39,210⎫⎛- ⎪⎝⎭D ．319,210⎫⎛- ⎪⎝⎭核心考点六：分段函数零点问题【典型例题】例16．（2023·山东青岛·高三期末）已知函数2|ln(1),1()(2),1x x f x x x ⎧+-=⎨+≤-⎩，若方程()0f x m -=有4个不相同的解，则实数m 的取值范围为（） A ．(0,1]B ．[0,1)C ．(0,1)D ．[0,1]例17．（2023·全国·高三专题练习）已知函数2log ,1()11,14x x f x x x >⎧⎪=⎨+≤⎪⎩，()()g x f x kx =-，若函数()g x 有两个零点，则k 的取值范围是（） A ．10,4⎛⎤⎥⎝⎦B ．10,ln 2e ⎛⎫ ⎪⎝⎭C ．10,e ⎡⎫⎪⎢⎣⎭D ．11,42eln ⎡⎫⎪⎢⎣⎭例18．（2023·江苏·高三专题练习）已知函数22,0()log ,0x x f x x x ⎧≤=⎨>⎩，函数()()g x f x x m =++，若()g x 有两个零点，则m 的取值范围是（）． A ．[1,)-+∞B ．(,1]-∞-C ．[0,)+∞D ．[1,0)-核心考点七：函数对称问题【典型例题】例19．（2023·安徽省滁州中学高三月考（文））已知函数()22ln ,03,02x x x x f x x x x ->⎧⎪=⎨--≤⎪⎩的图象上有且仅有四个不同的点关于直线1y =的对称点在10kx y +-=的图象上,则实数k 的取值范围是A ．1,12⎛⎫⎪⎝⎭B ．13,24⎛⎫ ⎪⎝⎭C ．1,13⎛⎫ ⎪⎝⎭D ．1,22⎛⎫ ⎪⎝⎭例20．（2023·全国·高一课时练习）若直角坐标平面内的两点P ，Q 满足条件：①P ，Q 都在函数()f x 的图象上；②P ，Q 关于原点对称，则称点对[],P Q 是函数()f x 的一个“友好点对”（注：点对[],P Q 与[],Q P 看作同一个“友好点对”）．已知函数()22log ,04,0x x f x x x x >⎧=⎨--≤⎩，则此函数的“友好点对”有（）A ．0个B ．1个C ．2个D ．3个例21．（2023·福建·厦门一中高一竞赛）若函数y ＝f (x )图象上存在不同的两点A ，B 关于y 轴对称，则称点对[A ，B ]是函数y ＝f (x )的一对“黄金点对”（注：点对[A ，B ]与[B ，A ]可看作同一对“黄金点对”）已知函数2229,0()4,041232,4x x f x x x x x x x +<⎧⎪=-+≤≤⎨⎪-+>⎩，则此函数的“黄金点对”有（）A ．0对B ．1对C ．2对D ．3对核心考点八：零点嵌套问题【典型例题】例22．（2023·湖北武汉·高三月考）已知函数2()()(1)()1x x f x xe a xe a =+-+-有三个不同的零点123,,x x x .其中123x x x <<，则3122123(1)(1)(1)x x x x e x e x e ---的值为（）A ．1B ．2(1)a -C ．1-D ．1a -例23．（2023·全国·模拟预测（理））已知函数2()e e x x x ax f x a ⎛⎫=+- ⎪⎝⎭有三个不同的零点123,,x x x （其中123x x x <<），则3122312111e e ex x x x x x ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为 A ．1B ．1-C ．aD ．a -例24．（2023·浙江省杭州第二中学高三开学考试）已知函数()()()2ln ln f x ax x x x x =+--，有三个不同的零点，（其中123x x x <<），则2312123ln ln ln 111x x x x x x ⎛⎫⎛⎫⎛⎫---⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为 A ．1a - B ．1a - C ．-1 D ．1核心考点九：函数零点问题之三变量问题【典型例题】例25．（2023·全国·高三）若存在两个正实数x 、y ，使得等式3(24)(ln ln )0x a y ex y x +--=成立，其中e 为自然对数的底数，则实数a 的取值范围是（）．A ．()0-∞，B ．3(0)[)2e-∞⋃+∞，， C ．3(0]2e，D ．3[)2e+∞，例26．（2023·山东枣庄·高二期末）对于任意的实数[1,e]x ∈，总存在三个不同的实数y ，使得ln 0ye xy x ay y--=成立，其中e 为自然对数的底数，则实数a 的取值范围是A ．2(,)4e -∞-B ．2(,0)4e -C ．2[,)4e -+∞D ．2(,)4e -+∞例27．（2023·四川省新津中学高三月考（理））若存在两个正实数,x y ，使得等式330yx x e ay -=成立，其中e 为自然对数的底数，则实数a 的取值范围为A ．2[,)8e +∞B ．3(0,]27eC ．3[,)27e +∞D ．2(0,]8e核心考点十：倍值函数【典型例题】例28．（河南省郑州市第一中学2022-2023学年高三上学期期中考试数学（理）试题）对于函数()y f x =，若存在区间[],a b ，当[],x a b ∈时的值域为[](),0ka kb k >，则称()y f x =为k 倍值函数.若()2xf x e x =+是k倍值函数，则实数k 的取值范围是（） A ．()1,e ++∞B ．()2,e ++∞C ．1,e e ⎛⎫++∞ ⎪⎝⎭D ．,e e 2⎛⎫++∞ ⎪⎝⎭例29．（2023·四川·内江市教育科学研究所高二期末（文））对于函数()y f x =，若存在区间,a b ，当[],x a b ∈时，()f x 的值域为[],ka kb ，则称()y f x =为k 倍值函数.若()xf x e =是k 倍值函数，则k 的取值范围为（）A ．10,e ⎛⎫⎪⎝⎭B ．()1,eC ．(),e +∞D ．1,e ⎛⎫+∞ ⎪⎝⎭例30．（2023·吉林·长春十一高高二期中（理））对于函数()y f x =，若存在区间[],a b ，当[],x a b ∈时，()f x 的值域为[],ka kb ，则称()y f x =为k 倍值函数．若()ln f x x x =+是k 倍值函数，则k 的取值范围为（） A ．10,e ⎛⎫ ⎪⎝⎭B ．1,e ⎛⎫+∞ ⎪⎝⎭C ．11,1e ⎛⎫+ ⎪⎝⎭D ．11,e ⎛⎫++∞ ⎪⎝⎭核心考点十一：函数不动点问题【典型例题】例31．（2023·广东海珠·高三期末）设函数()f x a R e ∈，为自然对数的底数），若曲线y x x =上存在点00()x y ，使得00()f y y =，则a 的取值范围是（） A ．1e[1]e-, B ．1e[e 1]e-+， C ．[1e 1]+， D ．[1,e]例32．（2023·山西省榆社中学高三月考（理））若存在一个实数t ，使得()F t t =成立，则称t 为函数()F x 的一个不动点.设函数()1(xg x e x a =+-(a R ∈，e 为自然对数的底数)，定义在R 上的连续函数()f x 满足()()2f x f x x -+=，且当0x ≤时，()f x x '<.若存在01|()(1)2x x f x f x x ⎧⎫∈+-+⎨⎬⎩⎭，且0x 为函数()g x 的一个不动点，则实数a 的取值范围为（）A ．⎛⎫-∞ ⎪ ⎪⎝⎭ B ．⎡⎫+∞⎪⎢⎪⎣⎭ C ．⎛⎤⎥ ⎝⎦ D ．⎛⎫+∞⎪ ⎪⎝⎭例33．（2023·四川自贡·高二期末（文））设函数()()1ln 2=+-∈f x x x a a R ，若存在[]1,b e ∈(e 为自然对数的底数)，使得()()f f b b =，则实数a 的取值范围是（） A ．1,122⎡⎤--⎢⎥⎣⎦eB ．e 1,ln 212⎡⎤--⎢⎥⎣⎦C ．1,ln 212⎡⎤--⎢⎥⎣⎦D ．1,02⎡⎤-⎢⎥⎣⎦核心考点十二：函数的旋转问题【典型例题】例34．（2023·上海市建平中学高三期末）双曲线2213x y -=绕坐标原点O 旋转适当角度可以成为函数f （x ）的图象，关于此函数f （x ）有如下四个命题，其中真命题的个数为（） ①f （x ）是奇函数；②f （x ）的图象过点32⎫⎪⎪⎝⎭或32⎫-⎪⎪⎝⎭； ③f （x ）的值域是33,,22⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭；④函数y ＝f （x ）－x 有两个零点． A ．4个B ．3个C ．2个D ．1个例35．（2023·山东青岛·高三开学考试）将函数2([3,3])y x =∈-的图象绕点(3,0)-逆时针旋转(0)ααθ≤≤，得到曲线C ，对于每一个旋转角α，曲线C 都是一个函数的图象，则θ最大时的正切值为（）A ．32B ．23C ．1D 例36．（2023·浙江·高三期末）将函数π2sin 0,22x y x ⎛⎫⎡⎤=∈ ⎪⎢⎥⎣⎦⎝⎭的图像绕着原点逆时针旋转角α得到曲线T ，当(]0,αθ∈时都能使T 成为某个函数的图像，则θ的最大值是（）A ．π6B ．π4C ．3π4D ．2π3核心考点十三：构造函数解不等式【典型例题】例37．（2023·江西赣州·高三期中（文））已知函数()()f x x R ∈满足(1)1f =，且()f x 的导数1()2f x '>，则不等式||1(||)22x f x <+的解集为（） A ．(,1)-∞-B ．(1,)+∞C ．(1,1)-D ．(,1][1,)-∞-+∞例38．（2023·全国·高二课时练习）设定义在R 上的函数()f x 的导函数为()'f x ，若()()'2f x f x +<，()02021f =，则不等式()22019x x e f x e >+（其中e 为自然对数的底数）的解集为（） A ．()0+∞，B ．()2019+∞，C ．()0-∞，D ．()()02019-∞+∞，，例39．（2023·全国·高二课时练习）已知()f x 的定义域为0,，()'f x 为()f x 的导函数，且满足()()f x xf x '<-，则不等式()()()2111f x x f x +>--的解集是（）A ．0,1B ．2,C ．1,2D ．1,核心考点十四：导数中的距离问题【典型例题】例40．（2023春•荔湾区期末）设函数22()()(22)f x x a lnx a =-+-，其中0x >，a R ∈，存在0x 使得04()5f x 成立，则实数a 的值是( ) A ．15B ．25C ．12D ．1例41．（2023•龙岩模拟）若对任意的正实数t ，函数33()()()3f x x t x lnt ax =-+--在R 上都是增函数，则实数a 的取值范围是( )A ．1(,]2-∞B ．(-∞C ．(-∞D ．(-∞，2]例42．（2023•淮北一模）若存在实数x 使得关于x 的不等式2221()22x e a x ax a -+-+成立，则实数a 的取值范围是( ) A ．1{}2B ．1{}4C ．1[2，)+∞D ．1[4，)+∞核心考点十五：导数的同构思想【典型例题】例43．（2023·全国·高三专题练习）已知关于x 的不等式ln ln(1)0x e mx x m ---+≥在(0,)+∞恒成立，则m 的取值范围是（） A ．(]1,1-B ．(]1,1e --C ．(]1,1e -D ．(]1,e例44．（2023·安徽·合肥一中高三月考（理））设实数0m ＞，若对任意的()1,x ∈+∞，不等式2ln 20mxxe m-≥恒成立，则实数m 的取值范围是（） A ．1,2e ⎡⎫+∞⎪⎢⎣⎭B ．1,2⎡⎫+∞⎪⎢⎣⎭C ．[)1,+∞D ．[),e +∞例45．（2023·宁夏·石嘴山市第一中学高二月考（理））若对任意()0,x ∈+∞，不等式ln 0ax ae x ->恒成立，则实数a 的取值范围为（）A ．1,e e ⎛⎫- ⎪⎝⎭B ．1,e⎛⎫+∞ ⎪⎝⎭C ．1e e ⎛⎫ ⎪⎝⎭,D ．(),e +∞核心考点十六：不等式恒成立之分离参数、分离函数、放缩法【典型例题】例46．（2023·浙江·高三月考）已知函数2()1x f x xe =-，不等式()ln f x mx x ≥+对任意(0,)x ∈+∞恒成立，则实数m 的取值范围是（） A ．(,2]-∞B ．[0,2]C ．(2,e 1⎤-∞-⎦D ．20,1e ⎡⎤-⎣⎦例47．（2023·四川省资中县第二中学高二月考（理））关于x 的不等式()32ln 113x x a x xe x+++-≥对任意0x >恒成立，则a 的取值范围是（）． A ．(],1-∞-B ．(){},1e -∞⋃C ．[],1e --D ．(],0-∞例48．（2023·全国·高三专题练习）已知,a b ∈R ，若关于x 的不等式2ln 0x a x a b -+-≥恒成立，则ab 的最大值为_______．核心考点十七：三次函数问题【典型例题】例49．（2023·全国·高三课时练习）设函数()y f x ''=是()y f x '=的导数，经过探究发现，任意一个三次函数()()320ax bx d a f x cx =+++≠的图象都有对称中心()()00,x f x ，其中0x 满足()00f x ''=，已知函数()3272392f x x x x =-+-，则12320212022202220222022f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（） A ．2021 B ．20212C ．2022D ．40212例50．（2023·安徽·东至县第二中学高三月考（理））人们在研究学习过程中，发现：三次整式函数()f x 都有对称中心，其对称中心为00(,())x f x （其中0''()0f x =）.已知函数32()345f x x x x =-++.若()4,()10f m f n ==，则m n +=（） A ．1B ．32C ．2D ．3例51．（2023·全国·高三月考（文））已知m ，n ，p ∈R ，若三次函数()32f x x mx nx p =+++有三个零点a ，b ，c ，且满足()()3112f f -=<，()()022f f =>，则111a b c ++的取值范围是（）A ．1,13⎛⎫ ⎪⎝⎭B ．11,43⎛⎫ ⎪⎝⎭C ．11,42⎛⎫⎪⎝⎭D ．11,32⎛⎫ ⎪⎝⎭核心考点十八：切线问题【典型例题】例52．（2023·云南红河·高三月考（理））下列关于三次函数32()(0)()f x ax bx cx d a x R =+++≠∈叙述正确的是（）①函数()f x 的图象一定是中心对称图形； ②函数()f x 可能只有一个极值点； ③当03bx a≠-时，()f x 在0x x =处的切线与函数()y f x =的图象有且仅有两个交点； ④当03bx a≠-时，则过点()()00,x f x 的切线可能有一条或者三条． A ．①③B ．②③C ．①④D ．②④例53．（2023·江西·南昌二中高三月考（文））若函数2()1f x x =+的图象与曲线C:()21(0)x g x a e a =⋅+>存在公共切线，则实数a 的取值范围为 A ．220,e ⎛⎤ ⎥⎝⎦B ．240,e ⎛⎤ ⎥⎝⎦C ．21,e ⎡⎫+∞⎪⎢⎣⎭D ．23,e ⎡⎫+∞⎪⎢⎣⎭例54．（2023·全国·高二单元测试）若过点(),a b 可以作曲线e x y =的两条切线，则( ) A ．e b a <B ．e b a >C ．0e b a <<D ．0e a b <<核心考点十九：任意存在性问题【典型例题】例55．（2023·河南·郑州外国语中学高三月考（理））若不等式()()()221212log 1log 3,,13x xa x x ++-≥-∈-∞恒成立，则实数a 的范围是（） A ．[0,)+∞B ．[1,)+∞C ．(,0]-∞D ．(,1]-∞.例56．（2023·全国·高三专题练习）已知函数2()=++f x x px q 对,∀∈p q R ，总有0[1,5]∃∈x ，使()0f x m≥成立，则m 的范围是（） A ．5,2⎛⎤-∞ ⎥⎝⎦B ．(,2]-∞C ．(,3]-∞D ．(,4]-∞例57．（2023·全国·高二课时练习）已知()()1ln f x x x =+，若k ∈Z ，且()()2k x f x -<对任意2x >恒成立，则k 的最大值为（） A ．3B ．4C ．5D ．6核心考点二十：双参数最值问题【典型例题】例58．（2023·浙江·宁波市北仑中学高三开学考试）已知,a b ∈R ，且0ab ≠，对任意0x >均有()()(ln )0x a b x a x b ----≥，则（） A ．0,0a b <<B ．0,0a b <>C ．0,0a b ><D ．0,0a b >>例59．（2023·山西运城·高三期中（理））已知在函数()()0,0f x ax b a b =+>>，()()ln 2g x x =+，若对2x ∀>-，()()f x g x ≥恒成立，则实数ba的取值范围为（）A ．[)0,+∞B ．[)1,+∞C ．[)2,+∞D ．[),e +∞例60．（2023·黑龙江·鹤岗一中高三月考（理））当(1,)x ∈+∞时，不等式ln(1)230(x ax b a --+，b R ∈，0)a ≠恒成立，则ba 的最大值为（）A ．1eB ．2C ．43D ．2e核心考点二十一：切线斜率与割线斜率【典型例题】例61．（2023·广东·佛山一中高三月考）已知函数2()ln (1)1h x a x a x =+-+(0)a < ，在函数()h x 图象上任取两点,A B ，若直线AB 的斜率的绝对值都不小于5，则实数a 的取值范围是（）A ．(,0)-∞B ．⎛-∞ ⎝⎦C ．,⎛-∞ ⎝⎦D ．⎫⎪⎪⎝⎭例62．（2023·山西大同·高一期中）已知函数(),()f x g x 是定义在R 上的函数，且()f x 是奇函数，()g x 是偶函数，()()f x g x +=2x ax +，记2()()()g x h x xf x x =+，若对于任意的1212x x <<<，都有()()12120h x h x x x -<-，则实数a 的取值范围为（） A ．1,02⎡⎫-⎪⎢⎣⎭B ．(0,)+∞C ．(,1]-∞-D ．(0,2]例63．（2023·全国·高一课时练习）已知函数(),142,12x a x f x a x x ⎧≥⎪=⎨⎛⎫-+< ⎪⎪⎝⎭⎩，若对任意的1x ，2x ，且12x x ≠，都有()()12120f x f x x x ->-成立，则实数a 的取值范围是（）A ．()1,+∞B ．[)1,8C ．()4,8D ．[)4,8核心考点二十二：最大值的最小值问题（平口单峰函数、铅锤距离）【典型例题】例64．设二次函数2()(2)32f x a x ax =-++在R 上有最大值，最大值为m （a ），当m （a ）取最小值时，(a =) A ．0B ．1C ．12D例65．（2023春•绍兴期末）已知函数2()||||f x x a x b =+++，[0x ∈，1]，设()f x 的最大值为M ，若M 的最小值为1时，则a 的值可以是( ) AB ．0 CD ．1例66．（2023•济南模拟）已知函数2()||2x f x ax b x -=--+，若对任意的实数a ，b ，总存在0[1x ∈-，2]，使得0()f x m 成立，则实数m 的取值范围是( ) A ．1(,]4-∞B ．(-∞，1]2C ．(-∞，2]3D ．(-∞，1]核心考点二十三：两边夹问题和零点相同问题【典型例题】例67．（2023春•湖州期末）若存在正实数x ，y 使得不等式22414lnx x lny ln y -++-成立，则(xy += ) ABCD 例68．（2023•上饶二模）已知实数x ，y 满足2(436)326x y ln x y e x y +-+--+-，则x y +的值为( ) A ．2B ．1C ．0D ．1-例69．（2023•崇明区期末）若不等式(||)sin()06x a b x ππ--+对[1x ∈-，1]恒成立，则a b +的值等于() A ．23B ．56C ．1D ．2核心考点二十四：函数的伸缩变换问题【典型例题】例70．（2023·天津一中高三月考）定义域为R 的函数()f x 满足()()22f x f x +=，当[]0,2x 时，()[)[)232,0,11,1,22x x x x f x x -⎧-∈⎪⎪=⎨⎛⎫-∈⎪ ⎪⎪⎝⎭⎩，若当[)4,2x ∈--时，不等式()2142m f x m ≥-+恒成立，则实数m 的取值范围是（） A ．[]2,3 B ．[]1,3 C ．[]1,4D ．[]2,4例71．（2023·浙江·杭州高级中学高三期中）定义域为R 的函数()f x 满足(2)3()f x f x +=，当[0,2]x ∈时，2()2f x x x =-，若[4,2]x ∈--时，13()()18≥-f x t t恒成立，则实数t 的取值范围是( ) A ．(](],10,3-∞-B．((,0,3⎤-∞⎦C ．[)[)1,03,-+∞D ．))3,⎡⎡+∞⎣⎣例72．（2023届山西省榆林市高三二模理科数学试卷）定义域为R 的函数()f x 满足()()22f x f x +=，当[)0,2x ∈时，()[)[)2213,0,1{ln ,1,2x x x f x x x x -+∈=∈，若当[)4,2x ∈--时，函数()22f x t t ≥+恒成立，则实数t 的取值范围为（） A ．30t -≤≤B ．31t -≤≤C ．20t -≤≤D ．01t ≤≤【新题速递】一、单选题1．（2023·广西南宁·南宁二中校考一模）已知函数()2,01,011x x f x x x x ⎧≤⎪=-≤<⎨≥，若函数()()()22231g x m f x mf x =-+，存在5个零点，则m =（） A ．1B ．12C ．1或12D ．1-2．（2023春·陕西西安·高三统考期末）已知函数()e ,03,0x x f x x x ⎧≥=⎨-<⎩，若函数()()()g x f x f x =--，则函数()g x 的零点个数为（）A ．1B ．3C ．4D ．53．（2023·江西景德镇·统考模拟预测）已知函数()11,041,0x xf x x x ⎧+<⎪⎪=⎨⎪->⎪⎩，若()()12f x f x =，则12x x -的最小值为（） A ．4B ．92C ．143D ．54．（2023春·内蒙古赤峰·高三统考阶段练习）已知实数0a >，0b >，1a b +=，则下列说法中，正确的是（）． A ．114a b+≤B ．存在a ，b ，使得223a b +≥C ．22log log 1a b ⋅≤D ．存在a ，b ，使得直线10ax by 与圆224x y +=相切5．（2023·全国·高三专题练习）已知()0,2A ，()(),00B t t <，动点C 在曲线T ：()2401y x x =≤≤上，若△ABC 面积的最小值为1，则t 不可能为（） A ．4-B ．3-C ．2-D ．1-6．（2023·浙江温州·统考模拟预测）已知P 为直线=1y x --上一动点，过点P 作抛物线2:2C x y =的两条切线，切点记为A ，B ，则原点到直线AB 距离的最大值为（） A ．1BCD ．27．（2023春·江西赣州·高三赣州市赣县第三中学校考期中）已知0a >，0b >，直线2e y x b -=+与曲线ln y x a =-相切，则11a b+的最小值是（） A ．16B ．12C ．8D ．48．（2023春·江苏苏州·高三苏州中学校考阶段练习）若关于x 的不等式(41ln )ln 3k x x x x --<-+对于任意(1,)x ∈+∞恒成立，则整数k 的最大值为（） A ．-2 B ．-1 C ．0 D ．1二、多选题9．（2023·江苏苏州·苏州中学校考模拟预测）已知函数()e xf x x =-，()lng x x x =-，则下列说法正确的是（）A ．()e xg 在()0,∞+上是增函数B ．1x ∀>，不等式()()2ln f ax f x ≥恒成立，则正实数a 的最小值为2eC ．若()f x t =有两个零点12,x x ，则120x x +>D ．若()()()122f x g x t t ==>，且210x x >>，则21ln t x x -的最大值为1e10．（2023春·重庆·高三统考阶段练习）已知函数32()e 3xf x ax =-有三个不同的极值点1x ，2x ，3x ，且123x x x <<，则下列结论正确的是（）A ．2e 8a >B ．11x <-C ．2x 为函数()f x 的极大值点D ．()23e 3f x <11．（2023春·福建宁德·高三校考阶段练习）已知函数()3f x x ax b =++，其中a ，b 为实数，则下列条件能使函数()f x 仅有一个零点的是（） A ．3a =-，3b =-B ．3a =-，2b =C ．0a =，3b =-D ．1a =，2b =12．（2023春·山东潍坊·高三统考期中）定义在R 上的函数()f x 的导函数为()f x '，对于任意实数x ，都有2()e ()x f x f x -=，且满足22()()21e x f x f x x -'+=+-，则（）A ．函数()e ()x F x f x =为偶函数B ．(0)0f =C ．不等式e ()e e x xxf x +<的解集为(1,)+∞ D ．若方程2()()0f x x a x--=有两个根12,x x ，则122x x a +> 13．（2023·浙江温州·统考模拟预测）若函数()y f x =的图象上存在两个不同的点P ，Q ，使得()f x 在这两点处的切线重合，则称函数()y f x =为“切线重合函数”，下列函数中是“切线重合函数”的是（） A ．sin cos y x x =+ B ．(sin c s )o y x = C ．sin y x x =+D ．2sin y x x =+14．（2023春·江苏南京·高三统考阶段练习）已知双曲线C ：224x y -=，曲线E ：2y ax x b =++，记两条曲线过点()1,0的切线分别为1l ，2l ，且斜率均为正数，则（） A ．若=0a ，1b =，则C 与E 有一个交点 B ．若=1a ，=0b ，则C 与E 有一个交点C ．若0a b ，则1l 与E 夹角的正切值为7-D ．若==1a b ，则1l 与2l 三、填空题15．（2023·河南郑州·高三阶段练习）正实数a ，b 满足1e 4a a +=+，()ln 3b b +=，则b a -的值为____________． 16．（2023·全国·高三校联考阶段练习）已知函数()234202312342023x x x x f x x =+-+-++，()234202312342023x x x x g x x =-+-+--，设()()()53F x f x g x =+⋅-，且函数()F x 的零点均在区间[](a b a b <，，a ，)b Z ∈内，则b a -的最小值为__________．17．（2023春·广东广州·高三统考阶段练习）方程e 0x ax a -+=有唯一的实数解，实数a 的取值范围为__________．18．（2023春·山东·高三山东省实验中学校考阶段练习）已知函数()()23e ,? 0e ,? 0x x xf x x a x ⎧->=⎨-≤⎩，若()()12f x f x =，且12x x -的最大值为4，则实数a 的值为_______．19．（2023·全国·高三专题练习）若存在0a >，0b >，满足(2e )ln (2e )ln a t b a b t b a a +-=-，其中e 为自然对数的底数，则实数t 的取值范围是___________．20．（2023·四川资阳·统考模拟预测）若2224ln x ax a x ->，则a 的取值范围是______．。

不规则容器的液体压强(原卷版)-2023年中考物理二轮复习核心考点精讲与必刷题型精练(全国通用)

专题16 不规则容器的液体压强【核心考点精讲】 1、液体对容器底部压力（1）比较大小（割补法）甲图中，液体对容器底部压力液G F >；乙图中，液体对容器底部压力液G F =；丙图中，液体对容器底部压力液G F <。

（2）计算数据【规则形容器】如图乙所示，液体对容器底部压力等于液体自身重力，液G F =。

【不规则容器】如图甲、丙所示，液体对容器底部压力的计算方法 ①求液体对容器底部压强：gh p 液ρ=； ②求液体对容器底部压力：pS F =。

2、液体对容器底部压强液体对容器底部压强gh p 液ρ=（与容器形状无关）。

【必刷题型精练】1．（2022•巴中中考）如图，甲、乙、丙是三个质量和底面积都相等的容器，若在容器中装入质量相等的水。

则三个容器底部受到水的压强（）A ．甲最大B ．乙最大C ．丙最大D ．一样大2．（2022•铜仁中考）如图所示，一密闭容器放在桌面上，如图（a ）所示，此时液体对容器底的压力为F 1，容器对桌面的压强为p 1；将容器倒立放置，此时液体对容器底的压力为F 2，容器对桌面的压强为p 2，如图（b ）所示。

则下列说法正确的是（）A．F1＝F2p1＝p2B．F1＞F2p1＜p2C．F1＞F2p1＞p2D．F1＜F2p1＜p23．（2022•安顺中考）如图所示，将一个密闭的圆柱形空筒放在装有水的深桶中，用手慢慢把它竖直压入水中（水未溢出）。

在空筒完全进入水中之前，空筒每下降相同距离，下列说法正确的是（）A．桶底受到水的压强的增加量不变B．桶底受到水的压强的增加量变大C．空筒底部受到水的压强的增加量不变D．空筒底部受到水的压强的增加量变小4．（2022•大连中考）如图所示，水平桌面上有甲、乙两个质量相同的薄壁容器，两个容器开口大小相同、底面积相同，分别装有质量相同的a、b两种液体，两个容器中的液面高度不同。

下列说法正确的是（）A．两种液体密度的大小关系是ρa＞ρbB．桌面对两个容器支持力的大小关系是F甲＞F乙C．两种液体对容器底压强的大小关系是p a＜p bD．两个容器对桌面压强的大小关系是p甲＜p乙5．（2022•桂林中考）如图所示，底面积和质量都相同的甲、乙两个规则容器（容器厚度不计），装有质量相同的A、B两种液体，放在水平桌面上，液面高度相同，若液体对容器底部的压强分别为p A、p B，液体对容器底部的压力分别为F A、F B；容器对桌面的压强分别为p甲、p乙，容器对桌面的压力分别为F甲、F乙，则它们的大小关系正确的是（）A．p A＞p B，F A＞F B；p甲＝p乙，F甲＝F乙B．p A＜p B，F A＜F B；p甲＝p乙，F甲＝F乙C．p A＝p B，F A＝F B；p甲＞p乙，F甲＞F乙D．p A＜p B，F A＜F B；p甲＞p乙，F甲＞F乙6．（2022•漳州模拟）如图所示，将一圆柱体从水中匀速提起直至下表面刚好离开水面，此过程容器底受到水的压强p随时间t变化的图象大致如下列图中的（）A．B．C．D．7．（2022•长春模拟）如图所示，容器中盛有水，其中h1＝100cm，h2＝60cm，容器底面积S＝20cm2，水对容器顶的压强是（）A．10000 Pa B．2000 Pa C．6000 Pa D．4000Pa 8．（2022•自贡模拟）甲、乙两个相同的容器分别装有质量相等的酒精和水，设容器底部受到水和酒精的压强分别为p甲和p乙，则二者的关系是（）A．p甲＞p乙B．p甲＜p乙C．p甲＝p乙D．无法确定9．（2022•常德模拟）如图所示，水平桌面上放有底面积和质量都相同的甲、乙两平底容器，分别装有深度相同、质量相等的不同液体。

初中物理考点讲练考第16讲—电功率(考点精讲)(解析版)

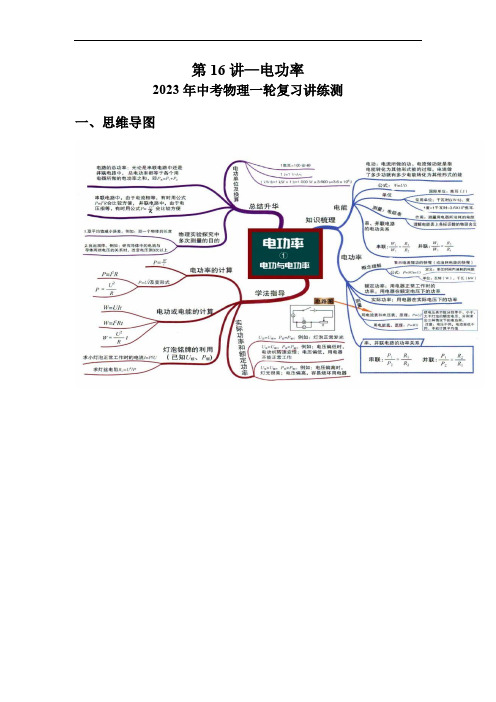
第16讲—电功率2023年中考物理一轮复习讲练测一、思维导图二、考点精讲考点1 电能1. 电功：（1）定义：电流所做的功叫电功。

电功的符号是W（2）单位：焦耳（焦，J）。

电功的常用单位是度，即千瓦时（kW·h）。

1kW·h ＝3.6×106J电流做功的过程，实际上就是电能转化为其他形式能的过程。

（3）公式：①W=UIt U=WIt I=WU t t =WU I②W=I2Rt I2= WRt I =WRt R=WI2 t t =WI2R③W=U2R t U2=WRt U =WRt R =U2 tW t =WRU2④W=UQ U=WQ Q =WU⑤W=Pt P=Wt t=WP（4）公式中的物理量：W—电能—焦耳（J）U—电压—伏特（V）I—电流—安培（A）t—时间—秒（s）R—电阻—欧姆（Ω）Q—电荷量—库伦（C）P—功率—瓦特（W）2. 电能表：测量电功的仪表是电能表（也叫电度表）。

下图是一种电能表的表盘。

表盘上的数字表示已经消耗的电能，单位是千瓦时，计数器的最后一位是小数，即1234.5 kW·h。

用电能表月底的读数减去月初的读数，就表示这个月所消耗的电能。

“220 V”表示这个电能表的额定电压是220V，应该在220V的电路中使用。

“10（20 A）”表示这个电能表的标定电流为10A，额定最大电流为20 A。

“50 Hz”表示这个电能表在50 Hz的交流电中使用；“600 revs/kW·h”表示接在这个电能表上的用电器，每消耗1千瓦时的电能，电能表上的表盘转过600转。

拓展：用电能表测量电路消耗电能的方法a．消耗电能较多时，电能表的计数器在一段时间内前后两次读数之差，就是这段时间内所消耗电能的总量．（最后一位表示小数点后第一位）b．消耗电能较少时，可通过转盘所转过的圈数（或指示灯闪烁的次数）间接计算出电路消耗的电能．如参数为Nr/（kW·h）的电能表，转盘转n转消耗的电能为W＝nN kW·h或W＝nN×3.6×106 J.3. 串并联电路电功特点：（1）在串联电路和并联电路中，电流所做的总功等于各用电器电功之和；（2）串联电路中，各用电器的电功与其电阻成正比，即W1W2=R1R2;（3）并联电路中，各用电器的电功与其电阻成反比，即W1W2=R2R1（各支路通电时间相同）。

专题16 全等三角形的核心知识点精讲(讲义)-备战2024年中考数学一轮复习考点帮

专题16 全等三角形的核心知识点精讲1.熟悉全等三角形常考5种模型2.掌握全等三角形性质，并运用全等三角形性质解答。

考点1：全等三角形的概念及性质考点2：全等三角形的判定模型一：平移型模型分析：此模型特征是有一组边共线或部分重合，另两组边分别平行，常要在移动的方向上加（减）公共线段，构造线段相等，或利用平行线性质找到对应角相等.模型示例概念两个能完全重合的三角形叫做全等三角形．性质1.两全等三角形的对应边相等，对应角相等．2.全等三角形的对应边上的高相等，对应边上的中线相等，对应角的平分线相等．3.全等三角形的周长、面积相等．模型二：轴对称模型模型分析:所给图形可沿某一直线折叠，直线两旁的部分能完全重合，重合的顶点就是全等三角形的对应顶点，解题时要注意隐含条件，即公共边或公共角相等.模型三：旋转型模型解读：将三角形绕着公共顶点旋转一定角度后，两个三角形能够完全重合，则称这两个三角形为旋转型三角形．旋转后的图形与原图形存在两种情况：①无重叠：两个三角形有公共顶点，无重叠部分，一般有一对隐含的等角②有重叠：两个三角形含有一部分公共角，运用角的和差可得到等角.模型四：一线三垂直型模型解读：一线：经过直角顶点的直线；三垂直：直角两边互相垂直，过直角的两边向直线作垂直，利用“同角的余角相等”转化找等角【题型1：平移型】【典例1】（2023•广州）如图，B是AD的中点，BC∥DE，BC＝DE．求证：∠C＝∠E．1．（2022•淮安）已知：如图，点A、D、C、F在一条直线上，且AD＝CF，AB＝DE，∠BAC＝∠EDF．求证：∠B＝∠E．2．（2022•柳州）如图，点A，D，C，F在同一条直线上，AB＝DE，BC＝EF．有下列三个条件：①AC＝D F，②∠ABC＝∠DEF，③∠ACB＝∠DFE．（1）请在上述三个条件中选取一个条件，使得△ABC≌△DEF．你选取的条件为（填写序号）（只需选一个条件，多选不得分），你判定△ABC≌△DEF的依据是（填“SSS”或“SAS”或“ASA”或“AAS”）；（2）利用（1）的结论△ABC≌△DEF．求证：AB∥DE．【题型2：对称型】【典例2】（2023•福建）如图，OA＝OC，OB＝OD，∠AOD＝∠COB．求证：AB＝CD．1．（2023•长沙）如图，AB＝AC，CD⊥AB，BE⊥AC，垂足分别为D，E．（1）求证：△ABE≌△ACD；（2）若AE＝6，CD＝8，求BD的长．2．（2022•西藏）如图，已知AD平分∠BAC，AB＝AC．求证：△ABD≌△ACD．【题型3：旋转型】【典例3】（2023•大连）如图，AC＝AE，BC＝DE，BC的延长线与DE相交于点F，∠ACF+∠AED＝180°．求证：AB＝AD．1．（2023•乐山）如图，已知AB与CD相交于点O，AC∥BD，AO＝BO，求证：AC＝BD．2．（2023•泸州）如图，点B在线段AC上，BD∥CE，AB＝EC，DB＝BC．求证：AD＝EB．3．（2023•西藏）如图，已知AB＝DE，AC＝DC，CE＝CB．求证：∠1＝∠2．【题型4：一线三等角】【典例4】（2023•陕西）如图，在△ABC中，∠B＝90°，作CD⊥AC，且使CD＝AC，作DE⊥BC，交BC 的延长线于点E．求证：CE＝AB．1．（2021•南充）如图，∠BAC＝90°，AD是∠BAC内部一条射线，若AB＝AC，BE⊥AD于点E，CF⊥A D于点F．求证：AF＝BE．一．选择题（共8小题）1．下列各组图案中，不是全等形的是（）A．B．C．D．2．已知图中的两个三角形全等，则∠1等于（）A．50°B．58°C．60°D．72°3．如图，△ABC≌△DEC，点E在AB边上，∠B＝70°，则∠ACD的度数为（）A．30°B．40°C．45°D．50°4．如图，△ABD≌△ACE，若AB＝6，AE＝4，则CD的长度为（）A．10B．6C．4D．25．如图，点B、F、C、E在一条直线上，∠A＝∠D＝90°，AB＝DE，添加下列选项中的条件，能用HL 判定△ABC≌△DEF的是（）A．AC＝DF B．∠B＝∠E C．∠ACB＝∠DFE D．BC＝EF6．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（）A．∠B＝∠C B．BE＝CD C．BD＝CE D．AD＝AE7．如图，BE⊥AC于点E，CF⊥AB于点F，若BE＝CF，则Rt△BCF≌Rt△CBE的理由是（）A．AAS B．HL C．SAS D．ASA8．如图所示，已知在△ABC中，∠C＝90°，AD＝AC，DE⊥AB交BC于点E，若∠B＝28°，则∠AEC ＝（）A．28°B．59°C．60°D．62°二．填空题（共4小题）9．如图是两个全等三角形，图中的字母表示三角形的边长，那么∠1的度数为．10．已知：如图，△ABC和△BAD中，∠C＝∠D＝90°，再添加一个条件就可以判断△ABC ≌△BAD．11．请仔细观察用直尺和圆规作一个角∠A'O'B'等于已知角∠AOB的示意图．请你根据所学的三角形全等的有关知识，说明画出∠A'O'B'＝∠AOB的依据是．12．如图，若AC平分∠BCD，∠B+∠D＝180°，AE⊥BC于点E，BC＝13cm，CD＝7cm，则BE＝．三．解答题（共4小题）13．如图，点B、E、C、F在一条直线上，AB＝DE，AC＝DF，BE＝CF．（1）求证：△ABC≌△DEF；（2）若∠D＝45°，求∠EGC的大小．14．如图，∠ACB＝90°，∠BAC＝45°，AD⊥CE，BE⊥CE，垂足分别是D，E，BE＝0.8，DE＝1.7，求AD的长．15．如图，点A，B，C在一条直线上，△ABD、△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q．（1）求证：△ABE≌△DBC；（2）求∠DMA的度数．16．如图，AC＝DC，E为AB上一点，EC＝BC，并且∠1＝∠2．（1）求证：△ABC≌△DEC；（2）若∠B＝75°，求∠3的度数．一．选择题（共7小题）1．如图，任意画一个∠A＝60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC＝120°；②AP平分∠BAC；③AP＝PC；④BD+CE＝BC；⑤S△PBA：S△PCA＝AB：AC，其中正确的个数是（）个．A．5B．4C．3D．22．如图，在△ABC中，∠BAC＝60°，BE、CD为△ABC的角平分线．BE与CD相交于点F，FG平分∠BFC，有下列四个结论：①∠BFC＝120°；②BD＝CE；③BC＝BD+CE；④若BE⊥AC，△BDF≌△CE F．其中正确的是（）A．①③B．②③④C．①③④D．①②③④3．如图，已知△ABC和△ADE都是等腰直角三角形，∠BAC＝∠EAD＝90°，BD，CE交于点F，连接A F，下列结论：①BD＝CE②∠AEF＝∠ADF③BD⊥CE④AF平分∠CAD⑤∠AFE＝45°其中结论正确的序号是（）A．①②③④B．①②④⑤C．①③④⑤D．①②③⑤4．如图，在Rt△AEB和Rt△AFC中，∠E＝∠F＝90°，BE＝CF，BE与AC相交于点M，与CF相交于点D，AB与CF相交于点N，∠EAC＝∠F AB．有下列结论：①∠B＝∠C；②ED＝FD；③AC＝BE；④△ACN≌△ABM．其中正确结论的个数是（）A．1个B．2个C．3个D．4个5．在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+2S2+2S3+S4＝（）A．6B．8C．10D．126．如图，△ABC和△CDE都是等边三角形，B，C，D三点在一条直线上，AD与BE相交于点P，AC、B E相交于点M，AD、CE相交于点N，则下列四个结论：①AD＝BE；②∠BMC＝∠ANC；③∠APM＝60°；④CP平分∠MCN．其中，一定正确的结论的个数是（）A．1B．2C．3D．47．如图，△ABC中，∠BAC＝60°，∠BAC的平分线AD与边BC的垂直平分线MD相交于D，DE⊥AB 交AB的延长线于点E，DF⊥AC于点F，现有下列结论：①DE＝DF；②DE+DF＝AD；③MD平分∠E DF；④若AE＝3，则AB+AC＝6．其中正确的个数为（）A．1个B．2个C．3个D．4个二．填空题（共5小题）8．如图，以△ABC的每一条边为边，在边AB的同侧作三个正三角形△ABD、△BCE和△ACF．已知这三个正三角形构成的图形中，甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和．则∠FCE＝°．9．如图，在△ACB中，∠ACB＝90°，AC＝BC，点C的坐标为（﹣2，0），点A的坐标为（﹣8，3），点B的坐标是．10．如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，则下列结论中，正确的是（填序号）．①∠AED＝90°；②∠ADE＝∠CDE；③DE＝BE；④AD＝AB+CD．11．如图，已知等腰△ABC中，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，下面的结论：①∠APO+∠DCO＝30°；②△OPC是等边三角形；③A C＝AO+AP；④S△ABC＝S四边形AOCP，其中正确的是．（填序号）12．如图，在等腰直角三角形ABC中，∠ACB＝90°，AC＝BC＝4，点D是AB的中点，E、F在射线AC 与射线CB上运动，且满足AE＝CF，则在运动过程中△DEF面积的最小值为．三．解答题（共4小题）13．如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．（1）如图1，若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°，求证：AD＝BE；（2）如图2，若∠ACB＝∠DCE＝90°，CF为△DCE中DE边上的高，试猜想AE，CF，BE之间的关系，并证明你的结论．14．如图所示，等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ．（1）求证：AP＝AQ；（2）试判断△APQ是什么形状的三角形？并说明你的理由．15．（1）【模型启迪】如图1，在△ABC中，D为BC边的中点，连接AD并延长至点H，使DH＝AD，连接BH，则AC与BH的数量关系为，位置关系为．（2）【模型探索】如图2，在△ABC中，D为BC边的中点，连接AD，E为AC边上一点，连接BE交A D于点F，且BF＝AC．求证：AE＝EF．16．如图1，AC＝BC，CD＝CE，∠ACB＝∠DCE＝α，AD、BE相交于点M，连接CM．（1）求证：BE＝AD；（2）用含α的式子表示∠AMB的度数（直接写出结果）；（3）当α＝90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图2，判断△CPQ的形状，并加以证明．1．（2023•甘孜州）如图，AB与CD相交于点O，AC∥BD，只添加一个条件，能判定△AOC≌△BOD的是（）A．∠A＝∠D B．AO＝BO C．AC＝BO D．AB＝CD2．（2023•北京）如图，点A，B，C在同一条直线上，点B在点A，C之间，点D，E在直线AC同侧，AB ＜BC，∠A＝∠C＝90°，△EAB≌△BCD，连接DE．设AB＝a，BC＝b，DE＝c，给出下面三个结论：①a+b＜c；②a+b＞；③（a+b）＞c．上述结论中，所有正确结论的序号是（）A．①②B．①③C．②③D．①②③3．（2022•黑龙江）如图，在四边形ABCD中，对角线AC，BD相交于点O，OA＝OC，请你添加一个条件，使△AOB≌△COD．4．（2023•成都）如图，已知△ABC≌△DEF，点B，E，C，F依次在同一条直线上．若BC＝8，CE＝5，则CF的长为．5．（2023•重庆）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D为BC上一点，连接AD．过点B 作BE⊥AD于点E，过点C作CF⊥AD交AD的延长线于点F．若BE＝4，CF＝1，则EF的长度为3．6．（2023•南通）如图，四边形ABCD的两条对角线AC，BD互相垂直，AC＝4，BD＝6，则AD+BC的最小值是．7．（2023•淮安）已知：如图，点D为线段BC上一点，BD＝AC，∠E＝∠ABC，DE∥AC．求证：DE＝B C．8．（2023•吉林）如图，点C在线段BD上，△ABC和△DEC中，∠A＝∠D，AB＝DE，∠B＝∠E．求证：AC＝DC．9．（2022•兰州）如图1是小军制作的燕子风筝，燕子风筝的骨架图如图2所示，AB＝AE，AC＝AD，∠B AD＝∠EAC，∠C＝50°，求∠D的大小．10．（2022•安顺）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝1，D是BC边上的一点，以AD为直角边作等腰Rt△ADE，其中∠DAE＝90°，连接CE．（1）求证：△ABD≌△ACE；（2）若∠BAD＝22.5°时，求BD的长．。