【数学】江苏省泰州市姜堰区2015届高三上学期期中考试(理)

合集下载

江苏省泰州市姜堰区高三上学期期中考试数学试题(Word版含答案).pdf

2013～2014学年度第一学期期中考试高数学试题(考试时间：120分钟总分160分) 命题人：审题人：注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的无效．一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸相应答题线上．），，则 ▲ ．”的否定是 ▲ ．函数的域为．函数的值域为． ▲ ．，则 ▲ ．满足，若，则 ▲ ．前项和为，若，则 ▲ ．设是定义在上的奇函数,当时, (为自然对数的底数),则的值为．集合，，，若，则实数的取值范围是 ▲ ．（其中）有两个相等的实根，则的最小值为 ▲ ．，若，则的取值范围是 ▲ ．，，则数列的前项和等于 ▲ ．是直线上三点，是直线外一点，，，，则＝ ▲ ．二、解答题：（6小题,共90分.解答应写出文字说明,证明过程或演算步骤．） 15．（本题满分14分），，其中． (Ⅰ)若，且，求的值； (Ⅱ)若，求的值． 16．（本题满分14分）表示的平面区域为A． (Ⅰ)画出平面区域A，并求面积； (Ⅱ)点在平面区域内，求的取值范围； (Ⅲ)一次函数的图像平分区域A的面积，求． 17．（本题满分1分）已知等差数列中，． (Ⅰ)求数列的前项和的最小值； (Ⅱ)求数列的前项和． 18．（本题满分1分） . (Ⅰ)若， (i)求曲线在点处的切线方程， (ii)求在区间上的最大值； (Ⅱ)若当时，恒成立，求实数的取值范围. 19．（本题满分16分）和互补，且AB=BC． (Ⅰ)设AB=x米，cosA=,求的解析式，并指出x的取值范围；求四边形ABCD面积的最大值． 20．(本题满分16分) 的三边长分别为，面积为，已知，. (Ⅰ)求数列的通项公式； (Ⅱ)求证：无论取何正整数，恒为定值； (Ⅲ)判断函数的单调性，并加以说明. 2013～2014学年度第一学期期中考试高数学试题(考试时间：分钟总分分) 命题人：审题人：注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的无效．(本题分分)有两个零点1,2，且在轴上的截距为3. (Ⅰ)求函数的解析式；(Ⅱ)求函数在区间[0,3]上的值域. B．在等比数列中. (Ⅰ)已知，求；(Ⅱ)已知，求. 22．(本题分)设平面向量,若存在实数和角,其中，使向量,且. 求的关系式; 若,求的最小值,并求出此时的值.(本题分). (Ⅰ)若函数在区间上有极值，求实数的取值范围； (Ⅱ)若关于的方程有实数解，求实数的取值范围； (Ⅲ)当，时，求证：.2013～2014学年度第一学期期中考试高数学 2. 3. 4. 5. 1 6. 7. 8 8.3 9. 10. 11. 12 . 13.2 14. 二、解答题 15.解：(Ⅰ)∵，∴，----------------2分 ∴，∴，----------------------4分而，∴，∴，即，------6分又，所以，---------------------------7分 (Ⅱ) ----------------------10分 ∴，即 ∴-------------------------14分 16.解：(Ⅰ)不等式表示直线及直线下方的平面区域；不等式表示直线及直线上方的平面区域；不等式表示直线及直线左侧的平面区域。

江苏省泰州市姜堰区2015届高三上学期期中考试试卷化学 Word版含答案.pdf

2014～2015学年度第一学期期中考试可能用到的相对原子质量H：1 N：14 O：16 Na：23 Al：27 S：32 Cl：35.5 Cr：52 Fe：56 Zn：65 I：127 选择题(共40分) 单项选择题：本题包括10小题，每小题2分，共计20分。

每小题只有一个选项符合题意。

1．A．B． C． D． 2．下列化学用语的表达或使用正确的是 A．氟离子的结构示意图： B．4的比例模型： C．的电子式 D．NaHCO3的电离方程式：NaHCO3==Na++H++CO32 3．下列有关物质的性质与应用相对应的是 A． B． C．铝合金的大量使用归功于人们能用焦炭等还原剂从氧化铝中获取铝 D．NH4Cl固体的试管， 4．以下实验方案可以从海洋动物柄海鞘中提取具有抗肿瘤活性的天然产物。

下列说法错误的是A．步骤需要过滤装置 B．步骤需要用到分漏斗 C．步骤需要用到坩埚 D．步骤需要蒸馏装置．下列实验装置与描述正确的是 ① ② ③ ④ A．装置 B．装置除去NO2中的NO C．装置配制1mol/L NaCl溶液定容操作 D．装置滴有淀粉碘化钾溶液的纸蝴蝶变蓝 FeCl3· 6H2O FeOOH 纳米四氧化三铁下列有关叙述不合理的是 A．．．．==2Fe3O4+3H2O+CO2 7．下列离子方程式正确的是 A．和硫酸反应：H＋==2Fe3＋H2↑ B．Na2O2溶于水产生O2：Na2O2+H2O==2Na＋+2OH+O2↑ C．+2H2O====Cl2↑+H2↑+2OH D．+3ClO+2Fe(OH)3==2FeO42+3Cl+5H2O 8．用NA表示阿伏加德罗常数的数值，下列说法正确的是 A．NA B．mol/L的氯化铁溶液中Fe3+的数目为NANA C．0.1 mol0.3molH2在一定条件下充分反应，转移电子数目为0.6NA D．常温常压下，NA 9．下列各组物质中，物质之间不可能实现如图转化的是选项XYZM A．NH3NONO2O2 B．NaOHNa2SO3NaHSO3SO2 C．Al2O3NaAlO2Al(OH)3NaOH D．MgCCOCO210．液体燃料电池相比于气体燃料电池具有体积小等优点。

江苏省泰州市姜堰区2015-2016学年高一上学期期中考试数学试题解析(解析版)

一、填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题卷相应的位置上）1.已知集合{}=12A ，,{}=23B ，,则A B ⋂= ．【答案】{}2考点：集合的交集运算2.函数()=f x 的定义域是【答案】[1,)+∞ 【解析】试题分析：要使函数有意义，需满足101x x -≥∴≥，因此定义域为[1,)+∞ 考点：函数定义域3.已知幂函数()f x x α=的图象过，则()f x = . 【答案】12x 【解析】试题分析：函数过点()()121222af a f x x ∴===∴=考点：函数求解析式4.函数2()log (2)f x x =-在[0,1]x ∈上的最大值为【答案】1 【解析】试题分析：函数由()2log ,2f t t t x ==-复合而成，由复合函数单调性的判定可知函数()f x 在定义域上是减函数，因此函数最大值为()()20log 201f =-=考点：函数单调性与最值 5.满足不等式1327x <的实数x 的取值范围是 . 【答案】3x <- 【解析】试题分析：等式1327x <转化为333x -<，结合指数函数3x y =是增函数可得3x <- 考点：指数不等式解法6.著名的Dirichlet 函数⎩⎨⎧=取无理数时取有理数时x x x D ,0,1)(，则)2(D =_________【答案】0 【解析】为无理数，当自变量x =0D =考点：分段函数求值7.若()2122,f x x x +=++，则()2f =___________.【答案】5考点：函数求值8.计算21()lg 2lg 52---=_______________ 【答案】3 【解析】试题分析：()221()lg 2lg 52lg 2lg 54lg104132---=-+=-=-= 考点：指数式对数式化简 9.已知函数2()21xf x a =-+是奇函数，则实数a 的值为______________ 【答案】1 【解析】试题分析：函数定义域为R ，函数为奇函数，可得()02000121f a a =∴-=∴=+ 考点：奇函数性质10.若函数2()(1)3f x kx k x =+-+是偶函数，则()f x 的递减区间是．【答案】(,0]-∞ 【解析】试题分析：函数为偶函数()()f x f x ∴-=恒成立()21013k k f x x ∴-=∴=∴=+，减区间为(,0]-∞考点：函数奇偶性与单调性11.若函数()lg(1)3f x x x =++-的零点为0x ，满足()0,1x k k ∈+且k Z ∈，则k= ．【答案】2考点：函数零点存在性定理12.已知函数log (3)(0,1)a y x a a =+>≠的图象过定点A ，若点A 也在函数()3xf x b =+的图象上，则3(log 2)f =【答案】179【解析】试题分析：当31x +=时0y =，所以定点()2,0A -，代入()3xf x b =+中得19b =-3log 231117(log 2)32999f =-=-= 考点：1.对数函数性质；2.对数式运算13.已知定义在R 上的函数)(x f 是满足()()0f x f x +-=，在(,0)-∞上()()12120f x f x x x -<-，且0)5(=f ，则使()0f x <的x 取值范围是___________【答案】(5,0)(5,)-⋃+∞ 【解析】试题分析：函数)(x f 是满足()()0f x f x +-=，所以函数为偶函数，由()()12120f x f x x x -<-可得函数在(,0)-∞是减函数，由0)5(=f 得(5)0f -=，结合图像可知不等式()0f x <的解集为(5,0)(5,)-+∞考点：1.函数奇偶性单调性；2.函数图像14.已知函数4log ,04()13,42x x f x x x ⎧<≤⎪=⎨-+>⎪⎩，若a b c <<且()()()f a f b f c ==，则(1)c ab +的取值范围是. 【答案】(16,64)考点：1.函数图像；2.指数函数性质二．解答题（本大题共6小题，共90分，解答时应写出文字说明、证明过程或演算步骤）15.（本题满分14分）已知全集U R =，集合{}|210,A x x =-≤{}22150B x x x =--=．（1）分别求A 、B ；（2）求U C A 和()U C A B ．【答案】（1）1(,]2A =-∞，{}3,5B =-（2）1(,)2u C A =+∞，{}()5u C A B =【解析】试题分析：解一元一次不等式得到的x 的取值范围即集合A ，解一元二次方程得到的x 的取值即集合B ，U C A为在全集中但不在集合A 中的所有元素构成的集合，()U C A B 为集合U C A 与集合B 的相同的元素构成的集合试题解析：（1）解不等式可得12x ≤，所以1(,]2A =-∞……………………………………………………3分解方程得35x =-或，所以{}3,5B =-……………………………………………………7分（2）1(,)2u C A =+∞……………………………………………………10分{}()5u C A B =……………………………………………………14分考点：1.一元一次不等式解法；2.一元二次方程解法；3.集合的交并补运算 16.（本题满分14分）已知函数f(x)＝22 , 02(1) 1 , 0x x x x ⎧<⎪⎨--≥⎪⎩．（1）写出函数f(x)的单调减区间；（2）求解方程1()2f x =．【答案】（1）单调减区间(0,1)；（2）方程的解为1,1-±试题解析：（1）当0x <时，由解析式可知不存在减区间；当0x ≥时，函数为二次函数，对称轴为1x =，因此减区间为(0,1)（2）由1()2f x =得1212x x =∴=-，或()2121112x x --=∴=1,1-±考点：1.函数单调性；2.函数求值 17.（本题满分14分）已知函数xmxx f +-=11)(．（1）当2m =时，用定义证明：)(x f 在(0,)x ∈+∞上的单调递减；（2）若不恒为0的函数)(lg )(x f x g =是奇函数，求实数m 的值．【答案】（1）详见解析（2）1=m 【解析】试题分析：（1）证明函数单调性一般采用定义法，首先在定义域内任取12x x <，判断()()12f x f x -的正负，若()()12f x f x <则函数是增函数，若()()12f x f x >则函数为减函数；（2）由()g x 是奇函数，则有()()g x g x -=-，代入函数式整理得1=m ，求解时要注意验证()g x 是否恒为零试题解析：（1）12()1xf x x -=+，设120x x <<()()()()()211212311x x f x f x x x -∴-=++12211200,10,10x x x x x x <<∴->+>+>()()120f x f x ∴->，()()12f x f x ∴>，因此函数在(0,)x ∈+∞上的单调递减；……………………………………………………7分（2）因为函数x mxx g +-=11lg)(是奇函数， mxxx mx x mx x g x g -+=+--=-+-=-∴11lg11lg 11lg ),()(， ,1111mxx x mx -+=-+∴即,11222x x m -=-∴ ,0)1(22=-∴x m .1±=∴m …………………12分当1-=m 时，011lg)(=++=xxx g 与不恒为0矛盾，所以1=m …………………14分考点：1.函数单调性证明；2.函数奇偶性判断 18.（本题满分16分）姜堰某化学试剂厂以x 千克/小时的速度匀速生产某种产品（生产条件要求110x ≤≤），每小时可获得的利润是351x x +-千元．．．（1）要使生产该产品2小时获得利润不低于30千元，求x 的取值范围；（2）要使生产120千克该产品获得的利润最大，问：该工厂应该选取何种生产速度？并求此最大利润．【答案】（1）310x ≤≤（2）该工厂应该选取6千克/小时生产速度，利润最大，且最大利润为610千元试题解析：（1）由题意可知：32(51)30,x x+-≥25143(51)(3)0,x x x x ∴--=+-≥13,5x x ∴≤-≥或…………………………………………4分又因为110x ≤≤，310x ∴≤≤…………………………………………………………………6分（2）2120331(51)120(5),[1,10]y x x x x x x=+-=-++∈…………………………………10分令11[,1]10t x =∈，2120(35)y t t ∴=-++ 当16t =即6x =时，max 610y ∴=千元。

2014-2015年江苏省泰州市姜堰区高一(上)期中数学试卷及参考答案

2014-2015学年江苏省泰州市姜堰区高一（上）期中数学试卷一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．（5分）集合A={1，2}，B={2，3}，则A∪B=．2．（5分）已知f（x+1）=x，则f（2）=．3．（5分）函数f（x）=的定义域为．4．（5分）已知幂函数f（x）=xα（α为实常数）的图象过点（2，），则f（16）=．5．（5分）已知集合M⊆{﹣1，0，2}，且M中含有两个元素，则符合条件的集合M有个．6．（5分）若函数f（x）=为奇函数，则实数a的值为．7．（5分）若函数f（x）=2x2﹣mx+3在[﹣2，+∞）上是增函数，则实数m的取值范围是．8．（5分）若不等式a≤x2﹣4x对任意x∈[0，4]恒成立，则a的取值范围是．9．（5分）已知定义域为（﹣∞，0）∪（0，+∞）的偶函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式f（x）＞0的解集为．10．（5分）若函数f（x）=lnx+2x﹣6的零点为x0，则满足x0∈（k，k+1）且k 为整数，则k=．11．（5分）设定义在R上的函数f（x）同时满足以下三个条件：①f（x）+f（﹣x）=0；②f（x+2）=f（x）；③当0＜x＜1时，，则=．12．（5分）已知实数m≠0，函数，若f（2﹣m）=f（2+m），则实数m的值为．13．（5分）已知函数f（x）=|log2x|，正实数m，n满足m＜n，且f（m）=f（n），若f（x）在区间[m2，n]上的最大值为2，则n+m=．14．（5分）已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣3x．则函数g（x）=f（x）﹣x+3的零点的集合为．二、解答题：（本大题共6小题，共90分.解答应写出文字说明，证明过程或演算步骤．）15．（14分）若函数f（x）=x2+2，g（x）=4x﹣1的定义域都是集合A，函数f（x）和g（x）的值域分别为S和T．（Ⅰ）若A=[1，2]，求S∩T；（Ⅱ）若A=[1，m]（m＞1），且S=T，求实数m的值．16．（14分）计算下列各式：（Ⅰ）lg5•lg20+（lg2）2（Ⅱ）0.027﹣﹣（﹣）﹣2+2560.75﹣+（）0．17．（14分）函数f（x）=k•a﹣x（k，a为常数，a＞0且a≠1）的图象过点A（0，1），B（3，8）．（1）求函数f（x）的解析式；（2）若函数，试判断函数g（x）的奇偶性．18．（16分）心理学家通过研究学生的学习行为发现；学生的接受能力与老师引入概念和描述问题所用的时间相关，教学开始时，学生的兴趣激增，学生的兴趣保持一段较理想的状态，随后学生的注意力开始分散，分析结果和实验表明，用f（x）表示学生掌握和接受概念的能力，x表示讲授概念的时间（单位：min），可有以下的关系：f（x）=（Ⅰ）开讲后第5min与开讲后第20min比较，学生的接受能力何时更强一些？（Ⅱ）开讲后多少min学生的接受能力最强？能维持多少时间？（Ⅲ）若一个新数学概念需要55以上（包括55）的接受能力以及13min时间，那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念？19．（16分）已知函数f（x）=log a（a＞0且a≠1）的图象经过点P（﹣，2）．（1）求函数y=f（x）的解析式；（2）设，用函数单调性的定义证明：函数y=g（x）在区间（﹣1，1）上单调递减；（3）解不等式：f（t2﹣2t﹣2）＜0．20．（16分）二次函数f（x）的图象顶点为A（1，16），且图象在x轴上截得线段长为8．（1）求函数f（x）的解析式；（2）令g（x）=（2﹣2a）x﹣f（x）；①若函数g（x）在x∈[0，2]上是单调增函数，求实数a的取值范围；②求函数g（x）在x∈[0，2]的最小值．2014-2015学年江苏省泰州市姜堰区高一（上）期中数学试卷参考答案与试题解析一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．（5分）集合A={1，2}，B={2，3}，则A∪B={1，2，3} ．【解答】解：∵A={1，2}，B={2，3}，∴A∪B={1，2，3}．故答案为：{1，2，3}2．（5分）已知f（x+1）=x，则f（2）=1．【解答】解：∵f（x+1）=x，∴f（2）=f（1+1）=1．故答案为：1．3．（5分）函数f（x）=的定义域为（﹣∞，1] ．【解答】解：由题意得：1﹣x≥0，解得：x≤1，故答案为：（﹣∞，1]．4．（5分）已知幂函数f（x）=xα（α为实常数）的图象过点（2，），则f（16）=4．【解答】解：由幂函数f（x）=xα（α为实常数）的图象过点（2，），得：所以，．则，所以，==4．故答案为4．5．（5分）已知集合M⊆{﹣1，0，2}，且M中含有两个元素，则符合条件的集合M有3个．【解答】解：由题意，M={﹣1，0}，{﹣1，2}，{0，2}共3个．故答案为：3．6．（5分）若函数f（x）=为奇函数，则实数a的值为1．【解答】解：∵函数f（x）=为奇函数，∴f（0）==0，解得a=1．经过验证满足题意．故答案为：1．7．（5分）若函数f（x）=2x2﹣mx+3在[﹣2，+∞）上是增函数，则实数m的取值范围是m≤﹣8．【解答】解：函数f（x）=2x2﹣mx+3的对称轴是x=，∵在[﹣2，+∞）上是增函数，∴≤﹣2，解得m≤﹣8，故答案为：m≤﹣8．8．（5分）若不等式a≤x2﹣4x对任意x∈[0，4]恒成立，则a的取值范围是（﹣∞，﹣4] ．【解答】解：令f（x）=x2﹣4x，x∈[0，4]，由f（x）的对称轴x=2，得：f（x）在[0，2）递减，在（2，4]递增，∴f（x）min=f（2）=﹣4，∴a≤﹣4，故答案为：（﹣∞，﹣4]．9．（5分）已知定义域为（﹣∞，0）∪（0，+∞）的偶函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式f（x）＞0的解集为（﹣∞，﹣1）∪（1，+∞）．【解答】解：∵偶函数f（x）在（0，+∞）上为增函数，且f（1）=0，∴不等式f（x）＞0等价为f（x）＞f（1），即f（|x|）＞f（1），则|x|＞1，解得x＞1或x＜﹣1，故答案为：（﹣∞，﹣1）∪（1，+∞）10．（5分）若函数f（x）=lnx+2x﹣6的零点为x0，则满足x0∈（k，k+1）且k 为整数，则k=2．【解答】解：∵函数的定义域为（0，+∞），且函数单调递增，∴f（2）=ln2+4﹣6=ln2﹣2＜0，f（3）=ln3+6﹣6=ln3＞0，即函数f（x）在（2，3）内存在唯一的一个零点，∵x0∈（k，k+1）且k为整数，∴k=2，故答案为：211．（5分）设定义在R上的函数f（x）同时满足以下三个条件：①f（x）+f（﹣x）=0；②f（x+2）=f（x）；③当0＜x＜1时，，则=．【解答】解：∵f（x）+f（﹣x）=0，∴f（x）是奇函数，∵f（x+2）=f（x），∴f（x）的周期为2，∴f（）=﹣f（﹣）=﹣f（﹣+2）=﹣f（），∴当x=时，f（）=，∴f（）=﹣，故答案为﹣．12．（5分）已知实数m≠0，函数，若f（2﹣m）=f（2+m），则实数m的值为和8．【解答】解：∵，∴f（x）在x≤2和x＞2时，函数均为一次函数，∵f（2﹣m）=f（2+m），∴2﹣m和2+m分别在x≤2和x＞2两段上各一个，①当2﹣m≤2，且2+m＞2，即m＞0时，∴f（2﹣m）=3（2﹣m）﹣m=6﹣4m，f（2+m）=﹣（2+m）﹣2m=﹣2﹣3m，∵f（2﹣m）=f（2+m），∴6﹣4m=﹣2﹣3m，∴m=8，；②当2﹣m＞2，且2+m≤2，即m＜0时，∴f（2﹣m）=﹣（2﹣m）﹣2m=﹣2﹣m，f（2+m）=3（2+m）﹣m=6+2m，∵f（2﹣m）=f（2+m），∴﹣2﹣m=6+2m，∴m=．综合①②，可得实数m的值为和8．故答案为：和8．13．（5分）已知函数f（x）=|log2x|，正实数m，n满足m＜n，且f（m）=f（n），若f（x）在区间[m2，n]上的最大值为2，则n+m=．【解答】解：∵f（x）=|log2x|，且f（m）=f（n），∴mn=1∵若f（x）在区间[m2，n]上的最大值为2∴|log2m2|=2∵m＜n，∴m=∴n=2∴n+m=故答案为：14．（5分）已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣3x．则函数g（x）=f（x）﹣x+3的零点的集合为{﹣2﹣，1，3} ．【解答】解：∵f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣3x，令x＜0，则﹣x＞0，∴f（﹣x）=x2+3x=﹣f（x）∴f（x）=﹣x2﹣3x，则，∵g（x）=f（x）﹣x+3∴，令g（x）=0，当x≥0时，x2﹣4x+3=0，解得x=1，或x=3，当x＜0时，﹣x2﹣4x+3=0，解得x=﹣2﹣或x=﹣2+（舍去）∴函数g（x）=f（x）﹣x+3的零点的集合为{﹣2﹣，1，3}故答案为：{﹣2﹣，1，3}．二、解答题：（本大题共6小题，共90分.解答应写出文字说明，证明过程或演算步骤．）15．（14分）若函数f（x）=x2+2，g（x）=4x﹣1的定义域都是集合A，函数f（x）和g（x）的值域分别为S和T．（Ⅰ）若A=[1，2]，求S∩T；（Ⅱ）若A=[1，m]（m＞1），且S=T，求实数m的值．【解答】解：（Ⅰ）由题意可得，S=[3，6]，T=[3，7]，所以S∩T=[3，6]；（Ⅱ）由题意可得，S=[3，m2+2]，T=[3，4m﹣1]，因为S=T，所以m2+2=4m﹣1，所以m2﹣4m+3=0 可得m=3 或m=1；又m＞1，所以m=3．16．（14分）计算下列各式：（Ⅰ）lg5•lg20+（lg2）2（Ⅱ）0.027﹣﹣（﹣）﹣2+2560.75﹣+（）0．【解答】解（Ⅰ）原式=（1﹣lg2）（1+lg2）+lg22=1﹣lg22+lg22=1．（Ⅱ）原式=﹣+﹣+1=﹣+64﹣+1=67．17．（14分）函数f（x）=k•a﹣x（k，a为常数，a＞0且a≠1）的图象过点A（0，1），B（3，8）．（1）求函数f（x）的解析式；（2）若函数，试判断函数g（x）的奇偶性．【解答】解：（1）将A（0，1），B（3，8）代入函数解析式，得，∴，∴f（x）=2x（2），其定义域为R，又∴函数g（x）为奇函数．18．（16分）心理学家通过研究学生的学习行为发现；学生的接受能力与老师引入概念和描述问题所用的时间相关，教学开始时，学生的兴趣激增，学生的兴趣保持一段较理想的状态，随后学生的注意力开始分散，分析结果和实验表明，用f（x）表示学生掌握和接受概念的能力，x表示讲授概念的时间（单位：min），可有以下的关系：f（x）=（Ⅰ）开讲后第5min与开讲后第20min比较，学生的接受能力何时更强一些？（Ⅱ）开讲后多少min学生的接受能力最强？能维持多少时间？（Ⅲ）若一个新数学概念需要55以上（包括55）的接受能力以及13min时间，那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念？【解答】解：（Ⅰ）由于f（x）=，由于f（5）=53.5，f（20）=47，则f（5）＞f（20）则开讲后第5min比开讲后第20min，学生的接受能力更强一些；（Ⅱ）当0＜x≤10时，f（x）=﹣0.1（x﹣13）2+59.9，则当x=10时，f（x）min=f（10）=59，当x＞16时，f（x）＜﹣3×16+109=59，故开讲后10min（包括10分钟）学生的接受能力最强，能维持6 min．（Ⅲ）由得6＜x≤10；由得16＜x则t=（10﹣6）+6+（﹣6）=＜13．答：老师不能在学生一直达到所需接受能力的状态下讲授完这个概念．19．（16分）已知函数f（x）=log a（a＞0且a≠1）的图象经过点P（﹣，2）．（1）求函数y=f（x）的解析式；（2）设，用函数单调性的定义证明：函数y=g（x）在区间（﹣1，1）上单调递减；（3）解不等式：f（t2﹣2t﹣2）＜0．【解答】解：（1），解得：a2=9，∵a＞0 且a≠1，∴a=3；函数y=f（x）的解析式：f（x）=log3…（3分）（2）设x1、x2为（﹣1，1）上的任意两个值，且x1＜x2，则x1+1＞0，x2+1＞0，x2﹣x1＞0∵g（x1）﹣g（x2）==…（6分）∴g（x1）﹣g（x2）＞0，∴g（x1）＞g（x2）．∴在区间（﹣，1）上单调递减．…（8分）（3）∵∴…（10分）由，得：t2﹣2t﹣2＞0或t2﹣2t﹣2＜﹣1；由得：﹣1＜t2﹣2t﹣2＜1，∴0＜t2﹣2t﹣2＜1…（13分）∴或．…（15分）20．（16分）二次函数f（x）的图象顶点为A（1，16），且图象在x轴上截得线段长为8．（1）求函数f（x）的解析式；（2）令g（x）=（2﹣2a）x﹣f（x）；①若函数g（x）在x∈[0，2]上是单调增函数，求实数a的取值范围；②求函数g（x）在x∈[0，2]的最小值．【解答】解：（1）由条件设二次函数f（x）=a（x﹣1）2+16=ax2﹣2ax+a+16，设f（x）=0的两根为：x1，x2，令x1＜x2，∵图象在x轴上截得线段长为8，由韦达定理得：（x2﹣x1）2=（x2+x1）2﹣4x2x1=（﹣2）2﹣4×a+16 a=64解得a=﹣1，∴函数的解析式为f（x）=﹣x2+2x+15．（2）①∵f（x）=﹣x2+2x+15，∴g（x）=（2﹣2a）x﹣f（x）=x2﹣2ax﹣15，而g（x）在x∈[0，2]上是单调增函数，∴对称轴x=a在[0，2]的左侧，∴a≤0．所以实数a的取值范围是{a|a≤0}．②g（x）=x2﹣2ax﹣15，x∈[0，2]，对称轴x=a，当a＞2时，g（x）min=g（2）=4﹣4a﹣15=﹣4a﹣11，当a＜0时，g（x）min=g（0）=﹣15，当0≤a≤2时，g（x）min=g（a）=a2﹣2a2﹣15=﹣a2﹣15．。

【精品】2015年江苏省泰州市姜堰区高二上学期期中数学试卷带解析答案(理科)

2014-2015学年江苏省泰州市姜堰区高二（上）期中数学试卷（理科）一、填空题（本大题共14小题，每小题5分，共70分）1．（5分）在直角坐标系中，直线2x﹣y﹣1=0的斜率是．2．（5分）圆x2+y2+2x﹣2y﹣7=0的半径是．3．（5分）椭圆+=1的焦点坐标是．4．（5分）抛物线x2=4y的准线方程为．5．（5分）双曲线的两条渐近线方程为．6．（5分）若圆x2+y2=4 与圆x2+y2﹣2mx+m2﹣1=0相外切，则实数m=．7．（5分）已知点P为直线x+y﹣4=0上一动点，则P到坐标原点的距离的最小值是．8．（5分）若方程表示椭圆，则k的取值范围是．9．（5分）已知两圆x2+y2=10和（x﹣1）2+（y﹣3）2=10相交于A，B两点，则直线AB的方程是．10．（5分）已知点P在抛物线y2=4x上运动，F为抛物线的焦点，点M的坐标为（3，2），当PM+PF取最小值时点P的坐标为．11．（5分）已知点P是圆C：x2+y2﹣4ax﹣2by﹣5=0（a＞0，b＞0）上任意一点，若点P关于直线x+2y﹣1=0的对称点仍在圆C上，则+的最小值是．12．（5分）已知O为坐标原点，点A（2，0），动点P与两点O、A的距离之比为1：，则P点轨迹方程是．13．（5分）设集合M={（x，y）|y=x+b}，N={（x，y）|y=3﹣}，当M ∩N≠∅时，则实数b的取值范围是．14．（5分）已知椭圆C：+=1（a＞b＞0）的左、右焦点分别F1、F2，过点F1的直线交椭圆C于A，B两点，若=3，且cos∠AF2B=，则椭圆C的离心率是．二、解答题（本题共6小题，共90分，解答时应写出文字说明、证明过程或演算步骤）15．（14分）已知点P为直线l1：2x﹣3y﹣1=0和直线l2：x+y+2=0的交点，M（1，2），N（﹣1，﹣5）．（Ⅰ）求过点P 且与直线l3：3x+y﹣1=0平行的直线方程；（Ⅱ）求过点P且与直线MN垂直的直线方程．16．（14分）已知三点P（5，2）、F1（﹣6，0）、F2（6，0）．（Ⅰ）求以F1、F2为焦点且过点P的椭圆标准方程；（Ⅱ）设点P、F1、F2关于直线y=x的对称点分别为P′、F1′、F2′，求以F1′、F2′为焦点且过点P′的双曲线的标准方程．17．（14分）某城市交通规划中，拟在以点O为圆心，半径为50m的高架圆形车道外侧P处开一个出口，以与圆形道相切的方式，引申一条直道连接到距圆形道圆心O正北250m的道路上C处（如图），以O为原点，OC为y轴建立如图所示的直角坐标系，求直道PC所在的直线方程，并计算出口P的坐标．18．（16分）过点P（﹣4，4）作直线l与圆O：x2+y2=4相交于A、B两点．（Ⅰ）若直线l变动时，求AB中点M的轨迹方程；（Ⅱ）若直线l的斜率为﹣，求弦AB的长；（Ⅲ）若一直线与圆O相切于点Q且与x轴的正半轴，y轴的正半轴围成一个三角形，当该三角形面积最小时，求点Q的坐标．19．（16分）在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A（1，2）其焦点F在x轴上．（Ⅰ）求抛物线C的标准方程；（Ⅱ）求过点F和OA的中点的直线的方程；（Ⅲ）设点P（﹣1，m），过点F的直线交抛物线C于B、D两点，记PB，PF，PD的斜率分别为k1，k2，k3，求证：k1+k3=2k2．20．（16分）在平面直角坐标系xOy中，已知定点A（﹣4，0），B（4，0），动点P与A、B连线的斜率之积为﹣．（Ⅰ）求点P的轨迹方程；（Ⅱ）设点P的轨迹与y轴负半轴交于点C，半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得弦长为r．（1）求圆M的方程；（2）当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如果不存在，说明理由．2014-2015学年江苏省泰州市姜堰区高二（上）期中数学试卷（理科）参考答案与试题解析一、填空题（本大题共14小题，每小题5分，共70分）1．（5分）在直角坐标系中，直线2x﹣y﹣1=0的斜率是2．【解答】解：直线2x﹣y﹣1=0可化为y=2x﹣1，由直线的斜截式可知直线斜率为：2故答案为：22．（5分）圆x2+y2+2x﹣2y﹣7=0的半径是3．【解答】解：圆x2+y2+2x﹣2y﹣7=0可化为圆（x+1）2+（y﹣1）2=9，∴圆x2+y2+2x﹣2y﹣7=0的半径是3，故答案为：33．（5分）椭圆+=1的焦点坐标是（1，0）和（﹣1，0）．【解答】解：∵椭圆+=1，∴a2=5，b2=4，∴c==1，∴椭圆焦点为（1，0）和（﹣1，0）．故答案为：（1，0）和（﹣1，0）．4．（5分）抛物线x2=4y的准线方程为y=﹣1．【解答】解：∵抛物线方程为x2=4y，∴其准线方程为：y=﹣1．故答案为：y=﹣1．5．（5分）双曲线的两条渐近线方程为．【解答】解：∵双曲线的a=4，b=3，焦点在x轴上而双曲线的渐近线方程为y=±x∴双曲线的渐近线方程为故答案为：6．（5分）若圆x2+y2=4 与圆x2+y2﹣2mx+m2﹣1=0相外切，则实数m=±3．【解答】解：圆x2+y2=4 的圆心为（0，0）、半径为2；圆x2+y2﹣2mx+m2﹣1=0，即（x﹣m）2+y2=1，表示圆心为（m，0）、半径等于1的圆．根据两圆相外切，可得圆心距等于半径之和，即|m|=2+1=3，求得m=±3，故答案为：±3．7．（5分）已知点P为直线x+y﹣4=0上一动点，则P到坐标原点的距离的最小值是．【解答】解：∵原点O（0，0）到直线x+y﹣4=0的距离为：，∴直线x+y﹣4=0上一动点P到坐标原点的距离的最小值为：．故答案为：：．8．（5分）若方程表示椭圆，则k的取值范围是（1，5）∪（5，9）．【解答】解：∵方程表示椭圆，∴9﹣k＞0，k﹣1＞0，9﹣k≠k﹣1∴k∈（1，5）∪（5，9）故答案为：（1，5）∪（5，9）．9．（5分）已知两圆x2+y2=10和（x﹣1）2+（y﹣3）2=10相交于A，B两点，则直线AB的方程是x+3y﹣5=0．【解答】解：把两圆x2+y2=10和（x﹣1）2+（y﹣3）2=10的方程相减可得x+3y ﹣5=0，此直线的方程既能满足第一个圆的方程、又能满足第二个圆的方程，故必是两个圆的公共弦所在的直线方程，故答案为：x+3y﹣5=0．10．（5分）已知点P在抛物线y2=4x上运动，F为抛物线的焦点，点M的坐标为（3，2），当PM+PF取最小值时点P的坐标为（1，2）．【解答】解：设点P在准线上的射影为D，由抛物线的定义可知PF=PD，∴要求PM+PF的最小值，即求PM+PD的最小值，只有当D，P，M三点共线时PM+PD最小，且最小值为3﹣（﹣1）=4令y=2，可得x=1，∴当PM+PF取最小值时点P的坐标为（1，2）．故答案为：（1，2）．11．（5分）已知点P是圆C：x2+y2﹣4ax﹣2by﹣5=0（a＞0，b＞0）上任意一点，若点P关于直线x+2y﹣1=0的对称点仍在圆C上，则+的最小值是18．【解答】解：x2+y2﹣4ax﹣2by﹣5=0表示的是以（2a，b）为圆心的圆，故由曲线x2+y2﹣4ax﹣2by﹣5=0上的任意一点关于直线x+2y﹣1=0的对称点仍在圆C上可得，直线x+2y﹣1=0过点（2a，b），则2a+2b﹣1=0，即a+b=（a＞0，b＞0），则+=2（a+b）（+）=2（5++）≥2（5+4）=18．（当且仅当=时，等号成立）故答案为：18．12．（5分）已知O为坐标原点，点A（2，0），动点P与两点O、A的距离之比为1：，则P点轨迹方程是（x+1）2+y2=3．【解答】解：设P（x，y），∵动点P到两点O、A的距离之比为1：，∴|PA|=|PO|，∴（x﹣2）2+y2=3（x2+y2），化简得（x+1）2+y2=3，故答案为：（x+1）2+y2=3．13．（5分）设集合M={（x，y）|y=x+b}，N={（x，y）|y=3﹣}，当M ∩N≠∅时，则实数b的取值范围是[1﹣2，3] ．【解答】解：∵集合M={（x，y）|y=x+b}，N={（x，y）|y=3﹣}，M∩N≠∅，∴直线y=x+b与半圆（x﹣2）2+（y﹣3）2=4（1≤y≤3）有交点，半圆（x﹣2）2+（y﹣3）2=4（1≤y≤3）表示：圆心在（2，3），半径为 2 的圆的下半部分，y=x+b表示斜率为1的平行线，其中b是直线在y轴上的截距，当直线与圆相切时，圆心到直线的距离等于半径，即圆心（2，3）到直线y=x+b的距离d==2，解得b=1﹣2或b=1+2（舍），由图知b的取值范围是[1﹣2，3]．∴实数b的取值范围是[1﹣2，3]．故答案为：[1﹣2，3]．14．（5分）已知椭圆C：+=1（a＞b＞0）的左、右焦点分别F1、F2，过点F1的直线交椭圆C于A，B两点，若=3，且cos∠AF2B=，则椭圆C的离心率是．【解答】解：设|F1B|=k（k＞0），则|AF1|=3k，|AB|=4k，∴|AF2|=2a﹣3k，|BF2|=2a﹣k∵cos∠AF2B=，∴（4k）2=（2a﹣3k）2+（2a﹣k）2﹣（2a﹣3k）（2a﹣k），化简可得a=3k，∴|AF2|=|AF1|=3k，|BF2|=5k∴|BF2|2=|AF2|2+|AB|2，∴AF1⊥AF2，∴△AF1F2是等腰直角三角形，∴c=a，∴e==．故答案为：．二、解答题（本题共6小题，共90分，解答时应写出文字说明、证明过程或演算步骤）15．（14分）已知点P为直线l1：2x﹣3y﹣1=0和直线l2：x+y+2=0的交点，M（1，2），N（﹣1，﹣5）．（Ⅰ）求过点P 且与直线l3：3x+y﹣1=0平行的直线方程；（Ⅱ）求过点P且与直线MN垂直的直线方程．【解答】解：由题意得：（Ⅰ），解得：，∴P（﹣1，﹣1）．∵所求直线与直线l3：3x+y﹣1=0平行，∴k=﹣3，∴所求直线方程为：3x+y+4=0．（Ⅱ）直线MN所在直线的斜率为：，∵所求直线与两点M（1，2），N（﹣1，﹣5）所在直线垂直，∴k=，则所求直线方程为：2x+7y+9=0．16．（14分）已知三点P（5，2）、F1（﹣6，0）、F2（6，0）．（Ⅰ）求以F1、F2为焦点且过点P的椭圆标准方程；（Ⅱ）设点P、F1、F2关于直线y=x的对称点分别为P′、F1′、F2′，求以F1′、F2′为焦点且过点P′的双曲线的标准方程．【解答】解：（1）由题意可设所求椭圆的标准方程为（a＞b＞0），其半焦距c=6∴，b2=a2﹣c2=9．所以所求椭圆的标准方程为（2）点P（5，2）、F1（﹣6，0）、F2（6，0）关于直线y=x的对称点分别为点P′（2，5）、F1′（0，﹣6）、F2′（0，6）．设所求双曲线的标准方程为由题意知，半焦距c1=6，，b12=c12﹣a12=36﹣20=16．所以所求双曲线的标准方程为．17．（14分）某城市交通规划中，拟在以点O为圆心，半径为50m的高架圆形车道外侧P处开一个出口，以与圆形道相切的方式，引申一条直道连接到距圆形道圆心O正北250m的道路上C处（如图），以O为原点，OC为y轴建立如图所示的直角坐标系，求直道PC所在的直线方程，并计算出口P的坐标．【解答】解：由题意可得圆形道的方程为x2+y2=502，引伸道与北向道路的交接点C的坐标为（0，250）．设CP的方程为y=kx+250，由图可知k＜0．又CP与圆O相切，∴O到CP距离=50，解得k=﹣7，∴CP的方程为y=﹣7x+250①．又OP⊥CP，∴K OP•K CP=﹣1，∴K OP=﹣=．则OP的方程是：y=x ②．由①②解得P点坐标为（35，5），∴引伸道所在的直线方程为7x+y﹣250=0，出口P的坐标是（35，5）．18．（16分）过点P（﹣4，4）作直线l与圆O：x2+y2=4相交于A、B两点．（Ⅰ）若直线l变动时，求AB中点M的轨迹方程；（Ⅱ）若直线l的斜率为﹣，求弦AB的长；（Ⅲ）若一直线与圆O相切于点Q且与x轴的正半轴，y轴的正半轴围成一个三角形，当该三角形面积最小时，求点Q的坐标．【解答】解：（Ⅰ）因为点M是AB的中点，所以OM⊥AB，则点M所在曲线是以OP为直径的圆，其方程为x（x+4）+y（y﹣4）=0，即（x+2）2+（y﹣2）2=8；…（4分）（Ⅱ）因为直线l的斜率为﹣，所以直线l的方程是：y﹣4=﹣（x+4），即x+2y﹣4=0，…（6分）设点O到直线l的距离为d，则d=，所以AB=2=；…（10分）（Ⅲ）设切点Q的坐标为（x0，y0）（x0＞0，y0＞0）．则切线斜率为﹣．所以切线方程为y﹣y0=﹣（x﹣x0）．又x02+y02=4，则x0x+y0y=4 …（12分）此时，两个坐标轴的正半轴于切线围成的三角形面积S==．…（14分）由x 02+y02=4≥2x0y0，知当且仅当x0=y0=时，x0y0有最大值．即S有最小值．因此点Q的坐标为（，）．…（16分）19．（16分）在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A（1，2）其焦点F在x轴上．（Ⅰ）求抛物线C的标准方程；（Ⅱ）求过点F和OA的中点的直线的方程；（Ⅲ）设点P（﹣1，m），过点F的直线交抛物线C于B、D两点，记PB，PF，PD的斜率分别为k1，k2，k3，求证：k1+k3=2k2．【解答】（Ⅰ）解：由题意可设抛物线的方程为：y2=2px，（p＞0），因为抛物线经过点A（1，2），所以4=2p，解得：p=2，则抛物线C的标准方程是：y2=4x．…（3分）（Ⅱ）解：由（1）知：F（1，0），OA的中点M的坐标为（），则k FM==﹣2，所以直线FM的方程是：2x+y﹣2=0．…（6分）（Ⅲ）证明：当直线的斜率不存在时，则F（1，0），B（1，2），D（1，﹣2），所以，，，则k1+k3=2k2，…（8分）当直线的斜率存在时，设为k，则直线的方程为y=k（x﹣1），设B（x1，y1），D（x2，y2），则=，同理可得：，所以=2k﹣（2k+m）﹣，…（12分）由方程组，消去y，并整理得：k2x2﹣2（k2+2）x+k2=0，所以x1x2=1，…（14分）则k1+k3=2k﹣（2k+m）×1=﹣m，又，所以k1+k3=2k2，综上所述：k1+k3=2k2．…（16分）20．（16分）在平面直角坐标系xOy中，已知定点A（﹣4，0），B（4，0），动点P与A、B连线的斜率之积为﹣．（Ⅰ）求点P的轨迹方程；（Ⅱ）设点P的轨迹与y轴负半轴交于点C，半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得弦长为r．（1）求圆M的方程；（2）当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如果不存在，说明理由．【解答】解：（Ⅰ）设P点的坐标为（x，y），则k PA=，x≠﹣4，k PB=，x≠4，因为动点P与A、B连线的斜率之积为﹣，所以，化简得：，所以点P的轨迹方程为（x≠±4）…（6分）（Ⅱ）（1）由题意知：C（0，﹣2），A（﹣4，0），所以线段AC的垂直平分线方程为y=2x+3，…（8分）设M（a，2a+3）（a＞0），则⊙M 的方程为（x﹣a）2+（y﹣2a﹣3）2=r2，因为圆心M到y轴的距离d=a，由，得：a=，…（10分）所以圆M的方程为．…（11分）（2）假设存在定直线l与动圆M均相切，当定直线l的斜率不存在时，不合题意，…（12分）当定直线l的斜率存在时，设直线l：y=kx+b，则对任意r＞0恒成立，由|k×﹣r﹣3+b|=r，得：（）2r2+（k﹣2）（b﹣3）r+（b﹣3）2=（1+k2）r2，…（14分）所以，解得：或，所以存在两条直线y=3和4x+3y﹣9=0与动圆M均相切．…（16分）赠送：初中数学几何模型举例【模型四】几何最值模型：图形特征：l运用举例：1. △ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为AP的中点，则MF的最小值为EM FB2.如图，在边长为6的菱形ABCD中，∠BAD＝60°，E为AB的中点，F为AC上一动点，则EF+BF的最小值为_________。

江苏省泰州二中2015届高三数学上学期一次限时试卷理(含解析)

2014-2015学年江苏省泰州二中高三（上）第一次限时数学试卷（理科）一、填空题（请把答案写在答题纸的指定位置上.）1．已知全集U={1，2，3，4，5}，A={1，2}，B={1，2，4}，则∁U（A∪B）= ．2．命题p：a∈M={x|x2﹣x＜0}；命题q：a∈N={x|x＜2}；p是q的条件．3．函数的定义域为（以区间作答）4．0.04﹣（﹣0.3）0+16= ．5．在△ABC中，∠A=45°，∠C=105°，BC=，则AC的长度为．6．若函数f（x）=x2+（a2﹣4a+1）x+2在区间（﹣∞，1]上是减函数，则a的取值范围是．7．设f（x）是定义在R上的奇函数，且当x＞0时，f（x）=2x﹣3，则f（﹣2）= ．8．已知向量夹角为45°，且，则= ．9．设函数．若f（x）+f′（x）是奇函数，则φ= ．10．已知S n，T n分别是等差数列{a n}，{b n}的前n项和，且=，（n∈N+）则+= ．11．如图，在直角梯形ABCD中，已知BC∥AD，AB⊥AD，AB=4，BC=2，AD=4，若P为CD的中点，则的值为．12．定义：F（x，y）=y x（x＞0，y＞0），设数列{a n}满足a n=，设S n为数列{}的前n项和，则S n1（填“＞”、“=”、“＜”）．13．设函数f（x）=x2+c，g（x）=ae x的图象的一个公共点为P（2，t），且曲线y=f（x），y=g（x）在P点处有相同的切线，若函数f（x）﹣g（x）的负零点在区间（k，k+1）（k∈Z）内，则k= ．14．下列命题中，正确的是①平面向量与的夹角为60°，=（2，0），||=1，则||=；②已知=（sinθ，），=（1，）其中θ∈（π，）则；③O是△ABC所在平面上一定点，动点P满足：+λ（+），λ∈（0，+∞），则直线AP一定通过△ABC的内心．二、解答题（将解答过程写在答题纸指定区域内）15．已知集合A={x|x2﹣2x﹣3≤0，x∈R}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}．（1）若A∩B=[0，3]，求实数m的值；（2）若A⊆∁R B，求实数m的取值范围．16．已知函数f（x）=2sin•cos+cos．（1）求函数f（x）的最小正周期及最值；（2）令g（x）=f，判断函数g（x）的奇偶性，并说明理由．17．已知向量=（m，cos2x），=（sin2x，n），函数f（x）=•，且y=f（x）的图象过点（，）和点（，﹣2）．（Ⅰ）求m，n的值；（Ⅱ）将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后得到函数y=g（x）的图象，若y=g（x）图象上的最高点到点（0，3）的距离的最小值为1，求y=g（x）的单调递增区间．18．将52名志愿者分成A，B两组参加义务植树活动，A组种植150捆白杨树苗，B组种植200捆沙棘树苗．假定A，B两组同时开始种植．（1）根据历年统计，每名志愿者种植一捆白杨树苗用时小时，种植一捆沙棘树苗用时小时．应如何分配A，B两组的人数，使植树活动持续时间最短？（2）在按（1）分配的人数种植1小时后发现，每名志愿者种植一捆白杨树苗仍用时小时，而每名志愿者种植一捆沙棘树苗实际用时小时，于是从A组抽调6名志愿者加入B组继续种植，求植树活动所持续的时间．19．已知首项为的等比数列{a n}不是递减数列，其前n项和为S n（n∈N*），且S3+a3，S5+a5，S4+a4成等差数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设，求数列{T n}的最大项的值与最小项的值．20．已知函数f（x）=xlnx，g（x）=﹣x2+ax﹣2．（1）求函数f（x）在[t，t+2]（t＞0）上的最小值；（2）若函数y=f（x）与y=g（x）的图象恰有一个公共点，求实数a的值；（3）若函数y=f（x）+g（x）有两个不同的极值点x1，x2（x1＜x2），且x2﹣x1＞ln2，求实数a的取值范围．2014-2015学年江苏省泰州二中高三（上）第一次限时数学试卷（理科）参考答案与试题解析一、填空题（请把答案写在答题纸的指定位置上.）1．已知全集U={1，2，3，4，5}，A={1，2}，B={1，2，4}，则∁U（A∪B）= {3，5} ．考点：交、并、补集的混合运算．专题：计算题．分析：首先求出A∪B，进而求出C U（A∪B）．解答：解：A∪B={1，2，4}；∴C U（A∪B）={3，5}故答案为：{3，5}．点评：本题考查了补、并的混合运算，属于基础题型．2．命题p：a∈M={x|x2﹣x＜0}；命题q：a∈N={x|x＜2}；p是q的充分不必要条件．考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：命题p：a∈M={x|x2﹣x＜0}，解出0＜x＜1；命题q：a∈N={x|x＜2}，然后判断充要条件．解答：解：命题p：a∈M={x|x2﹣x＜0}，可知x2﹣x＜0时M={x|0＜x＜1}；命题q：a∈N={x|x＜2}，显然a∈M则a∈N，即p⇒q；a∈N时则a不一定∈M，q不能推出p，p是q的充分不必要条件．故答案为：充分不必要．点评：判断充要条件的方法是：①若p⇒q为真命题且q⇒p为假命题，则命题p是命题q的充分不必要条件；②若p⇒q为假命题且q⇒p为真命题，则命题p是命题q的必要不充分条件；③若p⇒q为真命题且q⇒p为真命题，则命题p是命题q的充要条件；④若p⇒q为假命题且q⇒p为假命题，则命题p是命题q的即不充分也不必要条件．⑤判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．3．函数的定义域为[1，+∞）（以区间作答）考点：对数函数的定义域．专题：计算题．分析：欲使函数要有意义只需偶次根式下大于等于0，对数的真数大于0，建立不等式组，解之即可．解答：解：函数要有意义则即∴函数的定义域为{x|x≥1}故答案为：[1，+∞）点评：本题主要考查了偶次根式函数、对数函数的定义域，以及利用单调性解对数不等式，属于基础题．4．0.04﹣（﹣0.3）0+16= 12 ．考点：有理数指数幂的化简求值．专题：函数的性质及应用．分析：直接利用有理指数幂的运算法则求解即可．解答：解：0.04﹣（﹣0.3）0+16==﹣1+8=12．故答案为：12．点评：本题考查有理指数幂的运算，基本知识的考查．5．在△ABC中，∠A=45°，∠C=105°，BC=，则AC的长度为 1 ．考点：正弦定理．专题：解三角形．分析：由A与C的度数，利用三角形内角和定理求出B的度数，再由sinA，sinB及BC的长，利用正弦定理即可求出AC的长．解答：解：∵∠A=45°，∠C=105°，∴∠B=30°，∵BC=，∴由正弦定理=得：AC===1．故答案为：1点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．6．若函数f（x）=x2+（a2﹣4a+1）x+2在区间（﹣∞，1]上是减函数，则a的取值范围是[1，3] ．考点：二次函数的性质．专题：函数的性质及应用．分析：根据二次函数的对称轴方程为x=﹣，且函数在区间（﹣∞，1]上是减函数，可得﹣≥1，由此求得a的范围．解答：解：由于函数f（x）=x2+（a2﹣4a+1）x+2的对称轴方程为x=﹣，且函数在区间（﹣∞，1]上是减函数，故有﹣≥1，求得1≤a≤3，故答案为：[1，3]，点评：本题主要考查二次函数的性质的应用，属于基础题．7．设f（x）是定义在R上的奇函数，且当x＞0时，f（x）=2x﹣3，则f（﹣2）= ﹣1 ．考点：函数奇偶性的性质．专题：函数的性质及应用．分析：由奇函数性质得，f（﹣0）=﹣f（0），可得f（0）的值；再借助x＞0时，f（x）=2x﹣3，可将f（﹣2）转化为f（2）求解．解答：解：因为f（x）是定义在R上的奇函数，又x＞0时，f（x）=2x﹣3，所以f（﹣2）=﹣f（2）=﹣（22﹣3）=﹣1．故答案为：﹣1．点评：本题主要考查奇偶性的定义及其应用奇偶性求函数值，属基础题．8．已知向量夹角为45°，且，则= 3．考点：平面向量数量积的运算；平面向量数量积的坐标表示、模、夹角．专题：计算题；压轴题．分析：由已知可得，=，代入|2|====可求解答：解：∵，=1∴=∴|2|====解得故答案为：3点评：本题主要考查了向量的数量积定义的应用，向量的数量积性质||=是求解向量的模常用的方法9．设函数．若f（x）+f′（x）是奇函数，则φ= ．考点：余弦函数的奇偶性；导数的运算．专题：计算题；压轴题．分析：对函数求导结合两角差的正弦公式，代入整理可得，，根据奇函数的性质可得x=0时函数值为0，代入可求φ的值解答：解：，则f（x）+f′（x）=，为奇函数，令g（x）=f（x）+f′（x），即函数g（x）为奇函数，g（0）=0⇒2sin（φ）=0，∵0＜φ＜π，∴φ=．故答案为：．点评：本题主要考查了两角差的正弦公式，函数的求导公式，奇函数的性质：若函数f（x）为R上奇函数，则f（0）=0，属于对基础知识的综合考查，试题较易．10．已知S n，T n分别是等差数列{a n}，{b n}的前n项和，且=，（n∈N+）则+= ．考点：数列的求和．专题：计算题．分析：由等差数列的性质，知+==，由此能够求出结果．解答：解：∵S n，T n分别是等差数列{a n}，{b n}的前n项和，且=，（n∈N+），∴+====．故答案为：．点评：本题考查等差数列的通项公式和前n项和公式的应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．11．（2012•雁峰区校级模拟）如图，在直角梯形ABCD中，已知BC∥AD，AB⊥AD，AB=4，BC=2，AD=4，若P为CD的中点，则的值为 5 ．考点：平面向量数量积的性质及其运算律．专题：计算题；平面向量及应用．分析：由题意可得 cos∠PDA=，再由=（+）•（+）=（+2）•（﹣+），利用两个向量的数量积的定义运算求得结果．解答：解：由题意可得tan∠PDA=2，cos∠PDA=，=2，=﹣，||=||==．∴=（+）•（+）=（+2）•（﹣+）=﹣﹣•+2 =﹣5﹣×2 cos（π﹣∠PDA）+2×4=﹣5﹣×2×（﹣）+8=5，故答案为 5．点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，属于基础题．12．定义：F（x，y）=y x（x＞0，y＞0），设数列{a n}满足a n=，设S n为数列{}的前n项和，则S n＜1（填“＞”、“=”、“＜”）．考点：数列的求和．专题：等差数列与等比数列．分析：由F（x，y）=y x（x＞0，y＞0），知a n==，故===﹣，由此能求出结果．解答：解：∵F（x，y）=y x（x＞0，y＞0），∴a n==，∴===﹣，∴S n=1﹣+…+﹣=1﹣＜1．故答案为：＜．点评：本题考查数列的递推式的应用，是基础题．解题时要认真审题，仔细解答，注意裂项求和法的合理运用．13．设函数f（x）=x2+c，g（x）=ae x的图象的一个公共点为P（2，t），且曲线y=f（x），y=g（x）在P点处有相同的切线，若函数f（x）﹣g（x）的负零点在区间（k，k+1）（k∈Z）内，则k= ﹣1 ．考点：函数零点的判定定理；利用导数研究曲线上某点切线方程．专题：计算题；导数的综合应用．分析：由题意知f′（2）=g′（2），即4=ae2①，f（2）=g（2），即4+c=ae2②，联立①②可求a，c，从而得f（x）﹣g（x），利用导数可判断函数在（﹣∞，0）上的单调性，由零点判定定理可知零点的存在的区间，由此可求k．解答：解：f′（x）=2x，g′（x）=ae x，∵曲线y=f（x），y=g（x）在P（2，t）点处有相同的切线，∴f′（2）=g′（2），即4=ae2，①又P为两曲线的公共点，∴f（2）=g（2），即4+c=ae2，②由①②解得c=0，a=，令h（x）=f（x）﹣g（x）=x2﹣•e x=x2﹣4e x﹣2，则h′（x）=2x﹣4e x﹣2，当x≤0时，h′（x）＜0，∴h（x）在（﹣∞，0）上递减，又h（﹣1）=1﹣4e﹣3＞0，h（0）=﹣4e﹣2＜0，∴h（x）在（﹣1，0）内有唯一零点，由题意知（k，k+1）=（﹣1，0），∴k=﹣1．故答案为：﹣1．点评：本题考查利用导数研究曲线上某点的切线方程，考查函数的零点判定定理．曲线上某点处的切线的斜率，就是函数在该点处的导数值，是中档题14．下列命题中，正确的是①②③①平面向量与的夹角为60°，=（2，0），||=1，则||=；②已知=（sinθ，），=（1，）其中θ∈（π，）则；③O是△ABC所在平面上一定点，动点P满足：+λ（+），λ∈（0，+∞），则直线AP一定通过△ABC的内心．考点：命题的真假判断与应用．专题：综合题；压轴题．分析：①由，求出，在三个向量构成的三角形中，运用余弦定理求；②写出两个向量的数量积，运用同角三角函数的基本关系式整理即可得到结论；③把给出等式中的角的正弦值用对应边长和外接圆半径表示，移向整理后得即．由此式可知直线AP一定通过△ABC的内心．解答：解：①如图，因为=（2，0），所以，对应的向量是以和为邻边的平行四边形的对角线，由余弦定理得：=，所以①正确；②由=（sinθ，），=（1，），则==sinθ+|sinθ|，因为θ∈（π，），所以sinθ＜0，所以，所以，所以②正确；③如图，在△ABC中，由（R为三角形ABC外接圆半径），所以，所以+λ（+）=+=，即．所以直线AP一定通过△ABC的内心．所以③正确．故答案为①②③点评：本题考查了命题的真假的判断与运用，解答此题的关键是判断③，需要掌握的是表示方向上的单位向量，此题是中档题．二、解答题（将解答过程写在答题纸指定区域内）15．已知集合A={x|x2﹣2x﹣3≤0，x∈R}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}．（1）若A∩B=[0，3]，求实数m的值；（2）若A⊆∁R B，求实数m的取值范围．考点：交、并、补集的混合运算．分析：（1）根据一元二次不等式的解法，对A，B集合中的不等式进行因式分解，从而解出集合A，B，再根据A∩B=[0，3]，求出实数m的值；（2）由（1）解出的集合A，B，因为A⊆C R B，根据子集的定义和补集的定义，列出等式进行求解．解答：解：由已知得：A={x|﹣1≤x≤3}，B={x|m﹣2≤x≤m+2}．（4分）（1）∵A∩B=[0，3]∴（6分）∴，∴m=2；（8分）（2）C R B={x|x＜m﹣2，或x＞m+2}（10分）∵A⊆C R B，∴m﹣2＞3，或m+2＜﹣1，（12分）∴m＞5，或m＜﹣3．（14分）点评：此题主要考查集合的定义及集合的交集及补集运算，一元二次不等式的解法及集合间的交、并、补运算是高考中的常考内容，要认真掌握．16．已知函数f（x）=2sin•cos+cos．（1）求函数f（x）的最小正周期及最值；（2）令g（x）=f，判断函数g（x）的奇偶性，并说明理由．考点：三角函数的周期性及其求法；正弦函数的奇偶性；三角函数的最值．专题：计算题．分析：利用二倍角公式、两角和的正弦函数化简函数f（x）=2sin•cos+cos，为y=2sin，（1）直接利用周期公式求出周期，求出最值．（2）求出g（x）=f的表达式，g（x）=2cos．然后判断出奇偶性即可．解答：解：（1）∵f（x）=sin+cos=2sin，∴f（x）的最小正周期T==4π．当sin=﹣1时，f（x）取得最小值﹣2；当sin=1时，f（x）取得最大值2．（2）g（x）是偶函数．理由如下：由（1）知f（x）=2sin，又g（x）=f，∴g（x）=2sin=2sin=2cos．∵g（﹣x）=2cos=2cos=g（x），∴函数g（x）是偶函数．点评：本题是基础题，考查三角函数的化简与求值，考查三角函数的基本性质，常考题型．17．已知向量=（m，cos2x），=（sin2x，n），函数f（x）=•，且y=f（x）的图象过点（，）和点（，﹣2）．（Ⅰ）求m，n的值；（Ⅱ）将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后得到函数y=g（x）的图象，若y=g（x）图象上的最高点到点（0，3）的距离的最小值为1，求y=g（x）的单调递增区间．考点：平面向量数量积的运算；正弦函数的单调性；函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质；平面向量及应用．分析：（Ⅰ）由题意可得函数f（x）=msin2x+ncos2x，再由y=f（x）的图象过点（，）和点（，﹣2），解方程组求得m、n的值．（Ⅱ）由（Ⅰ）可得f（x）=2sin（2x+），根据函数y=Asin（ωx+φ）的图象变换规律求得g（x）=2sin（2x+2φ+）的图象，再由函数g（x）的一个最高点在y轴上，求得φ=，可得g（x）=2cos2x．令2kπ﹣π≤2x≤2kπ，k∈Z，求得x的范围，可得g（x）的增区间．解答：解：（Ⅰ）由题意可得函数f（x）=•=msin2x+ncos2x，再由y=f（x）的图象过点（，）和点（，﹣2），可得．解得 m=，n=1．（Ⅱ）由（Ⅰ）可得f（x）=sin2x+cos2x=2（sin2x+cos2x）=2sin（2x+）．将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后，得到函数g（x）=2sin[2（x+φ）+]=2sin（2x+2φ+）的图象，显然函数g（x）最高点的纵坐标为2．y=g（x）图象上各最高点到点（0，3）的距离的最小值为1，故函数g（x）的一个最高点在y轴上，∴2φ+=2kπ+，k∈Z，结合0＜φ＜π，可得φ=，故g（x）=2sin（2x+）=2cos2x．令2kπ﹣π≤2x≤2kπ，k∈Z，求得 kπ﹣≤x≤kπ，故y=g（x）的单调递增区间是[kπ﹣，kπ]，k∈Z．点评：本题主要考查两个向量的数量积公式，三角恒等变换，函数y=Asin（ωx+φ）的图象变换规律，余弦函数的单调性，体现了转化的数学思想，属于中档题．18．将52名志愿者分成A，B两组参加义务植树活动，A组种植150捆白杨树苗，B组种植200捆沙棘树苗．假定A，B两组同时开始种植．（1）根据历年统计，每名志愿者种植一捆白杨树苗用时小时，种植一捆沙棘树苗用时小时．应如何分配A，B两组的人数，使植树活动持续时间最短？（2）在按（1）分配的人数种植1小时后发现，每名志愿者种植一捆白杨树苗仍用时小时，而每名志愿者种植一捆沙棘树苗实际用时小时，于是从A组抽调6名志愿者加入B组继续种植，求植树活动所持续的时间．考点：简单线性规划的应用．专题：应用题；不等式的解法及应用．分析：（1）设A组的人数为x，则B组人数为52﹣x，可求出A组所用时间t1==，B组所用时间=令t1=t2，可求x，然后代入检验即可（2）先求出1小时后A组余下白杨，根据此时的人数可求还需时间，同理可求B组还需时间，两组所化时间进行比较即可求解植树持续时间解答：解：（1）设A组的人数为x，则B组人数为52﹣xA组所用时间t1==，B组所用时间=令t1=t2，则，解可得x=19.5①当 x=19时，t1=≈3.158，≈3.030＜3.158，总用时 3.158小时②当 x=20时，t1==3，=3.125＞3，总用时 3.125小时总用时 3.125小时＜3.158小时∴应分配 A组 20人，B组32人，总用时最短为小时（2）1小时后，A组已种=50捆，余150﹣50=100捆白杨，此后，A组20﹣6=14人，还需=≈2.857小时B组已种=48捆，余200﹣48=152捆，此后B组32+6=38人还需时间=≈2.687 小时＜2.857小时∴植树持续时间+1=点评：本题主要考查了线性规划知识在实际问题中的应用，解题的关键是要把实际问题转化为数学问题19．已知首项为的等比数列{a n}不是递减数列，其前n项和为S n（n∈N*），且S3+a3，S5+a5，S4+a4成等差数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设，求数列{T n}的最大项的值与最小项的值．考点：等差数列与等比数列的综合；等比数列的通项公式；数列的求和．专题：等差数列与等比数列．分析：（Ⅰ）设等比数列的公比为q，由S3+a3，S5+a5，S4+a4成等差数列，可构造关于q的方程，结合首项为的等比数列{a n}不是递减数列，求出q值，可得答案．（Ⅱ）由（Ⅰ）可得S n的表达式，由于数列为摆动数列，故可分类讨论求出在n为奇数和偶数时的范围，综合讨论结果，可得答案．解答：解：（Ⅰ）设等比数列的公比为q，∵S3+a3，S5+a5，S4+a4成等差数列．∴S5+a5﹣（S3+a3）=S4+a4﹣（S5+a5）即4a5=a3，故q2==又∵数列{a n}不是递减数列，且等比数列的首项为∴q=﹣∴数列{a n}的通项公式a n=×（﹣）n﹣1=（﹣1）n﹣1•（Ⅱ）由（Ⅰ）得S n=1﹣（﹣）n=当n为奇数时，S n随n的增大而减小，所以1＜S n≤S1=故0＜≤=﹣=当n为偶数时，S n随n的增大而增大，所以1＞S n≥S2=故0＞≥=﹣=综上，对于n∈N*，总有≤≤故数列{T n}的最大项的值为，最小项的值为点评：本小题主要考查等差数列的概念，等比数列的概念、通项公式、前n项和公式，数列的基本性质等基础知识，考查分类讨论思想，考查运算能力、分析问题和解析问题的能力．20．已知函数f（x）=xlnx，g（x）=﹣x2+ax﹣2．（1）求函数f（x）在[t，t+2]（t＞0）上的最小值；（2）若函数y=f（x）与y=g（x）的图象恰有一个公共点，求实数a的值；（3）若函数y=f（x）+g（x）有两个不同的极值点x1，x2（x1＜x2），且x2﹣x1＞ln2，求实数a的取值范围．考点：利用导数求闭区间上函数的最值；利用导数研究曲线上某点切线方程．专题：综合题；导数的综合应用．分析：（1）求导数，再分类讨论，确定函数在区间上的单调性，即可求得函数的最小值；（2）将函数图象只有一个公共点转化为方程只有一根，再分离参数，求出函数的最小值即可；（3）函数由两个不同的极值点转化为导函数等于0的方程有两个不同的实数根，进而转化为图象的交点问题，由此可得结论．解答：解：（1）由f′（x）=lnx+1=0，可得x=∴①时，函数f（x）在（t，）上单调递减，在（，t+2）上单调递增∴函数f（x）在[t，t+2]（t＞0）上的最小值为；②当t≥时，f（x）在[t，t+2]上单调递增，∴f（x）min=f（t）=tlnt，∴f（x）min=；（2）函数y=f（x）与y=g（x）的图象恰有一个公共点，等价于f（x）﹣g（x）=xlnx+x2﹣ax+2=0在（0，+∞）上有且只有一根，即a=在（0，+∞）上有且只有一根令h（x）=，则∴x∈（0，1）时，h′（x）＜0，函数单调递减；x∈（1，+∞）时，h′（x）＞0，函数单调递增∴a=h（x）min=h（1）=3（3）y=f（x）+g（x）=xlnx﹣x2+ax﹣2，则y′=lnx﹣2x+1+a题意即为y′=lnx﹣2x+1+a=0有两个不同的实根x1，x2（x1＜x2），即a=﹣lnx+2x﹣1有两个不同的实根x1，x2（x1＜x2），等价于直线y=a与函数G（x）=﹣lnx+2x﹣1的图象有两个不同的交点∵，∴G（x）在（0，）上单调递减，在（，+∞）上单调递增画出函数图象的大致形状（如右图），由图象知，当a＞G（x）min=G（）=ln2时，x1，x2存在，且x2﹣x1的值随着a的增大而增大而当x2﹣x1=ln2时，由题意两式相减可得∴x2=4x1代入上述方程可得此时所以，实数a的取值范围为．点评：本题考查导数知识的运用，考查函数的单调性与最值，考查分离参数法的运用，考查数形结合的数学思想，综合性强．。

2015-2016学年江苏省泰州市姜堰区高三上学期期中考试(文)

2015-2016学年江苏省泰州市姜堰区高三上学期期中考试（文）一、填空题（共14小题；共70分）1. 若复数（是虚数单位），则的实部为．2. 已知，，若，则实数的取值范围为．3. 若样本数据，，，的平均数为，则数据，，，的平均数为．4. 若，满足则的最大值为．5. 根据如图所示的伪代码，可知输出的结果为．S 1I 1While I<10S S+2I I+3End WhilePrint S6. 设，则" "是" "的条件（从“充分不必要”、“必要不充分”、“既不充分也不必要”、“充要”中选择）．7. 袋中有形状、大小都相同的只球，其中只白球、只红球、只黄球，从中一次随机摸出只球，则这只球颜色不同的概率为．8. 将函数图象上所有点的横坐标伸长到原来的倍（纵坐标不变），再将所得到的图象向右平移个单位长度得到函数，则．9. 设的内角，，的对边分别为，，，若，，，则．10. 在中，点，满足，．若，则，．11. 与直线平行且与圆相切的直线方程为．12. 过点作曲线的切线，切点为，设在轴上的投影是点，过点再作曲线的切线，切点为，设在轴上的投影是点，依次下去，得到第个切点，则点的坐标为．13. 如果函数在区间单调递减，那么的最大值为．14. 设，其中，均为实数，下列条件中，使得该三次方程仅有一个实根的有（写出所有正确条件的编号）．①，；②，；③，；④，；⑤，二、解答题（共6小题；共78分）15. 已知函数．（1）求的最小正周期；（2）求在区间上的最小值．16. 在平面直角坐标系中，已知向量，，．（1）若，求的值；（2）若与的夹角为，求的值．17. 已知的顶点是，，，为坐标原点．（1）求外接圆方程；（2）设为外接圆上任意一点，求的最大值和最小值．18. 强度分别为，的两个光源，间的距离为．已知照度与光的强度成正比，与光源距离的平方成反比，比例系数为（，为常数）．线段上有一点，设，点处总照度为．试就，，时回答下列问题．（注：点处的总照度为受，光源的照度之和）（1）试将表示成关于的函数，并写出其定义域；（2）问：为何值时，点处的总照度最小?19. 已知是各项均为正数的等比数列，是等差数列，且，，．（1）求和的通项公式；（2）设，，其前项和为．（i）求；（ii）若对任意恒成立，求的最大值．20. 已知函数．（1）求函数的单调递增区间；（2）证明：当时，；（3）确定实数的所有可能取值，使得存在，当，恒有．答案第一部分1.2.3.4.【解析】画出可行域如下图．由图知，当直线过点时，取到最大值．5.6. 充分不必要7.【解析】根据题意，记白球为，红球为，黄球为，，则一次取出只球，基本事件为，，，，，共种，其中只球的颜色不同的是，，，，共种；所以所求的概率是．8.9. 或【解析】因为，所以或．当时，，为直角三角形，；当时，，由正弦定理得，解得．所以或．10. ；【解析】．11.【解析】提示：设圆的切线方程为，所以有，解得．12.【解析】设，则，因为过点的切线方程的斜率为，所以，整理得，又，所以点的横坐标是以为首项，以为公差的等差数列，所以，所以点．13.【解析】当时，，若函数在区间上单调递减，则，所以，所以；当时，函数图象为开口向上的抛物线，若函数在区间上单调递减，则，即．因为，所以，即，当且仅当，即，时，取得最大值；当时，函数图象为开口向下的抛物线，若函数在区间上单调递减，则，即，所以．因为，所以．综上，的最大值为．14. ①②③⑤【解析】令，则．当时，，单调递增，①②正确；当时，若，则，此时函数的极大值为，极小值为，要使得只有一个零点，需或成立，解得或，所以③⑤正确，④错误．第二部分15. （1），所以的最小正周期．（2）因为，所以，所以当，即时，取最小值为．16. （1）若，则．由向量数量积的坐标公式得，．（2）与的夹角为，，即，．又，，，即．17. （1）设外接圆方程为，代入，，坐标，得解得所以外接圆的方程为．（2）设圆上任意一点，则，所以又外接圆的标准方程为，所以，所以最小值为，最大值为，即最小值为，最大值为．18. （1）由题意可知：点处受光源的照度为．点处受光源的照度为．从而，点的总照度为，其定义域为．（2）对函数求导，可得．令，得因为，所以，所以，解得当，；，，因此，时，取得极小值，且是最小值．答：时，点处的总照度最小．19. （1）设的公比为，的公差为，由题意，由已知，有解得所以的通项公式为，，的通项公式为，．（2）（i）由（1）有，则两式相减得所以（ii）令，由，得即解得对任意成立，即数列为单调递增数列，所以的最小项为因为对任意恒成立，所以，所以的最大值为．20. （1），．由，得解得．故的单调递增区间是．（2）令，，则有．当时，，所以在上单调递减，故当时，，即当时，．（3）由（2）知，当时，不存在满足题意．当时，对于，有，则，从而不存在满足题意．当时，令，，则有．由，得，解得当时，，故在内单调递增．从而当时，，即．综上，的取值范围是．。

江苏省姜堰市2015届高三上学期第一次诊断性考试数学试题 Word版

2014.92015届高三第一次诊断性考试数学试卷参考公式：样本数据1x ，2x ，… ，n x 的方差2211()n ii s x x n ==-∑，其中x =11n i i x n =∑．一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位．．．．．．置上．．． 1．设集合{}21A x x x =<∈R ，，{}20B x x =≤≤，则A B = ▲ ．2．若1i1i im n +=+（m n ∈R ，，i 为虚数单位），则mn 的值为▲ ．3．命题：“x ∃∈R ，0x ≤”的否定是 ▲ ． 4．在平面直角坐标系xOy 中，抛物线28y x =上横坐标为1的点到其焦点的距离为 ▲ ．5．设实数x ，y 满足0 0 3 24 x y x y x y ⎧⎪⎪⎨+⎪⎪+⎩≤≤≥，≥，，，则32z x y =+的最大值是▲ ．6．如图是一个算法的流程图．若输入x 的值为2，则输出y 的值是 ▲ ．7．则空气质量指数(AQI )较为稳定(方差较小)的城市为 ▲ （填甲或乙）．8．已知正三棱锥的侧棱长为1机选取两条棱，则这两条棱互相垂直的概率是 ▲ ．9．将函数()()sin 2f x x ϕ=+()0ϕ<<π的图象上所有点向右平移π6个单位后得到的图象关于原点对称，则ϕ等于 ▲ ．10．等比数列{a n }的首项为2，公比为3，前n 项和为S n ．若log 3［12a n (S 4m +1)］=9，则1n +4m 的最小值是 ▲ ．（第6题）11．若向量()cos sin αα=，a ，()cos sin ββ=，b ，且2+⋅≤a b a b ，则c o s ()αβ-的值是 ▲ ． 12．平面直角坐标系xOy 中，直线y x b =+是曲线ln y a x =的切线，则当a ＞0时，实数b 的最小值是 ▲ ．13．已知函数f (x )＝201,02(1),xx x x ⎧⎛⎫<⎪ ⎪⎨⎝⎭⎪-⎩≥，，若((2))()f f f k ->，则实数k 的取值范围为 ▲ ． 14．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若tan 7tan A B =，223a b c-=，则c =▲ ．二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答. 解答时应写出文字说明、证明过程或演算步骤．15．(本小题满分14分) 如图，在四棱柱1111ABCD A B C D -中，//AB CD ，1AB BC ⊥，且1AA AB =．（1）求证：AB ∥平面11D DCC ；（2）求证：1AB ⊥平面1A BC ．16．(本小题满分14分)在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边长，且c =－3b cos A ，tan C =34．（1）求tan B 的值；（2）若2c =，求△ABC 的面积．A 1B 1C 1CDD 1（第15题）17．(本小题满分14分)已知a 为实常数，y =f (x )是定义在(－∞，0)∪(0，+∞)上的奇函数，且当x <0时，f (x )=2x －a 3x2+1．（1）求函数f (x )的单调区间；（2）若f (x )≥a －1对一切x ＞0成立，求a 的取值范围．18．(本小题满分14分)某单位拟建一个扇环面形状的花坛(如图所示)，该扇环面是由以点O 为圆心的两个同心圆弧和延长后通过点O 的两条直线段围成．按设计要求扇环面的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为x 米，圆心角为θ（弧度）．（1）求θ关于x 的函数关系式；（2）已知在花坛的边缘(实线部分)进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为y ，求y 关于x的函数关系式，并求出x 为何值时，y 取得最大值？(第18题图)19．(本小题满分16分)已知ABC ∆的三个顶点(1,0)A -，(1,0)B ，(3,2)C ，其外接圆为H ．(1)若直线l 过点C ，且被H 截得的弦长为2，求直线l 的方程；(2)对于线段BH 上的任意一点P ，若在以C 为圆心的圆上都存在不同的两点,M N ，使得点M 是线段PN 的中点，求C 的半径r 的取值范围．20．（本小题满分16分）已知数列{}n a 满足1a x =，23a x =，2*1132(2,)n n n S S S n n n +-++=+∈N ≥，n S 是数列{}n a 的前n 项和．(1)若数列{}n a 为等差数列．（ⅰ）求数列的通项n a ；（ⅱ）若数列{}n b 满足2n a n b =，数列{}n c 满足221n n n n c t b tb b ++=--，试比较数列{}n b 前n 项和n B 与{}n c 前n 项和n C 的大小；(2)若对任意*n ∈N ，1n n a a +<恒成立，求实数x 的取值范围．。

江苏省泰州市姜堰区2014-2015学年高一上学期中考试数学 Word版含答案

2014～2015学年度第一学期期中考试试题高一数学(考试时间：120分钟总分160分)命题人：王光华王鸿审题人：孟太朱善宏注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的无效．一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．已知集合{}=12A ，,{}=23B ，,则A B = ▲ ．2．已知(1) f x x +=，则(2)f = ▲ ．3．函数()f x =的定义域为 ▲ .4．已知幂函数()f x x α=的图象过，则(16)f = ▲ .5．已知集合M {1,0,2}⊆-，且M 中含有两个元素，则符合条件的集合M 有 ▲ 个.6．若函数21() 1x a f x x +-=+为奇函数，则实数a 的值为 ▲ . 7．已知函数2()23f x x mx =-+在[)2,x ∈-+∞上是增函数，则m 范围是 ▲ .8．若不等式x x a 42-≤对任意[]0,4x ∈恒成立，则a 的取值范围是 ▲ . 9．已知定义域为()(),00,-∞+∞的偶函数()f x 在(0)+∞，上为增函数，且(1)0f =，则不等式()0f x >的解集为 ▲ .10．若函数()ln 26f x x x =+-的零点为0x ，则满足()0,1x k k ∈+且k 为整数，则k = ▲ ．11．设定义在R 上的函数()f x 同时满足以下三个条件：① ()()0f x f x +-=；② (2)()f x f x +=；③当01x <<时，()2x f x =，则3()2f = ▲ . 12．已知实数0m ≠,函数32()22x m x f x x m x -≤⎧=⎨-->⎩，()，()，若(2)(2)f m f m -=+，则实数m 的值为 ▲ ．13．设已知函数2()log f x x =，正实数m ，n 满足m n <，且()()f m f n =，若()f x 在区间2[,]m n 上的最大值为2，则n m += ▲ ．14．已知()f x 是定义在R 上的奇函数，当0x ≥时，2()3f x x x =-，则函数()()3g x f x x =-+的零点的集合为 ▲ .二、解答题：（本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤．）15．（本小题满分14分）若函数2()2f x x =+，()41g x x =-的定义域都是集合A ，函数)(x f 和)(x g 的值域分别为S 和T . （Ⅰ）若[]2,1=A ，求T S ；（Ⅱ）若[]1,(1)A m m =>，且S T =，求实数m 的值.16．（本小题满分14分）计算下列各式：（Ⅰ）2lg5lg20(lg2)∙+ （Ⅱ）120.75031110.027256639++---（-）-（）17．（本小题满分14分）函数()(,x f x k a k a -=⋅为常数，0a >且1)a ≠的图象过点)8,3(),1,0(B A（Ⅰ）求函数()f x 的解析式；（Ⅱ）若函数()1()()1f xg x f x -=+，试判断函数()g x 的奇偶性并给出证明．18．（本小题满分16分）心理学家通过研究学生的学习行为发现；学生的接受能力与老师引入概念和描述问题所用的时间相关，教学开始时，学生的兴趣激增，学生的兴趣保持一段较理想的状态，随后学生的注意力开始分散，分析结果和实验表明，用()x f 表示学生掌握和接受概念的能力, x 表示讲授概念的时间(单位:min )，可有以下的关系:()x f ()()()20.1 2.64301059101631071630.x x x x x x ⎧-++<≤⎪=<≤⎨⎪-+<≤⎩ （Ⅰ）开讲后第5min 与开讲后第20min 比较,学生的接受能力何时更强一些?（Ⅱ）开讲后多少min 学生的接受能力最强?能维持多少时间?（Ⅲ）若一个新数学概念需要55以上（包括55）的接受能力以及13min 时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?19．（本小题满分16分）已知函数1()log (01a x f x a x -=>+且1)a ≠的图象经过点4(,2)5P -．（Ⅰ）求函数()y f x =的解析式；（Ⅱ）设1()1x g x x-=+，用函数单调性的定义证明：函数()y g x =在区间(1,1)-上单调递减；（Ⅲ）求不等式的解集：2(22)0f t t --<．20．（本小题满分16分）二次函数()f x 的图像顶点为(1,16)A ，且图像在x 轴上截得线段长为8（Ⅰ）求函数()f x 的解析式；（Ⅱ）令()()(22)g x f x a x =+-①若函数()g x 在[]0,2x ∈上是单调函数，求实数a 的取值范围；②求函数()g x 在[]0,2x ∈的最大值。

2015年江苏姜堰中学高三数学期初试题及答案讲评

2015年江苏省姜堰中学高三期初学情检测数学试题与参考答案及评分标准一、填空题（本大题共14小题，每小题5分，共70分） 1．函数sin 2cos 2y x x =的最小正周期是 ▲ ．（全对）答案：2π；提示：变式：1sin 42y x =；242T ππ==．■ 2．设复数z 满足(4)32i z i -=+（i 是虚数单位），则z 的虚部为 ▲ ．答案：3-；提示：设 ()z a bi a b R =+∈、，(4)32(4)323i a bi i b a i i b +-=+⇒-+-=+⇒=-．■ 做错者．．．：王睿泽、吴桐．（要订正20条） 3．某用人单位从甲、乙、丙、丁4名应聘者中招聘2人，若每名应聘者被录用的机会均等，则甲、乙2人中至少有1人被录用的概率为 ▲ ．答案：56；提示：古典概型，正难则反；事件总数为246C =，无甲无乙仅1种，∴15166P =-=．■ 做错者．．．：李慧敏、郭大为、焦晓佳．（要订正20条） 4．某班有49位同学玩“数字接龙”游戏，具体规则按如图所示的程序框图执行（其中a 为座号），并以输出的值作为下一个输入的值；若第一次输入的值为8，则第三输出的值为 ▲ ．答案：8；提示：48152988→→→−−−→．■ 做错者．．．：陆冰冰、翟荣蓉、潘倩玉．（要订正20条） 5．已知圆锥的轴截面是边长为2的正三角形，则该圆锥的体积为 ▲ ．答案；提示：底面半径为12113V π=⋅．■ 做错者．．．：翟逸笑、蒋沛清．（要订正20条） 6．已知将函数sin y x =的图象上的所有点的横坐标伸长到原来的3倍（纵坐标不变），再向左平移4π个单位，可得到函数()y f x =的图象，则()f x = ▲ ．答案：sin()312x y π=+；提示：4sin sin sin sin()33312x x x y x y y ππ+=→=→==+．■ 做错者．．．：李慧敏、陈婷婷、卢稷楠．（要订正20条） 7．若实数, x y 满足102030x y x x y -+≥⎧⎪-≤⎨⎪+-≥⎩，则24x y z =的取值范围是 ▲ ．答案：1[, 1]16；提示：变式：2224x x y y z -==，设2t x y =-，则[4, 0]t ∈-，从而1[, 1]16z ∈．■做错者．．．：郑天宇、李慧敏、缪沁杨、陈煜琪、潘倩玉、徐雨桐．（要订正20条） 8．已知ABC ∆中，角A B C 、、的对边分别为a b c 、、，且22265tan acB a c b =+-，则sin B 的值是 ▲ ．答案：35；提示：“切化弦”、“正、余弦定理”同时发挥作用，通常着落在角．上，偶尔在边．上；变式：2225sin 35sin 33sin cos cos cos 52B B B B B B a c b ac=⇒=⇒=+-．■ 做错者．．．：王睿泽．（要订正20条） 9．已知椭圆2239x y +=的左焦点为1F ，点P 是椭圆上异于顶点的任意一点，O 为坐标原点，若点D 是线段1PF 的中点，则1F OD ∆的周长为 ▲ ．答案：3；提示：圆锥曲线的核心解法是“紧扣定义”；设右焦点为2F ，连结2PF ，则OD 是12PF F ∆的中位线，3a =，c ==3a c =+=做错者．．．：刘剑雨、王钱益、顾盼、窦慧星．（要订正20条） 10．已知函数()f x 对任意的x R ∈满足()()f x f x -=，且当0x ≥时，2()1f x x ax =-+；若()f x 有4个零点，则实数a 的取值范围是 ▲ ．答案：(2, )+∞；提示：偶函数，4个零点，则当0x ≥时，必有2个；由二次函数的性质可知：对称轴在y 轴右侧且顶点在x 轴下方；02a >且()02af <，即0a >且24a >，故2a >．■ 做错者．．．：黄少峰、仲建宇、刘剑雨、乔森、陈婷婷、许黄蓉、郭大为、贺文杰、陈子慧、窦慧星、卫世杰、徐雨桐．（要订正20条） 11．设a b R ∈、，已知关于x 的方程22(1)(1)0x ax x bx -+-+=的四个实数根构成以q 为公比的等比数列，若1[, 2]3q ∈，则实数ab 的取值范围是 ▲ ．答案：112[4,]9；提示：二次函数的灵魂是“开口方向．．．．、对称轴．．．、是否过定点．．．”；变式：2222(1)(1)010 1=0x ax x bx x ax x bx -+-+=⇔-+=-+或；（本题有点难）考察两个函数：2()1f x x ax =-+和2()1g x x bx =-+；开口向上，过共同的定点(0, 1)K ；故两函数的零点是同号的，又由于公比q 是正数，不妨设四个实数根均为正数，且a b <；令四个根为1234x x x x 、、、，1234(0)x x x x <<<<；它们构成以q 为公比的等比数列；由图象可知：23x x 、是()f x 的零点，14x x 、是()g x 的零点；∴23x x a +=，14x x b +=，23141x x x x ⋅=⋅=；再结合等比数列可得：21()x q q a += ①，31(1)x q b += ②，2311x q ⋅= ③；①⨯②÷③得：23321232()(1)(1)(1)q q q q q ab q q q q q q --++++===+++ 211()()2q q q q=+++-；令1t q q =+，则由于1[, 2]3q ∈，有10[2, ]3t ∈，再由22ab t t =+-在10[2, ]3t ∈上是增函数；故112[4,]9ab ∈．■ 做对者．．．：王宇嘉、武朝钦、季小淇、林芮、常毅琛、刘冬兰、石金鹏、韩婷婷、乔森、陆冰冰、陈胜、翟逸笑、李慧敏．共13人．12．在平面直角坐标系xOy 中，设直线2y x =-+与圆222x y r +=(0)r >交于A B 、两点，O 为坐标原点，若圆上一点C 满足5344OC OA OB =+，则r = ▲ ．答案提示：A B C 、、均在圆上，平方得：22225930cos 161616OC OA OB OA OB AOB =++⋅∠；即222225930cos 161616r r r r AOB =++∠，化简：3cos 5AOB ∠=-；设圆心到直线的距离为d ；则d =2231cos 2cos ()12152AOB AOB -=∠=∠-=⨯-；（画图便知）解得：210r =即r =（本题不难）做对者．．．：王宇嘉、武朝钦、季小淇、洪宇晨、王亚丽、杨晨、常毅琛、杭慧、袁峥嵘、袁鑫、王小雨、孙琴、陈胜、王倩、王睿泽、黄河清、缪沁杨、王荣、钱睿、徐亚敏、翟荣蓉、陈婷婷、许黄蓉、王钱益、郭大为、蒋沛清、焦晓佳．共27人．13．若x y z 、、均为正实数，且2221x y z ++=，则2(1)2z xyz+的最小值为 ▲ ．答案：3+提示：注意到：222x y xy +≥，考虑保留z ，构造关于z 的一元二次不等式；设2(1)2z t xyz +=，则2(1)2z xy tz +=，且0t >；结合题设，有：22(1)1z z tz+-≥，即2(1)(1)(1)tz z z z -+≥+；再由题设知：01z <<；有10z +>，10z -> ∴(1)1tz z z -≥+即2211112(1)(1)3(1)23[(1)]1z z z t z z z z z z z z +++≥===--+-+++--+++；∴考察上式右端分母的最小值为3-3+故所求式子的最小值为3+（本题有点难）做对者．．．：林芮、洪宇晨、王亚丽、杨晨、郑天宇．共5人．14．已知公差为d 的等差数列{}n a 满足0d >，且2a 是14a a 、的等比中项；记2n n b a =(*)n N ∈，则对任意的正整数n 均有121112nb b b ++⋅⋅⋅+<，则公差d 的取值范围是 ▲ ．答案：1[, )2+∞；提示：由题意可得：222141111()(3)a a a a d a a d a d =⇒+=+⇒=，从而n a nd =；从而21111222n nn n n n b a d b d d ==⇒==⋅；∴1111111111()(1)222nn n k k n k k k k b d d d ====⋅==-∑∑∑； ∴有11(1)22n d -<对任意正整数n 恒成立；易知：1[, )2d ∈+∞．■（本题不难）做对者．．．：季小淇、林芮、杨晨、刘冬兰、李慧敏．共5人．C 1C1二、解答题（本大题共6小题，共90分） 15．（本题满分14分）锐角ABC ∆的内角A B C 、、的对边分别为a b c 、、，已知2cos()2sin 2CB A -=；（1）求sin sin A B 的值；（2）若3a =，2b =，求ABC ∆的值．解析：（1）由条件可得cos()1cos 1cos()B A C B A -=-=++；………………………………………… 4分∴cos cos sin sin 1cos cos sin sin B A B A B A B A +=+-；即1sin sin 2B A =．…………………………………………………………………………… 7分（2）由正弦定理得：32sin sin sin sina b A B A B=⇒=，可设sin 3A k =，sin 2Bk =；（这里有点难）再由（1）得：2162k k =⇒=sinA ，sinB =；……………………… 9分由锐角三角形可得：1cos 2A =，cos B =；从而sin sin()sin cos cos sinC A B A B A B =+=+= 12分 ∴11sin 2322ABC S ab C ∆==⨯⨯= ……………………………… 14分失分者．．．：刘剑雨7-、陆冰冰7-、王倩7-、张楷文7-、许黄蓉7-、潘倩玉7-、陈子慧7-、缪沁杨4-、钱睿4-、吴桐4-、仲建宇4-．共11人．（要订正5条）16．（本题满分14分）如图，在直三棱柱111ABC A B C -中，AB AC =，点D 为BC 的中点，点E 为BD 的中点，点F 在1AC 上，且14AC AF =；（1）求证：平面ADF ⊥平面11BCC B ；（2）求证：直线//EF 平面11ABB A ．证明：（1）由直三棱柱的定义可知：1CC ⊥平面ABC ；而AD ⊂平面ABC ，∴1CC AD ⊥；………………… 2分 ∵AB AC =，点D 为BC 的中点，∴AD BC ⊥；∵1BC CC C = ，BC ⊂平面11BCC B ，1CC ⊂平面11BCC B ； ∴AD ⊥平面11BCC B ；……………………………… 5分而AD ⊂平面ADF∴平面ADF ⊥平面11BCC B ．……………………… 7分（2）连结CF 并延长交1AA 于G ，连结GB ；∵14AC AF =，11//AA CC ， ∴3CF FG =；∵D 是BC 的中点，E 是BD 的中点；∴//EF BG ；……………………………………… 11分而EF ⊄平面11ABB A ，BG ⊂平面11ABB A ；∴//EF ；平面11ABB A ．■ ……………………… 14分失．分者．．：王宇嘉4-、季小淇4-、王亚丽4-、杨晨3-、翟逸笑4-、张楷文7-、黄河清4-、王荣5-、钱睿4-、陈婷婷7-、王钱益5-、贺文杰7-、焦晓佳7-、窦慧星4-、徐雨桐5-．共15人．（要订正5条）如图，一楼房高AB 为米，某广告公司在楼顶安装一块宽BC 为4米的广告牌，CD 为拉杆，广告牌的倾角为60︒米的监理人员EF 站在楼前观察该广告牌的安装效果；为保证安全，该监理人员不得站在广告牌的正下方；设AE x =米，该监理人员观察广告牌的视角BFC θ∠=；（1）试将tan θ表示为x 的函数；（2）求点E 的位置，使θ取得最大值．解析：（1）作CG AE ⊥于G ，作FH AB ⊥于H ，交CG 于M ，作BN CG ⊥于N ，则CFM BFH θ=∠-∠；在直角BCN ∆中，4BC =，60CBN ∠=︒，则2BN =，CN = 在直角CFM ∆中，有tan CM CN NM CFM MF AE BN +∠===- 在直角BFH ∆中，有tan BH BFH HF ∠==； ∴tantan tan tan()1tan tan CFM BFHCFM BFH CFMBFHθ∠-∠=∠-∠=+∠⋅∠==；再由题意可知：监理人员只能在G 点右侧，即(2, )x ∈+∞．……………………… 7分（2）由（1）得：218tan 21080x x xθ+==-+；令18t x =+，则(20,)t ∈+∞； ∴221tan 1440(18)2(18)108038144038t t t t t t t tθ===≤---+-++- 当且仅当1440t t=即t =18x =；又易知：θ是锐角，即(0, )2πθ∈，而tan y θ=在(0, )2πθ∈是增函数；∴当18x =时，θ取最大值．■ ………………………………………………… 14分得满分者：王宇嘉、季小淇、洪宇晨、杭慧、袁鑫、孙琴、石金鹏、黄少峰、仲建宇、刘剑雨、翟逸笑、张楷文、李慧敏、陈婷婷、贺文杰．共15人．得0分者：韩婷婷、乔森、李继强、黄河清、缪沁杨、王荣、王赵晨、徐智雅、陈煜琪、郭大为、顾盼、刘晓宇、唐潇、贾幼、焦晓佳、陈子慧、窦慧星、徐雨桐．另加：曹伟（仅得2分），共19人．（要订正5条）如图，椭圆C 的中心在原点，左焦点为1(1, 0)F -，右准线方程为：4x =；（1）求椭圆C 的标准方程；（2）若椭圆C 上点N 到定点(, 0)M m (02)m <<的距离的最小值为1，求m 的值及点N 的坐标；（3）分别过椭圆C 的四个顶点作坐标轴的垂线，围成如图所示的矩形，A B 、是所围成的矩形在x 轴上方的两个顶点；若P Q 、是椭圆C 上两个动点，直线OP OQ 、与椭圆的另一个交点分别为11P Q 、；且有直线 OP OQ 、的斜率之积等于直线O A O B 、的斜率之积，试探求四边形11PQPQ 的面积是否为定值，并说明理由．解析：（1）设椭圆的方程为：2222 1 (0)x y a b a b+=>>，c 为半焦距；由题意可得：1c =，24a c=；解得：2a =，从而有2223b a c =-=；∴椭圆C 的方程为：22143x y +=．…………………………………………………… 4分（2）设(, )N x y ，由定点(,0)M m 则222()MN x m y =-+22()3(1)4x x m =-+-221234x mx m =-++；二次函数的图象对称轴为4x m =；由椭圆方程知：22x -≤≤；……… 6分由题设知：048m <<；分类讨论：①当042m <≤即102m <≤时，在4x m =时有22min331MN m =-+=；解得：22134m =>，不符合题意，舍去； ②当42m >即122m <<时，由单调性知：在2x =时有22min41MN m m =-+=；解得：1m =或3m =（舍）；综上可得：m 的值为2，点N 的坐标为(2, 0)．…………………………………… 10分（3）由椭圆方程可知：四条垂线的方程分别为：2x =±、y =；则(2,A 、(2,B -；∴34OA OB k k ⋅=-；设11(, )P x y 、22(, )Q x y ，则有1212OP OQ y y k k x x ⋅=；∴由题意可得：121234y y x x =-（*），而点P Q 、均在椭圆上，有22113(1)4x y =-、22223(1)4x y =-； ∴将（*）式平方并代入可得：2222221212129169(4)(4)x x y y x x==--，即22124x x +=； (12)分 ()a 若12x x =，则11P P Q Q 、、、分别是直线OA O B、与椭圆的交点；∴四个点的坐标分别为：、、(、( ； ∴四边形11PQPQ 的面积为 14分()b 若12x x ≠，则可设直线PQ 的方程为：211121()y y y y x x x x --=--；化简可得：21212112()()0y y x x x y x y x y ---+-=； ∴原点O 到直线PQ的距离为d =PQ∴12211122OPQ S PQ d x y x y ∆=⋅=-== 根据椭圆的对称性，该四边形11PQPQ 也是关于O 成中心对称； ∴四边形11PQPQ 的面积为4OPQ S ∆，即为定值综上所述：四边形11PQPQ的面积为定值，该定值为 ……………………… 16分得10分以上者：武朝钦15+、刘剑雨13+、季小淇12+、袁峥嵘12+、郑天宇12+、张楷文12+、许黄荣12+、潘倩玉12+、王亚丽11+、乔森11+、韩婷婷11+．共11人．19．（本题满分16分）对给定数列{}n c ，如果存在实常数p q 、使得1n n c pc q +=+对任意*n N ∈都成立，我们称数列{}n c 是“线性数列”；（1）若2n a n =，32n n b =⋅，*n N ∈，数列{}n a 、{}n b 是否为“线性数列”？若是，指出它对应的实常数p 和q ，若不是，请说明理由；（2）求证：若数列{}n a 是“线性数列”，则数列1{}n n a a ++也是“线性数列”；（3）若数列{}n a 满足12a =，132 (*)n n n a a t n N ++=⋅∈，t 为常数，求数列{}n a 的前n 项的和．解析：（1）本小题的思路是：紧扣定义．∵2n a n =，∴12n n a a +=+，(*)n N ∈；∴数列{}n a 是“线性数列”，对应的实常数分别为1，2；…………………………………… 2分 ∵32n n b =⋅，∴12n n b b +=，(*)n N ∈；∴数列{}n b 是“线性数列”，对应的实常数分别为2，0．…………………………………… 4分（2）本小题的思路依旧是：紧扣定义．∵数列{}n a 是“线性数列”，∴存在实常数p q 、，使得1n n a pa q +=+对任意*n N ∈恒成立；再进一步有：21n n a pa q ++=+对任意*n N ∈恒成立； ∴有121()()2n n n n a a p a a q ++++=++对任意*n N ∈都成立，∴数列1{}n n a a ++也是“线性数列”，对应的实常数分别为 2p q 、．……………………… 10分（3）本小题的思路是：成对出现，奇偶分清．当n 是偶数时，3112341()()()323232n n n n S a a a a a a t t t --=++++⋅⋅⋅++=⋅+⋅+⋅⋅⋅+⋅23112(14)3(222)32214nn n t t t t -+-=++⋅⋅⋅+=⋅=⋅--；…………………… 13分当n 是奇数时，241123451()()()2323232n n n n S a a a a a a a t t t --=+++++⋅⋅⋅++=+⋅+⋅+⋅⋅⋅+⋅1224114(14)23(222)2324214n n n t t t t --+-=+++⋅⋅⋅+=+⋅=⋅-+-；故1122, 242, n n n t t n S t t n ++⎧⋅-⎪=⎨⋅-+⎪⎩为偶数为奇数．■ …………………………………………………… 16分得满分者：王倩、缪沁杨．得10分及以上者32人．得4分以下者：李慧敏、卢稷楠、刘晓宇、徐雨桐．（要订正5条）20．（本题满分16分）已知函数32()f x ax bx cx d =+++()a b c d R ∈、、、，设直线12l l 、分别是曲线()y f x =的两条不同的切线；（1）若函数()f x 为奇函数，且当1x =时，()f x 有极小值为4-；()i 求a b c d 、、、的值；()ii 若直线3l 亦与曲线()y f x =相切，且三条不同的直线123l l l 、、交于点(, 4)G m ，求实数m 的取值范围；（2）若直线12//l l ，直线1l 与曲线()y f x =切于点B 且交曲线()y f x =于点D ，直线2l 与曲线()y f x =切于点C 且交曲线()y f x =于点A ，记点A B C D 、、、的横坐标分别为A B C D x x x x 、、、，求():():()A B B C C D x x x x x x ---的值．解析：（1）()i 本小题：紧扣定义，用好条件，注意检验．∵()f x 是奇函数，且x R ∈；∴(0)0f d ==，且3232a bx cx a bx cx -+-=---即0b =； ∴3()f x ax cx =+；∴2'()3f x ax c =+，而当1x =时有极小值4-； ………………… 2分 ∴3'(1)0302()26(1)446f a c a f x x x f a c c =+==⎧⎧⎧⇒⇒⇒=-⎨⎨⎨=-+=-=-⎩⎩⎩； …………………………… 4分经检验3()26f x x x =-满足题意，则2060a b c d ===-=、、、．…………………… 5分 ()ii 本小题：三次函数的切线处理方法要洞明．设00(,)P x y 是曲线()y f x =上的一点，由()i 知：300026y x x =-，200'()66f x x =-； ∴过P 点的切线方程为：2000(66)()y y x x x -=--，消去0y 即得：2300(66)4y x x x =--；由此切线方程形式可知：过某一点的切线最多有三条；又由奇函数性质可知：点3(1, 4)P -是极大值点；从而3:4l y =是一条切线且过点(, 4)m ；再设另两条切线的切点为111(, )P x y 、222(, )Px y ，其中121x x ≠≠-；则可令切线23111:(66)4l y x x x =--，23222:(66)4l y x x x =--；将(, 4)G m 代入12l l 、的方程中，并化简可得：23113(1)2(1)m x x -=+且23223(1)2(1)m x x -=+；从而有：21112(1)3(1)x x m x -+=-且22222(1)3(1)x x m x -+=-；………………………………………… 8分∴12x x 、是方程22(1)3(1)x x m x -+=-的两根；（下面考察m 取何值时，该方程有两个不相等的实根）构造函数：22(1)21()(11)3(1)31x x g x x x x -+==-++--， 221'()[1]3(1)g x x =--；由'()00 2g x x x =⇒==或，而2(0)3g =-，(2)2g =，结合图象可得：实数m 的取值范围是：2(, 1)(1, )(2, )3-∞---+∞ ．……………… 10分（2）注意：第1小题与第2小题没有递进关系．令1B x x =，2C x x =；由2'()32f x ax bx c =++及12//l l 可得：2211223232ax bx c ax bx c ++=++；而12x x ≠，化简可得：1223b x x a +=-，即2123bx x a=--；………………………………… 12分（下面求A x 和D x ）将切线1l 的方程21111(32)()y y ax bx c x x -=++-代入()y f x =中并化简得：（注意切点横坐标是其一解）322321111(32)20ax bx ax bx x ax bx +-+++=，即211()(2)0b a x x x x a -++=，∴12D b x x a=--；同理，21223A b b x x x a a =--=+；则13A B b x x x a -=+，1223B C b x x x a -=+，13C D bx x x a-=+；∴():():()1:2:1A B B C C D x x x x x x ---=．■ ……………………………………………… 16分得最高分者：王宇嘉9分；得最低分者：王荣1分．附加题与参考答案21．（本题满分20分）B ．（本小题满分10分，矩阵与变换）在平面直角坐标系xOy 中，设曲线:1C xy =在矩阵cos sin sin cos θθθθ⎡⎤⎢⎥-⎣⎦(0)2πθ≤<对应的变换作用下得到曲线F ，且F 的方程为222 (0)x y a a -=>，求θ和a 的值．解析：设00(, )P x y 是曲线C 上任意一点，00(, )P x y 在矩阵cos sin sin cos θθθθ⎡⎤⎢⎥-⎣⎦对应的变换下变为：00(, )P x y '''；则有0000cos sin sin cos x x y y θθθθ⎡⎤'⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥-⎢⎥'⎣⎦⎣⎦⎣⎦，∴000000cos sin sin cos x x y y x y θθθθ⎧'=+⎪⎨'⎪=-+⎩；代入到222x y a -=中，有：2220000(cos sin )(sin cos )x y x y a θθθθ+--+=，且001x y =；…………………………… 5分化简得：222220000()(cos sin )4sin cos x y x y a θθθθ--+=即2222200()(cos sin )4sin cos x y a θθθθ--+=； ∴22cos sin 0θθ-=且24sin cos a θθ=，而[0, )2πθ∈，0a >；∴4πθ=，a 10分被扣分者：陈子慧5-、徐亚敏10-、王倩5-、翟逸笑5-、潘倩玉5-、孙琴10-、刘晓宇5-、季小淇10-、田景明5-、许黄蓉10-、张慧雯10-、徐智雅10-、蒋沛清10-、黄河清5-、徐雨桐5-、贾幼5-、武朝钦5-、曹伟10-、陈胜10-、王睿泽5-、贺文杰5-、卫世杰10-．共22人．（要订正5条）C ．（本小题满分10分，极坐标系与参数方程）在平面直角坐标系xOy 中，直线l 的参数方程为54x t y t =+⎧⎨=--⎩（t 为参数）；圆C 的参数方程是cos sin x y θθ=⎧⎨=⎩（θ为参数），与直线l 交于两个不同的点A B 、，点P 在圆C 上运动，求PAB ∆面积的最大值．解析：直线l 的普通方程是：10x y +-=，圆C 的普通方程：221x y +=；它们的交点分别为(1, 0)A 、(0, 1)B ；………………………………………………………… 5分设点(cos , sin )P θθ(02)θπ≤<，则点P 到直线l 的距离为：d ，当54πθ=时，d；而AB =，∴当P为( 时，PAB S ∆．■…………………… 10分22．（本题满分10分）如图，PA ⊥平面ABCD ，//AD BC ，90ABC ∠=︒，1AB BC PA ===，3AD =，E 是PB 的中点；（1）求证：AE ⊥平面PBC ；（2）求二面角B PC D --的余弦值．解析：（1）分别以 AB AD AP、、为x 轴、y 轴、z 轴；建立如图所示的平面直角坐标系；则(0, 0, 0)A ，(1, 0, 0)B ，(1, 1, 0)C ，(0, 3, 0)D ，(0, 0, 1)P ，11(, 0, )22E ；∴11(, 0, )22AE = ，(0, 1, 0)BC = ，(1, 0, 1)BP =- ；∵0AE BC ⋅= ，0AE BP ⋅= ；∴AE BC ⊥ ，AE BP ⊥即AE BC ⊥，AE BP ⊥；而BC BP ⊂、平面PBC ，且BC BP B = ；∴AE ⊥平面PBC ．…………………………………………………………………… 4分（2）设平面的法向量为：(, , )n x y z = ，而(1, 2, 0)CD =- ，(0, 3, 1)PD =-；则由02023030n CD x y x y y z z y n PD ⎧⋅=-+==⎧⎧⎪⇒⇒⎨⎨⎨-==⋅=⎩⎩⎪⎩；取1y =，则2x =，3z =即(2, 1, 3)n = ；又由（1）AE ⊥平面PBC ，∴AE 是平面PBC 的法向量，而11(, 0, )22AE =；∴310cos , AE n AE n AE n++⋅<>===⋅，即AE 与n；故由图形可知：二面角B PC D --的余弦值为．■ …………………… 10分得满分者：共28人．被扣分者：洪宇晨5-、杭慧5-、石金鹏5-、翟逸笑5-、张楷文5-、刘正宇5-、李慧敏5-、郭大为5-、刘晓宇5-、焦晓佳5-；共10人．11 23．（本题满分10分）设正整数m n 、满足1n m <≤，1F ，2F ，3F ，…，k F 为集合{1, 2, 3, , }m ⋅⋅⋅的n 元子集，且1i j k ≤<≤；（1）若,k a b F ∀∈，满足1a b ->；()i 求证：12m n +≤；()ii 求满足条件的集合k F 的个数；（2）若i j F F 中至多有一个元素，求证：(1)(1)m m k n n -≤-．解析：（1）()i 本小题关键：写明白．．．题设条件，用好题设条件．设123{, , , , }k n F a a a a =⋅⋅⋅，其中1231n a a a a m ≤<<<⋅⋅⋅<≤，∵a b 、是正整数，∴12a b a b ->⇔-≥；则有：212a a -≥，322a a -≥，432a a -≥，…，12n n a a --≥；累加上述各式得：112(1)n m a a n -≥-≥-，即12m n +≤．………………………… 3分 ()ii 本小题关键：读懂．．题设条件，用好等价转化．由题设可知：“任意两个元素之差的绝对值大于1”⇔“子集中没有数值相邻的元素”；于是原题转化为：“从m 个元素中，任取n 个元素，其中任意两个元素都不是相邻整数，有多少种取法？”下面采用“插空重组法”求出k F 的个数．具体操作是：S1 插空 S2 重新编号．第一步：先取出n 个元素，后将剩下的m n -个元素排成一列，各元素之间，包括两端，一共有1m n -+空档，再将n 个元素放回这1m n -+空档中．第二步：记着放回的元素，它们都不相邻，重新进行编号；回放的元素相当于取的新号元素．计数：上述不同的放法，对应不同的一组新号，这些新号一定不相邻；这种放回的种数就是所求的k F 的个数；由排列组合知识可得：共有1n m n C -+个．故满足条件的k F 的个数是1n m n C -+．…………………………………………………… 6分（2）本小题关键：读懂．．题设条件，用好反证法．由题设知：集合(1, 2, 3, , )i F i k =⋅⋅⋅是n 元子集，i j F F (1)i j k ≤<≤没有相同的二元子集；否则与“至多有一个元素”矛盾；而每一个i F 的二元子集的个数为2n C ，其中1, 2, 3, , i k =⋅⋅⋅，则所有的i F 的二元子集的个数不超过2n kC ，又对于全集{1, 2, 3, , }m ⋅⋅⋅来说，所有的二元子集的个数是2m C ，故2222(1)(1)m n mn C m m kC C k k n n C -≤⇒≤⇒≤-．■ …………………………………………… 10分得2分者：王宇嘉、王亚丽、杭慧、潘倩玉；共4人．得1分者：季小淇、王小雨、陆冰冰、陈胜、李慧敏、徐亚敏、曹伟、卢稷楠、吴桐、贺文杰、窦慧星、徐雨桐；共12人．。

江苏省泰州市姜堰区2015届高三上学期期中考试物理

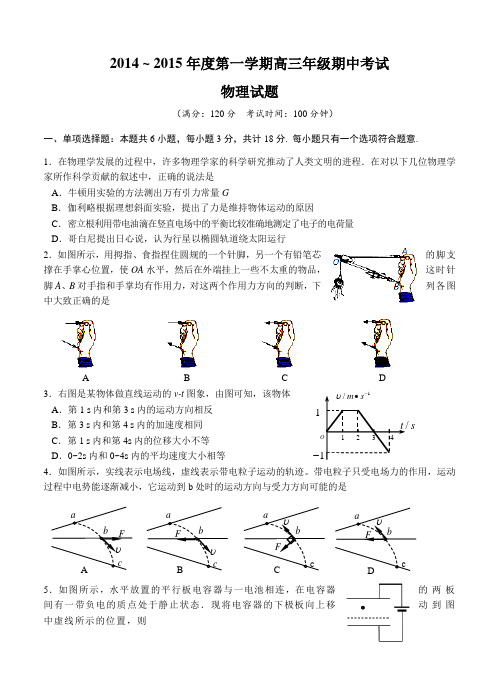
2014 ~ 2015年度第一学期高三年级期中考试物理试题（满分：120分考试时间：100分钟）一、单项选择题：本题共6小题，每小题3分，共计18分. 每小题只有一个选项符合题意. 1．在物理学发展的过程中，许多物理学家的科学研究推动了人类文明的进程．在对以下几位物理学家所作科学贡献的叙述中，正确的说法是 A ．牛顿用实验的方法测出万有引力常量GB ．伽利略根据理想斜面实验，提出了力是维持物体运动的原因C ．密立根利用带电油滴在竖直电场中的平衡比较准确地测定了电子的电荷量D ．哥白尼提出日心说，认为行星以椭圆轨道绕太阳运行 2．如图所示，用拇指、食指捏住圆规的一个针脚，另一个有铅笔芯的脚支撑在手掌心位置，使OA 水平，然后在外端挂上一些不太重的物品，这时针脚A 、B 对手指和手掌均有作用力，对这两个作用力方向的判断，下列各图中大致正确的是3．右图是某物体做直线运动的v-t 图象，由图可知，该物体 A ．第1 s 内和第3 s 内的运动方向相反 B ．第3 s 内和第4 s 内的加速度相同 C ．第1 s 内和第4s 内的位移大小不等 D ．0~2s 内和0~4s 内的平均速度大小相等4．如图所示，实线表示电场线，虚线表示带电粒子运动的轨迹。

带电粒子只受电场力的作用，运动过程中电势能逐渐减小，它运动到b 处时的运动方向与受力方向可能的是5．如图所示，水平放置的平行板电容器与一电池相连，在电容器的两板间有一带负电的质点处于静止状态．现将电容器的下极板向上移动到图中虚线所示的位置，则s1-ABCDA ．电容器的电容变大，质点向上运动B ．电容器的电容变小，质点向上运动C ．电容器的电容变大，质点向下运动D ．电容器的电容变小，质点向下运动6．如图，在倾角为α的固定光滑斜面上，有一用绳子拴着的长木板，木板上站着一只猫。

已知木板的质量是猫的质量的2倍，当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变。

江苏省泰州市姜堰区高三物理上学期期中试题(含解析)新人教版

江苏省泰州市姜堰区2015届高三上学期期中考试物理试卷一、单项选择题：本题共6小题，每小题3分，共计18分.每小题只有一个选项符合题意. 1．（3分）在物理学发展的过程中，许多物理学家的科学研究推动了人类文明的进程．在对以2．如图所示，用拇指、食指捏住圆规的一个针脚，另一个有铅笔芯的脚支撑在手掌心位置，使OA水平，然后在外端挂上一些不太重的物品，这时针脚A、B对手指和手掌均有作用力，对这两个作用力方向的判断，下列各图中大致正确的是（）B3．（3分）（2014•广东高考）如图是物体做直线运动的v﹣t图象，由图可知，该物体（）4．（3分）（2014•盐城一模）如图所示，实线表示电场线，虚线表示带电粒子运动的轨迹．带电粒子只受电场力的作用，运动过程中电势能逐渐减小，它运动到b处时的运动方向与受力D5．（3分）如图所示，水平放置的平行板电容器与一电池相连，在电容器的两板间有一带负电的质点处于静止平衡状态．现将电容器的下极板向上移动到图中虚线所示的位置，则（）C=C=可知，当6．（3分）如图，在倾角为α的固定光滑斜面上，有一用绳子栓着的长木板，木板上站着一只猫．已知木板的质量是猫的质量的2倍．当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变．则此时木板沿斜面下滑的加速度为（）B二、多项选择题：本题共4小题，每小题4分，共计16分.每小题有多个选项符合题意.全部选对的得4分，选对但不全的得2分，错选或不答的得0分.7．（4分）我国于2012年10月25日在西昌成功发射第16颗北斗导航卫星，这是二代北斗导航工程的最后一颗卫星．这次发射的北斗导航卫星是一颗地球同步卫星，如图所示，若第16颗北斗导航卫星先沿椭圆轨道1飞行，后在远地点P处点火加速，由椭圆轨道1变成地球同步圆轨道2．下列说法正确的是（）、根据地球的万有引力提供向心力得==a=8．（4分）已知雨滴下落时受到的空气阻力与速度大小成正比，若雨滴从空中由静止下落，下落过程中所受重力保持不变，下落过程中加速度用a 表示，速度用v 表示，下落距离用s 表B9．（4分）一带负电的粒子只在电场力作用下沿x 轴正向运动，其电势能E p 随位移x 变化的关系如图所示，其中0～x 2段是关于直线x=x 1对称的曲线，x 2～x 3段是直线，则下列说法正确的是（），结合分析图象斜率E=，，图象切线的斜率等于10．（4分）如图，质量分别为m和2m的两个小球A和B，中间用长为2L的轻杆相连，在杆的中点O处有一固定转动轴，把杆置于水平位置后由静止释放，在B球顺时针摆动到最低位置的过程中（）球摆动到最低位置时的速度大小为，解得：三、实验题（共2小题，共20分.请把答案填在答题卡相应的横线上．）11．（10分）某同学用如图甲所示的装置做“探究加速度与物体受力的关系”实验．（1）图乙是实验桌上的一把游标卡尺，该同学应该用游标卡尺 A 部分（填字母序号）测量小车上挡光片的宽度．测量结果如图丙所示，则挡光片的宽度为 1.015 cm；（2）实验中通过调节让小车匀速下滑，目的是平衡摩擦力；然后用细线通过定滑轮挂上重物让小车每次都从同一位置释放，此位置距光电门距离为l，设挡光片的宽度为d，光电门记录的挡光时间为t，则小车加速度的表达式a= ；（3）实验中多次改变所挂重物的质量，测出对应的加速度a，通过力传感器读出拉力F，则下列图象中能正确反映小车加速度a与拉力F关系的是 B ．a=；）平衡摩擦力；；12．（10分）用图甲所示装置验证机械能守恒定律时，所用交流电源的频率为50Hz，得到如图乙所示的纸带．选取纸带上打出的连续五个点A、B、C、D、E，测出A点距起点O的距离为s0=19.00cm，点A、C间的距离为s1=8.36cm，点C、E间的距离为s2=9.88cm，g取9.8m/s2，测得重物的质量为1kg．（1）下列做法正确的有AB ．A．图甲中两限位孔必须在同一竖直线上B．实验前，手应提住纸带上端，并使纸带竖直C．实验时，先放手松开纸带，再接通打点计时器电源D．数据处理时，应选择纸带上距离较近的两点作为初、末位置（2）选取O、C两点为初末位置研究机械能守恒．重物减少的重力势能是 2.68 J，打下C 点时重物的速度是 2.28 m/s．（结果保留三位有效数字）（3）继续根据纸带算出各点的速度v，量出下落距离s，以为纵轴、以s为横轴画出的图象，应是图丙中的 C ．（4）实验中，重物减小的重力势能总是略大于增加的动能，写出一条产生这一现象的原因重物受到空气阻力或纸带与打点计时器之间的摩擦阻力．=2.28m/s，并以为纵轴、以根据四、计算题：本题共5小题，共计66分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题，答案中必须明确写出数值和单位. 13．（12分）2014年10月8日，月全食带来的“红月亮”亮相天空，引起人们对月球的关注．我国发射的“嫦娥三号”探月卫星在环月圆轨道绕行n圈所用时间为t，如图所示．已知月球半径为R，月球表面处重力加速度为g月，引力常量为G．试求：（1）月球的质量M；（2）月球的第一宇宙速度v1；（3）“嫦娥三号”卫星离月球表面高度h．在月球表面的物体受到的重力等于万有引力根据万有引力提供向心力根据万有引力提供向心力）月球表面处引力等于重力，M=所以月球第一宇宙速度卫星周期）月球的质量为）月球的第一宇宙速度为；）“嫦娥三号”卫星离月球表面高度为14．（12分）如图所示，质量为m的小球沿光滑的水平面冲上一光滑的半圆形轨道，轨道半径为R，小球在轨道最高点对轨道压力等于0.5mg，重力加速度为g，求：（1）小球在最高点的速度大小；（2）小球落地时，距最高点的水平位移大小；（3）小球经过半圆轨道最低点时，对轨道的压力．t=2x=vt=）小球在最高点的速度大小为）小球落地时，距最高点的水平位移大小；15．（13分）2012年11月，“歼15”舰载机在“辽宁号”航空母舰上着舰成功．图1为利用阻拦系统让舰载机在飞行甲板上快速停止的原理示意图．飞机着舰并成功钩住阻拦索后，飞机的动力系统立即关闭，阻拦系统通过阻拦索对飞机施加一作用力，使飞机在甲板上短距离滑行后停止．若航母保持静止，在某次降落中，以飞机着舰为计时起点，飞机的速度随时间变化关系如图2所示．飞机在t1=0.4s时恰好钩住阻拦索中间位置，此时速度v1=70m/s；在t2=2.4s时飞机速度v2=10m/s．飞机从t1到t2的运动可看成匀减速直线运动．设飞机受到除阻拦索以外的阻力f大小不变，且f=5.0×104N，“歼15”舰载机的质量m=2.0×104kg．（1）若飞机在t1时刻未钩住阻拦索，仍立即关闭动力系统，仅在阻力f的作用下减速，求飞机继续滑行的距离x（假设甲板足够长）；（2）在t1～t2间的某个时刻，阻拦索夹角α=120°，求此时阻拦索中的弹力T的大小；（3）飞机钩住阻拦索并关闭动力系统后，在甲板上滑行的总距离为82m，求从t2时刻至飞机停止，阻拦索对飞机做的功W．=2Tcos16．（14分）如图所示，离子发生器发射一束质量为m，电荷量为+q的离子，从静止经PQ两板间的加速电压加速后，以初速度v0再从a点沿ab方向进入一匀强电场区域，abcd所围成的正方形区域是该匀强电场的边界，已知正方形的边长为L，匀强电场的方向与ad边平行且由a指向d．（1）求加速电压U0；（2）若离子恰从c点飞离电场，求ac两点间的电势差U ac；（3）若离子从abcd边界上某点飞出时的动能为mv02，求此时匀强电场的场强大小E．可知，离子射出电场时的速度v Eqy=m﹣；；17．（15分）（2011•泗阳县一模）在水平长直的轨道上，有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动．某时刻将一质量为m的小滑块轻放到车面的中点，滑块与车面间的动摩擦因数为μ．（1）证明：若滑块最终停在小车上，滑块和车摩擦产生的内能与动摩擦因数μ无关，是一个定值．（2）已知滑块与车面间动摩擦因数μ=0.2，滑块质量m=1kg，车长L=2m，车速v0=4m/s，取g=10m/s2，当滑块放到车面中点的同时对该滑块施加一个与车运动方向相同的恒力F，要保证滑块不能从车的左端掉下，恒力F大小应该满足什么条件？（3）在（2）的情况下，力F取最小值，要保证滑块不从车上掉下，力F的作用时间应该在什么范围内？）滑块不从左端掉下来，即滑块相对于车的位移不能大于；如果此时力继续作用，滑块将在（与动摩擦因数由④⑤⑥式代入数据解得，物体不从右端滑出，物体在力。

江苏省泰州市泰兴市2015届高三上学期期中考试数学试卷

2014-2015学年江苏省泰州市泰兴市高三（上）期中数学试卷一、填空题（每小题5分，共70分）1．已知集合A={x|y=lg（2x﹣x2）}，B={y|y=2x，x＞0}，则A∩B= ．2．已知，则= ．3．命题P：“若，则a、b、c成等比数列”，则命题P的否命题是（填“真”或“假”之一）命题．4．如果x﹣1+yi，与i﹣3x是共轭复数（x、y是实数），则x+y= ．5．在等差数列{a n}中，a7=m，a14=n，则a28= ．6．已知O、A、B三点的坐标分别为O（0，0），A（3，0），B（0，3），且P在线段AB上，=t（0≤t≤1）则•的最大值为．7．已知a n=（n∈N*），设a m为数列{a n}的最大项，则m= ．8．已知实数a≠0，函数，若f（1﹣a）=f（1+a），则a的值为．9．函数的图象与函数y=2sinπx（﹣2≤x≤4）的图象所有交点的横坐标之和等于．10．已知AD是△ABC的中线，若∠A=120°，，则的最小值是．11．如图，l1，l2，l3是同一平面内的三条平行直线，l1与l2间的距离是1，l3与l2间的距离是2，正△ABC的三顶点分别在l1，l2，l3上，则△ABC的边长是．12．将函数f（x）=2sin（ωx﹣）（ω＞0）的图象向左平移个单位，得到函数y=g（x）的图象，若y=g（x）在[0，]上为增函数，则ω的最大值为．13．定义f（x）是R上的奇函数，且当x≥0时，f（x）=x2．若对任意的x∈[a，a+2]均有f（x+a）≥2f（x），则实数a的取值范围为．14．对任意的x＞0，总有 f（x）=a﹣x﹣|lgx|≤0，则a的取值范围是．二、解答题（本大题6小题，共90分）15．设集合A={x|x2﹣（a+4）x+4a=0，a∈R}，B={x|x2﹣5x+4=0}．求（Ⅰ）若A∩B=A，求实数a的值；（Ⅱ）求A∪B，A∩B．16．已知函数f（x）=sincos+cos2（1）将f（x）写成Asin（ωx+φ）+b的形式，并求其图象对称中心的横坐标；（2）如果△ABC的三边a，b，c满足b2=ac，且边b所对的角为x，试求x 的范围及此时函数f（x）的值域．17．已知扇形AOB的半径等于1，∠AOB=120°，P是圆弧上的一点．（1）若∠AOP=30°，求的值．（2）若，①求λ，μ满足的条件；②求λ2+μ2的取值范围．18．为合理用电缓解电力紧张，某市将试行“峰谷电价”计费方法，在高峰用电时段，即居民户每日8时至22时，电价每千瓦时为0.56元，其余时段电价每千瓦时为0.28元．而目前没有实行“峰谷电价”的居民户电价为每千瓦时0.53元．若总用电量为S千瓦时，设高峰时段用电量为x 千瓦时．（1）写出实行峰谷电价的电费y1=g1（x）及现行电价的电费y2=g2（S）的函数解析式及电费总差额f（x）=y2﹣y1的解析式；（2）对于用电量按时均等的电器（在全天任何相同长的时间内，用电量相同），采用峰谷电价的计费方法后是否能省钱？说明你的理由．19．已知数列{a n}、{b n}，其中，a1=，数列{a n}的前n项和S n=n2a n（n∈N*），数列{b n}满足b1=2，b n+1=2b n．（1）求数列{a n}、{b n}的通项公式；（2）是否存在自然数m，使得对于任意n∈N*，n≥2，有1+恒成立？若存在，求出m的最小值；（3）若数列{c n}满足c n=，求数列{c n}的前n项和T n．20．已知函数f（x）=ax3+bx2+（b﹣a）x（a，b不同时为零的常数），导函数为f′（x）．（1）当时，若存在x∈[﹣3，﹣1]使得f′（x）＞0成立，求b的取值范围；（2）求证：函数y=f′（x）在（﹣1，0）内至少有一个零点；（3）若函数f（x）为奇函数，且在x=1处的切线垂直于直线x+2y﹣3=0，关于x的方程在[﹣1，t]（t＞﹣1）上有且只有一个实数根，求实数t的取值范围．　2014-2015学年江苏省泰州市泰兴市高三（上）期中数学试卷参考答案与试题解析一、填空题（每小题5分，共70分）1．已知集合A={x|y=lg（2x﹣x2）}，B={y|y=2x，x＞0}，则A∩B=　（1，2）　．考点：交集及其运算．专题：计算题．分析：求出A中函数的定义域确定出A，求出B中函数的值域确定出B，找出A与B的交集即可．解答：解：由A中的函数y=lg（2x﹣x2），得到2x﹣x2＞0，即x（x﹣2）＜0，解得：0＜x＜2，即A=（0，2），由B中的函数y=2x，x＞0，得到y＞1，即B=（1，+∞），则A∩B=（1，2）．故答案为：（1，2）点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．已知，则=　　．考点：运用诱导公式化简求值．专题：计算题．分析：根据诱导公式可知=sin（﹣α﹣），进而整理后，把sin（α+）的值代入即可求得答案．解答：解：=sin（﹣α﹣）=﹣sin（α+）=﹣故答案为：﹣点评：本题主要考查了运用诱导公式化简求值的问题．属基础题．　3．命题P：“若，则a、b、c成等比数列”，则命题P的否命题是　假　（填“真”或“假”之一）命题．考点：命题的真假判断与应用．专题：计算题．分析：写出命题的否命题，然后判断否命题的真假即可．解答：解：命题P：“若，则a、b、c成等比数列”，命题P的否命题是：“若，则a、b、c不成等比数列”．否命题中，，可以有ac=b2，a、b、c成等比数列，所以否命题不正确．故答案为：假．点评：本题考查命题的真假的判断，四种命题的关系，考查基本知识的应用．4．如果x﹣1+yi，与i﹣3x是共轭复数（x、y是实数），则x+y=　　．考点：复数的基本概念．专题：数系的扩充和复数．分析：利用共轭复数的定义即可得出．解答：解：∵x﹣1+yi，与i﹣3x是共轭复数，∴﹣3x=x﹣1，﹣y=1，解得x=，y=﹣1．∴x+y=．故答案为：﹣．点评：本题考查了共轭复数的定义，属于基础题．5．在等差数列{a n}中，a7=m，a14=n，则a28=　3n﹣2m　．考点：等差数列的性质．专题：计算题；等差数列与等比数列．分析：由等差数列的性质可得a28=3a14﹣2a7，代入已知的值可求．解答：解：等差数列{a n}中，由性质可得：a28=a1+27d，3a14﹣2a7=3（a1+13d）﹣2（a1+6d）=a1+27d，∴a28=3a14﹣2a7，∵a7=m，a14=n，∴a28=3n﹣2m．故答案为：3n﹣2m．点评：本题为等差数列性质的应用，熟练利用性质是解决问题的关键，属基础题．6．已知O、A、B三点的坐标分别为O（0，0），A（3，0），B（0，3），且P在线段AB上，=t（0≤t≤1）则•的最大值为　9　．考点：平面向量数量积的含义与物理意义．专题：计算题．分析：先利用响亮的三角形法则将用表达，再由数量积的坐标运算得到关于t的式子求最值即可．解答：解：•=====（1﹣t）9因为0≤t≤1，所以（1﹣t）9≤9，最大值为9，所以•的最大值为9故答案为：9点评：本题考查向量的表示、数量积运算等知识，属基本运算运算的考查．7．已知a n=（n∈N*），设a m为数列{a n}的最大项，则m=　8　．考点：数列的函数特性．专题：函数的性质及应用；等差数列与等比数列．分析：把数列a n==1+，根据单调性，项的符号判断最大项．解答：解：∵a n=（n∈N*），∴a n==1+根据函数的单调性可判断：数列{a n}在[1，7]，[8，+∞）单调递减，∵在[1，7]上a n＜1，在[8，+∞）上a n＞1，∴a8为最大项，故答案为：8点评：本题考查了数列与函数的结合，根据单调性求解，属于中档题．8．已知实数a≠0，函数，若f（1﹣a）=f（1+a），则a的值为　　．考点：函数的值；分段函数的应用．专题：函数的性质及应用．分析：对a分类讨论判断出1﹣a，1+a在分段函数的哪一段，代入求出函数值；解方程求出a．解答：解：当a＞0时，1﹣a＜1，1+a＞1∴2（1﹣a）+a=﹣1﹣a﹣2a解得a=舍去当a＜0时，1﹣a＞1，1+a＜1∴﹣1+a﹣2a=2+2a+a解得a=故答案为点评：本题考查分段函数的函数值的求法：关键是判断出自变量所在的范围．9．函数的图象与函数y=2sinπx（﹣2≤x≤4）的图象所有交点的横坐标之和等于　4　．考点：正弦函数的图象；函数的零点与方程根的关系．专题：计算题．分析：的图象由奇函数的图象向右平移1个单位而得，所以它的图象关于点（1，0）中心对称，再由正弦函数的对称中心公式，可得函数y2=2sinπx的图象的一个对称中心也是点（1，0），故交点个数为偶数，且对称点的横坐标之和为2解答：解：函数y1==2sinπx的图象有公共的对称中心（1，0），作出两个函数的图象，当1＜x≤4时，y1≥，而函数y2在（1，4）上出现1.5个周期的图象，在上是单调增且为正数函数，y2在（1，4）上出现1.5个周期的图象，在上是单调减且为正数，∴函数y2在x=处取最大值为2≥，而函数y2在（1，2）、（3，4）上为负数与y1的图象没有交点，所以两个函数图象在（1，4）上有两个交点（图中C、D），根据它们有公共的对称中心（1，0），可得在区间（﹣2，1）上也有两个交点（图中A、B），并且：x A+x D=x B+x C=2，故所求的横坐标之和为4，故答案为：4．点评：本题考查函数的零点与方程的根的关系，考查数形结合思想，发现两个图象公共的对称中心是解决本题的入口，讨论函数y2=2sinπx 的单调性找出区间（1，4）上的交点个数是本题的难点所在．10．已知AD是△ABC的中线，若∠A=120°，，则的最小值是　1　．考点：向量在几何中的应用．专题：压轴题；平面向量及应用．分析：利用向量的数量积公式，及三角形中线向量的表示，利用基本不等式，即可求的最小值．解答：解：∵=||||cosA，∠A=120°，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（7分）∴||||=4﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）∵=（+），∴||2=（||2+||2+2•）=（||2+||2﹣4）≥（2||||﹣4）=1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）∴min=1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）故答案为：1．点评：本题考查向量的数量积，基本不等式，考查学生的计算能力，属于中档题．11．如图，l1，l2，l3是同一平面内的三条平行直线，l1与l2间的距离是1，l3与l2间的距离是2，正△ABC的三顶点分别在l1，l2，l3上，则△ABC的边长是　　．考点：两点间的距离公式．专题：计算题；空间位置关系与距离．分析：过A，C作AE，CF垂直于L2，点E，F是垂足，将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处，延长DA交L2于点G，由此可得结论．解答：解：如图，过A，C作AE，CF垂直于L2，点E，F是垂足，将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处，延长DA交L2于点G．由作图可知：∠DBG=60°，AD=CF=2．在Rt△BDG中，∠BGD=30°．在Rt△AEG中，∠EAG=60°，AE=1，AG=2，DG=4．∴BD=在Rt△ABD中，AB==故答案为：点评：本题考查平行线的性质，等腰三角形，直角三角形的性质，考查学生的计算能力，属于基础题．12．（5分）（2015•德州一模）将函数f（x）=2sin（ωx﹣）（ω＞0）的图象向左平移个单位，得到函数y=g（x）的图象，若y=g（x）在[0，]上为增函数，则ω的最大值为　2　．考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题．分析：函数的图象向左平移个单位，得到函数y=g（x）的表达式，然后利用在上为增函数，说明，利用周期公式，求出ω的不等式，得到ω的最大值．解答：解：函数的图象向左平移个单位，得到函数y=g（x）=2sinωx，y=g（x）在上为增函数，所以，即：ω≤2，所以ω的最大值为：2．故答案为：2．点评：本题是基础题，考查由y=Asin（ωx+φ）的部分图象确定其解析式，注意函数的周期与单调增区间的关系，考查计算能力，常考题型，题目新颖．13．定义f（x）是R上的奇函数，且当x≥0时，f（x）=x2．若对任意的x∈[a，a+2]均有f（x+a）≥2f（x），则实数a的取值范围为　　．考点：函数恒成立问题．专题：函数的性质及应用．分析：利用函数奇偶性和单调性之间的关系，解不等式即可．解答：解：∵当x≥0时，f（x）=x2，∴此时函数f（x）单调递增，∵f（x）是定义在R上的奇函数，∴函数f（x）在R上单调递增，若对任意x∈[a，a+2]，不等式f（x+a）≥2f（x）恒成立，∵2f（x）=2x2=（x）2=f（x），∴f（x+a）≥f（x）恒成立，则x+a≥恒成立，即a≥﹣x+=恒成立，∵x∈[a，a+2]，∴（）max=（a+2），即a≥（a+2），解得a，即实数a的取值范围是故答案为．故答案为：．点评：本题主要考查函数奇偶性和单调性的应用，以及不等式恒成立问题，综合考查函数的性质，是中档题．14．对任意的x＞0，总有 f（x）=a﹣x﹣|lgx|≤0，则a的取值范围是　（﹣∞，lge﹣lglge]　．考点：函数恒成立问题．专题：函数的性质及应用．分析：把不等式变形，然后分x≥1和0＜x＜1两种情况讨论，对于0＜x ＜1时，借助于导数求函数的最小值得答案．解答：解：由 f（x）=a﹣x﹣|lgx|≤0，得a≤x+|lgx|．当x≥1时，化为a≤x+lgx，知a≤1；当0＜x＜1时，化为a≤x﹣lgx，令g（x）=x﹣lgx，则，由，得x=lge．当x∈（0，lge）时，g′（x）＜0，当x∈（lge，1）时，g′（x）＞0，∴当x=lge时，g（x）有最小值为lge﹣lglge．综上，a的取值范围是（﹣∞，lge﹣lglge]．故答案为：（﹣∞，lge﹣lglge]．点评：本题考查了函数恒成立问题，考查了数学转化思想方法，训练了利用导数求函数的最值，是中档题．二、解答题（本大题6小题，共90分）15．设集合A={x|x2﹣（a+4）x+4a=0，a∈R}，B={x|x2﹣5x+4=0}．求（Ⅰ）若A∩B=A，求实数a的值；（Ⅱ）求A∪B，A∩B．考点：交、并、补集的混合运算．专题：集合．分析：本题考察集合的运算中的交集和并集，先对集合A，B进行化简，然后按运算法则运算即可．解答：解：A={x|x=4，或x=a}，B={x|x=1，或x=4}．（Ⅰ）∵A∩B=A，∴A⊆B，由此得，a=1或a=4（Ⅱ）若a=1，则A=B={1，4}，∴A∪B={1，4}，A∩B={1，4}；若a=4，则A={4}，∴A∪B={1，4}，A∩B={4}；若a≠1、4，则A={4，a}，∴A∪B={1，4，a}，A∩B={4}．点评：本题考查集合运算，属于基础题．注意元素的互异性和确定性．16．已知函数f（x）=sincos+cos2（1）将f（x）写成Asin（ωx+φ）+b的形式，并求其图象对称中心的横坐标；（2）如果△ABC的三边a，b，c满足b2=ac，且边b所对的角为x，试求x 的范围及此时函数f（x）的值域．考点：余弦定理；两角和与差的正弦函数．专题：解三角形．分析：（1）f（x）解析式利用二倍角的正弦、余弦函数公式化简，整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数，令正弦函数为0求出x的值，即为其图象对称中心的横坐标；（2）利用余弦定理表示出cosx，把b2=ac代入并利用基本不等式变形，求出cosx的范围，确定出x的范围，求出这个角的范围，利用正弦函数的值域确定出f（x）的值域即可．解答：解：（1）f（x）=sin+（1+cos）=sin+cos+=sin（+）+，由sin（+）=0，得+=kπ（k∈Z），解得：x=，k∈Z，则对称中心的横坐标为（k∈Z）；（2）由已知b2=ac及余弦定理，得：cosx==≥=，∴≤cosx＜1，即0＜x≤，∴＜+≤，∴＜sin（+）+≤1+，即f（x）的值域为（，1+]，综上所述，x∈（0，]，f（x）值域为（，1+]．点评：此题考查了余弦定理，二倍角的正弦、余弦函数公式，以及正弦函数的定义域与值域，熟练掌握余弦定理是解本题的关键．17．已知扇形AOB的半径等于1，∠AOB=120°，P是圆弧上的一点．（1）若∠AOP=30°，求的值．（2）若，①求λ，μ满足的条件；②求λ2+μ2的取值范围．考点：余弦定理；平面向量数量积的运算．专题：解三角形．分析：（1）由题意确定出∠BOP为直角，即OP与OB垂直，得到数量积为0，原式变形后，利用平面向量数量积运算法则计算即可得到结果；（2）①利用余弦定理列出关系式，利用平面向量的数量积运算法则及特殊角的三角函数值化简，整理即可得到λ，μ满足的条件；②利用基本不等式求出λ2+μ2的取值范围即可．解答：解：（1）∵∠AOP=30°，∠AOB=120°，∴∠BOP=∠AOB﹣∠AOP=120°﹣30°=90°，∴•=0，则•=•（﹣）=•﹣•=﹣cos30°=﹣；（2）①由余弦定理，知=cos60°=，整理得：=，即λ2+μ2=1+λμ，则λ，μ满足的条件为；②由λ≥0，μ≥0，知λ2+μ2=1+λμ≥1（当且仅当λ=0或μ=0时取“=”），由λ2+μ2=1+λμ≤1+，得到λ2+μ2≤2（当且仅当λ=μ时取“=”），则λ2+μ2的取值范围为[1，2]．点评：此题考查了余弦定理，平面向量的数量积运算，以及基本不等式的运用，熟练掌握余弦定理是解本题的关键．18．为合理用电缓解电力紧张，某市将试行“峰谷电价”计费方法，在高峰用电时段，即居民户每日8时至22时，电价每千瓦时为0.56元，其余时段电价每千瓦时为0.28元．而目前没有实行“峰谷电价”的居民户电价为每千瓦时0.53元．若总用电量为S千瓦时，设高峰时段用电量为x 千瓦时．（1）写出实行峰谷电价的电费y1=g1（x）及现行电价的电费y2=g2（S）的函数解析式及电费总差额f（x）=y2﹣y1的解析式；（2）对于用电量按时均等的电器（在全天任何相同长的时间内，用电量相同），采用峰谷电价的计费方法后是否能省钱？说明你的理由．考点：函数模型的选择与应用．专题：应用题．分析：（1）总用电量为S千瓦时，高锋时段用电量为x千瓦时，则低谷时段用电量为（S﹣x）千瓦时；实行峰谷电价的电费y1=0.56x+（S﹣x）×0.28；现行电价的电费y2=0.53S；作差比较y2﹣y1即可．（2）省钱时y2﹣y1＞0，可得＜；对于用电量按时均等的电器，高峰用电时段的时间与总时间的比为．所以能省钱．解答：解：（1）若总用电量为S千瓦时，设高锋时段用电量为x千瓦时，则低谷时段用电量为（S﹣x）千瓦时；实行峰谷电价的电费为y1=0.56x+（S﹣x）×0.28=0.28S+0.28x；现行电价的电费为y2=0.53S；电费总差额f（x）=y2﹣y1=0.25S﹣0.28x，（0≤x≤S）（2）可以省钱，因为f（x）＞0，即0.25S﹣0.28x＞0，∴＜．对于用电量按时均等的电器，高峰用电时段的时间与总时间的比为．所以用电量按时均等的电器采用峰谷电价的计费方法后能省钱．点评：本题考查了与实际生活相关的峰谷用电问题，并通过作差来比较函数值的大小，属于基础题目．19．已知数列{a n}、{b n}，其中，a1=，数列{a n}的前n项和S n=n2a n（n∈N*），数列{b n}满足b1=2，b n+1=2b n．（1）求数列{a n}、{b n}的通项公式；（2）是否存在自然数m，使得对于任意n∈N*，n≥2，有1+恒成立？若存在，求出m的最小值；（3）若数列{c n}满足c n=，求数列{c n}的前n项和T n．考点：数列与不等式的综合．专题：综合题；不等式的解法及应用．分析：（1）根据题设条件用累乘法能够求出数列{a n}的通项公式．b1=2，b n+1=2b n可知{b n}是首项为2，公比为2的等比数列，由此能求出{b n}的通项公式．（2）b n=2n．假设存在自然数m，使得对于任意n∈N*，n≥2，有1+恒成立，由此能导出m的最小值．（3）当n是奇数时，，当n是偶数时，，由此能推导出当n是偶数时，求数列{c n}的前n项和T n．解答：解：（1）因为．当n≥2时，，所以所以（n+1）a n=（n﹣1）a n﹣1，即． …2分又，所以==．…4分当n=1时，上式成立，因为b1=2，b n+1=2b n，所以{b n}是首项为2，公比为2的等比数列，故．…6分（2）由（1）知，则．假设存在自然数m，使得对于任意n∈N*，n≥2，有恒成立，即恒成立，由，解得m≥16．…9分所以存在自然数m，使得对于任意n∈N*，n≥2，有恒成立，此时，m的最小值为16．…11分（3）当n为奇数时，=[2+4+…+（n+1）]+（22+24+…+2n﹣1）==；…13分当n为偶数时，=（2+4+…+n）+（22+24+…+2n）==．…15分因此． …16分．点评：本题是考查数列知识的综合运用题，难度较大，在解题时要认真审题，仔细作答．20．已知函数f（x）=ax3+bx2+（b﹣a）x（a，b不同时为零的常数），导函数为f′（x）．（1）当时，若存在x∈[﹣3，﹣1]使得f′（x）＞0成立，求b的取值范围；（2）求证：函数y=f′（x）在（﹣1，0）内至少有一个零点；（3）若函数f（x）为奇函数，且在x=1处的切线垂直于直线x+2y﹣3=0，关于x的方程在[﹣1，t]（t＞﹣1）上有且只有一个实数根，求实数t的取值范围．考点：利用导数研究函数的单调性；奇偶性与单调性的综合．专题：计算题；证明题；压轴题；转化思想．分析：（1）当时，f′（x）==，由二次函数的性质，分类讨论可得答案；（2）因为f′（x）=3ax2+2bx+（b﹣a），所以f′（0）=b﹣a，f'（﹣1）=2a﹣b，．再由a，b不同时为零，所以，故结论成立；（3）将“关于x的方程在[﹣1，t]（t＞﹣1）上有且只有一个实数根”转化为“函数f（x）与的交点”问题解决，先求函数f（x）因为f（x）=ax3+bx2+（b﹣a）x为奇函数，可解得b=0，所以f（x）=ax3﹣ax，再由“f（x）在x=1处的切线垂直于直线x+2y﹣3=0”解得a，从而得到f（x），再求导，由，知f（x上是増函数，在上是减函数，明确函数的变化规律，再研究两个函数的相对位置求解．解答：解：（1）当时，f′（x）==，其对称轴为直线x=﹣b，当，解得，当，b无解，所以b的取值范围为；（4分）（2）因为f′（x）=3ax2+2bx+（b﹣a），∴f′（0）=b﹣a，f'（﹣1）=2a﹣b，．由于a，b不同时为零，所以，故结论成立．（3）因为f（x）=ax3+bx2+（b﹣a）x为奇函数，所以b=0，所以f（x）=ax3﹣ax，又f（x）在x=1处的切线垂直于直线x+2y﹣3=0．所以a=1，即f（x）=x3﹣x．因为所以f（x）在上是増函数，在上是减函数，由f（x）=0解得x=±1，x=0，如图所示，当时，，即，解得；当时，或，解得；当时，或，即，解得；当时，或或，故．当时，或，解可得t=，当时，，无解．所以t的取值范围是或或t=．点评：本题主要考查利用导数法研究函数的单调性，主要涉及了函数的奇偶性，函数的图象和性质以及方程的根转化为函数图象的交点解决等问题．。

江苏省泰州市姜堰区高三上学期期中考试物理 Word版含答案.pdf

为g，引力常量为G，求：
（1）地球的质量M；
（2）卫星的向心加速度大小；
（3）地球的第一宇宙速度大小．
16．（15分）如图所示，一固定足够长的粗糙斜面与水平面夹角．一个质量的小物体（可视为质点），在F＝10
N的沿斜面向上的拉力作用下，由静止开始沿斜面向上运动．已知斜面与物体间的动摩擦因数，取．
于伸直状态，则
A．A在从C至E的过程中，先做匀加速运动，后做匀减速运动
B．A在从C至D的过程中，加速度大小
C．弹簧的最大弹性势能为
D．弹簧的最大弹性势能为
三、实验题（共2小题，共24分.请把答案填在答题卡相应的横线上．）
13.（12分）小叶同学利用图甲装置来探究加速度与力、质量之间的定性关系。
▲ (填“电火花”或“电磁”)打点计时器.
（3）打点计时器使用的交流电频率f=50Hz.，图丙是小叶同学在正确操作下获得的一条纸带，其中A、B、C、D、
E每两点之间还有4个点没有标出.写出用s1、s3以及f来表示小车加速度的计算式：a=▲
.根据纸带所提供的数据
，算得小车的加速度a大小为 ▲ m/s2（结果保留两位有效数字）
点，C为最低点，B、D与圆心O等高．球的质量为m，重力加速度为g，则
A．在C处板对球所需施加的力比A处大6mg
B．球在运动过程中机械能守恒
C．球在最低点C的速度最小值为
D．匀速圆周运动的速度越大，板在B处与水平方向倾斜角θ越小
二、多项选择题：本题共5小题，每小题4分，共计20分. 每小题有多个选项符合题意. 全部选对的得4分，选对但
Байду номын сангаас
②在B的下端挂上质量为m的物块C，让系统（重物A、B以及物块C）中的物体由静止开始运动，光电门记录挡光片挡

江苏省泰州市姜堰区2015届高三上学期期中考试-题目

江苏省泰州市姜堰区2015届高三上学期期中考试语文试题（考试时间：150分钟总分：160分）注意事项：1．本试卷共19题，1、2、3、4、5、7题为选择题，其余为非选择题。

2．所有试题的答案均填写到答题卡上，答案写在试卷上的无效。

一、语言文字运用（15分）1.下列语段横线处应填入的词语，最恰当的一组是（3分）有人曾同我争论：中国的是建设现代物质文明，然后才谈得上疗治文明的。

我只能怯生生地问道：难道几代人的灵魂寻求是无足轻重的吗?我承认我不是，因为我能感觉到时代的两难困境：野蛮的符咒尚未挣脱，文明的压抑接踵而至。

一方面，权贵贪欲的膨胀使得腐败丛生；另一方面，金钱力量的崛起导致精神平庸。

（选自周国平《困惑与坦然》）A．燃眉之急诟病理直气壮B．当务之急诟病义正词严C．当务之急弊病理直气壮D．燃眉之急弊病义正词严2．日前，《广州市拾遗物品管理规定（征求意见稿）》拟出新规，拾金不昧者可获得相当于失物价值10%的金钱奖励。

此消息一出，引发舆论热议，下面是四位网友的留言，表意最准确、鲜明、生动的一项是（3分）A.拾金不昧，虽是中华民族传统美德，但从失主的角度看，东西失而复得，对归还者给予一定钱物表示感谢，似乎是人之常情。

B.拾金不昧有偿，是否与传统美德相悖？是否就标志着道德的沦丧？是否会被不法分子利用，成为一种获利手段？这些问题值得思考。

C.拾金不昧有奖与拾金不昧，二者之间不是你死我活的敌对关系，而是更加务实开放的伙伴关系。

拾金不昧有奖更接地气，贴人心，我支持！D.对于拾金不昧，有奖才是王道，神马都是浮云。

子曾经曰过：“重赏之下必有勇夫。

”因此，对这一举措，我举双手赞成。

3．下面是旅居台湾的孔子第77代嫡传孙孔德成写给在大陆二姐的对联中的上联，最适合作为下联的一句是（3分）上联：风雨一杯酒下联：A.天涯共此时B.羁危万里身C. 婵娟千里共D. 江山万里心4．依次填入下面一段文字横线处的语句，衔接最恰当的一组是（3分）朱光潜的《谈美》一书中还谈论了美感与快感的区别，，，，，。