晶体结构
第一章 晶体结构(Crystal Structure)

基元( basis)
构成晶体的基本结构单元。 基元是化学组成、空间结构、排列取向、周 围环境相同的原子、分子、离子或离子团的集 合。 可以是一个原子(如铜、金、银等),可以是 两个或两个以上原子(如金刚石、氯化钠、磷化 镓等),有些无机物晶体的一个基元可有多达 100个以上的原子,如金属间化合物NaCd2的基 元包含1000 多个原子,而蛋白质晶体的一个基 元包含多达10000 个以上的原子。
六角密堆积晶格结构是一个复式晶格
基元为两个原子 2 1 1 (0,0,0)、( , , ) 3 3 2
c
a
b
三、致密度
反映粒子排列的紧密程度,或也称堆积因 子。 定义: 晶胞内所有粒子的体积与晶胞体积之比。
例1:计算简单立方晶胞的致密度
解: 3 简单立方晶胞的体积为 a,
晶胞内有一个原子,原 子半径为 0 .5 a
a ( a a ) 1 2 3
就是布拉菲格子的晶胞。 晶胞基矢的选取使得平行六面体有尽可能多的相等的棱和 角,有尽可能多的直角,尽可能地反映空间点阵的对称性。 ,一般 晶胞体积为 。 a ( b c )
c构成的最小的平行六面体 以不共面的晶胞基矢 a 、b 、
如果将A、B两个原子看作为一 个基元,则点阵结构就如前页所示 ,格子就是布拉菲格子了。
二维蜂窝格子 (非布拉菲格子)
二、布拉菲格子的原胞与晶胞 a3 以不共面的原胞基矢 a 、 、 a 1 2 构成的最小的平行六面体就是
布拉菲格子的原胞。其体积为:
基矢的取法不唯一,故原胞的取法也不唯一。 无论如何选取,原胞均有相同的体积。 对于布拉菲格子,原胞只含有一个基元(格点)。
原胞体积为:
晶体结构——精选推荐

第七章晶体结构第一节晶体的点阵结构一、晶体及其特性晶体是原子(离子、分子)或基团(分子片段)在空间按一定规律周期性重复地排列构成的固体物质。
晶体中原子或基团的排列具有三维空间的周期性,这是晶体结构的最基本的特征,它使晶体具有下列共同的性质:(1)自发的形成多面体外形晶体在生长过程中自发的形成晶面,晶面相交成为晶棱,晶棱会聚成顶点,从而出现具有几何多面体外形的特点。
晶体在理想环境中应长成凸多面体。
其晶面数(F)、晶棱数(E)、顶点数(V)相互之间的关系符合公式:F+V=E+2 八面体有8个面,12条棱,6个顶点,并且在晶体形成过程中,各晶面生长的速度是不同的,这对晶体的多面体外形有很大影响:生长速度快的晶面在晶体生长的时候,相对变小,甚至消失,生长速度小的晶面在晶体生长过程中相对增大。
这就是布拉维法则。
(2)均匀性:晶体中原子周期性的排布,由于周期极小,故一块晶体各部分的宏观性质完全相同。
如密度、化学组成等。
(3)各向异性:由于晶体内部三维的结构基元在不同方向上原子、分子的排列与取向不同,故晶体在不同方向的性质各不相同。
如石墨晶体在与它的层状结构中各层相平行方向上的电导率约为与各层相垂直方向上电导率的410倍。
(4)晶体有明显确定的熔点二、晶体的同素异构由于形成环境不同,同一种原子或基团形成的晶体,可能存在不同的晶体结构,这种现象称为晶体的同素异构。
如:金刚石、石墨和C60是碳的同素异形体。
三、晶体的点阵结构理论1、基本概念(1)点阵:伸展的聚乙烯分子具有一维周期性,重复单位为2个C原子,4个H 原子。
如果我们不管其重复单位的内容,将它抽象成几何学上的点,那么这些点在空间的排布就能表示晶体结构中原子的排布规律。
这些没有大小、没有质量、不可分辨的点在空间排布形成的图形称为点阵。
构成点阵的点称为点阵点。
点阵点所代表的重复单位的具体内容称为结构基元。
用点阵来研究晶体的几何结构的理论称为点阵理论。
(2)直线点阵:根据晶体结构的周期性,将沿着晶棱方向周期的重复排列的结构单元,抽象出一组分布在同一直线上等距离的点列,称直线点阵。
14种晶体结构

14种晶体结构晶体是由原子、分子或福隔离子按照一定的空间规则排列而成的有序固体。
晶体结构是指晶体中原子、离子或分子排列的规则和顺序。
在固体物质中,晶体结构的种类有很多种,其中比较常见的有以下14种:1. 立方晶体结构:最简单的晶体结构之一,具有三个等长的边和六个等角,包括简单立方、体心立方和面心立方三种类型。
2. 六方晶体结构:其晶胞的基本结构是六方密堆,其中最典型的就是六方晶体和螺旋晶体。
3. 正交晶体结构:晶胞具有三个不相互垂直的晶轴,分别被称为a、b 和c 轴,是最常见的晶体结构之一。
4. 单斜晶体结构:晶胞具有两个不相互垂直的晶轴,是晶体结构中的一种。
5. 三方晶体结构:具有三个相等的轴,夹角为60度,最常见的晶体结构之一是石英。
6. 菱晶体结构:晶胞内部有四面体结构,是一种简单的晶体结构。
7. 钙钛矿晶体结构:一种具有钙钛矿结构的晶体,包括钙钛矿结构和螺旋钙钛矿结构。
8. 蜗牛晶体结构:晶胞的形状像一只蜗牛的壳,是晶体结构中的一种。
9. 立方密排晶体结构:晶胞的结构是立方密排,是晶体结构中的一种。
10. 体心立方晶体结构:晶体结构的晶胞中有一个原子位于晶体的中心,是晶体结构中的一种。
11. 面心立方晶体结构:晶体结构的晶胞的各个面的中心有一个原子,是晶体结构中的一种。
12. 钻石晶体结构:晶体结构的晶胞构成了一种钻石结构,是晶体结构中的一种。
13. 银晶体结构:晶体结构的晶胞构成了一种银结构,是晶体结构中的一种。
14. 锶钛矿晶体结构:晶体结构的晶胞构成了一种锶钛矿结构,是晶体结构中的一种。
晶体结构的种类繁多,每种晶体结构都有其独特的结构特点和性质,对晶体的物理和化学性质有着重要的影响。
研究晶体结构不仅可以帮助我们更好地了解晶体的构成和性质,还有助于我们在材料科学、物理化学等领域的应用和研究。
因此,对晶体结构的研究具有重要的科学意义和应用价值。
常见晶体结构

常见晶体结构
FCC和HCP ➢配位数是一样的 ➢间隙相对大小是一样的 ➢间隙数和原子数比是一样的 ➢堆垛密度(致密度)是一样的
0.155R<100>
常见晶体结构
三、常见晶体结构及其几何特征
4 常见晶体的堆垛方式 任何晶体都可以看成由任给的{hkl}原子面一层一层堆垛而成的。 主要讨论FCC和HCP的密排面的堆垛次序。
➢这里,“最邻近”是就同种元素的原子 相比较而言,而配位数则是一个原子周 围的各元素的最近邻原子数之和。 ➢ 配位数通常用 CN 表示。例如, CN 12 表示配位数为12。
体心立方结构 CN8常见晶 Nhomakorabea结构四 面 体 配 位4
立方 体配
位 8
常见晶体结构
八 面 体 配 位6
十 四 面 体 配 位 12
体中的原子看成是有一定直径的刚球,则紧密系 数可以用刚球所占空间的体积百分数来表示。
以一个晶胞为例,致密度就等于晶胞中原子所 占体积与晶胞体积之比 即: 致密度 =晶胞中原子所占体积之和/晶胞的体积。
=nv/V n: 晶胞原子数 v:每个原子所占的体积 V: 晶胞的体积
常见晶体结构
三、常见晶体结构及其几何特征
1 常见晶体结构 (1)体心立方结构 简写为BCC 例如:V Nb Ta Cr Mo W (2)面心立方结构 简写为FCC 例如:Al Cu Ag Au (3)密排六方结构 简写为HCP 例如:-Ti -Zr -Hf
常见晶体结构
2 几何特征 2.1 配位数 简写CN 一个原子周围最邻近的原子数 ➢ 纯元素金属 这些最邻近的原子到所论原子的距离是相等的 ➢ 多元素晶体 不同元素的最邻近原子到所论原子的距离不一定相等
知识总结—— 晶体结构

第七章 晶体结构第一节 晶体的基本概念一、晶体概述固态物质按其组成粒子(分子、原子或离子等)在空间排列是否长程有序分成晶体(Crystal )和非晶体(又称为无定形体、玻璃体等)两类。
所谓长程有序,是指组成固态物质的粒子在三维空间按一定方式周期性的重复排列,从而使晶体成为长程有序结构。
长程有序体现了平移对称性等晶体的性质。
与晶体相反,非晶体(Non-crystal )内部的粒子(分子、原子或离子等)在空间排列不是长程有序的,而是杂乱无章的排列。
例如橡胶、玻璃等都是非晶体。
晶体内部各部分的宏观性质相同,称为晶体性质的均匀性。
非晶体也有均匀性,尽管起因与晶体不同。
晶体特有的性质是异向性、自范性、对称性、确定的熔点、X 光衍射效应、晶体的缺陷等。
对于长程有序的晶体结构来说,若了解了其周期性重复单位的结构及排列方式,就了解了整个晶体的结构。
可见,周期性重复单位对认识晶体结构非常重要。
在长程有序的晶体结构中,周期性重复的单位(一般是平行六面体)有多种不同的选取方法。
按照对称性高、体积尽量小的原则选择的周期性重复单位(平面上的重复单位是平行四边形,空间中的重复单位是平行六面体),就是正当晶胞,一般称为晶胞(Crystal cell )。
二、晶胞及以晶胞为基础的计算1. 晶胞的两个要素晶胞是代表晶体结构的最小单元,它有两个要素:一是晶胞的大小、型式,晶胞的大小可由晶胞参数确定,晶胞的型式是指素晶胞或复晶胞。
二是晶胞的内容,是指晶胞中原子的种类和位置,表示原子位置要用分数坐标。
晶体可由三个不相平行的矢量a , b , c 划分成晶胞,适量a , b , c 的长度a , b , c 及其相互之间的夹角α, β, γ称为晶胞参数,其中α是矢量b 和c 之间的交角,β是矢量a 和c 之间的交角,γ是矢量a 和b 之间的交角。
素晶胞是指只包含一个重复单位的晶胞,复晶胞是指只包含一个以上重复单位的晶胞。
分数坐标是指原子在晶胞中的坐标参数(x , y , z ),坐标参数(x , y , z )是由晶胞原点指向原子的矢量r 用单位矢量a , b , c 表达,即r = x a + y b + z c如图所示晶体,小球和大球的分数坐标分别为 小球:)21,21,21( ),21,0,0( ),0,21,0( ),0,0,21( 大球:)21,21,0( ),21,0,21( ),0,21,21( ),0,0,0( 2. 以晶胞为基础的计算(1)根据晶体的化学式计算密度:D =ZM/N A V ,M 是晶体化学式的相对式量,Z 是一个晶胞中包含化学式的个数,V 是晶胞的体积,N A 是阿佛加德罗常数。
晶体结构

金属能带理论中, 成键的实质是, 电子填充 在低能量的能级中, 使晶体的能量低于金属原子 单独存在时的能量总和.
2. 金属晶体的堆积模型
金属原子堆积在一起,形成金属晶体。金 属原子最外层价电子脱离核的束缚,在 晶体中自由运动,形成“自由电子”, 留下的金属正离子都是满壳层电子结构, 电子云呈球状分布,所以在金属结构模 型中,人们把金属正离子近似为等径圆 球。
面心立方紧密堆积, 配位数12, 空间利用率74% 六方紧密堆积: 配位数12,空间利用率74% 体心立方紧密堆积: 配位数8, 空间利用率68%
金属元素中具有面心立方,密集六
方和体心立方三种典型结构的金属占了 绝 大 多 数 , 如 表 3-33 所 示 。 许 多 金 属 中 存在多种结构转变现象,这说明三种结 构之间能量差异不大。
点阵是一组无限的点,点阵中每个点都
具有完全相同的周围环境。在平移的对 称操作下,(连结点阵中任意两点的矢 量,按此矢量平移),所有点都能复原, 满足以上条件的一组点称为点阵。
平移——点阵:
平移是晶体结构中最基本的对称操作,可用T 来表示 Tmnp=ma+nb+pc m,n,p为任意整数 即一个平移矢量Tmnp作用在晶体三维点阵上, 使点阵点在a方向平移m单位,b方向平移n单 位,c方向平移p单位后,点阵结构仍能复原。
3.4 金属晶体
1. 金属键
金属键的形象说法: “失去电子的金属 离子浸在自由电子的海洋中”. 金属离子 通过吸引自由电子联系在一起, 形成金属 晶体. 这就是金属键.
金属键无方向性, 饱和性。金属键的 强弱和自由电子的多少有关, 也和离子半 径、电子层结构等其它许多因素有关, 很 复杂. 金属键的强弱可以用金属原子化热 等来衡量. 金属原子化热是指 1mol 金属 变成气态原子所需要的热量. 金属原子化 热数值小时, 其熔点低, 质地软; 反之, 则 熔点高, 硬度大.
晶体结构
1、点阵:按连接其中任意两点的向量进行平移后,均能复原
的一组点。 如 等径密置球
. a. . . . . . . .
3a
特点:①点阵是由无限多个点组成;
②每个点周围的环境相同;
③同一个方向上相邻点之间的距离一样.
晶体结构 = 点阵+结构基元
1、直线点阵:一维点阵 如:结构 结构基元:
点阵
.
a
.
2a
六、晶面指标(符号)和有理指数定律: 由于不同方向的晶面结构微粒排列的情况不同,导致物理 性质不一样——各向异性。
用晶面表示不同的平面点阵组,那晶面在三个晶轴上的倒
易截数之比——晶面指标。 如图 某晶面在坐标轴上的截面 截距
z
4c
2a , 3b , 4c
y
c b 2 3 4 截数 a 3b 1 1 1 2a 倒易截数 (643) 2 3 4 x 倒易截数之比:1/2:1/3:1/4 = 6:4:3 ,为整数 1 1 1 符号化—倒易截数之比: : : h : k : l hkl 为晶面指标 r s t
a b c , 900
一个 6 或 6
一个 4 或 4 一个 3 或 3 三个 2 一个 2 无(仅有i )
1200
a b c, 900
a b c, 900
a b c, 900
C2V , D2 , D2 h
, , ;
V , M r , Z , DC 等
Beq ,U eq
原子坐标及等效温度因子: x , y , z;
分子结构参数:键长,键角,最小二乘平面等 绘出分子结构图,晶胞堆积图等 分析结构特征,解释结构与性能之间的关系。
晶体结构(共78张PPT)

山东大学材料科学基础
共价键结合,有方 向性和饱和性,键 能约80kJ/mol
Si,InSb, PbTe
金属键结合, 无方向性,配 位数高,键能 约80kJ/mol
Fe,Cu,W
范得华力结合 ,键能低, 约 8-40 kJ /mol
Ar,H2,CO2
熔点高
强度和硬度由中到 高,质地脆
闪锌矿〔立方ZnS〕结构 S
Zn
属于闪锌矿结构的晶体有β-SiC,GaAs,AlP,InSb
山东大学材料科学基础
•
•
•
•
萤石〔CaF2〕型结构
立方晶系Fm3m空间群,
a0=0.545nm, Z=4。 AB2型化合物, rc/ra>0.732〔0.975〕 配位数:8:4
Ca2+作立方紧密堆积,
F-填入全部四面体 空隙中。 注意:所有八面 体空隙都未被占据。
山东大学材料科学基础
钙钛矿〔CaTiO3〕结构
Ti
ABO3型
立方晶系:以
•
一个Ca2+和3个
O2-作面心立方
Ca
密堆积,
Ti4+占1/4八面体C空aT隙iO3。晶胞 配位多面体连接与Ca2+配位数
Ti4+配位数6,rc/ra=0.436(0.414-0.732)
Ca2+配位数12,rc/ra=0.96
O2-配位数6;
取决温度、组成、掺杂等条件,钙钛矿结构呈现立方、
四方、正交等结构形式。
山东大学材料科学基础
许多化学式为ABO3型的化合物,其中A与B两种阳 离子的半径相差颇大时常取钙钛矿型结构。在钙钛矿 结构中实际上并不存在一个密堆积的亚格子,该结构 可以看成是面心立方密堆积的衍生结构。较小的B离 子占据面心立方点阵的八面体格位,其最近邻仅是氧 离子。
第一章 晶体结构(Crystal Structure)

§1.3 晶格的周期性
一、布拉菲(Bravais)格子
布喇菲(A. Bravais),法国学者,1850年提出。 定义: 各晶体是由一些基元(或格点)按一定规则, 周期重 复排列而成。任一格点的位矢均可以写成形式 R n a n a n a n 1 n 2 n 3 、 、 a1 a2 。其中, 、 、 取整数, n 1 1 2 2 3 3 a Rn 为基矢, 为布拉菲格子的格矢,或称 正格矢。 3 能用上式表示的空间点阵称为布拉菲点阵,相应的 空间格子称为布拉菲格子.
§1.2 空间点阵
空间点阵定义: 晶体的内部结构可以概括为是由一些相同的 点子在空间有规则地作周期性的无限分布,这 些点子的总体称为点阵。 X射线衍射技术从实验上证明。
1、格点与基元 如果晶体是由完全相同的一种原子所组成 的,则格点代表原子或原子周围相应点的位置, 如铜的晶体结构。 点阵(lattice) 在空间任何方向 上均为周期排列的无 限个全同点的集合。
基元( basis)
构成晶体的基本结构单元。 基元是化学组成、空间结构、排列取向、周 围环境相同的原子、分子、离子或离子团的集 合。 可以是一个原子(如铜、金、银等),可以是 两个或两个以上原子(如金刚石、氯化钠、磷化 镓等),有些无机物晶体的一个基元可有多达 100个以上的原子,如金属间化合物NaCd2的基 元包含1000 多个原子,而蛋白质晶体的一个基 元包含多达10000 个以上的原子。
复式晶格:
如果晶体的基元中包含两种或两种以上的原 子。显然,每一种等价原子各构成与晶体基元代表 点的空间格子相同的网格 , 称为晶体的 子晶格 . 每 一种等价原子的子晶格具有相同的几何结构,整 个晶格可视为,子晶格相互位移套构而成。该晶 体晶格称为复式晶格. 例如:氯化钠晶体
晶体结构的基本结构单元

晶体结构的基本结构单元
晶体结构的基本结构单元主要有三种:原子、分子和离子。
这些基本结构单元在空间中按照一定的规律排列,形成了具有周期性的三维结构。
1.原子:原子是构成物质的基本粒子,它们按照一定的顺序排列在晶体中,形
成一种重复的模式。
原子的排列方式直接决定了晶体的物理和化学性质。
例如,金属原子按照一种被称为“金属键”的强力键合排列,这使得金属具有良好的导电性和导热性。
2.分子:分子是由两个或更多原子通过共价键结合在一起的。
在晶体中,分子
可以是链状、网状或者层状排列。
分子的排列方式会影响分子的化学性质和物理性质。
例如,在石墨中,碳原子以层状排列,每层之间的相互作用很弱,因此石墨可以轻易地在层之间滑动。
3.离子:离子是带有电荷的原子或分子。
在晶体中,离子通常通过离子键或者
共价键结合在一起。
离子的排列方式会影响晶体的离子导电性和耐压性。
例如,在食盐(NaCl)中,钠离子和氯离子通过离子键结合,这种键合方式使得食盐具有良好的导电性和耐压性。
常见九种典型的晶体结构
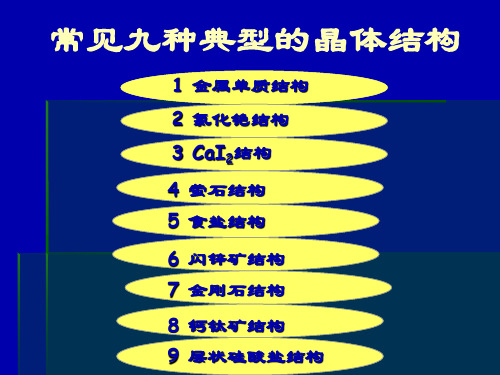
反萤石型结构
球键图
阳离子四面体配位 阴离子立方体配位
反萤石型结构可看作:阴离子做立方最紧密堆积,阳离 子充填在全部的四面体空隙中。
结构类型 物质名称 萤石(CaF2)
萤石型结 氯化锶(SrCl2)
构
氯化钡(BaCl2)
氟化铅(PbF2)
氧化钾(K2O)
反萤石型 结构
氧化钠(Na2O)
氧化锂(Li2O)
闪锌矿的晶体结构:球键图(左)、配位多面体连接图(右)
结构中,S2- 和Zn2+配位数都是4,配位多面体都 是四面体。四面体共角顶相联。
从图可看出,[SZn4] 四面体([ZnS4] 四面体 也是一样)共角顶联成的 四面体基元层与[111]方 向垂直。
由于S2-和Zn2+都呈配位四面体,所以闪锌矿只用一种配位 多面体结构形式表达(S和Zn互换是一样的)。
(Fe3+(Fe2+Fe3+)2O4)。
当结构中四、八面体孔隙被A2+和B3+无序占据时, 叫混合尖晶石结构,代表晶相是镁铁矿(Fe, Mg)3O4。
具有尖晶石型结构的部分物质
Fe3O4 VMn2O4 NiAl2O4 NiGa2O4 Co3S4 TiZn2O4 γ-Fe2O3 LiTi2O4 CoAl2O4 MgGa2O4 NiCo2S4 VZn2O4 MnFe2O4 MnTi2O4 ZnAl2O4 MnGa2O4 Fe2SiO4 SnMg2O4 MgFe2O4 ZnCr2O4 Co3O4 ZnIn2S4 Ni2SiO4 TiMg2O4 Ti Fe2O4 CoCr2O4 GeCo2O4 MgIn2O4 Co2SiO4 WNa2O4 LiMn2O4 CuMn2O4 VCo2O4 CuV2S4 Mg2SiO4 CdIn2O4
晶体结构

§1.1 晶格的周期性
一、布拉菲(Bravais)格子
布喇菲(A. Bravais),法国学者,1850年提出。
定义:
各晶体是由一些基元(或格点)按一定规则, 周期重
复排列而成。任一格点的位矢均可以写成形式
Ra为n3 基 n矢1a1, n。2为Ra其2n 布中n拉3a,3菲、格子、的取n格1整矢n数2,,n或3 称、正、格矢a。1
3、金刚石结构( diamond ):
碳的同素异构体。 经琢磨后的金刚石又称钻石。 无色透明、有光泽、折光力极强,最硬的物质。
金刚石结构是复式晶格结构,基元中有两个碳原子A、B, 布拉菲格子是面心立方。
或可视为两个面心立方子晶格,沿体对角线平移1/4 体对角 线长度套构而成,如图所示.
金刚石晶体的配位数是4, 这4个碳原子构成一个 正四面体,碳-碳键角为109º28´。
基元是化学组成、空间结构、排列取向、周 围环境相同的原子、分子、离子或离子团的集 合。
可以是一个原子(如铜、金、银等),可以是 两个或两个以上原子(如金刚石、氯化钠、磷化 镓等),有些无机物晶体的一个基元可有多达 100个以上的原子,如金属间化合物NaCd2的基 元包含1000 多个原子,而蛋白质晶体的一个基 元包含多达10000 个以上的原子。
具有金刚石结构的晶体有: 金刚石、元素半导体Si、Ge ,灰锡等。
4、闪锌矿(立方ZnS)结构:( cubic zinc sulfide )
与金刚石结构类似,金刚石的基元是化学性质相同的两个 原子A、B ,而闪锌矿结构的基元是两个不相同的原子.
闪锌矿结构也可视为是两个不同原子的面心立方子晶格, 沿体对角线平移1/4 体对角线长度套构而成.
例如,简立方晶格的几个晶列如图所示。
晶体结构

[SiO4]四面体
围绕c轴的螺旋状链
链连接形成的格架
α-石英平行(0001)的结构
β-石英平行(0001)的结构 空间群P642,ao=0.501nm,co=0.547nm。
α-石英晶体沿一个二次轴受压后正负电荷 重心分离,产生表面电荷
④ 赤铜矿(Cu 2 O)型结构
等轴晶系,空间群为Pn3m,a0=0.426nm,Z=2。 等效点的坐标为;O2- 是 0,0,0;1/2,1/2,1/2; Cu+ ,1/4,1/4,1/4;3/4,1/4,3/4;1/4,3/4,1/4; 3/4,3/4,1/4。
Th、U… ❖ 氧化物(AO),A=Sr2+、Ba2+、Ca2+、Ti2+、Sn2+、Pb2+ ❖ 氢化物 (AH), A=Li+、Na+、K+、Ru+、Cs+
典型结构分析
化学式为:NaCI CI-
Na+
典型结构分析
结构描述:
(1)立方晶系,a=0.563nm,Z=4
(2)Na+ CI-离子键,NaCI为离子晶体. (3)CN+=CN-=6 (4)--- CI-离子按立方最紧密堆积方式堆积, Na+离子充
均属于 A1 型。
6.3 非金属单质的晶体结构
原子之间多以共价键结合。 原子配位数一般符合CN = 8-N规则。 N:非金属原子在元素周期表中的族数。
① 金刚石型
共价键 covalent bond: 杂化
Carbon: | | 1s 2s 2p
金刚石的结构-sp3杂化
填于全部八面体空隙。
--- Na+ 离子的配位数是6,构成Na--Cl八面体。NaCI结 构是由Na--Cl八面体以共棱的方式相连而成。 --- Na+ 离子位 于面心格子的结点位置上, Cl-离子也位于另一套这样的格 子上,即后一个格子与前一个格子相距1/2晶棱的位移。
晶体的结构晶格与晶体缺陷

晶体的结构晶格与晶体缺陷晶体是由具有规则排列的原子、离子或分子构成的固态物质。
晶体结构的产生与晶格有着密切的关系,晶体缺陷则是晶格中存在的非完美的部分。
本文将依次介绍晶体的结构晶格以及晶体缺陷的相关内容。
一、晶体的结构晶格晶体的结构是由晶格确定的。
晶格是指在空间中规则排列的点阵或周期性结构。
不同的晶体结构有不同的晶格类型,最常见的晶格类型是立方晶格、六方晶格、四方晶格等。
1. 立方晶格立方晶格是最简单的晶格类型之一,它具有等边、等角的特点。
立方晶格可分为面心立方晶格、体心立方晶格和简单立方晶格。
其中,面心立方晶格具有最高的密堆率,每个原子周围都密集地包围着12个相邻的原子。
2. 六方晶格六方晶格是由一个六边形晶胞构成,其顶角分别为120度和60度。
六方晶格是较为常见的晶格类型,许多金属和陶瓷材料都具有这种结构。
3. 四方晶格四方晶格是晶格的一种,具有和立方晶格相似的特征,但其在z轴方向上具有不同的长度。
二、晶体缺陷及其分类晶体缺陷是指晶体中存在的非完美的部分,可以分为点缺陷、线缺陷和面缺陷三种类型。
1. 点缺陷点缺陷是指晶体中由于原子或离子的位置发生变化而产生的缺陷。
常见的点缺陷有原子空位、杂质原子和间隙原子等。
- 原子空位是指晶体中存在不被原子占据的空位,其产生原因可以是晶体生长过程中的缺陷或中子轰击等因素。
- 杂质原子是指进入晶体中的与主要晶体原子不同的原子。
杂质原子的存在可以影响晶体的导电性、光学性能等特性。
- 间隙原子是指位于晶体原子间隙处的原子,其存在可以引起晶格的畸变和物理性质的变化。
2. 线缺陷线缺陷是指沿晶体表面或晶体内部存在的缺陷线。
常见的线缺陷有位错、脆性裂纹和位移等。
- 位错是指晶体中原子排列出现的错位或位移,常见的有边界位错、螺位错和混合位错等。
- 脆性裂纹是晶体中的裂纹缺陷,由于内部应力超过晶体的强度而导致裂纹的产生和扩展。
- 位移是晶体中原子在晶体平面方向上的滑移或背斜,它对晶体材料的塑性形变和变形行为有着重要影响。
材料科学基础第一章2-1典型的晶体结构及几何特征
与相邻的8个晶胞共有,每个晶胞
实际上只占其1/8;位于晶胞棱上
的原子为相邻的4个晶胞所共有;
每个面心原子为相邻两个晶胞共
有;而晶胞中心原子为晶胞所独
有。
• FCC结构每个晶胞中的原子数:
1
1
8 6 4
8
2
1、FCC 面心立方
配位数
• 配位数是指晶体结构中任一原子周围
( )
3
4
3
4r 3
2
2、HCP 密排六方
••
•
• 原子半径:
上下底面的中心原子与周围六个
顶角上的原子相切
1
2 = , =
2
• 每个晶胞中的原子数:
1
1
12 2 3 6
6
2
•
••
•
•
•
•
•
••
•
•
••
2、HCP 密排六方
• 配位数:
C.N.= 6 + 3×2 =12
最邻近的原子数。常用CN
(coordination number)表示。
• 对于多元素晶体,“最近邻”是同种原
子比较而言,配位数是一个原子周围的
各元素的最近邻原子数之和。
• 晶体结构中每个原子的配位数愈大,
晶体中的原子排列就愈紧密。
• •
•
•
•
• • • •
•
•
•
•
•ห้องสมุดไป่ตู้
• FCC结构的配位数:
A面、B面、C面上各4个,等同点, 4×3=12
• 堆垛密度
2
c
3
常见九种典型的晶体结构

尖晶石通式是A2+B3+2O4,表示二价阳离子A占据了 晶胞四面体空隙,三价阳离子B占据八面体空隙,此即 尖晶石结构,代表是尖晶石(MgAl2O4),
当结构中的四面体空隙被B3+占据,而八面体空隙则 被B3+和A2+各占一半,即有分子式B3+ A2+B3+ 2O4时, 这种结构叫做反尖晶石结构,代表物质磁铁矿
▪ 值得指出的是,部分元素的单质可以在不同条件下 形成不同的结构,或者可以有不同的结构状态共存,
▪ 如单质铁:
▪ α-铁(Iron-alpha) ---(奥氏体) --立方体心 ▪ γ-铁(Iron-gama) --(马氏体)--立方面心 ▪ ε-铁(Iron- Epsilon) --六方结构
2 氯化铯 CsCl 结构
5 石盐结构
空间群:Fm3m,立方面心格子,
具有NaCl型结构的部分物质,
氯化物 碳化物
氯化钾
(KCl)
氯化铷
(RbCl)
碳化钛
(TiC)
碳化钒
(VC)
碳化锆
(ZrC)
氮化物
氮化钒
(VN)
氮化钛
(TiN)
氮化锆
(ZrN)
氮化钪
(ScN)
氮化铕
(EuN)
氧化物
氧化镁
(MgO)
氧化钴
(CoO)
氧化镍
金刚石的晶体结构可以看成是半数的C作立方最紧密堆积 蓝 球 ,另外一半C相间地充填在其中的四面体孔隙中(红球)而构成 的,
该晶体是典型的原子晶体,每个碳原子都以sp3杂化轨道与四个 碳原子形成强的共价键,键长为0.155nm,键角为109° 28′16″,即C的配位数4,配位多面体是四面体,碳-碳配位 四面体在三维空间共角顶相联,形成最坚强的晶体结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点阵类型
立方 六方 四方
14:42
P、I、F
=120
a=bc,===90
H P、I
88
三方 1)a=b=c, == 9060109.47 2)a=bc, ==90,=120
R*
H
14:42
89
abc, ===90 单斜* * abc, ==90,90 三斜 abc, 正交
14:42 40
平面点阵的五种类型: 正方形 (a=b,ab=90) 平面六方 (a=b,ab=120) 矩形 (ab,ab=90) 矩形带心 (ab,ab=90) 一般平行四边形 (ab,ab90) 平面点阵可以看成由平行四边形正 当单位平移共边连接而成。
14:42 41
棱心为1/4(因为四格共用)
面心为1/2(因为二格共用) 格子内为1.
晶胞中原子个数的计算
14:42
66
14:42
67
晶胞中所含原子数的计算
一个平行四边形的四个内角之和为2π即 一个圆的圆周(弧)角。 一个平行六面体的八个内顶角之和为4π 即一个球的立体(球面)角。
14:42
68
4、晶胞 晶胞是晶体中的一个平行六面体单 位,它相应于该晶体的点阵单位。所谓 胞类型是指晶体的点阵类型。晶体可以 看成是由晶胞平移共面连接而成的。
六个晶胞参数即相应点阵平行六面 体单位的点阵参数。 一般选取主轴为c轴,主轴即晶体中 轴次为最高的对称轴,若晶体中无对称 轴则以对称面的法线方向为c轴。
14:42
79
14:42
80
现
代
半导体的后起之秀——砷化镓
科
技
中
的
晶
体
作为半导体材料,GaAs的综合性能优于Si, 开关速
度仅为10-12 s(而Si为10-9 s), 用GaAs芯片制造计算机将使
CsCl型晶体的点阵——立方简单
14:42
73
NaCl型晶体中,按统一的方式将每一对离子A-B抽象 为一个点阵点. 于是,点阵成为立方面心. 请点击按钮打开晶胞模型动态观察
NaCl型晶体结构
NaCl型晶体的点阵—立方面心
这种所谓的“点阵”有一个致命错误:它本身就违反点 阵的数学定义,并不是点阵!更别说是金刚石晶体的点阵. 正确做法如下:
点击动画按钮,用播放键分步观察.
石墨层的平面点阵 (红线围成正当平面格子)
为什么不能将每个C原子都抽象成点
阵点?如果这样做,你会发现……
?
14:42
39
划分平面格子的要求是:在充分 反映平面点阵的对称性的前提下,使 平行四边形的面积尽可能地小(即包 含的点阵点数尽可能少);即所选平行 四边形单位的形状要尽可能地规则、 面积要尽可能地小。这样所得到的平 行四边形单位称为“正当单位”。
14:42
6
2、晶体的宏观通性 (1)自范性 在理想条件下,晶体有自发生长成 具有规则凸多面体外形的性质。如岩盐 为立方体,明矾为正八面体。以下是不 同外形的石英晶体。
14:42
7
14:42
8
晶 体 的 对 称 性
晶体的理想外形具有特定的对称性,这是内部 结构对称性的反映.
14:42
10
14:42
空间点阵划分为点阵单位即划分空间格子的原
则:在充分反映点阵对称性的前提下,使平行六面 体的体积尽可能小(即包含的点阵点数尽可能); 即所选平行六面体单位的形状要尽可能地规则,体 积要尽可能地小。在此原则下全部晶体点阵可以划 分为14种类型。这14种类型的空间点阵是由法国结 晶学家布拉菲(Bravais)在1866年确定的,因此常
运算速度提高千倍.GaAs是超级计算机、光信号处理和 卫星直接广播接收的理想材料。
14:42
82
14:42
83
14:42
84
14:42
85
从严格的意义上讲,应该从晶体 的对称性来界定晶胞,给晶胞下严格 的定义如下: 晶胞是晶体中能够充分反映晶体 结构对称性的一个最小平行六面单位. 对称性指一种晶体的平移对称性(即 点阵)和对称轴(旋转轴、反轴和螺 旋轴)、 对称面(镜面和滑移面)、 对称中心 等所有的微观对称性。
14:42
56
单斜:P、C(或I)
14:42
57
三斜:P
14:4258Fra bibliotek14:42
59
=
请点击按钮观看动画
不成功的“发明”,成功的学习!
(2)为什么NaCl型晶胞要抽象成立方面心格子(左)而不抽 象成三方R格子(右图红线所示)?尽管后者是一个素格子. 点击按钮打开晶格模型
点击按钮观看动画
14:42
14:42
45
14:42
46
14:42
47
正当空间格子的标准:
空间格子净含点阵点数: 顶点为1/8(因为八格共用)
空 间 点 阵 与 正 当 空 间 格 子
1. 平行六面体 2. 对称性尽可能高 3. 含点阵点尽可能少 正当空间格子有7种形状,14种型式
棱心为1/4(因为四格共用)
面心为1/2(因为二格共用) 格子内为1.
石墨的素晶胞与素格子
右:素格子
晶胞的两个要素: a)晶胞的大 小和形状。晶胞平行六面体的大小和 形状由其三边边长a、b、c及夹角 =bc,=ca,=ab确定,这六个 数称为晶胞参数。a、b、c三者常称为 三个晶轴。b)晶胞的内容,即晶胞中 原子的种类、数目及位置。
14:42
78
晶胞参数和点阵参数及晶轴
1、晶体结构的基本特征—周期性
周期性结构有两个要素:周期性重复 的结构基本单元和周期性重复分布的形式。 晶体中在三维空间作周期性重复的结构基 本单元简称为结构基元(motif)。周期性
重 复分布的形式可以用一组几何点来表
示,这组点称为点阵(lattice)。
14:42 18
因此有人提出这样一个关于晶体 结构的所谓公式: 晶体结构=点阵+结构基元
合物的固体都是晶体。
14:42 2
垂直于石墨层观察(蓝、黄球均为C). 注意第1、3
石 墨
层(蓝)对正而与第2层(黄)错开. 沿紫色菱形框,
垂直于石墨层,从第1层切到第3层,就得到一个晶胞:
晶态结构示意图
按周期性规律重复排列
非 晶 态 结 构 示 意 图
同一种晶体会呈现不同的外形。居里 —乌里夫对晶体生长应具有的外形拟订了 下述法则,称为居里—乌里夫原理:当晶 体与溶液或熔体处于平衡时,它所具有的 形态应使其总表面能最小。 有人认为,只有晶体才能称得上是标 准的固体。
14:42
28
(二)二维(平面)点阵 基本周期a 、b 基本平移向量 a 、b 在一平面点阵中,按选定的两个基 本向量的方向用直线将点阵点贯串起来, 将其划分为格子,则可见平面点阵被划 分成完全等同的平行四边形。因此,平 面点阵的类型可用其中的一个平行四边 形来表示。
14:42 29
实例:NaCl(100)晶面如何抽象成点阵?
11
(2)均匀性 (3)固定熔点 (4)各向异性 晶体的不同方向一般具有不同性 质。这是晶体区别与非晶体的一个重 要特征。(以石墨为例)
14:42
12
14:42
13
石墨在平行于层的方向上电导率高且为半金属性导电; 垂直于层的方向上电导率低且为半导体性导电.
图 中 红 、 蓝 球 均 为 C 原 子
14:42
21
(用简谐波来试看如何用点阵来表示结 构的周期。)
14:42
22
14:42
23
结构基元与点阵点
(一)一维(直线)点阵 基本周期a 基本平移向量a
14:42
25
一维周期性结构与直线点阵
14:42
27
•
由此可见,一维周期性结构是由 结构基元按照一维点阵所表示的周期 重复排列而成的。
矩形框中内容为一个结构基元,可抽象为一个点阵点.安 放点阵点的位置是任意的,但必须保持一致,这就得到点阵:
14:42
31
14:42
32
14:42
33
14:42
34
14:42
35
14:42
36
实例:如何从石墨层抽取出平面点阵
石墨层
小黑点为平面点阵. 为比较二者关系, 暂以
石墨层作为背景,其实点阵不保留这种背景.
14:42 86
三、晶体的7个晶系
1、晶系的划分 一般按国际晶体学会编制的“X-
射 线晶体学国际表”的做法,以晶体的宏 观 称性特征把晶体划分为7个晶系。7个晶 系及其晶胞参数的特征和相应的点阵类 型如下:
14:42
87
晶系
晶胞参数特征 a=b=c,===90 a=bc,==90,
14:42
69
CsCl型晶体结构
CsCl型晶体中A、B是不同的原子,不能都被抽象为点阵 点. 否则,将得到错误的立方体心点阵!这是一种常见的错误:
请点击按钮打开晶胞模型
14:42
71
正确做法是按统一取法把每一对离子A-B作为结构
基元,抽象为点阵点, 就得到正确的点阵——立方简单. 请点击按钮打开晶胞模型动态观察.
14:42
42
开普勒的老问题:为什么天上不下五角形雪花?
……从瓷砖铺地的二维问题来联想一下:
14:42
44
(三)三维(空间)点阵 基本周期 a、b、c 基本平移向量 a、b、c 空间点阵的形式用以基本周期a、 b、c为棱边长度的一个平行六面体单 位来表示。这个平行六面体单位称为 点阵单位。空间点阵可以看成由点阵 单位平移共面连接而成。
62
牵 一 发 而 动 全 身 !
下图是立方面心失去相对两个面心的结果. 试看:
