最新17.1变量与函数(1)课件pptPPT课件
合集下载
变量与函数(1)PPT课件

/份
总价
/元 0.4 0.8 1.2 1.6 2.0 2.4 2.8 40
y与X之间的关系是y= 0.4x ,在这个变化过程中,常量是 单价0.4, 变量是份数X、总价Y。
5、一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时 间t(小时)表示水箱中的剩水量y(吨)y= 30-0.5t ,t的取值 范围是0 ≤ t ≤ 60 。
拓展提高
如图:已知△ABC中,底边BC=15cm,高 AD可以任意伸宿。写出△ABC的面积S随AD变 化关系式并指出其中常量与变量。
通过本节课的学习与探索,
同学们学会了什么?还有什么 疑问吗?
-
7
课后作业
必做题:课本71—72页练习题和习题19.1复 习巩固的第一题
选做题:如图,每个图中是由若干个盆花组成 的图案,每条边(包括两个顶点)有n盆花,每 个图案的花盆总数是s,求s与n之间的关系式是 什么?
变式练习
1、小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元
)与他买这种笔记本的本数x之间的关系是( )C
A、Q=8x B、Q=8x-50 C、Q=50-8x
D、Q=8x+50
2、甲乙两地相距s千米,某人行完全程所用的时间t(时)与他的
速度v(千米/时)满足s=vt,在这个变化过程中,下列判断中错
误的是(A)
A、s是变量 B、t是变量 C、v是变量
D、s是常量
3、长方形相邻两边长分别为x、Y,面积为100,则用含x的式子
表示y,则y=100/X ,在这个问题中, 面积 是常量,X、Y是变
量。
4、某种报纸的价格是每份0.4元,买x份报纸的总价为y元,先填写 下表,再用含x的式子表示y。
总价
/元 0.4 0.8 1.2 1.6 2.0 2.4 2.8 40
y与X之间的关系是y= 0.4x ,在这个变化过程中,常量是 单价0.4, 变量是份数X、总价Y。
5、一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时 间t(小时)表示水箱中的剩水量y(吨)y= 30-0.5t ,t的取值 范围是0 ≤ t ≤ 60 。
拓展提高
如图:已知△ABC中,底边BC=15cm,高 AD可以任意伸宿。写出△ABC的面积S随AD变 化关系式并指出其中常量与变量。
通过本节课的学习与探索,
同学们学会了什么?还有什么 疑问吗?
-
7
课后作业
必做题:课本71—72页练习题和习题19.1复 习巩固的第一题
选做题:如图,每个图中是由若干个盆花组成 的图案,每条边(包括两个顶点)有n盆花,每 个图案的花盆总数是s,求s与n之间的关系式是 什么?
变式练习
1、小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元
)与他买这种笔记本的本数x之间的关系是( )C
A、Q=8x B、Q=8x-50 C、Q=50-8x
D、Q=8x+50
2、甲乙两地相距s千米,某人行完全程所用的时间t(时)与他的
速度v(千米/时)满足s=vt,在这个变化过程中,下列判断中错
误的是(A)
A、s是变量 B、t是变量 C、v是变量
D、s是常量
3、长方形相邻两边长分别为x、Y,面积为100,则用含x的式子
表示y,则y=100/X ,在这个问题中, 面积 是常量,X、Y是变
量。
4、某种报纸的价格是每份0.4元,买x份报纸的总价为y元,先填写 下表,再用含x的式子表示y。
八年级数学下册 17.1.2 变量与函数 自变量范围课件

x表示,纵向的加数用
y表示,试写出y与x的
函数关系式.
第六页,共二十页。
分析(fēnxī我): 们发现,横向的加数与纵向的加数之和为10, 即x+y=10,通过这个关于x,y的二元一次方程(yī cì fānɡ ,可 chénɡ) 以求出y与x之间的函数关系式:
y=10-x
12
11 10
(0<x<10 , x为整数)
练习(liànxí) :1.求下列(xiàliè)函数中自变量x的取值范围
(1) y =
;3-x
(2) y =
+x-1 .
1-x
第十六页,共二十页。
例3 在上面(shàng miɑn)试一试的问题(3)中,当MA=1 cm时,重叠 部分的面积是多少?
解 设重叠部分面积为ycm²,MA长为x cm,容易(róngyì)求出y与x之间的函数
先找出自变量x与函数y之间的等量关系
列出关于x, y的二元一次方程
然后用x表示y
最后还要考虑数量的实际意义
第十页,共二十页。
自变量的取值范围(fànwéi)
y=10-x (0<x<10 x为整数 ) (zhěngshù)
y=180-2x
(0<x<90)
y=
1 2
x²
(0 ≤ x≤10 )
使函数有意义的自变量的取值的全体,叫做(jiàozuò)函数自变量的
关系式为
y=
1 2
x²
(0 ≤ x≤10 )
当x=1时,
y=
1
y= 2
1 2
×1²
=
1 2
叫做(jiàozuò)当x=1时的函数值.
第十七页,共二十页。
y表示,试写出y与x的
函数关系式.
第六页,共二十页。
分析(fēnxī我): 们发现,横向的加数与纵向的加数之和为10, 即x+y=10,通过这个关于x,y的二元一次方程(yī cì fānɡ ,可 chénɡ) 以求出y与x之间的函数关系式:
y=10-x
12
11 10
(0<x<10 , x为整数)
练习(liànxí) :1.求下列(xiàliè)函数中自变量x的取值范围
(1) y =
;3-x
(2) y =
+x-1 .
1-x
第十六页,共二十页。
例3 在上面(shàng miɑn)试一试的问题(3)中,当MA=1 cm时,重叠 部分的面积是多少?
解 设重叠部分面积为ycm²,MA长为x cm,容易(róngyì)求出y与x之间的函数
先找出自变量x与函数y之间的等量关系
列出关于x, y的二元一次方程
然后用x表示y
最后还要考虑数量的实际意义
第十页,共二十页。
自变量的取值范围(fànwéi)
y=10-x (0<x<10 x为整数 ) (zhěngshù)
y=180-2x
(0<x<90)
y=
1 2
x²
(0 ≤ x≤10 )
使函数有意义的自变量的取值的全体,叫做(jiàozuò)函数自变量的
关系式为
y=
1 2
x²
(0 ≤ x≤10 )
当x=1时,
y=
1
y= 2
1 2
×1²
=
1 2
叫做(jiàozuò)当x=1时的函数值.
第十七页,共二十页。
《变量与函数》课件

解:因为0< 2 < 3 ,所以当 x=3时,收费为 10 元.
因为 5 >3 ,所以当 x=5 时,收费为 16 元.
0 ≤ x ≤ 20.
3.一盒中性笔有 10 支,价格为 15 元. 请写出购买中性 笔支数 x 与花费的总钱数 y 之间的关系式. 解:根据题意,得 10 支中性笔的价格为 15 元,则 1 支中性笔的价格为 1.5 元. 花费的总钱数 = 单价×购买中性笔数量,即 y =1.5x.
课堂小结
函
更多同类练习见RJ八下 《教材帮》19.1节方法帮
新知探究 跟踪训练
1.拖拉机开始工作时,油箱中有油 36 L,如果每小时
耗油4 L,那么油箱中剩余油量 y L 与工作时间 x h 之间的函数解析式是 y = 36- 4x ,自变量 x 的取值范 围是 0 ≤ x ≤ 9 ,当 x=4 时,函数值 y= 20 .
(1)请分别写出 x>3 和 0<x≤3 时,表示 y 与 x 的关系式;
分析:①当 0<x≤3 时,一律
按照 10 元收费,即 y=10. ②当 x>3 时,超过 3 公里的
解:y =
部分,每公里加收 3元,则 y
10 (0<x≤3), 3x+1 (x>3).
=10+3(x-3)=3x+1.
2.本市出租车的收费标准如下:乘坐公里数不超过 3 公里的,一律按照 10 元收费;超过 3 公里的部分,每 公里加收 3 元. 设乘坐公里数为 x 公里(x 为整数), 相对应的收费为 y 元. (2)直接写出当 x=2 和 x=5 时的函数值.
写 根据数量关系写出含有两个变量的等式. 将等式变形为用含自变量的式子表示因变量的
因为 5 >3 ,所以当 x=5 时,收费为 16 元.
0 ≤ x ≤ 20.
3.一盒中性笔有 10 支,价格为 15 元. 请写出购买中性 笔支数 x 与花费的总钱数 y 之间的关系式. 解:根据题意,得 10 支中性笔的价格为 15 元,则 1 支中性笔的价格为 1.5 元. 花费的总钱数 = 单价×购买中性笔数量,即 y =1.5x.
课堂小结
函
更多同类练习见RJ八下 《教材帮》19.1节方法帮
新知探究 跟踪训练
1.拖拉机开始工作时,油箱中有油 36 L,如果每小时
耗油4 L,那么油箱中剩余油量 y L 与工作时间 x h 之间的函数解析式是 y = 36- 4x ,自变量 x 的取值范 围是 0 ≤ x ≤ 9 ,当 x=4 时,函数值 y= 20 .
(1)请分别写出 x>3 和 0<x≤3 时,表示 y 与 x 的关系式;
分析:①当 0<x≤3 时,一律
按照 10 元收费,即 y=10. ②当 x>3 时,超过 3 公里的
解:y =
部分,每公里加收 3元,则 y
10 (0<x≤3), 3x+1 (x>3).
=10+3(x-3)=3x+1.
2.本市出租车的收费标准如下:乘坐公里数不超过 3 公里的,一律按照 10 元收费;超过 3 公里的部分,每 公里加收 3 元. 设乘坐公里数为 x 公里(x 为整数), 相对应的收费为 y 元. (2)直接写出当 x=2 和 x=5 时的函数值.
写 根据数量关系写出含有两个变量的等式. 将等式变形为用含自变量的式子表示因变量的
《变量与函数》精美课件1

小组讨论:
2
5
10 15 ······
120 300 600 900 ······
1.在这个行程问题中,我们所研究的对象有几个量?
2.在研究的这些量中,哪些是变化的量,哪些是 固定不变的量?他们之间存在怎样的数量关系? 请用含有t的式子表示s。
《变量与函数》精美课件1
《变量与函数》精美课件1
研究对象
时间是个常数,但也是个变数。 勤奋的人无穷多,懒惰的人无穷少。
一次 函数
(ቤተ መጻሕፍቲ ባይዱ一课时)
《变量与函数》精美课件1
创设情境 形成概念
(1)汽车以60 km/h 的速度匀速行驶,行驶时间为 t h, 行驶路程为 s km.s的值随t的值的变化而变化吗?
填一填:
t(h) ······ 1
S(km) ······ 60
《变量与函数》精美课件1
《变量与函数》精美课件1
3.弹簧原长22 cm,弹簧挂上物体后会伸长,测得一 弹簧的长度y(cm)与所挂物体的质量x(kg)有如下 关系:在这个问题中变化的量是什么?不变化的量 是什么?
x/kg 0 1 2 3 4 5 6 y/cm 22 22.5 23 23.5 24 24.5 25
票价,张数,票房收入 张数,收入
票价
Y=10x
面积,半径,圆周率π 面积,半径
圆周率π
S= π r 2
《变量与函数》精美课件1
《变量与函数》精美课件1
(4)用10 m长的绳子围一个矩形,当矩形的一边长 x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分 别为多少?y的值随x的值的变化而变化吗?
D
C
一边长x(m) 3 3.5 4 4.5
2
5
10 15 ······
120 300 600 900 ······
1.在这个行程问题中,我们所研究的对象有几个量?
2.在研究的这些量中,哪些是变化的量,哪些是 固定不变的量?他们之间存在怎样的数量关系? 请用含有t的式子表示s。
《变量与函数》精美课件1
《变量与函数》精美课件1
研究对象
时间是个常数,但也是个变数。 勤奋的人无穷多,懒惰的人无穷少。
一次 函数
(ቤተ መጻሕፍቲ ባይዱ一课时)
《变量与函数》精美课件1
创设情境 形成概念
(1)汽车以60 km/h 的速度匀速行驶,行驶时间为 t h, 行驶路程为 s km.s的值随t的值的变化而变化吗?
填一填:
t(h) ······ 1
S(km) ······ 60
《变量与函数》精美课件1
《变量与函数》精美课件1
3.弹簧原长22 cm,弹簧挂上物体后会伸长,测得一 弹簧的长度y(cm)与所挂物体的质量x(kg)有如下 关系:在这个问题中变化的量是什么?不变化的量 是什么?
x/kg 0 1 2 3 4 5 6 y/cm 22 22.5 23 23.5 24 24.5 25
票价,张数,票房收入 张数,收入
票价
Y=10x
面积,半径,圆周率π 面积,半径
圆周率π
S= π r 2
《变量与函数》精美课件1
《变量与函数》精美课件1
(4)用10 m长的绳子围一个矩形,当矩形的一边长 x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分 别为多少?y的值随x的值的变化而变化吗?
D
C
一边长x(m) 3 3.5 4 4.5
变量与函数-PPT课件全文

(2)在求自变量的取值范围时,要从两个方面来考虑: ①代数式要有意义;②要符合实际.
1、下列关系中,y不是x函数的是( D )
A. y x B. y x2 C. y x D. y x
2
2、求出下列函数中自变量的取值范围
(1)y=x-3 (2) y 1 x (3) y 3 2 x
(4)
大千世界万物皆变
行星在宇宙中的位置随时间而变化; 人体细胞的个数随年龄而变化; 气温随海拔而变化; 汽车行驶里程随行驶时间而变化;
……
这种一个量随另一个量的变化而变化的现象大量存在。
大千世界处在不停的运动变化之 中,如何来研究这些运动变化并寻找 规律呢?
数学上常用变量与函数 来刻画各种运动变化。
如果当x=a时y=b,那么b叫做当自 变量x的值为a时y的函数值。
t
1 2 3 4 ……
S
60 120 180 240 ……
思考下列问题?
(1)y 2x 中的y是x的函数吗 是
(2)一天中的气温是时刻的函数吗? 是
(3) y x 不是
判断是不是函数,我们可以看它的两个变量之间 是否满足函数的定义
例1求出下列函数中自变量的取值范围
(1)y=2x
(2)
y 3 x2
(3)m n 1 (4)y 3 x 1
(5) h 1 k
k 1
(7) y x 1 x 1
(6) y x2 1
确定函数自变量取值范围的条件:
(1)分母不等于0;【1a(a≠ 0】
(2)开偶数次方中的被开方数必须大
于等于0。【 a(a≥0】
(2)若教室座位共安排15排,座位总数
将达到多少个?
(1)m=25+n-1=n+24, p 25 24 n • n 1 n(n 49)
1、下列关系中,y不是x函数的是( D )
A. y x B. y x2 C. y x D. y x
2
2、求出下列函数中自变量的取值范围
(1)y=x-3 (2) y 1 x (3) y 3 2 x
(4)
大千世界万物皆变
行星在宇宙中的位置随时间而变化; 人体细胞的个数随年龄而变化; 气温随海拔而变化; 汽车行驶里程随行驶时间而变化;
……
这种一个量随另一个量的变化而变化的现象大量存在。
大千世界处在不停的运动变化之 中,如何来研究这些运动变化并寻找 规律呢?
数学上常用变量与函数 来刻画各种运动变化。
如果当x=a时y=b,那么b叫做当自 变量x的值为a时y的函数值。
t
1 2 3 4 ……
S
60 120 180 240 ……
思考下列问题?
(1)y 2x 中的y是x的函数吗 是
(2)一天中的气温是时刻的函数吗? 是
(3) y x 不是
判断是不是函数,我们可以看它的两个变量之间 是否满足函数的定义
例1求出下列函数中自变量的取值范围
(1)y=2x
(2)
y 3 x2
(3)m n 1 (4)y 3 x 1
(5) h 1 k
k 1
(7) y x 1 x 1
(6) y x2 1
确定函数自变量取值范围的条件:
(1)分母不等于0;【1a(a≠ 0】
(2)开偶数次方中的被开方数必须大
于等于0。【 a(a≥0】
(2)若教室座位共安排15排,座位总数
将达到多少个?
(1)m=25+n-1=n+24, p 25 24 n • n 1 n(n 49)
17.1.1变量与函数

⑵下列变化中,哪些y是x的函数?哪些不是? 说明理由。 xy=2 x+y=5 |y|=3x+1 y=x2-4x+5
表示函数关系的方法
300 000 2 f ,S r l
波长 l(m) 300 500 600 1000 1500 频率 f(kHz) 1000 600 500 300 200
例3、
求下列函数中自变量x的取值范围:
(2) y=2x2+7
(1) y=3x-1;
1 (3) y= x 2
(4) y= x 2
说明:四种基本类型的函数自变量取值范围 1 整式-----一切实数 2 分式-----分母不为零
偶次根式 (被开方数≥0)
3 根式----奇次根式 (被开方数为一切实数 ) 4 零指数-----底数≠0
解析法 列表法
图象法
图 17.1.1
• 例2 写出下列各问题中的函数关系式, 并指出其中的常量与变量: (1)圆的周长C与半径r的函数关系式; (2)火车以60千米/时的速度行驶,它驶 过的路程s(千米)与所用时间t(时) 的函数关系式; (3)n边形的内角和的度数S与边数n的函 数关系式.
(4)、矩形的周长是18 cm ,它的长是y, 宽是x cm ;
结论:任给一个存期x的确定值,年利率y都有 唯一的一个值和它对应
观 察:
3、收音机刻度盘上的波长和频率分别是用米 和千赫兹(kHz)为单位标刻的。下面是一些对应的数值:
波长 300 λ(m) 频率 ƒ(kHz) 1000
500
600
1000
1500
600
500
300
200
λƒ=300000
ƒ=
300000
《变量与函数》优质精ppt课件

ppt精选版
14
❖ 思考: 填表并回答问题:
2和-2 8和-8 18和-18 32和-32
(1)对于x的每一个值,y都有唯一的值与之 对应吗?答:不是 。
(2)y是x的函数吗?为什么?
答:不是,因为y的值不是唯一的。
ppt精选版
15
1. 指出下列变化关系中,哪些y是x的函数, 哪些不是?说出你的理由。
(2)当h=3时,面积s=__7_.5___,
(3)当h=10时,面积s=__2_5___;
ppt精选版
21
练习1:下列问题中哪些量是自变量?哪些量是自变量的函数
?试写出函数的解析式。
(1)秀水村的耕地面积是106m2,这个村人均耕地面积y
随着人数x的变化而变化
y 10 6
x
(2)正方形的面积S 随边长 x 的变化 S=x2
(2) y 1 x
(4) y ( x - 3)0
ppt精选版
18
请同学们想一想函数自变量的取 值范围有什么规律?
(1)有分母,分母不能为零
(2)开偶数次方,被开方数是非负数
(3)零次幂,底数不能为零
(4)是实际问题,要使实际问题有意义ppt精选版 Nhomakorabea19
例1:一辆汽车的油箱中现有汽油50L,如果不再 加油,那么油箱中的油量y(单位:L)随行驶里程 x(单位:km)的增加而减少,平均耗油量为 0.1L/km .
ppt精选版
4
问题4:你见过水中涟漪吗?如图所示,圆形 水波慢慢的扩大.在这一过程中,当圆的半径r分 别为10 cm,20 cm,30 cm时,圆的面积S分别为多 少?S的值随r的值的变化而变化吗? (1)填表:
半半径径r(rc(cmm)) 1010 2020 3300
《变量与函数》1精品PPT课件

问题3: 收音机刻度盘的波长和频率分别是用米(m) 和千赫兹(kHz)为单位标刻的.下面是一些对应 的数值:
波长 (m) 300 频率 f (khz) 1000
500 600 1000 1500 600 500 300 200
观察上表回答:
(1)波长 和频率f数值之间有什么关系?
与 f 的乘积是一个定值,即
变量与函数
问题1:
如图是某地一天内的气温变化图
·
·
看图回答:
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的 某一时刻,说出这一时刻的气温.
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
温度T随着时间t的变化而变化.
这里函数关系是用图象给出的
(图象法)
2下表是表示某水库存水量Q与水库的深度h的关系
水深h 0 5 10 15Q 0 20 40 90 160 275 437.5 650 (万方)
这里函数关系是用表格给出的
(列表法)
3、在S=30t中,S与t具有函数关系吗?
这里函数关系是用数学式子给出的 (解析法)
(3) y= 1
x2
(4) y= x 2
(1)因为x取任意实数,3x 1都有意义,
所以x的取值范围是任意实数.
(2)因为x取任意实数,2x2 7 都有意义,
所以x的取值范围是任意实1 数. (3)因为x+2不等于0时,x 2 才有意义,所以
x的取值范围是: x 2 0,即x 2.
(4)因为x≥2时, x 2 才有意义,所以x
问题2: 银行对各种不同的存款方式都规定了相应的 利率,下表是2006年8月中国人民银行为“整 存整取”的存款方式规定的年利率: 存期 x 三月 六月 一年 二年 三年 五年
《变量与函数》ppt完美课件

2
自变量x的取值范围 2<x≤5
《变量与函数》完美实用课件(PPT优 秀课件 )
解:时间T是自变量,水量V是T的函数 函数解析式为 V=10-0.05T
《变量与函数》完美实用课件(PPT优 秀课件 )
《变量与函数》完美实用课件(PPT优 秀课件 )
归纳
小结
1、一般地,在一个变化过程中,如果有两__个__
变量x和y,并且对于x
的
每一个确定的值
,y都有
_唯__一__确__定__的__值__与其对应,那么我们就说x
新课讲解
下列问题中哪些量是自变量?哪些量是自变量的 函数?试写出函数的解析式. (1)改变正方形的边长x,正方形的面积s随之 改变。
解:边长x是自变量 ,面积S是x的函数 函数解析式为 s=x2
(2)每分向一水池注水0.1m3,注水量y(单位: m3)随注水时间x(单位:min)的变化而变化。
解:时间x是自变量, 水量y是x的函数 函数解析式为 y=0.1x
(3) 汽车行驶200㎞时,油箱中还有多少汽油?
解:(1)y与x的函数关系式为y=_5_0_-_0_._1_x__
(2)因为x代表的实际意义为行驶路程,所以x不能
取 负数 .且行驶中的耗油量为 0.1x ,它不能超过油
箱中现有汽油量的值50,即
0.1x≤50
因此,自变量x
的取值范围是___0_≤___x__≤___5_0__
是
自变量
,y是x的 函数 。
2、如果当x=a时,y=b,那么 a 叫做当自变
量的值为 b 时的函数值.
3、用关于
自变量的式子 表示_变__量_____
之间的关系,这种式子叫做函数的解析式.
湖南省耒阳市冠湘中学八年级华师大版数学下册课件:171变量与函数(1)(共31张PPT)

图片欣赏
大千世界处在不停的运动变化之中,如何来研究 这些运动变化并寻找规律呢?
数学上常用变量与函数来刻画各种运动变化.
先看什么叫变量?
(1)你坐过 摩天轮吗?你 坐在摩天轮上 时,随着时间t的 变化,你离开地 面的高度h是如 何变化的?
h(米)
3
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
与单价 a(元)的关系式是 n 50 ,
其中变量是 a ,n ,常量是a 50
.
· 问题1:如图是某地一天内的气温变化图
·ห้องสมุดไป่ตู้
看图回答:
当时间t发生变化时,
(1)这天的6时、10时和14时的气温温分度别T为也多随少着?变任化意
给出这天中的某一时刻,说出这一时刻的气温.
(2)这一天中,最高气温是多少?最低气温是多少?
纵向的加数用y表示,试写出y与x的函数关系
式.
(2)试写出等腰三角形中顶角的度数 y与底角的度数x之间的函数关系式.
y 180 2x
y
x
等腰三角形两底角相等
在上面“试一试”中所出现的各个函 数中,自变量的取值有限制吗?如果 有,写出它的取值范围。
y 10 x (x取1到9的自然数)
y 180 2x (0 x 90 )
半径l(cm) 1 1.5 圆面积S(cm²) 3.14 7.07
2
2.6
12.56 21.23
3.2 …
32.15 …
圆的面积随着半径的增大而增大,
所以 r 和 S 是变量, 是常量。
柳暗花明
问题
变量 自变量 因变量
图 17.1.1
“气温变化问题”
波长 300 500 600 1000 1500
大千世界处在不停的运动变化之中,如何来研究 这些运动变化并寻找规律呢?
数学上常用变量与函数来刻画各种运动变化.
先看什么叫变量?
(1)你坐过 摩天轮吗?你 坐在摩天轮上 时,随着时间t的 变化,你离开地 面的高度h是如 何变化的?
h(米)
3
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
与单价 a(元)的关系式是 n 50 ,
其中变量是 a ,n ,常量是a 50
.
· 问题1:如图是某地一天内的气温变化图
·ห้องสมุดไป่ตู้
看图回答:
当时间t发生变化时,
(1)这天的6时、10时和14时的气温温分度别T为也多随少着?变任化意
给出这天中的某一时刻,说出这一时刻的气温.
(2)这一天中,最高气温是多少?最低气温是多少?
纵向的加数用y表示,试写出y与x的函数关系
式.
(2)试写出等腰三角形中顶角的度数 y与底角的度数x之间的函数关系式.
y 180 2x
y
x
等腰三角形两底角相等
在上面“试一试”中所出现的各个函 数中,自变量的取值有限制吗?如果 有,写出它的取值范围。
y 10 x (x取1到9的自然数)
y 180 2x (0 x 90 )
半径l(cm) 1 1.5 圆面积S(cm²) 3.14 7.07
2
2.6
12.56 21.23
3.2 …
32.15 …
圆的面积随着半径的增大而增大,
所以 r 和 S 是变量, 是常量。
柳暗花明
问题
变量 自变量 因变量
图 17.1.1
“气温变化问题”
波长 300 500 600 1000 1500
《变量与函数》课件

二、函数
1. 函数的定义
函数是一段可重复使用的代码,用于执行特定的任务。它可以接受参数并返回结果。
2. 函数的调用
我们可以通过调用函数来执行其中的代码,并传递参数给函数以获得所需的结果。
3. 函数的返回值
函数的返回值是函数执行完毕后返回给调用者的结果。我们可以通过获取函数的返回值来使 用它。
三、实例演示
《变量与函数》PPT课件
欢迎来到我们的《变量与函数》PPT课件。在本课程中,我们将一起探索变 量和函数的概念,学习它们在编程中的作用以及如何正确使用它们。让我们 开始吧!
一、变量
1. 变量的定义
什么是变量?变量是用于存储数据的容器,可 以在程序中赋过赋值语句,我们可以将值赋给变量并在程 序中使用这些值。
1
1. 变量实例
让我们通过一个实例了解如何定义、赋
2. 函数实例
2
值和使用变量,以及变量在程序中的作 用。
现在,我们将展示一个函数的实例,演
示如何定义函数、调用函数,并解释函
数返回值的概念。
四、总结
1. 变量和函数的区别
变量和函数在编程中有不同的角色和用途,理解它们之间的区别对于编写高效的代码至关重 要。
2. 变量和函数的应用
掌握变量和函数的概念和使用方法后,我们可以将它们应用于解决实际问题和开发创新的程 序。
3. 其他相关知识
除了变量和函数的基本概念外,我们还会介绍全局变量和局部变量、函数的递归调用,以及 在不同编程语言中的差异。
1变量与函数(第1课时)PPT课件(华师大版)
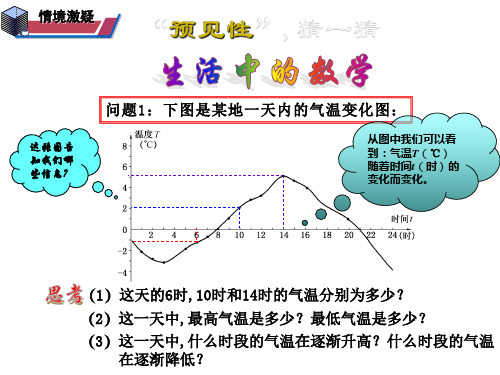
(1)题中有几个变量? T、t两个变量
(2)当横轴上的时间t取定一个值时,纵轴上气温T有几个值 与之对应?
探究发现
问题2:小蕾在过14岁生日的时候,看到了爸爸为她记录的各周岁的 体重,如下表:
周岁 1 2 3 4 5 6 7 8 9 10 11 12 13 体重 (kg)
(1)题中有几个变量? (2)每取一个周岁,与之相对应的体重有几个?
学以致用
例 1 列出下列关系式,并指出关系式中的变量。
(1)收音机刻度盘上的波长λ(m)与频率f (kHz)之间的关系:
(2)三角形的一边长5cm,它的面积S(cm2)与这边上的高h(cm)的 关系式:
(3)圆的周长C与半径r之间的关系:
C 2 r
探究发现
问题5:下面的例子中有一些始终不变的量,你能找出来吗? (1)收音机刻度盘上的波长λ(m)与频率f (kHz)之间的关系:
探究发现
问题2:小蕾在过14岁生日的时候,看到了爸爸为她记录的各周岁的 体重,如下表:
周岁 1 2 3 4 5 6 7 8 9 10 11 12 13 体重 (kg)
(1)视察上表,说一说随着年龄的增长,小蕾的体重如何变化的? (2)小蕾的体重在哪一段时间内增加较快? (3)通过上表,你发现了什么?
例 2 判断下面各量之间的关系式是不是函数关系,若是,请指出自变量
与因变量。 (1)长方形的宽b一定,其长a与周长C,其中C=2(a+b)
(2)y=|x|中的x和y;
(3)小刚计划用20元购买本子,所能购买的本子数n(本)与本子的单价a
(元),其中
.
学以致用
例 3 下列关系式中,y不是自变量x的函数的是( D )
探究发现
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑤y=x2-4x+5
表示函数关系的方法
f 30000, 0Sr2
l
波长 l(m)
300
500
600 1000 1500
频率 f(kHz) 1000
600
500 300 200
解析法 列表法
图17.1.1
图象法
例2 、写出下列各问题中的函数关系式,并指 出其中的常量与变量:
(1)圆的周长C与半径r的函数关系式;
C=2∏r
(2)火车以60千米/时的速度行驶,它驶过的路 程s(千米)与所用时间t(时)的函数关系
式;
S=60t
(3)n边形的内角和的度数S与边数n的函数关系 式.
S=(n-2)1800
如何书写函数的关系式呢? 函数的关系式是等式 通常等式的右边是含有自变量的代数式,
左边的一个字母表示函数 例2、根据所给的 条件,写出y与x的函数关系式 1、矩形的周长是18 cm ,它的长是y,宽是x cm ;
试一试:看谁的眼光准
例1、判断下列变量关系是不是函数? (1)等腰三角形的底边长与面积
(2)关系 y式 x中 ,y是 x的函数 ? 吗
判断是不是函数,我们可以看它的数学式 子中的变量之间是否满足函数的定义
⑵下列变化中,哪些y是x的函数?哪些不是?
说明理由。
xy=2
x2+y2=10
x+y=5
|y|=3x+1
变量:如:T和t, y和x,
ƒ 和λ, S和r。
常量: 如:问题3中的300000
和问题4中的
概括
2、一般地,在一个变化过程中有两个变量x 与y,如果对于x每 一个值,y都有唯一的值与 它对应,那么就说x是自变量,y是因变量,此 时也称 y是x的函数。
如: 当矩形的长一定时,矩形的面积依 赖宽的变化而变化, 他们之间是否存在函数 关系呢?
• 1、在y=3x+1中,如果x 是自变量, 是x的函数
2、下列说法中,不正确的是( ) A、函数不是数,而是 一种关系 B、多边形的内角和是边数的函数 C、一天中时间是温度的函数 D、一天中温度是时间的函数
3、正方形的边长为5 cm,当边长减 少x cm时,周长为y cm,求y与x 的函数关系式。
17.1变量与函数(1)课件 ppt
变量与函数(1)
大千世界处在不停的运动变化之中,如何 来研究这些运动变化并寻找规律呢?
数学上常用变量与函数来刻画各种运动变化.
观 察: 3、收音机刻度盘上的波长和频率分别是
用米(m)和千赫兹(kHz)为单位标刻的。下面是 一些对应的数值:
波长 λ(m) 300 500 600 频率 ƒ(kHz) 1000 600 500
2、y 是 x的 倒数的4倍
教你一招:
1、先认真审题,根据题意找出相等关系
2、按相等关系,写出含有两个变量的等式 3、将等式变形为用含有自变量的代数式
表示函数的式子
认真审题:你会有意外的收获
汽车由洪泽驶往相距500公里外的上海, 它的平均速度是100 公里/小时,则汽车距上 海的的距离s(公里)与行驶时间t(小时)的 函数关系式?
本案在审理时,农资公司的经理矢口否认他让秘书李某 签字,否定自己当时在场,声称自己不知道这回事。化肥厂却 到郭某曾经与匡某和李某住过的宾馆取证,找到了匡某与李某 的住房登记记录,宾馆开具有关证明。匡某承认自己在那里住 过,但还是否认知道这件事。法庭认为匡莱理由不足,认定李 某的签名是合法的代理,签名有效。
1000 1500 300 200
λƒ=300000 或 ƒ= 300000
波长 λ 越大,频率 f 就__越__小_.
结论:任给一个波长λ的确定值,频率ƒ都有唯一 的一个值和它对应
观 察:圆的面积随着半径的增大而增大。如果用r表
示圆的半径,S表示圆的面积,则S与r之间满 足下列关系:
r S=———— 2
课堂小结:
• 本节课我们学习主要内容是什么? • 你有什么收获?
某化肥厂诉某农资公司履行合同纠纷案
[案情]: 在2005年1月中,某化肥厂业务员郭某出差时在火车上碰 巧遇到某农资公司的经理匡某及其秘书李某,双方在火车上就开始谈论 生意。郭某介绍了厂里的主要产品及其价格,匡某对该化肥厂的钾肥感 兴趣,表示可以考虑买人一批,准备春耕季节的市场需求.下了火车后,郭 某决定与匡某等同佐一家宾馆。双方都看过对方的有关证件后,郭某拿 出已经盖了合同专用章的合同文本,填写了有关事项,签名,递给匡某签 名,匡某说不需要自己亲自签名,让秘书李某签名就行。李某按照匡某 的意思签了名。签完名才想到没有合同专用章。郭某说不要紧,只要双 方有意做生意就行。双方可以先签好合同,一式两份,等匡某和李某回到 公司后再益章,然后传真绘郭某,当做最后文件。匡某同意.合同上约定, 化肥厂出售10吨优质钾肥绘农资公司,价格为每吨2000元.共2万元,化肥 厂在3月15日之前送货上门,货到付款.李某与匡某回到公司后,因为忙于 年终收尾工作,把与郭某的合同一事忘记了。不久就放假过年。郭某回 到厂里却通知销售部,准备在3月15日之前发货并且送到农资公司。
[问题] :( l)李某的签名是否有效? (2)双方签审理]与 [分析]
[审理]:
法庭判决该合同是有效的合同,农资公司应该履行合同, 接收货物,支付款项。
[分析]:
《合同法》第33条 “ 当事人采用合同书形式订立合同的, 自双方当事人签字或者盖章时合同成立。”
请完成下表:
半径r(cm) 1
1.5 2
2.6 3.2 …
面积S(cm2) 2.25 4 6.76 10.24 …
可以看出:圆的半径越大,它的面积就越大
结论:任给一个半径r的确定值,面积S都有唯 一的一个值和它对应
概括
1、在某一变化过程中,可以取不同数值的 量 叫做变量.
在问题的研究过程中,还有一种量,它的 取值始终保持不变,我们称之为常量
在3月12日,化肥厂把货送到农资公司时,谁知农资公司却拒绝收货, 说不知道与化肥厂有购销合同,已经从别的厂采购了相同的化肥。农资 公司的经营人员通知经理匡某,匡某才想起与郭某的合同。但是他为了 维护公司的利益,随即说明签的只是合同草稿,没有盖章,合同还没有 成立。后来又说该草稿是李某签的,李某不是法定代表人,又不是业务 员,签字无效。化肥厂把化肥卸下堆在农资公司门口,用油布遮好,声 明对方必须接收并如数付款。双方僵持不下。化肥厂到法院起诉,要求 认定双方合同关系成立,判决对方履行合同。
