(完整版)复合梯形公式与复合辛普森公式对比

合集下载

(完整版)复合梯形公式与复合辛普森公式对比

SHANGHAI JIAO TONG UNIVERSITY题目名称：复合梯形公式与复合辛普森公式对比学生姓名:学生学号:班级:学院(系):目录1.概述 (3)2.问题提出 (4)3.算法推导 (5)4.算法框图 (6)4.1复合梯形公式算法流程图 (6)4.2 复合辛普森公式算法流程图 (7)5.MATLAB源程序 (8)6.结论与展望 (9)图表目录图4-1 复合梯形公式算法流程图 (6)图4-2 复合辛普森公式算法流程图 (7)图6-1 MATLAB计算结果 (9)表2-1函数计算结果表 (4)1.概述梯形求积公式和辛普森求积公式分别是牛顿-科斯特公式中n=1和n=2时的情形。

其中梯形求积公式可表示为由于牛顿-科斯特公式在n≥8时不具有稳定性，故不可能通过提高阶的方法来提高求积精度。

为了提高精度通常可把积分区间分成若干子区间（通常是等分），再在每个子区间上用低阶求积公式。

这种方法称为复合求积法。

本文主要讨论复合梯形公式和复合辛普森公式在同一数学问题中的应用。

首先给出了复合梯形公式和复合辛普森公式的推导过程以及其余项的表达形式，然后用流程图的形式介绍算法思路，再运用MATLAB编写代码计算结果，最后对结果进行对比讨论。

希望通过两个算法在同一个算例中的应用对比，更好的理解和掌握复合梯形公式和复合辛普森公式的适用范围和适用条件。

并且能够熟悉MATLAB编程求解问题的流程，掌握编程化的思想方法。

同时对两种方法的计算结果对比分析，讨论两种求积方法的计算精度。

2.问题提出对于函数f(x)=sinxx给出的函数表如下，试用复合梯形公式和复合辛普森公式计算积分I=∫sinxx dx1。

表 2-1函数计算结果表3. 算法推导3.1复合梯形公式根据梯形公式，将区间[a,b]划分为n 等份，分点x k =a +kℎ,h =b−a n,k =0,1,…,n ，在每个子区间[x k ,x k+1](k =0,1,…,n −1)上采用梯形公式，则得：记则T n 为复合梯形公式。

复化梯形公式和复化Simpson公式

一、计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。

1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x %定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。

f3='-(2*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果 Tn=等分数 n=7019已知值与计算值的误差 R=2. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果 Sn=等分数 n=24已知值与计算值的误差 R=用复化梯形公式计算的结果为：，与精确解的误差为：。

复合梯形公式与复合辛普森公式对比

4、1 复合梯形公式算法流程图
开始
输入区间断点 a,b 及等分数 n
求出步长 h,各节点及相应得
各函节数点值函数值,k=1,2求,、、与ns-u1m, k=1,2,、、n-1
输出积分值
结束
图 4-1 复合梯形公式算法流程图 4、2 复合辛普森公式算法流程图
开始
输入区间断点 a, b 及等分数 n
SHANGHAI JIAO TONG UNIVERSITY
题目名称：复合梯形公式与复合辛普森公式对比
学生姓名: 学生学号：班级：学院(系)：
目录
1、概述 .............................................................................................................. 1 2、问题提出 ...................................................................................................... 2 3、算法推导 ...................................................................................................... 3 4、算法框图 ...................................................................................................... 4
图表目录
图 4-1 复合梯形公式算法流程图 ...................................................................... 4 图 4-2 复合辛普森公式算法流程图 .................................................................. 5 图 6-1 MATLAB 计算结果..................................................................................6 表 2-1 函数计算结果表 .......................................................................................2

复合梯形公式和复合Simpson公式用法的比较

复合梯形公式和复合Simpson 公式用法的比较一、问题叙述由曲线y ()f x = ,a x b ≤≤绕x 轴旋转得到立体，其表面积计算公式为2(baS f x π=⎰分别用N=10的复合梯形公式和N=5的复合Simpson 公式求解下列每个的曲线绕x 轴旋转得到立方体的表面积。

（1）3(),01f x x x =≤≤ （2）()sin ,0/4f x x x π=≤≤ ；（3）()e ,01x f x x -=≤≤。

二、问题分析由叙述可知，三个函数在各自的定义域上函数值都大于0，且函数在各自的定义域上都是单调的。

（1）复合梯形公式取正整数n,令(b a)/n h =-,则点(k 0,1,,n)k x a kh =+=将[a,b]分为n 个小区间，利用定积分的性质可得11110011(x)(x)(x )f(x )2 =(a)f(b)2(x )2j jn n bx j j ax j j n j j h f dx f dx f h f f +--+==-=⎡⎤=≈+⎣⎦⎡⎤++⎢⎥⎣⎦∑∑⎰⎰∑所以，复合梯形公式的近似面积为：11(a)f(b)2(x )2n j j h S f f -=⎡⎤=++⎢⎥⎣⎦∑（2）复合Simpson 公式取正整数n,令h=(b-a)/2n,(j 0,1,,2n)j x a jh =+=.利用定积分的性质，以及Simpson 公式[]012(x)(x )4f(x )f(x )(f)3bahf dx f R =+++⎰在小区间222,j j x x -⎡⎤⎣⎦上的应用，有 2222221211(x)(x)(x )4f(x )f(x )3j nnbj j j j ax j j hf dx f dx f ---==⎡⎤=≈++⎣⎦∑∑⎰⎰整理可得，复合Simpson 公式的近似面积为：121211[f(a)f(b)4(x )2(x )]3n n j j j j hS f f --===+++∑∑。

复化梯形公式和复化辛普生公式

}
void main()
{
tixing ti;
ti.integration();
}
2）复化simpson
#include<iostream.h>
#include<math.h>
class simpson
{
private:
double result;
int n,k;//n是等分数，
double h;//h步长
cin>>b>>a;
cout<<"输入你要使用tixing法则的数目(即等分数)";
cin>>n;
h=(b-a)/n;
sum=0.0;
for(k=1;k<n;k++)
{
sum+=func(k*h);
}
integral=(h/2.0)*(2.0*sum+func(b)+1);
cout<<endl<<"积分值="<<integral<<endl;
public:
double sine(double);
void integration();//实现积分的函数
};
double simpson::sine(double a)
{
result=sin(a)/a;//被积函数
cout<<"sin("<<a<<")/"<<a<<"="<<result<<endl;
源程序：

复合梯形公式和复合辛普森公式例题

复合梯形公式和复合辛普森公式例题复合梯形公式和复合辛普森公式例题数值计算是现代科学技术中重要的研究领域之一，而数值积分是数值计算中的一个重要分支。

数值积分是指在一定区间上用数值方法来逼近求解定积分的过程。

综合考虑精度和效率，梯形公式和辛普森公式是数值积分中比较常用的方法，而复合梯形公式和复合辛普森公式则是对前两种方法的改进和完善。

一、复合梯形公式（一）基本原理梯形公式是数值积分中运用最广泛的一种方法，其基本思想是将被积函数在区间[a,b]上的曲线用若干条梯形逼近，然后计算梯形的面积之和，得到函数曲线下的面积。

若将区间[a,b]分为n个小区间，梯形公式还可以推广为复合梯形公式。

复合梯形公式的基本原理是将整个区间[a,b]等分为n 个小区间，每个小区间的长度为h=(b-a)/n，然后对于每个小区间求出梯形的面积，并将所有梯形面积加起来得到函数曲线下的面积，并作为积分的近似值。

具体地说，复合梯形公式的表达式为：$$\int_a^b f(x)dx \approx \frac{h}{2}[f(a)+2\sum_{i=1}^{n-1} f(x_{i})+f(b)]$$其中，$x_1=a+h,x_2=a+2h,...,x_{i+1}=x_i+h,...,x_{n}=b-h$，h是小区间长度。

（二）例题现在考虑如下的积分：$$I=\int_0^1 e^{x^2} dx$$将整个区间[0,1]等分为4个小区间，得到$h=0.25$，对于每个小区间，可以分别求出梯形的面积，得到：$$\frac{h}{2}[f(0)+2f(0.25)+2f(0.5)+2f(0.75)+f(1)]$$代入函数$f(x)=e^{x^2}$，得到近似积分值为$1.4627$。

使用Matlab代码进行计算，得到具体结果为：>> f=@(x) exp(x.^2); h=0.25; x=0:h:1;I=h/2*(f(x(1))+2*sum(f(x(2:end-1)))+f(x(end))) sprintf('%.5f',I)ans =1.46270可以发现，与精确值$1.46265$相比，误差很小，说明复合梯形公式是一种很有效的近似积分方法。

复合梯形公式和复合辛普森公式

复合梯形公式和复合辛普森公式1.复合梯形公式步骤1：将积分区间[a,b]均匀地分成n个小区间，每个小区间的长度为h=(b-a)/n，其中n为正整数。

步骤2：定义一个函数f(x)，并在每个小区间上求出函数在小区间两个端点的函数值，记作f(x0), f(x1), f(x2), ..., f(xn)。

步骤3：根据梯形公式，每个小区间上的定积分近似值为(h/2) * (f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn))。

步骤4：将所有小区间上的定积分近似值相加，得到最终的近似值。

复合辛普森公式是通过将积分区间划分成若干个小区间，然后在每个小区间上应用辛普森公式来逼近定积分的值。

具体的步骤如下：步骤1：将积分区间[a,b]均匀地分成n个小区间，每个小区间的长度为h=(b-a)/n，其中n为正偶数。

步骤2：定义一个函数f(x)，并在每个小区间上求出函数在小区间三个点的函数值，记作f(x0),f(x1),f(x2)。

步骤3：根据辛普森公式，每个小区间上的定积分近似值为(h/3)*(f(x0)+4f(x1)+f(x2))。

步骤4：将所有小区间上的定积分近似值相加，得到最终的近似值。

复合辛普森公式的误差主要取决于小区间的数量和函数在每个小区间上的变化情况。

与复合梯形公式相比，复合辛普森公式的精度更高，但计算复杂度也更高。

综上所述，复合梯形公式和复合辛普森公式是数值积分中常用的近似计算方法。

它们通过将积分区间划分成小区间，并在每个小区间上应用相应的公式来逼近定积分的值。

这两种方法都可以通过增加小区间的数量来提高近似的精度，但相应地也会增加计算的复杂度。

根据实际情况，我们可以选择合适的方法来计算需要求解的定积分。

复化梯形公式和复化辛普森公式

复化梯形公式和复化辛普森公式1. 引言嘿，大家好！今天我们来聊聊数学里那些看似高深莫测的公式，尤其是复化梯形公式和复化辛普森公式。

这些名字听起来就像是从某部科幻片里蹦出来的角色，但其实它们是我们在数值积分中不可或缺的好帮手。

你知道吗？它们就像是数学世界里的“超能英雄”，让我们轻松搞定积分，简直是妙不可言。

2. 复化梯形公式2.1 你知道什么是梯形吗？首先，咱们得聊聊复化梯形公式。

说白了，就是把一个复杂的积分任务，分解成几个小的梯形来求解。

想象一下，你在河边钓鱼，河水流得可欢了。

为了找一个合适的钓鱼点，你可能得把河分成几段，然后每一段的宽度就是你的小梯形。

你看，这就是复化梯形的魅力所在！2.2 如何运用复化梯形公式？用这个公式的时候，你只需把整个区间分成N个小区间，每个区间的宽度都是一样的。

然后，把每个小区间的函数值拿来加一加，再乘上宽度的一半，最后再把头尾的函数值加上。

这听起来是不是很简单？比如，你想算从0到1的某个函数的积分，只要把这个区间分成若干段，像切蛋糕一样，每一片都求个函数值，然后把结果合起来就行了。

简单得就像吃个冰淇淋，大家都喜欢。

3. 复化辛普森公式3.1 辛普森是谁？接下来，让我们来看看复化辛普森公式。

辛普森这个名字，大家可能都听过，或者说过“这是辛普森家的事儿”。

其实，他是一位牛逼的数学家，专门研究如何让积分变得更加简单。

辛普森公式就像是对梯形公式的一次升级，像换了个新款手机，功能更强大，效果更好。

3.2 如何运用复化辛普森公式？用复化辛普森公式的时候，我们也是把整个区间分成N个小区间，不过这里的N必须是偶数哦！每个小区间的宽度仍然是一样的。

然后，用函数值的加权平均法来计算。

换句话说，你把每个小区间的头尾和中间的函数值都考虑进来，像是为你的冰淇淋加上各种口味的配料。

最后，你的结果就会比单纯用梯形公式得来的要精准多了，仿佛一口下去，味蕾都在舞蹈。

4. 比较与应用4.1 谁更强？说到这儿，很多人就会问，复化梯形公式和复化辛普森公式，谁更厉害呢？其实，这就像问“苹果和橘子，哪个更好吃”。

复化梯形公式和复化Simpson公式

数值计算方法上机题目3一、计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。

1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。

f3='-(2*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果Tn= 7.3891等分数n=7019已知值与计算值的误差R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果Sn= 7.3891等分数n=24已知值与计算值的误差R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。

复化梯形公式和复化Simpson公式

1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。

f3='-(2*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果 Tn= 7.3891等分数 n=7019已知值与计算值的误差 R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果 Sn= 7.3891等分数 n=24已知值与计算值的误差 R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。

复化梯形公式和复化Simpson公式

数值计算方法上机题目3一、计算定积分的近似值：要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。

1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x %定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可 f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。

f3='-(2*exp(x) + x*exp(x))' %因fminbnd （）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果Tn= 7.3891等分数n=7019已知值与计算值的误差R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果Sn= 7.3891等分数n=24已知值与计算值的误差R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。

复合梯形公式与复合辛普森公式对比

SHANGHAI JIAO TONG UNIVERSITY题目名称：复合梯形公式与复合辛普森公式对比学生姓名:学生学号:班级:学院(系):目录1.概述 (3)2.问题提出 (4)3.算法推导 (5)4.算法框图 (6)4.1复合梯形公式算法流程图 (6)4.2 复合辛普森公式算法流程图 (7)5.MATLAB源程序 (8)6.结论与展望 (9)图表目录图4-1 复合梯形公式算法流程图 (6)图4-2 复合辛普森公式算法流程图 (7)图6-1 MATLAB计算结果 (9)表2-1函数计算结果表 (4)概述梯形求积公式和辛普森求积公式分别是牛顿-科斯特公式中n=1和n=2时的情形。

其中梯形求积公式可表示为其公式左端是以[a,b]区间上积分，右端为b-a为高、端点函数值为上下底的梯形的面积值，故通称为梯形公式，具有1次代数精确度。

类似的，辛普森求积公式可以表示为该公式一般在立体几何中用来求拟柱体的体积，由于偶数n阶牛顿-科特斯求积公式至少具有n+1次代数精确度，所以辛普森公式实际上具有3次代数精确度。

由于牛顿-科斯特公式在n≥8时不具有稳定性，故不可能通过提高阶的方法来提高求积精度。

为了提高精度通常可把积分区间分成若干子区间（通常是等分），再在每个子区间上用低阶求积公式。

这种方法称为复合求积法。

本文主要讨论复合梯形公式和复合辛普森公式在同一数学问题中的应用。

首先给出了复合梯形公式和复合辛普森公式的推导过程以及其余项的表达形式，然后用流程图的形式介绍算法思路，再运用MATLAB 编写代码计算结果，最后对结果进行对比讨论。

希望通过两个算法在同一个算例中的应用对比，更好的理解和掌握复合梯形公式和复合辛普森公式的适用范围和适用条件。

并且能够熟悉MATLAB编程求解问题的流程，掌握编程化的思想方法。

同时对两种方法的计算结果对比分析，讨论两种求积方法的计算精度。

问题提出对于函数给出的函数表如下，试用复合梯形公式和复合辛普森公式计算积分。

数值计算考题五——复合梯形求积公式与复合辛普森求积公式求积分

数值计算考题五1. 分别用复合梯形求积公式与复合辛普森求积公式求积分I=⎰102x e sinx dx 的近似值，要求误差不超过ε=0.5⨯10-5.解：方法一：复合梯形求积公式复合梯形求积公式是将积分区间划分为n 个很小的区间，然后将各个小区间的面积相加而得到在整个积分区间上的积分，当分成的小区间数n →∞时，求得的面积就等于积分的精确值。

由复合梯形求积公式的余项R n T 可得满足精度要求≤ε0.5⨯10-5时区间()b a ,被分成的区间数n 的最小值为700，所以在编程时循环次数应大于等于这个值，方可满足精度要求。

以下是编写的C 语言程序：#include<stdio.h>#include<math.h>void main(){int n=700,i;double x,f=0.0,t,h,T=0.0,c=2.0,a=0.0,b=1.0;h=(b-a)/n;for(i=0;i<n;i++){x=a+i*h;f=f+exp(pow(x,c))*sin(x);}t=(h/2)*(2*f+sin(1)*exp(1));printf("T=%f\n",t);}输出结果为T=0.778746.方法二：复合辛普森求积公式：复合辛普森求积法是将积分区间分割之后，在每个小区间[x i ,x i+1]上运用辛普森求积公式。

以下是编写的c 语言程序：#include<stdio.h>#include<math.h>void main(){int n=700,i;double x1,x2,f1=0.0,f2=0.0,t,h,T=0.0,c=2.0,a=0.0,b=1.0;h=(b-a)/n;for(i=0;i<n;i++){x1=a+i*h;x2=a+(i+0.5)*h;f1=f1+exp(pow(x1,c))*sin(x1);f2=f2+exp(pow(x2,c))*sin(x2); }t=(h/6)*(2*f1+sin(1)*exp(1)+4*f2); printf("T=%f\n",t);}程序输出结果为0.778745.2. 用高斯求积法求上述积分的近似值。

复化梯形公式和复化辛普森公式的精度比较(共7页)

- 让每一个人同等地提高(tí gāo)自我实验四、复化梯形(tīxíng)公式和复化Simpson 公式的精度(jīnɡ dù)比较（2 学时(xuéshí)）一、实验目的(mùdì)与要求1、熟习复化 Simpson 公式和复化梯形公式的结构原理；2、熟习并掌握两者的余项表达式；3、分别求出正确值，复化梯形的近似值，复化Simpson 的近似值，并比较后两者的精度；4、从余项表达式，即偏差曲线，来察看两者的精度，看哪个更靠近于正确值。

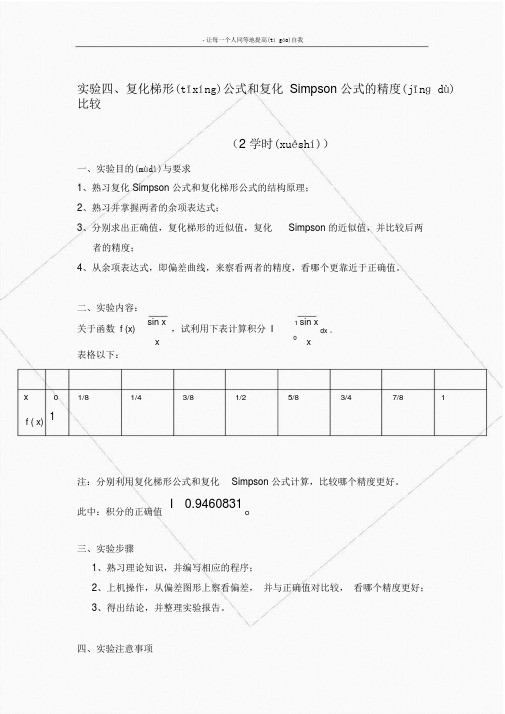
二、实验内容：关于函数 f (x) sin x，试利用下表计算积分 I 1sin xdx 。

x x表格以下：x 0 1/8 1/4 3/8 1/2 5/8 3/4 7/8 1 f ( x)1注：分别利用复化梯形公式和复化Simpson 公式计算，比较哪个精度更好。

此中：积分的正确值I0.9460831。

三、实验步骤1、熟习理论知识，并编写相应的程序；2、上机操作，从偏差图形上察看偏差，并与正确值对比较，看哪个精度更好；3、得出结论，并整理实验报告。

四、实验注意事项11- 让每一个人同等地提高(tí gāo)自我1、复化梯形公式，程序主体(zhǔtǐ)部分：for n=2:10T(n)=*T(n-1)for i=1:2^(n-2)；endend2、复化 Simpson 公式(gōngshì)，程序主体部分：for i=1:10n=2.^ix=0:1/n:1f=sin(x)./xf(1)=1s=0for j=1:n/2s=s+f(2*j)endt=0for j=1:(n/2-1)t=t+f(2*j-1)endS(i)=1/3/n*(f(1)+4*s+2*t+f(n+1))end五．实验(shíyàn)内容复化梯形(tīxíng)公式和复化辛普森公式的引入22- 让每一个(yī ɡè)人同等地提高自我复化梯形(tīxíng)公式：T n n 1 h [ f (x k f ( x k 1 )] ；k 0 2复化辛普森公式：S n n 1 h4 f ( x 1 ) f (x k 1 )] ；[ f (x kk 0 6k2依据题意(tí yì)和复化梯形公式、复化辛普森公式的原理编写程序求解代码以下：Matlab 代码(dài mǎ)clcs=quad( 'sin(x)./x',0,1)p1=zeros(10,1);p2=zeros(10,1);for k=6:15s1=0;s2=0;x=linspace(0,1,k);y=sin(x)./x;z=(1/(2*(k-1))):(1/(k-1)):1;sz=sin(z)./z;y(1)=1;for i=1:(k-1)s1=s1+*(x(i+1)-x(i))*(y(i)+y(i+1));endfor j=1:(k-1)s2=s2+(1/6)*(x(j+1)-x(j))*(y(j)+y(j+1)+4*sz(j));endp1(k-5)=s1-s;p2(k-5)=s2-s;endp1;33- 让每一个人同等地提高(tí gāo)自我p2;s1=s+p1(4)s2=s+p2(4)format longfor k=1:length(p1)p1(k)=abs(p1(k));p2(k)=abs(p2(k));endp1p2plot(6:1:15,p1,'-r' )hold onplot(6:1:15,10000*(p2),'-c' )hold off部分(bù fen)程序结果输出：s=s1 =s2 =结果剖析1 sin( x)；依据结果输出可知：积分 I dx 的正确值为： I=x44- 让每一个人同等(tóngděng)地提高自我经过复化梯形公式(gōngshì)和复化辛普森公式获得的积分值为：s1 =:s2 =;相对偏差为：S 1 I 100 4.15 10 4 ； 1I 100S 2 I 100 1.62 10 8 ； 2 I 100明显，从相对偏差可知经过辛普森公式获得(huòdé)的结果偏差小精度高。

复合梯形公式和复合辛普森公式误差

复合梯形公式和复合辛普森公式误差在我们学习数学的过程中，常常会遇到各种各样的公式，而复合梯形公式和复合辛普森公式就是其中比较重要的两个。

这两个公式在数值计算中发挥着重要的作用，可别小瞧它们，这里面的学问可大着呢！先来说说复合梯形公式。

它就像是一个勤劳的小工人，虽然简单直接，但也有自己的小脾气。

复合梯形公式的基本思想就是把区间分成很多小段，然后在每个小段上用梯形的面积来近似函数的积分值。

这就好像我们要计算一段山坡的面积，把山坡分成一段一段的，每一段都看成一个梯形，然后把这些梯形的面积加起来，就得到了山坡的近似面积。

我记得有一次在课堂上，老师给我们出了一道用复合梯形公式计算积分的题目。

那道题可把大家难住了，大家都在草稿纸上不停地写写画画。

我也不例外，一开始我总是算错，不是区间分错了，就是梯形面积计算有误。

但是我没有放弃，一遍又一遍地检查，终于发现了问题所在。

原来我在计算梯形面积的时候，忘记乘以二分之一了。

经过这次小小的挫折，我对复合梯形公式的理解更加深刻了，也明白了做数学题一定要细心，不能马虎。

再聊聊复合辛普森公式。

它可比复合梯形公式要“聪明”一些，精度也更高。

复合辛普森公式就像是一个精明的小管家，能够更准确地估计函数的积分值。

它把区间分成偶数段，然后用抛物线来近似函数，计算出的结果更接近真实值。

有一次我在做一个数学实验，要用复合辛普森公式计算一个复杂函数的积分。

我按照公式一步一步地计算，心里还挺紧张，生怕出错。

当我算出结果，和标准答案一对比，发现竟然相差无几，那一刻我心里别提多高兴了，就像是在黑暗中找到了光明一样。

那么，复合梯形公式和复合辛普森公式到底有什么误差呢？其实啊，复合梯形公式的误差与区间长度的平方成正比，而复合辛普森公式的误差与区间长度的四次方成正比。

这就意味着，在相同的区间长度下，复合辛普森公式的误差要比复合梯形公式小得多。

比如说，我们要计算一个函数在[0, 1]区间上的积分，如果用复合梯形公式，把区间分成 10 段，可能会有比较大的误差；但如果用复合辛普森公式，同样分成 10 段，误差就会小很多。

梯形法则和辛普森法则

梯形法则与辛普森法则1. 概述梯形法则和辛普森法则是数值积分中常用的近似方法。

它们通过将曲线或曲面分割成若干个由直线或弧线组成的小区间，并在每个小区间内估计函数值来求解定积分。

这两种方法具有较高的精度和广泛的应用领域，本文将详细介绍这两种方法的原理、应用和优缺点。

2. 梯形法则梯形法则是一种利用梯形来近似曲线下面积的方法。

假设我们要计算函数f(x)在区间[a, b]上的定积分，梯形法则将该区间分成n个小区间，每个小区间的宽度为Δx=(b-a)/n。

然后，我们可以将每个小区间内的函数值连接起来，形成若干个梯形，计算每个梯形的面积，并将它们相加，即可得到函数在整个区间上的近似积分值。

梯形法则的近似积分公式如下：∫[a, b] f(x) dx ≈ Δx/2 * [f(a) + 2f(x1) + 2f(x2) + ... + f(b)]其中，x1, x2, …, xn-1 是分割点。

梯形法则的优点是简单易懂，容易推广到多维积分，适用于一般的函数。

然而，它的缺点是存在一定的误差，特别是在曲线弯曲的区域，误差较大。

3. 辛普森法则辛普森法则是一种利用拟合曲线来近似曲线下面积的方法。

与梯形法则类似，辛普森法则也将函数f(x)在区间[a, b]上分成若干个小区间，每个小区间的宽度为Δx=(b-a)/n，但不同的是，辛普森法则采用二次多项式来拟合每个小区间内的曲线。

辛普森法则的近似积分公式如下：∫[a, b] f(x) dx ≈ Δx/3 * [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + ... + f(xn)]其中，x0, x1, x2, …, xn 是分割点，且n为偶数。

辛普森法则的优点是相比于梯形法则，它的精度更高，尤其适用于曲线较为平滑的情况。

然而，辛普森法则的缺点是计算量较大，对于需要较高精度的计算而言，分割的区间数需要相对较多。

4. 应用场景梯形法则和辛普森法则在数值计算中有广泛的应用，特别是在求解无法用解析方法求得精确解的积分问题时，这两种方法成为重要的工具。

复合梯形公式与复合辛普森公式对比

SHANGHAI JIAO TONG UNIVERSITY 题目名称：复合梯形公式与复合辛普森公式对比学生姓名:学生学号:班级:学院(系):目录1.概述 (3)2.问题提出 (4)3.算法推导 (5)4.算法框图 (6)复合梯形公式算法流程图 (6)复合辛普森公式算法流程图 (7)5.MATLAB源程序 (8)6.结论与展望 (9)图表目录图 4-1 复合梯形公式算法流程图 (6)图 4-2 复合辛普森公式算法流程图 (7)图 6-1 MATLAB计算结果 (9)表 2-1函数计算结果表 (4)1.概述梯形求积公式和辛普森求积公式分别是牛顿-科斯特公式中n=1和n=2时的情形。

由于牛顿-科斯特公式在n≥8时不具有稳定性，故不可能通过提高阶的方法来提高求积精度。

为了提高精度通常可把积分区间分成若干子区间（通常是等分），再在每个子区间上用低阶求积公式。

这种方法称为复合求积法。

本文主要讨论复合梯形公式和复合辛普森公式在同一数学问题中的应用。

希望通过两个算法在同一个算例中的应用对比，更好的理解和掌握复合梯形公式和复合辛普森公式的适用范围和适用条件。

并且能够熟悉MATLAB编程求解问题的流程，掌握编程化的思想方法。

同时对两种方法的计算结果对比分析，讨论两种求积方法的计算精度。

2.问题提出对于函数f(x)=sinxx给出的函数表如下，试用复合梯形公式和复合辛普森公式计算积分I=∫sinxx dx1。

复合梯形和复合辛普森MATLAB程序10页

复合梯形和复合辛普森MATLAB程序10页
复合梯形公式和复合辛普森公式都是数值积分方法中的常用方法。

本文将编写MATLAB 程序来实现这两种方法。

一、复合梯形公式
复合梯形公式是将被积函数在每个小区间内近似为一个梯形，再将这些梯形的面积相
加得到数值积分结果。

具体的，在区间$[a,b]$中，将其分成$n$个小区间，记每个小区间的长度为
$h=\frac{b-a}{n}$，则复合梯形公式的数值积分公式为：
$$
\int_a^bf(x)dx\approx \frac{h}{2}\sum_{i=1}^n(f(x_{i-1})+f(x_i))
$$
其中，$x_i=a+ih$，$i=0,1,\dots,n$。

将以上公式写成MATLAB代码：
function result=composite_trapezoidal(f,a,b,n)%f为被积函数,a,b为积分上下限，n为小区间数
h=(b-a)/n;
result=f(a)+f(b);
for i=1:n-1
x=a+i*h;
result=result+2*f(x);
end
result=result*h/2;
end
上述程序中，首先计算$h$，从而计算出$x_i$，然后使用循环遍历每个小区间内的中
点$x$，计算其所在梯形面积，并将所有梯形面积相加得到最终结果。

二、复合辛普森公式
最后需要指出的是，虽然复合辛普森公式的收敛速度比复合梯形公式快，但是当被积函数存在奇点或者发散点时，复合辛普森公式可能不收敛。

此时需要选择其他的数值积分方法来计算。

球体体积计算-梯形公式与辛普森公式

梯形公式和辛普森公式计算球体体积题目：分别用梯形公式和辛普森公式计算半径为1的球体体积解答：计算积分值：I=梯形公式：I=(b-a)/2*[]组合梯形公式：辛普森公式：I=(b-a)/6*[] 组合辛普森公式：+*（1）梯形公式计算定义函数function y=fx(x) function T_n=fht(a,b,n)源代码：function y=fx(x)y=3.14*(1-x^2);function T_n=fht(a,b,n)h=(b-a)/n;for k=0:nx(k+1)=a+k*h;endT_1=h/2*(fx(x(1))+fx(x(n+1)));for i=2:nF(i)=h*fx(x(i));endT_2=sum(F);T_n=T_1+T_2;（2）辛普森公式计算定义函数function G_n=sps(a,b,n)源代码：function G_n=sps(a,b,n)h=(b-a)/n;for k=0:nx(k+1)=a+k*hx_k(k+1)=x(k+1)+1/2*hendG_1=h/6*(fx(x(1))+fx(x(n+1)));for i=2:nF_1(i)=h/3*fx(x(i));endfor j=1:nF_2(j)=2*h/3*fx(x_k(j));endG_2=sum(F_1)+sum(F_2);G_n=G_1+G_2;结果分析：梯形公式：n=10,100,1000,T_n=fht(-1,1,10) T_n=4.1848T_n=fht(-1,1,100) T_n=4.1862T_n=fht(-1,1,1000) T_n=4.1867辛普森公式：n=10,100,1000G_n=sps(-1,1,10) G_n=4.1867G_n=sps(-1,1,10) G_n=4.1867G_n=sps(-1,1,10) G_n=4.1867通过对比，n值越大，球体体积的计算结果更加准确，并且辛普森公式计算比梯形公式更加准确V-n关系曲线梯形公式V-n曲线代码：辛普森公式V-n曲线代码：图形：。