高考数学一轮复习课件:02-6指数与指数函数
合集下载
2018届高三数学文一轮复习课件:2-6 指数与指数函数 精品

微知识❷ 有理数的指数幂
(1)幂的有关概念
m
①正分数指数幂:a n =
n am
(a>0,m、n∈N*,且 n>1);
1
1
②负分数指数幂:a-
m n
=
m
an
=
n am
(a>0,m、n∈N*,且 n>1)。
③0 的正分数指数幂等于 0 ,0 的负分数指数幂 无意义 。
(2)有理数指数幂的性质
①aras= ar+s (a>0,r,s∈Q); ②(ar)s= ars (a>0,r,s∈Q);
A.{x|x<-2 或 x>4}
B.{x|x<0 或 x>4}
C.{x|x<0 或 x>6}
D.{x|x<-2 或 x>2}
解析:f(x)为偶函数,当 x<0 时, f(x)=f(-x)=2-x-4。
2x-4,x≥0, 所以 f(x)=2-x-4,x<0, 当 f(x-2)>0 时,
x-2≥0,
x-2<0,
③(ab)r= arbr (a>0,b>0,r∈Q)。
微知识❸ 指数函数的图象与性质
y=ax
a>1
0<a<1
图象
定义域 值域
性质
R
(0,+∞)
(1)过定点 (0,1)
(2)当 x>0 时, y>1 ;x (2)当 x>0 时,0<y<1 ;
<0 时, 0<y<1
x<0 时, y>1
(3)在 R 上是 增函数 (3)在 R 上是 减函数
(3)∵x≥0,∴-x≤0,∴3-x≤3, ∴0<23-x≤23=8,∴0≤8-23-x<8, ∴函数 y=8-23-x 的值域为[0,8)。
微考场 新提升
考题选萃 随堂自测
高三第一轮复习指数及指数函数课件

THANKS
感谢观看
当 $a > 1$ 时,函数图像位于第 一象限和第四象限;当 $0 < a < 1$ 时,函数图像位于第一象 限和第二象限。
指数函数的过定点性质
无论 $a$ 的值是多少,函数图像 都会经过点 $(0,1)$。
指数函数的应用实例
01
02
03
复利计算
复利计算中,本金和利息 一起作为下一次的本金来 计算利息,可以使用指数 函数进行计算。
指数函数的图像与性质
指数函数的基本形式
$y = a^x$,其中 $a > 0$ 且 $a neq 1$
指数函数的单调性
当 $a > 1$ 时,函数在 $mathbf{R}$ 上单调递增;当 $0 < a < 1$ 时,函数在 $mathbf{R}$ 上单调递减。
01 02 03 04
指数函数的图像特点
详细描述:提升练习题在基础练习题的基础上,增加了难度和综合性,旨在提高学生的解题能力和思维水平,帮助学生掌握 更复杂的问题解决技巧。
综合练习题
总结词:综合运用
详细描述:综合练习题涉及的知识点更为广泛和深入,需要学生综合运用指数及指数函数的知识和其 他数学知识,解决复杂的问题。通过这类练习,可以提高学生的综合运用能力和问题解决能力。
复杂指数不等式的转化
将复杂的指数不等式转化为更容易处理的形式,如通过化简、分离 参数等手段。
指数函数与其他函数的综合应用
复合函数
理解复合函数的概念,掌 握如何将复合函数转化为 更简单的形式。
函数图像
理解指数函数图像的特点 ,掌握如何利用图像解决 一些实际问题。
导数与微积分
理解导数的概念和性质, 掌握如何利用导数研究函 数的单调性、极值等性质 。
高考数学(文)一轮复习课件第二章第6讲 指数与指数函数精选ppt版本

2.若函数 y=(a2-1)x 在(-∞,+∞)上为减函数,则实数 a
的取值范围是_(_-___2_,__-__1_)_∪__(1_,___2_)_. 解析: 由 y=(a2-1)x 在(-∞,+∞)上为减函数,得 0<a2- 1<1,所以 1<a2<2,即 1<a< 2或- 2<a<-1.
3.函数 y= 16-4x的值域是_[0_,__4_)___.
=245a0·b0=245.
考点二 指数函数的图象性质及应用(高频考点) (1)函数 y=a2 015-x+2 015(a>0,且 a≠1)恒过点
__(2__0_1_5_,__2_0_1_6_)_.
(2)方程 2x=2-x 的解的个数为_1_______.
(3)已知函数
f(x)
=
2 3
即 a+1a=0,即 a2+1=0,显然无解. 所以 f(x)不可能是奇函数. (2)因为 f(x)是偶函数,所以 f(-x)=f(x), 即eax+eax=ea-x+ea-x,整理得a-1a(ex-e-x)=0, 所以有 a-1a=0,得 a=1. 所以 f(x)=e-x+ex,以下讨论其单调性,
1
(2)14-2·
(
4ab-1)3 1.
0.1-2(a3b-3)2
解: (1)原式=1 20700-13-(-1)-217-2+29512-1
=130-49+53-1=-45.
13
42·42 3
33
3
(2)原式= 100 ·a2·a-2·b2·b-2
|x|-a
,
则
函
数
f(x)的单调递增区间为
_(-__∞__,__0_]__,单调递减区间为_[_0_,__+__∞__)__.若 f(x)的最大值
(人教A版)高考数学复习:2.6《指数与指数函数》ppt课件

且 f(x)是偶函数,则 m+μ=______1__.
第22页,共36页。
栏目 导引
第二章 基本初等函数、导数及其应用
解析:(1)由 f(x)=ax-b 的图象可以观察出函数 f(x)=ax-b 在 定义域上单调递减,所以 0<a<1.函数 f(x)=ax-b 的图象是
在 f(x)=ax 的基础上向左平移得到的,所以 b<0.
第5页,共36页。
栏目 导引
3.指数函数的图象与性质
y=ax
a>1
第二章 基本初等函数、导数及其应用
0<a<1
图象
定义域 值域
_____R_____ __(0_,__+__∞__)_ 过定点___(0_,__1_) ___
性质
当x>0时,_y_>_1___;当 x<0时,0_<__y<_1__
当x>0时,____0_<_y<_1___; 当x<0时,_____y>__1___
(2)由于 f(x)是偶函数, 所以 f(-x)=f(x), 即 e-(-x-μ)2 =e-(-x-μ)2 ,
∴(x+μ)2=(x-μ)2,∴μ=0,
∴f(x)=e-x2.又 y=ex 是 R 上的增函数,而-x2≤0, ∴f(x)的最大值为 e0=1=m,
∴m+μ=1.
第23页,共36页。
栏目 导引
③ 0 的 正 分 数 指 数 幂 等 于 ___0___ , 0 的 负 分 数 指 数 幂 ___无__意__义___.
第4页,共36页。
栏目 导引
第二章 基本初等函数、导数及其应用
(2)有理数指数幂的运算性质: ①aras=___a_r+_s_____ (a>0,r,s∈Q); ②(ar)s=___a_rs______ (a>0,r,s∈Q); ③(ab)r=__a_r_b_r _____ (a>0,b>0,r∈Q).
第22页,共36页。
栏目 导引
第二章 基本初等函数、导数及其应用
解析:(1)由 f(x)=ax-b 的图象可以观察出函数 f(x)=ax-b 在 定义域上单调递减,所以 0<a<1.函数 f(x)=ax-b 的图象是
在 f(x)=ax 的基础上向左平移得到的,所以 b<0.
第5页,共36页。
栏目 导引
3.指数函数的图象与性质
y=ax
a>1
第二章 基本初等函数、导数及其应用
0<a<1
图象
定义域 值域
_____R_____ __(0_,__+__∞__)_ 过定点___(0_,__1_) ___
性质
当x>0时,_y_>_1___;当 x<0时,0_<__y<_1__
当x>0时,____0_<_y<_1___; 当x<0时,_____y>__1___
(2)由于 f(x)是偶函数, 所以 f(-x)=f(x), 即 e-(-x-μ)2 =e-(-x-μ)2 ,
∴(x+μ)2=(x-μ)2,∴μ=0,
∴f(x)=e-x2.又 y=ex 是 R 上的增函数,而-x2≤0, ∴f(x)的最大值为 e0=1=m,
∴m+μ=1.
第23页,共36页。
栏目 导引
③ 0 的 正 分 数 指 数 幂 等 于 ___0___ , 0 的 负 分 数 指 数 幂 ___无__意__义___.
第4页,共36页。
栏目 导引
第二章 基本初等函数、导数及其应用
(2)有理数指数幂的运算性质: ①aras=___a_r+_s_____ (a>0,r,s∈Q); ②(ar)s=___a_rs______ (a>0,r,s∈Q); ③(ab)r=__a_r_b_r _____ (a>0,b>0,r∈Q).
高考数学大一轮总复习 第二章 第6讲 指数与指数函数课件 理

5
)
2
1
]2
+
44
3 4
+(2
3 2
)
2 3
-
1
+1
10
2
3
= 3 - 5 +43+2-1+1=64 7 ;
10 2
3
15
.
ppt精选
14
2 7 3 3-33 24-6 3 1+4 33 3
9
=7
1
33-3(3
1
23 )3-6
3
2 3
+4
4
33
=7
1
33-6
1
33
-2
3
3
2 3
1
+33
1
1
=2 33-2 33=0;
ppt精选
17
【跟踪训练 1】下列命题中,正确的是( )
n A.
an=a
B.若 a∈R,则(a2-a+1)0=1
4
C. x4+y3= x 3 y
3 D.
-5=6
-52
ppt精选
18
解析::对于 A,因为 n 为奇数时,n an=a;当 n 为偶
数时,n an=|a|,故 A 错;对于 B,因为 a2-a+1≠0,所以
ppt精选
1
第6讲 指数与指数函数
ppt精选
2
ppt精选
3
1.下列各函数中,是指数函数的是(D )
A.y=(-3)x
B.y=-3x
C.y=3x-1
D.y=(13)x
ppt精选
4
2.函数 f(x)= 1-2x的定义域是(D )
A.(-∞,+∞)
B.[0,+∞)
C.(-∞,0)
高三数学一轮复习--2-6指数与指数函数-北师大版PPT课件
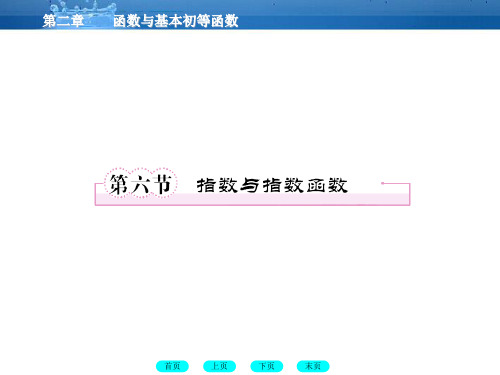
(2)根式的性质 ①当 n 为奇数时,正数的 n 次方根是一个正数,负数的 n 次方根是一个负数,这时,a 的 n 次方根用符号 n a 表示. ②当 n 为偶数时,正数的 n 次方根有两个,它们互为相 反数,这时,正数的正的 n 次方根用符号 n a 表示,负的 n 次方根用符号 -n a 表示.正负两个 n 次方根可以合写为 ±n a (a>0).
首页
上页
下页
末页
第二章 函数与基本初等函数
[例 1] 化简与计算 (1)(0.027)-13-17-2+27912-( 2-1)0; (2)56a13b-2·(-3a-12b-1)÷(4a23·b-3)12× ab;
=3-1 32+3+1 32=3+
32+3- 62
32=2642 =2346=23.
首页
上页
下页
末页
第二章 函数与基本初等函数
2.设y1=40.9,y2=80.48,y3= -1.5,则(
)
A.y3>y1>y2
B.y2>y1>y3
C.y1>y2>y3
D.y1>y3>y2
[答案] D
[解析] y1=21.8,y2=21.44,y3=21.5,∵y=2x在R上 是单调递增函数,∴y1>y3>y2.∴选D.
②(ar)s= ars
(a>0,r,s∈Q).
③(ab)r= arbr (a>0,b>0,r∈Q).
3.指数函数的图像与性质
首页
上页
下页
末页
第二章 函数与基本初等函数
a>1
0<a<1
定义域
(-∞,+∞) .
高三数学一轮复习26指数与指数函数PPT课件

指数幂的运算
[例 1] 求值与化简:
3 (1)2
-
1 3
1
×-670+8 4
×4
2+(3
2×
3)6-
-23
3 2
=____;
(2)
3 a3
·
5 b3=________;
5 b2
4 a3
4
1
a (3)
3
-8a 3
2
b+23
2
ab+4b 3
)÷1-2
3
a3
ba·3 a=________.
[自主解答]
1.化简下列各式(其中各字母均为正数).
2
(1)a
3
·b-1 2
1 2
·a
1 2
·b
1 3
6 ,
a·b5);
5 (2)6a
1 3
·b-2·-3a
1 2
b-1)÷4a23·b-3
1 2
.
解:(1)原式=a-
3 2
1
b2
1
·a
5
1 2
b
1 3
)==a
1 3
1 2
1 6
·b
1 2
1 3
5 6
=1a.
____ 当n是偶数时,正数相的反n次数方根有两
n a
零的n次
方根是零
n ± a(a>0) 负数没有
个,这两个数互为 _______
偶次方根
(2)两个重要公式:
a ,n为奇数,
①n
an=|a|=
a a≥0, -a a<0,
n为偶数.
②(n a)n= a (注意 a 必须使n a有意义).
2025版高考数学全程一轮复习第二章函数第六节指数与指数函数课件

提示:c>d>1>a>b>0.在第一象限内,底数越大,
函数图象越高,即“底大图高”.
关键能力·题型剖析
题型一 指数幂的运算
2
3
5
例1 (1)计算:(7+4 3)0+32 -2×
4
1
3 −83
2
2
3
4 3 +2 +3
(2)化简:
÷
2
−3
−
3
2
1 −3
3
+
8
2×
3
×5
a× a2
)
2
2
A.(0, )
B.(-∞, )
9
2
C.(-∞, )
3
2
D.(0, )
3
9
答案:A
解析:由函数f(x)=3x+b的图象经过第一、三、四象限,可得b<-1,
1
2 b 2 -1 2
2 b
b
b-1
b
所以g(b)=f(b)-f(b-1)=3 -3 =3 ·(1- )= ·3 < ·3 = ,又因为 ·3 >0,
2
2
当 0<a<1时,函数f(x)在区间[1,2]上单调递减,
a
1
由题意可得f(1)-f(2)=a-a2= ,解得a= 或a=0(舍去);
3
综上所述a= 或
2
1
a=2.
2
2
∴0<a<1,且b<0.
题型三 指数函数的性质及应用
角度一 比较指数式的大小
1
1
3 −3
3 −4
例3
,
,
函数图象越高,即“底大图高”.
关键能力·题型剖析
题型一 指数幂的运算
2
3
5
例1 (1)计算:(7+4 3)0+32 -2×
4
1
3 −83
2
2
3
4 3 +2 +3
(2)化简:
÷
2
−3
−
3
2
1 −3
3
+
8
2×
3
×5
a× a2
)
2
2
A.(0, )
B.(-∞, )
9
2
C.(-∞, )
3
2
D.(0, )
3
9
答案:A
解析:由函数f(x)=3x+b的图象经过第一、三、四象限,可得b<-1,
1
2 b 2 -1 2
2 b
b
b-1
b
所以g(b)=f(b)-f(b-1)=3 -3 =3 ·(1- )= ·3 < ·3 = ,又因为 ·3 >0,
2
2
当 0<a<1时,函数f(x)在区间[1,2]上单调递减,
a
1
由题意可得f(1)-f(2)=a-a2= ,解得a= 或a=0(舍去);
3
综上所述a= 或
2
1
a=2.
2
2
∴0<a<1,且b<0.
题型三 指数函数的性质及应用
角度一 比较指数式的大小
1
1
3 −3
3 −4
例3
,
,
高考数学一轮复习课件:第二篇函数与基本初等函数Ⅰ第4讲指数与指数函数

当 $a > 1$ 时,随着 $x$ 的增大,$y$ 的值无限增大;当 $0 < a < 1$ 时,随着 $x$ 的增大,$y$ 的值趋近于零。
指数函数的值域为 $(0, +infty)$。
指数函数的图象
指数函数的图象是经过原点的 一条单调曲线,其形状由底数 $a$ 的值决定。
当 $a > 1$ 时,图象位于第一 象限和第四象限;当 $0 < a < 1$ 时,图象位于第一象限和第 二象限。
指数函数在数学建模中的应用
生态种群模型
在生态学中,指数函数常 用于描述种群数量的增长 或减少。
经济模型
在经济学中,指数函数常 用于描述经济增长、消费 、投资等经济活动。
传染病模型
在流行病学中,指数函数 用于描述疾病的传播过程 。
指数函数与其他数学知识的综合应用
与导数结合
指数函数与导数结合,可以研究 函数的单调性、极值等问题。
基础习题2
已知$2^{x} = 4$,求$x$的值。
基础习题3
已知$x^{2} = 4$,求$x$的值。
提高习题
提高习题1
已知$a^{m} = 2$,$a^{n} = 8$ ,求$frac{a^{m + n}}{a^{m}}$ 的值。
提高习题2
已知$2^{x} = 4$,求$log_{2}4$ 的值。
已知$2^{x} = 4$,$log_{2}4 = y$, 求$x$和$y$的值。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
06
总结与回顾
本讲重点回顾
指数函数的定义与性质
指数函数是形如$y=a^x$ (其中 $a>0$且$aneq1$)的函数,具有增 长或减少的特性。
指数函数的值域为 $(0, +infty)$。
指数函数的图象
指数函数的图象是经过原点的 一条单调曲线,其形状由底数 $a$ 的值决定。
当 $a > 1$ 时,图象位于第一 象限和第四象限;当 $0 < a < 1$ 时,图象位于第一象限和第 二象限。
指数函数在数学建模中的应用
生态种群模型
在生态学中,指数函数常 用于描述种群数量的增长 或减少。
经济模型
在经济学中,指数函数常 用于描述经济增长、消费 、投资等经济活动。
传染病模型
在流行病学中,指数函数 用于描述疾病的传播过程 。
指数函数与其他数学知识的综合应用
与导数结合
指数函数与导数结合,可以研究 函数的单调性、极值等问题。
基础习题2
已知$2^{x} = 4$,求$x$的值。
基础习题3
已知$x^{2} = 4$,求$x$的值。
提高习题
提高习题1
已知$a^{m} = 2$,$a^{n} = 8$ ,求$frac{a^{m + n}}{a^{m}}$ 的值。
提高习题2
已知$2^{x} = 4$,求$log_{2}4$ 的值。
已知$2^{x} = 4$,$log_{2}4 = y$, 求$x$和$y$的值。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
06
总结与回顾
本讲重点回顾
指数函数的定义与性质
指数函数是形如$y=a^x$ (其中 $a>0$且$aneq1$)的函数,具有增 长或减少的特性。
文科数学高考第一轮复习 指数与指数函数(课堂PPT)

11
例 1、 化简求值:
(1)2350+2-2·214- -(0.01)0.5;
16 15
1 a
(3)(0.027) -17-2+279 -( 2-1)0; -45
5 (4)6a
·b-2·(-3a-
b-1)÷(4a ·b-3)
.
5 ab 4ab2
【新坐标】
12
考点 2 指数函数的图象及应用 1、画指数函数 y=ax 的图象,应抓住三个关键点: (1,a),(0,1),(-1,1a), 2、熟记指数函数 y=10x,y=2x,y=(110)x,y=(12)x 在同一坐标系中 图象的相对位置,由此掌握指数函数图象的位置与底数大小的关系. 3、对于图像问题的选择题,可以考虑特殊值法; 4、对于指数型复合函数的图像问题,一般从最基本的指数函数的 图像入手,通过平移、伸缩、对称变化而得到; 5、一些指数方程、不等式问题的求解,往往利用相应的指数型函 数图像数形结合求解. 6、需特别注底数 a>1 与 0<a<1 两种不同情况;
y
要使c<b<a且f(c)>f(a)>f(b)成立,
则有c<0且a>0.
o
x
16
例3 设 f(x)=|3x-1|,c<b<a,f(c)>f(a)>f(b),则
下列关系式中一定成立的是( D )
A.3c>3a
B.3c>3b
C.3c+3a>2
D.3c+3a<2.
【解析】画出 f(x)=|3x-1|的图象
关于y轴对称
8
问题2:如图是指数函数
(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx 的图象,底 数a,b,c,d与1之间的大小关系如何?你能得到什么规律?
例 1、 化简求值:
(1)2350+2-2·214- -(0.01)0.5;
16 15
1 a
(3)(0.027) -17-2+279 -( 2-1)0; -45
5 (4)6a
·b-2·(-3a-
b-1)÷(4a ·b-3)
.
5 ab 4ab2
【新坐标】
12
考点 2 指数函数的图象及应用 1、画指数函数 y=ax 的图象,应抓住三个关键点: (1,a),(0,1),(-1,1a), 2、熟记指数函数 y=10x,y=2x,y=(110)x,y=(12)x 在同一坐标系中 图象的相对位置,由此掌握指数函数图象的位置与底数大小的关系. 3、对于图像问题的选择题,可以考虑特殊值法; 4、对于指数型复合函数的图像问题,一般从最基本的指数函数的 图像入手,通过平移、伸缩、对称变化而得到; 5、一些指数方程、不等式问题的求解,往往利用相应的指数型函 数图像数形结合求解. 6、需特别注底数 a>1 与 0<a<1 两种不同情况;
y
要使c<b<a且f(c)>f(a)>f(b)成立,
则有c<0且a>0.
o
x
16
例3 设 f(x)=|3x-1|,c<b<a,f(c)>f(a)>f(b),则
下列关系式中一定成立的是( D )
A.3c>3a
B.3c>3b
C.3c+3a>2
D.3c+3a<2.
【解析】画出 f(x)=|3x-1|的图象
关于y轴对称
8
问题2:如图是指数函数
(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx 的图象,底 数a,b,c,d与1之间的大小关系如何?你能得到什么规律?
高考数学一轮复习课件25指数与指数函数

x-1
-20-
考点1
考点2
考点3
C
解析:因为y=0.6x在R上单调递减,所以b=0.61.5<a=0.60.6<1.
又c=1.50.6>1,所以b<a<c.
-21-
考点1
考点2
考点3
考向2 解简单的指数方程或指数不等式
例 4(2019 上海青浦区高三一模)不等式2
为 (-2,3)
.
2 -4-3
3
D,x =
1
1
3
=
1
3
x
-4
=
3
4
=
4
y 3
x
,故 C 正确;对于
,故 D 错误.故选 ABD.
-14-
考点1
考点2
考点3
指数函数的图象及其应用
D
D
[-1,1]
-15-
考点1
考点2
考点3
1
1
解析:(3)[-1,1] (1)函数 y=ax- 是由函数 y=ax 的图象向下平移 个单
值域不可能为R),故a的值为0.
-24-
考点1
考点2
考点3
解题心得1.比较两个指数幂的大小时,尽量化为同底或同指.当底
数相同,指数不同时,构造同一指数函数,然后比较大小;当指数相同,
底ห้องสมุดไป่ตู้不同时,构造同一幂函数,然后比较大小;当底数、指数均不同
时,可以利用中间值比较.
2.解决简单的指数方程或不等式的问题主要利用指数函数的单
1
A.0<a<
2
<a<1
<a<3
-20-
考点1
考点2
考点3
C
解析:因为y=0.6x在R上单调递减,所以b=0.61.5<a=0.60.6<1.
又c=1.50.6>1,所以b<a<c.
-21-
考点1
考点2
考点3
考向2 解简单的指数方程或指数不等式
例 4(2019 上海青浦区高三一模)不等式2
为 (-2,3)
.
2 -4-3
3
D,x =
1
1
3
=
1
3
x
-4
=
3
4
=
4
y 3
x
,故 C 正确;对于
,故 D 错误.故选 ABD.
-14-
考点1
考点2
考点3
指数函数的图象及其应用
D
D
[-1,1]
-15-
考点1
考点2
考点3
1
1
解析:(3)[-1,1] (1)函数 y=ax- 是由函数 y=ax 的图象向下平移 个单
值域不可能为R),故a的值为0.
-24-
考点1
考点2
考点3
解题心得1.比较两个指数幂的大小时,尽量化为同底或同指.当底
数相同,指数不同时,构造同一指数函数,然后比较大小;当指数相同,
底ห้องสมุดไป่ตู้不同时,构造同一幂函数,然后比较大小;当底数、指数均不同
时,可以利用中间值比较.
2.解决简单的指数方程或不等式的问题主要利用指数函数的单
1
A.0<a<
2
<a<1
<a<3
2025届高中数学一轮复习课件《指数函数》PPT

第29页
求解与指数函数有关的复合函数问题时,首先要熟知指数函数的定义域、值域、单调性 等相关性质,其次要明确复合函数的构成,当涉及单调性问题时,要借助“同增异减”这一 性质分析判断.
高考一轮总复习•数学
第30页
对点练 4(1)(2024·山东莱芜模拟)已知函数 f(x)=|-2x-x+15|,,xx≤>22,, 若函数 g(x)=f(x)-
解析:∵y=35x 是 R 上的减函数,∴35-13 >35-14 >350,即 a>b>1,又 c=32-34 <320 =1,∴c<b<a.
高考一轮总复习•数学
第11页
4.(2024·四川成都模拟)若函数 f(x)=13-x2+4ax 在区间(1,2)上单调递增,则 a 的取值范 围为___-__∞__,__12_ _.
在(4,+∞)上单调递增.令12x≤4,得 x≥-2,令12x>4,得 x<-2, 代入外层函数的单调递减区间,得到自变量 x 的取值范围,这才是复合函数的单调递增 区间. 而函数 t=12x 在 R 上单调递减,所以函数 y=122x-8·12x+17 的单调递增区间为[-2, +∞).
高考一轮总复习•数学
所谓“底大图高”,反映指数函数的排列规律.
高考一轮总复习•数学
第8页
1.判断下列结论是否正确. (1)函数 y=a-x(a>0,且 a≠1)是 R 上的增函数.( ) (2)函数 y=ax(a>0,且 a≠1)与 x 轴有且只有一个交点.( ) (3)若 am>an,则 m>n.( ) (4)函数 y=ax 与 y=a-x(a>0,且 a≠1)的图象关于 y 轴对称.( √ )
高考数学一轮复习 2.6指数与指数函数课件 文

解:由 f(x)=ab-x=1ax-b 的图象可知,0<1a<1,得 a>1;又 f(0) =ab∈(0,1),所以 b<0.
完整版ppt
33
考点三 指数函数的性质及其应用 对于指数函数性质的考查,以单调性为主,如比较函数值的
大小、解简单的指数不等式等.在解题过程中一是注意底数 a 的 取值,二是注意化为同底的指数这两个问题.
6
③(n a)n= a .
④当n为奇数时,n an= a ; a,
当n为偶数时,n an=|a|= -a,
⑤负数没有偶次方根.
a≥0, a<0.
完整版ppt
7
2.有理数指数幂 (1)幂的有关概念
①正整数指数幂: ②零指数幂:a0= 1 (a≠0);
1 ③负整数指数幂:a-p= ap (a≠0,p∈N*);
完整版ppt
42
从而 y=ax-a-x 为减函数, 所以 f(x)为增函数. 故当 a>0,且 a≠1 时,f(x)在定义域内单调递增. (3)由(2)知 f(x)在 R 上是增函数, 所以在区间[-1,1]上为增函数, 所以 f(-1)≤f(x)≤f(1), 所以 f(x)min=f(-1) =a2-a 1(a-1-a)
完整版ppt
45
2.画指数函数 y=ax(a>0,a≠1)的图象,应抓住三个关键点: (1,a)、(0,1)、-1,1a.
3.在有关根式、分数指数幂的变形、求值过程中,要注意 运用方程的观点处理问题,通过解方程(组)来求值,或用换元法 转化为方程来求解.
完整版ppt
46
名师讲坛
完整版ppt
47
忽视对参数的分类讨论造成漏解
【答案】 ((1)与指数函数有关的函数的图象的研究,往往利用相应指数 函数的图象,通过平移、对称变换得到其图象;(2)一些指数方程、 不等式问题的求解,往往利用相应的指数型函数图象数形结合求 解.
完整版ppt
33
考点三 指数函数的性质及其应用 对于指数函数性质的考查,以单调性为主,如比较函数值的
大小、解简单的指数不等式等.在解题过程中一是注意底数 a 的 取值,二是注意化为同底的指数这两个问题.
6
③(n a)n= a .
④当n为奇数时,n an= a ; a,
当n为偶数时,n an=|a|= -a,
⑤负数没有偶次方根.
a≥0, a<0.
完整版ppt
7
2.有理数指数幂 (1)幂的有关概念
①正整数指数幂: ②零指数幂:a0= 1 (a≠0);
1 ③负整数指数幂:a-p= ap (a≠0,p∈N*);
完整版ppt
42
从而 y=ax-a-x 为减函数, 所以 f(x)为增函数. 故当 a>0,且 a≠1 时,f(x)在定义域内单调递增. (3)由(2)知 f(x)在 R 上是增函数, 所以在区间[-1,1]上为增函数, 所以 f(-1)≤f(x)≤f(1), 所以 f(x)min=f(-1) =a2-a 1(a-1-a)
完整版ppt
45
2.画指数函数 y=ax(a>0,a≠1)的图象,应抓住三个关键点: (1,a)、(0,1)、-1,1a.
3.在有关根式、分数指数幂的变形、求值过程中,要注意 运用方程的观点处理问题,通过解方程(组)来求值,或用换元法 转化为方程来求解.
完整版ppt
46
名师讲坛
完整版ppt
47
忽视对参数的分类讨论造成漏解
【答案】 ((1)与指数函数有关的函数的图象的研究,往往利用相应指数 函数的图象,通过平移、对称变换得到其图象;(2)一些指数方程、 不等式问题的求解,往往利用相应的指数型函数图象数形结合求 解.
高考数学一轮复习课件:指数与指数函数
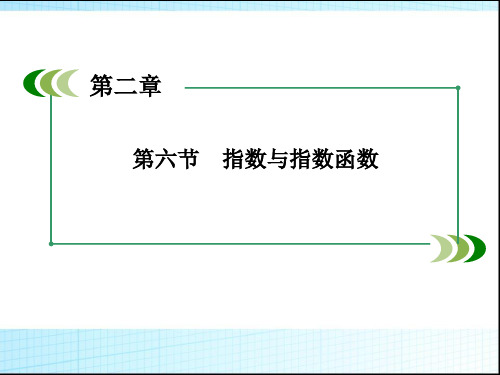
3.设指数函数 f(x)=ax(a>0 且 a≠1),则下列等式不正确
的是( )
Hale Waihona Puke A.f(x+y)=f(x)·f(y)
B.f[(xy)n]=fn(x)·fn(y)
C.f(x-y)=ffxy
D.f(nx)=fn(x)
[答案] B
[解析] 由 f(x)=ax,验证 B 知,f[(xy)n]=a(xy)n,fn(x)·fn(y) =(ax)n·(ay)n=axn·ayn=axn+yn,
[答案] A
[解析] ∵y=(12)x=2-x, ∴它与函数 y=2x 的图像关于 y 轴对称.
(理)已知函数 f(x)=
.
(1)若 a=-1,求 f(x)的单调区间;
(2)若 f(x)有最大值 3,求 a 的值.
[解析] (1)当 a=-1 时,f(x)=
,
令 g(x)=-x2-4x+3,由于 g(x)在(-∞,-2)上是增加
从而 y=ax-a-x 为减函数,∴f(x)为增函数. 故当 a>0,且 a≠1 时,f(x)在定义域内单调增加的. (3)由(2)知 f(x)在 R 上是增函数, ∴在区间[-1,1]上为增加的, ∴f(-1)≤f(x)≤f(1). ∴f(x)min=f(-1)=a2-a 1(a-1-a)
=a2-a 1·1-a a2=-1. ∴要使 f(x)≥b 在[-1,1]上恒成立,则只需 b≤-1. 故 b 的取值范围是(-∞,-1].
2.有理数指数幂
(1)分数指数幂的表示
①正数的正分数指数幂是
m
an =
n am
(a>0,m,n∈N+,n>1).
②正数的负分数指数幂是
1
高考数学一轮复习讲义 指数与指数函数课件 新人教A版

将函数(hánshù)写成分段函数(hánshù)的形式
作图象
写出单调区间
写出x的取值
第二十三页,共44页。
解 (1)由已知可得
y
( 1 )| x 1| 3
(
1) 3
x
1
3x1
(x 1) ,
(x 1)
其图象由两部分(bù fen)组成:
一部分(bù
feyn)是( 1:) x 3
(x
向左平移(pínɡ
2
1
1
2a 3b 3
2
b3
)
1
b3
1
1
1 b3
4a 3 2a3b3 b3
2a3 b3
1 1 根1 式运算1 或根式与指数式混合运算时,将
根 式b3化为b3指数b3式计(算b3较)3为(bj.iào wéi)方便,对于计算的结果,不
强探求究统(一tà用nj什iū么)形提式高来表示,如果有特殊要求,要根
⑤负数没有偶次方根.
2.有理数指数幂
(1)幂的有关概念
①正整数指数幂: an a•a••a
n个
②零指数幂:a0=__1__(a≠0);
③负整数指数幂:a-p=___1__(a≠0,p∈N*); ap
(n∈N*);
第三页,共44页。
④正分数指数(zhǐsahùmn)幂:n am=_______(a>0,m、n∈N*,
据要求写出结果.但结果不能同时含有根号和分数指
数,也不能既有分母又含有负指数.
第十四页,共44页。
知能迁移(qiānyí)1
(1)化简 :
1
(0.027) 3
( 1 )2
(2
7
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 a -3a+2=0 即 a>0且a≠1.
∴a=2.
3.设指数函数 f(x)=ax(a>0 且 a≠1),则下列等式不正确 的是( ) B.f[(xy)n]=fn(x)· fn(y) D.f(nx)=fn(x)
A.f(x+y)=f(x)· f(y) fx C.f(x-y)= fy
[答案] B
[解析]
由 f(x)=ax,验证 B 知,f[(xy)n]=a(xy)n,fn(x)· fn(y)
=(ax)n· (ay)n=axn· ayn=axn+yn, ∴f[(xy)n]≠fn(x)fn(y),而验证 A,C,D 都正确.
[答案] B
[解析]
(理)若 a=(2+ 3) 1,b=(2- 3) 1,则(a+1) 2+(b+1)
∴- 2<a<-1 或 1<a< 2. 即 a 的取值范围是(- 2,-1)∪(1, 2).
课堂典例讲练
幂式的化简与求值
[例 1]
化简下列各式(其中各字母均为正数):
[分析]
(1)因为题目中的式子既有根式又有分数指数幂,
先化为分数指数幂以便用法则运算; (2)题目中给出的是分数指数幂,先看其是否符合运算法 则的条件, 如符合用法则进行下去, 如不符合再创设条件去求.
第二章
第六节 指数与指数函数
高考目标
3
课堂典例讲练
课前自主预习
4
思想方法点拨
5
课后强化作业
高考目标
考纲解读 1.了解指数函数模型的实际背景. 2.理解有理数指数幂的含义,了解实数指数幂的意义, 掌握幂的运算. 3.理解指数函数的概念,理解指数函数的单调性,掌握 指数函数图像通过的特殊点. 4.知道指数函数是一类重要的函数模型.
3.指数函数的图像与性质
a>1 0<a<1
图像
定义域 值域
(-∞,+∞)
(0,+∞)
a>1
0<a<1 (1)过定点 (0,1)
(2)当 x>0 时, y>1;x<0 (2)当 x>0 时,0<y<1 ; 性 质 时, 0<y<1 x<0 时, y>1
(3)在(-∞,+∞)上是 (3)在(-∞,+∞)上是 减函数 增函数
fx+2,x<2, f(x)= -x 2 ,x≥2,
则 f(-3)=__________.
1 [答案] 8
[解析]
f(-3)=f(-3+2)=f(-1)=f(-1+2)=f(1)=f(1
-3Байду номын сангаас
1 +2)=f(3)=2 =8.
5-1 6.已知 a= ,函数 f(x)=ax,若实数 m,n 满足 2 f(m)>f(n),则 m,n 的大小关系为________.
③( a)n=a . ④当 n 为奇数时, an= a ;
a -a
n
n
当 n 为偶数时, an=|a|= ⑤负数没有偶次方根. ⑥零的任何次方根都是零.
n
a≥0 a<0
.
2.有理数指数幂 (1)分数指数幂的表示 ①正数的正分数指数幂是 n m a = a (a>0,m,n∈N+,n>1).
基 础 自 测
1.化简 16x8y4(x<0,y<0)得( A.2x2y C.4x2y
4
)
B.2xy D.-2x2y
[答案] D
[解析]
2.函数 y=(a2-3a+3)ax 是指数函数,则有( A.a=1 或 a=2 C.a=2 B.a=1 D.a>0 且 a≠1
)
[答案] C
[解析]
2 a -3a+3=1, 由已知,得 a>0且a≠1,
[解析]
[点评]
指数幂的化简与求值
(1)化简原则:①化根式为分数指数幂;②化负指数幂为 正指数幂;③化小数为分数;④注意运算的先后顺序. 提醒:有理数指数幂的运算性质中,其底数都大于零,否 则不能用性质来运算. (2)结果要求:①若题目以根式形式给出,则结果用根式 表示; ②若题目以分数指数幂的形式给出, 则结果用分数指数 幂的形式表示; ③结果不能同时含有根式和分数指数幂, 也不 能既有分母又有负分数指数幂.
- - - -2
的值是( A.1 2 C. 2
) 1 B.4 2 D. 3
[答案] D
[解析]
∵a=2- 3,b=2+ 3,
-2 -2
1 1 ∴(a+1) +(b+1) = 2+ 3- 3 3+ 32 3+ 32+3- 32 24 24 2 = = 62 =36=3. 62
5.函数
[答案] m<n
[解析]
本题主要考查指数函数的图像和性质.
5-1 ∵a= ,∴0<a<1, 2 函数 f(x)=ax 在 x∈R 上是单调递减的.又 f(m)>f(n), ∴m<n.
7.若函数 f(x)=(a2-1)x 在(-∞,+∞)上是减函数,求 a 的取值范围.
[解析] 由题意可得 0<a2-1<1,∴1<a2<2,
(2)根式的性质 ①当 n 为奇数时,正数的 n 次方根是一个正数,负数的 n n 次方根是一个负数,这时,a 的 n 次方根用符号 a 表示. ②当 n 为偶数时, 正数的 n 次方根有两个, 它们互为相反数, n 这时,正数的正的 n 次方根用符号 a 表示,负的 n 次方根用 n n - a 符号 表示.正负两个 n 次方根可以合写为 ± a (a>0).
m n
②正数的负分数指数幂是 1 1 n m a a = a = (a>0,m,n∈N+,n>1).
- m n
m n
③0 的正分数指数幂是 0 ,0 的负分数指数幂无意义.
(2)有理数指数幂的运算性质 ①aras= ar+s (a>0,r,s∈Q). ②(ar)s= ars (a>0,r,s∈Q). ③(ab)r= arbr (a>0,b>0,r∈Q).
考向预测 1.指数函数在高中数学中占有十分重要的地位,是高考 重点考查的对象,热点是指数函数的图像与性质的综合应 用.同时考查分类整合思想和数形结合思想. 2.幂的运算是解决与指数有关问题的基础,常与指数函 数交汇命题.
课前自主预习
知识梳理 1.指数幂的概念 (1)根式 如果一个数的 n 次方等于 a(n>1 且 n∈N+),那么这个数叫 做 a 的 n 次方根.也就是,若 xn=a,则 x 叫做 a 的 n 次方根, 其中 n>1 且 n∈N+.式子 a叫做 根式 ,这里 n 叫做 根指数 , a 叫做 被开方数. n
