信号与系统课件第二章
合集下载
信号与系统课件:第二章 LTI系统

第2章 线性时不变系统
2.1 离散时间LTI系统: 卷积和
(1)用移位单位抽样信号表示离散时间信号 (2)卷积和在离散时间信号LTI系统中的表征 (3)卷积和的计算 (4) 离散时间信号LTI系统的性质
(1)用单位抽样信号表示离散时间信号
x[n] ... x[1] n 1 x[0] n x[1] n 1... x[n][0] x[n 1][1]
(1)初始条件为n<0时,y(n)=0,求其单位抽样响应;
(2)初始条件为n≥0时,y(n)=0,求其单位抽样响应。
解:(1)设x(n) (n),且 y(1) h(1) 0 ,必有
y(n) h(n) 0, n 0
依次迭代
y(0) h(0) (0) 1 y(1) 1 0 1
2
当系统的初始状态为零,单位抽样响应h(n)就 能完全代表系统,那么对于线性时不变系统,任意 输入下的系统输出就可以利用卷积和求得。
差分方程在给定输入和边界条件下,可用迭代 的方法求系统的响应,当输入为δ(n)时,输出 (响应)就是单位抽样响应h(n)。
例:常系数差分方程
y(n) x(n) 1 y(n 1) 2
x[n]u[n] x[k]u[n k] x[k]
k
k
(ii)交换律:
yn xnhn hn xn
例子: 线性时不变系统中的阶跃响应 sn
sn unhn hnun
阶跃输入
输 单位抽样信号 入 响应的累加
n
sn hk
k
(iii)分配律:
xnh1n h2 n xnh1n xnh2 n
y(1) h(1) (1) 1 y(0) 0 1 1
2
22
y(2) h(2) (2) 1 y(1) 0 1 1 (1)2
2.1 离散时间LTI系统: 卷积和
(1)用移位单位抽样信号表示离散时间信号 (2)卷积和在离散时间信号LTI系统中的表征 (3)卷积和的计算 (4) 离散时间信号LTI系统的性质
(1)用单位抽样信号表示离散时间信号
x[n] ... x[1] n 1 x[0] n x[1] n 1... x[n][0] x[n 1][1]
(1)初始条件为n<0时,y(n)=0,求其单位抽样响应;
(2)初始条件为n≥0时,y(n)=0,求其单位抽样响应。
解:(1)设x(n) (n),且 y(1) h(1) 0 ,必有
y(n) h(n) 0, n 0
依次迭代
y(0) h(0) (0) 1 y(1) 1 0 1
2
当系统的初始状态为零,单位抽样响应h(n)就 能完全代表系统,那么对于线性时不变系统,任意 输入下的系统输出就可以利用卷积和求得。
差分方程在给定输入和边界条件下,可用迭代 的方法求系统的响应,当输入为δ(n)时,输出 (响应)就是单位抽样响应h(n)。
例:常系数差分方程
y(n) x(n) 1 y(n 1) 2
x[n]u[n] x[k]u[n k] x[k]
k
k
(ii)交换律:
yn xnhn hn xn
例子: 线性时不变系统中的阶跃响应 sn
sn unhn hnun
阶跃输入
输 单位抽样信号 入 响应的累加
n
sn hk
k
(iii)分配律:
xnh1n h2 n xnh1n xnh2 n
y(1) h(1) (1) 1 y(0) 0 1 1
2
22
y(2) h(2) (2) 1 y(1) 0 1 1 (1)2
信号与系统 第二章ppt剖析

网络拓扑约束:由网络结构决定的电压电流约束关系, KCL,KVL。
第
例1 求并联电路的端电压 vt 与激励 is t 间的关系。
7 页
电阻
iR t
1 R
vt
电感
iLt
1 L
t v d
ist
电容
iC
t
C
dv d
t
t
iR iL R LC
a ic
vt
b
根据KCL iRt iLt iC t iS t
系统的完全响应
第 17
页
求出齐次解rh t 和特解rp t 相加即得方程的完全解:
n
rt Aieit rp t i 1
利用初始条件求待定系数Ai 我们一般将激励信号加入的时刻定义为t=0,响应
的求解区间定为 t ,如0 果响应在0时刻没有跳变,通常
取t=0,这样对应的一组条件称为初始条件。
1
2
10
B1
, 3
B2
, 9
B3 27
所以,特解为
rp t
1 3
2 9
t
10 27
第 15
页
(2)
(原方程:
d2 rt
dt2
2
d rt
dt
3r t
d et
dt
et
)
当et et时, 很明显, 可选rt Bet。这里,B是待定系数。
代入方程后有:
Bet 2Bet 3Bet et et
于是,特解为 1 et。 3
B 1 3
几种典型激励函数相应的特解
第 16
页
激励函数e(t)
E(常数)
响应函数r(t)的特解
第
例1 求并联电路的端电压 vt 与激励 is t 间的关系。
7 页
电阻
iR t
1 R
vt
电感
iLt
1 L
t v d
ist
电容
iC
t
C
dv d
t
t
iR iL R LC
a ic
vt
b
根据KCL iRt iLt iC t iS t
系统的完全响应
第 17
页
求出齐次解rh t 和特解rp t 相加即得方程的完全解:
n
rt Aieit rp t i 1
利用初始条件求待定系数Ai 我们一般将激励信号加入的时刻定义为t=0,响应
的求解区间定为 t ,如0 果响应在0时刻没有跳变,通常
取t=0,这样对应的一组条件称为初始条件。
1
2
10
B1
, 3
B2
, 9
B3 27
所以,特解为
rp t
1 3
2 9
t
10 27
第 15
页
(2)
(原方程:
d2 rt
dt2
2
d rt
dt
3r t
d et
dt
et
)
当et et时, 很明显, 可选rt Bet。这里,B是待定系数。
代入方程后有:
Bet 2Bet 3Bet et et
于是,特解为 1 et。 3
B 1 3
几种典型激励函数相应的特解
第 16
页
激励函数e(t)
E(常数)
响应函数r(t)的特解
信号与系统课件第二章解读

8.1 Z变换的定义
fs (t) f (t) T (t) f (t) (t kT)
k
Fs (s)
f (t ) (t kT )estdt
k
f (kT )eskT
k
引入一个新的复变量z,令z esT或s 1 ln z T
则上式变为F (z) f (k )zk k
当 1时,级数收敛, 1时,级数发散, 1不定
8.1 Z变换的定义
3、有限长序列的收敛域
f (k) f (k) 0
k1 k k2 其它
k2
F (z) f (k )zk k k1
为有限项之和,最小收敛域为0 z
若k1 0, k2 0则存在负幂项,z 0 若k1 0, k2 0则只有正幂项,z 0,不含z , 0 z
Z[u(k)]
1 1 z1
z
z 1
即u(k) z z 1 z1
z 1
8.2 常用序列的Z变换
例3、求指数序列a k u(k )的z变换
解:Z[aku(k )] ak zk ( a )k
k0
k0 z
当 a 1即 z | a | 时,有 z
Z[aku(k)] 1 z 1 a za z
因为 a 1 ,所以 a z a1,则 f k 的双边Z变换存在
F z
z za
z z a1
z2
a a1 a a1
z z1
a z a1
若 a 1 ,则由于左边序列与右边序列的Z变换没有公共的收 敛域,此时该序列不存在双边Z变换。
8.3 Z变换的性质
1、线性性质
if
f1(k) F1(z) f2 (k) F2 (z)
| z || a |,
信号与系统 第二章ppt_part2
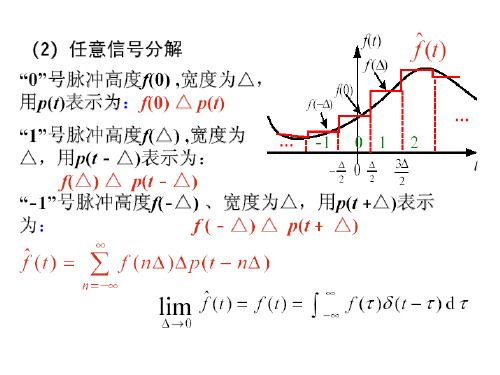
1
0 t 1
[1 e(t 1) ]
演示
[1 e(t 1) ]u(t 1) f1 (t ) f2 (t )
f1 (t )* f2 (t )
1
0
1
t
解法二:f 2 ( ) 不变,反褶 f1 ( ), f 2 ( ) f1 ( )
1 1 1
f1 (t ) f2 (t ) f 2 ( ) f1 (t )d
f
( 1) 2
t e d u ( ) e t u (t ) (1 e t )u (t ) (t ) e u ( )d 0
t
f1(t)*f2(t)=(1-e-t) u(t)- [(1-e-(t-2)] u(t-2)
n
即
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
n
当 t 0 时,t d , kt ,
t 0
t 0
lim
t k 0 0
s(t )
1 e
T
(t T )
e ]u(t T )
t
t
(t T )
]u(t T )
1
0
t
T
演示
例2-13 已知信号x(t)与h(t)如下图所示,求 h(t) x(t) 1 1
y(t ) x(t ) h(t )
-1/2 0 解:
1
t
0
2
t
y (t ) x( )h(t )d
h(t )
1
0 t 1
[1 e(t 1) ]
演示
[1 e(t 1) ]u(t 1) f1 (t ) f2 (t )
f1 (t )* f2 (t )
1
0
1
t
解法二:f 2 ( ) 不变,反褶 f1 ( ), f 2 ( ) f1 ( )
1 1 1
f1 (t ) f2 (t ) f 2 ( ) f1 (t )d
f
( 1) 2
t e d u ( ) e t u (t ) (1 e t )u (t ) (t ) e u ( )d 0
t
f1(t)*f2(t)=(1-e-t) u(t)- [(1-e-(t-2)] u(t-2)
n
即
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
n
当 t 0 时,t d , kt ,
t 0
t 0
lim
t k 0 0
s(t )
1 e
T
(t T )
e ]u(t T )
t
t
(t T )
]u(t T )
1
0
t
T
演示
例2-13 已知信号x(t)与h(t)如下图所示,求 h(t) x(t) 1 1
y(t ) x(t ) h(t )
-1/2 0 解:
1
t
0
2
t
y (t ) x( )h(t )d
h(t )
1
信号与线性系统分析第2章

t r ( Pmt m Pm1t m1 P 0的特征根) 1t P 0 )(有r重为
e t
cos t sin t
Pe t (不等于特征根) t (P t P )e (等于特征单根) 1 0
(Pr t r Pr 1t r 1 P0 )e t (等于r重特征根)
例:f1(t), f2(t)如图,求f1(t)* f2(t) 解: f1(t) = 2ε (t) –2ε (t –1) f2(t) = ε (t+1) –ε (t –1) f1(t)* f2(t) = 2 ε (t)* ε (t+1) –2 ε (t)* ε (t –1) –2ε (t –1)* ε (t+1) +2ε (t –1)* ε (t –1) 由于ε (t)* ε (t) = tε (t) 据时移特性,有 f1(t)* f2(t) = 2 (t+1) ε (t+1) - 2 (t –1) ε (t –1) –2 tε (t) +2 (t –2) ε (t –2)
f (t ) f1 ( ) f 2 (t )d
为f1(t)与f2(t)的卷积积分,简称卷积;记为 f(t)= f1(t)*f2(t) 注意:积分是在虚设的变量τ下进行的,τ为积分变量, t为参变量。结果仍为t 的函数。
y zs (t )
f ( )h(t ) d f (t ) * ) d
▲ ■ 第 13 页
2 .任意信号作用下的零状态响应
f ( t) 根据h(t)的定义: δ(t)
LTI系统 零状态
yzs(t) h(t) h(t -τ) f (τ) h(t -τ)
由时不变性:
e t
cos t sin t
Pe t (不等于特征根) t (P t P )e (等于特征单根) 1 0
(Pr t r Pr 1t r 1 P0 )e t (等于r重特征根)
例:f1(t), f2(t)如图,求f1(t)* f2(t) 解: f1(t) = 2ε (t) –2ε (t –1) f2(t) = ε (t+1) –ε (t –1) f1(t)* f2(t) = 2 ε (t)* ε (t+1) –2 ε (t)* ε (t –1) –2ε (t –1)* ε (t+1) +2ε (t –1)* ε (t –1) 由于ε (t)* ε (t) = tε (t) 据时移特性,有 f1(t)* f2(t) = 2 (t+1) ε (t+1) - 2 (t –1) ε (t –1) –2 tε (t) +2 (t –2) ε (t –2)
f (t ) f1 ( ) f 2 (t )d
为f1(t)与f2(t)的卷积积分,简称卷积;记为 f(t)= f1(t)*f2(t) 注意:积分是在虚设的变量τ下进行的,τ为积分变量, t为参变量。结果仍为t 的函数。
y zs (t )
f ( )h(t ) d f (t ) * ) d
▲ ■ 第 13 页
2 .任意信号作用下的零状态响应
f ( t) 根据h(t)的定义: δ(t)
LTI系统 零状态
yzs(t) h(t) h(t -τ) f (τ) h(t -τ)
由时不变性:
信号与系统-第2章

f (t)
K
两式相加:
cosωt =
1 2
(e
jωt
+
e
jωt )
(2-4)
0 K
t
两式相减:
sinωt =
1 2j
(e
jωt
-e
jωt )
(2-5)
(3) 复指数信号: f(t) = Ke st = Ke (σ+ jω)t
= Keσt (cosωt + j sinωt)
当 σ > 0 时为增幅振荡 ω = 0 时为实指数信号 σ < 0 时为衰减振荡
2
01
t
f(
1 2
t)
=
1 2
t
0
0<t <4 其它
f(12 t)
2 0
4t
注意: 平移、反折和展缩都是用新的时间变量去代换原来的
时间变量, 而信号幅度不变.
t +2 -2<t<0 例2-5:已知 f(t) = -2t + 2 0<t<1
f (t)
2
0
其它
-2 0 1
t
求 f(2t-1),
f(
1 2
(1) 相加和相乘
信号相加: f t f1t f2 t fn t 信号相乘: f t f1t f2 t fn t
0 t<0 例2-1:已知 f1(t) = sint t ≥ 0 , f2(t) =-sint, 求和积.
解: f1(t) + f2(t) =
-sint 0
t<0 t≥0
0
t<0
f1(t) f2(t) = -sin2t t ≥ 0 也可通过波形相加和相乘.
∞ t=0 作用: 方便信号运算.
信号与系统第二章课件.

先假定逆系统的冲击响应的结果为hi1(t),然后经逐步修 正找到最终的hi(t) 。
很遗憾以上关于hi1(t)的假定,虽然可以消除δ(t)项, 却引入了新的a2 δ(t-2T)项。不过回波信号的强度衰减了, 而且时间延迟了,使干扰效果明显减弱。可进一步设
可见若逆系统的冲激响应hi1(t)若采用此结果,回 波信号的强度可以衰减至无穷小,而且时间可以延迟 至无穷远。 实际问题中,我们只须将延时补偿采用几项,就 可达到理想效果。
其中N变量指所有的回波路径。Tm、源自m表示各条路径的延迟 时间和衰减系数。当T较小且a较小时,形成所谓的“混响”。
根据以上分析,可以很容易写出回波系统的冲击响应
这样一般信号的响应,可以很容易根据卷积关系写为
为了从含有干扰信号的回波信号中取出正常信号,我们需设 计一个“逆系统”,其方框图如下。
接下来的工作是从上式求出hi(t),这样的问题是卷 积的反问题,称为解卷积。 对已连续时间系统,解卷积一般难以给出普适的公式,而 对于离散时间问题,§7.7给出了一般的解法。采用变换域 解法(如付里叶变换、拉普拉斯变换),也可较方便给出此问 题冲激响应(或者系统函数)的解法。 下面我们给出此问题的尝试解法。
信号与系统
§2.10用算子符号表示微分方程
采用算子符号可以简化微分、积分方程的计算,本节给 出算子符号的一些基本运算规则,然后通过实例说明此方法 的方便之处。 (一)算子符号的基本规则
(一)用算子符号建立微分方程 用算子符号建立系统的微分方程不仅书写简单,而且非 常方便。电感、电容的等效算子符号为:
实例:用算子符号建立电路微分方程
R1=1
Lp=(1/4)p
1/CP=1/p C R2=3/2
线性电路微分方程求解借鉴课本,P81
信号与系统讲义-2

f (t) u 3 10
p
u pf (t) 2p 10
u(t) (Ae5t B)U(t)
2 du(t) 10u(t) df (t)
dt
dt
u(t) 5Ae5t U(t) (A B)(t)
2(A B) 1 B0
u(t) 1 e5tU(t)V 2
H
(
p)
2p2 8p 3 ( p 1)( p 3)2
求系统的响应 y(t)。
解: D(p) (p 1)(p 3)2 0 p1 1 p2 p3 3
y0 (t) K1e t K 2e3t K 3te3t
y0 (0 ) K1 K2 =2 y0 (0 ) K1 3K 2 K3=1
3、共轭复根:(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
,
d
02 2 , 0
1 LC
4
三、 RLC串联电路全响应
d 2uc dt 2
R L
duc dt
1 LC
uc
1 LC Us
(二阶常系数线性非齐次微分方程)
t<0 , K在2,有 uc (0 ) U0
C
uc Aep1t Be p2t Us
2、重根:(临界阻尼) 即
R2
L C
(自然频率、固有频率)
uc (A Bt)ept Us
3、共轭复根:(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
d 02 2
信号与系统课件(郑君里版)第二章

e ,t≥0;y(0)=2,y’(0)= 2 t ,t≥0;y(0)= 1, e
t
-1
y’(0)=0时的全解。
解: (1) 特征方程为
2 + 5λ+ 6 = 0
其特征根λ1= – 2,λ2= – 3。 齐次解为
yh (t ) C1e2t C2e2t
由表2-2可知,当f(t) = 2 e t
y fh (t ) C f 1e
2t
C f 2e
t
其特解为常数 3 , 于是有
y f (t ) C f 1e2t C f 2et 3
C1 1 C 2 4
根据初始值求得:
y f (t ) e2t 4et 3,t 0
四.系统响应划分
自由响应+强迫响应 (Natural+forced) 暂态响应+稳态响应 (Transient+Steady-state) 零输入响应+零状态响应 (Zero-input+Zero-state)
零输入响应
2.2 冲激响应和阶跃响应
一.冲激响应 1.定义 系统在单位冲激信号δ(t) 作用下产生的零状态响 应,称为单位冲激响应,简称冲激响应,一般用h(t)表 示。
t
ht
H
[例2.2.1] 描述某系统的微分方程为y”(t)+5y’(t)+6y(t)=f(t)求其 冲激响应h(t)。
相互关系
零输入响应是自由响应的一部分,零状态响应有自由响 应的一部分和强迫响应构成 。
y (t ) e 2t 3 y x (t ) y f (t ) (2e 2t 4e t ) (e 2t 4e t 3),t 0
信号与系统 第二章

( x1 ( t ) + x2 ( t ))* h( t ) = x1 ( t )* h( t ) + x2 ( t )* h( t )
Application: Parallel system a common system Can break a complicated convolution into several simpler ones
Signals & Systems
Example 2.10
1 n x[n] = ( ) u[ n] + 2n u[− n] 2 h[n] = u[n]
Signals & Systems
2.3.3 The Associative Property
x[n]* ( h1 [n]* h2 [n]) = ( x[n]* h1 [n])* h2 [n] x ( t )*[h1 ( t )* h2 ( t )] = [ x ( t )* h1 ( t )]* h2 ( t )
1 h[n] = 0 n = 0,1 otherwise
Example 2.9
If the system is LTI,determine the relationship between input and output If the system is not LTI,determine the relationship between input and output
Signals & Systems
2.2 Continuous-Time LTI System: The Convolution Integral
2.2.1 The Representation ContinuousTime Signals In Term Of Impulse
信号与系统第二章ppt课件

解 先画出f1(t-τ)|t=0, 即f1(-τ)和f2(τ)波形如题解图2.6(a)所 示。再令t从-∞ 开始增长,随f1(t-τ)波形右移,分区间计算卷 积积分:
30
第2章 连续信号与系统的时域分析 31
最后整理得
第2章 连续信号与系统的时域分析
波形如题解图2.6(b)所示。
32
第2章 连续信号与系统的时域分析
3
(2) 因为
第2章 连续信号与系统的时域分析
所以
4
第2章 连续信号与系统的时域分析
2.2 写出下列复频率s所表示的指数信号est的表达式,并画 出其波形。
(1) 2; (2) -2; (3) -j5; (4) -1+j2。
5
第2章 连续信号与系统的时域分析
解 (1) f1(t)=e2t,波形如题解图2.2(a)所示。 (2) f2(t)=e-2t, 波形如题解图2.2(b)所示。显然, f1(t)和f2(t)都 是实指数信号。 (3) f3(t)=e-j5t=cos5t-j sin5t。f3(t)是虚指数信号,其实部、 虚部分别是等幅余弦、正弦信号。实部信号波形如题解图2.2(c) 所示。 (4) f4(t)=e(-1+j2)t=e-t·ej2t=e-t(cos2t+j sin2t)。f4(t)是复指数信 号,其实部和虚部分别是幅度按指数规律衰减的余弦和正弦信 号。实部信号波形如题解图2.2(d)所示。
(4) 由于tε(t)|t=-∞=0,有 所以
38
第2章 连续信号与系统的时域分析
2.8 已知f1(t)和f2(t)如题图2.4所示。设f(t)=f1(t)*f2(t),试求 f(-1)、f(0)和f(1)的值。
题图 2.4
30
第2章 连续信号与系统的时域分析 31
最后整理得
第2章 连续信号与系统的时域分析
波形如题解图2.6(b)所示。
32
第2章 连续信号与系统的时域分析
3
(2) 因为
第2章 连续信号与系统的时域分析
所以
4
第2章 连续信号与系统的时域分析
2.2 写出下列复频率s所表示的指数信号est的表达式,并画 出其波形。
(1) 2; (2) -2; (3) -j5; (4) -1+j2。
5
第2章 连续信号与系统的时域分析
解 (1) f1(t)=e2t,波形如题解图2.2(a)所示。 (2) f2(t)=e-2t, 波形如题解图2.2(b)所示。显然, f1(t)和f2(t)都 是实指数信号。 (3) f3(t)=e-j5t=cos5t-j sin5t。f3(t)是虚指数信号,其实部、 虚部分别是等幅余弦、正弦信号。实部信号波形如题解图2.2(c) 所示。 (4) f4(t)=e(-1+j2)t=e-t·ej2t=e-t(cos2t+j sin2t)。f4(t)是复指数信 号,其实部和虚部分别是幅度按指数规律衰减的余弦和正弦信 号。实部信号波形如题解图2.2(d)所示。
(4) 由于tε(t)|t=-∞=0,有 所以
38
第2章 连续信号与系统的时域分析
2.8 已知f1(t)和f2(t)如题图2.4所示。设f(t)=f1(t)*f2(t),试求 f(-1)、f(0)和f(1)的值。
题图 2.4
信号与系统 第2章(3-5)

X
n = −∞
∑
k
x[n ]
1 k
n = −∞
∑ x[n]
2 1
k
3
单位阶跃序列可 用单位脉冲序列 的求和表示: 的求和表示:
0
k
k
u[ k ] =
n = −∞
∑ δ [n]
2.5 确定信号的时域分解
X
一、信号分解为直流分量与交流分量 二、信号分解为奇分量与偶分量之和 三、信号分解为实部分量与虚部分量 四、连续信号分解为冲激信号的线性组合 五、离散信号分解为脉冲序列的线性组合 六、信号分解为正交信号集
d
u[k ] =
u( t ) =
∫d ∫
t
−∞
δ (τ ) τ
n =−∞
∑ δ [ n] ∑ u [n]
k
k
u( t ) = d r ( t ) t r (t ) =
−∞
u[k ] = r[k + 1] − r[k ]
u(τ ) τ
d
r [ k + 1] =
n = −∞
2.4 离散时间信号的基本运算
一、序列相加与相乘
2. 序列相乘 序列相乘
x1[ k ]
0 1 k
2 1 y[k]=x1[k]× x2[k] 2 1.5
X
将若干序列同序号的数值相乘。 将若干序列同序号的数值相乘。
y[k ] = x1 [k ] × x2 [k ] × … × xn [k ]
x2 [ k ]
0
k
0
k
2.4.2 序列的相加、相乘、差分与求和
x[k] = x D C [k] + x A C [k]
k = N1
《信号与系统》第二版_(郑君里)_高等教育出版社课件

10
2021/4/2
零输入响应与零状态响应(cont.)
例2 7 设有如图所示的RC电路,电容两端有起始电压u( C 0),激 励源为e(t),求t 0时系统响应 电容两端电压u( C t)。 解:列写系统的微分方程为
d dt
uc (t)
1 RC
uc (t)
1 RC
e(t )
根
据微分方
程
的
一般表达式可
t
e RCuc (t) uc (0 )
1 RC
t
e RCe( )d
0-
R
+
+ e(t) uc (0 ) C
-
整
理
得:uc
(t
)=e
t RC
uc
(0
)
1 RC
t
e
t RC
e(
)d
0-
零输入响应
零状态响应
+
uc (t)
-
smilegs2001@
11
2021/4/2
零输入响应与零状态响应(cont.)
uR (t) RiL (t) 联立上式得
+
is (t)
-
R
iC (t) +
C
uc (t)
-
iL (t)
+
L uL (t)
-
带入(5)式得iL
(t )
iS
(t )
C
duC (t) dt
代入(3)式得
L
diL (t) dt
uC (t)
RiL (t)........................(1)
KVL:
uL
信号与系统第二章课件

(t 0)
18
连续系统的时域求解(例)
例.(2.4-1)系统 r (t ) r (t ) r (t ) e(t ) e(t ) 解: 2 1 0 1,2 0.5 j 0.5 3 求h (t)和g (t)。
1
在所选专用树的单树支割集、单连支回路方程中列方程
消去其它变量,得 i(t) 的微分方程
3 2 L C uc (t ) 1 H F 1 4
i(t ) 7i(t ) 10i(t ) e(t ) 6e(t ) 4e(t )
2nd.确定初始值/定解条件
i (0 ), i(0 )
[前例]
m n ( i ) ( j) ai rzs (t ) b j e (t ) j0 i 0 (k ) rzs (0 ) 0
求全响应:
13
第二章 连续时间信号与系统的时域分析
§2.5 系统的零状态响应 2.
n (i ) r(t )求解:先求零输入响应 a r i zi (t ) 0 即解零输入方程(即齐次方程)i 0 (k ) (k ) r ( t ) r ( t ) r ( 0 ) r 经典法得解为: zi h zi (0 ) zi
8
1st. i(t ) 7i(t ) 10i(t ) e(t ) 6e(t ) 4e(t ) nd i ( 0 ) 14 5 ( A ) i ( 0 ) 2( A) 2 .求出初始条件 3rd.解: 2 7 10 0 1 2, 2 5
[求取h(t) ]
1. 作为一种特殊的零状态响应(经典法) 例1:系统 r(t ) 4r(t ) 3r (t ) e(t ) 2e(t ) 求 h(t ) 解: 即解 h(t ) 4h(t ) 3h(t ) (t ) 2 (t ) h ( 0 ) h ( 0 ) 0(无初始储能 )
信号与系统第2章ppt课件

(B) u(t)Limetu(t) 0
假设u(t)的傅立叶变换为:
F ()A ()jB ()
e t u (t ) 的傅立叶变换为 :
依据傅立叶变换具有唯一性:
F e()A e()jB e()
F()li m0Fe()
所以
A()li m0Ae()精选pBpt()li m0Be()
第二章 傅立叶变换
F ()A ()jB () A()li m0Ae() B()li m0Be()
,这种频谱搬移技术在通信系统中
得到广泛的应用。调幅,调频都是
在该基础上进行的。
精选ppt
由此可见,将时间信号f(t)乘以Cs(ω0t) 或Sin(ω0t)
,等效于将f(t)的频谱一分
为二,即幅度减小一半,沿
频率轴向左和向右各平移ω0.
第二章 傅立叶变换
例2 求如下矩形调幅信号的频谱函数
f(t) G (t)c o s 0 t
例7 如图a所示系统,已知乘法器的输入为
f (t) sin(2t) s(t)co3st)(
t
系统的频率响应为:
求输出y(t).
精选ppt
第二章 傅立叶变换
f (t) sin(2t) s(t)co3st)(
t
乘法器的输出信号为: x(t)f(t)s(t)
依频域卷积定理可知:X(j)21F(j)*S(j) 这里 f(t)F(j) s(t)S(j)
精选ppt
第二章 傅立叶变换
11周期信号的傅里叶变换
周期信号的频谱------用傅里叶级数表示。 非周期信号的频谱——用傅里叶变换表示。 周期信号的频谱可以用傅里叶变换表示吗? (1)正弦、余弦信号的傅里叶变换 直流信号的博立叶变换为
信号与系统第二章(陈后金)2PPT课件

2 1 0 1 2
x [k]
3
22
1
k
2 1 0 1 2 3
x [ k ] 3 [ k 1 ] [ k ] 2 [ k 1 ] 2 [ k 2 ]
2021/4/8
28
二、基本离散时间序列
5.单位阶跃序列
定义:
u[k] 1
2 1 0 1 2
✓ [k]与u[k]的关系:
[k]u[k]u[k1]
2021/4/8
1 k 0 u[k]0 k 0
k
k
u[k] [n] n 29
二、基本离散时间序列
6.矩形序列
1 0kN1
RN[k]0 otherwise
N 1
R N[k]u[k]u[kN ][km ] m 0 RN[k] 1
k
21 0 1 2
N1
2021/4/8
30
二、基本离散时间序列
7.斜坡序列
即0N = m2p , m = 正整数时,信号是周期信号。
如果0 /2p m/N , N、m是不可约的整数, 则信号的周期为N。
2021/4/8
23
[例]判断下列离散序列是否为周期信号.
1) x1[k] = cos(kp/6)
0 /2p 1/12, 由于1/12是不可约的有理数,
故离散序列的周期N=12。
-1 0 1 2 3
k
➢ 序列的列表表示
表示k=0的位置
x[k]=[0, 2, 0, 1, 3, 1, 0]
2021/4/8
18
二、基本离散时间序列
1.实指数序列
r >1
x[k]Akr, kZ
0< r <1
r <1
x [k]
3
22
1
k
2 1 0 1 2 3
x [ k ] 3 [ k 1 ] [ k ] 2 [ k 1 ] 2 [ k 2 ]
2021/4/8
28
二、基本离散时间序列
5.单位阶跃序列
定义:
u[k] 1
2 1 0 1 2
✓ [k]与u[k]的关系:
[k]u[k]u[k1]
2021/4/8
1 k 0 u[k]0 k 0
k
k
u[k] [n] n 29
二、基本离散时间序列
6.矩形序列
1 0kN1
RN[k]0 otherwise
N 1
R N[k]u[k]u[kN ][km ] m 0 RN[k] 1
k
21 0 1 2
N1
2021/4/8
30
二、基本离散时间序列
7.斜坡序列
即0N = m2p , m = 正整数时,信号是周期信号。
如果0 /2p m/N , N、m是不可约的整数, 则信号的周期为N。
2021/4/8
23
[例]判断下列离散序列是否为周期信号.
1) x1[k] = cos(kp/6)
0 /2p 1/12, 由于1/12是不可约的有理数,
故离散序列的周期N=12。
-1 0 1 2 3
k
➢ 序列的列表表示
表示k=0的位置
x[k]=[0, 2, 0, 1, 3, 1, 0]
2021/4/8
18
二、基本离散时间序列
1.实指数序列
r >1
x[k]Akr, kZ
0< r <1
r <1
