运筹学实验报告2
管理运筹学实验报告

课程实验报告管理运筹学实验(二)专业年级课程名称指导教师学生姓名学号实验日期实验地点实验成绩教务处制2011年11月日所示.一种规格,问如何下料,才能使总的用料根数最少已知一名正式职工11点开始上班,工作4个小时后,休息1个小时,而后再工作4个小时;另一名正式职点开始上班,工作4个小时后,休息1个小时,而后再工作4个小时.又知临时工每小时的工资为在满足对职工需求的条件下,如何安排临时工的班次,使得使用临时工的成本最小?设按 14 种方案下料的原材料的根数分别为 x1,x2,x3,x4,x5,x6,x7x9,x10,x11,x12,x13,x14,则可列出下面的数学模型:min f=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14用管理运筹学软件我们可以求得此问题的解为x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0,x9=0,x10=0,x11=140用管理运筹学软件我们可以求得此问题的解如下。
x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0,x10=0,x11=0最优值为 320。
(1)在满足对职工需求的条件下,在 11 时安排 8 个临时工,13 时新安排 1 临时工,14时新安排 1 个临时工,16 时新安排 4 个临时工,18 时新安排 6 个临时工可使临时工的总成本用管理运筹学软件我们可以求得此问题的解如下。
x1=200,x2=250,x3=100,最优值为 6 400。
(1)在资源数量及市场容量允许的条件下,生产 A 200 件,B 250 件,C可使生产获利最多。
(2)A、B、C 的市场容量的对偶价格分别为 10元,12 元,14 元。
材料、台。
运筹学实验报告2讲解

实验报告《运筹学》2015~2016学年第一学期实验目的:加强学生分析问题的能力,锻炼数学建模的能力。
掌握WinQSB/Matlab 软件中线性规划、灵敏度问题的求解和分析。
用 WORD 书写实验报告:包括详细规划模型、试验步骤和结果分析。
实验内容:题1:某厂的一个车间有1B ,2B 两个工段可以生产123,,A A A 三种产品,各工段开工一天生产三种产品的数量和成本,以及合同对三种产品的每周最低需求量由表1给出。
问每周各工段对该生产任务应开工几天,可使生产合同的要求得到满足,并使成本最低。
建立模型。
表1生产定额(吨/天)工段B生产合同每周最低需求量(吨)ib iA 产品1A 2A 3A 1B 2B 11311310002000599成本(元/天)建立模型:WinQSB录入模型界面:运行结果界面:结果分析:决策变量:X1,X2最优解:X1=3,X2=2;目标系数:C1=1000,C2=2000;最优值:7000;其中X1贡献3000,X2贡献4000;检验数,或称缩减成本:0,0。
即当非基变量增加一个单位时,目标值的变动量。
目标系数的允许减量和允许增量;目标系数在此范围变量时,最优基不变。
约束条件约束条件:C1,C2,C3左端:5,11,9右端:5,9,9松弛变量或剩余变量:该端等于约束左端与约束优端之差;为0表示资源达到限制值。
题2:明兴公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,这三种产品都要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。
有关情况见表2;公司中可利用的总工时为:铸造8000小时,机加工12000小时和装配10000小时。
建立模型:解;假设公司选择甲产品自产X1件,外包协作X2件,乙产品自产X3件,外包协作X4件,丙产品生产X5件,则有;maxZ=15X1+13X2+10X3+9X4+7X5s.t. 5X1+10X3+7X5<=80006X1+6X2+4X3+4X4+8X5<=12000 3X1+3X2+2X3+2X4+2X5<=10000 X1-5>=0WinQSB录入模型界面:运行结果界面:结果分析:(1)X*=(1600,0,0,600,0), Z*=29400元,即:公司为了获得最大利润29400元,甲、乙、丙三种产品各生产1600件、600件、0件。
运筹学实验报告

《运筹学》实验报告成绩:班级:学号:姓名:实验一、线性规划(25分)一、实验目的:安装WinQSB软件,了解WinQSB软件在Windows环境下的文件管理操作,熟悉软件界面内容,掌握操作命令;利用WinQSB软件求解线性规划问题。
二、实验内容:安装与启动软件;建立新问题,输入模型,求解模型,结果的简单分析。
三、操作步骤:(1)安装与启动WinQSB软件(5分)1.安装双击Setup.exe,弹出窗口如下图0—1所示:图0—1输入安装的目标文件夹,点Continue按钮,弹出窗口如图0—2所示:图0—2输入用户名和公司或组织名称,点Continue按钮进行文件的复制,完成后弹出窗口如图0—3:图0—3显示安装完成,点“确定”退出。
WinQSB软件安装完毕后,会在开始→程序→WinQSB中生成19个菜单项,分别对应运筹学的19个问题。
如图0—4所示:图0—42.启动在开始菜单中选择Linear and Integer Programming,运行后出现启动窗口如下图0—5所示:图0—5(2)建立线性规划问题并输入模型(5分)选题:P32例八,题目如下:miz z=-3x1+x2+x3x1-2x2+x3≤11-4x1+x2+2x3≥3-2x1 +x3=1x1,x2,x3≥0输入数据,如下图所示:、(3)分析模型并求解(5分)计算结果:a) 运用软件计算的具体过程:b)计算的最终结果如下:(4)实验结果分析(5分)最优解=[4,1,9],即x1=4,x2=1,x3=9最优值=-2,min z=-2四、实验中遇到的主要问题及解决方法(5分)起初未能正确的Variable Type选择导致了计算结果出现错误,最后仔细的检查了操作过程,改变了Variable Type,得出了正确的结果。
实验二、运输问题(25分)一、实验目的:熟悉运用WinQSB软件求解运输问题和指派问题,掌握操作方法。
二、实验内容:求解实际中某一运输问题,建立、输入并求解模型,结果的简单分析。
运筹学实践教学报告范文(3篇)

第1篇一、引言运筹学作为一门应用数学分支,广泛应用于经济管理、工程技术、军事决策等领域。
本报告旨在通过运筹学实践教学,验证理论知识在实际问题中的应用效果,提高学生的实践能力和创新能力。
以下是对本次实践教学的总结和反思。
二、实践教学内容1. 线性规划问题本次实践教学选择了线性规划问题作为研究对象。
通过建立线性规划模型,我们尝试解决生产计划、资源分配等实际问题。
- 案例一:生产计划问题某公司生产A、B两种产品,每单位A产品需消耗2小时机器时间和3小时人工时间,每单位B产品需消耗1小时机器时间和2小时人工时间。
公司每天可利用机器时间为8小时,人工时间为10小时。
假设A、B产品的利润分别为50元和30元,请问如何安排生产计划以获得最大利润?- 建模:设A产品生产量为x,B产品生产量为y,目标函数为最大化利润Z = 50x + 30y,约束条件为:\[\begin{cases}2x + y \leq 8 \\3x + 2y \leq 10 \\x, y \geq 0\end{cases}\]- 求解:利用单纯形法求解该线性规划问题,得到最优解为x = 3,y = 2,最大利润为240元。
- 案例二:资源分配问题某项目需要分配三种资源:人力、物力和财力。
人力为50人,物力为100台设备,财力为500万元。
根据项目需求,每种资源的需求量如下:- 人力:研发阶段需20人,生产阶段需30人;- 物力:研发阶段需30台设备,生产阶段需50台设备;- 财力:研发阶段需100万元,生产阶段需200万元。
请问如何合理分配资源以满足项目需求?- 建模:设人力分配量为x,物力分配量为y,财力分配量为z,目标函数为最大化总效用U = x + y + z,约束条件为:\[\begin{cases}x \leq 20 \\y \leq 30 \\z \leq 100 \\x + y + z \leq 500\end{cases}\]- 求解:利用线性规划软件求解该问题,得到最优解为x = 20,y = 30,z = 100,总效用为150。
运筹学实验报告
运筹学实验报告一实验一:线性规划【例l】某制药厂用甲、乙两台机器生产A、B两种药物。
每种药物要经过两道工序,在甲机器上搅拌,在乙机器上包装。
生产每千克药物所需的加工时间以及机器1周可用于加工的总时间如下表1所示。
已知生产每千克药物A的利润是30元,B是25元,问应如何安排1周的生产计划才能使工厂获利最大?表 1 两种药物在各机器上所需加工时间及各机器可用于加工的总时间(1)写出数学模型,建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果。
(2)将电子表格格式转换成标准模型。
(3)将结果复制到Excel或Word文档中。
(4)分析结果。
解:(1)从已知条件写出该问题的数学模型:max Z=30x1+25x2;2x1+4x2<=40;3x1+2x2<=30;x1>=0,x2>=0.建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果:求解模型过程Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 3X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioX2 25.0000 0 1.0000 0.3750 -0.2500 7.5000X1 30.0000 1.0000 0 -0.2500 0.5000 5.0000C(j)-Z(j) 0 0 -1.8750 -8.7500 337.5000(2)将电子表格格式转换成标准模型。
运筹学实验2

实验内容及基本要求:
实验项目名称:运输问题实验
实验类型:验证
每组人数:1
实验内容及要求:
内容:运输问题建模与求解
要求:能够写出求解模型、运用excel和Lingo分别进行求解并对求解结果进行分析
实验背景:某企业集团有3个生产同类产品的工厂,生产的产品由4个销售中心出售,各工厂的生产量、各销售中心的销售量(假定单位均为吨)、各工厂到各销售点的单位运价(元/吨)示于表1中。要求研究产品如何调运才能使总运费最小。
成绩评定:
该生对待本次实验的态度□认真□良好□一般□比较差。
本次实验的过程情况□很好□较好□一般□比较差
对实验结果的分析□很好□良好□一般□比较差
文档书写符合规范程度□很好□良好□一般□比较差
综合意见:
成绩
指导教师签名
朱卫未
日期
2016.4.29
实验结果:
一,建立模型
根据题目要求结合表数据,建立数学模型如下:
设A1在各销地的运量分别为x1,x2,x3,x4,同理A2,A3在各销售地的运量为x5,x6,x7,x8,x9,x10,x11,x12,且总运价为Z则:
Min Z=3x11+11x12+3x313+9x14+x21+9x22+2x23+8x24+7x31+4x32+10x33+5x34
表1产销平衡表和单位运价表
销地
运价
产地
B1B2B3B4
产量
A1
A2
A3
3 11 3 9
1 9 2 8
7 4 10 5
6
4
9
运筹学实验报告

运筹学实验报告运筹学实验报告2实验内容:线性规划问题的建模和求解。
“炼油厂生产计划安排”,“长征医院的护士值班计划”两题目任选其一,每个小组最多3名同学,共同完成实验报告。
一、问题提出长征医院是长宁市的一所区级医院,该院每天各时间区段内需求的值班护士数如表1所示.该医院护士上班分五个班次,每班8h,具体上班时间为第一班2:00~10:00,第二班6:00~14:00,第三班10:00~18:00,第四班14:00~22:00,第五班18:00~2:00(次日).每名护士每周上5个班,并被安排在不同日子,有一名总护士长负责护士的值班安排计划.值班方案要做到在人员或经济上比较节省,又做到尽可能合情合理.下面是一些正在考虑中的值班方案:方案1 每名护士连续上班5天,休息2天,并从上班第一天起按从上第一班到第五班顺序安排.例如第一名护士从周一开始上班,则她于周一上第一班,周二上第二班,……,周五上第五班;另一名护士若从周三起上班,则她于周三上第一班,周四上第二班,……,周日上第五班,等等.方案2 考虑到按上述方案中每名护士在周末(周六、周日)两天内休息安排不均匀.于是规定每名护士在周六、周日两天内安排一天、且只安排一天休息,再在周一至周五期间安排4个班,同样上班的五天内分别顺序安排5个不同班次.在对第1、2方案建立线性规划模型并求解后,发现方案2虽然在安排周末休息上比较合理,但所需值班人数要比第1方案有较多增加,经济上不太合算,于是又提出了第3方案.方案3 在方案2基础上,动员一部分护士放弃周末休息,即每周在周一至周五间由总护士长给安排三天值班,加周六周日共上五个班,同样五个班分别安排不同班次.作为奖励,规定放弃周末休息的护士,其工资和奖金总额比其他护士增加a%.根据上述,帮助长征医院的总护士长分析研究:(x)对方案1、2建立使值班护士人数为最少的线性规划模型并求解;(b)对方案3,同样建立使值班护士人数为最少的线性规划模型并求解,然后回答a的值为多大时,第3方案较第2方案更经济;二、问题简述从该医院各时间段护士值班表可看出:五个时间段所需护士人数分别为18,20,19,17,12。
运筹学实验报告2

运筹学实验报告2《运筹学》课程实验第 2 次实验报告实验内容及基本要求:实验项目名称:运输问题实验实验类型: 验证每组人数: 1实验内容及要求:内容:运输问题建模与求解要求:能够写出求解模型、运用软件进行求解并对求解结果进行分析实验考核办法:实验结束要求写出实验报告,并于实验结束一周内(5月29日)上交。
实验结果:(附后)内容主要包括以下3点:1. 问题分析与建立模型,阐明建立模型的过程(一定要给出模型)。
2. 实验步骤,包含使用什么软件以及详细的实验过程。
3. 实验结果及其分析。
成绩评定:该生对待本次实验的态度 ?认真 ?良好 ?一般 ?比较差。
本次实验的过程情况 ?很好 ?较好 ?一般 ?比较差对实验结果的分析 ?很好 ?良好 ?一般 ?比较差文档书写符合规范程度 ?很好 ?良好 ?一般 ?比较差综合意见: 成绩指导教师签名刘长贤日期 2012.5.31实验背景:某农民承包了五块土地工206亩,打算种小麦、玉米和蔬菜三种农作物。
各种农作物的计划播种面积(亩)以及每块土地各种不同农作物的亩产量(公斤)如表1所示。
问如何安排种植计划,可使总产量最高,表1 每块土地种植不同农作物的亩产数量土地块别计划1 2 34 5 播种作物种类面积小麦 500 600650 1050 80086850 800 700 900 95070 玉米1000 950 850550 70050 蔬菜44 32 46 36 48土地亩数一(问题分析与建立模型 1.问题分析:总产量为目标函数maxZ;计划播种面积和土地亩数是约束条件;每块土地种植的不同农作物的亩产数量是决策变量2数学模型:目标函数1112131415MaxZ,500x,600x,650x,1050x,800x,2122232425 850x,800x,700x,900x,950x,1000x31,950x32,850x33,550x34,700x35约束条件x,x,x,x,x,861112131415x,x,x,x,x,702122232425x,x,x,x,x,503132333435x,x,x,36112131x,x,x,48122232x,x,x,44132333x,x,x,32142434 x,x,x,46152535xi,j,0,i,1,2,3,4,5;j,1,2,3二(实验步骤1.根据数学模型和题目要求,使用Excel软件建立如下表格2.单元格名称指定:选中要指定名称的单元格,点击“插入-名称-定义/指定”,则可对上图中的“亩产数量(=Sheet1!$C$3:$G$5),种植量(=Sheet1!$C$8:$G$10),实际面积(=Sheet1!$H$8:$H$10),计划面积(=Sheet1!$J$8:$J$10),实际亩数(=Sheet1!$C$11:$G$11),土地亩数(=Sheet1!$C$13:$G$13),总产量(=Sheet1!$L$12)”进行名称的指定3.单元格赋值:(1)利用“求和”函数对“实际面积”和“实际亩数”相应的单元格进行赋值,例如H8=SUM(小麦),C11=SUM(土地1)(2)利用“SUMPRODUCT”函数对“总产量”对应的单元格L12进行赋值,由于之前指定了单元格名称,故总产量=SUMPRODUCT(亩产数量,种植量) (3)由于当前各决策变量的值为0,故相应的实际面积,实际亩数,总产量为0 4.单击“工具”>“加载宏”>“规划求解”设置相关参数,如下图目标单元格为总产量可变单元格为每块土地种植的不同农作物对应的单元格约束条件为实际面积=计划面积;实际亩数=计划亩数5.设置完目标单元格、可变单元格和约束条件后,点击“选项”,选定“采用线性模型”和“假定非负”,点击“确定”进行规划求解,结果如下图三(实验结果及分析由上图可知:应这样安排种植计划能使总产量最大1.在土地1上种植34亩玉米和2亩蔬菜2.在土地2上种植48亩蔬菜3.在土地3上种植44亩小麦4.在土地4上种植32亩小麦5.在土地5上种植10亩小麦和36亩玉米。
运筹学实验报告案例二

安阳师范学院数学与统计学院实验报告实验课程名称:运筹学实验设计题目:配料问题专业:数学与应用数学班级:13级二班学生:常俊建 130800003 学生:刘翠宇 130800004 学生:李燃 130800022配料问题一、问题的描述某饲料公司生产鸡混合饲料,每千克饲料所需营养质量要求如表C-4所示。
表C-4每千克饲料所需营养质量要求公司计划使用的原料有玉米、小麦、麦麸、米糠、豆饼、菜子饼、鱼粉、槐叶粉、DL-蛋氨酸、骨粉、碳酸钙和食盐等12种。
各原料的营养成分含量及价格见表C-5。
表C-5原料的营养成分含量及价格公司根据原料来源,还要求1吨混合饲料中原料含量为:玉米不低于400kg、小麦不低于100kg、麦麸不低于100kg、米糠不超过150kg、豆饼不超过100kg、菜子饼不低于30kg、鱼粉不低于50kg、槐叶粉不低于30kg,DL-蛋氨酸、骨粉、碳酸钙适量。
(1)按照肉用种鸡公司标准,求1kg混合饲料中每种原料各配多少成本最低,建立数学模型并求解。
(2)按照肉用种鸡国家标准,求1kg混合饲料中每种原料各配多少成本最低。
(3)公司采购了一批花生饼,单价是0.6元/kg,代谢能到有机磷的含量分别为(2.4,38,120,0,0.92,0.15,0.17),求肉用种鸡成本最低的配料方案。
(4)求产蛋鸡的最优饲料配方方案。
(5)公司考虑到未来鱼粉、骨粉和碳酸钙将要涨价,米糠将要降价,价格变化率都r,试对两种产品配方方案进行灵敏度分析。
是原价的%说明:以上5个问题独立求解和分析,如在问题(3)中只加花生饼,其他方案则不加花生饼。
二、问题的分析与符号说明2.1模型的分析设公司计划使用的原料有玉米、小麦、麦麸、米糠、豆饼、菜子饼、鱼粉、槐叶粉、DL-蛋氨酸、骨粉、碳酸钙和食盐的用量分别为()1,2,,12i x i =,若将相应的原料单价分别用()1,2,,12i c i =,来表示,则其总成本可以用下面的线性函数来表示即121i i i w c x ==∑.2.2模型的符号说明三、模型建立与求解4.1问题(1)的模型建立与求解根据问题(1)所给数据及问题要求可列出约束条件,所以可建立混合饲料配料计划的线性规划模型如下:123456789101112123456781234567min 0.680.720.230.220.370.32 1.540.38230.56 1.120.423.35 3.08 1.78 2.10 2.40 1.62 2.80 1.61 2.73.35 3.08 1.78 2.10 2.40 1.62 2.80 1.6z x x x x x x x x x x x x x x x x x x x x x x x x x x x =++++++++++++++++++≥+++++++812345678123456812345678123456781135781141421174023604501701451622957249113108452.33.4 6.0 6.524.18.129.110.65.61.2 1.72.3 2.7 5.17.111.8 2.29x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ≥+++++++≤++++++≤+++++++≥++++++++91234567810111234567810121234567891011121234580 2.60.70.60.3 1.0 3.2 5.3634300400300.30.34101358.427414051000 3.710.4,0.1,0.10.15x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ≥+++++++++≥++++++++≥=+++++++++++=≥≥≥≤≤6780.10.030.050.030,(1,2, (12)j x x x x j ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪≥⎪⎪≥⎪≥⎪⎪≥=⎩ 问题(1)的lingo 程序如下:Min=0.68*x1+0.72*x2+0.23*x3+0.22*x4+0.37*x5+0.32*x6+1.54*x7+0.38*x8+23*x9+ 0.56*x10+1.12*x11+0.42*x12;3.35*x1+3.08*x2+1.78*x3+2.10*x4+2.40*x5+1.62*x6+2.80*x7+1.61*x8>=2.7; 78*x1+114*x2+142*x3+117*x4+402*x5+360*x6+450*x7+170*x8>=135; 78*x1+114*x2+142*x3+117*x4+402*x5+360*x6+450*x7+170*x8<=145; 16*x1+22*x2+95*x3+72*x4+49*x5+113*x6+108*x8<=45;2.3*x1+3.4*x2+6.0*x3+6.5*x4+24.1*x5+8.1*x6+29.1*x7+10.6*x8>=5.6; 1.2*x1+1.7*x2+2.3*x3+2.7*x4+5.1*x5+7.1*x6+11.8*x7+2.2*x8+980*x9>=2.6; 0.7*x1+0.6*x2+0.3*x3+1.0*x4+3.2*x5+5.3*x6+63*x7+4.0*x8+300*x10+400*x11>=30; 0.3*x1+0.34*x2+10.0*x3+13.0*x4+5.0*x5+8.4*x6+27*x7+4.0*x8+140*x10>=5; 1000*x12=3.7;X1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12=1; X1>=0.4; x2>=0.1; x3>=0.1; x4<=0.15; x5<=0.1; x6>=0.03; x7>=0.05; x8>=0.03;问题(1)Lingo 程序的结果:Global optimal solution found.Objective value: 0.6553693Infeasibilities: 0.000000Total solver iterations: 9Variable Value Reduced CostX1 0.5385030 0.000000X2 0.1000000 0.000000X3 0.1000000 0.000000X4 0.000000 0.1446276X5 0.7213126E-01 0.000000X6 0.3000000E-01 0.000000X7 0.5000000E-01 0.000000X8 0.3000000E-01 0.000000X9 0.3233949E-03 0.000000X10 0.4263719E-01 0.000000X11 0.3270518E-01 0.000000X12 0.3700000E-02 0.000000Row Slack or Surplus Dual Price1 0.6553693 -1.0000002 0.000000 -0.52187993 0.000000 -0.2339449E-034 10.00000 0.0000005 14.51952 0.0000006 0.3329203 0.0000007 0.000000 -0.2461224E-018 0.000000 -0.5600000E-029 4.247413 0.00000010 0.000000 -0.1540000E-0211 0.000000 1.12000012 0.1385030 0.00000013 0.000000 -0.160739414 0.000000 -0.329545515 0.1500000 0.00000016 0.2786874E-01 0.00000017 0.000000 -0.305907518 0.000000 -0.450236719 0.000000 -0.5434558所以按照肉用种鸡公司标准,1kg混合饲料中玉米约需要0.54kg,小麦约需要0.1kg,麦麸约需要0.1kg,米糠约需要0kg,豆饼约需要0.072kg,菜子饼约需要0.03kg,鱼粉约需要0.05kg,槐叶粉约需要0.03kg,DL蛋氨酸约需要0.0003kg,骨粉约需要0.042kg,碳酸钙约需要0.032kg,食盐约需要0.0037kg,此时成本最低为约为0.655元。
运筹学实验报告

目录实验一线性规划求解(1)实验二线性规划求解(2)实验三线性规划建模求解(1)实验四线性规划建模求解(2)实验五运输问题实验六 LINOG软件的初步使用实验一线性规划求解(1)实验属性:验证性实验时间:2013-6-29 实验目的1.理解线性规划解的基本概念;2.掌握管理运筹学软件的使用方法;3. 掌握线性规划的求解原理和方法。
实验内容1.认真阅读下列各题,注意每个问题的特征;2.用本书附带的《管理运筹学软件》求解下列问题,并记录结果;(对照书第3章有关软件的介绍理解计算结果的相关解释,要求包含全部运算结果及相关的敏感性分析结果)3.对结果作适当分析(与图解对比);4.完成实验报告。
(如有余力,以该软件做一下课后题,对单纯形法相对照)实验步骤(1) max z=6x1+4x2s.t. 2x1+x2<=10x1+x2<=8x1,x2>=0(2) max z=50x1+30x2 s.t. 4x1+3x2<=120 2x1+x2<=50x1,x2>=0(3) max z=x1+x2 s.t. x1+2x2<=4 x1-2x2>=5x1,x2>=0(4) max z=2x1+x2 s.t. x1+x2>=2 x1-2x2<=0x1,x2>=0(5) max z=40x1+30x2 s.t. 4x1+3x2<=1202x1+x2<50x1,x2>=0(6) min z=x1+x2+x3+x4+x5+x6 s.t. x1+x6>=60x1+x2>=70x2+x3>=60 x3+x4>=50 x4+x5>=20 x5+x6>=30 x1,…x6>=0实验结果分析线性规划问题的结果输出部分增加了线性规划的逐步运算过程。
更易了解掌握线性规划计算的全过程。
在本实验过程中,线性规划软件不仅可以输出正确的结果,还能同时得到目标函数最优值、松弛变量、对偶价格、目标函数系数范围和常数项范围。
哈工大运筹学实验报告 实验一,实验二

实验一一、实验目的1)了解Excel的基本功能,熟悉界面,掌握基本的操作命令;2)熟悉Matlab编程环境,了解Matlab的基本功能,掌握基本的编程语言;3)用Excel和Matlab求解话务排班线性规划问题。
二、实验器材1)PC机:20台。
2)Microsoft Excel软件(具备规划求解工具模块):20用户。
3)Matlab软件(具备优化工具箱):20用户。
三、实验原理:话务排班属于线性规划问题,通过对问题建立数学模型,根据Excel自身特点把数学模型在电子表格中进行清晰的描述,再利用规划求解工具设定相应的约束条件,最终完成对问题的寻优过程,具体可参见1.2;在Matlab中,根据Matlab 提供的线性规划求解函数,将数学模型转换成线性规划求解函数可传递的数值参数,最终实现对问题的寻优求解过程,具体可参见2中linprog函数描述和示例。
四、实验内容和步骤:某寻呼公司雇佣了多名话务员工作,他们每天工作3节,每节3小时,每节开始时间为午夜、凌晨3点钟、凌晨6点钟,上午9点、中午12点,下午3点、6点、9点,为方便话务员上下班,管理层安排每位话务员每天连续工作3节,根据调查,对于不同的时间,由于业务量不同,需要的话务员的人数也不相同,公司付的薪水也不相同,有关数据如下表所示。
问:如何安排话务员才能保证服务人数,又使总成本最低?第一步:建立线性规划模型设1x 为0点开始工作的人数,2x 是3点开始工作的人数,3x 是6点开始工作的人数,4x ……,8x 是21点开始工作的人数。
Z 为所支付的总薪水。
算出每个时间段的最低需求人数,如1x +2x +3x 为6-9点工作的人数。
由题意列出约束方程为:1x + 7x +8x ≥8 1x +2x + 8x ≥61x +2x +3x ≥152x +3x +4x ≥20 3x +4x +5x ≥25 4x +5x +6x ≥23 5x +6x +7x ≥186x +7x +8x ≥10 i x ≥0(i=1,.....8) 目标函数z min =841x +802x +703x +624x +625x +666x +727x +808xExcel 求解过程描述打开Excel ,选择“Excel 选项”通过“工具”菜单的“加载宏”选项打开“加载宏”对话框来添加“规划求解”。
运筹学实验报告_2

运筹学上机实验报告
5.用指令 linprog()实现 page 48 例 10
6. 用指令 linprog()实现 page 48 例 11
三、程序流程图: 1.用指令 linprog() 实现 page 15
f=-[2,3]'; a=[1,2;4,0;0,4]; b=[8,16,12]'; lb=[0,0]'; [x,fval,ex]=linprog(f ,a,b,[],[],lb,[])
2.用指令 linprog() 实现 page18 无穷多最优解
if exitflag==-3 fprintf('该线性规划为无界解')
end
4. 用指令 linprog()实现 page18 无可行解
f=-[1,1]'; a=[-2,1;1,-1]; b=[0,0]'; [x,fval,exitflag]=linprog(f,a,b,[],[],lb,[ ])
所e述xi问tf题la无g 可= 行解 5.用指-2令 linprog()实现 page 48 例 10
x=
2.5470 0.0000 0.0000 0.0000 0.0000
fval =
1.0043e-011
6. 用指令 linprog()实现 page 48 例 11
x=
100.0000 50.0000 50.0000
0.0000 0.0000 0.0000 0.0000 25.0000 0.0000
运筹学实验报告
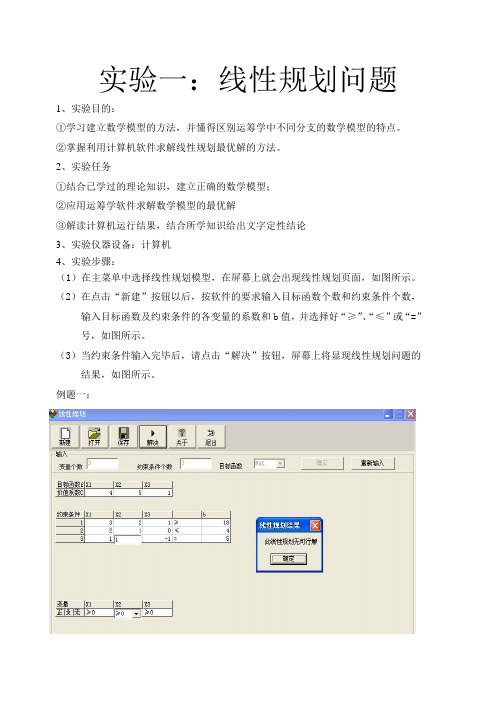
实验一:线性规划问题1、实验目的:①学习建立数学模型的方法,并懂得区别运筹学中不同分支的数学模型的特点。
②掌握利用计算机软件求解线性规划最优解的方法。
2、实验任务①结合已学过的理论知识,建立正确的数学模型;②应用运筹学软件求解数学模型的最优解③解读计算机运行结果,结合所学知识给出文字定性结论3、实验仪器设备:计算机4、实验步骤:(1)在主菜单中选择线性规划模型,在屏幕上就会出现线性规划页面,如图所示。
(2)在点击“新建”按钮以后,按软件的要求输入目标函数个数和约束条件个数,输入目标函数及约束条件的各变量的系数和b值,并选择好“≥”、“≤”或“=”号,如图所示。
(3)当约束条件输入完毕后,请点击“解决”按钮,屏幕上将显现线性规划问题的结果,如图所示。
例题一:例题二:例题三:例题四:例题五5、试验体会或心得运筹学是一门实用的学科,学习运筹学,结合生活实际运用运筹学,我们可以将资源最大化利用。
学习理论的目的就是为了解决实际问题。
线性规划的理论对我们的实际生活指导意义很大。
当我们遇到一个问题,需要认真考察该问题。
如果它适合线性规划的条件,那么我们就利用线性规划的理论解决该问题。
线性规划指的是在资源有限的条件下,为达到预期目标最优,而寻找资源消耗最少的方案。
其数学模型有目标函数和约束条件组成。
一个问题要满足一下条件时才能归结为线性规划的模型:⑴要求解的问题的目标能用效益指标度量大小,并能用线性函数描述目标的要求;⑵为达到这个目标存在很多种方案;⑶要到达的目标是在一定约束条件下实现的,这些条件可以用线性等式或者不等式描述。
所以,通过这次实验,不仅对运筹学的有关知识有了进一步的掌握,同时对在自己的计算机操作水准也有了很大的提高。
这次实验让我懂得了运筹学在电脑的应用,让我对运输与数学相结合的应用理解更深了。
实验二:整数规划与运输问题1、实验目的:①学习建立数学模型的方法,并懂得区别运筹学中不同分支的数学模型的特点。
运筹学实验报告2

运筹学实验报告2交通与汽车工程学院课程名称: 运筹学(汽车) 课程代码: 7100570 学院(直属系): 交通与汽车工程学院年级/专业/班: 2009级物流管理3班学生姓名: 学号: 实验总成绩: 任课教师: 黎青松开课学院: 交通与汽车工程学院实验中心名称: 物流管理实验室第 2 组西华大学实验报告西华大学实验报告开课学院及实验室:交通与汽车学院计算机中心实验时间: 年月日学生姓名学号实验成绩课程名称运筹学(汽车学院) 课程代码 8245050 实验项目名称炼油厂计划、菜篮子工程项目代码指导教师黎青松项目学分实验课考勤 10% 实验工作表现 20% 实验报告 70% 1、实验目的1.1训练建模能力1.2.应用EXCEL建模及求解的方法应用;1.3通过实验进一步掌握运筹学有关方法原理、求解过程,提高学生分析问题和解决问题能力。
2、实验设备、仪器及材料计算机、Excel3、实验内容3.1炼油厂产计划安排问题例一炼油厂的生产计划某炼油厂的工艺流程图如图 1-1所示。
炼油厂输入两种原油(原油 1和原油2)。
原油先进入蒸馏装置,每桶原油经蒸馏后的产品及份额见表1-1,其中轻、中、重石脑油的辛烷值分别为90、80和70。
1西华大学实验报告石脑油部分直接用于发动机油混合,部分输入重整装置,得辛烷值为115的重整汽油。
1桶轻、中、重石脑油经重整后得到的重整汽油分别为0.6、0.52、0.45桶。
蒸馏得到的轻油和重油,一部分直接用于煤油和燃料油的混合,一部分经裂解装置得到裂解汽油和裂解油。
裂解汽油的辛烷值为105。
1桶轻油经裂解后得0.68桶裂解油和0.28桶裂桶汽油;1桶重油裂解后得0.75桶裂解油和0.2桶裂解汽油。
其中裂解汽油用于发动机油混合,裂解油用于煤油和燃料油的混合。
渣油可直接用于煤油和燃料油的混合,或用于生产润滑油。
1桶渣油经处理后可得0.5桶润滑油。
混合成的高档发动机油的辛烷值应不低于 94,普通的发动机油辛烷值不低于84。
最新运筹学实践报告加工问题的(优质5篇)

最新运筹学实践报告加工问题的(优质5篇)(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如职场文书、公文写作、党团资料、总结报告、演讲致辞、合同协议、条据书信、心得体会、教学资料、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, this store provides various types of classic sample essays for everyone, such as workplace documents, official document writing, party and youth information, summary reports, speeches, contract agreements, documentary letters, experiences, teaching materials, other sample essays, etc. If you want to learn about different sample formats and writing methods, please pay attention!最新运筹学实践报告加工问题的(优质5篇)“报告”使用范围很广,按照上级部署或工作计划,每完成一项任务,一般都要向上级写报告,反映工作中的基本情况、工作中取得的经验教训、存在的问题以及今后工作设想等,以取得上级领导部门的指导。
运筹学上机实验报告

运筹学上机实验报告一、实验目的本次运筹学上机实验的目的是通过实践操作,加深对运筹学知识的理解和掌握,了解线性规划模型的建立和求解方法,并能够应用相关软件进行模型求解。
二、实验内容1. 线性规划模型建立在本次实验中,我们需要根据给定的问题情境,建立相应的线性规划模型。
具体来说,我们需要确定决策变量、约束条件和目标函数,并将其转化为标准形式。
2. 模型求解在建立好线性规划模型后,我们需要利用相关软件进行模型求解。
常用的求解方法包括单纯形法、对偶单纯形法等。
通过对不同方法的比较和分析,可以找到最优解并得出相应结论。
3. 结果分析与优化在得出最优解后,我们还需要对结果进行分析和优化。
可以通过灵敏度分析等方法来研究问题情境中各个因素对最终结果的影响程度,并提出相应改进意见。
三、实验过程1. 线性规划模型建立首先,我们需要确定决策变量。
例如,在一个生产计划问题中,决策变量可能是不同产品的生产数量。
然后,我们需要根据问题情境确定约束条件,例如生产线的产能限制、原材料的供应量等。
最后,我们需要确定目标函数,即需要最小化或最大化的目标。
2. 模型求解在建立好模型后,我们需要利用相关软件进行模型求解。
以MATLAB 为例,可以使用linprog函数进行线性规划求解。
具体步骤包括输入决策变量、约束条件和目标函数等参数,并调用linprog函数进行计算。
3. 结果分析与优化在得出最优解后,我们还需要对结果进行分析和优化。
例如,在灵敏度分析中,我们可以通过改变某些参数值来研究其对最终结果的影响程度。
如果发现某个因素对结果影响较大,则可以提出相应改进意见。
四、实验心得通过本次运筹学上机实验,我深刻认识到了线性规划模型在实际问题中的重要性,并学会了如何利用相关软件进行模型求解和结果分析。
同时,在实验过程中也遇到了一些困难和挑战,例如如何正确建立模型、如何选择合适的求解方法等。
但通过不断尝试和探索,我逐渐掌握了相关技能和方法,并取得了较好的实验成果。
运筹学实验报告 2

运筹学实验报告学院:专业班级:姓名:学号:实验一线性规划一、实验目的学习WinQSB软件的基本操作,利用Linear Programming功能求解线性规划问题。
掌握线性规划的基本理论与求解方法,重点在于单纯形法的应用以及灵敏度分析方法。
二、实验内容安装WinQSB软件,了解WinQSB软件在Windows环境下的文件管理操作,熟悉软件界面内容,掌握操作命令。
利用Linear Programming功能建立线性模型,输入模型,求解模型,并对求解结果进行简单分析。
三、实验步骤1.将WinQSB文件复制到本地硬盘;在WinQSB文件夹中双击setup.exe。
2.指定安装WinQSB软件的目标目录(默认为C:\ WinQSB)。
3.安装过程需要输入用户名和单位名称(任意输入),安装完毕之后,WinQSB菜单自动生成在系统程序中。
4.熟悉WinQSB软件子菜单内容及其功能,掌握操作命令。
5.求解下面线性规划问题:某工厂要用三种原材料C、P、H混合调配出三种不同规格的产品A、B、D。
已知产品的规格要求,产品单价,每天能供应的原材料数量及原材料单价分别见下表1和2。
该厂应如何安排生产,使利润收入为最大?表1产品名称规格要求单价(元/kg)A 原材料C不少于50%原材料P不超过25%50B 原材料C不少于25%原材料P 不超过50%35D 不限25表2原材料名称每天最多供应量(kg)单价(元/kg)C P H 10010060652535列出该线性规划问题的模型如下:以A C 表示产品A 中C 的成分,A P 表示产品A 中P 的成分,依次类推。
则约束条件为:A C +BC +D C ≤100 A P +B P +D P ≤100 A H +B H +D H ≤60在约束条件中共有9个变量,为计算和叙述方便,分别用x 1,…,x 9表示。
令x 1=A c , x 2=A p , x 3=A H , x 4=B C , x 5=B P , x 6=B H , x 7=D C , x 8=D P , x 9=D H . 则:启动程序 开始→程序→WinQSB →Linear and Integer Programming ,点击菜单栏File 中的New Problem 项,建立新问题。
实验二运筹学

实验二线性规划模型的对偶问题及灵敏度分析一、实验目的:进一步掌握线性规划模型的基本原理,理解线性规划的对偶问题,掌握R软件在线性规划问题灵敏度分析中的运用。
二、实验内容:(1)教材P127 习题1。
利用线性规划的最终单纯形表,对目标函数系数和约束方程的常数项进行灵敏度分析,并在R软件中验证你的计算结果;(2)教材P131 习题11。
写出该问题的对偶问题,并用R 软件求解原问题和对偶问题。
指出二者最优解与对偶价格之间的联系。
(3)建立教材P130 习题7的数学模型并用R软件分析。
三、实验要求:(1)利用线性规划基本原理对所求解问题建立数学模型;(2)熟练写出线性规划问题的对偶问题;(3)给出R软件中的输入并求解;(4)对目标函数系数及约束方程的常数项进行灵敏度分析四、实验报告要求:实验过程描述(包括变量定义、分析过程、分析结果及其解释、实验过程遇到的问题及体会)。
(1)maxz=20X1+8X2+6X38X1+3X2+2X3<=2502X1+X2<=504X1+3X3<=150X 1,X2,X3>=0> library(lpSolve)> obj<-c(20,8,6)> mat<-matrix(c(8,3,2,2,1,0,4,0,3),nrow=3,byrow=T) > dir<-c("<=","<=","<=")> rhs<-c(250,50,150)> x<-lp("max",obj,mat,dir,rhs,compute.sens=1)> x$status;x$solution;x$objval[1] 0[1] 0 50 50[1] 700> x$sens.coef.from;x$sens.coef.to[1] -1e+30 6e+00 3e+00[1] 2.4e+01 1.0e+30 1.0e+30C1范围是(-∞,24),C2范围是(6,+∞),C3范围是(3,+∞)> library(lpSolve)> obj<-c(20,8,6)> mat<-matrix(c(8,3,2,2,1,0,4,0,3),nrow=3,byrow=T) > dir<-c("<=","<=","<=")> rhs<-c(250,50,150)> x<-lp("max",obj,mat,dir,rhs,compute.sens=1)> x$status;x$solution;x$objval[1] 0[1] 0 50 50[1] 700> x$duals;x$duals.from;x$duals.to[1] 0 8 2 -4 0 0[1] -1.000000e+30 7.105427e-15 -2.842171e-14 0.000000e +00 -1.000000e+30 -1.000000e+30[1] 1.0e+30 5.0e+01 1.5e+02 2.5e+01 1.0e+30 1.0e+30b1,b2,b3的对偶价格分别为0、8、2;b1范围为(250,∞),b2范围为(0, 50),b3范围为(0, 150)。
运筹学实验报告 2

实验报告《运筹学》2015~2016学年第一学期学院(部)管理学院指导教师阎瑞霞班级代号 1511131姓名/学号周云佳151113172 同组人无提交时间成绩评定实验目的:加强学生分析问题的能力,锻炼数学建模的能力。
掌握WinQSB/Matlab 软件中线性规划、灵敏度问题的求解和分析。
用 WORD 书写实验报告:包括详细规划模型、试验步骤和结果分析。
实验内容:题1:某厂的一个车间有1B ,2B 两个工段可以生产123,,A A A 三种产品,各工段开工一天生产三种产品的数量和成本,以及合同对三种产品的每周最低需求量由表1给出。
问每周各工段对该生产任务应开工几天,可使生产合同的要求得到满足,并使成本最低。
建立模型。
表1生产定额(吨/天)工段B生产合同每周最低需求量(吨)ib iA 产品1A 2A 3A 1B 2B 11311310002000599成本(元/天)建立模型:WinQSB 录入模型界面:运行结果界面:结果分析:决策变量:X1,X2最优解:X1=3,X2=2;目标系数:C1=1000,C2=2000;最优值:7000;其中X1贡献3000,X2贡献4000;检验数,或称缩减成本:0,0。
即当非基变量增加一个单位时,目标值的变动量。
目标系数的允许减量和允许增量;目标系数在此范围变量时,最优基不变。
约束条件约束条件:C1,C2,C3左端:5,11,9右端:5,9,9松弛变量或剩余变量:该端等于约束左端与约束优端之差;为0表示资源达到限制值。
题2:明兴公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,这三种产品都要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。
有关情况见表2;公司中可利用的总工时为:铸造8000小时,机加工12000小时和装配10000小时。
建立模型:解;假设公司选择甲产品自产X1件,外包协作X2件,乙产品自产X3件,外包协作X4件,丙产品生产X5件,则有;maxZ=15X1+13X2+10X3+9X4+7X5s.t. 5X1+10X3+7X5<=80006X1+6X2+4X3+4X4+8X5<=120003X1+3X2+2X3+2X4+2X5<=10000X1-5>=0WinQSB录入模型界面:运行结果界面:结果分析:(1) X*=(1600,0,0,600,0), Z*=29400元,即:公司为了获得最大利润29400元,甲、乙、丙三种产品各生产1600件、600件、0件。
运筹学(二)实 验 报 告

《运筹学(二)》实验报告2011~2012学年第二学期学院(部):姓名/学号:实验目的:加强学生分析问题的能力,锻炼数学建模的能力。
利用所学知识,设计动态规划和决策树算法,并完成程序设计。
实验内容:题1(动态规划):(投资问题)现有资金5百万元,可对3个项目进行投资。
假设2#项目的投资不得超过3百万元,1#和3#项目的投资均不得超过4百万元,3#项目至少要投资1百万元。
投资5年后每个项目预计可获得的收益由表1给出。
问如何投资可获得最大的收益。
表1实验过程参考答案:建立模型:MATLAB程序代码:题2:在某单人理发店顾客到达为普阿松流,平均到达间隔为20分钟,理发时间服从负指数分布,平均时间为15分钟。
求(1)顾客来理发不必等待的概率;(2)理发店内顾客平均数;(3)顾客在理发馆内平均逗留时间;(4)若顾客在店内平均逗留时间超过1.25小时,则店主将考虑增加设备及理发员,问平均到达率提高多少时店主才做这样考虑呢?MATLAB程序代码:function[PO,Ls,Lp,Ws,Wq]=model6lenda=input('请输入到达速率:');mhu=input('请输入服务速率:');rho=lenda/mhu;PO=1-rho;Ls=lenda/(mhu-lenda);Lq=Ls-rho;Ws=1/(mhu-lenda);Wq=Ws-1/mhu;POLsLqWsWq结果分析:>> model6请输入到达速率:1/20请输入服务速率:1/15PO =0.2500Ls =3.0000Lq =2.2500Ws =60.0000Wq =45.0000ans =0.25001.PO=0.252.Ls=33.Ws=604.lenda=4/75(人/分钟)5.题3:某企业为了扩大某产品的生产,拟建设新厂。
据市场预测,产品销路好的概率为0.7,销路差的概率为0.3。
有三种方案可供企业选择:方案一、新建大厂,需投资300万元。
