一元二次方程根的分布
一元二次方程根的分布(2019年11月)

C.必要不充分条件 D.既不必要不充分条件
例5:求方程3x2-2mx+m+1=0一根在0,1之 间另一根在1,2之间的充要条件
例6 : 抛物线y=-x2+3x-m与直线y=3-x在 0<x<3时只有一个交点,求m的范围. -3<m≤0或m=1
例7 设m,n分别是关于x的二次方程ax2+bx+c=0
一、实系数一元二次方程ax2+bx+c=0 (a,b,c∈R,a≠0)的根的问题,常利用韦达 定理和判别式来解。常用结论有:1 方源自有两个正根2 方程有两个负根
3.方程有一个正根一个负根
x1 x2 0(或ac 0)
0
4.方程两根都大于m (x1 m) (x2 m) 0
(x1 m) (x2 m) 0
0
5 .方程两根都小于m (x1 m) (x2 m) 0
(x1 m) (x2 m) 0
6. 方程一根大于m另一根小于m
(x1 m) (x2 m) 0
• 例1: 方程x2+2ax+1=0有两个不等负
• 二、二次方程与二次函数联系紧密,关于二次 方程问题求解的另一思路是转化为二次函数来 解,因此一元二次方程根的分布问题可借助二 次函数图象来研究求解。(函数法) 抓△,对称轴的位置,特殊点的函数值
令f(x)=ax2+bx+c(a>0) 则有如下结论
1 .方程两根都大于m
2.方程两根都小于m 3.方程一个根大于m另一根小于m 4.方程两根都大于m且都小于n
5.x1<m<n<x2
6.若f(m) ·f(n)<0,则方程必有一根在m与n之间
不等式一元二次方程根的分布

布2023-11-07•定义和公式•根的分布情况•图像表示目录•实例分析•解题技巧和注意事项•练习题与答案01定义和公式定义一元二次方程的标准形式是$ax^2 + bx + c = 0$,其中$a \neq 0$。
说明一元二次方程的标准形式是解决一元二次方程问题的基础,通过配方等方法可以将非标准形式的一元二次方程转化为标准形式,便于分析其根的分布情况。
一元二次方程的标准形式一元二次方程的解是满足方程的根,记作$x_{1}, x_{2}$。
定义根据判别式的性质,一元二次方程的解的情况分为三种:有两个不相等的实数根、有两个相等的实数根和没有实数根。
判别式$b^2 - 4ac$是判断一元二次方程解的分布情况的依据。
说明一元二次方程的解02根的分布情况当判别式Δ大于0时,一元二次方程有两个不相等的实根。
两根不等实根与系数关系图像表示两个实根的和为-b/a,两个实根的积为c/a。
在实数平面上表示为两个不相交的直线。
030201当判别式Δ等于0时,一元二次方程有两个相等的实根。
两根相等两个实根的和为-b/a,两个实根的积为c/a。
实根与系数关系在实数平面上表示为一条直线。
图像表示当判别式Δ小于0时,一元二次方程有两个不相等的虚根。
两根不等且虚根两个虚根的实部为0。
实部为0两个虚根的虚部为√(-Δ)/a。
虚部与系数关系在复数平面上表示为两个相交的直线。
图像表示当Δ < 0时,方程的根的分布03图像表示图像表示一元二次方程的解实数根对于一元二次方程 $ax^2 + bx + c = 0$,如果 $a > 0$,那么该方程有两个实数根,分别是 $x_1 = \frac{-b + \sqrt{\Delta}}{2a}$ 和 $x_2 = \frac{-b - \sqrt{\Delta}}{2a}$。
虚数根如果 $a < 0$,那么该方程有两个共轭虚数根,分别是 $x_1 = \frac{-b + i\sqrt{4ac - b^2}}{2a}$ 和 $x_2 = \frac{-b - i\sqrt{4ac - b^2}}{2a}$。
一元二次方程根的分布

3 m 1 时,根 x 2 3,0 ,即 m 1 满足题意;当 m 时, 得出 m 1或 m 3 ,当 2 2
15 3 m 或 m 1 根 x 33,0 ,故 m 3 不满足题意;综上分析,得出 14 2
3.一根在(m,n)内,另一根在(p,q)内
0 f m 0 f n 0 b m n 2a
0 f m 0 f n 0 b m n 2a
2.两根有且仅有一根在(m,n)内
f m f n 0
综合结论 (不讨论 a)
一.一元二次方程根的基本分布——零分布
所谓一元二次方程根的零分布,指的是方程的 根相对于零的关系。比如二次方程有一正根, 有一负根,其实就是指这个二次方程一个根比 零大,一个根比零小,或者说,这两个根分布 在零的两侧。 设一元二次方程ax2+bx+c=0(a≠0)的两个 实根为x1,x2,且x1<x2。
f m 0 f n 0
已知关于 x 的方程 x2 (2m 1) x 4 2m 0 ,求满足下列条件的 m 的取值范围. (1) 两个正根 (2)有两个负根 (3) 两个根都小于 1 (4) 两个根都大于 1 2 (5)一个根大于 2,一个根小于 2 (6) 两个根都在 (0, 2) 内 (7) 两个根有且仅有一个在 (0, 2) 内 (8)一个根在 (2,0) 内,另一个根在 (1,3) 内 (9) 一个正根,一个负根且正根绝对值较大 (10)一个根小于 2,一个根大于 4
一元二次方程根的分布
知识要点
一元二次方程ax2+bx+c=0 (a≠0)的根从几 何意义上来说就是抛物线y=ax2+bx+c (a≠0)与 轴交点的横坐标,所以研究方程 ax2+bx+c=0 (a≠0)的实根的情况,可借助二次函数图象来研 究求解.(几何法) 若在 (- ∞ ,+ ∞)内研究方程ax2+bx+c=0 (a≠0)的实根情况,只需考察函数 y=ax2+bx+c (a≠0)与 x轴交点个数及交点横坐标的符号,利 用韦达定理和判别式来解,由 y=ax2+bx+c (a≠0) 的系数可判断出 △,x1+x2,x1x2的符号,从而判断 出实根的情况.(代数法)
一元二次方程根的分布情况归纳(完整版)

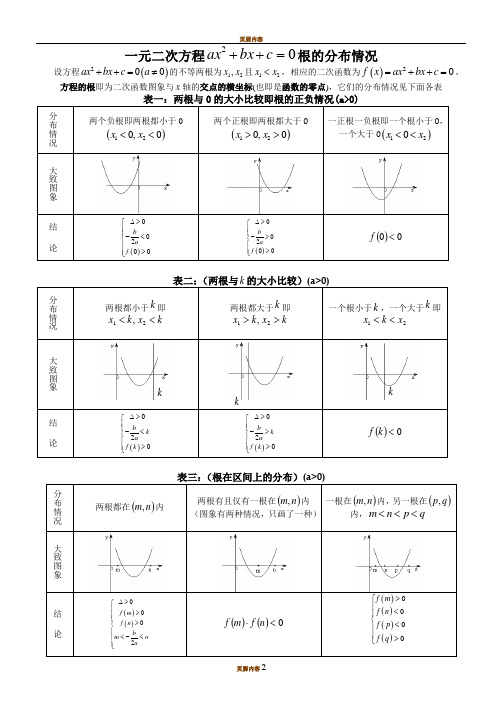
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求;方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
一元二次方程的根的分布

情形1 方程根的零分布 :
结论1 一元二次方程ax 2 bx c 0(a 0)有两个正根.
b2 x1 0 x 2 0 x1 x 2 y x1 x 2
c0 O x1
4ac 0 b 0 a c 0 a
2
k的根.
y
a0 0 x2 b k 2a
a0 0 x2 O b 0 k 2a
k x1 O
x
k x1
x
情形2: 方程根的k分布
结论2 一元二次方程ax 2 bx c 0(a〉 有两个小于 0) k的根. b 2 4ac 0 b 2 4ac 0 x1 k ( x1 k ) ( x 2 k ) 0 b k x2 k ( x k )( x k ) 0 2a 1 2
x x
一个正根和一个负根, 求k的范围。
x
结论4 一元二次方程ax bx c 0(a 0)在区间
2
(k1 , k2 )内有且只有一根x1.即k1 x1 k2
f (k1 ) f (k 2 ) 0
y
f (k1 ) 0
a0
x1 O k1
k2
x2
x
f (k 2 ) 0
结论4 一元二次方程ax bx c 0(a〉 的根满足 0)
求函数的零点有两种方法: ①代数法:求方程f(x)=0的实数根; ②几何法:将它与函数y=f(x)的图象联 系起来,并利用函数的性质找出零点。
连续函数在某个区间上存在零点的判别方法:
如果函数y=f(x)在区间[a,b]上的图 象是连续不断一条曲线,并且有 f(a)· f(b)<0,那么,函数y=f(x)在区间 (a,b)内有零点.即存在c∈(a,b),使得 f(c )=0,这个c也就是方程f(x)=0的根.
一元二次方程根的分布情况归纳总结
一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点的横坐标(也即是函数的零点),它们的分布情况见下面各表表一:两根与0的大小比较即根的正负情况(a>0)分布情况 两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0,一个大于0()120x x <<大致图象结论()00200ba f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200ba f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f分布情况两根都小于k 即 k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ,一个大于k 即21x k x <<大致图象结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f分布情况 两根都在()n m ,内两根有且仅有一根在()n m ,内(图象有两种情况,只画了一种)一根在()n m ,内,另一根在()q p ,内,q p n m <<< 大致图象结 论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩k kk函数与方程思想:(1)方程f (0x )=0有根⇔y =()f x 与x 轴有交点0x ⇔函数y=()f x 有零点0x (2)若y =f (x )与y =g (x )有交点(0x ,0y )⇔()f x =()g x 有解0x根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
一元二次方程根的分布

一元二次方程的形式为ax^2+bx+c=0,其中a、b、c为常数。
一元二次方程根的分布取决于方程的解的个数,有如下三种情况:1 两个不相等的实根:如果一元二次方程有两个不相等的实根,那么方程的解为x1=r1、x2=r2,其中r1和r2是方程的两个实根。
2 两个相等的实根:如果一元二次方程有两个相等的实根,那么方程的解为x1=x2=r,其中r是方程的两个相等的实根。
3 两个复数根:如果一元二次方程有两个复数根,那么方程的解为x1=r1+r2i、x2=r1-r2i,其中r1和r2是方程的两个复数根的实部和虚部。
一元二次方程的根分布可以通过求解方程的判别式来确定。
判别式为b^2-4ac,如果判别式>0,则方程有两个不相等的实根;如果判别式=0,则方程有两个相等的实根;如果判别式<0,则方程有两个复数根。
在数学中,一元二次方程是由一个二次项和一个一次项组成的方程。
它的形式为ax^2+bx+c=0,其中a、b、c为常数。
解决一元二次方程的方法有多种,常见的方法有求解公式法、因式分解法、二分法、牛顿迭代法等。
求解公式法是最常见的求解一元二次方程的方法,它的公式为:x1= (-b+sqrt(b^2-4ac))/(2a)x2= (-b-sqrt(b^2-4ac))/(2a)其中sqrt(b^2-4ac)表示根号内的值。
因式分解法是将一元二次方程写成两个一次方程的形式,然后分别求解两个一次方程的解。
二分法是一种数值解法,通过取方程的两个端点的中点来逐步缩小解的范围,最终得到方程的解。
牛顿迭代法是一种逐步迭代的方法,通过不断迭代来逼近方程的解,最终得到方程的解。
在解决一元二次方程时,应根据具体情况选择合适的方法。
一元二次方程根的分布

第九讲 一元二次方程根的分布一元二次方程根的分布是二次函数中的重要内容。
这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用。
知识点:1.为了本课教学内容的需要与方便,先介绍函数符号"f(x)".例如二次函数记作f(x)= ax 2+bx+c (a ≠0), x=1时的函数值记作f(1), 即f(1)=a+b+c. 2.韦达定理: 1212,b c x x x x a a+=-= 3.一元二次方程根的分布函数与方程思想:若y =()f x 与x 轴有交点0x ⇔f (0x )=0下面我们将主要结合二次函数图象的性质,系统地介绍一元二次方程实根的分布(1)开口方向; (2)对称轴位置; (3)判别式; (4)端点函数值符号。
例题:例1.若一元二次方程0)1(2)1(2=-++-m x m x m 有两个正根,求m 的取值范围。
例2.若一元二次方程0332=-++k kx kx 的两根都是负数,求k 的取值范围。
变式:k 在何范围内取值,一元二次方程0332=-++k kx kx 有一个正根和一个负根?例3.已知方程02112=-+-m x x 的两实根都大于1,求m 的取值范围。
变式(1)方程()f x =2ax bx c ++=0(a >0)的两个根都大于1的充要条件是 ( )A 、△≥0且f (1)>0B 、f (1)>0且-ab >2C 、△≥0且-a b >2,ca>1D 、△≥0且f (1)>0,-ab>2变式(2)若一元二次方程03)1(2=++-x m mx 的两个实根都大于-1,求m 的取值范围。
变式(3)若一元二次方程03)1(2=++-x m mx 的两实根都小于2,求m 的取值范围。
例4.已知方程032222=-++m mx x 有一根大于2,另一根比2小,求m 的取值范围。
一元二次方程根的分布情况归纳(完整版)
( 1)若 b m, n ,则 f x max max f m , f 2a
b ,f n
2a
, f x min
min f m , f
b ,f n
;
2a
( 2)若 b 2a
m, n ,则 f x max
max f m , f n , f x min
min f m , f n
另外,当二次函数开口向上时,自变量的取值离开
3a b 2 5 2b 2
b25 3a b 2 2
a 1; b0
a1 b3
解:对称轴 x0 a ( 1)当 a 1 时,ymin f 1 2 2a( 2)当 1 a 3 时,ymin f a 1 a2 ;( 3)当 a 3 时,ymin f 3 10 6a
'.
.
改: 1.本题若修改为求函数的最大值,过程又如何?
.
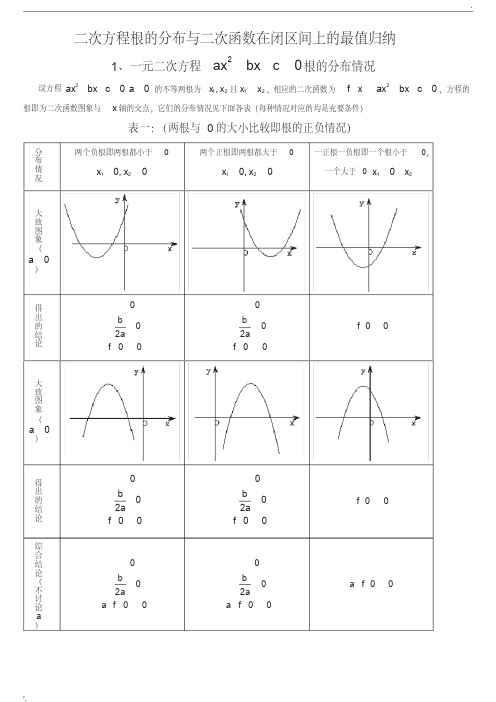
二次方程根的分布与二次函数在闭区间上的最值归纳
1、一元二次方程 ax2 bx c 0 根的分布情况
设方程 ax2 bx c 0 a 0 的不等两根为 x1, x2 且 x1 x2 ,相应的二次函数为 f x ax2 bx c 0 ,方程的 根即为二次函数图象与 x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)
解:对称轴 x0 1 2,3 ,故函数 f x 在区间 2,3 上单调。
( 1)当 a 0 时,函数 f x 在区间 2,3 上是增函数,故
f x max f x min
f3 f2
( 2)当 a 0 时,函数 f x 在区间 2,3 上是减函数,故
f x max f x min
f2 f3
例 2、求函数 f x x2 2ax 1, x 1,3 的最小值。
一元二次方程根的分布

0
5 .方程两根都小于m (x1 m) (x2 m) 0
(x1 m) (x2 m) 0
6. 方程一根大于m另一根小于m
(x1 m) (x2 m) 0
• 例1பைடு நூலகம் 方程x2+2ax+1=0有两个不等负
• 二、二次方程与二次函数联系紧密,关于二次 方程问题求解的另一思路是转化为二次函数来 解,因此一元二次方程根的分布问题可借助二 次函数图象来研究求解。(函数法) 抓△,对称轴的位置,特殊点的函数值
令f(x)=ax2+bx+c(a>0) 则有如下结论
1 .方程两根都大于m
2.方程两根都小于m 3.方程一个根大于m另一根小于m 4.方程两根都大于m且都小于n
C.必要不充分条件 D.既不必要不充分条件
例5:求方程3x2-2mx+m+1=0一根在0,1之 间另一根在1,2之间的充要条件
例6 : 抛物线y=-x2+3x-m与直线y=3-x在 0<x<3时只有一个交点,求m的范围. -3<m≤0或m=1
根,求实数a的取值范围。(a>1)
例2: 方程mx2+(2m-1)x-3(m-1)=0 两根都大于3,求实数m的取值范围。
;资质代办 /daiban/ 资质代办
;
替那些果实遮过阴凉、从枝头跌落、背井离乡的叶子。 祖母在秋天的离世毫无征兆,只是那一天刮了很大的风,院子里的那棵老柳树稀里哗啦地掉落了所有的叶子。其实,也只有风能让叶子喘息或者感叹。在叶子的生命中,风往往扮演着接生婆和送行者的双重角色,所以叶子的心思只 和风说,它只和风窃窃私语。 落叶也有遗言吗?在离开枝头的刹那,它和风都说了什么?谁
一元二次函数函数的根的分布(有图)

判别式
当判别式Δ=b^24ac大于0时,一元二 次方程有两个不相等 பைடு நூலகம்实根。
当判别式Δ=b^24ac小于0时,一元二 次方程没有实根。
当判别式Δ=b^24ac等于0时,一元二 次方程有两个相等的 实根。
02 根的分布条件
两个实根的条件
总结词
当判别式大于0时,一元二次函数有 两个实根。
详细描述
一元二次函数$ax^2+bx+c=0$的判 别式为$Delta=b^2-4ac$。当判别式 $Delta>0$时,一元二次函数有两个 不相等的实根。
一个实根的条件
总结词
当判别式等于0时,一元二次函数有一个实根。
详细描述
一元二次函数$ax^2+bx+c=0$的判别式为$Delta=b^2-4ac$。当判别式 $Delta=0$时,一元二次函数有一个实根。
无实根的条件
总结词
当判别式小于0时,一元二次函数无实根。
详细描述
一元二次函数$ax^2+bx+c=0$的判别式为$Delta=b^2-4ac$。当判别式$Delta<0$时,一元二次函 数无实根。
感谢您的观看
03 根的分布与图像关系
两个实根在图像上的表现
总结词:两个交点
详细描述:当一元二次函数有两个实根时,其图像与x轴会有两个交点。这两个交点的横坐标即为函 数的两个实根。
一个实根在图像上的表现
总结词:一个交点
详细描述:当一元二次函数有一个实根时,其图像与x轴会有一个交点。这个交点的横坐标即为函数的实根。
一元二次函数函数的根的分布(有 图)
目录
• 一元二次函数的基本性质 • 根的分布条件 • 根的分布与图像关系 • 根的分布的实际应用 • 总结与展望
一元二次方程根的分布

一元二次方程根的分布设一元二次方程ax 2+bx +c =0(a ≠0)的两个实根为x 1,x 2,且x 1<x 2,相应的一元二次函数为=)(x f ax 2+bx +c ,一元二次方程的根即为相应一元二次函数图象与x 轴的交点的横坐标,它们的分布情况可以分为以下三类:一.一元二次方程根的零分布:一元二次方程根的0分布,指的是方程的根相对于0的关系。
0分布的情况如下表所示:对于一元二次方程有两正根、两负根、一正一负根这三种情况,还可以用韦达定理解决如下,设一元二次方程ax 2+bx +c =0(a ≠0)的两个实根为x 1,x 2,且x 1≤x 2,则(1)x 1、x 2>0 ⇔ ⎩⎪⎨⎪⎧△=b 2-4ac ≥0x 1+x 2=-b a >0x 1x 2=c a >0;(2)x 1、x 2<0 ⇔ ⎩⎪⎨⎪⎧△=b 2-4ac ≥0x 1+x 2=-ba <0x 1x 2=c a>0;(3)x 1<0<x 2 ⇔ c a<0。
二.一元二次方程根的k分布:设一元二次方程ax2+bx+c=0(a≠0)的两实根为x1,x2,且x1<x2。
k为常数,则一元二次方程根的非12kk km n分布:二.一元二次方程根的(,)补充:对以上的根的分布表中一些特殊情况作说明:1.两根有且仅有一根在()n m ,内有以下特殊情况:若()0f m =或()0f n =,则此时0)()(<n f m f 不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值.如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求;2.对于方程有两个相等实根的情况,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数.3.总之,讨论一元二次方程根的分布问题实际上就是利用相应一元二次函数的图象及函数值来“控制”一元二次方程根的分布,因此必须从以下五个方面入手:①开口方向;②对称轴的位置;③判别式;④端点处的函数值;⑤与坐标轴(y 轴)的交点。
HXK一元二次方程根的分布

一元二次方程根的分布一.一元二次方程根的基本分布——零分布设一元二次方程()的两个实根为,,且。
1. 两根都是正数,【例1】若一元二次方程有两个正根,求的取值范围。
2. 两根都是负数,【例2】 若一元二次方程的两根都是负数,求的取值范围。
3. 两根一正一负【例3】在何范围内取值,一元二次方程有一个正根和一个负根?二.一元二次方程的非零分布——分布1. 两根都大于【例1】若一元二次方程的两根都大于2,求的取值范围。
2. 两根都小于【例2】若一元二次方程的两根都小于1,求的取值范围。
3. 一根大于,一根小于【例3】若一元二次方程的一根大于1,一根小于1,求的取值范围。
4. 两根都或【例4】是否存在实数,使方程的两根都在(2,4)内?5. 一根,另一根或【例5】为何值时,方程的一根大于且小于0,另一根大于1且小于3?6. 有且仅有一根【小结】三.闭区间问题1. 两根都2. 有且仅有一根【例1】 方程有且仅有一根,求的取值范围。
作业:1. 已知方程的两实根都大于1,求的取值范围。
2. 一元二次方程的两个实根都大于-1,求的取值范围。
3. 一元二次方程的两实根都小于2,求的取值范围。
4. 方程有一根大于2,另一根比2小,求的取值范围。
5. 方程的较小实根在0和1之间,求实数的取值范围。
6. 方程的两实根均在区间(、1)内,求的取值范围。
7. 方程的两根中,一根在0和1之间,另一根在1和2之间,求的取值范围。
8. 关于的方程的两根为且满足,求的取值范围。
9. 已知关于x的方程x2+2mx+2m+1=0,(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围; (2)若方程两根均在区间(0,1)内,求m的范围.10. 若方程有两个不相同的实根,求的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程根的分布
一.知识要点
二次方程02=++c bx ax 的根从几何意义上来说就是抛物线c bx ax y ++=2与x 轴交点的横坐标,所以研究方程02=++c bx ax 的实根的情况,可从c bx ax y ++=2的图象上进行研究.
若在),(+∞-∞内研究方程02=++c bx ax 的实根情况,只需考察函数c bx ax y ++=2与x 轴交点个数及交点横坐标的符号,根据判别式以及韦达定理,由c bx ax y ++=2的系数可判断出2121,,x x x x +∆的符号,从而判断出实根的情况.
若在区间),(n m 内研究二次方程02=++c bx ax ,则需由二次函数图象与区间关系来确定. 1.二次方程有且只有一个实根属于),(n m 的充要条件
若n m ,其中一个是方程的根,则由韦达定理可求出另一根.
若n m ,不是二次方程02=++c bx ax 的根,二次函数c bx ax x f ++=2)(的图象有以下几种可能:
(1)21,0x n x m a <<<> (2)n x m x a <<<>21,0
(3)21,0x n x m a <<<< (4)n x m x a <<<<21,0
由图象可以看出,)(x f 在m x =处的值)(m f 与在n x =处的值)(n f 符号总是相反,即0)()(<⋅n f m f ;反之,若0)()(<⋅n f m f ,)(x f 的图象的相对位置只能是图中四种情况之一.所以得出结论:若n m ,都不是方程)0(02≠=++a c bx ax 的根,记c bx ax x f ++=2)(,则0)(=x f 有且只有一个实根属于),(n m 的充要条件是0)()(<n f m f . 2.二次方程两个根都属于),(n m
方程)0(02≠=++a c bc ax 的两个实根都属于),(n m ,则二次函数c bx ax x f ++=2)(的图象与x 轴有两个交点或相切于点,且两个交点或切点的横坐标都大于m 小于n ,它的图象有以下
几种情形:
(1)n x x m a <<<>21,0 (2)n x x m a <=<>21,0
(3)n x x m a <<<<21,0 (4)n x x m a <=<<21,0
由此可得出结论:
方程)0(02≠=++a c bx ax 的两个实根都属于区间),(n m 的充要条件是:
⎪⎪⎪
⎩
⎪
⎪⎪
⎨⎧<-<>>≥-n a b m n af m af ac b 20)(0)(042
这里 c bx ax x f ++=2)(.
同理可得出:
3.二次方程02=++c bx ax 的两个实根分别在区间),(n m 的两侧(一根小于m ,另一根大于n )的充要条件是:
⎩
⎨⎧<<0)(0
)(n af m af
这里c bx ax x f ++=2)(.
4.二次方程02=++c bx ax 的两个实根都在),(n m 的右侧的充要条件是:
⎪⎪⎩⎪
⎪⎨⎧
>->≥-n a
b n af a
c b 20)(042
二次方程02=++c bx ax 的两个实根都在),(n m 的左侧(两根都小于m )的充要条件是:
⎪⎪⎩⎪
⎪⎨⎧
<->≥-m a
b m af a
c b 20)(042
这里c bx ax x f ++=2)(.
二.例题选讲
例1.设关于x 的方程∈=--+b b x x (0241R ),
(1)若方程有实数解,求实数b 的取值范围;
(2)当方程有实数解时,讨论方程实根的个数,并求出方程的解。
例2.设[2,4)A =-,2{40}B x x ax =--≤,若B A ⊆,求实数a 的取值范围.
变式:已知方程x 2 + (3m -1)x + (3m -2)=0的两个根都属于( -3, 3),且其中至少有一个根小于1,求m 的取值范围.
例5.求实数m 的范围,使关于x 的方程062)1(22
=++-+m x m x . (1)有两个实根,且一个比2大,一个比2小. (2)有两个实根βα,,且满足410<<<<βα. (3)至少有一个正根.
例6. 已知关于x 的二次方程x 2+2mx +2m +1=0.
(1) 若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m 的范围. (2) 若方程两根均在区间(0,1)内,求m 的范围.
例7.已知二次方程02)12(2=+--+m x m mx 的两个根都小于1,求m 的取值范围.
三.巩固练习
1.已知二次方程04)32()13(2=+-++-m x m x m 有且只有一个实根属于( -1, 1),求m 的取值范围.
2.已知方程02)12(22=+⋅-+⋅m m m x x 在)1,(-∞上有两个根,求m 的取值范围.。
