初中数学——最强胡不归专题
九年级培优专题:经典几何模型——“胡不归”

经典几何模型——“阿氏圆”与“胡不归” 一.“胡不归”模型典故从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路。
由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径 A →B (如图所示),而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭。
邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?…何以归”。
这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归问题”。
二.“胡不归”模型建立如图所示,已知sin ∠MBN =k ,点 P 为角∠MBN 其中一边 BM 上的一个动点,点A 在射线BM 、BN 的同侧,连接AP ,则当“PA +k ·PB ”最小时,P 点的位置如何确定? 分析:本题的关键在于如何确定“k ·PB ”的大小,过点P 作 PQ ⊥BN 垂足为Q ,则 k ·PB =PB ·sin ∠MBN =PQ , “PA +k ·PB ”的最小值转化为求“PA +PQ ”的最小值,即A 、P 、Q 三点共线时最小。
三.“胡不归”模型破解策略“胡不归”构造某角正弦值等于系数k (k 小于1)当k 值大于1时,则提取k ,构造某角正弦值等于系数k1 起点构造所需角(k =sin ∠CAE )→过终点作所构角边的垂线→利用垂线段最短解决四.“胡不归”典型例题讲解1.四边形ABCD 是菱形,AB =6,且∠ABC =60°,M 为对角线BD (不含B 点)上任意一点,则 AM +21BM 的最小值为 . 变式思考:(1)本题如要求“2AM +BM ”的最小值你会求吗?(2)本题如要求“AM +BM +CM ”的最小值你会求吗?A DBC 沙 砾 地 带2.如图,等腰△ABC 中,AB =AC =3,BC =2,BC 边上的高为AO ,点D为射线AO 上一点,一动点P 从点A 出发,沿AD -DC 运动,动点P 在AD 上运动速度3个单位每秒,动点P 在CD 上运动的速度为1个单位每秒,则当AD = 时,运动时间最短为 秒.3.如图,在菱形ABCD 中,AB =6,且∠ABC =150°,点P 是对角线AC 上的一个动点,则P A +2PB 的最小值为 .用费马点思想做下试试4.如图,在△ACE 中,CA =CE ,∠CAE =30°,⊙O 经过点C ,且圆的直径AB 在线段AE 上。
中考数学压轴题复习之胡不归

胡不归整理基本解法:构造直角三角形胡不归问题解法通法:第一步:在速度快的线段与起点相异的一侧,过终点作一射线,使之与该线段构成的角满足:1 sinVα=;第二步:过起点作该射线的垂线;第三步:该垂线与线段的交点即为所求.例题解析:例1、(2016•宜兴市一模)如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是s.【解答】解:过点E作y轴的平行线,再过D点作y轴的平行线,两线相交于点H,如图,∵EH∥AB,∴∠HEB=∠ABE,∴tan∠HED=tan∠EBA==,设DH=4m,EH=3m,则DE=5m,∴蚂蚁从D爬到E点的时间==4(s)若设蚂蚁从D爬到H点的速度为1单位/s,则蚂蚁从D爬到H点的时间==4(s),∴蚂蚁从D爬到E点所用的时间等于从D爬到H点所用的时间相等,∴蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点所用时间等于它从A以1单位/s的速度爬到D点,再从D点以1单位/s 速度爬到H点的时间,作AG⊥EH于G,则AD+DH≥AH≥AG,∴AD+DH的最小值为AQ的长,当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),直线BE交y轴于C点,如图,在Rt△OBC中,∵tan∠CBO==,∴OC=4,则C (0,4),设直线BE 的解析式为y=kx +b ,把B (3,0),C (0,4)代入得,解得,∴直线BE 的解析式为y=﹣x +4, 解方程组得或,则E 点坐标为(﹣,),∴AQ=,∴蚂蚁从A 爬到G 点的时间==(s ),即蚂蚁从A 到E 的最短时间为s . 故答案为.例2、(2014成都)如图,已知抛物线)4)(2(8-+=x x k y (k 为常数,且0>k )与x 轴从左至右依次交于A ,B 两点,与y 轴交于点C ,经过点B 的直线b x y +-=33与抛物线的另一交点为D .(1)若点D 的横坐标为-5,求抛物线的函数表达式; (2)若在第一象限的抛物线上有点P ,使得以A ,B ,P 为顶点的三角形与△ABC 相似,求k 的值;(3)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A 出发,沿线段AF 以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止。
2023年中考数学常见几何模型之最值模型胡不归问题

专题10 最值模型---胡不归问题最值问题在中考数学常以压轴题的形式考查,可将胡不归问题看作将军饮马衍生,主要考查转化与化归等的数学思想。
在各类考试中都以高档题为主,中考说明中曾多处涉及。
本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握。
在解决胡不归问题主要依据是:①两点之间,线段最短;②垂线段最短。
【模型背景】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?看到这里很多人都会有一个疑问,少年究竟能不能提前到家呢?假设可以提早到家,那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题.【模型解读】一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BC V V +的值最小.(注意与阿氏圆模型的区分)2驿道2M1)121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =,即求BC +kAC 的最小值. 2)构造射线AD 使得sin ∠DAN =k ,CH k AC=,CH =kAC ,将问题转化为求BC +CH 最小值. 3)过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【解题关键】在求形如“P A +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“P A +kPB ”型问题转化为“P A +PC ”型.(若k >1,则提取系数,转化为小于1的形式解决即可)。
【最值原理】两点之间线段最短及垂线段最短。
例1.(2022·内蒙古·中考真题)如图,在△ABC 中,AB =AC =4,∠CAB =30°,AD ⊥BC ,垂足为D ,P 为线段AD 上的一动点,连接PB 、PC .则P A +2PB 的最小值为 _____.在∠BAC 的外部作∠CAE =15°此时P A +2PB 最小,∴∠AFB ∴∠CAD =∠BAD =12BAC ∠1例2.(2022·湖北武汉·一模)如图,在ACE △中,CA CE =,30CAE ∠=︒,半径为5的O 经过点C ,CE 是圆O 的切线,且圆的直径AB 在线段AE 上,设点D 是线段AC 上任意一点(不含端点),则12OD CD +的最小值为______.//CH AB ,30CAE ∠=︒,OC OA =,sin HCD ∴∠当O ,例3.(2021·眉山市·中考真题)如图,在菱形中,,对角线、相交于点,点在线段上,且,点为线段上的一个动点,则的最小值是______.【分析】过M 点作MH 垂直BC 于H 点,与OB 的交点为P 点,此时的长度最小为MH ,再算出MC 的长度, 在直角三角形MPC 中利用三角函数即可解得MH 【详解】过M 点作MH 垂直BC 于H 点,与OB 的交点为P 点,此时的长度最小∵菱形中,∴AB =BC =AC =10,△ABC 为等边三角形ABCD 10AB AC ==AC BD O M AC 3AM =P BD 12MP PB +12MP PB +12MP PB +ABCD 10AB AC ==∴∠PBC =30°,∠ACB =60°∴在直角△PBH 中,∠PBH =30°∴PH = ∴此时得到最小值, ∵AC =10,AM =3,∴MC =7又∠MPC =60°∴MH =MC【点睛】本题主要考查了菱形的性质与三角函数,能够找到最小值时的P 点是解题关键. 例4.(2022·山东淄博·二模)如图,在平面直角坐标系中,点A 的坐标是(0,2),点C 的坐标是(0,2)−,点(,0)B x 是x 轴上的动点,点B 在x 轴上移动时,始终保持ABP 是等边三角形(点P 不在第二象限),连接PC ,求得12AP PC +的最小值为( )A .B .4C .D .2【答案】C【分析】如图1所示,以OA 为边,向右作等边△AOD ,连接PD ,过点D 作DE ⊥OA 于E ,先求出点D 的坐标,然后证明△BAO ≌△P AD 得到∠PDA =∠BOA =90°,则点P 在经过点D 且与AD 垂直的直线上运动,当点P 运动到y 轴时,如图2所示,证明此时点P 的坐标为(0,-2)从而求出直线PD 的解析式;如图3所示,作点A 关于直线PD 的对称点G ,连接PG ,过点P 作PF ⊥y 轴于F ,设直线PD 与x 轴的交点为H ,先求出点H 的坐1PB 212MP PB +1=2MP PB MP PH MH ++=当点P运动到y轴时,如图2所示,此时点∵△ABP是等边三角形,BO⊥AP,∴例5.(2021·资阳市·中考真题)抛物线与x 轴交于A 、B 两点,与y 轴交于点C ,且.(1)求抛物线的解析式;(2)如图1,点P 是抛物线上位于直线上方的一点,与相交于点E ,当时,求点P 的坐标;(3)如图2,点D 是抛物线的顶点,将抛物线沿方向平移,使点D 落在点处,且,点M 是平移后所得抛物线上位于左侧的一点,轴交直线于点N ,连结.当的值最小时,求的长. 2y x bx c =−++()()1,0,0,3B C −AC BP AC :1:2PE BE =CD D 2DD CD '=D //MN y OD 'CN 5D N CN '+MN【答案】(1);(2)或;(3). 【分析】(1)利用待定系数法即可得;(2)设点的坐标为,先利用待定系数法求出直线的解析式,再根据可得点的坐标,代入直线的解析式求解即可得;(3)先根据求出点的坐标,再根据二次函数图象的平移规律得出平移后的函数解析式,设点的坐标,从而可得点的坐标,然后根据两点之间的距离公式可得,最后根据两点之间线段最短、垂线段最短求解即可得. 【详解】解:(1)由题意,将点代入得:, 解得,则抛物线的解析式为; (2)对于二次函数,当时,,解得或,,设点的坐标为,点的坐标为, ,,解得,2y x 2x 3=−++(1,4)P (2,3)P 34P 2(,23)P a a a −++AC :1:2PE BE =E AC 2DD CD '=D MN 5D N CN '+()()1,0,0,3B C −2y x bx c =−++103b c c −−+=⎧⎨=⎩23b c =⎧⎨=⎩2y x 2x 3=−++2y x 2x 3=−++0y =2230x x −++=1x =−3x =(3,0)A ∴P 2(,23)(03)P a a a a −++<<E 11(,)E x y :1:2,(1,0)PE BE B =−1121111223102a x x a a y y −⎧=⎪+⎪∴⎨−++−⎪=⎪−⎩121213324233x a y a a ⎧=−⎪⎪⎨⎪=−++⎪⎩,设直线的解析式为, 将点代入得:,解得,则直线的解析式为,将点代入得:,解得或,当时,,此时,当时,,此时,综上,点的坐标为或;(3)二次函数的顶点坐标为,设点的坐标为,,,解得,, 则平移后的二次函数的解析式为,设直线的解析式为,将点代入得:,解得, 则直线的解析式为,设点的坐标为,则点的坐标为, 如图,连接,过点作于点,过点作于点,交于点,连接,22124(,2)3333E a a a ∴−−++AC y kx t =+(3,0),(0,3)A C 303k t t +=⎧⎨=⎩13k t =−⎧⎨=⎩AC 3y x =−+22124(,2)3333E a a a −−++22124323333a a a −++=−++1a =2a =1a =2231234a a −++=−++=(1,4)P 2a =22342233a a −++=−+⨯+=(2,3)P P (1,4)P (2,3)P 2223(1)4y x x x =−++=−−+D (1,4)D D 22(,)D x y '2,(0,3),(1,4)DD C D D C '=2212104243x y −⎧=⎪⎪−∴⎨−⎪=⎪−⎩2236x y =⎧⎨=⎩(3,6)D '∴22(3)663y x x x =−−+=−+−OD '0y k x =(3,6)D '036k =02k =OD '2y x =M 2(,63)(3)M m m m m −+−<N (,2)N m m AD 'N NF AD '⊥F C CG AD '⊥G OD 'N 'CF,轴,,, 由两点之间线段最短得:的最小值为,由垂线段最短得:当点与点重合时,取得最小值,此时点与点重合, 则点的纵坐标与点的纵坐标相等,即,解得, 则,,. 【点睛】本题考查了利用待定系数法求二次函数的解析式、二次函数图象的平移规律、垂线段最短等知识点,较难的是题(3),正确求出平移后的抛物线的解析式是解题关键. 例6.(2020·湖南·中考真题)已知直线与抛物线(b ,c 为常数,)的一个交点为,点是x 轴正半轴上的动点.(1)当直线与抛物线(b ,c 为常数,)的另一个交点为该抛物线的顶点E 时,求k ,b ,c 的值及抛物线顶点E 的坐标;(2)点D 在抛物线上,且点D 的横坐标为的最小值多时,求b 的值.【答案】(1)-2,2,-3,;(2)4或6;(3)3 (3,0),(3,6)D A 'AD x '∴⊥3FN m ∴=−35D N CN CN m CN FN CN '+==−+=+FN CN +CF F G CF CG N N 'N 'C 23m =32m =2263243MN m m m m m =−+−−=−+−233()4322=−+⨯−34=2y kx =−2y x bx c =−+0b >(1,0)A −(,0)M m 2y kx =−2y x bx c =−+0b >12b +2DM +4()1,4−【分析】(1)由题意可知直线经过,因而把代入直线即可求出k 的值,然后把代入抛物线得出含b 的代数式表达c ,再根据直线与抛物线(b ,c 为常数,)的另一个交点得出抛物线的顶点坐标E ,并代入直线,解方程即可求出b 的值,代入即可求解;(2)将点D 的横坐标代入抛物线(b ,c 为常数,),根据点A 的坐标得到含b 的代数式表达c ,求出点D 的纵坐标为,可知点D 在第四象限,且在直线的右侧,取点,过点D 作直线AN 的垂线,垂足为G ,DG 与x 轴相交于点M ,过点D 作QH ⊥x 轴于点H ,则点H,在Rt △MDH 中,可知,由题意可知点,用含b 的代数式表示m,可得方程,求解即可得出答案. 【详解】解:(1)∵直线经过,∴把代入直线,可得,解得; ∵抛物线(b ,c 为常数,)经过,∴把代入抛物线,可得,∵当直线与抛物线(b ,c 为常数,)的另一个交点为该抛物线的顶点E ,∴顶点的坐标为,把代入直线,可得,∴,解得,2y kx =−(1,0)A −(1,0)A −2y kx =−(1,0)A −2y kx =−2y xbx c =−+0b >24,24b c b ⎛⎫− ⎪⎝⎭22y x =−−12b +2y x bx c =−+0b >324b −−13,224b b ⎛⎫+−−⎪⎝⎭x b =(0,1)N 1,02b ⎛⎫+⎪⎝⎭45DMH MDH ︒∠=∠=(,0)M m 24DM +=2y kx =−(1,0)A −(1,0)A −2y kx =−02k =−−2k =−2y xbx c =−+0b >(1,0)A −(1,0)A −2y x bx c =−+1c b =−−2y kx =−2y x bx c =−+0b >E 24,24b c b ⎛⎫− ⎪⎝⎭E 24,24b c b ⎛⎫− ⎪⎝⎭22y x =−−242224b c b −−⨯−=()2412224b b b−−−−⨯−=2b =±∵,∴,∴,∴顶点的坐标为. (2)∵点D 在抛物线(b ,c 为常数,)上,且点D 的横坐标为, ∴,∵在抛物线(b ,c 为常数,)上,∴,即,∴,可知点D 在第四象限,且在直线的右侧.,∴可取点,如图2,过点D 作直线AN 的垂线,垂足为G ,DG 与x 轴相交于点M ,∴,得, 则此时点M 满足题意,过点D 作QH ⊥x 轴于点H ,则点H ,在Rt △MDH 中,可知,∴,∵点,∴,解得:,,∴,∴.0b >2b =213c =−−=−E ()1,4−2y xbx c =−+0b >12b +21122D y b b b c ⎛⎫⎛⎫=+−++ ⎪ ⎪⎝⎭⎝⎭(1,0)A −2y x bx c =−+0b >()210b c −+=+1c b =−−21131=2224D b y b b b b ⎛⎫⎛⎫=+−+−−−− ⎪ ⎪⎝⎭⎝⎭13,224b b ⎛⎫+−− ⎪⎝⎭x b =222DM AM DM ⎛⎫+=+ ⎪ ⎪⎝⎭(0,1)N 45GAM ︒∠=2AM GM =1,02b ⎛⎫+⎪⎝⎭45DMH MDH ︒∠=∠=,D DH MH M ==(,0)M m 310242b b m ⎛⎫⎛⎫−−−=+− ⎪ ⎪⎝⎭⎝⎭124b m =−24DM +=111(1)2242244b b b ⎤⎤⎛⎫⎛⎫⎛⎫−−−++−−= ⎪ ⎪ ⎪⎥⎥⎝⎭⎝⎭⎝⎭⎦⎦3b =【点睛】本题是二次函数综合题,主要考查了待定系数法求解析式、二次函数的性质、等腰三角形的性质、三角形的面积公式等知识点,解题的关键是学会使用待定系数法求出抛物线的解析式.例7.(2022·四川成都·中考模拟)6.如图,已知抛物线为常数,且与轴从左至右依次交于,两点,与轴交于点,经过点的直线与抛物线的另一交点为.(1)若点的横坐标为,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点,使得以,,为顶点的三角形与相似,求的值;(3)在(1)的条件下,设为线段上一点(不含端点),连接,一动点从点出发,沿线段以每秒1个单位的速度运动到,再沿线段以每秒2个单位的速度运动到后停止,当点的坐标是多少时,点在整个运动过程中用时最少?(2)(4)(8ky x x k =+−0)k >x A B y C B y b =+D D 5−P A B P ABC ∆k F BD AF M A AF F FD D F M解:(1)抛物线,令,解得或,,.直线经过点,,解得, 直线解析式为:.当时,,,. 点,在抛物线上,,.抛物线的函数表达式为:.即. (2)由抛物线解析式,令,得,,. 因为点在第一象限内的抛物线上,所以为钝角.因此若两个三角形相似,只可能是或. ①若,则有,如答图所示. 设,过点作轴于点,则,. ,即:,. ,代入抛物线解析式,得,整理得:, 解得:或(与点重合,舍去),.,,即. ②若,则有,如答图所示. 设,过点作轴于点,则,.,即:,. (2)(4)8ky x x =+−0y =2x =−4x =(2,0)A ∴−(4,0)B y b =+(4,0)B 40b +=b ∴BD 33y x =+5x =−y =(5D ∴−(5D −(2)(4)8k y x x =+−∴(52)(54)8k −+−−=k ∴=∴2)(4)y x x +−2y x =0x =y k =−(0,)C k ∴−OC k =P ABP ∠ABC APB ∆∆∽ABC PAB ∆∆∽ABC APB ∆∆∽BAC PAB ∠=∠21−(,)P x y P PN x ⊥N ON x =PN y =tan tan BAC PAB ∠=∠22k y x =+2k y x k ∴=+(,)2k P x x k ∴+(2)(4)8ky x x =+−(2)(4)82k kx x x k +−=+26160x x −−=8x =2x =−A (8,5)P k ∴ABC APB ∆∆∽∴AC AB AB AP ==5k =ABC PAB ∆∆∽ABC PAB ∠=∠22−(,)P x y P PN x ⊥N ON x =PN y =tan tan ABC PAB ∠=∠42k y x =+42k ky x ∴=+,代入抛物线解析式,得,整理得:, 解得:或(与点重合,舍去),. ,,,,综上所述,或(3)方法一:如答图3,由(1)知:,,如答图,过点作轴于点,则,,, ,. 过点作轴,则.过点作于点,则. 由题意,动点运动的路径为折线,运动时间:,,即运动的时间值等于折线的长度值.由垂线段最短可知,折线的长度的最小值为与轴之间的垂线段.(,)42k k P x x ∴+(2)(4)8ky x x =+−(2)(4)842k k kx x x +−=+24120x x −−=6x =2x =−A (6,2)P k ∴ABC PAB ∆∆∽AB CBAP AB=∴=k =0k >k ∴=k =k =(5D −22−D DN x ⊥N DN =5ON =459BN =+=tan DN DBA BN ∴∠===30DBA ∴∠=︒D //DK x 30KDF DBA ∠=∠=︒F FG DK ⊥G 12FG DF =M AF DF +12t AF DF =+t AF FG ∴=+AF FG +AF FG +DK x过点作于点,则,与直线的交点,即为所求之点. 点横坐标为,直线解析式为:,,. 综上所述,当点坐标为,时,点在整个运动过程中用时最少. 方法二:作,,交直线于点, ,,, 当且仅当时,最小,点在整个运动中用时为:, ,, 【点睛】本题考查单动点问题;二次函数和一次函数交点问题;曲线上点的坐标与方程的关系;勾股定理;相似三角形的判定;垂直线段最短的性质;分类思想和数形结合思想的应用.课后专项训练1.(2022·河北·九年级期中)如图,在△ABC 中,∠A =15°,AB =2,P 为AC 边上的一个动点(不与A 、C 重合),连接BP ,则AP +PB 的最小值是( )A AH DK ⊥H t AH =最小AH BD FA 2−BD 33y x =+(2)33y ∴=⨯−+=(2F ∴−F (2−M //DK AB AH DK ⊥AH BD F 30DBA ∠=︒30BDH ∴∠=︒sin302FDFH DF ∴=⨯︒=∴AH DK ⊥AF FH +M 12AF FDt AF FH =+=+:BD l y =+2X X F A ∴==−(F ∴−A.B.C.D.2【解答】解:如图,在△ABC内作∠MBA=30°过点A作AE⊥BM于点E,BM交AC于点P,∵∠BAC=15°,∴∠APE=45°∴EP=AP当BP⊥AE时,则AP+PB=PE+PB的值最小,最小值是BE的长,在Rt△ABE中,∠ABE=30°,AB=2∴BE=AB•cos30°=.∴AP+PB的最小值是.故选:B.2.(2022·江苏·九年级月考)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4,点D、F分别是边AB,BC上的动点,连接CD,过点A作AE⊥CD交BC于点E,垂足为G,连接GF,则GF+FB的最小值是()A.B.C.D.【解答】解:延长AC到点P,使CP=AC,连接BP,过点F作FH⊥BP于点H,取AC中点O,连接OG,过点O作OQ⊥BP于点Q,∵∠ACB=90°,∠ABC=30°,AB=4∴AC=CP=2,BP=AB=4∴△ABP 是等边三角形∴∠FBH =30°∴Rt △FHB 中,FH =FB ∴当G 、F 、H 在同一直线上时,GF +FB =GF +FH =GH 取得最小值 ∵AE ⊥CD 于点G ∴∠AGC =90°∵O 为AC 中点∴OA =OC =OG =AC ∴A 、C 、G 三点共圆,圆心为O ,即点G 在⊙O 上运动 ∴当点G 运动到OQ 上时,GH 取得最小值 ∵Rt △OPQ 中,∠P =60°,OP =3,sin ∠P =∴OQ =OP =∴GH 最小值为故选:C .3.(2022·山东·九年级月考)如图,在平面直角坐标系中,二次函数y =x 2﹣2x +c 的图象与x 轴交于A 、C 两点,与y 轴交于点B (0,﹣3),若P 是x 轴上一动点,点D (0,1)在y 轴上,连接PD +PC 的最小值是( )A .4B .2+C .D .32∵二次函数y =x 2﹣2x +c 的图象与∴二次函数的解析式为y =x 2解得x =﹣1或3,∴A (﹣1∵∠BOC =90°,∴∠OBC =∵D (0,1),∴OD =1,BD 设DH x =,则BH x =,∵DH4.(2022·重庆·九年级期中)如图所示,菱形ABCO 的边长为5,对角线OB 的长为,P为OB 上一动点,则AP +的最小值为( )A .4B .5C .D .解:如图,过点A 作AH OC ⊥于点H ,过点P 作PF OC ⊥于点F ,连接AC 交OB 于点J .四边形OABC 是菱形,AC OB ∴⊥,OJ JB ∴==,CJ ==2AC CJ ∴==,AH OC ⊥,12OC AH OB AC ∴⋅=⋅⋅,142AH ∴==,sin PF CJ POF OP OC ∴∠==,PF ∴,AP AP PF ∴+=+,AP PF AH +,4AP ∴,AP ∴+的最小值为4,故选:A .5.(2022·浙江宁波·九年级开学考试)如图,在平面直角坐标系中,一次函数y =分别交x 轴、y 轴于A 、B 两点,若C 为x 轴上的一动点,则2BC +AC 的最小值为__________.6.(2022·湖南·九年级月考)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形点E为△BCD围成的区域(包括各边)的一点过点E作EM∥AB,交直线AC于点M作EN∥AC交直线AB于点N,则AN+AM的最大值为.【解答】解:过E作EH⊥AC交AC的延长线于点H,∵EN∥AC,EM∥AB,∴四边形ANEM是平行四边形,∠HME=∠A=60°,设EM =AN =a ,AM =b ,Rt △HEM 中,∠HEM =30°,∴MH =ME =a ,∴AN +AM =a +b =MH +AM =AH ,当E 在点D 时,AH 的值最大是:3+4.5=7.5,AN +AM 的最大值为7.5,故答案为:7.5.7.(2022·湖北武汉·九年级期末)如图,▱ABCD 中60A ∠=︒,6AB =,2AD =,P 为边CD 2PB +的最小值为______.四边形8.(2022·成都市七中育才九年级期中)如图,在平面直角坐标系中,直线l 分别交x 、y 轴于B 、C 两点,点A 、C 的坐标分别为(3,0)、(0,﹣3),且∠OCB =60°,点P 是直线l 上一动点,连接AP ,则2AP PC +的最小值是______.在Rt △PCG 中,∠PCG =60°,则∠CPG =30°,1PC PG =3PC AP 9.(2022·四川自贡·一模)如图,ABC 中,10AB AC ==,tan 2A =,BE AC ⊥于点E ,D 是线段BE 上的一个动点,则CD 的最小值是__________.DH CM 即可求值.【详解】解:如图,过点∵BE AC ⊥,∴90AEB ∠=︒设AE a =,2BE a =,2AB AE =∴25a =或25−(舍弃),∴∵AB AC =,BE AC ⊥,CM ⊥DH CM ,∴45BD ,∴【点睛】本题主要考查解直角三角形,等腰三角形的性质,勾股定理,垂线段最短等,学会添加辅助线并利用转化的思想是解题的关键.10.(2022·广东·一模)已知抛物线243y x x =−+与x 轴交于A ,B 两点(A 在B 点左侧),与y 轴正半轴交于点C ,点P 是直线BC 上的动点,点Q 是线段OC 上的动点.(1)求直线BC 解析式.(2)如图①,求OP +P A 的和取最小值时点P 的坐标. 12+QC 的最小值. Rt A PB '∵B (3,0),C (0,3),∴又∠BOC =90°,∴∠OCB 由对称性可知OCP DCP ≌,OCB DCB ≌,∴∠DCB =∠OCB =45°,∠CDB =∠COB =90°,∴∠OCD =90°,∴四边形OCDB 为正方形,∴D 坐标为(又A (1,0),∴AB =2,BD =3,则AQ +QP =A Q PQ A '+≥在Rt A PB '中,∠OBP =45°为22;(4)解:如图,在x 轴负半轴上找点∴12HQ CQ =,∴12AQ +∴当A ,Q ,H 三点共线,且∵CO =3,∠COG =90°,∠∴GO =3,∠CGO =60°当AH ⊥CG 时,AH AG =11.(2022·江苏·中考模拟)如图,抛物线与直线交于,两212y x mx n =++132y x =−+A B点,交轴于,两点,连接,,已知,.(Ⅰ)求抛物线的解析式和的值;(Ⅱ)在(Ⅰ)条件下:(1)为轴右侧抛物线上一动点,连接,过点作交轴于点,问:是否存在点使得以,,为顶点的三角形与相似?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.(2)设为线段上一点(不含端点),连接,一动点从点出发,沿线段以每秒一个单位速度运动到点,再沿线段个单位的速度运动到后停止,当点的坐标是多少时,点在整个运动中用时最少?解:(Ⅰ)把,代入,得,解得:.抛物线的解析式为联立,解得:或,点的坐标为.如图1.,,,,,,,是直角三角形,,;(Ⅱ)方法一:(1)存在点,使得以,,为顶点的三角形与相似.过点作轴于,则.x D C AC BC(0,3)A(3,0)Ctan BAC∠P y PA P PQ PA⊥y Q P A P QACB∆PE AC DE M D DEE EA A EM(0,3)A(3,0)C212y x mx n=++31902nmx n=⎧⎪⎨⨯++=⎪⎩523mn⎧=−⎪⎨⎪=⎩∴215322y x x=−+213215322y xyx x⎧=−+⎪⎪⎨⎪=−+⎪⎩3xy=⎧⎨=⎩41xy=⎧⎨=⎩∴B(4,1)(3,0)C(4,1)B(0,3)A220AB∴=22BC=218AC=222BC AC AB∴+=ABC∴∆90ACB∴∠=︒1tan3BCBACAC∴∠===P A P Q ACB∆P PG y⊥G90PGA∠=︒设点的横坐标为,由在轴右侧可得,则.,,.若点在点的下方,①如图2①,当时,则. ,,,.. 则.把代入,得 ,整理得:解得:(舍去),(舍去). ②如图2②,当时,则.同理可得:,则, 把代入,得, 整理得:解得:(舍去),,,; 若点在点的上方,①当时,则,同理可得:点的坐标为.②当时,则.同理可得:点的坐标为,. 综上所述:满足条件的点的坐标为、,、,; 方法二:作的“外接矩形” ,易证,, 以,,为顶点的三角形与相似,或, 设,,, ①,,,, ②,,,(舍, 满足题意的点的坐标为、,、,; (2)方法一:过点作轴于,如图3.在中,,即, P x P y 0x >PG x =PQ PA ⊥90ACB ∠=︒90APQ ACB ∴∠=∠=︒G A PAQ CAB ∠=∠PAQ CAB ∆∆∽90PGA ACB ∠=∠=︒PAQ CAB ∠=∠PGA BCA ∴∆∆∽∴13PG BC AG AC ==33AG PG x ∴==(,33)P x x −(,33)P x x −215322y x x =−+21533322x x x −+=−20x x +=10x =21x =−PAQ CBA ∠=∠PAQ CBA ∆∆∽1133AG PG x ==1(,3)3P x x −1(,3)3P x x −215322y x x =−+215133223x x x −+=−21303x x −=10x =2133x =13(3P ∴14)9G A PAQ CAB ∠=∠PAQ CAB ∆∆∽P (11,36)PAQ CBA ∠=∠PAQ CBA ∆∆∽P 17(3P 44)9P (11,36)13(314)917(344)9APQ ∆AQGH AHP QGP ∆∆∽∴AP HP PQ QG=A P Q ACB ∆∴13AP HP BC PQ QG AC ===3AP HP AC PQ QG BC===2(2,253)P t t t −+(0,3)A (2,3)H t 13HP QG =232531||23t t t −−+∴=11323t ∴=21723t =3HP QG =23253||32t t t −−+∴=1211t ∴=221t =−)∴P (11,36)13(314)917(344)9E EN y ⊥N Rt ANE∆sin 452EN AE AE =⋅︒=AE =点在整个运动中所用的时间为. 作点关于的对称点,连接,则有,,,,.根据两点之间线段最短可得:当、、三点共线时,最小.此时,,四边形是矩形,,.对于, 当时,有,解得:,.,, ,,点的坐标为.方法二:作点关于的对称点,交于点,显然,作轴,垂足为,交直线于点,如图4,在中,,即, 当、、三点共线时,最小,,,,,,,,,,,, ∴M 1DE DE EN =+D AC D 'D E 'D E DE '=D C DC '=45D CA DCA ∠'=∠=︒90D CD ∴∠'=︒DE EN D E EN +='+D 'E N DE EN D E EN +='+90D CD D NO NOC ∠'=∠'=∠=︒∴OCD N '3ND OC ∴'==ON D C DC ='=215322y x x =−+0y =2153022x x −+=12x =23x =(2,0)D ∴2OD =321ON DC OC OD ∴==−=−=312NE AN AO ON ∴==−=−=∴E(2,1)D AC D 'DD 'AC M DE D E ='D N y '⊥N AC E Rt ANE∆sin 45EN AE AE =⋅︒=AE =∴D 'E N DE EN D E EN +='+(0,3)A (3,0)C :3AC l y x ∴=−+(,3)M m m ∴−+(2,0)D DM AC ⊥1DM AC K K ∴⨯=−3112m m −+∴−⨯=−−52m ∴=5(2M ∴1)2为的中点,,,.方法三:如图,5,过作射线轴,过作射线轴,与交于点. ,,.,,, ,..当且仅当时,取得最小值,点在整个运动中用时最少为: , 抛物线的解析式为,且,可求得点坐标为 则点横坐标为2,将代入,得.所以.12.(2020·四川乐山市·中考真题)已知抛物线与轴交于,两点,为抛物线的顶点,抛物线的对称轴交轴于点,连结,且,如图所示.(1)求抛物线的解析式;(2)设是抛物线的对称轴上的一个动点.①过点作轴的平行线交线段于点,过点作交抛物线于点,连结、,求的面积的最大值;②连结,求的最小值.【答案】(1);(2)①;②. 【分析】(1)先函数图象与x 轴交点求出D 点坐标,再由求出C 点坐标,用待定系数法设交点式,将C 点坐标代入即可求解;(2)①先求出BC 的解析式M DD '(3,1)D ∴'1Y Y E D ='=(2,1)E ∴A //AF x D //DF y DF AC E (0,3)A (3,0)C :3AC l y x ∴=−+OA OC =90AOC ∠=︒45ACO ∴∠=︒//AF OC 45FAE ∴∠=︒sin 45EF AE ∴=⋅︒∴AF DF ⊥DE EF +M 1DE t DE EF ==+215322y x x =−+(3,0)C ∴D (2,0)E 2x =:3AC l y x =−+1y =(2,1)E 2y ax bx c =++x (1,0)A −(50)B ,C x D BC 4tan 3CBD ∠=P P x BC E E EF PE ⊥F FB FC BCF ∆PB 35PC PB+241620999y x x =−++322454tan 3CBD ∠=,设E 坐标为,则F 点坐标为,进而用t 表示出的面积,由二次函数性质即可求出最大值;②过点作于,由可得,由此可知当BPH 三点共线时的值最小,即过点作于点,线段的长就是的最小值,根据面积法求高即可. 【详解】解:(1)根据题意,可设抛物线的解析式为:,∵是抛物线的对称轴,∴,又∵,∴,即,代入抛物线的解析式,得,解得 , ∴二次函数的解析式为 或; (2)①设直线的解析式为 ,∴ 解得 即直线的解析式为 ,设E 坐标为,则F 点坐标为, ∴, ∴的面积 ∴, 42033=−+y x 420,33t t ⎛⎫−+ ⎪⎝⎭241620999,t t t ⎛⎫ ⎪⎝−+⎭+BCF ∆P PG AC ⊥G 3sin 5PG PC ACD PC =⋅∠=35PC PB PG PB +=+35PC PB +B BH AC ⊥H BH 35PC PB +(1)(5)y a x x =+−CD (20)D ,4tan 3CBD ∠=tan 4CD BD CBD =⋅∠=(24)C ,4(21)(25)a =+−49a =−4(1)(5)9y x x =−+−241620999y x x =−++BC y kx b =+0542.k b k b =+⎧⎨=+⎩,4320.3k b ⎧=−⎪⎪⎨⎪=⎪⎩,BC 42033=−+y x 420,33t t ⎛⎫−+ ⎪⎝⎭241620999,t t t ⎛⎫ ⎪⎝−+⎭+22420341620428409999993EF t t t t t =−++−=−+⎛⎫⎛⎫−+ ⎪ ⎪⎝⎭−⎝⎭BCF ∆21142840322999S EF BD t t ⎛⎫=⨯⨯=−+− ⎪⎝⎭2273()322S t =−−+∴当时,的面积最大,且最大值为; ②如图,连接,根据图形的对称性可知 ,,∴,过点作于,则在中,, ∴,再过点作于点,则, ∴线段的长就是的最小值,∵, 又∵,∴,即,∴的最小值为. 【点睛】此题主要考查了二次函数的综合题型,其中涉及了待定系数法求解析式和三角形的面积最大值求法、线段和的最值问题.解(1)关键是利用三角函数求出C 点坐标,解(2)关键是由点E 、F 坐标表示线段EF 长,从而得到三角形面积的函数解析式,解(3)的难点是将的最小值转化为点B 到AC 的距离. 13.(2021·四川达州市·中考真题)如图,在平面直角坐标系中,抛物线交轴于点和,交轴于点,抛物线的对称轴交轴于点,交抛物线72t =BCF ∆32AC ACD BCD ∠=∠5AC BC ==3sin 5AD ACD AC ∠==P PG AC ⊥G Rt PCG ∆3sin 5PG PC ACD PC =⋅∠=35PC PB PG PB +=+B BH AC ⊥H PG PH BH +≥BH 35PC PB +11641222ABC S AB CD ∆=⨯⨯=⨯⨯=1522ABC S AC BH BH ∆=⨯⨯=5122BH =245BH =35PC PB +24535PC PB +2y x bx c =−++x A ()1,0C y ()0,3B x E于点.(1)求抛物线的解析式;(2)将线段绕着点沿顺时针方向旋转得到线段,旋转角为,连接,,求的最小值.(3)为平面直角坐标系中一点,在抛物线上是否存在一点,使得以,,,为顶点的四边形为矩形?若存在,请直接写出点的横坐标;若不存在,请说明理由;【答案】(1);(2;(3)存在,点的横坐标分别为:2,,或. 【分析】(1)待定系数法求二次函数解析式,设解析式为将,两点代入求得,c的值即可;(2)胡不归问题,要求的值,将折线化为直线,构造相似三角形将转化为,再利用三角形两边之和大于第三边求得最值;(3)分2种情形讨论:①AB 为矩形的一条边,利用等腰直角三角形三角形的性质可以求得N 点的坐标;②AB 为矩形的对角线,设R 为AB 的中点,RN =AB ,利用两点距离公式求解方程可得N 点的坐标. F OE О'OE ()090αα︒<<︒'AE 'BE 13''BE AE +M N A B M N N 223y x x =−−+N 1−12−+12−2y x bx c =−++()1,0C ()0,3B b 13''BE AE +13'AE 13'DE 13''BE AE +12【详解】解:(1)∵过,∴∴,∴抛物线的解析式为: (2)在上取一点,使得,连接,∵对称轴.∴, ,∴,∴ ∴ ∴ 当,,三点在同一点直线上时,最小为.在中,, ∴ 即. (3)情形①如图,AB 为矩形的一条边时,联立得 2y x bx c =−++()1,0C ()0,3B 103b c c −++=⎧⎨=⎩2b =−3c =223y x x =−−+OE D 13OD OE ='AE BD 11'33OD OE OE ==3112x −+==−()1,0E −1OE ='1OE OE ==3OA ='1'3OE OD OA OE ==''DOE E OA ∠=∠''DOE E OA ∆∆∽1''3DE AE =1''''3BE AE BE DE +=+B 'E D ''BE DE +BD Rt BOD ∆13OD =3OB =3BD ===13''BE AE +2023y y x x =⎧⎨=−−+⎩31,00x x y y =−=⎧⎧⎨⎨==⎩⎩是等腰,分别过 两点作的垂线,交于点,过作轴,轴,,也是等腰直角三角形 设,则,所以代入,解得,(不符题意,舍) 同理,设,则 ,所以代入,解得,(不符题意,舍)② AB 为矩形的对角线,设R 为AB 的中点,则 , 设 ,则 整理得: 解得:(不符题意,舍),(不符题意,(3,0),3A OA ∴−=3OB =ABO ∴Rt 45BAO ∠=︒,A B AB 223y x x =−−+12,N N 12,N N 1N Q y ⊥2N P x ⊥1245QBN PAN ∴∠=∠=︒∴1BN Q △2AN P △QB m =1N Q m =1(,3)N m m −+223y x x =−−+11m =20m =∴1(1,4)N −OP n ==3PN n +2(,3)N n n −−223y x x =−−+1n 2=23n =−2(2,-5)N∴12RN AB =()3,0,()0,3A B −33(,)22R ∴−AB ==122RB AB ∴==12RN AB==2RN ∴2(,23)N x x x −−+222233()(2)()222x x x +++−=2(3)(1)0x x x x ++−=1=0x 23x =−舍),, 综上所述:点的横坐标分别为:2,,【点睛】本题考查了二次函数的性质,待定系数法求解析式,三角形相似,勾股定理,二次函数与一次函数交点,矩形的性质,等腰直角三角形性质,平面直角坐标系中两点距离计算等知识,能正确做出辅助线,找到相似三角形是解题的关键.14.(2022·广西·南宁三中一模)如图,二次函数21y ax bx =++的图象交x 轴于点()2,0A −、()10B ,,交y 轴于点C ,点D 是第四象限内抛物线上的动点,过点D 作//DE y 轴交x 轴于点E ,线段CB 的延长线交DE 于点M ,连接OM 、BD 交于点N ,连接AD .(1)求二次函数的表达式;(2)当OEM DBE S S =时,求点D 的坐标及sin DAE ∠;(3)在(2)的条件下,点P 是x 轴上一个动点,求DP 的最小值. 31=2x −+41=2x −∴N 1−12−OEM DBE S S=,∴1BE a =−,EM【点睛】主要考查了待定系数法求函数的解析式,函数图象上点的坐标特征,勾股定理,垂线段最短,轴对称的性质,以及解直角三角形的知识,要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系,解决相关问题.15.(2022·广东·东莞市三模)已知,如图,二次函数2y ax bx c =++图像交x 轴于(1,0)A −,交y 交轴于点(0,3)C ,D 是抛物线的顶点,对称轴DF 经过x 轴上的点(1,0)F .(1)求二次函数关系式;(2)对称轴DF 与BC 交于点M ,点P 为对称轴DF 上一动点.①求AP 的最小值及取得最小值时点P 的坐标; ②在①的条件下,把APF 沿着x 轴向右平移t 个单位长度(04)t ≤≤时,设APF 与MBF 重叠部分面积记为S ,求S 与t 之间的函数表达式,并求出S 的最大值.则sinPH PD FDB=⋅∠=依“垂线段最短”得此时AH∵sinAH DF OBDAB DB ∠==16.(2022·天津·中考模拟)如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.(1)证明:CE是⊙O的切线;(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;(3)设点D是线段AC上任意一点(不含端点),连接OD,当CD+OD的最小值为6时,求⊙O的直径AB的长.【答案】(1)见解析;(2)(3)AB=【解析】(1)连接OC,如图,∵CA=CE,∠CAE=30°,∴∠E=∠CAE=30°,∠COE=2∠A=60°,∴∠OCE=90°,∴CE是⊙O的切线;(2)过点C作CH⊥AB于H,连接OC,如图,由题可得CH=h.在Rt△OHC中,CH=OC•sin∠COH,∴h=OC•sin60°=OC,∴OC=,∴AB=2OC=;(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图,则∠AOF=∠COF=∠AOC=(180°﹣60°)=60°.∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,∴四边形AOCF是菱形,∴根据对称性可得DF=DO.过点D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DC•sin∠DCH=DC•sin30°=DC,∴+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD CD+OD)最小,此时FH=OF•sin∠FOH==6,则OF=,AB=2OF=8.∴当CD+OD的最小值为6时,⊙O的直径AB的长为8.。
胡不归问题【模型专题】(含答案解析)

2.如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于________.
【答案】
【解析】
【分析】过点P作PQ⊥AD于点Q,由于∠PDQ=60°,因此 ,由此可知当B、P、Q三点共线时 有最小值,然后利用解直角三角形的知识进行求解即可.
一般的:更一般地:使mPA+nPB最短(不妨设m>n),我们只须在上式中提取m、n中的较大者,即可化归到上述类型.
,在类似的位置构造一个正弦等于 的角即可.
模型一:几何问题中的最值
例1:
1.如图, 中, , , 于点 , 是线段 上的一个动点,则 的最小值是__________.
【答案】
【解析】
【分析】过点D作 于 ,过点C作 于 ,首先通过勾股定理及 求出AE,BE的长度,然后根据等腰三角形两腰上的高相等得出 ,然后通过锐角三角函数得出 ,进而可得出 ,最后利用 即可求值.
∴当C'、E、F三点共线时,EF+CF的值最小为C'E,
设直线C'E的解析式为y=kx+b,
∵E(5,0),C'(-1,2 ),
则 ,
∴ ,
∴ ,
∴ ,
解得x=1,
∴F(1, ),
作第二、四象限的角平分线l3,,过点F作FQ⊥l3,,交y轴于点P,交l3,于点Q,
在Rt△PQO中,∠POQ=45°,
更一般地:使mPA+nPB最短(不妨设m>n)
思路:设所求P点在直线AN上,我们在直线AN异于B点的一侧构造∠NAM,使得sin∠NAM=m(相当于把mPA通过正弦打折化归到直角三角形的直角边上)
我们作BF⊥AM交AN于P点,毫无疑问P点即为所求!mPA=PF,mPA+PB=BF,BF即为mPA+PB的最小值(而mPA+PB<AB)
中考数学最值—胡不归问题(解析+例题)

中考数学最值——胡不归问题(点在直线上运动)(PA+k·PB型最值)【历史典故】从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路。
由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径A→B(如图所示),而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭。
邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?…”。
这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归问题”。
【知识储备】①三角形三边关系:两边之和大于第三边;两边之差小于第三边。
②两点之间线段最短。
③连接直线外一点和直线上各点的所有线段中,垂线段最短。
【模型分析】①条件:已知A、B为定点,P为射线AC上一动点。
②问题:P在何处时,BP+nm AP最短(nm<1)。
③方法:第一步在AC的一侧,PB的异侧构造∠CAE=α,使得sinα=nm 第二步做BH⊥AE,交AC于P,点P就是所求位置,BH就是其最小值。
【模型分析】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB的长度,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D 选在何处时,所用时间最短?个运动过程中用时最少,请求出最少时间和此时点F的坐标。
【巩固训练】练习1:如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上BM的最小值为_____。
任意一点,则AM+12练习2:如图,等腰ΔABC中,AB=AC=3,BC=2,BC边上的高为A0,点D为射线A0上一点,一动点P从点A出发,沿AD-DC运动,动点P在AD上运动速度3个单位每秒,动点P在CD上运动的速度为1个单位每秒,则当 AD= 时,运动时间最短为秒。
(完整word版)胡不归问题专题
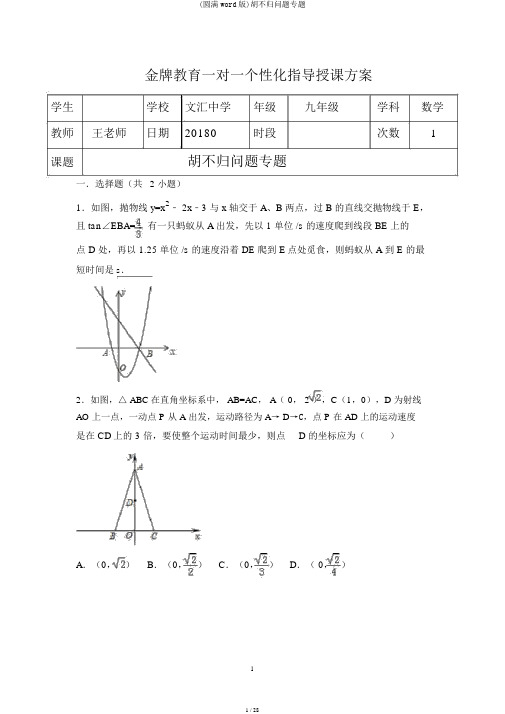
金牌教育一对一个性化指导授课方案学生学校文汇中学年级九年级学科数学教师王老师日期20180时段次数1课题胡不归问题专题一.选择题(共 2 小题)1.如图,抛物线 y=x2﹣ 2x﹣3 与 x 轴交于 A、B 两点,过 B 的直线交抛物线于 E,且 tan∠EBA= ,有一只蚂蚁从 A 出发,先以 1 单位 /s 的速度爬到线段 BE 上的点D 处,再以 1.25 单位 /s 的速度沿着 DE 爬到 E点处觅食,则蚂蚁从 A 到 E 的最短时间是s.2.如图,△ ABC在直角坐标系中, AB=AC, A( 0, 2 ),C(1,0),D 为射线AO 上一点,一动点 P 从 A 出发,运动路径为 A→ D→C,点 P 在 AD 上的运动速度是在 CD上的 3 倍,要使整个运动时间最少,则点 D 的坐标应为()A.(0,)B.(0,)C.(0,)D.( 0,)二.填空题(共 1 小题)3.如图,一条笔挺的公路l 穿过草原,公路边有一消防站A,距离公路5 千米的地方有一居民点 B,A、B 的直线距离是 10 千米.一天,居民点 B 着火,消防员授命欲前去救火.若消防车在公路上的最迅速度是 80 千米 / 小时,而在草地上的最迅速度是 40 千米 / 小时,则消防车在出发后最快经过小时可抵达居民点B.(友谊提示:消防车可从公路的随意地点进入草地行驶.)三.解答题(共 5 小题)4.如图,在平面直角坐标系中,二次函数 y=ax2+bx+c 的图象经过点 A(﹣ 1,0),B(0,﹣),C(2,0),其对称轴与x轴交于点D( 1)求二次函数的表达式及其极点坐标;( 2)若 P 为 y 轴上的一个动点,连结PD,则PB+PD 的最小值为;( 3) M(x,t)为抛物线对称轴上一动点①若平面内存在点N,使得以 A,B,M,N 为极点的四边形为菱形,则这样的点N 共有个;②连结 MA, MB,若∠ AMB 不小于 60°,求 t 的取值范围.5.如图,在△ ACE中, CA=CE,∠ CAE=30°,⊙ O 经过点 C,且圆的直径 AB 在线段AE 上.(1)试说明 CE是⊙ O 的切线;(2)若△ ACE中 AE 边上的高为 h,试用含 h 的代数式表示⊙ O 的直径 AB;(3)设点 D 是线段 AC 上随意一点(不含端点),连结 OD,当 CD+OD 的最小值为 6 时,求⊙ O 的直径 AB 的长.6.如图,已知抛物线y= ( x+2)(x﹣4)(k 为常数,且 k> 0)与 x 轴从左至右挨次交于 A,B 两点,与 y 轴交于点 C,经过点 B 的直线 y=﹣x+b 与抛物线的另一交点为 D.(1)若点 D 的横坐标为﹣ 5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点 P,使得以 A, B, P 为极点的三角形与△ABC相像,求 k 的值;( 3)在( 1)的条件下,设 F 为线段 BD 上一点(不含端点),连结 AF,一动点M 从点 A 出发,沿线段 AF以每秒 1 个单位的速度运动到 F,再沿线段 FD 以每秒 2 个单位的速度运动到 D 后停止,当点 F 的坐标是多少时,点 M 在整个运动过程顶用时最少?7.(1)如图 1,已知正方形 ABCD的边长为 4,圆 B 的半径为 2,点 P 是圆 B 上的一个动点,求PD+的最小值和PD﹣的最大值;( 2)如图 2,已知正方形 ABCD的边长为 9,圆 B 的半径为 6,点 P 是圆 B 上的一个动点,那么PD+的最小值为,PD﹣的最大值为.( 3)如图 3,已知菱形 ABCD的边长为 4,∠ B=60°,圆 B 的半径为 2,点 P 是圆B 上的一个动点,那么PD+的最小值为,PD﹣的最大值为.8.如图 1,抛物线 y=ax2+(a+3) x+3(a≠ 0)与 x 轴交于点 A(4,0),与 y 轴交于点 B,在 x 轴上有一动点 E(m, 0)(0<m< 4),过点 E 作 x 轴的垂线交直线AB 于点 N,交抛物线于点 P,过点 P 作 PM⊥ AB 于点M.( 1)求 a 的值和直线 AB 的函数表达式;( 2)设△ PMN 的周长为 C1,△ AEN的周长为 C2,若=,求m的值;(3)如图 2,在( 2)条件下,将线段 OE 绕点 O 逆时针旋转获得 OE′,旋转角为α(0°<α<90°),连结 E′A、E′B,求 E′A+ E′B的最小值.2018 年 05 月 25 日 187****4779 的初中数学组卷参照答案与试题解析一.选择题(共 2 小题)1.如图,抛物线 y=x2﹣ 2x﹣3 与 x 轴交于 A、B 两点,过 B 的直线交抛物线于 E,且 tan∠EBA= ,有一只蚂蚁从 A 出发,先以 1 单位 /s 的速度爬到线段 BE 上的点 D 处,再以 1.25 单位 /s 的速度沿着 DE 爬到 E点处觅食,则蚂蚁从 A 到 E 的最短时间是s.【解析】过点 E 作 x 轴的平行线,再过 D 点作 y 轴的平行线,两线订交于点 H,如图,利用平行线的性质和三角函数的定义获得 tan∠HED=tan∠EBA= = ,设DH=4m, EH=3m,则 DE=5m,则可判断蚂蚁从 D 爬到 E 点所用的时间等于从D 爬到 H 点所用的时间相等,于是获得蚂蚁从 A 出发,先以 1 单位 /s 的速度爬到线段 BE上的点 D 处,再以 1.25 单位 /s 的速度沿着 DE 爬到 E 点所用时间等于它从A 以 1 单位 /s 的速度爬到 D 点,再从 D 点以 1 单位 /s 速度爬到 H 点的时间,利用两点之间线段最短获得 AD+DH 的最小值为 AQ 的长,接着求出 A 点和 B 点坐标,再利用待定系数法求出BE的解析式,此后解由直线解析式和抛物线解析式所构成的方程组确立 E 点坐标,从而获得 AQ 的长,此后计算爬行的时间.【解答】解:过点 E 作 x 轴的平行线,再过 D 点作 y 轴的平行线,两线订交于点H,如图,∵EH∥AB,∴∠HEB=∠ABE,∴ tan∠ HED=tan∠ EBA= = ,设DH=4m,EH=3m,则 DE=5m,∴蚂蚁从 D 爬到 E 点的时间 ==4(s)若设蚂蚁从 D 爬到 H 点的速度为 1 单位 /s,则蚂蚁从 D 爬到 H 点的时间 = =4 ( s),∴蚂蚁从 D 爬到 E 点所用的时间等于从 D 爬到 H 点所用的时间相等,∴蚂蚁从 A 出发,先以 1 单位 /s 的速度爬到线段 BE上的点 D 处,再以 1.25 单位/s 的速度沿着 DE 爬到 E 点所用时间等于它从 A 以 1 单位 /s 的速度爬到 D 点,再从D 点以 1 单位 /s 速度爬到 H 点的时间,作 AG⊥EH于 G,则 AD+DH≥AH≥AG,∴ AD+DH 的最小值为 AQ 的长,当y=0 时, x2﹣2x﹣ 3=0,解得 x1=﹣1,x2=3,则 A(﹣ 1,0),B(3,0),直线 BE交 y 轴于 C 点,如图,在 Rt△OBC中,∵ tan∠CBO= = ,∴OC=4,则 C(0,4),设直线 BE的解析式为 y=kx+b,把 B(3,0), C( 0, 4)代入得,解得,∴直线 BE的解析式为 y=﹣x+4,解方程组得或,则E点坐标为(﹣,),∴AQ= ,∴蚂蚁从 A 爬到 G 点的时间 ==(s),即蚂蚁从 A 到 E 的最短时间为s.故答案为.【谈论】此题察看了二次函数与x 轴的交点:把求二次函数y=ax2+bx+c(a, b,c 是常数, a≠0)与 x 轴的交点坐标化为解对于x 的一元二次方程.解决此题的重点是确立蚂蚁在DH 和 DE上爬行的时间相等.2.如图,△ ABC在直角坐标系中, AB=AC, A( 0, 2 ),C(1,0),D 为射线AO 上一点,一动点 P 从 A 出发,运动路径为 A→ D→C,点 P 在 AD 上的运动速度是在 CD上的 3 倍,要使整个运动时间最少,则点 D 的坐标应为()A.(0,) B.(0,) C.(0,) D.( 0,)【解析】假定 P 在 AD 的速度为 3,在 CD的速度为 1,第一表示出总的时间,再依据根的鉴别式求出 t 的取值范围,从而求出 D 的坐标.【解答】解:假定 P 在 AD 的速度为 3,在 CD的速度为 1,设 D 坐标为( 0,y),则 AD=2﹣y,CD==,∴设 t=+,等式变形为: t+y﹣=,则 t 的最小值时考虑 y 的取值即可,∴ t2+( y﹣)t+( y﹣)2=y2 +1,∴ y2+(﹣t)y﹣t 2+t+1=0,△ =(﹣t)2﹣4×(﹣t2+t+1)≥ 0,∴ t 的最小值为,∴y= ,∴点 D 的坐标为( 0,),应选 D.解法二:假定 P 在 AD 的速度为 3V,在 CD的速度为 1V,总时间 t= + =(+CD),要使 t 最小,就要+CD最小,由于 AB=AC=3,过点 B 作 BH⊥AC 交 AC 于点 H,交 OA 于 D,易证△ ADH∽△ ACO,所以= =3,所以=DH,由于△ ABC 是等腰三角形,所以BD=CD,所以要+CD最小,就是要 DH+BD 最小,就要 B、 D、H 三点共线就行了.由于△AOC ∽△ BOD,所以=,即=,所以OD=,所以点 D 的坐标应为( 0,).【谈论】此题察看了勾股定理的运用、一元二次方程根的鉴别式(△=b2﹣ 4ac)判断方程的根的状况以及坐标于图形的性质题目的综合性较强,难度较大.二.填空题(共 1 小题)3.如图,一条笔挺的公路l 穿过草原,公路边有一消防站A,距离公路5 千米的地方有一居民点 B,A、B 的直线距离是 10 千米.一天,居民点 B 着火,消防员授命欲前去救火.若消防车在公路上的最迅速度是 80 千米 / 小时,而在草地上的最迅速度是40 千米 / 小时,则消防车在出发后最快经过小时可抵达居民点 B.(友谊提示:消防车可从公路的随意地点进入草地行驶.)【解析】要求所用行车时间最短,就要计算好行驶的路线,能够设在公路上行驶x千米,依据题意,找出能够运用勾股定理的直角三角形,运用勾股定理求解.【解答】解:以以以下图,公路上行驶的路线是 AD,草地上行驶的路线是 DB,设AD 的行程为 x 千米,由已知条件 AB=10千米,BC=5千米,BC⊥AC,知AC==15 千米.则CD=AC﹣AD=(15﹣x)千米,BD==km,设走的行驶时间为y,则y= +.整理为对于 x 的一元二次方程得3x2 +(160y﹣120)x﹣6400y2+1200=0.由于 x 必然存在,所以△≥ 0.即(160y﹣120)2﹣ 4× 3×( 1200﹣ 6400y2)≥0.化简得 102400y2﹣38400y≥0.解得 y≥,即消防车在出发后最快经过小时可抵达居民点B.故答案为:.【谈论】此题察看的是在直角三角形中勾股定理的运用,画出图形建立直角三角形是重点,依据一元二次不等式的求解,能够计算出解的最小值,以便求出最短行程.三.解答题(共 5 小题)4.如图,在平面直角坐标系中,二次函数 y=ax2+bx+c 的图象经过点 A(﹣ 1,0),B(0,﹣),C(2,0),其对称轴与x轴交于点D( 1)求二次函数的表达式及其极点坐标;( 2)若 P 为 y 轴上的一个动点,连结PD,则PB+PD 的最小值为;( 3) M(x,t)为抛物线对称轴上一动点①若平面内存在点N,使得以 A,B,M,N 为极点的四边形为菱形,则这样的点N 共有5个;②连结 MA, MB,若∠ AMB 不小于 60°,求 t 的取值范围.【解析】(1)利用待定系数法转变为解方程组解决问题.( 2)如图 1 中,连结 AB,作 DH⊥AB 于 H,交 OB 于 P,此时 PB+PD 最小.最小值就是线段 DH,求出 DH 即可.(3)①先在对称轴上找寻知足△ABM 是等腰三角形的点M,由此即可解决问题.②作 AB 的中垂线与 y 轴交于点 E,连结 EA,则∠ AEB=120°,以 E 为圆心,EB为半径作圆,与抛物线对称轴交于点 F、G.则∠ AFB=∠AGB=60°,从而线段FG上的点知足题意,求出 F、G 的坐标即可解决问题.【解答】解:(1)由题意解得,∴抛物线解析式为y= x2﹣x﹣,∵ y= x2﹣x﹣=(x﹣)2﹣,∴极点坐标(,﹣).( 2)如图 1 中,连结 AB,作 DH⊥AB 于 H,交 OB 于 P,此时PB+PD 最小.原因:∵ OA=1, OB=,∴tan∠ ABO= = ,∴∠ ABO=30°,∴PH= PB,∴PB+PD=PH+PD=DH,∴此时PB+PD 最短(垂线段最短).在Rt△ADH 中,∵∠ AHD=90°,AD= ,∠ HAD=60°,∴sin60 °= ,∴DH=,∴PB+PD 的最小值为.故答案为.(3)①以 A 为圆心 AB 为半径画弧与对称轴有两个交点,以 B 为圆心 AB 为半径画弧与对称轴也有两个交点,线段 AB 的垂直均分线与对称轴有一个交点,所以知足条件的点 M 有 5 个,即知足条件的点 N 也有 5 个,故答案为 5.②如图, Rt△AOB 中,∵ tan∠ ABO= =,∴∠ ABO=30°,作 AB 的中垂线与 y 轴交于点 E,连结 EA,则∠ AEB=120°,以E 为圆心, EB为半径作圆,与抛物线对称轴交于点 F、G.则∠ AFB=∠AGB=60°,从而线段 FG上的点知足题意,∵ EB==,∴ OE=OB﹣ EB=,2 2∵F(,t ),EF =EB,∴()2+(t+)2=()2,解得 t=或,故 F(,),G(,),∴ t 的取值范围≤ t≤【谈论】此题察看二次函数综合题、锐角三角函数、最短问题、圆等知识,解题的重点是掌握待定系数法确立函数解析式,学会利用垂线段最短解决实指责题中的最短问题,学会增添协助线,结构圆解决角度问题,属于中考压轴题.5.如图,在△ ACE中, CA=CE,∠ CAE=30°,⊙ O 经过点 C,且圆的直径 AB 在线段AE 上.(1)试说明 CE是⊙ O 的切线;(2)若△ ACE中 AE 边上的高为 h,试用含 h 的代数式表示⊙ O 的直径 AB;(3)设点 D 是线段 AC 上随意一点(不含端点),连结 OD,当 CD+OD 的最小值为 6 时,求⊙ O 的直径 AB 的长.【解析】(1)连结 OC,如图 1,要证 CE是⊙ O 的切线,只要证到∠ OCE=90°即可;(2)过点 C 作 CH⊥AB 于 H,连结 OC,如图 2,在 Rt△OHC中运用三角函数即可解决问题;(3)作 OF 均分∠ AOC,交⊙ O 于 F,连结 AF、CF、DF,如图 3,易证四边形 AOCF 是菱形,依据对称性可得DF=DO.过点 D 作 DH⊥ OC于 H,易得 DH= DC,从而有CD+OD=DH+FD.依据两点之间线段最短可得:当 F、D、H 三点共线时, DH+FD (即CD+OD)最小,此后在 Rt△ OHF中运用三角函数即可解决问题.【解答】解:(1)连结 OC,如图 1,∵CA=CE,∠ CAE=30°,∴∠ E=∠CAE=30°,∠ COE=2∠ A=60°,∴∠ OCE=90°,∴ CE是⊙ O 的切线;( 2)过点 C 作 CH⊥AB 于 H,连结 OC,如图 2,由题可得 CH=h.在Rt△OHC中, CH=OC?sin∠COH,∴ h=OC?sin60°= OC,∴ OC= =h,∴ AB=2OC= h;( 3)作 OF 均分∠ AOC,交⊙ O 于 F,连结 AF、 CF、DF,如图 3,则∠ AOF=∠COF= ∠AOC= ( 180°﹣60°)=60°.∵OA=OF=OC,∴△ AOF、△ COF是等边三角形,∴AF=AO=OC=FC,∴四边形 AOCF是菱形,∴依据对称性可得 DF=DO.过点 D 作 DH⊥OC于 H,∵ OA=OC,∴∠ OCA=∠ OAC=30°,∴DH=DC?sin∠DCH=DC?sin30°=DC,∴CD+OD=DH+FD.依据两点之间线段最短可得:当 F、D、H 三点共线时, DH+FD(即CD+OD)最小,此时 FH=OF?sin∠FOH=OF=6,则OF=4 , AB=2OF=8 .∴当CD+OD 的最小值为 6 时,⊙ O 的直径 AB 的长为 8.【谈论】此题主要察看了圆周角定理、切线的判断、等腰三角形的性质、三角函数的定义、特别角的三角函数值、等边三角形的判断与性质、菱形的判断与性质、两点之间线段最短等知识,把 CD+OD 转变为 DH+FD 是解决第( 3)小题的重点.6.如图,已知抛物线y= ( x+2)(x﹣4)(k 为常数,且 k> 0)与 x 轴从左至右挨次交于 A,B 两点,与 y 轴交于点 C,经过点 B 的直线 y=﹣x+b 与抛物线的另一交点为 D.(1)若点 D 的横坐标为﹣ 5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点 P,使得以 A, B, P 为极点的三角形与△ABC相像,求 k 的值;( 3)在( 1)的条件下,设 F 为线段 BD 上一点(不含端点),连结 AF,一动点M 从点 A 出发,沿线段 AF以每秒 1 个单位的速度运动到 F,再沿线段 FD 以每秒 2 个单位的速度运动到 D 后停止,当点 F 的坐标是多少时,点 M 在整个运动过程顶用时最少?【解析】(1)第一求出点 A、B 坐标,此后求出直线 BD 的解析式,求得点 D 坐标,代入抛物线解析式,求得 k 的值;( 2)由于点 P 在第一象限内的抛物线上,所以∠ABP 为钝角.所以若两个三角形相像,只可能是△ ABC∽△ APB或△ ABC∽△ PAB.如答图 2,依据以上两种状况进行分类谈论,分别计算;( 3)由题意,动点 M 运动的路径为折线AF+DF,运动时间: t=AF+DF.如答图3,作协助线,将 AF+ DF 转变为 AF+FG;再由垂线段最短,获得垂线段 AH 与直线 BD 的交点,即为所求的 F 点.【解答】解:(1)抛物线 y=(x+2)(x﹣4),令y=0,解得 x=﹣ 2 或 x=4,∴ A(﹣ 2,0), B( 4, 0).∵直线 y=﹣ x+b 经过点 B( 4,0),∴﹣×4+b=0,解得 b=,∴直线 BD解析式为: y=﹣x+.当 x=﹣5 时, y=3,∴ D(﹣ 5,3 ).∵点 D(﹣ 5, 3)在抛物线 y= (x+2)(x﹣4)上,∴(﹣ 5+2)(﹣ 5﹣ 4) =3,∴ k=.∴抛物线的函数表达式为: y=(x+2)(x﹣4).即 y=x2﹣x﹣.(2)由抛物线解析式,令 x=0,得 y=﹣k,∴ C( 0,﹣ k),OC=k.由于点 P 在第一象限内的抛物线上,所以∠ ABP为钝角.所以若两个三角形相像,只可能是△ ABC∽△ APB 或△ ABC∽△ PAB.①若△ ABC∽△ APB,则有∠ BAC=∠PAB,如答图 2﹣1 所示.设 P(x, y),过点 P 作 PN⊥ x 轴于点 N,则 ON=x,PN=y.tan∠BAC=tan∠PAB,即:,∴y= x+k.∴P( x, x+k),代入抛物线解析式 y= ( x+2)( x﹣4),得(x+2)(x﹣4)=x+k,整理得: x2﹣6x﹣ 16=0,解得: x=8 或 x=﹣ 2(与点 A 重合,舍去),∴P( 8,5k).∵△ABC∽△ APB,∴,即,解得: k=.②若△ ABC∽△ PAB,则有∠ ABC=∠PAB,如答图 2﹣2 所示.设P(x, y),过点 P 作 PN⊥ x 轴于点 N,则 ON=x,PN=y.tan∠ABC=tan∠PAB,即:=,∴y= x+ .∴P( x, x+ ),代入抛物线解析式 y= (x+2)(x﹣4),得(x+2)(x﹣4)=x+,整理得:x2﹣4x﹣12=0,解得: x=6 或 x=﹣ 2(与点 A 重合,舍去),∴P( 6,2k).∵△ ABC∽△19=,∴=,解得 k=±,∵ k> 0,∴ k=,综上所述, k=或k=.( 3)方法一:如答图 3,由( 1)知: D(﹣ 5,3),如答图 2﹣ 2,过点 D 作 DN⊥x 轴于点 N,则 DN=3,ON=5,BN=4+5=9,∴tan∠DBA= == ,∴∠ DBA=30°.过点 D 作 DK∥x 轴,则∠ KDF=∠DBA=30°.过点 F 作 FG⊥ DK于点 G,则 FG= DF.由题意,动点 M 运动的路径为折线AF+DF,运动时间: t=AF+DF,∴t=AF+FG,即运动的时间值等于折线 AF+FG的长度值.由垂线段最短可知,折线 AF+FG的长度的最小值为 DK与 x 轴之间的垂线段.过点 A 作 AH⊥DK 于点 H,则 t 最小 =AH,AH 与直线 BD 的交点,即为所求之 F 点.∵ A 点横坐标为﹣ 2,直线 BD 解析式为: y=﹣x+,∴ y=﹣×(﹣2)+=2,∴ F(﹣ 2, 2).综上所述,当点 F 坐标为(﹣ 2,2)时,点M在整个运动过程顶用时最少.方法二:作DK∥ AB, AH⊥DK,AH 交直线 BD 于点 F,∵∠ DBA=30°,∴∠ BDH=30°,∴ FH=DF×sin30 °= ,∴当且仅当 AH⊥DK 时, AF+FH 最小,点 M 在整个运动顶用时为: t=,∵ l BD:y=﹣x+,∴F X=A X=﹣ 2,∴F(﹣ 2,).【谈论】此题是二次函数压轴题,难度很大.第( 2)问中需要分类谈论,防范漏解;在计算过程中,解析式中含有未知数 k,增添了计算的难度,注意解题过程中的技巧;第(3)问中,运用了转变思想使得试题难度大大降低,需要仔细意会.7.(1)如图 1,已知正方形 ABCD的边长为 4,圆 B 的半径为 2,点 P 是圆 B 上的一个动点,求PD+的最小值和PD﹣的最大值;( 2)如图 2,已知正方形 ABCD的边长为 9,圆 B 的半径为 6,点 P 是圆 B 上的一个动点,那么 PD+的最小值为,PD﹣的最大值为.( 3)如图 3,已知菱形 ABCD的边长为 4,∠ B=60°,圆 B 的半径为 2,点 P 是圆B 上的一个动点,那么PD+的最小值为,PD﹣的最大值为.【解析】(1)如图 1 中,在 BC上取一点 G,使得 BG=1.由△ PBG∽△ CBP,推出= = ,推出 PG= PC,推出 PD+ PC=DP+PG,由 DP+PG≥DG,当 D、G、P 共线时, PD+ PC 的值最小,最小值为DG==5.由 PD﹣PC=PD﹣PG≤ DG,当点 P 在 DG 的延伸线上时, PD﹣PC的值最大(如图 2 中),最大值为DG=5;(2)如图 3 中,在 BC上取一点 G,使得 BG=4.解法近似( 1);(3)如图 4 中,在 BC上取一点 G,使得 BG=4,作 DF⊥BC于 F.解法近似( 1);【解答】解:(1)如图 1 中,在 BC上取一点 G,使得 BG=1.∵= =2, = =2,∴= ,∵∠ PBG=∠PBC,∴△ PBG∽△ CBP,∴= = ,∴PG= PC,∴PD+ PC=DP+PG,∵DP+PG≥ DG,∴当 D、G、 P共线时, PD+ PC的值最小,最小值为 DG==5.∵PD﹣ PC=PD﹣PG≤DG,当点 P 在 DG 的延伸线上时, PD﹣P C的值最大(如图 2 中),最大值为 DG=5.( 2)如图 3 中,在 BC上取一点 G,使得 BG=4.∵= = , = = ,∴= ,∵∠ PBG=∠PBC,∴△ PBG∽△ CBP,∴= = ,∴PG= PC,∴PD+ PC=DP+PG,∵DP+PG≥ DG,∴当 D、G、 P共线时, PD+ PC的值最小,最小值为DG==.∵PD﹣ PC=PD﹣PG≤DG,当点 P 在 DG 的延伸线上时, PD﹣PC的值最大,最大值为DG=.故答案为,( 3)如图 4 中,在 BC上取一点 G,使得 BG=4,作 DF⊥ BC于 F.∵= =2, = =2,∴= ,∵∠ PBG=∠PBC,∴△ PBG∽△ CBP,∴= = ,∴PG= PC,∴PD+ PC=DP+PG,∵DP+PG≥ DG,∴当 D、G、 P共线时, PD+ PC的值最小,最小值为DG,在Rt△CDF中,∠ DCF=60°, CD=4,∴ DF=CD?sin60°=2 ,CF=2,在 Rt△GDF中, DG==∵PD﹣ PC=PD﹣PG≤DG,当点 P 在 DG 的延伸线上时,PD﹣PC的值最大(如图 2 中),最大值为 DG=.故答案为,.【谈论】此题察看圆综合题、正方形的性质、菱形的性质、相像三角形的判断和性质、两点之间线段最短等知识,解题的重点是学会建立相像三角形解决问题,学会用转变的思想思虑问题,把问题转变为两点之间线段最短解决,题目比较难,属于中考压轴题.8.如图 1,抛物线 y=ax2+(a+3) x+3(a≠ 0)与 x 轴交于点 A(4,0),与 y 轴交于点 B,在 x 轴上有一动点 E(m, 0)(0<m< 4),过点 E 作 x 轴的垂线交直线AB 于点 N,交抛物线于点 P,过点 P 作 PM⊥ AB 于点M.( 1)求 a 的值和直线 AB 的函数表达式;( 2)设△ PMN 的周长为 C1,△ AEN的周长为 C2,若=,求m的值;(3)如图 2,在( 2)条件下,将线段 OE 绕点 O 逆时针旋转获得 OE′,旋转角为α(0°<α<90°),连结 E′A、E′B,求 E′A+ E′B的最小值.【解析】(1)令 y=0,求出抛物线与 x 轴交点,列出方程即可求出 a,依据待定系数法能够确立直线 AB 解析式.(2)由△ PNM∽△ ANE,推出 = ,列出方程即可解决问题.(3)在 y 轴上取一点 M 使得 OM′=,结构相像三角形,能够证明 AM′就是E′A+ E′B的最小值.【解答】解:(1)令 y=0,则 ax2+(a+3)x+3=0,∴ x=﹣1 或﹣,∵抛物线 y=ax2+( a+3)x+3(a≠0)与 x 轴交于点 A(4,0),∴﹣=4,∴a=﹣.∵ A( 4, 0),B(0,3),设直线 AB 解析式为 y=kx+b,则,解得,∴直线 AB 解析式为 y=﹣x+3.( 2)如图 1 中,∵PM⊥ AB, PE⊥OA,∴∠ PMN=∠ AEN,∵∠ PNM=∠ANE,∴△ PNM∽△ ANE,∴= ,∵NE∥OB,∴ = ,∴ AN= (4﹣m),∵抛物线解析式为y=﹣x2 + x+3,∴PN=﹣ m2 + m+3﹣(﹣ m+3)=﹣ m2 +3m,∴=,解得 m=2.( 3)如图 2 中,在 y 轴上取一点 M′使得 OM′=,连结 AM′,在 AM′上取一点E′使得 OE′ =OE.∵OE′=2,OM′?OB= × 3=4,2′,∴ OE′=OM ?OB∴=,∵∠ BOE′=∠ M′OE,′∴△ M′OE′∽△ E′OB,∴== ,∴M′E′=BE′,∴AE′+ BE′=AE+E′′M′=AM,′此时 AE′+ BE′最小(两点间线段最短, A、 M′、E′共线时),最小值 =AM′==.【谈论】此题察看相像三角形的判断和性质、待定系数法、最小值问题等知识,解题的重点是结构相像三角形,找到线段 AM′就是 E′A+ E′B的最小值,属于中考压轴题.。
专题+圆---利用“胡不归”模型求最值-2024年中考数学复习几何模型

那么OD+0.5BD的最小值为______.
K
E M
解析:作BK∥CA,DE⊥BK于E,OM⊥BK于M,连
接OB.由已知得∠BAC=30º,在Rt△DBE
中,DE=0.5BD,∴0D+0.5BD=0D+DE,根据垂线
段最短可知,当点E与M重合时,OD+0.5BD的
值最小,最小值为OM=√3.
B
D
A
O
C
典例精讲
胡不归模型
知识点一
【例2】如图,△ABC在直角坐标系中,AB=AC,A(0, ),C(1,0),D为射线
AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是
在CD上的3倍,要使整个运动时间最少,则点D的坐标应为_________.
解析:设点P在DC上的速度为v,则时间
第三步:根据两点之间线段最短,找到最小值的位置;
第四步:计算.
模型分析
胡不归模型
tanα+tanβ
tan(α+β)=
1-tanα·tanβ
预备知识
sin(a+β)=sinα·cosβ+cosa·sinβ
直角三角形斜边大于直角边,直角三角形中,斜边打一个折扣(sinα),
化归为这个角的对边.斜边·sinα=对边.
题情境(1)当m=___时,CP最短,理由是_________.
(2)当m为何值时,
问题再现
1
CP BP
的最小值?请求出最小值。小明的解
2
决方法:如图,作射线BA,使∠OBA=30º,交x轴于点A,过点C作
y
CF⊥AB于点F,请完善小明的解法.问题突破当m为何值时,CP+
中考数学复习《几何最值---胡不归》例题复习讲义PPT课件

,记 k
V1 V2
,
即求 BC+kAC 的最小值. 构造射线 AD 使得 sin∠DAN=k,CH/AC=k,CH=kAC.
将问题转化为求 BC+CH 最小值,过 B 点作 BH⊥AD 交 MN 于点 C,交 AD 于 H 点,此时 BC+CH 取到最小值,即 BC+kAC 最小.
在求形如“PA+kPB”的式子的最值问题中,关键是构造与 kPB 相等的线段,将“PA+kPB”型 问题转化为“PA+PC”型.
中考数学复习《几何最值---胡不归》例 题复习讲义PPT课件
胡不归模型问题解题步骤如下;
1、将所求线段和改写为“PA+ b PB”的形式( b <1),若 b >1,提取系数,转化为小于 1
a
a
a
的形式解决。
2、在 PB 的一侧,PA 的异侧,构造一个角度α,使得 sinα= b a
3、最后利用两点之间线段最短及垂线段最短解题
1.如图,△ABC 中,AB=AC=10,tanA=2,BE⊥AC 于点 E,D 是线段 BE 上的一个动点,则
CD 5 BD 的最小值是(
)
5
【答案】B
【详解】 如图,作 DH⊥AB 于 H,CM⊥A
∵tanA= BE =2,设 AE=a,BE=2a, AE
∴DH= 5 BD, 5
∴CD+ 5 BD=CD+DH, 5
∴CD+DH≥CM,
∴CD+ 5 BD≥4 5 ,
5
∴CD+ 5 BD 的最小值为 4 5 .
5 故选 B.
• 本课结束
【模型展示】 如图,一动点 P 在直线 MN 外的运动速度为 V1,在直线 MN 上运动的速度为 V2,且 V1<V2,A、 B 为定点,点 C 在直线 MN 上,确定点 C 的位置使 AC BC 的值最小.
中考数学专题:胡不归问题解析

3
3
y 3 x 2 x 4 ,化简为: y 3 x2 2 3 x 8 3 .另外为了突出问题,此处略去了
9
9
9
9
该题的第二小问.
点
M
运动的时间为
AF
y
1 2
DF
,即求
AF
1 2
DF
y
的最小值.
DF
H
D
M
F
AO C
B
x
AO C
B
x
接下来问题便是如何构造 DF ,考虑 BD 与 x 轴夹角为 30°,且 DF 方向不变,故过点 D 作 2
而这里的 PB 必须是一条方向不变的线段,方能构造定角利用三角函数得到 kPB 的等线段.
【2019 长沙中考】如图,△ABC 中,AB=AC=10,tanA=2,BE⊥AC 于点 E,D 是线段 BE 上的一个动点,则 CD 5 BD 的最小值是_______.
5
A
E D
B
C
【 分 析 】本 题 关 键 在 于处 理 “ 5 BD ” , 考 虑 tanA =2, △ABE 三 边 之 比为 1: 2 : 5 , 5
E D
B
C
则需自行构造α ,如下图,这一步正是 解决“ 胡不归” 问题关键所在.
A
E D
H
E
D
B
C
α
5
sinα= B
C
5
【2019 南通中考】如图,平行四边形 ABCD 中,∠DAB =60°,AB =6,BC=2,P 为边 CD 上的一动点,则 PB 3 PD 的最小值等于________.
2
饮马模型解题即可.
P
中考数学几何复习---最值系列之胡不归问题

中考数学几何复习--最值系列之“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如P A +PB 最值,除此之外我们还可能会遇上形如“P A +kPB ”这样的式子的最值,此类式子一般可以分为两类问题:(1)胡不归问题;(2)阿氏圆.本文简单介绍“胡不归”模型.【故事介绍】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?…”(“胡”同“何”)而如果先沿着驿道AC 先走一段,再走砂石地,会不会更早些到家?2驿道【模型建立】如图,一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BCV V +的值最小.2M【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =, 即求BC +kAC 的最小值.【问题解决】构造射线AD使得sin∠DAN=k,CH/AC=k,CH=kAC.M将问题转化为求BC+CH最小值,过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小.M【模型总结】在求形如“P A+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“P A+kPB”型问题转化为“P A+PC”型.而这里的PB必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB的等线段.【长沙中考】如图,△ABC 中,AB =AC =10,tan A =2,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,则CD 的最小值是_______.ABCDE【分析】本题关键在于处理”,考虑tan A =2,△ABE三边之比为1:2sin ∠,故作DH ⊥AB 交AB 于H点,则DH =. HEDCBAABCDEH问题转化为CD +DH 最小值,故C 、D 、H共线时值最小,此时CD DH CH BE +===.【小结】本题简单在于题目已经将BA 线作出来,只需分析角度的三角函数值,作出垂线DH ,即可解决问题,若稍作改变,将图形改造如下:EDCB则需自行构造α,如下图,这一步正是解决“胡不归”问题关键所在.αsin α5HEDC BAEDCB【南通中考】如图,平行四边形ABCD 中,∠DAB =60°,AB =6,BC =2,P 为边CD 上的一动点,则PB 的最小值等于________.ABCDP【分析】考虑如何构造”,已知∠A =60°,且sin60°,故延长AD ,作PH ⊥AD 延长线于H 点,即可得PH =,将问题转化为:求PB +PH 最小值. M HPDCBA当B 、P 、H 三点共线时,可得PB +PH 取到最小值,即BH 的长,解直角△ABH 即可得BH 长.ABCDPH M【成都中考】如图,已知抛物线()()248ky x x =+-(k 为常数,且k >0)与x 轴从左至右依次交于A ,B 两点,与y 轴交于点C ,经过点B的直线y b =+与抛物线的另一交点为D . (1)若点D 的横坐标为-5,求抛物线的函数表达式;(2)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A 出发,沿线段AF以每秒1个单位的速度运动到F ,再沿线段FD 以每秒2个单位的速度运动到D 后停止,当点F 的坐标是多少时,点M 在整个运动过程中用时最少?【分析】第一小问代点坐标,求解析式即可,此处我们直接写答案:A (y =+,D 点坐标为(-,故抛物线解析式为)()24y x x +-,化简为:2y =点M 运动的时间为12AF DF ⎛⎫+ ⎪⎝⎭,即求12AF DF ⎛⎫+ ⎪⎝⎭的最小值.接下来问题便是如何构造2DF,考虑BD 与x 轴夹角为30°,且DF 方向不变,故过点D 作DM ∥x 轴,过点F 作FH ⊥DM 交DM 于H 点,则任意位置均有FH =2DF. 当A 、F 、H 共线时取到最小值,根据A 、D 两点坐标可得结果.【重庆中考】抛物线2y x =x 轴交于点A ,B (点A 在点B 的左边),与y 轴交于点C .点P 是直线AC 上方抛物线上一点,PF ⊥x 轴于点F ,PF 与线段AC 交于点E ;将线段OB 沿x 轴左右平移,线段OB 的对应线段是O 1B 1,当12PE EC +的值最大时,求四边形PO 1B 1C 周长的最小值,并求出对应的点O 1的坐标.(为突出问题,删去了两个小问)【分析】根据抛物线解析式得A ()-、B )、C (,直线AC的解析式为:y =+知AC 与x 轴夹角为30°. 根据题意考虑,P 在何处时,PE +2EC取到最大值.过点E 作EH ⊥y 轴交y 轴于H 点,则∠CEH =30°,故CH =2EC,问题转化为PE +CH 何时取到最小值.考虑到PE 于CH并无公共端点,故用代数法计算,设2,P m ⎛- ⎝,则E m ⎛+ ⎝,H ⎛ ⎝,2PE =-,CH =,22=PE CH m +=+sin ABE ∠=当P点坐标为(-时,取到最小值,故确定P 、C 、求四边形面积最小值,运用将军饮马模型解题即可.。
中考数学几何最值模型第2讲胡不归问题

A
G
P
H
B
H
C
课堂练习
4.等边三角形ABC的边长为6,将其放置在如图所示的平面直角坐标系中,其中BC边
在X轴上,BC边的高OA在y轴上,一只电子虫从A出发,先沿y轴到达G点,再沿GC到
达C点,已知电子虫在y轴上运动的速度是在GC上运动速度的2倍。若电子虫走完全程
_x001A_0, −_x001A__x001B_3_x001B__x001B_
一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,
小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念
叨着“胡不归? 胡不归? …”(“胡”同“何”)而如果先沿着驿道AC先
走一段,再走砂石地,会不会更早些到家?
故事介绍
从前有个少年外出求学,某天不幸得知老父亲
病危的消息,便立即赶路回家.根据“两点之
H
∵AE⊥CD于点G,∴∠AGC=90°
Q
∵O为AC中点, ∴OA=OC=OG=_x001A_1_x001B_2_x001B_AC
P
∴A,C, G三点共圆, 圆心为O,即点G在圆O上运动,
课堂练习
1.如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,点M为对角线BD(不含点B)上的
一动点,则AM+_x001A_1_x001B_2_x001B_的最小值为_______.
BN=_x001A_1_x001B_2_x001B_=1,=_x001A__x001B
_3_x001B_,CN=2−_x001A__x001B_3_x001B_,
∴BC=_x001A__x001B__x001A__x001B_2_x001B_+_x00
1A_C_x001B_2_x001B__x001B_=_x001A__x001B__x001
初中数学知识点各个击破专项练习:一次函数综合最值问题“将军饮马、胡不归”(学生版)

一次函数综合最值问题“将军饮马、胡不归”一、解答题1已知一次函数y=4kx+5k+132k≠0.(1)无论k为何值,函数图象必过定点,求该定点的坐标;(2)如图1,当k=-12时,一次函数y=4kx+5k+132的图象交x轴,y轴于A、B两点,点Q是直线l2:y=x+1上一点,若S△ABQ=6,求Q点的坐标;(3)如图2,在(2)的条件下,直线l2:y=x+1交AB于点P,C点在x轴负半轴上,且S△ABC=203,动点M 的坐标为a,a,求CM+MP的最小值.2已知一次函数y=4kx+5k+132(k≠0).(1)无论k为何值,函数图象必过定点,则该定点的坐标;(2)如图1,当k=-12时,该直线交x轴,y轴于A,B两点,直线l2:y=x+1交AB于点P,点T是l2上一点,若S△ABT=9,求T点的坐标;(3)如图2,在第2问的条件下,已知D点在该直线上,横坐标为1,C点在x轴负半轴,∠ABC=45°,点M 是x轴上一动点,连接BM,并将线段BM绕点M顺时针旋转90°得到MQ,①求点C的坐标;②CQ+QD的最小值为.3如图,一次函数y=12x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.(可能用到的公式:若A(x1,y1),B(x2,y2),①AB中点坐标为x1+x2 2,y1+y22;②AB=x1-x22+y1-y22(1)求线段AB的长;(2)过B、C两点的直线对应的函数表达式.(3)点D是BC中点,在直线AB上是否存在一点P,使得PC+PD有最小值?若存在,则求出此最小值;若不存在,则说明理由.4已知一次函数y=kx+b(k≠0)与x轴交于点A(3,0),且过点7,8,回答下列问题.(1)求该一次函数解析式;(2)一次函数的解析式也称作该直线的斜截式方程,如解析式y=kx+b我们只需要将y向右移项就可以得到kx-y+b=0,将x前的系数k替代为未知数A,将y前的系数1替代为未知数B,将常数项b替代为未知数C,即可得到方程Ax+By+C=0,该二元一次方程也称为直线的一般方程(其中A一般为非负整数,且A、B不能同时为0).一般地,在平面直角坐标系中,我们求点到直线间的距离,可用下面的公式求解:点P x0,y0到直线Ax+By+C=0的距离d 公式是:d=Ax0+By0+CA2+B2如:求:点P1,1到直线y=-13x+32的距离.5如图,一次函数y=kx+b的图象交x轴于点A,OA=4,与正比例函数y=3x的图象交于点B,B 点的横坐标为1.(1)求一次函数y=kx+b的解析式;(2)若点C在y轴上,且满足S△BOC=12S△AOB,求点C的坐标;(3)若点D4,-2,点P是y轴上的一个动点,连接BD,PB,PD,是否存在点P,使得△PBD的周长有最小值?若存在,请直接写出△PBD周长的最小值.6在平面直角坐标系xoy中,一次函数y=34x+3的图像分别与x轴、y轴交于A、B两点,点C为x轴正半轴上的一个动点,设点C的横坐标为t.(1)求A、B两点的坐标;(2)点D为平面直角坐标系xoy中一点,且与点A、B、C构成平行四边形ABCD.①若平行四边形ABCD是矩形,求t的值;②在点C运动的过程中,点D的纵坐标是否发生变化,若不变,求出点D的纵坐标;若变化,说明理由;③当t为何值时,BC+BD的值最小,请直接写出此时t的值及BC+BD的最小值.7已知,一次函数y=(2-t)x+4与y=-(t+1)x-2的图像相交于点P,分别与y轴相交于点A、B.其中t为常数,t≠2且t≠-1.(1)求线段AB的长;(2)试探索△ABP的面积是否是一个定值?若是,求出△ABP的面积;若不是,请说明理由;(3)当t为何值时,△ABP的周长最小,并求出△ABP周长的最小值.8如图1,已知一次函数y=x+3与x轴,y轴分别交于B点,A点,x正半轴上有一点C,∠ACO= 60°,以A,B,C为顶点作平行四边形ABCD.(1)求C点坐标.(2)如图2,将直线AB沿y轴翻折,翻折后的直线交CD于E点,在y轴上有一个动点P,x轴上有一动点Q,当DP+PQ+QE取得最小值时,求此时(DP+PQ+QE)2的值.(3)如图3,将△AOC向左平移使得点C与坐标原点O重合,A的对应点为A ,O的对应点为O ,将△A O O绕点O顺时针旋转,旋转角为α0°≤α≤180°,在旋转过程中,直线AB与直线A O 、A O交于M,G两点,在旋转过程中,△A MG能否成为等腰三角形,若能,求出所满足条件的α,若不能,请说明理由.9(1)问题解决:如图1,在平面直角坐标系xOy中,一次函数y=1x+1与x轴交于点A,与y轴交于点B,4以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,点A、B、C的坐标分别为、、.(2)综合运用:①如图2,在平面直角坐标系xOy中,点A坐标(0,-6),点B坐标(8,0),过点B作x轴垂线l,点P是l上一动点,点D是在一次函数y=-2x+2图像上一动点,若△APD是以点D为直角顶点的等腰直角三角形,请求出点D的坐标.②如图2,在⑵的条件中,若M为x轴上一动点,连接AM,把AM绕M点逆时针旋转90°至线段NM,ON+AN的最小值是.10已知一次函数y =kx +32的图象与x 轴交于点A ,与y 轴交于点B ,点M 的坐标为0,m ,其中0<m <32.(1)若点A (-32,0),过点O 作OP ⊥AM ,连接BP 并延长与x 轴交于点C ,①求k 的值;②求证:BP PC =OM OC ;(2)若点A -2,0 ,求2AM +BM 的最小值.11如图1,一次函数y=43x+4的图象与x轴、y轴分别交于点A、B.(1)则点A的坐标为,点B的坐标为;(2)如图2,点P为y轴上的动点,以点P为圆心,PB长为半径画弧,与BA的延长线交于点E,连接PE,已知PB=PE,求证:∠BPE=2∠OAB;(3)在(2)的条件下,如图3,连接PA,以PA为腰作等腰三角形PAQ,其中PA=PQ,∠APQ=2∠OAB.连接OQ.①则图中(不添加其他辅助线)与∠EPA相等的角有;(都写出来)②试求线段OQ长的最小值.12如图一次函数y1=k1x+3的图象与坐标轴相交于点A-2,0和点B,与反比例函数y2=k2x (x>0)的图象相交于点C2,m.(1)求出一次函数与反比例函数的解析式;(2)若点P是反比例函数图象上的一点,连接CP并延长,交x轴正半轴于点D,若PD:CP=1:2时,求△COP的面积;(3)在(2)的条件下,在y轴上是否存在点Q,使PQ+CQ的值最小,若存在请直接写出PQ+CQ的最小值,若不存在请说明理由.13【定义】斜率,表示一条直线相对于横轴的倾斜程度.当直线l的斜率存在时,对于一次函数y=kx+b(k≠0),k即为该函数图象(直线)的斜率.当直线过点(x1,y1)、(x2,y2)时,斜率k=y2-y1x2-x1,特别的,若两条直线l1⊥l2,则它们的斜率之积k1•k2=-1,反过来,若两条直线的斜率之积k1•k2=-1,则直线l1⊥l2【运用】请根据以上材料解答下列问题:(1)已知平面直角坐标系中,点A(1,3)、B(m,-5)、C(3,n)在斜率为2的同一条直线上,求m、n的值;(2)在(1)的条件下,点P为y轴上一个动点,当∠APC为直角时,求点P的坐标;(3)在平面直角坐标系中另有两点D(3,2)、E(-1,-6),连接DA并延长至点G,使DA=AG,连接GE交直线AB于点F,M为线段FA上的一个动点,求DM+55MF的最小值.14如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(23,4),一次函数y= -3x+b的图象与边OC、AB、x轴分别交于点D、E、F,∠DFO=30°,并且满足OD=BE,点M是线3段DF上的一个动点.(1)求b的值;(2)连接OM,若ΔODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;(3)求OM+1MF的最小值.215如图1,一次函数y=34x-6的图象与坐标轴交于点A,B,BC平分∠OBA交x轴与点C,CD⊥AB,垂足为D.(1)求点A,B的坐标;(2)求CD所在直线的解析式;(3)如图2,点E是线段OB上的一点,点F是线段BC上的一点,求EF+OF的最小值.16如图,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B0,2,与正比例函数y=32x的图象交于点C4,c.(1)求k和b的值.(2)如图1,点P是y轴上一个动点,当PA-PC最大时,求点P的坐标.(3)如图2,设动点D,E都在x轴上运动,且DE=2,分别连结BD,CE,当四边形BDEC的周长取最小值时直接写出点D和E的坐标.17在平面直角坐标系中,一次函数y=-23x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.(1)当t=2秒时,OQ的长度为;(2)设MN、PN分别与直线y=-23x+4交于点C、D,求证:MC=NC;(3)在运动过程中,设正方形PQMN的对角线交于点E,MP与QD交于点F,如图2,求OF+EN的最小值.18已知一次函数y=4kx+5k+132k≠0,(1)无论k为何值,函数图像必过定点,求该点的坐标;(2)如图1,当k=-12时,该直线交x轴,y轴于A,B两点,直线l2:y=x+1交AB于点P,点Q是l2上一点,若SDABQ=6,求Q点的坐标;(3)如图2,在第2问的条件下,已知D点在该直线上,横坐标为1,C点在x轴负半轴,ÐABC=45°,动点M的坐标为(a,a),求CM+MD的最小值.19如图,在平面直角坐标系中,一次函数y=kx+b的图像经过点A(-2,0),B(0,-23)、过D(1,0)作平行于y轴的直线l;(1)求一次函数y=kx+b的表达式;PB+PD的最小值为.(2)若P为y轴上的一个动点,连接PD,则12(3)M(s,t)为直线l上的一个动点,若平面内存在点N,使得A、B、M、N为顶点的四边形为矩形,则求M,N点的坐标;+k(其中k·b≠0,且|k|≠|b|))为互助一次函数,例如:y=-2x+3和y=3x-2就是互助一次函数.如图1所示,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于点P,l1,l2与x轴、y轴分别交于点A,B 和点C,D.(1)如图1所示,当k=-1,b=5时,直接写出点P的坐标是.(2)如图2所示,已知点M(-1,1.5),N(-2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化,若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时点P的坐标.+k(其中k⋅b≠0,且|k|≠|b|)为互助一次函数,例如y=-23x+2和y=2x-23就是互助一次函数.如图,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于P点,l1,l2,与x轴,y轴分别交于A,B点和C,D点.(1)如图(1),当k=-1,b=3时,请回答下列问题:①直接写出P点坐标;②Q是射线CP上一点(与C点不重合),其横坐标为m,求四边形OCQB的面积S与m之间的函数关系式,并求当△BCQ与△ACP面积相等时m的值;(2)如图(2),已知点M(-1,2),N(-2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化?若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时的P点坐标.22如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线DE经过点C,过A作AD ⊥DE于点D,过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为 “K型全等”.(不需要证明)【模型应用】若一次函数y=kx+4(k≠0)的图像与x轴、y轴分别交于A、B两点.(1)如图2,当k=-1时,若点B到经过原点的直线l的距离BE的长为3,求点A到直线l的距离AD的长;(2)如图3,当k=-43时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标;(3)当k的取值变化时,点A随之在x轴上运动,将线段BA绕点B逆时针旋转90°得到BQ,连接OQ,求OQ长的最小值.。
中考数学最值—胡不归问题(解析+例题)

中考数学最值——胡不归问题(点在直线上运动)(PA+k·PB型最值)【历史典故】从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路。
由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径A→B(如图所示),而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭。
邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?…”。
这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归问题”。
【知识储备】①三角形三边关系:两边之和大于第三边;两边之差小于第三边。
②两点之间线段最短。
③连接直线外一点和直线上各点的所有线段中,垂线段最短。
【模型分析】①条件:已知A、B为定点,P为射线AC上一动点。
②问题:P在何处时,BP+nm AP最短(nm<1)。
③方法:第一步在AC的一侧,PB的异侧构造∠CAE=α,使得sinα=nm 第二步做BH⊥AE,交AC于P,点P就是所求位置,BH就是其最小值。
【模型分析】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB的长度,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D 选在何处时,所用时间最短?个运动过程中用时最少,请求出最少时间和此时点F的坐标。
【巩固训练】练习1:如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上BM的最小值为_____。
任意一点,则AM+12练习2:如图,等腰ΔABC中,AB=AC=3,BC=2,BC边上的高为A0,点D为射线A0上一点,一动点P从点A出发,沿AD-DC运动,动点P在AD上运动速度3个单位每秒,动点P在CD上运动的速度为1个单位每秒,则当 AD= 时,运动时间最短为秒。
初中数学胡不归问题

问题探究
【建立模型】
如图,一动点P在直线MN外的运动速度为v1,在直线MN上运动的
速度为v2,且v1>v2,A、B为定点,点C在直线MN上,确定点C的位置
使 BC AC 的值最小。
求最值。
C
M Aα
N
注意:这里的AC必须是一条方向不变的直线,且0<k<1,方
能构造定角利用三角函数得到和kAC相等的线段。
H D
类题演练
【2019 长沙中考】如图,△ABC 中,AB=AC=10,tanA=2,BE⊥AC 于点 E,D 是线段 BE 上的一个动点,则 CD 5 BD 的最小值是_______.
C,交AD于点H,此时BH+CH最小,即BC+kAC最小。
M M A Aα α
CH sinα= =k
AC
CH=kAC
C
C
H
H
BB
NN
D
D
【模型总结】
在求形如“BC+kAC”的式子的最值问题中,关 B
键是构造与kAC相等的线段,将“BC+kAC”型的问
题,转化为“BC+CH”型,然后根据“垂线段最短”
【小结】本题简单在于题目已经将 BA 线作出来,只需分析角度的三角函数值,作出垂线 DH ,即可解决问题,若稍 作改变,将图形改造如下:
E D
B
C
则需自行构造α ,如下图,这一步正是 解决“ 胡不归” 问题关键所在.
A
E D
H
E
D
B
C
α
5
胡不归问题解题方法和口诀

胡不归问题解题方法和口诀
胡不归问题是一种常见的计数问题,通常涉及到等差数列和等比数列的求和问题。
下面是胡不归问题的解题方法和口诀。
解题方法:
1. 对于等差数列的胡不归问题,可以通过求和公式求解。
设第 n 个数为 a_n,公差为 d,则前 n-1 个数的和为:
S(n-1) = n*(a_1 + a_2 + ... + a_n) = n*(a_1 + a_2 + ... + a_{n-1}) - n*a_n
当 n 趋近于无穷大时,S(n-1) 趋近于正无穷大,因此胡不归的时间点一定是在等差数列的最后一个数 a_n 取最大值或最小值的时候。
2. 对于等比数列的胡不归问题,可以通过乘法公式求解。
设第 n 个数为 a_n,公比为 q,则前 n-1 个数的和为:
S(n-1) = (a_1 + a_2 + ... + a_n)/n = a_1 + a_2 + ... + a_{n-1} + n*q^(n-1) - n*q^n
当 n 趋近于无穷大时,S(n-1) 趋近于正无穷大,因此胡不归的时间点一定是在等比数列的最后一个数 a_n 取最大值或最小值的时候。
口诀:
1. 胡不归问题,数列求解;等差数列求和,等比数列乘积;
2. 首项加末项,求和公式运用;数列趋近于正无穷大,胡不归时间确定;
3. 掌握等差数列和等比数列的特点,运用极限思想求解。
拓展:
胡不归问题不仅可以应用于计数问题,还可以应用于其他数学领域。
例如,在概率论中,胡不归问题可以应用于判断一个事件是否会发生;在组合数学中,胡不归问题可以应用于求解组合数的总和。
