42.染色问题
纺织染色工中级工四级题库

纺织染色工四级题库一、单选题(200题)1.下列纤维中()属于纤维素纤维。
AA.棉纤维B.涤纶纤维C.羊毛D.锦纶纤维2.红、黄、兰三色的余色分别为()。
CA.紫、绿、橙B.黑、棕、青C.绿、紫、橙D.橙、绿、紫3.染料的摩尔吸光度越大,则染料的染色()。
DA.越深B.越浅C.越淡D.越浓4.还原染料还原成隐色体时,一般用的还原剂是()。
AA.烧碱和保险粉B.雕白粉C.硫化钠D.亚硫酸钠5.食盐在阳离子染料染色时起()作用。
BA.促染B.缓染C.助溶D.氧化6.直接染料除可用于棉纤维的染色外,还常用于()的染色。
BA.涤纶纤维B.粘胶纤维C.腈纶纤维D.氨纶7.直接染料轧染时,初染液应该()。
BA.加浓B.冲淡C.与常规染液一致D.加深8.轧染时易产生头深现象的本质原因是()。
CA.轧液浓度太大B.染色温度太低C. 亲和力太大D.亲和力太小9.为了提高直接染料的耐洗牢度,通常可采用()固色剂来进行固色。
BA.阴电荷性B.阳电荷性C.电荷中性D.都可以10.直接染料当遇到还原剂时,染料被还原破坏,这时用氧化剂氧化()BA.可以恢复原来颜色B.不能恢复原料颜色C.不确定D. 恢复原料颜色11.当轧车轧液不均匀时,极易产生()。
BA.原样色差B.左中右色差C.前后色差D.正反面色差12.国产X型活性染料其活性基的学名为()。
BA.一氯均三嗪B.二氯均三嗪C.β-乙烯枫D.二氯嘧啶13.由于X型活性染料反应性较高,在()中就能固色,因此又叫普通型活性染料。
AA.低温和较弱碱剂B.高温和较弱碱剂C.低温和较强碱剂D.14.任何类型的活性染料,当它与纤维固色后,染浴的PH值一般将()。
CA.提高B.降低C.不变D.不确定15.在活性染料中加入尿素,能够帮助染料溶解,同时能提高()。
BA.染色牢度B.给色量C.固色温度D.染色温度16.一氯均三嗪型活性染料染色时,固色温度一般要控制在()。
CA.30℃左右B.60℃左右C.90℃左右D.100℃左右17.在相同的染色条件下,丝光后的织物一般比不丝光的织物色泽()。
染整工艺与原理——染色印花知到章节答案智慧树2023年青岛大学

染整工艺与原理——染色印花知到章节测试答案智慧树2023年最新青岛大学绪论单元测试1.泳移可使染色获得均匀的染色效果。
参考答案:错2.轧余率是浸轧后织物上带液质量占轧后湿布质量比。
参考答案:错3.颜色的三属性分别是色相、明度和饱和度。
参考答案:对4.染料拼色的三原色是红、黄、蓝(这里的红即减法混色的原色品红,蓝即是减法混色的原色青色)。
参考答案:对5.织物浸轧染液烘干时,为了防止织物上染料的泳移,烘筒温度通常应()。
参考答案:前低后高6.下列不属于轧染染色方法的特点是()参考答案:适合小批量生产7.浴比为1:10则表示1克织物需要用()参考答案:10ML水8.轧染时易产生头深尾浅现象的本质原因是()。
参考答案:亲和力太大9.当轧车轧液不匀时,极易产生()参考答案:左、中、右色差10.下列属于轧染方法的特点的是()参考答案:连续生产;适合大批量生产第一章测试1.上染过程的四个阶段中,决定上染速率的阶段是染料在纤维中的扩散阶段。
参考答案:对2.拼色时,选用半染时间相近的染料不容易获得前后一致的色泽。
参考答案:错3.通常,纤维的ζ电位与热力学电位符号相反,主观题绝对值较低。
参考答案:错4.在实际染色过程中,如直接染料染色过程中,加盐可以降低纤维表面的动电层电位。
参考答案:对5.在大多数染色体系中,染料的上染过程是吸热反应,因此高温会使染料解吸。
参考答案:错6.符合朗缪尔吸附等温线的染色过程,其染料在纤维中的吸附是非定位吸附。
参考答案:错7.符合弗莱因德利胥型吸附等温线的染色过程,存在染色饱和值。
参考答案:错8.提高染色温度,平衡上染百分率()参考答案:下降9.半染时间即达到平衡上染率一半所需要的时间的半染时间短,表明()参考答案:染料扩散速率快10.对于棉、黏胶和蚕丝等亲水性纤维,染料分子在纤维上的扩散特点可以用()模型来说明。
参考答案:孔道扩散模型第二章测试1.对于匀染性直接染料,染色时温度不宜过高,也无需加入大量电解质。
二年级上美术教案-染色游戏-人教新课标版

二年级上美术教案-染色游戏-人教新课标版一、教学目标1. 让学生了解色彩的基本知识,掌握染色技巧,培养学生的动手能力和审美能力。
2. 通过染色游戏,激发学生的想象力和创造力,提高学生的艺术素养。
3. 培养学生合作意识,学会与他人分享和交流,增强团队凝聚力。
二、教学内容1. 色彩知识:三原色、间色、互补色等。
2. 染色技巧:晕染、泼染、折叠染等。
3. 染色作品欣赏与评价。
三、教学重点与难点1. 教学重点:掌握染色技巧,创作出富有创意的染色作品。
2. 教学难点:如何运用染色技巧表现出丰富的层次和美感。
四、教具与学具准备1. 教具:多媒体设备、染色作品案例、教程视频等。
2. 学具:白纸、水彩笔、蜡笔、水粉颜料、画笔、调色盘、吸水纸等。
五、教学过程1. 导入:通过展示染色作品,激发学生的兴趣,引导学生关注染色艺术。
2. 新课内容:讲解色彩知识,示范染色技巧,让学生了解并掌握染色方法。
3. 实践操作:学生分组进行染色游戏,鼓励学生发挥想象,创作出独特的作品。
4. 作品展示与评价:学生展示自己的作品,互相评价,老师给予点评和建议。
5. 总结与反思:总结本次课程所学内容,让学生认识到染色艺术的魅力,激发继续学习的兴趣。
六、板书设计1. 二年级上美术教案-染色游戏2. 目录:教学目标、教学内容、教学重点与难点、教具与学具准备、教学过程、板书设计、作业设计、课后反思3. 正文:根据教学过程逐步展示板书内容,包括染色技巧、作品欣赏等。
七、作业设计1. 创作一幅染色作品,要求运用课堂所学染色技巧,表现出丰富的层次和美感。
2. 写一篇关于染色游戏的感受,内容包括:最喜欢的染色技巧、创作过程中的趣事、对染色艺术的看法等。
八、课后反思1. 教师反思:本次课程的教学效果、学生的参与度、教学方法的适用性等。
2. 学生反思:染色技巧的掌握程度、作品的创作思路、与同学的协作情况等。
通过本次课程,让学生在愉快的染色游戏中,掌握色彩知识和染色技巧,培养动手能力、审美能力和合作意识,提高艺术素养。
染整工艺原理试题库

1 .浓色染样的日晒牢度往往比淡色染样的要(),而水洗牢度要()。
2 .溶液中电解质如食盐浓度增加会()染料的聚集。
3 .加热溶解配制的染液在放置过程中其汲取光谱曲线上会消失一个新的波峰,这是由于染料()所引起的。
4 .染色时最常用的助溶剂为()。
5 .直接染料染色后用阳离子固色剂后处理其目的是提高(),但往往会使()牢度有所降低。
6 .还原染料隐色体电位负值越大,还原倾向越()。
7 .活性染料染色时,染料的采用率不高主要是由于染色过程中()。
8 . 1 : 2型酸性含媒染料中的比例关系是指()的比。
9 .匀染性酸性染料染羊毛时,等电点以下电解质起()作用,等电点以上电解质起()作用。
10 .两只染料拼混时,若要获得最佳配伍效果,其配伍性比值K应()°11 .染料能平均地汲取各种波长的可见光,则此染料是(),全部汲取可见光波则是()o12 .轧染中为防止染料泳移而实行的主要措施有()、()、加防泳移剂等。
13 . 一个水分子生成有四个氢键的结构,称为()结构,此时分子的能级()。
14 .在直接染料对纤维的染色中,半染时间差异很大,集中速率高的,半染时间(),上染比较(),要达到同样的上染速率,集中速率低的染料便需要()上染温度。
15 .还原速率低的染料可以()还原,还原速率高的染料可以()还原。
16 .和羊毛染色相比,酸性染料对聚酰胺纤维上染的pH相应较(),这说明酸性染料对聚酰胺纤维的亲和力比染羊毛的(),因此染料在聚酰胺纤维上更易发生()。
17 .暂溶性还原染料显色的必要条件为()和()。
18 .上染时,染料随着染液的流淌到达(),再通过染料自身的分子运动,()到纤维表面。
19 .上染过程中,分散染料与涤纶纤维的分子间作用力为()、()。
20 . 一般认为,染色焰成正值的现象是上染过程中,水分子混乱度(),类冰结构()而引起的。
21 .在直接染料对纤维素纤维的染色中,集中速率()的染料,移染性能(),水洗牢度(),属于A类染料。
20181125小学奥数练习卷(知识点:染色问题)含答案解析

小学奥数练习卷(知识点:染色问题)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.选择题(共5小题)1.连接正方形ABCD的对角线,并将四个顶点分别染成红色或黄色,将顶点颜色全相同的三角形称为同色三角形,则图中有同色三角形的染色方法共有()A.12B.17C.22D.102.由210块小正方体构成5×6×7的长方体,如果将其表面涂成红色,那么其中一面涂红的小正方体有()块,两面涂红的小正方体有()块.A.92,48B.94,48C.90,50D.94,463.一个由边长为1的小正方形组成的n×n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个角上的小正方形不全同色,那么正整数n的最大值是()A.3B.4C.5D.64.如图,一块草地被开垦出11块正六边形耕地,菲菲在这些耕地内种植向日葵、豌豆射手、闪电芦苇、冰冻西瓜4种植物,如果相邻的耕地种植的植物不能相同,她有()种不同的种植办法.(相邻耕地是指有公共边,每块耕地内只能种植一种植物)A.6912B.6144C.4608D.42245.将一个大三角形分割成36 个小三角形,并且将其中一部分小三角形涂成红色,另一部分涂成蓝色,并且使得两个有公共边的三角形的颜色不同,如果红色的三角形比蓝色的多,那么多()个.A.1B.4C.6D.7第Ⅱ卷(非选择题)二.填空题(共37小题)6.把一个正方体的表面积全涂成黑色,然后切成27个小正方体(如图),那么两面是黑色的小正方体共有个.7.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要种颜色.8.一个长方体的棱长都是整数,表面涂上色后,切成棱长为1的正方体,若没有颜色的小正方体共有12个,则一面有色的正方体最少有个.9.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要种颜色.10.一个宝库有9个藏宝室,成九宫格状排列,但只有一个进口和一个出口分别开在如图所示的藏宝室,每个藏宝室至多只能进去一次,相邻的藏宝室之间都有门相通,每个藏宝室中的宝贝价值已标在图中,大盗买通守护,夜间进入宝库,他能带走的宝物价值最多是.11.如图是一个由26个相同的小正方体堆成的几何体,它的底层由5×4个小正方体构成,如果把它的外表面(包括底面)全部涂成红色,那么当这个几何体被拆开后,有3个面是红色的小正方体有块.12.如图所示,用64个棱长为1的小立方体组成一个棱长为4的大立方体,再从上到下取走4个小立方体(图中阴影部分).将剩余立体图形的内外表面都染成红色,那么恰有两个面染色的小立方体共有个.13.一个5×5的方格由25个1×1的小方格组成,每个小方格都被分成四个相同的等腰直角三角形,其中三个被涂成了黑色(如图a所示).小正方形的边如果位于黑色部分,就称为黑边,反之就是白边.在5×5的方格内,相邻(有公共边)小方格的公共边必须是同色的,那么5×5方格的四条长边(如图b 所示)上最少有条黑边.14.将一个8×8×8的立方体的三个面染红色,三个面染蓝色(要求任意三个有公共顶点的面不能全都染同一种颜色),然后将其切割成512个1×1×1的小立方体.这512个小立方体中,有个小立方体上既有红色面又有蓝色面.15.如图,5×5的方格中有三个小方格已经染黑.现在要将一个1×3的白长方形(不能选已经染黑的方格)染黑,要求其不能与已经染黑的方格产生公共边或者公共点.有种选法.16.这是一个由72个相同小四边形组成的图形,有一些四边形被病毒感染变成黑色.当某个健康的小四边形(白色),其周围至少有两个相邻的小四边形被感染时,则该四边形也将被感染变黑,依次扩散开来.那么至少再增加个病毒源(即黑色小四边形),可以使整个大图形都被感染.(相邻是指两个小四边形有公共边).17.将一个4×4×4的立方体切割成64个1×1×1的小立方体,然后将其中16个1×1×1的小立方体染成红色,要求与任意一条棱平行的4个小立方体中,都正好有1个小正方体被染成红色,不同的染色方法有种(旋转后相同的染色方法也视为不同的染色方法).18.小明想要对图中的每个小三角形进行染色,要求任意一个三角形的三边都是一条染红色、一条染绿色、一条染蓝色.图中给出了某些边的颜色,则AB边应该染色.19.如图是一个被挖空的长方体,每个洞都是贯穿的,如果把它丢进染缸里,4个面染色的小正方体比3个面染色的小正方体多个.20.如图,一个长方形的表格有8列,将数字1,2,…按一定顺序填入表格中(从左往右填,等一行填满后进入下一行,还是从左往右填),一个学生先将填有数字1的格子涂黑,接下来跳过1个格子,将填有数字3的格子涂黑;接下来跳过2个格子,将填有数字6的格子涂黑;接下来跳过3个格子,将填有数字10的格子涂黑.依此类推,直到所有列都含有至少一个黑格为止(不再继续涂黑了).那么,他涂黑的最后一个格子里的数字为.21.将1,2,3,4,5填入如图表格中(表中的字母和数字用来标注行、列或者小方格,比如D3就表示D行3列那个白色小方格),要求每行每列上的五个数互不相同,接下来给出一些提示:(1)第4列的黑色小方格内的数之和为9;(2)第C行的黑色小方格内的数之和为7;(3)第2列的白色小方格内的数之和为8;(4)第B行的黑色小方格内的数之和小于第D行的黑色小方格内的数之和.则D4中填的数字为.22.图中的网格是由6个相同的小正方形构成,将其中4个小正方形涂上灰色,要求每行每列都有涂色的小正方形,经旋转后两种涂色的网格相同,则视为相同的涂法,那么有种不同的涂色方法.23.如图所示的多面体叫做正二十面体,是5个柏拉图立体(正多面体)中的一个,这个多面体由20个面(正三角形)围成,现将这20个面着色,要求有共同棱的两个面染有不同的颜色,则至少需要种颜色.24.由一些顶点和边构成的图形称为一个图,对一个图用不同颜色给顶点染色,要求具有相同边的两个顶点染不同的颜色.称为图的点染色,图的点染色通常要研究的问题是完成染色所需要的最少的颜色数,这个数称为图的色数.如图的图称为皮特森图,皮特森图的色数为.25.一块长、宽、高分别为15cm、12cm、9cm的长方体木块表面涂上红色后,将它切成大小相等的正方体且没有废料,至少可以切块,其中六个面都没有涂上红色的正方体有块.26.把一个棱长为n的大正方体表面涂上红色,然后切成n3个棱长为1的小正方体,经统计,恰好有一面涂红色的小正方体数量刚好是有三面涂红色的小正方体的12倍,那么n=.27.七个正方形拼成如图,我们要对其中的若干个正方形进行涂色,要求:(1)至少涂其中的两个正方形;(2)相邻正方形不能同时被涂色(有公共边或者公共顶点的正方形称为相邻正方形).那么,有种不同的涂色方法.28.我们有27个1×1×1的小立方体,将其拼成一个3×3×3的大立方体,其中的一些小立方体的某些面被涂成了灰色,最后拼成的大立方体如图所示,那么,六个面都是白色的小立方体最多有个.29.图2的8×8表格中共含有168个如图1的“T”形.现对图2中的每个小方格染成黑色或白色;如果一个“T”形中黑白小方格各2个,则称这个“T”形为“和谐”的;那么对图2的各种染色方案,“和谐”的“T”形至多有个.30.将图中的边染色,要求有共同顶点的两个相邻的边染不同的颜色,则至少需要中颜色.31.四个黑色1×1×1的正方体和四个白色1×1×1的正方体可以组成种不同的2×2×2的正方体(经过旋转得到相同的正方体视为同一种惰况).32.一个大正方形表面涂上红色后,按如图方式切成27个小正方形,这些小正方形中,恰好有三个面涂有红色的有个.33.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则至少需要种颜色.34.有9个表面涂有红漆的正方体,它们的棱长分别是2,3,4,…,9,10.将这些正方体都锯成棱长是1 的小正方体,在得到的小正方体中,至少有一个面是红色的有个.35.用1024个棱长是1的小正方体组成体积是1024的一个长方体.将这个长方体的六个面都涂上颜色,则六个面都没有涂色的小正方体最多有个.36.如图是64个小正方体组成的大正方体,把它的表面全部涂上绿色,请回答:三面涂上绿色的小正方体有个.没有涂上绿色的小正方体有个.两面涂上绿色的小正方体有个.37.将图中的圆圈染色.要求有连线的两个相邻的圆圈染不同的颜色,则最少需要种颜色.38.36个相同的小正方体叠成如图所示的长方体,取走A、B、C三个小正方体后,在这个几何体的整个表面涂满红漆,其中有个正方体是三面有漆的.39.x是一个正整数,将x×4×5的长方体的表面涂满红色后,锯成棱长全部是1的小正方体.这些正方体中,至少有一面是红色的小正方体有110个.那么,x=.40.由四个完全相同的正方体堆积成如图所示的立体,则立体的表面上(包括底面)所有黑点的总数至少是个.41.把一个大长方体表面涂满红色后,分割成若干个同样大小的长方体,其中只有两个面涂上红色的小长方体恰好是12块,那么可以把这个大长方体分割成个小长方体.A.20个B.27个C.32个D.42个.42.如图是一个变形的红十字一共分为六块区域.现在要用n种颜色对其染色,要求相邻的两块区域(有公共边的两块区域称为相邻)染成不同的颜色.如果颜色能反复使用,那么一共有种不同的染色方法(用n表示).三.解答题(共8小题)43.将图中的O分别涂成红色、黄色或绿色,要求有线段相连的两个相邻O涂不同的颜色,共有多少种不同的涂法?44.7×7的方格黑白染色,如果黑格比白格少的列的个数为m,黑格比白格多的行的个数为n,求m+n的最大值.45.如图是一个等边三角形,等分为4个小的等边三角形,用红和黄两种颜色涂染它们的顶点,要求每个顶点必须涂色,且只能涂一种颜色.涂完后,如果经过旋转,等边三角形的涂色相同,则认为是相同的涂色,则共有多少种不同的涂法?46.三阶魔方的国际标准配色:白顶黄底,绿前蓝后,橙左红右.现在规定:白色═1,黄色═2,绿色═3,蓝色═4,橙色═5,红色═6.一个复原状态三阶魔方放在桌面上(如图1所示),今天这个魔方按照动态图片的方式打乱,最终变成图2的形态.此时图片中可以看到7个角块,那么看不到的那一个角块儿中与桌面完全接触的颜色代码是.47.用红、绿、蓝三种颜色涂正八面体(如图)的八个面,要求相邻面涂不同的颜色(有一条公共棱的面称为相邻面),一共有多少种不同的涂色方法?(旋转后相同的视为同一种涂色方法)48.下面是一张把4×6的方格纸去掉两个角所得的图形.(1)请把其中的一些格子涂上阴影,使得每个1×2小长方形(不论横竖)的2个方格中都恰有1个阴影方格和1个空白方格;(2)能否用11个1×2小长方形恰好拼满这张方格纸?如果能,请给出一种方法;如果不能,请说明理由.49.将每个最简分数(其中m,n 互质的非零自然数)染成红色或蓝色,染色规则如下:(1)将1染成红色;(2)相差为1的两个数颜色不同,(3)不为1的数与其倒数颜色不同.问:和分别染成什么颜色?50.在给你的卡纸上画有分别由1、2、3、4、5、6、7、8个小正三角形组成的8块拼板,并涂上黑、白两种颜色.(1)请你把这8块拼板剪下并拼成图1所示大的正三角形,且小三角形间的黑、白两种颜色必须相间.请在图1中用粗线条直接画出拼法,并标上每块拼板的标号.(2)图1的三角形金字塔我们称其为边长为6的金字塔(计每个小正三角形的边长为1).图1金字塔中有个如图2所示的菱形.(注意,只要和图2中的形状一样即可,可旋转.)(3)是否存在整数n,使得边长为n的金字塔中菱形的个数为2012202201220132如果存在,请求出n;如果不存在,请证明.参考答案与试题解析一.选择题(共5小题)1.连接正方形ABCD的对角线,并将四个顶点分别染成红色或黄色,将顶点颜色全相同的三角形称为同色三角形,则图中有同色三角形的染色方法共有()A.12B.17C.22D.10【分析】本题考察染色问题.【解答】解:全部为红色或全部为黄色,2种;三红一黄或者三黄一红,4×2=8种,所以有同色三角形的染色方法有2+8=10(种),故选:D.【点评】本题只需简单分类进行枚举即可.2.由210块小正方体构成5×6×7的长方体,如果将其表面涂成红色,那么其中一面涂红的小正方体有()块,两面涂红的小正方体有()块.A.92,48B.94,48C.90,50D.94,46【分析】根据立体图形切拼可知:三个面均为红色的是各顶点处的小正方体,在各棱处,除去顶点处的正方体的有两面红色,在每个面上,除去棱上的正方体都是一面红色,所有的小正方体的个数减去有红色的小正方体的个数即是没有涂色的小正方体.根据上面的结论,即可求得答案.【解答】解:一面涂红的小正方体在每个面的中间,有:5﹣2=3(块),6﹣2=4(块),7﹣2=5(块)(3×4+3×5+4×5)×2=47×2=94(块)两面涂红的小正方体在12条棱的中间部分(除去顶点),有:(3+4+5)×4=12×4=48(块)答:其中一面涂红的小正方体有94块,两面涂红的小正方体有48块.故选:B.【点评】关键是理解正方体表面涂色的特点,知道切割后的小正方体涂色面的排列特点.注意数形结合与正方体表面涂色的特点的应用.3.一个由边长为1的小正方形组成的n×n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个角上的小正方形不全同色,那么正整数n的最大值是()A.3B.4C.5D.6【分析】此题要充分利用抽屉原理和假设推理.根据题目所给的选项不妨选一个中间的数5为假设n的值,进行一步步地推理,进而推出与题目要求矛盾.从而得出n的取值范围,即得出答案.【解答】解:①假设n=5,(由抽屉原理知)第一行中至少有3个格子颜色相同.不妨设前3格为黑色(如图1).在这3个黑格下方可以分割为4个横着的3×1的长方形,若其中有一个中有2个黑格(如图2),则存在着图中的粗线长方形4个角上的小正方形都是黑格;所以这4个横着的3×1的长方形中,每个至多1个黑格.②假设这4个横着的3×1的长方形中,有两个对应格子颜色都一样(如图3),则一样存在图中的粗线长方形4个角上的小正方形都是白格;而3×1的长方形中至多1个黑格的只有如图4的这4种.如果这4种都存在的话如图5,则同样存在图中粗线长方形4个角上的小正方形都是白格;这均与题目要求的矛盾.所以,n<5,正整数n的最大值是4.而图6给出了n=4的一种构造.故选:B.【点评】对于选择题(特别是类似本题的),我们可以用题目选项所给答案进行推理,而选项正确的答案.4.如图,一块草地被开垦出11块正六边形耕地,菲菲在这些耕地内种植向日葵、豌豆射手、闪电芦苇、冰冻西瓜4种植物,如果相邻的耕地种植的植物不能相同,她有()种不同的种植办法.(相邻耕地是指有公共边,每块耕地内只能种植一种植物)A.6912B.6144C.4608D.4224【分析】由题意,菲菲在这些耕地内种植向日葵、豌豆射手、闪电芦苇、冰冻西瓜4种植物,相邻的耕地种植的植物不能相同,如图所示,发现阴影六边形一圈是关键,中间选好种后,求出中间一圈3×25×[3×24﹣(3×23﹣3×2×1)]=66,即可得出结论.【解答】解:如图所示发现阴影六边形一圈是关键,中间选好种后,周围一圈3种植物,3×25﹣(A、F同色,相当于5个围一圈),5个围一圈=3×24﹣(4个围一圈),4个围一圈=3×23﹣(3个围一圈),3个围一圈=3×2×1=6,中间一圈3×25×[3×24﹣(3×23﹣3×2×1)]=66,所以总共有4×66×24=4224(种)故选:D.【点评】本题考查染色问题.分情况讨论,发现阴影六边形一圈是关键.5.将一个大三角形分割成36 个小三角形,并且将其中一部分小三角形涂成红色,另一部分涂成蓝色,并且使得两个有公共边的三角形的颜色不同,如果红色的三角形比蓝色的多,那么多()个.A.1B.4C.6D.7【分析】按题目要求来涂色的话,只有1 种涂法:红色比蓝色多:(1+2+3+4+5+6)﹣(1+2+3+4+5)=6个.【解答】解:根据分析,按题目要求来涂色的话,只有1 种涂法,如图:红色比蓝色多:(1+2+3+4+5+6)﹣(1+2+3+4+5)=6个.故选:C.【点评】本题考查染色问题,突破点是:逆向思维,推出按题意要求来染色只有一种符合条件,从而得出红色比蓝色的个数.二.填空题(共37小题)6.把一个正方体的表面积全涂成黑色,然后切成27个小正方体(如图),那么两面是黑色的小正方体共有12个.【分析】根据正方体表面涂色的特点,分别得出切割后的小正方体涂色面的排列特点:(1)三面涂色的在每个顶点处;(2)两面涂色的在每条棱长上(除去顶点处的小正方体);(3)一面涂色的都在每个面上(除去棱长上的小正方体);(4)没有涂色的都在内部.【解答】解:两面涂色的在每条棱长上(除去顶点处的小正方体),有:(3﹣2)×12=12(个)故答案为:12.【点评】解决此类问题的关键是抓住:三面涂色的在顶点处;两面涂色的在每条棱长的中间上;一面涂色的在每个面的中心上;没有涂色的在内部.7.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要4种颜色.【分析】要保证使用的颜色最少,则两个相邻的圆圈的颜色要尽可能多的相同,尝试2种颜色和3种颜色都不行,需要4种颜色,据此解答即可.【解答】解:尝试2种颜色和3种颜色都不行,需要4种颜色,如下图:【点评】本题考查染色问题.8.一个长方体的棱长都是整数,表面涂上色后,切成棱长为1的正方体,若没有颜色的小正方体共有12个,则一面有色的正方体最少有32个.【分析】设把表面涂色的小正方形去了,得到的长方体的长、宽、高分别为a、b、c,由题意abc=12,分有四种情形求解即可.【解答】解:设把表面涂色的小正方形去了,得到的长方体的长、宽、高分别为a、b、c,由题意abc=12,有四种情形:①1×1×12时,一面有色的正方体有2(1×1+1×12+1×12)=50个,②1×2×6时,一面有色的正方体有2(1×2+1×6+2×6)=40个,③1×3×4时,一面有色的正方体有2(1×3+1×4+3×4)=38个,④2×2×3时,一面有色的正方体有2×(2×2+2×3+2×3)=32个,综上所述,一面有色的正方体最少有32个.故答案为32.【点评】本题考查染色问题,记住长方体(a×b×c)的染色规律:①3面染色的有8个(与长方体的顶点有关);②2面染色的有4[(a﹣2)+(b﹣2)+(c ﹣2)]个(与长方体的棱长有关);③1面染色的有2[(a﹣2)(b﹣2)+(a ﹣2)(c﹣2)+(b﹣2)(c﹣2)]个(与长方体的表面积有关);④0面染色的有(a﹣2)(b﹣2)(c﹣2)个(与长方体的体积有关);9.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要2种颜色.【分析】可以用不同的字母或数字表示不同的颜色,在图中进行标示,本题要求是有线段相连的两个圆圈颜色不同.【解答】解:用字母A、B、C…表示不同的颜色,先在左上角的圆圈填入A,为了使用的颜色种类尽量少,下一步在与它相连的三个圆圈都填入B,最后得到下面的涂色方法:共使用了2种颜色.故本题答案为:2.【点评】简单涂色类题目可以用标字母的方法,方便分析和解答.10.一个宝库有9个藏宝室,成九宫格状排列,但只有一个进口和一个出口分别开在如图所示的藏宝室,每个藏宝室至多只能进去一次,相邻的藏宝室之间都有门相通,每个藏宝室中的宝贝价值已标在图中,大盗买通守护,夜间进入宝库,他能带走的宝物价值最多是39.【分析】本题首先能想到根据染色问题进行分析,可将房间黑白相间染色,根据进口和出口所染颜色不同可知大盗应该经过了偶数个房间,因此最多经过8个房间,据此解答.【解答】解:借助染色解题,给3×3的方格黑白相同染色(如图),进口为黑格,若全部走完9个方格,出口应为黑格,而图中出口为白格,故至少有一个黑格不能走到,标数最小的(进口除外)应为6,即标6的房间无法进入,所以大盗能带走的宝物最多是45﹣6=39.故答案为:39.【点评】本题的突破口在于能用染色的方法进行解题,难度较大.11.如图是一个由26个相同的小正方体堆成的几何体,它的底层由5×4个小正方体构成,如果把它的外表面(包括底面)全部涂成红色,那么当这个几何体被拆开后,有3个面是红色的小正方体有14块.【分析】首先分析染色的方法,3个面的红色的上层的角块和下层的边块是符合条件的.【解答】解:依题意可知:第一层的共有4个角满足条件.第二层的4个角是4面红色,去掉所有的角块其余的符合条件.分别是3+2+3+2=10(个);共10+4=14(个);故答案为:14【点评】本题考查对染色问题的理解和运用,关键是底面边长不同计算时要分开计算.同时注意底面是涂色的,问题解决.12.如图所示,用64个棱长为1的小立方体组成一个棱长为4的大立方体,再从上到下取走4个小立方体(图中阴影部分).将剩余立体图形的内外表面都染成红色,那么恰有两个面染色的小立方体共有28个.【分析】首先分析棱上的小块,面上的除了空心通道以外其他是没有的,空心通道的数字计算出来相加即可.【解答】解:依题意可知:在大正方体的棱上的,上下各有6个,侧面棱上8个,棱上共20个.空心通道产生的上下各有2个,通道内有4个共8个.共20+8=28(个).故答案为:28.【点评】本题考查对染色问题的理解和运用,关键问题是从棱上分析再分析空心通道即可,问题解决.13.一个5×5的方格由25个1×1的小方格组成,每个小方格都被分成四个相同的等腰直角三角形,其中三个被涂成了黑色(如图a所示).小正方形的边如果位于黑色部分,就称为黑边,反之就是白边.在5×5的方格内,相邻(有公共边)小方格的公共边必须是同色的,那么5×5方格的四条长边(如图b 所示)上最少有5条黑边.【分析】由题意,角上的小方格每个有2条边在外面,故其中至少有1条是黑边,这样5×5方格的四条长边上,黑边不少于1×4=4条.再判断内部的黑边的条数为偶数,则四条长边上的黑边的条数为奇数,所以5×5方格的四条长边上,黑边不少于5条.【解答】解:由题意,角上的小方格每个有2条边在外面,故其中至少有1条是黑边,这样5×5方格的四条长边上,黑边不少于1×4=4条.每个小方格有3条黑边,5×5=25个小方格一共有3×25=75条黑边,而在5×5方格内,相邻(有公共边)小方格的公共边必须是同色的,故内部的黑边的条数为偶数,则四条长边上的黑边的条数为奇数,所以5×5方格的四条长边上,黑边不少于5条,如图所示为5×5方格的四条长边上有5条黑边的例子,综上所述,5×5方格的四条长边(如图b所示)上最少有5条黑边.故答案为5.。
小学奥数专题15:染色问题
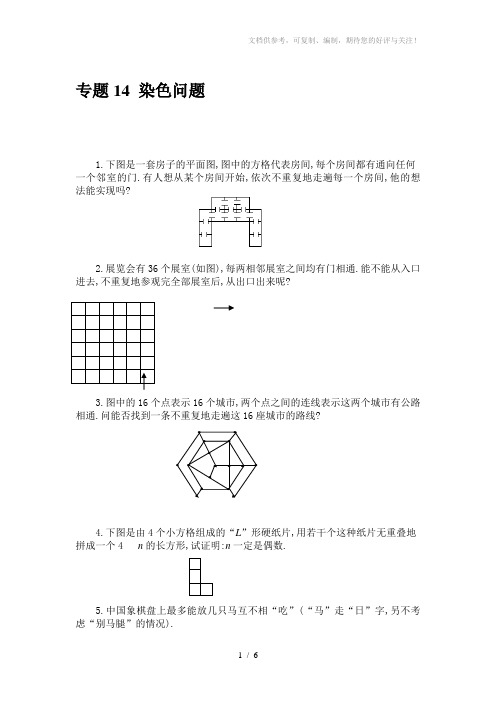
专题14 染色问题1.下图是一套房子的平面图,图中的方格代表房间,每个房间都有通向任何 一个邻室的门.有人想从某个房间开始,依次不重复地走遍每一个房间,他的想法能实现吗?2.展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入口 进去,不重复地参观完全部展室后,从出口出来呢?3.图中的16个点表示16个城市,两个点之间的连线表示这两个城市有公路 相通.问能否找到一条不重复地走遍这16座城市的路线?4.下图是由4个小方格组成的“L ”形硬纸片,用若干个这种纸片无重叠地 拼成一个4n 的长方形,试证明:n 一定是偶数.5.中国象棋盘上最多能放几只马互不相“吃”(“马”走“日”字,另不考虑“别马腿”的情况).6.能否用一个田字和15个41矩形覆盖88棋盘?7.能否用1个田字和15个T 字纸片,拼成一个88的正方形棋盘?8.在88棋盘上,马能否从左下角的方格出发,不重地走遍棋盘,最后回到起点?若能请找出一条路,若不能,请说明理由.9.下面三个图形都是从44的正方形分别剪去两个11的小方格得到的,问可否把它们分别剪成12的七个小矩形? (1) (2) (3)10.把三行七列的21个小格组成的矩形染色,每个小格染上红、蓝两种色中的一种.求证:总可以找到4个同色小方格,处于某个矩形的4个角上(如图)红 红 红 红11.17个科学家互相通信,在他们的通信中共讨论3个问题,而任意两个科学家之间仅讨论1个问题.证明:至少有3个科学家,他们彼此通信讨论的是同一个问题.12.用一批124的长方体木块,能不能把一个容积为666的正方体木箱充塞填满?说明理由.13.在平面上有一个2727的方格棋盘,在棋盘的正中间摆好81枚棋子,它们被罢成一个99的正方形.按下面的规则进行游戏:每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子,放进紧挨着这枚棋子的空格中,并把越过的这格棋子取出来.问:是否存在一种走法,使棋盘上最后恰好剩下一枚棋子?14.1212的超极棋盘上,一匹超级马每步跳至34矩形的另一角(如图).问能否从任一点出发遍历每一格恰一次,再回到出发点(这种情况又称马有“回 O12 3O———————————————答案——————————————————————1. 不能.对房间染色,使最下面的两个房间染成黑色,与黑色相邻的房染成白色,则图中有7个黑色房间和5个白色房间.如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.2. 不能.对展室进行染色,使相邻两房间分别是黑色和白色的.此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个展室,入口与出口展室的颜色应该不相同.3. 不能.对这16个城市进行黑白相间的染色,一种颜色有9个,另一种颜色有7个.而要不重复地走遍这16个城市,黑色与白色的个数应该相等.4. 如图,对4n长方形的各列分别染上黑色和白色.任一L形纸片所占的方格只有两类:第一类占3黑1白,第二类占3白1黑.n个设第一类有a个,第二类有b个,因为涂有两种颜色的方格数相等,故有3b+a=3a+b,即a=b,也就是说第一类与第二类相等,因此各种颜色的方格数都是4的倍数,总数是8的倍数,从而n是偶然.5. 将棋盘黑白相间染色,由“马”的走法可知,放在黑点上的“马”,只能吃放在某些白点上的马.整个棋盘上黑、白点的个数均为45,故可在45个黑点放上马,它们是不能互吃的.6. 如图的方式对棋盘染色.那么一个田字形盖住1个或3个白格,而一个41的矩形盖住2个白格.这样一来一个田字和15个41的矩形能盖住的白格数是一个奇数,但上图中的白格数是一个偶数,因此一个田字形和15个41.7. 将棋盘里黑白相间涂色.一个田字形盖住2个白格,一个T字形盖住3个或1个白格.故1个田字和15个T字盖住的白格数是一个奇数,但棋盘上的白格数是一个偶数.因此一个田字形和15个T字形不能盖住88的棋盘.8. 将棋盘黑白相间地染色后,马的走法是从一种颜色的格子跳到另一种颜色.棋盘上有32个白格与32个黑格,故马可能跳遍整个棋盘.图中给出了一种走法.56 41 58 35 50 39 60 3347 44 55 40 59 34 51 3842 57 46 49 36 53 32 6145 48 43 54 31 62 37 5220 5 30 63 22 11 16 1329 64 21 4 17 14 25 106 19 2 278 23 12 151 28 7 18 3 26 9 249. 先对44的棋盘黑白相间的涂色(如图),这道题的实际问题是问7个12矩形能否分别复盖剪去A、B;剪去A、C;剪去A、D的三个棋盘.若7个12矩形可以复盖剪残的棋盘,因为每个12矩形均可盖住一个白格和一个黑格,所以棋盘的白格与黑格数目应该相等.都是7个.而剪去A格和C格的棋盘(2)有5个白格8个黑格,剪去A、D的棋盘(3)有5个白格8个黑格,因此这两个剪损的棋盘均不能被7个12矩形复盖,也就不能剪成7个12的矩形. ABCD棋盘(1)可以被7个12的矩形所复盖.下面给出一种剪法:A 1 1 27 7 B 26 5 4 36 5 4 310. 在第一行的7格中必有4格同色,不妨设这4格位于前4个位置,且均为红色.然后考虑前4列构成的34矩形.若第二行和第3行中出现2个或2个以上的红色格子.则该行的两个红色格子与第一行的红色格子就组成一个4角同为红色格子的矩形.若不然,则第2、3行中都至少有3个蓝格在前4列中,不妨设第2行前3格为蓝色,显然第三行中的前3格中至少有2个蓝格,故在二、三行的前4列中必存在四角都是蓝色的矩形.11. 将17个科学家用17个点代表,两点之间连结的线段表示两个科学家之间讨论的问题.用三种颜色给这些线段染色,表示三个问题,于是问题就变成:给17个点之间的所有连结线段用三种颜色染色,必有同色三角形.从任意一点,不妨设从A 向其他16点A 1,A 2,…A 16共可连成16条线段,用三种颜色染色,由抽屉原则可知,必有6条线段同色.设这6条线段为AA 1,AA 2,…AA 6且同为红色.考虑A 1,A 2,A 3,A 4,A 5,A 6这六点之间的连线,若有一条为红色,(如A 1A 2为红色) ,则三角形AA 1A 2为红色的同色三角形.若这六点之间的连线中,没有一条是红色的,则它们之间只能涂两种颜色.考虑从A 1引出的五条线段A 1A 2 A 1A 3 A 1A 4 A 1A 5 A 1A 6,由抽屉原理知,其中必有三条是同色的.不妨设这三条为A 1A 2 A 1A 3 A 1A 4,且同为蓝色.若三角形A 2A 3A 4的三边中有一条为蓝色的,则有一个蓝色的三角形存在;若三角形A 2A 3A 4三边都不是蓝色的,则它的三边是同为第三色的同色三角形.12. 把正方体木箱分成27个小正方体,每个小正方体的体积为222=8.将这些正方体如右图黑白相间染上色.显然黑色222的正方体有14个,白色222小正方体有13个.每一个这样的正方体相当于8个111的小正方体.将124的长方体放入木箱,无论怎么放,每个长方体木块盖住8个边长为1的单位正方体,其中有4个黑色的,4个白色的.木箱共含666=216个单位正方体,26个长方体木块共盖住826=208个单位正方体,其中黑白各占104个,余下216-208=8个单位正方体是黑色的.但是第27个124长方体木块不管怎样放,也无法盖住这8个黑色单位正方体.13. 如图,将整个棋盘的每一格都分别染上红、白、黑三种颜色,这种染色方式将棋盘分成了三个部分.按照游戏规则,每走一步,有两种颜色方格中的棋子数分别减少了1个,而第三种颜色的棋子数增加了一个.这表明每走一步,每个部分的棋子的奇偶性要发生改变.AA 1 A 2A 3A 4A 5 A 6 A 1A 2 A 3 A 4因为一开始时,81枚棋子摆成一个99的正方形,显然三个部分的棋子数是相同的,从而每走一步,三部分中的棋子数的奇偶性是相同的.如果走了若干步以后,棋盘上恰好剩下一枚棋子,则两部分上的棋子数为偶数,而另一部分上的棋子数为奇数.这种结果是不可能出现的.14. 用两种方法对超级棋盘染色.首先,将棋盘黑白相间染色,则马每跳一步,它所在的方格就要改变一次颜色.不妨设第奇数步跳入白格.其次,将棋盘的第3,4,5及8,9,10这六行染成黑色,其余六行染成白色.在此种染色方式下,马从白格一定跳入黑格.又因黑白格总数相同,马要遍历每一格恰一次又回到出发点,因此,马从黑格只能跳入白格而不能跳入黑格.不妨设马第奇数步跳入白格.但是对于一种满足要求跳法,在两种染色方式下第奇数步跳入的格子的全体是不同的,这显然是不可能的,故题目要求的跳法是不存在的.。
小学奥数专题15:染色问题

专题14 染色问题1.下图是一套房子的平面图,图中的方格代表房间,每个房间都有通向任何 一个邻室的门.有人想从某个房间开始,依次不重复地走遍每一个房间,他的想法能实现吗?2.展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入口 进去,不重复地参观完全部展室后,从出口出来呢?3.图中的16个点表示16个城市,两个点之间的连线表示这两个城市有公路 相通.问能否找到一条不重复地走遍这16座城市的路线?4.下图是由4个小方格组成的“L ”形硬纸片,用若干个这种纸片无重叠地 拼成一个4 n 的长方形,试证明:n 一定是偶数.5.中国象棋盘上最多能放几只马互不相“吃”(“马”走“日”字,另不考虑“别马腿”的情况).6.能否用一个田字和15个4⨯1矩形覆盖8⨯8棋盘?7.能否用1个田字和15个T 字纸片,拼成一个8⨯8的正方形棋盘?8.在8⨯8棋盘上,马能否从左下角的方格出发,不重地走遍棋盘,最后回到起点?若能请找出一条路,若不能,请说明理由.9.下面三个图形都是从4⨯4的正方形分别剪去两个1⨯1的小方格得到的,问可否把它们分别剪成1⨯2的七个小矩形?10.把三行七列的21个小格组成的矩形染色,每个小格染上红、蓝两种色中的一种.求证:总可以找到4个同色小方格,处于某个矩形的4个角上(如图)11.17个科学家互相通信,在他们的通信中共讨论3个问题,而任意两个科学家之间仅讨论1个问题.证明:至少有3个科学家,他们彼此通信讨论的是同一个问题.12.用一批1⨯2⨯4的长方体木块,能不能把一个容积为6⨯6⨯6的正方体木箱充塞填满?说明理由.13.在平面上有一个27⨯27的方格棋盘,在棋盘的正中间摆好81枚棋子,它们被罢成一个9⨯9的正方形.按下面的规则进行游戏:每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子,放进紧挨着这枚棋子的空格中,并把越过的这格棋子取出来.问:是否存在一种走法,使棋盘上最后恰好剩下一枚棋子?14.12⨯12的超极棋盘上,一匹超级马每步跳至3⨯4矩形的另一角(如图).问能否从任一点出发遍历每一格恰一次,再回到出发点(这种情况又称马有“回12 3———————————————答 案——————————————————————1. 不能.对房间染色,使最下面的两个房间染成黑色,与黑色相邻的房染成白色,则图中有7个黑色房间和5个白色房间.如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.2. 不能.对展室进行染色,使相邻两房间分别是黑色和白色的.此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个展室,入口与出口展室的颜色应该不相同.3. 不能.对这16个城市进行黑白相间的染色,一种颜色有9个,另一种颜色有7个.而要不重复地走遍这16个城市,黑色与白色的个数应该相等.4. 如图,对4⨯n 长方形的各列分别染上黑色和白色.任一L 形纸片所占的方3黑1白,第二类占3白1黑.设第一类有a 个,第二类有b 个,因为涂有两种颜色的方格数相等,故有3b +a =3a +b ,即a =b ,也就是说第一类与第二类相等,因此各种颜色的方格数都是4的倍数,总数是8的倍数,从而n 是偶然.5. 将棋盘黑白相间染色,由“马”的走法可知,放在黑点上的“马”,只能吃放在某些白点上的马.整个棋盘上黑、白点的个数均为45,故可在45个黑点放上马,它们是不能互吃的.6. 如图的方式对棋盘染色.那么一个田字形盖住1个或3个白格,而一个4⨯1的矩形盖住2个白格.这样一来一个田字和15个4⨯1的矩形能盖住的白格数是一个奇数,但上图中的白格数是一个偶数,因此一个田字形和15个4⨯1的矩形n 个7. 将棋盘里黑白相间涂色.一个田字形盖住2个白格,一个T字形盖住3个或1个白格.故1个田字和15个T字盖住的白格数是一个奇数,但棋盘上的白格数是一个偶数.因此一个田字形和15个T字形不能盖住8⨯8的棋盘.8. 将棋盘黑白相间地染色后,马的走法是从一种颜色的格子跳到另一种颜色.棋盘上有32个白格与32个黑格,故马可能跳遍整个棋盘.图中给出了一种走法.9. 先对4⨯4的棋盘黑白相间的涂色(如图),这道题的实际问题是问7个1⨯2矩形能否分别复盖剪去A、B;剪去A、C;剪去A、D的三个棋盘.若7个1⨯2矩形可以复盖剪残的棋盘,因为每个1⨯2矩形均可盖住一个白格和一个黑格,所以棋盘的白格与黑格数目应该相等.都是7个.而剪去A格和C格的棋盘(2)有5个白格8个黑格,剪去A、D的棋盘(3)有5个白格8个黑格,因此这两个剪损的棋盘均不能被7个也就不能剪成7个1⨯2的矩形.棋盘(1).下面给出一种剪法:10. 在第一行的7格中必有4格同色,不妨设这4格位于前4个位置,且均为红色.然后考虑前4列构成的3⨯4矩形.若第二行和第3行中出现2个或2个以上的红色格子.则该行的两个红色格子与第一行的红色格子就组成一个4角同为红色格子的矩形.若不然,则第2、3行中都至少有3个蓝格在前4列中,不妨设第2行前3格为蓝色,显然第三行中的前3格中至少有2个蓝格,故在二、三行的前4列中必存在四角都是蓝色的矩形.11. 将17个科学家用17个点代表,两点之间连结的线段表示两个科学家之间讨论的问题.用三种颜色给这些线段染色,表示三个问题,于是问题就变成:给17个点之间的所有连结线段用三种颜色染色,必有同色三角形.从任意一点,不妨设从A向其他16点A1,A2,…A16共可连成16条线段,用三种颜色染色,由抽屉原则可知,必有6条线段同色.设这6条线段为AA1,AA2,…AA6且同为红色.考虑A1,A2,A3,A4,A5,A6这六点之间的连线,若有一条为红色,(如A1A2为红色) ,则三角形AA1A2为红色的同色三角形.若这六点之间的连线中,没有一条是红色的,则它们之间只能涂两种颜色.考虑从A1引出的五条线段A1A2A1A3A1A4A1A5A1A6,由抽屉原理知,其中必有三条是同色的.不妨设这三条为A1A2A1A3A1A4,且同为蓝色.若三角形A2A3A4的三边中有一条为蓝色的,则有一个蓝色的三角形存在;若三角形A2A3A4三边都不是蓝色的,则它的三边是同为第三色的同色三角形.12. 把正方体木箱分成27个小正方体,每个小正方体的体积为2⨯2⨯2=8.将这些正方体如右图黑白相间染上色.显然黑色2⨯2⨯2的正方体有14个,白色2⨯2⨯2小正方体有13个.每一个这样的正方体相当于8个1⨯1⨯1的小正方体.将1⨯2⨯4的长方体放入木箱,无论怎么放,每个长方体木块盖住8个边长为1的单位正方体,其中有4个黑色的,4个白色的.木箱共含6⨯6⨯6=216个单位正方体,26个长方体木块共盖住8⨯26=208个单位正方体,其中黑白各占104个,余下216-208=8个单位正方体是黑色的.但是第27个1⨯2⨯4长方体木块不管怎样放,也无法盖住这8个黑色单位正方体.13. 如图,将整个棋盘的每一格都分别染上红、白、黑三种颜色,这种染色方式将棋盘分成了三个部分.按照游戏规则,每走一步,有两种颜色方格中的棋子数分别减少了1个,而第三种颜色的棋子数增加了一个.这表明每走一步,每个部.AA1 A2A3A4A5A6A1A2A3A4因为一开始时,81枚棋子摆成一个9 9的正方形,显然三个部分的棋子数是相同的,从而每走一步,三部分中的棋子数的奇偶性是相同的.如果走了若干步以后,棋盘上恰好剩下一枚棋子,则两部分上的棋子数为偶数,而另一部分上的棋子数为奇数.这种结果是不可能出现的.14. 用两种方法对超级棋盘染色.首先,将棋盘黑白相间染色,则马每跳一步,它所在的方格就要改变一次颜色.不妨设第奇数步跳入白格.其次,将棋盘的第3,4,5及8,9,10这六行染成黑色,其余六行染成白色.在此种染色方式下,马从白格一定跳入黑格.又因黑白格总数相同,马要遍历每一格恰一次又回到出发点,因此,马从黑格只能跳入白格而不能跳入黑格.不妨设马第奇数步跳入白格.但是对于一种满足要求跳法,在两种染色方式下第奇数步跳入的格子的全体是不同的,这显然是不可能的,故题目要求的跳法是不存在的.。
考题染色基本知识

考题染⾊基本知识第⼀章染⾊基本知识1. 什么叫染⾊?它的⽬的和要求是什么?2. 物体为什么会有颜⾊?物体具有颜⾊的基本条件是什么?3. 什么叫染⾊牢度?常见的染⾊牢度有哪些?4. 什么叫浸染?什么叫轧染?各适⽤于何种织物的染⾊?第⼆章染⾊基本理论1. 亲和⼒和直接性有何不同?2. 酸性染料染⽺⽑或聚酰胺纤维有⽆饱和值?⽤什么法其求出它?3. 何谓平衡吸附等温线?它分为哪⼏种类型?有何特点,⽅程式如何?4. 什么叫上染?上染过程分哪⼏个阶段?它和染⾊过程是否相同?5. 什么叫上染百分率?平衡上染百分率?它们在上染速率曲线上各有何特征?6. 染料在纤维中的扩散与染⾊效果有什么关系?影响扩散速率的因素有哪些?染料的扩散活化能⼤⼩对扩散有什么影响?7. 试从染料的扩散速率、扩散活化能以及平衡吸附等⽅⾯说明温度对上染的影响。
8. 什么扩散边界层?染⾊时染液的流动对其有何影响?9. 染料在⽔溶液中有⼏种存在形式?染⾊时染料是以何种形式上染⾊?10. 浓度、温度及中性电解质对染料在溶液中的聚集有何影响?11. 在⼀般上染过程中,△H0和△S0为何是负值?根据△H0、△S0和T的关系式,讨论染⾊温度T对平衡上染百分率的影响?12. 试说明某些酸性染料上染蛋⽩质纤维时,△S0为正值,即整个染⾊体系混乱度增加的原因。
13. 什么叫稳态扩散、⾮稳态扩散?写出对应的Fick扩散⽅程式及其物理意义。
14. 什么叫⽆限染浴、有限染浴?它们在染⾊过程中各有何特点?15. 什么叫半染时间?在不同的染⾊条件下,其变化和哪些因素有关?16. 何谓孔道扩散模型和⾃由体积扩散模型?根据其基本理论简述纤维微结构的差异对染料扩散速率的影响。
17. 什么叫初染率、移染性?染料的标准亲和⼒及染料的扩散性能对其有何影响?18. 为获得满意的染⾊效果,⼀般可通过哪些⼯艺条件来控制染料的上染速率。
19. 什么叫泳移、半匀染时间?第三章直接染料的染⾊1. 直接染料染⾊时加⼊中性电解质的作⽤是什么?说明其作⽤原理。
第四十六章染色与覆盖问题

第四十六章染色与覆盖问题概念本讲我们将一起学习染色与覆盖。
而这里所说的染色问题并不是要求如何染色,然后有多少种染色方法等数学问题。
而是一种解决逻辑推理题的一种方法,一种将研究对象分类的形象化的方法。
通过将要解决的问题适当的染色,可以使我们更形象的观察分析其中所蕴含的关系,在经过一定的推理从而得到问题的答案。
具体介绍:一、座位染色问题分析题中规定每个座位的前后左右都是他的邻座,那么35名同学每个人都恰好坐到它的邻座上能否办到?像这种问题我们该如何考虑呢?直接一步一步操作吗?很显然是很不现实的,那么有什么方法能让我们更直接的找到答案呢?染色。
我们将35个座位染成黑白相间的形式,一眼就能看出,每个黑色的座位都是白色座位的邻座,也就是说如果35名同学每个人都恰好能坐到它的邻座上,那么必然是,黑白位置对换,但从图中我们看到黑色17格,白色18格,黑白个数不相等,所以无法办到。
二、路径问题分析如果一次次的操作的话很难看出是否能够按要求办到。
所以我们按例1的方法,将9个小格染成黑白相间的颜色,很明显就能看出是不能办到的。
因为从A格出去,第一步不管往哪走都会走入黑格,接着第二步又都会走入黑格,即走奇数步后进黑格,偶数步后进白格,这个人若要从A格出去又要回到A格,必须走9个格,所以最后一格必为黑才可以,而A格为白格,所以不可以。
三、结点问题分析与路径问题相似,只不过我们这回染得不再是小格而是点,染成黑白相间的点。
我们会发现一共14个点,6个黑点8个白点,每次的路线仍是从黑点走到白点或者从白点走到黑点,所以若想每个点不重复的都走一遍的话必须黑白相等或相差1个,但本题黑白差2个,所以不可以。
四、一般覆盖将这14个小格染成黑白相间的,那么7个相邻两方格应该是一黑一白的,所以如果能覆盖的话,14个格中的黑白格数应该是相等的,但图中有8个黑格,6个白格。
所以不可以。
五、特殊覆盖分析因为每次有两个数同时加上或减去同一个数(假设次数为a),因此经过一次这样的操作后,相当于加上或减去了a的2倍,那么9个数总和就会多或者少偶数个数,也就是说9个数的总和为45,经过1次操作后总和加上或减去一个偶数后应该还是奇数,但表(2)中的总和是4,所以不可能。
染色物理化学考试题及答案

染色物理化学(复习)1.何谓染色化学位?染色亲和力?写出染色亲和力与染料活度的关系,分析染色温度与染色亲和力的关系,并举例说明。
2.何谓化学位?染色直接性?染色亲和力?染色热?染色熵和染色饱和值?分析染色亲和力与温度的关系,并写出分散染料染涤纶时染色亲和力与浓度的关系。
3.何谓上染率,固色率,半染时间,染色提升性,竟染和染色加和性?并说明在什么条件下,半染时间与扩散系数保持反比关系。
4.何谓自由焓?化学平衡,写出化学反应的等温方程式,分析温度对化学平衡常数的影响,并举例说明。
5.何谓染色熵?说明它与染色亲和力的关系,比较染料从水和有机溶剂染液中上染纤维时体系中熵的变化,并分析纤维及染料化学结构与染色熵的关系。
6.何谓染色热和染色熵?它们分别说明上染过程中的什么结果?并写出它们与亲和力的关系。
染料上染纤维的亲和力主要决定于谁?在什么条件下染色熵才愈来愈重要,为什么?7.何谓染色饱和值?超当量吸附?举例说明哪些纤维染色存在饱和值和超当量吸附,并分析出现超当量吸附的原因。
8.何谓上染百分率?扩散活化能?移染?染料染色配伍指数?染色饱和值和染色加和性。
9.何谓反应历程?何谓反应活化能?分析温度对反应速度的影响,如何简便地求出反应活化能。
10.何谓吸附等温线。
阳离子染料上染腈纶的吸附等温线属哪种。
指出这种吸附等温线的特征,染料在纤维中的状态。
选用什么性质的阳离子染料拼色才能获得均匀效果,解释之。
11.何谓吸附等温线?通常有几种类型?写出它们的数学关系式?说明不同类型的物理意义,分析阳离子染料上染腈纶的吸附等温线,有何特点。
12.分散染料上染合成纤维属哪类吸附等温线?解释其吸附物理意义,分析温度对其吸附等温线的影响,解释之。
13.分散染料染涤纶主要有哪几种方法?解释它的上染机理,写出吸附等温线,并分别指出各种方法的固色温度范围,解释固色温度不同的原因。
14.染料在纤维中扩散有几种模型。
亲水性纤维用离子性染料染色属哪种扩散模型。
高考生物基因的本质梳理汇总(新教材答案版)

第3章基因的本质第1节DNA是主要的遗传物质1.P42问题探讨20世纪中叶,科学家发现染色依主要是由蛋白质和DNA组成的。
在这两种物质中,完竞哪一种是遗传物质呢?这个问题曾引起生畅学界激烈的争论。
讨论:(1)你认为遗传物质可能具有什么特点?提示:遗传物质应能够储存大量的遗传信息,可以准确地复制,并传递给下一代,结构比较稳定,等等。
(2)你认为证明某一种物质是遗传物质的可行方法有哪些?提示; 这是一道开放性问题,答案并不唯一,只要提出正确的思路即可。
例如,将特定的遗传物质转移给其他生物,观察后代的性状表现,等等。
2.P46思考.讨论:证明DNA是遗传遗传物质的实验(1)艾弗里与赫尔希等人选用细菌或病毒作为实验材料,以细菌或病每作为实验材科具有哪些优点?提示:细菌和病毒作为实验材料,具有以下优点: (1) 个体很小,结构简单,细菌是单细胞生物,病毒无细胞结构,只有核酸和蛋白质外壳。
易于观察因遗传物质改变导致的结构和功能的变化。
(2) 繁殖快,细菌20~ 30 min就可繁殖-一代,病毒短时间内可大量繁殖。
(2)从控制自变量的角度,艾弗里实验的基本思路是什么?在实际操作过程中最大的困难是什么?提示:从控制自变量的角度,艾弗里在每个实验组中特异性地去除了一种物质,然后观察在没有这种物质的情况下,实验结果会有什么变化。
最大的困难是,如何彻底去除细胞中含有的某种物质(如糖类、脂质、蛋白质等)。
(3)艾弗里和赫尔希等人都分别采用了哪些技术手段来实现他们的实验设计?这对于你认识科学与技术之间的相互关系有什么启示?提示:艾弗里采用的主要技术手段有细菌的培养技术、物质的提纯和鉴定技术等。
赫尔希采用的主要技术手段有噬菌体的培养技术、同位素标记技术,以及物质的提取和分离技术等(学生可能回答出其他技术,但只要回答出上述主要技术即可)。
科学成果的取得必须有技术手段作保证,技术的发展需要以科学原理为基础,因此,科学与技术是相互支持、相互促进的。
染色问题的求解方法

染色问题的求解方法某伞厂所生产的伞品种齐全,其中品牌为"太阳伞"的伞的伞蓬都由太阳光的七种颜色组成,这七种颜色分别涂在伞蓬的八个区域内,且恰有一种颜色涂在相对的区域内,则不同颜色图案的此类太阳伞至多有( )种(A )40320 (B )5040 (C )20160 (D )2520答案:B一、区域染色问题对区域的染色问题一般是(1)直接根据两个基本原理求解;(2)根据所用的颜色的种数分类;(3)根据某两个区域同色或不同色分类;(4)根据相间区域使用的种类分类。
用四种颜色给四川、青海、西藏、云南四省(区)的地图染色,每一省(区)一种颜色,只要求相邻的省(区)不同色,则不同的染色方法有多少种? 分析:给四川染色有4种方法,给青海染色有3种方法,给西藏染色有2种方法,给云南染色有2种方法,根据分步计数原理共有482234=⨯⨯⨯种方法。
点评:本例是直接利用两个基本原理来解决。
(2003全国)16.如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有 ________种。
(以数字作答)答案:72解法一:合并单元格法 分析:颜色相同的区域可能是②④,③⑤。
下面分情况讨论:(ⅰ)当②④颜色相同且③⑤颜色不同时,将②④合并成一个单元格,此时不同的着色方法相当于四个元素②④、①、③、⑤的全排列数44A 。
(ⅱ)当②④颜色不同且③⑤颜色相同时同情形(ⅰ)有44A 种着色方法。
(ⅲ)当②④及③⑤分别同色时,分别将②④及③⑤合并,这样仅有三个单元格,即②④、③⑤、①,从4种颜色中选3种来着色这三个单元格,即有3334A C 种方法。
由分类计数原理知,不同的着色方法共有7224482333444=+=+A C A (种)。
解法二:由题意可知至少要选三种颜色,依着色的种数分类:(ⅰ)当选用三种颜色时,区域②与④必须同色,区域③与⑤必须同色,故有34A 种。
奥数染色问题题目及答案.doc
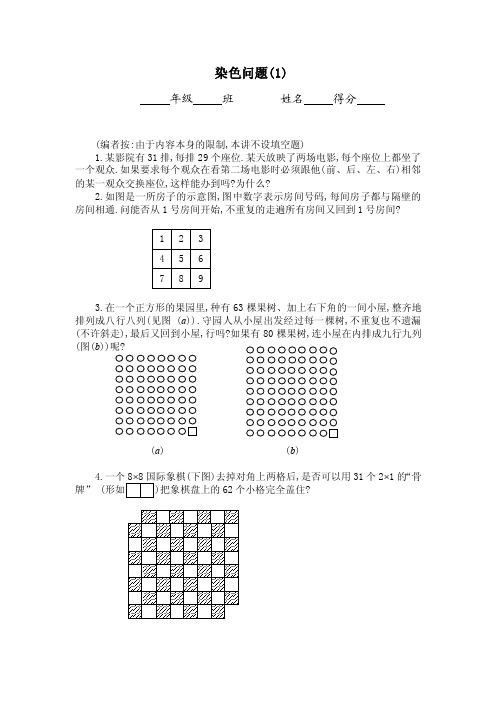
染色问题(1)年级班姓名得分(编者按:由于内容本身的限制,本讲不设填空题)1.某影院有31排,每排29个座位.某天放映了两场电影,每个座位上都坐了一个观众.如果要求每个观众在看第二场电影时必须跟他(前、后、左、右)相邻的某一观众交换座位,这样能办到吗?为什么?2.如图是一所房子的示意图,图中数字表示房间号码,每间房子都与隔壁的房间相通.问能否从1号房间开始,不重复的走遍所有房间又回到1号房间?1 2 34 5 67 8 93.在一个正方形的果园里,种有63棵果树、加上右下角的一间小屋,整齐地排列成八行八列(见图 (a)).守园人从小屋出发经过每一棵树,不重复也不遗漏(不许斜走),最后又回到小屋,行吗?如果有80棵果树,连小屋在内排成九行九列(图(b))呢?(a) (b)4.一个8⨯8国际象棋(下图)去掉对角上两格后,是否可以用31个2⨯1的“骨牌” (形如 )把象棋盘上的62个小格完全盖住?5.如果在中国象棋盘上放了多于45只马,求证:至少有两只马可以“互吃”.6.空间6个点,任三点不共线,对以它们为顶点的线段随意涂以红色或蓝色,是否必有两个同色三角形?7.如图,把正方体分割成27个相等的小正方体,在中心的那个小正方体中有一只甲虫,甲虫能从每个小正方体走到与这个正方体相邻的6个小正方体中的任一个中去.如果要求甲虫能走到每个小正方体一次,那么甲虫能走遍所有的正方体吗?8.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只马从起点出发,跳了n 步又回到起点.证明:n 一定是偶数.9.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只马能否跳遍这半张棋盘,每一点都不重复,最后一步跳回起点?10.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:ABA B证明:一只马不可能从位置B 出发,跳遍半张棋盘而每个点都只经过一次(不要求最后一步跳回起点).11.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只马能否从位置B 出发,用6步跳到位置A ?为什么?12.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只车从位置A 出发,在这半张棋盘上走,每步走一格,走了若干步后到了位置B .证明:至少有一个格点没被走过或被走了不止一次.13.8⨯8的国际象棋棋盘能不能被剪成7个2⨯2的正方形和9个4⨯1的长方形?如果可以,请给出一种剪法;如果不行,请说明理由.14.(表1)是由数字0,1交替构成的,(表2)是由(表1)中任选 、 、三种形式组成的图形,并在每个小方格全部加1或减1,如此反复多次进行形成的,试问(表2)中的A 格上的数字是多少?并说明理由.1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1ABABA B表 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 A 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 1 1表 2———————————————答案——————————————————————1. 把影院的座位图画成黑白相间的矩形.(29⨯31),共有899个小方格.不妨假定四角为黑格,则共有黑格450个,白格449个.要求看第二场电影,每位观众必须跟他相邻的某一观众交换位置,即要求每一黑白格必须互换,因黑白格的总数不相等,因此是不可能的.2. 将编号为奇数的房间染成黑色,编号为偶数的房间染成白色.从1号房间出发,只能按黑白黑白……的次序,当走遍九个房间时应在黑色房间中,这个房间不与1号房间相邻,故不能不重复地走遍所有房间又回到1号房间.3. 图(a)行,走法如图所示.图(a)图(b)不行,将小屋染成黑色,果树染成黑白相间的颜色,则图(b)中有41个黑色的,40个白色的.从小屋出发,按黑白黑白……的次序,当走遍80棵树后,到达的树的颜色还是黑色,与小屋不相邻,故不可能最后回到小屋.4. 不能.原因是每一个2⨯1的矩形骨牌一定恰好盖住一个黑格和一个白格,31个这样的骨牌恰好盖住31个黑格和31个白格.但是国际象棋棋盘上对角两格的颜色是相同的,把它们去掉后剩下的是30个白格,32个黑格,或32个白格,30个黑格,因此不能盖住.5. 中国象棋棋盘上有90个交叉点,把棋盘分成10个小部分,每部分有3 3=9个交叉点,由抽屉原则知,至少有一个小部分内含有6只马.将这一小部分的9个交叉点分别涂上黑色及白色.总有两只马在不同颜色交叉点上,故一定有两只马“互吃”.6. 设这六个点为A 、B 、C 、D 、E 、F.我们先证明存在一个同色的三角形: 考虑由A 点引出的五条线段AB 、AC 、AD 、AE 、AF,其中必有三条被染成了相同的颜色,不妨设AB 、AC 、AD 三条同为红色.再考虑三角形BCD 的三边:若其中有一条为红色,则存在一个红色三角形;若这三条都不是红色,则三角形BCD 为蓝色三角形.下面再来证明有两个同色三角形,不妨设三角形ABC 的三边同为红色. (1)若三角形DEF 也是红色三角形,则存在两个同色三角形.(2)若三角形DEF 中有一条边为蓝色(不妨设DE),下面考虑DA 、DB 、DC 三 条线段,其中必有两条同色.①若其中有两条是红色的,如DA 、DB 是红色的,则三角形DAB 为第二个同色三角形(图1).②若其中有两条是蓝色的,设DA 、DB 为蓝色(图2).此时在EA 、EB 两条线段中,若有一条为蓝色,则存在一个蓝色三角形;若两条都是红色的,则三角形EAB 为红色三角形.综上所述,一定有两个同色三角形.7. 甲虫不能走遍所有的立方体.我们将大正方体如图分割成27个小正方体,涂上黑白相间的两种颜色,使得中心的小正方体染成白色,再使两个相邻的小正方体染上不同的颜色.显然在27A B DCA BC D E (图1) A BCDE (图2)个小正文体中,14个是黑的,13个是白的.甲虫从中间的白色正方体出发,每走一步,小正方体就改变一种颜色.故它走27步,应该经过14个白色的小正方体,13个黑色的小正方体.因此在27步中至少有一个白色的小正方体,甲虫进去过两次.故若要求甲虫到每个小正方体只去一次,甲虫就不能走遍所有的小正方体.8. 将棋盘上的各点按黑白相间的方式染上黑白二色.由“马步”的行走规则,当“马”从黑点出发,下一步只能跳到白点,以后依次是黑、白、黑、白……要回到原出发点(黑点),它必须跳偶数步.9. 不能.半张象棋盘共有45个格点,马从起点出发跳遍半张棋盘,则起点与最后一步同色.故不可能从最后一步跳回起点.10. 与B 点同色的点(白点)有22个,异色的点(黑色)有23个.马从B 点出发,跳了42步时,已经跳遍了所有的白色,还剩下两个黑点,但是马不能够连续跳过两个黑点.11. 不能.因为A 、B 两点异色,从B 到A 所跳的步数是一个奇数.12. “车”每走一步,所在的格点就会改变一次颜色.因A 、B 两点异色,故从A 到B “车”走的步数是一个奇数.但半张棋盘共有45个格点,不重复地走遍半张棋盘要44步,但44是一个偶数.13. 如图对8⨯8的棋盘染色,则每一个4⨯1的长方形能盖住2白2黑小方格,而每一个2⨯2的正方形能盖住1白3黑或1黑3白小方格,那么7个2⨯2的正方形盖住的黑色小方格数总是一个奇数,但图中黑格数为32是一个偶数.故这种剪法是不存在的.14. 如下图所示,将表(1)黑白相间地染色.+1 +1 +1 +1-1 -1 -1 -1+1 +1 +1 +1 +1 +1-1 -1 -1 -1 -1 -1+1 +1 +1 +1+1 +1-1 -1 -1 -1-1 -1表(1)本题条件允许如图所示的6个操作,这6个操作无论实行在那个位置上,白格中的数字之和减去黑格中的数字之和总是一个常数,所以表1中白格中数字之和与黑格中数字之和的差即32,等于表2中白格中数字之和与黑格中数字之和的差即(31+A)-32,于是(31+A)-32=32,故A=33.。
四年级数学奥数题知识点《染色问题》专项训练及答案_题型归纳

四年级数学奥数题知识点《染色问题》专项训练及答案_题型归纳
题型:染色问题难度:★★
如图,把A、B、C、D、M这五个部分用5种不同的颜色染色,且相邻的部分不能使用同一种颜色,有的颜色也可以不用,不相邻的部分可以使用同一种颜色,那么这幅图一共有多少种不同的染色方法?
【答案解析】
如果5种颜色全部使用,那么共有5×4×3×2×1=120种染色方法。
如果只使用4种颜色,可以是B和D同色,也可以是A和C同色,那么共有5×4×3×2×2=240种染色方法。
如果只使用3种颜色,那么有B和D同色并且A和C同色,共有5×4×3=60种染色方法。
120+240+60=420,所以这幅图一共有420种不同的染色方法。
题型:染色问题难度:★★
如图,9条小线段组成了4个小三角形,现在将每条线段分别染上红、黄、蓝三种颜色之一,使得每个三角形三条边的颜色互不相同,那么共有多少种不同的染色方式?
【答案解析】
任选一个小三角形的一条边,当这条边的颜色确定时,这个小三角形的染色方法有2种,同时每种方法都会确定与其相邻的小三角形的一条边的颜色。
24×3=48,所以共有48种不同的染色方式。
六年级上册奥数试题-第19讲:简单染色问题_全国通用(含答案)

第19讲简单染色问题知识网络数学竞赛中的“染色”一般包括两个方面:染色问题和染色方法。
如果染色作为题目的条件给出,那么一般要考虑的是存在与否,有何性质以及有多少种染法等,这就是染色问题。
如果题目中没有提到染色,在解题中运用形象、直观的染色来进行分类,帮助解决问题这就是染色方法。
重点·难点我们在前面几讲中也涉及到染色问题。
一般来说,染色问题涉及分类、奇偶性、排列组合等多方面的知识。
因此如何应用这些相关的知识点解题,是很关键的。
在下面的例题中也可以看出,这些知识在解题中的应用。
学法指导染色作为一种数学思维方法,可以用来推证说理,使一些难以讲清楚的问题一目了然。
有时染色题可能很难想清楚,比如“四色问题”,但可以运用上面的知识点解决一些比较简单的染色问题。
经典例题[例1]如图1所示,一个长方形被分成6块区域,若给每一块区域都染色,并且要求相邻的区域颜色不同,请问至少需要多少种不同的颜色?思路剖析由于A、B、C两两相邻,所以要使相邻的区域颜色不同,至少A、B、C的颜色不能相同。
但是,仅有3种颜色够不够呢?对于区域较少的情形可以逐一试验,如果区域较多时,可以考虑取有多相邻区域的区域来先染色。
解答先考虑有最多相邻区域的A,染第1种颜色;其次考虑与A相邻的B、C、D、E中,有最多相邻区域的E,染第2种颜色;再考虑B,它与A、E都相邻,染第3种颜色。
由C 和E不相邻,故C可用第2种颜色,D与B不相邻,D可用第3种颜色,F和A不相邻,F 可染第一种颜色。
这样,用第一种颜色染在A和F上,用第二种颜色染在C和E上,用第三种颜色染在B和D上即可满足题意要求。
所以,满足条件的染色,至少需要三种颜色。
[例2]用红、黄、蓝三种颜色涂一个正方体的六个面,两个面涂一种颜色,那么共有几种涂法?思路剖析本题要用到分类和组合的一些思想,同进,在解题时要注意,如果两种所谓不同涂法的正方体经翻转或旋转之后得到同样的效果,它只能是一种涂法。
染整实用工艺原理(二)习题

染整工艺原理(二)习题一、染色理论部分1.名词解释染色亲和力染色熵染色热上染速率上染百分率匀染初染率菲克扩散定律吸附等温线移染泳移染色饱和值浴比稳态扩散非稳态扩散扩散活化能扩散边界层半染时间平衡吸附量带液率(轧余率)2.染料的上染过程包括几个阶段?影响各个阶段的因素有哪些?3.染料的聚集性能受哪些因素的影响?4.测定染料在纤维内扩散系数的方法有哪些?试举例说明。
5.说明染色亲和力或平衡吸附量与染色温度的关系。
6.吸附等温线有几类?解释每种吸附等温线的物理意义,写出其物理关系式。
7.何谓孔道和自由体积扩散模型?比较它们的扩散特点,分析加快扩散的可能途径。
8.说明染色温度对上染速率的影响。
二、直接染料染色1.直接染料分几类?比较其染色性能。
2.何谓温度效应?实际染色时如何合理制定染色温度?3.何谓盐效应?说明直接染料染色时加入中性电介质的促染机理。
4.说明直接染料染色时阳离子固色剂的固色机理,目前常用的阳离子固色剂有哪些品种?5.写出直接染料浸染纤维素纤维的工艺过程及工艺条件。
6.分析直接染料在纤维素纤维上的结合状态。
三、还原染料染色1.名词解释隐色体浸染悬浮体轧染干缸还原全浴还原隐色体电位二色性常数半还原时间2.还原染料的染色过程有哪几个基本步骤?3.影响还原染料还原速率的主要因素有哪些?4.还原染料有几种染色工艺?浸染的染色温度主要根据哪些因素决定?5.写出还原金黄GK、艳桃红R的还原反应历程,并比较它们的还原电位高低。
6.还原染料常有哪些不正常的还原现象产生,举例说明。
四、活性染料染色1.写出卤代氮杂环(X、K、KE型)和β-羟基乙砜硫酸酯(KN型)活性染料与纤维素纤维的反应历程,指出决定速率的阶段,影响反应过程主要有哪些因素?2.活性染料染色主要有几种工艺?写出工艺过程和固色条件。
3.何谓固色率、固色速率和固色效率?影响固色效率的因素主要有哪些?4.写出卤代杂环和β-羟基乙砜硫酸酯活性染料的断键反应历程。
纺织品设计与染色工艺考试 选择题 58题

1. 纺织品设计中,哪种纤维的吸湿性最好?A. 聚酯B. 棉C. 尼龙D. 丙烯酸2. 染色工艺中,哪种染料最适合用于棉织物?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料3. 在纺织品设计中,哪种图案设计方法最常用?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣4. 染色工艺中,哪种方法可以实现渐变色效果?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花5. 纺织品设计中,哪种纤维的弹性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯6. 染色工艺中,哪种染料最适合用于丝绸?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料7. 在纺织品设计中,哪种图案设计方法可以实现复杂的几何图案?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣8. 染色工艺中,哪种方法可以实现高精度的图案?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花9. 纺织品设计中,哪种纤维的耐磨性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯10. 染色工艺中,哪种染料最适合用于尼龙?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料11. 在纺织品设计中,哪种图案设计方法可以实现快速生产?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣12. 染色工艺中,哪种方法可以实现大面积的均匀染色?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花13. 纺织品设计中,哪种纤维的保暖性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯14. 染色工艺中,哪种染料最适合用于羊毛?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料15. 在纺织品设计中,哪种图案设计方法可以实现个性化定制?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣16. 染色工艺中,哪种方法可以实现多种颜色的混合效果?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花17. 纺织品设计中,哪种纤维的透气性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯18. 染色工艺中,哪种染料最适合用于聚酯?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料19. 在纺织品设计中,哪种图案设计方法可以实现高效率的生产?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣20. 染色工艺中,哪种方法可以实现快速染色?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花21. 纺织品设计中,哪种纤维的柔软性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯22. 染色工艺中,哪种染料最适合用于丙烯酸?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料23. 在纺织品设计中,哪种图案设计方法可以实现复杂的花卉图案?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣24. 染色工艺中,哪种方法可以实现高饱和度的颜色?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花25. 纺织品设计中,哪种纤维的抗皱性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯26. 染色工艺中,哪种染料最适合用于棉和聚酯混纺织物?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料27. 在纺织品设计中,哪种图案设计方法可以实现高精度的图案复制?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣28. 染色工艺中,哪种方法可以实现环保染色?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花29. 纺织品设计中,哪种纤维的耐光性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯30. 染色工艺中,哪种染料最适合用于户外纺织品?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料31. 在纺织品设计中,哪种图案设计方法可以实现快速迭代?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣32. 染色工艺中,哪种方法可以实现高耐洗性?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花33. 纺织品设计中,哪种纤维的抗菌性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯34. 染色工艺中,哪种染料最适合用于医疗纺织品?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料35. 在纺织品设计中,哪种图案设计方法可以实现高度的创意自由度?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣36. 染色工艺中,哪种方法可以实现高度的颜色稳定性?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花37. 纺织品设计中,哪种纤维的耐化学性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯38. 染色工艺中,哪种染料最适合用于工业纺织品?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料39. 在纺织品设计中,哪种图案设计方法可以实现高度的生产灵活性?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣40. 染色工艺中,哪种方法可以实现高度的染色均匀性?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花41. 纺织品设计中,哪种纤维的耐热性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯42. 染色工艺中,哪种染料最适合用于高温染色?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料43. 在纺织品设计中,哪种图案设计方法可以实现高度的图案复杂性?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣44. 染色工艺中,哪种方法可以实现高度的颜色深度?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花45. 纺织品设计中,哪种纤维的耐腐蚀性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯46. 染色工艺中,哪种染料最适合用于耐腐蚀纺织品?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料47. 在纺织品设计中,哪种图案设计方法可以实现高度的图案一致性?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣48. 染色工艺中,哪种方法可以实现高度的染色效率?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花49. 纺织品设计中,哪种纤维的耐撕裂性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯50. 染色工艺中,哪种染料最适合用于耐撕裂纺织品?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料51. 在纺织品设计中,哪种图案设计方法可以实现高度的图案多样性?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣52. 染色工艺中,哪种方法可以实现高度的染色稳定性?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花53. 纺织品设计中,哪种纤维的耐紫外线性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯54. 染色工艺中,哪种染料最适合用于耐紫外线纺织品?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料55. 在纺织品设计中,哪种图案设计方法可以实现高度的图案创新性?A. 手工绘制B. 计算机辅助设计C. 模板印刷D. 手工刺绣56. 染色工艺中,哪种方法可以实现高度的染色灵活性?A. 直接染色B. 印花C. 渐变染色D. 喷墨印花57. 纺织品设计中,哪种纤维的耐摩擦性最好?A. 棉B. 羊毛C. 尼龙D. 聚酯58. 染色工艺中,哪种染料最适合用于耐摩擦纺织品?A. 酸性染料B. 活性染料C. 分散染料D. 硫化染料答案1. B2. B3. B4. C5. C6. A7. B8. D9. D10. C11. B12. A13. B14. A15. B16. D17. A18. C19. B20. A21. A22. B23. B24. B25. D26. B27. B28. D29. D30. C31. B32. B33. C34. B35. B36. D37. D38. D39. B40. A41. D42. C43. B44. B45. D46. D47. B48. A49. C50. C51. B52. A53. D54. C55. B56. D57. C58. C。
染色工考试考试题(题库版)

染色工考试考试题(题库版)1、多选还原染料按还原条件及操作方法的不同分为()。
A.全浴还原法B.干缸还原法C.甲法D.乙法正确答案:A, B2、单选强酸性染料染羊毛的吸附等温线符合().A.能(江南博哥)斯忒(Nernst)型B.弗莱因德胥(Freundlich)型C.郎格谬尔(Langmuir)型正确答案:C3、单选下列还原染料中,最容易被还原的染料是().A.黄G(隐色体电位为-640mV)B.蓝2B(隐色体电位为-690mV)C.桃红R(隐色体电位为-730mV)D.灰M(隐色体电位为-760Mv)正确答案:A4、填空题涤纶织物转移印花的原理是().正确答案:通过高温使染料受热升华为气相凝聚在涤纶表面,然后向纤维大分子中无定型区渗透,经冷却后固着在纤维内部5、单选耐日晒牢度的等级共分()级。
A.5B.6C.8D.9正确答案:C6、单选下述现象中,哪种现象是还原染料染色常出现的().A.光敏脆损B.烟褪C.焦油化D.升华正确答案:A7、单选还原染料隐色体主要是通过()固着在纤维素纤维上。
A.离子键B.共价键C.氢键D.范德华力正确答案:A8、填空题活性染料浸染工艺包括()、二浴二步法、一浴一步法(全浴法)。
正确答案:一浴二步法9、单选下列牢度中,哪种牢度是分散染料所特有的牢度()。
A.耐升华牢度B.烟褪牢度C.耐氯漂牢度D.耐水洗牢度正确答案:A10、多选分散染料主要是通过()固着在涤纶纤维上。
A.离子键B.共价键C.氢键D.范德华力正确答案:C, D11、名词解释上染量正确答案:染色结束时,单位重量纤维所吸收到的染料量.12、填空题次氯酸钠漂白的有效成分是ClO-、()、Cl2。
正确答案:HClO13、单选耐水洗牢度的等级共分()级。
A.5B.6C.8D.9正确答案:A14、单选阳离子染料主要是通过()固着在腈纶纤维上。
A.离子键B.共价键C.氢键D.范德华力正确答案:A15、填空题纺纱过程中常用的浆料有天然淀粉、变性淀粉、()、聚乙烯醇PVA和聚丙烯酸。
纺织品染色与加工技术考试 选择题 61题

1题1. 下列哪种纤维素纤维染色时需要使用铜氨溶液?A. 棉B. 麻C. 粘胶纤维D. 醋酸纤维2. 酸性染料主要用于哪种纤维的染色?A. 棉B. 羊毛C. 尼龙D. 聚酯3. 分散染料主要用于哪种纤维的染色?A. 棉B. 羊毛C. 尼龙D. 聚酯4. 活性染料染色时,常用的固色剂是?A. 硫酸钠B. 碳酸钠C. 氯化钠D. 醋酸钠5. 下列哪种染料染色时需要使用还原剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料6. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯7. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料8. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯9. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料D. 活性染料10. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯11. 下列哪种染料染色时需要使用金属离子?A. 直接染料B. 酸性染料C. 分散染料D. 金属络合染料12. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯13. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料14. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯15. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料16. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯17. 下列哪种染料染色时需要使用金属离子?A. 直接染料B. 酸性染料C. 分散染料D. 金属络合染料18. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯19. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料20. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯21. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料D. 活性染料22. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯23. 下列哪种染料染色时需要使用金属离子?B. 酸性染料C. 分散染料D. 金属络合染料24. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯25. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料26. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯27. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料D. 活性染料28. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯29. 下列哪种染料染色时需要使用金属离子?A. 直接染料B. 酸性染料C. 分散染料D. 金属络合染料30. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙31. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料32. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯33. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料D. 活性染料34. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯35. 下列哪种染料染色时需要使用金属离子?A. 直接染料B. 酸性染料C. 分散染料D. 金属络合染料36. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯37. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料38. 下列哪种纤维染色时需要使用酸性条件?B. 羊毛C. 尼龙D. 聚酯39. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料D. 活性染料40. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯41. 下列哪种染料染色时需要使用金属离子?A. 直接染料B. 酸性染料C. 分散染料D. 金属络合染料42. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯43. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料44. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯45. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料46. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯47. 下列哪种染料染色时需要使用金属离子?A. 直接染料B. 酸性染料C. 分散染料D. 金属络合染料48. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯49. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料50. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯51. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料D. 活性染料52. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯53. 下列哪种染料染色时需要使用金属离子?B. 酸性染料C. 分散染料D. 金属络合染料54. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯55. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料56. 下列哪种纤维染色时需要使用酸性条件?A. 棉B. 羊毛C. 尼龙D. 聚酯57. 下列哪种染料染色时需要使用碱性条件?A. 直接染料B. 酸性染料C. 分散染料D. 活性染料58. 下列哪种纤维染色时需要使用还原剂?A. 棉B. 羊毛C. 尼龙D. 聚酯59. 下列哪种染料染色时需要使用金属离子?A. 直接染料B. 酸性染料C. 分散染料D. 金属络合染料60. 下列哪种纤维染色时需要使用高温高压染色机?A. 棉B. 羊毛C. 尼龙D. 聚酯61. 下列哪种染料染色时需要使用氧化剂?A. 直接染料B. 酸性染料C. 分散染料D. 还原染料答案1. C2. B3. D4. B5. D6. D7. D8. B9. D10. D11. D12. D13. D14. B15. D16. D17. D18. D19. D20. B21. D22. D23. D24. D25. D26. B27. D28. D29. D30. D31. D32. B33. D34. D35. D36. D37. D38. B39. D40. D41. D42. D43. D44. B45. D46. D47. D48. D49. D50. B51. D52. D53. D54. D55. D56. B57. D58. D59. D60. D61. D。
纺织染色工五级理论试卷A卷

绍兴市职业技能等级认定试卷机构类型:技工院校机构名称:柯桥区高级技工学校认定计划号:纺织染色工五级理论知识试卷A1、考试时间: 90分钟。
2、请首先按要求在试卷的标封处填写您的姓名、准考证号和所在单位的名称。
3、请仔细阅读各种题目的回答要求,在规定的位置填写您的答案。
~第50题。
将判断结果填入括号中。
正确的填“√”,错误的填“×”。
每题0.5分,满分25分。
)()1.麻类织物进行丝光处理,主要的目的是为了提高光泽。
()2.柞蚕丝精练与桑蚕丝相比,需要在较高的碱性条件下进行()3.热定形中,湿热定形温度要高于干热定形温度()4.涤/棉混纺织物一般不用次氯酸钠漂白()5.棉针织物的前处理加工一般不需要进行退浆工序()6.卷染机染色属于绳状染色()7.染色过程一般可分为二个阶段,即染料的吸附和染料的扩散()8.冰染料染色的过程可理解为色基与纤维上色酚的偶合过程()9.弱酸性染料染羊毛,元明粉是起促染作用()10.M型活性染料是一类含有双活性基团的活性染料()11.上染过程并不一定等于染色过程,而染色过程必须包括上染过程。
()12.物体具有颜色是物体对光波选择性吸收的结果。
()13.在印染工业中,拼色属于加法混色,其三元色为红、绿、蓝。
()14移染效果和泳移现象均可提高被染物的匀染性。
()15双活性基型活性染料染色可明显提高其固色率。
()16.冰染料色基直接印花,花色的深浅是由色酚来定的。
()17.冰涂共同印花时,为防止传色,可在冰染料色浆中加入一定量的还原剂。
()18.不溶性偶氮染料地色拔染印花染地色时,不宜进行皂煮。
()19.活性防活性印花,地色是K型活性染料,防染染料是X型活性染料()20.活性染料与涂料可以进行防染印花()21.分散染料印花常采用合成增稠剂作为原糊。
()22.活性防活性印花工艺均采用K型活性染料。
()23.共同印花与同浆印花是相同的印花工艺。
()24.为了保证色光的一致性,染同一批布要用同一产地厂家生产的染料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
染色问题
一、染色问题 (1)
一、 染色问题
1. (1991年全国初中数学联赛2试)将正方形ABCD 分割为2n 个相等的小方格(n
是自然数),把相对的顶点A ,C 染成红色,把B ,D 染成蓝色,其他交点任意染成红、蓝两色中的一种颜色,证明:恰有三个顶点同色的小方格的数目必是偶数.
【难度】 ★★★★
【解析】 证法1:用数代表颜色,将红色记为0,蓝色记为1,再将小方格编号,记为1,
2,3,…2n 。
又记第i 个小方格四个顶点数字之和为i A ,若恰有三顶点同色,则1i A =或3为奇数,否则i A 为偶数。
在212n A A A +++中,有如下事实:
对正方形内部的交点,各加了4次;
原正方形边上非端点的交点,各加了2次;
对原正方形的四个顶点,各加了1次(含两个0,两个1)。
因此212n A A A +++
4=⨯(内部交点相应的数之和)2+⨯(边上非端点的交点相应的数之和)2+,
必为偶数,于是,在1A ,2A ,…,2n A 中必有偶数个奇数,这就是说,恰有三个
顶点同色的小方格必有偶数个。
证法2:用数代表颜色,红色记为1,蓝色记为1-,将小方格编号,记为1,
2,…,2n 。
记第i 个小方格四个顶点数字之和为i A ,若恰有三顶点同色,则1i A =-否则
1i A =。
现在考虑乘积212n A A A ⨯⨯⨯。
对正方形内部交点,各点相应的数重复出现4
次;边上的不是端点的交点相应的数各出现2次;A ,B ,C ,D 四点相应的数的乘积为11(1)(1)1⨯⨯-⨯-=,
于是2121n A A A ⨯⨯⨯=,
因此,1A ,2A ,…,2n A 中1-的个数必为偶数,即恰有三顶点同色的小方格必有偶数个。
证法3:考虑染了色之后,改变一个交点的染色方式,这时以此点为顶点的小方格,要么由三顶点同色变为非三顶点同色,要么由非三顶点同色变成三顶点同
色。
注意:除A ,B ,C ,D 之外,每一次点必是偶数个小方格的顶点,因此,改变一个交点的染色并不改变三项点同色小方格数目的奇偶性。
n=时,结论显然成立,
当1
n>时,每次改变一个交点的染色,最终总可以使B,D之外的点皆为红色,当1
这时,三项点同色的小方格只有两个,为偶数。
因此,任意染色之下,三顶点同色的小方格有偶数个。
