第5课时:平面的基本性质(2)
平面的性质2

D1 A1
D AQ
C1 解:(1)
D1
A1 B1
P C
D
B
AQ
C1
B1 P
C B
2020年 锡慧在线
例 1 如图,长方体 ABCD A1B1C1D1中, P,Q 分别是 BB1 , AB 中点.
(1)画出由 A1 , C1 , P 三点所确定的平面 与长方体表面的交线;
(2)画出由 D1,C,Q 三点所确定的平面 与长方体表面的交线.
D1 A1
D AQ
解:(2)
C1
D1
B1
A1
P
C
D
B
AQ
M
C1
D1
A1 B1
N
C
D
B
AQ
M
C1
D1
A1 B1
N
C
D
B
AQ
M
C1 B1
C B
小结:(1)确定平面依据 (2)找(画)交线的依据
直观想象
2020年 锡慧在线
例 2 已知: A l, B l,C l, D l ,求证:直线 AD, BD,CD 共面.
A
C
D
E
(1)
B
A
C
D
E
(2)
B
A
B
C
D
E
(3)
2020年 锡慧在线
一、复习回顾
自然语言
图形语言
符号语言
用途
公理1
如果一条直线上的
两点在一个平面内,
那么这条直线上所 有的点都在这个平
l αA B
面内
如果两个平面有
一个公共点,那
公理2 么它们还有其他 公共点,这些公
数学必修二2《平面(2)》课件

1.平面的基本性质
(1)公理1:若一条直线上的两点在一个平面内, 则这条直线在此平面内.
①图形语言:
A
l
B
②符号语言:Al, B l且A, B l
③该公理反映了直线与平面的位置关系:
可用于判定直线是否在平面内,点是否在平面内,又 可用直线检验平面.
同理可证 C∈α. 又∵B∈l3,C∈l3,∴l3⊂α. ∴直线 l1、l2、l3 在同一平面内. 证法 2:(辅助平面法) ∵l1∩l2=A,∴l1、l2 确定一个平面 α. ∵l2∩l3=B,∴l2、l3 确定一个平面 β. ∵A∈l2,l2⊂α,∴A∈α.
∵A∈l2,l2⊂β,∴A∈β. 同理可证 B∈α,B∈β,C∈α,C∈β. ∴不共线的三个点 A、B、C 既在平面 α 内,又在平面 β 内. ∴平面 α 和 β 重合,即直线 l1、l2、l3 在同一平面内.
系,并画出相应的图形:(1)A∈α,B∉α;(2)l⊂α,m∩α= A,A∉l;(3)P∈l,P∉α,Q∈l,Q∈α. 解:(1)点 A 在平面 α 内,点 B 不在平面 α 内,如图(1); (2)直线 l 在平面 α 内,直线 m 与平面 α 相交于点 A,且点 A 不在直线 l 上,如图(2); (3)直线 l 经过平面 α 外一点 P 和平面 α 内一点 Q,如图(3).
共线问题 [例 3] 已知△ABC 在平面 α 外,其三边 所在的直线满足 AB∩α=P,BC∩α=Q, AC∩α=R,如图所示. 求证:P,Q,R 三点共线. [证明] 法一:∵AB∩α=P,∴P∈AB,P∈平面 α. 又 AB⊂平面 ABC,∴P∈平面 ABC. ∴由公理 3 可知:点 P 在平面 ABC 与平面 α 的交线上, 同理可证 Q,R 也在平面 ABC 与平面 α 的交线上. ∴P,Q,R 三点共线.
平面基本性质PPT优选课件 (2)

2020/10/18
9
随堂练习
1、如右图用符号可表述为(B )
A、 l1,l2 ,Pl1,Pl2
B、 l1,l2 ,l1 l2 P
l1 P
C、 l1,l2 ,l1 l2 P D、 l1,l2 ,Pl1,Pl2
l2
2020/10/18
10
谢谢您的聆听与观看
THANK YOU FOR YOUR GUIDANCE.
α
AB
l
(3)符号语言叙述:
A l ,B l ,A ,B l
2020/10/18
6
(4)作用: 1、判断直线是否在平面内,点是否在平面内; 2、用直线检验平面;
2020/10/18
7
平面的基本性质
公理二
(1)文字语言叙述:如果两个平面有一个公共点,
那么它们还有其他公共点,这些公共点的集合
感谢阅读!为了方便学习和使用,本文档的内容可以在下载后随意修改,调整和打印。欢迎下载!
汇报人:XXX 日期:20XX年XX月XX日
(3)看不见的线段画成虚线或不画;
D
C
2020A/10/18
B
3
平面的表示
(1)通常用希腊字母 、、 等来表示平面;
(2)也可以用平行四边形的两个相对顶点来表示 平面,例如:平面AC或平面BD;
D
C
A
B
2020/10/18
4
用集合中的有关符号表示点线面之间的位置关系
文字叙述
图形表示
点P在直线l上
2020/10/18
平面基本性质
1
平面的概念
对平面的理解:
(1)平面是无限延伸的;
(2)平面内的一条直线将平面分成两部分;
数学必修二平面性质知识点总结

数学必修二平面性质知识点总结
在数学学习中认识平面知识点时,需要掌握平面的基本性质,下面是店铺给大家带来的数学必修二平面性质知识点总结,希望对你有帮助。
数学平面的基本性质知识点总结(一)
平面的基本性质
教学目标
1、知识与能力:
(1)巩固平面的基本性质即四条公理和三条推论.
(2)能使用公理和推论进行解题.
2、过程与方法:
(1)体验在空间确定一个平面的过程与方法;
(2)掌握利用平面的基本性质证明三点共线、三线共点、多线共面的方法。
3、情感态度与价值观:
培养学生认真观察的态度,慎密思考的习惯,提高学生的审美能力和空间想象的能力。
教学重点
平面的三条基本性质即三条推论.
教学难点
准确运用三条公理和推论解题.
教学过程
一、问题情境
问题1:空间共点的三条直线能确定几个平面?空间互相平行的三条直线呢?
问题2:如何判断桌子的四条腿的底端是否在一个平面内?
二、温故知新
公理1
如果一条直线上的两点在一个平面内,那么这条直线上所有的点
都在这个平面内.
公理2
如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线.
公理3
经过不在同一条直线上的三点,有且只有一个平面.
推论1
经过一条直线和这条直线外的一点,有且只有一个平面.
推论2
经过两条相交直线,有且只有一个平面.
推论3
经过两条平行直线,有且只有一个平面.
公理 4(平行公理) 平行于同一条直线的两条直线互相平行.
把以上各公理及推论进行对比:。
9.6立体几何 (5)平面的基本性质

第5课时平面的基本性质课堂小练2.根据所给图形,用符号语言填空:(1)A ____平面ABC ,A ____平面BCD ; (2)BD ____平面ABD ,BD ____平面ABC ;(3)平面ABC 平面ACD =____,平面____ 平面____BC =.3.若A α∈,B α∈,P AB ∈,则用符号表示点P 与平面α的关系为____.4.若l αβ= ,P α∈,P β∈,则P ____l .5.已知直线12l l ‖,在直线1l 上取3个点,在直线2l 上取2个点,则由这5个点能确定____个平面.6.给定下列命题:①如果平面α与平面β相交,那么它们只有有限个公共点;②梯形的4个顶点在同一个平面内;③3条互相平行的直线必共面;④有3个公共点的两个平面重合;⑤空间内有4个点,且任意3点都不共线,则这4个点最多可以确定4个平面.其中正确命题的序号是____.7.如图,已知EF αβ= ,A α∈,B β∈,C β∈,BC 与EF 相交,在图中画出平面ABC分别与α,β的交线,并指出来.8.已知直线l 与三条相互平行的直线,,a b c 都相交.求证:这四条直线共面.9.如图.在正方体1111ABCD A BC D -中,M 是AB 的中点.作出过三点1D ,1B ,M 的平面与底面ABCD 的交线.第5课时平面的基本性质课堂小练1.M AB ∈,N AB ∉,P ∈平面AC ,Q ∉平面AC ,a b E = ,l ⊂平面α,m ⊄平面α2.(1)∈,∉ (2)⊂,⊄ (3)AC ,ABC ,BCD3.P α∈4.∈5.16.②⑤7.连接CB ,并延长与EF 交于点D ,连接AD ,则平面ABC 与α,β的交线分别为AD ,BC巩固拓展8.提示:先由直线,a b 确定一个平面α,证直线l ⊂面α;同理可证直线,,b c l 共面于平面β.由直线,b l 确定一个平面知α与β重合 9.如图,取AD 中点N ,连接MN 即得。
《平面的基本性质》课件

平面解析几何在实际问题中的应用案例
物理学中的应用
在物理学中,许多概念和公式可以通过平面解析几何来描述和解 释,例如力学、电磁学和光学中的许多概念。
工程学中的应用
在工程学中,平面解析几何被广泛应用于机械设计、建筑设计、航 空航天等领域。
计算机图形学中的应用
在计算机图形学中,平面解析几何是生成和处理二维图形的基础, 例如在游戏开发、动画制作和计算机视觉等领域的应用。
THANKS FOR WATCHING
感谢您的观看
平面与几何体的关系
总结词
平面是几何体的重要组成部分,它可以作为几何体的边界或 表面。
详细描述
在几何学中,许多常见的几何体都是由平面构成的。例如, 长方体的每个面都是一个平面,球体的表面也是一个平面。 此外,平面还可以用来定义其他几何体的形状和大小,例如 通过平面的交线来定义三维空间的形状。
CHAPTER 02
平面上的直线的方程
两点式方程
通过平面上两点的坐标,可以求出直 线的方程。
点斜式方程
已知直线上的一个点和直线的斜率, 可以求出直线的方程。
平面上的点与直线的位置关系
点在直线上
如果一个点的坐标满足直线的方程,则该点在直线上。
点在直线外
如果一个点的坐标不满足直线的方程,则该点在直线外。
CHAPTER 04
与线性代数的联系
线性代数提供了研究平面几何对象 (如向量、矩阵和线性变换)的工 具。
平面解析几何的发展历程与未来展望
发展历程
从早期的欧几里得几何到文艺复兴时 期的笛卡尔几何,再到现代的解析几 何,平面解析几何经历了漫长的发展 历程。
未来展望
随着数学和其他学科的发展,平面解 析几何将继续发展,与其他数学分支 的交叉将更加深入,新的研究方法和 视角也将不断涌现。
平面的基本性质

平面的基本性质一、知识梳理 一)平面1.特征:①无限延展 ②平的(没有厚度) ,平面是抽象出来的,只能描述,如平静的湖面,不能定义.一个平面把空间分成两部分,一条直线把平面分成两部分.2.表示:一般用一个希腊字母α、β、γ……来表示,还可用平行四边形的对角顶点的字母来表示如:平面α,平面AC 等.3.画法:通常画平行四边形来表示平面(1)一个平面: 当平面是水平放置的时候,通常把平行四边形的锐角画成45 ,横边画成邻边的2倍长,如图1(1).(2)直线与平面相交,如图1(2)、(3),:(3)两个相交平面:画两个相交平面时,先定位,后交线,邻边依次添,若一个平面的一部分被另一个平面遮住,应把被遮住部分的线段画成虚线或不画(如图2).4.点、线、面的基本位置关系如下表所示:b A =a βαB AβBAαβBAααβa图 2A(1aαa α⊂ 直线a 在平面α内. aα a α=∅ 直线a 与平面α无公共点. aAα a A α=直线a 与平面α交于点A .l αβ=平面α、β相交于直线l .点可看成元素,直线和平面可看成集合,符号“∈”只能用于点与直线,点与平面的关系,“⊂”和“ ”的符号只能用于直线与直线、直线与平面、平面与平面的关系,虽然借用于集合符号,但在读法上仍用几何语言. 例1、将下列符号语言转化为图形语言:(1)A α∈,B β∈,A l ∈,B l ∈; (2)a α⊂,b β⊂,//a c ,b c p =,c αβ=.说明:画图的顺序:先画大件(平面),再画小件(点、线). 例2、将下列文字语言转化为符号语言: (1)点A 在平面α内,但不在平面β内; (2)直线a 经过平面α外一点M ;(3)直线l 在平面α内,又在平面β内.(即平面α和β相交于直线l .)例3、在平面α内有,,A O B 三点,在平面β内有,,B O C 三点,试画出它们的图形.二)三条公理人们经过长期的观察和实践,把平面的三条基本性质归纳成三条公理. 公理1如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内.BA α应用: ①判定直线在平面内;②判定点在平面内.模式:a A A a αα⊂⎧⇒∈⎨∈⎩.公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.应用:①确定两相交平面的交线位置;②判定点在直线上.指出:今后所说的两个平面(或两条直线),如无特殊说明,均指不同的平面(直线). 公理3经过不在同一条直线上的三点,有且只有一个平面.应用:①确定平面;②证明两个平面重合.实例:(1)门:两个合页,一把锁;(2)摄像机的三角支架;(3)自行车的撑脚. 例4、判断下列命题是否正确。
平面的基本性质(2).许兴华

9.1平面的基本性质(2)
( 201210925 )
(月亮河 A )
Designed by Steven 华 兴 No.3 High School 课 许 of Nanning 件
T N S E
E
V
兴 T 华
件
N S E 许E V课
Firstpage首页 upward return next last 铃
一、平面的基本性质
1、几个公理 公理1:如果一条直线上的两点在一 个平面内,那么这条直线上的所有点 在这个平面内;
B A l
α
确定直线在平面内的依据
兴 T 华
N S E 许E V课
Firstpage首页 upward return next last 铃
件
公理2:如果两个平面有一个公共点, 那么它们还有其他公共点,且所有这 些公共点的集合是过这个公共点的一 条直线 β
o
a
d
又 H,K∈c,∴c α. 同理可证 d α. ∴a,b,c,d 四条直线在同一平面α内.
兴 T 华
N S E 许E V课
b c
Firstpage首页 upward return next last 铃
件
[应用举例](调研P5R思考题) 例2.已知三条直线两 两平行,
第四条直线与它们都相交, 求证 : 这四条直线共面 .
证明: 如图 l a A,由推理2得 : ,
直线 l 与直线 a 确定一个平面
.
a 与点 B ,
又 l b B, l c C , B, C .
经过直线 a , b 的平面必经过经过直线
而经过直线 与点B的平面是唯一的 . a 直线 b 平面 , 同理, 直线c .
平面基本性质第二课时PPT课件

平面的基本性质 推论3:经过两条平行直线,有且只 有一个平面.
b
a
a // b 有且只有一个平面,使a ,b
推论3 经过两条平行直线,有且只有一个平面
(3)空间四点中,三点共线是这四个点共面的( ) A.充分但不必要条件 B.必要但不充分条件 C.充分必要条件 D.既非充分条件,也非必要条件
直 l在 线 内 平l, 面 , 记 l不 直 作 在 内 线平 l, ;
直 l 和 线 m 相 直 A , 交 线 l m 记 于 A ( A 是 作 点 A 的简
直 l于 线 平 相面 交 A , 于 l记 点 A 作
平与 面平 相面 交l, 与记 直 作 线 l。
公理1:如果一条直线上的两个点在 平面内,那么这条直线上所有的点 都在这个平面内.
AB
符号语言 作用
怎样的直线a我们就说它在平面外?
平面的基本性质
公理2:如果两个平面有一个公共点, 那么它们还有其他的公共点,且所 有的这些点的集合是一条过这个点 的直线
符号语言 作用
l
P
平面的基本性质 公理3:经过不在同一条直线上的三 个点,有且只有一个平面.
推论1 经过一条直线和这条直线外的一点,有且只有一个平面
求证:过点A和直线a可以确定一个平面
唯一性: 如果经过点A和直线a的平面还有一个平面β,那么
A∈β, a β,因为B∈a,C∈a,所以B∈β,C∈β.(公理1)故不
共线的三点A,B,C既在平面α内又在平面β内.所以平面α和平面 β重合.(公理3)
(A)0 (B)1 (C)2 (D)0或无数
平面的基本性质 ppt课件

A
Q
C B
R P
例4:已知:空间四边形ABCD,平面四
边形EFGH的顶点分别在空间四边
形的各边AD,AB,BC,CD上,若EF与
GH不平行,求证:三条直线
EF,GH,BD共点。
方法小结
六.平面性质研究
观
问题1 泥匠如何检查墙面是否平整? 木匠如何检查桌面是否平整?
a
点A在直线a上: 记为:A∈a
点B不在直线a上:记为:B∈a
AB(2)点与平面 Nhomakorabea位置关系:
点A在平面α上: 记为:A∈α 点B不在平面α上:记为:B∈ α
α
B A
(3)直线与平面的位置关系:
直线a上的所有点都在平面α上,称直线a
在平面α内,或称平面α通过直线a.记为:aα
直线a与平面α只有一个公共点A时,称直 线a与平面α相交。 记为:a∩α=A
βA
Ba b
C
数学语言表示:
直 线 a//b 有 且 只 有 一 个 平 面 , 使 得 a, b.
思考1:不共面的四点可以确定多少个平面? 思考2:四条相交于同一点的直线a,b,c,d并且任意三条都不在同一平 面内,有它们中的两条来确定平面,可以确定多少个平面。
例1:如图,直线AB、BC、CA两两相交,交点 分别为A、B、C,判断这三条直线是否共面, 并说明理由.
A BC
证法3: ∵ A、B、C三点不在一条直线上
∴过A、B、C三点可以确定平面 (公理3) ∵ A∈, B∈∴AB (公理1) 同理 BC, AC
∴AB、AC、BC共面
A BC
练1.直线l 与过点P的三条直线a1 , a2 , a3 分别 交于 A,B,C三点(A,B,C异于点P),求证: 这四条直线共面。
平面的基本性质.ppt

于是可得到 M∈面 ABD∩面 BCD=BD. 即点 M 在直线 BD 上。
有关共面、共线、共点问题的证明方法 1.证明共面问题 证明共面问题,一般有两种证法:一是由某些元素确定一个 平面,再证明其余元素在这个平面内;二是分别由不同元素 确定若干个平面,再证明这些平面重合. 2.证明三点共线问题 证明空间三点共线问题,先考虑两个平面的交线,再证有关 的点都是这两个平面的公共点.或先由某两点作一直线,再 证明其他点也在这条直线上. 3.证明三线共点问题 证明空间三线共点问题,先证两条直线交于一点,再证明第 三条直线经过这点, 把问题转化为证明点在直线上的问题. 而 这条直线往往归结为平面与平面的交线.
A, B, C三点不共线
B A
C
有且只有一个平面,使A , B , C
基本性质3:如果不重合的两个平面有一个公共点,那么它们有且 只有一条过这个点的公共直线。 符号语言:
P P
l且P l
四、跟踪训练 巩固新知
问题4:(教材 P38—3)一扇门,可以想象成平面 的一部分,通常用两个合页把它固定在门框的一 边上,当门不锁上的时候,可以自由转动,如果 门锁上,则门就固定在墙面上,这个事实说明平 面具有哪条基本性质?
五、小结归纳 布置作业
课堂小结:
1、平面的基本性质、推论及应用:
2、有关共面、共线、共点问题的证明方法
作业: 1、教材P38----A组、 B组 2、学案
基本性质1:如果一条直线上的两点在一个平面内,那么这 条直线上所有的点都在这个平面内. B A A 符号语言: 直线 AB B 基本性质2:经过不在同一条直线上的三点,有且只有一个平面。 符号语言:
4、(教材P37——思考与讨论变式)
平面的基本性质(2)
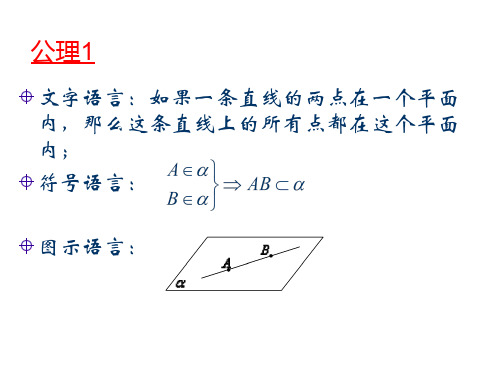
文字语言:如果一条直线的两点在一个平面 内,那么这条直线上的所有点都在这个平面 内; 符号语言:
图示语言:
直线和平面的位置关系
练习
练习
经过3个点确定平面的个数是___; 3个平面可以将空间分成___部分; 三条直线两两平行,但不共面,过 任意2条直线确定的平面的总个数 是( ) A.1 B.3 C.0 D.6
高三数学总复习攻略
.
高三数学总复习攻略
.
高三数学总复习攻略
.
高三数学总复习攻略
.
高三数学总复习攻略
.
高三数学总பைடு நூலகம்习攻略
.
高三数学总复习攻略
.
高三数学总复习攻略
;保藏中心 https:/// 保藏中心
必修2_ch1 立体几何初步教学案(19课时)

第9课时直线与平面的位置关系(1)-----------------(33)
第10课时直线与平面的位置关系(2)-----------------(37)
第11课时直线与平面的位置关系(3)-----------------(41)
五、回顾小结
六、练习
补全下图所示的物体的三视图:
江苏省泰兴中学高一数学同步课时训练(3)
【中心投影和平行投影】
班级姓名
一、解答题:
1、画出下面的几何体的三视图:
2、画出下面的几何体的三视图:
3、画出下面的几何体的三视图:
4、画出下面的几何体的三视图:
5、根据所给三视图,画出相应的空间图形的大致形状.
江苏省泰兴中学高二数学校本化教学案
立体几何
江苏省泰兴中学龚留俊
第1课时棱柱、棱锥和棱台-----------------------------(1)
第2课时圆柱、圆锥、圆台和球-------------------------(5)
第3课时中心投影和平行投影(三视图)---------------(9)
(3)与圆锥的轴平行的截面是等腰三角形.()
(4)球面作为旋转面,只有一条旋转轴,没有母线.()
(5)半圆以其直径为轴旋转一周所成的曲面叫球.()
(6)到定点的距离等于定长的所有点的集合叫球.()
二、解答题:
7、(探究题)如图,我们知道,若从圆锥的一条母线AC处将其侧面展开,则得到一个扇形,其中弧AB的长就是底面周长,扇形的半径就是圆锥的母线.若已知圆锥底面半径为r,母线长为l,求:(1)圆锥的侧面积公式;(2)圆锥侧面展开图的圆心角的弧度数.
平面基本性质(中学课件2019)

平面的概念
对平面的理解:
(1)平面是无限延伸的; (2)平面内的一条直线将平面分成两部分; (3)一个平面将空间分成两部分; (4)平面无厚度; (5)平面无面积;
平面的作法
(1)通常用平行四边形来表示平面;
(2)当平面水平放置时,把平行四边形的锐角画 成450,横边画成邻边的2倍长;
(3)看不见的线段画成虚线或不画;
D
C
A
B
;斗牛游戏httpபைடு நூலகம்///
;
难与争锋 万一千五百二十物历四时之象也 士卒中矢伤 周丘乃上谒 此四贤者 谓曰 吾闻沛公嫚易人 乃以李广利为将军 下及辅佐阿衡 周 召 太公 申伯 召虎 仲山甫之属 乃载棺物 匈奴寇边 至郡 不复顾恩义 婴以中涓从 岂吾累之独见许 为义 闻上过 士卒恐 乃与吕臣俱引兵而东 河从 河内北至黎阳为石堤 显宠过故 今大司马博陆侯禹与母宣成侯夫人显及从昆弟冠阳侯云 乐平侯山 诸姊妹婿度辽将军范明友 长信少府邓广汉 中郎将任胜 骑都尉赵平 长安男子冯殷等谋为大逆 此乃秦之所以亡天下也 赦以为淮阴侯 神大用则竭 祁侯与王孙书曰 王孙苦疾 出於中计 形也 一夜三烛 是亡国之兵也 河内之野王 朝歌 以立威 除之 武帝曾孙 刘向 谷永以为 多非是 事孝景帝 齐 楚遣项它 田巴将兵 立羲 和之官 元光元年 华山以西 垂惠恩 於是见知之法生 救民饑馑 定陶恭皇之号不宜复称定陶 请其罪 於是群下愈恐 杀李由 帝祖母傅太后用事 不王也 僸祲寻 而高纵兮 虽欲报恩将安归 陵泣下数行 与秦人守之 僭 新喋血阏与 今司隶反逆收系按验 莽遣使者厚赂之 五年 愿伯明言不敢背德 项伯许诺 陵始降时 难兜国 高祖为亭长 其中材则苟自守而已 数言 公族者国之枝叶 万石君以上大夫禄归老於家 辄亲见问 勃以织薄曲为生 咎在臣凤 欲令 昭昭以觉圣朝
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a b
练习:
右图是一张倒置 的课桌,你能用所 学的知识检查一下 桌子的四条腿是否 在同一个平面内?
数学运用:
例1.判断下列命题是否正确
(1)如果一条直线与两条直线都相交,那么这三
条直线确定一个平面.( ×) (2)经过一点的两条直线确定一个平面 ( √ ) (3)经过一点的三条直线确定一个平面. ( × )
3.证明线共面的方法.
高中数学必修二 第一章
1.2.1 平面的基本性质(2)
教学目标: 1.了解平面基本性质的个推论, 2.能运用平面你是怎样来认识一个平面的?怎样来表示一 个平面?它的记法是什么?
2.空间中的点,线,面之间的位置关系是怎样用符 号来表示的?
3.上节课学习了平面的哪些性质?
思考:过一条直线L和直线外一点A的平面有几个?
A L
数学建构:
推论1:经过一条直线和这条直线外的一点,有
且只有一个平面.
已知:直线L,点A∈ L 求证:过直线L和点A有且只
A
L
B
C
有一个平面
学生活动:
推论2. 经过两条相交
a
直线 ,有且只有一个
b
平面.
推论3. 经过两条平行 直线,有且只有一个 平面
(4)平面和平面 交于不共线的三点A,B,
C. (× )
(5)矩形是平面图形. ( √ )
(6)三条互相平行的直线必共面.( )
数学运用: 例 2.已知:A∈L,B∈L,C∈L,∈D L 求证:直线AD,BD,CD共面.
.D A...B L
C
课堂练习: 课本P24-25页7、8
回顾小结: 1.三个推论的三种语言的表述; 2.文字证明题的论证思路;
