浙江省富阳市第二中学高中数学 3.2.1直线的点斜式方程练习题(无答案)新人教A版必修2
浙江省富阳市第二中学高中数学 3.2.2直线的两点式方程练习题(无答案)新人教A版必修2

浙江省富阳市第二中学高中数学 3.2.2直线的两点式方程练习题(无答案)新人教A 版必修21.若三点A(t,-6),B (-1,t),C(0,2)在同一直线上,则t 的值是 ( )A.2或-2B. 4或-4C. 4或-2D.4或22.过点A(-1,1)和点B(2,2)的直线在x 轴上的截距是 ( ) A.-4 B.-3 C.4 D.33.如果直线l 沿x 轴负方向平移3个单位,再沿y 轴正方向平移1个单位后,又回到原来的位置,则直线l 的斜率是 ( )(A )31 (B )3 (C )31- (D )-34、过A(1,1)、B(0,-1)两点的直线方程是 ( )A. B. C. D.y=x5.已知0,0ab bc <<,则直线ax by c +=通过 ( )A .第一、二、三象限B .第一、二、四象限C .第一、三、四象限D .第二、三、四象限6.直线1x =的倾斜角和斜率分别是 ( )A .045,1B .0135,1-C .090,不存在D .0180,不存在7.直线xa yb 221-=在y 轴上的截距是 ( )A .bB .2b -C .b 2D .±b8.已知点(2,3),(3,2)A B --,若直线l 过点(1,1)P 与线段AB 相交,则直线l 的斜率k 的取值范围是 ( )A .34k ≥ B .324k ≤≤ C .324k k ≥≤或 D .2k ≤9. 过点M(2, 1)的直线与x 轴,y 轴分别交于P,Q两点,且|MP|=|MQ|,则l 的方程是A. x -2y +3=0B. 2x -y -3=0 C .2x +y -5=0 D. x +2y -4=010.过点P (1,-2),且在两坐标轴上截距的绝对值相等的直线有 ( )A.4条B.3条C.2条D.1条11. 直线l 1, l 2在x 轴上的截距都是m ,在y 轴上的截距都是n ,则l 1, l 2满足 ( )A .平行B .重合C .平行或重合D .相交或重合12.已知直线222(273)(9)30a a x a y a -++-+=的倾斜角为4π,则a 的值等于_______.13.直线L 1:(m+2)x+(1-m)y=0,L 2:(m-1)x+(2m+3)y+2=0,L 1⊥L 2,则m=___________.14.若方程22(62)(352)10a a x a a y a --+-++-=表示平行于y 轴的直线,则a=______.15.一直线过点(-3,4),并且在两坐标轴上截距之和为12,这条直线方程是_____ _____.16. 直线ax -6y -12a =0(a ≠0)在x 轴上的截距是它在y 轴上的截距的3倍,则a 等于 .17.过点()--54,作一直线l ,使它与两坐标轴相交且与两轴所围成的三角形面积为5.19.已知直线m与直线L:2x-y+3=0在y轴上的截距相等,且倾斜角是L的倾斜角的2倍,求直线m的方程.。
3.2.1直线的点斜式方程(小结练习)

第三章 直线与方程3.2.1直线的点斜式方程一、选择题1. 若两条直线y=ax-2和y=(a+2)x+1相互垂直,则实数a 等于( )A.2B.1C.0D.-12. 已知过点A(-2,m)和B(m ,4)的直线与直线2x+y-1=0平行,则m 的值为( )A.0B.-8C.2D.103.若直线l 在y 轴上的截距为3,且经过点(2,0),则直线l 的方程是( ) A. 332y x =+ B. 332y x =- C. 332y x =-+ D. 332y x =-- 4.直线y=3x 绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为( ) A. 1133y x =-+ B. 113y x =-+ C. 33y x =- D.113y x =+ 5.过点(1,0)且与直线x-2y-2=0平行的直线方程是( ) A. 210x y --= B. 210x y -+=C. 220x y +-=D. 210x y +-= 6.直线l 过点(1,2)且与直线2x-3y+4=0垂直,则l 的方程是( )A. 3210x y +-=B. 3270x y ++=C. 2310x y --=D. 2380x y -+=二、填空题7.将直线2)y x =-绕点(2,0)按顺时针方向旋转30°所得的直线方程是______.8. 无论k 为何值时,直线(21)(1)510k x k y k ++-++=恒过顶点________.9.直线l 过点M(2,1),其倾斜角是直线340x y -+=的倾斜角的2倍,则直线l 的方程是_________.10.直线l经过点P(2,倾斜角为60°,该直线方程是_____________.三、解答题11. 已知一条直线的倾斜角为α,且4cos5α=,该直线与两坐标轴围成的三角形的面积为6,求此直线方程.12. 求过点P(2,3),且在两坐标轴上截距相等的直线方程.。
3.2.1直线的点斜式方程(最新)
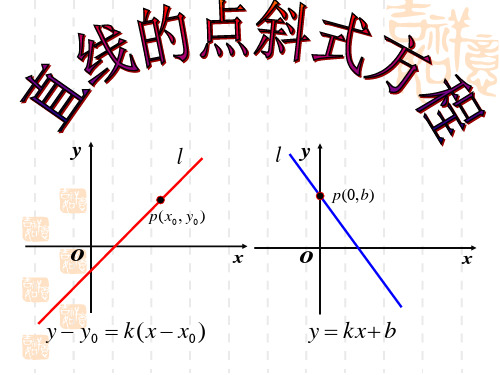
(点P不同于点A时)
y 3 2[ x (1)]
o
P( x, y)
1 直线 l 上每一点的坐标(x,y)都满足:
y 3 2[ x (1)];
x
l
2 坐标满足此方程的每一点都在直线 l 上.
问题2:若直线 l 经过点 P0 ( x0 , y0 ) ,斜率为k, 则此直线 的方程是?
若角A为直角, m 1 m 2, 解得: 7. 则 k AC
C4
3 所以,m 2或3,7.
讲授新课:
一、直线的点斜式方程
问题1: 若直线 l经过点A(-1,3),斜率为-2,点P在直线 l 上运动,则点P的坐标(x , y)满足怎样的关系式?
y
A(1,3)
y 3 2 x (1)
y2 y1 ( x1 x2 ) k x2 x1
温故知新 4、倾斜角
0 90
Байду номын сангаас 0
与斜率 k 的关系
k __ 0,
90
k0
k
越大 越大, k ___
k __ 0, 越大, k越大 ___ 90 180 5、若两条不重合直线斜率都存在时,
不能用点斜式求方程
O x0
直线上任意点 横坐标都等于x0
x x0 0 x x0 直线y轴的方程:
x=0
例1:直线l经过点P0(-2, 3),且倾斜角=45º , 求直线l的点斜式方程,并画出直线l. 解:直线l经过点P0(-2, 3),斜率 k tan45 1,
0
应用新知
代入点斜式方程得
y
l
3.2.1 直线的点斜式方程(练习)(解析版)

3.2.1直线的点斜式方程(练习)(建议用时:40分钟)一、选择题1.过点(-3,2),倾斜角为60°的直线方程为()A.y+2=3(x-3)B.y-2=33(x+3)C.y-2=3(x+3)D.y+2=33(x+3)【答案】C[因为直线的倾斜角为60°,所以其斜率k=tan60°=3,由直线方程的点斜式,可得方程为y-2=3(x+3).]2.已知直线的倾斜角为60°,在y轴上的截距为-2,则此直线的方程为()A.y=3x+2B.y=-3x+2C.y=-3x-2D.y=3x-2【答案】D[直线的倾斜角为60°,则其斜率为3,利用斜截式得y=3x-2.]3.直线y-b=2(x-a)在y轴上的截距为()A.a+b B.2a-bC.b-2a D.|2a-b|【答案】C[由y-b=2(x-a),得y=2x-2a+b,故在y轴上的截距为b-2a.]4.直线l过点(-3,0),且与直线y+1=2x垂直,则直线l的方程为()A.y=-12(x-3)B.y=-12(x+3)C.y=12(x-3)D.y=12(x+3)【答案】B[因为直线y=2x-1的斜率为2,所以直线l的斜率为-12.又直线l过点(-3,0),故所求直线的方程为y=-12(x+3),选B.]5.直线l1:y=ax+b与直线l2:y=bx+a(ab≠0,a≠b)在同一平面直角坐标系内的图象只可能是()【答案】D[对于A 选项,由l 1得a >0,b <0,而由l 2得a >0,b >0,矛盾;对于B 选项,由l 1得a <0,b >0,而由l 2得a >0,b >0,矛盾;对于C 选项,由l 1得a >0,b <0,而由l 2得a <0,b >0,矛盾;对于D 选项,由l 1得a >0,b >0,而由l 2得a >0,b >0.故选D.]二、填空题6.直线y =2x +1的斜率为________.【答案】27.设点A (-1,0),B (1,0),直线2x +y -b =0与线段AB 相交,则b 的取值范围是________.【答案】[-2,2][b 为直线y =-2x +b 在y 轴上的截距,如图,当直线y =-2x +b 过点A (-1,0)和点B (1,0)时b 分别取得最小值和最大值.∴b 的取值范围是[-2,2].]8.与直线l :y =34x +1平行,且在两坐标轴上截距之和为1的直线l 1的方程为________.【答案】y =34x -3[依题意设直线方程为y =34x +b ,令x =0可得纵截距为b ,令y =0可得横截距为-43b ,∴-43b +b =1,∴b =-3,所以直线方程为y=34x-3.]三、解答题9.一条直线经过点A(2,-3),并且它的倾斜角等于直线y=33x的倾斜角的2倍,求这条直线的点斜式方程.【答案】∵直线y=33x的斜率为33,∴它的倾斜角为30°,∴所求直线的倾斜角为60°,斜率为 3.又直线经过点A(2,-3),∴这条直线的点斜式方程为y+3=3(x-2).10.已知三角形的顶点坐标是A(-5,0),B(3,-3),C(0,2),试求这个三角形的三条边所在的斜截式方程.【答案】直线AB的斜率k AB=-3-03-(-5)=-38,过点A(-5,0),∴直线AB的点斜式方程为y=-38(x+5),即所求的斜截式方程为y=-38x-158.同理,直线BC的方程为y-2=-53 x,即y=-53x+2.直线AC的方程为y-2=25 x,即y=25x+2.∴直线AB,BC,AC的斜截式方程分别为y=-38x-158,y=-53x+2,y=25x+2.1.已知等边三角形ABC 的两个顶点A (0,0),B (4,0),且第三个顶点在第四象限,则BC 边所在的直线方程是()A .y =-3xB .y =-3(x -4)C .y =3(x -4)D .y =3(x +4)【答案】C[由题意,知直线BC 的倾斜角为60°,故直线BC 的斜率为3,由点斜式得所求直线的方程为y =3(x -4).]2.方程y =ax +1a表示的直线可能是图中的()【答案】B[直线y =ax +1a 的斜率是a ,在y 轴上的截距为1a.当a >0时,斜率a >0,在y轴上的截距1a >0,则直线y =ax +1a 过第一、二、三象限,四个选项都不符合;当a <0时,斜率a <0,在y 轴上的截距1a <0,则直线y =ax +1a过第二、三、四象限,仅有选项B 符合.]3.设直线l 的倾斜角是直线y =-3x +1的倾斜角的12,且与y 轴的交点到x 轴的距离是3,则直线l 的方程是________.【答案】y =3x ±3[直线y =-3x +1的倾斜角为120°,所以直线l 的倾斜角为60°,∴k l =tan 60°=3,又直线l 在y 轴上的截距为b =±3.所以直线l 的方程为y =3x ±3.]4.已知直线y =12x +k 与两坐标轴围成的三角形的面积不小于1,则实数k 的取值范围是________.【答案】(-∞,-1]∪[1,+∞)[令y =0,则x =-2k .令x =0,则y =k ,则直线与两坐标轴围成的三角形的面积为S =12|k |·|-2k |=k 2.由题意知,三角形的面积不小于1,可得k 2≥1,所以k 的取值范围是k ≥1或k ≤-1.]5.已知直线l :y =ax +3-a5.(1)求证:无论a 为何值,直线l 必经过第一象限;(2)若直线l 不经过第二象限,求实数a 的取值范围.【答案】(1)当x =15时,y =35,所以直线ll 必经过第一象限.(2)如图,直线OA 的斜率k OA =35-015-0=3.若直线l 不经过第二象限,则直线l 的斜率k l ≥3,即a ≥3.所以实数a 的取值范围为[3,+∞).。
高中数学 3.2.1直线的点斜式方程练习 新人教A版必修2

【成才之路】2015-2016学年高中数学 3.2.1直线的点斜式方程练习新人教A 版必修2基础巩固一、选择题1.已知直线的方程是y +2=-x -1,则( ) A .直线经过点(-1,2),斜率为-1 B .直线经过点(2,-1),斜率为-1 C .直线经过点(-1,-2),斜率为-1 D .直线经过点(-2,-1),斜率为1 [答案] C[解析] 直线方程y +2=-x -1可化为y -(-2)=-[x -(-1)],故直线经过点(-1,-2),斜率为-1.2.经过点(-2,2),倾斜角是60°的直线方程是( ) A .y +2=33(x -2) B .y -2=3(x +2) C .y -2=33(x +2) D .y +2=3(x -2)[答案] B[解析] k =tan60°=3,则点斜式方程为y -2=3(x +2). 3.直线y -3=-32(x +4)的斜率为k ,在y 轴上的截距为b ,则有( )A .k =-32,b =3B .k =-32,b =-2C .k =-32,b =-3D .k =-23,b =-3[答案] C[解析] 原方程可化为y =-32x -3,故k =-32,b =-3.4.与直线y =2x +1垂直,且在y 轴上的截距为4的直线的斜截式方程为( ) A .y =12x +4B .y =2x +4C .y =-2x +4D .y =-12x +4[答案] D5.已知两条直线y =ax -2和y =(2-a )x +1互相平行,则a 等于( )A .2B .1C .0D .-1[答案] B[解析] 根据两条直线的方程可以看出它们的斜率分别是k 1=a ,k 2=2-a .两直线平行,则有k 1=k 2.所以a =2-a ,解得a =1. 6.直线y =2x -6通过( ) A .第一、二、三象限 B .第一、二、四象限 C .第一、三、四象限 D .第二、三、四象限[答案] C[解析] y =2x -6过点(3,0)、T (0,-6),因此直线过一、三、四象限,选C . 二、填空题7.已知直线l 1过点P (2,1)且与直线l 2:y =x +1垂直,则l 1的点斜式方程为_________. [答案] y -1=-(x -2)[解析] 设l 1的斜率为k 1,l 2的斜率为k 2, ∵l 1⊥l 2,∴k 1k 2=-1. 又k 2=1,∴k 1=-1.∴l 1的点斜式方程为y -1=-(x -2).8.已知点(1,-4)和(-1,0)是直线y =kx +b 上的两点,则k =_________,b =_________.[答案] -2 -2[解析] 由题意,得⎩⎪⎨⎪⎧-4=k +b ,0=-k +b ,解得k =-2,b =-2.三、解答题9.已知直线l 1的方程为y =-2x +3,l 2的方程为y =4x -2,直线l 与l 1平行且与l 2在y 轴上的截距相同,求直线l 的方程.[解析] 由斜截式方程知直线l 1的斜率k 1=-2. 又∵l ∥l 1,∴l 的斜率k =k 1=-2. 由题意知l 2在y 轴上的截距为-2, ∴l 在y 轴上的截距b =-2,∴由斜截式可得直线l 的方程为y =-2x -2.10.已知△ABC 的三个顶点分别是A (-5,0),B (3,-3),C (0,2),试求BC 边上的高所在直线的点斜式方程.[分析] BC 边上的高与边BC 垂直,由此求得BC 边上的高所在直线的斜率,从而由点斜式得直线方程.[解析] 设BC 边上的高为AD ,则BC ⊥AD , ∴k BC k AD =-1. ∴2+30-3k AD =-1,解得k AD =35. ∴BC 边上的高所在直线的点斜式方程是y -0=35(x +5).即y =35x +3.能力提升一、选择题1.方程y -y 0=k (x -x 0)( ) A .可以表示任何直线 B .不能表示过原点的直线 C .不能表示与y 轴垂直的直线 D .不能表示与x 轴垂直的直线[答案] D[解析] 直线的点斜式方程不能表示没有斜率的直线,即不能表示与x 轴垂直的直线. 2.直线l 过点P (1,3),且与x 、y 轴正半轴所围成的三角形的面积等于6,则l 的方程是( )A .3x +y -6=0B .x +3y -10=0C .3x -y =0D .x -3y +8=0[答案] A[解析] 设y =kx +b ,由题意k <0,b >0,且 ⎩⎪⎨⎪⎧3=k +b ,12·|b |·|-b k |=6,解得⎩⎪⎨⎪⎧k =-3,b =6.3.方程y =ax +1a表示的直线可能是( )[答案] B[解析] 直线y =ax +1a 的斜率是a ,在y 轴上的截距是1a.当a >0时,斜率a >0,在y 轴上的截距是1a >0,则直线y =ax +1a过第一、二、三象限,四个选项都不符合;当a <0时,斜率a <0,在y 轴上的截距是1a <0,则直线y =ax +1a过第二、三、四象限,仅有选项B 符合.4.(2015·合肥高一检测)下列四个结论: ①方程k =y -2x +1与方程y -2=k (x +1)可表示同一直线; ②直线l 过点P (x 1,y 1),倾斜角为π2,则其方程为x =x 1;③直线l 过点P (x 1,y 1),斜率为0,则其方程为y =y 1; ④所有直线都有点斜式和斜截式方程. 其中正确的个数为( ) A .1 B .2 C .3 D .4[答案] B[解析] ①④不正确,②③正确,故选B . 二、填空题5.直线x +y +1=0上一点P 的横坐标是3,若该直线绕点P 逆时针旋转90°得直线l ,则直线l 的方程是_________.[答案] x -y -7=0[解析] P (3,-4),l 的倾斜角为135°-90°=45°,k =tan45°=1,则其方程为y +4=x -3,即x -y -7=0.6.(2015·山东师大附中)设直线l 的倾斜角是直线y =-3x +1的斜率角为12,且与y 轴的交点到x 轴的距离是3,则直线l 的方程是_________.[答案] y =3x ±3[解析] 因为已知直线的倾斜角是120°,所以直线l 的倾斜角是60°,又直线l 在y 轴上的截距b =±3,所以直线l 的方程为y =3x ±3.三、解答题 7.已知直线y =-33x +5的倾斜角是直线l 的倾斜角的大小的5倍,分别求满足下列条件的直线l 的方程.(1)过点P (3,-4); (2)在x 轴上截距为-2; (3)在y 轴上截距为3. [解析] 直线y =-33x +5的斜率k =tan α=-33,∴α=150°, 故所求直线l 的倾斜角为30°,斜率k ′=33. (1)过点P (3,-4),由点斜式方程得:y +4=33(x -3), ∴y =33x -3-4. (2)在x 轴截距为-2,即直线l 过点(-2,0), 由点斜式方程得:y -0=33(x +2),∴y =33x +233. (3)在y 轴上截距为3,由斜截式方程得y =33x +3. 8.求与直线x =43x +53垂直,并且与两坐标轴围成的三角形面积为24的直线l 的方程.[解析] 由直线l 与直线y =43x +53垂直,可设直线l 的方程为y =-34x +b ,则直线l 在x 轴,y 轴上的截距分别为x 0=43b ,y 0=b .又因为直线l 与两坐标轴围成的三角形的面积为24, 所以S =12|x 0||y 0|=24,即12|43b ||b |=24,b 2=36,解得b =6,或b =-6. 故所求的直线方程为y =-34x +6,或y =-34x -6.。
高中数学 3.2.1 直线的点斜式方程习题 新人教A版必修2

A.x-2y-1=0B.x-2y+1=0
C.2x+y-2=0D.x+2y-1=0
解析:选A与直线y= x-1平行的直线方程可设为:y= x+c,将点(1,0)代入得0= +c,解得c=- ,故直线方程为y= x- 即x-2y-1=0.
二、填空题
3、大自然的语言丰富多彩:从秋叶的飘零中,我们读出了季节的变换;从归雁的行列中,我读出了集体的力量;从冰雪的消融中,我们读出了春天的脚步;从穿石的滴水中,我们读出了坚持的可贵;从蜂蜜的浓香中,我们读出了勤劳的甜美。
4、成功与失败种子,如果害怕埋没,那它永远不能发芽。鲜花,如果害怕凋谢,那它永远不能开放。矿石,如果害怕焚烧(熔炉),那它永远不能成钢(炼成金子)。蜡烛,如果害怕熄灭(燃烧),那它永远不能发光。航船,如果害怕风浪,那它永远不能到达彼岸。
10.已知直线l的斜率与直线3x-2y=6的斜率相等,且直线l在x轴上的截距比在y轴上的截距大1,求直线l的方程.
解:由题意知,直线l的斜率为 ,故设直线l的方程为y= x+b,l在x轴上的截距为- b,在y轴上的截距为b,所以- b-b=1,b=- ,直线l的方程为y= x- ,即15x-10y-6=0.
三、解答题
9.已知三角形的顶点坐标是A(-5,0),B(3,-3),C(0,2),试求这个三角形的三条边所在直线的方程.
解:直线AB的斜率kAB= =- ,过点A(-5,0),由点斜式得直线AB的方程为y=- (x+5),即3x+8y+15=0;同理,kBC= =- ,kAC= = ,直线BC,AC的方程分别为5x+3y-6=0,2x-5y+10=0.
8、青春是一首歌,她拨动着我们年轻的心弦;青春是一团火,她点燃了我们沸腾的热血;青春是一面旗帜,她召唤着我们勇敢前行;青春是一本教科书,她启迪着我们的智慧和心灵。
高中数学第三章3.2.1直线的点斜式方程练习(含解析)新人教A版必修2
第22课时直线的点斜式方程A.直线经过点(-3,4),斜率为2B.直线经过点(4,-3),斜率为2C.直线经过点(3,-4),斜率为2D.直线经过点(-4,3),斜率为-2答案 C解析直线方程y+4=2x-6可化为y-(-4)=2(x-3),故直线经过点(3,-4),斜率为2.2.经过点(-3,2),倾斜角为60°的直线方程是( )A.y+2=3(x-3) B.y-2=33(x+3)C .y -2=3(x +3)D .y +2=33(x -3) 答案 C解析 直线的斜率k =tan60°=3,由点斜式可得直线的方程为y -2=3(x +3),所以选C .A .y =-x -3B .y =x +3C .y =-x +3D .y =x -3 答案 C解析 直线在y 轴上的截距为3的直线方程可以设为y =kx +3.将点A(-1,4)代入方程,得4=-k +3,解得k =-1,即所求直线方程为y =-x +3.4.直线y =ax +1a的图象可能是( )答案 B解析 根据斜截式方程,得其斜率与在y 轴上的截距同号,故选B .5.已知过点A(-2,m)和点B(m ,4)的直线为l 1,l 2:y =-2x +1,l 3:y =-n x -n .若l 1∥l 2,l 2⊥l 3,则m +n 的值为( )A .-10B .-2C .0D .8 答案 A解析 ∵l 1∥l 2,∴k AB =4-m m +2=-2,解得m =-8.又∵l 2⊥l 3,∴⎝ ⎛⎭⎪⎫-1n ×(-2)=-1,解得n =-2.∴m+n =-10.故选A .6.已知直线l 1的方程是y =ax +b ,l 2的方程是y =bx -a(ab≠0,a≠b),则下列各示意图形中,正确的是 ( )答案 D解析 逐一判定即可,对于选项A ,由l 1的图象知a>0,b>0,由l 2的图象知a<0,b<0,矛盾,故A 错误;对于选项B ,由l 1的图象知a>0,b<0,由l 2的图象知a<0,b>0,矛盾,故B 错误;对于选项C ,由l 1的图象知a<0,b>0,由l 2的图象知a<0,b<0,矛盾,故C 错误;对于选项D ,由l 1的图象知a<0,b>0,由l 2的图象知a<0,b>0,故D 正确.7.求斜率为4,且与坐标轴围成的三角形周长是12的直线l 的方程.解 设直线l 的方程为y =34x +b ,易求与x ,y 轴的交点分别为A ⎝ ⎛⎭⎪⎫-43b ,0,B(0,b), ∴|AB|=⎝ ⎛⎭⎪⎫-43b 2+b 2=53|b|.∴53|b|+43|b|+|b|=12,∴b=±3. ∴直线l 的方程为y =34x±3,即:3x -4y±12=0.8.已知直线l :3ax -5y -a +2=0,求证:不论a 为何值,直线l 总经过第一象限. 证明 方程3ax -5y -a +2=0可化为 5y -2=a(3x -1), 即y =35a ⎝ ⎛⎭⎪⎫x -13+25,∴它表示过点⎝ ⎛⎭⎪⎫13,25的直线. ∵点⎝ ⎛⎭⎪⎫13,25在第一象限, ∴直线l 不论a 取何值,总过第一象限.一、选择题1.直线y =k(x -1)+2恒过定点( )A .(-1,2)B .(1,2)C .(2,-1)D .(2,1) 答案 B解析 根据直线点斜式的定义可知,直线y =k(x -1)+2恒过定点(1,2). 2.过点(1,0)且与直线x -2y -2=0垂直的直线方程为( ) A .x -2y -1=0 B .x -2y +1=0 C .2x +y -2=0 D .x +2y -1=0 答案 C解析 ∵x-2y -2=0的斜率为12,由题意得,所求直线的斜率为-2,由点斜式得y -0=-2(x -1),即2x +y -2=0.3.在同一直角坐标系中,表示直线y =ax 与y =x +a 正确的是( )答案 C解析 解法一:(1)当a>0时,直线y =ax 的倾斜角为锐角且过原点,直线y =x +a 在y 轴上的截距a>0,A ,B ,C ,D 都不成立;(2)当a =0时,直线y =ax 的倾斜角为0°,所以A ,B ,C ,D 都不成立;(3)当a<0时,直线y =ax 的倾斜角为钝角且过原点,直线y =x +a 的倾斜角为锐角,且在y 轴上的截距a<0.C 正确.解法二(排除法):直线y =x +a 的倾斜角为锐角,排除B 、D ,A 选项中:直线y =ax 的倾斜角为锐角,所以a>0,而直线y =x +a 在y 轴上的截距a<0,所以不满足.从而得C 正确.4.下列叙述中正确的是( )A .点斜式方程y -y 1=k(x -x 1)适用于过点(x 1,y 1)且不垂直于x 轴的任何直线B .y -y 1x -x 1=k 表示过点P(x 1,y 1)且斜率为k 的直线方程 C .斜截式y =kx +b 适用于不平行于x 轴的任何直线 D .直线y =kx +b 与y 轴交于点B(0,b),其中截距b =|OB| 答案 A解析 对于选项A ,点斜式方程y -y 1=k(x -x 1)适用于过点(x 1,y 1)且不垂直于x 轴的任何直线,满足点斜式方程的条件,所以正确;对于选项B ,显然P(x 1,y 1)不满足方程,不正确;对于选项C ,斜截式y =kx +b 适用于不垂直于x 轴的任何直线,所以不正确;对于选项D ,直线y =kx +b 与y 轴交于点B(0,b),其中截距b =|OB|不正确,因为截距是b ,其值可正、可负、可为零.故选A .5.将直线y =3x 绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为( ) A .y =-13x +13 B .y =-13x +1C .y =3x -3D .y =13x +1答案 A解析 将直线y =3x 绕原点逆时针旋转90°,得到直线y =-13x ,再向右平移1个单位,所得到的直线为y =-13(x -1),即y =-13x +13.二、填空题6.已知直线l 在y 轴上的截距为1,且垂直于直线y =12x ,则l 的方程是________.答案 y =-2x +1解析 设垂直于直线y =12x 的直线l 的方程为y =-2x +m .因为直线l 在y 轴上的截距为1,所以m =1,所以直线l 的方程是y =-2x +1.7.已知点M 是直线l :y =3x +3与x 轴的交点,将直线l 绕点M 旋转30°,则所得到的直线l′的方程为________.答案 x +3=0或x -3y +3=0解析 在y =3x +3中,令y =0,得x =-3,即M(-3,0).因为直线l 的斜率为3,所以其倾斜角为60°.若直线l 绕点M 逆时针旋转30°,则得到的直线l′的倾斜角为90°,此时直线l′的斜率不存在,故其方程为x +3=0;若直线l 绕点M 顺时针旋转30°,则得到的直线l′的倾斜角为30°,此时直线l′的斜率为tan30°=33,故其方程为y =33(x +3).即x -3y +3=0.综上所述,所求直线l′的方程为x +3=0或x -3y +3=0.8.设点A(-1,0),B(1,0),直线2x +y -b =0与线段AB 相交,则b 的取值范围是________. 答案 [-2,2]解析 b 为直线y =-2x +b 在y 轴上的截距,如图,当直线y =-2x +b 过点A(-1,0)和点B(1,0)时b 分别取得最小值和最大值. ∴b 的取值范围是[-2,2]. 三、解答题9.求过点M(m ,0)和点N(2,1)的直线方程.解 当m =2时,过点M(m ,0)和点N(2,1)的直线斜率不存在,其方程为x =2. 当m≠2时,直线的斜率为k =0-1m -2=-1m -2.又直线过点N(2,1),∴直线的点斜式方程为y -1=-1m -2(x -2).综上,当m =2时,所求的直线方程为x =2. 当m≠2时,所求的直线方程为y -1=-1m -2(x -2).10.等腰△ABC 的顶点A(-1,2),AC 的斜率为3,点B(-3,2),求直线AC ,BC 及∠A 的平分线所在的直线方程.解 AC :y =3x +2+3. ∵AB∥x 轴,AC 的倾斜角为60°, ∴BC 的倾斜角α为30°或120°. 当α=30°时,BC 的方程为y =33x +2+3,∠A 平分线的倾斜角为120°, 即其所在直线方程为y =-3x +2-3.当α=120°时,BC 的方程为y =-3x +2-33, ∠A 平分线的倾斜角为30°,即其所在直线方程为y =33x +2+33.。
高中数学人教版必修2 3.2.1直线的点斜式方程 作业(系列四)

直线的点斜式一、选择题(每小题6分,共30分)1.直线y=-3x-6的斜率为k,在y轴上的截距为b,则()A.k=3,b=6B.k=-3,b=-6C.k=-3,b=6D.k=3,b=-62.(2013·济宁高一检测)直线y=23xa a--的倾斜角为120°,则a的值是()3.方程y=ax+1a表示的直线可能是()4.(2013·遵义高一检测)已知ab<0,bc<0,则直线y=a cxb b-+通过()A.第一、二、三象限B.第一、二、四象限C.第一、三、四象限D.第二、三、四象限5.(2013·佛山高一检测)已知两条直线y=ax-2和y=(a+2)·x+1互相垂直,则a=()A.2B.1C.0D.-1二、填空题(每小题8分,共24分)6.直线l1与直线l2:y=3x+1平行,又直线l1过点(3,5),则直线l1的方程为.7.求斜率为34,且与坐标轴所围成的三角形的周长是12的直线方程是.8.已知集合A={(x,y)|y=-mx-1},B={(x,y)|y=m2m-x-m1m+},若A∩B=∅,则m的值为.三、解答题(9题,10题14分,11题18分)9.设直线l的方程为y=-(a+1)x+a-2.(1)若l在两个坐标轴上的截距相等,求l的方程.(2)若l不经过第二象限,求a的取值范围.10.(2013·临沂高一检测)已知直线l 经过点(0,-2),其倾斜角是60°.(1)求直线l 的方程.(2)求直线l 与两坐标轴围成的三角形的面积.11.(能力挑战题)有一个可同时进出水的容器,每单位时间内的水量是一定的,设从某时刻开始10min 内只进水不出水,在随后的30min 内既进水又出水,得到时间x(min)与水量y(L )之间的关系如图所示.若40min后只放水不进水,求y 与x 的函数关系.答案解析1.【解析】选B.因为y=-3x-6,所以k=-3,b=-6.2.【解析】选A.由2a -=tan 120°,所以3.【解题指南】由直线的方程,可知直线的斜率与纵截距的符号相同,结合选项得出答案.【解析】选B.当a>0时,1a >0,即直线的斜率与截距大于0;当a<0时,1a <0,即直线的斜率与截距小于0,结合选项可知选B.4.【解析】选C.因为ab<0,bc<0,所以a b ->0,c b <0, 即直线y=a c x b b-+过第一、三、四象限. 5.【解析】选D.两条直线y=ax-2和y=(a+2)x+1互相垂直,所以a(a+2)=-1,所以a=-1. 【变式训练】过点P(-1,3)且垂直于直线y=13x 22+的直线方程为( ) A.y=-2x+1 B.y=-2x+5 C.y=15x 22+ D.y=17x 22- 【解析】选A.由所求直线与直线y=13x 22+垂直, 所以可设为y=-2x+m,把点P(-1,3)代入得m=1,即y=-2x+1.6.【解析】直线l 1与直线l 2:y=3x+1平行,故其斜率为3,又过点(3,5),所以方程为y-5=3(x-3),即y=3x-4. 答案:y=3x-4【变式训练】在x 轴上的截距是5,倾斜角为34π的直线方程为 . 【解析】在x 轴上的截距是5,故过点(5,0),倾斜角为34π,斜率为-1,所以直线方程为y-0=-(x-5),即y=-x+5. 答案:y=-x+57.【解析】设所求直线的方程为y=34x+b,与y 轴交点为A,与x 轴交点为B,令x=0,得y=b, 则|OA|=|b|,令y=0,得x=4b 3-, 则|OB|=|4b 3-|,所以|AB|=5b ||3==,又直线与坐标轴所围成的三角形的周长是12,所以|4b 3-|+|b|+|5b 3|=12,所以b=±3,所以所求直线的方程为 y=34x±3. 答案:y=34x±3 【举一反三】把题中“斜率为34”改为“过点(3,0)”,则直线的方程为 . 【解析】由题意可知,所求直线的斜率存在,设所求直线的方程为y=k(x-3),令x=0,得y=-3k,令y=0,得x=3, 由所求直线与坐标轴所围成的三角形的周长是12,所以所以k=±43,所以所求直线的方程为y=±43(x-3). 答案:y=±43(x-3)8.【解析】因为A∩B=∅,所以直线y=-mx-1与直线y=m 2m 1x m m -+-平行,由两条直线平行得-m=m 2m -,所以m=1或-2.答案:1或-29.【解析】(1)当x=0时,y=a-2,当y=0时, x=a 2a 1-+,所以a-2=a 2a 1-+,所以a 2-2a=0, 所以a=0或a=2.所以直线l 的方程为y=-x-2或y=-3x.(2)因为l 不经过第二象限,所以(a 1)0,a 20,-+≥⎧⎨-≤⎩所以a≤-1.10.【解析】(1)因为直线l 的倾斜角为60°,故其斜率为tan60°又直线l 经过点(0,-2),所以其方程为(2)由直线l 的方程知它在x 轴、y所以直线l 与两坐标轴围成的三角形的面积11.【解析】当0≤x≤10时,直线段过点O(0,0),A(10,20),所以k OA =2010=2,可以得OA 的点斜式方程为y=2x.当10≤x≤40时,直线段过点A(10,20),B(40,30),所以k AB =3020140103-=-, 所以AB 的点斜式方程为y-20=13(x-10),即y=150x 33+.当x≥40时,由题意可知直线段的斜率就是相应进水速度或放水速度.设进水的速度为v 1,放水的速度为v 2,在第①段中是只进水不放水的过程,所以v 1=2,在第②段中是既进水又放水的过程,所以v 1+v 2=13,所以v 2=53-,所以当x≥40时,可得直线段的方程为y-30= 53- (x-40), 即y=53-x+2903.若y=0,则x=58. 综上所述,y=y 2x,0x 10,150x ,10x 40,335290x ,40x 58.33⎧⎪=≤⎪⎪+≤⎨⎪⎪-+≤≤⎪⎩<<关闭Word 文档返回原板块。
-高中数学 3.2.1直线的点斜式方程练习 新人教a版必修2

3.2.1 直线的点斜式方程基础梳理1.直线的点斜式方程和斜截式方程.练习1:直线的点斜式方程能否表示平面上的所有直线?答案:不能不能表示垂直于x轴的直线2.直线l的截距.(1)直线在y轴上的截距:直线与y轴的交点(0,b)的纵坐标.(2)直线在x轴上的截距:直线与x轴的交点(a,0)的横坐标.练习2:(1)能否用斜截式表示平面内的所有直线?(2)y=kx+b中b的含义是什么?答案:(1)不能表示与x轴垂直的直线.(2)截距b就是函数图象与y轴交点的纵坐标.►思考应用1.直线方程的斜截式与我们学过的一次函数表达式比较你会得到什么结论?解析:当k≠0时,斜截式方程即为一次函数表达式.2.直线l的截距一定是非负吗?解析:截距不是距离,可正,可负,也可是0.自测自评1.直线的方程y-y0=k(x-x0)(D)A.可以表示任何直线B.不能表示过原点的直线C.不能表示与y轴垂直的直线D.不能表示与x轴垂直的直线2.已知直线的方程是y+2=-x-1,则(C)A.直线经过点(-1,2),斜率为-1B.直线经过点(2,-1),斜率为-1C.直线经过点(-1,-2),斜率为-1D.直线经过点(-2,-1),斜率为-1解析:由点斜式可知直线过(-1,-2),斜率为-1.3.直线y=ax+b(a+b=0,ab≠0)的图象可能是下列图中的(D)4.已知直线l1过点P(2,1)且与直线l2:y=x+1垂直,则l1的点斜式方程为y-1=-(x-2).5.已知直线l过点(0,7),且与直线y=-4x+2平行,则直线l的方程为(D)A.y=-4x-7 B.y=4x-7C.y=4x+7 D.y=-4x+7解析:过点(0,7)且与直线y=-4x+2平行的直线方程为y-7=-4x,即直线l的方程为y=-4x+7,故应选D.基础达标1.经过点(-3,2),倾斜角为60°的直线方程是(C )A .y +2=3(x -3)B .y -2=33(x +3) C .y -2=3(x +3) D .y +2=33(x -3) 2.如下图所示,方程y =ax +1a表示的直线可能是(B )3.直线y -2=-3(x +1)的倾斜角及在y 轴上的截距分别为(B )A .60°,2B .120°,2- 3C .60°,2- 3D .120°,2解析:该直线的斜率为-3,当x =0时,y =2-3,故其倾斜角为120°,在y 轴上的截距为2- 3.4.已知直线l 1:y =kx +b ,l 2:y =bx +k ,则它们的图象可能为(C )5.经过原点,且倾斜角是直线y =22x +1倾斜角2倍的直线(D ) A .x =0 B .y =0 C .y =2x D .y =22x6.欲使直线(m +2)x -y -3=0与直线(3m -2)x -y +1=0平行,则实数m 的值是(B )A .1B .2C .3D .不存在解析:把直线化为斜截式,得出斜率,通过直线平行的条件计算. 7.直线y =k(x -2)+3必过定点,该定点为(B )A .(3,2)B .(2,3)C .(2,-3)D .(-2,3)解析:直线方程改写为y -3=k(x -2),则过定点(2,3). 巩固提升8.若直线(m +2)x +(m 2-2m -3)y =2m 在x 轴上的截距是3,则m 的值是(D )A .25B .6C .-25D .-6解析:令y =0,得(m +2)x =2m ,将x =3代入得m =-6,故选D .9.求倾斜角为直线y =-3x +1的倾斜角的一半,且分别满足下列条件的直线方程: (1)经过点(-4,1); (2)在y 轴上的截距为-10.解析:∵直线l 1:y =-3x +1的斜率k 1=-3,∴直线的倾斜角为120°,由题意知,所求直线的倾斜角为60°,斜率k = 3. (1)∵过点(-4,1),∴直线方程为y -1=3(x +4). (2)∵在y 轴上截距为-10, ∴直线方程为y =3x -10.10.已知直线l :5ax -5y -a +3=0,(1)求证:不论a 为何值,直线l 总过第一象限; (2)为了使直线l 不过第二象限,求a 得取值范围.解析:(1)直线l 的方程可化为y -35=a(x -15),由点斜式方程可知直线l 的斜率为a ,且过定点A(15,35),由于点A 在第一象限,所以直线一定过第一象限.(2)如图,直线l 的倾斜角介于直线AO 与AP 的倾斜角之间,k AO =35-015-0=3,直线AP 的斜率不存在,故a≥3.1.直线方程的点斜式y -y 0=k(x -x 0)和斜截式y =kx +b 都是在斜率k 存在的前提下使用.2.注意区分截距和距离.截距可取一切实数,即可为正数、零、负数;距离必须大于等于0.3.数形结合解题.本章是用代数方法解决几何问题,因此画草图是必不可少的步骤,也是正确解题的前提和保证.3.2.1 直线的点斜式方程基础梳理1.直线的点斜式方程和斜截式方程.练习1:直线的点斜式方程能否表示平面上的所有直线?答案:不能不能表示垂直于x轴的直线2.直线l的截距.(1)直线在y轴上的截距:直线与y轴的交点(0,b)的纵坐标.(2)直线在x轴上的截距:直线与x轴的交点(a,0)的横坐标.练习2:(1)能否用斜截式表示平面内的所有直线?(2)y=kx+b中b的含义是什么?答案:(1)不能表示与x轴垂直的直线.(2)截距b就是函数图象与y轴交点的纵坐标.►思考应用1.直线方程的斜截式与我们学过的一次函数表达式比较你会得到什么结论?解析:当k≠0时,斜截式方程即为一次函数表达式.2.直线l的截距一定是非负吗?解析:截距不是距离,可正,可负,也可是0.自测自评1.直线的方程y-y0=k(x-x0)(D)A.可以表示任何直线B.不能表示过原点的直线C .不能表示与y 轴垂直的直线D .不能表示与x 轴垂直的直线2.已知直线的方程是y +2=-x -1,则(C )A .直线经过点(-1,2),斜率为-1B .直线经过点(2,-1),斜率为-1C .直线经过点(-1,-2),斜率为-1D .直线经过点(-2,-1),斜率为-1解析:由点斜式可知直线过(-1,-2),斜率为-1.3.直线y =ax +b(a +b =0,ab ≠0)的图象可能是下列图中的(D )4.已知直线l 1过点P(2,1)且与直线l 2:y =x +1垂直,则l 1的点斜式方程为y -1=-(x -2).5.已知直线l 过点(0,7),且与直线y =-4x +2平行,则直线l 的方程为(D )A .y =-4x -7B .y =4x -7C .y =4x +7D .y =-4x +7解析:过点(0,7)且与直线y =-4x +2平行的直线方程为y -7=-4x ,即直线l 的方程为y =-4x +7,故应选D .基础达标1.经过点(-3,2),倾斜角为60°的直线方程是(C )A .y +2=3(x -3)B .y -2=33(x +3) C .y -2=3(x +3) D .y +2=33(x -3) 2.如下图所示,方程y =ax +1a表示的直线可能是(B )3.直线y-2=-3(x+1)的倾斜角及在y轴上的截距分别为(B)A.60°,2 B.120°,2- 3C.60°,2- 3 D.120°,2解析:该直线的斜率为-3,当x=0时,y=2-3,故其倾斜角为120°,在y轴上的截距为2- 3.4.已知直线l1:y=kx+b,l2:y=bx+k,则它们的图象可能为(C)5.经过原点,且倾斜角是直线y=22x+1倾斜角2倍的直线(D)A.x=0 B.y=0C.y=2x D.y=22x6.欲使直线(m+2)x-y-3=0与直线(3m-2)x-y+1=0平行,则实数m的值是(B) A.1 B.2C.3 D.不存在解析:把直线化为斜截式,得出斜率,通过直线平行的条件计算.7.直线y=k(x-2)+3必过定点,该定点为(B)A .(3,2)B .(2,3)C .(2,-3)D .(-2,3)解析:直线方程改写为y -3=k(x -2),则过定点(2,3). 巩固提升8.若直线(m +2)x +(m 2-2m -3)y =2m 在x 轴上的截距是3,则m 的值是(D )A .25B .6C .-25D .-6解析:令y =0,得(m +2)x =2m ,将x =3代入得m =-6,故选D .9.求倾斜角为直线y =-3x +1的倾斜角的一半,且分别满足下列条件的直线方程: (1)经过点(-4,1); (2)在y 轴上的截距为-10.解析:∵直线l 1:y =-3x +1的斜率k 1=-3,∴直线的倾斜角为120°,由题意知,所求直线的倾斜角为60°,斜率k = 3. (1)∵过点(-4,1),∴直线方程为y -1=3(x +4). (2)∵在y 轴上截距为-10, ∴直线方程为y =3x -10.10.已知直线l :5ax -5y -a +3=0,(1)求证:不论a 为何值,直线l 总过第一象限; (2)为了使直线l 不过第二象限,求a 得取值范围.解析:(1)直线l 的方程可化为y -35=a(x -15),由点斜式方程可知直线l 的斜率为a ,且过定点A(15,35),由于点A 在第一象限,所以直线一定过第一象限.(2)如图,直线l 的倾斜角介于直线AO 与AP 的倾斜角之间,k AO =35-015-0=3,直线AP 的斜率不存在,故a≥3.1.直线方程的点斜式y-y0=k(x-x0)和斜截式y=kx+b都是在斜率k存在的前提下使用.2.注意区分截距和距离.截距可取一切实数,即可为正数、零、负数;距离必须大于等于0.3.数形结合解题.本章是用代数方法解决几何问题,因此画草图是必不可少的步骤,也是正确解题的前提和保证.。
浙江省富阳市第二中学高中数学 直线的方程练习题(无答案)新人教A版必修2

浙江省富阳市第二中学高中数学 直线的方程(1)练习题(无答案)新人教A 版必修2( )1.若直线y=kx+b 过原点,则A.k=0B.k ≠0C.b=0D.b ≠0( )2.设直线ax+by+c=0的倾斜角为α,且sin α+cos α=0,则a,b 满足A.a+b=1B. a-b=1C. a+b=0D. a-b=0( )3.过点(2,3)且在坐标轴上的截距相等的直线方程是A.x+y-5=0B.3x-2y=0 或x+y-5=0C.x-y+1=0D.x-y+1=0 或3x-2y=0( )4.两条直线ax+y+b=0与x+ay-1=0互相平行的条件是A.a=1±B.a=-1C.11a b =⎧⎨≠-⎩D. 11a b =⎧⎨≠-⎩或11a b =-⎧⎨≠⎩( )5.直线(2m-1)x+(3-m)y-8=0与(m+5)x+(2m+1)y+4=0互相垂直,则m 的值是 A.17 B.13- C.1 D.12 ( )6. 顺次连结A(-4,3),B(2,5),C(6,3),D(-3,0)四点所组成的图形是A.平行四边形B.直角梯形C.等腰梯形D.以上都不对( )7.已知点P(0,-1),点Q 在直线x-y+1=0上,若直线PQ 垂直于直线x+2y-5=0,则点Q 的坐标是A.(-2,1)B.(2,1)C.(2,3)D.(-2,-1)( )8.已知点A(1,1)和点B(3,4),P 是y 轴上一点,则PA PB +的最小值是A.13B.5C.29D.不存在( ) 9. 如图,直线aax y 1-=的图象可能是10、设直线l 的方程为(a +1)x +y -2+a =0,若l 经过第一象限,则a 的取值范围是___________.11.已知直线L:22(2)(32)50,m m x m m y +-+++-=若L 与x 轴平行,则m=____________;若L 与y 轴平行,则m=____________.12.点A(-1,2)关于直线:l 2x+y-1=0的对称点的坐标是_______________________.13.已知点M 是直线:l 2x -y-4=0与x 轴的交点,把直线l 绕点M 依逆时针方向旋转45o ,得到的直线方程____________________________.14.不论m 取何实数,直线:(2+m)x+(1-2m)y+4-3m=0必过定点,其定点坐标是____________.15. 已知三点A (m-1,2)、B (1,1)、C (3,m 2-m-1),若AB ⊥BC ,求m 的值..16.直线L过点P(-2,3),且与x轴,y轴分别交于A,B两点.若P恰为A,B的中点,求直线L的方程.17.倾斜角为直线3x-4y+7=0的倾斜角的一半,且在两坐标轴上的截距之和为1的直线L的方程.18.一束光线过A(3,2),被L:x+y+1=0反射后过点B(-1,1),求入射线及反射线所在的直线的方程.。
高中数学 第三章3.2.1直线的点斜式方程基础过关训练

§3.2 直线的方程3.2.1 直线的点斜式方程一、基础过关1.已知直线的倾斜角为60°,在y 轴上的截距为-2,则此直线方程为( ) A .y =3x +2B .y =-3x +2C .y =-3x -2D .y =3x -2 2.过点(-1,3)且平行于直线x -2y +3=0的直线方程为 ( ) A .2x +y -1=0B .x -2y -5=0C .x -2y +7=0D .2x +y -5=0 3.直线y =kx +b 通过第一、三、四象限,则有( ) A .k >0,b >0B .k >0,b <0C .k <0,b >0D .k <0,b <0 4.下列选项中,在同一直角坐标系中,表示直线y =ax 与y =x +a 正确的是( )5.将直线y =3x 绕原点逆时针旋转90°,再向右平移1个单位长度,所得到的直线为_______.6.已知一条直线经过点P (1,2)且与直线y =2x +3平行,则该直线的点斜式方程是________.7.求满足下列条件的直线方程:(1)过点P (-4,3),斜率k =-3;(2)过点P (3,-4),且与x 轴平行;(3)过点P (5,-2),且与y 轴平行;(4)过点P (-2,3),Q (5,-4)两点.8.已知△ABC 的三个顶点坐标分别是A (-5,0),B (3,-3),C (0,2),求BC 边上的高所在的直线方程.二、能力提升9.集合A ={直线的斜截式方程},B ={一次函数的解析式},则集合A 、B 间的关系是( )A .A =BB .B AC .A BD .以上都不对 10.直线kx -y +1-3k =0当k 变化时,所有的直线恒过定点( ) A .(1,3)B .(-1,-3)C .(3,1)D .(-3,-1) 11.下列四个结论:①方程k =y -2x +1与方程y -2=k (x +1)可表示同一直线; ②直线l 过点P (x 1,y 1),倾斜角为90°,则其方程是x =x 1;③直线l过点P(x1,y1),斜率为0,则其方程是y=y1;④所有的直线都有点斜式和斜截式方程.正确的为________(填序号).12.已知直线l:y=kx+2k+1.(1)求证:直线l恒过一个定点;(2)当-3<x<3时,直线上的点都在x轴上方,求实数k的取值范围.三、探究与拓展13.等腰△ABC的顶点A(-1,2),AC的斜率为3,点B(-3,2),求直线AC、BC及∠A的平分线所在直线的方程.答案1.D 2.C 3.B 4.C5.y =-13x +13 6.y -2=2(x -1)7.解 (1)∵直线过点P (-4,3),斜率k =-3,∴由直线方程的点斜式得直线方程为y -3=-3(x +4),即3x +y +9=0.(2)与x 轴平行的直线,其斜率k =0,由直线方程的点斜式可得直线方程为y -(-4)=0(x -3),即y =-4.(3)与y 轴平行的直线,其斜率k 不存在,不能用点斜式方程表示,但直线上点的横坐标均为5,故直线方程为x =5.(4)过点P (-2,3),Q (5,-4)的直线斜率k PQ =-4-35--2=-77=-1.又∵直线过点P (-2,3),∴由直线方程的点斜式可得直线方程为y -3=-1(x +2),即x +y -1=0.8.解 设BC 边上的高为AD ,则BC ⊥AD ,∴k AD ·k BC =-1,∴2+30-3·k AD =-1,解得k AD =35.∴BC 边上的高所在的直线方程为y -0=35(x +5),即y =35x +3.9.B 10.C11.②③12.解 (1)由y =kx +2k +1,得y -1=k (x +2).由直线方程的点斜式可知,直线恒过定点(-2,1).(2)设函数f (x )=kx +2k +1,显然其图象是一条直线(如图所示),若使当-3<x <3时,直线上的点都在x 轴上方,需满足⎩⎪⎨⎪⎧ f -3≥0,f 3≥0.即⎩⎪⎨⎪⎧ -3k +2k +1≥0,3k +2k +1≥0.解得-15≤k ≤1.所以,实数k 的取值范围是-15≤k ≤1.13.解 直线AC 的方程:y =3x +2+ 3.∵AB ∥x 轴,AC的倾斜角为60°,∴BC的倾斜角为30°或120°.当α=30°时,BC方程为y=33x+2+3,∠A平分线倾斜角为120°,∴所在直线方程为y=-3x+2- 3.当α=120°时,BC方程为y=-3x+2-33,∠A平分线倾斜角为30°,∴所在直线方程为y=33x+2+33.。
高中数学 第三章3.2.1 直线的点斜式方程练习 新人教A版必修2

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学习资料专题3.2.1 直线的点斜式方程【选题明细表】1.(2018·北京海淀期末)直线2x+y-1=0在y轴上的截距为( D )(A)-2 (B)-1 (C)- (D)1解析:直线2x+y-1=0化为y=-2x+1,则在y轴上的截距为1.故选D.2.(2018·深圳调研)在同一平面直角坐标系中,直线l1:ax+y+b=0和直线l2:bx+y+a=0有可能是( B )解析:当a>0,b>0时,-a<0,-b<0.选项B符合.故选B.3.已知直线的斜率是2,在y轴上的截距是-3,则此直线方程是( A )(A)2x-y-3=0 (B)2x-y+3=0(C)2x+y+3=0 (D)2x+y-3=0解析:由直线方程的斜截式得方程为y=2x-3,即2x-y-3=0.4.(2018·广东湛江高一期末)经过点A(-1,4)且在x轴上的截距为3的直线方程是( C )(A)x+y+3=0 (B)x-y+5=0(C)x+y-3=0 (D)x+y-5=0解析:过点A(-1,4)且在x轴上的截距为3的直线的斜率为=-1.所求的直线方程为y-4=-(x+1),即x+y-3=0.5.(2018·台山市华侨中学高二上期末)已知三角形的三个顶点A(4,3), B(-1,2),C(1,-3),则△ABC的高CD所在的直线方程是( A )(A)5x+y-2=0 (B)x-5y-16=0(C)5x-y-8=0 (D)x+5y+14=0解析:△ABC的高CD与直线AB垂直,故有直线CD的斜率k CD与直线AB的斜率k AB满足k CD·k AB=-1k AB==,所以k CD=-5.直线CD过点C(1,-3),故其直线方程是y+3=-5(x-1)整理得5x+y-2=0,选A.6.(2018·河南商丘期末)已知直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行,则a的值为( D )(A)±(B)±1 (C)1 (D)-1解析:直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行,所以a2-2=-1,2≠2a,解得a=-1.故选D.7.(2018·海口一中质检)根据条件写出下列直线的方程.(1)斜率为2,在y轴上的截距是3的直线方程: ;(2)过点(0,-2),斜率为-3的直线方程: .解析:有斜率,且知道直线在y轴上的截距可选直线的斜截式方程.(1)直线方程为y=2x+3,即2x-y+3=0;(2)因为过点(0,-2),所以直线在y轴上的截距是-2,故直线方程为3x+y+2=0.答案:(1)2x-y+3=0 (2)3x+y+2=08.求倾斜角是直线y=-x+1的倾斜角的,且分别满足下列条件的直线方程.(1)经过点(,-1);(2)在y轴上的截距是-5.解:因为直线y=-x+1的斜率k=-,所以其倾斜角α=120°.由题意得所求直线的倾斜角α1=α=30°,故所求直线的斜率k1=tan 30°=.(1)因为所求直线经过点(,-1),斜率为,所以所求直线方程是y+1=(x-),即x-3y-6=0.(2)因为所求直线的斜率是,在y轴上的截距为-5,所以所求直线的方程为y=x-5,即x-3y-15=0.9.(2018·深圳模拟)直线l1的斜率为2,l1∥l2,直线l2过点(-1,1)且与y轴交于点P,则P点坐标为.解析:因为l1∥l2,且l1的斜率为2,则直线l2的斜率k=2,又直线l2过点(-1,1),所以直线l2的方程为y-1=2(x+1),整理得y=2x+3,令x=0,得y=3,所以P点坐标为(0,3).答案:(0,3)10.写出下列直线的斜截式方程.(1)斜率是3,在y轴上的截距是-3;(2)倾斜角是60°,在y轴上的截距是5;(3)倾斜角是30°,在y轴上的截距是0.解:(1)y=3x-3.(2)因为k=tan 60°=,所以y=x+5.(3)因为k=tan 30°=,所以y=x.11.已知直线l:5ax-5y-a+3=0.(1)求证:不论a为何值,直线l总过第一象限;(2)为了使直线l不过第二象限,求a的取值范围.(1)证明:直线l的方程可化为y-=a(x-),由点斜式方程可知直线l的斜率为a,且过定点A(,),由于点A在第一象限,所以直线一定过第一象限.(2)解:如图,直线l的倾斜角介于直线AO与AP的倾斜角之间,k AO==3,直线AP的斜率不存在,故a≥3.即a的取值范围为[,+∞).。
高中数学二 3.2.1 直线的点斜式方程 (学生版)

3。
2。
1 直线的点斜式方程时间:30分钟,总分:70分班级:姓名:一、选择题(共6小题,每题5分,共30分)1.下面四个直线方程中,是直线的斜截式方程的是( )A.x=3 B.y=-5 C.2y=x D.x=4y-12.已知直线的方程为y+2=-x-1,则() A.直线过点(-1,2),斜率为-1B.直线过点(-1,2),斜率为1C.直线过点(-1,-2),斜率为-1[D.直线过点(-1,-2),斜率为13.倾斜角为135°,且在y轴上的截距为-1的直线方程是()A.x-y+1=0 B.x-y-1=0C.x+y-1=0 D.x+y+1=04.经过点(-错误!,2),且倾斜角是30°的直线方程是( )A.y+错误!=错误!(x-2)B.y+2=错误!(x-错误!)C.y-2=错误!(x+错误!) D.y-2=错误!(x+错误!) 5.已知直线l不经过第三象限,若其斜率为k,在y轴上的截距为b(b≠0),则()A.kb〈0 B.kb≤0 C.kb>0 D.kb≥06.直线kx-y+1-3k=0当k变化时,所有的直线恒过定点( )A.(1,3) B.(-1,-3)C.(3,1) D.(-3,-1)二、填空题(共4小题,每题5分,共20分)7、若直线l在y轴上的截距等于它的斜率,则直线l 一定经过点________.8、若直线y=kx+1与以A(3,2),B(2,3)为端点的线段有公共点,则k的取值范围是________.9.已知直线l的方程为y-a=(a-1)(x+2),若此直线在y轴上的截距为10,则a=________.10.过点(1,3)且与直线x+2y-1=0垂直的直线的方程是________.三、解答题(共2小题,每题10分,共20分)11、求经过点A(-2,2),并且和x轴的正半轴、y 轴的正半轴所围成的三角形的面积是1的直线的方程.12.已知△ABC的三个顶点坐标分别是A(-5,0),B(3,-3),C(0,2),求BC边上的高所在的直线方程.。
浙江省富阳市第二中学高中数学 3.1.1倾斜角与斜率练习题(无答案)新人教A版必修2

浙江省富阳市第二中学高中数学 3.1.1倾斜角与斜率练习题(无答案)新人教A 版必修21.已知直线经过点A (-2,0),B (-5,3),则该直线的倾斜角为( )A .1500B 。
1350C 。
750D 。
450 2.已知直线l 的倾斜角为︒-15α,则下列结论中正确的是 ( )A.︒<≤︒1800αB. ︒<<︒18015αC. ︒<≤︒18015αD. ︒<≤︒19515α3.下列各组中,三点共线的是 ( )A .(1,4),(-1,2),(3,5)B 。
(-2,-5),(7,6),(-5,3)C .(1,0),(0,31-),(7,2)D 。
(0,0),(2,4),(-1,3)4.若直线AB 的斜率为2,将直线绕点A 按逆时针方向旋转︒45后,所得直线的斜率是 ( )A.3- B.31- C.3 D. 31 5.直线l 的斜率为21m k -=(R m ∈),则直线l 的倾斜角的取值范围是 ( )A. ]4,0[πB. ),43[]4,0[πππ⋃C.),2(]4,0[πππ⋃ D. ),0[π 6.右图中的直线l 1、l 2、l 3的斜率分别为k 1、k 2、k 3,则( ).A .k 1<k 2<k 3 B. k 3<k 1<k 2 C. k 3<k 2<k 1 D. k 1<k 3<k 27.已知直线的斜率的绝对值为3,则直线的倾斜角为 ;8.已知直线l 的倾斜角为α,且1312cos =α,则此直线的斜率为 ; 9.倾斜角是过原点和)32,2(的直线倾斜角2倍的直线的斜率为 ;10(1)若直线l 的倾斜角取值范围为2[,],33ππ则斜率的取值范围是______ ______;(2)若直线l 的斜率的取值范围是[1,3]-,则其倾斜角的取值范围是__ _ ___;11.已知点A (cos700,sin700),B(cos200,sin200),则直线AB 的斜率为 ;12.直线l 的斜率为αcos ,则其倾斜角的取值范围是 ;13.已知直线l 过)1,2(),,12(-+m N m m M(1)当m 为多少时,直线l 的倾斜角为43π?(2)当m 为多少时,直线l 的倾斜角为2π?14.若三点)4,()0,4()8,0(--m C B A 共线,求实数m 的值。
人教版高一数学(必修2)导学案:3.2.1直线的点斜式方程(无答案)

3.2.1 直线的点斜式方程
班级: 姓名: 编者: 高一数学备课组 问题引航
2.直线的斜截式方程的形式是什么?适用范围是什么?截距的定义是什么? 自主探究
互动探究 例1. 一条直线经过点P 1(-2,3),且倾斜角045α=,求这条直线L 的点斜式方程,
并画出直线L.
例2.已知直线111222:,:l y k x b l y k x b =+=+,试讨论:(1)12l l P 的条件是什么?(2)12l l ⊥的条件是什么?
当堂检测
1.方程()331--=+x y 表示过点______、斜率是______、倾斜角是______、在y 轴上的截距是______的直线。
2.已知直线的点斜式方程是y +2=(x +1),那么此直线经过定点_______,直线的斜率是______,倾斜角是_______.
3.已知直线的点斜式方程是y -2=x -1,那么直线的斜率是_____,倾斜角是_____, 此直线必过定点______
4.经过点(-3,2)且与2x+3y-1=0平行的直线方程是
5.直线方程可表示成点斜式方程的条件是( )
(A )直线的斜率存在 (B )直线的斜率不存在
(C )直线不过原点 (D )不同于上述答案
6.已知直线经过点(6,4),斜率为43-,求直线的点斜式和斜截式.
知识拓展
1. 已知直线l 的方程为112
y x =-+,求过点(2,3)且垂直于l 的直线方程
2.求直线y=4x+8与坐标轴所围成的三角形的面积。
作业
课本第100页习题3.2 A 组第1题(1)(2)(3),第2题,第5题 自我评价
)
A.非常好 B.较好 C.一般 D.较差
E.很差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省富阳市第二中学高中数学 3.2.1直线的点斜式方程练习题(无答案)新人
教A 版必修2
1.若直线y=kx+b 过原点,则 ( ) A.k=0 B.k ≠0 C.b=0 D.b ≠0
2.设直线ax+by+c=0的倾斜角为α,且sin α+cos α=0,则a,b 满足 ( )
A.a+b=1
B. a-b=1
C. a+b=0
D. a-b=0
3.过点(2,3)且在坐标轴上的截距相等的直线方程是 ( )
A.x+y-5=0
B.3x-2y=0 或x+y-5=0
C.x-y+1=0
D.x-y+1=0 或3x-2y=0
4.两条直线ax+y+b=0与x+ay-1=0互相平行的条件是 ( )
A.a=1±
B.a=-1
C.11a b =⎧⎨≠-⎩
D. 11a b =⎧⎨≠-⎩或11
a b =-⎧⎨≠⎩
5.直线(2m-1)x+(3-m)y-8=0与(m+5)x+(2m+1)y+4=0互相垂直,则m 的值是 ( ) A.17 B.13- C.1 D.12
6.直线mx+4y-2=0与2x-5y+n=0垂直,垂足为(1,p),则m+n-p 的值为 ( )
A.-4
B.0
C.20
D.24
7.已知点P(0,-1),点Q 在直线x-y+1=0上,若直线PQ 垂直于直线x+2y-5=0,则
点Q 的坐标是 ( )
A.(-2,1)
B.(2,1)
C.(2,3)
D.(-2,-1)
8.已知点A(1,1)和点B(3,4),P 是y 轴上一点,则PA PB +的最小值是 ( )
A.13
B.5
C.29
D.不存在
9. 如图,直线a
ax y 1-=的图象可能是 ( )
10、设直线l 的方程为(a +1)x +y -2+a =0,若l 经过第一象限,则a 的取值范围是___________.
11.已知直线L:22
(2)(32)50,m m x m m y +-+++-=
若L 与x 轴平行,则m=____________;若L 与y 轴平行,则m=____________.
12.点A(-1,2)关于直线:l 2x+y-1=0的对称点的坐标是_______________________.
13.已知点M 是直线:l 2x-y-4=0与x 轴的交点,把直线l 绕点M 依逆时针方向旋转45o ,得到的直线方程____________________________.
14.不论m 取何实数,直线:(2+m)x+(1-2m)y+4-3m=0必过定点,其定点坐标是____________.
15.设θ是直线l 的倾斜角,且满足1sin cos 5
θθ+=-
,求直线l 的斜率.
16.直线L过点P(-2,3),且与x轴,y轴分别交于A,B两点.若P恰为A,B的中点,求直线L的方程.
17.倾斜角为直线3x-4y+7=0的倾斜角的一半,且在两坐标轴上的截距之和为1的直线L的方程.
18.一束光线过A(3,2),被L:x+y+1=0反射后过点B(-1,1),求入射线及反射线所在的直线的方程.。
