第八章 理想流体的有旋流动和无旋流动
工程流体力学总复习要点

1.狭缝流动、管内流动及平板降膜流 动的剪应力与速度分布
第六章
一、概念 1.连续性方程与质量守恒方程的关系 2.N-S方程的适用条件 3.N-S方程各项的含义 二、计算与推导 1. 三维不可压缩流体连续性方程
第七章 一、概念 1.势函数与流函数存在的条件 2.无旋流动的判别方法 二、计算 1.给定流场能求势函数和流函数, 反之亦然。
第一章
一、概念 1.流体的连续介质模型 2.流体的主要物理性质 3.牛顿剪切定律 4.牛顿流体与非牛顿流体 5.理想流体与实际流体 二、计算 1.拉普拉斯公式
第二章
一、概念 1.层流与湍流 2.稳态流动与非稳态流动 3.拉格朗日法与欧拉法 4.迹线与流线 5.有旋流动与无旋流动 二、计算 1.流线方程与迹线方程
第三 章
一、概念 1.质量力与表面力 2.流体静力学基本方程及静止条件 二、计算 1.非惯性坐标系中静止流体的计算 2.静止液体中平板的受力
第四章
一、概念 1.系统与控制体 2.输运公式的作用 二、计算 1.四大守恒方程的计算应用 2.各守恒方程的综合应用
第五章
一、概念
1.常见的边界条件有哪些? 2.建立流动微分方程的基本方法 3. 管内流动最大速度与平均速度的关 系
第八章 一、概念 1.流动相似包含哪几方面? 2.动力相似 3.量纲分析方法有几种?
第十章ห้องสมุดไป่ตู้
一、概念 1.边界层的定义 2.边界层分离的原因 3.逆压梯度 二、计算 1.平板层流边界层厚度的计算
谢谢观赏!
有旋流动和无旋流动

分析流体的速度场、流体性质和边界条件是否满 足有旋流动和无旋流动的转换条件。
转换过程的实现
通过改变流体的某些参数,如速度、压力、温度 等,促使有旋流动和无旋流动之间的转换。
转换的影响因素
能量损失
有旋流动和无旋流动之间的转换 会导致能量损失,包括摩擦损失
和能量转换损失。
流动稳定性
转换过程可能会影响流体的稳定性, 导致流体的状态发生波动或失稳。
产生条件
恒定流
在恒定流场中,流线是平行且均匀的,因此不会产生旋涡。
势流
在势流中,流体受到的力与流速的大小和方向无关,因此不会产生旋涡。
实例分析
河流中的平直河段
在平直河段中,水流是平顺的,没有旋涡产生。
飞机在空中飞行时,机翼下方的气流
由于机翼的形状和气流的速度,机翼下方的气流会形成无旋流动。
04
有旋流动和无旋流动的研究对 于理解流体运动规律、优化流 体机械设计、提高流体输送效 率等方面具有重要意义。
对未来的展望
未来研究可以进一步深入探索有旋流动和无旋流 动的内在机制和演化规律,以及它们在不同条件 下的表现和相互作用。
在实际应用方面,可以结合具体工程背景,研究 有旋流动和无旋流动在流体机械、能源利用、环 境保护等领域中的应用,提出更加高效、环保的 解决方案。
有旋流动与无旋流动的转换
转换条件
速度场条件
有旋流动和无旋流动的转换取决于速 度场的条件,包括速度的大小和方向。
流体性质
边界条件
流体的边界条件,如管道的形状、入 口和出口条件等,也会影响有旋流动 和无旋流动的转换。
流体的粘性、密度、弹性等物理性质 对转换过程也有重要影响。
转换过程
第八章 理想流体有旋流动和无旋流动

y
y vy vx x
v x t
vy
v y x
x
vx
vx x
x
v y t
线变形运动
x方向的速度差
v B x vA x v x x x v C x v D x v x x x
y方向的速度差
vD yvA y v y y y vC yvB y v y y y
AB、DC在δt时间内伸长
y
vx
vx x
x
vx y
y
vy
vy x
x
vx
vx x
x
平移运动
矩形ABCD各角 点具有相同的速 度 分 量 vx 、 vy 。 导 致 矩 形 ABCD 平 移 vxδt, 上 移 vyδt, ABCD的形 状不变。
vy
vy y
y
vx
vx y
y
vy
v y x
x
v y y
y
vx
vx x
x
vx y
角变形速度的平均值
z
1 2
vy x
vx y
x
1 2
vz y
vy z
y
1 2
vx z
vz x
v x y t y
y
x
v y x t x
旋转运动
v x y t y
y
x
vy x t x
流体微团只发生角变形
流体微团只发生旋转,不发生角变形
流体微团在发生角变形的同时,还要发生旋转运动
亥姆霍兹速度分解定理
在一般情况下微小流体质团的运动可以分解为三部分: (1)随质团中某点(基点)一起前进的平移运动; (2)绕该点的旋转运动; (3)含有线变形和角变形的变形运动。
流体力学课程自学辅导资料

流体力学课程自学辅导资料二○○八年十月教材:工程流体力学教材编者:孔珑出版社:中国电力出版社出版时间:2007年注:期中(第10周左右)将前半部分测验作业寄给班主任,期末面授时将后半部分测验作业直接交给任课教师。
总成绩中,作业占15分。
第一章绪论一、本章的核心、重点及前后联系(一)本章的核心流体力学的研究内容和研究方法(二)本章重点流体力学的研究内容和研究方法(三)本章前后联系为本书的其它章节内容做一介绍二、本章的基本概念、难点及学习方法指导(一)本章的基本概念研究内容:是力学的一个独立分支,是一门研究流体的平衡和运动规律及其实际应用的技术科学。
研究速度分布、压强分布、能量损失及作用力。
研究方法:理论分析、实验研究、数值计算(二)本章难点及学习方法指导流体力学研究内容三、典型例题分析(略)四、思考题、习题及习题解答(一)思考题、习题(略)(二)习题解答(只解答难题)(略)第二章流体及其物理性质一、本章的核心、重点及前后联系(一)本章的核心1、流体的几个性质2、流体的几个物理模型3、作用在流体上的力(二)本章重点1、流体的压缩性、粘性2、连续介质模型、不可压缩流体模型、理想流体模型3、作用在流体上的力:表面力和质量力(三)本章前后联系为本书的其它章节建立物理模型二、本章的基本概念、难点及学习方法指导(一)本章的基本概念1、流体力学定义:受任何微小剪切力都能连续变形的物质特征:流动性2、连续介质模型:(1)宏观上无限小(2)微观上足够大(3)有确定物理量连续介质假设(continuum/continuous medium model):把流体视为没有间隙地充满所占据的整个空间的一种连续介质,且其所有的物理量都是空间坐标和时间的连续函数的一种假设模型:f =f(t,x,y,z)。
特例:分子的自由行程和所涉及的最小有效尺寸可以相比拟时,如火箭在高空非常稀薄的空气中以及高真空技术3、压缩性:一定温度下、压强增加体积缩小的性质4、膨胀性:一定压强下、温度升高体积增大的性质5、不可压缩流体模型:通常情况下液体流速不高、压强变化小气体6、粘性:在运动的状态下,流体所产生的抵抗剪切变形的性质影响粘性的主要因素:流体种类、温度和压强7、牛顿流体:牛顿内摩擦定律和牛顿流体8、理想流体模型:粘度为09、作用在流体上的力:表面力和质量力(二)本章难点及学习方法指导1、流体的力学定义2、不可压缩流体模型3、理想流体模型三、典型例题分析1、P8. 例2-12、P14例2-4四、思考题、习题及习题解答(一)思考题、习题2-1、2-3、2-14(二)习题解答(只解答难题)(略)第三章流体静力学一、本章的核心、重点及前后联系(一)本章的核心流体静压强分布及作用在平面和曲面上的力(二)本章重点1、流体静压强特性2、流体静力学基本方程及其物理和几何意义3、液体相对平衡时压强分布及工程应用4、静止液体作用在平板上总压力大小和位置5、静止液体作用在曲面上总压力,压力体(三)本章前后联系流体静力学是力学的基础知识,最基本内容二、本章的基本概念、难点及学习方法指导(一)本章的基本概念1、流体静压强特性:方向沿作用面内法线方向,大小和作用面方位无关2、等压面:压强相等的点组成的面3、流体静力学基本方程及其物理和几何意义:水头、测压管水头、压强势能、重力势能4、帕斯卡原理、液柱式测压计5、液体相对平衡时压强分布及工程应用:离心式泵与风机、离心铸造机工作原理6、静止液体作用在平板上总压力大小和位置7、静止液体作用在曲面上总压力,压力体(二)本章难点及学习方法指导1、液体相对平衡时压强分布及工程应用:离心式泵与风机、离心铸造机工作原理2、静止液体作用在平板上总压力大小和位置3、静止液体作用在曲面上总压力,压力体三、典型例题分析1、P30. 例3-22、P37. 例3-63、P40. 例3-7四、思考题、习题及习题解答(一)思考题、习题1.相对平衡的流体的等压面是否为水平面?为什么?什么条件下的等压面是水平面?2.压力表和测压计上测得的压强是绝对压强还是相对压强 ?3、圆筒,H0=0.7m,R=0.4m, V=0.25m3, ω=10rad/s,中心开孔,顶盖m=5kg 。
流体力学:第八章 理想不可压缩流体平面流动

因为:ac dy,cb dx,所以
dq udy vdx dy dx d
y x
积分, q
2 d
1
2
1
在论证流函数存在及说明其特性时,仅用了平面 流动的条件,故以上结论对任何平面流动都适用, 不论势流和涡流。
一、无旋流动(有势流动) 旋转角速度为零,通常称为势流。
x
1 ( w 2 y
v ) z
0,
或 w y
v z
y
1 ( u 2 z
w ) 0, x
或 u z
w x
z
1 2
( v x
u ) y
0,
或 v u x y
流体质点本身是否发生旋转,与流体微团 本身运动时的轨迹形状无关。
由数学分析知,上式是使udx vdy wdz为某一函数的
Cylinder with Circulation
引言
平面势流理论在流体力学中占有非常重要的地位 Why? Example
本章将简要地介绍平面势流的基本理论,分析绕流 不同形状的物体势流长的压力分布,以及流体对被绕 流物体的作用力。
§8–1 无旋流动和有旋流动
根据流体微团是否存在旋转,将流动分为两大类型: 无旋流动和有旋流动。 Two examples
涡线
涡线的表达式:
dx dy dz
x y z 通过微元断面的涡线组成涡束,涡束的表面称为涡管。 涡束断面面积和2倍旋转角速度的乘积称为涡通量,以 I表示,则微元涡通量为:
dI 2dA dA
2
速度环量:在流场中取一封闭曲线,流速沿该曲线的
积分称为沿 流线L的速度环量,用 表示:
全微分的必要充分条件。
有旋流动和无旋流动_1~9

vx
v x dx v x dy x 2 y 2
vy
vy
v y dx v y dy x 2 y 2
Y方向速度: vy
Z方向速度:
vx
vx
vx dt
y
v x dx v x dy x 2 y 2
vz
vx
v x dx vx dy v x dz x 2 y 2 z 2
vx vx
vx dx v x dy v x dz x 2 y 2 z 2
vy
vx vx dx vx dy vx dz x 2 y 2 z 2
E
vx
vx dx v x dy v x dz x 2 y 2 z 2
vy
vx
v y dx v y dy x 2 y 2
v x dx v x dy x 2 y 2
vx
v x dx v x dy x 2 y 2
Y方向速度:
y
vy
vy
v y dx v y dy x 2 y 2
vx
vx
v x dx v x dy x 2 y 2
(
(
y
v y dy dy )(v y )dzdx y 2 y 2
z轴方向流体的净流入量:
( v z dz v z dz )dxdy ( v z )dxdydz z z z
o
z
x
每秒流入微元六面体的净流体质量
x轴方向流体的净流入量:
( v x dx v x dx )dydz ( v x )dxdydz x x x
dz v dz )( v z z )dxdy z 2 z 2
流体力学教案第8章边界层理论

第八章 边界层理论§8-1 边界层的基本概念实际流体和理想流体的本质区别就是前者具有粘性。
对层流而言,单位面积摩擦力的大小yud d μτ=,可以看出,对于确定的流体的等温流场,摩擦力的大小与速度梯度有关,其比例函数即动力粘度。
速度梯度yud d 大,粘性力也大,此时的流场称为粘性流场。
若速度梯度yud d 很小,则粘性力可以忽略,称为非粘性流场。
对于非粘性流场,则可按理想流体来处理。
则N-S 方程可由欧拉方程代替,从而使问题大为简化。
Vlv l lV v A y u V l tVl t u mρρμρρ======2223d d d d 粘性力惯性力当空气、蒸汽,水等小粘度的流体与其它物体作高速相对运动时,一般雷诺数很大。
由vVl==粘性力惯性力Re ,则在这些流动中,惯性力>>粘性力,所以可略去粘性力。
但在紧靠物体壁面存在一流体薄层,粘性力却与惯性力为同一数量级。
所以,在这一薄层中,两者均不能略去。
这一薄层就叫边界层,或叫速度边界层,由普朗特在1904年发现。
a .流体流过固体壁面,紧贴壁面处速度从零迅速增至主流速度,这一流体薄层,就叫边界层或速度边界层。
b .整个流场分为两部分 层外,0=∂∂yu,粘性忽略,无旋流动。
层内,粘性流,主要速度降在此,有旋流动。
c .由边界层外边界上∞=V u %99,来定义δ,δ为边界层厚度。
d .按流动状态,边界层又分为层流边界层和紊流边界层。
由于在边界层内,流体在物体表面法线方向(即yu∂∂)速度梯度很大,所以,边界层内的流体具有相当大的旋涡强度;而在层外,由于速度梯度很小。
所以,即使对于粘度很大的流体,粘性力也很小,故可忽略不计,所以可认为,图8-2空气沿平板边界层速度分布外部区域边界层边界层外的流动是无旋的势流。
边界层的基本特征有: (1)1<<Lδ⇒薄层性质,其中L 为物体的长度;沿流方向↑↑→δx 。
(2) 层内yu∂∂很大, 边界层内存在层流和紊流两种流态。
《流体力学》第八章绕流运动解析

( x, y ) d u dy u y dx C
x
实际上ψ(x,y)表示流场中的流线,C为任 意常数。不同的C,则对应不同的流线。 d dx dy ux , uy x y y x
ux , uy y x
第八章
绕流运动
在自然界和实际工程中,存在着大量的流体 绕流物体的流动问题,即绕流问题。 我们研究时,都是把坐标固结于物体,将物 体看作是静止的,而探讨流体相对于物体的 运动。 在大雷诺数的绕流中,由于流体的惯性力远 大于粘性力,可将流体视为理想流体。 在靠近物体的一薄层内,可以用附面层理论 处理。
d ( x, y, z) ux dx uy dy uz dz
展开势函数的全微分
d dx dy dz x y x
比较上两式的对应系数,得出:
ux uy uz x y z 即速度在三坐标上的投影,等于速度势函 数对于相应坐标的偏导数
工 业 液 槽 边 侧 吸 气
平面无旋运动是旋转角速度为零的平面运 动。在平面运动中,仅只有一个坐标方向 上的旋转角速度分量ωz,当ωz=0时,则 满足: u u
y
x
x
y
这时速度势函数全微分为:
d ux dx u y dy
对应的拉普拉斯方程为: 0 2 2 x y
流函数与势函数间关系为:
ux x y
两者交叉相乘得:
uy y x
0 y y x x
由高等数学得到,上式表明, φ(x,y)=C1和 ψ(x,y)=C2是互为正交的。由此表明:流线与等 势线是相互垂直的。当给出不同的常数C1,C2时, 就可得到一系列等势线和流线,它们间构成相互 正交的流网,应用流网的正交性,借助数值计算 方法和计算机,可以解决复杂的流场问题。
有旋流动和无旋流动.ppt

对于非粘性的不可压缩流体和可压缩正压流体, 在有势质量力作用下速度环量和旋涡都是不能自 行产生、也是不能自行消灭的。
❖ 正压流体
❖
内部任一点的压力只是密度的函数的流体。
❖ 斜压流体
❖
若流体压力不仅是密度的函数,而且还和其他热力学参量(例
如温度等)有关,则称为斜压流体。
❖
广义地说,正压流体是其力学特性与热学特性无关的流体。
第5章_有旋流动和无旋流动
在许多工程实际问题中,流动参数不仅在流动方 向上发生变化,而且在垂直于流动方向的横截面上 也要发生变化。要研究此类问题,就要用多维流的 分析方法。本章主要讨论理想流体多维流动的基本 规律,为解决工程实际中类似的问题提供理论依据,
也为进一步研究粘性流体多维流动奠定必要的基础。
但在更多的情况下,流体运动的有旋性并不是一眼就 能看得出来的,如当流体绕流物体时,在物体表面附近形 成的速度梯度很大的薄层内,每一点都有旋涡,而这些旋 涡肉眼却是观察不到的。
至于工程中大量存在着的紊流运动,更是充满着尺度 不同的大小旋涡。
流体的无旋流动虽然在工程上出现得较少,但 无旋流动比有旋流动在数学处理上简单得多,因 此,对二维平面势流在理论研究方面较成熟。
v
y
d dt
(dy) vz
d dt
(dz)]
[vxdvx vydvy vzdvz ]
d ( vx2 vy2 vz2 ) d ( v2 )
2
2
由理想流体的欧拉运动微分方程,等号右端第二项积分式可表
示为:
( dvx dx dvy dy dvz dz)
dt
dt
dt
[(
fx
1
p )dx ( x
有旋流动与无旋流动
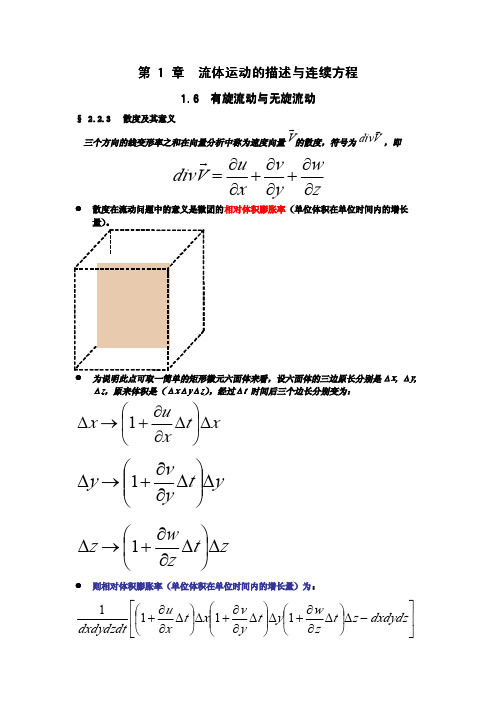
y
B A C D
B’ C’ 0
�
A’ D’
B’’ C’’
A’’ D’’
x
需要指出,一般并不是先有了速度后求φ,而是恰恰相反,先求出φ,然后再确 定速度分布的 。
§ 2.5 环量与涡
§ 2.5.1 环量与涡的概念 � 研究流动的问题,还有两面个极重要的概念,一个叫环量,一个叫做涡。 � 环量的定义:在流场中任取一条封闭曲线,速度沿该封闭曲线的线积分称为该封闭曲 线的速度环量。速度环量的符号不仅决定于流场的速度方向,而且与封闭曲线的绕行 方向有关,规定积分时逆时针绕行方向为正,即封闭曲线所包围的区域总在行进方向 的左侧。
旋流。一个流场,如果各处的
ωx x
� ω 都等于零,这种流场称为有很大的意义。无旋流多了一个 ω = 0 的条件。这个
条件就是 :
ω x = 0, ω y = 0, ω z = 0
∂v ∂w = ; ∂z ∂y
�
∂u ∂v = ; ∂y ∂x
∂u ∂v ∂w 略高次项后= + + ∂x ∂y ∂z
� � 可以证明任何形状微团的相对体积膨胀率均为上式。 流体微团在运动中不论它的形状怎么变,体积怎么变,它的质量总是不变的。而 质量等于体积乘密度,所以在密度不变的不可压流里,其速度的散度必为零:
� ω
� ∂u ∂v ∂w divV = + + =0 ∂x ∂y ∂z
∫ (udx + vdy + wdz ) = ∫ dφ = φ
A A
� 例. 设有一个二维流场其速度分布是
B
B
B
− φA
u = 2 ax,
v = −2 ay
,
问这个流动是有旋的还
第八章理想流体的有旋流动和无旋流动

vx vy vz 0
x
y
z
vx vy vz 0 x y z
vx vy 0
x
y
vx vy 0 x y
第二节 流体微团运动分解
刚体的一般运动可以分解为移动和转动两部分。 流体与刚体的主要不同在于它具有流动性,极易变
形。 因此,任一流体微团在运动过程中不但与刚体一样
可以移动和转动,而且还会发生变形运动。 所以,在一般情况下流体微团的运动可以分解为移
动、转动和变形运动三部分。
vMx
vx
vx x
x
vx y
y
vx z
z
vMy
vy
vy x
x
vy y
y
vy z
z
vMz
vz
vz x
x
vz y
y
vz z
z
图8-2 平行六面体微小流体质团
vMx
vx
vx x
x
1 2
v y x
vx y
y
1 vx 2 z
vz x
z
1 vx 2 z
vz x
z
1 2
v y x
vx
vx x
δ
x δ t
vx
δt
vx x
δ
x
δt
v y
vy y
δ
y t
vy
δt
vy x
δ
y
δt
vx x
δ xδt
vx
δ x δt x
vy y
δ
yδt
vy
δ y δ t y
vMx
vx
vx x
x
zy yz
yz zy
第8章_理想流体的有旋和无旋流动
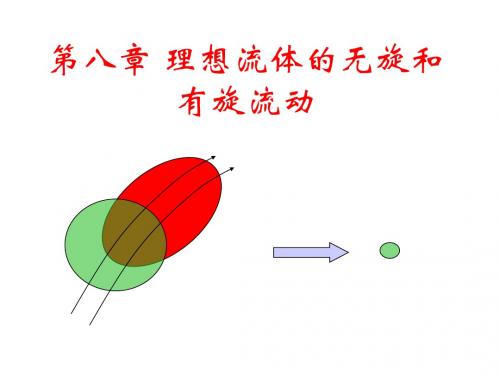
n
dA 0
即:控制体内流体质量的增长率+ 通过界面流出控制体的质量流量=0
( vx ) ( v y ) ( vz ) 0 t x y z
微分形式的连续方程
第一节 微分形式的连续方程
引入哈密顿算子
i j k x y z
v z 4x 4 y 0 z
f ( x, y ) 0
v z 4( x y) z
第二节 流体微团运动的分解
刚体任意参考点的平移速度 绕参考点的旋转速度
刚体的运动速度
流体任一质点速度
质点上任意参考点的平移速 度 绕通过该点的瞬时轴旋转速度 变形速度
第二节 流体微团运动的分解
2
1 n ! x
x
y
y
z
z f ( x, y , z )
n
15
分析流体微团运动用图
第二节 流体微团运动的分解
vFX vx vx vx vx dx dy dz x y z
v y x dx v y y dy v y z dz
A
D
B
C
同理y向线变形速度:
v y y
3.角变形运动
B、C在y方向有速度差:
vBy vCy
v y x
A
dx
d
在dt时间内BC线段将旋转:
d
C B
v y d tand x
dx dt dx
v y x
dt
v x 同理,AB在dt时间线段将旋转: dt y
div ( v) 0 t d div (v) 0 dt
微分形式的连续方程适用于所有流体(粘性、理 想),所有流态(层、紊、亚音速、超音速等)。
流体力学第8章

(1) 理想流体存在无旋流动; (2) 粘滞力很小的流体(水、空气)——可以看作理想流体; (3) 从静止到运动的理想流体。
(飞机对空气的扰动,紧贴固壁的部分为有旋的,其他地方为无旋的); (4) 吸风装置所形成的气流。
(吸风时工作区的气流从静止开始运动,故无旋;相反,送风装置所形 成
b dx c
ψ1
dy
ux a
dq d
x
积分:q=Δψ, 即:相邻两流线流函数数值之差=此两流线间的单宽流量。
用流线的疏密来反映流速的大小,两流 线之间的流速与流线间的距离成反比。 流线越密流速越大
14
§8-2 平面无旋流动
性质(3)的证明
dn为等势线间的网格长;dm为流线间的网格长。 证明dn/dm=定值
流体力学
主讲:周传辉
暖通教研室
二00二年十一月
1
第八章 绕流运动
§8-1 无旋运动 §8-2 平面无旋流动 §8-3 几种简单的平面无旋流动 §8-4 势流叠加 §8-6 绕流运动与附面层基本概念
§8-7 附面层动量方程 §8-8 附面层的近似计算 §8-10 曲面附面层的分离现象
与卡门涡街
§8-1 无旋运动
流线的绘制
原则:利用流线和等势线相互正交,并且网格相邻边长成正比,使网格形成曲线 正方形网格。
方法:先绘制流线,根据流动的大致方向,绘制一系列流线,然后,再绘制一些 等势线,当然,一次不可能绘制成功,要反复调整,直至基本符合流网特征。
关键:抓住边界条件,固壁边界、自由水面、入流断面,出流断面等。
固壁本身就是一条流线,自由水面也是一条流线。
y)
cos(S, z)
S x
y
8-第8讲 理想流体的有旋与无旋流动

21 2 2 0 x 2 y 2 2 2 2 2 0 x 2 y 2
则 1 2 也满足拉普拉斯方程,即有
2 2 0 x 2 y 2
同理,对于无旋运动的流函数也有这一特性,两个流函数叠加后可构成新的流函数。 这一结论推广的有限个势函数或流函数的叠加仍然成立。 3、 流函数与势函数满足科希-黎曼关系式 由(6-31)和(6-33)可知,势函数与流函数满足关系式
x y x y
此式称为科希-黎曼关系式。 4、 等流函数线与等势线正交 对于等流函数线,有 C ,即有
(6-35)
d
dx dy 0 x y
在等流函数线上一点 ( x, y ) 处曲线切线的斜率为
(6-53)
q q ( A B ) P 2 2
(6-54)
注: 设 常数 , 得到流线方程为 如图 6-13 所示。
这是一个经过点 A 和点 B 的圆线簇, P 常数 ,
y
等流函数线
☉ A
☉
B
x
图 6-13
点源与点汇的叠加流线
如果点源和点汇无限接近,即令 a 0 ,可得到一个无旋流动,称为偶极流。偶极流 的流函数与势函数的推导如下。 点源与点汇叠加后的势函数为
即流动一定是无旋的。 对于二元流动,不管是有旋还是无旋流动,我们都可以定义另外一个函数,称为流函 数,记作 ,定义如下
v x u y
这样的函数是天然满足连续性方程的,即有
(6-32)
u v 2 2 0 x y xy xy
流函数与势函数有如下基本特性。 1、 对于有势流动,流函数与势函数均为调和函数 若流场是有势的,即(6-31)式成立,则由连续性方程,有
流体力学 第八章 绕流运动

第八章绕流运动一、应用背景1、问题的广泛存在性:在自然界和工程实际中,存在着大量的流体绕物体的流动问题(绕流问题),如:飞机在空气中的飞行、河水流过桥墩、大型建筑物周围的空气流动、植物护岸(消浪,船行波),粉尘颗粒在空气中的飞扬和沉降,水处理中固体颗粒污染物在水中的运动。
(一种:流体运动;另外一种:物体运动),我们研究,将坐标系固结于物体上,将物体看成静止的,讨论流体相对于物体的运动。
2、问题的复杂性上一章的内容中可以看出,流体力学的问题可以归结为求解在一定边界条件和初始条件下偏微分方程组的求解。
但描述液体运动的方程式非常复杂的:一方面,是方程的非线性性质,造成方程求解的困难;另一方面,复杂的边界条件和初始条件都给求解流体力学造成了很多麻烦。
迄今为止,只有很少数的问题得到了解决。
平面泊萧叶流动,圆管coutte流动等等。
而我们所要解决的绕流问题正是有着非常复杂的边界条件。
3、问题的简化及其合理性流体力学对此的简化则是,简化原方程,建立研究理想液体的势流理论。
实际液体满足势流运动的条件:粘性不占主导地位,或者粘性还没有开始起作用。
正例:远离边界层的流体绕流运动、地下水运动、波浪运动、物体落入静止水体中,水的运动规律研究。
反例:研究阻力规律、能量损失、内能转换等等。
圆柱绕流(经典之一)半无限长平板绕流(经典之二)分成两个区域:一个区域是远离边界的地方,此区域剪切作用不明显,而且流体惯性力的影响远远大于粘性力的影响(理想液体)(引导n-s方程);另一个是靠近边界的地方(附面层,粘性底层),此区域有很强烈的剪切作用,粘性力的影响超强,据现代流体力学的研究表明,此区域是产生湍流的重要区域,有强烈的剪切涡结构,但此区域只有非常薄的厚度。
此区域对绕流物体的阻力、能量耗损、扩散、传热传质都产生重要影响。
4、本章的主要研究内容(1) 外部:理想液体,(简化方法,求解方式)、(2) 内部:附面层理论,(简化方法,求解方式,求解内容,现象描述) (3) 两者的衔接。
无旋流动与有旋流动

vz
从而,无旋流动条件也可以写作:
w v y z u w z x v u x y
充要条件
速度向量为有势向量,即:
v ( x, y, z )
u ,v ,w x y z
具有流速势的流动称为有势流动,无旋流动就是有势流动。
从场论的观点: 由于一个数量场 的梯度的旋度为零,即:
( ) 0
每个无旋的速度场
v 均可对应于某个梯度场 。
因此,无旋流场与速度有势场互为充要条件。
重要推论:
1)任意指定方向的速度为
x y z vs s x s y s z s ucos( s, x) vcos( s, y) wcos在该方向的分量。
2)对于无旋流,沿连接A,B的曲线进行速度的线积分,结果与路径
无关,只与两端点的 值之差有关。
B
A
v dl dl d B A
A A
B
B
涡量:
流体微团速度向量的旋度(curl)定义为流体
微团的涡量,以 表示,
无旋流动/有势流动
流体微团的旋转角速度写作矢量的形式为:
1 ω rot 2
一个流场,如果各处的
1 v v 2
ω0
都等于零,这样的流动称为
无旋流动,即在运动学分析中没有观察到微团的旋转现象。
速度的旋度在笛卡尔直角坐标系的运算表达式:
i rot
j y
k z
v
x
vx
vy
= curl v = v
涡量不为零的流动称为有旋流动或有涡流动,如
果一个流场中任一点的涡量均为零则为无旋流动
第八章 绕流问题

u
环流的速度分布规律
说明,纯环流中,任一包围原点的速度 环量等于常数。并称Γ为环流强度。
u rd
2
0
c rd 2c r
7
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
(8-5)
(8-4)
式(8-5)称为拉普拉斯方程。满足拉普拉斯方程的函数称 为调和函数
3
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
8.1.1 势函数和流函数
1 w v x 2 y z 1 u w y 2 z x 1 v u z 2 x y
在圆柱坐标系中,势函数为,且有:
2、源流和汇流 设想流体在单位时间内从源泉 点流出体积为 Q 的流体。如 果流体在间距为 1的平行平板 间向四周均匀扩散,这种流动 就称为源流。点称为源点,如 图所示。反过来,若流体从四 周向某汇合点集中,这种流动 称为汇流流动。点称为汇点。 由于流动是连续且对称的,任意点的速度为:
源流的势函数为 :
8.1.2 几种简单的平面势流 1、平行流(均匀直线流) 流场中各点的速度大小和方向都相同的流动称为平行流。 设x,y方向的速度分量分别为
8.1.2 几种简单的平面势流
显然,流线是一簇与轴成角的平行线,如 下图所示的实线。图中虚线为等势线,流 线和等势线正交。
ay bx ax by
y
2d
v
b dxc
dy
理想流体的有旋流动和无旋流动

Ω
S
C
n
速度环量(velocity circulation):速度在某一封闭周 线切线上的分量沿该封闭周线的积分。
K v ds vx dx v y dy vz dz
K
速度环量是标量,其正负号与速度和线积分绕行方向有关, 规定:其绕行正方向为逆时针方向,面积的法线与正方向 形成右手螺旋系统。
v yB v yC v xA v xB d dx dy 2 2 v v yA v xC v xD dx yD dy 2 2
0
x
将各点速度代入,并忽略高阶小量,得到
v y vx d x y dxdy
v y vx d 2 z dxdy x y
是研究非定常流动必不可少的定解条件 • 2、边界条件:方程组的解在流场边界上应当满足的条件。
A、固体壁面:壁面上流体质点的法向速度应等于对应点上壁面的法向速度
流体与固体壁面的作用力也必沿壁面法线方向;
B、流体交界面:在交界面同一点,两种流体法向速度相等,对于平面,压力相 等; C、无穷远处:一般给定参数; D、流道进、出口处,可根据具体情况确定。
v v v x y z x y z
v M i vi
vi xj x j
i 1, 2, 3
亥姆霍兹运动分解定理
平移运动
vM i
v vi i x j x j
vi 1 vi v j 1 vi v j ij ij ( ) ( ) x j 2 x j xi 2 x j xi
不可压缩流体 定常流动
即
常数
divv 0
vx v y vz 0 x y z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∂ (ρvx )dxdydz ∂x
(c1)
第八章
理想流体的有旋流动和无旋流动
同理可得 y和 方向单位时间通过微元体表面的净通量分别为: 方向单位时间通过微元体表面的净通量分别为: 净通量分别为
z
∂ (ρvy )dxdydz ∂y
c2) (c2) c3) (c3)
∂ (ρvz )dxdydz ∂z
因此,单位时间流过微元体控制面的总净通量为: 因此,单位时间流过微元体控制面的总净通量为:
变形运动
F点速度 点速度: 点速度
vFX ∂vx dx ∂vx dy ∂vx dz = vx + + + ∂x 2 ∂y 2 ∂z 2
∂vy dx ∂vy dy ∂vy dz = vy + + + ∂x 2 ∂y 2 ∂z 2
C B
G
vy
D dz
F
dy
vFY
vz vx
dx
E
h
A
y
vFZ ∂vz dx ∂vz dy ∂vz dz = vz + + + ∂x 2 ∂y 2 ∂z 2
r 1 r ω = ∇×V = 0 2 r r 1 ω = ∇×V ≠ 0
2
无旋流动 有旋流动
在笛卡儿坐标系中: 在笛卡儿坐标系中:
r ∂vz ∂vy r ∂vx ∂vz r ∂vy ∂vx r ∇×V = ∂y − ∂z i + ∂z − ∂x j + ∂x − ∂y k
第八章
理想流体的有旋流动和无旋流动
第一节 微分形式的连续性方程
当把流体的流动看作是连续介质的流动, 当把流体的流动看作是连续介质的流动,它必然遵守质量 守恒定律。对于一定的控制体,必须满足输运公式。 守恒定律。对于一定的控制体,必须满足输运公式。它表示在 控制体内由于流体密度变化所引起的流体质量随时间的变化率 等于单位时间内通过控制体的流体质量的净通量。 等于单位时间内通过控制体的流体质量的净通量。 首先推导在笛卡儿坐标系中微分形式的连续性方程。 首先推导在笛卡儿坐标系中微分形式的连续性方程。
vBy − vCy =
∂v y ∂x
A
dx
dβ
dt时间内 线段将旋转: 时间内BC线段将旋转 在dt时间内BC线段将旋转:
dα
C B
∂v y dα = tan dα = ∂x
dx ⋅ dt dx
=
∂v y ∂x
dt
∂v x 同理, 在 时间线段将旋转 时间线段将旋转: 同理,AB在dt时间线段将旋转: dt ∂y
即当流场速度同时满足: 即当流场速度同时满足:
∂vz ∂vy = ∂y ∂z
∂vx ∂vz = ∂z ∂x
∂vy
∂vx = ∂x ∂y
时流动无旋
需要指出的是, 需要指出的是,有旋流动和无旋流动仅由流体微团本身是 否发生旋转来决定,而与流体微团本身的运动轨迹无关。 否发生旋转来决定,而与流体微团本身的运动轨迹无关。
∂ ∂ ∂ ∫∫ ρvndA = ∂x (ρvx ) + ∂y (ρvy ) + ∂z (ρvz )dxdydz (c) CS
微元六面体内由于密度随时间的变化而引起的质量的变化率为: 微元六面体内由于密度随时间的变化而引起的质量的变化率为 质量的变化率
∂ ∂ ∂ρ ρdV = ∫∫∫ ρdxdydz = dxdydz ∂t ∫∫∫ ∂t CV ∂t CV
1 ∂vx ∂vy dy 1 ∂vx ∂vz dz +[ ( − ) + ( − ) ] 2 ∂y ∂x 2 2 ∂z ∂x 2
∂vx dx 1 ∂vx ∂vy dy 1 ∂vx ∂vz dz vFx = vx + +[ ( + ) + ( + ) ] ∂x 2 2 ∂y ∂x 2 2 ∂z ∂x 2
fxρdxdydz + ( p − = ρdxdydz dvx dt
C B F
G
= ma
∂p dx ∂p dx )dydz −( p + )dydz ∂x 2 ∂x 2
fy
dy
A D
fz
dx
fx
H E
两端同除以微元体的质量
1 ∂p dvx fx − = dt ρ ∂x 1 ∂p dvy fy − = ρ ∂y dt 1 ∂p dvz fz − = ρ ∂z dt
连续性方程表示了单位时间内控制体内流体质量的增量等于流体在控 制体表面上的净通量。 制体表面上的净通量。 在定常流动中,由于 在定常流动中,
∂ =0 ∂t
∂ (ρvx ) + ∂ (ρvy ) + ∂ (ρvz ) = 0 ∂x ∂y ∂z
对于不可压缩流体( 常数) 对于不可压缩流体(ρ =常数) ∂ y v ∂ x v ∂ z v + + =0 ∂ x ∂ y ∂ z
1 ∂vx ∂vz ωy = − =0 2 ∂z ∂x
1 ∂vy ∂vx 1 ωz = ∂x − ∂y = − 2 a ≠ 0 2
所以该流动是有旋运动。 所以该流动是有旋运动。
第三节 理想流体的运动方程 定解条件
一、运动微分方程 方向: 在x方向: F 方向
ω = ω +ω +ω
2 x 2 y
2 z
写成矢量形式为: 写成矢量形式为:
r 1 r r r ω = ωxi + ω y j + ωz k = ∇ × V 2 v v v i j k 1 ∂ ∂ ∂ = 2 ∂x ∂y ∂z vx v y vz r
三、有旋运动和无旋运动
根据流体微团在流动中是否旋转, 根据流体微团在流动中是否旋转,可将流体的流动分为两 有旋流动和无旋流动。 类:有旋流动和无旋流动。 数学条件: 数学条件: 当 当
( d)
第八章
理想流体的有旋流动和无旋流动
将式( ),( ),(d)代入下式, 将式(c),( )代入下式,取 dxdydz →0, , 则可得到流场中任一点的连续性方程的一般表达式为: 则可得到流场中任一点的连续性方程的一般表达式为:
∂ (ρvx ) + ∂ (ρvy ) + ∂ (ρvz ) + ∂ρ = 0 ∂x ∂y ∂z ∂t
第八章
理想流体的有旋流动和无旋流动
v、vy、vz, x
设该微元六面体中心点O( 设该微元六面体中心点 (x, y, z)上流体质点的速度为 )
轴垂直的两个平面上的质量流量如图所示。 密度为 ρ,于是和 x轴垂直的两个平面上的质量流量如图所示。 方向上,单位时间通过EFGH面流入的流体质量为: 面流入的流体质量为: 在 x 方向上,单位时间通过 面流入的流体质量为
x
z
方程两边加上两个和为0的项, 方程两边加上两个和为 的项,其值不变 的项 ∂vx d43; + + ∂x 2 ∂y 2 ∂z 2
组合
1 ∂vy dy 1 ∂vz dz ± ± 2 ∂x 2 2 ∂x 2
∂vx dx 1 ∂vx ∂vy dy 1 ∂vx ∂vz dz vFx = vx + +[ ( + ) + ( + ) ] ∂x 2 2 ∂y ∂x 2 2 ∂z ∂x 2
vz = −4(x + y)z
f (x, y) = 0
第二节 流体微团的运动分析
一、物理模型 刚体的运动速度
刚体任意参考点的平移速度 绕参考点的旋转速度
质点上任意参考点的平移速度 质点上任意参考点的平移速度
流体任一质点速度
绕通过该点的瞬时轴旋转速度 绕通过该点的瞬时轴旋转速度 变形速度
移动
流体微团的运动 转动
同理可得: 同理可得:
1 ∂v z ∂v y γ&x = ( + ) 2 ∂y ∂z
1 ∂v x ∂v z γ&y = ( + ) 2 ∂z ∂x
4.旋转运动 旋转运动
流体微团的旋转角速度的定义 为每秒内绕同一转轴的两条互 相垂直的微元线段旋转角度的 平均值。 平均值。 规定逆时针旋转角度为正: 规定逆时针旋转角度为正:
A
dβ
dα
C B
BC边旋转的角度为: 边旋转的角度为: 边旋转的角度为
∂x ∂v x BA边旋转的角度为: β =- 边旋转的角度为: 边旋转的角度为 d dt ∂y
dα =
∂v y
dt
轴旋转角速度为两个互相垂直边旋转角速度的一半: 轴旋转角速度为两个互相垂直边旋转角速度的一半:
1 ∂v z ∂v y − ω x = 2 ∂y ∂z 1 ∂v x ∂v z − ω y = 2 ∂z ∂x 1 ∂v y ∂v x ω z = ∂x − ∂y 2
vy = vz = 0 a是不为零 其中a 【例】某一流动速度场为 vx = ay , 其中 的常数,流线是平行于x轴的直线。 的常数,流线是平行于x轴的直线。试判别该流动是有旋流动还 是无旋流动。 是无旋流动。
1 ∂vz ∂vy 【解】 由于 ωx = ∂y − ∂z = 0 2
二、物理意义(以平面流动进行分析) 物理意义(以平面流动进行分析) 1.平移运动 平移运动 向左移动 向上移动
vxdt vxdt
vydt
vx
vy vydt
流体力学
2.线变形运动 线变形运动 每秒内单位长度的伸长(或缩短) 每秒内单位长度的伸长(或缩短)量称为线应变速度
B、C在x方向有速度差 、 在 方向有速度差
移动 线变形运动
角变形运动
1 ∂vx ∂vy dy 1 ∂vx ∂vz dz +[ ( − ) + ( − ) ] 2 ∂y ∂x 2 2 ∂z ∂x 2
