练_解直角三角形及其应用(沪科版)(解析版)

合集下载

沪科版九年级上册23.2.3解直角三角形及其应用

情景导入
如图，一艘轮船从A点出发，航行路线为AC、CB，你知道如何准确描述此过程轮船航行的方向吗？
情景导入
方位角：指北或指南方向与目标方向线所成的小于 90°的水平角，叫_方__位__角__．如右图中的目标方向线 OA、OB、OC、OD的方向角分别表示北__偏__东__60°， _南_偏__东__45°(或东__南__方__向__)，南__偏__西__80°及北__偏__西__30°
第(2)题图)
第(3)题图)
(3)如图，一艘船向正北航行，在A处看到灯塔S在船的北偏东30°的方向上，航行12海里到达B处，在B处看到灯塔S在船的北偏东60°的方向上，此船继续沿正北方向航行过程中，距灯塔S的最近距离是_6__3_海里．
知识模块二复杂的方位角问题
范例
如图所示，某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处，在点A处测得某岛C在北偏东60°的方向上．该货船航行30分钟后到达B处，此时又测得该岛在北偏东30°方向上，已知在岛C周围9海里的区域内有暗礁，若继续向正东方向航行，该货船有无触礁危险？试说明理由．
坡度通常写成 1∶m的形式，如i=1∶6.
自学互研
3. 坡度与坡角的关系
i h tan
l 即坡度等于坡角的正切值.
坡面
i= h : l
h
α
l 水平面
自学互研
范例
(德州中考)如图是拦水坝的横断面，斜坡AB的水平宽度为12m，斜面坡度为1∶2，则斜坡AB的长为 (B )
A．4 3 m C．12 5 m
BH＝4 5 (取正值)、AH＝8 5 .
在Rt△BCH中，BC＝40×
15 60
＝10，

沪科版数学九年级上册解直角三角形分课时习题及答案

沪科版数学九年级上册解直角三角形分课时习题及答案第1课时 30°、60°、45°角的三角函数值第2课时一般锐角的三角函数值第1课时解直角三角形练习第2课时解直角三角形的应用第3课时解直角三角形的应用第4课时解直角三角形的应用第1课时 30°、60°、45°角的三角函数值1．如图，每个小正方形的边长为1，A ，B ，C 是小正方形的顶点，则∠ABC 的度数为( )．A ．90°B ．60°C ．45°D ．30°2．将(－sin 30°)－2、()0、(3这三个实数按从小到大的顺序排列，正确的结果是( )．A ．(－sin 30°)－2＜()0＜()3B ．(－sin 30°)－2＜()3＜()0C ．(3＜()0＜(－sin 30°)－2D ．()0＜(3＜(－sin 30°)－23．在锐角△ABC 中，∠B＝α，∠C＝α－15°，且sin(α－15°)＝2，则∠A＝________.4．计算：(1)tan 30°sin 60°＋cos 230°－sin 245°tan 45°；(2)sin 60cos30︒︒；(3)cos 60°－sin 245°＋23tan 304︒－tan 245°.5．一个等腰三角形的腰是10，底边是12，求这个三角形顶角的正弦值、余弦值、正切值．6．在△ABC 中，cos A ＋21sin 2B ⎛⎫- ⎪⎝⎭＝0，求∠C．7．如图，海船以29.8海里/时的速度向正北方向航行，在A 处观察到灯塔C 在海船的北偏东30°方向上，半小时后航行到点B 处，发现此时灯塔C 与海船的距离最短．(1)在图上标出点B 的位置；(2)求灯塔C 到B 处的距离(精确到0.1海里)． 8．在某段限速公路BC 上(公路视为直线)，交通管理部门规定汽车的最高行驶速度不能超过60千米/时50/3⎛⎫⎪⎝⎭即米秒，并在离该公路100米处设置了一个监测点A ．在如图所示的直角坐标系中，点A 位于y 轴上，测速路段BC 在x 轴上，点B 在A 的北偏西60°方向上，点C 在A 的北偏东45°方向上，另外一条高等级公路在y 轴上，AO 为其中的一段．(1)求点B 和点C 的坐标．(2)一辆汽车从点B 匀速行驶到点C 所用的时间是15秒，通过计算，判断该汽车在这段限速路上是否超速？((3)若一辆大货车在限速路上由C 处向西行驶，一辆小汽车在高等级公路上由A 处向北行驶，设两车同时开出且小汽车的速度是大货车速度的2倍，求两车在匀速行驶过程中的最近距离是多少？9．(创新应用)如图，某居民小区内A 、B 两楼之间的距离MN ＝30 m ，两楼的高都是20 m ，A 楼在B 楼正南，B 楼窗户朝南．B 楼内一楼住户的窗台离小区地面的距离DN ＝2 m ，窗户高CD ＝1.8 m ．当正午时刻太阳光线与地面成30°角时，A 楼的影子是否影响B 楼的一楼住户采光？若影响，挡住该住户窗户多高？若不影响，请说明理由．(参考答案1解析：连接AC ，则AC BC AB∴AC 2＋BC 2＝AB 2.∴△ABC 为等腰直角三角形．∴∠ABC＝45°. 答案：C2解析：(－sin 30°)－2＝4，()0＝1，()3＝-，所以(3＜()0＜(－sin 30°)－2. 答案：C3解析：在锐角三角形中，sin(α－15°)＝2， ∴α＝75°，即∠B＝75°，∠C＝60°. ∴∠A＝180°－∠B－∠C＝45°. 答案：45°4解：(1)tan 30°sin 60°＋cos 230°－sin 245°tan 45°＝2213222⎛⎛+-⨯ ⎝⎭⎝⎭＝131242+-＝34.(2)sin 60|1cos30︒=︒＝1－1.(3)cos 60°－sin 245°＋23tan 304︒－tan 245°＝2213111311242244-+⨯-=-+-=⎝⎭⎝⎭. 5解：如图所示，AB ＝AC ＝10，BC ＝12，作A D⊥BC 于点D ，作CE⊥AB 于点E.∵AB＝AC ，AD⊥BC， ∴BD＝CD ＝6.在Rt△ABD 中，AD ＝=＝8.又∵S △ABC ＝12AB CE ⋅= 12BC AD ⋅， ∴10×CE＝12×8，CE ＝9.6.在Rt△ACE 中，AE = 2.8.∴sin∠BAC ＝9.610CE AC =＝0.96，cos∠BAC ＝ 2.810AE AC =＝0.28，tan∠BAC ＝9.62.8CE AE =＝247.6解：∵21cos sin 2A B ⎛⎫-+- ⎪⎝⎭＝0，由于cos A -≥0，21sin 2B ⎛⎫- ⎪⎝⎭≥0，∴cos A -0，21sin 2B ⎛⎫- ⎪⎝⎭＝0.∴cos A－2＝0，sin B －12＝0，即cos A ＝2，sin B ＝12.∴∠A＝45°，∠B＝30°.∴∠C＝180°－45°－30°＝105°.7解：(1)如图，作CB⊥AD，垂足为B ，则点B 即为所求．(2)在Rt△ABC 中，AB ＝29.8×0.5＝14.9(海里)，BC ＝AB×tan 30°＝14.9×3≈8.6(海里)．答：灯塔C 到B 处的距离约为8.6海里．8解：(1)在Rt△AOB 中，OA ＝100，∠BAO＝60°，OB ＝OA·tan∠BAO＝在Rt△AOC 中，∵∠CAO＝45°， ∴OC＝OA ＝100.∴B(-0)，C(100,0)．(2)∵BC＝BO ＋OC ＝＋100，∴10015≈18.∵18＞503，∴这辆车超速了．(3)设大货车行驶到某一时刻行驶了x 米，则此时小汽车行驶了2x 米，且两车之间的距离为y当x ＝60时，y =米)．答：两车相距的最近距离为9解：如图，设光线FE 影响到B 楼的E 处，作BG⊥FM于点G，由题知EG＝MN＝30 m，∠FEG＝30°，2.68(m)．∵DN＝2 m，CD＝1.8 m.∴ED＝2.68－2＝0.68(m)，即A楼影子影响到B楼一楼采光，挡住该户窗户0.68 m高．第2课时一般锐角的三角函数值1．如图，为测量一幢大楼的高度，在地面上距离楼底O 点20 m 的点A 处，测得楼顶B 点的仰角∠OAB＝65°，则这幢大楼的高度为(结果保留3个有效数字)( )．A ．42.8 mB ．42.80 mC ．42.9 mD ．42.90 m2．如图，沿AC 方向开山修路，为了加快施工进度，要在小山的另一边同时施工，从AC 上的一点B 取∠ABD＝148°，BD ＝480 m ，∠D＝58°，要使A ，C ，E 成一直线，那么开挖点E 离点D 的距离是( )．A ．480sin 58° mB ．480cos 58° mC ．480tan 58° mD ．480tan 58︒m3．因为sin 30°＝12，sin 210°＝12-，所以sin 210°＝sin(180°＋30°)＝－sin30°；因为，sin 225°＝-，所以sin 225°＝sin(180°＋45°)＝－sin 45°.由此猜想，推理知：一般地，当α为锐角时有sin(180°＋α)＝－sin α，由此可知：sin 240°等于( )．A ．12-B ．2-C ．2-D ．4．已知在△ABC 中，∠C＝90°，设sin B ＝n ，当∠B 是最小的内角时，n 的取值范围是( )．A ．0＜nB ．0＜n ＜12C ．0＜n ＜3D ．0＜n ＜25．如图，在坡屋顶的设计图中，AB ＝AC ，屋顶的宽度l 为10米，坡角α为35°，则坡屋顶的高度h 为______米．(结果精确到0.1米)6．如图，已知Rt△ABC 中，AC ＝3，BC ＝4，过直角顶点C 作CA 1⊥AB，垂足为A 1，再过A 1作A 1C 1⊥B C ，垂足为C 1，过C 1作C 1A 2⊥AB，垂足为A 2，再过A 2作A 2C 2⊥BC，垂足为C 2，…，这样一直作下去，得到了一组线段CA 1，A 1C 1，C 1A 2，…，则CA 1＝__________，4555C A A C ＝__________.7．(1)用计算器求图中∠A 的正弦值、余弦值、正切值．(2)已知sin A ＝0.328 6，tan B ＝10.08，利用计算器求其相应的锐角A 、B ． 8．若A ，B 是锐角△ABC 的两个内角且满足下列关系式|2sin B＝0，求∠C 的度数．9．(创新应用)在Rt△ABC 中，∠C＝90°，利用sin B ＝b c ，cos B ＝ac，证明对于同一个锐角的正弦和余弦之间存在着以下重要的关系式：sin 2B ＋cos 2B ＝1，并且0＜sin B ＜1,0＜cos B ＜1.1答案：C2解析：∵∠DBC＝32°，∠BDE＝58°， ∴∠BED＝90°.∴△BED 是直角三角形．∴DE＝BD·cos∠BDE＝480cos 58°(m)．答案：B3解析：sin 240°＝sin(180°＋60°)＝－sin 60°＝2-. 答案：C4解析：由题可知，∠A＞∠B，又∠A＋∠B＝90°， ∴0°＜∠B＜45°. ∴0＜n. 答案：A 5答案：3.56解析：由面积法，知AC·BC＝AB·CA 1，所以CA 1＝341255⨯=. 由图形知∠A 5C 4C 5＝∠A 1CB ＝∠A，因为sin A ＝45，而sin∠A 5C 4C 5＝5545A C C A ＝sin A ＝45，所以455554C A A C =.答案：125 547解：(1)sin A ＝0.868 3，cos A ＝0.496 2，tan A ＝1.75.(2)∠A＝19.18°，∠B＝84.33°.8解：根据题意，得1tan 0,2sin 0,A B -=⎧⎪⎨=⎪⎩∴∠A＝45°，∠B＝60°.∴∠C＝180°－∠A －∠B＝180°－45°－60°＝75°.9证明：在Rt△ABC 中，由勾股定理，得a 2＋b 2＝c 2.∴22a b c c ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭＝1. ∵sin B＝b c ，cos B ＝ac，∴sin 2B ＋cos 2B ＝1.① ∵sin B＝b c ＞0，cos B ＝ac＞0，由①，得sin 2B ＜1，cos 2B ＜1.∴0＜sin B ＜1,0＜cos B ＜1.(或者由b ＜c ，a ＜c ，得0＜sin B ＜1,0＜cos B ＜1)解直角三角形及其应用第1课时解直角三角形练习1．如图，在Rt△ABC 中，∠C＝90°，∠A＝30°，E 为AB 上一点且AE ∶EB＝4∶1，EF⊥AC 于F ，连接FB ，则tan∠CFB 的值等于( )．A BCD ．2．如图，在等腰Rt△ABC 中，∠C＝90°，AC ＝6，D 是AC 上一点，若tan∠DBA＝15，则AD 的长为( )．A ．2BCD ．13．如图，孔明同学背着一桶水，从山脚A 出发，沿与地面成30°角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家(B 处)，AB ＝80米，则孔明从A 到B 上升的高度BC 是__________米．4．将一副三角尺如图所示叠放在一起，若AB ＝14 cm ，则阴影部分的面积是______ c m 2.5．如图，在Rt△ABC 中，∠CAB＝90°，AD 是∠CAB 的平分线，tan B ＝12，则CD∶DB ＝__________.6．如图，在△ABC 中，∠B＝45°，cos C ＝35，AC ＝5a ，则△ABC 的面积用含a 的式子表示为________．7．如图，在平面直角坐标系内，O 为原点，点A 的坐标为(10,0)，点B 在第一象限内，BO ＝5，sin∠BOA＝35.求：(1)点B 的坐标；(2)cos∠BAO 的值．8．如图，在△ABC 中，AD 是BC 上的高，tan B ＝cos∠DAC．(1)求证：AC ＝BD ； (2)若sin C ＝1213，BC ＝12，求9．(创新应用)图(2)是图(1)中窗子开到一定位置时的平面图，若∠AOB＝45°，∠OAB＝30°，OA ＝60 cm ，求点B 到OA 边的距离．≈1.7，结果精确到整数)参考答案1解析：设EB ＝1，则AE ＝4，BC ＝52，AC .. 答案：C2解析：如图，过点D 作DE ⊥AB ，垂足为E.易证△ADE 为等腰直角三角形，AE=DE.在Rt △BDE 中，tan ∠DBA=15DE AE BE BE ==，所以BE=5AE.在等腰Rt △ABC 中，∠C=90°，AC=6，由勾股定理可求出AB=，所以.在等腰Rt △AD E 中，由勾股定理可求出AD 的长为2.2答案：A3答案：404解析：Rt△ABC 中，AB ＝14 cm ，∠B＝30°，则AC ＝7 cm ，易知CF ＝AC ＝7 cm ，所以阴影部分的面积为492cm 2. 答案：4925解析：过D 作DE⊥AB 于点E.∵tan B＝12，∴DE＝12EB ． ∵∠CAB＝90°，AD 是∠CAB 的平分线，∴∠DAE＝45°.∴∠ADE＝45°. ∴∠DAE＝∠ADE.∴AE＝DE.∵DE∥CA，∴CD∶DB＝AE∶EB＝1∶2. 答案：1∶26解析：过A 作AD ⊥BC 于点D ．在Rt △ADC 中，cos C=35，AC=5a ，∴DC=3a ，AD=4a .∵在Rt △ADB 中，∠B=45°， ∴BD=AD=4a . ∴S △ABC ＝12AD ·BC＝12×4a ×(4a ＋3a )＝14a 2. 答案：14a 27解：(1)如图，作BH⊥OA，垂足为H.在Rt△OHB 中，∵BO＝5，sin∠BOA＝35， ∴BH＝BO·sin∠BOA＝3.∴OH＝4. ∴点B 的坐标为(4,3)．(2)∵OA＝10，OH ＝4，∴AH＝6. 在Rt△AHB 中，BH ＝3，∴AB＝∴cos∠BAO＝5AH AB =. AD 的长．8(1)证明：∵AD⊥BC，∴△ABD 和△ADC 为直角三角形． ∴tan B＝AD BD ，cos∠DAC＝ADAC. ∵t an B ＝cos ∠DAC， ∴AD BD ＝AD AC，即AC ＝BD ． (2)解：在Rt△ADC 中，已知sin C ＝AD AC ＝1213，故可设AD ＝12k ，AC ＝13k.5k. ∵BC＝BD ＋CD ，又AC ＝BD ， ∴BC＝13k ＋5k ＝18k. 由已知BC ＝12， ∴18k＝12. ∴k ＝23.∴AD＝12k ＝8. 9解：如图，过点B 作BC ⊥OA 于点C ，∵∠AOB=45°， ∴∠CBO=45°， BC=OC ．设BC=OC=x ，∵∠OAB=30°，∴AC=tan 30BC=︒.∵OC+CA=OA ，∴x =60(cm)． ∴x22(cm)，即点B 到OA 边的距离是22 cm.第2课时解直角三角形的应用1．如图，已知一商场自动扶梯的长为10米，该自动扶梯到达的高度h 为6米，自动扶梯与地面所成的角为θ，则tan θ的值等于( )．A ．34B ．43C ．35D ．452．如图，为了加快施工进度，要在小山的另一边同时施工，从AC 上的一点B ，取∠ABD ＝145°，BD ＝500 m ，∠D＝55°，要A ，C ，E 成一直线，那么开挖点E 离点D 的距离是( )．A ．500sin 55° mB ．500cos 55° mC ．500tan 55° mD ．500m tan 553．如图，在坡度为1∶2的山坡上种树，要求株距(相邻两树间的水平距离)是6 m ，则斜坡上相邻两树间的坡面距离是__________ m.4．如图，小明在操场上距离旗杆18 m 的C 处，用测角仪测得旗杆AB 的顶端A 的仰角为30°，已知测角仪CD 的高为1.4 m ，那么旗杆AB 的高为________ m ．(保留三位有效数字)5. 如图，在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶．在航行到B 处时，发现灯塔A 在我军舰的正北方向500米处；当该军舰从B 处向正西方向行驶至C 处时，发现灯塔A 在我军舰的北偏东60°的方向．求该军舰行驶的路程(计算过程和结果均不取近似值)．6．如图，一枚运载火箭从地面O 处发射，当火箭到达A 点时，从地面C 处的雷达站测得AC 的距离是6 km ，仰角是43°.1 s 后，火箭到达B 点，此时测得BC 的距离是6.13 km ，仰角为45.54°，解答下列问题：(1)火箭到达B 点时距离发射点有多远(精确到0.01 km)? (2)火箭从A 点到B 点的平均速度是多少(精确到0.1 km/s )?7．某商场为缓解我市“停车难”问题，拟建造地下停车库，如图是该地下停车库坡道入口的设计示意图，其中，AB⊥BD，∠BAD ＝18°，C 在BD 上，BC ＝0.5 m ．根据规定，地下停车库坡道入口上方要张贴限高标志，以便告知驾驶员所驾车辆能否安全驶入．小明认为CD 的长就是所限制的高度，而小亮认为应该以CE 的长作为限制的高度．小明和小亮谁说的对？请你判断并计算出正确的结果．(结果精确到0.1 m)8．(创新应用)关于三角函数有如下的公式： sin(α＋β)＝sin αcos β＋cos αsin β，① cos(α＋β)＝cos αcos β－sin αsin β，② tan(α＋β)＝tan tan 1tan tan αβαβ+-⋅(1－tan α·tan β≠0)．③利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，如 tan 105°＝tan(45°＋60°)＝tan 45tan 601tan 45tan 60︒+︒===-︒⋅︒(2．根据上面的知识，你可以选择适当的公式解决下面的实际问题：如图，直升飞机在一建筑物CD 上方A 点处测得建筑物顶端D 点的俯角α为60°，底端C 点的俯角β为75°，此时直升飞机与建筑物CD 的水平距离BC 为42米，求建筑物CD 的高．参考答案1答案：A2解析：∵∠E＝180°－55°－35°＝90°，∴DE＝BD·cos D＝500cos 55°(m)．答案：B3答案：4解析：AEEB＝1.4 m，∴AB＝AE＋BE＝10.4＋1.4＝11.8(m)．答案：11.85解：由已知，可得∠ACB=30°.在Rt△ABC中，∠ACB=30°，AB=500.∵tan∠ACB=AB BC，∴BC=tan AB ACB ∠=500500tan30=÷=︒因此该军舰行驶的路程为6解：(1)在Rt△OCB中，sin 45.54°＝OBCB，OB＝6.13×sin 45.54°≈4.38(km)，答：火箭到达B点时距发射点约4.38 km.(2)在Rt△OCA中，sin 43°＝OA CA，∴OA＝6×sin 43°≈4.09(km)，v＝(OB－OA)÷t＝(4.38－4.09)÷1≈0.3(km/s)．答：火箭从A点到B点的平均速度约为0.3 km/s. 7解：小亮的说法正确．在△ABD中，∠ABD＝90°，∠BAD＝18°，BA＝10，∴tan∠BAD＝BD BA.∴BD＝10×tan 18°.∴CD＝BD―BC＝10×tan 18°－0.5.在△ABD中，∠CDE＝90°－∠BAD＝72°，∵CE⊥ED，∴sin∠CDE＝CE CD.∴CE＝sin∠CDE×CD＝sin 72°×(10×tan 18°－0.5)≈2.6(m)．答：CE为2.6 m，即限高为2.6 m.8解：过点D作DE⊥AB于E，依题意，在Rt△ADE中，∠ADE=∠α=60°，AE=ED·tan 60°=BC·tan 60°=在Rt△ACB中，∠ACB=∠β=75°，AB=BC·tan 75°. ∵tan 75°=tan(45°+30°)=tan45tan30 1tan45tan30︒+︒-︒⋅︒2=∴AB=42×)=84+CD=BE=AB-AE=84+米)．答：建筑物CD的高为84米．第3课时解直角三角形的应用1．王英同学从A地沿北偏西60°方向走100 m到B地，再从B地向正南方向走200 m 到C地，此时王英同学离A地( )．A．B．100 mC．150 m D． m2．如图，在把易拉罐中的水倒入一个圆水杯的过程中，若水杯中的水在点P与易拉罐刚好接触，则此时水杯中的水深为__________．3．海中有一个小岛P，它的周围18海里内有暗礁，渔船跟踪鱼群由西向东航行，在点A测得小岛P在北偏东60°方向上，航行12海里到达B点，这时测得小岛P在北偏东45°方向上．如果渔船不改变航线继续向东航行，有没有触礁危险？请说明理由．4．如图，一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出，继续在同一深度直线航行4 000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出，求海底黑匣子C点处距离海面的深度．(精确到米，参考数据：5．如图，某处山坡上一座发射塔被冰雪从C处压折，塔尖恰好落在坡面上的点B处，在B处测得点C的仰角为38°，塔基A的俯角为21°，又测得斜坡上点A到点B的坡面距离AB为15 m，求折断．．前．发射塔的高．(精确到0.1 m)6．如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°.已知A点的高度AB为2米，台阶AC的坡度为即，且B，C，E三点在同一条直线上．请根据以上条件求出树DE的高度(测倾器的高度忽略不计)．7．如图，某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救，便立即派三名救生员前去营救.1号救生员从A点直接跳入海中；2号救生员沿岸边(岸边看成是直线)向前跑到C点，再跳入海中；3号救生员沿岸边向前跑300 m到离B点最近的D点，再跳入海中．救生员在岸上跑的速度都是6 m/s，在水中游泳的速度都是2 m/s.若∠BAD＝45°，∠BCD＝60°，三名救生员同时从A点出发，请说明谁先到达营救地点B．(参考数据8．(创新应用)在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案(如图甲所示)：①在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE＝α；②量出测点A到旗杆底部N的水平距离AN＝m；③量出测倾器的高度AC＝h.根据上述测量数据，即可求出旗杆的高度MN.如果测量工具不变，请参照上述过程，重新设计一个方案测量某小山的高度．(1)在图乙中，画出你测量小山高度MN的示意图(标上适当的字母)；(2)写出你的设计方案．参考答案1解析：BD ＝100×sin 30°＝50 m ，AD ＝100×cos 30°＝，CD ＝200－50＝150 m ，在Rt△ADC 中，AC ==.答案：D2答案：6 cm3解：有触礁危险．理由：过点P 作PD⊥AC 于D ．设PD 为x ，在Rt△PBD 中，∠PBD＝90°－45°＝45°，∴BD＝PD ＝x . 在Rt△PAD 中，∵∠PAD＝90°－60°＝30°，∴AD＝tan 30x=︒.∵AD＝AB ＋BD ＝12＋x .∴x 1)=．∵1)＜18，∴渔船不改变航线继续向东航行，有触礁危险．4解：由C 点向AB 作垂线，交AB 的延长线于E 点，并交海面于F 点．已知AB ＝4 000(米)，∠BAC＝30°，∠EBC＝60°. ∵∠BCA＝∠EBC－∠BAC＝30°， ∴∠BAC＝∠BCA，∴BC ＝BA ＝4 000(米)．在Rt△BEC 中，EC ＝BC·sin 60°＝4 000×2＝(米)，∴CF＝CE ＋EF ＝＋500≈3 964(米)．答：海底黑匣子C 点处距离海面的深度约为3 964米． 4解：作BD ⊥AC 于D ．由已知，得∠CBD=38°，∠ABD=21°，AB=15 m.在Rt △ADB 中，∵sin ∠ABD=ADAB ， ∴AD=AB ·sin ∠ABD=15×sin 21°≈5.38(m)． ∵cos ∠ABD=BDAB， ∴BD=AB ·cos ∠ABD=15×cos 21°≈14.00(m)．在Rt △BDC 中，∵tan ∠CBD=CDBD， ∴CD=BD ·tan ∠CBD ≈14.00×tan 38°≈10.94(m)．∵cos ∠CBD=BDBC ， ∴BC=cos BD CBD ∠≈14.00cos38︒≈17.77(m)．∴AD+CD+BC ≈5.38+10.94+17.77=34.09≈34.1(m)．答：折断前发射塔的高约为34.1 m. 6解：如图，过点A 作AF⊥DE 于F ，则四边形ABEF 为矩形． ∴AF＝BE ，EF ＝AB ＝2.设DE ＝x ，在Rt△CDE 中，CE ＝tan tan 60DE DE x DCE ==∠︒.在Rt△ABC 中，∵AB BC =，AB ＝2，∴BC＝在Rt △AFD 中，DF ＝DE －EF ＝x －2，∴AF ＝22)tan tan 30DF x x DAF -==-∠︒．∵AF＝BE ＝BC ＋CE ，2)x x -=.解得x ＝6. 答：树DE 的高度为6米．7解：在△ABD 中，∠A＝45°，∠D＝90°，AD ＝300(m)，∴AB＝cos 45AD︒＝，BD ＝AD·t an 45°＝300(m)．在△BCD 中，∵∠BCD＝60°，∠D＝90°，∴BC＝sin 60BD=︒，CD ＝tan 60BD =︒．1号救生员到达B 点所用的时间为2＝s )；2号救生员到达B 点所用的时间为30062-+＝50＋3≈191.7(s )；3号救生员到达B 点所用的时间为30030062+＝200(s )． ∵191.7＜200＜210，∴2号救生员先到达营救地点B ． 8分析：仿照测量旗杆高度的方法去测量的话，不能测量出测量点到山顶的底部的距离，所以要选取两个测量点，进行两次测量，构造出两个直角三角形，解这两个直角三角形求出小山的高度．解：(1)如下图所示：(2)方案如下：①测点A 处安置测倾器，测得小山顶部M 的仰角∠MCE＝α；②测点B 处安置测倾器，测得小山顶部M 的仰角∠MDE＝β；③量出测点A 到测点B 的水平距离AB ＝m ； ④量出测倾器的高度AC ＝h.根据上述测量可以求出小山MN 的高度．第4课时解直角三角形的应用1．如图，坡角为30°的斜坡上两树间的水平距离AC为2 m，则两树间的坡面距离AB 为( )．A．4 m B m C m D．2．如图，一游人由山脚A沿坡角为30°的山坡AB行走600 m，到达一个景点B，再由B沿山坡BC行走200 m到达山顶C，若在山顶C处观测到景点B的俯角为45°，则山高CD ＝__________(结果用根号表示)．3．一段路基的横断面是直角梯形，如图(1)所示，已知原来坡面的坡角α的正弦值为0.6，现不改变土石方量，全部利用原有土石进行坡面改造，使坡度变小，达到如图(2)所示的技术要求．试求出改造后坡面的坡度是多少？4．如图所示，A、B两城市相距100 km，现计划在这两座城市间修建一条高速公路(即线段AB)，经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上，已知森林保护区的范围在以P点为圆心，50 km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区？为什么？(≈1.414)5．如图，在梯形ABCD中，AB∥CD，∠BCD＝90°，且AB＝1，BC＝2，tan∠ADC＝2.(1)求证：DC＝BC；(2)E是梯形内一点，F是梯形外一点，且∠EDC＝∠FBC，DE＝BF，试判断△ECF的形状，并证明你的结论；(3)在(2)的条件下，当BE∶CE＝1∶2，∠BEC＝135°时，求sin∠BFE的值．6．如图是某宾馆大厅到二楼的楼梯设计图，已知BC＝6 m，AB＝9 m，中间平台宽度DE为2 m，DM、EN为平台的两根支柱，DM、EN垂直于AB，垂足分别为M、N，∠EAB＝30°，∠CDF＝45°.求DM和BC的水平距离BM.(精确到0.1 m，≈1.73)7．如图，某堤坝的横截面是梯形ABCD，背水坡AD的坡度i(即tan α)为1∶1.2，坝高为5 m．现为了提高堤坝的防洪抗洪能力，市防汛指挥部决定加固堤坝，要求坝顶CD加宽1 m，形成新的背水坡EF，其坡度为1∶1.4.已知堤坝总长度为4 000 m.(1)完成该工程需要多少土方？(2)该工程由甲、乙两个工程队同时合作完成，按原计划需要20天．准备开工前接到上级通知，汛期可能提前，要求两个工程队提高工作效率．甲队工作效率提高30%，乙队工作效率提高40%，结果提前5天完成．问这两个工程队原计划每天各完成多少土方？8．(创新应用)腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①)．为了测量雕塑的高度，小明在二楼找到一点C，利用三角板测得雕塑顶端A点的仰角为30°，底部B点的俯角为45°，小华在五楼找到一点D，利用三角板测得A点的俯角为60°(如图②)．若已知CD为10米，请求出雕塑AB的高度．(结果精确到0.1 1.73)参考答案1解析：在Rt△ABC 中，ACAB ＝cos 30°，则AB ＝cos30AC︒ m.答案：C2解析：过点B 作B E⊥CD，垂足为E ，在Rt△BCE 中，CE ＝BE ＝BC×sin 45°＝，过点B 作BF⊥AD，垂足为F ，则在Rt△ABF 中，BF ＝ABsin 30°＝300(m)，∴CD＝CE ＋DE ＝CE ＋BF ＝300＋(m)．答案：(300＋) m3解：由题图(1)知BE⊥DC，BE ＝30 m ，sin α＝0.6. 在Rt△BEC 中， ∵sin α＝BE BC ，∴BC＝30sin 0.6BE α=＝50(m)．根据勾股定理，得EC ＝40 m.在不改变土石方量，全部充分利用原有土石方的前提下进行坡面改造，使坡度变小，则S 梯形ABCD ＝S 梯形A 1B 1C 1D 1. ∴20×30＋12×30×40＝20×20＋12×20·E 1C 1，解得E 1C 1＝80(m)． ∴改建后的坡度i ＝B 1E 1∶E 1C 1＝20∶80＝1∶4.4解：过点P 作PC⊥AB，垂足为C ，则∠APC＝30°，∠BPC＝45°，AC ＝PC·tan 30°，BC ＝PC·tan 45°. ∵AC＋BC ＝AB ，∴PC·tan 30°＋PC·tan 45°＝100.∴13⎛⎫+⎪ ⎪⎝⎭·PC＝100.∴PC＝50(3)≈50×(3－1.732)≈63.4＞50.答：森林保护区的中心与直线AB 的距离大于保护区的半径，∴计划修筑的这条高速公路不会穿越保护区．5解：(1)证明：过A 作DC 的垂线AM 交DC 于M(如图)，则AM ＝BC ＝2，AB ＝MC ＝1.又tan∠ADC＝AMDM＝2， ∴DM＝2AM＝1. 又MC ＝1，∴DC＝2，DC ＝CB ． (2)等腰直角三角形．证明：∵DE＝BF ，∠EDC＝∠FBC，DC ＝BC ， ∴△DEC≌△BFC．∴CE＝CF ，∠ECD＝∠BCF.∴∠ECF＝∠BCF＋∠BCE＝∠ECD＋∠BCE＝∠BCD ＝90°，即△ECF 是等腰直角三角形．(3)设BE ＝k ，则CE ＝CF ＝2k ，∴EF＝. ∵∠BEC＝135°，又∠CEF＝45°， ∴∠BEF＝90°.3k. ∴sin∠BFE＝133k k =. 6解：设DF ＝x m ．∵∠CDF＝45°，∠CFD＝90°， ∴CF＝DF ＝x m .∴BF＝BC －CF ＝(6－x ) m . ∴EN＝DM ＝BF ＝(6－x ) m .∵AB＝9 m ，DE ＝2 m ，DF ＝x m ， ∴AN＝AB －MN －BM ＝(7－x ) m .在△AEN 中，∠ANE＝90°，∠EAN＝30°，∴EN＝AN·tan 30°，即6－x (7－x )，解得x≈4.6.答：支柱DM 距BC 的水平距离约为4.6 m. 7解：(1)作DG ⊥AB 于G ，作EH ⊥AB 于H.∵CD ∥AB ， ∴EH=DG=5 m.∵11.2DG AG =，∴AG=6 m. ∵11.4EH FH =，∴FH=7 m. ∴FA=FH+GH-AG=7+1-6=2(m)． ∴S 梯形ADEF ＝12(ED ＋AF)·EH＝12×(1＋2)×5＝7.5(m 2)，V ＝7.5×4 000＝30 000(m 3)． (2)设甲队原计划每天完成x m 3土方，乙队原计划每天完成y m 3土方．根据题意，得20()30000,15[(130%)(140%)]30000.x y x y +=⎧⎨+++=⎩化简，得1500,1.3 1.42000,x y x y +=⎧⎨+=⎩解之，得1000,500.x y =⎧⎨=⎩答：甲队原计划每天完成1 000 m 3土方，乙队原计划每天完成500 m 3土方．8解：过点C 作CE ⊥AB 于E.∵∠D＝90°－60°＝30°，∠ACD＝90°－30°＝60°，∴∠CAD＝90°.∵CD＝10(米)， ∴AC＝12CD ＝5(米)．在Rt△A CE 中，AE ＝AC·sin∠ACE＝5×sin 30°＝52(米)，CE 米)．在Rt△BCE 中， ∵∠BCE＝45°，米)． ∴AB＝AE ＋BE＝52+＝51)2≈6.8(米)．∴雕塑AB 的高度约为6.8米．。

沪教版九年级(上)数学秋季课程第4讲解直角三角形(解析版)

解直角三角形是九年级上学期第二章第二节的内容，通过本节的学习，需要掌握直角三角形中，除直角外其余五个元素之间的关系，并熟练运用锐角三角比的意义解直角三角形，以及解直角三角形的相关应用．重点在于理解仰角、俯角、方向角、坡度、坡角等概念，并能利用其解决实际问题；难点在于，若一个三角形不是直角三角形，要有意识把它化归为解直角三角形的问题．1、解直角三角形在直角三角形中，由已知元素求出所有未知元素的过程，叫做解直角三角形．在t R ABC∆中，如果=90C∠︒，那么它的三条边和两个锐角之间有以下的关系：（1）三边之间的关系：222a b c+=（2）锐角之间的关系：90A B∠+∠=︒（3）边角之间的关系：sin cosaA Bc==，cos sinbA Bc==tan cotaA Bb==，cot tanbA Ba==解直角三角形内容分析知识结构模块一：解直角三角形知识精讲2 / 26【例1】ABC ∆中，90C ∠=︒，已知AB = 6.4，40B ∠=︒，则A ∠=______，AC =______，BC =______．（sin400.64︒≈，sin500.77︒≈，边长精确到0.1）【答案】50︒，4.1，4.9．【解析】9050A B ∠=︒-∠=︒，根据锐角三角形比的定义，sin ACB AB=，即得sin40 6.40.64 4.096 4.1AC AB =⋅︒≈⨯=≈，同理sin50 4.9BC AB =⋅︒≈．【总结】考查直角三角形中锐角三角比的定义和应用．【例2】若菱形的周长为8，相邻两内角之比为3 : 1，则菱形的高是______．【答案】2．【解析】菱形周长为8，则其边长为2，相邻两内角之比为3 : 1，则较小内角为1180454︒⨯=︒，则菱形高为2sin 452︒=．【总结】考查菱形性质和相关锐角三角比的应用．【例3】如图，OAB ∆中，OA = OB ，125AOB ∠=︒．已知点A 的坐标是（4，0），则点B的坐标是____________．（用锐角三角比表示）【答案】()4cos554sin55-︒︒，．【解析】过点B 作BM x ⊥轴交x 轴于点M ，则有18055BOM AOB ∠=︒-∠=︒，由4BO AO ==，可得cos55MO BO =⋅︒，sin55BM BO =⋅︒，点B 在第二象限，可知其坐标即为()4cos554sin55-︒︒，．【总结】考查平面直角坐标系中点坐标与线段长度的转换，结合锐角三角比相关知识解题．【例4】如图，在ABC ∆中，90BAC ∠=︒，AB = AC ，D 为边AC 的中点，DE BC ⊥于点E ，连接BD ，则tan DBC ∠的值为（）例题解析A BOxyMAB CDEOA ．13B ．21-C ．23-D ．14【答案】A【解析】设AB AC a ==，90BAC ∠=︒，可得2BC a =，45C ∠=︒，D 为AC 中点，则有1122CD AC a ==，DE BC ⊥，可得2sin 4DE CE CD C a ==⋅=，则324BE BC CE a =-=，214tan 3324aDE DBC BE a ∠===．【总结】考查等腰直角三角形中的锐角三角比的应用．【例5】如图，在矩形ABCD 中，对角线AC 、BD 相交于点O ，E 是边AD 的中点，若AC =10，DC =25，则BO =______，EBD ∠的度数约为____°____＇（参考数据：1tan 2634'2︒≈）．【答案】5，18，26．【解析】根据矩形性质，10BD AC ==，152BO BD ==，根据勾股定理，2245AB BD AB =-=，E 是AD 中点，则25AE AB ==，251tan 245AB ADB AD ∠===，则有2634'ADB ∠=︒，45AEB ∠=︒，即得：452634'1826'EBD AEB ADB ∠=∠-∠=︒-︒=︒．【总结】本题一方面考查矩形性质，另一方面考查锐角三角比的应用．【例6】在锐角ABC ∆中，AB = 14，BC = 14，84ABC S ∆=，求cot C 的值．【答案】7136-．【解析】作AD BC ⊥交BC 于D ，则有12ABC S AD BC ∆=⋅，得：22841214ABC S AD BC ∆⨯===，根据勾股定理可得22213BD AB AD =-=，则14213713cot 126CD C AD --===．【总结】解三角形，通过作高把线段放到直角三角形中即可．【例7】如图，ABC ∆中，23AB =，AC = 2，边BC 上的高3AD =，求ABC S ∆和BAC ∠的大小．【答案】23ABC S ∆=，90BAC ∠=︒．【解析】AD BC ⊥，根据锐角三角比的定义，则有AB CDEABCD4 / 2631sin 223AD B AB ===，3sin 2AD C AC ==，可得：30B ∠=︒，60C ∠=︒，可知90BAC ∠=︒，所以1232ABC S AB AC ∆=⋅=．【总结】解直角三角形的应用，直接采用特殊角锐角三角比，也可直接用勾股定理解题．【例8】如图，在锐角ABC ∆，4sin 5B =，tan 2C =，且40ABC S ∆=，求BC 的长．【答案】10【解析】作AD BC ⊥交BC 于点D ，由4sin 5B =，可设4AD a =，则有5AB a =，根据勾股定理得：223BD AB AD a =-=，因为tan 2C =，则2CD a =，5BC BD CD a =+=，11454022ABC S AD BC a a ∆=⋅=⋅⋅=，即24a =，解得：2a =，即得：510BC a ==．【总结】考查锐角三角比的应用，通过作高把线段放到直角三角形中即可．【例9】如图，ABC ∆中，30B ∠=︒，45C ∠=︒，22AB AC -=-，求BC 的长．【答案】31+．【解析】过点A 作AD BC ⊥交BC 于D ，设AD a =，由30B ∠=︒，45C ∠=︒，可得：2AB a =，3BD a =，CD a =，2AC a =．∵22AB AC -=-，∴2222a a -=-，解得：1a =，由此可得331BC BD CD a a =+=+=+．【总结】考查锐角三角比的应用，通过作高把线段放到直角三角形中，把题目中的线段用一条线段表示出来即可．【例10】如图，先将斜边AB 长6 cm ，30A ∠=︒的直角三角板ABC 绕点C 顺时针方向旋转 90°至''A B C ∆位置，再沿CB 向左平移，使点B 落在原三角板ABC 位置的斜边AB 上，则平移的距离为______．【答案】()33cm -． ''B 【解析】30A ∠=︒，得'sin303BC AB cm B C =⋅︒==，cos3033AC AB cm =⋅︒=，则有'333AB =-，得()()'''3tan 333333B B AB A cm =⋅=-⨯=-．ABCAB CDABCD【总结】考查锐角三角比的应用，通过作高把线段放到直角三角形中，把题目中的已知线段用一条线段表示出来即可．【例11】如图，正方形ABCD 中，E 为边BC 上一点，将正方形折叠，使A 点与E 点重合，折痕为MN ，若1tan 3AEN ∠=，DC + CE =10．（1）求ANE ∆的面积；（2）求sin ENB ∠的值．【答案】（1）103；（2）35．【解析】（1）设正方形边长为a ，由1tan 3AEN ∠=，可得：13BE a =，则有23CE a =，CD a =，DC + CE =10，即2103a a +=，解得：6a =，则123BE a ==，设AN m =，根据翻折的性质，则有EN AN m ==，6BN m =-，在Rt BNE ∆中用勾股定理，则有222BN BE NE +=，即()22262m m -+=，解得：103m =，11102223ANE S BE AN m ∆=⋅=⨯=；（2）由（1）可得2BE =，103NE =，则23sin 1053BE ENB NE ∠===．【总结】解直角三角形的应用，注意充分利用翻折的性质和其中的相关等量关系．【例12】如图，四边形ABCD 中，90A C ∠=∠=︒，120B ∠=︒，AB = 4，BC = 2，求四边形的面积．【答案】2633．【解析】延长AB 、DC 交于点E ，90A C ∠=∠=︒，120B ∠=︒，60D CBE ∴∠=∠=︒．由BC = 2，得tan 602324CE BC BE BC =︒⋅===，．由AB = 4，即得8AE AB BE =+=，则有83cot 603AD AE =⋅︒=． A BC D EN MABCD E6 / 26即得：1118312638223222323ABCD ADE BCE S S S AD AE BC CE ∆∆=-=⋅-⋅=⨯⨯-⨯⨯=．【总结】利用割补法求面积，关键在于对特殊角的利用，不能把特殊角分开，延长即可．【例13】如图，在四边形ABCD 中，已知AD = AB = BC ，连接AC ，且30ACD ∠=︒，23tan 3BAC ∠=，CD = 3，求AC 的长．【答案】635或63．【解析】过点B 作BE AC ⊥交AC 于E ，过点D 作DF AC ⊥交AC 于F ，则有12AE CE AC ==，设AE a =，由23tan 3BAC ∠=，可得：233BE a =，根据勾股定理即可得22213AB BE AE a BC AD =+===，由30ACD ∠=︒，CD = 3，可得3sin302DF CD =⋅︒=，33cos302CF CD =⋅︒=，在Rt ADF ∆中用勾股定理，则有222AF DF AD +=，即222333212223a a ⎛⎫⎛⎫⎛⎫-+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，整理，得：25183270a a -+=，解得：1335a =，233a =，均符合题意，即得6325AC a ==或63AC =．【总结】考查锐角三角比的应用，通过作高把线段放到直角三角形中，把题目中的线段用一条线段表示出来即可．【例14】小智在学习特殊角的三角比时发现，将如图所示的矩形纸片ABCD 沿过B 点的直线折叠，使点A 落在BC 上的点E 处，折痕BM ．还原后，再沿过点E 的直线折叠，使点A 落在BC 上的点F 处，折痕EN ．利用这种方法，可以求出tan67.5︒的值是21+，试证明之．【答案】略．【解析】证明：第一次折叠，由翻折的性质，得：AB BE =，有45AEB ∠=︒，第二次折叠，由翻折的性质，得：AE EF =，有2AEB AFB ∠=∠，则有22.5AFB ∠=︒，67.5FAB ∠=︒，设AB a =，则有BE a =，2AE a EF ==，则有()21BF a =+，A BCDEFNM AB CD E F仰角视线水平线俯角铅垂线()21tan 67.5tan 21a BFFAB ABa+︒=∠===+．【总结】考查翻折性质与特殊角锐角三角比的结合运用，注意线段长度的合理转换．【例15】在平面直角坐标系内，放置了5个如图所示的正方形（用阴影表示）．点1B 在y 轴上，点1C 、1E 、2E 、2C 、3E 、4E 、3C 在x 轴上．已知正方形1111A B C D 的边长为1， 1160B C O ∠=︒，11B C //22B C //33B C ，则点3A 到x 轴的距离是（）A ．3318+ B ．3118+ C ．336+ D ．316+ 【答案】D【解析】由1160B C O ∠=︒，11B C //22B C //33B C ，可得： 22233460B C E B C E ∠=∠=︒，由11122290B C D B C D ∠=∠=︒，得：11122360C D E C D E ∠=∠=︒， 1111221cos602D E C D B E =⋅︒==则2222223sin 603B E BC CD ===︒，2322343cos606D E C D B E =⋅︒==，由此可得3A 到x 轴的距离即为()3433311cot 601366B E ⎛⎫+⋅+︒=+⨯= ⎪ ⎪⎝⎭，故选D ．【总结】考查特殊角锐角三角比的应用，注意进行边角转化．1、仰角与俯角在测量过程中，常常会遇到仰角和俯角．如图，当我们进行测量时，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角．模块二：解直角三角形的应用知识精讲x yO8 / 26北北偏东30°南偏西45°北偏西70°南偏东50°30° 70° 45° 50°hl2、方向角指北或指南方向线与目标方向线所成的小于90°的角叫做方向角．如图：北偏东30°，北偏西70°，南偏东50°，南偏西45°．3、坡度（坡比）、坡角在修路、挖河、开渠等设计图纸上，都需要注明斜坡的倾斜程度．如图，坡面的铅垂高度h 和水平宽度l 的比叫做坡面的坡度（或坡比），记作i ，即h i l=．坡度通常写成1 : m 的形式，如1:1.5i =．坡面与水平面的夹角叫做坡角，记作α．坡度i 与坡角α之间的关系：tan hi l α==．【例16】如图，为测量一棵与地面垂直的树OA 的高度，在距离树的底端30米的B 处，测得树顶A 的仰角ABO ∠为α，则树OA 的高度为（）A ．30tan αB ．30sin αC ．30tan αD ．30cos α【答案】C【解析】转化为直角三角形中求长度的问题，根据锐角三角比定义可得tan OAOB α=，即得30tan OA α=，故选C ．【总结】考查锐角三角比在实际问题中的应用．例题解析A BO【例17】如图，一艘海轮位于灯塔P 的北偏东55°方向，距离灯塔2海里的点A 处．如果海轮沿着正南方向航行到灯塔的正东方向，那么海轮航行的距离AB 的长是（）海里A ．2B ．2sin 55°C ．2cos 55°D ．2tan 55°【答案】C【解析】转化为直角三角形中求长度的问题，根据锐角三角比定义可得cos ABPAB PA ∠=，即得2cos55OA =︒，故选C ．【总结】考查锐角三角比在实际问题中的应用．【例18】如图所示，某公园入口处原有三级台阶，每级台阶高为18厘米，深为30厘米，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A ，斜坡的起始点为C ，现设计斜坡BC 的坡度i = 1 : 5，那么AC 的长度是______厘米．【答案】210【解析】依题意可得31854BD =⨯=， 23060AD =⨯=，根据坡度的含义，可得：270BDCD i==，由此可得210AC CD AD cm =-=．【总结】考查坡度的实际应用和理解．【例19】如图，斜面AC 的坡度为1 : 2，AC =35米，坡顶有一旗杆BC ，旗杆顶端B 点与 A 点有一条彩带相连，若AB = 10米，则旗杆BC 的高度为（）米A ．5B ．6C ．8D ．3+5【答案】A【解析】斜坡坡度为1 : 2，即12CD AD =，设CD a =，则有2AD a =，根据勾股定理可得535AC a ==，解得3a =，即得：3CD =，6AD =，根据勾股定理可得228BD AB AD =-=，则5BC BD CD m =-=．【总结】考查坡度的实际应用和理解，结合勾股定理进行实际计算．C ABDABP 北ABC D10 / 26【例20】如图，要在宽为22米的大道AB 两边安装路灯，路灯的灯臂CD 长2米，且与灯柱BC 成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO 与灯臂CD 垂直．当灯罩的轴线DO 通过公路路面中心线时照明效果最佳．此时，路灯的灯柱BC 的高度应该设计为（）米 A ．1122- B ．1123-C ．11322-D ．1134-【答案】D【解析】延长OD 、DC 交于点E ．90B ODC ∠=∠=︒，120BCD ∠=︒， 60DOB DCE ∴∠=∠=︒，由BC = 2，tan 602324DE DC CE DC ∴=︒⋅===，．依题意可知：O B =11，即得：tan 60113BE OB =⋅︒=，则()1134BC BE CE m =-=-．【总结】考查利用锐角三角比求线段长度，关键在于对特殊角的利用，不能把特殊角分开，延长即可．【例21】如图，为测得一栋大厦CD 的高度，一人先在附近一楼房的底端A 点观测大厦顶端C 处的仰角是60°，然后爬到该楼房顶端B 处观测大厦底部D 处的俯角是30°，已知楼房高AB 约是45 m ，根据以上观测数据可求大厦的高CD 是______m ．【答案】135．【解析】90BAD ADC ∠=∠=︒，30ADB ∠=︒，60CAD ∠=︒，则有tan 60453AD AB =⋅︒=，tan60135CD AD m =⋅︒=．【总结】考查俯角仰角与特殊角锐角三角比的结合应用．【例22】如图，小智在大楼30米高（即PH = 30米）的A BCDABCH PQABC DO E窗口P 处进行观测，测得山坡上A 处的俯角为15°，山脚B 处的俯角为60°．已知山坡的坡度为1:3，点P 、H 、B 、C 、 A 在同一平面上，点H 、B 、C 在同一直线上，且PH HC ⊥．则山坡上A 、B 两点间的距离为______．【答案】203m ．【解析】依题意有60PBH ∠=︒，15QPA ∠=︒，山坡坡度为1:3，则有30ABC ∠=︒，由此可得:9030BPH PBH ∠=︒-∠=︒，90ABP ∠=︒， 9045APB BPH QPA ∠=︒-∠-∠=︒，则有203sin 60PHBP ==︒，203AB PB m ==．【总结】考查俯角仰角与特殊角锐角三角比的结合应用．【例23】某单位拟建造地下停车库，设计师提供了车库入口设计示意图（如图），按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你计算图中CE 的长．（参考数据：sin180.309︒≈，cos180.951︒≈，tan180.325︒≈，cot18 3.078︒≈，结果精确到0.1 m ）【答案】2.3m ．【解析】依题意得18BAD ∠=︒，tan 9tan18BD AB BAD =⋅∠=︒， 9tan180.5CD BD BD =-=︒-， 9072BDA BAD ∠=︒-∠=︒，则有9018DCE BDA ∠=︒-∠=︒，由此可得()cos 9tan180.5cos189sin180.5cos18CE CD DCE =⋅∠=︒-⨯︒=︒-︒由上述数据，即可得90.3090.50.951 2.3055 2.3CE m ≈⨯-⨯=≈．【总结】考查锐角三角比在解决实际问题中的具体应用，注意题目要求，考虑需要涉及到哪些相关的锐角三角比．ABC D E9 m0.5 m12 / 26【例24】小方在课外活动中观察吊车的工作过程，绘制了如图所示的平面图形．已知吊车吊臂的支点O 距离地面高'2OO =米．当吊臂顶端由点A 抬升至点'A （吊臂长度不变）时，地面B 处的重物（高度不计）被吊至'B 处，紧绷着的吊缆''A B AB =．AB 垂直地面'O B 于点B ，直线''A B 垂直地面'O B 于点C ，吊臂长度'10OA OA ==米，且3cos 5A =，1sin '2A =．（1）求重物在水平方向移动的距离BC ；（2）求重物在竖直方向提升的高度'B C ．【答案】（1）3m ；（2）()536m -．【解析】（1）如图，则有4sin 1085OD OA A m =⋅=⨯=， ''1sin 1052OF OA A m =⋅=⨯=，则3BC FD OD OF m ==-=；（2）由（1）可得：cos 6AD OA A m =⋅=，则'''8AB AD DB AD OO m A B =+=+==， ''2253A F OA OF m =-=，则()''''5328536B C A F FC A B m =+-=+-=-．【总结】考查锐角三角比在解决实际问题中的具体应用，注意题目要求，考虑需要涉及到哪些相关的锐角三角比，注意看清楚题目提供的条件．【例25】如图，是一座人行天桥的示意图，天桥的高度是10米，CB DB ⊥，坡面AC 的坡角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC 的坡度为3:3i =．若新坡角下需留3米宽的人行道，问离原坡角（A 点处）10米的建筑物是否需要拆除？（参考数据：2 1.414≈，3 1.732≈）【答案】需要拆除．【解析】依题意有45CAB ∠=︒，则10AB BC ==，DC 的坡度为3:3i =，即得：103CDBD i==，由此可得：10310AD BD AB =-=-，则点A 距人行道外侧距离至少为103103103710.3210-+=-≈>，由此可知建筑物需要拆除．【总结】考查锐角三角比在解决实际问题中的具体应用．【例26】数学兴趣小组准备利用所学的知识测量公路旁某广告牌的高度．如图所示，先在水平面上点A 处测得对广告牌上沿点C 的仰角为30°，然后沿AH 方向前进10米至点A BCD FDA BA ＇B ＇ O ＇OCC DG 广告牌B 处，测得对广告牌下沿点D 的仰角为60°．已知矩形广告牌垂直于地面的一边CD高2米．求广告牌的高度GH （结果保留根号）．【答案】()531m -．【解析】作DE BH ⊥交BH 于E ，设BE a =，则有tan 3DE BE DBE a =⋅∠=， 32CE CD DE a =+=+，由30CAE ∠=︒，得332310AE CE a AB BE a ==+=+=+，解得：53a =-，由此可得()()323532531GH CE a m ==+=⨯-+=-．【总结】考查锐角三角比在解决实际问题中的具体应用，注意线段长度的转化和等量关系．【例27】如图，轮船甲位于码头O 的正西方向A 处，轮船乙位于码头O 的正北方向C 处，测得45CAO ∠=︒．轮船甲自西向东匀速行驶，同时轮船乙沿正北方向匀速行驶，它们的速度分别为45 km /h 和36 km /h ．经过0.1 h ，轮船甲行驶至B 处，轮船乙行驶至D 处，测得58DBO ∠=︒．此时B 处距离码头O 有多远？（参考数据：sin580.85︒≈，cos580.53︒≈，tan58 1.60︒≈）【答案】13.5km ．【解析】依题意可得：450.1 4.5AB km =⨯=， 360.1 3.6CD km =⨯=，由45CAO ∠=︒，可知 4.5AO CO BO ==+，8.1DO CO CD BO =+=+，58DBO ∠=︒，得tan tan58DODBO BO∠==︒，即8.1 1.60BO BO+≈，解得：13.5BO km =．【总结】考查锐角三角比在解决实际问题中的具体应用，注意线段长度的转化和等量关系．【例28】如图，MN 表示一段笔直的高架道路，线段AB 表示高架道路旁的一排居民楼．已知点A 到MN 的距离为15米，BA 的延长线与MN 相交于点D ，且30BDN ∠=︒，假设汽车在高架道路上行驶时，周围39米以内会受到噪音的影响．A BCD O北东14 / 26（1）过点A 作MN 的垂线，垂足为H ．如果汽车沿着从M 到N 的方向在MN 上行驶，当汽车到达点P 处时，噪音开始影响这一排居民楼，那么此时汽车与点H 的距离为多少米？（2）降低噪音的一种方法是在高架道路旁安装隔音板．当汽车行驶到点Q 时，它与这一排居民楼的距离QC 为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？（结果精确到1米，参考数据：3 1.7≈）【答案】（1）36；（2）89．【解析】（1）39AP =，根据勾股定理可得：2222391536PH AP AH m =-=-=；（2）30BDN ∠=︒，得278DQ QC m ==， cot 30153DH AH m =⋅︒=，由此可得隔音板长度：361537811415389PQ PH DH DQ m =-+=-+=-≈．【总结】考查锐角三角比在解决实际问题中的具体应用，注意将题目中的语言转化为数学符号语言．【例29】台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形成气旋风暴，有极强的破坏力．据气象部门观测，某沿海城市A 正南方向相距220 km 的B 处有一台风中心，中心最大风力为12级，每远离台风中心20 km ，风力就会减弱一级．现台风中心正以15 km /h 的速度沿北偏东30°方向移动，如图所示．若城市所受风力达到或超过4级，则称为受台风影响．（1）设台风中心风力不变，该城市是否会受到这次台风的影响？请说明理由．（2）如该城市受台风影响，那么台风影响该城市的持续时间有多长？（3）该城市受到台风影响时的最大风力为几级？【答案】（1）会受影响；（2）415h ；（3）6.5级．【解析】（1）作AD BC ⊥交BC 于D ，则有sin 110AD AB B km =⋅=，不受台风影响的最小距离为()12420160km -⨯=，因为110160<，故该城市会受到台风影响；（2）设在E 点处该城市开始受到台风影响，则有160AE km =，根据勾股定理可得：223015DE AE AD =-=，则受影响时间为2301515415h ⨯÷=；（3）台风中心到达D 点处距该城市最近，受到最大风力影响，受到的最大风力即为1211020 6.5-÷=级．【总结】考查锐角三角比在解决实际问题中的具体应用，关键是找准题目要求的临界位置结AB CDP NMQH AB CD E合题意进行求解．【例30】某水库大坝的横截面积是如图所示的四边形ABCD ，其中AB // CD ．瞭望台PC 正前方水面上有两艘渔船M 、N ，观察员在瞭望台顶端P 处观测渔船M 的俯角31α=︒，观测渔船N 的俯角45β=︒．已知MN 所在直线与PC 所在直线垂直，垂足为E ，PE 长为30米．（1）求两渔船M 、N 之间的距离（结果精确到1米）（2）已知坝高24米，坝长100米，背水坡AD 的坡度i = 1 : 0.25．为了提高大坝的防洪能力，某施工队在大坝的背水坡填筑土石方加固，加固后坝顶加宽3米，背水坡FH 的坡度为i = 1 : 1.5．施工12天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的1.5倍，结果比原计划提前20天完成加固任务．施工队原计划平均每天填筑土石方多少立方米？（参考数据：tan310.60︒≈，sin310.52︒≈）【答案】（1）20m ；（2）600．【解析】（1）3050tan 0.60PE ME m α=≈=，30tan PENE m β==，由此可得：20MN ME NE m =-=；（2）作DG AB ⊥交AB 于G ，作 FQ BH ⊥交BH 于Q ．依题意有：24DG FQ ==，AD 坡度i = 1 : 0.25，即得：16DGAG i ==，FH 坡度i = 1 : 1.5，即得：236FQHQ i ==，AB C D E F NM P JHG Q16 / 26由此可得336633AH GQ HQ AG =+-=+-=，则填筑土石方总量为()()11005024333432002DG DF AH ⋅+⨯=⨯⨯+=方，设原计划每天填筑x 方，可列方程4320012 1.5122043200x x x ⎛⎫+--= ⎪⎝⎭，解得：600x =，经检验，600x =是原方程的根，即原计划每天填筑土石方600立方米．【总结】考查实际问题的应用，主要是对题目要求进行准确分析．【习题1】如图，菱形ABCD 的边长为15，3sin 5BAC ∠=，则对角线AC 的长为______．【答案】24．【解析】连结BD 交AC 于点O ，则有AC BD ⊥，2AC AO =，由3sin 5BAC ∠=，即35BO AB =，得9BO =，勾股定理得2212AO AO BO =-=，则224AC AO ==．【总结】考查菱形的性质结合锐角三角比基础知识的应用．【习题2】有一个相框的侧面抽象为如图所示的几何图形，已知BC = BD = 15 cm ， 40CBD ∠=︒，则点B 到CD 的距离为______cm ．（参考数据：sin200.342︒≈，cos200.940︒≈，sin400.642︒≈，cos400.766︒≈，结果精确到0.1 cm ）【答案】14.1．【解析】作BE CD ⊥，则有1202CBE CBD ∠=∠=︒，故B 到CD 的距离cos 150.94014.1BE BC CBE cm =⋅∠≈⨯=．【总结】考查锐角三角比和等腰三角形性质的结合应用．随堂检测AB CDOABC DEABCDE F G 【习题3】如图，为了测得电视塔的高度AB ，在D 处用高为1米的测角仪CD 测得电视塔顶端A 的仰角为30°，再向电视塔方向前进100米到达F 处，又测得电视塔顶端A 的仰角为60°，则这个电视塔的高度AB 为（）A ．503米B ．51米C ．()503+1米D ．101米【答案】C【解析】60AEG ∠=︒，得：tan 603AG EG EG =⋅︒=，30ACG ∠=︒，则有cot 3033CG AG AG EG =⋅︒==，则有2100CE CG EG EG =-==，得：50EG =，3503AG EG ==，()5031AB AG BG m =+=+．故选C ．【总结】考查特殊角锐角三角比的实际应用，相应线段长度转化．【习题4】如图，ABC ∆中，90C ∠=︒，3sin 5B =．D 是BC 上一点，已知45ADC ∠=︒，DC = 6，求tan BAD ∠的值．【答案】17．【解析】过点D 作DE AB ⊥交AB 于点E ．由90C ∠=︒，3sin 5B =，可设3AC a =，则5AB a =，根据勾股定理可得224BC AB AC a =-=，由45ADC ∠=︒，可得3CD AC a ==，则BD BC CD a =-=，由90C DEB B B ∠=∠=︒∠=∠，，即得ACB ∆∽DEB ∆，则有55AC BC AB a DE BE BD a ====，由此可得35DE a =，45BE a =，则215AE AB BE a =-=，即得315tan 2175aDE BAD AE a ∠===．【总结】解直角三角形，通过作高把线段放到直角三角形中再通过相应的线段比例关系把三角形中的相关线段表示出来即可．【习题5】如图，ABC ∆和ADE ∆都是等边三角形，AB = 2AD ，已知45BAD ∠=︒，AC 与DE 相交于点F ，ABC ∆的面积为3，求阴影部分的面积．【答案】334-【解析】作CG AB ⊥交AB 于点G ，作FH AE ⊥交AE 于点H ，则有6045E B EAF BAD ∠=∠=︒∠=∠=︒，．设ABC ∆边长为a ，则有1322BG a CG a ==，，ABCD EA BCDE FG H18 / 261133222ABC S CG AB a a ∆=⋅=⋅⋅=，即得24a =，解得：2a =，即22AB AD ==，得ADE ∆边长为1，则有1AE =，设FH h =，则有3cot 603EH EF h =⋅︒=，AH FH h ==，即得3113AE AH FH h ⎛⎫=+=+= ⎪ ⎪⎝⎭，解得332h -=，13324S AE FH -=⋅=阴．【总结】考查特殊角的锐角三角比与特殊图形的结合应用．【习题6】如图，在四边形ABCD 中，45A C ∠=∠=︒，105ADB ABC ∠=∠=︒．（1）若AD = 2，求AB ；（2）若232AB CD +=+，求AB ．【答案】（1）62+；（2）31+．【解析】（1）作DE AB ⊥交AB 于点E ，由45A ∠=︒，可得：cos452AE AD DE =⋅︒==，由105ADB ∠=︒，可得：30ABD ∠=︒，即得cot 306BE DE =⋅︒=，则62AB =+；（2）作BF CD ⊥交CD 于点F ，由（1）可得()31AB DE =+，设DE a =，则有2BD a =，由45A C ∠=∠=︒，105ADB ABC ∠=∠=︒，可得60BDC ∠=︒，则有cos60DF BD a =⋅︒=，3BF a CF ==，即得()31CD a AB =+=，由232AB CD +=+，即可得31AB =+．【总结】考查特殊角锐角三角比的应用，通过作高解直角三角形即可．【习题7】2015年4月25日14时11分，尼泊尔发生8.1级地震，震源深度为20千米．中国救援队火速赶往灾区救援，探测出某建筑物废墟下方C 处有生命迹象．在废墟一侧某面上选两探测点A 、B ，点A 、B 相距2米，探测线与该面的夹角分别是30°和45°（如图），试确定生命所在的点C 与探测面的距离（参考数据：2 1.414≈，3 1.732≈）【答案】2.732m ．【解析】作CD AB ⊥交直线AB 于点D ．由题意可得：30CAD ∠=︒，45CBD ∠=︒，则有cot 303AD CD CD =⋅︒=，BD CD =，即()312AB AD BD CD =-=-=，AB CDEFABC30°45° DEDCB A解得：31 2.732CD m =+≈【总结】考查特殊角锐角三角比的应用，通过作高解直角三角形即可．【习题8】利用几何图形，求sin 18°的值．【答案】514-．【解析】如图，ABC ∆为“黄金三角形”，AD 、BE 分别为其顶角和一底角角平分线，则有18BAD ∠=︒，12BD BC =，根据相似可证得“黄金三角形中”512BC AC -=，则有51sin184BD AC -︒==．【总结】考查“黄金三角形”的性质的应用．【习题9】如图，港口B 位于港口O 正西方向120 km 处，小岛C 位于港口O 北偏西60° 方向上．一艘游船从港口O 出发，沿OA 方向（北偏西30°）以v km /h 的速度驶离港口O ，同时一艘快艇从港口B 出发，沿北偏东30°的方向以60 km /h 的速度驶向小岛C ，在小岛C 用1 h 加装补给物资后，立即按原来的速度给游船送去．（1）快艇从港口B 到小岛C 需要多长时间？（2）若快艇从小岛C 到与游船相遇恰好用时1 h ，求v 的值及相遇处与港口O 的距离．【答案】（1）1h ；（2）40v =，相遇处与港口O 的距离120km ．【解析】（1）依题意可得60CBO ∠=︒，30BOC ∠=︒，则有90ACB ∠=︒，此时sin 60BC OB BOC km =⋅∠=，则快艇到小岛的时间为60601h ÷=；（2）延长BC 交AO 于点D ．由题意可知60CD BC ==，则有AB BO =，由30AOC ∠=︒，可得60BOD ∠=︒，即BOD ∆为等边三角形，相遇点D 与港口距离120OD OB km ==，船速()12011140/v km h =÷++=． A B CO北北东D20 / 26【总结】考查方位角的应用，计算速度时注意不要遗漏时间．【习题10】如图所示，已知边长为2的正三角形ABC 沿直线l 顺时针滚动．（1）当ABC ∆滚动一周到111A B C ∆的位置时，A 点所运动的路程约为______；（精确到0.1）（2）设ABC ∆滚动240°，C 点的位置为'C ，当ABC ∆滚动480°时，A 点的位置再'A ，请你利用正切的两角和公式()tan tan tan 1tan tan αβαβαβ++=-，求出''CAC CAA ∠+∠的度数．【答案】（1）8.4；（2）30︒．【解析】（1）A 点转过的圆心角度数为1202240︒⨯=︒，由此可得运动路程为：240288 3.148.418033ππ⨯⨯=≈≈；（2）作'C D AC ⊥交直线AC 于点D ，作'A E AC ⊥交直线AC 于点E ．则有''2sin 603C D A E ==︒=，2215AD =⨯+=，4219AE =⨯+=，则有''3tan 5C D CAC AD ∠==，''3tan 9A E CAA AE ∠==，根据上述公式，代值计算，则有()''''''33tan tan 359tan 1tan tan 333159CAC CAA CAC CAA CAC CAA +∠+∠∠+∠===-∠⋅∠-⨯，即得''30CAC CAA ∠+∠=︒．【总结】阅读题，抓住题目中的运动过程，准确分析即可进行解题应用．ABCA 1B 1C 1DE【作业1】如图，将正方形ABCD 的边BC 延长到点E ，使得CE = AC ，AE 与CD 相交于点F ，求E ∠的余切值．【答案】21+．【解析】设正方形边长为a ，则有2AC a CE ==， ()21BE BC CE a =+=+，()21cot 21aBEE ABa+===+．【总结】考查根据一些特殊角锐角三角比计算一些相关锐角三角比的思想方法．【作业2】如图，在矩形ABCD 中，AB = 8，BC = 12，E 是BC 的中点，连接AE ，将ABE ∆沿AE 折叠，点B 落在点F 处，连接FC ，则sin EFC ∠的值为______．【答案】45．【解析】连结BF ，根据翻折的性质，可得BE EF FC ==，可证得BFC ∆为直角三角形，AE BF ⊥，即得//AE CF ，所以EFC AEF AEB ∠=∠=∠．由8AB =，6BE =，勾股定理得：2210AE AB BE =+=，则84sin sin 105AB EFC AEB AE ∠=∠===．【总结】考查翻折性质的应用，通过等角转化求角的锐角三角比．课后作业AB C D EFA B CDEF22 / 26【作业3】如图，AD 是ABC ∆的中线，1tan 3B =，2cos 2C =，2AC =．求：（1）BC 的长；（2）sin ADC ∠的值．【答案】（1）4；（2）22．【解析】（1）作AE BC ⊥交BC 于点E ，则cos 1CE AC C AE =⋅==，由1tan 3AE B BE ==，即得：3BE =，则4BC CE CE =+=；（2）因为AD 是ABC ∆中线，则有2BD CD ==，即得：1DE CD CE =-=，由勾股定理，得：222AD AE DE =+=，则有12sin 22AE ADC AD ∠===．【总结】解三角形，通过作高把边转化到直角三角形中即可．【作业4】如图，轮船从B 处以每小时60海里的速度沿南偏东20°的方向匀速航行，在B 处观测灯塔A 位于南偏东50°方向上．轮船航行40分钟到达C 处，在C 处观测灯塔A 位于北偏东10°方向上，则C 处与灯塔A 的距离是（）A ．20海里B ．40海里C ．2033海里D ．4033海里【答案】D ．【解析】依题意可得：30ABC ACB ∠=∠=︒，则有AB AC =，作AD BC ⊥交BC 于D ，轮船行程即260403BC =⨯=，则有1202BD CD BC ===，403cos 3CD AC ACB ==∠．【总结】考查方位角知识的应用，本题重点在于准确分析相关角度的大小再利用特殊角的锐角三角比解决问题．ABCD EABC 北东D【作业5】如图，在ABC ∆中，45B ∠=︒，562AB =，D 是BC 上一点，AD = 5，CD = 3，求ADC ∠的度数及AC 的长．【答案】60ADC ∠=︒，19AC =．【解析】作AE BC ⊥交BC 于点E ，则有56253sin 222AE AB B =⋅=⨯=， 3sin 2AE ADE AD ∠==，即得sin 60ADE ∠=︒，则1522DE AD ==，则12CE CD DE =-=，勾股定理得2219AC AE CE =+=．【总结】考查特殊角锐角三角比的应用，作高把线段放到直角三角形中即可．【作业6】如图，点D 在ABC ∆的边BC 上，C BAD DAC ∠+∠=∠，4tan 7BAD ∠=，65AD =，CD = 13，求线段AC 的长．【答案】265．【解析】作DE AB ⊥交AB 于点E ，作AF BC ⊥交BC 于点F ，作DAG BAD ∠=∠交CD 于点G ，作DH AG ⊥交AG 于点H ． ∵4tan 7DE BAD AE ∠==，勾股定理得22265AE DE AD +==，∴4DE =，7AE =．∵AD 为角平分线，根据角平分线性质有4DH DE ==，7AH AE ==，C BAD DAC ∠+∠=∠，即C BAD DAH GAC ∠+∠=∠+∠，即得：C GAC ∠=∠．∴AG CG =，设AG a =，则有7GH a =-，13DG a =-，在Rt DGH ∆中，∵222DH HG DG +=，∴()()2224713a a +-=-，解得：263a =，即263AG GC ==，此时13133DG a =-=．在ADG ∆中用面积法，则有DH AG AF DG ⋅=⋅，即2613433AF ⨯=⋅，即得8AF =，Rt ADF ∆勾股定理，得()22226581DF AD AF =-=-=，则12CF CD DF =-=，由此可得2222812413AC AF CF =+=+=．【总结】本题综合性较强，综合应用了锐角三角比、角平分线的性质、面积法等解三角形常用的方法，主要是根据题目条件进行变化得出最终结果．【作业7】如图，一栋楼房AB 背后有一台阶CD ，台阶每层高0.2米，且AC = 17.2米．设太阳光线与水平地面的夹角为α，当60α=︒时，测得楼房在地面上的影长AE = 10米．现D AB CE HF EGABCD24 / 26有一只小猫睡在台阶的MN 这层上晒太阳．（参考数据：3 1.73≈）（1）楼房的高度约为多少米？（2）过了一会儿，当45α=︒时，问小猫能否还晒到太阳？请说明理由．【答案】（1）17.3m ；（2）能．【解析】（1）根据锐角三角比的含义，tan AB AE α=，则有tan 10317.3AB AE m α=⋅=≈；（2）45α=︒时，影长即为tan 17.3AB m α⋅=， 17.317.20.10.2m m -=<，即影子的落点正在在台阶侧面CM 上，此时小猫还是可以晒到太阳的．【总结】考查利用锐角三角比解决实际问题，化为实际三角形模型即可．【作业8】如图，CD 是ABC ∆的中线，已知90ACD ∠=︒，3cos 5A =，求tan BCD ∠的值．【答案】38．【解析】由90ACD ∠=︒，3cos 5AC A AD ==，可设3AC a =，则5AD a =，根据勾股定理，可得：224CD AD AC a =-=．延长CD 到E ，使DE CD =，连结AE ．由AD BD =，CDB ADE ∠=∠，可证CDB EDA ∆≅∆，则有BCD E ∠=∠，由此可得：33tan tan 248AC a BCD E CE a ∠=∠===⨯．【总结】考查“倍长中线法”在解三角形中的应用，可进行等角转化，将不便计算的角放到直角三角形中即可．【作业9】如图，在梯形ABCD 中，AD // BC ，AB = 4，BC = 6，DAC B AEF ∠=∠=∠，点E 、F 分别在BC 、AC 上（点E 与B 、C 不重合），设BE = x ，AF = y ．（1）求cos B ；ABCDENM ABCDE（2）求证：ABE ∆∽ECF ∆；（3）求y 关于x 的代数式；（4）当点E 在BC 上移动时，AEF ∆是否有可能是直角三角形？若有可能，请求出BE 的长；若不能，请说明理由．【答案】（1）34；（2）略；（3）26164x x y -+=；（4）23BE =或3BE =．【解析】（1）作AG BC ⊥交BC 于点G ， //AD BC ， DAC ACB ∴∠=∠． DAC B ∠=∠， B ACB ∴∠=∠．AB AC ∴=， 132BG CG BC ∴===．3cos 4BG B AB ∴==．（2）证明：AEC B BAE AEF FEC ∠=∠+∠=∠+∠，又B AEF ∠=∠， BAE FEC ∴∠=∠，B ACB ∠=∠，∴ABE ∆∽ECF ∆．（3）由ABE ∆∽ECF ∆，则有AB BEEC CF=，即464x x y =--，整理得：26164x x y -+=；（4）①90AEF B ∠=∠<︒，即AEF ∠不可能为直角；②90EAF ∠=︒，则有3cos cos 4AC ACE B EC ∠===，4AC AB ==，则有163EC =，则162633BE BC EC =-=-=；③90AFE ∠=︒，此时则有90AEB EFC ∠=∠=︒，此时点E 与点G 重合，即为BC 中点，此时3BE =；综上所述，23BE =或3BE =．【总结】考查“一线三等角”证相似的基本模型，同时对直角三角形的存在性问题可转化为固定角的锐角三角比不变的问题．【作业10】如图（a ）所示，已知正方形ABCD 在直线MN 的上方，BC 在直线MN 上，E是BC 上一点，以AE 为边在直线MN 的上方作正方形AEFG ．（1）连接GD ，求证：ADG ∆≌ABE ∆；（2）连接FC ，观察并猜测FCN ∠的度数，并说明理由；ABCDE FG。

沪科版九年级数学上册试题第23章《解直角三角形》章节测试卷(含解析)

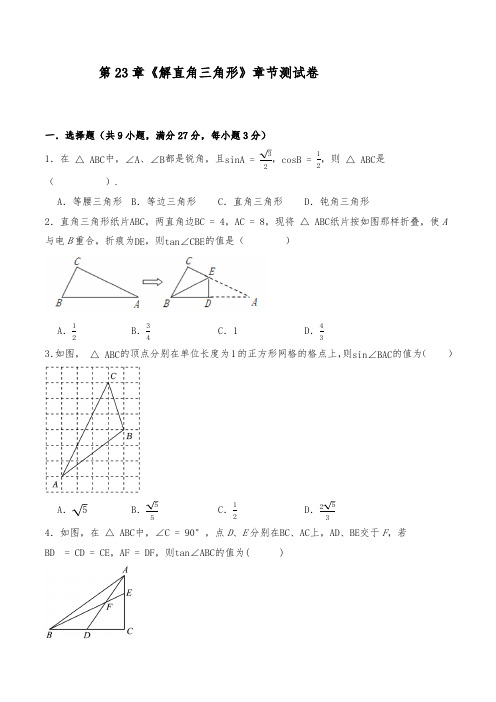
第23章《解直角三角形》章节测试卷一．选择题（共9小题，满分27分，每小题3分）1．在△ABC 中，∠A 、∠B 都是锐角，且sinA =32，cosB =12，则△ABC 是（）.A ．等腰三角形B ．等边三角形C ．直角三角形D ．钝角三角形2．直角三角形纸片ABC ，两直角边BC =4，AC =8，现将△ABC 纸片按如图那样折叠，使A 与电B 重合，折痕为DE ，则tan ∠CBE 的值是（）A ．12B ．34C ．1D ．433．如图，△ABC 的顶点分别在单位长度为1的正方形网格的格点上，则sin ∠BAC 的值为（）A ．5B ．55C ．12D ．2534．如图，在△ABC 中，∠C =90°，点D 、E 分别在BC 、AC 上，AD 、BE 交于F ，若BD=CD =CE ，AF =DF ，则tan ∠ABC 的值为( )A ．12B ．23C ．34D ．455．一块直角三角板ABC 按如图放置，顶点A 的坐标为(0,1)，直角顶点C 的坐标为(−3,0)，∠B =30°，则点B 的坐标为（）A. (−3−33,33)B ．(−3+3,3)C ．(−3+33,33)D ．(−3−3,33)6．在Rt △ABC 中，∠A =90°，有一个锐角为60°，BC =6，若点P 在直线AC 上（不与点A 、C 重合），且∠ABP =30°，则CP 的长为（）A ．6或23B ．6或43C ．23或43D ．6或23或437．如图，延长等腰Rt ΔABC 斜边AB 到D ，使BD =2AB ，连接CD ，则tan ∠BCD 的值为（）A ．23B ．1C ．13D ．128．如图，在△ABC 中，∠ACB =90∘，分别以AB ，AC ，BC 为边向外作正方形，连结CD ，若sin∠BCD=35，则tan ∠CDB 的值为（）A ．23B ．34C ．710D ．9139．如图1是由四个全等的直角三角形组成的“风车”图案，其中∠AOB =90°，延长直角三角形的斜边恰好交于另一直角三角形的斜边中点，得到如图2，若IJ =2，则该“风车”的面积为（）A ．2+1B ．22C ．4−2D ．42二．填空题（共6小题，满分18分，每小题3分）10．如图，在Rt △ABC 中，∠C =90°，点D ，E 分别在AC ，BC 边上，且AD =3，BE =4，连接AE ，BD ，交于点F ，BD=10，cos ∠AFD=32，则AE 的长为．11．如图，在菱形ABCD 中，tan ∠ABC =43，AE ⊥BC 于点E ，AE 的延长线与DC 的延长线交于点F ，则S △ECF :S 四边形ADCE = ．（S 表示面积）12．如图，在矩形ABCD中，AB=3,AD=4，E是对角线BD上一动点（点E不与点B，D重合），当△ABE是等腰三角形时，DE=．13．如图，已知点P是菱形ABCD的对角线AC延长线上一点，过点P分别作AD，DC延长线的垂线，垂足分别为点E，F．若∠ABC=120°，AB=6，则PE−PF的值为．14．如图，在正方形ABCD中，M，N分别是AB，CD的中点，P是线段MN上的一点，BP的延长线交4D 于点E，连接PD，PC，将△DEP绕点P顺时针旋转90°得△GFP，则下列结论：①CP=GP，②tan∠CGF=1；③BC垂直平分FG；④若AB=4，点E在AD边上运动，则D，F两点之间距离的2．其中结论正确的序号有．最小值是3215．如图，△A B1A1，△A1B2A2，△A2B3A3，…是等边三角形，直线y=33x+2经过它们的顶点A，A1，A2，A3，…，点B1，B2，B3，…在x轴上，则线段B2022B2023的长度是．16．如图，E、F、G、H分别是矩形的边AB、BC、CD、AD上的点，AH=CF，AE=CG，∠EHF=60°，∠GHF=45°，若AH=2，AD=5+3，则四边形EFGH的周长为．三．解答题（共7小题，满分52分）17．（6分）计算：(1)2sin60°−tan45°2−tan30°⋅tan60°−2cos30°+6sin245°． (2)(π−1)0+4sin45°−8+|−3|．18．（6分）如图，在△ABC中，AD⊥BC于点D，若AD=6，BC=12，tan∠ACD=32．求：(1)CD的长；(2)sin∠ABC的值．19．（8分）（2023春·河南南阳·九年级统考期中）如图，已知点A（7，8）、C（0，6），AB⊥x轴，垂足为点B，点D在线段OB上，DE∥AC，交AB于点E，EF∥CD，交AC于点F．（1）求经过A、C两点的直线的表达式；（2）设OD＝t，BE＝s，求s与t的函数关系式；（3）是否存在点D，使四边形CDEF为矩形？若存在，请直接写出点D的坐标；若不存在，请说明理由．20．（8分）（1）在如图1的正方形网格图中，每个小正方形的边长为1，A，B，C，D均为格点（小正方形的顶点)．求证：∠ABC=∠D．（2）在如图2所示的正方形网格图中，每个小正方形的边长为1，A，B，C均为格点，请你仅用无刻度的直尺在线段AC上求作一点P，使得∠PBA=∠C，并简要说明理由．21．（9分）如图，小明为测量宣传牌AB的高度，他站在距离建筑楼底部E处6米远的地面C处，测得宣传牌的底部B的仰角为60°．同时测得建筑楼窗户D处的仰角为30°（A、B、D、E在同一直线上．）然后，小明沿坡度为i=1:2.5的斜坡从C走到F处，此时DF正好与地面CE平行，小明在F处又测得宣传牌顶部A的仰角为45°．(1)填空：∠DAF=__________度，∠BDC=__________度；(2)求F距离地面CE的高度（结果保留根号）；(3)求宣传牌AB的高度（结果保留根号）．22．（9分）我们定义：等腰三角形中底边与腰的比叫做顶角正对（sad），如图①，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=底边腰=BCAB．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：(1)sad90°=________．(2)对于0°<A<180°，∠A的正对值sadA的取值范围是________．(3)如图②，已知sinA=35，其中∠A为锐角，试求sadA的值．23．（9分）已知：△ABC 中，AB =AC ，D 为直线BC 上一点．(1)如图1，BH ⊥AD 于点H ，若AD =BD ，求证：BC =2AH ．(2)如图2，∠BAC =120°，点D 在CB 延长线上，点E 在BC 上且∠DAE=120°，若AB =6，DB=23，求CE 的值．(3)如图3，D 在CB 延长线上，E 为AB 上一点，且满足：∠BAD=∠BCE ，AE BE=23，若tan ∠ABC =34，BD =5，求BC 的长．答案解析一.选择题1．B【分析】根据特殊角的三角函数值求出∠A=60°，∠B=60°，然后利用三角形内角和定理求出∠C的度数，即可解答．【详解】解：∵sinA=32，cosB=12，∴∠A=60°，∠B=60°，∴∠C=180°−∠A−∠B=60°，∴△ABC是等边三角形，故选：B．2．B【分析】根据折叠的性质得出BE=AE，设CE=x，则BE=AE=8−x，在Rt△BCE中，根据勾股定理得出B C2+C E2=B E2，列出方程求出x的值，最后根据正切的定义，即可解答．【详解】解：∵△ADE沿DE折叠得到△BDE，∴BE=AE，设CE=x，则BE=AE=8−x，在Rt△BCE中，根据勾股定理可得：B C2+C E2=B E2，即42+x2=(8−x)2，解得：x=3，∴tan∠CBE=CEBC =34，故选：B．3．B【分析】过B作BD⊥AC于点D，根据勾股定理得出AB,AC的值，再利用面积公式求出BD的值，由sin∠BAC=BDBA可得角的正弦值．【详解】解：如图，过B作BD⊥AC于点D根据勾股定理得：AB =32+42=5，AC =32+62=35∴S ΔABC =12AC ⋅BD =4×6−12×3×1−12×3×4−12×6×3=152, ∴BD =5∴sin ∠CAB=BD AB =55故选：B ．4．C 【分析】如图，过A 作AG ∥BC ，交BE 的延长线于G ，证明△AGF ≌△DBF (AAS )，则AG =BD =12BC ，证明△AEG ∽△CEB ，则AE CE =AG BC =12，解得AE =12CE ，AC =32CE ，根据tan ∠ABC =ACBC，计算求解即可．【详解】解：如图，过A 作AG ∥BC ，交BE 的延长线于G ，∴∠G =∠DBF ，在△AGF 和△DBF 中，∵{∠G =∠DBF∠AFG =∠DFB AF =DF，∴△AGF ≌△DBF (AAS )，∴AG =BD =12BC ，∵∠G =∠CBE ，∠AEG =∠CEB ，∴△AEG ∽△CEB ，∴AE CE =AG BC=12，解得AE =12CE ，∴AC =32CE ，∴tan ∠ABC=AC BC =32CE 2CE =34，故选：C ．5．D【分析】过点B 作BE ⊥OC 于点E ，根据ΔABC 为直角三角形可证明ΔBCE ∽ΔCAO ，求出AC =10，求出BC ，再由比例线段可求出BE ，CE 长，则答案可求出．【详解】解：过点B 作BE ⊥OC 于点E ，∵△ABC 为直角三角形，∴∠BCE +∠ACO =90°，∴ΔBCE ∽ΔCAO ，∴ BE OC =BC AC =EC OA ，在Rt △ACO 中，AC =A O 2+C O 2=12+32=10，在Rt △ABC 中，∠CBA=30°，∴ tan ∠CBA=CA BC ，∴ BC =CA tan ∠CBA =10tan30°=30，∴ BE3=3010=EC1，解得BE =33，EC =3，∴ EO =EC +CO =3+3，∴点B 的坐标为(−3−3，33)．故选：D ．6．D【分析】根据点P在直线AC上的不同位置，∠ABP=30°，利用特殊角的三角函数进行求解．【详解】如图1：当∠C=60°时，∠ABC=30°，与∠ABP=30°矛盾；如图2：当∠C=60°时，∠ABC=30°，∵∠ABP=30°，∴∠CBP=60°，∴△PBC是等边三角形，∴CP=BC=6；如图3：当∠ABC=60°时，∠C=30°，∵∠ABP=30°，∴∠PBC=60°−30°=30°，∴PC=PB，∵BC=6，∴AB=3，∴PC=PB=3cos30°=332=23如图4：当∠ABC=60°时，∠C=30°，∵∠ABP=30°，∴∠PBC=60°+30°=90°，∴PC=BCcos30°=632=43故选：D7．A【分析】过点D作DE垂直于CB的延长线于点E，设AC=BC=a，根据勾股定理得AB=2a，由等腰直角三角形的性质得∠ABC=∠BAC=45°，从而得BD=2AB=22a，在Rt△BDE中，解直角三角形得DE=2a，BE=2a，进而求得CE=BC+BE=3a即可求得tan∠BCD．【详解】解：过点D作DE垂直于CB的延长线于点E，如下图，设AC=BC=a，∵AC⊥BC，AC=BC=a，∴AB=A C2+B C2=2a，∠ABC+∠BAC=90°，∠ABC=∠BAC，∴∠ABC=∠BAC=45°，BD=2AB=22a，∴∠DBE=∠ABC=45°，∵DE⊥CE，∴DE=BD·sin∠DBE=22a·sin45°=2a，BE=BD·cos∠DBE=22a·cos45°=2a，∴CE=BC+BE=3a，∴tan∠BCD=DECE =2a3a=23，故选：A．8．D【分析】过点B作BE⊥CD于点E，过点C作CF⊥AB于点F，可得△ABC，△BED，△BEC，△BCF都是直角三角形，根据sin∠BCE＝BEBC =35，设BE＝3a，BC＝5 a，得CE＝B C2−B E2＝4 a，过点C作DB延长线于点G，得矩形CFBG，设AC＝x，AB＝y，然后利用勾股定理和三角形的面积可得y2−9＝133，进而利用锐角三角函数即可解决问题．【详解】解：如图，过点B作BE⊥CD于点E，过点C作CF⊥AB于点F，∴△ABC，△BED，△BEC，△BCF都是直角三角形，∵sin∠BCD＝35，∴sin∠BCE＝BEBC =35，设BE＝3a，BC＝5a，∴CE＝B C2−B E2＝4a，过点C作DB延长线于点G，得矩形CFBG，∴BF＝CG，设AC＝x，AB＝y，在Rt△ABC中，根据勾股定理，得AB2﹣AC2＝BC2，∴y2﹣x2＝25a2，∵S△ABC＝12×AB•CF＝12×AC•BC，∴y•CF＝5ax，∴CF＝5axy，在Rt△BCF中，根据勾股定理，得BF＝B C2−C F2＝25a2−(5axy )2＝25ya，∴BF＝CG＝25ya，在正方形ABDH中，AB＝BD＝y，在Rt△BDE中，根据勾股定理，得DE＝B D2−B E2＝y2−9a2，∴CD＝CE+ED＝4a +y2−9a2，∵S△CBD＝12×CD•BE＝12×BD•CG，∴CD•BE＝BD•CG，∴(4a +y2−9a2)×3＝y×25ya，∴y2−9a2＝133a，∴tan∠CDB＝tan∠EDB＝BEDE ＝3ay2−9a2＝913．故选：D．9．B【分析】连接AC,由题意可得Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH，进而说明△OAC为等腰直角三角形，再说明分CD、GI垂直平分AB，进而说明∠OBH=∠OHB=45°，然后再运用解直角三角形求得AI，然后再求得三角形AOB的面积，最后求风车面积即可．【详解】解：如图：连接AC由题意可得：Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH∴OA=OC, ∠OAB= ∠OCD∵∠AOC=∠AOB=90°∴△OAC为等腰直角三角形又∵∠OAB= ∠OCD：∴∠AJD=180°-∠ADJ-∠OAB=180°-∠ODC-∠OCD=90°，即AJ⊥CD又∵CJ=DJ∴AJ垂直平分CD同理：GI垂直平分AB∴AC=AD,AJ是等腰三角形顶角∠CAD的角平分线即∠DAJ=12∠CAD=12×45°=22.5°易得IH=BJ,IJ=IB+BJ=IB+IH 又∵IB=IA∴IJ=IB+BJ=IH+IA= 2在Rt△ABO中，∠ABH=∠BAH=22.5°∴∠OBH=OHB=45°设OB=OH=a，即AH=BH=2OB=2a∴tan∠A=BOAO =aa+2a=2−1∴IHIA=tan∠A=2−1设IH=（2−1）x，AI=x ∴IH+IA=2x=2，即x=1∴S△ABH =12×AB×IH=2−1又∵SΔBOHSΔABH =OHAH=12∴S△BOH =1−22∴S△AOB =S△ABH+S△BOH=2−1+1−22=22∴S风车=4S△AOB=4×22=22．故选B．二．填空题10．53【分析】过点A作AG∥BE，BG∥AE交于点G，连接DG，勾股定理求得DG，过点D作DH⊥BG，证明G,H重合，进而勾股定理即可求解．【详解】解：如图所示，过点A作AG∥BE，BG∥AE交于点G，连接DG，则四边形AGBE是平行四边形，∴AG=BE=4，∵∠C=90°，则BC⊥AC∴AG⊥AC∴△ADG是直角三角形，∴DG=5∵cos∠AFD=32∴∠AFD=30°∵AE∥BG∴∠DBG=30°∵DG=5,DB=10过点D作DH⊥BG，∵sin∠DBG=12∴DH=12DB=5,∴G,H重合，∴AE=BG=BH=53故答案为：53．11．4:21【分析】设AE=4k，则BE=3k，根据勾股定理求出AB=5k，然后证明△CEF∽△DAF，最后根据相似三角形的性质求解即可．【详解】解∶∵tan∠ABC=43，AE⊥BC，∴tan∠ABC=43=AEBE，设AE=4k，则BE=3k，∴AB =A E 2+B E 2=5k ，∵四边形ABCD 是菱形，∴CB ∥AD ，AD =BC =AB =5k ，∴CE =BC −BE =2k ，∵CB ∥AD ，∴△CEF ∽△DAF ，∴S △CEF S△DAF =(CE DA )2=(2k 5k )2=425，∴S △CEFS 四边形ADCE =S △CEF S △DAF −S △CEF =425−4=421．故答案为：4:21．12．2或52或75【分析】分AB =AE,BE =BA,EA =EB 三种情况，分别画出图形，即可求解．【详解】解：在矩形ABCD 中，AB =3,AD =4，∴∠BAD=90°，∴BD =A B 2+A D 2=32+42=5，当AB =AE 时，过点A 作AF ⊥AD 于点F ，则AF ⊥BD ，∴cos ∠ABD=AB BD =BF AB ，∴BF =AB 2BD =95∴DE =BD −BE =BD −2BF =5−185=75，当BA =BE 时，DE =BD −BE =5−3=2，当EA =EB 时，过点E 作EG ⊥AB 于点G ，∴EG ∥AD ，AG =GB ，∴BE ED=BG AG =1，∴DE =12BD=52，综上所述DE = 2或52或75，故答案为：2或52或75．13．33【分析】如图，延长BC 交EP 于M ，由菱形的性质可知，CP 为∠BCD ，∠FCM 的平分线，则PF =PM ，PE −PF =PE −PM =EM ，由题意知，EM 为△ABD 底边AD 上的高，由菱形ABCD ，∠ABC=120°，AB =6，可得∠BAD=60°，根据EM=AB ⋅sin ∠BAD ，计算求解，进而可得结果．【详解】解：如图，延长BC 交EP 于M ，由菱形的性质可知，CP为∠BCD，∠FCM的平分线，∵PF⊥CF，PM⊥CM，∴PF=PM，∴PE−PF=PE−PM=EM，由题意知，EM为△ABD底边AD上的高，∵菱形ABCD，∠ABC=120°，AB=6，∴∠BAD=60°，∴EM=AB⋅sin∠BAD=33，∴PE−PF=33，故答案为：33．14．①②③【分析】延长GF交AD于点H，连接FC，FB，FA，由已知可得MN为AB，CD的垂直平分线，由垂直平分线的性质和图形旋转的性质可得①的结论正确；利用三角形的内角和定理和等腰三角形的性质计算可得∠BCG=45°，由四边形内角和定理通过计算可得∠EHF=90°；利用平行线的性质可得BC⊥FG，则∠CGF=45°，可说明②的结论正确；通过证明点A，B，E，F在以点P为圆心，PA为半径的同一个圆上，利用圆周角定理可得∠FAB=45°，得到A，F，C三点共线，得到△CGF为等腰直角三角形，则③的结论正确；由题意点F在对角线AC上运动，当EF⊥AC时，EF的值最小，连接AC，解直角三角形的知识可得④的结论不正确．【详解】解：延长GF交AD于点H，连接FC，FB，FA，如图，∵正方形ABCD中，M，N分别是AB，CD的中点，∴MN是线段BA，CD的垂直平分线．∴PD=PC，PA=PB．∵△FPG是△PED绕点P顺时针旋转90°得到，∴△FPG≌△PED，∴PD=PG．∴PC=PG．∴①的结论正确；∵PD=PC，∴∠PDC=∠PCD=1(180°−∠DPC)．2∵PC=PG，∴∠PCG=∠PGC=1(180°−∠CPG)．2∴∠PCD+∠PCG=1[360°−(∠DPC+∠CPG)]．2∵∠DPC+∠CPG=90°，∴∠PCD+∠PCG=135°．∵∠BCD=90°，∴∠BCG=45°．∵△FPG≌△PED，∴∠DEP=∠GFP．∵∠HFP+∠PFG=180°，∴∠DEP+∠HFP=180°．∵∠DEP+∠HFP+∠EHF+∠EPF=360°，∴∠EHF+∠EPF=180°．∴∠EPF=90°，∴∠EHF=90°．即GH⊥AD．∵AD//BC，∴GF⊥BC．∴∠CGF=45°．∴tan∠CGF=1．∴②的结论正确；∵PA=PB，PM⊥AB，∴∠APM=∠BPM，∵PM//AE，∴∠PEA=∠BPM，∠PAE=APM．∴∠PEA=∠PAE．∴PA=PE．∵PE=PF，∴PA=PB=PE=PF．∴点A，B，E，F在以点P为圆心，PA为半径的同一个圆上．∴∠FAB=12∠FPB=12×90°=45°．∴点F在对角线AC上，∴∠FCB=45°．∵∠BCG=∠CGF=45°，∴△FCG为等腰直角三角形．∵BC平分∠FCG，∴BC垂直平分FG．∴③的结论正确；由以上可知：点F在正方形的对角线AC上运动，∴当EF⊥AC时，EF的值最小．此时点E与点D重合，∴DF=AD⋅sin45°=4×22=22．∴④的结论不正确．综上，结论正确的序号有：①②③，故答案为：①②③．15．220233【分析】设直线y=33x+2与x轴交于点C，求出点A、C的坐标，可得OA=2,OC=23，推出∠C B1A1=90°，∠C B1A=30°，然后求出C B1=2O B1=43=22×3，C B2=2C B1=83=23×3，C B3=2C B2=163=24×3，…，进而可得C B2022=22023×3，C B2023=22024×3，再求出B2022B2023即可．【详解】解：如图所示，设直线y =33x +2与x 轴交于点C ，当x =0时，y =2；当y =0时，x =−23，∴ A (0,2)，C (−23,0)，∴ OA=2，OC =23，∴ tan ∠ACO =OA OC=223=33，∴ ∠ACO=30°，∵ △A B 1A 1是等边三角形，∴ ∠A A 1B 1=∠A B 1A 1=60°，∴ ∠C B 1A 1=90°，∠C B 1A =30°，∴ AC =A B 1，∵ AO⊥C B 1，∴ O B 1=OC =23，∴ C B 1=2O B 1=43=22×3，同理，C B 2=2C B 1=83=23×3，C B 3=2C B 2=163=24×3，……，∴ C B 2022=22023×3，C B 2023=22024×3，∴ B 2022B 2023=22024×3−22023×3=220233，故答案为：220233．16．8+46【分析】先构造15° 的直角三角形，求得15° 的余弦和正切值；作EK ⊥FH ，可求得EH:EF =2:6；作∠ARH=∠BFT =15°，分别交直线AB 于R 和T ，构造“一线三等角”，先求得FT 的长，进而根据相似三角形求得ER ，进而求得AE ，于是得出∠AEH =30°，进一步求得结果．【详解】解：如图1，Rt △PMN 中，∠P =15°，NQ =PQ ，∠MQN =30°，设MN=1，则PQ =NQ =2，MQ=3，PN =6+2，∴cos15°=6+24，tan15°=2−3，如图2，作EK ⊥FH 于K ，作∠AHR =∠BFT =15°，分别交直线AB 于R 和T ，∵四边形ABCD 是矩形，∴∠A =∠C ，在△AEH 与△CGF 中，{AE =CG ∠A =∠C AH =CF，∴△AEH ≌△CGF(SAS)，∴EH =GF ，同理证得△EBF ≌△GDH ，则EF =GH ，∴四边形EFGH 是平行四边形，设HK=a ，则EH=2a ，EK =3a ，∴EF =2EK =6a ，∵∠EAH =∠EBF =90°，∴∠R=∠T =75°，∴∠R=∠T=∠HEF=75°，可得：FT=BFcos15°=3+36+24=26，AR=AH⋅tan15°=4−23，△FTE∽△ERH，∴FTER =EFEH，∴26ER =62，∴ER=4，∴AE=ER−AR=23，∴tan∠AEH=223=33，∴∠AEH=30°，∴HG=2AH=4，∵∠BEF=180°−∠AEH−∠HEF=75°，∴∠BEF=∠T，∴EF=FT=26，∴EH+EF=4+26=2(2+6)，∴2(EH+EF)=4(2+6)，∴四边形EFGH的周长为：8+46，故答案为：8+46．三．解答题17．（1）原式=2×32−12−33×3−2×32+6×(22)2=3−12−1−3+6×12=3−1−3+3=2．（2）原式=1+4×22−22+3 =1+22−22+3=4．18．（1）解：∵AD⊥BC，∴∠ADB=∠ADC=90°，在Rt△ADC中，tan∠ACD=ADCD =32，AD=6，∴CD=4；（2）解：由（2）得CD=4，∴BD=BC−CD=8，∴AB=A D2+B D2=10，在Rt△ABD中，sin∠ABD=ADAB =35，即sin∠ABC=35．19．解：（1）设直线AC的表达式为y＝kx+b 将点A、C的坐标代入，得得：{7k+b=8b=6，解得：{k=27b=6，故直线AC的表达式为：y＝27x+6；（2）∵OD＝t，BE＝s，AB⊥x轴∴则点D（t，0），点E（7，s）∵DE∥AC可设直线DE的解析式为y＝27x+c将点D的坐标代入0＝27t+c解得：c=﹣27t∴直线的表达式为：y＝27x﹣27t，将点E的坐标代入，得s＝2﹣27t（根据点D在线段OB上，可得0＜t＜7）；（3）存在，理由：设点D（t，0），由（2）BE＝2﹣27t，四边形CDEF为矩形，则∠CDE＝90°，∵∠EDB +∠CDO ＝90°，∠CDO +∠OCD ＝90°，∴∠OCD ＝∠BDE ，∴tan ∠OCD ＝tan ∠BDE ，∴ODOC ＝BE BD即t 6＝2−27t 7−t，解得：t ＝127或7（因为0＜t ＜7，故舍去7），故点D 的坐标为（127，0）．20．（1）如图所示，取格点E ，F ，连接BF,AF ，AE,CE ，∵BF =12+12=2，DF =32+32=32，∴tan ∠D =BF DF=232=13，∵CE =1，BE =3，∴tan ∠ABC=CE BE=13，∴tan ∠D =tan ∠ABC ，∴∠ABC=∠D ；（2）解：如图，取格点D ，E ，同理（1）可得，在Rt△AEC中，tan∠ACE=1，2，在Rt△ABD中，tan∠ABD=12∴tan∠ACE=tan∠ABD，∴∠ACE=∠ABD，直线BD与AC的交点为所求的点P．21．（1）解：由题意，得AD⊥DF，∴∠ADF=90°∴∠DAF=90°−∠AFD=90°−45°=45°，由题意，得FD∥CE，∴∠CDF=∠ECD=30°∴∠BDC=∠ADF+∠CDF=90°+30°=120°．（2）解：如图，过点F作FG⊥EC于G，由题意得，FG∥DE,DF∥GE,∠FGE=90°，∴四边形DEGF是矩形．∴FG=DE．在Rt △CDE 中，DE =CE ⋅tan ∠DCE=6×tan30°=23（米），∴FG =23（米）．答：F 距离地面CE 的高度为23米；（3）解：∵斜坡CF 的坡度为i =1:2.5，∴Rt △CFG 中，CG = 2.5FG =23× 2.5=53（米），∴FD =EG =(53+6)（米）．∴在Rt △AFD 中，∠AFD=45°，∴AD =FD =(53+6)米．在Rt △BCE 中，BE =CE ⋅tan ∠BCE =6×tan60°=63（米），∴AB =AD +DE −BE =53+6+23−63=(6+3)（米）．答：宣传牌AB 的高度约为(6+3)米．22．（1）解：如图，∠BAC=90°,AB =AC ,sad90°=BC AB ,∵cos45°=AB BC=22,∴sad90°=BCAB = 2.（2）解：如图，点A 在BC 的中垂线上，当点A 向BC 靠近时，∠A 增大，逐渐接近180°，腰长AB 接近12BC ，AB >12BC 相应的sadA =BC AB <2；当点A 远离BC 时，∠A 减小，逐渐接近0°，腰长AB 逐渐增大，相应的sadA =BCAB 逐渐接近0，sad A =BCAB >0；∴0<sadA <2（3）解：如图，在AB 上截取AH=AC ，过H 作HD ⊥AC 于D ，sinA =35=DH AH ，设HD =3x,AH =AC =5x ，则，AD =A H 2−H D 2=4x ,∴DC =AC −AD =5x −4x =x ．Rt △HDC 中，HC =C D 2+H D 2=10x ，∴sadA =CH AH =10x 5x =105．23．（1）解：证明：如图1，过点A 作AN ⊥BC 于N ，∵AB =AC ，∴BN =12BC ，∵AD =BD ，∴∠ABD =∠BAD ，在△ABN 和△BAH 中，{∠ANB=∠BHA=90°∠ABD=∠DABAB=BA，∴△ABN≌△BAH(AAS)，∴BN=AH，∴12BC=AH，∴BC=2AH；（2）如图2，在AC上取一点F，使EF=EC，连接EF，∵∠BAC=∠DAE=120°，∴∠DAB=∠EAC，∵AB=AC，∴∠ABE=∠C=∠CFE=30°，∴∠ABD=∠AFE=150°，∴△ABD∽△AFE，∴ABAF =BDEF，即6AF=23EF，∴AFEF=3，设EF=a，则AF=3a，∵EF=CE=a，∠C=30°，∴CF=2EF·cos30°=3a，∴6−3a=3a，∴a=3，∴CE=EF=3；（3）如图3，过点A作AP⊥BC于P，作AG∥CE交BC的延长线于G，设AE=2m，BE=3m，则AB=AC=5m，∵tan∠ABC=34=AP BP ，∴ BP AB =45，∴BP =CP =4m ，BC =8m ，∵∠BAD =∠BCE =∠G ，∠ABD =∠GCA ，∴△ABD ∽△GCA ，∴ CG AB =AC BD ，即CG 5m =5m 5，∴CG =5m 2，∵AG ∥CE ，∴ BE AE =BC CG ，∴ 3m 2m =8m5m 2，∴m =1615，∴BC =8m =12815．。

沪科版九年级数学习题-解直角三角形及其应用(第4课时)

第4課時解直角三角形及其應用（4）1．如圖，坡角為30°的斜坡上兩樹間的水準距離AC為2 m，則兩樹間的坡面距離AB 為()m D．mA．4 m B m C．2．如圖，一遊人由山腳A沿坡角為30°的山坡AB行走600 m，到達一個景點B，再由B沿山坡BC行走200 m到達山頂C，若在山頂C處觀測到景點B的俯角為45°，則山高CD＝__________(結果用根號表示)．3．一段路基的橫斷面是直角梯形，如圖(1)所示，已知原來坡面的坡角α的正弦值為0.6，現不改變土石方量，全部利用原有土石進行坡面改造，使坡度變小，達到如圖(2)所示的技術要求．試求出改造後坡面的坡度是多少？4．如圖所示，A、B兩城市相距100 km，現計畫在這兩座城市間修建一條高速公路(即線段AB)，經測量，森林保護中心P在A城市的北偏東30°和B城市的北偏西45°的方向上，已知森林保護區的範圍在以P點為圓心，50 km為半徑的圓形區域內，請問計畫修建的這條高速公路會不會穿越保護區？為什麼？(≈1.732≈1.414)5．如圖，在梯形ABCD中，AB∥CD，∠BCD＝90°，且AB＝1，BC＝2，tan∠ADC ＝2.(1)求證：DC＝BC；(2)E是梯形內一點，F是梯形外一點，且∠EDC＝∠FBC，DE＝BF，試判斷△ECF的形狀，並證明你的結論；(3)在(2)的條件下，當BE∶CE＝1∶2，∠BEC＝135°時，求sin∠BFE的值．6．如圖是某賓館大廳到二樓的樓梯設計圖，已知BC＝6 m，AB＝9 m，中間平臺寬度DE為2 m，DM、EN為平臺的兩根支柱，DM、EN垂直於AB，垂足分別為M、N，∠EAB＝30°，∠CDF＝45°.求DM和BC的水準距離BM.(精確到0.1 m， 1.41，1.73)7．如圖，某堤壩的橫截面是梯形ABCD，背水坡AD的坡度i(即tan α)為1∶1.2，壩高為5 m．現為了提高堤壩的防洪抗洪能力，市防汛指揮部決定加固堤壩，要求壩頂CD加寬1 m，形成新的背水坡EF，其坡度為1∶1.4.已知堤壩總長度為4 000 m.(1)完成該工程需要多少土方？(2)該工程由甲、乙兩個工程隊同時合作完成，按原計畫需要20天．準備開工前接到上級通知，汛期可能提前，要求兩個工程隊提高工作效率．甲隊工作效率提高30%，乙隊工作效率提高40%，結果提前5天完成．問這兩個工程隊原計畫每天各完成多少土方？8．(創新應用)騰飛中學在教學樓前新建了一座“騰飛”雕塑(如圖①)．為了測量雕塑的高度，小明在二樓找到一點C，利用三角板測得雕塑頂端A點的仰角為30°，底部B點的俯角為45°，小華在五樓找到一點D，利用三角板測得A點的俯角為60°(如圖②)．若已知CD為10米，請求出雕塑AB的高度．(結果精確到0.1＝1.73)參考答案1解析：在Rt △ABC 中，ACAB ＝cos 30°，則AB ＝cos30AC ︒＝2 m. 答案：C2解析：過點B 作BE ⊥CD ，垂足為E ，在Rt △BCE 中，CE ＝BE ＝BC ×sin 45°＝，過點B 作BF ⊥AD ，垂足為F ，則在Rt △ABF 中，BF ＝ABsin 30°＝300(m)，∴CD ＝CE ＋DE ＝CE ＋BF ＝300＋．答案：(300＋3解：由題圖(1)知BE ⊥DC ，BE ＝30 m ，sin α＝0.6.在Rt △BEC 中，∵sin α＝BE BC ，∴BC ＝30sin 0.6BE α=＝50(m)．根據畢氏定理，得EC ＝40 m.在不改變土石方量，全部充分利用原有土石方的前提下進行坡面改造，使坡度變小，則S 梯形ABCD ＝S 梯形A 1B 1C 1D 1.∴20×30＋12×30×40＝20×20＋12×20·E 1C 1，解得E 1C 1＝80(m)． ∴改建後的坡度i ＝B 1E 1∶E 1C 1＝20∶80＝1∶4.4解：過點P 作PC ⊥AB ，垂足為C ，則∠APC ＝30°，∠BPC ＝45°，AC ＝PC ·tan 30°，BC ＝PC ·tan 45°.∵AC ＋BC ＝AB ，∴PC ·tan 30°＋PC ·tan 45°＝100.∴1⎫⎪⎪⎝⎭·PC ＝100.∴PC ＝50(3≈50×(3－1.732)≈63.4＞50.答：森林保護區的中心與直線AB 的距離大於保護區的半徑，∴計畫修築的這條高速公路不會穿越保護區．5解：(1)證明：過A 作DC 的垂線AM 交DC 於M(如圖)，則AM ＝BC ＝2，AB ＝MC ＝1.又tan ∠ADC ＝AM DM＝2， ∴DM ＝2AM ＝1. 又MC ＝1，∴DC ＝2，DC ＝CB ．(2)等腰直角三角形．證明：∵DE ＝BF ，∠EDC ＝∠FBC ，DC ＝BC ，∴△DEC ≌△BFC ．∴CE ＝CF ，∠ECD ＝∠BCF.∴∠ECF ＝∠BCF ＋∠BCE ＝∠ECD ＋∠BCE ＝∠BCD ＝90°，即△ECF 是等腰直角三角形．(3)設BE ＝k ，則CE ＝CF ＝2k ，∴EF ＝.∵∠BEC ＝135°，又∠CEF ＝45°，∴∠BEF ＝90°.∴BF 3k.∴sin ∠BFE ＝133k k =. 6解：設DF ＝x m ．∵∠CDF ＝45°，∠CFD ＝90°，∴CF ＝DF ＝x m .∴BF ＝BC －CF ＝(6－x ) m .∴EN ＝DM ＝BF ＝(6－x ) m .∵AB ＝9 m ，DE ＝2 m ，DF ＝x m ，∴AN ＝AB －MN －BM ＝(7－x ) m .在△AEN 中，∠ANE ＝90°，∠EAN ＝30°，∴EN ＝AN ·tan 30°，即6－x ＝3(7－x )，解得x ≈4.6. 答：支柱DM 距BC 的水準距離約為4.6 m.7解：(1)作DG ⊥AB 於G ，作EH ⊥AB 於H.∵CD ∥AB ，∴EH=DG=5 m. ∵11.2DG AG =，∴AG=6 m. ∵11.4EH FH =，∴FH=7 m. ∴FA=FH+GH-AG=7+1-6=2(m)．∴S 梯形ADEF ＝12(ED ＋AF)·EH ＝12×(1＋2)×5＝7.5(m 2)，V ＝7.5×4 000＝30 000(m 3)．(2)設甲隊原計畫每天完成x m 3土方，乙隊原計畫每天完成y m 3土方．根據題意，得20()30000,15[(130%)(140%)]30000.x y x y +=⎧⎨+++=⎩ 化簡，得1500,1.3 1.42000,x y x y +=⎧⎨+=⎩解之，得1000,500.x y =⎧⎨=⎩ 答：甲隊原計畫每天完成1 000 m 3土方，乙隊原計畫每天完成500 m 3土方． 8解：過點C 作CE ⊥AB 於E.∵∠D ＝90°－60°＝30°，∠ACD ＝90°－30°＝60°，∴∠CAD ＝90°.∵CD ＝10(米)，∴AC ＝12CD ＝5(米)．在Rt △ACE 中，AE ＝AC ·sin ∠ACE ＝5×sin 30°＝52(米)， CE ＝AC ·cos ∠ACE ＝5×cos 30(米)．在Rt △BCE 中，∵∠BCE ＝45°，∴BE ＝CE ·tan 45(米)． ∴AB ＝AE ＋BE＝52＝51)2≈6.8(米)．∴雕塑AB 的高度約為6.8米．。

沪教版解直角三角形讲解练习

第二讲解直角三角形知识要点：1、锐角三角函数的定义.cot tan cos sin 90Rt 的对边的邻边＝，的邻边的对边＝，斜边的邻边＝，斜边的对边＝，＝中，△如图，在A A A A A A A A A A C ABC ∠∠∠∠∠∠︒∠ BACac2、特殊角的三角函数值3、互为余角的三角函数关系sinA ＝cos （90º－A ）， cos A ＝sin （90º－A ）， tan A ＝cot （90º－A ）， cot A ＝an （90º－A ）． 4、锐角三角函数值随角度的变化规律当角度在0—90°变化时，正弦、正切值随角度的增大（或减小）而增大（或减小）；余弦、余切值随角度的增大（或减小）而减小（或增大）．5、锐角的三角函数值的取值范围0＜sin α＜1， 0＜cos α＜1， tan α＞0， cot α＞0． 6、解直角三角形（1）由直角三角形中除直角外的已知两个元素（至少有一个是边），求出其余的三个未知元素的过程，叫做解直角三角形．（2）在Rt △ABC 中，∠C ＝90º，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，可供解直角三角形的依据是： ①直角三角形角的关系：∠A ＋∠B ＝90º； ②直角三角形边的关系：a 2＋b 2＝c 2；③直角三角形的边角的关系：．＝＝，＝＝，＝＝，＝＝abA B b aB A c bA B caB A cot tan cot tan cos sin cos sin （3）在实际问题中常用的几种角 ①俯角和仰角在测量时，视线与水平线所成的角中，视线在水平线上方的角叫做仰角；视线在水平线下方的角叫做俯角． ②坡度与坡角如图，通常坡面的竖直高度h 和水平宽度l 的比叫做坡度，用字母i 表示，即lhi ==αtan ，其中α是坡面与水平面的夹注意：三角函数值与梯子的倾斜程度的关系：tan A 的值越大，梯子越陡；sinA 的值越大，梯子越陡；cos A 的值越小，梯子越陡.7.解直角三角形通常应用在计算距离、高度、角度，应用于测量、工程、物理学中等方面的实际问题。

九年级数学上23.2解直角三角形及其应用课时练习(沪科版有答案和解释)

九年级数学上23.2解直角三角形及其应用课时练习（沪科版有答案和解释）九年级上学期数学课时练习题（23.2 解直角三角形及其应用）一、选择题 1.在△ABC中，∠C＝90°，若AB＝4，sinA＝，则斜边上的高等于（） A. B. C. D. 2.已知：△ABC中，∠C＝90°，∠A＝60°，BC+AC＝3+ ，则BC等于（） A. B.3 C.2 D. +1 3.在△ABC中，AB ＝12 ，AC＝13，cosB＝，则BC边长为（） A.7 B.8 C.8或17 D.7或17 4.等腰三角形的底边与底边上的高的比是2：，则顶角为（）A.60° B.90° C.120° D.150° 5.如图，在△ABC中，∠BAC＝90°，AB＝AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC 的值为（） A. B. －1 C.2－ D. 第5题图第6题图第7题图 6.如图，在△ABC中，∠C＝90°，AM是BC边上的中线，sin∠CAM＝，则tanB的值为（） A. B. C. D. 7.如图，在Rt△BAD中，延长斜边BD到点C，使DC＝ BD，连接AC，若tanB＝，则tan∠CAD的值为（） A. B. C. D. 8.如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进40海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD是（）A.20海里 B.40海里 C.20 海里 D.40 海里 9.如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF，tan ＝，则“人字梯”的顶端离地面的高度AD是（） A.144cm B.180cm C.240cm D.360cm 第8题图第9题图第10题图 10.如图，为了测得电视塔高度AB，在D处用高为1米的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进100米到达F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（） A.50 B.51 C.50 +1 D.101 二、填空题 11. 在△ABC中，，∠C＝90°，tana＝，AC＝6，则BC＝___________. 12.在平面直角坐标系xOy中，已知一次函数y＝kx+b（k＜0）的图象过点P(1，1)，与x轴交于点A，与y轴交于点B，且tan∠ABO＝3，那么点A的坐标是____________. 13.小明同学在距某电视塔底部水平距离500米处，看塔顶的仰角为20°（不考虑身高因素），则此电视塔高约为________________米.（结果保留整数，参考数据：sin20°≈0.3420，sin70°≈0.9397，tan20°≈0.3640，tan70°≈2.7475） 14.如图，铁路的路基横断面可看成是等腰梯形，斜坡AB的坡度为1：，斜坡AB的水平宽度BE ＝3 m，那么斜坡AB的长为_________m. 第14题图第15题图第16题图 15.4月26日，2015黄河口国际马拉松比赛拉开帷幕，中央电视台体育频道用直升机航拍技术全程直播．如图，在直升机的镜头下，观测马拉松景观大道A处的俯角为30°，B处的俯角为45°．如果此时直升机镜头C处的高度CD为200米，点A、D、B在同一直线上，则AB两点的距离是_________________米． 16.如图，在菱形ABCD中，AE⊥BC于点E，若cosB＝，EC＝2，P是AB边上的一动点，则线段PE的长度的最小值是___________. 三、解答题 17.已知：如图，在△ABC中，AD是边BC上的高，E为边AC的中点，BC＝14，AD ＝12，sinB＝，求：（1）线段DC的长；（2）tan∠EDC的值.18.如图，已知矩形ABCD的对角线AC、BD相交于点O，过点O作OE⊥AC 交AD于E，若AB＝6，AD＝8，求sin∠OEA的值．19.如图，平台AB高为12米，在B处测得楼房CD顶部点D的仰角为45°，底部点C的俯角为30°，求楼房CD的高度.( ≈1.7) 20.如图，某水上乐园有一个滑梯AB，高度AC为6米，倾斜角为60°，暑期将至，为改善滑梯AB的安全性能，把倾斜角由60°减至30°. （1）求调整后的滑梯AD的长度（2）调整后的滑梯AD比原滑梯AB增加多少米？（精确到0.1米）（参考数据：≈1.41，≈1.73，≈2.45）21.如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽为6米，坝高20米，斜坡AB的坡度i＝1：2.5，斜坡CD的坡角为30°，求坝底AD的长度.（结果精确到0.1米，参考数据：≈1.414，≈1.732）22.如图，AD是等腰△ABC底边上的高，且AD＝4，sinB＝，若E是AC边上的点，且满足AE：EC＝2：3，连接DE，求sin∠ADE的值.23.如图，在南北方向的海岸线MN上，有A、B两艘巡船，现均收到故障船C的求救信号．已知A，B两船相距100( +1)海里，船C在船A的北偏东60°方向上，船C在船B的东南方向上，MN上有一观测点D，测得船C正好在观测点D的南偏东75°方向上．已知距观测点D处100海里范围内有暗礁，若巡逻船A沿直线AC去营救船C，在去营救的途中有无触暗礁危险？（参考数据：≈1.41，≈1.73） 23.2解直角三角形及其应用课时练习题参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 B B D A A B D C B C 1.在Rt△ABC中，∠C ＝90°，若AB＝4，sinA＝，则斜边上的高等于（） A. B. C. D. 解答：∵在Rt△ABC中，sinA＝＝，AB＝4，∴BC＝，由勾股定理得：AC＝，∵在Rt△ADC中，sinA＝，∴CD＝× ＝ . 故选：B.2.已知：△ABC中，∠C＝90°，∠A＝60°，BC+AC＝3+ ，则BC等于（） A. B.3 C.2 D. +1 解答：设BC＝x，则AC＝＝ x，∵BC+AC ＝3+ ，∴x+ x＝3+ ，解得：x＝3，即BC＝3，故选：B.3.在△ABC 中，AB＝12 ，AC＝13，cosB＝，则BC边长为（） A.7 B.8 C.8或17 D.7或17 解答：∵cos∠B＝，∴∠B＝45°，当△ABC为钝角三角形时，如图1，∵AB＝12 ，∠B＝45°，∴AD＝BD＝12，∵AC ＝13，∴由勾股定理得CD＝5，∴BC＝BD�CD＝12�5＝7；当△ABC 为锐角三角形时，如图2， BC＝BD+CD＝12+5＝17，故选：D． 4.等腰三角形的底边与底边上的高的比是2：，则顶角为（）A.60° B.90° C.120° D.150° 解答：如图，AB＝AC，AD为BC边上的高，由题意得：BC：AD＝2：，由等腰三角形的“三线合一”得BD＝ BC，∴BD：AD＝1：，即＝，∴tanB＝，∴∠B＝60°，∴此三角形为等边三角形，故顶角为60°，故选：A. 5.如图，在△ABC中，∠BAC ＝90°，AB＝AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为（） A. B. －1 C.2－ D. 解答：∵在△ABC中，∠BAC＝90°，AB＝AC，∴∠ABC＝∠C＝45°，BC＝ AC．又∵点D 为边AC的中点，∴AD＝DC＝ AC．∵DE⊥BC于点E，∴∠CDE＝∠C ＝45°，∴DE＝EC＝ DC＝ AC．∴tan∠DBC＝＝＝，故选：A． 6.如图，在Rt△ABC中，∠C＝90°，AM是BC边上的中线，sin∠CAM ＝，则tanB的值为（） A. B. C. D. 解答：在Rt△ACM中，sin∠CAM ＝＝，设CM＝3x，则AM＝5x，根据勾股定理得：AC＝＝4x，又M为BC的中点，∴BC＝2CM＝6x，在Rt△ABC中，tanB＝＝＝，故选：B. 7.如图，在Rt△ABC中，延长斜边BD到点C，使DC＝ BD，连接AC，若tanB＝，则tan CAD的值为（） A. B. C. D. 解答：如图，延长AD，过点C作CE⊥AD，垂足为E，∵tanB＝，即＝，∴设AD＝5x，则AB＝3x，∵∠CDE＝∠BDA，∠CED＝∠BAD，∴△CDE∽△BDA，∴ ＝＝＝，∴CE＝ x，DE＝ x，∴AE＝ x，∴tan∠CAD＝＝，故选：D． 8.如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进40海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD是（） A.20海里 B.40海里 C.20 海里 D.40 海里解答：根据题意可知∠CAD＝30°，∠CBD＝60°，∵∠CBD＝∠CAD+∠ACB，∴∠CAD＝30°＝∠ACB，∴AB＝BC＝40海里，在Rt△CBD中，∠BDC ＝90°，∠DBC＝60°，sin∠DBC＝，∴sin60°＝，∴CD＝40×sin60°＝40× ＝20 （海里），故选：C． 9.如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF，tan ＝，则“人字梯”的顶端离地面的高度AD是（） A.144cm B.180cm C.240cm D.360cm 解答：根据题意可知：：△AFO∽△ABD，OF＝ EF＝30cm ∴ ＝，即＝，∴DC＝72cm，∵tan ＝，∴ ＝，∴AD＝×72＝180cm．故选：B． 10.如图，为了测得电视塔高度AB，在D处用高为1米的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进100米到达F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（） A.50 B.51 C.50 +1 D.101 解答：设AG＝x，在Rt△AEG中，∵tan∠AEG＝，∴EG＝＝ x，在Rt△ACG 中，∵tan∠ACG＝，∴CG＝＝ x，∴ x�x＝100，解得：x＝50 ，则AB＝50 +1（米），故选：C．二、填空题 11. 4 12. （4，0）.13. 182米. 14. 6. 15. 200 +200． 16. 4.8. 11.在Rt△ABC中，∠C＝90°，tanA＝，AC＝6，则BC＝___________. 解答：∵∠C＝90°，tanA＝，∴ ＝，∴BC＝6× ＝4，故答案为：4. 12.在平面直角坐标系xOy中，已知一次函数y＝kx+b（k＜0）的图象过点P(1，1)，与x轴交于点A，与y轴交于点B，且tan∠ABO＝3，那么点A的坐标是____________. 解答：如图，∵一次函数y＝kx+b（k＜0）的图象过点P(1，1)，∴k+b＝1①，点A，点B分别与x轴，y轴的正半轴相交，且点B坐标为（0，b），∴OB＝b，在Rt△AOB中，∵tan∠ABO＝3，∴OA＝3OB＝3b，∴点A的坐标为（3b，0），∴3bk+b ＝0，∴k＝－，把k＝－代入①得：b＝，∴点A的坐标为（4，0），故答案为：（4，0）. 13.小明同学在距某电视塔底部水平距离500米处，看塔顶的仰角为20°（不考虑身高因素），则此电视塔高约为________________米.（结果保留整数，参考数据：sin20°≈0.3420，s in70°≈0.9397，tan20°≈0.3640，tan70°≈2.7475）解答：设电视塔高为x米，由题意得：x＝500tan20°≈500×0.3640＝182（米），故答案为：182米. 14.如图，铁路的路基横断面可看成是等腰梯形，斜坡AB的坡度为1：，斜坡AB的水平宽度BE＝3 m，那么斜坡AB的长为_________m. 解答：∵斜坡AB的坡度为1：，∴tanB＝，∴∠B＝30°，∵cosB＝，∴AB＝＝6（m），故答案为：6. 15.4月26日，2015黄河口国际马拉松比赛拉开帷幕，中央电视台体育频道用直升机航拍技术全程直播．如图，在直升机的镜头下，观测马拉松景观大道A处的俯角为30°，B处的俯角为45°．如果此时直升机镜头C处的高度CD为200米，点A、D、B在同一直线上，则AB两点的距离是_________________米．解答：由已知，得∠A＝30°，∠B＝45°，CD＝200，∵CD⊥AB 于点D，∴在Rt△ACD中，∠CDA＝90°，tanA＝，∴AD＝＝200 ，在Rt△BCD中，∠CDB＝90°，∠B＝45° ∴DB＝CD＝200，∴AB＝AD+DB＝200 +200，故答案为：200 +200． 16.如图，在菱形ABCD 中，AE⊥BC于点E，若cosB＝，EC＝2，P是AB边上的一动点，则线段PE的长度的最小值是___________. 解答：设菱形ABCD的边长为x，则AB＝BC＝x，又EC＝2，所以BE＝x�2，因为AE⊥BC于E，所以在Rt△ABE中，cosB＝，又cosB＝，于是＝，解得x＝10，即AB＝10．所以易求BE＝8，AE＝6，当EP⊥AB时，PE取得最小值．故由三角形面积公式有： AB PE＝ BE AE，求得PE的最小值为4.8，故答案为 4.8. 三、解答题 17.已知：如图，在△ABC中，AD是边BC上的高，E为边AC的中点，BC＝14，AD＝12，sinB＝，求：（1）线段DC的长；（2）tan∠EDC的值. 解答：（1）∵AD是边BC上的高，AD＝12，∴sinB＝＝，∴AB＝15，在Rt△ABD中，BD＝＝9，∴DC＝BC－BD＝14－9＝5；（2）∵E是斜边AC的中点，∴DE＝EC，∴∠EDC＝∠C，在Rt△ADC中，tanC＝＝，∴tan∠EDC ＝tanC＝ . 18.如图，已知矩形ABCD的对角线AC、BD相交于点O，过点O作OE⊥AC交AD于E，若AB＝6，AD＝8，求sin∠OEA的值．解答：连结EC，∵四边形ABCD为矩形，∴BC＝AD＝8，OA＝OC，∠ABC ＝90°，由勾股定理得：AC＝＝10，则OA＝5，∵OE⊥AC，∴OE 是AC的垂直平分线，∴AE＝CE，在Rt△EDC中，设EC＝AE＝x，则有ED＝AD－AE＝8－x，DC＝AB＝6，根据勾股定理得：x2＝(8－x)2+62，解得：x＝，∴AE＝，在Rt△AOE中，sin∠OEA＝＝ . 19.如图，平台AB高为12米，在B处测得楼房CD顶部点D的仰角为45°，底部点C的俯角为30°，求楼房CD的高度.( ≈1.7) 解答：作BE⊥CD 于点E，则CE＝AB＝12，在Rt△BCE中，BE＝＝＝12 ，在Rt△BDE 中，DE＝BE tan∠DBE＝12 tan45°＝12 ，∴CD＝CE+DE＝12+12≈32.4，所以，楼房CD的高度约为32.4米. 20.如图，某水上乐园有一个滑梯AB，高度AC为6米，倾斜角为60°，暑期将至，为改善滑梯AB的安全性能，把倾斜角由60°减至30°. （1）求调整后的滑梯AD的长度（2）调整后的滑梯AD比原滑梯AB增加多少米？（精确到0.1米）（参考数据：≈1.41，≈1.73，≈2.45）解答：（1）Rt△ABD中，∵∠ADB＝30°，AC＝6米，∴AD＝2AC＝12（m）∴AD的长度为12米；（2）∵Rt△ABC中，AB＝＝4 （m），∴AD－AB＝12�4 ≈5.1（m）．∴改善后的滑梯会加长5.1m． 21.如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽为6米，坝高20米，斜坡AB的坡度i＝1：2.5，斜坡CD的坡角为30°，求坝底AD的长度.（结果精确到0.1米，参考数据：≈1.414，≈1.732）解答：作BE⊥AD，CF⊥AD，垂足分别为点E，F，则四边形BCFE是矩形，由题意知：BC＝EF＝6米，BE＝CF＝20米，斜坡AB的坡度i＝1：2.5，在Rt△ABE中，i＝＝，∴AE＝50米，在Rt△CFD中，∠D＝30°，∴DF＝＝20 米，∴AD＝AE+EF+DF＝50+6+20 ≈90.6（米），答：坝底AD的长度约为90.6米. 22.如图，AD是等腰△ABC底边上的高，且AD＝4，sinB＝，若E是AC边上的点，且满足AE：EC＝2：3，连接DE，求sin∠ADE的值. 解答：过点A作AF∥BC，交DE的延长线于F，∵AD是等腰△ABC底边上的高，∴BD＝CD，AB＝AC，在Rt△ABD 中，∵sinB＝＝，而AD＝4，∴AB＝5，∴BD＝＝3，∴CD＝BD ＝3，∵AF∥CD，∴∠DAF＝90°，△AEF∽△CED，∴ ＝，即＝，∴AF＝2，在Rt△DAF中，DF＝＝2 ，在Rt△DAF中，sin∠ADF ＝＝＝，即sin∠ADE的值为． 23.如图，在南北方向的海岸线MN上，有A、B两艘巡船，现均收到故障船C的求救信号．已知A，B 两船相距100( +1)海里，船C在船A的北偏东60°方向上，船C在船B的东南方向上，MN上有一观测点D，测得船C正好在观测点D的南偏东75°方向上．已知距观测点D处100海里范围内有暗礁，若巡逻船A沿直线AC去营救船C，在去营救的途中有无触暗礁危险？（参考数据：≈1.41，≈1.73）解答：过点C作CE⊥AB于点E，由题意得：∠ABC＝45°，∠BAC＝60°，设AE＝x海里，在Rt△AEC中，CE＝AE tan60°＝ x；在Rt△BCE中，BE＝CE＝ x，∴AE+BE＝x+ x＝100( +1)，解得：x＝100，∴AC＝＝2x＝200．在△ACD中，∠DAC＝60°，∠ADC＝75°，则∠ACD＝45°，过点D作DF⊥AC于点F，设AF＝y，则DF＝CF＝y，∴AC＝y+ y＝200，解得：y＝100( －1)，∴DF＝ AF＝×100( －1)≈126.3海里，∵126.3＞100，所以巡逻船A沿直线AC航线，在去营救的途中没有触暗礁危险.。

沪科版九年级数学习题-解直角三角形及其应用(第1课时)

第1課時解直角三角形及其應用（1）1．如圖，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，E 為AB 上一點且AE ∶EB ＝4∶1，EF ⊥AC 於F ，連接FB ，則tan ∠CFB 的值等於( )A ．3B ．3C ．3 D ．2．如圖，在等腰Rt △ABC 中，∠C ＝90°，AC ＝6，D 是AC 上一點，若tan ∠DBA ＝15，則AD 的長為( )A ．2BCD ．13．如圖，孔明同學背著一桶水，從山腳A 出發，沿與地面成30°角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家(B 處)，AB ＝80米，則孔明從A 到B 上升的高度BC 是__________米．4．將一副三角尺如圖所示疊放在一起，若AB ＝14 cm ，則陰影部分的面積是______ cm 2.5．如圖，在Rt △ABC 中，∠CAB ＝90°，AD 是∠CAB 的平分線，tan B ＝12，則CD ∶DB ＝__________.6．如圖，在△ABC 中，∠B ＝45°，cos C ＝35，AC ＝5a ，則△ABC 的面積用含a 的式子表示為________．7．如圖，在平面直角坐標系內，O為原點，點A的座標為(10,0)，點B在第一象限內，.BO＝5，sin∠BOA＝35求：(1)點B的座標；(2)cos∠BAO的值．8．如圖，在△ABC中，AD是BC上的高，tan B＝cos∠DAC．(1)求證：AC＝BD；(2)若sin C＝12，BC＝12，求AD的長.139．(創新應用)圖(2)是圖(1)中窗子開到一定位置時的平面圖，若∠AOB＝45°，∠OAB＝30°，OA＝60 cm，求點B到OA邊的距離． 1.7，結果精確到整數)參考答案1解析：設EB ＝1，則AE ＝4，BC ＝52，AC .∴CF∴tan ∠CFB . 答案：C2解析：如圖，過點D 作DE ⊥AB ，垂足為E.易證△ADE 為等腰直角三角形，AE=DE.在Rt △BDE 中，tan ∠DBA=15DE AE BE BE ==，所以BE=5AE.在等腰Rt △ABC 中，∠C=90°，AC=6，由畢氏定理可求出AB=.在等腰Rt △ADE 中，由畢氏定理可求出AD 的長為2.2答案：A 3答案：404解析：Rt △ABC 中，AB ＝14 cm ，∠B ＝30°，則AC ＝7 cm ，易知CF ＝AC ＝7 cm ，所以陰影部分的面積為492cm 2. 答案：4925解析：過D 作DE ⊥AB 於點E.∵tan B ＝12，∴DE ＝12EB ． ∵∠CAB ＝90°，AD 是∠CAB 的平分線， ∴∠DAE ＝45°.∴∠ADE ＝45°.∴∠DAE ＝∠ADE.∴AE ＝DE.∵DE ∥CA ，∴CD ∶DB ＝AE ∶EB ＝1∶2.答案：1∶26解析：過A 作AD ⊥BC 於點D ．在Rt △ADC 中，cos C=35，AC=5a ，∴DC=3a ，AD=4a .∵在Rt △ADB 中，∠B=45°，∴BD=AD=4a .∴S △ABC ＝12AD ·BC ＝12×4a ×(4a ＋3a )＝14a 2. 答案：14a 27解：(1)如圖，作BH ⊥OA ，垂足為H.在Rt △OHB 中，∵BO ＝5，sin ∠BOA ＝35， ∴BH ＝BO ·sin ∠BOA ＝3.∴OH ＝4. ∴點B 的座標為(4,3)．(2)∵OA ＝10，OH ＝4，∴AH ＝6.在Rt △AHB 中，BH ＝3，∴AB ＝∴cos ∠BAO ＝5AH AB =. AD 的長．8(1)證明：∵AD ⊥BC ，∴△ABD 和△ADC 為直角三角形．∴tan B ＝AD BD ，cos ∠DAC ＝AD AC. ∵tan B ＝cos ∠DAC ， ∴AD BD ＝AD AC，即AC ＝BD ． (2)解：在Rt △ADC 中，已知sin C ＝AD AC ＝1213，故可設AD ＝12k ，AC ＝13k.∴CD 5k.∵BC ＝BD ＋CD ，又AC ＝BD ，∴BC ＝13k ＋5k ＝18k.由已知BC ＝12，∴18k ＝12.∴k ＝23.∴AD ＝12k ＝8. 9解：如圖，過點B 作BC ⊥OA 於點C ，∵∠AOB=45°，∴∠CBO=45°，BC=OC ．設BC=OC=x ，∵∠OAB=30°，∴AC=tan 30BC=︒.∵OC+CA=OA ，∴x =60(cm)．∴x≈22(cm)，即點B 到OA 邊的距離是22 cm.。

沪科版九年级数学习题-解直角三角形及其应用(第2课时)

第2課時解直角三角形及其應用（2）1．如圖，已知一商場自動扶梯的長為10米，該自動扶梯到達的高度h為6米，自動扶梯與地面所成的角為θ，則tan θ的值等於()A．34B．43C．35D．452．如圖，為了加快施工進度，要在小山的另一邊同時施工，從AC上的一點B，取∠ABD ＝145°，BD＝500 m，∠D＝55°，要A，C，E成一直線，那麼開挖點E離點D的距離是()A．500sin 55°m B．500cos 55°mC．500tan 55°m D．500mtan553．如圖，在坡度為1∶2的山坡上種樹，要求株距(相鄰兩樹間的水準距離)是6 m，則斜坡上相鄰兩樹間的坡面距離是__________ m.4．如圖，小明在操場上距離旗杆18 m的C處，用測角儀測得旗杆AB的頂端A的仰角為30°，已知測角儀CD的高為1.4 m，那麼旗杆AB的高為________ m．(保留三位有效數字)5. 如圖，在亞丁灣一海域執行護航任務的我海軍某軍艦由東向西行駛．在航行到B處時，發現燈塔A在我軍艦的正北方向500米處；當該軍艦從B處向正西方向行駛至C處時，發現燈塔A在我軍艦的北偏東60°的方向．求該軍艦行駛的路程(計算過程和結果均不取近似值)．6．如圖，一枚運載火箭從地面O 處發射，當火箭到達A 點時，從地面C 處的雷達站測得AC 的距離是6 km ，仰角是43°.1 s 後，火箭到達B 點，此時測得BC 的距離是6.13 km ，仰角為45.54°，解答下列問題：(1)火箭到達B 點時距離發射點有多遠(精確到0.01 km)?(2)火箭從A 點到B 點的平均速度是多少(精確到0.1 km/s )?7．某商場為緩解我市“停車難”問題，擬建造地下停車庫，如圖是該地下停車庫坡道入口的設計示意圖，其中，AB ⊥BD ，∠BAD ＝18°，C 在BD 上，BC ＝0.5 m ．根據規定，地下停車庫坡道入口上方要張貼限高標誌，以便告知駕駛員所駕車輛能否安全駛入．小明認為CD 的長就是所限制的高度，而小亮認為應該以CE 的長作為限制的高度．小明和小亮誰說的對？請你判斷並計算出正確的結果．(結果精確到0.1 m)8．(創新應用)關於三角函數有如下的公式：sin(α＋β)＝sin αcos β＋cos αsin β，①cos(α＋β)＝cos αcos β－sin αsin β，②tan(α＋β)＝tan tan 1tan tan αβαβ+-⋅(1－tan α·tan β≠0)．③ 利用這些公式可以將一些不是特殊角的三角函數轉化為特殊角的三角函數來求值，如tan 105°＝tan(45°＋60°)＝tan 45tan 601tan 45tan 60︒+︒===-︒⋅︒＝－(2．根據上面的知識，你可以選擇適當的公式解決下麵的實際問題：如圖，直升飛機在一建築物CD 上方A 點處測得建築物頂端D 點的俯角α為60°，底端C 點的俯角β為75°，此時直升飛機與建築物CD 的水準距離BC 為42米，求建築物CD 的高．參考答案1答案：A2解析：∵∠E ＝180°－55°－35°＝90°，∴DE ＝BD ·cos D ＝500cos 55°(m)．答案：B3答案：4解析：AE ＝DE ·tan 30°＝18×3≈10.4(m)， EB ＝1.4 m ，∴AB ＝AE ＋BE ＝10.4＋1.4＝11.8(m)．答案：11.85解：由已知，可得∠ACB=30°.在Rt △ABC 中，∠ACB=30°，AB=500.∵tan ∠ACB=AB BC， ∴BC=tan AB ACB∠=500500tan 30==︒因此該軍艦行駛的路程為6解：(1)在Rt △OCB 中，sin 45.54°＝OB CB，OB ＝6.13×sin 45.54°≈4.38(km)，答：火箭到達B 點時距發射點約4.38 km.(2)在Rt △OCA 中，sin 43°＝OA CA， ∴OA ＝6×sin 43°≈4.09(km)， v ＝(OB －OA)÷t ＝(4.38－4.09)÷1≈0.3(km/s)．答：火箭從A 點到B 點的平均速度約為0.3 km/s.7解：小亮的說法正確．在△ABD 中，∠ABD ＝90°，∠BAD ＝18°，BA ＝10，∴tan ∠BAD ＝BD BA. ∴BD ＝10×tan 18°.∴CD ＝BD ―BC ＝10×tan 18°－0.5.在△ABD 中，∠CDE ＝90°－∠BAD ＝72°，∵CE ⊥ED ，∴sin ∠CDE ＝CE CD. ∴CE ＝sin ∠CDE ×CD ＝sin 72°×(10×tan 18°－0.5)≈2.6(m)．答：CE 為2.6 m ，即限高為2.6 m .8解：過點D 作DE ⊥AB 於E ，依題意，在Rt △ADE 中，∠ADE=∠α=60°，AE=ED ·tan 60°=BC ·tan 60°=在Rt △ACB 中，∠ACB=∠β=75°，AB=BC ·tan 75°.∵tan 75°=tan(45°+30°) =tan 45tan 301tan 45tan 30︒+︒-︒⋅︒2=∴AB=42×)=84+CD=BE=AB-AE=84+米)．答：建築物CD 的高為84米．。

沪科版-数学-九年级上册-24.3解直角三角形及其应用典型例题2

解直角三角形典型例题例1、在∆ABC 中, ∠C = 90︒, sin A =23, 求ctg B 。

解: 方法一, 设∠A 对边BC = 2a , 斜边AB 为3a , 由勾股定理, AC =5a , 由三角函数的定义, ctg B BC AC B a a ===,即ctg 25255 。

方法二; ∵sin A =23, 由同角三角函数关系式, sin cos 221A A +=, 得cos A =-⎛⎝ ⎫⎭⎪=123532, 则tgA A A ===sin cos 2353255。

又∵∠A 与∠B 互为余角, ∴sin A = cos B , tg A = ctg B , ∴ctg B = tg A =255。

说明: 当直角三角形中已知一个三角函数求其它三角函数值时, 用小三角形法, 即方法一是比较简单的, 因为三角函数的定义是比值, 因此可设一份为一个常量, 设出比值, 再去计算。

用同角三角函数关系式计算也应当会, 只是计算起来麻烦一些。

例2、在∆ABC 中, ∠C = 90︒, tg A =125,∆ABC 的周长为45cm, 求BC 的长。

解: 设BC = 12x , AC = 5x , 则AB = 13x , 则题意, 12x + 5x + 13x = 45cm, 30x = 45,∴x = 32, ∴BC = 123218⨯=(cm)例3、在∆ABC 中, ∠C = 90︒, a b ==1535,, 求∠A 及S ABC ∆。

解: ∵∠C = 90︒, a b ==1535,∴tg A ==153533, 又∵∠A 为锐角, ∴∠A = 30︒, ∴S ab ABC ∆==⨯⨯=121215351523。

说明: 当已知边求角时, 可利用三角函数的定义, 这里已知两直角边, 可以求锐角的正切或余切值, 再去求角。

例4、求值: cos cos 2237151548534245︒+︒︒+︒+︒-︒+︒tg ctg tg ctg tg · 分析: 所给的三角函数中, 只有45︒的三角函数是特殊角的三角函数值, 其它都不是特殊的三角函数值, 应当分析这些三角函数值之间的关系, 由分析可以看出37︒与53︒角互为余角, 因为互为余角的余函数相等, 因此tg48︒与ctg42︒也相等, 再进行计算就可以了。

沪科版九年级数学习题-解直角三角形及其应用(第3课时)

第3課時解直角三角形及其應用（3）1．王英同學從A地沿北偏西60°方向走100 m到B地，再從B地向正南方向走200 m 到C地，此時王英同學離A地()A．B．100 mC．150 m D．m2．如圖，在把易開罐中的水倒入一個圓水杯的過程中，若水杯中的水在點P與易開罐剛好接觸，則此時水杯中的水深為__________．3．海中有一個小島P，它的周圍18海裏內有暗礁，漁船跟蹤魚群由西向東航行，在點A測得小島P在北偏東60°方向上，航行12海裏到達B點，這時測得小島P在北偏東45°方向上．如果漁船不改變航線繼續向東航行，有沒有觸礁危險？請說明理由．4．如圖，一艘核潛艇在海面下500米A點處測得俯角為30°正前方的海底有黑匣子信號發出，繼續在同一深度直線航行4 000米後再次在B點處測得俯角為60°正前方的海底有黑匣子信號發出，求海底黑匣子C點處距離海面的深度．(精確到米，≈1.414，1.7322.236)5．如圖，某處山坡上一座發射塔被冰雪從C處壓折，塔尖恰好落在坡面上的點B處，在B處測得點C的仰角為38°，塔基A的俯角為21°，又測得斜坡上點A到點B的坡面距離AB為15 m，求折斷前發射塔的高．(精確到0.1 m)6．如圖，某校綜合實踐活動小組的同學欲測量公園內一棵樹DE的高度．他們在這棵樹正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°，朝著這棵樹的方向走到臺階下的點C處，測得樹頂端D的仰角為60°.已知A點的高度AB為2米，臺階AC的坡度為1(即AB∶BC＝1，且B，C，E三點在同一條直線上．請根據以上條件求出樹DE的高度(測傾器的高度忽略不計)．7．如圖，某邊防巡邏隊在一個海濱浴場岸邊的A點處發現海中的B點有人求救，便立即派三名救生員前去營救.1號救生員從A點直接跳入海中；2號救生員沿岸邊(岸邊看成是直線)向前跑到C點，再跳入海中；3號救生員沿岸邊向前跑300 m到離B點最近的D點，再跳入海中．救生員在岸上跑的速度都是 6 m/s，在水中游泳的速度都是 2 m/s.若∠BAD＝45°，∠BCD＝60°，三名救生員同時從A點出發，請說明誰先到達營救地點B．(參考數據≈1.4 1.7)8．(創新應用)在一次實踐活動中，某課題學習小組用測傾器、皮尺測量旗杆的高度，他們設計了如下的方案(如圖甲所示)：①在測點A處安置測傾器，測得旗杆頂部M的仰角∠MCE＝α；②量出測點A到旗杆底部N的水準距離AN＝m；③量出測傾器的高度AC＝h.根據上述測量數據，即可求出旗杆的高度MN.如果測量工具不變，請參照上述過程，重新設計一個方案測量某小山的高度．(1)在圖乙中，畫出你測量小山高度MN的示意圖(標上適當的字母)；(2)寫出你的設計方案．參考答案1解析：BD ＝100×sin 30°＝50 m ，AD ＝100×cos 30°＝m ，CD ＝200－50＝150 m ，在Rt △ADC 中，AC ==.答案：D2答案：6 cm3解：有觸礁危險．理由：過點P 作PD ⊥AC 於D ．設PD 為x ，在Rt △PBD 中，∠PBD ＝90°－45°＝45°，∴BD ＝PD ＝x .在Rt △PAD 中，∵∠PAD ＝90°－60°＝30°，∴AD ＝tan 30x =︒.∵AD ＝AB ＋BD ＝12＋x .∴x 1)=．∵1)＜18，∴漁船不改變航線繼續向東航行，有觸礁危險．4解：由C 點向AB 作垂線，交AB 的延長線於E 點，並交海面於F 點．已知AB ＝4 000(米)，∠BAC ＝30°，∠EBC ＝60°.∵∠BCA ＝∠EBC －∠BAC ＝30°，∴∠BAC ＝∠BCA ，∴BC ＝BA ＝4 000(米)．在Rt △BEC 中，EC ＝BC ·sin 60°＝4 000×2＝米)，∴CF ＝CE ＋EF ＝＋500≈3 964(米)．答：海底黑匣子C 點處距離海面的深度約為3 964米．5解：作BD ⊥AC 於D ．由已知，得∠CBD=38°，∠ABD=21°，AB=15 m.在Rt △ADB 中，∵sin ∠ABD=AD AB， ∴AD=AB ·sin ∠ABD=15×sin 21°≈5.38(m)．∵cos ∠ABD=BD AB， ∴BD=AB ·cos ∠ABD=15×cos 21°≈14.00(m)．在Rt △BDC 中，∵tan ∠CBD=CD BD， ∴CD=BD ·tan ∠CBD ≈14.00×tan 38°≈10.94(m)．∵cos ∠CBD=BD BC， ∴BC=cos BD CBD ∠≈14.00cos38︒≈17.77(m)． ∴AD+CD+BC ≈5.38+10.94+17.77=34.09≈34.1(m)．答：折斷前發射塔的高約為34.1 m.6解：如圖，過點A 作AF ⊥DE 於F ，則四邊形ABEF 為矩形．∴AF ＝BE ，EF ＝AB ＝2.設DE ＝x ，在Rt △CDE 中，CE ＝tan tan 603DE DE x DCE ==∠︒. 在Rt △ABC 中，∵AB BC =，AB ＝2，∴BC ＝在Rt △AFD 中，DF ＝DE －EF ＝x －2，∴AF ＝22)tan tan 30DF x x DAF -==-∠︒． ∵AF ＝BE ＝BC ＋CE ，∴2)x x -=.解得x ＝6. 答：樹DE 的高度為6米．7解：在△ABD 中，∠A ＝45°，∠D ＝90°，AD ＝300(m)，∴AB ＝cos 45AD ︒＝(m)，BD ＝AD ·tan 45°＝300(m)．在△BCD 中，∵∠BCD ＝60°，∠D ＝90°，∴BC ＝sin 60BD =︒(m)， CD ＝tan 60BD =︒(m)．1號救生員到達B 點所用的時間為2＝210(s )；2號救生員到達B 點所用的時間為30062-+＝50＋3≈191.7(s )； 3號救生員到達B 點所用的時間為30030062+＝200(s )． ∵191.7＜200＜210，∴2號救生員先到達營救地點B ．8分析：仿照測量旗杆高度的方法去測量的話，不能測量出測量點到山頂的底部的距離，所以要選取兩個測量點，進行兩次測量，構造出兩個直角三角形，解這兩個直角三角形求出小山的高度．解：(1)如下圖所示：(2)方案如下： ①測點A 處安置測傾器，測得小山頂部M 的仰角∠MCE ＝α；②測點B 處安置測傾器，測得小山頂部M 的仰角∠MDE ＝β；③量出測點A 到測點B 的水準距離AB ＝m ；④量出測傾器的高度AC ＝h.根據上述測量可以求出小山MN 的高度．。

沪科版数学九年级上册23.2解直角三角形及其应用同步练习(含答案)

23.2 解直角三角形及其应用一、选择题（共4题）1．如图，已知一商场自动扶梯的长为10米，该自动扶梯到达的高度h为6米，自动扶梯与地面所成的角为θ，则tan θ的值等于()．A． B． C． D．2．如图，为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B，取∠ABD ＝145°，BD＝500 m，∠D＝55°，要A，C，E成一直线，那么开挖点E离点D的距离是()．A．500sin 55° m B．500cos 55° mC．500tan 55° m D．3.等腰三角形的两条边长分别是4 cm、9 cm，则等腰三角形的底角的余弦值是( )A. B. C. D.4.如图，两建筑物的水平距离为a米，从A点测得D点的俯角为α，测得C点的俯角为β，则较低建筑物CD的高度为( )A.aB.atanαC.a(sinα－cosα)D.a(tanβ－tanα)二、填空题（共5题）5．如图，在坡度为1∶2的山坡上种树，要求株距(相邻两树间的水平距离)是6 m，则斜坡上相邻两树间的坡面距离是__________ m.6．如图，小明在操场上距离旗杆18 m的C处，用测角仪测得旗杆AB的顶端A的仰角为30°，已知测角仪CD的高为1.4 m，那么旗杆AB的高为________ m．(保留三位有效数字)7.有人说，数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高度（如图），他测得CB=10米，∠ACB=50°，请你帮他算出树高AB,约为________________米.（注：①树垂直于地面；②供选用数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.2）三、计算与解答题（共4题）8. 如图，在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶．在航行到B处时，发现灯塔A在我军舰的正北方向500米处；当该军舰从B处向正西方向行驶至C处时，发现灯塔A在我军舰的北偏东60°的方向．求该军舰行驶的路程(计算过程和结果均不取近似值)．9．如图，一枚运载火箭从地面O处发射，当火箭到达A点时，从地面C处的雷达站测得AC的距离是6 km，仰角是43°.1 s后，火箭到达B点，此时测得BC的距离是6.13 km，仰角为45.54°，解答下列问题：(1)火箭到达B点时距离发射点有多远(精确到0.01 km)?(2)火箭从A点到B点的平均速度是多少(精确到0.1 km/s)?10．某商场为缓解我市“停车难”问题，拟建造地下停车库，如图是该地下停车库坡道入口的设计示意图，其中，AB⊥BD，∠BAD＝18°，C在BD上，BC＝0.5 m．根据规定，地下停车库坡道入口上方要张贴限高标志，以便告知驾驶员所驾车辆能否安全驶入．小明认为CD的长就是所限制的高度，而小亮认为应该以CE的长作为限制的高度．小明和小亮谁说的对？请你判断并计算出正确的结果．(结果精确到0.1 m)11．关于三角函数有如下的公式：sin(α＋β)＝sin αcos β＋cos αsin β，①cos(α＋β)＝cos αcos β－sin αsin β，②tan(α＋β)＝(1－tan α·tan β≠0)．③利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，如tan 105°＝tan(45°＋60°)＝＝－(2＋)．根据上面的知识，你可以选择适当的公式解决下面的实际问题：如图，直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α为60°，底端C点的俯角β为75°，此时直升飞机与建筑物CD的水平距离BC为42米，求建筑物CD的高．参考答案1.A2.解析：∵∠E＝180°－55°－35°＝90°，∴DE＝BD·cos D＝500cos 55°(m)．答案：B3.解析：根据构成三角形的条件，该等腰三角形的三边长为9、9、4，∴其底角的余弦值为.答案：C4.解析:过D点作AB的垂线交AB于E点，在Rt△ADE中,∠ADE=α,DE=a,∴AE=a·tanα.在Rt△ABC中,∠ACB=β,BC=a,∴AB=a·tanβ.∴CD=AB－AE=a·tanβ－a·tanα.答案:D5.6.解析：AE＝DE·tan 30°＝18×≈10.4(m)，EB＝1.4 m，∴AB＝AE＋BE＝10.4＋1.4＝11.8(m)．答案：11.87.解析:AB=BC·tanC=12(米).答案:128.解：由已知，可得∠ACB=30°.在Rt△ABC中，∠ACB=30°，AB=500.∵tan∠ACB=，∴BC==.因此该军舰行驶的路程为米．9.解：(1)在Rt△OCB中，sin 45.54°＝，OB＝6.13×sin 45.54°≈4.38(km)，答：火箭到达B点时距发射点约4.38 km.(2)在Rt△OCA中，sin 43°＝，∴OA＝6×sin 43°≈4.09(km)，v＝(OB－OA)÷t＝(4.38－4.09)÷1≈0.3(km/s)．答：火箭从A点到B点的平均速度约为0.3 km/s.10.解：小亮的说法正确．在△ABD中，∠ABD＝90°，∠BAD＝18°，BA＝10，∴tan∠BAD＝.∴BD＝10×tan 18°.∴CD＝BD―BC＝10×tan 18°－0.5.在△ABD中，∠CDE＝90°－∠BAD＝72°，∵CE⊥ED，∴sin∠CDE＝.∴CE＝sin∠CDE×CD＝sin 72°×(10×tan 18°－0.5)≈2.6(m)．答：CE为2.6 m，即限高为2.6 m.11.解：过点D作DE⊥AB于E，依题意，在Rt△ADE中，∠ADE=∠α=60°，AE=ED·tan 60°=BC·tan 60°=.在Rt△ACB中，∠ACB=∠β=75°，AB=BC·tan 75°.∵tan 75°=tan(45°+30°)==，∴AB=42×(2+)=84+ ，CD=BE=AB-AE=84+ =84(米)．答：建筑物CD的高为84米．。

沪科版数学九年级上册24.3解直角三角形及其应用

考点1解直角三角形的依据（1）三边之间的关系（2）边角之间的关系（3）锐角之间的关系
考点2坡度（坡比）、坡角
（1）坡度也叫坡比，即i=h：m，
h是坡面的铅直高度，

m是对应的水平宽度。
α m
（2）坡角是坡面与水平面的夹角
（3）坡度与坡角的关系：i=tanα
6、在离地面高度为6米处引拉线固定电线杆，拉线和地面成B60°角，则拉线长为（）
A、6m3B、4mC、2mD3 、3m
3
7、一个小球由地面沿坡度 i=1：2的坡面上前进了10米，此时小球距离地面的高度为
（）B。 A、5米B、2米 5 C、4米5D、米 10
3
8、如图，某生产车间的人字
形屋架为等腰三角形，夸度 AB=12米，∠A=30°，则中柱CD=，2√3米上弦AC=。4√3米 C
理？（2）若2号救生员从A跑到C，
再跳水入海中游泳到B点救助，且
∠BCD=65°，请问谁先到达点B？
（所有数据精确到0·1，
sin65°≈0.9，cos65°≈0.4，
tan65°≈2.0，√2≈1.4
B
AC D
12、如图，平面镜PQ前有直线
MN∥PQ，MN与PQ的距离为1米，
在MN上一点A处观察物体B及B在
距离为。30米
A
B
C
11、某海滨浴场的沿岸可以看成直线，如图，1号救生员在岸边的 A点看到海中的B点有人求救，便立即向前跑了300米到离B点最近的D点，再跳入海中游到B点救助；若每位救生员在岸上跑步的速度都是每秒6米，在水中游泳的速度都是每秒2米，∠BAD=45°
（1）请问1号救生员的做法是否合
A
D

沪科版-数学-九年级上册--24.3解直角三角形及其应用

例5、某校九年级学生为了测量当地电视塔高AB ，因为不能直接到塔底B 处，他采用在发射塔院外与电视塔B 成一直线的C 、D 两地面处，用测角器测得顶部A的仰角450和300，同时测得CD=50m ，测角器高1m ，你能求电视塔的高度吗？解：设AB 1=xm在Rt ⊿AC 1B 1中，由∠AC 1B 1=450，得C 1B 1=AB 1=x又在Rt ⊿AD 1B 1，中由∠AD 1B 1=300，得tan ∠AD 1B 1=11AB1B D =1!111B C C D AB + 即tan300=xx +50 解方程，得X=25（3+1）≈68（m ）∴AB=AB 1+B 1B ≈68+1=69（m ）因而，电视塔的高约为69 m 。

一、新课讲解例6、一船以20 n mile/h 的速度向正东航行，在A 处测得灯塔C 在北偏东600，继续航行1h 到达B 处，再测得灯塔C 在北偏东300，已知灯塔C 四周10hmile 内有暗礁，问这船继续向东航行是否安全？分析：这船继续向东航行是否安全，取决于灯塔到航线的距离是否大于10n mile 。

解：作C D ⊥AB 于点D ，设CD=x n mi le在Rt ⊿ACD 中，AD=CAD CD ∠tan =30tan x 在Rt ⊿BCD 中，BD=CBD CD ∠tan =60tan x 由AB=AD-BD ，得AB=30tan x -60tan x =20 ∴CD=x=33320-=103>10 因而，船继续向东航行五触礁的危险。

练习：课本P 115,练习1、2二、自主探究例7、铁路路基的横断面是等腰梯形ABCD ，路基的上底宽BC=9.8m ，路基高BE=5.8m,斜坡的坡度1：1.6，求路基下底宽（精确到0.1m ）与斜坡的坡角。

（精确到10）三、课堂练习：课本P116页，练习1、2四、课堂小结解斜三角形和梯形：（1）基本思想是作高，将斜三角形转化为直角三角形求解；（2）几种情况：①已知两边及其夹角；②已知两角夹一边；③已知两角和一角的对边；④已知三边。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

练习12 解直角三角形及其应用一．选择题1．如图，在Rt ABC ∆中，90ABC ∠=︒，BD AC ⊥于点D ，2AB BC =，则tan ABD ∠的值为( )A ．2B ．12C ．5D ．25【解答】解：90ABC ∠=︒，90A C ∴∠+∠=︒，BD AC ⊥，90ADB ∴∠=︒，90A ABD ∴∠+∠=︒，ABD C ∴∠=∠，2AB BC =，tan tan 2ABABD C BC ∴∠=∠==，故选：A ．2．如图，小正方形的边长均为1，A 、B 、C 分别是小正方形的三个顶点，则sin BAC ∠的值为()A ．12 B 2C ．1D 3【解答】解：连接BC ，如图：每个小正方形的边长均为1， 22215AB ∴=+=，22215BC =+=，223110AC =+=，222AB BC AC +=，ABC ∴∆是直角三角形，52sin 10BC BAC AC ∴∠===，故选：B ．3．如图，在边长相同的小正方形组成的网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB 、CD 相交于点P ，则tan (APD ∠= )A 5B ．3C 10D ．2【解答】解：设小正方形的边长为1，由图形可知，2,2AD DC AC ==，ADC ∴∆是等腰直角三角形，AD DC ∴⊥．//AC BD ，∴2AC CP BD DP==， 2PC DP ∴=，3AD DC DP ∴==，∴tan 3AD APD DP∠==．故选：B ．二．填空题4．如图，河宽CD为1003米，在C处测得对岸A点在C点南偏西30︒方向、对岸B点在C点南偏东45︒方向，则A、B两点间的距离是米．（结果保留根号）【解答】解：在Rt ACD∆中，tanAD ACDCD∠=，则3tan1003100AD CD ACD=⨯∠=⨯=（米），在Rt CDB∆中，45BCD∠=︒，1003BD CD∴==（米），(1001003)AB AD BD∴=+=+米，故答案为：(1001003)+．5．平放在地面上的三角形铁板ABC的一部分被沙堆掩埋，其示意图如图所示，量得A∠为54︒，B∠为36︒，边AB的长为2.1m，BC边上露出部分BD的长为0.9m，则铁板BC边被掩埋部分CD的长是0.8m．（结果精确到0.1m．参考数据：sin540.81︒≈，cos540.59︒≈，tan54 1.38)︒≈．【解答】解：在直角三角形中，sinBCAAB =，则sin 2.1sin54 2.10.81 1.701BC AB A==︒≈⨯=，则 1.7010.9CD BC BD=-=-，0.8010.8()m=≈，故答案为：0.8．6．再如图，一艘船由A港沿北偏东65︒方向航行302km至B港，然后再沿北偏西40︒方向航行至C港，C 港在A港北偏东20︒方向，则A，C两港之间的距离为多少km．【解答】解：如图，过B 作BE AC ⊥于E ，过C 作//CF AD ，则////CF AD BG ，90AEB CEB ∠=∠=︒，20ACF CAD ∴∠=∠=︒，40BCF CBG ∠=∠=︒，204060ACB ∴∠=︒+︒=︒，由题意得，652045CAB ∠=︒-︒=︒，302AB km =，在Rt ABE ∆中，45ABE ∠=︒，ABE ∴∆是等腰直角三角形，302AB km =，230()AE BE AB km ∴===，在Rt CBE ∆中，60ACB ∠=︒，tan BE ACB CE ∠=， 103()tan 603BE CE km ∴===︒， 30103()AC AE CE km ∴=+=+，A ∴，C 两港之间的距离为(30103)km +，故答案为：(30103)+．三．解答题7．5月27日，2020珠峰高程测量登山队成功登顶珠穆朗玛峰完成峰顶测量任务，受此消息鼓舞，某数学小组开展了一次测量小山高度的活动，如图，该数学小组从地面A 处出发，沿坡角为53︒的山坡AB 直线上行一段距离到达B 处，再沿着坡角为22︒的山坡BC 直线上行600米到达C 处，通过测量数据计算出小山高500CD m =．求该数学小组行进的水平距离AD （结果精确到1)m ．（参考数据：sin220.37︒≈，cos220.92︒≈，tan220.32︒≈，sin530.8︒≈，cos530.6︒≈，tan53 1.3)︒≈【解答】解：过B 作BE CD ⊥于E ，过B 作BH AD ⊥于H ，则四边形BEDH 是矩形，DE BH ∴=，BE DH =，在Rt ACE ∆中，600BC =，22CBE ∠=︒，sin 226000.37222()CE BC m ∴=︒=⨯=，cos226000.92552()BE BC m =︒=⨯=，552DH BE m ∴==，500CD m =，500222278()BH DE CD CE m ∴==-=-=，在Rt ABH ∆中，53BAH ∠=︒，tan53BH AH ∴︒=， 278214()1.3AH m ∴=≈， 214552766()AD AH DH m ∴=+=+=，答：该数学小组行进的水平距离AD 为766m ．8．如图，某大楼的顶部竖有一块宣传牌AB ，小明在斜坡的坡脚D 处测得宣传牌底部B 的仰角为45︒，沿斜坡DE 向上走到E 处测得宣传牌顶部A 的仰角为31︒，已知斜坡DE 的坡度3:4，10DE =米，22DC =米，求宣传牌AB 的高度．（测角器的高度忽略不计，参考数据：sin310.52︒≈，cos310.86︒≈，tan310.6)︒≈【解答】解：过E 分别作CD 、AC 的垂线，设垂足为F 、G ，则CF EG =，CG EF =，在Rt EFD ∆中，斜坡DE 的坡度3:4，10DE =米，∴设3EF x =米，4DF x =米， 22510DE EF DF x ∴=+==，2x ∴=，6EF ∴=米，8DF =米，在Rt BCD ∆中，45BDC ∠=︒，22BC CD ∴==米，22616BG BC CG ∴=-=-=（米），在Rt AEG ∆中，tan31300.618AG EG =︒=⨯=（米），18162AB AG BG ∴=-=-=（米），答：宣传牌AB 的高度为2米．9．如图，A 市北偏东30︒方向有一旅游景点M ，在A 市北偏东60︒的公路上向前行1000米到C 处，测得M 位于C 的北偏西15︒，试求景点M 到C 处的距离MC 及景点M 到公路AC 的距离MN （结果保留根号）．【解答】解：由题意可知：603030MAC ∠=︒-︒=︒，156075MCN ∠=︒+︒=︒， 753045AMC MCN MAC ∴∠=∠-∠=︒-︒=︒，过C 作CH AM ⊥交AM 于点H ，如图所示：在Rt ACH ∆中，30MAC ∠=︒，1000AC m =， 1500()2HC AC m ∴=，35003()AH HC m ==，在Rt HMC ∆中，5002,500sin 45tan 45HC HC CM m HM m ====︒︒， ∴1122AMC S AM CH AC MN ∆==，即：(5003500)5001000MN +⨯=，∴(2503250)MN m =+，即MC 的长度为5002米，MN 的长度为(2503250)+米．1．如图，一艘渔船从点A 出发，沿正南方向航行了半小时到达点B ，再沿南偏西60︒方向航行了半小时到达点C ，此时测得码头D 在C 的正东方向，该渔船的速度为60海里/时，则B ，D 两点间的距离为( )A ．10海里B ．15海里C ．30海里D ．90海里【解答】解：由题意可得，160302AB BC ==⨯=（海里），在Rt BCD ∆中，90BDC ∠=︒，60CBD ∠=︒，30BCD ∴∠=︒，1152BD BC ∴==（海里），即点B 、D 之间的距离为15海里，故选：B ． 2．如图，在边长为1的正方形网格中，端点在格点上的两条线段相交形成1∠，则tan 1∠= ．【解答】解：如图，设小正方形ABCD 的边长为a ，连接AC ，BD 交于点O ，设EC 交BD 于J ．2BD a =，//CD EB ，∴13DJ CD JB EB ==， 124JD BD ∴=， 22OD OB OC OA ====， 222OJ OD JD ∴=-==， AC BD ⊥，90COJ ∴∠=︒，22tan 122a OC OJ a ∴∠===，故答案为2．3．小明家所在居民楼的对面有一座大厦74AB =米，为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C 处测得大厦顶部A 的仰角为37︒，大厦底部B 的俯角为48︒．求小明家所在居民楼与大厦的距离CD 的长度．（参考数据：3sin375︒≈，3tan374︒≈，7sin 4810︒≈，11tan 48)10︒≈【解答】解：设CD x =米．在Rt ACD ∆中，tan37AD CD ︒=，则34AD x=， 34AD x ∴=；在Rt BCD ∆中，tan 48BD CD ︒=，则1110BD x =， 1110BD x ∴=． AD BD AB +=，∴31174410x x +=，解得：40x =，答：小明家所在居民楼与大厦的距离CD 的长度是40米．4．我市里运河有一座人行天桥如图所示，天桥高为6米，坡面BC 的坡度为1:1，文化墙PM 在天桥底部正前方8米处(PB 的长），为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1:3．有关部门规定，文化墙距天桥底部小于3米时应拆除，天桥改造后，该文化墙PM 是否需要拆除？请说明理由．（参考数据：2 1.414=，3 1.732)=【解答】解：该文化墙PM 不需要拆除，理由：设新坡面坡角为α，新坡面的坡度为3，3tan 3α∴= 30α∴=︒．作CD AB ⊥于点D ，则6CD =米，新坡面的坡度为3，6tan 3CD CAD AD AD ∴∠==，解得，63AD =坡面BC 的坡度为1:1，6CD =米， 6BD ∴=米，(636)AB AD BD ∴=-=米，又8PB =米，8(636)1463146 1.732 3.6PA PB AB ∴=-=-=-≈-⨯≈米3>米，该文化墙PM不需要拆除．。