北师大版八年级数学下册 测培优试题(有难度)(无答案)
北师大版八年级数学下册-测培优试题(有难度)(无答案)

数学综合测试题(北师大版·八年级)一、选择题(每小题3分,共30分)1. 若21=+xx ,则221xx+=( )A . 1B .2C .3D .42. 已知关于x 的不等式组230320a x a x +>⎧⎨-≥⎩恰有3个整数解,则a 的取值范围是( )A .23≤a ≤32 B 。
43≤a ≤32 C .43<a ≤32 D .43≤a <323. 已知a b c d 满足20031200212001120001+=-=+=-d c b a 则a b c d 四个数的大小关系为( ) A . a >c >b >d ( B ) b 〉d 〉a >c (C ) d >b >a 〉c (D ) c 〉a >b >d 4. 已知x 为整数,且分式1222-+x x 的值为整数,则x 可取的值有( )A .1个B .2个C .3个D .4个 5. 要使a 5<a 3<a <a 2<a 4成立,则a 的取值范围是( )A .0<a <1B 。
a >1C 。
-1<a <0D . a <-16. 下列因式分解正确的是 ( )A .4x 2–4xy+y 2–1=(2x –y )2–1=(2x –y+1)(2x –y –1)B .4x 2–4xy+y 2–1=(2x –y )2–1=(2x –y+1)(2x+y –1)C .4x 2–4xy+y 2–1=(2x –y )2–1=(2x –y+1)(2x+y+1)D .4x 2–4xy+y 2–1=(2x+y)2–1=(2x+y+1)(2x+y –1) 7. 13。
数据8,10,12,9,11的平均数和方差分别是 ( )A .10和2B .10和2C .50和2D .50和28. 延长线段AB 到C,使得BC= AB ,则AC:AB=( )A .2:1B .3:1C .3:2D .4:39. 三角形三边之比为3:4:5,与它相似的另一个三角形的最短边为6cm ,则这个三角形的周长为( )A .12cmB .18cmC .24cmD .30cm10. 如图,已知梯形ABCD ,AD BC ∥,4AD DC ==,8BC =,点N 在BC 上,2CN =,E 是AB中点,在AC 上找一点M 使EM MN +的值最小,此时其最小值一定等于( ) A .6B .8C .4D .3二、填空题(每小题3分,共30分)AE BDN2. 若543zy x ==,则x z y x 562-+= .3. 若关于x 的不等式组⎪⎩⎪⎨⎧+++②m <x ①x >x 01456的解集为4x <,则m 的取值范围是 .4. 若不等式0432b <a x b a -+-)(的解集是49x >,则不等式032)4(b >a x b a -+-的解集是 .5. 数与数之间的关系非常奇妙.例如: ①21211=-,②34322=-,③49433=-,……根据式中所蕴含的规律可知第n 个式子是 .6. 如图,在梯形ABCD 中,AD ∥BC ,AB=AD=5cm ,CD=6cm,BC=10cm,E 是BC 上的一个动点,当四边形AECD 为平行四边形时,OA 的长为 cm ;7. 某数学课外实验小组想利用树影测量树高,他们在同一时刻测得一名身高为1。
八年级数学下学期第7周周末培优卷(无答案)北师大版
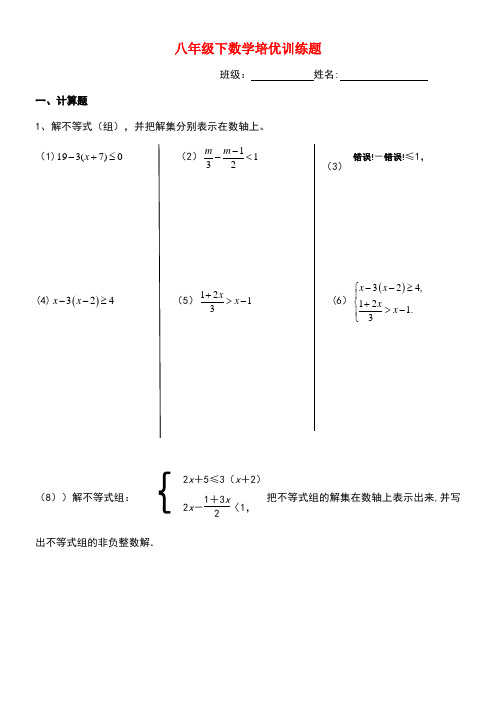
八年级下数学培优训练题班级: 姓名: 一、计算题1、解不等式(组),并把解集分别表示在数轴上。
(1)0)7(319≤+-x(2)1213<--m m (3)错误!-错误!≤1,(4)()324x x --≥ (5)1213x x +>- (6)()324,12 1.3x x x x --≥⎧⎪⎨+>-⎪⎩(8))解不等式组:{2x +5≤3(x +2)2x -1+3x 2〈1,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.BAFDEC二、填空题2、如果关于x 的不等式(a -1)x <a +5和2x <4的解集相同,则a 的值为________.3、 如图7,已知面积为1的正方形ABCD 的对角线相交于点O ,过点O 任作一条直线分别交AD BC ,于E F ,,则阴影部分的面积是 .4、 如图8所示,在平面内将Rt △ABC 绕直角顶点C 逆时针旋转90°得到Rt △EFC 。
若AB=5,BC=1,则线段BE 的长为 .5、 如图9,P 是正方形ABCD 内一点,将△ABP 绕点B 顺时针方向旋转一定的角度后能与△CB /P 重合.若PB=3,则P /P = .6、如图10,在正方形ABCD 中,E 为DC 边上的点,连结BE,将△BCE 绕点C 顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD 的度数为 .7、图11中两直线l 1与l 2的交点P 的坐标可以看成是方程组_________的解.图11三、解答题图7A E DOB 图108、在图12中,在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移.使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的像△A′B′C′(不写画法),并直接写出点B′、C′的坐标:B′( , )、C′(, );(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是( ,);(3)△ABC的面积为:_________.9、如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2.10、在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题:(1)将四边形ABCD先向左平移4个单位,再向下平移6个单位,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1;(2)将四边形A1B1C1D1绕点A1逆时针旋转90°,得到四边形A1B2C2D2,画出旋转后的四边形A1B2C2D2,并写出点C2的坐标.11、阅读下面材料:如图(1),把△ABC沿直线BC平行移动线段BC的长度,可以变到△DEC的位置;如图(2),以BC为轴,把△ABC翻折180º,可以变到△DBC的位置;如图(3),以点A为中心,把△ABC旋转180º,可以变到△AED的位置.像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.回答下列问题:①在下图中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使△ABE变到△ADF 的位置;②指图中线段BE与DF之间的关系,为什么?尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
北师大数学八下优辅难题培优

29级初二放学期数学优辅(8)--特别的平行四边形知识点概括:1.菱形:四条边相等的四边形。
(1)菱形拥有全部平行四边形的性质,其特别点在于:对角线相互垂直,对角线均分对角。
(2)菱形的对称性:菱形既是轴对称图形,也是(对称轴是对角线),它有两条对称轴。
( 3)在60°的菱形中,短对角线等于边长,长对角线是短对角线的 3 倍。
( 4)菱形的面积能够用对角线乘积的一半来计算。
对角线相互垂直,这个特征简单和勾股定理相联合。
2.矩形:四个角都是直角的四边形。
( 1)矩形拥有全部平行四边形的性质,其特别点在于: 四个角均为直角,对角线相等。
(2)矩形的对称性:矩形既是轴对称图形,也是(对称轴是任何一组对边中点的连线),它有两条对称轴。
3.正方形:四边相等且四个角都是直角的四边形。
(1)正方形拥有平行四边形的全部性质,切实的说,它是矩形和菱形的交集,所以拥有矩形和菱形的全部特征。
(2)正方形的对称性:既是,又是(有四条对称轴,分别是两条对角线和两条中点连线)。
( 3)正方形的两条对角线把正方形分红8 个等腰直角三角形。
典型例题解说及练习:例 1 已知菱形的一条对角线是另一条的对角线的 2 倍,面积为S,则它的边长是练习:________.1.边长为 13 的菱形 ABCD的对角线 BD长 10cm,则对角线 AC长为 _________, 面积是 ________.2.菱形两个邻角度数比是1: 3,边长是52,则高是 ________.3. 菱形 ABCD的周长为 16,一个内角为 60°,则这个菱形的两条对角线AC、BD的长度分别是 __________,菱形的面积是 __________.例 2 如图, CD为Rt ABC斜边 AB边上的高,BAC 的均分线交CD于 E,交 BC于 F,FG AB于G,求证:四边形EGFC是菱形。
练习:1.ABC中, AC的垂直均分线 MN交 AB于点 D,交 AC于点 O,CE AE CF 2 BDE BCF BEF BCF BDE AE BD 练习:1.在矩形 ABCD中,对角线 AC、 BD 订交于 O,AOB 60,AE均分BAD ,交BC于点E,则BOE =________.2.在矩形 ABCD中, E 为 BC中点,BAE30, AE=2, AC=________.3.在矩形 ABCD中 ,AD=12,AB=5,P 是 AD 上的动点,有PF BD,PE AC ,E、F为垂足,则PE+PF=__________.例 4练习1.2.3. 矩形 ABCD中, AB=12cm, BC=6cm,点 P 沿 AB边从点 A开始向 B 以 2cm/s的速度运动, Q沿 DA 边从点 D 向 A 以 1cm/s 的速度运动,若 P、Q同时出发, t 表示运动时间( 0<t<6 ).( 1)当 t 为什么值时,△ QAB是等腰三角形?D CQ( 2)试求四边形QABC的面积,并提出一个有关结论。
北师大八年级数学(下)全章节培优练习题

八年级数学下册培优讲稿、练习资料目录八年级数学下册培优讲稿、练习资料目录 (1)第一章一元一次不等式和一元一次不等式组 (3)不等关系、不等式的基本性质及解集 (3)知识要点 (3)易错易混点 (3)典型例题 (4)学习自评 (4)一元一次不等式、一元一次不等式与一次函数、一元一次不等式组 (6)知识要点 (6)易错易混点 (6)典型例题 (7)学习自评 (7)第二章分解因式 (14)分解因式 (14)知识要点 (14)易错易混点 (14)典型例题 (14)学习自评 (14)提公因式法、公式法 (16)知识要点 (16)易错易混点 (16)典型例题 (16)学习自评 (17)第三章分式 (19)分式 (19)知识要点 (19)易错易混点 (19)典型例题 (19)学习自评 (20)分式的乘除法、加减法 (21)知识要点 (21)易错易混点 (21)典型例题 (21)学习自评 (22)分式方程 (23)知识要点 (23)易错易混点 (24)典型例题 (24)学习自评 (25)第四章相似图形 (27)线段的比、黄金分割及形状相同的图形 (27)知识要点 (27)易错易混点 (28)典型例题 (28)学习自评 (29)相似多边形相似三角形及三角形相似的条件 (31)知识要点 (31)易错易混点 (31)典型例题 (31)学习自评 (33)相似形的应用、相似多边形的性质、图形的方法与缩小 (37)知识要点 (37)易错易混点 (38)典型例题 (38)学习自评 (40)第五章数据的收集与处理 (44)数据的收集 (44)知识要点 (44)易错易混点 (44)典型例题 (44)学习自评 (45)频数与频率、数据的波动 (47)知识要点 (47)易错易混点 (48)典型例题 (48)学习自评 (49)第六章证明(一) (53)肯定与否定定义与命题 (53)知识要点 (53)易错易混点 (53)典型例题 (54)学习自评 (55)平行线的判定及其性质三角形内角和定理、推论及应用 (58)知识要点 (58)易错易混点 (58)典型例题 (59)学习自评 (59)第一章 一元一次不等式和一元一次不等式组不等关系、不等式的基本性质及解集知识要点※要点1 不等式的概念及分类一般地,用符号“<”(或“≤”),“>”(或“≥”),≠,连接的式子叫做不等式。
北师大版数学八下培优4

初二年级数学培养试题(四)1、如图,已知梯形ABCD ,AD BC ∥,4AD DC ==,8BC =,点N 在BC 上,2CN =,E 是AB 中点,在AC 上找一点M 使EM MN +的值最小,此时其最小值一定等于( )A .6B .8C .4D .432、如图:矩形纸片ABCD ,AB=2,点E 在BC 上,且AE=EC .若将纸片沿AE 折叠,点B 恰好落在AC 上,则AC 的长是 .3、某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)如果工厂招聘)100(<<n n 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W (元)尽可能的少?4、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x (h ),两车之间的距离为y (km ),图中的折线表示y 与x 之间的函数关系.根据函数图象进行以下探究:信息读取 (1)甲、乙两地之间的距离为 km ;(2)请解释图中点B 的实际意义;图象理解 (3)求慢车和快车的速度; (4)求线段BC 所表示的y 与x问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?5、在平面直y ∕km B x ∕hO 12 A CD 900 4 AE B D A B C DE角坐标系中,一动点P (x ,y )从M (1,0)出发,沿由A (-1,1),B (-1,-1),C (1,-1),D (1,1)四点组成的正方形边线(如图①)按一定方向运动。
北师大版数学八下优辅(难题培优)(6)

分式与分式方程培优一、分式方程的解法1、不解下列方程,判断下列哪个数是方程21311323x x x x =+++--的解( ). A .x=1 B .x=-1 C .x=3 D .x=-3 2、关于x 的方程4332=-+x a ax 的解为x=1,则a=( )A 、1B 、3C 、-1D 、-33、当m = 时,方程1121=--+x m mx 的解与方程34=+x x 的解互为相反数. 4、当 时,分式1521221-++x x有意义5、已知分式xx x 2422+-的值为零,求x 的值 。
6、如果把代数式xyyx 22+中的x 和y 都扩大10倍,则分式的值( ) A. 扩大10倍 B.缩小10倍 C.缩小2倍 D. 不变A.不变B.扩大50倍C. 扩大10倍D.缩小到原来的10倍7、方程y x x =++13的整数解有 组。
8、解方程: (1) 2111x x x x ++=+ ⑵12241422-+=-+--xx x x x x9、已知,0232=--x x 求代数式11)1(23-+--x x x 的值 (3)51413121+-+=+-+x x x x (4)11117456x x x x +=+----10、(设参数法)已知432c b a ==,求cb a cb a +++-523的值12、(倒数法)已知三个数x ,y ,z 满足34,34,2-=+=+-=+x z zx z y yz y x xy ,求yxxz xy xyz++二、方程有增根、无解、正解、负解的问题:1、如果关于x 的方程xmx x -=--552无解,则m 等于( ) A.3 B. 4 C.-3 D.52、若方程xx x --=+-34731有增根,则增根为 . 3、若分式方程0123=---x ax 无解,那么a 的值应为 。
4、当k 时关于x 的方程4162222-=--+-x kx x x x 有解。
北师大版八年级下册数学培优试卷

八年级培优试卷(一)1.如图,矩形纸片ABCD 中,AB=12,BC=5,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,则AG 的长为__________2.如图所示,等边△ABC 内一点P 到三边距离分别为h 1,h 2,h 3,且h 1+h 2+h 3=3, 其中PD=h 1,PE=h 2,PF=h 3,则△ABC 的边BC 上的高为_________3.如图,一块四边形菜地ABCD ,已知∠B=90°,AB=9m ,BC=12m ,AD=8m ,CD=17m ,这块菜地的面积为________.4.若点M (x ,y )满足 2)(222-+=+y x y x ,则点M 所在的象限是( ) A. 第一象限或第三象限 B. 第二象限或第四象限 C. 第一象限或第二次象限 D. 不能确定5.化简aa 3-的结果是( )A.a 3- B. a 3 C. a 3-- D. 3-6. 若实数a 满足 1122=+-+a a a ,则a 的取值范围是( )A.B.C.D.7. 如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( ) A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<08. 若一次函数y=kx+b,当x 的值减小1,y 的值就减小2,则当x 的值增加2时,y 的值( ) A. 增加4 B. 减小4 C. 增加2 D. 减小29.一次函数y=ax+4与y=bx-2的图象在x 轴上相交于同一点,则ba的值是_______. 10. 直线y=2x+b 经过直线y=x-2与直线y=3x+4的交点,则b 的值为( ) A. -11 B. -1 C. 1 D. 611. 已知一次函数y=kx+b 的图象与y=2x+1的交点的横坐标为2,与直线y=-x-8的交点的纵坐标为-7,则直线y=kx+b 的表达式为__________12. 如图,在平面直角坐标系中,线段AB 的端点坐标为A (-1,2),B (3,1), 若直线y=kx-2与线段AB 有交点,则k 的值可能是( )A. -3B. -2C. -1D. 213. 如图,直线834+-=x y 与x 轴、y 轴分别交于A ,B 两点,则∠BAO 的平分线所在的直线AM 的解析式是( ) A. 2521+-=x y B. 321+-=x y C. 2721+-=x y D. 421+-=x yB D CA EF14. 已知一次函数y=kx+b的图象经过点(-3,3),且与x轴相交于点P,直线321+-=xy与x轴相交于点Q,点Q恰与点P关于y轴对称,则这个一次函数的表达式为( )A. y=x+6B. y=-x-6C. 231+-=xy D. y=-3x-615. 如图,直线AB: 121+=xy分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴、y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是( )A.25,3( B.(8,5) C. (4,3) D.45,21(16. 将一副三角尺按如图所示放置,已知AE∥BC,求∠AFD的度数。
八年级数学下学期第12周周末培优卷(无答案) 北师大版(2021年整理)

2016-2017学年八年级数学下学期第12周周末培优卷(无答案)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2016-2017学年八年级数学下学期第12周周末培优卷(无答案)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2016-2017学年八年级数学下学期第12周周末培优卷(无答案)北师大版的全部内容。
八年级下数学培优训练题班级: 姓名:一、计算题1、解不等式(组),并把解集在数轴上表示出来。
x x 21231)1(-≥- (2)⎪⎩⎪⎨⎧-≥+-<-x x x 2211322、分解因式(1)—4x 2—4y 2-8xy (2) (x 2+4) 2-16x 23、化简(1)323105a bc a b - = (2)a b b a -- = (3)22a a b ⎛⎫⎪-⎝⎭= 4、计算(1)xyyx x xy -÷-)2( (2) 43222)()()(a bc ab c c b a ÷-⋅-(3)24244422223-+-÷+-+-x x x x x x x x (4)222)11(11-+⋅-÷--m m m m m m m(5)22x x x x --+ (6)222)3(9)3(x yx y x -----(7)211x x x --- (8)22441m m m -+-÷21m m --+21m -5、先化简 )121(1212-+÷+-+x x x x ,然后从1,0,-1中选取一个你认为合适的数作为x 的值代入求值。
二、填空题1、当x =1时,分式nx mx -+2无意义,当x =4分式的值为零, 则n m +=__________. 2、分式35,3,x abx c ax b -的最简公分母是__________.3、计算=-+ab b a6543322 ;4、若ab=2,a+b=-1,则ba 11+ 的值为 ; 三、解答题1、如图,在平面直角坐标系中,△ABC 的三个顶点的坐标分别是A(﹣3,2),B(﹣1,4),C(0,2). (1)将△ABC 以点C 为旋转中心旋转180°,画出旋转后对应的△A 1B 1C;(2)平移△ABC,若A 的对应点A 2的坐标为(﹣5,﹣2),画出平移后的△A 2B 2C 2;(3)若将△A 2B 2C 2绕某一点旋转可以得到△A 1B 1C ,请直接写出旋转中心的坐标.2、如图,在△ABC 中,∠C=90°,∠B=30°,以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ,再分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ,连结AP 并延长交BC 于点D 求证:(1)点D 在AB 的中垂线上;(2)如果△ACD 的面积为1,求△ABD 的面积.BCNMA D BCNA D3、已知:正方形ABCD 中,∠MAN =45°,∠MAN 绕点A 顺时针旋转,它的两边分别交CB ,DC (或它们的延长线)于点M ,N .当∠MAN 绕点A 旋转到BM =DN 时(如图1),易证BM +DN =MN . (1)当∠MAN 绕点A 旋转到BM ≠DN 时(如图2),线段BM ,DN 和MN 之间有怎样的数量关系?写出猜想,并加以证明.(2)当∠MAN 绕点A 旋转到如图3的位置时,线段BM ,DN 和MN 之间又有怎样的数量关系?并说明理由.图1 图2 图3MBC NA D。
北师大版数学八下优辅(难题培优)()

29级初二下学期数学优辅(1)一元一次不等式【典例示范】例1、要使a 5<a 3<a <a 2<a 4成立,则a 的取值范围是( )A.0<a <1B. a >1C.-1<a <0D. a <-1 例2、已知6<a <10,2a≤b ≤a 2,b a c +=,则c 的取值范围是 。
例3、若不等式0432b <a x b a -+-)(的解集是49x >,则不等式的解集是0324b >a x b a -+-)( 。
例4、设7321x x x x ,,,, 均为自然数,且76321x x x x x <<<<< ,又201721=+++x x x ,则21x x +的最大值是 。
例5、设实数a 、b 、c 满足a <b <c (ac <0),且|c |<|b |<|a |,则|x -a |+|x -b |+|x +c |的最小值是( ) (A )3|c b a |++ (B )|b | (C )c -a (D )―c ―a例6、三角形的三条边各不相同,并且其三条高都是整数,其中有两条高分别是3和10,那么第三条高的长度为__________.【练习巩固】 一、选择题1、如果a 、b 表示两个负数,且a <b ,则 ( ).(A)1>ba(B)ba<1 (C)ba 11< (D)ab <12、a 、b 是有理数,下列各式中成立的是 ( ).(A)若|a |≠|b |,则a ≠b (B)若a 2>b 2,则a >b(C)若a ≠b ,则|a |≠|b | (D)若a >b ,则a 2>b 23、|a |+a 的值一定是( ).(A)大于零 (B)小于零 (C)不大于零 (D)不小于零4、若不等式(a +1)x >a +1的解集是x <1,则a 必满足( ).(A)a <0 (B)a >-1 (C)a <1 (D)a <-1 5、若由x <y 可得到ax ≥ay ,应满足的条件是 ( ).(A)a ≥0 (B)a ≤0 (C)a >0 (D)a <06、某市出租车的收费标准是:起步价7元,超过3km 时,每增加1km 加收2.4元(不足1km 按1km 计).某人乘这种出租车从甲地到乙地共支付车费19元,设此人从甲地到乙地经过的路程是x km ,那么x 的最大值是 ( ).(A)11 (B)8 (C)7 (D)5 7、若不等式组⎩⎨⎧>≤<k x x ,21有解,则k 的取值范围是 ( ).(A)k <1 (B)k ≥2(C)k <2(D)1≤k <28、不等式组⎩⎨⎧+>+<+1,159m x x x 的解集是x >2,则m 的取值范围是( ).(A)m ≤2 (B)m ≥2(C)m ≤1(D)m ≥1二、填空题9、对于整数a ,b ,c ,d ,定义bd ac c d b a -=,已知3411<<d b,则b +d 的值为_________. 10、如果-a 2x >-a 2y (a ≠0).那么x ______y . 11、若x 是非负数,则5231x-≤-的解集是______. 12、已知(x -2)2+|2x -3y -a |=0,y 是正数,则a 的取值范围是______. 13、6月1日起,某超市开始有偿..提供可重复使用的三种环保购物袋,每只售价分别为1元、2元和3元,这三种环保购物袋每只最多分别能装大米3千克、5千克和8千克.6月7日,小星和爸爸在该超市选购了3只环保购物袋用来装刚买的20千克散装大米,他们选购的3只环保购物袋至.少.应付给超市______元. 14、试用m 表示出不等式(5-m )x >1-m 的解集______.三、解下列不等式(组)15、 ).1(32)]1(21[21-<---x x x x⋅->+-+2503.0.02.003.05.09.04.0x x x16、解不等式组⎪⎩⎪⎨⎧-<-->-->+.3273,4536,7342x x x x x x四、解答题17、适当选择a 的取值范围,使1.7<x <a 的整数解:(1) x 只有一个整数解; (2) x 一个整数解也没有.18、已知A =2x 2+3x +2,B =2x 2-4x -5,试比较A 与B 的大小.19、某次数学竞赛活动,共有16道选择题,评分办法是:答对一题给6分,答错一题倒扣2分,不答题不得分也不扣分.某同学有一道题未答,那么这个学生至少答对多少题,成绩才能在60分以上?20、若干名学生,若干间宿舍,若每间住4人将有20人无法安排住处;若每间住8人,则有一间宿舍的人不空也不满.问学生有多少人?宿舍有几间?附加题:1.3|x-1|+2≥|x-1|+52.求不等式|x |>|x+5|的解集3.已知|x-1|+|x-5|=4,求x 的取值范围。
北师大版数学八下优辅(难题培优)(6)-精选.pdf

分式与分式方程培优一、分式方程的解法1、不解下列方程,判断下列哪个数是方程21311323x x xx的解().A .x=1B .x=-1 C.x=3 D.x=-32、关于x 的方程4332xaax 的解为x=1,则a=()A 、1B 、3C 、-1D 、-33、当m =时,方程1121x m mx 的解与方程34xx 的解互为相反数.4、当时,分式1521221x x 有意义5、已知分式xxx2422的值为零,求x 的值。
6、如果把代数式xyyx 22中的x 和y 都扩大10倍,则分式的值()A.扩大10倍B.缩小10倍C.缩小2倍D. 不变变式:如果把分式yxx 5的x 与y 都扩大10倍,那么这个代数式的值()A.不变B.扩大50倍C. 扩大10倍D.缩小到原来的10倍7、方程y x x 13的整数解有组。
8、解方程:(1)2111x x x x⑵12241422xx xx x x 9、已知,0232x x求代数式11)1(23x xx 的值(3)51413121xxxx (4)11117456x xxx10、(设参数法)已知432c b a ,求cbac b a 523的值12、(倒数法)已知三个数x ,y ,z 满足34,34,2x z zxz yyz yxxy ,求yxxz xy xyz 二、方程有增根、无解、正解、负解的问题:1、如果关于x 的方程xm x x 552无解,则m 等于()A.3B. 4C.-3D.52、若方程xx x34731有增根,则增根为 .3、若分式方程0123xax 无解,那么a 的值应为。
4、当k时关于x 的方程4162222xk xx x x 有解。
5、若关于x 的方程313292xx xm 有增根, 则增根是多少?产生增根的m 值又是多少?7、若关于x 的方程11122xx xkxx 不会产生增根,求k 的值。
8、知关于x 的方程323x m x x 解为正数,求m 的取值范围.9、当a 为何值时,)1)(2(21221x x ax x x x x 的解是负数?4、分式方程622132x xm xxx xx 的解不小于1,求m 的取值范围。
2022—2023学年北师大版数学八年级下册期末综合培优检测试题

2023学年北师大版八年级下册数学期末综合培优检测试题一、单选题1.一个凸多边形的每一个内角都等于150°,则这个多边形所有对角线的条数共有( )4353.下列说法正确的有( )∥4x =是31x ->的解;∥不等式30x -<的解有无数个;∥5x >是不等式23x +>的解集;∥3x =是21x +>的解;∥不等式25x +<有无数个正整数解;A .1个B .2个C .3个D .4个4.如图,ABC 中,36BAC ∠=︒,将ABC 绕点A 按顺时针方向旋转70︒,得到''AB C ,则'BAC ∠的度数为( )A .0B .6C .-6D .6±6.下列说法正确的是( )A .甲、乙两人10次测试成绩的方差分别是224,14S S ==甲乙,则乙的成绩更稳定7.如图,是ABC 中DE 垂直平分AC 边,若10cm BC =,6cm AB =,则ABD △的周长为( )A .2x =-B .2x =C .1222x x ==,D .以上答案都不对 9.下列长度的三条线段能组成直角三角形的是( )A .1,1,2B .1,2,3C .3,4,5D .5,10,13 10.下列四种基本尺规作图分别表示,则对应选项中作法错误的是( )A . 作一个角等于已知角B . 作一个角的平分线C . 作一条线段的垂直平分线D . 过直线外一点P 作已知直线的垂线二、填空题14.正多边形的一个内角的度数恰好等于它的外角的度数的3倍,则这个多边形的边数为.15.如图,等边三角形ABC的顶点在坐标轴上,边长为4,则点A的坐标是.16.如图,ABCD的对角线AC、BD相交于点O,且AC+BD=14,AB=4.则∥OCD的周长为.三、解答题个单位,ABC的顶点(1)在图∥中画出ABD △,使ABD △与ABC 关于直线AB 轴对称.(2)在图∥中画出MNF ,MNF 是由ABC 先向上平移1个单位,再向右平移2个单位得到;在平移过程中,线段AB 扫过的面积为___________.21.已知:如图1,∥ABC 中,AB =AC ,P 是BC 的中点,PD ∥AB ,PE ∥AC ,垂足分别是D 、E ,过点C 作直线AB 的垂线,垂足是F .(1)若∥BAC =120°,求证:PD +PE =CF ;(2)若∥BAC =100°,(1)中的结论是否仍然成立?并说明理由.(3)如图2,∥ABC 中,AB=AC ,P 是BC 边上任意一点,PD ∥AB ,PE ∥AC ,垂足分别是D 、E ,已知∥ABC 的面积为15,AB =6,则PD +PE =_____.22.解不等式组:()62318x x x <-+⎧⎨+≥⎩,并将不等式组的解集表示在如图所示的数轴上.23.如图,在平面直角坐标系中,点A (0,b ),点B (a ,0),点D (2,0),其中a 、b 满足 DE∥x 轴,且∥BED=∥ABO,直线AE 交x 轴于点C .(1)求A 、B 两点的坐标;(2)求直线AE的解析式;(3)若以AB为一边在第二象限内构造等腰直角三角形∥ABF,请直接写出点F的坐标.。
北师大版八年级下册数学培优试卷两套

EFD C B A EDBA试卷(一)一、选择题(每小题3分,共24分)1.如图2所示,如要将图(1)变成(2),可经过的变换是( )A .旋转、平移B .对称、旋转C .平移、旋转D .旋转、旋转2.下列几何图形中,既是轴对称图形又是中心对称图形的是( )A .等边三角形B .矩形C .平行四边形D .等腰梯形3.下列代数式:2x ,5x y +,11x -,12a -,1x π-,2xx A .2个B .3个C .4个D .5个4.若把分式2x y x+中的x ,y 都扩大为原来的2倍,则该分式的值( ) A .扩大为原来的2倍 B .缩小为原来的12 C .不变 D .5.若a b >,则下列不等式不一定成立的是( )A .a m b m +>+B .22(1)(1)a m b m +>+ C .22a b -<- D .22a b >6.下列多项式中,不能用平方差公式分解因式的是( )A .22x y -B .22x y --C .224x y -D .24y -+7.小玲家有不到40只鸡要放入家里的鸡笼中,若每个鸡笼里放4只,则有一只鸡无笼可放;若每个鸡笼里放5只,则有一笼无鸡可放,且有一笼中的鸡不足3只.小玲家有多少只鸡?多少个鸡笼?( )A .41,10B .36,9C .37,9D .38,98.如图,已知直线y kx b =+经过A (2-,1-),B (1,2)两点,则不等式组122x kx b <+<的解集为( ) A .122x << B .112x <<C .21x -<<D .112x -<<二、填空题(每小题3分,共21分)9.已知当2x =-时,分式x b x a -+无意义,当6x =时,该分式的值为0,则3a b ⎛⎫= ⎪⎝⎭___________.10.若112x y-=,则55x xy yx xy y +-=--______________. 11.若方程61(1)(1)1mx x x -=+--有增根,则m 的值为_________________.12.用反证法证明“在直角三角形中,至少有一个锐角不大于45°”时,应假设________________________________________________.13.若关于x 的不等式组3132>1x a x -⎧⎨--⎩≥有且只有3个整数解,则a 的取值范围是_____________.15.如图,在△ABC 中,∠BAC 的平分线交BC 于点D ,AD 的垂直平分线交AB 于点F ,交BC 的延长线于点E .则下列结论:①∠EAD =∠EDA ;②DF ∥AC ;③AD =AE ;④∠EAC =∠B .其中正确的有_____________________.(填写序号)三、解答题(本大题共6小题,满分55分)16.(8分)解不等式组12(1)532122x x x --⎧⎪⎨-<+⎪⎩≤,并把它的解集在数轴上表示出来. 17.(8分)把下列各式分解因式.(1)3223a ab ab b +--;(2)229()4(2)x y x y +--.18.(9分)化简分式2221121xx x x x x x x -⎛⎫-÷ ⎪---+⎝⎭,并从13x -≤≤中选取一个你认为合适的整数x 代入求值.19.(10分)解下列分式方程.(1)33122x x x-+=--; (2)2133193x x x +=--. 20.(9分)如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,∠BAC =90°,∠CED =45°,∠DCE =30°,DE =BE =CD 的长及四边形ABCD 的面积.21.(11分)某农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A ,B 两地区收割小麦,其中30台派往A 地区,20台派往B 地区.两地区与该农机租赁公司商定的每天租赁价格如下表:(1)设派往A 地区x 台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金总额为y 元,求y 与x 之间的函数关系式,并写出x 的取值范围.(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,则有多少种租赁方案?请将各种方案设计出来.(3)如何设计方案,才能使租赁公司这50台联合收割机一天获得的租金总额最高?3分,共24分)N1M1ED CBAFEDBAEDCBA1.下列代数式:1x,3a b+,32xπ,22a ba b-+,15m+,其中属于分式的有()A.1个B.2个C.3个D.4个2.下列各式从左到右的变形属于因式分解的是()A.22(1)2x x x x--=--B.22()()a b a b a b+-=-C.24(2)(2)x x x-=+-D.111x xx⎛⎫-=-⎪⎝⎭3.若0a b>>,则下列不等式不一定成立的是()A.ac bc>B.a c b c+>+C.11a b<D.2ab b>4.下列运算正确的是()A.y yx y x y=----B.2233x yx y+=+C.22x yx yx y+=++D.221y xx y x y-=--+5.如图,在44⨯的正方形网格中,△MNP绕某点旋转一定的角度得到△M1N1P1,则其旋转中心是()A.点A B.点B C.点C D.点D6.用反证法证明“一个三角形中至多有一个钝角”时,应假设()A.一个三角形中至少有两个钝角B.一个三角形中至多有一个钝角C.一个三角形中至少有一个钝角D.一个三角形中没有钝角7.用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装满8吨,则最后一辆汽车不满也不空.那么汽车共有()A.5辆B.6辆C.7辆D.8辆8.如图,已知直线y kx b=+经过A(2,1),B(1-,2-)两点,则不等式组122kx b x-<+<的解集为()A.1x<-或2x>B.21x-<<C.12x-<<D.2x>二、填空题(每小题3分,共21分)9.有意义,则x的取值范围是_________________.10.分解因式:32242a a a-+-=_____________________.11.已知113x y-=,则代数式21422x xy yx xy y----的值为__________.12.若关于x的不等式组721x mx+<⎧⎨-⎩≤的整数解共有4个,则m的取值范围是______________.13.若关于x的分式方程7311mx x+=--有增根,则m的值为_____________.14.如图,在矩形ABCD中,AB=2BC,点E在CD边上,且AE=AB,则∠EBC=________.15.如图,在△ABC中,已知AB=AC,点D,E分别在边AB,AC上,且DE垂直平分AB,BE⊥AC.若AF⊥BC于点F,则∠EFC=__________.三、解答题(本大题共6小题,满分55分)16.(8分)如图,在平面直角坐标系xOy中,已知点A,B,C的坐标分别为A(2-,3),B(3-,1),C(1-,2).(1)将△ABC向右平移4个单位,再向下平移2个单位,画出平移后的△A1B1C1;(2)将△ABC绕原点O逆时针旋转90°,画出旋转后的△A2B2C2.17(8分)解不等式组253(1)1132x xx x--⎧⎪-⎨-<⎪⎩≥,并把它的解集表示在数轴上.18.(8分)先化简:2344111x xxx x-+⎛⎫-+÷⎪++⎝⎭,然后从12x-≤≤中选取一个合适的整数x代入求值.19.(10分)解下列分式方程.(1)21124xx x-=--;(2)5412524236x xx x-+-=--.20.(10分)如图,在△ABC中,∠BAC=120°,以BC为边向外作等边三角形BCD,把△ABD绕点D按顺时针方向旋转60°,得到△ECD.若AB=3,AC=2,求∠BAD的度数及AD的长.21.(11分)某工程机械厂根据市场需求,计划生产A,B两种型号的大型挖掘机共100台.已知该厂所筹生产资金不少于22 400万元,但不超过22 500万元,所筹资金全部用于生产这两种型号的挖掘机,且所生产的挖掘机可全部售出.这两种型号挖掘机的生产成本和售价如下表:(1)该厂有哪几种生产方案?(2)该厂如何安排生产这两种型号的挖掘机,才能获得最大利润?(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(0m>),则该厂如何安排生产这两种型号的挖掘机,才能获得最大利润?一、选择题(每小题3分,共24分)1.下列各式属于最简分式的是()FEDGCBAA .22x y xB .4xπC .222244x y x y -+ D .22244x y xy x-- 2.下列图形中,既是轴对称图形又是中心对称图形的有( )A .4个B .3个C .2个D .1个3.已知不等式(1)2a x +>的解集是1x <-,则( )A .2a >B .3a -≤C .3a =D .3a =-4.若a ,b ,c 为△ABC 的三边长,且满足2222()()ac bc a b a b -=-+,则△ABC 是( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形5.在如图所示的单位正方形网格中,△ABC 经过平移后得到△A 1B 1C 1,已知AC 边上的点P (2.4,2)经过平移后的对应点为P 1,将点P 1绕点O 逆时针旋转180°,得到点P 2,则点P 2的坐标为( )A .( 1.6-,1-)B .(1.6,1)C .( 1.4-,1-)D .(1.4,1)6.下列命题的逆命题错误的是( )A .相等的角是对顶角B .到线段两端距离相等的点在这条线段的垂直平分线上C .全等三角形的对应角相等D .角平分线上的点到这个角两边的距离相等7.若不等式组1240x ax +>⎧⎨-⎩≤有解,则a 的取值范围是( )A .3a ≤B .3a <C .2a <D .2a ≤8.一段坡路,小明骑自行车上坡时的速度为每小时v 1千米,下坡时的速度为每小时v 2千米,则他在这段坡路上的平均速度为每小时( )千米.A .122v v + B .1212v v v v +C .12122v v v v + D .无法确定二、填空题(每小题3分,共21分)9..若分式1(3)(1)x x x -+-的值为0,则x 的值为_________________.10.若5x y +=,2xy =,则32232x y x y xy ++=________________.11.若关于x ,y 的方程组332x y kx y +=⎧⎨+=⎩的解满足1x y +>,则k 的取值范围是______________.12.如图,在△ABC 中,∠BAC 的平分线交BC 于点D ,DF ⊥AB 于点F ,点E ,G 分别在边AB ,AC上,且DE =DG .若△ADG 和△ADE 的面积分别为50和39,则△EDF 的面积为______________.13.如图,在Rt △ABC 中,∠C =90°,∠B =50°,点D 在BC 边上,且BD =2CD .把△ABC 绕着点D 逆时针旋转m (0180m <<)度后,若点B 恰好落在初始Rt △ABC 的边上,则m 的值为_________________.14.若关于x 的分式方程211x ax -=-的解是正数,则a 的取值范围是____________________. 15.如图,直线1y mx =与直线2y kx b =+交于点P (2,1),则不等式组12mx kx b -<<+的解集为三、三、解答题(本大题共6小题,满分55分)16.(8分)解不等式组331213(1)8x x x x-⎧+>+⎪⎨⎪---⎩≤,并把它的解集在数轴上表示出来.17.(8分)把下列各式因式分解.(1)22344xy x y y --;(2)22222()4a b a b +-.18.(9分)先化简,再求值:352242a a a a -⎛⎫÷-- ⎪--⎝⎭,其中3a =.(9分)已知:线段a .19.求作:△ABC ,使AB =AC ,且BC a =,高32AD a =.20.(10分)当k 为何值时,分式方程26251x k x x x x+=---有增根?21.(11分)某公司有A 型产品40件,B 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品时每件的利润(元)如下表:(1)设分配给甲店x 件A 型产品,这家公司卖出这100件产品的总利润为W (元),求W 与x 之间的函数关系式,并求出x 的取值范围.(2)若公司要求总利润不低于17 560元,请你为这家公司设计销售方案,并分析哪种方案所获利润最多.(3)为了促销,公司决定对甲店A 型产品让利销售,每件让利a 元,但让利后A 型产品的每件利润仍高于甲店B 型产品的每件利润.若甲店的B 型产品及乙店的A ,B 型产品的每件利润均不变,该公司又如何设计销售方案,才能使总利润达到最大?模拟试卷(一)(北师版)参考答案一、选择题 1.A2.B3.C4.B 5.D6.B7.C8.C二、填空题aC9.12710.3 11.3 12.在直角三角形中,两个锐角都大于45° 13.74a -<-≤ 14.(2-,0)或(1-, 15.①②④三、解答题16.13x -<≤,解集在数轴上的表示略. 17.(1)2()()a b a b +-; (2)(5)(7)x y x y -+.18.原式1x x =+,当2x =时,原式23=.(或当3x =时,原式34=.此题中x 只能取2或3)19.(1)1x =; (2)原方程无解.20.CD 的长为2,四边形ABCD的面积为3(32+.21.(1)20074000y x =+(1030x ≤≤,且x 为整数)(2)共有3种租赁方案.方案一,派往A 地区2台甲型联合收割机,28台乙型联合收割机;派往B 地区18台甲型联合收割机,2台乙型联合收割机.方案二,派往A 地区1台甲型联合收割机,29台乙型联合收割机;派往B 地区19台甲型联合收割机,1台乙型联合收割机.方案三,派往A 地区0台甲型联合收割机,30台乙型联合收割机;派往B 地区20台甲型联合收割机,0台乙型联合收割机.(3)选择方案三,才能使租赁公司这50台联合收割机一天获得的租金总额最高,即派往A 地区0台甲型联合收割机,30台乙型联合收割机;派往B 地区20台甲型联合收割机,0台乙型联合收割机.模拟试卷(二)(北师版)参考答案一、选择题 1.C2.C3.A4.D 5.B6.A 7.B 8.C 二、填空题9.1x ≥且2x ≠ 10.22(1)a a -- 11.4 12.76m -<-≤ 13.7 14.15° 15.45° 三、解答题 16.作图略. 17.32x -<-≤,解集在数轴上的表示略.18.原式22x x +=--,当0x =时,原式1=.(或当1x =时,原式3=.此题中x 只能取0或1)19.(1)32x=-; (2)原方程无解. 20.∠BAD =60°,AD =5. 21.(1)该厂共有3种生产方案.方案一,生产A 型号挖掘机38台,B 型号挖掘机62台; 方案二,生产A 型号挖掘机39台,B 型号挖掘机61台; 方案三,生产A 型号挖掘机40台,B 型号挖掘机60台.(2)按方案一安排生产,即生产A 型号挖掘机38台,B 型号挖掘机62台,才能获得最大利润.(3)当010m <<时,按方案一安排生产,即生产A 型号挖掘机38台,B 型号挖掘机62台,能获得最大利润;当10m =时,3种方案所获利润相同;当10m >时,按方案三安排生产,即生产A 型号挖掘机40台,B 型号挖掘机60台,能获得最大利润.模拟试卷(三)(北师版)参考答案一、选择题1.C2.C3.D4.D 5.B6.C7.B8.C二、填空题9.1- 10.50 11.2k> 12.11213.80或120 14.1a >且2a ≠ 15.12x -<<三、解答题16.21x -<≤,解集在数轴上的表示略. 17.(1)2(2)y x y --; (2)22()()a b a b +-.18.原式12(3)a =-+,当3a =时,原式6=-.19.作图略.20.当k 的值为52-或52时,原分式方程有增根. 21.(1)2016800W x =+(1040x ≤≤,且x 为整数)(2)共有3种销售方案.方案一,分配给甲店38件A 型产品,32件B 型产品;分配给乙店2件A 型产品,28件B 型产品. 方案二,分配给甲店39件A 型产品,31件B 型产品;分配给乙店1件A 型产品,29件B 型产品. 方案三,分配给甲店40件A 型产品,30件B 型产品;分配给乙店0件A 型产品,30件B 型产品.其中方案三所获利润最多.(3)当020a <<时,分配给甲店40件A 型产品,30件B 型产品;分配给乙店0件A 型产品,30件B 型产品,可使总利润达到最大.当20a =时,无论怎样分配总利润都一样.当2030a <<时,分配给甲店10件A 型产品,60件B 型产品;分配给乙店30件A 型产品,0件B 型产品,可使总利润达到最大.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学综合测试题(北师大版·八年级)
一、选择题(每小题3分,共30分)
1. 若21
=+x
x ,则221x
x
+
=( )
A . 1
B .2
C .3
D .4
2. 已知关于x 的不等式组230
320a x a x +>⎧⎨-≥⎩
恰有3个整数解,则a 的取值范围是( )
A .
23≤a ≤32 B . 43≤a ≤32 C .43<a ≤32 D .43≤a <3
2
3. 已知a b c d 满足
2003
1
200212001120001+=
-=+=-d c b a 则a b c d 四个数的大小关系为( ) A . a >c >b >d ( B ) b >d >a >c (C ) d >b >a >c (D ) c >a >b >d 4. 已知x 为整数,且分式
1
222-+x x 的值为整数,则x 可取的值有( )
A .1个
B .2个
C .3个
D .4个 5. 要使a 5<a 3<a <a 2<a 4成立,则a 的取值范围是( )
A .0<a <1
B . a >1
C .-1<a <0
D . a <-1
6. 下列因式分解正确的是 ( )
A .4x 2–4xy+y 2–1=(2x –y)2–1=(2x –y+1)(2x –y –1)
B .4x 2–4xy+y 2–1=(2x –y)2–1=(2x –y+1)(2x+y –1)
C .4x 2–4xy+y 2–1=(2x –y)2–1=(2x –y+1)(2x+y+1)
D .4x 2–4xy+y 2–1=(2x+y)2–1=(2x+y+1)(2x+y –1) 7. 13. 数据8,10,12,9,11的平均数和方差分别是 ( )
A .10和2
B .10和2
C .50和2
D .50和2
8. 延长线段AB 到C,使得BC= AB,则AC:AB=( )
A .2:1
B .3:1
C .3:2
D .4:3
9. 三角形三边之比为3:4:5,与它相似的另一个三角形的最短边为6cm ,则这个三角形的周长为( )
A .12cm
B .18cm
C .24cm
D .30cm
10. 如图,已知梯形ABCD ,AD BC ∥,4AD DC ==,8BC =,点N 在BC 上,2CN =,E 是
AB 中点,在AC 上找一点M 使EM MN +的值最小,此时其
最小值一定等于( ) A .6
B .8
C .4
D .3二、填空题(每小题3分,共30分)
1. 因式分解:x 3–4x= .
2. 若543z
y x =
=,则x z y x 562-+= .
A
E B
D
N
3. 若关于x 的不等式组⎪⎩⎪⎨⎧+++②
m <x ①x >x 01456的解集为4x <,则m 的取值范围是 。
4. 若不等式0432b <a x b a -+-)(的解集是
49
x >
,则不等式032)4(b >a x b a -+-的解集
是 。
5. 数与数之间的关系非常奇妙.例如: ①
21211=-
,②34322=-,③49433=-,……
根据式中所蕴含的规律可知第n 个式子是 .
6. 如图,在梯形ABCD 中,AD ∥BC,AB=AD=5cm ,CD=6cm ,BC=10cm ,E 是BC 上的一个动点,
当四边形AECD 为平行四边形时,OA 的长为 cm ;
7. 某数学课外实验小组想利用树影测量树高,他们在同一时刻测得一名身高为1.5米的同学落在地面
上的影子长为1.35米,因大树靠近一幢大楼,影子不会落在地面上(如图),他们测得地面部分的影子BC=3.6米,墙上影长CD=1.8米,则树高AB= 米.
A
B
C
D
O
E A
B
D
C
第7题 第8题
8. 如果 ,则 , 。
9. 已知 ,则
10. 已知:x:y:z=3:4:5,且x+y-z=6,则:2x-3y+2z= 三、计算题(每小题8分,共24分)
1. 因式分解:(1)2
221
2
1b ab a +- (2)x 4+4 (3)(x2+9y2)2–36x2y2
2. 18.(5分)解不等式组:⎪⎩⎪⎨⎧->-<--x
x x x 25)12(312
3
,并把解集在数轴上表示出来.
3. 19.化简:
⎪⎪⎭⎫ ⎝⎛-•⎪⎪⎭⎫ ⎝⎛--+y x x y y x y x 11
四、解答题(共66分)
1. 如图已知:△ABC 中,F 分AC 为1:2两部分,D 为BF 中点,AD 的延长线交BC 于E.求:BE:EC
2. 已知:如图,△ABC 中,AE =CE ,BC =CD ,求证:ED =3EF 。
3. 如图5—19,已知CE 、CB 分别是△ABC 和△ADC 的中线,且
AB=AC .求证:CD=2CE .(8分)
4. 甲、乙两个施工队各有若干名工人,现两施工队分别从东西两头同时修一条公路,甲队有1人每
A
B
C
D
E
F
x
y E
11
D C
B
A
O 天修路6米,其余每人每天修路11米;乙队有1人每天修路7米,其余每人每天修路10米.已知两队每天完成的工作量相同,且每队每天修路的工作量不少于100米也不超过200米,问甲、乙两队各有多少人?(10分)
5. 已知:如图,平面直角坐标系中,A (1,0),B (0,1),C (-1,0),过点C 的直线l 绕点C 旋
转,交y 轴于点D ,交线段AB 于点E.(10分) (1)求∠OAB 的度数及直线AB 的解析式; (2)若△OCD 与△BDE 的面积相等, ① 求直线CE 的解析式;
② 若y 轴上一点P 满足∠APE=45°,请直接写出P 点的坐标.
6. 图1、图2中,点C 为线段AB 上一点,△ACM 与△CBN 都是等边三角形.(12分)
(1) 如图1,线段AN 与线段BM 是否相等?证明你的结论;
(2) 如图2,AN 与MC 交于点E ,BM 与CN 交于点F ,探究△CEF 的形状,并证明你的结论.
图2
图1。
