辽宁省锦州市高二数学下学期期末考试试题 理(含解析)
辽宁省锦州市高二下学期期末考试(数学理).pdf

Lesson 4 The Wish Fill in the blanks with proper prepositions: Start each line in your poem _____ a word related ______ the scene. When others are speaking, you’d better listen _______ interruption. This song is ________ nature. Can you describe what is happening _______ this place_______ this moment? I know/learn it _______ heart. A Haiku is just a description ________ a scene. Let’s start this lesson ________ a song. to without about in at by of with with 根据句意用方框中词语的适当形式完成句子,每空一词: clear sleep expect simple poem form as set dark 1. I was too_______ to hear what he said. 2. Li Bai is one of the most famous _________ in China. 3. The teacher spoke very _________ so that we could hear every word. 4. The ____________ accident surprised everyone. 5. I _______ want to know what is happening in this place. 6. My uncle is __________ a policeman. 7. Haiku is an old ________ of Japanese poetry. 8. They do not tell a story, ______ some poems do. 9. A _______ number of chickens are killed every day. 10. The classroom is too _______ that I can’t see anything. sleepy poets clearly unexpected simply simply form as set dark A task: Fill in the blanks! Haiku Snow is very (so) _________(colour). See me run through it _______(adverb with ly at the end), It makes me feel _________(temperature). I wish I had a cherry without a stone. I wish I had a chicken without a bone. I wish I knew a story without an end. I wish I knew a language with no speaking. How can there be a cherry without a stone? How can there be a chicken without a bone? How can there be a story without an end? How can there be a language with no speaking? Enjoy the words of the song: 我希望我有一棵没有核的樱桃。
2020届辽宁省锦州市高二下学期期末数学(理)试题 解析版

绝密★启用前数学(理)试题一、单选题1.已知集合{}12,3A x y x B x x -⎧⎫===≥⎨⎬⎩⎭,则()R A C B =I ( )A .[)0,3B .(0,3)C .()3,+∞D .()0,∞+【答案】B 【解析】 【分析】先分别化简集合A,B,再利用集合补集交集运算求解即可 【详解】12A x y x -⎧⎫==⎨⎬⎩⎭=()0,∞+{}3B x x =≥=[3,)(,3]+ト-? ,则()0,3R A C B ⋂=()故选:B 【点睛】本题考查集合的运算,解绝对值不等式,准确计算是关键,是基础题 2.设i 为虚数单位,复数11ii i++-等于( ) A .2i - B .2iC .1i -+D .0【答案】B 【解析】 【分析】利用复数除法和加法运算求解即可 【详解】11i i i ++=-()2122i i i ++= 故选:B 【点睛】本题考查复数的运算,准确计算是关键,是基础题3.已知22,0()log ,0x x f x a x x ⎧<=⎨+≥⎩,若((1))1f f -=-.则实数a 的值为( )A .-2B .2C .0D .1【答案】C4.0sin xdx π⎰的值为( )A .2B .0C .-2D .1【答案】A5.若方程2210ax x -+=在区间(-1,1)和区间(1,2)上各有一根,则实数a 的取值范围是( ) A .31a -<<B .314a << C .334a -<<D .3a <-或34a >【答案】B6.若log 0.5log 0.50m n >>,则( ) A .1m n << B .1m n << C .1n m << D .1n m <<【答案】D7.已知过点(1,1)P 且与曲线3y x =相切的直线的条数有( ). A .0 B .1C .2D .3【答案】C8.2nx ⎫⎪⎭的展开式中的第7项是常数,则正整数n 的值为( )A .16B .18C .20D .22【答案】B9.甲、乙两位同学各自独立地解答同一个问题,他们能够正确解答该问题的概率分别是25和12,在这个问题已被正确解答的条件下,甲、乙两位同学都能正确回答该问题的概率为( ) A .27B .15C .29D .910【答案】A10.甲、乙、丙、丁四名同学组成一个4⨯100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( ) A .甲 B .乙C .丙D .丁【答案】C 11.函数ln ()(e 2.7128)exx f x ==L 的大致图象是( )A .B .C .D .【答案】A12.对于函教2()e (1)(2)xf x x x =--,以下选项正确的是( ) A .1是极大值点 B .有1个极小值C .1是极小值点D .有2个极大值【答案】A第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人 得分二、填空题13.幂函数()()222133m m f x m m x -+=-+在区间()0,∞+上是增函数,则m =________.【答案】214.若对甲、乙、丙3组不同的数据作线性相关性检验,得到这3组数据的线性相关系数依次为0.83,0.72,-0.90,则线性相关程度最强的一组是_______.(填甲、乙、丙中的一个) 【答案】丙15.将1,2,3,4,5,这五个数字放在构成“W ”型线段的5个端点位置,要求下面的两个数字分别比和它相邻的上面两个数字大,这样的安排方法种数为_______. 【答案】1616.已知函数()12ln ,e e f x a x x ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎣⎦⎝⎭的图象上存在点P ,函数()22g x x =--的图象上存在点Q ,且点P 和点Q 关于原点对称,则实数a 的取值范围是________.【答案】23,e ⎡⎤⎣⎦【解析】 【详解】函数y =﹣x 2﹣2的图象与函数y =x 2+2的图象关于原点对称, 若函数y =a +2lnx (x ∈[1e,e ])的图象上存在点P ,函数y =﹣x 2﹣2的图象上存在点Q ,且P ,Q 关于原点对称,则函数y =a +2lnx (x ∈[1e ,e ])的图象与函数y =x 2+2的图象有交点, 即方程a +2lnx =x 2+2(x ∈[1e ,e ])有解,即a =x 2+2﹣2lnx (x ∈[1e,e ])有解,令f (x )=x 2+2﹣2lnx ,则f ′(x )()221x x-=,当x ∈[1e,1)时,f ′(x )<0,当x ∈(1,e ]时,f ′(x )>0, 故当x =1时,f (x )取最小值3, 由f (1e )21e=+4,f (e )=e 2, 故当x =e 时,f (x )取最大值e 2, 故a ∈[3,e 2],故答案为23,e ⎡⎤⎣⎦三、解答题17.已知函数()ln(3)ln(3)f x x x =++-. (1)求函数()y f x =的定义域并判断奇偶性; (2)若(21)()f m f m -<,求实数m 的取值范围.【答案】(1)见解析;(2)113m -<<或12m <<. 【解析】 【分析】(1)由3030x x +⎧⎨-⎩>>,求得x 的范围,可得函数y =f (x )定义域,由函数y =f (x )的定义域关于原点对称,且满足 f (﹣x )=f (x ),可得函数y =f (x )为偶函数;(2)化简函数f (x )的解析式为()()2ln 9f x x=-所,结合函数的单调性可得,不等式()()21f m f m -<等价于32133321m m m m ⎧-<-<⎪-<<⎨⎪->⎩,由此求得m 的范围.【详解】(1)由3030x x +>⎧⎨->⎩得33x -<<,所以()f x 的定义域为()3,3-,又因为()()()()ln 3ln 3f x x x f x -=-++=,所以()f x 偶函数.(2)因为()()()()2ln 3ln 3ln 9f x x x x =++-=-所以()f x 是[0,3)上的减函数,又()f x 是偶函数.故32133321m m m m⎧-<-<⎪-<<⎨⎪->⎩解得113m -<<或12m <<.【点睛】本题主要考查求函数的定义域,函数的奇偶性的判断,复合函数的单调性,属于中档题. 18.袋中装有10个除颜色外完全一样的黑球和白球,已知从袋中任意摸出2个球,至少得到1个白球的概率是79. (1)求白球的个数;(2)从袋中任意摸出3个球,记得到白球的个数为X ,求随机变量X 的分布列. 【答案】(1)5个;(2)见解析. 【解析】 【分析】(1)设白球的个数为x ,则黑球的个数为10﹣x ,记“从袋中任意摸出2个球,至少得到1个白球”为事件A ,则两个都是黑球与事件A 为对立事件,由此能求出白球的个数;(2)随机变量X 的取值可能为:0,1,2,3,分别求出相应的概率,由此能求出X 的分布列. 【详解】(1)设白球的个数为x ,则黑球的个数为10﹣x ,记“从袋中任意摸出2个球,至少得到1个白球”为事件A ,则()210210719xC P A C -=-=,解得5x =.故白球有5个. (2)X 服从以10,5,3为参数的超几何分布,()355310,0,1,2,3k kC C P X k k C -===. 于是可得其分布列为:【点睛】本题主要考查离散型随机变量的分布列,超几何分布,求出离散型随机变量取每个值的概率,是解题的关键,属于中档题.19.设数列{}n a 的前n 项和为n S 且对任意的正整数n 都有:2(1)n n n S a S -=.(1)求123,,S S S ;(2)猜想n S 的表达式并证明. 【答案】(1)123,,234;(2)*()1n n S n N n =∈+,证明见解析. 【解析】 【分析】(1)分别代入1,2,3n =计算即可求解;(2)猜想:()*1n nS n N n =∈+,利用数学归纳法证明即可 【详解】当()2111111,1;2n S S S S =-=⇒=当()22222122,1;23n S S S S ⎛⎫=-=-⇒= ⎪⎝⎭ 当()23333233,1;34n S S S S ⎛⎫=-=-⇒= ⎪⎝⎭ (2)猜想:()*1n nS n N n =∈+. 证明:①当1n =时,显然成立;②假设当(1n k k =≥且*)k N ∈时,1k kS k =+成立. 则当1n k =+时,由()21111k k k S a S +++-=,得()()21111k k k k S S S S +++-=-,整理得()11111221121k k k k S k S k k k +++====-+++-+.即1n k =+时,猜想也成立.综合①②得()*1n nS n N n =∈+. 【点睛】本题考查递推数列求值,数学归纳法证明,考查推理计算能力,是基础题20.IC 芯片堪称“国之重器”其制作流程异常繁琐,制作IC 芯片核心部分首先需要制造单晶的晶圆,此过程主要是加入碳,以氧化还原的方式,将氧化硅转换为高纯度的硅.为达到这一高标准要求,研究工作人员曾就是否需采用西门子制程(Siemens process )这一工艺技术进行了反复比较,在一次实验中,工作人员对生产出的50片单晶的晶圆进行研究,结果发现使用了该工艺的30片单晶的晶圆中有28片合格,没有使用该工艺的20片单晶的晶圆中有12片合格.(1)请填写2⨯2列联表并判断:这次实验是否有99.5%的把握认为单晶的晶圆的制作效果与使用西门子制程(Siemens process )这一工艺技术有关?(2)在得到单晶的晶圆后,接下来的生产制作还前对单晶的晶圆依次进行金属溅镀,涂布光阻,蚀刻技术,光阻去除这四个环节的精密操作,进而得到多晶的晶圆,生产出来的多晶的晶圆经过严格的质检,确定合格后才能进入下一个流程,如果生产出来的多晶的晶圆在质检中不合格,那么必须依次对前四个环节进行技术检测并对所有的出错环节进行修复才能成为合格品.在实验的初期,由于技术的不成熟,生产制作的多晶的晶圆很难达到理想状态,研究人员根据以往的数据与经验得知在实验生产多晶的晶圆的过程中,前三个环节每个环节生产正常的概率为23,第四个环节生产正常的概率为34,且每个环节是否生产正常是相互独立的.前三个环节每个环节出错需要修复的费用均为20元,第四环节出错需要修复的费用为10元.问:一次实验生产出来的多晶的晶圆要成为合格品平均还需要消耗多少元费用?(假设质检与检测过程不产生费用)参考公式:22()n()()()(n ad bcK a b c da b c d a c b d-==+++ ++++,)参考数据:【答案】(1)见解析;(2)22.5元. 【解析】【分析】(1)先列出列联表,再根据列表求出K2253=>7.879,从而有99.5%的把握认为晶圆的制作效果与使用西门子制程这一工艺技术有关.(2)设A i表示检测到第i个环节有问题,(i=1,2,3,4),X表示成为一个合格的多晶圆需消耗的费用,则X的可能取值为:0,10,20,30,40,50,60,70,分别求出相应的概率,由此能求出X的分布列和数学期望.【详解】(1)()2250288212258.3337.879302040103K ⨯-⨯==≈>⨯⨯⨯ 故有99.5%的把握认为单晶的晶圆的制作效果与使用西门子制程这一工艺技术有关. (2)设X 表示成为一个合格的多晶的晶圆还需要消耗的费用,则X 的可能取值为:0,10,20,30,40,50,60,70.()32324034108P X ⎛⎫==⨯=⎪⎝⎭()32181034108P X ⎛⎫==⨯=⎪⎝⎭ ()2131233620334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()2131211230334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()2231231840334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭()223121650334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()31336034108P X ⎛⎫==⨯=⎪⎝⎭ ()31117034108P X ⎛⎫==⨯=⎪⎝⎭ 所以X 分布列为:故()24836121863101020304050607022.5108108108108108108108108E X =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=,故平均还需要耗费22.5元. 【点睛】本题考查独立检验的应用,考查离散型随机变量的分布列和数学期望的求法,考查离散型随机变量的分布列、数学期望等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.21.已知函数()2(0)f x a lnx ax a =+->. (1)求()f x 的最大值()a ϕ; (2)若()0f x ≤恒成立,求a 的值;(3)在(2)的条件下,设[]()()x f x ax g x x a+=-在(,)a +∞上的最小值为,m 求证:11()10f m -<<-.【答案】(1)()22ln 2ln2(0)a a a a ϕ=--+>;(2)2;(3)证明见解析. 【解析】 【分析】(1)()2'(0)axf x a x-=>,判断函数的单调性即可求解最大值;(2)要使()0f x ≤成立必须()22ln 2ln20a a a ϕ=--+≤,()2'a a aϕ-=,判断单调性求解()()min 20a ϕϕ==即可得解2a =;(3)()22ln 2x x xg x x +=-,得()()()222ln 4'2x x g x x --=-,令()2ln 4u x x x =--判断其单调性进而求得()()20000000min0022ln 2=22x x x x x g x g x x x x +-===--,得0m x =,再求()0f x 的范围进而得证【详解】 (1)()2'(0)axf x a x-=>, 由()'0f x >得20x a <<;()'0f x <得2x a >;所以()f x 在20,a ⎛⎫⎪⎝⎭上单调递增,在2,a ⎛⎫+∞ ⎪⎝⎭上单调递减.故()max 222ln 2ln2f x f a a a ⎛⎫==--+ ⎪⎝⎭, 即()22ln 2ln2(0)a a a a ϕ=--+>;(2)要使()0f x ≤成立必须()22ln 2ln20a a a ϕ=--+≤.因为()2'a a aϕ-=,所以当02a <<时,()'0a ϕ<;当2a >时,()'0a ϕ>.所以()a ϕ在()0,2上单调递减,在()2,+∞上单调递增.又()()min 20a ϕϕ==,所以满足条件的a 只有2,即2a =. (3)由(2)知()22ln 2x x x g x x +=-,所以()()()222ln 4'2x x g x x --=-. 令()2ln 4u x x x =--,则()2'0x u x x-=>,()u x 是()2,+∞上的增函数;又()()80,90u u ,所以存在()08,9x ∈满足()00u x =,即002ln 4x x =-,且当()02,x x ∈时,()()0,'0u x g x <<;当()0,x x ∈+∞,()()0,'0u x g x >>所以()g x 在()02,x 上单调递减;在()0,x +∞上单调递增.所以()()20000000min 0022ln 2=22x x x x x g x g x x x x +-===--,即0m x =. 所以()()000022ln 2=21110f m f x x x x ==+---∈--(,),即()1110f m -<<-.【点睛】本题考查了利用导数研究函数的单调性及最值,考查了零点存在定理和数学转化思想,在(3)的证明过程中,利用零点存在定理转化是难点属中档题.22.已知极坐标系的极点在直角坐标系的原点处,极轴与x 轴正半轴重合,直线l 的参数方程为:2cos sin x t y t αα=+⎧⎨=⎩(t 为参数,[0,)απ∈),曲线C 的极坐标方程为:4sin ρθ=.(1)写出曲线C 的直角坐标方程;(2)设直线l 与曲线C 相交于,P Q 两点,直线l 过定点M ,若MP MQ +=直线l 的斜率.【答案】(1)22(2)4x y +-=;(2)1-.【解析】【分析】(1)由4sin ρθ=,得24sin ρρθ=,由此能求出曲线C 的直角坐标方程;(2)把2cos sin x t y t αα=+⎧⎨=⎩代入()2224x y +-=,整理得()24cos sin 40t t αα+-+=,由1212MP MQ t t t t +=+=+,得34πα=,能求出直线l 的斜率. 【详解】 (1)曲线C 的极坐标方程为4sin ρθ=,所以24sin ρρθ=.即224x y y +=,即()2224x y +-=. (2)把直线l 的参数方程带入()2224x y +-=得()24cos sin 40t t αα+-+= 设此方程两根为12,t t ,易知()2,0M ,而定点M 在圆C 外,所以1212MP MQ t t t t +=+=+,4cos sin αα∴-=,cos sin αα∴-=[0,)απ∈,可得34πα=, ∴1k =-,所以直线l 的斜率为-1.【点睛】本题考查曲线的直角坐标方程的求法,考查直线的斜率的求法,考查极坐标方程、直角坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.23.已知()1f x x x m =+++,()232g x x x =++.(1)若0m >且()f x 的最小值为1,求m 的值;(2)不等式()3f x ≤的解集为A ,不等式()0g x ≤的解集为B ,B A ⊆,求m 的取值范围.【答案】(1)2m =;(2)04m ≤≤【解析】试题分析:(1)利用绝对值三角不等式可得()11f x m ≥-=,解出方程即可;(2)易得[]2,1B =--,()3f x ≤即4x m x +≤+,即42m x +≥-且4m ≤,再根据B A ⊆列出不等式即可得结果.试题解析:(1)()()()111f x x x m x x m m =+++≥+-+=-(当1x =-时,等号成立)∵()f x 的最小值为 1,∴11m -=,∴2m = 或0m =,又0m >,∴2m =.(2)由()0g x ≤得,[]2,1B =--,∵B A ⊆,∴(),3x B f x ∀∈≤,即()13x x m -+++≤44442m x m x x x m x x +⇔+≤+⇔--≤+≤+⇔≥-且4m ≤422m +⇔-≤-且404m m ≤⇔≤≤.。
2015-2016学年辽宁省锦州市高二(下)期末数学试卷(理科)(解析版)

2015-2016学年辽宁省锦州市高二(下)期末数学试卷(理科)一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知i是虚数单位,则复数z=在复平面内对应的点所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)已知集合M={1,(m2﹣3m﹣1)+(m2﹣5m﹣6)i},N={1,3},M∩N={1,3},则实数m的值为()A.4B.﹣1C.4或﹣1D.1或63.(5分)(2x+5y)n展开式中第k项的二项式系数为()A.B.2n﹣k5kC.D.2n+1﹣k5k﹣14.(5分)设函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),则f(3)=()A.B.C.1D.25.(5分)下列值等于1的积分是()A.xdx B.(x+1)dxC.1dx D.dx6.(5分)“因为对数函数y=log a x是增函数(大前提),而y=是对数函数(小前提),所以y=是增函数(结论).”上面推理的错误是()A.大前提错导致结论错B.小前提错导致结论错C.推理形式错导致结论错D.大前提和小前提都错导致结论错7.(5分)已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=a x+b的图象大致为()A.B.C.D.8.(5分)某班主任对全班50名学生进行了作业量的调查,数据如表则推断“学生的性别与认为作业量大有关”的把握大约为()附:Χ2=.独立性检验临界值表A.99%B.95%C.90%D.不确定9.(5分)下列命题中,正确的命题个数是()①用相关系数r来判断两个变量的相关性时,r越接近0,说明两个变量有较强的相关性;②将一组数据中的每个数据都加上同一个非零常数后,期望改变,方差不变;③某厂生产的零件外直径x~N(3,1),且p(2≤x≤4)=0.68,则p(x<4)=0.84④用数学归纳法证明不等式++…+<(n≥2,n∈{N*)的过程中,由n=k递推到n=k+1时不等式的左边增加项为﹣.A.1个B.2个C.3个D.4个10.(5分)甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A为“三个人去的景点不相同”,事件B为“甲独自去一个景点”,则概率P(A|B)等于()A.B.C.D.11.(5分)从1,2,3,4,9,18六个数中任取两个不同的数分别作为一个对数的底数和真数,得到不同的对数值有()A.21B.20C.19D.1712.(5分)已知函数f(x)=lnx+tanα(0<α<)的导函数为f'(x),若方程f'(x)=f (x)的根x0小于1,则α的取值范围为()A.B.C.D.二、填空题(本大题共4小题,每小题5分.共20分.)13.(5分)如果质点M按规律s=3+t2运动,则在一小段时间[2,2.1]中相应的平均速度是.14.(5分)用反证法证明命题“若a2+b2=0,则a,b全为0 (a,b为实数)”,其反设为.15.(5分)设a∈Z,且0≤a<13,若512016+a能被13整除,则a=.16.(5分)已知函数f(x)的定义域为(0,+∞),且f(x)=2f()﹣1,则f(x)=.三.解答题(解答应写出文字说明,证明过程或演算步骤.)17.(10分)已知i是虚数单位,z1=x+yi(x,y∈R),且x2+y2=1,z2=(3+4i)z1+(3﹣4i).(I)求证:z2∈R;(II)求z2的最大值和最小值.18.(12分)某公司在甲、乙两地销售同一种品牌的汽车,利润(单位:万元)分别为L1=5.06x﹣0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,求该公司能获得的最大利润为多少万元?19.(12分)已知a>b>0,求证:.20.(12分)设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.(I)求进入商场的1位顾客购买甲,乙两种商品中的一种的概率;(II)求进入商场的1位顾客至少购买甲,乙两种商品中的一种概率;(III)用ξ表示进入商场的3位顾客中至少购买甲,乙两种商品中的一种的人数,求ξ的分布列.21.(12分)对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b﹣1(a≠0).(1)当a=1,b=﹣2时,求函数f(x)的不动点;(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的范围;(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+对称,求b的最小值.22.(12分)已知函数f(x)=ax2﹣(2a+1)x+2lnx(a∈R).(Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;(Ⅱ)求f(x)的单调区间;(Ⅲ)设g(x)=x2﹣2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求a的取值范围.2015-2016学年辽宁省锦州市高二(下)期末数学试卷(理科)参考答案与试题解析一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的.)1.【解答】解:复数z====在复平面内对应的点所在的象限为第四象限.故选:D.2.【解答】解:根据题意,若M∩N={1,3},则3∈M,而M={1,(m2﹣3m﹣1)+(m2﹣5m﹣6)i},则有(m2﹣3m﹣1)+(m2﹣5m﹣6)i=3,即(m2﹣3m﹣1)=3且(m2﹣5m﹣6)=0,解可得m=﹣1,故选:B.3.【解答】解:(2x+5y)n展开式中第k项的二项式系数为∁n k﹣1,故选:C.4.【解答】解:函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),∴f(0)=0,∴且f(1)=f(﹣1+2)=f(﹣1)+f(2)=﹣f(1)+f(2),∴f(2)=2f(1)=1,则f(3)=f(1+2)=f(1)+f(2)=+1=,故选:B.5.【解答】解:选项A,xdx=x2=,不满足题意;选项B,(x+1)dx=(x2+x)=+1=,不满足题意;选项C,1dx=x=1﹣0=1,满足题意;选项D,dx=x=﹣0=,不满足题意;故选:C.6.【解答】解:当a>1时,对数函数y=log a x是增函数,当0<a<1时,对数函数y=log a x是减函数,故推理的大前提是错误的故选:A.7.【解答】解:由二次方程的解法易得(x﹣a)(x﹣b)=0的两根为a、b;根据函数零点与方程的根的关系,可得f(x)=(x﹣a)(x﹣b)的零点就是a、b,即函数图象与x轴交点的横坐标;观察f(x)=(x﹣a)(x﹣b)的图象,可得其与x轴的两个交点分别在区间(﹣∞,﹣1)与(0,1)上,又由a>b,可得b<﹣1,0<a<1;在函数g(x)=a x+b可得,由0<a<1可得其是减函数,又由b<﹣1可得其与y轴交点的坐标在x轴的下方;分析选项可得A符合这两点,BCD均不满足;故选:A.8.【解答】解:∵根据表中数据得到K2=≈5.059>3.841,∴推断“学生的性别与认为作业量大有关”的把握大约为95%故选:B.9.【解答】解:①两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值越接近于0,表示两个变量之间几乎不存在线性相关,故①不正确;②将一组数据中的每个数据都加上同一个非零常数后,期望改变,方差不变,正确,故②正确,③某厂生产的零件外直径x~N(3,1),且p(2≤x≤4)=0.68,则p(3≤x≤4)=0.34,则p(x<4)=0.34+0.5=0.84,故③正确,④用数学归纳法证明不等式++…+<(n≥2,n∈{N*)的过程中,当n=k时,左边为++…+,当n=k+1时,左边为+…+++=++…++(+﹣),故左边增加的项是+﹣,故④错误,故正确的是②③,故选:B.10.【解答】解:甲独自去一个景点,则有3个景点可选,乙丙只能在甲剩下的哪两个景点中选择,可能性为2×2=4所以甲独自去一个景点的可能性为3×2×2=12因为三个人去的景点不同的可能性为3×2×1=6,所以P(A|B)==.故选:C.11.【解答】解:当构成的对数式含有1时,得到的对数值为0;当构成的对数式不含1时,有=20种,其中log23=log49,log24=log39,log32=log94,log42=log93,重复4个,有20﹣4=16个;综上,可以得到1+16=17种不同的对数值,故选:D.12.【解答】解:∵f′(x)=,f′(x0)=,f′(x0)=f(x0),∴=ln x0+tan α,∴tan α=﹣ln x0,又∵0<x0<1,∴可得﹣ln x0>1,即tan α>1,∴α∈(,).故选:A.二、填空题(本大题共4小题,每小题5分.共20分.)13.【解答】解:∵质点M按规律s=s(t)=3+t2运动,∴在一小段时间[2,2.1]中相应的平均速度v====4.1,故答案为:4.114.【解答】解:用反证法证明命题的真假,先假设命题的结论不成立,所以用反证法证明命题“若a2+b2=0,则a,b全为0 (a,b为实数)”,其反设为a,b不全为0,故答案为:a,b不全为0.15.【解答】解:512016+a=(52﹣1)2016+a=•522016+•522015•(﹣1)1+•522014•(﹣1)2+…+•(﹣1)2016+a,除最后两项外,其余各项都有13的倍数52,故由题意可得•(﹣1)2016+a能被13整除,∵0≤a<13,∴a=12,故答案为:1216.【解答】解:考虑到所给式子中含有f(x)和f(),故可考虑利用换元法进行求解.在f(x)=2f()﹣1,用代替x,得f()=2f(x)﹣1,将f()=﹣1代入f(x)=2f()﹣1中,可求得f(x)=+.故答案为:+三.解答题(解答应写出文字说明,证明过程或演算步骤.)17.【解答】解:(Ⅰ)证明∵z1=x+yi,1=x﹣yi(x,y∈R),∴z1+1=2x,z1﹣1=2yi.∴z2=(3+4i)z1+(3﹣4i)1,=3(z 1+)+4i(z1﹣1).=6x+8yi2=(6x﹣8y)∈R(Ⅱ)解∵x2+y2=1,设u=6x﹣8y,代入x2+y2=1消去y得64x2+(6x﹣u)2=64.∴100x2﹣12ux+u2﹣64=0.∵x∈R,∴△≥0.∴144u2﹣4×100(u2﹣64)≥0.∴u2﹣100≤0.∴﹣10≤u≤10.∴z2的最大值是10,最小值是﹣1018.【解答】解:设甲地销售x辆,则乙地销售15﹣x辆,0≤x≤15,则该公司能获得的最大利润y=5.06x﹣0.15x2+2(15﹣x)=﹣0.15x2+3.06x+30,当x=10.2时,S取最大值又x必须是整数,故x=10,此时S max=45.6(万元).即甲地销售10辆,则乙地销售5辆时,该公司能获得的最大利润为45.6万元19.【解答】解:∵又==∵a>b>0,∴,所以上式大于1,故成立,同理可证20.【解答】(本小题满分12分)解:(Ⅰ)记A表示事件:进入商场的1位顾客购买甲种商品,B表示事件:进入商场的1位顾客购买乙种商品,C表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,D表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种.C=A•+•B.进入商场的1位顾客购买甲,乙两种商品中的一种的概率:P(C)=P(A•+•B)=P(A•)+P(•B)=P(A)•P()+P()•P(B)=0.5×0.4+0.5×0.6=0.5…(4分)(Ⅱ)=•,P()=P(•)=P()•P()=0.5×0.4=0.2,进入商场的1位顾客至少购买甲,乙两种商品中的一种概率P(D)=1﹣P()=0.8…(8分)(Ⅲ)ξ~B(3,0.8),P(ξ=0)=0.23=0.008,P(ξ=1)=×0.8×0.22=0.096,P(ξ=2)=×0.82×0.2=0.384,P(ξ=3)=0.83=0.512.ξ的分布列为…(12分)21.【解答】解:(1)∵a=1,b=﹣2时,f(x)=x2﹣x﹣3,f(x)=x⇒x2﹣2x﹣3=0⇒x=﹣1,x=3∴函数f(x)的不动点为﹣1和3;(2)即f(x)=ax2+(b+1)x+b﹣1=x有两个不等实根,转化为ax2+bx+b﹣1=0有两个不等实根,须有判别式大于0恒成立即b2﹣4a(b﹣1)>0⇒△=(﹣4a)2﹣4×4a<0⇒0<a<1,∴a的取值范围为0<a<1;(3)设A(x1,x1),B(x2,x2),则x1+x2=﹣,A,B的中点M的坐标为(,),即M(﹣,﹣)∵A、B两点关于直线y=kx+对称,又因为A,B在直线y=x上,∴k=﹣1,A,B的中点M在直线y=kx+上.∴﹣=⇒b=﹣=﹣利用基本不等式可得当且仅当a=时,b的最小值为﹣.22.【解答】解:(Ⅰ)∵函数,∴(x>0).∵曲线y=f(x)在x=1和x=3处的切线互相平行,∴f'(1)=f'(3),即,解得.(Ⅱ)(x>0).①当a≤0时,x>0,ax﹣1<0,在区间(0,2)上,f'(x)>0;在区间(2,+∞)上f'(x)<0,故f(x)的单调递增区间是(0,2),单调递减区间是(2,+∞).②当时,,在区间(0,2)和上,f'(x)>0;在区间上f'(x)<0,故f(x)的单调递增区间是(0,2)和,单调递减区间是③当时,,故f(x)的单调递增区间是(0,+∞).④当时,,在区间和(2,+∞)上,f'(x)>0;在区间上f'(x)<0,故f(x)的单调递增区间是和(2,+∞),单调递减区间是.(Ⅲ)由已知,在(0,2]上有f(x)max<g(x)max.由已知,g(x)max=0,由(Ⅱ)可知,①当时,f(x)在(0,2]上单调递增,故f(x)max=f(2)=2a﹣2(2a+1)+2ln2=﹣2a﹣2+2ln2,所以,﹣2a﹣2+2ln2<0,解得a>ln2﹣1,故.②当时,f(x)在上单调递增,在上单调递减,故.由可知,2lna>﹣2,﹣2lna<2,所以,﹣2﹣2lna<0,f(x)max<0,综上所述,a>ln2﹣1.。
辽宁省锦州市高二下学期期末数学试卷(理科)

辽宁省锦州市高二下学期期末数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)过原点和在复平面内对应点的直线的倾斜角为A .B .C .D . -2. (2分)已知复数(是虚数单位),它的实部和虚部的和是()A . 4B . 6C . 2D . 33. (2分)用系统抽样要从160名学生中抽取容量为20的样本,将160名学生从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,…,153~160号),若第16组抽出的号码为123,则第2组中应抽出的号码是()A . 10B . 11C . 12D . 134. (2分)(2017高一下·东丰期末) 在中,三个内角A,B,C的对边分别是则b等于()A . 4B .C . 6D .5. (2分)(2017·大庆模拟) 已知集合A={y|0≤y<2,y∈N},B={x|x2﹣4x﹣5≤0,x∈N},则A∩B=()A . {1}B . {0,1}C . [0,2)D . ∅6. (2分) (2017高一上·鞍山期末) 已知向量 =(1,x), =(x,4),若 =| |•| |,则x=()A . ﹣2B . 2C . 0D . ﹣2或27. (2分)与椭圆共焦点且过点的双曲线方程是()A .B .C .8. (2分)函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f (2013)+f(2014)+f(2015)+f(2016)的值分别为()A . f(x)=sin2πx+1,S=2016B . f(x)=sin2πx+1,S=2016C . f(x)=sin x+1,S=2017D . f(x)=sin x+1,S=20179. (2分)下列说法正确的是()A . 三点确定一个平面B . 四边形一定是平面图形C . 梯形一定是平面图形D . 平面α和平面β有不同在一条直线上的三个交点10. (2分) (2017高三上·湖南月考) 下列选项中为函数的一个对称中心为()A .B .C .11. (2分)若的展开式中项的系数为280,则()A .B . 2C .D .12. (2分)已知f(x)=x2ex(e为自然对数的底),若存在唯一的x0∈[﹣1,1],使得f(x0)=m在m∈[t ﹣2,t]上恒成立,则实数t的取值范围是()A . [1,e]B . (1+ ,e]C . (2,e]D . (2+ ,e]二、填空题 (共4题;共4分)13. (1分) (2019高二上·辽宁月考) 如果函数满足:对于任意给定的等比数列仍是等比数列,则称为“保等比数列函数”.在下列函数中所有“保等比数列函数”的序号为________① ② ③ ④⑤14. (1分) (2018高二上·宜昌期末) 某旅行社租用A、B两种型号的客车安排900名客人旅行,A、B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆.则租金最少为________元.15. (1分) (2016高一下·红桥期中) 执行如图所示的储蓄框图,若输出S的值为720,则判断框内可填入的条件是________.16. (1分)(2018·鞍山模拟) 在三棱锥中,,当三梭锥的体积最大时,其外接球的表面积为________.三、解答题 (共8题;共85分)17. (10分) (2016高二上·菏泽期中) 设数列{an}的前n项和为Sn ,且Sn=n2﹣4n﹣5.(1)求数列{an}的通项公式;(2)设bn=|an|,数列{bn}的前n项和为Tn,求Tn.18. (5分)(2017·南昌模拟) 网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商场购物,且参加者必须从淘宝和京东商城选择一家购物.(Ⅰ)求这4人中恰有1人去淘宝网购物的概率;(Ⅱ)用ξ、η分别表示这4人中去淘宝网和京东商城购物的人数,记X=ξη,求随机变量X的分布列与数学期望EX.19. (10分) (2016高二上·武邑期中) 如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=2,E为线段PD上一点,记=λ.当λ= 时,二面角D﹣AE﹣C的平面角的余弦值为.(1)求AB的长;(2)当时,求异面直线BP与直线CE所成角的余弦值.20. (20分)已知椭圆C:的离心率为,椭圆C上任意一点到椭圆两焦点的距离和为6.(1)求椭圆C的方程;(2)设直线l:y=kx,求直线DE的斜截式方程;(3)设椭圆C的弦DE的中点为(﹣1,1),求直线DE的斜截式方程;(4)设直线l:y=x﹣2与椭圆C交于M、N两点,O是原点,求△OMN的面积.21. (10分)(2018·重庆模拟) 已知函数(,).(1)若在上单调递减,求的取值范围;(2)当时,判断关于的方程的解的个数.22. (10分)(2017·来宾模拟) 如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.(1)求证:BD⊥AD;(2)若AC=BD,AB=6,求弦DE的长.23. (10分)(2018·河南模拟) 已知直线:,曲线: .(1)求直线的直角坐标方程与曲线的普通方程;(2)设直线与曲线交于,两点,若,求实数的取值范围.24. (10分) (2015高三上·连云期末) 已知数列{an}满足an=3n﹣2,f(n)= + +…+ ,g(n)=f(n2)﹣f(n﹣1),n∈N* .(1)求证:g(2)>;(2)求证:当n≥3时,g(n)>.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共8题;共85分) 17-1、17-2、18-1、19-1、19-2、20-1、20-2、20-3、20-4、21-1、21-2、22-1、22-2、23-1、23-2、24-1、24-2、。
辽宁锦州市数学高二下期末复习题(含答案)

一、选择题1.已知,a b 是单位向量,且,a b 的夹角为3π,若向量c 满足22c a b -+=,则||c 的最大值为( )A.2B .2C 2D 22.( ) A .sin2cos2+ B .cos2sin2- C .sin2cos2-D .cos2sin2±-3.将函数sin y x =图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图象上所有的点向左平移π4个单位长度,则所得图象对应的函数解析式为( ) A .sin(2)4y x π=+B .sin()24x y π=+C .cos 2x y =D .cos 2y x =4.已知2sin2α=1+cos2α,则tan2α=( ) A .43-B .43C .43-或0 D .43或0 5.已知P (14,1),Q (54,-1)分别是函数()()cos f x x ωϕ=+0,2πωϕ⎛⎫>< ⎪⎝⎭的图象上相邻的最高点和最低点,则ωϕ-=( ) A .54π-B .54πC .-34π D .34π 6.若将函数y =cos2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为( ) A .x =kπ2−π6(k ∈Z ) B .x =kπ2+π6(k ∈Z )x C .x =kπ2−π12(k ∈Z )D .x =kπ2+π12(k ∈Z )7.已知2sin()3,且(,0)2απ∈-,则tan(2)πα-= ( )A B . C D .8.已知向量(3,4),(sin ,cos )a b αα==,且//a b ,则tan α=( ) A .34B .34-C .43D .43-9.若平面四边形ABCD 满足0,()0AB CD AB AD AC +=-⋅=,则该四边形一定是( )A .正方形B .矩形C .菱形D .直角梯形10.已知a ,b 是平面内两个互相垂直的单位向量,若向量c 满足()()0a c b c -⋅-=,则c 的最大值是( ) A .1B .2C .D .11.若()2sin sinsin777n n S n N πππ︒=+++∈,则在中,正数的个数是( ) A .16 B .72C .86D .10012.已知角6πα-的顶点在原点,始边与x 轴正半轴重合,终边过点()5,12P -, 则7cos 12πα⎛⎫+= ⎪⎝⎭( ) A .17226-B .7226-C .7226D .1722613.已知向量(2,0)OB =,向量(2,2)OC =,向量(2cos ,2sin )CA αα=,则向量OA 与向量OB 的夹角的取值范围是( ).A .π0,4⎡⎤⎢⎥⎣⎦B .π5π,412⎡⎤⎢⎥⎣⎦C .5ππ,122⎡⎤⎢⎥⎣⎦ D .π5π,1212⎡⎤⎢⎥⎣⎦ 14.已知非零向量a ⃑ =(t,0),b ⃑ =(−1,√3),若a ⃑ ⋅b ⃑ =−4,则a ⃑ +2b ⃑ 与b⃑ 的夹角( ) A .π3B .π2C .π6D .2π315.已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的最小正周期为6π,且其图象向右平移23π个单位后得到函数()sin g x x ω=的图象,则ϕ=( ) A .6π B .3π C .29π D .49π 二、填空题16.已知向量()1,1a =,()3,2b =-,若2ka b -与a 垂直,则实数k =__________. 17.如图,已知△ABC 中,∠BAC =90°,∠B =30°,点P 在线段BC 上运动,且满足CP CB λ=,当PA PC ⋅取到最小值时,λ的值为_________ .18.求()22sin cos 2,,63f x x x x ππ⎡⎤=-+∈-⎢⎥⎣⎦的值域____.19.将函数()2sin(2)6f x x π=-的图象向左平移(0)φφ>个单位,若所得到图象关于原点对称,则φ的最小值为__________. 20.在平面上,12OB OB ⊥,122MB MB ==12OP OB OB =+.若1MP <,则OM 的取值范围是_______.21.设(1,3,2)a =-,(2,+1,1)b m n =-,且a //b ,则实数m n -=_____. 22.若sincos022αα<<,则角α的终边落在第________象限.23.为得到函数2y sin x =的图象,要将函数24y sin x π⎛⎫=+ ⎪⎝⎭的图象向右平移至少__________个单位. 24.若()1sin 3πα-=,且2παπ≤≤,则cos α的值为__________. 25.已知()()2,1,,3a b λ=-=,若a 与b 的夹角为钝角,则λ的取值范围是___________.(用集合表示)三、解答题26.已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+(Ⅰ)求函数()f x 的最小正周期和图象的对称轴方程 (Ⅱ)求函数()f x 在区间[,]122ππ-上的值域 27.在ABC ∆ 中,角A B C 、、所对的边分别为a b c 、、sin cC=, (1)求A 的大小;(2)若6a =,求b c +的取值范围. 28.已知向量(1,2),(,1)a b x →→==(1)当(2)(2)a b a b +⊥-时,求x 的值;(2)若,a b <>为锐角,求x 的范围. 29.已知ABC ∆中,角,,A B C 的对边分别为,,a b c ,且2cos cos (1tan tan )1A B A B -=-,c =,ABC ∆的面积为2.(1)求C 的大小; (2)求+a b 的值.30.已知平面内向量(17)(51)(21)OA OB OP ===,,,,,,点Q 是直线OP 上的一个动点. (1)当QA QB ⋅取最小值时,求OQ 的坐标;的值.(2)当点Q满足(1)中的条件时,求cos AQB【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.B2.C3.D4.D5.B6.C7.A8.A9.C10.C11.C12.B13.D14.A15.C二、填空题16.-1【解析】【分析】由题意结合向量垂直的充分必要条件得到关于k的方程解方程即可求得实数k的值【详解】由平面向量的坐标运算可得:与垂直则即:解得:【点睛】本题主要考查向量的坐标运算向量垂直的充分必要条17.【解析】【分析】将用表示出来注意的数量关系再根据的二次函数求最值【详解】设因为所以;所以故当时有最小值【点睛】图形中向量的数量积问题主要是将未知的向量用已知的向量表示这样可以方便计算18.【解析】【分析】由条件利用同角三角函数的基本关系化简函数解析式再利用正弦函数的定义域和值域二次函数的性质求得函数在上的值域【详解】设故在上值域等价于在上的值域即的值域为【点睛】本题考查同角三角函数的19.【解析】分析:先根据图像平移得解析式再根据图像性质求关系式解得最小值详解:因为函数的图象向左平移个单位得所以因为所以点睛:三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟20.【解析】【分析】本题可以通过建立平面直角坐标系将给的向量条件坐标化然后把所求的也用坐标表示出来最后根据式子采用适当的方法得出结果【详解】设则有因为所以①②③因为所以①+②得即由①②可知带入③中可知综21.8【解析】由题意得22.二【解析】由题意结合三角函数的性质可得:则据此可得角的终边落在第二象限23.【解析】函数的解析式:则要将函数的图象向右平移至少个单位点睛:由y=sinx的图象利用图象变换作函数y=Asin(ωx+φ)(A>0ω>0)(x∈R)的图象要特别注意:当周期变换和相位变换的先后顺序24.【解析】由题意得25.【解析】∵向量与的夹角为钝角∴即;解得即的取值范围是故答案为三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1.B 解析:B 【解析】不妨设(1,0)a =,13(,2b =,(,)c x y =,则2(,c a b x y -+=+,所以22(3)2c a b x -+=+=,即22(4x y +=,点(,)x y 在以(0,为圆心,2为半径的圆上,所以2c x =+2+.故选B .2.C解析:C 【解析】 【分析】先利用诱导公式化简角,然后利用正弦的二倍角公式和完全平方式结合角在各个象限中的符号化简即可得到答案. 【详解】==,∵22ππ<<,∴sin2cos20->.∴原式sin2cos2=-. 故选C. 【点睛】本题考查诱导公式和二倍角公式以及三角函数在各个象限中的符号的应用,属于基础题.3.D解析:D 【解析】 【分析】由正弦函数的周期变换以及平移变换即可得出正确答案. 【详解】函数sin y x =图象上所有点的横坐标缩短到原来的12倍(纵坐标不变)得到sin 2y x =,再将所得图象上所有的点向左平移π4个单位长度,得到sin 2sin 2cos 242y x x x ππ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭故选:D 【点睛】本题主要考查了正弦函数的周期变换以及平移变换,属于中档题.4.D解析:D 【解析】 【分析】 【详解】试题分析:把2sin 21cos2αα=+的两边平方得224sin 2(1cos 2)αα=+,整理可得2244cos 412cos 2cos 2ααα-=++,即25cos 22cos 230αα+-=,所以(5cos 23)(cos 21)0αα-+=,解得3cos 25α=或cos21α=-,当2312sin 5α-=时,1cos 244sin 2,tan 2253ααα+===;当cos21α=-时,1cos 2sin 20,tan 202ααα+===,所以4tan 23α=或0,故选D. 考点:三角函数的基本关系式及三角函数的化简求值.5.B解析:B 【解析】 【分析】由点P,Q 两点可以求出函数的周期,进而求出ω,再将点P 或点Q 的坐标代入,求得ϕ,即求出ωϕ-. 【详解】 因为512244πω⎛⎫-=⎪⎝⎭,所以ωπ=,把1,14P ⎛⎫ ⎪⎝⎭的坐标代入方程()cos y x πϕ=+,得 ()24k k Z ϕππ=-+∈,因为2πϕ<,所以5,44ππϕωϕ=--=,故选B . 【点睛】本题主要考查利用三角函数的性质求其解析式.解析:C 【解析】 【分析】 【详解】试题分析:由题意得,将函数y =cos2x 的图象向左平移π12个单位长度,得到y =cos2(x +π12)=cos (2x +π6),由2x +π6=kπ,k ∈Z ,得x =kπ2−π12,k ∈Z ,即平移后的函数的对称轴方程为x =kπ2−π12(k ∈Z ),故选C .7.A解析:A 【解析】 【分析】由三角函数的诱导公式,求得2sin3,再由三角函数的基本关系式,求得5cos α3, 最后利用三角函数的基本关系式,即可求解tan(2)πα-的值,得到答案. 【详解】由三角函数的诱导公式,可得2sin()sin 3παα-==-,因为(,0)2απ∈-,所以cos α==,又由sin tan(2)tan cos απααα-=-=-=,故选A. 【点睛】本题主要考查了三角函数的诱导公式和三角函数的基本关系式的化简、求值问题,其中解答中熟练应用三角函数的诱导公式和三角函数的基本关系式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.8.A解析:A 【解析】 【分析】直接利用向量平行的充要条件列方程求解即可. 【详解】由//a b 可得到sin 34sin 3cos 0tan cos 4ααααα-=⇒==. 故选A利用向量的位置关系求参数是出题的热点,主要命题方式有两个:(1)两向量平行,利用12210x y x y -=解答;(2)两向量垂直,利用12120x x y y +=解答.9.C解析:C 【解析】试题分析:因为0,AB CD AB DC +=∴=,所以四边形ABCD 为平行四边形,又因为()0,0AB AD AC DB AC -⋅=∴⋅=,所以BD 垂直AC ,所以四边形ABCD 为菱形.考点:向量在证明菱形当中的应用.点评:在利用向量进行证明时,要注意向量平行与直线平行的区别,向量平行两条直线可能共线也可能平行.10.C解析:C 【解析】 【分析】 【详解】 试题分析:由于垂直,不妨设,,,则,,表示到原点的距离,表示圆心,为半径的圆,因此的最大值,故答案为C .考点:平面向量数量积的运算.11.C解析:C 【解析】 【分析】 【详解】 令7πα=,则7n n πα=,当1≤n≤14时,画出角序列n α终边如图,其终边两两关于x 轴对称,故有均为正数,而,由周期性可知,当14k-13≤n≤14k 时,Sn>0, 而,其中k=1,2,…,7,所以在中有14个为0,其余都是正数,即正数共有100-14=86个,故选C.12.B解析:B 【解析】分析:利用三角函数的定义求得66cos sin ππαα⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭, 结果,进而利用两角和的余弦函数公式即可计算得解.详解:由三角函数的定义可得512,613613cos sin ππαα⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭, 则773cos cos cos 12661264ππππππααα⎛⎫⎛⎫⎛⎫+=-++=-+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ 33=cos cos sin sin 6464ππππαα⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭5212272=1313⎛⎛⎫--= ⎪ ⎝⎭⎝⎭ 点睛:本题考查任意角的三角函数的定义,两角和与差的余弦函数公式,考查了计算能力和转化思想,属于基础题.13.D解析:D 【解析】 不妨设(0,0)O∵(2,2)OC =,(22)CA αα=. ∴(2,2)C 、(22,22)A cos αα+. ∴点A 在以(2,2)2的圆上. ∴OA 与OB 的夹角为直线OA 的倾斜角. 设:OA l y kx = ∴22121k d r k -=≤=+即2410k k -+≤,则[23,23]k ∈-+. 又∵π23tan12=,523tanπ12+=. ∴OA 、OB 夹角[23,23]θ∈.故选D .14.A解析:A 【解析】 【分析】根据条件容易求出t=4,从而得出a ⃑ =(4,0),从而得出a ⃑ +2b ⃑ =(2,2√3)可设a ⃑ +2b ⃑ 与b⃑ 的夹角为θ,这样根据cosθ=(a ⃑ +2b ⃑ )·b ⃑ |a⃑ +2b ⃑ ||b ⃑ | 即可求出cosθ,进而得出θ的值.【详解】因a ⃑ ⋅b⃑ =−4=−t ∴t=4;∴a ⃑ =(4,0),b ⃑ =(−1,√3),a ⃑ +2b⃑ =(2,2√3) 设a ⃑ +2b ⃑ 与b ⃑ 的夹角为θ,则:cosθ=(a ⃑ +2b⃑ )·b ⃑ |a ⃑ +2b ⃑ ||b ⃑ |=-2+64×2=12, ∴θ=π3 故答案为A . 【点睛】本题主要考查向量的模及平面向量数量积公式、余弦定理的应用,属于中档题.平面向量数量积公式有两种形式,一是a ⃑ ⋅b ⃑ =|a ⃑ ||b ⃑ |cosθ,二是a ⃑ ⋅b ⃑ =x 1x 2+y 1y 2,主要应用以下几个方面:(1)求向量的夹角, cosθ=a⃑ ·b ⃑ |a ⃑ |·|b ⃑ | (此时a⃑ ·b ⃑ 往往用坐标形式求解);(2)求投影,a ⃑ 在b ⃑ 上的投影是a ⃑⋅b ⃑ |b ⃑ |;(3)a ⃑ ,b ⃑ 向量垂直则a ⃑ ⋅b ⃑ =0;(4)求向量ma ⃑ +nb ⃑ 的模(平方后需求a ⃑ ⋅b ⃑ ). 15.C解析:C 【解析】 【分析】利用函数()y f x =的周期求出ω的值,利用逆向变换将函数()y g x =的图象向左平行23π个单位长度,得出函数()y f x =的图象,根据平移规律得出ϕ的值. 【详解】由于函数()y f x =的周期为6π,2163πωπ∴==,则()1sin 3g x x =, 利用逆向变换,将函数()y g x =的图象向左平移23π个单位长度,得到函数()y f x =的图象,所以()1212sin sin 3339f x x x ππ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,因此,29πϕ=,故选:C. 【点睛】本题考查正弦型函数周期的计算,同时也考查了三角函数图象的平移变换,本题利用逆向变换求函数解析式,可简化计算,考查推理能力与运算求解能力,属于中等题.二、填空题16.-1【解析】【分析】由题意结合向量垂直的充分必要条件得到关于k 的方程解方程即可求得实数k 的值【详解】由平面向量的坐标运算可得:与垂直则即:解得:【点睛】本题主要考查向量的坐标运算向量垂直的充分必要条 解析:-1 【解析】 【分析】由题意结合向量垂直的充分必要条件得到关于k 的方程,解方程即可求得实数k 的值. 【详解】由平面向量的坐标运算可得:()()()21,123,26,4ka b k k k -=--=+-,2ka b -与a 垂直,则()20ka b a -⋅=,即:()()61410k k +⨯+-⨯=,解得:1k =-. 【点睛】本题主要考查向量的坐标运算,向量垂直的充分必要条件等知识,意在考查学生的转化能力和计算求解能力.17.【解析】【分析】将用表示出来注意的数量关系再根据的二次函数求最值【详解】设因为所以;所以故当时有最小值【点睛】图形中向量的数量积问题主要是将未知的向量用已知的向量表示这样可以方便计算解析:18【解析】 【分析】将PA PC ⋅用AB ,AC 表示出来,注意AB ,AC 的数量关系,再根据λ的二次函数求最值. 【详解】设AC a =,因为90BAC ∠=︒,30B ∠=︒,所以3AB a =,2BC a =;22()()PA PC PC CA PC BC CA BC BC BC CA λλλλ⋅=+⋅=+⋅=+⋅,所以22222142cos1204()816a PA PC a a a a λλλ⋅=+⋅⋅⋅︒=--,故当18λ=时,PA PC⋅有最小值. 【点睛】图形中向量的数量积问题,主要是将未知的向量用已知的向量表示,这样可以方便计算.18.【解析】【分析】由条件利用同角三角函数的基本关系化简函数解析式再利用正弦函数的定义域和值域二次函数的性质求得函数在上的值域【详解】设故在上值域等价于在上的值域即的值域为【点睛】本题考查同角三角函数的解析:3,34⎡⎤⎢⎥⎣⎦【解析】 【分析】由条件利用同角三角函数的基本关系化简函数解析式,再利用正弦函数的定义域和值域、二次函数的性质,求得函数()f x 在2,63ππ⎡⎤-⎢⎥⎣⎦上的值域。
辽宁省锦州市2024_2025学年高二数学下学期期末考试试题含解析

辽宁省锦州市2024-2025学年高二数学下学期期末考试试题(含解析)一、单选题(本大题共8小题,每小题5分,共40分)1.已知P(B|A)=,P(A)=,则P(AB)等于( )A. B.C.D.2.在数列中,,,则()A. -2B. -1C. D. 23.播种用的一等小麦种子中混有2%的二等种子,1.5%的三等种子,1%的四等种子.用一、二、三、四等种子长出的穗含50颗以上麦粒的概率分别为0.5,0.15,0.1,0.05,则这批种子所结的穗含50颗以上麦粒的概率为()A. 0.8B. 0.8325 C. 0.5325 D. 0.482 54.《周髀算经》是我国古老的天文学和数学著作,其书中记载:一年有二十四个节气,每个节气晷长损益相同(晷是依据日影测定时刻的仪器,晷长即为所测影子的长度),夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降是连续的九个节气,其晷长依次成等差数列,经记录测算,这九个节气的全部晷长之和为49.5尺,夏至、大暑、处暑三个节气晷长之和为10.5尺,则立秋的晷长为()A. 1.5尺B. 2.5尺 C. 3.5尺 D. 4.5尺5.李克强总理提出,要在960万平方公里土地上掀起“大众创业”、“草根创业”的新浪潮,形成“万众创新”、“人人创新”的新势态.为响应国家激励青年创业的号召,小王开了两家店铺,每个店铺招收了两名员工,若某节假日每位员工的休假概率均为,且是否休假互不影响,若一家店铺的员工全部休假,而另一家无人休假,则调剂1人到该店铺,使得该店铺能够正常营业,否则该店就停业.则两家店铺该节假日能正常开业的概率为()A. B . C.D.6.已知,若对随意两个不等的正实数,,都有恒成立,则a的取值范围是()A. B.C.D.7.今年元旦,市民小王向挚友小李借款100万元用于购房,双方约定年利率为5%,按复利计算(即本年利息计入次年本金生息),借款分三次等额归还,从明年的元旦起先,连续三年都是在元旦还款,则每次的还款额约是()万元.(四舍五入,精确到整数)(参考数据:,,)A. 36B.37 C.38 D. 39 8.下列函数图象中,函数的图象不行能的是()A.B.C.D.二、多选题(本大题共4小题,每小题5分,共20分)9.下列命题正确的是()A. 将一组数据中的每个数据都乘以同一个非零常数后,方差也变为原来的倍B. 抛掷匀称硬币一次,出现正面的次数是随机变量C. 线性相关系数越大,两个变量的线性相关性越强;反之,线性相关性越弱D. 若回来直线的斜率估计值为0.25,,,则回来直线的方程为10.“杂交水稻之父”袁隆平一生致力于杂交水稻技术的探讨、应用与推广,独创了“三系法”籼型杂交水稻,胜利探讨出“两系法”杂交水稻,创建了超级杂交稻技术体系,为我国粮食平安、农业科学发展和世界粮食供应做出了杰出贡献;某杂交水稻种植探讨所调查某地水稻的株高,得出株高(单位:cm)听从正态分布,其密度曲线函数为,则下列说法正确的是()A. 该地水稻的平均株高为100cmB. 该地水稻株高的方差为10C. 随机测量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大D. 随机测量一株水稻,其株高在(80,90)和在(100,110)(单位:cm)的概率一样大11.已知函数的定义域,部分对应值如表,的导函数的图象如图所示,下列关于函数的结论正确的是()-1 0 4 51 2 2 1A. 函数的极大值点有2个B. 函数在上是减函数C. 若时,的最大值是2,那么的最大值为4D. 当时,函数有4个零点12.已知数列均为递增数列,的前n项和为的前n项和为且满意,则下列结论正确的是()A. B.C.D.三、填空题(本大题共4小题,每小题5分,共20分)13.随机变量,若,,则 ________.14.写出一个满意下列条件的三次多项式函数:① 上的奇函数;②在处的切线斜率为4,则可以为________.15.已知函数,,若存在,,使得成立,则的最小值为________.16.已知等比数列的前项和为,,则 ________; ________ .(填“ ”,“ ”或“ ”)四、解答题(本大题共70分)17.已知数列满意:,且___________,其中,从① ,②,③ 三个条件中任选一个填入上面的横线中,并完成下列问题解答. (1)求数列的通项公式;(2)设,为数列的前项和,求 .18.为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:单价(元/件)8 8.2 8.4 8.6 8.8 9销量(万件)90 84 83 80 75 68(1)依据以上数据,求关于的线性回来方程;(2)若该产品成本是7元/件,假设该产品全部卖出,预料把单价定为多少时,工厂获得最大利润?(参考公式:回来方程,其中,)19.设为实数,函数, .(1)求函数的单调区间与极值;(2)求证:当,且时,有 .20.受新冠疫情影响,来我市旅游人数与前几年同期相比有所削减,某土特产超市为预估2024年暑假期间游客购买土特产的状况来制定进货方案,对2024年暑假期间的90位游客购买状况进行统计,得到如下购买金额及人数分布表:购买金额(元)人数10 15 20 15 20 10(1)依据以上数据完成列联表,并推断是否有95%的把握认为购买金额是否少于60元与性别有关;不少于60元少于60元合计男40女18合计(2)售货员佳佳发觉:沟帮子烧鸡、锦州小菜、真空包装干豆腐这三种特产成为了本店的“明星”商品.若有一位顾客须要在预选的包括这三种“明星”商品在内的7件(种类均不同)产品中选择4件特产带回家,求购买的4件特产中包含“明星”商品的件数的分布列及期望.附:参考公式和数据:, .附表:k0 2.072 2.706 3.841 6.635 7.879P(K2≥k0)0.150 0.100 0.050 0.010 0.00521.已知函数 .(1)当时,证明: 在上有唯一零点;(2)若对恒成立,求实数的取值范围.22.(1)某中学理学社为了汲取更多新社员,在校团委的支持下,在高一学年组织了抽签赠书活动.月初报名,月末抽签,最初有30名同学参与.社团活动主动分子甲同学参与了活动.①第一个月有18个中签名额.甲先抽签,乙和丙紧随其后抽签.求这三名同学同时中签的概率.②理学社设置了第 ( )个月中签的名额为,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,假如某次抽签的同学全部中签,则活动立即结束.求甲同学参与活动时间的期望.(2)某出版集团为了扩大影响,在全国组织了抽签赠书活动.报名和抽签时间与(1)中某中学理学社的报名和抽签时间相同,最初有30万人参与,甲同学在其中.每个月抽中的人退出活动,同时补充新人,补充的人数与中签的人数相同.出版集团设置了第 ( )个月中签的概率为,活动进行了个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参与活动时间的均值小于个月.答案解析部分一、单选题1.已知P(B|A)=,P(A)=,则P(AB)等于( )A. B.C.D.【答案】 C【考点】条件概率与独立事务【解析】【解答】由条件概率公式变形得P(AB)=P(B|A)·P(A)=,故答案为:C.【分析】由已知条件利用条件概率计算公式干脆求解.2.在数列中,,,则()A. -2B. -1C. D. 2【答案】 B【考点】数列递推式【解析】【解答】由题意,数列中,,,可得。
2021-2022学年辽宁省锦州市高二下学期期末考试数学试题(解析版)

2021-2022学年辽宁省锦州市高二下学期期末考试数学试题一、单选题1.已知等差数列{}n a 的通项公式53n a n =-+,则它的公差为( ) A .3 B .3- C .5 D .5-【答案】D【分析】由21a a -求得公差.【详解】依题意,等差数列{}n a 的通项公式53n a n =-+, 122,7a a =-=-,所以公差为215a a -=-. 故选:D2.已知随机变量X 服从正态分布()2,N μσ,若()()241P X P X >-+≥=,则μ=( )A .1-B .1C .2-D .2【答案】B【分析】根据正态分布的对称性求得正确答案. 【详解】由于随机变量X 服从正态分布()2,N μσ,且()()241P X P X >-+≥=,而()()221P X P X >-+≤-=, 所以()()42P X P X ≥=≤-, 所以()4212μ+-==. 故选:B3.函数()y f x =的图象如图所示,则(1)f ' 与(3)f '的大小关系是( )A .(1)(3)f f ''<B .(1)=(3)''f fC .(1)(3)f f ''>D .(1)(3)0f f ''+> 【答案】A【分析】根据导数的几何意义,函数在点()00,x y 处的导数值,即函数在这一点的切线的斜率,结合图象即可得解;【详解】解:由图可知(1)0f '<,(3)0f '<且(1)(3)f f ''<; 故选:A4.某铁球在0℃时,半径为1dm .当温度在很小的范围内变化时,由于热胀冷缩,铁球的半径会发生变化,且当温度为t ℃时铁球的半径为()1dm at +,其中a 为常数,则在0=t 时,铁球体积对温度的瞬时变化率为( )(参考公式:34π3V R =球)A .0B .4πC .4πaD .4π3a【答案】C【分析】先求得铁球体积关于温度t 的表达式,再对其求导,进而即可求得在0=t 时,铁球体积对温度的瞬时变化率. 【详解】3344ππ(1+)33V R at ==球, 则'224π3(1+)4π(1+)3V at a a at =⨯⨯=球 则204π(1+0)4πt V a a a '==⨯=球,即在0=t 时,铁球体积对温度的瞬时变化率为4πa 故选:C5.针对某种突发性的流感病毒,各国的医疗科研机构都在研制疫苗.已知甲、乙两个机构各自研制成功的概率分别为13和14,而且两个机构互不影响,则恰有一个机构研制成功的概率为( ) A .920B .512C .720D .112【答案】B【分析】根据相互独立事件概率计算方法,计算出正确答案.【详解】依题意,有一个机构研制成功的概率为1111511343412⎛⎫⎛⎫⨯-+-⨯= ⎪ ⎪⎝⎭⎝⎭.故选:B6.随机变量X 的分布列是若()212E X +=,则()D X =( )A .1 B .4 C .117 D .74【答案】D【分析】根据()212E X +=以及113a b ++=求得(),,a b E X ,进而求得()D X .【详解】依题意121,33a b a b ++=+=①,()()227,2121222333E X a b E X a b a b ⎛⎫=-+++=-+++=-++= ⎪⎝⎭,整理得16a b -=②,由①②解得51,124a b ==,且()512112432E X =-++=. 所以()222151111711221224234D X ⎛⎫⎛⎫⎛⎫=--⨯+-⨯+-⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:D7.英国物理学家牛顿用“作切线”的方法求函数的零点时,给出的“牛顿数列”在航空航天中应用广泛,若数列{}n x 满足()()1n n n n f x x x f x +=-',则称数列{}n x 为牛顿数列,如果()22f x x x =--,数列{}n x 为牛顿数列,设1ln2n n n x a x +=-且11a =,2n x >,数列{}n a 的前n 项和为n S ,则2022S =( )A .202221- B .202222-C .20221122⎛⎫- ⎪⎝⎭D .2022122⎛⎫- ⎪⎝⎭【答案】A【分析】先求得n a ,然后等比数列的前n 项和公式求得n S ,进而求得正确答案. 【详解】依题意11a =,2n x >,()22f x x x =--,()'12f x x =-,依题意()()1n n n n f x x x f x +=-', 即21221n n n n n x x x x x +--=--,则()22121211121nn n n n n n x x x x x x x +--=-+=-+-+,()22122221221n n n n n n n x x x x x x x +--=--=----(由于2n x >,所以12n x +≠), 则()()12211122n n n n x x x x ++++=--,两边取对数得121111ln ln 2ln222n n n n n n x x x x x x ++⎛⎫+++== ⎪---⎝⎭,即12n n a a +=, 所以数列{}n a 是首项为11a =,公比为2的等比数列,所以12n n a .所以122112n n n S -==--,所以2022202221S =-. 故选:A8.已知定义在R 上的函数()f x 的导函数()f x ',且()()0f x f x <'<,则( ) A .()()e 21f f >,()()2e 1f f > B .()()e 21f f >,()()2e 1f f < C .()()e 21f f <,()()2e 1f f < D .()()e 21f f <,()()2e 1f f >【答案】D【分析】根据已知不等式构造函数,结合导数的性质进行求解即可. 【详解】构造函数()()()()()e e x xf x f x f xg x g x '-'=⇒=,因为()()f x f x '<,所以()0g x '>,因此函数()g x 是增函数, 于是有2(2)(1)(2)(1)(2)e (1)e ef fg g f f >⇒>⇒>, 构造函数()()e ()e [()()]x x h x f x h x f x f x ''=⋅⇒=+,因为()()0f x f x <'<, 所以()0h x '<,因此()h x 是单调递减函数, 于是有2(2)(1)e (2)e (1)e (2)(1)h h f f f f <⇒<⇒<, 故选:D【点睛】关键点睛:根据不等式的形式构造新函数,再利用导数的性质是解题的关键.二、多选题9.函数()f x 的定义域为R ,它的导函数()y f x '=的部分图像如图所示,则下列结论正确的是( )A .()()21f f ->-B .1x =是()f x 的极小值点C .函数()f x 在()1,1-上有极大值D .3x =-是()f x 的极大值点【答案】AD【分析】根据函数极值的定义,结合导数的性质和导函数的图象逐一判断即可. 【详解】由()y f x '=的图象可知:当(,3)x ∈-∞-时,()0f x '>,所以函数()f x 单调递增;当(3,1)x ∈--时,()0f x '<,所以函数()f x 单调递减,因此有()()21f f ->-,3x =-是()f x 的极大值点,所以选项A 、D 正确;当(1,1)x ∈-,或(1,)x ∈+∞时,()0f x '>,所以函数()f x 单调递增,因此函数()f x 在()1,1-上没有极大值,且1x =不是()f x 的极小值点,所以选项B 、C 不正确,故选:AD10.有3台车床加工同一型号零件,第1台次品率为6%,第2,3台次品率为5%,加工的零件混在一起,已知第1,2,3台车床加工的零件分别占总数的25%,30%,45%,记事件B =“任取一个零件为次品”,事件=i A “零件为第i 台车床加工”(1i =,2,3),则( )A .()10.06PB A = B .()20.015P A B =C .()0.0525P B =D .()137P A B =【答案】ABC【分析】利用相互独立事件概率的乘法公式及条件概率公式分别求出各个选项的值即可判断各个选项的正误.【详解】解:根据题意()6%25%5%30%5%45%0.0525P B =⨯+⨯+⨯=,故C 正确;()()120.25,0.3P A P A ==,则()16%0.250.060.25P B A ⨯==,故A 正确;()20.35%0.015P A B =⨯=,故B 正确;()16%0.2536%4P A B ⨯==,故D 错误. 故选:ABC.11.已知在数列{}n a 中,11a =,()10nn n a a b b ++=>,其前n 项和为n S ,则( )A .当1b =时,9951S =B .当1b >时,数列{}n a 是递增数列C .30a >D .对任意0b >,存在R λ∈,使得数列{}nn a b λ-成等比数列【答案】CD【分析】通过计算判断AC 选项的正确性,利用特殊值判断B 选项错误,根据等比数列的知识判断D 选项的正确性.【详解】A 选项,当1b =时,11n n a a ++=, 由于11a =,所以213210,11a a a a =-==-=,……,以此类推,可知此时数列{}n a 的奇数项为1,偶数项为0,9950S =,所以A 选项错误.C 选项,11a =,()10nn n a a b b ++=>,212,1a a b a b +==-,2222323213,1024a a b a b a b b b ⎛⎫+==-=-+=-+> ⎪⎝⎭,所以C 选项正确.B 选项,不妨设2b =,根据C 选项的分析可知121,11a a b ==-=, 此时数列{}n a 不是递增数列,所以B 选项错误.D 选项,当0b >时,由1n n n a a b ++=得1nn n a a b +=-+,()1111n n nn n n n b b a b b b a a λλλ+++⎡⎤-+-=---⋅-⎣=⎦, 要使数列{}nn a b λ-成等比数列,则()11,11,1b b bλλλλ=-+==+, 即任意0b >,存在11b λ=+,使数列{}nn a b λ-成首项为11110111b a b b b b-⋅=-=>+++, 公比为1-的等比数列,所以D 选项正确.故选:CD12.对于函数()ln xf x x=,下列说法正确的是( ) A .()f x 在()0,e 上单调递减,在()e,+∞上单调递增 B .当1201x x 时,1221ln ln x x x x ⋅>⋅ C .若函数()y f x k =-有两个零点,则0k <D .设()2g x x a =+,若对1x ∀∈R ,()21,x ∃∈+∞,使得()()12g x f x =成立,则e a ≥【答案】BD【分析】利用函数的定义域判断A 选项的正确性;利用()f x 的单调性来判断B 选项的正确性;结合()y f x =的图象来判断C 选项的正确性;通过求()f x 和()g x 在给定区间上的取值范围来判断D 选项的正确性. 【详解】对于A 选项,()ln xf x x=的定义域为()()0,11,+∞,所以A 选项错误.对于B 选项,()()'2ln 1ln x f x x -=,当01x <<时,()'0f x <,()f x 递减.由于1201x x ,所以()()121212,ln ln x xf x f x x x >>, 由于()()1212ln 0,ln 0,ln ln 0x x x x <<⋅>,所以由1212ln ln x x x x >两边乘以()()12ln ln x x ⋅得 1221ln ln x x x x ⋅>⋅,所以B 选项正确. 对于C 选项,令()()0,y f x k f x k =-==,由于()()'2ln 1ln x f x x -=,所以在区间()()()()'0,1,1,e ,0,f x f x <递减;在区间()()()'e,,0,f x f x +∞>递增.当01x <<时,()0ln x f x x =<;当1x >时,()0ln x f x x=>;()e e f =. 函数()y f x =是定义域为()()()(),11,00,11,-∞-⋃-⋃⋃+∞的偶函数. 由此画出()y f x =的图象如下图所示,由图可知,直线e y =与()y f x =的图象有两个交点,即当e =k 时, 函数()y f x k =-有两个零点,所以C 选项错误.对于D 选项,由上述分析可知,()21,x ∈+∞,则()[)2e,g x ∈+∞,1R x ∈,()1g x a ≥,要使“对1x ∀∈R ,()21,x ∃∈+∞,使得()()12g x f x =成立”,则需e a ≥,所以D 选项正确. 故选:BD【点睛】利用导数研究函数的单调性,首先要求函数的定义域,单调性必须在定义域这个大前提下进行求解.求解恒成立、存在性问题,可转化为求最值或取值范围来进行求解.三、填空题13.已知函数()f x 的导函数为()f x ',且满足()()3e ln f x xf x '=+,则()e f '=______. 【答案】12e-【分析】运用导数的运算公式,结合代入法进行求解即可. 【详解】由()()()()()()113e ln 3e e 3e ef x xf x f x f f f x '''''=+⇒=+⇒=+, 解得()1e 2ef '=-, 故答案为:12e-14.如图,抛物线y x =x 轴上的点构成等边三角形11OPQ ,122OP Q ,1n n n Q P Q -⋯,⋯其中点nP 在抛物线上,点n Q 的坐标为(n x ,0),猜测数列{}n x 的通项公式为________.【答案】(1)3n n n x +=【分析】求出1133P ⎛ ⎝⎭,, 24233P ⎛ ⎝⎭,,(33P ,12||3OQ =,124||3Q Q =,236||3Q Q =,可猜测12||3n n nQ Q -=,利用累加法,即可求解 【详解】1OP 的方程为3y x =,代入抛物线y x =1133P ⎛ ⎝⎭,,12||3OQ =.同理可得24233P ⎛ ⎝⎭,,(33P ,124||3Q Q =,236||3Q Q =, 可猜测12||3n n nQ Q -=, 证明:记三角形1n n n Q P Q -的边长为n a , 由题意可知,当2n ≥时,121132n n n n P a a a a -⎛⎫++++⎪ ⎪⎝⎭在抛物线y x =可得21213142n n n a a a a a -=++++,当3n ≥时,2112213142n n n a a a a a ---=++++,两式相减得:221133114422n n n n a a a a ---=+ 化简得:123n n a a --=, 则数列{}n a 是等差数列,()122133n n a a n =+-⨯=, 12||3n n n Q Q -=, 123n n n x x -∴-=, 1462333n n x x ∴-=++⋯+, 2(1)(12)33n n n x n +∴=++⋯+=.故答案为:(1)3n n n x +=.15.若实数a ,b ,c ,d 满足2ln b a a =-,2d c =-,则()()22a cb d -+-的最小值是______. 【答案】2【分析】利用两点间距离公式,将()()22a cb d -+-转化为函数2()ln f x x x =-上任意一点P 与函数()2h x x =-上任意一点Q 间距离的最小值的平方,再利用导数的几何意义去求解PQ 最小值即可解决.【详解】设点(),P a b 为函数2()ln f x x x =-上任意一点, 点(),Q c d 为函数()2h x x =-上任意一点, 则()()222=a b Q c d P -+-由2()ln f x x x =-,可得1()2f x x x'=-设与直线()2h x x =-平行的直线与函数2()ln f x x x =-相切于()00,M x y ,()00x > 则00121x x -=,解之得01x =或012x =-(舍)则切点()1,1M 又切点()1,1M 到直线()2h x x =-的距离d ==则PQ,()()22a cb d -+-的最小值为2 故答案为:2四、双空题16.某产品的研发投入费用x (单位:万元)与销售量y (单位:万件)之间的对应数据如表所示:根据表中的数据可得回归直线方程 2.27y x a =-,则a =______;该产品的研发投入费用每提高3万元,销售量估计能提高______万件. 【答案】 1.33 6.81【分析】根据样本中心点求得a ,利用回归直线方程进行估计.【详解】 2.2 2.6 4.3 5.0 5.945x ++++==,3.8 5.47.010.3512.27.755y ++++==,所以7.75 2.274a =⨯-,解得 1.33a =. 所以为回归直线方程 2.27 1.33y x =-.所以该产品的研发投入费用每提高3万元,销售量估计能提高2.273 6.81⨯=万件. 故答案为:1.33;6.81五、解答题17.等差数列{}n a 的前n 项和记为n S ,且3720a a +=,526a a -=. (1)求数列{}n a 的通项公式n a ;(2)记数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和为n T ,若97100n T >,求n 的最小值.【答案】(1)2n a n = (2)33【分析】(1)根据已知条件求得等差数列{}n a 的首项和公差,从而求得n a . (2)利用裂项求和法求得n T ,由此化简不等式97100n T >并求得n 的最小值. 【详解】(1)设等差数列{}n a 的公差为d , 依题意3720a a +=,526a a -=,则1282036a d d +=⎧⎨=⎩,解得12a d ==,所以2n a n =.(2)()122122n n a a n S n n n n ++=⋅=⋅=+,1111n S n n =-+,所以1111111122311n T n n n =-+-++-=-++, 由97100n T >,得197131,,33100,39711001100n n n n -><+>>++, 9713233n >=+,由于*N n ∈,所以n 的最小值为33. 18.某水果经营户对出售的苹果按大小和色泽两项指标进行分类,最大横切面直径不小于70毫米则大小达标,着色度不低于90%则色泽达标,大小和色泽均达标的苹果为一级果;大小和色泽有一项达标另一项不达标的苹果为二级果;两项均不达标的苹果为三级果.已知该经营户购进一批苹果,从中随机抽取100个进行检验,得到如下统计表格:(1)根据以上数据,判断是否有95%的把握认为该经营户购进的这批苹果的大小达标和色泽达标有关;(2)该经营户对三个等级的苹果按照分层抽样从样本中抽取10个苹果,再从中随机抽取3个,求抽到二级果个数X 的概率分布列和数学期望. 附:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.【答案】(1)有95%的把握认为该经营户购进的这批苹果的大小达标和色泽达标有关 (2)分布列见解析,()910E X =【分析】(1)根据已知表格中的数据,由2K 的计算公式求出2K ,再结合临界值表即可求解;(2)由分层抽样可得一级果6个,二级果3个,三级果1个,从而根据离散型随机变量分布列的求解步骤及期望公式即可求解.【详解】(1)解:由于()22100106015154 3.84125757525K ⨯⨯-⨯==>⨯⨯⨯,所以有95%的把握认为该经营户购进的这批苹果的大小达标和色泽达标有关; (2)解:对三个等级的苹果按照分层抽样从样本中抽取10个,则一级果6个,二级果3个,三级果1个.由题意,二级果的个数X 的可能值为0,1,2,3,则()()312737331010C C C 7210,1C 24C 40P X P X ======,()()213373331010C C C 712,3C 40C 120P X P X ======.所以X 的分布列为:所以X 的数学期望()721719012324404012010E X =⨯+⨯+⨯+⨯=. 19.已知函数()324f x x ax =-+-,其中a 为实常数.(1)当3a =时,求曲线()y f x =在点()()1,1f 处的切线方程; (2)讨论()f x 的单调性;(3)若存在()00,x ∈+∞,使得不等式()00f x >成立,求实数a 的取值范围. 【答案】(1)35y x =- (2)答案详见解析 (3)()3,+∞【分析】(1)利用切点和斜率求得切线方程.(2)求得()'f x ,对a 进行分类讨论,由此求得()f x 的单调区间.(3)结合(2),对a 进行分类讨论,结合()f x 的单调区间、最值,求得a 的取值范围.【详解】(1)()()32'234,36f x x x f x x x =-+-=-+,所以()()'12,13f f =-=,所以切线方程为()()231,35y x y x --=-=-.(2)()f x 的定义域为R ,()'223233f x x ax x x a ⎛⎫=-+=-- ⎪⎝⎭,当0a <时,()f x 在区间()()()'2,,0,,0,3a f x f x ⎛⎫-∞+∞< ⎪⎝⎭递减;在区间()()'2,0,0,3a f x f x ⎛⎫> ⎪⎝⎭递增.当0a =时,()'0f x ≤,()f x 在R 上递减.当0a >时,()f x 在区间()()()'2,0,,,0,3a f x f x ⎛⎫-∞+∞< ⎪⎝⎭递减;在区间()()'20,,0,3a f x f x ⎛⎫> ⎪⎝⎭递增.(3)由(2)知:当0a ≤时,()f x 在()0,∞+上递减,()()040f x f <=-<,不符合题意. 当0a >时,在区间()0,∞+上,()3max 244327a f x f a ⎛⎫==- ⎪⎝⎭,依题意可知344027a ->,解得3a >.综上所述,a 的取值范围是()3,+∞.20.已知数列{}n a 是首项为1,公差不为0的等差数列,且248,,a a a 成等比数列.数列{}n b 的前n 项的和为n S ,且满足()()*112n n S b n N =-∈. (1)求数列{}{},n n a b 的通项公式; (2)求数列{}n n a b 的前n 项和n T .【答案】(1)n a n =,13nn b ⎛⎫= ⎪⎝⎭(2)3314243nn n T ⎛⎫⎛⎫=-+ ⎪⎪⎝⎭⎝⎭【分析】(1)设数列{}n a 公差为()d d ≠0,由248,,a a a 成等比数列求得d ,可得n a . 利用2n 1n n n S S b --=求得n b ; (2)利用错位相减求和n T 即可.【详解】(1)设数列{}n a 公差为()d d ≠0,由248,,a a a 成等比数列有:()()2117(13)d d d ++=+,解得:1d =,所以()111n a n n =+-⨯=, 数列{}()()*1:12n n n b S b n N =-∈,当1n =即,()11112b b =-,解得:113b =,当2n 时,有()11112n n S b --=-,所以()()11111122n n n n S S b b ---=---, 得:13n n b b -=.又11110,33n n b b b -=≠=, 所以数列{}n b 为以113b =为首项,公比为13的等比数列,所以数列{}n b 的通项公式为:13nn b ⎛⎫= ⎪⎝⎭.(2)1122n n n T a b a b a b =+++,211112333nn T n ⎛⎫⎛⎫=⋅+⋅++ ⎪ ⎪⎝⎭⎝⎭, 231111123333n n T n +⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,得212111133333nn n T n +⎛⎫⎛⎫⎛⎫=+++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,1211113233n n n T n +⎡⎤⎛⎫⎛⎫=--⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦, 化简得:3314243nn n T ⎛⎫⎛⎫=-+ ⎪⎪⎝⎭⎝⎭.21.2022年2月6日,中国女足在两球落后的情况下,以3比2逆转击败韩国女足,成功夺得亚洲杯冠军,在之前的半决赛中,中国女足通过点球大战6:5惊险战胜日本女足,其中门将朱钰两度扑出日本队员的点球,表现神勇.(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有12的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑出点球的个数X 的分布列和期望;(2)好成绩的取得离不开平时的努力训练,甲、乙、丙、丁4名女足队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外3人中的1人,接球者接到球后再等可能地随机传向另外3人中的1人,如此不停地传下去,假设传出的球都能接住.记第n 次传球之前球在甲脚下的概率为n p ,易知121,0==p p .①试证明14n p ⎧⎫-⎨⎬⎩⎭为等比数列;②设第n 次传球之前球在乙脚下的概率为n q ,比较10p 与10q 的大小. 【答案】(1)分布列见解析,1()2E X = (2)①证明见解析;②1010p q <【分析】(1)先计算门将每次可以扑出点球的概率,再列出其分布列,进而求得数学期望;(2)递推求解,记第n 次传球之前球在甲脚下的概率为n p ,则当2n ≥时,第1n -次传球之前球在甲脚下的概率为1n p -,满足()11111101333n n n n p p p p ---=⋅+-⋅=-+.【详解】(1)解析1:分布列与期望依题意可得,门将每次可以扑出点球的概率为111133326p =⨯⨯⨯=,门将在前三次扑出点球的个数X 可能的取值为0,1,2,3,030315125(0)66216P X C ⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭,12131525(1)6672P X C ⎛⎫⎛⎫==⨯⨯=⎪ ⎪⎝⎭⎝⎭, 2123155(2)6672P X C ⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭,3033151(3)66216P X C ⎛⎫⎛⎫==⨯⨯=⎪ ⎪⎝⎭⎝⎭,X 的分布列为:期望12525511()012321672722162E X =⨯+⨯+⨯+⨯=. (1)解析2:二项分布依题意可得,门将每次可以扑出点球的概率为111133326p =⨯⨯⨯=,门将在前三次扑出点球的个数X 可能的取值为0,1,2,3,易知13,6X B ⎛⎫~ ⎪⎝⎭,3315()66k k kP X k C -⎛⎫⎛⎫==⨯⨯ ⎪ ⎪⎝⎭⎝⎭,0,1,2,3k =.X 的分布列为:期望11()362E X =⨯=.(2)解析:递推求解①第n 次传球之前球在甲脚下的概率为n p ,则当2n ≥时,第1n -次传球之前球在甲脚下的概率为1n p -,第1n -次传球之前球不在甲脚下的概率为11n p --,则()11111101333n n n n p p p p ---=⋅+-⋅=-+,从而1111434n n p p -⎛⎫-=-- ⎪⎝⎭,又11344p -=,∴14n p ⎧⎫-⎨⎬⎩⎭是以34为首项.公比为13-的等比数列.②由①可知1311434n n p -⎛⎫=-+ ⎪⎝⎭,91031114344p ⎛⎫=-+< ⎪⎝⎭,()101011134q p =->,故1010p q <. 22.已知函数()e 1xf x x =-,()()lng x a x x =+.(1)若2a =,证明:()42g x x ≤-;(2)若不等式()()f x g x ≥恒成立,求正实数a 的值;(3)证明:()2e 2ln 2sin xx x x x >++.【答案】(1)证明详见解析 (2)1a = (3)证明详见解析【分析】(1)将()42g x x ≤-转化为ln 10x x -+≤,然后利用构造函数法,结合导数证得不等式成立.(2)利用换元法,将不等式()()f x g x ≥恒成立,转化为10t e at --≥恒成立,利用构造函数法,结合导数求得正实数a 的值.(3)结合(1)(2),将所要证明的不等式转化为证明222sin x x x -+>,结合二次函数的性质证得不等式成立.【详解】(1)2a =时,()42ln 10g x x x x ≤-⇔-+≤,设()ln 1t x x x =-+,11()1(0)x t x x x x'-=-=>, 所以()t x 在区间()()()'0,1,0,t x t x >递增;在区间()()()'1,,0,t x t x +∞<递减.所以()()10t x t ≤=,即ln 10x x -+≤, 所以2a =时,()42g x x ≤-.(2)依题意,ln e 1(ln )e (ln )10x x x x a x x a x x +-≥+⇔-+-≥, 令ln t x x =+,ln y x x =+在()0,∞+上递增,且R t ∈, 所以10t e at --≥对任意R t ∈恒成立.设()()()'e 10,e t th t at a h t a =-->=-,所以函数()h t 在区间()()()',ln ,0,a h t h t -∞<递减;在区间()()()'ln ,,0,a h t h t +∞>递增.所以()()min ln ln 1h t h a a a a ==--, 所以ln 10--≥a a a ,111ln1,ln 1a a a a a+≥≥-, 由(1)知ln 10x x -+≤,即ln 1≤-x x ,即11ln 1a a≤-, 所以11ln1a a =-,当且仅当11a=,即1a =时成立. (3)由(2)得,当1a =时,()e (ln )1x f x x x x =-+≥对任意0x >恒成立. 所以()0,x ∀∈+∞,e ln 1x x x x ≥++,当且仅当1x =时等号成立.则()22e ln 0x x x x x x x ≥++>,要证明()()2e 2ln 2sin 0xx x x x x >++>,只需证明2ln (2)ln 2sin (0)x x x x x x x x ++>++>, 即证22ln 2sin (0)x x x x x +>+>, 由(1)知()ln 10x x x ≤->,所以只需证()22(1)2sin 0x x x x x +>-+>,即证()222sin 0x x x x -+>>,①当1x >时,()221222sin x x x x x -+=-+>≥,不等式成立.②当01x <≤时,221772()244x x x -+=-+≥, π72sin 2sin12sin34x ≤<=<,不等式成立.所以()222sin 0x x x x -+>>成立,所以()()2e 2ln 2sin 0xx x x x x >++>成立.【点睛】利用导数研究不等式恒成立问题,可对不等式进行转化,然后利用构造函数法,结合导数求得所构造函数的单调性、极值、最值等,从而求得参数的取值范围.。
辽宁省锦州市数学高二下学期理数期末联考试卷

辽宁省锦州市数学高二下学期理数期末联考试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)复数的值是()A . 1B . -1C . iD . -i2. (2分)(2018·杭州模拟) 二项式的展开式中含项的系数是()A . 80B . 48C . -40D . -803. (2分)(2019·枣庄模拟) 空间直角坐标系O-xyz中,某四面体的顶点坐标分别为(0,0,0),(0,1,1),(1,0,1),(1,1,0),画该四面体三视图时,以yOz平面为投影面所得到的视图为正视图,则该四面体的侧视图是()A .B .C .D .4. (2分)某单位为了了解用电量Y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温数据如表格所示.若由表中数据得回归直线方程y=bx+a中b=﹣2,据此预测当气温为15℃时,用电量的度数约为()气温(℃)141286用电量(度)22263438A . 20B . 25C . 30D . 355. (2分) (2019高二下·张家口月考) 调查研究某项运动与性别是否有关系得到列联表如图,若这两个变量没有关系,则的可能值为()男性女性合计爱好运动100a100+a不爱好运动120600720合计220600+a820+aA . 720B . 500D . 2006. (2分) (2018高二下·中山月考) 12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变.则不同调整方法的种数是()A .B .C .D .7. (2分)长方体的一条体对角线与长方体的棱所组成的异面直线有()A . 2对B . 3对C . 6对D . 12对8. (2分) (2019高一上·成都月考) 函数在区间[2,5)上的最大值,最小值分别是()A . 无最大值,最小值是4B .C . 最大值是4,无最小值D . 4,09. (2分) (2018高二上·淮北月考) 抛物线的焦点为,准线为,是抛物线上的两个动点,且满足,设线段的中点在上的投影为,则的最大值是()B .C .D . 110. (2分) (2016高一下·南沙期末) 在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:(1)对任意a∈R,a*0=a;(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).则函数f(x)=(ex)* 的最小值为()A . 2B . 3C . 6D . 811. (2分) (2017高二下·桃江期末) 五位同学去听同时进行的4个课外知识讲座,每个同学可自由选择,则不同的选择种数是()A . 54B . 5×4×3×2C . 45D . 5×412. (2分)定义在R上的函数满足,为的导函数,已知的图像如图所示,若两个正数a、b满足,则的取值范围是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)全称命题的否定是________。
2022届辽宁省锦州市高二第二学期数学期末教学质量检测试题含解析

2022届辽宁省锦州市高二第二学期数学期末教学质量检测试题一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意) 1.已知函数()f x 是定义在R 上的奇函数,当(),0x ∈-∞时,()322f x x x =+,则()2f =( )A .12B .20C .28D .14-2.曲线()cos sin cos xf x x x =-在点33,44M f ππ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭处的切线的斜率为( ) A .12 B .12-C .22-D .223.甲、乙、丙三人每人准备在个旅游景点中各选一处去游玩,则在“至少有个景点未被选择”的条件下,恰有个景点未被选择的概率是( ) A .B .C .D .4.设函数()f x 是(,0)-∞上的可导函数其导函数为()f x ',且有2()()0f x xf x '+>,则不等式2(2016)(2016)x f x ++9(3)0f -->的解集为( )A .(,2013)-∞-B .(2016,0)-C .(,2019)-∞-D .(2019,0)-5.椭圆()222210x y a b a b +=>>短轴的一个端点和两个焦点相连构成一个三角形,若该三角形内切圆的半径为5b,则该椭圆的离心率为( ) A .12 B .13C .14D .296.已知曲线()cos 3f x x x x =+在点()()0,0f 处的切线与直线410ax y ++=垂直,则实数a 的值为( ) A .-4B .-1C .1D .47.《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( ) A .288种B .144种C .720种D .360种8.从5名男生和4名女生中选出3名学生参加一项活动,要求至少一名女生参加,不同的选法种数是( ) A .70B .74C .84D .5049.在ABC ∆中,43,5,tan ,3AB BC AB BC ===-u u u v u u u v u u u v u u u v,则CA CB ⋅=u u u v u u u v ( ) A .16-B .16C .9D .9-10.已知函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象如图所示,则函数()y f x ω=+的对称中心坐标为( )A .()23,3242k k Z ππ⎛⎫+∈⎪⎝⎭B .()323,83k k Z ππ⎛⎫-∈ ⎪⎝⎭C .()153,282k k Z ππ⎛⎫+∈⎪⎝⎭ D .()332,283k k Z ππ⎛⎫-∈⎪⎝⎭ 11.设函数()()ln 21f x x x =--的极小值为a ,则下列判断正确的是 A .1a = B .0ln 2a << C .ln 2a =D .ln 21a <<12.已知直线2:2l y x =与双曲线()2222:10,0x y E a b a b -=>>分别交于点,A B ,若,A B 两点在x 轴上的射影恰好是双曲线E 的两个焦点,则双曲线E 的离心率为( ) A .2B .3C .4D .5二、填空题(本题包括4个小题,每小题5分,共20分)13.若从4名男生和3名女生中任选2人参加演讲比赛,则至少选出1名女生的概率为_______(结果用分数表示).14.如图所示,在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别是1CC ,AD 的中点,那么异面直线1D E 和1A F 所成角的余弦值等于________________.15.定义在R 上的偶函数()f x 满足()()3f x f x +=-,且()12019f -=,则()2020f =______. 16.圆22420x y x y +-+=的圆心到直线3430x y ++=的距离__________. 三、解答题(本题包括6个小题,共70分) 17.已知函数()(1)x f x x e =-.(1)求()f x 的单调区间;(2)证明:当0a >时,方程()f x a =在区间(1,)+∞上只有一个解;(3)设()()ln(1)h x f x a x ax =---,其中0a >.若()0h x ≥恒成立,求a 的取值范围.18.已知p :方程2216x ym m +=-表示焦点在x 轴上的椭圆;q :双曲线2215y x m-=的实轴长大于虚轴长.若命题“p q ∨”为真命题,“p q ∧”为假命题,求m 的取值范围.19.(6分)如图,在三棱锥P ABC -中,22AB BC ==,4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.20.(6分) “绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到月生产销售的统计规律如下:①月固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③月生产x 百台的销售收入20.540.504()7.54x x x R x x ⎧-+-≤≤=⎨>⎩,,(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).(1)为使该产品的生产不亏本,月产量x 应控制在什么范围内? (2)该产品生产多少台时,可使月利润最大?并求出最大值.21.(6分)已知椭圆的中心在原点,焦点在x 轴上,长轴长是短轴长的2倍且经过点()2,1M ,平行于OM 的直线l 在y 轴上的截距为()0m m ≠,l 交椭圆于,A B 两个不同点. (1)求椭圆的标准方程以及m 的取值范围;(2)求证直线,MA MB 与x 轴始终围成一个等腰三角形. 22.(8分)在ABC ∆3cos 1A A -=,cos 45B =,AB 43=(1)求内角A 的大小;(2)求边BC 的长.参考答案一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意) 1.A 【解析】 【分析】 先计算出()2f -的值,然后利用奇函数的性质得出()()22f f =--可得出()2f 的值。
2020年辽宁省锦州市数学高二下期末综合测试试题含解析

2020年辽宁省锦州市数学高二(下)期末综合测试试题一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意) 1.幂函数的图象过点(14,2) ,那么(8)f 的值为( )A .24B .64C .22D .1642.已知函数()1,0f 11,02x e x x x x ⎧-≤⎪=⎨->⎪⎩,若m n <且()()f m f n =,则n-m 的最小值为( )A .2ln2-1B .2-ln2C .1+ln2D .23.正项等比数列{}n a 中,2018201620172a a a =+,若2116m n a a a =,则41m n +的最小值等于( ) A .1 B .35C .136D .324.已知函数2()()f x x a =-,且'(1)2f =,则a =( ) A .1-B .2C .1D .05.下列说法正确的是( )A .命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠”B .已知()y f x =是R 上的可导函数,则“()00f x '=”是“x 0是函数()y f x =的极值点”的必要不充分条件C .命题“存在x ∈R ,使得210x x ++<”的否定是:“对任意x ∈R ,均有210x x ++<”D .命题“角α的终边在第一象限角,则α是锐角”的逆否命题为真命题 6.下列命题中为真命题的是( ) A .若10,2x x x≠+≥ B .命题:若21x =,则1x =或1x =-的逆否命题为:若1x ≠且1x ≠-,则21x ≠ C .“=1a ”是“直线0x ay -=与直线0x ay +=互相垂直”的充要条件 D .若命题2:,10p x R x x ∃∈-+<,则2:,10p x R x x ⌝∀∈-+> 7.函数()1f x x=与两条平行线x e =,4x =及x 轴围成的区域面积是( ) A .2ln21-+B .2ln 21-C .ln 2-D .ln 28.设a=log 20.3,b=10lg0.3,c=100.3,则 A .a<b<cB .b<c<aC .c<a<bD .c<b<a颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )A .120种B .240种C .144种D .288种10.如图,在矩形OABC 中的曲线分别是sin y x =,cos y x =的一部分,,02A π⎛⎫⎪⎝⎭,()0,1C ,在矩形OABC 内随机取一点,则此点取自阴影部分的概率为( )A .()421π-B .()321π-C .()221π-D .21π-11.函数y 5ln x x=的图象大致为( )A .B .C .D .12.设函数()f x 是定义在()0-∞,上的可导函数,其导函数为()'f x ,且有()()3'0f x xf x +<,则不等式()()()320192019820x f x f +++-<的解集为( )A .()20212019--,B .()2021-∞-,C .()20192017--,D .()2021-+∞, 二、填空题(本题包括4个小题,每小题5分,共20分) 13.复数21i+(i 是虚数单位)的虚部是______. 14.某校毕业典礼由6个节目组成,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在前三位,且节目丙、丁必须排在一起,则该校毕业典礼节目演出顺序的编排方案共有______种.16.已知复数z 满足||||2z i z a ++-=,若z 在复平面上对应点的轨迹是椭圆,则实数a 的取值范围是______;三、解答题(本题包括6个小题,共70分)17.如图(1)是一个仿古的首饰盒,其左视图是由一个半径为r 分米的半圆和矩形ABCD 组成,其中AD 长为a 分米,如图(2).为了美观,要求2r a r ≤≤.已知该首饰盒的长为4r 分米,容积为4立方分米(不计厚度),假设该首饰盒的制作费用只与其表面积有关,下半部分的制作费用为每平方分米2百元,上半部制作费用为每平方分米4百元,设该首饰盒的制作费用为y 百元.(1)写出y 关于r 的函数解析式;(2)当r 为何值时,该首饰盒的制作费用最低? 18.已知函数()ln ()f x x a x a R =-∈.(Ⅰ)当2a =时,求曲线y =()f x 在点(1,(1))A f 处的切线方程; (Ⅱ)求函数()f x 的极值.19.(6分)如图,多面体P ABCD -,平面ABCD ⊥平面PBC ,DC BC ⊥,DA BC P ,090BCP ∠=,M 是AP 的中点,N 是DP 上的点.(Ⅰ)若MN ∥平面PBC ,证明:N 是DP 的中点;(Ⅱ)若3CB CD CP ===,1AD =,求二面角A BP C --的平面角的余弦值.20.(6分)在四棱锥P-ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,4PA AD ==,2AB =, 以AC 的中点O 为球心,AC 为直径的球面交PD 于点M ,交PC 于点N.(1)求证:平面ABM ⊥平面PCD ;(2)求直线CD 与平面ACM 所成角的大小; (3)求点N 到平面ACM 的距离.21.(6分)数列{}n a 满足2(n n S n a n =-∈N *). (1)计算1234,,,a a a a ,并由此猜想通项公式n a ; (2)用数学归纳法证明(1)中的猜想.22.(8分)某保险公司拟推出某种意外伤害险,每位参保人交付50元参保费,出险时可获得2万元的赔付,已知一年中的出险率为0.15%,现有6000人参保.(1)求保险公司获利在[)6,12(单位:万元)范围内的概率(结果保留小数点后三位); (2)求保险公司亏本的概率.(结果保留小数点后三位) 附:()6000600000.00150.9985ktt t i P k C-==⨯⨯∑.k 9 10 11 12 13 1415()P k0.587 0.706 0.803 0.876 0.926 0.959 0.978参考答案一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意) 1.A 【解析】 【分析】 【详解】设幂函数的解析式为f x x α=(), ∵幂函数f x ()的图象过点1(4)2,,121124882248f αα-∴=∴=-∴===,.(). 选A 2.C 【解析】 【分析】作出函数()f x 的图象,由题意可得0m …,求得2m n e =,可得()2mg m n m e m =-=-,0m …,求出导数和单调区间,可得极小值,且为最小值,即可得解. 【详解】解:作出函数()1,011,02x e x f x x x ⎧-⎪=⎨->⎪⎩…的图象如下,m n <,且()()f m f n =,可得0m …,1112n m e -=-,即为2m n e =, 可得()2mg m n m e m =-=-,0m …,()'21m g m e =-,令()'0g m =,则1ln 2m = 当1ln 2m <时,()'0g m <,()g m 递减; 当1ln02m <…时,()'0g m >,()g m 递增. 则()g m 在1ln 2m =处取得极小值,也为最小值1ln 211ln 2ln 1ln222g e ⎛⎫=-=+ ⎪⎝⎭,故选C . 【点睛】本题考查分段函数及应用,注意运用转化思想和数形结合思想,运用导数求单调区间和极值、最值,考查【解析】分析:先求公比,再得m,n 关系式,最后根据基本不等式求最值.详解:因为2018201620172a a a =+,所以2202q q q q =+>∴=Q , 因为2116m n a a a =,所以211211216246m n a a m n m n -+-=∴+-=∴+=,因此41411413()(5)(5,6662m n n m m n m n m n ++=+=++≥+= 当且仅当24m n ==时取等号 选点睛:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误. 4.D 【解析】 【分析】求出函数()y f x =的导数,结合条件()12f '=,可求出实数a 的值. 【详解】因为'()22f x x a =-,所以'(1)2122f a =⨯-=,解得0a =,故选D . 【点睛】本题考查导数的计算,考查导数的运算法则以及基本初等函数的导数,考查运算求解能力,属于基础题. 5.B 【解析】试题分析:对于A ,命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠”,不满足否命题的定义,所以A 不正确;对于B ,已知()y f x =是R 上的可导函数,则“()00f x '=”函数不一定有极值,“0x 是函数()y f x =的极值点”一定有导函数为0,所以已知()y f x =是R 上的可导函数,则“()00f x '=”是“0x 是函数()y f x =的极值点”的必要不充分条件,正确;对于C ,命题“存在x R ∈,使得210x x ++<”的否定是:“对任意x R ∈,均有210x x ++<”,不满足命题的否定形式,所以不正确;对于D ,命题“角α的终边在第一象限角,则α是锐角”是错误命题,则逆否命题为假命题,所以D 不正确;故选B . 考点:命题的真假判断与应用. 6.B分析:对四个命题,分别进行判断,即可得出结论. 详解:对于A ,0x >,利用基本不等式,可得12x x+≥,故不正确; 对于B ,命题:若21x =,则1x =或1x =-的逆否命题为:若1x ≠且1x ≠-,则21x ≠ ,正确;对于C ,“1a =± ”是“直线0x ay -=与直线0x ay +=互相垂直”的充要条件,故不正确; 对于D ,命题命题2:,10p x R x x ∃∈-+<,则2:,10p x R x x ⌝∀∈-+≥ ,故不正确. 故选:B .点睛:本题考查命题的真假判断与应用,考查学生分析解决问题的能力,属基础题. 7.B 【解析】 【分析】根据定积分的几何意义直接求出()f x 在区间[,4]e 的定积分,即可得出答案。
辽宁省锦州市第二十四中学2022年高二数学理下学期期末试题含解析

辽宁省锦州市第二十四中学2022年高二数学理下学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 某班级有一个7人小组,现任选其中3人相互调整座位,其余4人座位不变,则不同的调整方法的种数有()A.35 B.70 C.210 D.105参考答案:B2. 过点()引直线l与曲线y=相交于A,B两点,O为坐标原点,当△ABO的面积取得最大值时,直线l的斜率等于()A.B.C.D.参考答案:B【考点】直线与圆的位置关系;直线的斜率.【专题】压轴题;直线与圆.【分析】由题意可知曲线为单位圆在x轴上方部分(含与x轴的交点),由此可得到过C点的直线与曲线相交时k的范围,设出直线方程,由点到直线的距离公式求出原点到直线的距离,由勾股定理求出直线被圆所截半弦长,写出面积后利用配方法转化为求二次函数的最值.【解答】解:由y=,得x2+y2=1(y≥0).所以曲线y=表示单位圆在x轴上方的部分(含与x轴的交点),设直线l的斜率为k,要保证直线l与曲线有两个交点,且直线不与x轴重合,则﹣1<k<0,直线l的方程为y﹣0=,即.则原点O到l的距离d=,l被半圆截得的半弦长为.则===.令,则,当,即时,S△ABO有最大值为.此时由,解得k=﹣.故答案为B.【点评】本题考查了直线的斜率,考查了直线与圆的关系,考查了学生的运算能力,考查了配方法及二次函数求最值,解答此题的关键在于把面积表达式转化为二次函数求最值,是中档题.3. 若三棱锥P-ABC的三条侧棱与底面所成的角都相等,则点P在底面ABC上的射影一定是 ABC的()A. 外心B. 垂心C. 内心D. 重心参考答案:略4. 下列函数f(x)中,满足“对任意x1,x2∈(-∞,0),当x1<x2时,都有f(x1)<f(x2)”的函数是()A.f(x)=-x+1 B f(x)=2xC. f(x)=x2-1D.f(x)=ln(-x)参考答案:B略5. 已知双曲线的渐近线与圆相交,则双曲线的离心率的取值范围是()A. B. C. D.参考答案:C6. 已知两点M(-2,0),N(2,0),点P满足=12,则点P的轨迹方程为A. B. C. D.参考答案:C7. 用反证法证明命题“若自然数a,b,c的积为偶数,则a,b,c中至少有一个偶数”时,对结论正确的反设为()A、a,b,c中至多有一个偶数B、a,b,c都是奇数C、a,b,c至多有一个奇数D、a,b,c都是偶数参考答案:B【考点】反证法与放缩法【解答】解:用反证法法证明数学命题时,应先假设要证的命题的反面成立,即要证的命题的否定成立,而命题:“自然数a,b,c中至少有一个是偶数”的否定为:“a,b,c中一个偶数都没有”,即a,b,c都是奇数,故选:B.【分析】用反证法法证明数学命题时,应先假设命题的反面成立,求出要证的命题的否定,即为所求.8. 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是( )A.B.C.D.参考答案:A【考点】平面图形的直观图.【专题】作图题;空间位置关系与距离.【分析】根据斜二测画法知,平行于x轴的线段长度不变,平行于y的线段变为原来的,由此得出原来的图形是什么.【解答】解:根据斜二测画法知,平行于x轴的线段长度不变,平行于y的线段变为原来的,∵O′C′=1,O′A′=,∴OC=O′C′=1,OA=2O′A′=2;由此得出原来的图形是A.故选:A.【点评】本题考查了平面图形的斜二测画法应用问题,是基础题目.9. 对于上可导的任意函数,若满足,则必有()A BC D参考答案:C略10. 如图所示,正三棱锥S-ABC, SB⊥AC,SB=AC=2, E、F分别是SC和AB的中点,则EF的长是()A.1 B. C. D.参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 已知、是椭圆(>>0)的两个焦点,为椭圆上一点,且.若的面积为9,则=____________ .参考答案:略12. 已知函数 若,则实数_________.参考答案:13. (5分)(2011?福建模拟)在△ABC 中,若a=7,b=8,,则最大角的余弦值是.参考答案:【考点】余弦定理.【专题】计算题.【分析】先利用余弦定理求得边c 的长度,进而根据大角对大边的原则推断出B 为最大角,最后利用余弦定理求得cosB 的值.【解答】解:c==3,∴b 边最大,∴B 为最大角,cosB==﹣,故答案为﹣.【点评】本题主要考查了余弦定理的应用.解题的关键是判断出三角形中的最大角.14. 二项式的展开式中含的项的系数是参考答案:15. 已知向量,,且,则.参考答案:-616. 已知双曲线的离心率为,则双曲线的离心率为 。
辽宁省锦州市太和区中学高二数学理下学期期末试卷含解析

辽宁省锦州市太和区中学高二数学理下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设在上连续,则在上的平均值是()A.B.C.D.参考答案:D2. 若直线的倾斜角为,则实数的值为【】.A. B. C.D.或参考答案:C略3. 设三棱锥的顶点在平面上的射影是,给出以下命题:①若两两互相垂直,则是的垂心②若,是斜边上的中点,则③若,则是的外心④若到的三边的距离相等,则为的内心其中正确命题的是()A.①③④ B.②③④ C.①②③ D.①②③④参考答案:C 略4. 函数的图象上关于轴对称的点共有A. 1对B. 2对C. 3对D. 4对参考答案:C5. A是圆上固定的一点,在圆上其他位置任取一点A′,连接AA′如右图,它是一条弦,它的长度大于等于半径长的概率为()A. B. C. D.参考答案:B略6. 抛物线的焦点到准线的距离为( )A. B. C.8 D.2参考答案:D7. 已知异面直线a、b的方向向量分别为、,平面α、β的法向量分别为、,则下列命题中是假命题的是( ▲ )A.对于,若存在实数x、y使得,则共面B.若∥,则a⊥αC.若=,则l与所成角大小为D.若二面角α—l—β的大小为γ,则γ=<,>或π-<,>.参考答案:C略8. 函数的导数是( )A. B.C. D.参考答案:A9. 等差数列{a n}的前n项和为S n,若,则()A. -1B. 1C. -2D. 2参考答案:A【分析】根据等差数列的性质化简已知条件,由此求得的值.【详解】依题意,故选A.【点睛】本小题主要考查等差数列性质的应用,考查化归与转化的数学思想方法,属于基础题.10. 已知等比数列{a n}满足,a3a5=4(a4﹣1),则a2=()A.2 B.1 C.D.参考答案:C【考点】等比数列的通项公式.【专题】等差数列与等比数列.【分析】利用等比数列的通项公式即可得出.【解答】解:设等比数列{a n}的公比为q,∵,a3a5=4(a4﹣1),∴=4,化为q3=8,解得q=2则a2==.故选:C.【点评】本题考查了等比数列的通项公式,属于基础题.二、填空题:本大题共7小题,每小题4分,共28分11. 观察下列等式:由以上等式推测到一个一般的结论:对于=参考答案:略12. 二项式展开式中含项的系数是________(用数字回答).参考答案:40【分析】利用二项式展开式的通项公式进行求解即可.【详解】二项式展开式的通项公式为:.令,所以二项式展开式中含项的系数是.故答案为:40【点睛】本题考查了求二项式展开式中某项问题,考查了数学运算能力,属于基础题.13. 甲、乙两队各有n个队员,已知甲队的每个队员分别与乙队的每个队员各握手一次(同队的队员之间不握手),从这n2次的握手中任意取两次.记事件A:两次握手中恰有3个队员参与.若事件A发生的概率P<,则n的最小值是_____________.参考答案:2014. 函数y=log a(x﹣3)+3(a>0且a≠1)恒过定点.参考答案:(4,3)【考点】4O:对数函数的单调性与特殊点.【分析】根据对数函数的图象恒过定点(1,0),求出该题的答案即可.【解答】解:当x﹣3=1,即x=4时,y=log a(x﹣3)+3=0+3=3,∴函数y=2log a(x﹣3)+3的图象恒过定点(4,3).故答案为:(4,3).【点评】本题考查了对数函数的图象与性质的应用问题,是基础题目.15. 设等比数列的前项和为,若,则= 。
辽宁省锦州市08-09学年高二下学期期末考试(数学理)

2008-2009学年度第二学期高二质量检测数学(理)一、选择题(每题5分,共60分) (1)已知全集,集合,,那么集合等于 (A ) ( B ) (C ) ( D )(2)复数(3+i )m -(2+i )对应的点在第三象限内,则实数m 的取值范围是 (A )m <23 (B )m <1 (C )23<m <1 (D )m >1(3)直线与圆的位置关系是(A )相离 (B )相交 (C )相切 (D )不确定 (4)已知p :关于x 的不等式x 2+2a x -a>0的解集是R ,q :-1<a<0,则p 是q 的那么 (A )充分非必要条件 (B ) 必要非充分条件 (C ) 充要条件 (D ) 既非充分又非必要条件(5)某校举办奥运知识竞赛,有6个代表队参赛,每队有2名学生,若12名参赛同学中有4人获奖,且这4人来自3个不同的代表队,则不同的获奖种数共有 (A ) (B ) (C ) (D )(6)在的展开式中,含项的系数是通项公式为的数列的 (A )第3项 (B )第11项 (C )第20项 (D )第24项 (7)对于下列命题① ② ③; ④的充要条件是。
其中正确命题的个数是 (A )0 (B )1 (C )2 (D )3(8)函数,对任意有,且,那么等于 A (A ) (B ) (C ) (D ) (9)若顺次成等差数列,则(A )有最大值1,无最小值 (B )有最小值,无最大值 (C )有最小值,最大值1 (D )有最小值,最大值1 (10)在中,,则角等于(A ) (B ) (C ) (D )(11)在平面直角坐标系中,设直线与抛物线相交于两点,给定下列三个条件:①②; ③直线过定点(2,0)。
如果将上面①、②、③中的任意一个作为条件,余下两个作为结论,则构成的三个命题中,真命题的个数是(A )3 (B )2 (C )1 (D )0 (12)已知,则的值为(A )1 (B )0 (C )5 (D )8 二、填空题(每题5分,共20分)(13)阅读右图的程序框图,若输入,则输出 .(14)在等差数列中,有,其中分别是的前项和,用类比推理的方法,在等比数列中,有________. (15)已知平面区域,向区域内任意掷点,若点落在曲线下方的概率是,则实数的值是________. (16)已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 .三、解答题:本大题共6小题,共70分。
辽宁省锦州市第五中学高二数学理期末试题含解析

辽宁省锦州市第五中学高二数学理期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 直线y=kx+2与双曲线有且只有一个交点,那么实数k的值是A. B. C. 或 D.参考答案:C略2. 在复平面内,复数对应的点位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限参考答案:B3. 若圆(x-3)2+(y+5)2=r2上有且只有两个点到直线4x-3y-2=0距离等于1,则半径r的取值范围是().A.(4,6) B.[4,6) C.(4,6] D.[4,6]参考答案:A4. 已知等差数列共有10项、其中奇数项之和为15,偶数项之和为30,则其公差是()A.5B.4C. 3D.2参考答案:C5. 定义域为的函数对任意的都有,且其导函数满足:,则当时,下列成立的是()A. B.C. D.参考答案:B6. 如果为偶函数,且导数存在,则的值为()A、2B、1C、0D、-1参考答案:C7. 点P是双曲线(a>0,b>0)左支上的一点,其右焦点为F(c,0),若M为线段FP的中点,且M到坐标原点的距离为,则双曲线的离心率e范围是()A.(1,8] B.C.D.(2,3]参考答案:B【考点】双曲线的简单性质.【分析】直接利用双曲线的定义,结合三角形的中位线定理,推出a,b,c的关系,求出双曲线的离心率.【解答】解:设双曲线的左焦点为F1,因为点P是双曲线(a>0,b>0)左支上的一点,其右焦点为F(c,0),若M为线段FP的中点,且M到坐标原点的距离为,由三角形中位线定理可知:OM=PF1,PF1=PF﹣2a,PF≥a+c.所以,1.故选B.【点评】本题是中档题,考查双曲线的基本性质,找出三角形的中位线与双曲线的定义的关系,得到PF≥a+c.是解题的关键.8. 椭圆短轴上的两个三等分点与两个焦点构成一个正方形,则椭圆的离心率为()A. B.C. D.参考答案:A略9. 不等式表示的区域在直线的()A.右上方B.右下方C.左上方D.左下方参考答案:B略10. 在中,已知,,,P为线段AB上的一点,且.,则的最小值为( )A.B.C.D.参考答案:C二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数有两个极值点,则实数a的取值范围是__________.参考答案:.,令函数有两个极值点,则在区间上有两个实数根,,当时,,则函数在区间单调递增,因此在区间上不可能有两个实数根,应舍去,当时,令,解得,令,解得,此时函数单调递增,令,解得,此时函数单调递减,当时,函数取得极大值,当近于与近于时,,要使在区间有两个实数根,则,解得实数的取值范围是,故答案为.12. 圆锥曲线的准线方程是.参考答案:略13. 定义某种运算?,S=a?b的运算原理如图,则式子6?3+3?4= .参考答案:20【考点】程序框图.【专题】计算题;图表型;分类讨论;算法和程序框图.【分析】通过程序框图判断出S=a?b的解析式,求出6?3+3?4的值.【解答】解:有框图知S=a?b=,∴6?3+3?4=6×(3﹣1)+4×(3﹣1)=20. 故答案为:20.【点评】新定义题是近几年常考的题型,要重视.解决新定义题关键是理解题中给的新定义.14. 若函数在上无极值点,则实数的取值范围是____.参考答案:15. 全集U ={1,2,3,4,5},M ={1,3},N ={1,2},则?U (M ∪N )= ▲ 参考答案:{4,5}略16. 不等式|x 2-2|≤2x +1的解集为__________________.参考答案:17. 若直线和曲线恰有一个公共点,则b的取值范围是 ;参考答案:三、 解答题:本大题共5小题,共72分。
辽宁省锦州市10-11学年高二下学期期末考试(数学理)扫描版

2010—2011学年度第二学期期末考试高 二 数 学(理)参考答案及评分标准一、选择题:(1)~(12)(13)24(14)95 (15)30302110201211b b b b b b ⋅⋅⋅=⋅⋅⋅ (16)①③④ 三、解答题:(17)(本小题满分10分)解:(Ⅰ) 列联表补充如下:-----------------------(5分)(Ⅱ)∵2250(2015105)8.3337.87930202525K ⨯⨯-⨯=≈>⨯⨯⨯---------------------(9分) ∴有99.5%的把握认为喜爱打篮球与性别有 ---------------------------(10分)(18)(本小题满分12分)(Ⅰ)证明:()f x 在(1,)-+∞上是增函数121,x x ∀-<<则 -----------------------------(1分) 1212121222()()()11x x x x f x f x a a x x ---=+--=++21212123()(1)(1)(1)x x x x x a a x x --=-+++ --------------------------------------------------(3分)12121,10,x x x x a --<<∴-<且2120,10,10x a x x >+>+>,所以12()()0f x f x -< -------------------------------------------(5分) 即12()()f x f x <故()f x 在(1,)-+∞上是增函数. --------------------------------------(6分) (Ⅱ)证明:设存在000(1)x x <≠-满足0()0f x = -----------------------(8分)则0002(0,1)1x x a x -=-∈+ 解得0122x << -----------------------------------------(10分) 与假设矛盾,故方程无负数根. -------------------------------------(12分)(19)(本小题满分12分)解:(3分) 即31p =,则答:走公路②堵车的概率p 的值为 ---------------------(6分)(Ⅱ)解:X 可能的取值为0,1,2,3 -----------------------(7分) ()332304438P X ==⋅⋅= ; ()7116P X == : ()12112131124434436P X C ==⋅⋅+⋅⋅= ()1111344348P X ==⋅⋅= --------------------------(10分)X 的分布列为:----------------------------(11分) 所以(E X--------------------------------------(12分) (20)(本小题满分12分) 解:(Ⅰ)依题意,销售价提高后为6000(1+x )元/台,月销售量为2(1)a x -台---(2分)则[]2(1)6000(1)4500y a x x =-+- -------------------(4分) 即321500(441)(01)y a x x x x =--++<<. -------------------(6分)(Ⅱ)21500(1224)y a x x '=--+令0y '=,得2620x x +-=, 解得12,(23x x ==-舍去). -------------------(9分) 当10,0;2x y '<<>时 当11,0.2x y '<<<时 --------------(11分) 当12x =时,y 取得最大值. 此时销售价为3600090002⨯=元. 答:笔记本电脑的销售价为9000元时,电脑企业的月利润最大.------------ (12分)(21)(本小题满分12分)解:(Ⅰ)由题得121+=+n n n a a a ,又21=a , 则3412112=+=a a a ,7812223=+=a a a ,151612334=+=a a a ----------(6分) (Ⅱ)猜想122-=n nn a 。
辽宁省锦州市2023-2024学年高二下学期期末考试+数学 解析版

2023~2024学年度第二学期期末考试高二数学注意事项:1.本试卷考试时间为120分钟,满分150分.2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.3.答选择题时,选出每小题答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答题标号;答非选择题时,将答案写在答题卡上相应区域内,超出答题区域或写在本试卷上无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列函数的求导正确的是()A.()e e xx--'= B.22(ln )x x'=C.()1e ln 3e 3x x '+=+D.()22x -'=-2.已知等比数列{}n a 满足202318a a -=,2024224a a -=,则q =()A.1B.1- C.3D.3-3.2021年7月30日,东京奥运会女子七人制橄榄球中国队29:0完胜日本队,该事件吸引了大批大学生开始练习橄榄球,某大学橄榄球社团先对报名者的力量和速度进行综合评分,评分达标者方能被吸收为正式社员.现有400人报名,他们的综合评分服从正态分布()250,15N ,若80分以上为达标,则估计能被吸收为正式社员的人数为()(附:若随机变量()2,X N μσ~,则()0.6826P X μσμσ-<≤+=,()220.9544P X μσμσ-<≤+=,()330.9974P X μσμσ-<≤+=.)A.18B.13C.9D.54.有3台车床加工同一型号的零件,第1,2,3台加工的次品率分别为5%,2%,4%,加工出来的零件混放在一起.己知第1,2,3台车床加工的零件数的比为4: 5: 11,现任取一个零件,记事件=i A “零件为第i 台车床加工”(1,2,3)i =,事件B =“零件为次品”,则()1P A B =()A.0.2B.0.05C.537 D.10375.已知数列{}n a 满足:11,3,231,nn n n n a a a a a a +⎧⎪==⎨⎪+⎩为偶数为奇数,则25a =()A.1B.2C.3D.46.如果方程0(),F x y =能确定y 是x 的函数,那么称这种方式表示的函数是隐函数.隐函数的求导方法如下:在方程0(),F x y =中,把y 看成x 的函数()y y x =,则方程可看成关于x 的恒等式()(),0F x y x =,在等式两边同时对x 求导,然后解出()y x '即可.例如,求由方程221x y +=所确定的隐函数的导数y ',将方程221x y +=的两边同时对x 求导,则220x y y '+⋅=(()y y x =是中间变量,需要用复合函数的求导法则),得(0)xy y y'=-≠.那么曲线ln 2xy y +=在点()2,1处的切线方程为()A.310x y -+=B.350x y +-=C.350x y --= D.2370x y +-=7.现有一货物堆,从上向下查,第一层有1个货物,第二层比第一层多2个,第三层比第二层多3个,以此类推,记第n 层货物的个数为n a ,则数列221{}nn a +的前2023项和为()A.212[1(]2024- B.212[1()]2023-C.214[1()]2023- D.214[1()]2024-8.若310ea -=,0.30.3e b =,13ln1.310c =,则()A.a b c >>B.a c b>> C.b a c>> D.c b a>>二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知随机事件,A B 的概率分别为()(),P A P B ,且11(),(),()()32P A P B P A B P A B ===∣∣,则()A.事件A 与事件B 相互独立B.事件A 与事件B 相互对立C.()23P A B +=D.1(6P ABB =∣10.已知函数()1e ,01ln ,04x x x f x x x +⎧-≤⎪=⎨->⎪⎩,下列选项中正确的是()A.()f x 在(),1-∞-上单调递增,在()1,0-上单调递减B.()f x 有极大值C.()f x 无最小值D.若函数()()()()2[]24h x f x af x a =-+∈R 恰有6个零点,则实数a 的取值范围是5,2⎛⎫+∞⎪⎝⎭11.已知各项都是正数的数列{}n a 的前n 项和为n S ,且122n n na S a =+,则下列结论正确的是()A.当()*m n m n >∈N,时,mn aa > B.212n n n S S S +++<C.数列{}2n S 是等差数列D.1ln n nS n S -≥三、填空题:本题共3小题,每小题5分,共15分.12.已知随机变量()2,X Nμσ ,()6,Y B p ~,且()132P X ≥=,()()32E X E Y =,则p =__________.13.已知数列{}n a 满足()()1113,3114n n n n a a a a a ++=-++=-,则n a =__________.14.已知函数()f x 及其导函数()f x '的定义域均为R ,且()()()()()4220,4e x x f x f x f x f x -⎡⎤-->-'=⎣⎦,则不等式()()3e ln 3f x xf <的解集是__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知0m >,函数()e 2xf x x m =-+的图象在点()()0,0f 处的切线与两坐标轴围成的三角形的面积为2.(1)求m 的值;(2)求()f x 在[]1,2-上的值域.16.记n S 为数列{}n a 的前n 项和,已知11a =,n n S a ⎧⎫⎨⎬⎩⎭是公差为12的等差数列.(1)求{}n a 的通项公式;(2)记m b 为{}n a 在区间(()1*2,2mm m +⎤∈⎦N 中的项的个数,求数列{}m m a b 的前m 项和m T .17.2024年1月18日是中国传统的“腊八节”,“腊八”是中国农历十二月初八(即腊月初八)这一天.腊八节起源于古代祭祀祖先和神灵的仪式,后逐渐成为民间节日,盛行于中国北方.为调查不同年龄人群对“腊八节”民俗文化的了解情况,某机构抽样调查了某市的部分人群.(1)在100名受调人群中,得到如下数据:年龄了解程度不了解了解30岁以下162450岁以上1644根据小概率值0.1α=的2χ独立性检验,分析受调群体中对“腊八节”民俗的了解程度是否存在年龄差异;(2)调查问卷共设置10个题目,选择题、填空题各5个.受调者只需回答8个题:其中选择题必须全部回答,填空题随机抽取3个进行问答.某位受调者选择题每题答对的概率为0.8,知道其中3个填空题的答案,但不知道另外2个的答案.求该受调者答对题目数量的期望.参考公式:①()()()()()22n ad bc a b c d a c b d χ-=++++.独立性检验常用小概率值和相应临界值:α0.10.050.010.0050.001x α2.7063.8416.6357.87910.828②随机变量X ,Y 的期望满足:()()()E X Y E X E Y +=+18.某排球教练带领甲、乙两名排球主力运动员训练排球的接球与传球,首先由教练第一次传球给甲、乙中的某位运动员,然后该运动员再传回教练.每次教练接球后按下列规律传球:若教练上一次是传给某运动员,则这次有13的概率再传给该运动员,有23的概率传给另一位运动员.已知教练第一次传给了甲运动员,且教练第n 次传球传给甲运动员的概率为n p .(1)求2p ,3p ;(2)求n p 的表达式;(3)设21n n q p =-,证明:()()1111sin sin 2ni i i i i qq q q ++=--<∑.19.固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程为e e 2x xccc y -⎛⎫+ ⎪⎝⎭=,其中c 为参数.当1c =时,就是双曲余弦函数()e e ch 2x x x -+=,类似地我们可以定义双曲正弦函数()e e sh 2x xx --=.它们与正、余弦函数有许多类似的性质.(1)类比正、余弦函数导数之间的关系,()sin cos x x '=,()cos sin x x '=-,请写出()sh x ,()ch x 具有的类似的性质(不需要证明);(2)当0x >时,()sh x ax >恒成立,求实数a 的取值范围;(3)求()()2ch cos f x x x x =--的最小值.2023~2024学年度第二学期期末考试高二数学注意事项:1.本试卷考试时间为120分钟,满分150分.2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.3.答选择题时,选出每小题答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答题标号;答非选择题时,将答案写在答题卡上相应区域内,超出答题区域或写在本试卷上无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列函数的求导正确的是()A.()e e xx--'= B.22(ln )x x'=C.()1e ln 3e 3x x '+=+D.()22x -'=-【答案】B 【解析】【分析】根据基本初等函数的导数公式和复合函数的求导法则,可对选项一一判断即得.【详解】对于A 项,因()x x --'=-e e ,故A 项错误;对于B 项,2222(ln )x x xx'==,故B 项正确;对于C 项,()e ln 3e x x '+=,故C 项错误;对于D 项,()23322x x x --'=-=-,故D 项错误.故选:B.2.已知等比数列{}n a 满足202318a a -=,2024224a a -=,则q =()A.1B.1- C.3D.3-【答案】C 【解析】【分析】两式相除即可得解.【详解】因为202318a a -=,2024224a a -=,20242023a a q =⋅,21a a q =⋅,所以202422023202311202312438a a a a q a a a a q q ⋅--==⋅==--.故选:C3.2021年7月30日,东京奥运会女子七人制橄榄球中国队29:0完胜日本队,该事件吸引了大批大学生开始练习橄榄球,某大学橄榄球社团先对报名者的力量和速度进行综合评分,评分达标者方能被吸收为正式社员.现有400人报名,他们的综合评分服从正态分布()250,15N ,若80分以上为达标,则估计能被吸收为正式社员的人数为()(附:若随机变量()2,X N μσ~,则()0.6826P X μσμσ-<≤+=,()220.9544P X μσμσ-<≤+=,()330.9974P X μσμσ-<≤+=.)A.18B.13C.9D.5【答案】C 【解析】【分析】利用正态分布的对称性求出80分以上的概率,即可求解.【详解】因为X 服从正态分布()250,15N ,所以()()()8050215P X P X >=>+⨯=10.95440.02282-=,则估计能被吸收为正式社员的人数为4000.02289.129⨯=≈(人).故选:C4.有3台车床加工同一型号的零件,第1,2,3台加工的次品率分别为5%,2%,4%,加工出来的零件混放在一起.己知第1,2,3台车床加工的零件数的比为4: 5: 11,现任取一个零件,记事件=i A “零件为第i 台车床加工”(1,2,3)i =,事件B =“零件为次品”,则()1P A B =()A.0.2B.0.05C.537 D.1037【答案】D 【解析】【分析】根据题意,由全概率公式、条件概率公式和贝叶斯公式,结合已知条件,求解即可.【详解】根据题意可得:()()()12341511111,,4511545114451120P A P A P A ======++++++;()()()123|0.05, |0.02, |0.04P B A P B A P B A ===;由全概率公式可得:()()()()()()()112233|||P B P A P B A P A P B A P A P B A =++1111370.050.020.0454201000=⨯+⨯+⨯=;故()()()()()1111110.05(|)10510037373710001000P A B P A P B A P A B P B P B ⨯=====.故选:D.5.已知数列{}n a 满足:11,3,231,nn n n n a a a a a a +⎧⎪==⎨⎪+⎩为偶数为奇数,则25a =()A.1B.2C.3D.4【答案】B 【解析】【分析】根据递推公式列出数列的前几项,即可找到规律,从而得解.【详解】因为11,3,231,nn n n n a a a a a a +⎧⎪==⎨⎪+⎩为偶数为奇数,所以213110a a =+=,2352a a ==,433116a a =+=,4582aa ==,5642a a ==,6722a a ==,7812a a ==,98314a a =+=, ,可知从第6项起数列为周期为3的周期数列,又255362=+⨯+,所以2572a a ==.故选:B6.如果方程0(),F x y =能确定y 是x 的函数,那么称这种方式表示的函数是隐函数.隐函数的求导方法如下:在方程0(),F x y =中,把y 看成x 的函数()y y x =,则方程可看成关于x 的恒等式()(),0F x y x =,在等式两边同时对x 求导,然后解出()y x '即可.例如,求由方程221x y +=所确定的隐函数的导数y ',将方程221x y +=的两边同时对x 求导,则220x y y '+⋅=(()y y x =是中间变量,需要用复合函数的求导法则),得(0)xy y y'=-≠.那么曲线ln 2xy y +=在点()2,1处的切线方程为()A.310x y -+=B.350x y +-=C.350x y --= D.2370x y +-=【解析】【分析】利用给定隐函数的导数求法确定斜率,再求出切线方程即可.【详解】由给定定义得,对ln 2xy y +=左右两侧同时求导,可得10y xy y y+⨯'+=',将点()2,1代入,得120y y ++'=',解得13y '=-,故切线斜率为13-,得到切线方程为()1123y x -=--,化简得方程为350x y +-=,故B 正确.故选:B7.现有一货物堆,从上向下查,第一层有1个货物,第二层比第一层多2个,第三层比第二层多3个,以此类推,记第n 层货物的个数为n a ,则数列221{}nn a +的前2023项和为()A.212[1(]2024- B.212[1()]2023-C.214[1()]2023- D.214[1()]2024-【答案】D 【解析】【分析】由累加法可得n a ,利用裂项相消求和法求出n S ,即可得解.【详解】依题意,11a =,213212,3,,n n a a a a a a n --=-=-= ,2n ≥,N n *∈,则由累加法得,123n a n a =+-++ ,因此(1)(1)1222n n n n n a n n -+=+++=+= ,而11a =满足上式,即()12n n n a +=,则()2222242121114[](1)(1)n n n a n n n n ++==-++,所以2222221111114[1]4[1]223(1)(1)n S n n n =-+-++-=-++ ,2202314[1()]2024S =-.故选:D 8.若310ea -=,0.30.3eb =,13ln1.310c =,则()A.a b c >>B.a c b>> C.b a c>> D.c b a>>【答案】A【分析】利用作商法可得a b >;构建函数()e 1xg x x =--,0x >,利用导数判断()g x 的单调性,可得0.3e1.3>,构建()ln f x x x =,1ex >,利用导数判断()f x 的单调性,可得b c >.【详解】显然310ea -=>,0.30.3e 0b =>,因为0.30.63100.3e 0.3e 0.3e 0.91e b a-==<<<,所以a b >;又因为0.30.30.30.3e e ln e b ==,13ln1.310c ==1.3ln1.3,令()e 1xg x x =--,0x >.则()e 10xg x ='->,可知()g x 在()0,∞+上单调递增,则()()0.300g g >=,可得0.31e 10.3 1.3e>+=>,令()ln f x x x =,1e x >,则()ln 10f x x +'=>在1,e ∞⎛⎫+ ⎪⎝⎭内恒成立,可知()f x 在1,e∞⎛⎫+ ⎪⎝⎭内单调递增,则()()0.3e1.3f f >,即0.30.3eln e 1.3ln1.3>,所以b c >;综上所述:a b c >>.故选:A .二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知随机事件,A B 的概率分别为()(),P A P B ,且11(),(),()()32P A P B P A B P A B ===∣∣,则()A.事件A 与事件B 相互独立B.事件A 与事件B 相互对立C.()23P A B += D.1(6P ABB =∣【答案】AC 【解析】【分析】根据题意可求得1(),2P B =再利用条件概率公式可得1()()6P AB P AB ==,由相互独立事件的定义可知()()()P AB P A P B =,即事件A 与事件B 相互独立;显然(16)5()P A P B +=≠,即事件A 与事件B 不是相互对立事件;由概率的加法公式和条件概率公式计算可得C 正确,D 错误.【详解】对A ,根据题意可得1()1(),2P B P B =-=由条件概率公式可得()()(),()()()P AB P AB P AB P A B P B P B ==∣∣,又1()(),2P B P B ==所以()()P AB P AB =,又易知1()()()3P AB P AB P A +==,所以1()(6P AB P AB ==;即满足()()()P AB P A P B =,所以事件A 与事件B 相互独立,即A 正确;对B ,又115()()1326P A P B +=+=≠,不满足()1()P A P B =-,所以事件A 与事件B 不是相互对立事件,即B 错误;对C ,易知()()11()()212363P P P A P B A B AB +-=++==-,即C 正确;对D ,由条件概率公式可得()()()13P AB P ABB P B ==∣,所以D 错误.故选:AC10.已知函数()1e ,01ln ,04x x x f x x x +⎧-≤⎪=⎨->⎪⎩,下列选项中正确的是()A.()f x 在(),1-∞-上单调递增,在()1,0-上单调递减B.()f x 有极大值C.()f x 无最小值D.若函数()()()()2[]24h x f x af x a =-+∈R 恰有6个零点,则实数a 的取值范围是5,2⎛⎫+∞ ⎪⎝⎭【答案】ABD 【解析】【分析】对于A ,利用导数判断()f x 在(,0)-∞的单调性,对于B ,由选项A 中的单调性进行判断,对于C ,分别求出0x ≤和0x >时的值域分析判断,对于D ,作出()f x 的图象,结合函数图象,根据一元二次方程根的分布得到关于a 的不等式,解不等式即可得到实数a 的取值范围.【详解】对于A ,当0x ≤时,1()e x f x x +=-,则111()(e e )e (1)x x x f x x x +++'=-+=-+,当1x <-时,()0f x '>,当10x -<<时,()0f x '<,所以()f x 在(),1∞--上单调递增,在()1,0-上单调递减,所以A 正确,对于B ,由选项A 可知()f x 在(),1∞--上单调递增,在()1,0-上单调递减,所以()f x 在=1x -处取得极大值,所以B 正确,对于C ,当0x >时,14141ln ,e 14()ln 41ln ,0e 4x x f x x x x ⎧-≥⎪⎪=-=⎨⎪-<<⎪⎩,当14e x ≥时,1ln 04x -≥,当140e x <<时,1ln 04x ->,所以当0x >时,()0f x ≥,因为()f x 在(),1∞--上单调递增,在()1,0-上单调递减,且当0x ≤时,()0f x ≥恒成立,综上,()f x 的值域为[0,)+∞,所以()f x 有最小值0,所以C 错误,对于D ,因为()f x 在(),1∞--上单调递增,在()1,0-上单调递减,()11f -=,(0)0f =,14141ln ,e 14()ln 41ln ,0e 4x x f x x x x ⎧-≥⎪⎪=-=⎨⎪-<<⎪⎩所以()f x的大致图象如图所示由()0h x =,得()()2[]240f x af x -+=,令()f x t =,则2240t at -+=,由()f x 的图象可知,要使()h x 有6个零点,则方程2240t at -+=有两个不相等的实数根12,t t ,不妨令12t t <,若120,01t t =<<,则由图可知()h x 有6个零点,但202040a -⨯+≠,所以不符合题意,所以1201,1t t <<>,因为2020440a -⨯+=>,所以21240a -+<,解得52a >,即实数a 的取值范围是5,2∞⎛⎫+ ⎪⎝⎭,所以D 正确,故选:ABD【点睛】关键点点睛:此题考查导数的综合应用,考查利用导数求函数的单调区间、极值和最值,利用导数解决函数零点问题,选项D 解题的关键是根据题意画出函数的大致图象,换元后根据图象将问题转化为方程有两个不等的实根,考查计算能力和数学转化思想,属于较难题.11.已知各项都是正数的数列{}n a 的前n 项和为n S ,且122n n na S a =+,则下列结论正确的是()A.当()*m n m n >∈N,时,mn aa > B.212n n n S S S +++<C.数列{}2n S 是等差数列D.1ln n nS n S -≥【答案】BCD 【解析】【分析】计算数列首项及第二项可判定A ,利用等差数列的定义及,n n S a 的关系可判定C ,从而求出n S 的通项公式结合基本不等式、函数的单调性可判定B 、D .【详解】对A ,由题意可知211111122a a a a =+⇒=,所以11a =,则2212222121022a a a a a a +=+⇒+-=,所以211a a =<,故A 错误;对C ,由()()2211111122222n n n n n n n n n n a S S S S S S n a S S ----=+⇒=+⇒-=≥-,故C 正确;对C ,所以()211n n S n n S =+-=⇒=则212n n n S S S +++=,故B 正确;对D,易知1n n S S -=()()12ln 1f x x x x x=--≥,则()22121110f x x x x ⎛⎫=+-=-≥ ⎪⎝⎭',则()f x 单调递增,所以()()10ln f x f n ≥=⇒,即1ln n nS n S -≥,故D 正确.故选:BCD三、填空题:本题共3小题,每小题5分,共15分.12.已知随机变量()2,X Nμσ ,()6,Y B p ~,且()132P X ≥=,()()32E X E Y =,则p =__________.【答案】13【解析】【分析】根据正态曲线的性质求出3μ=,即可得到()3E X =,从而求出()E Y ,再由二项分布的期望公式计算可得.【详解】因为()2,X N μσ 且()132P X ≥=,所以3μ=,则()3E X =,又()()32E X E Y =,所以()2E Y =,因为()6,Y B p ~,所以()62E Y p ==,解得13p =.故答案为:1313.已知数列{}n a 满足()()1113,3114n n n n a a a a a ++=-++=-,则n a =__________.【答案】331n n -+【解析】【分析】依题意可得()()()()1113111n n n n a a a a ++-++++=,两边同除()()111n n a a +++得到111311n n a a +-=++,即可得到11n a ⎧⎫⎨⎬+⎩⎭是以4为首项,3为公差的等差数列,即可求出11n a +的通项,即可得解.【详解】因为134a =-,()()11311n n n n a a a a ++++=-,则()()()()1113111n n n n a a a a ++-++++=,因为1114a +=,显然10n a +≠,所以111311n n a a +-=++,所以11n a ⎧⎫⎨+⎩⎭是以1141a =+为首项,3为公差的等差数列,所以1311n n a =++,所以1131n a n +=+,则1313131n na n n -=-+=++.故答案为:331nn -+14.已知函数()f x 及其导函数()f x '的定义域均为R ,且()()()()()4220,4e x x f x f x f x f x -⎡⎤-->-'=⎣⎦,则不等式()()3e ln 3f x xf <的解集是__________.【答案】()3e,e 【解析】【分析】根据题意可构造函数()()exf x F x =,求得()F x 的单调性,再利用函数对称性解不等式即可求得结果.【详解】构造函数()()e xf x F x =,则()()()exf x f x F x '-'=;因为()()()20x f x f x ⎡⎤-->⎣⎦',所以当2x >时,()()0f x f x '->,即()0F x '>,此时()F x 在()2,+∞上单调递增;当2x <时,()()0f x f x '-<,即()0F x '<,此时()F x 在(),2-∞上单调递减;又()()424exf x f x --=,所以()()44eexxf x f x --=,即()()4F x F x -=;所以函数()F x 图像上的点()(),x F x 关于2x =的对称点()()4,x F x -也在函数图像上,即函数()F x 图像关于直线2x =对称,不等式()()3e ln 3f x xf <变形为()()3ln 3ef x f x<,即()()ln 3ln 3eexf x f <;可得()()()ln 31F x F F <=,又()F x 在()2,+∞上单调递增,在(),2-∞上单调递减,所以1ln 3x <<,解得3e e x <<.则不等式的解集为()3e,e .故答案为:()3e,e【点睛】关键点点睛:本题关键在于根据()()()20x f x f x ⎡⎤-->⎣⎦'的结构特征构造函数()()ex f x F x =,判断出其单调性,再由()()424exf x f x --=得出其对称性解不等式即可.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知0m >,函数()e 2xf x x m =-+的图象在点()()0,0f 处的切线与两坐标轴围成的三角形的面积为2.(1)求m 的值;(2)求()f x 在[]1,2-上的值域.【答案】(1)1m =(2)232ln2,e 3⎡⎤--⎣⎦.【解析】【分析】(1)根据导数的几何意义,求出切线的斜率,利用点斜式求出切线方程1y x m =-++,求出切线在坐标轴上的截距,利用三角形面积公式可得结果;(2)由(1)可得()f x 在(]ln2,2上单调递增,在[)1,ln2-上单调递减,求出()1f -,()2f ,()ln2f 的值可得结果.【小问1详解】因为()e 2xf x x m =-+,所以()e 2x f x '=-,则()01k f '==-.因为()01f m =+,所以切点坐标为()0,1m +,所以()f x 的图象在点()()0,0f 处的切线方程为1y x m =-++.令0y =,得1x m =+,又0m >,所以()()11122m m ⨯+⨯+=,所以1m =.【小问2详解】由(1)可知()e 2xf x '=-,令()0f x ¢>,解得ln2x >,所以()f x 在(]ln2,2上单调递增.令()0f x '<,解得ln2x <,所以()f x 在[)1,ln2-上单调递减,又()113ef -=+,()22e 3f =-,()ln232ln2f =-,所以()f x 在[]1,2-上的值域为232ln2,e 3⎡⎤--⎣⎦.16.记n S 为数列{}n a 的前n 项和,已知11a =,n n S a ⎧⎫⎨⎬⎩⎭是公差为12的等差数列.(1)求{}n a 的通项公式;(2)记m b 为{}n a 在区间(()1*2,2mm m +⎤∈⎦N 中的项的个数,求数列{}m m a b 的前m 项和m T .【答案】(1)n a n =(2)()11·22m m T m +=-+.【解析】【分析】(1)先利用等差数列的通项公式求得n S ,再利用n S 求n a 即可得解;(2)利用“错位相减求和法”即可得解.【小问1详解】因为11a =,故111S a =,所以数列n n S a ⎧⎫⎨⎬⎩⎭是以1为首项,12为公差的等差数列,所以12n n S n a +=,即12n n n S a +=,则1122n n n S a +++=,两式相减得112122n n n n n a a a ++++=-,即1122n n n n a a ++=,所以11111n n a a a n n +====+ ,因此{}n a 的通项公式为n a n =.【小问2详解】由题可知1222m m m m b +=-=,则2mm m a b m =⨯,所以()1211222122m m m T m m -=⨯+⨯++-+⨯ ,()23121222122m m m T m m +=⨯+⨯++-+⨯ ,两式相减得()()12111212222221·2212m m m m m m T m m m +++--=+++-⨯=-⨯=--- ,所以()11·22m m T m +=-+.17.2024年1月18日是中国传统的“腊八节”,“腊八”是中国农历十二月初八(即腊月初八)这一天.腊八节起源于古代祭祀祖先和神灵的仪式,后逐渐成为民间节日,盛行于中国北方.为调查不同年龄人群对“腊八节”民俗文化的了解情况,某机构抽样调查了某市的部分人群.(1)在100名受调人群中,得到如下数据:年龄了解程度不了解了解30岁以下162450岁以上1644根据小概率值0.1α=的2χ独立性检验,分析受调群体中对“腊八节”民俗的了解程度是否存在年龄差异;(2)调查问卷共设置10个题目,选择题、填空题各5个.受调者只需回答8个题:其中选择题必须全部回答,填空题随机抽取3个进行问答.某位受调者选择题每题答对的概率为0.8,知道其中3个填空题的答案,但不知道另外2个的答案.求该受调者答对题目数量的期望.参考公式:①()()()()()22n ad bc a b c d a c b d χ-=++++.独立性检验常用小概率值和相应临界值:α0.10.050.010.0050.001x α2.7063.8416.6357.87910.828②随机变量X ,Y 的期望满足:()()()E X Y E X E Y +=+【答案】(1)答案见解析(2)5.8【解析】【分析】(1)计算出2χ参考独立性检验常用小概率值和相应临界值表比较可得答案;(2)用X Y 、分别表示受调者答对选择题、填空题的个数,求出()E X 、()E Y ,由()()()E X Y E X E Y +=+可得答案.【小问1详解】()2210016442416 1.961 2.70640603268χ⨯⨯-⨯=≈<⨯⨯⨯,根据小概率值0.1α=的独立性检验,认为受调群体中对“腊八节”民俗的了解程度不存在年龄差异;【小问2详解】用X Y 、分别表示受调者答对选择题、填空题的个数,则()5,0.8X B ~,所以()50.84E X =⨯=,则Y 可取则1,2,3,所以()123235C C 31C 10P X ===,()213235C C 62C 10P X ===,()3335C 13C 10P X ===,所以()361123 1.8101010E Y =⨯+⨯+⨯=,由()()()4 1.8 5.8E X Y E X E Y +=+=+=,该受调者答对题目数量的期望为5.8.18.某排球教练带领甲、乙两名排球主力运动员训练排球的接球与传球,首先由教练第一次传球给甲、乙中的某位运动员,然后该运动员再传回教练.每次教练接球后按下列规律传球:若教练上一次是传给某运动员,则这次有13的概率再传给该运动员,有23的概率传给另一位运动员.已知教练第一次传给了甲运动员,且教练第n 次传球传给甲运动员的概率为n p .(1)求2p ,3p ;(2)求n p 的表达式;(3)设21n n q p =-,证明:()()1111sin sin 2ni i i i i q q q q ++=--<∑.【答案】(1)213p =,359p =(2)1111223n n p -⎛⎫=+- ⎪⎝⎭(3)证明见解析【解析】【分析】(1)根据题意,结合互斥事件和独立事件概率公式进行求解即可;(2)根据互斥事件和独立事件概率公式,结合等比数列的定义和通项公式进行求解即可;(3)利用构造函数法,结合导数与函数单调性的关系、等比数列的前n 项和公式进行证明即可.【小问1详解】11p =,213p =,()3221251339p p p =+-=;【小问2详解】由已知()1112133n n n p p p --=+-,∴11233n n p p -=-+,即1111232n n p p -⎛⎫-=-- ⎪⎝⎭,∴12n p ⎧⎫-⎨⎬⎩⎭是以13-为公比的等比数列,∴11111223n n p p -⎛⎫⎛⎫-=-- ⎪⎪⎝⎭⎝⎭,∴1111223n n p -⎛⎫=+- ⎪⎝⎭.【小问3详解】(]11210,13n n n q p -=-=∈.设()sin h x x x =-,(]0,1x ∈,∴()1cos 0h x x '=->,∴()h x 在(]0,1上单调递增,显然1n n q q +>,则()()1n n h q h q +>,∴11sin sin n n n n q q q q ++->-,则112sin sin 3n n n n nq q q q ++=->-,即()()()()11114sin sin sin sin 9n n n n n n n n n q q q q q q q q ++++--=--<,∴()()1111141119sin sin 11929219nn i i i i n i q q q q ++=-⎛⎫--<⋅=-< ⎪⎝⎭-∑.【点睛】关键点睛:本题的关键是根据题意利用独立事件概率公式得到递推关系式()1112133n n n p p p --=+-.19.固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程为e e 2x xccc y -⎛⎫+ ⎪⎝⎭=,其中c 为参数.当1c =时,就是双曲余弦函数()e ech 2x x x -+=,类似地我们可以定义双曲正弦函数()e e sh 2x xx --=.它们与正、余弦函数有许多类似的性质.(1)类比正、余弦函数导数之间的关系,()sin cos x x '=,()cos sin x x '=-,请写出()sh x ,()ch x 具有的类似的性质(不需要证明);(2)当0x >时,()sh x ax >恒成立,求实数a 的取值范围;(3)求()()2ch cos f x x x x =--的最小值.【答案】(1)()()()sh ch x x '=,()()()ch sh x x '=(2)(],1-∞(3)0【解析】【分析】(1)求导即可得结论;(2)构造函数()()sh F x x ax =-,求导,并结合分类讨论确定函数的最小值即可求解;(3)多次求导最终判断函数()f x 单调在[)0,∞+内单调递增,且函数为偶函数从而确定最小值.【小问1详解】求导易知()()()sh ch x x '=,()()()ch sh x x '=.【小问2详解】构造函数()()sh F x x ax =-,[)0,x ∈+∞,由(1)可知()()ch F x x a ='-,①当1a ≤时,由()e e ch 12x xx a -+=≥=≥,可知,()0F x '≥,故()F x 单调递增,此时()()00F x F ≥=,故对任意0x >,()sh x ax >恒成立,满足题意;②当1a >时,令()()G x F x =',[)0,x ∈+∞,则()()sh 0G x x ='≥,可知()G x 单调递增,由()010G a =-<与()()1ln 204G a a=>可知,存在唯一()()00,ln 2x a ∈,使得()00G x =,故当()00,x x ∈时,()()()00F x G x G x =<=',则()F x 在()00,x 内单调递减,故对任意()00,x x ∈,()()00F x F <=,即()sh x ax <,矛盾;综上所述,实数a 的取值范围为(],1-∞.【小问3详解】()()2ch cos f x x x x =--,()()sh sin 2f x x x x =+-',令()()g x f x =',则()()ch cos 2g x x x =+-';令()()h x g x =',则()()sh sin h x x x -'=,当[)0,x ∈+∞时,由(2)可知,()sh x x ≥,则()()sh sin sin h x x x x x =≥-'-,令()sin u x x x =-,则()1cos 0u x x ='-≥,故()u x 在[)0,∞+内单调递增,则()()()00h x u x u ≥'≥=,故()h x 在[)0,∞+内单调递增,则()()()00g x h x h ≥'==,故()g x 在[)0,∞+内单调递增,则()()()00f x g x g ≥'==,故()f x 在[)0,∞+内单调递增,因为()()()()22ch cos ()ch cos f x x x x x x x f x -=-----=--=,即()f x 为偶函数,故()f x 在(],0-∞内单调递减,则()()min 00f x f ==,故当且仅当0x =时,()f x 取得最小值0.。
2018-2019辽宁省锦州市高二下学期期末数学(理)试题 解析版

绝密★启用前辽宁省锦州市2018-2019学年高二下学期期末数学(理)试题一、单选题1.已知集合{}12,3A x y x B x x -⎧⎫===≥⎨⎬⎩⎭,则()R A C B =( ) A .[)0,3B .(0,3)C .()3,+∞D .()0,∞+【答案】B【解析】【分析】 先分别化简集合A,B,再利用集合补集交集运算求解即可【详解】12A x y x -⎧⎫==⎨⎬⎩⎭=()0,∞+ {}3B x x =≥=[3,)(,3] ,则()0,3R A C B ⋂=()故选:B【点睛】 本题考查集合的运算,解绝对值不等式,准确计算是关键,是基础题2.设i 为虚数单位,复数11i i i ++-等于( ) A .2i -B .2iC .1i -+D .0【答案】B【解析】【分析】利用复数除法和加法运算求解即可【详解】 11i i i++=-2122i i i故选:B【点睛】 本题考查复数的运算,准确计算是关键,是基础题3.已知22,0()log ,0x x f x a x x ⎧<=⎨+≥⎩,若((1))1f f -=-.则实数a 的值为( ) A .-2B .2C .0D .1【答案】C【解析】【分析】 由函数()22,0log ,0x x f x a x x ⎧<=⎨+≥⎩,将x ==-1,代入,构造关于a 的方程,解得答案. 【详解】∵函数()22,0log ,0x x f x a x x ⎧<=⎨+≥⎩, ∴f (﹣1)=12, ∴f [f (﹣1)]112f a ⎛⎫==-=- ⎪⎝⎭1, 解得:a =0,故选:C .【点睛】本题考查的知识点是分段函数的应用,函数求值,难度不大,属于基础题. 4.0sin xdx π⎰的值为( )A .2B .0C .-2D .1【答案】A【解析】【分析】 根据的定积分的计算法则计算即可.【详解】sin xdx π⎰=(-cos x )0|2π= 故选:A .【点睛】本题考查了定积分的计算,关键是求出原函数,属于基础题.5.若方程2210ax x -+=在区间(-1,1)和区间(1,2)上各有一根,则实数a 的取值范围是( )A .31a -<<B .314a <<C .334a -<<D .3a <-或34a > 【答案】B【解析】【分析】函数f (x )=221ax x -+在区间(﹣1,1)和区间(1,2)上分别存在一个零点,则()()()()110120f f f f ⎧-⎪⎨⎪⎩<<,解得即可. 【详解】∵函数f (x )=ax 2﹣2x +1在区间(﹣1,1)和区间(1,2)上分别存在一个零点, ∴()()()()110120f f f f ⎧-⎪⎨⎪⎩<<, 即()()()()3101430a a a a ⎧+-⎪⎨--⎪⎩<<, 解得34<a <1,故选:B .【点睛】本题考查函数零点的判断定理,理解零点判定定理的内容,将题设条件转化为关于参数的不等式组是解本题的关键.6.若log 0.5log 0.50m n >>,则( )A .1m n <<B .1m n <<C .1n m <<D .1n m << 【答案】D【解析】【分析】由于两个对数值均为正,故m 和n 一定都小于1,再利用对数换底公式,将不等式等价变形为以10为底的对数不等式,利用对数函数的单调性比较m 、n 的大小即可【详解】∵log 0.5log 0.50m n >>∴0<n <1,0<m <1 且0.50.50lg lg lgm lgn>> 即lg 0.5(11lgm lgn -)>0⇔lg 0.5(lgn lgm lgm lgn -⨯)>0 ∵lg 0.5<0,lgm <0,lgn <0∴lgn ﹣lgm <0即lgn <lgm ⇔n <m∴1>m >n >0故选:D .【点睛】本题考查了对数函数的图象和性质,对数的运算法则及其换底公式的应用,利用图象和性质比较大小的方法7.已知过点(1,1)P 且与曲线3y x =相切的直线的条数有( ).A .0B .1C .2D .3【答案】C【解析】【分析】设切点为()00x ,y ,则300y x =,由于直线l 经过点()1,1,可得切线的斜率,再根据导数的几何意义求出曲线在点0x 处的切线斜率,建立关于0x 的方程,从而可求方程.【详解】若直线与曲线切于点()()000x ,y x 0≠,则32000000y 1x 1k x x 1x 1x 1--===++--, 又∵2y'3x =,∴200y'x x 3x ==,∴2002x x 10--=,解得0x 1=,01x 2=-, ∴过点()P 1,1与曲线3C :y x =相切的直线方程为3x y 20--=或3x 4y 10-+=,故选:C .【点睛】本题主要考查了利用导数求曲线上过某点切线方程的斜率,求解曲线的切线的方程,其中解答中熟记利用导数的几何意义求解切线的方程是解答的关键,着重考查了运算与求解能力,属于基础题.8.2nx ⎫⎪⎭的展开式中的第7项是常数,则正整数n 的值为( ) A .16B .18C .20D .22 【答案】B【解析】【分析】利用通项公式即可得出.【详解】 2nx ⎫⎪⎭的展开式的第7项66672()()n n T x x -=-=6622x n n ﹣9, 令902n =0,解得n =18. 故选:B .【点睛】本题考查了二项式定理的应用、方程思想,考查了推理能力与计算能力,属于中档题. 9.甲、乙两位同学各自独立地解答同一个问题,他们能够正确解答该问题的概率分别是25和12,在这个问题已被正确解答的条件下,甲、乙两位同学都能正确回答该问题的概率为( )A .27B .15C .29D .910【答案】A【解析】【分析】设事件A 表示“甲能回答该问题”,事件B 表示“乙能回答该问题”,事件C 表示“这个问题被解答”,则P (A )=0.4,P (B )=0.5,求出P (C )=P (A B )+P (AB )+P (AB )=0.7,由此利用条件概率计算公式能求出在这个问题已被解答的条件下,甲乙两位同学都能正确回答该问题的概率.【详解】设事件A 表示“甲能回答该问题”,事件B 表示“乙能回答该问题”,事件C 表示“这个问题被解答”,则P(A)=0.4,P(B)=0.5,P(C)=P(A B)+P(AB)+P(AB)=0.2+0.3+0.2=0.7,∴在这个问题已被解答的条件下,甲乙两位同学都能正确回答该问题的概率:P(AB|C)()()0.40.520.77P ABP C⨯===.故选:A【点睛】本题考查条件概率的求法,是基础题,解题时要认真审题,注意等可能事件概率公式的合理运用.10.甲、乙、丙、丁四名同学组成一个4⨯100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( )A.甲B.乙C.丙D.丁【答案】C【解析】【分析】跑第三棒的只能是乙、丙中的一个,当丙跑第三棒时,乙只能跑第二棒,这时丁跑第一棒,甲跑第四棒,符合题意;当乙跑第三棒时,丙只能跑第二棒,这里四和丁都不跑第一棒,不合题意.【详解】由题意得乙、丙均不跑第一棒和第四棒,∴跑第三棒的只能是乙、丙中的一个,当丙跑第三棒时,乙只能跑第二棒,这时丁跑第一棒,甲跑第四棒,符合题意;当乙跑第三棒时,丙只能跑第二棒,这里四和丁都不跑第一棒,不合题意.故跑第三棒的是丙.故选:C.【点睛】本题考查推理论证,考查简单的合情推理等基础知识,考查运算求解能力、分析判断能力,是基础题.11.函数ln ()(e 2.7128)e x x f x ==的大致图象是( )A .B .C .D .【答案】A【解析】【分析】利用函数的奇偶性,排除选项B,D ,再利用特殊点的函数值判断即可.【详解】函数为非奇非偶函数,排除选项B,D ;当-10x << ,f (x )<0,排除选项C ,故选:A .【点睛】本题考查函数的图象的判断,函数的奇偶性以及函数的图象的变化趋势是判断函数的图象的常用方法.12.对于函教2()e (1)(2)x f x x x =--,以下选项正确的是( )A .1是极大值点B .有1个极小值C .1是极小值点D .有2个极大值 【答案】A【解析】【分析】求出函数的导数,解关于导函数的不等式,求出函数的极值点,再逐项判断即可.【详解】 '213x f xe x x 当'031,3fx x x 当'013,3f x x x ,故1是极大值点,且函数有两个极小值点 故选:A【点睛】本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题13.幂函数()()2221 33m m f x m m x -+=-+在区间()0,∞+上是增函数,则m =________.【答案】2【解析】【分析】根据幂函数的定义求出m 的值,判断即可.【详解】若幂函数()()222133m m f x m m x -+=-+在区间(0,+∞)上是增函数,则由m 2﹣3m +3=1解得:m =2或m =1,m =2时,f (x )=x ,是增函数,m =1时,f (x )=1,是常函数(不合题意,舍去),故答案为:2.【点睛】本题考查了幂函数的定义,考查函数的单调性问题,是一道基础题.14.若对甲、乙、丙3组不同的数据作线性相关性检验,得到这3组数据的线性相关系数依次为0.83,0.72,-0.90,则线性相关程度最强的一组是_______.(填甲、乙、丙中的一个)【答案】丙【解析】【分析】根据两个变量y 与x 的回归模型中,相关系数|r |的绝对值越接近于1,其相关程度越强即可求解.【详解】两个变量y 与x 的回归模型中,它们的相关系数|r |越接近于1,这个模型的两个变量线性相关程度就越强,在甲、乙、丙中,所给的数值中﹣0.90的绝对值最接近1,所以丙的线性相关程度最强.故答案为:丙.【点睛】本题考查了利用相关系数判断两个变量相关性强弱的应用问题,是基础题. 15.将1,2,3,4,5,这五个数字放在构成“W ”型线段的5个端点位置,要求下面的两个数字分别比和它相邻的上面两个数字大,这样的安排方法种数为_______.【答案】16【解析】【分析】由已知1和2必须在上面,5必须在下面,分两大类来计算:(1)下面是3和5时,有2(1+1)=4种情况;(2)下面是4和5时,有233A =12种情况,继而得出结果.【详解】由已知1和2必须在上面,5必须在下面,分两大类来计算:(1)下面是3和5时,有2(1+1)=4种情况;(2)下面是4和5时,有233A =12种情况,所以一共有4+12=16种方法种数.故答案为:16.【点睛】本题考查的是分步计数原理,考查分类讨论的思想,是基础题16.已知函数()12ln ,e e f x a x x ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎣⎦⎝⎭的图象上存在点P ,函数()22g x x =--的图象上存在点Q ,且点P 和点Q 关于原点对称,则实数a 的取值范围是________.【答案】23,e ⎡⎤⎣⎦【解析】【分析】由题可以转化为函数y =a +2lnx (x ∈[1e,e ])的图象与函数y =x 2+2的图象有交点,即方程a +2lnx =x 2+2(x ∈[1e ,e ])有解,即a =x 2+2﹣2lnx (x ∈[1e ,e ])有解,令f (x )=x 2+2﹣2lnx ,利用导数法求出函数的值域,可得答案.【详解】函数y =﹣x 2﹣2的图象与函数y =x 2+2的图象关于原点对称, 若函数y =a +2lnx (x ∈[1e,e ])的图象上存在点P ,函数y =﹣x 2﹣2的图象上存在点Q ,且P ,Q 关于原点对称,则函数y =a +2lnx (x ∈[1e ,e ])的图象与函数y =x 2+2的图象有交点, 即方程a +2lnx =x 2+2(x ∈[1e ,e ])有解,即a =x 2+2﹣2lnx (x ∈[1e,e ])有解,令f (x )=x 2+2﹣2lnx ,则f ′(x )()221x x-=,当x ∈[1e,1)时,f ′(x )<0,当x ∈(1,e ]时,f ′(x )>0, 故当x =1时,f (x )取最小值3, 由f (1e )21e=+4,f (e )=e 2, 故当x =e 时,f (x )取最大值e 2, 故a ∈[3,e 2],故答案为23,e ⎡⎤⎣⎦【点睛】本题考查的知识点是函数图象的对称性,函数的值域,难度中档.三、解答题17.已知函数()ln(3)ln(3)f x x x =++-. (1)求函数()y f x =的定义域并判断奇偶性; (2)若(21)()f m f m -<,求实数m 的取值范围.【答案】(1)见解析;(2)113m -<<或12m <<. 【解析】 【分析】 (1)由3030x x +⎧⎨-⎩>>,求得x 的范围,可得函数y =f (x )定义域,由函数y =f (x )的定义域关于原点对称,且满足 f (﹣x )=f (x ),可得函数y =f (x )为偶函数;(2)化简函数f (x )的解析式为()()2ln 9f x x=-所,结合函数的单调性可得,不等式()()21f m f m -<等价于32133321m m m m ⎧-<-<⎪-<<⎨⎪->⎩,由此求得m 的范围.【详解】 (1)由3030x x +>⎧⎨->⎩得33x -<<,所以()f x 的定义域为()3,3-,又因为()()()()ln 3ln 3f x x x f x -=-++=,所以()f x 偶函数.(2)因为()()()()2ln 3ln 3ln 9f x x x x =++-=-所以()f x 是[0,3)上的减函数,又()f x 是偶函数.故32133321m m m m⎧-<-<⎪-<<⎨⎪->⎩解得113m -<<或12m <<.【点睛】本题主要考查求函数的定义域,函数的奇偶性的判断,复合函数的单调性,属于中档题. 18.袋中装有10个除颜色外完全一样的黑球和白球,已知从袋中任意摸出2个球,至少得到1个白球的概率是79. (1)求白球的个数;(2)从袋中任意摸出3个球,记得到白球的个数为X ,求随机变量X 的分布列. 【答案】(1)5个;(2)见解析. 【解析】 【分析】(1)设白球的个数为x ,则黑球的个数为10﹣x ,记“从袋中任意摸出2个球,至少得到1个白球”为事件A ,则两个都是黑球与事件A 为对立事件,由此能求出白球的个数;(2)随机变量X 的取值可能为:0,1,2,3,分别求出相应的概率,由此能求出X 的分布列. 【详解】(1)设白球的个数为x ,则黑球的个数为10﹣x ,记“从袋中任意摸出2个球,至少得到1个白球”为事件A ,则()210210719xC P A C -=-=,解得5x =.故白球有5个.(2)X 服从以10,5,3为参数的超几何分布,()355310,0,1,2,3k kC C P X k k C -===. 于是可得其分布列为:【点睛】本题主要考查离散型随机变量的分布列,超几何分布,求出离散型随机变量取每个值的概率,是解题的关键,属于中档题.19.设数列{}n a 的前n 项和为n S 且对任意的正整数n 都有:2(1)n n n S a S -=.(1)求123,,S S S ;(2)猜想n S 的表达式并证明. 【答案】(1)123,,234;(2)*()1n n S n N n =∈+,证明见解析. 【解析】 【分析】(1)分别代入1,2,3n =计算即可求解;(2)猜想:()*1n nS n N n =∈+,利用数学归纳法证明即可 【详解】当()2111111,1;2n S S S S =-=⇒=当()22222122,1;23n S S S S ⎛⎫=-=-⇒= ⎪⎝⎭ 当()23333233,1;34n S S S S ⎛⎫=-=-⇒= ⎪⎝⎭ (2)猜想:()*1n nS n N n =∈+. 证明:①当1n =时,显然成立; ②假设当(1n k k =≥且*)k N ∈时,1k kS k =+成立.则当1n k =+时,由()21111k k k S a S +++-=,得()()21111k k k k S S S S +++-=-,整理得()11111221121k k k k S k S k k k +++====-+++-+.即1n k =+时,猜想也成立.综合①②得()*1n nS n N n =∈+. 【点睛】本题考查递推数列求值,数学归纳法证明,考查推理计算能力,是基础题20.IC 芯片堪称“国之重器”其制作流程异常繁琐,制作IC 芯片核心部分首先需要制造单晶的晶圆,此过程主要是加入碳,以氧化还原的方式,将氧化硅转换为高纯度的硅.为达到这一高标准要求,研究工作人员曾就是否需采用西门子制程(Siemens process )这一工艺技术进行了反复比较,在一次实验中,工作人员对生产出的50片单晶的晶圆进行研究,结果发现使用了该工艺的30片单晶的晶圆中有28片合格,没有使用该工艺的20片单晶的晶圆中有12片合格.(1)请填写2⨯2列联表并判断:这次实验是否有99.5%的把握认为单晶的晶圆的制作效果与使用西门子制程(Siemens process )这一工艺技术有关?(2)在得到单晶的晶圆后,接下来的生产制作还前对单晶的晶圆依次进行金属溅镀,涂布光阻,蚀刻技术,光阻去除这四个环节的精密操作,进而得到多晶的晶圆,生产出来的多晶的晶圆经过严格的质检,确定合格后才能进入下一个流程,如果生产出来的多晶的晶圆在质检中不合格,那么必须依次对前四个环节进行技术检测并对所有的出错环节进行修复才能成为合格品.在实验的初期,由于技术的不成熟,生产制作的多晶的晶圆很难达到理想状态,研究人员根据以往的数据与经验得知在实验生产多晶的晶圆的过程中,前三个环节每个环节生产正常的概率为23,第四个环节生产正常的概率为34,且每个环节是否生产正常是相互独立的.前三个环节每个环节出错需要修复的费用均为20元,第四环节出错需要修复的费用为10元.问:一次实验生产出来的多晶的晶圆要成为合格品平均还需要消耗多少元费用?(假设质检与检测过程不产生费用)参考公式:22()n ()()()(n ad bc K a b c d a b c d a c b d -==+++++++,)参考数据:【答案】(1)见解析;(2)22.5元. 【解析】 【分析】(1)先列出列联表,再根据列表求出K 2253=>7.879,从而有99.5%的把握认为晶圆的制作效果与使用西门子制程这一工艺技术有关.(2)设A i 表示检测到第i 个环节有问题,(i =1,2,3,4),X 表示成为一个合格的多晶圆需消耗的费用,则X 的可能取值为:0,10,20,30,40,50,60,70,分别求出相应的概率,由此能求出X 的分布列和数学期望. 【详解】 (1)()2250288212258.3337.879302040103K ⨯-⨯==≈>⨯⨯⨯ 故有99.5%的把握认为单晶的晶圆的制作效果与使用西门子制程这一工艺技术有关. (2)设X 表示成为一个合格的多晶的晶圆还需要消耗的费用,则X 的可能取值为:0,10,20,30,40,50,60,70.()32324034108P X ⎛⎫==⨯=⎪⎝⎭()32181034108P X ⎛⎫==⨯=⎪⎝⎭ ()2131233620334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()2131211230334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()2231231840334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭()223121650334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()31336034108P X ⎛⎫==⨯=⎪⎝⎭ ()31117034108P X ⎛⎫==⨯=⎪⎝⎭ 所以X 分布列为:故()24836121863101020304050607022.5108108108108108108108108E X =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=,故平均还需要耗费22.5元. 【点睛】本题考查独立检验的应用,考查离散型随机变量的分布列和数学期望的求法,考查离散型随机变量的分布列、数学期望等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.21.已知函数()2(0)f x a lnx ax a =+->. (1)求()f x 的最大值()a ϕ; (2)若()0f x ≤恒成立,求a 的值;(3)在(2)的条件下,设[]()()x f x ax g x x a+=-在(,)a +∞上的最小值为,m 求证:11()10f m -<<-.【答案】(1)()22ln 2ln2(0)a a a a ϕ=--+>;(2)2;(3)证明见解析. 【解析】 【分析】(1)()2'(0)axf x a x-=>,判断函数的单调性即可求解最大值;(2)要使()0f x ≤成立必须()22ln 2ln20a a a ϕ=--+≤,()2'a a aϕ-=,判断单调性求解()()min 20a ϕϕ==即可得解2a =;(3)()22ln 2x x xg x x +=-,得()()()222ln 4'2x x g x x --=-,令()2ln 4u x x x =--判断其单调性进而求得()()20000000min0022ln 2=22x x x x x g x g x x x x +-===--,得0m x =,再求()0f x 的范围进而得证【详解】 (1)()2'(0)axf x a x-=>, 由()'0f x >得20x a <<;()'0f x <得2x a >;所以()f x 在20,a ⎛⎫⎪⎝⎭上单调递增,在2,a ⎛⎫+∞ ⎪⎝⎭上单调递减.故()max222ln 2ln2f x f a a a ⎛⎫==--+ ⎪⎝⎭, 即()22ln 2ln2(0)a a a a ϕ=--+>;(2)要使()0f x ≤成立必须()22ln 2ln20a a a ϕ=--+≤.因为()2'a a aϕ-=,所以当02a <<时,()'0a ϕ<;当2a >时,()'0a ϕ>.所以()a ϕ在()0,2上单调递减,在()2,+∞上单调递增.又()()min 20a ϕϕ==,所以满足条件的a 只有2,即2a =.(3)由(2)知()22ln 2x x x g x x +=-,所以()()()222ln 4'2x x g x x --=-. 令()2ln 4u x x x =--,则()2'0x u x x-=>,()u x 是()2,+∞上的增函数;又()()80,90u u ,所以存在()08,9x ∈满足()00u x =,即002ln 4x x =-,且当()02,x x ∈时,()()0,'0u x g x <<; 当()0,x x ∈+∞,()()0,'0u x g x >>所以()g x 在()02,x 上单调递减;在()0,x +∞上单调递增.所以()()20000000min0022ln 2=22x x x x x g x g x x x x +-===--,即0m x =.所以()()000022ln 2=21110f m f x x x x ==+---∈--(,),即()1110f m -<<-.【点睛】本题考查了利用导数研究函数的单调性及最值,考查了零点存在定理和数学转化思想,在(3)的证明过程中,利用零点存在定理转化是难点属中档题.22.已知极坐标系的极点在直角坐标系的原点处,极轴与x 轴正半轴重合,直线l 的参数方程为:2cos sin x t y t αα=+⎧⎨=⎩(t 为参数,[0,)απ∈),曲线C 的极坐标方程为:4sin ρθ=.(1)写出曲线C 的直角坐标方程;(2)设直线l 与曲线C 相交于,P Q 两点,直线l 过定点M ,若MP MQ +=求直线l 的斜率.【答案】(1)22(2)4x y +-=;(2)1-. 【解析】 【分析】(1)由4sin ρθ=,得24sin ρρθ=,由此能求出曲线C 的直角坐标方程;(2)把2cos sin x t y t αα=+⎧⎨=⎩代入()2224x y +-=,整理得()24cos sin 40t t αα+-+=,由1212MP MQ t t t t +=+=+,得34πα=,能求出直线l 的斜率. 【详解】(1)曲线C 的极坐标方程为4sin ρθ=,所以24sin ρρθ=.即224x y y +=,即()2224x y +-=.(2)把直线l 的参数方程带入()2224x y +-=得()24cos sin 40t t αα+-+=设此方程两根为12,t t ,易知()2,0M ,而定点M 在圆C 外,所以1212MP MQ t t t t +=+=+,4cos sin αα∴-=cos sin αα∴-=[0,)απ∈,可得34πα=, ∴1k =-,所以直线l 的斜率为-1. 【点睛】本题考查曲线的直角坐标方程的求法,考查直线的斜率的求法,考查极坐标方程、直角坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.23.已知()1f x x x m =+++,()232g x x x =++.(1)若0m >且()f x 的最小值为1,求m 的值;(2)不等式()3f x ≤的解集为A ,不等式()0g x ≤的解集为B ,B A ⊆,求m 的取值范围.【答案】(1)2m =;(2)04m ≤≤ 【解析】试题分析:(1)利用绝对值三角不等式可得()11f x m ≥-=,解出方程即可;(2)易得[]2,1B =--,()3f x ≤即4x m x +≤+,即42m x +≥-且4m ≤,再根据B A ⊆列出不等式即可得结果.试题解析:(1)()()()111f x x x m x x m m =+++≥+-+=-(当1x =-时,等号成立)∵()f x 的最小值为 1,∴11m -=,∴2m = 或0m =,又0m >,∴2m =. (2)由()0g x ≤得,[]2,1B =--,∵B A ⊆, ∴(),3x B f x ∀∈≤,即()13x x m -+++≤44442m x m x x x m x x +⇔+≤+⇔--≤+≤+⇔≥-且4m ≤ 422m +⇔-≤-且404m m ≤⇔≤≤.。
辽宁省锦州市2022届数学高二(下)期末质量检测试题含解析

辽宁省锦州市2022届数学高二(下)期末质量检测试题一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意) 1.点的极坐标,它关于极点的对称点的一个极坐标是A .B .C .D .【答案】C 【解析】 【分析】在点极径不变,在极角的基础上加上,可得出与点关于极点对称的点的一个极坐标。
【详解】设点关于极点的对称点为,则,,所以点的一个极坐标为.故选:C 。
【点睛】本题考查点的极坐标,考查具备对称性的两点极坐标之间的关系,把握极径与极角之间的关系,是解本题的关键,属于基础题。
2.在三棱锥P ABC -中,PA ⊥平面ABC ,2π,43BAC AP ∠==,23AB AC ==则三棱锥P ABC -的外接球的表面积为( ) A .32π B .48πC .64πD .72π【答案】C 【解析】 【分析】先求出ABC V 的外接圆的半径,然后取ABC V 的外接圆的圆心G ,过G 作//GO AP ,且122GO AP ==,由于PA ⊥平面ABC ,故点O 为三棱锥P ABC -的外接球的球心,OA 为外接球半径,求解即可. 【详解】在ABC V 中,23AB AC ==23BAC π∠=,可得6ACB π∠=, 则ABC V 的外接圆的半径2332sin 2sin6AB r ACB ===ABC V 的外接圆的圆心G ,过G 作//GO AP ,且122GO AP ==, 因为PA ⊥平面ABC ,所以点O 为三棱锥P ABC -的外接球的球心, 则222OA OG AG =+,即外接球半径()222234R =+=,则三棱锥P ABC -的外接球的表面积为24π4π1664πR =⨯=. 故选C.【点睛】本题考查了三棱锥的外接球表面积的求法,考查了学生的空间想象能力,属于中档题.3.在四棱锥P ABCD -中,底面ABCD 是正方形,顶点P 在底面的射影是底面的中心,且各顶点都在同一球面上,11,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:()3322()a b a b a ab b -=-++)A .2B .116 C .4D .113【答案】B 【解析】 【分析】如图所示,设底面正方形ABCD 的中心为'O ,正四棱锥P ABCD -的外接球的球心为O ,半径为R .则在'Rt PO D ∆中,有221112a h +=,再根据体积为4可求3h =及2a =,在'Rt OO D ∆中,有222(3)(2)R R -+=,解出R 后可得正确的选项.【详解】如图所示,设底面正方形ABCD 的中心为'O ,正四棱锥P ABCD -的外接球的球心为O ,半径为R .设底面正方形ABCD 的边长为a ,正四棱锥的高为()*h h ∈N,则22O D a '=. 因为该正四棱锥的侧棱长为11,所以222112a h ⎛⎫+= ⎪ ⎪⎝⎭,即221112a h +=……① 又因为正四棱锥的体积为4,所以2143a h =• ……②由①得()22211a h=-,代入②得31160hh -+=,配凑得32711330h h --+=,()2(3)3911(3)0h h h h -++--=,即()2(3)320h h h -+-=,得30h -=或2h +320h -=.因为*h ∈N ,所以3h =,再将3h =代入①中,解得2a =, 所以22O D a '==,所以OO PO '='-3PO R =-. 在Rt OO D ∆'中,由勾股定理,得222OO O D OD '+'=, 即222(3)(2)R R -+=,解得116R =,所以此球的半径等于116.故选B. 【点睛】正棱锥中,棱锥的高、斜高、侧棱和底面外接圆的半径可构成四个直角三角形,它们沟通了棱锥各个几何量之间的关系,解题中注意利用它们实现不同几何量之间的联系.4.针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的女生人数是男生人数的,男生喜欢抖音的人数占男生人数的,女生喜欢抖音的人数占女生人数,若有的把握认为是否喜欢抖音和性别有关,则男生至少有( ) 参考公式:0.10 0.05 0.025 0.010 0.005 0.0012.7063.8415.0246.6357.87910.828A .12人B .18人C .24人D .30人【答案】B 【解析】 【分析】设男生人数为,女生人数为,完善列联表,计算解不等式得到答案.【详解】设男生人数为,女生人数为喜欢抖音 不喜欢抖音 总计男生女生总计男女人数为整数 故答案选B 【点睛】本题考查了独立性检验,意在考查学生的计算能力和应用能力.5.设曲线(1)ln y a x x =--在点()1,0处的切线方程为33y x =-,则a =( ) A .1 B .2C .3D .4【答案】D 【解析】 【分析】利用导数的几何意义得直线的斜率,列出a 的方程即可求解 【详解】因为1y a x'=-,且在点()1,0处的切线的斜率为3,所以13a -=,即4a =. 故选:D 【点睛】本题考查导数的几何意义,考查运算求解能力,是基础题 6.设0a >,0b >,若21a b +=,则21a b+的最小值为A .B .8C .9D .10【答案】C 【解析】 【分析】根据题意可知,利用“1”的代换,将21a b +化为()2()21a ba b ++,展开再利用基本不等式,即可求解出答案。
2022届辽宁省锦州市高二第二学期数学期末教学质量检测试题含解析
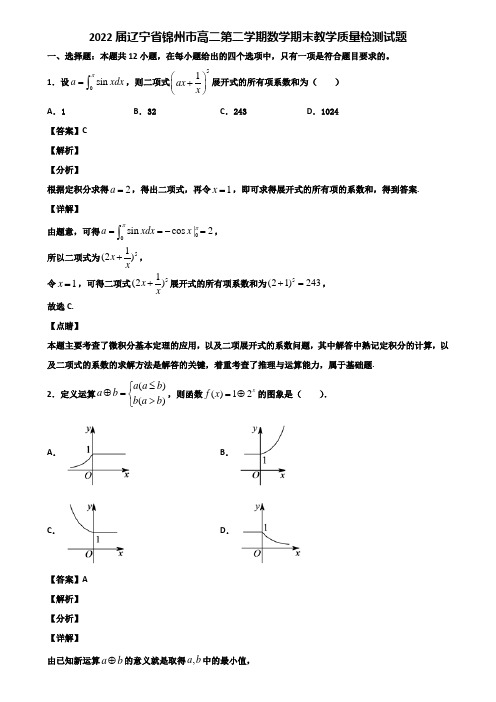
2022届辽宁省锦州市高二第二学期数学期末教学质量检测试题一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设0sin a xdx π=⎰,则二项式51ax x ⎛⎫+ ⎪⎝⎭展开式的所有项系数和为( ) A .1B .32C .243D .1024 【答案】C【解析】【分析】根据定积分求得2a =,得出二项式,再令1x =,即可求得展开式的所有项的系数和,得到答案.【详解】由题意,可得00sin cos |2a xdx x ππ==-=⎰,所以二项式为51(2)x x +,令1x =,可得二项式51(2)x x +展开式的所有项系数和为5(21)243+=, 故选C.【点睛】本题主要考查了微积分基本定理的应用,以及二项展开式的系数问题,其中解答中熟记定积分的计算,以及二项式的系数的求解方法是解答的关键,着重考查了推理与运算能力,属于基础题.2.定义运算()()a ab a b b a b ≤⎧⊕=⎨>⎩,则函数()12x f x =⊕的图象是( ). A . B .C .D .【答案】A【解析】【分析】【详解】由已知新运算的意义就是取得,a b 中的最小值,因此函数()1,0122,0x x x f x x >⎧=⊕=⎨≤⎩, 只有选项A 中的图象符合要求,故选A.3.已知扇形的圆心角为23π弧度,半径为2,则扇形的面积是( ) A .83π B .43 C .2π D .43π 【答案】D【解析】【分析】利用扇形面积公式212S R α=(α为扇形的圆心角的弧度数,R 为扇形的半径),可计算出扇形的面积. 【详解】由题意可知,扇形的面积为21242233S ππ=⨯⨯=,故选D. 【点睛】本题考查扇形面积的计算,意在考查扇形公式的理解与应用,考查计算能力,属于基础题.4.圆柱形容器内盛有高度为6 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,如图所示.则球的半径是( )A .1 cmB .2 cmC .3 cmD .4 cm【答案】C【解析】【分析】 设出球的半径,根据题意得三个球的体积和水的体积之和,等于柱体的体积,结合体积公式求解即可.【详解】设球半径为r ,则由3V V V +=球水柱,可得32243663r r r r πππ⨯+⨯=⨯,解得3r =,故选C.【点睛】本题主要考查了几何体的体积公式的应用,考查学生空间想象能力以及计算能力,是基础题. 5.用数学归纳法证明11151236n n n ++⋅⋅⋅+≥++时,从n k =到1n k =+,不等式左边需添加的项是A .111313233k k k +++++ B .112313233k k k +-+++ C .11331k k -++ D .133k + 【答案】B【解析】 分析:分析n k =,1n k =+时,左边起始项与终止项,比较差距,得结果.详解:n k =时,左边为111123k k k++⋅⋅⋅+++, 1n k =+时,左边为111111233313233k k k k k k ++⋅⋅⋅++++++++++, 所以左边需添加的项是 11111123132331313233k k k k k k k ++-=+-+++++++,选B. 点睛:研究n k =到1n k =+项的变化,实质是研究式子变化的规律,起始项与终止项是什么,中间项是如何变化的.6.从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是( )A .至少有一个红球与都是红球B .至少有一个红球与都是白球C .恰有一个红球与恰有二个红球D .至少有一个红球与至少有一个白球【答案】C【解析】【详解】从装有5个红球和3个白球的口袋内任取3个球,不同的取球情况共有以下几种:3个球全是红球;2个红球和1个白球;1个红球2个白球;3个全是白球.选项A 中,事件“都是红球”是事件“至少有一个红球”的子事件;选项B 中,事件“至少有一个红球”与事件“都是白球”是对立事件;选项D 中,事件“至少有一个红球”与事件“至少有一个白球”的事件为“2个红球1个白球”与“1个红球2个白球”;选项C 中,事件“恰有一个红球”与事件“恰有2个红球”互斥不对立,故选C.7.为了考察两个变量x 和y 之间的线性相关性,甲、乙两个同学各自独立做了15次和20次试验,并且利用线性回归方法,求得回归直线为l 1和l 2,已知在两人的试验中发现对变量x 的观测数据的平均值恰好相等,都为s ,对变量y 的观测数据的平均值也恰好相等,都为t ,那么下列说法正确的是( ) A .直线l 1和直线l 2有交点(s ,t )B .直线l 1和直线l 2相交,但交点未必是点(s ,t )C .直线l 1和直线l 2必定重合D .直线l 1和直线l 2由于斜率相等,所以必定平行【答案】A根据回归直线过样本数据中心点,并结合回归直线的斜率来进行判断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁省锦州市2018-2019学年高二数学下学期期末考试试题 理(含解析)第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}12,3A x y x B x x -⎧⎫===≥⎨⎬⎩⎭,则()R A C B =I ( ) A. [)0,3B. (0,3)C. ()3,+∞D. ()0,∞+【答案】B【解析】【分析】 先分别化简集合A,B,再利用集合补集交集运算求解即可 【详解】12A x y x -⎧⎫==⎨⎬⎩⎭=()0,∞+ {}3B x x =≥=[3,)(,3]+ト-? ,则()0,3R A C B ⋂=()故选:B【点睛】本题考查集合的运算,解绝对值不等式,准确计算是关键,是基础题2.设i 为虚数单位,复数11i i i ++-等于( ) A. 2i -B. 2iC. 1i -+D. 0 【答案】B【解析】【分析】利用复数除法和加法运算求解即可 详解】11i i i ++=-()2122i i i ++= 故选:B【点睛】本题考查复数的运算,准确计算是关键,是基础题3.已知22,0()log ,0x x f x a xx ⎧<=⎨+≥⎩,若((1))1f f -=-.则实数a 的值为( )A. -2B. 2C. 0D. 1【答案】C【解析】【分析】由函数()22,0log ,0x x f x a x x ⎧<=⎨+≥⎩,将x ==-1,代入,构造关于a 的方程,解得答案.【详解】∵函数()22,0log ,0x x f x a x x ⎧<=⎨+≥⎩,∴f (﹣1)=12 ,∴f [f (﹣1)]112f a ⎛⎫==-=- ⎪⎝⎭1,解得:a =0,故选:C .【点睛】本题考查的知识点是分段函数的应用,函数求值,难度不大,属于基础题.4.0sin xdx π⎰的值为( )A. 2B. 0C. -2D. 1【答案】A【解析】【分析】根据的定积分的计算法则计算即可.【详解】0sin xdx π⎰=(-cos x )0|2π=故选:A .【点睛】本题考查了定积分的计算,关键是求出原函数,属于基础题.5.若方程2210ax x -+=在区间(-1,1)和区间(1,2)上各有一根,则实数a 的取值范围是( )A. 31a -<<B. 314a <<C. 334a -<<D. 3a <-或34a > 【答案】B【解析】【分析】函数f (x )=221ax x -+在区间(﹣1,1)和区间(1,2)上分别存在一个零点,则()()()()110120f f f f ⎧-⎪⎨⎪⎩<<,解得即可. 【详解】∵函数f (x )=ax 2﹣2x +1在区间(﹣1,1)和区间(1,2)上分别存在一个零点, ∴()()()()110120f f f f ⎧-⎪⎨⎪⎩<<, 即()()()()3101430a a a a ⎧+-⎪⎨--⎪⎩<<, 解得34<a <1,故选:B .【点睛】本题考查函数零点的判断定理,理解零点判定定理的内容,将题设条件转化为关于参数的不等式组是解本题的关键.6.若log 0.5log 0.50m n >>,则( )A. 1m n <<B. 1m n <<C. 1n m <<D. 1n m <<【答案】D【解析】【分析】由于两个对数值均为正,故m 和n 一定都小于1,再利用对数换底公式,将不等式等价变形为以10为底的对数不等式,利用对数函数的单调性比较m 、n 的大小即可【详解】∵log 0.5log 0.50m n >>∴0<n <1,0<m <1 且0.50.50lg lg lgm lgn>> 即lg 0.5(11lgm lgn -)>0⇔lg 0.5(lgn lgm lgm lgn-⨯)>0 ∵lg 0.5<0,lgm <0,lgn <0∴lgn ﹣lgm <0即lgn <lgm ⇔n <m∴1>m >n >0故选:D .【点睛】本题考查了对数函数的图象和性质,对数的运算法则及其换底公式的应用,利用图象和性质比较大小的方法7.已知过点(1,1)P 且与曲线3y x =相切的直线的条数有( ).A. 0B. 1C. 2D. 3【答案】C【解析】【分析】设切点为()00x ,y ,则300y x =,由于直线l 经过点()1,1,可得切线的斜率,再根据导数的几何意义求出曲线在点0x 处的切线斜率,建立关于0x 的方程,从而可求方程.【详解】若直线与曲线切于点()()000x ,y x 0≠,则32000000y 1x 1k x x 1x 1x 1--===++--, 又∵2y'3x =,∴200y'x x 3x ==,∴2002x x 10--=,解得0x 1=,01x 2=-, ∴过点()P 1,1与曲线3C :y x =相切的直线方程为3x y 20--=或3x 4y 10-+=,故选:C .【点睛】本题主要考查了利用导数求曲线上过某点切线方程的斜率,求解曲线的切线的方程,其中解答中熟记利用导数的几何意义求解切线的方程是解答的关键,着重考查了运算与求解能力,属于基础题.8.2n x ⎫⎪⎭的展开式中的第7项是常数,则正整数n 的值为( ) A. 16B. 18C. 20D. 22 【答案】B【解析】【分析】利用通项公式即可得出.【详解】2nx ⎫⎪⎭的展开式的第7项66672()n n T x -=-=C 6622x n n C ﹣9, 令902n -= =0,解得n =18. 故选:B .【点睛】本题考查了二项式定理的应用、方程思想,考查了推理能力与计算能力,属于中档题.9.甲、乙两位同学各自独立地解答同一个问题,他们能够正确解答该问题的概率分别是25和12,在这个问题已被正确解答的条件下,甲、乙两位同学都能正确回答该问题的概率为( ) A. 27 B. 15 C. 29 D. 910【答案】A【解析】【分析】设事件A 表示“甲能回答该问题”,事件B 表示“乙能回答该问题”,事件C 表示“这个问题被解答”,则P (A )=0.4,P (B )=0.5,求出P (C )=P (A B )+P (AB )+P (AB )=0.7,由此利用条件概率计算公式能求出在这个问题已被解答的条件下,甲乙两位同学都能正确回答该问题的概率.【详解】设事件A 表示“甲能回答该问题”,事件B 表示“乙能回答该问题”,事件C 表示“这个问题被解答”,则P(A)=0.4,P(B)=0.5,P(C)=P(A B)+P(AB)+P(AB)=0.2+0.3+0.2=0.7,∴在这个问题已被解答的条件下,甲乙两位同学都能正确回答该问题的概率:P(AB|C)()()0.40.520.77P ABP C⨯===.故选:A【点睛】本题考查条件概率的求法,是基础题,解题时要认真审题,注意等可能事件概率公式的合理运用.10.甲、乙、丙、丁四名同学组成一个4⨯100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( )A. 甲B. 乙C. 丙D. 丁【答案】C【解析】【分析】跑第三棒的只能是乙、丙中的一个,当丙跑第三棒时,乙只能跑第二棒,这时丁跑第一棒,甲跑第四棒,符合题意;当乙跑第三棒时,丙只能跑第二棒,这里四和丁都不跑第一棒,不合题意.【详解】由题意得乙、丙均不跑第一棒和第四棒,∴跑第三棒的只能是乙、丙中的一个,当丙跑第三棒时,乙只能跑第二棒,这时丁跑第一棒,甲跑第四棒,符合题意;当乙跑第三棒时,丙只能跑第二棒,这里四和丁都不跑第一棒,不合题意.故跑第三棒的是丙.故选:C.【点睛】本题考查推理论证,考查简单的合情推理等基础知识,考查运算求解能力、分析判断能力,是基础题.11.函数ln ()(e 2.7128)e x xf x ==L 的大致图象是( )A. B. C. D.【答案】A【解析】【分析】利用函数的奇偶性,排除选项B,D ,再利用特殊点的函数值判断即可.【详解】函数为非奇非偶函数,排除选项B,D ;当-10x << ,f (x )<0,排除选项C ,故选:A .【点睛】本题考查函数的图象的判断,函数的奇偶性以及函数的图象的变化趋势是判断函数的图象的常用方法.12.对于函教2()e (1)(2)x f x x x =--,以下选项正确的是( )A. 1是极大值点B. 有1个极小值C. 1是极小值点D. 有2个极大值【答案】A【解析】【分析】求出函数的导数,解关于导函数的不等式,求出函数的极值点,再逐项判断即可.【详解】()()()'213x fx e x x =-- 当()'031,3fx x x >?<当()'013,3f x x x <?<-1是极大值点,且函数有两个极小值点故选:A【点睛】本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.幂函数()()2221 33m m f x m m x -+=-+在区间()0,∞+上是增函数,则m =________.【答案】2【解析】【分析】根据幂函数的定义求出m 的值,判断即可.【详解】若幂函数()()222133m m f x m m x -+=-+在区间(0,+∞)上是增函数, 则由m 2﹣3m +3=1解得:m =2或m =1, m =2时,f (x )=x ,是增函数,m =1时,f (x )=1,是常函数(不合题意,舍去),故答案为:2.【点睛】本题考查了幂函数的定义,考查函数的单调性问题,是一道基础题.14.若对甲、乙、丙3组不同的数据作线性相关性检验,得到这3组数据的线性相关系数依次为0.83,0.72,-0.90,则线性相关程度最强的一组是_______.(填甲、乙、丙中的一个)【答案】丙【解析】【分析】根据两个变量y 与x 的回归模型中,相关系数|r |的绝对值越接近于1,其相关程度越强即可求解.【详解】两个变量y 与x 的回归模型中,它们的相关系数|r |越接近于1,这个模型的两个变量线性相关程度就越强,在甲、乙、丙中,所给的数值中﹣0.90的绝对值最接近1,所以丙的线性相关程度最强.故答案为:丙.【点睛】本题考查了利用相关系数判断两个变量相关性强弱的应用问题,是基础题.15.将1,2,3,4,5,这五个数字放在构成“W ”型线段的5个端点位置,要求下面的两个数字分别比和它相邻的上面两个数字大,这样的安排方法种数为_______.【答案】16【解析】【分析】由已知1和2必须在上面,5必须在下面,分两大类来计算:(1)下面是3和5时,有2(1+1)=4种情况;(2)下面是4和5时,有233A =12种情况,继而得出结果.【详解】由已知1和2必须在上面,5必须在下面,分两大类来计算:(1)下面是3和5时,有2(1+1)=4种情况;(2)下面是4和5时,有233A =12种情况,所以一共有4+12=16种方法种数.故答案为:16.【点睛】本题考查的是分步计数原理,考查分类讨论的思想,是基础题16.已知函数()12ln ,e e f x a x x ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎣⎦⎝⎭的图象上存在点P ,函数()22g x x =--的图象上存在点Q ,且点P 和点Q 关于原点对称,则实数a 的取值范围是________.【答案】23,e ⎡⎤⎣⎦【解析】【分析】由题可以转化为函数y =a +2lnx (x ∈[1e,e ])的图象与函数y =x 2+2的图象有交点,即方程a +2lnx =x 2+2(x ∈[1e ,e ])有解,即a =x 2+2﹣2lnx (x ∈[1e ,e ])有解,令f (x )=x 2+2﹣2lnx ,利用导数法求出函数的值域,可得答案.【详解】函数y =﹣x 2﹣2的图象与函数y =x 2+2的图象关于原点对称,若函数y =a +2lnx (x ∈[1e,e ])的图象上存在点P ,函数y =﹣x 2﹣2的图象上存在点Q ,且P ,Q 关于原点对称,则函数y =a +2lnx (x ∈[1e,e ])的图象与函数y =x 2+2的图象有交点, 即方程a +2lnx =x 2+2(x ∈[1e,e ])有解, 即a =x 2+2﹣2lnx (x ∈[1e ,e ])有解, 令f (x )=x 2+2﹣2lnx ,则f ′(x )()221x x -=, 当x ∈[1e,1)时,f ′(x )<0,当x ∈(1,e ]时,f ′(x )>0, 故当x =1时,f (x )取最小值3,由f (1e )21e=+4,f (e )=e 2, 故当x =e 时,f (x )取最大值e 2, 故a ∈[3,e 2],故答案为23,e ⎡⎤⎣⎦【点睛】本题考查的知识点是函数图象的对称性,函数的值域,难度中档.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.已知函数()ln(3)ln(3)f x x x =++-.(1)求函数()y f x =的定义域并判断奇偶性;(2)若(21)()f m f m -<,求实数m 的取值范围.【答案】(1)见解析;(2)113m -<<或12m <<. 【解析】【分析】 (1)由3030x x +⎧⎨-⎩>>,求得x 的范围,可得函数y =f (x )定义域,由函数y =f (x )的定义域关于原点对称,且满足 f (﹣x )=f (x ),可得函数y =f (x )为偶函数;(2)化简函数f (x )的解析式为()()2ln 9f x x=-所,结合函数的单调性可得,不等式()()21f m f m -<等价于32133321m m m m ⎧-<-<⎪-<<⎨⎪->⎩,由此求得m 的范围. 【详解】(1)由3030x x +>⎧⎨->⎩得33x -<<,所以()f x 的定义域为()3,3-,又因为()()()()ln 3ln 3f x x x f x -=-++=,所以()f x 偶函数.(2)因为()()()()2ln 3ln 3ln 9f x x x x =++-=-所以()f x 是[0,3)上的减函数,又()f x 是偶函数.故32133321m m m m⎧-<-<⎪-<<⎨⎪->⎩解得113m -<<或12m <<.【点睛】本题主要考查求函数的定义域,函数的奇偶性的判断,复合函数的单调性,属于中档题.18.袋中装有10个除颜色外完全一样的黑球和白球,已知从袋中任意摸出2个球,至少得到1个白球的概率是79. (1)求白球的个数;(2)从袋中任意摸出3个球,记得到白球的个数为X ,求随机变量X 的分布列. 【答案】(1)5个;(2)见解析. 【解析】 【分析】(1)设白球的个数为x ,则黑球的个数为10﹣x ,记“从袋中任意摸出2个球,至少得到1个白球”为事件A ,则两个都是黑球与事件A 为对立事件,由此能求出白球的个数;(2)随机变量X 的取值可能为:0,1,2,3,分别求出相应的概率,由此能求出X 的分布列. 【详解】(1)设白球的个数为x ,则黑球的个数为10﹣x ,记“从袋中任意摸出2个球,至少得到1个白球”为事件A ,则()210210719xC P A C -=-=,解得5x =.故白球有5个.(2)X 服从以10,5,3为参数的超几何分布,()355310,0,1,2,3k kC C P X k k C -===. 于是可得其分布列为:【点睛】本题主要考查离散型随机变量的分布列,超几何分布,求出离散型随机变量取每个值的概率,是解题的关键,属于中档题.19.设数列{}n a 的前n 项和为n S 且对任意的正整数n 都有:2(1)n n n S a S -=.(1)求123,,S S S ;(2)猜想n S 的表达式并证明. 【答案】(1)123,,234;(2)*()1n n S n N n =∈+,证明见解析. 【解析】 【分析】(1)分别代入1,2,3n =计算即可求解;(2)猜想:()*1n nS n N n =∈+,利用数学归纳法证明即可详解】当()2111111,1;2n S S S S =-=⇒=当()22222122,1;23n S S S S ⎛⎫=-=-⇒= ⎪⎝⎭ 当()23333233,1;34n S S S S ⎛⎫=-=-⇒= ⎪⎝⎭ (2)猜想:()*1n nS n N n =∈+. 证明:①当1n =时,显然成立;②假设当(1n k k =≥且*)k N ∈时,1k kS k =+成立.则当1n k =+时,由()21111k k k S a S +++-=,得()()21111k k k k S S S S +++-=-,整理得()11111221121k k k k S k S k k k +++====-+++-+.即1n k =+时,猜想也成立.综合①②得()*1n nS n N n =∈+. 【点睛】本题考查递推数列求值,数学归纳法证明,考查推理计算能力,是基础题20.IC 芯片堪称“国之重器”其制作流程异常繁琐,制作IC 芯片核心部分首先需要制造单晶的晶圆,此过程主要是加入碳,以氧化还原的方式,将氧化硅转换为高纯度的硅.为达到这一高标准要求,研究工作人员曾就是否需采用西门子制程(Siemens process )这一工艺技术进行了反复比较,在一次实验中,工作人员对生产出的50片单晶的晶圆进行研究,结果发现使用了该工艺的30片单晶的晶圆中有28片合格,没有使用该工艺的20片单晶的晶圆中有12片合格.(1)请填写2⨯2列联表并判断:这次实验是否有99.5%的把握认为单晶的晶圆的制作效果与使用西门子制程(Siemens process )这一工艺技术有关?(2)在得到单晶的晶圆后,接下来的生产制作还前对单晶的晶圆依次进行金属溅镀,涂布光阻,蚀刻技术,光阻去除这四个环节的精密操作,进而得到多晶的晶圆,生产出来的多晶的晶圆经过严格的质检,确定合格后才能进入下一个流程,如果生产出来的多晶的晶圆在质检中不合格,那么必须依次对前四个环节进行技术检测并对所有的出错环节进行修复才能成为合格品.在实验的初期,由于技术的不成熟,生产制作的多晶的晶圆很难达到理想状态,研究人员根据以往的数据与经验得知在实验生产多晶的晶圆的过程中,前三个环节每个环节生产正常的概率为23,第四个环节生产正常的概率为34,且每个环节是否生产正常是相互独立的.前三个环节每个环节出错需要修复的费用均为20元,第四环节出错需要修复的费用为10元.问:一次实验生产出来的多晶的晶圆要成为合格品平均还需要消耗多少元费用?(假设质检与检测过程不产生费用)参考公式:22()n ()()()(n ad bc K a b c d a b c d a c b d -==+++++++,)参考数据:【答案】(1)见解析;(2)22.5元. 【解析】 【分析】(1)先列出列联表,再根据列表求出K 2253=>7.879,从而有99.5%的把握认为晶圆的制作效果与使用西门子制程这一工艺技术有关.(2)设A i 表示检测到第i 个环节有问题,(i =1,2,3,4),X 表示成为一个合格的多晶圆需消耗的费用,则X 的可能取值为:0,10,20,30,40,50,60,70,分别求出相应的概率,由此能求出X 的分布列和数学期望. 【详解】(1)()2250288212258.3337.879302040103K ⨯-⨯==≈>⨯⨯⨯故有99.5%的把握认为单晶的晶圆的制作效果与使用西门子制程这一工艺技术有关. (2)设X 表示成为一个合格的多晶的晶圆还需要消耗的费用,则X 的可能取值为:0,10,20,30,40,50,60,70.()32324034108P X ⎛⎫==⨯=⎪⎝⎭()32181034108P X ⎛⎫==⨯=⎪⎝⎭ ()2131233620334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()2131211230334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()2231231840334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭()223121650334108P X C ⎛⎫==⨯⨯⨯=⎪⎝⎭ ()31336034108P X ⎛⎫==⨯=⎪⎝⎭ ()31117034108P X ⎛⎫==⨯=⎪⎝⎭ 所以X 分布列为:故()24836121863101020304050607022.5108108108108108108108108E X =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=,故平均还需要耗费22.5元.【点睛】本题考查独立检验的应用,考查离散型随机变量的分布列和数学期望的求法,考查离散型随机变量的分布列、数学期望等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.21.已知函数()2(0)f x a lnx ax a =+->. (1)求()f x 的最大值()a ϕ;(2)若()0f x ≤恒成立,求a 的值;(3)在(2)的条件下,设[]()()x f x ax g x x a+=-在(,)a +∞上的最小值为,m 求证:11()10f m -<<-.【答案】(1)()22ln 2ln2(0)a a a a ϕ=--+>;(2)2;(3)证明见解析. 【解析】 【分析】 (1)()2'(0)axf x a x-=>,判断函数的单调性即可求解最大值;(2)要使()0f x ≤成立必须()22ln 2ln20a a a ϕ=--+≤,()2'a a aϕ-=,判断单调性求解()()min 20a ϕϕ==即可得解2a =;(3)()22ln 2x x xg x x +=-,得()()()222ln 4'2x x g x x --=-,令()2ln 4u x x x =--判断其单调性进而求得()()20000000min0022ln 2=22x x x x x g x g x x x x +-===--,得0m x =,再求()0f x 的范围进而得证【详解】(1)()2'(0)axf x a x-=>, 由()'0f x >得20x a <<;()'0f x <得2x a >;所以()f x 在20,a ⎛⎫⎪⎝⎭上单调递增,在2,a ⎛⎫+∞ ⎪⎝⎭上单调递减.故()max222ln 2ln2f x f a a a ⎛⎫==--+ ⎪⎝⎭,即()22ln 2ln2(0)a a a a ϕ=--+>;(2)要使()0f x ≤成立必须()22ln 2ln20a a a ϕ=--+≤.因为()2'a a aϕ-=,所以当02a <<时,()'0a ϕ<;当2a >时,()'0a ϕ>.所以()a ϕ在()0,2上单调递减,在()2,+∞上单调递增.又()()min 20a ϕϕ==,所以满足条件的a 只有2,即2a =.(3)由(2)知()22ln 2x x x g x x +=-,所以()()()222ln 4'2x x g x x --=-. 令()2ln 4u x x x =--,则()2'0x u x x-=>,()u x 是()2,+∞上的增函数;又()()80,90u u ,所以存在()08,9x ∈满足()00u x =,即002ln 4x x =-,且当()02,x x ∈时,()()0,'0u x g x <<; 当()0,x x ∈+∞,()()0,'0u x g x >>所以()g x 在()02,x 上单调递减;在()0,x +∞上单调递增.所以()()20000000min0022ln 2=22x x x x x g x g x x x x +-===--,即0m x =.所以()()000022ln 2=21110f m f x x x x ==+---∈--(,),即()1110f m -<<-.【点睛】本题考查了利用导数研究函数的单调性及最值,考查了零点存在定理和数学转化思想,在(3)的证明过程中,利用零点存在定理转化是难点属中档题.请考生从第22、23题中任选一题作答. 选修4-4:坐标系与参数方程22.已知极坐标系的极点在直角坐标系的原点处,极轴与x 轴正半轴重合,直线l 的参数方程为:2cos sin x t y t αα=+⎧⎨=⎩(t 为参数,[0,)απ∈),曲线C 的极坐标方程为:4sin ρθ=.(1)写出曲线C 的直角坐标方程;(2)设直线l 与曲线C 相交于,P Q 两点,直线l 过定点M ,若MP MQ +=求直线l 的斜率.【答案】(1)22(2)4x y +-=;(2)1-. 【解析】 【分析】(1)由4sin ρθ=,得24sin ρρθ=,由此能求出曲线C 的直角坐标方程;(2)把2cos sin x t y t αα=+⎧⎨=⎩代入()2224x y +-=,整理得()24cos sin 40t t αα+-+=,由1212MP MQ t t t t +=+=+,得34πα=,能求出直线l 的斜率. 【详解】(1)曲线C 的极坐标方程为4sin ρθ=,所以24sin ρρθ=.即224x y y +=,即()2224x y +-=.(2)把直线l 的参数方程带入()2224x y +-=得()24cos sin 40t t αα+-+=设此方程两根为12,t t ,易知()2,0M ,而定点M 在圆C 外,所以1212MP MQ t t t t +=+=+,4cos sin αα∴-=cos sin αα∴-=[0,)απ∈,可得34πα=, ∴1k =-,所以直线l 的斜率为-1.【点睛】本题考查曲线的直角坐标方程的求法,考查直线的斜率的求法,考查极坐标方程、直角坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.选修4-5:不等式选讲23.已知()1f x x x m =+++,()232g x x x =++.(1)若0m >且()f x 的最小值为1,求m 的值; (2)不等式()3f x ≤解集为A ,不等式()0g x ≤的解集为B ,B A ⊆,求m 的取值范围.【答案】(1)2m =;(2)04m ≤≤ 【解析】试题分析:(1)利用绝对值三角不等式可得()11f x m ≥-=,解出方程即可;(2)易得[]2,1B =--,()3f x ≤即4x m x +≤+,即42m x +≥-且4m ≤,再根据B A ⊆列出不等式即可得结果.试题解析:(1)()()()111f x x x m x x m m =+++≥+-+=-(当1x =-时,等号成立) ∵()f x 的最小值为 1,∴11m -=,∴2m = 或0m =,又0m >,∴2m =. (2)由()0g x ≤得,[]2,1B =--,∵B A ⊆, ∴(),3x B f x ∀∈≤,即()13x x m -+++≤44442m x m x x x m x x +⇔+≤+⇔--≤+≤+⇔≥-且4m ≤ 422m +⇔-≤-且404m m ≤⇔≤≤.。
