离散数学 第11讲 布尔代数
离散数学中的布尔函数和布尔代数

离散数学是一门研究离散结构和离散对象的数学学科,它在计算机科学等领域扮演着重要的角色。
布尔函数和布尔代数是离散数学中的重要概念之一,它们在逻辑电路设计、计算机编程等方面具有广泛的应用。
布尔函数是一种将布尔域上的值映射为布尔域上的值的函数。
布尔域上的值只有两个:真和假。
布尔函数的输入和输出都是布尔值。
布尔函数可以通过真值表、函数表达式或者逻辑电路图表示。
常见的布尔运算有与运算、或运算、非运算等。
布尔函数可以定义在不同的布尔变量上,而布尔变量可以取真或假两个值。
通过组合不同的布尔运算,可以构造出复杂的布尔函数。
布尔代数是研究布尔函数性质和运算规则的代数系统。
布尔代数的基本操作有与运算、或运算、非运算等。
与运算、或运算和非运算是布尔函数的基本运算,在布尔代数中具有特殊的性质。
例如,与运算满足交换律、结合律和分配律;或运算满足交换律、结合律和分配律;非运算满足德摩根定律。
布尔代数还有很多其他的运算规则,如吸收律、零元律、幂等律等。
这些运算规则可以用来简化布尔函数,使其更加简洁明了。
布尔函数和布尔代数在逻辑电路设计中起着重要的作用。
逻辑电路是一种基础的电子电路,用来完成逻辑运算。
布尔函数可以用来描述逻辑电路的功能,布尔代数可以用来简化逻辑电路。
通过布尔函数和布尔代数可以设计出各种复杂的逻辑电路,如逻辑门、多路选择器、时序电路等。
逻辑电路在计算机硬件中广泛应用,是计算机工作的基础。
因此,研究布尔函数和布尔代数不仅有助于理解离散数学的基本概念,也对计算机科学和工程领域有着重要的实际意义。
此外,布尔函数和布尔代数在计算机编程中也具有重要的应用。
计算机程序是一系列指令的集合,通过执行这些指令实现特定的功能。
布尔函数可以用来描述程序中的条件和逻辑关系,判断某个条件是否成立,从而确定程序的执行路径。
布尔代数可以用来简化程序的逻辑表达式,使程序更加高效和可读。
在编程语言中,布尔变量和布尔运算是基础数据类型和基本运算符之一,它们与布尔函数和布尔代数密切相关。
离散数学中的代数系统和布尔代数

离散数学是数学的一个重要分支,研究的是离散结构和离散对象的性质。
代数系统和布尔代数是离散数学中的两个重要概念。
代数系统是研究集合上的运算的一种数学结构。
它由集合和一组运算所组成,其中运算可以是两个对象相互运算得到一个新的对象,也可以是一个对象自身经过某种运算得到一个新的对象。
代数系统包括了很多种类,例如群、环、域等等。
其中,布尔代数是代数系统的一种重要类型。
布尔代数是一种二元代数系统,它研究的是关于真值和逻辑运算的代数。
在布尔代数中,我们考虑的对象是命题,而运算包括了与、或、非等等。
布尔代数主要用于逻辑运算和电路设计中。
布尔代数中的命题可以用真和假来表示,它们分别对应于数学中的1和0。
与、或、非等运算在布尔代数中也有对应的符号,分别是∧、∨、¬。
这些符号在逻辑运算中扮演重要角色。
布尔代数的运算有很多有趣的性质。
比如,与运算满足交换律、结合律、分配律等等;或运算满足交换律、结合律、分配律等等;非运算满足逆运算和恒等律。
这些性质使得布尔代数具有很强的推理和运算能力。
布尔代数在逻辑运算中有着广泛的应用。
在计算机科学中,布尔代数被用于电路设计和逻辑推理;在人工智能领域,布尔代数被用于知识表示和推理;在运筹学中,布尔代数被用于约束求解和优化问题。
布尔代数的应用广泛而深入,是离散数学中的重要工具之一。
总结起来,离散数学中的代数系统和布尔代数是两个重要的概念。
代数系统研究的是集合上的运算,而布尔代数研究的是关于真值和逻辑运算的代数。
布尔代数具有许多有趣的性质和广泛的应用,是离散数学中的一个重要工具。
布尔代数的基本公式和定律

布尔代数的基本公式和定律布尔代数是数学中的一个重要概念,在计算机科学、电子工程等领域都有着广泛的应用。
对于咱们从小学到高中的学习来说,虽然不会深入到特别复杂的层面,但了解其基本公式和定律,对于培养逻辑思维可是大有益处的。
先来说说布尔代数中的基本公式。
就比如说,A + 0 = A ,这就好像你兜里已经有了一些糖果 A ,别人再给你 0 颗糖,你兜里还是只有原来的那些糖果 A 。
再比如,A · 1 = A ,这就好比你有一个书包 A ,里面装满了书,然后你又把一整个图书馆的书(1)都装进去,可实际上书包还是只能装下原来的那些书 A 。
还有 A + 1 = 1 ,想象一下,你正在参加一个比赛,已经有了自己的一些分数 A ,然后比赛规则说,不管你之前多少分,只要你完成了某个超级难的任务就能直接得到满分 1 ,那最终你的成绩就是满分 1 啦。
布尔代数的定律也很有趣。
交换律,A + B = B + A ,这就好像你和朋友交换礼物,不管谁先给谁,结果都是一样的,都完成了礼物的交换。
结合律,(A + B) + C = A + (B + C) ,就像你们三个人排队,不管是你先和第二个排好,再一起和第三个排,还是第二个和第三个先排好,你再加入,最终的队伍顺序都是一样的。
我还记得之前给学生们讲布尔代数的时候,有个小同学一脸迷糊地问我:“老师,这布尔代数到底有啥用啊?”我笑着回答他:“就像你搭积木,每一块积木都有自己的位置和作用,布尔代数就是帮你找到这些位置和作用的工具呀。
”他似懂非懂地点点头,然后在接下来的练习中,努力地去理解和运用这些公式和定律。
分配律,A · (B + C) = A · B + A · C ,这就好像你有一堆水果,一部分是苹果(B ),一部分是香蕉(C ),然后你要把它们分别装在几个盒子(A )里,不管是先把水果混合再分装,还是先分开再分别装,最终装在盒子里的水果数量都是一样的。
离散数学中的布尔代数与逻辑电路

离散数学是一门研究离散对象及其性质与关系的数学学科。
而在离散数学中,布尔代数与逻辑电路是其中的重要部分。
布尔代数是一种关于逻辑和关系的代数体系,而逻辑电路则是利用布尔代数运算实现各种逻辑运算的电路。
布尔代数作为一种逻辑代数,旨在研究命题之间的逻辑关系。
其中最基本的运算包括与运算、或运算和非运算。
与运算表示的是两个命题在同一时间都为真的情况;或运算表示的是两个命题至少一个为真的情况;非运算表示的是对一个命题取反。
此外,布尔代数还有其他一些常见的运算符,比如异或运算、析取运算以及蕴含运算等。
逻辑电路是应用布尔代数于电子技术中的一种实现方式。
逻辑电路通过不同的布尔运算实现各种逻辑操作,如与门、或门、非门、异或门等。
与门用于实现与运算,只有当所有输入都为真时,输出才为真;或门用于实现或运算,只要有一个输入为真,输出就为真;非门用于实现非运算,对输入取反得到输出。
而异或门则表示的是两个输入不同时为真的情况下输出为真。
逻辑电路在计算机科学和电子工程中起到了至关重要的作用。
无论是计算机控制器还是数字电路,都离不开逻辑电路的应用。
逻辑电路通过布尔代数的运算实现各种逻辑功能,将电子元件之间的关系转化为人们可以理解的逻辑操作。
通过逻辑电路的设计和实现,可以对电子信号进行加工处理,从而实现各种复杂的功能。
在现实生活中,布尔代数和逻辑电路的应用无处不在。
无论是家庭电器、车载电子设备还是航空航天技术,都需要利用布尔代数和逻辑电路来实现各种控制和运算。
例如,家庭中的电视机、洗衣机、空调等都需要通过逻辑电路实现各种操作控制。
汽车上的引擎控制单元、车载导航仪等也都需要逻辑电路的支持。
而在航空航天领域,逻辑电路更是发挥着至关重要的作用,可以实现航空器的导航、通信、控制等功能。
总之,离散数学中的布尔代数与逻辑电路是一对密不可分的概念。
布尔代数为逻辑运算提供了严密的理论基础,而逻辑电路则是将布尔代数应用于实际电子技术中的一种实现方式。
离散数学格与布尔代数

§7.1 格
例 < P(S) , >是格 表示为<P(S), , * > 又可表示为< P(S) ,∪,∩>
例 <Z+,≤>,或 <Z+,|> <Z+, , * > <Z+, LCM,GCD>
§7.2 格——代数系统
格〈L,≤〉中自然存在两个运算 和 * ,从而 派生出一个代数系统〈L,,*〉
6
<S15,|>,
2
2019/10/5
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/5
§7.1 格
例 设Z+为正整数集合,对于a,b Z+,关系“≤”定义为: a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格,
并、交 运算的性质
定理1 设〈L,≤〉是一个格,并运算与交运算 * 满足 如下性质:
L1 a a = a
a*a=a
(幂等律)
L2 a b = b a a * b = b * a (交换律)
L3 (a b) c = a (b c)
离散数学-格和布尔代数

的次序图如下
-1 的次序图如下
6 2 1 3 2
1 3 6
若 < L; > 是一个偏序集,则对于任意元素 l1, l2, l3 L,有以 下六个关系式成立: l1 l1 若 l1 l2,l2 l1,则 l1 = l2 若 l1 l2,l2 l3,则 l1 l3 l1 l1 若 l1 l2,l2 l1,则 l1 = l2 (7-1) (7-2) (7-3) (7-1) (7-2)
60以上说明与格一样布尔代数也是一个代数系统该代数系统可取交换律分配律同一律和互补律作为公二元运算是一元运算若这些运算满足交换律分配律同一律和互补律则称称作集合代数它是一个布尔代数
第二部分 抽象代数
0
第七章
格和布尔代数
格是 Birkhoff (1884 - 1944) 在 20 世纪 30 年代提出的,格的提出 以子集为背景。 历史上最初出现的格是英国数学家 George Boole 于 1854 年提出 的,是他在研究命题演算中发现的,通常称为布尔格或布尔代 数。 格和布尔代数的理论成为计算机硬件设计和通讯系统设计中的 重要工具。格论是计算机语言的指称语义的理论基础。格是一 种特殊的偏序集,也可以看作是有两个二元运算的代数系统, 布尔代数是一种特殊的格。在保密学、开关理论、计算机理论 和逻辑设计以及其他一些科学和工程领域中,都直接应用了格 与布尔代数。 1
7.2 格及其性质
一、格的定义
定义7-5 设 < L; > 是一个偏序集,如果 L 中任意两个元素都 存在着最大下界和最小上界,则称 < L; > 是格。 由于每对元素的最大下界和最小上界唯一,故引入记号: l1 l2 = glb(l1, l2),l1 l2 = lub(l1, l2), 其中 和 均可看作是集合 L 上的二元运算,分别称为交和并。 注:若 < L; > 是一个格,则意味着 < L; > 也是一个形为 < L; , > 的代数系统,其中 和 是 L 上的两个二元运算, 对于任意 l1, l2 L,l1 l2 表示在偏序 “ ” 意义下,l1 和 l2 的最小上界,l1 l2 表示 l1 和 l2 的最大下界。
离散数学布尔代数

一个非零元素b,至少存在一个原子a,使得a ≤ b。 1
证明:若b本身就是一个原子,则b ≤ b,得证。c
df
若b不是原子,肯定存在b1,使得0 ≤ b1 ≤ b, a
be
若b1是原子,则定理得证;
0
否则,若b1不是原子,则必存在b2,使得0 ≤ b2 ≤ b1 ≤ b
∵<A, ≤>是一个有全下界的有限格,
定理1:对于布尔代数中任意两个元素 a, b,必定有
(1) ( a ) = a, (2) a∨b = a∧b , (3) a∧b = a∨b
3
❖ 布尔代数
定义3:设<A,∨1,∧1, - > 和<B,∨2,∧2, ~ >是两个布尔代数, 如果存在A到B的双射 f,对于a,bA,有
f (a∨1b) = f (a) ∨2 f (b)
2、对a,bA,有 f (a∧b) = f (a)∩f (b)
9
❖ 格与布尔代数
定理3 ( Stone表示定理 ) :
设<A,∨,∧, - >是由有限布尔格<A, ≤>所诱导的一个有 限布尔代数,S是布尔格<A, ≤>中的所有原子的集合,则 < A,∨,∧, - >< P(S),∪,∩, ~ >同构。 分析:要证两个代数系统同构,分为以下几步:
1、找一个双射函数 f: A P(S)
∴a ≤ c ,又∵a ≤ c, ∴a ≤ c ∧ c,即 a ≤ 0,
这与a是原子相矛盾, ∴假设错
∴b ∧ c = 0,由引理1得: b≤c ∴b=c,即:b= a1∨a2∨... ∨ak
7
❖ 格与布尔代数
证明(2):设b的另一种表示形式为 b = aj1∨aj2∨... ∨ajt 其中aj1,aj2,……,ajt是A中原子。∵b是 aj1,aj2,……,ajt 的最小上界, ∴有aj1≤b, aj2≤b,…,ajt≤b,而a1,a2,……,ak是A中满足 a j ≤b的所有原子, {aj1,aj2,…,ajt}是{a1,a2,…,ak}的子集,即 |{aj1,aj2,…,ajt}|<=|{a1,a2,…,ak}|, 即:t ≤ k。(下面证 t < k 是不可能的)
布尔代数基础

布尔代数基础和布尔函数的化简和实现布尔代数是分析和设计数字逻辑电路的数学工具。
因此这里从应用的角度向读者介绍布尔代数,而不是从数学的角度去研究布尔代数。
一、布尔代数的基本概念1、布尔代数的定义域和值域都只有“0”和“1”。
布尔代数的运算只有三种就是“或”(用+表示),“与”(用·表示)和“非”(用 ̄表示,以后用’表示)。
因此布尔代数是封闭的代数系统,可记为B=(k,+,·, ̄,0,1),其中k表示变量的集合。
2、布尔函数有三种表示方法。
其一是布尔表达式,用布尔变量和“或”、“与”和“非”三种运算符所构成的式子。
其二是用真值表,输入变量的所有可能取值组合及其对应的输出函数值所构成的表格。
其三是卡诺图,由表示逻辑变量所有可能取值组合的小方格所构成的图形。
3、布尔函数的相等可以有两种证明方法,一种是从布尔表达式经过演绎和归纳来证明。
另一种就是通过列出真值表来证明,如两个函数的真值表相同,则两个函数就相等。
二、布尔代数的公式、定理和规则1、基本公式有交换律、结合律、分配律、0—1律、互补律、重叠律、吸收律、对合律和德·摩根律。
值得注意的是分配律有两个是:A·(B+C)=A·B+A·C和A+B·C=(A+B)·(A+C),另外就是吸收律,A+AB=A;A+A’B=A+B它们是代数法化简的基本公式。
2、布尔代数的主要定理是展开定理(教材中称为附加公式)。
3、布尔代数的重要规则有对偶规则和反演规则。
三、基本逻辑电路1、与门F=A·B2、或门F=A+B3、非门F=A’(为了打字的方便,以后用单引号“’”表示非运算,不再用上划线表示非运算)4、与非门F=(A·B)’5、或非门F=(A+B)’6、与或非门F=(A·B+C·D)’7、异或门F=A’B+AB’=A⊕B8、同或门F=A’B’+AB=A⊙B四、布尔函数的公式法化简同一个布尔函数可以有许多种布尔表达式来表示它,一个布尔表达式就相应于一种逻辑电路。
离散数学中的布尔代数知识点介绍

离散数学中的布尔代数知识点介绍离散数学是计算机科学和数学中的一个重要分支,而布尔代数则是离散数学中的一个基础概念。
布尔代数是一种逻辑推理和计算的数学体系,其基本概念和运算规则直接应用于计算机计算和逻辑设计中。
一、布尔代数的基本概念布尔代数有两个基本元素:命题和逻辑操作符。
命题是关于真(True)和假(False)的陈述,可以用字母或其他符号表示。
逻辑操作符包括与(AND)、或(OR)、非(NOT)三种基本运算符,用于对命题进行逻辑运算。
二、布尔代数的基本运算规则1. 与运算(AND):只有当两个命题都为真时,与运算的结果才为真。
用符号“∧”表示,例如命题A∧B表示“命题A和命题B都为真”。
2. 或运算(OR):只要两个命题中有一个为真,或运算的结果就为真。
用符号“∨”表示,例如命题A∨B表示“命题A或命题B为真”。
3. 非运算(NOT):将命题的真值取反,即将真变为假,将假变为真。
用符号“¬”表示,例如¬A表示“命题A的取反”。
三、布尔代数的重要性布尔代数在计算机科学和逻辑设计中具有重要的应用。
布尔代数提供了一种形式化的工具,可以对逻辑关系和计算过程进行精确的描述和处理。
利用布尔代数的运算规则,可以进行逻辑推理、逻辑运算和逻辑设计。
布尔代数为计算机的基本运算提供了理论基础,是计算机科学不可或缺的一部分。
四、布尔代数的应用领域1. 逻辑电路设计:布尔代数的基本运算规则可以用于逻辑门电路的设计与分析。
逻辑门电路由与门、或门、非门等基本门电路组成,通过布尔代数的运算规则可以进行电路的优化和逻辑设计。
2. 程序设计与算法分析:布尔代数在程序设计和算法分析中具有重要地位。
利用布尔代数的运算规则,可以对程序的逻辑关系进行抽象和分析,确保程序的正确性和可靠性。
3. 数据库查询与管理:布尔代数可用于数据库查询和管理中的条件表达式构建。
通过布尔代数的运算规则,可以对数据库数据进行选择、过滤和计算,实现对数据的高效管理与查询。
离散数学中的布尔代数与逻辑运算

离散数学是数学中的一个分支,主要研究离散、离散结构及其性质。
其中,布尔代数和逻辑运算是离散数学中的重要内容。
布尔代数是离散数学中的一个分支,它是建立在两个元素的集合上的一种数学结构。
布尔代数的基本元素是0和1,分别表示假和真。
在布尔代数中,有四种基本运算:与(AND)、或(OR)、非(NOT)和异或(XOR)。
这些运算在逻辑中起着至关重要的作用。
布尔代数可以应用于计算机科学、电路分析和逻辑推理等领域。
逻辑运算是根据一定的规则对命题进行运算的过程。
逻辑运算包括命题的合取(AND)、析取(OR)、否定(NOT)和条件(IF-THEN)等。
布尔代数是逻辑运算的数学基础,在逻辑运算中起着重要的作用。
通过布尔代数的运算规则,可以对逻辑表达式进行简化,并得出正确的逻辑推理结果。
布尔代数和逻辑运算在计算机科学中有广泛的应用。
在计算机中,所有的数据都是以二进制形式存储和运算的。
布尔代数的基本元素0和1对应于计算机中的假和真。
通过布尔代数的运算规则,可以实现复杂的逻辑运算,如逻辑与、逻辑或、逻辑非等。
这些逻辑运算在编程中经常使用,可以实现条件判断、循环控制等逻辑功能。
布尔代数的运算规则也被应用于逻辑电路的设计和分析,如与门、或门和非门等。
此外,布尔代数和逻辑运算还广泛应用于电路分析和数字电子技术中。
在电路分析中,逻辑门是一个重要的电路元件,用于实现布尔运算。
通过逻辑门的组合,可以实现不同逻辑函数的实现。
逻辑门通过电平的输入和输出来进行逻辑运算,具有高可靠性和稳定性。
逻辑门的组合可以实现各种电路和系统的设计和实现,如计算机的中央处理器、存储器和输入输出接口等。
总而言之,离散数学中的布尔代数和逻辑运算在计算机科学、电路分析和逻辑推理等领域起着重要的作用。
通过对布尔代数和逻辑运算的理解和应用,可以优化电路设计、简化逻辑运算和提高计算机编程的效率。
布尔代数和逻辑运算是离散数学中的重要内容,深入研究和应用布尔代数和逻辑运算对于理解计算机科学和电子技术具有重要意义。
离散数学-格与布尔代数1PPT课件
证明:如果a≤b,又b≤b∨d, 由传递性得a≤b∨d,
类似由c≤d, d≤b∨d,由传递性得c≤b∨d,
这说明b∨d是a,c的一个上界
而a∨c是a,c的最小上界
所以 a∨c≤b∨d。
类似可证 a∧c≤b∧d。
推论:在一个格中,任何 a,b,c∈A,如果b≤c,则
a∨b≤a∨c,a∧b≤a∧c。
此性质称为格的保序性。
∴ (a∨b)∨c ≤a∨(b∨c)
⑵同理可证 a∨(b∨c)≤(a∨b)∨c
最后由反对称性得 (a∨b)∨c = a∨(b∨c)
类似可证 (a∧b)∧c =a∧(b∧c) 。
2021/3/12
8
6. ∨和∧都满足吸收律。即 a∨( a∧b) =a, a∧(a∨b) =a。
证明:⑴显然有 a≤a∨( a∧b) ⑵再证 a∨( a∧b) ≤a
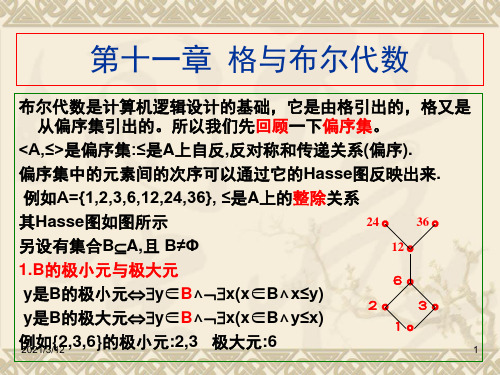
24。 36。 12。 6。
2。 3。 1。
y是B的下界y∈A∧x(x∈By≤x)
y是B的上界y∈A∧x(x∈Bx≤y)
{2,3,6}的下界:1 上界: 6,12,24,36
4.B的最大下界(下确界)与最小上界(上确界)
y是B的最大下界(下确界):B的所有下界x,有x≤y。
y是B的最小上界(上确界):B的所有上界x,有y≤x。
∵ a≤ a a∧b ≤a ∴ a∨( a∧b) ≤a 最后由反对称得 a∨( a∧b) =a, 类似可证 a∧(a∨b) =a。
2021/3/12
9
7. ∨和∧不满足分配律。但有分配不等式:
<B,≤><C,≤>
。 12 6。
6。 2。 3。
2。
1。
10。 3。
1。
离散数学格与布尔代数ppt课件

精选ppt
14
定理11.2
(3) 证明<S,≤>构成格。 即证明a∨b=ab,a∧b=a*b 。
a,b∈S 有 a(ab)=(aa)b=ab
说明 通过规定运算及其基本性质可以给出格的定义。
精选ppt
12
定理11.2
(1)证明在S中*和运算都适合幂等律。 a∈S,由吸收律得 a*a = a*(a(a*a)) = a
同理有 aa=a。
(2)在S上定义二元关系R, a,b∈S 有 <a,b>∈R ab=b
下面证明R在S上的偏序。
根据幂等律, a∈S都有aa=a,即<a,a>∈R,
6
例11.3
例11.3 设G是群,L(G)是G的所有子群的集合。即 L(G)={ H|H≤G }
对任意的H1,H2∈L(G),H1∩H2也是G的子群,而<H1∪H2>是由 H1∪H2生成的子群(即包含着H1∪H2的最小的子群)。 在L(G)上定义包含关系,则L(G)关于包含关系构成一个格, 称为G的子群格。 易见在L(G)中,H1∧H2就是H1∩H2,H1∨H2就是<H1∪H2>。
(1)交换律 a,b∈L 有
a∨b=b∨a
a∧b=b∧a
(2)结合律 a,b,c∈L 有
(a∨b)∨c=a∨(b∨c) (a∧b)∧c=a∧(b∧c)
(3)幂等律 a∈L 有
a∨a=a
a∧a=a
(4)吸收律 a,b∈L 有
a∨(a∧b)=a
a∧(a∨b)=a
精选ppt
9
定理11.1
(1)a∨b和b∨a分别是{a,b}和{b,a}的最小上界。 由于{a,b}={b,a},所以a∨b=b∨a。 由对偶原理,a∧b=b∧a得证。
布尔代数的基本公式

布尔代数的基本公式
哎呀,说起布尔代数,这玩意儿听起来就像是数学书里那些让人头疼的公式,但你知道吗?其实它就像是我们生活中的小玩意儿,挺有趣的。
记得有一回,我在超市里挑东西,就遇到了一个布尔代数的“现实版”。
我站在一排排的饮料架前,脑子里突然冒出个问题:如果我想买一瓶不含糖的果汁,那我应该拿哪一种呢?这就像是布尔代数里的一个基本公式,比如 A 代表“果汁”,B 代表“不含糖”,那么我要找的就是 A 且非B 的饮料。
我扫了一眼货架,有的果汁是“含糖”的,有的果汁是“不含糖”的,还有的果汁是“含糖”和“不含糖”都有的。
这就像是布尔代数里的“或”和“与”运算。
我得找到那个“不含糖”的果汁,也就是A 且非B 的饮料。
我仔细地看了看标签,有的果汁写着“无糖”,有的写着“低糖”,还有的写着“全糖”。
我得找到那个“无糖”的,也就是 A 且非B 的果汁。
我就像侦探一样,一个一个地检查,最后终于找到了一瓶写着“无糖”的果汁。
我拿起那瓶果汁,心里想,这不就是布尔代数的现实应用吗?我得找到那个既满足“果汁”又满足“不含糖”的饮料,这不就是 A 且非B 吗?
所以,你看,布尔代数其实并不是那么遥远和枯燥,它就在我们身边,只是我们可能没有意识到。
就像我挑果汁的时候,其实就用了布尔代数的基本公式。
最后,我拿着那瓶无糖果汁,心里美滋滋的,因为我不仅找到了我想要的东西,还意外地复习了一下数学知识。
这大概就是生活中的小确幸吧,不是吗?
所以,下次当你在超市里挑东西的时候,不妨也试试用布尔代数的公式来思考问题,说不定会有意想不到的乐趣哦!。
离散数学布尔代数与逻辑

离散数学布尔代数与逻辑离散数学是数学的一个分支,研究离散的、离散的结构和离散的现象。
而布尔代数是离散数学的重要组成部分,是代数学中关于二元关系的理论。
同时,与布尔代数密切相关的是逻辑学,研究命题的真值、论证的正确性以及推理的方法。
一、布尔代数基础布尔代数是一种逻辑代数,它使用逻辑运算符号和变量,描述和分析命题逻辑关系。
在布尔代数中,变量只有两个取值,即真(用1表示)和假(用0表示)。
布尔代数的基本运算包括逻辑与、逻辑或和逻辑非。
逻辑与表示当且仅当两个变量都为真时,结果为真;逻辑或表示当至少有一个变量为真时,结果为真;逻辑非表示当某个变量为真时,结果为假,反之亦然。
在布尔代数中,可以使用真值表来描述和分析布尔函数的取值情况。
布尔函数是指由布尔代数运算符组成的表达式,它接受一个或多个输入变量,并产生一个输出变量。
布尔函数在逻辑电路设计、计算机科学、编程等领域中有广泛的应用。
通过真值表分析布尔函数的取值规律,可以优化逻辑电路的设计和布尔函数的运算。
二、逻辑学与命题逻辑逻辑学是研究推理和论证的科学,其中命题逻辑是逻辑学的一个重要分支。
命题逻辑的基本概念是命题,它是陈述句,可以被判断为真或假。
命题逻辑使用逻辑连接词和命题变量来组成复合命题,并通过逻辑运算符来描述复合命题之间的关系。
逻辑连接词包括逻辑与、逻辑或、逻辑非、蕴涵和等价。
逻辑与表示两个命题同时为真时,复合命题为真;逻辑或表示两个命题至少有一个为真时,复合命题为真;逻辑非表示命题的否定,即真变为假,假变为真;蕴涵表示如果第一个命题为真,则第二个命题为真,否则为假;等价表示两个命题具有相同的真值。
逻辑学通过推理规则和推理方法来分析和判断复合命题的真假。
其中包括代入规则、假言推理、拒取否定、双重否定等推理规则。
通过应用这些推理规则,可以推导出逻辑上正确的结论,并解决实际问题中的逻辑推理和决策问题。
三、离散数学中的应用离散数学是计算机科学和信息技术的基础学科,广泛应用于计算机算法、数据结构、数据库、图论等领域。
布尔代数

任何有限布尔代数的基数为2n, n是自然数。
设B是有限代数系统,A是B中所有原子的集合。 则:B≅P(A), ∴|B|=|P(A)|=2|A|
等势的布尔代数系统均同构
设B1和B2是有限布尔代数,且|B1|=|B2|;A1,A2分别是相应 的原子的集合。由同构关系的传递性,只需证明: P(A1)≅P(A2)。
则称ϕ是B1到B2的同态映射。(若ϕ是双射,则是同构)
其实,上述3个等式不是独立的。
(2)+(3)⇒(1): ϕ(a∨b)=ϕ(((a∨b)')')= -ϕ((a∨b)')= -ϕ(a'∧ b')= -(ϕ(a')⋂ϕ(b'))= -(-ϕ(a)⋂-ϕ(b))=ϕ(a)⋃ϕ(b) 同理:(1)+(3)⇒(2)
有限布尔代数的表示定理的证明
ϕ: B → P(A), ∀x∈B, ϕ(x)=T(x)是同态映射。
ϕ(x∧y) = T(x∧y) = {b|b∈A, b≼x∧y} = {b|(b∈A, b≼x)且 (b∈A, b≼y)} = {b|b∈A,b≼x}⋂{b|b∈A,b≼y} = T(x)⋂T(y) = ϕ(x)⋂ϕ(y) 令x=a1 ∨ a2 ∨ … ∨ an , y=b1 ∨ b2 ∨ … ∨ bm 。 则x ∨ y= a1 ∨ … ∨ an ∨ b1 ∨ … ∨ bm , 显然:ϕ(x∨y) = T(x∨y) = T(x)⋃T(y) = ϕ(x) ⋃ ϕ(y) 设x'是x在B中的补元。注意: ϕ(x)⋃ϕ(x')=ϕ(x ∨ x')=ϕ(1)=A 且 ϕ(x)⋂ϕ(x')=ϕ(x ∧ x')=ϕ(0)=∅ ∴ϕ(x') = ∼ϕ(x)
离散数学中的布尔代数应用

离散数学中的布尔代数应用离散数学是数学中的一个分支,它研究离散化的对象和运算符,并不依赖于连续性或可测度性的概念。
而布尔代数是离散数学中的重要内容之一,它是以数学逻辑为基础,研究由命题变量和逻辑运算符组成的代数系统。
布尔代数在离散数学中扮演着重要的角色,并在现实生活中有广泛的应用。
一、基础概念布尔代数以数学逻辑为基础,由命题变量和逻辑运算符构成。
命题变量可以取两个值:真或假,用1或0表示。
逻辑运算符包括非(NOT)、与(AND)、或(OR)等几种基本运算。
以布尔代数的符号形式表示,可以用符号表达式来表示命题逻辑。
符号表达式由命题变量、基本命题和逻辑运算符组成。
通过运算符的组合,可以得到复合命题。
在离散数学中,布尔代数的应用广泛,如在电路设计、计算机科学、人工智能等领域都有重要的应用。
二、应用领域1. 电路设计在电路设计中,布尔代数被广泛应用于逻辑电路的设计和分析。
逻辑门是电子电路中最基本的构建单元,通过不同的逻辑门的组合可以实现各种逻辑功能。
逻辑门可以表示为布尔代数中的逻辑运算符,通过对输入信号进行逻辑运算,得到输出信号。
例如,与门(AND gate)可以实现两个输入信号的与运算,输出为1当且仅当两个输入信号都为1;或门(OR gate)可以实现两个输入信号的或运算,输出为1当且仅当至少一个输入信号为1。
通过对逻辑门的组合与连接,可以实现复杂的逻辑功能,如加法器、多路选择器等。
2. 计算机科学在计算机科学中,布尔代数是计算机逻辑和数字电路设计的基础。
计算机内部的大部分操作都是通过逻辑门的组合实现的。
计算机的数据存储、运算和控制等功能都离不开布尔代数的运算。
例如,计算机的加法器可以使用逻辑门实现。
在二进制加法中,每一位的相加可以看作是两个输入信号的异或运算,而进位可以看作是两个输入信号的与运算。
通过逻辑门的组合,可以实现多位二进制数的加法。
3. 人工智能在人工智能领域,布尔代数被应用于逻辑推理和知识表示等方面。
离散数学布尔代数

离散数学布尔代数离散数学(discrete mathematics)是研究离散量的结构及其相互关系的数学学科,是现代数学的一个重要分支。
离散的含义是指不同的连接在一起的元素,主要是研究基于离散量的结构和相互间的关系,其对象一般是有限个或可数个元素。
简介离散数学在各学科领域,特别在计算机科学与技术领域有著广为的应用领域,同时离散数学也就是计算机专业的专业课程,例如程序设计语言、数据结构、操作系统、编程技术、人工智能、数据库、算法设计与分析、理论计算机科学基础等必不可少的先行课程。
通过离散数学的自学,不但可以掌控处置线性结构的叙述工具和方法,为时程课程的自学创造条件,而且可以提升抽象思维和严苛的逻辑推理能力,为将来参予创新性的研究和研发工作奠定稳固的基础。
发展随着信息时代的到来,工业革命时代以微积分为代表的已连续数学占到主流的地位已经出现了变化,离散数学的重要性逐渐被人们重新认识。
离散数学课程所传授的思想和方法,广为地彰显在计算机科学技术及有关专业的诸领域,从科学计算至信息处理,从理论计算机科学至计算机应用技术,从计算机软件至计算机硬件,从人工智能至心智系统,无不与离散数学密切相关。
由于数字电子计算机就是一个线性结构,它就可以处置线性的或线性化后了的数量关系,因此,无论计算机科学本身,还是与计算机科学及其应用领域密切相关的现代科学研究领域,都遭遇着如何对线性结构建立相应的数学模型;又如何将已用已连续数量关系创建出来的数学模型线性化,从而可以由计算机予以处置。
离散数学是传统的逻辑学,集合论(包括函数),数论基础,算法设计,组合分析,离散概率,关系理论,图论与树,抽象代数(包括代数系统,群、环、域等),布尔代数,计算模型(语言与自动机)等汇集起来的一门综合学科。
离散数学的应用遍及现代科学技术的诸多领域。
离散数学也可以说道就是计算机科学的基础核心学科,在离散数学中的存有一个知名的典型例子-四色定理又称四色悖论,这就是世界近代三小数学难题之一,它就是在年,由英国的一名绘图员弗南西斯·格思里明确提出的,他在展开地图着色时,辨认出了一个现象,“每幅地图都可以仅用四种颜色着色,并且共同边界的国家都可以被着上时相同的颜色”。
离散数学--十一章格与布尔代数

离散数学--⼗⼀章格与布尔代数格的定义与性质:布尔代数是计算机逻辑设计的基础,它是由格引出的。
格⼜是从偏序集引出的。
所以我们先回顾⼀下偏序集中的⼀些概念。
偏序集简单来说就是集合A中有⾃反,反⾃反,传递的关系具体可以看第七章我们结合Hasse图看如下关系:假如 A={1,2,3,6,12,24,36} 且有如下关系如果:B={2,3,6}最⼤|⼩元定义:y是B的最⼩元⇔∃y∈B∧∀x(x∈B→y≤x)y是B的最⼤元⇔∃y∈B∧∀x(x∈B→x≤y)最⼤|⼩元是唯⼀的(类⽐函数的最值)⽽极⼤|⼩元不唯⼀B最⼤元6 ,最⼩元⽆B中Hasse图的最底(顶)层,且这⼀层只有⼀个点才能是最⼩(⼤)元极⼤|⼩元定义:y是B的极⼩元⇔∃y∈B∧¬∃x(x∈B∧x≤y)y是B的极⼤元⇔∃y∈B∧¬∃x(x∈B∧y≤x)这⾥⾯B的极⼩元是 {2,3},极⼤元是 {6}B中Hasse图的最底(顶)层,则是极⼩(⼤)元上下界定义:y是B的下界⇔∃y∈A∧∀x(x∈B→y≤x)y是B的上界⇔∃y∈A∧∀x(x∈B→x≤y)⽐如 B上界 {12,24,36} 下界 {1}Hasse图中B的最底(顶)层,包括这⼀层和这⼀层下⾯(上⾯)的所有元素构成的集合则是下(上)界确界定义:B的上确界(最⼩上界)下确界(最⼤下界)就是上界的min,下界的max结合Hasse 图理解若B={2,3,6} 有如上图的关系格讲这么多终于到格的定义了其实只要⼀个偏序集中任意⼦集都有上下确界就是格了莫名很简洁暗⽰判断格要疯狂枚举格诱导的代数系统交并运算设<A, ≤>是格,在A上定义⼆元运算∨和∧为:∀a,b∈Aa∨b=LUB {a,b} |{a,b}的最⼩上界.Least Upper Bounda∧b=GLB {a,b} |{a,b}的最⼤下界.Greatest Lower Bound称<A,∨,∧>是由格<A,≤>诱导的代数系统. (∨-并,∧-交)就是⽤符号定义了上下确界⽽已并且有:设<L, ≼>是格则有运算∨和∧适合交换律、结合律、幂等律和吸收律<==> 设<S, ∗, ◦ >是代数系统, ∗和◦是⼆元运算, 如果∗和◦满⾜交换律、结合律和吸收律, 则<S, ∗,◦>构成格.注意⼀下吸收率就好了:a∨(a∧b) = a, a∧(a∨b) = a各种格分配格如果交并还满⾜分配率就叫分配格有界格如果B是A时仍有上下确界则此时的格为有界格,这个确界分别称为全上|下界⼀般将全上界记为1 ,全下界记为0,⼀般将有界格L记为<L,∧,∨,0,1>.有限格L={a1,a2,…,an}是有界格, 则a1∧a2∧…∧an是L的全下界, a1∨a2∨…∨an是L的全上界.0是关于∧运算的零元,∨运算的单位元;1是关于∨运算的零元,∧运算的单位元.有补格有补元的格称为有补格a∧b = 0 和 a∨b = 1成⽴, 则称b是a的补元在任何有界格中, 全下界0与全上界1互补对于⼀般元素, 可能存在补元, 也可能不存在补元. 如果存在补元, 可能是惟⼀的, 也可能是多个补元.对于有界分配格, 如果元素存在补元, ⼀定是惟⼀的⼦群格没有特别懂对⼀个群先找出它的所有⼦群⽐如Z12 <0>,<1>,<2>,<3> ,<6>就是所有⼦群|也满⾜格的定义?也是⼦格然后再画所有⼦群(⼦格)的Hasse图就⾏了布尔代数本质上就是⼀个集合如果⼀个格是有补分配格, 则称它为布尔格或布尔代数. 布尔代数标记为<B,∧,∨,′, 0, 1>, ′为求补运算这⾥⾯的 ' 的运算规律相当于 ‘否’(a' )' =a∀a,b∈B, (a∧b)′ = a′∨b′, (a∨b) ′= a′∧b′(0∧b)∨(a∧0) = 0∨0 = 0(1∨b′)∧(a′∨1) = 1∧1 = 1(a∧b)∧(a′∨b′) = (a∧b∧a′)∨(a∧b∧b′)注意⼀下:Sn代表 n的因⼦所构成的集合|别到时候不知道⽐如 s6={1,2,3,6}。
布尔代数-张艳

LOGO
4. 布尔代数的一些特殊定律
同一律: A· =A , A A+A=A 德· 摩根定律: A · · · ·= A + B + C + · · B C · · A + B + C · ·= A · · · · · B C ·
吸收律:
A+A· =A B
A · + B) = A (A
A+A· =A+B B
• 交换律: A · = B · B A
• • • A+B=B+A (A + B) + C = A + (B + C) A + (B · = (A+B) · C) (A+C)
• 结合律: (A · · = A · · B) C (B C) • 分配律: A · + C) = A · + A · (B B C
例如:求 F = A B + CD 的反函数,可根据上述规 则写成:
F = (A + B)· + D) (C
但不能写成
F=A+B· +D C
பைடு நூலகம்
LOGO
对偶法则
对于任意一个逻辑函数表达式 F,如果把 F 中所 有的“· ”换成“+”,“+”换成“· ”;“0”换成 “1”,“1”换成“0”,那么得到一个新的逻辑函 数表达式,就叫做逻辑函数 F 的对偶式,记做 F‘ 。
摩根在19世纪前半叶卷入了一场著名的争论,布尔知道摩根是对的, 于是在1848年出版了一本薄薄的小册子来为朋友辩护。这本书是他6 年后更伟大的东西的预告,它一问世,立即激起了摩根的赞扬,肯定 他开辟了新的、棘手的研究科目。布尔此时已经在研究逻辑代数,即 布尔代数。他把逻辑简化成极为容易和简单的一种代数。在这种代数 中,适当的材料上的“推理 ”,成了公式的初等运算的事情,这些 公式比过去在中学代数第二年级课程中所运用的大多数公式要简单得 多。这样,就使逻辑本身受数学的支配。为了使自己的研究工作趋于 完善,布尔在此后6年的漫长时间里,又付出了不同寻常的努力。 1854年,他发表了《思维规律》这部杰作,当时他已39岁,布尔代数 问世了,数学史上树起了一座新的里程碑。几乎像所有的新生事物一 样,布尔代数发明后没有受到人们的重视。欧洲大陆著名的数学家蔑 视地称它为没有数学意义的、哲学上稀奇古怪的东西,他们怀疑英伦 岛国的数学家能在数学上做出独特贡献。布尔在他的杰作出版后不久 就去世了。20世纪初,罗素在《数学原理》中认为,“纯数学是布尔 在一部他称之为《思维规律》的著作中发现的。”此说一出,立刻引 起世人对布尔代数的注意。今天,布尔发明的逻辑代数已经发展成为 纯数学的一个主要分支。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)描述代数系统
证明<A,∨,∧, ′,0,1 >和<(S),∪,∩, ¯, Ø, S>同构. 推论1 有限布尔格的元素个数必定等于2n,其中n是该布尔格中所有原 子的个数。 推论2 任何一个具有2n个元素的有限布尔代数都是同构的。
离散数学(二)
1
布尔代数
主要内容:
11 布尔代数两个定义 2 3
布尔同态 有限布尔代数的结构
重点和难点:
重点: 布尔代数的定义 难点: 有限布尔代数的结构
一、布尔代数两个定义
布尔代数的定义:
定义1 布尔代数:有界有补的分配格<L,∧,∨, ', 0, 1>.
定义1′ <B,*,⊕>是代数系统, *和⊕是B上的二元运算,如果对任意 的元素a,b,c∈B,满足下列4条,则称<B,*,⊕>为布尔代数:
定理1:设<B,∧,∨, ′,0,1>是布尔代数, a∈B是原子的充分必要条件 是a≠0且对B中任何元素x有
x∧a=a 或 x∧a=0
定理1的证明:
(I)
先证必要性.
设a是原子,显然a≠0. 另设x∧a≠a, 由于x∧a ≤ a, 故x∧a < a. 据原 子的定义和0 ≤ x∧a,可得x∧a=0.
(1) 交换律 a*b=b*a 和 a⊕b=b⊕a
(2) 分配律 a*(b⊕c)=(a*b)⊕(a*c)和 a⊕(b*c)=(a⊕b)*(a⊕c) (3) 全上(下)界 B中存在两个元素0和1, 对B中任意元素a,满足 a*1=a 和 a⊕0=a (4)补元存在性 对B中每一元素a都存在一元素a′,满足 a*a′=0 理4: 设<A,∨,∧, ′, 0,1>是一个有限布尔代数,若x是A中任意非零 元素, a1, a2, … ,ak是A中满足aj≤x的所有原子(j=1,2,…,k),则x =
a1∨a2∨…∨ak是将x表示为原子之并的唯一形式。
证明: 设有另一种表示形式为x= b1∨b2∨…∨bt,其中b1,b2,…,bt是原子。 因为x是b1,b2,…,bt的最小上界, 所以必有b1≤ x, b2≤ x,..., bt≤ x。而a1,
三、有限布尔代数的结构
定义4 <L, ≤>(<L,∧,∨>)是格,有全下界0, a∈L,满足 (1) a≠0; (2) 不∃b∈L使得0<b<a; 则称a为该布尔代数的一个原子。 盖住关系:设a, b是一个格中的两个元素,如果b≤a且b≠a,即b<a,并且在此 格中再没有别的元素c,使得b<c和c<a,则称元素a覆盖元素b。 定义5 设<L, ≤> 是一个格,且具有全下界0,如果有元素a盖住0,则称 元素a为原子。原子:与0相邻且比0“大” 例子(参见右图) d, e均是原子。实际上,在布尔代数中, 原子是B-{0}的极小元,因为原子与0之 间不存在其他元素。
三、有限布尔代数的结构
引理2说明: 原子是这样的元素,它把B中的元素分为两类,第一类是 与自己可比较的(包括自身),它小于等于这一类中的任一元素。第二 类是与自己不可比较的或是0,它小于等于这一类中任一元素的补元。 为了加深对原子和定理 7.4―2 的认识 , 试考察图 7.4―3,(a) 中 ,a1 是原 子; (b)中,a1和a2是原子;(c)中,a1,a2和a3是原子. 在(a),(b)(c)三图中,虚 线都是表示原子a1将B的元素划分成两类。
三、有限布尔代数的结构
第(1)部分证明: 构造函数f: A→(S), ∀aA, 当a=0时, f(0)=Ø;当a=1时, f(1)=S. 当a≠0时, f(a)= {ai|ai S∧ai ≤ a}. 令S1 = {ai|ai S∧ai ≤ a} f满射: ∀一S1∈(S) ,令S1 ={a1,a2 ,…, ak},则由于运算∨的封闭性, 所以 a1∨a2∨…∨ak = aA 这就说明对∀S1∈(S),必存在aA,使得f(a)=S1。 f单射: 证明∀ a, bA, 当a≠b时有f(a)≠f(b). 等价于证明若f(a)=f(b),则a=b. 令f(a)=f(b)= {a1,a2 ,…, ak}(S), 由f(a)= {a1,a2 ,…, ak}知 a= a1∨a2∨…∨ak 由f(b)= {a1,a2 ,…, ak}知 b= a1∨a2∨…∨ak 所以a=b.
a∧b=0。
定理2的证明: (反证法) 假如a∧b≠0, 令a∧b=c, 若a, b是原子且a∧b≠0, 则 0<c≤ a 0<c ≤ b c < a 时与a为原子相矛盾. c=a时, 结合0 < c ≤ b 得0 < a< b,与b为原子相矛盾.所以a∧b=0.
三、有限布尔代数的结构
引理1: 设<B,∨,∧, ′, 0, 1>是一有限布尔代数, 则对于B中任一非 零元素b, 恒有一原子a∈B, 使a≤b。 证明: 任取b∈B且b≠0. 若b为原子, 有b≤b, 则命题已得证。 若b不是原子, 则必有b1∈B, 使得0 < b1 < b。 若b1不是原子,存在b2使0<b2<b1<b,对b2重复上面的讨论。 因为B有限,这一过程必将中止,上述过程产生的元素序列满足 0 < …<b2 < b1 < b 即存在br, br为原子,且0 < br < b, 否则此序列无限长。
三、有限布尔代数的结构
引理2: 设<B,∨,∧, ′, 0,1>是有限布尔代数, 则 (1) 任意b,c∈B, 有b∧c'=0当且仅当b ≤ c; (2) 对于B中任一原子a和任一非零元素b, a≤b 和a≤b'两式中有且仅 有一式成立。 (1)证明: 必要性⇒ 若b∧c'=0, 证明b ≤ c. (b∨c)∧(c'∨c)=(b∧c')∨c=0∨c=c (b∨c)∧(c'∨c)=(b∨c)∧1=b∨c 所以b∨c=c,故b ≤ c. 充分性 ⇐ 若b ≤ c, 证明b∧c'=0. c'≤ c',且b ≤ c,有b∧c'≤ c∧c'=0, 所 以b∧c'=0.
结论:
(1)每一正整数n∈N,一定存在2n个元素的布尔代数。 S={a1,…,an}, |ρ(S)|=2n, <ρ(S),∩,∪, ¯ , Ø, S>; (2) 反之, 对于任一有限布尔代数L, 总存在自然数n∈N,使得|L|=2n
(它的元素个数必为2的幂次)。
二、布尔同态
定义2 具有有限个元素的布尔代数称为有限布尔代数. 定义3 设<A,*,⊕,′,0,1>和<B,∩,∪, - ,α,β>是两个布尔代数。定义一 个映射f:A→B,如果在f的作用下能够保持布尔代数的所有运算,且 常数相对应,亦即对于任何a,b∈A有: f(a*b)=f (a)∩f(b) f(a⊕b)=f (a)∪f(b) f(a′)=f(a) f(0)=α f(1)=β 则称映射f:A→B是一个布尔同态。
一、布尔代数两个定义
定义1→定义1′, 显然。下面证明定义1←定义1′:
(1) 交换律:运算*和⊕是可交换的
(2) 吸收律 :要证明 a*(a⊕b)=a 和 a⊕(a*b)=a a *(a⊕b)=(a⊕0)*(a⊕b)=a⊕(0*b)=a⊕0=a 同理可证 a⊕(a*b)=a
一、布尔代数两个定义
三、有限布尔代数的结构
引理3: 设<A,∨,∧, ′, 0, 1>是一个有限布尔代数,若x是A中任意非 零元素, a1, a2, … , ak是A中满足aj ≤ x的所有原子(j=1,2,…,k),则 x = a1∨a2∨…∨ak
证明: (1) 先证 a1∨a2∨…∨ak ≤ x. 记a1∨a2∨…∨ak =c,因为aj ≤ x,所以c ≤ x。 (2)再证 x ≤ a1∨a2∨…∨ak =c. 由引理2(1)知,要证x ≤ c只需证x∧c' =0, 反设x∧c' ≠0,于是必有一个原子a,使得a ≤ x∧c'。 又因x∧c' ≤ x ,和 x∧c'≤c', 所以 a ≤ x 和 a ≤ c'. 因为a是原子,且a ≤ x,所以a必是a1, a2, …, ak中的一 个,因此 a≤c,已有 a≤c', 得a ≤ c∧c', 即a ≤ 0, 与a是原子矛盾。x∧c' ≠0假设不成立。 综合(1)和(2)引理得证。
三、有限布尔代数的结构
布尔代数的原子有以下性质: 定理1:设<B,∧,∨, ′,0,1>是布尔代数, a∈B是原子的充分必要条件
是a≠0且对B中任何元素x有
x∧a=a 或 x∧a=0 定理2: 设a, b为布尔代数<B,∨,∧,′,0,1>中任意两个原子且a≠b, 则
a∧b=0。
三、有限布尔代数的结构
三、有限布尔代数的结构
引理2: 设<B,∨,∧, ′, 0,1>是有限布尔代数, 则 (1) 任意b,c∈B, 有b∧c'=0当且仅当b ≤ c; (2) 对于B中任一原子a和任一非零元素b, a≤b 和a≤b'两式中有且仅 有一式成立。 (2)证明: 先证a ≤ b 和a ≤ b'两式不可能同时成立. 假如a ≤ b 和a ≤ b'同时 成立, 就有a ≤ b∧b'=0, 这与a是原子相矛盾。 再证a ≤ b 和a ≤ b'两式中必有一式成立. 因为a∧b ≤ a, a是原子, 所以只能是a∧b=0或a∧b=a. 若a∧b=0,则 a∧(b')'=0, 由(1)得a ≤ b'; 若a∧b=a, 得a≤b. 命题得证.
再证充分性. 设a≠0, 且对任意x∈B, 有x∧a=a或x∧a=0成立. 若a不是原子, 那 么必有 b∈B, 使0 < b < a. 于是, b∧a=b. 因为b≠0, b≠a, 故b∧a=b 与式(I)矛盾. 因此, a只能是原子.
