黑龙江省哈尔滨市第六中学2014-2015学年高二数学下学期期中试题 文
黑龙江省哈尔滨市第六中学2014-2015学年高二12月月考化学试卷word版无答案

哈尔滨第六中学2014-2015学年高二年级化学试题3.下列各组原子中,彼此化学性质一定相似的是A.原子核外电子排布式为1s2的X原子与原子核外电子排布式为1s22s2的Y原子B.原子核外M层上仅有两个电子的X原子与原子核外N层上仅有两个电子的Y原子C.2p轨道上有一个空轨道的X原子与3p轨道上有一个空轨道的Y原子D.最外层都只有一个电子的X、Y原子4.对Na、Mg、Al的有关性质的叙述正确的是A.碱性:NaOH<Mg(OH)2<Al(OH)3B.第一电离能:Na<Mg<AlC.电负性:Na>Mg>AlD.还原性:Na>Mg>Al5.下列说法错误的是A.ns电子的能量不一定高于(n-1)p电子的能量B.6C的电子排布式1s22s22p2x违反了洪特规则C.电子排布式(21Sc)1s22s22p63s23p63d3违反了能量最低原理D.电子排布式(22Ti)1s22s22p63s23p10违反了泡利原理6.具有以下结构的原子,一定属于主族元素的是A.最外层有8个电子的原子B.最外层电子排布为ns2的原子C.次外层无未成对电子的原子D.最外层有3个未成对电子的原子7.下列关于元素第一电离能的说法不正确的是A.钾元素的第一电离能小于钠元素的第一电离能,故钾的活泼性强于钠B.因同周期元素的原子半径从左到右逐渐减小,故第一电离能必依次增大C.外围电子排布为ns2np6(当只有K层时为1s2)的原子,第一电离能较大D.对于同一元素而言,原子的电离能I1<I2<I3<…8. 下列原子序数所对应的元素组中,两者可形成离子键的是A.1和17B.12和9C.14和6D.15和89. 下列离子中,电子数大于质子数且质子数大于中子数的是A、D3O+B、Li+C、ODˉD、OHˉ10. 下列分子中所有原子都满足最外层为8电子结构的是A.BF3B.H2OC.SiCl4D.PCl511. 酸HX的下列性质中,可以证明它是弱电解质的是A.1 mol/L HX溶液的pH值约为2 B.HX能与水以任意比例互溶C.10 mL 1mol/L HX恰好与10 mL l mol/L NaOH溶液完全反应D.HX溶液的导电性比强酸溶液的弱12. 在已达到电离平衡的0.1 mol·L一的醋酸溶液中,欲使平衡向电离的方向移动,同时使溶液的pH降低,应采取的措施是A.加少量盐酸B.加热C.加少量醋酸钠晶体D.加氢氧化钠13. 分别在等体积等pH或等物质的量浓度的盐酸和醋酸溶液中,加入足量锌粉,氢离子浓度c(H+)及氢气的体积V(H2)(同温同压下测定)的变化图示如下,其中正确的是①②③④A.①②③B.②④C.①③D.①②③④14. 取0.2 mol·L—HX溶液与0.2mol·L—NaOH溶液等体积混合(忽略混合后溶液体积的变化),测得混合溶液的pH=8(25℃),则下列说法(或关系式)正确的是A.混合溶液中由水电离出的c(OH一)=1×10—8mol·L。
哈六中2014年高二下数学期末试卷含答案文科

哈六中2014年高二下数学期末试卷(含答案文科)考试说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合}12|{},31|{<<-=<<-=x x B x x M ,则=⋂B M ( ))1,2.(-A )1,1.(-B )3,1.(C )3,2.(-D2.命题“对任意的01,23≤+-∈x x R x ”的否定是 ( ).A 不存在01,23≤+-∈x x R x .B 存在01,23≥+-∈x x R x .C 存在01,23>+-∈x x R x .D 对任意的01,23>+-∈x x R x3.已知某程序框图如图所示,则执行该程序后输出的结果是 ( ).A 1- .B 21.C 2 .D 1 4.函数43)1ln(2+--+=x x x y 的定义域为 ( ))1,4.(--A )1,4.(-B )1,1.(-C ]1,1.(-D5.已知函数)(x f y =在R 上是减函数,则)3(-=x f y 的单调减区间是 ( ).A ),(+∞-∞ .B ),3[+∞ .C ),3[+∞- .D ]3,(-∞6.设函数)(),(x g x f 的定义域为R ,且)(x f 是奇函数,)(x g 是偶函数,则下列结论中正确的是 ( ))()(.x g x f A 是偶函数 )(|)(|.x g x f B 是奇函数 |)(|)(.x g x f C 是奇函数 |)()(|.x g x f D 是奇函数7.为调查哈市高中三年级男生的身高情况,选取了5000人作为样本,右图是此次调查中的某一项流程图,若其输出的结果是3800,则身高在cm 170以下的频率为 ( ).A 24.0 .B 38.0 .C 62.0 .D 76.08.下列各组函数中,表示同一函数的是 ( ).A y y ==.B 112+-=x x y 与1-=x y.C ln ln x x y e y e ==与 .D 001y x y x==与9.已知2211)11(xx x x f +-=+-,则)(x f 的解析式是 ( ) .A 21x x + .B 212x x +- .C 212x x+.D 21x x +- 10. 已知函数)0,(1cos )(≠∈-=x R x xx x f ,则)1(f '值为 ( ) .A 1sin 1-- .B 1sin 1+ .C 1sin 1+- .D 1sin 1-11.已知命题1:≠x p 或2≠y ,命题3:≠+y x q ,则命题p 是q 的( ).A 充分不必要 .B 必要不充分 .C 充要条件 .D 既不充分也不必要12.定义在R 上的函数)(x f 满足1)1(=f ,且)(x f 的导数)(x f '在R 上恒有21)(<'x f ,则不等式212)(22+<x x f 的解集是( ) .A ),1(+∞ .B )1,(--∞ .C )1,1(- .D ),1()1,(+∞⋃--∞第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分.13.甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服种选择1种,则他们选择相同颜色运动服的概率为______14.设函数⎪⎩⎪⎨⎧≥<=-1,1,)(311x x x e x f x ,则使得2)(≤x f 成立的x 的取值范围是15.已知)3,1(,)2()(2-∈-=x x x f ,函数)1(+x f 的单调减区间为 16.函数1]3,0[142≠∈-+=x x x x y 且的值域为 三、解答题:解答应写出必要的文字说明,证明过程或演算步骤. 17.(本小题满分10分)已知命题p :方程012=++mx x 有两个不等的负根;命题q :方程244(2)10x m x +-+=无实根.若p 或q 为真,p 且q 为假,求m 的取值范围.18. (本小题满分12分)已知函数)(x f 是定义在R 上的偶函数,当0≥x 时,17)(2++-=x x xx f(1)求0<x 时,)(x f 的解析式; (2)求)(x f 的值域。
黑龙江省哈尔滨市第六中学2014届高三9月月考数学(文)试题 Word版含答案

黑龙江省哈尔滨市第六中学2014届高三9月月考数学(文)试题第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分) 1. 集合}12|{Z xN x ∈∈*中含有的元素个数为 ( ) A.4 B. 6 C.8 D. 122. 已知函数⎩⎨⎧≤>=0,30,log )(2x x x x f x ,则))41((f f 的值是( )A. 9B. 91C.9-D. 91- 3. 命题:P 不等式1|1|->-x xx x 的解集为)1,0(;命题:q 在ABC ∆中“B A >”是“B A sin sin >”成立的必要充分条件,则下列命题为真命题的为 ( )A.q p ∧B. q p ∧⌝C.q p ⌝∧D. q p ⌝∧⌝ 4. 已知32cos sin =+θθ,则)252cos(πθ+的值为( ) A.97 B. 97- C. 924- D. 9245. 在△ABC 中,角C B A ,,的对边为,,a b c ,若22241c b a +=,则cBa cos 的值为( ) A.41 B. 45 C. 85 D.83 6.已知函数x x P x f -⋅-=22)(,则下列结论正确的是( )A .1=P ,)(x f 为奇函数且为R 上的减函数B .1-=P ,)(x f 为偶函数且为R 上的减函数C .1=P ,)(x f 为奇函数且为R 上的增函数D .1-=P ,)(x f 为偶函数且为R 上的增函数7. 已知函数()sin()f x A x ωϕ=+,R x ∈(其中πϕπω<<->>,0,0A ),其部分图象如图所示,则ϕω,的值为( )A.4,4πϕπω==B. 43,4πϕπω-==C. 4,2πϕπω==D. 43,2πϕπω-==8. 已知51)4cos(22cos =+πx x ,(π<<x 0)则x tan 的值等于( ) A.34- B. 43-C.2D. 2- 9. 已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ上单调递减,则ω取值范围是( )A.]45,21[B. ]43,21[C. ]21,0( D. ]2,0( 10.若函数x x x f ln 2)(2-=在其定义域内的一个子区间)1,1(+-k k 内不是单调函数,则实数k 的取值范围是 ( )A. ),1[+∞B. )23,1[C.)2,1[D. )2,23[11. 已知)(x g 为三次函数cx ax x a x f ++=233)(的导函数,则函数)(x g 与)(x f 的图像可能是( )12. 函数)1(|12|)(<-=x x f x 则关于x 的方程0)()(2=++c x bf x f 有个不同实数解的充分条件是( )A.01<<-b 且0>cB. 10<<b 且0<cC.01<<-b 且0=cD. 10<≤b 且0<c二、填空题(本大题共4个小题,每小题5分,共20分)13. 函数)3(log 231x x y -=的单调递减区间是14. 若存在常数m 使得210cos 70sin 32=︒-︒-m ,则实数m 的值为15. 已知函数b a bx ax x f +++=3)(2是定义在]2,1[a a -(R b a ∈,)上的偶函数,则)(x f 的值域为 16.对于函数⎪⎩⎪⎨⎧>+-≤=0,2120,2)(2x x x x xe x f x ,①过该函数图像上一点()2(,2--f )的切线的斜率为22e - ②函数)(x f 的最小值为e2-③该函数图像与x 轴有4个交点④函数)(x f 在]1,(--∞上为减函数,在]1,0(上也为减函数 其中正确命题的序号为第Ⅱ卷(非选择题 共90分)三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤 17. (本小题满分10分)ABC ∆中角C B A ,,的对边分别为c b a ,,,且0222=+-+bc a c b ,(1)求角A 的大小;(2)若3=a ,求ABC ∆面积ABC S ∆的最大值。
2014-2015年黑龙江省哈尔滨六中高二(下)期中数学试卷(文科)和答案

2014-2015学年黑龙江省哈尔滨六中高二(下)期中数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.(5分)已知x与y之间的一组数据如表,则y与x的线性回归方程=x+必过()A.点(2,2)B.点(1.5,0)C.点(1,2)D.点(1.5,4)2.(5分)下列结论正确的是()①当a<0时,(a2)=a3;②函数f(x)=(x﹣2)﹣(3x﹣7)0的定义域是{x|x≥2且x≠};③=|a|(n∈N*,n是偶数);④若2x=16,3y=,则x+y=7.A.①②B.②③C.③④D.②④3.(5分)函数f(x)=的值域为()A.(﹣∞,﹣1)B.(﹣1,0)∪(0,+∞)C.(﹣1,+∞)D.(﹣∞,﹣1)∪(0,+∞)4.(5分)下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间(0,+∞)上是减函数;(3)是偶函数.这样的函数是()A.y=x3+1B.y=log2(|x|+2)C.y=()|x|D.y=2|x|5.(5分)一个几何体的正视图和俯视图如图所示,其中俯视图为边长为的正三角形,且圆与三角形内切,则该几何体侧视图的面积为()A.4+πB.C.6+3πD.6+π6.(5分)双曲线x2+ky2=1的一条渐近线斜率是2,则k的值为()A.4B.C.﹣4D.7.(5分)根据如图所示的求公约数方法的程序框图,输入m=2146,n=1813,则输出的m的值为()A.36B.37C.38D.398.(5分)下列说法正确的个数为()①“p∨q为真”是“p∧q为真”的充分不必要条件;②∃m∈R,使f(x)=(m﹣1)•x是幂函数,且在(0,+∞)上递减;③已知点A(﹣2,1)在抛物线y2=2px(p>0)的准线上,记其焦点为F,则直线AF的斜率等于﹣4;④命题“∃x∈R,x2+x+1<0”的否定是“∀x∈R,x2+x+1<0”;⑤在正三棱锥S﹣ABC内任取一点P,使得V P﹣ABC <V S﹣ABC的概率是.A.1B.2C.3D.49.(5分)已知函数f(x)的定义域为[﹣1,4],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数y=f(x)﹣a 的零点的个数为()A.1B.2C.3D.410.(5分)已知定义在R上的奇函数f(x)满足f(x+2)=﹣f(x),若f(﹣1)>﹣2,f(﹣7)=,则实数a的取值范围为()A.B.(﹣2,1)C.D.11.(5分)已知y=f (x)是奇函数,当x∈(0,2)时,f (x)=ln x﹣ax (a >),当x∈(﹣2,0)时,f (x)的最小值为1,则a的值等于()A.B.C.D.112.(5分)已知双曲线﹣=1(a>0,b>0)的右焦点为F(2,0),设A、B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,直线AB的斜率为,则双曲线的离心率为()A.B.C.2D.4二、填空题:本大题共4小题,每小题5分,共20分.将答案填在机读卡上相应的位置.13.(5分)已知集合{0,﹣1,2a}={a﹣1,﹣|a|,a+1},则实数a的值为.14.(5分)利用计算机在区间(0,1)上产生两个随机数a和b,则方程x=﹣2a ﹣无实根的概率为.15.(5分)已知A,B,C三点在同一球面上,若球心到平面ABC的距离为1,AB=1,AC=2,∠BAC=60°,则球的体积为.16.(5分)设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),当x∈[0,1]时,f(x)=2x﹣1则(1)2是函数f(x)的周期;(2)函数f(x)在(2,3)上是增函数;(3)函数f(x)的最大值是1,最小值是0;(4)直线x=2是函数f(x)的一条对称轴.其中正确的命题是.三、选修题【选修4-4:坐标系与参数方程】17.(10分)极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线C的极坐标方程为ρ=2(cosθ+sin θ),斜率为的直线l交y轴于点E(0,1).(I)求C的直角坐标方程,l的参数方程;(Ⅱ)直线l与曲线C交于A、B两点,求|EA|+|EB|.四、解答题:本大题共5小题,共60分.解答时应写出必要的文字说明、证明过程或演算步骤.18.(12分)近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽9人,其中女性抽多少人?(2)为了研究三高疾病是否与性别有关,请计算出统计量K2,并说明你有多大的把握认为三高疾病与性别有关?下面的临界值表供参考:(参考公式K2=,其中n=a+b+c+d)19.(12分)如图,在四棱锥S﹣ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.(Ⅰ)求证:PQ∥平面SAD;(Ⅱ)求证:AC⊥平面SEQ;(Ⅲ)如果SA=AB=2,求三棱锥S﹣ABC的体积.20.(12分)已知函数f(x)=lnx,g(x)=ax2﹣bx(a、b为常数).(1)求函数f(x)在点(1,f(1))处的切线方程;(2)当函数g(x)在x=2处取得极值﹣2.求函数g(x)的解析式;(3)当时,设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围.21.(12分)已知函数f(x)=lnx﹣ax,其中a>0.(1)当a=1时,求f(x)在[1,e]上的最大值;(2)若1≤x≤e时,函数f(x)的最大值为﹣4,求函数f(x)的表达式.22.(12分)已知椭圆C:=1(a>b>0)的离心率为,椭圆的短轴端点与双曲线=1的焦点重合,过P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.(Ⅰ)求椭圆C的方程;(Ⅱ)求的取值范围.2014-2015学年黑龙江省哈尔滨六中高二(下)期中数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.(5分)已知x与y之间的一组数据如表,则y与x的线性回归方程=x+必过()A.点(2,2)B.点(1.5,0)C.点(1,2)D.点(1.5,4)【解答】解:由题意知,y与x的线性回归方程=x+必过样本中心点,==1.5,==4,∵=x+=x+(﹣=(x﹣)+,∴线性回归方程必过(1.5,4).故选:D.2.(5分)下列结论正确的是()①当a<0时,(a2)=a3;②函数f(x)=(x﹣2)﹣(3x﹣7)0的定义域是{x|x≥2且x≠};③=|a|(n∈N*,n是偶数);④若2x=16,3y=,则x+y=7.A.①②B.②③C.③④D.②④【解答】解:①当a<0时,(a2)=﹣a3,因此不正确;②由函数f(x)=(x﹣2)﹣(3x﹣7)0,可得,解得x≥2且x≠,因此其定义域是{x|x≥2且x≠},正确;③=|a|(n∈N*,n是偶数),正确;④若2x=16,3y=,则x=4,y=﹣3,则x+y=1,因此不正确.故选:B.3.(5分)函数f(x)=的值域为()A.(﹣∞,﹣1)B.(﹣1,0)∪(0,+∞)C.(﹣1,+∞)D.(﹣∞,﹣1)∪(0,+∞)【解答】解:∵2x>0,∴2x﹣2>﹣2,由f(x)=得2x﹣2≠0,若2x﹣2>0,则f(x)>0,若﹣2<2x﹣2<0,则,则<﹣1,即此时f(x)<﹣1,综上f(x)>0或f(x)<﹣1,即函数的值域为(﹣∞,﹣1)∪(0,+∞),故选:D.4.(5分)下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间(0,+∞)上是减函数;(3)是偶函数.这样的函数是()A.y=x3+1B.y=log2(|x|+2)C.y=()|x|D.y=2|x|【解答】解:当x=0时,对于A:y=x3+1=1;对于B:y=log2(|x|+2)=1;对于C:y=()|x|;对于D:y=2|x|=1.故四个函数都满足性质(1),而满足性质(2)在区间(0,+∞)上是减函数的只有C.且C:y=()|x|是偶函数.故选:C.5.(5分)一个几何体的正视图和俯视图如图所示,其中俯视图为边长为的正三角形,且圆与三角形内切,则该几何体侧视图的面积为()A.4+πB.C.6+3πD.6+π【解答】解:由题设条件,俯视图为边长为2的正三角形,且圆与三角形内切知俯视图中三角形的高为=3,故此三角形的面积为×3×2=3,此三角形的周长为6,又此三角形的面积又可表示为×r×6,故可解得内切圆的半径为1,则侧视图上部圆的表面积为π侧视图下部是一个矩形由图示及求解知,此两边长分别为为3与2,故其面积为6由上计算知侧视图的面积为6+π故选:D.6.(5分)双曲线x2+ky2=1的一条渐近线斜率是2,则k的值为()A.4B.C.﹣4D.【解答】解:∵双曲线的方程为x2+ky2=1即,所以焦点在x轴上,其中∵一条渐近线斜率是2,∴,∴解得k=故选:D.7.(5分)根据如图所示的求公约数方法的程序框图,输入m=2146,n=1813,则输出的m的值为()A.36B.37C.38D.39【解答】解:∵2146÷1813=1 (333)1813÷333=5 (148)333÷148=2 (37)148÷37=4∴m=2146,n=1813的最大公约数是37故选:B.8.(5分)下列说法正确的个数为()①“p∨q为真”是“p∧q为真”的充分不必要条件;②∃m∈R,使f(x)=(m﹣1)•x是幂函数,且在(0,+∞)上递减;③已知点A(﹣2,1)在抛物线y2=2px(p>0)的准线上,记其焦点为F,则直线AF的斜率等于﹣4;④命题“∃x∈R,x2+x+1<0”的否定是“∀x∈R,x2+x+1<0”;⑤在正三棱锥S﹣ABC内任取一点P,使得V P﹣ABC <V S﹣ABC的概率是.A.1B.2C.3D.4【解答】解:对于①“p∨q”为真,说明p,q中至少一个为真,故不能推出“p ∧q”为真,而“p∧q”为真,说明p,q同为真,故能推出“p∨q”为真,故前者是后者的必要不充分条件,故不正确;对于②m=2时,f(x)=x﹣1是幂函数,且在(0,+∞)上递减,故正确;对于③∵点A(﹣2,1)在抛物线C:y2=2px的准线上,∴=2,∴F(2,0),则直线AF的斜率为=﹣,故不正确;对于④命题“∃x∈R,x2+x+1<0”的否定是“∀x∈R,x2+x+1≥0”;故不正确;对于⑤如图所示,O是正△ABC的中心,分别取棱SA,SB,SC的中点D,E,F,则在△DEF及其内部任取一点P,则V P﹣ABC=S△ABC×SO=V S﹣ABC,因此使得使得V P﹣ABC <V S﹣ABC的概率是1﹣=,故正确;故选:B.9.(5分)已知函数f(x)的定义域为[﹣1,4],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数y=f(x)﹣a 的零点的个数为()A.1B.2C.3D.4【解答】解:根据导函数图象,可得2为函数的极小值点,函数y=f(x)的图象如图所示:因为f(0)=f(3)=2,1<a<2,所以函数y=f(x)﹣a的零点的个数为4个.故选:D.10.(5分)已知定义在R上的奇函数f(x)满足f(x+2)=﹣f(x),若f(﹣1)>﹣2,f(﹣7)=,则实数a的取值范围为()A.B.(﹣2,1)C.D.【解答】解:∵f(x)是定义在R上的奇函数,且满足f(x+2)=﹣f(x),∴f(x+4)=﹣f(x+2)=f(x),函数的周期为4,则f(﹣7)=f(8﹣7)=f(1)=﹣f(﹣1),又f(﹣1)>﹣2,f(﹣7)==﹣f(﹣1),∴﹣>﹣2,即,即解得a∈,故选:D.11.(5分)已知y=f (x)是奇函数,当x∈(0,2)时,f (x)=ln x﹣ax (a >),当x∈(﹣2,0)时,f (x)的最小值为1,则a的值等于()A.B.C.D.1【解答】解:∵f(x)是奇函数,∴f(x)在(0,2)上的最大值为﹣1,当x∈(0,2)时,,令f'(x)=0得,又,∴.令f'(x)>0时,,f(x)在上递增;令f'(x)<0时,,f(x)在上递减;∴,∴,得a=1.故选:D.12.(5分)已知双曲线﹣=1(a>0,b>0)的右焦点为F(2,0),设A、B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,直线AB的斜率为,则双曲线的离心率为()A.B.C.2D.4【解答】解:根据题意,设A(x1,y1),则B(﹣x1,﹣y1),∵AF的中点为M,BF的中点为N,∴M((x1+2),y1),N((﹣x1+2),﹣y1).∵原点O在以线段MN为直径的圆上,∴∠NOM=90°,可得=(4﹣)﹣=0.…①又∵点A在双曲线上,且直线AB的斜率为,∴,…②.由①②联解消去x1、y1,得﹣=,…③又∵F(2,0)是双曲线的右焦点,可得b2=c2﹣a2=4﹣a2,∴代入③,化简整理得a4﹣8a2+7=0,解之得a2=1或7,由于a2<c2=4,所以a2=7不合题意,舍去.故a2=1,得a=1,离心率e==2.故选:C.二、填空题:本大题共4小题,每小题5分,共20分.将答案填在机读卡上相应的位置.13.(5分)已知集合{0,﹣1,2a}={a﹣1,﹣|a|,a+1},则实数a的值为±1.【解答】解:令A={0,﹣1,2a},B={a﹣1,﹣|a|,a+1},∵{0,﹣1,2a}={a﹣1,﹣|a|,a+1},若a﹣1=0,则a=1,则A={0,﹣1,2},B={0,﹣1,2},满足要求;若﹣|a|=0,则a=0,则A={0,﹣1,0},不满足集合元素的互异性;若a+1=0,则a=﹣1,则A={0,﹣1,﹣2},B={0,﹣1,﹣2},满足要求;故实数a的值为±1故答案为:±114.(5分)利用计算机在区间(0,1)上产生两个随机数a和b,则方程x=﹣2a﹣无实根的概率为.【解答】解:设在区间(0,1)上产生两个随机数a和b,记为(a,b),对于区域的面积为边长为1的正方形的面积1,而在此条件下满足方程x=﹣2a﹣整理得x2+2ax+b2=0,方程有实根,△≥0即4a2﹣4b2≥0∴b≤a.在aOb坐标系中画出图形.如图.∴方程有实根的概率为P==故答案为:.15.(5分)已知A,B,C三点在同一球面上,若球心到平面ABC的距离为1,AB=1,AC=2,∠BAC=60°,则球的体积为.【解答】解:在三角形ABC中,∠BAC=60°,AB=1,AC=2,∴BC=,则三角形ABC是以AC为斜边的直角三角形,如图所示:取AC的中点M,则球面上A、B、C三点所在的圆即为⊙M,连接OM,则OM 即为球心到平面ABC的距离,在Rt△OMB中,OM=1,MA=1,∴OA=,即球球的半径为.∴球的体积为:=.故答案为:.16.(5分)设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),当x∈[0,1]时,f(x)=2x﹣1则(1)2是函数f(x)的周期;(2)函数f(x)在(2,3)上是增函数;(3)函数f(x)的最大值是1,最小值是0;(4)直线x=2是函数f(x)的一条对称轴.其中正确的命题是(1)(2)(4).【解答】解:(1)由函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),取x=x+1则f(x+1+1)=f(x+1﹣1)=f(x),即f(x+2)=f(x),所以2是函数f(x)的周期,所以(1)正确;(2)因为当x∈[0,1]时,f(x)=2x﹣1为增函数,又因为函数f(x)的周期是2,所以函数在[2,3]上的图象与在[0,1]上的图象完全相同,所以函数f(x)在(2,3)上是增函数,所以(2)正确;(3)因为当x∈[0,1]时,f(x)=2x﹣1为增函数,且函数f(x)为偶函数,所以在[﹣1,1]上函数的最小值为f(0)=,再由函数图象以2为周期周期出现,所以函数f(x)的最小值是,所以(3)不正确;(4)由函数f(x)的周期是2,且函数f(x)是偶函数,所以f(4+x)=f(x)=f(﹣x),所以函数的一条对称轴是x=2,所以(4)正确.故答案为(1)(2)(4).三、选修题【选修4-4:坐标系与参数方程】17.(10分)极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线C的极坐标方程为ρ=2(cosθ+sin θ),斜率为的直线l交y轴于点E(0,1).(I)求C的直角坐标方程,l的参数方程;(Ⅱ)直线l与曲线C交于A、B两点,求|EA|+|EB|.【解答】解:(Ⅰ)由ρ=2(cosθ+sinθ),得ρ2=2(ρcosθ+ρsinθ),即x2+y2=2x+2y,即(x﹣1)2+(y﹣1)2=2.l 的参数方程为(t为参数,t∈R),(Ⅱ)将代入(x﹣1)2+(y﹣1)2=2得t2﹣t﹣1=0,解得,t1=,t2=.则|EA|+|EB|=|t1|+|t2|=|t1﹣t2|=.四、解答题:本大题共5小题,共60分.解答时应写出必要的文字说明、证明过程或演算步骤.18.(12分)近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽9人,其中女性抽多少人?(2)为了研究三高疾病是否与性别有关,请计算出统计量K 2,并说明你有多大的把握认为三高疾病与性别有关? 下面的临界值表供参考:(参考公式K 2=,其中n=a+b+c+d )【解答】(本题满分12分) 解:(1)表格如下:…(3分)在患三高疾病人群中抽9人,则抽取比例为∴女性应该抽取人.…(6分)(2)∵…(8分)=10>7.879,…(10分)那么,我们有99.5%的把握认为是否患三高疾病与性别有关系.…(12分) 19.(12分)如图,在四棱锥S ﹣ABCD 中,底面ABCD 为菱形,∠BAD=60°,平面SAD ⊥平面ABCD ,SA=SD ,E ,P ,Q 分别是棱AD ,SC ,AB 的中点. (Ⅰ)求证:PQ ∥平面SAD ; (Ⅱ)求证:AC ⊥平面SEQ ;(Ⅲ)如果SA=AB=2,求三棱锥S ﹣ABC 的体积.【解答】(Ⅰ)证明:取SD中点F,连结AF,PF.因为P,F分别是棱SC,SD的中点,所以FP∥CD,且FP=CD.又因为菱形ABCD中,Q是AB的中点,所以AQ∥CD,且AQ=CD.所以FP∥AQ且FP=AQ.所以AQPF为平行四边形.所以PQ∥AF.又因为PQ⊄平面SAD,AF⊂平面SAD,所以PQ∥平面SAD.…(5分)(Ⅱ)证明:连结BD,因为△SAD中SA=SD,点E棱AD的中点,所以SE⊥AD.又平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,SE⊂平面SAD,所以SE⊥平面ABCD,所以SE⊥AC.因为底面ABCD为菱形,E,Q分别是棱AD,AB的中点,所以BD⊥AC,EQ∥BD.所以EQ⊥AC,因为SE∩EQ=E,所以AC⊥平面SEQ.…(11分)(Ⅲ)解:因为菱形ABCD中,∠BAD=60°,AB=2,=AB•BCsin∠ABC=.所以S△ABC因为SA=AD=SD=2,E是AD的中点,所以SE=.由(Ⅱ)可知SE⊥平面ABC,•SE=1.…(14分)所以三棱锥S﹣ABC的体积V=S△ABC20.(12分)已知函数f(x)=lnx,g(x)=ax2﹣bx(a、b为常数).(1)求函数f(x)在点(1,f(1))处的切线方程;(2)当函数g(x)在x=2处取得极值﹣2.求函数g(x)的解析式;(3)当时,设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围.【解答】解:(1)由f(x)=lnx(x>0),可得f′(x)=(x>0),∴f(x)在点(1,f(1))处的切线方程是y﹣f(1)=f′(1)(x﹣1),即y=x﹣1,所求切线方程为y=x﹣1;(2)∵又g(x)=ax2﹣bx可得g′(x)=2ax﹣b,且g(x)在x=2处取得极值﹣2.∴,可得解得,b=2.所求g(x)=(x∈R).(3)∵,h′(x)=(x>0).依题存在x>0使h′(x)=(x>0).h′(x)<0(x>0)即存在x>0使x2﹣bx+1<0,∵不等式x2﹣bx+1<0等价于(*)令,∵.∴λ(x)在(0,1)上递减,在[1,+∞)上递增,故,+∞),∵存在x>0,不等式(*)成立,∴b>2.所求b∈(2,+∞).21.(12分)已知函数f(x)=lnx﹣ax,其中a>0.(1)当a=1时,求f(x)在[1,e]上的最大值;(2)若1≤x≤e时,函数f(x)的最大值为﹣4,求函数f(x)的表达式.【解答】解:f′(x)=﹣a=,(a>0,x>0)(1)当a=1时,f′(x)=,∴x∈[1,e]时,f′(x)<0,∴f(x)在[1,e]上单调递减,最大值为f(1)=﹣1.(2)∵f′(x)=﹣a,令f(x)在(0,)上单调递增,在(,+∞)上单调递减.①当0<<1,即a>1时,f(x)max=f(1)=﹣4,解得a=4符合题意;②当1≤≤e,即≤a≤1时,f(x)max=f()=﹣4,解得:a=e3>1(舍去);③当>e,即0<a<时,f(x)max=f(e)=﹣4,解得:a=>(舍去).综上,f(x)=lnx﹣4x.22.(12分)已知椭圆C:=1(a>b>0)的离心率为,椭圆的短轴端点与双曲线=1的焦点重合,过P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.(Ⅰ)求椭圆C的方程;(Ⅱ)求的取值范围.【解答】解:(I)由双曲线=1得焦点,得b=.又,a2=b2+c2,联立解得a2=4,c=1.故椭圆C的方程为;(II)由题意可知直线l的斜率存在,设直线l的方程为y=k(x﹣4),联立,(4k2+3)x2﹣32k2x+64k2﹣12=0,由△=(﹣32k2)2﹣4(4k2+3)(64k2﹣12)>0得.设A(x1,y1),B(x2,y2),则,,∴=,∴=x1x2+y1y2==,∵,∴,∴.故的取值范围为.。
黑龙江省哈尔滨市第六中学2014-2015学年高一下学期期中考试数学试题 Word版含答案

哈尔滨市第六中学2014—2015学年度下学期期中考试高一数学试题考试时间:120分钟 满分:150分一、选择题:(本大题共12小题,每小题5分,共60分) 1.若R,a b c a b ∈>、、,则下列不等式成立的是 ( )A.b a 11<B.22b a >C.22(1)(1)a c b c +>+D.||||c b c a > 2.已知非零向量,a b 满足12a b=,)b a -⊥,则向量a 与b的夹角大小为( ) A .30 B .60 C .120 D .150 3.设等差数列{}n a 的前n 项和为n S ,若3613S S =,则612SS 的值为( ) A .103 B .310C .43D .344.在等比数列{}n a 中,若243119753=a a a a a ,则1129a a 的值为( )A . 1-B . 1C .2D .35. 向量,a b 的夹角为120,2a b ==,4c =,则a b c +-的最大值为( ) A . 2 B .4 C .6 D .86. 如果数列}{n a 中,满足123121,,,,-n n a a a a a a a 是首项为1公比为3的等比数列,则100a 等于( ) A .1003B.903 C.49503 D.505037.数列}{n a 是等比数列,若21a =,518a =,设12231n n n S a a a a a a +=+++,若232n S m m ≤+对任意n N *∈恒成立,则m 的取值范围为( )A .42m -≤≤B .4m ≤-或2m ≥C .24m -≤≤D .2m ≤-或4m ≥8.等差数列{}n a 中1091a a <-,它的前n 项和n S 有最大值,则当n S 取得最小正值时,=n ( ) A .17 B .18 C .19 D .209.已知O 是ABC ∆内部一点,0OA OB OC ++=,6AB AC ⋅=,60BAC ∠=,则OBC ∆的面积为( ) A . B .1 CD .310.已知正项等比数列{}n a 满足:6542a a a =+,若存在两项,m n a a ,12a =,则19m n+的最小值为( ) A. 6 B. 5 C.283 D.4 11.平行四边形ABCD 中,60,1=∠=BAD AD ,E 为CD 中点.若1=⋅BE AC ,则=||AB ( )A .1B .21C .31D .41 12.定义np p p n+++ 21为n 个正数n p p p ,,,21 的“均倒数”.若已知数列}{n a 的前n 项的“均倒数”为121+n ,又41+=n n a b ,则11103221111b b b b b b +++ =( ) A .111 B .109 C .1110 D .1211二、填空题:(本大题共4小题,每小题5分,共20分) 13.当2x >时,不等式12x a x +≥-恒成立,则实数a 的最大值是__________ 14.已知n S 是等差数列{}n a 的前n 项和,36S =,216n n a a -+=,若50n S =,则n 的值为_____15.如图,在直角梯形ABCD 中,AB ∥CD ,90BAD ∠=,且122A B A D C D ===,3CB CM =,则D M A C ⋅的值为_____________16.若数列{}n a 与{}n b 满足11(1)1n n n n n b a b a +++=-+,13(1),2n n b n N -*+-=∈,且12a =,设数列{}n a 的前n 项和为n S ,则63___________S =三、解答题(本大题共6小题,共70分,解答时写出必要的文字说明,证明过程或解题步骤) 17.(满分10分)等差数列{}n a 的前n 项和为n S ,已知2=1a ,1045S =.(1)求数列{}n a 的通项公式; (2)若数列{}n b 满足na nb -=2,求数列{}n b 的前n 项和n T .18.(满分12分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,, 若(sin ,sin )m A B =,(sin ,sin )n B C =,1cos2m n B ⋅=-(1)求证:c b a ,,成等差数列; (2)若32π=C ,求ba的值.A BC D M19.(满分12分)解关于x 的不等式 (1)34x x -+>(2)2(1)10ax a x -++< ()a R ∈20.(满分12分)已知函数2()2)(0)f x x =≥,数列{}n a 满足:14a =,1()n n a f a +=,数列{}n b 满足:321)23nb b b b n N n*++++=∈(1)求证数列}1是等比数列,并求数列{}n a 的通项公式;(2)求数列{}n b 的通项公式和它的前n 项和n T ;21.(满分12分)在锐角ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知向量1(sin ,)2=m A ,(3,sin )=n A A ,且m ∥n ,(1)求角A 的大小; (2)求b ca+的取值范围22.(满分12分)已知各项都是正数的数列{}n a 的前n 项和为n S ,212n n n S a a =+,n N *∈ (1) 求数列{}n a 的通项公式;(2) 设数列{}n b 满足:11b =,12(2)n n n b b a n --=≥,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T (3) 若(4)n T n λ≤+对任意n N *∈恒成立,求λ的取值范围2017届高一下学期期中考试数学试题参考答案13、4; 14、10; 15.、12; 16、560 三、解答题:17.解:(1)1111011045451n a d a a n a d d +==⎧⎧⇒⇒=-⎨⎨+==⎩⎩ —————————————————5分 (2)12nn b -= 211222n n n n b b -+-== {}n b ∴是以1为首项,2为公比的等比数列122112nn n T -∴==--————————————————————————————————10分18.解:(1)2sin sin sin sin 1cos22sin m n A B B C B B ⋅=+=-= sin 0B ≠ sin sin 2sin A C B ∴+= 2a c b ∴+=————————————————— 6分(2)22222232cos (2)5a c ab ab C b a a b ab b =+-⇒-=++⇒=———————————12分19.解:(1)3x ≥时,734,2x x x -+>∴>03x <<时,34x x -+>,不成立4x ≤时,34x x -->,12x <-∴解集为17(,)(,)22-∞-⋃+∞————————————————————————6分(2)0a =时, 解集为(1,)+∞01a <<时,解集为1(1,)a1a =时, 解集为φ1a >时, 解集为1(,1)a0a <时, 解集为1(,)(1,)a-∞⋃+∞——————————————————————12分20.解:(1211)==13=}1∴是以3为首项,以3为公比的等比数列 13n =,2(31)n n a ∴=-————4分(2)3213123n n b b b b n++++=- 1312131(2)231n n bb b b n n --++++=-≥-123(2)n n bn n-∴=⋅≥,123(2)n n b n n -∴=≥, 12b =符合上式, 123()n n b n n N -*∴=∈—————————————————————————————8分(3)11()322n n T n =-+——————————————————————————————12分21.解:(1)3sin (sin )2A A A =,sin(2)16A π∴-=,(0,)2A π∈,52(,)666A πππ∴-∈-262A ππ∴-=,3A π∴=——————————————————————————————4分(2)sin sin sin()]2sin()sin 36b c B C B B B a A ππ++==++=+———————————8分02262032B B πππππ⎧<<⎪⎪⇒<<⎨⎪<<⎪⎩————————————————————————————10分 2(,)633B πππ⇒+∈sin()6b cB aπ+⇒+∈⇒∈—————————————12分 22.解:(1)1n =时,211111122a a a a =+∴=21112211211121222n n n n n n nn n n n S a a a a a a a S a a+++--⎧=+⎪⎪⇒=-+-⎨⎪=+⎪⎩ 111()()02n n n n a a a a --⇒+--= 1102n n n a a a ->∴-=∴{}n a 是以12为首项,12为公差的等差数列 12n a n ∴=———————————4分(2)1n n b b n --=21321123(2)(1)(1)22n nn n b b b b n n n n b b b b b n--=⎧⎪-=+-+⎪⇒-=⇒=⎨⎪⎪-=⎩————————————————6分 12112()(1)1n b n n n n ==-++,11111122(1)2(1)223111n n T n n n n ∴=-+-++-=-=+++——9分 224(1)(4)5n n n n n λ≥=++++ 当且仅当2n =时,245n n++有最大值29,29λ∴≥ ———12分。
黑龙江省哈尔滨市第六中学2014-2015学年高二下学期期末考试数学(理)试题 Word版含答案

哈尔滨市第六中学2014-2015学年度下学期期末考试高二理科数学一、选择题(本大题共12个小题,每小题5分,共60分)1.已知集合}2|||{≤=x x M ,集合},03|{2Z x x x x N ∈≥+=,则)(N C M Z ⋂等于( ) A.}20|{≤<x x B.}02|{<≤-x x C.}2,1{ D.}1,2{--2.设函数⎩⎨⎧≤+>=-0,140,log )(2x x x x f x ,则)3log ()2(2-+f f 的值为( )A.9B.10C. 11D. 12 3.已知)2(+x f 是偶函数,且函数)(x f 在),2[+∞上是单调递增,则( )A.)0()3(f f >B.)1()3(f f >C.)1()0(f f <D.)1()4(f f > 4.设2.03=a ,3log 4=b ,)1(log 25.0+=m c ,则( )A.c b a <<B.c a b <<C.a b c << D .b c a <<5. 若ax x x g --=2)(在区间),3(+∞上是减函数,则a 的取值范围是( ) A.3≤a B.32≤<a C.2>a D .2<a6.由直线x y e x y 2,,0===及曲线xy 2=所围成的封闭的图形的面积为( )A.2ln 23+B.3C.322-e D.e 7. 有下列四个命题::1p 若幂函数m kx x f =)(过)9,3(,则2=mk ;:2p 函数x e x f =)(的反函数为x x g ln )(=; :3p “1,1>>b a ”是“)1,0()(≠>-=a a b a x f x ”的图象不过第二象限的必要不充分条件; :4p “q p ∨”为假是“q p ∧”为假的充分不必要条件。
黑龙江省哈尔滨师范大学附属中学2014-2015学年高二下学期期中考试数学(文)试题Word版含答案
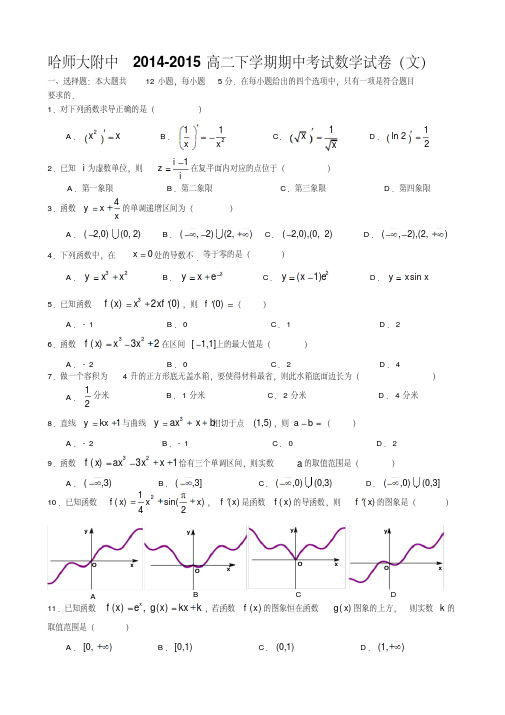
哈师大附中2014-2015高二下学期期中考试数学试卷(文)一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.对下列函数求导正确的是()A .2xxB .211x xC .1xxD .1ln 222.已知i 为虚数单位,则1i zi在复平面内对应的点位于()A .第一象限B .第二象限C .第三象限D .第四象限3.函数4y xx的单调递增区间为()A .(2,0)(0,2)B .(,2)(2,)C .(2,0),(0,2)D .(,2),(2,)4.下列函数中,在0x处的导数不.等于零的是()A .32y xxB .xy x eC .2(1)y x eD .sin y x x5.已知函数3()2(0)f x xxf ,则(0)f ()A .-1 B .0C .1D .26.函数32()32f x xx在区间[1,1]上的最大值是()A .-2B .0C .2D .47.做一个容积为4升的正方形底无盖水箱,要使得材料最省,则此水箱底面边长为()A .12分米B .1分米C .2分米D .4分米8.直线1ykx 与曲线3y axxb相切于点(1,5),则a b ()A .-2B .-1C .0D .2 9.函数32()31f x axxx 恰有三个单调区间,则实数a 的取值范围是()A .(,3)B .(,3]C .(,0)(0,3)D .(,0)(0,3]10.已知函数21()sin()42f x xx ,()f x 是函数()f x 的导函数,则()f x 的图象是()11.已知函数(),()xf x eg x kx k ,若函数()f x 的图象恒在函数()g x 图象的上方,则实数k 的取值范围是()A .[0,)B .[0,1)C .(0,1)D .(1,)OyxOyxOyxO yxABCD12.可导函数()f x 满足()()f x f x 对x R 恒成立,则()A .(1)(0)f ef ,2015(2015)(0)f e f B .(1)(0)f ef ,2015(2015)(0)f e f C .(1)(0)f ef ,2015(2015)(0)f ef D .(1)(0)f ef ,2015(2015)(0)f ef 二、填空题:本大题共4小题,每小题5分.13.函数()2ln f x x x 的单调递减区间为____________.14.函数2()1xaf x x 在0x 处取得极值,则a ____________.15.经过点(2,0)且与曲线4yx相切的直线方程为____________.16.已知函数()(ln )f x x xax 有两个极值点,则实数a 的取值范围是____________.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本题满分10分)已知函数2xf xx e .(Ⅰ)求f x 的单调区间;(Ⅱ)求f x 在2,0上的最值.18.(本题满分12分)已知在平面直角坐标系xOy 中曲线C 的参数方程为2cos ,3sinx y(为参数),直线l 的参数方程为11232x tyt (t 为参数),曲线C 与直线l 相交于点,,A B 且定点P 的坐标为(1,0).(Ⅰ)求曲线C 的普通方程;(Ⅱ)求PA PB 的值.19.(本题满分12分)已知函数321132f xxaxx x R .(Ⅰ)若函数y f x 在0,上为增函数,求a 的取值范围;(Ⅱ)若1a ,当1x 时,求证:()1f x x .已知函数x mx xxf ln 2.(Ⅰ)当0m时,求曲线y)(x f 在1,1f 处的切线方程;(Ⅱ)令2x xf xg ,当e x,0(e 是自然常数)时,3xg ,求实数m 的取值范围.21.(本题满分12分)已知函数36)2(23)(23x xa axx f .(Ⅰ)当2a 时,求函数)(x f 的极值;(Ⅱ)当2a时,讨论函数)(x f 零点的个数.yxMPB AO在平面直角坐标系xOy 中,已知椭圆C :22221(0)x y a bab的离心率为22,且经过点(2,1),过椭圆的左顶点A 作直线l ⊥x 轴,点M 为直线l 上的动点(点M 与点A 不重合),点B为椭圆右顶点,直线BM 交椭圆C 于点P .(Ⅰ)求椭圆C 的方程;(Ⅱ)求证:AP ⊥OM ;(Ⅲ)试问OP OM 是否为定值?若是定值,请求出该定值;若不是,请说明理由.哈师大附中2014-2015高二下学期期中数学(文)参考答案一、选择题:本大题共12小题,每小题5分.题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BADCB CCACDBA二、填空题:本大题共4小题,每小题5分.13.(0,2);14.0;15.480x y ;16.1(0,)2.三、解答题:本大题共6小题,共70分.17.解:(Ⅰ)1xf x x e .…………2分当1x 时,0f x;当1x时,0fx .∴f x 的单调减区间为(,1),增区间为(1,).…………6分(Ⅱ)由(Ⅰ)知,f x 在[0,1]上递减,在[1,2]上递增.又(0)2,(2)f f ∴max()(2)0f x f ;min()(1)f x f e .…………10分18.解:(Ⅰ)曲线C 的普通方程为22143xy…………4分(Ⅱ)将直线l 的参数方程代入曲线C 的普通方程得22133(1)4()1222t t ,即254120t t ,△>0设其两根为12,t t ,12125t t 1212121255PA PB t t t t .…………12分19.解:(Ⅰ)由已知210fxx ax ,即21xax对0,x 恒成立.∵0x 时,2112xx xx(当且仅当1x 取等号)∴2a …………5分(Ⅱ)1a时,321132f x xxx ,设3211()132g x xx,则2()(1)g x xx x x 当1x时,()0g x ,∴()g x 在[1,)单调递减.∴当1x 时,5()(1)06g x g ,即()1f x x .…………12分20.解:(Ⅰ)当0m 时,2ln f x xx ,∴12fxxx ,∴(1)1kf ,又(1)1f ∴切线方程为yx…………4分(Ⅱ)(方法一)当e x ,0时,ln 3g xmx x ,即3ln xmx对e x ,0恒成立.设3ln ()(0)x h x xe x,则2ln ()xh x x当210xe时,()0h x ;当21x e e时,()0h x ∴()h x 的增区间为21(0,)e,减区间为21(,)e e∴2max 21()()h x h ee∴2me .…………12分(方法二)ln (0)g xmx x xe ,则1g x mx当e x,0时,11xe①1m e时,0g x ,∴g x 在0,e 单调递减∴min()10g xg e em 矛盾,(舍)②1m e时,当10xm时,()0g x ;当1xe m时,()0g x ∴g x 在1(0,)m 单调递减,1(,)e m单调递增∴min1()1ln 3g x g mm,解得2me综上,实数m 的取值范围为2[,)e .…………12分21.解:)1)(2(36)2(332x axxaaxx f (Ⅰ)当2a时,)1)(1(6x x x f 令x f =0得1,121x x x)1,(1)1,1(1),1(()f x - 0 + 0 -()f x ↘极小值↗极大值↘∴7)1()(f x f 极小值,1)1()(f x f 极大值.…………4分(Ⅱ))1)(2(36)2(332x ax xa axxf …………5分①若0a ,则2)13)(x x f (,由()0f x ,得1x∴)(x f 只有一个零点.…………6分②若0a,则12a∴当ax2或x >1时,x f <0;当12xa时,x f >0∴)(x f 的单调递减区间为2(,)a 和),1(,单调递增区间为2(,1)a ∵极大值)(x f 02)1(a f ,且极小值)(x f 2246()30f a aa∴)(x f 有三个零点.…………9分③若20a ,则12a∴当1x或a x2时,x f >0;当12xa时,x f <0 ∴)(x f 的单调递增区间为(,1)和2(,)a,单调递减区间为2(1,)a ∴极大值)(x f 02)1(a f ∴)(x f 有一个零点.…………11分综上,02a时,)(x f 只有一个零点;0a时,)(x f 有三个零点.…………12分22.解:(Ⅰ)由已知22c a,则222ab ,又22211ab,∴224,2ab∴椭圆C 的方程为22142xy …………4分(Ⅱ)由(Ⅰ)知,(2,0),(2,0)A B ,直线BM 斜率显然存在,设BM 方程为(2)y k x ,则(2,4)M k 由22(2)142yk x xy ,得2222(21)8840kxkk,△>0则2284221Pkxk,∴224221Pkxk,24(2)21P Pky k xk,即222424(,)2121k kPk k………7分又22284(,)2121k kAPk k,(2,4)OM k∴222216162121k kAP OMk k,即AP⊥OM.…………10分(Ⅲ)22222222424841684(,)(2,4)421212121k k k k kOP OM kk k k k∴OP OM为定值4.…………12分。
黑龙江省哈六中高二数学下学期期中试题理

黑龙江省哈六中 高二数学下学期期中试题 理一、选择题(本大题共12个小题,每个小题5分,共60分) 1.曲线11-+=x x y 在点)1,0(-处的切线方程为( ) A.12--=x y B.12-=x y C.12+-=x y D.12+=x y 2.已知随机变量X 服从正态分布),2(2σN ,8.0)40(=<<X P ,则)4(>X P 的值等于( )A.0.1B.0.2C.0.4D.0.6 3.函数)cos()(2x x x f +=导数是( )A.)sin(2x x +- B. )sin()12(2x x x ++- D. )sin()12(2x x x ++ C. )sin(22x x x +- 4. 甲、乙等5人站成一排,其中甲、乙不相邻的不同排法共有( )A.144种B.72种C.36 种D.12种 5.二项式5)12(x x -的展开式中含21x项的系数为( ) A.10 B. 10- C.40 D.40-6. 现进行医药下乡活动,某医院的4名男医生和4名女医生及2名护士要去两个不同的山区进行义诊,若每个山区去男、女医生各2名,并带1名护士,则不同的分配方法有( ) A.144 B.72 C.36 D.167. 若x x f x f x f ln 4)1(')2(2)(-+-=,则)1(f 等于 ( ) A.2- B.4- C.2 D. 0 8.取一根长度为5米的绳子,拉直后在任意位置剪断,则剪得两段的长度都不小于1米,且以剪得的两段绳为两边的矩形的面积都不大于6平方米的概率为( ) A.31 B.41 C.52 D.539.若nxx )2(+的展开式中各项系数和为n -99,则展开式中系数最大的项为( ) A.第3项 B.第4项 C.第5项 D.第6项 10. 某5个同学进行投篮比赛,已知每个同学投篮命中率为8.0,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记X 为5个同学的得分总和,则X 的数学期望为( )A.400B.200C.100D.80 11.由3个2,3个8,2个6可以组成n 个8位电话号码,若后四位是由含3个8或2个6和2个8组成的电话号码,则称这个电话号码为“吉祥号”.现某人从这n 个电话号码中随机选取一个,则是“吉祥号”的概率为( ) A.51 B. 354 C.101 D. 3516 12.已知)(x f 是定义在R 上的函数,若12)('-<x x f 且0)1(=f ,则x x x f ->2)(的解集为( )A.),0(+∞B. )0,(-∞C. ),1(+∞D. )1,(-∞ 二、填空题:(本大题共4小题,每小题5分,共20分.将答案填在机读卡上相应的位置) 13. 已知函数xxx f ln )(=,若0)('0=x f ,则0x 的值为 14.已知a +⨯10102(110<≤a )能被11整除,则实数a 的值为15.教育局组织直属学校的老师去新疆地区支教,现甲学校有2名男老师和3名女老师愿意去支教,乙学校有3名男老师和3名女老师愿意去支教,由于名额有限,教育局决定从甲学校选2人去支教,乙学校选1人去支教,若被选去支教的5名老师中必须有男老师,则乙学校被选去支教的老师是女老师的概率为_______16.已知曲线方程)(31)(23R a ax x x f ∈-=,若对任意实数m ,直线0:=++m y x l ,都不是曲线)(x f y =的切线,则实数a 的取值范围是_______三、解答题(本大题共6个小题,共70分,解答时写出必要的文字说明和演算步骤) 17. (本小题满分10分)延迟退休年龄的问题,近期引发社会的关注.人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数月收入(元) [1000,2000) [2000,3000) [3000,4000) [4000,5000) [5000,6000) [6000,7000)频数 5 10 15 10 5 5 反对人数4812521(1)由以上统计数据估算月收入高于4000的调查对象中,持反对态度的概率;(2)若对月收入在[1000,2000),[4000,5000)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为X ,求X 的分布列和数学期望. 18. (本小题满分12分)已知函数b e ax x x f x++=)()(2,R b a ∈,,若函数)(x f 在0=x 处的切线方程为12+-=x y ,(1)求b a ,的值;(2)求函数)(x f 的单调区间。
黑龙江省哈尔滨市第六中学高二数学下学期期中试题 理
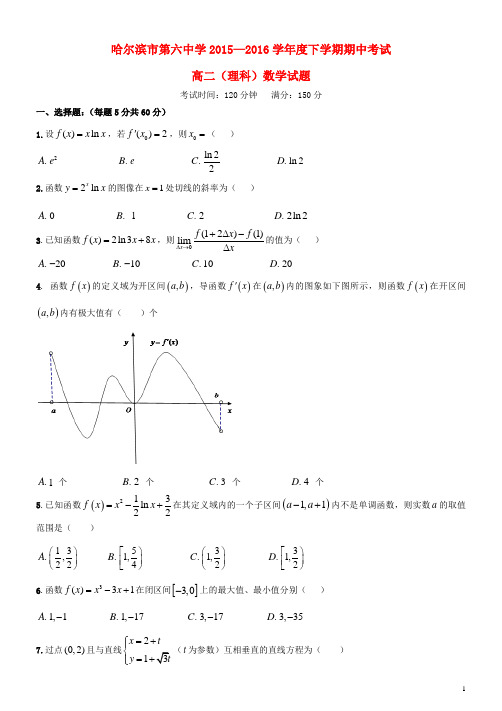
哈尔滨市第六中学2015—2016学年度下学期期中考试高二(理科)数学试题考试时间:120分钟 满分:150分一、选择题:(每题5分共60分)1.设()ln f x x x =,若0()2f x '=,则0x =( ).A 2e .B e .C ln 22.D ln 2 2.函数2ln xy x =的图像在1x =处切线的斜率为( ).A 0 .B 1 .C 2 .D 2ln 23.已知函数()2ln 38f x x x =+,则0(12)(1)limx f x f x∆→+∆-∆的值为( ).A 20- .B 10- .C 10 .D 204. 函数()f x 的定义域为开区间(),a b ,导函数()f x '在(),a b 内的图象如下图所示,则函数()f x 在开区间(),a b 内有极大值有( )个。
.A 1 个 .B 2 个 .C 3 个 .D 4 个5.已知函数()213ln 22f x x x =-+在其定义域内的一个子区间()1,1a a -+内不是单调函数,则实数a 的取值范围是( ).A 13,22⎛⎫ ⎪⎝⎭ .B 51,4⎡⎫⎪⎢⎣⎭ .C 31,2⎛⎫ ⎪⎝⎭ .D 31,2⎡⎫⎪⎢⎣⎭6.函数3()31f x x x =-+在闭区间[]3,0-上的最大值、最小值分别( ).A 1,1- .B 1,17- .C 3,17- .D 3,35-7.过点(0,2)且与直线2x t =+⎧⎪⎨(t 为参数)互相垂直的直线方程为( ).A 2x y t ⎧=⎪⎨=+⎪⎩ .B 2x y t ⎧=⎪⎨=+⎪⎩ .C 2x y t ⎧=⎪⎨=-⎪⎩ .D 2x y t⎧=⎪⎨=⎪⎩ 8.由曲线3y x = 与直线4y x = 所围成的平面图形的面积为( ).A 4 .B 8 .C 12 D .169.在极坐标系中,直线l 的方程为224sin =⎪⎭⎫⎝⎛+πθρ,则点⎪⎭⎫ ⎝⎛43,2πA 到直线l 的距离为( ) .A 22 .B 2 .C 222-.D 222+ 10. 设函数()f x '是函数))((R x x f ∈的导函数,1)0(=f ,且3)()(3-'=x f x f ,则)()(4x f x f '>的解集是( )A B C D 11.若曲线21:(0)C y ax a => 与曲线2:xC y e = 存在公切线,则a 有( ).A 最大值28e .B 最大值24e .C 最小值28e .D 最小值24e12.已知函数)()(ln )(2R b x b x x x f ∈-+=.若存在]2,21[∈x ,使得)()(x f x x f '⋅->,则实数b 的取值范围是( ).A (-∞ B C .D (),3-∞二、填空题(每题5分共20分)13.在直角坐标系xOy 中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,设点,A B 分别在曲线13cos :4sin x C y θθ=+⎧⎨=+⎩(θ 为参数)和曲线2:1C ρ=上,则AB 的最小值为 ; 14.函数()ln f x x x =-的单调减区间为 ; 15.函数3411()34f x x x =- 在区间[]3,3-上的极值点为 ; 16.设函数()2x g x e x a =+-(a R ∈,e 为自然对数底数),定义在R 上函数()f x 满足:2()()f x f x x -+=,且当0x <时,()f x x '<,若存在01|()(1)2x x f x f x x ⎧⎫∈+≥-+⎨⎬⎩⎭, 使[]00()g g x x =,则实数a 的取值范围为 。
黑龙江省哈尔滨六中高二数学下学期期中试题 文(含解析

2012-2013学年黑龙江省哈尔滨六中高二(下)期中数学试卷(文科)参考答案与试题解析一、选择题:(每题5分,共60分)1.(5分)(2010•天津)命题“若f(x)是奇函数,则f(﹣x)是奇函数”的否命题是()A.若f(x)是偶函数,则f(﹣x)是偶函数B.若f(x)不是奇函数,则f(﹣x)不是奇函数C.若f(﹣x)是奇函数,则f(x)是奇函数D.若f(﹣x)不是奇函数,则f(x)不是奇函数考点:四种命题.分析:用否命题的定义来判断.解答:解:否命题是同时否定命题的条件结论,故由否命题的定义可知B项是正确的.故选B点评:本题主要考查否命题的概念,注意否命题与命题否定的区别.2.(5分)(2011•福州模拟)若曲线y=x2+ax+b在点(0,b)处的切线方程是x﹣y+1=0,则()A.a=1,b=1 B.a=﹣1,b=1 C.a=1,b=﹣1 D.a=﹣1,b=﹣1考点:导数的几何意义.专题:计算题;数形结合.分析:根据导数的几何意义求出函数y在x=0处的导数,从而求出切线的斜率,建立等量关系求出a,再根据点(0,b)在切线x﹣y+1=0上求出b即可.解答:解:∵y'=2x+a|x=0=a,∵曲线y=x2+ax+b在点(0,b)处的切线方程x﹣y+1=0的斜率为1,∴a=1,又切点在切线x﹣y+1=0,∴0﹣b+1=0∴b=1.故选:A点评:本题考查了导数的几何意思即求曲线上一点处的切线方程,属于基础题.3.(5分)(2012•汕头二模)如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为()A.7.68 B.16.32 C.17.32 D.8.68考点:几何概型.专题:计算题.分析:欲估计出椭圆的面积,可利用概率模拟,只要利用平面图形的面积比求出落在椭圆外的概率即可.解答:解:∵黄豆落在椭圆外的概率为:即:解得:S=16.32.故选B.点评:本题考查几何概型.如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,称为几何概型.4.(5分)(2010•四川)一个单位有职工800人,期中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是()A.12,24,15,9 B.9,12,12,7 C.8,15,12,5 D.8,16,10,6考点:分层抽样方法.分析:先求得比例,然后各层的总人数乘上这个比例,即得到样本中各层的人数.解答:解:因为=,故各层中依次抽取的人数分别是=8,=16,=10,=6,故选D.点评:本题主要考查分层抽样方法.5.(5分)(2008•福建)如果函数y=f(x)的图象如图,那么导函数y=f′(x)的图象可能是()A.B.C.D.考点:函数的单调性与导数的关系.专题:压轴题.分析:由y=f(x)的图象得函数的单调性,从而得导函数的正负.解答:解:由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负,故选A.点评:导数的正负决定函数的单调性.6.(5分)(2007•海南)曲线y=e x在点(2,e2)处的切线与坐标轴所围三角形的面积为()A.e2B.2e2C.e2D.考点:利用导数研究曲线上某点切线方程.专题:计算题.分析:欲求切线与坐标轴所围三角形的面积的大小,只须求出其斜率得到切线的方程即可,故先利用导数求出在x=4处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.解答:解:∵点(2,e2)在曲线上,∴切线的斜率k=y′|x•2=e x|x•2=e2,∴切线的方程为y﹣e2=e2(x﹣2).即e2x﹣y﹣e2=0.与两坐标轴的交点坐标为(0,﹣e2),(1,0),∴S△=×1×e2=.故选D.点评:本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.7.(5分)(2012•吉林二模)某几何体的三视图如图所示,则其侧面积为()A.B.C.D.考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:从三视图可以推知,几何体是四棱锥,底面是一个直角梯形,一条侧棱垂直底面,易求侧面积.解答:解:几何体是四棱锥,底面是一个直角梯形,一条侧棱垂直底面.且底面直角梯形的上底为1,下底为2,高为1,四棱锥的高为1.四个侧面都是直角三角形,其中△PBC的高PB===故其侧面积是S=S△PAB+S△PBC+S△PCD+S△PAD==故选A点本题考查三视图求面积、体积,考查空间想象能力,是中档题.评:8.(5分)(2010•北京)从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是()A.B.C.D.考点:等可能事件的概率.专题:计算题.分析:由题意知本题是一个古典概型,试验包含的所有事件根据分步计数原理知共有5×3种结果,而满足条件的事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果.解答:解:由题意知本题是一个古典概型,∵试验包含的所有事件根据分步计数原理知共有5×3种结果,而满足条件的事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果,∴由古典概型公式得到P==,故选D.点评:本题考查离散型随机变量的概率问题,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.9.(5分)(2012•辽宁)在长为12cm的线段AB上任取一点C.现做一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小于32cm2的概率为()A.B.C.D.考点:几何概型.专题:计算题.分析:设AC=x,则0<x<12,若矩形面积为小于32,则x>8或x<4,从而利用几何概型概率计算公式,所求概率为长度之比解答:解:设AC=x,则BC=12﹣x,0<x<12若矩形面积S=x(12﹣x)<32,则x>8或x<4即将线段AB三等分,当C位于首段和尾段时,矩形面积小于32,故该矩形面积小于32cm2的概率为P==故选 C点评:本题主要考查了几何概型概率的意义及其计算方法,将此概率转化为长度之比是解决本题的关键,属基础题10.(5分)(2008•广东)设a∈R,若函数y=e x+ax,x∈R,有大于零的极值点,则()A.a<﹣1 B.a>﹣1 C.D.考点:利用导数研究函数的极值.专题:压轴题;数形结合.分析:先对函数进行求导令导函数等于0,原函数有大于0的极值故导函数等于0有大于0的根,然后转化为两个函数观察交点,确定a的范围.解答:解:∵y=e x+ax,∴y'=e x+a.由题意知e x+a=0有大于0的实根,令y1=e x,y2=﹣a,则两曲线交点在第一象限,结合图象易得﹣a>1⇒a<﹣1,故选A.点评:本题主要考查函数的极值与其导函数的关系,即函数取到极值时一定有其导函数等于0,但反之不一定成立.11.(5分)已知正棱锥S﹣ABC的底面边长为4,高为3,在正棱锥内任取一点P,使得V S﹣ABC的概率是()A.B.C.D.考点:几何概型.专题:计算题.分析:本题利用几何概型解决.根据题中条件:“V S﹣ABC”得点P所在的区域为棱锥的中截面以下,结合大棱锥与小棱锥的体积比即可求得结果.解答:解:由题意知,当点P在三棱锥的中截面以下时,满足:V S﹣ABC故使得V S﹣ABC的概率:==.故选B.点评:本题主要考查了几何概型划,以及空间想象能力,属于基础题.简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型,解本题的关键是理解体积比是相似比的平方.12.(5分)若f(x)=x2﹣2x﹣4lnx,不等式f′(x)>0的解集为p,关于x的不等式x2+(a﹣1)x﹣a>0的解集记为q,已知p是q的充分不必要条件,则实数a的取值范围是()A.(﹣2,﹣1] B.[﹣2,﹣1] C.∅D.[﹣2,+∞)考点:必要条件、充分条件与充要条件的判断;一元二次不等式的解法.专题:不等式的解法及应用.分析:分别求解解集p与q,由p是q的充分不必要条件可知p是q的真子集,利用集合的包含关系可以求得.解答:解:不等式f′(x)>0即2x﹣2﹣>0(其中x>0)的解集p为(2,+∞),不等式x2+(a﹣1)x﹣a>0可化为(x﹣1)(x+a)>0,由于p是q的充分不必要条件可知p是q的真子集,①当﹣a<1时,不等式x2+(a﹣1)x﹣a>0的解集为(﹣∞,﹣a)∪(1,+∞),此时满足题意;②当﹣a=1时,不等式x2+(a﹣1)x﹣a>0的解集为(﹣∞,1)∪(1,+∞),此时满足题意;③当﹣a>1时,不等式x2+(a﹣1)x﹣a>0的解集为(﹣∞,1)∪(﹣a,+∞),必须有﹣a≤2,即﹣1<a≤﹣2.∴实数a的取值范围是[﹣2,+∞).故选D.点评:本题重点考查四种条件,考查集合之间的包含关系,利用集合的包含关系解决有关四种条件问题是一种行之有效的方法,注意细细体会.二、填空题:(每题5分,共20分)13.(5分)(2010•辽宁)三张卡片上分别写上字母E、E、B,将三张卡片随机地排成一行,恰好排成英文单词BEE的概率为.考点:排列及排列数公式.专题:计算题.分析:由题意知本题是一个古典概型,试验包含的所有事件可以列举出三张卡片随机地排成一行,而满足条件的只有一种,根据概率公式得到结果.解答:解:由题意知本题是一个古典概型,∵试验包含的所有事件可以列举出三张卡片随机地排成一行,共有三种情况:BEE,EBE,EEB,而满足条件的只有一种,∴概率为:.故答案为:点评:字母排列问题是概率中经常出现的题目,一般可以列举出要求的事件,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的可以借助于排列数和组合数来表示.14.(5分)(2010•安徽)某地有居民100000户,其中普通家庭99000户,高收入家庭1000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取100户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收人家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 5.7 %.考点:分层抽样方法.专题:压轴题.分析:首先根据拥有3套或3套以上住房的家庭所占的比例,得出100 000户中居民中拥有3套或3套以上住房的户数,它除以100 000得到的值,为该地拥有3套或3套以上住房的家庭所占比例的合理估计.解答:解:该地拥有3套或3套以上住房的家庭可以估计有:99000×+1000×=5700户,所以所占比例的合理估计是5700÷100000=5.7%.点评:本题分层抽样问题的运用,首先要注意分层抽样的方法与特点,进而根据合理估计的计算方法,得到答案.15.(5分)函数的单调递增区间是(0,).考点:利用导数研究函数的单调性.专题:计算题.分析:依题意,利用f′(x)=﹣>0即可求得f(x)=的单调递增区间.解答:解:∵f′(x)=﹣,∴由f′(x)=﹣>0得:lnx+1<0,∴x<,又x>0,∴0<x<.故答案为:(0,).点评:本题考查利用导数研究函数的单调性,求得f′(x)=﹣是关键,考查运算与推理能力,属于中档题.16.(5分)两人相约在7:30到8:00之间相遇,早到者应等迟到者10分钟方可离去,如果两人出发是各自独立的,在7:30到8:00之间的任何时刻是等可能的,问两人相遇的可能性有多大.考点:几何概型.专题:概率与统计.分析:由题意知本题是一个几何概型,视30分钟为一个单位.试验包含的所有事件是Ω={(x,y)|0<x<1,0<y<1},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|0<x<1,0<y<1,|x﹣y|<},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.解答:解:视30分钟为一个单位1.设两人到达约会地点的时刻分别为x,y,依题意,必须满足|x﹣y|≤才能相遇.我们把他们到达的时刻分别作为横坐标和纵坐标,于是两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内,如图所示,而相遇现象则发生在阴影区域G内,即甲、乙两人的到达时刻(x,y)满足|x﹣y|≤,所以两人相遇的概率为区域G与区域Ⅰ的面积之比:P===.故答案为:.点评:本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.三、解答题:17.(12分)(2013•潮州二模)口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(1)甲、乙按以上规则各摸一个球,求事件“甲赢且编号的和为6”发生的概率;(2)这种游戏规则公平吗?试说明理由.考点:等可能事件的概率.专题:计算题.分析:(1)由题意知本题是一个等可能事件的概率,试验发生包含的事件是甲、乙二人取出的数字共有5×5等可能的结果,满足条件的事件包含的基本事件可以列举出,根据概率公式得到结果.(2)这种游戏规则不公平,甲胜即两数字之和为偶数所包含的基本事件数为13个,做出甲胜的概率,根据对立事件的概率做出乙胜的概率,两者相比较得到结论.解答:解:(1)由题意知本题是一个等可能事件的概率,设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为(1,5),(2,4)(3,3),(4,2),(5,1)共5个.又甲、乙二人取出的数字共有5×5=25等可能的结果,∴.即编号的和为6的概率为.(2)这种游戏规则不公平.设甲胜为事件B,乙胜为事件C,则甲胜即两数字之和为偶数所包含的基本事件数为13个:(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).∴甲胜的概率P(B)=,从而乙胜的概率P(C)=1﹣=.由于P(B)≠P(C),∴这种游戏规则不公平.点评:本题主要考查古典概型,解决古典概型问题时最有效的工具是列举,大纲中要求能通过列举解决古典概型问题,也有一些题目需要借助于排列组合来计数.18.(12分)如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,,M是线段EF的中点.(1)证明:CM∥平面DFB(2)求异面直线AM与DE所成的角的余弦值.考点:直线与平面平行的判定;异面直线及其所成的角.专题:空间位置关系与距离.分析:(1)设正方形的对角线AC和BD相交于点O,由条件证明MF和CO平行且相等,四边形COFM为平行四边形,故CM∥OF,再由直线和平面平行的判定定理证得 CM∥平面DFB.(2)建立空间直角坐标系,求得点C、点A、点E、,点D、点M的坐标,可得和的坐标,以及||、||和的值.再利用两个向量的夹角公式求得、的夹角θ 的余弦值,再取绝对值,即得所求.解答:解:(1)设正方形的对角线AC和BD相交于点O,∵M为的中点,ACEF为矩形,故MF 和CO平行且相等,故四边形COFM为平行四边形,故CM∥OF,而OF⊂平面DFB,CM不在平面DFB内,∴CM∥平面DFB.(2)以点C为原点,CD为x轴,CB为y轴,CE为z轴,建立空间直角坐标系,则点C(0,0),点A(,,0),点E(0,0,1),点D(,0,0),点M(,,1),∴=(﹣,﹣,1),=(﹣,0,1),||=,||=,=1+0+1=2.设、的夹角为θ,cosθ===,故异面直线AM与DE所成的角的余弦值为.点评:本题主要考查直线和平面平行的判定定理的应用,求异面直线所成的角的余弦值,两个向量的夹角公式的应用,体现了转化的数学思想,属于中档题.19.(12分)(2012•东莞一模)某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.组号分组频数频率第1组[160,165) 5 0.050第2组[165,170)①0.350第3组[170,175) 30 ②第4组[175,180) 20 0.200第5组[180,185) 10 0.100合计100 1.00(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?考点:频率分布直方图.专题:计算题;作图题.分析:(1)由频率的意义可知,每小组的频率=,由此计算填表中空格;(2)先算出第3、4、5组每组学生数,分层抽样得按比例确定每小组抽取个体的个数,求得第3、4、5组每组各抽取多少名学生进入第二轮面试.(3)根据概率公式计算,事件“六位同学中抽两位同学”有15种可能,而且这些事件的可能性相同,其中事件“第4组的2位同学为B1,B2至少有一位同学入选”可能种数是9,那么即可求得事件A的概率.解答:解:(1)由题可知,第2组的频数为0.35×100=35人,(1分)第3组的频率为,(2分)频率分布直方图如图所示:(5分)(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为:第3组:人,(6分)第4组:人,(7分)第5组:人,(8分)所以第3、4、5组分别抽取3人、2人、1人.(3)设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,则从六位同学中抽两位同学有15种可能如下:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),(10分)其中第4组的2位同学为B1,B2至少有一位同学入选的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(B1,B2),(A3,B2),(B1,C1),(B2,C1),9中可能,(12分)所以其中第4组的2位同学为B1,B2至少有一位同学入选的概率为.(15分)点评:此题考查了对频数分布直方图的掌握情况,考查的是概率的求法.如果一个事件有n 种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.20.(12分)(2012•道里区三模)如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.(Ⅰ)求证:平面AEC⊥平面PDB;(Ⅱ)当,且直线AE与平面PBD成角为45°时,确定点E的位置,即求出的值.考点:用空间向量求直线与平面的夹角;平面与平面垂直的判定;直线与平面所成的角.专题:综合题;空间位置关系与距离;空间向量及应用.分析:(Ⅰ)设AC交BD于O,连接OE,由PD⊥平面ABCD,知PD⊥AC,由BD⊥AC,知AC⊥平面PBD,由此能够证明平面ACE⊥平面PBD.(Ⅱ)法一:由平面ACE⊥平面PBD,知AO⊥PBD,由直线AE与平面PBD成角为45°,知∠AEO=45°,由此能够求出.法二:以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,利用向量法能够求出的值.解答:解:(Ⅰ)设AC交BD于O,连接OE,∵PD⊥平面ABCD,∴PD⊥AC,∵BD⊥AC,∴AC⊥平面PBD,又∵AC⊆平面AEC,∴平面ACE⊥平面PBD.…(6分)(Ⅱ)(方法一)∵平面ACE⊥平面PBD,∴AO⊥PBD,∵直线AE与平面PBD成角为45°,∴∠AEO=45°,设,则OE=1,∴.…(12分)(方法二)以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,如图平面BDE法向量为,设,,,令,则,,得或λ=1(舍),∴.…(12分)点评:本题考查平面与平面垂直的证明,考查点的位置的确定.解题时要认真审题,仔细解答,注意空间思维能力的培养.21.(12分)已知函数.,其中a,b∈R(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=3x+1,求函数f(x)的解析式;(2)讨论函数f(x)的单调区间.考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.专题:导数的综合应用.分析:(1)先求函数的导数,再由导数的几何意义和切线方程列方程f′(2)=3,再由切点在切线上和曲线上列方程,分别求出a和b;(2)由解析式求出函数的定义域,根据导数的表达式对a进行分类:a≥0和a<0,分别求出f'(x)<0和f'(x)>0的解集,再表示成区间的形式.解答:解:(1)由题意得=,∵在点P(2,f(2))处的切线方程为y=3x+1,∴f′(2)==3,且f(2)=7=,解得,a=﹣16,b=17,故函数f(x)的解析式:,(2)函数f(x)的定义域为(﹣∞,0)∪(0,+∞),且=,当a≥0时,恒有f'(x)≤0,f(x)的单调递减区间为(﹣∞,0),(0,+∞);当a<0时,令f'(x)=0,解得x=,当x>或x<﹣时,f'(x)<0;当﹣<x<且x≠0时,f'(x)>0,∴f(x)单调递减区间为(﹣∞,﹣),(,+∞),单调递增区间为(﹣,0),(0,),综上得,当a≥0时,函数的f(x)的减区间为(﹣∞,0),(0,+∞);当a<0时,减区间为(﹣∞,﹣),(,+∞),增区间为(﹣,0),0,).点评:本题考查了导数与函数的单调性关系,以及导数的几何意义、切点在曲线上和切线上的应用等,考查了分类讨论思想.22.(12分)已知函数f(x)=x2﹣(2a+1)x+alnx(1)当a=1时,求函数f(x)的单调增区间;(2)当时,求函数f(x)在区间[1,e]上的最小值.考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性.专题:导数的综合应用.分析:(1)先求出导函数,根据x=1时f(x)取得极值求出a=2;再令导函数大于0求出增区间,导函数小于0求出减区间即可;(2)先求出导函数f'(x),然后讨论a研究函数在[1,e]上的单调性,将f(x)的各极值与其端点的函数值比较,其中最小的一个就是最小值.解答:解:(1)当a=1时,f(x)=x2﹣3x+lnx,令,解得x>1或.则函数f(x)的单调增区间为(2)f(x)=x2﹣(2a+1)x+alnx,令①当,x∈[1,e],f'(x)>0,f(x)单调增.f(x)min=g(1)=﹣2a.②当1<a<e,x∈(1,a),f'(x)<0,f(x)单调减.,x∈(a,e),f'(x)>0,f(x)单调增.③当a≥e,x∈[1,e],f'(x)<0,f(x)单调减,故函数f(x)在区间[1,e]上的最小值点评:本题主要考查了利用导数研究函数的单调性,以及利用导数求闭区间上函数的最值,属于中档题.。
黑龙江省哈六中高二数学下学期期中试题 文

满分150分 时间120分钟一、选择题:(每题5分,共60分)1.命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是( )A .若f(x) 是偶函数,则f(-x)是偶函数 B.若f(x)不是奇函数,则f(-x)不是奇函数 C.若f(-x)是奇函数,则f(x)是奇函数 D.若f(-x)不是奇函数,则f(x)不是奇函数 2.若曲线2y x ax b =++在点(0,)b 处的切线方程是10x y -+=,则( ) A.1,1a b == B.1,1a b =-= C.1,1a b ==- D.1,1a b =-=- 3.如右图所示,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆, 数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( )A .8.68B .16.32C .17.32D .7.684.一个单位有职工800人,期中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( ) A.12,24,15,9 B.9,12,12,7 C. 8,16,10,6 D. 8,15,12,55. 如果函数()y f x =的图象如左图,那么导函数()y f x '=的图象可能是( )6. 曲线xy e =在点2(2)e ,处的切线与坐标轴所围三角形的面积为( )A .294eB .22eC .2eD .22e7.某几何体的三视图如右图所示,则其侧面积为( )A .3+2+62 B .2+3+62 C .6+2+32 D .3+228.从{1,2,3,4,5}中随机选取一个数为a ,从{1,2,3}中随机选取一个数为b ,则a b >的概率是( ) A.45 B.35C.25 D.159.在长为cm 12的线段AB 上任取一点C 现作一矩形,领边长分别等于线段CB AC ,的长,则该矩形面积小于232cm 的概率为( ) A .16B .13 C .23 D .4510.设a R ∈,若函数xy e ax =+,x R ∈,有大于零的极值点,则( ) A.1a <- B.1a >- C.1a e <- D.1a e>-11.已知正三棱锥ABC S -的底面边长为4,高为3,在正三棱锥内任取一点P ,使得ABC S ABC P V V --<21的概率为( ) A .87B .43C .21D .4112.若()224ln f x x x x =--,不等式()'0fx >的解集为p ,关于x 的不等式2(1)0x a x a +--> 的解集记为q ,已知p 是q 的充分不必要条件,则实数a 的取值范围是( )A .(]2,1--B .[]2,1-- C. φ D. [)2,-+∞二、填空题:( 每题5分,共20分 )13.三张卡片上分别写上字母E 、E 、B ,将三张卡片随机地排成一行,恰好排成英文单词BEE的概率为 .14.某地有居民100000户,其中普通家庭99000户,高收入家庭1000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取l00户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收人家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 . 15.函数xx x f ln 1)(=的单调递增区间是 . 16.两人相约在7:30到8:00之间相遇,早到者应等迟到者10分钟方可离去,如果两人出发是各自独立的,在7:30到8:00之间的任何时刻是等可能的,问两人相遇的可能性有多大 .MFDCBEA三、解答题: 17.(本小题满分12分)一个口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(Ⅰ)求甲赢且编号的和为6的事件发生的概率; (Ⅱ)这种游戏规则公平吗?试用概率说明理由. 18.(本小题满分12分)如图所示,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,,1,2==AF AB M 是线段EF 的中点。
哈六中-高二数学下学期期末试卷文科含答案

哈六中2014-2015高二数学下学期期末试卷(文科含答案)哈六中2014-2015高二数学下学期期末试卷(文科含答案)第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.1.设集合=,,为虚数单位,∈,则为()A.(0,1)B.(0,1]C.[0,1)D.[0,1]2.对于向量、、和实数,下列命题中真命题是()A.若,则B.若,则或C.若,则D.若,则或3.已知是等差数列,,其前10项和,则其公差()A.B.C.D.4.已知=2,=3,=,则向量与向量的夹角是()A.B.C.D.5.已知正项等比数列的前项和为,若,则()A.9B.C.18D.396.函数(其中)的图象如图所示,为了得到的图象,只需把的图象上所有点()A.向右平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向左平移个单位长度7.若函数在区间内单调递增,则可以是()A.B.C.D.8.已知向量a=(1,k),b=(2,2),且a+b与a共线,那么ab的值为()A.4B.3C.2D.19.中,D是边AC上的点,且AB=AD,2AB=BD,BC=2BD,则()A.B.C.D.10.已知函数,若,则实数的取值范围是()A.B.C.D.11.已知P是边长为的正三角形ABC的边BC上的动点,则()A.最大值为18B.是定值24C.最小值为20D.与P的位置有关12.已知函数,当时,只有一个实数根;当3个相异实根,现给出下列4个命题:①函数有2个极值点;②函数有3个极值点;③,有一个相同的实根;④和有一个相同的实根;其中正确命题的个数是()A.1B.2C.3D.4第Ⅱ卷(非选择题共60分)二、填空题(本大题共4小题,每小题5分,共20分.) 13.已知,则14.已知为奇函数,,则__________.15.数列的通项公式,其前项和为,则=16.函数的零点个数为个.三、解答题:(本大题共6小题,共70分)17.(本题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系中,以坐标原点为极点,轴非负半轴为极轴建立极坐标系.已知直线过点,斜率为,曲线:.(Ⅰ)写出直线的一个参数方程及曲线的直角坐标方程;(Ⅱ)若直线与曲线交于两点,求的值.18.(本题满分12分)从一批草莓中,随机抽取个,其重量(单位:克)的频率分布表如下:分组(重量)频数(个)已知从个草莓中随机抽取一个,抽到重量在的草莓的概率为.(Ⅰ)求出,的值;(Ⅱ)用分层抽样的方法从重量在和的草莓中共抽取个,再从这个草莓中任取个,求重量在和中各有个的概率.19.(本题满分12分)设是等差数列,是各项都为正数的等比数列,且,,.(Ⅰ)求,的通项公式;(Ⅱ)求数列的前项和.20.(本题满分12分)已知分别为三个内角的对边,.(Ⅰ)求的值;(Ⅱ)若,求的最大值.21.(本小题满分12分)如图:三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=,D是侧棱AA1的中点.(Ⅰ)证明:平面BDC1⊥平面BDC;(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.22.(本题满分12分)已知函数.(Ⅰ)讨论函数在定义域内的极值点的个数;(Ⅱ)若函数在处取得极值,对任意的恒成立,求实数的取值范围.2016届高二下文数期末考试试题答案1-5CDDCA6-10CBADDTE11-12BC13.14.15.16.17.解:(Ⅰ)∵直线过点,斜率为,∴直线的一个参数方程为;∵,∴,即得,∴,∴曲线的直角坐标方程为.(Ⅱ)把代入整理得:,设点对应的参数分别为,则,∴.18.解:(1)依题意可得,,从而得.(2)若采用分层抽样的方法从重量在和的草莓中共抽取5个,则重量在的个数为;记为,,在的个数为;记为,,,从抽出的5个草莓中,任取个共有,,,,,,,,,10种情况.其中符合“重量在和中各有一个”的情况共有,,,,,6种.设事件表示“抽出的5个草莓中,任取个,重量在和中各有一个”,则.答:从抽出的5个草莓中,任取个,重量在和中各有一个的概率为.19.解:设的公差为,的公比为,由题意得,且,.解得,因此,,,①,②由①-②得,则.20.解:(Ⅰ)因为,所以应用正弦定理可得:,而,将其代入上式即可得到:,整理得:,又因为,所以,所以,即,所以或,即或,又因为,所以.(Ⅱ)由(Ⅰ)知,应用正弦定理可得:,所以,所以,所以的最大值为.21.解:(1)证明:由题设可知,,.6分(2)设棱锥的体积为,,又三棱柱的体积为V=1,故平面分棱柱所得两部分的体积比为1:1.12分22.解:(Ⅰ)当时在上恒成立,函数在上单调递减,所以函数在上没有极值点,当时得得,函数在上单调递减,函数在上单调递增,所以函数在时有有极小值,所以当时,函数在上没有极值点,当时,函数在上有一个极值点(Ⅱ)函数在处取得极值,所以,令可得在上递减,在上递增。
黑龙江省哈六中高二数学下学期期中试题 文

哈尔滨市第六中学2013—2014学年度下学期期中考试高二(文科)数学试题考试时间:120分钟 满分:150分一、选择题:(每题5分共60分) 1.下列关于回归分析的说法中错误的是( )A. 回归直线一定过样本中心(y x ,)B. 残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适C. 两个模型中残差平方和越小的模型拟合的效果越好D .甲、乙两个模型的2R 分别约为98.0和80.0,则模型乙的拟合效果更好 2.一个容量为20的样本,数据的分组及各组的频数如下:(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2. 则样本在区间(10,50]上的频率为( )A .0.5B .0.7C .0.25D .0.053.按ABO 血型系统学说,每个人的血型为A ,B ,O ,AB 型四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB 型时,子女的血型一定不是O 型,若某人的血型的O 型,则父母血型的所有可能情况有( )A .12种B .6种C .10种D .9种4.有五条线段长度分别为1,3,5,7,9,从这5条线段中任取3条,则所取3条线段能构成一个锐角三角形的概率为( ) A101 B 103 C 0 D 107 5.设x x x f ln )(=,若2)(0='x f ,则=0x( )A.2e B.e C.22ln D.2ln 6.从装有4粒大小、形状相同,颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率 ( )A.小B.大C.相等D.大小不能确定7.已知实数[]1,9x ∈,执行如右图所示的程序框图,则输出的x 不小于55的概率为 ( )A.58B.38C.23D.13 8.若右面的程序框图输出的S是126,则①应为( )A .5n ≤? B.6n ≤?C .7n ≤? D.8n ≤?(7题图) (8题图)9.设x x f ln )(=,若10<<<<a b c ,则a a f )(,bb f )(,c c f )(的大小关系为 ( )A c c f b b f a a f )()()(>>B a a f b b f c c f )()()(>> C c c f a a f b b f )()()(>> D bb fc c f a a f )()()(>> 10.已知函数ax x x x f ++=2ln 2)(,若曲线)(x f y =存在与直线02=-y x 平行的切线,则实数a 的取值范围是( )A. (,2]-∞-B. (,2)-∞-C. (2,)-+∞D. [2,)-+∞ 11.在一次独立性检验中,有300人按性别和是否色弱分类如下表:由此表计算得统计量2=( ) .(参考公式:22()()()()(()ad bc a b c d K a b a c b d c d -+++=++++))A. 2B. 3C. 2.4D. 3.612.已知)(x f y =在R 上开导,且2)1(=f ,若2)('>x f ,则不等式x x f 2)(>的解集为( )A. )1,(-∞B. ),1(+∞C. )0,(-∞D. ),0(+∞二、填空题(每题5分共20分)13.在区间(0,1)上任意取两个实数a ,b ,则b a +<56的概率为 14.某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某3由表中数据能 .(参考公式:x b y a xnxy x n yx bni ini ii -=--=∑∑==,1221)15.阅读下面的程序,当输入2000x =时,输出的y = .16.已知极坐标系的极点与直角坐标系的原点重合,极轴与x 轴的正半轴重合,直线l 的倾斜角为,参数方程为(t 为参数,),圆C 的极坐标方程为,直线l 与圆C 交于A ,B 两点,则|OA|+|OB|= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈尔滨市第六中学2016届期中考试
高二文科数学试卷
考试说明:本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分, 满分150分,考试时间120分钟.
(1)答题前,考生先将自己的姓名、准考证号码填写清楚;
(2)选择题必须使用2B 铅笔填涂, 非选择题必须使用0.5毫米黑色字迹的签字笔书写, 字体工整, 字迹清楚;
(3)请在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效;
(4)保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀. 第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是
符合题目要求的.
1.已知x 与y 之间的一组数据:
则y 与x 的线性回归方程为ˆy =bx +∧
a 必过
( )
A .点()2,2
B .点()0,5.1
C .点()2,1
D .点()4,5.1
2.下列结论正确的是 ( ) ① 当0a <时,3232()a a =;② 函数102()(2)(37)f x x x =---的定义域是7
{|2}3x x x ≥≠且;
③ ||a (*
,n N n ∈是偶数); ④ 若
1
216,327x y ==
,则7x y +=.
A .①②
B .②③
C .③④
D .②④
3.函数222
)(-=
x x f 的值域为 ( )
A .
)1,(--∞ B .),0()0,1(+∞⋃- C .),1(+∞- D .),0()1,(+∞⋃--∞
4.下列函数中,同时具有性质:①图像过点(0,1); ②在区间)
,0(+∞上
是减函数;
③是偶函数.这样的函数是 ( )
A .13+=x y
B .)2|(|log 2+=x y
C .||)21(x y =
D .|
|2x y = 5.一个几何体的正视图和俯视图如图所示,其中俯视图为边长为
( )
A .6π+
B .4π+
C .63π+ D
.3π
6.双曲线
122=+ky x 的一条渐近线的斜率是2,则k 的值为( ) A .
41
-
B .41
C .4
D .4-
7.根据如图所示的求公约数方法的程序框图,
输入,1813,2146
==n m 则输出的实数m 的值为 ( ) A .36 B .37 C .38 D .39
8.下列说法正确的个数为 ( ) ① “p q ∨为真”是“p q ∧为真”的充分不必要条件;
② m R ∃∈,使2
43
()(1)m
m f x m x
-+=-⋅是幂函数,且在(0,)+∞上递减;
③ 已知点
()
2,1A -在抛物线
()
220y px p =>的准线上,
记其焦点为F ,则直线AF 的斜率等于4-;
④ 命题“2,10x R x x ∃∈++<”的否定是“2
,10x R x x ∀∈++<”;
⑤ 在正三棱锥S ABC -内任取一点P ,使得12P ABC S ABC
V V --<的概率是7
8;
A .1
B . 2
C .3
D .4
9.已知函数()f x 的定义域为[1,4]-,部分对应值如下表,
()f x 的导函数()y f x '=的图象如上图所示.
当12a <<时,函数()y f x a =-的零点的个数为 ( ) A.1 B.2 C.3 D.4
10.已知定义在R 上的奇函数
()
f x 满足
()()
2f x f x +=-,
若
()12
f ->-,
()1
732a f a +-=
-,则实数a 的取值范围为 ( )
A .3,12
⎛⎫-- ⎪⎝⎭ B .()2,1- C .31,2⎛⎫ ⎪⎝⎭ D .()3,1,2⎛⎫-∞+∞ ⎪
⎝⎭ 11.已知)(x f y =是奇函数,当)2,0(∈x 时,)21
( ln )(>-=a ax x x f ,当)0,2(-∈x 时,)
(x f 的最小值为1,则a 的值为 ( )
A .32
B .54
C .1
D .21
12.已知双曲线22
2
21x y a b -=(a >0,b >0)的右焦点为)0,2(F ,设B A ,为双曲线上关于原
点对称
的两点,AF 的中点为BF M ,的中点N ,若原点
O 在以线段MN 为直径的圆上,且直线AB
的斜率为,则双曲线的离心率为 (
)
A
C .2
D .4 第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.将答案填在机读卡上相应的位置. 13.已知集合
{0,1,2}{1,||,1}
a a a a -=--+,则实数a 的值为 ;
14.利用计算机在区间
01(,)上产生两个随机数a 和b , 则方程
2
42b x a x =--
无实根的概率为 ; 15.已知C B A ,,三点在同一球面上,若球心到平面ABC 的距离为1, ︒=∠==60,2,1BAC AC AB , 则球的体积为 ;
16.设函数()f x 是定义在R 上的偶函数,且对任意的R x ∈恒有)
1()1(-=+x f x f ,
已知当
]1,0[∈x 时,1
2)(-=x x f ,有下列命题:
① 2是函数
)
(x f 的周期; ② 函数
)
(x f 在(2,3)上是增函数;
③ 函数)(x f 的最大值是1,最小值是0; ④ 直线2=x 是函数)(x f 图像的一条对称轴 其中所有正确命题的序号是 ;
三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分10分)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系xOy 的原点,极轴为x 轴的非负半轴,两种坐标系中的长度单位
相同;已知曲线C 的极坐标方程为2(cos sin )ρθθ=+的直线l 交y 轴于点
(0,1)E ;
(1)求C 的直角坐标方程,l 的参数方程;
(2)直线l 与曲线C 交于A 、B 两点,求||||EA EB +;
18.(本小题满分12分)
近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽9人,其中女性抽 多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量2
K ,并说明你有多大的把握认为三高疾病
与性别有关? 下面的临界值表供参考:
(参考公式
2
2
()()()()()n ad bc K a b c d a c b d -=
++++,其中n a b c d =+++)
19.(本小题满分12分)
如图,在四棱锥S-ABCD 中,底面ABCD 为菱形, ∠BAD=60°,平面SAD ⊥平面ABCD ,SA=SD ,E ,P ,Q 分别是棱AD ,SC ,AB 的中点. (Ⅰ)求证:PQ ∥平面SAD ;
(Ⅱ)求证:AC ⊥平面SEQ ;
(Ⅲ)如果SA=AB=2,求三棱锥S-ABC 的体积.
20.(本小题满分12分)
已知函数x x f ln )(=,
bx ax x g -=2
)((a 、b 为常数). (1) 求函数)(x f 在点(1,)1(f )处的切线方程;
(2) 当函数g(x)在x=2处取得极值2-,求函数)(x g 的解析式;
(3) 当21
=
a 时,设)()()(x g x f x h +=,若函数)(x h 在定义域上存在单调减区间,
求实数b 的取值范围;
21.(本小题满分12分) 已知函数
()ln f x x ax
=-,其中0a >;
(1)当1a =时,求()f x 在[]1,e 上的最大值;
(2)若1x e ≤≤时,函数()f x 的最大值为4-,求函数()f x 的解析式;
22.(本小题满分12分)
已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,椭圆的短轴端点与双曲线2
212y x -=的焦点重合,过点(4,0)P 且不垂直于x 轴的直线l 与椭圆C 相交于,A B 两点;
(1)求椭圆C 的方程;(2)求OA OB ⋅的取值范围;。
