6.3 向量的减法课件下载
合集下载
向量减法ppt(1) 下载

A
b
b
ab
B “首首相连,尾尾连,
指向被减”
b BA a
BA a b 代数式:OA-OB=BA
作法:
1在平面内任取一点O A
2作OA a,OB b
a
Байду номын сангаас
ab
3则向量BA a b
O
B
b
a
b
•特殊情况
1.共线同向 a
b
ab
OB
A
2.共线反向 a
b
ab
A
OB
思考:|| a | | b ||、| a-b |、| a | | b |的关系 (1)若a、b不共线,则|| a | | b ||| a-b || a | | b |
用 a,b 表示向量AC, DB
D
C
b
解:有向量加法的平行四边形法则,
得
AC a b;
Aa
B
由向量的减法可得,
DB AB AD a b.
例2.已知向量 a,b, c, d, 求作向量 a b, c d.
A
BD
C
bd c
bd
a
a
c
O•
作法:
1.在 平 面 上 任 取 点O, 作OA a, OB b, OC
记作: | AB |
向量是不能比较大小的,但
a向量的模是可| 以a 进|行| b大| 小比较的. 有意义
b
a b
没有意义
3.相等的向量 相等向量:长度相等,方向相同的两个向量。
a
b
记为:a b
与a长度相等,方向相反的向量叫a相反向量,
记为 a
a
( a) a
《向量的加减法》课件

《向量的加减法》PPT课 件
欢迎来到《向量的加减法》课件!在本课程中,我们将深入探讨向量的定义、 加法、减法、平移和线性组合等概念。
1. 概述
向量是一个常见且重要的数学概念,它既可以用于表示物理量,也可以用于 描述几何关系。本节将介绍向量的定义和基本性到一个新的向量。我们将讨论加法的几何意义、计算方法和运算规律。
3. 向量的减法
向量的减法是指将一个向量从另一个向量中减去,从而得到一个新的向量。 我们将探讨减法的几何意义、计算方法和运算规律。
4. 向量的平移
向量的平移是指将一个向量从一个点移动到另一个点,从而得到一个平移后 的向量。我们将研究平移的定义、几何意义和计算方法。
5. 向量的线性组合
向量的线性组合是指用标量乘以向量再相加的运算。我们将介绍线性组合的 定义、概念、计算方法和应用。
6. 例题解析
通过解析一些实例题,我们将加深对向量加减法、平移和线性组合的理解, 并学会如何应用这些概念解决实际问题。
7. 总结
在本课程的总结中,我们将回顾重点概念、整理知识点,并提供学习建议,帮助你更好地掌握向量的加减法。
欢迎来到《向量的加减法》课件!在本课程中,我们将深入探讨向量的定义、 加法、减法、平移和线性组合等概念。
1. 概述
向量是一个常见且重要的数学概念,它既可以用于表示物理量,也可以用于 描述几何关系。本节将介绍向量的定义和基本性到一个新的向量。我们将讨论加法的几何意义、计算方法和运算规律。
3. 向量的减法
向量的减法是指将一个向量从另一个向量中减去,从而得到一个新的向量。 我们将探讨减法的几何意义、计算方法和运算规律。
4. 向量的平移
向量的平移是指将一个向量从一个点移动到另一个点,从而得到一个平移后 的向量。我们将研究平移的定义、几何意义和计算方法。
5. 向量的线性组合
向量的线性组合是指用标量乘以向量再相加的运算。我们将介绍线性组合的 定义、概念、计算方法和应用。
6. 例题解析
通过解析一些实例题,我们将加深对向量加减法、平移和线性组合的理解, 并学会如何应用这些概念解决实际问题。
7. 总结
在本课程的总结中,我们将回顾重点概念、整理知识点,并提供学习建议,帮助你更好地掌握向量的加减法。
向量的加减法课件

题目2
已知向量$overset{longrightarrow}{a} = (2,3)$,$overset{longrightarrow}{b} = ( - 1,2)$,求$overset{longrightarrow}{a} overset{longrightarrow}{b}$。
进阶练习题
题目3
三角形法则的几何解释
向量减法的三角形法则可以理解为两个向量在起点和终点之间形成的闭合三角形,减数向量是三角形的一条边。
向量减法的向量场意义
向量场
向量场是由一组有序的向量所组成的集合,每个向量都有一个起点和一个终点。
向量场中向量的加减法
在向量场中,向量的加减法可以通过将减数的起点移动到被减数的起点来实现,然后按照向量的加法 法则进行计算。
感谢您的观看
THANKS
02 向量加法的几何意义
向量加法的平行四边形法则
总结词
向量加法的平行四边形法则是向量的基本运算法则之一,它 基于平行四边形的性质,将两个向量相加得到一个新的向量 。
详细描述
向量加法的平行四边形法则是通过构造一个平行四边形,其 中两个相邻的边分别表示要相加的向量,然后连接对角线来 表示这两个向量的和。
详细描述
在向量场中,向量加法运算可以看作 是将一个向量从一个点平移到另一个 点,这种平移过程可以用来描述物体 在空间中的运动和力的作用。
03 向量减法的几何意义
向量减法的三角形法则
三角形法则
向量减法可以通过作平行四边形并取对角线来实现,也可以通过连接两个向量的起点,并作与减数平行的向量来 实现。
答案3
$2overset{longrightarrow}{a} + overset{longrightarrow}{b} = (5,5)$
向量的减法运算(课件)高一数学(人教A版2019必修第二册)

经典例题
题型二 利用已知向量表示其他向量
总结 三个技巧 1.搞清楚图形中的相等向量、相反向量、共线向量以及构成三角形的三 个向量之间的关系,确定已知向量与被表示向量的转化渠道. 2.注意综合应用向量加法、减法的几何意义以及向量加法的结合律、交 换律来分析解决问题. 3.注意在封闭图形中利用向量加法的多边形法则.
又|A→D+C→D|=|D→A+D→C|=|D→B|,|C→D-C→B|=|B→D|=|D→B|,∴D 正确;
A 肯定不正确,故选 BCD.
当堂达标
4.已知 A,B,C 为三个不共线的点,P 为△ABC 所在平面内一点,若P→A +P→B =P→C +A→B ,则下列结论正确的是( ) A.点 P 在△ABC 内部 B.点 P 在△ABC 外部
经典例题
题型一 向量加减法法则的应用
例1 化简(A→B-C→D)-(A→C-B→D). 解:方法一(统一成加法) (A→B-C→D)-(A→C-B→D)=A→B-C→D-A→C+B→D=A→B+D→C+C→A+B→D= A→B+B→D+D→C+C→A=A→D+D→A=0. 方法二(利用减法)
(A→B-C→D)-(A→C-B→D)=A→B-C→D-A→C+B→D=(A→B-A→C)-C→D+B→D
课堂小结
知识点: 1.相反向量 2.向量减法 3.|a-b|与|a|,|b|之间的关系 题型: 1. 向量加减法法则的应用 2.利用已知向量表示其他向量 3.向量减法的应用
课后作业
对应课后练习
C.点 P 在直线 AB 上 √D.点 P 在直线 AC 上
解析:因为P→A +P→B =P→C +A→B ,所以P→B -P→C =A→B -P→A , 所以C→B =A→B +A→P ,C→B -A→B =A→P ,即C→A =A→P . 故点 P 在边 AC 所在的直线上.
向量减法PPT课件

04
向量减法的应用
向量减法在物理中的应用
01 速度与加速度
在物理中,向量减法常用于计算速度和加速度。 例如,在平抛运动中,通过向量减法可以计算出 物体在任意时刻的速度和加速度。
02 力的合成与分解
在力学中,向量减法用于计算合力与分力。通过 将多个力向量进行减法运算,可以确定合力的大 小和方向。
03 振动分析
在振动分析中,向量减法用于描述振动位移、速 度和加速度的变化。通过向量减法,可以分析振 动的相位差和振动模式。
向量减法在解析几何中的应用
01 向量模的计算
在解析几何中,向量减法用于计算向量的模长。 通过向量减法,可以得出向量的起点和终点坐标 ,进而计算出向量的长度。
02 向量夹的角度。通过 向量减法,可以计算出两个向量的夹角,进一步 分析向量的方向和关系。
光照计算
在3D渲染中,光照是一个重要的因素。通过向量减法,可 以计算出光线与物体表面的角度和方向,进而确定光照的 强度和颜色。
动画制作
在动画制作中,向量减法用于描述动画帧之间的变化。通 过向量减法,可以计算出动画帧之间的位移、旋转和缩放 ,进而生成平滑的动画效果。
05
练习题
基础练习题
总结词:掌握向量减法的 定义和性质
向量减法的零向量性质
总结词
零向量性质表明,任何向量减去零向量都等于原向量本身。
详细描述
如果向量a减去零向量(即没有任何向量),结果仍然是向量 a本身。在数学表达式上,这可以表示为:a - 0 = a。这一性 质是向量减法的基本定义之一,它确保了任何向量都可以通 过减去零向量来获得其本身。
03
向量减法的运算规则
通过比较向量的各个分量,计算出两个 向量的差值。
6.1.3 《向量的减法》课件人教B版(2019)高中数学必修第二册

解:因为 = − ,||=8,||=5,|||-|||≤| −
|≤||+||,
所以 3≤||≤13,
当与同向时,||=3;
当与反向时,||=13.
所以||的取值范围是[3,13].
探究一
探究二
探究三
当堂检测
延伸探究 2 本例条件不变,求| + |的取值范围.
)
A.菱形
B.任意四边形
C.矩形
D.平行四边形
解析:由题意得| − |=| − |,可得||=| |,又∵ ∥ ,
∴四边形 ABCD 是平行四边形.故选 D.
答案:D
探究一
探究二
探究三
3.化简: + + − − =
当堂检测
.
解析:原式= + + -( + )=0- = .
解:方法一:先作 a-b,再作 a-b-c 即可.
如图①所示,以 A 为起点分别作向量和,使=a,=b.连接
CB,得向量=a-b,再以 C 为起点作向量,使=c,连接 DB,得向
量.则向量即为所求作的向量 a-b-c.
探究一
探究二
探究三
当堂检测
方法二:先作-b,-c,再作 a+(-b)+(-c),如图②.
A.a-b B.b-a
C.b+a D.-a-b
)
解析:根据向量的运算法则,可得 = − =- − =-a-b,故
选 D.
答案:D
探究一
探究二
探究三
当堂检测
2.O 是四边形 ABCD 所在平面上任一点, ∥ ,且| −
|=| − |,则四边形 ABCD 一定为(
(3)零向量的相反向量仍是零向量.
|≤||+||,
所以 3≤||≤13,
当与同向时,||=3;
当与反向时,||=13.
所以||的取值范围是[3,13].
探究一
探究二
探究三
当堂检测
延伸探究 2 本例条件不变,求| + |的取值范围.
)
A.菱形
B.任意四边形
C.矩形
D.平行四边形
解析:由题意得| − |=| − |,可得||=| |,又∵ ∥ ,
∴四边形 ABCD 是平行四边形.故选 D.
答案:D
探究一
探究二
探究三
3.化简: + + − − =
当堂检测
.
解析:原式= + + -( + )=0- = .
解:方法一:先作 a-b,再作 a-b-c 即可.
如图①所示,以 A 为起点分别作向量和,使=a,=b.连接
CB,得向量=a-b,再以 C 为起点作向量,使=c,连接 DB,得向
量.则向量即为所求作的向量 a-b-c.
探究一
探究二
探究三
当堂检测
方法二:先作-b,-c,再作 a+(-b)+(-c),如图②.
A.a-b B.b-a
C.b+a D.-a-b
)
解析:根据向量的运算法则,可得 = − =- − =-a-b,故
选 D.
答案:D
探究一
探究二
探究三
当堂检测
2.O 是四边形 ABCD 所在平面上任一点, ∥ ,且| −
|=| − |,则四边形 ABCD 一定为(
(3)零向量的相反向量仍是零向量.
《向量的加减法》课件

03 向量的数乘
数乘的定义
定义
对于向量$overset{longrightarrow}{a}$ 和实数$k$,数乘 $koverset{longrightarrow}{a}$是一个 向量,其长度为 $|k||overset{longrightarrow}{a}|$,方 向与$overset{longrightarrow}{a}$相同 或相反,取决于$k$的正负。
向量加法的性质
向量加法满足结合律
即$(overset{longrightarrow}{a} + overset{longrightarrow}{b}) + overset{longrightarrow}{c} = overset{longrightarrow}{a} + (overset{longrightarrow}{b} + overset{longrightarrow}{c})$。
谢谢聆听
02
当$k < 0$时,$koverset{longrightarrow}{a}$表示向 量$overset{longrightarrow}{a}$按比例缩小$-k$倍。
03
当$k = 0$时,$0overset{longrightarrow}{a} = mathbf{0}$,即零向量。
数乘的性质
箭头表示法
详细描述
向量通常用带箭头的线段表示,箭头指向代表方向,长度代表大小。
向量的模
总结词
向量的长度
详细描述
向量的模表示向量的长度,记作$|overrightarrow{AB}|$,计算公式为$sqrt{x^2+y^2}$。
02 向量的加法
向量加法的定义
定义
向量加法是指将两个向量首尾相接,以第一个向量的起点为 共同起点,以第二个向量的终点为共同终点,连接第一个向 量的终点与第二个向量的起点的向量。
向量的减法运算(优秀经典公开课课件)

[素养聚焦] 利用向量减法的几何意义,把直观想象、逻辑推理等核心素养体现在解题过 程中.
[规律方法] 1.用向量法解决平面几何问题的步骤 (1)将平面几何问题中的量抽象成向量. (2)化归为向量问题,进行向量运算. (3)将向量问题还原为平面几何问题. 2.用向量法证明四边形为平行四边形的方法和解题关键 (1)利用向量证明线段平行且相等,从而证明四边形为平行四边形,只需证明 对应有向线段所表示的向量相等即可. (2)根据图形灵活应用向量的运算法则,找到向量之间的关系是解决此类问题 的关键.
(1)可以转化为向量的加法来进行,如 a-b,可以先作-b,然后作 a+(-b) 即可.
(2)可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为 连接两个向量的终点,指向被减向量的终点的向量.
[触类旁通] 2.如图,已知向量 a,b,c,求作向量 a-b-c.
解析 在平面内任取一点 O,作向量O→A=a,O→B=b,则向量 a-b=B→A,再 作向量B→C=c,则向量C→A=a-b-c.
2.几何意义: 在平面内任取一点 O,作O→A=a,O→B=b,则向量 a-b=B→A,如图所示.
3.文字叙述:如果把两个向量的__起__点____放在一起,那么这两个向量的差 是以减向量的终点为__起__点____,被减向量的终点为__终__点____的向量.
[基础自测] 1.判断正误(正确的打“√”,错误的打“×”) (1)两个相等向量之差等于 0.( ) (2)两个相反向量之差等于 0.( ) (3)两个向量的差仍是一个向量.( ) (4)向量的减法实质上是向量的加法的逆运算.( ) 答案 (1)√ (2)× (3)√ (4)√
[答案] B
(2)[解析] ∵||A→B|-|A→D||≤|A→B-A→D|≤|A→B|+|A→D|, 且|A→D|=9,|A→B|=6,∴3≤|A→B-A→D|≤15. 当A→D与A→B同向时,|A→B-A→D|=3; 当A→D与A→B反向时,|A→B-A→D|=15. ∴|A→B-A→D|的取值范围为[3,15].
向量的运算向量的减法ppt市公开课一等奖省优质课获奖课件
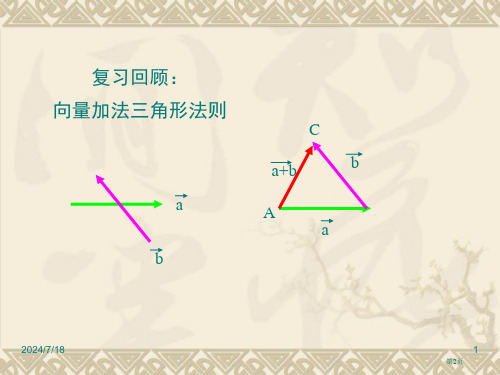
复习回顾: 向量加法三角形法则
a b
C
a+b
b
A a
2024/7/18
1
第2页
一、向量减法定义
1、定义:向量a加上向量b相反向量, 叫a与b差,即a-b=a+(-b)
求两个向量差运算叫向量减法
说明:1、与b长度相等、方向相反向量, 叫做b相反向量
2、零向量相反向量仍是零向量
3、任一向量和它相反向量和是零向量
向量终点字母为终点
2024/7/18
7
第8页
例题2
化简 AB-AC+BD-CD 解:原式:=CB+BD-CD=CD-CD=0
化简OA+OC+BO+CO 解:原式=(OA+BO)+(OC+CO)
=(OA-OB)+0=BA
4/7/18
8
第9页
思索:
已知OA=a,OB=b,且|a|=|b|=4,角 AOB为600, (1)求|a+b|,|a-b| (2)求a+b与a夹角,a-b与a夹角
法则有b+(a-b)=a
即a-b=CB
2024/7/18
4
第5页
例1:
❖如图:已知向量a, b, c, d,求 作
❖向量 a-b,c-d.
bd
a
c
2024/7/18
5
第6页
2024/7/18
结论
a-b B
D
A
d c-d
b
C a
c
O
6
第7页
深入了解
两个向量相减,则表示两个向量 起点字母必须相同(不然无法相 减),这么两个向量差向量是以 减向量终点字母为起点,以被减
a b
C
a+b
b
A a
2024/7/18
1
第2页
一、向量减法定义
1、定义:向量a加上向量b相反向量, 叫a与b差,即a-b=a+(-b)
求两个向量差运算叫向量减法
说明:1、与b长度相等、方向相反向量, 叫做b相反向量
2、零向量相反向量仍是零向量
3、任一向量和它相反向量和是零向量
向量终点字母为终点
2024/7/18
7
第8页
例题2
化简 AB-AC+BD-CD 解:原式:=CB+BD-CD=CD-CD=0
化简OA+OC+BO+CO 解:原式=(OA+BO)+(OC+CO)
=(OA-OB)+0=BA
4/7/18
8
第9页
思索:
已知OA=a,OB=b,且|a|=|b|=4,角 AOB为600, (1)求|a+b|,|a-b| (2)求a+b与a夹角,a-b与a夹角
法则有b+(a-b)=a
即a-b=CB
2024/7/18
4
第5页
例1:
❖如图:已知向量a, b, c, d,求 作
❖向量 a-b,c-d.
bd
a
c
2024/7/18
5
第6页
2024/7/18
结论
a-b B
D
A
d c-d
b
C a
c
O
6
第7页
深入了解
两个向量相减,则表示两个向量 起点字母必须相同(不然无法相 减),这么两个向量差向量是以 减向量终点字母为起点,以被减
向量的减法运算课件-高一数学人教A版(2019)必修第二册

C
a+b-c
c
B
a+b
O
法一:几何意义法
b
a
A
在平面内任取一点O,作 =a, =b,
则 =a+b,再作 =c,
则 =a+b-c.
题型突破
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
O
a+b
B
a+b-c b
-c
a
法二:定义法
在平面内任取一点O,
作=a, =b,则 =a+b,
∴| - |的取值范围为[3,15].
题型突破
多维探究
变式1 将本例(2)的条件改为“||=8,||=5”,求||的取值范围.
因为= - ,||=8,||=5,
|||-|||≤| - |≤||+||,
所以3≤||≤13,
当与同向时,||=3;
(1)转化为向量的加法,如 a-b,可以先作-b,再作 a+(-b).
(2)直接用向量减法的三角形法则,两向量的起点重合,则差向量为
连接两个向量的终点,指向被减向量的终点的向量.
探索新知
同时有二向量和与差,则作平行四边形
例4 如图,平行四边形ABCD,AB=a,AD =b,用a,b表示向量 AC,DB .
a b OA OB BA
(1) 在平面内任取一点 O
A
→
→
(2) 作OA=a,OB= b
→
(3) 连接 BA,则 BA=a-b
注意
ab
a
O
.
b
共起点,连终点,指向被减向量.
B
a-b可以表示为从向
量b的终点指向向量a
的终点,这就是向量
减法的几何意义
a+b-c
c
B
a+b
O
法一:几何意义法
b
a
A
在平面内任取一点O,作 =a, =b,
则 =a+b,再作 =c,
则 =a+b-c.
题型突破
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
O
a+b
B
a+b-c b
-c
a
法二:定义法
在平面内任取一点O,
作=a, =b,则 =a+b,
∴| - |的取值范围为[3,15].
题型突破
多维探究
变式1 将本例(2)的条件改为“||=8,||=5”,求||的取值范围.
因为= - ,||=8,||=5,
|||-|||≤| - |≤||+||,
所以3≤||≤13,
当与同向时,||=3;
(1)转化为向量的加法,如 a-b,可以先作-b,再作 a+(-b).
(2)直接用向量减法的三角形法则,两向量的起点重合,则差向量为
连接两个向量的终点,指向被减向量的终点的向量.
探索新知
同时有二向量和与差,则作平行四边形
例4 如图,平行四边形ABCD,AB=a,AD =b,用a,b表示向量 AC,DB .
a b OA OB BA
(1) 在平面内任取一点 O
A
→
→
(2) 作OA=a,OB= b
→
(3) 连接 BA,则 BA=a-b
注意
ab
a
O
.
b
共起点,连终点,指向被减向量.
B
a-b可以表示为从向
量b的终点指向向量a
的终点,这就是向量
减法的几何意义
6.2.2向量的减法运算PPT课件(人教版)

——本课须掌握的三大问题 1.向量减法的实质是向量加法的逆运算.利用相反向量的定义,-A→B=B→A就 可以把减法转化为加法.即:减去一个向量等于加上这个向量的相反向量.如 a- b=a+(-b).
2.在用三角形法则作向量减法时,要注意“差向量连接两向量的终点,箭头 指向被减数”.解题时要结合图形,准确判断,防止混淆.
水平二:掌握向量的加减运算法则及其几何意义,并能运用它们解决相应的向 量问题.(直观想象)
知识点一 相反向量
[填一填] (1)我们规定,与向量 a 长度相等 , 方向相反 的向量,叫做 a 的相反向量, 记作 -a . (2)-(-a)= a ,a+(-a)=(-a)+ a = 0 . (3)零向量的相反向量仍是 零向量 ,即 0= -0 .
[解] ∵四边形 ACDE 为平行四边形, ∴C→D=A→E=c,B→C=A→C-A→B=b-a, ∴B→D=B→C+C→D=b-a+c, B→E=A→E-A→B=c-a,C→E=A→E-A→C=c-b.
解决这类问题时,要根据图形的几何性质,正确运用向量的加法、减法以及共 线相等向量,要注意向量的方向及运算式中向量之间的关系.当运用三角形法则 时,要注意两个向量起点的位置,当两个向量共起点时,可以考虑向量的减法.,常 用结论:任意一个非零向量一定可以表示为两个不共线向量的和差,即A→M= A→B+B→M以及A→B=N→B-N→AM,N 均是与A→B在同一平面内的任意点.
[变式训练 3] 已知△ABC 是等腰直角三角形,∠ACB =90°,M 是斜边 AB 的中点,C→M=a,C→A=b. 求证:
(1)|a-b|=|a|. (2)|a+(a-b)|=|b|.
证明:在等腰直角三角形 ABC 中,由 M 是斜边 AB 的中点,得|C→M|=|A→M|,|C→A |=|C→B|.
新教材人教b版必修第二册第六章613向量的减法课件

于( )
A.B→A
B.C→D
C.A→C
D.A→D
【解析】选 AB.C→M -B→M -D→B =C→M +M→B +B→D =C→D =B→A .
【补偿训练】 如图所示,已知O→A =a,O→B =b,O→C =c,O→D =d,O→E =e,O→F =f,试用 a,b,c,d,e,f 表示:
(1)A→D -A→B ;(2)A→B +C→F ;(3)B→F -B→D)
A.e1-3e2 C.-3e1+e2
B.e1+3e2 D.-e1+3e2
【解析】选 D.由图可得,a=e1+4e2,b=2e1+e2,所以 a-b=-e1+3e2.
2.(多选题)在平行四边形 ABCD 中,M 为 DC 上任一点,则C→M -B→M -D→B 等
【解析】选 A.如图,设O→A =a,O→B =b,
则 a-b=O→A
-O→B
=B→A
,又 tan
∠OBA=OO→→AB
=
3 3
,所以∠OBA=30°,
且B→A = O→A2+O→B2 =20(km),故 a-b 表示向南偏西 30°方向走 20 km.
【补偿训练】 如图,已知向量 a,b,c,求作向量 a-b-c.
2.本例中的条件“点 B 是该平行四边形 ACDE 外一点”若换为“点 B 是平行四边形 ACDE 内一点”,其他条件不变,其结论又如何呢?
【解析】因为四边形 ACDE 是平行四边形 所以C→D =A→E =c,B→C =A→C -A→B =b-a, B→D =B→C +C→D =b-a+c.
【类题通法】利用已知向量表示其他向量的一个关键及三点注意 (1)一个关键: 一个关键是确定已知向量与被表示向量的转化渠道. (2)三点注意: ①注意相等向量、相反向量、共线向量与构成三角形三向量之间的关系; ②注意应用向量加法、减法的几何意义以及它们的运算律; ③注意在封闭图形中利用多边形法则.
