定积分求曲边图形面积精析
定积分求曲边梯形面积的步骤

定积分求曲边梯形面积1. 概述曲边梯形是一种特殊的梯形,其上底和下底的长度不同,且两个底之间的边是一条曲线。
要计算曲边梯形的面积,可以通过定积分来实现。
本文将介绍使用定积分求解曲边梯形面积的步骤。
2. 基本原理定积分是微积分中的一个重要概念,用于计算曲线下的面积。
在本问题中,我们需要将曲边梯形划分为无穷多个无限小的矩形区域,并计算这些矩形区域的面积之和。
通过取极限,我们可以得到曲边梯形的面积。
3. 求解步骤步骤一:确定曲线方程首先需要确定曲线方程,以便后续计算。
假设曲线为y=f(x),其中f(x)为定义在[a, b]上的函数。
步骤二:确定上下底边界将[a, b]区间划分为n个小区间,每个小区间宽度为Δx。
根据题目给定条件或要求,确定上底和下底的边界。
步骤三:确定高度函数高度函数h(x)定义为上底和下底之间的距离,即h(x) = f(x) - g(x),其中g(x)为下底的方程。
步骤四:计算矩形面积将[a, b]区间划分为n个小区间,每个小区间宽度为Δx。
计算每个小区间内的矩形面积,即ΔA = h(x) * Δx。
步骤五:求和将所有矩形面积ΔA相加,得到曲边梯形的近似面积S:S ≈ Σ(ΔA)步骤六:取极限当n趋向于无穷大时,Δx趋向于0,曲边梯形的近似面积逐渐接近真实面积。
通过取极限得到定积分公式:S = ∫[a, b] h(x) dx4. 实例演示假设我们要计算曲边梯形的面积,其中上底为曲线y = x^2,下底为直线y = 2x,且x的范围为[0, 1]。
步骤一:确定曲线方程曲线方程为y = x^2。
步骤二:确定上下底边界上底为曲线y = x^2,下底为直线y = 2x。
步骤三:确定高度函数高度函数h(x) = f(x) - g(x) = x^2 - 2x。
步骤四:计算矩形面积将区间[0, 1]划分为n个小区间,每个小区间宽度为Δx。
计算每个小区间内的矩形面积ΔA = h(x) * Δx。
步骤五:求和将所有矩形面积ΔA相加,得到近似面积S:S ≈ Σ(ΔA)步骤六:取极限当n趋向于无穷大时,Δx趋向于0,曲边梯形的近似面积逐渐接近真实面积。
定积分在特殊图形面积问题中的应用

% ’ # .’! 得直线% ’ #.’ 解析 ! 解方程组 #! ! %’ 槡
,
! # ! " ! # ! 因此它们所围 # 有且只有两个交点 " # # ! # .’ 成 的图形在直线# ’#及# ’!之间 ! 可以不画图 ! 也 ! +上 两 曲 线 的 上 $ 不考虑在区间 * 下 位 置 关 系! 而 # ! 直接将两函数式相减并取绝对值 ! 然后积分 !
’
! & ! ! ! ! 令# )# 由 题意 ! 则% ’ % ’& . !# ! % )#! /
!
$
#
# $’
#
(
’
’
’ # ! %
槡
! & ! ! 故该椭圆在 第 一 象 限 内 的 # # # # /# ! & . !# " /
点评 ! 实际上 ! 图"中阴影部分的面积除了可 以用 ( 补 )的方法 " 求和 #来计算之外 ! 还可以用 ( 割)
!
!
出直线 % ’ # .’! 曲线 % ’ 槡 # ! " ! 草图 # 则它们 与 # 轴 所 围 成 的 图 形为图 " 中的阴影部分 ! 故所求面积 A ’
( ’ #
! # 7 #$ 5槡
% !
图" !槡 ! " # . # " ! %
% !
5
!! *槡 # + ! # ." #.’ # ’ 槡# 7 ’ %
! # ! #
的 方法 " 求差 # 来计算 ! 即A ’ ’ !槡 ! # %
% !
( #
! # 7 #. H’H’ ! 5槡
定积分求曲边梯形面积公式

定积分求曲边梯形面积公式定积分求曲边梯形面积的公式是一个较为复杂的问题,它涉及到曲线的函数表达式、积分的概念以及曲线与横轴所围成的面积等知识。
在解答这个问题前,我们先来了解一下什么是定积分。
定积分是微积分中的一个重要概念,它可以用来求函数在某一区间上的面积。
对于一个给定的函数f(x),它在区间[a,b]上的定积分可以表示为:∫[a,b]f(x)dx其中,∫是积分符号,f(x)是被积函数,dx表示积分变量。
定积分的运算过程即求解被积函数在[a,b]区间上与x轴之间的面积。
现在我们来讨论如何使用定积分来求解曲边梯形的面积。
曲边梯形是指在平面内,上底和下底平行,且一边为曲线的梯形。
为简化问题,假设我们要求解的曲边梯形位于x轴上,并且曲线可以用一个函数f(x)表示。
我们将曲边梯形分成无数个微小的矩形条,并将它们的面积加起来,即可得到曲边梯形的面积。
假设曲边梯形的底边长为a,顶边长为b,宽度为dx(即微小矩形条的宽度),则每个微小矩形条的面积可以表示为(a+kb)dx,其中k表示微小矩形条的位置。
将上述微小矩形条的面积加起来,即得到曲边梯形的面积:∫[a,b](a+k(x)b)dx接下来,我们将这个定积分进行求解。
首先将被积函数展开:∫[a,b](a+bk(x))dx = a∫[a,b]dx + b∫[a,b]k(x)dx其中,a∫[a,b]dx表示在[a,b]区间上的积分,由于dx仅与x有关,所以其结果为(a+b)(b-a)。
b∫[a,b]k(x)dx表示曲线所围成的面积,即曲边梯形的面积。
综上所述,曲边梯形的面积可以表示为:面积 = (a+b)(b-a) + b∫[a,b]k(x)dx这就是曲边梯形面积的定积分求解公式。
需要注意的是,该公式仅适用于曲边梯形位于x轴上,且曲线函数f(x)可求解的情况。
对于非x轴上的曲边梯形,可以通过变量换元或者函数变换的方法将其转化为在x轴上的曲边梯形,然后使用上述公式求解。
曲边梯形的面积与定积分

n i 1 i 1 1 Sn S f ( )x ( )2 n n n i 1 i 1 i 1 n ' i n
y
S lim Sn
1 1 1 lim 1 2 n 6 n n 1 . 3 y x2
问题探究 例1.求抛物线y=x2、直线x=1和y=0所围成的
曲边梯形的面积。
(1)分割:将曲边梯形分成 n个小曲边梯形 (2)近似代替 :用小矩形的面积代替小曲边 y 梯形的面积, 于是曲边梯形的面积S近似为:
S S1+ S2 + + Sn
y x2
O
1 n
2 n
k n
n n
x
(1)分割 把区间[0,1]等分成n个小区间:
, 记作 f x dx, a, b 上的 定积分 a
b
n 1
即 f ( x)dx lim
b a
n 1 i 0
0
这里, a与b分别叫做积分下限与积分上限,区间
ba f (i ) xi lim f i . n n i 1
n
a, b 叫做积分区间,函数f x 叫做被积函数, x叫 做积分变量, f x dx叫做被积式.
n
课题:曲边梯形面积
我行 我能 我要成功 我能成功
(4)求极限 当分割无限变细,即 x 0(亦即n )时, 1 2 2 1 1 2 2 [0 1 2 (n 1) ] 3 (n 1)n (2n 1) 3 n n 6 1 1 1 1 (1 )(2 ) 6 n n 3 1 1 所以S ,即所求曲边三角形的 面积为 。 3 3
(2)近似代替 i 1 i 1 2 1 Si f ( )x ( ) n n n (3)求和
三角函数的定积分计算与曲边梯形面积应用

三角函数的定积分计算与曲边梯形面积应用三角函数是数学中的一种重要函数类型,它在物理学、工程学等领域中具有广泛的应用。
本文将介绍三角函数的定积分计算方法,以及如何利用三角函数求解曲边梯形的面积。
一、三角函数的定积分计算定积分是微积分中的一个重要概念,表示曲线下的面积。
对于三角函数来说,我们可以利用其周期性和性质进行定积分的计算。
1. 正弦函数的定积分计算正弦函数的定义域是整个实数集,其周期为2π。
对于正弦函数sin(x),其定积分可以表示为∫sin(x)dx。
利用正弦函数的性质可以得到该定积分的计算方法。
我们知道,正弦函数的一个周期(0到2π)的定积分为0,即∫[0,2π]sin(x)dx = 0。
由于正弦函数是周期性函数,所以在每个周期内的定积分都是相等的。
例如,要计算∫[0, 4π]sin(x)dx,可以将其分解成四个周期内的定积分的和:∫[0, 2π]sin(x)dx + ∫[2π, 4π]sin(x)dx + ∫[4π, 6π]sin(x)dx + ∫[6π,8π]sin(x)dx。
由于每个周期内的定积分都为0,所以该定积分的结果为0。
2. 余弦函数的定积分计算与正弦函数类似,余弦函数也是一个周期性函数,其周期为2π。
对于余弦函数cos(x),其定积分可以表示为∫cos(x)dx。
同样地,余弦函数一个周期(0到2π)内的定积分为0,即∫[0,2π]cos(x)dx = 0。
由于余弦函数也是周期性函数,所以在每个周期内的定积分都是相等的。
例如,要计算∫[0, 6π]cos(x)dx,可以将其分解成三个周期内的定积分的和:∫[0, 2π]cos(x)dx + ∫[2π, 4π]cos(x)dx + ∫[4π, 6π]cos(x)dx。
由于每个周期内的定积分都为0,所以该定积分的结果为0。
二、曲边梯形的面积应用曲边梯形是一个由曲线和直线围成的四边形,其中有一条边为曲线边,其余三条边为直线边。
对于曲边梯形的面积计算,我们可以利用三角函数进行求解。
定积分 曲边三角形的面积

定积分曲边三角形的面积可以通过以下步骤计算:
1. 确定积分上下限:根据所选择的定积分区间,确定积分上下限。
2. 计算曲边三角形的面积:根据定积分的公式,将区间分成多个小区间,每个小区间的长度可以根据需要选择。
每个小区间的左侧边和右侧边的纵坐标之差,就是曲边三角形在相应区间上的高度。
将所有曲边三角形的高度乘以对应的区间长度,再将所有结果相加,即可得到定积分曲边三角形的面积。
以下是一个简单的例子:
假设定积分区间为[a, b],将区间分成n个小区间,每个小区间的长度为Δx。
曲边三角形的面积为S = (b-a) * (Δx/2) * (Δx/√(3)) + √(3) * Δx / 4 * (N-n),其中N为总区间数。
可以参考以下的诗句:
* "独在异乡为异客,每逢佳节倍思亲。
遥知兄弟登高处,遍插茱萸少一人。
"(王维《九月九日忆山东兄弟》)
* "月落乌啼霜满天,江枫渔火对愁眠。
姑苏城外寒山寺,夜半钟声到客船。
"(张继《枫桥夜泊》)
* "中秋谁与共孤光,把盏凄然北望。
"(苏轼《西江月·世事一场大梦》)
这些诗句都表达了错过中秋时的孤独和思乡之情。
定积分的应用求面积与弧长

定积分的应用求面积与弧长定积分是微积分中的一个重要概念,它有着广泛的应用。
其中之一就是通过定积分来求解曲线的面积和弧长。
本文将介绍定积分在求解面积和弧长问题中的应用方法。
一、定积分求解曲线下面积在平面直角坐标系中,考虑曲线y=f(x)与x轴所围成的封闭曲线。
我们希望求解这个封闭曲线所包围的面积。
设x的取值范围为[a, b]。
根据定积分的定义,可以用无穷小的矩形近似曲线下面积。
即将[a, b]区间分成n个小区间,每个小区间的长度为Δx=(b-a)/n,并在每个小区间内选择任意一个点xi。
那么第i个小区间的面积即为f(xi)Δx。
将所有小区间的面积累加起来,即可得到近似曲线下面积的总和:S≈Σf(xi)Δx当n趋向于无穷大时,即Δx趋向于0,这个近似值趋于真实的曲线下面积。
所以我们可以得到曲线下面积的定积分表示:S=∫[a, b] f(x) dx其中,f(x)是曲线的函数,而dx表示对x的积分。
通过计算定积分,就可以得到所求曲线下的面积。
二、定积分求解曲线的弧长另一个常见的问题是求解曲线的弧长。
考虑曲线y=f(x)在[a, b]区间上的一部分弧段。
我们可以将弧段分割成n个小弧段,每个小弧段的长度为Δs。
与求解面积类似,我们可以得到每个小弧段的长度:Δs≈√(Δx)²+(Δy)²其中Δy=f(xi+1)-f(xi),Δx=xi+1-xi。
将所有小弧段的长度累加起来,即可得到对曲线的弧长的近似值:L≈ΣΔs当n趋向于无穷大时,即Δx趋向于0,这个近似值趋于真实的曲线弧长。
所以我们可以得到曲线的弧长的定积分表示:L=∫[a, b] √(1+(f'(x))²) dx其中,f'(x)是曲线函数的导数。
通过计算定积分,就可以得到所求曲线的弧长。
综上所述,定积分的应用可以帮助我们求解曲线的面积与弧长问题。
无论是求解面积还是弧长,都可以通过将曲线划分为无穷小的小区间或小弧段,并使用定积分的方法进行累加求和,最终得到准确的结果。
定积分应用求面积
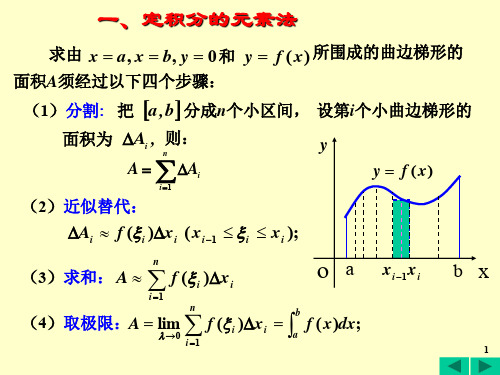
y2 2
4
y3
4
4y 2
6
2
18
8
注:如果取x为积分变量
X型 在 0,8 上任取小区间x, x dx,
则 dA 2 x1xdx
A
8
0
2 x
y穿出
1 x
y穿入
dx
y
dA
o (2,2)
(8,4)
以 f ( x)dx作为 A的近似值。
即: A f ( x)dx
f ( x)dx 叫做面积元素, 记为
dA f ( x)dx
Oa
y f (x)
A
dx
x x dx
b
x
b
(3)写出A的积分表达式,即:A f ( x)dx a
3
一般地,如果某一实际问题中的所求量 U符合下列条件:
以极点O为圆心,以 a为半径的的圆的极坐标方程: r a.
P(r, )
P(r, )
r
O
(a,0) x O (a,0)
x
P(r, )
3
3
O
x
以点(a,0) 为圆心,以 a 为半径的的圆的极坐标方程 r 2a cos
过极点O,且与极轴的夹角为 的直线方程 .
(1)U是与一个变量x的变化区间[a,b]有关的量; (2)U对于区间[a,b]具有可加性;
(3)部分量
U
的近似值可表为
i
f i xi
那么这个量就
可以用积分来表示。
具体步骤是:
(1)确定积分变量,和它的变化区间[a,b]; (2)写出积分元素
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定积分求曲边图形面积精析
曾玲莉 熊明军
定积分是课标教材的新增内容,在数学方面主要包括平面图形的面积及微积分基本定理,而利用定积分求含曲边的平面图形面积问题在平面几何中是难以用常规方法加以解决的。
定积分知识的引入,为此类问题的解决提供了强有力的方法工具,也充分体现了新内容引进的必要性。
一、利用定积分求平面曲边图形面积的步骤及理论
基本步骤:①画图形→②求交点→③写积分→④算面积。
基本理论:①如果函数()x f 和()x g 在],[b a 上可积,并且满足()()],[,b a x x g x f ∈∀≥, 那么介于直线b x a x ==,和曲线()()x g y x f y ==,之间的图形面积可以表示为定积分:
()()dx x g x f S b
a ⎰-=][图形面积. ②如果函数()y ϕ和()y φ在],[
b a 上可积,并且满足()()],[,b a y y y ∈∀≥φϕ, 那么介于直线b y a y ==,和曲线()()y x y x φϕ==,之间的图形面积可以表示为定积分:
()()dy y y S b
a ⎰-=][φϕ图形面积. *注意:在基本步骤中,第③步怎样写出图形面积对应的定积分表达式是重点也是难点,由于定积分值不一定为正,但平面曲边图形的面积总是正值,因此,在这里要注意准确把握基本理论,就是根据所画图形查找是否有一条曲线(直线)在另一条曲线(直线)之上,x 做积分变量不行就换y 做积分变量。
即:
①对于x 做积分变量时,()()],[,b a x x g x f ∈∀≥;
②对于y 做积分变量时,()()],[,b a y y y ∈∀≥φϕ。
二、定积分求平面曲边图形面积的典例精析
例1:求曲线x y sin =与x 轴在区间]2,0[π上所围成阴影部分的面积。
x
解析:①画图形:如上图已知;②求交点:()()()0,2,0,,0,0ππ;③写积分:以x 作为积分变量,在],0[π上,0sin ≥x ,直线0=y 与曲线x y sin =所围成的曲边图形面积:()dx x dx x S ⎰⎰=-=π
π00sin 0sin 图形面积;在]2,[ππ上,x sin 0≥,同理可得图形面积为
()()dx x dx x dx x S ⎰⎰⎰-=-=-=ππππππ
222sin sin sin 0图形面积。
④算面积:求得阴影部分面积:()()()422sin sin sin 00sin 2020
=--=-=-+-=⎰⎰⎰⎰dx x dx x dx x dx x S ππππππ图形面积。
【点评:】本题严格按照文中所列方法步骤解题,条理清晰,形成固定算法,不易出错。
例2:求抛物线x y 22=与直线04=--y x 所围成图形的面积。
解析:①画图形:
②求交点:联立⎩⎨⎧=--=0
422y x x y ,解得交点为()()4,8,2,2-
③写积分:先以x 作为积分变量,在积分]8,0[上不是任意点都满足()4-≥x x f (在]2,0[上04=--y x 没有参与围成曲边图形面积),所以不选择;再以y 作为积分变量,
在]4,2[-上,242y y ≥+,直线04=--y x 与曲线x y 22=所围图形面积:()dy y y S ⎰-⎥⎦⎤⎢⎣
⎡-+=42224。
④算面积:直线04=--y x 与曲线x y 22
=所围曲边图形面积(如上图所示):
()1842161421244223422422=⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛++-=⎥⎦⎤⎢⎣⎡-+=---⎰⎰y y y dy y y dy y y S 图形面积。
【点评:】根据基本理论,为了满足不等关系,适当选取积分变量,会使计算变得简洁。
