【评测练习】指数函数
指数函数测试卷试卷含详解

2
a 2
x
2,
x
2
在
R
上是增函数,则实数
a
的取值范围是
ax1, x 2
()
A. 2 a 4
B. 2 a 4
C. 3 a 4
D. 3 a 4
9.不等式
1 2
x2 8
22 x
0
的解集是(
)
A.[2, 4] B. (, 2] [4, )
C.[4, 2] D. [2,0]
10.设
y1
f
(x)
1 3
ax2
4
x
3
,
(1)若 a 1 ,求 f (x) 的单调区间;(2)若 f (x) 有最大值 3,求 a 的值.
(3)若 f (x) 的值域是 (0, ) ,求 a 的取值范围.
19(本小题满分 12 分).已知二次函数 f x ax2 bx 满足 f x 1 f x x 1 .
12.函数 y ax (a 0,a 1) 在0,2 上的最大值与最小值的差为 2,则 a 的值为( )
A. 2
B. 3
C. 2
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分.)
D. 3
f (x)
13.பைடு நூலகம்数
6 5x x2 x 1
1
4
1 2
x
的定义域为__________.
14.已知当
x
0 时,函数
f
x
2a
1x
a
0, a
1 2
的值总大于
1,则函数
y a2xx2 的单调增区间是______. 15.已知关于 x 的方程 4x 3 2x a 0 有解,则实数 a 的取值范围是_________. 16.若函数 f (x) 2 xa (a R) 满足 f (1 x) f (1 x) ,且 f (x) 在[m, ) 单调递增,
指数函数与幂函数练习题

指数函数与幂函数练习题1. 指数函数练习题(1) 求解方程:2^x = 8(2) 计算:3^(1/2) × 3^(3/2)(3) 简化表达式:4^(x+2) × 2^(3-x) ÷ 8^2x(4) 求函数 y = 2^x 的定义域和值域2. 幂函数练习题(1) 求解方程:x^2 = 16(2) 计算:(2^3)^x - 2^(2x + 2)(3) 简化表达式:(5^3)^(x+2) ÷ (5^4)^x(4) 求函数 y = 3^x 的定义域和值域3. 综合练习题(1) 求解方程:2^x = x^2(2) 计算:(3^2)^(x+1) × 3^(2x-1) - (9^x) ÷ (3^2x)(3) 简化表达式:(4^x)^(1/3) × (8^x)^(1/2)(4) 求函数 y = 5^x - 2 的定义域和值域解答:1. 指数函数练习题(1) 2^x = 8由指数函数与对数函数的互反关系可知,等式两边取对数,得到 x = log2(8) = 3。
(2) 3^(1/2) × 3^(3/2)由指数函数的乘法法则可知,指数相加,底数不变。
因此,3^(1/2) × 3^(3/2) = 3^(1/2 + 3/2) = 3^2 = 9。
(3) 4^(x+2) × 2^(3-x) ÷ 8^2x首先简化指数部分:4^(x+2) × 2^(3-x) ÷ 8^2x = 2^2(x+2) × 2^(3-x) ÷ (2^3)^2x = 2^(2x+4) × 2^(3-x) ÷ 2^(6x) = 2^(2x+4+3-x-6x) = 2^(2-3x)。
简化后的表达式为 2^(2-3x)。
(4) 函数 y = 2^x 的定义域和值域指数函数的定义域为实数集,即 x ∈ℝ。
(完整版)指数函数对数函数专练习题(含答案)
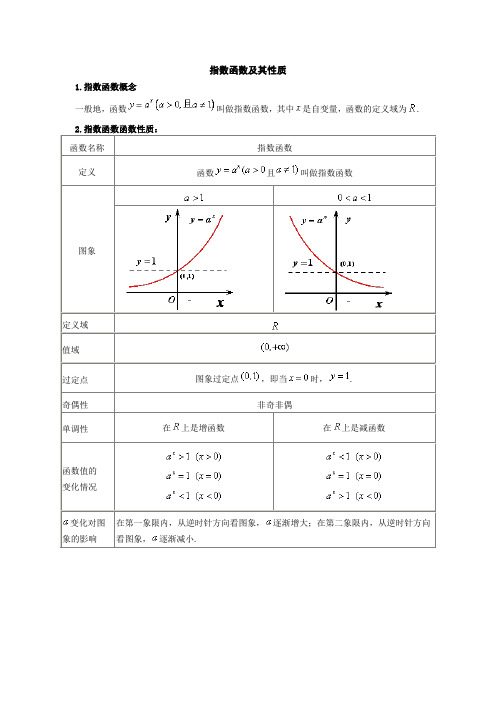
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.函数名称指数函数定义函数且叫做指数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.函数名称对数函数定义函数且叫做对数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.指数函数习题一、选择题1.定义运算a ⊗b =⎩⎪⎨⎪⎧a (a ≤b )b (a >b ),则函数f (x )=1⊗2x的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x)的大小关系是( )A .f (b x )≤f (c x)B .f (b x )≥f (c x)C .f (b x )>f (c x)D .大小关系随x 的不同而不同3.函数y =|2x-1|在区间(k -1,k +1)内不单调,则k 的取值范围是( ) A .(-1,+∞) B .(-∞,1) C .(-1,1) D .(0,2)4.设函数f (x )=ln [(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x-2x-1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( ) A .a >3 B .a ≥3 C .a > 5D .a ≥ 55.已知函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( ) A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x(a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.8.若曲线|y |=2x+1与直线y =b 没有公共点,则b 的取值范围是________.9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题10.求函数y =2的定义域、值域和单调区间.11.(2011·银川模拟)若函数y =a 2x +2a x-1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.1.解析:由a ⊗b =⎩⎪⎨⎪⎧a (a ≤b )b (a >b )得f (x )=1⊗2x=⎩⎨⎧2x(x ≤0),1 (x >0).答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增. 若x ≥0,则3x≥2x≥1,∴f (3x)≥f (2x).若x <0,则3x<2x<1,∴f (3x)>f (2x).∴f (3x)≥f (2x).答案:A3.解析:由于函数y =|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4. 解析:由题意得:A =(1,2),a x-2x>1且a >2,由A ⊆B 知a x-2x>1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3.答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a 8-6>(3-a )×7-3,所以⎩⎨⎧a >13-a >0a 8-6>(3-a )×7-3,解得2<a <3.答案:C6. 解析:f (x)<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =ax在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x+1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x+1与直线y =b没有公共点,则b 应满足的条件是b ∈[-1,1].答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1.∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =2341()2x x --+的值域为[28,1]. 由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =2341()2x x --+[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x=t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a+2=18⇒3a=2⇒a =log 32.(2)此时g (x )=λ·2x-4x,设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立. 由于2x 2+2x 1>20+20=2,所以实数λ的取值范围是λ≤2. 法二:(1)同法一. (2)此时g (x )=λ·2x-4x,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x-ln4·4x=ln2[-2·(2x )2+λ·2x ]≤0成立.设2x=u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立.因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.对数与对数函数同步练习一、选择题1、已知32a =,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、 23a a -2、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或13、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a a a x m n x+==-则等于( )A 、m n +B 、m n -C 、()12m n +D 、()12m n -4、如果方程2lg (lg5lg 7)lg lg5lg 70x x +++=g的两根是,αβ,则αβg 的值是( )A 、lg5lg 7gB 、lg35C 、35D 、351 5、已知732log [log (log )]0x =,那么12x -等于( )A 、13 B C D 6、函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y x =对称7、函数(21)log x y -= )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭UB 、()1,11,2⎛⎫+∞ ⎪⎝⎭UC 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a <,则a 的取值范围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭UB 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭U11、下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+ B 、2log y =C 、21log y x = D 、2log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a +=是( )A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。
指数函数的练习题

指数函数的练习题指数函数是高中数学中的重要内容,它在数学和实际生活中都有广泛的应用。
通过练习题的形式,我们可以更好地理解和掌握指数函数的相关概念和性质。
下面,我将给大家提供一些指数函数的练习题,希望能够对大家的学习有所帮助。
练习题一:简单指数函数计算1. 计算 $2^3$ 和 $(-3)^2$ 的值。
2. 计算 $10^{-2}$ 和 $\left(\frac{1}{2}\right)^{-3}$ 的值。
练习题二:指数函数的性质1. 如果 $a > 1$,那么 $a^x$ 是否是递增函数?为什么?2. 如果 $0 < a < 1$,那么 $a^x$ 是否是递增函数?为什么?3. 如果 $a > 1$,那么 $a^x$ 是否有上界?为什么?练习题三:指数函数的图像1. 画出函数 $y = 2^x$ 和 $y = \left(\frac{1}{2}\right)^x$ 的图像。
2. 画出函数 $y = 3^x$ 和 $y = \left(\frac{1}{3}\right)^x$ 的图像。
练习题四:指数函数的应用1. 假设某种细菌的数量每小时增加50%,现在有1000个细菌,经过多少小时后细菌的数量会达到5000个?2. 一笔投资每年以5%的利率复利计算,如果初始投资为10000元,经过多少年后投资会翻倍?练习题五:指数函数的方程1. 解方程 $2^x = 8$。
2. 解方程 $3^{2x-1} = \frac{1}{9}$。
通过以上的练习题,我们可以加深对指数函数的理解和运用。
在计算指数函数的值时,我们需要注意底数的正负以及指数的大小。
指数函数的性质也是我们需要掌握的重要内容,它们对于理解函数的增减性和图像的变化有着重要的影响。
通过绘制指数函数的图像,我们可以更直观地观察函数的特点和变化趋势。
指数函数在实际生活中也有广泛的应用。
在金融领域中,复利计算常常使用指数函数的概念。
指数函数练习题(包括详细答案)

1.给出以下结论:②na n=|a|(n>1,n∈N*,n为偶数);④假设2x=16,3y=127,那么x+y=7.其中正确的选项是( )A.①②B.②③C.③④D.②④答案 B解析∵2x=16,∴x=4,∵3y=127,∴y=-3.∴x+y=4+(-3)=1,故④错.2.函数y=16-4x的值域是() A.[0,+∞) B.[0,4] C.[0,4) D.(0,4) 答案 C3.函数f(x)=3-x-1的概念域、值域是() A.概念域是R,值域是RB.概念域是R,值域是(0,+∞)C.概念域是R,值域是(-1,+∞)D.以上都不对答案 C解析f(x)=(13)x-1,∵(13)x >0,∴f (x )>-1.4.设y 1=,y 2=,y 3=(12)-,那么( )A .y 3>y 1>y 2B .y 2>y 1>y 3C .y 1>y 2>y 3D .y 1>y 3>y 2答案 D解析 y 1=,y 2=,y 3=,∵y =2x 在概念域内为增函数,∴y 1>y 3>y 2.5.函数f (x )=a x -b 的图像如图,其中a ,b 为常数,那么以下结论正确的选项是( )A .a >1,b <0B .a >1,b >0C .0<a <1,b >0D .0<a <1,b <0答案 D6.(2021·成都二诊)假设函数f (x )=(a +1e x -1)cos x 是奇函数,那么常数a 的值等于( )A .-1B .1C .-12答案 D7.(2021·山东师大附中)集合A ={(x ,y )|y =a },集合B ={(x ,y )|y =b x +1,b >0,b ≠1},假设集合A ∩B 只有一个子集,那么实数a 的取值范围是( )A .(-∞,1)B .(-∞,1]C .(1,+∞)D .R 答案 B8.函数f (x )=3·4x -2x 在x ∈[0,+∞)上的最小值是( )1A.-12B.0C .2D .10答案 C 解析 设t =2x ,∵x ∈[0,+∞),∴t ≥1.∵y =3t 2-t (t ≥1)的最小值为2,∴函数f (x )的最小值为2.9.已知函数f (x )=⎩⎨⎧x -1,x >0,2-|x |+1,x ≤0.假设关于x 的方程f (x )+2x -k =0有且只有两个不同的实根,那么实数k 的取值范围为( )A .(-1,2]B .(-∞,1]∪(2,+∞)C .(0,1]D .[1,+∞) 答案 A解析 在同一坐标系中作出y =f (x )和y =-2x +k 的图像,数形结合即可.10.函数y =2|x |的概念域为[a ,b ],值域为[1,16],当a 转变时,函数b =g (a )的图像能够是( )答案 B解析 函数y =2|x |的图像如图.当a =-4时,0≤b ≤4;当b =4时,-4≤a ≤0.11.假设函数y =(a 2-1)x 在(-∞,+∞)上为减函数,那么实数a 的取值范围是________.答案(-2,-1)∪(1,2)解析函数y=(a2-1)x在(-∞,+∞)上为减函数,那么0<a2-1<1,解得1<a<2或-2<a<-1.12.函数y =a x 在[0,1]上的最大值与最小值的和为3,那么a =________. 答案 2解析 ∵y =a x 在[0,1]上为单调函数,∴a 0+a 1=3,∴a =2.13.(2021·沧州七校联考)假设函数f (x )=a |2x -4|(a >0,a ≠1)知足f (1)=19,那么f (x )的单调递减区间是________.答案 [2,+∞)解析 f (1)=a 2=19,a =13,f (x )=⎩⎪⎨⎪⎧ (13)2x -4,x ≥2,(13)4-2x , x <2.∴单调递减区间为[2,+∞).14.假设0<a <1,0<b <1,且,那么x 的取值范围是________.答案 (3,4)解析 log b (x -3)>0,∴0<x -3<1,∴3<x <4.15.假设函数y =2-x +1+m 的图像不通过第一象限,那么m 的取值范围是______. 答案 m ≤-216.是不是存在实数a ,使函数y =a 2x +2a x -1(a >0且a ≠1)在[-1,1]上的最大值是14?答案 a =3或a =13解析 令t =a x ,那么y =t 2+2t -1.(1)当a >1时,∵x ∈[-1,1],∴a x ∈[1a ,a ],即t ∈[1a ,a ].∴y =t 2+2t -1=(t +1)2-2在[1a ,a ]上是增函数(对称轴t =-1<1a ).∴当t =a 时,y max =(a +1)2-2=14.∴a =3或a =-5.∵a >1,∴a =3.(2)当0<a <1时,t ∈[a ,1a ].∵y =(t +1)2-2在[a ,1a ]上是增函数,∴y max =(1a +1)2-2=14.∴a =13或a =-15.∵0<a <1,∴a =13.综上,a =3或a =13.17.(2020·上海)已知函数f (x )=a ·2x +b ·3x ,其中a ,b 知足a ·b ≠0.(1)假设a ·b >0,判定函数f (x )的单调性;(2)假设a ·b <0,求f (x +1)>f (x )时的x 的取值范围.答案 (1)a >0,b >0时,f (x )增函数;a <0,b <0时,f (x )减函数(2)a <0,b >0时,x >;a >0,b <0时,x <解析 (1)当a >0,b >0时,任意x 1,x 2∈R ,x 1<x 2,∴f (x 1)-f (x 2)<0,∴函数f (x )在R 上是增函数.当a <0,b <0时,同理,函数f (x )在R 上是减函数.(2)f (x +1)-f (x )=a ·2x +2b ·3x >0.当a <0,b >0时,⎝ ⎛⎭⎪⎫32x >-a 2b ,那么x >; 当a >0,b <0时,⎝ ⎛⎭⎪⎫32x <-a 2b ,那么x <. 18.已知函数f (x )=-2x2x +1. (1)用概念证明函数f (x )在(-∞,+∞)上为减函数;(2)假设x ∈[1,2],求函数f (x )的值域;(3)假设g (x )=a 2+f (x ),且当x ∈[1,2]时g (x )≥0恒成立,求实数a 的取值范围.45,-23](3)a≥85答案(1)略(2)[-(2)∵f (x )在(-∞,+∞)上为减函数,∴f (x )的值域为[-45,-23]. (3)当x ∈[1,2]时,g (x )∈[a 2-45,a 2-23].∵g (x )≥0在x ∈[1,2]上恒成立, ∴a 2-45≥0,∴a ≥85.。
指数函数练习题

指数函数练习题一、选择题1. 下列函数中,哪一个函数是指数函数?A. y = 2xB. y = x^2C. y = 3^xD. y = log2xA. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 若指数函数f(x) = 2^x的图象向右平移1个单位,得到新函数g(x),则g(x)的表达式为?A. g(x) = 2^(x+1)B. g(x) = 2^(x1)C. g(x) = 2^x + 1D. g(x) = 2^x 1二、填空题1. 指数函数的一般形式为______,其中底数a满足______。
2. 若f(x) = 3^x,则f(0) =______,f(1) =______。
3. 已知指数函数f(x) = a^x(a > 0且a ≠ 1)的图象过点(2,9),则a =______。
三、解答题1. 判断下列函数是否为指数函数,并说明理由:(1)y = 5^(2x)(2)y = (1/2)^x(3)y = 4^x + 12. 已知指数函数f(x) = 2^x,求f(x)在x = 1处的切线方程。
3. 讨论指数函数f(x) = a^x(a > 0且a ≠ 1)的单调性,并说明理由。
4. 已知指数函数f(x) = 3^x,求证:对于任意实数x1、x2(x1 < x2),都有f(x1) < f(x2)。
5. 设指数函数f(x) = a^x(a > 0且a ≠ 1),若f(1) = 3,f(2) = 9,求f(x)的表达式。
四、综合题1. 已知指数函数f(x) = 2^x和g(x) = 4^x,求证:f(x)和g(x)的图象关于y轴对称。
2. 设指数函数f(x) = a^x(a > 0且a ≠ 1),若f(x)的图象经过点(1, 2),求f(x)在x = 0处的切线方程。
3. 已知指数函数f(x) = 2^x,求证:对于任意实数x,都有f(x) > 0。
指数函数检测题

指数函数检测题A 卷(基础训练)一、选择题(每小题6分,共36分)1. 函数f (x )=a x (a >0且a≠1)对于任意的实数x ,y 都有( ) (A ) f (xy )= f (x )f (y ) (B ) f (xy )= f (x )+f (y )(C )f (x+y )= f (x )f (y ) (D )f (x+y )= f (x )+f (y )2. 已知奇函数f (x )和偶函数g (x )满足f (x )+g (x )= a x -a -x +2,且g (2)=a ,则f (2)等于( )(A )154(B )2 (C )174(D )43. 集合A={y ∈R|y=2x },B={-1,0,1},则下列结论正确的是( ) (A )A∩B={0,1} (B )A ∪B=(0,+∞) (C )(C R A )∪B=(-∞,0) (D )(C R A )∩B={-1,0}4. 函数f (x )=xx 214-的图象关于( ) (A )原点对称 (B )直线y=x 对称 (C )直线y=-x 对称 (D )y 轴对称 5. 设a >1,函数()xf x a =的图象大致是 ( )6. 函数f (x )=3x (0<x ≤2)的反函数的定义域为 ( )(A )(0,+∞) (B )(0,1) (C )(1,9] (D )[9,+∞) 二、填空题(每小题6分,共24分)7. 化简)31()3)((656131212132b a b a b a ÷-的结果是 .8. 定义a b ad bc c d =-,若2142x=0,则x= 。
9. 已知函数y=f (x )是定义在R 上的奇函数,当0>x 时,xx f 2)(=,则f (-3)= .10. 已知函数221,1,(),1,x x f x x ax x ⎧+<⎪=⎨+≥⎪⎩若f (f (0))=4a ,则实数a=三、解答题(共40分)11. 已知全集为R ,集合A={x│-1≤x ≤3},B ={x│12x -<1}。
指数函数及其性质练习题及答案

指数函数及其性质练习题及答案1、若指数函数y=(a+1)^x在(-∞,+∞)上是减函数,那么()A、0<a<1 B、-1<a<0 C、a=-1 D、a<-12、已知3^x=10,则这样的x()A、存在且只有一个B、存在且不止一个 C、存在且x<2 D、根本不存在3、函数f(x)=2^(3-x)在区间(-∞,3)上的单调性是()A、增函数 B、减函数 C、常数 D、有时是增函数有时是减函数4、下列函数图象中,函数y=ax(a>0且a≠1),与函数y=(1-a)^x的图象只能是()A、ABCD中都有 B、ABCD中都没有 C、AB中有,CD中没有 D、CD中有,AB中没有5、函数f(x)=2^(x+1)-3在区间(-∞,1]上是()A、增函数B、减函数C、常数D、有时是增函数有时是减函数6、函数f(x)=2^x,g(x)=x+2,使f(x)=g(x)成立的x的值的集合()A、是∅B、有且只有一个元素C、有两个元素D、有无数个元素7、若函数y=a+(b-1)(a>0且a≠1)的图象不经过第二象限,则有()A、a>1且b1 D、a>1且b≤18、F(x)=(1+2^(1-x))⋅f(x)(x≠1)是偶函数,且f(x)不恒等于零,则f(x)是()A、奇函数 B、可能是奇函数,也可能是偶函数 C、偶函数 D、不是奇函数,也不是偶函数二、填空题9、函数y=2^(x+1)-3的定义域是_________。
10、指数函数f(x)=a^x的图象经过点(2,16),则底数的值是_________。
11、将函数f(x)=2^x的图象向右平移2个单位,就可以得到函数g(x)=2^(x-2)的图象。
12、函数f(x)=(2^x-1)/(x+1),使f(x)是增函数的区间是_________。
13、已知函数f(x)=2^(x+1)-3,x∈R,证明:f(x)在区间(-∞,1]上是减函数。
指数函数习题(经典 含答案及详细解析)

指数函数习题一、选择题1.定义运算⎩⎨⎧>≤=⊗ba b b a a b a ,则函数xx f 21)(⊗=的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x )的大小关系是( ) A .f (b x )≤f (c x ) B .f (b x )≥f (c x ) C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,则k 的取值范围是( ) A .(-1,+∞) B .(-∞,1) C .(-1,1) D .(0,2) 4.设函数f (x )=ln[(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x -2x -1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( ) A .a >3 B .a ≥3 C .a > 5D .a ≥ 55.已知函数⎩⎨⎧>≤--=-77)3)(3()(6x a x x a x f x ,若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( ) A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x (a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.8.若曲线|y |=2x +1与直线y =b 没有公共点,则b 的取值范围是________. 9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题10.求函数y =211.(2011·银川模拟)若函数y =a 2x +2a x -1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.指数函数答案1.解析:由a ⊗b =⎩⎪⎨⎪⎧aa ≤b b a >b得f (x )=1⊗2x=⎩⎪⎨⎪⎧2xx ,1 x答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x).若x <0,则3x <2x <1,∴f (3x )>f (2x).∴f (3x )≥f (2x). 答案:A3.解析:由于函数y =|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x>1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3. 答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a 8-6>(3-a )×7-3,所以⎩⎪⎨⎪⎧a >13-a >0a 8-6-a -3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =ax在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x+1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x+1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1. ∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =1()2[28,1].由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =1()2[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x=t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a +2=18⇒3a=2⇒a =log 32.(2)此时g (x )=λ·2x -4x,设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,所以实数λ的取值范围是λ≤2.法二:(1)同法一.(2)此时g (x )=λ·2x -4x,因为g (x )在区间[0,1]上是单调减函数,所以有g′(x)=λln2·2x-ln4·4x=ln2[-2·(2x)2+λ·2x]≤0成立.设2x=u∈[1,2],上式成立等价于-2u2+λu≤0恒成立.因为u∈[1,2],只需λ≤2u恒成立,所以实数λ的取值范围是λ≤2.。
指数函数基础练习题

指数函数基础练习题一、选择题1. 若 f(x) = 2^x,则 f(3) 的值为:A. 2B. 4C. 8D. 162. 若 g(x) = 5^x,则 g(0) 的值为:A. 0B. 1C. 5D. 103. 若 h(x) = (1/3)^x,则 h(2) 的值为:A. 1/9B. 1/6C. 1/3D. 9/14. 若 k(x) = 10^x,则 k(-1) 的值为:A. 0.1B. 1C. 10D. 1005. 若 p(x) = e^x,则 p(1) 的值为:A. 1B. eC. e^2D. e^-1二、填空题1. 若 f(x) = 2^x,解方程 f(x) = 64,x 的值为 _______。
2. 若 g(x) = 5^x,解不等式 g(x) < 1,x 的取值范围为 _______。
3. 若 h(x) = (1/4)^x,解不等式 h(x) > 16,x 的取值范围为 _______。
4. 若 k(x) = 10^x,解方程 k(x) = 1000,x 的值为 _______。
5. 若 p(x) = e^x,解方程 p(x) = 5,x 的值约为 _______(保留两位小数)。
三、计算题1. 计算 f(2) + f(0) + f(-1) 的值。
2. 计算 g(3) - g(2) 的值。
3. 计算 h(1/2) + h(1/3) 的值。
4. 计算 k(-2) - k(0) 的值。
5. 若指数函数 f(x) = a * b^x,已知 f(0) = 3,f(2) = 27,求 a 和 b 的值。
四、解答题1. 将函数 f(x) = 4 * 2^x 的图像完整地画在坐标系中,并标出至少三个点的坐标。
2. 设函数 f(x) = 3 * 5^x,求函数 f(x) 的反函数,并说明反函数的定义域和值域。
3. 证明:指数函数 f(x) = b^x (其中 b > 0 且b ≠ 1)的图像经过点(0, 1)。
指数函数的概念-练习题

3.答案:a(1+n%)12
解析:2007年的产值为a(1+n%),
2008年的产值为a(1+n%)2,…,
2018年的产值为a(1+n%)12.
4.答案:6倍
解析:设x天后变为原来的f(x)倍,则f(x)=1.0625x(x≥0),利用计算工具可得f(30)=1.062530≈6.16.所以经过30天,该湖泊的蓝藻会变为原来的6倍.
.
4.在某个时期,某湖泊中的蓝藻每天以6.25%的增长率呈指数增长,那么经过30天,该湖泊的蓝藻会变为原来的多少倍?
【答案】
1.答案:C
解析:A为y=3×3x,不是指数函数;B为y=-1×3x,故不是指数函数;D中底数中含自变量x,故不是指数函数,答案选C.
2.答案:a> 且a≠1
解析:函数y=(2a-1)x为指数函数,则
指数函数的概念
课后练习
1.下列以x为自变量的函数中是指数函数的是()
A.y=3x+1B.y=-3x
C.y=3-xD.y=(2x+1)x
.
2.若函数y=(2a-1)x为指数函数,则实数a的取值范围是_____.
3.某厂2006年的产值为a万元,预计产值每年以n%递增,则该厂到2018年的产值(单位:万元)是________.
指数函数习题及答案(经典)

指数函数习题一、选择题1.定义运算a ⊗b =⎩⎨⎧a a ≤b b a >b,则函数f (x )=1⊗2x 的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x )的大小关系是( )A .f (b x )≤f (c x )B .f (b x )≥f (c x )C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,则k 的取值范围是( ) A .(-1,+∞) B .(-∞,1) C .(-1,1) D .(0,2) 4.设函数f (x )=ln[(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x -2x -1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( ) A .a >3 B .a ≥3 C .a > 5D .a ≥ 55.已知函数f (x )=⎩⎪⎨⎪⎧3-a x -3,x ≤7,a x -6,x >7.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( ) A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x (a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.8.若曲线|y |=2x +1与直线y =b 没有公共点,则b 的取值范围是________. 9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题 10.求函数y =2342x x --+11.(2011·银川模拟)若函数y =a 2x +2a x -1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.指数函数答案1.解析:由a ⊗b =⎩⎪⎨⎪⎧aa ≤b b a >b得f (x )=1⊗2x=⎩⎪⎨⎪⎧2xx ≤0,1 x >0.答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x).若x <0,则3x <2x <1,∴f (3x )>f (2x).∴f (3x )≥f (2x). 答案:A3.解析:由于函数y =|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x>1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3. 答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a 8-6>(3-a )×7-3,所以⎩⎪⎨⎪⎧a >13-a >0a 8-6>3-a ×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =ax在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x+1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x+1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1. ∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =2341()2x x --+[28,1].由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =1()2[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x=t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a +2=18⇒3a=2⇒a =log 32.(2)此时g (x )=λ·2x -4x, 设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,所以实数λ的取值范围是λ≤2. 法二:(1)同法一.(2)此时g (x )=λ·2x -4x,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x]≤0成立.设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立. 因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.。
指数函数专题训练

指数函数专题训练1. 指数函数的定义和特性- 指数函数可以用如下形式表示:f(x) = a^x,其中a是一个常数,称为底数,x是指数。
- 指数函数的定义域是所有实数,值域是正实数。
- 当底数a大于1时,指数函数是增长函数;当0 < a < 1时,指数函数是减少函数。
- 指数函数的图像为一个逐渐增长或减少的曲线,且不会与x 轴相交。
- 指数函数有以下的性质:- a^0 = 1,任何数的0次方都等于1。
- a^x * a^y = a^(x+y),指数相加时,底数相乘。
- a^x / a^y = a^(x-y),指数相减时,底数相除。
2. 指数函数的图像和性质探究- 结合实际情境,探究指数函数的图像和性质。
例如,比较a 为2和a为0.5时的指数函数图像,观察它们的变化趋势。
- 使用计算工具绘制指数函数的图像,并根据图像,讨论指数函数在不同区间上的增长或减少速度。
- 研究指数函数的性质,例如指数函数的导数和二阶导数,沿着它的图像观察变化趋势,并探究导数和二阶导数与指数函数相关的规律。
3. 指数函数的应用- 研究指数函数在实际问题中的应用,如金融领域中的复利计算,人口增长模型等。
- 研究指数函数在自然科学中的应用,如放射性衰变的模型,生态系统中的物种扩张模型等。
- 研究指数函数在工程领域中的应用,如电路中的电流增长和衰减模型,生物医学工程中的光强度计算模型等。
4. 指数函数的变形和拓展- 研究具有不同底数和指数的指数函数,探索它们的图像和性质。
- 研究含有常数和其他函数的指数函数,例如f(x) = a^x + b,探讨对图像和性质造成的影响。
- 考虑复数底数和指数的指数函数,研究它们的图像和性质。
5. 指数函数的计算和求解问题- 学习如何计算和化简含有指数函数的复合函数。
- 学习如何解指数函数的方程和不等式,例如a^x = b,a^x > b 等。
- 学习如何利用指数函数求解实际应用问题,例如利用指数函数计算复利、模拟人口增长等。
高中试卷-专题4.2 指数函数(含答案)

专题4.2 指数函数1、指数函数的概念:一般地,函数x y a = 叫做指数函数,其中x 是自变量,函数的定义域为R .注意:指数函数的底数的取值范围,底数不能是负数、零和1.即 a>0且a ≠12、指数函数的图象和性质0<a<1a>1图像定义域R , 值域(0,+∞)(1)过定点(0,1),即x=0时,y=1(2)在R 上是减函数(2)在R 上是增函数性质(3)当x>0时,0<y<1;当x<0时,y>1(3)当x>0时,y>1;当x<0时,0<y<1图象特征函数性质向x 轴正负方向无限延伸函数的定义域为R 函数图象都在x 轴上方函数的值域为R +图象关于原点和y 轴不对称非奇非偶函数共性函数图象都过定点(0,1)过定点(0,1)自左向右看,图象逐渐下降减函数在第一象限内的图象纵坐标都小于1当x>0时,0<y<1;在第二象限内的图象纵坐标都大于1当x<0时,y>10<a<1图象上升趋势是越来越缓函数值开始减小极快,到了某一值后减小速度较慢;自左向右看,图象逐渐上升增函数在第一象限内的图象纵坐标都大于1当x>0时,y>1;在第二象限内的图象纵坐标都小于1当x<0时,0<y<1a>1图象上升趋势是越来越陡函数值开始增长较慢,到了某一值后增长速度极快;注意: 指数增长模型:y=N(1+p)x 指数型函数: y=ka x 3 考点:(1)a b =N, 当b>0时,a,N 在1的同侧;当b<0时,a,N 在1的 异侧。
(2)指数函数的单调性由底数决定的,底数不明确的时候要进行讨论。
掌握利用单调性比较幂的大小,同底找对应的指数函数,底数不同指数也不同插进1(=a 0)进行传递或者利用(1)的知识。
(3)求指数型函数的定义域可将底数去掉只看指数的式子,值域求法用单调性。
考点09 指数函数(练习)(解析版)

考点9指数函数【题组一定义辨析】1.下列函数中指数函数的个数是。
①y =2x ;②y =x 2;③y =2x +1;④y =x x ;⑤y =(6a –3)x 12(23a a >≠,且.【答案】2【解析】只有①⑤是指数函数;②底数不是常数,故不是指数函数;③1222x x y +==⨯是2与指数2x y =的乘积;④中底数x 不是常数,不符合指数函数的定义,所以指数函数的个数是2.2.下列函数中,指数函数的个数为。
①112x y -⎛⎫= ⎪⎝⎭②y =a x ()01a a >≠且;③y =1x ;④2112xy ⎛⎫=- ⎪⎝⎭【答案】1【解析】由指数函数的定义可判定,只有②正确.3.函数2(232)xy a a a =-+是指数函数,则a 的取值范围是。
【答案】12⎧⎫⎨⎬⎩⎭【解析】 函数2(232)x y a a a =-+是指数函数,22321a a ∴-+=且0a >,1a ≠,由22321a a -+=解得1a =或12a =,12a ∴=,4.已知函数2()(1)(1)x f x a a a =+-+为指数函数,则a =.【答案】1【解析】 函数()()()211xf x a a a =+-+为指数函数,21110a a a ⎧+-=∴⎨+>⎩解得1a =【题组二定义域】1.函数()1f x x =+-的定义域为__________.【答案】(2,1)-【解析】函数()1f x x =-x 满足:2650140210xx x x ⎧--≥⎪⎪⎛⎫->⎨⎪⎝⎭⎪⎪-≠⎩,解得6121x x x -≤≤⎧⎪>-⎨⎪≠⎩即21x -<<.故答案为:(2,1)-2.函数31()log f x x=的定义域为。
【答案】{}1|0x x <<【解析】要使函数有意义,则01220x x x >⎧⎪≠⎨⎪-≥⎩,解得0<x <1,3.设函数()f x =,则函数2(log )y f x =的定义域为。
指数函数练习题

指数函数练习题1.指数函数的基本概念指数函数是数学中一类重要的函数,常用于描述指数增长或指数衰减的情况。
其一般形式为:$y = a \cdot b^x$,其中 $a$ 和$b$ 是常数,$b。
0$ 且 $b \neq 1$。
指数函数的特点包括:当 $b。
1$ 时,函数呈指数增长趋势;当 $0 < b < 1$ 时,函数呈指数衰减趋势;当 $b = 1$ 时,函数退化为常数函数。
2.指数函数的求解与应用指数函数的求解主要涉及确定常数 $a$ 和 $b$ 的值,以及利用函数的性质进行计算。
示例1.已知函数 $y = 3 \cdot 2^x$,求当 $x = 2$ 时的函数值。
示例1.已知函数 $y = 3 \cdot 2^x$,求当 $x = 2$ 时的函数值。
解答:将 $x = 2$ 代入函数表达式中,得到 $y = 3 \cdot 2^2 = 12$。
因此,当 $x = 2$ 时,函数值为 12.示例2.某车辆的初始价格为 10 万元,每年贬值 5%,求经过 5 年后车辆的价格。
示例2.某车辆的初始价格为 10 万元,每年贬值5%,求经过 5 年后车辆的价格。
解答:设经过 $x$ 年后车辆的价格为 $y$,则满足指数衰减的函数关系为 $y = 10 \times (1-0.05)^x$。
代入 $x = 5$,得到 $y = 10 \times (1-0.05)^5 \approx 7.788$ 万元。
因此,经过 5 年后车辆的价格约为 7.788 万元。
指数函数在实际生活中有广泛的应用,例如金融领域的复利计算、生物学中的指数增长模型、电子电路中的放大器响应曲线等。
3.指数函数的练习题练习题1.若指数函数 $y = a \cdot b^x$ 过点 $(1,4)$,并且在$x = 2$ 处的斜率为 1,求函数的表达式。
练习题1.若指数函数 $y = a \cdot b^x$ 过点 $(1,4)$,并且在 $x = 2$ 处的斜率为 1,求函数的表达式。
