二年级思维第9讲 简单数列求和(二)讲义
数列的求和方法(ppt)

错位相减法:形如An=BnCn,其中{Bn}为等差数列,首项为b1,公差为d;{Cn}为等 比数列,首项为c1,公比为q。对数列{An}进行求和,首先列出Sn,记为①式;再把① 式中所有项同乘等比数列{Cn}的公比q,即得qSn,记为②式;然后①②两式错开一位 做差,从而得到{An}的前n项和。这种数列求和方式叫作错位相减。
数列的求和方法(ppt)
演讲人
目录
01
数列概念
02
等差数列思维导图
数列求和的七种方法:倒序相加法、分组求和法、错位相减法、裂项相消法、乘 公比错项相减(等差×等比)、公式法、迭加法。
倒序相加法:如果一个数列{an},与首末两端等“距离”的两项和相等或者等于 同一个常数,则求该数列的前n项和即可用倒序相加法。例如等差数列的求和公 式,就可以用该方法进行证明。
等差数列思维导图
一般地来说如果一个数列从第2项起,每一项与它的前一项的差等于同一个常 数,这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字 母d表示,前n项和用Sn表示。
谢谢
裂项相消法:裂项相消法把数列的通项拆成两项之差,在求和时中间的一些项可以相互 抵消,从而求得其和。
乘公比错项相减(等差×等比):这种方法是在推导等比数列的前 n 项和公式时所用的 方法,这种方法主要用于求数列(anxbn)的前n项和,其中(an),(bn)分别是 等差数列和等比数列。
公式法:对等差数列、等比数列,求前n项和Sn可直接用等差、等 比数列的前n项和公式进行求解。运用公式求解的注意事项:首先 要注意公式的应用范围,确定公式适用于这个数列之后,再计算。
数列求和PPT课件

1 2n-1
-
1 2n+1
)]
=
3n 2n+1
.
11.已知 {an} 是 首 项 为 a1, 公 比 为 q 的 等 比 数 列. (1)求和: a1C20-a2C12+a3C22, a1C03-a2C13+a3C23-a4C33 ; (2)由(1)的结果归纳概 括出关于正整数 n 的一个结论, 并加以证明; (3)设q≠1, Sn是{an} 的前 n 项和, 求 S1Cn0-S2C1n+S3C2n-S4C3n+ … +(-1)nSn+1Cnn.
n+1 项
∵lgx+lgy=a, ∴lg(xy)=a.
∴Sn=
n(n+1) 2
lg(xy)=
n(n2+1)a.
注: 本题亦可用对数的运算性质求解:
∵Sn=lg[xn+(n-1)+…+3+2+1y1+2+3+…+(n-1)+n],
∴Sn=
n(n+1) 2
lg(xy)=
n(n2+1)a.
7.求证: Cn0+3Cn1+5Cn2+…+(2n+1)Cnn=(n+1)2n.
-nn2+,1 2
,
n 为偶数时, n 为奇数时.
将数列的每一项拆(裂开)成两项之差, 使得正负项能相互
抵消, 剩下首尾若干项.
例
求和
Sn=
1×1 2+
1 2×3
+…+
1 n(n+1)
.
n n+1
二年级下 数学思维训练 奥数 第9讲-简便运算

=(15+15)+58 =30+58 =88
28+67+2
=(28+2)+67 =30+67 =97
34+39+16
=(34+16)+39 =50+39 =89
例题三
计算: 46+99
141—102
例题三
计算:1. 46+99
1. 46+99 =46+(100—1) =46+100—1 =146-1 =145
=19+(9+71) =19+80 =99
46+7+23
=46+(7+23) =46+30 =76
38+46+2
=(38+2)+46 =40+46 =86
习题二
2.用简便方法计算 。 45+32+5
28+67+2
15+58+15
34+39+16
习题二
2.用简便方法计算 。 45+32+5
=(45+5)+32 =50+32 =82
65+24+6 =65+(24+6) =65+30 =95
32+35+8 =(32+8)+35 = 40+35 =75
习题二
1.用简便方法计算 。 78+16+4
46+7+23
19+9+71
第9讲-等比数列-简单难度-讲义

等比数列引入庄子曰“一尺之棰,日取其半,万世不竭.”意思:“一尺长的木棒,每日取其一半,永远也取不完”.如果将“一尺之棰”视为一份,则每日剩下的部分依次为:1111,,,,248L从上述数列看到了什么规律?他的递推公式是什么?解读1、等比数列概念如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,常用字母(0)q q ≠表示.即数列{}n a 的递推公式为1n na q a +=(常数)(*N n ∈). 【注意】(1)由于等比数列每一项都可能作为分母,故每一项均不为0,因此q 也不为0;(2)从第二项开始,因此首项没有前一项; (3)1n na a +均为同一个常数,即比值相等; (4)常数列都是等差数列,但不一定是等比数列.若常数列各项都为0的数列,它就不是等比数列,当常数列各项不为0时,是等比数列.2、等比数列的通项公式及推导等比数列的通项公式为:1*1n n a a q n N -=∈,.等比数列的公式的推导:累乘法等比数列通项公式的推导:2132121n n nn a q a a q a a q a a q a ---====L L,将这1n -个式子的等号两边分别相乘得:11n na q a -=, 即11n n a a q -=.由等差数列的通项公式易知:n mm n a a q -=.3、等差中项如果三个数x G y ,,组成等比数列,那么G 叫做x 和y 的等比中项,即2G xy =. 由等比数列的定义可知G yx G=,得2G xy =. 两个正数(或两个负数)的等比中项有两个,它们互为相反数;一个正数与一个负数没有等比中项.4、等比数列的常用性质(1)公比为q 的等比数列的各项同乘以一个不为零的数m ,所得数列仍为等比数列,公比仍为q ;(2)若*(,,,)p q m n m n p q N +=+∈,则有p q m n a a a a ⋅=⋅;由等比数列的通项公式可知1111p q p q a a a q a q --⋅=⋅⋅⋅,1111m n m n a a a q a q --⋅=⋅⋅⋅,如果p q m n +=+,则p q m n a a a a ⋅=⋅若2m p q =+,则有2m p q a a a =⋅;(3)等距离取出若干项也构成一个等比数列,即n a ,n m a +,2n m a +,L L 为等比数列,公比为mq .由等比数列定义可知(1)1(1)1(1)1km m n kmk m n k ma a q q aa q-+--+-⋅==⋅*(N )k ∈. (4)若等比数列{}n a 的公比为q ,则1n a ⎧⎫⎨⎬⎩⎭是以1q 为公比的等比数列; (5)若{}n a 与{}n b 均为等比数列,则{}n n a b 也为等比数列;(6)101a q >⎧⎨>⎩或{}1001n a a q <⎧⇔⎨<<⎩递增;1001a q >⎧⎨<<⎩或{}101n a a q <⎧⇔⎨>⎩递减;{}1n q a =⇔为常数列;{}0n q a <⇔为摆动数列.5、等比数列的前n 项和及推导过程等比数列前n 项和公式:111(1)(1)(1)11n n n na q S a a q a q q q q =⎧⎪=--⎨=≠⎪--⎩等比数列由等比数列的定义知公式的推导:方法一:由等比数列的定义知2132121n n n n a a q a a q a a q a a q ---====L ,,,,,将这n 个等式的两边分别相加得:23121()n n a a a a a a q -+++=+++L L ,即1()n n n S a S a q -=-,整理得111(1)n n n S q a a q a a q -=-=-,当1q ≠时,1(1)(2)1n n a q S n q-=-≥,显然此式对1n =也成立; 当1q =时,1n S na =.方法二:由前n 项定义知211111n n S a a q a q a q -=++++L , 将上式两边同乘以q 得:n qS =231111n a q a q a q a q ++++L 两式相减得:11(1)n n q S a a q -=-, 以下讨论同法一.方法二称为错位相减法,是数列求和中常用的一种方法.错位相减求和法:非零的等差数列{}n a 、等比数列{}n b 构造数列{},{}n n n na ab b ,数列称为差比数列,求它的前n 项和可用错位相减法.6、等比数列前n 项和的性质(1)公比为q 的等比数列,按m 项分组,每m 项之和组成一个新数列,仍为等比数列,其公比为m q (也就是说:232m m m m m S S S S S --,,,L L 为等比数列,公比为m q ,可知12=m m S a a a +++L ,212212=m m mm m m m m m S S a a a a q a q a q ++-=+++⋅+⋅++L L ,222322122312=,m m m m m m m m n S S a a a a q a q a q ++-=+++⋅+⋅++⋅L L L(1)*(1)()(2,N )()k m km m km k m S S q m m S S +--=≥∈-(2)对于项数为*2()k k N ∈的等比数列,有=S qS 偶奇.探究图中的三角形称为希尔宾斯基(Sierpinski )三角形.在下图5个三角形中,黑色三角形的个数依次构成一个数列的前5项1、请写出这个数列的一个递推公式?答:如题图这5个三角形中黑色三角形个数分别为1,3,9,27,81,从第二项开始每一项都是前一项的3倍则所求数列递推通项公式是13n n a a +=.2、请写出这个数列的一个通项公式?答:如题图这5个三角形中黑色三角形个数分别为1,3,9,27,81,则所求数列的前5项都是3的指数幂,指数为序号建议.猜想这个数列的通项公式是1=3n n a -.典例精讲一.选择题(共16小题)1.(2018秋•龙岩期中)在等比数列{a n }中,a 4•a 8=16,则a 2•a 10=( ) A .12 B .16 C .20 D .242.(2018秋•龙岩期中)已知等比数列{a n }的公比q =−13,则a 1+a 3+a 5+a 7a 3+a 5+a 7+a 9等于( )A .−13B .﹣3C .19D .93.(2018秋•偃师市校级月考)等比数列{a n }中,16a 6=a 2,则公比q=( )A .12B .±12C .2D .±24.(2018秋•太原期中)已知等比数列{a n }中,a 1+a 2=12,a 1﹣a 3=34,则a 4=( )A .﹣18B .18C .﹣4D .45.(2018春•南昌期末)若实数x 为2与8的等比中项,则x=( ) A .16 B .4C .﹣4D .±46.(2018春•南部县期末)在等比数列{a n}中,已知a2a4a6=8,则a3a5=()A.3B.5C.4D.27.(2018春•金牛区校级期中)在等比数列{a n}中,若a1和a4033是函数f(x)=x+ 5x+k,(k<0)的两个零点,则a2016a2017a2018的值为()A.±5√5B.5√5C.−5√5D.258.(2018春•涪城区校级期中)若a,b为正实数,A是a,b的等差中项,G是a,b的等比中项,则()A.A≥G B.A>G C.A≤G D.A<G9.(2018春•金牛区校级期中)若等比数列{a n}的前n项和S n=2×3n−1+a,则a等于()A.3B.2C.−23D.−1310.(2018春•金牛区校级期中)若某等比数列前12项的和为21,前18项的和为49,则该等比数列前6项的和为()A.7B.9C.63D.7或6311.(2018春•东湖区校级期中)设等比数列{a n }的前n 项和为S n ,若S 3S 6=3,则S 6S 9=( ) A .2 B .83C .37D .312.(2018•聊城二模)已知等比数列{a n }的公比为3,a 1=2,前n 项和S n =242,则n=( ) A .3 B .4 C .5 D .613.(2018•洛阳一模)已知等比数列{a n },a 2=14,a 5=132,则数列{log 2a n }的前10项之和是( ) A .45 B .﹣35 C .55 D .﹣5514.(2018•呼和浩特二模)已知等比数列{a n }满足a 1+a 2=6,a 4+a 5=48,则数列{a n }前8项的和S n =( ) A .510 B .126 C .256 D .51215.(2018•泰安二模)等比数列{a n }的前n 项和为S n ,已知S 2=a 1+2a 3,a 4=1,则S 4=( )A .78B .158C .14D .1516.(2018•迎泽区校级一模)已知等比数列{a n}前n项和为S n,则下列一定成立的是()A.若a3>0,则a2015<0B.若a4>0,则a2014<0C.若a3>0,则S2015>0D.若a4>0,则S2014>0二.填空题(共5小题)17.(2018春•保定期末)在正项等比数列{a n}中,1a1+1a2=1,1a3+1a4=2,则公比q=.18.(2018•江苏模拟)已知各项均为正数的等比数列{a n}满足a1=12,且a2a8=2a5+3,则a9=.19.(2017秋•龙岗区期末)设f(n)=2+24+27+210+⋅⋅⋅+23n+1(n∈N*),则f(n)=.20.(2018•浦东新区二模)已知{a n}是等比数列,它的前n项和为S n,且a3=4,a4=﹣8,则S5=21.(2016春•无锡校级期末)各项均为正数的等比数列{a n}的前n项和为S n,若S4 S2=4,则S8S4=.三.解答题(共3小题)22.(2016•衡水校级一模)设数列{a n}的前n项和为S n,且首项a1≠3,a n+1=S n+3n (n∈N*).(1)求证:{S n﹣3n}是等比数列;(2)若{a n}为递增数列,求a1的取值范围.23.(2018秋•洋县校级月考)已知数列{a n}中,a1=2,a n+1=2a n.(1)求a n;(2)求数列{a n}的前n项和.24.(2018秋•长汀县校级月考)已知等比数列{a n}中,a1=1,a4=8.(⋅)求数列{a n}的通项公式;(⋅)若等差数列{b n}满足b1=a1,b2=a2,求数列{b n}的前10项和.归纳总结1、等比数列概念如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,常用字母(0)q q ≠表示.即数列{}n a 的递推公式为1n na q a +=(常数)(*N n ∈). 【注意】(1)由于等比数列每一项都可能作为分母,故每一项均不为0,因此q 也不为0;(2)从第二项开始,因此首项没有前一项; (3)1n na a +均为同一个常数,即比值相等; (4)常数列都是等差数列,但不一定是等比数列.若常数列各项都为0的数列,它就不是等比数列,当常数列各项不为0时,是等比数列.2、等比数列的通项公式及推导等比数列的通项公式为:1*1n n a a q n N -=∈,.等比数列的公式的推导:累乘法等比数列通项公式的推导:2132121n n nn a q a a q a a q a a q a ---====L L ,将这1n -个式子的等号两边分别相乘得:11n na q a -=,即11n n a a q -=.由等差数列的通项公式易知:n mm n a a q -=.3、等差中项如果三个数x G y ,,组成等比数列,那么G 叫做x 和y 的等比中项,即2G xy =. 两个正数(或两个负数)的等比中项有两个,它们互为相反数;一个正数与一个负数没有等比中项.4、等比数列的常用性质(1)公比为q 的等比数列的各项同乘以一个不为零的数m ,所得数列仍为等比数列,公比仍为q ;(2)若*(,,,)p q m n m n p q N +=+∈,则有p q m n a a a a ⋅=⋅;若2m p q =+,则有2m p q a a a =⋅;(3)等距离取出若干项也构成一个等比数列,即n a ,n m a +,2n m a +,L L 为等比数列,公比为mq .(4)若等比数列{}n a 的公比为q ,则1n a⎧⎫⎨⎬⎩⎭是以1q 为公比的等比数列;(5)若{}n a 与{}n b均为等比数列,则{}n n a b 也为等比数列;(6)101a q >⎧⎨>⎩或{}1001na a q <⎧⇔⎨<<⎩递增;1001a q >⎧⎨<<⎩或{}101n a a q <⎧⇔⎨>⎩递减;{}1n q a =⇔为常数列;{}0n q a <⇔为摆动数列.5、等比数列的前n 项和及推导过程等比数列前n 项和公式:111(1)(1)(1)11n n n na q S a a q a q q q q =⎧⎪=--⎨=≠⎪--⎩等比数列由等比数列的定义知公式的推导:方法一:由等比数列的定义知2132121n n n n a a q a a q a a q a a q ---====L ,,,,, 将这n 个等式的两边分别相加得:23121()n n a a a a a a q -+++=+++L L , 即1()n n n S a S a q -=-,整理得111(1)n n n S q a a q a a q -=-=-,当1q ≠时,1(1)(2)1n n a q S n q-=-≥,显然此式对1n =也成立;当1q =时,1n S na =.方法二:由前n 项定义知211111n n S a a q a q a q -=++++L , 将上式两边同乘以q 得:n qS =231111n a q a q a q a q ++++L 两式相减得:11(1)n n q S a a q -=-, 以下讨论同法一.方法二称为错位相减法,是数列求和中常用的一种方法.错位相减求和法:非零的等差数列{}n a 、等比数列{}n b 构造数列{},{}n n n na ab b ,数列称为差比数列,求它的前n 项和可用错位相减法.6、等比数列前n 项和的性质(1)公比为q 的等比数列,按m 项分组,每m 项之和组成一个新数列,仍为等比数列,其公比为m q (也就是说:232m m m m m S S S S S --,,,L L 为等比数列,公比为mq ,(2)对于项数为*2(N )k k ∈的等比数列,有=S qS 偶奇.。
数列求和方法总结PPT课件

有一类数列,既不是等差数列,也不是等比 数列,若将这类数列适当拆开,可分为几个等差、 等比或常见的数列,然后分别求和,再将其合并 即可.
-
6
例2:求数列的前n项和:1 1, 1 4, 1 7, , 1 3n 2,…
a a2
a n1
-
7
练习 : 求数列1 1 2
,3 1 4
,5
1 8
-
1
本节概要 数列求和的常用方法
-
2
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
(q
1)
.
自然数方幂和公式:1 2 3 n 1 n(n 1) 2
12 22 32 n2 1 n(n 1)(2n 1) 6
2n 2n
…………………………………①
1 2
Sn
2 22
4 23
6 24
2n 2 n1
………………………………②
(设制错位)
①-②得(1
1 2
)S
n
2 2
2 22
2 23
2 24
2 2n
2n 2 n 1
2 1 2n 2n1 2n1
∴
Sn
4
n2 2 n 1
-
17
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
-
18
例
5.设
f
(x)
4 x , 则f 4x 2
第讲数列的求和精选课件

【互动探究】 1.(2019 年陕西)已知{an}是公差不为零的等差数列,a1=1,
且 a1,a3,a9 成等比数列. (1)求数列{an}的通项公式; (2)求数列{2 a n}的前 n 项和 Sn.
4.数列 112,214,318,…,n+21n,…的前 n 项和 Sn=______ __12_n_(n_+__1_)_+__1_-__21_n___.
5.数列{an}的通项公式 an=
1 n+
n+1,若前
n
项的和为
10,
则项数 n=___1_2_0___.
考点1 利用公式或分组法求和
例1:(2011 年重庆)设{an}是公比为正数的等比数列,a1=2, a3=a2+4.
数列求和常用的方法
1.公式法 (1)等差数列{an}的前
n
项和公式:Sn=nnaa1+ 12+nann2-,1d.
(2)等比数列{an}的前n项和Sn:①当q=1时,Sn=__n_a_1_;
a11-qn
a1-anq
②当 q≠1 时,Sn=____1_-__q___=____1_-__q__.
2.分组求和法 把一个数列分成几个可以直接求和的数列. 3.错位相减法 适用于一个等差数列和等比数列对应项相乘构成的数列求 和. 4.裂项相消法 有时把一个数列的通项公式分成两项差的形式,相加过程消 去中间项,只剩有限项再求和.
解析:(1)P1(-1,0),an=n-2,bn=2n-2. (2)f(n)=n2- n-2, 2,n为 n为奇偶数数,. 假设存在符合条件. ①若 k 为偶数,则 k+5 为奇数. 有 f(k+5)=k+3,f(k)=2k-2. 如果 f(k+5)=2f(k)-2,则 k+3=4k-6⇒k=3 与 k 为偶数矛 盾.故不符(舍去). ②若 k 为奇数,则 k+5 为偶数, 有 f(k+5)=2k+8,f(k)=k-2. ∴2k+8=2(k-2)-2 这样的 k 也不存在. 综上所述:不存在符合条件的 k.
数列求和的几种方法课件ppt
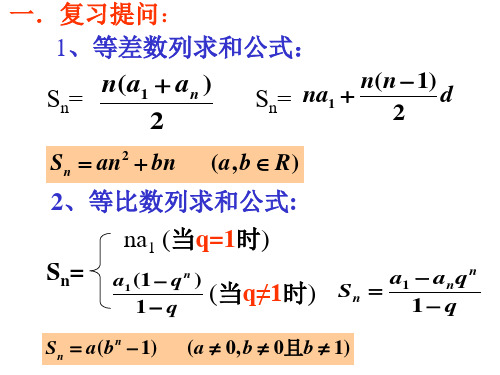
(2)乘公比,错位相减(对“A·G”型);
(3)裂通项,交替相消
1、转化成等差、等比数列求和
(公式法、分组求和法、错位相减法、 裂(并)项法求和)
练习: 指出下列求和的方法:
合并项求和
特殊的数列,在求数列的和时,可将一些项放在一起先求和,然后再求Sn.
[例] 在各项均为正数的等比数列中,若
的值.
求和: (1)Sn=1+(3+4)+(5+6+7)+…+(2n-1+2n+ …+3n-2); (2)Sn=12-22+32-42+…+(-1)n-1·n2.
(1)一般应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为适用特点的形式,从而求和.
数列求和的方法
(2)解决非等差、等比和,两种思路: ①转化的思想,即化为等差或等比数列. ②裂项相消法、错位相减法、倒序相加法等求和.
数列求和的常用方法:
(1) 拆项(对A±G型 如果拆项不明显,写出通项,如例2 )
na1+ d
n(n+1)(2n+1)
n2(n+1)2
倒序相加
令
例题1. 求和
(1)
[解Байду номын сангаас原式=
n(n+3)/2
(x≠1)
(x=1)
分析:原式=(1+2+3+…+n)+
我们把这种类型的数列称为“A+G”型。而求此类数列的和,一般是把数列的每一项分成两项,再分别利用等差和等比数列的求和公式求解。此方法称为分组求和法。
二年级思维拓展-简单数列求和

简单数列求和知识要点本讲的主要内容:1.数列的概念。
2.数列求和公式。
基本方法与要求:世界著名的德国数学家高斯(1777年~1855年),幼年时代,曾很快算出1+2+3+4+......+99+100的结果,高斯的算法是:1+100=101,2+99=101,......,50+51=101。
把1~100采用上述方式两两配对相加,共配对50对,它们的和都等于101,因而1+2+3+4+......+99+100=101×50=5050。
1, 2, 3, 4, (99)100这列数中的规律是相邻两数的差相等。
按照一定的次序排列的一列数叫数列。
排在数列最前面的一项称为首项,最后一项称为末项,从第二项起,任一项与前一项的差称为公差。
高斯的解法表明:数列和=(首项+末项)×项数÷2项数=(末项-首项)÷公差+1末项=首项+公差×(项数-1)学习数列要注意经常观察、分析和推敲推敲,这些都有助于学生数学能力的提高和实践创新能力的培养。
☜精选例题【例1】:计算:(1)1+2+3+4+5+6+7+8(2)2+4+6+8+10+12(3)3+6+9+12+15☝思路点拨:(1)先根据数的规律,看相邻两个数的差是否相等,从第二项起,任意一项与前一项的差是1,即公差为1,首项为1,末项为8,项数为8,根据数列和公式可以求得它们的和。
(2)根据这一数列的变化规律,可以发现后一项总比前一项多2,即公差是2,首项是2,末项是12,项数是6,根据数列求和公式可以求得它们的和。
(3)根据这一数列的变化规律,可以发现后一项总比前一项多3,即公差是3,首项是3,末项是15,项数是5,根据数列求和公式可以求得它们的和。
☝标准答案:(1)原式=(1+8)×8÷2=36(2)原式=(2+12)×6÷2=42(3)原式=(3+15)×5÷2=45✌活学巧用1.计算:(1)1+2+3+4+5+6+7+8+9(2)0+2+4+6+8+10+12(3)2+4+6+8+10+12+14+162.计算:(1)0+3+6+9+12+15+18(2)3+5+7+9+11+13+15+17(3)0+5+10+15+20【例2】:(1)求首项是2,末项是14,公差是2的这个数列的和是多少?(2)求首项是2,公差是3的数列的前8项的和是多少?思路点拨:(1)根据题意可寻址它们排列的变化规律及项数,2,4,6,8,10,12,14,即项数是7,再根据数列求和公式求解。
掌握小学数学中的数列求和

掌握小学数学中的数列求和数列求和是小学数学中的基础概念,也是后续学习数学的重要基础。
通过掌握数列求和的方法和技巧,学生可以更加深入地理解数学运算的规律,提高数学思维和解题能力。
本文将介绍小学数学中的数列求和的概念、方法和应用。
一、数列求和的基本概念数列是按照一定规律排列的一组数,在小学数学中常常以字母表示。
数列中的每个数称为项,用数学符号表示为an,其中n表示项的位置。
求和就是将数列中的每个项相加的运算,用数学符号表示为Σ(an)。
二、等差数列求和的方法等差数列是指数列中的每两个相邻的数之间的差值相等的数列,常用的等差数列求和方法有以下两种:1. 数列之和的公式当已知等差数列的首项a1、末项an和项数n时,就可以使用数列之和的公式来求得该等差数列的和。
公式如下:S(n) = 1/2 * n * (a1 + an)其中,S(n)表示等差数列的和。
2. 首尾项求和的方法另一种求等差数列之和的方法是将首项和末项对应相加再乘以项数的一半。
具体步骤如下:(1)计算首项a1和末项an;(2)计算项数n;(3)使用公式S(n) = 1/2 * n * (a1 + an)计算等差数列的和。
三、等比数列求和的方法等比数列是指数列中的每两个相邻的数之比相等的数列,常用的等比数列求和方法有以下两种:1. 数列之和的公式当已知等比数列的首项a1、公比q和项数n时,就可以使用数列之和的公式来求得该等比数列的和。
公式如下:S(n) = a1 * (1 - q^n) / (1 - q)其中,S(n)表示等比数列的和。
2. 迭加法另一种求等比数列之和的方法是迭加法,即将每一项逐个相加求和,具体步骤如下:(1)计算首项a1和公比q;(2)计算项数n;(3)使用迭加法将数列中的每一项相加求和。
四、数列求和的应用数列求和不仅在小学数学中有重要意义,在日常生活和其他学科中也有广泛应用。
以下是数列求和的一些应用案例:1. 等差数列求和应用于日常计算。
小学数学认识简单的数列的递推和求和

小学数学认识简单的数列的递推和求和数列是数学中重要的概念之一,它在小学数学中也有着重要的地位。
在小学的数学课堂上,老师会教给我们怎样认识简单的数列,并且学习数列的递推和求和。
本文将介绍小学数学中有关数列的基本知识,包括数列的定义、递推和求和方法。
一、数列的定义数列是由一列有序的数按照一定的规律排列而成的。
数列中的每个数称为数列的项,用字母表示时通常用An表示第n项,其中n表示项的位置。
例如,1, 3, 5, 7, 9就是一个数列,其中1是第1项,3是第2项,5是第3项,以此类推。
二、数列的递推数列的递推是指通过已知的前一项或前几项来推导后一项的方法。
简单的数列递推通常可以通过观察规律或运用简单的算法来得到。
下面是几种常见的数列递推方法:1. 等差数列等差数列是指数列中的每一项与前一项之差都相等的数列。
我们可以通过前两项的差值来推导后面的项。
设第一项为a,公差为d,则等差数列的通项公式为An=a+(n-1)d。
2. 等比数列等比数列是指数列中的每一项与前一项之比都相等的数列。
通过计算前两项的比值,我们可以得到等比数列的通项公式。
设第一项为a,公比为r,则等比数列的通项公式为An=a*r^(n-1)。
3. 斐波那契数列斐波那契数列是一个特殊的数列,它的前两项均为1,从第三项开始,每一项都是前两项之和。
斐波那契数列的通项公式为An=An-1+An-2。
三、数列的求和数列的求和是指将数列中的所有项加起来得到的结果。
常见的数列求和方法有两种:等差数列求和和等比数列求和。
1. 等差数列求和对于等差数列,我们可以利用以下公式来求和:Sn = (a1+an)*n/2,其中,Sn表示数列的前n项和,a1表示第一项,an表示第n项,n 表示项数。
例如,对于数列1, 3, 5, 7, 9,当n=5时,利用等差数列求和公式可以得到Sn = (1+9)*5/2 = 25。
2. 等比数列求和对于等比数列,我们可以利用以下公式来求和:Sn = a*(1-r^n)/(1-r),其中,Sn表示数列的前n项和,a表示第一项,r表示公比,n表示项数。
数列求和各种方法总结归纳课件PPT

[冲关锦囊]
用错位相减法求和时,应注意 (1)要善于识别题目类型,特别是等比数列公比为负数
的情形; (2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“
错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
[精析考题] [例3] (2011·全国新课标卷)等比数列{an}的各项均为正数,且2a1+ 3a2=1,a32=9a2a6. (1)求数列{an}的通项公式; (2)设bn=log3a1+log3a2+…+log3an,求数列{b1n}的前n项和.
(1)an=kn+b,利用等差数列前n项和公式直接求解;
所以,当n>1时,①-②得 用错位相减法求和时,应注意
①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成.
①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成.
数列求和各种方法总结归纳
二、非等差、等比数列求和的常用方法 1.倒序相加法
如果一个数列{an},首末两端等“距离”的两项的和相等 或等于同一常数,那么求这个数列的前n项和即可用倒 序相加法,如等差数列的前n项和即是用此法推导的.
2.分组求和法 若一个数列的通项公式是由若干个等差数列或等比数列 或可求和的数列组成,则求和时可用分组转化法,分别 求和而后相加减.
∴bn+1+1=2bn+2=2(bn+1).
∴((11b))要a1n=善=0于k,n识b+1别b+,题1利=目用1类≠等0型.差n1,数-特列别n前是+n1等项比1和数公列=式公直-比接为求n负解2+数n;1.
所以数列{b1n}的前n项和为-n2+n1.
[巧练模拟]—————(课堂突破保分题,分分必保!)
北师大版二年级上册数学 第9招 巧求连续的数 知识点梳理重点题型练习课件

7
8 =30
5
技 巧 4 巧求连续的数,解决生活中的实际问题
4.元旦到了,合唱队的 27 名学生站成 3 排进行表 演,要求后面一排的人数都比前面一排多 1。你 知道每一排各站多少人吗? 27÷3=9(人) 9-1=8(人) 9+1=10(人) 答:第一排站8人,第二排站9人,第三排站10人。
解析:要求后面一排的人数都比前面一排多1,说明 这3排的人数是连续的三个数。连续的3个数的和÷3 =中间数,则中间排的人数为27÷3=9(人)。所以前 面一排的人数为9-1=8(人),后面一排的人数为9+ 1=10(人)。
3 5
技 巧 2 已知连续的 3 个数的和,巧求连续的数
2.在下面的 23 56
里填上连续的 3 个数,使等式成立。
4 =9
6
7
8 =21
7 =18 8
9 10 =27
3
技 巧 3 已知连续的 5 个数的和,巧求连 续的数
3.在下面的 里填上连续的 5 个数,使等式成立。
12
34
5的数
技 巧 1 已知单数个连续的数,巧求和
1.算一算,填一填。 1+2+3=2× 3 = 6 2+3+4+5+6=4× 5 = 20 4+5+6=5× 3 = 15 1+2+3+4+5=3× 5 = 15
3+4+5= 4 × 3 = 12 3+4+5+6+7= 5 × 5 = 25
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9讲:简单数列求和(二)姓名:
知识要点
在学习这一讲内容之前,让我们一起来认识“数学王子”——高斯。
高斯(1777年—1855年)是德国著名数学家。
有关高斯最出名的故事就是他十岁时,小学老师出了一道数学难题:“计算1+2+3+4+…+99+100=?”这可难为了初学数学的学生,但是高斯却在几秒后将答案解了出来。
他把这些数首尾配对:1+100=101,2+99=101,…,50+51=101。
也就是首末两项两两相加,共有50对,它们的和都是101,因此,1+2+3+4+…+99+100=101×50=5050。
据说最后只有高斯的答案是正确无误的。
现在让我们来看看这道题目。
1、2、3、4…99、100正好组成一个等差数列,1是首项,100是末项,一共有100个项数。
在高斯的解法中,101表示前后两项两两相加的得数,也就是首项+末项=101;50表示有50对这样的数,也就是项数÷2。
由此可得到:数列和=(首项+末项)×项数÷2。
运用等差数列求和的方法还可以帮助我们解决生活中的一些实际问题呢。
例1:求等差数列3、4、5、6……前6项的和。
练习1:求等差数列6、10、14、18……前8项的和。
例2:计算:1+3+5+7+9+11的和。
练习2:计算:10+12+14+16+18+20
例3:一个数列首项是2,公差是3,求这个数列前7项的和是多少。
练习3:一个数列首项是2,公差是4,求这个数列前5项的和是多少。
例4:一个小型剧院共有6排座位,第一排有10个座位,以后的每一排总比前一排多2个座位,这个小型剧院共有多少个座位?
练习4:这是歌剧院的一个厅,共有7排座位,第一排有8个座位,以后的每一排总比前一排多4个座位,这个厅共有多少个座位?
例5:一次有8个朋友聚会,见面时,每人和其余的每个人只握一次手,那么这8个人共握手多少次?
练习5:有9个同学聚会,如果参加聚会的每个人和其余的每个人只握手一次,请问这9个同学共握手多少次?
总结归纳
一个等差数列的项数无论是奇数还是偶数,都可以运用同样的求和公式:(首项+末项)×项数÷2来求和,不分奇数项与偶数项。
这是对任意项等差数列都通用的公式,在解决问题时可以直接运用这个求和公式。
奥赛点击
用3根一样长的火柴棒拼成一个等边三角形,再用这样的等边三角形拼成一个大的等边三角形,如图。
如果这个大的等边三角形的底边放了6根火柴,那么这个大的等边三角形中一共放了多少根火柴?
自我检测得分:.
1. 求等差数列2、3、4……前6项的和。
2. 求等差数列3、6、9……前6项的和。
3. 求等差数列1、3、5……前8项的和。
4. 计算:1+2+3+4+5+6+7+8。
5. 计算:2+4+6+8+10+12。
6. 计算:0+3+6+9+12+15+18+21。
7. 一个数列首项是0,公差是1,求这个数列前8项的和是多少。
8. 一个数列首项是2,公差是2,求这个数列前9项的和是多少。
9. 一个数列公差是4,首项是0,求这个数列前6项的和是多少。
10. 某个小型会场有8排座位,第一排有4个座位,后一排都比前一排多2个座位。
这个小型会场一共有多少个座位?
自我检测(二)
1. 一个数列首项是3,公差是2,求这个数列前6项的和是多少。
2. 水果摊上有6篮苹果,第一篮有4个苹果,以后每一篮都比前一篮多3个,这个水果摊上共有多少个苹果?
3. 7个小朋友下棋,每人和其余的每个人都要下一局,这7个小朋友共下了多少局?
4. 有10支足球队参加比赛,如果每两个队必须踢一场,那么这10支足球队一共要踢几场?
5. 如图所示,一堆砖中央最高的一摞有7块,它的左右两边各是6块,再往两边分别是5块、4块、3块、2块、1块。
这堆砖一共有多少块?。
