第20课时6.2.2 频率分布直方图和折线图

合集下载

第20课时《频率分布直方图和折线图》

第20课时频率分布直方图和折线图【学习导航】知识网络学习要求1．频率分布直方图的作法，频率分布直方图更加直观形象地反映出总体分布的情况；2．频率分布折线图的作法，优点是反映了数据的变化趋势，如果样本容量足够大，分组的组距足够小，则这条折线将趋于一条曲线，称为总体分布的密度曲线。

【课堂互动】自学评价案例1 下表是某学校一个星期中收交来的失物件数，请将5天中收交来的失物数用条（1）在EXCEL工作表中输入数据，光标停留在数据区中;（2）选择“插入/图表”，在弹出的对话框中点击“柱形图”；（3）点击“完成”，即可看到如下频数条形图．案例2 从某校高一年级的1002名新生中用系统抽样的方法抽取一个容量为100的身高样本，数据如下(单位：cm)。

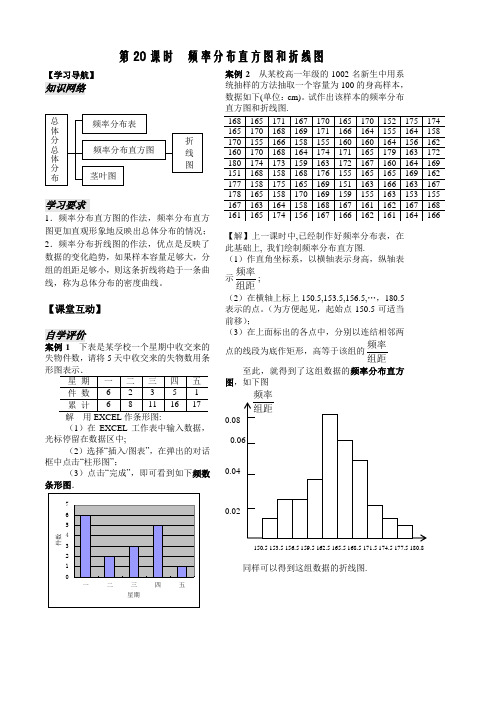
试作出该样本的频率分布直方图和折线图.【解】上一课时中,已经制作好频率分布表，在此基础上, 我们绘制频率分布直方图.（1）作直角坐标系，以横轴表示身高，纵轴表示组距频率;（2）在横轴上标上150.5,153.5,156.5,…，180.5表示的点。

（为方便起见，起始点150.5可适当前移）；（3）在上面标出的各点中，分别以连结相邻两点的线段为底作矩形，高等于该组的组距频率至此，就得到了这组数据的频率分布直方图，如下图150.5 153.5 156.5 159.5 162.5 165.5 168.5 171.5 174.5 177.5 180.8同样可以得到这组数据的折线图.150.5 153.5 156.5 159.5 162.5 165.5 168.5 171.5 174.5 177.5180.8【小结】1．利用直方图反映样本的频率分布规律,这样的直方图称为频率分布直方图(frequency histogram),简称频率直方图。

2. 频率直方图比频率分布表更直观、形象地反映了样本的分布规律。

3．如果将频率分布直方图中相邻的矩形的上底边的中点顺次连结起来，就得到一条折线，我们称这条折线为本组数据的频率折线图(frequency polygon)4．频率分布折线图的的首、尾两端如何处理: 取值区间两端点须分别向外延伸半个组距，并取此组距上的x 轴上的点与折线的首、尾分别相连5．如果将样本容量取得足够大，分组的组距取得足够小，则这条折线趋于一条曲线，这一曲线称为总体分布的密度曲线。

统计学》课程习题参考答案(部分)

《统计学》课程部分习题参考答案(龚凤乾）1．试针对统计学的三种任务各举一例。

答：见授课题板。

2．举例说明统计分组可以完成的任务。

答：见授课题板。

3．举一个单向复合分组表的例子，再举一个双向复合分组表的例子。

答：单向复合分组表的例如下4．某市拟对该市专业技术人员进行调查，想要通过调查来研究下列问题：（1）通过描述专业技术人员队伍的学历结构来反映队伍的整体质量；（2）研究专业技术人员总体的职称结构比例是否合理；（3）描述专业技术人员总体的年龄分布状况；（4）研究专业技术人员完成的科研成果数是否与其最后学历有关。

请回答：（1）该项调查研究的调查对象是该市全部专业技术人员；（2）该项调查研究的调查单位是该市每一位专业技术人员；（3）该项调查研究的报告单位是该市每一位专业技术人员；（4）为完成该项调查研究任务，对每一个调查单位应询问下列调查项目学历、职称、年龄、科研成果数。

5根据上表指出：（1）上表变量数列属于哪一种变量数列；（2）上表中的变量、变量值、上限、下限、次数（频数）；（3）计算各组组距、组中值、频率。

答：（1）连续型组距式分组；（2）连续型组距式分组的组距=本组上限—本组下限；组中值=（上限+下限）/2；频率= ii f f /6．某地区人口统计数据如下表，请在此表的空白处添加以下数字：组距、组中值、频率、上限以下累计频数。

注：年龄以“岁”为单位计算，小数部分按舍尾法处理。

7．对下列指标进行分类。

（只写出字母标号即可）A 手机拥有量B 商品库存额C 市场占有率D 人口数E 出生人口数F 单位产品成本G 人口出生率H 利税额（1）时期性总量指标有： EH ；（2）时点性总量指标有： ABD ；（3）质量指标有： CFG ；（4）数量指标有： ABDEH ；（5）离散型变量有： ADE ；（6）连续型变量有： BCFGH 。

8．现在把某地区1999年末全部个体经营工业单位作为研究对象。

对这个统计总体，设计了“1999年末全部个体经营工业单位总数”和上述这个个体经营工业单位总体的“1999年全年产品销售收入”两个统计指标。

频率分布直方图与折线图优秀课件1

2.能否根据频率分布表来绘制频率直方图？
3.能否根据频数情况来绘制频数条形图？
频率分布直方图与折线图
引例2
下表是某校一个星期中收来的失物件数，请将5天中收交来的失物数用条形图来表示。
星期件数累计一 6 6 二 2 8 三 3 11 四 5 16 五 1 17
星期件数累计
7 6 5 4 3 2 1 0 一
(1)什么是频数？什么是频率?
（2）什么是全距？全距与组数、组距之间的关系是什么？（3）如何绘制频率分布图？
问题情境
1.列频率分布表的一般步骤是什么？
一般地编制频率分布表的步骤如下：（1）求全距，决定组数和组距；全距是指整个取值区间的长度，组距是指分成的区间的长度; （2）分组，通常对组内的数值所在的区间取左闭右开区间，最后一组取闭区间；（3）登记频数，计算频率，列出频率分布表．
54.5 56.5 58.5 60.5 62.5 64.5 66.5 68.5 70.5 72.5 74.5 76.5
频率组距
体重（kg）
（5）为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如下，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为 a，视力在4.6到5.0之间的学生数为b，则a, b的值分别 A 为（） A．0.27,78 B．0.27,83 C．2.7,78 D．2.7,83
[165.5, 168.5) [168.5, 171.5) [171.5, 174.5) [174.5, 177.5) [177.5, 180.5] 合计
19 14 7 4 3 100
0.19 0.14 0.07 0.04 0.03 1

频数分布直方图_课件

小结
画频数分布直方图的一般步骤:
极差: 注意：一般情况
(1) 计算最大值与最小值的差(极差). (2) 决定组距与组数: 极差/组距=________ （1）可以由组距来求组数； (3) 决定分点. 当数据个数40—100个时，组数为7－10 (4)列频数分布表. 组；
数据分成_____组. （2）当数据个数小于40时，组数为6－8组；
8 6 4 2 0 22.5 24.5 26.5 28.5 30.5 32.5 数据
1、一个样本含有20个数
据:35,31,33,35,37,39,35,38,40,39,36,3
4,35,37,36,32,34,35,36,34. 在列频数分布表时,如果组距为2, 那么应分成___组,32.5~34.5这组的频数为 _____.
7 6 5 4 3 2 1
99.5 299.5 499.5 699.5 899.5 最小能见度(米)
练习：一次统计八年级若干名学生每分钟跳绳次数的频数分布直方图，请根据这个直方图回答下列问题： ⑴ 参加测试的总人数是多少？ 15人 ⑵ 自左至右最后一组的频数、频率分别是多少？
3，0.2
⑶ 数据分组时，组距是多少？
（2）视力在4.85及4.85以上的同学约占全校学生比例为 37.5% ,全校学生的平均视力是 4.76 .（精确到百分位）（3）如果视力在第1，2，3组范围内均属视力不良，那么该校约共有 1250 名学生视力不良，应给予治疗、矫正。
50
40 30 第3组第2组第1组
3.95 4.25 4.55 4.85
数出每一组频数
(5)绘制频数分布直方图.
横轴表示各组数据，纵轴表示频数，该组内的频数为高，画出一个个矩形。

(中考复习)第20 讲统计的应用

3．(2013· 玉林)如图20－1所示是某手机店今年1－5月份音乐手
机销售额统计图．根据图中信息，可以判断相邻两个月音乐手机销售额变化最大的是 (
C )
基础知识 · 自主学习
题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考
图20－1
A．1月至2月
C．3月至4月
B．2月至3月
D．4月至5月
基础知识 · 自主学习
题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考 (3)补全折线统计图和条形统计图如图．解：补全后的统计图如图20－7所示．
图20－7
基础知识 · 自主学习题组分类 · 深度剖析
积极践行“节约用水，从我做起”，下表是从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况：
基础知识 · 自主学习
题组分类 · 深度剖析
课堂回顾 · 巩固
0.25 2
0.3 2
0.4 4
0.5 1 ( A )
那么这组数据的众数和平均数分别是 A．0.4和0.34 C．0.25和0.34 B．0.4和0.3 D．0.25和0.3
课堂回顾 · 巩固提升
浙派名师中考 5．(2013· 日照)如图20－3所示是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则，如年龄为36
岁统计在36≤x＜38小组，而不在34≤x＜36小组)，根据图形
提供的信息，下列说法中错误的是 ( D )
图20－3
基础知识 · 自主学习题组分类 · 深度剖析
(1)小丽看了统计图后说：“该市2011年新建保障房的套数比 2010年少了．”你认为小丽说法正确吗？请说明理由；

数学教材梳理频率分布直方图与折线图

庖丁巧解牛知识·巧学一、关于频率分布直方图的概念由于频率分布表数字较多，阅读困难，为了将频率分布表中的结果直观形象地表示出来，我们通常画频率分布直方图.画图时，应以横轴表示分组，纵轴表示频率与组距的比值。

以每个组距为底，以各频率除以组距的商为高,分别画成矩形,这样得到的直方图就是频率分布直方图.二、关于频率分布直方图的绘制方法频率分布直方图是在频率分布表的基础上绘制而成的，它的前期工作就是准确列出频率分布表，然后在平面直角坐标系中画出频率分布直方图，具体步骤如下：（1）求极差，即计算最大值与最小值的差。

(2）决定组距和组数。

组距与组数的确定没有固定标准，需要尝试、选择，力求有合适的组数，以能把数据的规律较清楚地呈现为准.太多或太少都不好,不利对数据规律的发现.组数应与样本的容量有关，样本容量越大组数越多。

(3)决定分点,将数据分组。

分组时，通常规定分组的区间是“左闭右开”的，避免数据被重复计算.（4）列频率分布表。

一般分“分组”“频数”“频率”三列，最后一行是“合计”。

注意频数的合计应是样本容量,频率合计应是1。

（5）画频率分布直方图。

建立直角坐标系，图中横轴为分组，图中的纵轴表示“频率/组距”。

各组数据以小长方形表示，其中，小长方形的宽为组距，小长方形的高=组距频率，频率=样本容量频率=组距×组距频率=小长方体的面积.各小长方形的面积总和为1。

由此可以看出，直方图中的各小长方形的面积表示相应的各组的频率。

这样频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小.误区警示直方图中小长方形的高并不表示各组数据的频率，而是频率与组距之比,小长方形的面积才是各组数据的频率.辨析比较频率分布表在数量表示上比较确切,但不够直观、形象,分析数据的总体态势不太方便,频率分布直方图形象、直观，与频率分布表相比较,频率直方图能直观地表明数据的分布形状,但原始数据不能在图中表示，说明直方图丢失了一些信息.从频率分布直方图可以清楚地看出数据分布的总体态势，但是从直方图本身得不出原始的数据内容。

高中数学2.2.1 2频率分布直方图与折线图.ppt

分组频数频率
[50.5,60.5) 4 0.08
[60.5,70.5)
0.16
[70.5,80.5) 10
[80.5,90.5) 16 0.32
[90.5,100.5)
合计
50
课前探究学习
课堂讲练互动
活页规范训练
(1)填充频率分布表的空格(将答案直接填在表格内)；
(2)补全频率分布直方图；
(3)学校决定成绩在[75.5,85.5)分的学生为二等奖，问该校
活页规范训练
[规范解答] (1)二、三两组的人数和为 50－(0.004＋0.044＋
0.012＋0.008)×10×50＝16，
第一组人数为 0.004×10×50＝2，
(2 分)
解得第二组人数为 6 人，第三组人数为 10，
∴第二组的频率是560＝0.12，第三组的频率是1500＝0.20，(4 分)
课前探究学习
课堂讲练互动
活页规范训练
【变式2】下表给出了某校500名12岁男孩的身高(单位：c m)资料：
身高 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 20
35
40
90
140
身高 [142,146) [146,150) [150,154) [154,158)
课前探究学习
课堂讲练互动
活页规范训练
根据上面的数据列出频率分布表、绘制出频率分布直方图，并估计长度在5.75～6.05 cm之间的麦穗在这批麦穗中所占的百分比．
[思路探索] 主要考查了频率分布直方图的作法以及用频率分布表或频率分布直方图分析样本，先求极差，决定组数和组距，然后列频率分布表，再在直角坐标系中，横轴表示高度，纵轴表示频率与组距的比值，得到频率分布直方图．

课下能力提升：(十一) 频率分布表频率分布直方图与折线图 Word版含答案

课下能力提升(十一) 频率分布表频率分布直方图与折线图一、填空题1．如图是容量为100的样本的频率分布直方图，试根据图形中的数据填空．(1)样本数据在范围[6,10)内的频率为________；(2)样本数据落在范围[10,14)内的频数为________．2．为了调查某厂工人生产某种产品的能力，随机抽查了20名工人某天生产该产品的数量，产品数量的分组区间为[45,55)，[55,65)，[65,75)，[75,85)，[85,95]，由此得到频率分布直方图如下图，则这20名工人中一天生产该产品数量在[55,75)的人数是________．3．将容量为100的样本数据，按从小到大的顺序分成8个组，如下表：4．为提高公众对健康的自我管理能力和科学认识，某调查机构共调查了200人在一天中的睡眠时间．现将数据整理分组，如下表所示．由于操作不慎，表中A，B，C，D四处数据污损，统计员只记得A处的数据比C处的数据大4，由此可知B处的数据为________.5.(如图)，但是年龄组为[25,30)的数据不慎丢失，则依据此图可得：(1)[25,30)年龄组对应小矩形的高度为________；(2)据此估计该市“四城同创”活动中志愿者年龄在[25,35)的人数为________．二、解答题6.某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96,106]，样本数据分组为[96,98)，[98,100)，[100,102)，[102,104)，[104,106)．已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是多少？7.根据空气质量指数API(为整数)的不同，可将空气质量分级如下表：对某城市一年(365天)的空气质量进行监测，获得的API 数据按照区间[0,50]，(50,100]，(100,150]，(150,200]，(200,250]，(250,300]进行分组，得到频率分布直方图如图．(1)求频率分布直方图中x 的值；(2)计算一年中空气质量为良和轻微污染的总天数．(提示：结果用分数表示．已知57＝78 125,27＝128，31 825＋2365＋71 825＋31 825＋89 125＝1239 125，365＝73×5)8．为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量(单位：千克)，并将所得数据分组，画出频率分布直方图(如图所示)．(1)求出各组相应的频率；(2)估计数据落在[1.15，1.30]中的概率为多少；(3)将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中还有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数．答案1．解析：(1)样本数据在[6,10)内频率为0.08×4＝0.32.(2)在[10,14)内的频数为0.09×4×100＝36.答案：(1)0.32 (2)362．解析：由题意得，这20名工人中一天生产该产品数量在[55,75)的人数是20×[(0.040＋0.025)×10]＝13(人)．答案：133．解析：9＋14＋14＋13＋12＋x＋13＋10＝100，x＝15.P＝15100＝0.15. 答案：0.154．解析：设A处的数据为x，则C处的数据为x－4，则x＋x－4＋8＋52＋20＋4＝200，x＝60，则B 处数据为60200＝0.3.答案：0.35．解析：设[25,30)年龄组对应小矩形的高度为h ，则5×(0.01＋h ＋0.07＋0.06＋0.02)＝1，h ＝0.04.志愿者年龄在[25,35)的频率为5×(0.04＋0.07)＝0.55，故志愿者年龄在[25,35)的人数约为0.55×800＝440.答案：0.04 4406．解：产品净重小于100克的频率为(0.050＋0.100)×2＝0.300，已知样本中产品净重小于100克的个数是36，设样本容量为n ，则36n＝0.300，所以n ＝120，净重大于或等于98克并且小于104克的产品的频率为(0.100＋0.150＋0.125)×2＝0.750，所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.750＝90.7．解：(1)由图可知50x ＝1－(31 825＋2365＋71 825＋31 825＋89 125)×50＝1－1239 125×50，解得x ＝11918 250；(2)365×(11918 250×50＋2365×50)＝219.答：一年中空气质量为良和轻微污染的总天数为219天． 8．解：(1)由频率分布直方图和频率＝组距×(频率组距)可得下表(2)0.30＋0.15＋0.02＝中的概率约为0.47.(3)由分层抽样中每个个体被抽到的概率相同知：设水库中鱼的总条数为N ，则120N ＝6100，即N ＝2 000，故水库中鱼的总条数约为2 000条．。

频数分布折线图PPT课件

2020年10月2日
10
通过本节课的学习，请谈谈你的收获？
2020年10月2日
11
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
请制作上述数据的频数分布表。
2020年10月2日
7
81，73，77，79，80，78，85，80，68，90， 80，89，82，81，84，72，83，77，79，75。
20名学生每分钟脉搏跳动的次数的频数分布表
组别（次）组中值（次）
频数
67.5~72.5 72.5~77.5 77.5~82.5
尺寸（码）
2由020年上10月2日图中你可以得到什么信息？ 4
知识要点
➢ 用来表示频数分布的
基本统计图叫做频数分布直方频图，简称直方图。
数
边界值
组中值
2020年10月2日
5
➢ 一次统计八年级若干名学生每分钟跳绳次数的频数分布直方图，请根据这个直方图回答下列问题： ⑴ 参加测试的总人数是多少？ ⑵ 自左至右最后一组的频数、频率分别是多少？ ⑶ 数据分组时，组距是多少？
82.5~87.5 87.5~92.5
根据频数分布表画出频数分布直方图
2020年10月2日
8
20名学生每分脉搏跳动次数的频数分布直方图
频
数12
（
人10

频率分布直方图与折线图知识学习

频率分布直方图与折线图知识讲解分析数据的一种基本方法是用图将它们画出来，基者用紧凑的表格改变数据的排列方式，作图可以达到两个目的，一是从数据中提取信息，二是利用图形传递信息。

本节学习的重点在于通过实例体会分布的意义和作用，在表示样本数据过程中，学会列出频率分布表，画频率分布直方图、频率折线图，体会它们各自的特点。

本节的学习，难点在理解频率分布直方图的含义，利用频率分布直方图、折线图、估计总体的数据落在某一范围的频率。

本节内容是初中“统计初步”的继续和提高，概念多，要准确地把握各个概念的内涵，统计内容实践性较强，要多动手，于解决实际问题的实践中巩固巩固掌握知识，提高解决问题能力。

我们在初中曾学过一种直观体现数据分布规律的方法------频数分布直方图，纵轴高度表示各组的频数。

1、频率分布直方图：对于样本数据，分组后把横轴分成若干段，每一段对应一个组距，然后以线段为底作一矩形，它的高度等于该组的频率/组距，这样得出一系列的矩形，每个矩形的面积恰好是该组上的频率。

这些矩形就构成了频率分布直方图。

这里要注意频率分布直方图的横轴表示样本数据，纵轴表示各组的频率/组距。

图中小长方形的面积是相应分组的频率。

在频率分布直方图中，每个小矩形的面积等于相应各组的频率，而各组的频率的和等于1。

因此各小矩形的面积和等于1。

频率分布直方图能够很容易地表示大量数据，非常直观地表明分布的形状，使我们能够看到在频率分布表中看不出原始的数据模式。

但是从频率分布在直方图本身不能得出原始数据的内容，也就是说，把数据表示成频率分布直方图后，原有的具体数据信息就补抹掉了。

2、频率分布折线图：把频率分布直方图中的各个矩形上边中点用线段连接起来，就得到频率分布折线图。

一般为方便看图，习惯上绘制折线图时：按照分组原则，再在左边和右边各加一个区间，从所加左边区间中点开始，将频率分布直方图中各相邻矩形的上底边的中点顺次连接起来，直至右边区间的中点，就得到折线图。

高中数学北师大版必修一频率分布直方图课件

主
堂
预习
[提示]
因为通过抽样获得的原始数据多而且杂乱，无法直接从
小结
·
探
提
新中理解它们的含义，并提取信息，也不便于我们用它来传递信息．正素
知
养
因为如此我们才用频率分布直方图来整理数据．
合
作探
2．为什么要对样本数据进行分组？
课时
究
分
[提示] 不分组很难看出样本中的数字所包含的信息，分组后，层
层作
疑
业
难
大小．
返首页
·
5
·
自
课
主
堂
预
小
习
结
·
探新
2．频率分布直方图的应用
提素
知
养
当考虑数据落在若干个组内的频率之和时，可以用相应矩形面积
合
作
课
探之和来表示．
时
究
分
层释作来自疑业难
返首页
·
6
·
自
课
主
3．画频率分布直方图的步骤
堂
预
小
习
结
探
(1)计算极差：即一组数据中_最__大__值_和最__小__值__的差；
堂小
习探
生，实测身高数据(单位：cm)如下：
·
结提
新
素
知
171 163 163 166 166 168 168 160 168 165
养
·
·
合
171 169 167 169 151 168 170 160 168 174
作探
165 168 174 159 167 156 157 164 169 180

《2.2.2频率分布直方图与折线图》教案新部编本1

教师学科教案[ 20 – 20 学年度第__学期]任教学科：_____________任教年级：_____________任教老师：_____________xx市实验学校1．列频率分布表的一般步骤是什么？能否根据频率分布表来绘制频率直方图？2．作频率分布直方图的方法为：3．如果将频率分布直方图中各相邻矩形的上底边中点并顺次连结起来，就得到_________，简称___________．4．频率折线图的优点是：__________________________．如果样本容量取得足够大，分组的组距取得足够小，那么相应的频率折线图将趋于一条光滑的曲线，我们称这条光滑的曲线为总体分布的___________．例题剖析例1 下表是某学校一个星期中收交来的失物件数，请将5天中收交来的失物数用条形图表示．例2 作出例1中数据的频率分布直方图．例3 为了了解一大片经济林生长情况，随机测量其中的100株的底部周长，得到如下数据表(单位：cm)(2)绘制频率分布直方图；(3)估计该片经济林中底部周长小于100cm 的树木约占多少，周长不小于120cm 的树木约占多少．巩固练习1．在频率分布直方图中，所有矩形的面积和为_________．2．200辆汽车通过某一段公路时的时速如下图所示，则时速在的汽车大约有______辆．km ）.0.0.0.0课堂小结什么是频数条形图、频率直方图、折线图、密度曲线．课后训练一基础题1．在100人中，有40个学生，21个干部，29个工人，10个农民，则29.0是工人( )A．频数B．频率C．累计频率D．累计频数2．对于样本频率分布折线图与总体密度曲线的关系，下列说法中正确的是( ) A．频率分布折线图与总体密度曲线无关；B．频率分布折线图就是总体密度曲线；C．样本容量很大的频率分布折线图就是总体密度曲线；D．如果样本容量无限增大，分组的组距无限减小，那么频率分布折线图就会无限接近于总体密度曲折线．3．在频率分布直方图中，各个小长方形的面积表示( ) A．落在相应各组的数据的频数B．相应各组的频率.C．该样本所分成的组数D．该样本的样本容量4．容量为100的某个样本数据拆分为10组，并填写频率分布表，若前七组频率之和为79.0，则剩下的三组中频率最大的一组的.0，而剩下的三组的频率依次差为05频率为_________．5．在一个小时内统计一传呼台接收到用户的呼唤次数，按每分钟统计如下：00121223410125312224 24311323461202313141 12023425021103213120写出一分钟内传呼呼唤次数的频率分布表，并画出频率分布图．二提高题6．在一个容量为的样本，数据的分组及各组的频数如下：[)5.15,5.123[)5.18,5.158[)5.21,5.189[)5.24,5.2111[)5.27,5.2410[)5.30,5.275[)5.33,5.304(1)列出样本的频率分布表；(2)画出频率分布直方图；(3)根据频率分布直方图估计，数据落在[)5.24,5.15的可能性约是多少？7．姚明在2004NBA赛季常规赛82场比赛的前80场中，带领休斯顿火箭队取2003-得了较好的战绩，提前锁定了季后赛资格．以下是姚明在这80场比赛中的得分表现：20,,2112,1218,,21,,,,1219,19201016,16,,2312,,10,21,,18,,141112,2019,8,14,,,152216,22,,21,2117,2913,,15,,12,211615,4,10,,6,22,1416,29,41371720,,,12,,25,9,12,7,16,16,,1717,1929,10,,3314,13．11,,29,27,23,15,2112,15,12,,,6,25,2814,,,1627(1)如果将这个数据分为组，作出这组数据的频率分布表；(2)画出频率分布直方图并作出频率折线图；(3)在频率分布直方图中作出密度曲线．。

频率分布直方图与折线图共23页

频率分布直方图与折线图
21、没有人陪你走一辈子，所以你要适应孤独，没有人会帮你一辈子，所以你要奋斗一生。 22、当眼泪流尽的时候，留下的应该是坚强。 23、要改变命运，首先改变自己。
24、勇气很有理由被当作人类德性之首，因为这种德性保证了所有其余的德性。--温斯顿．丘吉尔。 25、梯子的梯阶从来不是用来搁脚的，它只是让人们的脚放上一段时间，以便让别一只脚能够再往上登。
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利

频率分布直方图与折线图

（2）在横轴上标上表示的点；
身高/cm
（3）在上面各点中，分别以连接相邻两点的线段为底作矩形，高等于该组的频率/组距．
问题：如何作出例1数据的频率分布折线图？
在频率分布直方图中，取相邻矩形上底边的中点顺次连结起来，就得到频率分布折线图（简称频率折线图）
取值区间两端点须分别向外延伸半个组距，取此组距上在x轴上的点与折线的首尾分别相连
合计
频数 1 2 4 14 24 15 12 9 11 6 2
100
频率频率/组距
分组 [80，85) [85，90) [90，95 [95，100) [100，105) [105，110) [110，115) [115，120) [120，125) [125，130] [130，135]
合计
频数 1 2 4 14 24 15 12 9 11 6 2
（1）编制频率分布表；（2）绘制频率分直方图，折线图；（3）估计该片经济林中底部周长小于
100cm的树木约占多少，周长不小于120cm的树木约占多少。
分组 [80，85) [85，90) [90，95 [95，100) [100，105) [105，110) [110，115) [115，120) [120，125) [125，130] [130，135]
100
频率 0.01 0.02 0.04 0.14 0.24 0.15 0.12 0.09 0.11 0.06 0.02
1
频率/组距 0.002 0.004 0.008 0.028 0.048 0.030 0.024 0.018 0.022 0.012 0.004 0.2
（2）直方图如图：
（3）从频率分布表得，
示频率/组距；

频率分布直方图

［30.5, 33.5）
频数
3 0.06 8 0.16 9 0.18 11 0.22 10 0.20 5 0.10 4 0.08
频率
0.020 0.053 0.060 0.073 0.067 0.033 0.027
精品课件
频率分布直方图如下：
频率组距
0.070 0.060 0.050 0.040 0.030 0.020 0.010
12.5 15.5 18.5 21.5 24.5 27.5
精品课件
频率/ 组距
0.020 0.053 0.060 0.073 0.067 0.033 0.027
所得到的结论的统计意义
• 一般的，统计得到的结果，是对于总体较为合理的估计或预测，但其误差应该控制在合理的范围之内。
• 也正因为这样，统计结果的好坏，往往需要进一步的评价，或通过理论方法的检验，或通过实际应用的检验。
组数：将数据分组，当数据在100个以内时，
按数据多少常分5-12组。
组距：指每个小组的两个端点的距离，
组数=
极差组距
=
4.1 0.5
=
8.2
3.将数据分组
［0，0.5 )，［0.5，1 )，…，［4，4.5］
精品课件
4.列频率分布表 100位居民月平均用水量的频率分布表
注意：这里出来了条形图中条形的宽度。频率不仅与条形的高度有关，而且与它的宽度有关。
分析：样本容量越大，这种估计越精确。但随着样本容量的增加，作图时所分的组数增加，组距减小，相应的频率折线图会越来越接近于一条光滑曲线.
精品课件
总体密度曲线
当样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近一条光滑曲线——总体密度曲线．