2003高教社杯全国大学生数学建模竞赛B题竞赛参考答案
全国大学生数学建模竞赛题目B题

B题公交车调度
公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
2003年全国大学生数学建模竞赛题目

高教社杯全国大学生数学建模竞赛B题参考答案.docx

交巡警服务平台的设置与调度优化分析摘要本文以实现警察的刑事执法、治安管理、交通管理、服务群众四大职能为宗旨,利用有限的警务资源,根据城市的实际情况与需求合理地设置了交巡警服务平台、分配各平台的管辖范围及调度警务资源。
并分别对题目的各问,作了合理的解答。
问题一:(1)、根据题目所给数据,确定各节点之间的相邻关系和距离,利用Floyd 算法及 matlab 编程求出两点之间的最短距离,使其尽量满足能在 3 分钟内有交巡警平台警力到达案发结点的原则,节点去选择平台,把节点分配给离节点距离最近的平台管辖,据此,我们得到了平台的管辖区域划分。
(2)、我们对进出该区的 13 条交通要道实现快速全封锁的问题,我们认定在所有调度方案中,某种方案中耗时最长的的围堵时间最短即最佳方案,利用 0-1 变量确定平台的去向,并利用线性规划知识来求解指派问题,求得了最优的调度方案。
(3)、在确定增添平台的个数和具体位置的问题中,我们将尽量保证每个节点都有一个平台可以在三分钟内到达作为主要原则来求解。
我们先找出到达每个平台的时间都超过三分钟的节点,并尝试在这些节点中选取若干个作为新的平台,求出合理的添加方案。
问题二:(1)、按照设置交巡警服务平台的原则和任务,分析现有的服务平台的设置是否合理,我们以各区覆盖率作为服务平台分布合不合理的评价标准,得到C、 D、 E、F区域平台设置不合理。
并尝试一些新的设置方案使得设置更为合理,最后以覆盖率最低的E 区为例,使用一种修改方案得到一个比原方案更合理的交巡警服务平台的设置方案。
(2)、追捕问题要求在最快的时间内抓到围堵罪犯,在罪犯和警察的行动速度一致的前提假设下,我们先设定一个具体较小的时间,编写程序检验在这个时间内是否可以成功抓捕罪犯,不行则以微小时间间隔增加时间,当第一次成功围堵时,这个时间即为最佳围堵方案。
关健字: MATLAB软件, 0-1 规划,最短路, Floyd 算法,指派问题一、问题重述“有困难找警察” ,是家喻户晓的一句流行语。
高教社杯全国大学生数学建模竞赛B题参考答案

交巡警服务平台的设置与调度优化分析摘要本文以实现警察的刑事执法、治安管理、交通管理、服务群众四大职能为宗旨,利用有限的警务资源,根据城市的实际情况与需求合理地设置了交巡警服务平台、分配各平台的管辖范围及调度警务资源。
并分别对题目的各问,作了合理的解答。
问题一:(1)、根据题目所给数据,确定各节点之间的相邻关系和距离,利用Floyd 算法及matlab编程求出两点之间的最短距离,使其尽量满足能在3分钟内有交巡警平台警力到达案发结点的原则,节点去选择平台,把节点分配给离节点距离最近的平台管辖,据此,我们得到了平台的管辖区域划分。
(2)、我们对进出该区的13条交通要道实现快速全封锁的问题,我们认定在所有调度方案中,某种方案中耗时最长的的围堵时间最短即最佳方案,利用0-1变量确定平台的去向,并利用线性规划知识来求解指派问题,求得了最优的调度方案。
(3)、在确定增添平台的个数和具体位置的问题中,我们将尽量保证每个节点都有一个平台可以在三分钟内到达作为主要原则来求解。
我们先找出到达每个平台的时间都超过三分钟的节点,并尝试在这些节点中选取若干个作为新的平台,求出合理的添加方案。
问题二:(1)、按照设置交巡警服务平台的原则和任务,分析现有的服务平台的设置是否合理,我们以各区覆盖率作为服务平台分布合不合理的评价标准,得到C、D、E、F区域平台设置不合理。
并尝试一些新的设置方案使得设置更为合理,最后以覆盖率最低的E区为例,使用一种修改方案得到一个比原方案更合理的交巡警服务平台的设置方案。
(2)、追捕问题要求在最快的时间内抓到围堵罪犯,在罪犯和警察的行动速度一致的前提假设下,我们先设定一个具体较小的时间,编写程序检验在这个时间内是否可以成功抓捕罪犯,不行则以微小时间间隔增加时间,当第一次成功围堵时,这个时间即为最佳围堵方案。
关健字: MATLAB软件,0-1规划,最短路,Floyd算法,指派问题一、问题重述“有困难找警察”,是家喻户晓的一句流行语。
2003数学建模B题(国家一等奖)-参考

露天矿生产的车辆安排摘要:本文讨论了铁矿运输问题中,在满足卸点产量和品位要求的前提下,针对不同的原则建立一般的最优生产计划的模型。
用LINDO软件求解,速度很快,在实例求解的过程中,迭代次数分别为47次和45次。
与经典的线性规划方法相比,具有一定的优越性。
针对原则一:列出多目标规划模型。
然后将模型简化,分为两阶段求解。
第一阶段为单目标线性规划模型,用LINDO软件求解,得出运输路线及运输次数。
第二阶段采用MATLAB软件求解,用到第一阶段的结果,得出最优生产计划。
结果:需要13辆卡车;7辆电铲,电铲分布在铲点1,2,3,4,8,9,10;总运量为8.57万吨公里。
针对原则二:列出多目标规划模型。
然后分为三阶段来求解,前两阶段为单目标线性规划,第三阶段是分析的过程。
采用LINDO软件求解。
结果:需要20辆卡车;7辆电铲,电铲分布在铲点1,2,3,4,8,9,10;总产量为10.087万吨,其中矿石6.0022万吨,岩石4.0848万吨。
关键词:多目标规划模型化简分阶段求解快速算法一、问题的提出钢铁工业是国家工业的基础之一,铁矿的运输工程的重要性由此可见。
本题要求根据两个原则分别建立模型,在满足卸点的数量和品位的前提下,求解出最优生产计划。
原则一:总运量(吨公里)最小,同时出动最少的卡车,从而运输成本最小;原则二:利用现有车辆运输,获得最大的产量(岩石产量优先;在产量相同的情况下,取总运量最小的解)。
生产计划包括:出动几台电铲,分别在那些铲位上;出动几辆卡车,分别在那些路线上各运输多少次;在卡车不等待条件下满足产量和品位要求。
二、问题的假设1.铁矿的运输是周期性的,虽然本题只要求给出一个班次的生产计划,我们仍然把它放在一个周期性的运输过程当中来考虑,卡车完成本班次的运输任务以后仍回到出发点。
2在确定生产计划时,不考虑随机因素的影响,即装车与卸车的时间严格遵守题目所给的时间。
3运输成本不包括铲车的运行费用。
最新2022高教社杯全国大学生数学建模竞赛B题竞赛参考答案

2022高教社杯全国大学生数学建模竞赛B题竞赛参考答案2022高教社杯全国大学生数学建模竞赛B题参考答案注意:以下答案是命题人给出的,仅供参考。
各评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
问题:钢铁工业是国家工业的根底之一,铁矿是钢铁工业的主要原料基地。
许多现代化铁矿是露天开采的,它的生产主要是由电动铲车〔以下简称电铲〕装车、电动轮自卸卡车〔以下简称卡车〕运输来完成。
提高这些大型设备的利用率是增加露天矿经济效益的首要任务。
露天矿里有假设干个爆破生成的石料堆,每堆称为一个铲位,每个铲位已预先根据铁含量将石料分成矿石和岩石。
一般来说,平均铁含量不低于 25%的为矿石,否那么为岩石。
每个铲位的矿石、岩石数量,以及矿石的平均铁含量〔称为品位〕都是的。
每个铲位至多能安置一台电铲,电铲的平均装车时间为 5 分钟。
卸货地点〔以下简称卸点〕有卸矿石的矿石漏、2 个铁路倒装场〔以下简称倒装场〕和卸岩石的岩石漏、岩场等,每个卸点都有各自的产量要求。
从保护国家资源的角度及矿山的经济效益考虑,应该尽量把矿石按矿石卸点需要的铁含量〔假设要求都为29.5% 1%,称为品位限制〕搭配起来送到卸点,搭配的量在一个班次〔8 小时〕内满足品位限制即可。
从长远看,卸点可以移动,但一个班次内不变。
卡车的平均卸车时间为3 分钟。
所用卡车载重量为 154 吨,平均时速 28kmh 。
卡车的耗油量很大,每个班次每台车消耗近 1 吨柴油。
发动机点火时需要消耗相当多的电瓶能量,故一个班次中只在开始工作时点火一次。
卡车在等待时所消耗的能量也是相当可观的,原那么上在安排时不应发生卡车等待的情况。
电铲和卸点都不能同时为两辆及两辆以上卡车效劳。
卡车每次都是满载运输。
每个铲位到每个卸点的道路都是专用的宽 60 m 的双向车道,不会出现堵车现象,每段道路的里程都是的。
一个班次的生产方案应该包含以下内容:出动几台电铲,分别在哪些铲位上;出动几辆卡车,分别在哪些路线上各运输多少次〔因为随机因素影响,装卸时间与运输时间都不精确,所以排时方案无效,只求出各条路线上的卡车数及安排即可〕。
数学建模2003高教杯年b题matlab代码

数学建模2003高教杯年b题matlab代码
(最新版)
目录
一、数学建模竞赛简介
二、2003 年高教杯数学建模竞赛 B 题概述
三、Matlab 代码应用
四、结论
正文
一、数学建模竞赛简介
数学建模竞赛是一项面向全球高校大学生的竞技活动,旨在通过对现实问题进行抽象、建模和求解,培养学生的创新意识、团队协作精神和实际问题解决能力。
竞赛题目一般来源于工程、物理、经济、社会等多个领域,参赛选手需要运用自己所学的数学知识,对题目进行深入研究,并撰写论文说明模型建立和求解过程。
二、2003 年高教杯数学建模竞赛 B 题概述
2003 年高教杯全国大学生数学建模竞赛(大专组)的 B 题为“抢渡长江”,要求参赛选手建立一个合适的数学模型,对抢渡长江的过程进行优化。
题目中涉及到的问题包括船只的调度、航行速度的控制等,需要参赛选手充分考虑长江的实际情况,如长江的宽度、水流速度等。
三、Matlab 代码应用
在解决该问题时,可以使用 Matlab 编程语言进行建模和求解。
Matlab 是一种广泛应用于科学计算和工程设计的语言,具有强大的数值计算和数据分析功能。
在解决“抢渡长江”问题时,可以首先建立长江的简化模型,包括长江的宽度、水流速度等参数,然后运用 Matlab 中的优化算法,如遗传算法、粒子群算法等,对船只的调度和航行速度进行优化,
从而实现最短时间抢渡长江的目标。
四、结论
通过以上分析,我们可以得出结论:在 2003 年高教杯全国大学生数学建模竞赛(大专组)中,B 题“抢渡长江”可以通过运用 Matlab 编程语言进行建模和求解。
案例四2003高教社杯全国大学生数学建模竞赛题目B题露天矿生产

案例四:2003高教社杯全国大学生数学建模竞赛题目B题露天矿生产的车辆安排钢铁工业是国家工业的基础之一,铁矿是钢铁工业的主要原料基地。
许多现代化铁矿是露天开采的,它的生产主要是由电动铲车(以下简称电铲)装车、电动轮自卸卡车(以下简称卡车)运输来完成。
提高这些大型设备的利用率是增加露天矿经济效益的首要任务。
露天矿里有若干个爆破生成的石料堆,每堆称为一个铲位,每个铲位已预先根据铁含量将石料分成矿石和岩石。
一般来说,平均铁含量不低于25%的为矿石,否则为岩石。
每个铲位的矿石、岩石数量,以及矿石的平均铁含量(称为品位)都是已知的。
每个铲位至多能安置一台电铲,电铲的平均装车时间为5分钟。
卸货地点(以下简称卸点)有卸矿石的矿石漏、2个铁路倒装场(以下简称倒装场)和卸岩石的岩石漏、岩场等,每个卸点都有各自的产量要求。
从保护国家资源的角度及矿山的经济效益考虑,应该尽量把矿石按矿石卸点需要的铁含量(假设要求都为29.5%1%,称为品位限制)搭配起来送到卸点,搭配的量在一个班次(8小时)内满足品位限制即可。
从长远看,卸点可以移动,但一个班次内不变。
卡车的平均卸车时间为3分钟。
所用卡车载重量为154吨,平均时速28。
卡车的耗油量很大,每个班次每台车消耗近1吨柴油。
发动机点火时需要消耗相当多的电瓶能量,故一个班次中只在开始工作时点火一次。
卡车在等待时所耗费的能量也是相当可观的,原则上在安排时不应发生卡车等待的情况。
电铲和卸点都不能同时为两辆及两辆以上卡车服务。
卡车每次都是满载运输。
每个铲位到每个卸点的道路都是专用的宽60的双向车道,不会出现堵车现象,每段道路的里程都是已知的。
一个班次的生产计划应该包含以下内容:出动几台电铲,分别在哪些铲位上;出动几辆卡车,分别在哪些路线上各运输多少次(因为随机因素影响,装卸时间与运输时间都不精确,所以排时计划无效,只求出各条路线上的卡车数及安排即可)。
一个合格的计划要在卡车不等待条件下满足产量和质量(品位)要求,而一个好的计划还应该考虑下面两条原则之一:1.总运量(吨公里)最小,同时出动最少的卡车,从而运输成本最小;2.利用现有车辆运输,获得最大的产量(岩石产量优先;在产量相同的情况下,取总运量最小的解)。
2002高教社杯全国大学生数学建模竞赛B题参考答案

2002高教社杯全国大学生数学建模竞赛B 题 彩票中的数学 参考答案注意:以下答案是命题人给出的,仅供参考。
各评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
评价一个方案的优劣,或合理性如何,主要取决于彩票公司和广大彩民两方面的利益。
事实上,公司和彩民各得销售总额的50%是确定的,双方的利益主要就取决于销售总额的大小,即双方的利益都与销售额成正比。
因此,问题是怎样才能有利于销售额的增加?即公司采用什么样的方案才能吸引广大的彩民积极踊跃购买彩票?具体地讲,问题涉及到一个方案的设置使彩民获奖的可能性有多大、奖金额有多少、对彩民的吸引力有多大、广大彩民如何看待各奖项的设置,即彩民的心理曲线怎样?另外,一个方案对彩民的影响程度可能与区域有关,即与彩民所在地区的经济状况以及收入和消费水平有关。
为此,我们要考查一个方案的合理性问题,需要考虑以上这些因素的影响,这是我们建立模型的关键所在。
1. 模型假设与符号说明彩票摇奖是公平公正的,各号码的出现是随机的; 彩民购买彩票是随机的独立事件;对同一方案中高级别奖项的奖金比例或奖金额不应低于相对低级别的奖金比例或奖金额;根据我国的现行制度,假设我国居民的平均工作年限为T =35年。
jr ---第j 等(高项)奖占高项奖总额的比例,3,2,1=j ;i x ----第i 等奖奖金额均值,71≤≤i ; i p ----彩民中第i 等奖i x 的概率,71≤≤i ;)(i x μ----彩民对某个方案第i 等奖的满意度,即第i 等奖对彩民的吸引力,71≤≤i ;λ----某地区的平均收入和消费水平的相关因子,称为“实力因子”,一般为常数; F ----彩票方案的合理性指标,即方案设置对彩民吸引力的综合指标;2. 模型的准备(1)彩民获各项奖的概率从已给的29种方案可知,可将其分为四类,1K :10选6+1(6+1/10)型、2K : n 选m )/(n m 型、3K :n 选1+m )/1(n m +型和4K :n 选m )/(n m 无特别号型,分别给出各种类型方案的彩民获各奖项的概率公式:● ● 1K :10选6+1(6+1/10)型7611021051-⨯=⨯=p ,7621081054-⨯=⨯=p ,56193101.8102-⨯=⨯=C p 461919110194102.61102-⨯=+=C C C C p , 361101919110110195103.421022-⨯=+=C C C C C C p 261919191101101919110110110196104.199510)23(32-⨯=⨯+⨯⨯-⨯+⨯=C C C C C C C C C C C p● ● 2K :n 选m )/(n m 型m n C p 11=,m n m m C C p 12-=,m n m n m m C C C p 1)1(13+--=,mn m n m m C C C p 1)1(24+--=,m n m n m m C C C p 2)1(25+--=,m n m n m m C C C p 2)1(36+--=,mn m n m m C C C p 3)1(37+--=。
全国大学生数学建模竞赛题目B题
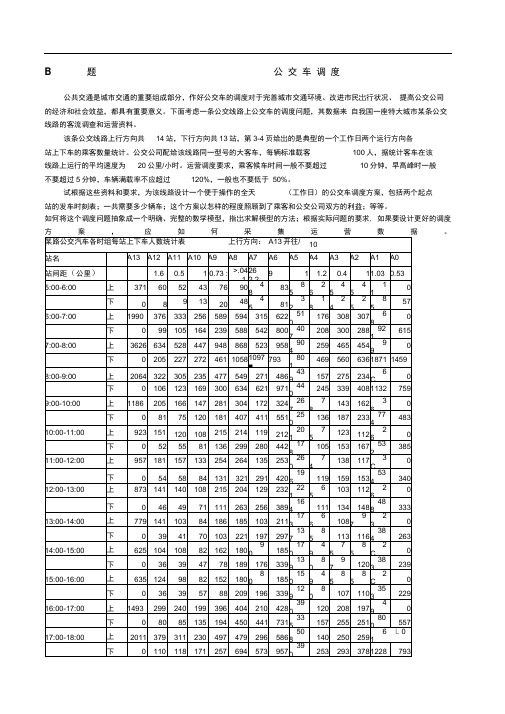
B 题公交车调度
公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民岀行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给岀的是典型的一个工作日两个运行方向各
站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100人,据统计客车在该
线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般
不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点
站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指岀求解模型的方法;根据实际问题的要求, 如果要设计更好的调度方案,应如何采集运营数据。
全国大学生数学建模竞赛题目B题

B题公交车调度公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过 120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
数学建模2003高教杯年b题matlab代码

数学建模是数学与现实问题结合的一门学科,旨在利用数学知识和方法解决实际生活和工程中的问题。
而2003年高教杯数学建模竞赛是我国高校数学建模领域的重要比赛之一,吸引了大量对数学研究和应用感兴趣的学生参与。
其中,B题是竞赛中的一道问题,下面我们将介绍这道题目并给出对应的Matlab代码。
一、B题题目概述B题的题目较为复杂,主要是关于某公司的生产调度问题。
具体来说,题目要求在考虑生产线上各机器时间限制的条件下,设计出最佳的生产调度方案,以最大化生产效率并确保各产品按时完成。
二、问题分析1. 我们需要建立数学模型来描述该生产调度问题。
可以考虑引入作业调度理论中的相关概念,如作业、机器、加工时间等。
2. 需要考虑问题的约束条件,例如各种产品的生产时间限制、各机器的最大工作时间等。
3. 需要确定优化目标,即在满足约束条件的前提下,如何设计出最佳的生产调度方案。
三、Matlab代码实现在解决这一问题时,可以使用Matlab编程来实现数学模型的构建和优化算法的求解。
以下是一个简单的Matlab代码示例,用于对B题中所描述的生产调度问题进行建模和求解。
```matlab假设产品数为n,机器数为mn = 10;m = 5;初始化生产时间矩阵,其中A(i, j)表示第i个产品在第j台机器上的加工时间A = rand(n, m);设定机器的最大工作时间,假设为100machine_time_limit = 100 * ones(1, m);构建优化模型cvx_beginvariables x(n, m) 定义决策变量x(i, j),表示第i个产品在第j台机器上是否加工maximize(sum(sum(x))) 最大化生产效率subject tofor j = 1:msum(x(:, j).*A(:, j)) <= machine_time_limit(j) 确保每台机器的工作时间不超过限制endsum(x, 2) == ones(n, 1) 确保每个产品都按时完成x >= 0, x <= 1 约束x的取值范围为0到1cvx_end```以上代码利用了Matlab中的cvx工具箱,通过建立数学模型和求解优化问题,可以得到最佳的生产调度方案。
2003高教社杯全国大学生数学建模竞赛题目第四问.

2003年的阳春三月,本是个杨柳吐翠,树木萌芽的美好季节,可是,在此时此刻,我国部分地区却爆发了一种可怕的疾病—— SARS 。
一场没有硝烟的战争打破了人们平静祥和的生活, 无情的病魔, 威胁着广大人民群众的健康和生命安全, 这是生命与疾病的斗争, 是人类与病魔的斗争。
没有谁能够想象 SARS 竟然这么大杀伤力出现在人们面前,从轻微的咳嗽,发烧到大范围的扩散, 引起的部分死亡。
一时间,人心惶惶,谣言四起, 每个人都畏惧这种疾病却又无能为力。
在这个关键时刻,伟大的科学研究者向“非典”做出有力的反击。
在迎击这场天灾的战斗中, 医疗战线的英雄冲锋在前, 前仆后继地用汗水和生命筑起了一道血肉堤防。
在全国人民齐心协力,同舟共济,在科学和团结面前, “非典”低下了头。
在这场“非典”攻坚战中,是“传染病数学模型”在安抚民心,使得人们在消灭这种病毒有了一定的勇气与信心, 才能在后来打败了 SARS 这种大传播性的, 恢复正常安宁的生活。
传染病数学模型是指科技工作者分析了这次“非典” 爆发的部分数据后, 建立模型来描述 SARS 病毒的宏观传播过程,有助于从量的方面来分析受感染人数的变化趋势,掌握 SARS 的流行规律,从而及时对疫情进行控制, 提供科学的数据,认清传染的基本要素, 为防病提供必要的依据。
这种措施需要有一个预见性, 这就需要人们通过模型的建立对 SARS 的发病周期、发病人数的变化趋势、疑似人数的变化趋势等来分析和预测。
并为政府和医疗卫生部门进行决策和资料调配提供直接的服务,为相关的研究部门提供科学的数据。
SARS作为新发传染病之一,虽有着其特殊性,但也符合一般传染病的传播规律。
从 SARS 对人民身体健康造成严重危害可以看出及时对传染病建立模型并进行分析和预测对人类的生命健康有着至关重要的作用。
非典已经过去, “传染病模型”却这一概念深入人心,它也在后来一些传染病中被应用广泛,解决了很多问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2003高教社杯全国大学生数学建模竞赛B题参考答案注意:以下答案是命题人给出的,仅供参考。
各评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
问题:钢铁工业是国家工业的基础之一,铁矿是钢铁工业的主要原料基地。
许多现代化铁矿是露天开采的,它的生产主要是由电动铲车(以下简称电铲)装车、电动轮自卸卡车(以下简称卡车)运输来完成。
提高这些大型设备的利用率是增加露天矿经济效益的首要任务。
?露天矿里有若干个爆破生成的石料堆,每堆称为一个铲位,每个铲位已预先根据铁含量将石料分成矿石和岩石。
一般来说,平均铁含量不低于?25%的为矿石,否则为岩石。
?每个铲位的矿石、岩石数量,以及矿石的平均铁含量(称为品位)都是已知的。
每个铲?位至多能安置一台电铲,电铲的平均装车时间为?5?分钟。
卸货地点(以下简称卸点)有卸矿石的矿石漏、2?个铁路倒装场(以下简称倒装场)?和卸岩石的岩石漏、岩场等,每个卸点都有各自的产量要求。
从保护国家资源的角度及?矿山的经济效益考虑,应该尽量把矿石按矿石卸点需要的铁含量(假设要求都为29.5%?1%,称为品位限制)搭配起来送到卸点,搭配的量在一个班次(8?小时)内满足?品位限制即可。
从长远看,卸点可以移动,但一个班次内不变。
卡车的平均卸车时间为3?分钟。
所用卡车载重量为?154?吨,平均时速?28kmh?。
卡车的耗油量很大,每个班次每台车消耗近?1?吨柴油。
发动机点火时需要消耗相当多的电瓶能量,故一个班次中只在开始?工作时点火一次。
卡车在等待时所耗费的能量也是相当可观的,原则上在安排时不应发?生卡车等待的情况。
电铲和卸点都不能同时为两辆及两辆以上卡车服务。
卡车每次都是满载运输。
?每个铲位到每个卸点的道路都是专用的宽?60?m?的双向车道,不会出现堵车现象,每段道路的里程都是已知的。
一个班次的生产计划应该包含以下内容:出动几台电铲,分别在哪些铲位上;出动几辆卡车,分别在哪些路线上各运输多少次(因为随机因素影响,装卸时间与运输时间?都不精确,所以排时计划无效,只求出各条路线上的卡车数及安排即可)。
一个合格的计划要在卡车不等待条件下满足产量和质量(品位)要求,而一个好的计划还应该考虑下面两条原则之一:?1.总运量(吨公里)最小,同时出动最少的卡车,从而运输成本最小;?2.利用现有车辆运输,获得最大的产量(岩石产量优先;在产量相同的情况下,取总运量最小的解)。
?请你就两条原则分别建立数学模型,并给出一个班次生产计划的快速算法。
针对下面的实例,给出具体的生产计划、相应的总运量及岩石和矿石产量。
?某露天矿有铲位?10?个,卸点?5?个,现有铲车?7?台,卡车?20?辆。
各卸点一个班次的?产量要求:矿石漏?1.2?万吨、倒装场Ⅰ1.3?万吨、倒装场Ⅱ1.3?万吨、岩石漏?1.9?万吨、?岩场?1.3?万吨问题分析:本题目与典型的运输问题明显有以下不同: 1. 运输矿石与岩石两种物资; 2. 产量大于销量的不平衡运输; 3. 在品位约束下矿石要搭配运输; 4. 产地、销地均有单位时间的流量限制; 5. 运输车辆每次都是满载,154吨/车次;6. 铲位数多于铲车数意味着最优的选择不多于7个产地; 7. 最后求出各条路线上的派出车辆数及安排。
运输问题对应着线性规划,以上第1、2、3、4条可通过变量设计、调整约束条件实现;第5条使其变为整数线性规划;第6条用线性模型实现的一种办法,是从120710C 个整数规划中取最优的即得到最佳物流;对第7条由最佳物流算出各条路线上的最少派出车辆数(整数),再给出具体安排即完成全部计算。
对于这个实际问题,要求快速算法,计算含50个变量的整数规划比较困难。
另外,这是一个二层规划,第二层是组合优化,如果求最优解计算量较大,现成的各种算法都无能为力。
于是问题变为找一个寻求近优解的近似解法,例如可用启发式方法求解。
调用120次整数规划可用三种方法避免:(1)先不考虑电铲数量约束运行整数线性规划,再对解中运量最少的几个铲位进行筛选;(2)在整数线性规划的铲车约束中调用sign 函数来实现;(3)增加10个0-1变量来标志各个铲位是否有产量。
这是一个多目标规划,第一问的目标有两层:第一层是总运量(吨公里)最小,第二层是出动卡车数最少,从而实现运输成本最小。
第二问的目标有:岩石产量最大;矿石产量最大;运量最小,三者的重要性应按此序。
合理的假设主要有:1.卡车在一个班次中不应发生等待或熄火后再启动的情况;2.在铲位或卸点处因两条路线(及以上)造成的冲突时,只要平均时间能完成任务即可,不进行排时讨论;3.空载与重载的速度都是28km/h,耗油相差却很大,因此总运量只考虑重载运量;4.卡车可提前退出系统。
符号:x ij ~ 从i号铲位到j号卸点的石料运量单位吨;c ij~ 从i号铲位到j号卸点的距离公里;T ij ~ 从i号铲位到j号卸点路线上运行一个周期平均所需时间分;A ij ~ 从i号铲位到j号卸点最多能同时运行的卡车数辆;B ij ~ 从i号铲位到j号卸点路线上一辆车最多可以运行的次数次;p i ~ i号铲位的矿石铁含量。
%p =(30,28,29,32,31,33,32,31,33,31)q j ~j 号卸点任务需求吨q =(1.2,1.3,1.3,1.9,1.3)*10000ck i ~ i 号铲位的铁矿石储量万吨 cy i ~ i 号铲位的岩石储量万吨f i : ~ 描述第i 号铲位是否使用的0-1开关变量,取1为使用;取0为关闭。
模型建立、算法设计与模型求解: 问题一、求运输成本最小的生产计划一.以总运量最小为目标函数求解最佳物流—-第一层规划 (1)道路能力约束:一个电铲(卸点)不能同时为两辆卡车服务,一条路线上最多能同时运行的卡车数是有限制的。
卡车从i 号铲位到j 号卸点运行一个周期平均所需时间为53/2+平均速度+距离到⨯=j i T ij (分钟)。
由于装车时间5分钟大于卸车时间3分钟,所以这条路线上在卡车不等待条件下最多能同时运行的卡车数为:⎣⎦5/ijijT A =;其中最后开始发车的一辆卡车一个班次中在这条路线上最多可以运行的次数为(其他卡车可能比此数多1次)⎣⎦ij ij ij T A B /)5)1(608(⨯-⨯=-,这里5)1(⨯-ij A 是开始装车时最后一辆车的延时时间。
一个班次中这条固定路线上最多可能运行的总车次大约为:ij ij ij B A L ⨯=,总吨数ij L ⨯154。
(2)电铲能力约束:一台电铲不能同时为两辆卡车服务,所以一台电铲在一个班次中的最大可能产量为8×60/5×154(吨)。
(3)卸点能力约束:卸点的最大吞吐量为每小时60/3=20车次,于是一个卸点在一个班次中的最大可能产量为8×20×154(吨)。
(4)铲位储量约束:铲位的矿石和岩石产量都不能超过相应的储藏量。
(5)产量任务约束:各卸点的产量不小于该卸点的任务要求。
(6)铁含量约束:各矿石卸点的平均品位要求都在指定的范围内。
(7)电铲数量约束:电铲数量约束无法用普通不等式表达,可以引入10个0—1变量来标志各个铲位是否有产量。
(8)整数约束:当把问题作为整数规划模型时,流量x ij 除以154为非负整数。
(9)卡车数量约束:不超过20辆。
得到的一种模型为c x iji j ij⨯∑∑==10151min(0)s.t. 5,,1,10,,1,154 ==⨯≤⨯j i BA x ijijij(1)10,,1,1545/60851 =⨯⨯⨯≤∑=i f x i j ij (2)5,,1,154208101=⨯⨯≤∑=j i ijx(3)10,,1,100001000043521=⨯≤+⨯≤++i cy xx ck x x x ii i ii i i (4)5,,1,101=≥∑=j qx ji ij(5)5,2,1,0)5.28(0)5.30(101101=⎪⎪⎭⎪⎪⎬⎫≥-⨯≤-⨯∑∑==j p x p x i i ij i i ij (6) 5,,1,10,,1,154154 ===⎥⎥⎦⎥⎢⎢⎣⎢j i x x ijij . (7) 7101≤∑=i if(8)20154,≤⨯∑ji ijij B x (9)二.对最佳物流的结果进行派车—-第二层规划这是组合优化中的一维背包模型,针对快速算法的要求,用启发式方法求近优解。
先用最佳物流修正B ij , 确定卡车一个班次中在这条路线上实际最多可以运行的次数。
然后在以目标为出动总卡车数最少的各路线派车中,把各路线需要的卡车数)*154/(ij ij ij B x e =分成整数部分⎣⎦ij e 和小数部分⎣⎦ij ij e e -,进而可以分配任务让⎣⎦ij e 辆车在i 到j 路线上,每辆往返运输B ij 次。
为了最后实现第二层规划的目标,只需联合处理所有的⎣⎦ij ij e e -时把这些小数组合成最少的整数卡车数。
所需总卡车数的下界显然是⎥⎥⎤⎢⎢⎡=∑ji ij e Y ,0。
如果某种派车方案恰好派出Y 0辆车实现了所有的x ij ,则其即为第二层目标意义下近优解的最优方案。
但由于有联合派车而总公里数不一定最小,故不一定为全局意义下的最佳方案。
出动卡车数最少,意味着出动的卡车利用率要最大。
容易出现的一辆卡车为两个以上路线服务的联合派车,可分为两种情况:⑴有共同铲位(或卸点)的联合派车(V 字形或更复杂);⑵不同铲位且不同卸点之间的联合派车(Z 字形或四边形或更复杂)。
派车方案的空载路线应尽量安排在第一层规划的最佳物流路线内,即使有的超出也要保证超出的路程总和最小,这样才能实现重载路程最小且使卡车空载路程也最小。
而情况⑴的路线不会超出第一层规划的最佳物流路线。
只有情况⑵才会有一部分不在第一层规划的最佳物流路线内。
问题:各路线都是小数的需车数,如何组合使总卡车数最少且如果出现情况⑵时空载超出部分总和尽量小。
如果存在情况⑴,则整体考虑情况⑴形路线需要的卡车数相加的和,先确定和的整数部分的车数并对这些车分配任务(任务的形式为在哪条路线上运几趟,再在哪条路线上运几趟,等等)。
之后已无情况⑴了,再对各个小数进行组合相加试探,在所有动用卡车数最少的情况中,选择超出第一层最佳物流路线的总和最小的,即为最后派车方案,再对这些车分配任务。
由于属情况⑴的为多数,故后面的组合搜索比较简单,常常只有一两个任务属情况⑵。
根据最后派车方案,回代计算出各车辆在各路线的运输次数。
由于整数部分已分配完运输次数,小数乘以对应路线上的B ij取整计算出小数部分对应的具体运输次数.进一步计算出实际总运量与矿石和岩石的产量。
三、求解过程:(一)第一层规划求解前面给出的整数规划模型可计算出最优值为总运量85628.62吨公里。
