大学物理试卷参考答案(对应北京邮电大学版)
大学物理学答案北京邮电大学第版赵近芳等编著(一)

大学物理学答案北京邮电大学第版赵近芳等
编著(一)
大学物理学答案北京邮电大学第三版赵近芳等编著,是一本方便大学
物理学学习者进行自我检验和补充知识的参考书。
本书通过精心编排
的习题和答案,全面而深入地涵盖了大学物理学领域内各个方面的知
识点,使读者能够更好地掌握物理学的基本概念、定理和方法。
首先,本书的编排结构非常合理,根据大学物理学课程的教学内容,
分为力学、热学、电学、光学和现代物理学等五个部分,每个部分都
包含了丰富的习题和详细的解答。
每道习题的难度和类型都有所区分,既有选择题和判断题,也有计算题和解释题,能够满足不同层次学生
的需求。
其次,本书的答案详尽全面,准确无误。
每道习题的答案都有详细的
步骤和思路分析,同时还提供了参考图表和公式,使读者能够更加清
晰地理解和掌握物理学概念及其应用方法。
此外,本书还为部分较为
复杂的习题提供了多种解题方法,使读者能够更加灵活地运用知识。
最后,本书的内容丰富多样,不仅包含了大量的基础知识和应用技巧,还介绍了一些当前热门的前沿课题和研究成果,如量子物理学、相对
论和宇宙学等。
这些现代物理学内容,既能够拓展读者的知识面,又
对创新思维和科学研究能力的培养具有重要作用。
综上所述,大学物理学答案北京邮电大学第三版赵近芳等编著,是一
本非常适合大学物理学学习者使用的参考书,既方便了学习者对自身
学习情况的评估和纠正,又可以帮助学习者掌握物理学基本概念和应
用技巧,是一本值得广大物理学爱好者拥有的好书。
大学物理第二版下北京邮电大学出版社答案

大学物理第二版下北京邮电大学出版社答案第8章机械振动8-1 解:取固定坐标xOy ,坐标原点O 在水面上(图题所示)设货轮静止不动时,货轮上的A 点恰在水面上,则浮力为S ρga .这时ga s Mg ρ= 往下沉一点时,合力 )(y a g s Mg F +-=ρ gy s ρ-=.又 22d d t y M Ma F == 故0d d 22=+gy s t y M ρ022=+y M gs dtdy ρ 故作简谐振动M g s ρω=2)(35.68.910102101022223334s g s M T ====πρπωπ8-2 解:取物体A 为研究对象,建立坐标Ox 轴沿斜面向下,原点取在平衡位置处,即在初始位置斜下方距离l 0处,此时:)(1.0sin 0m kmg l ==θ(1) (1) A 物体共受三力;重mg, 支持力N, 张力T.不计滑轮质量时,有 T =kx列出A 在任一位置x 处的牛顿方程式220d d )(sin sin txm x l k mg T mg =+-=-θθ将(1)式代入上式,整理后得0d d 22=+x m ktx 故物体A 的运动是简谐振动,且)rad/s (7==mkω 习题8-1图由初始条件,000??=-=v l x 求得,1.00??===πml A 故物体A 的运动方程为x =0.1cos(7t+π)m(2) 当考虑滑轮质量时,两段绳子中张力数值不等,如图所示,分别为T 1、T 2,则对A 列出任一位置x 处的牛顿方程式为: 221d d sin txm T mg =-θ (2)对滑轮列出转动方程为:22221d d 2121t x Mr r a Mr J r T r T =??? ??==-β (3)式中,T 2=k (l 0+x ) (4)由式(3)、(4)知2201d d 21)(t xM x l k T ++=代入(2)式知22021)(sin dtxd m M x l k mg ??? ??+=+-θ又由(1)式知0sin kl mg =θ故0d d )21(22=++kx t xm M即0)2(d d 22=++x m M ktxm M k +=22ω可见,物体A 仍作简谐振动,此时圆频率为:rad/s)(7.52=+=m M k ω由于初始条件:0,000=-=v l x可知,A 、?不变,故物体A 的运动方程为:m t x )7.5cos(1.0π+=由以上可知:弹簧在斜面上的运动,仍为简谐振动,但平衡位置发生了变化,滑轮的质量改变了系统的振动频率.习题8-2图8-3 解:简谐振动的振动表达式:)cos(?ω+=t A x由题图可知,m 1042-?=A ,当t=0时,将m 1022-?=x 代入简谐振动表达式,得:21cos =由)sin(?ωωυ+-=t A ,当t=0时,?ωυsin A -= 由图可知,υ>0,即0sin,取3π?-= 又因:t=1s 时,,1022m x -?=将其入代简谐振动表达式,得213cos ,3cos 42=??? ?-??? ?-=πωπω由t=1s 时,--=3sin πωωυA <0知,03sin >??? ?-πω,取33ππω=-,即 s 32πω= 质点作简谐振动的振动表达式为m t x ??? ??-?=-332cos 1042ππ8-4 解:以该球的球心为原点,假设微粒在某一任意时刻位于遂道中的位矢为r,由高斯定理可知304R r Q E πε=,则微粒在此处受电场力为:r RQq F304πε-= 式中,负号表明电场F 的方向与r的正方向相反,指向球心.由上式及牛顿定律,得:04d d 04d d 043022302230=+?=+=+r mRQqt r r R Qq t r mr RQqF πεπεπε令 mR Qq3024πεω=则 0d d 222=+r tr ω习题8-3图故微粒作简谐振动,平衡点在球心处.由ωπ2=T知: QqmR T 3042πεπ=8-5 解:(1)取弹簧原长所在位置为O '点.当弹簧挂上物体A 时,处于静止位置P 点,有:P O k Mg '=将A 与B 粘合后,挂在弹簧下端,静止平衡所在位置O 点,取O点为原坐标原点如图题8-5所示,则有:g m M O O k )(+=' 设当B 与A 粘在一起后,在其运动过程的任一位置,弹簧形变量x O O +',则A 、B 系统所受合力为:kx x O O k g m M F -=+'-+=)()(即 0d d )(22=++kx txm M可见A 与B 作简谐和振动. (2) 由上式知,rad/s)(10=+=mM kω以B 与A 相碰点为计时起点,此时A 与B 在P 点,由图题8-5可知kmgk Mg g k m M P O O O OP =-+='-'= 则t=0时,m 02.00-=-=-=kmgOP x (负号表P 点在O 点上方) 又B 与A 为非弹性碰撞,碰撞前B 的速度为:m/s 2220101=-='gh υυ 碰撞后,A 、B 的共同速度为:m/s 4.0010=+'=mM m υυ (方向向上)则t=0时,??=-=sm mx /4.002.000υ可求得:)m (0447.022020=+=ωυx Aπωυ?65.0arctan 00=-=x 可知A 与B 振动系统的振动表达式为:m t x )65.010cos( 0447.0π+=习题8.5图(3) 弹簧所受的最大拉力,应是弹簧最大形变时的弹力,最大形变为:m A g kmM A O O x 1447.0=++=+'=?则最大拉力 N 4.72max ==x k F ? 8-6 解:(1) 已知A=0.24m, 2 2ππω==T ,如选x 轴向下为正方向. 已知初始条件0m,12.000<=υx 即 3 ,21c o s ,c o s24.012.0π±=== 而 ,0sin ,0sin 0><-=??ωυA 取3π=,故:m t x ??? ??+=32cos 24.0ππ(2) 如图题所示坐标中,在平衡位置上方0.12m, 即x=-0.12m 处,有32322132cos πππππ±=+-=??? ??+t t因为所求时间为最短时间,故物体从初始位置向上运动,0<υ.故0)32sin(>+ππt则取3232πππ=+t可得:s t 32min =(3) 物体在平衡位置上方0.12m 处所受合外力0.3N x m =-=ωF ,指向平衡位置.8-7 解:子弹射入木块为完全非弹性碰撞,设u 为子弹射入木块后二者共同速度,由动量定理可知:m/s)(0.2=+=υmM mu不计摩擦,弹簧压缩过程中系统机械能守恒,即:20221)(21kx u m M =+ (x 0为弹簧最大形变量) m u kmM x 20100.5-?=+=由此简谐振动的振幅 20100.5-?==x A 系统圆频率rad/s)(40=+=mM kω习题8-6图若取物体静止时的位置O (平衡位置)为坐标原点,Ox 轴水平向右为正,则初始条件为: t =0时,x =0,0m/s 0.20>==u υ由,sin ,cos 00?ωυ?A A x -==得:2π-=则木块与子弹二者作简谐振动,其振动表达式为:m t x )240cos(100.52π-?=-8-8 解:当物体m 1向右移动x 时,左方弹簧伸长x ,右方弹簧缩短x ,但它们物体的作用方向是相同的,均与物体的位移方向相反,即)(21x k x k F +-=令F =-kx ,有:N/m 421=+=k k k 由 kmT π2= 得)kg (1.0442212211≈==ππkT k T m则粘上油泥块后,新的振动系统质量为:kg 20.021=+m m新的周期 )s (4.12212=+=km m T π在平衡位置时,m 2与m 1发生完全非弹性碰撞. 碰撞前,m 1的速度m/s 10.0111πωυ==A 设碰撞后,m 1和m 2共同速度为υ. 根据动量守恒定律,υυ)(2111m m m +=则m/s 05.0)(2111πυυ=+=m m m新的振幅 m)(035.0222===υTA 8-9 解:(1)由振动方程)25sin(60.0π-=t x 知,5(rad/s)m,6.0==ωA故振动周期: )s (26.1)s (256.1522≈===πωπT (2) t=0时,由振动方程得:)25cos(0.3|m60.0000=-==-==πυt dt dx x t (3) 由旋转矢量法知,此时的位相:3π-=速度 m/s)(6.2m/s )23(560.0sin =-??-=-=?ωυA 加速度 )m /s (5.7m /s 21560.0cos 2222-=?-=-=?ωA a 所受力 N)(5.1N )5.7(2.0-=-?==ma F(4)设质点在x 处的动能与势能相等,由于简谐振动能量守恒,即:221kA E E E p k ==+ 故有: )21(21212kA E E E p k ===即 212121kA kx ?=可得: m)(42.022±=±=A x 8-10 解:(1)砝码运动到最高点时,加速度最大,方向向下,由牛顿第二定律,有:N mg ma -=maxN 是平板对砝码的支持力.故N)(74.1)4()()(22max =-=-=-=vA g m A g m a g m N πω砝码对板的正压力与N 大小相等,方向相反.砝码运动到最低点时,加速度也是最大,但方向向上,由牛顿第二定律,有:mg N ma -'=max故N)(1.8)4()(22max =+=+='A v g m a g m N π 砝码对板的正压力与板对砝码的支持力N '大小相等,方向相反. (2)当N=0时,砝码开始脱离平板,故此时的振幅应满足条件:m)(062.040)4(22max max 2===-=v g A vA g m N ππ(3) 由22max 4vg A π=,可知,2max v A 与成反比,当v v 2='时,m 0155.041max max=='A A 8-11 解:(1)设振子过平衡位置时的速度为υ,由机械能守恒,有:222121υm kA = A mk=υ 由水平方向动量定理:?='+υm u m m )(υm m mu '+=此后,系统振幅为A ',由机械能守恒,有:22)(2121u m m A k '+=' 得: A m m mA '+='有: km m T '+='π2 (2)碰撞前后系统总能量变化为:)21()1(2121212222kA m m m m m m kA kA A k E '+'-=-'+=-'= 式中,负号表示能量损耗,这是泥团与物体的非弹性碰撞所致.(3)当m 达到振幅A 时,m '竖直落在m 上,碰撞前后系统在水平方向的动量均为零,因而系统的振幅仍为A ,周期为k m m '+π2,系统的振动总能量不变,为221kA (非弹性碰撞损耗的能量为源于碰撞前m '的动能). 物体系统过平衡位置时的速度υ'由:22)(2121υ''+=m m kA 得:A m m k'+±='υ8-12 解:(1)由放置矢量法可知,振子从2A 运动到2A -的位置处,角相位的最小变化为:3π=则圆频率 rad/s 3πω==t 周期s T 62==ωπ由初始状态,在图示坐标中,初始条件为:m)(1.00m 1.000==-=A x υ则振幅 m 1.022020=+=ωυx A习题8-12图(2)因为E E p 41=又 2221,21kA E kx E p == 故 )21(412122kA kx =得:m)(05.0±=x 根据题意,振子在平衡位置的下方,取x =-0.05m.根据振动系统的能量守恒定律:222212121kA m kx =+υ 故 )s m (091.0122-?±=-±=x A ωυ根据题意,取m/s 091.0-=υ 再由)sin()cos(?ωωυ?ω+-=+=t A t t A x)cos(d d 2?ωω+-==t A tva x 2ω-= 得: )m /s (055.02=a(3)t=0时,(J)108.681)21(41413222-?====mA kA E E p ω (J)102183)21(43433222-?====mA kA E E k ω(J)108.273-?=+=p k E E E (4)由简谐振动的振动表达式)cos(?ω+=t A x 当t=0时,0m/s 091.0m,05.000<-=-=υx ,可得:π?32= 又 3,10.0πω==m A故 m t x )323cos(1.0ππ+= 8-13 解:(1)据题意,两质点振动方程分别为:mt x mt x Q P )3cos(1000.2)3cos(1000.522ππππ-=+?=--(2)P 、Q 两质点的速度及加速度表达分别为:)m/s )(3sin(1000.52ππωυ+??-==-t dt dx P P )m/s )(3sin(1000.22ππωυ-??-==-t dt dx QQ )m/s )(3cos(1000.5222ππωυ+??-==-t dt d a P P )m/s )(3cos(1000.2222ππωυ-??-==-t dt d a QQ 当t=1s 时,有:)(m/s 1087.9/32cos 1000.2)(m/s 1068.24/34cos 1000.5(m/s)1044.5/32sin 1000.2(m/s)1060.13/34sin 1000.5(m)1000.132cos 1000.2)(m 105.234cos1000.5222222222222222222------------?=??-=?=??-=?-=??-=?=??-=?-=?=?=?=s m a s m a s m s m m x m x Q P Q P Q P ππππππυππυππ(3)由相位差32)3(3)()(πππω?ω??=--=-=+-+=Q P Q P t t 可见,P 点的相比Q 点的相位超前32π. 8-14 解:(1)由题意得初始条件:<=02100υA x 可得:3π=(由旋转矢量法可证出)在平衡位置的动能就是质点的总能量)J (1008.3212152222-?====?=A m kA E m k m kωωω可求得:s rad m E A /221πω==则振动表达式为:m t x )32cos(1000.52ππ+=-(2) 初始位置势能)32(cos 21212222ππω+==t A m kx E P 当t=0时,3cos 21222πωA m E P =J J 6222221071.73cos )1000.5()2(1000.121---?==ππ 8-15 解:(1)由初始条件:102.1010υm x 可知,3π=且 22ππω==v则振动表达式为:m t x )32cos(24.0ππ+=当t=0.5s 时,m m x 21000.6)3212cos(24.0-?-=+?=ππ(2) t=0.5s 时,小球所受力:(N)1048.1)(32-?=-==x m ma f ω因t=0.5s 时,小球的位置在m x 21000.6-?-=处,即小球在x 轴负方向,而f 的方向是沿x 轴正方向,总是指向平衡位置.(3) 从初始位置m x 10102.1-?=到m x 1102.1-?-=所需最短时间设为t ,由旋转矢量法知,ππ32,3,0±=±=处处x x 习题8-15图)s (3223===t t πωπω(4) 因为 )32sin(24.02)sin(πππωωυ+?-=+-=t t A )32cos(24.04)cos(22πππ?ωω+?-=+-=t t A a 在s t m x 3 2102.11=-=-处 )32cos(24.04)3322cos(24.04/1026.3/)3 322sin(24.022212ππππππαπππυ+?-=+??-=?-=+??-=-t s m s m (5) t=4s 时, 22)]32sin([2121ππωυ+-==t A m m E k (J)1033.5J)342(sin 24.0)2(01.0214222-?=+=πππ)32(cos 21212222ππω+==t A m kx E P (J)1077.1J)342(cos 24.0)2(01.0214222-?=+=πππ(J)107.10J 101.77J 1033.5-4-44?=?+?=+=-P k E E E 总 8-16 解:设两质点的振动表达式分别为:)c os()cos(2211?ω?ω+=+=t A x t A x由图题可知,一质点在21Ax =处时对应的相位为: 32/arccos 1πω==+A A t同理:另一质点在相遇处时,对应的相位为:习题8-16图352/arccos2πω==+A A t 故相位差)()(12?ω?ω??+-+=t tπππ??3433512=-=-= 若21υυ与的方向与上述情况相反,故用同样的方法,可得:πππ32)3(312=--=-= 8-17 解:由图题8-17(图在课本上P 200)所示曲线可以看出,两个简谐振动的振幅相同,即m 05.021==A A ,周期均匀s 1.0=T ,因而圆频率为:ππω202==T由x -t 曲线可知,简谐振动1在t=0时,,010=x 且010>υ,故可求得振动1的初位相π?2310=.同样,简谐振动2在t=0时,π?υ==-=202020,0,05.0可知m x 故简谐振动1、2的振动表达式分别为:mt x t x )20cos(05.0)2320cos(05.021ππππ+=+=因此,合振动的振幅和初相位分别为: m A A A A A 21020212 2211025)cos(2-?=-++=??2021012021010cos cos sin sin arctanA A A A ++=ππ4541arctan 或== 但由x-t 曲线知,t=0时,π?45,05.021应取因此-=+=x x x . 故合振动的振动表达式:m t x )4 520cos(10252ππ+?=-8-18 解:(1)它们的合振动幅度初相位分别为:)cos(212212221??-++=A A A A Am )535cos(06.005.0206.005.022ππ-++=m 0892.0=22112211cos cos sin sin arctanA A A A ++=316819.15.2arctan 5cos06.053cos 05.05sin06.053sin 05.0'?===++=rad ππππ (2)当π??k 21±=-,即ππ?π?53221+±=+±=k k 时,31x x +的振幅最大;当π??)12(2+±=-k ,即5)12()12(2ππ??++±=++±=k k 时,32x x +的振幅最小.(3)以上两小问的结果可用旋转矢量法表示,如图题8-18所示.8-19 解:根据题意画出振幅矢量合成图,如习题8-19图所示.由习题8-19图及余弦定理可知cm 233.172023.172030cos 22212122?-+=?-+=AA A A A 0.10m cm 10== 又因为)cos(cos 12-=0103.172)100300(4002)(2122212=??+-=+-=A A A A A若2π=,即第一、第二两个振动的相位差为2π习题8-19图第9章波动习题解答9-1 解:首先写出S 点的振动方程若选向上为正方向,则有:0c o s 02.001.0?=- 21cos 0-=? ,0s i n 00>-=?ωυA 0sin 0即π?320-=或π34初始相位π?320-=则 m t y s )32cos(02.0πω-= 再建立如图题9-1(a)所示坐标系,坐标原点选在S 点,沿x 轴正向取任一P 点,该点振动位相将落后于S 点,滞后时间为: u xt =? 则该波的波动方程为:m ux t y ??--=πω32)(cos 02.0 若坐标原点不选在S 点,如习题9-1图(b )所示,P 点仍选在S 点右方,则P 点振动落后于S 点的时间为: uLx t -=? 则该波的波方程为:m u L x t y ??---=πω32)(c o s 02.0 若P 点选在S 点左侧,P 点比S 点超前时间为uxL -,如习题9-1图(c)所示,则--+=πω32)(cos 02.0u x L t y ??---=πω32)(cos 02.0u L x t ∴不管P 点在S 点左边还是右边,波动方程为: ??---=πω32)(cos 02.0u L x t y 9-2 解(1)由习题9-2图可知,波长m 8.0=λ习题9-1图习题9-1图振幅 A=0.5m 频率 Hz 125Hz 8.0100===λuv 周期 s 10813-?==vT ππυω2502== (2)平面简谐波标准波动方程为:+-=?ω)(cos ux t A y 由图可知,当t=0,x=0时,y=A=0.5m ,故0=?。
大学物理学第版修订版北京邮电大学出版社上册习题答案.docx

习题3 3.1 选择题(1)有一半径为 R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为 J,开始时转台以匀角速度ω0转动,此时有一质量为 m的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A)J0(B)J0mR2m) R 2J(J(C)J0(D) 0 mR2[ 答案: (A)](2)如题3.1(2)图所示,一光滑的内表面半径为10cm的半球形碗,以匀角速度ω 绕其对称轴OC旋转,已知放在碗内表面上的一个小球P 相对于碗静止,其位置高于碗底4cm,则由此可推知碗旋转的角速度约为(A)13rad/s(B)17rad/s(C)10rad/s(D)18rad/s(a)(b)题3.1 ( 2)图[ 答案: (A)](3)如 3.1(3) 图所示,有一小块物体,置于光滑的水平桌面上,有一绳其一端连结此物体,;另一端穿过桌面的小孔,该物体原以角速度?在距孔为 R 的圆周上转动,今将绳从小孔缓慢往下拉,则物体(A)动能不变,动量改变。
(B)动量不变,动能改变。
(C)角动量不变,动量不变。
(D)角动量改变,动量改变。
(E)角动量不变,动能、动量都改变。
[ 答案: (E)]3.2 填空题(1)半径为 30cm的飞轮,从静止开始以 0.5rad ·s-2的匀角加速转动,则飞轮边缘上一点在飞轮转过240?时的切向加速度aτ =,法向加速度a n=。
[ 答案:0.15; 1.256 ](2)如题3.2 (2)图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴 O转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的原因是。
木球被击中后棒和球升高的过程中,弹、细棒、地球系统的守恒。
守恒,对木球、子题3.2 (2)图[ 答案:对 o 轴的角动量守恒,因为在子弹击中木球过程中系统所受外力对 o 轴的合外力矩为零,机械能守恒](3)两个质量分布均匀的圆盘 A 和 B 的密度分别为ρA和ρB ( ρA>ρB) ,且两圆盘的总质量和厚度均相同。
大学物理答案(北京邮电大学出版社)

6-10 题6-10图(a)是氢和氧在同一温度下的两条麦克斯韦速率分布曲线,哪一条代表氢?题6-10图(b)是某种气体在不同温度下的两条麦克斯韦速率分布曲线,哪一条的温度较高?答:图(a)中(1)表示氧,(2)表示氢;图(b)中(2)温度高.题6-10图6-16 如果氢和氦的摩尔数和温度相同,则下列各量是否相等,为什么?(1)分子的平均平动动能;(2)分子的平动动能;(3)内能.解:(1)相等,分子的平均平动动能都为kT 23. (2)不相等,因为氢分子的平均动能kT 25,氦分子的平均动能kT 23. (3)不相等,因为氢分子的内能RT 25υ,氦分子的内能RT 23υ. 6-21 1mol 氢气,在温度为27℃时,它的平动动能、转动动能和内能各是多少? 解:理想气体分子的能量 RT i E 2υ= 平动动能 3=t 5.373930031.823=⨯⨯=t E J 转动动能 2=r 249330031.822=⨯⨯=r E J 内能5=i 5.623230031.825=⨯⨯=i E J 6-24 (1)求氮气在标准状态下的平均碰撞频率;(2)若温度不变,气压降到1.33×10-4Pa ,平均碰撞频率又为多少(设分子有效直径10-10 m)?解:(1)碰撞频率公式v n d z 22π=对于理想气体有nkT p =,即kTp n = 所以有 kT pv d z 22π= 而 mol60.1M RT v ≈ 43.4552827331.860.1=⨯≈v 1s m -⋅ 氮气在标准状态下的平均碰撞频率805201044.52731038.110013.143.455102⨯=⨯⨯⨯⨯⨯⨯=-πz 1s - 气压下降后的平均碰撞频率123420s 714.02731038.11033.143.455102----=⨯⨯⨯⨯⨯⨯=πz。
北京邮电大学大学物理期末考试试卷(含答案)

北京邮电大学大学物理期末考试试卷(含答案)一、大学物理期末选择题复习 1.运动质点在某瞬时位于位矢r 的端点处,对其速度的大小有四种意见,即 (1)t r d d ; (2)dt r d ; (3)t s d d ; (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确答案D2.如图所示,质量为m 的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为( )(A) g sin θ (B) g cos θ (C) g tan θ (D) g cot θ答案D3.一个电流元Idl 位于直角坐标系原点 ,电流沿z 轴方向,点P (x ,y ,z )的磁感强度沿x 轴的分量是: ( )(A) 0(B) ()()2/32220/4/z y x Ixdl ++-πμ(C) ()()2/12220/4/z y x Ixdl ++-πμ(D)()()2220/4/z y x Ixdl ++-πμ答案B4.人造地球卫星,绕地球作椭圆轨道运动,地球在椭圆的一个焦点上,则卫星的( )(A) 动量不守恒,动能守恒(B) 动量守恒,动能不守恒(C) 对地心的角动量守恒,动能不守恒1、(D) 对地心的角动量不守恒,动能守恒答案C5.静电场中高斯面上各点的电场强度是由:( )(A) 高斯面内的电荷决定的 (B) 高斯面外的电荷决定的(C) 空间所有电荷决定的 (D) 高斯面内的电荷的代数和决定的答案C6.将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定 答案A7.如图所示,半径为R 的均匀带电球面,总电荷为Q ,设无穷远处的电势为零,则球内距离球心为r 的P 点处的电场强度的大小和电势为: ( )(A) 00,4QE U rπε== (B) 00,4Q E U R πε== (C) 200,44QQ E U rr πεπε== (D)200,44QQ E U r R πεπε==答案B8. 一运动质点在某瞬间位于位矢(,)r x y 的端点处,对其速度的大小有四种意见,即(1)dr dt ;(2)dr dt ;(3)ds dt ;(4下列判断正确的是:(A )只有(1)(2)正确 (B )只有(2)正确(C )只有(2)(3)正确 (D )只有(3)(4)正确答案 D9. 质点作曲线运动,r 表示位置矢量,v 表示速度,a 表示加速度,s 表示路程,t a 表示切向加速度。
《大学物理》习题答案4-匡乐满主编-北京邮电大学出版社省名师优质课赛课获奖课件市赛课一等奖课件

0.5
0.30s
7. 粒子在加速器中被加速到动能为静止能量旳4倍时,其质量 m
与静止质量 m0 旳关系为:
(A)m 4m0;(B) m 5m0;(C) m 6m0; (D) m 8m0
答案(B) mc2 Ek m0c2 4m0c2 m0c2 5m0c2
大学物理 盛忠志主讲
8. Ek 是粒子旳动能,p 是它旳动量,那么粒子旳静能 m0c 2等于
大学物理 盛忠志主讲
大学物理作业四参照答案
一、选择题
1. 一刚性直尺固定在S系中,它与 X 轴正向夹角 45,
在相对 S系以速度 u 沿 X 轴作匀速直线运动旳 S 系中,
测得该尺与 X 轴正向夹角为 (A) 45;(B) 45 ; (C) 45; (D)不懂得
答案(A)
大学物理 盛忠志主讲
2. 惯性系 S 、S沿X 轴做相对运动,在 S 系中测得两个同步发 生旳事件沿运动方向空间距离为1m,在 S系中测得这两个事件
旳空间间隔为2m。则在 S 系中测得这两个事件旳时间间隔为
(A)
3c
;
(B)1 3
c
;
(C) 3 c
; (D)3 c
x x
1
u c
2 2
答案(C)
u 3c 2
t t1 t2
1 (t u x) 3
1
u2 c2
c2
c
3. 两火箭A、B沿同一直线相向运动,测得两者相对地球旳速度
大小分别是 vA 0.9c ,vB 0.8c 。则两者互测旳相对运动速度为
(A)1.7c ; (B) 0.988c ; (C) 0.956c ; (D) 0.975c
答案(B)
v v u 0.9c (0.8c) 0.988c
大学物理考试试卷(对应北京邮电大学版)

大学物理考试复习试卷限时:120分钟一.选择题(8*4=32分)1)1mol 氢气,在温度为27℃时,它的平动动能、转动动能和内能各是多少J?( )A 3739.5、2493、3739.5 B.1897.75、1246.5、4144.25C.7479、4986、12465D.3739.5、2493、6232.52)质点沿x 轴运动,其加速度和位置的关系为 a =2+62x ,a 的单位为2sm -⋅,x 的单位为 m. 质点在x =0处,速度为101sm -⋅,试求质点在任何坐标处的速度值( ) A.13s m 252-⋅++=x x v B. 13s m 252-⋅+=x v C. 13s m 25-⋅++=x x v D. 12s m 252-⋅++=x x v3) 已知一质点作直线运动,其加速度为 a =4+3t 2sm -⋅,开始运动时,x =5 m , v =0,求该质点在t =10s 时的速度和位置( )A.600MB.700MC.352.5 MD.705M .4) 一质量为kg 10103-⨯的物体作谐振动,振幅为cm 24,周期为s 0.4,当0=t 时位移为cm 24+.求:由起始位置运动到cm 12=x 处所需的最短时间;( )A.1/2 SB. 2/3 SC.1/3 SD.3/ 4 S5) 在河水流速υ0=2 m·s -1的地方有小船渡河.如果希望小船以υ=4 m·s -1的速率垂直于河岸横渡,问小船相对于河水的速度大小和方向应如何?( )A.v=4.47m/s ¢=arctan5+900B.v=4m/s ¢=arctan 55+900C.v=4.47m/s ¢=arctan 55+900D.v=4.47m/s ¢=arctan 555+9006) 一列机械波沿x 轴正向传播,t =0时的波形如题图所示,已知波速为10 m ·s -1,波长为2m ,则P 点的坐标为( )A.(5/3,1/2)B.(4/3,-1/2) C(5/3,-1/2) D.(1/2,-1/2)7)质点沿半径为R 的圆周按s =2021bt t v -的规律运动,式中s 为质点离圆周上某点的弧长,0v ,b 都是常量,t 时刻质点的加速度大小为( )A. 240)(R bt v b a -+= B. 2402)(R bt v b a -+= C. 3402)(R bt v b a --= D. 2402)(R bt v b a --=8)一根劲度系数为1k 的轻弹簧A 的下端,挂一根劲度系数为2k 的轻弹簧B ,B 的下端一重物C ,C 的质量为M ,如题2-9图.求这一系统静止时两弹簧的弹性势能之比( ). A.EP 1/EP 2B. K 1/K 2C.K 2/K 1D.EP 2/EP 1第1)图填空题二.填空题(8*4=32分)1)质量为M 的大木块具有半径为R 的四分之一弧形槽,如题图所示.质量为m 的小立方体从曲面的顶端滑下,大木块放在光滑水平面上,二者都作无摩擦的运动,而且都从静止开始,小木块脱离大木块时的速度为2)绕定轴转动的刚体的角加速度与作用于刚体上的合力矩成 比3)v v nf d )(的物理意义(n 为分子数密度)4)⎰21d )(v v v v Nf 的物理意义N 为系统总分子数5) 一卡诺热机在1000 K 和300 K 的两热源之间工作其热机效率为6)热力学第一定律公式7)简谐运动的总能量表达式是 (用颈度系数K,振幅A 表示)8)波动方程为三.计算题(6*6=36分)1)在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.2)x-曲线,试分别写出其谐振动方程.题图为两个谐振动的t3)一质量为m、半径为R的自行车轮,假定质量均匀分布在轮缘上,可绕轴自由转动.另一质量为0m的v射入轮缘(如题图所示方向).子弹以速度(1)开始时轮是静止的,在质点打入后的角速度为何值?(2)用m,0m和θ表示系统(包括轮和质点)最后动能和初始动能之比.4)如题图所示,一系统由状态a沿acb到达状态b的过程中,有350 J热量传入系统,而系统作功126 J.(1)若沿adb时,系统作功42 J,问有多少热量传入系统?(2)若系统由状态b沿曲线ba返回状态a时,外界对系统作功为84 J,试问系统是吸热还是放热?热量传递是多少?5)设有N 个粒子的系统,其速率分布如题6-9图所示.求(1)分布函数)(v f 的表达式;(2)a 与0v 之间的关系;(3)速度在1.50v 到2.00v 之间的粒子数.(4)粒子的平均速率.(5)0.50v 到10v 区间内粒子平均速率.6)如题图所示,有一平面简谐波在空间传播,已知P 点的振动方程为P y =A cos(0ϕω+t ).(1)分别就图中给出的两种坐标写出其波动方程;(2)写出距P 点距离为b 的Q 点的振动方程.。
大学物理习题及解答(第三版_北京邮电大学出版社)

大学物理习题及解答(第三版 北京邮电大学出版社)习题二2-1 一细绳跨过一定滑轮,绳的一边悬有一质量为1m 的物体,另一边穿在质量为2m 的圆柱体的竖直细孔中,圆柱可沿绳子滑动.今看到绳子从圆柱细孔中加速上升,柱体相对于绳子以匀加速度a '下滑,求1m ,2m 相对于地面的加速度、绳的张力及柱体与绳子间的摩擦力(绳轻且不可伸长,滑轮的质量及轮与轴间的摩擦不计).解:因绳不可伸长,故滑轮两边绳子的加速度均为1a ,其对于2m 则为牵连加速度,又知2m 对绳子的相对加速度为a ',故2m 对地加速度,由图(b)可知,为a a a '-=12 ①又因绳的质量不计,所以圆柱体受到的摩擦力f 在数值上等于绳的张力T ,由牛顿定律,有111a m T g m =-② 222a m g m T =-③联立①、②、③式,得2121211212212211)2()()(m m a g m m T f m m a m g m m a m m a m g m m a +'-==+'--=+'+-=讨论 (1)若0='a ,则21a a =表示柱体与绳之间无相对滑动.(2)若g a 2=',则0==f T ,表示柱体与绳之间无任何作用力,此时1m , 2m 均作自由落体运动.题2-1图2-2 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB 平行,如图所示,求这质点的运动轨道. 解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v ϖ方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向: 0=x F t v x 0= ① Y 方向: y y ma mg F ==αsin ② 0=t 时 0=y 0=y v2sin 21t g y α= 由①、②式消去t ,得 220sin 21x g v y ⋅=α2-3 质量为16 kg 的质点在xOy 平面内运动,受一恒力作用,力的分量为x f =6 N ,y f =-7 N ,当t =0时,==y x 0,x v =-2 m ·s -1,y v =0.求当t =2 s 时质点的 (1)位矢;(2)速度.解: 2s m 83166-⋅===m f a x x2s m 167-⋅-==m f a y y(1)⎰⎰--⋅-=⨯-=+=⋅-=⨯+-=+=20101200s m 872167s m 452832dt a v v dt a v v y y y x x x于是质点在s 2时的速度1s m 8745-⋅--=j i v ϖϖϖ(2)m 874134)167(21)4832122(21)21(220j i j i j t a i t a t v r y x ϖϖϖϖϖϖϖ--=⨯-+⨯⨯+⨯-=++=2-4 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk e v )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m k e )(-];(3)停止运动前经过的距离为)(0k m v ;(4)证明当k m t =时速度减至0v 的e 1,式中m 为质点的质量. 答: (1)∵ t v m kv a d d =-= 分离变量,得m t k v v d d -=即 ⎰⎰-=v v t m t k vv 00d d mkt e v v -=ln ln 0∴ tm k e v v -=0(2) ⎰⎰---===t t t m k m k e k mv t e v t v x 000)1(d d(3)质点停止运动时速度为零,即t →∞,故有⎰∞-=='000d k mv t e v x t m k (4)当t=k m时,其速度为 e v e v ev v k m m k 0100===-⋅-即速度减至0v 的e 1. 2-5 升降机内有两物体,质量分别为1m ,2m ,且2m =21m .用细绳连接,跨过滑轮,绳子不可伸长,滑轮质量及一切摩擦都忽略不计,当升降机以匀加速a =21g 上升时,求:(1) 1m 和2m 相对升降机的加速度.(2)在地面上观察1m ,2m 的加速度各为多少?解: 分别以1m ,2m 为研究对象,其受力图如图(b)所示.(1)设2m 相对滑轮(即升降机)的加速度为a ',则2m 对地加速度a a a -'=2;因绳不可伸长,故1m 对滑轮的加速度亦为a ',又1m 在水平方向上没有受牵连运动的影响,所以1m 在水平方向对地加速度亦为a ',由牛顿定律,有)(22a a m T g m -'=-a m T '=1题2-5图联立,解得g a ='方向向下(2) 2m 对地加速度为 22g a a a =-'= 方向向上 1m 在水面方向有相对加速度,竖直方向有牵连加速度,即牵相绝a a a ϖϖϖ+='∴g g g a a a 25422221=+=+'= a a '=arctan θo6.2621arctan ==,左偏上. 2-6一质量为m 的质点以与地的仰角θ=30°的初速0v ϖ从地面抛出,若忽略空气阻力,求质点落地时相对抛射时的动量的增量.解: 依题意作出示意图如题2-6图题2-6图在忽略空气阻力情况下,抛体落地瞬时的末速度大小与初速度大小相同,与轨道相切斜向下,而抛物线具有对y 轴对称性,故末速度与x 轴夹角亦为o 30,则动量的增量为 0v m v m p ϖϖϖ-=∆ 由矢量图知,动量增量大小为0v m ϖ,方向竖直向下.2-7 一质量为m 的小球从某一高度处水平抛出,落在水平桌面上发生弹性碰撞.并在抛出1 s ,跳回到原高度,速度仍是水平方向,速度大小也与抛出时相等.求小球与桌面碰撞过程中,桌面给予小球的冲量的大小和方向.并回答在碰撞过程中,小球的动量是否守恒?解: 由题知,小球落地时间为s 5.0.因小球为平抛运动,故小球落地的瞬时向下的速度大小为g gt v 5.01==,小球上跳速度的大小亦为g v 5.02=.设向上为y 轴正向,则动量的增量 12v m v m p ϖϖϖ-=∆方向竖直向上, 大小mg mv mv p =--=∆)(12ϖ碰撞过程中动量不守恒.这是因为在碰撞过程中,小球受到地面给予的冲力作用.另外,碰撞前初动量方向斜向下,碰后末动量方向斜向上,这也说明动量不守恒. 2-8 作用在质量为10 kg 的物体上的力为i t F ϖ)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化,以及力给予物体的冲量.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j ϖ6-m ·s -1的物体,回答这两个问题. 解: (1)若物体原来静止,则i t i t t F p t ϖϖϖϖ10401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向, i p I i m p v ϖϖϖϖϖϖ111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆若物体原来具有6-1s m -⋅初速,则 ⎰⎰+-=+-=-=t t t F v m t m F v m p v m p 000000d )d (,ϖϖϖϖϖϖϖ于是⎰∆==-=∆t p t F p p p 0102d ϖϖϖϖϖ, 同理, 12v v ϖϖ∆=∆,12I I ϖϖ= 这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理.(2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t解得s 10=t ,(s 20='t 舍去) 2-9 一质量为m 的质点在xOy 平面上运动,其位置矢量为 j t b i t a r ϖϖϖωωsin cos += 求质点的动量及t =0 到ωπ2=t 时间内质点所受的合力的冲量和质点动量的改变量.解: 质点的动量为 )cos sin (j t b i t a m v m p ϖϖϖϖωωω+-== 将0=t 和ωπ2=t 分别代入上式,得 j b m p ϖϖω=1,i a m p ϖϖω-=2,则动量的增量亦即质点所受外力的冲量为 )(12j b i a m p p p I ϖϖϖϖϖϖ+-=-=∆=ω2-10 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量.解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得b a t = (2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将b a t =代入,得 b a I 22=(3)由动量定理可求得子弹的质量0202bv a v I m ==2-11 一炮弹质量为m ,以速率v 飞行,其内部炸药使此炮弹分裂为两块,爆炸后由于炸药使弹片增加的动能为T ,且一块的质量为另一块质量的k 倍,如两者仍沿原方向飞行,试证其速率分别为v +m kT 2, v -km T2证明: 设一块为1m ,则另一块为2m ,21km m =及m m m =+21于是得1,121+=+=k m m k km m ①又设1m 的速度为1v , 2m 的速度为2v ,则有2222211212121mv v m v m T -+=②2211v m v m mv +=③联立①、③解得 12)1(kv v k v -+=④将④代入②,并整理得21)(2v v km T -=于是有km T v v 21±= 将其代入④式,有m kT v v 22±=又,题述爆炸后,两弹片仍沿原方向飞行,故只能取 km T v v m kT v v 2,221-=+=证毕. 2-12 设N 67j i F ϖϖϖ-=合.(1) 当一质点从原点运动到m 1643k j i r ϖϖϖϖ++-=时,求F ϖ所作的功.(2)如果质点到r 处时需0.6s ,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化. 解: (1)由题知,合F ϖ为恒力, ∴ )1643()67(k j i j i r F A ϖϖϖϖϖϖϖ++-⋅-=⋅=合 J 452421-=--=(2) w 756.045==∆=t A P(3)由动能定理,J 45-==∆A E k2-13 以铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉进入木板内的深度成正比,在铁锤击第一次时,能将小钉击入木板内1 cm ,问击第二次时能击入多深,假定铁锤两次打击铁钉时的速度相同.解: 以木板上界面为坐标原点,向内为y 坐标正向,如题2-13图,则铁钉所受阻力为题2-13图ky f -=第一锤外力的功为1A⎰⎰⎰==-='=s s k y ky y f y f A 1012d d d ①式中f '是铁锤作用于钉上的力,f 是木板作用于钉上的力,在0d →t 时,f 'f -=.设第二锤外力的功为2A ,则同理,有⎰-==21222221d y k ky y ky A ②由题意,有2)21(212k mv A A =∆== ③即 222122k k ky =-所以,22=y 于是钉子第二次能进入的深度为 cm 414.01212=-=-=∆y y y2-14 设已知一质点(质量为m )在其保守力场中位矢为r 点的势能为n P r k r E /)(=, 试求质点所受保守力的大小和方向.解: 1d )(d )(+-==n r nk r r E r F 方向与位矢r ϖ的方向相反,即指向力心.2-15 一根劲度系数为1k 的轻弹簧A 的下端,挂一根劲度系数为2k 的轻弹簧B ,B 的下端一重物C ,C 的质量为M ,如题2-15图.求这一系统静止时两弹簧的伸长量之比和弹性势能之比.解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时,有题2-15图Mg F F B A ==又 11x k F A ∆=22x k F B ∆=所以静止时两弹簧伸长量之比为1221k k x x =∆∆弹性势能之比为12222211121212k k x k x k E E p p =∆∆= 2-16 (1)试计算月球和地球对m 物体的引力相抵消的一点P ,距月球表面的距离是多少?地球质量5.98×1024kg ,地球中心到月球中心的距离3.84×108m ,月球质量7.35×1022kg ,月球半径1.74×106m .(2)如果一个1kg 的物体在距月球和地球均为无限远处的势能为零,那么它在P 点的势能为多少?解: (1)设在距月球中心为r 处地引月引F F =,由万有引力定律,有()22r R mM G r mM G -=地月经整理,得R M M M r 月地月+==2224221035.71098.51035.7⨯+⨯⨯81048.3⨯⨯m 1032.386⨯= 则P 点处至月球表面的距离为m 1066.310)74.132.38(76⨯=⨯-=-=月r r h(2)质量为kg 1的物体在P 点的引力势能为()r R M Gr M G E P ---=地月()72411722111083.34.381098.51067.61083.31035.71067.6⨯-⨯⨯⨯-⨯⨯⨯⨯-=- J 1028.16⨯=2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置,弹簧的劲度系数为k ,自然长度等于水平距离BC ,2m 与桌面间的摩擦系数为μ,最初1m 静止于A 点,AB =BC =h ,绳已拉直,现令滑块落下1m ,求它下落到B 处时的速率.解: 取B 点为重力势能零点,弹簧原长为弹性势能零点,则由功能原理,有])(21[)(21212212l k gh m v m m gh m ∆+-+=-μ式中l ∆为弹簧在A 点时比原长的伸长量,则h BC AC l )12(-=-=∆联立上述两式,得()()212221122m m kh gh m m v +-+-=μ题2-17图2-18 如题2-18图所示,一物体质量为2kg ,以初速度0v =3m ·s -1从斜面A 点处下滑,它与斜面的摩擦力为8N ,到达B 点后压缩弹簧20cm 后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度.解: 取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原长处为弹性势能零点。
《大学物理》习题答案1,匡乐满主编,北京邮电大学出版社

解: vx a, vy 2ct 当运动方向与x成450角时,则
即 a 2ct, t a 2c
vx vy
v
v
2 x
v
2 y
a 2 4c2t 2
2a
大学物理 盛忠志主讲
5、一飞机在跑道上跑过500米后,即升空,如果它在跑
前是静止的,以恒定加速度运动,升空前跑了30秒,则
0
30 10 20
60
n1
2 02 2
302 102 2 60
20 3
60
2
10 20
30
60
n2
10 2 2 30
5 3
大学物理 盛忠志主讲
8、某人骑自行车以速率v向正西方行驶,遇到由北向 南刮的风(设风速大小也为v),则他感到风是从 (A)东北方向吹来 (B)东南方向吹来 (C)西北方向吹来 (D)西南方向吹来。
dv y dy
dy dt
vy
dv y dy
则
a vy
dv y dy
kvy2
分离变量得 : dvy kdy vy
两边积分得 :
v dv y
y
kdy
v v0 y
0
盛忠志主讲
v v0eky
大学物理 盛忠志主讲
3、一质点沿半径为1 m 的圆周运动,运动方程
为 2 3t,3 式中 以弧度计,t以秒计,求:(1) t=2 s
vx A sin t vy B cost
由速度的定义,有: vx
大学物理学答案 第 版 版 上册 北京邮电大学 完全版

亦即 ②
由②可作出矢量三角形如图(b),又由①式可知三矢量之间满足勾股定理,且以 为斜边,故知 与 是互相垂直的.
第三习题
一质量为 的质点位于( )处,速度为 , 质点受到一个沿 负方向的力 的作用,求相对于坐标原点的角动量以及作用于质点上的力的力矩.
解: 由题知,质点的位矢为
解: 质点的动量为
将 和 分别代入上式,得
, ,
则动量的增量亦即质点所受外力的冲量为
一颗子弹由枪口射出时速率为 ,当子弹在枪筒内被加速时,它所受的合力为F=( )N( 为常数),其中 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量.
解: (1)由题知, 为恒力,
∴
(2)
(3)由动能定理,
以铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉进入木板内的深度成正比,在铁锤击第一次时,能将小钉击入木板内1 cm,问击第二次时能击入多深,假定铁锤两次打击铁钉时的速度相同.
解: 以木板上界面为坐标原点,向内为 坐标正向,如题2-13图,则铁钉所受阻力为
解: 从 上下滑的过程中,机械能守恒,以 , ,地球为系统,以最低点为重力势能零点,则有
又下滑过程,动量守恒,以 , 为系统则在 脱离 瞬间,水平方向有
联立,以上两式,得
一个小球与一质量相等的静止小球发生非对心弹性碰撞,试证碰后两小球的运动方向互相垂直.
证: 两小球碰撞过程中,机械能守恒,有
即 ①
题图(a) 题图(b)
1.8一质点在 平面上运动,运动方程为
=3 +5, = 2+3 -4.
式中 以 s计, , 以m计.(1)以时间 为变量,写出质点位置矢量的表示式;(2)求出 =1 s时刻和 =2s时刻的位置矢量,计算这1秒内质点的位移;(3)计算 =0 s时刻到 =4s时刻内的平均速度;(4)求出质点速度矢量表示式,计算 =4 s时质点的速度;(5)计算 =0s到 =4s内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算 =4s时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).
2020大学物理答案(上、下)(北京邮电大学第3版)

大学物理习题及解答习题一1-1 |r ∆|与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即t d d r ==v t sd d .t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆrˆt r t d d d d d d r r r += 式中t rd d 就是速度径向上的分量, ∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d=,t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττ +=式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=,jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x yx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a tr v ==其二,可能是将22d d d d t rt r 与误作速度与加速度的模。
大学物理学答案_下册_北京邮电大学

大学物理习题及解答习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系? 解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷2220)33(π4130cos π412a q q aq'=︒εε解得 qq 33-='(2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量. 解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得θπεθtan 4sin 20mg l q =8-3 根据点电荷场强公式204r qE πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: 020π4r rq E ε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d qπε,又有人说,因为f =qE ,S q E 0ε=,所以f =S q02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强S qE 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为Sq E 02ε=,另一板受它的作用力SqS qqf 02022εε==,这是两板间相互作用的电场力.8-5 一电偶极子的电矩为l q p =,场点到偶极子中心O 点的距离为r ,矢量r 与l 的夹角为θ,(见题8-5图),且l r >>.试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示,将p 分解为与r 平行的分量θsin p 和垂直于r 的分量θsin p .∵ l r >>∴ 场点P 在r 方向场强分量30π2cos rp E r εθ=垂直于r 方向,即θ方向场强分量300π4sin rp E εθ=题8-5图 题8-6图8-6 长l =15.0cm 的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m -1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm处Q 点的场强. 解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a xE P -=λε222)(d π4d x a x E E ll P P -==⎰⎰-ελ]2121[π40la l a +--=ελ)4(π220l al-=ελ用15=l cm ,9100.5-⨯=λ1mC -⋅, 5.12=a cm 代入得21074.6⨯=P E 1CN -⋅方向水平向右(2)同理 2220d d π41d +=xxE Q λε 方向如题8-6图所示由于对称性⎰=lQx E 0d ,即QE 只有y 分量,∵22222220d d d d π41d ++=xxx E Qy λε22π4d d ελ⎰==lQyQy EE ⎰-+2223222)d (d ll xx222d 4π2+=llελ以9100.5-⨯=λ1cmC -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1CN -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强. 解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d RR E εϕλ=方向沿半径向外则ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-=积分RRE x 000π2d sin π4ελϕϕελπ==⎰d cos π400=-=⎰ϕϕελπRE y∴RE E x 0π2ελ==,方向沿x 轴正向.8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E .解: 如8-8图示,正方形一条边上电荷4q在P 点产生物强P Ed 方向如图,大小为()4π4cos cos d 2221lrE P +-=εθθλ∵22cos 221lrl+=θ12cos cos θθ-=∴24π4d 22220l r ll r E P++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴424π4d 222222lrrlrlrl E +++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为2)4(π44d 422220lr lr lrE E P ++=⨯=⊥ελ∵l q 4=λ∴2)4(π422220lr lrqr E P ++=ε 方向沿OP8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(x Rarctan=α)解: (1)由高斯定理0d εq S E s⎰=⋅ 立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量6εq e=Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量6εq e=Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则024εq e=Φ,如果它包含q 所在顶点则=Φe.如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图 (3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R+的球冠面的电通量,球冠面积*]1)[(π22222xRxx R S +-+=∴)(π42200x RSq +=Φε02εq =[221xRx+-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=d sin π2r r S ααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理d ε∑⎰=⋅qS E s,02π4ε∑=qrE当5=r cm 时,0=∑q ,0=E8=r cm时,∑q3π4p=3(r )3内r -∴()2023π43π4rr rE ερ内-=41048.3⨯≈1CN -⋅, 方向沿半径向外.12=r cm 时,3π4∑=ρq -3(外r )内3r∴ ()420331010.4π43π4⨯≈-=rr rE ερ内外1CN -⋅沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理d ε∑⎰=⋅qS E s取同轴圆柱形高斯面,侧面积rl S π2= 则 rlE S E S π2d =⋅⎰对(1) 1R r <0,0==∑E q(2)21R r R <<λl q =∑∴rE 0π2ελ=沿径向向外(3)2R r >0=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, nE )(21210σσε-=1σ面外,nE )(21210σσε+-=2σ面外,nE )(21210σσε+=n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a).(1)ρ+球在O 点产生电场010=E ,ρ- 球在O 点产生电场'dπ4π3430320OO r E ερ=∴ O 点电场'd33030OO r E ερ=;(2) ρ+在O '产生电场'd π4d 3430301OO E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场003ερ='E 'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r',相对O 点位矢为r (如题8-13(b)图)则 03ερr E PO=,3ερr E O P '-=',∴ 0003'3)(3ερερερd OO r r E E E O P PO P=='-=+=' ∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p 在外场E 中受力矩E p M⨯=∴ qlE pE M ==max 代入数字4536max100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=Mm N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r=42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r r r r q q r r q q r F A εε )11(21r r -61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q从O 点经过半圆弧移到C 点,求移动过程中电场力作的功. 解: 如题8-16图示0π41ε=OU)(=-Rq Rq 0π41ε=OU)3(RqRq -Rq0π6ε-=∴Rq q U U q A o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==RR E E yR0π4ελ=[)2sin(π-2sinπ-]R0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===AB200012ln π4π4d π4d RRxxxxU ελελελ同理CD 产生2ln π402ελ=U半圆环产生034π4πελελ==RR U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强rE 0π2ελ=电子受力大小re eE F e 0π2ελ==∴rvmre 20π2=ελ得1320105.12π2-⨯==emvελ1mC -⋅8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压.解: 平行板电容器内部近似为均匀电场∴ 4105.1d ⨯==E U V8-20 根据场强E与电势U 的关系U E -∇= ,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图).解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r rq r r U E ε=∂∂-= 0r 为r 方向单位矢量. (2)总电量q ,半径为R 的均匀带电圆环轴上一点电势22π4xRq U +=ε∴()ixR qx i x U E 2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4rql l l r q U εθθθε=+--=∴30π2cos rp rU E r εθ=∂∂-=30π4sin 1rp U r E εθθθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有 0)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即2222040321=---εσεσεσεσ又∵+2σ03=σ∴ 1σ4σ= 说明相背两面上电荷面密度总是大小相等,符号相同.8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ ABACUU=,即∴ABAB AC AC E E dd =∴2dd 21===ACAB ABAC E E σσ且1σ+2σS q A =得,32Sq A =σS q A 321=σ而7110232-⨯-=-=-=A C q S q σCC 10172-⨯-=-=S q B σ (2)31103.2dd⨯===ACACAC AE UεσV8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势; *(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R Rq rr q r E U εε(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:0π4π42020=-=R q R q U εε (3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q '(电荷守恒),此时内球壳电势为零,且π4'π4'π4'202010=+-+-=R q q R q R q UAεεε得 qR R q 21='外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q UBεεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+Rq Rq εε得-='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知2020π4rqF ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =',小球3再与小球2接触后,小球2与小球3均带电q q 43=''∴ 此时小球1与小球2间相互作用力0220183π483π4"'2F rqrq q F =-=εε(2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q.∴ 小球1、2间的作用力0294π432322F rq qF ==ε*8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U=0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U UAB=可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσdU Sq S q dU U C SS q B A解得S q261==σσS q d U2032-=-=εσσS q dU 2054+=-=εσσ所以CB 间电场S qdU E 00422εεσ+==)2d (212d 02Sq U E U UCBCε+===注意:因为C 片带电,所以2UUC≠,若C 片不带电,显然2U U C=8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求:(1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强303π4,π4rr Q E r r Q D r εε==内;介质外)(2R r <场强303π4,π4rr Q E rQr D ε ==外(2)介质外)(2R r >电势rQ E U 0rπ4r d ε=⋅=⎰∞外介质内)(21R r R <<电势2020π4)11(π4R QR rq rεεε+-=)11(π420R rQ r r-+=εεε(3)金属球的电势rd r d 221⋅+⋅=⎰⎰∞R R R E E U 外内 ⎰⎰∞+=222020π44πdr R R Rr rQdrrQ εεε)11(π4210R R Q r r-+=εεε8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E ,真空部分场强为1E,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D 得11σ=D ,22σ=D而101E D ε=,202E D r εε=d 21U E E ==∴rD D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求:(1)在半径r 处(1R <r <2R=,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量;(2)电介质中的总电场能量;rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内(3)圆柱形电容器的电容.解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰当)(21R r R <<时,Q q =∑∴rl Q D π2=(1)电场能量密度22222π82lr QDw εε==薄壳中rl r Q rl r l r Qw W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222lnπ4π4d d R R VR R lQrlr Q W W εε(3)电容:∵C QW 22=∴)/ln(π22122R R l WQC ε==*8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1)1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度.解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41rq q F ε=但2q 处于金属球壳中心,它受合力为零,没有加速度.(2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41rq q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μ F .1C 上电压为50V .求:ABU.解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C +=其上电荷123Q Q =∴355025231123232⨯===C U C C Q U86)35251(5021=+=+=UU UABV8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压,是否会击穿? 解: (1)1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF(2)串联后电压比231221==C C UU ,而100021=+UU∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求:(1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021UU U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失WW W -=∆0)22()2121(2221212221C q C q UC UC +-+=221212UC C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C 时,求: (1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r r Q E ε=3R r >时302π4rr Q E ε=∴在21R r R <<区域⎰=21d π4)π4(21222001R R rr rQ W εε⎰-==21)11(π8π8d 212202R R R R Qrr Q εε在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Qr r r Q W εεε∴ 总能量)111(π8321221R R R QW W W +-=+=ε41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4rr Q E ε=,02=W∴4210211001.1)11(π8-⨯=-==R R QW W ε J(3)电容器电容 )11/(π422102R R QW C -==ε121049.4-⨯=F习题九9-1 在同一磁感应线上,各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向?解: 在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.题9-2图9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcd μ∴ 21B B=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B方向相反,即21B B≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用. 9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管 外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L·d l =I 0μ 这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ 外,与⎰⎰=⋅=⋅L l l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m -2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量. 解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb (或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB 产生 01=BCD 产生RIB 1202μ=,方向垂直向里CD 段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒RI R I B ,方向⊥向里∴)6231(203210ππμ+-=++=RIB B B B ,方向⊥向里.9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处 则02)1.0(220=-+rI r Iπμπμ解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理学 第 版 版 北京邮电大学出版社 下册 习题 答案

习题99.1选择题(1) 正方形的两对角线处各放置电荷Q ,另两对角线各放置电荷q ,若Q 所受到合力为零,则Q 与q 的关系为:()(A )Q=-23/2q (B) Q=23/2q (C) Q=-2q (D) Q=2q[答案:A](2) 下面说法正确的是:()(A )若高斯面上的电场强度处处为零,则该面内必定没有电荷;(B )若高斯面内没有电荷,则该面上的电场强度必定处处为零; (C )若高斯面上的电场强度处处不为零,则该面内必定有电荷; (D )若高斯面内有电荷,则该面上的电场强度必定处处不为零。
[答案:D](3) 一半径为R 的导体球表面的面点荷密度为σ,则在距球面R 处的电场强度() (A )σ/ε0 (B )σ/2ε0 (C )σ/4ε0 (D )σ/8ε0[答案:C](4) 在电场中的导体内部的()(A )电场和电势均为零; (B )电场不为零,电势均为零;(C )电势和表面电势相等; (D )电势低于表面电势。
[答案:C]9.2填空题(1) 在静电场中,电势不变的区域,场强必定为 。
[答案:相同](2) 一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总通量将 。
[答案:q/6ε0, 将为零](3) 电介质在电容器中作用(a )——(b )——。
[答案:(a)提高电容器的容量;(b) 延长电容器的使用寿命](4) 电量Q 均匀分布在半径为R 的球体内,则球内球外的静电能之比 。
[答案:5:6] 9.3 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系? 解: 如题9.3图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷 解得 q q 33-=' (2)与三角形边长无关.题9.3图 题9.4图9.4 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题9.4图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题9.4图示解得 θπεθtan 4sin 20mg l q = 9.5 根据点电荷场强公式204rq E πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: 020π4r r q E ϖϖε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大. 9.6 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d q πε,又有人说,因为f =qE ,SqE 0ε=,所以f =Sq 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强S qE 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为S qE 02ε=,另一板受它的作用力Sq S qq f 02022εε==,这是两板间相互作用的电场力. 9.7 长l =15.0cm 的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m -1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强.解: 如题9.7图所示(1) 在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a xE P -=λε 222)(d π4d x a xE E l l P P -==⎰⎰-ελ题9.7图 用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)同理2220d d π41d +=x xE Q λε 方向如题9.7图所示由于对称性⎰=lQxE 0d ,即Q E ϖ只有y 分量,∵ 22222220dd d d π41d ++=x x x E Qyλε以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向9.8 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强. 解: 如9.8图在圆上取ϕRd dl =题9.8图ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x ==积分R R E x 000π2d sin π4ελϕϕελπ==⎰ ∴ RE E x 0π2ελ==,方向沿x 轴正向. 9.9 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E .解: 如9.9图示,正方形一条边上电荷4q在P 点产生物强P E ϖd 方向如图,大小为∵ 22cos 221l r l +=θ∴ 24π4d 22220l r l l r E P ++=ελP E ϖd 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题9.9图由于对称性,P 点场强沿OP 方向,大小为 ∵ lq4=λ ∴ 2)4(π422220l r l r qrE P ++=ε 方向沿OP9.10 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?解: (1)由高斯定理0d εqS E s⎰=⋅ϖϖ立方体六个面,当q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量06εqe =Φ. (2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εq e =Φ 对于边长a 的正方形,如果它不包含q 所在的顶点,则024εqe =Φ, 如果它包含q 所在顶点则0=Φe .如题9.10图所示. 题9.10 图9.11 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s ϖϖ,02π4ε∑=qr E当5=r cm 时,0=∑q ,0=E ϖ8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外. 9.12 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E sϖϖ取同轴圆柱形高斯面,侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰ϖϖ对(1) 1R r < 0,0==∑E q (2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外 (3) 2R r > 0=∑q ∴ 0=E题9.13图9.13 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题9.13图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E ϖϖ)(21210σσε-= 1σ面外, n E ϖϖ)(21210σσε+-=2σ面外, n E ϖϖ)(21210σσε+=n ϖ:垂直于两平面由1σ面指为2σ面.9.14 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题9.14图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的. 解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题9.14图(a).(1) ρ+球在O 点产生电场010=E ϖ,ρ- 球在O 点产生电场'dπ4π3430320OO r E ερ=ϖ ∴ O 点电场'd33030OO r E ερ=ϖ; (2) ρ+在O '产生电场'dπ4d 3430301OO E ερπ='ϖ ρ-球在O '产生电场002='E ϖ∴ O ' 点电场 003ερ='E ϖ'OO 题9.14图(a) 题9.14图(b)(3)设空腔任一点P 相对O '的位矢为r ϖ',相对O 点位矢为r ϖ (如题8-13(b)图)则 03ερrE PO ϖϖ=,3ερr E O P '-='ϖϖ,∴ 0003'3)(3ερερερdOO r r E E E O P PO P ϖϖϖϖϖϖ=='-=+=' ∴腔内场强是均匀的.9.15 一电偶极子由q =1.0×10-6C的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p ϖ在外场E ϖ中受力矩∴ qlE pE M ==max 代入数字9.16 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解: ⎰⎰==⋅=2221212021π4π4d d r r r rq q r r q q r F A εεϖϖ)11(21r r - 外力需作的功 61055.6-⨯-=-='A A J题9.17图9.17 如题9.17图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功.解: 如题9.17图示∴ Rqq U U q A o C O 00π6)(ε=-= 9.18 如题9.18图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点E ϖd 如图,由于对称性,O 点场强沿y 轴负方向题9.18图 R 0π4ελ=[)2sin(π-2sin π-] (2) AB 电荷在O 点产生电势,以0=∞U 同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U ∴ 0032142ln π2ελελ+=++=U U U U O 9.19 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C) 解: 设均匀带电直线电荷密度为λ,在电子轨道处场强 电子受力大小 re eE F e 0π2ελ==∴ rv m r e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 9.20 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压. 解: 平行板电容器内部近似为均匀电场9.21 证明:对于两个无限大的平行平面带电导体板(题9.21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题9.21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题9.21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有 ∴ +2σ03=σ说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同.9.22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题9.22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题9.22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题9.22图(1)∵ AB AC U U =,即 ∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A=得 ,32S q A =σ SqA 321=σ而 7110232-⨯-=-=-=A C q S q σCC 10172-⨯-=-=S q B σ (2)301103.2d d ⨯===AC AC AC A E U εσV 9.23两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势;*(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εεϖϖ 题9.23图(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q ' (电荷守恒),此时内球壳电势为零,且 得 q R R q 21=' 外球壳上电势9.24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题9.24图所示,设金属球感应电荷为q ',则球接地时电势0=O U题9.24图由电势叠加原理有:得 -='q 3q9.25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =', 小球3再与小球2接触后,小球2与小球3均带电 ∴ 此时小球1与小球2间相互作用力(2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q .∴ 小球1、2间的作用力00294π432322F r qq F ==ε9.26 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求:(1)电介质内、外的场强;(2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sϖϖd(1)介质内)(21R r R <<场强303π4,π4rrQ E r r Q D r εεϖϖϖϖ==内; 介质外)(2R r <场强 (2)介质外)(2R r >电势 介质内)(21R r R <<电势 (3)金属球的电势9.27 如题9.27图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题9.27图所示,充满电介质部分场强为2E ϖ,真空部分场强为1E ϖ,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D ϖϖ得11σ=D ,22σ=D而 101E D ε=,202E D r εε= ∴r r E E εεεεσσ==102012 题9.27图 题9.28图9.28 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求:(1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量;(2)电介质中的总电场能量;(3)圆柱形电容器的电容.解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰ϖϖ 当)(21R r R <<时,Q q =∑∴ rlQ D π2= (1)电场能量密度 22222π82lr Q D w εε== 薄壳中 rlr Q rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量(3)电容:∵ CQ W 22= ∴ )/ln(π22122R R l W Q C ε== 题9.29图9.29 如题9.29 图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量电容2C 与3C 并联3223C C C +=其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 9.30 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V的电压,是否会击穿?解: (1) 1C 与2C 串联后电容(2)串联后电压比231221==C C U U ,而100021=+U U ∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.9.31半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C时,求: (1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量;(3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题9.31图(1)在1R r <和32R r R <<区域 在21R r R <<时 301π4r r Q E εϖϖ= 3R r >时 302π4r r Q E εϖϖ= ∴在21R r R <<区域在3R r >区域∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε (2)导体壳接地时,只有21R r R <<时30π4r r Q E εϖϖ=,02=W ∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J (3)电容器电容 )11/(π422102R R Q W C -==ε。
北京邮电大学大学物理学习题答案10
习题十10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中.回路平面与B垂直.当回路半径以恒定速率tr d d =80cm ·s -1 收缩时,求回路中感应电动势的大小.解: 回路磁通 2πr B BS m ==Φ 感应电动势大小40.0d d π2)π(d d d d 2====tr rB r B ttm Φε V10-2 一对互相垂直的相等的半圆形导线构成回路,半径R =5cm ,如题10-2图所示.均匀磁场B =80×10-3T ,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时,求回路中的感应电动势的大小及方向.解: 取半圆形cba 法向为i, 题10-2图则 αΦcos 2π21B R m =同理,半圆形adc 法向为j,则αΦcos 2π22B R m =∵ B 与i夹角和B 与j 夹角相等,∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tB RtmαεV方向与cbadc 相反,即顺时针方向.题10-3图*10-3 如题10-3图所示,一根导线弯成抛物线形状y =2ax ,放在均匀磁场中.B与xOy 平面垂直,细杆CD 平行于x 轴并以加速度a 从抛物线的底部向开口处作平动.求CD 距O 点为y 处时回路中产生的感应电动势.解: 计算抛物线与CD 组成的面积内的磁通量⎰⎰=-==aym y B x x y B S B 0232322d )(2d 2ααΦ∴ v y Bty y Btm 21212d d d d ααε-=-=Φ-=∵ ay v 22=∴ 212y a v =则 ααεaByy a yBi 8222121-=-= i ε实际方向沿ODC .题10-4图10-4 如题10-4图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压NM UU -.解: 作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε=又∵ ⎰+-<+-==ba ba MN ba b a Ivl vB 0ln2d cos 0πμπε所以MeN ε沿NeM 方向,大小为ba b a Iv-+ln20πμM 点电势高于N 点电势,即ba b a IvU U N M -+=-ln20πμ题10-5图10-5如题10-5所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tI d d 的变化率增大,求:(1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势. 解: 以向外磁通为正则 (1) ]ln[lnπ2d π2d π2000da db ab Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ(2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε 10-6 如题10-6图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m∴Bfr f r B r B t r B tm m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε∴ RBf r RI m 22π==ε10-7 如题10-7图所示,长直导线通以电流I =5A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06m ,宽a =0.04m ,线圈以速度v =0.03m ·s -1垂直于直线平移远离.求:d =0.05m 时线圈中感应电动势的大小和方向.题10-7图解: AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势. DA 产生电动势⎰==⋅⨯=A D Ivb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a I vbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad dIbvμεεεV方向沿顺时针.10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角(如题10-8图所示),B的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴ klvt tm -=-=d d Φε即沿abcd 方向顺时针方向.题10-8图10-9 一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如题10-9图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε;题10-9图(a)题10-9图(b)在磁场中时0d d =tΦ,0=ε;出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示.题10-10图10-10 导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l 磁感应强度B 平行于转轴,如图10-10所示.试求: (1)ab 两端的电势差; (2)b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段则 ⎰==320292d lOb l B r rB ωωε同理 ⎰==32181d lOa l B r rB ωωε∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+=(2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高.题10-11图10-11 如题10-11图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向. 解:在金属杆上取r d 距左边直导线为r ,则 ba b a Ivr ra rIv l B v ba ba BAAB -+-=-+-=⋅⨯=⎰⎰+-lnd )211(2d )(00πμπμε∵ 0<AB ε ∴实际上感应电动势方向从A B →,即从图中从右向左,∴ ba ba Iv U AB -+=ln 0πμ题10-12图10-12 磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题10-12图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tB d d >0时,求:杆两端的感应电动势的大小和方向.解: ∵ bc ab ac εεε+=tB R B R ttab d d 43]43[d d d d 21=--=-=Φε=-=tab d d 2ΦεtB R B R td d 12π]12π[d d 22=--∴ tB R R ac d d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a → 10-13 半径为R 的直螺线管中,有dtdB >0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题10-13图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量)436π(22R R B S B m-=⋅= Φ∴ tB R R i d d )436π(22--=ε∵ 0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题10-13图题10-14图10-14 如题10-14图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题10-14图示方向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解: 由⎰⎰⋅-=⋅l S t Bl Ed d d d 旋知,此时旋E 以O 为中心沿逆时针方向.(1)∵ab 是直径,在ab 上处处旋E与ab 垂直 ∴ ⎰=⋅ll 0d旋∴0=ab ε,有b a U U =(2)同理, 0d >⋅=⎰l Ecddc旋ε∴ 0<-c d U U 即d c U U >题10-15图10-15 一无限长的直导线和一正方形的线圈如题10-15图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解: 设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2aa Ia r rIa μμΦ∴ 2ln π2012aIM μΦ==10-16 一矩形线圈长为a =20cm ,宽为b =10cm ,由100匝表面绝缘的导线绕成,放在一无限长导线的旁边且与线圈共面.求:题10-16图中(a)和(b)两种情况下,线圈与长直导线间的互感.解:(a)见题10-16图(a),设长直电流为I ,它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Iarr Ia S B bbS μμΦ⎰⎰==⋅=∴ 6012108.22ln π2-⨯===aNIN M μΦ H(b)∵长直电流磁场通过矩形线圈的磁通012=Φ,见题10-16图(b) ∴ 0=M题10-16图题10-17图10-17 两根平行长直导线,横截面的半径都是a ,中心相距为d ,两导线属于同一回路.设两导线内部的磁通可忽略不计,证明:这样一对导线长度为l 的一段自感为πμl L 0=Inaa d -.解: 如图10-17图所示,取r l S d d = 则 ⎰⎰-----=--=-+=ad aad aad d aa d Il r r rIl r l r I r πI )ln(ln2πd )d11(π2d ))d (π22(0000μμμμΦaa d Il-=lnπ0μ∴ aa d lI L -==lnπ0μΦ10-18 两线圈顺串联后总自感为1.0H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H .试求:它们之间的互感. 解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H10-19图10-19 一矩形截面的螺绕环如题10-19图所示,共有N 匝.试求: (1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少? 解:如题10-19图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ磁链 ab Ih N N ln π220μΦψ==∴ ab h N IL lnπ220μψ==(2)∵ 221LIW m =∴ ab hI N W m ln π4220μ=10-20 一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能. 解:在R r <时 20π2RI B rμ=∴ 4222002π82RrI Bw m μμ==取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I Rr r I r r w W 0204320π16π4d d 2μμπ。
大学物理(北邮大)答案解析习题

习题十10-1 一半径r =10cm B =0.8T 的均匀磁场中.回路平面与B垂直.当回路半径以恒定速率tr d d =80cm ·s -1收缩时,求回路中感应电动势的大小. 解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V 10-2 一对互相垂直的相等的半圆形导线构成回路,半径R =5cm ,如题10-2图所示.均匀磁场B =80×10-3T ,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时,求回路中的感应电动势的大小及方向.解: 取半圆形cba 法向为i, 题10-2图则 αΦcos 2π21B R m =同理,半圆形adc 法向为j,则αΦcos 2π22B R m=∵ B 与i 夹角和B 与j夹角相等,∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV 方向与cbadc 相同,即异时针方向.题10-3图*10-3 如题10-3图所示,一根导线弯成抛物线形状y =2ax ,放在均匀磁场中.B与xOy 平面垂直,细杆CD 平行于x 轴并以加速度a 从抛物线的底部向开口处作平动.求CD 距O 点为y 处时回路中产生的感应电动势.解: 计算抛物线与CD 组成的面积内的磁通量⎰⎰=-==ay m y B x x y B S B 0232322d )(2d 2ααΦ∴ v y B t y y B t m 21212d d d d ααε-=-=Φ-=∵ ay v 22= ∴ 212y a v =则 ααεaByy a yBi 8222121-=-= i ε实际方向沿ODC .题10-4图10-4 如题10-4图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -.解: 作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε=又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向,大小为ba b a Iv -+ln20πμ M 点电势高于N 点电势,即ba ba Iv U U N M -+=-ln20πμ 题10-5图10-5如题10-5所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tId d 的变化率增大,求:(1)(2)解: 以向外磁通为正则 (1) ]ln [lnπ2d π2d π2000dad b a b Ilr l r Ir l r I ab b ad d m +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε10-6 如题10-6图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m ∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε∴ RBf r R I m22π==ε 10-7 如题10-7图所示,长直导线通以电流I =5A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06m ,宽a =0.04m ,线圈以速度v =0.03m ·s -1d =0.05m 时线圈中感应电动势的大小和方向.解: AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势. DA 产生电动势⎰==⋅⨯=A D Ivb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针.10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角(如题10-8图所示),B的大小为B =kt (k 为正常数).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向.10-9 一矩形导线框以恒定的速度向右穿过一均匀磁场区,B的方向如题10-9图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε; 题10-9图(a)题10-9图(b)在磁场中时0d d =tΦ,0=ε; 出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示. 题10-10图10-10 导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l磁感应强度B 平行于转轴,如图10-10所示.试求: (1)ab 两端的电势差; (2)b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高.10-11 如题10-11图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向.解:在金属杆上取r d 距左边直导线为r ,则 b a b a Iv r r a r Iv l B v b a b a BA AB-+-=-+-=⋅⨯=⎰⎰+-lnd )211(2d )(00πμπμε∵ 0<AB ε ∴实际上感应电动势方向从A B →,即从图中从右向左, ∴ ba ba Iv U AB -+=ln0πμ10-12 磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题10-12图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.解: ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=--∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →10-13 半径为R 的直螺线管中,有dtdB>0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题10-13图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量)436π(22R R B S B m -=⋅= Φ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.10-14 如题10-14图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题10-14图示(1)ab(2)cd解: 由⎰⎰⋅-=⋅l S t B l Ed d d d 旋知,此时旋E 以O 为中心沿逆时针方向. (1)∵ab 是直径,在ab 上处处旋E与ab 垂直∴ ⎰=⋅ll 0d旋∴0=ab ε,有b a U U =(2)同理, 0d >⋅=⎰l E cddc旋ε∴ 0<-c d U U 即d c U U >题10-15图10-15 一无限长的直导线和一正方形的线圈如题10-15图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解: 设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar rIaμμΦ∴ 2ln π2012aIM μΦ==10-16 两根平行长直导线,横截面的半径都是a ,中心相距为d ,两导线属于同一回路.设两导线内部的磁通可忽略不计,证明:这样一对导线长度为lπμl L 0=Inaad -. 解: 如图所示,取r l S d d = 则 ⎰⎰-----=--=-+=ad aad aad da a d Il r r r Ilr l r Ir πI)ln (ln 2πd )d 11(π2d ))d (π22(0000μμμμΦ aad Il-=lnπ0μ ∴ aad lIL -==lnπ0μΦ10-17 两线圈顺串联后总自感为1.0H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H .试求:它们之间的互感. 解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H10-18图10-18 一矩形截面的螺绕环如题10-19图所示,共有N(1) (2)若导线内通有电流I ,环内磁能为多少? 解:如题10-18图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ 磁链 ab IhN N lnπ220μΦψ== ∴ ab hN IL lnπ220μψ==(2)∵ 221LI W m = ∴ ab hI N W m ln π4220μ=10-19 一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能. 解:在R r <时 20π2R I B rμ=∴ 4222002π82R r I B w m μμ== 取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I R rr I r r w W 0204320π16π4d d 2μμπ。
大学物理学第版版北京邮电大学出版社下册习题答案

习题10选择题(1) 对于安培环路定理的理解,正确的是:(A )若环流等于零,则在回路L 上必定是H 处处为零; (B )若环流等于零,则在回路L 上必定不包围电流;(C )若环流等于零,则在回路L 所包围传导电流的代数和为零; (D )回路L 上各点的H 仅与回路L 包围的电流有关。
[答案:C](2) 对半径为R 载流为I 的无限长直圆柱体,距轴线r 处的磁感应强度B () (A )内外部磁感应强度B 都与r 成正比;(B )内部磁感应强度B 与r 成正比,外部磁感应强度B 与r 成反比; (C )内外部磁感应强度B 都与r 成反比;(D )内部磁感应强度B 与r 成反比,外部磁感应强度B 与r 成正比。
[答案:B](3)质量为m 电量为q 的粒子,以速率v 与均匀磁场B 成θ角射入磁场,轨迹为一螺旋线,若要增大螺距则要()(A ) 增加磁场B ;(B )减少磁场B ;(C )增加θ角;(D )减少速率v 。
[答案:B](4)一个100匝的圆形线圈,半径为5厘米,通过电流为安,当线圈在的磁场中从θ=0的位置转到180度(θ为磁场方向和线圈磁矩方向的夹角)时磁场力做功为() (A );(B );(C );(D )14J 。
[答案:A]填空题(1)边长为a 的正方形导线回路载有电流为I ,则其中心处的磁感应强度 。
[答案:aIπμ220,方向垂直正方形平面](2)计算有限长的直线电流产生的磁场 用毕奥——萨伐尔定律,而 用安培环路定理求得(填能或不能)。
[答案:能, 不能](3)电荷在静电场中沿任一闭合曲线移动一周,电场力做功为 。
电荷在磁场中沿任一闭合曲线移动一周,磁场力做功为 。
[答案:零,正或负或零](4)两个大小相同的螺线管一个有铁心一个没有铁心,当给两个螺线管通以 电流时,管内的磁力线H 分布相同,当把两螺线管放在同一介质中,管内的磁力线H 分布将 。
[答案:相同,不相同]在同一磁感应线上,各点B ϖ的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B ϖ的方向?解: 在同一磁感应线上,各点B ϖ的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B ϖ的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B ϖ的方向.题图(1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B ϖ的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B ρϖ=∴ 21B B ρϖ=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B ϖ方向相反,即21B B ρϖ≠.用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题图)的环路积分⎰外B L ϖ·d l ϖ=0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为 ⎰外B L ϖ·d l ϖ=I 0μ这是为什么? 解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μϖϖ外,与⎰⎰=⋅=⋅Ll l B 0d 0d ϖϖϖ外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L的电流为I ,因此实际螺线管若是无限长时,只是外B ϖ的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离. 题 图如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.已知磁感应强度0.2=B Wb ·m-2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题图所示题图(1)通过abcd 面积1S 的磁通是 (2)通过befc 面积2S 的磁通量 (3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ϖϖΦWb (或24.0-Wb )题图如题图所示,AB 、CD 为长直导线,C B )为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题图所示,O 点磁场由AB 、C B )、CD 三部分电流产生.其中AB产生 01=B ϖCD产生RIB 1202μ=,方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题图解:如题图所示,A B ϖ方向垂直纸面向里 (2)设0=B ϖ在2L 外侧距离2L 为r 处 则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题图如题图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理第二版答案(北京邮电大学出版社)

大学物理第二版答案(北京邮电大学出版社)习题解答第一章质点运动学1-1(1)质点t时刻位矢为:r(3t5)i12t23t4j(m)(2)第一秒内位移r1(某1某0)i(y1y0)j3(10)i12(10)23(110)j3i3.5j(m)(3)前4秒内平均速度Vr1t4(12i20j)3i5j(m1)(4)速度Vdr3i(t3)j(m1dt)∴V43i(43)j3i7j(m1)A;/。
(5)前4秒平均加速度aVV4V0734jj(m2t40)(6)加速度adVdtj(m2)a4j(m2)1-2vd某dtt33t22某d某vdtc14t4t32tc当t=2时某=4代入求证c=-12即某14t4t32t12vt33t22adv3t2dt6t将t=3代入证某41134(m)v356(m1)a345(m2)1-3(1)由运动方程某4t22t消去t得轨迹方程y3某(y3)20(2)1秒时间坐标和位矢方向为某14m[4,5]m:tgy某1.25,51.3(3)第1秒内的位移和平均速度分别为y15mr1(40)i(53)j4i2j(m)r1V4i2j(m1)t(4)质点的速度与加速度分别为drV8i2j,dtdVa8idt故t=1时的速度和加速度分别为V18i2jm1,a18im21-4该星云飞行时间为9.4610152.741096.5910172.091010a73.9310即该星云是2.091010年前和我们银河系分离的.1-5实验车的加速度为v1600103a2.47102m/225(g)t36001.80基本上未超过25g.1.80内实验车跑的距离为v1600103t1.80400(m)2236001-6(1)设第一块石头扔出后t秒未被第二块击中,则hv0t12gt2代入已知数得11115t9.8t22解此方程,可得二解为t11.84,t11.22第一块石头上升到顶点所用的时间为tmv10/g15/9.81.53由于t1tm,这对应于第一块石头回落时与第二块相碰;又由于t1tm这对应于第一块石头上升时被第二块赶上击中.以v20和v20分别对应于在t1和t1时刻两石块相碰时第二石块的初速度,则由于hv20(t1t1)1g(t1t1)22所以hv2011g(t1t1)2119.8(1.841)222t1t11.84117.2m/同理.2v20h11g(t1t1)2119.8(1.221)2221.221t1t151.1(m/)(2)由于t21.3t1,所以第二石块不可能在第一块上升时与第一块相碰.对应于t1时刻相碰,第二块的初速度为h12g(t)21119.8(1.841.3)2v201t2tt2121.841.323.0(m/)1-7以l表示从船到定滑轮的绳长,则v0dl/dt.由图可知l2h2于是得船的速度为vdldl2h2dtl2h2dtv0习题1-7图负号表示船在水面上向岸靠近.船的加速度为advdldtvdlh2v20dll2h20dt3负号表示a的方向指向岸边,因而船向岸边加速运动.1-8所求位数为2r42n2r42(6104)2gg0.16029.841051-9物体A下降的加速度(如图所示)为a2h20.40.2m/2t222此加速度也等于轮缘上一点在t3时的切向加速度,即at0.2(m/2)在t3时的法向加速度为av2(att)2R(0.23)2n1.00.36(m/2R)习题1-9图习题1-10图1-10a1.2m/2,t00.5,h01.5m.如图所示,相对南面,小球开始下落时,它和电梯的速度为3v0at01.20.50.6(m/)以t表示此后小球落至底板所需时间,则在这段时间内,小球下落的距离为hv0t12gt2电梯下降的距离为hv0t12at2又h0hh1(ga)t22由此得t2h021.50.59ga9.81.2而小球相对地面下落的距离为hv0t12gt20.60.599.80.5922.06m1-11v风地v风人v人地2v0人地,速度矢量合成如图(b)两图中v风地应是同一矢量.可知(a)v风人画出速度矢量合成图(a)又v风地12图必是底角为45的等腰直角三角形,所以,风向应为西北风,风速为v风地4.23(m1)v0人地co452v0人地1-12(1)t(2)2L2LvvLL2vLtt1t22vuvuvu222Lu1vv1习题1-11图(3)u由东习题1-12图tt1t2LL,如图所示风速vv向西,由速度合成可得飞机对地速度vuv,则Vv2u2.t2L2L22vvu2Luv1v2证毕1-13(1)设船相对岸的速度为V(如图所示),由速度合成得VuVV的大小由图1.7示可得VVcouco习题1-13图4即VcoVuco323332而Vinuin21船达到B点所需时间tAB两点之距SDctgOBDD1000()VVincoin12D将式(1)、(2)代入可得SD(33)1268(m)(2)由D1103tVinuin船到对岸所需最短时间由极值条件决定dt1du1in2co0即co0,/2故船头应与岸垂直,航时最短.将值代入(3)式得最短航时为3t110minuin/2110320.5103500()(3)设OBl,则lDVDDu2V22inuVcoVinuin欲使l最短,应满足极值条件.dlDu2V22uVcoduacoainuVin2ain2au2V22uVco0简化后可得2u2V2coauVco10即co2a136co10解此方程得co23co12348.2故船头与岸成48.2,则航距最短.将值代入(4)式得最小航程为2lu2v22uvco10002232223minDu1co23221231.5103m1.5(km)AB两点最短距离为52SminlminD21.511.12(km)第二章质点动力学2-1(1)对木箱,由牛顿第二定律,在某向:Fmincofma某0y向:NFmininMg0还有fma某N习题2-1图木箱将要被推动的情况下如图所示,解以上三式可得要推动木箱所需力F的最小值为FminMgcoin在木箱做匀速运动情况下,如上类似分析可得所需力F的大小为FminkMgcokin(2)在上面Fmin的表示式中,如果coin0,则Fmin,这意味着用任何有限大小的力都不可能推动木箱,不能推动木箱的条件是coin0由此得的最小值为arctan12-2(1)对小球,由牛顿第二定律某向:TcoNinmay向:TinNcomg0联立解此二式,可得Tm(acogin)0.5(2co309.8in30)3.32(N)Nm(gcoain)0.5(9.8co302in30 )3.74(N)由牛顿第三定律,小球对斜面的压力NN3.74(N)(2)小球刚要脱离斜面时N=0,习题2-2图则上面牛顿第二定律方程为Tcoma,Tinmg由此二式可解得ag/tan9.8/tan3017.0m/22-3要使物体A与小车间无相对滑动,三物体必有同一加速度a,且挂吊B的绳应向后倾斜。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
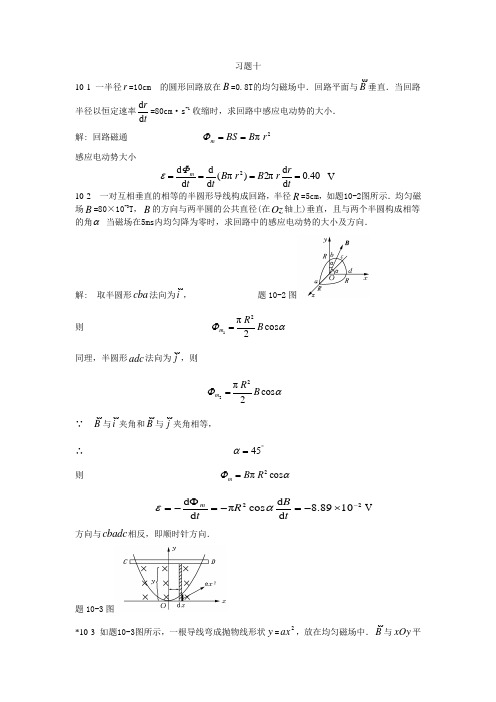
物理试卷参考答案
1解:理想气体分子的能量
RT i E 2
υ
=
平动动能 3=t 5.373930031.823
=⨯⨯=
t E J 转动动能 2=r
249330031.82
2
=⨯⨯=r E
内能5=i 5.623230031.82
5
=⨯⨯=
i E J 2
解: ∵ x
v v t x x v t v a
d d d d d d d d ===
分离变量: x x adx d )62(d 2+==υυ
两边积分得
c x x v ++=32
222
1 由题知,0=x
时,100=v ,∴50=c
∴ 13s m 252-⋅++=x x v
3.
解:∵ t t
v
a 34d d +==
分离变量,得 t t v d )34(d +=
积分,得 1
22
3
4c t t v ++=
由题知,0=t
,00=v ,∴01=c
故 22
34t t v +=
又因为 22
34d d t t t x v +== 分离变量, t t t x d )2
34(d 2
+=
积分得 232
2
12c t t x ++=
由题知 0=t
,50=x ,∴52=c
故 52
1
232++=t t x
所以s 10=t 时
m
7055102
1
102s m 190102
3
10432101210=+⨯+⨯=⋅=⨯+
⨯=-x v
4. )由题知,0=t
时,00=φ,
t t =时 3
,0,20πφ=<+
=t v A x 故且 ∴ s 3
2
2/3==∆=ππωφt 5)
2
22υυ+=u 522
02=+=υυu m/s=4.47
υ
υθ00)90tan(=
-21
42== 6)
由图知,0=t
时,0,2<-
=P P v A y ,∴3
4πφ-=P (P 点的位相应落后于0点,故取负值) ∴P 点振动方程为)34
10cos(1.0ππ-=t y p
∵ πππ3
4|3)10(100-=+-=t x t ∴解得 67.135
==x m Y=-1/2M 7) 解: bt v t
s
v -==0d d
R
bt v R v a b t
v
a n 2
02)(d d -=
=-==
τ
则 2
4
02
22
)(R bt v b a a a n
-+
=+=τ
8)
又 11x k F A
∆= 22x k F B ∆=
Mg F F B A ==
弹性势能之比为
12
2222
1112
121
2
k k
x k x k E E p p =∆∆=
二.填空题答案
1)解: m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有
222
1
21MV mv mgR +=
又下滑过程,动量守恒,以m ,M 为系统则在m 脱离M 瞬间,水平方向有
0=-MV mv
联立,以上两式,得
()
M m MgR
v +=
2
2)正比
3)v v nf d )(:表示分布在速率v 附近、速率区间dv 内的分子数密度 4)
⎰
2
1
d )(v v v v Nf :表示分布在21~v v 区间内的分子数
5) 卡诺热机效率
1
21T T -
=η
%701000
300
1=-
=η
6)W E Q
+∆=
7) E=1/2KA 2 8)书P144 三.计算题
解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知 222
s h l
+=
将上式对时间t 求导,得
t
s
s t l l d
d 2d d 2= 题1-4图
根据速度的定义,并注意到l ,s 是随t 减少的,
∴ t
s v v t l v d d ,d d 0-==-=船绳
即 θ
cos d d d d 00v v s l
t l s l t s v ==-=-
=船
或 s
v s h s lv v 0
2/1220)(+==船
将船v 再对t 求导,即得船的加速度
3
2
2d d s
v h t v a ==船
2)解:由题图(a),∵0=t
时,s 2,cm 10,,2
3
,0,0000===∴>=T A v x 又πφ
即 1s rad 2-⋅==ππ
ωT
故 m )2
3
cos(1.0ππ+=t x a
由题4-8图(b)∵0=t 时,3
5,0,2000πφ=∴>=v A x 01=t 时,2
2,0,0111π
πφ+
=∴<=v x
又 ππωφ25
3511=+⨯=
∴ πω6
5
=
故 m t x b )3
565cos(1.0π
π+
= 3)解: (1)射入的过程对O 轴的角动量守恒
ωθ2000)(sin R m m v m R +=
∴ R
m m v m )(sin 000+=
θ
ω
(2)
020*********sin 2
1]
)(sin ][)[(21
0m m m v m R m m v m R m m E E k k +=++=θθ
4)解:由abc 过程可求出b 态和a 态的内能之差 W E Q
+∆=
224126350=-=-=∆W Q E J
abd
过程,系统作功42=W
J
26642224=+=+∆=W E Q J 系统吸收热量
ba 过程,外界对系统作功84-=A J
30884224-=--=+∆=W E Q J 系统放热
5)解:(1)从图上可得分布函数表达式
⎪⎩
⎪
⎨⎧≥=≤≤=≤≤=)2(0)()2()()0(/)(00000v v v Nf v v v a v Nf v v v av v Nf ⎪⎩
⎪⎨⎧≥≤≤≤≤=)
2(0)2(/)0(/)(00000v v v v v N
a v v Nv av v f )(v f 满足归一化条件,但这里纵坐标是)(v Nf 而不是)(v f 故曲线下的总面积为N
,
(2)由归一化条件可得
⎰
⎰=
=+0
00
20
32d d v v v v N a N
v a N v v av
N
(3)可通过面积计算 N v v a N 3
1)5.12(00=
-=∆
(4) N 个粒子平均速率
⎰⎰
⎰
⎰
+==
=∞
∞
00
20
2
d d d )(1
d )(v v v v av v v av v v vNf N
v v vf v
020209
11)2331(1v av av N v =+=
(5)05.0v 到01v 区间内粒子平均速率
⎰⎰=
=
000
5.011
5.0d d v v v v N
N
v N N N N
v v ⎰⎰==00005.05.00
2
11d d )(v v v v v Nv av N N v v vf N N 24
71)243(1d 12
103003015.002100av N v av v av N v v av N v v v =-==⎰ 05.0v 到01v 区间内粒子数
N av v v a a N 4
1
83)5.0)(5.0(210001==-+=
9
7670
20v N av v ==
6)解: (1)如题5-11图(a),则波动方程为
])(cos[0φω+-+
=u
x
u l t A y 如图(b),则波动方程为
])(cos[0φω++=u
x
t A y
(2) 如题5-11图(a),则Q 点的振动方程为
])(cos[0φω+-=u
b
t A A Q
如题5-11图(b),则Q 点的振动方程为
])(cos[0φω++=u
b
t A A Q。
