线性代数试题1

合集下载

线性代数试题1及答案

线性代数试题1及答案一. 填空题（每空3分，共15分）1. 设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333222111c b a c b a c b a A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333222111d b a d b a d b a B 且4=A ,1=B 则=+B A 20 2. 二次型233222213214),,(x x tx x x x x x f +-+=是正定的，则t 的取值范围是44 t -3. A 为3阶方阵，且21=A ，则=--*12)3(A A 2716-4. 设n 阶矩阵A 的元素全为1，则A 的n 个特征值是0,21====n n λλλ5. 设A 为n 阶方阵，n βββ ,,21为A 的n 个列向量，若方程组0=AX 只有零解，则向量组(n βββ ,,21)的秩为 n二. 选择题（每题3分，共15分）6. 设线性方程组⎪⎩⎪⎨⎧=+=+--=-0322313221ax cx bc bx cx ab ax bx ，则下列结论正确的是（A ） (A)当c b a ,,取任意实数时，方程组均有解 (B)当a ＝0时，方程组无解 (C) 当b ＝0时，方程组无解 (D)当c ＝0时，方程组无解 7. A.B 同为n 阶方阵，则（C ）成立(A) B A B A +=+ (B) BA AB =(C) BA AB = (D) 111)(---+=+B A B A8. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=331332123111131211232221a a a a a a a a a a a a B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1000010101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1010100012P 则（C ）成立 (A)21P AP (B) 12P AP (C) A P P 21 (D) A P P 12 9. A ,B 均为n 阶可逆方阵，则AB 的伴随矩阵=*)(AB （D ） (A) **B A (B) 11--B A AB (C) 11--A B (D)**A B 10. 设A 为n n ⨯矩阵，r A r =)(＜n ，那么A 的n 个列向量中（B ）（A ）任意r 个列向量线性无关 (B) 必有某r 个列向量线性无关(C) 任意r 个列向量均构成极大线性无关组(D) 任意1个列向量均可由其余n －1个列向量线性表示三. 计算题（每题7分，共21分）11. 设⎪⎪⎪⎭⎫⎝⎛=300041003A 。

线性代数模拟题1

一、选择题1.设向量()()()=-1,0,1=2,-3,=,3,1T T Tx y αβγ-，，，且2αβγ+=，则x =（）..1A - .0B .2C .1D 2.已知()11=1,2,3=1,,=23TT T A αβαβ⎛⎫ ⎪⎝⎭，，,则n A =（） 111213212223212223111213313233311132123313123.,010100100,010,001101a a a a a a A a a a B a a a a a a a a a a a a P P ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭设则（）A. 12APP B =B. 21AP P B =C. 12PP A B =D. 21P PA B =4.排列2413的逆序数()τ=5.如果方程组⎪⎩⎪⎨⎧=+=-=-+0404033232321kx x xx x kx x 有非零解,则 k =（）A.-2B.-1C.1D.26.若3阶行列式1023145x x 的代数余子式121A =-，则代数余子式21A =（）.1A - B ．4 C ．-2 D ．27．设A 、B 为同阶可逆矩阵，则以下结论正确的是（）A ．|AB|=|BA|B ．|A+B|=|A|+|B|C ．（AB ）-1=A -1B -1D ．（A+B ）2=A 2+2AB+B 28．设A 为3阶方阵，且|A |＝2，则|2A -1|=（）A ．-4B ．-1C ．1D ．49.若矩阵A 满足()12,A A E A E -+=+=则（）.A A E - .B A E + .2C A E -+ .D A10.设123,,,,αααβγ均为4维列向量，且4阶行列式321,,,2,αααβ=-123,,,1,βγααα+=-则4阶行列式1232,,,γααα=（）A ．0B ．2C ．1D ．-111.设A 为三阶矩阵，且|A |=2，则|（A *）-1|=（） A.41B.1C.2D.412．设A 为5×4矩阵，若秩（A ）=4，则秩（5A T ）为（）A ．2B ．3C ．4D ．513.设α1=[1，2，1]，α2=[0，5，3]，α3=[2，4，2]，则向量组α1，α2，α3的秩是（）A ．0B ．1C ．2D ．314．若向量组α1=（1，t+1，0），α2=（1，2，0），α3=（0，0，t 2+1）线性相关，则实数t=（）A ．0B ．1C ．2D ．315．设3元非齐次线性方程组Ax=b 的两个解为α=（1，0，2）T ， β=（1，-1，3）T ，且系数矩阵A 的秩r(A )=2，则对于任意常数k , k 1, k 2, 方程组的通解可表为（）A ．k 1(1,0,2)T +k 2(1,-1,3)TB ．(1,0,2)T +k (1,-1,3)TC ．(1,0,2)T +k (0,1,-1)TD ．(1,0,2)T +k (2,-1,5)T16．对非齐次线性方程组A m ×n x =b ，设秩（A ）=r ，则（）A ．r =m 时，方程组Ax =b 有解B ．r =n 时，方程组Ax =b 有唯一解C ．m =n 时，方程组Ax =b 有唯一解D ．r <n 时，方程组Ax =b 有无穷多解17．若A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡10001000210100002B x 与相似，则x=（） A ．-1 B ．0 C ．1 D ．218.设()21,103T a A ξ⎛⎫== ⎪⎝⎭是的特征向量，则a =（） A ．1 B ．0 C ．-1D ．2 19．设λ=2是可逆矩阵A 的一个特征值，则矩阵（A 2）-1必有一个特征值等于（）A ．41B ．21C ．2D ．420.设A 为3阶方阵，其特征值分别为2,1,0则| A +2E |=( )A.0B.2C.3D.2421.若向量α=（1，-2,1）与β=(2，3，t )正交，则t =( )A.-2B.0C.2D.422.三元二次型f （x 1，x 2，x 3）=233222312121912464x x x x x x x x x +++++的矩阵为（）A.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963642321B.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963640341C.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡960642621D.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡9123042321 23．若实对称矩阵A =⎪⎪⎪⎭⎫ ⎝⎛a a a 000103为正定矩阵，则a 的取值应满足().0A a <<.0B a <<.C a <<.1D a <<二、计算题1.已知矩阵A=011110124⎛⎫ ⎪ ⎪ ⎪-⎝⎭，B=101332⎛⎫⎪- ⎪ ⎪⎝⎭，（1）判断A 是否可逆，如可逆，求A 的逆矩阵A -1以及秩；（2）解矩阵方程AX=B.2．求行列式01121102(1)12102110-----(2)a b b b a bb b a的值.3. .已知矩阵A=111011002⎛⎫⎪⎪ ⎪⎝⎭，B=121011-⎛⎫⎪-⎝⎭，（1）求A 的逆矩阵A -1；（2）解矩阵方程XA=B.4．求线性方程组123412341234221245224x x x x x x x x x x x x -++=⎧⎪+++=⎨⎪---+=-⎩（1）求导出组的基础解系；（2）求方程组的一般解。

自考本科_线性代数_历年真题[1]

第 1 页全国2010年1月自考线性代数（经管类）试题课程代码：04184说明：本卷中，A T 表示矩阵A 的转置，αT 表示向量α的转置，E 表示单位矩阵，|A |表示方阵A 的行列式，A -1表示方阵A 的逆矩阵，r （A ）表示矩阵A 的秩.一、单项选择题（本大题共10小题，每小题2分，共30分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将代码填写在题后的括号内。

错选、多选或未选均无分。

1.设行列式==1111034222,1111304z y x zy x则行列式( ) A.32B.1C.2D.38 2.设A ，B ，C 为同阶可逆方阵，则（ABC ）-1=( ) A. A -1B -1C -1 B. C -1B -1A -1 C. C -1A -1B -1D. A -1C -1B -13.设α1，α2，α3，α4是4维列向量，矩阵A =（α1，α2，α3，α4）.如果|A |=2，则|-2A |=( ) A.-32 B.-4 C.4D.324.设α1，α2，α3，α4 是三维实向量，则( ) A. α1，α2，α3，α4一定线性无关 B. α1一定可由α2，α3，α4线性表出 C. α1，α2，α3，α4一定线性相关D. α1，α2，α3一定线性无关5.向量组α1=（1，0，0），α2=（1，1，0），α3=（1，1，1）的秩为( ) A.1 B.2 C.3D.46.设A 是4×6矩阵，r （A ）=2，则齐次线性方程组Ax =0的基础解系中所含向量的个数是( )A.1B.2C.3D.47.设A 是m ×n 矩阵，已知Ax =0只有零解，则以下结论正确的是( ) A.m ≥n B.Ax =b (其中b 是m 维实向量)必有唯一解 C.r (A )=mD.Ax =0存在基础解系第 2 页8.设矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---496375254，则以下向量中是A 的特征向量的是( ) A.（1，1，1）T B.（1，1，3）T C.（1，1，0）TD.（1，0，-3）T9.设矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--111131111的三个特征值分别为λ1，λ2，λ3，则λ1+λ2+λ3 = ()A.4B.5C.6D.710.三元二次型f (x 1，x 2，x 3)=233222312121912464x x x x x x x x x +++++的矩阵为( )A.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963642321 B.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963640341 C.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡960642621 D.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡9123042321 二、填空题（本大题共10小题，每小题2分，共20分）请在每小题的空格中填上正确答案。

线性代数试题与答案1

（试卷一）一、填空题（本题总计20分，每小题2分） 1. 排列7623451的逆序数是_______。

2. 若122211211=a a a a ，则=16030322211211a a a a 3. 已知n 阶矩阵A 、B 和C 满足E ABC =，其中E 为n 阶单位矩阵，则CAB =-1。

4. 若A 为n m ⨯矩阵，则非齐次线性方程组AX b =有唯一解的充分要条件是_________5. 设A 为86⨯的矩阵，已知它的秩为4，则以A 为系数矩阵的齐次线性方程组的解空间维数为__2___________。

6. 设A 为三阶可逆阵，⎪⎪⎪⎭⎫ ⎝⎛=-1230120011A，则=*A 7.若A 为n m ⨯矩阵，则齐次线性方程组0Ax =有非零解的充分必要条件是8.已知五阶行列式1234532011111112140354321=D ，则=++++4544434241A A A A A 9. 向量α=(2,1,0,2)T-的模（范数）______________。

10.若()Tk11=α与()T121-=β正交，则=k二、选择题（本题总计10分，每小题2分） 1. 向量组r ααα,,,21 线性相关且秩为s ，则(D) Ａ．s r = Ｂ．s r ≤Ｃ．r s ≤ Ｄ．r s <2. 若A 为三阶方阵，且043,02,02=-=+=+E A E A E A ，则=A (A)Ａ．8Ｂ．8-Ｃ．34 Ｄ．34-3．设向量组A 能由向量组B 线性表示，则( d )Ａ．)()(A R B R ≤ Ｂ．)()(A R B R <Ｃ．)()(A R B R =Ｄ．)()(A R B R ≥4. 设n 阶矩阵A 的行列式等于D ，则()*kA 等于_____。

c)(A *kA )(B *A k n)(C *-A k n 1)(D *A5. 设n 阶矩阵A ，B 和C ，则下列说法正确的是_____。

线性代数总复习题(一)

九．设 A、B 都是 n 阶对称阵，证明 AB 是对称阵的充分必要条件是 AB = BA ．证明：∵ A, B 都是 n 阶对称阵．
∴ AT = A ， B T = B ．
∴ AB 是对称阵 ⇔ ( AB ) = AB
T
⇔ B T AT = AB ⇔ BA = AB
十．求下面矩阵的特征值和特征向量：
1．设 D1 =
a11 a21 an1
a12 a22 an 2
a1n a2 n ann
， D2 =
an1 an −1,1 a11
an 2 an −1,2 a12
ann an −1, n a1n
，则 D1 与 D2 的关系是（
C
）．
（A） D2 = D1 分析： rn 依次与 rn −1 , rn − 2 ,
∴ i = 2 ， k = 5 ；或 i = 5 ， k = 2 ．
．若 i = 2 ， k = 5 ，则列标排列 32145 的逆序数为 3，这一项的符号为“ − ” ．若 i = 5 ， k = 2 ，则列标排列 35142 的逆序数为 6，这一项的符号为“ + ”
∴ i =5，k = 2．
（2） R ( A ) = 2 ；（3） R ( A ) = 3 ．（1） R ( A ) = 1 ；
−2 3k ⎞ ⎛ 1 −2 3k ⎞ ⎛ 1 ⎟ ⎜ ⎟ ⎜ 3 ( k − 1) 解： A = ⎜ −1 2k −3 ⎟ ∼ ⎜ 0 2 ( k − 1) ⎟． ⎜ k −2 3 ⎟ ⎜ 0 0 −3 ( k + 2 )( k − 1) ⎟ ⎝ ⎠ ⎝ ⎠ ∴ （1）当 k ≠ −2 且 k ≠ 1 时， 2 ( k − 1) ≠ 0 ， −3 ( k + 2 )( k − 1) ≠ 0 ， R ( A ) = 3 ． ⎛ 1 −2 −6 ⎞ ⎜ ⎟ （2）当 k = −2 时， A ∼ ⎜ 0 −6 −9 ⎟ ， R ( A ) = 2 ． ⎜0 0 0 ⎟ ⎝ ⎠ ⎛ 1 −2 3 ⎞ ⎜ ⎟ （3）当 k = 1 使， A ∼ ⎜ 0 0 0 ⎟ ， R ( A ) = 1 ． ⎜0 0 0⎟ ⎝ ⎠

线性代数习题及答案1

线性代数测试题（线性代数测试题（--）一、单项选择题（每小题3分，共15分。

）1.1.已知已知B A ,是同阶方阵，下列等式中正确的是【【】 A. ||||||B A AB = ； B. T T T B A AB =)(； C.111)(---=B A AB ； D. kk k B A AB =)(.2.2.设设A 是n m ´矩阵，齐次线性方程组0=Ax 有非零解的充要条件是【】A.n A r =)(；B.n A r <)(；C.0||=A ；D.n m > .3.3.设设A 是45´矩阵矩阵,,则下列命题正确的是【】A.A 的行向量组线性无关；B.A 的行向量组线性相关；C.A 的列向量组线性无关；D.A 的列向量组线性相关的列向量组线性相关..4.4.设设A 是n 阶可逆矩阵，l 是A 的一个特征值，则*A 的一个特征值是【】 A.n A ||1-l ； B.||1A -l ； C.||A l ； D.n A ||l .5.5.设设n 阶方阵A 与B 相似，则下列命题不正确的是【】A.A 与B 有相同的特征值；B.)()(B r A r =；C.||||B A =；D.A 与B 有相同的特征向量有相同的特征向量. .二、填空题（每小题3分，共15分。

） 1.1.已知已知)1,3,2(),1,1,1(),,2,1(321=-==a a a t ，当t t 时，时，321,,a a a 线性无关线性无关.. 2.yy y y y y f 212112)(---=中3y 的系数是的系数是 .3. .3. .3.设设A 为3阶方阵，A 的特征值为的特征值为-1-1-1，，1，2，则|3|1-A = . 4.设321,,a a a 是三元线性方程组b Ax =的三个解，且2)(=A r ，÷÷÷øöçççèæ=+40221a a ，÷÷÷øöçççèæ=-11132a a ，则b Ax =的通解为 5.设二次型31212322212224x x x tx x x x f ++++=是正定的，则t 的范围是的范围是三、（本题10分）已知÷÷÷øöçççèæ-=221011324A ，矩阵X满足X A AX 2+=，求矩阵X四、（本题10分）求下列向量组的秩和一个最大无关组求下列向量组的秩和一个最大无关组. .)3,4,3,4(,)3,2,1,1(,)1,1,3,2(,)1,1,1,1(4321-=-=--==a a a a . 五、（本题14分）已知线性方程组ïïîïïíì=+-=-=-=-.,,,41433221k kx x k x kx k x kx k x kx (1)(8分)k 为何值时，方程组有惟一解为何值时，方程组有惟一解? ? ? 无解？无穷多解？无解？无穷多解？无解？无穷多解？(2)(6分)在有无穷多解的情况下求出其通解.六、（本题10分）已知三阶方阵A 的特征值为的特征值为-1-1-1，，1，2.2.设设3223A A I B +-=. (1)(5分)求矩阵A 的行列式及A 的秩；的秩；(2)(5分)求矩阵B 的特征值及其相似对角矩阵的特征值及其相似对角矩阵. .七、（本题14分）设úúúûùêêêëé=011101110A ，求正交矩阵P 使得L =-AP P 1为对角矩阵为对角矩阵. . 八、证明题（本大题2小题，每小题6分，共12分）分）1.1.向量组向量组321,,a a a 线性无关，试证向量组32121132,2,a a a a a a +++ 线性无关线性无关.. 2.2.设设A 为n m ´矩阵矩阵,,B 为m n ´矩阵矩阵,,且n m >. . 证明：证明：.0||=AB线性代数测试题答案线性代数测试题答案((一)一、单项选择题(每小题3分，共15分) 1.A 1.A；； 2.B 2.B；； 3.B 3.B；； 4.B 4.B；； 5.D. 二、填空题（每小题3分，共15分）1.2¹t； 2.-4 2.-4；； 3.227-； 4.)()1,1,1()2,0,1(R k k T T Î+； 5.22<<-t .三、（10分）解：由X A AX 2+=得A X I A =-）（2 （（1分）分）30210113222=--=-|I A | （（2分）所以A I A X 12--=）（（2分）分）÷÷÷øöçççèæ--=--3423111012021//I A ）（（（3分）故÷÷÷øöçççèæ--=35432230241//X . . （（2分）分）四、（10分）解：对A 进行初等行变换进行初等行变换÷÷÷÷÷øöçççççèæ-@÷÷÷÷÷øöçççççèæ----=00001100011041213311421131314121A （（5分）此向量组的秩为：分）此向量组的秩为：3 3 3 （（2分）分）它的一个最大无关组为.,,321a a a （（3分）分）五、（14分）解：解：(1)(1)(1)系数矩阵系数矩阵A 的行列式为的行列式为10011000100014-=----=k kk k k |A | （（5分）当1±¹k 时，方程组有惟一解；时，方程组有惟一解；（（1分）分）当1=k 时，4)(,3)(==Ab r A r ，方程组无解；，方程组无解；（1分）当1-=k 时，3)()(==Ab r A r ，方程组有无穷多解；（1分）分）(2)(2)对增广矩阵进行行初等变换：对增广矩阵进行行初等变换：÷÷÷÷øöççççèæ-@÷÷÷÷øöççççèæ------------=0000011100010101100111001111001011010011)Ab （（（3分）分） \原方程组的通解为：)R k (),,,(k ),,,(x T T Î--+=11110101 （（3分）分）六、（10分）解：解：(1)(1)2-=A （3分）3=)A (r （（2分）分） (2)(2)设设l 为A 的特征值，x 为A 的对应于l 的特征向量，则：的特征向量，则： x x A A I Bx )231()23(3232l l +-=+-=B \的特征值为的特征值为-4-4-4，，0，5 5 （（4分）分）B 的相似对角矩阵为：÷÷÷øöçççèæ-504 . . （（1分）分）七、解：0)2()1(1111112=+-+=---=-l l l l l l I A 得到特征值2,121=-=l l （3分）11-=l 时，÷÷÷øöçççèæ÷÷÷øöçççèæ=+000000111~111111111I A ，对应于11-=l 的两个正交的特征向量为÷÷÷øöçççèæ-÷÷÷øöçççèæ-101,121 ，单位化得÷÷÷øöçççèæ-÷÷÷øöçççèæ-10121,12161 （6分）22=l 时，÷÷÷øöçççèæ--÷÷÷øöçççèæ---=-000110101~2111211122I A ，对应于22=l 的一个特征向量为÷÷÷øöçççèæ111，位化得÷÷÷øöçççèæ11131（3分）正交阵÷÷÷÷øöççççèæ--=3/12/16/13/106/23/12/16/1P . . （（2分）分）八、（共 12分）1.1.证：令证：令0)32()2(321321211=+++++a a a a a a x x x （（2分）分）整理得：03)22()(332321321=+++++a a a x x x x x x(1分) 由于321,,a a a 线性无关，所以有：.0,0,0321===x x x （2分）则向量组32121132,2,a a a a a a +++线性无关线性无关. . . （（1分）分）证：A 为n m ´矩阵，B 为m n ´矩阵，且n m >，n AB r n B r n A r £££\)(,)(,)( （4分）分）又AB 为m 阶方阵，则0||=AB . （2分）分）。

线性代数1-8试题2011.10.11

《线性代数》试题1一、单项选择题（本大题共6小题，每小题3分，共18分，每题只有一个正确答案，错选、多选或未选均不给分。

）1. 若1112132122233132332a a a a a a a a a =，则111211132122212331323133232323a a a a a a a a a a a a ++=+【】 A ．2 B. 4 C. 8 D.16 2．设A 是n 阶方阵，且3A =，则13A =【】 A ．113n -B ．13n -C ． 3nD ．13．设a b A c d ⎛⎫= ⎪⎝⎭且，则A 的伴随矩阵A *=【】 A ．d b ca ⎛⎫⎪⎝⎭ B ．a b c d -⎛⎫ ⎪-⎝⎭ C ．d b c a -⎛⎫ ⎪-⎝⎭ D. a b c d -⎛⎫ ⎪-⎝⎭4．设给向量组 321,,:αααA ； :B 4321,,,αααα ，则下列命题中正确的是【】A.若A 线性无关，则B 线性无关；B. 若B 线性无关，则A 线性无关；C.若A 线性无关，则B 线性相关；D. 若B 线性相关，则A 线性相关。

5．设21,ηη是非齐次线性方程组β=Ax 的解，则下列向量中齐次线性方程组0=Ax 的解的是【】.A ． 121233ηη+ B ．12ηη+ C ．12ηη-D ． 122ηη-6．设λ是可逆阵A 的一个特征值，则23A -必有一个特征值是【】A ．23λB ．32λC ．13λD ．23λ二、填空题(本大题共6小题，每小题3分，共18分)1.四阶行列式|a |D ij =中,含有因子1221a a 且带负号的项为 2．若方阵A 满足2230A A E +-=，则=-1A .3．设三阶方阵A 等价于122111231-⎛⎫⎪ ⎪⎪-⎝⎭，则()R A =____ _4．设101n A ⎛⎫= ⎪⎝⎭，则nA = 5．若2112A ⎛⎫= ⎪⎝⎭与00xB y ⎛⎫= ⎪⎝⎭相似，则x = ，y = 。

[理学]线性代数习题1-8

习题一向量及其线性运算一、填空题：1．下列等式何时成立： 1）βαβα-=+，当2,πβα=；2）βαβα+=+，当0,=βα；3）βαβα-=+，当βαπβα≥=且,,；4）ββαα=，),(为非零向量βα，当0=β，。

2．βαβα->+，当为非零向量，且βαπβα2,0<≤。

3．指出下列向量组是线性相关还是线性无关： 1）},{αθ是线性相关；2）βα,不平行，},{βα是线性无关； 3）γβα,,共面，},,{γβα是线性相关 ; 4），γβα,,不共面，},,{γβα是线性无关。

二、用几何作图证明：1）αβαβα2)()(=-++ 2）)(21)21()21(βααββα-=+-+ 证明：三、设P OB OA ,,βα==为线段AB 上任一点，证明：存在数λ，使得λβαλ+-=)1(OP 。

证明： AP AP OA OP ,+=与BA 平行，∴可设BA AP λ-=所以，λβαλλλλλ+-=+-=--=-=)1()1()(OB OA OB OA OA BA OA OP 。

四、已知向量313221,,e e e e e e +=+=+=γβα，问向量αγγββα---,,是否共面？如果共面，写出它们的线性表示式。

解：因为 ,)()()(θαγγββα=-+-+- （1）所以向量αγγββα---,,共面。

线性表示式为（1）式。

习题二空间直角坐标系一、填空题：1．在空间直角坐标系中，点)5,3,2(-M 关于xoy 平面的对称点的坐标是)5,3,2(--；关于yoz 平面的对称点是)5,3,2(--；关于xoz 平面的对称点是)5,3,2(；关于原点的对称点是)53,2(--。

2．在空间直角坐标系中，点轴关于x M )4,3,1(-的对称点的坐标是)4,3,1(---；关于y 轴的对称点是)4,3,1(-；关于z 轴的对称点是)4,3,1(-。

3．在空间直角坐标系中，点)6,5,2(--M 在xoy 平面上的投影点坐标是)0,5,2(--；在yoz 平面上的投影点是)6,5,0(-；在xoz 平面上的投影点是)6,0,2(-；在x 轴上的投影点是)0,0,2(-；在y 轴上的投影点是)0,5,0(-；在z 轴上的投影点是)6,0,0(。

线代第一章测试题及答案

线代第一章测试题及答案一、选择题（每题5分，共20分）1. 以下哪个选项不是线性代数的研究对象？A. 向量空间B. 线性方程组C. 矩阵D. 微分方程答案：D2. 矩阵的秩是指：A. 矩阵的行数B. 矩阵的列数C. 矩阵中非零行（或列）的最大数目D. 矩阵的元素个数答案：C3. 以下哪个矩阵是可逆的？A. 零矩阵B. 单位矩阵C. 奇异矩阵D. 任意矩阵答案：B4. 向量空间的基是指：A. 空间中的任意一组向量B. 空间中的一组线性无关的向量C. 空间中的一组线性相关的向量D. 空间中的一组正交向量答案：B二、填空题（每题5分，共20分）1. 矩阵的元素个数称为矩阵的______。

答案：阶数2. 如果一个矩阵的行向量组线性无关，则该矩阵是______矩阵。

答案：满秩3. 向量空间中，一组向量如果满足线性组合的系数全为零，则称这组向量是______的。

答案：线性无关4. 一个n阶方阵的行列式等于______。

答案：0三、简答题（每题10分，共20分）1. 请简述什么是线性方程组的解。

答案：线性方程组的解是指满足方程组中所有方程的未知数的取值。

2. 请解释什么是矩阵的转置。

答案：矩阵的转置是指将矩阵的行向量变成列向量，列向量变成行向量，即交换矩阵的行和列。

四、计算题（每题15分，共40分）1. 计算矩阵A的行列式，其中A = \[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\]。

答案：\[ \text{det}(A) = (1)(4) - (2)(3) = 4 - 6 = -2 \]2. 已知矩阵B = \[\begin{bmatrix} 2 & 1 \\ 4 & 2\end{bmatrix}\]，求B的逆矩阵。

答案：\[ B^{-1} = \frac{1}{(2)(2) - (1)(4)} \begin{bmatrix} 2 & -1 \\ -4 & 2 \end{bmatrix} = \begin{bmatrix} 1 & -0.5 \\-2 & 1 \end{bmatrix} \]。

线性代数1

线性代数试题1说明：在本卷中，A T 表示矩阵A 的转置矩阵，A *表示矩阵A 的伴随矩阵，E 表示单位矩阵，A 表示方阵A 的行列式，r (A )表示矩阵A 的秩。

一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．3阶行列式011101110---=ij a 中元素a 21的代数余子式A 21=（） A ．-2 B ．-1C ．-1D ．22．设n 阶可逆矩阵A 、B 、C 满足ABC =E ，则B -1=（）A ．A -1C -1B ．C -1A -1C ．ACD ．CA3．设3阶矩阵A =⎪⎪⎪⎭⎫ ⎝⎛000100010，则A 2的秩为（）A ．0B ．1C ．2D ．3 4．设矩阵A =⎪⎪⎭⎫ ⎝⎛22211211a a a a ，B =⎪⎪⎭⎫ ⎝⎛++121112221121a a a a a a ，P 1=⎪⎪⎭⎫ ⎝⎛0110，P 2=⎪⎪⎭⎫ ⎝⎛1101，则必有（） A ．P 1P 2A =B B ．P 2P 1A =BC ．AP 1P 2=BD ．AP 2P 1=B5．设向量组α1, α2, α3, α4线性相关，则向量组中（）A ．必有一个向量可以表为其余向量的线性组合B ．必有两个向量可以表为其余向量的线性组合C ．必有三个向量可以表为其余向量的线性组合D ．每一个向量都可以表为其余向量的线性组合6．设α1, α2, α3, α4是一个4维向量组，若已知α4可以表为α1, α2, α3,的线性组合，且表示法惟一，则向量组α1, α2, α3, α4的秩为（）A ．1B ．2C ．3D ．47．设α1, α2, α3是齐次线性方程组Ax =0的一个基础解系，则下列解向量组中，可以作为该方程组基础解系的是（）A ．α1, α2, α1+α 2B ．α1, α2, α1-α 2C ．α1+α2, α2+α3, α3+α 1D ．α1-α2，α2-α3，α3-α18．设A 为3阶矩阵，且E A 32-=0，则A 必有一个特征值为（）A ．-23B ．-32C ．32D ．23 9．设实对称矩阵A =⎪⎪⎪⎭⎫ ⎝⎛--120240002，则3元二次型f (x 1,x 2,x 3)=x T Ax 的规范形为（）A ．21z +22z +23zB ．21z +22z -23zC ．21z +22zD ．21z -22z10．设2元二次型f (x 1,x 2)=x T Ax 正定，则矩阵A 可取为（）A ．⎪⎪⎭⎫ ⎝⎛--2112 B ．⎪⎪⎭⎫ ⎝⎛--2112 C ．⎪⎪⎭⎫ ⎝⎛--1221 D ．⎪⎪⎭⎫ ⎝⎛1221 二、填空题（本大题共10小题，每小题2分，共20分）请在每小题的空格中填上正确答案。

线性代数1-5章习题1

线性代数习题集第一章行列式一、判断题1．行列式如果有两列元素对应成比例，则行列式等于零. ( )2. 213210 124121 012342=-.( )3. 13434121.42042=-( )4.123213123213123213.a a ab b bb b b a a ac c c c c c=( )5.123123123123123123.a a a a a ab b b b b bc c c c c c---------=---( )6. n阶行列式n D中元素ij a的代数余子式ij A为1n-阶行列式. ( )7. 312143 245328 836256=.( )8.111213212223313233a a aa a aa a a122r r+111213211122122313313233222+++a a aa a a a a aa a a( )9．如果齐次线性方程组有非零解，则它的系数行列式必等于零. ( )10. 如果方程个数与未知数个数相等，且系数行列式不为零，则方程组一定有解. ( )二、选择题1．若12532453r sa a a a a是5阶行列式中带正号的一项，则,r s的值为（）．A.1,1r s ==B.1,4r s ==C.4,1r s ==D.4,4r s ==2.下列排列是偶排列的是（）A. 4312B. 51432C. 45312D. 6543213.若行列式210120312x --=-，则x =( ).A.–2B. 2C. -1D. 14.行列式0000000000a bc d e f的值等于（）. A. abcdef B. abdf - C. abdf D. cdf5.设abc ≠0，则三阶行列式00000d c b a的值是（）.A ．aB ．-bC ．0D ．abc 6.设行列式2211b a b a =1，2211c a c a =2，则222111c b a c b a ++=（）.A ．-3B ．-1C ．1D ．37.设非齐次线性方程组123123123238223105ax x x ax x x x x bx ++=⎧⎪++=⎨⎪++=⎩有唯一解，则,a b 必须满足（）..0,0A a b ≠≠ 2.,03B a b ≠≠ 23.,32C a b ≠≠ 3.0,2D a b ≠≠ 8. 215152521112223030223-=---是按（）展开的.A ．第2列B ．第2行C ．第1列D ．第1行9.设111211212ni i inn n nna a a D a a a a a a =则下式中（）是正确的. 1122.0i i i i in in A a A a A a A +++= 1122.0i j i j ni nj B a A a A a A +++=1122.i i i i in ni C a A a A a A D +++= 1122.i j i j ni nj D D a A a A a A =+++10. 349571214的23a 的代数余子式23A 的值为（）.A. 3B. -3C. 5D. -5 三、填空题1．排列36715284的逆序数是________.2．四阶行列式中的一项14322341a a a a 应取的符号是_______. 3.若,0211=k 则k=___________. 4.行列式1694432111中32a 元素的代数余子式A 32=____________.5.598413111=__________. 6.行列式0001001010000100=______.7.行列式0004003002001000=__________. 8.非零元素只有1n -行的n 阶行列式的值等于__________.9. 1231231238,a a a b b b c c c =则123123123222c c c b b b a a a ---=__________. 10.n 阶行列式nD 中元素ij a 的代数余子式ij A 与余子式ij M 之间的关系是ij A =__________，n D 按第j 列展开的公式是n D =__________.四、计算题1.写出五阶行列式中含1325a a 并带有正号的所有项.2.计算四阶行列式1002210002100021的值.3.求4阶行列式1111112113114111的值.4.计算行列式D =1111123414916182764的值.5. 计算行列式122224242λλλ--+---+6.计算n 阶行列式011110111101111.7. 计算n 阶行列式 00 n a D a⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅, 其中对角线上元素都是a , 未写出的元素都是0;8. 计算n 阶行列式 n x a a a xaD a ax⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅五、证明题1.33()ax byay bz az bx x y z ay bzaz bx ax by a b yz x az bx ax byay bzzxy++++++=++++2.2222222222222222(1)(2)(3)(1)(2)(3)0(1)(2)(3)(1)(2)(3)a a a a b b b b cc c cd d d d ++++++=++++++六.用克拉默法则解方程1. 12341234123412345242235232110x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩； 2.121232343454556156056056051x x x x x x x x x x x x x +=⎧⎪++=⎪⎪++=⎨⎪++=⎪⎪+=⎩.七. 问λ取何值时, 齐次线性方程组123123123(1)2402(3)0(1)0x x x x x x x x x λλλ--+=⎧⎪+-+=⎨⎪++-=⎩有非零解？第二章矩阵一、判断题1.若A 是23⨯矩阵，B 是32⨯矩阵，则AB 是22⨯矩阵. ( )2.若,AB O =且,A O ≠则.=B O ( )3. 12103425X ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭的解110122534X -⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭. ( ) 4.若A 是n 阶对称矩阵，则2A 也是n 阶对称矩阵. ( ) 5. n 阶矩阵A 为零矩阵的充分必要条件是0.A = ( )6. 若,A B 为同阶可逆矩阵，则11()kA kA --=. ( )7. 42042069126232110110⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭. ( )8. n 阶矩阵A 为逆矩阵的充分必要条件是0.A ≠ ( )9.设,A B 为同阶方阵，则 A B A B +=+. ( )10.设 ,A B 为n 阶可逆矩阵，则 111A O A O O B OB ---⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭.( ) 二、选择题1. 若,A B 为n 阶矩阵，则下式中（）是正确的.22.()()A A B A B A B -+=- .(),=.-=≠B A B C O A O B C 且，必有222.(+)+2+B A B A AB B = .D AB A B =2.若,s n n l A B ⨯⨯，则下列运算有意义的是（）..T T A B A .B BA .+C A B .+T D A B3.若,m n s t A B ⨯⨯，做乘积AB 则必须满足（）..=A m t .=B m s .=C n s .=D n t4.矩阵1111A --⎛⎫=⎪⎝⎭的伴随矩阵*=A （）A ．⎪⎪⎭⎫ ⎝⎛--1111B ．⎪⎪⎭⎫ ⎝⎛--1111C ．⎪⎪⎭⎫ ⎝⎛--1111D ．⎪⎪⎭⎫ ⎝⎛--11115.设2阶矩阵a b A c d ⎛⎫= ⎪⎝⎭，则*=A （） A ．⎪⎪⎭⎫ ⎝⎛--a c b d B ．⎪⎪⎭⎫ ⎝⎛--a b c d C ．⎪⎪⎭⎫ ⎝⎛--a cb dD ．⎪⎪⎭⎫⎝⎛--a b c d 6. 矩阵⎪⎪⎭⎫⎝⎛-0133的逆矩阵是（）A ．⎪⎪⎭⎫ ⎝⎛-3310B ．⎪⎪⎭⎫ ⎝⎛-3130C ．⎪⎪⎭⎫⎝⎛-13110 D ．⎪⎪⎪⎭⎫ ⎝⎛-01311 7. 设2阶方阵A 可逆，且A -1=⎪⎭⎫ ⎝⎛--2173，则A=（）.A ．⎪⎭⎫ ⎝⎛--3172 B ．⎪⎭⎫ ⎝⎛3172 C ．⎪⎭⎫ ⎝⎛--3172 D ．⎪⎭⎫ ⎝⎛21738. n 阶矩阵A 行列式为,A 则kA 的行列式为（）.A. kA B. n k A C. k A D. -k A9. 设,A B 为n 阶矩阵满足=,AB A 且A 可逆，则有（）..==A A B E .=B A E .=B B E .,D A B 互为逆矩阵10.设A 是任意阶矩阵，则（）是对称阵..(+)T T A A A .+T B A A .T C AA .T T D A AA三、填空题1.设矩阵120210001A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，100021013B ⎛⎫⎪= ⎪ ⎪⎝⎭，则2+=A B _____________2.设A=⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤411023，B=,010201⎢⎣⎡⎥⎦⎤则AB =___________. 3.设矩阵A=⎪⎪⎭⎫ ⎝⎛21，B=⎪⎪⎭⎫ ⎝⎛31，则A TB =____________. 4.⎪⎪⎪⎭⎫⎝⎛321(1，2，3)=__________. 5.n1111⎪⎪⎭⎫ ⎝⎛=__________. 6.⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-0410******** ＝______________________. 7.设2阶矩阵A =⎪⎪⎭⎫⎝⎛3202，则A *A =_____________.8.设矩阵A=⎪⎭⎫⎝⎛4321，则行列式|A 2|=__________. 9.设A=⎪⎪⎭⎫ ⎝⎛d c b a ，且det(A)=ad-bc≠0，则A -1=__________ .10. 设 ,A B 为n 阶可逆矩阵，则 1O A B O -⎛⎫= ⎪⎝⎭_______________.四、计算题1．已知110123011,124,111021A B ⎡⎤⎡⎤⎢⎥⎢⎥=----⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求()TA B +.2.计算下列乘积1).431712325701⎛⎫⎛⎫ ⎪⎪- ⎪⎪ ⎪⎪⎝⎭⎝⎭;2).3(123)21⎛⎫⎪⎪ ⎪⎝⎭；3).)21(312-⎪⎪⎭⎫⎝⎛；4).13121400121134131402⎛⎫⎪-⎛⎫ ⎪⎪ ⎪--⎝⎭⎪-⎝⎭；5).111213112312222321323333()a a a xx x x a a a xa a a x⎛⎫⎛⎫⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭.3.求矩阵方程.1)25461321X-⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭;2)211113210432111X-⎛⎫-⎛⎫⎪=⎪⎪⎝⎭⎪-⎝⎭;3)142031121101X⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭;4）010100143100001201001010120X-⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-⎪ ⎪ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭.4.设矩阵21=53A⎛⎫⎪⎝⎭，13=20B⎛⎫⎪⎝⎭，求矩阵方程=XA B的解X.5.设321=111101A ⎡⎤⎢⎥⎢⎥⎢⎥⎦⎣，求-1A .6.设101=210,325A ⎛⎫ ⎪⎪ ⎪--⎝⎭求-1A7.设101=210325A ⎛⎫ ⎪ ⎪ ⎪--⎝⎭，求-1A .8.设⎪⎪⎪⎪⎪⎭⎫⎝⎛=2500380000120025A ，⎪⎪⎪⎪⎪⎭⎫⎝⎛=2600140000540023B . 求：AB BA 和9. 设A 为3阶矩阵, , 求-1(2)-5A A *.10.设(1,2,1),28,A diag A BA BA E *=-=- 求.B11.设34432022O A O ⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭, 求8A |及4A .五、证明题1. 设,A B 为n 阶矩阵，且A 为对称矩阵，证明TB AB 也是对称矩阵.2.设,A B 为n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是AB BA =.3.设为n 阶矩阵A 满足235,A A E O --=试证A E +可逆，且()14A E A E -+=-.4. 设A 为n 阶矩阵，且2,A A =且A E ≠，证明A 是不可逆矩阵.第三章矩阵的初等变换与线性方程组一、选择题1．设n 元齐次线性方程组0AX =的系数矩阵的秩为r ，则0AX =有非零解的充分必要条件是（）(A) r n = (B) r n <(C) r n ≥ (D) r n >2．设A 是m n ⨯矩阵，则线性方程组AX b =有无穷解的充要条件是（）(A) ()r A m < (B) ()r A n < (C) ()()r Ab r A m =< (D) ()()r Ab r A n =<3．设A 是m n ⨯矩阵，非齐次线性方程组AX b =的导出组为0AX =，若m n <，则（）(A) AX b =必有无穷多解 (B) AX b =必有唯一解 (C) 0AX =必有非零解 (D) 0AX =必有唯一解4．已知12,ββ是非齐次线性方程组AX b =的两个不同的解，12,αα是导出组0AX =的基础解系，12,k k 为任意常数，则AX b =的通解是（） (A) 1211212()2k k ββααα-+++(B) 1211212()2k k ββααα++-+(C) 1211212()2k k ββαββ-+++ (D) 1211212()2k k ββαββ++-+5．设A 为m n ⨯矩阵，则下列结论正确的是（）(A) 若0AX =仅有零解，则AX b =有唯一解 (B) 若0AX =有非零解，则AX b =有无穷多解 (C) 若AX b =有无穷多解，则0AX =仅有零解(D) 若AX b =有无穷多解，则0AX =有非零解6．线性方程组123123123123047101x x x x x x x x x ++=⎧⎪++=⎨⎪++=⎩ （）(A) 无解 (B) 有唯一解 (C) 有无穷多解 (D) 其导出组只有零解二、判断题1．若,αβ是线性方程组Ax b =的两个解向量，则αβ-是方程组0Ax =的解。

线性代数练习册(第1章)

第一章习题一（行列式的基本概念）一、填空题1. 按自然数从小到大为标准次序，排列2413的逆序数是 .2. 按自然数从小到大为标准次序，排列4637251的逆序数是 .3. 按自然数从小到大为标准次序，排列()n n 2241213 -的逆序数是 .4.若排列4153972j i 为偶排列，则=i ，=j . 5. 四阶行列式中含有因子2311a a 的项是 . 6. 在5级行列式中，项4524513213a a a a a 前带的符号是 . 二、解答题 1. 求行列式的值.（1） 200146213-；（2） 987654321.2. 证明（1）))()((111222a c c b b a c b a c b a---=.（2）()32211122b a b b a a b aba -=+.（3）()()4242313144312211000000y y x x y y x x x y x y y x y x --=.第一章习题二（行列式的性质）一、填空题1.行列式403212101的值是 .2. 行列式211312707458-的值是 .3. 行列式322000000111d d c dc b a = .；=dcb a .二、解答题1. 计算下列各行列式：（1）71100251020214214.（2）2605232112131412-.（3）efcfbf de cd bdae ac ab ---. 2. 证明（1）2222222224c b a b a bccabc a c ab ca ab c b =+++.（2）()()()()()()()()()()()()03213213213212222222222222222=++++++++++++d d d d c c c c b b b b a a a a .（3）()()()()()()()d c b a d c d b c b d a c a b a d c b a d c b a dc b a+++------=444422221111.第一章习题三（行列式按行或列展开）一、填空题1．设4阶行列式1221304312107301----=D ,则（1)D 的代数余子式14A = ；（2) 1413121122A A A A -+-= ；2．行列式12334152--=aD 的代数余512=A ，则a = .3．行列式xd d d x c c c x b b b x a a a D 3213213213214=，则=+++41312111A A A A .二、解答题1.设1121013=z y x ，求111314111zy x ---.2. 计算n 阶行列式n222232222222221.3．证明1221100001001n nn n x xD x a a a a a x----=-+12121,(2)n n n n n x a x a x a x a n ---=+++++≥.4．计算行列式00100200100000n D n n =-.5．计算n 阶行列式0001000000000001000n a a a D a a=.第一章习题四（克拉默法则）一、填空题1.如果线性方程组的系数行列式D ，则线性方程组一定有解且解是 .2.如果齐次线性方程组的系数行列式0≠D ，则齐次线性方程组没有解.3.当=λ 时，齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=+=+=-=+02,0,02,043214131x x x x x x x x λλ有非零解.二、解答题1.用克拉默法则解线性方程组.⎪⎪⎩⎪⎪⎨⎧=-+=-+-=+--=+-.5534,12523,432,543321421431432x x x x x x x x x x x x2.已知齐次线性方程组()()()⎪⎩⎪⎨⎧=-+-=--=++-0124,02,0332132321x x x x x x x x λλλ有非零解，求λ的值.3.问μλ,取何值时，齐次线性方程组⎪⎩⎪⎨⎧=++=++=++02,0,0321321321x x x x x x x x x μμλ有非零解？4.问λ取何值时，齐次线性方程组()()()⎪⎩⎪⎨⎧=-++=+-+=+--01,032,0421321321321x x x x x x x x x λλλ有非零解？5（思考题）．计算行列式βααββαβααββααββα+++++=10000010001000n D .。

《线性代数》试题一

等于
()
A. r
B. n
线
C. n + r
D. n − r
4．设矩阵 A = (a1, a2 , a3) ，且 a1 + a2 = a3 ，若 A 经过有限次初等行变换变为矩阵
B = (b1,b2 ,b3) ，那么一定有
()
A． b1 + b2 = b3 B． b3 + b2 = b1 C． b1 + b3 = b2 D． b1 − b2 = b3
3,
⎪⎩ 2x1 + 3x2 + 3x3 + 5x4 = 5.
第2页, 共 4 页
⎛1⎞ ⎛1⎞ ⎛ 0⎞ ⎛ 2⎞
4.
设有向量组
A:
a1
=
⎜⎜1⎟⎟ , a2
=
⎜ ⎜
2
⎟ ⎟
,
a3
=
⎜ ⎜
1
⎟ ⎟
,
a4
=
⎜ ⎜
4
⎟ ⎟
，求向量组
A
的一个最大无
⎜⎝1⎟⎠
⎜⎝ 3⎟⎠
⎜⎝ 3⎟⎠
⎜⎝ 3⎟⎠
关组，并把其余向量用此最大无关组线性表示.
.
2. 已知 3 阶矩阵 A 的特征值为 1, 1,2, 则 A3 − A − 2E =
.
3. 设 n 阶矩阵 A 的秩为 n −1，则 A 的伴随矩阵的秩为
.
4.
设
n
阶矩阵
A
及
s
阶矩阵
B
都可逆，则
⎛ ⎜ ⎝
A 0
C B
⎞−1 ⎟ ⎠
=
.
5. 设 λ 是 A 的特征值，则 A3 + 2A − E 的特征值为

线性代数习题1(附答案)

线性代数复习题1（广工卷）一．填空题(每小题4分,共20分) 1.设五阶矩阵 123230,2A A A A A ⎡⎤=⎢⎥⎣⎦是3阶方阵,122,1A A ==，则 A = .2.设 123,,a a a 线性无关,若 112223331,,b a ta b a ta b a ta =+=+=+ 线性无关,则 t 应满足条件 .3.向量组112α⎛⎫⎪= ⎪⎪⎝⎭，⎪⎪⎪⎭⎫ ⎝⎛-=113β，⎪⎪⎪⎭⎫ ⎝⎛-=201γ线性关4.如果矩阵 14000400x x x x A x xx ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭是不可逆的，则 x = . 5.设 n 阶(3n ≥)矩阵 1111a a a a a a A aa a a aa⎛⎫ ⎪⎪⎪= ⎪ ⎪ ⎪⎝⎭的秩为 1n -, 则 a 必为二.单项选择题(每小题4分,共20分)1. 设 ,A B 为同阶可逆矩阵，则 ( ) (A) .A B B A = (B) 存在可逆矩阵 ,P 使 1.P AP B -= (C) 存在可逆矩阵,C 使 .TC AC B = (D)存在可逆矩阵P 和,Q 使 .PAQ B = 2.设A,B 都是n 阶非零矩阵,且 0A B =,则A 与B 的秩是 ( ). (A) 必有一个等于零. (B) 都小于n.(C) 都等于n. (D) 一个小于n, 一个等于n.3. 设n 元齐次线性方程组 0A x =中 ()R A r =, 则0A x = 有非零解的充要条件是 ( )(A) r n =. (B) r n ≥. (C) .r n < (D) .r n >4. 若向量组,,a b c 线性无关,,,a b d 线性相关, 则 ( )(A) a 必可由 ,,b c d 线性表示. (B) b 必不可由 ,,a c d 线性表示. (C) d 必可由 ,,a b c 线性表示. (D) d 必不可由 ,,a b c 线性表示.5. 设⎪⎪⎭⎫ ⎝⎛=1011A ，则12A 等于 ( ) (A ) ⎪⎪⎭⎫ ⎝⎛1101111 (B ) ⎪⎪⎭⎫ ⎝⎛10121 (C ) ⎪⎪⎭⎫ ⎝⎛11121(D ) ⎪⎪⎭⎫⎝⎛1201212三.(14分) 设 3521110513132413D --=----D 的(,)i j 元的余子式和代数余子式依次记作,,ij ij M A 求11121314112131.A A A A M M M M ++++++及四. (10分) 已知 21311122,20,13225A B --⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦求 X AX B =使.五.(10分) 判定下列向量组的线性相关性, 求出它的一个极大线性无关组, 并将其余向量用极大线性无关组线性表示.()()()()()123451,1,2,4,0,3,1,2,3,0,7,141,2,2,0,2,1,5,10a a a a a =-===-=六.(10分) 用基础解系表示下面方程组的全部解:12341234123422124522x x x x x x x x x x x x a+-+=⎧⎪+++=⎨⎪++-=⎩七(16分) 已知A 是n 阶方阵,且满足 220(A A E E +-=是n 阶单位阵). (1) 证明 A E + 和 3A E - 可逆,并求逆矩阵； (2) 证明 2A E +不可逆线性代数复习题1（广工卷）一．填空题(每小题4分, 共24分) 1．144。

线性代数考试题库及答案(一)

线性代数考试题库及答案(一)1.下面是线性代数考试题库及答案的第一部分专项同步练第一章行列式的格式正确版本：一、单项选择题1.下列排列是5阶偶排列的是(A) (B) (C) (D) .2.如果n阶排列j1j2…jn的逆序数是k，则排列jn…j2j1的逆序数是(B) n-k。

3.n阶行列式的展开式中含a11a12的项共有(D) (n-1)。

项。

4.1/1 = (D) 2.5.1/(-1) = (B) -1.6.在函数f(x) = (2x-1)/(2-x^3)中x^3项的系数是(A) 0.7.若D = |a11 a12 a13| |a21 a22 a23| |1 a32 a33|，则D1 =2a11a33 - 4a13a31 - 2a12a32.8.若 |a11 a12| |a21 a22| = a，则 |a12 a11| |ka22 ka21| = (-k^2)a。

9.已知4阶行列式中第1行元依次是-4.0.1.3，第3行元的余子式依次为-2.5.1.x，则x = 3.10.若D = |4 3 1 5| |-1 3 4 1| |2 -1 6 3| |-2 1 3 4|，则D中第一行元的代数余子式的和为(B) -2.11.若D = |-1 5| |3 -2|，则D = (A) -1.12.k等于下列选项中哪个值时，齐次线性方程组x1 + kx2 + x3 = 0，kx1 + x2 + x3 = 0，x2 + x3 = 0有非零解。

(B) -2.二、填空题1.2n阶排列24…(2n)13…(2n-1)的逆序数是n(2n-1)。

2.在六阶行列式中项a32a41a25a13a56a64的符号为-。

改写后的文章：线性代数考试题库及答案第一部分专项同步练第一章行列式一、单项选择题1.下列排列是5阶偶排列的是(A) (B) (C) (D) .2.如果n阶排列j1j2…jn的逆序数是k，则排列jn…j2j1的逆序数是(B) n-k。

线性代数(经管类)试题及答案解析(试卷+答案+解析) (1)

全国2011年7月高等教育自学考试线性代数（经管类）试题（课程代码：04184）说明：本卷中，A T表示方阵A的转置钜阵，A*表示矩阵A的伴随矩阵，E表示单位矩阵，|A|表示方阵A的行列式.一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1. 设101350041A-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，则TAA=（）A. -49B. -7C. 7D. 492. 设A为3阶方阵，且4A=，则2A-=（）A. -32B. -8C. 8D. 323. 设A，B为n阶方阵，且A T=-A，B T=B，则下列命题正确的是（）A. （A+B）T=A+BB. （AB）T=-ABC. A2是对称矩阵D. B2+A是对称阵4. 设A，B，X，Y都是n阶方阵，则下面等式正确的是（）A. 若A2=0，则A=0B. （AB）2=A2B2C. 若AX=AY，则X=YD. 若A+X=B，则X=B-A5. 设矩阵A =11310214000500⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦，则秩（A ）=（）A. 1B. 2C. 3D. 46. 若方程组02020kx z x ky z kx y z +=⎧⎪++=⎨⎪-+=⎩仅有零解，则k ≠（）A. -2B. -1C. 0D. 27. 实数向量空间V={（x 1，x 2，x 3）|x 1 +x 3=0}的维数是（） A. 0 B. 1 C. 2D. 38. 若方程组12323232132(3)(4)(2)x x x x x x x λλλλλλ+-=-⎧⎪-=-⎨⎪-=--+-⎩有无穷多解，则λ=（） A. 1 B. 2 C. 3 D. 49. 设A =100010002⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，则下列矩阵中与A 相似的是（）A. 100020001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ B. 110010002⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦C. 10001102⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦D. 10102001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦10. 设实二次型2212323(,,)f x xx x x =-，则f （）A. 正定B. 不定C. 负定D. 半正定二、填空题（本大题共10小题，每小题2分，共20分）请在每小题的空格中填上正确答案。

大一线性代数试卷1含答案

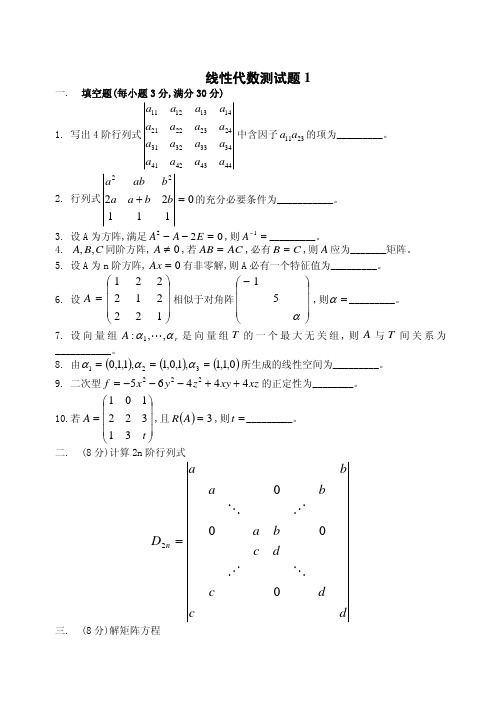
111
3. 设 A 为方阵,满足 A2 A 2E 0 ,则 A1 _________。 4. A, B,C 同阶方阵, A 0 ,若 AB AC ,必有 B C ,则 A 应为_______矩阵。
5. 设 A 为 n 阶方阵, Ax 0 有非零解,则 A 必有一个特征值为_________。
2 2 4
3 1 3
X
2 5
13
1 2 3
3 0 1
求X ?
四. (10 分)设向量组 A:
1 1,4,1,0,2 2,1,1,3,3 1,0,3,1,4 0,2,6,3
求向量组 A 的秩及一个最大无关组.
五. 12 分)讨论方程组的解的情况
x1 x1
x2 x2
x3 x3
9. 二次型 f 5x2 6 y2 4z2 4xy 4xz 的正定性为________。
1 10.若 A 2
0 2
1 3 ,且
RA
3
,则 t
_________。
1 3 t
二. (8 分)计算 2n 阶行列式
a
b
a
0
b
0
ab
0
D2n
cd
c
0
d
c
d
三. (8 分)解矩阵方程
1 2 3
1 (1, 1, 0)T 2
3
3
3, 2 2,2
2
(0,
1, 1)T
，标准化3
1 (0, 1, 1)T 2
因而 P (1 ,2 ,3 ) ，且 f 3 y22 3 y32
九. 令
1
2
3
n
1 1 1 1
2 2
2

考研线性代数习题及答案（一）

考研线性代数基础习题及答案（一）1．计算下列二阶行列式：．计算下列二阶行列式：（1）3125--；（2）log 11log a b b a )1b ,a 0,¹>且（b a ；（3）x x y x yx+-；（4）21111t t t +-+. 解：1）= (-3)×5-(-1)×2=-132）=log log 10b aa b ×-= 3）=22()()x x y x y y -+-= 4）=(t +1)(t 2-t +1)-1=t 32．计算下列三阶行列式：．计算下列三阶行列式：（1）111101112---；（2）12111516312---；（3）0230ba cbc a-；（4）111c b ca b a---. 解：1) =1×0×(-2)+1×1×(-1)+(-1)×1×1-(-1)×0×(-1)-1×1×1-(-2)×1×1=-1 2) =1×15×(-2)+2×16×3+(-1)×(-1)×1-(-1)×15×3-16×1×1-(-2)×2×(-1)=92 3) =2()30000b c ac a b c abc ´´+-´´+---= 4) =22222211abc abc b a c a b c +-+++=+++3．求下列各排列的逆序数，并说明它们的奇偶性：．求下列各排列的逆序数，并说明它们的奇偶性：（1）264315；（2）542163. 解：1）6G = 偶排列偶排列 2）9G = 奇排列奇排列4．确定i 和j 的值，使得9级排列级排列（1）1 2 7 4 i 5 6 j 9成偶排列；成偶排列；（2）3 9 7 2 i 1 5 j 4成奇排列. 解：1）当8,3i j ==时成偶排列时成偶排列 2）当8,6i j ==时成奇排列时成奇排列5．利用行列式定义计算下列行列式．利用行列式定义计算下列行列式（1）010010100101001D =；（2）12340000000000a a D a a =. 解：1）(2143)21124334(1)1D a a a a G =-= 2）(2143)142332411234(1)D a a a a a a a a G=-=6．利用行列式性质计算下列行列式：．利用行列式性质计算下列行列式：（1）313023429722203-；（2）3211040220110102；（3）1234234134124123；（4）213131071242115-----. （5）xy x y y x y x x yxy+++; （6）222a b c a b c b c a b cac a b++++++. 解：1) =312103430455223121--=-=--- 2) =10100002602100302=--3) =100010001113110010101601222124411111104-==-------- 4) =10001001138100085521005725401151143==------5) =00x x x y x x y yx y x x y x xx y y x y +++++=0000xyx y y x x y x y y x y x yx y x-++--- 332()x yxyx y x y xy x x y y =+=-+-+-6) =222a b c a bc b c a b c a c a b++++++ =22a b ca b c a b c c b c ab ca c ab ++------++++ 111()22a b c cb c ab cac a b--=++++++=111()022022a b c b c a b c a c c a b --++++++++ 111()0()022a b c a b c a b a cc a b--=++++-++++ =32()a b c ++7．计算下列行列式：．计算下列行列式：（1）1123103230n n nD --=--；（2）111222121212n n n n a a a n a a a nD a a a n++++++=+++（n ≥2）；（3）11221110001100011000010011n n n n a a a a D a a a +-----=---；（4）0121111111000101210001n i n na a a D a i n a a +-=¹=（其中0，，，，，）.解：1) 10001200!1n D n n-==-2) 1°当n =2时，12n D a a =-2°当n ＞2时，11111222222122120212n nn n n n a a a n a a na a a n a a n D a a a na a n++++++++=+=++++3) 110000110000110010001000011n D+--==-4) 01211201111110000000010000nn n i i n na a a D a a a a a a a +=-æö==-ç÷èøå8．解方程：．解方程：（1）2212134526032113212x x ---=--+-- （2）11001()01001x y z x x y z y z=其中、、均为实数. 解：1)22(9)(1)0x x --=3x =±或1x =± 2)22211x y z ---=0x y z ===9．用克拉默法则解下列线性方程组：．用克拉默法则解下列线性方程组：（1）123123133243421132411x x x x x x x x x --=ìï+-=íï-+=î（2）1234123423412342513232222420x x x x x x x x x x x x x x x -++=ìï++-=ïí++=-ïï-++=î解：1)1234112412141142311234111124311432113,,1211211211342342342324324324x xx --------====------------2) 12251115112111113121311231032223220222214201422042D D D -----===----34251125111121113243220322211214D D ----==---- 312412341,0,,1DDDDx x x x DDDD\=======-10．k 取何值时，下面的方程组仅有零解？取何值时，下面的方程组仅有零解？（1）320720230x y z kx y z x y z +-=ìï+-=íï-+=î（2）0020kx y z x ky z x y z ++=ìï+-=íï-+=î解：1) ) 当当32163725630,,5213kk k --=-¹¹-即时仅有零解仅有零解2) ) 当当1111(1)(4)0,14,211kk k k k k -=+-¹¹¹-即且时仅有零解仅有零解（B ）1．填空题．填空题（1）设1234134()124123x f x x x=，则方程f (x )=0的根为____________；（2）1111111111111111xx y y +-+-=________________；（3）设行列式3040222207005322--，则第四行各元素余子式之和的值为__________；（4）n 阶行列式阶行列式00010000001n a a D a a==__________ （5）设n 阶行列式阶行列式13521120010301n n D n-=则D n 的第一行各元素的代数余子式之和11121n A A A +++= ______________. 解：1) ()(2)(3)(4)0f x x x x =---= 2,3,4x x x \===2) =22x y 3) -284) 2nn a a--5) 21!(1)nk nk =-å2．选择题．选择题（1）下列行列式中，不等于零的是（）下列行列式中，不等于零的是（）. A ．1231110.50.50.5---B. 1231110.5 1.5 2.5 C. 1531210.54 2.5D. 111412125---- （2）已知2122231112132122233111321233133132331121122213232223322a a a a a a a a a m a a a a a a a a a a a a a a a =---+++，则=（）. A ．6m B ．-6m C ．12m D ．-12m（3）多项式10223()71043173x x x f x x-=--中的常数项是（中的常数项是（）. A ．3 B ．-3 C ．15 D ．-15 （4）设行列式1234123412341234()a a a a x a a a x a f x a a xa a a xa a a --=--，则方程()f x =0的根为（的根为（）. A ．1234,a a a a ++ B ．12340,a a a a +++ C ．1234,a a a a --D ．12340,a a a a ----（5）n 阶行列式D n 为零的充分条件是（为零的充分条件是（）. A ．主对角线上的元素全为零．主对角线上的元素全为零B ．有(1)2n n -个元素都等于零个元素都等于零 C ．至少有一个（n -1）阶子式为零）阶子式为零D ．所有（n -1）阶子式均为零）阶子式均为零解：D 、A 、A 、B 、D 3．证明：32222()22a b c a a b b c a b a b c ccc a b----=+---. 证明证明: : : 左左=111()2222a b c bb c a bc cc a b++---- 33111()00()0a b c b c aa b c c a b=++---=++---4．证明：1111111112222222222a bb cc aa b c a b b c c a a b c a b b c c a a b c ++++++=+++. 解：11111111112222222222ab c c a b b c c a ab c c a b b c c a a b c c a b b c c a ++++=+++++++++左 =1112222ab cab c a b c5．计算下列n 阶行列式：阶行列式：（1）0000100002001000000nD n n=-；（2）123121221321321221n n n n n D n n nn n ---=---- ；（3）210001210000021012n D ---=--；（4）12323413452121n n D n n =-. 解：解： 1) (1)(2)((1),(2)1,)2(1)!(1)!n n n n nnD n n --G --=-=-2) 11111111110222111120022211111nn n n n Dn n n ------------=--=---12(1)2(1)n nn --=-+3) 100000210001200100012n D n ---=--=+-- 4) 1231341(1)145221111n n n n D n +=- =1230111(1)01112111n n n n n-+-(1)12(1)(1)2n n n n n +-+=-×6．用数学归纳法证明．用数学归纳法证明2112122222122122121111n n n n n n na a a a a a a a a a D a a a a a a a a ++==++++12cos sin(1)sin n q qq+=2cos sin 3sin q q q==sin(1)sin k qq=sin(2)sin k qq=又又111x x x =解：211112122212111()1n n i j j i n n nn n a a a a a a D a a a a a --£££-==-Õ123,0n D D D x D ===== 11231,0n D x x x x D \======10．若齐次线性方程且．若齐次线性方程且1234123412341234020300x x x ax x x x x x x x x x x ax bx +++=ìï+++=ïí+-+=ïï+++=î有非零解，则a 、b 应满足什么条件？应满足什么条件？解：当11112110113111a a b =-即2(1)4a b +=时,方程组有非零解方程组有非零解..。

线性代数练习题及答案解析(一)

线性代数练习题及答案解析（一）一、行列式1、排列25341的逆序数为 7 ；2、排列643125的逆序数是 9 ；3、方程211123049x x =的根为 2,3 ；（范德蒙行列式） 4、行列式D=162021304---中，元素－3的代数余子式是（ A ）（A ）10 （B ）2 （C ）－10 （D ）－2 考点：代数余子式定义5、(1)三阶行列式det()ij D a =中含有因子1322a a 的项为 132231-a a a ，含有因子1223a a 的项为 122331a a a . 考点：行列式展开式的定义规则(2)四阶行列式det()ij D a =中含有因子1123a a 的项为 12233144a a a a 或12233441-a a a a .6、设n 阶行列式60D =，且D 中的每列的元素之和为6，则D 中的第三行的代数余子式之和为 10 .考点：行列式的性质6，行列式按行（列）展开7、(1)设n 阶行列式det()ij D a =，j i A 是D 中元素j i a 的代数余子式，则下列各式中正确的是（ C ）. 考点：行列式按自己的行（列）展开等于行列式，如行（列）与代数余子式的行（列）不一致则等于零。

A 、10nijij i aA ==∑；B 、10nijij j aA ==∑； C 、1nijij j aA D ==∑； D 、121ni i i aA D==∑(2)若4阶行列式D 中第2行的元素212223242,1,3,0,a a a a ====余子式212M =,2223241,3,0M M M ===则D= -12 .注意：代数余子式与余子式的区别。

行列式的展开只与代数余子式有关。

(3)若3阶行列式D 中第1行的元素1112133,2,5,a a a ===代数余子式114A =,12131,2,A A =-=则D= 20 .8、行列式112233440000000a b a b b a b a =（ B ）。

线性代数试题1