自相关过程
计量经济学:自相关

所以在实际应用中,对于序列相关问题一般只进行D.W.检验。
3、LM检验(或BG检验)
• 此方法不仅适用于一阶自相关检验,也适用于高阶自相关的检验。 • 检验步骤: 1、用OLS对回归模型进行,得到残差序列et;
1、经济变量固有的惯性 大多数经济时间序列数据都有一个明显的特点——惯性,表现为 滞后值对本期值具有影响。
例如:GDP、价格指数、生产、就业与失业等时间序列都呈周期性,如周期 中的复苏阶段,大多数经济序列均呈上升势,序列在每一时刻的值都高于前 一时刻的值,似乎有一种内在的动力驱使这一势头继续下去,直至某些情况 (如利率或课税的升高)出现才把它拖慢下来。
证明:由于 DW
e
t 2
T
t
e t 1
2 t T
2
e
t 1
T
e e
t 2 2 t t 2 T T
T
T
2 t 1
2 e t e t 1
t 2 2 t
T
e
t 1 t 2 2 t 1
T
若样本容量足够大,有 则 e e
t 2 2 t
et2
3、数据的“加工整理”
在实际经济问题中,有些数据是通过已知数据生成的。因此,新生
成的数据与原数据间就有了内在的联系,从而表现出序列相关性。
例如:季度数据来自月度数据的简单平均,这种平均的计算减弱了每 月数据的波动而引进了数据中的平滑性,这种平滑性本身就能使干扰项 中出现系统性的因素,从而出现序列相关。 还有就是两个时间点之间的“内插”技术往往导致随机项的序列相关性。
第二节 自相关性

D-W检验原理简单,检验方便,是目前最常用 的自相关检验方法.Eviews软件在回归分析的输 出结果中直接给出了DW统计量的值。
在使用D-W检验时应注意以下几个问题:
(1)DW检验只能判断是否存在一阶自相关性。 (2)DW检验有两个无法判定的区域。如DW值落入该 两个区域时,一般改用其他检验方法来判断。 (3)如果模型的解释变量中含有滞后的被解释变量,例如:
t 2 t 2 t 2 n n n
(*)
et 2 ~
t 1
n
D.W . 2(1
ee ~~
t 2 n
n
t t 1
e ~
t 1
) 2(1 )
2
t
D.W . 2(1
ee ~~
t 2 n
n
t t 1
这里:
~~ et et 1 ~2 et
~2 et
三、自相关性的检验
基本思路:
序列相关性检验方法有多种,但基本思路相同:
首先, 采用 OLS 法估计模型, 以求得随机误差项的
~ ei “近似估计量” ,用
表示:
~ ˆ ei Yi (Yi ) 0ls
然后,通过分析这些“近似估计量”之间的相 关性,以判断随机误差项是否具有序列相关性。
1、残差图分析法
3、变量的显著性检验失去意义
在变量的显著性检验中,统计量是建立在参 数方差正确估计基础之上的,这只有当随机误差 项具有同方差性和互相独立性时才能成立。
其他检验也是如此。
4、降低模型的预测精度!(模型的预 测失效)
区间预测与参数估计量的方差有关,在 方差有偏误的情况下,使得预测估计不准 确,预测精度降低。 所以,当模型出现序列相关性时,它的 预测功能失效。
自相关分析

i=1i-1+2i-2+Li-L+i
关于迭代的次数,可根据具体的问题来定。
一般是事先给出一个精度,当相邻两次 1,2, ,L的估计值之差小于这一精度时,迭 代终止。
实践中,有时只要迭代两次,就可得到 较满意的结果。两次迭代过程也被称为科克 伦—奥科特两步法。
(2)杜宾(durbin)两步法 该方法仍是先估计1,2,,l,再对差分模型 进行估计。
D.W检验步骤: (1)计算DW值 (2)给定,由n和k的大小查DW分布表,得临 界值dL和dU (3)比较、判断 若 0<D.W.<dL dL<D.W.<dU dU <D.W.<4-dU 存在正自相关 不能确定 无自相关
4-dU <D.W.<4- dL 4-dL <D.W.<4
不 能 确 定 无自相关
对(3)运用OLS 估计,得到 (1 ) 1和 2的估计值,进而算出
(3)
1, 2
应用广义最小二乘法或广义差分法,必须已知随机误差项的
相关系数1, 2, … , L 。
实际上,人们并不知道它们的具体数值,所以必须首先对它
们进行估计。
简单的方法有:(1)由DW-d统计量中估计
ˆ ˆ ˆ ˆ Yi 1Yi1 l Yil 0 (1 1 l ) 1 ( X i 1 X i1 l X i l ) i
i 1 l,2 l,, n
求出i新的“近拟估计值”, 并以之作为样本 观测值,再次估计:
ˆ ˆ ˆ 第二步,将估计的 1 , 2 , , l 代入差分模型
Yi 1Yi 1 l Yi l 0 (1 1 l ) 1 ( X i 1 X i 1 l X i l ) i
自相关(序列相关)

高阶序列相关的广义差分法
如果原模型存在:
i 1 i 1 2 i 2 l i l i
(2.5.11)
可以将原模型变换为:
Yi 1Yi 1 l Yi l 0 (1 1 l ) 1 ( X i 1 X i 1 l X i l ) i
yt 0 1x1t 2 x2t k xkt yt 1 ut
(4)回归含有截距项; (5)没有缺落数据。
一阶自相关的Dubin-watson检验
自相关存在时,有 ut ut 1 v,vt无自相关。 t Covut , ut 1 相关系数: ,
三、序列相关性的后果
1、参数估计量无偏但非有效 ; 2、变量的显著性检验失去意义 ; 3、模型的预测失效 ;
1、参数估计量无偏但非有效
OLS参数估计量仍具无偏性
OLS估计量不具有有效性
在大样本情况下,参数估计量仍然不具有渐近有效 性,这就是说参数估计量不具有一致性
2、变量的显著性检验失去意义
i 1 l ,2 l , , n
(2.5.12) 模型(2.5.12)为广义差分模型,该模型不存在序列相 关问题。采用OLS法估计可以得到原模型参数的无偏、 有效的估计量。 广义差分法可以克服所有类型的序列相关带来的问题, 一阶差分法是它的一个特例。
随机误差项相关系数的估计
应用广义差分法,必须已知不同样本点之间随机误差 项的相关系数1, 2,…, l 。实际上,人们并不知道它 们的具体数值,所以必须首先对它们进行估计。
Euiu j 0, i j
i
如果仅是Eut ut 1 0 ,称有一阶自相关 二、实际经济问题中的序列相关性
自相关的操作过程
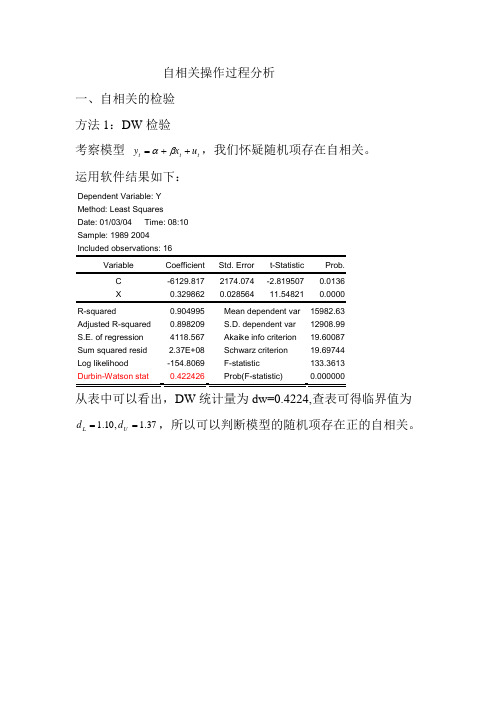
自相关操作过程分析一、自相关的检验 方法1:DW 检验考察模型 t t t u x y ++=βα,我们怀疑随机项存在自相关。
运用软件结果如下:Dependent Variable: Y Method: Least Squares Date: 01/03/04 Time: 08:10 Sample: 1989 2004 Included observations: 16C -6129.817 2174.074 -2.819507 0.0136 X0.3298620.02856411.548210.0000 R-squared0.904995 Mean dependent var 15982.63 Adjusted R-squared 0.898209 S.D. dependent var 12908.99 S.E. of regression 4118.567 Akaike info criterion 19.60087 Sum squared resid 2.37E+08 Schwarz criterion 19.69744 Log likelihood -154.8069 F-statistic 133.3613 Durbin-Watson stat0.422426 Prob(F-statistic)0.000000从表中可以看出,DW 统计量为dw=0.4224,查表可得临界值为37.1,10.1==U L d d ,所以可以判断模型的随机项存在正的自相关。
方法2:直接检验法(回归检验法) 一阶自相关形式为:t t t v u u +=-1ρ即对模型t t tv e e +=-1ρ进行回归,进行T 检验,判断系数是否为0.结果如下:在EVIEW 软件中常用)(k X -表示变量的X 的滞后k 阶变量。
Dependent Variable: E Method: Least Squares Date: 01/03/04 Time: 08:19 Sample(adjusted): 1990 2004R-squared0.565485 Mean dependent var -167.2139 Adjusted R-squared 0.565485 S.D. dependent var 4059.960 S.E. of regression 2676.235 Akaike info criterion 18.68655 Sum squared resid 1.00E+08 Schwarz criterion 18.73375 Log likelihood-139.1491 Durbin-Watson stat0.750574可写出模型为19818.0ˆ-=t t e e ,因为1-t e 的系数的T 检验的犯错概率为0.0008,远远地小于0.05,这说明系数显著地不为0。
3个样本函数的随机过程求自相关函数

题目:三个样本函数的随机过程求自相关函数在统计学和概率论中,我们经常需要研究各种随机过程的性质。
其中,自相关函数是一个非常重要的概念,它能够帮助我们理解不同时间点的随机变量之间的相关性。
在本文中,我们将探讨三个样本函数的随机过程如何求取自相关函数,并对其进行深入分析。
1.样本函数的随机过程及自相关函数的概念在开始探讨三个样本函数的随机过程求自相关函数之前,我们首先要了解两个重要概念:样本函数的随机过程和自相关函数。
对于一个具体的概率空间Ω和一个指定的测度p,如果我们对每一个固定的ω∈Ω,都有一个随机变量X(t, ω)与之对应,则称X(t, ω)为一个随机过程。
当固定t后,X(t, ω)就成为关于ω的函数,我们称之为样本函数。
而自相关函数则是用来描述同一随机过程中不同时间点的随机变量之间的相关性的函数。
它在信号处理、时间序列分析等领域中扮演着非常重要的角色。
2.三个样本函数的随机过程求自相关函数的方法接下来,我们将介绍如何对三个样本函数的随机过程求取自相关函数。
根据统计学中相关性的定义,自相关函数的定义如下:R(t1, t2) = E[X(t1)X(t2)]其中,E[•]表示期望值的运算符。
对于离散情况下的随机过程,我们可以通过计算期望值来求取自相关函数。
而对于连续情况下的随机过程,我们则需要使用积分来表示期望值。
对于三个不同的样本函数,我们分别记为X1(t)、X2(t)和X3(t),我们可以按照上述定义分别求取它们之间的自相关函数。
在实际计算中,我们可以利用数值模拟或者数学分析的方法来求取自相关函数。
3.对三个样本函数的随机过程求自相关函数的分析在获得三个样本函数的自相关函数之后,我们需要对其进行深入分析,以便更好地理解随机过程的特性。
我们可以比较三个样本函数的自相关函数的形状和特点,从而发现它们之间的关联和差异。
通过图表或者数学分析的方法,我们可以清晰地展现这些信息。
我们可以探讨自相关函数的物理意义和应用价值。
第六章自相关性详解

y A bx vt
* t * t
其中,A=a(1- ρ )。
ˆ /(1 利用OLS法估计A、b,进而得到: a ˆA
若ρ =1,则可得到一阶差分模型 yt-yt-1=b(xt-xt-1) +υ 如果为高阶自回归形式: ε t=ρ 1ε t-1+ρ 2ε t-2+…+ρ pε
(2)构造检验统计量:
DW
(e
2
n
t
et 1 )
2
2 e t 1
n
DW统计量与ρ 之间的关系: 因为对于大样本,
2 2 e e t et 1 2 t 1 2 2 n n n
所以:
DW
2
2 2 ( e 2 e e e t t t 1 t 1 )
e
2 t
2 2 e 2 e e e t t t 1 t 1 ) 2 e t
2( e t et et 1 )
2 e t
et et 1 21 2 2 1 et
Байду номын сангаас
e
et et 1
2 t
ˆ) S (b
2
( xt x )
2
ˆ2 ( xt x ) 2
三、t检验失效。 四、模型的预测精度降低。
第三节 自相关性的检验
一、残差图检验 二、德宾-沃森(Durbin-Watson,DW)检验 适用条件:随机项一阶自相关性;解释变量 与随机项不相关;不含有滞后的被解释变量, 截距项不为零;样本容量较大。 基本原理和步骤: (1) 提出假设 H0: ρ =0一
③在大样本情况下,有 nR2~χ 2(p) 给定α ,若nR2大于临界值,拒绝H0。 EViews软件操作:在方程窗口中点击View\ Residual Test \Serial Correlation LM Test。
自相关过程的质量控制方法_残差控制图

© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
2005
年第
6
期
Science
and
科技管理研究 Technology Management
Research
2005
No16
文章编号 : 1000 - 7695 (2005) 06 - 0139 - 02
自相关过程的质量控制方法 ———残差控制图
王斌会 , 张志雷
有效使用控制图能够在生产过程中科学地保证预防原 则的实现 , 减少质量的异常波动 , 从而提高产品品质 、增 强市场竞争力 。但是 , 人们在生产实践中逐渐认识到在使 用常规控制图对过程进行控制时 , 存在着一些不足之处 , 并陆续提出一些改进方法 。本文仅研究当过程存在自相关 现象从而违背常规控制图独立性假定时 , 对质量特性值控 制的残差图理论 , 希望以此对实际质量管理者提供有益的 参考 。
σ2Y = Var ( Yt)
σε2
= 1-
<2
假设在受控状态下质量特性观测值呈现自相关的系统
机理可用式 (3) 表达 , 则过程残差 et 为 : et ≡Yt - ^Yt| t - 1 , t - 2 , …
其中 ^Yt| t - 1 , t - 2 , …是 Yt 的估计值 , 令 Yt 的最小均方误 差线性估计值为 E ( Yt | Yt - 1 , Yt - 2 , …) 。在 t 时刻的估计值 是: ^Yt| t - 1 , t - 2 , … = E ( Yt| Yt - 1 , Yt - 2 , …) =μ^ + ^< ( Yt - 1 - μ^ )
第六章 自相关(序列相关)

可以证明: 1- 2 - 1 C= 0 2 1- 0
2
0 0 1 0 0 - 0 0 0 - 1 0
1- 2 Cy 以 1- C左乘原模型,并定义y 1- 2 CX, 1- 2 C X
则变换后的扰动项 满足球型扰动项的假设, 故高斯-马尔可夫定理成立(因为这种变换是 GLS的一个特例)
1- 2 - 1- 2 Cy= 0 y 0
0 0 y1 1 0 0 y2 - 0 0 yn 0 - 1 0
第六章 自相关(序列相关)
一、自相关的后果 违反球型扰动项假定的另一情形是自相关。若存在 i j使得E i j X 0,即扰动项的协方差阵Var X 的非主对角线元素不全为0,则称存在“自相关” (autocorrelation)或“序列相关”(serial correlation)
其中, Var u t ,而1= ,
2 u 2
1 2 故一阶自相关系数 = 2 = 0
由课件第三章p21, 2= , , n-1= ,故
2 2 n-1 2
1 2 Var X = n-1
1
1- 2 y1= 1- 2 1+ 1- 2 2 x12++ 1- 2 k x1k+1 y 2- y1=1- 1+ 2 x 22- x12 ++ k x 2k- x1k + 2 y n- y n-1=1- 1+ 2 x n 2- x n-1, ++ k x nk- x n-1,k 2 + 2
因此辅助回归的解释变量e t-1, ,e t-p必与扰动项相 关,导致不一致的估计。这就是所谓的随机解释变 量问题,后面会介绍。若引入解释变量x t1, ,x tk 将使BG检验更加稳健 由于使用了滞后残差值e t-p,损失了p个样本值,故
自相关(序列相关)

常用的方法有: (1)科克伦-奥科特(Cochrane-Orcutt)迭代法。 (2)杜宾(durbin)两步法
附:杜宾(durbin)两步法
该方法仍是先估计1,2,,L,再对差分 模型进行估计。
第一步,变换差分模型为下列形式:
Yi 1Yi 1 l Yi l 0 (1 1 l ) 1 ( X i 1 X i 1 l X i l ) i
利用
ut ut 1 vt
有
ut 1 ut 2 vt 1,, ut m1 ut m vt m1
ut mut m m1vt ( m1) m2vt ( m2) vt 1 vt
1 2 Cov N , N u n 1
i 1 l ,2 l , , n
(2.5.13)
采用 OLS 法估计该方程,得各Y j ( j i 1, i 2, i l ) 前的
ˆ1 , ˆ 2 , , ˆl 。 系数 1 , 2 , , l 的估计值
ˆ1 , ˆ 2 ,, ˆ l 代入差分模型 第二步,将估计的
i
对各方程估计并进行显著性检验,如果存在某 一种函数形式,使得方程显著成立,则说明原模 型存在序列相关性。
具体应用时需要反复试算。 回归检验法的优点是:
一旦确定了模型存在序列相关性,也就同时知 道了相关的形式;
它适用于任何类型的序列相关性问题的检验。
(2)杜宾-瓦森(Durbin-Watson)检验法
三、序列相关性的后果
1、参数估计量无偏但非有效 ; 2、变量的显著性检验失去意义 ; 3、模型的预测失效 ;
自相关——精选推荐

第六章 自相关一、什么是自相关及其来源 二、自相关的后果三、自相关的检验 四、自相关的修正五、应用实例6.1自相关的概念及其来源例如:研究中国工业总产值指数(Y )和国有企业工业总产值指数(X )的关系,利用1977年至1997年的历史资料,运用OLS 方法得到如下模型。
2ˆ0.0568 1.0628(37.8666)(0.3502)(0.0015)(3.0348)0.32650.37679.2099t t Y X t R DW F =+====给定显著性水平a=0.05,自由度为19,查t 分布表得0.025(19) 2.093t =。
以模型的计算结果t=3.0348,且0.025(19)t t >,表明t X 对t Y 的影响比较显著,但可决系数并不理想。
这种情况下,随机扰动项之间有可能存在序列自相关。
一、自相关的概念自相关(auto correlation )又称序列相关(serial correlation ),是指总体回归模型的随机误差项i u 之间存在的相关关系。
更一般的,自相关是指某一随机变量在时间上与其滞后项之间的相关。
经典回归模型中,曾假定随机误差项无自相关,即i u 在不同观测点之间是不相关的。
(,)(,)0()i j i j Cov u u E u u i j ==≠如果该假设不成立,就称i u 与j u 存在自相关,即不同观测点上的误差项彼此相关。
二、自相关产生的原因 1)经济系统的惯性。
自相关现象大多出现在时间序列数据中,其本期值往往受滞后值影响,突出特征就是惯性和低灵敏度。
例如:居民总消费函数模型01(1,2,,)t t tC Y u t n ββ=++=总消费受收入(t Y )的影响,事实上消费也受消费习惯的影响。
把消费习惯并列随机扰动项中,就可能出现序列相关性。
2)经济行为的滞后性例如,基础设施的建设需要一定的建设周期,那么产出效益的发挥有一定滞后时间。
数字信号处理中的自相关与互相关

数字信号处理中的自相关与互相关数字信号处理(Digital Signal Processing,DSP)是一门关于对离散信号进行数字化处理的学科。
在数字信号处理的领域中,自相关与互相关是两个重要的概念和技术,在信号分析和处理中具有广泛的应用。
本文将重点讨论数字信号处理中的自相关与互相关的原理、计算以及应用。
一、自相关自相关是指一个信号与其自身之间的相关性。
在数字信号处理中,自相关常用于分析信号的周期性、相干性以及计算信号的功率谱密度。
自相关函数(Autocorrelation Function,ACF)是用来衡量信号在不同时刻的相似程度的一种数学工具。
自相关函数可以通过以下公式计算:\[R_x(k) = \sum_{n=0}^{N-k-1} x(n)x(n+k)\]其中,$R_x(k)$表示信号$x(n)$在延迟$k$时刻的自相关函数值,$N$表示信号的长度,$k$为延迟时间。
通过计算不同的延迟时间,可以得到自相关序列,进而对信号进行周期性和相干性的分析。
自相关函数在信号处理中具有广泛的应用。
例如,在音频处理中,可以通过自相关函数分析音频信号的周期性,从而实现音频信号的去噪和频率分析;在图像处理中,自相关函数可以用于图像的模板匹配和边缘检测。
二、互相关互相关是指两个不同的信号之间的相关性。
在数字信号处理中,互相关常用于信号的匹配、滤波和信号相似度的衡量。
互相关函数(Cross-Correlation Function,CCF)是用来衡量两个信号之间相似性的一种数学工具。
互相关函数可以通过以下公式计算:\[R_{xy}(k) = \sum_{n=0}^{N-k-1} x(n)y(n+k)\]其中,$R_{xy}(k)$表示信号$x(n)$和$y(n)$在延迟$k$时刻的互相关函数值,$N$表示信号的长度,$k$为延迟时间。
通过计算不同的延迟时间,可以得到互相关序列,进而分析两个信号之间的相似度和相对偏移。
第10章-自相关:如果误差项相关会有什么后果

第10章 自相关:如果误差项相关会有什么后果本章主要讲授如下内容:10.1 自相关的性质 10.2 自相关的后果 10.3 自相关的诊断 10.4 自相关的补救措施10.1 自相关的性质1.定义对于模型:t kt k t t t X B X B X B B Y μ+++++= 33221如果随机误差项的各期值之间存在着相关关系,即0)(),cov(≠=j i j i E μμμμ,j i ≠,k j i ,,2,1, =这时,称随机误差项之间存在自相关(autocorrelation )或序列相关(serial correlation )。
最常见的类型是随机误差项之间存在一阶自相关,即0)(),cov(11≠=--t t t t E μμμμ或t t t νρμμ+=-1其中,ρ是μt 与μt-1的相关系数,νt 是满足经典假设的随机误差项。
自相关的一般形式可以表示成t p t p t t t νμρμρμρμ++++=--- 2211称之为p 阶自回归形式,或模型存在p 阶自相关。
2.判断由于我们无法观察到误差项μt ,只能通过残差项e t 来判断μt 的行为。
如果残差项e t 随时间呈现有规律的变化,则表示残差项e t 存在自相关。
否则,不存在自相关。
如图10-1所示。
3.类型主要有正的自相关和负的自相关两类,如图10-2所示。
4.自相关产生的原因(1)经济变量的惯性作用 如GDP 、就业、货币供给、价格指数等时间序列都呈现出周期性。
(2)经济行为的滞后性 如投资对其后若干年内经济的影响等。
(3)一些随机因素的干扰或影响 如战争、自然灾害、错误政策的后果、金融危机等随机因素,不仅对当期经济造成影响,而且对以后若干时期的经济产生影响,反映在模型中即容易形成随机误差序列的自相关。
(4)模型设定误差 如果模型中遗漏了重要的变量,或选择了不正确的函数形式,则得到的残差会出现自相关。
(5)数据的“编造” 在实证分析中,有些数据是通过已知数据生成的,如对原始数据进行内插或平滑处理等。
计量经济学-第12章 自相关

但我们拟合了以下模型:
边际成本 i
1
2
产出 i
vi
于是有:
vi
产出2
3
i
ui
(12.1.4) (12.1.5)
由于函数形式的错误使用,残差将反映出自相关性质
蛛网现象(Cobweb phenomenon)
供给对价格的反应要滞后一个时期
供给 t
1
价格
2
t 1
ut
(12.1.6)
t期产量太多,则t期价格下降,从而t+1期产量减少
滞后效应
在消费支出对收入的时间序列回归中,当期消费还 会受到前期消费水平的影响:
消费 t
1
2收入t
3消费t1
ut
(12.1.7)
这种带有因变量的滞后值的回归也叫自回归“编造”
从月度数据计算得出季度数据,会减小波动,引进 匀滑作用,使扰动项出现系统性模式
并获得具有BLUE性质的估计量
— —这种方法即GLS
未知
一次差分法:因为 落在-1到+1之间,
当 = +1时,广义差分方程(12.6.5)便化为一阶差
分方程:
或:
Yt Yt1 2 ( X t X t1 ) (ut ut1 )
2 ( X t X t1 ) t
xt2
xt2
n
xt2
t 1
n
xt2
t 1
n t 1
xt2
对照:没有自相关情形:
(12.2.5) (12.2.6)
var( 2 )
自相关函数与偏自相关函数

自相关函数与偏自相关函数上一节介绍了随机过程的几种模型。
实际中单凭对时间序列的观察很难确定其属于哪一种模型,而自相关函数和偏自相关函数是分析随机过程和识别模型的有力工具。
1、自相关函数定义在给出自相关函数定义之前先介绍自协方差函数概念。
由第一节知随机过程{t x }中的每一个元素t x ,t = 1, 2, … 都是随机变量。
对于平稳的随机过程,其期望为常数,用μ表示,即()t E x μ=,1,2,t=随机过程的取值将以 μ 为中心上下变动。
平稳随机过程的方差也是一个常量2()t xVar x σ=,1,2,t=2x σ用来度量随机过程取值对其均值μ的离散程度。
相隔k 期的两个随机变量t x 与t k x -的协方差即滞后k 期的自协方差,定义为:(,)[()()]k t t k t t k Cov x x E x x γμμ--==--自协方差序列:k γ,0,1,2,k=称为随机过程{t x }的自协方差函数。
当k = 0 时,20()t x Var x γσ==。
自相关系数定义:k ρ=因为对于一个平稳过程有:2()()t t k x Var x Var x σ-==所以220(,)t t k k kk x x Cov x x γγρσσγ-===,当 k = 0 时,有01ρ=。
以滞后期k 为变量的自相关系数列k ρ(0,1,2,k =)称为自相关函数。
因为k k ρρ-=,即(,)t k t Cov x x -= (,)t t k Cov x x +,自相关函数是零对称的,所以实际研究中只给出自相关函数的正半部分即可。
2、自回归过程的自相关函数 (1)平稳AR(1)过程的自相关函数 AR(1) 过程:11t t t x x u φ-=+,|φ1| < 1。
已知()0t E x =(why?)。
用t k x -同乘上式两侧t x t k x -11t t k t t k x x u x φ---=+上式两侧同取期望:k γ11k φγ-=其中()0t t k E u x -=(why?)(由于x t = u t + φ1 u t -1 + φ12u t -2 +… ,所以x t-k = u t-k + φ1u t-k-1 + φ12 u t-k-2 +…,而u t 是白噪音与其t - k 期及以前各项都不相关)。
检验自相关的方法

d t2
n
2 t
t2
t2
t2
n
2 t
t 1
t 1
对于大样本(即n很大)来说,可以认为
n
n
n
2 t 1
2 t
2 t
t2
t2
t 1
于是(6.3.2)式可以改写成
n
n
2
2 t 1
2
t
t
1
n
t t 1
d t2
t2
n
2 t 1
2(1
t
2 n
)
2 t 1
t2
t2
(6.3.2) (6.3.3)
注意εt是随机项ut的估计量,根据(6.1.3)便有
图6.3.5
由图6.3.5知,相关系数和偏相关系数都具有一阶自相关。
(1 d ) ( k 1 )2
ˆ 2
n
1 (k 1 )2
n
(6.3.6)
来计算 ˆ ,式中k是模型中自变量的个数。此公
式可以使的偏倚程度减少。
三、回归检验法 它的具体步骤如下: (1)对样本观测值用OLS法建立线性回归模型, 然后计算残差εt。
(2)由于事先不知道u自相关的类型,可以对不同形
(4)根据样本容量n,自变量个数和显著水平0.05 (或0.01)从D-W检验临界值表中查出dL和du。 (5)将d 的现实值与临界值进行比较: ①若d < dL,则否定H0,即u存在一阶线性正自相关; ②若d > 4- dL,则否定H0,即u存在一阶线性负自相关; ③若du< d < 4- du,则不否定 H0,即u不存在(一阶)线 性自相关;
§6.3 检验自相关的方法
一、图解法 (一)
自相关的计算过程

自相关的计算过程自相关是时间序列分析中一个重要的概念,用于衡量时间序列中自身的相关性。
自相关函数(ACF)是一个可以显示时间序列与其自身在不同滞后值下的相关性的图形。
计算自相关函数通常采用两种方法:计算公式法和计算函数法。
下面将分别介绍这两种方法。
一、计算公式法:假设我们有一个长度为N的时间序列X = {X1, X2, ..., XN},其平均值为μ。
那么它的自相关函数ACF(lag)可以用以下公式计算:ACF(lag) = (1/N) * sum((Xi-μ)(Xi+lag-μ)), i=1 to N-lag其中,lag为滞后值,Xi表示时间序列的第i个值。
该公式计算了时间序列与其在不同滞后值下的自相关性。
计算过程如下:1.计算时间序列的平均值:μ = (1/N) * sum(Xi), i=1 to N2. 计算ACF(lag):a. 选择一个合适的滞后值lag。
b. 对每个滞后值,计算(1/N) * sum((Xi-μ)(Xi+lag-μ))。
重复以上步骤,可以得到时间序列在不同滞后值下的自相关系数。
二、计算函数法:在实际应用中,可以借助统计软件或编程语言中的函数来计算自相关函数。
例如,在Python中,可以使用numpy库中的corrcoef函数来计算自相关系数。
下面是一个使用Python的示例代码:import numpy as npdef autocorrelation(x):x = np.array(x)n = len(x)x = x - np.mean(x)autocorr = np.correlate(x, x, mode='full')[-n:]autocorr /= autocorr[0]return autocorr#假设有一个时间序列X=[1,2,3,4,5,6,7,8,9,10]X=[1,2,3,4,5,6,7,8,9,10]#计算自相关函数acf = autocorrelation(X)print(acf)在上述代码中,autocorrelation函数实现了自相关的计算过程。
自相关的计算过程

自相关的计算过程自相关(Autocorrelation)是一种统计方法,用于衡量一个随机过程的自相似性或相关性。
它是时间序列分析中一个重要的工具,能够帮助我们研究随机变量的变化规律和预测未来的变化。
1.理解自相关的概念和公式:自相关是通过计算变量与其自身的相关系数来衡量随机变量序列内部的相关性。
一般情况下,我们使用皮尔逊相关系数来度量两个随机变量之间的线性相关性。
对于时间序列来说,自相关可以直观地表示为变量在不同时刻的相关程度。
自相关的公式为:R(t,t+k)=(X(t)-μ)*(X(t+k)-μ)/σ^2其中,R(t,t+k)表示在时间t和时间t+k的两个变量的自相关系数,X(t)和X(t+k)分别表示这两个时间点的变量值,μ表示变量的均值,σ^2表示变量的方差。
2.计算均值和方差:为了计算自相关,首先需要计算变量的均值和方差。
均值可以通过对时间序列中的每个变量值求平均来得到,即:μ=(X(1)+X(2)+...+X(n))/n其中,X(1)到X(n)表示时间序列中的变量值,n表示时间序列的长度。
方差可以通过计算每个变量值与均值的差的平方的平均值来得到,即:σ^2=[(X(1)-μ)^2+(X(2)-μ)^2+...+(X(n)-μ)^2]/n3.计算自相关系数:利用均值和方差,我们可以计算时间序列中任意两个变量之间的自相关系数。
假设我们想计算时间点t和时间点t+k的自相关系数,其中k表示时间差:R(t,t+k)=[(X(t)-μ)*(X(t+k)-μ)]/σ^2其中,X(t)和X(t+k)分别表示时间序列在时间点t和时间点t+k的变量值。
4.可视化自相关函数:将自相关系数R(t,t+k)与时间差k进行可视化,可以得到自相关函数。
自相关函数用来显示时间序列中不同时间差下的相关性。
自相关函数的图形通常是一个波动的曲线,其中波峰表示正相关,波谷表示负相关,而自相关系数为0的时间差表示无相关性。
5.解释自相关图形:自相关图形可以帮助我们理解时间序列中的周期性和趋势性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自相关过程控制院系:管理科学与工程专业:质量与可靠性工程学号:110510335 姓名:张华威自相关过程质量控制引论:自相关过程质量控制概述当质量过程呈现自相关现象时,常规控制图已经不能准确反映生产中质量的波动.常规控制图理论:质量管理的观点认为:质量具有变异性其特性值是波动的,具有规律性,但它不是通常的确定性现象的确定性规律,而是随机现象的统计规律,用数学语言来讲,就是服从某种分布。
如果出现异常情况,就必然使波动偏离原来的分布,利用统计技术就可以发现这种波动。
在现代质量管理学中,通常使用休哈特控制图进行质量控制,但休哈特控制图的原理要求数据必须复合独立正态性,即要求数据服从正态分布,所以说如果数据之间彼此具有相关性的话,休哈特控制图便不再使用。
基于以上理论基础绘制的常规控制图虽然使用简便且易于理解,但对于受控状态下一般性原因的认知过于简化。
因此为了提高控制图对特殊性原因的检测能力,当过程相关时设计控制图,必须考虑质量过程的自相关结构。
为了解决过程自相关情况下的质量控制问题,统计学家们陆续提出了一些改进方法,其中主要方法之一就是引入时间序列分析法。
以ARMA以及ARIMA 模型为基础,我们便可以对具有相关性的一组数据进行相关性分析,方差分析,以及残差分析等,通过一系列控制图,便可以达到对具有自相关性的数据进行质量控制和质量改进的目的。
一、收集或生成反应自相关生产过程的平稳时间序列ARMA(p,q)数据:0.5377 0.1183 -0.6593 -1.8273 -0.93062.3339 0.5832 -1.9769 -1.5564 -1.2791-0.9306 -0.887 -1.0862 -1.3611 -0.59951.097 -1.3821 -1.6807 -1.9456 -0.37060.5881 -0.964 -0.8627 -0.3625 -1.2301-0.6845 0.636 -1.5359 -0.8981 -0.7563-0.5994 -0.7409 -0.5368 -1.2723 -0.912-0.1624 0.1918 0.0102 0.4458 -0.05523.3173 -0.352 1.556 -0.3836 0.79214.3794 0.9989 0.5869 -0.6471 1.48871.835 -0.6952 -1.3781 -0.7324 -0.9085.2662 -0.0154 -1.3526 -1.4082 -0.42463.909 0.3363 0.2649 -2.044 0.23763.4713 1.2641 -1.3455 1.0815 2.57693.6231 2.2772 0.3677 1.5831 0.69282.648 1.6038 -0.0958 1.4235 1.30682.2868 -0.0066 1.4991 -0.0704 0.77883.4275 -0.2645 -1.2401 -0.4736 -1.15163.8088 -1.1958 -0.368 -0.4345 -0.78114.3498 1.6732 -1.7639 0.4321 -2.53073.9891 -0.1377 1.9157 -1.2463 -0.3442.092 1.1812 1.2539 -2.8234 -0.59092.96 0.3569 2.5806 -3.2347 -2.14883.7378 1.4214 0.6083 -2.1308 -1.5373 3.2458 0.0529 0.6097 -1.6445 -2.2447 3.7789 -0.9494 0.2149 -1.0098 -2.5627 3.5901 -1.8812 1.3888 -1.1285 -3.1112 2.6253 -0.7372 0.481 -0.6835 -2.858 2.6835 -1.1103 1.3587 -1.1565 -4.3651.3421 -0.9724 -1.2282 0.0787 -2.07562.3645 0.6 -0.5603 -1.6693 0.3241 0.4378 0.2999 -1.4722 -0.356 0.1171 -0.1406 0.5277 -2.4813 -1.5275 -0.1473 -0.7485 1.9415 -1.1743 -1.2054 -0.0155 -3.3607 0.3246 -1.0496 -0.5082 -0.0006 -0.4665 1.4414 -0.8436 0.4234 0.8211 -0.9163 1.6532 -2.0703 -1.0584 1.9373 -1.353 1.0153 -0.1608 0.8585 1.6819 0.4189 1.2193 -0.3513 0.7719 1.2125 -1.908 -0.2516 -0.5229 0.5756 1.736二、建立过程的时间序列模型建模步骤:a :传统修哈特控制图分析:首先对所生成数据作正态性检验概率图P值大于0.05,服从正态分布作均值极差控制图控制图X 的Xbar 控制图检验结果检验1。
1 个点,距离中心线超过3.00 个标准差。
检验出下列点不合格: 6, 23, 35, 38, 40* 警告* 如果使用新数据更新图形,以上结果可能不再正确。
极差图比较稳定,但均值相对不稳定,出界点比较多。
b、自相关和偏自相关函数计算自相关函数: X滞后 ACF T LBQ1 0.727177 10.28 107.352 0.678401 6.69 201.264 0.485630 3.64 309.625 0.443131 3.12 350.316 0.428990 2.88 388.637 0.359051 2.32 415.628 0.375852 2.37 445.349 0.278182 1.70 461.7110 0.305383 1.84 481.5411 0.244883 1.45 494.3612 0.250115 1.47 507.8013 0.196341 1.14 516.1314 0.186023 1.07 523.6515 0.099887 0.57 525.8216 0.074984 0.43 527.0617 0.003639 0.02 527.0618 0.007837 0.04 527.0819 0.012380 0.07 527.1120 -0.013296 -0.08 527.1521 -0.021272 -0.12 527.2522 -0.011947 -0.07 527.2823 -0.037200 -0.21 527.6024 -0.015564 -0.09 527.6625 -0.063402 -0.36 528.5826 -0.044974 -0.26 529.0527 -0.011008 -0.06 529.0829 0.051372 0.29 529.8630 0.007681 0.04 529.8831 0.033461 0.19 530.1432 0.027212 0.16 530.3233 0.027991 0.16 530.5134 0.055998 0.32 531.2835 0.079038 0.45 532.8036 0.054507 0.31 533.5437 0.085359 0.49 535.3438 0.073699 0.42 536.7039 0.075304 0.43 538.1240 0.050118 0.28 538.7541 0.069264 0.39 539.9742 0.073646 0.42 541.3643 0.092007 0.52 543.5444 0.055604 0.32 544.3445 0.071869 0.41 545.6946 0.007542 0.04 545.7047 0.030062 0.17 545.9448 -0.017241 -0.10 546.0249 -0.031052 -0.18 546.2850 -0.045935 -0.26 546.84自相关拖尾偏自相关函数: X滞后 PACF T1 0.727177 10.282 0.317509 4.493 -0.065540 -0.934 0.039569 0.565 0.092228 1.306 0.083726 1.187 -0.081558 -1.158 0.109569 1.559 -0.114016 -1.6110 0.092335 1.3111 -0.026630 -0.3812 0.020699 0.2913 -0.056106 -0.7914 0.000014 0.0015 -0.116225 -1.6416 -0.057514 -0.8117 -0.040725 -0.5818 0.007370 0.1019 0.102724 1.4520 -0.102616 -1.4521 0.023942 0.3422 0.043098 0.6123 0.000943 0.0124 -0.001718 -0.0225 -0.065507 -0.9326 0.039754 0.5627 0.130916 1.8528 -0.041215 -0.5829 0.150788 2.1330 -0.109011 -1.5431 0.040996 0.5832 -0.020660 -0.2933 -0.004306 -0.0634 0.049428 0.7035 0.025736 0.3636 -0.040926 -0.5837 -0.003730 -0.0538 0.059449 0.8439 -0.071464 -1.0140 -0.043371 -0.6141 0.007420 0.1042 0.061468 0.8743 -0.031528 -0.4544 -0.012511 -0.1845 0.011844 0.1746 -0.112511 -1.5947 0.078713 1.1148 -0.117750 -1.6749 -0.029906 -0.4250 0.027278 0.39偏自相关函数截尾自相关函数拖尾,偏自相关函数拖尾,拟合ARMA模型C模型拟合(模型识别及参数估计)d 回归显著性方差分析拟合AR(2)模型回归分析: X 与X1, X2回归方程为X = 0.0144 + 0.492 X1 + 0.325 X2自变量系数系数标准误 T P常量 0.01436 0.07728 0.19 0.853X1 0.49179 0.06744 7.29 0.000X2 0.32547 0.06776 4.80 0.000S = 1.09107 R-Sq = 58.2% R-Sq(调整) = 57.8%方差分析来源自由度 SS MS F P回归 2 326.91 163.45 137.30 0.000残差误差 197 234.52 1.19合计 199 561.42来源自由度 Seq SSX1 1 299.44X2 1 27.47异常观测值拟合值标准化观测值 X1 X 拟合值标准误残差残差2 -0.93 2.3339 -0.0863 0.1495 2.4202 2.24R7 -0.16 -0.5994 1.0142 0.2445 -1.6136 -1.52 X8 3.32 -0.1624 3.0711 0.2128 -3.2335 -3.02R10 1.84 4.3794 2.6308 0.2875 1.7486 1.66 X11 5.27 1.8350 3.8765 0.2500 -2.0415 -1.92 X12 3.91 5.2662 3.0666 0.1959 2.1996 2.05R 31 0.44 2.3645 0.1839 0.0851 2.1806 2.00R 35 -0.47 -3.3607 -0.5133 0.0907 -2.8474 -2.62R 117 -1.24 1.4991 -0.7153 0.1046 2.2144 2.04R 119 -1.76 -0.3680 -0.2296 0.2445 -0.1384 -0.13 X 120 1.92 -1.7639 1.3646 0.1144 -3.1285 -2.88R 149 -2.08 -4.3650 -1.6011 0.1280 -2.7639 -2.55R 163 1.08 -2.0440 1.0615 0.1039 -3.1055 -2.86Re、时间序列平稳性检验特征方程为x^2-0.492x - 0.325=0x=solve('x^2-0.492*x - 0.325=0')x =-0.374899347720707466358940097205870.86689934772070746635894009720587根的模abs(x)ans =0.374899347720707466358940097205870.86689934772070746635894009720587由上可知,特征方程的根都在单位圆内,时间序列平稳f、模型优化模型无需优化g、残差正态性及独立性分析见第三部分三作残差控制图残差的Xbar-R 控制图残差的R 控制图检验结果概率图P值大于0.01,符合正态分布。
