运动的合成与分解和平抛运动
4.2抛体运动讲义
4.2抛体运动【知识梳理】1.平抛运动(1)定义:将物体以一定的初速度沿方向抛出,物体只在作用下的运动。
(2)性质:平抛运动是加速度为g的运动,运动轨迹是。
(3)研究方法:运动的合成与分解。
①水平方向:运动;②竖直方向:运动。
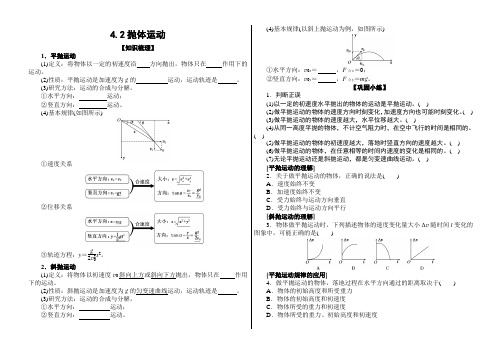
(4)基本规律(如图所示)①速度关系②位移关系③轨迹方程:y=g2v20x2。
2.斜抛运动(1)定义:将物体以初速度v0斜向上方或斜向下方抛出,物体只在作用下的运动。
(2)性质:斜抛运动是加速度为g的匀变速曲线运动,运动轨迹是。
(3)研究方法:运动的合成与分解。
①水平方向:运动;②竖直方向:运动。
(4)基本规律(以斜上抛运动为例,如图所示)①水平方向:v0x=,F合x=0;②竖直方向:v0y=,F合y=mg。
【巩固小练】1.判断正误(1)以一定的初速度水平抛出的物体的运动是平抛运动。
( )(2)做平抛运动的物体的速度方向时刻变化,加速度方向也可能时刻变化。
( )(3)做平抛运动的物体的速度越大,水平位移越大。
( )(4)从同一高度平抛的物体,不计空气阻力时,在空中飞行的时间是相同的。
( )(5)做平抛运动的物体的初速度越大,落地时竖直方向的速度越大。
( )(6)做平抛运动的物体,在任意相等的时间内速度的变化是相同的。
( )(7)无论平抛运动还是斜抛运动,都是匀变速曲线运动。
( )[平抛运动的理解]2.关于做平抛运动的物体,正确的说法是()A.速度始终不变B.加速度始终不变C.受力始终与运动方向垂直D.受力始终与运动方向平行[斜抛运动的理解]3.物体做平抛运动时,下列描述物体的速度变化量大小Δv随时间t变化的图象中,可能正确的是()[平抛运动规律的应用]4.做平抛运动的物体,落地过程在水平方向通过的距离取决于()A.物体的初始高度和所受重力B.物体的初始高度和初速度C.物体所受的重力和初速度D.物体所受的重力、初始高度和初速度【考点一】 平抛运动的基本规律 问题一 平抛运动(1)飞行时间:由t =2hg知,时间取决于下落高度h ,与初速度v 0无关。
高中物理【抛体运动】知识点规律总结

19
(2)如图乙所示,小球恰好沿 B 点的切线方向进入圆轨道,此时半径 OB 垂直于速度 方向,圆心角 α 与速度的偏向角相等.
(3)如图丙所示,小球恰好从圆柱体 Q 点沿切线飞过,此时半径 OQ 垂直于速度方向, 圆心角 θ 与速度的偏向角相等.
20
考点三 平抛运动中的临界问题
师生互动
1.临界点的确定
(2)做平抛(或类平抛)运动的物体在任意时刻任意位置处,设其末速度方向与水平方 向的夹角为 α,位移与水平方向的夹角为 θ,则 tan α=2tan θ.
12
第 2 维度:多个物体的平抛运动 对多体平抛问题的四点提醒 (1)两条平抛运动轨迹的交点是两物体的必经之处,两物体要在此处相遇,必须同时 到达此处.即轨迹相交是物体相遇的必要条件. (2)若两物体同时从同一高度抛出,则两物体始终处在同一高度. (3)若两物体同时从不同高度抛出,则两物体高度差始终与抛出点高度差相同. (4)若两物体从同一高度先后抛出,则两物体高度差随时间均匀增大.
vt= vx2+v2y= v20+2gh
与初速度 v0、下落高度 h 和重力加速度 g 有关
Δv=gΔt,方向恒为竖直向下
速度改变量
由重力加速度 g 和时间间隔 Δt 共同决 定
11
2.关于平抛(类平抛)运动的两个重要推论 (1)做平抛(或类平抛)运动的物体任意时刻的瞬时速度的反向延长线一定通过此时水 平位移的中点,如图中 A 点和 B 点所示,即 xB=x2A.
1
第 2 讲 抛体运动
一、平抛运动 1.定义:将物体以一定的初速度沿水平方向抛出,物体只在_重__力___作用下的运动. 2.性质:平抛运动是加速度为 g 的__匀__变__速__曲线运动,运动轨迹是抛物线. 3.研究方法:运动的合成与分解 (1)水平方向:_匀__速___直线运动. (2)竖直方向:_自__由__落__体___运动.
(浙江选考)2021高考物理二轮复习专题一力与运动第4讲运动的合成与分解平抛运动学案

第4讲运动的合成与分解平抛运动[历次选考考情分析]章知识内容考试要求历次选考统计必考加试2021 /102021/042021/102021/042021/112021/04曲线运动曲线运动 b b运动的合成与分解b c平抛运动 d d 2、10 7131920考点一曲线运动的理解1.曲线运动(1)速度方向:沿曲线上该点的切线方向.(2)条件:合外力与速度不共线.(3)运动轨迹:在速度与合外力方向所夹的区间内,向合外力的方向弯曲.2.运动的合成与分解的运算法那么(1)运动的合成与分解是指描述运动的各物理量即位移、速度、加速度的合成与分解,由于它们均是矢量,故合成与分解都遵守平行四边形定那么.(2)合运动是物体的实际运动,合运动的性质是由合初速度与合加速度决定的.1.[曲线运动方向](2021·绍兴市期末)翻滚过山车是大型游乐园里的一种比拟刺激的娱乐工程.如图1所示,翻滚过山车(可看成质点)从高处冲下,过M点时速度方向如下图,在圆形轨道内经过A、B、C三点.以下说法正确的选项是( )图1A.过A点时的速度方向沿AB方向B.过B点时的速度方向沿水平方向C.过A、C两点时的速度方向一样D.圆形轨道上与M点速度方向一样的点在AB段上答案 B2.[曲线运动条件]如图2所示,水平桌面上一小钢球沿直线运动.假设在钢球运动的正前方A处或旁边B处放一块磁铁,假设小钢球受到的摩擦力大小恒定,那么以下关于小球运动的说法正确的选项是( )图2A.磁铁放在A处时,小球可能做匀加速直线运动B.磁铁放在A处时,小球做曲线运动C.磁铁放在B处时,小球做曲线运动D.磁铁放在B处时,小球可能做匀速圆周运动答案 C解析磁铁放在A处时,合力向前,加速度向前,小钢球做加速直线运动,但磁力大小与距离有关,故加速度是变化的,不是匀加速直线运动,故A、B错误;磁铁放在B处时,合力与速度不共线,故小钢球向磁铁一侧偏转;磁力大小与距离有关,故加速度是变化的,所以小球做变加速曲线运动,故C正确,D错误.3.[小船渡河](2021·绍兴市期末)唐僧、悟空、八戒、沙僧师徒四人想划船渡过一条宽180 m的河,他们在静水中划船的速度为3 m/s,现在他们观测到河水的流速为4 m/s,对于这次划船过河,他们有各自的看法,其中正确的选项是( ) A.唐僧说:我们要想到达正对岸就得使船头朝向正对岸B.悟空说:我们要想到达正对岸船头必须朝向上游划船C.八戒说:我们要想少走点路就得朝着正对岸划船D.沙僧说:今天这种情况我们是不可能到达正对岸的答案 D解析当静水速度垂直于河岸时,渡河的时间最短,t=dv c=1803s=60 s,此时船将运动到下游,故A错误;由于静水速度小于水流速度,合速度不可能垂直于河岸,不可能到达正对岸,当静水速度的方向与合速度方向垂直时,渡河位移最短,故B、C错误,D正确.4.[运动轨迹分析]如图3甲所示,在一次海上救援行动中,直升机和伤员一起沿水平方向匀速飞行,同时悬索系住伤员匀速上拉,以地面为参考系,伤员从A至B的运动轨迹可能是图乙中的( )图3A.折线ACB B.线段ABC.曲线AmB D.曲线AnB答案 B解析伤员参与了两个分运动,水平方向匀速移动,竖直方向匀速上升,合速度是两个分速度的矢量和,遵循平行四边形定那么,由于两个分速度大小和方向都恒定,故合速度固定不变,即合运动是匀速直线运动,故轨迹是线段AB,故A、C、D错误,B正确.5.[运动的合成与分解](2021·桐乡中学期末)手持滑轮把悬挂重物的细线拉至如图4所示的实线位置,然后滑轮水平向右匀速移动,运动中始终保持悬挂重物的细线竖直,那么重物运动的速度( )图4A.大小和方向均不变B.大小不变,方向改变C.大小改变,方向不变D.大小和方向均改变答案 A解析 滑轮水平向右匀速运动过程中,悬挂重物的细线保持竖直,重物具有与滑轮一样的水平速度,同时重物竖直方向匀速上升,其上升的距离与滑轮水平向右移动的距离一样,故重物竖直上升的速度恒定不变,且与水平方向速度大小相等,因此重物运动的速度方向斜向右上方,与水平方向成45°角,大小恒定,A 正确.考点二 平抛运动根本规律的应用 1.飞行时间:t =2hg,取决于下落高度h ,与初速度v 0无关.2.水平射程:x =v 0t =v 02hg,由初速度v 0和下落高度h 共同决定,与其他因素无关.3.落地速度:v =v x 2+v y 2=v 02+2gh ,与水平方向的夹角的正切值tan α=v y v x=2gh v 0,所以落地速度只与初速度v 0和下落高度h 有关.4.某时刻速度的反向延长线通过此时水平位移的中点,速度方向与水平方向夹角的正切值是位移方向与水平方向夹角的正切值的2倍.例1 (2021·稽阳联考)现有一玩具枪,其枪管长度L =20 cm ,枪口直径d =6 mm ,子弹质量为m =2 g ,在测试中,让玩具枪在高度h =1.8 m 处水平发射,实测子弹射程为12 m ,不计子弹受到的阻力,g 取10 m/s 2,求: (1)子弹出枪口的速度大小;(2)假设在枪管内子弹始终受到恒定的推力,试求此推力的大小. 答案 (1)20 m/s (2)2 N解析 (1)子弹离开枪口后做平抛运动,运动时间t =2hg= s =0.6 s由x =vt ,那么v =x t =120.6m/s =20 m/s(2)在枪管内,由运动学公式得v 2=2aL ,那么a =v 22L=1 000 m/s 2,根据牛顿第二定律得F=ma =2 N.6.(2021·浙江4月选考·10)某卡车在公路上与路旁障碍物相撞.处理事故的警察在泥地中发现了一个小的金属物体,经判断,它是相撞瞬间车顶上一个松脱的零件被抛出而陷在泥里的.为了判断卡车是否超速,需要测量的量是( ) A .车的长度、车的重量B .车的高度、车的重量C .车的长度、零件脱落点与陷落点的水平距离D .车的高度、零件脱落点与陷落点的水平距离 答案 D解析 物体从车顶平抛出去,根据平抛运动知识可知h =12gt 2,x =vt ,因此要知道车顶到地面的高度,即可求出时间.测量零件脱落点与陷落点的水平距离即可求出抛出时(事故发生时)的瞬时速度,故答案为D.7.某同学将一篮球斜向上抛出,篮球恰好垂直击中篮板反弹后进入篮筐,忽略空气阻力,假设抛射点远离篮板方向水平移动一小段距离,仍使篮球垂直击中篮板一样位置,且球击中篮板前不会与篮筐相撞,那么以下方案可行的是( ) A .增大抛射速度,同时减小抛射角 B .减小抛射速度,同时减小抛射角 C .增大抛射角,同时减小抛出速度 D .增大抛射角,同时增大抛出速度 答案 A解析 应用逆向思维,把篮球的运动看成平抛运动,由于竖直高度不变,水平位移增大,篮球从抛射点到篮板的时间t =2hg不变,竖直分速度v y =2gh 不变,水平方向由x =v x t 知x 增大,v x 增大,抛射速度v =v x 2+v y 2增大,与水平方向的夹角的正切值tan θ=v yv x减小,故θ减小,可知A 正确.8.(2021·杭州市五校联考)在同一竖直线上的不同高度分别沿同一方向水平抛出两个小球A 和B ,两球在空中相遇,其运动轨迹如图5所示,不计空气阻力,以下说法正确的选项是( )图5A .相遇时A 球速度一定大于B 球 B .相遇时A 球速度一定小于B 球C .相遇时A 球速度的水平分量一定等于B 球速度的水平分量D .相遇时A 球速度的竖直分量一定大于B 球速度的竖直分量 答案 D解析 根据t =2hg,v y =gt ,h A >h B ,x =v x t ,知t A >t B ,v yA >v yB ,v xA <v xB ,选项D 正确.9.(2021·七彩阳光联盟期中)一条水平放置的水管,横截面积S =4.0 cm 2,距地面高度h =1.8 m .水从管口以不变的速度源源不断地沿水平方向射出,水落地的位置到管口的水平距离约为0.6 m .假设管口横截面上各处水的速度都一样,那么每秒内从管口射出的水的体积约为(g 取10 m/s 2)( ) A .400 mL B .600 mL C .800 mL D .1 000 mL答案 A解析 根据h =12gt 2得:t =2h g = s =0.6 s ,那么平抛运动的初速度为:v 0=x t=1.0 m/s ,流量为:Q =vS =1.0×4.0×10-4 m 3/s =4×10-4 m 3/s =400 mL/s ,故V =Qt =400×1 mL=400 mL.考点三 与斜面有关的平抛运动问题1.从斜面开场平抛到落回斜面的过程(1)全过程位移的方向沿斜面方向,即竖直位移与水平位移的比值等于斜面倾角的正切值. (2)竖直速度与水平速度之比等于斜面倾角正切值的两倍.方法内容斜面 总结分解位移水平:x =v 0t竖直:y =12gt 2合位移:s =x 2+y 2分解位移,构建位移三角形2.从斜面外抛出的物体落到斜面上,注意找速度方向与斜面倾角的关系方法内容 斜面 总结分解速度水平:v x =v 0竖直:v y =gt 合速度:v =v x 2+v y 2分解速度,构建速度三角形分解速度水平:v x =v 0竖直:v y =gt 合速度:v =v x 2+v y 2分解速度,构建速度三角形例2 如图6所示,一小球从平台上水平抛出,恰好落在临近平台的一倾角为α=53°的固定斜面顶端,并刚好沿斜面下滑,小球与斜面间的动摩擦因数μ=0.5,斜面顶端与平台的高度差h =0.8 m ,g =10 m/s 2,sin 53°=0.8,cos 53°=0.6,空气阻力不计,那么:图6(1)小球水平抛出的初速度是多大?(2)斜面顶端与平台边缘的水平距离s 是多少?(3)假设平台与斜面底端高度差H =6.8 m ,那么小球离开平台后经多长时间到达斜面底端? 答案 (1)3 m/s (2)1.2 m (3)1.4 s 解析 (1)由于刚好沿斜面下滑,竖直方向有v y 2=2gh 据题有tan 37°=v 0v y解得v 0=3 m/s (2)由h =12gt 12s =v 0t 1解得s =1.2 m ,t 1=0.4 s(3)小球沿斜面下滑时,受力分析如图,沿斜面方向根据牛顿第二定律有mg sin 53°-μmg cos 53°=ma设斜面长度为L ,由几何关系有cos 37°=H -hL小球刚落到斜面上时的速度v =vycos 37°小球在斜面上运动的过程有L =vt 2+12at 22联立解得:t 2=1 s 因此t 总=t 1+t 2=1.4 s.10.如图7是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB 、水平的起跳平台BC 和着陆雪道CD 组成,AB 与BC 平滑连接.运发动从助滑雪道AB 上由静止开场在重力作用下下滑,滑到C 点后水平飞出,落到CD 上的F 点,E 是运动轨迹上的某一点,在该点运发动的速度方向与轨道CD 平行,E ′点是E 点在斜面上的垂直投影.设运发动从C 到E 与从E 到F 的运动时间分别为t CE 和t EF .不计飞行中的空气阻力,下面说法或结论不正确的选项是( )图7A .运发动在F 点的速度方向与从C 点飞出时的速度大小无关B .t CE ∶t EF =1∶1C .CE ′∶E ′F 可能等于1∶3D .CE ′∶E ′F 可能等于1∶2 答案 C解析 设运发动在F 点的速度方向与水平方向的夹角为α,CD 斜面的倾角为θ,那么有tanα=v y v 0,tan θ=y x =v y2tv 0t =v y2v 0,那么得tan α=2tan θ,θ一定,那么α一定,那么知运发动在F 点的速度方向与从C 点飞出时的速度大小无关,故A 正确;将运发动的运动分解为沿斜面方向和垂直于斜面方向,那么知垂直斜面方向上先做匀减速直线运动(类似于竖直上抛运动),当运动到E 点,垂直斜面方向上的速度减为零,然后做匀加速直线运动,根据运动的对称性,知时间相等,t CE ∶t EF =1∶1,故B 正确;在沿斜面方向上做匀加速直线运动,根据匀加速直线运动规律知,初速度为零时,在连续相等时间内的位移为1∶3,又因为沿斜面方向上的初速度不为零,那么相等时间内的水平位移之比大于1∶3,可能等于1∶2,故D 正确,C 错误.11.(2021·宁波市3月选考)如图8所示,以10 3 m/s 的水平初速度v 0抛出的物体,飞行一段时间后,撞在倾角为30°的斜面上时,速度方向与斜面成60°角,这段飞行所用的时间为(g取10 m/s2)( )图8A.1 s B.2 s C.3 s D.6 s答案 A解析由速度关系v y=v0tan 60°=10 m/s,又由v y=gt可知t=1 s,故A正确.考点四 平抛运动的临界问题1.确定运动性质——平抛运动.2.确定临界状态,一般用极限法分析,即把平抛运动的初速度增大或减小,使临界状态呈现出来.3.确定临界状态的运动轨迹,并画出轨迹示意图,画示意图可以使抽象的物理情景变得直观,更可以使有些隐藏于问题深处的条件暴露出来.例3 某同学将小球从P 点水平抛向固定在水平地面上的圆柱形桶,小球沿着桶的直径方向恰好从桶的左侧上边沿进入桶内并打在桶的底角,如图9所示,P 点到桶左边沿的水平距离s =0.80 m ,桶的高度h 0=0.45 m ,直径d =0.20 m ,桶底和桶壁的厚度不计,不计空气阻力,取重力加速度g =10 m/s 2,那么( )图9A .P 点离地面的高度为2.5 mB .P 点离地面的高度为1.25 mC .小球抛出时的速度大小为1.0 m/sD .小球经过桶的左侧上边沿时的速度大小为2.0 m/s 答案 B解析 设小球从P 点运动到桶左侧上边沿的时间为t 1,从P 点运动到桶的底角的总时间为t 2 从P 点运动到桶左侧上边沿过程中有:h 1-h 0=12gt 12① s =v 0t 1②从P 点运动到桶的底角过程中有:h 1=12gt 22③由几何知识有s +d =v 0t 2④由①②③④式并代入数据可得:h 1=1.25 m ,v 0=2.0 m/s设小球运动到桶的左侧上边沿时速度大小为v 1,与水平方向的夹角为θ,由平抛运动的规律有:竖直方向的速度:v ⊥=gt 1⑤ 此时小球的速度:v 1=v ⊥2+v 02⑥tan θ=v ⊥v 0⑦ 联立解得v 1=2 5 m/s ,tan θ=2.12.如图10所示,B 为竖直圆轨道的左端点,它和圆心O 的连线与竖直方向的夹角为α.一小球在圆轨道左侧的A 点以速度v 0平抛,恰好沿B 点的切线方向进入圆轨道.重力加速度为g ,不计空气阻力,那么A 、B 之间的水平距离为( )图10A.v 02tan αgB.2v 02tan αgC.v 02g tan αD.2v 02g tan α答案 A解析 由小球恰好沿B 点的切线方向进入圆轨道可知小球在B 点时的速度方向与水平方向夹角为α.由tan α=gt v 0,x =v 0t ,联立解得AB 之间的水平距离为x =v 02tan αg,选项A 正确.专题强化练1.(2021·宁波市期末)如图1所示,某同学让带有水的伞绕伞柄旋转,可以看到伞面上的水滴沿伞边水平飞出,假设不考虑空气阻力,水滴飞出后做的运动是( )图1A .匀速直线运动B .平抛运动C .自由落体运动D .圆周运动 答案 B2.如图2所示,一辆汽车沿着弯曲的水平公路行驶,依次通过公路上的abcde 各位置,其中汽车速度方向与它在e 位置的速度方向大致一样的是( )图2A.位置a B.位置bC.位置c D.位置d答案 A解析a、b、c、d、e各点的速度方向为该点的切线方向,所以a和e的切线方向都是偏向左下的,速度方向大致一样.3.如图3,乒乓球从斜面上滚下,它以一定的速度沿直线运动,在与乒乓球路径相垂直的方向上放一个纸筒(纸筒的直径略大于乒乓球的直径),当乒乓球经过筒口时,对着球横向吹气,那么关于乒乓球的运动,以下说法中正确的选项是( )图3A.乒乓球将保持原有的速度继续前进B.乒乓球将偏离原有的运动路径,但不进入纸筒C.乒乓球一定能沿吹气方向进入纸筒D.只有用力吹气,乒乓球才能沿吹气方向进入纸筒答案 B解析当乒乓球经过筒口时,对着球横向吹气,乒乓球沿着原方向做匀速直线运动的同时也会沿着吹气方向做加速运动,实际运动是两个运动的合运动,故一定不会进入纸筒.4.一轮船以一定的速度垂直河岸向对岸行驶,当河水流速均匀时,轮船所通过的路程、过河所用的时间与水流速度的正确关系是( )A.水速越大,路程和时间都不变B.水速越大,路程越长,时间不变C.水速越大,路程越长,时间越长D.水速越大,路程越长,时间越短答案 B解析运用运动分解的思想,求过河时间只分析垂直河岸的速度,当轮船以一定的速度垂直河岸向对岸行驶,即垂直河岸的速度不变,过河所用的时间不变,与水速无关;水越越大,由平行四边形定那么知,轮船的合速度越大,轮船所通过的路程越长,故A、C、D错误,B正确.5.(2021·温州市期末)公园里,经常可以看到大人和小孩都喜欢玩的一种游戏——“套圈〞,如图4所示是“套圈〞游戏的场景.某小孩和大人分别水平抛出圆环,大人抛出的圆环时运动高度大于小孩抛出时的高度,结果恰好都套中前方同一物体,假设圆环的水平位移一样.如果不计空气阻力,圆环的运动可以视为平抛运动,那么以下说法正确的选项是( )图4A.大人和小孩抛出的圆环发生的位移相等B.大人抛出圆环的加速度小于小孩抛出圆环的加速度C.大人和小孩抛出的圆环在空中飞行的时间相等D.大人抛出圆环的初速度小于小孩抛出圆环的初速度答案 D解析大人和小孩抛出的圆环发生的水平位移相等,竖直位移不同,所以大人和小孩抛出的圆环发生的位移不相等,故A错误;圆环做平抛运动,加速度a=g,所以大人、小孩抛出的圆环的加速度相等,故B错误;平抛运动的时间由下落高度决定,可知大人抛出的圆环运动时间较长,故C错误;大人抛出的圆环运动时间较长,如果要让大人与小孩抛出的圆环的水平位移相等,那么大人要以较小的初速度抛出圆环,故D正确.6.(2021·嘉兴市期末)某同学对着墙壁练习打网球,假定球在墙面上以20 m/s的速度沿水平方向反弹,球在墙面上反弹点的高度在1.25 m至1.80 m之间,忽略空气阻力,那么球反弹后到第一次落地(g取10 m/s2)( )A.飞行的最短时间为0.6 sB.飞行的最长时间为1.1 sC.最远水平距离为10 mD.最大位移将超过12 m答案 D7.飞镖运动于15世纪兴起于英格兰,20世纪初成为流行甚广的日常休闲活动.如图5所示,某同学在离墙一定距离的O点,将飞镖水平掷出,飞镖插在墙壁的靶上且与墙壁的夹角为θ,不计空气阻力的影响,那么以下说法正确的选项是( )图5A .飞镖的质量越大,θ角越大B .飞镖的初速度越大,θ角越大C .飞镖离墙的距离越大,θ角越大D .飞镖离墙的距离越大,θ角不变 答案 B解析 设飞镖与墙的距离为d ,那么飞镖运动的时间t =dv 0,竖直方向速度v y =gt =dg v 0,tan θ=v 0v y =v 02dg,所以v 0越大,θ角越大;d 越大,θ角越小,B 项正确. 8.(2021·金华市十校期末)如图6所示,在一次海上救援行动中,直升机用悬索系住伤员,直升机和伤员一起在水平方向以v 1=8 m/s 的速度匀速运动,同时悬索将伤员在竖直方向以v 2=6 m/s 的速度匀速上拉,那么伤员实际运动速度v 的大小是( )图6A .6 m/sB .8 m/sC .10 m/sD .14 m/s答案 C解析 由速度的合成知,实际速度v =v 12+v 22=10 m/s.9.(2021·湖州、衢州、丽水高三期末)如图7为利用稳定的细水柱显示平抛运动轨迹的装置.圆柱形饮料瓶的底面积为S ,每秒钟瓶中水位下降Δh ,形成的局部水柱末端P 离出水口的水平距离为x 时,竖直距离为h ,重力加速度为g ,那么(所有物理量均用国际单位)( )图7A .为防止漏水,A 处口子应该堵住B .为保证水柱稳定,瓶中的水应少一些C .出水口的截面积数值大小约为S Δh x2h gD .出水口的截面积数值大小约为S Δhg答案 C解析 左侧竖直管上端与空气相通,A 处水的压强始终等于大气压,不受瓶内水面上下的影响,因此,在水面降到A 处以前的一段时间内,可以得到稳定的细水柱,故A 、B 错误;根据题意可知水流离开管口做平抛运动,设初速度为v ,竖直方向下落的时间为:t =2hg,那么有:v =x t =xg2h,圆柱形饮料瓶的底面积为S ,每秒钟瓶中水位下降Δh ,那么有:S Δh =vS ′,解得出水口的截面积数值大小约为S Δh x2hg,故C 正确,D 错误.10.模拟飞机投弹游戏中,从飞机上水平抛出物块击中斜面上的某一个点,如图8所示,AB =BC =CD ,不计空气阻力.方式一:假设飞机盘旋在A 点的正上方某一不变的位置以不同的初速度v 1、v 2抛出两个物块,分别击中斜面上的B 点与C 点.方式二:假设飞机匀速运动,每隔一样的时间放下一个物块,前两个物块分别落在了B 、C 点,那么( )图8A .方式一,v 1∶v 2=1∶2B .方式二,第三个物块恰好落在D 点C .方式二,第三个物块落在C 、D 之间 D .方式二,第三个物块落在水平面上 答案 C11.如图9所示,球网高出桌面H ,网到左、右桌边缘的距离为L .某人在乒乓球训练中,从左侧L2处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧桌边缘.设乒乓球的运动为平抛运动.那么( )图9A .击球点的高度与网高度之比为2∶1B .乒乓球在网左右两侧运动时间之比为2∶1C .乒乓球过网时与落到桌边缘时竖直方向速率之比为1∶2D .乒乓球在网左、右两侧运动速度变化量之比为1∶2 答案 D解析 根据平抛运动规律,乒乓球在网左、右两侧运动时间之比为1∶2,由Δv =g Δt 可得,乒乓球在左、右两侧运动速度变化量之比为1∶2,选项D 正确,B 错误.由y =12gt 2可得击球点的高度与网高度之比为9∶8,乒乓球过网时与落到桌边缘时竖直方向速率之比为1∶3,选项A 、C 错误.12.如图10所示,一长为2L 的木板,倾斜放置,倾角为45°,今有一弹性小球,从与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板夹角相等,欲使小球一次碰撞后恰好落到木板下端,那么小球释放点距木板上端的水平距离为(不计空气阻力)( )图10A.12LB.13LC.14LD.15L 答案 D解析 由于小球释放位置与木板上端等高,设小球释放位置距木板上端的水平距离为x ,小球与木板碰撞前有v 2=2gx ,小球与木板碰撞后做平抛运动,那么水平方向上有L -x =vt ,竖直方向上有L -x =12gt 2,由以上三式联立解得x =15L ,故D 正确.13.(2021·温州市九校联盟期末)如图11所示,倾角θ=30°的斜面AB ,在斜面顶端B 向左水平抛出小球1、同时在底端A 正上方某高度处水平向右抛出小球2,小球1、2同时落在P 点,P 点为斜边AB 的中点,不计空气阻力,那么( )图11A .小球2 一定垂直撞在斜面上B .小球1、2的初速度可以不相等C .小球1落在P 点时与斜面的夹角为30°D .改变小球1的初速度,小球1落在斜面上的速度方向都平行 答案 D解析 两个小球同时做平抛运动,又同时落在P 点,说明运动时间一样,水平位移大小相等,由x =v 0t 知初速度相等.小球1落在斜面上时,有 tan θ=12gt 2v0t =gt2v 0小球2落在斜面上的速度与竖直方向的夹角的正切值tan α=v 0gt =12tan θ,α≠θ,所以小球2没有垂直撞在斜面上,故A 、B 错误.小球1落在P 点时速度与水平方向的夹角的正切值tan β=gt v 0=2tan θ=233<3,β<60°,所以小球1落在P 点时与斜面的夹角小于30°,故C 错误.改变小球1的初速度,根据tan β=2tan θ知,小球1落在斜面上的速度方向与水平方向的夹角一样,相互平行,故D 正确.14.俄罗斯苏-34轰炸机对叙利亚的两个恐惧分子车队进展了打击,消灭了40辆油罐汽车.如图12所示的一辆油罐汽车被准确击中.假设飞机投弹时正在距地面180 m 高度以速度80 m/s 沿水平方向匀速飞行(炸弹离开飞机时相对飞机的初速度为零),而该车当时正在飞机正前方下的平直公路上以20 m/s 的速度匀速前进(运动方向与飞机的飞行方向一样),不计空气阻力.(取g =10 m/s 2)求:图12(1)炸弹从被投出到落地的时间; (2)炸弹刚落地时的速度大小;(3)飞机是从距油罐汽车水平距离多远时开场投弹的. 答案 (1)6 s (2)100 m/s (3)360 m解析 (1)根据h =12gt 2得,炸弹抛出到落地的时间t =2h g=2×18010s =6 s. (2)炸弹落地时的竖直分速度v y =gt =10×6 m/s=60 m/s.根据平行四边形定那么知,落地时的速度大小v =v x 2+v y 2=802+602m/s =100 m/s. (3)炸弹的水平位移x 1=v x t =80×6 m=480 m ,油罐汽车的位移x 2=v ′t =20×6 m=120 m ,那么Δx =x 1-x 2=480 m -120 m =360 m.15.如图13所示,水平台面AB 距地面的高度h =0.8 m .有一滑块从A 点以v 0=6 m/s 的初速度在台面上自由滑行,滑块与平台间的动摩擦因数μB 点后垂直于平台边缘水平飞出.x AB =2.2 m ,不计空气阻力,g 取10 m/s 2.求:图13(1)滑块从B 点飞出时的速度大小; (2)滑块落地点到平台边缘的水平距离. 答案 (1)5 m/s (2)2 m解析 滑块在平台上做匀减速直线运动的加速度大小为a =F f m=μg =2.5 m/s 2(1)由v B 2-v 02=-2ax AB , 得v B =5 m/s(2)滑块从B 点飞出后做平抛运动,竖直方向,h =12gt 2水平方向,x =v B t 解得x =2 m故滑块落地点到平台边缘的水平距离为2 m.。
新课程沪科版必修2第1章 怎样研究抛体运动-新课标[原创][全套]
![新课程沪科版必修2第1章 怎样研究抛体运动-新课标[原创][全套]](https://img.taocdn.com/s3/m/e73d67273169a4517723a36a.png)
第1章怎样研究抛体运动1.1 飞机投弹和运动的合成与分解【目标导航】1、了解物体做曲线运动的条件及求解方法。
2、掌握运动合成与分解简单问题的求解。
【知能点拨】1.知识概要(1)平抛运动:将物体沿水平方向抛出,物体只在重力作用下的运动。
(2)合运动与分运动的关系①等时性:合运动和分运动经历的时间相等,即同时开始、同时进行、同时停止。
②独立性:一个物体同时参与几个分运动,各分运动独立进行,不受其它分运动的影响。
③等效性:各分运动的规律叠加起来与合运动的规律有完全相同的效果。
2.探究方略对事物的研究和探索通常都要经过从感性认识到理性认识的过程,我们这一章要研究抛体运动,首先要感受什么是抛体运动,当然飞机投弹的实验并不是每个人都可以做的,但我们可以在运动的汽车上、自行车上模拟、感受这一运动。
有条件的同学,可以借助家用摄像机,从不同的角度和位置拍摄物体的运动,不仅可以细致观察运动情况,而且还可以进一步体会在必修1中学习的有关参考系的知识。
为了能更好地研究抛体运动,本节中用了大量的篇幅介绍了运动的合成与分解。
这部分知识较难理解,所以课本中利用实验和日常生活中的经验进行了讲解。
3.我的认识(1)有人认为两个直线运动的合运动一定是直线运动,你认为这句话对吗?如果是两个匀速直线运动的合运动呢?(2)合运动的速度一定大于分运动的速度吗?(3)做曲线运动的物体所受的合外力一定是变力,这种观点对吗?【例题精析】例1.下列说法正确的是A.两匀速直线运动的合运动的轨迹必是直线B.两匀变速直线运动的合运动的轨迹必是直线C.一个匀变速直线运动和一个匀速直线运动的合运动的轨迹一定是曲线D.两个初速度为零的匀变速直线运动的合运动的轨迹一定是直线解析:物体做曲线运动的条件是所受的合外力方向与初速度方向不在一条直线上。
当物体所受合外力方向与初速度方向在一条直线上时,物体做直线运动。
物体做匀速直线运动时,合外力为零,两个匀速直线运动合成时,合外力仍为零,物体仍做匀速直线运动,A正确。
学业水平测试专题05运动的合成分及平抛运动

学业水平测试专题五运动的合成分及平抛运动1.曲线运动的速度方向沿轨迹的切线方向,曲线运动速度方向一直在变;例1.(1).做曲线运动的物体的速度方向必变化(对/错);(2).速度变化的运动必是曲线运动(对/错);(3).平抛运动是变速运动(对/错);(4).匀速圆周运动是变速运动(对/错);2.船渡河模型例2.船在静水中的速度为5m/s,河岸笔直,河宽30m,水流的速度为3m/s,求:(1).船要行驶到正对岸,船头方向为(偏上游/正对对面河岸/偏下游);(2).船过河的最短时间为;船头方向为(偏上游/正对对面河岸/偏下游);(3).若船头朝正对岸行驶,行驶至河中间时,水流速度变大,则过河时间(变大/小/不变);例3.在长为80cm的玻璃管中注满清水,水中放一个可以匀速上浮的红蜡烛,将此玻璃管竖直放置,让红蜡烛沿玻璃管从底部匀速上升,与此同时,让玻璃管沿水平方向向右匀速移动,若红蜡烛在玻璃管中沿竖直方向向上运动的速度为8cm/s,玻璃管沿水平方向移动的速度为6cm/s,则红蜡烛运动的速度大小是cm/s,红蜡烛上升到水面的时间为S。
3.平抛运动的分解(水平方向匀速直线运动/竖直方向自由落体运动);加速度为g;例4.关于平抛运动,下列说法正确的是()A.平抛运动是非匀变速运动B.平抛运动是匀速运动C.平抛运动是匀变速运动D.平抛运动的物体落地时速度方向一定是竖直向下的4.平抛运动的公式(水平:X水平=V0t;竖直:h/Vy按匀变速公式求解)例5.将一个物体以10 m/s的速度从5m 的高度水平抛出,求落地所用时间和落地时它的速度方向与地面的夹角为多少?例6.如图所示,高为h=1.25 m的平台上,覆盖一层薄冰,现有一质量为60 kg的滑雪爱好者,以5.0 m/s的初速度向平台边缘匀速滑去,(取重力加速度g=10 m/s2).求:(1)滑雪者在空中运动的时间(2)滑雪者着地点到平台边缘的水平距离5.平抛运动的公式tgθ=Vy /Vx;例7.从某一高度平抛一物体,当抛出2s后它的速度方向与水平方向成45°角,落地时速度方向与水平成60°角。
运动分解之平抛运动基础知识归纳

运动分解之平抛运动基础知识归纳1.曲线运动的特点(1)在曲线运动中,运动质点在某一点的瞬时速度的方向,确实是通过这一点曲线的切线方向。
因此,曲线运动中能够确信速度方向在变化,故曲线运动一定是变速运动。
(2)曲线运动中一定有加速度且加速度和速度不能在一条直线上,加速度方向一定指向曲线轨迹凹的那一边。
2.物体做曲线运动的条件物体所受合外力与速度方向不在同一直线上。
中学时期实际处理的合外力与速度的关系常有以下三种情形①合外力为恒力,合外力与速度成某一角度。
如在重力作用下平抛,带电粒子垂直进人匀强电场的类平抛等。
②合外力为变力,大小不变,仅方向变,且合外力与速度垂直,如匀速圆周运动.③一样情形,合外力既是变力,又与速度不垂直,高中时期只做定性分析。
3.运动的合成与分解(1)运动的合成与分解的法则:平行四边形定则。
(2)合运动与分运动是等效的关系,能够相互替代。
具有等时性、等效性和独立性。
(3)确定合运动与分运动的方法:物体相对参照物的实际运动的方向确实是合运动方向。
(4)运动的合成与分解是设法把曲线运动分解成直线运动,再用直线运动规律求解。
常见模型:船渡河问题、绳通过定滑轮拉物体运动问题。
4.运动的独立作用原理一个物体可同时参与几个分运动,各分运动独立进行,各自产生成效而不互相干扰,这确实是运动的独立作用原理。
运动的独立作用原理是运动的合成与分解的理论依据。
5.平抛运动(1)特点:仅受重力作用,水平方向匀速直线运动,竖直方向自由落体,是一种匀变速曲线运动;轨迹是条抛物线。
(2)处理方法:将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
运动的合成与分解问题归纳

抛体运动;运动的合成与分解问题归纳一. 教学内容:抛体运动;运动的合成与分解问题归纳二. 学习目标:1、理解曲线运动的条件,能够根据条件判断运动的性质及轨迹。
2、掌握运动的合成与分解的方法,理解合运动是物体的实际运动,合运动与分运动的关系。
3、重点理解牵连速度的分解问题及小船渡河类问题的分析方法。
三. 考点地位:曲线运动的条件及运动的合成与分解问题是高中物理问题的难点所在,特别是绳子的牵连速度问题,小般渡河问题是学生们学习曲线运动问题的难点,同时这部分内容也是学习和理解好平抛运动问题的基础,对于本部分内容的考查,在出题的形式上既可以通过选择题的形式单独考查,也可以融合在大型的计算题当中,如2007年广东卷理科基础卷的第5题,第6题,2005年上海卷的第10题是通过选择题目的形式出现的。
四. 重难点解析:(一)抛体运动:1、曲线运动的概念及性质:所有物体的运动从轨迹的不同可以分为两大类,即直线运动和曲线运动。
运动轨迹是直线的运动称为直线运动;运动轨迹是曲线的运动称为曲线运动。
2、曲线运动的速度:曲线运动中质点在某一时刻的(或在某一点的瞬时速度方向,就是质点从该时刻(或该点)脱离曲线后自由运动的方向,也就是曲线上这一点的切线方向。
3、曲线运动的性质速度是矢量,速度的变化,不仅指速度大小的变化,也包括速度方向的变化。
物体曲线运动的速度(即轨迹上各点的切线方向)时刻在发生变化,所以曲线运动是一种变速运动,一定具有加速度。
4、物体做曲线运动的条件曲线运动既然是一种变速运动,就一定有加速度,由牛顿第二定律可知,也一定受到合外力的作用。
当运动物体所受合外力的方向跟物体的速度方向在一条直线上(同向或反向)时,物体做直线运动。
这时合外力只改变速度大小,不改变速度的方向,当合外力的方向跟速度方向不在同一直线上时,可将合外力分解到沿着速度方向和垂直于速度方向上,沿着速度方向的分力改变速度大小,垂直于速度方向的分力改变速度的方向,这时物体做曲线运动。
曲线运动、运动的分解与合成、平抛运动

第五章曲线运动一、曲线运动1.曲线运动的位移(1)水平位移(2)竖直位移(3)合位移(某一时刻的位移)2.曲线运动的速度(1)水平速度(2)竖直速度(3)合速度(某一时刻的位移)(4)方向切线方向二、运动的合成与分解1、合运动与分运动(1)、合运动:物体实际发生的运动(2)、分运动:两个方向上的运动(垂直关系)2.运动的合成与分解的本质(1)速度、加速度、位移的合成与分解.(2)正交关系、正交分解或合成(垂直关系)。
3合运动与分运动的关系(1)等时性:合运动与分运动的时间相等。
(2)独立性:两个分运动之间相互无影响。
(3)等效性:两个分运动描述的运动和合运动描述的运动相同。
4、几种分运动和合运动的合成分解情况(1)两个分运动都是匀速直线运动,合运动是匀速直线运动。
(2)一个匀速直线运动、另一个是匀变速直线运动,合运动是匀变速曲线运动。
(3)两个都是匀变速直线运动,合运动是:A.匀变速直线运动B.匀变速曲线运动5、常见的运动合成与分解问题(1)小船过河A.时间最短B.位移最小a.船速大 a.船速大b.船速小 b.船速小(2)小船靠岸A.细绳模型:绳上的力、速度等全是相等的B.合速度为小船(物体)实际运行的速度(3)风雨交加、车上观雨风速、雨速、车速、参照物三、抛体运动1.平抛运动(匀变速曲线运动)(1)运动特点:轨迹是抛物线;初速度不是零;(2)受力情况:仅受重力;a=g;合外力与初速度垂直;(3)平抛运动的解决方法:运动的合成与分解X:匀速直线运动F=0 V≠V0Y:匀加速直线运动F=mg V y=gt y=1/2gt²V²=2gy (4)重要推论(不可以直接用)θ=2tan tan a(5)平抛运动八个基本量示意图任意知道其中的两个量,都要会求其它的六个量。
2.斜抛运动(1)运动特点:初速度不是零;初速度方向不水平/竖直。
(2)受力情况:合力为重力,加速度g ;(3)解决方法:速度的合成与分解X :匀速直线运动 F=0 V ≠V 0Y :匀加速直线运动 V y =V 0-gt y=V 0t -1/2gt ² V ²-V 0²=-2gy(4)最高点问题 V y =0(5)斜面中距离斜面最远问题当V y =0时物体不再远离斜面此时离斜面最远。
1、运动的合成与分解、竖直方向上的抛体运动解析

课 题运动的合成与分解、竖直方向上的抛体运动教学目标 1、理解合运动与分运动 2、理解竖直方向上的抛体运动的分解 重 点 运动的合成与分解 难 点 竖直方向上的抛体运动 作 业 附 后基础知识梳理一、运动的合成与分解1、合运动与分运动合运动就是物体的实际运动,一个运动可以看作物体同时参与了几个分运动,这几个分运动就是物体实际运动的分运动。
2、运动的合成与分解(1)定义:物体的实际运动往往是由几个独立的分运动合成的,由已知的分运动求跟它们等效的合运动叫做运动的合成;由已知的合运动求跟它等效的分运动叫做运动的分解。
(2)合运动与分运动的关系:①等时性:合运动和分运动经历的时间相等.即同时开始,同时进行,同时停止 ②独立性:一个物体同时参与几个分运动,各分运动独立进行,不受其他分运动的影响 ③等效性:各分运动的规律叠加起来与合运动的规律有完全相同的效果 (3)运动的合成与分解的运算原则运动的合成与分解是指描述运动的物理量,包括位移、速度、加速度的合成和分解。
它们与力的合成和分解一样都遵守平行四边形定则,基本方法如下:A .两个分运动在同一直线上时,矢量运算转化为代数运算。
先选定一正方向,凡与正方向相同的取正,相反取负,合运动为各分运动的代数和。
B .不在同一直线上,按照平行四边形法则合成,如下图所示:C .两分运动垂直或正交分解后的合成:22y x a a a +=合,22y x s s s +=合D .两个分运动必须是同一质点在同一时间内相对于同一参考系的运动。
3、合运动轨迹的几种可能情况:两直线运动的合运动的性质和轨迹由各分运动的性质即合初速度与合加速度的方向关系决定:①两个匀速直线运动的合运动仍是匀速直线运动.②一个匀速直线运动和一个匀变速直线运动的合运动仍是匀变速运动。
二者共线时为匀变速直线运动,如竖直上抛运动或竖直下抛运动;二者不共线时匀变速曲线运动,如平抛运动。
③两个匀变速直线运动的合运动仍为匀变速运动,当合初速度与合加速度共线时为匀变速直线运动;当合初速度与合加速度不共线时为匀变速曲线运动.4、运动分解的基本方法根据运动的实际效果将描述合运动规律的各物理量(位移、速度、加速度)按平行四边形定则分别分解,或进行正交分解。
2022年人教版高中物理必修二第五章抛体运动第4节抛体运动的规律

第五章抛体运动4.抛体运动的规律【课标定向】1.会用运动合成与分解的方法分析平抛运动。
2.体会将复杂运动分解为简单运动的物理思想。
3.能分析生产生活中的抛体运动。
【素养导引】1.认识平抛运动,理解平抛运动的规律,会用运动合成和分解的方法分析平抛运动。
(物理观念) 2.运用运动的合成与分解的思想,分析生产生活中的抛体运动。
(科学思维)3.能体会物理学规律的运用对生产生活的影响。
(科学探究)一、平抛运动的速度将物体以初速度v0水平抛出,由于物体只受重力作用,t时刻的速度水平方向v x=v0竖直方向v y=gt合速度大小:v=v2x+v2y=v2+g2t2方向:tan θ=v yv x=gtv0将物体以初速度v0水平抛出,经时间t,物体的位移水平方向x=v0t竖直方向y=21gt2合位移大小:s=x2+y2=()v0t2+⎝⎛⎭⎪⎫12gt22方向:tan α=yx=gt2v0轨迹y=g2v2x2,是一条抛物线1.定义:初速度沿斜向上或斜向下方向的抛体运动。
2.初速度:v x =v 0cos__θ,v y =v 0sin__θ。
3.性质:斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下抛运动的合运动。
[思考] 在某次乒乓球比赛中,乒乓球先后两次落台后恰好在等高处水平越过球网,过网时的速度方向均垂直于球网,把两次落台的乒乓球看成完全相同的两个球,球1和球2,如图,不计乒乓球的旋转和空气阻力。
(1)乒乓球自起跳到最高点的过程中,球1与球2的飞行时间相等吗? (2)过网时球1与球2的速度哪个大?提示:(1)由h =12gt 2可得两球飞行时间相等。
(2)由x =vt 可知,球1的水平位移较大,运动时间相同,则球1的水平速度较大。
许多的极限运动项目由滑板项目延伸而来。
如图所示,某滑板运动员以某一初速度从某一高处水平飞出,落在水平地面上。
(忽略空气阻力,运动员和滑板可视为质点)由以上叙述判断下列问题:1.初速度越大,运动员在空中运动时间越长。
第一讲运动和合成与分解抛体运动

第一讲运动的合成与分解抛体运动(共同专题)本讲学习提要1.理解运动的合成与分解。
2.掌握平抛运动,会用运动的合成与分解方法分析平抛运动的规律,导出平抛运动的基本公式,了解平抛运动的特点和平抛运动的轨迹,求解平抛运动问题。
*3.理解斜抛运动,会用运动的各成与分解方法分析斜抛运动的规律,导出斜抛运动的基本公式,了解斜抛运动的特点和斜抛运动的轨迹,求解斜抛运动问题。
本章从拓展型课程Ⅰ部分中初速不为零的匀变速直线运动出发,介绍运动的合成与分解的方法。
然后将这种方法应用于平抛运动和斜抛运动。
通过本章学习,认识到某些较为复杂的曲线运动(如平抛和斜抛运动)的规律可通过简单的直线运动(入匀速直线运动和初速为零的匀变速直线运动)的规律来描述和掌握;体会从特殊到一般、从简单到复杂的科学探究过程;感悟科学分析和综合方法在人类认识和应用自然规律过程中的作用和价值。
A运动的合成与分解一、学习要求理解运动的合成与分解。
学会用平行四边形定则解决运动的合成与分解问题,通过运动的合成与分解方法的学习,体验科学分析和综合方法的普遍性、简单性。
二、要点辨析1.什么是运动的合成与分解?运动的合成与分解是指描写运动状态的物理量(包括位移、速度、加速度等)的合成与分解。
运动的合成与分解是针对同一个研究对象的运动进行的,因此合运动以及它的各分运动中的时间参量是相同的。
2.为什么要讨论运动的合成与分解?将一个物体的运动(称为“合运动”)分解为两个或几个“分运动”的目的是,通过已知的较为简单的分运动的规律性,认识和掌握较为复杂的合运动的规律性。
运动的合成与分解方法是科学分析和综合方法在物理学中的体现。
3.用“平行四边形定则”对运动进行合成或分解速度、位移与力一样,都是矢量,他们的合成与分解都遵循平行四边形定则。
由同一起点作出表示两个分运动的速度或位移矢量的线段,以它们为邻边作一平行四边形,由起点所作的对角线即表示合运动的速度或位移矢量,实际上,矢量可理解为遵循平行四边形定则的量。
平抛运动各种变化

知识点:运动的合成与分解 1. 合运动与分运动的关系等时性:各分运动经历的时间与合运动经历的时间相等。
独立性:一个物体同时参与的几个分运动,个分运动独立进展,不受其他分运动的影响。
等效性:各分运动的叠加与合运动有完全一样的效果 2.平抛运动特点:思考:求下面三种情况下平抛时间〔思考斜面提供了什么条件〕 〔1〕以v 0平抛的物体垂直落在对面倾角为θ的斜面上 〔2〕从倾角θ为的斜面顶端以v 0平抛的物体落在斜面上 〔2〕从倾角θ为的斜面顶端以v 0平抛的物体离斜面最远时1如左图一水平抛出的小球落到一倾角为θ的斜面上时,其速度方向与斜面垂直,运动轨迹如右图中虚线所示。
小球在竖直方向下落的距离与在水平方向通过的距离之比为〔 〕 A .1tan θ B .12tan θC .tan θD .2tan θ 2如中图,一物体自倾角为θ的固定斜面顶端平抛后落在斜面上,物体与斜面接触时速度与水平方向的夹角α满足〔 〕A 、tan α=sin θB 、tan α=cos θC 、tan α=tan θD 、tan α=2tan θ3:如右图物体从倾角θ为的斜面顶端以v 0平抛,求物体距斜面的最大距离?4如右图物体从倾角θ为的斜面顶端以v 0平抛,从抛出到离斜面最远所用的时间为t 1,沿斜面位移为s 1,从离斜面最远到落到斜面所用时间为t 2,沿斜面位移为s 2,那么( ) A 、t 1 =t 2 B 、t 1<t 2 C 、s 1=s 2 D 、s 1<s 2α θ θ v 0 θ θxy v 0 θv θ v x v yθ5:倾角θ为的斜面底端为足够大的水平平面,小球从斜面顶端以v 0平抛一物体路落在斜面上,当增大平抛的水平初速,那么飞行时间〔 〕 A 、一定变长 B 、可能变长 C 、可能变短 D 、可能不变6:一小球从某点开场做平抛运动,抛出点有一点光源,距抛出点L 有一竖直墙,小球在点光源照射下在墙上产生的影子做〔 〕运动 A 、自由落体 B 、匀速直线 C 、变加速直线 D 、无法确定7:光滑斜面顶端同时有两个小球开场运动,甲球做平抛运动,乙球由静止开场沿斜面下滑,当甲球落在斜面上P 点时,乙球〔 〕 A 、还没到达p 点B 、正好到达p 点C 、已经经过p 点D 、无法确定8:在水平地面上固定一倾角θ=30,外表光滑的斜面体,物体A 以v 1=6m/s 的初速度沿斜面上滑,同时在物体A 的正上方,有一物体B 以某一初速水平抛出,如果当A 上滑到最高点时,恰好被B 物体击中〔A 、B 均可视为质点,取g=10m/s 2〕 〔1〕物体A 上滑到最高点所用的时间:〔2〕物体B 抛出时的初速度: 〔3〕物体A 、B 间初始位置的高度差:9:如图,斜面倾角为θ,斜面顶端A 球平抛的同时,斜面底端B 球以v 0沿斜面向上运动,那么〔1〕A 球初始高度为h ,抛出后,A 、B 恰好在斜面上相遇,,求A 球的速度和相遇时间 〔2〕要使从开场到相遇所经历的时间最长,A 的初始高度h 应为多少/ABBO xyA O xyBO xyCO xyD1. 以下说法中正确的选项是〔〕A、合速度的大小一定比每个分速度大B、两个匀速直线运动的合运动一定是匀速直线运动C、只要两个分运动是直线运动,那么他们的合运动一定也是直线运动D、两个分运动的时间一定与他们的合运动的时间相等E、物体在恒力作用下一定作直线运动F、曲线运动一定是变速运动G、变速运动一定是曲线运动H、匀速圆周运动就是速度不变的运动2.一质点在xoy平面内的运动轨迹如下列图,下面判断正确的选项是〔〕A.假设质点在x方向始终匀速运动,那么在y方向上先作加速运动后作减速运动B.假设质点在x方向始终匀速运动,那么在y方向上先作减速运动后作加速运动C.假设质点在y方向始终匀速运动,那么在x方向上先作加速运动后作减速运动D.假设质点在y方向始终匀速运动,那么在x方向上先作减速运动后作加速运动3.一物体由静止开场自由下落,一小段时间后突然受一恒定水平向右的风力的影响,但着地前一段时间风突然停顿,那么其运动的轨迹可能是图中的哪一个?( )4.如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h。
2024高考物理复习重难点解析—运动的合成与分解、抛体运动

2024高考物理复习重难点解析—运动的合成与分解、抛体运动这部分知识单独考查一个知识点的试题非常少,大多数情况都是同时涉及到几个知识点,而且都是运动的合成与分解、动量、动能定理的内容结合起来考查,考查时注重物理思维与物理能力的考核.命题趋势有平抛运动和斜抛运动,而且三维坐标系考查三维立体空间的分解能力增多。
例题1.(2022·山东·高考真题)如图所示,某同学将离地1.25m 的网球以13m/s 的速度斜向上击出,击球点到竖直墙壁的距离4.8m 。
当网球竖直分速度为零时,击中墙壁上离地高度为8.45m 的P 点。
网球与墙壁碰撞后,垂直墙面速度分量大小变为碰前的0.75倍。
平行墙面的速度分量不变。
重力加速度g 取210m/s ,网球碰墙后的速度大小v 和着地点到墙壁的距离d 分别为()A .5m/s v =B .v =C . 3.6m =dD . 3.9m=d【答案】BD【解析】设网球飞出时的速度为0v ,竖直方向20=2()v g H h -竖直代入数据得012m/sv =竖直则05m/sv =水平排球水平方向到P 点的距离0006m v x v t v g==⋅=竖直水平水平水平根据几何关系可得打在墙面上时,垂直墙面的速度分量0044m/s5v v =⋅=水平⊥水平平行墙面的速度分量0033m/s5v v =⋅=水平∥水平反弹后,垂直墙面的速度分量'00.753m/sv v =⋅=水平⊥水平⊥则反弹后的网球速度大小为v 水平网球落到地面的时间' 1.3s t ===着地点到墙壁的距离'' 3.9md v t ⊥==水平故BD 正确,AC 错误。
故选BD 。
例题2.(2022·全国·高考真题)将一小球水平抛出,使用频闪仪和照相机对运动的小球进行拍摄,频闪仪每隔0.05s 发出一次闪光。
某次拍摄时,小球在抛出瞬间频闪仪恰好闪光,拍摄的照片编辑后如图所示。
导与练必修二物理运动的合成和分解

导与练必修二物理运动的合成和分解下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!物质的运动是宇宙中无处不在的现象,而物理运动作为研究物质运动规律的一门学科,对于我们了解世界、改造世界、服务社会具有重要意义。
高中物理必修二54抛体运动的规律(解析版)

5.4 抛体运动的规律【学习目标】1. 知道平抛运动的概念及条件,会用运动的合成与分解的方法分析平抛运动.2. 理解平抛运动可以看作是水平方向的匀速直线运动与竖直方向上的自由落体运动的合运动,且这两个分运动互不影响.3.知道平抛运动的规律,并能运用规律解答相关问题. 【知识要点】 一、平抛运动的特点1.平抛运动的定义:将物体以一定的初速度沿水平方向抛出,不考虑空气的阻力,物体只在重力作用下所做的运动,叫做平抛运动.2.平抛运动的特点:水平方向上为匀速直线运动,竖直方向上为自由落体运动. 二、平抛运动的规律1.研究方法:通常采用“化曲为直”的方法.即以抛出点为原点,取水平方向为x 轴,正方向与初速度v0方向相同;竖直方向为y 轴,正方向竖直向下.分别在x 方向和y 方向研究. 2.平抛运动的规律在水平方向,物体的位移和速度分别为:⎩⎪⎨⎪⎧x =v x tv x =v 0在竖直方向,物体的位移和速度分别为:⎩⎪⎨⎪⎧y =12gt 2v y =gt某时刻实际速度的大小和方向:v t =v 2x +v 2y ,合速度与水平方向成θ角,且满足tan θ=v y v x =gt v 0. t 时间内合位移的大小和方向:l =x 2+y 2,合位移与水平方向成α角,且满足tan α=y x =gt2v 0.三、平抛运动的两个推论1.推论一:某时刻速度、位移与初速度方向的夹角θ、α的关系为tan θ=2tan_α.2.推论二:平抛运动的物体在任意时刻瞬时速度的反向延长线一定通过此时水平位移的中点. 【题型分类】题型一、平抛运动的理解例1 关于平抛物体的运动,以下说法正确的是( ) A .做平抛运动的物体,速度和加速度都随时间增大B .做平抛运动的物体仅受到重力的作用,所以加速度保持不变C .平抛物体的运动是匀变速运动D .平抛物体的运动是变加速运动解析 做平抛运动的物体,速度随时间不断增大,但由于只受恒定不变的重力作用,所以加速度是恒定不变的,选项A 、D 错误,B 、C 正确. 答案 BC 【同类练习】1.关于平抛运动,下列说法正确的是( ) A .平抛运动是非匀变速运动 B .平抛运动是匀速运动 C .平抛运动是匀变速曲线运动D .平抛运动的物体落地时的速度可能是竖直向下的 答案 C解析 做平抛运动的物体只受重力作用,产生恒定的加速度,是匀变速运动,其初速度与合外力垂直不共线,是曲线运动,故平抛运动是匀变速曲线运动,A 、B 错误,C 正确;平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,故落地时的速度是水平方向的分速度和竖直方向的分速度的合速度,其方向一定与竖直方向(或水平方向)有一定的夹角,D 错误. 题型二、平抛运动规律的应用例2 如图所示,排球运动员站在发球线上正对球网跳起从O 点向正前方先后水平击出两个速度不同的排球。
高三物理运动的合成与分解

v2
【名师支招】船在过河时,同时参与了两个运动,一是 船随水沿岸方向的运动,二是船本身相对水的运动。假如 我们将船的运动沿平行于河岸方向(称平行方向)和垂直于河 岸方向(称垂直方向)进行分解,于是船的划速v1可分解为平 行分量v∥和垂直方向的分量v⊥,如图4-1-7所示,而水的速 度v2则总是沿平行于河岸的正方向。根据运动的独立性原理, 平行于河岸的运动对小船过河没有影响,只有垂直于河岸 的运动才能使小船渡河到达对岸。
【答案】v0cosα
【解析】方法一:岸上重物的速度等于绳的速度,我们找 到绳与轮船的连接点,此点的实际运动速度就是轮船的速度, 是合速度,则沿绳的速度为分速度,作出速度的分解图如图 4-1-9所示,可知沿绳方向的分速度v∥=v0cosα。 方法二:从连接点参与的两分运动的效果上判定分运动 方向。设当船在短时间内从A到B(图4-1-10),绳从CA到CB, 可见船的运动产生了两个效果(1)使船沿绳的方向运动;(2)使 绳绕C点转动。 因此,任一时刻船的速度都可按效果沿绳的 方向及垂直绳的方向分解,如图4-1-11所示,则 v1=v0cosα,而滑轮两边沿绳方向的速度大小是 相等的(绳的总长度不变),故v1=v0cosα即为 图4-1-10 绳拉动重物移动的速度。 图4-1-8
图4-1-7
2 小船过河,河宽为90 m,船在静水中航行速度是3 m/s,水 流速度是4 m/s,则( A C ) A.船渡过河的最短时间为30 s B.小船渡河的最短路程为90 m C.船头偏向上游某一角度可使船以最短路程过河 D.小船渡河的最短路程为150 m
热点三
绳连物体问题
【例3】如图4-1-8所示,轮船以恒定的水平速度v0沿水面向远离河岸方向运动,通过跨越滑轮的钢丝绳拉动 岸上水平轨道上的重物,当钢丝绳与水平面夹角为α的瞬间,岸上重物移动的速度多大?
第二讲:平抛运动解析版

第二讲:平抛运动一、平抛运动1.定义:将物体以一定的初速度沿水平方向抛出,物体只在重力作用下的运动.2.性质:平抛运动是加速度为g 的匀变速曲线运动,运动轨迹是抛物线.3.研究方法:运动的合成与分解 (1)水平方向:匀速直线运动; (2)竖直方向:自由落体运动. 4.基本规律如图,以抛出点O 为坐标原点,以初速度v 0方向(水平方向)为x 轴正方向,竖直向下为y 轴正方向.(1)位移关系(2)速度关系(3)轨迹方程:h =g2v 02x 25.基本应用例题、如图所示,x 轴在水平地面上,y 轴在竖直方向.图中画出了从y 轴上沿x 轴正方向水平抛出的三个小球a 、b 和c 的运动轨迹.不计空气阻力,下列说法正确的是( )A .a 和b 的初速度大小之比为2∶1B .a 和b 在空中运动的时间之比为(1)飞行时间由t =2hg知,时间取决于下落高度h ,与初速度v 0无关.(2)水平射程x =v 0t =v 02hg,即水平射程由初速度v 0和下落高度h共同决定,与其他因素无关. (3)落地速度v =v x 2+v y 2=v 02+2gh ,以θ表示落地速度与水平正方向的夹角,有tan θ=v y v x=2ghv 0,落地速度与初速度v 0和下落高度h 有关. (4)速度改变量因为平抛运动的加速度为恒定的重力加速度g ,所以做平抛运动的物体在任意相等时间间隔Δt 内的速度改变量Δv =g Δt 是相同的,方向恒为竖直向下,如图所示.(5)两个重要推论①做平抛运动的物体在任意时刻的瞬时速度的反向延长线一例题、如图甲所示是网球发球机,某次室内训练时将发球机放在距地面一定的高度,然后向竖直墙面发射网球.假定网球均水平射出,某两次射出的网球碰到墙面时速度与水平方向夹角分别为30°和60°,若不考虑空气阻力,则( )A.两次发射的初速度大小之比为3∶1定通过此时水平位移的中点,如图所示,即x B =x A2.推导:⎭⎪⎬⎪⎫tan θ=y Ax A -x Btan θ=v yv 0=2y Ax A→x B=x A2①做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α. 推导:⎭⎪⎬⎪⎫tan θ=v y v 0=gtv 0tan α=y x =gt 2v 0→tan θ=2tan α二、与斜面结合的平抛运动1.顺着斜面平抛(如图)方法:分解位移.x =v 0t ,y =12gt 2,tan θ=y x,可求得t =2v 0tan θg.2.对着斜面平抛(垂直打到斜面,如图) 方法:分解速度.v x =v 0, v y =gt ,tan θ=v x v y =v 0gt,可求得t =v 0g tan θ.三、斜抛运动1.定义:将物体以初速度v 0斜向上方或斜向下方抛出,物体只在重力作用下的运动.2.性质:斜抛运动是加速度为g 的匀变速曲线运动,运动轨迹是抛物线.3.研究方法:运动的合成与分解(1)水平方向:匀速直线运动;(2)竖直方向:匀变速直线运动.例题、某同学在练习投篮时将篮球从同一位置斜向上抛出,其中有两次篮球垂直撞在竖直放置的篮板上,运动轨迹如图所示,不计空气阻力,关于这两次篮球从抛出到撞击篮板的过程( )4.基本规律(以斜上抛运动为例,如图所示)(1)水平方向:v 0x =v 0cos θ,F 合x =0;做匀速直线运动,v 0x =v 0cos θ,x =v 0tcos θ. (2)竖直方向:v 0y =v 0sin θ,F 合y =mg .做竖直上抛运动,v 0y =v 0sin θ,y =v 0tsin θ-12gt2四、类平抛运动1.类平抛运动物体受到与初速度垂直的恒定的合外力作用时,其轨迹与平抛运动相似,称为类平抛运动.类平抛运动的受力特点是物体所受合力为恒力,且与初速度的方向垂直.2.类平抛运动问题的求解技巧(1)常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性.(2)特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度a 分解为a x 、a y ,初速度v 0分解为v x 、v y ,然后分别在x 、y 方向上列方程求解.针对训练题型1:平抛运动性质例题、如图所示的光滑斜面ABCD 是边长为l 的正方形,倾角为30°,一物块(视为质点)沿斜面左上方顶点A 以平行于AB 边的初速度v 0水平射入,到达底边CD 中点E ,则( )A .初速度2glB .初速度4glC .物块由A 点运动到E 点所用的时间2lt g= D .物块由A 点运动到E 点所用的时间lt g=1.关于平抛运动的性质,以下说法中正确的是()A.变加速运动B.匀变速运动C.匀速率曲线运动D.不可能是两个直线运动的合运动【解答】解:A、平抛运动是匀变速曲线运动,速率不断增加。
平抛运动总结6页

平抛运动总结6页1.平抛运动是一种典型的曲线运动,是运动的合成与分解的实际应用。
2.平抛运动的定义:将物体用一定的初速度沿水平方向抛出,不考虑空气阻力,物体只在重力作用下所做的运动,叫做平抛运动。
是加速度恒为重力加速度g的匀变速曲线运动。
(1)因平抛运动只受竖直向下的重力G=mg,故由牛顿第二定律可知,实际加速度就是重力加速度g(方向竖直向下),因为速度方向与合力G(或加速度g)的方向不在同一直线上(开始运动时初速度方向与加速度方向垂直,以后速度方向与加速度方向的夹角越来越小,但是永远不重合),所以做曲线运动。
(2)平抛物体的初速度不太大,发生在离地不太高的范围内,地面可以看作是水平面,重力G和重力加速度g是恒量,方向竖直向下,始终垂直于水平面,所以平抛运动是匀变速曲线运动。
(3)可以证明,平抛运动轨迹是抛物线。
(4)平抛运动发生在同一个竖直平面内。
平抛运动是比较复杂的曲线运动,利用运动的合成和分解的观点,把它看做是水平方向(沿初速度方向向前)的匀速直线运动与竖直向下方向的自由落体运动的合运动。
把曲线运动转换成两个简单的直线运动,就可以用直线运动的规律来处理,研究起来简单方便。
这是一种重要的思想方法。
1、曲线运动产生条件物体在光滑的水平面上受到两个水平恒力的作用而做匀速直线运动,若突然撤去其中一个力,另一个保持不变,它可能做()A.匀速直线运动B.匀加速直线运动C.匀减速直线运动D.曲线运动[解答]BCD2、认识曲线运动关于曲线运动,下列说法中正确的是()A.曲线运动一定是变速运动B.曲线运动速度的方向不断变化,但速度的大小可以不变C.曲线运动的速度方向可能不变D.曲线运动的速度大小和方向一定同时改变[解答]AB3、认识曲线运动的特点一物体在一组共点力F1、F2……Fn的共同作用下做匀速直线运动,若突然撤去力F1,其他力不变,则该物体()A.必定沿F1的方向做直线运动B.必定沿F1的反方向做匀减速直线运动C.可能做曲线运动D.可能做匀加速直线运动,也可能做匀减速直线运动,但不可能做曲线运动[解答]C4、船渡河型一艘船在静水中的速度为3m/s,今欲过一条宽为60m的河,若已知水的流速为4m/s,则船过河的最短时间为()A.20sB.15sC.12sD.因为水速大于船在静水中的速度,故船不能过到对岸[解答]A5、竖直上抛运动物体做竖直上抛运动时,下列说法中正确的是()A.将物体以一定初速度竖直向上抛出,且不计空气阻力,则其运动为竖直上抛运动B.做竖直上抛运动的物体,其加速度与物体重力有关,重力越大的物体,加速度越小C.竖直上抛运动的物体达到最高点时速度为零,加速度为零,处于平衡状态D.竖直上抛运动过程中,其速度和加速度的方向都可改变[解答]A6、平抛运动“逆”型如图所示,在水平地面上的A点以速度v1射出一弹丸,方向与地面成θ角,经过一段时间,弹丸恰好以v2的速度垂直穿入竖直壁上的小孔B,不计空气阻力.下面说法正确的是()A.如果在B点以与v2大小相等的速度,水平向左射出弹丸,则它必定落在地面上A点B.如果在B点以与v1大小相等的速度,水平向左射出弹丸,则它必定落在地面上A点C.如果在B点以与v2大小相等的速度,水平向左射出弹丸,那它必定落在地面上A点左侧D.如果在B点以与v1大小相等的速度,水平向左射出弹丸,那它必定落在地面上A点右侧[解答]A7、平抛运动综合型如图所示,一小球自平台上水平抛出,恰好落在临近平台的一倾角为α=53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8m,g=10m/s2,sin53°=0.8,cos53°=0.6,则⑴小球水平抛出的初速度υ0是多少?⑵斜面顶端与平台边缘的水平距离s是多少?⑶若斜面顶端高H=20.8m,则小球离开平台后经多长时间t 到达斜面底端?[解答]解:⑴由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以υy=υ0tan53°(2分)υy2=2gh(1分)代入数据,得υy=4m/s,υ0=3m/s(2分)⑵由υy=gt1得t1=0.4s(1分)s=υ0t1=3×0.4m=1.2m(1分)⑶小球沿斜面做匀加速直线运动的加速度a=8m/s2(1分)初速度υ0=5m/s(1分)=υt2+at22(1分)代入数据,整理得4t22+5t2-26=0解得t2=2s或t2=-13s(不合题意舍去)(1分)所以t=t1+t2=2.4s(1分)8、平抛运动定性型如图所示,在同一竖直平面内,小球a、b从高度不同的两点分别以初速度va和vb沿水平方向抛出,分别经过时间ta和tb后落到与两抛出点水平距离相等的P点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲线运动
建立运动的合成与分解的基本思想,竖直面内圆周运动的绳模型、杆模型是高考的热点,尤其是在最高点和最低点的临界问题要给予充分重视.人造卫星问题最基本的关系是万有引力提供向心力。
曲线运动轨迹特征:曲线运动的轨迹始终夹在合力的方向与速度的方向之间,而且向合力的一侧弯曲,或者说合力的方向总指向曲线的“凹”侧.
例1.质点仅在恒力F的作用下,由O点运动到A点的轨
迹如图22-2所示,在A点时速度的方向与x轴平行,则
恒力F的方向可能沿()
A.x轴正方向
B. x轴负方向
C. y轴正方向
D. y轴负方向
例2.质点在一水平面内沿曲线由P运动到Q,如果用v、a、F分别表示质点运动过程中的速度、加速度和受到的合外力,图22-3中有可能正确的是()
1.运动的合成与分解实质是对描述物体运动的参量(位移、速度、加速度)进行合成与分解,与力的合成与分解一样,遵从平行四边形定则.
2.合运动的性质可由合初速度与合加速度进行判断:
(1)两个匀速直线运动的合运动一定为匀速直线运动;
(2)合初速度与合加速度共线,物体做直线运动;
(3)合初速度与合加速度不共线,物体做曲线运动,合外力恒定时物体做匀变速曲线运动.
3.运动合成与分解的常见问题主要有拉船问题(又称绳端问题)、渡河问题,准确确定合运动(物体的实际运动为合运动)是分析
这两类问题的关键.
如人拉小船运动问题(如图22-4所示),船的实
际速度为合速度,小船沿绳方向的速度为分速度
v1,小船绕滑轮转动的速度为分速度v2,人拉绳的
速度与小船速度满足v人=v1=v船cosθ.
例3.船在静水中的速度为v ,流水的速度为u ,河宽为L.(1)为使渡河时间最短,应向什么方向划船?此时渡河所经历的时间和位移各为多大?(2)当v >u 时,为使渡河通过的位移最短,应向什么方向划船?此时渡河所经历的时间和所通过的位移各为多大?(3)当v <u 时,为使渡河通过的位移最短,应向什么方向划船?此时渡河所经历的时间和所通过的位移各为多大?
例4.如图22-5所示,一块橡皮用细线悬挂于O 点,
用铅笔靠着线的左侧水平向右匀速移动,运动中始终
保持悬线竖直,则橡皮运动的速度( )
A.大小和方向均不变
B.大小不变,方向改变
C.大小改变,方向不变
D.大小和方向均改变
绳或杆连接体的问题:物体的实际运动就是合运动,分运动应该按照运动的效果分解:沿绳方向伸长或收缩的分运动和垂直于绳子方向转动的分运动.把与杆端点连接的物体的实际速度分解为垂直于杆和平行于杆两个分量,根据各端点沿绳方向的分速度大小相同求解.
特别提醒:沿着绳(杆)的方向上的两个分速度相等是绳(杆)连接物问题的研究关键.
例5.如图22-6所示,一个长直轻杆两端分别固定一个小球A 和B ,两球的质量均为m ,两球半径忽略不计,杆AB 的长度为l ,现将杆AB 竖直靠放在竖直墙上,轻轻振动小球B ,使小球B 在水平地面上由静止向右运动,求当A 球沿墙
下滑距离为l 2
时A 、B 两球的速度v A 和v B 的关系.(不计一切摩擦) 例6.A 、B 两物体通过一根跨过定滑轮的轻绳相连放在水平面上,现物体A 以v 1的速度向右匀速运动,当绳被拉成与水平面夹角分别是α、β时,如图22-7所示,物体B 的运动速度v
B 为(绳始终有拉力)( )
A.v1sinαsinβ
B.v1cosαsinβ
C.v1sinαcosβ
D.v1cosαcosβ
平抛运动:
条件:(1)初速度沿________方向;(2)只受________作用.
性质:________曲线运动,其运动轨迹为________.
推论:1.做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移与水平方向的夹角为φ,则tanθ=2tanφ
2.做平抛(或类平抛)运动的物体,任意时刻的瞬时速度方向的反向延长线一定通过此时水平位移的中点
平抛运动研究方法:分解成水平方向的________运动和竖直方向的________运动两个方向的分运动.
飞行时间t =2h g 水平射程:x =v 0t =v 02h g
例1.在同一平台上的O 点抛出的3个物体,做平抛运
动的轨迹如图23-1所示,则3个物体做平抛运动的初
速度v A 、v B 、v C 的关系及落地时间t A 、t B 、t C 的关系分
别是( )
A.v A >v B >v C ,t A >t B >t C B .v A =v B =v C ,t A =t B =t C
C.v A <v B <v C ,t A >t B >t C D .v A <v B <v C ,t A <t B <t C
例2.如图23-2所示,一物体自倾角为θ的固定斜
面顶端沿水平方向抛出后落在斜面上.物体与斜面
接触时速度与水平方向的夹角φ满足( )
A.tanφ=sinθ B .tanφ=cosθ
C.tanφ=tanθ D .tanφ=2tanθ
例3.如图23-3所示,某同学为了找出平抛运动物
体的初速度之间的关系,用一个小球在O 点对准前
方的一块竖直放置的挡板,O 与A 在同一高度,小
球的水平初速度分别是v1、v2、v3,打在挡板上的
位置分别是B 、C 、D ,且AB ∶BC ∶CD =1∶3∶5.
则v1、v2、v3之间的正确关系是( )
A.v1∶v2∶v3=3∶2∶1
B.v1∶v2∶v3=5∶3∶1
C.v1∶v2∶v3=6∶3∶2
D.v1∶v2∶v3=9∶4∶1
例4.如图23-4所示,斜面倾角为θ,从此斜面
上的A 点以速度v0将一小球水平抛出,它落在
斜面的B 点处,则小球从A 点到B 点的运动时
间和从A 点到离开斜面最远处的运动时间之比
为( )
A.2 B .2sinθ C .2cosθ D .2tanθ
例5.一水平抛出的小球落到一倾角为θ的斜面上
时,其速度方向与斜面垂直,运动轨迹如图23-5
中虚线所示.小球在竖直方向下落的距离与在水平
方向通过的距离之比为( )
A.tanθ
B.2tanθ
C.1tanθ
D.12tanθ
1.D
2.B
3.(1)垂直河岸
L v L v
u 2+v 2 (2)偏上游与河岸夹角α=arccos u v L v 2-u
2 L (3)最短渡河位移确定方法如下:以船随流水的分运动速度v 2末端为圆心,以船相对静水的分速度v 1为半径画圆,则v 2起点向圆弧所作的切线的方向就是航程最短情况下的合速度方向.船过河最短航程x 短=d sinα=v1v2d. 最短航程x 短=d sinα=v1v2
d 4.A 5.由题意知,θ=30°,由运动的合成与分解得v A sinθ=v B cosθ, vA vB =cosθsinθ
= 3. 6.D \
1.C
2.D
3.C
4.A
5.D。
