线性规划案例
管理运筹学第二章 线性规划的图解法

B、约束条件不是等式的问题:
若约束条件为 ai1 x1+ai2 x2+ … +ain xn ≤ bi 可以引进一个新的变量si ,使它等于约束右 边与左边之差 si=bi–(ai1 x1 + ai2 x2 + … + ain xn ) 显然,si 也具有非负约束,即si≥0, 这时新的约束条件成为 ai1 x1+ai2 x2+ … +ain xn+si = bi
第二章 线性规划 的图解法
一、线性规划的概念 二、线性规划问题的提出 三、线性规划的数学模型 四、线性规划的图解法 五、线性规划解的情况 六、LP图解法的灵敏度分析
一、线性规划的概念
线性规划Linear Programming 简称LP,是一 种解决在线性约束条件下追求最大或最小的 线性目标函数的方法。 线性规划的目标和约束条件都可以表示成线 性的式子。
max z 3 x1 2 x2
2 x1 x2 ≤ 10 设备B台时占用 s.t. x1 x2 ≤ 8 x , x ≥ 0 产量非负 1 2
决策变量 (decision variable) 目标函数 (objective function) 约束条件 (subject to)
-ai1
x1-ai2 x2- … -ain xn = -bi 。
例1.3:将以下线性规划问题转化为标准形式 Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7 4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x 1 , x 2 , x3 ≥ 0
线性规划应用案例分析

线性规划应用案例分析线性规划是一种在数学和运营管理中常见的优化技术。
它涉及到在一组线性不等式约束下,最大化或最小化一个线性目标函数。
这种技术可以应用于许多不同的领域,包括供应链管理、资源分配、投资组合优化等。
本文将探讨几个线性规划应用案例,以展示其在实际问题中的应用和价值。
某制造公司需要计划生产三种产品,每种产品都需要不同的原材料和生产时间。
公司的目标是最大化利润,但同时也受到原材料限制、生产能力限制以及每种产品市场需求限制的约束。
通过使用线性规划,该公司能够找到最优的生产计划,即在满足所有约束条件下,最大化利润。
某物流公司需要计划将货物从多个产地运输到多个目的地。
公司的目标是最小化运输成本,但同时也受到运输能力、货物量和目的地需求的约束。
通过使用线性规划,该公司能够找到最优的运输方案,即在满足所有约束条件下,最小化运输成本。
某投资公司需要将其资金分配给多个不同的投资项目。
每个项目都有不同的预期回报率和风险水平。
公司的目标是最大化回报率,同时也要保证投资风险在可接受的范围内。
通过使用线性规划,该公司能够找到最优的投资组合,即在满足所有约束条件下,最大化回报率。
这些案例展示了线性规划在实践中的应用。
然而,线性规划的应用远不止这些,它还可以用于诸如资源分配、时间表制定、路线规划等问题。
线性规划是一种强大的工具,可以帮助决策者解决复杂的问题并找到最优解决方案。
线性规划是一种广泛应用的数学优化技术,适用于在多种资源限制下寻求最优解。
这种技术涉及到各种领域,包括工业、商业、运输、农业、金融等,目的是在给定条件下最大化或最小化线性目标函数。
下面我们将详细讨论线性规划的应用。
线性规划是一种求解最优化问题的数学方法。
它的基本思想是在一定的约束条件下,通过线性方程组的求解,求得目标函数的最优解。
这里的约束条件通常表现为一组线性不等式或等式,而目标函数则通常表示为变量的线性函数。
工业生产:在工业生产中,线性规划可以用于生产计划、物料调配、人力资源分配等方面。
线性规划应用案例

线性规划应用案例线性规划是一种在约束条件下寻找最优解的数学优化方法。
它在实际应用中广泛使用,涉及许多领域和行业。
本文将介绍两个典型的线性规划应用案例:运输问题和产能规划问题。
一、运输问题运输问题是线性规划最早发展起来的一个领域,它是指如何在各个供应地和需求地之间运输商品,以使得总运输成本最小。
一个典型的运输问题可以描述为:有m个供应地和n个需求地,每个供应地和需求地之间有一个固定的运输成本和一个固定的供应和需求量。
问题是如何确定每对供需地之间的运输量,以使得总运输成本最小。
举例来说,假设有三个供应地A、B、C,三个需求地X、Y、Z。
运输成本如下表所示:\begin{array}{ c c c c c c }&X&Y&Z&供应量\\A&10&12&8&100\\B&6&8&7&200\\C&9&10&11&300\\需求量&150&175&125&\\\end{array}求解此问题的线性规划模型如下:目标函数:minimize \quad Z = 10x_{11} + 12x_{12} + 8x_{13} + 6x_{21} + 8x_{22} + 7x_{23} + 9x_{31} + 10x_{32} + 11x_{33}约束条件:x_{11} + x_{12} + x_{13} \leq 100x_{21} + x_{22} + x_{23} \leq 200x_{31} + x_{32} + x_{33} \leq 300x_{11} + x_{21} + x_{31} \geq 150x_{12} + x_{22} + x_{32} \geq 175x_{13} + x_{23} + x_{33} \geq 125x_{ij} \geq 0, i = 1,2,3 \quad j = 1,2,3其中x_{ij}表示从供应地i到需求地j的运输量。
(一)线性规划

(一)线性规划
案例分析1
例1.10飞乐公司经营一个回收中心,专门混合三种废弃原材料C、P和h,以生产三
种不同规格的产品abd。
根据混合过程中各种材料的比例,产品可分为不同等级(见表
1.12)。
尽管混合不同等级的产品时允许一定的流动性,各等级产品中各种材料的最大值
和最小值必须符合下列质量标准的规定(最大值和最小值根据材料重量占该等级产品总重
量的比例确定)。
在两种更高级的产品中,一种特定材料的比例是固定的。
规格要求、单价、原材料数量、每天可供原材料单价见表1.12、表1.13。
工厂应该如何安排生产以实
现利润最大化?表1.12
产品名称abd
本规范要求原料C不小于50%,原料P不大于25%,原料C不小于25%,原料P不大于50%
不限
单价(元/公斤)
503525
回收中心可以定期从某些渠道收集所需的固体废物,从而获得处理能力,保持稳定运行。
表1.13显示了中心每天可以收集的每种材料的数量和单价。
表1.13
原料名称
cph
最大日供应量(千克)
10010060
单价(元/公斤)
652535
飞乐公司是格陵兰组织的全资子公司,格陵兰组织是一家专门从事环境相关业务的组织。
管理层决定在表1.12和表1.13所列的限制范围内,有效地向各级产品分配各种材料,以使每周的总利润最大化。
线性规划应用案例
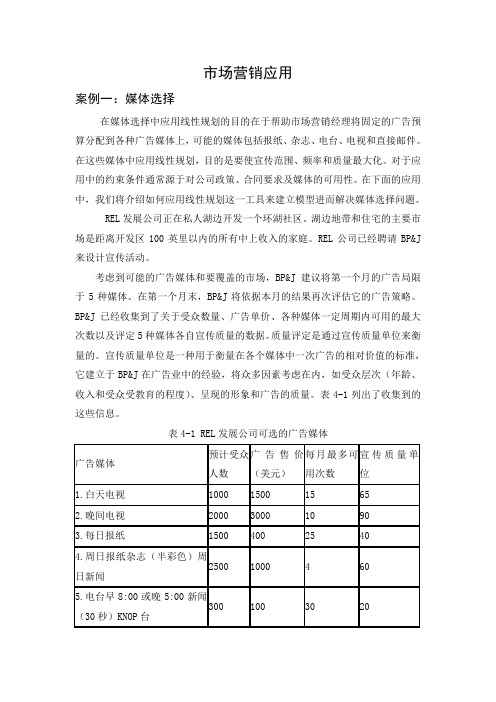
市场营销应用案例一:媒体选择在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。
在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。
对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。
在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。
REL发展公司正在私人湖边开发一个环湖社区。
湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。
REL公司已经聘请BP&J 来设计宣传活动。
考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。
在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。
BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。
质量评定是通过宣传质量单位来衡量的。
宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。
表4-1列出了收集到的这些信息。
表4-1 REL发展公司可选的广告媒体REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。
而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。
应当推荐何种广告媒体选择计划呢?案例二:市场调查公司开展市场营销调查以了解消费者个性特点、态度以及偏好。
专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。
市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。
线性规划 实际案例

线性规划是一种数学优化模型,用于解决在有一些约束条件下,如何使一个目标函数达到最优解的问题。
线性规划广泛应用于许多实际案例中,其中一些常见的案例如下:
1.生产规划:在生产过程中,企业可能需要在有限的生产资源和需求的限制下,决策
生产的数量、成本、产品组合等,以使生产效益最大化。
这就需要用到线性规划模
型来解决。
2.交通规划:在城市规划过程中,市政部门可能需要决策道路的建设、扩建、维护等,
以满足城市交通需求,并考虑到道路建设的成本和环境影响等因素。
这时候可以使
用线性规划模型来解决。
3.财务规划:在进行财务管理时,企业或个人可能需要在有限的资金和资产的限制下,
决策投资、储蓄、借贷等,以使财务效益最大化。
这时候可以使用线性规划模型来
解决。
4.供应链管理:在供应链管理过程中,企业可能需要决策采购、生产、运输、库存等
各个环节,以保证供应链的流畅运行并达到最优的效益。
这时候可以使用线性规划
模型来解决。
这些都是线性规划在实际案例中的应用,线性规划能够帮助企业和组织在有限的条件下,有效地规划和决策,并取得较好的效益。
线性规划案例(2)

饮食规划问题分析摘要本案例旨在解决一个与饮食规划相关的管理问题。
通过应用线性规划方法,我们将建立一个模型来帮助一个人根据营养需求和食材成本,制定最佳的饮食计划。
问题描述希望根据自己的营养需求,在预算限制下制定每日的饮食计划。
1确保摄入足够的蛋白质、碳水化合物、脂肪和维生素,并且希望最小化食材的总成本。
2已知不同食材的营养含量和价格,确定每种食材的最佳购买量,以满足所需的营养需求并节约成本。
模型的构建1. 变量定义:- Xi:购买的食材i的数量(单位:克)2. 目标函数:Minimize: ∑(i) Pi * Xi其中,Pi表示食材i的价格(单位:货币单位/克)3. 约束条件:蛋白质约束:∑(i) Ni * Xi ≥P碳水化合物约束:∑(i) Ci * Xi ≥C脂肪约束:∑(i) Fi * Xi ≥ F维生素约束:∑(i) Vi * Xi ≥V预算约束:∑(i) Pi * Xi ≤ B非负约束:Xi ≥0为了模拟数据,我们将使用一个简化的饮食规划问题来说明。
假设我们有以下食材和相关参数:4 变量确定鸡胸肉:价格0.3 货币单位/克,蛋白质含量20g/100g,碳水化合物含量0g/100g,脂肪含量2g/100g,维生素含量0g/100g米饭:价格0.1 货币单位/克,蛋白质含量7g/100g,碳水化合物含量28g/100g,脂肪含量0.3g/100g,维生素含量0g/100g鸡蛋:价格0.2 货币单位/克,蛋白质含量13g/100g,碳水化合物含量1.1g/100g,脂肪含量10g/100g,维生素含量0.2g/100g个人营养需求:蛋白质需求:每日需要摄入至少50g碳水化合物需求:每日需要摄入至少150g脂肪需求:每日需要摄入至少30g维生素需求:每日需要摄入至少0.5g预算限制:每日食材购买总成本不超过10 货币单位5建立线性规划模型(1)变量定义:X1:购买的鸡胸肉数量(单位:克)X2:购买的米饭数量(单位:克)X3:购买的鸡蛋数量(单位:克)(2)目标函数:Minimize: 0.3 * X1 + 0.1 * X2 + 0.2 * X3(3)约束条件:蛋白质约束:20/100 * X1 + 7/100 * X2 + 13/100 * X3 ≥50碳水化合物约束:0/100 * X1 + 28/100 * X2 + 1.1/100 * X3 ≥150脂肪约束:2/100 * X1 + 0.3/100 * X2 + 10/100 * X3 ≥30维生素约束:0/100 * X1 + 0/100 * X2 + 0.2/100 * X3 ≥0.5预算约束:0.3 * X1 + 0.1 * X2 + 0.2 * X3 ≤10非负约束:X1 ≥0, X2 ≥0, X3 ≥06 模型的spss求解与分析我们将根据上述数据和模型构建的线性规划模型来进行分析。
线性规划应用案例分析

通过整理,得到以下模型:
15
例6.(续)
目标函数:Max z = -15x11+25x12+15x13-30x21+10x22-40x31-10x33 约束条件: s.t. 0.5 x11-0.5 x12 -0.5 x13 ≥ 0 (原材料1不少于50%) -0.25x11+0.75x12 -0.25x13 ≤ 0 (原材料2不超过25%)
标准汽油
表 4
辛烷数
蒸汽压力(g/cm2)
库存量(L)
1
2 3 4
107.5
93.0 87.0 108.0
7.11×10-2
11.38 ×10-2 5.69×10-2 28.45 ×10-2 蒸汽压力(g/cm2)
380000
265200 408100 130100 产量需求
表 4 7
---
6
飞机汽油 辛烷数 1 2 不小于91 不小于100
0.75x21-0.25x22 -0.25x23 ≥ 0 (原材料1不少于25%)
-0.5 x21+0.5 x22 -0.5 x23 ≤ 0 (原材料2不超过50%)
x11+
x21 +
x31 ≤ 100
(供应量限制)
x12+
x13+
x22 +
x23 +
x32 ≤ 100
x33 ≤ 60
(供应量限制)
约束条件: 从第1个表中有:
x11≥0.5(x11+x12+x13)
x12≤0.25(x11+x12+x13)
x21≥0.25(x21+x22+x23) x22≤0.5(x21+x22+x23)
线性规划的应用

线性规划的应用引言:线性规划是一种优化问题的数学建模方法,广泛应用于各个领域,包括经济学、管理学、工程学等。
本文将介绍线性规划的基本概念、模型构建方法以及几个典型的应用案例。
一、线性规划的基本概念1. 目标函数:线性规划的目标是最大化或者最小化一个线性函数,该函数被称为目标函数。
目标函数通常表示为一个或者多个决策变量的线性组合。
2. 约束条件:线性规划问题还包括一组约束条件,这些条件限制了决策变量的取值范围。
约束条件通常表示为一组线性不等式或者等式。
3. 决策变量:决策变量是问题中需要确定的变量,它们的取值将影响目标函数的值。
决策变量通常表示为一个向量。
二、线性规划模型的构建方法1. 确定决策变量:根据问题的特点,确定需要决策的变量,并给出变量的取值范围。
2. 建立目标函数:根据问题的目标,构建一个线性函数,该函数描述了需要最大化或者最小化的目标。
3. 建立约束条件:根据问题中的限制条件,建立一组线性不等式或者等式,限制决策变量的取值范围。
4. 求解线性规划模型:使用线性规划求解方法,如单纯形法或者内点法,求解得到最优解。
三、线性规划的应用案例1. 生产计划优化:假设一个工厂有多个产品需要生产,每一个产品的生产需要一定的资源和时间。
通过线性规划,可以确定每一个产品的生产数量,以最大化总利润或者最小化总成本。
2. 运输问题:假设有多个供应商和多个需求点,每一个供应商的供应量和每一个需求点的需求量已知。
通过线性规划,可以确定每一个供应商向每一个需求点运输的数量,以最小化总运输成本。
3. 投资组合优化:假设有多个投资标的可供选择,每一个标的的收益率和风险已知。
通过线性规划,可以确定投资组合中每一个标的的投资比例,以最大化预期收益或者最小化预期风险。
4. 人力资源分配:假设一个公司有多个项目需要人力资源支持,每一个项目需要的人力资源和每一个人的能力已知。
通过线性规划,可以确定每一个项目分配的人力资源,以最大化项目的总产出或者最小化总成本。
线性规划应用案例

线性规划应⽤案例案例1 ⼴告战⽕烈鸟烤⾁饭店是⼀家位于佛罗⾥达的⾯向⾼消费阶层的⼀家饭店。
为了帮助计划下⼀季度的⼴告宣传计划,该饭店雇⽤了HJ⼴告公司。
饭店的管理层要求HJ推荐如何将⼴告预算分配在电视、⼴播和报纸上。
总的⼴告预算费⽤为279000美元。
在与⽕烈鸟烤⾁饭店管理层的⼀次会议上,HJ顾问提供了以下信息:关于每种⼴告媒体在⾏业内的宣传率、每则⼴告能达到的新受众数以及各⾃的⼴告成本。
⼴告媒体每则⼴告的宣传率每则⼴告能达到的新受众数成本(美元)电视90 4000 10000⼴播25 2000 3000报纸10 1000 1000宣传率被视作衡量⼴告对现有客户和潜在新客户的价值。
它是图像、消息反馈、可视程度、可闻形象等的函数。
正如预料的那样,最贵的电视⼴告有最⼤的宣传率,同时可达到最多的潜在新客户。
在这⼀点上,HJ顾问指出,关于每种媒体的宣传率和达到率的数据只在最初的⼏次⼴告应⽤中有效。
例如电视,它的90的宣传率和达到4000个潜在客户的数据只在头10次⼴告中有效,10次以后,电视⼴告的效⽤值会下降。
HJ顾问指出第10次以后播出的⼴告,宣传率降到55,同时到达的潜在客户也降到了1500。
对于⼴播媒体,上表中的数据在头15次⼴告中是有效的,到第15次后,宣传率降为20,能到达的潜在客户降为1200。
类似地,对于报纸,上表中的数据在头20次⼴告中是有效的,到第20次后,宣传率降为5,能到达的潜在客户为800.⽕烈鸟公司管理层接受了最⼤化各种媒体总宣传率作为这次⼴告运动的⽬标。
由于管理层很在意吸引新的客户,因此希望这次⼴告活动⾄少能达到100000个新客户。
为了平衡⼴告宣传活动以及充分利⽤⼴告媒体,⽕烈鸟公司管理团队还采纳了以下⽅针:1)⼴播⼴告运⽤的次数⾄少是电视⼴告的2倍;2)电视⼴告不能运⽤超过20次;3)电视⼴告的预算⾄少为140000美元;4)⼴播⼴告的预算最多不能超过99000美元;5)报纸⼴告的预算⾄少为30000美元。
【精品】线性规划案例

1。
人力资源分配问题例1.某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。
设司机和乘务人员分别在各时间段开始时上班,并连续工作8小时,问该公交线路应怎样安排司机和乘务人员,既能满足工作需要,又使配备司机和乘务人员的人数最少?解:设x i表示第i班次时开始上班的司机和乘务人员数,这样我们建立如下的数学模型。
目标函数:Min x1+x2+x3+x4+x5+x6约束条件:s.t.x1+x6≥60x1+x2≥70x2+x3≥60x3+x4≥50x4+x5≥20x5+x6≥30x1,x2,x3,x4,x5,x6≥0运用lingo求解:Objectivevalue:150。
0000ariableValueReducedCostX160。
000000。
000000X210.000000.000000X350。
000000。
000000X40.0000000.000000X530.000000.000000X60.0000000.000000例2.一家中型的百货商场,它对售货员的需求经过统计分析如下表所示。
为了保证售货人员充分休息,售货人员每周工作5天,休息两天,并要求休息的两天是连续的。
问应该如何安排售货人员的作息,既满足工作需要,又使配备的售货人员的人数最少?解:设x i(i=1,2,…,7)表示星期一至日开始休息的人数,这样我们建立如下的数学模型。
目标函数:Min x1+x2+x3+x4+x5+x6+x7约束条件:s.t.x1+x2+x3+x4+x5≥28x2+x3+x4+x5+x6≥15x3+x4+x5+x6+x7≥24x4+x5+x6+x7+x1≥25x5+x6+x7+x1+x2≥19x6+x7+x1+x2+x3≥31x7+x1+x2+x3+x4≥28x1,x2,x3,x4,x5,x6,x7≥0lingo求解Objectivevalue:36。
00000VariableValueReducedCostX112.000000。
线性规划应用案例

出售价格 ($/码)
可变成本 ($/码)
购买价格 ($/码)
1
16500
0.99
0.66
0.80
2
22000
0.86
0.55
0.70
3
62000
1.10
0.49
0.60
4
7500
1.24
0.51
0.70
5
62000
0.70
0.50
0.70
工厂有两种纺织机:帝备纺织机和常规纺织机。帝备纺织机更加多
样化,可以用于生产5种织物,常规纺织机只能生产3种织物。工厂共有 38台纺织机,包括8台帝备纺织机和30台常规纺织机。各种纺织机生产 各种织物的生产率如表2所示。从生产一种织物转换生产另一种织物的 时间可以忽略。
以及各自的广告成本。
广告媒体 电视 广播 报纸
每则广告的宣传 每则广告能达到
率
的新受众数
90
4000
25
2000
10
1000
成本(美元)
10000 3000 1000
宣传率被视作衡量广告对现有客户和潜在新客户的价值。它是图
像、消息反馈、可视程度、可闻形象等的函数。正如预料的那样,最贵
的电视广告有最大的宣传率,同时可达到最多的潜在新客户。 在这一点上,HJ顾问指出,关于每种媒体的宣传率和达到率的数据
的不同。(目标函数系数的取值范围在这两种模型中的含义 有什么不同)
案例3 Cinergy煤分配
Cinergy公司为位于印第安纳、肯塔基及俄亥俄州的客户发电并配 送电力。该公司每年运作其燃煤及燃气发电厂所需的燃料花费为7.25亿 —7.5亿美元。发电厂所需的燃料中,92%—95%为煤炭。Cinergy公司 有10家燃煤发电厂,5家坐落在内陆,另外5家坐落在俄亥俄河上,有的 工厂不止一套发电设备。作为全美第7大燃煤单位,Cinergy公司每年使 用2800万—2900万吨煤,平均每天花费约200万元。
线性规划应用案例
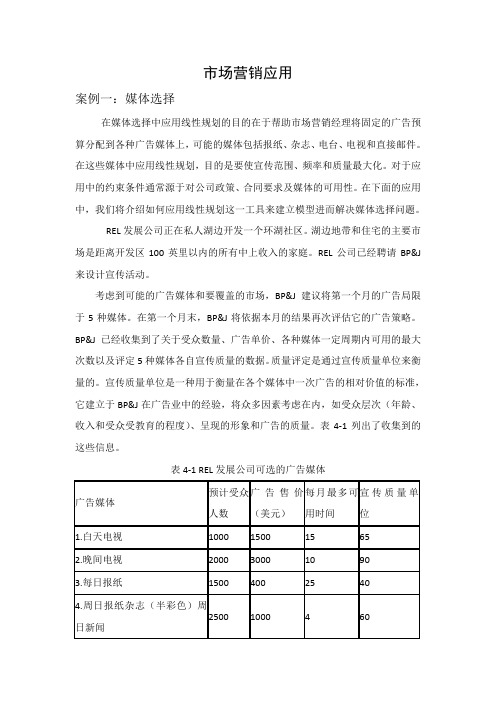
市场营销应用案例一:媒体选择在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。
在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。
对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。
在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。
REL发展公司正在私人湖边开发一个环湖社区。
湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。
REL公司已经聘请BP&J 来设计宣传活动。
考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。
在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。
BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。
质量评定是通过宣传质量单位来衡量的。
宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。
表4-1列出了收集到的这些信息。
表4-1 REL发展公司可选的广告媒体5.电台早8:00或晚5:00新闻3001003020(30秒)KNOP台REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。
而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。
应当推荐何种广告媒体选择计划呢案例二:市场调查公司开展市场营销调查以了解消费者个性特点、态度以及偏好。
专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。
市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。
运筹学线性规划案例

运筹学线性规划案例线性规划是运筹学中的一个重要分支,它主要研究如何利用数学模型来解决最优化问题。
在实际应用中,线性规划可以帮助企业做出最佳的决策,使资源得到最大化利用。
本文将通过一个实际案例来介绍线性规划的应用,以便读者更好地理解和掌握这一方法。
假设某公司生产两种产品A和B,它们分别需要机器加工和人工装配。
公司拥有的机器和人工资源分别为每周80小时和60人天。
产品A每单位需要机器加工2小时,人工装配3人天;产品B每单位需要机器加工3小时,人工装配2人天。
每单位产品A的利润为2000元,产品B的利润为3000元。
现在的问题是,如何安排生产计划,才能使得利润最大化呢?首先,我们可以将该问题建立成数学模型。
假设x1和x2分别表示生产产品A 和B的单位数,则该问题可以表示为:Max Z=2000x1+3000x2。
约束条件为:2x1+3x2≤80。
3x1+2x2≤60。
x1≥0,x2≥0。
接下来,我们可以通过线性规划的方法来求解最优解。
在这里,我们不妨使用单纯形法来进行求解。
首先,我们将约束条件转化成标准形式,得到:2x1+3x2+s1=80。
3x1+2x2+s2=60。
x1≥0,x2≥0。
然后,我们构造初始单纯形表,并进行单纯形法的迭代计算。
最终得到最优解为x1=20,x2=10,此时利润最大为80000元。
通过这个简单的案例,我们可以看到线性规划在实际中的应用。
通过建立数学模型和运用线性规划方法,我们可以很好地解决类似的最优化问题,使得资源得到最大化利用,从而帮助企业做出更加科学合理的决策。
总之,线性规划作为运筹学中的重要方法,具有广泛的应用前景。
通过不断地学习和实践,我们可以更好地掌握线性规划的原理和方法,为实际问题的解决提供更加科学的支持。
希望本文的案例能够帮助读者更好地理解线性规划的应用,从而在实际工作中能够更好地运用这一方法,取得更好的效果。
线性规划案例及应用

案例及应用:麦基油漆公司麦基油漆公司在新英格兰、太平洋西岸中部和中西部地区诸州经营4个工厂和5个仓库。
该公司生产的油漆,85%供国内外用户消费,其余的供应公司在纽约地区开设的15家商店,再由它们零售分配给600个独立的特许专营商。
最近几年,麦基公司的油漆占市场销售量的比例下降了6个百分点。
15家最好的零售商已转向经营其他公司的油漆。
店主们说售货盈利太少。
销售经理维恩在了解和认真研究了这种情况后,在一份报告中写道:“在产品质量和交货期方面,我们和多数竞争对手一样一直做得不错,或者说比他们还要好一些,但是在价格方面我们未能占上风。
在4种销售量最大的油漆中,我们有3种定价最高。
为了提高我们的市场占有率,我认为我们至少必须把各种油漆的定价削减5% ,能削减7% 则更好。
我还建议在各地多开设一些自己的零售商店,这将有助于补偿因削价造成的损失,同时能促使整个销售量达到应有的水平。
”T.A麦基是公司的常务付总经理,他的哥哥H.B麦基任总经理兼司库。
在研究维恩的报告时,T.A麦基说:“汉克,你关于推进降低成本的想法或许是对的。
我们的毛利已很微薄,而金融市场的行情你比我更清楚。
如果你认为我们无法以合适的条件获得资金在纽约市外增设联营零售店的话,我们就只能通过降低成本来弥补削价所造成的损失。
”麦基公司的4个工厂的设备都能生产公司销售的各种油漆。
因种种原因,各厂的平均直接单位成本并不一致。
有一个工厂的颜料粉碎机和调和装置已使用了20年之久,而其余3个厂的才分别使用了3年、5年和6年,因此,老厂的每工时劳动生产率和设备的运行与维修的劳动成本较高。
由于运输距离和费用的不同,各厂按离岸价格计算的原料(如颜料、化工产品和调和机械器具等,成本也不相同。
另外,各厂在工资方面也略有差异)。
麦基公司生产油漆的工艺简单地说包含三个过程。
首先,在两个旋转的大钢罐内把颜料彻底粉碎成糊状,使它们达到规定的颜色、浓度和均匀度。
其次,把粉碎后的颜料同选好的载色剂(通常用油或清漆)投入巨大的容器中,通过机械搅拌器进行调和。
线性规划的应用总结

线性规划的应用总结线性规划是一种常见的数学优化问题,它可以在给定的约束条件下,寻找一个线性目标函数的最优解。
线性规划广泛应用于各个领域,如经济学、工程学、生产管理等。
本文将对线性规划的应用进行总结,并介绍一些常见的应用案例。
一、线性规划的介绍线性规划的基本形式可以表示为:Max(或Min)Z = C1X1 + C2X2 + … + CnXnSubject to:A11X1 + A12X2 + … + A1nXn ≤ B1A21X1 + A22X2 + … + A2nXn ≤ B2…Am1X1 + Am2X2 + … + AmnXn ≤ Bm其中,X1, X2, …, Xn为决策变量;C1, C2, …, Cn为目标函数的系数;A11, A12, …, Amn为约束条件矩阵的系数;B1, B2, …, Bm为约束条件的右侧常数。
二、经济学领域中的应用在线性规划中,经济学领域是最常见的应用之一。
其中一个典型的案例是生产计划。
假设一个工厂生产多种产品,通过线性规划可以确定每种产品的产量,以实现最大利润。
约束条件包括生产成本、原材料数量和市场需求。
另一个经济学中的应用是资产组合。
投资者想要构建一个资产组合,通过线性规划可以确定每种资产的投资比例,以实现最大的收益或最小的风险。
约束条件包括投资额度、收益率和风险指标。
三、工程学领域中的应用在工程学领域,线性规划被广泛应用于资源分配和调度问题。
例如,在项目管理中,可以使用线性规划来优化资源的分配,以满足项目的时间和成本约束。
另一个常见的应用是运输问题。
假设有多个供应地和多个需求地,通过线性规划可以确定每个供应地到需求地的货物运输量,以实现最低的运输成本。
约束条件包括供应地的产能、需求地的需求量和运输通路的限制。
四、生产管理领域中的应用线性规划在生产管理领域中也有广泛的应用。
一个典型的应用是生产调度问题。
假设一个工厂有多个订单需要完成,通过线性规划可以确定每个订单的开始时间和完成时间,以及每个订单的生产量,以最大化生产效率。
线性规划案例5

问题描述:
靠近某河流有两个化工厂(见图1-1),流经第一化工厂的河流流量为每天500万立方米,在两个工厂之间有一条流量为每天200万立方米的支流。
化工厂1每天排放含有某种有害物质的工业污水2万立方米,化工厂2每天排放的工业污水为1.4万立方米。
从化工厂1排出的污水流到化工厂2前,有20%可自然净化。
根据环保要求,河流中工业污水的含量应不大于0.2%。
因此两个工厂都需处理一部分工业污水。
化工厂1处理污水的成本是1000元/万立方米,化工厂2处理污水的成本是800元/万立方米。
问:
在满足环保要求的条件下,每厂各应处理多少工业污水,使两个工厂处理工业污水的总费用最小。
线性规划与圆

线性规划与圆线性规划是一种数学优化方法,广泛应用于工程、经济、管理等领域。
它的目标是在给定的约束条件下,寻觅一个线性模型的最优解。
而圆是一个具有无限多个点的几何形状,由一个固定的中心点和与中心点距离相等的所有点组成。
线性规划与圆之间的联系并不直接,但在某些情况下可以通过线性规划来解决与圆相关的问题。
下面将介绍两个与线性规划与圆相关的实际应用案例。
案例一:最小圆覆盖问题在一个平面上给定一组点,求一个圆,使得这个圆能够覆盖所有的点,并且圆的半径尽可能小。
这个问题可以转化为一个线性规划问题。
首先,我们可以定义一个变量x表示圆心的横坐标,变量y表示圆心的纵坐标,变量r表示圆的半径。
然后,我们可以设置一组约束条件,确保圆能够覆盖所有的点。
例如,对于每一个点(xi, yi),我们可以设置一个约束条件(x-xi)^2 + (y-yi)^2 ≤ r^2,表示该点在圆的内部。
此外,我们还可以设置一个约束条件,确保圆的半径尽可能小,例如r ≥ 0。
最后,我们可以设置一个目标函数,使得圆的半径最小化,例如minimize r。
通过求解这个线性规划问题,我们可以得到最小圆覆盖问题的最优解。
案例二:圆的最大包含问题在一个平面上给定一个圆和一组点,求一个半径最大的圆,使得这个圆能够彻底包含所有的点。
同样,这个问题也可以转化为一个线性规划问题。
首先,我们可以定义一个变量x表示圆心的横坐标,变量y表示圆心的纵坐标,变量r表示圆的半径。
然后,我们可以设置一组约束条件,确保圆能够彻底包含所有的点。
例如,对于每一个点(xi, yi),我们可以设置一个约束条件(x-xi)^2 + (y-yi)^2 ≤ r^2,表示该点在圆的内部。
此外,我们还可以设置一个约束条件,确保圆的半径尽可能大,例如r ≥ 0。
最后,我们可以设置一个目标函数,使得圆的半径最大化,例如maximize r。
通过求解这个线性规划问题,我们可以得到圆的最大包含问题的最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.人力资源分配问题设司机和乘务人员分别在各时间段开始时上班,并连续工作8小时,问该公交线路应怎样安排司机和乘务人员,既能满足工作需要,又使配备司机和乘务人员的人数最少?解:设x i 表示第i班次时开始上班的司机和乘务人员数,这样我们建立如下的数学模型。
目标函数:Min x1 + x2 + x3 + x4 + x5 + x6约束条件:s.t. x1 + x6 ≥60x1 + x2 ≥70x2 + x3 ≥60x3 + x4 ≥50x4 + x5 ≥20x5 + x6 ≥30x1,x2,x3,x4,x5,x6 ≥0运用lingo求解:Objective value: 150.0000ariable Value Reduced Cost X1 60.00000 0.000000X2 10.00000 0.000000X3 50.00000 0.000000X4 0.000000 0.000000X5 30.00000 0.000000X6 0.000000 0.000000例2.一家中型的百货商场,它对售货员的需求经过统计分析如下表所示。
为了保证售货人员充分休息,售货人员每周工作5天,休息两天,并要求休息的两天是连续的。
问应该如何安排售货人员的作息,既满足工作需要,又使配备的售货人员的人数最少?解:设x i ( i = 1,2,…,7)表示星期一至日开始休息的人数,这样我们建立如下的数学模型。
目标函数:Min x1 + x2 + x3 + x4 + x5 + x6 + x7约束条件:s.t. x1 + x2 + x3 + x4 + x5 ≥28x2 + x3 + x4 + x5 + x6 ≥15x3 + x4 + x5 + x6 + x7 ≥24x4 + x5 + x6 + x7 + x1 ≥25x5 + x6 + x7 + x1 + x2 ≥19x6 + x7 + x1 + x2 + x3 ≥31x7 + x1 + x2 + x3 + x4 ≥28x1,x2,x3,x4,x5,x6,x7 ≥0lingo求解Objective value: 36.00000Variable Value Reduced Cost X1 12.00000 0.000000X2 0.000000 0.3333333 X3 11.00000 0.000000X4 5.000000 0.000000X5 0.000000 0.000000X6 8.000000 0.000000X7 0.000000 0.000000例3. 某储蓄所每天的营业时间为上午9:00到下午17:00,根据经验,每天不同时间段所需要储蓄所可以雇佣全时和半时两类服务员。
全时服务员每天报酬为100元,从上午9:00到下午17:00工作,但中午12:00到下午14:00之间必须安排1小时的午餐时间;储蓄所每天可以雇佣不超过3名的半时服务员,每个半时服务员必须连续工作4小时,报酬为40元。
问:1) 储蓄所应该如何雇佣全时和半时两类服务员?2) 如果不能雇佣半时服务员,每天至少增加多少经费?3) 如果雇佣半时服务员的数量没有限制,每天可以减少多少经费?解:设x1, x2分别表示12~13,13~14进行午餐的全时服务人员,y1,y2,y3,y4,y5分别表示9~10,10~11,11~12,12~13,13~14开始工作的半时服务人员,则问题1的模型如下所示:min=100*x1+100*x2+40*y1+40*y2+40*y3+40*y4+40*y5;x1+x2+y1>4;x1+x2+y1+y2>3;x1+x2+y1+y2+y3>4;x2+y1+y2+y3+y4>6;x1+y2+y3+y4+y5>5;x1+x2+y3+y4+y5>6;x1+x2+y4+y5>8;x1+x2+y5>8;y1+y2+y3+y4+y5<3;@gin(x1);@gin(x2);@gin(y1);@gin(y2);@gin(y3);@gin(y4);@gin(y5); Objective value: 820.0000Variable Value Reduced Cost X1 3.000000 100.0000 X2 4.000000 100.0000 Y1 0.000000 40.00000 Y2 2.000000 40.00000 Y3 0.000000 40.00000 Y4 0.000000 40.00000 Y5 1.000000 40.000002)把y1+y2+y3+y4+y5<3;修改为y1+y2+y3+y4+y5=0;min=100*x1+100*x2+40*y1+40*y2+40*y3+40*y4+40*y5;x1+x2+y1>4;x1+x2+y1+y2>3;x1+x2+y1+y2+y3>4;x2+y1+y2+y3+y4>6;x1+y2+y3+y4+y5>5;x1+x2+y3+y4+y5>6;x1+x2+y4+y5>8;x1+x2+y5>8;y1+y2+y3+y4+y5=0;@gin(x1);@gin(x2);@gin(y1);@gin(y2);@gin(y3);@gin(y4);@gin(y5); Objective value: 1100.000Variable Value Reduced Cost X1 5.000000 0.000000 X2 6.000000 0.000000 Y1 0.000000 100.0000 Y2 0.000000 0.000000 Y3 0.000000 0.000000 Y4 0.000000 0.000000 Y5 0.000000 100.00003)把y1+y2+y3+y4+y5<3;去掉min=100*x1+100*x2+40*y1+40*y2+40*y3+40*y4+40*y5;x1+x2+y1>4;x1+x2+y1+y2>3;x1+x2+y1+y2+y3>4;x2+y1+y2+y3+y4>6;x1+y2+y3+y4+y5>5;x1+x2+y3+y4+y5>6;x1+x2+y4+y5>8;x1+x2+y5>8;@gin(x1);@gin(x2);@gin(y1);@gin(y2);@gin(y3);@gin(y4);@gin(y5);运用lingo求解Objective value: 560.0000Variable Value Reduced CostX1 0.000000 100.0000X2 0.000000 100.0000Y1 6.000000 40.00000Y2 0.000000 40.00000Y3 0.000000 40.00000Y4 0.000000 40.00000Y5 8.000000 40.000002. 生产计划问题例4.某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。
数据如表。
问:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应解:设x1,x2,x3 分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数,x4,x5 分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。
求x i 的利润:利润= 售价- 各成本之和产品甲全部自制的利润=23-(3+2+3)=15产品甲铸造外协,其余自制的利润=23-(5+2+3)=13产品乙全部自制的利润=18-(5+1+2)=10产品乙铸造外协,其余自制的利润=18-(6+1+2)=9产品丙的利润=16-(4+3+2)=7可得到x i (i = 1,2,3,4,5)的利润分别为15、10、7、13、9 元。
通过以上分析,可建立如下的数学模型:目标函数:Max 15x1 + 10x2 + 7x3 + 13x4 + 9x5约束条件:5x1 + 10x2 + 7x3 ≤80006x1 + 4x2 + 8x3 + 6x4 + 4x5 ≤120003x1 + 2x2 + 2x3 + 3x4 + 2x5 ≤10000x1,x2,x3,x4,x5 ≥0lingo求解Objective value: 29400.00Variable Value Reduced Cost X1 1600.000 0.000000X2 0.000000 2.000000X3 0.000000 13.10000X4 0.000000 0.5000000X5 600.0000 0.000000例5.永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A 工序;有三种规格的设备B1、B2、B3能完成B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工。
数据如表。
问:为使该厂获得最大利润,应如何制定产品加工方案?解:设x ijk 表示第j 个工序在第k 种设备上加工的第i 种产品的数量。
建立如下的数学模型:s.t. 5x111 + 10x211 ≤6000 (设备A1 )7x112 + 9x212 + 12x312 ≤10000 (设备A2 )6x121 + 8x221 ≤4000 (设备B1 )4x122 + 11x322 ≤7000 (设备B2 )7x123 ≤4000 (设备B3 )x111+ x112- x121- x122- x123 = 0 (Ⅰ产品在A、B工序加工的数量相等)x211+ x212- x221 = 0 (Ⅱ产品在A、B工序加工的数量相等)x312 - x322 = 0 (Ⅲ产品在A、B工序加工的数量相等)x ijk ≥0 , i = 1,2,3; j = 1,2; k = 1,2,3目标函数为计算利润最大化,利润的计算公式为:利润= [(销售单价- 原料单价)* 产品件数]之和-(每台时的设备费用*设备实际使用的总台时数)之和。
这样得到目标函数:Max(1.25-0.25)(x111+x112)+(2-0.35)x221+(2.80-0.5)x312 –300/6000(5x111+10x211)-321/10000(7x112+9x212+12x312)-250/4000(6x121+8x221)-783/7000(4x122+11x322)-200/4000(7x123).经整理可得:Max0.75x111+0.7753x112+1.15x211+1.3611x212+1.9148x312-0.375x121-0.5x221-0.4475x122-1.2304x322-0.35x123运用lingo求解Objective value: 1146.514Variable Value Reduced CostX111 1200.000 0.000000X112 230.0493 0.000000X211 0.000000 0.3101897X212 500.0000 0.000000X312 324.1379 0.000000X121 0.000000 0.2530095X221 500.0000 0.000000X122 858.6207 0.000000X322 324.1379 0.000000X123 571.4286 0.000000近似有X111=1200,X112=230,X211=0,X212=500,X312=324, X121=0,X221=500 X122=859, X322=324,X123=571Objective value: 1146.362利用整数规划Objective value: 1146.362Variable Value Reduced CostX111 1200.000 -0.7500000X112 230.0000 -0.7753000X211 0.000000 -1.150000X212 500.0000 -1.361100X312 324.0000 -1.914800X121 0.000000 0.3750000X221 500.0000 0.5000000X122 859.0000 0.4475000X322 324.0000 1.230400X123 571.0000 0.3500000例6. 双层卷焊钢管是光明制造厂1990从意大利引进的主导民用产品,生产流程为:钢带镀铜→镀铜带精剪→制管。
