高中数学苏教版高二选修2-2学业分层测评:第二章_推理与证明_14 含解析
苏教版数学高二- 选修2-2第二章《推理与证明》综合检测

综合检测(二)第2章推理与证明(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分.请把正确的答案填在题中横线上)1.下面几种推理是合情推理的序号的是________.①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°;③某次考试张军成绩是100分,由此推出全班同学成绩都是100分;④三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得凸多边形内角和是(n-2)·180°.【解析】①是类比推理;②是归纳推理;③不属于合情推理;④是归纳推理.【答案】①②④2.若大前提是:任何实数的平方都大于0,小前提是:a∈R,结论是:a2>0,那么这个演绎推理错在________(填“大前提”,“小前提”或“推理过程”).【解析】a=0时,a2=0,因此大前提错误.【答案】大前提3.用数学归纳法证明12+22+…+(n-1)2+n2+(n-1)2+…+22+12=n(2n2+1)3时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是________.【解析】由等式的特征,左边应添加(k+1)2+k2.【答案】(k+1)2+k24.下列四个图形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为________.图1【解析】由图形可知,着色三角形的个数依次为:1,3,9,27,…,故a n=3n-1.【答案】3n-15.已知a>0,b>0,m=lg a+b2,n=lga+b2,则m与n的大小关系为________.【解析】∵(a+b)2=a+b+2ab>a+b>0,∴a+b>a+b>0,则a+b2>a+b2.∴lg a+b2>lga+b2,则m>n.【答案】m>n6.已知圆x2+y2=r2(r>0)的面积为S=πr2,由此类比椭圆x2a2+y2b2=1(a>b>0)的面积最有可能是________.【解析】将圆看作椭圆的极端情况,即a=b情形.∴类比S圆=πr2,得椭圆面积S=πab.【答案】πab7.已知结论“若a1,a2∈{正实数},且a1+a2=1,则1a1+1a2≥4”,请猜想若a1,a2,…,a n∈{正实数},且a1+a2+…+a n=1,则1a1+1a2+…+1a n≥________.【解析】左边是2项,右边为22,猜想:左边是n项,右边为n2.【答案】n2图28.现有一个关于平面图形的命题:如图2,在一个平面内有两个边长都是a 的正方形,其中一个正方形的某个顶点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为a24,类比到空间,有两个棱长均为a的正方体,其中一个正方体的某个顶点在另一个正方体的中心,则这两个正方体重叠部分的体积恒为________.【解析】正方形类比到正方体,重叠面积类比到重叠体积,则S=a24,类比得V=(a2)3=a38.【答案】a3 89.将全体正整数排成一个三角形数阵:12 345 6789101112131415根据以上排列规律,数阵中第n(n≥3)行的从左到右的第三个数是________.【解析】前n-1行共有正整数1+2+3+…+(n-1)=n2-n2个,∴第n行第3个数是n2-n2+3=n2-n+62.【答案】n2-n+6210.(2013·南京高二检测)已知数列{a n}为等差数列,数列{b n}是各项均为正数的等比数列,且公比q>1,若a1=b1,a2 013=b2 013,则a1 007与b1 007的大小关系是________.【解析】 由2a 1 007=a 1+a 2 013,得a 1 007=a 1+a 2 0132.又b 21 007=b 1·b 2 013,得b 1 007=b 1·b 2 013,∵a 1=b 1>0,a 2 013=b 2 013>0,且a 1≠a 2 013, ∴a 1 007>b 1 007. 【答案】 a 1 007>b 1 00711.一切奇数都不能被2整除,2100+1是奇数,所以2100+1不能被2整除,其“三段论”的形式为:大前提:一切奇数都不能被2整除. 小前提:________.结论:所以2100+1不能被2整除. 【答案】 2100+1是奇数12.求证:1+5<23的证明如下:因为1+5和23都是正数,所以为了证明1+5<23, 只需证明(1+5)2<(23)2, 展开得6+25<12,即5<3, 只需证明5<9.因为5<9成立. 所以不等式1+5<23成立. 上述证明过程应用的方法是________. 【答案】 分析法13.用反证法证明命题“a ,b ∈N *,ab 可被5整除, 那么a ,b 至少有1个能被5整除”,则假设的内容是________.【解析】 “a 、b 中至少有一个能被5整除”的否定为“a ,b 都不能被5整除”.【答案】 a ,b 都不能被5整除14.(2013·徐州高二检测)在平面几何中,△ABC 的内角平分线CE 分AB 所成线段的比AE EB =ACBC ,把这个结论类比到空间:在三棱锥A —BCD 中(如图3所示),面DEC 平分二面角A —CD —B 且与AB 相交于E ,则得到的类比的结论是________.图3【解析】 CE 平分角ACB ,而面CDE 平分二面角A —CD —B. ∴AC BC 可类比成S △ACD S △BCD ,故结论为AE EB =S △ACDS △BCD .【答案】 AE EB =S △ACDS △BCD二、解答题(本大题共6小题,共90分.解答时应写出必要的文字说明,证明过程或演算步骤)15.(本小题满分14分)观察:(1)sin 210°+cos 240°+sin 10°cos 40°=34; (2)sin 26°+cos 236°+sin 6°cos 36°=34.由上面两题的结构规律,你能否提出一个猜想?并证明你的猜想. 【解】 观察40°-10°=30°,36°-6°=30°,由此猜想: sin 2α+cos 2(30°+α)+sin α·cos(30°+α)=34. 证明:sin 2α+cos 2(30°+α)+sin α·cos(30°+α)=1-cos 2α2+1+cos (60°+2α)2+sin α(32cos α-12sin α) =1-cos 2α2+12[1+(12cos 2α-32sin 2α)]+34sin 2α-12sin 2α =1-14cos 2α-34sin 2α+34sin 2α-12×1-cos 2α2=3 4.16.(本小题满分14分)已知0<a<1,求证:1a+41-a≥9.【证明】∵0<a<1,∴1-a>0.欲证1a +41-a≥9成立,只需证明1-a+4a≥9a(1-a).整理移项9a2-6a+1≥0.即证明(3a-1)2≥0.∵a∈(0,1),∴(3a-1)2≥0显然成立.故1 a +41-a≥9成立.17.(本小题满分14分)(2013·无锡高二检测)已知函数f(x)=log2(x+2),a,b,c,是两两不相等的正数,且a,b,c成等比数列,试判断f(a)+f(c)与2f(b)的大小关系,并证明你的结论.【解】f(a)+f(c)>2f(b),证明如下:∵a,b,c是不相等的正数,∴a+c>2ac,∵b2=ac,∴ac+2(a+c)>b2+4b,即ac+2(a+c)+4>b2+4b+4,从而(a+2)(c+2)>(b+2)2,∵f(x)=log2x是增函数,∴log2(a+2)(c+2)>log2(b+2)2,即log2(a+2)+log2(c+2)>2log2(b+2)故f(a)+f(c)>2f(b).18.(本小题满分16分)如图4甲,在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;若类比该命题,如图乙,三棱锥A—BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题?图4【解】命题是:三棱锥A—BCD中,AD⊥面ABC,若A点在三角形BCD 所在平面内的射影为M,则有S2△ABC=S△BCM·S△BCD,是一个真命题.证明如下:在图乙中,连结DM,并延长交BC于E,连结AE,则有DE⊥BC,AE⊥BC.因为AD⊥面ABC,所以AD⊥AE.因为AM⊥DE,所以AE2=EM·ED.于是S2△ABC=(12BC·AE)2=(12BC·EM)·(12BC·ED)=S△BCM·S△BCD.19.(本小题满分16分)已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.【解】(1)当a=1,b=2时,f(x)=(x-1)2(x-2).∴f′(x)=(x-1)(3x-5),则f′(2)=1.又f(2)=(2-1)2(2-2)=0.∴f(x)在点(2,0)处的切线方程为y =x -2. (2)因为f′(x)=3(x -a)(x -a +2b3), 由于a <b ,故a <a +2b 3,所以f(x)的两个极值点为x =a ,x =a +2b 3. 不妨设x 1=a ,x 2=a +2b3, 因为x 3≠x 1,x 3≠x 2, 且x 3是f(x)的零点. 故x 3=b.又因为a +2b 3-a =2(b -a +2b3), 故可令x 4=12(a +a +2b 3)=2a +b 3,此时,a ,2a +b 3,a +2b3,b 依次成等差数列, 所以存在实数x 4满足题意,且x 4=2a +b3.20.(本小题满分16分)已知f(n)=1+123+133+143+…+1n 3,g(n)=32-12n 2,n ∈N *.(1)当n =1,2,3时,试比较f(n)与g(n)的大小关系; (2)猜想f(n)与g(n)的大小关系,并给出证明.【解】 (1)当n =1时,f(1)=1,g(1)=1,所以f(1)=g(1); 当n =2时,f(2)=98,g(2)=118,所以f(2)<g(2);当n =3时,f(3)=251216,g(3)=312216, 所以f(3)<g(3).(2)由(1),猜想f(n)≤g(n),下面用数学归纳法给出证明: ①当n =1,2,3时,不等式显然成立. ②假设当n =k(k ≥3)时不等式成立, 即1+123+133+143+…+1k 3<32-12k 2, 那么,当n =k +1时, f(k +1)=f(k)+1(k +1)3<32-12k 2+1(k +1)3, 因为12(k +1)2+1(k +1)3-12k 2=k +32(k +1)3-12k 2=-3k -12(k +1)3k 2<0, ∴-12k 2+1(k +1)3<-12(k +1)2,因此32-12k 2+1(k +1)3<32-12(k +1)2, ∴f(k +1)<32-12(k +1)2, ∴当n =k +1时成立. 由①②可知,对一切n ∈N *, 都有f(n)≤g(n)成立.。
苏教版高中数学必修2学业分层测评14 两点式 Word版含解析

学业分层测评(十四)(建议用时:45分钟)[学业达标]一、填空题1.直线l过点(-1,2)和点(2,5),则直线l的方程为________________.【解析】由直线的两点式方程得y-25-2=x-(-1)2-(-1),整理得x-y+3=0.【答案】x-y+3=02.一条直线不与坐标轴平行或重合,则它的方程________.①可以写成两点式或截距式;②可以写成两点式或斜截式或点斜式;③可以写成点斜式或截距式;④可以写成两点式或截距式或斜截式或点斜式.【解析】由于直线不与坐标轴平行或重合,所以直线的斜率存在,且直线上任意两点的横坐标及纵坐标都不相同,所以直线能写成两点式或斜截式或点斜式.由于直线在坐标轴上的截距有可能为0,所以直线不一定能写成截距式.【答案】②3.直线xa+yb=1过第一、二、三象限,则a________0,b________0.【解析】因为直线l在x轴上的截距为a,在y轴上的截距为b,且经过第一、二、三象限,故a<0,b>0.【答案】<>4.若直线l过定点(-1,-1)和(2,5),且点(2 017,a)在l上,则a的值为________.【解析】∵(-1,-1),(2,5),(2 017,a)三点共线,∴5-(-1)2-(-1)=a-52 017-2,∴a=4 035.【答案】 4 0355.经过点A(2,1),在x轴上的截距为-2的直线方程是________. 【导学号:60420059】【解析】 由题意知直线过两点(2,1),(-2,0),由两点式方程可得所求直线的方程为y -01-0=x +22+2,即x -4y +2=0. 【答案】 x -4y +2=06.两条直线l 1:x a -y b =1和l 2:x b -y a =1在同一直角坐标系中的图象可以是________.图2-1-5【解析】 化为截距式x a +y -b =1,x b +y -a=1. 假定l 1,判断a ,b ,确定l 2的位置.【答案】 ①7.已知A (3,0),B (0,4),动点P (x 0,y 0)在线段AB 上移动,则4x 0+3y 0的值等于________.【解析】 AB 所在直线方程为x 3+y 4=1,则x 03+y 04=1,即4x 0+3y 0=12.【答案】 128.直线mx +ny +p =0(mn ≠0)在两坐标轴上的截距相等,则m ,n ,p 满足的条件是________.【解析】 当p =0时,直线在两轴上的截距相等,当p ≠0时,因mn ≠0,∴-p m =-p n ,即m =n .【答案】 p =0或p ≠0且m =n二、解答题9.已知直线l 与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l 的方程:(1)过定点A (-3,4);(2)斜率为16.【解】 (1)设直线l 的方程是y =k (x +3)+4,它在x 轴,y 轴上的截距分别是-4k -3,3k +4,由已知,得(3k +4)⎝ ⎛⎭⎪⎫-4k -3=±6, 解得k 1=-23或k 2=-83.故直线l 的方程为2x +3y -6=0或8x +3y +12=0.(2)设直线l 在y 轴上的截距为b ,则直线l 的方程是y =16x +b ,它在x 轴上的截距是-6b ,由已知,得|-6b ·b |=6,∴b =±1.∴直线l 的方程为x -6y +6=0或x -6y -6=0.10.已知直线l 过点P (-5,-4)且与两坐标轴围成的三角形面积为5,求直线l 的方程.【解】 设直线l 的方程为x a +y b =1,则有⎩⎪⎨⎪⎧ -5a +-4b =1,12|a |·|b |=5,解得⎩⎨⎧ a =5,b =-2或⎩⎪⎨⎪⎧ a =-52,b =4.故直线l 的方程为x 5-y 2=1或-2x 5+y 4=1.即2x -5y -10=0或8x -5y +20=0.[能力提升]1.过点P (2,-1),在x 轴和y 轴上的截距分别为a ,b ,且满足a =3b ,则直线的方程为__________.【解析】 当b =0时,设直线方程为y =kx ,则2k =-1,所以k =-12,所以直线方程为y =-12x ,即x +2y =0.当b ≠0时,设直线方程为x 3b +y b =1,则23b +-1b =1,解得b =-13.所以直线方程为-x -3y =1,即x +3y +1=0.【答案】 x +2y =0或x +3y +1=02.已知实数x ,y 满足y =-2x +8,且2≤x ≤3,求y x 的取值范围是______.【解析】 如图所示,由于点(x ,y )满足关系式2x +y =8,且2≤x ≤3,可知点P (x ,y )在线段AB 上移动,并且A ,B 两点的坐标可分别求得为A (2,4),B (3,2).由于y x 的几何意义是直线OP 的斜率,且k OA =2,k OB =23,所以y x ∈⎣⎢⎡⎦⎥⎤23,2. 【答案】 ⎣⎢⎡⎦⎥⎤23,2 3.已知两点A (3,0),B (0,4),动点P (x ,y )在线段AB 上运动,则xy 的最大值为________.【解析】 由A ,B ,P 三点共线,得y -0x -3=4-00-3, 即y =-43(x -3),x ∈[0,3].∴xy =x ·⎣⎢⎡⎦⎥⎤-43(x -3)=-43(x 2-3x ) =-43⎝ ⎛⎭⎪⎫x -322+3. 当x =32时,xy 取得最大值3,此时x =32,y =2,即点P ⎝ ⎛⎭⎪⎫32,2. 【答案】 34.直线l 与两坐标轴在第一象限所围成的三角形的面积为2,两截距之差的绝对值为3,求直线l 的方程.【解】 由题意可知,设直线l 与两坐标轴的交点分别为(a,0),(0,b ),且有a >0,b >0,根据题中两个条件,可得⎩⎪⎨⎪⎧ S =12ab =2,|a -b |=3,解得⎩⎨⎧ a =4,b =1,或⎩⎨⎧a =1,b =4.所以直线l 的方程为x 4+y =1或x +y 4=1.。
苏教版高中数学必修二第2章学业分层测评12.docx

高中数学学习材料马鸣风萧萧*整理制作学业分层测评(十二)(建议用时:45分钟)[学业达标]一、填空题1.对于样本频率分布折线图与总体密度曲线的关系,下列说法中正确的是________.(填序号)①频率分布折线图与总体密度曲线无关;②频率分布折线图就是总体密度曲线;③样本容量很大的频率分布折线图就是总体密度曲线;④如果样本容量无限增大、分组的组距无限减小,那么频率分布折线图就会无限接近总体密度曲线.【解析】由总体密度曲线定义知④正确.【答案】④2.为了解高二年级女生的身高情况,从中抽出20名进行测量,所得结果如下:(单位:cm)149159142160156163145150148151156144148149153143168168152155在列样本频率分布表的过程中,如果设组距为4 cm,那么组数为________.【解析】极大值为168,极小值为142,极差为168-142=26,根据组距=极差组数,知组数为7. 【答案】 73.一个容量为40的样本数据,分组后,组距与频数如下:[5,10)5个;[10,15)14个;[15,20)9个;[20,25)5个;[25,30)4个;[30,35]3个.则样本在区间[20,+∞)上的频率为________.【解析】 由题意知在区间[20,+∞)上的样本数为5+4+3=12个,故所求频率为1240=0.3.【答案】 0.34.如图2-2-5是容量为100的样本的频率分布直方图,试根据图中的数据填空.图2-2-5(1)样本数据在范围[6,10)内的频率为________; (2)样本数据落在范围[10,14)内的频数为________. 【解析】 (1)样本数据在[6,10)内频率为0.08×4=0.32. (2)在[10,14)内的频数为0.09×4×100=36. 【答案】 (1)0.32 (2)365.在样本频率分布直方图中,共有11个小矩形,若中间一个小矩形的面积等于其他10个小矩形的面积的和的14,且样本容量为100,则中间一组的频数为________.【解析】 设中间一个小矩形的面积为x ,由题意得x 1-x =14,解得x =15,故中间一组的频数为100×15=20.【答案】 206.为了了解某地区10 000名高三男生的身体发育情况,抽查了该地区100名年龄为17~18岁的高三男生体重(kg),得到频率分布直方图如图2-2-6.根据图示,请你估计该地区高三男生中体重在[56.5,64.5]的学生人数是________.图2-2-6【解析】 依题意得,该地区高三男生中体重在[56.5,64.5]的学生人数是10 000×(0.03+2×0.05+0.07)×2=4 000.【答案】 4 0007.某班的全体学生参加英语测试,成绩的频率分布直方图如图2-2-7,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是________.【导学号:11032040】图2-2-7【解析】 成绩在[20,40)和[40,60)的频率分别是0.1,0.2,则低于60分的频率是0.3.设该班学生总人数为m ,则15m =0.3,m =50.【答案】 508.对某市“两学一做”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图2-2-8),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:图2-2-8(1)[25,30)年龄组对应小矩形的高度为________;(2)据此估计该市“两学一做”活动中志愿者年龄在[25,35)的人数为________.【解析】 设[25,30)年龄组对应小矩形的高度为h ,则5×(0.01+h +0.07+0.06+0.02)=1,h =0.04.志愿者年龄在[25,35)的频率为5×(0.04+0.07)=0.55,故志愿者年龄在[25,35)的人数约为0.55×800=440.【答案】 (1)0.04 (2)440 二、解答题9.某工厂对一批产品进行了抽样检测,图2-2-9是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是多少?图2-2-9【解】 产品净重小于100克的频率为(0.050+0.100)×2=0.300,已知样本中产品净重小于100克的个数是36,设样本容量为n ,则36n =0.300,所以n =120,净重大于或等于98克并且小于104克的产品的频率为(0.100+0.150+0.125)×2=0.750,所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.750=90.10.下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高(单位:cm).分组 [122, 126) [126, 130) [130, 134) [134, 138) [138, 142) 人数58102233分组 [142, 146) [146, 150) [150, 154) [154, 158] 人数201165(1)列出样本频率分布表; (2)画出频率分布直方图;(3)估计身高小于134 cm 的人数占总人数的百分比. 【解】 (1)样本频率分布表如下:分组 频数 频率 [122,126) 5 0.04 [126,130) 8 0.07 [130,134) 10 0.08 [134,138) 22 0.18 [138,142) 33 0.28 [142,146) 20 0.17 [146,150) 11 0.09 [150,154) 6 0.05 [154,158] 5 0.04 合计1201(2)其频率分布直方图如下:(3)由样本频率分布表可知身高小于134 cm 的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134 cm 的人数占总人数的19%.[能力提升]1.某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下,则表中字母m、n、M、N所对应的数值分别为________、________、________、________.组别频数频率[145.5,149.5)80.16[149.5,153.5)60.12[153.5,157.5)140.28[157.5,161.5)100.20[161.5,165.5)80.16[165.5,169.5]m n合计M N【解析】由题意知样本容量为80.16=50,故M=50,从而m=50-(8+6+14+10+8)=4,所以n=450=0.08;N=1.【答案】40.0850 12.从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图2-2-10).由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为________.图2-2-10【解析】由题意知1-(0.005+0.035+0.020+0.010)×10=0.3,故a=0.3 10=0.030;由分层抽样的方法知,在[140,150]内的学生中选取的人数为18×0.010.03+0.02+0.01=18×16=3人.【答案】 0.030 33.某市数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图2-2-11所示,已知130~140分数段的人数为90人,求90~100分数段的人数a =________,则下边的流程图(图2-2-12)的功能是________.图2-2-11 图2-2-12【解析】 ①在频率分布图中,由题意可得900.05=a0.45,∴a =810. ②在图2中,∵a =810, n ←1时,S ←1,S ←1×1, n ←2时,S ←1×1,S ←1×1×2, n ←3时,S ←1×2,S ←1×2×3, 依此循环,n >810时终止循环,输出S . 此时S =1×2×3×4× (810)故该流程图的功能是计算并输出1×2×3×4×…×810的值. 【答案】 810 计算并输出1×2×3×…×810的值4.从某学校高三年级800名学生中随机抽取50名测量身高,被抽取的学生的身高全部介于155 cm 和195 cm 之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195],如图2-2-13是按上述分组方法得到的频率分布直方图.图2-2-13(1)根据已知条件填写下面表格:组别12345678样本数(2)估计这所学校高三年级800名学生中身高在180 cm以上(含180 cm)的人数.【解】(1)由频率分布直方图得第七组的频率为1-(0.008×2+0.016×2+0.04×2+0.06)×5=0.06,∴第七组的人数为0.06×50=3.同理可得各组人数如下:组别12345678样本数2410101543 2(2)由频率分布直方图得后三组的频率为0.016×5+0.06+0.008×5=0.18.估计这所学校高三年级身高在180 cm以上(含180 cm)的人数为800×0.18=144.。
高中数学选修2-2分层测评 第二章 推理与证明 2.2.1 含答案

学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.在证明命题“对于任意角θ,cos 4θ-sin 4 θ=cos 2θ”的过程:“cos 4 θ-sin 4 θ=(cos 2 θ+sin 2 θ)(cos 2 θ-sin 2 θ)=cos 2 θ-sin 2 θ=cos 2θ”中应用了( )A .分析法B .综合法C .分析法和综合法综合使用D .间接证法【解析】 此证明符合综合法的证明思路.故选B. 【答案】 B2.要证a 2+b 2-1-a 2b 2≤0,只需证( ) A .2ab -1-a 2b 2≤0 B .a 2+b 2-1-a 2+b 22≤0C.(a +b )22-1-a 2b 2≤0 D .(a 2-1)(b 2-1)≥0【解析】 要证a 2+b 2-1-a 2b 2≤0, 只需证a 2b 2-a 2-b 2+1≥0, 只需证(a 2-1)(b 2-1)≥0,故选D. 【答案】 D3.在集合{a ,b ,c ,d }上定义两种运算⊕和⊗如下:那么,d⊗(a⊕c)等于()A.a B.bC.c D.d【解析】由⊕运算可知,a⊕c=c,∴d⊗(a⊕c)=d⊗c.由⊗运算可知,d⊗c=a.故选A.【答案】 A4.欲证2-3<6-7成立,只需证()A.(2-3)2<(6-7)2B.(2-6)2<(3-7)2C.(2+7)2<(3+6)2D.(2-3-6)2<(-7)2【解析】∵2-3<0,6-7<0,故2-3<6-7⇔2+7<3+6⇔(2+7)2<(3+6)2.故选C. 【答案】 C5.对任意的锐角α,β,下列不等式中正确的是()A.sin(α+β)>sin α+sin βB.sin(α+β)>cos α+cos βC.cos(α+β)>sin α+sin βD.cos(α+β)<cos α+cos β【解析】因为0<α<π2,0<β<π2,所以0<α+β<π,若π2≤α+β<π,则cos(α+β)≤0,因为cos α>0,cos β>0.所以cos α+cos β>cos (α+β).若0<α+β<π2,则α+β>α且α+β>β,因为cos(α+β)<cos α,cos(α+β)<cos β,所以cos(α+β)<cos α+cos β,总之,对任意的锐角α,β有cos(α+β)<cos α+cos β.【答案】 D二、填空题6.命题“函数f(x)=x-x ln x在区间(0,1)上是增函数”的证明过程“对函数f(x)=x-x ln x求导得f′(x)=-ln x,当x∈(0,1)时,f′(x)=-ln x>0,故函数f(x)在区间(0,1)上是增函数”应用了________的证明方法.【解析】该证明方法是“由因导果”法.【答案】综合法7.如果a a>b b,则实数a,b应满足的条件是__________.【解析】要使a a>b b,只需使a>0,b>0,(a a)2>(b b)2,即a>b>0.【答案】a>b>08.若对任意x>0,xx2+3x+1≤a恒成立,则a的取值范围是__________.【导学号:05410046】【解析】若对任意x>0,xx2+3x+1≤a恒成立,只需求y=xx2+3x+1的最大值,且令a 不小于这个最大值即可.因为x >0,所以y =x x 2+3x +1=1x +1x +3≤12x ·1x +3=15,当且仅当x =1时,等号成立,所以a 的取值范围是⎣⎢⎡⎭⎪⎫15,+∞.【答案】 ⎣⎢⎡⎭⎪⎫15,+∞三、解答题9.已知倾斜角为60°的直线L 经过抛物线y 2=4x 的焦点F ,且与抛物线相交于A ,B 两点,其中O 为坐标原点.(1)求弦AB 的长; (2)求三角形ABO 的面积.【解】 (1)由题意得,直线L 的方程为y =3(x -1), 代入y 2=4x ,得3x 2-10x +3=0. 设点A (x 1,y 1),B (x 2,y 2), 则x 1+x 2=103.由抛物线的定义,得弦长|AB |=x 1+x 2+p =103+2=163. (2)点O 到直线AB 的距离d =|-3|3+1=32,所以三角形OAB 的面积为S =12|AB |·d =433.10.已知三角形的三边长为a ,b ,c ,其面积为S ,求证:a 2+b 2+c 2≥43S . 【证明】 要证a 2+b 2+c 2≥43S ,只要证a 2+b 2+(a 2+b 2-2ab cos C )≥2 3 ab sin C ,即证a 2+b 2≥2ab sin(C +30°),因为2ab sin(C +30°)≤2ab ,只需证a 2+b 2≥2ab ,显然上式成立.所以a2+b2+c2≥43S.[能力提升]1.设a>0,b>0,若3是3a与3b的等比中项,则1a+1b的最小值为()A.8 B.4C.1 D.1 4【解析】3是3a与3b的等比中项⇒3a·3b=3⇒3a+b=3⇒a+b=1,因为a>0,b>0,所以ab≤a+b2=12⇒ab≤14,所以1a+1b=a+bab=1ab≥114=4.【答案】 B2.(2016·石家庄高二检测)已知关于x的方程x2+(k-3)x+k2=0的一根小于1,另一根大于1,则k的取值范围是()A.(-1,2)B.(-2,1)C.(-∞,-1)∪(2,+∞)D.(-∞,-2)∪(1,+∞)【解析】令f(x)=x2+(k-3)x+k2.因为其图象开口向上,由题意可知f(1)<0,即f(1)=1+(k-3)+k2=k2+k-2<0,解得-2<k<1.【答案】 B3.如果a a+b b>a b+b a,则实数a,b应满足的条件是__________.【导学号:05410047】【解析】a a+b b>a b+b a⇔a a-a b>b a-b b⇔a(a-b)>b(a -b)⇔(a-b)(a-b)>0⇔(a+b)(a-b)2>0,故只需a ≠b 且a ,b 都不小于零即可. 【答案】 a ≥0,b ≥0且a ≠b4.(2016·天津高二检测)已知α,β≠k π+π2,(k ∈Z )且sin θ+cos θ=2sin α,sin θcos θ=sin 2β.求证:1-tan 2 α1+tan 2 α=1-tan 2 β2(1+tan 2 β).【证明】 要证1-tan 2 α1+tan 2 α=1-tan 2 β2(1+tan 2 β)成立,即证1-sin 2 αcos 2 α1+sin 2 αcos 2 α=1-sin 2 βcos 2 β2⎝ ⎛⎭⎪⎫1+sin 2 βcos 2 β. 即证cos 2α-sin 2α=12(cos 2β-sin 2β), 即证1-2sin 2α=12(1-2sin 2β), 即证4sin 2α-2sin 2β=1, 因为sin θ+cos θ=2sin α, sin θcos θ=sin 2β,所以(sin θ+cos θ)2=1+2sin θcos θ=4sin 2α,所以1+2sin 2β=4sin 2 α, 即4sin 2α-2sin 2β=1. 故原结论正确.。
高中数学苏教版高二选修2-2学业分层测评:第二章_推理与证明_17 含解析

高中数学苏教版高二选修2-2学业分层测评:第二章_推理与证明_17 含解析学业分层测评(十七)(建议用时:45分钟)学业达标]一、填空题1.设f(n)=1+12+13+…+13n-1(n∈N*),那么f(n+1)-f(n)等于________.【解析】f(n+1)-f(n)=1+12+13+…+13n-1+13n+13n+1+13n+2-f(n)=13n+13n+1+13n+2.【答案】13n+13n+1+13n+22.(2016·无锡高二期末)用数学归纳法证明不等式“1n+1+1n+2+1n+3+…+13n+1>2512”,当n=1时,不等式左边的项为:________.【解析】不等式左边分子是1,分母是从n+1一直到3n+1的分数之和,当n=1时,n+1=2,3n+1=4,左边项为12+13+14.【答案】12+13+143.用数学归纳法证明:“2n>n2+1对于n≥n0的正整数n都成立”时,第一步证明中的起始值n0应取值________.【导学号:01580053】【解析】∵当n=1时,21=12+1;当n=2时,22<22+1,当n=3时,23<32+1;当n=4时,24<42+1;当n≥5时,2n>n2+1恒成立.∴n0=5.【答案】 54.若f(n)=12+22+32+…+(2n)2,n∈N*,则f(k+1)-f(k)=______________.【解析】f(k)=12+22+32+…+(2k)2,f (k +1)=12+22+32+…+(2k )2+(2k +1)2+(2k +2)2,则f (k +1)-f (k )=(2k +1)2+(2k +2)2.【答案】 (2k +1)2+(2k +2)25.已知数列{a n }的前n 项和S n =n 2a n (n ≥2),而a 1=1,通过计算a 2,a 3,a 4,猜想a n =________.【解析】 a 1=1=21×2,a 2=22×3,a 3=23×4,a 4=24×5,猜想a n =2n (n +1). 【答案】 2n (n +1)6.用数学归纳法证明a n +b n 2≥⎝ ⎛⎭⎪⎫a +b 2n (a ,b 是非负实数,n ∈N *)时,假设n =k 命题成立之后,证明n =k +1时命题也成立的关键是两边同乘以________.【解析】 要想办法出现a k +1+b k +1,两边同乘以a +b 2,右边也出现了要证的⎝ ⎛⎭⎪⎫a +b 2k +1. 【答案】 a +b 27.以下是用数学归纳法证明“n ∈N *时,2n >n 2”的过程,证明:(1)当n =1时,21>12,不等式显然成立.(2)假设当n =k (k ∈N *)时不等式成立,即2k >k 2.那么,当n =k +1时,2k +1=2×2k =2k +2k >k 2+k 2≥k 2+2k +1=(k +1)2. 即当n =k +1时不等式也成立.根据(1)和(2),可知对任何n ∈N *不等式都成立.其中错误的步骤为________(填序号).【解析】 在2k +1=2×2k =2k +2k >k 2+k 2≥k 2+2k +1中用了k 2≥2k +1,这是一个不确定的结论.如k =2时,k 2<2k +1.【答案】 (2)8.用数学归纳法证明12+22+…+(n -1)2+n 2+(n -1)2+…+22+12=n (2n 2+1)3时,由n =k 的假设到证明n =k +1时,等式左边应添加的式子是_____.【解析】 当n =k 时,左边=12+22+…+(k -1)2+k 2+(k -1)2+…+22+12. 当n =k +1时,左边=12+22+…+k 2+(k +1)2+k 2+(k -1)2+…+22+12,所以左边添加的式子为(k +1)2+k 2.【答案】 (k +1)2+k 2二、解答题9.用数学归纳法证明:当n ∈N *时,1+22+33+…+n n <(n +1)n .【证明】 (1)当n =1时,左边=1,右边=2,1<2,不等式成立.(2)假设当n =k (k ∈N *)时不等式成立,即1+22+33+…+k k <(k +1)k ,那么,当n =k +1时,左边=1+22+33+…+k k +(k +1)k +1<(k +1)k +(k +1)k +1=(k +1)k (k +2)<(k +2)k +1=(k +1)+1]k +1=右边,即左边<右边,即当n =k +1时不等式也成立.根据(1)和(2),可知不等式对任意n ∈N *都成立.10.已知数列{a n }满足a n +1=12-a n ,a 1=0.试猜想{a n }的通项公式,并用数学归纳法证明. 【解】 由a n +1=12-a n ,a 1=0,得 a 2=12-0=12,a 3=12-12=23,a 4=12-23=34, a 5=12-34=45,….归纳上述结果,可得猜想a n =n -1n (n =1,2,3,…).下面用数学归纳法证明这个猜想:(1)当n =1时,猜想显然成立.(2)假设当n =k 时猜想成立,即a k =k -1k ,那么,当n =k +1时,a k +1=12-a k=12-k -1k=k k +1=(k +1)-1k +1, 即当n =k +1时,猜想也成立.根据(1)和(2),可知猜想a n =n -1n 对所有正整数都成立,即为数列{a n }的通项公式.能力提升]1.用数学归纳法证明“当n 为正偶数时x n -y n 能被x +y 整除”第一步应验证n =________时,命题成立;第二步归纳假设应写成________.【解析】 由于n 为正偶数,第一步应检验n =2时,命题成立.第二步,应假设n =2k (k ∈N *)时命题成立,即n =2k (k ∈N *)时x 2k -y 2k 能被x +y 整除.【答案】 2 假设n =2k (k ∈N *)时x 2k -y 2k 能被x +y 整除2.用数学归纳法证明:凸n 边形对角线的条数f (n )=12n (n -3)(n ≥4)时,f (k +1)与f (k )的关系是_______________________________________________.【解析】假设n=k(k≥4,k∈N*)时成立,则f(k)=12k(k-3),当n=k+1时,多出一条边,实际上增加的对角线条数为k+1-2=k-1条,所以f(k+1)=f(k)+k-1.【答案】f(k+1)=f(k)+k-13.用数学归纳法证明:“1+12+13+…+12n-1<n(n>1)”,由n=k(k>1)不等式成立,推证n=k+1时,左边应增加的项的项数是________.【解析】当n=k+1时,左边是1+12+13+…+12k-1+12k+…+12k+1-1增加的是12k+12k+1+…+12k+1-1,共有2k+1-1-2k+1=2k项,故左边应增加的项的项数是2k.【答案】2k4.用数学归纳法证明34n+2+52n+1能被14整除的过程中,当n=k+1时,34(k+1)+2+52(k+1)+1应变形为__________.【导学号:01580054】【解析】当n=k+1时,34(k+1)+2+52(k+1)+1=81·34k+2+25·52k+1=25(34k+2+52k+1)+56·34k +2.【答案】25(34k+2+52k+1)+56·34k+25.设函数y=f(x)对任意实数x,y都有f(x+y)=f(x)+f(y)+2xy.(1)求f(0)的值;(2)若f(1)=1,求f(2),f(3),f(4)的值;(3)在(2)的条件下,猜想f(n)(n∈N*)的表达式,并用数学归纳法加以证明.【解】(1)令x=y=0,得f(0+0)=f(0)+f(0)+2×0×0⇒f(0)=0.(2)f(1)=1,f(2)=f(1+1)=1+1+2=4,f(3)=f(2+1)=4+1+2×2×1=9,f(4)=f(3+1)=9+1+2×3×1=16.(3)猜想f(n)=n2,下面用数学归纳法证明.当n=1时,f(1)=1满足条件.假设当n=k(k∈N*)时成立,即f(k)=k2,则当n=k+1时,f(k+1)=f(k)+f(1)+2k=k2+1+2k=(k+1)2,从而可得当n=k+1时满足条件,所以对任意的正整数n,都有f(n)=n2.。
高中数学苏教版高二选修2-2学业分层测评:章末综合检测_02

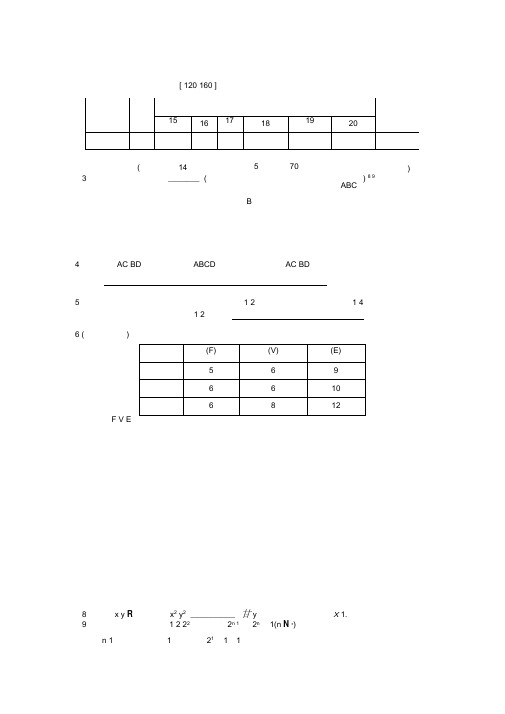
章末综合测评(二)(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分,请把答案填在题中的横线上)1.有一段“三段论”推理是这样的:对于可导函数f(x),若f(x0)=0,则x=x0是函数f(x)的极值点.因为f(x)=x3在x=0处的导数值f′(0)=0,所以x=0是f(x)=x3的极值点.以上推理中________错误.【解析】大前提是错误的,若f′(x0)=0,x=x0不一定是函数f(x)的极值点.【答案】大前提2.下列四个图形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为________.图1【解析】由图形可知,着色三角形的个数依次为:1,3,9,27,…,故a n=3n-1.【答案】3n-13.(2016·日照联考)已知f(n)=1+12+13+…+1n(n∈N*),计算得f(22)>2,f(23)>52,f(24)>3,f(25)>72,由此推测,当n≥2时,有________.【解析】因为f(22)>42,f(23)>52,f(24)>62,f(25)>72,所以推测,当n≥2时,f(2n)>n+22.【答案】f(2n)>n+2 24.已知圆x2+y2=r2(r>0)的面积为S=πr2,由此类比椭圆x2a2+y2b2=1(a>b>0)的面积最有可能是________.【解析】将圆看作椭圆的极端情况,即a=b情形.∴类比S圆=πr2,得椭圆面积S=πab.【答案】πab5.已知a>0,b>0,m=lg a+b2,n=lga+b2,则m与n的大小关系为________.【解析】∵(a+b)2=a+b+2ab>a+b>0,∴a +b >a +b >0,则a +b 2>a +b2.∴lga +b 2>lg a +b2,则m >n .【答案】 m >n6.已知数列{a n }为等差数列,数列{b n }是各项均为正数的等比数列,且公比q >1,若a 1=b 1,a 2 013=b 2 013,则a 1 007与b 1 007的大小关系是________.【解析】 由2a 1 007=a 1+a 2 013,得a 1 007=a 1+a 2 0132.又b 21 007=b 1·b 2 013,得b 1 007=b 1·b 2 013, ∵a 1=b 1>0,a 2 013=b 2 013>0,且a 1≠a 2 013, ∴a 1 007>b 1 007. 【答案】 a 1 007>b 1 007 7.利用数学归纳法证明不等式1n +1+1n +2+…+1n +n>12(n >1,n ∈N *)的过程中,第一步的代数式为____________________.【解析】 第一步:n =2时,左边为12+1+12+2,故代数式为12+1+12+2>12. 【答案】12+1+12+2>12 8.(2016·江西一模)观察下列等式: (1+x +x 2)1=1+x +x 2,(1+x +x 2)2=1+2x +3x 2+2x 3+x 4,(1+x +x 2)3=1+3x +6x 2+7x 3+6x 4+3x 5+x 6,(1+x +x 2)4=1+4x +10x 2+16x 3+19x 4+16x 5+10x 6+4x 7+x 8,由以上等式推测:对于n ∈N *,若(1+x +x 2)n =a 0+a 1x +a 2x 2+…+a 2n x 2n ,则a 2=________. 【解析】 观察知,a 2为数列1,3,6,10,…中的第n 项,而1=22=1×22,3=62=2×32,6=122=3×42,10=202=4×52,…,归纳得a 2=n (n +1)2.【答案】n (n +1)29.将全体正整数排成一个三角形数阵:图2根据以上排列规律,数阵中第n (n ≥3)行从左到右的第三个数是________. 【解析】 前n -1行共有正整数1+2+3+…+(n -1)=n 2-n2个, ∴第n 行第3个数是n 2-n 2+3=n 2-n +62.【答案】 n 2-n +6210.(2016·东北三校二模)观察下列等式:13=12,13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第n 个等式为________.【解析】 由题知13=12; 13+23=⎝⎛⎭⎪⎫2×322; 13+23+33=⎝⎛⎭⎪⎫3×422; 13+23+33+43=⎝⎛⎭⎪⎫4×522; …∴13+23+33+43+…+n 3=⎣⎢⎡⎦⎥⎤n (n +1)22. 【答案】 13+23+33+43+…+n 3=⎣⎢⎡⎦⎥⎤n (n +1)2211.已知点A (x 1,3x 1),B (x 2,3x 2)是函数y =3x 的图象上任意不同两点,依据图象可知,线段AB 总是位于A ,B 两点之间函数图象的上方,因此有结论3x 1+3x 22>3x 1+x 22成立.运用类比思想方法可知,若点A (x 1,tan x 1),B (x 2,tan x 2)是函数y =tan x ⎝ ⎛⎭⎪⎫-π2<x <0的图象上任意不同两点,则类似地有____________成立.【解析】 因为y =tan x ⎝ ⎛⎭⎪⎫-π2<x <0图象是上凸的,因此线段AB 的中点的纵坐标tan x 1+tan x 22总是小于函数y =tan x ⎝ ⎛⎭⎪⎫-π2<x <0图象上的点⎝ ⎛⎭⎪⎫x 1+x 22,tan x 1+x 22的纵坐标,即有tan x 1+tan x 22<tan x 1+x 22成立.【答案】 tan x 1+tan x 22<tan x 1+x 2212.定义映射f :A →B ,其中A ={(m ,n )|m ,n ∈R },B =R ,已知对所有的有序正整数对(m ,n )满足下述条件:①f (m,1)=1;②若n >m ,则f (m ,n )=0;③f (m +1,n )=nf (m ,n )+f (m ,n -1)].则f (2,2)=________,f (n,2)=________.【解析】 根据定义得f (2,2)=f (1+1,2)=2f (1,2)+f (1,1)]=2f (1,1)=2×1=2. f (3,2)=f (2+1,2)=2f (2,2)+f (2,1)]=2×(2+1)=6=23-2,f (4,2)=f (3+1,2)=2f (3,2)+f (3,1)]=2×(6+1)=14=24-2,f (5,2)=f (4+1,2)=2f (4,2)+f (4,1)]=2×(14+1)=30=25-2,所以根据归纳推理可知f (n,2)=2n -2.【答案】 2 2n -213.(2014·陕西高考)观察分析下表中的数据:猜想一般凸多面体中F ,V ,E所满足的等式是_______________________________________________.【解析】 观察表中数据,并计算F +V 分别为11,12,14,又其对应E 分别为9,10,12,易观察并猜想F +V -E =2.【答案】 F +V -E =214.(2016·北京顺义区统考)数列{a n }的前n 项和为S n ,若数列{a n }的各项按如下规则排列: 12;13,23;14,24,34;15,25,35,45;…1n ,2n ,…,n -1n ….则a 15=______;若存在正整数k ,使S k -1<10,S k >10,则a k =________.【解析】 从题中可看出分母n +1出现n 次,当分母为n +1时,分子依次是1,2,3,…n 共n 个,由于1+2+3+4+5=15.因此a 15=56.计算分母为n +1的各分数的和,依次为12,1,32,2,52,3,…,而12+1+32+2+52+3=10.5>10,但12+1+32+2+52=7.5<10,再计算17+27+3 7+47+57=217,而712+217=9914<10,故a k=67.【答案】5667二、解答题(本大题共6小题,共90分.解答时应写出文字说明,证明过程或演算步骤)15.(本小题满分14分)用反证法证明:如果x>12,那么x2+2x-1≠0.【导学号:01580057】【证明】假设x2+2x-1=0,则x=-1±2.容易看出-1-2<12,下面证明-1+2<12.要证:-1+2<12,只需证:2<32,只需证:2<94.上式显然成立,故有-1+2<12.综上,x=-1±2<12.而这与已知条件x>12相矛盾,因此假设不成立,也即原命题成立.16.(本小题满分14分)设数列{a n}的前n项和S n=n(a n+1)2(n∈N*),a2=2.(1)求{a n}的前三项a1,a2,a3;(2)猜想{a n}的通项公式,并证明.【解】(1)由S n=n(a n+1)2得a1=1,又由a2=2,得a3=3.(2)猜想:a n=n.证明如下:①当n=1时,猜想成立.②假设当n=k(k≥2)时,猜想成立,即a k=k,那么当n=k+1时,a k+1=S k+1-S k=(k+1)(a k+1+1)2-k(a k+1)2.=(k+1)(a k+1+1)2-k(k+1)2.所以a k+1=k2k-1-1k-1=k+1,所以当n=k+1时,猜想也成立.根据①②知,对任意n∈N*,都有a n=n.17.(本小题满分14分)已知△ABC的三边长分别为a,b,c,且其中任意两边长均不相等,若1a,1b,1c成等差数列.(1)比较ba与cb的大小,并证明你的结论;(2)求证:角B不可能是钝角.【解】(1)ba<cb.证明如下:要证ba<cb,只需证ba<cb.∵a,b,c>0,∴只需证b2<ac.∵1a,1b,1c成等差数列,∴2b=1a+1c≥21ac,∴b2≤ac.又a,b,c均不相等,∴b2<ac.故所得大小关系正确.(2)法一:假设角B是钝角,则cos B<0.由余弦定理得,cos B=a2+c2-b22ac≥2ac-b22ac>ac-b22ac>0,这与cos B<0矛盾,故假设不成立.所以角B不可能是钝角.法二:假设角B是钝角,则角B的对边b为最大边,即b>a,b>c,所以1a>1b>0,1c>1b>0,则1a+1c>1b+1b=2b,这与1a+1c=2b矛盾,故假设不成立.所以角B不可能是钝角.18.(本小题满分16分)(2016·南通月考)诺贝尔奖的发放方式为:每年一次,把奖金总额平均分成6份,奖励在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类作出了最有益贡献的人.每年发放奖金的总金额是基金在该年度所获利息的一半,另一半利息用于增加基金总额,以便保证奖金数逐年递增.假设基金平均年利率为r=6.24%.资料显示:2002年诺贝尔奖发奖后基金总额约为19 800万美元.设f(x)表示为第x(x∈N*)年诺贝尔奖发奖后的基金总额(2002年记为f(1)).(1)用f(1)表示f(2)与f(3),并根据所求结果归纳出函数f(x)的表达式;(2)试根据f(x)的表达式判断网上一则新闻“2012年度诺贝尔各项奖金高达150万美元”是否为真,并说明理由.(参考数据:1.031 29≈1.32)【解】(1)由题意知:f(2)=f(1)(1+6.24%)-12f(1)·6.24%=f(1)(1+3.12%),f(3)=f(2)(1+6.24%)-12f(2)·6.24%=f(1)·(1+3.12%)2,∴f(x)=19 800·(1+3.12%)x-1(x∈N*).(2)2011年诺贝尔奖发奖后基金总额为f(10)=19 800×(1+3.12%)9=26 136万美元,∴2012年度诺贝尔奖各项奖金额为16×12×f(10)×6.24%≈136万美元,与150万美元相比少了约14万美元.所以新闻“2012年度诺贝尔奖各项奖金高达150万美元”不真,是假新闻.19.(本小题满分16分)(2016·南通三模)各项均为正数的数列{x n}对一切n∈N*均满足x n+1x n+1<2.证明:(1)x n<x n+1;(2)1-1n<x n<1.【证明】(1)因为x n>0,x n+1x n+1<2,所以0<1x n+1<2-x n,所以x n+1>12-x n,且2-x n>0.因为12-x n -x n=x2n-2x n+12-x n=(x n-1)22-x n≥0,所以12-x n≥x n,所以x n ≤12-x n <x n +1,即x n <x n +1. (2)下面先证明x n ≤1.假设存在自然数k ,使得x k >1,则一定存在自然数m ,使得x k >1+1m . 因为x k +1x k +1<2,x k +1>12-x k >12-⎝ ⎛⎭⎪⎫1+1m =mm -1. x k +2>12-x k +1>12-⎝ ⎛⎭⎪⎫1+1m -1>m -1m -2,…,x k +m -1>m -(m -2)m -(m -1)=2, 与题设x k +1x k +1<2矛盾,所以x k ≤1. 若x k =1,则x k +1>x k =1,根据上述证明可知存在矛盾. 所以x k <1成立.下面用数学归纳法证明:x n >1-1n .①当n =1时,由题设x 1>0可知结论成立; ②假设n =k 时,x k >1-1k ,当n =k +1时,由(1)得,x k +1>12-x k >12-⎝ ⎛⎭⎪⎫1-1k =k k +1=1-1k +1,故x n >1-1n .20.(本小题满分16分)在数列{a n },{b n }中,a 1=2,b 1=4,且a n ,b n ,a n +1成等差数列,b n ,a n +1,b n +1成等比数列(n ∈N *).(1)求a 2,a 3,a 4及b 2,b 3,b 4,由此归纳出{a n },{b n }的通项公式,并证明你的结论; (2)证明:1a 1+b 1+1a 2+b 2+1a 3+b 3+…+1a n +b n <512. 【解】 (1)由条件得2b n =a n +a n +1,a 2n +1=b n b n +1,由此可得a 2=6,b 2=9,a 3=12,b 3=16,a 4=20,b 4=25.猜测a n =n (n +1),b n =(n +1)2. 用数学归纳法证明:①当n =1时,由上可得结论成立. ②假设当n =k 时,结论成立,即a k =k (k +1),b k =(k +1)2, 那么当n =k +1时,a k +1=2b k -a k =2(k +1)2-k (k +1)=(k +1)(k +2),b k +1=a 2k +1b k=(k +2)2.所以当n =k +1时,结论也成立.由①②,可知a n =n (n +1),b n =(n +1)2对一切正整数n 都成立. (2)1a 1+b 1=16<512. 当n ≥2时,由(1)知a n +b n =(n +1)(2n +1)>2(n +1)n . 1a 1+b 1+1a 2+b 2+1a 3+b 3+…+1a n +b n <16+12⎣⎢⎡⎦⎥⎤12×3+13×4+…1n (n +1)=16+12⎝ ⎛⎭⎪⎫12-13+13-14+…+1n -1n +1 =16+12⎝ ⎛⎭⎪⎫12-1n +1 <16+14=512.综上,原不等式成立.。
【推荐】高中数学选修22第2章《推理与证明》单元测试题

选修2-2第二章《推理与证明》单元测试题一.选择题: (以下题目从4项答案中选出一项,每小题5分,共50分) 1. 集合P ={1, 4, 9, 16…},若a ∈P , b ∈P 则a ⊕b ∈P ,则运算⊕可能是( ) A .加法 B .减法 C .除法 D .乘法2. 若平面四边形ABCD 满足0AB CD +=,()0AB AD AC -⋅=,则该四边形一定是( ) A .直角梯形 B .矩形 C .正方形 D .菱形3.给出下面类比推理命题(其中Q 为有理数集,R 为实数集,C 为复数集): ①“若a,b b a b a R =⇒=-∈0,则”类比推出“若a,b b a b a C =⇒=-∈0,则”; ②“若a,b,c,d d b c a di c bi a R ==⇒+=+∈,,则复数”类比推出“若a,b,c,d ,Q ∈ 则d b c a d c b a ==⇒+=+,22”;③“若a,b b a b a R >⇒>-∈0,则” 类比推出“若a,b b a b a C >⇒>-∈0,则”; 其中类比结论正确的个数是( ) (A)0 (B)1 (C)2(D)34.平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到(3)n n ≥维向量,n 维向量可用 123(,,,,)n x x x x 表示.设123(,,,,)n a a a a a =,123(,,,,)n b b b b b =,规定向量a 与b 夹角θ的余弦为∑∑∑====n i ni i i ni ii b a ba 11221))((cos θ.当(1,1,1,1)a =,(1,1,1,1)b =--时,cos θ=( )A .n n 1- B .nn 3- C .n n 2- D .n n 4- 5. 下列函数中,在区间02π⎛⎫⎪⎝⎭,上为增函数且以π为周期的函数是( )A .sin2xy = B . sin y x = C . tan y x =- D . cos 2y x =- 6. 若一系列函数的解析式相同、值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为 y =x 2、值域为{0,4}的“同族函数”共有( )个. A. 2 B. 3 C. 4 D.无数7.对于使22x x M -+≤成立的所有常数M 中,我们把M 的最小值1叫做22x x -+的上确界,若 ,,1a b R a b +∈+=且,则122a b--的上确界为( ) A .92 B .92- C .41D .4- 8.如图,圆周上按顺时针方向标有1,2,3,4,5五个点。
高二数学苏教版选修2-2阶段质量检测(二)推理与证明
3 _______ () 8 9 4AC BD ABCD AC BD51 21 21 46 ( )F V E8 x y R x 2 y 2 __________ 甘y X 1.91 2 22 2n 1 2n 1(n N *) n 1121 1 1[ 120 160 ](14)5 70ABCB②假设当n = k(k € N *)时,等式成立,即 1+ 2 + 22+…+ 2k 「1 = 2k — 1; 高中数学14 .(湖北高考)古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数 1,3,6,10,…,第n 个三角形数为 中+1 = *n 2+切.记第n 个k 边形数为N(n , k)(k >3),以下列出了部分k 边形数中第n 个数的表达式:三角形数 1 2 1N(n ,3) = ?n +尹 正方形数 N(n,4) = n 2, 五边形数3 2 1 N(n,5) = ?n 2—1n ,六边形数N( n,6) = 2n 2— n ,可以推测N(n , k)的表达式,由此计算 N(10,24) = _________、解答题(本大题共6个小题,共90分.解答应写出文字说明、 证明过程或演算步骤)③则当n = k + 1时,k + 11+ 2+尸+…十2k —1 + 2k=等—T =2k +1 -1则当n = k + 1时等式* »成立•由此可知,对任何 n € N ,等式都成立.上述证明步骤中错误的是 _________ •2 2 210.如图,在平面直角坐标系 xOy 中,圆x + y = r (r > 0)内切于正 方形 ABCD ,任取圆上一点 P ,若 OP = m OA + n OB (m , n € R ), 则和2 2m 2, n 2的等差中项;现有一椭圆 X 2+ y ^= 1(a >b > 0)内切于矩形 ABCD ,a b任取椭圆上一点 P ,若OP = m OA + n OB (m , n € R ),贝U m 2, n 2的等差中项为 ____________11.(安徽高考)如图,在等腰直角三角形 ABC 中,斜边BC = 2 . 2. 过点A 作BC 的垂线,垂足为A 1 ;过点A 1作AC 的垂线,垂足为A 2; 过点A 2作A 1C 的垂线,垂足为 A 3 ;…,依此类推.设 BA = a 1 , AA 1 =a 2 , A 1A 2= a 3,…, A 5A 6= a 7,贝a 7=___________________________________________ .1 4 27 a12 .已知 x>0,不等式 x +-> 2, x + -2 >3, x + r > 4,…,可推广为 x + n + 1,则x x x xa 的值为 _________ .13.如图,第n 个图形是由正n + 2边形“扩展”而来(n = 1,2,3,…),则第n 个图形中 共有 ________ 个顶点.15 ( 14 ) a>0 b>0 a b 1 1 1 1 a b ab16 (14 ) {a n}a1 a3 52a n 5n 3 b n 6T n 5n a n{b n}1 a n a n 1 g"n N *)T n a1 a2 5n17 ( 14 ) sin210 2cos 40 sin 10 cos 402 si n262cos 36 sin 6 cos 3634.18 ( 16 ) a b c 0<a b c<2 (2 a)b (2 b)c1.(2 c)a19. (本小题满分16分)数列{a n}满足S n= 2n-a n(n € N ).(1)计算a i, a2, a3, a4,并由此猜想通项a n的表达式;⑵用数学归纳法证明(1)中的猜想.1 320. (本小题满分16分)已知函数f(x) = 3X -x,数列{a n}满足条件:a1> 1, a n+1>f' (a n+ 1),(1) 证明:a n> 2n- 1(n€ N ).1 1 1(2) 试比较一 + -一+…+ —与1的大小,并说明理由.1 + a1 1 + a2 1 + a n答案1. 解析:由甲、丙的回答易知甲去过A城市和C城市,乙去过A城市或C城市,结合乙的回答可得乙去过A城市.答案:A2. 解析:平面图形中的图类比空间几何体中的球,周长类比表面积,面积类比体积.故可以得到的结论是:表面积一定的空间几何体中,球的体积最大.答案:表面积一定的空间几何体中,球的体积最大3. 解析:如果演绎推理的大前提和小前提都正确,则结论一定正确.大前提和小前提中,只要有一项不正确,则结论一定也不正确•故②错误.答案:①③④4. 形对角线互相垂直且平分V1_竺_包也」1_ 15.解析:V2 1 S2 h2 4 2 8'1站2答案:1 : 8高中数学12x6 6 10 26 8 12 2F V E 2.8x y 4x 2 122222x (1 y ) 1 y (1 x ) 2yp1 x 2y x 2 1 x 2 y 2.y)2 0 yx 2 y 2 1.1944 2 XT XT x xa n n n n10P(x y) 227 p 2 1 A(a b) B( a b)m OA n OBn 2(m n a (m n p22 , m n 1 ~~24m 2 n 21 4.11 ABCBC 2^2 ABAC a 1AA 1 a 2 V 2 A 1A 2a 3 1 ABCAn 1A nan 12 /(m n) (m A 5A 6 a 7 a 11 4.2 , 2A 2a7a 1 2 AA 13 27 3 P x4 x xn n -n n x13 a n a1 3 3 3 a2 4 4 4高中数学12 xa n -2 = n + n •,22a n = (n + 2) + n + 2 = n + 5n + 6. 答案:n 5+ 5n + 614. 解析:N(n , k) = a k n 2 + b k n(k 》3),其中数列{a k }是以舟为首项,2为公差的等差数列; 数列{b k }是以*为首项,一1为公差的等差数列;所以N(n,24) = 11n 2- 10n,当n = 10时,N(10,24)=11 x 102- 10 x 10= 1 ooo.答案:1 00015. 证明:•/ a>0, b>0, a + b = 1.1 11 = a + b >2 ab , ab <㊁,ab <4, •-存4当a = 2, b = 2时等号成立 又 a +6=(a +b) 1+b当a =1,b =2■时等号成立 1 1 1 •1+ b +新 8. 16. 解:因为 T n = a 1 + a2 5+ a3 52+ …+ an 5nS ① 所以 5T n = a 1 5+ a 2 5 + a 3 5 + …+ a n -1 5 1+a n 5,② 由①+②得:6T n = a 1+ (a 1 + a ?) 5+ @+ 83) 52 + …+ (a n -1+ a *) 5n 1+ a * 5n=1 + 5x 5+ 1 2x 52+-+n -1x 5n -1 + a n 5n=n+ an 5 ,所以 6T n — 5n a n = n ,所以数列{ b n }的通项公式为b n = n.17•解:观察 40。
高中数学苏教版选修2-2学业分层测评:第二章 推理与证明 16含解析

学业分层测评(十六)(建议用时:45分钟)学业达标]一、填空题1.(2016·西安高二检测)△ABC中,若AB=AC,P是△ABC内的一点,∠APB>∠APC,求证:∠BAP<∠CAP.用反证法证明时的假设为________.【答案】∠BAP≥∠CAP2.(2016·无锡高二期末)用反证法证明命题“在一个三角形的三个内角中,至少有两个锐角”时,假设命题的结论不成立的正确叙述是“在一个三角形的三个内角中,________个锐角.”【解析】“至少有两个”的否定是“至多有一个”.【答案】至多有一个3.(2014·山东高考改编)用反证法证明命题“设a,b为实数,则方程x3+ax +b=0至少有一个实根”时,要做的假设是________.【解析】因为“方程x3+ax+b=0至少有一个实根”等价于“方程x3+ax+b=0的实根的个数大于或等于1”,所以要做的假设是“方程x3+ax+b=0没有实根”.【答案】方程x3+ax+b=0没有实根4.命题“a,b是实数,若|a-1|+|b-1|=0,则a=b=1”用反证法证明时应假设为________.【01580049】【解析】“a=b=1”是“a=1且b=1”,又因“p且q”的否定为“綈p或綈q”,所以“a=b=1”的否定为“a≠1或b≠1”.【答案】a≠1或b≠15.若下列两个方程x2+(a-1)x+a2=0,x2+2ax-2a=0中至少有一个方程有实根,则实数a的取值范围是______________.【解析】若两个方程均无实根,则⎩⎨⎧ Δ1=(a -1)2-4a 2<0,Δ2=4a 2+8a<0,解得⎩⎨⎧ a>13或a<-1,-2<a<0.∴-2<a<-1. 因此两方程至少有一个有实根时,应有a ≤-2或a ≥-1.【答案】 {a|a ≤-2或a ≥-1}6.用反证法证明命题“若a 2+b 2=0,则a ,b 全为0(a ,b 为实数)”,其反设为____________.【解析】 “a ,b 全为0”即是“a =0且b =0”,因此它的反设为“a ≠0或b ≠0”,即a ,b 不全为0.【答案】 a ,b 不全为07.若a ,b ,c 是不全相等的正数,给出下列判断:①(a -b)2+(b -c)2+(c -a)2≠0;②a>b 与a<b 及a =b 中至少有一个成立;③a ≠c ,b ≠c ,a ≠b 不能同时成立.其中正确的是________(填序号).【解析】 因为a ,b ,c 不全相等,所以①正确;②显然正确,③中的a ≠c ,b ≠c ,a ≠b 可以同时成立,所以③错.【答案】 ①②8.完成反证法证题的全过程.题目:设a 1,a 2,…,a 7是由数字1,2,…,7任意排成的一个数列,求证:乘积p =(a 1-1)(a 2-2)…(a 7-7)为偶数.证明:假设p 为奇数,则__________均为奇数.①因7个奇数之和为奇数,故有(a 1-1)+(a 2-2)+…+(a 7-7)为__________.②而(a 1-1)+(a 2-2)+…+(a 7-7)=(a 1+a 2+…+a 7)-(1+2+…+7)=__________.③②与③矛盾,故p 为偶数.【解析】 由假设p 为奇数可知(a 1-1),(a 2-2),…,(a 7-7)均为奇数,故(a 1-1)+(a 2-2)+…+(a 7-7)=(a 1+a 2+…+a 7)-(1+2+…+7)=0为奇数,这与0为偶数矛盾.【答案】 ①a 1-1,a 2-2,…,a 7-7 ②奇数 ③0二、解答题9.已知x ,y ,z 均大于零,求证:x +4y ,y +4z ,z +4x这三个数中至少有一个不小于4.【证明】 假设x +4y ,y +4z ,z +4x都小于4, 即x +4y <4,y +4z <4,z +4x<4, 于是得⎝⎛⎭⎪⎫x +4y +⎝ ⎛⎭⎪⎫y +4z +⎝ ⎛⎭⎪⎫z +4x <12, 而⎝⎛⎭⎪⎫x +4y +⎝ ⎛⎭⎪⎫y +4z +⎝ ⎛⎭⎪⎫z +4x =⎝ ⎛⎭⎪⎫x +4x +⎝ ⎛⎭⎪⎫y +4y +⎝ ⎛⎭⎪⎫z +4z ≥2 x ·4x +2 y ·4y +2 z ·4z=12, 这与⎝⎛⎭⎪⎫x +4y +⎝ ⎛⎭⎪⎫y +4z +⎝ ⎛⎭⎪⎫z +4x <12矛盾, 因此假设错误,即x +4y ,y +4z ,z +4x中至少有一个不小于4. 10.等差数列{a n }的前n 项和为S n ,a 1=1+2,S 3=9+3 2.(1)求数列{a n }的通项a n 与前n 项和S n ;(2)设b n =S n n(n ∈N *),求证:数列{b n }中任意不同的三项都不可能成为等比数列.【解】 (1)设公差为d ,由已知得⎩⎪⎨⎪⎧ a 1=2+1,3a 1+3d =9+32,∴d =2,故a n =2n -1+2,S n =n(n +2).(2)证明:由(1)得b n =S n n =n + 2.。
2016-2017学年高二数学苏教版选修2-2学业分层测评14 推理案例赏析

学业分层测评(十四)(建议用时:45分钟)[学业达标]一、填空题1.如图2119所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成的规律,a 所表示的数是________.【导学号:01580042】图2119【解析】 由图形中数字,不难得出每行两头数字均为1,其它数字均为其肩上两数字之和,∴a =3+3=6.【答案】 62.对于大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”:23=Error! 33=Error! 43=Error!….仿此,若m 3的“分裂数”中有一个是2 015,则m =________.【解析】 根据分裂特点,设最小数为a 1,则ma 1+×2=m 3,∴a 1=m 2-m +1.m (m -1)2∵a 1为奇数,又452=2 025,∴猜想m =45.验证453=91 125=.(1 979+2 071)×452【答案】 453.对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:________________________.【解析】 平面几何中的线与立体几何中的面相类比,可得:夹在两个平行平面间的平行线段相等.【答案】 夹在两个平行平面间的平行线段相等4.观察下面不等式:1+<,1++<,1+++<,…,猜122321221325312213214274想第n 个不等式为________.【解析】 当n ≥2时,则不等式左端就为1+++…+,而右端的1221321n 2分母正好是n ,分子是2n -1,因此可以猜想,n ≥2时,满足的不等式为1+++…+<.1221321n 22n -1n故可归纳式子为:1+++…+<(n ≥2).1221321n 22n -1n【答案】 1+++…+<(n ≥2)1221321n 22n -1n5.若a 1,a 2,a 3,a 4∈R +,有以下不等式成立:,≥,≥.由a 1+a 22a 1a 2a 1+a 2+a 333a 1a 2a 3a 1+a 2+a 3+a 444a 1a 2a 3a 4此推测成立的不等式是_______________________________________________.(要注明成立的条件)【答案】 (a 1,a 2,a 3,…,a n ∈R +)a 1+a 2+a 3+…+annna 1a 2a 3…an 6.观察下列各式:55=3 125,56=15 625,57=78 125,…则52 015的末四位数字为________.【解析】 ∵55=3 125,56=15 625,57=78 125,58末四位数字为0 625,59末四位数字为3 125,510末四位数字为5 625,511末四位数字为8 125,512末四位数字为0 625,…,由上可得末四位数字周期为4,呈规律性交替出现,∴52 015=54×503+3末四位数字为8 125.【答案】 8 1257.(2016·湖北调研)如图2120①②③④所示,它们都是由小圆圈组成的图案.现按同样的排列规则进行排列,记第n 个图形包含的小圆圈个数为f (n ),则图2120(1)f (5)=________;(2)f (2 015)的个位数字为________.【解析】 观察规律可知:f (5)=4×5+1=21,f (2 015)=2 014×2015+1,它的个位数字是1.【答案】 (1)21 (2)18.(2016·江西稳派调研)将2n 按如表所示的规律填在5列的数表中,设22015排在数表的第n 行,第m 列,则第m -1列中的前n 个数的和S n =________.212223242827262529210211212216215214213……………【解析】 由于2 015=4×503+3,故22 015位于表格的第504行第4列,所以n =504,m =4.所以S n ==.22[1-(24)504]1-2422 018-415【答案】 22 018-415二、解答题9.数列{a n }的前n 项和记为S n ,已知a 1=1,a n +1=S n (n ∈N *),证明:n +2n (1)数列是等比数列;{Snn }(2)S n +1=4a n .【导学号:01580043】【证明】 (1)∵a n +1=S n +1-S n ,a n +1=S n ,n +2n ∴(n +2)S n =n (S n +1-S n ),即nS n +1=2(n +1)S n .故=2·,数列是以1为首项,2为公比的等比数列.Sn +1n +1Snn {Snn }(2)由(1)知=4·(n ≥2).Sn +1n +1Sn -1n -1∴S n +1=4(n +1)·=4··S n -1=4a n (n ≥2).Sn -1n -1n -1+2n -1又∵a 2=3S 1=3,S 2=a 1+a 2=4=4a 1,∴对任意正整数n ,都有S n +1=4a n .10.在平面几何中,研究正三角形内任意一点与三边的关系时,我们有真命题:边长为a 的正三角形内任意一点到各边的距离之和是定值a .类比上述32命题,请你写出关于正四面体内任意一点与四个面的关系的一个真命题,并给出简要的证明.【解】 类比所得的真命题是:棱长为a 的正四面体内任意一点到四个面的距离之和是定值a .63证明:设M 是正四面体P ABC 内任意一点,M 到面ABC ,面PAB ,面PAC ,面PBC 的距离分别为d 1,d 2,d 3,d 4.由于正四面体四个面的面积相等,故有:V P ABC =V M ABC +V M PAB +V M PAC +V M PBC=·S △ABC ·(d 1+d 2+d 3+d 4),13而S △ABC =a 2,V P ABC =a 3,34212故d 1+d 2+d 3+d 4=a (定值).63[能力提升]1.(2016·盐城高二期终)已知=2,=3,=4,…类比这些等式,若2+23233+38384+415415=6(a ,b 均为正实数),则a +b =______.6+ab ab 【解析】 类比已知的3个等式,知a =6,b =62-1=35.所以a +b =41.【答案】 412.已知结论:“在正三角形ABC 中,若D 是边BC 的中点,G 是三角形ABC 的重心,则=2”.若把该结论推广到空间,则有结论:在棱长都相等的AGGD 四面体ABCD 中,若△BCD 的中心为M ,四面体内部一点O 到四面体各面的距离都相等,则等于________.AOOM 【解析】 如图,设正四面体的棱长为1,则易知其高AM =,此时点63O 即为正四面体内切球的球心,设其半径为r ,利用等体积法有4××r =××⇒r =,故AO =AM -MO =-=,故13341334636126361264AO ∶OM =∶=3.64612【答案】 33.(2016·湖北宜昌高三模拟)观察下列等式:①sin 2θ=cos θ·2sin θ;②sin 4θ=cos θ(4sin θ-8sin 3θ);③sin 6θ=cos θ(6sin θ-32sin 3θ+32sin 5θ);④sin 8θ=cos θ(8sin θ-80sin 3θ+192sin 5θ-128sin 7θ);⑤sin 10θ=cos θ(10sin θ-160sin 3θ+m sin 5θ-1 024sin 7θ+n sin 9θ).则可以推测(1)n =________,(2)m =________.【解析】 由给定等式的规律可知奇数式的最后一项系数为正数.数值为2n ,n 的值与sin θ的次数相同,所以式子⑤中n =29=512.另一特征为括号中所有系数的和奇数式与θ的系数相等,偶数式与θ的系数相反,所以⑤式中10-160+m -1 024+512=10,∴m =672.【答案】 512 672【答案】 145.设f (x )=,g (x )=(其中a >0,a ≠1).ax +a -x2ax -a -x2(1)请你推测g (5)能否用f (2),f (3),g (2),g (3)来表示.(2)如果(1)中获得一个结论,请你推测能否推广并加以证明.【解】 (1)由题意可得f (2)=,f (3)=,g (2)a 2+a -22a 3+a -32=,g (3)=.a 2-a -22a 3-a -32则f (3)·g (2)+g (3)·f (2)==.a 5-a +a -1-a -5+a 5+a -a -1-a -54a 5-a -52又g (5)=,a 5-a -52因此,g (5)=f (3)·g (2)+g (3)·f (2).(2)g (5)=f (3)·g (2)+g (3)·f (2),即g (3+2)=f (3)·g (2)+g (3)·f (2).于是猜测g (x +y )=f (x )·g (y )+g (x )·f (y ).证明:∵f (x )=,g (x )=,ax +a -x2ax -a -x2∴g (x +y )=,a (x +y )-a -(x +y )2g (y )=,f (y )=,ay -a -y 2ay +a -y2所以f (x )·g (y )+g (x )·f (y )=·+·ax +a -x 2ay -a -y 2ax -a -x 2ay +a -y 2==g (x +y ).a (x +y )-a -(x +y )2故g (x +y )=f (x )·g (y )+g (x )·f (y ).。
苏教版数学高二数学苏教版选修2-2单元测试 第2章推理与证明

第2章过关检测(时间90分钟,满分100分)一、填空题(本大题共14小题,每小题4分,满分56分)1.如果f (x +y )=f (x )f (y ),且f (1)=1,则f (2)f (1)+f (3)f (2)+…+f (2 010)f (2 009)等于__________.2.若从点O 所作的两条射线OM 、ON 上分别有点M 1、M 2与点N 1、N 2,则三角形面积之比为:S △OM 1N 1S △OM 2N 2=OM 1OM 2·ON 1ON 2.若从点O 所作的不在同一个平面内的三条射线OP 、OQ和OR 上分别有点P 1、P 2与点Q 1、Q 2和R 1、R 2,则类似的结论为:__________.3.根据图中的5个图形及相应的点的个数的变化规律,试猜测第n 个图中有__________个点.4.三段论:“①只有船准时起航,才能准时到达目的港;②这艘船是准时到达目的港的;③所以这艘船是准时起航的.”中的“小前提”是__________.5.设S (n )=1n +1n +1+1n +2+1n +3+…+1n 2,则S (n )共有__________项,S (2)=__________.6.用数学归纳法证明1+2+22+…+2n -1=2n -1(n ∈N *)的过程如下: ①当n =1时,左边=1,右边=21-1=1,等式成立. ②假设当n =k 时,等式成立,即1+2+22+…+2k -1=2k -1, 则当n =k +1时,1+2+22+…+2k -1+2k =1-2k +11-2=2k +1-1,所以当n =k +1时等式成立. 由此可知对任何n ∈N *,等式都成立. 上述证明的错误是__________.7.F (n )是一个关于自然数n 的命题,若F (k )(k ∈N *)真,则F (k +1)真,现已知F (7)不真,则有①F (8)不真;②F (8)真;③F (6)不真;④F (6)真;⑤F (5)不真;⑥F (5)真.其中真命题是__________.8.从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,归纳出一般的式子是__________.9.已知a >b >0,且ab =1,若0<c <1,p =log c a 2+b 22,q =log c (1a +b )2,则p 、q的大小关系是__________.10.在椭圆中,我们有如下结论:椭圆x 2a 2+y 2b 2=1上斜率为1的弦的中点在直线x a 2+yb 2=0上,类比上述结论,得到正确的结论为:双曲线x 2a 2-y 2b 2=1上斜率为1的弦的中点在直线__________上.11.在等差数列{a n }中,当a r =a s (r ≠s )时,数列{a n }必定是常数列.然而在等比数列{a n }中,对某些正整数r ,s (r ≠s ),当a r =a s 时,非常数数列{a n }的一个例子是__________.12.将正奇数排列如下表,其中第i 行第j 个数表示a ij (i ∈N *,j ∈N *),例如a 32=9,a ij=2 009,则i +j =__________.13.在平面上的n 个圆中,每两个圆都相交,每三个圆不交于一点,则它们把平面分成__________部分.14.{a n }是由非负整数组成的数列,满足a 1=0,a 2=3,a n +1a n =(a n -1+2)(a n -2+2),n =3,4,5,…,则a 3=__________.二、解答题(本大题共4小题,满分44分)15.(10分)如图,已知平面α∩平面β=直线a ,直线b ⊂α,直线c ⊂β,b ∩a =A ,c ∥a .求证:b 与c 是异面直线.16.(10分)已知数列{a n}满足a1=1,且4a n+1-a n a n+1+2a n=9(n∈N*).(1)求a2,a3,a4;(2)由(1)猜想{a n}的通项公式a n,并用数学归纳法证明你的猜想.17.(12分)下列命题是真命题还是假命题,用分析法证明你的结论.命题:若a>b>c且a+b+c=0,则b2-aca< 3.18.(12分)已知f (n )=(2n +7)·3n +9,是否存在自然数m ,使对任意n ∈N *,都有m 整除f (n )?若存在,求出最大值的m 值,并证明你的结论;若不存在,说明理由.参考答案1.2 009 解析:令x =n (n ∈N *),y =1得f (n +1)=f (n )·f (1)=f (n ),所以f (n +1)f (n )=1,所以f (2)f (1)+f (3)f (2)+…+f (2 010)f (2 009)=1+1+…+1=2 009. 2.VO —P 1Q 1R 1VO —P 2Q 2R 2=OP 1OP 2·OQ 1OQ 2·OR 1OR 23.n 2-n +1 解析:如设第n 个图中的点数为a n ,则有a 1=1,a 2=3=22-1,a 3=7=32-2,a 4=13=42-3,a 5=21=52-4.故a n =n 2-(n -1)=n 2-n +1.4.② 解析:①的意思是:如果船不准时起航,那么它就不能准时到达目的港,它的逆否命题是:如果船准时到达目的港,那么它是准时起航.由此可知,①是大前提,②是小前题.5.n 2-n +1 1312解析:从n 到n 2共有n 2-n +1个自然数,即S (n )共有n 2-n +1项.S (2)=12+13+14=1312. 6.在证明n =k +1时,没有用假设n =k 时的结论7.③⑤ 解析:“F (k )真⇒F (k +1)真”等价于“F (k +1)假⇒F (k )假”.8.1-4+9-16+…+(-1)n +1n 2=(-1)n -1·n (n +1)2(n ∈N *) 解析:1-4=-(1+2)=(-1)2-1·2(2+1)2,1-4+9=1+2+3=(-1)3-13(3+1)2,1-4+9-16=-(1+2+3+4)=(-1)4-14(4+1)2,由此可归纳出结论. 9.p >q 解析:∵a 2+b 22≥ab =1,∴p =log c a 2+b 22<0.又q =log c (1a +b )2=log c 1a +b +2ab>log c 14ab =log c 14>0,∴q >p . 10.x a 2-yb2=0 11.1,-1,1,-1,…(不唯一)12.60 解析:2 009是正奇数1,3,5,…中的第1 005个,则1 005=1+2+3+…+(i -1)+j =(i -1)i2+j .估算:当i =45时,(i -1)i2=990,j =15,所以i +j =60.13.n 2-n +2 解析:n =1时,a 1=2; n =2时,a 2=4=a 1+2=a 1+2×1; n =3时,a 3=8=a 2+4=a 2+2×2; n =4时,a 4=14=a 3+6=a 3+2×3; …a n +1=a n +2n .由⎩⎪⎨⎪⎧a 1=2a n +1=a n+2n⇒a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 2-a 1)+a 1=2(n -1)+2(n -2)+…+2×1+2=n 2-n +2.14.2 解析:由已知a 4a 3=(a 2+2)(a 1+2)=5×2=10×1, ∴a 3可能取值1,2,5,10. 若a 3=1,a 4=10,从而a 5=(a 3+2)(a 2+2)a 4=1510=32,显然a 5不是非负整数,与题设矛盾. 若a 3=10,则a 4=1,从而a 5=60. 但再计算a 6=35,也与题设矛盾.∴a 3=2,a 4=5(或a 3=5,a 4=2⇒a 5∉N *,舍去). 15.证明:假设b 、c 不是异面直线,即b 与c 共面, 设b 与c 确定的平面为γ,则γ∩α=b ,γ∩β=c , ∵a ∥c ,∴α∥γ.又a ⊂α,且α∩γ=b , ∴a ∥b ,这与a ∩b =A 矛盾.因此b 与c 不可能共面,故b 与c 是异面直线. 16.解:(1)由4a n +1-a n a n +1+2a n =9得 a n +1=9-2a n 4-a n =2-1a n -4,求得a 2=73,a 3=135,a 4=197.(2)猜想a n =6n -52n -1.证明:①当n =1时,猜想成立.②设当n =k 时(k ∈N +)时,猜想成立,即a k =6k -52k -1,则当n =k +1时,有a k +1=2-1a k -4=2-16k -52k -1-4=6k +12k +1=6(k +1)-52(k +1)-1,所以当n =k +1时猜想也成立.③综合①②,猜想对任何n ∈N +都成立. 17.解:此命题是真命题.∵a +b +c =0,a >b >c ,∴a >0,c <0. 要证b 2-ac a <3成立,只要证b 2-ac <3a ,即证b 2-ac <3a 2,也就是证(a +c )2-ac <3a 2,即证(a-c)(2a+c)>0,∵a-c>0,2a+c=(a+c)+a=a-b>0,∴(a-c)(2a+c)>0成立.故原不等式成立.18.解:由f(1)=36,f(2)=108,f(3)=360,f(4)=1 224,猜想f(n)被36整除.证明:①当n=1时,猜想显然成立.②设n=k时,f(k)能被36整除.则n=k+1时,f(k+1)=[2(k+1)+7]·3k+1+9=3[(2k+7)·3k+9]+18(3k-1-1),根据假设3[2(k+7)·3k+9]被36整除,而3k-1-1是偶数,∴18(3k-1-1)能被36整除,从而f(k+1)能被36整除.综上所述,n∈N*时,f(n)能被36整除,由于f(1)=36,故36是整除f(n)的自然数中的最大数.。
(完整版)数学选修2-2练习题及答案

目录:数学选修2-2第一章 导数及其应用 [基础训练A 组] 第一章 导数及其应用 [综合训练B 组] 第一章 导数及其应用 [提高训练C 组] 第二章 推理与证明 [基础训练A 组] 第二章 推理与证明 [综合训练B 组]第二章 推理与证明 [提高训练C 组] 第三章 复数 [基础训练A 组] 第三章 复数 [综合训练B 组]第三章 复数 [提高训练C 组](数学选修2-2)第一章 导数及其应用[基础训练A 组]一、选择题1.若函数()y f x =在区间(,)a b 内可导,且0(,)x a b ∈则000()()limh f x h f x h h→+--的值为( )A .'0()f xB .'02()f xC .'02()f x - D .02.一个物体的运动方程为21t t s +-=其中s 的单位是米,t 的单位是秒, 那么物体在3秒末的瞬时速度是( ) A .7米/秒 B .6米/秒 C .5米/秒 D .8米/秒 3.函数3yx x 的递增区间是( )A .),0(+∞B .)1,(-∞C .),(+∞-∞D .),1(+∞4.32()32f x ax x =++,若'(1)4f -=,则a 的值等于( )A .319 B .316C .313 D .310 5.函数)(x f y =在一点的导数值为0是函数)(x f y =在这点取极值的( )A .充分条件B .必要条件C .充要条件D .必要非充分条件6.函数344+-=x x y 在区间[]2,3-上的最小值为( )A .72B .36C .12D .0二、填空题1.若3'0(),()3f x x f x ==,则0x 的值为_________________;2.曲线x x y 43-=在点(1,3)- 处的切线倾斜角为__________; 3.函数sin xy x=的导数为_________________; 4.曲线x y ln =在点(,1)M e 处的切线的斜率是_________,切线的方程为_______________; 5.函数5523--+=x x x y 的单调递增区间是___________________________。
苏教版数学高二-数学苏教版选修2-2 第二章 推理与证明 章末检测

第二章《推理与证明》章末检测 一、填空题 1.由1=12,1+3=22,1+3+5=32,1+3+5+7=42,…,得到1+3+…+(2n -1)=n 2用的是________推理.2.在△ABC 中,E 、F 分别为AB 、AC 的中点,则有EF ∥BC ,这个问题的大前提为________________________.3.用反证法证明命题 “三角形的内角至多有一个钝角”时,反设为________.4.用数学归纳法证明:1+11+2+11+2+3+…+11+2+3+…+n =2n n +1时,由n =k 到n =k +1左边需要添加的项是________.5.已知f (x +1)=2f (x )f (x )+2,f (1)=1(x ∈N *),猜想f (x )的表达式为________. 6.下列四个图形中,着色三角形的个数依次构成一个数列的前4页,则这个数列的一个通项公式为________.7.对“a ,b ,c 是不全相等的正数”,给出下列判断:①(a -b )2+(b -c )2+(c -a )2≠0;②a =b 与b =c 及a =c 中至少有一个成立;③a ≠c ,b ≠c ,a ≠b 不能同时成立.其中判断正确的个数为________.8.我们把平面几何里相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.下列几何体中,一定属于相似体的有________个. ①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱椎.9.数列{a n }满足a 1=12,a n +1=1-1a n,则a 2 013=________. 10.从1=12,2+3+4=32,3+4+5+6+7=52中,可得到一般规律为____________________________________.11.f (n )=1+12+13+…+1n (n ∈N *),经计算得f (2)=32,f (4)>2,f (8)>52,f (16)>3,f (32)>72,推测当n ≥2时,有____________.12.如图所示是按照一定规律画出的一列“树型”图,设第n 个图有a n 个“树枝”,则a n+1与a n (n ∈N *)之间的关系是______.13.在平面几何中,△ABC 的内角平分线CE 分AB 所成线段的比为AE EB =AC BC,把这个结论类比到空间:在三棱锥A —BCD 中(如图所示),面DEC 平分二面角A —CD —B 且与AB 相交于E ,则得到的类比的结论是________.二、解答题14.把下面在平面内成立的结论类比地推广到空间,并判断类比的结论是否成立:(1)如果一条直线和两条平行线中的一条相交,则必和另一条相交;(2)如果两条直线同时垂直于第三条直线,则这两条直线互相平行.15.1,3,2能否为同一等差数列中的三项?说明理由.16.设a ,b 为实数,求证:a 2+b 2≥22(a +b ).17.设a ,b ,c 为一个三角形的三边,s =12(a +b +c ),且s 2=2ab ,试证:s <2a .18.数列{a n }满足a 1=16,前n 项和S n =n (n +1)2a n . (1)写出a 2,a 3,a 4;(2)猜出a n 的表达式,并用数学归纳法证明.19.设f (n )=1+12+13+ (1),是否存在关于自然数n 的函数g (n ),使等式f (1)+f (2)+…+f (n -1)=g (n )·[f (n )-1]对于n ≥2的一切自然数都成立?并证明你的结论.答案1.归纳2.三角形的中位线平行于第三边3.假设至少有两个钝角4.2(k +1)(k +2)5.f (x )=2x +16.a n =3n -1(n ∈N *,n ≥1)7.18.29.-110.n +(n +1)+(n +2)+…+(3n -2)=(2n -1)211.f (2n )>2+n 2(n ≥2) 12.a n +1=2a n +113.AE EB =S △ACD S △BCD14.解 (1)类比为:如果一个平面和两个平行平面中的一个相交,则必和另一个相交.结论是正确的:证明如下:设α∥β,且γ∩α=a ,则必有γ∩β=b ,若γ与β不相交,则必有γ∥β,又α∥β,∴α∥γ,与γ∩α=a 矛盾,∴必有γ∩β=b .(2)类比为:如果两个平面同时垂直于第三个平面,则这两个平面互相平行,结论是错误的,这两个平面也可能相交.15.解 假设1,3,2能为同一等差数列中的三项,但不一定是连续的三项,设公差为d ,则1=3-md,2=3+nd ,m ,n 为两个正整数,消去d 得m =(3+1)n .∵m 为有理数,(3+1)n 为无理数,∴m ≠(3+1)n .∴假设不成立.即1,3,2不可能为同一等差数列中的三项.16.证明 当a +b ≤0时,∵a 2+b 2≥0, ∴a 2+b 2≥22(a +b )成立. 当a +b >0时,用分析法证明如下:要证a 2+b 2≥22(a +b ), 只需证(a 2+b 2)2≥⎣⎡⎦⎤22(a +b )2, 即证a 2+b 2≥12(a 2+b 2+2ab ),即证a 2+b 2≥2ab . ∵a 2+b 2≥2ab 对一切实数恒成立,∴a 2+b 2≥22(a +b )成立. 综上所述,对任意实数a ,b 不等式都成立. 17.证明 要证s <2a ,由于s 2=2ab ,所以只需证s <s 2b ,即证b <s . 因为s =12(a +b +c ),所以只需证2b <a +b +c ,即证b <a +c . 由于a ,b ,c 为一个三角形的三条边,所以上式成立.于是原命题成立.18.解 (1)令n =2,∵a 1=16,∴S 2=2×(2+1)2a 2, 即a 1+a 2=3a 2.∴a 2=112. 令n =3,得S 3=3×(3+1)2a 3, 即a 1+a 2+a 3=6a 3,∴a 3=120. 令n =4,得S 4=4×(4+1)2a 4, 即a 1+a 2+a 3+a 4=10a 4,∴a 4=130. (2)猜想a n =1(n +1)(n +2),下面用数学归纳法给出证明. ①当n =1时,a 1=16=1(1+1)(1+2),结论成立. ②假设当n =k 时,结论成立,即a k =1(k +1)(k +2), 则当n =k +1时,S k =k (k +1)2a k =k (k +1)2·1(k +1)(k +2)=k 2(k +2), S k +1=(k +1)(k +2)2a k +1, 即S k +a k +1=(k +1)(k +2)2a k +1. ∴k 2(k +2)+a k +1=(k +1)(k +2)2a k +1.∴a k +1=k 2(k +2)(k +1)(k +2)2-1=k k (k +3)(k +2) =1(k +2)(k +3). 当n =k +1时结论成立.由①②可知,对一切n ∈N *都有a n =1(n +1)(n +2). 19.解 当n =2时,由f (1)=g (2)·[f (2)-1],得g (2)=f (1)f (2)-1=1(1+12)-1=2, 当n =3时,由f (1)+f (2)=g (3)·[f (3)-1],得g (3)=f (1)+f (2)f (3)-1=1+(1+12)(1+12+13)-1=3, 猜想g (n )=n (n ≥2).下面用数学归纳法证明:当n ≥2时,等式f (1)+f (2)+…+f (n -1)=n [f (n )-1]恒成立. ①当n =2时,由上面计算可知,等式成立.②假设n =k (k ∈N *且k ≥2)时,等式成立,即f (1)+f (2)+…+f (k -1)=k [f (k )-1](k ≥2)成立, 那么当n =k +1时,f (1)+f (2)+…+f (k -1)+f (k )=k [f (k )-1]+f (k )=(k +1)f (k )-k=(k +1)[f (k +1)-1k +1]-k =(k +1)[f (k +1)-1],∴当n =k +1时,等式也成立.由①②知,对一切n ≥2的自然数n ,等式都成立,故存在函数g (n )=n ,使等式成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学苏教版高二选修2-2学业分层测评:第二章_推理与证明_14 含解析学业分层测评(十四)(建议用时:45分钟)学业达标]一、填空题1.如图2-1-19所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成的规律,a 所表示的数是________.【导学号:01580042】图2-1-19【解析】 由图形中数字,不难得出每行两头数字均为1,其它数字均为其肩上两数字之和,∴a =3+3=6.【答案】 62.对于大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”: 23=⎩⎨⎧3,5,33=⎩⎨⎧7,9,11,43=⎩⎨⎧13,15,17,19,….仿此,若m 3的“分裂数”中有一个是2 015,则m =________. 【解析】 根据分裂特点,设最小数为a 1, 则ma 1+m (m -1)2×2=m 3,∴a 1=m 2-m +1. ∵a 1为奇数,又452=2 025, ∴猜想m =45.验证453=91 125=(1 979+2 071)×452.【答案】 453.对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:________________________.【解析】 平面几何中的线与立体几何中的面相类比,可得:夹在两个平行平面间的平行线段相等.【答案】 夹在两个平行平面间的平行线段相等4.观察下面不等式:1+122<32,1+122+132<53,1+122+132+142<74,…,猜想第n 个不等式为________.【解析】 当n ≥2时,则不等式左端就为1+122+132+…+1n 2,而右端的分母正好是n ,分子是2n -1,因此可以猜想,n ≥2时,满足的不等式为1+122+132+…+1n 2<2n -1n .故可归纳式子为:1+122+132+…+1n 2<2n -1n (n ≥2). 【答案】 1+122+132+…+1n 2<2n -1n (n ≥2) 5.若a 1,a 2,a 3,a 4∈R +,有以下不等式成立:a 1+a 22≥a 1a 2,a 1+a 2+a 33≥3a 1a 2a 3,a 1+a 2+a 3+a 44≥4a 1a 2a 3a 4.由此推测成立的不等式是_______________________________________________.(要注明成立的条件) 【答案】a 1+a 2+a 3+…+a n n≥na 1a 2a 3…a n (a 1,a 2,a 3,…,a n ∈R +)6.观察下列各式:55=3 125,56=15 625,57=78 125,…则52 015的末四位数字为________. 【解析】 ∵55=3 125,56=15 625,57=78 125, 58末四位数字为0 625,59末四位数字为3 125, 510末四位数字为5 625,511末四位数字为8 125, 512末四位数字为0 625,…,由上可得末四位数字周期为4,呈规律性交替出现, ∴52 015=54×503+3末四位数字为8 125. 【答案】 8 1257.(2016·湖北调研)如图2-1-20①②③④所示,它们都是由小圆圈组成的图案.现按同样的排列规则进行排列,记第n 个图形包含的小圆圈个数为f (n ),则图2-1-20(1)f (5)=________;(2)f (2 015)的个位数字为________.【解析】 观察规律可知:f (5)=4×5+1=21,f (2 015)=2 014×2 015+1,它的个位数字是1.【答案】 (1)21 (2)18.(2016·江西稳派调研)将2n 按如表所示的规律填在5列的数表中,设22 015排在数表的第n 行,第m 列,则第m -1列中的前n 个数的和S n =________.【解析】 由于2 015=4×503+3,故22 015位于表格的第504行第4列,所以n =504,m =4.所以S n =22[1-(24)504]1-24=22 018-415. 【答案】22 018-415 二、解答题9.数列{a n }的前n 项和记为S n ,已知a 1=1,a n +1=n +2n S n (n ∈N *),证明:(1)数列⎩⎨⎧⎭⎬⎫S n n 是等比数列;(2)S n +1=4a n .【导学号:01580043】【证明】 (1)∵a n +1=S n +1-S n ,a n +1=n +2n S n , ∴(n +2)S n =n (S n +1-S n ),即nS n +1=2(n +1)S n .故S n +1n +1=2·S nn ,数列⎩⎨⎧⎭⎬⎫S n n 是以1为首项,2为公比的等比数列.(2)由(1)知S n +1n +1=4·S n -1n -1(n ≥2).∴S n +1=4(n +1)·S n -1n -1=4·n -1+2n -1·S n -1=4a n (n ≥2).又∵a 2=3S 1=3,S 2=a 1+a 2=4=4a 1, ∴对任意正整数n ,都有S n +1=4a n .10.在平面几何中,研究正三角形内任意一点与三边的关系时,我们有真命题:边长为a 的正三角形内任意一点到各边的距离之和是定值32a .类比上述命题,请你写出关于正四面体内任意一点与四个面的关系的一个真命题,并给出简要的证明.【解】 类比所得的真命题是:棱长为a 的正四面体内任意一点到四个面的距离之和是定值63a .证明:设M 是正四面体P -ABC 内任意一点,M 到面ABC ,面P AB ,面P AC ,面PBC 的距离分别为d 1,d 2,d 3,d 4.由于正四面体四个面的面积相等,故有:V P -ABC =V M -ABC +V M -P AB +V M -P AC +V M -PBC =13·S △ABC ·(d 1+d 2+d 3+d 4), 而S △ABC =34a 2,V P -ABC=212a 3,故d1+d2+d3+d4=63a(定值).能力提升]1.(2016·盐城高二期终)已知2+23=223,3+38=338,4+415=4415,…类比这些等式,若6+ab=6ab(a,b均为正实数),则a+b=______.【解析】类比已知的3个等式,知a=6,b=62-1=35.所以a+b=41.【答案】412.已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则AGGD=2”.若把该结论推广到空间,则有结论:在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则AOOM等于________.【解析】如图,设正四面体的棱长为1,则易知其高AM=63,此时点O即为正四面体内切球的球心,设其半径为r,利用等体积法有4×13×34r=13×34×63⇒r=612,故AO=AM-MO=63-612=64,故AO∶OM=64∶612=3.【答案】 33.(2016·湖北宜昌高三模拟)观察下列等式:①sin 2θ=cos θ·2sin θ;②sin 4θ=cos θ(4sin θ-8sin3θ);③sin 6θ=cos θ(6sin θ-32sin3θ+32sin5θ);④sin 8θ=cos θ(8sin θ-80sin3θ+192sin5θ-128sin7θ);⑤sin 10θ=cos θ(10sin θ-160sin3θ+m sin5θ-1 024sin7θ+n sin9θ).则可以推测(1)n=________,(2)m=________.【解析】由给定等式的规律可知奇数式的最后一项系数为正数.数值为2n,n的值与sinθ的次数相同,所以式子⑤中n =29=512.另一特征为括号中所有系数的和奇数式与θ的系数相等,偶数式与θ的系数相反,所以⑤式中10-160+m -1 024+512=10,∴m =672.【答案】 512 672【答案】 145.设f (x )=a x +a -x 2,g (x )=a x -a -x2(其中a >0,a ≠1). (1)请你推测g (5)能否用f (2),f (3),g (2),g (3)来表示. (2)如果(1)中获得一个结论,请你推测能否推广并加以证明.【解】 (1)由题意可得f (2)=a 2+a -22,f (3)=a 3+a -32,g (2)=a 2-a -22,g (3)=a 3-a -32. 则f (3)·g (2)+g (3)·f (2)=a 5-a +a -1-a -5+a 5+a -a -1-a -54=a 5-a -52.又g (5)=a 5-a -52,因此,g (5)=f (3)·g (2)+g (3)·f (2). (2)g (5)=f (3)·g (2)+g (3)·f (2), 即g (3+2)=f (3)·g (2)+g (3)·f (2). 于是猜测g (x +y )=f (x )·g (y )+g (x )·f (y ). 证明:∵f (x )=a x +a -x 2,g (x )=a x -a -x 2,∴g(x+y)=a(x+y)-a-(x+y)2,g(y)=a y-a-y2,f(y)=a y+a-y2,所以f(x)·g(y)+g(x)·f(y)=a x+a-x2·a y-a-y2+a x-a-x2·a y+a-y2=a(x+y)-a-(x+y)2=g(x+y).故g(x+y)=f(x)·g(y)+g(x)·f(y).。
