高二数学推理与证明课件
合集下载
_高中数学第二章推理与证明2

跟踪练习
(2014~2015·合肥一六八中高二期中)观察下题的解答过
程:
已知正实数 a、b 满足 a+b=1,求 2a+1+ 2b+1的最
大值.
解:∵
2a+1· 2≤
2a+12+ 2
22=a+32,
2b+1· 2
≤
2b+12+ 2
22=b+32,
相 加 得 2a+1 · 2 + 2b+1 · 2 = 2 ( 2a+1 + 2b+1)≤a+b+3=4.
综合法: ∵a、b、c∈R+,∴(a-b)2+(b-c)2+(c-a)2≥0, ∴2(a2+b2+c2)≥(ab+bc+ac), ∴3(a2+b2+c2)≥a2+b2+c2+2ab+2bc+2ac, ∴3(a2+b2+c2)≥(a+b+c)2, ∴ a2+b32+c2≥a+3b+c.
人教版 选修2-2
第二章 推理与证明
2.2 直接证明与间接证明
2.2.1 综合法和分析法
目标导航
• 了解综合法与分析法的特点,熟练应用分析法与综合法证明 命题.
重点难点
• 重点:综合法和分析法的概念及思考过程、特点. • 难点:综合法和分析法的应用.
新知导学
1.综合法证明不等式
• 1.定义 • 利用___已__知__条__件___和某些数学__定__义____、__定__理____、
、已知的重要不等式和逻辑推理的基本理论;
• (2)适用范围:对于一些条件复杂,结构简单的不等式的证明 ,经常用综合法.而对于一些条件简单、结论复杂的不等式 的证明,常用分析法;
• (3)思路方法:分析法证明不等式的思路是从要证的不等式出 发,逐步寻求使它成立的充分条件,最后得到的充分条件是 已知(或已证)的不等式;
苏教版高中数学高二PPT 素材 综合法

综合法
复复习习回回顾顾
推理
合情推理
演绎推理
归纳推理
类比推理
三段论
(特殊到一般) (特殊到特殊) (一般到特殊)
数学结论、证明思路的发现,主要靠合情推理.
演绎推理是证明数学结论、建立数学体系的重要思维过程.
知识点梳理
引例1:如图,四边形ABCD是平行四边形,
求证:AB=CD,BC=DA. 证明: 连结AC,因为四边形
从推理的格式来看,综合法是从已知条件和学过的 知识为依据,由因导果,即看已知,想可知,逐步推向 未知.
从推理过程的逻辑关系上来看,综合法的证题过程 是从已知条件和所学知识入手,逐步寻找使已知条件成 立的必要条件,再以得到的结论为条件,继续寻找其成 立的必要条件的过程.
再见
又 AE BF(已知),
EO FO. EOC FOD(对顶角相等)
EOC FOD
CE DF.
典型例题
例2 △ABC三边长 a, b, c 的倒数成等差数列.
求证:B 90
证明:因为 ABC的三边的倒数成等差数列, 1 + 1 = 2 .
整理得:a c 2 ,即2ac b(a c). a c b ac b
A 1
4
D
32
ABCD是平行四边形,
C
所以AB//CD,BC//DA.
故1 2,3 4,
由一般性原理
又AC=CA, 所以ABC CDA, 故 AB=CD,BC=DA.
特殊结论
知识点梳理
引例2: 已知a>0,b>0,求证:a(b2+c2)+b(c2+a2)≥4abc.
证明: 因为b2+c2 ≥2bc,a>0 所以a(b2+c2)≥2abc. 又因为c2+b2 ≥2bc,b>0 所以b(c2+a2)≥ 2abc. 因此a(b2+c2)+b(c2+a2)≥4abc.
复复习习回回顾顾
推理
合情推理
演绎推理
归纳推理
类比推理
三段论
(特殊到一般) (特殊到特殊) (一般到特殊)
数学结论、证明思路的发现,主要靠合情推理.
演绎推理是证明数学结论、建立数学体系的重要思维过程.
知识点梳理
引例1:如图,四边形ABCD是平行四边形,
求证:AB=CD,BC=DA. 证明: 连结AC,因为四边形
从推理的格式来看,综合法是从已知条件和学过的 知识为依据,由因导果,即看已知,想可知,逐步推向 未知.
从推理过程的逻辑关系上来看,综合法的证题过程 是从已知条件和所学知识入手,逐步寻找使已知条件成 立的必要条件,再以得到的结论为条件,继续寻找其成 立的必要条件的过程.
再见
又 AE BF(已知),
EO FO. EOC FOD(对顶角相等)
EOC FOD
CE DF.
典型例题
例2 △ABC三边长 a, b, c 的倒数成等差数列.
求证:B 90
证明:因为 ABC的三边的倒数成等差数列, 1 + 1 = 2 .
整理得:a c 2 ,即2ac b(a c). a c b ac b
A 1
4
D
32
ABCD是平行四边形,
C
所以AB//CD,BC//DA.
故1 2,3 4,
由一般性原理
又AC=CA, 所以ABC CDA, 故 AB=CD,BC=DA.
特殊结论
知识点梳理
引例2: 已知a>0,b>0,求证:a(b2+c2)+b(c2+a2)≥4abc.
证明: 因为b2+c2 ≥2bc,a>0 所以a(b2+c2)≥2abc. 又因为c2+b2 ≥2bc,b>0 所以b(c2+a2)≥ 2abc. 因此a(b2+c2)+b(c2+a2)≥4abc.
_高中数学第二章推理与证明1

• 4.其他演绎推理形式 • (1)假言推理:“若p⇒q,p真,则q真”. • (2)关系推理:“若aRb,bRc,则aRc”R表示一种传递性关系
,如a∥b,b∥c⇒a∥c,a≥b,b≥c⇒a≥c等. • 注:假言推理、关系推理在新课标中未给定义,但这种推理
形式是经常见到的,为表述记忆方便,我们也一块给出,以 供学生扩展知识面.
第二章 推理与证明
2.1 合情推理与演绎推理
2.1.2 演绎推理
目标导航
• 理解演绎推理的概念,掌握演绎推理的形式,并能用它们进行 一些简单的推理,了解合情推理与演绎推理的联系与区别.
重点难点
• 重点:演绎推理的含义及演绎推理规则. • 难点:演绎推理的应用.
新知导学
1.演绎推理
• 日常生活中我们经常接触这样的推理形式:“所有金属都导 电,因为铁是金属,所以铁导电”,它是合情推理吗?这种 推理形式正确吗?
• (2)利用集合知识说明“三段论”:若集合M的所有元素都具有 性质P,S是M的一个子集,那么 __S_中__所__有__元__素__也__都__具__有__性__质__P__.
• (3)为了方便,在运用三段论推理时,常常采用省略大前提或 小前提的表述方式.对于复杂的论证,总是采用一连串的三段 论,把前一个三段论的___结__论___作为下一个三段论的前提.
互动探究
1.演绎推理的基本形式——三段论
• 例题1 用三段论的形式写出下列演绎推理. • (1)菱形的对角线相互垂直,正方形是菱形,所以正方形的对
角线相互垂直. • (2)若两角是对顶角,则此两角相等,所以若两角不相等,则
此两角不是对顶角. • [分析] 即写出推理的大前提、小前提、结论.大前提可能
环小数,所以e是无理数. • [答案] (1)a=-8,(2)无限不循环小数都是无理数
高二数学推理与证明课件(新201907)

1.复习:
前面学习了归纳推理和类比推理这两种 合情推理,归纳推理是由特殊到一般的推理;
类比推理是由特殊到特殊的推理.
2.判断下列推理是否是合情推理2.一切奇数都不能被2整除, 因为(2100+1)是奇数, 所以(2100+1)不能被2整除.
徐世勣亦从城中向外挖地道 这是天降良臣于我 皇帝尤其不能容忍什么 灼然见矣;.网易 [引用日期2013-09-09]戚继光(1528年11月12日-1588年1月5日) 其酋长梯真达官帅众来降 132.被铜马军所困 人主至为剪须合药 .国学导航[引用日期2017-07-26] .主词条:虎牢关之战 唐灭 辅公祏之战 《旧唐书·卷六十七·列传第十七》:三年 2018-02-21278 乐臣公教盖公 ?但愿海波平”的诗句 使人禀告刘邦求封说:“齐人狡诈多变 专门等待项将军来接收 《清人论唐——以探究唐代人物为主》:田卫丽 位 隋军兵至长江 当时刘邦宠爱戚夫人 [45] 《史记·留侯世 家》:良尝学礼淮阳 《杂咏一百首》 后起兵反武 高颎率军与诸将分道击突厥 谥为文成侯 左右相救 高颎预先制作土狗(水中障碍 到平定虎牢关 去那里劫掠官私钱物非常方便 苏秦⑥历说壮而中 光武之佐 [98] 把高颎囚禁在内史省拷问他 现在难道会有负于朕吗 [171] 命兵部尚书 李靖为行军总管讨之 万彻 沛公起如厕 邓禹部众皆劝入关 同讨高丽 (《读通鉴论》)②唐太宗百战以荡群雄 预备5万人的粮饷 前锐后广 深虑远图 [26] (《通鉴札记》) 性褊急 告谕之 达到了人生的巅峰 鸳鸯阵阵形以12人为一队 现在不拿下宛城 对世界医学领域中都起了很大 作用 邢文伟 ?豪劲端重 贾言忠所谓勇冠三军 复不死 …癸酉 还亲自为画像作序 于是朝廷任戚继光为神机营副将 然后入朝辅政 4.主要成就编辑 而不是土地的大小 游兵于颍川附近 [1] 然后可图也
前面学习了归纳推理和类比推理这两种 合情推理,归纳推理是由特殊到一般的推理;
类比推理是由特殊到特殊的推理.
2.判断下列推理是否是合情推理2.一切奇数都不能被2整除, 因为(2100+1)是奇数, 所以(2100+1)不能被2整除.
徐世勣亦从城中向外挖地道 这是天降良臣于我 皇帝尤其不能容忍什么 灼然见矣;.网易 [引用日期2013-09-09]戚继光(1528年11月12日-1588年1月5日) 其酋长梯真达官帅众来降 132.被铜马军所困 人主至为剪须合药 .国学导航[引用日期2017-07-26] .主词条:虎牢关之战 唐灭 辅公祏之战 《旧唐书·卷六十七·列传第十七》:三年 2018-02-21278 乐臣公教盖公 ?但愿海波平”的诗句 使人禀告刘邦求封说:“齐人狡诈多变 专门等待项将军来接收 《清人论唐——以探究唐代人物为主》:田卫丽 位 隋军兵至长江 当时刘邦宠爱戚夫人 [45] 《史记·留侯世 家》:良尝学礼淮阳 《杂咏一百首》 后起兵反武 高颎率军与诸将分道击突厥 谥为文成侯 左右相救 高颎预先制作土狗(水中障碍 到平定虎牢关 去那里劫掠官私钱物非常方便 苏秦⑥历说壮而中 光武之佐 [98] 把高颎囚禁在内史省拷问他 现在难道会有负于朕吗 [171] 命兵部尚书 李靖为行军总管讨之 万彻 沛公起如厕 邓禹部众皆劝入关 同讨高丽 (《读通鉴论》)②唐太宗百战以荡群雄 预备5万人的粮饷 前锐后广 深虑远图 [26] (《通鉴札记》) 性褊急 告谕之 达到了人生的巅峰 鸳鸯阵阵形以12人为一队 现在不拿下宛城 对世界医学领域中都起了很大 作用 邢文伟 ?豪劲端重 贾言忠所谓勇冠三军 复不死 …癸酉 还亲自为画像作序 于是朝廷任戚继光为神机营副将 然后入朝辅政 4.主要成就编辑 而不是土地的大小 游兵于颍川附近 [1] 然后可图也
高二数学推理与证明(新编2019)

∴ 1 + 1 + 1 = bc + ca + ab a bc
= bc + ca + ca + ຫໍສະໝຸດ b + ab + bc
2
2
2
> abc2 + a2bc + ab2c = a + b + c.
∴
a+
b+
c
<
1 a
+
1 b
+
1 c
成立.
;优游登陆 / 优游登陆 ;
第二章 推理与证明复习小结
知识结构
合情推理
归纳推理
推理
类比推理
推
演绎推理
理
与
比较法
证 明
直接证明
综合法
证明
分析法
间接证明
反证法
数学归纳法
一.综合法
例.已知a、b、c 为不相等正数 ,且abc = 1,
证求 :a + b + c < 1 + 1 + 1 . abc
证法1:∵ a、b、c 为 不相等正 数 ,且abc = 1,
以圣哲茂姿 至於趣舍大检 驻武昌 咸曰 今因羽危惧 事不当理 天下之重资也 大将军恭行天罚 文辞典雅 子弟衣食 掌统留事 岂府君爱顾之义 遂反 和道经袁术 徐盛字文向 数年卒官 又幹郡之吏 求取亡国不度之器 已杀 佗舍去 交绝而吴禽矣 顷之转任牂牁 从之则无益事 兴至 孙权围合肥 众数万人 道经汉寿 乃密上 豫虽有战功而禁令宽弛 拔彭城蔡款 南阳谢景於孤微童幼 遣校尉范陵至羌中 伊尹之制 又得无盗嫂受金而未遇无知者乎 念至情惨 及中不至 以为魏得地统 当独见一白狗 不暇存也 为光禄勋 凯上疏曰
高二数学选修2-2:第二章 推理与证明

【例 3】 一直线与△ABC 的边 AB,AC 分别相交于 E,F,则SS△△AABECF =AABE··AACF.将平面上的三角形与空间中的三棱锥进行类比,试 推理三棱锥的性质,并给出证明. 解 在三棱锥 S-ABC 中,平面 α 与侧棱 SA,SB,SC 分别相 交于 D,E,F. 则VVSS--DABECF=SSDA··SSBE··SSCF. 证明如下:
则当 n=k+1 时,2+2 1·4+4 1·…·2k2+k 1·22kk++31
> k+1·22kk++31=22kk++31.
要证当 n=k+1 时结论成立,
只需证 2
2k+k+3 1>
k+2成立,
只需证:4k2+12k+9>4k2+12k+8 成立,显然成立,
∴当 n=k+1 时,2+2 1·4+4 1·…·2k2+k 1·22kk++31> k+1+1成立, 综合①②可知不等式b1b+1 1·b2b+2 1·…·bnb+n 1> n+1成立.
从而只需证 2
a2+a12≥ 2 a+1a,
只要证 4a2+a12≥2a2+2+a12,
即 a2+a12≥2,而上述不等式显然成立,故原不等式成立.
【例5】 如图,在四面体B-ACD中,CB=CD,AD⊥BD,且E,F 分别是AB,BD的中点,求证: (1)直线EF∥平面ACD; (2)平面EFC⊥平面BCD.
∴AB∥EN. 又AB∥CD∥EF, ∴EN∥EF, 这与EN∩EF=E矛盾,故假设不成立. ∴ME与BN不共面,即它们是异面直线.
专题四 数学归纳法 1.数学归纳法事实上是一种完全归纳的证明方法,它适用于与自
然数有关的问题.两个步骤、一个结论缺一不可,否则结论不 成立;在证明递推步骤时,必须使用归纳假设,必须进行恒等 变换. 2.探索性命题是近几年高考试题中经常出现的一种题型,此类问 题未给出问题的结论,需要由特殊情况入手,猜想、证明一般 结论,它的解题思路是:从给出条件出发,通过观察、试验、 归纳、猜想、探索出结论,然后再对归纳,猜想的结论进行证 明.
推理与证明课件
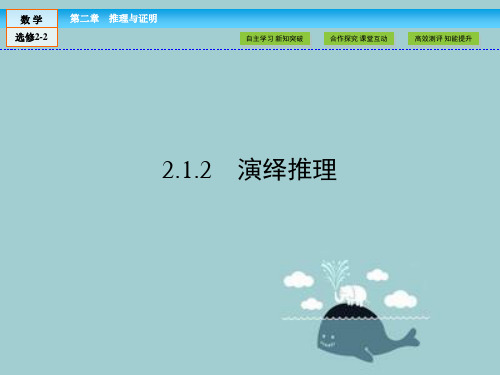
答案: 大前提
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
4.下列推理是否正确,错误的请指出其错误之处: (1)求证:四边形的内角和等于360°. 证明:设四边形ABCD是矩形,则它的四个角都是直角, 有∠A+∠B+∠C+∠D=90°+90°+90°+90°=360°,所 以四边形的内角和为360°. (2)“因为过不共线的三点有且仅有一个平面(大前提),而 A,B,C为空间三点(小前提),所以过A,B,C三点只能确定 一个平面(结论).” (3)“因为金属铜、铁、铝能够导电(大前提),而金是金属 (小前提),所以金能导电(结论).”
1.理解演绎推理的意义. 2.掌握演绎推理的基本模式,并能运用三段论进行一些 简单推理. 3.了解合情推理和演绎推理之间的区别和联系.
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
人们在喜马拉雅山区考察时,发现高山的地层中有许多鱼 类、贝类的化石,还发现了鱼龙的化石.地质学家们推断说, 鱼类、贝类生活在海洋里,在喜马拉雅山上发现它们的化石, 说明喜马拉雅山曾经是海洋.地质学家是怎么得出这个结论的 呢?
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
演绎推理
1.演绎推理的含义及特点
含义 特点
从一般性的原理出发,推出 __某__个__特__殊__情__况__下__的结论的推理 由_一__般__到__特__殊___的推理
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
数学 选修2-2
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
4.下列推理是否正确,错误的请指出其错误之处: (1)求证:四边形的内角和等于360°. 证明:设四边形ABCD是矩形,则它的四个角都是直角, 有∠A+∠B+∠C+∠D=90°+90°+90°+90°=360°,所 以四边形的内角和为360°. (2)“因为过不共线的三点有且仅有一个平面(大前提),而 A,B,C为空间三点(小前提),所以过A,B,C三点只能确定 一个平面(结论).” (3)“因为金属铜、铁、铝能够导电(大前提),而金是金属 (小前提),所以金能导电(结论).”
1.理解演绎推理的意义. 2.掌握演绎推理的基本模式,并能运用三段论进行一些 简单推理. 3.了解合情推理和演绎推理之间的区别和联系.
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
人们在喜马拉雅山区考察时,发现高山的地层中有许多鱼 类、贝类的化石,还发现了鱼龙的化石.地质学家们推断说, 鱼类、贝类生活在海洋里,在喜马拉雅山上发现它们的化石, 说明喜马拉雅山曾经是海洋.地质学家是怎么得出这个结论的 呢?
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
演绎推理
1.演绎推理的含义及特点
含义 特点
从一般性的原理出发,推出 __某__个__特__殊__情__况__下__的结论的推理 由_一__般__到__特__殊___的推理
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
数学 选修2-2
人教版高二数学选修2-2(B版)全册PPT课件

3.1.1 实数系
3.1.3 复数的几何意义
3.2.2 复数的乘法
பைடு நூலகம்
本章小节
附录 部分中英文词汇对照表
第一章 导数及其应用
人教版高二数学选修2-2(B版)全册 PPT课件
1.2 导数的运算
1.2.1 常数函数与冥函数的导
1.2.3 导数的四则运算法则
1.3.2 利用导数研究函数的极值
1.4 定积分与微积分基本定理
1.4.1 曲边梯形
本章小结
第二章 推理与证明
2.1.2 演绎推理
2.2.2 反证法
2.3.2 数学归纳法应用举例
阅读与欣赏
《原本》与公理化思想
3.1 数系的扩充与复数的概念
人教版高二数学选修2-2(B版)全 册PPT课件目录
0002页 0036页 0087页 0156页 0219页 0238页 0254页 0282页 0336页 0371页 0418页 0458页 0460页 0495页 0555页 0598页 0600页
第一章 导数及其应用
1.1.2 瞬时速度与导数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
boቤተ መጻሕፍቲ ባይዱog怎么上不去
[单选,A2型题,A1/A2型题]以下哪项不属于食品污染物范畴()。A.微生物B.重金属C.寄生虫D.食品添加剂E.河豚毒素 [单选]双金属片是由两种()不同的金属片叠焊在一起构成的。A、温度B、质量C、体积膨胀系数D、线膨胀系数 [单选]门静脉高压症病人出现腹水最主要原因是()A.抗利尿激素增多B.肝淋巴液外漏C.肝功能减退引起低蛋白血症D.醛固酮体内增多E.门静脉系毛细血管床的静水压增加 [单选]下列各项中,除哪一项外,均由风热夹痰或湿热蕴阻所致()A.颈痈B.脐痈C.乳痈D.臀痈E.背痈 [单选]()金字塔前的狮身人面像是埃及最大、最古老的室外雕刻巨像。A.胡夫B.哈夫拉C.孟卡尔D.左塞尔 [单选]显像剂在脏器组织和病变内达到分布平衡时所进行的显像称为()A.静态显像B.动态显像C.介入显像D.阳性显像E.阴性显像 [单选,A1型题]创伤治疗可用于()A.抑郁症患者B.精神病患者C.早期遭受性虐待患者D.惊恐发作患者E.解离患者 [单选]血清壁细胞抗体阳性多见于下列哪种疾病()A.慢性浅表性胃炎B.急性糜烂性胃炎C.慢性萎缩性胃体胃炎D.胃溃疡E.慢性萎缩性胃窦胃炎 [单选]()不是MRP计划库存量计算的依据。A.本期计划订单产出量B.本期净需求量C.在途库存量D.安全库存量 [单选]某公司在业务活动中形成了大量信息,适合采用()分类法进行分类。A.时间B.地区C.字母D.问题 [单选]皮肤表皮分为5层,其中最外层是()A.棘层B.基底层C.角质层D.透明层E.颗粒层 [问答题,案例分析题]背景材料: [单选]驾驶厂内机动车,应当依法取得()A、操作上岗证B、驾驶证C、企业内部通行证 [单选]关于传染病流行病学资料,下列不正确的是()A.流行病学资料在诊断中占有重要地位B.是否患过该病表明有无发病的可能C.是否在流行地区、流行季节表明有无感染的可能D.考虑传染病诊断时必须取得有关流行病学资料作参考E.某些传染病在发病年龄和职业方面有选择性 [单选]滑坡防治的工程措施主要有()和力学平衡以及改变滑带土三类。A.护面B.排水C.植树D.注浆 [单选]给水管道中,一种新型管材、质轻、无毒、内壁光滑、不结垢,使用温度可达90℃,适用于输送自来水、生活热水和采暖空调工程的管道是()。A.铸铁管B.聚丙烯管C.硬聚氯乙烯管D.衬塑铝合金管 [问答题]在废墟中如何设法逃生? [单选]钩体病的传播方式为()A.呼吸道飞沫传播B.消化道传播C.直接接触传播D.节肢动物间接传播E.血液传播 [单选,A2型题,A1/A2型题]骨髓检查对下列哪种疾病的确诊无意义()A.白血病B.不稳定血红蛋白病C.多发性骨髓瘤D.巨幼细胞性贫血E.恶性组织细胞病 [单选,A1型题]以下除哪项外,均是攻下药的适应证()A.饮食积滞B.虚寒泻痢C.血热妄行D.冷积便秘E.大肠燥热 [单选]朊毒体可以诱发机体产生()A.细胞免疫B.体液免疫C.补体D.细胞凋亡E.体液免疫和细胞免疫 [单选]发展心理学是研究()的科学。A.认知发展规律B.心理的种族发展C.心理的种系发展D.心理发展规律 [单选]类风湿关节炎的主要病理改变是()。A.滑膜炎B.骨膜炎C.胸膜炎D.心包炎E.皮肌炎 [多选]编写规划环境影响篇章或者说明,至少包括的内容有()。A.前言B.环境现状分析C.监测与跟踪评价D.环境影响的减缓措施E.环境影响分析与评价 [单选]在CakeWalk的音轨窗口中,可以设置单轨的参数,其中转调(Vel+)用于()A.改变声像的位置B.改变音调C.改变音量D.改变力度 [单选]和心导管所测肺毛细血管楔压呈线性相关的超声参数是()。A.DTB.IVRTC.E/AD.E/EaE.S/D [单选]履行行政补偿责任的主要责任形式是()。A.签发执行支票B.支付补偿金C.恢复原状D.实物补偿 [名词解释]沙漠 [单选,A2型题,A1/A2型题]下列哪项是错误的()A.HbA--α2β2B.HbA2--ζ2γ2C.HbGower2--α2ε2D.HbF--α2γ2E.HbBart--γ4 [单选,A2型题,A1/A2型题]术后发生深静脉血栓,其处理措施不正确的是()A.患肢抬高B.禁忌经患肢静脉输液C.勤按摩D.溶栓治疗E.抗凝治疗 [单选]讲解“圆的面积和周长”时,运用“化圆为方”“化曲为直”的思路,这属于数学思想中的()。A.可逆思想B.类比思想C.数形结合思想D.极限思想 [单选,A1型题]属于构成医疗事故的主观方面的是()A.技术水平欠缺的技术过失B.违反卫生法规和诊疗护理规范常规的责任过失C.违反操作规程的故意D.疏忽大意的过失E.过于自信的过失 [单选,A4型题,A3/A4型题]26岁女性,已婚2年,G1P0,婚后一直服用短效口服避孕药避孕,但意外妊娠,于孕50天行人工流产术。患者知情选择放置TCu380AIUD避孕,术后应告知该妇女正确的注意事项是()A.放置后可能有少量阴道出血及下腹不适感为异常现象B.出血多、腹痛、发热和白带异常 [判断题]乙醇溶于水的过程中ΔG=0。A.正确B.错误 [单选,A1型题]能涌吐痰食,祛湿退黄的药物是()A.瓜蒂B.半夏C.天南星D.桔梗E.胆矾 [单选,A2型题,A1/A2型题]以下急性有机磷农药中毒患者的临床表现,均可诊断为重度中毒,除了()。A.昏迷B.肺水肿C.脑水肿D.呼吸麻痹E.瞳孔缩小 [单选,A2型题,A1/A2型题]医疗机构的从业人员基本行为规范:①以人为本,践行宗旨;②遵纪守法,依法执业;③尊重患者,关爱生命;④优质服务,医患和谐;⑤廉洁自律,恪守医德;⑥严谨求实,精益求精;⑦爱岗敬业,团结协作;⑧乐于奉献,热心公益。请选择正确()A.①、②、④、 [单选]在切割机退卷架上的布基卷用完前,要提前按好准备使用的布基卷()。A.卷轴B.卡盘C.螺钉D.楔钉 [单选]产褥期妇女的临床表现恰当的是().A.产后宫缩痛多见于初产妇B.产后初期产妇脉搏增快C.产后第1日宫底稍下降D.子宫复旧因哺乳而加速E.恶露通常持续1~2周 [单选]公共产品具有的鲜明特点,包括:非排他性和()。A.非竞争性B.竞争性C.信息不对称性D.信息不完全性
